Difference between revisions of "ספר חשבון"
(→Primary Definitions) |
(→Proportions with fractions) |
||
| (114 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
|- | |- | ||
| | | | ||
| − | |style="width:45%;text-align:right;"|‫<ref>31v</ref><big>ספר חשבון</big | + | |style="width:45%;text-align:right;"|‫<ref>31v</ref><big>ספר חשבון</big> |
|- | |- | ||
| | | | ||
| Line 12: | Line 12: | ||
| | | | ||
|- | |- | ||
| − | |One, from one aspect, is a number and the foundation of the numbers | + | |One, from one aspect, is a number and the foundation of the numbers; from another aspect it is not a number. |
| − | |style="text-align:right;"|<big>האחד מדרך אחד‫<ref>אחד: MS Cambridge א‫' MS Ithaca חשבון< | + | |style="text-align:right;"|<big>האחד מדרך אחד הוא מן המספר</big> ועיקר המספר ומדרך אחר אינו מספר‫<ref>MS Cambridge: title is missing<br> |
| + | אחד: MS Cambridge א‫' MS Ithaca חשבון<br> | ||
| + | מן המספר: MS Cambridge מספר; Ithaca: המספר ומדרך א<br> | ||
| + | ועיקר המספר: MS Cambridge om.</ref> | ||
|- | |- | ||
| − | |The proof that indicates that | + | |The proof that indicates that it is not a number is that every number is half [the sum of the numbers on] its both sides and also [the sum of the numbers on] the sides of its both sides and so on until the end of its sides. |
:<math>\scriptstyle{\color{OliveGreen}{n=\frac{1}{2}\sdot\left[\left(n-a\right)+\left(n+a\right)\right]}}</math> | :<math>\scriptstyle{\color{OliveGreen}{n=\frac{1}{2}\sdot\left[\left(n-a\right)+\left(n+a\right)\right]}}</math> | ||
| − | |style="text-align:right;"|והאות המורה כי אננו מספר הוא | + | |style="text-align:right;"|והאות המורה כי אננו מספר הוא כי כל מספר הוא מחצית שני צדיו וכן הוא מחצית שני צדי צדיו על תכלית כל צדיו‫<ref>הוא: MS Cambridge om.<br> |
| + | על: MS Cambridge עד</ref> | ||
|- | |- | ||
| | | | ||
| Line 32: | Line 36: | ||
:It is also half [the sum of the numbers on] the sides of the sides of its sides, which are 13 and 7. | :It is also half [the sum of the numbers on] the sides of the sides of its sides, which are 13 and 7. | ||
:<math>\scriptstyle{\color{blue}{10=\frac{1}{2}\sdot\left(7+13\right)}}</math> | :<math>\scriptstyle{\color{blue}{10=\frac{1}{2}\sdot\left(7+13\right)}}</math> | ||
| − | |style="text-align:right;"|וכן הוא מחצית שני צדי | + | |style="text-align:right;"|וכן הוא מחצית שני צדי צדי צדיו שהם י"ג וז‫'‫<ref>צדי: MS Ithaca om.</ref> |
|- | |- | ||
|Ans so on, every number is half [the sum of the numbers on] its both sides. | |Ans so on, every number is half [the sum of the numbers on] its both sides. | ||
| Line 39: | Line 43: | ||
| | | | ||
:Since one is not a number, you do not find two sides of it. | :Since one is not a number, you do not find two sides of it. | ||
| − | |style="text-align:right;"|והאחד מפני שאינו‫<ref>שאינו: MS Cambridge שהוא אינו</ref> | + | |style="text-align:right;"|והאחד מפני שאינו מספר אי אתה מוצא לו ב' צדדים‫<ref>שאינו: MS Cambridge שהוא אינו</ref> |
|- | |- | ||
| | | | ||
| Line 47: | Line 51: | ||
|- | |- | ||
|Another proof that indicates that one is not a number is that every number is either integer or a fraction. | |Another proof that indicates that one is not a number is that every number is either integer or a fraction. | ||
| − | |style="text-align:right;"|<big>ואות אחר</big> מורה | + | |style="text-align:right;"|<big>ואות אחר</big> מורה שהאחד אינו מספר כי כל מספ' הוא או מספר שלם או שבר מספר‫<ref>מורה: MS Cambridge מוראה<br> |
| + | שבר: MS Ithaca <s>חצי</s> marg. שבר</ref> | ||
|- | |- | ||
| | | | ||
| Line 57: | Line 62: | ||
::As 2 times 2, which is 4. | ::As 2 times 2, which is 4. | ||
::<math>\scriptstyle{\color{blue}{2<2\times2=4}}</math> | ::<math>\scriptstyle{\color{blue}{2<2\times2=4}}</math> | ||
| − | |style="text-align:right;"|כגון ב' פעמי' ב'<ref>ב'פ'ב‫'‫ MS Cambridge :ב' פעמי' ב‫'</ref> | + | |style="text-align:right;"|כגון ב' פעמי' ב' ד‫'‫<ref>ב'פ'ב‫'‫ MS Cambridge :ב' פעמי' ב‫'</ref> |
|- | |- | ||
| | | | ||
::3 times 3, which is 9. | ::3 times 3, which is 9. | ||
::<math>\scriptstyle{\color{blue}{3<3\times3=9}}</math> | ::<math>\scriptstyle{\color{blue}{3<3\times3=9}}</math> | ||
| − | |style="text-align:right;"|ג' פעמי' ג'<ref>ג'פ'ג‫'‫ MS Cambridge :ג' פעמי' ג‫'</ref> | + | |style="text-align:right;"|ג' פעמי' ג' ט‫'‫<ref>ג'פ'ג‫'‫ MS Cambridge :ג' פעמי' ג‫'</ref> |
|- | |- | ||
| | | | ||
| Line 103: | Line 108: | ||
| | | | ||
|- | |- | ||
| + | !<span style=color:green>Units by Tens</span> | ||
| | | | ||
| − | + | |- | |
| − | :<math>\scriptstyle a\times\left(10\sdot b\right)</math> | + | |When we want to multiply units by tens. |
| + | :<math>\scriptstyle{\color{OliveGreen}{a\times\left(10\sdot b\right)}}</math> | ||
|style="text-align:right;"|<big>כשנרצה<ref>כשנרצה: MS Cambridge ואם נרצה</ref> לרבות<ref>לרבות: MS Cambridge לדעת</ref> אחדים</big> עם עשרות | |style="text-align:right;"|<big>כשנרצה<ref>כשנרצה: MS Cambridge ואם נרצה</ref> לרבות<ref>לרבות: MS Cambridge לדעת</ref> אחדים</big> עם עשרות | ||
|- | |- | ||
| | | | ||
| − | : | + | *As 6 times 40. |
| + | :<math>\scriptstyle6\times40</math> | ||
|style="text-align:right;"|כגון ו' פעמי' מ‫' | |style="text-align:right;"|כגון ו' פעמי' מ‫' | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{6\times40=\left(6\sdot4\right)\sdot10=24\sdot10=240}}</math> | + | :We take their analogous from the corresponding units: since 40 is 4 tens multiplied 6 times, and since 4 times 6 is 24, then 6 times 40 is 24 tens, which is 240. |
| + | :<math>\scriptstyle{\color{blue}{6\times40=\left(6\sdot4\right)\sdot10=24\sdot10=240}}</math> | ||
|style="text-align:right;"|נקח<ref>נקח: MS Cambridge om.</ref> דמיונם<ref>דמיונם: MS Cambridge שדמיונם</ref> מן האחדים הדומים להם ובעבור שמ' הם ד' עשרות מניינם הוא ו' פעמים וכמו<ref>מן ... וכמו: MS Cambridge om.</ref> שו' פעמי' ד'<ref>ו'פ'ד‫'‫ MS Cambridge :שו' פעמי' ד‫'</ref> הם<ref>הם: MS Cambridge שהם</ref> כ"ד כן ו' פעמים מ'<ref>‫כן ... מ‫': MS Cambridge om.</ref> הם<ref>הם: MS Cambridge בין יהיו</ref> כ"ד עשרות שהם ר"מ | |style="text-align:right;"|נקח<ref>נקח: MS Cambridge om.</ref> דמיונם<ref>דמיונם: MS Cambridge שדמיונם</ref> מן האחדים הדומים להם ובעבור שמ' הם ד' עשרות מניינם הוא ו' פעמים וכמו<ref>מן ... וכמו: MS Cambridge om.</ref> שו' פעמי' ד'<ref>ו'פ'ד‫'‫ MS Cambridge :שו' פעמי' ד‫'</ref> הם<ref>הם: MS Cambridge שהם</ref> כ"ד כן ו' פעמים מ'<ref>‫כן ... מ‫': MS Cambridge om.</ref> הם<ref>הם: MS Cambridge בין יהיו</ref> כ"ד עשרות שהם ר"מ | ||
|- | |- | ||
| | | | ||
| − | : | + | *The same for 3 times 30. |
| + | :<math>\scriptstyle3\times30</math> | ||
|style="text-align:right;"|וכן<ref>וכן: MS Cambridge <s>וג'</s> וכן</ref> ג' פעמים ל‫'<ref>ג'פ'ל‫'‫ MS Cambridge :ג' פעמים ל‫'</ref> | |style="text-align:right;"|וכן<ref>וכן: MS Cambridge <s>וג'</s> וכן</ref> ג' פעמים ל‫'<ref>ג'פ'ל‫'‫ MS Cambridge :ג' פעמים ל‫'</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{3\times30=\left(3\sdot3\right)\sdot10=9\sdot10=90}}</math> | + | :Their analogous is 3 times 3, which is 9. So, it is 9 tens, which is 90. |
| − | |style="text-align:right;"|דמיונם הוא<ref>הוא: MS Cambridge om.</ref> ג' פעמים ג' שהם ט' ויהיו<ref>ויהיו: MS Cambridge כן ג'פ'ל' יהיו</ref> ט' עשרות שהם צ' ועל זה הדרך הם כלם‫<ref>כשנרצה ... כלם: MS Cambridge the discussion on multiplication of units by tens appears after the discussion on multiplication of tens by tens</ref> | + | :<math>\scriptstyle{\color{blue}{3\times30=\left(3\sdot3\right)\sdot10=9\sdot10=90}}</math> |
| + | |style="text-align:right;"|דמיונם הוא<ref>הוא: MS Cambridge om.</ref> ג' פעמים ג' שהם ט' ויהיו<ref>ויהיו: MS Cambridge כן ג'פ'ל' יהיו</ref> ט' עשרות שהם צ‫' | ||
| + | |- | ||
| + | |This way for all of them. | ||
| + | |style="text-align:right;"|ועל זה הדרך הם כלם‫<ref>כשנרצה ... כלם: MS Cambridge the discussion on multiplication of units by tens appears after the discussion on multiplication of tens by tens</ref> | ||
|- | |- | ||
| + | !<span style=color:green>Tens by Tens</span> | ||
| | | | ||
| − | + | |- | |
| − | :<math>\scriptstyle\left(a\sdot10\right)\times\left(10\sdot b\right)</math> | + | |If we multiply tens by tens. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(a\sdot10\right)\times\left(10\sdot b\right)}}</math> | ||
|style="text-align:right;"|ואם נרבה<ref>ואם נרבה: MS Cambridge כשתרבה</ref> עשרות עם עשרות | |style="text-align:right;"|ואם נרבה<ref>ואם נרבה: MS Cambridge כשתרבה</ref> עשרות עם עשרות | ||
|- | |- | ||
| | | | ||
| − | : | + | *As 30 times 30. |
| + | :<math>\scriptstyle30\times30</math> | ||
|style="text-align:right;"|כגון ל' פעמים ל‫' | |style="text-align:right;"|כגון ל' פעמים ל‫' | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{30\times30=\left(3\sdot3\right)\sdot100=9\sdot100=900}}</math> | + | :We take their analogous from the corresponding units: since 30 is 3 tens, their analogous is 3 times 3 and as 3 times 3 is 9, so 30 times 30 is 9 hundred. |
| + | :<math>\scriptstyle{\color{blue}{30\times30=\left(3\sdot3\right)\sdot100=9\sdot100=900}}</math> | ||
|style="text-align:right;"|ניקח דמיונם מן האחדים הדומים להם ובעבור היות ל'<ref>של' הם‫ MS Cambridge :היות ל‫'</ref> ג'‫<ref>ל' ג': MS Ithaca ג' ל'</ref> עשרו' דמיונם הוא ג' פעמי' ג'<ref>ג'פ'ג‫'‫ MS Cambridge :ג' פעמי' ג‫'</ref> וכמו שג' פעמים ג'<ref>שג'פ'ג‫'‫ MS Cambridge :שג' פעמים ג‫'</ref> הם ט' כן ל' פעמים ל' הם ט' מאות | |style="text-align:right;"|ניקח דמיונם מן האחדים הדומים להם ובעבור היות ל'<ref>של' הם‫ MS Cambridge :היות ל‫'</ref> ג'‫<ref>ל' ג': MS Ithaca ג' ל'</ref> עשרו' דמיונם הוא ג' פעמי' ג'<ref>ג'פ'ג‫'‫ MS Cambridge :ג' פעמי' ג‫'</ref> וכמו שג' פעמים ג'<ref>שג'פ'ג‫'‫ MS Cambridge :שג' פעמים ג‫'</ref> הם ט' כן ל' פעמים ל' הם ט' מאות | ||
|- | |- | ||
| | | | ||
| − | : | + | *Also 40 times 40. |
| + | :<math>\scriptstyle40\times40</math> | ||
|style="text-align:right;"|וכן מ' פעמים מ‫'<ref>מ'פ'מ‫'‫ MS Cambridge :מ' פעמים מ‫'</ref> | |style="text-align:right;"|וכן מ' פעמים מ‫'<ref>מ'פ'מ‫'‫ MS Cambridge :מ' פעמים מ‫'</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{40\times40=\left(4\sdot4\right)\sdot100=16\sdot100=1600}}</math> | + | :Their analogous is 4 times [4], which is 16 hundred. |
| + | :<math>\scriptstyle{\color{blue}{40\times40=\left(4\sdot4\right)\sdot100=16\sdot100=1600}}</math> | ||
|style="text-align:right;"|דמיונם הוא ד' פעמים שהם י"ו‫<ref>י"ו: MS Ithaca: י"ו וכן מ' פעמי' מ' הם י"ו</ref> מאות‫<ref>ד' ד'פ'ד' י"ו וכן מ'פ'מ' י"ו מאות‫ MS Cambridge :ד' ... מאות</ref> | |style="text-align:right;"|דמיונם הוא ד' פעמים שהם י"ו‫<ref>י"ו: MS Ithaca: י"ו וכן מ' פעמי' מ' הם י"ו</ref> מאות‫<ref>ד' ד'פ'ד' י"ו וכן מ'פ'מ' י"ו מאות‫ MS Cambridge :ד' ... מאות</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | *Also 30 times 40. |
| + | :<math>\scriptstyle30\times40</math> | ||
|style="text-align:right;"|וכן ל' פעמים מ‫'<ref>ל'פ'מ‫'‫ MS Cambridge :ל' פעמים מ‫'</ref> | |style="text-align:right;"|וכן ל' פעמים מ‫'<ref>ל'פ'מ‫'‫ MS Cambridge :ל' פעמים מ‫'</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{30\times40=\left(3\sdot4\right)\sdot100=12\sdot100=1200}}</math> | + | :Their analogous is 3 times 4, which is 12. So, 30 times 40 is 12 hundred. |
| − | |style="text-align:right;"|דמיונם הוא ג' פעמים ד'<ref>ג'פ'ד‫'‫ MS Cambridge :הוא ... ד‫'</ref> שהם י"ב וכן ל' פע' מ'<ref>ל'פ'מ‫'‫ MS Cambridge :ל' פע' מ‫'</ref> הם י"ב מאות | + | :<math>\scriptstyle{\color{blue}{30\times40=\left(3\sdot4\right)\sdot100=12\sdot100=1200}}</math> |
| + | |style="text-align:right;"|דמיונם הוא ג' פעמים ד'<ref>ג'פ'ד‫'‫ MS Cambridge :הוא ... ד‫'</ref> שהם י"ב וכן ל' פע' מ'<ref>ל'פ'מ‫'‫ MS Cambridge :ל' פע' מ‫'</ref> הם י"ב מאות | ||
|- | |- | ||
| − | |The rule for | + | |The same for all. |
| + | |style="text-align:right;"|וכן כלם | ||
| + | |- | ||
| + | |The rule for this is that when we multiply units by tens, we take their analogous from the multiplication of the units by the units and the result is tens. | ||
|style="text-align:right;"|והכלל המסור לזה הוא כשנרבה אחדים עם עשרות נקח דמיונם מרבוי האחדים עם האחדים ויהיו העולה עשרות | |style="text-align:right;"|והכלל המסור לזה הוא כשנרבה אחדים עם עשרות נקח דמיונם מרבוי האחדים עם האחדים ויהיו העולה עשרות | ||
|- | |- | ||
| − | | | + | |If we multiply tens by tens the result is hundreds. |
|style="text-align:right;"|ואם נרבה עשרות עם עשרות יהיה העולה מאות‫<ref>ואם נרבה עשרות עם עשרות... מאות: MS Ithaca om.</ref> | |style="text-align:right;"|ואם נרבה עשרות עם עשרות יהיה העולה מאות‫<ref>ואם נרבה עשרות עם עשרות... מאות: MS Ithaca om.</ref> | ||
|- | |- | ||
| + | !<span style=color:green>Tens by Hundreds</span> | ||
| | | | ||
| − | + | |- | |
| − | :<math>\scriptstyle\left(a\sdot10\right)\times\left(100\sdot b\right)</math> | + | |If we multiply tens by hundreds, the result is thousands. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(a\sdot10\right)\times\left(100\sdot b\right)}}</math> | ||
|style="text-align:right;"|ואם נרבה עשרות‫<ref>עשרות: MS Ithaca עשרי'</ref>עם מאות יהיה<ref>יהיה: MS Cambridge יהיו</ref> העולה אלפים | |style="text-align:right;"|ואם נרבה עשרות‫<ref>עשרות: MS Ithaca עשרי'</ref>עם מאות יהיה<ref>יהיה: MS Cambridge יהיו</ref> העולה אלפים | ||
|- | |- | ||
| | | | ||
| − | : | + | *As 20 times 2 hundreds. |
| + | :<math>\scriptstyle20\times200</math> | ||
|style="text-align:right;"|כגון כ' פעמים ב' מאות‫<ref>ב'פ'ר‫'‫ MS Cambridge :כ' פעמים ב' מאות</ref> | |style="text-align:right;"|כגון כ' פעמים ב' מאות‫<ref>ב'פ'ר‫'‫ MS Cambridge :כ' פעמים ב' מאות</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{20\times200=\left(2\sdot2\right)\sdot1000=4\sdot1000=4000}}</math> | + | :Their analogous is 2 times 2, which is 4. So, it is 4 thousand. |
| + | :<math>\scriptstyle{\color{blue}{20\times200=\left(2\sdot2\right)\sdot1000=4\sdot1000=4000}}</math> | ||
|style="text-align:right;"|דמיונם שהם ב' פעמים ב'<ref>ב': MS Ithaca om.</ref> שהם ד' והם<ref>כן ב'פ'ר‫'‫ MS Cambridge :והם</ref> ד' אלפים | |style="text-align:right;"|דמיונם שהם ב' פעמים ב'<ref>ב': MS Ithaca om.</ref> שהם ד' והם<ref>כן ב'פ'ר‫'‫ MS Cambridge :והם</ref> ד' אלפים | ||
|- | |- | ||
| | | | ||
| − | : | + | *Also 50 times 500. |
| + | :<math>\scriptstyle50\times500</math> | ||
|style="text-align:right;"|וכן נ' פעמי' ת"ק | |style="text-align:right;"|וכן נ' פעמי' ת"ק | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{50\times500=\left(5\sdot5\right)\sdot1000=25\sdot1000=25000}}</math> | + | :Their analogous is 5 times 5, which is 25. So, it is 25 thousand. |
| − | |style="text-align:right;"|דמיונם ה' פעמי' ה'<ref>ה'פ'ה‫'‫ MS Cambridge :ה' פעמי' ה‫'</ref> שהם<ref>שהם: MS Cambridge יהיו</ref> כ"ה והם<ref>והם: MS Cambridge כן נ' פ' ת"ק יהיו</ref> כ"ה אלפים | + | :<math>\scriptstyle{\color{blue}{50\times500=\left(5\sdot5\right)\sdot1000=25\sdot1000=25000}}</math> |
| + | |style="text-align:right;"|דמיונם ה' פעמי' ה'<ref>ה'פ'ה‫'‫ MS Cambridge :ה' פעמי' ה‫'</ref> שהם<ref>שהם: MS Cambridge יהיו</ref> כ"ה והם<ref>והם: MS Cambridge כן נ' פ' ת"ק יהיו</ref> כ"ה אלפים | ||
|- | |- | ||
| + | |The same for all. | ||
| + | |style="text-align:right;"|וכן כלם | ||
| + | |- | ||
| + | !<span style=color:green>Hundreds by Hundreds</span> | ||
| | | | ||
| − | + | |- | |
| − | :<math>\scriptstyle\left(a\sdot100\right)\times\left(100\sdot b\right)</math> | + | |If we multiply hundreds by hundreds the result is tens of thousands. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(a\sdot100\right)\times\left(100\sdot b\right)}}</math> | ||
|style="text-align:right;"|ואם נרבה מאות עם מאות יהיה העולה עשרות מאלפים | |style="text-align:right;"|ואם נרבה מאות עם מאות יהיה העולה עשרות מאלפים | ||
|- | |- | ||
| | | | ||
| − | : | + | *As 200 times 200. |
| + | :<math>\scriptstyle200\times200</math> | ||
|style="text-align:right;"|כגון ר' פעמים ר‫'‫<ref>ר'פ'ר‫'‫ MS Cambridge :ר' פעמים ר‫'</ref> | |style="text-align:right;"|כגון ר' פעמים ר‫'‫<ref>ר'פ'ר‫'‫ MS Cambridge :ר' פעמים ר‫'</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{200\times200=\left(2\sdot2\right)\sdot10000=4\sdot10000=40000}}</math> | + | :Their analogous is 2 times 2, which is 4. So, it is 4 tens of thousands. |
| + | :<math>\scriptstyle{\color{blue}{200\times200=\left(2\sdot2\right)\sdot10000=4\sdot10000=40000}}</math> | ||
|style="text-align:right;"|דמיונם הם<ref>הם: MS Cambridge om.</ref> ב' פעמים ב'‫<ref>ב'פ'ב‫'‫ MS Cambridge :ב' פעמים ב‫'</ref> שהם<ref>שהם: MS Cambridge כגון ר'פ'ר' יהיו</ref> ד' ‫<ref>32r</ref>והם ד' עשרות מאלפים‫<ref>מאלפים: MS Cambridge מאלפים והם מ' אלפים</ref> | |style="text-align:right;"|דמיונם הם<ref>הם: MS Cambridge om.</ref> ב' פעמים ב'‫<ref>ב'פ'ב‫'‫ MS Cambridge :ב' פעמים ב‫'</ref> שהם<ref>שהם: MS Cambridge כגון ר'פ'ר' יהיו</ref> ד' ‫<ref>32r</ref>והם ד' עשרות מאלפים‫<ref>מאלפים: MS Cambridge מאלפים והם מ' אלפים</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | *Also 500 times 500. |
| + | :<math>\scriptstyle500\times500</math> | ||
|style="text-align:right;"|וכן ת"ק פעמים ת"ק | |style="text-align:right;"|וכן ת"ק פעמים ת"ק | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{500\times500=\left(5\sdot5\right)\sdot10000=25\sdot10000=250000}}</math> | + | :Their analogous is 5 times 5, which is 25. So, it is 25 tens of thousands. |
| − | |style="text-align:right;"|דמיונם ה' פעמים ה'<ref>ה'פ'ה‫'‫ MS Cambridge :ה' פעמים ה‫'</ref> שהם כ"ה והם<ref>והם: MS Cambridge ויהיו ת"ק פ' ת"ק</ref> כ"ה עשרות מאלפים וכן כלם | + | :<math>\scriptstyle{\color{blue}{500\times500=\left(5\sdot5\right)\sdot10000=25\sdot10000=250000}}</math> |
| + | |style="text-align:right;"|דמיונם ה' פעמים ה'<ref>ה'פ'ה‫'‫ MS Cambridge :ה' פעמים ה‫'</ref> שהם כ"ה והם<ref>והם: MS Cambridge ויהיו ת"ק פ' ת"ק</ref> כ"ה עשרות מאלפים | ||
| + | |- | ||
| + | |The same for all. | ||
| + | |style="text-align:right;"|וכן כלם | ||
|- | |- | ||
| | | | ||
| − | == <span style=color:green>The Decimal Ranks</span> == | + | == <span style=color:green>The Decimal Ranks</span>‫<ref>MS Ithaca om.</ref> == |
| − | + | | | |
| − | + | |- | |
| + | |The ranks of numbers one above the other: | ||
| + | |style="text-align:right;"|<big>מדרגות</big> המספרים זו למעלה מזו | ||
|- | |- | ||
| | | | ||
| − | * | + | *The units are in the first rank. |
|style="text-align:right;"|האחדים הם במדרגה הראשונה | |style="text-align:right;"|האחדים הם במדרגה הראשונה | ||
|- | |- | ||
| | | | ||
| − | * | + | *The tens are in the second rank. |
|style="text-align:right;"|העשרות הם במדרגה השנית | |style="text-align:right;"|העשרות הם במדרגה השנית | ||
|- | |- | ||
| | | | ||
| − | * | + | *The hundreds are in the third rank. |
|style="text-align:right;"|המאות הם במדרגה השלישית | |style="text-align:right;"|המאות הם במדרגה השלישית | ||
|- | |- | ||
| | | | ||
| − | * | + | *The thousands are in the fourth rank. |
|style="text-align:right;"|האלפים הם במדרגה הרביעית | |style="text-align:right;"|האלפים הם במדרגה הרביעית | ||
|- | |- | ||
| | | | ||
| − | * | + | *The tens of thousands are in the fifth rank. |
|style="text-align:right;"|העשרות מהאלפים הם במדרגה החמישית | |style="text-align:right;"|העשרות מהאלפים הם במדרגה החמישית | ||
|- | |- | ||
| | | | ||
| − | * | + | *The hundreds of Thousands are in the sixth rank. |
|style="text-align:right;"|המאות מהאלפים הם במדרגה השישית | |style="text-align:right;"|המאות מהאלפים הם במדרגה השישית | ||
| + | |- | ||
| + | |So they rise from rank to rank. | ||
| + | |style="text-align:right;"|וכן עולים ממדרגה למדרגה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *If we want to multiply 600 by 4 thousand. |
| + | :<math>\scriptstyle600\times4000</math> | ||
| + | |style="text-align:right;"|<big>ואם</big> נרצה לרבות‫<ref>ואם נרצה לרבות: MS Cambridge אם נרבה</ref> ת"ר‫<ref>ת"ר: MS Cambridge ת"ר <s>אלפים</s></ref> בד' אלפים | ||
|- | |- | ||
| | | | ||
| − | : | + | :Their analogous is 6 times 4, which is 24. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{600\times4000=\left(6\sdot4\right)\sdot100000=24\sdot100000}}</math> |
| + | |style="text-align:right;"|דמיונם ו'פ'ד' שהם‫<ref>שהם: MS Cambridge הם</ref> כ"ד | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{ | + | :If you want to know what [is the rank of] this 24, take the [positional value of] the rank of hundreds, which is three, and count 3 ranks from the thousands. The rank you will reach is the rank of 24 that you have kept and it is the rank of hundreds of thousands. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{OliveGreen}{\left(a\sdot10^n\right)\times\left(b\sdot10^m\right)=\left(a\sdot b\right)\sdot\left(10^n\sdot10^m\right)}}</math> |
| + | |style="text-align:right;"|ואם תרצה לדעת אלו הכ"ד מה יורו קח מעלת המאות שהוא שלשה ומנה מן האלפים ג' מעלות והמעלה שתגיע אליה היא מעלת כ"ד ששמרת‫<ref>ששמרת: MS Cambridge המשמרת</ref> והיא מעלת מאות האלפים‫<ref>מאות האלפים: MS Cambridge המאות מהאלפים</ref> | ||
|- | |- | ||
| | | | ||
| − | + | :Likewise, if you count 4 ranks, which is the rank of thousands, from the rank of hundreds, you reach also the rank of hundreds of thousands. | |
| − | : | + | |style="text-align:right;"|<big>וכן</big> אם אתה מונה מעלת האלפים והוא ד' ממעלת המאות אתה מגיע גם כן<ref>גם כן: MS Cambridge ג"כ</ref> אל מעלת מאות האלפים |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | : | + | :Know then that the units of the number you have kept, which is 24, is in the rank of hundreds of thousands, and its tens are in the rank of thousands of thousands. So, the 24 you have kept are 2 thousands of thousands and 400 thousand, because its units are four and its tens are 2. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותדע מכאן כי האחדים מהמספר אשר שמרת והוא כ"ד הוא ממעלת מאות האלפים ועשרותיו הם ממעלת אלפי האלפים<ref>האלפים: MS Cambridge אלפים</ref> יהיו אם כן<ref>אם כן: MS Cambridge א"כ</ref> כ"ד אשר שמרת ב' אלפי אלפים ות' אלף כי אחדיו הם ארבעה ועשרותיו הם ב‫' |
|- | |- | ||
| − | | | + | |Another method: consider [the positional values] of the two ranks and know their [sum]. Subtract 1 from it; the remainder is the rank of the product. |
| − | |style="text-align:right;"|דרך אחרת תחשוב אישי [פי' אחדי'] ב' המעלות ותדע מספרם ותפחות מהם א'<ref>אחד | + | |style="text-align:right;"|<big>דרך</big> אחרת תחשוב אישי [פי' אחדי'] ב' המעלות ותדע מספרם ותפחות מהם א'‫<ref>אחד: MS Cambridge א'</ref> והנשאר יהיה מעלת הנכלל |
|- | |- | ||
| | | | ||
| − | : | + | :As if you take [the positional value of] the rank of hundreds in this example, which is 3, and [the positional value of] the rank of thousands, which is 4; they are 7. Subtract 1 from it; 6 remains and this number is [the positional value of] the rank of hundreds of thousands. |
| + | :<math>\scriptstyle{\color{blue}{\left(3+4\right)-1=7-1=6}}</math> | ||
|style="text-align:right;"|כאלו תקח במשל הזה אוש המאות והוא ג' ואוש האלפים והוא ד' יהיו ז' ותפחות מהם א' וישארו ו' וזה המספר הוא אוש מאות האלפים | |style="text-align:right;"|כאלו תקח במשל הזה אוש המאות והוא ג' ואוש האלפים והוא ד' יהיו ז' ותפחות מהם א' וישארו ו' וזה המספר הוא אוש מאות האלפים | ||
|- | |- | ||
| | | | ||
| − | == <span style=color:green>Three Types of Numbers</span> | + | == <span style=color:green>Three Types of Numbers</span>‫<ref>MS Ithaca om.</ref> == |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |The numbers are [of] three [types]: perfect number, abundant number, deficient number. |
| − | + | |style="text-align:right;"|<big>המספרים</big> הם ג' <big>מספר שלם מספר עודף מספר חסר</big> | |
| − | |style="text-align:right;"|מספר חסר | ||
|- | |- | ||
| − | | | + | |The perfect number, as the number 6, its parts divide it and complete it [= it is equal to the sum of its divisors]; they do not exceed it, nor less than it. Because its parts are a half, a sixth, and a third. If you sum them up, they are six, which is the same as it. |
:<math>\scriptstyle{\color{blue}{\left(\frac{1}{6}\sdot6\right)+\left(\frac{1}{3}\sdot6\right)+\left(\frac{1}{2}\sdot6\right)=6}}</math> | :<math>\scriptstyle{\color{blue}{\left(\frac{1}{6}\sdot6\right)+\left(\frac{1}{3}\sdot6\right)+\left(\frac{1}{2}\sdot6\right)=6}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|מספר שלם הוא כמו מספר ו' אשר חלקיו המונים אותו ממלאים אותו ואינם עודפים עליו ואינם‫<ref>ואינם: MS Cambridge ולא</ref> חסרים ממנו כי חלקיו הם חצי ושתות ושליש ואם תקבצם יהיו ששה כמוהו |
| − | |||
|- | |- | ||
| − | | | + | |The same for the number 28 - its parts are: one part of 28, one part of 14, a seventh, a quarter, and a half. If you sum them up, they are 28, which is the same as it. |
|style="text-align:right;"|וכן מספר כ"ח חלקיו הם חלק מכ"ח וחלק מי"ד ושביע ורביע וחצי ואם תקבצם יהיו כ"ח כמוהו | |style="text-align:right;"|וכן מספר כ"ח חלקיו הם חלק מכ"ח וחלק מי"ד ושביע ורביע וחצי ואם תקבצם יהיו כ"ח כמוהו | ||
|- | |- | ||
| Line 287: | Line 328: | ||
:<math>\scriptstyle{\color{blue}{\left(\frac{1}{28}\sdot28\right)+\left(\frac{1}{14}\sdot28\right)+\left(\frac{1}{7}\sdot28\right)+\left(\frac{1}{4}\sdot28\right)+\left(\frac{1}{2}\sdot28\right)=28}}</math> | :<math>\scriptstyle{\color{blue}{\left(\frac{1}{28}\sdot28\right)+\left(\frac{1}{14}\sdot28\right)+\left(\frac{1}{7}\sdot28\right)+\left(\frac{1}{4}\sdot28\right)+\left(\frac{1}{2}\sdot28\right)=28}}</math> | ||
|- | |- | ||
| − | | | + | |The abundant number, as 12, whose parts are one part of 12, a sixth, a third, a quarter, and a half. If you sum them up, they are 16. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>ומספר עודף</big> הוא י"ב שחלקיו הם חלק מי"ב ושתות ושליש ורביע וחצי ואם תקבצם יהיו כלם י"ו |
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
:<math>\scriptstyle{\color{blue}{\left(\frac{1}{12}\sdot12\right)+\left(\frac{1}{6}\sdot12\right)+\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)+\left(\frac{1}{2}\sdot12\right)=16>12}}</math> | :<math>\scriptstyle{\color{blue}{\left(\frac{1}{12}\sdot12\right)+\left(\frac{1}{6}\sdot12\right)+\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)+\left(\frac{1}{2}\sdot12\right)=16>12}}</math> | ||
|- | |- | ||
| − | | | + | |The deficient number, as 14, whose parts are one part of 14, its half, and its seventh. If you sum them up, they are ten. |
:<math>\scriptstyle{\color{blue}{\left(\frac{1}{14}\sdot14\right)+\left(\frac{1}{7}\sdot14\right)+\left(\frac{1}{2}\sdot14\right)=10<12}}</math> | :<math>\scriptstyle{\color{blue}{\left(\frac{1}{14}\sdot14\right)+\left(\frac{1}{7}\sdot14\right)+\left(\frac{1}{2}\sdot14\right)=10<12}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>ומספר חסר</big> כגון מספר י"ד שחלקיו הם חלק מי"ד וחציו ושביעו ואם תקבצם יהיו כלם עשר |
|- | |- | ||
| | | | ||
| − | == <span style=color:green>The Ten Numerals</span> == | + | == <span style=color:green>The Ten Numerals</span>‫<ref>MS Ithaca om.</ref> == |
| | | | ||
|- | |- | ||
| − | | | + | |The sages of India made the shapes of their digits like these: |
|style="text-align:right;"|וחכמי הודו עשו צורות אותיותם כמו אלו | |style="text-align:right;"|וחכמי הודו עשו צורות אותיותם כמו אלו | ||
|- | |- | ||
| Line 310: | Line 351: | ||
| | | | ||
| − | == Finding the Square Numbers == | + | == <span style=color:green>The Method of Finding the Square Numbers</span>‫<ref>MS Ithaca om.</ref> == |
| − | + | |style="text-align:right;"|<big>הסדר למצא המספרים המרובעים</big> | |
|- | |- | ||
| − | |<math>\scriptstyle n^2+\left(2n+1\right)=\left(n+1\right)^2</math> | + | |It is that you sum the first square with the odd number that follows it and you will find the second square. |
| + | :<math>\scriptstyle{\color{OliveGreen}{n^2+\left(2n+1\right)=\left(n+1\right)^2}}</math> | ||
|style="text-align:right;"|הוא שתקבץ המרובע הראשון עם המספר הנפרד הבא אחריו ותמצא המרובע השני | |style="text-align:right;"|הוא שתקבץ המרובע הראשון עם המספר הנפרד הבא אחריו ותמצא המרובע השני | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{1^2+3=4=2^2}}</math> | + | *As if you sum one, which is the first square, with 3, which is the first of the odd numbers; you find 4, which is the second square, whose root is 2. |
| + | :<math>\scriptstyle{\color{blue}{1^2+3=4=2^2}}</math> | ||
|style="text-align:right;"|כמו אם תקבץ האחד שהוא המרובע הראשון עם הג' שהוא ראש<ref>ראש: MS Cambridge תחלת</ref> הנפרדים<ref>הנפרדים: MS Cambridge הנפרדות</ref> תמצא ד' שהוא המרובע השני אשר צלעו ב‫' | |style="text-align:right;"|כמו אם תקבץ האחד שהוא המרובע הראשון עם הג' שהוא ראש<ref>ראש: MS Cambridge תחלת</ref> הנפרדים<ref>הנפרדים: MS Cambridge הנפרדות</ref> תמצא ד' שהוא המרובע השני אשר צלעו ב‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{2^2+5=4+5=9=3^2}}</math> | + | *If you sum 4, which is the second square, with 5, which is the second odd number, they are 9, which is the third square, whose root is 3. |
| + | :<math>\scriptstyle{\color{blue}{2^2+5=4+5=9=3^2}}</math> | ||
|style="text-align:right;"|ואם תקבץ ד' שהוא המרובע השני עם ה' שהוא הנפרד השני יהיו ט' והוא המרובע השלישי אשר צלעו ג‫' | |style="text-align:right;"|ואם תקבץ ד' שהוא המרובע השני עם ה' שהוא הנפרד השני יהיו ט' והוא המרובע השלישי אשר צלעו ג‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{3^2+7=9+7=16=4^2}}</math> | + | *If you add the third odd number, which is 7, to 9, which is the third square, you find 16, which is the fourth square, whose root is 4. |
| + | :<math>\scriptstyle{\color{blue}{3^2+7=9+7=16=4^2}}</math> | ||
|style="text-align:right;"|ואם אתה מוסיף על ט' שהוא המרובע השלישי המספר הנפרד השלישי שהוא<ref>שהוא: MS Cambridge והוא</ref> ז' תמצא י"ו שהוא המרובע הרביעי אשר צלעו ד‫' | |style="text-align:right;"|ואם אתה מוסיף על ט' שהוא המרובע השלישי המספר הנפרד השלישי שהוא<ref>שהוא: MS Cambridge והוא</ref> ז' תמצא י"ו שהוא המרובע הרביעי אשר צלעו ד‫' | ||
|- | |- | ||
| − | | | + | |This way you find all of them. |
|style="text-align:right;"|ועל זה הסדר תמצאם כלם | |style="text-align:right;"|ועל זה הסדר תמצאם כלם | ||
|- | |- | ||
| | | | ||
| − | == <span style=color:green>Cubic Numbers</span> == | + | == <span style=color:green>Cubic Numbers</span>‫<ref>MS Ithaca om.</ref> == |
| − | |||
| | | | ||
|- | |- | ||
| − | | | + | |Anything whose length, breadth, and depth are equal is called cubic. |
| − | |style="text-align:right;"|כל דבר שארכו ורחבו ועמקו שוים יקרא | + | |style="text-align:right;"|<big>כל</big> דבר שארכו ורחבו ועמקו שוים יקרא מעוקב |
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{1^3=1}}</math> | + | *1 is the first cubic number. It is a place that is 1 in length, 1 in width, 1 in height and 1 in depth. |
| + | :<math>\scriptstyle{\color{blue}{1^3=1}}</math> | ||
|style="text-align:right;"|והנה א' הוא המעוקב הראשון והוא מקום שארכו א' ורחבו א' וגבהו א' ועמקו א‫' | |style="text-align:right;"|והנה א' הוא המעוקב הראשון והוא מקום שארכו א' ורחבו א' וגבהו א' ועמקו א‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{2^3=8}}</math> | + | *8 is the second cubic number derived from a place whose length, width, and depth are 2. |
| + | :<math>\scriptstyle{\color{blue}{2^3=8}}</math> | ||
|style="text-align:right;"|וח' הוא המעקב השני היוצא ממקום שארכו ורחבו ועמקו ב‫' | |style="text-align:right;"|וח' הוא המעקב השני היוצא ממקום שארכו ורחבו ועמקו ב‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{3^3=27}}</math> | + | *27 is the third cubic number derived from a place whose length, width, and depth are 3. |
| + | :<math>\scriptstyle{\color{blue}{3^3=27}}</math> | ||
|style="text-align:right;"|וכ"ז הוא המעוקב השלישי היוצא ממקום שארכו ורחבו ועמקו ג‫' | |style="text-align:right;"|וכ"ז הוא המעוקב השלישי היוצא ממקום שארכו ורחבו ועמקו ג‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{4^3=64}}</math> | + | *64 is the fourth cubic number derived from a place whose length, width, and depth are 4. |
| + | :<math>\scriptstyle{\color{blue}{4^3=64}}</math> | ||
|style="text-align:right;"|וס"ד הוא המעקב הרביעי היוצא ממקום שארכו ורחבו ועמקו ד‫' | |style="text-align:right;"|וס"ד הוא המעקב הרביעי היוצא ממקום שארכו ורחבו ועמקו ד‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{5^3=125}}</math> | + | *125 is the fifth cubic number derived from a place whose length, width, and depth are 5. |
| + | :<math>\scriptstyle{\color{blue}{5^3=125}}</math> | ||
|style="text-align:right;"|וקכ"ה הוא המעוקב החמשי היוצא ממקום שארכו ורחבו ועמקו ועמקו ה‫' | |style="text-align:right;"|וקכ"ה הוא המעוקב החמשי היוצא ממקום שארכו ורחבו ועמקו ועמקו ה‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{6^3=216}}</math> | + | *216 is the sixth cubic number derived from a place whose length, width, and depth are 6. |
| + | :<math>\scriptstyle{\color{blue}{6^3=216}}</math> | ||
|style="text-align:right;"|ורי"ו הוא המעוקב הששי היוצא ממקום שארכו ורחבו ועמקו ו‫' | |style="text-align:right;"|ורי"ו הוא המעוקב הששי היוצא ממקום שארכו ורחבו ועמקו ו‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{7^3=343}}</math> | + | *343 is the seventh cubic number derived from a place whose length, width, and depth are 7. |
| + | :<math>\scriptstyle{\color{blue}{7^3=343}}</math> | ||
|style="text-align:right;"|ושמ"ג הוא המעקב השבעי היוצא ממקום שארכו ורחבו ועמקו ז‫' | |style="text-align:right;"|ושמ"ג הוא המעקב השבעי היוצא ממקום שארכו ורחבו ועמקו ז‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{8^3=512}}</math> | + | *512 is the eighth cubic number derived from a place whose length, width, and depth are 8. |
| + | :<math>\scriptstyle{\color{blue}{8^3=512}}</math> | ||
|style="text-align:right;"|ותקי"ב הוא המעוקב השמני היוצא ממקום שארכו ורחבו ועמקו ח‫' | |style="text-align:right;"|ותקי"ב הוא המעוקב השמני היוצא ממקום שארכו ורחבו ועמקו ח‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{9^3=729}}</math> | + | *729 is the ninth cubic number derived from a place whose length, width, and depth are 9. |
| + | :<math>\scriptstyle{\color{blue}{9^3=729}}</math> | ||
|style="text-align:right;"|ותשכ"ט הוא המעוקב התשעי היוצא ממקום שארכו ורחבו ועמקו ט‫' | |style="text-align:right;"|ותשכ"ט הוא המעוקב התשעי היוצא ממקום שארכו ורחבו ועמקו ט‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{10^3=1000}}</math> | + | *One thousand is the tenth cubic number derived from a place whose length, width, and depth are 10. |
| + | :<math>\scriptstyle{\color{blue}{10^3=1000}}</math> | ||
|style="text-align:right;"|ואלף הוא המעוקב העשרי היוצא ממקום שארכו ורחבו ועמקו י‫' | |style="text-align:right;"|ואלף הוא המעוקב העשרי היוצא ממקום שארכו ורחבו ועמקו י‫' | ||
|- | |- | ||
| − | |<math>\scriptstyle\left(2n\right)^3=8\sdot n^3</math> | + | |You see that every cubic number, [when it is] doubled, is 8 times the original [cubic] number. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(2n\right)^3=8\sdot n^3}}</math> | ||
|style="text-align:right;"|והנך רואה כי כל מעוקב [זוג] יהיה ח' פעמי' מהמספר הראשון | |style="text-align:right;"|והנך רואה כי כל מעוקב [זוג] יהיה ח' פעמי' מהמספר הראשון | ||
|- | |- | ||
| | | | ||
| + | *Because the cube of 1 is 1. | ||
| + | :<math>\scriptstyle{\color{blue}{1^3=1}}</math> | ||
|style="text-align:right;"|כי כל מעקב א' הוא א‫' | |style="text-align:right;"|כי כל מעקב א' הוא א‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{2^3=\left(2\sdot1\right)^3=8=8\sdot1^3}}</math> | + | *The cube of 2, which is double 1, is 8. |
| + | :<math>\scriptstyle{\color{blue}{2^3=\left(2\sdot1\right)^3=8=8\sdot1^3}}</math> | ||
|style="text-align:right;"|ומעקב ב' שהוא כפל א' הוא ח‫' | |style="text-align:right;"|ומעקב ב' שהוא כפל א' הוא ח‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{4^3=\left(2\sdot2\right)^3=64=8\sdot2^3}}</math> | + | *The cube of 4, which is double 2, is 64, which is 8 times the cube of 2. |
| + | :<math>\scriptstyle{\color{blue}{4^3=\left(2\sdot2\right)^3=64=8\sdot2^3}}</math> | ||
|style="text-align:right;"|ומעקב ד' שהוא כפל ב' הוא ס"ד שהוא ח' פ' במעקב ב‫' | |style="text-align:right;"|ומעקב ד' שהוא כפל ב' הוא ס"ד שהוא ח' פ' במעקב ב‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle{\color{blue}{6^3=8\sdot3^3}}</math> | + | *Also the cube of 6 is 8 times the cube of 3. |
| − | |style="text-align:right;"|וכן מעקב ו' הוא ח' פ' במעקב ג' וכן לעולם | + | :<math>\scriptstyle{\color{blue}{6^3=8\sdot3^3}}</math> |
| + | |style="text-align:right;"|וכן מעקב ו' הוא ח' פ' במעקב ג‫' | ||
| + | |- | ||
| + | |And so on. | ||
| + | |style="text-align:right;"|וכן לעולם | ||
|- | |- | ||
| − | + | !<span style=color:green>Word Problem - Payment Problem</span> | |
| | | | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:digging a hole|612|QJWz}} | + | *{{#annot:digging a hole|612|QJWz}}Therefore, if someone says: dig me a hole 2 in length, 2 in breadth, 2 in depth, the payment should be 40 liṭra, which is 8 times 5 liṭra. |
:<math>\scriptstyle{\color{blue}{2^3\sdot5=8\sdot5=40}}</math> | :<math>\scriptstyle{\color{blue}{2^3\sdot5=8\sdot5=40}}</math> | ||
| − | |style="text-align:right;"|ולכן מי שיאמר חפור לי בור שיהיה ב' ארכו ב' רחבו ב' עמקו יהיה שכרו מ' ליט' שהוא ח' פעמי' ה' ליט'{{#annotend:QJWz}} | + | |style="text-align:right;"|ולכן מי שיאמר חפור לי בור שיהיה ב' ארכו ב' רחבו ב' עמקו יהיה שכרו מ' ליט' שהוא ח' פעמי' ה' ליט‫'{{#annotend:QJWz}} |
|- | |- | ||
| − | | | + | |Because every cubic number, when it is doubled, is 8 times the original [cubic] number. |
|style="text-align:right;"|כי כל מעקב כשיכפול יהיה ח' פעמים מהמספר הראשון | |style="text-align:right;"|כי כל מעקב כשיכפול יהיה ח' פעמים מהמספר הראשון | ||
|- | |- | ||
| | | | ||
| − | == <span style=color:green>Primary Definitions</span> == | + | == <span style=color:green>Primary Definitions</span>‫<ref>MS Ithaca om.</ref> == |
| − | |||
| | | | ||
|- | |- | ||
| | | | ||
| − | * | + | *<big>The unity</big> is the issue by which every one of the beings in the world is called one. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|האחדות הוא הענין אשר בו קוראים לכל אחד מהנמצאי' בעולם אחד |
|- | |- | ||
| | | | ||
| − | * | + | *<big>The number</big> is the multitude summed from units. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|המספר הוא הרבוי הנקבץ מן האחדים |
|- | |- | ||
| | | | ||
| − | * | + | *<big>The number counted by another number</big> is the product of the counted number multiplied a number of times that equals to the number of the units contained in the other number by which it is counted. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|המספר המנוי במספר אחר הוא מספר הנקבץ מכפל המספר המנוי פעמי' אשר מניינם כמניין האחדים אשר במספר השני אשר הוא נמנה בו |
|- | |- | ||
| | | | ||
| − | * | + | *<big>The square number</big> is the product of a number by the number of the units contained in that number itself. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|המספר המרובע הוא המספר הנקבץ מכפל מספר במספר אחדיו הנמצאי' בו באותו המספר עצמו |
|- | |- | ||
| | | | ||
| − | * | + | *<big>The the original number</big> is the root of the square number. |
| − | |style="text-align:right;"|המספר הראשון הוא | + | |style="text-align:right;"|המספר הראשון הוא גדר המרובע |
|- | |- | ||
| | | | ||
| − | :: | + | ::As the number nine, which is called a square, because it is a product of three times three. |
| + | ::<math>\scriptstyle{\color{blue}{9=3^2}}</math> | ||
|style="text-align:right;"|כגון מספר תשעה נקרא מרובע מפני שהוא נקבץ מכפל השלשה שלשה פעמי‫' | |style="text-align:right;"|כגון מספר תשעה נקרא מרובע מפני שהוא נקבץ מכפל השלשה שלשה פעמי‫' | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::The number three is called the root of the square. |
| + | ::<math>\scriptstyle{\color{blue}{3=\sqrt{9}}}</math> | ||
|style="text-align:right;"|ומספר השלשה נקרא גדר המרובע | |style="text-align:right;"|ומספר השלשה נקרא גדר המרובע | ||
|- | |- | ||
| | | | ||
| − | * | + | *<big>The cubic number</big> is an equilateral body, whose length, breadth and depth are equal and this number is the product of a square number by its root. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והמספר מעקב הוא הגוף השוה שארכו ורחבו ועמקו שוים והמספר הזה הוא המספר הנקבץ מכפל מספר המרובע כמנין גדרו |
|- | |- | ||
| | | | ||
| − | :: | + | ::As the number 9, which is a square; if you multiply it by 3, which is its root, the product is 27 and this number is called a cubic number. |
| + | ::<math>\scriptstyle{\color{blue}{27=9\sdot3=3^2\sdot3}}</math> | ||
|style="text-align:right;"|כגון מספר ט' שהוא 9 מרובע אם אתה כופל אותו במניין ג' שהוא גדרו יהיה הנקבץ מזה כ"ז והמספר הזה הוא הנקרא מספר מעוקב | |style="text-align:right;"|כגון מספר ט' שהוא 9 מרובע אם אתה כופל אותו במניין ג' שהוא גדרו יהיה הנקבץ מזה כ"ז והמספר הזה הוא הנקרא מספר מעוקב | ||
|- | |- | ||
| | | | ||
| − | * | + | *Relating a number to another number, or a shape to another shape - ? |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הקשת מניין אל מניין או תמונה לתמונה או ערך אחר כן השני |
|- | |- | ||
| | | | ||
| − | == Multiplication == | + | == <span style=color:green>Multiplication</span> == |
| | | | ||
|- | |- | ||
| | | | ||
| − | === Units and tens by units and tens === | + | === <span style=color:green>Units and tens by units and tens</span> === |
| − | + | | | |
| − | !style="text-align:right;"|דרך רבוי ב' אותיות כנגד ב' אותיות | + | |- |
| + | !The method of multiplying two digits by two digits | ||
| + | |style="text-align:right;"|<big>דרך רבוי ב' אותיות כנגד ב' אותיות</big>‫<ref>דרך...ב' אותיות: MS Ithaca om.</ref> | ||
|- | |- | ||
| − | | | + | |When we wish to multiply two digits by two digits: |
| − | |style="text-align:right;"|כשנרצה<ref>כשנרצה: MS Cambridge כשתרצה</ref> לרבות ב' אותיות כנגד ב' אותיות | + | |style="text-align:right;"|<big>כשנרצה</big>‫<ref>כשנרצה: MS Cambridge כשתרצה</ref> לרבות ב' אותיות כנגד ב' אותיות |
|- | |- | ||
| − | | | + | |We multiply them three times one after another: first, we multiply the units by the units; then we multiply the units by the tens; and then we multiply the tens by the tens. |
|style="text-align:right;"|נרבה אותם ג' פעמי' זה אחר זה<br> | |style="text-align:right;"|נרבה אותם ג' פעמי' זה אחר זה<br> | ||
בראשונה נרבה האחדים עם האחדים<br> | בראשונה נרבה האחדים עם האחדים<br> | ||
| − | ואחרי כן<ref>ואחרי כן: MS Cambridge ואח"כ</ref> נרבה האחדים עם העשרות<br> | + | ואחרי כן<ref>ואחרי כן: MS Cambridge ואח"כ</ref> נרבה האחדים עם <s>ב</s> העשרות<br> |
ואחרי כן<ref>ואחרי כן: MS Cambridge ואח"כ</ref> נרבה העשרות עם העשרות | ואחרי כן<ref>ואחרי כן: MS Cambridge ואח"כ</ref> נרבה העשרות עם העשרות | ||
|- | |- | ||
| − | | | + | |Here is the example of the [ordered] multiplications: |
|style="text-align:right;"|והנה דמיון הריבוי הקודם והמתאחר | |style="text-align:right;"|והנה דמיון הריבוי הקודם והמתאחר | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle22\times22</math> | + | *We wish to multiply 22 times 22. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle22\times22</math> |
| + | |style="text-align:right;"|<big>רצינו</big> לרבות כ"ב פעמים כ"ב | ||
|- | |- | ||
| | | | ||
| Line 517: | Line 585: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נרבה | + | :First, we multiply the units by each other and say: 2 times 2 is 4. We write 4 above the units on the right. |
| − | אחרי כן נרבה האחדים עם העשרות ונאמר ב' פעמי' ד' וב' פעמים ד' הרי ח' ונכתוב ח‫' | + | |style="text-align:right;"|נרבה בתחילת האחדים זה עם זה ונאמר ב' פעמים ב' הם ד' ונכתוב ד' למעלה מן האחדים מצד ימין |
| − | אחרי כן נרבה העשרות זו עם זו ונאמר ב' פעמים ב' ד' ונכתוב ד‫' | + | |- |
| − | יצא לנו כי כ"ב פעמים כ"ב הם תפ"ד | + | | |
| + | :Then, we multiply the units by the tens and say: 2 times [2] and 2 times [2] is 8. We write 8. | ||
| + | |style="text-align:right;"|אחרי כן נרבה האחדים עם העשרות ונאמר ב' פעמי' ד' וב' פעמים ד' הרי ח' ונכתוב ח‫' | ||
| + | |- | ||
| + | | | ||
| + | :Then, we multiply the tens by each other and say: 2 times 2 is 4. We write 4. | ||
| + | |style="text-align:right;"|אחרי כן נרבה העשרות זו עם זו ונאמר ב' פעמים ב' ד' ונכתוב ד‫' | ||
| + | |- | ||
| + | | | ||
| + | :We receive that 22 times 22 is 484. | ||
| + | |style="text-align:right;"|יצא לנו כי כ"ב פעמים כ"ב הם תפ"ד | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 534: | Line 612: | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle44\times44</math> | + | *Also if we wish to multiply 44 times 44. |
| + | :<math>\scriptstyle44\times44</math> | ||
|style="text-align:right;"|וכן אם רצינו לרבות מ"ד פעמים מ"ד | |style="text-align:right;"|וכן אם רצינו לרבות מ"ד פעמים מ"ד | ||
|- | |- | ||
| Line 554: | Line 633: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נרבה האחדים זה עם זה בתחילה ונאמר ד' | + | :First, we multiply the units by each other and say: 4 times 4 is 16. We write 6 and keep the ten, which is 1. |
| − | אחר כן נרבה האחדים עם העשרות ונאמר ד' פעמי' ד' י"ו וד' פעמים ד' י"ו הרי ל"ב וצרף עמהם הא' שהחזקת בידך הרי ל"ג ונכתוב ג' ונחזיק בידינו ג‫' | + | |style="text-align:right;"|נרבה האחדים זה עם זה בתחילה ונאמר ד' פעמי' ד' הם י"ו ונכתוב ו' ונחזיק‫<ref>ונחזיק: MS Ithaca ונכתוב</ref> בידינו העשרון שהוא א‫' |
| − | אחרי כן נרבה העשרות עם העשרות נאמר ד' פעמים ד' י"ו ועם הג' שהחזקנו בידינו הרי י"ט ונכתוב י"ט | + | |- |
| − | היוצא מזה כי מ"ד פעמים מ"ד הם אלף ות"תקל"ו | + | | |
| + | :Then, we multiply the units by the tens and say: 4 times 4 is 16 and 4 times 4 is 16; it is 32. Add to it the 1 you have kept; it is 33. We write 3 and keep 3. | ||
| + | |style="text-align:right;"|אחר כן נרבה האחדים עם העשרות ונאמר ד' פעמי' ד' י"ו וד' פעמים ד' י"ו הרי ל"ב וצרף עמהם הא' שהחזקת בידך הרי ל"ג ונכתוב ג' ונחזיק בידינו ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :Then, we multiply the tens by the tens and say: 4 times 4 is 16; with the 3 we have kept, it is 19. We write 19. | ||
| + | |style="text-align:right;"|אחרי כן נרבה העשרות עם העשרות נאמר ד' פעמים ד' י"ו ועם הג' שהחזקנו בידינו הרי י"ט ונכתוב י"ט | ||
| + | |- | ||
| + | | | ||
| + | :The result is that 44 times 44 is 1936. | ||
| + | |style="text-align:right;"|היוצא מזה כי מ"ד פעמים מ"ד הם אלף ות"תקל"ו | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 570: | Line 659: | ||
|- | |- | ||
| | | | ||
| − | *<math>\ | + | *Also if we wish to multiply 20 times 20. |
| + | :<math>\scriptstyle20\times20</math> | ||
|style="text-align:right;"|וכן אם רצינו לרבות כף פעמים כף | |style="text-align:right;"|וכן אם רצינו לרבות כף פעמים כף | ||
|- | |- | ||
| Line 607: | Line 697: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נאמר ציפרא פעם ציפרא ציפרא ונכתבנה | + | :We say: zero times zero is zero. We write it. |
| − | + | |style="text-align:right;"|נאמר ציפרא פעם ציפרא ציפרא ונכתבנה | |
| − | |||
| − | |||
|- | |- | ||
| − | | colspan="2"| | + | | |
| − | :{| | + | :Then, we say: zero times 2 and 2 times zero is zero. We write it. |
| + | |style="text-align:right;"|אחר כך נאמר ציפרא פעמים פעם ב' וב' פעמים ציפרא ציפרא ונכתבנה | ||
| + | |- | ||
| + | | | ||
| + | :Then, we sa: 2 times 2 is 4. We write it. | ||
| + | |style="text-align:right;"|ואחר כך נאמ' ב' פעמים ב' הם ד' ונכתבם | ||
| + | |- | ||
| + | | | ||
| + | :We receive that 20 times 20 is four hundred. | ||
| + | |style="text-align:right;"|יצא לנו כי כ פעמים כ הם ארבע מאות | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :{| | ||
|- | |- | ||
| ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{2\times0}}={\color{blue}{0}}}</math>|| <span style="color:#0000FF>0</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{\left(2\times0\right)+ | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{2\times0}}={\color{blue}{0}}}</math>|| <span style="color:#0000FF>0</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{\left(2\times0\right)+ | ||
| Line 625: | Line 725: | ||
| | | | ||
| − | === Units by units and tens === | + | === <span style=color:green>Units by units and tens</span> === |
| − | + | | | |
| − | |style="text-align:right;"|ואם רצינו לרבות אות אחד שנגד ב אותיות | + | |- |
| + | |If we want to multiply one digit by two digits. | ||
| + | |style="text-align:right;"|<big>ואם רצינו</big> לרבות אות אחד שנגד ב אותיות | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle7\times45</math> | + | *For example, when we wish to know [how much is] 7 times 45, as you see in the diagram: |
| + | :<math>\scriptstyle7\times45</math> | ||
|style="text-align:right;"|כגון שרצינו לדעת ז' פעמים מ"ה כמו שתראה בצורה | |style="text-align:right;"|כגון שרצינו לדעת ז' פעמים מ"ה כמו שתראה בצורה | ||
|- | |- | ||
| Line 662: | Line 765: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|נרבה אותם עם הציפרא כדי | + | :We multiply them [by adding] a zero, so that they will be two digits by two digits and this will be done easily. |
| + | :<math>\scriptstyle{\color{blue}{07\times45}}</math> | ||
| + | |style="text-align:right;"|נרבה אותם עם הציפרא כדי שיהיו ב' אותיות כנגד ב' אותיות ויעשה אותם בנקל | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונאמר ה' פעמי' ז' ל"ה ונכתוב האחדים שהם ה' ונחזיק בידינו העשרות שהם ג‫' | + | :We say: 5 times 7 is 35. We write the units, which is 5, and keep the tens that are 3. |
| − | אחר כך נאמר ציפרא פע' ה' ציפרא וד' פעמים ז' כ"ח וצרף עמהם הג' שהחזקנו בידינו יהיו ל"א ונכתוב ל"א כי מעתה לא נשאר לנו לרבות דבר אחר | + | |style="text-align:right;"|ונאמר ה' פעמי' ז' ל"ה ונכתוב האחדים שהם ה' ונחזיק בידינו העשרות שהם ג‫' |
| − | כי ציפרא פעם ד' שנשאר לנו לרבות הוא ציפרא ואינם עולים לכלום | + | |- |
| − | יצא לנו כי ז' פעמים מ"ה הם שט"ו | + | | |
| + | :Then, we say: zero times 5 is zero and 4 times 7 is 28. Add the 3 that we have kept; it is 31. We write 31, for we have nothing left to multiply. | ||
| + | |style="text-align:right;"|אחר כך נאמר ציפרא פע' ה' ציפרא וד' פעמים ז' כ"ח וצרף עמהם הג' שהחזקנו בידינו יהיו ל"א ונכתוב ל"א כי מעתה לא נשאר לנו לרבות דבר אחר | ||
| + | |- | ||
| + | | | ||
| + | :Because, zero times 4 we have left to multiply is zero; so the result is nothing. | ||
| + | |style="text-align:right;"|כי ציפרא פעם ד' שנשאר לנו לרבות הוא ציפרא ואינם עולים לכלום | ||
| + | |- | ||
| + | | | ||
| + | :We receive that 7 times 45 is 315. | ||
| + | |style="text-align:right;"|יצא לנו כי ז' פעמים מ"ה הם שט"ו | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 683: | Line 798: | ||
| | | | ||
| − | === Check === | + | ==== <span style=color:green>Check</span> ==== |
| − | + | | | |
| + | |- | ||
| + | |If we want to check if the number we received is correct: | ||
|style="text-align:right;"|ואם נרצה לבחון אם החשבון שיצא לנו הוא אמתי | |style="text-align:right;"|ואם נרצה לבחון אם החשבון שיצא לנו הוא אמתי | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle22\times22</math> | + | *We do this way with the calculation of 22 times 22: |
| + | :<math>\scriptstyle22\times22</math> | ||
|style="text-align:right;"|נעשה על זה הדרך בזה החשבון שהוא כ"ב פעמים כ"ב | |style="text-align:right;"|נעשה על זה הדרך בזה החשבון שהוא כ"ב פעמים כ"ב | ||
|- | |- | ||
| Line 711: | Line 826: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נקבץ הב' אותיות העליונות ונאמר ב' וב' הם ד' ונכתוב אותם אצל שתי האותיות התחתונות | + | :We sum up the upper digits and say: 2 and 2 is 4. We write it next to the two bottom digits. |
| − | אחרי כן נרבה אלו שתי | + | |style="text-align:right;"|נקבץ הב' אותיות העליונות ונאמר ב' וב' הם ד' ונכתוב אותם אצל שתי האותיות התחתונות |
| − | וכמו שנשארו בידינו כן צריך שישארו בידינו ז' מן ת'פ'ד' שעולה החשבון אחר שנשליך מהם הט‫' | + | |- |
| + | | | ||
| + | :Then, we multiply the two digits we wrote one above the other and say: 4 times [4] is 16. | ||
| + | |style="text-align:right;"|אחרי כן נרבה אלו שתי אותיות שכתבנו זו עם זו ונאמר ד' פעמי' י"ו | ||
| + | |- | ||
| + | | | ||
| + | :We cast out the 9 from it; 7 remains. We write 7 between the two mentioned digits. | ||
| + | |style="text-align:right;"|נשליך מהם הט' ישארו ז' ונכתוב ז' בתוך שתי האותיות הנזכרות | ||
| + | |- | ||
| + | | | ||
| + | :As the 7 we have left, so we should have 7 left from 484, which is the result of the calculation, after we cast out the 9 from it. | ||
| + | |style="text-align:right;"|וכמו שנשארו בידינו ז' כן צריך שישארו בידינו ז' מן ת'פ'ד' שעולה החשבון אחר שנשליך מהם הט‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| − | + | :<math>\scriptstyle{\color{blue}{\begin{cases}\scriptstyle2+2=4\\\scriptstyle2+2=4\end{cases}\longrightarrow 4\times4=16\longrightarrow16\equiv_97}}</math> | |
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{4+8+4=16\longrightarrow16\equiv_97}}</math> | + | :If we sum up 4, 8, and 4, which are the digits indicating 484; it is 16. |
| − | |style="text-align:right;"|והנה אם נקבץ ד' וח' וד' שהם האותיות המורות ת'פ'ד' יהיו י"ו | + | :<math>\scriptstyle{\color{blue}{4+8+4=16\longrightarrow16\equiv_97}}</math> |
| − | + | |style="text-align:right;"|והנה אם נקבץ ד' וח' וד' שהם האותיות המורות ת'פ'ד' יהיו י"ו | |
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle44\times44</math> | + | :If we cast out 9 from it, 7 remains. So, the calculation is correct. |
| + | |style="text-align:right;"|ואם נשליך מהם הט' ישארו <s>ד</s> ז' והוא חשבון אמתי | ||
| + | |- | ||
| + | | | ||
| + | *Also in the second calculation we did, which is 44 times 44. | ||
| + | :<math>\scriptstyle44\times44</math> | ||
|style="text-align:right;"|וכן בחשבון השני שעשינו שהם מ"ד פעמים מ"ד | |style="text-align:right;"|וכן בחשבון השני שעשינו שהם מ"ד פעמים מ"ד | ||
|- | |- | ||
| Line 744: | Line 875: | ||
|- | |- | ||
| | | | ||
| − | :: | + | :We sum up the upper digits and say: 4 and 4 is 8. We write it. |
| − | |style="text-align:right;"|נקבץ ‫<ref>32v</ref>האותיות העליונות ונאמר ד' וד' הם ח' ונכתבם | + | |style="text-align:right;"|נקבץ ‫<ref>32v</ref>האותיות העליונות ונאמר ד' וד' הם ח' ונכתבם |
| − | |||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{ | + | :We multiply them by each other and say: 8 times 8 is 64. |
| − | |style="text-align:right;"|וכן צריך להשאר מאלף ת"תק'ל'ו' שסימנם הוא א' וט' וג' וו‫'< | + | |style="text-align:right;"|ונרבה אותם זו עם זו ונאמר ח' פע' ח' הם ס"ד |
| − | + | |- | |
| + | | | ||
| + | :Cast out the nines from it; 1 remains. | ||
| + | |style="text-align:right;"|השליכם מהם ט' ט' ישאר מהם א‫' | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\begin{cases}\scriptstyle4+4=8\\\scriptstyle4+4=8\end{cases}\longrightarrow 8\times8=64\longrightarrow64\equiv_91}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :The same should remain from 1936, whose digits are 1, 9, 3, 6. | ||
| + | |style="text-align:right;"|וכן צריך להשאר מאלף ת"תק'ל'ו' שסימנם הוא א' וט' וג' וו‫' | ||
| + | |- | ||
| + | | | ||
| + | :Sum them up; it is 19. Cast out the nines from it; the remainder is 1. | ||
| + | |style="text-align:right;"|ואם <s>תכ</s> תקבצם יהיו י"ט ותשליך אותם ט'ט' יהיה הנשאר א‫' | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{1+9+3+6\longrightarrow19\equiv_91}}</math> | ||
|- | |- | ||
| | | | ||
| − | === Units, tens, and hundreds by units, tens, and hundreds === | + | === <span style=color:green>Units, tens, and hundreds by units, tens, and hundreds</span> === |
| − | + | | | |
| + | |- | ||
| + | |If we want to multiply three digits by three digits. | ||
|style="text-align:right;"|<big>ואם נרצה</big> לרבות ג' אותיות כנגד ג' אותיות | |style="text-align:right;"|<big>ואם נרצה</big> לרבות ג' אותיות כנגד ג' אותיות | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle222\times222</math> | + | *As when we wish to know [the product of] 222 times 222. |
| + | :<math>\scriptstyle222\times222</math> | ||
|style="text-align:right;"|כגון שרצינו לדעת רכ"ב פעמים רכ"ב פעמים | |style="text-align:right;"|כגון שרצינו לדעת רכ"ב פעמים רכ"ב פעמים | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|נרבה אותם ה' פעמים | + | :We multiply them five times [= i.e. five phases of multiplication, five ranks in the final result of multiplication] and this is the method of multiplication: |
| + | |style="text-align:right;"|נרבה אותם ה' פעמים וזהו דרך ריבויים | ||
| + | |- | ||
| + | | | ||
| + | :We write them 5 times, so that the first, second, third, fourth, and fifth multiplications will be clear to the eye. | ||
| + | |style="text-align:right;"|ונכתוב אותם ה' פעמים כדי שיתבאר למראית העין הרבוי הראשון והשני והשלישי והרביעי וחמשי | ||
|- | |- | ||
| − | | | + | | |
| − | | | + | | |
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| Line 783: | Line 938: | ||
|- | |- | ||
| | | | ||
| + | :If we want to multiply 222 times 222. | ||
|style="text-align:right;"|ואם נרצה לרבות רכ"ב פעמים רכ"ב | |style="text-align:right;"|ואם נרצה לרבות רכ"ב פעמים רכ"ב | ||
| − | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | + | |- |
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| | | | ||
| Line 799: | Line 958: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נתחיל לרבות האחדים ונאמר ב' פעמים ב' הם ד' ונכתבם | + | :We start to multiply the units and say: 2 times 2 is 4. We write it. |
| − | אחר זה נרבה האחדי' עם העשרות ונאמר ב' פעמי' ב' הם ד' וב' פעמים ב' הם ד' הרי ח' ונכתבם | + | |style="text-align:right;"|נתחיל לרבות האחדים ונאמר ב' פעמים ב' הם ד' ונכתבם |
| + | |- | ||
| + | | | ||
| + | :Then, we multiply the units by the tens and say: 2 times 2 is 4 and 2 times 2 is 4; so, it is 8. We write it. | ||
| + | |style="text-align:right;"|אחר זה נרבה האחדי' עם העשרות ונאמר ב' פעמי' ב' הם ד' וב' פעמים ב' הם ד' הרי ח' ונכתבם‫<ref>ונכתבם: MS Ithaca om.</ref> | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 813: | Line 976: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אחר זה נרבה שלשתם ביחד ונאמר ב' פעמים ב' ד' וב' פעמים ב' ד' הרי ח' וב' | + | :Then, we multiply all three together and say: 2 times 2 is 4; 2 times 2 is 4; so it is 8; and 2 times 2 is 4; so it is 12. We write 2 and keep 1. |
| + | |style="text-align:right;"|אחר זה נרבה שלשתם ביחד ונאמר ב' פעמים ב' ד' וב' פעמים ב' ד' הרי ח'‫<ref>אחר זה נרבה... הרי ח': MS Ithaca om.</ref> וב'פעמים ב' ד' הרי י"ב ונכתוב ב' ונחזי' בידינו א‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 826: | Line 990: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אחר זה נרבה העשרות עם המאות ונאמר ב' פעמים ב' ד' וב' פעמי' ב' ד' הרי ח' וא' שהחזקנו בידינו הרי ט' ונכתבם | + | :We multiply the tens by the hundreds and say: 2 times 2 is 4 and 2 times 2 is 4; so it is 8; with the 1 we have kept, it is 9. We write it. |
| − | אחר זה נרבה המאות עם המאות ונאמר ב' פעמי' ב' ד' ונכתבם | + | |style="text-align:right;"|אחר זה נרבה העשרות עם המאות ונאמר ב' פעמים ב' ד' וב' פעמי' ב' ד' הרי ח' וא' שהחזקנו בידינו הרי ט' ונכתבם |
| − | יצא לנו כי רכ"ב פעמים רכ"ב הם מ"ט אלפים ורפ"ד | + | |- |
| + | | | ||
| + | :We multiply the hundreds by the hundreds and say: 2 times 2 is 4. We write it. | ||
| + | |style="text-align:right;"|אחר זה נרבה המאות עם המאות ונאמר ב' פעמי' ב' ד' ונכתבם | ||
| + | |- | ||
| + | | | ||
| + | :We receive that 222 times 222 is 49284. | ||
| + | |style="text-align:right;"|יצא לנו כי רכ"ב פעמים רכ"ב הם מ"ט אלפים ורפ"ד | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 840: | Line 1,011: | ||
|} | |} | ||
|- | |- | ||
| − | |Check | + | | |
| + | ==== <span style=color:green>Check</span> ==== | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | |To check if the calculation is correct: | ||
|style="text-align:right;"|<big>ולבחון אם החשבון אמת</big> | |style="text-align:right;"|<big>ולבחון אם החשבון אמת</big> | ||
|- | |- | ||
| Line 860: | Line 1,036: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|קבצנו רכ"ב העליונים שסימנם ב'ב'ב' ועלו ו' וכתבנום אצלם | + | :We sum up the upper 222, whose digits are 2, 2, 2; the result is 6. We write it next to them. |
| − | רבינו ו' על ו' ועלו ל"ו השלכנו אותם ט'ט' ולא נשאר בידינו ונתננו ציפרא באמצעם | + | |style="text-align:right;"|קבצנו רכ"ב העליונים שסימנם ב'ב'ב' ועלו ו' וכתבנום אצלם |
| + | |- | ||
| + | | | ||
| + | :We multiply 6 by 6; the result is 36. | ||
| + | |style="text-align:right;"|רבינו ו' על ו' ועלו ל"ו | ||
| + | |- | ||
| + | | | ||
| + | :We cast out the nines; we are left with nothing. We write a zero between them. | ||
| + | |style="text-align:right;"|השלכנו אותם ט'ט' ולא נשאר בידינו ונתננו ציפרא באמצעם | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| − | + | :<math>\scriptstyle{\color{blue}{\begin{cases}\scriptstyle2+2+2=6\\\scriptstyle2+2+2=6\end{cases}\longrightarrow 6\times6=36\longrightarrow36\equiv_90}}</math> | |
| + | |- | ||
| + | | | ||
| + | :So, a zero should also remain from the sum of the calculation result, which is 49284, whose digits are 4, 9, 2, 8, 4. The sum is 27. | ||
| + | :<math>\scriptstyle{\color{blue}{4+9+2+8+4=27\longrightarrow27\equiv_90}}</math> | ||
| + | |style="text-align:right;"|וכן צריך להשאר הציפרא מן הסכום מן היוצא מן החשבון שהם מ"ט אלפים ורפ"ד אשר דמיונם הם ד' ט' ב' ח' ד' ועולה כ"ז‫<ref>כ"ז: MS Ithaca י"ח</ref> | ||
| + | |- | ||
| + | | | ||
| + | :If you cast out the nines, a zero remains. | ||
| + | |style="text-align:right;"|ואם תשליכם ט"ט ישאר ציפרא | ||
|- | |- | ||
| | | | ||
| − | : | + | :We find that the calculation is correct. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נמצא שהחשבון הוא אמת |
| − | |||
|- | |- | ||
| | | | ||
| − | === Units and tens by units, tens, and hundreds === | + | === <span style=color:green>Units and tens by units, tens, and hundreds</span> === |
| − | + | | | |
| + | |- | ||
| + | |If we want to multiply two digits by three [digits]. | ||
|style="text-align:right;"|<big>ואם רצינו</big> לרבות ב' אותיות כנגד ג‫' | |style="text-align:right;"|<big>ואם רצינו</big> לרבות ב' אותיות כנגד ג‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle22\times222</math> | + | *For example, when we wish to [find the product of] 222 times 22, as you see in the diagram: |
| − | |style="text-align:right;"|כגון שרצינו לומר ר'כ'ב' פעמים כ"ב כאשר תראה בצורה | + | :<math>\scriptstyle22\times222</math> |
| + | |style="text-align:right;"|כגון שרצינו לומר <s>כ</s> ר'כ'ב' פעמים כ"ב כאשר תראה בצורה‫<ref>בצורה: MS Ithaca אותה</ref> | ||
| + | |- | ||
| + | | | ||
| + | | | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| Line 894: | Line 1,092: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | |
| + | :We match them by [adding] a zero, so they are three digits by three digits and then the procedure is easier. | ||
|style="text-align:right;"|נשוה אותה עם הציפרא כדי שיהיו ג' אותיות כנגד ג' אותיות ויקל עשייתו | |style="text-align:right;"|נשוה אותה עם הציפרא כדי שיהיו ג' אותיות כנגד ג' אותיות ויקל עשייתו | ||
|- | |- | ||
| | | | ||
| − | === Units by units, tens, and hundreds === | + | === <span style=color:green>Units by units, tens, and hundreds</span> === |
| − | + | | | |
| − | |style="text-align:right;"|וכן אם רצינו לרבות אות אחת כנגד שלשה | + | |- |
| + | |If we want to multiply one digit by three [digits]. | ||
| + | |style="text-align:right;"|וכן אם רצינו לרבות אות‫<ref>אות: MS Ithaca אותו</ref> אחת כנגד שלשה | ||
|- | |- | ||
| − | | | + | |We match them also by [adding] zeros. |
|style="text-align:right;"|נשוה אותה עם הציפרא ג"כ | |style="text-align:right;"|נשוה אותה עם הציפרא ג"כ | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle9\times222</math> | + | *As when we wish to know [the product of] 9 times 222. |
| − | |style="text-align:right;"|כגון שרצינו לדעת ט' פעמים ר'כ'ב' נכתוב אותם בזה הדרך כאשר תראה בצורה | + | :<math>\scriptstyle9\times222</math> |
| + | |style="text-align:right;"|כגון שרצינו לדעת ט' פעמים ר'כ'ב' <s>כ</s> | ||
| + | |- | ||
| + | | | ||
| + | :We write them this way, as you see in the diagram: | ||
| + | |style="text-align:right;"|נכתוב אותם בזה הדרך כאשר תראה בצורה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| Line 924: | Line 1,133: | ||
|- | |- | ||
| | | | ||
| − | |||
| − | |style="text-align:right;"|אם נרצה לרבות ד' אותיות כנגד ד' אותיות | + | === <span style=color:green>Units, tens, hundreds, and thousands by units, tens, hundreds, and thousands</span> === |
| + | | | ||
| + | |- | ||
| + | |If we want to multiply four digits by four digits. | ||
| + | |style="text-align:right;"|<big>אם‫<ref>אם: MS Ithaca om.</ref> נרצה לרבות</big> ד'‫<ref>ד': MS Ithaca ג'</ref> אותיות כנגד ד'‫<ref>ד': MS Ithaca ג'</ref> אותיות | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle2222\times2222</math> | + | *As when we wish to multiply 2222 times 2222. |
| − | |style="text-align:right;"|כגון שרצינו לרבות ב' אלפים ור'כ'ב' פעמי' ב' אלפים ור'כ'ב‫' | + | :<math>\scriptstyle2222\times2222</math> |
| + | |style="text-align:right;"|כג כגון שרצינו לרבות ב' אלפים ור'כ'ב' פעמי' ב' אלפים ור'כ'ב‫' | ||
|- | |- | ||
| − | | | + | | |
| − | + | :We multiply them seven times and write them seven times, in order that it will be clear to the quick and slow observer. | |
| − | |style="text-align:right;"|נרבה אותם ז' פעמים ונכתוב אותם ז' פעמי' כדי שיתבאר למעיין הקודם והמתאחר | + | |style="text-align:right;"|נרבה אותם ז' פעמים ונכתוב אותם ז' פעמי'‫<ref>ונכתוב אותם ז' פעמי': MS Ithaca om.</ref> כדי שיתבאר למעיין הקודם והמתאחר‫<ref>Here ends this chapter in MS Ithaca</ref> |
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 952: | Line 1,165: | ||
|- | |- | ||
| | | | ||
| + | :If we wish to multiply 2222 by 2222. | ||
|style="text-align:right;"|ואם רצינו לרבות ב' אלפי' ור'כ'ב' עם ב' אלפי' ור'כ'ב‫' | |style="text-align:right;"|ואם רצינו לרבות ב' אלפי' ור'כ'ב' עם ב' אלפי' ור'כ'ב‫' | ||
|- | |- | ||
| Line 970: | Line 1,184: | ||
|- | |- | ||
| | | | ||
| + | :We do as we did in the previous calculations. | ||
|style="text-align:right;"|נעשה כאשר עשינו בחשבונו' הקודמי‫' | |style="text-align:right;"|נעשה כאשר עשינו בחשבונו' הקודמי‫' | ||
|- | |- | ||
| | | | ||
| + | :The result of the calculation is 4937284. | ||
|style="text-align:right;"|ויעלה החשבון ד' אלפי אלפים ות'ת'ק'ל'ז' אלפי' ור'פ'ד‫' | |style="text-align:right;"|ויעלה החשבון ד' אלפי אלפים ות'ת'ק'ל'ז' אלפי' ור'פ'ד‫' | ||
|- | |- | ||
| | | | ||
| − | === Units, tens, hundreds, and thousands by units, tens, and hundreds === | + | === <span style=color:green>Units, tens, hundreds, and thousands by units, tens, and hundreds</span> === |
| − | + | | | |
| + | |- | ||
| + | |If we want to multiply four digits by three digits. | ||
|style="text-align:right;"|ואם רצינו לרבות ד' אותיות כנגד ג' אותיות | |style="text-align:right;"|ואם רצינו לרבות ד' אותיות כנגד ג' אותיות | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle2222\times222</math> | + | *As when we want to multiply 2222 by 222. |
| + | :<math>\scriptstyle2222\times222</math> | ||
|style="text-align:right;"|כגון שרצינו לרבות ב' אלפים ור'כ'ב' כנגד ר'כ'ב‫' | |style="text-align:right;"|כגון שרצינו לרבות ב' אלפים ור'כ'ב' כנגד ר'כ'ב‫' | ||
|- | |- | ||
| − | | | + | | |
| + | :We match them by [adding] a zero, as you see in the diagram: | ||
|style="text-align:right;"|נשוה אותם עם הציפרא כאשר תראה בצורה | |style="text-align:right;"|נשוה אותם עם הציפרא כאשר תראה בצורה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| Line 1,002: | Line 1,225: | ||
|- | |- | ||
| | | | ||
| + | :The result is 493284. | ||
|style="text-align:right;"|ועולים ת'צ'ג' אלפים ור'פ'ד‫' | |style="text-align:right;"|ועולים ת'צ'ג' אלפים ור'פ'ד‫' | ||
|- | |- | ||
| | | | ||
| − | === Units, tens, hundreds, and thousands by units and tens === | + | === <span style=color:green>Units, tens, hundreds, and thousands by units and tens</span> === |
| − | + | | | |
| + | |- | ||
| + | |If we want to multiply two digits by four [digits]. | ||
|style="text-align:right;"|וכן אם רצינו לרבות ב' אותיות כנגד ד‫' | |style="text-align:right;"|וכן אם רצינו לרבות ב' אותיות כנגד ד‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle2222\times22</math> | + | *As when we wish to multiply 2222 by 22. |
| + | :<math>\scriptstyle2222\times22</math> | ||
|style="text-align:right;"|כגון שרצינו לרבות ב' אלפים ור'כ'ב' כנגד כ"ב | |style="text-align:right;"|כגון שרצינו לרבות ב' אלפים ור'כ'ב' כנגד כ"ב | ||
|- | |- | ||
| − | | | + | | |
| + | :We match them by [adding] zeros, as you see in the diagram: | ||
|style="text-align:right;"|נשוה אותם עם הציפרא כאשר תראה בצורה | |style="text-align:right;"|נשוה אותם עם הציפרא כאשר תראה בצורה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| Line 1,031: | Line 1,262: | ||
|- | |- | ||
| | | | ||
| + | :The result is 48884. | ||
|style="text-align:right;"|ועולים מ"ח אלפים ות'ת'פ'ד‫' | |style="text-align:right;"|ועולים מ"ח אלפים ות'ת'פ'ד‫' | ||
|- | |- | ||
| | | | ||
| − | === Units, tens, hundreds, and thousands by units === | + | === <span style=color:green>Units, tens, hundreds, and thousands by units</span> === |
| − | + | | | |
| + | |- | ||
| + | |If we want to multiply one digit by four digits. | ||
|style="text-align:right;"|וכן אם רצינו לרבות אות אחד כנגד כנגד ד' אותיות | |style="text-align:right;"|וכן אם רצינו לרבות אות אחד כנגד כנגד ד' אותיות | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle2\times2222</math> | + | *As 2 by 2222. |
| + | :<math>\scriptstyle2\times2222</math> | ||
|style="text-align:right;"|כגון ב' עם ב' אלפים ור'כ'ב‫' | |style="text-align:right;"|כגון ב' עם ב' אלפים ור'כ'ב‫' | ||
|- | |- | ||
| − | | | + | | |
| + | :We match them by [adding] zeros, as you see in the diagram: | ||
|style="text-align:right;"|נשוה אותם עם הציפרא כאשר תראה בצורה | |style="text-align:right;"|נשוה אותם עם הציפרא כאשר תראה בצורה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| Line 1,060: | Line 1,299: | ||
|- | |- | ||
| | | | ||
| + | :The result is 4444. | ||
|style="text-align:right;"|ועולים ד' אלפים ות'מ'ד‫' | |style="text-align:right;"|ועולים ד' אלפים ות'מ'ד‫' | ||
|- | |- | ||
| | | | ||
| − | === Units, tens, hundreds, thousands, and tens of thousands by units, tens, hundreds, thousands, and tens of thousands === | + | === <span style=color:green>Units, tens, hundreds, thousands, and tens of thousands by units, tens, hundreds, thousands, and tens of thousands</span> === |
| − | + | | | |
| + | |- | ||
| + | |If we want to multiply five digits by five digits. | ||
|style="text-align:right;"|אם נרצה לרבות ה' אותיות כנגד ה' אותיות | |style="text-align:right;"|אם נרצה לרבות ה' אותיות כנגד ה' אותיות | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle22222\times22222</math> | + | *As when we wish to know [the product of] 22222 by 22222. |
| + | :<math>\scriptstyle22222\times22222</math> | ||
|style="text-align:right;"|כגון שרצינו לדעת כ"ב אלפים ור'כ'ב' כ"ב אלפי' ור'כ'ב‫' | |style="text-align:right;"|כגון שרצינו לדעת כ"ב אלפים ור'כ'ב' כ"ב אלפי' ור'כ'ב‫' | ||
|- | |- | ||
| − | | | + | | |
| − | + | :We multiply them nine times and this is the method of multiplication: | |
| − | |style="text-align:right;"|נרבה אותם ט' פעמים וזה דרך רבויים | + | |style="text-align:right;"|נרבה אותם ט' פעמים וזה דרך רבויים |
| − | ונכתוב אותם ט' פעמי' כדי שיתבאר למעיין הקודם הקודם והמתאחר | + | |- |
| + | | | ||
| + | :We write them nine times, in order that it will be clear to the quick and slow observer. | ||
| + | |style="text-align:right;"|ונכתוב אותם ט' פעמי' כדי שיתבאר למעיין הקודם הקודם והמתאחר | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,094: | Line 1,340: | ||
| | | | ||
| − | === Units, tens, hundreds, thousands, tens of thousands, and hundreds of thousands by units, tens, hundreds, thousands, tens of thousands, and hundreds of thousands === | + | === <span style=color:green>Units, tens, hundreds, thousands, tens of thousands, and hundreds of thousands by units, tens, hundreds, thousands, tens of thousands, and hundreds of thousands</span> === |
| − | + | | | |
| + | |- | ||
| + | |If we want to multiply six digits by six digits. | ||
|style="text-align:right;"|ואם נרצה לרבות ו' אותיות כנגד ו' אותיות | |style="text-align:right;"|ואם נרצה לרבות ו' אותיות כנגד ו' אותיות | ||
|- | |- | ||
| − | | | + | |We multiply them 11 times. |
|style="text-align:right;"|נרבה אותם י"א פעמי‫' | |style="text-align:right;"|נרבה אותם י"א פעמי‫' | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle222222\times222222</math> | + | *As when we wish to multiply 222222 by 222222. |
| + | :<math>\scriptstyle222222\times222222</math> | ||
|style="text-align:right;"|כגון שרצינו לרבות ר'כ'ב' אלפי' ור'כ'ב' ר'כ'ב' אלפים ור'כ'ב‫' | |style="text-align:right;"|כגון שרצינו לרבות ר'כ'ב' אלפי' ור'כ'ב' ר'כ'ב' אלפים ור'כ'ב‫' | ||
|- | |- | ||
| | | | ||
| + | :We multiply them 11 times, in order that it will be clear to the quick and slow observer. | ||
|style="text-align:right;"|ונרבה אותם י"א פעמי' כדי שיתבאר למעיין הקודם והמתאחר | |style="text-align:right;"|ונרבה אותם י"א פעמי' כדי שיתבאר למעיין הקודם והמתאחר | ||
|} | |} | ||
| Line 1,126: | Line 1,376: | ||
| | | | ||
| − | == | + | == The Method of Summing Up Separate Numbers Called Congregare or Riunire == |
| − | |style="width:45%;text-align:right;"|<big>דרך קיבוץ חשבונות נפרדים | + | |style="width:45%;text-align:right;"|<big>דרך קיבוץ חשבונות נפרדים הנקראים קונגרייג</big> או ריונרייי |
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |If we want to sum up separate numbers and bring them into one sum, we do this way: we write them successively one beneath the other: the units beneath the units, the tens corresponding the tens, the hundreds corresponding the hundreds and the thousands corresponding the thousands. |
| − | |style="text-align:right;"|נעשה על זאת הדרך שנכתוב אותם על הסדר זה תחת זה האחדי' תחת האחדים והעשרות נכח העשרות | + | |style="text-align:right;"|אם רצינו לקבץ חשבונות נפרדים ולהביאם לסכום אחד נעשה על זאת הדרך שנכתוב אותם על הסדר זה תחת זה האחדי' תחת האחדים והעשרות נכח העשרות והמאות נכח המאות והאלפים נכח האלפים |
|- | |- | ||
| − | | | + | |We start summing the units and write [their sum]. |
| − | |||
|style="text-align:right;"|ונתחיל לקבץ האחדי' ולכותבם | |style="text-align:right;"|ונתחיל לקבץ האחדי' ולכותבם | ||
|- | |- | ||
| − | | | + | |If [the sum] is more than ten, we write the units and keep the tens. |
| − | |||
|style="text-align:right;"|אם יעלו על עשר נכתוב האחדים ונחזיק בידינו העשרות | |style="text-align:right;"|אם יעלו על עשר נכתוב האחדים ונחזיק בידינו העשרות | ||
|- | |- | ||
| − | | | + | |Then, we sum the hundreds, then the thousands, as you see in this diagram: |
|style="text-align:right;"|אחרי כן נקבץ המאות אחרי כן נקבץ האלפים כמו שתראה בצורה הזאת | |style="text-align:right;"|אחרי כן נקבץ המאות אחרי כן נקבץ האלפים כמו שתראה בצורה הזאת | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle12345+67891+23456+78912+34567</math> | + | *Example: we wish to sum up 12345 with 67891, 23456, 78912, and 34567. |
| − | |style="text-align:right;"|‫<ref>33r</ref>דמיון זה רצינו לקבץ י"ב אלפים וש'מ'ה' וס"ז אלפי' ות'ת'צ'א' וכ"ג אלפים ת'נ'ו' וע"ח אלפים ות'ת'ק'י'ב' ול"ד אלפים ות'ק'ס'ז' | + | :<math>\scriptstyle12345+67891+23456+78912+34567</math> |
| + | |style="text-align:right;"|‫<ref>33r</ref>דמיון זה רצינו לקבץ י"ב‫<ref>י"ב: MS Ithaca י"ג</ref> אלפים וש'מ'ה' וס"ז אלפי' ות'ת'צ'א' וכ"ג אלפים ת'נ'ו' וע"ח אלפים ות'ת'ק'י'ב' ול"ד אלפים ות'ק'ס'ז'‫<ref>תקס"ז: MS Ithaca תתקס"ז</ref> | ||
|- | |- | ||
| | | | ||
| Line 1,194: | Line 1,440: | ||
|- | |- | ||
| | | | ||
| − | :: | + | :We start summing the units and say: 5, 1, 6, 2, 7 are 21. We write 1 and keep 2. |
| + | :<math>\scriptstyle{\color{blue}{5+1+6+2+7={\color{green}{2}}1}}</math> | ||
|style="text-align:right;"|נתחיל לקבץ האחדים ונאמר ה' וא' וו' וב' וז' הם כ"א נכתוב א' ונחזי' בידינו ב‫' | |style="text-align:right;"|נתחיל לקבץ האחדים ונאמר ה' וא' וו' וב' וז' הם כ"א נכתוב א' ונחזי' בידינו ב‫' | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Then, we sum the tens and say: 4, 9, 5, 1, 6 are 25; with the 2 we have kept, they are 27. We write 7 and keep 2. |
| − | |style="text-align:right;"|נקבץ אחרי כן העשרות ונאמר ד' וט' וה' וא' וו' הם כ"ה וב' | + | :<math>\scriptstyle{\color{blue}{\left(4+9+5+1+6\right)+{\color{green}{2}}=25+2={\color{green}{2}}7}}</math> |
| + | |style="text-align:right;"|נקבץ אחרי כן העשרות ונאמר ד' וט' וה' וא' וו' הם כ"ה וב' שה<sup>ח</sup>זקנו בידינו הם כ"ז נכתו' ז' ונחזיק בידינו ב‫' | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Then, we sum the hundreds and say: 3, 8, 4, 9, 5 are 29; with the 2 we have kept, they are 31. We write 1 and keep 3. |
| + | :<math>\scriptstyle{\color{blue}{\left(3+8+4+9+5\right)+{\color{green}{2}}=29+2={\color{green}{3}}1}}</math> | ||
|style="text-align:right;"|נקבץ אחרי כן המאות ונאמ' ג' וח' וד' וט' וה' הם כ"ט וב' שהחזקנו בידינו הרי ל"א נכתוב א' ונחזיק בידינו ג‫' | |style="text-align:right;"|נקבץ אחרי כן המאות ונאמ' ג' וח' וד' וט' וה' הם כ"ט וב' שהחזקנו בידינו הרי ל"א נכתוב א' ונחזיק בידינו ג‫' | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Then, we sum the thousands and say: 2, 7, 3, 8, 4 are 24; with the 3 we have kept, they are 27. We write 7 and keep 2. |
| + | :<math>\scriptstyle{\color{blue}{\left(2+7+3+8+4\right)+{\color{green}{3}}=24+3={\color{green}{2}}7}}</math> | ||
|style="text-align:right;"|נקבץ אחרי כן האלפים ונאמר ב' וז' וג' וח' וד' הם כ"ד וג' שהחזקנו בידינו הרי כ"ז ונכתוב ז' ונחזיק בידינו ב‫' | |style="text-align:right;"|נקבץ אחרי כן האלפים ונאמר ב' וז' וג' וח' וד' הם כ"ד וג' שהחזקנו בידינו הרי כ"ז ונכתוב ז' ונחזיק בידינו ב‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :Then, we sum the tens of thousands and say: 1, 6, 2, 7, 3 are 19; with the 2 we have kept, they are 21. We write everything, because we do not have another number to sum. |
| − | |style="text-align:right;"|נקבץ אחר זה העשרות מן האלפים | + | :<math>\scriptstyle{\color{blue}{\left(1+6+2+7+3\right)+{\color{green}{2}}=19+2=21}}</math> |
| + | |style="text-align:right;"|נקבץ אחר זה העשרות מן האלפים ונאמ' א' וו' וב'‫<ref>וב': MS Ithaca om.</ref> וז' וג' הם י"ט‫<ref>הם י"ט: MS Ithaca om.</ref> וב' שהחזקנו בידינו הרי כ"א נכתוב אותם כלם כי אין לנו לקבץ חשבון אחר | ||
|- | |- | ||
| | | | ||
| + | :The total result is 217171. | ||
|style="text-align:right;"|עלו כלם רי"ז אלפים וקע"א | |style="text-align:right;"|עלו כלם רי"ז אלפים וקע"א | ||
|- | |- | ||
| − | | | + | |If we want to sum up numbers, some of which have three digits, some have four, some have two, and some have more or less: |
| − | |||
|style="text-align:right;"|<big>ואם רצינו</big> לקבץ חשבונות נפרדים שקצתם הם מג' אותיות וקצתם מד' וקצתם מב' וקצתם מיותר או פחות | |style="text-align:right;"|<big>ואם רצינו</big> לקבץ חשבונות נפרדים שקצתם הם מג' אותיות וקצתם מד' וקצתם מב' וקצתם מיותר או פחות | ||
|- | |- | ||
| − | | | + | |We always write the units corresponding to the units, the tens corresponding to the tens and so on and we match them by [adding] zeros to make the procedure easier. |
| − | |||
|style="text-align:right;"|נכתוב לעולם האחדים נוכח האחדי' והעשרות נוכח העשרות וכן כלם ונשוה אותם עם הציפרי כדי שיקל העניין | |style="text-align:right;"|נכתוב לעולם האחדים נוכח האחדי' והעשרות נוכח העשרות וכן כלם ונשוה אותם עם הציפרי כדי שיקל העניין | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle12345+06789+00123+45600+80912+03406</math> | + | *Example: we wish to sum up 12345 with 6789, 123, 45600, 80912, and 3406. |
| + | :<math>\scriptstyle12345+06789+00123+45600+80912+03406</math> | ||
|style="text-align:right;"|<big>דמיון זה</big> רצינו לקבץ י"ב אלפים וש'מ'ה' וו' אלפים ות"שפ"ט וקכ"ג ומ"ה אלפים ות"ר ופ' אלפי' ות"תקי"ב וג' אלפים ות"ו | |style="text-align:right;"|<big>דמיון זה</big> רצינו לקבץ י"ב אלפים וש'מ'ה' וו' אלפים ות"שפ"ט וקכ"ג ומ"ה אלפים ות"ר ופ' אלפי' ות"תקי"ב וג' אלפים ות"ו | ||
|- | |- | ||
| Line 1,272: | Line 1,523: | ||
|- | |- | ||
| | | | ||
| − | :: | + | :We start summing the units and say: 5, 9, 3, 2, 6 are 25. We write [5] and keep 2. |
| + | :<math>\scriptstyle{\color{blue}{5+9+3+2+6={\color{green}{2}}5}}</math> | ||
|style="text-align:right;"|התחלנו לקבץ האחדים ואמרנו ה' וט' וג' וב' וו' הם כ"ה כתבנו כ"ה והחזקנו בידינו ב‫' | |style="text-align:right;"|התחלנו לקבץ האחדים ואמרנו ה' וט' וג' וב' וו' הם כ"ה כתבנו כ"ה והחזקנו בידינו ב‫' | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Then, we sum the tens and say: 4, 8, 2, 1 are 15; with the 2 we have kept, they are 17. We write 7 and keep 1. |
| − | |style="text-align:right;"|קבצנו אחר כן העשרות ואמרנו ד' וח' וב' וא' הם ט"ו ועם הב' שהחזקנו בידינו הם י"ז כתבנו ז' והחזקנו בידינו א‫' | + | :<math>\scriptstyle{\color{blue}{\left(4+8+2+1\right)+{\color{green}{2}}=15+2={\color{green}{1}}7}}</math> |
| + | |style="text-align:right;"|קבצנו אחר כן‫<ref>אחר כן: MS Ithaca בידינו</ref> העשרות ואמרנו ד' וח' וב' וא' הם ט"ו ועם הב' שהחזקנו בידינו הם י"ז כתבנו ז' והחזקנו בידינו א‫' | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Then, we sum the hundreds and say: 3, 7, 1, 6, 9, 4 are 30; with the 1 we have kept, they are 31. We write 1 and keep 3. |
| + | :<math>\scriptstyle{\color{blue}{\left(3+7+1+6+9+4\right)+{\color{green}{1}}=30+1={\color{green}{3}}1}}</math> | ||
|style="text-align:right;"|קבצנו אחרי כן המאות ואמרנו ג' וז' וא' וו' וט' וד' הם ל' ועם הא' שהחזקנו בידינו הם ל"א כתבנו א' והחזקנו בידינו ג‫' | |style="text-align:right;"|קבצנו אחרי כן המאות ואמרנו ג' וז' וא' וו' וט' וד' הם ל' ועם הא' שהחזקנו בידינו הם ל"א כתבנו א' והחזקנו בידינו ג‫' | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Then, we sum the thousands and say: 2, 6, 5, 3 are 16; with the 3 we have kept, they are 19. We write 9 and keep 1. |
| + | :<math>\scriptstyle{\color{blue}{\left(2+6+5+3\right)+{\color{green}{3}}=16+3={\color{green}{1}}9}}</math> | ||
|style="text-align:right;"|קבצנו אחרי כן האלפים ואמרנו ב' וו' וה' וג' הם י"ו ועם הג' שהחזקנו בידינו הם י"ט כתבנו ט' והחזקנו בידינו א‫' | |style="text-align:right;"|קבצנו אחרי כן האלפים ואמרנו ב' וו' וה' וג' הם י"ו ועם הג' שהחזקנו בידינו הם י"ט כתבנו ט' והחזקנו בידינו א‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :Then, we sum the tens of thousands and say: 1, 4, 8 are 13; with the 1 we have kept, they are 14. We write 14, because we have summed everything. |
| − | |style="text-align:right;"|קבצנו אחר זה העשרות מן האלפי' ואמרנו א' וד' וח' הם י"ג ועם א' שהחזקנו בידינו הם י"ד וכתבנו י"ד כי מעתה קבצנו הכל | + | :<math>\scriptstyle{\color{blue}{\left(1+4+8\right)+{\color{green}{1}}=13+1=14}}</math> |
| + | |style="text-align:right;"|קבצנו אחר זה העשרות מן האלפי' ואמרנו א' וד' וח' הם י"ג ועם א' שהחזקנו בידינו הם י"ד‫<ref>ועם... י"ד: MS Ithaca om.</ref> וכתבנו י"ד כי מעתה קבצנו הכל | ||
|- | |- | ||
| | | | ||
| + | :Their sum is 149175. | ||
|style="text-align:right;"|ועולה סכומם קמ"ט אלפים וקע"ה | |style="text-align:right;"|ועולה סכומם קמ"ט אלפים וקע"ה | ||
|- | |- | ||
| | | | ||
| − | == | + | == The Method of Subtracting a Number from a Number Called Sottrarre == |
|style="text-align:right;"|<big>דרך הוצאת מספר ממספר הנק' סורטראיירי</big> | |style="text-align:right;"|<big>דרך הוצאת מספר ממספר הנק' סורטראיירי</big> | ||
|- | |- | ||
| − | | | + | |If we want to subtract a number from a number: |
| − | + | |style="text-align:right;"|אם רצינו לגרוע מספר ממספר | |
| − | |style="text-align:right;"| | + | |- |
| + | |If all the [digits] of the larger number, from which you want to subtract another number, are greater than the [digits] of that number, the procedure is easy. | ||
| + | |style="text-align:right;"|אם המספר הגדול אשר אתה רוצה לגרוע ממנו מספר אחר כל חלקיו גדולי' מחלקי המספר הוא דרך נקל | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle987654-645232</math> | + | *Example: we wish to subtract 645232 from 987654. |
| − | |style="text-align:right;"|דמיון זה רצינו לגרוע מתת"קפ"ז אלפים ותרנ"ד ת"רמ"ה אלפים ורל"ב | + | :<math>\scriptstyle987654-645232</math> |
| + | |style="text-align:right;"|<big>דמיון זה</big> רצינו לגרוע מתת"קפ"ז אלפים ותרנ"ד ת"רמ"ה אלפים ורל"ב | ||
|- | |- | ||
| | | | ||
| Line 1,326: | Line 1,586: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|נעשה על זה הדרך | + | :We do this way: |
| + | |style="text-align:right;"|נעשה על זה הדרך | ||
|- | |- | ||
| | | | ||
| − | :: | + | :We start from the units and say: subtract 2 from 4; 2 remains. We write 2 beneath them. |
| − | |style="text-align:right;"|ונאמר מד' הוצא ב' ישארו ב' ונכתוב ב' תחתיהם | + | :<math>\scriptstyle{\color{blue}{4-2=2}}</math> |
| + | |style="text-align:right;"|נתחיל מן האחדים ונאמר מד' הוצא ב' ישארו ב' ונכתוב ב' תחתיהם | ||
|- | |- | ||
| | | | ||
| − | : | + | :Subtract 3 from 5; 2 remains. Write 2 beneath them. |
| + | :<math>\scriptstyle{\color{blue}{5-3=2}}</math> | ||
|style="text-align:right;"|ומן ה' הוצא ג' ישארו ב' ותכתוב ב' תחתיהם | |style="text-align:right;"|ומן ה' הוצא ג' ישארו ב' ותכתוב ב' תחתיהם | ||
|- | |- | ||
| | | | ||
| − | : | + | :Subtract 2 from 6; 4 remains. Write 4 beneath them. |
| + | :<math>\scriptstyle{\color{blue}{6-2=4}}</math> | ||
|style="text-align:right;"|ומן ו' הוצא ב' ישארו ד' ותכתוב ד' תחתיהם | |style="text-align:right;"|ומן ו' הוצא ב' ישארו ד' ותכתוב ד' תחתיהם | ||
|- | |- | ||
| | | | ||
| − | : | + | :Subtract 5 from 7; 2 remains. Write 2 beneath them. |
| + | :<math>\scriptstyle{\color{blue}{7-5=2}}</math> | ||
|style="text-align:right;"|ומן ז' תוצא ה' ישארו ב' ונכתוב ב' תחתיהם | |style="text-align:right;"|ומן ז' תוצא ה' ישארו ב' ונכתוב ב' תחתיהם | ||
|- | |- | ||
| | | | ||
| − | : | + | :Subtract 4 from 8; 4 remains. Write 4 beneath them. |
| − | |style="text-align:right;"|ומן ח' הוצא ד' ישארו ד' ונכתוב ד' תחתיהם | + | :<math>\scriptstyle{\color{blue}{8-4=4}}</math> |
| + | |style="text-align:right;"|ומן ח' הוצא ד' ישארו ד' ונכתוב ד' תחתיהם‫<ref>ומן ז'... ד' תחתיהם: MS Ithaca om.</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | :Subtract 6 from 9; 3 remains. Write 3 beneath them. |
| + | :<math>\scriptstyle{\color{blue}{9-6=3}}</math> | ||
|style="text-align:right;"|ומן ט' הוצא ו' ישארו ג' ותכתוב ג' תחתיהם | |style="text-align:right;"|ומן ט' הוצא ו' ישארו ג' ותכתוב ג' תחתיהם | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הרי שאם נוציא מת"תק'פ'ז' אלפים ות"רנ"ד ת"רמ"ה אלפים ורל"ב ישארו ש'מ'ב' אלפים ות'כ'ב' וזהו דרך נקל | + | :So, if we subtract 645232 from 987654, 342422 remains and this procedure is easy. |
| + | |style="text-align:right;"|הרי שאם נוציא מת"תק'פ'ז' אלפים <s>ת</s> ות"רנ"ד ת"רמ"ה אלפים <s>ול</s> ורל"ב ישארו ש'מ'ב' אלפים ות'כ'ב' וזהו דרך נקל | ||
|- | |- | ||
| − | |Check: | + | |<span style="color:green">'''Check - addition:'''</span> If you want to check if your calculation is correct, sum the digits you subtracted with the digits that remained and if [their sums] are the same as the digits from which you subtracted the other digits, it is correct. |
| − | |style="text-align:right;"|ואם תרצה לבחון אם החשבון שעשית הוא אמתי תקבץ המספרים שהוצאת עם המספרים שנשארו ואם יסכימו עם המספרים שהוצאת המספרים האחרי' ההם הוא אמתי | + | |style="text-align:right;"|<big>ואם תרצה לבחון</big> אם החשבון שעשית הוא אמתי תקבץ המספרים שהוצאת עם המספרים שנשארו ואם יסכימו עם המספרים שהוצאת המספרים האחרי' ההם הוא אמתי |
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle645232+342422=987654</math> | + | :Example: We sum 2 with 2; it is 4. We sum 3 with 2; it is 5. We sum 2 with 4; it is 6. We sum 5 with 2; it is 7. We sum 4 with 4; it is 8. We sum 6 with 3; it is 9. They are the same as the greater digits from which you subtracted the smaller digits. This indicates that the calculation is correct. |
| − | |style="text-align:right;"|דמיון זה קבצנו ב' עם ב' והיו ד' וקבצנו ג' וב' והיו ה' וקבצנו ב' עם ד' והיו ו' וקבצנו ה' עם ב' והיו ז' וקבצנו ד' עם ד' והיו ח' וקבצנו ו' עם ג' והיו ט' והם מסכימים עם המספרים הגדולים אשר הוצאת ממספר הקטנים מהם וזה יורה כי החשבון הוא אמתי | + | :<math>\scriptstyle645232+342422=987654</math> |
| + | |style="text-align:right;"|<big>דמיון</big> זה קבצנו ב' עם ב' והיו ד' וקבצנו ג' וב' והיו ה' וקבצנו ב' עם ד' והיו ו' וקבצנו ה' עם ב' והיו ז' וקבצנו ד' עם ד' והיו ח' וקבצנו ו' עם ג' והיו ט' והם מסכימים עם המספרים הגדולים אשר הוצאת ממספר הקטנים מהם וזה יורה כי החשבון הוא אמתי | ||
|- | |- | ||
| − | | | + | |If you want to subtract a number from a number, but some of the digits of the smaller number that you want to subtract from the greater number are greater than some of the [corresponding] digits of the greater number, you should use another procedure: |
| − | + | |style="text-align:right;"|<big>אמנם</big> אם תרצה לגרוע מספר ממספר ויהיו קצת חלקי המספר הקטן שאתה רוצה לפחות מהמספר הגדול גדולים מקצת מספר חלקי המספר הגדול אתה צריך לעשות על דרך אחרת | |
| − | |style="text-align:right;"|אמנם אם תרצה לגרוע מספר ממספר ויהיו קצת חלקי המספר הקטן שאתה רוצה לפחות מהמספר הגדול גדולים מקצת מספר חלקי המספר הגדול אתה צריך לעשות על דרך אחרת | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle93432-27654</math> | + | *Example: we wish to subtract 27654 from 93432. |
| − | |style="text-align:right;"|דמיון זה רצינו לגרוע מצ"ג אלפים ותל"ב כ"ז אלפים ות"רנ"ד | + | :<math>\scriptstyle93432-27654</math> |
| + | |style="text-align:right;"|<big>דמיון זה</big> רצינו לגרוע מצ"ג אלפים ותל"ב כ"ז אלפים ות"רנ"ד | ||
|- | |- | ||
| | | | ||
| Line 1,390: | Line 1,659: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נתחיל מן | + | :We start from the units and say: subtract 4 from 2; we cannot. |
| − | ונחזור אל הג' שפחתנו ממנו א' וישארו ב' ונאמר מב' | + | |style="text-align:right;"|נתחיל מן האחדי' ותאמר מב' תוצי' ד' לא נוכל |
| + | |- | ||
| + | | | ||
| + | :We subtract 1 from the 3 next to it and add it to the 2; they are 12. | ||
| + | |style="text-align:right;"|נפחות א' מן הג' שבצדה ונחבר אותה אל הב' ויהיו י"ב | ||
| + | |- | ||
| + | | | ||
| + | :We say: subtract 4 from 12; 8 remains. We write it. | ||
| + | |style="text-align:right;"|ונאמר מי"ב הוצא ד' ישארו ח'‫<ref>ישארו ח': MS Ithaca marg.</ref> ונכתבם | ||
| + | |- | ||
| + | | | ||
| + | :We return to the 3, from which we have subtracted 1; 2 remains. | ||
| + | |style="text-align:right;"|ונחזור אל הג' שפחתנו ממנו א' וישארו ב‫' | ||
| + | |- | ||
| + | | | ||
| + | :We say: subtract 5 from 2; we cannot. | ||
| + | |style="text-align:right;"|ונאמר מב' הוצא ה' לא נוכל | ||
| + | |- | ||
| + | | | ||
| + | :We subtract 1 from the 4 next to it and say: subtract 5 from 12; 7 remains. We write it. | ||
| + | |style="text-align:right;"|נפחות א' מהד' אשר בצדה ונאמר מי"ב הוצא ה' ישארו ז' ונכתבם | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,404: | Line 1,693: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונחזור אל הד' שפחתנו ממנה א' ונשארו ג' | + | :We return to the 4, from which we have subtracted 1; 3 remains. |
| − | + | |style="text-align:right;"|ונחזור אל הד' שפחתנו ממנה א' ונשארו ג‫' | |
| − | |||
| − | |||
|- | |- | ||
| − | + | | | |
| − | ::: | + | :We say: subtract 6 from 3; we cannot. |
| + | |style="text-align:right;"|ונאמר מג' הוצא ו' ולא נוכל | ||
|- | |- | ||
| − | | | + | | |
| + | :We subtract 1 from the 3 next to it and say: subtract 6 from 13; 7 remains. We write it. | ||
| + | |style="text-align:right;"|נפחות א' מן הג' אשר בצדה ונאמר מי"ג הוצא ו' וישארו ז' ונכתבם | ||
|- | |- | ||
| − | |2 | + | | |
| + | :We return to the 3, from which we have subtracted 1; 2 remains. | ||
| + | |style="text-align:right;"|ונחזור אל הג' שפחתנו ממנו א' ונשארו ב‫' | ||
|- | |- | ||
| − | | | + | | |
| − | | | + | :We say: subtract 7 from 2; we cannot. |
| + | |style="text-align:right;"|ונאמר מב' הוצא ז' לא נוכל | ||
|- | |- | ||
| − | |Check: | + | | |
| − | |style="text-align:right;"|והנה אם תקבץ מה שהוצאתו מהמספר הנזכר עם הנשאר יהיה כמספר הראשון | + | :We subtract 1 from the 9 next to it and say: subtract 7 from 12; 5 remains. We write it. |
| + | |style="text-align:right;"|נפחות א' מן הט' אשר בצדה ונאמר מי"ב הוצא ז' ישארו ה' ונכתבם | ||
| + | |- | ||
| + | | | ||
| + | :We return to the 9, from which we have subtracted 1; 8 remains. | ||
| + | |style="text-align:right;"|ונחזור אל הט' אשר פחתנו ממנה א' ונשארו ח‫' | ||
| + | |- | ||
| + | | | ||
| + | :We say: subtract 2 from 8; 6 remains. We write it. | ||
| + | |style="text-align:right;"|ונאמר מח' הוצא ב' ישארו ו' ונכתבנו | ||
| + | |- | ||
| + | | | ||
| + | :Hence, we subtract 27654 from 93432 and 65778 remains | ||
| + | |style="text-align:right;"|הרי שהוצאנו מצ"ג אלפים ותל"ב כ"ז אלפים ות"רנ"ד‫<ref>ותרנ"ד: MS Ithaca ותרנ"ב</ref> ונשארו ס"ה אלפים ות"שע"ח | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :::{| | ||
| + | |- | ||
| + | |rowspan="3"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{3-1}}={\color{green}{2}}\\&\scriptstyle{\color{green}{13}}{\color{red}{-6}}={\color{blue}{7}}\\\end{align}}</math>||9<span style="color:red">3</span>432||rowspan="3"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{9-1}}={\color{green}{8}}\\&\scriptstyle{\color{green}{12}}{\color{red}{-7}}={\color{blue}{5}}\\\end{align}}</math>||<span style="color:red">9</span>3432||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{green}{8}}{\color{red}{-2}}={\color{blue}{6}}}</math>||93432 | ||
| + | |- | ||
| + | |2<span style="color:red">7</span>654||<span style="color:red">2</span>7654||27654 | ||
| + | |- | ||
| + | |  <span style="color:#0000FF>7</span>78|| <span style="color:#0000FF>5</span>778||<span style="color:#0000FF>6</span>5778 | ||
| + | |} | ||
| + | |- | ||
| + | |<span style="color:green">'''Check - addition:'''</span> If you sum what you subtracted from the mentioned number with the remainder, it will be the same as the original number. | ||
| + | |style="text-align:right;"|והנה אם תקבץ מה שהוצאתו מהמספר הנזכר עם הנשאר יהיה כמספר הראשון | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle27654+65778=93432</math> | ||
| + | :If we sum 4 with 8; they are 12. We write 2 and keep 1. | ||
| + | |style="text-align:right;"|וזה שאם נקבץ ד' וח' יהיו י"ב ונכתוב ב' ונחזיק בידינו א‫' | ||
| + | |- | ||
| + | | | ||
| + | :If we sum 5 with 7; they are 12. With the 1 we have left, they are 13. We write 3 and keep 1. | ||
| + | |style="text-align:right;"|ואם נקבץ ה' וז' יהיו י"ב ועם הא' שנשארה בידינו יהיו י"ג ונכתוב ג' ונחזיק א‫' | ||
| + | |- | ||
| + | | | ||
| + | :If we sum 6 with 7; they are 13. With the 1 we have left, they are 14. We write 4 and keep 1. | ||
| + | |style="text-align:right;"|ואם נקבץ ו' וז' יהיו י"ג וא' שנשאר בידינו הרי י"ד ונכתוב ד' ונחזיק א‫' | ||
| + | |- | ||
| + | | | ||
| + | :If we sum 7 with 5; they are 12. With the 1 we have left, they are 13. We write 3 and keep 1. | ||
| + | |style="text-align:right;"|ואם נקבץ ז' וה' יהיו י"ב וא' שנשאר בידינו הרי י"ג ונכתוב ג' ונחזיק א‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :If we sum 2 with 6; they are 8. With the 1 we have left, they are 9. We write it. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואם נקבץ ב' וו' יהיו ח' וא' שנשאר בידינו הרי ט' ונכתבם |
| − | + | |- | |
| − | + | | | |
| − | + | :So, the final number is the same as the original [number]. | |
| − | ואם נקבץ ב' וו' יהיו ח' וא' שנשאר בידינו הרי ט' ונכתבם | + | |style="text-align:right;"|הרי שהמספר האחרון שוה עם הראשון |
| − | הרי שהמספר האחרון שוה עם הראשון דרך חילוק | + | |- |
| + | |The method of division. | ||
| + | |style="text-align:right;"|דרך חילוק | ||
|- | |- | ||
| | | | ||
| − | == | + | == The Method of Dividing a Number by a Number Called Dividere or Partire == |
|style="text-align:right;"|‫<ref>34r</ref><big>דרך חילוק מספר על מספר הנק' דיבי' או פארטיר‫'</big> | |style="text-align:right;"|‫<ref>34r</ref><big>דרך חילוק מספר על מספר הנק' דיבי' או פארטיר‫'</big> | ||
|- | |- | ||
| − | | | + | |If we want to divide a larger number by a smaller number: |
| − | |style="text-align:right;"|אם נרצה לחלוק מספר גדול על מספר קטן אם כל חלקי המספר הגדול הם גדולי מהמספר שאתה רוצה לחלק אותם בו הוא דרך נקל | + | |style="text-align:right;"|אם נרצה לחלוק מספר גדול על מספר קטן |
| + | |- | ||
| + | |If all the digits of the large number are larger than the number by which you want to divide them, the procedure is easy. | ||
| + | |style="text-align:right;"|אם כל חלקי המספר הגדול הם גדולי מהמספר שאתה רוצה לחלק אותם בו הוא דרך נקל | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle98756\div4</math> | + | *Example: we wish to divide 98756 by 4. |
| + | :<math>\scriptstyle98756\div4</math> | ||
|style="text-align:right;"|<big>דמיון זה</big> רצינו לחלק צ"ח אלפים ות'ש'נ'ו' על ד‫' | |style="text-align:right;"|<big>דמיון זה</big> רצינו לחלק צ"ח אלפים ות'ש'נ'ו' על ד‫' | ||
|- | |- | ||
| Line 1,472: | Line 1,814: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נעשה בזה הדרך | + | :We do this way: |
| − | ואותו הא' נחבר עם הח' הסמוך לו ויהיו י"ח ונאמר נחלק י"ח על ד' יהיו ד' ונכתבם וישארו בידינו ב‫' | + | |style="text-align:right;"|נעשה בזה הדרך |
| + | |- | ||
| + | | | ||
| + | :We start from the large number and say: we divide 9 by 4; it is 2. We write it and we are left with 1. | ||
| + | |style="text-align:right;"|נתחי' מן המספר הגדול ונאמר נחלק ט' על ד' יהיו ב' ונכתבם וישאר בידינו א‫' | ||
| + | |- | ||
| + | | | ||
| + | :We add this 1 to the 8 next to it; they are 18. | ||
| + | |style="text-align:right;"|ואותו הא' נחבר עם הח' הסמוך לו <s>וישאר י"ח</s> ויהיו י"ח | ||
| + | |- | ||
| + | | | ||
| + | :We say: we divide 18 by 4; it is 4. We write it and we are left with 2. | ||
| + | |style="text-align:right;"|ונאמר נחלק י"ח על ד' יהיו ד' ונכתבם וישארו בידינו ב‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,486: | Line 1,840: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואלו הב' נחבר עם הז' הבא אחריו ויהיו כ"ז ונחלקם על ד' ויהיו ו' ונכתבם וישארו בידינו ג‫' | + | :We add this 2 to the 7 that follows it; they are 27. |
| − | ואילו הג' נחבר עם הבא אחריו ויהיו ל"ה ונחלקם על ד' יהיו ח' ונכתבם וישארו בידינו ג‫' | + | |style="text-align:right;"|ואלו הב' נחבר עם הז' הבא אחריו ויהיו כ"ז |
| + | |- | ||
| + | | | ||
| + | :We divide it by 4; it is 6. We write it and we are left with 3. | ||
| + | |style="text-align:right;"|ונחלקם על ד' ויהיו ו' ונכתבם וישארו בידינו ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :We add this 3 to the [5] that follows it; they are 35. | ||
| + | |style="text-align:right;"|ואילו הג' נחבר עם הבא אחריו ויהיו ל"ה | ||
| + | |- | ||
| + | | | ||
| + | :We divide it by 4; it is 8. We write it and we are left with 3. | ||
| + | |style="text-align:right;"|ונחלקם על ד' יהיו ח' ונכתבם וישארו בידינו ג‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| − | + | ::{| | |
|- | |- | ||
|rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{{\color{green}{2}}7\div4}}={\color{blue}{6}}+{\color{green}{r3}}}</math>||987<span style="color:red>5</span>6||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{{\color{green}{3}}5\div4}}={\color{blue}{8}}+{\color{green}{r3}}}</math>||9875<span style="color:red>6</span> | |rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{{\color{green}{2}}7\div4}}={\color{blue}{6}}+{\color{green}{r3}}}</math>||987<span style="color:red>5</span>6||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{{\color{green}{3}}5\div4}}={\color{blue}{8}}+{\color{green}{r3}}}</math>||9875<span style="color:red>6</span> | ||
| Line 1,500: | Line 1,866: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואילו הג' נחבר עם ו' הבא אחריו ויהיו ל"ו | + | :We add this 3 to the 6 that follows it; they are 36. |
| − | + | |style="text-align:right;"|ואילו הג' נחבר עם ו' הבא אחריו ויהיו ל"ו | |
|- | |- | ||
| − | | | + | | |
| − | + | :We divide it by 4; it is 9. We write it. | |
| + | |style="text-align:right;"|ונחלקם על ד' ויהיו ט' ונכתבם | ||
|- | |- | ||
| − | |rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{{\color{green}{3}}6\div4}}={\color{blue}{9}}}</math>||98756 | + | | |
| + | :Hence, we divide 98756 by 4 and the result is 24689. | ||
| + | |style="text-align:right;"|הרי שחלקנו צ"ח אלפים ותשנ"ו על ד' ועלו כ"ד אלפי' ות"רפ"ט | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :::{| | ||
| + | |- | ||
| + | |rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{{\color{green}{3}}6\div4}}={\color{blue}{9}}}</math>||98756 | ||
|- | |- | ||
|2468<span style="color:#0000FF>9</span> | |2468<span style="color:#0000FF>9</span> | ||
| Line 1,513: | Line 1,887: | ||
|} | |} | ||
|- | |- | ||
| − | |If | + | |If we had 1, or 2, or 3 left at the end, they were parts of the 4 by which we divided the number. |
|style="text-align:right;"|ואם היה נשאר בידינו באחרונה א' או ב' או ג' היו חלקי' מד' שחלקנו עליו החשבון | |style="text-align:right;"|ואם היה נשאר בידינו באחרונה א' או ב' או ג' היו חלקי' מד' שחלקנו עליו החשבון | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle8976\div5</math> | + | *If we want to divide the number 8976 by 5. |
| + | :<math>\scriptstyle8976\div5</math> | ||
|style="text-align:right;"|וכן אלו רצינו לחלק החשבון ח' אלפים ותת"קע"ו על ה‫' | |style="text-align:right;"|וכן אלו רצינו לחלק החשבון ח' אלפים ותת"קע"ו על ה‫' | ||
|- | |- | ||
| Line 1,535: | Line 1,910: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נעשה על זה הדרך ונאמר חלק ח' על ה' יהיה א' ונכתבנו ישאר ג‫' | + | :We do this way: |
| − | ואילו הג' נחבר עם הט' הבא אחריו ויהיו ל"ט נחלקם על ה' יהיו ז' ונכתבם וישארו ד‫' | + | |style="text-align:right;"|נעשה על זה הדרך |
| + | |- | ||
| + | | | ||
| + | :We say: divide 8 by 5; it is 1. We write it. 1 remains. | ||
| + | |style="text-align:right;"|ונאמר חלק ח' על ה' יהיה א' ונכתבנו ישאר ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :We add this 3 to the 9 that follows it; they are 39. | ||
| + | |style="text-align:right;"|ואילו הג' נחבר עם הט' הבא אחריו ויהיו ל"ט | ||
| + | |- | ||
| + | | | ||
| + | :We divide it by 5; it is 7. We write it. 4 remains. | ||
| + | |style="text-align:right;"|נחלקם על ה' יהיו ז' ונכתבם וישארו ד‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,549: | Line 1,936: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואלו הד' נחברם עם הז' הבא אחריו יהיו מ"ז נחלקם על ה' ויהיו ט' ונכתבם וישארו בידינו ב‫' | + | :We add this 4 to the 7 that follows it; they are 47. |
| − | ואלו הב' נחברם עם ו' הבא אחריו ויהיו כ"ו נחלקם על ה' ויהיו ה' ונכתבם וישאר בידינו א' ונכתבנו על ה' אשר חלקנו עליו החשבון | + | |style="text-align:right;"|ואלו הד' נחברם עם הז' הבא אחריו יהיו מ"ז |
| − | ויהי היוצא מן החלוקה הנזכר' אלף ות"שצ"ה וא' חומש | + | |- |
| + | | | ||
| + | :We divide it by 5; it is 9. We write it and we are left with 2. | ||
| + | |style="text-align:right;"|נחלקם על ה' ויהיו ט' ונכתבם וישארו בידינו ב‫' | ||
| + | |- | ||
| + | | | ||
| + | :We add this 2 to the 6 that follows it; they are 26. | ||
| + | |style="text-align:right;"|ואלו הב' נחברם עם ו' הבא אחריו ויהיו כ"ו | ||
| + | |- | ||
| + | | | ||
| + | :We divide it by 5; it is 5. We write it and we are left with 1. We write it above the 5, by which we divided the number. | ||
| + | |style="text-align:right;"|נחלקם על ה' ויהיו ה' ונכתבם וישאר בידינו א' ונכתבנו על ה' אשר חלקנו עליו החשבון | ||
| + | |- | ||
| + | | | ||
| + | :The result of the division mentioned is 1795 and a fifth. | ||
| + | |style="text-align:right;"|ויהי היוצא מן החלוקה הנזכר' אלף ות"שצ"ה וא' חומש | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,563: | Line 1,965: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | |If we want to divide a number by a number and the digits of the number you want to divide are smaller than the number by which you want to divide them, you should do this way: |
|style="text-align:right;"|<big>אמנם</big> אילו רצינו לחלק מספר על מספר וחלקי המספר שאתה רוצה לחלק קטנים מהמספר שתרצה לחלקם בו אתה צריך לעשות על זה הדרך | |style="text-align:right;"|<big>אמנם</big> אילו רצינו לחלק מספר על מספר וחלקי המספר שאתה רוצה לחלק קטנים מהמספר שתרצה לחלקם בו אתה צריך לעשות על זה הדרך | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle12345\div9</math> | + | *Example: we wish to divide 12345 by 9. |
| + | :<math>\scriptstyle12345\div9</math> | ||
|style="text-align:right;"|<big>דמיון זה</big> רצינו לחלק י"ב אלפי' ושמ"ה על ט‫' | |style="text-align:right;"|<big>דמיון זה</big> רצינו לחלק י"ב אלפי' ושמ"ה על ט‫' | ||
| + | |- | ||
| + | | | ||
| + | | | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| Line 1,582: | Line 1,988: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :We say: divide 1 by 9; we cannot. |
| − | ונחברם עם הג' הבא אחריו ויהיו ל"ג חלקם בט' ויהיו ג' ונכתבם וישארו בידינו ו‫' | + | |style="text-align:right;"|אמרנו חלק א' על ט' לא נוכל‫<ref>נוכל: MS Ithaca illegible</ref> |
| + | |- | ||
| + | | | ||
| + | :We add 1 to the 2 that follows it; they are 12. | ||
| + | |style="text-align:right;"|נחבר א' עם הב' הבא אחריו ויהיו י"ב | ||
| + | |- | ||
| + | | | ||
| + | :Divide it by 9; it is 1. We write it and we are left with 3. | ||
| + | |style="text-align:right;"|חלקם על ט' יהיה א' ונכתבנו וישארו בידינו ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :We add it to the 3 that follows it; they are 33. | ||
| + | |style="text-align:right;"|ונחברם עם הג' הבא אחריו ויהיו ל"ג | ||
| + | |- | ||
| + | | | ||
| + | :Divide it by 9; it is 3. We write it and we are left with 6. | ||
| + | |style="text-align:right;"|חלקם בט' ויהיו ג' ונכתבם וישארו בידינו ו‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,596: | Line 2,018: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונחבר אלו הו' עם הד' הבא אחריו ויהיו ס"ד חלקם בט' ויהיו ז' ונכתבם וישאר בידינו א‫' | + | :We add this 6 to the 4 that follows it; they are 64. |
| − | + | |style="text-align:right;"|ונחבר אלו הו' עם הד' הבא אחריו ויהיו ס"ד | |
| − | והיוצא מזה הוא שאם נחלק י"ב אלפים וש'מ'ה' על ט' יהיה היוצא מן החלוקה אלפים וש'ע'א' וו' תשיעיות | + | |- |
| + | | | ||
| + | :Divide it by 9; it is 7. We write it and we are left with 1. | ||
| + | |style="text-align:right;"|חלקם בט' <s>ו</s> ויהיו ז' ונכתבם וישאר בידינו <s>ו' ונחבר אילו הו'</s> א‫' | ||
| + | |- | ||
| + | | | ||
| + | :We add the 1 to the 5 that follows it; they are 15. | ||
| + | |style="text-align:right;"|נחבר הא' עם הה' הבא אחריו יהיו ט"ו | ||
| + | |- | ||
| + | | | ||
| + | :We say: divide 15 by 9; it is 1 and we are left with 6. We write it above the 9, by which we divided the whole number. | ||
| + | |style="text-align:right;"|ונאמר חלק ט"ו בט' יהיו א'‫<ref>א': MS Ithaca om.</ref> וישארו בידינו ו' ונכתוב אותם על‫<ref>ונכתוב אותם על: MS Ithaca ונחלקנו על ח'</ref> הט' אשר בו חלקנו כל‫<ref>כל: MS Ithaca om.</ref> החשבון | ||
| + | |- | ||
| + | | | ||
| + | :The result is that if we divide 12345 by 9, the result of division is 2371 and 6-ninths. | ||
| + | |style="text-align:right;"|והיוצא מזה הוא שאם נחלק י"ב אלפים וש'מ'ה' על ט' יהיה היוצא מן החלוקה‫<ref>יהיה היוצא מן החלוקה: MS Ithaca om.</ref> אלפים וש'ע'א' וו' תשיעיות | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,610: | Line 2,047: | ||
|} | |} | ||
|- | |- | ||
| − | |'''Check''' | + | |<span style="color:green>'''Check:'''</span> If you want to check if our calculation is correct, we do as follows: |
| − | |style="text-align:right;"|ואם תרצה לבחון אם החשבון שעשינו הוא אמתי נעשה על זה הדרך | + | |style="text-align:right;"|ואם תרצה לבחון אם החשבון שעשינו הוא אמתי נעשה על זה הדרך |
| − | היינו שנקבץ המספרים המחולקים ונשליכם ט' ט' ומה שנשאר נחזיק בידינו | + | |- |
| − | אחר כן נקבץ מה שעלה בידינו בחלוק ונשליכם ט' ט' ומה שעלה בידינו נרבה אותו עם המחלק | + | |We sum up the digits of the dividend, cast out the nines and keep the remainder. |
| − | ומה שעלה בידינו מהרבוי נשליכם ט' ט‫' | + | |style="text-align:right;"|היינו שנקבץ המספרים המחולקים ונשליכם ט' ט' ומה שנשאר נחזיק בידינו |
| − | ואם החשבון הוא אמתי יעלה בידינו כמו שעלה בידינו בקבצנו המספרים המחולקים | + | |- |
| + | |Then, we sum up [the digits of] the result of division, cast out the nines and multiply what we received by the divisor. | ||
| + | |style="text-align:right;"|אחר כן נקבץ מה שעלה בידינו בחלוק ונשליכם ט' ט' ומה שעלה בידינו נרבה אותו עם המחלק | ||
| + | |- | ||
| + | |We cast out the nines from the product we received. | ||
| + | |style="text-align:right;"|ומה שעלה בידינו מהרבוי נשליכם ט' ט‫' | ||
| + | |- | ||
| + | |If the calculation is correct, we receive the same as what we received when we summed the digits of the dividend. | ||
| + | |style="text-align:right;"|ואם החשבון הוא אמתי יעלה בידינו כמו שעלה בידינו בקבצנו המספרים המחולקים | ||
|- | |- | ||
| | | | ||
| − | :: | + | *We will illustrate this in the calculation we wrote above: |
| + | :<math>\scriptstyle98756\div4</math> | ||
|style="text-align:right;"|וזה הדמיון נעשו בחשבון שכתבנו לעיל | |style="text-align:right;"|וזה הדמיון נעשו בחשבון שכתבנו לעיל | ||
|- | |- | ||
| Line 1,643: | Line 2,089: | ||
|- | |- | ||
| | | | ||
| − | :: | + | :First, we sum up the digits of the dividend and say: 6, 5, 7, 8, 9; the total is 35. |
| − | |style="text-align:right;"|היינו בתחלה נקבץ המספרי' המחולקים ונאמ' ו' וה' ז' וח' וט' בין כלם ל"ה | + | |style="text-align:right;"|היינו בתחלה נקבץ המספרי' המחולקים ונאמ' ו' וה' ז' וח' וט' בין כלם ל"ה |
|- | |- | ||
| | | | ||
| − | : | + | :We cast out the nines; 8 remains. We write it next to the digits of the dividend. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{9+8+7+5+6=35\longrightarrow35\equiv_98}}</math> |
| − | + | |style="text-align:right;"|נשליכם ט' ט' ישארו ח' ונכת' ונכתבם אצל המספרי' המחולקים | |
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | :Then, we sum up [the digits of] the result of division and say: 9, 8, 6, 4, 2; the total is 29. |
| − | + | |style="text-align:right;"|אחר כן נקבץ מה שעלה בחלוק ונאמ' ט' וח' וו' וד' ב' בין כלם כ"ט | |
| − | |||
|- | |- | ||
| | | | ||
| − | + | :We cast out the nines; 2 remains. We write it next to the result of division. | |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{2+4+6+8+9=29\longrightarrow29\equiv_92\longrightarrow2\times4=8}}</math> |
| + | |style="text-align:right;"|נשליכם ט' ט' וישארו ב' ונכתבם אצל מה שעלה בחלוק | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Then, we multiply it by the divisor and say: 2 times 4 is 8. Therefore, we receive the same as we received when we summed the digits of the dividend, so the calculation is correct. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אחר כן נרבה אותו עם המחלק ונאמ' ב' פעמי' ד' ח' והנה עלה בידינו מה שעלה בקבצנו המספרי' המחולקים אם כן החשבון אמתי |
| + | |- | ||
| + | |If 1, or 2, or 3 remains from the division [procedure], we do this way: | ||
| + | |style="text-align:right;"|ואם ישארו מן החלוק א' או ב' או ג' נעשה על זה הדרך | ||
| + | |- | ||
| + | |After we sum up [the digits of] the result of division and cast out the nines, we add [what remains] to what we have left [= to the remainder from the division]. | ||
| + | |style="text-align:right;"|וזה שקבצנו אחר מה שעלה בחלוק והשלכנו אותם ט' ט' נקבצם עם מה שנשאר בידינו | ||
| + | |- | ||
| + | |If the calculation is correct, what we receive is the same as what we received when we summed the digits of the dividend. | ||
| + | |style="text-align:right;"|ואם החשבון אמתי יעלה בידינו כמו שעלה בידינו בקבצנו המספרים המחולקים | ||
|- | |- | ||
| | | | ||
| + | *We will illustrate this in the second calculation we wrote above: | ||
| + | :<math>\scriptstyle8976\div5</math> | ||
| + | |style="text-align:right;"|וזה הדמיון נעשו כחשבון השני שכתבנו למעלה | ||
| + | |- | ||
| | | | ||
| − | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | + | :First, we sum up the digits of the dividend and say: 6, 7, 8, 9; the total is 30. |
| + | |style="text-align:right;"|היינו בתחלה נקבץ המספרי' המחולקים ונאמר ו' וז' וח' וט' בין כלם ל‫' | ||
| + | |- | ||
| + | | | ||
| + | :We cast out the nines; we are left with 3. We write it next to the digits of the dividend. | ||
| + | :<math>\scriptstyle{\color{blue}{8+9+7+6=30\longrightarrow30\equiv_93}}</math> | ||
| + | |style="text-align:right;"|נשליכם ט' ט' וישאר בידינו ג' ונכתבנו אצל המספרי' המחולקים | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
|- | |- | ||
| | | | ||
| Line 1,693: | Line 2,162: | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Then, we sum up [the digits of] the result of division and say: 5, 9, 7, 1; the total is 22. |
| − | |style="text-align:right;"|אחר כן נקבץ מה שעלה בידינו בחלוק ונאמר ה' וט' וז' וא' בין כלם כ"ב | + | |style="text-align:right;"|אחר כן נקבץ מה שעלה בידינו בחלוק ונאמר ה' וט' וז' וא' בין כלם כ"ב |
| − | |||
| − | |||
|- | |- | ||
| − | |''' | + | | |
| + | :We cast out the nines; we are left with 4. We write it next to the result of division. | ||
| + | |style="text-align:right;"|נשליכם ט' ט' וישאר בידינו ד' ונכתבנו אצל מה שעלה בחלוק | ||
| + | |- | ||
| + | | | ||
| + | :Then, we multiply it by the divisor and say: 4 times 5 is 20. | ||
| + | |style="text-align:right;"|אחר כן נרבה אותו עם המחלק ונאמ' ד' פעמי' ה' הם כ‫' | ||
| + | |- | ||
| + | | | ||
| + | :We cast out the nines; we are left with 2. We add it to the 1 we received from the division, which is written above the 5; they are 3. | ||
| + | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle1+7+9+5=22&\scriptstyle\longrightarrow22\equiv_94\longrightarrow4\times5=20\\&\scriptstyle\longrightarrow20\equiv_92\longrightarrow2+1=3\\\end{align}}}</math> | ||
| + | |style="text-align:right;"|ונשליכם ט'ט' וישאר בידינו ב' ונחבר עם הב' הא' שעלה בידינו מן החלוק הכתוב על ה' ויהיו ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :Therefore, we receive the same as we received when we summed the digits [of the dividend], so the calculation is correct. | ||
| + | |style="text-align:right;"|הנה שעלה בידינו כמו שעלה בידינו בקבצנו המספרים אם כך הוא החשבון אמתי‫<ref>ואם תרצה לבחון... אם כך הוא החשבון אמתי: MS Ithaca om.</ref> | ||
| + | |- | ||
| + | !Another method of dividing a number by a number | ||
|style="text-align:right;"|<big>דרך מספר על מספר בדרך אחרת</big> | |style="text-align:right;"|<big>דרך מספר על מספר בדרך אחרת</big> | ||
|- | |- | ||
| − | | | + | |If we want to divide a known number by another number and it is difficult for us to divide it by this number, we divide it twice and we receive as if we divided it once by that number. |
|style="text-align:right;"|‫<ref>34v</ref>אם נרצה לחלק מספר ידוע על מספר אחר ויקשה עלינו לחלקו על המספר ההוא נחלק אותו ב' פעמים ויעלה בידינו כאלו חלקנוהו פעם אחת על המספר ההוא | |style="text-align:right;"|‫<ref>34v</ref>אם נרצה לחלק מספר ידוע על מספר אחר ויקשה עלינו לחלקו על המספר ההוא נחלק אותו ב' פעמים ויעלה בידינו כאלו חלקנוהו פעם אחת על המספר ההוא | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle89765\div12</math> | + | *Example: we wish to divide 89765 by 12. |
| + | :<math>\scriptstyle89765\div12</math> | ||
|style="text-align:right;"|<big>דמיון זה</big> רצינו לחלק פ"ט אלפים ות"שס"ה על י"ב | |style="text-align:right;"|<big>דמיון זה</big> רצינו לחלק פ"ט אלפים ות"שס"ה על י"ב | ||
|- | |- | ||
| Line 1,725: | Line 2,210: | ||
|- | |- | ||
| | | | ||
| − | : | + | :If we divide it by 12 once the result is 7480 and 5 parts of 12 and this is the order of the procedure: |
|style="text-align:right;"|והנה אם חלקנוה על י"ב בפעם אחת יעלה ז' אלפים ות"פ וה' חלקים מי"ב וזה סדר עשייתו | |style="text-align:right;"|והנה אם חלקנוה על י"ב בפעם אחת יעלה ז' אלפים ות"פ וה' חלקים מי"ב וזה סדר עשייתו | ||
|- | |- | ||
| Line 1,743: | Line 2,228: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אמרנו חלק ח' על י"ב לא נוכל נחבר אל ח' הט' הבא אחריו יהיו פ"ט חלקם בי"ב יהיו ז' ונכתבם וישאר בידינו ה‫' | + | :We say: divide 8 by 12; we cannot. |
| − | ונחבר אליה ז' הבא אחריו ויהיו נ"ז | + | |style="text-align:right;"|אמרנו חלק ח' על י"ב לא נוכל |
| + | |- | ||
| + | | | ||
| + | :We add the 8 to the 9 that follows it; they are 89. | ||
| + | |style="text-align:right;"|נחבר אל ח' הט' הבא אחריו יהיו פ"ט | ||
| + | |- | ||
| + | | | ||
| + | :Divide it by 12; it is 7. We write it and we are left with 5. | ||
| + | |style="text-align:right;"|חלקם בי"ב יהיו ז' ונכתבם וישאר בידינו ה‫' | ||
| + | |- | ||
| + | | | ||
| + | :We add it to the 7 that follows it; they are 57. | ||
| + | |style="text-align:right;"|ונחבר אליה ז' הבא אחריו ויהיו נ"ז | ||
| + | |- | ||
| + | | | ||
| + | :Divide it by 12; it is 4. We write it and we are left with 9. | ||
| + | |style="text-align:right;"|חלקים בי"ב יהיו ד' ונכתבם וישארו בידינו ט‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,757: | Line 2,258: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונחבר אליהם ו' הבא אחריו יהיו צ"ו חלקים בי"ב יהיו ח' ונכתבם | + | :We add it to the 6 that follows it; they are 96. |
| − | ונאמר חלק ה' על יב לא נוכל ותכתוב ציפרא תחת הה' וה' תכתוב על י"ב יהיו ז' אלפים ותש"פ וה' חלקים מי"ב | + | |style="text-align:right;"|ונחבר אליהם ו' הבא אחריו יהיו צ"ו |
| + | |- | ||
| + | | | ||
| + | :Divide it by 12; it is 8. We write it. | ||
| + | |style="text-align:right;"|חלקים בי"ב יהיו ח' ונכתבם | ||
| + | |- | ||
| + | | | ||
| + | :We say: divide 5 by 12; we cannot. | ||
| + | |style="text-align:right;"|ונאמר חלק ה' על יב לא נוכל | ||
| + | |- | ||
| + | | | ||
| + | :Write a zero beneath the 5 and write the 5 above 12; it is 7780 and 5 parts of 12. | ||
| + | |style="text-align:right;"|ותכתוב ציפרא תחת הה' וה' תכתוב על י"ב יהיו ז' אלפים ותש"פ וה' חלקים מי"ב | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,771: | Line 2,284: | ||
|- | |- | ||
| | | | ||
| − | : | + | :If we want to divide this same number in another way, we divide it by 3 once, then we divide the result by 4, so it is divided into 12 parts also. |
| − | + | :<math>\scriptstyle\left(89765\div3\right)\div4</math> | |
| − | |style="text-align:right;"|ואם נרצה לחלק זה החשבון בעצמו בעניין אחר נחלק אותו על ג' פעם אחת והעולה נחלק אותו על ד' ויהיה נחלק לי"ב ג"כ ונכתוב זה החשבון שנית ונחלקנו על ג' בתחילה ואחר זה נחלקנו על ד‫' | + | |style="text-align:right;"|ואם נרצה לחלק זה החשבון בעצמו בעניין אחר נחלק אותו על ג' פעם אחת והעולה נחלק אותו על ד' ויהיה נחלק לי"ב חלקים ג"כ |
| + | |- | ||
| + | | | ||
| + | :We write this number again and divide it first by 3, then we divide it by 4. | ||
| + | |style="text-align:right;"|ונכתוב זה החשבון שנית ונחלקנו על ג' בתחילה ואחר זה נחלקנו על ד‫' | ||
|- | |- | ||
| | | | ||
| Line 1,792: | Line 2,309: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונאמר ח' חלק אותו על ג' יהיו ב' ונכתבם וישארו ב‫'< | + | :We say: divide 8 by 3; it is 2. We write it and 2 remains. |
| − | ונחבר אותם עם | + | |style="text-align:right;"|ונאמר ח' חלק אותו על ג' יהיו ב' ונכתבם וישארו ב‫' |
| + | |- | ||
| + | | | ||
| + | :We add it to the 9 that follows it; they are 29. | ||
| + | |style="text-align:right;"|ונחבר‫<ref>ונחבר: MS Ithaca ונכתבם ונחבר</ref> אותם עם ט' הבא אחריו ויהיו כ"ט | ||
| + | |- | ||
| + | | | ||
| + | :Divide it by 3; it is 9. We write it and 2 remains. | ||
| + | |style="text-align:right;"|חלקם בג' יהיו ט' ונכתבם וישארו ב‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,806: | Line 2,331: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונחברם עם הז' הבא אחריו ויהיו כ"ז ונחלקם על ג' יהיו ט' ונכתבם | + | :We add it to the 7 that follows it; they are 27. |
| − | ונאמר אחר זה ו' חלק בג' יהיו ב' ונכתבם | + | |style="text-align:right;"|ונחברם עם הז' הבא אחריו ויהיו כ"ז |
| − | ונאמר אחר זה ה' חלק בג' יהיו א' ונכתבנו וישארו ב' ונכתבם על הג' אשר בו חלקנו זה המספר | + | |- |
| + | | | ||
| + | :We divide it by 3; it is 9. We write it. | ||
| + | |style="text-align:right;"|ונחלקם על ג' יהיו ט' ונכתבם | ||
| + | |- | ||
| + | | | ||
| + | :Then, we say: divide 6 by 3; it is 2. We write it. | ||
| + | |style="text-align:right;"|ונאמר אחר זה ו' חלק בג' יהיו ב' ונכתבם | ||
| + | |- | ||
| + | | | ||
| + | :Then, we say: divide 5 by 3; it is 1. We write it and 2 remains. We write it above the 3, by which we divided this number. | ||
| + | |style="text-align:right;"|ונאמר אחר זה ה' חלק בג' יהיו א' ונכתבנו וישארו ב' ונכתבם על הג' אשר בו חלקנו זה המספר | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,821: | Line 2,357: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אחר זה נחלק זה המספר שעלה בידינו מן החלוקה על ד' ונאמר חלק ב' בד' לא נוכל | + | :Then, we divide by 4 the number we received from the division and say: divide 2 by 4; we cannot. |
| − | + | |style="text-align:right;"|אחר זה נחלק זה המספר שעלה בידינו מן החלוקה על ד' ונאמר חלק ב' בד' לא נוכל | |
| − | |||
|- | |- | ||
| − | | | + | | |
| − | + | :Add 2 to the 9 that follows it; they are 29. | |
| + | |style="text-align:right;"|חבר ב' עם הט' הבא אחריו יהיו כ"ט | ||
|- | |- | ||
| − | | | + | | |
| + | :Divide it by 4; it is 7. We write it and we are left with 1. | ||
| + | |style="text-align:right;"|חלקם בד' יהיו ז' ונכתבם וישאר בידינו א'‫<ref>א': MS Ithaca ונכתוב א'</ref> | ||
|- | |- | ||
| − | | | + | | |
| + | :We add 1 to the 9 that follows it; they are 19. | ||
| + | |style="text-align:right;"|ונחבר א' עם הט' הבא אחריו יהיו י"ט | ||
|- | |- | ||
| − | | <span style="color:#0000FF>7</span>   || 7<span style="color:#0000FF>4</span>  || 74<span style="color:#0000FF>8</span>  | + | | |
| + | :Divide it by 4; it is 4. We write it and we are left with 3. | ||
| + | |style="text-align:right;"|חלקם בד' יהיו ד' ונכתבם וישארו בידינו ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :We add it to the 2 that follows it; they are 32. | ||
| + | |style="text-align:right;"|ונחברם עם הב' הבא אחריו ויהיו ל"ב | ||
| + | |- | ||
| + | | | ||
| + | :We divide it by 4; it is 8. We write it. | ||
| + | |style="text-align:right;"|ונחלקם בד' יהיו ח' ונכתבם | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :::{| | ||
| + | |- | ||
| + | |rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{29\div4}}={\color{blue}{7}}+{\color{green}{r1}}}</math>||89765||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{{\color{green}{1}}9\div4}}={\color{blue}{4}}+{\color{green}{r3}}}</math>||89765||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{{\color{green}{3}}2\div4}}={\color{blue}{8}}}</math>||89765 | ||
| + | |- | ||
| + | |29<span style="color:red>9</span>21<math>\scriptstyle\frac{2}{3}</math>||299<span style="color:red>2</span>1<math>\scriptstyle\frac{2}{3}</math>||29921<math>\scriptstyle\frac{2}{3}</math> | ||
| + | |- | ||
| + | | <span style="color:#0000FF>7</span>   || 7<span style="color:#0000FF>4</span>  || 74<span style="color:#0000FF>8</span>  | ||
|- | |- | ||
|    <span style="color:red">4</span>||    <span style="color:red">4</span>||    4 | |    <span style="color:red">4</span>||    <span style="color:red">4</span>||    4 | ||
| Line 1,838: | Line 2,397: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונחלק א' בד' ולא נוכל ונכתוב ציפרא תחת הא' והא' שלא נוכל לחלקה בד' נכתוב אותה על הד' אשר עליה נחלק החשבון | + | :We divide 1 by 4; we cannot. We write a zero beneath the 1 and we write the 1, which we cannot divide by 4, above the 4, by which we divide the number. |
| + | |style="text-align:right;"|ונחלק א' בד' ולא נוכל ונכתוב ציפרא‫<ref>ציפרא: MS Ithaca twice</ref> תחת הא' והא' שלא נוכל לחלקה בד' נכתוב אותה על הד' אשר עליה נחלק החשבון | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,853: | Line 2,413: | ||
|- | |- | ||
| | | | ||
| − | : | + | :So, you have divided the number by 3 and 4 and it is as if you have divided it by 12. |
| − | |style="text-align:right;"|הרי שחלקת החשבון בג' וד' והוא כאלו חלקתו בי"ב | + | :<math>\scriptstyle{\color{blue}{\left(\frac{2}{3}\div4\right)+\frac{1}{4}=\frac{2+\left(3\sdot1\right)}{12}=\frac{2+3}{12}=\frac{5}{12}}}</math> |
| − | ותרבה אחר זה הא' שעל הד' עם הג' ואמור א' פעם ג' ג' וב' שעל הג' הרי ה' והם ה' חלקים מי"ב | + | |style="text-align:right;"|הרי שחלקת החשבון בג' וד' והוא כאלו חלקתו בי"ב |
| − | היוצא מדברינו שאם | + | |- |
| + | | | ||
| + | :Multiply the 1 above the 4 by the 3 and say: 1 time 3 is 3; with the 2 above the 3, it is 5 and they are 5 parts of 12. | ||
| + | |style="text-align:right;"|ותרבה אחר זה הא' שעל הד' עם הג' ואמור א' פעם ג' ג' וב' שעל הג' הרי ה' והם ה' חלקים מי"ב | ||
| + | |- | ||
| + | | | ||
| + | :It follows from this that if we first divide by 3, then we divide the result by 4 as we did, the result of division is 7480 and 5 parts of 12, as we received when we divided it once by 12 and this is clear. | ||
| + | |style="text-align:right;"|היוצא מדברינו שאם נחלק בראשונ' על ג' והיוצא נחלק על ד' על הדרך שעשינו יעלה מן החלוקה ז' אלפי' ות"פ וה' חלקים מי"ב כאשר עלה בידינו בעת שחלקנוהו פעם אחת על י"ב וזה מבואר | ||
|- | |- | ||
| | | | ||
| − | == | + | == The Method of Knowing the Numbers Summed One after the Other Successively == |
|style="text-align:right;"|‫<ref>35r</ref><big>דרך ידיעת המספרים המקובצים זה אחר זה על</big> הסדר | |style="text-align:right;"|‫<ref>35r</ref><big>דרך ידיעת המספרים המקובצים זה אחר זה על</big> הסדר | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:1-10|669|QIjG}}If a person says: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 - how much | + | *{{#annot:1-10|669|QIjG}}If a person says: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 - how much is the total? |
:<math>\scriptstyle1+2+3+4+5+6+7+8+9+10=\sum_{i=1}^{10} i</math> | :<math>\scriptstyle1+2+3+4+5+6+7+8+9+10=\sum_{i=1}^{10} i</math> | ||
|style="text-align:right;"|אם יאמר אדם א' וב' וג' וד' וה' וו' וז' וח' וטי' וי' כמה שוי בין כלם{{#annotend:QIjG}} | |style="text-align:right;"|אם יאמר אדם א' וב' וג' וד' וה' וו' וז' וח' וטי' וי' כמה שוי בין כלם{{#annotend:QIjG}} | ||
|- | |- | ||
| − | | | + | |You should understand, if the last term is an even number as this number or similar to it, always add one to the last term and multiply it by half the last term. |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} i=\left(n+1\right)\sdot\left(\frac{1}{2}\sdot n\right)}}</math> | |
| − | |style="text-align:right;"|יש לך להבין אם המספר האחרון הוא מספר זוג כמו זה מספר והדומה לו | + | |style="text-align:right;"|יש לך להבין אם המספר האחרון הוא מספר זוג כמו זה מספר והדומה לו תוסיף מספר אחד לעולם על הי' המספר האחרון ותרבה אותו על חצי המספר האחרו‫' |
|- | |- | ||
| | | | ||
| − | : | + | :Say: half 10 is 5. Multiply it by 11: 5 times 11 is 54 and so is [the sum of] the numbers mentioned. |
| − | + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=\left(10+1\right)\sdot\left(\frac{1}{2}\sdot10\right)=11\sdot5=55}}</math> | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואמור החצי מי' הוא ה' ותרבה אותו על י"א ה' פעמי' י"א נ"ה וכן יהיו המספרים הנזכרי‫' |
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-12|669|kTQb}}If he continues his question until 12. | |
| + | :<math>\scriptstyle\sum_{i=1}^{12} i</math> | ||
|style="text-align:right;"|ואם הלך בשאלתו עד י"ב{{#annotend:kTQb}} | |style="text-align:right;"|ואם הלך בשאלתו עד י"ב{{#annotend:kTQb}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{12} i=6\sdot13=78}}</math> | + | :Say: 6 times 13 is 78 and so is [their sum]. |
| − | |style="text-align:right;"|אמור ו' פעמי' י"ג ע"ח יהיו | + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{12} i=6\sdot13=78}}</math> |
| + | |style="text-align:right;"|אמור ו'‫<ref>ו': MS Ithaca י'</ref> פעמי' י"ג ע"ח‫<ref>ע"ח: MS Ithaca וכן</ref> יהיו | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-20|669|u3dY}}If he continues his question until 20. | |
| + | :<math>\scriptstyle\sum_{i=1}^{20} i</math> | ||
|style="text-align:right;"|ואם הלך בשאלתו עד כ‫'{{#annotend:u3dY}} | |style="text-align:right;"|ואם הלך בשאלתו עד כ‫'{{#annotend:u3dY}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{20} i=10\sdot21}}</math> | + | :Say: 10 times 21 and so is [their sum]. |
| + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{20} i=10\sdot21}}</math> | ||
|style="text-align:right;"|אמור י' פעמים כ"א וכן יהיו | |style="text-align:right;"|אמור י' פעמים כ"א וכן יהיו | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-100|669|YfUq}}If he continues his question until one hundred. | |
| + | :<math>\scriptstyle\sum_{i=1}^{100} i</math> | ||
|style="text-align:right;"|ואם הלך עד מאה{{#annotend:YfUq}} | |style="text-align:right;"|ואם הלך עד מאה{{#annotend:YfUq}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{100} i=50\sdot101}}</math> | + | :Say: 50 times 101 and so is [their sum]. |
| + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{100} i=50\sdot101}}</math> | ||
|style="text-align:right;"|אמור נ' פעמים ק"א וכן יהיו | |style="text-align:right;"|אמור נ' פעמים ק"א וכן יהיו | ||
|- | |- | ||
| − | | | + | |Always calculate this way when the last term is even. |
|style="text-align:right;"|ואתה תחשוב לעולם בזה הדרך כשיהיה מספר האחרון זוג | |style="text-align:right;"|ואתה תחשוב לעולם בזה הדרך כשיהיה מספר האחרון זוג | ||
|- | |- | ||
| − | | | + | |If the last term is an odd number, multiply the greater half of this last term by the whole last term. |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} i=\left[\left(n+1\right)\sdot\frac{1}{2}\right]\sdot n}}</math> | |
| − | + | |style="text-align:right;"|ואם יהיה מספר האחרון מספר נפרד תרבה הרוב מהמספר ההוא האחרון על כל המספר האחרון | |
| − | |||
| − | |||
| − | |||
| − | |style="text-align:right;"|תרבה הרוב מהמספר ההוא האחרון על כל המספר האחרון | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-7|669|Hvdz}}As the one who says: I continue my calculation until 7. How much is the total? | |
| + | :<math>\scriptstyle\sum_{i=1}^{7} i</math> | ||
|style="text-align:right;"|כגון האומר הלכתי בחשבוני עד ז' כמה יהיו כלם{{#annotend:Hvdz}} | |style="text-align:right;"|כגון האומר הלכתי בחשבוני עד ז' כמה יהיו כלם{{#annotend:Hvdz}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{7} i=\left[\left(7+1\right)\sdot\frac{1}{2}\right]\sdot7=4\sdot7=28}}</math> | + | :Say: the greater half of 7 is 4. Multiply it by 7; it is 28 and so is [their sum]. |
| − | |style="text-align:right;"|אמור הרוב מז' הם ד' תרבה אותם על ז' יהיו כ"ח וכן יהיו | + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{7} i=\left[\left(7+1\right)\sdot\frac{1}{2}\right]\sdot7=4\sdot7=28}}</math> |
| + | |style="text-align:right;"|אמור הרוב מז' הם ד' תרבה אותם על <s>נ"ח</s> ז' יהיו כ"ח וכן יהיו | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-9|669|2b1t}}If he continues his question until 9. | |
| + | :<math>\scriptstyle\sum_{i=1}^{9} i</math> | ||
|style="text-align:right;"|וכן אם הלך בשאלתו עד ט‫'{{#annotend:2b1t}} | |style="text-align:right;"|וכן אם הלך בשאלתו עד ט‫'{{#annotend:2b1t}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{9} i=\left[\left(9+1\right)\sdot\frac{1}{2}\right]\sdot9=5\sdot9=45}}</math> | + | :Say: the greater half of 9 is 5. Multiply it by 9; it is 45 and so is [their sum]. |
| + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{9} i=\left[\left(9+1\right)\sdot\frac{1}{2}\right]\sdot9=5\sdot9=45}}</math> | ||
|style="text-align:right;"|אמור הרוב מט' הוא ה' מנה אותם בט' יהיו מ"ה וכן יהיו | |style="text-align:right;"|אמור הרוב מט' הוא ה' מנה אותם בט' יהיו מ"ה וכן יהיו | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-17|669|T2rf}}If he continues until 17. | |
| + | :<math>\scriptstyle\sum_{i=1}^{17} i</math> | ||
|style="text-align:right;"|ואם הלך עד י"ז{{#annotend:T2rf}} | |style="text-align:right;"|ואם הלך עד י"ז{{#annotend:T2rf}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{17} i=9\sdot17}}</math> | + | :Multiply 9 by 17 and so is [their sum]. |
| − | |style="text-align:right;"|תרבה ט' על י"ז וכן יהיו | + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{17} i=9\sdot17}}</math> |
| + | |style="text-align:right;"|תרבה ט' על‫<ref>על: MS Ithaca עד</ref> י"ז וכן יהיו | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-19|669|CIoT}}If he continues until 19. | |
| + | :<math>\scriptstyle\sum_{i=1}^{19} i</math> | ||
|style="text-align:right;"|ואם הלך עד י"ט{{#annotend:CIoT}} | |style="text-align:right;"|ואם הלך עד י"ט{{#annotend:CIoT}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{19} i=10\sdot19}}</math> | + | :Multiply 10 by 19 and so is [their sum]. |
| − | |style="text-align:right;"|תרבה י' עם י"ט וכן יהיו | + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{19} i=10\sdot19}}</math> |
| − | + | |style="text-align:right;"|תרבה י' עם י"ט וכן <s>ה</s> יהיו | |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :< | + | === <span style=color:green>Sum of Evens</span> === |
| + | |||
| | | | ||
| + | |- | ||
| + | |If he says: I summed all the even numbers successively. | ||
| + | |style="text-align:right;"|ואם יאמר קבצתי מספרים כלם זוגות על הסדר | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:2-12|671|Gsfn}}As 2, 4, 6, 8, 10, 12 - how much is the total? | |
| + | :<math>\scriptstyle2+4+6+8+10+12=\sum_{i=1}^{6} 2i</math> | ||
|style="text-align:right;"|כמו ב' וד' וו' וח' וי' וי"ב כמה יהיה בין כלם{{#annotend:Gsfn}} | |style="text-align:right;"|כמו ב' וד' וו' וח' וי' וי"ב כמה יהיה בין כלם{{#annotend:Gsfn}} | ||
| + | |- | ||
| + | |Multiply half the last term by the number that follows this half. | ||
| + | |style="text-align:right;"|תרבה החצי מן המספר האחרון על המספר אשר אחרי החצי ההוא | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 2i=\left(\frac{1}{2}\sdot2n\right)\sdot\left[\left(\frac{1}{2}\sdot2n\right)+1\right]}}</math> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :Say: half 12 is 6 and the number that follows 6 is 7. 6 times 7 is 42 and so is [their sum]. |
| + | |style="text-align:right;"|ואמור החצי מי"ב הוא ו' והמספר שהוא אחר ו' הוא ז' ו' פעמים ז' הם <s>י"ב</s> מ"ב וכן יהיו | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,963: | Line 2,549: | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:2-20|671|qYPE}}If he says: I continued until twenty. | |
| + | :<math>\scriptstyle2+\ldots+20=\sum_{i=1}^{10} 2i</math> | ||
|style="text-align:right;"|ואם אומר הלכתי עד עשרי‫'{{#annotend:qYPE}} | |style="text-align:right;"|ואם אומר הלכתי עד עשרי‫'{{#annotend:qYPE}} | ||
|- | |- | ||
| | | | ||
| + | :Say: half twenty is 10 and the number that follows 10 is 11. 10 times [11] is 110 and so is [their sum]. | ||
|style="text-align:right;"|אמור החצי מעשרי' הוא י' והמספר שאחר י' הוא י"א י' פעמים הם ק"י וכן יהיו | |style="text-align:right;"|אמור החצי מעשרי' הוא י' והמספר שאחר י' הוא י"א י' פעמים הם ק"י וכן יהיו | ||
|- | |- | ||
| Line 1,972: | Line 2,560: | ||
:<math>\scriptstyle{\color{blue}{2+\ldots+20=\sum_{i=1}^{10} 2i=\left(\frac{1}{2}\sdot20\right)\sdot\left[\left(\frac{1}{2}\sdot20\right)+1\right]=10\sdot\left(10+1\right)=10\sdot11=110}}</math> | :<math>\scriptstyle{\color{blue}{2+\ldots+20=\sum_{i=1}^{10} 2i=\left(\frac{1}{2}\sdot20\right)\sdot\left[\left(\frac{1}{2}\sdot20\right)+1\right]=10\sdot\left(10+1\right)=10\sdot11=110}}</math> | ||
|- | |- | ||
| − | | | + | |Always calculate this way. |
|style="text-align:right;"|ועל זה הדרך תחשוב לעולם | |style="text-align:right;"|ועל זה הדרך תחשוב לעולם | ||
|- | |- | ||
| − | + | | | |
| − | + | === <span style=color:green>Sum of Odds</span> === | |
| + | | | ||
|- | |- | ||
| − | | | + | |If he says: I summed all the odd numbers successively. |
| − | + | |style="text-align:right;"|ואם יאמר קבצתי מספרים כלם נפרדי' על הסדר | |
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-9|670|rGAn}}As 1, 3, 5, 7, 9 - how much is the total? | |
| + | :<math>\scriptstyle1+3+5+7+9=\sum_{i=1}^{5} \left(2i-1\right)</math> | ||
|style="text-align:right;"|כגון א' וג' וה' וז' וט' כמה הם בין כלם{{#annotend:rGAn}} | |style="text-align:right;"|כגון א' וג' וה' וז' וט' כמה הם בין כלם{{#annotend:rGAn}} | ||
| + | |- | ||
| + | |Take the greater half of the last term and multiply it by itself. | ||
| + | |style="text-align:right;"|קח הרוב מהמספר האחרון ותרבה הרוב בעצמו | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} \left(2i-1\right)=\left[\left[\left(2n-1\right)+1\right]\sdot\frac{1}{2}\right]^2}}</math> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :Say: the greater half of 9 is 5. 5 times 5 is 25 and so is [their sum]. |
| + | |style="text-align:right;"|ואמור הרוב מט' הוא ה' וה' פעמים ה' הוא כ"ה וכן יהיו כלם | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 1,992: | Line 2,589: | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-11|670|NxSy}}If he continues his question until 11. | |
| + | :<math>\scriptstyle1+\ldots+11=\sum_{i=1}^{6} \left(2i-1\right)</math> | ||
|style="text-align:right;"|ואם הלך בשאלתו עד י"א{{#annotend:NxSy}} | |style="text-align:right;"|ואם הלך בשאלתו עד י"א{{#annotend:NxSy}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{1+\ldots+11=\sum_{i=1}^{6} \left(2i-1\right)=\left[\left(11+1\right)\sdot\frac{1}{2}\right]^2=6^2}}</math> | + | :Say: 6 times 6 and so is [their sum]. |
| + | :<math>\scriptstyle{\color{blue}{1+\ldots+11=\sum_{i=1}^{6} \left(2i-1\right)=\left[\left(11+1\right)\sdot\frac{1}{2}\right]^2=6^2}}</math> | ||
|style="text-align:right;"|אמור ו' פעמי' ו' וכן יהיו | |style="text-align:right;"|אמור ו' פעמי' ו' וכן יהיו | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-13|670|2g6v}}If he continues until 13. | |
| + | :<math>\scriptstyle1+\ldots+13=\sum_{i=1}^{7} \left(2i-1\right)</math> | ||
|style="text-align:right;"|ואם הלך עד י"ג{{#annotend:2g6v}} | |style="text-align:right;"|ואם הלך עד י"ג{{#annotend:2g6v}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{1+\ldots+13=\sum_{i=1}^{7} \left(2i-1\right)=\left[\left(13+1\right)\sdot\frac{1}{2}\right]^2=7^2}}</math> | + | :Say: 7 times 7 and so is [their sum]. |
| + | :<math>\scriptstyle{\color{blue}{1+\ldots+13=\sum_{i=1}^{7} \left(2i-1\right)=\left[\left(13+1\right)\sdot\frac{1}{2}\right]^2=7^2}}</math> | ||
|style="text-align:right;"|אמור ז' פעמי' ז' וכן יהיו | |style="text-align:right;"|אמור ז' פעמי' ז' וכן יהיו | ||
| + | |- | ||
| + | |Always calculate this way. | ||
| + | |style="text-align:right;"|ועל זה הדרך תחשוב לעולם | ||
|- | |- | ||
| | | | ||
| − | + | === <span style=color:green>Sum of Powers of Two</span> === | |
| + | |||
| + | | | ||
|- | |- | ||
| − | + | |If a man says: I summed the doubles to each other. | |
| − | + | :<math>\scriptstyle\sum_{i=m}^{n} 2^i</math> | |
| + | |style="text-align:right;"|ואם יאמר אדם קבצתי מספרים כפולי' זה על זה | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-32|674|y2at}}As 1, 2, 4, 8, 16, 32. | |
| + | :<math>\scriptstyle1+2+4+8+16+32=\sum_{i=1}^{6} 2^{i-1}</math> | ||
|style="text-align:right;"|כגון א' וב' וד' וח' וי"ו ול"ב{{#annotend:y2at}} | |style="text-align:right;"|כגון א' וב' וד' וח' וי"ו ול"ב{{#annotend:y2at}} | ||
|- | |- | ||
| − | | | + | |He starts with whichever [number] he wants to start and ends with whichever number he wants to end: double the last term and subtract the first term. |
| − | :<math>\scriptstyle\sum_{i=m}^{n} 2^i=\left(2\sdot2^n\right)-2^m</math> | + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 2^i=\left(2\sdot2^n\right)-2^m}}</math> |
|style="text-align:right;"|בכל מקום שירצה להתחיל יתחיל ובכל חשבון שיחפוץ לסיים יסיים כפול המספר האחרון וחסר המספר הראשון | |style="text-align:right;"|בכל מקום שירצה להתחיל יתחיל ובכל חשבון שיחפוץ לסיים יסיים כפול המספר האחרון וחסר המספר הראשון | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-32|674|6kg5}}Example: one says: I summed the doubles from 1 to 32. How much is their sum? | |
| + | :<math>\scriptstyle1+\ldots+32=\sum_{i=1}^{6} 2^{i-1}</math> | ||
|style="text-align:right;"|<big>דמיון זה</big> האומר קבצתי מספרים כפולי' מא' ועד ל"ב כמה הם{{#annotend:6kg5}} | |style="text-align:right;"|<big>דמיון זה</big> האומר קבצתי מספרים כפולי' מא' ועד ל"ב כמה הם{{#annotend:6kg5}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{1+\ldots+32=\sum_{i=1}^{6} 2^{i-1}=\left(2\sdot32\right)-1=64-1=63}}</math> | + | :Double 32, which is the last term; it is 64. Subtract the first term, which is 1; 63 remains and so is [their sum]. |
| − | |style="text-align:right;"|ואתה כפול ל"ב שהוא המספר האחרון ויהיו ס"ד וחסר המספר הראשון שהוא א' וישארו ס"ג וכן יהיו | + | :<math>\scriptstyle{\color{blue}{1+\ldots+32=\sum_{i=1}^{6} 2^{i-1}=\left(2\sdot32\right)-1=64-1=63}}</math> |
| + | |style="text-align:right;"|ואתה כפול ל"ב שהוא המספר האחרון ויהיו ס"ד וחסר המספר הראשון שהוא א' וישארו ס"ג‫<ref>ס"ג: MS Ithaca ג'</ref> וכן יהיו | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-64|674|WJGn}}If he says: I started from 1 and doubled until 64. How much is [their sum]? | |
| − | |style="text-align:right;"|ואם יאמ' התחלתי מא' וכפלתי עד ס"ד כמה יהיו{{#annotend:WJGn}} | + | :<math>\scriptstyle1+\ldots+64=\sum_{i=1}^{7} 2^{i-1}</math> |
| + | |style="text-align:right;"|ואם יאמ' התחלתי מא' וכפלתי עד ס"ד‫<ref>ס"ד: MS Ithaca קכ"ח</ref> כמה יהיו{{#annotend:WJGn}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{1+\ldots+64=\sum_{i=1}^{7} 2^{i-1}=\left(2\sdot64\right)-1=128-1=127}}</math> | + | :Double 64; it is 128. Subtract one; it is 127. |
| − | + | |style="text-align:right;"|כפול <s>קכ"ח</s> ס"ד יהיו קכ"ח חסר אחת יהיו קכ"ז | |
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{1+\ldots+64=\sum_{i=1}^{7} 2^{i-1}=\left(2\sdot64\right)-1=128-1=127}}</math> | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-128|674|IUR1}}If he says: I started from one and doubled until 128. How much is [their sum]? | |
| − | |style="text-align:right;"|ואם יאמר התחלתי מאחד וכפלתי עד קכ"ח כמה יהיו{{#annotend:IUR1}} | + | :<math>\scriptstyle1+\ldots+128=\sum_{i=1}^{8} 2^{i-1}</math> |
| + | |style="text-align:right;"|ואם יאמר התחלתי מאחד וכפלתי עד <s>ס"ד</s> קכ"ח כמה יהיו{{#annotend:IUR1}} | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|כפול קכ"ח יהיו רנ"ו חסר א' | + | :Double 128; it is 256. Subtract 1; it is 255. |
| + | |style="text-align:right;"|כפול קכ"ח יהיו רנ"ו חסר א' יהיה רנ"ה | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 2,048: | Line 2,664: | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:4-32|674|ghpP}}If he says: I started from 4 and doubled until 32. How much is their sum? | |
| + | :<math>\scriptstyle4+\ldots+32=\sum_{i=3}^{6} 2^{i-1}</math> | ||
|style="text-align:right;"|ואם יאמר התחלתי מד' וכפלתי עד ל"ב כמה יהיו{{#annotend:ghpP}} | |style="text-align:right;"|ואם יאמר התחלתי מד' וכפלתי עד ל"ב כמה יהיו{{#annotend:ghpP}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{4+\ldots+32=\sum_{i=3}^{6} 2^{i-1}=\left(2\sdot32\right)-4=64-4=60}}</math> | + | :Double 32; it is 64. Subtract 4; it is 60. |
| − | |style="text-align:right;"|כפול ל"ב | + | :<math>\scriptstyle{\color{blue}{4+\ldots+32=\sum_{i=3}^{6} 2^{i-1}=\left(2\sdot32\right)-4=64-4=60}}</math> |
| + | |style="text-align:right;"|כפול ל"ב יהיה ס"ד חסר ד' יהיו ס‫' | ||
|- | |- | ||
| + | |The procedure is to double the last and subtract the first. | ||
| + | |style="text-align:right;"|והחשבון המסור לזה לכפול הא <s>ל</s> האחרון ולחסר הראשון | ||
| + | |- | ||
| + | | | ||
| + | === <span style=color:green>Sum of Powers of Three</span> === | ||
| + | |||
| | | | ||
| − | |||
|- | |- | ||
| − | + | |If a man asks about [the sum of] the triples to each other. | |
| − | + | :<math>\scriptstyle\sum_{i=m}^{n} 3^i</math> | |
| + | |style="text-align:right;"|‫<ref>35v</ref><big>ואם ישאל</big> אדם על מספרי' משולשים זה על זה | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:1-27|675|mIQm}}As 1, 3, 9, 27. | |
| + | :<math>\scriptstyle1+3+9+27=\sum_{i=1}^{4} 3^{i-1}</math> | ||
|style="text-align:right;"|כגון א' ג' ט' כ"ז{{#annotend:mIQm}} | |style="text-align:right;"|כגון א' ג' ט' כ"ז{{#annotend:mIQm}} | ||
| + | |- | ||
| + | |He adds to the last its half after subtracting the first, with which he starts, then adds the first to it. | ||
| + | |style="text-align:right;"|יוסיף על האחרון <s>כ"ז</s> חציו אחר גרעון הראשון שהתחיל בו ועוד יוסיף הראשון עמו | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| − | :<math>\scriptstyle\sum_{i=m}^{n} 3^i=\left(3^n-3^m\right)+\left[\frac{1}{2}\sdot\left(3^n-3^m\right)\right]+3^m</math> | + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 3^i=\left(3^n-3^m\right)+\left[\frac{1}{2}\sdot\left(3^n-3^m\right)\right]+3^m}}</math> |
| + | |- | ||
| + | | | ||
| + | :He subtracts the first term, which is 1, from the last term, which is 27; 26 remains. | ||
| + | |style="text-align:right;"|דהיינו שיגרע מכ"ז שהוא המספר האחרון המספר הראשון שהוא א' ישארו כ"ו | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :He says: 26 plus its half, which is 13, is 39. With 1, which is the first term, it is 40 and this is the [sum of] 1, 3, 9, 27. |
| + | |style="text-align:right;"|יאמר כ"ו וחציו שהוא י"ג הם ל"ט וא' שהוא החשבון הראשון הרי מ' וכן הם א'ג'ט' כ"ז | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
:<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle1+3+9+27&\scriptstyle=\sum_{i=1}^{4} 3^{i-1}=\left(27-1\right)+\left[\frac{1}{2}\sdot\left(27-1\right)\right]+1\\&\scriptstyle=26+\left(\frac{1}{2}\sdot26\right)+1=26+13+1=39+1=40\\\end{align}}}</math> | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle1+3+9+27&\scriptstyle=\sum_{i=1}^{4} 3^{i-1}=\left(27-1\right)+\left[\frac{1}{2}\sdot\left(27-1\right)\right]+1\\&\scriptstyle=26+\left(\frac{1}{2}\sdot26\right)+1=26+13+1=39+1=40\\\end{align}}}</math> | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :*{{#annot:1-16|676|aAn8}}<math>\scriptstyle1+4+16=\sum_{i=1}^{3} 4^{i-1}</math> | + | === <span style=color:green>Sum of Powers of Four</span> === |
| + | |||
| + | | | ||
| + | |- | ||
| + | |If he asks about the quadruples. | ||
| + | :<math>\scriptstyle\sum_{i=m}^{n} 4^i</math> | ||
| + | |style="text-align:right;"|<big>ואם ישאל</big> על מספרי מרובעים | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:1-16|676|aAn8}}As 1, 4, 16. | ||
| + | :<math>\scriptstyle1+4+16=\sum_{i=1}^{3} 4^{i-1}</math> | ||
|style="text-align:right;"|כגון א' ד' י"ו{{#annotend:aAn8}} | |style="text-align:right;"|כגון א' ד' י"ו{{#annotend:aAn8}} | ||
| + | |- | ||
| + | |He adds to the last its third after subtracting the first, then adds the first to it. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 4^i=\left(4^n-4^m\right)+\left[\frac{1}{3}\sdot\left(4^n-4^m\right)\right]+4^m}}</math> | ||
| + | |style="text-align:right;"|יוסיף על האחרון שליש אחר גרעון הראשון ועוד יוסיף הראשון עמו | ||
|- | |- | ||
| | | | ||
| − | : | + | :Example: 1, 4, 16 are 21. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>דמיון זה</big> א' ד' י"ו הם כ"א |
| + | |- | ||
| + | | | ||
| + | :The last term is 16. Subtract the first term, which is 1; 15 remains. | ||
| + | |style="text-align:right;"|המספר האחרון הוא י"ו חסר המספר הראשון א שהוא א' ישארו ט"ו | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :Add to 15 its third, which is 5; it is 20. Add to it [the first] term; it is 21. |
| + | |style="text-align:right;"|הוסף על ט"ו שלישו שהוא ה' יהיו כ' הוסף עליהם המספר יהיו כ"א | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
:<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle1+4+16&\scriptstyle=\sum_{i=1}^{3} 4^{i-1}=\left(16-1\right)+\left[\frac{1}{3}\sdot\left(16-1\right)\right]+1\\&\scriptstyle=15+\left(\frac{1}{3}\sdot15\right)+1=15+5+1=20+1=21\\\end{align}}}</math> | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle1+4+16&\scriptstyle=\sum_{i=1}^{3} 4^{i-1}=\left(16-1\right)+\left[\frac{1}{3}\sdot\left(16-1\right)\right]+1\\&\scriptstyle=15+\left(\frac{1}{3}\sdot15\right)+1=15+5+1=20+1=21\\\end{align}}}</math> | ||
|- | |- | ||
| − | | | + | |And so on. |
| − | : | + | |style="text-align:right;"|וכן לעולם |
| − | : | + | |- |
| − | : | + | |The rule: |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} a^i=\left(a^n-a^m\right)+\left[\frac{1}{a-1}\sdot\left(a^n-a^m\right)\right]+a^m}}</math> | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והכלל המסור לזה |
| − | + | |- | |
| − | + | |For the triples he adds a half. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 3^i=\left(a^n-a^m\right)+\left[\frac{1}{2}\sdot\left(a^n-a^m\right)\right]+a^m}}</math> | |
| − | + | |style="text-align:right;"|למשולש יוסיף החצי | |
| − | ועל הדרך הזה יעשה לעולם | + | |- |
| + | |For the quadruples he adds a third. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 4^i=\left(a^n-a^m\right)+\left[\frac{1}{3}\sdot\left(a^n-a^m\right)\right]+a^m}}</math> | ||
| + | |style="text-align:right;"|ולמרובע יוסיף השלישי | ||
| + | |- | ||
| + | |For the quintuples he adds a quarter. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 5^i=\left(a^n-a^m\right)+\left[\frac{1}{4}\sdot\left(a^n-a^m\right)\right]+a^m}}</math> | ||
| + | |style="text-align:right;"|ולמחומש יוסיף <s>ר</s> הרביע | ||
| + | |- | ||
| + | |For the sextuples he adds a fifth. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 6^i=\left(a^n-a^m\right)+\left[\frac{1}{5}\sdot\left(a^n-a^m\right)\right]+a^m}}</math> | ||
| + | |style="text-align:right;"|ולמשושה יוסיף החומש | ||
| + | |- | ||
| + | |It is always done this way. | ||
| + | |style="text-align:right;"|ועל הדרך הזה יעשה לעולם | ||
|- | |- | ||
| | | | ||
| − | === Motion Problems - Pursuit === | + | |
| + | === <span style=color:green>Motion Problems - Pursuit</span> === | ||
| | | | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:two men|657|hue5}}A man is walking ten miles a day. | + | *{{#annot:two men|657|hue5}}If it is said: A man is walking ten miles a day. |
:Another man is walking one mile on the first day, two miles on the second day, three miles on the third day, four miles on the fourth day, and so on he goes on walking in each day [one mile more]. | :Another man is walking one mile on the first day, two miles on the second day, three miles on the third day, four miles on the fourth day, and so on he goes on walking in each day [one mile more]. | ||
| − | :In how many days will [ | + | :In how many days will they walk the same [total distance]? |
:<math>\scriptstyle10X=\sum_{i=1}^x i</math> | :<math>\scriptstyle10X=\sum_{i=1}^x i</math> | ||
| − | |style="text-align:right;"|אם יאמר אדם אחד הולך בכל יום ויום י' מילי‫'<br> | + | |style="text-align:right;"|<big>אם יאמר אדם</big> אחד הולך בכל יום ויום י' מילי‫'<br> |
ואדם אחר הולך ביום אחד א' מיל וביום ב' ב' מילי' וביום ג' ג' מילים וביום ד' ד' מילי' וכן מוסיף והולך בכל יום ויום<br> | ואדם אחר הולך ביום אחד א' מיל וביום ב' ב' מילי' וביום ג' ג' מילים וביום ד' ד' מילי' וכן מוסיף והולך בכל יום ויום<br> | ||
כמה ימים יעמדו בשוה{{#annotend:hue5}} | כמה ימים יעמדו בשוה{{#annotend:hue5}} | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle{\color{blue}{x=\left(2\sdot10\right)-1=20-1=19}}</math> | + | :Double the 10 miles that the one who walks 10 miles every day walks; it is 20. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אתה כפול הי' מילי' שמהלך אותו שמהלך בכל יום ויום י' מילין ויהיו כ‫' |
| − | תפחות מהם א' ישארו י"ט | + | |- |
| − | נמצא שבי"ט יעמדו בשוה | + | | |
| + | :Subtract 1 from it; 19 remains. | ||
| + | :<math>\scriptstyle{\color{blue}{x=\left(2\sdot10\right)-1=20-1=19}}</math> | ||
| + | |style="text-align:right;"|תפחות מהם א' ישארו י"ט | ||
| + | |- | ||
| + | | | ||
| + | :We find that in 19 [days] they walk the same [total distance]. | ||
| + | |style="text-align:right;"|נמצא שבי"ט יעמדו בשוה | ||
|- | |- | ||
| | | | ||
| − | :Check: | + | :<span style=color:green>'''Check:'''</span> |
| − | : | + | :The one who walks 10 miles a day walks in 19 days 190 miles, as the product of 10 by 19, which is 190. |
| − | |style="text-align:right;"|שצד אותו שמהלך בכל יום י' מילי' בי"ט ימים יהלך ק"צ מילי' | + | :<math>\scriptstyle{\color{blue}{10\sdot19=190}}</math> |
| + | |style="text-align:right;"|שצד אותו שמהלך בכל יום י' מילי' בי"ט ימים יהלך ק"צ מילי' כמניין י' על י"ט שהם ק"צ | ||
|- | |- | ||
| | | | ||
| − | : | + | :The one who adds another mile each day walks in 19 days 190 miles also: take the greater half of 19; it is 10. Multiply it by 19; it is 190. |
| − | :<math>\scriptstyle{\color{blue}{1+\ldots+19=\left[\left(19+1\right)\sdot\frac{1}{2}\right]\sdot19=10\sdot19=190}}</math> | + | :<math>\scriptstyle{\color{blue}{1+\ldots+19=\left[\left(19+1\right)\sdot\frac{1}{2}\right]\sdot19=10\sdot19=190}}</math> |
|style="text-align:right;"|ואותו שמוסיף בכל יום מיל אחד בי"ט ימים יהלך ג"כ ק"צ מילין<br> | |style="text-align:right;"|ואותו שמוסיף בכל יום מיל אחד בי"ט ימים יהלך ג"כ ק"צ מילין<br> | ||
| − | כיצד תפוש הרוב מי"ט והם י' ותכפול אותו על י"ט | + | כיצד תפוש הרוב מי"ט והם י' ותכפול אותו על י"ט ויהיה ק"צ |
|- | |- | ||
| − | | | + | |Always double the [number] of miles that the one who walks the same distance [each day] walks, then subtract one from it and this is the number of days, in which they walk the same [total distance]. |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{ax=\sum_{i=1}^x i\longrightarrow x=2a-1}}</math> | |
| − | :<math>\scriptstyle ax=\sum_{i=1}^x i\longrightarrow x=2a-1</math> | ||
|style="text-align:right;"|וכן לעולם תכפול המילי' שמהלך המילי' שמהלך הקבוע ותפחות מהם אחד וכמספרם יהיו הימים שיעמדו בשוה | |style="text-align:right;"|וכן לעולם תכפול המילי' שמהלך המילי' שמהלך הקבוע ותפחות מהם אחד וכמספרם יהיו הימים שיעמדו בשוה | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:two men|657|54en}}A man is walking ten miles a day. | + | *{{#annot:two men|657|54en}}If it is said: A man is walking ten miles a day. |
:Another man is walking two miles on the first day, four [miles] on the second day, six [miles] on the third day, eight [miles] on the fourth day, and so on he adds two [miles more each day]. | :Another man is walking two miles on the first day, four [miles] on the second day, six [miles] on the third day, eight [miles] on the fourth day, and so on he adds two [miles more each day]. | ||
| − | :In how many days will [ | + | :In how many days will they walk the same [total distance]? |
:<math>\scriptstyle10X=\sum_{i=1}^x 2i</math> | :<math>\scriptstyle10X=\sum_{i=1}^x 2i</math> | ||
| − | |style="text-align:right;"|ואם יאמר אדם אחד הולך בכל יום י' מילי‫'<br> | + | |style="text-align:right;"|<big>ואם יאמר</big> אדם אחד הולך בכל יום י' מילי‫'<br> |
| − | ואדם אחר הולך ביום אחד ב' מילין וביום שני ד' וביום שלישי ו' וביום רביעי ח' וכן לעולם הוא מוסיף ב' והולך על הסדר<br> | + | ואדם‫<ref>אחד הולך... ואדם: MS Ithaca twice</ref> אחר הולך ביום אחד ב' מילין וביום שני ד' וביום שלישי ו' וביום רביעי ח' וכן לעולם הוא מוסיף ב' והולך על הסדר<br> |
בכמה ימים יעמדו בשוה{{#annotend:54en}} | בכמה ימים יעמדו בשוה{{#annotend:54en}} | ||
|- | |- | ||
| | | | ||
| + | :Subtract 1 from the miles that the one who walks the same distance every day walks; 9 remains. | ||
:<math>\scriptstyle{\color{blue}{x=10-1=9}}</math> | :<math>\scriptstyle{\color{blue}{x=10-1=9}}</math> | ||
| − | |style="text-align:right;"|אתה תפחות אחת מן המילין שמהלך הקבוע בכל יום ישאירו ט‫' | + | |style="text-align:right;"|אתה תפחות אחת מן המילין שמהלך הקבוע בכל יום ישאירו ט‫' |
| − | נמצא שבט' ימים יעמדו בשוה | + | |- |
| + | | | ||
| + | :We find that in 9 days they walk the same [total distance]. | ||
| + | |style="text-align:right;"|נמצא שבט' ימים יעמדו בשוה | ||
|- | |- | ||
| | | | ||
| − | :Check: | + | :<span style=color:green>'''Check:'''</span> |
| − | : | + | :The one who walks 10 miles a day walks in 9 days 90 miles. |
| + | :<math>\scriptstyle{\color{blue}{10\sdot9=90}}</math> | ||
|style="text-align:right;"|כיצד אותו שמהלך בכל יום י' מילין בט' ימים מהלך צ' מילי‫' | |style="text-align:right;"|כיצד אותו שמהלך בכל יום י' מילין בט' ימים מהלך צ' מילי‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :For the one who walks an increasing even number of miles [each day], i.e. 2, 4, 6, 8, 10, 12, 14, 16, 18: |
| − | |style="text-align:right;"|ואותו שמהלך זוגות ר"ל ב' וד' וו' וח' וי' וי"ב וי"ד וי"ו וי"ח | + | |style="text-align:right;"|ואותו שמהלך זוגות ר"ל ב' וד' וו' וח' וי' וי"ב וי"ד וי"ו וי"ח |
| − | אמור החצי מי"ח הם ט‫' | + | |- |
| − | תרבה אותם עם י' שהוא החשבון הבא אחר ט' יהיו צ‫' | + | | |
| − | נמצא שבט' ימים יעמדו בשוה | + | :Say: the half of 18 is 9 |
| + | |style="text-align:right;"|אמור החצי מי"ח הם ט‫' | ||
| + | |- | ||
| + | | | ||
| + | :Multiply it by 10, which is the number that follows 9; it is 90. | ||
| + | |style="text-align:right;"|תרבה אותם עם י' שהוא החשבון הבא אחר ט' יהיו צ‫' | ||
| + | |- | ||
| + | | | ||
| + | :We find that in 9 days they walk the same [total distance]. | ||
| + | |style="text-align:right;"|נמצא שבט' ימים יעמדו בשוה | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
:<math>\scriptstyle{\color{blue}{2+4+6+8+10+12+14+16+18=\left(18\sdot\frac{1}{2}\right)\sdot\left(9+1\right)=9\sdot10=90}}</math> | :<math>\scriptstyle{\color{blue}{2+4+6+8+10+12+14+16+18=\left(18\sdot\frac{1}{2}\right)\sdot\left(9+1\right)=9\sdot10=90}}</math> | ||
|- | |- | ||
| − | | | + | |Always subtract [one] from the [number] of miles that the one who walks the same distance [each day] walks and this is the number of days, in which they walk the same [total distance]. |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{ax=\sum_{i=1}^x 2i\longrightarrow x=a-1}}</math> | |
| − | :<math>\scriptstyle ax=\sum_{i=1}^x 2i\longrightarrow x=a-1</math> | ||
|style="text-align:right;"|וכן לעולם תפחות מן המיל' שמהלך הקבוע וכמספרם יהיו הימים יעמדו בשוה | |style="text-align:right;"|וכן לעולם תפחות מן המיל' שמהלך הקבוע וכמספרם יהיו הימים יעמדו בשוה | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:two men|657|5kbx}}A man is walking ten miles a day. | + | *{{#annot:two men|657|5kbx}}If it is said: A man is walking ten miles a day. |
| − | :Another man is walking one mile on the first day, three miles on the second day, five miles on the third day, seven miles on the fourth day, and so on he goes on walking [in each day] an odd number of miles | + | :Another man is walking one mile on the first day, three miles on the second day, five miles on the third day, seven miles on the fourth day, and so on he goes on walking [in each day] an odd number of miles. |
:<math>\scriptstyle10X=\sum_{i=1}^x \left(2i-1\right)</math> | :<math>\scriptstyle10X=\sum_{i=1}^x \left(2i-1\right)</math> | ||
| − | |style="text-align:right;"|ואם יאמר אדם אחד הולך בכל יום י' מילי‫'<br> | + | |style="text-align:right;"|<big>ואם יאמר</big> אדם אחד הולך בכל יום י' מילי‫'<br> |
| − | ואדם אחר הולך בכל ביום אחד א' מיל וביום ב' ג' מילי' וביום ג' ה' מילי' וביום ד' ז' מילי' וכן מוסיף והולך לעולם החשבונות נפרדים{{#annotend:5kbx}} | + | ואדם אחר הולך <s>בכל</s> ביום אחד א' מיל וביום ב' ג' מילי' וביום ג' ה' מילי' וביום ד' ז' מילי' וכן מוסיף והולך לעולם החשבונות נפרדים{{#annotend:5kbx}} |
|- | |- | ||
| − | | | + | |Know that the number of miles that the one who walks the same [distance] [each day] walks each day is the same as the number of days, in which they walk the same [total distance]. |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{ax=\sum_{i=1}^x \left(2i-1\right)\longrightarrow x=a}}</math> | |
| − | :<math>\scriptstyle ax=\sum_{i=1}^x \left(2i-1\right)\longrightarrow x=a</math> | + | |style="text-align:right;"|דע כי כמספר המילין מהלך ק הקבוע בכל יום כן מספר הימים שיעמדו בשוה |
| − | |style="text-align:right;"|דע כי כמספר המילין מהלך הקבוע בכל יום כן מספר הימים שיעמדו בשוה | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{x=10}}</math> | + | :I.e. in 10 days. |
| + | :<math>\scriptstyle{\color{blue}{x=10}}</math> | ||
|style="text-align:right;"|דהיינו בי' ימים | |style="text-align:right;"|דהיינו בי' ימים | ||
|- | |- | ||
| | | | ||
| − | :Check: | + | :<span style=color:green>'''Check:'''</span> |
| − | : | + | :Because, the one who walks 10 miles a day walks in 10 days 100 miles. |
| + | :<math>\scriptstyle{\color{blue}{10\sdot10=100}}</math> | ||
|style="text-align:right;"|כי אותו שמהלך בכל יום י' מילי' ‫<ref>36r</ref>מהלך בי' ימי' ק' מילי‫' | |style="text-align:right;"|כי אותו שמהלך בכל יום י' מילי' ‫<ref>36r</ref>מהלך בי' ימי' ק' מילי‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :The one who walks 1 mile on the first day, 3 miles on the second day, and so on this way, walks 19 miles on the tenth day. |
| − | |style="text-align:right;"|ואותו שמהלך ביום אחד א' מיל וביום שני ג' מילי' ומוסיף והולך על הדרך הזה | + | |style="text-align:right;"|ואותו שמהלך ביום אחד א' מיל וביום שני ג' מילי' ומוסיף והולך על הדרך הזה ביום העשירי מהלך י"ט מילי‫' |
| − | ביום העשירי מהלך י"ט מילי | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| + | :The greater half of 19 is 10. | ||
| + | |style="text-align:right;"|והרוב מי"ט הוא י‫' | ||
| + | |- | ||
| + | | | ||
| + | :If you multiply 10 by itself, it is 100. | ||
| + | :<math>\scriptstyle{\color{blue}{1+3+\ldots+19=\left[\left(19+1\right)\sdot\frac{1}{2}\right]^2=10^2=100}}</math> | ||
| + | |style="text-align:right;"|ואם תרבה י' בעצמם הוא ק‫' | ||
| + | |- | ||
| + | |Do this way for any number you want. | ||
|style="text-align:right;"|ועל זה הדרך תעשה לכל חשבון שתרצה | |style="text-align:right;"|ועל זה הדרך תעשה לכל חשבון שתרצה | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | == Word Problems - The Rule of Three == | + | == <span style=color:green>Word Problems - The Rule of Three</span> == |
| − | + | | | |
| + | |- | ||
| + | |General Rule - A Selection of all the Rules in the World | ||
|style="text-align:right;"|<big>ריגולא כללית והיא מבחר כל הריגולא שבעולם</big> | |style="text-align:right;"|<big>ריגולא כללית והיא מבחר כל הריגולא שבעולם</big> | ||
|- | |- | ||
| Line 2,221: | Line 2,911: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:eggs|629|3fQk}}3 eggs are worth 4 pešiṭim. | + | *{{#annot:eggs|629|3fQk}}A man says: 3 eggs are worth 4 pešiṭim. |
:How many pešiṭim are 5 eggs worth at this price? | :How many pešiṭim are 5 eggs worth at this price? | ||
:<math>\scriptstyle\frac{4}{3}=\frac{X}{5}</math> | :<math>\scriptstyle\frac{4}{3}=\frac{X}{5}</math> | ||
| Line 2,228: | Line 2,918: | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Do this way: return the calculation back: he asks if 3 is equal to 4, how much is 5 equal to? |
:<math>\scriptstyle{\color{blue}{3:4=5:X}}</math> | :<math>\scriptstyle{\color{blue}{3:4=5:X}}</math> | ||
|style="text-align:right;"|עשה על זה הדרך שתחזיר החשבון לאחורנית הוא שואל אם ג' שוה ד' ה' כמה שוה | |style="text-align:right;"|עשה על זה הדרך שתחזיר החשבון לאחורנית הוא שואל אם ג' שוה ד' ה' כמה שוה | ||
|- | |- | ||
| | | | ||
| + | :Say: 5 times 4; divide it by 3; it is 6 and 2-thirds. | ||
:<math>\scriptstyle{\color{blue}{X=\frac{5\sdot4}{3}=6+\frac{2}{3}}}</math> | :<math>\scriptstyle{\color{blue}{X=\frac{5\sdot4}{3}=6+\frac{2}{3}}}</math> | ||
|style="text-align:right;"|ואתה אמור ה' פעמים ד' חלקם בג' יהיו ו' וב' שלישיו‫' | |style="text-align:right;"|ואתה אמור ה' פעמים ד' חלקם בג' יהיו ו' וב' שלישיו‫' | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:general|629|FApQ}}5 | + | *{{#annot:general|629|FApQ}}If he asks: if 5 is equal to 7, how much is 9 equal to? |
:<math>\scriptstyle\frac{7}{5}=\frac{X}{9}</math> | :<math>\scriptstyle\frac{7}{5}=\frac{X}{9}</math> | ||
|style="text-align:right;"|וכן אם שואל אם ה' שוה ז' ט' כמה שוי{{#annotend:FApQ}} | |style="text-align:right;"|וכן אם שואל אם ה' שוה ז' ט' כמה שוי{{#annotend:FApQ}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Say: 9 times 7 is 63. Divide it by 5 and so it is. |
:<math>\scriptstyle{\color{blue}{X=\frac{9\sdot7}{5}=\frac{63}{5}}}</math> | :<math>\scriptstyle{\color{blue}{X=\frac{9\sdot7}{5}=\frac{63}{5}}}</math> | ||
|style="text-align:right;"|אמור ט' פעמים ז' ס"ג<br> | |style="text-align:right;"|אמור ט' פעמים ז' ס"ג<br> | ||
| Line 2,248: | Line 2,939: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:general|629|hM80}}11 are worth 17 | + | *{{#annot:general|629|hM80}}If he says: 11 are worth 17 |
:How much are 31 worth at this price? | :How much are 31 worth at this price? | ||
:<math>\scriptstyle\frac{17}{11}=\frac{X}{31}</math> | :<math>\scriptstyle\frac{17}{11}=\frac{X}{31}</math> | ||
| Line 2,255: | Line 2,946: | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Say: 31 times 17; divide it by 11. |
:<math>\scriptstyle{\color{blue}{X=\frac{31\sdot17}{11}}}</math> | :<math>\scriptstyle{\color{blue}{X=\frac{31\sdot17}{11}}}</math> | ||
| − | |style="text-align:right;"|אמור ל"א פעמים י"ז וחלקם בי"א וכן על זה הדרך לעולם | + | |style="text-align:right;"|אמור ל"א פעמים י"ז וחלקם בי"א |
| + | |- | ||
| + | |It is always this way. | ||
| + | |style="text-align:right;"|וכן על זה הדרך לעולם | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:kor|629|lMNX}}10 korim are worth 6 dinar. | + | *{{#annot:kor|629|lMNX}}If he says: 10 korim are worth 6 dinar. |
:How much are 4 korim worth at this price? | :How much are 4 korim worth at this price? | ||
:<math>\scriptstyle\frac{6}{10}=\frac{X}{4}</math> | :<math>\scriptstyle\frac{6}{10}=\frac{X}{4}</math> | ||
| Line 2,267: | Line 2,961: | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Say: 4 times 6 is 24. Divide it by 10; the result is 2 and 4-tenths that are 2 dinar and 2-fifths of a dinar. |
| − | :<math>\scriptstyle{\color{blue}{X=\frac{4\sdot6}{10}=\frac{24}{10}=2+\frac{4}{10}=2+\frac{2}{5}}}</math> | + | :<math>\scriptstyle{\color{blue}{X=\frac{4\sdot6}{10}=\frac{24}{10}=2+\frac{4}{10}=2+\frac{2}{5}}}</math> |
|style="text-align:right;"|אמור ד' פעמי' ו' כ"ד<br> | |style="text-align:right;"|אמור ד' פעמי' ו' כ"ד<br> | ||
חלקם בי' יבואו ב' וד' עשיריות שהם ב' דינרי' וב' חומשי דינר | חלקם בי' יבואו ב' וד' עשיריות שהם ב' דינרי' וב' חומשי דינר | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:sheaves|629|oN2h}}3 sheaves are worth 4 dinar. | + | *{{#annot:sheaves|629|oN2h}}If it is said: 3 sheaves are worth 4 dinar. |
:How much are 10 sheaves worth at this price? | :How much are 10 sheaves worth at this price? | ||
:<math>\scriptstyle\frac{4}{3}=\frac{X}{10}</math> | :<math>\scriptstyle\frac{4}{3}=\frac{X}{10}</math> | ||
| Line 2,280: | Line 2,974: | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Say: 10 times 4 is 40. Divide it by 3; it is 13 dinar and a third of a dinar. |
| − | :<math>\scriptstyle{\color{blue}{X=\frac{10\sdot4}{3}=\frac{40}{3}=13+\frac{1}{3}}}</math> | + | :<math>\scriptstyle{\color{blue}{X=\frac{10\sdot4}{3}=\frac{40}{3}=13+\frac{1}{3}}}</math> |
|style="text-align:right;"|אמור י' פעמים ד' מ‫'<br> | |style="text-align:right;"|אמור י' פעמים ד' מ‫'<br> | ||
חלקם בג' יהיו י"ג דינרי' ושליש דינר | חלקם בג' יהיו י"ג דינרי' ושליש דינר | ||
| Line 2,289: | Line 2,983: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:wheat|630|1vZH}}I bought 10 korim of wheat for 6 dinar. | + | *{{#annot:wheat|630|1vZH}}Say: if it is said: I bought 10 korim of wheat for 6 dinar. |
:How many korim could I buy for 4 dinar? | :How many korim could I buy for 4 dinar? | ||
:<math>\scriptstyle\frac{6}{10}=\frac{X}{4}</math> | :<math>\scriptstyle\frac{6}{10}=\frac{X}{4}</math> | ||
| Line 2,296: | Line 2,990: | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Say: if we find 10 korim for 6 dinar, how many korim will we find for 4 dinar? |
:<math>\scriptstyle{\color{blue}{6:10=4:X}}</math> | :<math>\scriptstyle{\color{blue}{6:10=4:X}}</math> | ||
|style="text-align:right;"|אמור אם בו' דינרי' נמצא י' כורי' חטה בד' דינרי' כמה כורי' נמצא | |style="text-align:right;"|אמור אם בו' דינרי' נמצא י' כורי' חטה בד' דינרי' כמה כורי' נמצא | ||
|- | |- | ||
| | | | ||
| + | :Say: 4 times 10 is 40. Divide it by 6; it is 6 and 4-sixths, which is 6 and 2-thirds. | ||
:<math>\scriptstyle{\color{blue}{X=\frac{4\sdot10}{6}=\frac{40}{6}=6+\frac{4}{6}=6+\frac{2}{3}}}</math> | :<math>\scriptstyle{\color{blue}{X=\frac{4\sdot10}{6}=\frac{40}{6}=6+\frac{4}{6}=6+\frac{2}{3}}}</math> | ||
|style="text-align:right;"|אמור ד' פעמי' י' מ‫'<br> | |style="text-align:right;"|אמור ד' פעמי' י' מ‫'<br> | ||
| Line 2,306: | Line 3,001: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:kor|630|I3ZQ}}6 korim of wheat are worth 4 dinar. | + | *{{#annot:kor|630|I3ZQ}}If it is said: 6 korim of wheat are worth 4 dinar. |
| − | :How many | + | :How many korim could I buy for 7 dinar? |
:<math>\scriptstyle\frac{4}{6}=\frac{7}{X}</math> | :<math>\scriptstyle\frac{4}{6}=\frac{7}{X}</math> | ||
| − | |style="text-align:right;"|וכן אם יאמר שש כורי' שוי' ד' דינרי‫'<br> | + | |style="text-align:right;"|וכן אם יאמר שש כורי' שוי' ד'‫<ref>ד': MS Ithaca ו'</ref> דינרי‫'<br> |
כמה כורי אוכל לקנות בז' דינרי{{#annotend:I3ZQ}} | כמה כורי אוכל לקנות בז' דינרי{{#annotend:I3ZQ}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Say: if 4 dinar are worth 6 korim, how many korim are worth 7 dinar? |
:<math>\scriptstyle{\color{blue}{4:6=7:X}}</math> | :<math>\scriptstyle{\color{blue}{4:6=7:X}}</math> | ||
|style="text-align:right;"|אמור אם ד' דינרי' שוי' ו' כורי' ז' דינרי' כמה כורי' שוי‫' | |style="text-align:right;"|אמור אם ד' דינרי' שוי' ו' כורי' ז' דינרי' כמה כורי' שוי‫' | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle{\color{blue}{X=\frac{7\sdot6}{4}=\frac{42}{4}=10+\frac{2}{4}=10+\frac{1}{2}}}</math> | + | :Say: 7 times 6 is 42. Divide it by 4; it is 10 korim and 2-quarters that are 10 korim and half a kor. |
| + | :<math>\scriptstyle{\color{blue}{X=\frac{7\sdot6}{4}=\frac{42}{4}=10+\frac{2}{4}=10+\frac{1}{2}}}</math> | ||
|style="text-align:right;"|אמור ז' פעמים ו' מ"ב<br> | |style="text-align:right;"|אמור ז' פעמים ו' מ"ב<br> | ||
| − | חלקם בד' יהיו י' כורי' וב' רביעיות שהם י' כורי' וחצי | + | חלקם בד' יהיו <s>ד' כורי</s> י' כורי' וב' רביעיות שהם <s>ו' כורי</s> י' כורי' וחצי כור |
|- | |- | ||
| | | | ||
| − | === Employment Problems - Payment Problems === | + | === <span style=color:green>Employment Problems - Payment Problems</span> === |
| − | + | | | |
| + | |- | ||
| + | |The same for the issue of employment. | ||
|style="text-align:right;"|וכן לעניין השכירות | |style="text-align:right;"|וכן לעניין השכירות | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:one worker|612|J3UH}}I hired a worker for 30 days for 10 zuzim but he worked with me 8 days. | + | *{{#annot:one worker|612|J3UH}}Example: the one who says: I hired a worker for 30 days for 10 zuzim but he worked with me 8 days. |
:How much should his payment be? | :How much should his payment be? | ||
:<math>\scriptstyle\frac{10}{30}=\frac{X}{8}</math> | :<math>\scriptstyle\frac{10}{30}=\frac{X}{8}</math> | ||
| Line 2,336: | Line 3,034: | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Say: if for 30 days, his payment is 10 zuz, how much is his payment for 8 days? |
:<math>\scriptstyle{\color{blue}{30:10=8:X}}</math> | :<math>\scriptstyle{\color{blue}{30:10=8:X}}</math> | ||
|style="text-align:right;"|אמור אם בל' יום יהיה שכרו י' זוז בח' ימים כמה שכרו | |style="text-align:right;"|אמור אם בל' יום יהיה שכרו י' זוז בח' ימים כמה שכרו | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{X=\frac{8\sdot10}{30}=\frac{80}{30}=2+\frac{20}{30}=2+\frac{2}{3}=3-\frac{1}{3}}}</math> dinar | + | :Say: 8 times 10 is 80. Divide it by 30; the result is 2 zuzim and 20 parts of 30, which are 2 and 2-thirds, which are 3 dinar minus a third of a dinar. |
| + | :<math>\scriptstyle{\color{blue}{X=\frac{8\sdot10}{30}=\frac{80}{30}=2+\frac{20}{30}=2+\frac{2}{3}=3-\frac{1}{3}}}</math> dinar | ||
|style="text-align:right;"|אמור ח' פעמים י' הם כזה פ‫'<br> | |style="text-align:right;"|אמור ח' פעמים י' הם כזה פ‫'<br> | ||
| − | חלקם בל' יבואו ב' זוזי' וכ' חלקי' מל | + | חלקם בל' יבואו ב' זוזי' וכ' חלקי' מל' שהם ב' וב' שלישיות שהם ג' דינרי' פחות שליש דינר |
| − | שהם ב' וב' שלישיות | ||
| − | שהם ג' דינרי' | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| Line 2,354: | Line 3,048: | ||
== Calculation of Fractions == | == Calculation of Fractions == | ||
| − | + | |style="text-align:right;"|<big>חֶשְׁבּוֹן הַשְׁבָרִים</big> | |
|- | |- | ||
| − | |||
| | | | ||
| − | + | *If you divide one into two [equal] parts, each part will be a half and the two halves are one whole. | |
| − | + | :<math>\scriptstyle{\color{blue}{1=\frac{1}{2}+\frac{1}{2}}}</math> | |
| − | |||
|style="text-align:right;"|אם תחלק האחד בב' חלקים יהיה בכל חלק מהם חצי ושני החצאי' הם אחד שלם | |style="text-align:right;"|אם תחלק האחד בב' חלקים יהיה בכל חלק מהם חצי ושני החצאי' הם אחד שלם | ||
|- | |- | ||
| | | | ||
| − | *<math>\ | + | *If you divide one into three [equal] parts, each part is a third and three thirds are one whole. |
| + | :<math>\scriptstyle{\color{blue}{1=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}}}</math> | ||
|style="text-align:right;"|וכן אם החלק האחד בג' חלקי' יהיה כל חלק מהם שליש ושלש השלישיות הם אחד שלם | |style="text-align:right;"|וכן אם החלק האחד בג' חלקי' יהיה כל חלק מהם שליש ושלש השלישיות הם אחד שלם | ||
|- | |- | ||
| | | | ||
| − | *<math>\ | + | *If you divide one into four [equal] parts, each part is a quarter and four quarters are one whole. |
| + | :<math>\scriptstyle{\color{blue}{1=\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}}}</math> | ||
|style="text-align:right;"|וכן אם תחלק האחד בד' חלקי' יהיה כל אחד מהם רביע וד' הרביעיי' הם אחד שלם | |style="text-align:right;"|וכן אם תחלק האחד בד' חלקי' יהיה כל אחד מהם רביע וד' הרביעיי' הם אחד שלם | ||
|- | |- | ||
| − | | | + | |This way for all. |
|style="text-align:right;"|ועל זה הדרך הם כלם | |style="text-align:right;"|ועל זה הדרך הם כלם | ||
|- | |- | ||
| | | | ||
| − | === Addition of Fractions === | + | === <span style=color:green>Addition of Fractions</span> === |
| | | | ||
|- | |- | ||
| − | |<math>\scriptstyle\frac{1}{a}+\frac{1}{b}=\frac{\left[\frac{1}{a}\sdot\left(a\sdot b\right)\right]+\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}</math> | + | |<math>\scriptstyle{\color{OliveGreen}{\frac{1}{a}+\frac{1}{b}=\frac{\left[\frac{1}{a}\sdot\left(a\sdot b\right)\right]+\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}}}</math> |
| | | | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:½+⅓|677|Prkw}}<math>\scriptstyle\frac{1}{2}+\frac{1}{3}</math> | + | *{{#annot:½+⅓|677|Prkw}}If it is said: whoever has a half and a third of one thing, how much does he have of that thing? |
| + | :<math>\scriptstyle\frac{1}{2}+\frac{1}{3}</math> | ||
|style="text-align:right;"|ואם יאמ' מי שיש לו החצי והשליש מדבר אחד כמה חלק יש לו מן הדבר ההוא{{#annotend:Prkw}} | |style="text-align:right;"|ואם יאמ' מי שיש לו החצי והשליש מדבר אחד כמה חלק יש לו מן הדבר ההוא{{#annotend:Prkw}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a half and a third are found in 2 times 3, which is 6. |
:<math>\scriptstyle{\color{blue}{2\sdot3=6}}</math> | :<math>\scriptstyle{\color{blue}{2\sdot3=6}}</math> | ||
| − | |style="text-align:right;"|אמור חצי ושליש ימצא בב' פעמים ג' שהם ו‫' | + | |style="text-align:right;"|אמור חצי ושליש ‫<ref>36v</ref>ימצא בב' פעמים ג' שהם ו‫' |
|- | |- | ||
| | | | ||
| + | :Its half is 3 and its third is 2. If you sum them, they are 5. So, the one who has a half and a third of the thing, has 5 parts of 6 of that thing. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{2}+\frac{1}{3}=\frac{\left(\frac{1}{2}\sdot6\right)+\left(\frac{1}{3}\sdot6\right)}{6}=\frac{3+2}{6}=\frac{5}{6}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{2}+\frac{1}{3}=\frac{\left(\frac{1}{2}\sdot6\right)+\left(\frac{1}{3}\sdot6\right)}{6}=\frac{3+2}{6}=\frac{5}{6}}}</math> | ||
|style="text-align:right;"|חציי ג' ושלישיתו ב' ואם תקבצו יהיו ה' הרי שאותו שיש לו החצי והשליש מן הדבר יש לו ה' חלקי' מו' מן הדבר ההוא | |style="text-align:right;"|חציי ג' ושלישיתו ב' ואם תקבצו יהיו ה' הרי שאותו שיש לו החצי והשליש מן הדבר יש לו ה' חלקי' מו' מן הדבר ההוא | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓+¼|677|595p}}<math>\scriptstyle\frac{1}{3}+\frac{1}{4}</math> | + | *{{#annot:⅓+¼|677|595p}}Whoever has a third and a quarter of the thing, how much does he have of that thing? |
| − | |style="text-align:right;"|ואם מי שיש לו השליש והרביעי מן הדבר כמה חלק יש לו ממנו{{#annotend:595p}} | + | :<math>\scriptstyle\frac{1}{3}+\frac{1}{4}</math> |
| + | |style="text-align:right;"|<big>ואם</big> מי שיש לו השליש והרביעי מן הדבר כמה חלק יש לו ממנו{{#annotend:595p}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third and a quarter are found in 3 times 4, which is 12. |
:<math>\scriptstyle{\color{blue}{3\sdot4=12}}</math> | :<math>\scriptstyle{\color{blue}{3\sdot4=12}}</math> | ||
|style="text-align:right;"|אמור שליש ורביע ימצא בג' פעמים ד' שהם י"ב | |style="text-align:right;"|אמור שליש ורביע ימצא בג' פעמים ד' שהם י"ב | ||
|- | |- | ||
| | | | ||
| + | :Its third is 4 and its quarter is 3. If you sum them, they are 7. So, the one who has a third and a quarter of the thing, has 7 parts of 12 of that thing. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}+\frac{1}{4}=\frac{\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)}{12}=\frac{4+3}{12}=\frac{7}{12}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}+\frac{1}{4}=\frac{\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)}{12}=\frac{4+3}{12}=\frac{7}{12}}}</math> | ||
|style="text-align:right;"|השליש מהם הם ד' והרביעי הוא ג' ואם תקבצם הם ז' הרי שמי שיש לו השליש והרביע מן הדבר יש לו ז' חלקי' מי"ב מן הדבר ההוא | |style="text-align:right;"|השליש מהם הם ד' והרביעי הוא ג' ואם תקבצם הם ז' הרי שמי שיש לו השליש והרביע מן הדבר יש לו ז' חלקי' מי"ב מן הדבר ההוא | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓+⅕|677|Asm1}}<math>\scriptstyle\frac{1}{3}+\frac{1}{5}</math> | + | *{{#annot:⅓+⅕|677|Asm1}}Whoever has a third and a fifth of the thing. |
| + | :<math>\scriptstyle\frac{1}{3}+\frac{1}{5}</math> | ||
|style="text-align:right;"|וכן מי שיש לו השליש והחומש מן הדבר{{#annotend:Asm1}} | |style="text-align:right;"|וכן מי שיש לו השליש והחומש מן הדבר{{#annotend:Asm1}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third and a fifth are found in 3 times 5, which is 15. |
:<math>\scriptstyle{\color{blue}{3\sdot5=15}}</math> | :<math>\scriptstyle{\color{blue}{3\sdot5=15}}</math> | ||
|style="text-align:right;"|אמור שליש וחומש ימצא בג' פעמים ה' שהם ט"ו | |style="text-align:right;"|אמור שליש וחומש ימצא בג' פעמים ה' שהם ט"ו | ||
|- | |- | ||
| | | | ||
| + | :Its third is 5 and its fifth is 3. Together they are 8. So, the one who has a third and a fifth of the thing, has 8 parts of 15 of that thing. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}+\frac{1}{5}=\frac{\left(\frac{1}{3}\sdot15\right)+\left(\frac{1}{5}\sdot15\right)}{15}=\frac{5+3}{15}=\frac{8}{15}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}+\frac{1}{5}=\frac{\left(\frac{1}{3}\sdot15\right)+\left(\frac{1}{5}\sdot15\right)}{15}=\frac{5+3}{15}=\frac{8}{15}}}</math> | ||
|style="text-align:right;"|השליש מהם הוא ה' והחומש ג' ושניהם יחד הם ח' אם כן מי שיש לו השליש והחומש מן הדבר יש לו ח' חלקים מט"ו מן הדבר ההוא | |style="text-align:right;"|השליש מהם הוא ה' והחומש ג' ושניהם יחד הם ח' אם כן מי שיש לו השליש והחומש מן הדבר יש לו ח' חלקים מט"ו מן הדבר ההוא | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:¼+⅕|677|nQTO}}<math>\scriptstyle\frac{1}{4}+\frac{1}{5}</math> | + | *{{#annot:¼+⅕|677|nQTO}}Whoever has a quarter and a fifth of the thing. |
| + | :<math>\scriptstyle\frac{1}{4}+\frac{1}{5}</math> | ||
|style="text-align:right;"|וכן מי שיש לו הרביע והחומש מן הדבר{{#annotend:nQTO}} | |style="text-align:right;"|וכן מי שיש לו הרביע והחומש מן הדבר{{#annotend:nQTO}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a quarter and a fifth are found in 4 times 5, which is 20. |
:<math>\scriptstyle{\color{blue}{4\sdot5=20}}</math> | :<math>\scriptstyle{\color{blue}{4\sdot5=20}}</math> | ||
|style="text-align:right;"|אמור רביע וחומש ימצא בד' פעמי' ה' שהם כ‫' | |style="text-align:right;"|אמור רביע וחומש ימצא בד' פעמי' ה' שהם כ‫' | ||
|- | |- | ||
| | | | ||
| + | :Its quarter is 5 and its fifth is 4. Together they are 9. So, he has 9 parts of 20 of that thing. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{4}+\frac{1}{5}=\frac{\left(\frac{1}{4}\sdot20\right)+\left(\frac{1}{5}\sdot20\right)}{20}=\frac{5+4}{20}=\frac{9}{20}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{4}+\frac{1}{5}=\frac{\left(\frac{1}{4}\sdot20\right)+\left(\frac{1}{5}\sdot20\right)}{20}=\frac{5+4}{20}=\frac{9}{20}}}</math> | ||
| − | |style="text-align:right;"|הרביע הוא ה' והחומש הוא ד' ושניהם יחד הם ט' אם כן יש לו ט' חלקים מכ' מן הדבר ההוא | + | |style="text-align:right;"|הרביע הוא‫<ref>הוא: MS Ithaca הם</ref> ה' והחומש הוא ד'‫<ref>והחומש הוא ד': MS Ithaca om.</ref> ושניהם יחד הם ט'‫<ref>ט': MS Ithaca ד'</ref> אם כן יש לו ט' חלקים מכ' מן הדבר ההוא |
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓+⅐|677|c6OW}}<math>\scriptstyle\frac{1}{3}+\frac{1}{7}</math> | + | *{{#annot:⅓+⅐|677|c6OW}}Whoever has a third and a seventh of the thing. |
| + | :<math>\scriptstyle\frac{1}{3}+\frac{1}{7}</math> | ||
|style="text-align:right;"|וכן מי שיש לו שליש ושביע מן הדבר{{#annotend:c6OW}} | |style="text-align:right;"|וכן מי שיש לו שליש ושביע מן הדבר{{#annotend:c6OW}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third and a seventh are found in 3 times 7, which is 21. |
:<math>\scriptstyle{\color{blue}{3\sdot7=21}}</math> | :<math>\scriptstyle{\color{blue}{3\sdot7=21}}</math> | ||
|style="text-align:right;"|אמור שליש ושביע ימצאו בג' פעמים ז' שהם כ"א | |style="text-align:right;"|אמור שליש ושביע ימצאו בג' פעמים ז' שהם כ"א | ||
|- | |- | ||
| | | | ||
| + | :Its third is 7 and its seventh is 3. Together they are 10. So, he has 10 parts of 21. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}+\frac{1}{7}=\frac{\left(\frac{1}{3}\sdot21\right)+\left(\frac{1}{7}\sdot21\right)}{21}=\frac{7+3}{21}=\frac{10}{21}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}+\frac{1}{7}=\frac{\left(\frac{1}{3}\sdot21\right)+\left(\frac{1}{7}\sdot21\right)}{21}=\frac{7+3}{21}=\frac{10}{21}}}</math> | ||
| − | |style="text-align:right;"|השליש ז' והשביעי ג' ושניהם יחד הם י' א"כ יש לו י' חלקי' מכ"א | + | |style="text-align:right;"|השליש ז' והשביעי ג' ושניהם יחד הם י' א"כ יש לו י'‫<ref>י': MS Ithaca ו'</ref> חלקי' מכ"א |
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓+¼+⅕+⅙|677|pvs7}}<math>\scriptstyle\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}</math> | + | *{{#annot:⅓+¼+⅕+⅙|677|pvs7}}Whoever has a third, a quarter, a fifth, and a sixth of the thing. |
| + | :<math>\scriptstyle\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}</math> | ||
|style="text-align:right;"|וכן מי שיש לו שליש ורביע וחומש ושתות מן הדבר{{#annotend:pvs7}} | |style="text-align:right;"|וכן מי שיש לו שליש ורביע וחומש ושתות מן הדבר{{#annotend:pvs7}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third, a quarter, a fifth and a sixth are found in 60. |
|style="text-align:right;"|אמור שליש ורביע וחומש ושתות אם ימצאו בס‫' | |style="text-align:right;"|אמור שליש ורביע וחומש ושתות אם ימצאו בס‫' | ||
|- | |- | ||
| | | | ||
| + | :Its third is 20, its quarter is 15, its fifth is 12 and its sixth is 10. If you sum them, they are 57. So, he has 57 parts of 60 of that thing. | ||
|style="text-align:right;"|השליש הוא כ' הרבי' ט"ו והחומש י"ב והשתות י' ואם תקבצם יהיו נ"ז הרי שיש לו נ"ז חלקים מס' מן הדבר ההוא | |style="text-align:right;"|השליש הוא כ' הרבי' ט"ו והחומש י"ב והשתות י' ואם תקבצם יהיו נ"ז הרי שיש לו נ"ז חלקים מס' מן הדבר ההוא | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}=\frac{\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)}{60}=\frac{20+15+12+10}{60}=\frac{57}{60}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}=\frac{\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)}{60}=\frac{20+15+12+10}{60}=\frac{57}{60}}}</math> | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| Line 2,469: | Line 3,173: | ||
| | | | ||
|- | |- | ||
| − | |<math>\scriptstyle\frac{1}{a}-\frac{1}{b}=\frac{\left[\frac{1}{a}\sdot\left(a\sdot b\right)\right]-\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}</math> | + | |<math>\scriptstyle{\color{OliveGreen}{\frac{1}{a}-\frac{1}{b}=\frac{\left[\frac{1}{a}\sdot\left(a\sdot b\right)\right]-\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}}}</math> |
| | | | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓-¼|678|Gem8}}<math>\scriptstyle\frac{1}{3}-\frac{1}{4}</math> | + | *{{#annot:⅓-¼|678|Gem8}}If a man says: by how much is the third greater than the quarter? |
| + | :<math>\scriptstyle\frac{1}{3}-\frac{1}{4}</math> | ||
|style="text-align:right;"|אמנם אם יאמר אדם כמה הוא יותר השליש מן הרביע{{#annotend:Gem8}} | |style="text-align:right;"|אמנם אם יאמר אדם כמה הוא יותר השליש מן הרביע{{#annotend:Gem8}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Do this way, say: a third and a quarter are found in 3 times 4, which is 12. |
:<math>\scriptstyle{\color{blue}{3\sdot4=12}}</math> | :<math>\scriptstyle{\color{blue}{3\sdot4=12}}</math> | ||
|style="text-align:right;"|עשה על זה הדרך אמור שליש ורביע ימצאו בג' פעמי' ד' שהם י"ב | |style="text-align:right;"|עשה על זה הדרך אמור שליש ורביע ימצאו בג' פעמי' ד' שהם י"ב | ||
|- | |- | ||
| | | | ||
| + | :Its third is 4 and its quarter is 3. By how much is 4, which is the third, greater than 3, which is the quarter? By 1. So, the third is greater than the quarter by 1 part of 12. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}-\frac{1}{4}=\frac{\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)}{12}=\frac{4-3}{12}=\frac{1}{12}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}-\frac{1}{4}=\frac{\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)}{12}=\frac{4-3}{12}=\frac{1}{12}}}</math> | ||
|style="text-align:right;"|השליש הוא ד' והרביעי הוא ג' כמה יותר ד' שהוא השליש מג' שהוא הרביעי א' א"כ השליש הוא יותר מן הרביע א' חלק מי"ב | |style="text-align:right;"|השליש הוא ד' והרביעי הוא ג' כמה יותר ד' שהוא השליש מג' שהוא הרביעי א' א"כ השליש הוא יותר מן הרביע א' חלק מי"ב | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:¼-⅕|678|wkXD}}<math>\scriptstyle\frac{1}{4}-\frac{1}{5}</math> | + | *{{#annot:¼-⅕|678|wkXD}} If a man says: by how much is the quarter greater than the fifth? |
| + | :<math>\scriptstyle\frac{1}{4}-\frac{1}{5}</math> | ||
|style="text-align:right;"|וכן אם יאמר אדם כמה הוא יותר הרביע מן החומש{{#annotend:wkXD}} | |style="text-align:right;"|וכן אם יאמר אדם כמה הוא יותר הרביע מן החומש{{#annotend:wkXD}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a quarter and a fifth are found in 4 times 5, which is 20. |
:<math>\scriptstyle{\color{blue}{4\sdot5=20}}</math> | :<math>\scriptstyle{\color{blue}{4\sdot5=20}}</math> | ||
|style="text-align:right;"|אמור רביע וחומש ימצאו בד' פעמי' ה' שהוא כ‫' | |style="text-align:right;"|אמור רביע וחומש ימצאו בד' פעמי' ה' שהוא כ‫' | ||
|- | |- | ||
| | | | ||
| + | :Its quarter is 5 and its fifth is 4. By how much is 5 greater than 4? By 1. So, the quarter is greater than the fifth by 1 part of twenty. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{4}-\frac{1}{5}=\frac{\left(\frac{1}{4}\sdot20\right)-\left(\frac{1}{5}\sdot20\right)}{20}=\frac{5-4}{20}=\frac{1}{20}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{4}-\frac{1}{5}=\frac{\left(\frac{1}{4}\sdot20\right)-\left(\frac{1}{5}\sdot20\right)}{20}=\frac{5-4}{20}=\frac{1}{20}}}</math> | ||
|style="text-align:right;"|הרביעי הוא ה' והחומש הוא ד' כמה הוא יותר ה' מד' א' אם כן הרביע הוא יותר מן החומש א' חלק מעשרים | |style="text-align:right;"|הרביעי הוא ה' והחומש הוא ד' כמה הוא יותר ה' מד' א' אם כן הרביע הוא יותר מן החומש א' חלק מעשרים | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓-⅐|678|ebvM}}<math>\scriptstyle\frac{1}{3}-\frac{1}{7}</math> | + | *{{#annot:⅓-⅐|678|ebvM}} If it is said: by how much is the third greater than the seventh? |
| + | :<math>\scriptstyle\frac{1}{3}-\frac{1}{7}</math> | ||
|style="text-align:right;"|וכן אם יאמר כמה הוא יותר השליש מן השביע{{#annotend:ebvM}} | |style="text-align:right;"|וכן אם יאמר כמה הוא יותר השליש מן השביע{{#annotend:ebvM}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third and a seventh are found in 3 times 7, which is 21. |
:<math>\scriptstyle{\color{blue}{3\sdot7=21}}</math> | :<math>\scriptstyle{\color{blue}{3\sdot7=21}}</math> | ||
|style="text-align:right;"|אמור שליש ושביע ימצאו בג' פעמים ז' שהם כ"א | |style="text-align:right;"|אמור שליש ושביע ימצאו בג' פעמים ז' שהם כ"א | ||
|- | |- | ||
| | | | ||
| + | :Its third is 7 and its seventh is 3. By how much is 7 greater than 3? By 4. So, the third is greater than the seventh by 4 parts of 21. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}-\frac{1}{7}=\frac{\left(\frac{1}{3}\sdot21\right)-\left(\frac{1}{7}\sdot21\right)}{21}=\frac{7-3}{21}=\frac{4}{21}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}-\frac{1}{7}=\frac{\left(\frac{1}{3}\sdot21\right)-\left(\frac{1}{7}\sdot21\right)}{21}=\frac{7-3}{21}=\frac{4}{21}}}</math> | ||
|style="text-align:right;"|השליש הוא ז' השביע הוא ג' כמה הוא יותר ז' על ג' ד' וא"כ השליש יותר מן השביע ד' חלקי' מכ"א | |style="text-align:right;"|השליש הוא ז' השביע הוא ג' כמה הוא יותר ז' על ג' ד' וא"כ השליש יותר מן השביע ד' חלקי' מכ"א | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:(⅓+¼)-(⅕+⅙)|678|e3Ts}}<math>\scriptstyle\left(\frac{1}{3}+\frac{1}{4}\right)-\left(\frac{1}{5}+\frac{1}{6}\right)</math> | + | *{{#annot:(⅓+¼)-(⅕+⅙)|678|e3Ts}} If it is said: by how much are the third and the quarter greater than the fifth and the eighth? |
| + | :<math>\scriptstyle\left(\frac{1}{3}+\frac{1}{4}\right)-\left(\frac{1}{5}+\frac{1}{6}\right)</math> | ||
|style="text-align:right;"|ואם יאמר כמה הם יותר השליש והרביע מן החומש ושתות{{#annotend:e3Ts}} | |style="text-align:right;"|ואם יאמר כמה הם יותר השליש והרביע מן החומש ושתות{{#annotend:e3Ts}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third, a quarter, a fifth and a sixth are found in 60. |
|style="text-align:right;"|אמור שליש ורביע וחומש ושתות ימצאו בס‫' | |style="text-align:right;"|אמור שליש ורביע וחומש ושתות ימצאו בס‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|השליש הוא כ' הרביע ט"ו אם תקבצם יהיו ל"ה והחומש מס' הוא י"ב השתות י' אם תקבצם יהיו כ"ב כמה הם יותר ל"ה שהם השליש והרביע מכ"ב שהם החומש והשתות י"ג אם כן השליש והרביע הם יותר מן החומש והשתות י"ג חלקים מס‫' | + | :Its third is 20 and its quarter is 15. If you sum them, they are 35. The fifth of 60 is 12 and its sixth is 10. If you sum them, they are 22. By how much is 35, which is the third and the quarter, greater than 22, which is the fifth and the sixth? By 13. So, the third and the quarter are greater than the fifth and the sixth by 13 parts of 60. |
| + | |style="text-align:right;"|השליש הוא כ' הרביע ט"ו אם תקבצם יהיו ל"ה והחומש מס' הוא ל"ב י"ב השתות י' אם תקבצם יהיו כ"ב כמה הם יותר ל"ה שהם השליש והרביע מכ"ב שהם החומש והשתות י"ג אם כן השליש והרביע הם יותר מן החומש והשתות י"ג חלקים מס‫' | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 2,533: | Line 3,245: | ||
| | | | ||
|- | |- | ||
| − | |<math>\scriptstyle\frac{1}{a}\sdot\frac{1}{b}=\frac{\frac{1}{a}\sdot\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}</math> | + | |<math>\scriptstyle{\color{OliveGreen}{\frac{1}{a}\sdot\frac{1}{b}=\frac{\frac{1}{a}\sdot\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}}}</math> |
| | | | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓·¼|668|KdCj}}<math>\scriptstyle\frac{1}{3}\sdot\frac{1}{4}</math> | + | *{{#annot:⅓·¼|668|KdCj}}If it is said: whoever has a third of a quarter of the thing, how much does he have of [that thing]? |
| + | :<math>\scriptstyle\frac{1}{3}\sdot\frac{1}{4}</math> | ||
|style="text-align:right;"|אמנם אם יאמר מי שיש לו השליש מן הרביע מן הדבר כמה חלק יש לו ממנו{{#annotend:KdCj}} | |style="text-align:right;"|אמנם אם יאמר מי שיש לו השליש מן הרביע מן הדבר כמה חלק יש לו ממנו{{#annotend:KdCj}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third and a quarter are found in 12. |
|style="text-align:right;"|אמור שליש ורביע ימצא בי"ב | |style="text-align:right;"|אמור שליש ורביע ימצא בי"ב | ||
|- | |- | ||
| | | | ||
| + | :Whoever has a quarter of 12, has 3 parts of 12. Whoever has a third of these three that are a quarter, has 1 part of 12. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}\sdot\frac{1}{4}=\frac{\frac{1}{3}\sdot\left(\frac{1}{4}\sdot12\right)}{12}=\frac{\frac{1}{3}\sdot3}{12}=\frac{1}{12}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}\sdot\frac{1}{4}=\frac{\frac{1}{3}\sdot\left(\frac{1}{4}\sdot12\right)}{12}=\frac{\frac{1}{3}\sdot3}{12}=\frac{1}{12}}}</math> | ||
|style="text-align:right;"|ומי שיש לו הרביע מי"ב יש לו ג' חלקים מי"ב ומי שיש לו השליש מאלו הג' שהם הרביע יהיה לו א' חלק מי"ב | |style="text-align:right;"|ומי שיש לו הרביע מי"ב יש לו ג' חלקים מי"ב ומי שיש לו השליש מאלו הג' שהם הרביע יהיה לו א' חלק מי"ב | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓·⅕|668|dqBo}}<math>\scriptstyle\frac{1}{3}\sdot\frac{1}{5}</math> | + | *{{#annot:⅓·⅕|668|dqBo}}If it is said: whoever has a third of a fifth [of the thing], how much does he have of [that thing]? |
| + | :<math>\scriptstyle\frac{1}{3}\sdot\frac{1}{5}</math> | ||
|style="text-align:right;"|ואם יאמר מי שיש לו השליש מן החומש כמה חלק יש לו{{#annotend:dqBo}} | |style="text-align:right;"|ואם יאמר מי שיש לו השליש מן החומש כמה חלק יש לו{{#annotend:dqBo}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third and a fifth are found in 3 times 5, which is 15. |
:<math>\scriptstyle{\color{blue}{3\sdot5=15}}</math> | :<math>\scriptstyle{\color{blue}{3\sdot5=15}}</math> | ||
|style="text-align:right;"|אמור שליש וחומש ימצא בג' פעמים ה' שהם ט"ו | |style="text-align:right;"|אמור שליש וחומש ימצא בג' פעמים ה' שהם ט"ו | ||
|- | |- | ||
| | | | ||
| + | :The fifth of 15 is 3. Whoever has a third of the 3, which is the fifth, has 1 part of 15. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}\sdot\frac{1}{5}=\frac{\frac{1}{3}\sdot\left(\frac{1}{5}\sdot15\right)}{15}=\frac{\frac{1}{3}\sdot3}{15}=\frac{1}{15}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}\sdot\frac{1}{5}=\frac{\frac{1}{3}\sdot\left(\frac{1}{5}\sdot15\right)}{15}=\frac{\frac{1}{3}\sdot3}{15}=\frac{1}{15}}}</math> | ||
|style="text-align:right;"|החומש מט"ו הם ג' ומי שיש לו השליש מג' שהוא החומש יש לו א' חלק מט"ו | |style="text-align:right;"|החומש מט"ו הם ג' ומי שיש לו השליש מג' שהוא החומש יש לו א' חלק מט"ו | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅕·⅑|668|3ST2}}<math>\scriptstyle\frac{1}{5}\sdot\frac{1}{9}</math> | + | *{{#annot:⅕·⅑|668|3ST2}}Whoever has a fifth of a ninth. |
| − | |style="text-align:right;"|וכן מי שיש לו החומש מן התשיעית{{#annotend:3ST2}} | + | :<math>\scriptstyle\frac{1}{5}\sdot\frac{1}{9}</math> |
| + | |style="text-align:right;"|‫<ref>37r</ref>וכן מי שיש לו החומש מן התשיעית{{#annotend:3ST2}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a fifth and a ninth are found in 5 times 9, which is 45. |
:<math>\scriptstyle{\color{blue}{5\sdot9=45}}</math> | :<math>\scriptstyle{\color{blue}{5\sdot9=45}}</math> | ||
|style="text-align:right;"|אמור חומש ותשיע ימצא בה' פעמים ט' שהם מ"ה | |style="text-align:right;"|אמור חומש ותשיע ימצא בה' פעמים ט' שהם מ"ה | ||
|- | |- | ||
| | | | ||
| + | :The ninth of 45 is 5 and the fifth of 5 is 1. So, whoever has a fifth of a ninth, has 1 part of 45 of that thing. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot\frac{1}{9}=\frac{\frac{1}{5}\sdot\left(\frac{1}{9}\sdot45\right)}{45}=\frac{\frac{1}{5}\sdot5}{45}=\frac{1}{45}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot\frac{1}{9}=\frac{\frac{1}{5}\sdot\left(\frac{1}{9}\sdot45\right)}{45}=\frac{\frac{1}{5}\sdot5}{45}=\frac{1}{45}}}</math> | ||
|style="text-align:right;"|והתשיעי ממ"ה הוא ה' והחומש מה' הוא א' א"כ מי שיש לו החומש מן התשיעית יש לו א' חלק ממ"ה מן הדבר ההוא | |style="text-align:right;"|והתשיעי ממ"ה הוא ה' והחומש מה' הוא א' א"כ מי שיש לו החומש מן התשיעית יש לו א' חלק ממ"ה מן הדבר ההוא | ||
| Line 2,581: | Line 3,299: | ||
|- | |- | ||
| | | | ||
| − | *How many tenths there are in three eighths | + | *If a man says: How many tenths there are in three eighths? |
|style="text-align:right;"|אם יאמר אדם ג' שמיניות כמה עשיריות הם | |style="text-align:right;"|אם יאמר אדם ג' שמיניות כמה עשיריות הם | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :Do this way: |
| + | |style="text-align:right;"|עשה על זה הדרך | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Common denominator:'''</span> Say: an eighth and a tenth are found in 8 times 10, which is 80. | ||
:<math>\scriptstyle{\color{blue}{8\sdot10=80}}</math> | :<math>\scriptstyle{\color{blue}{8\sdot10=80}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אמור שמינית ועשירי' ימצאו בח' פעמי' י' שהם פ‫' |
|- | |- | ||
| | | | ||
| + | :3-eighths are 30. | ||
:<math>\scriptstyle{\color{blue}{\frac{3}{8}\sdot80=30}}</math> | :<math>\scriptstyle{\color{blue}{\frac{3}{8}\sdot80=30}}</math> | ||
|style="text-align:right;"|וג' שמיניות הם ל‫' | |style="text-align:right;"|וג' שמיניות הם ל‫' | ||
|- | |- | ||
| | | | ||
| + | :Because 10 is one-eighth of 80. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{8}\sdot80=10}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{8}\sdot80=10}}</math> | ||
| − | |style="text-align:right;"|כי י' הוא שמינית פ‫' | + | |style="text-align:right;"|כי י' הוא שמינית פ'‫<ref>וג'...שמינית פ': MS Ithaca om.</ref> |
|- | |- | ||
| | | | ||
| + | :And 8 is one-tenth of 80. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{10}\sdot80=8}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{10}\sdot80=8}}</math> | ||
|style="text-align:right;"|וח' הוא עשירית פ‫' | |style="text-align:right;"|וח' הוא עשירית פ‫' | ||
|- | |- | ||
| | | | ||
| + | :If you wish to know how many tenths are the 3-eighth of 80, divide 30, which is 3-eighths, by 8, which is one-tenth of 80; it is 3-tenths and 6 parts of 80. | ||
:<math>\scriptstyle{\color{blue}{\frac{3}{8}=\frac{\frac{3}{8}\sdot80}{80}=\frac{30}{80}=\frac{\frac{30}{8}}{10}=\frac{3}{10}+\frac{6}{80}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{3}{8}=\frac{\frac{3}{8}\sdot80}{80}=\frac{30}{80}=\frac{\frac{30}{8}}{10}=\frac{3}{10}+\frac{6}{80}}}</math> | ||
| − | |style="text-align:right;"|ואם תרצה לידע כמה עשיריות הם הג' שמיניות מפ' חלק הל' שהוא הג' שמיניות חלקם בח' שהוא עשירית פ' הם ג' עשריות וו' ואותם הו' הם ו' חלקים מפ‫' | + | |style="text-align:right;"|ואם תרצה לידע כמה עשיריות הם הג' שמיניות מפ' חלק הל' שהוא הג' שמיניות חלקם‫<ref>שהוא הג' שמיניות חלקם: MS Ithaca om.</ref> בח' שהוא עשירית פ' הם ג' עשריות וו' ואותם הו' הם ו' חלקים מפ'‫<ref>שהוא עשירית פ'...חלקים מפ': MS Ithaca יהיה ג‫'</ref> |
|- | |- | ||
| | | | ||
| Line 2,612: | Line 3,338: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅜+⁷/₁₀|677|tIym}}<math>\scriptstyle\frac{3}{8}+\frac{7}{10}</math> | + | *{{#annot:⅜+⁷/₁₀|677|tIym}}If one says: add 3-eighths to 7-tenths, how much are they? |
| − | |style="text-align:right;"|ואם יאמר הוסף ג' שמיניות על ז' עשיריות כמה יהיו{{#annotend:tIym}} | + | :<math>\scriptstyle\frac{3}{8}+\frac{7}{10}</math> |
| + | |style="text-align:right;"|ואם יאמר הוסף ג' שמיניות על ז' עשיריות כמה יהיו{{#annotend:tIym}}‫<ref>ואם יאמר... כמה יהיו: MS Ithaca om.</ref> | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: an eighth and a tenth are found in 8 times 10, which is 80. |
:<math>\scriptstyle{\color{blue}{8\sdot10=80}}</math> | :<math>\scriptstyle{\color{blue}{8\sdot10=80}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אמור שמינית ועשירי' ימצאו בח' פעמים י' שהם פ‫' |
|- | |- | ||
| | | | ||
| + | :Add [its] 3-eighths, which is 30, to its 7-tenths, which is 56; the total is 86 parts of 80, which is 1 integer and 6 parts of 80. | ||
:<math>\scriptstyle{\color{blue}{\frac{3}{8}+\frac{7}{10}=\frac{\left(\frac{3}{8}\sdot80\right)+\left(\frac{7}{10}\sdot80\right)}{80}=\frac{30+56}{80}=\frac{86}{80}=1+\frac{6}{80}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{3}{8}+\frac{7}{10}=\frac{\left(\frac{3}{8}\sdot80\right)+\left(\frac{7}{10}\sdot80\right)}{80}=\frac{30+56}{80}=\frac{86}{80}=1+\frac{6}{80}}}</math> | ||
| − | |style="text-align:right;"|ותוסיף ג' שמיניות והם ל' על ז' | + | |style="text-align:right;"|ותוסיף ג' שמיניות והם ל' על ז' עשרותיו והם נ"ו יהיו הכל פ"ו חלקים מפ' שהם א' שלם וו' חלקים מפ‫' |
|- | |- | ||
| | | | ||
| − | *{{#annot:⅔-³/₇|678|mJ1K}}<math>\scriptstyle\frac{2}{3}-\frac{3}{7}</math> | + | *{{#annot:⅔-³/₇|678|mJ1K}}If one says: subtract 3-sevenths from 2-thirds. |
| + | :<math>\scriptstyle\frac{2}{3}-\frac{3}{7}</math> | ||
|style="text-align:right;"|ואם יאמר השלך ג' שביעיות מב' שלישיות{{#annotend:mJ1K}} | |style="text-align:right;"|ואם יאמר השלך ג' שביעיות מב' שלישיות{{#annotend:mJ1K}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third and a seventh are found in 3 times 7, which is 21. |
:<math>\scriptstyle{\color{blue}{3\sdot7=21}}</math> | :<math>\scriptstyle{\color{blue}{3\sdot7=21}}</math> | ||
|style="text-align:right;"|אמו' שלישית ושביעית ימצאו בג' פעמ' ז' שהם כ"א | |style="text-align:right;"|אמו' שלישית ושביעית ימצאו בג' פעמ' ז' שהם כ"א | ||
|- | |- | ||
| | | | ||
| + | :Take its 2-thirds, which is 14, and subtract from it its 3-sevenths, which is 9; 5 parts of 21 remain. | ||
:<math>\scriptstyle{\color{blue}{\frac{2}{3}-\frac{3}{7}=\frac{\left(\frac{2}{3}\sdot21\right)-\left(\frac{3}{7}\sdot21\right)}{21}=\frac{14-9}{21}=\frac{5}{21}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{2}{3}-\frac{3}{7}=\frac{\left(\frac{2}{3}\sdot21\right)-\left(\frac{3}{7}\sdot21\right)}{21}=\frac{14-9}{21}=\frac{5}{21}}}</math> | ||
| − | |style="text-align:right;"|וקח ב' שלישיותיו והם י"ד ותשלך מהם ג' שביעיותיו והם ט' וישארו ה' חלקים מכ"א | + | |style="text-align:right;"|וקח ב' שלישיותיו והם י"ד ותשלך מהם ג' שביעיותיו והם ט' וישארו ה' חלקים מכ"א‫<ref>ואם יאמר השלך... חלקים מכ"א: MS Ithaca om.</ref> |
|- | |- | ||
| | | | ||
| − | *{{#annot:⅖-⅜|678|fRT6}}<math>\scriptstyle\frac{2}{5}-\frac{3}{8}</math> | + | *{{#annot:⅖-⅜|678|fRT6}}If one says: how much greater are 3-eighths than 2-fifths? |
| + | :<math>\scriptstyle\frac{2}{5}-\frac{3}{8}</math> | ||
|style="text-align:right;"|ואם יאמר כמה הם יותר ג' שמניות מב' חמשיות{{#annotend:fRT6}} | |style="text-align:right;"|ואם יאמר כמה הם יותר ג' שמניות מב' חמשיות{{#annotend:fRT6}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a fifth and an eighth are found in 5 times 8, which is 40. |
:<math>\scriptstyle{\color{blue}{5\sdot8=40}}</math> | :<math>\scriptstyle{\color{blue}{5\sdot8=40}}</math> | ||
|style="text-align:right;"|אמו' חמישיות ושמינית ימצא בה' פעמ' ח' שהם מ‫' | |style="text-align:right;"|אמו' חמישיות ושמינית ימצא בה' פעמ' ח' שהם מ‫' | ||
|- | |- | ||
| | | | ||
| + | :2-fifths are 16; 3-eighths are 15. We find that 2-fifths are greater that 3-eighths by one part of 40. | ||
:<math>\scriptstyle{\color{blue}{\frac{2}{5}-\frac{3}{8}=\frac{\left(\frac{2}{5}\sdot40\right)-\left(\frac{3}{8}\sdot40\right)}{40}=\frac{16-15}{40}=\frac{1}{40}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{2}{5}-\frac{3}{8}=\frac{\left(\frac{2}{5}\sdot40\right)-\left(\frac{3}{8}\sdot40\right)}{40}=\frac{16-15}{40}=\frac{1}{40}}}</math> | ||
| − | |style="text-align:right;"|ב' חמישיות הם י"ו וג' שמיניות הם ט"ו נמצא שהב' חמישיות הם יותר מג' שמיניות חלק אחת ממ‫' | + | |style="text-align:right;"|ב' חמישיות הם י"ו וג' שמיניות הם ט"ו נמצא שהב' חמישיות הם יותר מג' שמיניות חלק אחת ממ'‫<ref>ואם יאמר כמה הם יותר...חלק אחת ממ': MS Ithaca om.</ref> |
|- | |- | ||
| | | | ||
| − | *{{#annot:⅜·⅖|668|8Loc}}<math>\scriptstyle\frac{3}{8}\sdot\frac{2}{5}</math> | + | *{{#annot:⅜·⅖|668|8Loc}}If one says: how much are 3-eighths of 2-fifths? |
| + | :<math>\scriptstyle\frac{3}{8}\sdot\frac{2}{5}</math> | ||
|style="text-align:right;"|ואם יאמ' כמה הם ג' שמיניות מב' חמישיות{{#annotend:8Loc}} | |style="text-align:right;"|ואם יאמ' כמה הם ג' שמיניות מב' חמישיות{{#annotend:8Loc}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: an eighth and a fifth are found in 5 times 8, which is 40. |
:<math>\scriptstyle{\color{blue}{5\sdot8=40}}</math> | :<math>\scriptstyle{\color{blue}{5\sdot8=40}}</math> | ||
|style="text-align:right;"|אמור שמינית וחמישית ימצאו בה' פע' ח' שהם מ‫' | |style="text-align:right;"|אמור שמינית וחמישית ימצאו בה' פע' ח' שהם מ‫' | ||
|- | |- | ||
| | | | ||
| + | :2-fifths of 40 are 16; 3-eighths of 16 are 6; so they are 6 parts of 40. | ||
:<math>\scriptstyle{\color{blue}{\frac{3}{8}\sdot\frac{2}{5}=\frac{\frac{3}{8}\sdot\left(\frac{2}{5}\sdot40\right)}{40}=\frac{\frac{3}{8}\sdot16}{40}=\frac{6}{40}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{3}{8}\sdot\frac{2}{5}=\frac{\frac{3}{8}\sdot\left(\frac{2}{5}\sdot40\right)}{40}=\frac{\frac{3}{8}\sdot16}{40}=\frac{6}{40}}}</math> | ||
|style="text-align:right;"|וב' חמישיות מ' הם י"ו וג' שמיניות י"ו הם ו' א"כ הם ו' חלקי' ממ‫' | |style="text-align:right;"|וב' חמישיות מ' הם י"ו וג' שמיניות י"ו הם ו' א"כ הם ו' חלקי' ממ‫' | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅜÷⅖|552|gX0D}}<math>\scriptstyle\frac{3}{8}\div\frac{2}{5}</math> | + | *{{#annot:⅜÷⅖|552|gX0D}}If one says: divide 3-eighths by 2-fifths |
| + | :<math>\scriptstyle\frac{3}{8}\div\frac{2}{5}</math> | ||
|style="text-align:right;"|ואם יאמ' חלק ג' שמיניות על ב' חמשיות{{#annotend:gX0D}} | |style="text-align:right;"|ואם יאמ' חלק ג' שמיניות על ב' חמשיות{{#annotend:gX0D}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: an eighth and a fifth are found in 5 times 8, which is 40. |
:<math>\scriptstyle{\color{blue}{5\sdot8=40}}</math> | :<math>\scriptstyle{\color{blue}{5\sdot8=40}}</math> | ||
|style="text-align:right;"|אמו' שמינית וחומש ימצאו בה' פעמ' ח' שהם מ‫' | |style="text-align:right;"|אמו' שמינית וחומש ימצאו בה' פעמ' ח' שהם מ‫' | ||
|- | |- | ||
| | | | ||
| + | :3-eighths of 40 are 15; its 2-fifths are 16; divide 15 by 16. | ||
:<math>\scriptstyle{\color{blue}{\frac{3}{8}\div\frac{2}{5}=\frac{\frac{3}{8}\sdot40}{\frac{2}{5}\sdot40}=\frac{15}{16}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{3}{8}\div\frac{2}{5}=\frac{\frac{3}{8}\sdot40}{\frac{2}{5}\sdot40}=\frac{15}{16}}}</math> | ||
|style="text-align:right;"|וג' שמניות מ' הם ט"ו וב' חמשיותיו הם י"ו חלק ט"ו על י"ו | |style="text-align:right;"|וג' שמניות מ' הם ט"ו וב' חמשיותיו הם י"ו חלק ט"ו על י"ו | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅔×⅖|17|BRVP}}<math>\scriptstyle\frac{2}{3}\times\frac{2}{5}</math> | + | *{{#annot:⅔×⅖|17|BRVP}}If one says: multiply 2-thirds by 2-fifths. |
| + | :<math>\scriptstyle\frac{2}{3}\times\frac{2}{5}</math> | ||
|style="text-align:right;"|ואם יאמר חשוב ב' שלישים עם ב' חמישיות{{#annotend:BRVP}} | |style="text-align:right;"|ואם יאמר חשוב ב' שלישים עם ב' חמישיות{{#annotend:BRVP}} | ||
|- | |- | ||
| | | | ||
| + | :Multiply three by 5, which are the names of the parts; they are 15. | ||
| + | |style="text-align:right;"|תחשוב שלשה על ה' שהם שמות החלקים יהיו ט"ו | ||
| + | |- | ||
| + | | | ||
| + | :Say: 2 times 2, because they are the [numbers] of the parts; they are 4. | ||
| + | |style="text-align:right;"|ואמור ב' פעמ' ב' כי ב' הם שמות החלקים ויהיו ד‫' | ||
| + | |- | ||
| + | | | ||
| + | :So, 2-thirds by 2-fifths are 4 parts of 15. | ||
:<math>\scriptstyle{\color{blue}{\frac{2}{3}\times\frac{2}{5}=\frac{2\sdot2}{3\sdot5}=\frac{4}{15}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{2}{3}\times\frac{2}{5}=\frac{2\sdot2}{3\sdot5}=\frac{4}{15}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הרי שב' שלישיות על ב' חמישיות הם ד' חלקים מט"ו מן האחד |
|- | |- | ||
| | | | ||
| − | *{{#annot:²/₁₁ײ/₁₃|17|md7k}}<math>\scriptstyle\frac{2}{11}\times\frac{2}{13}</math> | + | *{{#annot:²/₁₁ײ/₁₃|17|md7k}}If one says: multiply 2 parts of 11 by 2 parts of 13. |
| + | :<math>\scriptstyle\frac{2}{11}\times\frac{2}{13}</math> | ||
|style="text-align:right;"|ואם יאמר חשוב ב' חלקים מי"א באחד על ב' חלקים מי"ג מן האחד{{#annotend:md7k}} | |style="text-align:right;"|ואם יאמר חשוב ב' חלקים מי"א באחד על ב' חלקים מי"ג מן האחד{{#annotend:md7k}} | ||
|- | |- | ||
| | | | ||
| + | :Multiply the names of the parts, which are 11 by 13; the result is 143. | ||
| + | |style="text-align:right;"|תחשוב שמות החלקים והם י"א על י"ג שעולים קמ"ג | ||
| + | |- | ||
| + | | | ||
| + | :Multiply the numbers of the parts, which are 2; say: 2 times 2 is 4. | ||
| + | |style="text-align:right;"|ותרבה מספר החלקים שהם ב' ואמור ב' פעמים ב' ד‫' | ||
| + | |- | ||
| + | | | ||
| + | :So, the result is 4 parts of 143. | ||
:<math>\scriptstyle{\color{blue}{\frac{2}{11}\times\frac{2}{13}=\frac{2\sdot2}{11\sdot13}=\frac{4}{143}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{2}{11}\times\frac{2}{13}=\frac{2\sdot2}{11\sdot13}=\frac{4}{143}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הרי שעולים ד' חלקים מקמ"ג בא‫' |
|- | |- | ||
| | | | ||
| − | *{{#annot:⅖×⅒×⅔|17|q3mD}}<math>\scriptstyle\frac{2}{5}\times\frac{1}{10}\times\frac{2}{3}</math> | + | *{{#annot:⅖×⅒×⅔|17|q3mD}}If one says: how much are 2 parts of 5 by one-tenth by 2-thirds? |
| + | :<math>\scriptstyle\frac{2}{5}\times\frac{1}{10}\times\frac{2}{3}</math> | ||
|style="text-align:right;"|ואם יאמ' ב' חלקים מה' בעשירית האחד בב' שלישי האחר כמה הם{{#annotend:q3mD}} | |style="text-align:right;"|ואם יאמ' ב' חלקים מה' בעשירית האחד בב' שלישי האחר כמה הם{{#annotend:q3mD}} | ||
|- | |- | ||
| | | | ||
| + | :Know that the name of one [fraction] is fifty, which is five by ten. Multiply this 50 by 3, which is the name of the other fraction; the total is 150. | ||
| + | |style="text-align:right;"|דע כי שם האחד הם חמשים בעניין חמשה בעשרה ותמנה אלו הנ' בג' שהוא שם החלק השני ויהיה הכל ק"נ | ||
| + | |- | ||
| + | | | ||
| + | :Say: 2 times 2 is 4, because 2 is the number of the fractions. | ||
| + | |style="text-align:right;"|ואמור ב' פעמ' ב' ד' כי ב' הוא מספר החלקי‫' | ||
| + | |- | ||
| + | | | ||
| + | :So, this product is 4 parts of 150. | ||
:<math>\scriptstyle{\color{blue}{\frac{2}{5}\times\frac{1}{10}\times\frac{2}{3}=\frac{2\sdot2}{\left(5\sdot10\right)\sdot3}=\frac{4}{50\sdot3}=\frac{4}{150}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{2}{5}\times\frac{1}{10}\times\frac{2}{3}=\frac{2\sdot2}{\left(5\sdot10\right)\sdot3}=\frac{4}{50\sdot3}=\frac{4}{150}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הרי שהחשבו' הזה הוא ד' חלקי' מק"נ מהאחר |
|- | |- | ||
| | | | ||
| − | *{{#annot:⅖×⅒ײ/₈×⅓|17|aUsg}}<math>\scriptstyle\frac{2}{5}\times\frac{1}{10}\times\frac{2}{8}\times\frac{1}{3}</math> | + | *{{#annot:⅖×⅒ײ/₈×⅓|17|aUsg}}If one says: 2 parts of five by one-tenth by two parts of eight by one-third. |
| + | :<math>\scriptstyle\frac{2}{5}\times\frac{1}{10}\times\frac{2}{8}\times\frac{1}{3}</math> | ||
|style="text-align:right;"|ואם יאמ' ב' חלקים מחמשה בעשירית האחד בשני חלקים משמנה בשלישית האחד{{#annotend:aUsg}} | |style="text-align:right;"|ואם יאמ' ב' חלקים מחמשה בעשירית האחד בשני חלקים משמנה בשלישית האחד{{#annotend:aUsg}} | ||
|- | |- | ||
| | | | ||
| + | :You need to know the names of the fractions: | ||
| + | |style="text-align:right;"|אתה צריך לדעת את שמות החלקים | ||
| + | |- | ||
| + | | | ||
| + | :Multiply 5 by 10; it is 50 and this is the name of one fraction. | ||
| + | |style="text-align:right;"|ותחשוב ה' בי' והם נ' והוא שם החלק האחד | ||
| + | |- | ||
| + | | | ||
| + | :Multiply 8 by 3; it is 24 and this is the name of the other fraction. | ||
| + | |style="text-align:right;"|ותחשוב עוד ח' בג' ויהיו כ"ד והוא שם החלק השני | ||
| + | |- | ||
| + | | | ||
| + | :Then, multiply 50 by 24; it is one thousand and two hundred. | ||
| + | |style="text-align:right;"|וחשוב אחר כן נ' על כ"ד ויהיה אלף ומאתים | ||
| + | |- | ||
| + | | | ||
| + | :Say: 2 times 2; i.e. 4. | ||
| + | |style="text-align:right;"|ואמו' אחר כן ב' פעמ' ב' ר"ל ד‫' | ||
| + | |- | ||
| + | | | ||
| + | :So, they are 4 parts of one thousand and two hundred. | ||
:<math>\scriptstyle{\color{blue}{\frac{2}{5}\times\frac{1}{10}\times\frac{2}{8}\times\frac{1}{3}=\frac{2\sdot2}{\left(5\sdot10\right)\sdot\left(8\sdot3\right)}=\frac{4}{50\sdot24}=\frac{4}{1200}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{2}{5}\times\frac{1}{10}\times\frac{2}{8}\times\frac{1}{3}=\frac{2\sdot2}{\left(5\sdot10\right)\sdot\left(8\sdot3\right)}=\frac{4}{50\sdot24}=\frac{4}{1200}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הרי שהם ד' חלקים מאלף ומאתים מן האחר‫<ref>ואם יאמר חלק ג'... ומאתים מן האחר: MS Ithaca om.</ref> |
|- | |- | ||
| | | | ||
| Line 2,715: | Line 3,503: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓×1|17|dp1H}}<math>\scriptstyle\frac{1}{3}\times1=\frac{1}{3}</math> | + | *{{#annot:⅓×1|17|dp1H}}When we multiply the third by one, it is a third. |
| − | |style="text-align:right;"|כשנרבה השליש באחד הוא שליש{{#annotend:dp1H}} | + | :<math>\scriptstyle\frac{1}{3}\times1=\frac{1}{3}</math> |
| + | |style="text-align:right;"|<big>כשנרבה השליש באחד</big> הוא שליש{{#annotend:dp1H}} | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓×2|17|CmHn}}<math>\scriptstyle\frac{1}{3}\times2=\frac{2}{3}</math> | + | *{{#annot:⅓×2|17|CmHn}}When we multiply the third by two it is 2-thirds. |
| + | :<math>\scriptstyle\frac{1}{3}\times2=\frac{2}{3}</math> | ||
|style="text-align:right;"|וכשנרבה השליש בשנים הוא ב' שלישי האחד{{#annotend:CmHn}} | |style="text-align:right;"|וכשנרבה השליש בשנים הוא ב' שלישי האחד{{#annotend:CmHn}} | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓×⅓|17|p54W}}<math>\scriptstyle\frac{1}{3}\times\frac{1}{3}=\frac{1}{3}\sdot\frac{1}{3}</math> | + | *{{#annot:⅓×⅓|17|p54W}}When we multiply a third by a third, it is a third of a third. |
| + | :<math>\scriptstyle\frac{1}{3}\times\frac{1}{3}=\frac{1}{3}\sdot\frac{1}{3}</math> | ||
|style="text-align:right;"|וכשנרבה שליש בשליש הוא שליש בשליש{{#annotend:p54W}} | |style="text-align:right;"|וכשנרבה שליש בשליש הוא שליש בשליש{{#annotend:p54W}} | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:¼×¼|17|q5Pm}}<math>\scriptstyle\frac{1}{4}\times\frac{1}{4}=\frac{1}{4}\sdot\frac{1}{4}</math> | + | *{{#annot:¼×¼|17|q5Pm}}The quarter by a quarter is a quarter of a quarter. |
| + | :<math>\scriptstyle\frac{1}{4}\times\frac{1}{4}=\frac{1}{4}\sdot\frac{1}{4}</math> | ||
|style="text-align:right;"|והרביע ברביע הוא רביע הרביע{{#annotend:q5Pm}} | |style="text-align:right;"|והרביע ברביע הוא רביע הרביע{{#annotend:q5Pm}} | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅕×⅕|17|GtWm}}<math>\scriptstyle\frac{1}{5}\times\frac{1}{5}=\frac{1}{5}\sdot\frac{1}{5}</math> | + | *{{#annot:⅕×⅕|17|GtWm}}The fifth by a fifth is a fifth of a fifth. |
| − | |style="text-align:right;"|וחומש בחומש הוא חומ' החומש | + | :<math>\scriptstyle\frac{1}{5}\times\frac{1}{5}=\frac{1}{5}\sdot\frac{1}{5}</math> |
| + | |style="text-align:right;"|וחומש בחומש הוא חומ' החומש{{#annotend:GtWm}} | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅔×⅔|17|Nlzy}}<math>\scriptstyle\frac{2}{3}\times\frac{2}{3}</math> | + | :And so on. |
| + | |style="text-align:right;"|וכן כלם | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:⅔×⅔|17|Nlzy}}If we multiply 2-thirds by 2-thirds. | ||
| + | :<math>\scriptstyle\frac{2}{3}\times\frac{2}{3}</math> | ||
|style="text-align:right;"|ואם נרבה ב' שלישי בב' שלישי{{#annotend:Nlzy}} | |style="text-align:right;"|ואם נרבה ב' שלישי בב' שלישי{{#annotend:Nlzy}} | ||
|- | |- | ||
| | | | ||
| + | :Say: 3 times 3 is 9. | ||
| + | |style="text-align:right;"|אמור ג' פעמים [.] ג' ט‫' | ||
| + | |- | ||
| + | | | ||
| + | :Then, say: 2 times 2 is 4. | ||
| + | |style="text-align:right;"|ואחר כך אמור ב' פעמים ב' פעמים הרי ד‫' | ||
| + | |- | ||
| + | | | ||
| + | :So, if we multiply 2-thirds by 2-thirds, they are 4 parts of 9. | ||
:<math>\scriptstyle{\color{blue}{\frac{2}{3}\times\frac{2}{3}=\frac{2\sdot2}{3\sdot3}=\frac{4}{9}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{2}{3}\times\frac{2}{3}=\frac{2\sdot2}{3\sdot3}=\frac{4}{9}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הרי שאם נרבה ב' שלישי על ב' שלישי הם ד' חלקי' מט' באחד |
|- | |- | ||
| | | | ||
| Line 2,749: | Line 3,556: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:⅓÷¼=⅕÷X|567|D0xp}}<math>\scriptstyle\frac{1}{3}:\frac{1}{4}=\frac{1}{5}:X</math> | + | *{{#annot:⅓÷¼=⅕÷X|567|D0xp}}When a man says: if a third is worth a quarter, how much is a fifth worth according to this calculation? |
| + | :<math>\scriptstyle\frac{1}{3}:\frac{1}{4}=\frac{1}{5}:X</math> | ||
|style="text-align:right;"|אם יאמר אדם אם שליש שוה רביע החומש כפי זה החשבון כמה שוה{{#annotend:D0xp}} | |style="text-align:right;"|אם יאמר אדם אם שליש שוה רביע החומש כפי זה החשבון כמה שוה{{#annotend:D0xp}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Common denominator:'''</span> | + | :<span style=color:green>'''Common denominator:'''</span> Say: a third, a quarter and a fifth are found in 60. |
|style="text-align:right;"|אמור שליש ורביע וחומש ימצאו בס‫' | |style="text-align:right;"|אמור שליש ורביע וחומש ימצאו בס‫' | ||
|- | |- | ||
| | | | ||
| + | :The third of 60 is 20. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}\sdot60=20}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}\sdot60=20}}</math> | ||
|style="text-align:right;"|השליש מס' הוא כ‫' | |style="text-align:right;"|השליש מס' הוא כ‫' | ||
|- | |- | ||
| | | | ||
| + | :The quarter is 15. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{4}\sdot60=15}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{4}\sdot60=15}}</math> | ||
|style="text-align:right;"|א"כ הרביע הוא ט"ו | |style="text-align:right;"|א"כ הרביע הוא ט"ו | ||
|- | |- | ||
| | | | ||
| + | :The fifth is 12. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot60=12}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot60=12}}</math> | ||
|style="text-align:right;"|והחומש הוא י"ב | |style="text-align:right;"|והחומש הוא י"ב | ||
|- | |- | ||
| | | | ||
| − | :<span style=color:green>'''Rule of Three:'''</span> | + | :<span style=color:green>'''Rule of Three:'''</span> Say: if 20, which is one-third of 60, is worth 15, which is the quarter, how much is the fifth, which is 12, worth? |
:<math>\scriptstyle{\color{blue}{20:15=12:\left(X\sdot60\right)}}</math> | :<math>\scriptstyle{\color{blue}{20:15=12:\left(X\sdot60\right)}}</math> | ||
|style="text-align:right;"|ואמור אם כ' שהוא שליש מס' שוה ט"ו שהוא הרביע החומש שהוא י"ב כמה שוה | |style="text-align:right;"|ואמור אם כ' שהוא שליש מס' שוה ט"ו שהוא הרביע החומש שהוא י"ב כמה שוה | ||
|- | |- | ||
| | | | ||
| + | :Say: 12 times 15 is 180 parts. | ||
| + | |style="text-align:right;"|אמור י"ב פעמי' ט"ו הם ק"פ חלקים | ||
| + | |- | ||
| + | | | ||
| + | :Divide it by 20; the result is 9 and they are 9 parts of 60. | ||
:<math>\scriptstyle{\color{blue}{X=\frac{\frac{12\sdot15}{20}}{60}=\frac{\frac{180}{20}}{60}=\frac{9}{60}}}</math> | :<math>\scriptstyle{\color{blue}{X=\frac{\frac{12\sdot15}{20}}{60}=\frac{\frac{180}{20}}{60}=\frac{9}{60}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|חלקם בכ' יבאו ט' והם ט' חלקים מס' באחד |
|- | |- | ||
| | | | ||
*{{#annot:3⅓÷4¼=5⅕÷X|567|JsBk}}<math>\scriptstyle\left(3+\frac{1}{3}\right):\left(4+\frac{1}{4}\right)=\left(5+\frac{1}{5}\right):X</math> | *{{#annot:3⅓÷4¼=5⅕÷X|567|JsBk}}<math>\scriptstyle\left(3+\frac{1}{3}\right):\left(4+\frac{1}{4}\right)=\left(5+\frac{1}{5}\right):X</math> | ||
| − | |style="text-align:right;"|אם יאמר אדם אם ג' ושליש שוים ד' ורביע ה' [ו]חומש כמה שוים{{#annotend:JsBk}} | + | |style="text-align:right;"|<big>אם יאמר אדם</big> אם ג' ושליש שוים ד' ורביע ה' [ו]חומש כמה שוים{{#annotend:JsBk}} |
|- | |- | ||
| | | | ||
| Line 2,787: | Line 3,603: | ||
| | | | ||
:<math>\scriptstyle{\color{blue}{5+\frac{1}{5}=\frac{\left(5\sdot5\right)+1}{5}=\frac{25+1}{5}=\frac{26}{5}}}</math> | :<math>\scriptstyle{\color{blue}{5+\frac{1}{5}=\frac{\left(5\sdot5\right)+1}{5}=\frac{25+1}{5}=\frac{26}{5}}}</math> | ||
| − | |style="text-align:right;"|תפוש ה' וחומש ואמור ה' פעמים ה' הם כ"ה וא' חומש הרי כ"ו | + | |style="text-align:right;"|תפוש ה' וחומש ואמור ה' פעמים ה' הם‫<ref>ה' הם: MS Ithaca om.</ref> כ"ה וא' חומש הרי כ"ו |
|- | |- | ||
| | | | ||
| Line 2,800: | Line 3,616: | ||
:converting to thirds: | :converting to thirds: | ||
:<math>\scriptstyle{\color{blue}{\left(5+\frac{1}{5}\right)\sdot\left(4+\frac{1}{4}\right)=22+\frac{1}{10}=\frac{3\sdot\left(22+\frac{1}{10}\right)}{3}=\frac{66+\frac{3}{10}}{3}}}</math> | :<math>\scriptstyle{\color{blue}{\left(5+\frac{1}{5}\right)\sdot\left(4+\frac{1}{4}\right)=22+\frac{1}{10}=\frac{3\sdot\left(22+\frac{1}{10}\right)}{3}=\frac{66+\frac{3}{10}}{3}}}</math> | ||
| − | |style="text-align:right;"|ובעבור שנצטרך לחלקם לג' ושליש עשה מכ"ב וא' | + | |style="text-align:right;"|ובעבור שנצטרך לחלקם לג' ושליש עשה מכ"ב וא' עשירית כולם שלישיות ואמור ג"פ כ"ב ס"ו וג' פעמי' א' עשירית הרי ג' עשיריות הרי ס"ו וג' עשיריות |
|- | |- | ||
| | | | ||
| Line 2,808: | Line 3,624: | ||
| | | | ||
|style="text-align:right;"|ואם נחלק ס"ו בי' חלקים יבואו ו' וו' עשיריות<br> | |style="text-align:right;"|ואם נחלק ס"ו בי' חלקים יבואו ו' וו' עשיריות<br> | ||
| − | נחלק אח"כ ג' עשיריות בי' חלקי' ישאר ג' חלקי' ממאה<br> | + | נחלק אח"כ ג' עשיריות בי' חלקי' ישאר ג' חלקי' ממאה‫<ref>ממאה: MS Ithaca ומאה</ref><br> |
| − | הרי שעולה החשבון ו' וו' עשיריות וג' חלקי' ממאה<br> | + | הרי שעולה החשבון ו' וו' עשיריות וג' חלקי' ממאה‫<ref>ממאה: MS Ithaca ומאה</ref><br> |
וכדי שנוכל לקבץ הכל יחד ו' עשיריות חלקים ממאה ויהיו ס' חלקים מק' וג' חלקים מק' שהיו בידינו הרי ס"ג<br> | וכדי שנוכל לקבץ הכל יחד ו' עשיריות חלקים ממאה ויהיו ס' חלקים מק' וג' חלקים מק' שהיו בידינו הרי ס"ג<br> | ||
תמצא מדברינו שאם ג' ושליש שוי' ד' ורביע ה' וחומש שוי' ו' וס"ג חלקים ממאה | תמצא מדברינו שאם ג' ושליש שוי' ד' ורביע ה' וחומש שוי' ו' וס"ג חלקים ממאה | ||
| Line 2,922: | Line 3,738: | ||
:Divide them by 3; the result is 1333 [liṭra], 6 dinar and 8 pešuṭim and so are a thousand liṭra of Pisa worth in Cortona. | :Divide them by 3; the result is 1333 [liṭra], 6 dinar and 8 pešuṭim and so are a thousand liṭra of Pisa worth in Cortona. | ||
:<math>\scriptstyle{\color{blue}{X=\frac{1000\sdot4}{3}=\frac{4000}{3}=1333+\frac{6}{20}+\frac{\frac{8}{12}}{20}}}</math> | :<math>\scriptstyle{\color{blue}{X=\frac{1000\sdot4}{3}=\frac{4000}{3}=1333+\frac{6}{20}+\frac{\frac{8}{12}}{20}}}</math> | ||
| − | |style="text-align:right;"|חלקם בג' יבואו אלף ושל"ג וו' די' וח' פשוטי' וכן שוים אלף ליט' פיסאני לקוטרניסי | + | |style="text-align:right;"|חלקם בג' יבואו אלף ושל"ג וו' די' וח' פשוטי' וכן שוים אלף ליט' פיסאני לקוטרניסי‫<ref>אם יאמר אדם ז' פיסאני... אלף ליט' פיסאני לקוטרניסי: MS Ithaca om.</ref> |
|- | |- | ||
| | | | ||
*{{#annot:two currencies|632|QWOi}}If a man says: if 7 silver ounces and a third are worth 73 liṭra and a quarter, how much are 19 silver ounces worth? | *{{#annot:two currencies|632|QWOi}}If a man says: if 7 silver ounces and a third are worth 73 liṭra and a quarter, how much are 19 silver ounces worth? | ||
:<math>\scriptstyle\frac{7+\frac{1}{3}}{73+\frac{1}{4}}=\frac{19}{X}</math> | :<math>\scriptstyle\frac{7+\frac{1}{3}}{73+\frac{1}{4}}=\frac{19}{X}</math> | ||
| − | |style="text-align:right;"|ואם יאמר אדם אם ז' אונקיו' ושליש מכסף שוי' ע"ג ליטרי' ורביע<br> | + | |style="text-align:right;"|‫<ref>37v</ref><big>ואם יאמר</big> אדם אם ז' אונקיו' ושליש מכסף שוי' ע"ג ליטרי' ורביע<br> |
י"ט אונקיו' מכסף כמה ישוו לפי חשבון זה{{#annotend:QWOi}} | י"ט אונקיו' מכסף כמה ישוו לפי חשבון זה{{#annotend:QWOi}} | ||
|- | |- | ||
| Line 3,246: | Line 4,062: | ||
:If you want to know how much gold the one whose gold is worth 3 liṭra for an ounce contributes, say: the third of 120 is 40. Multiply it by the number of ounces, which is 40; it is 1600. Divide it by 79; the result is 20 ounces and 20 parts of 79. | :If you want to know how much gold the one whose gold is worth 3 liṭra for an ounce contributes, say: the third of 120 is 40. Multiply it by the number of ounces, which is 40; it is 1600. Divide it by 79; the result is 20 ounces and 20 parts of 79. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}X=\frac{\left(\frac{1}{3}\sdot120\right)\sdot40}{79}=\frac{40\sdot40}{79}=\frac{1600}{79}=20+\frac{20}{79}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}X=\frac{\left(\frac{1}{3}\sdot120\right)\sdot40}{79}=\frac{40\sdot40}{79}=\frac{1600}{79}=20+\frac{20}{79}}}</math> | ||
| − | |style="text-align:right;"|<big>ואם תרצה</big> | + | |style="text-align:right;"|<big>ואם תרצה</big> לדעת כמה זהב ישים אותו שהזהב שלו שוה ג' ליטרי' האונקי‫'<br> |
| − | אמור השליש מק"כ הוא מ' ותרבה אותו עם סך האונקיות ‫<ref>38v</ref>שהם מ' יהיו אלף ות"ר | + | אמור השליש מק"כ הוא מ' ותרבה אותו עם סך האונקיות ‫<ref>38v</ref>שהם מ' יהיו אלף ות"ר‫<ref>לדעת כמה זהב ישים... יהיו אלף ות"ר: MS ithaca twice</ref><br> |
חלקם בע"ט יביאו כ' אונקיו' זהב וכ' חלקי' מע"ט | חלקם בע"ט יביאו כ' אונקיו' זהב וכ' חלקי' מע"ט | ||
|- | |- | ||
| Line 3,258: | Line 4,074: | ||
:<span style=color:green>'''Rule of Three:'''</span> for the 20 parts of 79 say: if 79, which is 1 ounce, is worth 720 pešuṭim that are 3 liṭra, how much are 20 parts of 79 worth? | :<span style=color:green>'''Rule of Three:'''</span> for the 20 parts of 79 say: if 79, which is 1 ounce, is worth 720 pešuṭim that are 3 liṭra, how much are 20 parts of 79 worth? | ||
:<math>\scriptstyle{\color{blue}{1:720=\frac{20}{79}:X}}</math> | :<math>\scriptstyle{\color{blue}{1:720=\frac{20}{79}:X}}</math> | ||
| − | |style="text-align:right;"|ומן הכ' חלקי' מע"ט אמור אם ע"ט שהוא כ' ליטרי' א' אונקי' שוה תש"כ | + | |style="text-align:right;"|ומן הכ' חלקי' מע"ט אמור אם ע"ט שהוא כ' ליטרי' א' אונקי' שוה תש"כ פשוטי' שהם ג' ליט' כ' חלקים מע"ט כמה שווים |
|- | |- | ||
| | | | ||
:Say: 20 times 720 is 14400. Divide it by 79; the result is 182 pešiṭim and 22 parts of 79. | :Say: 20 times 720 is 14400. Divide it by 79; the result is 182 pešiṭim and 22 parts of 79. | ||
:<math>\scriptstyle{\color{blue}{\frac{720\sdot20}{79}=\frac{14400}{79}=182+\frac{22}{79}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{720\sdot20}{79}=\frac{14400}{79}=182+\frac{22}{79}}}</math> | ||
| − | |style="text-align:right;"|אמו' כ' פעמ' תש"כ | + | |style="text-align:right;"|אמו' כ' פעמ' תש"כ‫<ref>פשוטי' שהם ג'... תש"כ: MS Ithaca om.</ref> יהיו <s>ד</s> י"ד אלפי' ות‫'<br> |
חלקם בע"ט יבואו קפ"ב פשיטי' וכ"ב חלקים מע"ט | חלקם בע"ט יבואו קפ"ב פשיטי' וכ"ב חלקים מע"ט | ||
|- | |- | ||
| Line 3,269: | Line 4,085: | ||
:Which are [60 liṭra], 15 dinar, 2 pešuṭim and 22 parts of 79. | :Which are [60 liṭra], 15 dinar, 2 pešuṭim and 22 parts of 79. | ||
:<math>\scriptstyle{\color{blue}{X=60+\frac{182+\frac{22}{79}}{20\sdot12}=60+\frac{15}{20}+\frac{2+\frac{22}{79}}{20\sdot12}}}</math> | :<math>\scriptstyle{\color{blue}{X=60+\frac{182+\frac{22}{79}}{20\sdot12}=60+\frac{15}{20}+\frac{2+\frac{22}{79}}{20\sdot12}}}</math> | ||
| − | |style="text-align:right;"|שהם | + | |style="text-align:right;"|שהם ס' ליט'‫<ref>ס' ליט': MS Ithaca כ"ה אלפים</ref> וט"ו דינרי' וב"פ וכ"ב חלקים מע"ט |
|- | |- | ||
| | | | ||
| Line 3,275: | Line 4,091: | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{5}X=\frac{\left(\frac{1}{5}\sdot120\right)\sdot40}{79}=\frac{24\sdot40}{79}=\frac{960}{79}=12+\frac{12}{79}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{5}X=\frac{\left(\frac{1}{5}\sdot120\right)\sdot40}{79}=\frac{24\sdot40}{79}=\frac{960}{79}=12+\frac{12}{79}}}</math> | ||
|style="text-align:right;"|<big>ואם תרצה לדעת</big> כמה זהב ישים אותו שהזהב שלו שוה ה' ליטרי' האונ‫'<br> | |style="text-align:right;"|<big>ואם תרצה לדעת</big> כמה זהב ישים אותו שהזהב שלו שוה ה' ליטרי' האונ‫'<br> | ||
| − | אמור החומש <s>מק"פ</s> | + | אמור החומש <s>מק"פ</s> מק"כ‫<ref>מק"כ: MS Ithaca marg.</ref> הם כ"ד תרבה אותם עם מ' שהוא סכום האונקי' עולים תתק"ס<br> |
חלקם בע"ט י"ב אונקיו' וי"ב חלקי' מע"ט | חלקם בע"ט י"ב אונקיו' וי"ב חלקי' מע"ט | ||
|- | |- | ||
| Line 3,286: | Line 4,102: | ||
:<span style=color:green>'''Rule of Three:'''</span> for the 12 parts of 79 say: if 79, which is 1 ounce, is worth 1200 pešuṭim that are 5 liṭra, how much are 12 parts of 79 worth? | :<span style=color:green>'''Rule of Three:'''</span> for the 12 parts of 79 say: if 79, which is 1 ounce, is worth 1200 pešuṭim that are 5 liṭra, how much are 12 parts of 79 worth? | ||
:<math>\scriptstyle{\color{blue}{1:1200=\frac{12}{79}:X}}</math> | :<math>\scriptstyle{\color{blue}{1:1200=\frac{12}{79}:X}}</math> | ||
| − | |style="text-align:right;"|ומן הי"ב | + | |style="text-align:right;"|ומן הי"ב חלקים‫<ref>חלקים: MS Ithaca ליטרי'</ref> מע"ט [אמור אם ע"ט שהוא א' אונקי' עולה אלף ור' פשוטי' שהם ה' ליט' הי"ב חלקים מע"ט כמה שווים |
|- | |- | ||
| | | | ||
| Line 3,359: | Line 4,175: | ||
| | | | ||
:Now that it is said "the sum of what all the three have is 60", do this way: | :Now that it is said "the sum of what all the three have is 60", do this way: | ||
| − | |style="text-align:right;"|ועתה שאמר ומחובר שלשתם | + | |style="text-align:right;"|ועתה שאמר ומחובר שלשתם ס'‫<ref>ס': MS Ithaca om.</ref> עשה על זה הדרך |
|- | |- | ||
| | | | ||
| Line 3,370: | Line 4,186: | ||
:<math>\scriptstyle{\color{blue}{a_1=\frac{60\sdot1}{13}=\frac{60}{13}=4+\frac{8}{13}}}</math> | :<math>\scriptstyle{\color{blue}{a_1=\frac{60\sdot1}{13}=\frac{60}{13}=4+\frac{8}{13}}}</math> | ||
|style="text-align:right;"|אמור ס' פעמי' א' הם ס‫'<br> | |style="text-align:right;"|אמור ס' פעמי' א' הם ס‫'<br> | ||
| − | חלקם בי"ג יהיו | + | חלקם בי"ג יהיו ד' וח'‫<ref>ד' וח': MS Ithaca י"ג וי"א</ref> חלקים מי"ג |
|- | |- | ||
| | | | ||
:<span style=color:green>'''Rule of Three:'''</span> To know the share of the second, say: if, when the sum is 13, the share of the second is 3, now that the sum is 60, how much is his share? | :<span style=color:green>'''Rule of Three:'''</span> To know the share of the second, say: if, when the sum is 13, the share of the second is 3, now that the sum is 60, how much is his share? | ||
:<math>\scriptstyle{\color{blue}{13:3=60:a_2}}</math> | :<math>\scriptstyle{\color{blue}{13:3=60:a_2}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ולדעת חלק השיני אמור אם בהיות המחובר י"ג יהיה החלק‫<ref>החלק: MS Ithaca המחובר</ref> השני ג'‫<ref>ג': MS Ithaca om.</ref> עתה שהמחובר ס' כמה הוא חלקו |
|- | |- | ||
| | | | ||
| Line 3,381: | Line 4,197: | ||
:<math>\scriptstyle{\color{blue}{a_2=\frac{60\sdot3}{13}=\frac{180}{13}=13+\frac{11}{13}}}</math> | :<math>\scriptstyle{\color{blue}{a_2=\frac{60\sdot3}{13}=\frac{180}{13}=13+\frac{11}{13}}}</math> | ||
|style="text-align:right;"|אמו' ס' פעמי' ג' הם ק"פ<br> | |style="text-align:right;"|אמו' ס' פעמי' ג' הם ק"פ<br> | ||
| − | חלקם בי"ג יהיו י"ג וי"א חלקים מי"ג | + | חלקם בי"ג יהיו י"ג וי"א חלקים מי"ג‫<ref>ולדעת חלק השיני... וי"א חלקים מי"ג: MS Ithaca twice</ref> |
|- | |- | ||
| | | | ||
| Line 3,462: | Line 4,278: | ||
:<span style=color:green>'''Rule of Three:'''</span> If you want to find Reuven's share, say: if, when the amount of money is 35 dinar, Reuven's share is 15, when the amount of money is 60, how much is his share? | :<span style=color:green>'''Rule of Three:'''</span> If you want to find Reuven's share, say: if, when the amount of money is 35 dinar, Reuven's share is 15, when the amount of money is 60, how much is his share? | ||
:<math>\scriptstyle{\color{blue}{35:15=60:a_1}}</math> | :<math>\scriptstyle{\color{blue}{35:15=60:a_1}}</math> | ||
| − | |style="text-align:right;"|אם תרצה לדעת חלק ראובן אמור אם בהיות סכום המעות | + | |style="text-align:right;"|אם תרצה לדעת חלק ראובן אמור אם בהיות סכום המעות ל"ה היה חלק ראובן ט"ו בהיות סכום‫<ref>ל"ה... בהיות סכום: MS Ithaca om.</ref> הדינרי' ס' כמה הוא חלקו |
|- | |- | ||
| | | | ||
:Say: 60 times 15 is 900. Divide it by 35; it is 25 and 25 parts of 35. | :Say: 60 times 15 is 900. Divide it by 35; it is 25 and 25 parts of 35. | ||
:<math>\scriptstyle{\color{blue}{a_1=\frac{60\sdot15}{35}=\frac{900}{35}=25+\frac{25}{35}}}</math> | :<math>\scriptstyle{\color{blue}{a_1=\frac{60\sdot15}{35}=\frac{900}{35}=25+\frac{25}{35}}}</math> | ||
| − | |style="text-align:right;"|אמור ס' פעמים | + | |style="text-align:right;"|אמור ס' פעמים ט"ו‫<ref>ט"ו: MS Ithaca om.</ref> הם תת"ק<br> |
חלקם בל"ה יהיו כ"ה וכ"ה חלקים מל"ה | חלקם בל"ה יהיו כ"ה וכ"ה חלקים מל"ה | ||
|- | |- | ||
| Line 3,478: | Line 4,294: | ||
:Say: 60 times 5 is 300. Divide it by 35; it is 8 and 20 parts of 35. | :Say: 60 times 5 is 300. Divide it by 35; it is 8 and 20 parts of 35. | ||
:<math>\scriptstyle{\color{blue}{a_3=\frac{60\sdot5}{35}=\frac{300}{35}=8+\frac{20}{35}}}</math> | :<math>\scriptstyle{\color{blue}{a_3=\frac{60\sdot5}{35}=\frac{300}{35}=8+\frac{20}{35}}}</math> | ||
| − | |style="text-align:right;"|אמור ס' פעמי' | + | |style="text-align:right;"|אמור ס' פעמי' ה'‫<ref>ה': MS Ithaca om.</ref> הם ש‫'<br> |
חלקם בל"ה יהיו ח' דינרי' וכ' חלקים מל"ה | חלקם בל"ה יהיו ח' דינרי' וכ' חלקים מל"ה | ||
|- | |- | ||
| Line 3,484: | Line 4,300: | ||
:<span style=color:green>'''Rule of Three:'''</span> To find Issachar's share, say: if, when the amount of money is 35 dinar, his share is 3, when the amount of money is 60, how much is [his share]? | :<span style=color:green>'''Rule of Three:'''</span> To find Issachar's share, say: if, when the amount of money is 35 dinar, his share is 3, when the amount of money is 60, how much is [his share]? | ||
:<math>\scriptstyle{\color{blue}{35:3=60:a_4}}</math> | :<math>\scriptstyle{\color{blue}{35:3=60:a_4}}</math> | ||
| − | |style="text-align:right;"|ולדעת חלק יששכר אמור אם בהיות סך המעות ל"ה דינרי' היה חלקו | + | |style="text-align:right;"|ולדעת חלק יששכר אמור אם בהיות סך המעות ל"ה דינרי' היה חלקו ג'‫<ref>ג': MS Ithaca om.</ref> בהיות סך המעות ס' כמה יהיו |
|- | |- | ||
| | | | ||
| Line 3,876: | Line 4,692: | ||
|- | |- | ||
| | | | ||
| − | :Take | + | :Take the total sum of the ounces of gold; take also the sum of the carat; divide the [sum of] the carat by the sum of the ounces. |
|style="text-align:right;"|ואתה קח סכום כל הא' ‫<ref>40r</ref>על האוקיו' של זהב וקח סכום הקראטי ג"כ וחלק הקראטי לסכום האוקיו‫' | |style="text-align:right;"|ואתה קח סכום כל הא' ‫<ref>40r</ref>על האוקיו' של זהב וקח סכום הקראטי ג"כ וחלק הקראטי לסכום האוקיו‫' | ||
|- | |- | ||
| Line 3,891: | Line 4,707: | ||
| | | | ||
:5 ounces of 18 carat are 90 carat. | :5 ounces of 18 carat are 90 carat. | ||
| − | :<math>\scriptstyle{\color{blue}{5\sdot18=90}}</math> | + | :<math>\scriptstyle{\color{blue}{5\sdot18=90}}</math> |
|style="text-align:right;"|והה' אונקיו' מי"ח קראטי עולות צ' קאראטי | |style="text-align:right;"|והה' אונקיו' מי"ח קראטי עולות צ' קאראטי | ||
|- | |- | ||
| Line 5,211: | Line 6,027: | ||
|pešuṭim | |pešuṭim | ||
|style="text-align:right;"|ותרבה רכ"ז עם רע"ז יהיו ס"ב אלפי' ותתע"ט<br> | |style="text-align:right;"|ותרבה רכ"ז עם רע"ז יהיו ס"ב אלפי' ותתע"ט<br> | ||
| − | חלקם בס' פעמי' ס' שהם ג' אלפים ות"ר יבאו | + | חלקם בס' פעמי' ס' שהם ג' אלפים ות"ר יבאו י"ז פשוטי'‫<ref>י"ז פשוטי': MS Ithaca ה"פ</ref> ואלף ותרע"ט חלקים מג' אלפים ות"ר מן הפשוט |
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 5,356: | Line 6,172: | ||
::= 36 pešiṭim | ::= 36 pešiṭim | ||
|style="text-align:right;"|אמור ו' פעמי' ק"נ תת"ק<br> | |style="text-align:right;"|אמור ו' פעמי' ק"נ תת"ק<br> | ||
| − | ותפוש מכל | + | ותפוש מכל כ"ה‫<ref>כ"ה: MS Ithaca אלף</ref> א' פשוט שיבואו ל"ו פשיטי' וכן יבא הליט‫' |
|- | |- | ||
|1 ounce of gold = 30 terri; | |1 ounce of gold = 30 terri; | ||
| Line 5,377: | Line 6,193: | ||
::take 8 pešiṭim for every liṭra and ⅖ for every dinar | ::take 8 pešiṭim for every liṭra and ⅖ for every dinar | ||
::<math>\scriptstyle{\color{red}{X=\left(5\sdot8\right)+\left(\frac{2}{5}\sdot15\right)}}</math> | ::<math>\scriptstyle{\color{red}{X=\left(5\sdot8\right)+\left(\frac{2}{5}\sdot15\right)}}</math> | ||
| − | |style="text-align:right;"|תפוש מכל ליטר' ח"פ ומכל דינר | + | |style="text-align:right;"|תפוש מכל ליטר' ח"פ ומכל דינר ב'‫<ref>ב': MS Ithaca ח'</ref> חמשיות וכן לכל חשבון שתרצה |
|- | |- | ||
| | | | ||
| Line 5,442: | Line 6,258: | ||
וזה תוכל לדעת שתתן לאחד מהם א' מטבע ולשני ב' ולשליש ד‫'<br> | וזה תוכל לדעת שתתן לאחד מהם א' מטבע ולשני ב' ולשליש ד‫'<br> | ||
ואמור להם שאותו שיש לו הזהב יכפול ד' פעמי' המטבעות שנתת לו באחרונה<br> | ואמור להם שאותו שיש לו הזהב יכפול ד' פעמי' המטבעות שנתת לו באחרונה<br> | ||
| − | ובעל הכסף יכפול | + | ובעל הכסף יכפול ה'‫<ref>ה': MS Ithaca ב'</ref> פעמים המטבעות שנתת לו באחרונה<br> |
ובעל הנחושת יכפול המטבעות שנתת לו באחרונה<br> | ובעל הנחושת יכפול המטבעות שנתת לו באחרונה<br> | ||
ויקבצו הכל וישליכו ז"ז<br> | ויקבצו הכל וישליכו ז"ז<br> | ||
| Line 5,459: | Line 6,275: | ||
| | | | ||
:[(3·1)+(2·2)+(4·4)] mod 7 = 2 → silver, copper, gold | :[(3·1)+(2·2)+(4·4)] mod 7 = 2 → silver, copper, gold | ||
| − | |style="text-align:right;"|ואם נשאר בידם ב' יהיה | + | |style="text-align:right;"|ואם נשאר בידם ב' יהיה הסדר‫<ref>הסדר: MS Ithaca הכסף</ref> כסף נחושת זהב |
|- | |- | ||
| | | | ||
| Line 5,485: | Line 6,301: | ||
אחר כן ישליך מה שחשב ה' ה' ושאל הנשאר<br> | אחר כן ישליך מה שחשב ה' ה' ושאל הנשאר<br> | ||
אחר זה ישליך מה שחשב ז' ז' ושאל הנשאר<br> | אחר זה ישליך מה שחשב ז' ז' ושאל הנשאר<br> | ||
| − | ומכל מה שנשאר אחר שהשליכם ג' ג' | + | ומכל מה שנשאר אחר שהשליכם ג' ג' תחשוב‫<ref>תחשוב: MS Ithaca om.</ref> לכל אחד הנ[ות]ר מן הג' ע‫'<br> |
| − | + | ומכל מה שנשאר אחר שהשליכם ה'ה' תחשוב לכל אחד‫<ref>ומכל... לכל אחד: MS Ithaca ולכל הנשאר מן הה'</ref> כ"א<br> | |
ומכל הנשאר אחר שהשליכם ז' ז' קח לכל אחד ט"ו<br> | ומכל הנשאר אחר שהשליכם ז' ז' קח לכל אחד ט"ו<br> | ||
וצרפם והשלך אותם ק"ה והנותר יהיה מה שחשב <big>והסימן ג"ע הכ"א זט"ו</big>{{#annotend:Quwt}} | וצרפם והשלך אותם ק"ה והנותר יהיה מה שחשב <big>והסימן ג"ע הכ"א זט"ו</big>{{#annotend:Quwt}} | ||
| Line 5,495: | Line 6,311: | ||
| | | | ||
:*If he chose [the number] 17 | :*If he chose [the number] 17 | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|דמיון זה כאלו חשב י"ז |
|- | |- | ||
| | | | ||
| Line 5,505: | Line 6,321: | ||
ומה שנשאר כשהשליכם ז'ז' דהיין ג' תחשוב לכל אחד ט"ו ויהיו מ"ה<br> | ומה שנשאר כשהשליכם ז'ז' דהיין ג' תחשוב לכל אחד ט"ו ויהיו מ"ה<br> | ||
קבץ הכל ויהיו רכ"ז<br> | קבץ הכל ויהיו רכ"ז<br> | ||
| − | השליכם ק"ה ק"ה ישארו בידך י"ז כמו שחשב חברך | + | השליכם ק"ה ק"ה ישארו בידך י"ז כמו שחשב חברך‫<ref>דמיון זה... כמו שחשב חברך: according to MS Verona; MS Ithaca om.</ref> |
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 5,524: | Line 6,340: | ||
:<math>\scriptstyle\left(2-\frac{5}{3}\right)X+\left(3-\frac{5}{3}\right)X=5</math> | :<math>\scriptstyle\left(2-\frac{5}{3}\right)X+\left(3-\frac{5}{3}\right)X=5</math> | ||
|style="text-align:right;"|‫<ref>44r</ref><big>שני אנשים היו יושבים לאכול</big><br> | |style="text-align:right;"|‫<ref>44r</ref><big>שני אנשים היו יושבים לאכול</big><br> | ||
| − | <big>לאחד</big> היו <s>ב'</s> | + | <big>לאחד</big> היו <s>ב'</s> ג'‫<ref>ג': MS Ithaca marg.</ref> לחמים ולשני ב' לחמים<br> |
בא אדם אחד שלישי ואכל עמהם ואכלו בין שלשתם אילו הה' לחמים<br> | בא אדם אחד שלישי ואכל עמהם ואכלו בין שלשתם אילו הה' לחמים<br> | ||
לאחר שאכלו נתן אותו השליש שאכל עמהם ה' פשיטי שיחלקום ביניהם<br> | לאחר שאכלו נתן אותו השליש שאכל עמהם ה' פשיטי שיחלקום ביניהם<br> | ||
| Line 5,572: | Line 6,388: | ||
| | | | ||
::it climbs up one cubit in 12 days | ::it climbs up one cubit in 12 days | ||
| − | |style="text-align:right;"|הרי | + | |style="text-align:right;"|הרי שי"ב ימים היא<ref>שי"ב ימים היא: MS Ithaca twice</ref> עולה א' אמה |
|- | |- | ||
| | | | ||
| Line 5,594: | Line 6,410: | ||
:<math>\scriptstyle X-\left(\frac{1}{3}X+\frac{1}{4}X+\frac{1}{5}X\right)=X-9</math> | :<math>\scriptstyle X-\left(\frac{1}{3}X+\frac{1}{4}X+\frac{1}{5}X\right)=X-9</math> | ||
|style="text-align:right;"|<big>הרי שיש לך מעות בכיס</big><br> | |style="text-align:right;"|<big>הרי שיש לך מעות בכיס</big><br> | ||
| − | והוצאת מהם השליש והרביע והחומש | + | והוצאת מהם השליש והרביע והחומש והם ט'<ref>והם ט': MS ithaca twice</ref> פשיטים<br> |
כמה יהיו הנשארים{{#annotend:Y4nv}} | כמה יהיו הנשארים{{#annotend:Y4nv}} | ||
|- | |- | ||
| Line 5,622: | Line 6,438: | ||
| | | | ||
::the money that was in the purse: <math>\scriptstyle{\color{blue}{X=11+\frac{23}{47}}}</math> pešiṭim | ::the money that was in the purse: <math>\scriptstyle{\color{blue}{X=11+\frac{23}{47}}}</math> pešiṭim | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נמצא שהיו בתוך הכיס י"א פשו' וכ"ג חלקים ממ"ז‫<ref>נמצא שהיו... ממ"ז: MS Ithaca om.</ref> |
|- | |- | ||
| | | | ||
| Line 5,642: | Line 6,458: | ||
ורוצה לחלקו לב' אנשי' וליתן לכל אחד ד' מנות<br> | ורוצה לחלקו לב' אנשי' וליתן לכל אחד ד' מנות<br> | ||
אמנם אין לו רק ב' כלים שהאחד מהם מחזיק ג' והאחר מחזיק ה‫'<br> | אמנם אין לו רק ב' כלים שהאחד מהם מחזיק ג' והאחר מחזיק ה‫'<br> | ||
| − | היאך יעשה אותם לחלק | + | היאך יעשה אותם לחלק זה היין‫<ref>זה היין: MS Ithaca אותם</ref> לחצי{{#annotend:Dsq4}} |
|- | |- | ||
| | | | ||
| Line 6,067: | Line 6,883: | ||
*{{#annot:four coins|652|vSHO}}Four coins are worth all in all 80 pešuṭim: | *{{#annot:four coins|652|vSHO}}Four coins are worth all in all 80 pešuṭim: | ||
:The first is equal to a half and a sixth of the second. | :The first is equal to a half and a sixth of the second. | ||
| − | :What is left from the second equals | + | :What is left from the second equals 2-thirds of the third. |
:The third is equal to a third, a quarter, and a sixth of the first. | :The third is equal to a third, a quarter, and a sixth of the first. | ||
| − | :The fourth is equal to | + | :The fourth is equal to 4-fifths of the [third]. |
:How much does each [of the coins] worth? | :How much does each [of the coins] worth? | ||
|style="text-align:right;"|ד' מט' מטבעות שוים בין ארבעתם פ' פשוטי‫'<br> | |style="text-align:right;"|ד' מט' מטבעות שוים בין ארבעתם פ' פשוטי‫'<br> | ||
| Line 6,075: | Line 6,891: | ||
הנשאר מן השני הם ב' שלישיות מן השלישי<br> | הנשאר מן השני הם ב' שלישיות מן השלישי<br> | ||
השלישי הוא שליש ורביע ושתות מן הראשו‫'<br> | השלישי הוא שליש ורביע ושתות מן הראשו‫'<br> | ||
| − | הרביעי הוא ד' חומשים | + | הרביעי הוא ד' חומשים מהשני<br> |
ותרצה לידע כמה שוה כל אחד ואחד{{#annotend:vSHO}} | ותרצה לידע כמה שוה כל אחד ואחד{{#annotend:vSHO}} | ||
|- | |- | ||
| Line 6,082: | Line 6,898: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|עשה על זה הדרך בעבו' שהראשו' שוה החצי והשתות מהשני<br> | + | ::Do it this way: |
| + | |style="text-align:right;"|עשה על זה הדרך | ||
| + | |- | ||
| + | | | ||
| + | ::Since the first is equal to a half and a sixth of the second, say: a half and a sixth are found in 6. The half is 3; the sixth is 1; their sum is 4; so they are 2-thirds. | ||
| + | |style="text-align:right;"|בעבו' שהראשו' שוה החצי והשתות מהשני<br> | ||
אמור חצי ושתות ימצאו בו‫'<br> | אמור חצי ושתות ימצאו בו‫'<br> | ||
החצי ג' השתות א‫'<br> | החצי ג' השתות א‫'<br> | ||
| Line 6,088: | Line 6,909: | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| − | :<math>\scriptstyle{\color{blue}{\frac{1}{2}+\frac{1}{6}=\frac{\left(\frac{1}{2}\sdot6\right)+\left(\frac{1}{6}\sdot6\right)}{6}=\frac{3+1}{6}=\frac{4}{6}=\frac{2}{3}}}</math> | + | ::<math>\scriptstyle{\color{blue}{\frac{1}{2}+\frac{1}{6}=\frac{\left(\frac{1}{2}\sdot6\right)+\left(\frac{1}{6}\sdot6\right)}{6}=\frac{3+1}{6}=\frac{4}{6}=\frac{2}{3}}}</math> |
|- | |- | ||
| | | | ||
| + | ::Therefore, the one that is equal to a half and a sixth of the second is as saying 2-thirds of the second. | ||
::<math>\scriptstyle{\color{blue}{a_1=\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2=\frac{2}{3}a_2}}</math> | ::<math>\scriptstyle{\color{blue}{a_1=\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2=\frac{2}{3}a_2}}</math> | ||
|style="text-align:right;"|אם כן זה ששוה חצי ושתות מן השני הוא כאלו אמר שוה ב' שלישייו' מן השני | |style="text-align:right;"|אם כן זה ששוה חצי ושתות מן השני הוא כאלו אמר שוה ב' שלישייו' מן השני | ||
|- | |- | ||
| | | | ||
| + | ::The third is equal to a third, a quarter, and a sixth of the first. Say: a third, a quarter, and a sixth are found in 60. The third is 20; the quarter is 15; the sixth is 10; their sum is 45 parts of 60, which are 3-quarters. | ||
|style="text-align:right;"|והשלישי ששוה שליש ורביע ושתות מן הראשו‫'<br> | |style="text-align:right;"|והשלישי ששוה שליש ורביע ושתות מן הראשו‫'<br> | ||
אמו' שליש ורביע ושתות ימצאו בס‫'<br> | אמו' שליש ורביע ושתות ימצאו בס‫'<br> | ||
| Line 6,101: | Line 6,924: | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| − | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{1}{3}+\frac{1}{4}+\frac{1}{6}&\scriptstyle=\frac{\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)}{60}\\&\scriptstyle=\frac{20+15+10}{60}=\frac{45}{60}=\frac{3}{4}\\\end{align}}}</math> | + | ::<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{1}{3}+\frac{1}{4}+\frac{1}{6}&\scriptstyle=\frac{\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)}{60}\\&\scriptstyle=\frac{20+15+10}{60}=\frac{45}{60}=\frac{3}{4}\\\end{align}}}</math> |
|- | |- | ||
| | | | ||
| + | ::It is as saying: the third is equal to 3-quarters of the first. | ||
::<math>\scriptstyle{\color{blue}{a_3=\frac{3}{4}a_1}}</math> | ::<math>\scriptstyle{\color{blue}{a_3=\frac{3}{4}a_1}}</math> | ||
|style="text-align:right;"|והוא כאלו אמר השלישי שוה ג' רבעייו' מן הראשון | |style="text-align:right;"|והוא כאלו אמר השלישי שוה ג' רבעייו' מן הראשון | ||
|- | |- | ||
| | | | ||
| + | ::The fourth is equal to 4-fifths of the third; this is clear. | ||
::<math>\scriptstyle{\color{blue}{a_4=\frac{4}{5}a_3}}</math> | ::<math>\scriptstyle{\color{blue}{a_4=\frac{4}{5}a_3}}</math> | ||
|style="text-align:right;"|והרביעי שוה ד' חמישייו' מהשלישי הוא מבואר | |style="text-align:right;"|והרביעי שוה ד' חמישייו' מהשלישי הוא מבואר | ||
|- | |- | ||
| | | | ||
| + | ::So the order is as follows: | ||
| + | ::The first is equal to 2-thirds of the second. | ||
| + | ::The third is equal to 3-quarters of the first. | ||
| + | ::The fourth is equal to 4-fifths of the [third]. | ||
::<math>\scriptstyle{\color{blue}{\begin{cases}\scriptstyle a_1=\frac{2}{3}a_2\\\scriptstyle a_3=\frac{3}{4} a_1\\\scriptstyle a_4=\frac{4}{5}a_3\end{cases}}}</math> | ::<math>\scriptstyle{\color{blue}{\begin{cases}\scriptstyle a_1=\frac{2}{3}a_2\\\scriptstyle a_3=\frac{3}{4} a_1\\\scriptstyle a_4=\frac{4}{5}a_3\end{cases}}}</math> | ||
| − | |style="text-align:right;"|אם כן הסדר הוא כך הראשו' שוה ב' שלשייו' מהשני<br> | + | |style="text-align:right;"|אם כן הסדר הוא כך<br> |
| + | הראשו' שוה ב' שלשייו' מהשני<br> | ||
והשלישי שוה ג' רביעייו' מן הראשון<br> | והשלישי שוה ג' רביעייו' מן הראשון<br> | ||
| − | הרביעי שוה ד' חמישיו | + | הרביעי שוה ד' חמישיו' מהשני |
|- | |- | ||
| | | | ||
| Line 6,357: | Line 7,187: | ||
:<span style=color:green>'''Rule of Three:'''</span> Multiply 6, which is a third of 18, by 9, which is the number of dinar, and say: 6 times 9 is 54. Divide it by 17 [parts] of one dinar; it is 3 dinar and 3 parts of 17 of one dinar. | :<span style=color:green>'''Rule of Three:'''</span> Multiply 6, which is a third of 18, by 9, which is the number of dinar, and say: 6 times 9 is 54. Divide it by 17 [parts] of one dinar; it is 3 dinar and 3 parts of 17 of one dinar. | ||
:<math>\scriptstyle{\color{blue}{\frac{1}{3}X=\frac{\left(\frac{1}{3}\sdot18\right)\sdot9}{17}=\frac{6\sdot9}{17}=\frac{54}{17}=3+\frac{3}{17}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{1}{3}X=\frac{\left(\frac{1}{3}\sdot18\right)\sdot9}{17}=\frac{6\sdot9}{17}=\frac{54}{17}=3+\frac{3}{17}}}</math> | ||
| − | |style="text-align:right;"|תרבה ו' שהוא השליש מי"ח עם ט' שהוא סכום הדינרי' ואמור ו' פעמי' | + | |style="text-align:right;"|תרבה ו' שהוא השליש מי"ח עם ט' שהוא סכום הדינרי' ואמור ו' פעמי' ט' נ"ד‫<ref>ט' נ"ד: MS Ithaca om.</ref><br> |
| − | חלקם בי"ז מהדינר | + | חלקם בי"ז מהדינר יבואו ג' די' וג' חלקים מי"ז מן הדי‫'‫<ref>יבואו ג'... מן הדי': MS Ithaca om.</ref> |
|- | |- | ||
| | | | ||
| Line 6,415: | Line 7,245: | ||
:The 3 parts of 17 of one liṭra are 3 times 14 pešuṭim and 3 times 2 parts of 17 of one pašuṭ. | :The 3 parts of 17 of one liṭra are 3 times 14 pešuṭim and 3 times 2 parts of 17 of one pašuṭ. | ||
:<math>\scriptstyle{\color{blue}{\frac{3}{17}=\frac{3\sdot\left(14+\frac{2}{17}\right)}{20\sdot12}}}</math> | :<math>\scriptstyle{\color{blue}{\frac{3}{17}=\frac{3\sdot\left(14+\frac{2}{17}\right)}{20\sdot12}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והג' חלקים מי"ז מן הליט'‫<ref>והג'... מן הליט': MS Ithaca om.</ref> הם ג' פעמים יד"פ וג' פעמים ב' חלקים מי"ז מהפשוט |
|- | |- | ||
| | | | ||
| Line 6,626: | Line 7,456: | ||
ושאל הנשאר ותקח דמיונם<br> | ושאל הנשאר ותקח דמיונם<br> | ||
דהיינו שאם נשארו ק' שדמיונם א' אמור כי חשב א‫'<br> | דהיינו שאם נשארו ק' שדמיונם א' אמור כי חשב א‫'<br> | ||
| − | ואם נשארו | + | ואם נשארו ר'‫<ref>ר': MS Ithaca om.</ref> שדמיונם ב' אמור כי חשב ב‫'<br> |
ואם נשארו ש' שדמיונם ג' אמור כי חשב ג‫'<br> | ואם נשארו ש' שדמיונם ג' אמור כי חשב ג‫'<br> | ||
וכן לעולם{{#annotend:nr3t}}‫<ref>MS Ithaca end.</ref> | וכן לעולם{{#annotend:nr3t}}‫<ref>MS Ithaca end.</ref> | ||
Latest revision as of 07:33, 19 November 2024
Contents
- 1 The Nature of One
- 2 Shortcuts - Products of Ranks by Ranks
- 3 The Decimal Ranks[61]
- 4 Three Types of Numbers[71]
- 5 The Ten Numerals[73]
- 6 The Method of Finding the Square Numbers[75]
- 7 Cubic Numbers[79]
- 8 Primary Definitions[80]
- 9 Multiplication
- 9.1 Units and tens by units and tens
- 9.2 Units by units and tens
- 9.3 Units, tens, and hundreds by units, tens, and hundreds
- 9.4 Units and tens by units, tens, and hundreds
- 9.5 Units by units, tens, and hundreds
- 9.6 Units, tens, hundreds, and thousands by units, tens, hundreds, and thousands
- 9.7 Units, tens, hundreds, and thousands by units, tens, and hundreds
- 9.8 Units, tens, hundreds, and thousands by units and tens
- 9.9 Units, tens, hundreds, and thousands by units
- 9.10 Units, tens, hundreds, thousands, and tens of thousands by units, tens, hundreds, thousands, and tens of thousands
- 9.11 Units, tens, hundreds, thousands, tens of thousands, and hundreds of thousands by units, tens, hundreds, thousands, tens of thousands, and hundreds of thousands
- 10 The Method of Summing Up Separate Numbers Called Congregare or Riunire
- 11 The Method of Subtracting a Number from a Number Called Sottrarre
- 12 The Method of Dividing a Number by a Number Called Dividere or Partire
- 13 The Method of Knowing the Numbers Summed One after the Other Successively
- 14 Word Problems - The Rule of Three
- 15 Calculation of Fractions
- 16 Word Problems
- 16.1 Exchange Problems
- 16.2 Divide a Quantity Problems
- 16.3 Partnership - for the same time
- 16.4 Multiple Quantities Problems
- 16.5 Joint Purchase Problem - If You Give Me - Amounts of Money
- 16.6 Multiple Quantities Problems
- 16.7 Mixture and Alligation Problem
- 16.8 Pricing Problems
- 16.9 Shared Work Problem - Four rivers
- 16.10 Multiple Quantities Problems
- 16.11 Rent Problems
- 16.12 Pricing Problems[185]
- 16.13 Interest and Discount Problems - Find the Earned Interest
- 16.14 Interest and Discount Problems (MS Verona)
- 16.15 Find a Number Problems
- 16.16 Find the Price - Cubits of Cloth
- 16.17 Interest and Discount Problem - Compound Interest
- 16.18 Pricing Problems
- 16.19 Guessing Problems
- 16.20 Divide a Quantity Problem
- 16.21 Motion Problem - To and From
- 16.22 Find a Quantity Problem - First from Last
- 16.23 Ordering Problems
- 16.24 Find a Quantity Problem - Whole from Parts[214]
- 16.25 Divide a Quantity Problem - Proportional Division[215]
- 16.26 Buy and Sell Problem
- 16.27 Ordering Problems
- 16.28 Multiple Quantities Problems
- 16.29 Fractions of Fractions (MS Firenze)[219]
- 16.30 Pricing Problems[220]
- 16.31 Divide a Quantity Problems
- 16.32 Guessing a chosen number (MS Verona)
- 16.33 Divisibility of the Numbers 1-112 (MS Ithaca)
- 17 Notes
- 18 Appendix: Bibliography
| [1]ספר חשבון | ||||||||||||||||||||||||||||||||
The Nature of One |
||||||||||||||||||||||||||||||||
| One, from one aspect, is a number and the foundation of the numbers; from another aspect it is not a number. | האחד מדרך אחד הוא מן המספר ועיקר המספר ומדרך אחר אינו מספר[2] | |||||||||||||||||||||||||||||||
| The proof that indicates that it is not a number is that every number is half [the sum of the numbers on] its both sides and also [the sum of the numbers on] the sides of its both sides and so on until the end of its sides.
|
והאות המורה כי אננו מספר הוא כי כל מספר הוא מחצית שני צדיו וכן הוא מחצית שני צדי צדיו על תכלית כל צדיו[3] | |||||||||||||||||||||||||||||||
|
המשל בזה י' צדו האחד י"א וצדו האחר ט' ושניהם כ' וי' הוא חצי שני הצדדים[4] | |||||||||||||||||||||||||||||||
|
וכן הוא חצי שני צדי צדיו שהם י"ב וח' | |||||||||||||||||||||||||||||||
|
וכן הוא מחצית שני צדי צדי צדיו שהם י"ג וז'[5] | |||||||||||||||||||||||||||||||
| Ans so on, every number is half [the sum of the numbers on] its both sides. | וכן כל המספר הוא מחצית ב' צידיו | |||||||||||||||||||||||||||||||
|
והאחד מפני שאינו מספר אי אתה מוצא לו ב' צדדים[6] | |||||||||||||||||||||||||||||||
|
ומצד היותו מספר הוא מחצית חצי צדו האחד ר"ל חצי מספר ב' | |||||||||||||||||||||||||||||||
| Another proof that indicates that one is not a number is that every number is either integer or a fraction. | ואות אחר מורה שהאחד אינו מספר כי כל מספ' הוא או מספר שלם או שבר מספר[7] | |||||||||||||||||||||||||||||||
|
ומדרך המספר השלם כשתרבה אותו בעצמו יוסיף | |||||||||||||||||||||||||||||||
|
כגון ב' פעמי' ב' ד'[8] | |||||||||||||||||||||||||||||||
|
ג' פעמי' ג' ט'[9] | |||||||||||||||||||||||||||||||
|
וכן כלם | |||||||||||||||||||||||||||||||
|
ושבר מספר כשתרבה[10] אותו בעצמו יחסר | |||||||||||||||||||||||||||||||
|
כגון[11] חצי פעם חצי[12] שהוא רביע | |||||||||||||||||||||||||||||||
|
שליש פעם א' שליש[13] שהוא[14] תשיע | |||||||||||||||||||||||||||||||
|
רביע פעם רביע[15] שהוא[16] חלק מי"ו | |||||||||||||||||||||||||||||||
|
וכן כלם | |||||||||||||||||||||||||||||||
|
והאחד שאינו מוסיף על חשבונו כשתמנהו בעצמו כדרך השלמים ולא גורע [ממניינו][17] כדרך השברים יורה שאיננו[18] מספר | |||||||||||||||||||||||||||||||
Shortcuts - Products of Ranks by Ranks |
||||||||||||||||||||||||||||||||
| Units by Tens | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| When we want to multiply units by tens.
|
כשנרצה[19] לרבות[20] אחדים עם עשרות | |||||||||||||||||||||||||||||||
|
כגון ו' פעמי' מ' | |||||||||||||||||||||||||||||||
|
נקח[21] דמיונם[22] מן האחדים הדומים להם ובעבור שמ' הם ד' עשרות מניינם הוא ו' פעמים וכמו[23] שו' פעמי' ד'[24] הם[25] כ"ד כן ו' פעמים מ'[26] הם[27] כ"ד עשרות שהם ר"מ | |||||||||||||||||||||||||||||||
|
וכן[28] ג' פעמים ל'[29] | |||||||||||||||||||||||||||||||
|
דמיונם הוא[30] ג' פעמים ג' שהם ט' ויהיו[31] ט' עשרות שהם צ' | |||||||||||||||||||||||||||||||
| This way for all of them. | ועל זה הדרך הם כלם[32] | |||||||||||||||||||||||||||||||
| Tens by Tens | ||||||||||||||||||||||||||||||||
| If we multiply tens by tens.
|
ואם נרבה[33] עשרות עם עשרות | |||||||||||||||||||||||||||||||
|
כגון ל' פעמים ל' | |||||||||||||||||||||||||||||||
|
ניקח דמיונם מן האחדים הדומים להם ובעבור היות ל'[34] ג'[35] עשרו' דמיונם הוא ג' פעמי' ג'[36] וכמו שג' פעמים ג'[37] הם ט' כן ל' פעמים ל' הם ט' מאות | |||||||||||||||||||||||||||||||
|
וכן מ' פעמים מ'[38] | |||||||||||||||||||||||||||||||
|
דמיונם הוא ד' פעמים שהם י"ו[39] מאות[40] | |||||||||||||||||||||||||||||||
|
וכן ל' פעמים מ'[41] | |||||||||||||||||||||||||||||||
|
דמיונם הוא ג' פעמים ד'[42] שהם י"ב וכן ל' פע' מ'[43] הם י"ב מאות | |||||||||||||||||||||||||||||||
| The same for all. | וכן כלם | |||||||||||||||||||||||||||||||
| The rule for this is that when we multiply units by tens, we take their analogous from the multiplication of the units by the units and the result is tens. | והכלל המסור לזה הוא כשנרבה אחדים עם עשרות נקח דמיונם מרבוי האחדים עם האחדים ויהיו העולה עשרות | |||||||||||||||||||||||||||||||
| If we multiply tens by tens the result is hundreds. | ואם נרבה עשרות עם עשרות יהיה העולה מאות[44] | |||||||||||||||||||||||||||||||
| Tens by Hundreds | ||||||||||||||||||||||||||||||||
| If we multiply tens by hundreds, the result is thousands.
|
ואם נרבה עשרות[45]עם מאות יהיה[46] העולה אלפים | |||||||||||||||||||||||||||||||
|
כגון כ' פעמים ב' מאות[47] | |||||||||||||||||||||||||||||||
|
דמיונם שהם ב' פעמים ב'[48] שהם ד' והם[49] ד' אלפים | |||||||||||||||||||||||||||||||
|
וכן נ' פעמי' ת"ק | |||||||||||||||||||||||||||||||
|
דמיונם ה' פעמי' ה'[50] שהם[51] כ"ה והם[52] כ"ה אלפים | |||||||||||||||||||||||||||||||
| The same for all. | וכן כלם | |||||||||||||||||||||||||||||||
| Hundreds by Hundreds | ||||||||||||||||||||||||||||||||
| If we multiply hundreds by hundreds the result is tens of thousands.
|
ואם נרבה מאות עם מאות יהיה העולה עשרות מאלפים | |||||||||||||||||||||||||||||||
|
כגון ר' פעמים ר'[53] | |||||||||||||||||||||||||||||||
|
דמיונם הם[54] ב' פעמים ב'[55] שהם[56] ד' [57]והם ד' עשרות מאלפים[58] | |||||||||||||||||||||||||||||||
|
וכן ת"ק פעמים ת"ק | |||||||||||||||||||||||||||||||
|
דמיונם ה' פעמים ה'[59] שהם כ"ה והם[60] כ"ה עשרות מאלפים | |||||||||||||||||||||||||||||||
| The same for all. | וכן כלם | |||||||||||||||||||||||||||||||
The Decimal Ranks[61] |
||||||||||||||||||||||||||||||||
| The ranks of numbers one above the other: | מדרגות המספרים זו למעלה מזו | |||||||||||||||||||||||||||||||
|
האחדים הם במדרגה הראשונה | |||||||||||||||||||||||||||||||
|
העשרות הם במדרגה השנית | |||||||||||||||||||||||||||||||
|
המאות הם במדרגה השלישית | |||||||||||||||||||||||||||||||
|
האלפים הם במדרגה הרביעית | |||||||||||||||||||||||||||||||
|
העשרות מהאלפים הם במדרגה החמישית | |||||||||||||||||||||||||||||||
|
המאות מהאלפים הם במדרגה השישית | |||||||||||||||||||||||||||||||
| So they rise from rank to rank. | וכן עולים ממדרגה למדרגה | |||||||||||||||||||||||||||||||
|
ואם נרצה לרבות[62] ת"ר[63] בד' אלפים | |||||||||||||||||||||||||||||||
|
דמיונם ו'פ'ד' שהם[64] כ"ד | |||||||||||||||||||||||||||||||
|
ואם תרצה לדעת אלו הכ"ד מה יורו קח מעלת המאות שהוא שלשה ומנה מן האלפים ג' מעלות והמעלה שתגיע אליה היא מעלת כ"ד ששמרת[65] והיא מעלת מאות האלפים[66] | |||||||||||||||||||||||||||||||
|
וכן אם אתה מונה מעלת האלפים והוא ד' ממעלת המאות אתה מגיע גם כן[67] אל מעלת מאות האלפים | |||||||||||||||||||||||||||||||
|
ותדע מכאן כי האחדים מהמספר אשר שמרת והוא כ"ד הוא ממעלת מאות האלפים ועשרותיו הם ממעלת אלפי האלפים[68] יהיו אם כן[69] כ"ד אשר שמרת ב' אלפי אלפים ות' אלף כי אחדיו הם ארבעה ועשרותיו הם ב' | |||||||||||||||||||||||||||||||
| Another method: consider [the positional values] of the two ranks and know their [sum]. Subtract 1 from it; the remainder is the rank of the product. | דרך אחרת תחשוב אישי [פי' אחדי'] ב' המעלות ותדע מספרם ותפחות מהם א'[70] והנשאר יהיה מעלת הנכלל | |||||||||||||||||||||||||||||||
|
כאלו תקח במשל הזה אוש המאות והוא ג' ואוש האלפים והוא ד' יהיו ז' ותפחות מהם א' וישארו ו' וזה המספר הוא אוש מאות האלפים | |||||||||||||||||||||||||||||||
Three Types of Numbers[71] |
||||||||||||||||||||||||||||||||
| The numbers are [of] three [types]: perfect number, abundant number, deficient number. | המספרים הם ג' מספר שלם מספר עודף מספר חסר | |||||||||||||||||||||||||||||||
| The perfect number, as the number 6, its parts divide it and complete it [= it is equal to the sum of its divisors]; they do not exceed it, nor less than it. Because its parts are a half, a sixth, and a third. If you sum them up, they are six, which is the same as it.
|
מספר שלם הוא כמו מספר ו' אשר חלקיו המונים אותו ממלאים אותו ואינם עודפים עליו ואינם[72] חסרים ממנו כי חלקיו הם חצי ושתות ושליש ואם תקבצם יהיו ששה כמוהו | |||||||||||||||||||||||||||||||
| The same for the number 28 - its parts are: one part of 28, one part of 14, a seventh, a quarter, and a half. If you sum them up, they are 28, which is the same as it. | וכן מספר כ"ח חלקיו הם חלק מכ"ח וחלק מי"ד ושביע ורביע וחצי ואם תקבצם יהיו כ"ח כמוהו | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| The abundant number, as 12, whose parts are one part of 12, a sixth, a third, a quarter, and a half. If you sum them up, they are 16. | ומספר עודף הוא י"ב שחלקיו הם חלק מי"ב ושתות ושליש ורביע וחצי ואם תקבצם יהיו כלם י"ו | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| The deficient number, as 14, whose parts are one part of 14, its half, and its seventh. If you sum them up, they are ten.
|
ומספר חסר כגון מספר י"ד שחלקיו הם חלק מי"ד וחציו ושביעו ואם תקבצם יהיו כלם עשר | |||||||||||||||||||||||||||||||
The Ten Numerals[73] |
||||||||||||||||||||||||||||||||
| The sages of India made the shapes of their digits like these: | וחכמי הודו עשו צורות אותיותם כמו אלו | |||||||||||||||||||||||||||||||
| [74]10 9 8 7 6 5 4 3 2 1 | ||||||||||||||||||||||||||||||||
The Method of Finding the Square Numbers[75] |
הסדר למצא המספרים המרובעים | |||||||||||||||||||||||||||||||
| It is that you sum the first square with the odd number that follows it and you will find the second square.
|
הוא שתקבץ המרובע הראשון עם המספר הנפרד הבא אחריו ותמצא המרובע השני | |||||||||||||||||||||||||||||||
|
כמו אם תקבץ האחד שהוא המרובע הראשון עם הג' שהוא ראש[76] הנפרדים[77] תמצא ד' שהוא המרובע השני אשר צלעו ב' | |||||||||||||||||||||||||||||||
|
ואם תקבץ ד' שהוא המרובע השני עם ה' שהוא הנפרד השני יהיו ט' והוא המרובע השלישי אשר צלעו ג' | |||||||||||||||||||||||||||||||
|
ואם אתה מוסיף על ט' שהוא המרובע השלישי המספר הנפרד השלישי שהוא[78] ז' תמצא י"ו שהוא המרובע הרביעי אשר צלעו ד' | |||||||||||||||||||||||||||||||
| This way you find all of them. | ועל זה הסדר תמצאם כלם | |||||||||||||||||||||||||||||||
Cubic Numbers[79] |
||||||||||||||||||||||||||||||||
| Anything whose length, breadth, and depth are equal is called cubic. | כל דבר שארכו ורחבו ועמקו שוים יקרא מעוקב | |||||||||||||||||||||||||||||||
|
והנה א' הוא המעוקב הראשון והוא מקום שארכו א' ורחבו א' וגבהו א' ועמקו א' | |||||||||||||||||||||||||||||||
|
וח' הוא המעקב השני היוצא ממקום שארכו ורחבו ועמקו ב' | |||||||||||||||||||||||||||||||
|
וכ"ז הוא המעוקב השלישי היוצא ממקום שארכו ורחבו ועמקו ג' | |||||||||||||||||||||||||||||||
|
וס"ד הוא המעקב הרביעי היוצא ממקום שארכו ורחבו ועמקו ד' | |||||||||||||||||||||||||||||||
|
וקכ"ה הוא המעוקב החמשי היוצא ממקום שארכו ורחבו ועמקו ועמקו ה' | |||||||||||||||||||||||||||||||
|
ורי"ו הוא המעוקב הששי היוצא ממקום שארכו ורחבו ועמקו ו' | |||||||||||||||||||||||||||||||
|
ושמ"ג הוא המעקב השבעי היוצא ממקום שארכו ורחבו ועמקו ז' | |||||||||||||||||||||||||||||||
|
ותקי"ב הוא המעוקב השמני היוצא ממקום שארכו ורחבו ועמקו ח' | |||||||||||||||||||||||||||||||
|
ותשכ"ט הוא המעוקב התשעי היוצא ממקום שארכו ורחבו ועמקו ט' | |||||||||||||||||||||||||||||||
|
ואלף הוא המעוקב העשרי היוצא ממקום שארכו ורחבו ועמקו י' | |||||||||||||||||||||||||||||||
| You see that every cubic number, [when it is] doubled, is 8 times the original [cubic] number.
|
והנך רואה כי כל מעוקב [זוג] יהיה ח' פעמי' מהמספר הראשון | |||||||||||||||||||||||||||||||
|
כי כל מעקב א' הוא א' | |||||||||||||||||||||||||||||||
|
ומעקב ב' שהוא כפל א' הוא ח' | |||||||||||||||||||||||||||||||
|
ומעקב ד' שהוא כפל ב' הוא ס"ד שהוא ח' פ' במעקב ב' | |||||||||||||||||||||||||||||||
|
וכן מעקב ו' הוא ח' פ' במעקב ג' | |||||||||||||||||||||||||||||||
| And so on. | וכן לעולם | |||||||||||||||||||||||||||||||
| Word Problem - Payment Problem | ||||||||||||||||||||||||||||||||
|
ולכן מי שיאמר חפור לי בור שיהיה ב' ארכו ב' רחבו ב' עמקו יהיה שכרו מ' ליט' שהוא ח' פעמי' ה' ליט' | |||||||||||||||||||||||||||||||
| Because every cubic number, when it is doubled, is 8 times the original [cubic] number. | כי כל מעקב כשיכפול יהיה ח' פעמים מהמספר הראשון | |||||||||||||||||||||||||||||||
Primary Definitions[80] |
||||||||||||||||||||||||||||||||
|
האחדות הוא הענין אשר בו קוראים לכל אחד מהנמצאי' בעולם אחד | |||||||||||||||||||||||||||||||
|
המספר הוא הרבוי הנקבץ מן האחדים | |||||||||||||||||||||||||||||||
|
המספר המנוי במספר אחר הוא מספר הנקבץ מכפל המספר המנוי פעמי' אשר מניינם כמניין האחדים אשר במספר השני אשר הוא נמנה בו | |||||||||||||||||||||||||||||||
|
המספר המרובע הוא המספר הנקבץ מכפל מספר במספר אחדיו הנמצאי' בו באותו המספר עצמו | |||||||||||||||||||||||||||||||
|
המספר הראשון הוא גדר המרובע | |||||||||||||||||||||||||||||||
|
כגון מספר תשעה נקרא מרובע מפני שהוא נקבץ מכפל השלשה שלשה פעמי' | |||||||||||||||||||||||||||||||
|
ומספר השלשה נקרא גדר המרובע | |||||||||||||||||||||||||||||||
|
והמספר מעקב הוא הגוף השוה שארכו ורחבו ועמקו שוים והמספר הזה הוא המספר הנקבץ מכפל מספר המרובע כמנין גדרו | |||||||||||||||||||||||||||||||
|
כגון מספר ט' שהוא 9 מרובע אם אתה כופל אותו במניין ג' שהוא גדרו יהיה הנקבץ מזה כ"ז והמספר הזה הוא הנקרא מספר מעוקב | |||||||||||||||||||||||||||||||
|
הקשת מניין אל מניין או תמונה לתמונה או ערך אחר כן השני | |||||||||||||||||||||||||||||||
Multiplication |
||||||||||||||||||||||||||||||||
Units and tens by units and tens |
||||||||||||||||||||||||||||||||
| The method of multiplying two digits by two digits | דרך רבוי ב' אותיות כנגד ב' אותיות[81] | |||||||||||||||||||||||||||||||
| When we wish to multiply two digits by two digits: | כשנרצה[82] לרבות ב' אותיות כנגד ב' אותיות | |||||||||||||||||||||||||||||||
| We multiply them three times one after another: first, we multiply the units by the units; then we multiply the units by the tens; and then we multiply the tens by the tens. | נרבה אותם ג' פעמי' זה אחר זה בראשונה נרבה האחדים עם האחדים | |||||||||||||||||||||||||||||||
| Here is the example of the [ordered] multiplications: | והנה דמיון הריבוי הקודם והמתאחר | |||||||||||||||||||||||||||||||
|
רצינו לרבות כ"ב פעמים כ"ב | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נרבה בתחילת האחדים זה עם זה ונאמר ב' פעמים ב' הם ד' ונכתוב ד' למעלה מן האחדים מצד ימין | |||||||||||||||||||||||||||||||
|
אחרי כן נרבה האחדים עם העשרות ונאמר ב' פעמי' ד' וב' פעמים ד' הרי ח' ונכתוב ח' | |||||||||||||||||||||||||||||||
|
אחרי כן נרבה העשרות זו עם זו ונאמר ב' פעמים ב' ד' ונכתוב ד' | |||||||||||||||||||||||||||||||
|
יצא לנו כי כ"ב פעמים כ"ב הם תפ"ד | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
וכן אם רצינו לרבות מ"ד פעמים מ"ד | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נרבה האחדים זה עם זה בתחילה ונאמר ד' פעמי' ד' הם י"ו ונכתוב ו' ונחזיק[85] בידינו העשרון שהוא א' | |||||||||||||||||||||||||||||||
|
אחר כן נרבה האחדים עם העשרות ונאמר ד' פעמי' ד' י"ו וד' פעמים ד' י"ו הרי ל"ב וצרף עמהם הא' שהחזקת בידך הרי ל"ג ונכתוב ג' ונחזיק בידינו ג' | |||||||||||||||||||||||||||||||
|
אחרי כן נרבה העשרות עם העשרות נאמר ד' פעמים ד' י"ו ועם הג' שהחזקנו בידינו הרי י"ט ונכתוב י"ט | |||||||||||||||||||||||||||||||
|
היוצא מזה כי מ"ד פעמים מ"ד הם אלף ות"תקל"ו | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
וכן אם רצינו לרבות כף פעמים כף | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נאמר ציפרא פעם ציפרא ציפרא ונכתבנה | |||||||||||||||||||||||||||||||
|
אחר כך נאמר ציפרא פעמים פעם ב' וב' פעמים ציפרא ציפרא ונכתבנה | |||||||||||||||||||||||||||||||
|
ואחר כך נאמ' ב' פעמים ב' הם ד' ונכתבם | |||||||||||||||||||||||||||||||
|
יצא לנו כי כ פעמים כ הם ארבע מאות | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Units by units and tens |
||||||||||||||||||||||||||||||||
| If we want to multiply one digit by two digits. | ואם רצינו לרבות אות אחד שנגד ב אותיות | |||||||||||||||||||||||||||||||
|
כגון שרצינו לדעת ז' פעמים מ"ה כמו שתראה בצורה | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נרבה אותם עם הציפרא כדי שיהיו ב' אותיות כנגד ב' אותיות ויעשה אותם בנקל | |||||||||||||||||||||||||||||||
|
ונאמר ה' פעמי' ז' ל"ה ונכתוב האחדים שהם ה' ונחזיק בידינו העשרות שהם ג' | |||||||||||||||||||||||||||||||
|
אחר כך נאמר ציפרא פע' ה' ציפרא וד' פעמים ז' כ"ח וצרף עמהם הג' שהחזקנו בידינו יהיו ל"א ונכתוב ל"א כי מעתה לא נשאר לנו לרבות דבר אחר | |||||||||||||||||||||||||||||||
|
כי ציפרא פעם ד' שנשאר לנו לרבות הוא ציפרא ואינם עולים לכלום | |||||||||||||||||||||||||||||||
|
יצא לנו כי ז' פעמים מ"ה הם שט"ו | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Check |
||||||||||||||||||||||||||||||||
| If we want to check if the number we received is correct: | ואם נרצה לבחון אם החשבון שיצא לנו הוא אמתי | |||||||||||||||||||||||||||||||
|
נעשה על זה הדרך בזה החשבון שהוא כ"ב פעמים כ"ב | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נקבץ הב' אותיות העליונות ונאמר ב' וב' הם ד' ונכתוב אותם אצל שתי האותיות התחתונות | |||||||||||||||||||||||||||||||
|
אחרי כן נרבה אלו שתי אותיות שכתבנו זו עם זו ונאמר ד' פעמי' י"ו | |||||||||||||||||||||||||||||||
|
נשליך מהם הט' ישארו ז' ונכתוב ז' בתוך שתי האותיות הנזכרות | |||||||||||||||||||||||||||||||
|
וכמו שנשארו בידינו ז' כן צריך שישארו בידינו ז' מן ת'פ'ד' שעולה החשבון אחר שנשליך מהם הט' | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
והנה אם נקבץ ד' וח' וד' שהם האותיות המורות ת'פ'ד' יהיו י"ו | |||||||||||||||||||||||||||||||
|
ואם נשליך מהם הט' ישארו | |||||||||||||||||||||||||||||||
|
וכן בחשבון השני שעשינו שהם מ"ד פעמים מ"ד | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נקבץ [86]האותיות העליונות ונאמר ד' וד' הם ח' ונכתבם | |||||||||||||||||||||||||||||||
|
ונרבה אותם זו עם זו ונאמר ח' פע' ח' הם ס"ד | |||||||||||||||||||||||||||||||
|
השליכם מהם ט' ט' ישאר מהם א' | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וכן צריך להשאר מאלף ת"תק'ל'ו' שסימנם הוא א' וט' וג' וו' | |||||||||||||||||||||||||||||||
|
ואם | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
Units, tens, and hundreds by units, tens, and hundreds |
||||||||||||||||||||||||||||||||
| If we want to multiply three digits by three digits. | ואם נרצה לרבות ג' אותיות כנגד ג' אותיות | |||||||||||||||||||||||||||||||
|
כגון שרצינו לדעת רכ"ב פעמים רכ"ב פעמים | |||||||||||||||||||||||||||||||
|
נרבה אותם ה' פעמים וזהו דרך ריבויים | |||||||||||||||||||||||||||||||
|
ונכתוב אותם ה' פעמים כדי שיתבאר למראית העין הרבוי הראשון והשני והשלישי והרביעי וחמשי | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
ואם נרצה לרבות רכ"ב פעמים רכ"ב | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נתחיל לרבות האחדים ונאמר ב' פעמים ב' הם ד' ונכתבם | |||||||||||||||||||||||||||||||
|
אחר זה נרבה האחדי' עם העשרות ונאמר ב' פעמי' ב' הם ד' וב' פעמים ב' הם ד' הרי ח' ונכתבם[87] | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
אחר זה נרבה שלשתם ביחד ונאמר ב' פעמים ב' ד' וב' פעמים ב' ד' הרי ח'[88] וב'פעמים ב' ד' הרי י"ב ונכתוב ב' ונחזי' בידינו א' | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
אחר זה נרבה העשרות עם המאות ונאמר ב' פעמים ב' ד' וב' פעמי' ב' ד' הרי ח' וא' שהחזקנו בידינו הרי ט' ונכתבם | |||||||||||||||||||||||||||||||
|
אחר זה נרבה המאות עם המאות ונאמר ב' פעמי' ב' ד' ונכתבם | |||||||||||||||||||||||||||||||
|
יצא לנו כי רכ"ב פעמים רכ"ב הם מ"ט אלפים ורפ"ד | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Check |
||||||||||||||||||||||||||||||||
| To check if the calculation is correct: | ולבחון אם החשבון אמת | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
קבצנו רכ"ב העליונים שסימנם ב'ב'ב' ועלו ו' וכתבנום אצלם | |||||||||||||||||||||||||||||||
|
רבינו ו' על ו' ועלו ל"ו | |||||||||||||||||||||||||||||||
|
השלכנו אותם ט'ט' ולא נשאר בידינו ונתננו ציפרא באמצעם | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וכן צריך להשאר הציפרא מן הסכום מן היוצא מן החשבון שהם מ"ט אלפים ורפ"ד אשר דמיונם הם ד' ט' ב' ח' ד' ועולה כ"ז[89] | |||||||||||||||||||||||||||||||
|
ואם תשליכם ט"ט ישאר ציפרא | |||||||||||||||||||||||||||||||
|
נמצא שהחשבון הוא אמת | |||||||||||||||||||||||||||||||
Units and tens by units, tens, and hundreds |
||||||||||||||||||||||||||||||||
| If we want to multiply two digits by three [digits]. | ואם רצינו לרבות ב' אותיות כנגד ג' | |||||||||||||||||||||||||||||||
|
כגון שרצינו לומר | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נשוה אותה עם הציפרא כדי שיהיו ג' אותיות כנגד ג' אותיות ויקל עשייתו | |||||||||||||||||||||||||||||||
Units by units, tens, and hundreds |
||||||||||||||||||||||||||||||||
| If we want to multiply one digit by three [digits]. | וכן אם רצינו לרבות אות[91] אחת כנגד שלשה | |||||||||||||||||||||||||||||||
| We match them also by [adding] zeros. | נשוה אותה עם הציפרא ג"כ | |||||||||||||||||||||||||||||||
|
כגון שרצינו לדעת ט' פעמים ר'כ'ב' | |||||||||||||||||||||||||||||||
|
נכתוב אותם בזה הדרך כאשר תראה בצורה | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Units, tens, hundreds, and thousands by units, tens, hundreds, and thousands |
||||||||||||||||||||||||||||||||
| If we want to multiply four digits by four digits. | אם[92] נרצה לרבות ד'[93] אותיות כנגד ד'[94] אותיות | |||||||||||||||||||||||||||||||
|
כג כגון שרצינו לרבות ב' אלפים ור'כ'ב' פעמי' ב' אלפים ור'כ'ב' | |||||||||||||||||||||||||||||||
|
נרבה אותם ז' פעמים ונכתוב אותם ז' פעמי'[95] כדי שיתבאר למעיין הקודם והמתאחר[96] | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
ואם רצינו לרבות ב' אלפי' ור'כ'ב' עם ב' אלפי' ור'כ'ב' | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
נעשה כאשר עשינו בחשבונו' הקודמי' | |||||||||||||||||||||||||||||||
|
ויעלה החשבון ד' אלפי אלפים ות'ת'ק'ל'ז' אלפי' ור'פ'ד' | |||||||||||||||||||||||||||||||
Units, tens, hundreds, and thousands by units, tens, and hundreds |
||||||||||||||||||||||||||||||||
| If we want to multiply four digits by three digits. | ואם רצינו לרבות ד' אותיות כנגד ג' אותיות | |||||||||||||||||||||||||||||||
|
כגון שרצינו לרבות ב' אלפים ור'כ'ב' כנגד ר'כ'ב' | |||||||||||||||||||||||||||||||
|
נשוה אותם עם הציפרא כאשר תראה בצורה | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
ועולים ת'צ'ג' אלפים ור'פ'ד' | |||||||||||||||||||||||||||||||
Units, tens, hundreds, and thousands by units and tens |
||||||||||||||||||||||||||||||||
| If we want to multiply two digits by four [digits]. | וכן אם רצינו לרבות ב' אותיות כנגד ד' | |||||||||||||||||||||||||||||||
|
כגון שרצינו לרבות ב' אלפים ור'כ'ב' כנגד כ"ב | |||||||||||||||||||||||||||||||
|
נשוה אותם עם הציפרא כאשר תראה בצורה | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
ועולים מ"ח אלפים ות'ת'פ'ד' | |||||||||||||||||||||||||||||||
Units, tens, hundreds, and thousands by units |
||||||||||||||||||||||||||||||||
| If we want to multiply one digit by four digits. | וכן אם רצינו לרבות אות אחד כנגד כנגד ד' אותיות | |||||||||||||||||||||||||||||||
|
כגון ב' עם ב' אלפים ור'כ'ב' | |||||||||||||||||||||||||||||||
|
נשוה אותם עם הציפרא כאשר תראה בצורה | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
ועולים ד' אלפים ות'מ'ד' | |||||||||||||||||||||||||||||||
Units, tens, hundreds, thousands, and tens of thousands by units, tens, hundreds, thousands, and tens of thousands |
||||||||||||||||||||||||||||||||
| If we want to multiply five digits by five digits. | אם נרצה לרבות ה' אותיות כנגד ה' אותיות | |||||||||||||||||||||||||||||||
|
כגון שרצינו לדעת כ"ב אלפים ור'כ'ב' כ"ב אלפי' ור'כ'ב' | |||||||||||||||||||||||||||||||
|
נרבה אותם ט' פעמים וזה דרך רבויים | |||||||||||||||||||||||||||||||
|
ונכתוב אותם ט' פעמי' כדי שיתבאר למעיין הקודם הקודם והמתאחר | |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Units, tens, hundreds, thousands, tens of thousands, and hundreds of thousands by units, tens, hundreds, thousands, tens of thousands, and hundreds of thousands |
||||||||||||||||||||||||||||||||
| If we want to multiply six digits by six digits. | ואם נרצה לרבות ו' אותיות כנגד ו' אותיות | |||||||||||||||||||||||||||||||
| We multiply them 11 times. | נרבה אותם י"א פעמי' | |||||||||||||||||||||||||||||||
|
כגון שרצינו לרבות ר'כ'ב' אלפי' ור'כ'ב' ר'כ'ב' אלפים ור'כ'ב' | |||||||||||||||||||||||||||||||
|
ונרבה אותם י"א פעמי' כדי שיתבאר למעיין הקודם והמתאחר | |||||||||||||||||||||||||||||||
|
The Method of Summing Up Separate Numbers Called Congregare or Riunire |
דרך קיבוץ חשבונות נפרדים הנקראים קונגרייג או ריונרייי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we want to sum up separate numbers and bring them into one sum, we do this way: we write them successively one beneath the other: the units beneath the units, the tens corresponding the tens, the hundreds corresponding the hundreds and the thousands corresponding the thousands. | אם רצינו לקבץ חשבונות נפרדים ולהביאם לסכום אחד נעשה על זאת הדרך שנכתוב אותם על הסדר זה תחת זה האחדי' תחת האחדים והעשרות נכח העשרות והמאות נכח המאות והאלפים נכח האלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We start summing the units and write [their sum]. | ונתחיל לקבץ האחדי' ולכותבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If [the sum] is more than ten, we write the units and keep the tens. | אם יעלו על עשר נכתוב האחדים ונחזיק בידינו העשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Then, we sum the hundreds, then the thousands, as you see in this diagram: | אחרי כן נקבץ המאות אחרי כן נקבץ האלפים כמו שתראה בצורה הזאת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[97]דמיון זה רצינו לקבץ י"ב[98] אלפים וש'מ'ה' וס"ז אלפי' ות'ת'צ'א' וכ"ג אלפים ת'נ'ו' וע"ח אלפים ות'ת'ק'י'ב' ול"ד אלפים ות'ק'ס'ז'[99] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נתחיל לקבץ האחדים ונאמר ה' וא' וו' וב' וז' הם כ"א נכתוב א' ונחזי' בידינו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקבץ אחרי כן העשרות ונאמר ד' וט' וה' וא' וו' הם כ"ה וב' שהחזקנו בידינו הם כ"ז נכתו' ז' ונחזיק בידינו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקבץ אחרי כן המאות ונאמ' ג' וח' וד' וט' וה' הם כ"ט וב' שהחזקנו בידינו הרי ל"א נכתוב א' ונחזיק בידינו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקבץ אחרי כן האלפים ונאמר ב' וז' וג' וח' וד' הם כ"ד וג' שהחזקנו בידינו הרי כ"ז ונכתוב ז' ונחזיק בידינו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקבץ אחר זה העשרות מן האלפים ונאמ' א' וו' וב'[100] וז' וג' הם י"ט[101] וב' שהחזקנו בידינו הרי כ"א נכתוב אותם כלם כי אין לנו לקבץ חשבון אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עלו כלם רי"ז אלפים וקע"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we want to sum up numbers, some of which have three digits, some have four, some have two, and some have more or less: | ואם רצינו לקבץ חשבונות נפרדים שקצתם הם מג' אותיות וקצתם מד' וקצתם מב' וקצתם מיותר או פחות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We always write the units corresponding to the units, the tens corresponding to the tens and so on and we match them by [adding] zeros to make the procedure easier. | נכתוב לעולם האחדים נוכח האחדי' והעשרות נוכח העשרות וכן כלם ונשוה אותם עם הציפרי כדי שיקל העניין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה רצינו לקבץ י"ב אלפים וש'מ'ה' וו' אלפים ות"שפ"ט וקכ"ג ומ"ה אלפים ות"ר ופ' אלפי' ות"תקי"ב וג' אלפים ות"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
התחלנו לקבץ האחדים ואמרנו ה' וט' וג' וב' וו' הם כ"ה כתבנו כ"ה והחזקנו בידינו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קבצנו אחר כן[102] העשרות ואמרנו ד' וח' וב' וא' הם ט"ו ועם הב' שהחזקנו בידינו הם י"ז כתבנו ז' והחזקנו בידינו א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קבצנו אחרי כן המאות ואמרנו ג' וז' וא' וו' וט' וד' הם ל' ועם הא' שהחזקנו בידינו הם ל"א כתבנו א' והחזקנו בידינו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קבצנו אחרי כן האלפים ואמרנו ב' וו' וה' וג' הם י"ו ועם הג' שהחזקנו בידינו הם י"ט כתבנו ט' והחזקנו בידינו א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קבצנו אחר זה העשרות מן האלפי' ואמרנו א' וד' וח' הם י"ג ועם א' שהחזקנו בידינו הם י"ד[103] וכתבנו י"ד כי מעתה קבצנו הכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועולה סכומם קמ"ט אלפים וקע"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The Method of Subtracting a Number from a Number Called Sottrarre |
דרך הוצאת מספר ממספר הנק' סורטראיירי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we want to subtract a number from a number: | אם רצינו לגרוע מספר ממספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If all the [digits] of the larger number, from which you want to subtract another number, are greater than the [digits] of that number, the procedure is easy. | אם המספר הגדול אשר אתה רוצה לגרוע ממנו מספר אחר כל חלקיו גדולי' מחלקי המספר הוא דרך נקל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה רצינו לגרוע מתת"קפ"ז אלפים ותרנ"ד ת"רמ"ה אלפים ורל"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נעשה על זה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נתחיל מן האחדים ונאמר מד' הוצא ב' ישארו ב' ונכתוב ב' תחתיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן ה' הוצא ג' ישארו ב' ותכתוב ב' תחתיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן ו' הוצא ב' ישארו ד' ותכתוב ד' תחתיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן ז' תוצא ה' ישארו ב' ונכתוב ב' תחתיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן ח' הוצא ד' ישארו ד' ונכתוב ד' תחתיהם[104] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן ט' הוצא ו' ישארו ג' ותכתוב ג' תחתיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הרי שאם נוציא מת"תק'פ'ז' אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check - addition: If you want to check if your calculation is correct, sum the digits you subtracted with the digits that remained and if [their sums] are the same as the digits from which you subtracted the other digits, it is correct. | ואם תרצה לבחון אם החשבון שעשית הוא אמתי תקבץ המספרים שהוצאת עם המספרים שנשארו ואם יסכימו עם המספרים שהוצאת המספרים האחרי' ההם הוא אמתי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה קבצנו ב' עם ב' והיו ד' וקבצנו ג' וב' והיו ה' וקבצנו ב' עם ד' והיו ו' וקבצנו ה' עם ב' והיו ז' וקבצנו ד' עם ד' והיו ח' וקבצנו ו' עם ג' והיו ט' והם מסכימים עם המספרים הגדולים אשר הוצאת ממספר הקטנים מהם וזה יורה כי החשבון הוא אמתי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you want to subtract a number from a number, but some of the digits of the smaller number that you want to subtract from the greater number are greater than some of the [corresponding] digits of the greater number, you should use another procedure: | אמנם אם תרצה לגרוע מספר ממספר ויהיו קצת חלקי המספר הקטן שאתה רוצה לפחות מהמספר הגדול גדולים מקצת מספר חלקי המספר הגדול אתה צריך לעשות על דרך אחרת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה רצינו לגרוע מצ"ג אלפים ותל"ב כ"ז אלפים ות"רנ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נתחיל מן האחדי' ותאמר מב' תוצי' ד' לא נוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נפחות א' מן הג' שבצדה ונחבר אותה אל הב' ויהיו י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר מי"ב הוצא ד' ישארו ח'[105] ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחזור אל הג' שפחתנו ממנו א' וישארו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר מב' הוצא ה' לא נוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נפחות א' מהד' אשר בצדה ונאמר מי"ב הוצא ה' ישארו ז' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחזור אל הד' שפחתנו ממנה א' ונשארו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר מג' הוצא ו' ולא נוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נפחות א' מן הג' אשר בצדה ונאמר מי"ג הוצא ו' וישארו ז' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחזור אל הג' שפחתנו ממנו א' ונשארו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר מב' הוצא ז' לא נוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נפחות א' מן הט' אשר בצדה ונאמר מי"ב הוצא ז' ישארו ה' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחזור אל הט' אשר פחתנו ממנה א' ונשארו ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר מח' הוצא ב' ישארו ו' ונכתבנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הרי שהוצאנו מצ"ג אלפים ותל"ב כ"ז אלפים ות"רנ"ד[106] ונשארו ס"ה אלפים ות"שע"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check - addition: If you sum what you subtracted from the mentioned number with the remainder, it will be the same as the original number. | והנה אם תקבץ מה שהוצאתו מהמספר הנזכר עם הנשאר יהיה כמספר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שאם נקבץ ד' וח' יהיו י"ב ונכתוב ב' ונחזיק בידינו א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם נקבץ ה' וז' יהיו י"ב ועם הא' שנשארה בידינו יהיו י"ג ונכתוב ג' ונחזיק א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם נקבץ ו' וז' יהיו י"ג וא' שנשאר בידינו הרי י"ד ונכתוב ד' ונחזיק א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם נקבץ ז' וה' יהיו י"ב וא' שנשאר בידינו הרי י"ג ונכתוב ג' ונחזיק א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם נקבץ ב' וו' יהיו ח' וא' שנשאר בידינו הרי ט' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הרי שהמספר האחרון שוה עם הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The method of division. | דרך חילוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The Method of Dividing a Number by a Number Called Dividere or Partire |
[107]דרך חילוק מספר על מספר הנק' דיבי' או פארטיר' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we want to divide a larger number by a smaller number: | אם נרצה לחלוק מספר גדול על מספר קטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If all the digits of the large number are larger than the number by which you want to divide them, the procedure is easy. | אם כל חלקי המספר הגדול הם גדולי מהמספר שאתה רוצה לחלק אותם בו הוא דרך נקל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה רצינו לחלק צ"ח אלפים ות'ש'נ'ו' על ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נעשה בזה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נתחי' מן המספר הגדול ונאמר נחלק ט' על ד' יהיו ב' ונכתבם וישאר בידינו א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואותו הא' נחבר עם הח' הסמוך לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר נחלק י"ח על ד' יהיו ד' ונכתבם וישארו בידינו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואלו הב' נחבר עם הז' הבא אחריו ויהיו כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחלקם על ד' ויהיו ו' ונכתבם וישארו בידינו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואילו הג' נחבר עם הבא אחריו ויהיו ל"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחלקם על ד' יהיו ח' ונכתבם וישארו בידינו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואילו הג' נחבר עם ו' הבא אחריו ויהיו ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחלקם על ד' ויהיו ט' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הרי שחלקנו צ"ח אלפים ותשנ"ו על ד' ועלו כ"ד אלפי' ות"רפ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we had 1, or 2, or 3 left at the end, they were parts of the 4 by which we divided the number. | ואם היה נשאר בידינו באחרונה א' או ב' או ג' היו חלקי' מד' שחלקנו עליו החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אלו רצינו לחלק החשבון ח' אלפים ותת"קע"ו על ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נעשה על זה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר חלק ח' על ה' יהיה א' ונכתבנו ישאר ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואילו הג' נחבר עם הט' הבא אחריו ויהיו ל"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחלקם על ה' יהיו ז' ונכתבם וישארו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואלו הד' נחברם עם הז' הבא אחריו יהיו מ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחלקם על ה' ויהיו ט' ונכתבם וישארו בידינו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואלו הב' נחברם עם ו' הבא אחריו ויהיו כ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחלקם על ה' ויהיו ה' ונכתבם וישאר בידינו א' ונכתבנו על ה' אשר חלקנו עליו החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהי היוצא מן החלוקה הנזכר' אלף ות"שצ"ה וא' חומש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we want to divide a number by a number and the digits of the number you want to divide are smaller than the number by which you want to divide them, you should do this way: | אמנם אילו רצינו לחלק מספר על מספר וחלקי המספר שאתה רוצה לחלק קטנים מהמספר שתרצה לחלקם בו אתה צריך לעשות על זה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה רצינו לחלק י"ב אלפי' ושמ"ה על ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמרנו חלק א' על ט' לא נוכל[108] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחבר א' עם הב' הבא אחריו ויהיו י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על ט' יהיה א' ונכתבנו וישארו בידינו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחברם עם הג' הבא אחריו ויהיו ל"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם בט' ויהיו ג' ונכתבם וישארו בידינו ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחבר אלו הו' עם הד' הבא אחריו ויהיו ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם בט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחבר הא' עם הה' הבא אחריו יהיו ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר חלק ט"ו בט' יהיו א'[109] וישארו בידינו ו' ונכתוב אותם על[110] הט' אשר בו חלקנו כל[111] החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והיוצא מזה הוא שאם נחלק י"ב אלפים וש'מ'ה' על ט' יהיה היוצא מן החלוקה[112] אלפים וש'ע'א' וו' תשיעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check: If you want to check if our calculation is correct, we do as follows: | ואם תרצה לבחון אם החשבון שעשינו הוא אמתי נעשה על זה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We sum up the digits of the dividend, cast out the nines and keep the remainder. | היינו שנקבץ המספרים המחולקים ונשליכם ט' ט' ומה שנשאר נחזיק בידינו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Then, we sum up [the digits of] the result of division, cast out the nines and multiply what we received by the divisor. | אחר כן נקבץ מה שעלה בידינו בחלוק ונשליכם ט' ט' ומה שעלה בידינו נרבה אותו עם המחלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We cast out the nines from the product we received. | ומה שעלה בידינו מהרבוי נשליכם ט' ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the calculation is correct, we receive the same as what we received when we summed the digits of the dividend. | ואם החשבון הוא אמתי יעלה בידינו כמו שעלה בידינו בקבצנו המספרים המחולקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה הדמיון נעשו בחשבון שכתבנו לעיל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
היינו בתחלה נקבץ המספרי' המחולקים ונאמ' ו' וה' ז' וח' וט' בין כלם ל"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשליכם ט' ט' ישארו ח' ונכת' ונכתבם אצל המספרי' המחולקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן נקבץ מה שעלה בחלוק ונאמ' ט' וח' וו' וד' ב' בין כלם כ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשליכם ט' ט' וישארו ב' ונכתבם אצל מה שעלה בחלוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן נרבה אותו עם המחלק ונאמ' ב' פעמי' ד' ח' והנה עלה בידינו מה שעלה בקבצנו המספרי' המחולקים אם כן החשבון אמתי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If 1, or 2, or 3 remains from the division [procedure], we do this way: | ואם ישארו מן החלוק א' או ב' או ג' נעשה על זה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| After we sum up [the digits of] the result of division and cast out the nines, we add [what remains] to what we have left [= to the remainder from the division]. | וזה שקבצנו אחר מה שעלה בחלוק והשלכנו אותם ט' ט' נקבצם עם מה שנשאר בידינו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the calculation is correct, what we receive is the same as what we received when we summed the digits of the dividend. | ואם החשבון אמתי יעלה בידינו כמו שעלה בידינו בקבצנו המספרים המחולקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה הדמיון נעשו כחשבון השני שכתבנו למעלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
היינו בתחלה נקבץ המספרי' המחולקים ונאמר ו' וז' וח' וט' בין כלם ל' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשליכם ט' ט' וישאר בידינו ג' ונכתבנו אצל המספרי' המחולקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן נקבץ מה שעלה בידינו בחלוק ונאמר ה' וט' וז' וא' בין כלם כ"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשליכם ט' ט' וישאר בידינו ד' ונכתבנו אצל מה שעלה בחלוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן נרבה אותו עם המחלק ונאמ' ד' פעמי' ה' הם כ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשליכם ט'ט' וישאר בידינו ב' ונחבר עם הב' הא' שעלה בידינו מן החלוק הכתוב על ה' ויהיו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה שעלה בידינו כמו שעלה בידינו בקבצנו המספרים אם כך הוא החשבון אמתי[113] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Another method of dividing a number by a number | דרך מספר על מספר בדרך אחרת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| If we want to divide a known number by another number and it is difficult for us to divide it by this number, we divide it twice and we receive as if we divided it once by that number. | [114]אם נרצה לחלק מספר ידוע על מספר אחר ויקשה עלינו לחלקו על המספר ההוא נחלק אותו ב' פעמים ויעלה בידינו כאלו חלקנוהו פעם אחת על המספר ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה רצינו לחלק פ"ט אלפים ות"שס"ה על י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה אם חלקנוה על י"ב בפעם אחת יעלה ז' אלפים ות"פ וה' חלקים מי"ב וזה סדר עשייתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמרנו חלק ח' על י"ב לא נוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחבר אל ח' הט' הבא אחריו יהיו פ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם בי"ב יהיו ז' ונכתבם וישאר בידינו ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחבר אליה ז' הבא אחריו ויהיו נ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקים בי"ב יהיו ד' ונכתבם וישארו בידינו ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחבר אליהם ו' הבא אחריו יהיו צ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקים בי"ב יהיו ח' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר חלק ה' על יב לא נוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותכתוב ציפרא תחת הה' וה' תכתוב על י"ב יהיו ז' אלפים ותש"פ וה' חלקים מי"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם נרצה לחלק זה החשבון בעצמו בעניין אחר נחלק אותו על ג' פעם אחת והעולה נחלק אותו על ד' ויהיה נחלק לי"ב חלקים ג"כ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב זה החשבון שנית ונחלקנו על ג' בתחילה ואחר זה נחלקנו על ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר ח' חלק אותו על ג' יהיו ב' ונכתבם וישארו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחבר[115] אותם עם ט' הבא אחריו ויהיו כ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם בג' יהיו ט' ונכתבם וישארו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחברם עם הז' הבא אחריו ויהיו כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחלקם על ג' יהיו ט' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר אחר זה ו' חלק בג' יהיו ב' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר אחר זה ה' חלק בג' יהיו א' ונכתבנו וישארו ב' ונכתבם על הג' אשר בו חלקנו זה המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר זה נחלק זה המספר שעלה בידינו מן החלוקה על ד' ונאמר חלק ב' בד' לא נוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חבר ב' עם הט' הבא אחריו יהיו כ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם בד' יהיו ז' ונכתבם וישאר בידינו א'[116] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחבר א' עם הט' הבא אחריו יהיו י"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם בד' יהיו ד' ונכתבם וישארו בידינו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחברם עם הב' הבא אחריו ויהיו ל"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחלקם בד' יהיו ח' ונכתבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחלק א' בד' ולא נוכל ונכתוב ציפרא[117] תחת הא' והא' שלא נוכל לחלקה בד' נכתוב אותה על הד' אשר עליה נחלק החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הרי שחלקת החשבון בג' וד' והוא כאלו חלקתו בי"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבה אחר זה הא' שעל הד' עם הג' ואמור א' פעם ג' ג' וב' שעל הג' הרי ה' והם ה' חלקים מי"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
היוצא מדברינו שאם נחלק בראשונ' על ג' והיוצא נחלק על ד' על הדרך שעשינו יעלה מן החלוקה ז' אלפי' ות"פ וה' חלקים מי"ב כאשר עלה בידינו בעת שחלקנוהו פעם אחת על י"ב וזה מבואר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The Method of Knowing the Numbers Summed One after the Other Successively |
[118]דרך ידיעת המספרים המקובצים זה אחר זה על הסדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם יאמר אדם א' וב' וג' וד' וה' וו' וז' וח' וטי' וי' כמה שוי בין כלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You should understand, if the last term is an even number as this number or similar to it, always add one to the last term and multiply it by half the last term.
|
יש לך להבין אם המספר האחרון הוא מספר זוג כמו זה מספר והדומה לו תוסיף מספר אחד לעולם על הי' המספר האחרון ותרבה אותו על חצי המספר האחרו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמור החצי מי' הוא ה' ותרבה אותו על י"א ה' פעמי' י"א נ"ה וכן יהיו המספרים הנזכרי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הלך בשאלתו עד י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ו'[119] פעמי' י"ג ע"ח[120] יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הלך בשאלתו עד כ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור י' פעמים כ"א וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הלך עד מאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור נ' פעמים ק"א וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Always calculate this way when the last term is even. | ואתה תחשוב לעולם בזה הדרך כשיהיה מספר האחרון זוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the last term is an odd number, multiply the greater half of this last term by the whole last term.
|
ואם יהיה מספר האחרון מספר נפרד תרבה הרוב מהמספר ההוא האחרון על כל המספר האחרון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון האומר הלכתי בחשבוני עד ז' כמה יהיו כלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור הרוב מז' הם ד' תרבה אותם על | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם הלך בשאלתו עד ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור הרוב מט' הוא ה' מנה אותם בט' יהיו מ"ה וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הלך עד י"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תרבה ט' על[121] י"ז וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הלך עד י"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תרבה י' עם י"ט וכן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sum of Evens |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If he says: I summed all the even numbers successively. | ואם יאמר קבצתי מספרים כלם זוגות על הסדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ב' וד' וו' וח' וי' וי"ב כמה יהיה בין כלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiply half the last term by the number that follows this half. | תרבה החצי מן המספר האחרון על המספר אשר אחרי החצי ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמור החצי מי"ב הוא ו' והמספר שהוא אחר ו' הוא ז' ו' פעמים ז' הם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם אומר הלכתי עד עשרי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור החצי מעשרי' הוא י' והמספר שאחר י' הוא י"א י' פעמים הם ק"י וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Always calculate this way. | ועל זה הדרך תחשוב לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sum of Odds |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If he says: I summed all the odd numbers successively. | ואם יאמר קבצתי מספרים כלם נפרדי' על הסדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון א' וג' וה' וז' וט' כמה הם בין כלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Take the greater half of the last term and multiply it by itself. | קח הרוב מהמספר האחרון ותרבה הרוב בעצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמור הרוב מט' הוא ה' וה' פעמים ה' הוא כ"ה וכן יהיו כלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הלך בשאלתו עד י"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ו' פעמי' ו' וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הלך עד י"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ז' פעמי' ז' וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Always calculate this way. | ועל זה הדרך תחשוב לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sum of Powers of Two |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If a man says: I summed the doubles to each other.
|
ואם יאמר אדם קבצתי מספרים כפולי' זה על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון א' וב' וד' וח' וי"ו ול"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| He starts with whichever [number] he wants to start and ends with whichever number he wants to end: double the last term and subtract the first term.
|
בכל מקום שירצה להתחיל יתחיל ובכל חשבון שיחפוץ לסיים יסיים כפול המספר האחרון וחסר המספר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה האומר קבצתי מספרים כפולי' מא' ועד ל"ב כמה הם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואתה כפול ל"ב שהוא המספר האחרון ויהיו ס"ד וחסר המספר הראשון שהוא א' וישארו ס"ג[122] וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יאמ' התחלתי מא' וכפלתי עד ס"ד[123] כמה יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יאמר התחלתי מאחד וכפלתי עד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול קכ"ח יהיו רנ"ו חסר א' יהיה רנ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יאמר התחלתי מד' וכפלתי עד ל"ב כמה יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול ל"ב יהיה ס"ד חסר ד' יהיו ס' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The procedure is to double the last and subtract the first. | והחשבון המסור לזה לכפול הא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sum of Powers of Three |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If a man asks about [the sum of] the triples to each other.
|
[124]ואם ישאל אדם על מספרי' משולשים זה על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון א' ג' ט' כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| He adds to the last its half after subtracting the first, with which he starts, then adds the first to it. | יוסיף על האחרון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דהיינו שיגרע מכ"ז שהוא המספר האחרון המספר הראשון שהוא א' ישארו כ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יאמר כ"ו וחציו שהוא י"ג הם ל"ט וא' שהוא החשבון הראשון הרי מ' וכן הם א'ג'ט' כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sum of Powers of Four |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If he asks about the quadruples.
|
ואם ישאל על מספרי מרובעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון א' ד' י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| He adds to the last its third after subtracting the first, then adds the first to it.
|
יוסיף על האחרון שליש אחר גרעון הראשון ועוד יוסיף הראשון עמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה א' ד' י"ו הם כ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המספר האחרון הוא י"ו חסר המספר הראשון א שהוא א' ישארו ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוסף על ט"ו שלישו שהוא ה' יהיו כ' הוסף עליהם המספר יהיו כ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on. | וכן לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The rule:
|
והכלל המסור לזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For the triples he adds a half.
|
למשולש יוסיף החצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For the quadruples he adds a third.
|
ולמרובע יוסיף השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For the quintuples he adds a quarter.
|
ולמחומש יוסיף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For the sextuples he adds a fifth.
|
ולמשושה יוסיף החומש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| It is always done this way. | ועל הדרך הזה יעשה לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Motion Problems - Pursuit |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם יאמר אדם אחד הולך בכל יום ויום י' מילי' ואדם אחר הולך ביום אחד א' מיל וביום ב' ב' מילי' וביום ג' ג' מילים וביום ד' ד' מילי' וכן מוסיף והולך בכל יום ויום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אתה כפול הי' מילי' שמהלך אותו שמהלך בכל יום ויום י' מילין ויהיו כ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תפחות מהם א' ישארו י"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נמצא שבי"ט יעמדו בשוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שצד אותו שמהלך בכל יום י' מילי' בי"ט ימים יהלך ק"צ מילי' כמניין י' על י"ט שהם ק"צ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואותו שמוסיף בכל יום מיל אחד בי"ט ימים יהלך ג"כ ק"צ מילין כיצד תפוש הרוב מי"ט והם י' ותכפול אותו על י"ט ויהיה ק"צ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Always double the [number] of miles that the one who walks the same distance [each day] walks, then subtract one from it and this is the number of days, in which they walk the same [total distance].
|
וכן לעולם תכפול המילי' שמהלך המילי' שמהלך הקבוע ותפחות מהם אחד וכמספרם יהיו הימים שיעמדו בשוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יאמר אדם אחד הולך בכל יום י' מילי' ואדם[125] אחר הולך ביום אחד ב' מילין וביום שני ד' וביום שלישי ו' וביום רביעי ח' וכן לעולם הוא מוסיף ב' והולך על הסדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אתה תפחות אחת מן המילין שמהלך הקבוע בכל יום ישאירו ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נמצא שבט' ימים יעמדו בשוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כיצד אותו שמהלך בכל יום י' מילין בט' ימים מהלך צ' מילי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואותו שמהלך זוגות ר"ל ב' וד' וו' וח' וי' וי"ב וי"ד וי"ו וי"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור החצי מי"ח הם ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תרבה אותם עם י' שהוא החשבון הבא אחר ט' יהיו צ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נמצא שבט' ימים יעמדו בשוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Always subtract [one] from the [number] of miles that the one who walks the same distance [each day] walks and this is the number of days, in which they walk the same [total distance].
|
וכן לעולם תפחות מן המיל' שמהלך הקבוע וכמספרם יהיו הימים יעמדו בשוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יאמר אדם אחד הולך בכל יום י' מילי' ואדם אחר הולך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that the number of miles that the one who walks the same [distance] [each day] walks each day is the same as the number of days, in which they walk the same [total distance].
|
דע כי כמספר המילין מהלך ק הקבוע בכל יום כן מספר הימים שיעמדו בשוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דהיינו בי' ימים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי אותו שמהלך בכל יום י' מילי' [126]מהלך בי' ימי' ק' מילי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואותו שמהלך ביום אחד א' מיל וביום שני ג' מילי' ומוסיף והולך על הדרך הזה ביום העשירי מהלך י"ט מילי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והרוב מי"ט הוא י' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תרבה י' בעצמם הוא ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Do this way for any number you want. | ועל זה הדרך תעשה לכל חשבון שתרצה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Word Problems - The Rule of Three |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| General Rule - A Selection of all the Rules in the World | ריגולא כללית והיא מבחר כל הריגולא שבעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pricing Problems |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Find the Price | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם יאמ' אדם ג' ביצות שוי ד' פשיטים ה' ביצות לזה החשבון כמה פשיטים עולי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עשה על זה הדרך שתחזיר החשבון לאחורנית הוא שואל אם ג' שוה ד' ה' כמה שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואתה אמור ה' פעמים ד' חלקם בג' יהיו ו' וב' שלישיו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם שואל אם ה' שוה ז' ט' כמה שוי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ט' פעמים ז' ס"ג חלקם בה' וכן יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם יאמר י"א שוים י"ז ל"א לזה החשבון כמה שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ל"א פעמים י"ז וחלקם בי"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| It is always this way. | וכן על זה הדרך לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם יאמ' י' כורי' שוי' ו' דינרי' ד' כורי' לחשבון זה כמה שוי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ד' פעמי' ו' כ"ד חלקם בי' יבואו ב' וד' עשיריות שהם ב' דינרי' וב' חומשי דינר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם יאמר ג' עמרים שוי ד' דינרי' י' עומרי' לחשבון זה כמה הם שוי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור י' פעמים ד' מ' חלקם בג' יהיו י"ג דינרי' ושליש דינר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Find the Amount | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור אם יאמר קניתי י' כורי חטה בו' דינרי' כמה כורי' אוכל ליקח בד' דינרי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור אם בו' דינרי' נמצא י' כורי' חטה בד' דינרי' כמה כורי' נמצא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ד' פעמי' י' מ' חלקם בו' יהיו ו' וד' ששיות שהם ו' וב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם יאמר שש כורי' שוי' ד'[127] דינרי' כמה כורי אוכל לקנות בז' דינרי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור אם ד' דינרי' שוי' ו' כורי' ז' דינרי' כמה כורי' שוי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ז' פעמים ו' מ"ב חלקם בד' יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Employment Problems - Payment Problems |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The same for the issue of employment. | וכן לעניין השכירות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון האומר שכרתי פועל לל' יום בי' זוזים ועשה עמי ח' ימים כמה שכרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור אם בל' יום יהיה שכרו י' זוז בח' ימים כמה שכרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור ח' פעמים י' הם כזה פ' חלקם בל' יבואו ב' זוזי' וכ' חלקי' מל' שהם ב' וב' שלישיות שהם ג' דינרי' פחות שליש דינר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Calculation of Fractions |
חֶשְׁבּוֹן הַשְׁבָרִים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם תחלק האחד בב' חלקים יהיה בכל חלק מהם חצי ושני החצאי' הם אחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם החלק האחד בג' חלקי' יהיה כל חלק מהם שליש ושלש השלישיות הם אחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם תחלק האחד בד' חלקי' יהיה כל אחד מהם רביע וד' הרביעיי' הם אחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This way for all. | ועל זה הדרך הם כלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Addition of Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![\scriptstyle{\color{OliveGreen}{\frac{1}{a}+\frac{1}{b}=\frac{\left[\frac{1}{a}\sdot\left(a\sdot b\right)\right]+\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}}}](/mediawiki/images/math/2/6/4/264a022ee3bfdc1d622c23b20b6c5ffe.png)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יאמ' מי שיש לו החצי והשליש מדבר אחד כמה חלק יש לו מן הדבר ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור חצי ושליש [128]ימצא בב' פעמים ג' שהם ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חציי ג' ושלישיתו ב' ואם תקבצו יהיו ה' הרי שאותו שיש לו החצי והשליש מן הדבר יש לו ה' חלקי' מו' מן הדבר ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם מי שיש לו השליש והרביעי מן הדבר כמה חלק יש לו ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור שליש ורביע ימצא בג' פעמים ד' שהם י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השליש מהם הם ד' והרביעי הוא ג' ואם תקבצם הם ז' הרי שמי שיש לו השליש והרביע מן הדבר יש לו ז' חלקי' מי"ב מן הדבר ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן מי שיש לו השליש והחומש מן הדבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור שליש וחומש ימצא בג' פעמים ה' שהם ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השליש מהם הוא ה' והחומש ג' ושניהם יחד הם ח' אם כן מי שיש לו השליש והחומש מן הדבר יש לו ח' חלקים מט"ו מן הדבר ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן מי שיש לו הרביע והחומש מן הדבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור רביע וחומש ימצא בד' פעמי' ה' שהם כ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הרביע הוא[129] ה' והחומש הוא ד'[130] ושניהם יחד הם ט'[131] אם כן יש לו ט' חלקים מכ' מן הדבר ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן מי שיש לו שליש ושביע מן הדבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור שליש ושביע ימצאו בג' פעמים ז' שהם כ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השליש ז' והשביעי ג' ושניהם יחד הם י' א"כ יש לו י'[132] חלקי' מכ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן מי שיש לו שליש ורביע וחומש ושתות מן הדבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור שליש ורביע וחומש ושתות אם ימצאו בס' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השליש הוא כ' הרבי' ט"ו והחומש י"ב והשתות י' ואם תקבצם יהיו נ"ז הרי שיש לו נ"ז חלקים מס' מן הדבר ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subtraction of Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![\scriptstyle{\color{OliveGreen}{\frac{1}{a}-\frac{1}{b}=\frac{\left[\frac{1}{a}\sdot\left(a\sdot b\right)\right]-\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}}}](/mediawiki/images/math/c/0/6/c0629aecee310d90e051b57b2c593d46.png)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמנם אם יאמר אדם כמה הוא יותר השליש מן הרביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עשה על זה הדרך אמור שליש ורביע ימצאו בג' פעמי' ד' שהם י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השליש הוא ד' והרביעי הוא ג' כמה יותר ד' שהוא השליש מג' שהוא הרביעי א' א"כ השליש הוא יותר מן הרביע א' חלק מי"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם יאמר אדם כמה הוא יותר הרביע מן החומש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור רביע וחומש ימצאו בד' פעמי' ה' שהוא כ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הרביעי הוא ה' והחומש הוא ד' כמה הוא יותר ה' מד' א' אם כן הרביע הוא יותר מן החומש א' חלק מעשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם יאמר כמה הוא יותר השליש מן השביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור שליש ושביע ימצאו בג' פעמים ז' שהם כ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השליש הוא ז' השביע הוא ג' כמה הוא יותר ז' על ג' ד' וא"כ השליש יותר מן השביע ד' חלקי' מכ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יאמר כמה הם יותר השליש והרביע מן החומש ושתות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור שליש ורביע וחומש ושתות ימצאו בס' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השליש הוא כ' הרביע ט"ו אם תקבצם יהיו ל"ה והחומש מס' הוא ל"ב י"ב השתות י' אם תקבצם יהיו כ"ב כמה הם יותר ל"ה שהם השליש והרביע מכ"ב שהם החומש והשתות י"ג אם כן השליש והרביע הם יותר מן החומש והשתות י"ג חלקים מס' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fractions of Fractions |
|||||||||||||||||||||||||||
![\scriptstyle{\color{OliveGreen}{\frac{1}{a}\sdot\frac{1}{b}=\frac{\frac{1}{a}\sdot\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}}}](/mediawiki/images/math/6/a/0/6a0cf9b7b8a099931ff2b5d1e5906c1a.png)
|
|||||||||||||||||||||||||||
|
אמנם אם יאמר מי שיש לו השליש מן הרביע מן הדבר כמה חלק יש לו ממנו | ||||||||||||||||||||||||||
|
אמור שליש ורביע ימצא בי"ב | ||||||||||||||||||||||||||
|
ומי שיש לו הרביע מי"ב יש לו ג' חלקים מי"ב ומי שיש לו השליש מאלו הג' שהם הרביע יהיה לו א' חלק מי"ב | ||||||||||||||||||||||||||
|
ואם יאמר מי שיש לו השליש מן החומש כמה חלק יש לו | ||||||||||||||||||||||||||
|
אמור שליש וחומש ימצא בג' פעמים ה' שהם ט"ו | ||||||||||||||||||||||||||
|
החומש מט"ו הם ג' ומי שיש לו השליש מג' שהוא החומש יש לו א' חלק מט"ו | ||||||||||||||||||||||||||
|
[133]וכן מי שיש לו החומש מן התשיעית | ||||||||||||||||||||||||||
|
אמור חומש ותשיע ימצא בה' פעמים ט' שהם מ"ה | ||||||||||||||||||||||||||
|
והתשיעי ממ"ה הוא ה' והחומש מה' הוא א' א"כ מי שיש לו החומש מן התשיעית יש לו א' חלק ממ"ה מן הדבר ההוא | ||||||||||||||||||||||||||
Conversion of fractions |
|||||||||||||||||||||||||||
|
אם יאמר אדם ג' שמיניות כמה עשיריות הם | ||||||||||||||||||||||||||
|
עשה על זה הדרך | ||||||||||||||||||||||||||
|
אמור שמינית ועשירי' ימצאו בח' פעמי' י' שהם פ' | ||||||||||||||||||||||||||
|
וג' שמיניות הם ל' | ||||||||||||||||||||||||||
|
כי י' הוא שמינית פ'[134] | ||||||||||||||||||||||||||
|
וח' הוא עשירית פ' | ||||||||||||||||||||||||||
|
ואם תרצה לידע כמה עשיריות הם הג' שמיניות מפ' חלק הל' שהוא הג' שמיניות חלקם[135] בח' שהוא עשירית פ' הם ג' עשריות וו' ואותם הו' הם ו' חלקים מפ'[136] | ||||||||||||||||||||||||||
Operations with fractions - numerator greater than 1 |
|||||||||||||||||||||||||||
|
ואם יאמר הוסף ג' שמיניות על ז' עשיריות כמה יהיו[137] | ||||||||||||||||||||||||||
|
אמור שמינית ועשירי' ימצאו בח' פעמים י' שהם פ' | ||||||||||||||||||||||||||
|
ותוסיף ג' שמיניות והם ל' על ז' עשרותיו והם נ"ו יהיו הכל פ"ו חלקים מפ' שהם א' שלם וו' חלקים מפ' | ||||||||||||||||||||||||||
|
ואם יאמר השלך ג' שביעיות מב' שלישיות | ||||||||||||||||||||||||||
|
אמו' שלישית ושביעית ימצאו בג' פעמ' ז' שהם כ"א | ||||||||||||||||||||||||||
|
וקח ב' שלישיותיו והם י"ד ותשלך מהם ג' שביעיותיו והם ט' וישארו ה' חלקים מכ"א[138] | ||||||||||||||||||||||||||
|
ואם יאמר כמה הם יותר ג' שמניות מב' חמשיות | ||||||||||||||||||||||||||
|
אמו' חמישיות ושמינית ימצא בה' פעמ' ח' שהם מ' | ||||||||||||||||||||||||||
|
ב' חמישיות הם י"ו וג' שמיניות הם ט"ו נמצא שהב' חמישיות הם יותר מג' שמיניות חלק אחת ממ'[139] | ||||||||||||||||||||||||||
|
ואם יאמ' כמה הם ג' שמיניות מב' חמישיות | ||||||||||||||||||||||||||
|
אמור שמינית וחמישית ימצאו בה' פע' ח' שהם מ' | ||||||||||||||||||||||||||
|
וב' חמישיות מ' הם י"ו וג' שמיניות י"ו הם ו' א"כ הם ו' חלקי' ממ' | ||||||||||||||||||||||||||
|
ואם יאמ' חלק ג' שמיניות על ב' חמשיות | ||||||||||||||||||||||||||
|
אמו' שמינית וחומש ימצאו בה' פעמ' ח' שהם מ' | ||||||||||||||||||||||||||
|
וג' שמניות מ' הם ט"ו וב' חמשיותיו הם י"ו חלק ט"ו על י"ו | ||||||||||||||||||||||||||
|
ואם יאמר חשוב ב' שלישים עם ב' חמישיות | ||||||||||||||||||||||||||
|
תחשוב שלשה על ה' שהם שמות החלקים יהיו ט"ו | ||||||||||||||||||||||||||
|
ואמור ב' פעמ' ב' כי ב' הם שמות החלקים ויהיו ד' | ||||||||||||||||||||||||||
|
הרי שב' שלישיות על ב' חמישיות הם ד' חלקים מט"ו מן האחד | ||||||||||||||||||||||||||
|
ואם יאמר חשוב ב' חלקים מי"א באחד על ב' חלקים מי"ג מן האחד | ||||||||||||||||||||||||||
|
תחשוב שמות החלקים והם י"א על י"ג שעולים קמ"ג | ||||||||||||||||||||||||||
|
ותרבה מספר החלקים שהם ב' ואמור ב' פעמים ב' ד' | ||||||||||||||||||||||||||
|
הרי שעולים ד' חלקים מקמ"ג בא' | ||||||||||||||||||||||||||
|
ואם יאמ' ב' חלקים מה' בעשירית האחד בב' שלישי האחר כמה הם | ||||||||||||||||||||||||||
|
דע כי שם האחד הם חמשים בעניין חמשה בעשרה ותמנה אלו הנ' בג' שהוא שם החלק השני ויהיה הכל ק"נ | ||||||||||||||||||||||||||
|
ואמור ב' פעמ' ב' ד' כי ב' הוא מספר החלקי' | ||||||||||||||||||||||||||
|
הרי שהחשבו' הזה הוא ד' חלקי' מק"נ מהאחר | ||||||||||||||||||||||||||
|
ואם יאמ' ב' חלקים מחמשה בעשירית האחד בשני חלקים משמנה בשלישית האחד | ||||||||||||||||||||||||||
|
אתה צריך לדעת את שמות החלקים | ||||||||||||||||||||||||||
|
ותחשוב ה' בי' והם נ' והוא שם החלק האחד | ||||||||||||||||||||||||||
|
ותחשוב עוד ח' בג' ויהיו כ"ד והוא שם החלק השני | ||||||||||||||||||||||||||
|
וחשוב אחר כן נ' על כ"ד ויהיה אלף ומאתים | ||||||||||||||||||||||||||
|
ואמו' אחר כן ב' פעמ' ב' ר"ל ד' | ||||||||||||||||||||||||||
|
הרי שהם ד' חלקים מאלף ומאתים מן האחר[140] | ||||||||||||||||||||||||||
Multiplication of fractions |
|||||||||||||||||||||||||||
|
כשנרבה השליש באחד הוא שליש | ||||||||||||||||||||||||||
|
וכשנרבה השליש בשנים הוא ב' שלישי האחד | ||||||||||||||||||||||||||
|
וכשנרבה שליש בשליש הוא שליש בשליש | ||||||||||||||||||||||||||
|
והרביע ברביע הוא רביע הרביע | ||||||||||||||||||||||||||
|
וחומש בחומש הוא חומ' החומש | ||||||||||||||||||||||||||
|
וכן כלם | ||||||||||||||||||||||||||
|
ואם נרבה ב' שלישי בב' שלישי | ||||||||||||||||||||||||||
|
אמור ג' פעמים [.] ג' ט' | ||||||||||||||||||||||||||
|
ואחר כך אמור ב' פעמים ב' פעמים הרי ד' | ||||||||||||||||||||||||||
|
הרי שאם נרבה ב' שלישי על ב' שלישי הם ד' חלקי' מט' באחד | ||||||||||||||||||||||||||
Proportions with fractions |
|||||||||||||||||||||||||||
|
אם יאמר אדם אם שליש שוה רביע החומש כפי זה החשבון כמה שוה | ||||||||||||||||||||||||||
|
אמור שליש ורביע וחומש ימצאו בס' | ||||||||||||||||||||||||||
|
השליש מס' הוא כ' | ||||||||||||||||||||||||||
|
א"כ הרביע הוא ט"ו | ||||||||||||||||||||||||||
|
והחומש הוא י"ב | ||||||||||||||||||||||||||
|
ואמור אם כ' שהוא שליש מס' שוה ט"ו שהוא הרביע החומש שהוא י"ב כמה שוה | ||||||||||||||||||||||||||
|
אמור י"ב פעמי' ט"ו הם ק"פ חלקים | ||||||||||||||||||||||||||
|
חלקם בכ' יבאו ט' והם ט' חלקים מס' באחד | ||||||||||||||||||||||||||
|
|
אם יאמר אדם אם ג' ושליש שוים ד' ורביע ה' [ו]חומש כמה שוים | ||||||||||||||||||||||||||
|
|
אמור ה' וחומש פעמים ד' ורביע וחלקם בג' ושליש וזה סדר עשייתו | ||||||||||||||||||||||||||
|
|
תפוש ה' וחומש ואמור ה' פעמים ה' הם[141] כ"ה וא' חומש הרי כ"ו | ||||||||||||||||||||||||||
|
|
אחר זה תפוש ד' ורביע ואמור ד' פעמים ד' י"ו וא' רביע הרי י"ז | ||||||||||||||||||||||||||
|
|
ותרבה י"ז עם כ"ו ויעלו תמ"ב ונחלק אותם בד' פעמים ה' שהם כ' יבואו כ"ב וא' עשירי' | ||||||||||||||||||||||||||
|
ובעבור שנצטרך לחלקם לג' ושליש עשה מכ"ב וא' עשירית כולם שלישיות ואמור ג"פ כ"ב ס"ו וג' פעמי' א' עשירית הרי ג' עשיריות הרי ס"ו וג' עשיריות | ||||||||||||||||||||||||||
|
|
וצריך שנחלק אותם בג' ושליש וסדר חילופו שתעשה מג' ושליש כלם שלישיות ואמור ג'פ'ג' ט' וא' הרי י' | ||||||||||||||||||||||||||
| ואם נחלק ס"ו בי' חלקים יבואו ו' וו' עשיריות נחלק אח"כ ג' עשיריות בי' חלקי' ישאר ג' חלקי' ממאה[142] | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
Word Problems |
|||||||||||||||||||||||||||
Exchange Problems |
|||||||||||||||||||||||||||
|
אם יאמר אדם ז' פיסאני שוים ט' קונטוניסי ק' ליט' פיסאני כמה ליט' קוטורניסי שוים | ||||||||||||||||||||||||||
|
עשה על זה הדרך | ||||||||||||||||||||||||||
|
ידוע כי אם ז' פיסאני שוים ט' קוטורניסי ז' דינ' פיסאני שוים ט' דנרי' קוטורניסי וז' ליט' פיסאני שוים ט' ליט' קוטורניסי ות"ש ליט' פיסאני שוים תת"ק ליט' קוטורניסי וכן לכל מטבע שתרצה | ||||||||||||||||||||||||||
|
א"כ השאלה הזאת היא כאלו שאל אם ת"ש ליט' פיסאני שוים תת"ק ליט' קוטורניסי ק' ליט' פיסאני כמה שוים | ||||||||||||||||||||||||||
|
ולהקל החשבון נאמר אם ז' שוים ט' ק' כמה שוים | ||||||||||||||||||||||||||
|
אמור ק' פעמי' ט' תת"ק | ||||||||||||||||||||||||||
|
חלקם בז' יהיו קכ"ח ליט' וי"א דינ' וא' שביע וכן ישוו הק' ליט' פיסא' לקוטורניסי | ||||||||||||||||||||||||||
|
אם יאמר אדם אם ה' פיסאני ורביע שוים ז' קוטורניסי אלף ליט' פיסאני כמה ליט מקוטורניסי שוים | ||||||||||||||||||||||||||
|
הנך רואה כי זה החשבון הוא שבור מחלק אחד וזה השבור הוא רביע | ||||||||||||||||||||||||||
|
לכן נרבה הב' חלקים שהם ה' ורביע וז' בד' דהיינו שנעשה כלם רביעיים | ||||||||||||||||||||||||||
|
ואמ' ד' פעמי' ה' פיסאני ורביע יבואו כ"א פיסאני | ||||||||||||||||||||||||||
|
וד' פעמי' ז' קוטורניסי יבואו כ"ח קוטורניסי | ||||||||||||||||||||||||||
|
הרי שכ"א פיסאני שוים כ"ח קוטורניסי | ||||||||||||||||||||||||||
|
ולהקל הענין נחלקם בשביע בעבור שבשני החלקים ימצא שביע | ||||||||||||||||||||||||||
|
השביע מכ"א הוא ג' | ||||||||||||||||||||||||||
|
והשביע מכ"ח הוא ד' | ||||||||||||||||||||||||||
|
נמצא שג' פיסאני שוים ד' קוטורניסי | ||||||||||||||||||||||||||
|
ואנו רוצים לדעת כמה שוים אלף ליט' פיסאני | ||||||||||||||||||||||||||
|
אמור א"כ אם ג' פיסאני שוים ד' קוטורניסי אלף ליט' פיסאני כמה שוים | ||||||||||||||||||||||||||
|
אמור אלף פעמי' ד' יבואו ד' אלפים | ||||||||||||||||||||||||||
|
חלקם בג' יבואו אלף ושל"ג וו' די' וח' פשוטי' וכן שוים אלף ליט' פיסאני לקוטרניסי[144] | ||||||||||||||||||||||||||
|
[145]ואם יאמר אדם אם ז' אונקיו' ושליש מכסף שוי' ע"ג ליטרי' ורביע י"ט אונקיו' מכסף כמה ישוו לפי חשבון זה | ||||||||||||||||||||||||||
|
עשה על זה הדרך השברי' שהם בזה החשבון הם שליש ורביע ושליש ורביע ימצאו בי"ב | ||||||||||||||||||||||||||
|
לכן יש לנו לרבות הב' חלקי' שהם ז' ושליש וע"ג ורביע בי"ב דהיינו לעשות מכלם חלקים מי"ב | ||||||||||||||||||||||||||
|
ואמור י"ב פעמי' ז' ושליש יבואו פ"ח אונקיו' כסף | ||||||||||||||||||||||||||
|
וי"ב פעמים ע"ג ליטרי' וה' דינרי' יהיו ת"תע"ט ליט' | ||||||||||||||||||||||||||
|
הרי שפ"ח אונקיו' כסף שוי' תתע"ט ליטרי' | ||||||||||||||||||||||||||
|
ואנו רוצי' לידע כמה שוי' הי"ט אונקיו' לחשבון זה | ||||||||||||||||||||||||||
|
אמור אם כן אם פ"ח אונקיו' כסף שוי' תתע"ט ליטרי' ואנו רוצי' לידע כמה שוי הי"ט אונקיו' לחשבון זה | ||||||||||||||||||||||||||
|
אמור י"ט פעמי' תתע"ט יהיו י"ו אלפים ותש"א ליט' | ||||||||||||||||||||||||||
|
חלק אותם בפ"ח דהיינו בח' ובי"א יבואו קפ"ט ליטרי' וט"ו דינרי' וח' פשיטי' וב' חלקי' מי"א מהפשוט וכן ישוו הי"ט אונקיו' כסף לפי חשבון זה | ||||||||||||||||||||||||||
Divide a Quantity Problems |
|||||||||||||||||||||||||||
|
אם תרצה לחלק ה' פשיטים לשליש ולרביע ולא ישארו מהם כלל | ||||||||||||||||||||||||||
|
אמור שליש ורביע ימצא בג' פעמים ד' שהם י"ב | ||||||||||||||||||||||||||
|
השליש הוא ד' הרביע הוא ג' וכללם הוא ז' והוא המחלק | ||||||||||||||||||||||||||
|
ואם יאמר תרצה לדעת כמה הוא חלק אותו שיש לו השליש אמור ד' פעמי' ה' בעבור שהם ה' יבואו כ' | ||||||||||||||||||||||||||
|
ואם תרצה לדעת חלק אותו שיש לו הרביע אמור ג' פעמי' ה' ט"ו | ||||||||||||||||||||||||||
|
ואם תקבץ ב' וו' חלקים מז' וב' וא' חלק מז' יהיו ה' פשיטי' כמספר המעות שחלקת | ||||||||||||||||||||||||||
|
ואם תרצה לחלק י"ב פשי' לחצי לשליש ולרביע | ||||||||||||||||||||||||||
|
אמור חצי ושליש ורביע ימצאו בי"ב | ||||||||||||||||||||||||||
|
החצי הוא ו' השליש הוא ד' הרביע ג' וכללם י"ג והוא המחלק | ||||||||||||||||||||||||||
|
ואם תרצה לדעת חלק מי שיש לו החצי | ||||||||||||||||||||||||||
|
אמור החצי מי"ב הוא ו' תרבה אותם עם י"ב שהוא סך המעות יהיו ע"ב חלקם בי"ג יהיו ה' וז' חלקים מי"ג | ||||||||||||||||||||||||||
|
ואם תרצה לדעת חלק אותו שיש לו השליש | ||||||||||||||||||||||||||
|
אמור השליש מי"ב הוא ד' ותרבה אותם עם סך המעות שהם י"ב ויהיו מ"ח וחלקם בי"ג יהיו ג' וט' חלקים מי"ג | ||||||||||||||||||||||||||
|
ואם תרצה לדעת חלק אותו שיש לו הרביע | ||||||||||||||||||||||||||
|
אמור הרביע מי"ב הוא ג' תרבה אותו עם סך המעות שהם י"ב ויהיו ל"ו חלקם בי"ג יהיו ב' וי' חלקי' מי"ג | ||||||||||||||||||||||||||
|
ואם תקבץ ג' החלקים האלה יהיו י"ב כמספר המעו' שחלקת | ||||||||||||||||||||||||||
|
וכן אם תרצה לחלק י"ב פשיטי' לשליש ולרביע | ||||||||||||||||||||||||||
|
אמור שליש ורבי' ימצאו א בי"ב | ||||||||||||||||||||||||||
|
השליש הוא ד' והרביע הוא ג' וכללם ז' והוא המחלק | ||||||||||||||||||||||||||
|
ואם תרצה לדעת מי שיש לו השליש כמה יהיו | ||||||||||||||||||||||||||
|
אמור שליש מי"ב הם ד' תרבה אותם על סך המעות שיהיו י"ב ויהיו מ"ח חלקם בז' יהיו ו' וו' חלקי' מז' | ||||||||||||||||||||||||||
|
ולדעת אותו שיש לו הרביע | ||||||||||||||||||||||||||
|
אמור הרביע מי"ב הוא ג' תרבה [146]אותם עם י"ב יהיה הרביע ל"ו חלקם בז' יהיו ה' וא' חלק מז' | ||||||||||||||||||||||||||
|
ושניהם י"ב | ||||||||||||||||||||||||||
|
ואם יהיו בידך ל' פשיטי' ותרצה לחלק אותם לשליש ולרביע ולחומש ולשתות | ||||||||||||||||||||||||||
|
אמור החלקי' האלה ימצאו בס' | ||||||||||||||||||||||||||
|
השליש הוא כ' הרביע ט"ו החומש י"ב השתות י' וכלם נ"ז והוא המחלק | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
ואותו שיש לו השליש יאמר השליש מס' הוא כ' ותרבה אותם עם ל' שהוא סך המעות יהיו ת"ר חלקי' בנ"ז יבואו י' ול' חלקי' מנ"ז | ||||||||||||||||||||||||||
|
ואותו שיש לו הרביע שהוא ט"ו יאמר ט"ו פעמי' ל' הם ת"ן חלקם בנ"ז יהיו ז' ונ"א חלקי' מנ"ז | ||||||||||||||||||||||||||
|
ואותו שיש לו החומש מי"ב שהוא י"ב יאמר י"ב פעמי' ל' הם ש"ס חלקם בנ"ז יבאו ו' וי"ח חלקי' מנ"ז | ||||||||||||||||||||||||||
|
ואותו שיש לו השתות שהוא י' יאמר י' פעמי' ל' הם ש"ס ש' חלקם בנ"ז יהיו ה' וט"ו חלקי' מנ"ז | ||||||||||||||||||||||||||
|
וכלל כל החלקי' הנזכרי' הם ל' פשיטי' | ||||||||||||||||||||||||||
|
לחלק ס' ליטרי' לחצי לשליש ולרביע | ||||||||||||||||||||||||||
|
אמור חצי ושליש ורביע ימצאו בי"ב | ||||||||||||||||||||||||||
|
וכללם י"ג והוא המחלק | ||||||||||||||||||||||||||
|
ואם תרצה לדעת חלק אותו שיש לו החצי | ||||||||||||||||||||||||||
|
אמור החצי מי"ב הוא ו' תרבה אות' עם ס' שהוא סכום ה' ליטרי' יהיו ש"ס חלקם בי"ג יהיו כ"ז וט' חלקים מי"ג מהליטר' | ||||||||||||||||||||||||||
|
ואם תרצה לדעת חלק אותו שיש לו השליש | ||||||||||||||||||||||||||
|
אמור השליש מי"ב הם ד' תרבה אותם עם ס' יהיו ר"מ חלקם בי"ג יהיו יהיו י"ח וו' חלקי' מי"ג מן הליטר' | ||||||||||||||||||||||||||
|
ואם תרצה לדעת אותו שיש לו הרביע | ||||||||||||||||||||||||||
|
אמור הרביע מי"ב הוא ג' תרבה אותם עם ס' יהיו ק"פ חלקם בי"ג הוא י"ג וי"א חלקי' מי"ג מן הליט' | ||||||||||||||||||||||||||
|
וא' חלק מי"ג מן הליטר' הוא י"ח פשיטי' וב' חלקי' מי"ג | ||||||||||||||||||||||||||
|
יהיה אם כן חלק אותו שיש לו החצי כ"ז ליטרי' וי"ג דינרי' וי' פשיטי' וב' חלקי' מי"ג מן הפשוט | ||||||||||||||||||||||||||
|
וחלק אותו שיש לו השליש הוא י"ח ליטרי' וט' דינרי' וב' פשיטי' וי' חלקי' מי"ג מן הפשוט | ||||||||||||||||||||||||||
|
וחלק אותו שיש לו הרביע הוא י"ג ליטרי' וי"ו דינרי' וי"א פשיטי' וא' חלק מי"ג מן הפשוט | ||||||||||||||||||||||||||
|
ואם תקבץ כל החלקים הנזכרי' יהיו ס' ליטרי' | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
Partnership - for the same time |
|||||||||||||||||||||||||||
|
שלשה אנשים עשו חברותה ושמו בין שלשתם א' אונקי' זהב לאחד היה זהב שוה ג' ליטרי' האונקי' | ||||||||||||||||||||||||||
|
אמור שליש וחומש ושמין ימצאו בק"כ | ||||||||||||||||||||||||||
|
השליש הוא מ' החומש הוא כ"ד השמינית ט"ו וכללם ע"ט והוא המחלק | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה זהב ישים אותו שהזהב שלו שוה ג' ליטרי' האונקי' אמור השליש מק"כ הוא מ' ותרבה אותו עם סך האונקיות [147]שהם מ' יהיו אלף ות"ר[148] | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה שוה חלקו אמור הכ' אונקיו' לחשבון ג' לי' האונ' עולי' ס' ליטרי' | ||||||||||||||||||||||||||
|
ומן הכ' חלקי' מע"ט אמור אם ע"ט שהוא כ' ליטרי' א' אונקי' שוה תש"כ פשוטי' שהם ג' ליט' כ' חלקים מע"ט כמה שווים | ||||||||||||||||||||||||||
|
אמו' כ' פעמ' תש"כ[149] יהיו חלקם בע"ט יבואו קפ"ב פשיטי' וכ"ב חלקים מע"ט | ||||||||||||||||||||||||||
|
שהם ס' ליט'[150] וט"ו דינרי' וב"פ וכ"ב חלקים מע"ט | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה זהב ישים אותו שהזהב שלו שוה ה' ליטרי' האונ' אמור החומש | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה שוה חלקו אמור הי"ב אונקיו' לחשבון ה' ליטרי' האונקי' עולי' ס' ליטרי' | ||||||||||||||||||||||||||
|
ומן הי"ב חלקים[152] מע"ט [אמור אם ע"ט שהוא א' אונקי' עולה אלף ור' פשוטי' שהם ה' ליט' הי"ב חלקים מע"ט כמה שווים | ||||||||||||||||||||||||||
|
אמו' י"ב פעמ' אלף ור' הם י"ד אלפים ות' חלקם בע"ט יבואו קפ"ב פשוטי' וכ"ב חלקים מע"ט | ||||||||||||||||||||||||||
|
הרי ששווה חלקו ס' ליט' וט"ו די' וב"פ וכ"ב חלקים מע"ט כמו הראשון | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה זהב ישים אותו שהזהב שלו שווה ח' ליט' האונק' אמו' השמינית מק"כ הם ט"ו תרבה אותם עם מ' שהם סכום האונק' יהיו ת"ר | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה שוה חלקו שלזה אמו' הז' אונק' לחשבו' ח' ליט' עולים נ"ו ליט' | ||||||||||||||||||||||||||
|
ומן המ"ז חלקים מע"ט אמו' אם ע"ט שהוא א' אונק' שוה אלף ותתק"כ פשוט' שהוא ח' ליט' המ"ז חלקים מע"ט כמה שווים | ||||||||||||||||||||||||||
|
אמו' מ"ז פעמ' אלף ותתק"כ הם צ' אלפים ור"מ חלקם בע"ט יהיו אלף וקמ"ב פשוטי' וכ"ב חלקים מע"ט | ||||||||||||||||||||||||||
|
שהם ד' ליט' וט"ו די' וב"פ וכ"ב חלקים מע"ט | ||||||||||||||||||||||||||
|
צרף אותם עם הנ"ו ליט' הרי ששווה חלקו שלזה כחלק כל אחד מחבריו ס' ליט' וט"ו די' וב"פ וכ"ב חלקים מע"ט][153] | ||||||||||||||||||||||||||
Multiple Quantities Problems |
|||||||||||||||||||||||||||
|
שלשה אחים לשיני יש יותר מן הראשו' על אחת ג' ולשלישי יש לאחת על אחת שיני ג' | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
עשה לך מורה שיוסיף לך זה על זה כזה הדמיון והם א' ג' ט' ומחובר שלשתם י"ג יהיה לראשון א' ולשני ג' ולשלישי ט' | ||||||||||||||||||||||||||
|
ועתה שאמר ומחובר שלשתם ס'[154] עשה על זה הדרך | ||||||||||||||||||||||||||
|
ולדעת כמה יש לראשון אמור אם בהיות המחובר י"ג יהיה החלק הראשון א' עתה שהמחובר ס' כמה יש לו | ||||||||||||||||||||||||||
|
אמור ס' פעמי' א' הם ס' חלקם בי"ג יהיו ד' וח'[155] חלקים מי"ג | ||||||||||||||||||||||||||
|
ולדעת חלק השיני אמור אם בהיות המחובר י"ג יהיה החלק[156] השני ג'[157] עתה שהמחובר ס' כמה הוא חלקו | ||||||||||||||||||||||||||
|
אמו' ס' פעמי' ג' הם ק"פ חלקם בי"ג יהיו י"ג וי"א חלקים מי"ג[158] | ||||||||||||||||||||||||||
|
ולדעת חלק השלישי אמור אם בהיות המחובר י"ג היה חלק השלישי ט' עתה בהיות המחובר ס' כמה הוא חלקו | ||||||||||||||||||||||||||
|
אמור ס' פעמי' ט' הם תק"מ חלקם בי"ג יהיו | ||||||||||||||||||||||||||
|
ואם תקבצם יהיו כלם ס' | ||||||||||||||||||||||||||
|
וכן אם יהיו זה על זה ב' או ד' או ה' וכן אם יהיו יותר מג' חברים כמו כן עשה המורה על דרך הראוי ותמצא חפצך | ||||||||||||||||||||||||||
|
יעקב חלק לחמשה בניו ל"ה דינרים והיה חלק ראובן גדול משל לוי ושל לוי גדול משל יששכר | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
והנה [159]לפי זה חלק ראובן ט"ו | ||||||||||||||||||||||||||
|
וחלק לוי ה' | ||||||||||||||||||||||||||
|
וחלק יששכר ג' | ||||||||||||||||||||||||||
|
וחלק שמעון י' | ||||||||||||||||||||||||||
|
וחלק יהודה ב' | ||||||||||||||||||||||||||
|
וכך כלם ל"ה | ||||||||||||||||||||||||||
|
והנה אמר השואל יעקב חלק לה' בניו ס' דינרי' כפי השאלה הקודמ' | ||||||||||||||||||||||||||
|
עשה כפי זה הדרך | ||||||||||||||||||||||||||
|
אם תרצה לדעת חלק ראובן אמור אם בהיות סכום המעות ל"ה היה חלק ראובן ט"ו בהיות סכום[160] הדינרי' ס' כמה הוא חלקו | ||||||||||||||||||||||||||
|
אמור ס' פעמים ט"ו[161] הם תת"ק חלקם בל"ה יהיו כ"ה וכ"ה חלקים מל"ה | ||||||||||||||||||||||||||
|
ולדעת חלק לוי אמור אם בהיות סכום הדינרי' ל"ה היה חלק לוי ה' בהיות סכום המעות ח' כמה יהיו | ||||||||||||||||||||||||||
|
אמור ס' פעמי' ה'[162] הם ש' חלקם בל"ה יהיו ח' דינרי' וכ' חלקים מל"ה | ||||||||||||||||||||||||||
|
ולדעת חלק יששכר אמור אם בהיות סך המעות ל"ה דינרי' היה חלקו ג'[163] בהיות סך המעות ס' כמה יהיו | ||||||||||||||||||||||||||
|
אמור ס' פעמים ג' הם ק"פ חלקם בל"ה יהיו ה' וה' חלקים מל"ה | ||||||||||||||||||||||||||
|
ולדעת חלק [שמעון שהוא כעודף ראובן על לוי יהיה חלקו י"ז וה' חלקים מל"ה | ||||||||||||||||||||||||||
|
ולדעת חלק][164] יהודה שהוא כעודף לוי על יששכר יהיו חלקו ג' וט"ו חלקי' מל"ה | ||||||||||||||||||||||||||
|
ואם תקבץ כל המספרים יהיו ס' ותמצ' [חלק][165] | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
Joint Purchase Problem - If You Give Me - Amounts of Money |
|||||||||||||||||||||||||||
|
שלשה חברים אומר הראשון לשני כל מה שבכיסי וחצי שניכם עולה ס' ענה השיני כל מה שבכיסי ושליש שניכם עולה ס' | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
מצאנו ג' מספרי' והם ה' י"א י"ג שהם כעין השאילה הזאת | ||||||||||||||||||||||||||
|
כי ה' אומ' לי"א ולי"ג אני וחצי שניכם י"ז | ||||||||||||||||||||||||||
|
וי"א אומ' לי"ג [וה'][166] אני ושליש שניכם י"ז | ||||||||||||||||||||||||||
|
י"ג אומרת לי"א ולה' אני ורביע שניכם י"ז | ||||||||||||||||||||||||||
|
והנך רואה שאמרו מחובר שלשתינו י"ז יהיה לאחד ה' ולשני י"א ולשלישי י"ג ועכשיו שאמרו מחובר שלשתינו ס' נשיב לערכים | ||||||||||||||||||||||||||
|
ונאמר כערך ה' לי"ז כן ערך ראשון לס' הוא ששאל לחביריו החצי | ||||||||||||||||||||||||||
|
וכערך י"א לי"ז כן ערך האמצעי [לס'][167] הוא ששאל לחבירו השליש | ||||||||||||||||||||||||||
|
וכערך י"ג לי"ז כן ערך הגדול אל ס' והוא ששאל לחביריו הרביע | ||||||||||||||||||||||||||
|
וכן תעריך לכל הסכומים שיאמרו שלשתם | ||||||||||||||||||||||||||
| תשיב המורה ה' י"א י"ג | |||||||||||||||||||||||||||
|
ודרך הערכים הוא בעניין הזה | ||||||||||||||||||||||||||
|
[אם תרצה לדעת חלק הקטון אמור אם בעת שהמחובר י"ז יהיה חלק הקטן ה' בהיות המחובר ס' כמה הם חלקו | ||||||||||||||||||||||||||
|
אמור ס' פעמי' ה' הם ש' חלקם בי"ז יהיו י"ז וי"א חלקים מי"ז | ||||||||||||||||||||||||||
|
ולדעת חלק האמצעי אמור אם בעת שהמחבר י"ז שוה החלק האמצעי י"א בהיות המחבר ס' כמה הוא חלקו | ||||||||||||||||||||||||||
|
אמור ס' פעמי' י"א הם תר"ס חלקם בי"ז יהיו ל"ח וי"ד חלקים מי"ז | ||||||||||||||||||||||||||
|
ולדעת חלק הגדול אמור אם בעת שהמחבר הוא י"ז יהיה חלק הגדול י"ג בהיות המחובר ס' כמה הוא חלקו | ||||||||||||||||||||||||||
|
אמור ס' פעמי' י"ג הם תש"פ חלקם בי"ז יהיו מ"ה וט"ו חלקים מי"ז | ||||||||||||||||||||||||||
|
ויהיה סדר העניין כן | ||||||||||||||||||||||||||
|
אומר הקטן אני שאני י"ז וי"א חלקים מי"ז וחצי האמצעי שהם י"ט וז' חלקים מי"ז וחצי הגדול שהם כ"ב וי"ו חלקים מי"ז מחובר שלשתינו עולה ס' | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
ואומר האמצעי אני שאני ל"ח וי"ד חלקים מי"ז ושליש הקטן שהם ה' וט"ו חלקים מי"ז ושליש הגדול שהם ט"ו וה' חלקים מי"ז מחובר שלשתינו עולה שהם ס' | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
ואמר הגדול אני שאני מ"ה וט"ו חלקים מי"ז רביע הקטן שהוא ד' וז' חלקים מי"ז ורביע האמצעי שהוא ט' וי"ב חלקים מי"ז מחובר שלשתינו עולה ס'][168] | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
Multiple Quantities Problems |
|||||||||||||||||||||||||||
Three Brothers - Money |
|||||||||||||||||||||||||||
|
שאלה יעקב חלק [כ"ד][169] דינרים לג' בניו והיה חלק ראובן גדול משל שמעון וחלק שמעון גדול מחלק לוי | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
אמור כי החלק האחד היה ד' והחלק השני ז' והחלק השלישי י"ג | ||||||||||||||||||||||||||
|
ונמצא באחרונה חלק כל אחד מהם ח' שוה בשוה | ||||||||||||||||||||||||||
|
והיה חלק ראובן י"ג וחלק שמעו' ז' וחלק לוי ד' | ||||||||||||||||||||||||||
|
והנה התחיל ראובן ונתן מן הי"ג שלו ז' לשמעון כפי חלקו וד' [ל]לוי כפי חלקו | ||||||||||||||||||||||||||
|
[ושמעון שחלקו מעתה הם י"ד נתן ב' לראובן כפי חלקו וח' ללוי כפי חלקו][170] | ||||||||||||||||||||||||||
|
ולוי שחלקו הם מעתה י"ו נתן ד' לראובן וד' לשמעון | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
מעתה יש לכל אחד ואחד מהם ח' | ||||||||||||||||||||||||||
Selling Cloth |
|||||||||||||||||||||||||||
|
אדם אחד נתן לשלש[ת] [בניו][171] [172]שלשי' אמות בגד למכור הלכו בשוק למכרו האחד מכר בד' דינרי' האמה והשני מכר בה' דינרי' האמה והשלישי מכר בו' דינרי' האמה | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
אמור תחלה רביע וחומש ושתות ימצאו בס' | ||||||||||||||||||||||||||
|
הרביע הוא ט"ו והחומש הוא י"ב והשתות י' וכללם ל"ז והוא המחלק | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה בגד מכר אותו שמכר בד' דינרי' האמה | ||||||||||||||||||||||||||
|
אמור הרביע מט"ו מס' הוא ט"ו ותרבה אותו על סך הבגד שהו' ל' אמות ואמור ט"ו פעמים ל' הם ת"נ חלקם בל"ז שהוא המחלק יבאו י"ב אמות וו' חלקי' מל"ז מן האמה | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה מעות קבל זה שמכר בד' דינרי' האמה | ||||||||||||||||||||||||||
|
אמור מי"ב אמות קבל מ"ח דינרי' | ||||||||||||||||||||||||||
|
ומן הו' חלקים מל"ז עשה על זה הדרך אמור אם ל"ז שהם אמה שלמה שוה מ"ח פשיטי' שהם ד' דינרי' הו' חלקי' מל"ז כמה שוי' | ||||||||||||||||||||||||||
|
אמור ו' פעמי' מ"ח הם רפ"ח חלקם בל"ז יבואו ז"פ וכ"ט חלקים מל"ז | ||||||||||||||||||||||||||
|
הרי שמכר י"ב אמות וו' חלקי' מל"ז | ||||||||||||||||||||||||||
|
וקיבל מ"ח דינרי' וז"פ וכ"ט חלקי' מל"ז | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה בגד מכר אותו שמכר בה' דינרי' האמה | ||||||||||||||||||||||||||
|
אמור החומש מס' הוא י"ב תרבה אותם עם סכום הבגד שהם ל' אמות ואמור י"ב פעמים ל' והם ש"ס חלקם בל"ז שהוא המחלק יבואו ט' אמות וכ"ז חלקים מל"ז מן האמה | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה מעות קבל אותו שמכר בה' דינרי' האמה | ||||||||||||||||||||||||||
|
אמור מט' אמות [בה' די' האמה][173] קבל מ"ה דינרי' | ||||||||||||||||||||||||||
|
ומן ה"ז הכ"ז חלקים מל"ז עשה על דרך הראשון ואמור אם מל"ז שהוא א' שלם שוי' ס' פשיטי' שהם ה' דינרי' הכ"ז חלקי' מל"ז כמה הם שוי' | ||||||||||||||||||||||||||
|
אמור כ"ז פעמי' ס' הם אלף ותר"כ חלקם בל"ז יבואו מ"ג פשיטים וכ"ט חלקי' מל"ז | ||||||||||||||||||||||||||
|
[וצרף אותם עם המ"ה די' שקבל מט' אמות בגד שמכר הרי שזה שמכר בה' די' האמה | ||||||||||||||||||||||||||
|
ומכר ט' אמו' וכ"ז חלקים מל"ז | ||||||||||||||||||||||||||
|
קבל מ"ח די' וז' פשו' וכ"ט חלקים מל"ז][174] כמו הראשון | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה בגד מכר אותו שמכר בו' דינרי' האמה | ||||||||||||||||||||||||||
|
אמור [השתות מס' הוא י' תרבה אותם עם סכום הבגד שהם ל' אמות ואמו' י' פעמ' ל' הם ש' חלקם בל"ז יהיו ח' אמות וד' חלקים מל"ז | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה מעות קבל זה שמכר בו' די' האמה | ||||||||||||||||||||||||||
|
אמו'][175] מן הח' אמות קבל מ"ח דינרי' | ||||||||||||||||||||||||||
|
ומן הד' חלקים מל"ז אמור אם ל"ז שהוא אחד שלם שוה ע"ב פשיטי' שהם ו' דינרי' הד' חלקי' מל"ז כמה הם שוי' | ||||||||||||||||||||||||||
|
אמור ד' פעמים ע"ב הוא רפ"ח חלקם בל"ז יהיו ז"פ וכ"ט חלקים מל"ז | ||||||||||||||||||||||||||
|
הרי שזה שמכר בו' דינרי' האמה מכר ח' אמות וד' חלקי' מל"ז אמות | ||||||||||||||||||||||||||
|
וקבל מ"ח וז"פ וכ"ט חלקי' מל"ז ככל אחד מחבירו | ||||||||||||||||||||||||||
Mixture and Alligation Problem |
|||||||||||||||||||||||||||
|
הרי שנתת לצורף י' אונקיות זהב לעשות ממנו מעות הב' אונקיות מהם היה זהב מי"ד קראטי האונקי' | ||||||||||||||||||||||||||
|
ואתה קח סכום כל הא' [176]על האוקיו' של זהב וקח סכום הקראטי ג"כ וחלק הקראטי לסכום האוקיו' | ||||||||||||||||||||||||||
|
כיצד הב' אוקיו' לי"ד קראטי האוקי' עולות כ"ח קראטי | ||||||||||||||||||||||||||
|
והג' אונקיו' מי"ו קראטי האוקיו' עולי' מ"ח קראטי | ||||||||||||||||||||||||||
|
והה' אונקיו' מי"ח קראטי עולות צ' קאראטי | ||||||||||||||||||||||||||
|
עולי' קס"ו קראטי בין הכל | ||||||||||||||||||||||||||
|
חלקם בעשרות כמניין האוקיו' יבא לכל אונקי' י"ו קראטי וג' חומשי קראטי | ||||||||||||||||||||||||||
|
וכן לכל חשבון שתרצה | ||||||||||||||||||||||||||
Pricing Problems |
|||||||||||||||||||||||||||
|
כשתדע שהזהב הוא מי"ח קראטי האונקי' ותרצה לדעת כמה פרחי' שוה האוקי' | ||||||||||||||||||||||||||
|
עשה מכל י"ח קראטי שלישיות וי"ח שלישיות הם ו' שלמים הרי שהזהב שהוא מי"ח קראטי שוה האונקי' ממנו ו' פרחי' | ||||||||||||||||||||||||||
|
אמת שאתה צרי' לפחות מכל קראטי ו' פשי' בעבור שזה הזהב אינו קוניינטו | ||||||||||||||||||||||||||
|
ואם הזהב מעשרי' קראטי ותרצה לדע' כמה שוה האונקי' | ||||||||||||||||||||||||||
|
עשה מן הכ' קראטי שלישיות הרי שהזהב שהוא מכ' קראטי שוה אונקי' ממנו ו' פרחי' וב' שלישי פרח | ||||||||||||||||||||||||||
|
ואתה צרי' לעולם לפחות ו"פ לכל קראטו | ||||||||||||||||||||||||||
|
וכן אם הזהב הוא מכ"א קראטי | ||||||||||||||||||||||||||
|
אמור כ"א שלישיות הם ז' שלימים הרי | ||||||||||||||||||||||||||
|
וכן אם הזהב הוא מכ"ד קראטי | ||||||||||||||||||||||||||
|
אמור כ"ד שלישיות הם ח' שלימים הרי שהאוקי' שוה ח' פרחי' | ||||||||||||||||||||||||||
|
ואתה צריך לפחות ו' פשיטי לכל קראטו | ||||||||||||||||||||||||||
|
שיבואו י"ב דינרי' בין כל האונקיו' | ||||||||||||||||||||||||||
|
והאונקי' שוקלת ח' פרחי' שיבואו | ||||||||||||||||||||||||||
|
הרי שהזהב מפרח שאינו קוניינטו שוה י"ח פ' פחו' מא' פרח | ||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
ארבע נהרות רצים אל מעיין אחד האחד ממלאו ביום אחד | ||||||||||||||||||||||||||
|
עשה על זה הדרך אמור ראשון ושליש ורביע ימצאו י"ב | ||||||||||||||||||||||||||
|
הראשון הוא י"ב | ||||||||||||||||||||||||||
|
החצי ו' | ||||||||||||||||||||||||||
|
השליש ד' | ||||||||||||||||||||||||||
|
הרביעי ג' | ||||||||||||||||||||||||||
|
חבר אותם יחד יהיו כ"ה והוא המחלק | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
וכשתתבונן תמצא שי"ב ימים ימלאו כ"ה מעיינות | ||||||||||||||||||||||||||
|
כיצד הממלאו ביום אחד ביום בי"ב ימים ימלא י"ב מעיינות | ||||||||||||||||||||||||||
|
והממלאו בב' ימים | ||||||||||||||||||||||||||
|
והממלאו בג' ימים בי"ב ימים ימלא [ד'][178] מעיינות | ||||||||||||||||||||||||||
|
והממלאו בד' ימים בי"ב ימים ימלא ג' מעיינות | ||||||||||||||||||||||||||
|
הרי שארבעתם יחד ימלאו בי"ב ימים כ"ה מעיינות | ||||||||||||||||||||||||||
|
אמור אם כן כ"ה מעיינות יתמלאו בי"ב ימים א' מעיין בכמה חלק מן היום יתמלא | ||||||||||||||||||||||||||
|
אמור א' פעם י"ב י"ב חלקם בכ"ה יבואו י"ב חלקים מכ"ה הרי שי"ב חלקים מכ"ה [179]מהיום ממלאים אותו כשירוצו מארבעתם יחד | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה חלק מן המים שם כל אחד מן הנהרות במעיין | ||||||||||||||||||||||||||
|
אמור הראשון הוא י"ב וי"ב פעמים א' בעבור המעיין שהוא א' הרי י"ב חלקם בכ"ה יבואו י"ב חלקים מכ"ה | ||||||||||||||||||||||||||
|
ואותו הממלאו בב' ימים אמור החצי מי"ב הוא ו' אמור ו' פעמי' א' בעבור המעיין הם ו' חלקם בכ"ה יבואו ו' חלקים מכ"ה הרי ששם במעיין ו' חלקים מכ"ה | ||||||||||||||||||||||||||
|
והממלאו בג' ימים אמור השליש מי"ב הוא ד' אמו' ד' פעמי' א' ד' חלקם בכ"ה יבואו ד' חלקים מכ"ה | ||||||||||||||||||||||||||
|
והממלאו בד' ימים אמור הרביע מי"ב הוא ג' אמור ג' פעמים א' ג' חלקם בכ"ה הרי ששם במעיין ג' חלקי' מכ"ה מן המים | ||||||||||||||||||||||||||
|
ועל זה הדרך תעשה לכל חשבון שתרצה | ||||||||||||||||||||||||||
Multiple Quantities Problems |
|||||||||||||||||||||||||||
|
אדם אחד היה לו בנים לא נדע מספרם והיו לו פרחי' לא אומר לך כמה | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
עשה על זה הדרך בעבור שהחשבון השבור שבזה החשבון הוא עשירית קח דוגמתו עשרה ותפחות מהם אחד ישארו ט' וט' היו הבנים | ||||||||||||||||||||||||||
|
וט' פעמים ט' היו הפרחים והם פ"א | ||||||||||||||||||||||||||
|
וט' פרחים היה חלק כל אחד ואחד | ||||||||||||||||||||||||||
|
כיצד הראשון קבל א' פרח מן הפ"א ועשירית הנשאר שהוא ח' הרי שקיבל ט' פרחי' | ||||||||||||||||||||||||||
|
ונשארו ע"ב | ||||||||||||||||||||||||||
|
השני קבל ב' פרחים מן הע"ב ועשירית הנשאר שהם ז' הרי שקיבל ט' פרחי' | ||||||||||||||||||||||||||
|
ונשארו ס"ג | ||||||||||||||||||||||||||
|
השלישי קיבל ג' פרחי' מן הס"ג ועשירית הנשאר שהם ו' הרי שקבל ט' פרחי' | ||||||||||||||||||||||||||
|
ונשארו נ"ד | ||||||||||||||||||||||||||
|
הרביעי קבל ד' מן הנ"ד ועשירית הנשאר שהם ה' פרחי' הרי שקבל ט' | ||||||||||||||||||||||||||
|
ונשארו מ"ה | ||||||||||||||||||||||||||
|
החמשי קבל ה' פרחי' מן המ"ה ועשירית מן הנשאר שהם ד' הרי שקיבל ט' | ||||||||||||||||||||||||||
|
ונשארו ל"ו | ||||||||||||||||||||||||||
|
הששי קבל ו' פרחי' א מן הל"ו ועשירית מן הנשאר שהם ג' | ||||||||||||||||||||||||||
|
ונשארו כ"ז | ||||||||||||||||||||||||||
|
השביעי קיבל ז' פרחי' מן הכ"ז ועשירית הכ' הנשארי' שהם ב' הרי שקבל ט' פרחי' | ||||||||||||||||||||||||||
|
ונשארו י"ח | ||||||||||||||||||||||||||
|
השמיני לקח ח' פר' מן הי"ח ועשירית הי' הנשארים שהוא א' הרי שקבל ט' פרחי' | ||||||||||||||||||||||||||
|
ונשארו ט' | ||||||||||||||||||||||||||
|
התשיעי שהוא האחרון הלך ולקח הכל שהם הט' פרחי' הנשארי' | ||||||||||||||||||||||||||
|
הרי שט' היו הבני' וט' פע' ט' היו הפרחי' וט' פרחי' היה חלק כל אחד ואחד | ||||||||||||||||||||||||||
|
[180]ודע כי זאת הריגולא היא כללם | ||||||||||||||||||||||||||
|
וכמו כן אם אמר לראשון קח א' פרח ותשיעית הנשאר ולשני ב' ותשיעית הנשאר | ||||||||||||||||||||||||||
|
יעשה על דרך הנזכר דהיינו בעבור שהחשבון השבור בזה החשבון הוא תשיעית יקח דוגמתו תשעה ויפחות מהם אחד וישארו שמנה ושמנה היו הבנים | ||||||||||||||||||||||||||
|
וח' פע' ח' שהם ס"ד וס"ד היו הפרחים | ||||||||||||||||||||||||||
|
וח' פרחי' יבואו לכל אחד ואחד | ||||||||||||||||||||||||||
|
וכן לכל חשבון שתרצה | ||||||||||||||||||||||||||
Rent Problems |
|||||||||||||||||||||||||||
|
אם יהיה שכירות הבית ו' ליטרין לשנה או אם יהיה לך חשבון שירויח השנה ו' ליטרי' ותרצה לידע כמה יבא היום | ||||||||||||||||||||||||||
|
תפוש הב' שלישיות מו' שהם ד' וכן יבואו אילו ד"פ ליום אחד | ||||||||||||||||||||||||||
|
וכן אם יהיה שכירות הבית או ריוח החשבון ט' ליטרי' השנה ותרצה לדעת כמה יבא היום | ||||||||||||||||||||||||||
|
קח מב' חלקים מט' שהם ו' יבואו ו"פ ליום | ||||||||||||||||||||||||||
|
וכן יהיה שכירות הבית או ריוח החשבון י"ב ליטרי' השנה | ||||||||||||||||||||||||||
|
קח שני שלשיות והם ח' וכן יבואו ח' פשיטים בכל יום | ||||||||||||||||||||||||||
| Or, do this way: double the [number of] liṭra earned a year, then divide them into a third; the result are the pešiṭim earned a day.
|
או תעשה בעניין זה תכפול הליטר' שיבואו השנה וחלקם לשליש וכמספר העולה יהיו הפשיטי' שיבואו ליום | ||||||||||||||||||||||||||
|
דמיון זה אם יהיה השכירו ו' ליטרין השנה | ||||||||||||||||||||||||||
|
תכפלם יהיו י"ב חלקם לשליש יהיו ד' הרי שיבואו ד"פ ליום | ||||||||||||||||||||||||||
|
וכן אם יהיה השכירות ט' ליטרי' השנה | ||||||||||||||||||||||||||
|
כפלם יהיו י"ח חלקם לשליש יהיו ו' הרי שיבואו ו' פשיטי' ליום | ||||||||||||||||||||||||||
|
וכן אם יהיה השכירות י"ב ליט' השנה | ||||||||||||||||||||||||||
|
כפלם יהיו כ"ד חלקם לשליש יהיו [ח'][181] וכן יהיו ח"פ ליום | ||||||||||||||||||||||||||
|
ועל זה הדרך תעשה לכל חשבון הדומה לזה | ||||||||||||||||||||||||||
|
ואם יאמר אדם [שכירות הבית או ריוח חשבון אחד עולה ד"פ ליום כמה ליט' יבואו השנה | ||||||||||||||||||||||||||
|
הוסף על ד' חציים שהם ב' ויהיו ו' וכן יבואו לחשבון זה ו' ליטרי' [השכיר'][182] השנה][183] | ||||||||||||||||||||||||||
|
[184]וכן אם יאמר שכירות הבית ו' ליטרי' בשנה ו' פשיטי' ליום כמה ליטרי' יבואו השנה | ||||||||||||||||||||||||||
|
הוסף על ו' חציים ג' הוא ט' וכן יבא ט' לשנה | ||||||||||||||||||||||||||
|
וכן אם יאמר שכירות הבית הוא ח' פשיטים ליום כמה ליטרי' יבאו השנה | ||||||||||||||||||||||||||
|
הוסף על ח' חציים שהם ד' יהיו י"ב וכך יהיו י"ב ליטרי' לשנ' | ||||||||||||||||||||||||||
|
ועל זה הדרך תעשה כל חשבון שתרצה | ||||||||||||||||||||||||||
Pricing Problems[185] |
|||||||||||||||||||||||||||
|
אם תקנה הככר מן הלוחות או מאיזה דבר שתרצה בז' ליט' ותרצה לדעת כמה יבא האחד | ||||||||||||||||||||||||||
|
קח לכל ליט' ב' פשוטי' וב' חמישייו' | ||||||||||||||||||||||||||
|
אם כן תכפול ז' ויהיו י"ד פשוטי' וי"ד חומשים הרי בן כולם י"ז פשוטי' פחו' מחומש | ||||||||||||||||||||||||||
|
וכן אם תקנה הככר בה' ליט' | ||||||||||||||||||||||||||
|
כפול ה' יהיו י' הרי שיבוא לזה החשבו' י' פשוטי' וי' חמשייו' שהם י"ב פשוטים | ||||||||||||||||||||||||||
|
וכן אם תקנה הככר בט' ליט' ליט' | ||||||||||||||||||||||||||
|
כפול ט' יהיו יהיו י"ח וי"ח חמשיות שהם כ"א פשו' וג' חמשיות | ||||||||||||||||||||||||||
|
וכן לחשבון כ"ה ליט' הככר | ||||||||||||||||||||||||||
|
יבא האחד נ' פשו' ונ' חמשיות שהם ה' | ||||||||||||||||||||||||||
|
וכן לחשבון ל' ליט' הככר | ||||||||||||||||||||||||||
|
יבא האחד ס' פשו' וס' חמשיות שהם ו' דינ' | ||||||||||||||||||||||||||
|
ואם יהיו שם די' כגון שיבא הככר י' ליט' וג' די' | ||||||||||||||||||||||||||
|
קח לכל די' ג' חלקים מכ"ה | ||||||||||||||||||||||||||
|
ומן הי' ליט' יבואו ב' די' כמו שידעת | ||||||||||||||||||||||||||
|
ובעבו' הג' די' יבואו ט' חלקים מכ"ה | ||||||||||||||||||||||||||
|
וכן לעולם תוסיף לכל די' ג' חלקים מכ"ה | ||||||||||||||||||||||||||
Interest and Discount Problems - Find the Earned Interest |
|||||||||||||||||||||||||||
|
[ואם תתן י"ב ליט' מן הככר לשנה ותרצה לידע לחשבו' כמה פשוטי' הליט' יבוא החודש | ||||||||||||||||||||||||||
|
תפוש מכל ליט' שיבא הככר א' חומש | ||||||||||||||||||||||||||
|
אם כן יבא לחשבו' י"ב חומשי' דהיינו לחשבו' ב' פשוטי' וב' חמישייו' החודש הליט' | ||||||||||||||||||||||||||
|
ולחשבו' ז' ליט' הככר לשנה יבוא הליט' א' חודש | ||||||||||||||||||||||||||
|
לחשבו' ז' חומשים שהוא א' פשוט וב' חמישייו' | ||||||||||||||||||||||||||
|
ולחשבון ח' ליט' הככר לשנה | ||||||||||||||||||||||||||
|
יבא חמשים שהם א' פשוט וג' חמשי' פשוטי' לליט' בחדש | ||||||||||||||||||||||||||
|
ולחש[ב]ון י' ליט' הככר לשנה | ||||||||||||||||||||||||||
|
יבא לחשבון י' חמשים שהוא לחשבון ב' פשו' החדש לליט' | ||||||||||||||||||||||||||
|
וכן לכל חשבון שתרצה][186] | ||||||||||||||||||||||||||
|
אם תלוה שלשה דינרי' לחשבון ו' פשיטי' החדש הליטר' ותרצה לידע כמה יבא החדש | ||||||||||||||||||||||||||
|
אמור אם מכ' דינרים יבא ו' פשיטי' מג' דינרי' כמה יעלו יבאו | ||||||||||||||||||||||||||
|
אמור ג"פ ו' י"ח חלקם בכ' יבואו י"ח חלקים מכ' בפשוט | ||||||||||||||||||||||||||
|
[וכן אם תלוה ה' דינרי' לחשבון][187] ז' פשיטי' הלי' השנה ותרצה לידע כמה יבא בחדש | ||||||||||||||||||||||||||
|
אמור אם מכ' דינרי' יבא ז' פשי' מה' דינרי' כמה יבואו | ||||||||||||||||||||||||||
|
אמור ה' פעמים ז' ל"ה חלקם בכ' יבואו א' פשוט וט"ו חלקים מכ' בפשוט | ||||||||||||||||||||||||||
|
ועל זה הדרך תעשה לעולם | ||||||||||||||||||||||||||
|
אם תלוה שלשה דינרי' לחשבון [ו' פשו' הליט' בחדש][188] ועמדו ט' חדשי' ותרצה לידע כמה יבואו | ||||||||||||||||||||||||||
|
אמור ג' פעמים [ט'][189] הם כ"ז וכמו שיבואו כ"ז דינרי' א' חודש לחשבון ול ו"פ הלי' השנה כן יבאו ג' דינרי' ט' חדשים | ||||||||||||||||||||||||||
|
וכן אם תלוה ט ז' דינרי' לחשבון ה' פשיטי' הלי' השנה ועמדו יד י' חדשים ותרצה לדעת כמה יבאו | ||||||||||||||||||||||||||
|
אמור ז' פעמי' י' הם ע' וכמו שיבאו ע' דינרי' שהם ג' ליטרין וחצי א' חדש הליט' לחשבון ה' פשיטי' הליט' השנה כן יבואו הז' דינרי' י' חדשים | ||||||||||||||||||||||||||
|
וכן אם תלוה ט' דינרי' לחשבון ה' פשי' הליט' השנה ועמדו ה' חדשים ותרצה לדעת כמה יבואו | ||||||||||||||||||||||||||
|
אמור ה' פעמי' ט' מ"ה וכמו שיבואו מ"ה דינרי' א' חדש לחשבון ד"פ הלי' השנה כן יבואו הט' דינרי' ה' חדשים | ||||||||||||||||||||||||||
|
וכן לכל חשבון שתרצה | ||||||||||||||||||||||||||
|
אם תלוה הככר בי"ב ליטרי' [190]השנה ותרצה לידע כמה יבא החדש | ||||||||||||||||||||||||||
|
דרך ריגולא תרבה הליט' שיבואו השנה לעולם על ה' ומה שיעלה יהיה ידות | ||||||||||||||||||||||||||
|
דמיון זה אמור י"ב פעמים ה' הם ס' נמצא שהם ס' ידות שהם כ' דינרי' | ||||||||||||||||||||||||||
|
ואם תלוה הכיכר לחשבון ה' ליטרי' לשנה ותרצה לידע כמה יבא החדש | ||||||||||||||||||||||||||
|
אמור ה' פעמים [ה'][191] כ"ה והם כ"ה ידות שהם ח' דינרי' וד' פשיטי' וכן יבא החדש | ||||||||||||||||||||||||||
|
וכן אם תלוה הכיכר לחשבון ו' ליטרי' השנה | ||||||||||||||||||||||||||
|
אמור ה' פעמים ו' הם ל' והם ל' ידות שהם י' דינרי' וכן יבא החדש | ||||||||||||||||||||||||||
|
ולחשבון ח' ליטרי' הככר לשנה אם תרצה לידע כמה יבא החדש | ||||||||||||||||||||||||||
|
אמור ה' פעמי' ח' הם מ' והם מ' ידות שהם י"ג דינרי' וד"פ | ||||||||||||||||||||||||||
|
ואם יהיו שם דינרי' תפוש מכל דינר א' פשוט | ||||||||||||||||||||||||||
|
וכן לכל חשבון שתרצה | ||||||||||||||||||||||||||
Interest and Discount Problems (MS Verona) |
|||||||||||||||||||||||||||
|
הלוויתי כ' דינ' לחשבון ד' פשו' לליט' בחדש עמדו שנה אחת והחזיר קצת מהמעות והנשארים עמדו שנה אחת והחזיר קצת מהמעו' כמו שנתן בראשונה | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
עולים הג' פרעונות כ"ח דינ' וה' פשוטים וע"ג חלקים מצ"א | ||||||||||||||||||||||||||
|
הרי שיבא בכל פרעון ופרעון ט' די' וה' פשו' ופ"ה חלקים מצ"א | ||||||||||||||||||||||||||
|
אם ישאלך אדם הלוותי מעות לחשבון ג' פשוטי' לליט' בחדש כמה יבואו לס' ליט' בח' חדשים | ||||||||||||||||||||||||||
|
תרבה אלו הג' פשו' עם החדשים ואמור ג' פעמי' ח' הם כ"ד כ"ד פשוטי' שהם ב' דינ' | ||||||||||||||||||||||||||
|
אחר כך תרבה אלו הב' די' עם הס' ליט' ואמור ס' פעמים ב' הם ק"כ דינ' שהם ו' ליט' נמצא הס' ליט' לחשבון ג' פשוטי' הליט' לחדש יבואו ו' ליט' לח' חדשים | ||||||||||||||||||||||||||
|
אם יאמר אדם הלויתי מעות לחשבון כך וכך לליט' לחדש כמה ליט' ירוויחו ביום אחד א' פשו' | ||||||||||||||||||||||||||
|
נחלק ל' ליט' בכל כך חלקים כמו המעו' שהרויח הליט' לחדש | ||||||||||||||||||||||||||
|
המשל בזה הרי שהלוותי הליט' בב' פשו' וחצי לחדש ותרצה לידע כמה ליט' ירוויחו ביום אחד א' פשו' לפי זה החשבון | ||||||||||||||||||||||||||
|
נחלק ל' ליט' בב' וחצי יבואו י"ב ליט' נמצא שבי"ב ליט' יבואו ביום אחד א' פשוט ביום אחד א' פשוט | ||||||||||||||||||||||||||
|
אם יאמר אדם הככר מריוח השנה ל"ז ליט' וי"ח דינ' וז' פשוטי' ס"ה ליט' בכמה זמן ירוויחו כהם | ||||||||||||||||||||||||||
|
תרבה הק' ליט' עם י"ב חדשי השנה ואמור י"ב פעמים ק' הם אלף ור' חלקם על ס"ה יבואו לכל חלק י"ב חדשים וי"ג ימים וי"א חלקים מי"ג ביום ר"ל חלקים מס"ה ובזה הזמן ירוויחו ס"ה ליט' כמו שירויח הככר לשנה | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
בין לחשבון ל"ז ליט' וי"ח דינ' וז' פשו' הככר לשנה כמו שעשינו בין לחשבון כ' ליט' בין לחשבון כ"ה בין לחשבון ל' בין לאי זה חשבון שיהיה | ||||||||||||||||||||||||||
|
וכן אם יאמר כ' ליט' ירוויחו לשנה ד' ליט' ל' ליט' בכמה זמן ירוויחו כהם | ||||||||||||||||||||||||||
|
עשה כמו שעשית למעלה ואמור כ' פעמים י"ב הם ר"מ חלקם בל' חלקים יבואו ח' חדשים | ||||||||||||||||||||||||||
|
אם יאמר הלוויתי הליט' לחשבון ג' ג' פשו' הליט' בחדש ותרצה לידע בכמה ימים תרוויח הליט' א' פשוט | ||||||||||||||||||||||||||
|
תחלק ל' יום בג' חלקים יבואו י' ימים לכל חלק הרי שבי' ימים תרויח הליט' א' פשו' לחשבון ג' פשו' הליט' לחדש | ||||||||||||||||||||||||||
|
וזה החשבון יוצא כך אמור אם ג' פשו' ירויחו לא' ליט' בא' יום א' פשוט בכמה ימים ירויח | ||||||||||||||||||||||||||
|
אמור א' פעם ל' הוא ל' חלקם בג' יבואו י' ימים | ||||||||||||||||||||||||||
|
אם הככר ירוויח בשנה כך וכך וכך ליט' כמה ליט' ירויחו ביום א' פשוט | ||||||||||||||||||||||||||
|
חלק ק"נ בכל כך חלקים כמו הליט' שירויח הככר לשנה | ||||||||||||||||||||||||||
|
המשל בזה הככר ירויח י"ב ליט' בשנה ותרצה לידע כמה ליט' ירויחו ביום אחד א' פשוט | ||||||||||||||||||||||||||
|
חלק ק"נ ליט' בי"ב חלקים ויעלו י"ב ליט' וחצי בכל חלק הרי שי"ב ליט' וחצי ירויחו ביום אחד א' פשוט | ||||||||||||||||||||||||||
|
וכן לכל חשבון כזה | ||||||||||||||||||||||||||
|
אם הככר ירויח כל כך ליט' השנה בכמה ימים תרויח הליט' א' פשו' | ||||||||||||||||||||||||||
|
חלק ק"נ ימים בכל כך חלקים כמו הליט' שירויח הככר לשנה | ||||||||||||||||||||||||||
|
המשל בזה הככר ירויח ט' ליט' השנה ותרצה לידע בכמה ימים תרויח הליט' א' פשו' | ||||||||||||||||||||||||||
|
חלק ק"נ ימים בט' חלקים שהם י"ו ימים וב' שלישי יום הרי שבי"ו ימים וב' שלישי יום תרויח הליט' ט' פשוט | ||||||||||||||||||||||||||
|
אם יאמר אדם כל [כך] ליט' בכל כך זמן תרויח כך וכך הליט' כמה ליט' בכך וכך זמן ירויח כהם | ||||||||||||||||||||||||||
|
תרבה סכום החדשי' כנגד סכום הליט' וחלקם בכך וכך חלקים כמו החדשי' שנרצה לידע | ||||||||||||||||||||||||||
|
המשל בזה כ"ה ליט' ירויחו בח' חדשים מ' די' בכמה ליט' ירויחו כהם בו' חדשים | ||||||||||||||||||||||||||
|
תרבה סכום החדשים כנגד סכום הליט' ואמור ו' פעמי' כ"ה יבוא ק"נ חלקם בח' חדשים יבואו י"ח ליט' וט"ו די' | ||||||||||||||||||||||||||
|
אם יאמר אדם הלוויתי הליטרא בכך וכך לחדש כל כך כל כך ליט בכמה זמן יכפלו מבלתי שישים ריוח בקרן | ||||||||||||||||||||||||||
|
חלק כ' שנים בכל כך חלקים כמו המעות שתרוויח הליט' בחדש | ||||||||||||||||||||||||||
|
המשל בזה הלוותי הליט' בג' פשו' לחדש צ"ה ליט' בכמה זמן יכפלו | ||||||||||||||||||||||||||
|
חלק כ' שנים בג' חלקים ויבא שבו' שנים וח' חדשים יכפלו הצ"ה ליט' | ||||||||||||||||||||||||||
|
וזה החשבון יוצא כך אחרי שהליט' היא בג' פשוטי' לחדש אם כן מרווחו בשנה ג' די' ויכפלו הג' די' בו' שנים וב' שלישי שנה כי בו' שנים יבואו י"ח די' ובח' חדשים ב' די' הרי כ' דינ' | ||||||||||||||||||||||||||
|
אם יאמר אדם הככר ירויח כל כך ליט' בשנה כך וכך ליט בכמה זמן יכפלו בלא ריוח וקרן | ||||||||||||||||||||||||||
|
חלק ק' שנים בכל כך חלקים כמו הליט' שירויח הככר לשנה | ||||||||||||||||||||||||||
|
המשל בזה הככר ירויח ח' ליט' לשנה מ"ה ליט' בכמה זמן יכפלו | ||||||||||||||||||||||||||
|
חלק ק' שנים בח' חלקים יבואו י"ב שנים וו' חדשים נמצא שבי"ב שנים וו' חדשים יכפלו מ"ה ליט' | ||||||||||||||||||||||||||
|
וזה החשבון יוצא כך ידוע כי בזמן שיכפול הככר באותו הזמן עצמו יכפול כל חלק וחלק מן הככר בין לחשבון י' בין לכל חשבון שיהיה וכדי להקל החשבון חשוב המ"ה ליט' יהיו ככר שלם | ||||||||||||||||||||||||||
|
אם יאמר אדם הככר ירויח בשנה כ"ט ליט' וי"ג די' ו' פשו' כמה ליט' ירויחו כהם בז' חדשים | ||||||||||||||||||||||||||
|
תרבה חדשי השנה עם הסך הליט' דהינו עם ק' ליט' וחלקם בכל כך חלקים כמו החדשים שנרצה לידע דהיינו הז' חדשים | ||||||||||||||||||||||||||
| ודע כי זה הוא חשבון חשבון כללי וכן תוכל לאמר הככר ירויח לשנה כ' ליט' או ל' או כ"ה וכן בכל עניין שתרצה הכל [...] | |||||||||||||||||||||||||||
|
אם יאמר אדם הלויתי הליט' לחשבון ב' פשו' וחצי לחדש בכמה זמן יכפלו מבלתי שנשים רויח בקרן | ||||||||||||||||||||||||||
|
|
חלק כ' שנים בכל כך חלקים כמו המעו' שירויח הליט' לחדש | ||||||||||||||||||||||||||
|
המשל בזה הלוויתי כ' דינ' לחשבון ב' פשו' וחצי הליט' לחדש ותרצה לידע בכמה זמן יכפלו | ||||||||||||||||||||||||||
|
חלק כ' דינ' בב' וחצי יבואו ח' שנים נמצא שבח' שנים יכפלו זה | ||||||||||||||||||||||||||
|
וזה החשבון יוצא כך כבר ידוע כי לחשבון ב' פשו' וחצי הליט' יבא בשנה ב' דינ' וחצי | ||||||||||||||||||||||||||
|
אמור אם כן אם ב' דינ' וחצי יהיו בא' שנה כ' דינ' כ' דינ' דהיינו שיכפלו בכמה זמן יהיו | ||||||||||||||||||||||||||
|
אמור כ' פעמים א' כ' חלקם בב' וחצי יבואו ח' | ||||||||||||||||||||||||||
|
אם יאמר אדם הלוותי הליט' לחשבון כך וכך לחדש כמה יעלה לך ליט' ביום | ||||||||||||||||||||||||||
|
תרבה ג' ושליש כנגד מעו' הרבית | ||||||||||||||||||||||||||
|
המשל בזה הלוותי הליט' לחשבון ג' פשו' הליט' לחדש ותרצה לדעת כמה ירויחו היום ק' ליט' | ||||||||||||||||||||||||||
|
תרבה ג' ושליש עם ג' ואמור ג' ושליש פעמי' ג' הם י' פשו' נמצא שק' ליט' ירויחו ביום אחד י' פשו' | ||||||||||||||||||||||||||
|
וזה החשבון תוכל לדעת בעניין זה כי לחשבון ג' פשו' הליט' לחדש יבא הככר לשנה ט"ו ליט' | ||||||||||||||||||||||||||
|
ומהשנה תוכל לדעת כמה יבא ביום ותכפול אותו ותפוש השליש | ||||||||||||||||||||||||||
|
ואם תכפול ט"ו יהיו ל' ותפוש השליש והם י' או תפוש הרוב מט"ו והם י' | ||||||||||||||||||||||||||
|
וכן לעולם | ||||||||||||||||||||||||||
|
אם יאמר אדם כל כך ליט' ירויחו א' פשו' ביום לאי זה סך יעלה בחדש הליט' | ||||||||||||||||||||||||||
|
חלק ל' פשו' בכל כך חלקים כמו הליט' שירוויחו ביום א' פשו' | ||||||||||||||||||||||||||
|
המשל בזה י"ב ליט' ירויחו ליום א' פשו' ותרצה לידע כמה יגיע לליט' בחדש | ||||||||||||||||||||||||||
|
חלק ל' פשו' לי"ב חלקים יבואו ב' וחצי נמצא שיבא לחשבון ב' פשו' וחצי הליט' | ||||||||||||||||||||||||||
|
וזה החשבון יוצא כך שאחרי שהי"ב ליט' מרויחים בכל יום א' פשו' אם כן מרויחים בל' יום שהוא א' חדש א' פשו' | ||||||||||||||||||||||||||
Find a Number Problems |
|||||||||||||||||||||||||||
|
אם ישאלך אדם חשבון שהסרות ממנו הי' ומן הנשאר הסרות ממנו העשירית פעם שנית ונשארו ק' כמה היה כל החשבון בטרם שהסרת ממנו ב' העשיריות | ||||||||||||||||||||||||||
|
עשה על זה הדרך אמור אלו על זה הדרך אלו היה החשבון ק' ופחתת ממנו ב' עשיריות ישארו פ"א | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
אמור [אם כן אם בחשבו' שנשארו פ"א אחר שהסרת ממנו הב' עשיריו' כמה היו הב' עשרייו' י"ט][192] | ||||||||||||||||||||||||||
|
|
אם כן ק' פעמים חלק בפ"א יהיו כ"ג ול"ז חלקים מפ"א | ||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
| הסר מהם העשיריות שהם י"ב וכ"ח חלקים מפ"א | |||||||||||||||||||||||||||
|
|
כיצד העשירית מק"כ הם י"ב | ||||||||||||||||||||||||||
|
|
והג' והל"ז חלקים מפ"א הם ר"פ חלקים מפ"א והעשירית מהם הם כ"ח חלקים מפ"א | ||||||||||||||||||||||||||
|
הרי שהמעשר הראשון היה י"ב וכ"ח חלקים מפ"א | ||||||||||||||||||||||||||
|
נשארו ק"ח ורנ"ב חלקי' מפ"א שהם קי"א וט' חלקי' מפ"א | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| הסר מהם עוד העשירית שהם י"א וט' חלקים מפ"א ישארו ק' | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
|
כיצד העשיריות מק"י הוא י"א | ||||||||||||||||||||||||||
|
|
וה[א'] והט' חלקי' מפ"א הם צ' חלקי' מפ"א והעשירית מהם הוא ט' חלקי' מפ"א | ||||||||||||||||||||||||||
|
הרי [193]שהמעשר הראשון היה י"ב וכ"ח חלקים מפ"א | ||||||||||||||||||||||||||
|
ונשארו קי"א וט' חלקי' מפ"א | ||||||||||||||||||||||||||
|
והמעשר השני היה י"א וט' חלקי' מפ"א | ||||||||||||||||||||||||||
|
ונשארו ק' | ||||||||||||||||||||||||||
|
אם תרצה לדעת ג' ושליש פעמים ד' ורביע כמה עולי' | ||||||||||||||||||||||||||
|
עשה מן הג' ושליש כלם שלישיות ואמור ג' פעמים ג' ט' וא' שליש הרי י' ותכתבם | ||||||||||||||||||||||||||
|
אחרי כן עשה מן הד' ורביע כלם רביעיות ואמור ד' פעמים ד' י"ו וא' רביע הרי י"ז ותכתבם | ||||||||||||||||||||||||||
| הרי שיש לנו י' שלישיות וי"ז רביעיות תרבה אותם זה עם זה ואמור י' פעמי' י"ז הם ק"ע | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| ועל זה הדרך תעשה כלם | |||||||||||||||||||||||||||
Find the Price - Cubits of Cloth |
|||||||||||||||||||||||||||
|
ואם תרצה לדעת ג' אמות בגד ושליש ורביע וחומש לחשבון ד"פ ורביע וחומש ושתות כמה יבואו | ||||||||||||||||||||||||||
|
|
אמור שליש ורביע וחומש ימצאו בס' השליש כ' הרביע ט"ו החומש י"ב וכללם מ"ז | ||||||||||||||||||||||||||
|
וכאלו השאילה היא ג' אמות ומ"ז חלקים מס' | ||||||||||||||||||||||||||
|
|
וכן רביע וחומש ושתות ימצאו בס' הרביע ט"ו והחומש י"ב והשתות י' וכללם ל"ז | ||||||||||||||||||||||||||
|
והוא כאלו אמר לחשבון ד"פ ול"ז חלקים מס' | ||||||||||||||||||||||||||
| ותכתבם כאשר תראם בצורה[194] ותרבה האותיות העליונות ואמור ג' פעמי' ס' הם ק"פ וצרף עמהם המ"ז הם רכ"ז ותכתבם | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| ותרבה אחרי כן האותיות התחתונות ואמור ד' פעמי' ס' ר"מ ול"ז הכתובים למעלה הרי רע"ז רכ"ז ותכתבם | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| pešuṭim | ותרבה רכ"ז עם רע"ז יהיו ס"ב אלפי' ותתע"ט חלקם בס' פעמי' ס' שהם ג' אלפים ות"ר יבאו י"ז פשוטי'[195] ואלף ותרע"ט חלקים מג' אלפים ות"ר מן הפשוט | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| ועל זה הדרך תעשה לעולם | |||||||||||||||||||||||||||
Interest and Discount Problem - Compound Interest |
|||||||||||||||||||||||||||
| Summing several loans for different times and converting them to one time | מי שרוצה לקבץ חשבונות הלואות רבות שנעשו בזמנים שונים | ||||||||||||||||||||||||||
|
יקבץ מספר החדשים ויחלקם במספר המעות | ||||||||||||||||||||||||||
|
המשל בזה הרי שהלוית ק' פרחי' א' חדש וק' פרחי' הרי ב' חדשי' וק' פרחי' הרי ג' [196]חדשי' וק' פרחי' הרי ד' חדשי' וק' פרחי' הרי ה' חדשי' | ||||||||||||||||||||||||||
|
עשה על זה הדרך אמור א' וב' וג' וד' וה' שהם חשבון החדשי' עולי' ט"ו חלק הסכום הככרים שהם ה' יהיו ג' וכאלו עמדו ג' חדשי' | ||||||||||||||||||||||||||
| וכן לכל חשבון כיוצא בזה | |||||||||||||||||||||||||||
Pricing Problems |
|||||||||||||||||||||||||||
|
[197]המוייולו מן האדמה הם י"ב שטארו אם תקנה המוייולו בעשרה ליט' או פחו' או יתר ותרצה לדעת כמה יבא השטארו | ||||||||||||||||||||||||||
|
תפוש מכל ליט' כ' פשוטי' ומכל די' א' פשוט' וכן לכל חשבו' שתרצה | ||||||||||||||||||||||||||
|
והוא הדין לליט' מן המשי שהוא י"ב אונק' עשה על זה הדרך | ||||||||||||||||||||||||||
|
אם האלף נמכר קי"א ליט' וז' די' כמה יבא הככר | ||||||||||||||||||||||||||
|
תפוש מכל ליט' כ' די' ומכל די' א' פשוט וחומש | ||||||||||||||||||||||||||
|
אם יאמר אדם האונקיא של פלפל נמכרה ז' פשיטי' כמה יבא הכיכר | ||||||||||||||||||||||||||
|
תפוש מכל פשוט ה' ליטרי' וכן כלם | ||||||||||||||||||||||||||
|
ואם יאמר האונקי' נמכרה ח' פשיטי' כמה יבא האלף | ||||||||||||||||||||||||||
|
תפוש מכל פשוט נ' ליטרי' | ||||||||||||||||||||||||||
|
ואמור ח' פעמי' נ' ליט' הם ת' ליטרי' | ||||||||||||||||||||||||||
|
אם יאמר אדם המארקו של כסף שהוא ח' אונקי' שוה ז' ליטרי' וח' וה' דינרי' כמה בא האונקי' | ||||||||||||||||||||||||||
|
תפוש מכל ליטרא כ' דינרי' וחצי ומכל דינר א' פשוט וחצי | ||||||||||||||||||||||||||
|
ואם יאמר הליט' שוה ה' דינרי' ותרצה לידע כמה יבא האלף | ||||||||||||||||||||||||||
|
תפוש מכל דינר נ' ליט' | ||||||||||||||||||||||||||
|
ואם היו שם פשיטי' | ||||||||||||||||||||||||||
|
תפוש מכל פשוט א' ד' ליטרי' וי' פשיטי' וכן תעשה לכל חשבון שתרצה | ||||||||||||||||||||||||||
|
ואם האלף שוה ק"נ ליטרי' ותרצה לידע כמה שוה הליט' | ||||||||||||||||||||||||||
|
אמור ו' פעמי' ק"נ תת"ק ותפוש מכל כ"ה[198] א' פשוט שיבואו ל"ו פשיטי' וכן יבא הליט' | ||||||||||||||||||||||||||
| 1 ounce of gold = 30 terri; | האונקיא של זהב הוא ל' טרי | ||||||||||||||||||||||||||
| 1 terri = 5 groni; | והטרי הם גארוני | ||||||||||||||||||||||||||
| 1 groni = 4 grani | והגרוני הם ד' גראניו | ||||||||||||||||||||||||||
|
ואם יאמר אדם האונקיא של זהב נמכרה ה' ליטרי' וט"ו דינרי' כמה יבא הטרי' | ||||||||||||||||||||||||||
|
תפוש מכל ליטר' ח"פ ומכל דינר ב'[199] חמשיות וכן לכל חשבון שתרצה | ||||||||||||||||||||||||||
|
ואם יאמר האונקי' של זהב שוה ו' ליטרי' כמה יבא הגרונא | ||||||||||||||||||||||||||
|
תפוש מכל ליטר' א' פשיט וג' חמישיות | ||||||||||||||||||||||||||
|
[ואם יהיו שם דינרי' [200]תפוש מכל דינר ג' חלקי' מכ"ה | ||||||||||||||||||||||||||
|
ואם יאמר כמה יבא הגראנו' | ||||||||||||||||||||||||||
|
תפוש מכל ליטר' ב' חומשי | ||||||||||||||||||||||||||
|
הרי שיבא הגראנו לחשבון | ||||||||||||||||||||||||||
|
ואם יהיו שם דינרי' תפוש מכל דינר א' חלק מחמשים | ||||||||||||||||||||||||||
|
ואם יאמר הטרי שוה כמה יבא האוקי' | ||||||||||||||||||||||||||
|
תפוש מכל דינר ל' דינרי' ומכל פשוט ל' פשיטי' | ||||||||||||||||||||||||||
Guessing Problems |
|||||||||||||||||||||||||||
|
תן לג' אנשים ג' מטבעות שונות הא' מזהב וא' מכסף וא' מנחשת ויחלקום ביניהם בלתי ידיעתך וזה תוכל לדעת שתתן לאחד מהם א' מטבע ולשני ב' ולשליש ד' | ||||||||||||||||||||||||||
|
וביאור זה אם נשאר בידם ד' יהיה הסדר זהב כסף ונחושת | ||||||||||||||||||||||||||
|
ואם נשאר בידם ו' יהיה הנשאר יהיה הנשאר זהב ונחושת כסף | ||||||||||||||||||||||||||
|
ואם נשאר בידם ב' יהיה הסדר[202] כסף נחושת זהב | ||||||||||||||||||||||||||
|
ואם נשאר בידם ה' יהיה הסדר כסף זהב נחושת | ||||||||||||||||||||||||||
|
ואם נשאר בידם א' יהיה הסדר | ||||||||||||||||||||||||||
|
ואם נשאר בידם ג' יהיה הסדר נחושת כסף זהב | ||||||||||||||||||||||||||
|
תאמר לאיש שיחשוב אך לא פחות מז' וישליכם ג' ג' ג' ושאל הנשאר אחר כן ישליך מה שחשב ה' ה' ושאל הנשאר | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
דמיון זה כאלו חשב י"ז | ||||||||||||||||||||||||||
| אמרנו שישליכם ג'ג' וישאר בידו ב' אחר כן אמרנו לו שישליכם ה'ה' וישאר בידו ב' | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
Divide a Quantity Problem |
|||||||||||||||||||||||||||
|
[206]שני אנשים היו יושבים לאכול לאחד היו | ||||||||||||||||||||||||||
|
אמור כמה חלק מן הלחם אכל כל אחד מהם א' לחם וב' שלישיות לחם | ||||||||||||||||||||||||||
|
אם כן אותו שהיו לו ב' לחמים ואכל א' לחם וב' שלישיות לא הפסיד כי אם שליש לחם | ||||||||||||||||||||||||||
|
ואותו שהיו לו ג' לחמים ואכל א' לחם וב' שלישיות | ||||||||||||||||||||||||||
|
אם כן אותו שיש לו ב' לחמים יקבל א' פשוט בעבור שהפסיד שליש לחם | ||||||||||||||||||||||||||
|
ואותו שיש לו ג' לחמים יקבל ד' פשיטי' כי הפסיד ד' שלישי לחם | ||||||||||||||||||||||||||
Motion Problem - To and From |
|||||||||||||||||||||||||||
|
מגדל שהוא גבוה עשרים אמה ונמלה אחת רוצה לעלות למעלה | ||||||||||||||||||||||||||
|
|
אמור תחלה כמה הוא יותר השליש מן הרביע א' חלק מי"ב | ||||||||||||||||||||||||||
|
הרי שי"ב ימים היא[208] עולה א' אמה | ||||||||||||||||||||||||||
|
ובעבור שהמגדל הוא גבוה כ' אמה אמור י"ב פעמים כ' הם ר"מ הרי שבר"מ ימים תגיע בראש המגדל | ||||||||||||||||||||||||||
| וכן כלם | |||||||||||||||||||||||||||
Find a Quantity Problem - First from Last |
|||||||||||||||||||||||||||
|
הרי שיש לך מעות בכיס והוצאת מהם השליש והרביע והחומש והם ט'[209] פשיטים | ||||||||||||||||||||||||||
|
|
אמור שליש ורביע וחומש ימצאו בס' השליש הוא כ' הרביע הוא ט"ו החומש י"ב וכללם מ"ז | ||||||||||||||||||||||||||
|
הרי שהשליש והרביע והחומש שהם ט"פ הם מ"ז חלקים מס' | ||||||||||||||||||||||||||
|
|
נמצא שהנשאר בכיס הם י"ג חלקי' מס' | ||||||||||||||||||||||||||
|
ולכן אמור אם מ"ז חלקי' מס' שוי' ט"פ י"ג חלקי' מס' כמה שוים | ||||||||||||||||||||||||||
|
|
אמור י"ג פעמי' [210]ט' קי"ז חלקם במ"ז יבאו ב' וכ"ג חלקים ממ"ז | ||||||||||||||||||||||||||
|
נמצא שהיו בתוך הכיס י"א פשו' וכ"ג חלקים ממ"ז[211] | ||||||||||||||||||||||||||
|
ומה שהוציא היו ט' ומה שנשאר היו ב' וכ"ג חלקים ממ"ז וכן לכל חשבון שתרצה | ||||||||||||||||||||||||||
Ordering Problems |
|||||||||||||||||||||||||||
|
אדם שיש לו צלוחית אחת שהיא מחזקת ח' כוסות יין ורוצה לחלקו לב' אנשי' וליתן לכל אחד ד' מנות | ||||||||||||||||||||||||||
|
ימלא הכלי שמחזיק ג' וישי' אותם בכלי שמחזיק ה' | ||||||||||||||||||||||||||
|
אחרי כן ימלא שנית הכלי שמחזיק ג' וישים מהם בכלי שמחזיק ה' ב' נמצא שהכלי שמחזיק ה' הוא מלא והכלי שמחזיק ג' יש שם א' והכלי שמחזיק ח' יש שם ב' | ||||||||||||||||||||||||||
|
ישים אחר כן הכלי שמחזיק ה' שהוא מלא לתוך הכלי שמחזיק ח' נמצא שיש באותו הכלי ז' כוסות | ||||||||||||||||||||||||||
|
ישים אחרי כן אותו הכוס האחד שהוא בכלי שמחזיק ג' בתוך הכלי שמחזיק ה' וימלא הכלי שמחזיק ג' וישים אותם בכלי שמחזיק ה' | ||||||||||||||||||||||||||
|
[213]אדם אחד שהיו לו י"ב חביות יין הא' מחזקת א' משואי | ||||||||||||||||||||||||||
|
יחלקם על זה הסדר כגון זה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
Find a Quantity Problem - Whole from Parts[214] |
|||||||||||||||||||||||||||
|
הרי שיש לפניך דג ונחתך ראשו וזנבו והגוף שוקל י' ליט' | ||||||||||||||||||||||||||
|
אמור תחלה שליש ורביע וחומש ושתות ימצאו בס' שהם כ' וט"ו וי"ב וי' | ||||||||||||||||||||||||||
|
ובין כולם הם נ"ז חלקים מס' שהוא השלם | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
ואותם הג' חלקים שנשארו מנ"ז עד ס' הוא הגוף ששוקל י' ליט' | ||||||||||||||||||||||||||
|
אמו' א"כ אם ג' חלקים מס' דהיינו הגוף שוקל י' ליט' הנ"ז חלקים מס' שהם הראש והזנב כמה שוקל | ||||||||||||||||||||||||||
|
אמו' נ"ז פעמ' י' הם תק"ע | ||||||||||||||||||||||||||
|
חלקם בג' יבואו ק"צ | ||||||||||||||||||||||||||
|
נמצא שהראש והזנב שוקלים ק"צ ליט' והגוף שוקל י' ליט' | ||||||||||||||||||||||||||
|
הרי שכל הדג שקל מאתים ליט' | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה שוקל הראש | ||||||||||||||||||||||||||
|
כבר ידעת שהראש השליש והרביע מכל הדג שהם כ' וט"ו חלקים מס' ובין כולם ל"ה | ||||||||||||||||||||||||||
|
ואמו' אם ג' חלקים מס' שהוא הגוף שוקל י' ליט' ל"ה חלקים מס' כמה הם | ||||||||||||||||||||||||||
|
אמו' י' פעמ' ל"ה ש"נ | ||||||||||||||||||||||||||
|
חלקם בג' יבואו קי"ו ליט' וב' שלישייות והוא משק' הראש | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה שוקל הזנב | ||||||||||||||||||||||||||
|
כבר ידעת שהזנב שוקל החומש והשתות מס' שהם י"ב וי' ובין כולם הוא כ"ב חלקים מס' | ||||||||||||||||||||||||||
|
ואמו' אם ג' חלקים מס' שוקל י' ליט' כ"ב חלקים מס' כמה שוקלים | ||||||||||||||||||||||||||
|
אמו' כ"ב פעמ' י' הם ר"כ | ||||||||||||||||||||||||||
|
חלקם בג' יבואו ע"ג ליט' ושליש והוא משקל הזנב | ||||||||||||||||||||||||||
|
נמצא שהגוף שוקל י' ליט' והראש שוקל קי"ו ליט' וב' שלשייו' והזנב שוקל ע"ג ליט' ושליש | ||||||||||||||||||||||||||
|
סך הכל מאתים ליט' | ||||||||||||||||||||||||||
Divide a Quantity Problem - Proportional Division[215] |
|||||||||||||||||||||||||||
|
הרי שג' אנשים קנו א' דג בט' פשוטי' האחד יש לו החצי והשני יש לו השליש והשלישי יש לו התשיע | ||||||||||||||||||||||||||
|
עשה על זה הדרך אמור חצי ושליש ותשיע ימצאו בי"ח | ||||||||||||||||||||||||||
|
חציו ט' שלישיתו ו' תשיעיתו ב' חבר אותם יחד יהיו י"ז והוא המחלק | ||||||||||||||||||||||||||
|
ואותו שיש לו החצי מן הדג אמו' החצי מי"ח הוא ט' | ||||||||||||||||||||||||||
|
ואם תרצה לידע כמה ופרע בעבור חלקו שהוא החצי אמו' החצי מי"ח הוא ט' ותרבה אותו בט' שהוא סך מכירת הדג יבא פ"א | ||||||||||||||||||||||||||
|
ואותו שיש לו השליש מן הדג אמו' השליש מי"ח הוא ו' ותרבה אותו על הדג שהוא א' ואמו' ו' פעמ' א' ו' | ||||||||||||||||||||||||||
|
ואם תרצה לידע כמה מעות יפרע בעבור חלקו שהוא השליש אמור השליש מי"ח הוא ו' ותרבה אותם על ט' פשוטי' שנמכר הדג ואמו' ו' פעמ' ט' הם נ"ד | ||||||||||||||||||||||||||
|
ואותו שיש לו התשיע אמו' התשיע מי"ז הוא ב' ותרבה אותם על א' שהוא הדג ואמו' ב' פעמ' א' ב' | ||||||||||||||||||||||||||
|
ואם תרצה לידע כמה מעות יפרע בעבו' חלקו שהוא התשיע אמו' התשיע מי"ח הוא ב' ותרבה אותם על מה שנמכר הדג שהוא ט' ואמו' ב' פעמ' ט' הם י"ח | ||||||||||||||||||||||||||
Buy and Sell Problem |
|||||||||||||||||||||||||||
|
אדם אחד אמר לחבירו הנה שני כלכלות של תאנים בכל אחת מהן ק' תאנים מכור היפות כ' בפשוט והרעות ל' בפשוט עולה חשבונם ח' פשיטי ושליש | ||||||||||||||||||||||||||
|
כי אותם שהם כ' בפשוט עולי' ה' פשיטים | ||||||||||||||||||||||||||
|
ואותם שהם ל' בפשוט עולי' ג' פעמי' ושליש פשוט | ||||||||||||||||||||||||||
Ordering Problems |
|||||||||||||||||||||||||||
|
אדם שיש לו שכיר אחד לשלשים יום בל' פשיטי' ורוצה לקבל פרעונו בכל יום ואי' לשוכר רק ו' מטבעי' שוי' ל' פשיטי' בין כלם | ||||||||||||||||||||||||||
|
צריכין להיות על זה הסדר | ||||||||||||||||||||||||||
|
שהאחת שי[ם] א' והשנית ב' והשלישית ג' והרביעית ד' והחמשית ח' והששית י"ב | ||||||||||||||||||||||||||
| ובזה יתכן העניין | |||||||||||||||||||||||||||
Multiple Quantities Problems |
|||||||||||||||||||||||||||
Four Coins[217] |
|||||||||||||||||||||||||||
|
ד' מטבעות שוים בין ארבעתן ק' פשוטי' הראשון שוה שליש ורביע ושתות מן השני | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| אמו' הראשון ששוה שליש ורביע ושתות מן השני כמה חלקים משלם הם אמו' שליש ורביע ושתות ימצאו בי"ב השליש ד' הרביע ג' השתות ב' | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
|
אם כן הראשון שוה ג' רביעייו' מהשני | ||||||||||||||||||||||||||
| וימצאו כל אילו השברים בארבעים אם כן השני הוא מ' | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
Selling Eggs |
|||||||||||||||||||||||||||
|
אדם אחד נתן לשלשת בניו ביצות למכור לאחד נתן נ' ביצות ולשלישי ל' ולשלישי י' | ||||||||||||||||||||||||||
|
הלכו ונתנו ז' ביצות בפשוט | ||||||||||||||||||||||||||
|
אותו שהיו לו נ' ביצות מכר ז' פ' מ"ט ביצות בז' פשיטי' ונשארה לו ביצה אחת | ||||||||||||||||||||||||||
|
ואותו שהיו לו ל' ביצות מכר כ"ח ביצות בד"פ ונשארו לו ב' ביצות | ||||||||||||||||||||||||||
|
ואותו שהיו לו י' ביצות מכר א' ביצה בז' פשיטי' ונשארו לו ג' ביצי' | ||||||||||||||||||||||||||
|
הלכו פעם שניה ומכרו הביצות שנשארו בג' פשיטי' הביצה | ||||||||||||||||||||||||||
|
הראשון הרי שקיבל י' פשיטי' | ||||||||||||||||||||||||||
|
והשיני שנשארו לו ב' ביצות קיבל ו' פשיטי' וד"פ שקיבל במכירה ראשונה הרי שקבל י' פשיטי' | ||||||||||||||||||||||||||
|
והשלישי שנשארו ג' הרי שקיבל י"פ | ||||||||||||||||||||||||||
|
הרי | ||||||||||||||||||||||||||
Four Coins[218] |
|||||||||||||||||||||||||||
|
ד' מט' מטבעות שוים בין ארבעתם פ' פשוטי' הראשון שוה החצי והשתות מן השני | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
עשה על זה הדרך | ||||||||||||||||||||||||||
|
בעבו' שהראשו' שוה החצי והשתות מהשני אמור חצי ושתות ימצאו בו' | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
אם כן זה ששוה חצי ושתות מן השני הוא כאלו אמר שוה ב' שלישייו' מן השני | ||||||||||||||||||||||||||
|
והשלישי ששוה שליש ורביע ושתות מן הראשו' אמו' שליש ורביע ושתות ימצאו בס' | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
והוא כאלו אמר השלישי שוה ג' רבעייו' מן הראשון | ||||||||||||||||||||||||||
|
והרביעי שוה ד' חמישייו' מהשלישי הוא מבואר | ||||||||||||||||||||||||||
|
אם כן הסדר הוא כך הראשו' שוה ב' שלשייו' מהשני | ||||||||||||||||||||||||||
|
ואמו' תחלה השברים הנזכרי' בזה החשבו' הם חצי ושליש ורביע ושתות מי' וימצאו כולם בס' | ||||||||||||||||||||||||||
|
|
אם כן השיני הוא ס' הראשון ששוה ב' שלישיו' מהשני הוא מ' | ||||||||||||||||||||||||||
|
|
והנשאר מן השני שהוא ב' שלישייו' מהשלישי עשה על זה הדרך אמו' כמה נשאר מהשני שהוא ס' אחר שהוצאת ממנו הראשון שהוא מ' נשארו כ' | ||||||||||||||||||||||||||
|
והרי שהראשו' הוא מ' והשני ס' והשלישי ל' והרביעי כ"ד צרף אותם יחד יהיו קנ"ד והוא המחלק | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה שוה הראשו' אמו' מ' פעמ' פ' ג' אלפים ומאתים חלקם בקנ"ד יבואו כ' וק"כ חלקים מקנ"ד | ||||||||||||||||||||||||||
|
ואם תרצה לדעת כמה שוה השני אמו' ס' פעמ' פ' ד' אלפים ות"ת חלקם בקנ"ד יבואו ל"א פשוטי' וכ"ו חלקים מקנ"ד | ||||||||||||||||||||||||||
|
ולדעת חלק השלישי אמו' ל' פעמי' פ' ב' אלפים ות' חלקם בקנ"ד יבואו ט"ו פשוטי' וצ' חלקים מקנ"ד | ||||||||||||||||||||||||||
|
ולדעת חלק הרביעי אמ' כ"ד פעמי' פ' הם אלף ותתק"כ חלקם בקנ"ד יבואו י"ב וע"ב חלקים מקנ"ד | ||||||||||||||||||||||||||
|
וכן תעש' ג"כ אם יהיו שוים ד' המטבעו' האילו ק' פשוטי' בין כולם | ||||||||||||||||||||||||||
|
לדעת הראשו' אמו' מ' פעמ' ק' וחלקם בקנ"ד | ||||||||||||||||||||||||||
|
ולדעת השני אמו' ס' פעמ' ק' וחלקם בקנ"ד | ||||||||||||||||||||||||||
|
ולדעת השלישי אמו' ל' פעמ' ק' וחלקם בקנ"ד | ||||||||||||||||||||||||||
|
ולדעת הרביעי אמו' כ"ד פעמ' ק' וחלקם בקנ"ד | ||||||||||||||||||||||||||
| וכן לכל חשבו' שתרצה תפוש אותו על זה הדרך | |||||||||||||||||||||||||||
Fractions of Fractions (MS Firenze)[219] |
|||||||||||||||||||||||||||
|
מי שיש לו השליש מן הרביע מן החומש | ||||||||||||||||||||||||||
|
|
יש לו א' חלק מס' | ||||||||||||||||||||||||||
|
|
כי החומש מס' הוא י"ב והרביע מי"ב הוא ג' | ||||||||||||||||||||||||||
|
ומי שיש לו השליש מן הרביע מן החומש מן השתות | ||||||||||||||||||||||||||
|
|
יש לו א' חלק מש"ס | ||||||||||||||||||||||||||
|
|
וש"ס יוצא מו' פעמ' ס' | ||||||||||||||||||||||||||
|
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע | ||||||||||||||||||||||||||
|
|
יש לו א' חלק מב' אלפי' ותק"כ | ||||||||||||||||||||||||||
|
|
וזה יוצא מן ז' פעמ' ש"ס | ||||||||||||||||||||||||||
|
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין | ||||||||||||||||||||||||||
|
|
יש לו א' חלק מכ' אלפי' וק"ס | ||||||||||||||||||||||||||
|
|
וזה יוצא מח' פעמ' ב' אלפים ותק"כ | ||||||||||||||||||||||||||
|
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע | ||||||||||||||||||||||||||
|
|
יש לו א' חלק מקפ"א אלפי' ות"כ | ||||||||||||||||||||||||||
|
|
וזה יוצא מט' פעמ' כ' אלפים וק"ס | ||||||||||||||||||||||||||
|
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע מן העשור | ||||||||||||||||||||||||||
|
|
יש לו א' חלק מאלף אלפים ותתי"ד אלפי' ור' | ||||||||||||||||||||||||||
|
|
וזה יוצא מי' פעמ' קפ"א אלפי' ות"כ | ||||||||||||||||||||||||||
Pricing Problems[220] |
|||||||||||||||||||||||||||
|
האלף של שמן הוא מ' מיטרי א' אם האלף שווה כ"ז ליט' וה' די' כמה יבא המיטרו | ||||||||||||||||||||||||||
|
תפוש מכל ליט' ו' פשו' ומכל די' א' חומש וחצי שהם ג' עשירייו' | ||||||||||||||||||||||||||
|
הככר מן המלח הוא מאתים בוטינילי אם תקנה הככר מן המלח בכ"ה ליט' ותרצה לידע כמה יבא הבוטינילו | ||||||||||||||||||||||||||
|
תפוש מכל ליט' א' פשוט וחומש | ||||||||||||||||||||||||||
Divide a Quantity Problems |
|||||||||||||||||||||||||||
|
לחלק ט' דינרי' לחצי לשליש ולתשיע | ||||||||||||||||||||||||||
|
אמור חצי ושליש ותשיע ימצאו בי"ח החצי ט' השליש ו' התשיע ב' וכללם י"ז והוא המחלק | ||||||||||||||||||||||||||
|
ולדעת חלק אותו שיש לו החצי | ||||||||||||||||||||||||||
|
אמור מי"ח הוא ט' ותרבה אותם עם סך הדינרי' שהם ט' ואמור ט' פעמים ט' הם פ"א חלקם בי"ז יהיו י"ד דינרי' וי"ג חלקים מי"ז מן הדינר | ||||||||||||||||||||||||||
|
נצטרך אם כן לחלק הדינר בי"ז חלקים ויהיה החלק י"ב חלקי' מי"ז מן הפשוט | ||||||||||||||||||||||||||
|
ואם נרצה לדעת הי"ג חלקים מי"ז מן הדינר כמה הם נאמר י"בי"ג פעמים י"ג הם קנ"ו | ||||||||||||||||||||||||||
|
הרי אותו שיש לו החצי יש לו לחלקו ד' דינרי' וט"פ וג' חלקי' מי"ז מהפשוט | ||||||||||||||||||||||||||
|
ולדעת חלק אותו שיש לו השליש | ||||||||||||||||||||||||||
|
תרבה ו' שהוא השליש מי"ח עם ט' שהוא סכום הדינרי' ואמור ו' פעמי' ט' נ"ד[221] חלקם בי"ז מהדינר יבואו ג' די' וג' חלקים מי"ז מן הדי'[222] | ||||||||||||||||||||||||||
|
ולדעת כמה הם אילו הג' חלקים מי"ז מהדינר אמור ג' פעמים י"ב ל"ו | ||||||||||||||||||||||||||
|
[223]ולדעת חלק אותו שיש לו התשיע | ||||||||||||||||||||||||||
|
תרבה ב' שהוא התשיע מי"ח עם הדינר שהוא סך הדינר חלקם בי"ז יהיו א' דינר וא' חלק מי"ז מהדינר שהוא י"ב חלקי' מי"ז מהפשוט | ||||||||||||||||||||||||||
|
הרי שבעל התשיע יש לו א' דינר וי"ב חלקי' מי"ז מהפשוט | ||||||||||||||||||||||||||
|
ולחלק ט' ליט' לחצי לשליש ולתשיע | ||||||||||||||||||||||||||
|
יהיה א"כ לבעל החצי ד' ליטרי' וי"ג חלקי' מי"ז מהלי' | ||||||||||||||||||||||||||
|
ולדעת כמה הם הי"ג חלקי' מהי"ז מן הליטרי' חלק הליט' שהו' ר"מ פשיטי' בי"ז חלקים יהיה כל חלק יד"פ וב' חלקי' מי"ז מן הפשוט | ||||||||||||||||||||||||||
|
ואם תרצה לדעת הי"ג חלקי' מי"ז מן הליטרא אמור י"ג פעמים יד"פ וב' חלקי' מי"ז הם ט"ו דינרים וג"פ וט' חלקי' מי"ז | ||||||||||||||||||||||||||
|
הרי שבעל החצי יש לו ד' ליטרי' וט"ו דינרי' וג"פ וט"ו חלקי' מי"ז מהפשוט | ||||||||||||||||||||||||||
|
ואותו שיש לו השליש יש לו ג' ליטרי' וג' חלקים מי"ז | ||||||||||||||||||||||||||
|
והג' חלקים מי"ז מן הליט'[224] הם ג' פעמים יד"פ וג' פעמים ב' חלקים מי"ז מהפשוט | ||||||||||||||||||||||||||
|
שהם בין הכל ג' ליטרי' וג' דינרי' וו' פשיטי' וו' חלקי' מי"ז מהפשוט | ||||||||||||||||||||||||||
|
ואותו שיש לו התשיע יש לו א' ליטר' וא' חלק מי"ז מהליט' | ||||||||||||||||||||||||||
|
וא' חלק מי"ז הליט' הוא יד"פ וב' חלקי' מי"ז מהפשוט | ||||||||||||||||||||||||||
|
ואם תקבץ כל החלקי' יהיו ט' ליטרין ממש | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
Guessing a chosen number (MS Verona) |
|||||||||||||||||||||||||||
|
לדעת מה יחשוב האדם אמור לאדם שיחשוב כרצונו ויכפלם פעמים או שלוש או ארבע כמו שתרצה לומ' לו א"כ תאמ' לו שיחלקם כפי המחשבה הראשונה שחשב | ||||||||||||||||||||||||||
|
דמיון זה כאלו חשב ד' | ||||||||||||||||||||||||||
|
כפול אותם פעם אחת יהיו ח' | ||||||||||||||||||||||||||
|
כפול אותם שנית יהיו י"ו | ||||||||||||||||||||||||||
|
כפול אותם שלישית יהיה ל"ב | ||||||||||||||||||||||||||
|
כפול אותם רביעית יהיו ס"ד | ||||||||||||||||||||||||||
|
חלקם על ד' שחשב בראשונה נשארו י"ו | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
ואתה חשבת א' | ||||||||||||||||||||||||||
|
כפלת אותו פעם אחת יהיו ב' | ||||||||||||||||||||||||||
|
כפלת ב' יהיו ד' | ||||||||||||||||||||||||||
|
כפלת ד' יהיו ח' | ||||||||||||||||||||||||||
|
כפול ח' יהיו י"ו | ||||||||||||||||||||||||||
|
חלקם על א' יהיו כמוהו י"ו בשוה | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
אחר אמו' שיחשוב דינרי' ויוסיף עליו כך וכך פשו' בכל לי' ויכפלם ויקנה מהם דגים שיתן לכל אחד כמספר התוספת שהוסיף בין כל הלי' וזה תוכל לדעת שתעשה החשבון בינך לבינך על י"ב | ||||||||||||||||||||||||||
|
דמיון זה שחשב ג' לי' ואמרנו לו שיוסיף בכל די' ג' פ' | ||||||||||||||||||||||||||
| והנה עלו כל הפשו' מ"ה | |||||||||||||||||||||||||||
| עו' אמרנו לו שיכפלם ועלו צ' פשו' | |||||||||||||||||||||||||||
| וכאשר אמרנו לו שיקנה מהם דגים ויתן בכל אחד ג' פשו' כמספר התוספת שאמרנו לו שיוסיף הנה קנה ל' דגים | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
|
והנה כשתעשה החשבון בינך לבינך על י"ב שתאמר שחשב א' לי' והוא י"ב פשו' | ||||||||||||||||||||||||||
| הנה כאשר הוסיף ג' פשו' עליהם ועלו ט"ו | |||||||||||||||||||||||||||
| וכפלם ועלו ל' | |||||||||||||||||||||||||||
| וקנה מהם דגים ונתן בכל אחד ג' פשו' שהוא מספר התוספת ועלו הדגים י' | |||||||||||||||||||||||||||
|
הנה תידע שאם יאמ' שקנה י' דגים תידע שחשב א' לי' | ||||||||||||||||||||||||||
|
וכן אם אמר שקנה כ דגים תידע שחשב ב' לי' | ||||||||||||||||||||||||||
|
אחר אמור לו שיחשוב ויכפלם פי שנים ויחלקם לחצי אם יש שם חצי יחשבהו שלם ויכפול זה החצי פי שנים וישליכם ט' ט' | ||||||||||||||||||||||||||
|
דמיון זה כאילו חשב כ' | ||||||||||||||||||||||||||
| אמרנו לו שיכפלם פי שנים ועלו ס' | |||||||||||||||||||||||||||
| ואמרנו לו שיחלקם לחצי ועלו ל' | |||||||||||||||||||||||||||
| והנה יש לנו חצי עו' אמרנו לו שיכפול זה החצי שהוא ל' פי שנים ועלו צ' | |||||||||||||||||||||||||||
| עו' אמרנו לו שישליכם ט'ט' והנה לא ישאר בידו כלום | |||||||||||||||||||||||||||
| הרי שיש שם י' פעמים ט' ובעבו' כל ט' תקח ב' ועלו כ' כמו שהוא חשב כ' | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
דמיון לכשישאר בידו יותר מט' כגון שחשב ט' | ||||||||||||||||||||||||||
| אמרנו לו שיכפלם פי שנים ועלו כ"ז | |||||||||||||||||||||||||||
| ואמרנו לו שיחלקם לחצי ועלו י"ג וחצי | |||||||||||||||||||||||||||
| ולפי שיש כן חצי אמרנו שיחשבהו שלם ויהיו י"ד | |||||||||||||||||||||||||||
| עו' אמרנו לו שיכפול אלו הי"ד פי שנים ועלו מ"ב | |||||||||||||||||||||||||||
| עו' אמרנו לו שישליכם ט'ט' ונשארו בידו ו' | |||||||||||||||||||||||||||
| הרי שיש בהם ד' פעמים ט' ובעבו' כל ט' תקח ב' הרי ח' | |||||||||||||||||||||||||||
| ובעבו' הנשארי' תקח א' הרי ט' כמו ט' שחשב הוא | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
[225]לדעת מה שיחשוב האדם[226] אמור לו שיחשוב ויכפלם ויוסיף עליהם ה' וירבה אותם על ה' ויוסיף עליהם י' וירבה אותם על י' וישליך מהם ש"נ | ||||||||||||||||||||||||||
|
דמיון זה כגון שחשב י' | ||||||||||||||||||||||||||
| אמרנו לו שיכפלם ויהיו כ' | |||||||||||||||||||||||||||
| גם אמרנו לו שיוסיף עליהם ה' ויהיו כ"ה | |||||||||||||||||||||||||||
| גם אמרנו לו שירבה אותם על ה' ויהיו קכ"ה | |||||||||||||||||||||||||||
| עו' אמרנו לו שיוסיף עליהם י' ויהיו קל"ה | |||||||||||||||||||||||||||
| גם אמרנו לו שירבה אותם על י' ויהיו אלף וש"נ | |||||||||||||||||||||||||||
| השלך מהם ש"נ ישארו אלף | |||||||||||||||||||||||||||
| ונקח דמיונם והוא י' כמו שחשב | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
אחר אמור שיחשוב ויכפול מה שחשב על ג' כן יכפלהו על ד' א"כ יכפלהו על ה' ויחלקהו על מה שחשב בראשונה ותוכל לדעת הנשאר בעשותך החשבון הזה על א' | ||||||||||||||||||||||||||
|
דמיון זה כגון שחשב ד' | ||||||||||||||||||||||||||
| כפול אותם על ג' ויהיו י"ב | |||||||||||||||||||||||||||
| כפול אותם על ד' ויהיו מ"ח | |||||||||||||||||||||||||||
| כפול אותם על ה' ויהיו ר"מ | |||||||||||||||||||||||||||
| חלקם על ד' שחשב בראשונה נשארו בידו ס' | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| ואתה חשבת א' | |||||||||||||||||||||||||||
| כפלת אותו על ג' היו ג' | |||||||||||||||||||||||||||
| כפלת אותו על ד' יהיו י"ב | |||||||||||||||||||||||||||
| כפלת אותו על ה' היו ס' | |||||||||||||||||||||||||||
| חלקת אותו על א' יהיו ס' כמו שנשאר בידו | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
אחר אמור שיחשוב אי זה מספר שירצה אך לא יהיה פחות מד' ויוסיף עליו פי שנים ויחלק העולה לחצאים אם יש בחצי שבר יחשבהו שלם ואם לאו אין צריך תקון אחר | ||||||||||||||||||||||||||
| endnote - MS Verona | תמו אלו הדרכים ברוך שוכן עליונים אמן חזק הכותב ואמץ הקורא | ||||||||||||||||||||||||||
| additional problem - another version of a guessing problem discussed above | |||||||||||||||||||||||||||
|
ג"ע הכ"א קט"ו כשתרצה לעשות זה החשבון אמור לחברך שיחשוב אי זה חשבון שתרצה | ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
דמיון זה הרי שחשב חברך י"א | ||||||||||||||||||||||||||
| השליכם ג' ג' ישאר ב' | |||||||||||||||||||||||||||
| השליכם [ה' ה'] ישאר א' | |||||||||||||||||||||||||||
| השליכם ז' ז' ישאר [ד'] | |||||||||||||||||||||||||||
| [...] כלול הכל | |||||||||||||||||||||||||||
| שתי פעמי' ע' הם ק"מ | |||||||||||||||||||||||||||
| א' פעם כ"א הוא כ"א | |||||||||||||||||||||||||||
| ד' פעמי' ט"ו הם ס' | |||||||||||||||||||||||||||
| חבר ק"מ וכ"א וס' יעלו רכ"א | |||||||||||||||||||||||||||
| השלך מהם שתי פעמים ק"ה ישאר י"א כמו שחשב חברך | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
ודע שאם שלש מאות או יותר תשליך מהם ג' פעמי' ק"ה | ||||||||||||||||||||||||||
|
וכן לה' ד' פעמי' ק"ה | ||||||||||||||||||||||||||
|
וכן כלם | ||||||||||||||||||||||||||
Divisibility of the Numbers 1-112 (MS Ithaca) |
|||||||||||||||||||||||||||
| endnote - MS Ithaca | נשלם ספר החשבון | ||||||||||||||||||||||||||
| תהלה לאל המחכים לכל חכם ונבון | |||||||||||||||||||||||||||
| תם ונשלם | |||||||||||||||||||||||||||
| A list of the fractions [= divisors] of each of the numbers 1-112 | [229]אלו הם חשבונות שיש להם ריגולא ר"ל שיש להם חלוק לחצי ולשליש ולרביע ולדומים ואותן שאין להם ריגולא | ||||||||||||||||||||||||||
|
א' אין לו ריגולא | ||||||||||||||||||||||||||
|
ב' יש לו ריגולא כי יש לו חצי | ||||||||||||||||||||||||||
|
ג' יש לו שליש | ||||||||||||||||||||||||||
|
ד' יש לו חצי ורביע | ||||||||||||||||||||||||||
|
ה' אין לו ריגולא | ||||||||||||||||||||||||||
|
ו' יש לו חצי ושליש והוא שוה בחלקיו | ||||||||||||||||||||||||||
|
ז' אין לו ריגולא | ||||||||||||||||||||||||||
|
ח' יש לו חצי ורביע | ||||||||||||||||||||||||||
|
ט' יש לו שליש | ||||||||||||||||||||||||||
|
י' יש לו חצי וחמש | ||||||||||||||||||||||||||
|
י"א אין לו ריגולא | ||||||||||||||||||||||||||
|
י"ב יש לו חצי ושליש ורביע ושתות | ||||||||||||||||||||||||||
|
י"ג אין לו ריגולא | ||||||||||||||||||||||||||
|
י"ד יש לו חצי ושביע | ||||||||||||||||||||||||||
|
ט"ו יש לו שליש וחמש | ||||||||||||||||||||||||||
|
י"ו יש לו חצי ורביע ושמיני | ||||||||||||||||||||||||||
|
י"ז אין לו ריגולא | ||||||||||||||||||||||||||
|
י"ח יש לו חצי ושליש ושתות | ||||||||||||||||||||||||||
|
י"ט אין לו ריגולא | ||||||||||||||||||||||||||
|
כ' יש לו חצי ורביע וחמש | ||||||||||||||||||||||||||
|
כ"א יש לו שליש ושביע | ||||||||||||||||||||||||||
|
כ"ב יש לו חצי ואחד מי"א | ||||||||||||||||||||||||||
|
כ"ג אין לו ריגולא | ||||||||||||||||||||||||||
|
כ"ד יש לו חצי ושליש ורביע ושתות [ו]שמיני | ||||||||||||||||||||||||||
|
כ"ה יש לו חמש | ||||||||||||||||||||||||||
|
כ"ו יש לו חצי ואחד מי"ג | ||||||||||||||||||||||||||
|
כ"ז יש לו שליש ותשיע | ||||||||||||||||||||||||||
|
כ"ח יש לו חצי ורביע ושביע ואחד מי"ד | ||||||||||||||||||||||||||
|
כ"ט אין לו רגולא | ||||||||||||||||||||||||||
|
ל' יש לו חצי ושליש ועשירית ואחד מט"ו | ||||||||||||||||||||||||||
|
ל"א אין לו ריגולא | ||||||||||||||||||||||||||
|
ל"ב יש לו חצי ורביעי' ושמינית ואחד מי"ו | ||||||||||||||||||||||||||
|
ל"ג יש לו שליש ואחד מי"א | ||||||||||||||||||||||||||
|
ל"ד יש לו חצי ואחד מי"ז | ||||||||||||||||||||||||||
|
ל"ה יש לו חמש ושביע | ||||||||||||||||||||||||||
|
ל"ו יש לו חצי ושליש ותשיע ורביע | ||||||||||||||||||||||||||
|
ל"ז אין לו ריגולא | ||||||||||||||||||||||||||
|
ל"ח יש לו חצי ואחד מי"ט | ||||||||||||||||||||||||||
|
ל"ט יש לו שליש ואחד מי"ג | ||||||||||||||||||||||||||
|
מ' יש לו חצי ורביע וחמש ושמין ועשירי | ||||||||||||||||||||||||||
|
מ"א אין לו ריגולא | ||||||||||||||||||||||||||
|
מ"ב יש לו חצי ושליש ושתות ושביע וי"ד וכ"א | ||||||||||||||||||||||||||
|
מ"ג אין לו ריגולא | ||||||||||||||||||||||||||
|
מ"ד יש לו חצי ורביע וי"א וכ"ב | ||||||||||||||||||||||||||
|
מ"ה יש לו חמש ותשיע וט"ו | ||||||||||||||||||||||||||
|
מ"ו יש לו חצי ואחד מכ"ג | ||||||||||||||||||||||||||
|
מ"ז אין לו ריגולא | ||||||||||||||||||||||||||
|
מ"ח יש לו חצי ושליש ורביע ושתות ושמין י"ב וי"ו וכ"ד | ||||||||||||||||||||||||||
|
מ"ט יש לו שביע | ||||||||||||||||||||||||||
|
נ' יש לו חצי וחמש ועשירית וכ"ה | ||||||||||||||||||||||||||
|
נ"א יש לו שליש וי"ז | ||||||||||||||||||||||||||
|
נ"ב יש לו חצי ורביע וי"ג וכ"ו | ||||||||||||||||||||||||||
|
נ"ג אין לו ריגולא | ||||||||||||||||||||||||||
|
נ"ד יש לו חצי ושליש ושתות ותשיע וכ"ז | ||||||||||||||||||||||||||
|
נ"ה יש לו חמש וי"א | ||||||||||||||||||||||||||
|
נ"ו יש לו חצי ורביע ושביע ושמיני וי"ד וכ"ח | ||||||||||||||||||||||||||
|
נ"ז יש לו שליש וי"ט | ||||||||||||||||||||||||||
|
נ"ח יש לו חצי וכ"ט | ||||||||||||||||||||||||||
|
נ"ט אין לו ריגולא | ||||||||||||||||||||||||||
|
[230]ס' יש לו חצי ושליש ורביע וחמש ושתות ועשירי וי"ב וט"ו וכ' ול' | ||||||||||||||||||||||||||
|
ס"א אין לו ריגולא | ||||||||||||||||||||||||||
|
ס"ב יש לו חצי ול"א | ||||||||||||||||||||||||||
|
ס"ג יש לו שליש ושביע ותשיע | ||||||||||||||||||||||||||
|
ס"ד יש לו חצי ורביע ושמיני וי"ו ול"ב | ||||||||||||||||||||||||||
|
ס"ה יש לו חמש וי"ג | ||||||||||||||||||||||||||
|
ס"ו יש לו חצי ושליש ושתות וי"א וכ"ב ול"ג | ||||||||||||||||||||||||||
|
ס"ז אין לו ריגולא | ||||||||||||||||||||||||||
|
ס"ח יש לו חצי ורביע וי"ז ול"ד | ||||||||||||||||||||||||||
|
ס"ט יש לו שליש וכ"ג | ||||||||||||||||||||||||||
|
ע' יש לו חצי ושביע וחמש וי"ד ול"ה | ||||||||||||||||||||||||||
|
ע"א אין לו ריגולא | ||||||||||||||||||||||||||
|
ע"ב יש לו חצי ושליש ורביע ושתות ושמיני ותשיע י"ב י"ח כ"ד ל"ו | ||||||||||||||||||||||||||
|
ע"ג אין לו ריגולא | ||||||||||||||||||||||||||
|
ע"ד יש לו חצי ול"ז | ||||||||||||||||||||||||||
|
ע"ה יש לו חמש וט"ו וכ"ה | ||||||||||||||||||||||||||
|
ע"ו יש לו חצי ורביע וי"ט ול"ח | ||||||||||||||||||||||||||
|
ע"ז יש לו שביע וי"א | ||||||||||||||||||||||||||
|
ע"ח יש לו חצי ושתות וי"ג ול"ט | ||||||||||||||||||||||||||
|
ע"ט אין לו ריגולא | ||||||||||||||||||||||||||
|
פ' יש לו חצי ורביע וחמש ושמיני ועשירי וי"ו וכ' ומ' | ||||||||||||||||||||||||||
|
פ"א יש לו תשיע | ||||||||||||||||||||||||||
|
פ"ב יש לו חצי ומ"א | ||||||||||||||||||||||||||
|
פ"ג אין לו ריגולא | ||||||||||||||||||||||||||
|
פ"ד יש לו חצי ושליש ורביע ושתות וי"ב וכ"א ומ"ב | ||||||||||||||||||||||||||
|
פ"ה יש לו שביע וי"ז | ||||||||||||||||||||||||||
|
פ"ו יש לו חצי ומ"ג | ||||||||||||||||||||||||||
|
פ"ז יש לו שליש וכ"ט | ||||||||||||||||||||||||||
|
פ"ח יש לו חצי וי"א ושמיני ורביע וכ"ב ומ"ד | ||||||||||||||||||||||||||
|
פ"ט אין לו ריגולא | ||||||||||||||||||||||||||
|
צ' יש לו חצי ושלישי וחמש ושתות ותשיעי ועשירי וט"ו ול' ומ"ה | ||||||||||||||||||||||||||
|
צ"א יש לו שביע וי"ג | ||||||||||||||||||||||||||
|
צ"ב יש לו חצי ושליש ורביע ושתות ומ"ו | ||||||||||||||||||||||||||
|
צ"ג יש לו שליש ול"א | ||||||||||||||||||||||||||
|
צ"ד יש לו חצי ומ"ז | ||||||||||||||||||||||||||
|
צ"ה יש לו חמש וי"ט | ||||||||||||||||||||||||||
|
צ"ו יש לו חצי ושליש ורביע ושתות ושמיני וי"ב וי"ו וכ"ד ול"ב ומ"ח | ||||||||||||||||||||||||||
|
צ"ז אין לו ריגולא | ||||||||||||||||||||||||||
|
צ"ח יש לו חצי ושביע | ||||||||||||||||||||||||||
|
צ"ט יש לו תשיע וי"א | ||||||||||||||||||||||||||
|
ק' יש לו חצי ורביע וחמש ועשירי וכ' וכ"ה ונ' | ||||||||||||||||||||||||||
|
ק"א אין לו ריגולא | ||||||||||||||||||||||||||
|
ק"ב יש לו ריגולא חצי ושליש ושתות וי"ז ול"ד ונ"א | ||||||||||||||||||||||||||
|
ק"ג אין לו ריגולא | ||||||||||||||||||||||||||
|
ק"ד יש לו חצי ורביע וי"ג וכ"ו ונ"ב ושמיני | ||||||||||||||||||||||||||
|
ק"ה יש לו שליש וחמש ושביע וט"ו וכ"א ול"ה | ||||||||||||||||||||||||||
|
ק"ו יש לו חצי ונ"ג | ||||||||||||||||||||||||||
|
ק"ז אין לו ריגולא | ||||||||||||||||||||||||||
|
ק"ח יש לו חצי ושליש ורביע ושתות ותשיע וי"ב וי"ח ול"ו ונ"ד | ||||||||||||||||||||||||||
|
ק"ט אין לו ריגולא | ||||||||||||||||||||||||||
|
ק"י יש לו חצי וחמש ועשירי וי"א וכ"ב ונ"ה | ||||||||||||||||||||||||||
|
קי"א אין לו ריגולא | ||||||||||||||||||||||||||
|
קי"ב יש לו חצי ורביע וכ"ח ונ"ו | ||||||||||||||||||||||||||
| סליק | |||||||||||||||||||||||||||
| [231]כתבים כ"ז, מהשר החכם דון בנבנשית בן לביא | |||||||||||||||||||||||||||
Notes
- ↑ 31v
- ↑ MS Cambridge: title is missing
אחד: MS Cambridge א' MS Ithaca חשבון
מן המספר: MS Cambridge מספר; Ithaca: המספר ומדרך א
ועיקר המספר: MS Cambridge om. - ↑ הוא: MS Cambridge om.
על: MS Cambridge עד - ↑ הצדדים: MS Ithaca צדי הצדדים
- ↑ צדי: MS Ithaca om.
- ↑ שאינו: MS Cambridge שהוא אינו
- ↑ מורה: MS Cambridge מוראה
שבר: MS Ithacaחציmarg. שבר - ↑ ב'פ'ב' MS Cambridge :ב' פעמי' ב'
- ↑ ג'פ'ג' MS Cambridge :ג' פעמי' ג'
- ↑ כשתרבה: MS Cambridge כשאתה מרבה
- ↑ כגון: MS Cambridge כמו
- ↑ חצי פעם חצי: MS Cambridge חצי פעם חצי פעם
- ↑ שליש פעם שליש: MS Cambridge שליש פעם שליש פעם
- ↑ שהוא: MS Cambridge הוא
- ↑ רביע פעם רביע: MS Cambridge רביע פעם רביע פעם
- ↑ שהוא: MS Cambridge הוא
- ↑ MS Ithaca om.
- ↑ שאיננו: MS Cambridge כי אינו
- ↑ כשנרצה: MS Cambridge ואם נרצה
- ↑ לרבות: MS Cambridge לדעת
- ↑ נקח: MS Cambridge om.
- ↑ דמיונם: MS Cambridge שדמיונם
- ↑ מן ... וכמו: MS Cambridge om.
- ↑ ו'פ'ד' MS Cambridge :שו' פעמי' ד'
- ↑ הם: MS Cambridge שהם
- ↑ כן ... מ': MS Cambridge om.
- ↑ הם: MS Cambridge בין יהיו
- ↑ וכן: MS Cambridge
וג'וכן - ↑ ג'פ'ל' MS Cambridge :ג' פעמים ל'
- ↑ הוא: MS Cambridge om.
- ↑ ויהיו: MS Cambridge כן ג'פ'ל' יהיו
- ↑ כשנרצה ... כלם: MS Cambridge the discussion on multiplication of units by tens appears after the discussion on multiplication of tens by tens
- ↑ ואם נרבה: MS Cambridge כשתרבה
- ↑ של' הם MS Cambridge :היות ל'
- ↑ ל' ג': MS Ithaca ג' ל'
- ↑ ג'פ'ג' MS Cambridge :ג' פעמי' ג'
- ↑ שג'פ'ג' MS Cambridge :שג' פעמים ג'
- ↑ מ'פ'מ' MS Cambridge :מ' פעמים מ'
- ↑ י"ו: MS Ithaca: י"ו וכן מ' פעמי' מ' הם י"ו
- ↑ ד' ד'פ'ד' י"ו וכן מ'פ'מ' י"ו מאות MS Cambridge :ד' ... מאות
- ↑ ל'פ'מ' MS Cambridge :ל' פעמים מ'
- ↑ ג'פ'ד' MS Cambridge :הוא ... ד'
- ↑ ל'פ'מ' MS Cambridge :ל' פע' מ'
- ↑ ואם נרבה עשרות עם עשרות... מאות: MS Ithaca om.
- ↑ עשרות: MS Ithaca עשרי'
- ↑ יהיה: MS Cambridge יהיו
- ↑ ב'פ'ר' MS Cambridge :כ' פעמים ב' מאות
- ↑ ב': MS Ithaca om.
- ↑ כן ב'פ'ר' MS Cambridge :והם
- ↑ ה'פ'ה' MS Cambridge :ה' פעמי' ה'
- ↑ שהם: MS Cambridge יהיו
- ↑ והם: MS Cambridge כן נ' פ' ת"ק יהיו
- ↑ ר'פ'ר' MS Cambridge :ר' פעמים ר'
- ↑ הם: MS Cambridge om.
- ↑ ב'פ'ב' MS Cambridge :ב' פעמים ב'
- ↑ שהם: MS Cambridge כגון ר'פ'ר' יהיו
- ↑ 32r
- ↑ מאלפים: MS Cambridge מאלפים והם מ' אלפים
- ↑ ה'פ'ה' MS Cambridge :ה' פעמים ה'
- ↑ והם: MS Cambridge ויהיו ת"ק פ' ת"ק
- ↑ MS Ithaca om.
- ↑ ואם נרצה לרבות: MS Cambridge אם נרבה
- ↑ ת"ר: MS Cambridge ת"ר
אלפים - ↑ שהם: MS Cambridge הם
- ↑ ששמרת: MS Cambridge המשמרת
- ↑ מאות האלפים: MS Cambridge המאות מהאלפים
- ↑ גם כן: MS Cambridge ג"כ
- ↑ האלפים: MS Cambridge אלפים
- ↑ אם כן: MS Cambridge א"כ
- ↑ אחד: MS Cambridge א'
- ↑ MS Ithaca om.
- ↑ ואינם: MS Cambridge ולא
- ↑ MS Ithaca om.
- ↑ וחכמי ... 10: MS Cambridge om.
- ↑ MS Ithaca om.
- ↑ ראש: MS Cambridge תחלת
- ↑ הנפרדים: MS Cambridge הנפרדות
- ↑ שהוא: MS Cambridge והוא
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ דרך...ב' אותיות: MS Ithaca om.
- ↑ כשנרצה: MS Cambridge כשתרצה
- ↑ ואחרי כן: MS Cambridge ואח"כ
- ↑ ואחרי כן: MS Cambridge ואח"כ
- ↑ ונחזיק: MS Ithaca ונכתוב
- ↑ 32v
- ↑ ונכתבם: MS Ithaca om.
- ↑ אחר זה נרבה... הרי ח': MS Ithaca om.
- ↑ כ"ז: MS Ithaca י"ח
- ↑ בצורה: MS Ithaca אותה
- ↑ אות: MS Ithaca אותו
- ↑ אם: MS Ithaca om.
- ↑ ד': MS Ithaca ג'
- ↑ ד': MS Ithaca ג'
- ↑ ונכתוב אותם ז' פעמי': MS Ithaca om.
- ↑ Here ends this chapter in MS Ithaca
- ↑ 33r
- ↑ י"ב: MS Ithaca י"ג
- ↑ תקס"ז: MS Ithaca תתקס"ז
- ↑ וב': MS Ithaca om.
- ↑ הם י"ט: MS Ithaca om.
- ↑ אחר כן: MS Ithaca בידינו
- ↑ ועם... י"ד: MS Ithaca om.
- ↑ ומן ז'... ד' תחתיהם: MS Ithaca om.
- ↑ ישארו ח': MS Ithaca marg.
- ↑ ותרנ"ד: MS Ithaca ותרנ"ב
- ↑ 34r
- ↑ נוכל: MS Ithaca illegible
- ↑ א': MS Ithaca om.
- ↑ ונכתוב אותם על: MS Ithaca ונחלקנו על ח'
- ↑ כל: MS Ithaca om.
- ↑ יהיה היוצא מן החלוקה: MS Ithaca om.
- ↑ ואם תרצה לבחון... אם כך הוא החשבון אמתי: MS Ithaca om.
- ↑ 34v
- ↑ ונחבר: MS Ithaca ונכתבם ונחבר
- ↑ א': MS Ithaca ונכתוב א'
- ↑ ציפרא: MS Ithaca twice
- ↑ 35r
- ↑ ו': MS Ithaca י'
- ↑ ע"ח: MS Ithaca וכן
- ↑ על: MS Ithaca עד
- ↑ ס"ג: MS Ithaca ג'
- ↑ ס"ד: MS Ithaca קכ"ח
- ↑ 35v
- ↑ אחד הולך... ואדם: MS Ithaca twice
- ↑ 36r
- ↑ ד': MS Ithaca ו'
- ↑ 36v
- ↑ הוא: MS Ithaca הם
- ↑ והחומש הוא ד': MS Ithaca om.
- ↑ ט': MS Ithaca ד'
- ↑ י': MS Ithaca ו'
- ↑ 37r
- ↑ וג'...שמינית פ': MS Ithaca om.
- ↑ שהוא הג' שמיניות חלקם: MS Ithaca om.
- ↑ שהוא עשירית פ'...חלקים מפ': MS Ithaca יהיה ג'
- ↑ ואם יאמר... כמה יהיו: MS Ithaca om.
- ↑ ואם יאמר השלך... חלקים מכ"א: MS Ithaca om.
- ↑ ואם יאמר כמה הם יותר...חלק אחת ממ': MS Ithaca om.
- ↑ ואם יאמר חלק ג'... ומאתים מן האחר: MS Ithaca om.
- ↑ ה' הם: MS Ithaca om.
- ↑ ממאה: MS Ithaca ומאה
- ↑ ממאה: MS Ithaca ומאה
- ↑ אם יאמר אדם ז' פיסאני... אלף ליט' פיסאני לקוטרניסי: MS Ithaca om.
- ↑ 37v
- ↑ 38r
- ↑ 38v
- ↑ לדעת כמה זהב ישים... יהיו אלף ות"ר: MS ithaca twice
- ↑ פשוטי' שהם ג'... תש"כ: MS Ithaca om.
- ↑ ס' ליט': MS Ithaca כ"ה אלפים
- ↑ מק"כ: MS Ithaca marg.
- ↑ חלקים: MS Ithaca ליטרי'
- ↑ MS Ithaca om. שלשתי ארבעי' אונקיו' זהב
- ↑ ס': MS Ithaca om.
- ↑ ד' וח': MS Ithaca י"ג וי"א
- ↑ החלק: MS Ithaca המחובר
- ↑ ג': MS Ithaca om.
- ↑ ולדעת חלק השיני... וי"א חלקים מי"ג: MS Ithaca twice
- ↑ 39r
- ↑ ל"ה... בהיות סכום: MS Ithaca om.
- ↑ ט"ו: MS Ithaca om.
- ↑ ה': MS Ithaca om.
- ↑ ג': MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ MS Ithaca ראשון ס'
- ↑ MS Ithaca om.
- ↑ MS Ithaca עשרים
- ↑ MS Ithaca om.
- ↑ MS Ithaca illegible
- ↑ 39v
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ 40r
- ↑ MS Ithaca פרחי' כ'
- ↑ MS Ithaca ג'
- ↑ 40v
- ↑ 41r
- ↑ MS Ithaca י"ח
- ↑ MS Ithaca om.
- ↑ MS Ithaca twice
- ↑ 41v
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ MS Ithaca twice
- ↑ MS Ithaca ופה"ה
- ↑ MS Ithaca om.
- ↑ 42r
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ 42v
- ↑ MS Ithaca marg.: חסר הצורה
- ↑ י"ז פשוטי': MS Ithaca ה"פ
- ↑ 43r
- ↑ This problem is missing in MS Ithaca
- ↑ כ"ה: MS Ithaca אלף
- ↑ ב': MS Ithaca ח'
- ↑ 43v
- ↑ ה': MS Ithaca ב'
- ↑ הסדר: MS Ithaca הכסף
- ↑ תחשוב: MS Ithaca om.
- ↑ ומכל... לכל אחד: MS Ithaca ולכל הנשאר מן הה'
- ↑ דמיון זה... כמו שחשב חברך: according to MS Verona; MS Ithaca om.
- ↑ 44r
- ↑ ג': MS Ithaca marg.
- ↑ שי"ב ימים היא: MS Ithaca twice
- ↑ והם ט': MS ithaca twice
- ↑ 44v
- ↑ נמצא שהיו... ממ"ז: MS Ithaca om.
- ↑ זה היין: MS Ithaca אותם
- ↑ This problem is missing in MS Ithaca; it appears in MS Verona, Cambridge
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ 45r
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ MS Ithaca om.
- ↑ ט' נ"ד: MS Ithaca om.
- ↑ יבואו ג'... מן הדי': MS Ithaca om.
- ↑ 45v
- ↑ והג'... מן הליט': MS Ithaca om.
- ↑ MS Ithaca: this problem appears at the end of the treatise, 46v
- ↑ MS Verona אחר
- ↑ ר': MS Ithaca om.
- ↑ MS Ithaca end.
- ↑ 46r
- ↑ 46v
- ↑ MS Ithaca end
Appendix: Bibliography
Anonymous Hebrew-Italian Textbook
Manuscripts:
- 1) Cambridge, University Library Add. 553 (IMHM: f 16842), ff. 64r-86r (17th century)
- 2) Firenze, Biblioteca Medicea Laurenziana Plut.44.3/2 (IMHM: f 17826), ff. 62r-69v (15th century)
- Plut.44.3/2
- 3) Ithaca (NY), Cornell University A 26/3 (IMHM: f 46122), ff. 31r-46v (15th century)
- 4) Paris, Bibliothèque Nationale de France heb. 1049/2 (IMHM: f 27767), ff. 35r-41v (14th-15th century)
- heb. 1049/2
- 5) Verona, Biblioteca Civica 33 (83.1)/2 (IMHM: f 32674), ff. 8r-84v; 222r-v (Cento, 1461)
The transcript is based mainly on manuscript Ithaca 26
![\scriptstyle{\color{OliveGreen}{n=\frac{1}{2}\sdot\left[\left(n-a\right)+\left(n+a\right)\right]}}](/mediawiki/images/math/f/c/8/fc83d38a8c331161825ee73003f3089d.png)
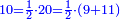
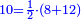

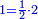
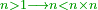
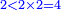
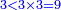
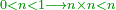
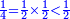
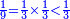
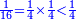
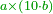
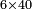
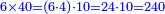
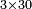
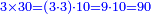
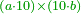
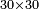
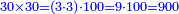
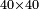

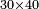

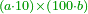
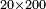

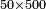

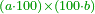
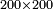

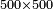

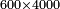
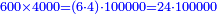
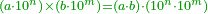
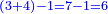
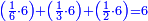
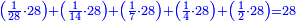
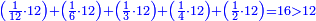
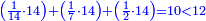
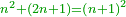
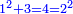
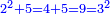
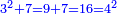
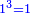
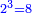
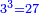
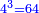
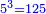

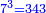
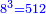
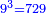
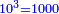
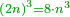
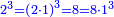
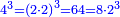
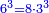
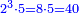
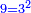
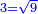
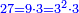
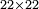
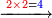

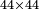
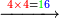
![\scriptstyle\xrightarrow{{\color{red}{\left[\left(4\times4\right)+\left(4\times4\right)\right]+{\color{green}{1}}}}={\color{green}{3}}{\color{blue}{3}}}](/mediawiki/images/math/1/e/c/1ececf5d034ec70c94f031bf071152aa.png)
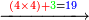
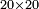
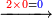

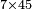
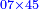
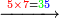
![\scriptstyle\xrightarrow{{\color{red}{\left[\left(5\times0\right)+\left(4\times7\right)\right]+{\color{green}{3}}}}={\color{green}{3}}{\color{blue}{1}}}](/mediawiki/images/math/4/c/4/4c410dd17897b37e2487c14c1d8e6e79.png)
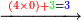
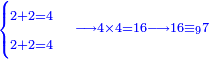
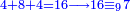
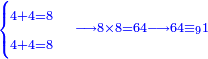
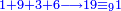
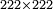

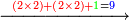
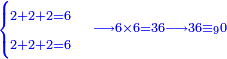
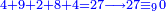
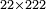
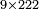
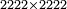
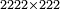
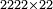
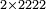
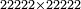
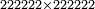
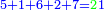
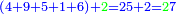
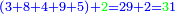
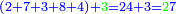
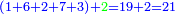
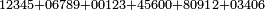
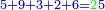
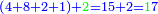
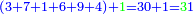
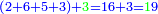
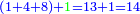



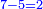
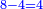

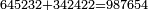
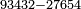
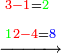
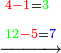
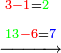
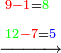
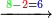
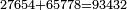
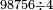
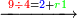
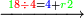
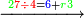
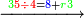
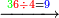
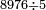

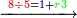
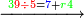
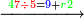
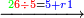

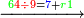
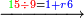
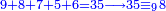

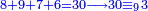
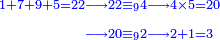
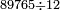
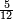
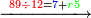
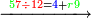

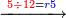
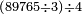
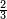

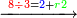
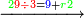
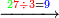
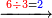
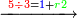
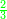
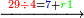
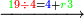
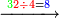
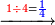

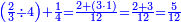
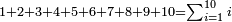
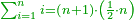
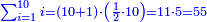
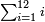
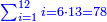
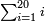
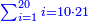
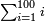
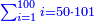
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} i=\left[\left(n+1\right)\sdot\frac{1}{2}\right]\sdot n}}](/mediawiki/images/math/3/d/7/3d7cb5864c46cebad79f69e1ed67f5c8.png)
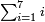
![\scriptstyle{\color{blue}{\sum_{i=1}^{7} i=\left[\left(7+1\right)\sdot\frac{1}{2}\right]\sdot7=4\sdot7=28}}](/mediawiki/images/math/4/0/3/403b7a86e997584f797dd94f6688ef6f.png)
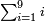
![\scriptstyle{\color{blue}{\sum_{i=1}^{9} i=\left[\left(9+1\right)\sdot\frac{1}{2}\right]\sdot9=5\sdot9=45}}](/mediawiki/images/math/b/5/8/b5841f529a3f589200f8bcc430afb0c9.png)
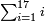
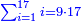
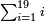
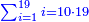
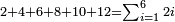
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 2i=\left(\frac{1}{2}\sdot2n\right)\sdot\left[\left(\frac{1}{2}\sdot2n\right)+1\right]}}](/mediawiki/images/math/b/7/9/b79eac562b9965aac8017cc090032f1c.png)
![\scriptstyle{\color{blue}{2+4+6+8+10+12=\sum_{i=1}^{6} 2i=\left(\frac{1}{2}\sdot12\right)\sdot\left[\left(\frac{1}{2}\sdot12\right)+1\right]=6\sdot\left(6+1\right)=6\sdot7=42}}](/mediawiki/images/math/8/4/b/84bc9cf5d332930a5d680c1926fa1f38.png)
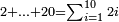
![\scriptstyle{\color{blue}{2+\ldots+20=\sum_{i=1}^{10} 2i=\left(\frac{1}{2}\sdot20\right)\sdot\left[\left(\frac{1}{2}\sdot20\right)+1\right]=10\sdot\left(10+1\right)=10\sdot11=110}}](/mediawiki/images/math/6/5/f/65f93f84aefe0ee6c312325aea59ea7a.png)
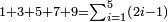
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} \left(2i-1\right)=\left[\left[\left(2n-1\right)+1\right]\sdot\frac{1}{2}\right]^2}}](/mediawiki/images/math/1/d/1/1d1c10bb903db4adabe6da43fd22af4f.png)
![\scriptstyle{\color{blue}{1+3+5+7+9=\sum_{i=1}^{5} \left(2i-1\right)=\left[\left(9+1\right)\sdot\frac{1}{2}\right]^2=5^2=25}}](/mediawiki/images/math/1/d/c/1dcff7ce3101deb7b2e30dcb2f08ed18.png)
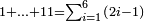
![\scriptstyle{\color{blue}{1+\ldots+11=\sum_{i=1}^{6} \left(2i-1\right)=\left[\left(11+1\right)\sdot\frac{1}{2}\right]^2=6^2}}](/mediawiki/images/math/a/2/1/a21f6f972f899caabdb7042fe46b9ec5.png)
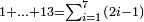
![\scriptstyle{\color{blue}{1+\ldots+13=\sum_{i=1}^{7} \left(2i-1\right)=\left[\left(13+1\right)\sdot\frac{1}{2}\right]^2=7^2}}](/mediawiki/images/math/4/6/3/46389700419bba26592720e86211a619.png)
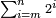
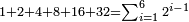
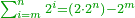
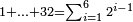
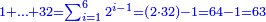
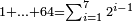
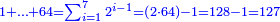
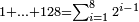
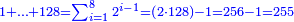
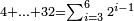
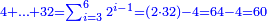
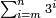
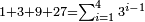
![\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 3^i=\left(3^n-3^m\right)+\left[\frac{1}{2}\sdot\left(3^n-3^m\right)\right]+3^m}}](/mediawiki/images/math/0/f/e/0fe2a83d5cf283c31e438b4be07d53ea.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle1+3+9+27&\scriptstyle=\sum_{i=1}^{4} 3^{i-1}=\left(27-1\right)+\left[\frac{1}{2}\sdot\left(27-1\right)\right]+1\\&\scriptstyle=26+\left(\frac{1}{2}\sdot26\right)+1=26+13+1=39+1=40\\\end{align}}}](/mediawiki/images/math/4/6/8/468339323fbfef4643a3d7badc4bb367.png)
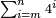
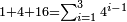
![\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 4^i=\left(4^n-4^m\right)+\left[\frac{1}{3}\sdot\left(4^n-4^m\right)\right]+4^m}}](/mediawiki/images/math/3/4/e/34e7297d6bec511e29f39a48f6cc5e12.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle1+4+16&\scriptstyle=\sum_{i=1}^{3} 4^{i-1}=\left(16-1\right)+\left[\frac{1}{3}\sdot\left(16-1\right)\right]+1\\&\scriptstyle=15+\left(\frac{1}{3}\sdot15\right)+1=15+5+1=20+1=21\\\end{align}}}](/mediawiki/images/math/6/c/e/6ce02e32a7ae9e3b4e927b4dec037172.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} a^i=\left(a^n-a^m\right)+\left[\frac{1}{a-1}\sdot\left(a^n-a^m\right)\right]+a^m}}](/mediawiki/images/math/a/c/4/ac4afed104d1c66d05263a2f17a27b9f.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 3^i=\left(a^n-a^m\right)+\left[\frac{1}{2}\sdot\left(a^n-a^m\right)\right]+a^m}}](/mediawiki/images/math/1/4/6/14646db7744151cb1835b9db18b1761a.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 4^i=\left(a^n-a^m\right)+\left[\frac{1}{3}\sdot\left(a^n-a^m\right)\right]+a^m}}](/mediawiki/images/math/7/b/a/7baf00c471e186dfc57af24c608c0970.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 5^i=\left(a^n-a^m\right)+\left[\frac{1}{4}\sdot\left(a^n-a^m\right)\right]+a^m}}](/mediawiki/images/math/4/7/8/47870f6eaa8697dba682894aa300e11c.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=m}^{n} 6^i=\left(a^n-a^m\right)+\left[\frac{1}{5}\sdot\left(a^n-a^m\right)\right]+a^m}}](/mediawiki/images/math/6/b/9/6b9bf1c9b3a3edcba79e5aa84b937b99.png)
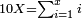
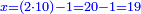
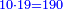
![\scriptstyle{\color{blue}{1+\ldots+19=\left[\left(19+1\right)\sdot\frac{1}{2}\right]\sdot19=10\sdot19=190}}](/mediawiki/images/math/f/a/e/faeed332110ad1840749b98d43980b97.png)
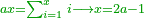
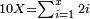
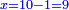
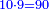
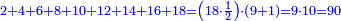
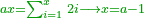
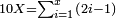
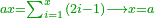
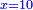
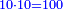
![\scriptstyle{\color{blue}{1+3+\ldots+19=\left[\left(19+1\right)\sdot\frac{1}{2}\right]^2=10^2=100}}](/mediawiki/images/math/6/5/c/65c4a0a762c7bcdc615f67afe71ce259.png)
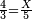
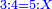
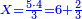
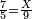
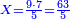
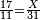
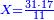
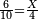
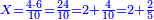
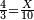
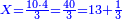
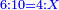
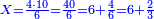
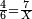
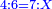
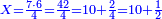
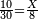
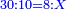
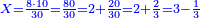 dinar
dinar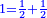
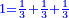
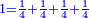
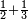

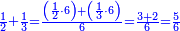
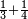
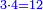
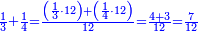
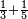
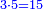
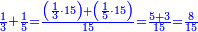
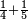
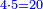
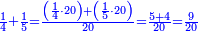
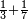
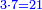
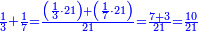
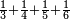
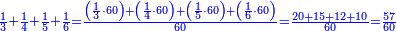
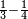
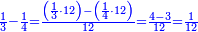
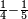
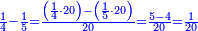
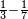
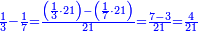
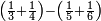
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{3}+\frac{1}{4}\right)-\left(\frac{1}{5}+\frac{1}{6}\right)&\scriptstyle=\frac{\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)\right]-\left[\left(\frac{1}{5}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)\right]}{60}\\&\scriptstyle=\frac{\left(20+15\right)-\left(12+10\right)}{60}=\frac{35-22}{60}=\frac{13}{60}\\\end{align}}}](/mediawiki/images/math/5/4/1/541b98460a6ac41c9f4c06a81eb94563.png)
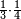
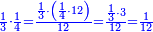
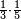
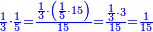
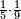
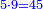
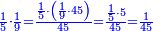
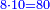
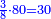
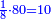
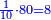
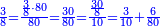
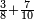
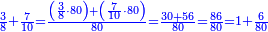
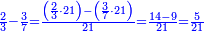
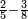
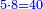
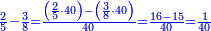
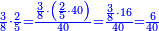
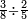
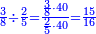
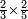
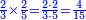
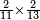
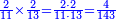
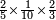
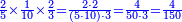
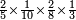
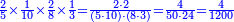
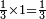
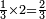
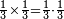
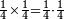
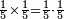
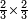
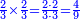
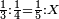



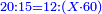
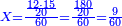
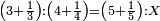
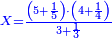
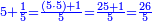
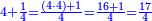
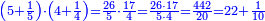
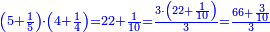
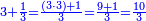
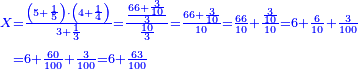
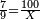
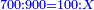
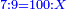
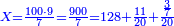
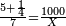
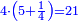
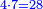
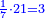
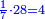
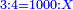
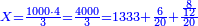
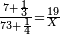
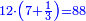
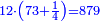
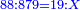
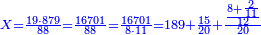
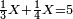
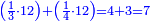
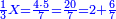
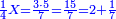
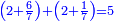
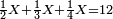
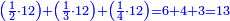
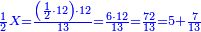
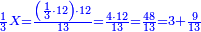
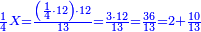
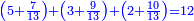
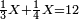
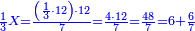
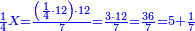
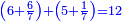
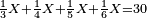
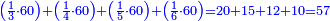
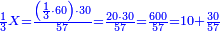
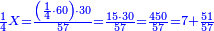
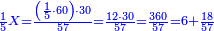
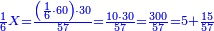
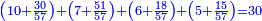
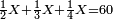
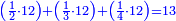
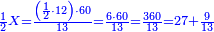
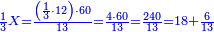
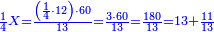
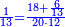
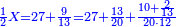
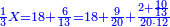
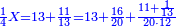
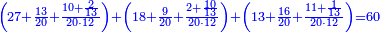
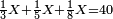
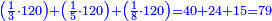
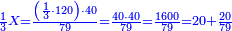
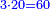
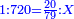
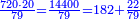
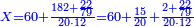
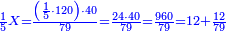
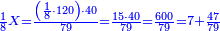
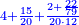
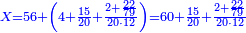
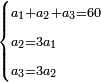
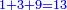
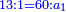
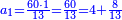
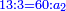
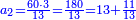
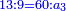
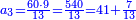
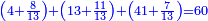
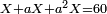
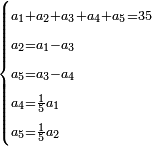
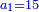
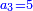
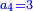

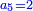

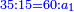
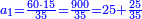
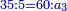
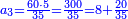
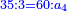
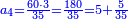
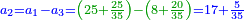
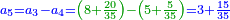
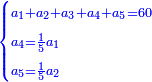
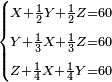
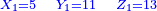
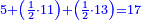
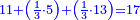
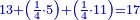
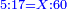
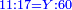
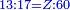
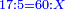
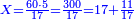
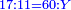
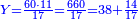
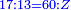
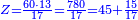
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle X+\frac{1}{2}Y+\frac{1}{2}Z &\scriptstyle=\left(17+\frac{11}{17}\right)+\left[\frac{1}{2}\sdot\left(38+\frac{14}{17}\right)\right]+\left[\frac{1}{2}\sdot\left(45+\frac{15}{17}\right)\right]\\&\scriptstyle=\left(17+\frac{11}{17}\right)+\left(19+\frac{7}{17}\right)+\left(22+\frac{16}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/4/b/c/4bcb7f884b3194f26cbd6e0d5126a31d.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Y+\frac{1}{3}X+\frac{1}{3}Z &\scriptstyle=\left(38+\frac{14}{17}\right)+\left[\frac{1}{3}\sdot\left(17+\frac{11}{17}\right)\right]+\left[\frac{1}{3}\sdot\left(45+\frac{15}{17}\right)\right]\\&\scriptstyle=\left(38+\frac{14}{17}\right)+\left(5+\frac{15}{17}\right)+\left(15+\frac{5}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/0/f/5/0f5bf6410e0eac1e6fcd1aeb019afee0.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Z+\frac{1}{4}X+\frac{1}{4}Y &\scriptstyle=\left(45+\frac{15}{17}\right)+\left[\frac{1}{4}\sdot\left(17+\frac{11}{17}\right)\right]+\left[\frac{1}{4}\sdot\left(38+\frac{14}{17}\right)\right]\\&\scriptstyle=\left(45+\frac{15}{17}\right)+\left(4+\frac{7}{17}\right)+\left(9+\frac{12}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/1/7/8/17829b09028256de1e18da1ebdbc1e04.png)
![\scriptstyle\begin{cases}\scriptstyle a_1+a_2+a_3=24\\\scriptstyle2\sdot\left[2\sdot\left[a_1-\left(a_2+a_3\right)\right]\right]\\\scriptstyle=2\sdot\left[\left(2\sdot a_2\right)-\left[\left[a_1-\left(a_2+a_3\right)\right]+\left(2\sdot a_3\right)\right]\right]\\\scriptstyle=\left[2\sdot\left(2\sdot a_3\right)\right]-\left[\left[2\sdot\left[a_1-\left(a_2+a_3\right)\right]\right]+\left[\left(2\sdot a_2\right)-\left[\left[a_1-\left(a_2+a_3\right)\right]+\left(2\sdot a_3\right)\right]\right]\right]\end{cases}](/mediawiki/images/math/8/f/b/8fb4979948b7a0b2c6bd3a05006620b0.png)
 ]; Shimon's share was 7 [
]; Shimon's share was 7 [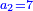 ]; and Levi's share was 4 [
]; and Levi's share was 4 [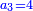 ].
].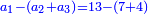
![\scriptstyle{\color{blue}{\left(2\sdot a_2\right)-\left[\left[a_1-\left(a_2+a_3\right)\right]+\left(2\sdot a_3\right)\right]=14-\left(2+8\right)}}](/mediawiki/images/math/3/a/a/3aa7dffab5cd2b56d52aefc2feb2dfed.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2\sdot\left(2\sdot a_3\right)\right]-\left[\left[2\sdot\left[a_1-\left(a_2+a_3\right)\right]\right]+\left[\left(2\sdot a_2\right)-\left[\left[a_1-\left(a_2+a_3\right)\right]+\left(2\sdot a_3\right)\right]\right]\right]\\&\scriptstyle=16-\left(4+4\right)\\\end{align}}}](/mediawiki/images/math/8/e/1/8e1b722eb36c5d205287f003ffcba2d0.png)
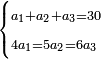
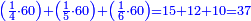
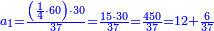
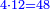

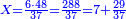
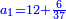
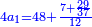
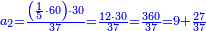
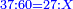
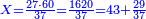
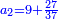
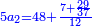
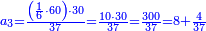
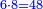
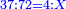
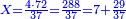 pešuṭim
pešuṭim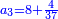
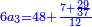
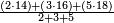
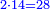
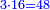

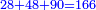
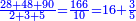
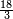
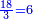
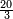
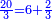
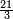
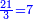
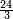
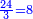
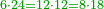
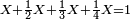
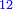
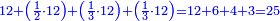
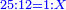
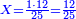
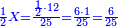
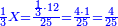
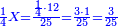
![\scriptstyle1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]=2+\frac{1}{10}\sdot\left[X-\left[\left[1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]\right]+2\right]\right]](/mediawiki/images/math/0/4/e/04ec9fa2f7109a05d7c4e8fa7ce5d879.png)
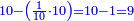
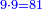
![\scriptstyle{\color{blue}{1+\left[\frac{1}{10}\sdot\left(81-1\right)\right]=1+8=9}}](/mediawiki/images/math/f/e/d/fedbd212f521d3490fb30e969942fcf1.png)
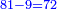
![\scriptstyle{\color{blue}{2+\left[\frac{1}{10}\sdot\left(72-2\right)\right]=2+7=9}}](/mediawiki/images/math/4/a/2/4a2f9ffedfc7ee8a418c144ec2910b39.png)

![\scriptstyle{\color{blue}{3+\left[\frac{1}{10}\sdot\left(63-3\right)\right]=3+6=9}}](/mediawiki/images/math/e/d/5/ed59c7cf92babd7c3ebf0a2fe199fe09.png)

![\scriptstyle{\color{blue}{4+\left[\frac{1}{10}\sdot\left(54-4\right)\right]=4+5=9}}](/mediawiki/images/math/1/5/c/15cbb37cff191d838c4d6807bb6f9562.png)

![\scriptstyle{\color{blue}{5+\left[\frac{1}{10}\sdot\left(45-5\right)\right]=5+4=9}}](/mediawiki/images/math/d/8/2/d82e44ebc852412b5d6902cc7868fc31.png)

![\scriptstyle{\color{blue}{6+\left[\frac{1}{10}\sdot\left(36-6\right)\right]=6+3=9}}](/mediawiki/images/math/f/7/6/f76d22ebfc6983540f2c6700d894c3d1.png)

![\scriptstyle{\color{blue}{7+\left[\frac{1}{10}\sdot\left(27-7\right)\right]=7+2=9}}](/mediawiki/images/math/d/4/3/d43701a6dcad19e91c64da436ff385c4.png)
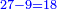
![\scriptstyle{\color{blue}{8+\left[\frac{1}{10}\sdot\left(18-8\right)\right]=8+1=9}}](/mediawiki/images/math/f/6/a/f6adf9374a14c5dd4c57219d2e303d0d.png)
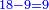
![\scriptstyle1+\left[\frac{1}{9}\sdot\left(X-1\right)\right]=2+\frac{1}{9}\sdot\left[X-\left[\left[1+\left[\frac{1}{9}\sdot\left(X-1\right)\right]\right]+2\right]\right]](/mediawiki/images/math/b/9/2/b920738ab0daea7167e2198d8a749244.png)
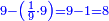
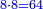
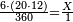
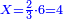
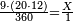
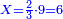
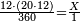
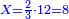
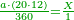
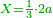
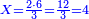
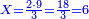
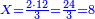
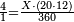
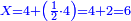
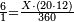
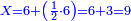
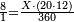
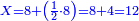
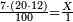
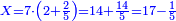
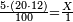
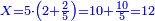
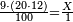
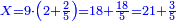
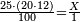
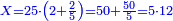
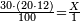
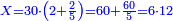
![\scriptstyle\frac{\left[10\sdot\left(20\sdot12\right)\right]+\left(3\sdot12\right)}{100}=\frac{X}{1}](/mediawiki/images/math/0/6/a/06aeda1bcfaef707f30841ae44efbf63.png)
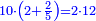
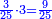
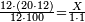
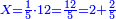
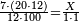
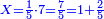
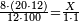
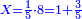
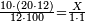
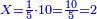
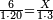
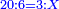
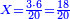
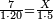
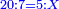
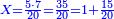
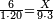
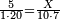
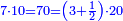
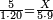
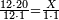

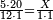
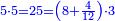
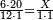
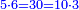
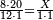
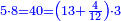
![\scriptstyle20+4-X+\left[\frac{4}{20}\sdot\left(20+4-X\right)\right]-X+\left[\frac{4}{20}\sdot\left[20+4-X+\left[\frac{4}{20}\sdot\left(20+4-X\right)\right]-X\right]\right]=X](/mediawiki/images/math/6/0/5/6053a7f78280380c9d2df6cfc64c3c4f.png)
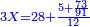
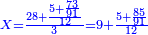
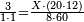
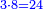

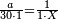
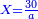
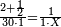
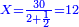
![\scriptstyle\frac{\left[37\sdot\left(20\sdot12\right)\right]+\left(18\sdot12\right)+7}{12\sdot100}=\frac{\left[37\sdot\left(20\sdot12\right)\right]+\left(18\sdot12\right)+7}{X\sdot65}](/mediawiki/images/math/6/2/6/6267dd6bf1a7b786414ead3141a07b0a.png)
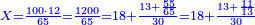
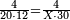
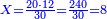
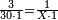
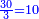
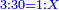
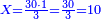
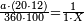
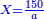
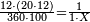
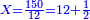
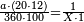
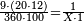
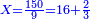
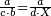
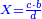
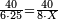
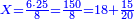
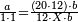
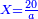
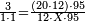
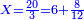
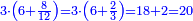 dinar
dinar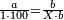
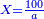
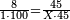
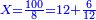
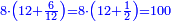
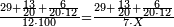
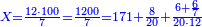
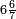 pešuṭim
pešuṭim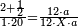
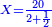
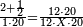
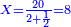 years
years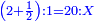
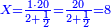 years
years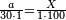
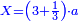
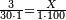
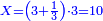
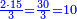 pešuṭim a day
pešuṭim a day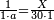
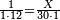
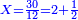
![\scriptstyle X-\frac{1}{10}X-\left[\frac{1}{10}\sdot\left(X-\frac{1}{10}X\right)\right]=100](/mediawiki/images/math/c/a/9/ca950635d00da924119bda8eef8b09bd.png)
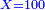
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle100-\left(\frac{1}{10}\sdot100\right)-\left[\frac{1}{10}\sdot\left[100-\left(\frac{1}{10}\sdot100\right)\right]\right]&\scriptstyle=100-10-\left[\frac{1}{10}\sdot\left(100-10\right)\right]\\&\scriptstyle=90-\left(\frac{1}{10}\sdot90\right)=81\\\end{align}}}](/mediawiki/images/math/b/3/2/b3276194f4c15a48cc259a94d7c3dee4.png)
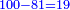
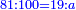
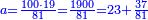


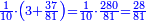
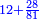
![\scriptstyle{\color{blue}{\left(123+\frac{37}{81}\right)-\left[\frac{1}{10}\sdot\left(123+\frac{37}{81}\right)\right]=\left(123+\frac{37}{81}\right)-\left(12+\frac{28}{81}\right)=108+\frac{252}{81}=111+\frac{9}{81}}}](/mediawiki/images/math/4/4/0/4406d671acff270a34129cc050078489.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(123+\frac{37}{81}\right)-\left[\frac{1}{10}\sdot\left(123+\frac{37}{81}\right)\right]-\left[\frac{1}{10}\sdot\left[\left(123+\frac{37}{81}\right)-\left[\frac{1}{10}\sdot\left(123+\frac{37}{81}\right)\right]\right]\right]\\&\scriptstyle=111+\frac{9}{81}-\left[\frac{1}{10}\sdot\left(111+\frac{9}{81}\right)\right]\\&\scriptstyle=111+\frac{9}{81}-\left(11+\frac{9}{81}\right)=100\\\end{align}}}](/mediawiki/images/math/7/6/6/7662441c4157441bc7ff9bb9661a2ac7.png)
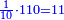
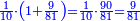
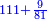
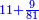
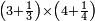
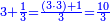
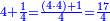
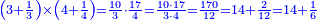
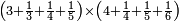
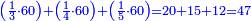
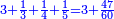 cubits
cubits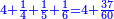 pešuṭim
pešuṭim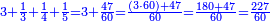
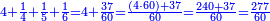
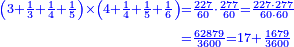
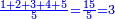
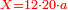
![\scriptstyle\frac{12\sdot\left[\left(20\sdot111\right)+7\right]}{1000}=\frac{X}{100}](/mediawiki/images/math/2/d/b/2db7116d7bb6f92861c3a5e513cce1da.png)
![\scriptstyle{\color{red}{X=\left[\left(20\sdot111\right)+7\right]\sdot\left(1+\frac{1}{5}\right)}}](/mediawiki/images/math/8/e/5/8e5d7f5ae4a8353f43a9fe4549563d65.png)
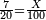
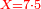
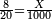
 liṭra
liṭra![\scriptstyle\frac{12\sdot\left[\left(20\sdot7\right)+5\right]}{8}=\frac{X}{1}](/mediawiki/images/math/2/2/a/22a88268d43fe4494d2d24fb2a0eeb02.png)
![\scriptstyle{\color{red}{X=\left[\left(20\sdot7\right)+5\right]\sdot\left(1+\frac{1}{2}\right)}}](/mediawiki/images/math/2/4/4/244aaefa49979d4e1bed720bed7d4e60.png)
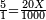
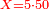
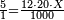
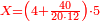
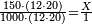
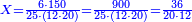
![\scriptstyle\frac{\left[5\sdot\left(12\sdot20\right)\right]+\left(15\sdot12\right)}{30}=\frac{X}{1}](/mediawiki/images/math/5/5/1/551d078a6e34f3b19f2d74db4a60a0a6.png)

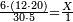
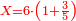
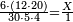
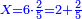 pešiṭim
pešiṭim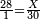

![\scriptstyle\left[\left[\left(x\, mod3\right)\sdot70\right]+\left[\left(x\, mod5\right)\sdot21\right]+\left[\left(x\, mod7\right)\sdot15\right]\right]mod105=x](/mediawiki/images/math/6/e/d/6ed986b78c38e68ce735d1213629da15.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle=\left[\left[\left(17\, mod3\right)\sdot70\right]+\left[\left(17\, mod5\right)\sdot21\right]+\left[\left(17\, mod7\right)\sdot15\right]\right]mod105\\&\scriptstyle=\left[\left(2\sdot70\right)+\left(2\sdot21\right)+\left(3\sdot15\right)\right]mod105\\&\scriptstyle=\left(140+42+45\right)mod105\\&\scriptstyle=227mod105=17\\\end{align}}}](/mediawiki/images/math/b/f/7/bf7be060d27859937ffa1cb19cb427ab.png)
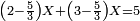
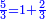 loaves of bread
loaves of bread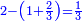 of a loaf
of a loaf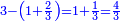 of a loaf
of a loaf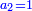 pašuṭ
pašuṭ 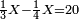
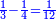
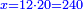 days
days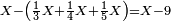
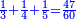
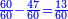
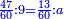
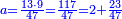
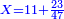 pešiṭim
pešiṭim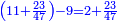
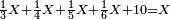
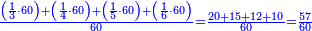
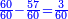
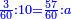
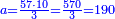
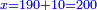
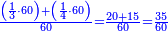
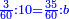
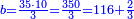
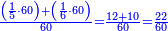
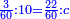
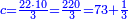
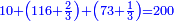
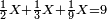
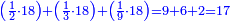
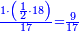
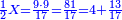 pešuṭim
pešuṭim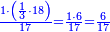 of the fish
of the fish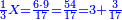 pešuṭim
pešuṭim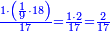 of the fish
of the fish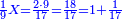 pešuṭim
pešuṭim![\scriptstyle{\color{blue}{\left(\frac{100}{20}+\frac{100}{30}\right)-8=\left[5+\left(3+\frac{1}{3}\right)\right]-8=\left(8+\frac{1}{3}\right)-8=\frac{1}{3}}}](/mediawiki/images/math/3/1/9/31933c8028d20c68279519e49dfe4676.png)
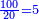 pešuṭim
pešuṭim

![\scriptstyle\begin{cases}\scriptstyle a_1+a_2+a_3+a_4=100\\\scriptstyle a_1=\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{6}\right)\sdot a_2\\\scriptstyle a_2-\left[\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{6}\right)\sdot a_2\right]=\frac{2}{5}a_3\\\scriptstyle a_3=\left(\frac{1}{2}+\frac{1}{3}\right)\sdot a_1\\\scriptstyle a_4=\frac{1}{5}a_3\end{cases}](/mediawiki/images/math/b/0/2/b022c165253164a670109c624280d783.png)
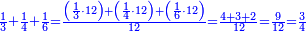
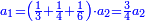
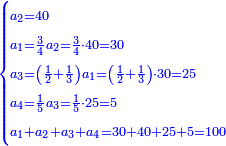
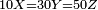
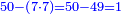
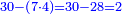
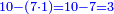

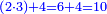
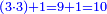
![\scriptstyle\begin{cases}\scriptstyle a_1+a_2+a_3+a_4=80\\\scriptstyle a_1=\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\\\scriptstyle a_2-\left[\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\right]=\frac{2}{3}a_3\\\scriptstyle a_3=\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{6}\right)\sdot a_1\\\scriptstyle a_4=\frac{4}{5}a_3\end{cases}](/mediawiki/images/math/e/6/1/e61594e5bed663d7d2049121054974b5.png)
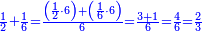
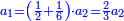
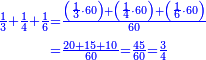
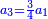
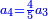
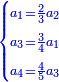
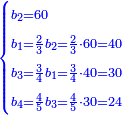
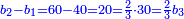
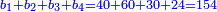


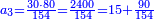

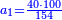
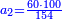
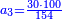
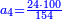
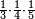
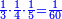
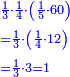
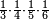
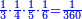
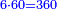
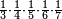
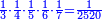
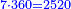
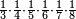
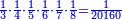
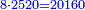
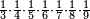
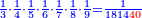
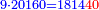
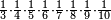
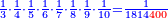
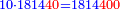
![\scriptstyle\frac{\left[27\sdot\left(20\sdot12\right)\right]+\left(5\sdot12\right)}{40}=\frac{X}{1}](/mediawiki/images/math/0/e/2/0e2454ca1e9e4d9db562dc71456dcaea.png)
![\scriptstyle{\color{red}{X=\left(27\sdot6\right)+\left(5\sdot\frac{3}{10}\right)=\left(27\sdot6\right)+\left[5\sdot\left[\frac{1}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\right]}}](/mediawiki/images/math/6/9/f/69fdab2f308ea4e93fde502a43bc5162.png)
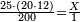
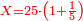
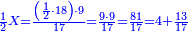
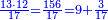
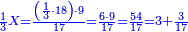
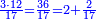
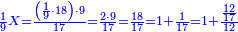
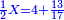
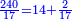
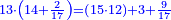
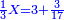
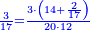
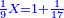
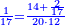
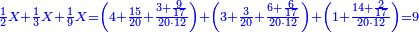
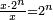
![\scriptstyle{\color{blue}{\frac{4\sdot2^4}{4}=\frac{\left[\left[\left(4\sdot2\right)\sdot2\right]\sdot2\right]\sdot2}{4}=\frac{\left[\left(8\sdot2\right)\sdot2\right]\sdot2}{4}=\frac{\left(16\sdot2\right)\sdot2}{4}=\frac{32\sdot2}{4}=\frac{64}{4}=16}}](/mediawiki/images/math/a/1/8/a18ada1d2c3e942f95b244551d7dfddb.png)
![\scriptstyle{\color{blue}{\frac{1\sdot2^4}{1}=\frac{\left[\left[\left(1\sdot2\right)\sdot2\right]\sdot2\right]\sdot2}{1}=\frac{\left[\left(2\sdot2\right)\sdot2\right]\sdot2}{1}=\frac{\left(4\sdot2\right)\sdot2}{1}=\frac{8\sdot2}{1}=\frac{16}{1}=16}}](/mediawiki/images/math/8/1/7/817177d1d689d0c2bb941b861fc1a916.png)
![\scriptstyle\frac{\left[12x+\left(a\sdot x\right)\right]\sdot2}{a}=](/mediawiki/images/math/7/2/a/72a9b6b9f640c674f2cc135e100f8460.png) the number of fishes that can be bought
the number of fishes that can be bought![\scriptstyle{\color{blue}{\frac{\left[\left(12\sdot3\right)+\left(3\sdot3\right)\right]\sdot2}{3}=\frac{45\sdot2}{3}=\frac{90}{3}=30}}](/mediawiki/images/math/c/5/4/c5416935be7a1852ae70ff33e3bba16d.png)
![\scriptstyle{\color{blue}{\left[\left(12\sdot1\right)+\left(3\sdot1\right)\right]\sdot2=\left(12+3\right)\sdot2=15\sdot2=30}}](/mediawiki/images/math/9/e/4/9e49687ba5b88f12039e865ac04c1bb5.png)
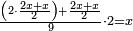
![\scriptstyle{\color{blue}{\frac{\left[2\sdot\frac{\left(2\sdot20\right)+20}{2}\right]+\frac{\left(2\sdot20\right)+20}{2}}{9}\sdot2=\frac{\left(2\sdot\frac{60}{2}\right)+\frac{60}{2}}{9}\sdot2=\frac{\left(2\sdot30\right)+30}{9}\sdot2=\frac{90}{9}\sdot2=10\sdot2=20}}](/mediawiki/images/math/7/e/c/7ec98b7c230d51f22a040960558b4f74.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{\left[2\sdot\frac{\left(2\sdot9\right)+9}{2}\right]+\frac{\left(2\sdot9\right)+9}{2}}{9}\sdot2&\scriptstyle=\frac{\left(2\sdot\frac{27}{2}\right)+\frac{27}{2}}{9}\sdot2=\frac{\left[2\sdot\left(13+\frac{1}{2}\right)\right]+\left(13+\frac{1}{2}\right)}{9}\sdot2\\&\scriptstyle\approx\frac{\left(2\sdot14\right)+14}{9}\sdot2=\frac{42}{9}\sdot2=\left(4+\frac{6}{9}\right)\sdot2\\&\scriptstyle\approx\left(4\sdot2\right)+1=8+1=9\\\end{align}}}](/mediawiki/images/math/e/c/4/ec480403fee8138a16803203e96e4057.png)
![\scriptstyle\frac{\left[10\sdot\left[\left[5\sdot\left[\left(2\sdot x\right)+5\right]\right]+10\right]\right]-350}{100}=x](/mediawiki/images/math/3/7/a/37a8d2fab4f5a34c96abb0250eb906ca.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{\left[10\sdot\left[\left[5\sdot\left[\left(2\sdot10\right)+5\right]\right]+10\right]\right]-350}{100}&\scriptstyle=\frac{\left[10\sdot\left[\left[5\sdot\left(20+5\right)\right]+10\right]\right]-350}{100}\\&\scriptstyle=\frac{\left[10\sdot\left[\left(5\sdot25\right)+10\right]\right]-350}{100}\\&\scriptstyle=\frac{\left[10\sdot\left(125+10\right)\right]-350}{100}\\&\scriptstyle=\frac{\left(10\sdot135\right)-350}{100}\\&\scriptstyle=\frac{1350-350}{100}=\frac{1000}{100}=10\\\end{align}}}](/mediawiki/images/math/d/0/3/d033b85e358a1413f6d87f195b81387b.png)
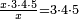
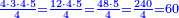
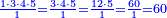
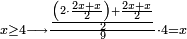
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle=\left[\left[\left(11\, mod3\right)\sdot70\right]+\left[\left(11\, mod5\right)\sdot21\right]+\left[\left(11\, mod7\right)\sdot15\right]\right]mod105\\&\scriptstyle=\left[\left(2\sdot70\right)+\left(1\sdot21\right)+\left(4\sdot15\right)\right]mod105\\&\scriptstyle=\left(140+21+60\right)mod105\\&\scriptstyle=221mod105=221-\left(2\sdot105\right)=11\\\end{align}}}](/mediawiki/images/math/d/a/b/daba8e39e6cb9e50938de81f423d8193.png)