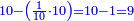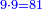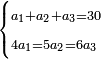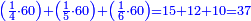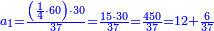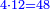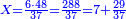Difference between revisions of "ספר הכללים במספר"
(→Arc, smaller than half a circle) |
(→Additional Problems - MS Mantova) |
||
| (70 intermediate revisions by the same user not shown) | |||
| Line 852: | Line 852: | ||
:Know that if 7 of Pisa equal 9 of Cortona: 7 dinar of Pisa are equal to 9 dinar of Cortona; 7 liṭra of Pisa are equal 9 liṭra of Cortona; 700 liṭra of Pisa are equal to 900 liṭra of Cortona. | :Know that if 7 of Pisa equal 9 of Cortona: 7 dinar of Pisa are equal to 9 dinar of Cortona; 7 liṭra of Pisa are equal 9 liṭra of Cortona; 700 liṭra of Pisa are equal to 900 liṭra of Cortona. | ||
|style="text-align:right;"|ודע כי אם ז' פיסני' שוים ט' קורטו' הז' דינרי' פיסני' שוים ט' דינרי' קורטוני' והז' ליט' מפיסני' שוים ט' ליט' קורטו' ות"ש ליט' מפיסני' שוים תת"ק ליט' קורטו‫' | |style="text-align:right;"|ודע כי אם ז' פיסני' שוים ט' קורטו' הז' דינרי' פיסני' שוים ט' דינרי' קורטוני' והז' ליט' מפיסני' שוים ט' ליט' קורטו' ות"ש ליט' מפיסני' שוים תת"ק ליט' קורטו‫' | ||
| + | |- | ||
| + | |? | ||
| + | |style="text-align:right;"|וכן יבא בין פפריני' ופריביסיני' ולכל [חשבון] כזה | ||
| + | |- | ||
| + | | | ||
| + | :20) <span style=color:green>'''Rule of Three - with fractions:'''</span> If you are asked for a calculation of these three categories, where both parts involve fractions: | ||
| + | |style="text-align:right;"|כ <big>אם</big> ישאל לך חשבון שיהיה בו מאלו הג' מינים ולפני הב' חלקי' יהיו שבורים | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :We know what number has these fractions. |
| + | |style="text-align:right;"|נדע באיזה המספר ימצאו אלו השבורים | ||
| + | |- | ||
| + | | | ||
| + | :Once you find the number in which these fractions are found, we multiply both parts by that number, in which these fractions are found. | ||
| + | |style="text-align:right;"|ואחר שידעת באי זה המספר ימצאו אלו השבורים נרבה הב' חלקי' באותו המספר שימצאו בו אלו השבורים | ||
|- | |- | ||
| | | | ||
| − | : | + | :Then, we multiply the thing we want to know by the thing that is not of its own kind and divide it by the third. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אחרי כן נרבה אותו הדבר שנרצה לדעת כנגד אותו הדבר שאנינה ממינה עצמה ונחלק אותה על השלישית וכה"ל |
| − | |||
| − | |||
| − | אחרי כן נרבה אותו הדבר שנרצה לדעת כנגד אותו הדבר שאנינה ממינה עצמה | ||
| − | ונחלק אותה על השלישית וכה"ל | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 868: | Line 876: | ||
|- | |- | ||
| | | | ||
| − | :21) <span style=color:green>'''Rule of Three:'''</span> | + | :21) <span style=color:green>'''Rule of Three - with one fraction:'''</span> If you are asked for another calculation in which one part involves fractions: |
| − | |style="text-align:right;"|כא <big>ואם</big> נשאל לך חשבון אחר שיהיה שבור מחלק אחד | + | |style="text-align:right;"|כא <big>ואם</big> נשאל לך חשבון אחר שיהיה שבור מחלק אחד |
| − | נרבה הב' חלקי' באותו המספר דהיינו עם אותו השבור | + | |- |
| − | אחרי כן נרבה אותו הדבר שנרצה לידע כנגד אותו הדבר שאנינה ממינה | + | | |
| − | ונחלק אותה על השלישית | + | :We multiply both parts by that number, i.e. by the [denominator of] the fraction. |
| + | |style="text-align:right;"|נרבה הב' חלקי' באותו המספר דהיינו עם אותו השבור | ||
| + | |- | ||
| + | | | ||
| + | :Then, we multiply the thing we want to know by the thing that is not of its kind and divide it by the third. | ||
| + | |style="text-align:right;"|אחרי כן נרבה אותו הדבר שנרצה לידע כנגד אותו הדבר שאנינה ממינה ונחלק אותה על השלישית | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
:<math>\scriptstyle{\color{OliveGreen}{\frac{a_1}{b_1}:a_2=a_3:x \longrightarrow\left(\frac{a_1}{b_1}\sdot b_1\right):\left(a_2\sdot b_1\right)=a_3:x\longrightarrow x=\frac{\left(a_2\sdot b_1\right)\sdot a_3}{\frac{a_1}{b_1}\sdot b_1}}}</math> | :<math>\scriptstyle{\color{OliveGreen}{\frac{a_1}{b_1}:a_2=a_3:x \longrightarrow\left(\frac{a_1}{b_1}\sdot b_1\right):\left(a_2\sdot b_1\right)=a_3:x\longrightarrow x=\frac{\left(a_2\sdot b_1\right)\sdot a_3}{\frac{a_1}{b_1}\sdot b_1}}}</math> | ||
|- | |- | ||
| − | | | + | |We give an example for the two cases - one for a calculation in which one part involves a fraction and the other in which the two parts involve fractions: |
|style="text-align:right;"|ונשים המשל בשני פנים האחד בעבור החשבון שהוא שבור מחלק אחד והאחר שהוא שבור מב' חלקי‫' | |style="text-align:right;"|ונשים המשל בשני פנים האחד בעבור החשבון שהוא שבור מחלק אחד והאחר שהוא שבור מב' חלקי‫' | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:two currencies|632|ppYb}}If | + | *{{#annot:two currencies|632|ppYb}}If 5 and a quarter of Pisa are worth 7 of Cortona, how many of Cortona are 1000 liṭra of Pisa worth? |
:<math>\scriptstyle\frac{5+\frac{1}{4}}{7}=\frac{1000}{X}</math> | :<math>\scriptstyle\frac{5+\frac{1}{4}}{7}=\frac{1000}{X}</math> | ||
| − | |style="text-align:right;"|אם ה' פיסני' ורביע שוים ז' | + | |style="text-align:right;"|אם ה' פיסני' ורביע שוים ז' קורטונו' כמה ישוו אלף ליט' מפיסני‫'{{#annotend:ppYb}} |
|- | |- | ||
| | | | ||
| − | : | + | :This is a calculation in which one part involves a fraction and this fraction is a quarter. So, we multiply both parts by 4. |
|style="text-align:right;"|וזה החשבון הוא שבור מחלק אחד וזה השיבור הוא הרביע<br> | |style="text-align:right;"|וזה החשבון הוא שבור מחלק אחד וזה השיבור הוא הרביע<br> | ||
לכן נרבה הב' חלקי' עם ד‫' | לכן נרבה הב' חלקי' עם ד‫' | ||
|- | |- | ||
| | | | ||
| − | :::<math>\scriptstyle{\color{blue}{4\sdot\left(5+\frac{1}{4}\right)=21}}</math> | + | :Say: 4 times 5 pisani and a quarter; the result is 21 pisani. |
| + | :<math>\scriptstyle{\color{blue}{4\sdot\left(5+\frac{1}{4}\right)=21}}</math> | ||
|style="text-align:right;"|ואמור ד' פעמי' ה' פיסני' ורביע יבוא כ"א פיסני‫' | |style="text-align:right;"|ואמור ד' פעמי' ה' פיסני' ורביע יבוא כ"א פיסני‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :4 times 7 corto; the result is 28 corto. |
| + | :<math>\scriptstyle{\color{blue}{4\sdot7=28}}</math> | ||
|style="text-align:right;"|וד' פעמי' ז' קורטו' בא כ"ח קורטו‫' | |style="text-align:right;"|וד' פעמי' ז' קורטו' בא כ"ח קורטו‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :So, 21 pisani are worth 28 of corto. |
|style="text-align:right;"|הרי שכ"א פיסני' שוים כ"ח קורטו‫' | |style="text-align:right;"|הרי שכ"א פיסני' שוים כ"ח קורטו‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :We reduce by 7 [lit. divide by a seventh], because both parts has a seventh. |
|style="text-align:right;"|ונחלק לשביע בעבור ‫<ref>90r</ref>שבשני החלקי' ימצא שביע | |style="text-align:right;"|ונחלק לשביע בעבור ‫<ref>90r</ref>שבשני החלקי' ימצא שביע | ||
|- | |- | ||
| | | | ||
| − | : | + | :The seventh of 21 is 3. |
| + | :<math>\scriptstyle{\color{blue}{\frac{1}{7}\sdot21=3}}</math> | ||
|style="text-align:right;"|השביע מכ"א הוא ג‫' | |style="text-align:right;"|השביע מכ"א הוא ג‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :The seventh of 28 is 4. |
| + | :<math>\scriptstyle{\color{blue}{\frac{1}{7}\sdot28=4}}</math> | ||
|style="text-align:right;"|השביע מכ"ח הוא ד‫' | |style="text-align:right;"|השביע מכ"ח הוא ד‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :We find that 3 pisani are worth 4 corto. |
|style="text-align:right;"|נמצא שג' פיסני' שוים ד' קורטו‫' | |style="text-align:right;"|נמצא שג' פיסני' שוים ד' קורטו‫' | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''Rule of Three:'''</span> We want to know how much are a thousand liṭra of Pisa worth. The pisani is the thing we want to know and the corto is the thing that is not of its own type. | |
| − | |style="text-align:right;"|ואנחנו נרצה לידע כמה ישוו אלף ליט' מפיסני' הפיסני הוא הדבר שנרצה לידע והקורטו' הוא הדבר שאנינה ממינה עצמה | + | :<math>\scriptstyle{\color{blue}{3:4=1000:X}}</math> |
| + | |style="text-align:right;"|ואנחנו נרצה לידע כמה ישוו אלף ליט' מפיסני‫'<br> | ||
| + | הפיסני הוא הדבר שנרצה לידע והקורטו' הוא הדבר שאנינה ממינה עצמה | ||
|- | |- | ||
| | | | ||
| − | : | + | :Therefore, we multiply 4 times a thousand; the result is 4 thousand of Cortona. |
| − | + | |style="text-align:right;"|לכן נרבה ד' פעמים אלף יבא ד' אלפי' מקורטו‫' | |
| − | |style="text-align:right;"|לכן נרבה ד' פעמים אלף יבא ד' אלפי' מקורטו | ||
| − | |||
|- | |- | ||
| | | | ||
| − | *{{#annot:two measures|867|p0EU}}If | + | :We divide it by 3; the result is 1333 liṭra, 6 dinar and 8 pešuṭim and so the thousand liṭra of of Pisa are worth in Cortona. |
| + | :<math>\scriptstyle{\color{blue}{X=\frac{1000\sdot4}{3}=\frac{4000}{3}=1333+\frac{6}{20}+\frac{\frac{8}{12}}{20}}}</math> | ||
| + | |style="text-align:right;"|ונחלק בג' שיבא אלף ושל"ג ליט' וו' דינרי' וח"פ וכן ישוו אלף ליט' מפיסני לקורטוט‫' | ||
| + | |- | ||
| + | |We give an example of a calculation in which both parts involve fractions: | ||
| + | |style="text-align:right;"|ונשים המשל אל החשבון שהוא שבור מב' חלקיו | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:two measures|867|p0EU}}If 7 silver ounces and a third are worth 73 liṭra and 5 dinar of Pisa, how many are 19 silver ounces worth? | ||
:<math>\scriptstyle\frac{7+\frac{1}{3}}{73+\frac{1}{4}}=\frac{19}{X}</math> | :<math>\scriptstyle\frac{7+\frac{1}{3}}{73+\frac{1}{4}}=\frac{19}{X}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם ז' אונקיו' ושליש כסף שוים ע"ג ליט' וה' דינרי' מפיסני‫'<br> |
כמה ישוו הי"ט אונקיו' כסף לפי זה החשבון{{#annotend:p0EU}} | כמה ישוו הי"ט אונקיו' כסף לפי זה החשבון{{#annotend:p0EU}} | ||
|- | |- | ||
| | | | ||
| − | : | + | :These fractions are a third and a quarter and they are found in 12. |
| − | |style="text-align:right;"|ואלו השבורים הם שליש ורביע אנה ימצאו בי"ב | + | |style="text-align:right;"|ואלו השבורים הם שליש ורביע אנה ימצאו בי"ב |
| − | לכן יש לנו לרבות הב' חלקי' בי"ב | + | |- |
| + | | | ||
| + | :So, we must multiply both parts by 12. | ||
| + | |style="text-align:right;"|לכן יש לנו לרבות הב' חלקי' בי"ב | ||
|- | |- | ||
| | | | ||
| − | :::<math>\scriptstyle{\color{blue}{12\sdot\left(7+\frac{1}{3}\right)=88}}</math> | + | :Say: 12 times 7 ounces and a third; the result is 88 silver ounces. |
| + | :<math>\scriptstyle{\color{blue}{12\sdot\left(7+\frac{1}{3}\right)=88}}</math> | ||
|style="text-align:right;"|ואמור י"ב פעמי' ז' אונקיו' ושליש יבא פ"ח אונקיו' כסף | |style="text-align:right;"|ואמור י"ב פעמי' ז' אונקיו' ושליש יבא פ"ח אונקיו' כסף | ||
|- | |- | ||
| | | | ||
| − | : | + | :12 times 73 liṭra and 5 dinar are 879 liṭra of Pisa. |
| + | :<math>\scriptstyle{\color{blue}{12\sdot\left(73+\frac{1}{4}\right)=879}}</math> | ||
|style="text-align:right;"|וי"ב פעמי' ע"ג ליט' וה' דינרי' יהיו תתע"ט ליט' מפסני‫' | |style="text-align:right;"|וי"ב פעמי' ע"ג ליט' וה' דינרי' יהיו תתע"ט ליט' מפסני‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :Therefore, 88 silver ounces are worth 879 liṭra. |
|style="text-align:right;"|הרי שפ"ח אונקיות כסף שוים תתע"ט ליט‫' | |style="text-align:right;"|הרי שפ"ח אונקיות כסף שוים תתע"ט ליט‫' | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''Rule of Three:'''</span> We want to know how much are 19 silver ounces worth. | |
| + | :<math>\scriptstyle{\color{blue}{88:879=19:X}}</math> | ||
|style="text-align:right;"|ונרצה לידע כמה ישוו הי"ט אונקיו' כסף | |style="text-align:right;"|ונרצה לידע כמה ישוו הי"ט אונקיו' כסף | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{X=\frac{19\sdot879}{88}=\frac{16701}{88}=\frac{16701}{8\sdot11}=189+\frac{15}{20}+\frac{\frac{8+\frac{2}{11}}{12}}{20}}}</math> | + | :We multiply 19 times 879 liṭra; they are 16701. |
| − | + | |style="text-align:right;"|נרבה י"ט פעמי' תתע"ט ליט' יהיו י"ו אלפי' ותש"א | |
| − | |style="text-align:right;"| | + | |- |
| − | חלקם בפ"ח יבא קפ"ט ליט' וט"ו די' וח"פ וב' חלקי' מי"א וכן ישוו הי"ט אונקיו' כסף באותו החשבון | + | | |
| + | :Divide them by 88; the result is 189 liṭra, 15 dinar, 8 pešuṭim and 2 parts of 11 and so the 19 silver ounce are worth. | ||
| + | :<math>\scriptstyle{\color{blue}{X=\frac{19\sdot879}{88}=\frac{16701}{88}=\frac{16701}{8\sdot11}=189+\frac{15}{20}+\frac{\frac{8+\frac{2}{11}}{12}}{20}}}</math> | ||
| + | |style="text-align:right;"|חלקם בפ"ח יבא קפ"ט ליט' וט"ו די' וח"פ וב' חלקי' מי"א וכן ישוו הי"ט אונקיו' כסף באותו החשבון | ||
|- | |- | ||
| | | | ||
| Line 2,705: | Line 2,739: | ||
|- | |- | ||
| | | | ||
| − | : | + | :Double 10 ; the result is 20. Subtract 1 from 20; it is 19. So, in 19 days they will [walk the same distance]. |
:<math>\scriptstyle{\color{blue}{x=\left(2\sdot10\right)-1=20-1=19}}</math> | :<math>\scriptstyle{\color{blue}{x=\left(2\sdot10\right)-1=20-1=19}}</math> | ||
|style="text-align:right;"|כפול י' עם י' ויבוא כ' תפחות א' מכ' יהיו י"ט הרי שבי"ט ימים יעמדו בשוה וכה"ל | |style="text-align:right;"|כפול י' עם י' ויבוא כ' תפחות א' מכ' יהיו י"ט הרי שבי"ט ימים יעמדו בשוה וכה"ל | ||
| Line 6,079: | Line 6,113: | ||
|style="text-align:right;"|הרי שכל הקוטר מן העגול שזה הקשת נקטם ממנו הוא י' וכה"ל | |style="text-align:right;"|הרי שכל הקוטר מן העגול שזה הקשת נקטם ממנו הוא י' וכה"ל | ||
|- | |- | ||
| − | | | + | | |
| + | :To clarify the matter well, complete the whole circle: | ||
|style="text-align:right;"|ולראות העניין באר הטב הוי משלים העגולה הזאת כלה | |style="text-align:right;"|ולראות העניין באר הטב הוי משלים העגולה הזאת כלה | ||
|- | |- | ||
| | | | ||
| + | :Draw line BD that reaches the circumference of the circle on the other side, as line BDZ. | ||
|style="text-align:right;"|והוצא קו ב"ד עד שיגיע אל עקמימות העגולה מן הצד השני כגון קו בד"ז | |style="text-align:right;"|והוצא קו ב"ד עד שיגיע אל עקמימות העגולה מן הצד השני כגון קו בד"ז | ||
|- | |- | ||
| | | | ||
| + | :If you want to know the area of this shape: | ||
|style="text-align:right;"|ואם תרצה לידע תשבורת הצורה הזאת | |style="text-align:right;"|ואם תרצה לידע תשבורת הצורה הזאת | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|חלק קו ב"ז לב' חלקי' שוים על | + | :Divide line BZ into two equal parts at point C, which will be the center of the circle |
| − | נקודת ח' ותהיה הנקודה הזאת {{#annot:term|1108,2178|0qCr}}ציר העגולה{{#annotend:0qCr}} ותרצה והוצא ממנה ב' קווים אל נקודת א' ואל נקודת ג' והם קוי ח"א וח"ג | + | |style="text-align:right;"|חלק קו ב"ז לב' חלקי' שוים על נקודת ח' ותהיה הנקודה הזאת {{#annot:term|1108,2178|0qCr}}ציר העגולה{{#annotend:0qCr}} |
| + | |- | ||
| + | | | ||
| + | :Draw from it two lines to point A and point G, which are lines CA and CG. | ||
| + | |style="text-align:right;"|ותרצה והוצא ממנה ב' קווים אל נקודת א' ואל נקודת ג' והם קוי ח"א וח"ג | ||
|- | |- | ||
| | | | ||
| Line 6,097: | Line 6,138: | ||
|- | |- | ||
| | | | ||
| − | :: | + | :If you multiply line AC, which is half the diameter of the circle, by half the arc, which is arc AG, this product is the area of the triangle, whose two sides are the two lines AC and CG. |
| + | :<math>\scriptstyle{\color{blue}{\triangle_{ACG}=AC\sdot\left(\frac{1}{2}\sdot AG\right)}}</math> | ||
|style="text-align:right;"|ואם אתה מרבע קו א"ח שהוא חצי הקוטר העגול בחצי הקשת אשר הוא עוקם א"ג יהיה מנין הזה תשבורת המשולש אשר ב' צלעיו הם ב' קוי א"ח וח"ג | |style="text-align:right;"|ואם אתה מרבע קו א"ח שהוא חצי הקוטר העגול בחצי הקשת אשר הוא עוקם א"ג יהיה מנין הזה תשבורת המשולש אשר ב' צלעיו הם ב' קוי א"ח וח"ג | ||
|- | |- | ||
| | | | ||
| − | : | + | :Subtract the area of triangle ACG from the area of [sector] ABG and you are left with the area of [segment] ABGD. |
|style="text-align:right;"|ותשבורת קשת אב"ג הוצא מן המנין תשבורת המשולש אח"ג וישאר בידך תשבורת הצורה שעליה אבג"ד | |style="text-align:right;"|ותשבורת קשת אב"ג הוצא מן המנין תשבורת המשולש אח"ג וישאר בידך תשבורת הצורה שעליה אבג"ד | ||
|- | |- | ||
| | | | ||
| + | :The area of this triangle is the product of line CD, which is 3 cubits in this shape, by half line AG, which is 4 cubits; their product is 12. | ||
| + | :<math>\scriptstyle{\color{blue}{ACG_{\triangle}=CD\sdot\left(\frac{1}{2}\sdot AG\right)=3\sdot4=12}}</math> | ||
|style="text-align:right;"|ותשבורת המשולש הזה הוא רבוע קו ח"ד שהוא בצורה הזאת ג' אמות בחצי קו א"ג והוא ד' אמות ורבועם י"ב | |style="text-align:right;"|ותשבורת המשולש הזה הוא רבוע קו ח"ד שהוא בצורה הזאת ג' אמות בחצי קו א"ג והוא ד' אמות ורבועם י"ב | ||
|- | |- | ||
| | | | ||
| + | :Subtract this number from the product of the straight line AC by the arc AB; the remainder is the area of shape ABGD, which is the arc that is smaller than a semicircle. | ||
|style="text-align:right;"|והוא הסך אשר תוציא מרבוע קו א"ח הישר בקו א"ב העקום ויהיה הנשאר תשבורת צורת אבג"ד שהוא צורת הקשת שהוא פחות מחצי עגול | |style="text-align:right;"|והוא הסך אשר תוציא מרבוע קו א"ח הישר בקו א"ב העקום ויהיה הנשאר תשבורת צורת אבג"ד שהוא צורת הקשת שהוא פחות מחצי עגול | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
| − | :<math>\scriptstyle{\color{blue}{AG_{sector}- | + | :<math>\scriptstyle{\color{blue}{ABGD=AG_{sector}-ACG_{\triangle}=AH\sdot\left(\frac{1}{2}\sdot AG_{arc}\right)-ACG_{\triangle}=\left[r\sdot\left(\frac{1}{2}\sdot AG_{arc}\right)\right]-ACG_{\triangle}}}</math> |
|- | |- | ||
| − | |the area of the | + | | |
| + | :Therefore, you say that the area of the arc that is smaller than a semicircle is [found] by that you multiply half the whole diameter of the circle, from which the arc is cut off, by half the arc; keep it. | ||
|style="text-align:right;"|ומכאן אתה אומ' כי {{#annot:term|816,1531|9C3m}}רבוע{{#annotend:9C3m}} הקשת שהוא פחות מחצי עגול הוא שתרבע חצי כל הקוטר מן העגול שהקשת נקטם ממנו בחצי הקשת ותשמור אותו | |style="text-align:right;"|ומכאן אתה אומ' כי {{#annot:term|816,1531|9C3m}}רבוע{{#annotend:9C3m}} הקשת שהוא פחות מחצי עגול הוא שתרבע חצי כל הקוטר מן העגול שהקשת נקטם ממנו בחצי הקשת ותשמור אותו | ||
|- | |- | ||
| | | | ||
| + | :Then, you subtract the versed sine of the arc by half the diameter and multiply what remains from half the diameter by half the chord. | ||
|style="text-align:right;"|ואחרי כן תוציא מחצי הקוטר קו החץ אשר לקשת והנשאר מחצי הקוטר מנה אותו במחצית המיתר | |style="text-align:right;"|ואחרי כן תוציא מחצי הקוטר קו החץ אשר לקשת והנשאר מחצי הקוטר מנה אותו במחצית המיתר | ||
|- | |- | ||
| | | | ||
| + | :You subtract the product from the number you kept and what you have left is the area of the arc that is less than a semicircle. | ||
|style="text-align:right;"|והעולה בידך תפחות אותו מן המנין אשר שמרת בידך והנשאר בידך הוא תשבורת הקשת שהוא ‫<ref>113r</ref>פוחת מחצי עגול | |style="text-align:right;"|והעולה בידך תפחות אותו מן המנין אשר שמרת בידך והנשאר בידך הוא תשבורת הקשת שהוא ‫<ref>113r</ref>פוחת מחצי עגול | ||
|- | |- | ||
| Line 6,132: | Line 6,180: | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:shape greater than half a circle|680|DEQW}}125) The shape of the arc that is greater than half the circle, which is arc ABG; its chord AG | + | :{{#annot:shape greater than half a circle|680|DEQW}}125) The shape of the arc that is greater than half the circle, which is arc ABG; its chord AG is 12 in length. |
|style="text-align:right;"|קכה <big>צורת</big> ''הקשת העודף על חצי העגול''<br> | |style="text-align:right;"|קכה <big>צורת</big> ''הקשת העודף על חצי העגול''<br> | ||
והוא קשת אשר עליו אב"ג ומיתרו א"ג ואורכו י"ב{{#annotend:DEQW}} | והוא קשת אשר עליו אב"ג ומיתרו א"ג ואורכו י"ב{{#annotend:DEQW}} | ||
| Line 6,140: | Line 6,188: | ||
|[[File:כללים במספר - קכה.png|thumb|200px]] | |[[File:כללים במספר - קכה.png|thumb|200px]] | ||
|- | |- | ||
| − | |the area of the shape | + | | |
| − | <math>\scriptstyle\left[\left[\frac{1}{2}\sdot\left(2r\right)\right]\sdot\left(\frac{1}{2}\sdot\rm{arc}\right)\right]+\rm{Area}_{\triangle}</math> | + | :If you want to know the area of this shape, draw the diameter of the whole circle, from which this shape is cut off. Multiply half the diameter by half the arc, then add to it the area of the triangle, whose base is the chord. The total is the area of this shape. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[\left[\frac{1}{2}\sdot\left(2r\right)\right]\sdot\left(\frac{1}{2}\sdot\rm{arc}\right)\right]+\rm{Area}_{\triangle}}}</math> | ||
|style="text-align:right;"|ואם תרצה לדעת תשבורת הצורה הזאת תוציא קוטר כל העגול שזאת הצורה נקטמת ממנו ותרבה חצי הקוטר בחצי הקשת ותוסיף עליו תשבורת המשולש אשר המיתר הוא תושבתו ויהיה סך הכל תשבורת כל זאת הצורה | |style="text-align:right;"|ואם תרצה לדעת תשבורת הצורה הזאת תוציא קוטר כל העגול שזאת הצורה נקטמת ממנו ותרבה חצי הקוטר בחצי הקשת ותוסיף עליו תשבורת המשולש אשר המיתר הוא תושבתו ויהיה סך הכל תשבורת כל זאת הצורה | ||
|- | |- | ||
| | | | ||
| − | ::the | + | :In this shape, multiply half the chord, which is 6, by itself; the result is 36. |
| − | ::<math>\scriptstyle{\color{blue}{\frac{\left(\frac{1}{2}\sdot12\right)^2}{12}+12=\frac{6^2}{12}+12=\frac{36}{12}+12=3+12=15}}</math> | + | |style="text-align:right;"|ובצורה הזאת תרבע חצי המיתר שהוא ו' בעצמו שיבואו ל"ו |
| − | |style="text-align:right;"| | + | |- |
| − | + | | | |
| − | הוסיפם על החץ יהיה סך הכל ט"ו והוא אורך כל הקוטר מן העגול שזאת הצורה נקטמת ממנה | + | :Divide it by the versed sine, which is 12; the quotient is 3. |
| + | |style="text-align:right;"|חלק אותם על החץ שהוא י"ב ויהיה החלוקה ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :Add it to the versed sine; the total is 15 and this is the length of the whole diameter of the circle, from which this shape is cut off. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{\left(\frac{1}{2}\sdot12\right)^2}{12}+12=\frac{6^2}{12}+12=\frac{36}{12}+12=3+12=15}}</math> | ||
| + | |style="text-align:right;"|הוסיפם על החץ יהיה סך הכל ט"ו והוא אורך כל הקוטר מן העגול שזאת הצורה נקטמת ממנה | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Its half is half the diameter and it is line BZ in this shape, so line BZ is 7 and a half. |
| + | :<math>\scriptstyle{\color{blue}{BZ=r=\frac{1}{2}\sdot15=7+\frac{1}{2}}}</math> | ||
|style="text-align:right;"|ומחציתו הוא מחצית הקוטר והוא בצורה הזאת קו ב"ז הרי שקו ב"ז הוא ז' וחצי | |style="text-align:right;"|ומחציתו הוא מחצית הקוטר והוא בצורה הזאת קו ב"ז הרי שקו ב"ז הוא ז' וחצי | ||
|- | |- | ||
| | | | ||
| + | :Multiply it by half the arc; the result is the area of the segment encompassed by the two lines GZ and AZ and arc ABG. | ||
:<math>\scriptstyle{\color{blue}{ABGZA=BZ\sdot\left(\frac{1}{2}\sdot\rm{arc}_{ABG}\right)}}</math> | :<math>\scriptstyle{\color{blue}{ABGZA=BZ\sdot\left(\frac{1}{2}\sdot\rm{arc}_{ABG}\right)}}</math> | ||
|style="text-align:right;"|מנה אותו במחצית הקשת ומה שיעלה יהיה תשבורת הצורה העקומה אשר יקיפו אותה ב' קווי ג"ז וא"ז עם קשת א'ב'ג‫' | |style="text-align:right;"|מנה אותו במחצית הקשת ומה שיעלה יהיה תשבורת הצורה העקומה אשר יקיפו אותה ב' קווי ג"ז וא"ז עם קשת א'ב'ג‫' | ||
|- | |- | ||
| | | | ||
| + | :Add to it the area of triangle AZG, which is the product of line DZ by half line AG. When you sum all, it is the area of this segment. | ||
|style="text-align:right;"|הוסף עליהם תשבורת משולש א'ז'ג' והוא המספר הנקבץ מרובע קו ד"ז במחצית קו א"ג וכשתקבץ הכל יהיה תשבורת העקמומית הזאת | |style="text-align:right;"|הוסף עליהם תשבורת משולש א'ז'ג' והוא המספר הנקבץ מרובע קו ד"ז במחצית קו א"ג וכשתקבץ הכל יהיה תשבורת העקמומית הזאת | ||
|- | |- | ||
| Line 6,165: | Line 6,223: | ||
:<math>\scriptstyle{\color{blue}{ABGDA=ABGZA+AZG=ABGZA+\left[DZ\sdot\left(\frac{1}{2}\sdot AG\right)\right]}}</math> | :<math>\scriptstyle{\color{blue}{ABGDA=ABGZA+AZG=ABGZA+\left[DZ\sdot\left(\frac{1}{2}\sdot AG\right)\right]}}</math> | ||
|- | |- | ||
| − | |the area of the | + | | |
| − | |style="text-align:right;"|ומכאן אתה למד הרוצה לדעת תשבורת העקום העודף על חצי העגול יהיה מרבע חצי הקוטר בחצי הקשת וישמור המספר | + | :You learn from this that whoever wants to know the area of the segment that is greater than the semicircle, multiplies half the diameter by half the arc and keeps the number. |
| − | ואחרי כן יפחות חצי הקוטר מן החץ | + | |style="text-align:right;"|ומכאן אתה למד הרוצה לדעת תשבורת העקום העודף על חצי העגול יהיה מרבע חצי הקוטר בחצי הקשת וישמור המספר |
| − | [והנשאר מן החץ] ירבע אותו בחצי המיתר | + | |- |
| − | והמספר העולה יאספינו אל המספר אשר שמר ויהיה הכל סך תשבורת העקומה העודפת על חצי העגול | + | | |
| + | :Then, subtracts half the diameter from the versed sine. | ||
| + | |style="text-align:right;"|ואחרי כן יפחות חצי הקוטר מן החץ | ||
| + | |- | ||
| + | | | ||
| + | :Multiplies what remains from the versed sine by half the chord. | ||
| + | |style="text-align:right;"|‫[והנשאר מן החץ] ירבע אותו בחצי המיתר | ||
| + | |- | ||
| + | | | ||
| + | :Adds the result to the number he kept and the total is the area of the segment that is greater than the semicircle. | ||
| + | |style="text-align:right;"|והמספר העולה יאספינו אל המספר אשר שמר ויהיה הכל סך תשבורת העקומה העודפת על חצי העגול | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
| Line 6,190: | Line 6,258: | ||
|- | |- | ||
| | | | ||
| − | * | + | *As triangle ABG, whose top is point A and its base is BG, and you want to divide it in half: |
| − | + | |style="text-align:right;"|כגון משולש א'ב'ג' אשר ראשו נקודת א' ותושבתו ב"ג ותרצה לחלקו לחצי | |
| − | |style="text-align:right;"|כגון משולש א'ב'ג' אשר ראשו נקודת א' ותושבתו ב"ג ותרצה לחלקו לחצי | + | |- |
| − | אתה צריך לחלק כל אחד מצלעי א"ב וא"ג לב' חלקי' בענין שיהיה מרובע הצלע כולו כפליים ממרובע הצלע החלק הגדול מחלקיו | + | | |
| + | :You should divide each of the sides AB and AG in two parts, so that the square of the whole side is twice the square of the larger portion of that side. | ||
| + | |style="text-align:right;"|אתה צריך לחלק כל אחד מצלעי א"ב וא"ג לב' חלקי' בענין שיהיה מרובע הצלע כולו כפליים ממרובע הצלע החלק הגדול מחלקיו | ||
|- | |- | ||
| | | | ||
| + | :As if you divide line AB in two parts at point D and line AG in two parts at point H. | ||
|style="text-align:right;"|כגון שתהיה חולק קו א"ב לב' חלקים על נקודת ד' וקו א"ג לב' חלקי' על נקודת ה‫' | |style="text-align:right;"|כגון שתהיה חולק קו א"ב לב' חלקים על נקודת ד' וקו א"ג לב' חלקי' על נקודת ה‫' | ||
|- | |- | ||
| Line 6,203: | Line 6,274: | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{AD^2=\frac{1}{2}\sdot AB^2}}</math> | + | :Let the square of AD be half the square of AB. |
| + | :<math>\scriptstyle{\color{blue}{AD^2=\frac{1}{2}\sdot AB^2}}</math> | ||
|style="text-align:right;"|ויהיה מרובע א"ד מחצית מרובע א | |style="text-align:right;"|ויהיה מרובע א"ד מחצית מרובע א | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{AH^2=\frac{1}{2}\sdot AG^2}}</math> | + | :Let also the square of AH be half the square of AG. |
| + | :<math>\scriptstyle{\color{blue}{AH^2=\frac{1}{2}\sdot AG^2}}</math> | ||
|style="text-align:right;"|וכן מרובע א"ה מחצית מרובע א"ג | |style="text-align:right;"|וכן מרובע א"ה מחצית מרובע א"ג | ||
|- | |- | ||
| | | | ||
| − | ::ADH = DHBG | + | :Draw a line from D to H, so that the triangle is divided into two equal parts: one part is triangle ADH and the other part is quadrilateral DHBG. |
| + | :<math>\scriptstyle{\color{blue}{\triangle_{ADH}=DHBG}}</math> | ||
|style="text-align:right;"|ותוציא קו מד' על ה' והיה משולש נחלק לב' חלקי' שוים החלק האחד משולש א'ד'ה' וחלק השני נפתל ד'ה'ב'ג‫' | |style="text-align:right;"|ותוציא קו מד' על ה' והיה משולש נחלק לב' חלקי' שוים החלק האחד משולש א'ד'ה' וחלק השני נפתל ד'ה'ב'ג‫' | ||
|- | |- | ||
| − | |The | + | | |
| − | |style="text-align:right;"|ודרך חשבון המרובעים האלה יהיה אם תהיה לוקח מאורך הקו מנקודת א' אשר הוא הראש ה' חלקי' מז' בו פחות חצי עשירית השביעית | + | :The way to calculate these squares is that you take 5 parts of 7 minus half a tenth of a seventh of the length of the line from point A, which is the top. The rule: you take 99 parts of 140 of the line. |
| − | והכלל המסור לזה הוא שתהיה לוקח מן הקו צ"ט חלקי' מק"מ חלקי' בו | + | :<math>\scriptstyle{\color{OliveGreen}{\frac{5}{7}a-\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{7}\right)a=\frac{99}{140}a}}</math> |
| + | |style="text-align:right;"|ודרך חשבון המרובעים האלה יהיה אם תהיה לוקח מאורך הקו מנקודת א' אשר הוא הראש ה' חלקי' מז' בו פחות חצי עשירית השביעית והכלל המסור לזה הוא שתהיה לוקח מן הקו צ"ט חלקי' מק"מ חלקי' בו | ||
|- | |- | ||
| | | | ||
| − | * | + | *As if the length of side AB is 7 cubits. |
| − | |||
|style="text-align:right;"|כאילו היה אורך צלע א"ב ז' אמות | |style="text-align:right;"|כאילו היה אורך צלע א"ב ז' אמות | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Line AD is 5 cubits minus one part of twenty of a cubit. |
| + | :<math>\scriptstyle{\color{blue}{AD=5-\frac{1}{20}}}</math> | ||
|style="text-align:right;"|יהיה קו א"ד מהם ה' אמות פחות חלק אחד מעשרים באמה | |style="text-align:right;"|יהיה קו א"ד מהם ה' אמות פחות חלק אחד מעשרים באמה | ||
|- | |- | ||
| | | | ||
| − | : | + | :The length of side AG is 10 cubits. |
|style="text-align:right;"|וצלע א"ג היה אורכו י' אמות | |style="text-align:right;"|וצלע א"ג היה אורכו י' אמות | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Line AH is 7 cubits and one part of 14 of a cubit. |
| + | :<math>\scriptstyle{\color{blue}{AH=7+\frac{1}{14}}}</math> | ||
|style="text-align:right;"|יהיה קו א"ה ז' אמות וחלק אחד מי"ד באמה | |style="text-align:right;"|יהיה קו א"ה ז' אמות וחלק אחד מי"ד באמה | ||
|- | |- | ||
| | | | ||
| + | :Divide both sides according to this calculation, and draw a line from one part to the other, then the triangle is divided into two equal parts. | ||
|style="text-align:right;"|ועל החשבון הזה אתה חולק את שתי הצלעות האלה ותוציא קו מן החלק האחד אל השני ויחלק המשולש לב' חלקים שוים | |style="text-align:right;"|ועל החשבון הזה אתה חולק את שתי הצלעות האלה ותוציא קו מן החלק האחד אל השני ויחלק המשולש לב' חלקים שוים | ||
|- | |- | ||
| Line 6,244: | Line 6,321: | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:triangular field - three owners|686|a7VB}}127) If you have to divide a triangular field to three owners and each asks his share in accordance with one of the sides of the triangle | + | :{{#annot:triangular field - three owners|686|a7VB}}127) If you have to divide a triangular field to three owners and each asks for his share in accordance with one of the sides of the triangle |
|style="text-align:right;"|‫<ref>113v</ref>קכז <big>ואם</big> יהיה קרקע המשולש לג' בעלים ואתה צריך לחלקו ביניהם וכל אחד מהבעלים מבקש חלקו נגד צלע אחד מצלעי המשולש{{#annotend:a7VB}} | |style="text-align:right;"|‫<ref>113v</ref>קכז <big>ואם</big> יהיה קרקע המשולש לג' בעלים ואתה צריך לחלקו ביניהם וכל אחד מהבעלים מבקש חלקו נגד צלע אחד מצלעי המשולש{{#annotend:a7VB}} | ||
|- | |- | ||
| | | | ||
| − | * | + | *Let the triangle be triangle ABG. |
|style="text-align:right;"|ויהיה המשולש הזה משולש א'ב'ג‫' | |style="text-align:right;"|ויהיה המשולש הזה משולש א'ב'ג‫' | ||
|- | |- | ||
| | | | ||
| − | ::AD = BD | + | :You divide side AB into two equal parts at point D. |
| − | |style="text-align:right;"|ואתה בא וחלק צלע א"ב לב' חלקי' שוים על נקודת ד' | + | :<math>{\color{blue}{\scriptstyle AD=BD}}</math> |
| − | והוצא קו מד' אל ג' ויחלק המשולש לב' חלקי' שוי‫' | + | |style="text-align:right;"|ואתה בא וחלק צלע א"ב לב' חלקי' שוים על נקודת ד‫' |
| + | |- | ||
| + | | | ||
| + | :Draw a line from D to G, so the triangle is divided into two equal parts. | ||
| + | |style="text-align:right;"|והוצא קו מד' אל ג' ויחלק המשולש לב' חלקי' שוי‫' | ||
|- | |- | ||
| | | | ||
| Line 6,261: | Line 6,342: | ||
|- | |- | ||
| | | | ||
| − | ::<math>{\color{blue}{\scriptstyle DH=\frac{1}{3}\sdot DG}}</math> | + | :Then, measure a third of line DG, which is the height if the triangle, from point D that is on the base. Let this part be line DH. |
| − | |style="text-align:right;"|ואחר כן מדוד מקו ד"ג אשר הוא קומת המשולש שלישיתו מנגד נקודת ד' אשר על התושבת ויהיה החלק הזה קו ד"ה והוצא מנקודת ה' ב' קוים אל נקודת א' ואל נקודת ב‫' | + | :<math>{\color{blue}{\scriptstyle DH=\frac{1}{3}\sdot DG}}</math> |
| + | |style="text-align:right;"|ואחר כן מדוד מקו ד"ג אשר הוא קומת המשולש שלישיתו מנגד נקודת ד' אשר על התושבת ויהיה החלק הזה קו ד"ה | ||
| + | |- | ||
| + | | | ||
| + | :Draw from point H two lines to point A and to point B. | ||
| + | |style="text-align:right;"|והוצא מנקודת ה' ב' קוים אל נקודת א' ואל נקודת ב‫' | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle\triangle GHA=\triangle AHB=\triangle GHB</math> | + | :The triangle is divided into three equal parts: triangle GHA, triangle AHB, and triangle GHB. |
| + | :<math>\scriptstyle{\color{blue}{\triangle GHA=\triangle AHB=\triangle GHB}}</math> | ||
|style="text-align:right;"|ויחלק המשולש לג' חלקים שוים והם משולש ג'ה'א' ומשולש א'ה'ב' ומשולש ג'ה'ב‫' | |style="text-align:right;"|ויחלק המשולש לג' חלקים שוים והם משולש ג'ה'א' ומשולש א'ה'ב' ומשולש ג'ה'ב‫' | ||
|- | |- | ||
| Line 6,275: | Line 6,362: | ||
|- | |- | ||
| | | | ||
| − | : | + | :{{#annot:rhombus|679|n38W}}128) Questions concerning the rhombus mentioned above - one of its diagonals is 16 and the other is 12. |
| − | |||
| − | |||
| − | |||
| − | |||
:How much is the side? | :How much is the side? | ||
| − | |style="text-align:right;"|אשר אחד מאלכסוניו י"ו והשני י"ב<br> | + | |style="text-align:right;"|קכח <big>שאלות</big> במעויין הנז' למעלה אשר אחד מאלכסוניו י"ו והשני י"ב<br> |
כמה הוא צלעו{{#annotend:n38W}} | כמה הוא צלעו{{#annotend:n38W}} | ||
|- | |- | ||
| − | |the | + | | |
| + | :Answer: take half of each of its diagonals, square them, sum the two squares and extract the root [of their sum]; then you will find the side. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sqrt{\left(\frac{1}{2}\sdot\rm{diagonal}_1\right)^2+\left(\frac{1}{2}\sdot\rm{diagonal}_2\right)^2}}}</math> | ||
|style="text-align:right;"|תשובה קח מחצית כל אחד מאלכסוניו ורבע אותם וקבץ שני המרובעי' וקח את גדרם ותמצא הצלע | |style="text-align:right;"|תשובה קח מחצית כל אחד מאלכסוניו ורבע אותם וקבץ שני המרובעי' וקח את גדרם ותמצא הצלע | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Explanation of the answer: |
| − | |style="text-align:right;"|ופירוש התשובה | + | |style="text-align:right;"|ופירוש התשובה |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | | |
| − | : | + | :Take the half of 16; it is 8 and its square is 64. |
| + | |style="text-align:right;"|קח מחצית י"ו והוא ח' וריבועו ס"ד | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:rhombus|683|EFrZ}} | + | :Take the half of 12; it is 6 and its square is 36. |
| − | :How much is the other diagonal? | + | |style="text-align:right;"|וקח מחצית י"ב והוא ו' וריבועו ל"ו |
| + | |- | ||
| + | | | ||
| + | :The sum of these two squares is 100. | ||
| + | |style="text-align:right;"|ומניין שני המרובעים האלו הם ק‫' | ||
| + | |- | ||
| + | | | ||
| + | :The root of 100 is 10 and this is the side of the rhombus. | ||
| + | |style="text-align:right;"|וגדר ק' הם י' והוא צלע המרובע | ||
| + | |- | ||
| + | |colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{\left(\frac{1}{2}\sdot16\right)^2+\left(\frac{1}{2}\sdot12\right)^2}=\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:rhombus|683|EFrZ}}If it is said: the area of the rhombus is 96, and one of its diagonals is 16. | ||
| + | :How much is the other diagonal? | ||
|style="text-align:right;"|ואם יאמר {{#annot:term|1095,1526|gBop}}מעויין{{#annotend:gBop}} שתשברתו צ"ו ואלכסון האחד י"ו<br> | |style="text-align:right;"|ואם יאמר {{#annot:term|1095,1526|gBop}}מעויין{{#annotend:gBop}} שתשברתו צ"ו ואלכסון האחד י"ו<br> | ||
כמה הוא האלכסון השני{{#annotend:EFrZ}} | כמה הוא האלכסון השני{{#annotend:EFrZ}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle\rm{diagonal}_2= | + | :Divide 96, which is the area, by the diagonal that is known to be 16; you find that half the other diagonal is 6; its double is 12 and this is the other diagonal. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\rm{diagonal}_2=2\sdot\frac{\rm{area_{rhombus}}}{diagonal_1}}}{\color{blue}{=2\sdot\frac{96}{16}=2\sdot6=12}}</math> | ||
|style="text-align:right;"|חלק צ"ו אשר הוא התשבורת על האלכסון אשר ידעת שהוא י"ו ותמצא מחצית האלכסון השני ו' וכפלה י"ב והוא האלכסון השני | |style="text-align:right;"|חלק צ"ו אשר הוא התשבורת על האלכסון אשר ידעת שהוא י"ו ותמצא מחצית האלכסון השני ו' וכפלה י"ב והוא האלכסון השני | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:rhombus|683|R9Pd}} | + | *{{#annot:rhombus|683|R9Pd}}If it is said: the side of the rhombus is 10 and its area is 96. |
:How much are its diagonals? | :How much are its diagonals? | ||
|style="text-align:right;"|ואם יאמ' מעויין צלעו י' ותשברתו צ"ו<br> | |style="text-align:right;"|ואם יאמ' מעויין צלעו י' ותשברתו צ"ו<br> | ||
| Line 6,316: | Line 6,413: | ||
|- | |- | ||
| | | | ||
| + | :Take the square of the side, which is 100. Add the area to it; it is 196. The root of this number is 14 and this is [the sum of] the two halves of the diagonals. | ||
|style="text-align:right;"|קח מרובע הצלע והוא ק' הוסף עליו התשבורת ויהיו קצ"ו וגדר המספר הזה הוא י"ד והם שני חציי האלכסונות | |style="text-align:right;"|קח מרובע הצלע והוא ק' הוסף עליו התשבורת ויהיו קצ"ו וגדר המספר הזה הוא י"ד והם שני חציי האלכסונות | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
| − | :<math>\scriptstyle{\color{ | + | :<math>\scriptstyle{\color{OliveGreen}{\frac{1}{2}\sdot\rm{diagonal}_1+\frac{1}{2}\sdot\rm{diagonal}_2=\sqrt{\rm{side^2+area}}}}{\color{blue}{=\sqrt{10^2+96}=\sqrt{100+96}=\sqrt{196}=14}}</math> |
| + | |- | ||
| + | | | ||
| + | :Take halve the number, which is 7. Its square is 49. | ||
| + | |style="text-align:right;"|קח מחצית המספר והוא ז' ומרובעו מ"ט | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :Subtract from it half the area, which is 48; you are left with 1. |
| − | הוצא ממנו מחצית התשבורת אשר הוא מ"ח וישאר בידך א‫' | + | |style="text-align:right;"|הוצא ממנו מחצית התשבורת אשר הוא מ"ח וישאר בידך א‫' |
| − | וגדר הא' הוא א' אם אתה מוסיף אותו על ז' יהיו ח' והוא מחצית האלכסון האחד | + | |- |
| + | | | ||
| + | :The root of 1 is 1. If you add it to 7, they are 8 and this is a half of the one diagonal. | ||
| + | |style="text-align:right;"|וגדר הא' הוא א' אם אתה מוסיף אותו על ז' יהיו ח' והוא מחצית האלכסון האחד | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
| − | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{1}{2}\sdot\rm{diagonal}_1&\scriptstyle=\left(\frac{1}{2}\sdot14\right)+\sqrt{\left(\frac{1}{2}\sdot14\right)^2-\left(\frac{1}{2}\sdot\rm{area}\right)}=7+\sqrt{7^2-\left(\frac{1}{2}\sdot96\right)} | + | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{1}{2}\sdot\rm{diagonal}_1&\scriptstyle=\left(\frac{1}{2}\sdot14\right)+\sqrt{\left(\frac{1}{2}\sdot14\right)^2-\left(\frac{1}{2}\sdot\rm{area}\right)}=7+\sqrt{7^2-\left(\frac{1}{2}\sdot96\right)}=7+\sqrt{49-48}\\&\scriptstyle=7+\sqrt{1}=7+1=8\\\end{align}}}</math> |
|- | |- | ||
| | | | ||
| + | :If you subtract it from 7, six remains and this is a half of the second diagonal. | ||
|style="text-align:right;"|ואם אתה פוחת אותו מן ז' ישאר ששה והוא מחצית האלכסון השני | |style="text-align:right;"|ואם אתה פוחת אותו מן ז' ישאר ששה והוא מחצית האלכסון השני | ||
|- | |- | ||
| Line 6,340: | Line 6,446: | ||
| | | | ||
:{{#annot:triangle - two parts|686|80ZX}}129) Question: a triangle, its one side AB is 12 cubits; the second side BG is 10 cubits and the third side AG is 15 cubits. | :{{#annot:triangle - two parts|686|80ZX}}129) Question: a triangle, its one side AB is 12 cubits; the second side BG is 10 cubits and the third side AG is 15 cubits. | ||
| − | :You want to divide it to two owners equally | + | :You want to divide it to two owners equally. |
|style="text-align:right;"|קכט <big>שאילה</big> משולש אשר צלעו האחד י"ב אמות והוא צלע א"ב וצלע ב"ג השני י' אמות וצלע א"ג השלישי ט"ו אמות<br> | |style="text-align:right;"|קכט <big>שאילה</big> משולש אשר צלעו האחד י"ב אמות והוא צלע א"ב וצלע ב"ג השני י' אמות וצלע א"ג השלישי ט"ו אמות<br> | ||
ואתה רוצה לחלקו לב' בעלים לכל אחד חלק שוה{{#annotend:80ZX}} | ואתה רוצה לחלקו לב' בעלים לכל אחד חלק שוה{{#annotend:80ZX}} | ||
| Line 6,349: | Line 6,455: | ||
|- | |- | ||
| | | | ||
| − | : | + | :We mark point D two cubits away from point B on side AB. |
| − | : | + | :<math>\scriptstyle{\color{blue}{D_1B=2}}</math> |
|style="text-align:right;"|והנה נשים נקודות ד' אשר הוא המיתר רחוקה מנקודת ב' על צלע א"ב שתי אמות | |style="text-align:right;"|והנה נשים נקודות ד' אשר הוא המיתר רחוקה מנקודת ב' על צלע א"ב שתי אמות | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Line AD remains 10 cubits long. |
| + | :<math>\scriptstyle{\color{blue}{AD_1=AB-D_1B=10}}</math> | ||
|style="text-align:right;"|וישאר קו א"ד י' אמות | |style="text-align:right;"|וישאר קו א"ד י' אמות | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Half line AB [is marked by] point Z. So, line AZ is six cubits, because we said that the whole side AB is 12 cubits long. |
| + | :<math>\scriptstyle{\color{blue}{AZ=BZ=\frac{1}{2}\sdot AB=6}}</math> | ||
|style="text-align:right;"|ויהיה מחצית צלע א"ב על נקודת ז' ויהיה קו א"ז שש אמות כי כן מסרנו צלע א"ב כולו י"ב אמות | |style="text-align:right;"|ויהיה מחצית צלע א"ב על נקודת ז' ויהיה קו א"ז שש אמות כי כן מסרנו צלע א"ב כולו י"ב אמות | ||
|- | |- | ||
| | | | ||
| − | : | + | :Between line AZ, which is the half [of AB], and line AD there are four cubits and they are two-fifths of line AD. |
| − | + | :<math>\scriptstyle{\color{blue}{D_1Z=AZ-AD_1=4=\frac{2}{5}\sdot AD_1}}</math> | |
|style="text-align:right;"|ובין קו א"ז שהוא המחצית ובין קו א"ד ארבע אמות<br> | |style="text-align:right;"|ובין קו א"ז שהוא המחצית ובין קו א"ד ארבע אמות<br> | ||
והם שני חמישיות קו א"ד | והם שני חמישיות קו א"ד | ||
|- | |- | ||
| | | | ||
| − | : | + | :Mark point H two-fifths from the top of line AG that is next to AD. |
| − | |style="text-align:right;"|ואתה קח מצלע א"ג הנדבק אל א"ד שני חמשיותיו אשר היא הראש על | + | |style="text-align:right;"|ואתה קח מצלע א"ג הנדבק אל א"ד שני חמשיותיו אשר היא הראש על נקודת ה‫' |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\ | + | :So, line GH is six cubits, because the whole side AG is 15 cubits. |
| + | :<math>\scriptstyle{\color{blue}{GH_1=\frac{2}{5}\sdot AG=\frac{2}{5}\sdot15=6}}</math> | ||
| + | |style="text-align:right;"|ויהיה קו ג"ה שש אמות כי כל צלע א"ג היה ט"ו אמה | ||
| + | |- | ||
| + | | | ||
| + | :Mark the half [by drawing a line] from point D to point H. | ||
| + | |style="text-align:right;"|והוצא המחצה מנקודת ד' עד נקודת ה‫' | ||
| + | |- | ||
| + | | | ||
| + | :The triangle is divided into two equal parts: one part is triangle DAH and the other part is quadrilateral DHGB. | ||
| + | :<math>\scriptstyle{\color{blue}{\triangle D_1AH_1=D_1H_1GB}}</math> | ||
|style="text-align:right;"|ויהיה המשולש הזה נחלק לשני חלקי' שוים החלק האחד משולש ד'א'ה' והחלק השני נפתל ד"ה ג"ב | |style="text-align:right;"|ויהיה המשולש הזה נחלק לשני חלקי' שוים החלק האחד משולש ד'א'ה' והחלק השני נפתל ד"ה ג"ב | ||
|- | |- | ||
| | | | ||
| − | : | + | :If point D [is closer to the other side] so that AD is two cubits, you should find the half of side BG instead of [the half of] side AG. |
| + | :<math>\scriptstyle{\color{blue}{AD_2=2}}</math> | ||
|style="text-align:right;"|ואילו היה המיצר אשר הוא נקודת ד' נופל לצד אחד עד שיהיה א"ד שתי אמות לא היית מוצא המחצה אל הצלע א"ג אבל אל צלע ב"ג | |style="text-align:right;"|ואילו היה המיצר אשר הוא נקודת ד' נופל לצד אחד עד שיהיה א"ד שתי אמות לא היית מוצא המחצה אל הצלע א"ג אבל אל צלע ב"ג | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Mark point H two-fifths from point G on line BG, which is 10 cubits. |
| − | |style="text-align:right;"|והיית לוקח מצלע ב"ג אשר הוא י' אמות שני חמשיותיו על נקודת ה' מנגד נקודת ג‫' | + | :<math>\scriptstyle{\color{blue}{GH_2=\frac{2}{5}\sdot BG=\frac{2}{5}\sdot10=4}}</math> |
| − | ויהיה קו ג"ה ‫<ref>114r</ref>בצלע ב"ג ד' אמות | + | |style="text-align:right;"|והיית לוקח מצלע ב"ג אשר הוא י' אמות שני חמשיותיו על נקודת ה' מנגד נקודת ג‫' |
| + | |- | ||
| + | | | ||
| + | :So, line GH is 4 cubits on side BG. | ||
| + | |style="text-align:right;"|ויהיה קו ג"ה ‫<ref>114r</ref>בצלע ב"ג ד' אמות | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{ | + | :Mark the half [by drawing a line] from point D to point H as you see in this shape. |
| + | :<math>\scriptstyle{\color{blue}{\triangle D_2BH_2=D_2H_2GA}}</math> | ||
|style="text-align:right;"|ותוציא המחצה מנקודת ד' אל נקודת ה' כאשר אתה רואה בצורה הזאת | |style="text-align:right;"|ותוציא המחצה מנקודת ד' אל נקודת ה' כאשר אתה רואה בצורה הזאת | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|כי המחצה בדמיון הזה היא יוצאה לעולם אל החלק הארוך | + | :Because the [crossing line] in this example is always drawn from the longer part: |
| − | אם יהיה הארוך ב"ד אתה מוציא המחצה אל צלע ב"ג | + | |style="text-align:right;"|כי המחצה בדמיון הזה היא יוצאה לעולם אל החלק הארוך |
| − | ואם יהיה הארוך א"ד אתה מוציא המחצה אל צלע א"ג | + | |- |
| − | ואתה מתחיל למדוד את שתי החמשיות מנקודת ג' אשר היא הראש ואל הנקודה הזאת הייתה המחצה יוצאה אלו היה המיצר נופל על מחצית צלע א"ב ומדת מרחק המיצר מן המחצית אתה מתרחק מנקודת ג' אשר הוא הראש | + | | |
| + | :If the longer [part] is BD - you draw the [crossing line] to side BG. | ||
| + | |style="text-align:right;"|אם יהיה הארוך ב"ד אתה מוציא המחצה אל צלע ב"ג | ||
| + | |- | ||
| + | | | ||
| + | :If the longer [part] is AD - you draw the [crossing line] to side AG. | ||
| + | |style="text-align:right;"|ואם יהיה הארוך א"ד אתה מוציא המחצה אל צלע א"ג | ||
| + | |- | ||
| + | | | ||
| + | :You start measuring the two-fifths from point G, which is the top vertex, and the [crossing line] is drawn from that point [to a point that is as far from the midpoint of side AB as that point is] from point G, which is the top vertex. | ||
| + | |style="text-align:right;"|ואתה מתחיל למדוד את שתי החמשיות מנקודת ג' אשר היא הראש ואל הנקודה הזאת הייתה המחצה יוצאה אלו היה המיצר נופל על מחצית צלע א"ב ומדת מרחק המיצר מן המחצית אתה מתרחק מנקודת ג' אשר הוא הראש | ||
|- | |- | ||
| − | | | + | | |
| + | :You can understand this issue without the numerical illustration, but I mentioned the numbers in order to make it easier for the student and bring the matter closer to the heart of the teacher. | ||
|style="text-align:right;"|ואתה יכול להבין את העניין הזה אם לא היית מדמה אותו במספר<br> | |style="text-align:right;"|ואתה יכול להבין את העניין הזה אם לא היית מדמה אותו במספר<br> | ||
אלא שזכרתי המספר כדי להקל על הלומד ולהקריב העניין ללב המלמד | אלא שזכרתי המספר כדי להקל על הלומד ולהקריב העניין ללב המלמד | ||
| Line 6,412: | Line 6,545: | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:polygon|680|TQAX}}130) | + | :{{#annot:polygon|680|TQAX}}130) Question in the measurement of shapes whose sides are more the four sides [= polygons]. These shapes are numerous, some of them are pentagonal, some of them are hexagonal and octagonal and so on, some of them have equal sides and angles and some are scalene. |
| − | |style="text-align:right;"|קל <big>שאלה</big> במדידת הצורות אשר צלעותיו עודפות על ארבע הצלעות | + | |style="text-align:right;"|קל <big>שאלה</big> במדידת הצורות אשר צלעותיו עודפות על ארבע הצלעות והצורות האלה הם על תמונות רבות מהם מחומשות ומהם משותתות ומשובעות ולמעלה מהם יש מהם שצלעותם וזוויותם שוות ויש שלא יהיו שוות אלא מתחלפות{{#annotend:TQAX}} |
| − | והצורות האלה הם על תמונות רבות מהם מחומשות ומהם משותתות ומשובעות ולמעלה מהם | ||
| − | יש מהם שצלעותם וזוויותם שוות ויש שלא יהיו שוות אלא מתחלפות{{#annotend:TQAX}} | ||
|- | |- | ||
| − | | | + | | |
| + | :First, I give you a rule for the measurement of equilateral polygons: | ||
|style="text-align:right;"|ואני נותן לך כלל ראשונה במדידת הצורות אשר צלעותן וזוויותן שוות | |style="text-align:right;"|ואני נותן לך כלל ראשונה במדידת הצורות אשר צלעותן וזוויותן שוות | ||
|- | |- | ||
| − | |the | + | | |
| + | :This rule is that for every shape that has straight lines, if you circle a circle inside it that touches its sides, it is known that the product of half the diameter of this circle by half of all the sides of that shape is its area. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(\frac{1}{2}\sdot\rm{diameter_{incircle}}\right)\sdot\frac{1}{2}\sdot\sum \rm{sides}}}</math> | ||
|style="text-align:right;"|והכלל הזה הוא כל תבנית וכל צורה אשר אין לה קוים ישרים אם אתה מעגיל בתוכה עגול שיהיה מושש לצלעיה ידוע הוא כי רבוע קוטר חצי העגול הזה במחצית כל צלעי הצורה ההיא א"ו היא תשברתה | |style="text-align:right;"|והכלל הזה הוא כל תבנית וכל צורה אשר אין לה קוים ישרים אם אתה מעגיל בתוכה עגול שיהיה מושש לצלעיה ידוע הוא כי רבוע קוטר חצי העגול הזה במחצית כל צלעי הצורה ההיא א"ו היא תשברתה | ||
|- | |- | ||
| − | | | + | | |
| + | :For every [polygon] from the square onward whose sides and angles are equal to each other, you can draw a circle in it that touches all its sides. | ||
|style="text-align:right;"|וכל צורה מן המרבע ולמעלה אשר צלעיה וזוויותיה שוות זו לזו אתה יכול {{#annot:term|2498,2218|Wkts}}לחוק בה עגול{{#annotend:Wkts}} שיהיה מושש לכל צלעיה | |style="text-align:right;"|וכל צורה מן המרבע ולמעלה אשר צלעיה וזוויותיה שוות זו לזו אתה יכול {{#annot:term|2498,2218|Wkts}}לחוק בה עגול{{#annotend:Wkts}} שיהיה מושש לכל צלעיה | ||
|- | |- | ||
| − | | | + | | |
| + | :If their sides and angles are not equal to each other, for some of [these shapes] it is impossible to draw a circle in them that touches all their sides. | ||
|style="text-align:right;"|ואם אין צלעיה וזוויותיה שוות יש מהם שלא יתכן {{#annot:term|2498,2218|CyVl}}לחוק בעגול{{#annotend:CyVl}} שיהיה מושש לכל צלעיה | |style="text-align:right;"|ואם אין צלעיה וזוויותיה שוות יש מהם שלא יתכן {{#annot:term|2498,2218|CyVl}}לחוק בעגול{{#annotend:CyVl}} שיהיה מושש לכל צלעיה | ||
|- | |- | ||
| − | |the | + | | |
| + | :If you have an [equilateral] triangle, square, pentagon or onward and you draw a circle inside it that touches its sides, know that the product of half the diameter of that circle by half [the sum] of the sides of this shape is its area. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(\frac{1}{2}\sdot\rm{diameter_{incircle}}\right)\sdot\frac{1}{2}\sdot\sum \rm{sides}}}</math> | ||
|style="text-align:right;"|ואם תבא לידך צורה מכל התמונות מן משולש או מרובע או מחומש או למעלה מהם ואתה מחיק בתוכה עגולה מוששת לצלעיה<br> | |style="text-align:right;"|ואם תבא לידך צורה מכל התמונות מן משולש או מרובע או מחומש או למעלה מהם ואתה מחיק בתוכה עגולה מוששת לצלעיה<br> | ||
הוי יודע כי רבוע חצי קוטר העגול ההוא במחצית כל צלעי התמונה הוא תשברתה | הוי יודע כי רבוע חצי קוטר העגול ההוא במחצית כל צלעי התמונה הוא תשברתה | ||
|- | |- | ||
| − | | | + | | |
| + | :We do not need to give an example for the triangle and the square, because the way [to find] their area has already been explained. | ||
|style="text-align:right;"|ואין אנו צריכין לתת דמיון מן המשולש ולא מן המרובע כי כבר פורש דרך רבועם | |style="text-align:right;"|ואין אנו צריכין לתת דמיון מן המשולש ולא מן המרובע כי כבר פורש דרך רבועם | ||
|- | |- | ||
| − | | | + | | |
| − | *{{#annot:pentagon|680|jZu4}} | + | *{{#annot:pentagon|680|jZu4}}However, we give an example for [finding the area of] the pentagon whose five angles are A, B, G, D, H, all its sides are equal in length and all its angles are equal to each other. |
|style="text-align:right;"|אבל אנו נותנין דמיון מן המחומש והוא אשר על חמש זוויותיו א'ב'ג'ד'ה' וכל צלע וצלע מצלעותיו שוות באורכן וכן זוויותיו כלם שוות זו לזו{{#annotend:jZu4}} | |style="text-align:right;"|אבל אנו נותנין דמיון מן המחומש והוא אשר על חמש זוויותיו א'ב'ג'ד'ה' וכל צלע וצלע מצלעותיו שוות באורכן וכן זוויותיו כלם שוות זו לזו{{#annotend:jZu4}} | ||
|- | |- | ||
| | | | ||
| − | : | + | :We draw a circle in it that touches its five sides at five points Z, C, T, K, L. |
|style="text-align:right;"|ואנו מעגילים בתוכן עגול מושש לה' צלעותיו על חמש נקודות ז'ח'ט'כ'ל‫' | |style="text-align:right;"|ואנו מעגילים בתוכן עגול מושש לה' צלעותיו על חמש נקודות ז'ח'ט'כ'ל‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :The center of the circle is point M. |
|style="text-align:right;"|ו{{#annot:term|1108,2178|a6OG}}ציר העגול{{#annotend:a6OG}} הזה הנקרא מרכז הוא נקודת מ‫' | |style="text-align:right;"|ו{{#annot:term|1108,2178|a6OG}}ציר העגול{{#annotend:a6OG}} הזה הנקרא מרכז הוא נקודת מ‫' | ||
|- | |- | ||
| Line 6,455: | Line 6,594: | ||
|- | |- | ||
| | | | ||
| − | : | + | :We say that the product of half the diameter of that circle by half [the sum] of all the sides of the pentagon is its area. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(\frac{1}{2}\sdot\rm{diameter_{incircle}}\right)\sdot\frac{1}{2}\sdot\sum_{i=1}^5 \rm{side}_i}}</math> | ||
|style="text-align:right;"|ואנו אומרים כי רבוע חצי קוטר העגול הזה במחצית כל צלעי המחומש הוא תשברתו | |style="text-align:right;"|ואנו אומרים כי רבוע חצי קוטר העגול הזה במחצית כל צלעי המחומש הוא תשברתו | ||
|- | |- | ||
| | | | ||
| − | : | + | :Half the diameter is any line that goes from point M to one of the points where the circle touches the pentagon. |
|style="text-align:right;"|וחצי הקוטר הוא קו יוצא מנקודת מ' אל אחת הנקודות אשר העגול מושש עליהם את המחומש | |style="text-align:right;"|וחצי הקוטר הוא קו יוצא מנקודת מ' אל אחת הנקודות אשר העגול מושש עליהם את המחומש | ||
|- | |- | ||
| | | | ||
| − | : | + | :Now, if we draw a line from point M, which is the center, to the two points A and B that are vertices of the pentagon, it gives us triangle MAB. |
|style="text-align:right;"|ועתה אם אנו מוצאים קו מנקודת מ' אשר הוא המרכז על שתי נקודות א' וב' מן זווית המחומש נתן לנו משולש אשר עליו מ'א'ב‫' | |style="text-align:right;"|ועתה אם אנו מוצאים קו מנקודת מ' אשר הוא המרכז על שתי נקודות א' וב' מן זווית המחומש נתן לנו משולש אשר עליו מ'א'ב‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :The area of this triangle is the product of the height drawn to its base by half the base. |
| − | |||
|style="text-align:right;"|ותשבורת המשולש הזה הוא ברבוע העמוד היוצא אל תושבתו בחצי התושבת | |style="text-align:right;"|ותשבורת המשולש הזה הוא ברבוע העמוד היוצא אל תושבתו בחצי התושבת | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | :If we draw a line from point M to point L, where the circle touches side AB, this line is the height of triangle MAB, which is half the diameter of the circle. |
| − | : | + | |style="text-align:right;"|ואם אנו מוציאים קו מנקודת מ' אל נקודת ל' אשר משש עליה העגול את צלע א"ב יהיה הקו הזה עמוד במשולש מ'א'ב' והוא חצי קוטר העגול |
| + | |- | ||
| + | | | ||
| + | :If we multiply this height by half the side AB, the product is the area of the triangle. | ||
| + | |style="text-align:right;"|ואם מרבע העמוד הזה בחצי צלע א"ב יהיה רבועו תשבורת המשולש | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\rm{height}\sdot\left(\frac{1}{2}\sdot AB\right)=ML\sdot\left(\frac{1}{2}\sdot AB\right)=\frac{1}{2}\sdot\rm{diameter}\sdot\left(\frac{1}{2}\sdot AB\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :This way you can construct five triangles on the five sides of the pentagon, the area of each triangle is the product of half the diameter by half the side, as [illustrated] for side [AB], and [the sum of] the area of the five triangles is the area of the pentagon, so it is a product of half the diameter by [the sum of] half the five sides. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(\frac{1}{2}\sdot diameter_{incircle}\right)\sdot\frac{1}{2}\sdot\sum_{i=1}^5 side_i}}</math> | ||
|style="text-align:right;"|ועל הדרך הזה אתה יכול לעשות חמשה משולשים על ‫<ref>114v</ref>חמש צלעי המשולש המחומש ויהיה תשבורת כל משולש מהם ברבוע חצי הקוטר בחצי הצלע כאשר היה בצלע הזה ותשבורת חמש המשולשים כולם הוא תשבורת המחומש והוא מרבוע חצי הקוטר בחצי כל חמש הצלעות | |style="text-align:right;"|ועל הדרך הזה אתה יכול לעשות חמשה משולשים על ‫<ref>114v</ref>חמש צלעי המשולש המחומש ויהיה תשבורת כל משולש מהם ברבוע חצי הקוטר בחצי הצלע כאשר היה בצלע הזה ותשבורת חמש המשולשים כולם הוא תשבורת המחומש והוא מרבוע חצי הקוטר בחצי כל חמש הצלעות | ||
|- | |- | ||
| | | | ||
| + | :This is the case for any similar shape, which has many or few sides: if you draw a circle inside it that touches its sides, its area is the product of half the diameter of the circle by [the sum of] half of the sides. | ||
|style="text-align:right;"|והוא יהיה העניין לכל צורה כמוה אשר צלעותיה רבים או מעטים אם אתה מעגיל בתוכה עגול מושש לצלעיה יהיה תשברתה ברבוע חצי קוטר העגול במחצית הצלעות וזאת היא צורתה | |style="text-align:right;"|והוא יהיה העניין לכל צורה כמוה אשר צלעותיה רבים או מעטים אם אתה מעגיל בתוכה עגול מושש לצלעיה יהיה תשברתה ברבוע חצי קוטר העגול במחצית הצלעות וזאת היא צורתה | ||
|- | |- | ||
| − | | | + | | |
| + | :Since you cannot draw in every shape a circle that touches all its sides, this rule is not enough for you in measuring the shapes that have more than four sides. | ||
|style="text-align:right;"|ומפני שאין אתה יכול להוציא בכל תמונה ותמונה עגול שיהיה מושש לכל צלעיה אין הכלל הזה מספיק לך במדידת כל העודפות על ד' צלעות | |style="text-align:right;"|ומפני שאין אתה יכול להוציא בכל תמונה ותמונה עגול שיהיה מושש לכל צלעיה אין הכלל הזה מספיק לך במדידת כל העודפות על ד' צלעות | ||
|- | |- | ||
| − | | | + | | |
| + | :Therefore, I give you another rule that you can apply for any shape whose sides are straight [= polygons] [no proof is given]: | ||
|style="text-align:right;"|ומפני זה אני נותן לך כלל אחר שיהיה נוהג לך בכל צורה אשר צלעותיה ישרות | |style="text-align:right;"|ומפני זה אני נותן לך כלל אחר שיהיה נוהג לך בכל צורה אשר צלעותיה ישרות | ||
|- | |- | ||
| − | | | + | | |
| + | :Know that any plane shape whose sides are straight is divided into triangles [whose number] is less than the number of sides by two. | ||
|style="text-align:right;"|הוי יודע כי כל תמונה שטוחה שצלעותיה ישרות מתחלקת למשולשים שהם חסרים מן מניין הצלעות שנים | |style="text-align:right;"|הוי יודע כי כל תמונה שטוחה שצלעותיה ישרות מתחלקת למשולשים שהם חסרים מן מניין הצלעות שנים | ||
|- | |- | ||
| | | | ||
| − | : | + | :As the square that has four sides is divided into two triangles, whose number is less than the number of sides by two. |
|style="text-align:right;"|כגון המרובע אשר לו ד' צלעות יתחלק לב' משולשים אשר מניינם פוחת ב' ממספר הצלעות | |style="text-align:right;"|כגון המרובע אשר לו ד' צלעות יתחלק לב' משולשים אשר מניינם פוחת ב' ממספר הצלעות | ||
|- | |- | ||
| | | | ||
| − | : | + | :The hexagon is divided into four triangles. |
| − | |style="text-align:right;"|והמשושה יתחלק לד' משולשים וכן למעלה מזה | + | |style="text-align:right;"|והמשושה יתחלק לד' משולשים |
| + | |- | ||
| + | | | ||
| + | :And so on. | ||
| + | |style="text-align:right;"|וכן למעלה מזה | ||
|- | |- | ||
| − | | | + | | |
| + | :According to this rule, divide any shape you have into the triangles into which it is divided, and find the area of each triangle according to the way you have learned; [the sum of] all their areas is the area of the shape from which they were divided. | ||
|style="text-align:right;"|ואתה בא מן הכלל הזה וחלק כל תמונה שיבוא לידך אל המשולשים אשר היא נחלקת אליהם ורבע כל משולש מהם על הדרך אשר למדת ויהיה מרובע כולם תשבורת התמונה אשר נחלקו ממנה | |style="text-align:right;"|ואתה בא מן הכלל הזה וחלק כל תמונה שיבוא לידך אל המשולשים אשר היא נחלקת אליהם ורבע כל משולש מהם על הדרך אשר למדת ויהיה מרובע כולם תשבורת התמונה אשר נחלקו ממנה | ||
|- | |- | ||
| | | | ||
| − | * | + | *As if you draw a line from point A to point G and another line to point D in the pentagon that I have drawn for you above, so the pentagon is divided into three triangles. |
|style="text-align:right;"|כאלו היית מוצא במחומש אשר ציירתי לך למעלה קו מנקודת א' אל נקודת ג' וקו אחר אל נקודת ד' ויהיה המחומש נחלק לג' משולשים | |style="text-align:right;"|כאלו היית מוצא במחומש אשר ציירתי לך למעלה קו מנקודת א' אל נקודת ג' וקו אחר אל נקודת ד' ויהיה המחומש נחלק לג' משולשים | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|ואין אתה יכול לפחות מהמשולשים האלה ואם אתה מרבע אותם יהיה רבוע שלשתם תשבורת המחומש כגון הצורה הזאת | + | :You cannot reduce [the number of] these triangles. |
| + | |style="text-align:right;"|ואין אתה יכול לפחות מהמשולשים האלה | ||
| + | |- | ||
| + | | | ||
| + | :If you find their areas, [the sum of] the areas of the three is the area of the pentagon. | ||
| + | |style="text-align:right;"|ואם אתה מרבע אותם יהיה רבוע שלשתם תשבורת המחומש כגון הצורה הזאת | ||
|- | |- | ||
| | | | ||
| + | |||
==== <span style=color:green>Square</span> ==== | ==== <span style=color:green>Square</span> ==== | ||
| Line 6,514: | Line 6,677: | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:square|680|5Xvk}}131) | + | :{{#annot:square|680|5Xvk}}131) You have a square of 10 cubits by 10 cubits within it a smaller square of 4 cubits by 4 cubits is drawn. |
| − | :You want to know how much is the area of the larger square after subtracting the area of the smaller square from it | + | :You want to know how much is the area of the larger square after subtracting the area of the smaller square from it. |
|style="text-align:right;"|קלא <big>הרי</big> שיש לפניך א' מרובע מי' אמה על י' אמה ובאמצע הוא חקוק ופוחת ד' אמות על ד' אמות<br> | |style="text-align:right;"|קלא <big>הרי</big> שיש לפניך א' מרובע מי' אמה על י' אמה ובאמצע הוא חקוק ופוחת ד' אמות על ד' אמות<br> | ||
ותרצה לדעת כמה הוא המרובע בשיבור אחר הוצאת הד' אמות על ד' אמות מן החקק{{#annotend:5Xvk}} | ותרצה לדעת כמה הוא המרובע בשיבור אחר הוצאת הד' אמות על ד' אמות מן החקק{{#annotend:5Xvk}} | ||
| Line 6,524: | Line 6,687: | ||
|- | |- | ||
| | | | ||
| − | :: | + | :Say: if the square were complete, you would say 10 times 10 is 100 and its area were 100. |
| − | + | |style="text-align:right;"|תאמר אלו היה הטבלה מרובעת שלימה בלתי שום חקיקה היית אומר י' פעמ' י' הם ק' ותשברתו היה ק‫' | |
| − | |style="text-align:right;"|תאמר אלו היה הטבלה מרובעת שלימה בלתי שום חקיקה היית אומר י' פעמ' י' הם ק' ותשברתו היה ק‫' | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| + | :Now, that 4 times 4 is missing in the middle, say 4 times 4 is 16. | ||
| + | |style="text-align:right;"|ועתה שפוחת באמצע ד' על ד' תאמ' ד' פעמ' ד' הם י"ו | ||
| + | |- | ||
| + | | | ||
| + | :Subtract it from 100; 84 remains. | ||
| + | |style="text-align:right;"|תפחתם מק' ישארו פ"ד | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\rm{area_{big\ square}}-\rm{area_{small\ square}}=10^2-4^2=100-16=84}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :So, the area of a square of 10 by 10 that is missing 4 by 4 in the middle is 84. | ||
| + | |style="text-align:right;"|א"כ א' טבלה מרובעת שהיא י' על י' ופוחת באמצעה ד' על ד' תשברתה פ"ד | ||
| + | |- | ||
| + | | | ||
| + | :The same for everything similar to it. | ||
| + | |style="text-align:right;"|וכן כל הדומה לו | ||
| + | |- | ||
| + | | | ||
| + | |||
==== <span style=color:green>Scalene Trapezoid</span> ==== | ==== <span style=color:green>Scalene Trapezoid</span> ==== | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:scalene trapezoid|680|JXCu}}132) | + | :{{#annot:scalene trapezoid|680|JXCu}}132) A trapezoid that has two parallel sides: line AG is 8 cubits long, line BD is 22 cubits long; and two unequal sides: line AB is 15 [cubits] long, and line GD is 13 cubits long. |
:It is called scalene trapezoid. | :It is called scalene trapezoid. | ||
|style="text-align:right;"|‫<ref>115r</ref>קלב <big>קטומה</big> שיש לה ב' קוים נכוחיים קו א"ג ואורכו ח' אמות וקו ב"ז ואורכו כ"ב אמות וב' צלעים שאינם שוות והם קו א"ב ואורכו ט"ו וקו ג"ד ואורכו י"ג אמות<br> | |style="text-align:right;"|‫<ref>115r</ref>קלב <big>קטומה</big> שיש לה ב' קוים נכוחיים קו א"ג ואורכו ח' אמות וקו ב"ז ואורכו כ"ב אמות וב' צלעים שאינם שוות והם קו א"ב ואורכו ט"ו וקו ג"ד ואורכו י"ג אמות<br> | ||
| Line 6,547: | Line 6,726: | ||
[[File:Kelalim ba-Mispar 132-1.png|thumb|250px|center]] | [[File:Kelalim ba-Mispar 132-1.png|thumb|250px|center]] | ||
|- | |- | ||
| − | |The area of | + | | |
| + | :The area of this shape is found by finding the height, as you did with the first [trapezoid] I described above. | ||
|style="text-align:right;"|וריבוע הצורה הזאת יהיה בהוצאת עמוד ה' כאשר עשית בראשונה שכתבתיה למעלה | |style="text-align:right;"|וריבוע הצורה הזאת יהיה בהוצאת עמוד ה' כאשר עשית בראשונה שכתבתיה למעלה | ||
|- | |- | ||
| − | | | + | | |
| + | :In this trapezoid you should find the long segment and the short segment of the base [= the distances between the heights and the meeting points of the longer and shorter sides with the basis] and you do it this way: | ||
|style="text-align:right;"|ואתה צריך בקטומה הזאת לגבל מעמד העמודים ולדעת מעמד הגדול ומעמד הקטון ואתה נוהג בהם המנהג הזה | |style="text-align:right;"|ואתה צריך בקטומה הזאת לגבל מעמד העמודים ולדעת מעמד הגדול ומעמד הקטון ואתה נוהג בהם המנהג הזה | ||
|- | |- | ||
| − | | | + | | |
| − | + | :Square the short side; subtract its square from the square of the long side; take half the difference between them and divide it by the excess of the bottom base over the upper base. If you add the result of division to half the excess of the bottom base, you find the long segment of the height, which is its distance from the longer side. | |
|style="text-align:right;"|תרבע הצלע הקצורה וגרע מרובעה ממרובע הצלע הארוך והעודף שבהם תקח מחציתו ותחלק אותו על עודף התושבת על הראש ואשר יצא מהחלוקה הזאת אם אתה מוסיף אותו על מחצית עדף התושבת תמצא המעמד הגדול אשר לעמוד והוא מרחקו מן הצלע הארוך | |style="text-align:right;"|תרבע הצלע הקצורה וגרע מרובעה ממרובע הצלע הארוך והעודף שבהם תקח מחציתו ותחלק אותו על עודף התושבת על הראש ואשר יצא מהחלוקה הזאת אם אתה מוסיף אותו על מחצית עדף התושבת תמצא המעמד הגדול אשר לעמוד והוא מרחקו מן הצלע הארוך | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | <math>\scriptstyle\left[\frac{1}{2}\sdot\left(\rm{base_{bottom}-base_{top}}\right)\right] | + | :<math>\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{base_{bottom}-base_{top}}\right)\right]+\frac{\frac{1}{2}\sdot\left(\rm{side_1^2-side_2^2}\right)}{\rm{base_{bottom}-base_{top}}}}}</math> |
| + | |- | ||
| + | | | ||
| + | :If you subtract it from half the excess, you find the short segment of the height, which is its distance from the short side. | ||
|style="text-align:right;"|ואם תגרעינו ממחצית העודף תמצא המעמד הקטן אשר לעמוד והוא מרחקו מן הצלע הקצר | |style="text-align:right;"|ואם תגרעינו ממחצית העודף תמצא המעמד הקטן אשר לעמוד והוא מרחקו מן הצלע הקצר | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{base_{bottom}-base_{top}}\right)\right]-\frac{\frac{1}{2}\sdot\left(\rm{side_1^2-side_2^2}\right)}{\rm{base_{bottom}-base_{top}}}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :In this shape, if you square 13, which is the length of the short side GD, its square is 169. | ||
| + | |style="text-align:right;"|ואם אתה מרבע בצורה הזאת י"ג שהוא אורך צלע ג"ד הקצור יהיה מרובעו ק'ס'ט‫' | ||
| + | |- | ||
| + | | | ||
| + | :Subtract it from the square of AB, which is the long side; 56 remains. | ||
| + | |style="text-align:right;"|פחות אותו ממרובע א"ב שהוא מרובע הצלע הארוך ישאר נ"ו | ||
| + | |- | ||
| + | | | ||
| + | :Take half this number; it is 28. | ||
| + | |style="text-align:right;"|קח מחצית המניין הזה והוא כ"ח | ||
| + | |- | ||
| + | | | ||
| + | :Divide it by 14, which is the excess of the bottom base over the upper base; the quotient is 2. | ||
| + | |style="text-align:right;"|חלק אותו על י"ד שהוא עודף התושבת על הראש תהיה החלוקה ב‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :If you add 2 to 7, which is half the excess of the bottom base, it is 9 and this is the length of BH, which is the distance of the height from the long side. |
| − | + | |style="text-align:right;"|ואם תוסיף ב' על ז' אשר הוא חצי עדף התושבת יהיה ט' והוא אורך קו ב"ה אשר הוא מרחק העמוד מהצלע הארוך | |
| − | |||
| − | |||
| − | ואם תוסיף ב' על ז' אשר הוא חצי עדף התושבת יהיה ט' והוא אורך קו ב"ה אשר הוא מרחק העמוד מהצלע הארוך | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
| Line 6,572: | Line 6,772: | ||
|- | |- | ||
| | | | ||
| + | :If you subtract 2 from 7, you find the distance of the height from the short side. | ||
:<math>\scriptstyle{\color{blue}{CD=\left[\frac{1}{2}\sdot\left(BD-AG\right)\right]-\frac{\frac{1}{2}\sdot\left(AB^2-GD^2\right)}{BD-AG}=7-2}}</math> | :<math>\scriptstyle{\color{blue}{CD=\left[\frac{1}{2}\sdot\left(BD-AG\right)\right]-\frac{\frac{1}{2}\sdot\left(AB^2-GD^2\right)}{BD-AG}=7-2}}</math> | ||
|style="text-align:right;"|ואם תפחות ב' מז' תמצא מרחק העמוד מהצלע הקצר | |style="text-align:right;"|ואם תפחות ב' מז' תמצא מרחק העמוד מהצלע הקצר | ||
|- | |- | ||
| − | | | + | | |
| + | :The proof of this matter is that you examine what I explained above regarding the height of the scalene triangle: | ||
|style="text-align:right;"|והאות על העניין הזה התבונן לך מאשר פירשתי למעלה בעמוד המשולש מתחלף הצלעות | |style="text-align:right;"|והאות על העניין הזה התבונן לך מאשר פירשתי למעלה בעמוד המשולש מתחלף הצלעות | ||
|- | |- | ||
| Line 6,582: | Line 6,784: | ||
| | | | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|כי בהוציאך מן התושבת את הרחב הראש והוא ה' ישאר קו ט"ח ג' אמות פחות שביע והוא עודף מעמד עמוד המשולש על מעמד עמוד הקטומה הקצר | + | :Because, when you subtract the upper base, which is 5, from the bottom base, the remainder is line TC, which is 3 cubits minus a seventh, and this is the excess of the segment of the height of the triangle over the distance of the height of the trapezoid from its short side. |
| − | והעודף הזה רבע בצלע הקטומה הקצר שהוא י"ג יהיה ל"ז ושביעית | + | |style="text-align:right;"|כי בהוציאך מן התושבת את הרחב הראש והוא ה' ישאר קו ט"ח ג' אמות פחות שביע והוא עודף מעמד עמוד המשולש על מעמד עמוד הקטומה הקצר |
| − | בוא וחלק המספר הזה על מעמד העמוד הקצר בקטומה והוא ה' תהיה החלוקה הזאת ז' וג' שביעיות והוא עודף צלע המשולש על צלע הקטומה הקצרה והוא קו ג"ז היוצא מצד הקצר | + | |- |
| + | | | ||
| + | :Multiply this excess by the short side of the trapezoid, which is 13; it is 37 and a seventh. | ||
| + | |style="text-align:right;"|והעודף הזה רבע בצלע הקטומה הקצר שהוא י"ג יהיה ל"ז ושביעית | ||
| + | |- | ||
| + | | | ||
| + | :Divide this number by the short segment of the trapezoid, which is 5; the quotient is 7 and 3-sevenths and this is the excess of the side of the triangle over the short side of the trapezoid, which is line GZ that is drawn from the short side. | ||
| + | |style="text-align:right;"|בוא וחלק המספר הזה על מעמד העמוד הקצר בקטומה והוא ה' תהיה החלוקה הזאת ז' וג' שביעיות והוא עודף צלע המשולש על צלע הקטומה הקצרה והוא קו ג"ז היוצא מצד הקצר | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
:<math>\scriptstyle{\color{blue}{GZ=\frac{TC\sdot GD}{CD}=\frac{\left(DT-CD\right)\sdot GD}{CD}=\frac{\left(3-\frac{1}{7}\right)\sdot13}{5}=\frac{37+\frac{1}{7}}{5}=7+\frac{3}{7}}}</math> | :<math>\scriptstyle{\color{blue}{GZ=\frac{TC\sdot GD}{CD}=\frac{\left(DT-CD\right)\sdot GD}{CD}=\frac{\left(3-\frac{1}{7}\right)\sdot13}{5}=\frac{37+\frac{1}{7}}{5}=7+\frac{3}{7}}}</math> | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|ואם תרצה לדעת קו א"ז הארוך הוצא המעמד הארוך במשולש על העניין שהוצאת הקצר | + | :If you want to find the short line AZ, find the long segment of the triangle according to the way you found the short segment. |
| − | ותמצא אותו י"ד ושביעית | + | |style="text-align:right;"|ואם תרצה לדעת קו א"ז הארוך הוצא המעמד הארוך במשולש על העניין שהוצאת הקצר |
| − | והוא מעדיף על מעמד הארוך ה' ושביעית | + | |- |
| − | מנה אותו בצלע הארוך שהוא ט"ו יהיה המניין ע"ז ושביעית | + | | |
| − | חלק המספר הזה על ט' שהוא המעמד הארוך בקטומה תהיה החלוקה ח' וד' שביעיות והוא עודף צלע המשולש על צלע הקטומה הא' הארוך והוא א"ז | + | :You find it is 14 and a seventh and it exceeds the long segment by 5 and a seventh. |
| + | |style="text-align:right;"|ותמצא אותו י"ד ושביעית והוא מעדיף על מעמד הארוך ה' ושביעית | ||
| + | |- | ||
| + | | | ||
| + | :Multiply it by the long side, which is 15; the product is 77 and a seventh. | ||
| + | |style="text-align:right;"|מנה אותו בצלע הארוך שהוא ט"ו יהיה המניין ע"ז ושביעית | ||
| + | |- | ||
| + | | | ||
| + | :Divide this number by 9, which is the long segment of the trapezoid; the quotient is 8 and 4-sevenths and this is the excess of the side of the triangle over the long side of the trapezoid, which is AZ. | ||
| + | |style="text-align:right;"|חלק המספר הזה על ט' שהוא המעמד הארוך בקטומה תהיה החלוקה ח' וד' שביעיות והוא עודף צלע המשולש על צלע הקטומה הא' הארוך והוא א"ז | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
:<math>\scriptstyle{\color{blue}{AZ=\frac{HT\sdot AB}{HB}=\frac{\left(BT-HB\right)\sdot AB}{HB}=\frac{\left[\left(14+\frac{1}{7}\right)-9\right]\sdot 15}{9}=\frac{\left(5+\frac{1}{7}\right)\sdot15}{9}=\frac{77+\frac{1}{7}}{9}=8+\frac{4}{7}}}</math> | :<math>\scriptstyle{\color{blue}{AZ=\frac{HT\sdot AB}{HB}=\frac{\left(BT-HB\right)\sdot AB}{HB}=\frac{\left[\left(14+\frac{1}{7}\right)-9\right]\sdot 15}{9}=\frac{\left(5+\frac{1}{7}\right)\sdot15}{9}=\frac{77+\frac{1}{7}}{9}=8+\frac{4}{7}}}</math> | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|ואם תבוא לדעת עמוד המשולש הזה הוי מונה עודף המעמד הקטן והוא ג' פחות שביע בעמוד הקטומה שהוא י"ב | + | :If you want to find the height of this triangle, multiply the excess of the short segment, which is 3 minus a seventh, by the height of the trapezoid, which is 12. |
| − | + | |style="text-align:right;"|ואם תבוא לדעת עמוד המשולש הזה הוי מונה עודף המעמד הקטן והוא ג' פחות שביע בעמוד הקטומה שהוא י"ב | |
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | | |
| − | : | + | :Then, divide it by the short segment, which is 5. |
| − | : | + | |style="text-align:right;"|וחלק אותו על מעמד הקטן והוא ה‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :Or, multiply the excess of the long segment, which is 5 and a seventh, by the height of the trapezoid, which is 12. |
| − | + | |style="text-align:right;"|או הוי מונה עודף המעמד הגדול והוא ה' ושביע בעמוד הקטומה שהוא י"ב | |
| − | |||
|- | |- | ||
| | | | ||
| − | + | :We divide it by the long segment, which is 9. | |
| − | + | |style="text-align:right;"|נחלקהו על המעמד הגדול והוא ט‫' | |
| − | + | |- | |
| | | | ||
| + | :You find both results are the same number, which is 7 minus a seventh, and this is the excess of the height of the triangle over the height of the trapezoid. | ||
| + | |style="text-align:right;"|תמצא שניהם מוציאים אל חשבון אחד והוא ז' פחות שביע והוא עודף עמוד המשולש על עמוד הקטומה | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:right trapezoid|680,683|Tojz}}133) The third | + | :Add it to 12, which is the height of the trapezoid; the total is 19 minus a seventh and this is the length of line ZT, which is the height of the triangle in this shape. |
| − | :For example: [right] trapezoid ABGD - its upper base AG is 8, its lower base BD is 20, its long leg AB is 15, and its short leg GD is 9 which is the height of BD. | + | |style="text-align:right;"|הוסף אותו על י"ב שהוא עמוד הקטומה ויהיה הכל י"ט פחות שביע והוא אורך קו ז"ט אשר הוא עמוד המשולש בצורה הזאת |
| − | |style="text-align:right;"|קלג התמונה השלישית הקטומה שראשה נכוחי לתושבתה ואחד מצלעיה עמוד עליה והתמונה הזאת נקראת ''חצי קטומה''<br> | + | |- |
| − | והדמיון לצורה הזאת קטומה שעליה א'ב'ג'ד' וראשה א"ג והיא ח' ותושבתה ב"ד והיא כ' וצלע א"ב הארוך ט"ו וצלע ג"ד הקצור ט' אמות והוא עמוד על תושבת ב"ד{{#annotend:Tojz}} | + | |colspan=2| |
| + | :<math>\scriptstyle{\color{blue}{ZT=\frac{TC\sdot GC}{CD}+GC=\frac{\left(3-\frac{1}{7}\right)\sdot12}{5}+12=\left(7-\frac{1}{7}\right)+12=19-\frac{1}{7}}}</math> | ||
| + | :<math>\scriptstyle{\color{blue}{ZT=\frac{HT\sdot AH}{BH}+AH=\frac{\left(5+\frac{1}{7}\right)\sdot12}{9}+12=\left(7-\frac{1}{7}\right)+12=19-\frac{1}{7}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :This matter is clear as we said above. | ||
| + | |style="text-align:right;"|‫<ref>116r</ref><big>גליון</big> וזה דבר ברור הוא כאשר אמרנו למעלה | ||
| + | |- | ||
| + | | | ||
| + | :Because, [the ratio of] line HT to line AH is the same as [the ratio of] line BH to the line of the excess of the height of the triangle over the height of the trapezoid, which is AH. | ||
| + | |style="text-align:right;"|כי קו ה"ט בקו א"ה כקו ב"ה בקו עודף עמוד המשולש על עמוד הקטומה שהיה א"ה | ||
| + | |- | ||
| + | | | ||
| + | :Therefore, if we multiply line HT by line AH and divide by line BH, we get the excess. | ||
| + | |style="text-align:right;"|על כן אם נרבע קו ה"ט בקו א"ה ונחלק על קו ב"ה יצא לנו העודף | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Right Trapezoid</span> ==== | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :{{#annot:right trapezoid|680,683|Tojz}}133) The third shape is the trapezoid whose upper base is parallel to its lower base and one of its legs is its height. This shape is called "right trapezoid". | ||
| + | :For example: [right] trapezoid ABGD - its upper base AG is 8, its lower base BD is 20, its long leg AB is 15, and its short leg GD is 9 cubits, which is the height of BD. | ||
| + | |style="text-align:right;"|קלג התמונה השלישית הקטומה שראשה נכוחי לתושבתה ואחד מצלעיה עמוד עליה והתמונה הזאת נקראת ''חצי קטומה''<br> | ||
| + | והדמיון לצורה הזאת קטומה שעליה א'ב'ג'ד' וראשה א"ג והיא ח' ותושבתה ב"ד והיא כ' וצלע א"ב הארוך ט"ו וצלע ג"ד הקצור ט' אמות והוא עמוד על תושבת ב"ד{{#annotend:Tojz}} | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 6,636: | Line 6,877: | ||
| | | | ||
|- | |- | ||
| − | | | + | | |
| − | <math>\scriptstyle \left[\frac{1}{2}\sdot\left(\rm{base_{top}+base_{bottom}}\right)\right]\sdot\rm{height}</math> | + | :The calculation of the area of this trapezoid is by adding its upper base to its lower base, then taking its half, and multiplying it by the height; this is the area of the trapezoid. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{base_{top}+base_{bottom}}\right)\right]\sdot\rm{height}}}</math> | ||
|style="text-align:right;"|וחשבון רבוע הקטומה הזאת הוא באסיפת ראשה אל תושבתה ולקחת מחציתם וימנה בעמוד ויהיה תשבורת הקטומה | |style="text-align:right;"|וחשבון רבוע הקטומה הזאת הוא באסיפת ראשה אל תושבתה ולקחת מחציתם וימנה בעמוד ויהיה תשבורת הקטומה | ||
|- | |- | ||
| | | | ||
| − | ::the area | + | :In this shape, if you add its upper base to its lower base, their sum is 28 and its half is 14. |
| − | + | |style="text-align:right;"|ואם תאסוף בצורה הזאת ראשה אל תושבתה יהיה כללם כ"ח ומחציתם י"ד | |
| − | |style="text-align:right;"| | + | |- |
| − | + | | | |
| − | ואם תרבע המספר הזה באורך העמוד והוא ט' יהיה ק'כ'ו' והוא תשבורת הקטומה הזאת | + | :If you multiply this number by the length of the height, which is 9, it is 126 and this is the area of this trapezoid. |
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{1}{2}\sdot\left(8+20\right)\right]\sdot9=\left(\frac{1}{2}\sdot28\right)\sdot9=14\sdot9=126}}</math> | ||
| + | |style="text-align:right;"|ואם תרבע המספר הזה באורך העמוד והוא ט' יהיה ק'כ'ו' והוא תשבורת הקטומה הזאת | ||
|- | |- | ||
| − | |The | + | | |
| + | :The proof of this is explained above regarding the complete trapezoid. | ||
|style="text-align:right;"|ואות לזה מפורש למעלה בקטומה הנשלמת | |style="text-align:right;"|ואות לזה מפורש למעלה בקטומה הנשלמת | ||
|- | |- | ||
| | | | ||
| − | : | + | :If you want to know its short diagonal, which is AD: |
| − | |style="text-align:right;"|ואם תבוא לדעת אלכסונה הקצור והוא א"ד | + | |style="text-align:right;"|ואם תבוא לדעת אלכסונה הקצור והוא א"ד |
| − | הוי מרבע את הראש והוא ח' ומרובעו ס"ד | + | |- |
| − | ואסוף אליו מרובע העמוד והוא הצלע הקצור והוא פ"א ויהיו שניהם יחד ק'מ'ה' והוא מרובע האלכסון | + | | |
| − | וגדר המספר הזה הוא אורך אלכסון הקצור | + | :Square the upper base, which is 8; its square is 64. |
| + | |style="text-align:right;"|הוי מרבע את הראש והוא ח' ומרובעו ס"ד | ||
| + | |- | ||
| + | | | ||
| + | :Add to it the square of the height, which is the short side that is 81; together they are 145 and this is the square of the diagonal. | ||
| + | |style="text-align:right;"|ואסוף אליו מרובע העמוד והוא הצלע הקצור והוא פ"א ויהיו שניהם יחד ק'מ'ה' והוא מרובע האלכסון | ||
| + | |- | ||
| + | | | ||
| + | :The root of this number is the length of the short diagonal. | ||
| + | |style="text-align:right;"|וגדר המספר הזה הוא אורך אלכסון הקצור | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
| Line 6,661: | Line 6,915: | ||
|- | |- | ||
| | | | ||
| − | : | + | :If you want to know the long diagonal: |
| − | |style="text-align:right;"|ואם תרצה לדעת אלכסון הארוך אסוף מרובע התושבת למרובע העמוד ויהיו שניהם ת'פ'א' והוא מרובע אלכסון הארוך | + | |style="text-align:right;"|ואם תרצה לדעת אלכסון הארוך |
| + | |- | ||
| + | | | ||
| + | :Add the square of the bottom base to the square of the height; they are 481 and this is the square of the long diagonal. | ||
| + | |style="text-align:right;"|אסוף מרובע התושבת למרובע העמוד ויהיו שניהם ת'פ'א' והוא מרובע אלכסון הארוך | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
:<math>\scriptstyle{\color{blue}{GB=\sqrt{\rm{base_{bottom}^2+height^2}}=\sqrt{20^2+9^2}=\sqrt{481}}}</math> | :<math>\scriptstyle{\color{blue}{GB=\sqrt{\rm{base_{bottom}^2+height^2}}=\sqrt{20^2+9^2}=\sqrt{481}}}</math> | ||
|- | |- | ||
| − | | | + | | |
| + | :This calculation is correct, because both angles at point G and point D on side GD are right angles, since this side is perpendicular to the lower base and the upper base that are parallel. | ||
|style="text-align:right;"|ונתכוון לך החשבון הזה מפני ששתי זוויות אשר על נקודת ג' ונקודת ד' מן צלע ג"ד הן ניצבות כי הצלע הזה הוא עמוד על התושבת ועל הראש אשר הם {{#annot:term|825,1821|uvqN}}נכוחיים{{#annotend:uvqN}} | |style="text-align:right;"|ונתכוון לך החשבון הזה מפני ששתי זוויות אשר על נקודת ג' ונקודת ד' מן צלע ג"ד הן ניצבות כי הצלע הזה הוא עמוד על התושבת ועל הראש אשר הם {{#annot:term|825,1821|uvqN}}נכוחיים{{#annotend:uvqN}} | ||
|- | |- | ||
| | | | ||
| − | : | + | :Diagonal AD is the hypotenuse opposite the right angle G. |
|style="text-align:right;"|ואלכסון א"ד הוא מיתר לזוית ג' הניצבה | |style="text-align:right;"|ואלכסון א"ד הוא מיתר לזוית ג' הניצבה | ||
|- | |- | ||
| | | | ||
| − | : | + | :Diagonal GB is the hypotenuse opposite the right angle D. |
| − | |style="text-align:right;"|ואלכסון ג"ב הוא מיתר לזוית ד' הניצבה ומרובע מיתר זוית הניצבה הוא שוה לשם מרובעי ב' הצלעות אשר הן מקיפות לה כאשר ידעת וזה לך האות על חשבון האלכסונות בצורה הזאת | + | |style="text-align:right;"|ואלכסון ג"ב הוא מיתר לזוית ד' הניצבה |
| + | |- | ||
| + | | | ||
| + | :The square of the hypotenuse opposite the right angle is equal to [the sum of] the squares of the two sides comprising it, as you know. | ||
| + | |style="text-align:right;"|ומרובע מיתר זוית הניצבה הוא שוה לשם מרובעי ב' הצלעות אשר הן מקיפות לה כאשר ידעת | ||
| + | |- | ||
| + | | | ||
| + | :This is your proof of calculating the diagonals in this shape. | ||
| + | |style="text-align:right;"|וזה לך האות על חשבון האלכסונות בצורה הזאת | ||
|- | |- | ||
| − | | | + | | |
| + | :If you want to complete this trapezoid and draw the top of the triangle from which it is cut off: | ||
|style="text-align:right;"|ואם תרצה להשלים הקטומה הזאת ולהוציא ראש המשולש הנקטמת ממנה | |style="text-align:right;"|ואם תרצה להשלים הקטומה הזאת ולהוציא ראש המשולש הנקטמת ממנה | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | :Apply the procedure you learned for the previous trapezoid: |
| + | |style="text-align:right;"|עשה כמעשה שלמדת מן הקטומה שלפניה | ||
| + | |- | ||
| + | | | ||
| + | :Find the excess of the lower base over the upper base, which is 12 in this shape. | ||
| + | |style="text-align:right;"|והוא שתהיה יודע עודף התושבת על הראש והוא י"ב בצורה הזאת | ||
| + | |- | ||
| + | | | ||
| + | :If you multiply the upper base by line AB, then divide it by the excess of the lower base, you get the length of the line drawn from the height [of the trapezoid] to the top of the triangle. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{\rm{base_{top}}\times\rm{long\ side_{trapezoid}}}{\rm{base_{bottom}-base_{top}}}}}</math> | ||
| + | |style="text-align:right;"|ואם תמנה הראש בקו א"ב וחלקנו על עודף התושבת יצא לך אורך הקו היוצא מהעמוד אל ראש המשולש | ||
| + | |- | ||
| + | | | ||
| + | :You can apply it the way you learned for the other shapes. | ||
| + | |style="text-align:right;"|ואתה יכול להוציאו למעשה מן הדרך שלמדת בצורות האחרות | ||
|- | |- | ||
| | | | ||
| Line 6,692: | Line 6,974: | ||
| | | | ||
:{{#annot:obtuse trapezoid|680,685,683|dvwi}}134) A trapezoid whose upper base is parallel to its lower base and one of its legs is at obtuse angle to the lower base. | :{{#annot:obtuse trapezoid|680,685,683|dvwi}}134) A trapezoid whose upper base is parallel to its lower base and one of its legs is at obtuse angle to the lower base. | ||
| − | : | + | :This trapezoid has two inner heights and one outer height. |
:It is an obtuse trapezoid | :It is an obtuse trapezoid | ||
:For example: [obtuse] trapezoid ABGD - its upper base AG is 14, its lower base BD is 21, its long leg AB is 20, and its short leg GD is 15. | :For example: [obtuse] trapezoid ABGD - its upper base AG is 14, its lower base BD is 21, its long leg AB is 20, and its short leg GD is 15. | ||
| Line 6,711: | Line 6,993: | ||
|- | |- | ||
| | | | ||
| − | :First, you should find [the distance between the height and the meeting | + | :First, you should find [the distance between the height and the meeting points of the sides with the basis]: |
|style="text-align:right;"|ואתה צריך תחלה להגביל מעמד העמוד | |style="text-align:right;"|ואתה צריך תחלה להגביל מעמד העמוד | ||
|- | |- | ||
| Line 6,731: | Line 7,013: | ||
|- | |- | ||
| | | | ||
| − | :The total is 16, which is the [distance between the height and the meeting point of the longer side AB with the basis. | + | :The total is 16, which is the [distance between the height and the meeting point of the longer side AB with the basis]. |
:<math>\scriptstyle{\color{blue}{HB=16}}</math> | :<math>\scriptstyle{\color{blue}{HB=16}}</math> | ||
|style="text-align:right;"|ויהיה הכל י"ו והוא גבול מעמד העמוד מנגד קו א"ב הארוך | |style="text-align:right;"|ויהיה הכל י"ו והוא גבול מעמד העמוד מנגד קו א"ב הארוך | ||
|- | |- | ||
| | | | ||
| − | :The 9 you have found is | + | :The 9 you have found is short segment. |
|style="text-align:right;"|ואלו הט' אשר מצאת הם המרחק הקצר | |style="text-align:right;"|ואלו הט' אשר מצאת הם המרחק הקצר | ||
|- | |- | ||
| Line 6,742: | Line 7,024: | ||
:<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle CD &\scriptstyle=\frac{\frac{1}{2}\sdot\left[AB^2-\left[\left(BD-AG\right)^2+GD^2\right]\right]}{BD-AG}=\frac{\frac{1}{2}\sdot\left[20^2-\left[\left(21-14\right)^2+15^2\right]\right]}{21-14}=\frac{\frac{1}{2}\sdot\left[20^2-\left(7^2+15^2\right)\right]}{7}\\&\scriptstyle=\frac{\frac{1}{2}\sdot\left(400-274\right)}{7}=\frac{\frac{1}{2}\sdot126}{7}=\frac{63}{7}=9\\\end{align}}}</math> | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle CD &\scriptstyle=\frac{\frac{1}{2}\sdot\left[AB^2-\left[\left(BD-AG\right)^2+GD^2\right]\right]}{BD-AG}=\frac{\frac{1}{2}\sdot\left[20^2-\left[\left(21-14\right)^2+15^2\right]\right]}{21-14}=\frac{\frac{1}{2}\sdot\left[20^2-\left(7^2+15^2\right)\right]}{7}\\&\scriptstyle=\frac{\frac{1}{2}\sdot\left(400-274\right)}{7}=\frac{\frac{1}{2}\sdot126}{7}=\frac{63}{7}=9\\\end{align}}}</math> | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|וכן מרחק העמוד שעליו ג"ח אשר הוא יוצא חוצה מן קו ב"ד התושבת | + | :So is the distance of the outer height GC from line BD, which is the lower base, and from the middle height DT, which falls on point D. |
| − | וכן מרחק העמוד התיכוני הנופל על נקודת ד' שעליו ד"ט | + | |style="text-align:right;"|וכן מרחק העמוד שעליו ג"ח אשר הוא יוצא חוצה מן קו ב"ד התושבת וכן מרחק העמוד התיכוני הנופל על נקודת ד' שעליו ד"ט |
|- | |- | ||
| | | | ||
| − | : | + | :If you want to know the length of the height: |
| − | |style="text-align:right;"|ואם תבוא לדעת | + | |style="text-align:right;"|ואם תבוא לדעת אורך העמוד |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | | |
| − | : | + | :Square the segment you want. |
| − | : | + | |style="text-align:right;"|הוי מרבע את מעמד שתרצה |
|- | |- | ||
| − | |the | + | | |
| − | <math>\scriptstyle\left[\frac{1}{2}\sdot\left(\rm{base_{top}+base_{bottom}}\right)\right]\sdot\rm{height}</math> | + | :If you square the long segment, which is 16, subtract it from the square of the long side, which is 20. |
| + | |style="text-align:right;"|ואם [אתה] מרבע המעמד הארוך שהוא י"ו הוציאנו ממרובע הצלע הארוך אשר הוא כ‫' | ||
| + | |- | ||
| + | | | ||
| + | :If you square the short segment, subtract it from the square of the short side. | ||
| + | |style="text-align:right;"|ואם תרבע המעמד הקצור הוציאנו ממרובע הצלע הקצר | ||
| + | |- | ||
| + | | | ||
| + | :The remainder in both calculations is 144 and this is the square of the height. | ||
| + | |style="text-align:right;"|ויהיה המותר מן כל אחד משני החשבונים האלה ק'מ'ד' והוא מרובע העמוד בק | ||
| + | |- | ||
| + | | | ||
| + | :Its root is 12 and this is the length of the height. | ||
| + | |style="text-align:right;"|וגדרו י"ב והוא אורך העמוד | ||
| + | |- | ||
| + | |colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{AH=\sqrt{AB^2-HB^2}=\sqrt{20^2-16^2}=\sqrt{144}=12}}</math> | ||
| + | :<math>\scriptstyle{\color{blue}{GC=\sqrt{GD^2-CD^2}=\sqrt{15^2-9^2}=\sqrt{144}=12}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :The area of this trapezoid is [found] by multiplying the height by [the sum of] half the upper base and half the lower base, as you did for the previous trapezoids. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{base_{top}+base_{bottom}}\right)\right]\sdot\rm{height}}}</math> | ||
|style="text-align:right;"|ותשבורת הקטומה הוא ברבוע העמוד בחצי הראש ובחצי התושבת כאשר עשית בשאר הקטומות שלפניה | |style="text-align:right;"|ותשבורת הקטומה הוא ברבוע העמוד בחצי הראש ובחצי התושבת כאשר עשית בשאר הקטומות שלפניה | ||
|- | |- | ||
| | | | ||
| − | :: | + | :The area is 210. |
| − | |style="text-align:right;"|והתשבורת הוא ר"י והאות על החשבון הזה שהוצאת בו את העמוד הוא מעניין האות שהורתיך בקטומה שאין צלעותיה שוות | + | :<math>\scriptstyle{\color{blue}{\left[\frac{1}{2}\sdot\left(14+21\right)\right]\sdot12=210}}</math> |
| + | |style="text-align:right;"|והתשבורת הוא ר"י | ||
| + | |- | ||
| + | | | ||
| + | :The proof for this calculation in which you extract the height is as the proof that I taught you for the scalene trapezoid. | ||
| + | |style="text-align:right;"|והאות על החשבון הזה שהוצאת בו את העמוד הוא מעניין האות שהורתיך בקטומה שאין צלעותיה שוות | ||
| + | |- | ||
| + | | | ||
| + | :Because, when you subtract the upper base from the lower base, and you are left with 7, this line is a side of an obtuse triangle, whose one side is 7 and the other is 15, and they are the sides comprising the obtuse angle. | ||
| + | |style="text-align:right;"|כי בהוציאך הראש מהתושבת ונשארו בידך ז' היה הקו ההוא צלע ל{{#annot:triangle|1105,2184|iUfN}}משולש מרויח הזויות{{#annotend:iUfN}} א' שצלעו האחת ז' והשינית ט"ו והם הצלעות המקיפות זוית הנרווחת | ||
| + | |- | ||
| + | | | ||
| + | :The hypotenuse of this angle is 20 cubits, which is the length of line AB in this trapezoid. | ||
| + | |style="text-align:right;"|ומיתר הזוית הזאת הוא כ' אמה אשר הוא אורך קו א"ב מן הקטומה הזאת | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | :If you draw an outer height in this obtuse triangle, you find its position outside, as you find in this shape. |
| − | + | |style="text-align:right;"|ואם אתה מוציא במשולש הזה המרויח הזויות עמוד שיהיה נופל חוצה אתה מוצא מעמדו חוצה כאשר מצאת בחשבונך בצורה הזאת | |
| − | ואם אתה מוציא במשולש הזה המרויח הזויות עמוד שיהיה נופל חוצה אתה מוצא מעמדו חוצה כאשר מצאת בחשבונך בצורה הזאת | ||
|- | |- | ||
| | | | ||
| Line 6,779: | Line 7,087: | ||
|- | |- | ||
| | | | ||
| − | : | + | :You can find the long diagonal of the trapezoid, if you add the segment of the outer height to the lower base, then square the total. |
| − | |style="text-align:right;"|ואתה יכול להוציא {{#annot:term|1106,1878|HaZi}}אלכסון{{#annotend:HaZi}} הקטומה הארוך אם אתה מאסף אל התושבת מעמד העמוד החיצוני וכולל את הכל ומרבע אותו | + | |style="text-align:right;"|ואתה יכול להוציא {{#annot:term|1106,1878|HaZi}}אלכסון{{#annotend:HaZi}} הקטומה הארוך אם אתה מאסף אל התושבת מעמד העמוד החיצוני וכולל את הכל ומרבע אותו |
| − | כאילו היית מאסף בצורה הזאת כ"א שהוא אורך התושבת אל ט' שהוא אורך מעמד העמוד חוצה ויהיה הכל ל‫' | + | |- |
| − | ואתה מרבע המניין הזה ומוסיף עליו מרובע העמוד ויהיה הכל אלף ומ"ד והוא מרובע האלכסון הארוך | + | | |
| − | וגדר המספר הזה הוא אורך האלכסון בקטומה הזאת מנקודת ג' אל נקודת ב‫' | + | :As if you add 21, which is the length of the lower base in this shape, to 9, which is the length of the segment of the outer height; the total is 30. |
| + | |style="text-align:right;"|כאילו היית מאסף בצורה הזאת כ"א שהוא אורך התושבת אל ט' שהוא אורך מעמד העמוד חוצה ויהיה הכל ל‫' | ||
| + | |- | ||
| + | | | ||
| + | :You square this number and add the square of the height to it; the total is 1044 and this is the square of the long diagonal. | ||
| + | |style="text-align:right;"|ואתה מרבע המניין הזה ומוסיף עליו מרובע העמוד ויהיה הכל אלף ומ"ד והוא מרובע האלכסון הארוך | ||
| + | |- | ||
| + | | | ||
| + | :The root of this number is the length of the diagonal from point G to point B in this trapezoid. | ||
| + | |style="text-align:right;"|וגדר המספר הזה הוא אורך האלכסון בקטומה הזאת מנקודת ג' אל נקודת ב‫' | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
| Line 6,789: | Line 7,106: | ||
|- | |- | ||
| | | | ||
| − | : | + | :If you want to find the short diagonal going from A to D: |
| − | |style="text-align:right;"|ואם תרצה להוציא אלכסון הקצור היוצא מן א' ועד ד‫' | + | |style="text-align:right;"|ואם תרצה להוציא אלכסון הקצור היוצא מן א' ועד ד‫' |
| − | תאסוף אל מרובע העמוד מרובע עודף התושבת על המעמד הארוך והוא בצורה הזאת ה' ויהיו שני המרובעים ק'ס'ט' והוא מרובע האלכסון הקצור | + | |- |
| − | וגדרו הוא אורך האלכסון | + | | |
| + | :Add the square of the height to the square of the excess of the lower base over the long segment, which is 5 in this shape; [the sum of] the two squares is 169 and this is the square of the short diagonal. | ||
| + | |style="text-align:right;"|תאסוף אל מרובע העמוד מרובע עודף התושבת על המעמד הארוך והוא בצורה הזאת ה' ויהיו שני המרובעים ק'ס'ט' והוא מרובע האלכסון הקצור | ||
| + | |- | ||
| + | | | ||
| + | :Its root is the length of the diagonal. | ||
| + | |style="text-align:right;"|וגדרו הוא אורך האלכסון | ||
|- | |- | ||
|colspan=2| | |colspan=2| | ||
:<math>\scriptstyle{\color{blue}{AD=\sqrt{\left(BD-HB\right)^2+AH^2}=\sqrt{\left(21-16\right)^2+12^2}=\sqrt{5^2+12^2}=\sqrt{169}}}</math> | :<math>\scriptstyle{\color{blue}{AD=\sqrt{\left(BD-HB\right)^2+AH^2}=\sqrt{\left(21-16\right)^2+12^2}=\sqrt{5^2+12^2}=\sqrt{169}}}</math> | ||
|- | |- | ||
| − | | | + | | |
| + | :You can understand the proof of this matter from the proofs above, when you look at right triangles formed by these diagonals, the sides of the trapezoid, and the heights, as I showed you above. | ||
|style="text-align:right;"|והאות אל העניין הזה אתה יכול להבין מהאותות אשר למעלה אם אתה מביט אל ה{{#annot:triangle|1104,1341|1xD2}}משולשים מוצבי זוית{{#annotend:1xD2}} אשר הם מתיילדים מהאלכסונות האלה עם צלעי הקטומה והעמודים כאשר הראיתך למעלה | |style="text-align:right;"|והאות אל העניין הזה אתה יכול להבין מהאותות אשר למעלה אם אתה מביט אל ה{{#annot:triangle|1104,1341|1xD2}}משולשים מוצבי זוית{{#annotend:1xD2}} אשר הם מתיילדים מהאלכסונות האלה עם צלעי הקטומה והעמודים כאשר הראיתך למעלה | ||
|- | |- | ||
| − | |The short diagonal of | + | | |
| + | :The short diagonal of this shape can be also the height of the trapezoid itself. | ||
|style="text-align:right;"|ויכול הוא בצורה הזאת שיהיה אלכסון הקצור הוא עמוד בקטומה בעצמו | |style="text-align:right;"|ויכול הוא בצורה הזאת שיהיה אלכסון הקצור הוא עמוד בקטומה בעצמו | ||
|- | |- | ||
| Line 6,810: | Line 7,135: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:obtuse trapezoid|683|RYHe}} | + | *{{#annot:obtuse trapezoid|683|RYHe}}As if the length of the upper base of the trapezoid [AG] is 9 cubits, its lower base [BD] is 16, and the size of the other two sides is the same as in the first shape. |
|style="text-align:right;"|כאילו היה בצורה הזאת אורך ראש הקטומה ט' אמות ותושבתה י"ו ומניין ב' הצלעות הנשארות המניין אשר היה להם בצורה הראשונה{{#annotend:RYHe}} | |style="text-align:right;"|כאילו היה בצורה הזאת אורך ראש הקטומה ט' אמות ותושבתה י"ו ומניין ב' הצלעות הנשארות המניין אשר היה להם בצורה הראשונה{{#annotend:RYHe}} | ||
|- | |- | ||
| | | | ||
| − | : | + | :You find the height in this second shape falling from point A to point D and this height is the length of the short diagonal [= AD]. |
|style="text-align:right;"|והיית מוצא בצורה הזאת השינית העמוד נופל מנקודת א' אל נקודת ד' ויהיה העמוד ההוא אורך האלכסון הקצר | |style="text-align:right;"|והיית מוצא בצורה הזאת השינית העמוד נופל מנקודת א' אל נקודת ד' ויהיה העמוד ההוא אורך האלכסון הקצר | ||
|- | |- | ||
| | | | ||
| − | : | + | :The long diagonal going from G to B is the root of 769, which is [the sum of] the square of the height AD with the square of line AG and line BD that are the upper base and the lower base of the trapezoid together in one line. |
|style="text-align:right;"|והאלכסון הארוך אשר הוא יוצא מג' עד ב' הוא גדר ת'ש'ס'ט' אשר הוא מרבע עמוד א"ד ‫<ref>117r</ref>עם מרובע קו א"ג עם קו ב"ד אשר ראש הקטומה ותושבת שניהם יחד בקו אחד | |style="text-align:right;"|והאלכסון הארוך אשר הוא יוצא מג' עד ב' הוא גדר ת'ש'ס'ט' אשר הוא מרבע עמוד א"ד ‫<ref>117r</ref>עם מרובע קו א"ג עם קו ב"ד אשר ראש הקטומה ותושבת שניהם יחד בקו אחד | ||
|- | |- | ||
| Line 6,825: | Line 7,150: | ||
|- | |- | ||
| | | | ||
| + | :You understand the proofs of all this calculation in place if you examine it properly. | ||
|style="text-align:right;"|ואתה מבין אותות כל החשבון הזה על מכונו אם אתה מעיין בה עיון יפה | |style="text-align:right;"|ואתה מבין אותות כל החשבון הזה על מכונו אם אתה מעיין בה עיון יפה | ||
|- | |- | ||
| Line 6,834: | Line 7,160: | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:quadrangle|680|pQjb}}135) The second type of shapes that have four sides are all the quadrangles that none of their sides is parallel to another side | + | :{{#annot:quadrangle|680|pQjb}}135) The second type of the rest of the shapes that have four sides are all the quadrangles that none of their sides is parallel to another side. |
| − | |style="text-align:right;"|קלה <big>המין</big> השני הנשאר מן התמונות אשר יש להם ד' צלעות הוא כל | + | |style="text-align:right;"|קלה <big>המין</big> השני הנשאר מן התמונות אשר יש להם ד' צלעות הוא כל ''מרובע שאין אחת מצלעותיו נכוחי לצלע אחרת''{{#annotend:pQjb}} |
|- | |- | ||
| − | | | + | | |
| + | :You find the areas of these shapes only by finding the areas of the triangles into which they are divided. | ||
|style="text-align:right;"|ובתמונות האלו אי אתה מוצא רבועם אלא מרבוע המשולשי' אשר הם נחלקי' עליהם | |style="text-align:right;"|ובתמונות האלו אי אתה מוצא רבועם אלא מרבוע המשולשי' אשר הם נחלקי' עליהם | ||
|- | |- | ||
| | | | ||
| − | : | + | :You can divide every quadrangle in the world into two triangles. |
|style="text-align:right;"|וכל מרובע בעולם אתה יכול לחלקו לשני משולשין | |style="text-align:right;"|וכל מרובע בעולם אתה יכול לחלקו לשני משולשין | ||
|- | |- | ||
| | | | ||
| − | : | + | :It is known that whoever divides it into these two triangles, then sums up their areas, finds the area of the quadrangle they are parts of. |
|style="text-align:right;"|וידוע הוא כי המשבר שני המשולשי' ההם ומצרף תשברתם ימצא התשבורת המרובע אשר הם חלקיו | |style="text-align:right;"|וידוע הוא כי המשבר שני המשולשי' ההם ומצרף תשברתם ימצא התשבורת המרובע אשר הם חלקיו | ||
|- | |- | ||
| − | | | + | | |
| + | :This way you can find the area of all quadrangles of different types, whose sides are equal or parallel, from the areas of the triangles into which they are divided. | ||
|style="text-align:right;"|ועל הענין הזה תוכל למצא התשבורת כל מרובע על חלופי מיניהן מן השוים בצלעותיו והנכוחיים מתשבורת המשולשים שהן נחלקים עליהם | |style="text-align:right;"|ועל הענין הזה תוכל למצא התשבורת כל מרובע על חלופי מיניהן מן השוים בצלעותיו והנכוחיים מתשבורת המשולשים שהן נחלקים עליהם | ||
|- | |- | ||
| − | | | + | | |
| + | :But, you can find the area of the quadrangles whose sides are equal or parallel in another method and you do not need to find the areas of the triangles into which they are divided. | ||
|style="text-align:right;"|אלא שהמרובעים השוים בצלעותיו והנכוחיים בהם אתה יכול להגיע אל תשברתן מדרך אחרת ואינך צריך לרבע בהן את המשולשים הנחלקים עליהם | |style="text-align:right;"|אלא שהמרובעים השוים בצלעותיו והנכוחיים בהם אתה יכול להגיע אל תשברתן מדרך אחרת ואינך צריך לרבע בהן את המשולשים הנחלקים עליהם | ||
|- | |- | ||
| − | | | + | | |
| + | :You can find the area of the other quadrangles that do not have parallel sides only by [calculating] the areas of the triangles into which they are divided. | ||
|style="text-align:right;"|ושאר המרובעים הנפתלים ואין בהם צלע {{#annot:term|825,1821|Jegs}}נכוחי{{#annotend:Jegs}} ובצלע אחד אי אתה יכול למצוא תשברתם אלא מתשבורת המשולש אשר יחלקו עליהם | |style="text-align:right;"|ושאר המרובעים הנפתלים ואין בהם צלע {{#annot:term|825,1821|Jegs}}נכוחי{{#annotend:Jegs}} ובצלע אחד אי אתה יכול למצוא תשברתם אלא מתשבורת המשולש אשר יחלקו עליהם | ||
|- | |- | ||
| | | | ||
| − | * | + | *I give you an example for this case and it will be enough for you for the other shapes. This example is of the shape whose explanation I have completed. |
| + | |style="text-align:right;"|ואני נותן לך דמיון בעניין זה ויהיה מספיק לך בשאר הצורות והדמיון הזה הוא מהצורה שהשלמתי פירושה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
:[[File:Kelalim ba-Mispar 135-1.png|thumb|200px|left]] | :[[File:Kelalim ba-Mispar 135-1.png|thumb|200px|left]] | ||
| − | |||
|- | |- | ||
| | | | ||
| − | : | + | :This is the fourth obtuse trapezoid [ABGD] in which side AG is 14 cubits, side BD is 21 cubits, side AB is 20 cubits, and side GD is 15 cubits. |
|style="text-align:right;"|והיא הקטומה הרביעית ה{{#annot:trapezoid|1105,2209|Bzov}}מתמוטטת{{#annotend:Bzov}} אשר צלע א"ג היה בה י"ד אמה וצלע ב"ד כ"א אמה וצלע א"ב כ' אמות וצלע ג"ד ט"ו אמה | |style="text-align:right;"|והיא הקטומה הרביעית ה{{#annot:trapezoid|1105,2209|Bzov}}מתמוטטת{{#annotend:Bzov}} אשר צלע א"ג היה בה י"ד אמה וצלע ב"ד כ"א אמה וצלע א"ב כ' אמות וצלע ג"ד ט"ו אמה | ||
|- | |- | ||
| | | | ||
| − | : | + | :You find that the short diagonal in this trapezoid is 13 cubits, as we calculated above. |
| + | :<math>\scriptstyle{\color{blue}{AD=13}}</math> | ||
|style="text-align:right;"|ומצאת האלכסון הקצור בקטומה הזאת כאשר חשבונו למעלה י"ג אמה | |style="text-align:right;"|ומצאת האלכסון הקצור בקטומה הזאת כאשר חשבונו למעלה י"ג אמה | ||
|- | |- | ||
| | | | ||
| − | : | + | :When you measure it, you find the area [of the quadrangle] is greater or smaller [than the area of the given trapezoid]. |
|style="text-align:right;"|וכשמדדת אותו אתה מרבע לא מצאת בו המידה הזאת אלא יותר ממנה או פחות ממנה | |style="text-align:right;"|וכשמדדת אותו אתה מרבע לא מצאת בו המידה הזאת אלא יותר ממנה או פחות ממנה | ||
|- | |- | ||
| | | | ||
| − | : | + | :We say that if you find that diagonal BG is 16 cubits, you know that this shape is not a trapezoid, because none of its sides is parallel to the other, for if they were parallel, its long or short diagonals would have to be exactly the same as they are in the [given] trapezoid. |
| − | + | |style="text-align:right;"|ואנו מוסרין כאילו מצאת אותה יתר ב"ג י"ו אמה ונודע לך מזה כי אין הצורה הזאת קטומת הראש כי אין אחת מצלעיה {{#annot:term|825,1821|E7Zk}}נכוחית{{#annotend:E7Zk}} עם צלע אחרת לפי אם היו נרוחיות לא היה אלכסונה הארוך או הקצר מתחלף מחשבונו שהיא בקטומה | |
| − | |style="text-align:right;"|ואנו מוסרין כאילו מצאת אותה יתר ב"ג י"ו אמה ונודע לך מזה כי אין הצורה הזאת קטומת הראש | ||
| − | כי אין אחת מצלעיה {{#annot:term|825,1821|E7Zk}}נכוחית{{#annotend:E7Zk}} עם צלע אחרת | ||
| − | לפי אם היו נרוחיות לא היה אלכסונה הארוך או הקצר מתחלף מחשבונו שהיא בקטומה | ||
|- | |- | ||
| | | | ||
| Line 6,886: | Line 7,217: | ||
|- | |- | ||
| | | | ||
| − | : | + | :Therefore, you should find the areas of the two triangles into which the diagonal you draw divides this quadrangle; they are triangles ADB and ADG, the sides of each are known. |
| + | :<math>\scriptstyle{\color{blue}{ABGD=\triangle_{ADB}+\triangle_{ADG}}}</math> | ||
|style="text-align:right;"|ומפני זה אתה צריך לרבע שני המשולשים אשר נחלק עליהן המרבע הזה באלכסון שהוצאת בו והוא שני משולשי א'ד'ב' וא'ד'ג' וכל אחד מהם צלעותיו ידועות | |style="text-align:right;"|ומפני זה אתה צריך לרבע שני המשולשים אשר נחלק עליהן המרבע הזה באלכסון שהוצאת בו והוא שני משולשי א'ד'ב' וא'ד'ג' וכל אחד מהם צלעותיו ידועות | ||
|- | |- | ||
| | | | ||
| − | : | + | :You can find their areas by finding their heights, as you learned regarding the area of triangles. |
|style="text-align:right;"|ואתה יכול להגיע אל ריבועם בהוצאת העמודים כאשר למדת בריבוע המשולשים | |style="text-align:right;"|ואתה יכול להגיע אל ריבועם בהוצאת העמודים כאשר למדת בריבוע המשולשים | ||
|- | |- | ||
| | | | ||
| − | :: | + | :If you apply the procedure on them, you find the area of triangle ADB is 96 and a third minus something. |
| + | :<math>\scriptstyle{\color{blue}{\triangle_{ADB}=96+\frac{1}{3}-\ldots}}</math> | ||
|style="text-align:right;"|ואם אתה נוהג בהם המנהג הזה תמצא תשבורת משולש א'ד'ב' מהן צ"ו ושליש פחות משהו | |style="text-align:right;"|ואם אתה נוהג בהם המנהג הזה תמצא תשבורת משולש א'ד'ב' מהן צ"ו ושליש פחות משהו | ||
|- | |- | ||
| | | | ||
| − | :: | + | :The area of triangle ADG is 150 and 2-thirds minus something. |
| + | :<math>\scriptstyle{\color{blue}{\triangle_{ADG}=150+\frac{2}{3}-\ldots}}</math> | ||
|style="text-align:right;"|ומשולש א'ד'ג' תהיה תשברתו ק"נ וב' שלישיים פחות משהו | |style="text-align:right;"|ומשולש א'ד'ג' תהיה תשברתו ק"נ וב' שלישיים פחות משהו | ||
|- | |- | ||
| | | | ||
| − | :: | + | :The whole area in this case is 247 minus something. |
| − | |style="text-align:right;"|ויהיה כל התשבורת בעניין הזה ר'מ'ז' פחות משהו | + | :<math>\scriptstyle{\color{blue}{ABGD=247-\ldots}}</math> |
| + | |style="text-align:right;"|ויהיה כל התשבורת בעניין הזה ר'מ'ז' פחות משהו | ||
|- | |- | ||
| | | | ||
| − | : | + | :We have found the area of the obtuse trapezoid, but we find that the area of this shape is greater, because its diagonal is greater. |
| − | |style="text-align:right;"|ונמצא הריבוע עודף בתמונה הזאת מפני עדיפת האלכסון | + | |style="text-align:right;"|ואנו מצאנו רבועו בקטומה המתמוטטת ה' ונמצא הריבוע עודף בתמונה הזאת מפני עדיפת האלכסון |
|- | |- | ||
| | | | ||
| − | :If the diagonal | + | :If the diagonal were smaller, the area would have been smaller. |
|style="text-align:right;"|ואילו היה האלכסון מתמעט היה הריבוע פוחת | |style="text-align:right;"|ואילו היה האלכסון מתמעט היה הריבוע פוחת | ||
|- | |- | ||
| − | | | + | | |
| − | + | :From this case you can deduce a general rule for quadrangles: | |
| − | |style="text-align:right;"|ומהעניין הזה אתה יכול למסור לך גדול במרובעת | + | |style="text-align:right;"|ומהעניין הזה אתה יכול למסור לך גדול במרובעת |
| − | |||
|- | |- | ||
| − | | | + | | |
| − | <math>\scriptstyle\left[\frac{1}{2}\sdot\left(\rm{height_1+height_2}\right)\right]\sdot\rm{diagonal}</math> | + | :I say that the quadrangle whose diagonal you are drawing is divided into two triangles. |
| − | |style="text-align:right;"|ותאסוף את שני העמודים ותקח את מחציתם ותצרף המחצית הזה במניין כל האלכסון אתה מוציא תשבורת המרבע | + | |style="text-align:right;"|ואומר מרובע אשר אתה מוציא את אלכסונו נחלק לב' משולשים |
| + | |- | ||
| + | | | ||
| + | :If you draw the height in both triangles, then sum the two heights, take half [their sum] and multiply that half by the whole diagonal, you find the area of the quadrangle. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{height_1+height_2}\right)\right]\sdot\rm{diagonal}}}</math> | ||
| + | |style="text-align:right;"|אם אתה מוציא עמוד של האלכסון בשני המשולשין ותאסוף את שני העמודים ותקח את מחציתם ותצרף המחצית הזה במניין כל האלכסון אתה מוציא תשבורת המרבע | ||
|- | |- | ||
| − | | | + | | |
| − | <math>\scriptstyle\left(\rm{height_1+height_2}\right)\sdot\left(\frac{1}{2}\sdot\rm{diagonal}\right)</math> | + | :Or, multiply [the sum of] the two heights by half the diagonal and you will also find the area of the quadrangle. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(\rm{height_1+height_2}\right)\sdot\left(\frac{1}{2}\sdot\rm{diagonal}\right)}}</math> | ||
|style="text-align:right;"|או תצרף שני העמודים במחצית האלכסון וגם בא תמצא תשבורת המרובע | |style="text-align:right;"|או תצרף שני העמודים במחצית האלכסון וגם בא תמצא תשבורת המרובע | ||
|- | |- | ||
| − | | | + | | |
| + | :I do not need to give you an example for this calculation, because you can understand it from the examples of finding the area of triangles and I do not need to elaborate the explanation of the quadrangle further than that. | ||
|style="text-align:right;"|ואיני צריך להביא לך ‫<ref>117v</ref>להביא לך משל מן החשבון הזה מפני שאתה מבין אותו מהדמיונות אשר במשיחת המשולשין ואיני נזקק להאריך בפירוש המרובעי' יותר מזה | |style="text-align:right;"|ואיני צריך להביא לך ‫<ref>117v</ref>להביא לך משל מן החשבון הזה מפני שאתה מבין אותו מהדמיונות אשר במשיחת המשולשין ואיני נזקק להאריך בפירוש המרובעי' יותר מזה | ||
|} | |} | ||
| Line 6,941: | Line 7,282: | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:two men|657|ZNBI}}136) A man is walking ten miles a day. | + | :{{#annot:two men|657|ZNBI}}136) If it is said: A man is walking ten miles a day. |
| − | :Another man is walking one mile on the first day, two miles on the second day, three miles on the third day, and so on he goes on walking in each day [one mile more]. | + | :Another [man] is walking one mile on the first day, two miles on the second day, three miles on the third day, and so on he goes on walking in each day [one mile more]. |
:In how many days will [the total distance each of them walked] be equal? | :In how many days will [the total distance each of them walked] be equal? | ||
:<math>\scriptstyle10X=\sum_{i=1}^x i</math> | :<math>\scriptstyle10X=\sum_{i=1}^x i</math> | ||
| Line 6,954: | Line 7,295: | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{x=\left(2\sdot10\right)-1=20-1=19}}</math> | + | :Double the miles of the one who walks the same distance [each day]; they are 20. |
| − | |style=" | + | |style="width:45%;text-align:right;"|תכפול המילים שמהלך הקבוע יהיו כ‫' |
| + | |- | ||
| + | | | ||
| + | :Subtract one from them; 19 remains. So, in 19 days they will [walk] the same [distance]. | ||
| + | :<math>\scriptstyle{\color{blue}{x=\left(2\sdot10\right)-1=20-1=19}}</math> | ||
| + | |style="text-align:right;"|וגרע מהם אחד ישארו י"ט הרי שבי"ט ימים יהיו בשוה | ||
|- | |- | ||
| | | | ||
| − | : | + | :Always double [the miles] of the one who walks a fixed distance [each day] and subtract one from them. |
|style="text-align:right;"|וכן לעולם תכפול שמהלך הקבוע ותגרע מהם אחד | |style="text-align:right;"|וכן לעולם תכפול שמהלך הקבוע ותגרע מהם אחד | ||
|- | |- | ||
| | | | ||
| − | :{{#annot:two men|657|GFZ9}}137) A man is walking ten miles a day. Another man is walking one mile on the first day, three miles on the second day, five miles on the third day, and so on he goes on walking in each day an odd number of miles. | + | :{{#annot:two men|657|GFZ9}}137) if it is said: A man is walking ten miles a day. |
| + | :Another [man] is walking one mile on the first day, three miles on the second day, five miles on the third day, and so on he goes on walking in each day an odd number of miles. | ||
:In how many days will [the total distance each of them walked] be equal? | :In how many days will [the total distance each of them walked] be equal? | ||
:<math>\scriptstyle10X=\sum_{i=1}^x \left(2i-1\right)</math> | :<math>\scriptstyle10X=\sum_{i=1}^x \left(2i-1\right)</math> | ||
| Line 6,970: | Line 7,317: | ||
|- | |- | ||
| | | | ||
| − | :the | + | :Know that as the number of miles of the one who walks a fixed distance each day so is the number of days in which they will [walk] the same [distance]. |
|style="text-align:right;"|דע כי כמספר המילים שמהלך הקבוע ליום כן מספר הימים שיעמדו בשוה | |style="text-align:right;"|דע כי כמספר המילים שמהלך הקבוע ליום כן מספר הימים שיעמדו בשוה | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{x=10}}</math> | + | :If the one [who walks the same distance each day] walks 10 miles each day, they will [walk] the same [distance] in 10 days. |
| + | :<math>\scriptstyle{\color{blue}{x=10}}</math> | ||
|style="text-align:right;"|ואם הקבוע מהלך י' מילים ביום בי' ימים יעמדו בשוה | |style="text-align:right;"|ואם הקבוע מהלך י' מילים ביום בי' ימים יעמדו בשוה | ||
|- | |- | ||
| | | | ||
| − | : | + | :If he walks 9 miles a day, they will [walk] the same [distance] in 9 days. |
| + | :<math>\scriptstyle{\color{blue}{x=9}}</math> | ||
|style="text-align:right;"|ואם מהלך ט' מילים ביום בט' ימים יעמדו בשוה וכה"ל | |style="text-align:right;"|ואם מהלך ט' מילים ביום בט' ימים יעמדו בשוה וכה"ל | ||
|- | |- | ||
| | | | ||
:{{#annot:two men|657|FF3W}}138) A man is walking ten miles a day. | :{{#annot:two men|657|FF3W}}138) A man is walking ten miles a day. | ||
| − | :Another man is walking two miles on the first day, four miles on the second day, six miles on the third day, and so on he goes on walking in each day an even number of miles. | + | :Another [man] is walking two miles on the first day, four miles on the second day, six miles on the third day, and so on he goes on walking in each day an even number of miles. |
:In how many days will [the total distance each of them walked] be equal? | :In how many days will [the total distance each of them walked] be equal? | ||
:<math>\scriptstyle10X=\sum_{i=1}^x 2i</math> | :<math>\scriptstyle10X=\sum_{i=1}^x 2i</math> | ||
| Line 6,991: | Line 7,340: | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{x=10-1=9}}</math> | + | :Subtract one from the miles of the one who walks a fixed distance [each day], which are 10; they are 9. So, in 9 days they will [walk] the same [distance]. |
| − | |style="text-align:right;"|תחסר אחד מן המילים שמהלך הקבוע שהם י' יהיו ט | + | :<math>\scriptstyle{\color{blue}{x=10-1=9}}</math> |
| − | הרי שבט' ימים יעמדו בשוה | + | |style="text-align:right;"|תחסר אחד מן המילים שמהלך הקבוע שהם י' יהיו ט' הרי שבט' ימים יעמדו בשוה |
|- | |- | ||
| | | | ||
| − | : | + | :Always subtract one from the number of miles. The same for everything similar to it. |
|style="text-align:right;"|וכן לעולם תחסר אחד ממספר המילים וכן כל הדומה לו | |style="text-align:right;"|וכן לעולם תחסר אחד ממספר המילים וכן כל הדומה לו | ||
|- | |- | ||
| Line 7,014: | Line 7,363: | ||
|- | |- | ||
| | | | ||
| − | ::from the top of the tree | + | :The answer: divide the square of the distance from the roots of the tree to its top, which is 25 in our example, by the height of the tree, which is 10; the result is 2 and a half. |
| − | |style="text-align:right;"|תשובה תחלק מרובע הרוחק שמשרש האילן לראש שהם כ"ה במשלנו על גובה האילן שהם י' ויצאו ב' וחצי | + | |style="text-align:right;"|תשובה תחלק מרובע הרוחק שמשרש האילן לראש שהם כ"ה במשלנו על גובה האילן שהם י' ויצאו ב' וחצי |
| − | נחברם עם הי' ונקח חציים שהם ו' ורביע וזהו כמות האילן עד מקום השבירה | + | |- |
| + | | | ||
| + | :We add it to the 10, then take a half [of the sum], which is 6 and a quarter and this is the measure from the top of the tree to the breaking spot. | ||
| + | |style="text-align:right;"|נחברם עם הי' ונקח חציים שהם ו' ורביע וזהו כמות האילן עד מקום השבירה | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| Line 7,022: | Line 7,374: | ||
|- | |- | ||
| | | | ||
| − | : | + | :The complement to ten, which is 3 and 3-quarters, is the number of cubits from the breaking spot to the foot of the tree. |
| − | + | :<math>\scriptstyle{\color{blue}{10-x=10-\left(6+\frac{1}{4}\right)=3+\frac{3}{4}}}</math> | |
|style="text-align:right;"|והנשאר עד תשלום הי' שהם ג' וג' רביעיות הם כמות האמות שממקום השבירה עד שרש האילן | |style="text-align:right;"|והנשאר עד תשלום הי' שהם ג' וג' רביעיות הם כמות האמות שממקום השבירה עד שרש האילן | ||
|- | |- | ||
| − | + | | | |
| + | === <span style=color:green>Additional Problems - MS Mantova</span> === | ||
| + | | | ||
| + | |- | ||
| + | !<span style=color:green>Multiple Quantities - Boys Sharing Property of Their Father</span> | ||
| | | | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:sons|652|yRsW}}A man who had sons, their number is unknown, said to one of them: take one peraḥ for yourself, and a tithe of the remaining. | + | *{{#annot:sons|652|yRsW}}A man who had sons, their number is unknown, said to one of them: go to the box and take one peraḥ for yourself, and a tithe of the remaining. |
:To the second he said: take two peraḥim and a tithe of the remaining. | :To the second he said: take two peraḥim and a tithe of the remaining. | ||
:And so [he said] to the third [son] and the fourth [son] and the fifth [son] until the last [son]. | :And so [he said] to the third [son] and the fourth [son] and the fifth [son] until the last [son]. | ||
| Line 7,036: | Line 7,392: | ||
:They went and took [the peraḥim] and found out that they all took the same share equally, the number of the peraḥim corresponded to the number of the boys. | :They went and took [the peraḥim] and found out that they all took the same share equally, the number of the peraḥim corresponded to the number of the boys. | ||
:How many were the sons and how many were the peraḥim? | :How many were the sons and how many were the peraḥim? | ||
| − | |style="text-align:right;"|אדם שהיו לו בנים ולא נודע מספרם<br> | + | |style="text-align:right;"|‫<ref>Mantova 79r</ref>אדם שהיו לו בנים ולא נודע מספרם<br> |
| − | ואמר לאחד לך | + | ואמר לאחד לך בארגז וקח לך פרח אחד והעשירית מכל הנשאר<br> |
ולשני אמ' קח ב' פרחים והעשירית מכל הנשאר<br> | ולשני אמ' קח ב' פרחים והעשירית מכל הנשאר<br> | ||
וכן לשלישי וכן לרביעי ולחמשי עד האחרון<br> | וכן לשלישי וכן לרביעי ולחמשי עד האחרון<br> | ||
| Line 7,048: | Line 7,404: | ||
|- | |- | ||
| | | | ||
| − | :: | + | :According to the calculation the fraction is a tenth. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|לפי חשבון השבור [.....] הוא עשירית |
| − | תפחות א' מעשרה ישארו ט' הרי שט' היו הבנים | + | |- |
| + | | | ||
| + | :Subtract 1 from ten; 9 remains, so the sons are 9. | ||
| + | :<math>\scriptstyle{\color{blue}{10-\left(\frac{1}{10}\sdot10\right)=10-1=9}}</math> | ||
| + | |style="text-align:right;"|תפחות א' מעשרה ישארו ט' הרי שט' היו הבנים | ||
| + | |- | ||
| + | | | ||
| + | :Then, say: 9 times 9 is 81 and so are the peraḥim. | ||
| + | :<math>\scriptstyle{\color{blue}{9\sdot9=81}}</math> | ||
| + | |style="text-align:right;"|אמור אחר זה ט' פעמי' ט' הם פ"א וככה היו הפרחים | ||
|- | |- | ||
| | | | ||
| − | : | + | :If they take as their father commanded, each has an equal share. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואם יקחו כאשר צוה אביהם יהיה לכל אחד חלק שוה |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :Likewise for any number you wish, do the same: subtract 1 from the denominator of the fraction; this is the number of the sons. Square it; this is the number of the peraḥim. As the number of the sons so is the number of peraḥim the each gets. |
| + | |style="text-align:right;"|וכן לכל חשבון שתרצה עשה כן שתפחות א' מהחשבון השבור והוא חשבון הבנים ותרבע אותו והוא חשבון הפרחי' וכמספר הבנים יהיו ‫<ref>Mantova 79v</ref>מספר הפרחים שיבא לכל אחד ודו"ק | ||
|- | |- | ||
!<span style=color:green>MS Mantova; MS Amsterdam: Multiple Quantities - Boys Selling Cubits of a Cloth</span> | !<span style=color:green>MS Mantova; MS Amsterdam: Multiple Quantities - Boys Selling Cubits of a Cloth</span> | ||
| Line 7,074: | Line 7,440: | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''False Position:'''</span> First, I say that a quarter, a fifth and a sixth are found in 60. | |
|style="text-align:right;"|אומר תחילה רביע וחומש ושתות נמצא בס‫' | |style="text-align:right;"|אומר תחילה רביע וחומש ושתות נמצא בס‫' | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''Denominator:'''</span> Their sum is 37 and this is the denominator. | |
| + | :<math>\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)=15+12+10=37}}</math> | ||
|style="text-align:right;"|וכללם הוא ל"ז והוא המחלק | |style="text-align:right;"|וכללם הוא ל"ז והוא המחלק | ||
|- | |- | ||
| | | | ||
| − | : | + | :If you want to know how many cubits the one who sold [one cubit] for 4 dinar sold: |
| − | ::<span style=color: | + | |style="text-align:right;"|ואם תרצה לדעת כמה אמות מכר אותו שמכר בד' דינרי‫' |
| − | |style="text-align:right;"| | + | |- |
| − | + | | | |
| − | חלקם בל"ז יבא י"ב ו' חלקי' מל"ז | + | :<span style=color:green>'''Rule of Three:'''</span> Take the quarter of 60, which is 15. Multiply it by the measure of the cloth, which is 30; say: 15 times 30 is 450. |
| − | הרי שמכר [הה] י"ב אמות ו' חלקי' מל"ז | + | |style="text-align:right;"|תפוס הרביע מס' שהוא ט"ו ותרבע אותו על סך הבגד שהוא ל' ואמור ט"ו פעמי' ל' ת"נ |
| + | |- | ||
| + | | | ||
| + | :Divide it by 37; the result is 12 and 6 parts of 37. | ||
| + | :<math>\scriptstyle{\color{blue}{a_1=\frac{\left(\frac{1}{4}\sdot60\right)\sdot30}{37}=\frac{15\sdot30}{37}=\frac{450}{37}=12+\frac{6}{37}}}</math> | ||
| + | |style="text-align:right;"|חלקם בל"ז יבא י"ב ו' חלקי' מל"ז | ||
| + | |- | ||
| + | | | ||
| + | :So, he sold 12 cubits and 6 parts of 37. | ||
| + | |style="text-align:right;"|הרי שמכר [הה] י"ב אמות ו' חלקי' מל"ז | ||
|- | |- | ||
| | | | ||
| − | : | + | :If you want to know how much money he received: |
|style="text-align:right;"|ואם תרצה לדעת כמה מעות קבל | |style="text-align:right;"|ואם תרצה לדעת כמה מעות קבל | ||
|- | |- | ||
| | | | ||
| − | :::<math>\scriptstyle{\color{blue}{4\sdot12=48}}</math> | + | :First, say: he received 48 dinar for 12 cubits. |
| + | :<math>\scriptstyle{\color{blue}{4\sdot12=48}}</math> | ||
|style="text-align:right;"|אמור תחילה מי"ב אמות קבל מ"ח דינ‫' | |style="text-align:right;"|אמור תחילה מי"ב אמות קבל מ"ח דינ‫' | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''Rule of Three:'''</span> For the 6 parts of 37 do this way: if 37, which is a whole cubit, is worth 48 pešuṭim, how much are 6 parts of 37 worth? | |
| + | :<math>\scriptstyle{\color{blue}{37:48=6:X}}</math> | ||
|style="text-align:right;"|ומן הו' חלקי' מל"ז עשה על זה הדרך אם ל"ז שהוא אמה שלמה שוה מ"ח פשי' הו' חלקי' מל"ז כמה שוים | |style="text-align:right;"|ומן הו' חלקי' מל"ז עשה על זה הדרך אם ל"ז שהוא אמה שלמה שוה מ"ח פשי' הו' חלקי' מל"ז כמה שוים | ||
|- | |- | ||
| | | | ||
| − | :::<math>\scriptstyle{\color{blue}{X=\frac{6\sdot48}{37}=\frac{288}{37}=7+\frac{29}{37}}}</math> | + | :Say: 6 times 48 is 288. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אמור ו' פעמי' מ"ח רפ"ח |
| − | חלקם בל"ז יבא ז' פשי' וכ"ט חלקים מל"ז | + | |- |
| + | | | ||
| + | :Divide it b 37; the result is 7 pešuṭim and 29 parts of 37. | ||
| + | :<math>\scriptstyle{\color{blue}{X=\frac{6\sdot48}{37}=\frac{288}{37}=7+\frac{29}{37}}}</math> | ||
| + | |style="text-align:right;"|חלקם בל"ז יבא ז' פשי' וכ"ט חלקים מל"ז | ||
|- | |- | ||
| | | | ||
| − | : | + | :Do the same for the others and you will get the answer. |
|style="text-align:right;"|וכזה תעשה האחרי' ויצא לך העניין | |style="text-align:right;"|וכזה תעשה האחרי' ויצא לך העניין | ||
|- | |- | ||
Latest revision as of 18:43, 22 May 2023
Contents
- 1 Problems of Various Types
- 1.1 Find a Number Problem - Subtraction of Fractions
- 1.2 Find a Number Problem - Addition of Fractions
- 1.3 Find a Quantity Problem - Whole from Parts Problem - Lance
- 1.4 How Much Problem - Money
- 1.5 Find a Quantity Problem - First from Last Problem – Money
- 1.6 How Much Problem – Money
- 1.7 How Much Problem – Money
- 1.8 Pricing Problem - Find the Amount
- 1.9 Pricing Problem - Find the Price
- 1.10 Exchange Problem - Currencies
- 1.11 Motion Problem – Pursuit
- 1.12 Motion Problem – Encounter
- 1.13 How Many Problem - Group of People
- 1.14 Buy and Sell Problem
- 1.15 Boiling Problem
- 1.16 Partnership Problem - For the Same Time
- 1.17 Purchase Problem – Moneychanger
- 1.18 Payment Problem - Digging a Hole
- 1.19 Buy and Sell Problem
- 2 Exchange Problems
- 3 Interest and Pricing Problems
- 4 Problems of Various Types
- 4.1 Rent Problem
- 4.2 Exchange Problems
- 4.3 Proportions of Fractions
- 4.4 Find a Quantity Problem - Whole from Parts – Tree
- 4.5 Motion Problem - To and From - an Ant Climbing a Tower
- 4.6 Find a Quantity Problem - First from Last Problem – Money
- 4.7 Divide a Quantity – Money
- 4.8 Divide a Quantity – Money
- 4.9 Ordering Problem - Six Coins
- 4.10 Find a Number Problem - Ratio of Integers and Fractions
- 4.11 Multiple Quantities - Boys Selling Eggs
- 4.12 Find a Quantity Problem - Whole from Parts – Fish
- 4.13 Simultaneous Division - Money in a Purse
- 4.14 Partnership - for the same time
- 4.15 Give and Take Problem - gatekeeper
- 4.16 Shared Work Problem - Rivers Filling a Fountain
- 4.17 Motion Problem – Pursuit
- 4.18 Mixture and Alligation Problem - Goldsmith making rings from several kinds of coins
- 4.19 Divide a Quantity - Price of a Fish Paid by a Group of People
- 4.20 Joint Purchase Problem - If You Give Me - two men - Amounts of Money
- 4.21 Interest and Discount Problem - find the fund
- 4.22 Exchange Problems
- 4.23 Interest and Discount Problem
- 4.24 Pricing Problem - Find the Amount
- 4.25 Divide a Quantity - Sharing Food
- 4.26 Find a Number Problems - Multiplication of fractions
- 4.27 Multiple Quantities - Coins that Worth an Amount of Money
- 4.28 Find a Number Problems - Sums
- 4.29 Find a Number Problem - Multiplication of integers and fractions
- 4.30 Interest and Discount Problems
- 4.31 Multiple Quantities Problem - Five Weights
- 4.32 Guessing - coins
- 4.33 Payment Problem - three workers, three different daily wages, the same actual payment
- 4.34 Divide a Quantity Problem - Proportional Division – Inheritance
- 5 Geometrical Problems
- 5.1 Triangulation Problem - Two towers
- 5.2 Rectangle
- 5.3 Quadrangle
- 5.4 Triangulation Problem - Tree leaning against a wall
- 5.5 Transformation Problems
- 5.6 Volume
- 5.7 Questions about Rectangles
- 5.8 Square
- 5.9 Area
- 5.10 Equilateral Triangle
- 5.11 Scalene Triangle
- 5.12 Isosceles Triangle
- 5.13 Area
- 5.14 Divide a Figure
- 5.15 Rhombus
- 5.16 Area
- 6 Additional Problems
- 7 Apparatus
- 8 Appendix: Bibliography
Problems of Various Types |
|||||||||||
| [Gold Weights: 1 kikkar = 100 liṭra; 1 liṭra = 20 dinar/zuz; 1 dinar/zuz = 12 pešiṭim/pešuṭim] | |||||||||||
Find a Number Problem - Subtraction of Fractions |
|||||||||||
|
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
[1]א אם ישאלך אדם כמה הוא יותר השליש מן הרביע | ||||||||||
|
אמור ג' פעמים ד' הם י"ב | ||||||||||
|
השליש הוא ד' דנריצימו | ||||||||||
|
הרביע הוא ג' דנריציסמו | ||||||||||
|
נמצא שהשליש הוא יותר מן הרביע א' תריציסמו | ||||||||||
|
וכן אם ישאלך כמה יותר הרביע מן החומש | ||||||||||
|
תעשה כמו שעשינו למעלה ואמור ד' פעמים ה' הם כ' | ||||||||||
|
הרביע הוא ה' בינטיני | ||||||||||
|
החומש הוא ד' בינטיני | ||||||||||
|
נמצא שהרביע הוא יותר מן החומש א' בינטינו | ||||||||||
| Likewise for everything similar to it. | וכן כל הדומה לו | ||||||||||
|
וכן אם ישאלך כמה הוא יותר השליש מן החמישית | ||||||||||
|
אמור ג' פעמים ה' הם ט"ו | ||||||||||
|
השליש הוא ה' קוויניציסמי | ||||||||||
|
והחומש הוא ג' קוויניציס | ||||||||||
|
נמצא שהשליש הוא יותר מן החומש ב' קוויניציסמו | ||||||||||
Find a Number Problem - Addition of Fractions |
|||||||||||
|
ב אם ישאלך אדם כמה הוא שליש פשוט ורביע וחומש ושתות ושביעית | ||||||||||
|
תצטרך לחלק הפשוט לכל כך חלקי' שתמצא בו כל אלו השעורים | ||||||||||
|
וכלך לדרך זו ואמור ג' פעמים ד' הם י"ב ה' פעמין י"ב הם ס' | ||||||||||
|
| |||||||||||
|
השליש הוא תת"מ חלקי' | ||||||||||
|
הרביע הוא תר"ל חלקי' | ||||||||||
|
החומש הוא תק"ד חלקי' | ||||||||||
|
השתות הוא ת"כ חלקי' | ||||||||||
|
השבעית הוא ש"ס חלקי' | ||||||||||
|
הרי שמן כולם הם אלפי' ותשנ"ד חלקי' | ||||||||||
|
תוציא מהם אלפים ותק"כ חלקי' שהוא אחד שלם נשארו בידך רל"ד חלקי' | ||||||||||
|
נמצא ששליש פשוט ורבע וחומש ושתות ושביעי הוא א' פשוט שלם ורל"ד חלקי' מפשוט אחד שתחלקהו לאלפי' ותק"כ חלקי' שהוא קי"ז חלקי' מאלף ור"ס וכה"ל | ||||||||||
|
| |||||||||||
Find a Quantity Problem - Whole from Parts Problem - Lance |
|||||||||||
|
ג שאלה רומח אחד שלישיתו במים ורביעיתו בעפר ולמעלה מן המים י' אמות כמה אמות כל הרומח | ||||||||||
|
נבקש מניין שיש לו שלישית ורביעית והוא י"ב | ||||||||||
|
ושלישיתו ורביעיתו מחוברים ז' | ||||||||||
|
נחסרם מי"ב ישארו ה' | ||||||||||
|
כפלנו הקצוות עלו ק"כ | ||||||||||
|
חלקנום על ה' עלה כ"ד וזהו גבהות כל הרומח | ||||||||||
|
שלישיתו ח' ורביעיתו ו' נחסרם מכ"ד ישארו י' שלמים בלי תוספת ומגרעת וכה"ל | ||||||||||
How Much Problem - Money |
|||||||||||
|
ד שאלה ממון חברנו חמישיתו ושביעיתו ותשיעיתו והיו י' כמה הממון | ||||||||||
|
נבקש המורה והוא שט"ו והחלקי' ההם קמ"ג | ||||||||||
|
כאשר החלק שט"ו של ה' יעלו ס"ג | ||||||||||
|
וכשהחלק של ז' יעלו מ"ה | ||||||||||
|
וכשהחלק של ט' יעלו ל"ה | ||||||||||
|
חברם יחד יעלו קמ"ג | ||||||||||
|
נכפול שט"ו על י' עלו ג' אלפי' וק"נ | ||||||||||
|
חלקנום על קמ"ג עלו כ"ב שלמי' וד' חלקי' מן קמ"ג וככה הממון | ||||||||||
|
קח חמישית כ"ב הם ד' נשאר ב' שהם ב' פעמי' קמ"ג והם רפ"ו | ||||||||||
|
חבר עליהם ד' חלקי' הרי ר"צ | ||||||||||
|
חלקם בה' יעלו נ"ח חלקי' מקמ"ג | ||||||||||
|
|
|||||||||||
|
וכן עשה מן התשיעית והשבעית ויעלו י' | ||||||||||
|
|
|||||||||||
|
עוד יש בו כלל אחר | ||||||||||
|
שתאמר החלקי' שהוספת שהם י' הם קמ"ג והממון הראשון היה קע"ב | ||||||||||
|
אמור אם קמ"ג שוים י' קע"ב כמה שוים | ||||||||||
|
אמור י' פעמי' קע"ב הם אלף תש"כ חלקם על קמ"ג יבאו י"ב שלמי' וד' חלקי' מקמ"ג | ||||||||||
|
חבר אליהם הי' יהיו כ"ב שלמי' וד' חלקי' מקמ"ג בלי תוספת ומגרעת | ||||||||||
|
וכן כ.. מה הכלל ג"כ הוא טוב לדעת מדת הרומח הכתוב למעלה | ||||||||||
Find a Quantity Problem - First from Last Problem – Money |
|||||||||||
|
[2]ה נעשה להפך ממון חסרנו ממנו חמשיתו ושבעיתו ותשיעיתו ונשארו י' | ||||||||||
|
נחסר קמ"ג שהם השברי' משט"ו שהוא המורה ישאר קע"ב | ||||||||||
|
ונעשה כך כפלנו י' על שט"ו עלו ג' אלפי' וק"נ חלקנום על קע"ב עלו י"ח שלמי' ונ"ד חלקי' מקע"ב | ||||||||||
|
לקחנו חמשית ושבעית ותשעית של זה המספר ישאר י' שלמי' | ||||||||||
|
| |||||||||||
How Much Problem – Money |
|||||||||||
|
ו שאלה ממון הוספנו עליו מחציתו ושלישיתו וחמישיתו וששיתו ובסך הכל היה מ' כמה היה הממון | ||||||||||
|
ידענו כי החצי והשלישית והששית הוא אחד שלם ונחשוב כי היה אלו אחד הרי שנים יש לו תוספת החמישית | ||||||||||
|
| |||||||||||
|
עתה יש לנו לחלק מ' על ב' וחמישית והעולה הוא הממון הנה נקח לכל אחד מן השלמים ה' ונשים עמהם החמשית יהיו אלף | ||||||||||
How Much Problem – Money |
|||||||||||
|
ז שאלה לקחנו חמישית ממון גם שביעיתו ותשיעיתו כמה הוא מערך הממון | ||||||||||
|
נבקש המורה והוא שט"ו | ||||||||||
|
ונחבר חמישית ושביעית ותשיעית יהיו קמ"ג | ||||||||||
|
נחלקה על ל"ה והנה הם ד' תשעיות ונשארו ג' חלקי' מל"ה כי ל"ה הוא התשיעית וה' הוא שביעית התשיעית | ||||||||||
|
| |||||||||||
Pricing Problem - Find the Amount |
|||||||||||
|
ח שאלה אדם מוכר י"ג מדות בכ"ג כמה מדות יתן בז' פשוטי' | ||||||||||
|
נאמר ז' פעמי' י"ג יהיו צ"א נחלקם על כ"ג בא ג' מדות וכ"ב מכ"ג חלקי' במדה אחת | ||||||||||
Pricing Problem - Find the Price |
|||||||||||
|
ועת' נהפוך חשבון שנבקש לדעת בכמה יתן לו ז' מדות | ||||||||||
|
נאמר ז' פעמים כ"ג הם קס"א נחלקם על י"ז יהיו י"ב וה' חלקי' מי"ג בפשוט | ||||||||||
Exchange Problem - Currencies |
|||||||||||
|
וכן אם יאמר לך אדם אם ג' תרוביסים שוים ד' קורטונוס ה' תרוביסיט' כמה קורטונוס שוים | ||||||||||
|
אמור ה' פעמי' ד' הם כ' חלקם על ג' בא ו' קורטוניס וב' שלשי' וכה"ל | ||||||||||
Motion Problem – Pursuit |
|||||||||||
|
ט שאלה אדם שלח רץ שילך בכל יום כ"ט מילים אחר מהלך י' ימי' שלח רץ אחר אחריו שילך בכל יום ל"ז מילי' | ||||||||||
|
נכפול המילים שהלך בי' ימי' יהיו ר"צ נחלקם על היתרון שבין שני המהלכים שהוא ח' והנו ל"ו ימים ורבע יום | ||||||||||
Motion Problem – Encounter |
|||||||||||
|
י שאלה ראובן יצא מעירו ללכת לקראת שמעון לעירו בקר יום ראשון של ר"ח ובאותו יום עצמו יצא שמעון מעירו ללכת לעיר ראובן | ||||||||||
|
ככה תעשה חבר שני המהלכי' הם ל"ו חלק עליו הק' מילים יהיו ב' ימים ישארו כ"ח חלקי' מל"ו ביום אחד שהם ז' תשעיו' יום | ||||||||||
How Many Problem - Group of People |
|||||||||||
|
יא שאלה אדם עבר על אנשים אמר להם שלו' לכם מאה איש | ||||||||||
|
והנה נקח למספרם אחד ואחד כמונו והנה שנים ומחציתנו חצי אחד הנה שנים וחצי נוסיף רבעיתו יהיו [3]ג' רבעיות | ||||||||||
|
ובעבור שיש לנו רבעית נקח לכל שלם ד' ויהיו ח' נחבר אליהם הג' רבעים יהיו י"א | ||||||||||
|
| |||||||||||
|
ובעבור שאמרו שיהיו עמו מאה יהיה מספרם עם התוספת צ"ט | ||||||||||
|
נשיבם מהדרך הד' יהיו שצ"ו | ||||||||||
|
נחלקם על י"א יהיו ל"ו וככה מספרם | ||||||||||
Buy and Sell Problem |
|||||||||||
|
יב שאלה אדם קנה בק' זהובים ק' ליט' אחרי כן מכר הנ' ליט' ורבע ליט' בזהוב והנ' ליט' מכר ליט' פחות רבע ליט' בזהוב | ||||||||||
|
נשיב הנ' ראשונים ר' כי רבעים הם נחלקם על ה' כי ליט' ורבע ליט' מכר בזהוב יהיו מ' זהובי' | ||||||||||
|
גם נכפול הנ' אחרים על ד' יהיו ר' נחלקם על ג' כי ג' רבעים מכר בזהוב והנה יהיו ס"ו זהובים ושני שלישי זהוב | ||||||||||
|
וחבר אליהם המ' יהיה הריוח ו' זהובים ושני שלישי זהוב וכה"ל | ||||||||||
|
| |||||||||||
Boiling Problem |
|||||||||||
|
יג שאלה אדם היו לו י' מדות משמש ורוצה לבשלם עד שלא ישאר כי אם השלישית והנה החל לבשל עד שנשארו מהם ח' מדות | ||||||||||
|
ועתה יש לך ג' מספרים ידועים | ||||||||||
|
האחד שליש י' והוא ג' ושליש | ||||||||||
|
והשני ח' הם המדות שנתבשלו | ||||||||||
|
והשלישי ו' שנשארו מן הנשפך | ||||||||||
|
והנה נכפול ו' על ג' ושליש יהיו כ' וחלקם על ח' יהיו ב' וחצי | ||||||||||
Partnership Problem - For the Same Time |
|||||||||||
|
יד שאלה ד' אנשים יש לאחד מהם י"א דינרי' ולשני י"ג די' ולשלישי ט"ו דינרי' ולרבעי י"ז דינרי' והרויחו י"ט דינרי' | ||||||||||
|
נחבר ראשי' כל ד' ממונם ויהיו נ"ו | ||||||||||
|
ובערך כל אחד אל נ"ו ככה יקח מי"ט | ||||||||||
|
ונעשה כך נכפול י"א על י"ט יעלו ר"ט נחלק על נ"ו יעלו ג' שלמי' ומ"א חלקי' | ||||||||||
|
עשינו כן בי"ג עלו רמ"ז חלקנום על נ"ו עלו ד' שלמי' וכ"ג חלקי' | ||||||||||
|
עשינו כן בט"ו יהיו רפ"ה חלקנום על נ"ו עלו ה' שלמי' וה' חלקי' | ||||||||||
|
עשינו כן בי"ז עלו שכ"ג חלקנום על נ"ו עלו ה' שלמי' ומ"ג חלקי' | ||||||||||
|
חברנו אלו השלמי' ואלו החלקי' עלו י"ט שלמי' כי החלקי' האלו חלקי נ"ו הם | ||||||||||
Purchase Problem – Moneychanger |
|||||||||||
|
טו שאלה יש אצל המחליף ג' מטבעים והזהוב שוה ממטבע אחד ג' דינרי ומן השני ד' ומן השלישי ו' ובא אדם אחד ובקש למחליף שיתן לו מג' המטבעים בזהוב ויהיה המספר שוה מן היקרים כמו משאינם יקרים | ||||||||||
|
בקש היתרה שיהיה בו שלישית ורבעית וששית והוא י"ב | ||||||||||
|
החלקי' הם ט' והוא דינר | ||||||||||
|
נחלק המורה על זה המספר יהיו י"ב תשי' וככה לקח מכל מטבע | ||||||||||
|
אחר על זאת השאלה שתאמר מה ערך י"ב אל ט' והיה כמות שלישיתו והנה נוסיף על י"ב ד' יהיו י"ו | ||||||||||
Payment Problem - Digging a Hole |
|||||||||||
|
יו שאלה ראובן שכר שמעון שיחפור לו בקרקע ז' באורך וו' ברוחב וה' בעומק ויתן לו י"א פשיטי' והוא חפר ו' באורך ה' ברוחב ד' בעומק | ||||||||||
|
נעשה כך ז' פעמים ו' הם מ"ב כפלם על ה' שהוא העומק ויהיו ר"י | ||||||||||
|
גם נכפול המספר השני שהוא ו' על ה' והם ל' גם נכפול זה על ד' שהוא העומק יהיו ק"כ | ||||||||||
|
ונכפול י"א פעמי' [4]ק"כ הם אלף וש"כ חלקם על ר"י עלו ו' שלמי' ונשאר ס' שהם ב' שבעיות פשוט וכה"ל | ||||||||||
Buy and Sell Problem |
|||||||||||
|
יז שאלה אדם קנה ג' חמשיות ליט' בפשוט ומכר ד' שבעיות ליט' בפשוט והרויח פשוט כמה היה ממונו | ||||||||||
|
בקש המורה הוא ל"ה וכפול ה' על ז' | ||||||||||
|
והיה ג' חמשיותיו כ"א | ||||||||||
|
וד' שבעיותיו כ' והממון היה כ' וכה"ל | ||||||||||
|
נראה שרוצה לו' שהוצ' כ' פשוטי' וזהו | ||||||||||
|
יח שאלה אדם קנה ד' שבעיות ליט' בפשוט ומכר ה' תשעיות ליט' בפשוט והרויח פשוט כמה היה הממון | ||||||||||
|
ידוע הוא כי ד' שבעיות אחד הוא יותר מה' תשעיות אחד | ||||||||||
|
והנה המורה ס"ג | ||||||||||
|
וה' תשיעיותיו ל"ה | ||||||||||
|
וד' שבעיותיו ל"ו | ||||||||||
|
ותוכל לבחון זה כי אחר שקנה ד' שבעיות ליט' בפשוט ממונו ל"ה הנה יש לו כ' ליט' | ||||||||||
|
עשה מהם תשעיו' יהיו ק"פ | ||||||||||
|
חלק זה המספר על ה' כי ה' תשעיו' מכר בפשוט יעלו בידך ל"ו | ||||||||||
|
ואילו אמר כי הרויח ב"פ | ||||||||||
|
כפלם על ל"ה יהיו הפשוטי' שהוציא | ||||||||||
|
|
כי הממון יהיה מ' ליט' | ||||||||||
|
ואם אמר ג"פ | ||||||||||
|
יכפלם על ל"ה | ||||||||||
|
וככה עד סוף החשבון | ||||||||||
Exchange Problems |
|||||||||||
|
יט כלל כל החשבונות הוא על שלשה פנים במדה או במשקל או במספר | ||||||||||
|
על כן נאמר הריגולי' הנאותים לשלשתם | ||||||||||
|
אם ישאל לך שום חשבון שיהיה בו אחד מאלו הג' מינים נרבה אותו הדבר שנרצה לידע כנגד אותה שאיננה ממינה עצמה ממש | ||||||||||
|
המשל בזה אם ז' פיסט' שוים ט' קורטוניס כמה ישוו ק' ליט' מפיסני' לקורטו' | ||||||||||
|
כבר ידעת כי הקורטו' הוא הדבר שאינה ממינה עצמה ממש לכן נרבה ט' פעמי' ק' יהיו תת"ק | ||||||||||
|
וחלקם על ז' קכ"ח ליט' וי"א דינרי' והם וכך ישוו הק' ליט' מפיסני' לקורטו' | ||||||||||
|
ודע כי אם ז' פיסני' שוים ט' קורטו' הז' דינרי' פיסני' שוים ט' דינרי' קורטוני' והז' ליט' מפיסני' שוים ט' ליט' קורטו' ות"ש ליט' מפיסני' שוים תת"ק ליט' קורטו' | ||||||||||
| ? | וכן יבא בין פפריני' ופריביסיני' ולכל [חשבון] כזה | ||||||||||
|
כ אם ישאל לך חשבון שיהיה בו מאלו הג' מינים ולפני הב' חלקי' יהיו שבורים | ||||||||||
|
נדע באיזה המספר ימצאו אלו השבורים | ||||||||||
|
ואחר שידעת באי זה המספר ימצאו אלו השבורים נרבה הב' חלקי' באותו המספר שימצאו בו אלו השבורים | ||||||||||
|
אחרי כן נרבה אותו הדבר שנרצה לדעת כנגד אותו הדבר שאנינה ממינה עצמה ונחלק אותה על השלישית וכה"ל | ||||||||||
|
| |||||||||||
|
כא ואם נשאל לך חשבון אחר שיהיה שבור מחלק אחד | ||||||||||
|
נרבה הב' חלקי' באותו המספר דהיינו עם אותו השבור | ||||||||||
|
אחרי כן נרבה אותו הדבר שנרצה לידע כנגד אותו הדבר שאנינה ממינה ונחלק אותה על השלישית | ||||||||||
|
| |||||||||||
| We give an example for the two cases - one for a calculation in which one part involves a fraction and the other in which the two parts involve fractions: | ונשים המשל בשני פנים האחד בעבור החשבון שהוא שבור מחלק אחד והאחר שהוא שבור מב' חלקי' | ||||||||||
|
אם ה' פיסני' ורביע שוים ז' קורטונו' כמה ישוו אלף ליט' מפיסני' | ||||||||||
|
וזה החשבון הוא שבור מחלק אחד וזה השיבור הוא הרביע לכן נרבה הב' חלקי' עם ד' | ||||||||||
|
ואמור ד' פעמי' ה' פיסני' ורביע יבוא כ"א פיסני' | ||||||||||
|
וד' פעמי' ז' קורטו' בא כ"ח קורטו' | ||||||||||
|
הרי שכ"א פיסני' שוים כ"ח קורטו' | ||||||||||
|
ונחלק לשביע בעבור [5]שבשני החלקי' ימצא שביע | ||||||||||
|
השביע מכ"א הוא ג' | ||||||||||
|
השביע מכ"ח הוא ד' | ||||||||||
|
נמצא שג' פיסני' שוים ד' קורטו' | ||||||||||
|
ואנחנו נרצה לידע כמה ישוו אלף ליט' מפיסני' הפיסני הוא הדבר שנרצה לידע והקורטו' הוא הדבר שאנינה ממינה עצמה | ||||||||||
|
לכן נרבה ד' פעמים אלף יבא ד' אלפי' מקורטו' | ||||||||||
|
ונחלק בג' שיבא אלף ושל"ג ליט' וו' דינרי' וח"פ וכן ישוו אלף ליט' מפיסני לקורטוט' | ||||||||||
| We give an example of a calculation in which both parts involve fractions: | ונשים המשל אל החשבון שהוא שבור מב' חלקיו | ||||||||||
|
אם ז' אונקיו' ושליש כסף שוים ע"ג ליט' וה' דינרי' מפיסני' כמה ישוו הי"ט אונקיו' כסף לפי זה החשבון | ||||||||||
|
ואלו השבורים הם שליש ורביע אנה ימצאו בי"ב | ||||||||||
|
לכן יש לנו לרבות הב' חלקי' בי"ב | ||||||||||
|
ואמור י"ב פעמי' ז' אונקיו' ושליש יבא פ"ח אונקיו' כסף | ||||||||||
|
וי"ב פעמי' ע"ג ליט' וה' דינרי' יהיו תתע"ט ליט' מפסני' | ||||||||||
|
הרי שפ"ח אונקיות כסף שוים תתע"ט ליט' | ||||||||||
|
ונרצה לידע כמה ישוו הי"ט אונקיו' כסף | ||||||||||
|
נרבה י"ט פעמי' תתע"ט ליט' יהיו י"ו אלפי' ותש"א | ||||||||||
|
חלקם בפ"ח יבא קפ"ט ליט' וט"ו די' וח"פ וב' חלקי' מי"א וכן ישוו הי"ט אונקיו' כסף באותו החשבון | ||||||||||
Interest and Pricing Problems |
|||||||||||
| Find the Time | |||||||||||
|
כב שאלה הככר ירויח השנה ל"ו ליט' וי"ח די' נוסף הס"ה ליט' בכמה זמן ירויחו כהם | ||||||||||
|
תרבה הק' ליט' כנגד י"ב חדשי השנה ואמור י"ב פעמי' ק' חדשים הם אלף ור' | ||||||||||
|
חלקם על ס"ה יבא לכל חלק י"ח חדשי' וי"ג ימים וי"א חלקי' מי"ג חלקי' ביום | ||||||||||
|
נמצא שבי"ח חדשי' וי"ג ימי' וי"א חלקי' מי"ג ביום ירויחו ס"ה ליט' כלכך כמו שירויח הככר השנה | ||||||||||
| Find the Earned Interest | |||||||||||
|
כג שאלה אם יאמר אדם הלותי מעות לחשבון גפה"ח הליט' החדש כמה יבואו הס' ליט' ח' חדשים | ||||||||||
|
תרבה מעות הרבית עם החדשים ואמור ג' פעמי' ח' כ"ד שהם ב' דינרי' | ||||||||||
|
אחר כן תרבה אלו הב' די' עם הס' ליט' ואמור ס' פעמי' ב' דינרי' הם ק"כ די' שהם ו' ליט' | ||||||||||
|
נמצא שבס' ליט' לחשבון גפה"ח יבוא ו' ליט' לח' חדשים וכה"ל | ||||||||||
| Find the Fund | |||||||||||
|
כד אם ישאלך אדם הלותי מעות הליט' לחשבון כך וכך החדש כמה ליט' ירויחו היום א"פ | ||||||||||
|
נחלק ל' ליט' בכל כך חלקי' כמו המעות שירויח הליט' החדש | ||||||||||
|
המשל בזה הרי שהלותי הליט' בב' פשוטי' וחצי החדש ותרצה לידע כמה ליט' ירויחו היום א"פ | ||||||||||
|
נחלק ל' ליט' בב' וחצי שיבוא י"ב ליט' | ||||||||||
|
נמצא שבי"ב ליט' ירויחו היום א"פ וכה"ל | ||||||||||
| Find the Time | |||||||||||
|
כה אם ישאלך אדם הלותי הליט' לחשבון כך וכך החודש בכמה ימים ירויח הליט' א"פ | ||||||||||
|
חלק ל' יום בכל כך חלקי' כמו המעות שירויח הליט' החדש | ||||||||||
|
המשל בזה הרי שהלוית לחשבון ג' ותרצה לידע כמה ימים ירויח הליט' א"פ | ||||||||||
|
חלק ל' יום בג' חלקי' שיבוא י' ימים | ||||||||||
|
הרי שבי' ימים ירויח הליט' א"פ | ||||||||||
| Find the Fund | |||||||||||
|
כו אם ישאלך אדם הככר ירויח כל השנה כל כך ליט' כמה ליט' ירויחו היום א"פ | ||||||||||
|
חלק ק"נ ליט' בכל כך חלקי' כמו הליט' שירויח הככר השנה | ||||||||||
|
המשל בזה הככר ירויח י"ב ליט' השנה ותרצה לידע כמה ליט' ירויחו היום א"פ | ||||||||||
|
חלק ק"נ ליט' בי"ב חלקי' שיבוא [6]י"ב וחצי | ||||||||||
|
הרי שבי"ב ליט' וחצי ירויחו ביום א"פ וכה"ל | ||||||||||
| Find the Time | |||||||||||
|
כז אם ישאלך אדם הככר ירויח כל כך ליט' השנה בכמה ימים ירויח הליט' א"פ | ||||||||||
|
חלק ק"נ ימים בכל כך חלקי' כמו הליט' שירויח הככר השנה | ||||||||||
|
המשל בזה הככר ירויח ט' ליט' השנה ותרצה לידע בכמה ימים ירויח הליט' א"פ | ||||||||||
|
חלק ק"נ ימים בט' חלקי' שיבואו י"ו ימים וב' שלשי הרי שבי"ו ימים וב' שלישי ירויח הליט' א"פ וכה"ל | ||||||||||
|
כח אם ישאלך אדם כל כך ליט' ירויחו כל כך בכל כך זמן | ||||||||||
|
תרבה סכום הליט' כנגד סכום החדשים וחלק בכל כך חלקי' כמו שהם ליט' או חדשים | ||||||||||
|
המשל בזה נ' ליט' ירויחו ג' ליט' בד' חדשים הע"ה ליט' בכמה זמן ירויחו כהם | ||||||||||
|
הרבה סכום הליט' כנגד סכום החדשים ואמור נ' פעמי' ד' חדשים יבא ר' חדשים וחלקם בע"ה יבא ב' חדשים וכ' ימים נמצא שבב' חדשי' וב' ימים ירויחו הע"ה ליט' כל כך כמו הנ' ליט' ד' חדשים וכה"ל | ||||||||||
| Find the Fund | |||||||||||
|
כט אם ישאלך אדם כל כך ליט' ירויחו בכל כך זמן כל כך ליט' כמה ליט' בכל כך זמן ירויחו כהם | ||||||||||
|
תרבה סכום החדשים כנגד סכום הליט' וחלקם בכל כך חלקי' כמו החדשי' או הליט' שנרצה לידע | ||||||||||
|
המשל בזה כ"ה ליט' ירויחו בו' חדשי' מ' דינרי' כמה ליט' ירויחו בהם בח' חדשים | ||||||||||
|
תרבה סכום החדשים כנגד סכום הליט' ואמור ו' פעמי' כ"ה ליט' יבא ק"נ ליט' חלקם בח' חלקי' יבא י"ח ליט' וט"ו דינרי' | ||||||||||
| Find the Time | |||||||||||
|
ל אם ישאלך אדם הלותי הליט' בכך וכך החדש כל כך ליט' בכמה זמן יכפלו בלתי לשים ריוח אקרן | ||||||||||
|
חלק כ' שנים בכל כך חלקי' כמו המעות שירויח הליט' החדש | ||||||||||
|
המשל בזה הלותי הליט' בגפ"ה הצ"ה ליט' בכמה זמן יכפלו | ||||||||||
|
חלק כ' שנים בג' חלקי' שיבא ו' שנים וח' חדשי' נמצא שבו' שנים וח' חדשים יכפלו הצ"ה ליט' | ||||||||||
|
לא אם ישאלך אדם הככר ירויח השנה כל כך ליט'
כל כך ליט' בכמה זמן יכפלו בלתי לשים ריוח אקרן | ||||||||||
|
חלק ק' שנים בכל כך חלקי' כמו הליט' שירויח הככר | ||||||||||
|
המשל בזה הככר ירויח ח' ליט' השנה המ"ה ליט' בכמה זמן יכפלו | ||||||||||
|
חלק ק' שנים בח' חלקי' שיבא י"ב שנים וחצי נמצא שבי"ב שנים וחצי יכפלו המ"ה ליט' | ||||||||||
| Pricing Problem - Find the Price | |||||||||||
|
לב אם ישאלך אדם הקנטרו' מן המוך שוה י"ז ליט' וה' דינרי' כמה ישוה הליט' | ||||||||||
|
חלק אלו הי"ז ליט' וה' דינרי' בג' חלקי' שיבא לכל חלק ה' ליט' וט"ו די' | ||||||||||
|
אחרי כן חלק אלו הה' ליט' וט"ו די' בה' חלקי' שיבא לכל חלק כ"ג דינרי' | ||||||||||
|
עת' תחלק אלו הכ"ג דינרי' בי"א חלקי' שיבא לכל חלק בה"פ וא' חלק מי"א נמצא שהליט' מן המוך שוה בה"פ וא' חלק מי"א בפשוט | ||||||||||
| Find the Earned Interest | |||||||||||
|
[7]לג אם ישאלך אדם כל כך ליט' ירויחו היום א"פ לאי זה חשבון יבא החדש הליט' | ||||||||||
|
חלק ליט' בכל כך חלקי' כמו הליט' שירויחו היום א"פ | ||||||||||
|
המשל בזה י"ב ליט' ירויחו היום א"פ ותרצה לידע לאי זה חשבון יבא החדש הליט' | ||||||||||
|
חלק ל"פ בי"ב חלקי' שיבא ב"פ וחצי נמצא שיבא החדש הליט' ב"פ וחצי וכה"ל | ||||||||||
|
לד אם ישאלך אדם כל כך ליט' ירויחו היום א"פ כמה ליט' ירויחו ק' ליט' א' שנה | ||||||||||
|
חלק ק"נ ליט' בכל כך חלקי' כמו הליט' שירויחו היום א"פ | ||||||||||
|
המשל בזה ט"ו ליט' ירויחו היום א"פ כמה ירויחו ק' ליט' א' שנה' | ||||||||||
|
חלק ק"נ ליט' בט"ו חלקי' שיבא י' ליט' נמצא שק' ליט' ירויחו א' שנה י' ליט' | ||||||||||
|
לה) אם ישאלך אדם הככר ירויח השנה כ"ט ליט' וי"ג דינרי' וז"פ כמה ליט' ירויחו בהם ז' חדשי' | ||||||||||
|
תרבה חדשי השנה עם סכום הליט' דהיינו ק' ליט' וחלקם בכל כך חלקי' כמו החדשי' שנרצה לידע דהיינו הז' חדשים | ||||||||||
|
ואמור י"ב פעמי' ק' ליט' יבא אלף ור' | ||||||||||
|
חלקם על ז' שיבא קע"א ליט' וח' דינרי' וחצי וו' חלקי' מז' בפשוט | ||||||||||
|
נמצא שקע"א ליט' וח' די' וחצי וו' חלקי' מז' בפשוט ירויחו כ"כ בז' חדשי' כמו הככר א' שנה וכה"ל | ||||||||||
| Find the Time | |||||||||||
|
לו אי"א הככר ירויח כ"כ ליט' השנה בכמה זמן יכפלו בלתי לשים ריוח אקרן | ||||||||||
|
חלק ק' שנים בכל כך חלקי' כמו הליט' שירויח הככר השנה | ||||||||||
|
המשל בזה הככר ירויח י"ד ליט' השנה ותרצה לידע בכמה זמן יכפלו | ||||||||||
|
חלק ק' שנים בי"ד חלקי' שיבא ז' שנים וא' חדש וכ"א ימים וג' חלקי' מז' ביום נמצא שבז' שנים וא' חדש וכ"א ימים וג' חלקי' מז' ביום יכפלו | ||||||||||
|
לז אי"א הלויתי הליט' לחשבון ב"פ וחצי החדש בכמה זמן יכפלו בלתי לשים רבית אקרן | ||||||||||
|
חלק כ' שנים בכל כך חלקים כמו המעות שירויח הליט' החדש | ||||||||||
|
המ"ב הלותי כ' דינרי' לחשבון ב"פ וחצי החדש הליט' ותרצה לידע בכמה זמן יכפלו | ||||||||||
|
חלק כ' שני' בב' וחצי שיבא ח' שני' נמצא שבח' שנים יכפלו וכה"ל | ||||||||||
| Find the Earned Interest | |||||||||||
|
לח אם ישאלך אדם הככר ירויח כ"כ ליט' השנה כמה ליט' ירויחו היום א"פ | ||||||||||
|
חלק ק"נ ליט' בכל כך חלקי' | ||||||||||
|
כמו הליט' שירויחו הככר השנה הב' הככר ירויח י"ג ליט' השנה ותרצה לידע כמה ליט' ירויחו היום א"פ | ||||||||||
|
חלק ק"נ ליט' בי"ג חלקי' שיבא י"א ליט' וי' די' וט"פ וג' חלקי' מי"ג בפשוט וכל כך מעות ירויחו היום א"פ | ||||||||||
|
לט אי"א הלותי הליט' החדש לחשבון כך וכך כמה ירויחו היום ק' ליט' | ||||||||||
|
תרבה ג' ושליש כנגד מעות הרבית | ||||||||||
|
המשל בזה הלותי הליט' לחשבון ג"פ החדש ותרצה לידע כמה ירויחו היום ק' ליט' | ||||||||||
|
תרבה ג' ושליש עם ג' ואמור ג' פעמי' ושליש ג' י"פ נמצא שק' ליט' ירויחו היום י"פ וכה"ל | ||||||||||
|
מ אם ישאלך אדם הככר ירויח כ"כ פשוטי' היום כמה ירויח הככר השנה | ||||||||||
|
תרבה א' וחצי [8]עם המעות שירויח הככר היום | ||||||||||
|
המשל בזה הככר ירויח היום י"פ ותרצה לידע כמה יבוא השנה | ||||||||||
|
תרבה א' וחצי עם י' ואמור א' וחצי פעמי' י' ליט' יבא ט"ו ליט' נמצא שירויח הככר ט"ו ליט' השנה | ||||||||||
|
מא אם ישאלך אדם הככר ירויח היום כ"כ פשוטי' כמה יבא החדש הליט' | ||||||||||
|
חלק בג' ושליש המעות שירויח הככר היום | ||||||||||
|
המשל בזה הככר ירויח היום י"פ ותרצה לידע כמה יבא החדש הליט' | ||||||||||
|
חלק י"פ בג' ושליש יבא ג"פ נמצא שיבא לחשבון גפה"ה וכה"ל | ||||||||||
|
מב אי"א הככר ירויח כל כך ליט' השנה כמה יבא החדש הליט' | ||||||||||
|
חלק לחומש הליט' שירויח הככר השנה ותחשבם פשוט' | ||||||||||
|
המשל בזה הככר ירויח י"ב ליט' השנה ותרצה לידע כמה יבא החדש הליט' | ||||||||||
|
חלק י"ב ליט' | ||||||||||
|
נמצא שיבא החדש הליט' ב"פ וב' חמשי' וכה"ל | ||||||||||
|
מג אם תלוה ק' ליט' א' חדש לחשבון ח' ליט' השנה ותרצה לידע כמה יבא בדרך קצרה | ||||||||||
|
כלך לדרך זו ואמור אם היית מלוה אותם א' חדש לחשבון ח' ליט' השנה היה עולה הריוח ק' פשוטי' שהם ח' די' וד"פ | ||||||||||
|
שיבא לכל ליט' א"פ בחדש | ||||||||||
|
וכשאתה מוסיף עוד ח' ליט' הרי שעולה הריוח בכל ליט' בא' חדש א' פשוט וג' חמשי פשוט | ||||||||||
|
שיבא הככר ק' פשוטי' וס' חומשי פשוט שהוא סך הכל י"ג די' וד"פ וכך יבא הככר החדש | ||||||||||
|
| |||||||||||
|
ולחש' ז' ליט' השנה | ||||||||||
|
יבא לכל ליט' א"פ וב' חומשי פשוט בחדש | ||||||||||
|
שיבא הככר בחדש י"ב די' פד"פ פחות ד' פשוטי' וכה"ל | ||||||||||
|
אחר על זאת השאלה הכתובה למעלה | ||||||||||
|
אם תלוה ק' ליט' א' חדש לחשבון ח' ליט' השנה ותרצה לידע כמה יבא בדרך קצרה | ||||||||||
|
כלך לדרך זו ואמור אם היית מלוה ק' ליט' א' חדש לחשבון כ' די' השנה | ||||||||||
|
יבא החדש כ"פ שהם ה' ידות שלישיון דינר | ||||||||||
|
ואמור ה' פעמי' ח' ידות ח' ליט' הם מ' ידות שלישיון שהם י"ג די' וד"פ | ||||||||||
|
ולחשבון זה תאמ' ג"כ ה' פעמי' ז' ידות הם ל"ה ידות שהם י"ב די' פחות ד"פ וכה"ל | ||||||||||
| Find the Interest | |||||||||||
|
מד) אם ישאלך אדם הלותי כ' די' שנה אחת לחש' דפ"ה ובסוף השנה פרעתי מהם קצת הלותים שנה שניה לחשבון דפ"ה כמו כן ופרעתי מהם קצת | ||||||||||
|
| |||||||||||
|
עלו כל הפרעונות כ"ח דינרי' וה' פשו' וע"ג חלקי' מצ"א בפשוט | ||||||||||
|
שיבא לכל פרעון ט' די' וה' פשוטי' ופ"ה חלקי' מצ"א | ||||||||||
|
ודרך עשיית החשבון הוא על זה הדרך שתתפוש החשבון אחר ותשים קצת הפרעון שבכל שנה ושנה ו' די' | ||||||||||
|
ותתפוש החשבון מסופו דהיינו שבסוף שנה שלישית נשארו ו' דינרי' | ||||||||||
|
ונרצה לדעת כמה נשארו בראש שנה שלישית שהוא סוף שנה שנייה | ||||||||||
|
אמור אם בסוף שנה שלישית נשארו ו' דינרי' הסר מהם השתות והנשאר הוא הקרן שנשאר בסוף שנה שנייה | ||||||||||
|
כי לעולם בכל חשבון עולה בו ריוח לחשבון דפה"ה החומש מלגין שהוא שתות מלבד | ||||||||||
|
ולכן כשתסיר ממנו [9]השתות ישאר הקרן לבד | ||||||||||
|
א"כ בראש שנה שלישית נשארו ה' די' | ||||||||||
|
ואז פרעת ו' די' עבור שנה שנייה הרי שבסוף שנה שנייה היו י"א | ||||||||||
|
הסר מהם השתות שהוא הריוח שעלה בהם בשנה שנייה נשארו ט' די' וב"פ | ||||||||||
|
ואז פרעת ו' די' בעבור שנה ראשונה הרי שבסוף שנה ראשונה היו ט"ו די' וב"פ | ||||||||||
|
הסר מהם השתות ישארו י"ב די' וז"פ וב' שלישי פשוט | ||||||||||
|
אם כן ידענו שאם הקרן הוא י"ב די' וז"פ וב' שלישי פשוט הפרעון הוא ו' די' בכל שנה ונרצה לידע אם הקרן הוא כ' די' כמה הוא הפרעון | ||||||||||
|
עשהו בדרך זה אם ג' שוה ד' ה' כמה שוה | ||||||||||
|
והבן זה כי עמוק הוא וכה"ל | ||||||||||
|
גם נוכל לעשותו בדרך אחרת | ||||||||||
|
ותאמר א"פ וב' שלשיות כמה חלק הוא מי"ב די' וז"פ וב' שלישיות הוא חלק אחד מצ"א | ||||||||||
|
אם תסירהו מן הקרן ישארו י"ב די' וחצי | ||||||||||
|
תסיר ממנו עוד מן הנשאר החומש ישארו י' די' | ||||||||||
|
כפלהו יעלה כ' די' | ||||||||||
|
וכן תעשה בפרעון תסיר מו' די' חלק אחד מצ"א אחרי כן תסיר מן הנשאר החומש ותכפול המותר | ||||||||||
| Pricing Problem - Find the Price | |||||||||||
|
מה פרי שקנית תגרות בכל כך ליט' הככר ותרצה לידע כמה יבא הליט' התגרות בדרך קצרה | ||||||||||
|
תפוש החומש מסכום החשבון המעות וד' חומשי' תשליך ומכל ליט' שנשאר בידך קח די' וכל כך מעות יבא הליט' מן התגרות | ||||||||||
|
המשל בזה הרי שקניתי ק' ליט' מפלפל לחשבון מ' ליט' ותרצה לידע כמה יבא הליט' | ||||||||||
|
תפוש החומש שהם ח' ליט' ומכל הליט' תקח די' הרי שיבא ח' די' הרי שיבא הליט' מן הפלפל ח' די' וה"ל | ||||||||||
|
אחר שבכל ליט' ממעות שהוציא בככר אחד מן התגרות יגיע לכל ליט' ב"פ וב' חמשי' | ||||||||||
|
והרי שקנית הככר מן התגרות במ' ליט' ותרצה לידע כמה יבא הליט' | ||||||||||
|
תאמר ב"פ מ"פ וב' פעמי' מ' חומשי פשוט הם ח' די' וכה"ל | ||||||||||
| Find the Earned Interest | |||||||||||
|
מו אם ישאלך אדם כמה יעלה הריוח מק' ליט' א' יום לחשבון ח' ליט' השנה | ||||||||||
|
תאמר ב' פעמי' ח' הם י"ו תפוש השליש בפרוטות שהם ה"פ ושליש וכן יבא וכה"ל | ||||||||||
Problems of Various Types |
|||||||||||
Rent Problem |
|||||||||||
|
מז אם תשכיר בית אחד לחשבון כך וכך ליט' השנה ותרצה לידע כמה יבא היום | ||||||||||
|
עשה כן מכל ליט' שתוציא בבית השנה יבא ליום ב' שלישי פשוט | ||||||||||
|
והרי שהשכרת בית אחד לחשבון כ' ליט' השנה | ||||||||||
|
תאמ' כ' פעמי' ב שלשיים הם מ' שהם י"ג פשו' ושלי' וכן יבא לזו | ||||||||||
Exchange Problems |
|||||||||||
|
מח אם ישאלך אדם הכ"ב פיסני שוים כ"ה בולייניני' כמה יתן חלוף הליט' מן הבולונייני' לליט' מן הפיסני' | ||||||||||
|
תרבה כ"ה פעמי' א' ליט' מבולנייני' יהיו כ"ה ליט' מבולנייני' חלקם על כ"ב יבא כ' די' וח"פ וח' חלקי' מי"א בפשוט | ||||||||||
Proportions of Fractions |
|||||||||||
|
מט אם שליש שוה רביע חומש כמה שוה | ||||||||||
|
אמור תחלה אנה ימצאו שליש ורביע וחומש אמור ג' פעמי' ד' י"ב | ||||||||||
|
השליש הוא כ' | ||||||||||
|
הרביע הוא ט"ו | ||||||||||
|
החומש הוא י"ב | ||||||||||
|
ואמור אם כ' שוה ט"ו י"ב כמה שוה | ||||||||||
|
אמור י"ב פעמי' ט"ו הם ק"פ חלקם בכ' חלקי' הרי שיבא ט' שהם ט' חלקי' מס' | ||||||||||
Find a Quantity Problem - Whole from Parts – Tree |
|||||||||||
|
[10]נ אם ישאלך אדם יש לי אי אילן שהחצי והשליש ממנו הוא עומד במים תחת הארץ והשליש והרבע מן הנשאר הוא מכוסה תקוע בארץ | ||||||||||
|
| |||||||||||
|
בקש המורה והוא ע"ב בכפלך ג' על ב' והם ו' וג' פעמי' ו' הם י"ח וד' פעמי' י"ח הם ע"ב | ||||||||||
|
ובע"ב תמצא חצי ושליש ושליש ורבע | ||||||||||
|
והוצא שליש וחצי מע"ב והם ס' וישארו י"ב | ||||||||||
|
א"כ בעבור החלק האחד שהוא בארץ הוצא השליש והרבע מי"ב והם ז' | ||||||||||
|
ועתה אסוף ז' עם ס' והם ס"ז וישארו ה' | ||||||||||
|
אם כן עשה אם ה' היו ג' ע"ב כמה היו | ||||||||||
|
ע"ב פעמי' ג' הם רי"ו | ||||||||||
|
חלקם בה' בא מ"ג וחומש | ||||||||||
|
א"כ אורך כל האילן היה מ"ג זרתות וחומש וכה"ל | ||||||||||
Motion Problem - To and From - an Ant Climbing a Tower |
|||||||||||
|
נא הרי שיש לפניך מגדל גבוה כ' אמה ונמלה אחת רוצה לעלות למעלה | ||||||||||
|
אמור תחלה כמה יותר השליש מן הרביע א' חלק מי"ב | ||||||||||
|
נמצא שבכל יום יש לה יתרון א' חלק מי"ב מן האמה | ||||||||||
|
הרי שבי"ב ימים היא עולה אמה אחת | ||||||||||
|
אמור י"ב פעמים כ' בעבור המגדל שגובהו כ' הרי ר"מ הרי שבר"מ ימים תעלה על המגדל | ||||||||||
Find a Quantity Problem - First from Last Problem – Money |
|||||||||||
|
נב הרי שיש לך מעות בכיס והוצאת מהם השליש והרביע והחומש והם ט' | ||||||||||
|
אמור תחלה אנה ימצאו שליש ורביע וחומש בס' | ||||||||||
|
השליש הוא כ' | ||||||||||
|
והרביע ט"ו | ||||||||||
|
והחומש י"ב | ||||||||||
|
וכללם מ"ז חלקי' מס' | ||||||||||
|
נמצא שהנשארי' הם י"ג חלקי' מס' | ||||||||||
|
ואמור אם מ"ז חלקי' מס' שוים ט' פשוט י"ג חלקי' מס' כמה יבואו | ||||||||||
|
אמור י"ג פעמי' ט' הם קי"ז חלקם במ"ז בא ב' וכ"ג חלקי' ממ"ז | ||||||||||
|
נמצא שהיו בתוך הכיס י"א וכ"ג חלקי' ממ"ז | ||||||||||
|
ומה שהוציא היו ט' ומה שנשאר היו ב' וכ"ג חלקי' ממ"ז וכה"ל | ||||||||||
|
נג אם ישאלך אדם היו לי מעות בכיס והוצאתי מהם העשירית ונשאר י' | ||||||||||
|
תפוש חשבון אחד ואמור מי' כשתקח ממנו העשירית ישארו ט' | ||||||||||
|
ואם כן הדרך היא כך אם ט' היו י' א' כמה היא | ||||||||||
|
כפול א' על י' הם י' חלקם על ט' יהיו א' ותשיעי' | ||||||||||
|
והוסיפם על הי' יהיו י"א ותשיעי' | ||||||||||
|
הוצא מהם העשירית ישארו י' שלמי' וכה"ל | ||||||||||
|
ואם יאמר כי נשארו י' ושתות | ||||||||||
|
עשה כן | ||||||||||
|
אחר שידעת כי האחר היא אחד ותשיעי' תאמ' אם אחת היא אחת ותשיעי' השתות כמה היא | ||||||||||
|
תפוש השתות מא' ותשיעי' | ||||||||||
|
והוסיפם על הי"א ותשיעי' וכן יצא | ||||||||||
Divide a Quantity – Money |
|||||||||||
|
נד אם תרצה לחלק ה"פ לשליש ולרביע ולא ישאר ממנו כלל | ||||||||||
|
אמור תחלה שליש ורביע נמצא בי"ב | ||||||||||
|
השליש הוא ד' | ||||||||||
|
הרביע הוא ג' | ||||||||||
|
חברם יחד הם ז' והוא המחלק | ||||||||||
|
ואם תרצה לידע כמה יבא למי שיש לו השליש שהוא ד' אמור ד' פעמי' ה' בעבור שהם הפ' יבא כ' | ||||||||||
|
ומי שהוא שיש לו הרביע שהוא ג' אמור ג' פעמי' ה' ט"ו | ||||||||||
|
חברם יחד יעלו ה' כמספר המעות הרי [11]שנחלקו לשליש ולרביע ולא נשאר מהם כלל וכה"ל | ||||||||||
Divide a Quantity – Money |
|||||||||||
|
נה אם תרצה לחלק י"ב פשוט לחצי ולשליש ולרביע | ||||||||||
|
אמור תחלה אנה ימצאו בי"ב | ||||||||||
|
החצי הוא ו' | ||||||||||
|
והשליש ד' | ||||||||||
|
והרביע ג' | ||||||||||
|
חברם הם י"ג והוא המחלק | ||||||||||
|
ומי שיש לו החצי אמור החצי מי"ב הוא ו' ואמור ו' פעמי' י"ב בעבור המעות שהם י"ב יבואו ע"ב | ||||||||||
|
ומי שיש לו השליש שהוא ד' אמור ד' י"ב הם מ"ח | ||||||||||
|
ומי שיש לו הרביע שהוא ג' אמור ג' פעמי' י"ב הם ל"ו | ||||||||||
|
ואם תאסוף כלם יבאו יב"פ כמספ' המעו' | ||||||||||
Ordering Problem - Six Coins |
|||||||||||
|
נו הרי שאדם יש לו שכיר אחד לשלשי' יום בל' פשו' ורוצה לקבל פרעונו בכל יום ואין לשוכר רק ו' מטבעות כסף ששוים ל"פ סך כולם | ||||||||||
|
סימ' א' ב' ג' ד' ח' י"ב | ||||||||||
Find a Number Problem - Ratio of Integers and Fractions |
|||||||||||
|
נז אם ג' ושליש שוים ד' ורביע ה' וחומש כמה שוים | ||||||||||
|
אמור ה' וחומש פעמי' ד' ורביע ומה שיבא חלקהו בג' ושליש | ||||||||||
|
וזה סדר עשייתו | ||||||||||
|
תפוש ה' וחומש ואמור ה' פעמי' כ"ה וא' הרי כ"ו הרי שעשית מה' וחומש כ"ו חמשיות ותזמן אותם כאשר תראה | ||||||||||
|
אחרי כן תפוש ד' ורביע ואמור ד' פעמי' ד' י"ו וא' הרי י"ז הרי שעשית מד' ורביע י"ז רבעיות | ||||||||||
|
ובעבור שאנו צריכים לומ' ה' וחומש פעמי' ד' ורביע תרבה כ"ו עם י"ז יעלו תמ"ב ונחלק אותם אחרי כן לרביע וחומש ונאמ' ד' פעמי' ה' כ' | ||||||||||
|
| |||||||||||
|
ובעבור שאנו צריכים לחלק בג' ושליש עשה מכ"ב וא' עשירי' כולם שלישייות ואמור ג' פעמי' כ"ב ס"ו וג' פעמי' א' עשירי' הם ג' עשריות הרי ס"ו וג' עשירייות | ||||||||||
|
חלק אותם אחרי כן בג' ושליש וזהו דרך חלוקו שתעשה מג' ושליש כולם שלישייות ואמור ג' פעמי' ג' ט' וא' הרי י' | ||||||||||
|
א"כ נחלק ס"ו בי' חלקי' יבואו ו' וו' עשירייות | ||||||||||
|
נחלק אחרי כן ג' עשיריות בי' חלקי' יבואו' ג' חלקי' מק' | ||||||||||
|
הרי שעולה החשבון ו' שלמים וו' עשירייות וג' חלקי' מק' | ||||||||||
|
נקבץ אותם יחד ונעשה מו' עשיריות חלקי' מק' ויהיו ס' וג' חלקי' שהיו לנו הרי ס"ג נמצא שיבא ו' שלמים וס"ג חלקי' ממאה | ||||||||||
|
| |||||||||||
Multiple Quantities - Boys Selling Eggs |
|||||||||||
|
נח אדם נתן לבניו ביצות למכור לאחד נתן נ' בצים ולשני ל' ולשלישי י' ואמ' להם לכו ומכרו הבצים בשוה וכולכם תביאו לי מעות בשוה | ||||||||||
|
הלכו ונתנו ז' בצים בפשוט | ||||||||||
|
אותו שהיו לו נ' בצים מכר מ"ט בצי' בז"פ ונשארה לו ביצה אחת | ||||||||||
|
ואותו שהיו לו ל' בצים מכר כ"ח בצים בד' פשו' ונשארו לו ב' בצים | ||||||||||
|
ואותו שהיו לו י' בצים מכר ז' בצים בפשו' ונשארו לו ג' בצים | ||||||||||
|
הילכו פעם שנייה ומכרו הבצים שנשארו להם בג"פ הביצה | ||||||||||
|
הראשון שנשארה לו ביצה אחת קבל ג' פשוט וז' שקבל במכירה ראשונה הרי י' פשו' | ||||||||||
|
והשני שנשארו לו ב' בצים קבל ו"פ וד"פ שקבל במכירה ראשונה הרי י"פ | ||||||||||
|
[12]והשלישי שנשארו לו ג' בצים קבל ט"פ וא"פ שקבל במכירה ראשונה הרי שקבל י"פ | ||||||||||
|
נמצא שכולם מכרו הבצים בשוה וכולם קיבלו מעות בשוה | ||||||||||
Find a Quantity Problem - Whole from Parts – Fish |
|||||||||||
|
נט הרי שיש לפניך דג ונחתך ראשו וזנבו והגוף שוקל י' ליט' | ||||||||||
|
אמור תחלה שליש ורביע וחומש ושתות נמצא בס' | ||||||||||
|
שהם כ' וט"ו וי"ב וי' שהם נ"ז חלקי' מס' | ||||||||||
|
נמצא שהראש והזנב ששקלו סך שניהם שליש ורביע וחומש ושתות הם נ"ז חלקי' מס' שהוא השלם | ||||||||||
|
| |||||||||||
|
ואותם הג' חלקי' שנשארו עד ס' הוא הגוף ששוקל י' ליט' | ||||||||||
|
אמור א"כ אם ג' חלקי' מס' שוקלים י' ליט' דהיינו הגוף הנשאר הנ"ז חלקי' מס' דהיינו השליש והרביע והחומש ושתות שהם הראש והזנב כמה שוקלי' | ||||||||||
|
אמור נ"ז פעמי' י' הם תק"ע | ||||||||||
|
חלקם בג' חלקי' יבוא ק"צ ליט' | ||||||||||
|
נמצא שהראש והזנב שוקלים ק"צ ליט' | ||||||||||
|
והגוף שוקל י' ליט' שהוא סך הכל ר' ליט' | ||||||||||
|
ואם תרצה לידע כמה שוקל הראש לבדו | ||||||||||
|
כבר ידעת כי הראש שוקל השליש והרביע והשליש והרביע מס' הם ל"ה חלקי' מס' | ||||||||||
|
ואמור אם ג' חלקי' מס' דהיינו הגוף שוקל י' ליט' אלו הל"ה חלקי' דהיינו הראש ששוקל שליש ורביע כמה שוקל | ||||||||||
|
אמור ל"ה פעמי' י' ש"נ | ||||||||||
|
חלקם בג' יבא קי"ו וב' שלשיות והוא משקל הראש | ||||||||||
|
ובזה הדרך תעשה גם הזנב ויצא לך הענין וכה"ל | ||||||||||
Simultaneous Division - Money in a Purse |
|||||||||||
|
ס ב אנשים היו להם מעות בא' כיס אמ' זה לזה שמעני אחי כך הם השליש והרביע ממעותי כמו השתות והשבע ממעותיך | ||||||||||
|
תמצא חשבון שימצא בו שליש ורביע וימצא בי"ב וכך מעות היו לו | ||||||||||
|
קח מהם שליש ורביע והם ז"פ | ||||||||||
|
ועבור האיש האחר שהיה לו שתות ושביע שהם י"ג חלקי' ממ"ב | ||||||||||
|
ואמור אם י"ג היו ז' כמה היו מ"ב | ||||||||||
|
אמור ז' פעמי' מ"ב רצ"ד חלקם בי"ג יהיו כ"ב וח' חלקי' מי"ג וכך מעות היו לו | ||||||||||
|
תוציא השתות והשביע מהם ויהיו ז"פ | ||||||||||
Partnership - for the same time |
|||||||||||
|
סא הרי שג' אנשים רצו להתחבר ולשים בחברותה מ' אונקי' זהב לאחד יש לו זהב ששוה ג' ליט' האונ' | ||||||||||
|
עשה על זה הדרך אמור שליש וחומש ושמינית אנה ימצאו בקש המורה והוא ק"כ | ||||||||||
|
השלשי הוא מ' | ||||||||||
|
החומש הוא כ"ד | ||||||||||
|
השמינית הוא ט"ו | ||||||||||
|
צרף כולם יהיו ע"ט והוא המחלק | ||||||||||
|
ואם תרצה לידע כמה זהב ישים אותו שיש לו הזהב ששוה ג' ליט' האונקי' אמור השלשי הוא מ' ותרבה אותו עם סך האונקי' שהם מ' ואמור מ' פעמי' מ' אלף ות"ר | ||||||||||
|
ואם תרצה לידע כמה שוה חלקו של זה אמור מן הכ' אונקי' יבוא ס' ליט' | ||||||||||
|
ומן הכ' חלקי' מע"ט אמור אם ע"ט שהוא אחד שלם שוה תש"כ פש' הכ' חלקי' מע"ט כמה שוים | ||||||||||
|
אמור כ' פעמי' תש"כ י"ד אלפי' ות' חלקם [13]בע"ט יבואו קפ"ב פשוטי' וכ"ב חלקי' מע"ט | ||||||||||
|
הרי ששוה חלקו של זה ס' ליט' וט"ו די' וב"פ וכ"ב חלקי' מע"ט | ||||||||||
|
וכן תעשה מן האחרים ויצא לך הענין וכה"ל | ||||||||||
Give and Take Problem - gatekeeper |
|||||||||||
|
סב איש אחד מהלך בד' עיירות ובעיר ראשונה הכפיל כל מעותיו ובצאתו מן העיר לקח לו השוער ח"פ | ||||||||||
|
אם תרצה לידע אותו עבור כי זה האיש הלך בד' עיירות ובכל עיר פרע ח"פ | ||||||||||
|
עבור העיר ראשונה צריך אלו הח"פ לחלק לחצי ויהיו ד"פ | ||||||||||
|
ועבו' העיר השנית אלו הד"פ חלק לחצי ויהיו ב"פ | ||||||||||
|
ועבו' העיר השלישית אלו הב"פ חלק לחצי ויהיה א"פ | ||||||||||
|
וזה הפשוט חלק לחצי ויהיה חצי פשוט | ||||||||||
|
ואסוף אחרי כן כולם יחד ויהיו ז' פשו' וחצי וכך היה הקרן וכה"ל | ||||||||||
|
|
|||||||||||
|
סג ד נהרות רצים אל מעיין אחד האחד ממלאו ביום אחד | ||||||||||
|
עשה על זה הדרך אמור ראשון וחצי ושליש ורביע ימצא בי"ב | ||||||||||
|
הראשון י"ב | ||||||||||
|
החצי ו' | ||||||||||
|
השליש ד' | ||||||||||
|
הרביע ג' | ||||||||||
|
חברם יחד הם כ"ה והוא המחלק | ||||||||||
|
הרי שבי"ב ימי' ימלאו כ"ה מעינות | ||||||||||
|
כיצד אותו שממלאהו ביום אחד א"כ בי"ב ימים ימלא י"ב מעינות | ||||||||||
|
ואותו שממלאהו בב' ימים א"כ בי"ב ימים ימלא ו' מעינות | ||||||||||
|
ואותו שממלאהו בג' ימים א"כ בי"ב ימים ימלא ד' מעיינות | ||||||||||
|
ואותו שממלאהו בד' ימים א"כ בי"ב ימים ימלא ג' מעיינו' | ||||||||||
|
נמצא שארבעתם יחד ימלאו בי"ב ימים כ"ה מעיינות | ||||||||||
|
אמור א"כ אם כ"ה מעיינות מתמלאי' בי"ב ימים א' מעיין בכמה מתמלא | ||||||||||
|
אמור א' פעם י"ב הם י"ב חלקם בכ"ה יבא י"ב חלקי' מכ"ה הרי שבי"ב חלקי' מכ"ה מתמלא ביום המעיין | ||||||||||
|
ואם תרצה לידע כמה חלק מן המים שם כל אחד מן הנהרות במעיין | ||||||||||
|
אמור הראשון הוא י"ב אמור י"ב פעמי' א' בעבו' המתמלא שהוא א' הם י"ב חלקם בכ"ה יבוא י"ב חלקי' מכ"ה | ||||||||||
|
ובזה הדרך תעשה מן האחרים וכה"ל | ||||||||||
|
ואם תרצה לידע כמה מעיינות ימלאו ביום אחד תאמ' א' פעם כ"ה הם כ"ה חלקם בי"ב יבואו ב' מעיינות וא' חלק מי"ב וכה"ל | ||||||||||
Motion Problem – Pursuit |
|||||||||||
|
סד הרי אדם אחד שהוא מהלך בכל יום י' מילין ואדם אחר מהלך ביום אחד א' מיל וביום שני ב' וביום ג' ג' והוא מוסיף בכל יום מיל אחד | ||||||||||
|
כפול י' עם י' ויבוא כ' תפחות א' מכ' יהיו י"ט הרי שבי"ט ימים יעמדו בשוה וכה"ל | ||||||||||
|
ואם הצולע מהלך אגה"ז ובכל יום מוסיף והולך פרדים ולא זוגות | ||||||||||
|
תפוס הי' מילים שמהלך הקבוע ודע שבי' ימים ישיגנו | ||||||||||
|
ואם הצולע מהלך בדו"ח וכן מוסיף והולך זוגות ולא פרדים | ||||||||||
|
תפחות א' מן הי' מילין שמהלך הקבוע [14]ואמור כי בט' ישיגנו ימים וכה"ל | ||||||||||
Mixture and Alligation Problem - Goldsmith making rings from several kinds of coins |
|||||||||||
|
סה הרי שנתתה לצורף י' אונקיו' זהב לעשות ממנו טבעות והב' אונקיו' מהם היה זהב מי"ד קראטי' האונקי' | ||||||||||
|
תפוש סכום האונק' והקרטי' וכפול הקרטי' בס | ||||||||||
|
כיצד הב' אונ' מי"ד קרטי' האונ' ת..ם כ"ח | ||||||||||
|
והג' אונק' מי"ו קרטי' האונ' ת..ם מ"ח | ||||||||||
|
והה' אונק' מי"ח קרטי' האונ' ת..ם צ' | ||||||||||
|
חברם יחד הם קס"ו קרטי' | ||||||||||
|
חלקם לי' חלקי' כמנין האונ' יבא לכל אונק' י"ו קרטי' וג' חומשי קרטי' וכה"ל | ||||||||||
Divide a Quantity - Price of a Fish Paid by a Group of People |
|||||||||||
|
סו הרי שג' אנשים קנו א' דג בט"פ לאחד יש לו החצי ולשני יש לו השליש ולשלישי יש לו התשיעי | ||||||||||
|
עשה על זה הדרך אמור אנה ימצא חצי ושליש ותשיעי בי"ח | ||||||||||
|
החצי הוא ט' | ||||||||||
|
השליש הוא ו' | ||||||||||
|
התשיעי הוא ב' | ||||||||||
|
חברם יחד הם י"ז והוא המחלק | ||||||||||
|
ואותו שיש לו החצי מן הדג אמור החצי הוא ט' | ||||||||||
|
ותרבה אותו על הדג שהוא א' ואמור ט' פעמי' א' הוא ט' חלקהו בי"ז יבא לחלקו ט' חלקי' מי"ז | ||||||||||
|
וכן תעשה מן האחרים ויצא לך הענין וכה"ל | ||||||||||
Joint Purchase Problem - If You Give Me - two men - Amounts of Money |
|||||||||||
|
סז אם יאמר אדם לחבירו תן לי ו"פ יהיה לי כאשר יש לך והאחר אמ' אם תתן לי ו"פ יהיה לי פי שנים ממך | ||||||||||
|
תאמ' ו' פעמי' ז' מ"ב וכך מעות היו לאיש שאמר תן לי ו"פ יהיה לי כפול ממך | ||||||||||
|
ולמעות האחר תאמ' ה' פעמ' ו' ל' וכן היו לו כה"ל | ||||||||||
Interest and Discount Problem - find the fund |
|||||||||||
|
סח אם נאמר לך אני פלני עשיתי מא"פ ב' ומב' עשיתי ג' ומג' ד' ומד' ה' ומה' ו' והיו לי בין קרן וריוח ת"פ אשאלך כמה היה הקרן | ||||||||||
|
עשה כן עת' כי מאחד עשית ב' ומב' ג' ומג' ד' ומד' ה' ומה' ו' א"כ צריך לראות כי ו' יצאו מא' א"כ מאיין מצים לצאת ת"פ | ||||||||||
|
עשה כן א' פעם ת"פ וחלקם בו' יהיו ס"ו פשו' וב' שלישי פשוט וכן היה הקרן | ||||||||||
Exchange Problems |
|||||||||||
|
סט כ די' אונקוניטני לחילוף בולייניני' לא"פ וחצי הליט' שוה פחות מן הבולונייני' כמה יבא לל"ז די' וחצי מאנקונטני' מחלוף | ||||||||||
|
עשה כן ל"ז פעמי' ל"א הם אלף וקמ"ז | ||||||||||
|
ואחר אמור איזהו החצי מל"א הוא ט"ו וחצי | ||||||||||
|
ומהו החצי מל"ז והוא י"ח וחצי | ||||||||||
|
ומהו החצי מן החצי הוא רביע | ||||||||||
|
ואסוף ט"ו וחצי וי"ח וחצי ורביע יהיו אלף וקפ"א ורביע חלק אותם לכ' חלקי' יבא נ"ט פשו' וא' חלק מכ' וא' חלק מפ' | ||||||||||
|
| |||||||||||
|
ואם יאמר לצ"א די' ורביע כמה יבא כמו כן | ||||||||||
|
תרבה צ"א פעמי' ל"א והם אלפיים ותתכ"א | ||||||||||
|
ואחר אמור איזהו הרביע מל"א הוא ז' וג' רבעי' | ||||||||||
|
ומה הוא החצי מצ"א והוא מ"ה וחצי | ||||||||||
|
ומהו החצי מן הרביע הוא שמינית | ||||||||||
|
ואסוף עם אלפים ותתכ"א ויהיו אלפי' ותתע"ד וא' רביע וא' שמינית וחלקם בכ' חלקי' ויהיו [15]קמ"ג פשו' וג' רבעים וא' חלק מכ' | ||||||||||
|
| |||||||||||
Interest and Discount Problem |
|||||||||||
|
ע חשבון אחר שבין קרן וריוח היו בשנה אחת י"ז ליט' לחשבון גפה"ה כמה היה הקרן | ||||||||||
|
תפוס חשבון אחד ואמור כ"ג ליט' לחשבון גפה"ה היו בסוף השנה כ' ליט' מקרן וג' ליט' מריוח | ||||||||||
|
ואמור אם כ"ג היה כ' י"ז כמה היה | ||||||||||
|
אמור י"ז פעמי' כ' ש"מ חלקם על כ"ג יהיו י"ד ליט' וט"ו די' נוס' וט"ו חלקי' מכ"ג בפשוט וכה"ל | ||||||||||
Pricing Problem - Find the Amount |
|||||||||||
|
עא אם נשאלת בכ"א ליט' וחצי הככר מן העורות עבור י"ב ליט' ורביע כמה עורות יבא | ||||||||||
|
עשה כ"א וחצי וכ"א וחצי ויהיו מ"ג וזהו המחלק | ||||||||||
|
ואחר עשה ב' פעמי' ק' והם מאתיי' | ||||||||||
|
ותרבה י"ב ליט' ורביע עם מאתיים ויהיו אלפיי' ות"נ וחלק במ"ג חלקים ויהיו נ"ו עורות ומ"ב חלקי' ממ"ג מא' עור וכה"ל | ||||||||||
|
ואם יאמר בע"א ליט' וחצי כמה עורות יבואו לו כמו כן | ||||||||||
|
תרבה ע"א ליט' וחצי עם ר' ויהיו קמ"ג ככרים וחלק במ"ג ויהיו של"ב עורות וכ"ד חלקי' ממ"ג מא' עור וכה"ל | ||||||||||
Divide a Quantity - Sharing Food |
|||||||||||
|
עב ב אנשים היו יושבים לאכול לאחד יש לו ב' לחמים ולשני ג' | ||||||||||
|
אמור כמה חלקי' מן הלחם אכל כל אחד ואחד א' לחם וב' שלישיות | ||||||||||
|
א"כ אותו שהיו לו ב' לחמים ואכל א' לחם וב' שלשיות לא הפסיד כי אם שליש לחם | ||||||||||
|
ואותו שהיו לו ג' לחמים ואכל א' לחם וב' שלשיות הפסיד א' לחם ושליש דהיינו ד' שלשיות | ||||||||||
|
א"כ אותו שהיו לו ב' לחמי' יקבל א"פ | ||||||||||
|
והאחר יקבל ד"פ | ||||||||||
Find a Number Problems - Multiplication of fractions |
|||||||||||
Fractions by Fractions |
|||||||||||
|
עג אם ישאלך אדם כמה הוא ד' חמשיות על ד' חמשיות | ||||||||||
|
תאמר אם היה שואל א' חמישית על א' חמישית | ||||||||||
|
הייתה אומר ה' פעמי' ה' כ"ה והיה עולה א' חלק מכ"ה | ||||||||||
|
ועתה שהוא שואל ד' חמשיות על ד' חמשיות עדיין תאמ' ד' פעמי' ד' י"ו נמצא שיבא י"ו חלקי' מכ"ה | ||||||||||
|
עד אי"א כמה הוא ז' תשיעיות על ד' שבעיות | ||||||||||
|
תאמ' אם היה שואל א' תשיעית על א' שבעית | ||||||||||
|
הייתה אומ' ז' פעמ' ט' הם ס"ג נמצא שהיה עולה א' חלק מס"ג | ||||||||||
|
ועתה שהוא שואל ז' תשעיות על ד' שבעיות עדיין תאמ' ז' פעמ' ד' כ"ח נמצא שיבא כ"ח חלקי' מס"ג וכה"ל | ||||||||||
Integers and Fractions |
|||||||||||
|
אי"א ג' שלמים וב' חמשיות על ב' שלמים וד' שבעיות כמה הוא | ||||||||||
|
תאמ' ג' פעמ' ב' הם ו' שלמים | ||||||||||
|
אח"כ תאמר ג' פעמ' ד' שבעיות הם י"ב שהוא אחד שלם וה' שבעיות שהוא כ"ה חלקי' מל"ה | ||||||||||
|
אח"כ תאמ' ב' פעמ' ב' חמשיות הם ד' חמשיות שהם כ"ח חלקי' מל"ה | ||||||||||
|
ואחרי כן תאמ' ב' חמשיות על ד' שבעיות הוא ח' חלקי' מל"ה | ||||||||||
|
צרף כלם יחד יבא ח' שלמים וכ"ו חלקי' מל"ה וכן יבא וכה"ל | ||||||||||
|
| |||||||||||
|
עה אי"א א' וה' שבעיות על א' וד' חמשיות כמה הוא | ||||||||||
|
אמור א' פעם א' א' | ||||||||||
|
א"כ תאמ' [16]א' פעם ד' חמשיות הם כ"ח חלקי' מל"ה | ||||||||||
|
אח"כ תאמ' א' פעם ה' שבעיות הם כ"ה חלקי' מל"ה | ||||||||||
|
אחר כן תאמ' ד' חמשיות על ה' שבעיות הם כ' חלקי' מל"ה | ||||||||||
|
צרפם יחד יבא ג' שלמים וג' חלקי' מל"ה וכה"ל | ||||||||||
|
| |||||||||||
Multiple Quantities - Coins that Worth an Amount of Money |
|||||||||||
|
עו הרי שיש לך ד' מטבעות ששוים סך ארבעתם פ' פשוטי' והראשון שוה החצי והשתות מן השני | ||||||||||
|
| |||||||||||
|
עשה על זה הדרך | ||||||||||
|
אמור הראשון ששוה החצי והשתות מן השני | ||||||||||
|
אמור חצי ושתות אנה ימצא בו' | ||||||||||
|
החצי הוא ג' השתות הוא א' הרי ד' חלקי' מו' שהם ב' שלשיות | ||||||||||
|
| |||||||||||
|
א"כ זה ששוה חצי ושתות מן השני הוא כאלו אמר הראשון שוה ב' שלשיות מהשני | ||||||||||
|
והשלשי ששוה שליש ורביע ושתות מן הראשון | ||||||||||
|
אמור אנה ימצא שליש ורביע ושתות בס' | ||||||||||
|
השליש הוא כ' הרביע ט"ו והשתות י' הרי למ"ה | ||||||||||
|
| |||||||||||
|
א"כ השלשי ששוה שליש ורביע ושתות מן הראשון שהם מ"ה חלקי' מס' הוא כאלו אמר ג' רבעיות מן הראשון | ||||||||||
|
והרבעי ששוה ד' חמשיות מהשלשי הוא מבואר | ||||||||||
|
א"כ הסדר כך הוא הראשון ששוה ב' שלשיות מהשני והשלשי שוה ג' רבעיות מן הראשון | ||||||||||
|
| |||||||||||
|
אמור תחלה השברים הנז' בזה החשבון הם חצי ושליש ורבע וחומש ושתות וימצאו כלם בס' | ||||||||||
|
א"כ השני הוא ס' | ||||||||||
|
והראשון שהוא שוה ב' שלשיות מן השני שהוא ס' הוא מ' כי מ' הוא ב' שלשיות מס' | ||||||||||
|
והשלשי ששוה ג' רבעיות מהראשון שהוא מ' א"כ הוא ל' כי ל' הם ג' רבעיות ממ' | ||||||||||
|
והרבעי ששוה ד' חמשיות מהשלשי שהוא ל' הוא כ"ד כי כ"ד הוא ד' חמשיות מל' | ||||||||||
|
| |||||||||||
|
והנשאר מהשני שהוא ב' שלשיות מהשלשי עשה על זה הדרך | ||||||||||
|
אמור כמה נשאר מן השני שהוא ס' אחר שהוצאת ממנו הראשון שהוא מ' נשארו כ' | ||||||||||
|
א"כ כ' שהוא הנשאר מהשני הם ב' שלשיות מן השלשי שהוא ל' כי כ' הם ב' שלשיות מל' | ||||||||||
|
הרי שהראשון הוא מ' והשני הוא ס' והשלשי ל' והרבעי כ"ד צרף אותם יחד יעלו קנ"ד והוא המחלק | ||||||||||
|
ואם תרצה לידע כמה שוה הראשון שהוא מ' אמור מ' פעמ' פ' בעבור שכלם שוים פ' יהיו ג' אלפי' ומאתיים | ||||||||||
|
ובזה הדרך תעשה מן האחרים ויצא לך הענין השוה וכה"ל | ||||||||||
Find a Number Problems - Sums |
|||||||||||
|
עז א ב' ג' ד' ה' ו' ז' ח' | ||||||||||
|
שהם נחלקי' לחצי | ||||||||||
|
תוסיף א' על הסך ותרבה אותו על החצי | ||||||||||
|
ואמור ד' פעמ' ט' ל"ו וכן יהיה מספרם ל"ו וכה"ל | ||||||||||
|
עח א ב' ג' ד' ה' ו' ז' | ||||||||||
|
שאינם נחלקים לחצי | ||||||||||
|
תפוס הרוב ותרבה אותו על הסך | ||||||||||
|
ואמור ד' פעמ' ז' כ"ח וכה"ל | ||||||||||
|
עט א ג' ה' ז' ט' שהם פרדים | ||||||||||
|
תרבה הרוב בעצמו | ||||||||||
|
ואמור הרוב מט' הוא ה' ואמ' ה' פעמ' ה' כ"ה וכן יבאו וכה"ל | ||||||||||
|
פ ב ד' ו' ח' שהם כלם זוגות | ||||||||||
|
תרבה חציים על הבא לאחריו | ||||||||||
|
ואמור החצי מח' ד' [17]ואמור ד' פעמ' ה' הם כ' וכן יבא וכה"ל | ||||||||||
Find a Number Problem - Multiplication of integers and fractions |
|||||||||||
|
פא אם ישאלך אדם א' ורביע על א' וחמישית כמה הוא | ||||||||||
|
אמור תחלה א' פעם א' א' | ||||||||||
|
אח"כ תאמ' פעם אחת רביע ופעם אחת חמישית הם ט' בנטיני' | ||||||||||
|
אחר כך תאמ' א' רביע על א' חמישית הוא א' חלק מכ' | ||||||||||
|
נמצא שיבא הכל א' וי' בנטיני' דהיינו א' וחצי | ||||||||||
Interest and Discount Problems |
|||||||||||
Find the Earned Interest |
|||||||||||
|
פב אם ישאלך אדם הלותי מעות לחשבון כך וכך פשו' החדש הליט' כמה יעלה ריוח בק' ליט' א' שנה | ||||||||||
|
תרבה ה' פעמ' כנגד המעות שירויח הליט' החדש | ||||||||||
|
המשל בזה הרי שהלוית ק' ליט' א' חדש לחשבון ז"פ החדש הליט' | ||||||||||
|
תאמ' ה' פעמ' ז' ל"ה | ||||||||||
|
נמצא שיבא הק' ליט' השנה ל"ה ליט' וכה"ל | ||||||||||
Compound Interest |
|||||||||||
|
פג) מי שרוצה לקבץ חשבונות הלוואות רבים שנעשו בזמנים שונים להביאם בזמן אחד | ||||||||||
|
יקבץ חשבונות החדשים כלם ויחלקם כחשבון המעות או הפרחי' או כמטבע ההלוואות ההם | ||||||||||
|
המשל בזה הרי שהלוית ק' פרחי' זהב א' חדש וק' פרחי' ב' חדשים וק' פרחי' ג' חדשי' וק' פרחי' ד' חדשי' וק' פרחי' ה' חדשי' | ||||||||||
|
עשה כן אחד ושנים ושלשה וארבעה וחמשה שהם החדשי' הרי ט"ו | ||||||||||
|
חלקם בסכום המעות שהם ה' יגיע לכל חלק מהם ג' | ||||||||||
|
הרי שעמדו כלם ג' חדשי' | ||||||||||
|
וכן הדומה לכל מטבע ולכל מנין וכה"ל | ||||||||||
Find the Earned Interest |
|||||||||||
|
פד הרוצה לידע לחשבון כך וכך הככר כמה יבואו קצתם לחדש | ||||||||||
|
תרבה חשבון הככר כסכום המעות שתרצה וחלקם בחמשה והחלק שיצא יגיע לכל חדש כסכום ההוא | ||||||||||
|
המשל בזה לחשבון ז' ליט' הככר לשנה כמה יבא ל' ליט' חדש אחד או ב' חדשי' או יותר | ||||||||||
|
תרבה ל' בז' והם ר"י | ||||||||||
|
חלקם בחמשה יגיע לכל חלק מהם מ"ב | ||||||||||
|
הרי שבמב"פ יבא לכל לחדש אחד | ||||||||||
|
אחרי כן תרבה החדשים שתרצה ויצא לך הענין וכה"ל | ||||||||||
Multiple Quantities Problem - Five Weights |
|||||||||||
|
פה אם הקצב מוכר בשר ואין לו רק ה' משקלות ששוקלות בין כולם קכ"א ליט' כמה ישקול כל משקל לעצמו שיוכל הקצב לשקול הבשר באלו המשקלות למי רב ולמי מעט | ||||||||||
|
שמי שירצה לקנות קכ"א ליט' בשר ישים כל המשקלות כנגד הבשר | ||||||||||
|
ואם ירצה לקנות נ' ליט' בשר או יותר או פחות ישים כל כך משקלות בצד המאזנים שכנגד הבשר שישקלו כמו הבשר שהוא רוצה לקנות | ||||||||||
|
ואם לא יבא בכיוון יחליף המשקלות | ||||||||||
|
ולפעמים צריך שישים אחד ושנים ושלשה משקלות עם הבשר כנגד משקל אחד להפיק רצון הקונה | ||||||||||
|
ועתה אשאלך כמה ישקול כל משקל לעצמו | ||||||||||
|
האחד ישקול א' ליט' | ||||||||||
|
והשני ישקול ג' ליט' | ||||||||||
|
והשלישי ט' ליט' | ||||||||||
|
והרבעי כ"ז ליט' | ||||||||||
|
והחמשי פ"א ליט' | ||||||||||
|
צרפם יחד יהיו קכ"א ליט' לא פחות ולא יותר | ||||||||||
|
ובאלו המשקלות יוכל הקצב למכור כרצונו למי רב ולמי מעט וכה"ל | ||||||||||
Guessing - coins |
|||||||||||
|
פו חשבון הג' מטבעות שונות לג' אנשים שונים להגידם לראשון תן א"פ ולשני ב' ולשלשי ד' ובעל המטבע הגדול יכפול חלקו ד' פעמ' והשני ג' פעמים [18]ובעל המטבע הקטן יכפול חלקו פעם אחד | ||||||||||
|
וסימן א' כסף זהב נחשת | ||||||||||
|
ב' זהב נחשת כסף | ||||||||||
|
ג' זהב כסף נחשת | ||||||||||
|
ד' נחשת כסף זהב | ||||||||||
|
ה' נחשת זהב כסף | ||||||||||
|
ו' כסף נחשת זהב וכה"ל | ||||||||||
Payment Problem - three workers, three different daily wages, the same actual payment |
|||||||||||
|
פז אדם שכר ג' אחים ראובן שמעון לוי שיעשו עבודתו כ' ימים מן הבקר עד הערב מאיזה מהם שיהיה ולא תשבות המלאכה והנה אם עבד ראובן כל הימים יתן לו ה' זהובים ואם שמעון ד' ואם לוי ג' | ||||||||||
|
דע כי ראובן ישמש ד' ימים בזהוב אחד | ||||||||||
|
ושמעון ה' ימים | ||||||||||
|
ולוי ו' ימים וב' שלישיות יום | ||||||||||
|
והנה הכל ט"ו ימים וב' שלישיות אחד | ||||||||||
|
נחלק כ' על זה המספר ועלה אחד שלם ונשארו ד' שלמים ושלישית | ||||||||||
|
והנה בעבור השלישית נשים הכל שלישיות | ||||||||||
|
והנה נשיב הכ' ימים ס' שלשיות והט"ו וב' שלישיו' מ"ז שלשיות והד' ושלישית י"ג | ||||||||||
|
והנה כל אחד לקח זהוב אחד וי"ג פשו' ממטבע מ"ז בזהוב | ||||||||||
|
| |||||||||||
|
ועתה נבקש כמה חייב כל אחד לעבוד עד שישלימו הכ' ימים | ||||||||||
|
והנה נחל מלוי שחייב לשמש בזהוב שלקח ו' ימים וב' שלישיות | ||||||||||
|
ונעשה מאלו שלשיות ויהיו כ' | ||||||||||
|
ונבקש לדעת כמה יש לו לעבוד בעבור יג"פ שלקח | ||||||||||
|
כפלנו י"ג על כ' היו ר"ס | ||||||||||
|
חלקנום על מ"ז עלו ה' נשארו כ"ה חלקי' | ||||||||||
|
חברנו ה' עם כ' היו כ"ה שלשיות וכ"ה חלקי' ממ"ז | ||||||||||
|
חלקנו אלו השלישיות על ג' עלו ח' שלמים ונשאר אחד | ||||||||||
|
נקח לו ד' שעות שהם שלישית יום | ||||||||||
|
נכפול כ"ה על ד' עלו ק' | ||||||||||
|
נחלקם על מ"ז עלו ב' שעות ונשארו ו' חלקי' | ||||||||||
|
| |||||||||||
|
והנה לוי עבד ח' ימים ו' שעות ו' חלקי' | ||||||||||
|
נבקש לדעת כמה עבד שמעון הוא חייב לעבוד בעבור הזהוב ה' ימים שהם ט"ו שלישיות | ||||||||||
|
ונבקש לדעת כמה יעבוד בעבור יג"פ שלקח | ||||||||||
|
נכפול י"ג על ט"ו עלו קצ"ה | ||||||||||
|
נחלקם על מ"ז יעלו ד' ונשאר ז' חלקי' | ||||||||||
|
נחבר הד' אל הט"ו כי שלשיות הם יהיו י"ט שלשיות | ||||||||||
|
נחלקם על ג' יהיו ו' ימים שלמים | ||||||||||
|
ונקח לאחד הנשאר ד' שעו' | ||||||||||
|
גם נכפול ז' על ד' יהיו כ"ח | ||||||||||
|
| |||||||||||
|
והנה הם ו' ימים וד' שעות וכ"ח חלקי' וככה עבד שמעון | ||||||||||
|
נבקש לדעת כמה עבד ראובן והנה עבד בשביל הזהוב ד' ימים שהם י"ב שלשיות | ||||||||||
|
ונעשה בעבור היג"פ שלקח הערך | ||||||||||
|
|||||||||||
|
נחלקם על מ"ז עלו ג' ונשארו ט"ו חלקים | ||||||||||
|
חברנו אלו הג' עם הי"ב שהיו לנו היו ט"ו והם שלשיות | ||||||||||
|
והנה עבד ה' ימים | ||||||||||
|
גם הט"ו חלקי' נכפול על ד' עלו ס' | ||||||||||
|
נחלקם על מ"ז עלתה שעה אחת ונשארו י"ג חלקי' משעה שעבד ראובן | ||||||||||
|
| |||||||||||
|
וכאשר תחבר אלה החלקי' יעלה מהם שעה אחת בלי תוספת ומגרעת | ||||||||||
|
וכאשר תחבר שעה זו לשעות הנזכרות יהיו י"ב שעות שהוא יום אחד | ||||||||||
|
וכאשר תחבר היום לימים הנז' יהיו כ' ימים בלי תוספת ומגרעת וכה"ל | ||||||||||
|
| |||||||||||
Divide a Quantity Problem - Proportional Division – Inheritance |
|||||||||||
|
פח שאלה יעקב מת והוציא ראובן שטר בשני עדים כשרים שנתן לו יעקב אביו כל [19]הממון שהיה לו וציוה כן מחמת מיתה | ||||||||||
| Three methods to divide the property between the four sons each according to his relative portion: | |||||||||||
|
והנה חכמי ישראל מחלקים אותו על דרך בקשת כל אחד | ||||||||||
|
וחכמי הגוים על דרך ערך הממון של כל אחד | ||||||||||
|
וחכמי החשבון יחשבו כי הממון היה אחד וכאשר תחבר אליו חציתו ושלשיתו ורבעיתו יהיו הכל שנים וחצי ששית | ||||||||||
|
והנה נשים האחד שלם ס' שיש לו כל החלקי' הנז' ויהיו בין הכל קכ"ה | ||||||||||
|
או נשים האחד שלם י"ב והשברים הנז' י"ג | ||||||||||
|
ושוה יצא המספר באחרונה אי זה מהם שתקח | ||||||||||
|
ועתה נבקש כמה יקח ראובן לפי ערך ממונו ונעשה הערך ככה על דרך ס' כי הוא מבקש כל הממון ונעשה כי הממון י' די' שהם ק"כ פ' | ||||||||||
|
וזה צורת ערך הממון שיקח ראובן | ||||||||||
|
| ||||||||||
|
כפלנו הקצוות עלו ז' אלפי' ור' חלקנום על קכ"ה עלו נ"ז פשו' וע"ה חלקי' וזה חלק ראובן | ||||||||||
|
וזה צורת ערך שמעון | ||||||||||
|
| ||||||||||
|
נכפול הקצוות ונחלק כמשפט | ||||||||||
|
וזה צורת חלק לוי | ||||||||||
|
| ||||||||||
|
ונכפול ונחלק כמשפט | ||||||||||
|
וזו צורת חלק יהודה | ||||||||||
|
| ||||||||||
|
ונכפול ונחלק כמשפט | ||||||||||
|
ענין אחר בדרך קצרה | ||||||||||
|
יקח שמעון חצי חלק ראובן | ||||||||||
|
ולוי יקח שליש חלק ראובן | ||||||||||
|
ויהודה יקח רביע חלק ראובן | ||||||||||
|
וכאשר תחבר אלו כל החלקי' והשלמים יהיו ק"כ פ' שהם י' די' | ||||||||||
|
ועל דרך חכמי ישראל | ||||||||||
|
יאמר הג' אחים הגדולים ליהודה אין אתה מערער רק על ל"פ וערעור כל אחד ממנו שוה בהם קח ז' וחצי שהוא הרבעית ולך מעמנו | ||||||||||
|
וכמו כן יקח כל אחד מהג' אחים | ||||||||||
|
ועוד יאמר ראובן ללוי אין אתה מערער רק על מ"פ וכבר לקחת חלקך מהל' שהארבעתינו חלקנו עליו קח אתה שלישית י' שהוא רבעית מ' ולך מעמנו | ||||||||||
|
והנה חלק לוי י' וה' ששיות פשוטי כי החצי מן הז' וחצי שלקח כבר הם ג' ששיות ושליש אחד מן הי' הם ב' ששיות הרי ה' ששיות | ||||||||||
|
| |||||||||||
|
גם ראובן יאמ' לשמעון אין אתה מערער רק על חצי האחד שהוא ס' וחצי האחר כולו שלי וכבר לקחת חלק מהמ' והנה שנשאר בינך ובני הערעור קח חציים ולך מעלי | ||||||||||
|
והנה חלק שמעון כ' וה' ששיות פשוט | ||||||||||
|
| |||||||||||
|
וחלק ראובן פ' וה' ששיות פשוט | ||||||||||
|
| |||||||||||
|
וכאשר תחבר אלו החלקי' יהיו י' די' וכה"ל | ||||||||||
Geometrical Problems |
||
Triangulation Problem - Two towers |
||
|
פט ב מגדלים אחד גבוה ט"ו אמות ואחד גבוה י"ב אמות ושם ב' יונים ומעיין אחד ביניהם ומגיעים ברגע אחד במעיין | |
|
|
||
|
שים הרוחק שבניהם כמדת גובה שתיהם דהיינו י"ב וט"ו שהם כ"ז | |
|
וחלק כ"ז לי"ב ולט"ו | |
|
ושים הט"ו אצל המגדל שהוא גבוה י"ב | |
|
ושים הי"ב אצל המגדל שהוא גבוה ט"ו | |
|
ובגבול הט"ו והי"ב מן התושבת שם המעיין וכה"ל | |
Rectangle |
||
| Figure Problem - Side; Diagonal; Area – Rectangle | ||
|---|---|---|
|
צ שאלה מרובע ארוך אשר אלכסונו עם צלעו האחד י"ח וצלעו השנית ו' כמה הוא ריבועו ואלכסונו וצלעו המנויה עם האלכסון | |
|
||
|
והמשיב על השאלה הזאת [20]ירבע את הצלע הידועה והוא ו' ויהיה רביעו ל"ו | |
|
ויחלקם על מניין האלכסון והצלע השנית שהוא י"ח ותהיה החלוקה ב' | |
|
ויוסיף ב' על י"ח ויהיו כ' | |
|
וידע כי מחצית כ' הוא האלכסון | |
|
| ||
|
והנשאר מי"ח הוא הצלע השנית והוא ח' | |
|
ורבועם ח' בו' והוא התשבורת | |
Quadrangle |
||
| Figure Problem - Area - Quadrangle | ||
|
צא הרי שיש לפניך א' מרובע שאין ארכו כרחבו ואינו שוה האורך האחד לאורך השני וגם רוחב האחד אינו שוה לרוחב השני | |
|
צרף האורך וחלקהו לחצי ותפוש חציו | |
|
וצרף הרוחב עם הרוחב ותפוש חציו | |
|
ותרבה החצי משני הארכים על החצי משני הרחבים וכפי מספר אותם הרבויים יהיו מספר שבריו | |
|
| ||
|
||
|
והמשל בזה הרי שהיה מקום אחד ארכו האחד ד' ואורכו השני ו' ורחבו האחד ה' ורחבו השני ג' כזה | |
|
|
||
|
צרף האורך עם האורך ואמ' ו' וד' הרי י' תפוס חציו הרי ה' ויהיה ד' ארכו ו' לך למשמר | |
|
אחרי כן צרף הרוחב עם הרוחב ואמור ג' וה' הרי ח' תפוס חציו שהוא ד' רחבו ה' | |
|
ותרבה אותו עם הה' שהוא מחצית ב' האורכים ואמור ד' פעמ' ה' הם כ' הרי שמידת שבריו הם כ' וכה"ל | |
|
| ||
Triangulation Problem - Tree leaning against a wall |
||
|
צב הרי שעץ אחד גבוה ל' אמות וזקוף בצד חומה אחת והוסר מלמטה י' אמות נרצה לידע מזה כמה הורד ראש העץ ממקום שהיה | |
|
||
|
אתה יודע כי החומה דהיינו מראש העץ עד הקרקע והקרקע דהיינו מן החומה עד סוף העץ הם שני זוויות על זוית נצבה | |
|
||
|
והאלכסון שלהם הוא העץ שהוא ל' אמות ושברי מרובע שיוצא ממנו הם תת"ק | |
|
ואחר כן תרבע קו הקרקע שהוא י' ושבריו הם ק' | |
|
והוציאם מן התת"ק ישארו ת"ת | |
|
ומצא השורש והוא קו החומה ויהיה מעט יותר מכ"ח ורביע | |
|
| ||
|
והוציאם מן הל' שהיה קו החומה כשהיה העץ זקוף ישארו מעט פחות מא' וג' רבעי' וכן הורד העץ | |
|
ולפעמי' יבא בכיוון וכה"ל | |
|
צג וכן אם היה עץ אחד גבוה י' אמות וזקוף בצד חומה והוסר מלמטה ו' אמות כמה הורד ראש העץ ממקום שהיה | |
|
||
|
עשה כמו שעשינו למעלה ותרבע מדת העץ והם ק' | |
|
אחר כן תרבע הו' אמות שהורד מלמטה והם ל"ו | |
|
והוציאם מן הק' ישארו ס"ד | |
|
ומצא השורש דהיינו ח' והוא קו החומה | |
|
| ||
|
והוציאם מן הי' שהיה קו החומה כשהיה העץ זקוף ומה שישאר בידך הורד העץ דהיינו ב' אמות | |
|
ועתה בא בכיוון וכה"ל | |
Transformation Problems |
||
| Square to Circle | ||
|
צד מרובע שוה צלעות ושבריו ל"ח וחצי ותרצה לעשות מהם עגול שיהיו שבריו כשברי זה המרובע | |
|
| ||
|
תרבה ל"ח וחצי על י"ב וד' שבעיות עולים תפ"ד | |
|
ותמצא השורש מתפ"ד והם כ"ב והוא יהיה מספר העגול יהיו שבריו כשבר המרובע שמספר שבריו ל"ח וחצי וכה"ל | |
|
| ||
| Circle to Square | ||
|
צה עגול שבריו ק' ותרצה לעשות ממנו מרובע שוה צלעות | |
|
| ||
|
תפוס השורש מק' והוא י' והוא יהיה מדת כל צלע מצלעו וכה"ל | |
Volume |
||
Sphere |
||
|
[21]צו תשבורת הכדור | |
|
כאשר זכרו אנשי חכמת השיעור הוא שתהיה מרבע את קוטר הכדור ותכפול המרובע הזה ג' פעמ' ושביעית פעם ויעלה בידך משיחת שטח הכדור | |
|
מנה אותו בשתות הקוטר ויעלה בידך תשבורת גוף הכדור | |
|
כגון כדור אשר קוטרו ז' אמות | |
|
יהיה מרובע הקטר מ"ט אמה | |
|
וכשאתה כופל המספר הזה ג' פעמ' ושביעית פעם יהיה קנ"ד והם מניין שטח אמות הכדור | |
|
מנה אותו בשתות הקוטר והוא אחד ושתות ויהיה ק"פ פחות שליש והוא תשבורת גוף הכדור הזה | |
Segment of a Sphere |
||
|
ומתוך החשבון הזה אתה יכול להבין תשבורת שברי הכדור | |
|
כגון בריכת מים אשר גופה מבפנים מעוגל ופיה עגול ורחבו ז' אמות ועומקו ג' אמות וחצי | |
|
ואתה יודע כי הבריכה הזאת היא חצי כדור ובא ומנה עומקה ברחב פיה אשר הוא קוטר הכדור והנקבץ בידך כפליהו ג' פעמי' ושביעית פעם כאשר עשית בכדור ויעלה ע"ז והוא משיחת שטח הבריכה | |
|
מנה אותו בשתות הקוטר יהיה צ' פחות שתות והוא תשבורת גוף הבריכה אשר היא חצי כדור | |
|
ואלו היה העומק פחות ממחצית הרוחב תהיה יודע שהבריכה הזאת מעוטה מחצי הכדור | |
|
כגון עגולת גוף שעמקה ב' אמות ורוחב עגולת פיה גדר מ' שהוא ו' ושליש בקירוב | |
|
ואתה יודע שהבריכה הזאת אין בה חצי כדור מפני שעומקה פחות ממחצית רוחב פיה | |
|
ואם אתה מוציא את קוטרה כאשר למדת תמצאנו ז' | |
|
ובא ומנה ב' שהוא עומק הבריכה בז' שהוא קוטר הכדור יהיו י"ד | |
|
כפול אותם ג' פעמי' ושביעית יהיו מ"ד והוא משיחת שטח הבריכה | |
|
מנה אותו בשתות הקוטר והוא אחד ושתות יהיו נ"א ושליש והוא תשבורת גוף הבריכה | |
|
ואם היית אומר עומק הבריכה ה' אמות ורוחב פיה גדר מ' | |
|
היות מוצא קוטרה ז' | |
|
ואם אתה מונה העומק בקוטר יהיה ל"ה | |
|
כפליהו ג' פעמ' ושביעית יהיה ק"י והוא משיחת שטח הבריכה | |
|
מנה אותו בשתות הקוטר יהיה קכ"ח ושליש והוא תשבורת רבוע הבריכה וכה"ל | |
Triangular Prism |
||
|
צז מצבה חצויה וקורים למצבה משולשת חצויה מפני שהיא מחצית המרובעת | |
|
מצבה חצויה אשר ראשה ותושבתה משולש נצב הזוית אשר צלעו האחת ג' אמות והשני ד' והשלישית ה' וגובהו י' אמות | |
|
[this figure does not appear in the text] |
||
|
אתה יודע תשבורת המשולש הזה והוא ו' אמות | |
|
מנה אותם בי' שהוא הגובה יהיו ס' אמה והוא תשבורת המצבה חצוית הראש | |
Pentagonal / Hexagonal Prism |
||
|
וכן אלו היה הגולם ראשו ותושבתו שטחים מחומשות או משושתות היא נקראת מצבה מחומשת או משותתת | |
|
תהיה יודע משיחת המחומש או המשותת הזה אשר היא תושבתו או ראשו ותהיה מונה משיחתו במניין הגובה ויעלה בידך תשבורת המצבה ההיא | |
|
| ||
Cylinder |
||
|
ואם יהיה הגולם ראשו ותשברתו שטחים עגולים וכל גופו עולה בעגול עם הראש | |
|
ואתה מונה תשבורת התמונה הזאת על הדרך אשר ידעת התמונות הראשונות | |
|
אם אתה מרבע העגול שהוא התושבת או הראש ואתה מונה מרובעו במניין הגובה יעלה בידך תשבורת התמונה [22]הזאת והיא נקראת מצבה עגולה | |
|
ואני נותן לך דמיון מזה מצבה עגולה אשר ראשה וכן תושבתה שטח עגול אשר קוטרו י' אמות וגובה המצבה י"ד | |
|
||
|
ואתה יכול להגיע אל תשבורת המצבה הזאת אם אתה מונה את קוטר העגול שהוא י' אמות במנין עצמם ויהיו ק' אמות ומנה ק' בי"ד שהם אמות הגובה ויהיו אלף ות' אמות וזה הוא תשבורת התמונה הזאת אלו היתה מרובעת | |
|
הוצא מהמספר הזה שבעיתו וחצי שבעיתו והם ג' מאות אמה ונשאר בידך אלף ומאה אמה והוא תשבורת המצבה העגולה | |
|
| ||
|
וכן אלו היית מוציא מן ק' אמה שהוא רביע התושבת שביעיתו ומחצית שבעיתו והוא כ' אמה וג' חלקי' מז' חלקי' באמה וישאר בידך ע"ח אמה וג' חלקי' מז' באמה והם משיחת העגול אשר היא תושבת המצבה | |
|
| ||
|
מנה אותה בגובה אשר הוא י"ד יעלה המניין לאלף ומאה אמה והוא תשבורת המצבה הזאת העגולה | |
|
| ||
|
ונראה לך שדרך כל המין הזה נוהג מנהג אחד ואם אתה יודע מספר תשבורת מזה התושבת מן התושבת או הראש מאיזו תמונה הייתה ותמנה תשברתה במנין הגובה י' אתה מוצא תשבורת הגוף ההוא ואין שם חילוף | |
Questions about Rectangles |
שאלות במרובע ארוך | |
| Figure Problem - Diagonal - Rectangle | ||
|
צח מרובע ארוך שיש בצלעו האחד ח' אמות ובצלעו השנית ו' כמה הוא אלכסונו | |
|
|
||
|
תשובה מנה ח' שהוא צלע האחת בו' שהוא הצלע השנית ויהיה רבועם מ"ח | |
|
וכפול המרובע הזה והם צ"ו | |
|
ואם תוסיף עליו מרובע ב' אשר היא תוספת הצלע האחת אל השנית יהיה הכל ק' | |
|
וגדר ק' הוא י' והוא אלכסון מן המרובע הזה | |
|
| ||
|
וכללו של ענין שכל מרובע ארוך אם אתה מוסיף רבוע העודף אשר בן שתי צלעיו על כפל תשברתו יהיו אלה שניהם שוים למרובע אלכסונו | |
|
| ||
| Figure Problem - Side; Area - Rectangle | ||
|
צט שאלה אחרת מרובע ארוך אשר באלכסונו י' אמה וארכו מוסיף על רחבו ב' אמות כמה הוא ארכו וכמה הוא רחבו וכמה תשברתו | |
|
|
||
|
תשובה אתה יודע כי מרובע האלכסון הוא ק' | |
|
הוצא ממנו רבוע עדף האורך על הרחב אשר הוא ב' וריבועו ד' ישאר בידך מהם צ"ו | |
|
חלק אותם לשנים ויהיו מ"ח והוא תשבורת המרובע | |
|
| ||
|
ואם תרצה לדעת צלעותיו אשר האחד מוספת על השנית ב' בא וחלק העודף הזה לשנים ויהיה א' וריבועו א' | |
|
הוסיפנו על התשבורת ויהיה מ"ט | |
|
וגדר המניין הזה הוא ז' | |
|
ואם תוסיף עליו אחת שהוא מחצית העודף יהיה ח' והוא קו האורך | |
|
| ||
|
ואם תפחות ממנו א' ישאר ו' והוא קו הרוחב | |
|
ומנין ח' בו' הוא מ"ח והוא התשבורת | |
|
ואם יאמר מרובע בתשברתו מ"ח וקו ארכו עם קו רחבו שניהם יחד י"ד כמה הוא ארכו וכמה הוא רחבו | |
|
ולתשובת השאלה הזאת תקח מחצית י"ד והוא ז' | |
|
ותרבע אותו ויהיה מ"ט | |
|
הוצא מהם מ"ח הוא התשבורת וישאר בידך א' | |
|
וגדר הא' הוא א' | |
|
אם תוסיפנו על ז' יהיה ח' והוא אורך המרובע | |
|
| ||
|
ואם תפחות האחד מן הז' ישאר בידך ו' והוא רוחב המרובע | |
|
והוי יודע כי אם ישאל בענין זה שאלה אשר יהיה בה התשבורת עודף על מרובע מחצית הצלעות כי שאלה זאת שקר וכזב | |
|
כגון האומר לך מרובע שתשברתו מ"ח וקו ארכו עם רחבו י"ג | |
|
טעות הוא בידו [23]או מנסה הוא לך ואינך צריך להשיב | |
Square |
||
| Figure Problem - Diagonal - Square | ||
|
ק שאלה מרובע השוה ונצב הצ' הזוית שארכו י' ורחבו י' כמה הוא אורך אלכסונו | |
|
תשובה האלכסון הזה הוא גדר מאתים כי מרובע האלכסון ימצא ברבועו מאתי' | |
|
מפני שכל מרובע נצב הזוויות רבוע אלכסונו כפלים מהמרובע ההוא | |
|
ומפני זה אמרנו על האלכסון הזה שהוא גדר מאתיי' אשר הוא כפלים מרובע י' על י' | |
| Figure Problem - Side - Square | ||
|
ואם יאמר מרובע שאלכסונו גדר מאתים כמה צלעו | |
|
חלק מרובע האלכסון לשנים ויהיה ק' האחד | |
|
ואמור גדר ק' הוא הצלע המרובע והוא י' | |
|
| ||
|
והאלכסון הזה י"ד ושביעית בקרוב | |
| Figure Problem - Side; Area - Square | ||
|
קא שאלה אחרת מרובע שוה שהוצאת מן מניין תשברתו מניין צלעותיו הארבעה ונשאר בידך מהתשבורת כ"א אמה כמה הוא התשבורת וכמה מניין כל צלע וצלע מהמרובע | |
|
תשובה חלק מנין הצלעות שהוא ד' לשנים | |
|
ומנה השנים בעצמם כלומר רבעם יהיו ד' | |
|
הוסף המניין הזה על המניין המסודר לך הנשאר לך מן המרובע ויהיה הכל כ"ה | |
|
ודע גדר כ"ה והוא ה' | |
|
ותוסיף עליו חצי מניין הצלעות והוא ב' ויהיה הכל ז' והוא צלע המרובע | |
|
| ||
|
ותשברתו מ"ט | |
|
ואם יאמר מרובע אשר הוספת מניין כל ד' צלעותיו על מניין תשברתו ויהיה הכל ע"ז כמה הוא המרובע הזה | |
|
ואתה בשאלה הזאת קח מניין חצי הצלעות והוא ב' | |
|
ותמנה אותו בעצמו ויהיו ד' | |
|
והוסיפנו על המניין שמסר לך והוא ע"ז ויהיו פ"א | |
|
וקח גדר המספר הזה והוא ט' | |
|
הוצא ממנו חצי מספר הצלעות שהוספת וישארו בידך ז' והוא צלע המרובע | |
|
| ||
|
ותשברתו מ"ט | |
| Figure Problem - Side - Square | ||
|
קב שאלה שלישית מרובע השלכת תשברתו ממניין ד' צלעותיו ונשאר בידך ג' | |
|
חלק מניין הצלעות על ב' וחציים הוא ב' | |
|
וריבועם הוא ד' | |
|
הוצא מהם השלשה שנשארו בידך וישאר א' | |
|
אשר גדרו א' | |
|
פחות אותו ממחצית הצלעות וישאר אחד והוא צלע המרובע | |
|
| ||
|
או הוסף עליו גדר האחד שנשאר בידך על מחצית הצלעות יהיו ג' ויהיו גם הם צלע המרובע | |
|
כי יכול יהיה א' הגדר ויכול יהיה ג' כי שני חשבונות לשאלה הזאת | |
Area |
||
Circle |
||
|
קג אם תרצה לדעת תשבורת העגול התמים אם תדע אלכסונו והוא הקוטר | |
|
תכפול אותו ג' פעמי' ושבעית פעם והוא יהיה אורך הקו הסובב | |
|
ואחר כן הוי מרבע מחצית הקוטר במחצית הקו הסובב והוא יהיה תשבורת העגול | |
|
והדמיון לענין הזה עגולה שהקוטר שלה י"ד | |
|
|
||
|
ואתה כופל אותו ג' פעמ' ושביעית ויהיה מ"ד והוא מדת הקו הסובב | |
|
ואם אתה מונה מחצית הקוטר והוא ז' במחצית הקו הסובב והוא כ"ב יהיה המניין קנ"ד אמות והוא תשבורת העגול | |
Triangle |
||
|
קד הרי שיש לפניך אי' משולש כזה ותרצה לידע מדת שבריו | |
|
|
||
|
תרבה חצי צלע העליון על כל העמוד וכן יהיו מדת שבריו | |
|
המשל בזה הרי שהיה צלע העליון י' אמות והעמוד שלו י"ב אמות | |
|
תקח [24]חצי צלע העליון שהוא ה' ותרבה אותו על כל העמוד שהוא י"ב ואמור ה' פעמ' י"ב ס' וכן יבא | |
Square |
||
|
קה המרובע שהוא שוה הצלעות וכל זוויותיו נצבות ותרצה לידע תשברתו | |
|
תמדוד אחד מצלעיו ותרבה אותו בעצמו וכפי מה שיעלה כן יהיה | |
|
המשל בזה מרובע אחד שכל אחד מצלעותיו ד' וזוויותיו נצבות | |
|
|
||
|
תמדוד אחד מצלעותיו שהוא ד' ותרבה אותו בעצמו ואמור ד' פעמ' ד' י"ו וכן יהיה מניין תשברתו וכה"ל | |
Triangle whose base is an arc - Sector |
||
|
קו משולש אשר תושבתו עקמימות ב"ג וב' צלעיו הם קוים ישרים והם כצורה אשר אני מצייר לך ב' קוים א"ב וא"ג והתושבת קו עקום אשר עליו בד"ג | |
|
ואם אתה עושה כצורה הזאת קו כגון קו ב"ג יהיה לך משולש ישר אשר עליו אב"ג וצורת העקום אשר עליה בד"ג והיא שבר עגולה | |
|
|
||
|
ואתה מרבע כל אחד מהם לבד ותאסוף שני המרובעים ויהיו תשבורת הצורה | |
Rectangle |
||
|
קז המרובע ארוך שלא תהיינה צלעותיו שוות זו לזו אבל הנכוחים לבד הם שוות דהיינו שיהיו שני הארוכים שוים ושני הרחבים שוים וכל הזוויות הם נצבות ותרצה לידע תשברתו | |
|
תרבה צלע האורך עם צלע הרוחב וכאשר יעלה כן יהיה תשברתו | |
|
כגון מרובע ארוך ששתי צלעותיו האורך כל אחד מהם ט' אמות ושתי צלעות הרוחב כל אחד מהם ה' אמות כזה | |
|
|
||
|
תרבה האורך עם הרוחב ואמור ה' ט' הם מ"ה וכן יהיה מניין תשברתו וכה"ל | |
Rhombus |
||
|
קח המרובע שהוא שוה הצלעות ואינו נצב הזוויות והוא הנקרא מרובע המעויין כגון מרובע שיש בכל צלעותיו י' אמות ואינו נצב הזוויות ואתה מוצא אלכסונותיו שאינן שוים כגון שיהיה האלכסון האחד י"ב אמות ואלכסון השני י"ו אמות | |
|
|
||
|
תמנה האלכסון האחד במחצית האלכסון השני | |
|
ואמור י"ו פעמי' ו' הם צ"ו וכן יהיה מנין תשברתו | |
|
או אמור י"ב פעמ' ח' צ"ו וכן יהיה מניין תשברתו וזו היא הצורה | |
Equilateral Triangle |
||
|
קט משולש שוה הצלעות ותרצה לדעת תשברתו | |
|
|
||
|
דע כי תשברתו הוא שלישית מרובע צלעו ועשירית מרובע הצלע | |
|
כגון משולש שכל אחד מצלעיו ט"ו | |
|
תרבה אחת מצלעיו ואמור ט"ו פעמי' ט"ו הם רכ"ה | |
|
קח שלישית רכ"ה שהוא ע"ה ועשירית רכ"ה שהוא כ"ב וחצי ויהיה הכל צ"ז וחצי וכן יהיה תשבורת זה המשולש וכה"ל וזאת היא הצורה | |
|
| ||
|
ואם תרצה לדעת תשבורת המשולש בעניין אחר | |
|
תרבע העמוד [25]היוצא בו במחצית התושבת או תרבע התושבת במחצית העמוד | |
|
כגון משולש שכל אחד מצלעותיו ט"ו ועמודו י"ג כזה | |
|
תרבה העמוד שהוא י"ג במחצית התושבת שהוא ז' וחצי ואמור י"ג פעמ' ז' וחצי הם צ"ז וחצי וכן יהיה תשבורת המשולש | |
|
או תרבע התושבת שהוא ט"ו במחצית העמוד שהוא ו' וחצי ואמור ט"ו פעמ' ו' וחצי צ"ז וחצי וכן יהיה תשברתו וכה"ל | |
Equilateral Triangle |
||
| Figure Problem - height; Area - Equilateral Triangle | ||
|
קי ואם תרצה לדעת שבור העמוד מן המשולש שהוא שוה הצלעות עשה כענין זה כגון משולש שכל אחד מצלעותיו י' כזה | |
|
|
||
|
תרבה הצלע האחד בעצמו ואמור י' פעמ' י' הם ק' | |
|
ותרבה חצי התושבת שהוא ה' בעצמו ואמור ה' פעמ' ה' כ"ה | |
|
ותפחות אותם מק' ישארו ע"ה | |
|
ותמצא הגדר של ע"ה והנו ח' וב' שלישי בקירוב והוא יהיה מספר העמוד | |
|
| ||
|
ואם תרצה לדעת שברי זה המשולש | |
|
תרבה כל העמוד עם חצי התושבת שהוא ה' | |
|
או תרבה כל התושבת במחצית העמוד | |
| Figure Problem - height; Area; Side - Equilateral Triangle | ||
|
קיא ואם תרצה לדעת שיעור העמוד בעניין אחר מן המשולש שהוא שוה הצלעות | |
|
תפחות לעולם מן הצלע שלמשולש שוה הצלעות ב' חלקי' מט"ו והוא יהיה מספר העמוד | |
|
כגון משולש שכל אחד מצלעותיו [ט"ו]
הוי יודע כי עמודו י"ג | |
|
תרבה י"ג שהוא העמוד בז' וחצי שהוא חצי התושבת | |
|
או כל התושבת שהוא ט"ו בו' וחצי שהוא חצי השיעור מן העמוד | |
|
ואם תדע העמוד מן המשולש השוה הצלעות ותרצה לדעת הצלע מן העמוד ההוא | |
|
תרבע העמוד בעצמו והוסיף על זה המרובע שלישיתו ותידע כמה הוא גדר הכל והוא יהיה מדת כל צלע מצלעי המשולש שוה הצלעות | |
|
כגון משולש שהעמוד שלו הוא י"ג ותרצה לידע מידת הצלע | |
|
תרבה העמוד בעצמו ואמור י"ג פעמ' י"ג קס"ט | |
|
הוסף עליהם שלישית קס"ט שהם נ"ו ושליש יהיו רכ"ה ושליש | |
|
תמצא הגדר של רכ"ה ושליש שהם ט"ו בקירוב והוא יהיה מספר הצלע | |
|
| ||
Scalene Triangle |
||
| Figure Problem - Side - Scalene Triangle | ||
|
קיב אם יאמר לך אדם משולש מתחלף עמודו י"ב והצלע האחר המקפת את ראשו י"ג והשנית ט"ו כמה תהיה התושבת | |
|
והתשובה בשאלה הזאת תרבע הצלע האחת כגון י"ג שריבועה קס"ט | |
|
ותוציא ממנו מרובע העמוד והוא קמ"ד ישאר כ"ה שגדרו ה' והוא המעמד האחד | |
|
ושוב ורבע את הצלע השנית ומרובעה רכ"ה | |
|
הוצא ממנה מרובע העמוד ישאר פ"א וגדרו ט' והוא המעמד השני | |
|
וב' המעמדי' האלה הם י"ד והוא אורך התושבת | |
|
| ||
| Figure Problem - height - Scalene Triangle | ||
|
ואם יאמר לך משולש מתחלף בתשברתו עם העמוד צ"ו ותושבת העמוד י"ד כמה הוא העמוד | |
|
תשובה קח מחצית התושבת והוסף אחד לעולם וחלק עליה את המספר אשר בידך ותמצא העמוד | |
|
כאילו היית מחלק בשאלה הזאת התושבת לשנים ומחציתה הוסף עליה אחד יהיו ח' חלק עליהם צ"ו יהיה י"ב והוא אורך העמוד | |
Isosceles Triangle |
||
| Figure Problem - Area; height; Side - Isosceles Triangle | ||
|
קיג משולש שוה השוקים והוא משולש ששוקיו שוים והתושבת אינו שוה עמהם [26]כגון זה המשולש שכל אחד משוקיו ט"ו והתושבת היא י"ח | |
|
|
||
|
נדע מספר העמוד תחלה ונעשה בענין זה | |
|
נרבע אחד מן השוקים בעצמו ואמור ט"ו פעמי' ט"ו הם רכ"ה | |
|
ונפחות מרכ"ה מרובע חצי התושבת וחצי התושבת הוא ט' ומרובעו פ"א ונפחות אותם מרכ"ה ישארו קמ"ד | |
|
ותמצא השורש מקמ"ד והוא י"ב וכן יהיה מספר העמוד הזה י"ב | |
|
| ||
|
ואם תרצה לדעת תשבורת המשולש הזה | |
|
תרבה כל העמוד שהוא י"ב על חצי התושבת שהוא ט' ואמור ט' פעמ' י"ב הוא ק"ח והוא תשבורת זה המשולש | |
|
או תרבה כל התושבת שהוא י"ח על חצי העמוד שהוא ו' ואמ' ו' פעמ' י"ח הוא ק"ח והוא יהיה תשברתו וכה"ל | |
|
ואם תדע מדת העמוד ומדת התושבת ממשולש שוה השוקים ותרצה לדעת מדת כל אחד מהשוקים כגון זה המשולש שעמודו י"ב ותושבתו י"ח | |
|
תרבע העמוד בעצמו שהוא י"ב ואמור י"ב פעמ' י"ב הם קמ"ד | |
|
הוסף עליהם מרובע חצי התושבת שהוא ט' שיבא פ"א וקבצם יהיו רכ"ה | |
|
תמצא השורש מרכ"ה והוא ט"ו וכן יהיה מדת כל אחד מהשוקיים וכה"ל | |
|
| ||
Area |
||
Scalene Triangle |
||
|
קיד משולש מתחלף הצלעות כגון משולש אב"ג שצלע א"ב י"ג וצלע ב"ג י"ד וצלע א"ג ט"ו | |
|
|
||
|
וזה המשולש לא נוכל לדעת תשברתו אלא מן העמוד | |
| [Although later on (problem 116) a general formula is given for finding the area of any triangle according to its three sides without needing to know the height] | ||
|
כי כל משולש בין שוה הצלעות בין מתחלף הצלעות תשברתו הוא ברבוע העמוד על חצי התושבת או בריבוע כל התושבת בחצי העמוד | |
|
| ||
|
ולכן נצטרך להוציא העמוד ולהגביל מעמדו בתושבת | |
|
כי העמוד במשולש הזה אינו עומד במחצית התושבת אבל נוטה ממחצית התושבת אל צד אחד | |
|
והצד הארוך מגבול מעמדו אנו קוראים לו מעמד ארוך והצד השני מעמד קצר | |
|
ואם נרצה להוציא המעמד הארוך | |
|
נקח מרובע הצלע משתי הצלעות אשר העמוד יוצא מבניהם והוא צלע א"ג שהוא ט"ו ומרבעו רכ"ה | |
|
ונחבר המרובע הזה אל מרובע התושבת שהוא י"ד ומרובעו קצ"ו ויהיו שני המרובעים תכ"א | |
|
נוציא מהם מרובע צלע הקצר שהוא צלע א"ב שהוא י"ג ומרובעו קס"ט וישארו רנ"ב | |
|
נחלק רנ"ב לשנים ויהיה המחצית קכ"ו | |
|
נחלק קכ"ו על התושבת שהוא י"ד יהיו ט' והוא מרחק גבול מעמד העמוד מן הצלע הארוך הרי שקו ג"ד הוא ט' | |
|
| ||
|
ואם נרצה לדעת המעמד הקצר | |
|
נקח מרובע הצלע הקצר שהוא י"ג ומרובעו קס"ט | |
|
עם מרובע התושבת שהוא קצ"ו ויהיו שני המרובעי' שס"ה | |
|
נוציא מהם רכ"ה שהוא מרובע קו א"ג שהוא הצלע הארוך שהוא ט"ו ישארו ק"מ | |
|
חלקם לשנים ויהיה המחצית ע' | |
|
נחלקם על התושבת שהוא י"ד יהיו ה' וכן מרחק מעמד העמוד מן הצלע הקצר | |
|
| ||
|
ואם תרצה לדעת אורך זה העמוד | |
|
נרבע הצלע ונוציא ממרובעו מרובע המעמד הדבק בו ונקח גדר הנשאר והוא יהיה אורך העמוד | |
|
| ||
|
המשל בזה נרבע הצלע הקצר שהוא י"ג בזה המשולש יהיו קס"ט | |
|
נפחות מקס"ט מרובע המעמד הקצר הדבק בו דהיינו קו ד"ב שהוא ה' ומרובעו כ"ה ישארו קמ"ד | |
|
וגדר קמ"ד הוא י"ב [27]הרי שמספר העמוד הוא י"ב | |
|
| ||
|
וכן אם נרבע הצלע הארוך שהוא ט"ו ומרובעו רכ"ה | |
|
ונפחות ממנו מרובע המעמד הארוך דהיינו קו ג"ד שהוא ט' ומרובעו פ"א ישארו קמ"ד כמו שנשאר מן הצלע הקצר | |
|
וגדר קמ"ד הוא י"ב והוא אורך העמוד | |
|
| ||
|
ואם תרצה לדעת תשבורת זה המשולש | |
|
תרבה כל העמוד שהוא י"ב בחצי התושבת שהוא ז' שיבואו פ"ד והוא תשברתו | |
|
או תרבה כל התושבת שהוא י"ד בחצי העמוד שהוא ו' ויהיו פ"ד והוא תשברתו וכה"ל וזאת היא צורתה | |
Right Triangle |
||
|
קטו המשולש הזה נקרא משולש נצב הזויות ואם תרצה לדעת תשברתו | |
|
תרבה הצלע האחד מן הצלעות המקיפות בזוית הנצבה בחצי הצלע האחרת | |
|
כגון אם היה קו ב"א י' וקו ב"ג ג"כ י' | |
|
|
||
|
אמור י' פעמ' ה' הם נ' והוא תשברתו | |
|
כי אתה רואה שהוא חצי מרובע שוה הצלעות נצב הזוויות | |
|
ואם היה מרובע שלם היינו אומרי' י' פעמ' י' הם ק' | |
|
ועכשיו שהוא חצי מרובע נאמר י' פעמ' ה' הם נ' וכן לכל חשבון כזה | |
|
| ||
Heron's Theorem |
||
|
קיו כלל גדול לדעת תשבורת המשולש שאינך צריך בו אל הוצאת העמוד והחשבון הזה נקרא חשבון המותרות | |
|
והוא שתדע מחצית כל אחד מצלעי המשולש ותקבץ כל המחציות האלה | |
|
ותדע מותר כללם על כל צלע וצלע ותשמור המותרות האלה | |
|
ותמנה אחד מהם בשיני והמספר הנקבץ מנה אותו בשלישי במספר | |
|
ואשר יכנס בידך מהחשבון הזה מנה אותו בכל כלל המחציות אשר קבצת | |
|
ויהיה המספר הזה מרובע תשבורת המשולש | |
|
ואם תוציא גדר המספר הזה תמצא התשבורת | |
|
| ||
|
המשל בזה משולש שצלעו האחד י' והשני ח' והשלישי ו' | |
|
|
||
|
ואם אתה מקבץ מחצית ג' הצלעות האלה יהיה המספר י"ב | |
|
ומותר י"ב על הצלע האחד ב' ועל השני ד' ועל השלישי ו' | |
|
ואתה בוא ומנה ב' שהוא מותר הצלע האחד בד' שהוא מותר הצלע השני יהיו ח' | |
|
בוא ומנה אלו הח' בו' שהוא מותר הצלע השלישי ויהיו מ"ח | |
|
שוב ומנה מ"ח בי"ב שהוא כלל המחציות ויהיו תקע"ו ותקע"ו הוא מרובע התשבורת | |
|
ואם תמצא הגדר של תקע"ו יהיו כ"ד והוא יהיה תשבורת זה המשולש וכה"ל | |
|
| ||
Parallelogram |
||
|
קיז מרובע ששני אורכיו שוים וכל אחד מהם כ"ה ושני רחביו שוים וכל אחד מהם ט"ו ואין זוויותיו נצבות כגון זה | |
|
|
||
|
כשנבוא לרבעו נמדוד בו אלכסון א"ג והיה כ' אמה והוא החולק הזה המרובע לב' משולשים שוים ואין אנו יכולין לדעת שברי זה המרובע אלא מתוך ריבוע ב' המשולשים האלה | |
|
ומפני זה אם אנו מוציאים את העמוד באחד מהם נדע תשבורת המשולש ההוא ונכפול אותו ונמצא תשבורת שני המשולשים דהיינו תשבורת כל זה המרובע | |
|
ואם תוציא עמוד [28]במשולש אב"ג על צלע א"ב יהיה העמוד י"ב ותשבורת המשולש ק"נ וכפל ק"נ הוא ש' והוא תשבורת המרובע הזה | |
|
ומי שלא היה מבין זה הדרך והיה מרבע האורך עם הרוחב כשאר המרובעים שהם על זוויות נצבות והיה אומ' כ"ה פעמ' ט"ו היו עולים שע"ה ראה כמה טעות בין שני החשבונות המרובע עודף | |
| Additional segment: the differences between the square and its inner circle and the inner square of the inner circle | ||
|
המרובע עודף על העגול שבתוכו העגול עודף על המרובע שבתוכו | |
|
||
Trapezoid |
||
Isosceles Trapezoid |
||
|
קיח קטומת הראש כגון זאת הצורה שיש לה ד' צלעות ועליהם אבג"ד וצלע א"ב וג"ד הם שוות וכל אחד מהם י"ג | |
|
והצורה הזאת נקראת קטומת הראש שוה | |
|
וצלע א"ג שהיא הקצרה משתי צלעות הנכוחייות נקראת ראש הקטומה | |
|
וצלע ב"ד הארוכה נקראת תושבת הקטומה | |
|
|
||
|
והרוצה למדוד הצורה הזאת יוציא עמודה ראשונה | |
|
ודרך הוצאתו הוא שיפחות ראש הקטומה משרשה מתושבתה | |
|
והעודף ביניהם יחלק אותו לשנים | |
|
וידע מרובע המחצית | |
|
ויפחות מהמרובע הזה מרובע אחת מן הצלעות השוות | |
|
והנשאר ממרובע הצלע ידע שרשו והוא יהיה מספר העמוד | |
|
ובצורה הזאת נפחות מנין ח' שהוא ראש הקטומה מן י"ח שהוא התושבת ישאר י' | |
|
והמחצית מי' הוא ה' והוא יהיה ודאי חלק העודף האחד מנקודת ה' קו ב"ה ומנקודת ז' קו ד"ז | |
|
ונוציא קו מא' אל ה' ומן ג' אל ז' ובידוע שכל קו מהם הוא עמוד על תושבת ב"ד | |
|
ויהיה משולש אה"ב נצב הזוית ומיתר הזוית הזאת הוא קו א"ב | |
|
ובידוע כי מרובע המיתר הזה שהוא י"ג שוה למרובע ב"ה שהוא אשר ידענו שהוא ה' ולמרובע א"ה שאנו רוצים לדעתו | |
|
ואם נפחות מרובע ה' שהוא כ"ה ממרובע י"ג שהוא קס"ט ישאר קמ"ד | |
|
ובידוע שגדר קמ"ד והוא י"ב יהיה מדת העמוד | |
|
| ||
|
ואם תרצה לדעת תשבורת זאת הצורה | |
|
תכניס הראש עם התושבת ויהיו כ"ו | |
|
קח מחציתם והם י"ג | |
|
ומנה אותם בי"ב שהוא מדת העמוד יהיו קנ"ו והוא תשברתו | |
|
| ||
|
ואם תרצה להאריך למעלה שני צלעי הקטומה שהם קו א"ב וג"ד עד שיפגשו אל נקודת ז' כמו שתראה בצורה ותהיה הצורה דומה למשולש | |
|
|
||
|
ותרצה לדעת אורך הקוים העולים למעלה והם קוי א"ז וג"ז | |
|
תדע עודף התושבת על הראש שהוא י' בצורה הזאת ותשמור אותו עמך | |
|
ושוב ותראה הראש שהוא ח' בכל הצלע [29]שהוא י"ג ויהיה הכל ק"ד | |
|
חלקם על י' אשר הוא העודף אשר שמרת ותהיה החלוקה י' ושני חומשי' והוא אורך קו א"ז וכמו כן קו ג"ז העולים עד הנקודה | |
|
| ||
|
או תעשה על זה הדרך שתדע ערך ח' אמות שהוא אורך הראש מי' שהוא עודף התושבת על הראש | |
|
וערך ח' אל י' הוא ד' חמשי' דהיינו א' פחות חומש | |
|
וכערך ח' אל י' כן יהיה ערך הקו העולה עד נקודת הז' אל י"ג שהוא הצלע | |
|
| ||
|
דהיינו שיהיו י"ג פחות י"ג חומשי' שהם י' וב' חמשים וכה"ל | |
Trapezoid |
||
|
קיט רבוע הקטומה הזאת הוא בריבוע אחד מעמודה במחצית הראש והתושבת יחד | |
|
|
||
|
והוא שתהיה מקבץ בצורה הזאת ח' שהוא אורך הראש כ"ב שהוא התושבת ויהיה הכל ל' | |
|
קח מחציתו והוא ט"ו ומנה אותו בי"ב שהוא אורך העמוד ויהיה הכל ק"פ והוא יהיה תשבורת הקטומה הזאת וזאת היא הצורה | |
Right Trapezoid |
||
|
קכ רבוע הקטומה הזאת | |
|
|
||
|
הוא באסיפת ראשה אל תושבתה ותקח מחצית' וימנה בעמוד והוא יהיה תשברתה | |
|
ואם תאסוף בצורה הזאת ראשה אל תושבתה יהיה כללם כ"ח | |
|
קח מחציתם שהוא י"ד ותרבה אותו בט' שהוא אורך העמוד יהיו קכ"ו והוא תשבורת הקטומה הזאת | |
Trapezoid |
||
|
קכא תשבורת הקטומה הזאת | |
|
|
||
|
הוא ברבוע העמוד בחצי הראש וחצי התושבת | |
|
וחצי הראש וחצי התושבת הם י"ז וחצי | |
|
תרבה אותם על י"ב שהוא העמוד יהיו ר"י והוא תשברתו וכה"ל | |
| Figure Problem - Quadrangle whose two sides are equal to its diagonal | ||
|
קכב מרובע שני קוויה כמרובע אלכסונה | |
|
||
Arc |
||
Half a Circle; Arc |
||
|
קכג צורת חצי עגול אם תרצה לדעת תשבורת הצורה הזאת | |
|
תרבע חצי המיתר שהוא חצי קוטר העגול בחצי הקו העקום הנקרא קשת ותמצא התשבורת | |
|
ואם תרצה לדעת מדת הקשת תכפול חצי המיתר שהוא ד' ג' פעמ' ושביעי' פעם [30]ויהיו י"ב אמות וד' שבעיות וכן יהיה מדת הקשת ר"ל הקו הסובב עקמומית זה החצי העגול | |
|
|
||
|
ואם תרצה לדעת שברי זה החצי העגול תרבע כאשר אמרנו חצי המיתר בחצי הקו הסובב דהיינו שתאמ' ד' פעמ' ו' וב' שבעיות יהיו כ"ה ושביעית וכן יהיה תשבורת חצי העגול וכה"ל | |
|
או תעשה על דרך זה תרבע את המיתר בעצמו ותוציא מזה המרובע שביעיתו וחצי שביעיתו וקח מחצית הנשאר והוא יהיה תשבורת חצי העגול | |
|
ובצורה הזאת אשר עשינו תרבע המיתר שהוא ח' בעצמו יהיו ס"ד | |
|
הוצא ממנו שבעיתו וחצי שביעיתו שהם י"ג אמות וה' שבעיות ישארו נ' אמות וב' שביעי אמה | |
|
קח מחציתם שהם כ"ה ושביעית והוא יהיה תשבורת חצי העגול | |
|
| ||
Arc, smaller than half a circle |
||
|
קכד קשת פחות מחצי עגול הדמיון לצורה המעוטה מחצי העגולה היא צורת קשת אב"ג ומיתרה א"ג ואורכו ח' וחיצה ד"ב ואורכו ב' | |
|
|
||
|
ואי אתה יכול להגיע לתשבורת הצורה הזאת אם אינך יודע כל קוטר העגול שזה הקשת נקטם ממנו | |
|
ותוכל לדעת קוטר העגול בעניין זה תרבע מחצית המיתר ותחלק מרובעו על החץ והוסף מדת החץ עליו ותדע סך הכל והוא יהיה אורך כל הקוטר | |
|
ומצורה הזאת אשר עשינו | |
|
תרבע מחצית המיתר שהוא ד' בעצמו יהיו י"ו | |
|
וחלק אותו על החץ שהוא ב' יהיו ח' והוא האורך הנשאר מן הקוטר | |
|
הוסף עליהם ב' שהוא החץ יהיו י' | |
|
הרי שכל הקוטר מן העגול שזה הקשת נקטם ממנו הוא י' וכה"ל | |
|
ולראות העניין באר הטב הוי משלים העגולה הזאת כלה | |
|
והוצא קו ב"ד עד שיגיע אל עקמימות העגולה מן הצד השני כגון קו בד"ז | |
|
ואם תרצה לידע תשבורת הצורה הזאת | |
|
חלק קו ב"ז לב' חלקי' שוים על נקודת ח' ותהיה הנקודה הזאת ציר העגולה | |
|
ותרצה והוצא ממנה ב' קווים אל נקודת א' ואל נקודת ג' והם קוי ח"א וח"ג | |
|
|
||
|
ואם אתה מרבע קו א"ח שהוא חצי הקוטר העגול בחצי הקשת אשר הוא עוקם א"ג יהיה מנין הזה תשבורת המשולש אשר ב' צלעיו הם ב' קוי א"ח וח"ג | |
|
ותשבורת קשת אב"ג הוצא מן המנין תשבורת המשולש אח"ג וישאר בידך תשבורת הצורה שעליה אבג"ד | |
|
ותשבורת המשולש הזה הוא רבוע קו ח"ד שהוא בצורה הזאת ג' אמות בחצי קו א"ג והוא ד' אמות ורבועם י"ב | |
|
והוא הסך אשר תוציא מרבוע קו א"ח הישר בקו א"ב העקום ויהיה הנשאר תשבורת צורת אבג"ד שהוא צורת הקשת שהוא פחות מחצי עגול | |
|
| ||
|
ומכאן אתה אומ' כי רבוע הקשת שהוא פחות מחצי עגול הוא שתרבע חצי כל הקוטר מן העגול שהקשת נקטם ממנו בחצי הקשת ותשמור אותו | |
|
ואחרי כן תוציא מחצי הקוטר קו החץ אשר לקשת והנשאר מחצי הקוטר מנה אותו במחצית המיתר | |
|
והעולה בידך תפחות אותו מן המנין אשר שמרת בידך והנשאר בידך הוא תשבורת הקשת שהוא [31]פוחת מחצי עגול | |
|
| ||
Arc, greater than half a circle |
||
|
קכה צורת הקשת העודף על חצי העגול והוא קשת אשר עליו אב"ג ומיתרו א"ג ואורכו י"ב | |
|
|
||
|
ואם תרצה לדעת תשבורת הצורה הזאת תוציא קוטר כל העגול שזאת הצורה נקטמת ממנו ותרבה חצי הקוטר בחצי הקשת ותוסיף עליו תשבורת המשולש אשר המיתר הוא תושבתו ויהיה סך הכל תשבורת כל זאת הצורה | |
|
ובצורה הזאת תרבע חצי המיתר שהוא ו' בעצמו שיבואו ל"ו | |
|
חלק אותם על החץ שהוא י"ב ויהיה החלוקה ג' | |
|
הוסיפם על החץ יהיה סך הכל ט"ו והוא אורך כל הקוטר מן העגול שזאת הצורה נקטמת ממנה | |
|
ומחציתו הוא מחצית הקוטר והוא בצורה הזאת קו ב"ז הרי שקו ב"ז הוא ז' וחצי | |
|
מנה אותו במחצית הקשת ומה שיעלה יהיה תשבורת הצורה העקומה אשר יקיפו אותה ב' קווי ג"ז וא"ז עם קשת א'ב'ג' | |
|
הוסף עליהם תשבורת משולש א'ז'ג' והוא המספר הנקבץ מרובע קו ד"ז במחצית קו א"ג וכשתקבץ הכל יהיה תשבורת העקמומית הזאת | |
|
| ||
|
ומכאן אתה למד הרוצה לדעת תשבורת העקום העודף על חצי העגול יהיה מרבע חצי הקוטר בחצי הקשת וישמור המספר | |
|
ואחרי כן יפחות חצי הקוטר מן החץ | |
|
[והנשאר מן החץ] ירבע אותו בחצי המיתר | |
|
והמספר העולה יאספינו אל המספר אשר שמר ויהיה הכל סך תשבורת העקומה העודפת על חצי העגול | |
|
| ||
Divide a Figure |
||
Triangle |
||
|
קכו אם תרצה לחלק המשולש לב' חלקי' שוים וישאר החלק האחד משולש והשני דומה למרובע | |
|
כגון משולש א'ב'ג' אשר ראשו נקודת א' ותושבתו ב"ג ותרצה לחלקו לחצי | |
|
אתה צריך לחלק כל אחד מצלעי א"ב וא"ג לב' חלקי' בענין שיהיה מרובע הצלע כולו כפליים ממרובע הצלע החלק הגדול מחלקיו | |
|
כגון שתהיה חולק קו א"ב לב' חלקים על נקודת ד' וקו א"ג לב' חלקי' על נקודת ה' | |
|
|
||
|
ויהיה מרובע א"ד מחצית מרובע א | |
|
וכן מרובע א"ה מחצית מרובע א"ג | |
|
ותוציא קו מד' על ה' והיה משולש נחלק לב' חלקי' שוים החלק האחד משולש א'ד'ה' וחלק השני נפתל ד'ה'ב'ג' | |
|
ודרך חשבון המרובעים האלה יהיה אם תהיה לוקח מאורך הקו מנקודת א' אשר הוא הראש ה' חלקי' מז' בו פחות חצי עשירית השביעית והכלל המסור לזה הוא שתהיה לוקח מן הקו צ"ט חלקי' מק"מ חלקי' בו | |
|
כאילו היה אורך צלע א"ב ז' אמות | |
|
יהיה קו א"ד מהם ה' אמות פחות חלק אחד מעשרים באמה | |
|
וצלע א"ג היה אורכו י' אמות | |
|
יהיה קו א"ה ז' אמות וחלק אחד מי"ד באמה | |
|
ועל החשבון הזה אתה חולק את שתי הצלעות האלה ותוציא קו מן החלק האחד אל השני ויחלק המשולש לב' חלקים שוים | |
Triangular Field |
||
|
[32]קכז ואם יהיה קרקע המשולש לג' בעלים ואתה צריך לחלקו ביניהם וכל אחד מהבעלים מבקש חלקו נגד צלע אחד מצלעי המשולש | |
|
ויהיה המשולש הזה משולש א'ב'ג' | |
|
ואתה בא וחלק צלע א"ב לב' חלקי' שוים על נקודת ד' | |
|
והוצא קו מד' אל ג' ויחלק המשולש לב' חלקי' שוי' | |
|
|
||
|
ואחר כן מדוד מקו ד"ג אשר הוא קומת המשולש שלישיתו מנגד נקודת ד' אשר על התושבת ויהיה החלק הזה קו ד"ה | |
|
והוצא מנקודת ה' ב' קוים אל נקודת א' ואל נקודת ב' | |
|
ויחלק המשולש לג' חלקים שוים והם משולש ג'ה'א' ומשולש א'ה'ב' ומשולש ג'ה'ב' | |
Rhombus |
||
|
קכח שאלות במעויין הנז' למעלה אשר אחד מאלכסוניו י"ו והשני י"ב כמה הוא צלעו | |
|
תשובה קח מחצית כל אחד מאלכסוניו ורבע אותם וקבץ שני המרובעי' וקח את גדרם ותמצא הצלע | |
|
ופירוש התשובה | |
|
קח מחצית י"ו והוא ח' וריבועו ס"ד | |
|
וקח מחצית י"ב והוא ו' וריבועו ל"ו | |
|
ומניין שני המרובעים האלו הם ק' | |
|
וגדר ק' הם י' והוא צלע המרובע | |
|
| ||
|
ואם יאמר מעויין שתשברתו צ"ו ואלכסון האחד י"ו כמה הוא האלכסון השני | |
|
חלק צ"ו אשר הוא התשבורת על האלכסון אשר ידעת שהוא י"ו ותמצא מחצית האלכסון השני ו' וכפלה י"ב והוא האלכסון השני | |
|
ואם יאמ' מעויין צלעו י' ותשברתו צ"ו כמה אלכסונו | |
|
קח מרובע הצלע והוא ק' הוסף עליו התשבורת ויהיו קצ"ו וגדר המספר הזה הוא י"ד והם שני חציי האלכסונות | |
|
| ||
|
קח מחצית המספר והוא ז' ומרובעו מ"ט | |
|
הוצא ממנו מחצית התשבורת אשר הוא מ"ח וישאר בידך א' | |
|
וגדר הא' הוא א' אם אתה מוסיף אותו על ז' יהיו ח' והוא מחצית האלכסון האחד | |
|
| ||
|
ואם אתה פוחת אותו מן ז' ישאר ששה והוא מחצית האלכסון השני | |
|
| ||
| Figure Problem - Divide a Figure - Triangle | ||
|
קכט שאילה משולש אשר צלעו האחד י"ב אמות והוא צלע א"ב וצלע ב"ג השני י' אמות וצלע א"ג השלישי ט"ו אמות ואתה רוצה לחלקו לב' בעלים לכל אחד חלק שוה | |
|
|
||
|
והנה נשים נקודות ד' אשר הוא המיתר רחוקה מנקודת ב' על צלע א"ב שתי אמות | |
|
וישאר קו א"ד י' אמות | |
|
ויהיה מחצית צלע א"ב על נקודת ז' ויהיה קו א"ז שש אמות כי כן מסרנו צלע א"ב כולו י"ב אמות | |
|
ובין קו א"ז שהוא המחצית ובין קו א"ד ארבע אמות והם שני חמישיות קו א"ד | |
|
ואתה קח מצלע א"ג הנדבק אל א"ד שני חמשיותיו אשר היא הראש על נקודת ה' | |
|
ויהיה קו ג"ה שש אמות כי כל צלע א"ג היה ט"ו אמה | |
|
והוצא המחצה מנקודת ד' עד נקודת ה' | |
|
ויהיה המשולש הזה נחלק לשני חלקי' שוים החלק האחד משולש ד'א'ה' והחלק השני נפתל ד"ה ג"ב | |
|
ואילו היה המיצר אשר הוא נקודת ד' נופל לצד אחד עד שיהיה א"ד שתי אמות לא היית מוצא המחצה אל הצלע א"ג אבל אל צלע ב"ג | |
|
והיית לוקח מצלע ב"ג אשר הוא י' אמות שני חמשיותיו על נקודת ה' מנגד נקודת ג' | |
|
ויהיה קו ג"ה [33]בצלע ב"ג ד' אמות | |
|
ותוציא המחצה מנקודת ד' אל נקודת ה' כאשר אתה רואה בצורה הזאת | |
|
כי המחצה בדמיון הזה היא יוצאה לעולם אל החלק הארוך | |
|
אם יהיה הארוך ב"ד אתה מוציא המחצה אל צלע ב"ג | |
|
ואם יהיה הארוך א"ד אתה מוציא המחצה אל צלע א"ג | |
|
ואתה מתחיל למדוד את שתי החמשיות מנקודת ג' אשר היא הראש ואל הנקודה הזאת הייתה המחצה יוצאה אלו היה המיצר נופל על מחצית צלע א"ב ומדת מרחק המיצר מן המחצית אתה מתרחק מנקודת ג' אשר הוא הראש | |
|
ואתה יכול להבין את העניין הזה אם לא היית מדמה אותו במספר אלא שזכרתי המספר כדי להקל על הלומד ולהקריב העניין ללב המלמד | |
Area |
||
Polygons |
||
|
קל שאלה במדידת הצורות אשר צלעותיו עודפות על ארבע הצלעות והצורות האלה הם על תמונות רבות מהם מחומשות ומהם משותתות ומשובעות ולמעלה מהם יש מהם שצלעותם וזוויותם שוות ויש שלא יהיו שוות אלא מתחלפות | |
|
ואני נותן לך כלל ראשונה במדידת הצורות אשר צלעותן וזוויותן שוות | |
|
והכלל הזה הוא כל תבנית וכל צורה אשר אין לה קוים ישרים אם אתה מעגיל בתוכה עגול שיהיה מושש לצלעיה ידוע הוא כי רבוע קוטר חצי העגול הזה במחצית כל צלעי הצורה ההיא א"ו היא תשברתה | |
|
וכל צורה מן המרבע ולמעלה אשר צלעיה וזוויותיה שוות זו לזו אתה יכול לחוק בה עגול שיהיה מושש לכל צלעיה | |
|
ואם אין צלעיה וזוויותיה שוות יש מהם שלא יתכן לחוק בעגול שיהיה מושש לכל צלעיה | |
|
ואם תבא לידך צורה מכל התמונות מן משולש או מרובע או מחומש או למעלה מהם ואתה מחיק בתוכה עגולה מוששת לצלעיה הוי יודע כי רבוע חצי קוטר העגול ההוא במחצית כל צלעי התמונה הוא תשברתה | |
|
ואין אנו צריכין לתת דמיון מן המשולש ולא מן המרובע כי כבר פורש דרך רבועם | |
|
אבל אנו נותנין דמיון מן המחומש והוא אשר על חמש זוויותיו א'ב'ג'ד'ה' וכל צלע וצלע מצלעותיו שוות באורכן וכן זוויותיו כלם שוות זו לזו | |
|
ואנו מעגילים בתוכן עגול מושש לה' צלעותיו על חמש נקודות ז'ח'ט'כ'ל' | |
|
וציר העגול הזה הנקרא מרכז הוא נקודת מ' | |
|
ואנו אומרים כי רבוע חצי קוטר העגול הזה במחצית כל צלעי המחומש הוא תשברתו | |
|
וחצי הקוטר הוא קו יוצא מנקודת מ' אל אחת הנקודות אשר העגול מושש עליהם את המחומש | |
|
ועתה אם אנו מוצאים קו מנקודת מ' אשר הוא המרכז על שתי נקודות א' וב' מן זווית המחומש נתן לנו משולש אשר עליו מ'א'ב' | |
|
ותשבורת המשולש הזה הוא ברבוע העמוד היוצא אל תושבתו בחצי התושבת | |
|
ואם אנו מוציאים קו מנקודת מ' אל נקודת ל' אשר משש עליה העגול את צלע א"ב יהיה הקו הזה עמוד במשולש מ'א'ב' והוא חצי קוטר העגול | |
|
ואם מרבע העמוד הזה בחצי צלע א"ב יהיה רבועו תשבורת המשולש | |
|
| ||
|
ועל הדרך הזה אתה יכול לעשות חמשה משולשים על [34]חמש צלעי המשולש המחומש ויהיה תשבורת כל משולש מהם ברבוע חצי הקוטר בחצי הצלע כאשר היה בצלע הזה ותשבורת חמש המשולשים כולם הוא תשבורת המחומש והוא מרבוע חצי הקוטר בחצי כל חמש הצלעות | |
|
והוא יהיה העניין לכל צורה כמוה אשר צלעותיה רבים או מעטים אם אתה מעגיל בתוכה עגול מושש לצלעיה יהיה תשברתה ברבוע חצי קוטר העגול במחצית הצלעות וזאת היא צורתה | |
|
ומפני שאין אתה יכול להוציא בכל תמונה ותמונה עגול שיהיה מושש לכל צלעיה אין הכלל הזה מספיק לך במדידת כל העודפות על ד' צלעות | |
|
ומפני זה אני נותן לך כלל אחר שיהיה נוהג לך בכל צורה אשר צלעותיה ישרות | |
|
הוי יודע כי כל תמונה שטוחה שצלעותיה ישרות מתחלקת למשולשים שהם חסרים מן מניין הצלעות שנים | |
|
כגון המרובע אשר לו ד' צלעות יתחלק לב' משולשים אשר מניינם פוחת ב' ממספר הצלעות | |
|
והמשושה יתחלק לד' משולשים | |
|
וכן למעלה מזה | |
|
ואתה בא מן הכלל הזה וחלק כל תמונה שיבוא לידך אל המשולשים אשר היא נחלקת אליהם ורבע כל משולש מהם על הדרך אשר למדת ויהיה מרובע כולם תשבורת התמונה אשר נחלקו ממנה | |
|
כאלו היית מוצא במחומש אשר ציירתי לך למעלה קו מנקודת א' אל נקודת ג' וקו אחר אל נקודת ד' ויהיה המחומש נחלק לג' משולשים | |
|
ואין אתה יכול לפחות מהמשולשים האלה | |
|
ואם אתה מרבע אותם יהיה רבוע שלשתם תשבורת המחומש כגון הצורה הזאת | |
Square |
||
|
קלא הרי שיש לפניך א' מרובע מי' אמה על י' אמה ובאמצע הוא חקוק ופוחת ד' אמות על ד' אמות ותרצה לדעת כמה הוא המרובע בשיבור אחר הוצאת הד' אמות על ד' אמות מן החקק | |
|
|
||
|
תאמר אלו היה הטבלה מרובעת שלימה בלתי שום חקיקה היית אומר י' פעמ' י' הם ק' ותשברתו היה ק' | |
|
ועתה שפוחת באמצע ד' על ד' תאמ' ד' פעמ' ד' הם י"ו | |
|
תפחתם מק' ישארו פ"ד | |
|
| ||
|
א"כ א' טבלה מרובעת שהיא י' על י' ופוחת באמצעה ד' על ד' תשברתה פ"ד | |
|
וכן כל הדומה לו | |
Scalene Trapezoid | ||
|
[35]קלב קטומה שיש לה ב' קוים נכוחיים קו א"ג ואורכו ח' אמות וקו ב"ז ואורכו כ"ב אמות וב' צלעים שאינם שוות והם קו א"ב ואורכו ט"ו וקו ג"ד ואורכו י"ג אמות והצורה הזאת נקראת קטומת הראש חלופה | |
|
וריבוע הצורה הזאת יהיה בהוצאת עמוד ה' כאשר עשית בראשונה שכתבתיה למעלה | |
|
ואתה צריך בקטומה הזאת לגבל מעמד העמודים ולדעת מעמד הגדול ומעמד הקטון ואתה נוהג בהם המנהג הזה | |
|
תרבע הצלע הקצורה וגרע מרובעה ממרובע הצלע הארוך והעודף שבהם תקח מחציתו ותחלק אותו על עודף התושבת על הראש ואשר יצא מהחלוקה הזאת אם אתה מוסיף אותו על מחצית עדף התושבת תמצא המעמד הגדול אשר לעמוד והוא מרחקו מן הצלע הארוך | |
|
| ||
|
ואם תגרעינו ממחצית העודף תמצא המעמד הקטן אשר לעמוד והוא מרחקו מן הצלע הקצר | |
|
| ||
|
ואם אתה מרבע בצורה הזאת י"ג שהוא אורך צלע ג"ד הקצור יהיה מרובעו ק'ס'ט' | |
|
פחות אותו ממרובע א"ב שהוא מרובע הצלע הארוך ישאר נ"ו | |
|
קח מחצית המניין הזה והוא כ"ח | |
|
חלק אותו על י"ד שהוא עודף התושבת על הראש תהיה החלוקה ב' | |
|
ואם תוסיף ב' על ז' אשר הוא חצי עדף התושבת יהיה ט' והוא אורך קו ב"ה אשר הוא מרחק העמוד מהצלע הארוך | |
|
| ||
|
ואם תפחות ב' מז' תמצא מרחק העמוד מהצלע הקצר | |
|
והאות על העניין הזה התבונן לך מאשר פירשתי למעלה בעמוד המשולש מתחלף הצלעות | |
|
|
||
|
כי בהוציאך מן התושבת את הרחב הראש והוא ה' ישאר קו ט"ח ג' אמות פחות שביע והוא עודף מעמד עמוד המשולש על מעמד עמוד הקטומה הקצר | |
|
והעודף הזה רבע בצלע הקטומה הקצר שהוא י"ג יהיה ל"ז ושביעית | |
|
בוא וחלק המספר הזה על מעמד העמוד הקצר בקטומה והוא ה' תהיה החלוקה הזאת ז' וג' שביעיות והוא עודף צלע המשולש על צלע הקטומה הקצרה והוא קו ג"ז היוצא מצד הקצר | |
|
| ||
|
ואם תרצה לדעת קו א"ז הארוך הוצא המעמד הארוך במשולש על העניין שהוצאת הקצר | |
|
ותמצא אותו י"ד ושביעית והוא מעדיף על מעמד הארוך ה' ושביעית | |
|
מנה אותו בצלע הארוך שהוא ט"ו יהיה המניין ע"ז ושביעית | |
|
חלק המספר הזה על ט' שהוא המעמד הארוך בקטומה תהיה החלוקה ח' וד' שביעיות והוא עודף צלע המשולש על צלע הקטומה הא' הארוך והוא א"ז | |
|
| ||
|
ואם תבוא לדעת עמוד המשולש הזה הוי מונה עודף המעמד הקטן והוא ג' פחות שביע בעמוד הקטומה שהוא י"ב | |
|
וחלק אותו על מעמד הקטן והוא ה' | |
|
או הוי מונה עודף המעמד הגדול והוא ה' ושביע בעמוד הקטומה שהוא י"ב | |
|
נחלקהו על המעמד הגדול והוא ט' | |
|
תמצא שניהם מוציאים אל חשבון אחד והוא ז' פחות שביע והוא עודף עמוד המשולש על עמוד הקטומה | |
|
הוסף אותו על י"ב שהוא עמוד הקטומה ויהיה הכל י"ט פחות שביע והוא אורך קו ז"ט אשר הוא עמוד המשולש בצורה הזאת | |
|
| ||
|
[36]גליון וזה דבר ברור הוא כאשר אמרנו למעלה | |
|
כי קו ה"ט בקו א"ה כקו ב"ה בקו עודף עמוד המשולש על עמוד הקטומה שהיה א"ה | |
|
על כן אם נרבע קו ה"ט בקו א"ה ונחלק על קו ב"ה יצא לנו העודף | |
Right Trapezoid |
||
|
קלג התמונה השלישית הקטומה שראשה נכוחי לתושבתה ואחד מצלעיה עמוד עליה והתמונה הזאת נקראת חצי קטומה והדמיון לצורה הזאת קטומה שעליה א'ב'ג'ד' וראשה א"ג והיא ח' ותושבתה ב"ד והיא כ' וצלע א"ב הארוך ט"ו וצלע ג"ד הקצור ט' אמות והוא עמוד על תושבת ב"ד | |
|
וחשבון רבוע הקטומה הזאת הוא באסיפת ראשה אל תושבתה ולקחת מחציתם וימנה בעמוד ויהיה תשבורת הקטומה | |
|
ואם תאסוף בצורה הזאת ראשה אל תושבתה יהיה כללם כ"ח ומחציתם י"ד | |
|
ואם תרבע המספר הזה באורך העמוד והוא ט' יהיה ק'כ'ו' והוא תשבורת הקטומה הזאת | |
|
ואות לזה מפורש למעלה בקטומה הנשלמת | |
|
ואם תבוא לדעת אלכסונה הקצור והוא א"ד | |
|
הוי מרבע את הראש והוא ח' ומרובעו ס"ד | |
|
ואסוף אליו מרובע העמוד והוא הצלע הקצור והוא פ"א ויהיו שניהם יחד ק'מ'ה' והוא מרובע האלכסון | |
|
וגדר המספר הזה הוא אורך אלכסון הקצור | |
|
| ||
|
ואם תרצה לדעת אלכסון הארוך | |
|
אסוף מרובע התושבת למרובע העמוד ויהיו שניהם ת'פ'א' והוא מרובע אלכסון הארוך | |
|
| ||
|
ונתכוון לך החשבון הזה מפני ששתי זוויות אשר על נקודת ג' ונקודת ד' מן צלע ג"ד הן ניצבות כי הצלע הזה הוא עמוד על התושבת ועל הראש אשר הם נכוחיים | |
|
ואלכסון א"ד הוא מיתר לזוית ג' הניצבה | |
|
ואלכסון ג"ב הוא מיתר לזוית ד' הניצבה | |
|
ומרובע מיתר זוית הניצבה הוא שוה לשם מרובעי ב' הצלעות אשר הן מקיפות לה כאשר ידעת | |
|
וזה לך האות על חשבון האלכסונות בצורה הזאת | |
|
ואם תרצה להשלים הקטומה הזאת ולהוציא ראש המשולש הנקטמת ממנה | |
|
עשה כמעשה שלמדת מן הקטומה שלפניה | |
|
והוא שתהיה יודע עודף התושבת על הראש והוא י"ב בצורה הזאת | |
|
ואם תמנה הראש בקו א"ב וחלקנו על עודף התושבת יצא לך אורך הקו היוצא מהעמוד אל ראש המשולש | |
|
ואתה יכול להוציאו למעשה מן הדרך שלמדת בצורות האחרות | |
Obtuse Trapezoid |
||
|
קלד קטומה שראשה נכוחי לתושבתה והצלע אחת נופלת על התושבת על זוית נרווחת ולקטומה הזאת שני עמודים תכונים ועמוד חצוני | |
|
ואתה יודע תשבורת הקטומה הזאת בהוצאת עמודיה | |
|
ואתה צריך תחלה להגביל מעמד העמוד | |
|
והוא שתהיה פוחת הראש והוא י"ד מן התושבת והוא כ"א ישאר בידך ז' והוא עודף התושבת | |
|
ובוא ורבע העודף הזה ואסוף מרובעו אל מרובע הצלע הקצור ותמצא ב' מרובעים אילו ר'ע'ד' | |
|
הוצא המספר ממרובע הצלע הארוך שהוא ת' ישאר בידך ק'כ'ו' | |
|
קח המחצית [37]והוא ס"ג חלק אותו על ז' והוא עודף התושבת | |
|
ויהיה הכל י"ו והוא גבול מעמד העמוד מנגד קו א"ב הארוך | |
|
ואלו הט' אשר מצאת הם המרחק הקצר | |
|
| ||
|
וכן מרחק העמוד שעליו ג"ח אשר הוא יוצא חוצה מן קו ב"ד התושבת וכן מרחק העמוד התיכוני הנופל על נקודת ד' שעליו ד"ט | |
|
ואם תבוא לדעת אורך העמוד | |
|
הוי מרבע את מעמד שתרצה | |
|
ואם [אתה] מרבע המעמד הארוך שהוא י"ו הוציאנו ממרובע הצלע הארוך אשר הוא כ' | |
|
ואם תרבע המעמד הקצור הוציאנו ממרובע הצלע הקצר | |
|
ויהיה המותר מן כל אחד משני החשבונים האלה ק'מ'ד' והוא מרובע העמוד בק | |
|
וגדרו י"ב והוא אורך העמוד | |
|
| ||
|
ותשבורת הקטומה הוא ברבוע העמוד בחצי הראש ובחצי התושבת כאשר עשית בשאר הקטומות שלפניה | |
|
והתשבורת הוא ר"י | |
|
והאות על החשבון הזה שהוצאת בו את העמוד הוא מעניין האות שהורתיך בקטומה שאין צלעותיה שוות | |
|
כי בהוציאך הראש מהתושבת ונשארו בידך ז' היה הקו ההוא צלע למשולש מרויח הזויות א' שצלעו האחת ז' והשינית ט"ו והם הצלעות המקיפות זוית הנרווחת | |
|
ומיתר הזוית הזאת הוא כ' אמה אשר הוא אורך קו א"ב מן הקטומה הזאת | |
|
ואם אתה מוציא במשולש הזה המרויח הזויות עמוד שיהיה נופל חוצה אתה מוצא מעמדו חוצה כאשר מצאת בחשבונך בצורה הזאת | |
|
|
||
|
ואתה יכול להוציא אלכסון הקטומה הארוך אם אתה מאסף אל התושבת מעמד העמוד החיצוני וכולל את הכל ומרבע אותו | |
|
כאילו היית מאסף בצורה הזאת כ"א שהוא אורך התושבת אל ט' שהוא אורך מעמד העמוד חוצה ויהיה הכל ל' | |
|
ואתה מרבע המניין הזה ומוסיף עליו מרובע העמוד ויהיה הכל אלף ומ"ד והוא מרובע האלכסון הארוך | |
|
וגדר המספר הזה הוא אורך האלכסון בקטומה הזאת מנקודת ג' אל נקודת ב' | |
|
| ||
|
ואם תרצה להוציא אלכסון הקצור היוצא מן א' ועד ד' | |
|
תאסוף אל מרובע העמוד מרובע עודף התושבת על המעמד הארוך והוא בצורה הזאת ה' ויהיו שני המרובעים ק'ס'ט' והוא מרובע האלכסון הקצור | |
|
וגדרו הוא אורך האלכסון | |
|
| ||
|
והאות אל העניין הזה אתה יכול להבין מהאותות אשר למעלה אם אתה מביט אל המשולשים מוצבי זוית אשר הם מתיילדים מהאלכסונות האלה עם צלעי הקטומה והעמודים כאשר הראיתך למעלה | |
|
ויכול הוא בצורה הזאת שיהיה אלכסון הקצור הוא עמוד בקטומה בעצמו | |
|
כאילו היה בצורה הזאת אורך ראש הקטומה ט' אמות ותושבתה י"ו ומניין ב' הצלעות הנשארות המניין אשר היה להם בצורה הראשונה | |
|
והיית מוצא בצורה הזאת השינית העמוד נופל מנקודת א' אל נקודת ד' ויהיה העמוד ההוא אורך האלכסון הקצר | |
|
והאלכסון הארוך אשר הוא יוצא מג' עד ב' הוא גדר ת'ש'ס'ט' אשר הוא מרבע עמוד א"ד [38]עם מרובע קו א"ג עם קו ב"ד אשר ראש הקטומה ותושבת שניהם יחד בקו אחד | |
|
| ||
|
ואתה מבין אותות כל החשבון הזה על מכונו אם אתה מעיין בה עיון יפה | |
Quadrangle which has no parallel sides |
||
|
קלה המין השני הנשאר מן התמונות אשר יש להם ד' צלעות הוא כל מרובע שאין אחת מצלעותיו נכוחי לצלע אחרת | |
|
ובתמונות האלו אי אתה מוצא רבועם אלא מרבוע המשולשי' אשר הם נחלקי' עליהם | |
|
וכל מרובע בעולם אתה יכול לחלקו לשני משולשין | |
|
וידוע הוא כי המשבר שני המשולשי' ההם ומצרף תשברתם ימצא התשבורת המרובע אשר הם חלקיו | |
|
ועל הענין הזה תוכל למצא התשבורת כל מרובע על חלופי מיניהן מן השוים בצלעותיו והנכוחיים מתשבורת המשולשים שהן נחלקים עליהם | |
|
אלא שהמרובעים השוים בצלעותיו והנכוחיים בהם אתה יכול להגיע אל תשברתן מדרך אחרת ואינך צריך לרבע בהן את המשולשים הנחלקים עליהם | |
|
ושאר המרובעים הנפתלים ואין בהם צלע נכוחי ובצלע אחד אי אתה יכול למצוא תשברתם אלא מתשבורת המשולש אשר יחלקו עליהם | |
|
ואני נותן לך דמיון בעניין זה ויהיה מספיק לך בשאר הצורות והדמיון הזה הוא מהצורה שהשלמתי פירושה | |
|
| ||
|
והיא הקטומה הרביעית המתמוטטת אשר צלע א"ג היה בה י"ד אמה וצלע ב"ד כ"א אמה וצלע א"ב כ' אמות וצלע ג"ד ט"ו אמה | |
|
ומצאת האלכסון הקצור בקטומה הזאת כאשר חשבונו למעלה י"ג אמה | |
|
וכשמדדת אותו אתה מרבע לא מצאת בו המידה הזאת אלא יותר ממנה או פחות ממנה | |
|
ואנו מוסרין כאילו מצאת אותה יתר ב"ג י"ו אמה ונודע לך מזה כי אין הצורה הזאת קטומת הראש כי אין אחת מצלעיה נכוחית עם צלע אחרת לפי אם היו נרוחיות לא היה אלכסונה הארוך או הקצר מתחלף מחשבונו שהיא בקטומה | |
|
|
||
|
ומפני זה אתה צריך לרבע שני המשולשים אשר נחלק עליהן המרבע הזה באלכסון שהוצאת בו והוא שני משולשי א'ד'ב' וא'ד'ג' וכל אחד מהם צלעותיו ידועות | |
|
ואתה יכול להגיע אל ריבועם בהוצאת העמודים כאשר למדת בריבוע המשולשים | |
|
ואם אתה נוהג בהם המנהג הזה תמצא תשבורת משולש א'ד'ב' מהן צ"ו ושליש פחות משהו | |
|
ומשולש א'ד'ג' תהיה תשברתו ק"נ וב' שלישיים פחות משהו | |
|
ויהיה כל התשבורת בעניין הזה ר'מ'ז' פחות משהו | |
|
ואנו מצאנו רבועו בקטומה המתמוטטת ה' ונמצא הריבוע עודף בתמונה הזאת מפני עדיפת האלכסון | |
|
ואילו היה האלכסון מתמעט היה הריבוע פוחת | |
|
ומהעניין הזה אתה יכול למסור לך גדול במרובעת | |
|
ואומר מרובע אשר אתה מוציא את אלכסונו נחלק לב' משולשים | |
|
אם אתה מוציא עמוד של האלכסון בשני המשולשין ותאסוף את שני העמודים ותקח את מחציתם ותצרף המחצית הזה במניין כל האלכסון אתה מוציא תשבורת המרבע | |
|
או תצרף שני העמודים במחצית האלכסון וגם בא תמצא תשבורת המרובע | |
|
ואיני צריך להביא לך [39]להביא לך משל מן החשבון הזה מפני שאתה מבין אותו מהדמיונות אשר במשיחת המשולשין ואיני נזקק להאריך בפירוש המרובעי' יותר מזה | |
Additional Problems |
|
| Motion Problem - Pursuit | |
|---|---|
|
קלו אם יאמר הרי אדם שהוא מהלך י' מלים בכל יום ואחר הוא מהלך ביום ראשון א' מיל וביום שני ב' מילים וביום השלישי ג' ומוסיף והולך בכל יום |
|
|
|
תכפול המילים שמהלך הקבוע יהיו כ' |
|
וגרע מהם אחד ישארו י"ט הרי שבי"ט ימים יהיו בשוה |
|
וכן לעולם תכפול שמהלך הקבוע ותגרע מהם אחד |
|
קלז ואם יאמר הרי אדם שהוא מהלך י' מילים בכל יום והאחר מהלך ביום אחד א' מיל וביום שני ג' וביום שלישי ה' וביום רבעי ז' ומוסיף והולך בכל יום חשבון נפרד |
|
דע כי כמספר המילים שמהלך הקבוע ליום כן מספר הימים שיעמדו בשוה |
|
ואם הקבוע מהלך י' מילים ביום בי' ימים יעמדו בשוה |
|
ואם מהלך ט' מילים ביום בט' ימים יעמדו בשוה וכה"ל |
|
קלח וכן אדם שמהלך בכל יום י' מילים והאחר מהלך ביום ראשון ב' וביום שני ד' וביום שלשי ו' ומוסיף והולך בכל יום מספר זוג כגון בדוח"י י"ב י"ד י"ו |
|
תחסר אחד מן המילים שמהלך הקבוע שהם י' יהיו ט' הרי שבט' ימים יעמדו בשוה |
|
וכן לעולם תחסר אחד ממספר המילים וכן כל הדומה לו |
| Triangulation Problem - Tree | |
|
שאלה אילן שגובהו י' אמות ובא רוח חזק ושברתו לשנים חלקים ולא נערכו חלקיו אך נטז ממקו' השבירה והגיע ראשו לארץ |
|
תשובה תחלק מרובע הרוחק שמשרש האילן לראש שהם כ"ה במשלנו על גובה האילן שהם י' ויצאו ב' וחצי |
|
נחברם עם הי' ונקח חציים שהם ו' ורביע וזהו כמות האילן עד מקום השבירה |
|
| |
|
והנשאר עד תשלום הי' שהם ג' וג' רביעיות הם כמות האמות שממקום השבירה עד שרש האילן |
Additional Problems - MS Mantova |
|
| Multiple Quantities - Boys Sharing Property of Their Father | |
|
[40]אדם שהיו לו בנים ולא נודע מספרם ואמר לאחד לך בארגז וקח לך פרח אחד והעשירית מכל הנשאר |
|
| |
|
לפי חשבון השבור [.....] הוא עשירית |
|
תפחות א' מעשרה ישארו ט' הרי שט' היו הבנים |
|
אמור אחר זה ט' פעמי' ט' הם פ"א וככה היו הפרחים |
|
ואם יקחו כאשר צוה אביהם יהיה לכל אחד חלק שוה |
|
וכן לכל חשבון שתרצה עשה כן שתפחות א' מהחשבון השבור והוא חשבון הבנים ותרבע אותו והוא חשבון הפרחי' וכמספר הבנים יהיו [41]מספר הפרחים שיבא לכל אחד ודו"ק |
| MS Mantova; MS Amsterdam: Multiple Quantities - Boys Selling Cubits of a Cloth | |
|
הרי אדם שנתן לג' בניו ל' אמות בגד והלכו לשוק למכרו האחד מכר בד' דנרי' האמה והשני בה' והשלישי בו' |
|
אומר תחילה רביע וחומש ושתות נמצא בס' |
|
וכללם הוא ל"ז והוא המחלק |
|
ואם תרצה לדעת כמה אמות מכר אותו שמכר בד' דינרי' |
|
תפוס הרביע מס' שהוא ט"ו ותרבע אותו על סך הבגד שהוא ל' ואמור ט"ו פעמי' ל' ת"נ |
|
חלקם בל"ז יבא י"ב ו' חלקי' מל"ז |
|
הרי שמכר [הה] י"ב אמות ו' חלקי' מל"ז |
|
ואם תרצה לדעת כמה מעות קבל |
|
אמור תחילה מי"ב אמות קבל מ"ח דינ' |
|
ומן הו' חלקי' מל"ז עשה על זה הדרך אם ל"ז שהוא אמה שלמה שוה מ"ח פשי' הו' חלקי' מל"ז כמה שוים |
|
אמור ו' פעמי' מ"ח רפ"ח |
|
חלקם בל"ז יבא ז' פשי' וכ"ט חלקים מל"ז |
|
וכזה תעשה האחרי' ויצא לך העניין |
Apparatus
Appendix: Bibliography
Anonymous
Sefer ha-Kelalim ba-Mispar
Manuscripts:
- 1) Amsterdam, Portugees Israelitisch Seminarium Ets Haim 47 D 20/43 (IMHM: f 3576), ff. 227r-232v (15th century)
- Ets Haim 47 D 20/43
- 2) Cambridge, University Library Add. 553 (IMHM: f 16842), ff. 90r-95r; 101r-104r (17th century)
- 3) Mantova, Comunità Ebraica MS ebr. 8/16 (IMHM: f 788), ff. 72r-82v (Porto, 1464-1471)
- ebr. 8/16
- 4) Moscow, Russian State Library, Ms. Guenzburg 698/2 (IMHM: f 47914), ff. 10r-40v (14th-15th century)
- 5) Oxford, Bodleian Library MS Mich. 536/6 (IMHM: f 22082), ff. 88r-99v; 110r-117v (cat. Neub. 1268, 6); (1518-1520)
The transcript is based mainly on manuscript Oxford 536
Bibliography:
Steinschneider, Moritz. 1906. Mathematik bei den Juden, Band II: 1551-1840. Monatsschrift für die Geschichte und Wissenschaft des Judenthums 50, p. 214. repr.: ed. Gad Freudenthal, Hildesheim, Zürich, New York: Olms, 2014, p. 137.
![\scriptstyle{\color{OliveGreen}{\frac{1}{a}-\frac{1}{b}=\frac{\left[\frac{1}{a}\sdot\left(a\sdot b\right)\right]-\left[\frac{1}{b}\sdot\left(a\sdot b\right)\right]}{a\sdot b}}}](/mediawiki/images/math/c/0/6/c0629aecee310d90e051b57b2c593d46.png)
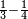
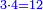
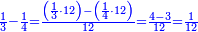
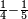
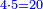
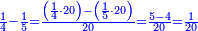
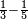
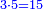
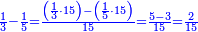
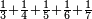
![\scriptstyle{\color{blue}{\left[\left[\left(3\sdot4\right)\sdot5\right]\sdot6\right]\sdot7=\left[\left(12\sdot5\right)\sdot6\right]\sdot7=\left(60\sdot6\right)\sdot7=360\sdot7=2520}}](/mediawiki/images/math/6/0/8/6087f1e952aeacad37a6f010aec8851d.png)
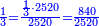
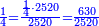
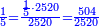
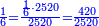
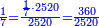

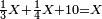
![\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=12-7=5}}](/mediawiki/images/math/9/9/4/994410b776b40d19b554ba92d759d4ae.png)
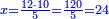
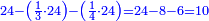
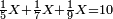
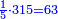
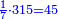
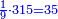
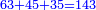
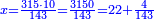
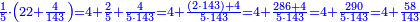
![\scriptstyle{\color{blue}{\left[\frac{1}{5}\sdot\left(22+\frac{4}{143}\right)\right]+\left[\frac{1}{7}\sdot\left(22+\frac{4}{143}\right)\right]+\left[\frac{1}{9}\sdot\left(22+\frac{4}{143}\right)\right]=10}}](/mediawiki/images/math/3/6/5/3657322cf92ee517a021923fd6effa87.png)
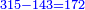
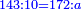
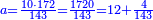
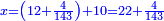
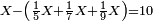
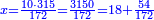
![\scriptstyle{\color{blue}{\left(18+\frac{54}{172}\right)-\left[\left[\frac{1}{5}\sdot\left(18+\frac{54}{172}\right)\right]+\left[\frac{1}{7}\sdot\left(18+\frac{54}{172}\right)\right]+\left[\frac{1}{9}\sdot\left(18+\frac{54}{172}\right)\right]\right]=10}}](/mediawiki/images/math/1/0/f/10f16522c9ec6736af054beb8758e910.png)
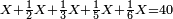
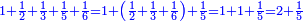
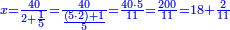
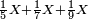
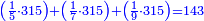
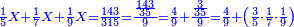
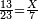
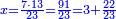
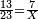
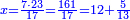
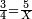
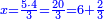 of Cortona
of Cortona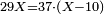
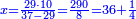
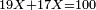
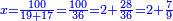
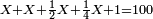
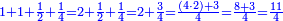
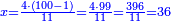
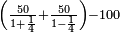
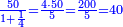
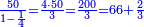
![\scriptstyle{\color{blue}{\left(\frac{50}{1+\frac{1}{4}}+\frac{50}{1-\frac{1}{4}}\right)-100=\left[40+\left(66+\frac{2}{3}\right)\right]-100=6+\frac{2}{3}}}](/mediawiki/images/math/5/4/e/54e344679b45d90141508c4ca499d0a6.png)
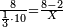

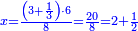
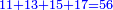
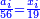
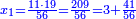
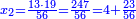
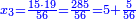
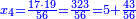
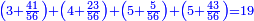
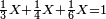
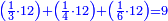
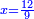
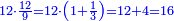
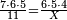
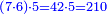
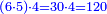
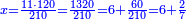
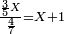
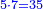
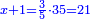
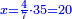
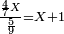
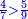

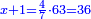
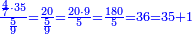
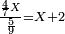

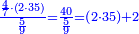
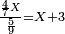


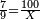
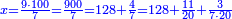
![\scriptstyle{\color{OliveGreen}{\frac{a_1}{b_1}:\frac{a_2}{b_2}=a_3:x\longrightarrow\left[\frac{a_1}{b_1}\sdot\left(b_1\sdot b_2\right)\right]:\left[\frac{a_2}{b_2}\sdot\left(b_1\sdot b_2\right)\right]=a_3:x\longrightarrow x=\frac{\left[\frac{a_2}{b_2}\sdot\left(b_1\sdot b_2\right)\right]\sdot a_3}{\frac{a_1}{b_1}\sdot\left(b_1\sdot b_2\right)}}}](/mediawiki/images/math/9/2/0/920461717fa923d2d19528270f52a2f0.png)
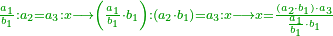
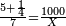
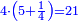
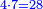
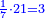
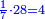
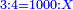
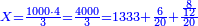
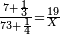
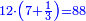
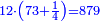
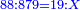
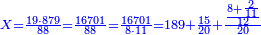
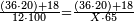
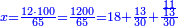
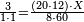
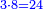

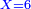
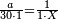
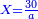
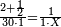
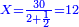
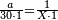
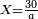
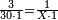
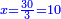
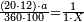
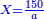
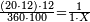
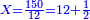
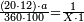
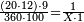
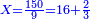
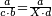
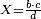
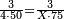
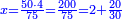
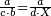
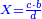
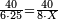
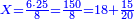
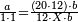
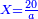
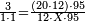
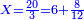
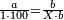
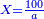
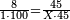
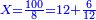
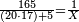
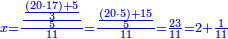
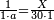
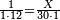
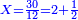
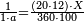
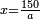
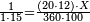
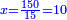
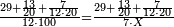
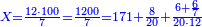
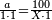
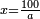
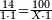
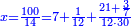
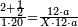
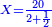
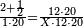
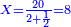
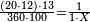
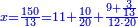
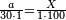
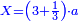
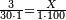
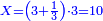
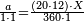
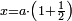
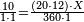
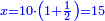
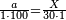
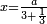
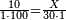
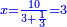
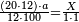
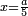
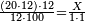
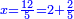
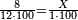
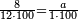
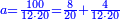
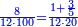
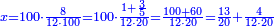
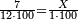
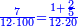
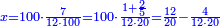
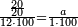
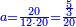
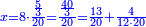
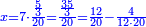
![\scriptstyle20+4-X+\left[\frac{4}{20}\sdot\left(20+4-X\right)\right]-X+\left[\frac{4}{20}\sdot\left[20+4-X+\left[\frac{4}{20}\sdot\left(20+4-X\right)\right]-X\right]\right]=X](/mediawiki/images/math/6/0/5/6053a7f78280380c9d2df6cfc64c3c4f.png)
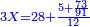
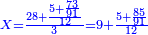
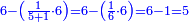
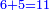
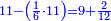
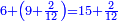
![\scriptstyle{\color{blue}{\left(15+\frac{2}{12}\right)-\left[\frac{1}{6}\sdot\left(15+\frac{2}{12}\right)\right]=12+\frac{7+\frac{2}{3}}{12}}}](/mediawiki/images/math/e/0/4/e04d582e4f2552e03545f8aea59a9acc.png)
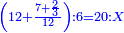
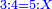
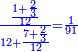
![\scriptstyle{\color{blue}{\left(12+\frac{7+\frac{2}{3}}{12}\right)-\left[\frac{1}{91}\sdot\left(12+\frac{7+\frac{2}{3}}{12}\right)\right]=12+\frac{1}{2}}}](/mediawiki/images/math/0/0/1/001e79fcd8b418bff28beebf4357d454.png)
![\scriptstyle{\color{blue}{\left(12+\frac{1}{2}\right)-\left[\frac{1}{5}\sdot\left(12+\frac{1}{2}\right)\right]=10}}](/mediawiki/images/math/5/1/3/513a14bb897c7a135c180395427a107b.png)
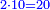
![\scriptstyle{\color{blue}{2\sdot\left[\left[6-\left(\frac{1}{91}\sdot6\right)\right]-\left[\frac{1}{5}\sdot\left[6-\left(\frac{1}{91}\sdot6\right)\right]\right]\right]=9+\frac{5+\frac{85}{91}}{12}}}](/mediawiki/images/math/a/f/2/af2f9548897783cb78fe90e3cbf580ef.png)
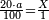
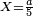
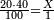
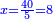

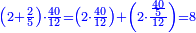
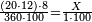
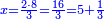
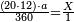
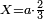
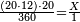
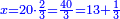
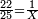
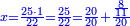
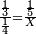
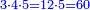



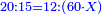
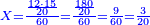
![\scriptstyle\left(\frac{1}{2}X+\frac{1}{3}X\right)+\left[\left(\frac{1}{3}+\frac{1}{4}\right)\sdot\left[X-\left(\frac{1}{2}X+\frac{1}{3}X\right)\right]\right]+3=X](/mediawiki/images/math/d/2/7/d276452e72993e94f14cd2ca6943159c.png)
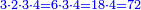
![\scriptstyle{\color{blue}{72-\left[\left(\frac{1}{2}\sdot72\right)+\left(\frac{1}{3}\sdot72\right)\right]=72-60=12}}](/mediawiki/images/math/0/d/c/0dc83d6b1571da9c902b55fe76608387.png)
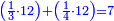
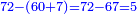
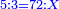
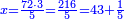
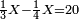
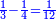
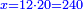
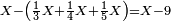
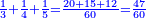
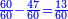
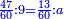
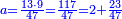
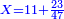
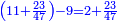
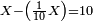
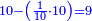
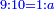
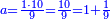
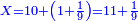
![\scriptstyle{\color{blue}{11+\frac{1}{9}-\left[\frac{1}{10}\sdot\left(11+\frac{1}{9}\right)\right]=10}}](/mediawiki/images/math/3/9/7/3977bd1a0169a0611a83ac0edf208b44.png)
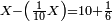
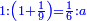
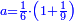
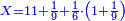
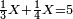
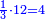
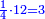
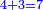
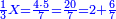
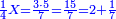
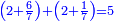
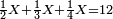
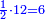
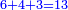
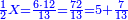
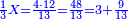
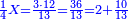
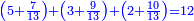

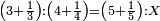
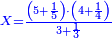
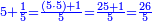
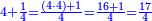
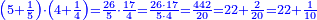
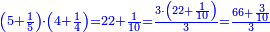
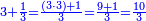
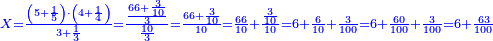
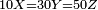
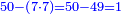
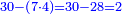
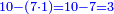

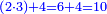
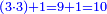
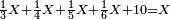
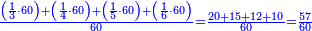
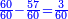
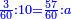
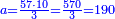
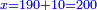
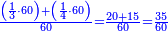
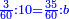
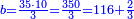
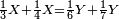
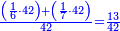
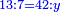
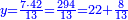
![\scriptstyle{\color{blue}{\left[\frac{1}{6}\sdot\left(22+\frac{8}{13}\right)\right]+\left[\frac{1}{7}\sdot\left(22+\frac{8}{13}\right)\right]=7}}](/mediawiki/images/math/7/b/8/7b872fc19ecb7a6fb8b3ed6bc94a0c38.png)
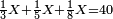





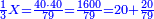
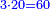
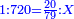
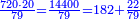
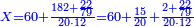
![\scriptstyle2\sdot\left[2\sdot\left[2\sdot\left(2x-8\right)-8\right]-8\right]=8](/mediawiki/images/math/b/7/c/b7c0d41d3d5b00c11ff0cfe8764fe1d2.png)
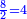
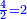
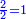

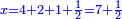
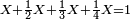

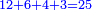
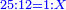
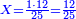
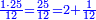
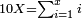
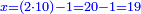
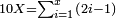
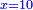
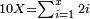
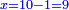
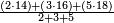
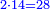
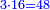

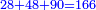
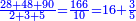
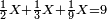
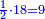
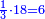
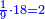
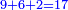
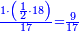
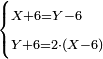
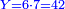
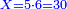
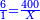
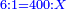
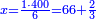
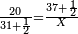
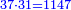
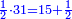
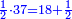
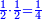
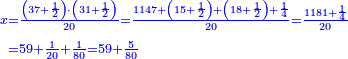
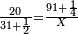
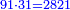
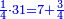
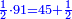
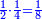
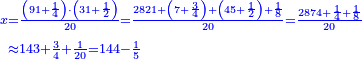
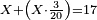
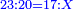
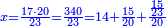
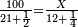
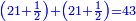
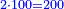
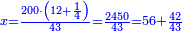
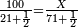
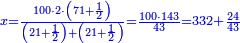
![\scriptstyle\left[\left(2-\frac{5}{3}\right)\sdot X\right]+\left[\left(3-\frac{5}{3}\right)\sdot X\right]=5](/mediawiki/images/math/b/3/9/b39a89f5f9f01ae578ff87165913ffb8.png)
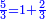
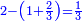
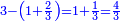
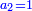
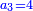
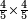
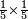
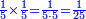
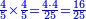
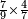
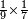
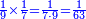
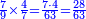
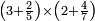

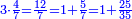
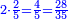
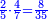
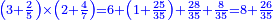
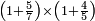
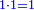
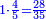
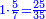
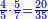
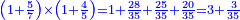
![\scriptstyle\begin{cases}\scriptstyle a_1+a_2+a_3+a_4=80\\\scriptstyle a_1=\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\\\scriptstyle a_2-\left[\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\right]=\frac{2}{3}a_3\\\scriptstyle a_3=\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{6}\right)\sdot a_1\\\scriptstyle a_4=\frac{4}{5}a_3\end{cases}](/mediawiki/images/math/e/6/1/e61594e5bed663d7d2049121054974b5.png)
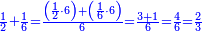
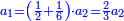
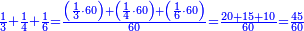
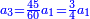
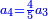
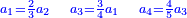
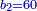
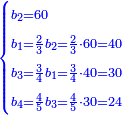
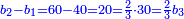
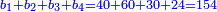

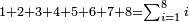
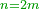 ]:
]: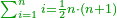
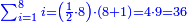
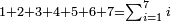
 ]:
]:![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^n i=\left[\frac{1}{2}\sdot\left(n+1\right)\right]\sdot n}}](/mediawiki/images/math/f/0/5/f05c82d98b93f64fdea1180201df1e54.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^7 i=\left[\frac{1}{2}\sdot\left(7+1\right)\right]\sdot7=4\sdot7=28}}](/mediawiki/images/math/a/7/c/a7cd0bfcbccb015720bd6dde810dd809.png)
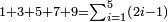
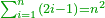
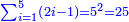
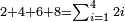
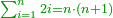
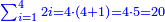
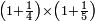
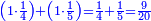
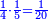
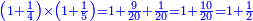
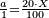

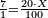

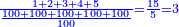
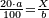
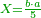
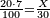
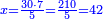
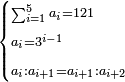
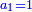
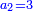
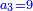

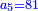

![\scriptstyle{\color{OliveGreen}{\left[\left(2\sdot1\right)+\left(4\sdot2\right)+\left(3\sdot4\right)\right]\bmod7=}}](/mediawiki/images/math/b/d/8/bd8cd8d9a5a69f4e75325dca7bdeca93.png) 1 → copper, gold, silver.
1 → copper, gold, silver.![\scriptstyle{\color{OliveGreen}{\left[\left(3\sdot1\right)+\left(2\sdot2\right)+\left(4\sdot4\right)\right]\bmod7=}}](/mediawiki/images/math/e/d/9/ed9c3072d779e894dc7d9bd6b1518106.png) 2 → silver, copper, gold.
2 → silver, copper, gold.![\scriptstyle{\color{OliveGreen}{\left[\left(2\sdot1\right)+\left(3\sdot2\right)+\left(4\sdot4\right)\right]\bmod7=}}](/mediawiki/images/math/d/2/9/d290492501dc1ca670dce7fdde74810a.png) 3 → copper, silver, gold.
3 → copper, silver, gold.![\scriptstyle{\color{OliveGreen}{\left[\left(4\sdot1\right)+\left(3\sdot2\right)+\left(2\sdot4\right)\right]\bmod7=}}](/mediawiki/images/math/d/b/8/db8690da87d43dafcdc91b8de3bc2800.png) 4 → gold, silver, copper.
4 → gold, silver, copper.![\scriptstyle{\color{OliveGreen}{\left[\left(3\sdot1\right)+\left(4\sdot2\right)+\left(2\sdot4\right)\right]\bmod7=}}](/mediawiki/images/math/1/7/a/17ae82029f9b50d7ab20ae9d9e3aed2c.png) 5 → silver, gold, copper.
5 → silver, gold, copper.![\scriptstyle{\color{OliveGreen}{\left[\left(4\sdot1\right)+\left(2\sdot2\right)+\left(3\sdot4\right)\right]\bmod7=}}](/mediawiki/images/math/4/0/f/40fea3c45e9afe81fc065fc0c9851fdf.png) 6 → gold, copper, silver.
6 → gold, copper, silver.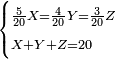
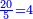
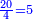
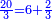
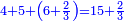 days
days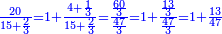
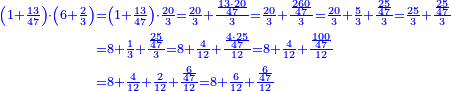
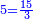
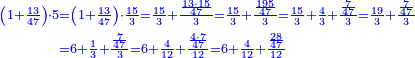
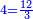
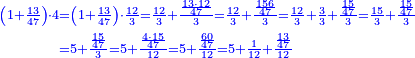
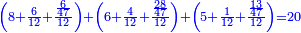
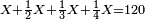
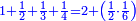
![\scriptstyle{\color{blue}{\left[2+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot60=125}}](/mediawiki/images/math/f/e/e/feee1688775c37c50f8c73a0ca686bf5.png)
![\scriptstyle{\color{blue}{\left[2+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot12=12+13}}](/mediawiki/images/math/c/8/4/c84d44d55e4f0aecc61dd6b809638c69.png)
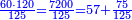
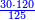
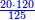
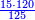
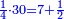
![\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot30\right)+\left[\frac{1}{3}\sdot\left(\frac{1}{4}\sdot40\right)\right]=\left(7+\frac{1}{2}\right)+\left(\frac{1}{3}\sdot10\right)=\left(7+\frac{3}{6}\right)+\left(3+\frac{2}{6}\right)=10+\frac{5}{6}}}](/mediawiki/images/math/8/0/2/8025548d7ffea180aaf74b2aa258a187.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot30\right)+\left[\frac{1}{3}\sdot\left(\frac{1}{4}\sdot40\right)\right]+\left[\frac{1}{2}\sdot\left(\frac{1}{3}\sdot60\right)\right]=20+\frac{5}{6}}}](/mediawiki/images/math/6/3/9/639c2256db341185f9c23923c2b05f10.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot30\right)+\left[\frac{1}{3}\sdot\left(\frac{1}{4}\sdot40\right)\right]+\left[\frac{1}{2}\sdot\left(\frac{1}{3}\sdot60\right)\right]+\left(\frac{1}{2}\sdot120\right)=80+\frac{5}{6}}}](/mediawiki/images/math/4/b/7/4b7c4c6a1a27b51b2f61f1452a8a65a0.png)
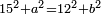
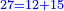
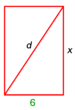
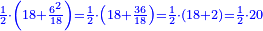
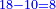

![\scriptstyle\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{length_1+length_2}\right)\right]\sdot\left[\frac{1}{2}\sdot\left(\rm{breadth_1+breadth_2}\right)\right]}}](/mediawiki/images/math/0/5/4/0541cff5b82ef3ad6443caeeaba42f0c.png)
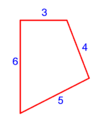
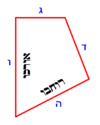
![\scriptstyle{\color{blue}{\left[\frac{1}{2}\sdot\left(4+6\right)\right]\sdot\left[\frac{1}{2}\sdot\left(5+3\right)\right]=\left(\frac{1}{2}\sdot10\right)\sdot\left(\frac{1}{2}\sdot8\right)=5\sdot4=20}}](/mediawiki/images/math/6/b/e/6be403d9d0da87e677138195512e3aaa.png)
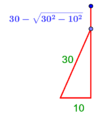
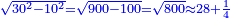
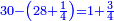


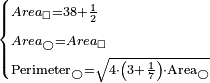
![\scriptstyle{\color{blue}{\sqrt{\left(38+\frac{1}{2}\right)\sdot\left[4\sdot\left(3+\frac{1}{7}\right)\right]}=\sqrt{\left(38+\frac{1}{2}\right)\sdot\left(12+\frac{4}{7}\right)}=\sqrt{484}=22}}](/mediawiki/images/math/7/b/7/7b7dca044063af8f374417378f76a6a1.png)
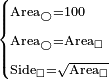

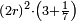
![\scriptstyle{\color{OliveGreen}{\rm{Surface_{sphere}}\sdot\left[\frac{1}{6}\sdot\left(2r\right)\right]}}](/mediawiki/images/math/1/c/5/1c52cc720d920cee8198165189e5281f.png)

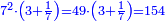
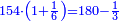
![\scriptstyle{\color{blue}{\left[7\sdot\left(3+\frac{1}{2}\right)\right]\sdot\left(3+\frac{1}{7}\right)=77}}](/mediawiki/images/math/7/4/5/7457b23543f85dd128179a780b2b2382.png)
![\scriptstyle{\color{blue}{77\sdot\left[\frac{1}{6}\sdot\left(2r\right)\right]=90-\frac{1}{6}}}](/mediawiki/images/math/4/d/2/4d2d28f827869eea6319d87dc150ff02.png)
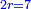
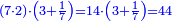
![\scriptstyle{\color{blue}{44\sdot\left[\frac{1}{6}\sdot\left(2r\right)\right]=44\sdot\left(1+\frac{1}{6}\right)=51+\frac{1}{3}}}](/mediawiki/images/math/4/c/c/4cc6a351ee80703dd6fdbd7965782c9e.png)
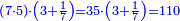
![\scriptstyle{\color{blue}{110\sdot\left[\frac{1}{6}\sdot\left(2r\right)\right]=128+\frac{1}{3}}}](/mediawiki/images/math/1/b/d/1bd0a32a24afbf4ad5cbbfff01b1a358.png)



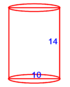
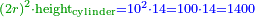
![\scriptstyle{\color{blue}{1400-\left[\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\sdot1400\right]=1400-300=1100}}](/mediawiki/images/math/9/6/8/968c893b6e831904d39545b4738b1cda.png)
![\scriptstyle{\color{blue}{100-\left[\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\sdot100\right]=100-\left(21+\frac{3}{7}\right)=78+\frac{4}{7}}}](/mediawiki/images/math/f/1/8/f18ddd8d864724be886adef0829db8d2.png)


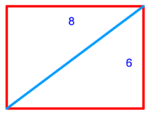
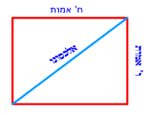
![\scriptstyle{\color{blue}{\sqrt{\left[2\sdot\left(8\sdot6\right)\right]+\left(8-6\right)^2}=\sqrt{\left(2\sdot48\right)+2^2}=\sqrt{96+2^2}=\sqrt{100}=10}}](/mediawiki/images/math/b/a/6/ba6094813180dc06f481c47295a2e833.png)

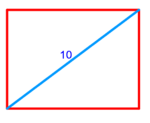
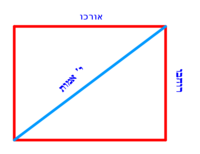
![\scriptstyle{\color{blue}{\frac{1}{2}\sdot\left[diagonal^2-\left(side_1-side_2\right)^2\right]=\frac{1}{2}\sdot\left(10^2-2^2\right)=\frac{1}{2}\sdot\left(100-4\right)=\frac{1}{2}\sdot96=48}}](/mediawiki/images/math/a/d/9/ad9a0fe0dcb662818d3ab0d7c95a9c00.png)
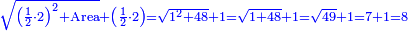

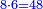
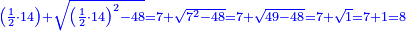
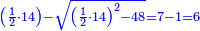
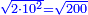
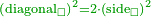
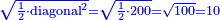

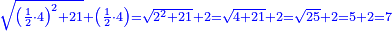

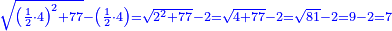
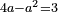
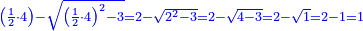
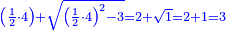
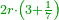
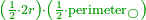
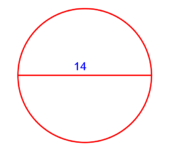

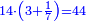
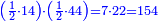
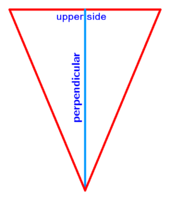
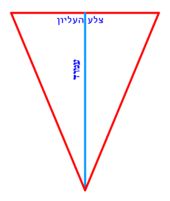
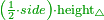

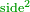
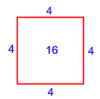
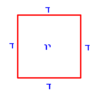
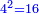
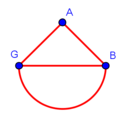
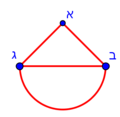

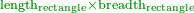
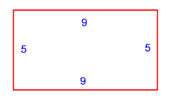
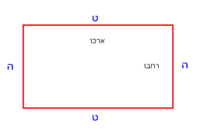
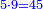
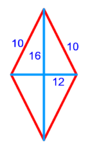
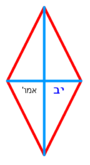
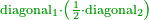
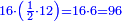
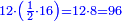
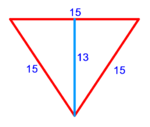
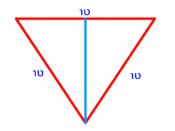
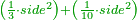
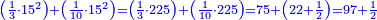
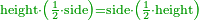
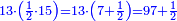
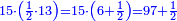
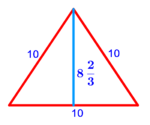
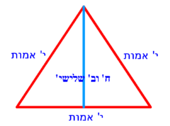
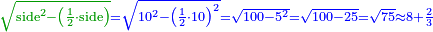
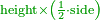
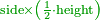
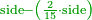
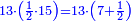
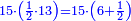
![\scriptstyle{\color{OliveGreen}{\sqrt{\rm{height}^2+\left[\frac{1}{3}\sdot\left(\rm{height}^2\right)\right]}}}](/mediawiki/images/math/1/b/8/1b868584da526e782eefe9f61ecdf63b.png)
![\scriptstyle{\color{blue}{\sqrt{13^2+\left[\frac{1}{3}\sdot\left(13^2\right)\right]}=\sqrt{169+\left(\frac{1}{3}\sdot169\right)}=\sqrt{169+\left(56+\frac{1}{3}\right)}=\sqrt{225+\frac{1}{3}}\approx15}}](/mediawiki/images/math/1/b/e/1be4eaaa35521be3c6f64424d6b16ded.png)
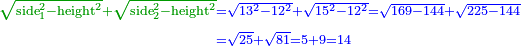
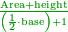
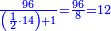
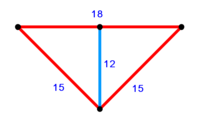
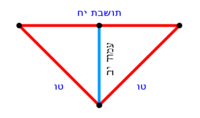
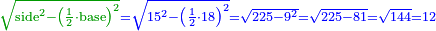
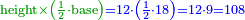
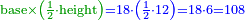
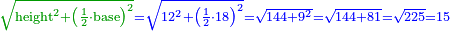
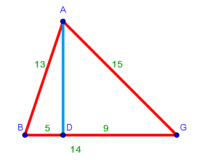
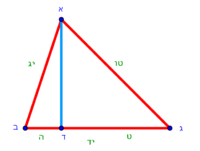
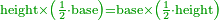
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{\frac{1}{2}\sdot\left[\left(AG^2+BG^2\right)-AB^2\right]}{BG}&\scriptstyle=\frac{\frac{1}{2}\sdot\left[\left(15^2+14^2\right)-13^2\right]}{14}=\frac{\frac{1}{2}\sdot\left[\left(225+196\right)-169\right]}{14}=\frac{\frac{1}{2}\sdot\left(421-169\right)}{14}\\&\scriptstyle=\frac{\frac{1}{2}\sdot252}{14}=\frac{126}{14}=9\\\end{align}}}](/mediawiki/images/math/3/9/b/39bf1d911e6e3d0c22577ed996e7967e.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{\frac{1}{2}\sdot\left[\left(AB^2+BG^2\right)-AG^2\right]}{BG}&\scriptstyle=\frac{\frac{1}{2}\sdot\left[\left(13^2+14^2\right)-15^2\right]}{14}=\frac{\frac{1}{2}\sdot\left[\left(169+196\right)-225\right]}{14}=\frac{\frac{1}{2}\sdot\left(365-225\right)}{14}\\&\scriptstyle=\frac{\frac{1}{2}\sdot140}{14}=\frac{70}{14}=5\\\end{align}}}](/mediawiki/images/math/e/b/f/ebffa7c5aa53ccfd67e5875218757ecd.png)

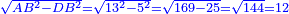
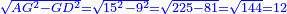
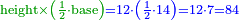
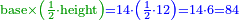
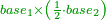
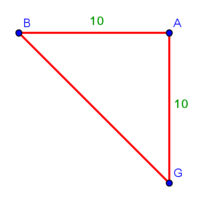
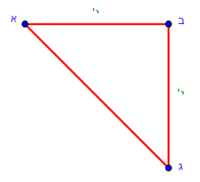
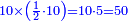
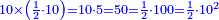
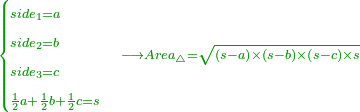
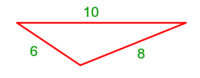
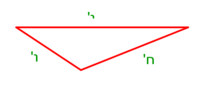
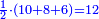
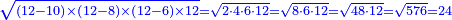
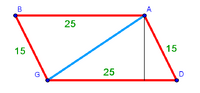
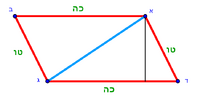
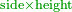
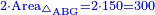
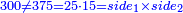
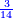 ; the inner circle exceeds its inner square by
; the inner circle exceeds its inner square by 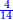 .
.
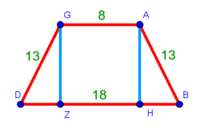
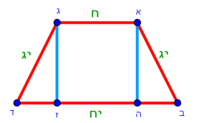
![\scriptstyle{\color{OliveGreen}{\sqrt{\rm{side}^2-\left[\frac{1}{2}\sdot\left[\left(\rm{bottom\ base}\right)-\left(\rm{upper\ base}\right)\right]\right]^2}}}](/mediawiki/images/math/4/d/d/4dd4d916db1f6b96bf6ff97a571571d7.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle AH&\scriptstyle=\sqrt{AB^2-\left[\frac{1}{2}\sdot\left(BD-AG\right)\right]^2}=\sqrt{13^2-\left[\frac{1}{2}\sdot\left(18-8\right)\right]^2}=\sqrt{169-\left(\frac{1}{2}\sdot10\right)^2}\\&\scriptstyle=\sqrt{169-5^2}=\sqrt{169-25}=\sqrt{144}=12\\\end{align}}}](/mediawiki/images/math/f/2/3/f234251db56850fb612e1a426a4c951a.png)
![\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left[\left(\rm{top\ base}\right)+\left(\rm{bottom\ base}\right)\right]\right]\sdot\rm{height}}}{\color{blue}{=\left[\frac{1}{2}\sdot\left(8+18\right)\right]\sdot12=\left[\frac{1}{2}\sdot26\right]\sdot12=13\sdot12=156}}](/mediawiki/images/math/f/b/6/fb69e96bf102ceb9d99d5e46825f03a0.png)
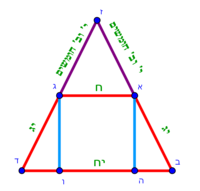

![\scriptstyle{\color{blue}{\begin{align}\scriptstyle AC:13=AC:BC=GC:13&\scriptstyle=GC:DC=AG:\left(BD-AG\right)\\&\scriptstyle={\color{OliveGreen}{\left(\rm{top\ base}\right):\left[\left(\rm{bottom\ base}\right)-\left(\rm{top\ base}\right)\right]}}\\&\scriptstyle=8:\left(18-8\right)=8:10=\frac{4}{5}=1-\frac{1}{5}\\\end{align}}}](/mediawiki/images/math/0/c/4/0c4d197b6c60509ca901c349a7530857.png)
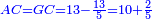
![\scriptstyle{\color{OliveGreen}{\rm{height}\sdot\left[\frac{1}{2}\sdot\left[\left(\rm{top\ base}\right)+\left(\rm{bottom\ base}\right)\right]\right]}}](/mediawiki/images/math/5/b/5/5b521955d63ba10eb7311e9a47d6fe46.png)
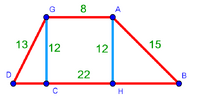
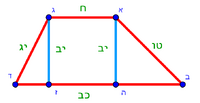
![\scriptstyle{\color{blue}{12\sdot\left[\frac{1}{2}\sdot\left(8+22\right)\right]=12\sdot\left(\frac{1}{2}\sdot30\right)=12\sdot15=180}}](/mediawiki/images/math/d/6/d/d6d1aad37c46030ca055b78ae6edd836.png)
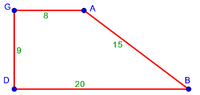
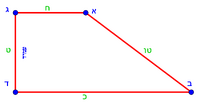
![\scriptstyle{\color{OliveGreen}{height\sdot\left[\frac{1}{2}\sdot\left[\left(top\ base\right)+\left(bottom\ base\right)\right]\right]}}](/mediawiki/images/math/b/1/d/b1df4ea4bb7e3bb8fba4815bd773d7dc.png)
![\scriptstyle{\color{blue}{9\sdot\left[\frac{1}{2}\sdot\left(8+20\right)\right]=9\sdot\left(\frac{1}{2}\sdot28\right)=9\sdot14=126}}](/mediawiki/images/math/6/8/b/68b1007c14e93b43f21b6fecffbb9f64.png)
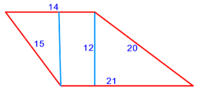
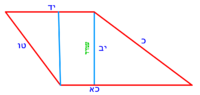
![\scriptstyle{\color{blue}{12\sdot\left[\frac{1}{2}\sdot\left(14+21\right)\right]=12\sdot\left(17+\frac{1}{2}\right)=210}}](/mediawiki/images/math/5/0/f/50f1b9c85f19e17260ef8843108adc68.png)
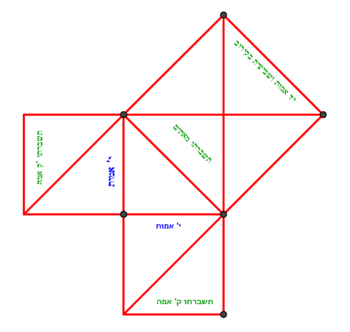
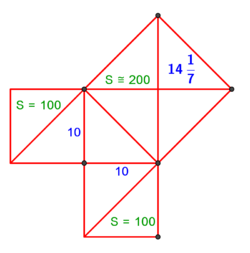

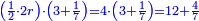
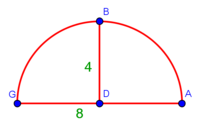
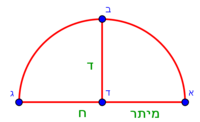
![\scriptstyle{\color{blue}{4\sdot\left[\frac{1}{2}\sdot\left(12+\frac{4}{7}\right)\right]=4\sdot\left(6+\frac{2}{7}\right)=25+\frac{1}{7}}}](/mediawiki/images/math/7/6/4/764622b2cd768983aec6d8c70c988879.png)
![\scriptstyle{\color{OliveGreen}{\frac{1}{2}\sdot\left[\left(2r\right)^2-\left[\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\sdot\left(2r\right)^2\right]\right]}}](/mediawiki/images/math/6/b/6/6b6e41a83d19b7fa663f7310300898cb.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{1}{2}\sdot\left[8^2-\left[\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\sdot8^2\right]\right]&\scriptstyle=\frac{1}{2}\sdot\left[64-\left[\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\sdot64\right]\right]=\frac{1}{2}\sdot\left[64-\left(13+\frac{5}{7}\right)\right]\\&\scriptstyle=\frac{1}{2}\sdot\left(50+\frac{2}{7}\right)=25+\frac{1}{7}\\\end{align}}}](/mediawiki/images/math/b/9/a/b9a4238e71f7081b6fab96916d3c3a15.png)
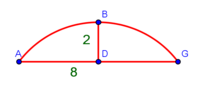
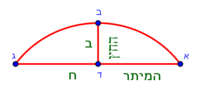
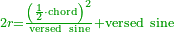
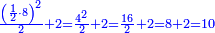
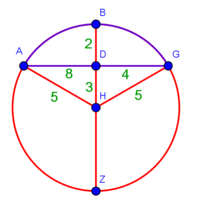
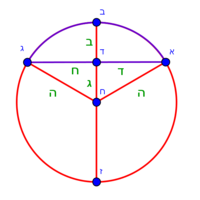
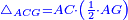
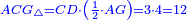
![\scriptstyle{\color{blue}{ABGD=AG_{sector}-ACG_{\triangle}=AH\sdot\left(\frac{1}{2}\sdot AG_{arc}\right)-ACG_{\triangle}=\left[r\sdot\left(\frac{1}{2}\sdot AG_{arc}\right)\right]-ACG_{\triangle}}}](/mediawiki/images/math/c/3/3/c331f26055d92bc081ccfe8c2793bc17.png)
![\scriptstyle{\color{OliveGreen}{\left[\left[\frac{1}{2}\sdot\left(2r\right)\right]\sdot\left(\frac{1}{2}\sdot\rm{arc}\right)\right]-\left[\left[\left[\frac{1}{2}\sdot\left(2r\right)\right]-\rm{versed\ sine}\right]\sdot\left(\frac{1}{2}\sdot\rm{chord}\right)\right]}}](/mediawiki/images/math/d/6/0/d605d4f78e9bef02470d63d9544f369b.png)
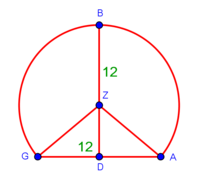

![\scriptstyle{\color{OliveGreen}{\left[\left[\frac{1}{2}\sdot\left(2r\right)\right]\sdot\left(\frac{1}{2}\sdot\rm{arc}\right)\right]+\rm{Area}_{\triangle}}}](/mediawiki/images/math/d/1/6/d16d06efbeaef35e417b2c19bff017b0.png)
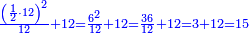
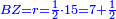
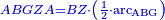
![\scriptstyle{\color{blue}{ABGDA=ABGZA+AZG=ABGZA+\left[DZ\sdot\left(\frac{1}{2}\sdot AG\right)\right]}}](/mediawiki/images/math/d/7/a/d7a5b97626d14c9dc6d3d9b48ea613a6.png)
![\scriptstyle{\color{OliveGreen}{\left[\left[\frac{1}{2}\sdot\left(2r\right)\right]\sdot\left(\frac{1}{2}\sdot\rm{arc}\right)\right]+\left[\left[\rm{versed\ sine}-\left[\frac{1}{2}\sdot\left(2r\right)\right]\right]\sdot\left(\frac{1}{2}\sdot\rm{chord}\right)\right]}}](/mediawiki/images/math/6/d/4/6d432194c21ae92fef81e69b723c15a3.png)
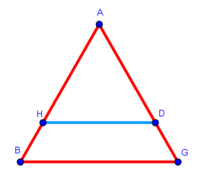
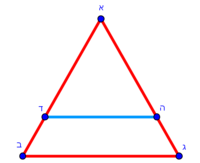
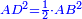
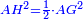
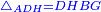
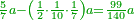
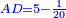
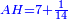

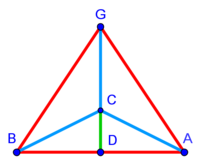
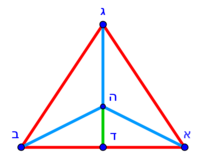
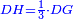
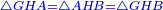
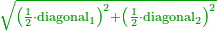



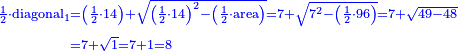
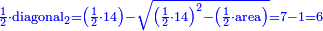

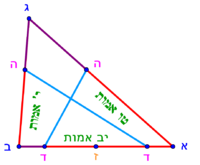
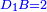
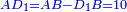
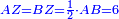
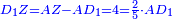
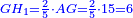
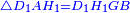

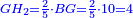
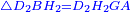

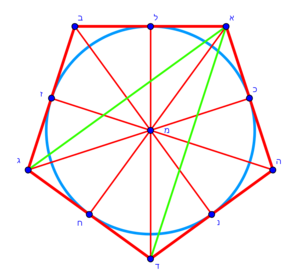
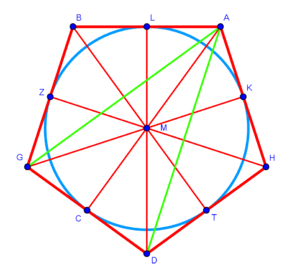




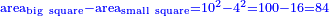
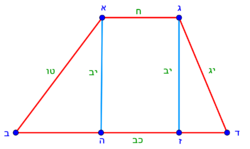
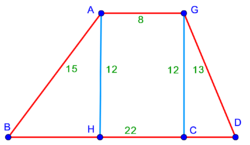
![\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{base_{bottom}-base_{top}}\right)\right]+\frac{\frac{1}{2}\sdot\left(\rm{side_1^2-side_2^2}\right)}{\rm{base_{bottom}-base_{top}}}}}](/mediawiki/images/math/8/c/9/8c9b6d1d38374842b7d95e80879134c9.png)
![\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{base_{bottom}-base_{top}}\right)\right]-\frac{\frac{1}{2}\sdot\left(\rm{side_1^2-side_2^2}\right)}{\rm{base_{bottom}-base_{top}}}}}](/mediawiki/images/math/a/b/0/ab088396870fa8692f26053d4809f487.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle BH &\scriptstyle=\left[\frac{1}{2}\sdot\left(BD-AG\right)\right]+\frac{\frac{1}{2}\sdot\left(AB^2-GD^2\right)}{BD-AG}=\left[\frac{1}{2}\sdot\left(22-8\right)\right]+\frac{\frac{1}{2}\sdot\left(15^2-13^2\right)}{22-8}\\&\scriptstyle=\left(\frac{1}{2}\sdot14\right)+\frac{\frac{1}{2}\sdot\left(15^2-169\right)}{14}=7+\frac{\frac{1}{2}\sdot56}{14}=7+\frac{28}{14}=7+2=9\\\end{align}}}](/mediawiki/images/math/a/7/8/a7855f2dfb8394a9f6ed7785513f77d2.png)
![\scriptstyle{\color{blue}{CD=\left[\frac{1}{2}\sdot\left(BD-AG\right)\right]-\frac{\frac{1}{2}\sdot\left(AB^2-GD^2\right)}{BD-AG}=7-2}}](/mediawiki/images/math/1/0/2/1027a9c6e067c0548a875e01e5376d46.png)
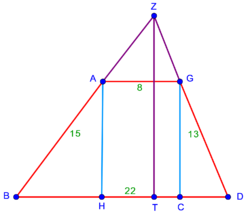
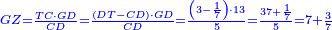
![\scriptstyle{\color{blue}{AZ=\frac{HT\sdot AB}{HB}=\frac{\left(BT-HB\right)\sdot AB}{HB}=\frac{\left[\left(14+\frac{1}{7}\right)-9\right]\sdot 15}{9}=\frac{\left(5+\frac{1}{7}\right)\sdot15}{9}=\frac{77+\frac{1}{7}}{9}=8+\frac{4}{7}}}](/mediawiki/images/math/5/a/8/5a8bdc31cf4a115ef3b3e6869789c4e0.png)
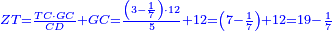
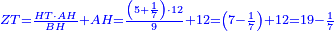
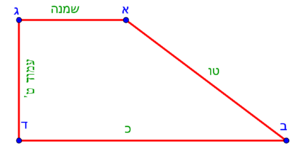
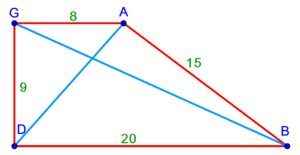
![\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{base_{top}+base_{bottom}}\right)\right]\sdot\rm{height}}}](/mediawiki/images/math/0/a/4/0a462b7f7ae6f829c66786fc98113e09.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{2}\sdot\left(8+20\right)\right]\sdot9=\left(\frac{1}{2}\sdot28\right)\sdot9=14\sdot9=126}}](/mediawiki/images/math/8/a/2/8a2be587e347ec5a64296a52ea860b9f.png)
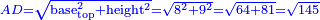


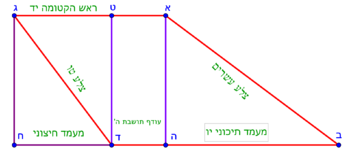
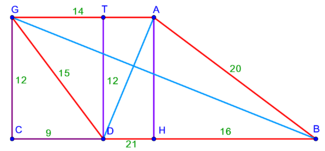
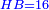
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle CD &\scriptstyle=\frac{\frac{1}{2}\sdot\left[AB^2-\left[\left(BD-AG\right)^2+GD^2\right]\right]}{BD-AG}=\frac{\frac{1}{2}\sdot\left[20^2-\left[\left(21-14\right)^2+15^2\right]\right]}{21-14}=\frac{\frac{1}{2}\sdot\left[20^2-\left(7^2+15^2\right)\right]}{7}\\&\scriptstyle=\frac{\frac{1}{2}\sdot\left(400-274\right)}{7}=\frac{\frac{1}{2}\sdot126}{7}=\frac{63}{7}=9\\\end{align}}}](/mediawiki/images/math/b/2/8/b28bbc6bd98c9e3890aa1105e145e1d1.png)
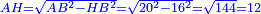
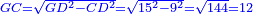
![\scriptstyle{\color{blue}{\left[\frac{1}{2}\sdot\left(14+21\right)\right]\sdot12=210}}](/mediawiki/images/math/8/c/b/8cb8b983e66e5f5777b2663053b8e239.png)
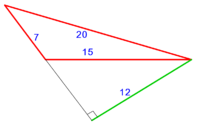
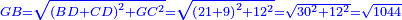
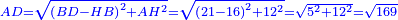
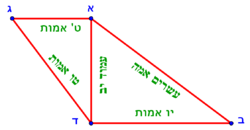
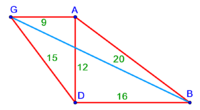
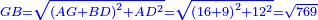
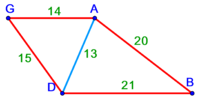
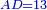
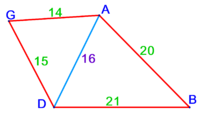
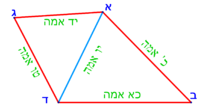
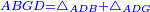
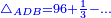
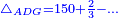
![\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(\rm{height_1+height_2}\right)\right]\sdot\rm{diagonal}}}](/mediawiki/images/math/3/1/1/311d7ab92aed0202cb3874127b6a5a58.png)

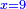
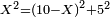
![\scriptstyle{\color{blue}{x=\frac{1}{2}\sdot\left(10+\frac{5^2}{10}\right)=\frac{1}{2}\sdot\left(10+\frac{25}{10}\right)=\frac{1}{2}\sdot\left[10+\left(2+\frac{1}{2}\right)\right]=6+\frac{1}{4}}}](/mediawiki/images/math/2/1/f/21f4dd1709c59b361a8076494299eed2.png)
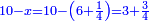
![\scriptstyle1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]=2+\frac{1}{10}\sdot\left[X-\left[\left[1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]\right]+2\right]\right]](/mediawiki/images/math/0/4/e/04ec9fa2f7109a05d7c4e8fa7ce5d879.png)