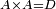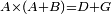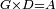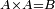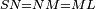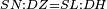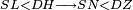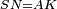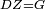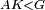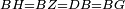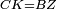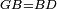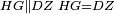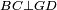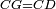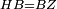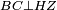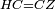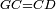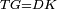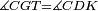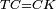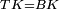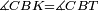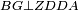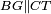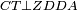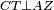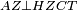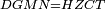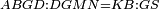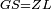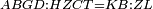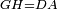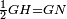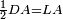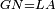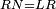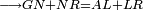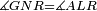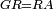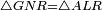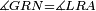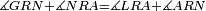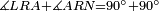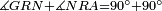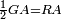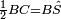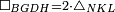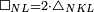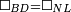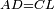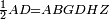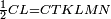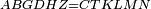Difference between revisions of "ספר היסודות לאקלידס"
(→Proposition 19) |
(→The Second Section of Euclid's Book) |
||
| (114 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
|- | |- | ||
| | | | ||
| − | === Definitions === | + | === <span style=color:green>Definitions</span> === |
| | | | ||
|- | |- | ||
| | | | ||
*{{#annot:definition|833,1606|I0Aq}}The '''point''' is a thing that has no part. | *{{#annot:definition|833,1606|I0Aq}}The '''point''' is a thing that has no part. | ||
| − | |style="text-align:right;"|<big>הנקודה</big> היא דבר אין לה חלק ולא הנחה{{#annotend:I0Aq}} | + | |style="width:45%;text-align:right;"|<big>הנקודה</big> היא דבר אין לה חלק ולא הנחה{{#annotend:I0Aq}} |
|- | |- | ||
| | | | ||
| Line 21: | Line 21: | ||
| | | | ||
:The ends of the line are points. | :The ends of the line are points. | ||
| − | |style="text-align:right;"|ותכליות הקו שתי נקודות | + | |style="width:45%; text-align:right;"|ותכליות הקו שתי נקודות |
|- | |- | ||
| | | | ||
| Line 52: | Line 52: | ||
|- | |- | ||
| | | | ||
| − | :*{{#annot:definition|1093, | + | :*{{#annot:definition|1093,2524|szjV}}The greater than a right angle is called an '''obtuse angle'''. |
|style="text-align:right;"|ואשר היא גדולה מנצבת תקרא <big>נרוחת</big>{{#annotend:szjV}} | |style="text-align:right;"|ואשר היא גדולה מנצבת תקרא <big>נרוחת</big>{{#annotend:szjV}} | ||
|- | |- | ||
| Line 73: | Line 73: | ||
| | | | ||
:*This point is the '''center''' of the circle. | :*This point is the '''center''' of the circle. | ||
| − | |style="text-align:right;"|והנקודה ההיא הוא <big>{{#annot: | + | |style="text-align:right;"|והנקודה ההיא הוא <big>{{#annot:center of a circle|1108,2234|C6ny}}מרכז העגולה{{#annotend:C6ny}}</big> |
|- | |- | ||
| | | | ||
| Line 124: | Line 124: | ||
|- | |- | ||
| | | | ||
| − | :*{{#annot:definition|1104, | + | :*{{#annot:triangle-definition|1104,1341|BAtH}}The '''right-angled triangle''' is that which has a right angle. |
|style="text-align:right;"|<big>המשולש נצב הזוית</big> והוא אשר לו זוית נצבת{{#annotend:BAtH}} | |style="text-align:right;"|<big>המשולש נצב הזוית</big> והוא אשר לו זוית נצבת{{#annotend:BAtH}} | ||
|- | |- | ||
| | | | ||
| − | :*{{#annot:definition|1105,2524|g9wm}}The '''obtuse-angled triangle''' is that which has an obtuse angle. | + | :*{{#annot:triangle-definition|1105,2524|g9wm}}The '''obtuse-angled triangle''' is that which has an obtuse angle. |
|style="text-align:right;"|<big>והמשולש הנרוח הזוית</big> והוא אשר לו זוית נרוחת{{#annotend:g9wm}} | |style="text-align:right;"|<big>והמשולש הנרוח הזוית</big> והוא אשר לו זוית נרוחת{{#annotend:g9wm}} | ||
|- | |- | ||
| | | | ||
| − | :*{{#annot:definition|1103,1343|pQ2M}}The '''acute-angled triangle''' is that whose three angles are acute. | + | :*{{#annot:triangle-definition|1103,1343|pQ2M}}The '''acute-angled triangle''' is that whose three angles are acute. |
|style="text-align:right;"|<big>ומשולש חד הזויות</big> והוא אשר כל אחת מזויותיו השלש חדה{{#annotend:pQ2M}} | |style="text-align:right;"|<big>ומשולש חד הזויות</big> והוא אשר כל אחת מזויותיו השלש חדה{{#annotend:pQ2M}} | ||
|- | |- | ||
| Line 162: | Line 162: | ||
*{{#annot:definition|825,1821|Zac6}}The '''parallel straight lines''' are those that are in the same plane such that if they are drawn endlessly in both directions, they do not meet one another in either direction. | *{{#annot:definition|825,1821|Zac6}}The '''parallel straight lines''' are those that are in the same plane such that if they are drawn endlessly in both directions, they do not meet one another in either direction. | ||
|style="text-align:right;"|<big>והקוים הישרים הנכחיים</big> הם אשר יהיו על שטח אחד שוה ואם הוצאו בשני הצדדים אל לא תכלית לא יפגשו באחד מהם{{#annotend:Zac6}} | |style="text-align:right;"|<big>והקוים הישרים הנכחיים</big> הם אשר יהיו על שטח אחד שוה ואם הוצאו בשני הצדדים אל לא תכלית לא יפגשו באחד מהם{{#annotend:Zac6}} | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | === Postulates === | + | === <span style=color:green>Postulates</span> === |
| | | | ||
|- | |- | ||
| Line 174: | Line 172: | ||
|- | |- | ||
| | | | ||
| − | *<span style=color: | + | *<span style=color:green>'''The first postulate:'''</span> any straight line can be drawn from any point to any point. |
|style="text-align:right;"|מהם שימשך קו ישר מכל נקודה אל כל נקודה | |style="text-align:right;"|מהם שימשך קו ישר מכל נקודה אל כל נקודה | ||
|- | |- | ||
| | | | ||
| − | *<span style=color: | + | *<span style=color:green>'''The second postulate:'''</span> any finite straight line can be extended indefinitely. |
|style="text-align:right;"|ושיוצא קו ישר בעל תכלית על יושר ודבקות לבלתי תכלית | |style="text-align:right;"|ושיוצא קו ישר בעל תכלית על יושר ודבקות לבלתי תכלית | ||
|- | |- | ||
| | | | ||
| − | *<span style=color: | + | *<span style=color:green>'''The third postulate:'''</span> circle can be drawn at any point [= center] and any measure of a distance [= radius] |
|style="text-align:right;"|וש{{#annot:term|2549,2498|Pgvr}}נקוה עגולה{{#annotend:Pgvr}} על כל נקודה ובשיעור כל מרחק | |style="text-align:right;"|וש{{#annot:term|2549,2498|Pgvr}}נקוה עגולה{{#annotend:Pgvr}} על כל נקודה ובשיעור כל מרחק | ||
|- | |- | ||
| | | | ||
| − | *<span style=color: | + | *<span style=color:green>'''The fourth postulate:'''</span> all right angles are equal to one another. |
|style="text-align:right;"|ושכל הזויות הנצבות שוות קצתם אל קצתם | |style="text-align:right;"|ושכל הזויות הנצבות שוות קצתם אל קצתם | ||
|- | |- | ||
| | | | ||
| − | *<span style=color: | + | *<span style=color:green>'''The fifth postulate:'''</span> if a straight line falls on two straight lines, forming two interior angles on the same side that sum to less than two right angles, then the two straight lines, when extended [indefinitely], meet on that side. |
|style="text-align:right;"|ואם נפל קו ישר על שני קוים ישרים ושם באחד משני הצדדים שתי הזויות הפנימיות פחות משתי נצבות הנה שני הקוים הישרים כאשר יוצאו בצד ההוא יפגשו | |style="text-align:right;"|ואם נפל קו ישר על שני קוים ישרים ושם באחד משני הצדדים שתי הזויות הפנימיות פחות משתי נצבות הנה שני הקוים הישרים כאשר יוצאו בצד ההוא יפגשו | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | === Common Notions === | + | === <span style=color:green>Common Notions</span> === |
| | | | ||
| Line 249: | Line 245: | ||
| | | | ||
|- | |- | ||
| − | | | + | |We wish to construct an equilateral triangle on a given finite straight line. |
|style="text-align:right;"|<big><span style=color:red>א</span> נרצה</big> שנעמיד משולש שוה הצלעות על קו ישר בעל תכלית מונח | |style="text-align:right;"|<big><span style=color:red>א</span> נרצה</big> שנעמיד משולש שוה הצלעות על קו ישר בעל תכלית מונח | ||
|- | |- | ||
| − | |Example: line AB | + | |Example: let line AB be the finite straight line. |
|style="text-align:right;"|<big>המשל</big> שיהיה הקו הישר הבעל תכלי' קו א"ב | |style="text-align:right;"|<big>המשל</big> שיהיה הקו הישר הבעל תכלי' קו א"ב | ||
|- | |- | ||
| − | | | + | |We wish to construct an equilateral triangle on the straight line AB. |
|style="text-align:right;"|ונרצה ש{{#annot:term|2550,1015|yirg}}נעמיד על{{#annotend:yirg}} קו א"ב הישר משולש שוה הצלעות | |style="text-align:right;"|ונרצה ש{{#annot:term|2550,1015|yirg}}נעמיד על{{#annotend:yirg}} קו א"ב הישר משולש שוה הצלעות | ||
| + | |- | ||
| + | |The procedure: | ||
| + | |style="text-align:right;"|המעשה | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''Postulate 3:'''</span> we draw around the center A a circle with radius AB, which is the circle GDB. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה {{#annot:term|1855,2498|Wj8n}}נקיף על{{#annotend:Wj8n}} מרכז א' ובמרחק א"ב עגולה והיא עגולת גד"ב |
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''Postulate 3:'''</span> we draw also around the center B a circle with radius BA, which is the circle AGH. | |
|style="text-align:right;"|ונקיף גם כן על מרכז ב' ובמרחק ב"א עגולה והיא עגולת אג"ה | |style="text-align:right;"|ונקיף גם כן על מרכז ב' ובמרחק ב"א עגולה והיא עגולת אג"ה | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''Postulate 1:'''</span> we join two straight lines, which are GB and GA, from the point G, at which the two circles cut one another, to the two points A and B | |
|style="text-align:right;"|ונגיע מנקודת ג' אשר יחתכו עליה שתי העגולות בשתי נקודות א"ב שני קוים ישרים והם ג"ב ג"א <span style=color:red>מא' מהפתיחה</span> | |style="text-align:right;"|ונגיע מנקודת ג' אשר יחתכו עליה שתי העגולות בשתי נקודות א"ב שני קוים ישרים והם ג"ב ג"א <span style=color:red>מא' מהפתיחה</span> | ||
|- | |- | ||
| | | | ||
| + | :We say that we have already constructed an equilateral triangle on line AB, which is triangle AGB. | ||
|style="text-align:right;"|ונאמ' שכבר העמדנו על קו א"ב משלש שוה הצלעות והוא משלש אג"ב | |style="text-align:right;"|ונאמ' שכבר העמדנו על קו א"ב משלש שוה הצלעות והוא משלש אג"ב | ||
|- | |- | ||
| Line 276: | Line 276: | ||
|[[File:אוקלידס I 1.png|thumb|200px]] | |[[File:אוקלידס I 1.png|thumb|200px]] | ||
|- | |- | ||
| − | | | + | |The proof: |
| − | + | |style="text-align:right;"|<big>המופת</big> | |
| − | |||
| − | |style="text-align:right;"|<big>המופת</big> | ||
|- | |- | ||
| | | | ||
| − | : | + | :<span style=color:green>'''def. circle:'''</span> Since point A is the center of the circle BGD, therefore line AG is equal to line AB. |
| − | |style="text-align:right;"|הנה יהיה קו א"ג שוה לקו א"ב <span style=color:red>מהפתיחה</span> | + | :<math>\scriptstyle{\color{blue}{AG=AB}}</math> |
| + | |style="text-align:right;"|הנה מפני שנקודת א' היא מרכז עגולת בג"ד<br> | ||
| + | הנה יהיה קו א"ג שוה לקו א"ב <span style=color:red>מהפתיחה</span> | ||
|- | |- | ||
| | | | ||
| − | ::B the center of <math>\scriptstyle\ | + | :<span style=color:green>'''def. circle:'''</span> Also, since point B is the center of the circle AGH, therefore line BG is equal to line AB. |
| − | |style="text-align:right;"|וגם כן הנה מפני שנקודת ב' היא מרכז עגולת אג"ה | + | :<math>\scriptstyle{\color{blue}{BG=AB}}</math> |
| + | |style="text-align:right;"|וגם כן הנה מפני שנקודת ב' היא מרכז עגולת אג"ה<br> | ||
| + | הנה קו ב"ג שוה לקו א"ב | ||
|- | |- | ||
| | | | ||
| − | : | + | :But, it has already been proven that line AG is equal to line AB. |
| − | + | :<math>\scriptstyle{\color{blue}{AG=AB}}</math> | |
| − | |||
| − | |||
| − | : | ||
|style="text-align:right;"|וכבר התבאר כי קו א"ג שוה לקו א"ב | |style="text-align:right;"|וכבר התבאר כי קו א"ג שוה לקו א"ב | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''C.N.:'''</span> So, line AG is equal to line GB. | |
| + | :<math>\scriptstyle{\color{blue}{AG=GB}}</math> | ||
|style="text-align:right;"|אם כן קו א"ג שוה לקו ג"ב <span style=color:red>מהפתיחה</span> | |style="text-align:right;"|אם כן קו א"ג שוה לקו ג"ב <span style=color:red>מהפתיחה</span> | ||
|- | |- | ||
| | | | ||
| − | + | :Therefore, the three lines AG, GB, and AB are equal. | |
| + | :<math>\scriptstyle{\color{blue}{AG=GB=AB}}</math> | ||
|style="text-align:right;"|אם כן קוי א"ג ג"ב וא"ב השלשה שוים | |style="text-align:right;"|אם כן קוי א"ג ג"ב וא"ב השלשה שוים | ||
|- | |- | ||
| − | |<span style=color: | + | | |
| + | :<span style=color:green>'''def. equilateral triangle:'''</span> Hence, the triangle ABG is equilateral. | ||
|style="text-align:right;"|אם כן משולש אב"ג שוה הצלעות <span style=color:red>מהפתיחה</span> | |style="text-align:right;"|אם כן משולש אב"ג שוה הצלעות <span style=color:red>מהפתיחה</span> | ||
|- | |- | ||
| − | | | + | |So, an equilateral triangle has already been constructed on the given finite line AB. |
|style="text-align:right;"|וכבר נעשה על קו א"ב בעל תכלית המונח משולש שוה הצלעות | |style="text-align:right;"|וכבר נעשה על קו א"ב בעל תכלית המונח משולש שוה הצלעות | ||
|- | |- | ||
| Line 319: | Line 321: | ||
| | | | ||
|- | |- | ||
| − | |We wish to attach to a given point a straight line that is equal to a given | + | |We wish to attach to a given point a straight line that is equal to a given line. |
|style="text-align:right;"|<big><span style=color:red>ב</span> נרצה</big> שנחבר אל נקודה מונחת קו ישר שוה לקו ישר מונח | |style="text-align:right;"|<big><span style=color:red>ב</span> נרצה</big> שנחבר אל נקודה מונחת קו ישר שוה לקו ישר מונח | ||
|- | |- | ||
| − | | | + | |Let A be the given point and BG the given straight line. |
|style="text-align:right;"|תהיה הנקודה המונחת א' והקו הישר המונח ב"ג | |style="text-align:right;"|תהיה הנקודה המונחת א' והקו הישר המונח ב"ג | ||
|- | |- | ||
| − | | | + | |We wish to attach a straight line to the given point A that is equal to the given straight line BG. |
|style="text-align:right;"|ונרצה שנחבר אל נקודת א' המונחת קו ישר שוה לקו ב"ג הישר המונח | |style="text-align:right;"|ונרצה שנחבר אל נקודת א' המונחת קו ישר שוה לקו ב"ג הישר המונח | ||
|- | |- | ||
| − | | | + | |We join the straight line AB from point A to point B. |
|style="text-align:right;"|הנה נגיע בין נקודת א' ונקודת ב' קו ישר והוא א"ב | |style="text-align:right;"|הנה נגיע בין נקודת א' ונקודת ב' קו ישר והוא א"ב | ||
|- | |- | ||
| − | |<span style=color: | + | |<span style=color:green>'''I.1:'''</span> we construct an equilateral triangle DAB on AB. |
|style="text-align:right;"|ונעמיד על א"ב משולש שוה הצלעות והוא משולש דא"ב <span style=color:red>מאשר לפניה</span> | |style="text-align:right;"|ונעמיד על א"ב משולש שוה הצלעות והוא משולש דא"ב <span style=color:red>מאשר לפניה</span> | ||
|- | |- | ||
| − | |< | + | | |
| + | :<span style=color:green>'''Postulate 2:'''</span> we draw two straight lines AH and BZ in a straight line with the straight lines DA and DB. | ||
|style="text-align:right;"|ונוציא שני קוי א"ה ב"ז הישרים על יושר ב' קוי ד"א ד"ב הישרים | |style="text-align:right;"|ונוציא שני קוי א"ה ב"ז הישרים על יושר ב' קוי ד"א ד"ב הישרים | ||
|- | |- | ||
| | | | ||
| − | :: | + | :<span style=color:green>'''Postulate 3:'''</span> we draw the circle CZG around the center B with radius BC. |
|style="text-align:right;"|ונקיף על מרכז ב' ובמרחק ב"ג עגולת חז"ג | |style="text-align:right;"|ונקיף על מרכז ב' ובמרחק ב"ג עגולת חז"ג | ||
|- | |- | ||
| | | | ||
| − | :: | + | :<span style=color:green>'''Postulate 3:'''</span> we also draw the circle ZTH around the center D with radius DZ. |
|style="text-align:right;"|ונקיף גם כן על מרכז ד' ובמרחק ד"ז עגולת זט"ה | |style="text-align:right;"|ונקיף גם כן על מרכז ד' ובמרחק ד"ז עגולת זט"ה | ||
|- | |- | ||
| | | | ||
| − | : | + | :<span style=color:green>'''def. circle:'''</span> Since point B is the center of the circle CZG, therefore line BZ is equal to line BG. |
| + | :<math>\scriptstyle{\color{blue}{BZ=BG}}</math> | ||
|style="text-align:right;"|הנה מפני שנקודת ב' מרכז עגולת חז"ג יהיה קו ב"ז שוה לקו ב"ג <span style=color:red>מהפתיחה</span> | |style="text-align:right;"|הנה מפני שנקודת ב' מרכז עגולת חז"ג יהיה קו ב"ז שוה לקו ב"ג <span style=color:red>מהפתיחה</span> | ||
|- | |- | ||
| | | | ||
| − | : | + | :<span style=color:green>'''def. circle:'''</span> Also, since point D is the center of the circle HZT, therefore line HD is equal to line DZ. |
| + | :<math>\scriptstyle{\color{blue}{HD=DZ}}</math> | ||
|style="text-align:right;"|ומפני שנקודת ד' גם כן מרכז עגולת הז"ט יהיה קו ה"ד שוה לקו ד"ז <span style=color:red>מהפתיחה</span> | |style="text-align:right;"|ומפני שנקודת ד' גם כן מרכז עגולת הז"ט יהיה קו ה"ד שוה לקו ד"ז <span style=color:red>מהפתיחה</span> | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle AD=BD</math> | + | :Line AD of one of them is equal to line BD of the other, since triangle DAB is equilateral. |
| − | |style="text-align:right;"|וקו א"ד מאחד מהם שוה לקו ב"ד מן האחר | + | :<math>\scriptstyle{\color{blue}{AD=BD}}</math> |
| − | + | |style="text-align:right;"|וקו א"ד מאחד מהם שוה לקו ב"ד מן האחר<br> | |
| − | + | מפני שמשולש דא"ב שוה הצלעות | |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle AH=BZ</math> | + | :Therefore, the remainder line AH is equal to the remainder line BZ. |
| + | :<math>\scriptstyle{\color{blue}{AH=BZ}}</math> | ||
|style="text-align:right;"|אם כן קו א"ה הנשאר שוה לקו ב"ז הנשאר | |style="text-align:right;"|אם כן קו א"ה הנשאר שוה לקו ב"ז הנשאר | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle BG=BZ</math> | + | :But, it has already been proven that line BG is equal to line BZ. |
| + | :<math>\scriptstyle{\color{blue}{BG=BZ}}</math> | ||
|style="text-align:right;"|וכבר התבאר שקו ב"ג שוה לקו ב"ז | |style="text-align:right;"|וכבר התבאר שקו ב"ג שוה לקו ב"ז | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle\ | + | :So, line AH is equal to line BG. |
| + | :<math>\scriptstyle{\color{blue}{AH=BG}}</math> | ||
|style="text-align:right;"|אם כן קו א"ה שוה לקו ב"ג | |style="text-align:right;"|אם כן קו א"ה שוה לקו ב"ג | ||
|- | |- | ||
| | | | ||
| + | :We have already attached to the given point A a straight line equal to the given straight line BG and this is line AH. | ||
|style="text-align:right;"|הנה כבר חברנו אל נקודת א' המונחת קו ישר שוה לקו ב"ג הישר המונח והוא קו א"ה | |style="text-align:right;"|הנה כבר חברנו אל נקודת א' המונחת קו ישר שוה לקו ב"ג הישר המונח והוא קו א"ה | ||
|- | |- | ||
| Line 387: | Line 394: | ||
|style="text-align:right;"|<big><span style=color:red>ג</span> נרצה</big> שנבדיל מאחד מב' קוי' מונחים ישרים בלתי שוים מן היותר גדול קו שוה ליותר קטן מהם | |style="text-align:right;"|<big><span style=color:red>ג</span> נרצה</big> שנבדיל מאחד מב' קוי' מונחים ישרים בלתי שוים מן היותר גדול קו שוה ליותר קטן מהם | ||
|- | |- | ||
| − | |Example: | + | |Example: Let the two given unequal straight lines be AB and G, of which line AB is the greater. |
| + | :<math>\scriptstyle{\color{blue}{AB>G}}</math> | ||
|style="text-align:right;"|ויהיו שני הקוים הישרים המונחים אשר הם בלתי שוים א"ב וג' והיותר גדול מהם קו א"ב | |style="text-align:right;"|ויהיו שני הקוים הישרים המונחים אשר הם בלתי שוים א"ב וג' והיותר גדול מהם קו א"ב | ||
|- | |- | ||
| Line 396: | Line 404: | ||
|[[File:אוקלידס I 3.png|thumb|150px]] | |[[File:אוקלידס I 3.png|thumb|150px]] | ||
|- | |- | ||
| − | |<span style=color: | + | |<span style=color:green>'''I.2:'''</span> attaching to point A a straight line AD equal to line G. |
| + | :<math>\scriptstyle{\color{blue}{AD=G}}</math> | ||
|style="text-align:right;"|הנה נחבר אל נקודת א' קו ישר שוה לקו ג' והוא קו א"ד <span style=color:red>מב' מזה</span> | |style="text-align:right;"|הנה נחבר אל נקודת א' קו ישר שוה לקו ג' והוא קו א"ד <span style=color:red>מב' מזה</span> | ||
|- | |- | ||
| | | | ||
| − | + | :A center, AD radius | |
|style="text-align:right;"|ו{{#annot:term|2549,2498|MoiN}}נקוה{{#annotend:MoiN}} על מרכז א' ובמרחק א"ד עגולת הז"ד | |style="text-align:right;"|ו{{#annot:term|2549,2498|MoiN}}נקוה{{#annotend:MoiN}} על מרכז א' ובמרחק א"ד עגולת הז"ד | ||
|- | |- | ||
| | | | ||
| − | :*<span style=color: | + | :*<span style=color:green>'''def. circle:'''</span> <math>\scriptstyle{\color{blue}{AZ=AD}}</math> |
|style="text-align:right;"|הנה מפני כי נקודת א' מרכז עגולת הז"ד יהיה קו א"ז שוה לקו א"ד <span style=color:red>מהפתיח'</span> | |style="text-align:right;"|הנה מפני כי נקודת א' מרכז עגולת הז"ד יהיה קו א"ז שוה לקו א"ד <span style=color:red>מהפתיח'</span> | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle AD=G</math> | + | :<math>\scriptstyle{\color{blue}{AD=G}}</math> |
| − | |style="text-align:right;"|אבל קו א"ד שוה לקו ג' | + | |style="text-align:right;"|אבל קו א"ד שוה לקו ג‫' |
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle\ | + | :<math>\scriptstyle{\color{blue}{AZ=G}}</math> |
| − | |style="text-align:right;"|אם כן א"ז שוה לקו ג' | + | |style="text-align:right;"|אם כן א"ז שוה לקו ג‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה כבר הבדלנו מן היותר גדול משני קוי א"ב וג' הישרים המונחים אשר הם בלתי שוים והוא א"ב קו שוה ליותר קטן משניהם והוא ג' | + | |style="text-align:right;"|הנה כבר הבדלנו מן היותר גדול משני קוי א"ב וג' הישרים המונחים אשר הם בלתי שוים והוא א"ב קו שוה ליותר קטן משניהם והוא ג‫' |
|- | |- | ||
|Q.E.D. | |Q.E.D. | ||
| Line 429: | Line 438: | ||
|style="text-align:right;"|<span style=color:red>ד</span> <big>כאשר</big> ישתוו שתי צלעות ממשולש אחד לשתי צלעות ממשולש אחר כל צלע לגילו וישתוו שתי הזויות משניהם אשר יקיפו בהם הקוים הישרים השוים הנה התושבת שוה לתושבת והמשולש שוה למשולש ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשנה | |style="text-align:right;"|<span style=color:red>ד</span> <big>כאשר</big> ישתוו שתי צלעות ממשולש אחד לשתי צלעות ממשולש אחר כל צלע לגילו וישתוו שתי הזויות משניהם אשר יקיפו בהם הקוים הישרים השוים הנה התושבת שוה לתושבת והמשולש שוה למשולש ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשנה | ||
|- | |- | ||
| − | | | + | |Let ABG and DHZ be the two triangles. |
|style="text-align:right;"|ויהיו שני המשולשים עליהם אב"ג דה"ז | |style="text-align:right;"|ויהיו שני המשולשים עליהם אב"ג דה"ז | ||
|- | |- | ||
| − | | | + | |Let the two sides BA and AG of the one be equal to the two sides HD and DZ of the other. |
|style="text-align:right;"|ויהיו שני צלעי ב"א א"ג מאחד משניהם שוים לשני צלעי ה"ד ד"ז מן האחר | |style="text-align:right;"|ויהיו שני צלעי ב"א א"ג מאחד משניהם שוים לשני צלעי ה"ד ד"ז מן האחר | ||
|- | |- | ||
| | | | ||
| − | : | + | :<math>\scriptstyle{\color{blue}{AB=DH}}</math>. |
|style="text-align:right;"|אולם צלע א"ב שוה לצלע ד"ה | |style="text-align:right;"|אולם צלע א"ב שוה לצלע ד"ה | ||
|- | |- | ||
| | | | ||
| − | : | + | :<math>\scriptstyle{\color{blue}{AG=DZ}}</math>. |
|style="text-align:right;"|וצלע א"ג לצלע ד"ז | |style="text-align:right;"|וצלע א"ג לצלע ד"ז | ||
|- | |- | ||
| Line 446: | Line 455: | ||
|style="text-align:right;"|ותהיה הזוית אשר יקיפו בה שתי צלעות ב"א א"ג שוה לזוית אשר יקיפו בה שתי צלעות ה"ד ד"ז | |style="text-align:right;"|ותהיה הזוית אשר יקיפו בה שתי צלעות ב"א א"ג שוה לזוית אשר יקיפו בה שתי צלעות ה"ד ד"ז | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that the base BG is also equal to the base HZ, triangle ABG is equal to triangle DZH and the remaining angles are equal to the remaining angles respectively, whose opposite side is the side that equals the opposite side of the former. |
|style="text-align:right;"|הנה אומר כי תושבת ב"ג גם כן שוה לתושבת ה"ז ושמשולש אב"ג שוה למשולש דה"ז ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשנה | |style="text-align:right;"|הנה אומר כי תושבת ב"ג גם כן שוה לתושבת ה"ז ושמשולש אב"ג שוה למשולש דה"ז ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשנה | ||
|- | |- | ||
| Line 465: | Line 474: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונפלה נקודת ב' על נקודת ה' ונקודת ג' על נקודת ז' | + | |style="text-align:right;"|ונפלה נקודת ב' על נקודת ה' ונקודת ג' על נקודת ז‫' |
|- | |- | ||
| | | | ||
| Line 496: | Line 505: | ||
|style="text-align:right;"|<span style=color:red>ה</span> <big>שתי</big> הזויות אשר על תושבת מן המשולשים שוי השוקים שוות ואם הוצאו הקוים הישרים השוים הנה שתי הזויות אשר תחת התושבת תהיינה שוות | |style="text-align:right;"|<span style=color:red>ה</span> <big>שתי</big> הזויות אשר על תושבת מן המשולשים שוי השוקים שוות ואם הוצאו הקוים הישרים השוים הנה שתי הזויות אשר תחת התושבת תהיינה שוות | ||
|- | |- | ||
| − | | | + | |Let ABG be an isosceles triangle. |
|style="text-align:right;"|ויהיה משולש שוה שתי השוקים עליו אב"ג | |style="text-align:right;"|ויהיה משולש שוה שתי השוקים עליו אב"ג | ||
|- | |- | ||
| − | | | + | |Let side AB be equal to side AG. |
| − | : | + | :<math>\scriptstyle{\color{blue}{AB=AG}}</math> |
|style="text-align:right;"|ויהיה צלע א"ב שוה לצלע א"ג | |style="text-align:right;"|ויהיה צלע א"ב שוה לצלע א"ג | ||
|- | |- | ||
| | | | ||
| + | *We draw the two straight lines BD and GH in a straight line with the two lines AB and AG. | ||
|style="text-align:right;"|ונוציא שני קוי ב"ד ג"ה הישרים על יושר שני קוי א"ב א"ג הישרים | |style="text-align:right;"|ונוציא שני קוי ב"ד ג"ה הישרים על יושר שני קוי א"ב א"ג הישרים | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that angle ABG is equal to angle BGA and angle GBD is equal to angle BGH. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle ABG=\measuredangle BGA\quad\measuredangle GBD=\measuredangle BGH}}</math> | |
| − | + | |style="text-align:right;"|הנה אומר כי זוית אב"ג שוה לזוית בג"א וזוית גב"ד שוה לזוית בג"ה | |
| − | |||
| − | |style="text-align:right;"|וזוית גב"ד שוה לזוית בג"ה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה נרשום על ב"ד נקודה איך מה שקרה והיא ז' | + | *We draw an arbitrary point Z on BD. |
| + | |style="text-align:right;"|הנה נרשום על ב"ד נקודה איך מה שקרה והיא ז‫' | ||
|- | |- | ||
| | | | ||
| + | *We cut off line AC from line AH equal to line AZ. | ||
| + | :<math>\scriptstyle{\color{blue}{AC=AZ}}</math> | ||
|style="text-align:right;"|ונבדיל מקו א"ה קו ישוה לקו א"ז והוא א"ח | |style="text-align:right;"|ונבדיל מקו א"ה קו ישוה לקו א"ז והוא א"ח | ||
|- | |- | ||
| | | | ||
| + | *We join the two lines GZ and BC. | ||
|style="text-align:right;"|ונגיע שני קוי ג"ז ב"ח | |style="text-align:right;"|ונגיע שני קוי ג"ז ב"ח | ||
|- | |- | ||
| − | | | + | |Line ZA is equal to line AC. |
| + | :<math>\scriptstyle{\color{blue}{ZA=AC}}</math> | ||
|style="text-align:right;"|הנה מפני כי קו ז"א שוה לקו א"ח | |style="text-align:right;"|הנה מפני כי קו ז"א שוה לקו א"ח | ||
|- | |- | ||
| − | |<math>\scriptstyle GA=AB</math> | + | |Line GA is equal to line AB. |
| + | :<math>\scriptstyle{\color{blue}{GA=AB}}</math> | ||
|style="text-align:right;"|וקו ג"א שוה לקו א"ב | |style="text-align:right;"|וקו ג"א שוה לקו א"ב | ||
|- | |- | ||
| − | | | + | |Therefore, each of the two lines BA and AC is equal to one of the two lines GA and AZ, respectively. |
|style="text-align:right;"|יהיו כל שני קוי ב"א א"ח שוים לכל שני קוי ג"א א"ז כל אחד לגילו | |style="text-align:right;"|יהיו כל שני קוי ב"א א"ח שוים לכל שני קוי ג"א א"ז כל אחד לגילו | ||
|- | |- | ||
| − | | | + | |These sides contain a common angle, which is angle ZAC. |
|style="text-align:right;"|ואלו הצלעות יקיפו בזוית אחת משותפת והיא זוית זא"ח | |style="text-align:right;"|ואלו הצלעות יקיפו בזוית אחת משותפת והיא זוית זא"ח | ||
|- | |- | ||
| − | |<math>\scriptstyle GZ=BC</math> | + | |Hence, base GZ is equal to base BC. |
| − | |style="text-align:right;"|אם כן תושבת ג"ז שוה לתושבת ב"ח | + | :<math>\scriptstyle{\color{blue}{GZ=BC}}</math> |
| + | |style="text-align:right;"|אם כן ‫<ref>2r</ref>תושבת ג"ז שוה לתושבת ב"ח | ||
|- | |- | ||
| − | |<math>\scriptstyle\ | + | |Triangle AZG is equal to triangle ABC. |
| + | :<math>\scriptstyle{\color{blue}{\triangle AZG=\triangle ABC}}</math> | ||
|style="text-align:right;"|ומשולש אז"ג שוה למשולש אב"ח | |style="text-align:right;"|ומשולש אז"ג שוה למשולש אב"ח | ||
|- | |- | ||
| − | | | + | |The remaining angles are equal to the remaining angles respectively, namely those that are opposite to the equal sides. |
| − | |style="text-align:right;"|ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר | + | |style="text-align:right;"|ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשונה |
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle AGZ=\measuredangle ABC</math> | + | |Angle AGZ is equal to angle ABC. |
| − | |style="text-align:right;"|אולם זוית אג"ז שוה לזוית אב"ח | + | :<math>\scriptstyle{\color{blue}{\measuredangle AGZ=\measuredangle ABC}}</math> |
| + | |style="text-align:right;"|אולם זוית אג"ז [שוה] לזוית אב"ח | ||
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle | + | |Angle AZG is equal to angle ACB. |
| − | |style="text-align:right;"|ואולם זוית | + | :<math>\scriptstyle{\color{blue}{\measuredangle AZG=\measuredangle ACB}}</math> |
| + | |style="text-align:right;"|ואולם זוית אז"ג [שוה] לזוית אח"ב | ||
|- | |- | ||
| − | | | + | |Line ZA is also equal to line AC. |
| − | |style="text-align:right;"|ומפני כי קו ז"א גם כן שוה לקו א"ח | + | :<math>\scriptstyle{\color{blue}{ZA=AC}}</math> |
| + | |style="text-align:right;"|ומפני כי קו ז"א גם כן שוה לקו א"ח <span style=color:red>מהפתיחה</span> | ||
|- | |- | ||
| − | | | + | |Lines BA and AG in them are equal. |
| + | :<math>\scriptstyle{\color{blue}{BA=AG}}</math> | ||
|style="text-align:right;"|וקוי ב"א א"ג משניהם שוים | |style="text-align:right;"|וקוי ב"א א"ג משניהם שוים | ||
|- | |- | ||
| − | | | + | |Therefore, the remainder line BZ is equal to the remainder line GC. |
| − | |style="text-align:right;"|יהיה קו ב"ז הנשאר שוה לקו ג"ח הנשאר | + | :<math>\scriptstyle{\color{blue}{BZ=GC}}</math> |
| + | |style="text-align:right;"|יהיה קו ב"ז הנשאר שוה לקו ג"ח הנשאר <span style=color:red>מד' מפתיחה</span> | ||
|- | |- | ||
| − | | | + | |It has already been proven that line GZ is equal to line BC. |
| − | |style="text-align:right;"|והנה ראוי שיהיה קו ג"ז שוה לקו ב"ח | + | :<math>\scriptstyle{\color{blue}{GZ=BC}}</math> |
| + | |style="text-align:right;"|<s>והנה ראוי שיהיה</s> <sup>וכבר התבאר ש</sup>קו ג"ז שוה לקו ב"ח | ||
|- | |- | ||
| − | | | + | |Therefore, each of the two lines BZ and ZG is equal to one of the two lines GC and CB, respectively. |
|style="text-align:right;"|הנה כל שני קוי ב"ז ז"ג שוים לכל שני קוי ג"ח ח"ב כל אחד לגילו | |style="text-align:right;"|הנה כל שני קוי ב"ז ז"ג שוים לכל שני קוי ג"ח ח"ב כל אחד לגילו | ||
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle BZG=\measuredangle GCB</math> | + | |Angle BZG is equal to angle GCB. |
| − | |style="text-align:right;"|וזוית בז"ג שוה לזוית גח"ב | + | :<math>\scriptstyle{\color{blue}{\measuredangle BZG=\measuredangle GCB}}</math> |
| + | |style="text-align:right;"|וזוית בז"ג <sup>שוה</sup> לזוית גח"ב | ||
|- | |- | ||
| − | |BG is common to both triangles. | + | |Base BG is common to both triangles. |
|style="text-align:right;"|ותושבת ב"ג משותפת לשני המשולשים | |style="text-align:right;"|ותושבת ב"ג משותפת לשני המשולשים | ||
|- | |- | ||
| − | | | + | |So, triangle BZG is equal to triangle GCB. |
| − | |style="text-align:right;"|אם כן משלש בז"ג שוה למשולש גח"ב | + | :<math>\scriptstyle{\color{blue}{\triangle BZG=\triangle GCB}}</math> |
| + | |style="text-align:right;"|אם כן משלש בז"ג <sup>שוה</sup> למשולש גח"ב <span style=color:red>מד‫'</span> | ||
|- | |- | ||
| − | | | + | |The remaining angles are equal to the remaining angles respectively, namely those that are opposite to the equal sides. |
| − | |style="text-align:right;"|ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה | + | |style="text-align:right;"|ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה הראשונה |
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle BGZ=\measuredangle GBC</math> | + | |But, angle BGZ is equal to angle GBC. |
| + | :<math>\scriptstyle{\color{blue}{\measuredangle BGZ=\measuredangle GBC}}</math> | ||
|style="text-align:right;"|אולם זוית בג"ז לזוית גב"ח | |style="text-align:right;"|אולם זוית בג"ז לזוית גב"ח | ||
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle GBZ=\measuredangle BGC</math> | + | |Angle GBZ is equal to angle BGC. |
| + | :<math>\scriptstyle{\color{blue}{\measuredangle GBZ=\measuredangle BGC}}</math> | ||
|style="text-align:right;"|ואולם זוית גב"ז לזוית בג"ח | |style="text-align:right;"|ואולם זוית גב"ז לזוית בג"ח | ||
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle AGZ=\measuredangle ABC</math> | + | |It has already been proven that the whole angle AGZ is equal to the whole angle ABC. |
| + | :<math>\scriptstyle{\color{blue}{\measuredangle AGZ=\measuredangle ABC}}</math> | ||
|style="text-align:right;"|וכבר התבאר כי כל זוית אג"ז שוה לכל זוית אב"ח | |style="text-align:right;"|וכבר התבאר כי כל זוית אג"ז שוה לכל זוית אב"ח | ||
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle BGZ=\measuredangle GBC</math> | + | |The two angles BGZ and GBC are equal. |
| − | |style="text-align:right;"|ושתי זויות בג"ז גב"ח משניהם שוות | + | :<math>\scriptstyle{\color{blue}{\measuredangle BGZ=\measuredangle GBC}}</math> |
| − | + | |style="text-align:right;"|ושתי זויות בג"ז גב"ח <s>משניהם</s> שוות | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |Therefore, the remaining angle BGA is equal to the remaining angle GBA, and they are at the base [of the triangle ABG]. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{\measuredangle BGA=\measuredangle GBA}}</math> |
| + | |style="text-align:right;"|אם כן זוית בג"א הנשארת שוה לזוית גב"א הנשארת <span style=color:red>מד' מפתיחה</span><br> | ||
| + | והם שתי הזויות אשר על התושבת | ||
|- | |- | ||
| − | | | + | |But, it has already been proven that angle GBD is equal to the angle BGH, and they are under the base. |
| − | |style="text-align:right;"|והם שתי הזויות אשר תחת התושבת | + | :<math>\scriptstyle{\color{blue}{\measuredangle GBD=\measuredangle BGH}}</math> |
| + | |style="text-align:right;"|וכבר התבאר כי זוית גב"ד שוה לזוית בג"ה‫<ref>marg.: פי' מאמרו אולם זוית גב"ז שוה לזוית בג"ח ומ"ח ל"ה כמו ל"ז ל"ד</ref><br> | ||
| + | והם שתי הזויות אשר תחת התושבת | ||
|- | |- | ||
| − | | | + | |Therefore, the two angles at the base of the isosceles triangle are equal to one another; and if the equal straight lines are drawn further, the [external] angles under the base are equal to one another. |
| − | |style="text-align:right;"|אם כן שתי הזויות אשר על התושבת מן המשולש | + | |style="text-align:right;"|אם כן שתי הזויות אשר על התושבת מן המשולש שווי שתי השוקים שוות ואם הוצאו הקוים הישרים השוים <sup>ההם</sup> הנה <sup>יהיו</sup> שתי הזויות אשר תחת התושבת שוות |
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
| − | |||
| − | |||
| − | |||
|style="text-align:right;"|וזה מה שרצינו לבאר | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
|- | |- | ||
| Line 614: | Line 637: | ||
|- | |- | ||
|When two angles of a triangle are equal to one another, then the two sides that are opposite to them are equal [to one another]. | |When two angles of a triangle are equal to one another, then the two sides that are opposite to them are equal [to one another]. | ||
| − | |style="text-align:right;"|<span style=color:red>ו</span> <big>כאשר</big> השתוו שתי זויות ממשולש הנה | + | |style="text-align:right;"|<span style=color:red>ו</span> <big>כאשר</big> השתוו שתי זויות ממשולש הנה שתי הצלעות אשר יהיו מיתר שתיהן יהיו שוות‫<ref>marg.: הפוך התמונה הנזכרת</ref> |
|- | |- | ||
| − | | | + | |Let angle ABG of triangle ABG be equal to angle AGB. |
| − | |style="text-align:right;"|ותהיה זוית אב"ג | + | :<math>\scriptstyle{\color{blue}{\measuredangle ABG=\measuredangle AGB}}</math> |
| + | |style="text-align:right;"|<big>ותהיה</big> זוית אב"ג ממשולש אב"ג שוה לזוית אג"ב ממנו | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that side BA is equal to side AG. |
| + | :<math>\scriptstyle{\color{blue}{BA=AG}}</math> | ||
|style="text-align:right;"|הנה אומר כי צלע ב"א שוה לצלע א"ג | |style="text-align:right;"|הנה אומר כי צלע ב"א שוה לצלע א"ג | ||
|- | |- | ||
| − | | | + | |If side BA does not equal side AG, then one of them is greater than the other. |
| − | |style="text-align:right;"|ואם לא יהיה צלע ב"א שוה לצלע א"ג הנה אחד משניהם יותר גדול מן האחר | + | |style="text-align:right;"|ואם לא יהיה צלע ב"א שוה לצלע א"ג הנה <sup>ה</sup>אחד משניהם יותר גדול מן האחר |
|- | |- | ||
| − | | | + | |Let AB be the greater if possible. |
| + | :<math>\scriptstyle{\color{blue}{AB>AG}}</math> | ||
|style="text-align:right;"|ויהיה היותר גדול א"ב אם אפשר זה | |style="text-align:right;"|ויהיה היותר גדול א"ב אם אפשר זה | ||
|- | |- | ||
| − | | | + | |We cut off BD from AB the greater equal to AG the less. |
| − | |style="text-align:right;"|ונבדיל מן א"ב היותר גדול קו | + | :<math>\scriptstyle{\color{blue}{BD=AG}}</math> |
| + | |style="text-align:right;"|ונבדיל מן א"ב היותר גדול קו השוה לקו א"ג היותר קטן והוא ב"ד <span style=color:red>מג‫'</span> | ||
|- | |- | ||
| − | | | + | |We join DG. |
| − | |style="text-align:right;"|ונגיע ד"ג | + | |style="text-align:right;"|ונגיע ד"ג <span style=color:red>מפתיחה ל"ז</span> |
|- | |- | ||
| − | | | + | |Line DB is equal to line AG. |
| − | |style="text-align:right;"|הנה | + | :<math>\scriptstyle{\color{blue}{BD=AG}}</math> |
| + | |style="text-align:right;"|הנה קו ד"ב שוה לקו א"ג | ||
|- | |- | ||
|Line BG is common | |Line BG is common | ||
|style="text-align:right;"|וקו ב"ג משותף | |style="text-align:right;"|וקו ב"ג משותף | ||
|- | |- | ||
| − | | | + | |Therefore, the two lines DB and BG are equal to the two lines AG and GB respectively. |
|style="text-align:right;"|יהיו כל שני קוי ד"ב ב"ג שוים לכל שני קוי א"ג ג"ב כל אחד לגילו | |style="text-align:right;"|יהיו כל שני קוי ד"ב ב"ג שוים לכל שני קוי א"ג ג"ב כל אחד לגילו | ||
|- | |- | ||
| − | | | + | |Angle AGB is equal to angle DBG. |
| − | |style="text-align:right;"|וזוית דב"ג שוה לזוית אג"ב | + | :<math>\scriptstyle{\color{blue}{\measuredangle AGB=\measuredangle DBG}}</math> |
| + | |style="text-align:right;"|וזוית דב"ג שוה <s>שוה</s> לזוית אג"ב | ||
|- | |- | ||
| − | | | + | |So, base DG is equal to base AB. |
| − | |style="text-align:right;"|אם כן תושבת ד"ג שוה לתושבת א"ב | + | :<math>\scriptstyle{\color{blue}{DG=AB}}</math> |
| + | |style="text-align:right;"|אם כן תושבת ד"ג שוה לתושבת א"ב <span style=color:red>מד‫'</span> | ||
|- | |- | ||
| − | | | + | |Triangle DBG equals triangle ABG. |
| + | :<math>\scriptstyle{\color{blue}{\triangle DBG=\triangle ABG}}</math> | ||
|style="text-align:right;"|ומשולש דב"ג שוה למשולש אב"ג | |style="text-align:right;"|ומשולש דב"ג שוה למשולש אב"ג | ||
|- | |- | ||
| − | | | + | |The smaller triangle equals the greater, which is impossible. |
| − | |style="text-align:right;"|וישוה | + | |style="text-align:right;"|וישוה המשולש הקטן לגדול וזה בלתי אפשר <span style=color:red>נ' מפתיחה</span> |
|- | |- | ||
| − | | | + | |Therefore, BA is not greater than AG. |
|style="text-align:right;"|אם כן אין ב"א יותר גדול מן א"ג | |style="text-align:right;"|אם כן אין ב"א יותר גדול מן א"ג | ||
|- | |- | ||
| − | | | + | |It is also clear that it is not smaller than it. |
|style="text-align:right;"|וכן יתבאר שאינו קטן ממנו | |style="text-align:right;"|וכן יתבאר שאינו קטן ממנו | ||
|- | |- | ||
| − | | | + | |Hence, line BA equals line AG. |
| + | :<math>\scriptstyle{\color{blue}{BA=AG}}</math> | ||
|style="text-align:right;"|אם כן קו ב"א שוה לקו א"ג | |style="text-align:right;"|אם כן קו ב"א שוה לקו א"ג | ||
|- | |- | ||
| − | | | + | |Therefore, when two angles of a triangle are equal to one another, then the two sides that are opposite to them are equal [to one another]. |
|style="text-align:right;"|אם כן כאשר השתוו שתי זויות ממשולש הנה שתי הצלעות אשר יהיו מיתרי שתיהן יהיו שוות | |style="text-align:right;"|אם כן כאשר השתוו שתי זויות ממשולש הנה שתי הצלעות אשר יהיו מיתרי שתיהן יהיו שוות | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| Line 675: | Line 707: | ||
| | | | ||
|- | |- | ||
| − | |Two straight lines that are equal to two other straight lines cannot stand on one straight line so that their meeting and the meeting of the | + | |Two straight lines that are equal to two other straight lines cannot stand on one straight line, so that their meeting and the meeting of the others are on the same side at two different points, and their two ends are the two ends of the two lines that are equal to them. |
| − | |style="text-align:right;"|<span style=color:red>ז</span> <big>לא יעמדו</big> על קו אחד ישר | + | |style="text-align:right;"|<span style=color:red>ז</span> <big>לא יעמדו</big> על קו אחד ישר שתי קוים ישרים שוים לשני קוים אחרים ישרים כל אחד לגילו ותהיה פגישתם ופגישת האחרים ‫<ref>2v</ref>בצד אחד על שתי נקודות מתחלפות ושתי תכליותיהם שתי תכליות שני הקוים השוים לשניהם |
|- | |- | ||
| − | | | + | |If possible, let the two straight lines AG and GB stand on the straight line AB. |
| − | |style="text-align:right;"|שאם היה אפשר | + | |style="text-align:right;"|<big>שאם</big> היה אפשר יעמדו על קו א"ב הישר שני קוים א"ג ג"ב הישרים |
|- | |- | ||
| − | | | + | |Let the two other lines AD and DB be equal to the former two respectively. |
|style="text-align:right;"|ושני קוים אחרים שוים לשניהם כל אחד לגילו והם א"ד ד"ב | |style="text-align:right;"|ושני קוים אחרים שוים לשניהם כל אחד לגילו והם א"ד ד"ב | ||
|- | |- | ||
| − | | | + | |Let their meeting and the meeting of the others be on the same side at the two different points G and D. |
| − | |style="text-align:right;"|ותהיה פגישתם ופגישת האחרים בצד אחד על שתי נקודות מתחלפות והם ג"ד | + | |style="text-align:right;"|ותהיה פגישתם ופגישת האחרים <s>שוים לשניהם</s> בצד אחד על שתי נקודות מתחלפות והם ג"ד |
|- | |- | ||
| − | | | + | |Let their two ends be the two ends of the two lines equal to them. |
| − | |style="text-align:right;"|ושתי תכליות שניהם | + | |style="text-align:right;"|ושתי תכליות שניהם שני תכליות שני הקוים השוים להם |
|- | |- | ||
| − | | | + | |But, the two ends of the two lines AG and AD is point A. |
| − | |style="text-align:right;"|אולם שתי תכליות שני קוי א"ג א"ד הוא נקודת א' | + | |style="text-align:right;"|אולם שתי תכליות שני קוי א"ג א"ד הוא נקודת א‫' |
|- | |- | ||
| − | | | + | |Also, the end of the two lines GB and BD is point B. |
| − | |style="text-align:right;"|ואולם | + | |style="text-align:right;"|ואולם תכלית שני קוי ג"ב ב"ד <s>הנה</s> היא נקודת ב‫' |
|- | |- | ||
| − | | | + | |We join line GD. |
| − | |style="text-align:right;"|ונגיע קו ג"ד | + | |style="text-align:right;"|ונגיע קו ג"ד <span style=color:red>מהפתיחה</span> |
|- | |- | ||
| − | | | + | |Line AG is equal to line AD. |
| + | :<math>\scriptstyle{\color{blue}{AG=AD}}</math> | ||
|style="text-align:right;"|הנה מפני כי קו א"ג שוה לקו א"ד | |style="text-align:right;"|הנה מפני כי קו א"ג שוה לקו א"ד | ||
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle GDA=\measuredangle DGA</math> | + | |Angle GDA equals angle DGA. |
| − | |style="text-align:right;"|תהיה זוית גד"א שוה לזוית דג"א | + | :<math>\scriptstyle{\color{blue}{\measuredangle GDA=\measuredangle DGA}}</math> |
| + | |style="text-align:right;"|תהיה זוית גד"א שוה לזוית דג"א <span style=color:red>מה‫'</span> | ||
|- | |- | ||
| − | | | + | |Therefore, angle GDA is greater than the angle DGB. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle GDA>\measuredangle DGB}}</math> | |
| − | |||
| − | |||
|style="text-align:right;"|אם כן זוית גד"א יותר גדולה מזוית דג"ב | |style="text-align:right;"|אם כן זוית גד"א יותר גדולה מזוית דג"ב | ||
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle GDB>\measuredangle DGB</math> | + | |So, angle GDB is much greater than angle DGB. |
| + | :<math>\scriptstyle{\color{blue}{\measuredangle GDB>\measuredangle DGB}}</math> | ||
|style="text-align:right;"|אם כן זוית גד"ב יותר גדולה הרבה מזוית דג"ב | |style="text-align:right;"|אם כן זוית גד"ב יותר גדולה הרבה מזוית דג"ב | ||
|- | |- | ||
| − | |<math>\scriptstyle GB=DB</math> | + | |Line GB equals line DB. |
| + | :<math>\scriptstyle{\color{blue}{GB=DB}}</math> | ||
|style="text-align:right;"|ומפני כי קו ג"ב גם כן שוה לקו ד"ב | |style="text-align:right;"|ומפני כי קו ג"ב גם כן שוה לקו ד"ב | ||
|- | |- | ||
| − | |<math>\scriptstyle\measuredangle GDB=\measuredangle DGB</math> | + | |Therefore, angle GDB equals angle DGB. |
| − | |style="text-align:right;"|תהיה זוית גד"ב שוה לזוית דג"ב | + | :<math>\scriptstyle{\color{blue}{\measuredangle GDB=\measuredangle DGB}}</math> |
| + | |style="text-align:right;"|תהיה זוית גד"ב <s>יותר גדולה</s> שוה לזוית דג"ב <span style=color:red>מה‫'</span> | ||
|- | |- | ||
| − | | | + | |But, it has already been proven that it is much greater than it, which is impossible. |
|style="text-align:right;"|וכבר התבאר שהיא יותר גדולה ממנה וזה בלתי אפשר | |style="text-align:right;"|וכבר התבאר שהיא יותר גדולה ממנה וזה בלתי אפשר | ||
|- | |- | ||
| − | | | + | |Therefore, two straight lines that are equal to two other straight lines cannot stand on one straight line, so that their meeting and the meeting of the others are on the same side at two different points, and the ends of both are the ends of the two lines that are equal to them. |
| − | |style="text-align:right;"|אם כן לא | + | |style="text-align:right;"|אם כן לא יעמדו על קו אחד ישר שני קוים ישרים שוים לשני קוים אחרים ישרים כל אחד לגילו ותהיה פגישת שניהם ופגישת האחרים בצד אחד על שתי נקודות מתחלפות ותכליות שניהם תכליות שני הקוים השוים להם |
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
|style="text-align:right;"|וזה מה שרצינו לבאר | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
|- | |- | ||
| Line 737: | Line 772: | ||
|style="text-align:right;"|<span style=color:red>ח</span> <big>כאשר</big> השתוו שתי צלעות ממשולש אחד לשתי צלעות ממשולש אחר כל אחת לגילה והשתותה תושבתו לתושבתו הנה שתי הזויות אשר יקיפו בהם הצלעות השוות הם שוות | |style="text-align:right;"|<span style=color:red>ח</span> <big>כאשר</big> השתוו שתי צלעות ממשולש אחד לשתי צלעות ממשולש אחר כל אחת לגילה והשתותה תושבתו לתושבתו הנה שתי הזויות אשר יקיפו בהם הצלעות השוות הם שוות | ||
|- | |- | ||
| − | | | + | |Let ABG and DHZ be the two triangles. |
|style="text-align:right;"|ויהיו שני המשלשים אב"ג דה"ז | |style="text-align:right;"|ויהיו שני המשלשים אב"ג דה"ז | ||
|- | |- | ||
| Line 744: | Line 779: | ||
|- | |- | ||
| | | | ||
| − | :*<math>\scriptstyle AB=HD</math> | + | :*<math>\scriptstyle{\color{blue}{AB=HD}}</math> |
|style="text-align:right;"|אולם צלע א"ב לצלע ה"ד | |style="text-align:right;"|אולם צלע א"ב לצלע ה"ד | ||
|- | |- | ||
| | | | ||
| − | :*<math>\scriptstyle AG=DZ</math> | + | :*<math>\scriptstyle{\color{blue}{AG=DZ}}</math> |
|style="text-align:right;"|ואולם צלע א"ג לצלע ד"ז | |style="text-align:right;"|ואולם צלע א"ג לצלע ד"ז | ||
|- | |- | ||
| | | | ||
| − | :*<math>\scriptstyle BG=HZ</math> | + | :*<math>\scriptstyle{\color{blue}{BG=HZ}}</math> |
|style="text-align:right;"|ותהיה תושבת ב"ג שוה לתושבת ה"ז | |style="text-align:right;"|ותהיה תושבת ב"ג שוה לתושבת ה"ז | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that angle BAG is equal to angle HDZ. |
|style="text-align:right;"|הנה אומר כי זוית בא"ג שוה לזוית הד"ז | |style="text-align:right;"|הנה אומר כי זוית בא"ג שוה לזוית הד"ז | ||
|- | |- | ||
| Line 1,010: | Line 1,045: | ||
|style="text-align:right;"|ויהיה כל אחד מן א"ב ג"ד נכחי לקו ה"ז | |style="text-align:right;"|ויהיה כל אחד מן א"ב ג"ד נכחי לקו ה"ז | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that AB is parallel to GD. |
|style="text-align:right;"|הנה אומר כי א"ב נכחי אל ג"ד | |style="text-align:right;"|הנה אומר כי א"ב נכחי אל ג"ד | ||
|- | |- | ||
| Line 1,095: | Line 1,130: | ||
|style="text-align:right;"|ויהיה משלש עליו אב"ג ותצא אחת מצלעותיו הוא ב"ג אל נקדת ד' | |style="text-align:right;"|ויהיה משלש עליו אב"ג ותצא אחת מצלעותיו הוא ב"ג אל נקדת ד' | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that the exterior angle AGD is equal [the sum of] the two interior angles A and B; and that [the sum of] the three interior angles ABG, BGA and GAB of the triangle equals two right angles. |
|style="text-align:right;"|הנה אומר כי זוית אג"ד החיצונה שוה לשתי זויות א"ב הפנימיו' ושזויות אב"ג בג"א גא"ב השלשה אשר תוך המשולש שוות לשתי זויות נצבות | |style="text-align:right;"|הנה אומר כי זוית אג"ד החיצונה שוה לשתי זויות א"ב הפנימיו' ושזויות אב"ג בג"א גא"ב השלשה אשר תוך המשולש שוות לשתי זויות נצבות | ||
|- | |- | ||
| Line 1,154: | Line 1,189: | ||
|style="text-align:right;"|ונגיע שני קוי א"ג ב"ד הישרים במה שבין קצוות שני קוי א"ב ג"ד אשר בצד אחד | |style="text-align:right;"|ונגיע שני קוי א"ג ב"ד הישרים במה שבין קצוות שני קוי א"ב ג"ד אשר בצד אחד | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that AG and BD are also equal and parallel. |
|style="text-align:right;"|הנה אומר כי א"ג ב"ד גם כן שוים נכחיים | |style="text-align:right;"|הנה אומר כי א"ג ב"ד גם כן שוים נכחיים | ||
|- | |- | ||
| Line 1,216: | Line 1,251: | ||
|style="text-align:right;"|ויהיה שטח א"ב ג"ד {{#annot:term|2555,1096|ERBz}}נכחי הצלעות{{#annotend:ERBz}} ויהיה קטרו ד"ב | |style="text-align:right;"|ויהיה שטח א"ב ג"ד {{#annot:term|2555,1096|ERBz}}נכחי הצלעות{{#annotend:ERBz}} ויהיה קטרו ד"ב | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> |
|style="text-align:right;"|הנה אומר כי צלעות שטח א"ב ג"ד נכחי הצלעות הצלעות המתנגדות וזויותיו המתנגדות שוות קצתם אל קצתם ושהקוטר יחלקהו לשני חצאיים | |style="text-align:right;"|הנה אומר כי צלעות שטח א"ב ג"ד נכחי הצלעות הצלעות המתנגדות וזויותיו המתנגדות שוות קצתם אל קצתם ושהקוטר יחלקהו לשני חצאיים | ||
|- | |- | ||
| Line 1,284: | Line 1,319: | ||
|style="text-align:right;"|ויהיו שני {{#annot:term|2555,1096|9qdL}}השטחים נכחיי הצלעות{{#annotend:9qdL}} א"ב ג"ד ה"ב ג"ז על תושבת אחת והיא ב"ג ובמה שבין שני קוים א"ז ב"ג הנכחים | |style="text-align:right;"|ויהיו שני {{#annot:term|2555,1096|9qdL}}השטחים נכחיי הצלעות{{#annotend:9qdL}} א"ב ג"ד ה"ב ג"ז על תושבת אחת והיא ב"ג ובמה שבין שני קוים א"ז ב"ג הנכחים | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that the parallelogram ABGD is equal to the parallelogram BHGZ. |
|style="text-align:right;"|הנה אומר כי שטח א"ב ג"ד נכחי הצלעות שוה לשטח ב"ה ג"ז נכחי הצלעות | |style="text-align:right;"|הנה אומר כי שטח א"ב ג"ד נכחי הצלעות שוה לשטח ב"ה ג"ז נכחי הצלעות | ||
|- | |- | ||
| Line 1,343: | Line 1,378: | ||
|style="text-align:right;"|ויהיו שני שטחים נכחיים הצלעות עליהם א"ב ג"ד ה"ז ח"ט על שתי תושבות שוות והם ב"ג ז"ח ובמה שבין שני קוים א"ט ב"ח הנכחיים | |style="text-align:right;"|ויהיו שני שטחים נכחיים הצלעות עליהם א"ב ג"ד ה"ז ח"ט על שתי תושבות שוות והם ב"ג ז"ח ובמה שבין שני קוים א"ט ב"ח הנכחיים | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that the parallelogram ABGD is equal to the parallelogram HZCT. |
|style="text-align:right;"|הנה אומר כי שטח א"ב ג"ד הנכחי הצלעות שוה לשטח ה"ז ח"ט הנכחי הצלעות | |style="text-align:right;"|הנה אומר כי שטח א"ב ג"ד הנכחי הצלעות שוה לשטח ה"ז ח"ט הנכחי הצלעות | ||
|- | |- | ||
| Line 1,399: | Line 1,434: | ||
|style="text-align:right;"|ובמה שבין שני קוי ב"ג א"ד הנכחיים | |style="text-align:right;"|ובמה שבין שני קוי ב"ג א"ד הנכחיים | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that triangle ABG is equal to triangle DBG. |
|style="text-align:right;"|הנה אומר כי משולש אב"ג שוה למשולש דב"ג | |style="text-align:right;"|הנה אומר כי משולש אב"ג שוה למשולש דב"ג | ||
|- | |- | ||
| Line 1,461: | Line 1,496: | ||
|style="text-align:right;"|ובמה שבין שני קוי א"ד ב"ז הנכחים | |style="text-align:right;"|ובמה שבין שני קוי א"ד ב"ז הנכחים | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that triangle ABG is equal to triangle DHZ. |
|style="text-align:right;"|הנה אומר שמשלש אב"ג שוה למשולש דה"ז | |style="text-align:right;"|הנה אומר שמשלש אב"ג שוה למשולש דה"ז | ||
|- | |- | ||
| Line 1,523: | Line 1,558: | ||
|style="text-align:right;"|ונמשיך קו א"ד | |style="text-align:right;"|ונמשיך קו א"ד | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that AD is parallel to BG. |
|style="text-align:right;"|אומר שא"ד נכחי אל ב"ג | |style="text-align:right;"|אומר שא"ד נכחי אל ב"ג | ||
|- | |- | ||
| Line 1,582: | Line 1,617: | ||
|style="text-align:right;"|ונמשיך קו א"ד | |style="text-align:right;"|ונמשיך קו א"ד | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that AD is parallel to BZ. |
|style="text-align:right;"|אומר שא"ד נכחי לב"ז | |style="text-align:right;"|אומר שא"ד נכחי לב"ז | ||
|- | |- | ||
| Line 1,595: | Line 1,630: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|מפני שהם על תושבות שוות והם ב"ג ה"ז הישרי' | + | |style="text-align:right;"|מפני שהם על תושבות שוות והם ב"ג ה"ז הישרי‫' |
|- | |- | ||
| | | | ||
| Line 1,624: | Line 1,659: | ||
|style="text-align:right;"|הנה שני המשולשים השוים אשר על שתי התושבות ושתי התושבות על קו ישר ובצד אחד יכלו במה שבין שני קוים נכחים | |style="text-align:right;"|הנה שני המשולשים השוים אשר על שתי התושבות ושתי התושבות על קו ישר ובצד אחד יכלו במה שבין שני קוים נכחים | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
|style="text-align:right;"|וזה מש"ל | |style="text-align:right;"|וזה מש"ל | ||
|- | |- | ||
| Line 1,633: | Line 1,668: | ||
|- | |- | ||
|When a parallelogram and a triangle are on the same base and are between the same parallel lines, then the parallelogram is double the triangle. | |When a parallelogram and a triangle are on the same base and are between the same parallel lines, then the parallelogram is double the triangle. | ||
| − | |style="text-align:right;"|<span style=color:red>מא</span> <big>כאשר</big> היה שטח נכחי הצלעות ומשולש על תושבת אחת ובין שני קוי בעינם נכחיים הנה השטח הנכחי הצלעות היא כפל המשולש | + | |style="text-align:right;"|<div id="Elements_I_41"></div><span style=color:red>מא</span> <big>כאשר</big> היה שטח נכחי הצלעות ומשולש על תושבת אחת ובין שני קוי בעינם נכחיים הנה השטח הנכחי הצלעות היא כפל המשולש |
|- | |- | ||
| | | | ||
| + | *Let parallelogram ABGD and triangle ABG have the same base, which is BG, and let them be between the same two parallels lines BG and AD. | ||
|style="text-align:right;"|יהיה שטח נכחי הצלעות עליו א"ב ג"ד ומשלש אב"ג והבעל תושבת אחת והיא ב"ג ובמה שבין שני קוי ב"ג א"ד הנכחיים | |style="text-align:right;"|יהיה שטח נכחי הצלעות עליו א"ב ג"ד ומשלש אב"ג והבעל תושבת אחת והיא ב"ג ובמה שבין שני קוי ב"ג א"ד הנכחיים | ||
|- | |- | ||
| − | |Supposition: | + | |<span style=color:green>'''Supposition:'''</span> I say that the parallelogram ABGD is double the triangle ABG. |
|style="text-align:right;"|הנה אומר כי שטח א"ב ג"ד נכחי הצלעות כפל משלש אב"ג | |style="text-align:right;"|הנה אומר כי שטח א"ב ג"ד נכחי הצלעות כפל משלש אב"ג | ||
|- | |- | ||
| | | | ||
| + | :For both are on the same base, which is BG, and between the two parallels lines BG and AD. | ||
|style="text-align:right;"|מפני כי שניהם על תושבת אחת והיא ב"ג ובמה שבין שני קוי נכחיים והם ב"ג א"ד | |style="text-align:right;"|מפני כי שניהם על תושבת אחת והיא ב"ג ובמה שבין שני קוי נכחיים והם ב"ג א"ד | ||
|- | |- | ||
| − | | | + | |But, double triangle ABG is parallelogram ABGD. |
| + | :<math>\scriptstyle{\color{blue}{ABGD=2\sdot\triangle_{ABG}}}</math> | ||
|style="text-align:right;"|אבל כפל משולש אב"ג הוא שטח אבג"ד הנכחי הצלעות | |style="text-align:right;"|אבל כפל משולש אב"ג הוא שטח אבג"ד הנכחי הצלעות | ||
|- | |- | ||
| | | | ||
| + | :Because its diameter is AG. | ||
|style="text-align:right;"|מפני כי קטרו א"ג | |style="text-align:right;"|מפני כי קטרו א"ג | ||
|- | |- | ||
| − | | | + | |So, parallelogram ABGD is double triangle ABG. |
| + | :<math>\scriptstyle{\color{blue}{ABGD=2\sdot\triangle_{ABG}}}</math> | ||
|style="text-align:right;"|אם כן יהיה שטח א"ב ג"ד נכחי הצלעות כפל משולש אב"ג | |style="text-align:right;"|אם כן יהיה שטח א"ב ג"ד נכחי הצלעות כפל משולש אב"ג | ||
|- | |- | ||
| − | | | + | |Hence, when a parallelogram and a triangle are on the same base and are between the same parallel lines, then the parallelogram is double the triangle. |
|style="text-align:right;"|אם כן כאשר היא שטח נכחי הצלעות ומשולש על תושבת אחת ומה שבין שני קוים בעצמם נכחים הנה השטח הנכחי הצלעות כפל המשולש | |style="text-align:right;"|אם כן כאשר היא שטח נכחי הצלעות ומשולש על תושבת אחת ומה שבין שני קוים בעצמם נכחים הנה השטח הנכחי הצלעות כפל המשולש | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
|style="text-align:right;"|וזה מש"ל | |style="text-align:right;"|וזה מש"ל | ||
|- | |- | ||
| Line 1,668: | Line 1,708: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה יהיה המשולש המונח עליו אב"ג והזוית המונחת ישרת הקוים זוית ד' | + | *Let ABG be the given triangle, and angle D be the given rectilinear angle. |
| + | |style="text-align:right;"|הנה יהיה המשולש המונח עליו אב"ג והזוית המונחת ישרת הקוים זוית ד‫' | ||
|- | |- | ||
| − | | | + | |We wish to construct a parallelogram equal to triangle ABG, whose angle is equal to the rectilinear angle D. |
|style="text-align:right;"|ונרצה שנעמיד שטח נכחי הצלעות שוה למשולש אב"ג המונח שוה זויתו לזוית ד' ישרת הקוים | |style="text-align:right;"|ונרצה שנעמיד שטח נכחי הצלעות שוה למשולש אב"ג המונח שוה זויתו לזוית ד' ישרת הקוים | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה נחלק ב"ג לחציים על נקודת ה' | + | *We cut BG in half at point H. |
| + | :<math>\scriptstyle{\color{blue}{BH=HG}}</math> | ||
| + | |style="text-align:right;"|הנה נחלק ב"ג לחציים על נקודת ה‫' | ||
|- | |- | ||
| | | | ||
| + | *We join A and H. | ||
|style="text-align:right;"|ונגיע א"ה | |style="text-align:right;"|ונגיע א"ה | ||
|- | |- | ||
| | | | ||
| + | *We construct angle GHZ on the straight line HG at point H equal to the rectilinear angle D. | ||
| + | :<math>\scriptstyle{\color{blue}{\measuredangle GHZ=\measuredangle D}}</math> | ||
|style="text-align:right;"|ונעמיד על קו ה"ג הישר על נקודת ה' ממנו זוית ישרת הקוים שוה לזוית ד' ישרת הקוים והיא זוית גה"ז | |style="text-align:right;"|ונעמיד על קו ה"ג הישר על נקודת ה' ממנו זוית ישרת הקוים שוה לזוית ד' ישרת הקוים והיא זוית גה"ז | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונוציא מנקודת ג' קו ג"ח נכחי לקו ה"ז הישר | + | *We draw line GC through point G parallel to the straight line HZ, and line AC through point C parallel to the straight line BG. |
| + | :<math>\scriptstyle{\color{blue}{GC\parallel HZ\quad AC\parallel BG}}</math> | ||
| + | |style="text-align:right;"|ונוציא מנקודת ג' קו ג"ח נכחי לקו ה"ז הישר ומנקודת ח' קו א"ח נכחי לקו ב"ג הישר | ||
|- | |- | ||
| − | | | + | |Then, ZHGC is a parallelogram. |
| − | |||
| − | |||
| − | |||
|style="text-align:right;"|אם כן שטח ז"ה ג"ח נכחי הצלעות | |style="text-align:right;"|אם כן שטח ז"ה ג"ח נכחי הצלעות | ||
|- | |- | ||
| − | | | + | |BH equals HG. |
| + | :<math>\scriptstyle{\color{blue}{BH=HG}}</math> | ||
|style="text-align:right;"|ומפני כי ב"ה שוה אל ה"ג | |style="text-align:right;"|ומפני כי ב"ה שוה אל ה"ג | ||
|- | |- | ||
| − | | | + | |Therefore triangle ABH equals triangle AHG. |
| + | :<math>\scriptstyle{\color{blue}{\triangle_{ABH}=\triangle_{AHG}}}</math> | ||
|style="text-align:right;"|יהיה משולש אב"ה שוה למשלש אה"ג | |style="text-align:right;"|יהיה משולש אב"ה שוה למשלש אה"ג | ||
|- | |- | ||
| | | | ||
| + | :For they are on two equal bases and both between the two parallels lines BG and AC. | ||
|style="text-align:right;"|מפני כי שניהם על שתי תושבות שוות ושניהם בין שני קוי ב"ג א"ח הנכחים | |style="text-align:right;"|מפני כי שניהם על שתי תושבות שוות ושניהם בין שני קוי ב"ג א"ח הנכחים | ||
|- | |- | ||
| − | | | + | |So, triangle ABG is double triangle AHG. |
| + | :<math>\scriptstyle{\color{blue}{\triangle_{ABG}=2\sdot\triangle_{AHG}}}</math> | ||
|style="text-align:right;"|אם כן משלש אב"ג כפל משלש אה"ג | |style="text-align:right;"|אם כן משלש אב"ג כפל משלש אה"ג | ||
|- | |- | ||
| − | | | + | |But, parallelogram HZGC is also double triangle AHG. |
| + | :<math>\scriptstyle{\color{blue}{HZGC=2\sdot\triangle_{AHG}}}</math> | ||
|style="text-align:right;"|ושטח ה"ז ג"ח נכחי הצלעות גם כן כפל משלש אה"ג | |style="text-align:right;"|ושטח ה"ז ג"ח נכחי הצלעות גם כן כפל משלש אה"ג | ||
|- | |- | ||
| | | | ||
| + | :For both are on the same base, which is HG, and between the two parallels lines HG and AC. | ||
|style="text-align:right;"|מפני כי שניהם על תושבת אחת והיא ה"ג ובמה שבין שני קוי ה"ג א"ח הנכחים | |style="text-align:right;"|מפני כי שניהם על תושבת אחת והיא ה"ג ובמה שבין שני קוי ה"ג א"ח הנכחים | ||
|- | |- | ||
| − | | | + | |Therefore parallelogram ZHGC is equal to triangle ABG. |
| + | :<math>\scriptstyle{\color{blue}{ZHGC=\triangle_{ABG}}}</math> | ||
|style="text-align:right;"|אם כן שטח ז"ה ג"ח נכחי הצלעות שוה למשלש אב"ג | |style="text-align:right;"|אם כן שטח ז"ה ג"ח נכחי הצלעות שוה למשלש אב"ג | ||
|- | |- | ||
| | | | ||
| + | :Since those that are double of the the same thing are equal to each other. | ||
|style="text-align:right;"|מפני כי מה שהם כפל לדבר אחד בעינו הם שוים | |style="text-align:right;"|מפני כי מה שהם כפל לדבר אחד בעינו הם שוים | ||
|- | |- | ||
| − | | | + | |Hence, we have already constructed the parallelogram ZCGH equal to triangle ABG, whose angle ZHG is equal to angle D. |
| − | |style="text-align:right;"|הנה כבר העמדנו שטח ז"ח ג"ה הנכחי הצלעות שוה למשולש אב"ג וזוית זה"ג ממנו שוה לזוית ד' | + | :<math>\scriptstyle{\color{blue}{ZCGH=\triangle_{ABG}\quad\measuredangle ZHG=\measuredangle D}}</math> |
| + | |style="text-align:right;"|הנה כבר העמדנו שטח ז"ח ג"ה הנכחי הצלעות שוה למשולש אב"ג וזוית זה"ג ממנו שוה לזוית ד‫' | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
|style="text-align:right;"|וזה מש"ל | |style="text-align:right;"|וזה מש"ל | ||
|- | |- | ||
| Line 1,730: | Line 1,784: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה שטח נכחי הצלעות עליו אב"ג ג"ד | + | *Let ABGD be the parallelogram. |
| + | |style="text-align:right;"|ויהיה שטח נכחי הצלעות עליו אב"ג ג"ד | ||
|- | |- | ||
| | | | ||
| + | *Let DB be its diameter. | ||
| + | |style="text-align:right;"|ויהיה קטרו ד"ב | ||
| + | |- | ||
| + | | | ||
| + | *Let DHZC and ZTBK be parallelograms about the diameter DB. | ||
| + | |style="text-align:right;"|ויהיה על קוטר ד"ב שני שטחי ד"ה ז"ח ז"ט ב"כ נכחי הצלעות | ||
| + | |- | ||
| + | | | ||
| + | *Let the two surfaces ATZH and ZKGC be the so-called complements. | ||
|style="text-align:right;"|ויהיו שני השטחים אשר יקרא לשניהם המתמימים שטח א"ט ז"ה ז"כ ג"ח | |style="text-align:right;"|ויהיו שני השטחים אשר יקרא לשניהם המתמימים שטח א"ט ז"ה ז"כ ג"ח | ||
|- | |- | ||
| − | |Supposition: <math>\scriptstyle\Box_{ATZH}=\Box_{ZKGC}</math> | + | |<span style=color:green>'''Supposition:'''</span> I say that the two surfaces ATZH and ZKGC are equal. |
| + | :<math>\scriptstyle{\color{blue}{\Box_{ATZH}=\Box_{ZKGC}}}</math> | ||
|style="text-align:right;"|ואומר ששני שטחי א"ט ז"ה ז"כ ג"ח שוים | |style="text-align:right;"|ואומר ששני שטחי א"ט ז"ה ז"כ ג"ח שוים | ||
|- | |- | ||
| − | |Proof: | + | |<span style=color:green>'''Proof:'''</span> |
| + | | | ||
| + | |- | ||
| + | |ABGD is a parallelogram, and DB is its diameter. | ||
|style="text-align:right;"|הנה מפני כי א"ב ג"ד נכחי הצלעות וקטרו ד"ב | |style="text-align:right;"|הנה מפני כי א"ב ג"ד נכחי הצלעות וקטרו ד"ב | ||
|- | |- | ||
| − | |<math>\scriptstyle\triangle_{ABD}=\triangle_{DGB}</math> | + | |Therefore, triangle ABD is equal to triangle DGB. |
| + | :<math>\scriptstyle{\color{blue}{\triangle_{ABD}=\triangle_{DGB}}}</math> | ||
|style="text-align:right;"|יהיה משולש אב"ד שוה למשולש דג"ב | |style="text-align:right;"|יהיה משולש אב"ד שוה למשולש דג"ב | ||
|- | |- | ||
| − | | | + | |DHZC is also a parallelogram, and DZ is its diameter. |
|style="text-align:right;"|ומפני כי שטח ד"ה ז"ח גם כן נכחי הצלעות וקטרו ד"ז | |style="text-align:right;"|ומפני כי שטח ד"ה ז"ח גם כן נכחי הצלעות וקטרו ד"ז | ||
|- | |- | ||
| − | | | + | |Therefore, triangle ZHD is equal to triangle ZCD. |
| − | : | + | :<math>\scriptstyle{\color{blue}{\triangle_{ZHD}=\triangle_{ZCD}}}</math> |
|style="text-align:right;"|יהיה משולש זה"ד שוה למשלש זח"ד | |style="text-align:right;"|יהיה משולש זה"ד שוה למשלש זח"ד | ||
|- | |- | ||
| − | | | + | |For the same reason, triangle ZTB is also equal to triangle ZKB. |
| − | : | + | :<math>\scriptstyle{\color{blue}{\triangle_{ZTB}=\triangle_{ZKB}}}</math> |
|style="text-align:right;"|ולזה גם כן יהיה משולש זט"ב שוה למשולש זכ"ב | |style="text-align:right;"|ולזה גם כן יהיה משולש זט"ב שוה למשולש זכ"ב | ||
|- | |- | ||
| − | | | + | |Hence, the two triangles DHZ and ZTB are equal to the two triangles DCZ and ZKB. |
| − | :<math>\scriptstyle\triangle_{ | + | :<math>\scriptstyle{\color{blue}{\triangle_{DHZ}+\triangle_{ZTB}=\triangle_{DCZ}+\triangle_{ZKB}}}</math> |
|style="text-align:right;"|אם כן שני משלשי דה"ז זט"ב שוים לשני משולשי דח"ז זכ"ב | |style="text-align:right;"|אם כן שני משלשי דה"ז זט"ב שוים לשני משולשי דח"ז זכ"ב | ||
|- | |- | ||
| − | |<math>\scriptstyle\triangle_{ABD}=\triangle_{DBG}</math> | + | |It has already been explained also that the whole triangle ABD is equal to the whole triangle BBG. |
| + | :<math>\scriptstyle{\color{blue}{\triangle_{ABD}=\triangle_{DBG}}}</math> | ||
|style="text-align:right;"|וכבר התבאר גם כן כי כל משולש אב"ד שוה לכל משולש דב"ג | |style="text-align:right;"|וכבר התבאר גם כן כי כל משולש אב"ד שוה לכל משולש דב"ג | ||
|- | |- | ||
| − | |<math>\scriptstyle\Box_{ATZH}=\Box_{ZKGC}</math> | + | |Therefore the remaining complement ATZH must be equal to the remaining complement ZKGC. |
| + | :<math>\scriptstyle{\color{blue}{\Box_{ATZH}=\Box_{ZKGC}}}</math> | ||
|style="text-align:right;"|הנה יחוייב שיהיה שטח א"ט ז"ה המתמים הנשאר שוה לשטח ז"כ ג"ח המתמים הנשאר | |style="text-align:right;"|הנה יחוייב שיהיה שטח א"ט ז"ה המתמים הנשאר שוה לשטח ז"כ ג"ח המתמים הנשאר | ||
|- | |- | ||
| − | | | + | |Thus, for every parallelogram, the complements [of the two parallelograms] on both sides of its the diameter are equal to one another. |
|style="text-align:right;"|אם כן כל שטח נכחי הצלעות אשר משני צדדי קטרו אשר יקרא לשניהם המתמימים שוים | |style="text-align:right;"|אם כן כל שטח נכחי הצלעות אשר משני צדדי קטרו אשר יקרא לשניהם המתמימים שוים | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum. |
|style="text-align:right;"|וזמש"ל | |style="text-align:right;"|וזמש"ל | ||
|- | |- | ||
| Line 1,780: | Line 1,851: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה הקו הישר המונח א"ב ומשולש המונח גד"ה והזוית המונחת ישרת הקוים זוית ז' | + | *Let AB be the given straight line, GDH the given triangle and angle Z the given rectilinear angle. |
| + | |style="text-align:right;"|ויהיה הקו הישר המונח א"ב ומשולש המונח גד"ה והזוית המונחת ישרת הקוים זוית ז‫' | ||
|- | |- | ||
| − | | | + | |We wish to construct on the given straight line AB a parallelogram equal to the given triangle GDH, whose angle is equal to the given rectilinear angle Z. |
|style="text-align:right;"|ונרצה שנעשה על קו א"ב הישר המונח שטח נכחי הצלעות שוה למשולש גד"ה המונח שוה זויתו לזוית ז' המונחת ישרת הקוים | |style="text-align:right;"|ונרצה שנעשה על קו א"ב הישר המונח שטח נכחי הצלעות שוה למשולש גד"ה המונח שוה זויתו לזוית ז' המונחת ישרת הקוים | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה נעמיד שטח נכחי הצלעות עליו ח"ב כ"ט שוה למשולש גד"ה המונח שוה זויתו לזוית ז' | + | *We construct the parallelogram CBKT equal to the given triangle GDH, whose angle is equal to angle Z. |
| + | :<math>\scriptstyle{\color{blue}{CBKT=\triangle_{GDH}}}</math> | ||
| + | |style="text-align:right;"|הנה נעמיד שטח נכחי הצלעות עליו ח"ב כ"ט שוה למשולש גד"ה המונח שוה זויתו לזוית ז‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה ב"כ ממנו על יושר | + | *Let BK on it be in a straight line with BA. |
| + | |style="text-align:right;"|ויהיה ב"כ ממנו על יושר ב"א | ||
|- | |- | ||
| | | | ||
| + | *We draw parallelogram LABC. | ||
|style="text-align:right;"|ונתמים שטח ל"א ב"ח הנכחי הצלעות | |style="text-align:right;"|ונתמים שטח ל"א ב"ח הנכחי הצלעות | ||
|- | |- | ||
| | | | ||
| + | *We join line LB. | ||
|style="text-align:right;"|ונגיע קו ל"ב | |style="text-align:right;"|ונגיע קו ל"ב | ||
|- | |- | ||
| − | | | + | |LA is parallel to TB. |
| + | :<math>\scriptstyle{\color{blue}{LA\parallel TB}}</math> | ||
|style="text-align:right;"|הנה מפני כי ל"א נכחי אל ט"ב | |style="text-align:right;"|הנה מפני כי ל"א נכחי אל ט"ב | ||
|- | |- | ||
| − | | | + | |The straight line LT falls upon both. |
|style="text-align:right;"|וכבר נפל על שניהם קו ל"ט הישר | |style="text-align:right;"|וכבר נפל על שניהם קו ל"ט הישר | ||
|- | |- | ||
| − | | | + | |Therefore [the sum of] the interior angles ALT and LTK equals two right angles. |
|style="text-align:right;"|יהיו שתי זויות אל"ט לט"כ הפנימיות שוות לשתי נצבות | |style="text-align:right;"|יהיו שתי זויות אל"ט לט"כ הפנימיות שוות לשתי נצבות | ||
|- | |- | ||
| − | | | + | |So, [the sum of] the angles BLT and LTK is less than two right angles. |
|style="text-align:right;"|אם כן שתי זויות בל"ט לט"כ פחות משתי זויות נצבות | |style="text-align:right;"|אם כן שתי זויות בל"ט לט"כ פחות משתי זויות נצבות | ||
|- | |- | ||
| − | | | + | |The lines produced indefinitely from [angles] less than two right angles meet. |
|style="text-align:right;"|והקוים אשר יצאו בפחות משתי נצבות אשר לא תכלית יפגשו | |style="text-align:right;"|והקוים אשר יצאו בפחות משתי נצבות אשר לא תכלית יפגשו | ||
| + | |- | ||
| + | |Therefore the two lines LB and TK, when produced indefinitely, will meet | ||
| + | |style="text-align:right;"|אם כן שני קוי ל"ב ט"כ כאשר יצאו אל לא תכלית יפגשו | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *Let them be produced and meet at point M. |
| + | |style="text-align:right;"|ויוצאו ויפגשו על נקודת מ‫' | ||
|- | |- | ||
| | | | ||
| + | *We draw MN through point M parallel to both BA and LT. | ||
|style="text-align:right;"|ונוציא מנקודת מ' קו נכחי לשני קוי ב"א ל"ט והוא מ"נ | |style="text-align:right;"|ונוציא מנקודת מ' קו נכחי לשני קוי ב"א ל"ט והוא מ"נ | ||
|- | |- | ||
| | | | ||
| + | *We draw the two lines AN and KH in straight lines with both lines LA and CB. | ||
|style="text-align:right;"|ונוציא שני קוי א"נ כ"ה על יושר שני קוי ל"א ח"ב | |style="text-align:right;"|ונוציא שני קוי א"נ כ"ה על יושר שני קוי ל"א ח"ב | ||
|- | |- | ||
| − | | | + | |LN is a parallelogram and its diameter is ML. |
|style="text-align:right;"|הנה מפני כי ל"נ נכחי הצלעות וקטרו מ"ל | |style="text-align:right;"|הנה מפני כי ל"נ נכחי הצלעות וקטרו מ"ל | ||
|- | |- | ||
| − | | | + | |LABC and BSMK are two parallelograms on diameter LM. |
|style="text-align:right;"|ועל קוטר ל"מ שני שטחי ל"א ב"ח ב"ס מ"כ נכחי הצלעות | |style="text-align:right;"|ועל קוטר ל"מ שני שטחי ל"א ב"ח ב"ס מ"כ נכחי הצלעות | ||
|- | |- | ||
| − | | | + | |ANCB and CBKT are the complements. |
| − | |style="text-align:right;"|ושני שטחי א"נ ח"ב ח" | + | |style="text-align:right;"|ושני שטחי א"נ ח"ב ח"ב כ"ט הם המתמימים |
|- | |- | ||
| − | | | + | |Therefore the parallelogram CBKT equals the parallelogram ANHB. |
| + | :<math>\scriptstyle{\color{blue}{CBTK=ANHK}}</math> | ||
|style="text-align:right;"|אם כן שטח ח"ב כ"ט נכחי הצלעות שוה לשטח א"נ ה"ב נכחי הצלעות | |style="text-align:right;"|אם כן שטח ח"ב כ"ט נכחי הצלעות שוה לשטח א"נ ה"ב נכחי הצלעות | ||
|- | |- | ||
| − | | | + | |But, surface CBTK equals the triangle GDH. |
| − | |style="text-align:right;"|אבל שטח ח"ב ט" | + | :<math>\scriptstyle{\color{blue}{CBTK=\triangle_{GDH}}}</math> |
| + | |style="text-align:right;"|אבל שטח ח"ב ט"כ שוה למשולש גד"ה | ||
|- | |- | ||
| − | | | + | |Therefore the parallelogram ANHK equals the triangle GDH. |
| + | :<math>\scriptstyle{\color{blue}{ANHK=\triangle_{GDH}}}</math> | ||
|style="text-align:right;"|אם כן שטח א"נ ה"כ הנכחי הצלעות שוה למשלש גד"ה | |style="text-align:right;"|אם כן שטח א"נ ה"כ הנכחי הצלעות שוה למשלש גד"ה | ||
|- | |- | ||
| − | | | + | |Angle CBK equals angle ABH. |
| + | :<math>\scriptstyle{\color{blue}{\measuredangle CBK=\measuredangle ABH}}</math> | ||
|style="text-align:right;"|ומפני כי זוית חב"כ שוה לזוית אב"ה | |style="text-align:right;"|ומפני כי זוית חב"כ שוה לזוית אב"ה | ||
|- | |- | ||
| − | | | + | |Angle CBK equals angle Z. |
| − | |style="text-align:right;"|וזוית חב"כ שוה לזוית ז' | + | :<math>\scriptstyle{\color{blue}{\measuredangle CBK=\measuredangle Z}}</math> |
| + | |style="text-align:right;"|וזוית חב"כ שוה לזוית ז‫' | ||
|- | |- | ||
| − | | | + | |Then, angle ABH equals angle Z. |
| − | |style="text-align:right;"|תהיה זוית אב"ה שוה לזוית ז' | + | :<math>\scriptstyle{\color{blue}{\measuredangle ABH=\measuredangle Z}}</math> |
| − | + | |style="text-align:right;"|תהיה זוית אב"ה שוה לזוית ז‫' | |
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |Hence, a parallelogram equal to the given triangle GDH has been constructed on the given straight line AB, whose angle ABH is equal to the given rectilinear angle Z. |
| − | |style="text-align:right;"|וזוית אב"ה ממנו שוה לזוית ז' המונחת ישרת הקוים | + | :<math>\scriptstyle{\color{blue}{ANHK=\triangle_{GDH}\quad\measuredangle ABH=\measuredangle Z}}</math> |
| + | |style="text-align:right;"|הנה כבר נעשה על קו א"ב הישר המונח שטח נכחי הצלעות שוה למשולש גד"ה המונח וזוית אב"ה ממנו שוה לזוית ז' המונחת ישרת הקוים | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum. |
|style="text-align:right;"|וזה מש"ל | |style="text-align:right;"|וזה מש"ל | ||
|- | |- | ||
| Line 1,866: | Line 1,954: | ||
|- | |- | ||
| | | | ||
| + | *Let ABGD be the given rectilinear figure. | ||
|style="text-align:right;"|ותהיה התמונה ישרת הקוים המונחת א"ב ג"ד | |style="text-align:right;"|ותהיה התמונה ישרת הקוים המונחת א"ב ג"ד | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ותהיה הזוית המונחת ישרת הקוים זוית ל' | + | *Let angle L be the given rectilinear angle. |
| + | |style="text-align:right;"|ותהיה הזוית המונחת ישרת הקוים זוית ל‫' | ||
|- | |- | ||
| − | | | + | |We wish to construct a parallelogram equal to the rectilinear figure ABGD, whose angle is equal to angle L. |
| − | |style="text-align:right;"|ונרצה שנעמיד שטח נכחי הצלעות שוה לתמונה א"ב ג"ד ישרת הקוים שוה זויתו לזוית ל' | + | |style="text-align:right;"|ונרצה שנעמיד שטח נכחי הצלעות שוה לתמונה א"ב ג"ד ישרת הקוים שוה זויתו לזוית ל‫' |
|- | |- | ||
| | | | ||
| + | *We join B and G. | ||
|style="text-align:right;"|הנה נגיע ב"ג | |style="text-align:right;"|הנה נגיע ב"ג | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונעמיד שטח נכחי הצלעות שוה למשולש אב"ג והוא ה"ז כ"ט | + | *We construct the parallelogram HZKT equal to the triangle ABD, whose angle ZHT is equal to angle L. |
| − | + | :<math>\scriptstyle{\color{blue}{HZKT=\triangle_{ABD}\quad\measuredangle ZHT=\measuredangle L}}</math> | |
| − | + | |style="text-align:right;"|ונעמיד שטח נכחי הצלעות שוה למשולש אב"ג והוא ה"ז כ"ט שוה זוית זה"ט ממנו לזוית ל‫' | |
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|שוה זוית חז"כ ממנו לזוית ל' | + | *We make on ZK the parallelogram ZCKM equal to the triangle BGD, whose angle CZK is equal to angle L. |
| + | :<math>\scriptstyle{\color{blue}{ZCKM=\triangle_BGD\quad\measuredangle CZK=\measuredangle L}}</math> | ||
| + | |style="text-align:right;"|ונעשה על ז"כ שטח נכחי הצלעות שוה למשולש בג"ד והוא ז"ח כ"מ שוה זוית חז"כ ממנו לזוית ל‫' | ||
|- | |- | ||
| − | | | + | |Since each of the angles ZHT and CZK equals angle L, then angle CZK equals angle ZHT. |
| − | |style="text-align:right;"|הנה מפני שכל אחת משתי זויות זה"ט חז"ב שוות לזוית ל' | + | :<math>\scriptstyle{\color{blue}{\measuredangle CZK=\measuredangle L=\measuredangle ZHT}}</math> |
| − | + | |style="text-align:right;"|הנה מפני שכל אחת משתי זויות זה"ט חז"ב שוות לזוית ל' תהיה זוית חז"כ שוה לזוית זה"ט | |
| − | |||
| − | |||
|- | |- | ||
| − | |We | + | |We make angle HZK common [to each]. |
|style="text-align:right;"|ונשים זוית הז"כ משותפת | |style="text-align:right;"|ונשים זוית הז"כ משותפת | ||
|- | |- | ||
| − | | | + | |Therefore [the sum of] the two angles ZHT and HZK equals [the sum of] the two angles CZK and KZH. |
|style="text-align:right;"|א"כ שתי זויות זה"ט הז"כ שוות לשתי זויות חז"כ כז"ה | |style="text-align:right;"|א"כ שתי זויות זה"ט הז"כ שוות לשתי זויות חז"כ כז"ה | ||
|- | |- | ||
| − | | | + | |But, [the sum of] the two angles ZHT and HZK equals two right angles. |
|style="text-align:right;"|אבל שתי זויות זה"ט הז"כ שוות לשתי נצבות | |style="text-align:right;"|אבל שתי זויות זה"ט הז"כ שוות לשתי נצבות | ||
|- | |- | ||
| − | | | + | |Therefore [the sum of] the angles CZK and KZH =equals two right angles. |
|style="text-align:right;"|אם כן זויות חז"כ כז"ה שוות לשתי נצבות | |style="text-align:right;"|אם כן זויות חז"כ כז"ה שוות לשתי נצבות | ||
|- | |- | ||
| − | | | + | |Hence, HZ is in a straight line with line ZC. |
|style="text-align:right;"|אם כן ה"ז על יושר קו ז"ח | |style="text-align:right;"|אם כן ה"ז על יושר קו ז"ח | ||
|- | |- | ||
| − | | | + | |So, line TB is also in a straight line with line KM. |
|style="text-align:right;"|ולכן גם כן קו ט"ב על יושר קו כ"מ | |style="text-align:right;"|ולכן גם כן קו ט"ב על יושר קו כ"מ | ||
|- | |- | ||
| − | | | + | |HZ is equal to KT and parallel to it. |
| + | :<math>\scriptstyle{\color{blue}{HZ=KT\quad HZ\parallel KT}}</math> | ||
|style="text-align:right;"|ומפני כי ה"ז שוה אל כ"ט ונכחי לו | |style="text-align:right;"|ומפני כי ה"ז שוה אל כ"ט ונכחי לו | ||
|- | |- | ||
| − | | | + | |ZC is equal to KM and parallel to it. |
| + | :<math>\scriptstyle{\color{blue}{ZC=KM\quad ZC\parallel KM}}</math> | ||
|style="text-align:right;"|וז"ח שוה אל כ"מ ונכחי לו | |style="text-align:right;"|וז"ח שוה אל כ"מ ונכחי לו | ||
|- | |- | ||
| − | | | + | |Therefore, the whole HC is equal to TB and parallel to it. |
| + | :<math>\scriptstyle{\color{blue}{HC=TB\quad HC\parallel TB}}</math> | ||
|style="text-align:right;"|יהיה כל ה"ח שוה אל ט"ב ונכחי לו | |style="text-align:right;"|יהיה כל ה"ח שוה אל ט"ב ונכחי לו | ||
|- | |- | ||
| − | | | + | |Hence the parallelogram HCTM is equal to the rectilinear figure ABGD. |
| + | :<math>\scriptstyle{\color{blue}{HCTM=ABGD}}</math> | ||
|style="text-align:right;"|אם כן שטח ה"ח ט"מ נכחי הצלעות שוה לתמונה א"ב ג"ד ישרת הקוים | |style="text-align:right;"|אם כן שטח ה"ח ט"מ נכחי הצלעות שוה לתמונה א"ב ג"ד ישרת הקוים | ||
|- | |- | ||
| − | | | + | |And angle ZHT is equal to angle L. |
| − | |style="text-align:right;"|וזוית זה"ט שוה לזוית ל' | + | :<math>\scriptstyle{\color{blue}{\measuredangle ZHT=\measuredangle L}}</math> |
| + | |style="text-align:right;"|וזוית זה"ט שוה לזוית ל‫' | ||
|- | |- | ||
| − | | | + | |Therefore we constructed a parallelogram equal to the rectilinear figure ABGD, whose angle equals the given rectilinear angle. |
|style="text-align:right;"|הנה כבר העמדנו שטח נכחי הצלעות שוה לתמונת א"ב ג"ד ישרת הקוים שוה זויותו לזוית מונחת ישרת הקוים | |style="text-align:right;"|הנה כבר העמדנו שטח נכחי הצלעות שוה לתמונת א"ב ג"ד ישרת הקוים שוה זויותו לזוית מונחת ישרת הקוים | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum. |
|style="text-align:right;"|וזה מש"ל | |style="text-align:right;"|וזה מש"ל | ||
|- | |- | ||
| Line 1,942: | Line 2,034: | ||
|style="text-align:right;"|<span style=color:red>מו</span> <big>נרצה</big> שנעשה על קו ישר מונח מרובע | |style="text-align:right;"|<span style=color:red>מו</span> <big>נרצה</big> שנעשה על קו ישר מונח מרובע | ||
|- | |- | ||
| − | | | + | |Let AB be the straight line. |
|style="text-align:right;"|ויהיה הקו הישר א"ב | |style="text-align:right;"|ויהיה הקו הישר א"ב | ||
|- | |- | ||
| − | |We wish to construct a square on AB. | + | |We wish to construct a square on line AB. |
|style="text-align:right;"|ונרצה לעשות על קו א"ב מרובע | |style="text-align:right;"|ונרצה לעשות על קו א"ב מרובע | ||
|- | |- | ||
| Line 1,953: | Line 2,045: | ||
|- | |- | ||
| | | | ||
| − | *We | + | *We make AG equal to AB. |
| + | :<math>\scriptstyle{\color{blue}{AG=AB}}</math> | ||
|style="text-align:right;"|ונשים א"ג כמו א"ב | |style="text-align:right;"|ונשים א"ג כמו א"ב | ||
|- | |- | ||
| Line 1,964: | Line 2,057: | ||
|style="text-align:right;"|ונוציא מנקודת ב' קו נכחי לקו א"ג והוא ב"ד | |style="text-align:right;"|ונוציא מנקודת ב' קו נכחי לקו א"ג והוא ב"ד | ||
|- | |- | ||
| − | | | + | |Then, GABD is a parallelogram. |
| − | |||
|style="text-align:right;"|אם כן שטח ג"א ב"ד נכחי הצלעות | |style="text-align:right;"|אם כן שטח ג"א ב"ד נכחי הצלעות | ||
|- | |- | ||
| | | | ||
| − | : | + | :Line AB equals line GD. |
| + | :<math>\scriptstyle{\color{blue}{AB=GD}}</math> | ||
|style="text-align:right;"|וקו א"ב שוה לקו ג"ד | |style="text-align:right;"|וקו א"ב שוה לקו ג"ד | ||
|- | |- | ||
| | | | ||
| − | : | + | :Line AG equals line BD. |
| + | :<math>\scriptstyle{\color{blue}{AG=BD}}</math> | ||
|style="text-align:right;"|וקו א"ג לקו ב"ד | |style="text-align:right;"|וקו א"ג לקו ב"ד | ||
|- | |- | ||
| − | | | + | |But, line AB equals line AG. |
| − | + | :<math>\scriptstyle{\color{blue}{AB=AG}}</math> | |
|style="text-align:right;"|אבל קו א"ב שוה לקו א"ג | |style="text-align:right;"|אבל קו א"ב שוה לקו א"ג | ||
|- | |- | ||
| − | | | + | |So, line GD also equals line DB. |
| − | + | :<math>\scriptstyle{\color{blue}{GD=DB}}</math> | |
|style="text-align:right;"|אם כן קו ג"ד שוה אל קו ד"ב | |style="text-align:right;"|אם כן קו ג"ד שוה אל קו ד"ב | ||
|- | |- | ||
|Therefore, lines AB, BD, DG, GA are equal to one another. | |Therefore, lines AB, BD, DG, GA are equal to one another. | ||
| + | :<math>\scriptstyle{\color{blue}{AB=BD=DG=GA}}</math> | ||
|style="text-align:right;"|אם כן קוי א"ב ב"ד ד"ג ג"א הם שוים | |style="text-align:right;"|אם כן קוי א"ב ב"ד ד"ג ג"א הם שוים | ||
|- | |- | ||
| Line 1,990: | Line 2,085: | ||
|style="text-align:right;"|אם כן שטח א"ג ד"ב שוה הצלעות | |style="text-align:right;"|אם כן שטח א"ג ד"ב שוה הצלעות | ||
|- | |- | ||
| − | |Supposition: it is also right-angled. | + | |<span style=color:green>'''Supposition:'''</span> I say that it is also right-angled. |
| − | |style="text-align:right;"|ואומר גם כן כי הוא נצב הזוי' | + | |style="text-align:right;"|ואומר גם כן כי הוא נצב הזוי‫' |
|- | |- | ||
| − | | | + | |Line GA falls upon the two parallel lines AB and GD. |
| − | |||
|style="text-align:right;"|כי מפני שהוא כבר נפל על שני קוי א"ב ג"ד הנכחיים קו ג"א | |style="text-align:right;"|כי מפני שהוא כבר נפל על שני קוי א"ב ג"ד הנכחיים קו ג"א | ||
|- | |- | ||
| − | | | + | |Therefore, [the sum of] the two angles BAG and AGD equals [the sum of] two right angles |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle BAG+\measuredangle AGD=90^\circ+90^\circ}}</math> | |
|style="text-align:right;"|יהיו שתי זויות בא"ג אג"ד שוות לשתי זויות נצבות | |style="text-align:right;"|יהיו שתי זויות בא"ג אג"ד שוות לשתי זויות נצבות | ||
|- | |- | ||
| − | | | + | |But, angle BAG is right. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle BAG=90^\circ}}</math> | |
|style="text-align:right;"|אבל זוית בא"ג נצבת | |style="text-align:right;"|אבל זוית בא"ג נצבת | ||
|- | |- | ||
| − | | | + | |So, angle AGD is also right. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle AGD=90^\circ}}</math> | |
|style="text-align:right;"|אם כן זוית אג"ד גם כן נצבת | |style="text-align:right;"|אם כן זוית אג"ד גם כן נצבת | ||
|- | |- | ||
| − | |Opposite sides and angles in | + | |Opposite sides and angles in parallelograms are equal to one another. |
|style="text-align:right;"|והזויות והצלעות המתנגדות מן השטחים נכחי הצלעות שוים | |style="text-align:right;"|והזויות והצלעות המתנגדות מן השטחים נכחי הצלעות שוים | ||
|- | |- | ||
| − | | | + | |Therefore, each of the angles ABD and BDG that are opposite to the above mentioned are right. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle ABD=\measuredangle BDG=90^\circ}}</math> | |
|style="text-align:right;"|אם כן כל אחת משתי זויות אב"ד בד"ג המתנגדות לאשר זכרנו שוות | |style="text-align:right;"|אם כן כל אחת משתי זויות אב"ד בד"ג המתנגדות לאשר זכרנו שוות | ||
|- | |- | ||
| − | |AGDB is right-angled and it was already proved equilateral. | + | |So, surface AGDB is right-angled and it was already proved to be equilateral. |
|style="text-align:right;"|אם כן שטח א"ב ג"ד נצב הזויות וכבר התבאר שהוא שוה הצלעות | |style="text-align:right;"|אם כן שטח א"ב ג"ד נצב הזויות וכבר התבאר שהוא שוה הצלעות | ||
|- | |- | ||
| − | | | + | |Therefore, surface AGDB is a square and it is constructed on line AB. |
| − | + | :<math>\scriptstyle{\color{blue}{AB\times GD=AB^2}}</math> | |
|style="text-align:right;"|אם כן שטח א"ב ג"ד מרובע והוא עשוי על קו א"ב | |style="text-align:right;"|אם כן שטח א"ב ג"ד מרובע והוא עשוי על קו א"ב | ||
|- | |- | ||
| − | | | + | |Hence, we have constructed a square on the given line AB. |
|style="text-align:right;"|הנה כבר קוינו מקו א"ב המונח מרובע | |style="text-align:right;"|הנה כבר קוינו מקו א"ב המונח מרובע | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum. |
|style="text-align:right;"|וזה מה שרצינו לבאר | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
|- | |- | ||
| Line 2,034: | Line 2,128: | ||
| | | | ||
|- | |- | ||
| − | |The square | + | |The square formed by the hypotenuse in right-angled triangles equals [the sum of] the two squares formed by the two sides containing the right angle. |
|style="text-align:right;"|<span style=color:red>מז</span> <big>המרובע</big> ההוה מן הצלע אשר יהיה מיתר הזוית הנצבת מן המשולשים נצבי הזויות שוה לשני המרובעים ההוים משתי צלעות המקיפות הזוית הנצבת | |style="text-align:right;"|<span style=color:red>מז</span> <big>המרובע</big> ההוה מן הצלע אשר יהיה מיתר הזוית הנצבת מן המשולשים נצבי הזויות שוה לשני המרובעים ההוים משתי צלעות המקיפות הזוית הנצבת | ||
|- | |- | ||
| − | | | + | |Let ABG be the right-angled triangle. |
|style="text-align:right;"|ויהיה המשולש נצב הזוית אב"ג | |style="text-align:right;"|ויהיה המשולש נצב הזוית אב"ג | ||
|- | |- | ||
| − | | | + | |Let angle BAG be its right angle. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle BAG=90^\circ}}</math> | |
|style="text-align:right;"|ותהיה זויתו הנצבת זוית בא"ג | |style="text-align:right;"|ותהיה זויתו הנצבת זוית בא"ג | ||
|- | |- | ||
| − | |Supposition: <math>\scriptstyle BG^2=BA^2+AG^2</math> | + | |<span style=color:green>'''Supposition:'''</span> I say that the square formed by BG is equal to [the sum of] the two squares formed by BA and AG. |
| + | :<math>\scriptstyle{\color{blue}{BG^2=BA^2+AG^2}}</math> | ||
|style="text-align:right;"|הנה אומר כי המרובע ההווה מן ב"ג שוה לשני המרובעים ההוים מן ב"א וא"ג | |style="text-align:right;"|הנה אומר כי המרובע ההווה מן ב"ג שוה לשני המרובעים ההוים מן ב"א וא"ג | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle\Box_{BDHG}=BG^2</math> | + | *We draw the square BDHG on BG. |
| + | :<math>\scriptstyle{\color{blue}{\Box_{BDHG}=BG^2}}</math> | ||
|style="text-align:right;"|הנה {{#annot:term|2549,819|kY7l}}נקוה{{#annotend:kY7l}} מן ב"ג מרובע ב"ד ה"ג | |style="text-align:right;"|הנה {{#annot:term|2549,819|kY7l}}נקוה{{#annotend:kY7l}} מן ב"ג מרובע ב"ד ה"ג | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle\Box_{BCZA}=BA^2\quad\Box_{GATK}=AG^2</math> | + | *Also the two squares BCZA and GATK on BA and AG. |
| + | :<math>\scriptstyle{\color{blue}{\Box_{BCZA}=BA^2\quad\Box_{GATK}=AG^2}}</math> | ||
|style="text-align:right;"|ומן ב"א א"ג שני מרובעים ב"ח ז"א ג"א ט"כ | |style="text-align:right;"|ומן ב"א א"ג שני מרובעים ב"ח ז"א ג"א ט"כ | ||
|- | |- | ||
| | | | ||
| − | *We draw line AL from point A parallel to BD and GH. | + | *We draw line AL from point A parallel to each of the two lines BD and GH. |
|style="text-align:right;"|ונוציא מנקודת א' קו נכחי לכל אחד משני קוי ב"ד ג"ה והוא א"ל | |style="text-align:right;"|ונוציא מנקודת א' קו נכחי לכל אחד משני קוי ב"ד ג"ה והוא א"ל | ||
|- | |- | ||
| | | | ||
| − | *We join lines CG and AD. | + | *We join the two lines CG and AD. |
|style="text-align:right;"|ונגיע שני קוי ח"ג א"ד | |style="text-align:right;"|ונגיע שני קוי ח"ג א"ד | ||
|- | |- | ||
| − | | | + | |Angle BAG is right. |
| − | : | + | :<math>\scriptstyle{\color{blue}{\measuredangle BAG=90^\circ}}</math> |
|style="text-align:right;"|הנה מפני זוית בא"ג נצבת | |style="text-align:right;"|הנה מפני זוית בא"ג נצבת | ||
|- | |- | ||
| − | | | + | |Angle BAZ is also right. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle BAZ=90^\circ}}</math> | |
|style="text-align:right;"|וזוית בא"ז גם כן נצבת | |style="text-align:right;"|וזוית בא"ז גם כן נצבת | ||
|- | |- | ||
| − | |When two straight lines ZA and AG are drawn from point A, but are not lying on the same side, the adjacent angles on both sides are equal to two right angles. | + | |When two straight lines ZA and AG are drawn from point A, but are not lying on the same side, the two [adjacent] angles GAB and BAZ on both sides are equal to two right angles. |
|style="text-align:right;"|יהיה כאשר הוצא מנקודת א' ממנו שני קוי ז"א א"ג הישרים ואינם בצד אחד ויהיו שתי זויות גא"ב בא"ז אשר משני הצדדים שוות לשתי נצבות | |style="text-align:right;"|יהיה כאשר הוצא מנקודת א' ממנו שני קוי ז"א א"ג הישרים ואינם בצד אחד ויהיו שתי זויות גא"ב בא"ז אשר משני הצדדים שוות לשתי נצבות | ||
|- | |- | ||
| − | | | + | |Therefore line ZA is in a straight line with GA. |
| − | + | :<math>\scriptstyle{\color{blue}{ZA\parallel GA}}</math> | |
|style="text-align:right;"|אם כן קו ז"א על יושר ג"א | |style="text-align:right;"|אם כן קו ז"א על יושר ג"א | ||
|- | |- | ||
| − | | | + | |So, line AT is in a straight line with AB. |
| − | + | :<math>\scriptstyle{\color{blue}{AT\parallel AB}}</math> | |
|style="text-align:right;"|ולכן יהיה קו א"ט על יושר קו א"ב | |style="text-align:right;"|ולכן יהיה קו א"ט על יושר קו א"ב | ||
|- | |- | ||
| − | | | + | |Angle CBA is equal to the angle DBG, for each is right. |
| − | : | + | :<math>\scriptstyle{\color{blue}{\measuredangle CBA=90^\circ=\measuredangle DBG}}</math> |
|style="text-align:right;"|ומפני כי זוית חב"א שוה לזוית דב"ג<br> | |style="text-align:right;"|ומפני כי זוית חב"א שוה לזוית דב"ג<br> | ||
וזה כי כל אחת משתיהן נצבות | וזה כי כל אחת משתיהן נצבות | ||
|- | |- | ||
| − | |We | + | |We add angle ABG common to both. |
|style="text-align:right;"|נשים זוית אב"ג משותפת | |style="text-align:right;"|נשים זוית אב"ג משותפת | ||
|- | |- | ||
| − | | | + | |So, the whole angle CBG is equal to the whole angle ABD. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle CBG=\measuredangle ABD}}</math> | |
|style="text-align:right;"|יהיה כל זוית חב"ג שוה לכל זוית אב"ד | |style="text-align:right;"|יהיה כל זוית חב"ג שוה לכל זוית אב"ד | ||
|- | |- | ||
| − | | | + | |CB is equal to BA. |
| − | : | + | :<math>\scriptstyle{\color{blue}{CB=BA}}</math> |
|style="text-align:right;"|ומפני כי ח"ב שוה אל ב"א | |style="text-align:right;"|ומפני כי ח"ב שוה אל ב"א | ||
|- | |- | ||
| − | | | + | |BG [is equal] to BD. |
| − | : | + | :<math>\scriptstyle{\color{blue}{BG=BD}}</math> |
|style="text-align:right;"|וב"ג אל ב"ד | |style="text-align:right;"|וב"ג אל ב"ד | ||
|- | |- | ||
| − | | | + | |Therefore, the two lines CB and BG are equal to the two lines AB and BD respectively. |
| − | |||
|style="text-align:right;"|יהיו כל שני קוי ח"ב ב"ג שוים לכל שני קוי א"ב ב"ד כל אחד לגילו | |style="text-align:right;"|יהיו כל שני קוי ח"ב ב"ג שוים לכל שני קוי א"ב ב"ד כל אחד לגילו | ||
|- | |- | ||
| − | | | + | |Angle CBG equals angle ABD. |
| − | : | + | :<math>\scriptstyle{\color{blue}{\measuredangle CBG=\measuredangle ABD}}</math> |
|style="text-align:right;"|וזוית חב"ג שוה לזוית אב"ד | |style="text-align:right;"|וזוית חב"ג שוה לזוית אב"ד | ||
|- | |- | ||
| − | | | + | |So, the base CG is equal to the base AD. |
| − | + | :<math>\scriptstyle{\color{blue}{CG=AD}}</math> | |
|style="text-align:right;"|אם כן תושבת ח"ג שוה לתושבת א"ד | |style="text-align:right;"|אם כן תושבת ח"ג שוה לתושבת א"ד | ||
|- | |- | ||
| − | | | + | |Also, triangle CBG [is equal] to triangle ABD. |
| − | + | :<math>\scriptstyle{\color{blue}{\triangle_{CBG}=\triangle_{ABD}}}</math> | |
|style="text-align:right;"|ומשולש חב"ג למשולש אב"ד | |style="text-align:right;"|ומשולש חב"ג למשולש אב"ד | ||
|- | |- | ||
| − | | | + | |But the parallelogram BDLM is double the triangle ABD. |
| − | + | :<math>\scriptstyle{\color{blue}{BDLM=2\sdot\triangle_{ABD}}}</math> | |
|style="text-align:right;"|אבל שטח ב"ד ל"מ נכחי הצלעות כפל משולש אב"ד | |style="text-align:right;"|אבל שטח ב"ד ל"מ נכחי הצלעות כפל משולש אב"ד | ||
|- | |- | ||
| | | | ||
| − | : | + | :For both are of the same base BD. |
|style="text-align:right;"|מפני כי שניהם על תושבת אחת והיא ב"ד | |style="text-align:right;"|מפני כי שניהם על תושבת אחת והיא ב"ד | ||
|- | |- | ||
| | | | ||
| − | : | + | :Also, they are between the two parallel lines BD and AL. |
|style="text-align:right;"|ובמה שבין שני קוים נכחיים והם ב"ד א"ל | |style="text-align:right;"|ובמה שבין שני קוים נכחיים והם ב"ד א"ל | ||
|- | |- | ||
| − | | | + | |The surface BAZC is double the triangle CBG. |
| − | + | :<math>\scriptstyle{\color{blue}{\square_{BAZC}=2\sdot\triangle_{CBG}}}</math> | |
|style="text-align:right;"|ושטח ב"א ז"ח כפל משולש חב"ג | |style="text-align:right;"|ושטח ב"א ז"ח כפל משולש חב"ג | ||
|- | |- | ||
| | | | ||
| − | : | + | :For both are of the same base BC. |
|style="text-align:right;"|מפני שניהם על תושבת אחת והיא ב"ח | |style="text-align:right;"|מפני שניהם על תושבת אחת והיא ב"ח | ||
|- | |- | ||
| | | | ||
| − | : | + | :Also, they are between the same parallel lines CB and ZG. |
|style="text-align:right;"|ובמה שבין קוים נכחיים והם ח"ב ז"ג הנכחיים | |style="text-align:right;"|ובמה שבין קוים נכחיים והם ח"ב ז"ג הנכחיים | ||
|- | |- | ||
| Line 2,145: | Line 2,241: | ||
|style="text-align:right;"|ואשר הם כפל לדבר אחד שוה הנה הם גם כן שוים | |style="text-align:right;"|ואשר הם כפל לדבר אחד שוה הנה הם גם כן שוים | ||
|- | |- | ||
| − | | | + | |Therefore, the parallelogram BDLM equals the square CBAZ. |
| − | + | :<math>\scriptstyle{\color{blue}{BDLM =\square_{CBAZ}}}</math> | |
|style="text-align:right;"|אם כן שטח ב"ד ל"מ הנכחי הצלעות שוה למרובע חבא"ז | |style="text-align:right;"|אם כן שטח ב"ד ל"מ הנכחי הצלעות שוה למרובע חבא"ז | ||
|- | |- | ||
| − | | | + | |Similarly, it is clear that the parallelogram MLHG equals the square TA. |
| − | + | :<math>\scriptstyle{\color{blue}{MLHG=TA^2}}</math> | |
|style="text-align:right;"|וכן יתבאר כי שטח מ"ל ה"ג הנכחי הצלעות שוה למרובע ט"א | |style="text-align:right;"|וכן יתבאר כי שטח מ"ל ה"ג הנכחי הצלעות שוה למרובע ט"א | ||
|- | |- | ||
| − | | | + | |Therefore, parallelogram BDHG is equal to [the sum of] the two squares CBAZ and TZGB that are formed by BA and AG. |
| − | + | :<math>\scriptstyle{\color{blue}{BDHG =\square_{CBAZ}+\square_{TZGB}=BA^2+AG^2}}</math> | |
|style="text-align:right;"|אם כן ב"ד ה"ג הנכחיי הצלעות שוה לשני מרובעי ח"ב א"ז ט"ז ג"ב והם הווים מן ב"א א"ג | |style="text-align:right;"|אם כן ב"ד ה"ג הנכחיי הצלעות שוה לשני מרובעי ח"ב א"ז ט"ז ג"ב והם הווים מן ב"א א"ג | ||
|- | |- | ||
| − | | | + | |Hence, the square formed by the hypotenuse in right-angled triangles equals [the sum of] the two squares formed by the [two] sides containing the right angle. |
|style="text-align:right;"|אם כן המרובע ההוה מן הצלע אשר תהיה מיתר הזוית הנצבת מן המשולשים נצבי הזויות שוים לשני המרובעים ההוים מהצלעות המקיפות בזוית הנצבת | |style="text-align:right;"|אם כן המרובע ההוה מן הצלע אשר תהיה מיתר הזוית הנצבת מן המשולשים נצבי הזויות שוים לשני המרובעים ההוים מהצלעות המקיפות בזוית הנצבת | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum. |
|style="text-align:right;"|וזה מה שרצינו לבאר | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
|- | |- | ||
| Line 2,168: | Line 2,264: | ||
| | | | ||
|- | |- | ||
| − | |When the square | + | |When the square formed by one of the sides of the triangle equals [the sum of] the squares formed by the remaining sides, then the angle contained by those remaining two sides of the triangle is right. |
|style="text-align:right;"|<span style=color:red>מח</span> <big>כאשר</big> היה המרובע ההווה מן הצלע מצלעות המשלש שוה למרובעים ההוים מן הצלעות הנשארות הנה הזוית אשר יקיפו בה שתי צלעות ההם מן המשולש נצבת | |style="text-align:right;"|<span style=color:red>מח</span> <big>כאשר</big> היה המרובע ההווה מן הצלע מצלעות המשלש שוה למרובעים ההוים מן הצלעות הנשארות הנה הזוית אשר יקיפו בה שתי צלעות ההם מן המשולש נצבת | ||
|- | |- | ||
| − | | | + | |Let ABG be the triangle. |
|style="text-align:right;"|ויהיה המשלש עליו אב"ג | |style="text-align:right;"|ויהיה המשלש עליו אב"ג | ||
|- | |- | ||
| − | | | + | |Let the square formed by BG be equal to [the sum of] the two squares formed by AG [and AB] |
| − | + | :<math>\scriptstyle{\color{blue}{BG^2=AG^2+}}{\color{red}{AB^2}}</math> | |
|style="text-align:right;"|ויהיה המרובע ההוה מן ב"ג ממנו שוה לשני המרובעים ההוים מן א"ג | |style="text-align:right;"|ויהיה המרובע ההוה מן ב"ג ממנו שוה לשני המרובעים ההוים מן א"ג | ||
|- | |- | ||
| − | |Supposition: <math>\scriptstyle\measuredangle BAG=90^\circ</math> | + | |<span style=color:green>'''Supposition:'''</span> I say that the angle BAG is right. |
| + | :<math>\scriptstyle{\color{blue}{\measuredangle BAG=90^\circ}}</math> | ||
|style="text-align:right;"|<big>הנה</big> אומר כי זוית בא"ג נצבת | |style="text-align:right;"|<big>הנה</big> אומר כי זוית בא"ג נצבת | ||
|- | |- | ||
| Line 2,186: | Line 2,283: | ||
|- | |- | ||
| | | | ||
| − | *We | + | *We make line AD equal to line AB. |
| + | :<math>\scriptstyle{\color{blue}{AD=AB}}</math> | ||
|style="text-align:right;"|ונשים קו א"ד שוה לקו א"ב | |style="text-align:right;"|ונשים קו א"ד שוה לקו א"ב | ||
|- | |- | ||
| Line 2,194: | Line 2,292: | ||
|- | |- | ||
| | | | ||
| − | : | + | :The square BG is equal to [the sum of] the two squares formed by BA and AG. |
| + | ::<math>\scriptstyle{\color{blue}{BG^2=BA^2+AG^2}}</math> | ||
|style="text-align:right;"|הנה מפני כי מרובע ב"ג שוה לשני המרובעים ההוים מן ב"א א"ג | |style="text-align:right;"|הנה מפני כי מרובע ב"ג שוה לשני המרובעים ההוים מן ב"א א"ג | ||
|- | |- | ||
| | | | ||
| − | : | + | :Line BA equals line AD. |
| + | ::<math>\scriptstyle{\color{blue}{BA=AD}}</math> | ||
|style="text-align:right;"|וקו ב"א שוה לקו א"ד | |style="text-align:right;"|וקו ב"א שוה לקו א"ד | ||
|- | |- | ||
| − | | | + | |Therefore the square formed by BG is equal to [the sum of] the two squares formed by AG anf AD. |
| − | + | :<math>\scriptstyle{\color{blue}{BG^2=AG^2+AD^2}}</math> | |
|style="text-align:right;"|יהיה המרובע ההוה מן ב"ג שוה לשני המרובעים ההוים מן א"ג א"ד | |style="text-align:right;"|יהיה המרובע ההוה מן ב"ג שוה לשני המרובעים ההוים מן א"ג א"ד | ||
|- | |- | ||
| − | | | + | |But, [the sum of] the two squares formed by AG and AD is equal to the square formed by DG. |
| − | : | + | :<math>\scriptstyle{\color{blue}{AG^2+AD^2=DG^2}}</math> |
|style="text-align:right;"|אבל שני המרובעים ההוים מן א"ג א"ד שוים למרובע ההוה מן ד"ג | |style="text-align:right;"|אבל שני המרובעים ההוים מן א"ג א"ד שוים למרובע ההוה מן ד"ג | ||
|- | |- | ||
| | | | ||
| − | ::Since <math>\scriptstyle\measuredangle DAG=90^\circ</math> | + | ::Since angle DAG is right. |
| + | ::<math>\scriptstyle{\color{blue}{\measuredangle DAG=90^\circ}}</math> | ||
|style="text-align:right;"|מפני כי זוית דא"ג נצבת | |style="text-align:right;"|מפני כי זוית דא"ג נצבת | ||
|- | |- | ||
| − | | | + | |Therefore the square formed by DG equals the square formed by BG. |
| − | + | :<math>\scriptstyle{\color{blue}{DG^2=BG^2}}</math> | |
|style="text-align:right;"|הנה המרובע ההוה מן ד"ג שוה למרובע ההוה מן ב"ג | |style="text-align:right;"|הנה המרובע ההוה מן ד"ג שוה למרובע ההוה מן ב"ג | ||
|- | |- | ||
| − | | | + | |So, line BG equals line GD. |
| − | + | :<math>\scriptstyle{\color{blue}{BG=GD}}</math> | |
|style="text-align:right;"|אם כן קו ב"ג שוה לקו ג"ד | |style="text-align:right;"|אם כן קו ב"ג שוה לקו ג"ד | ||
|- | |- | ||
| − | | | + | |Line BA equals line AD. |
| − | : | + | :<math>\scriptstyle{\color{blue}{BA=AD}}</math> |
|style="text-align:right;"|ומפני כי קו ב"א שוה אל קו א"ד | |style="text-align:right;"|ומפני כי קו ב"א שוה אל קו א"ד | ||
|- | |- | ||
| | | | ||
| − | : | + | :Line AG is common. |
|style="text-align:right;"|וקו א"ג משותף | |style="text-align:right;"|וקו א"ג משותף | ||
|- | |- | ||
| | | | ||
| − | + | :Then, the two lines BA and AG equal the two lines DA and AG respectively. | |
|style="text-align:right;"|יהיו כל שני קוי ב"א א"ג שוים לכל שני קוי ד"א א"ג כל אחת לגילו | |style="text-align:right;"|יהיו כל שני קוי ב"א א"ג שוים לכל שני קוי ד"א א"ג כל אחת לגילו | ||
|- | |- | ||
| − | | | + | |The base BG equals the base GD. |
| − | + | :<math>\scriptstyle{\color{blue}{BG=GD}}</math> | |
|style="text-align:right;"|ותושבת ב"ג שוה לתושבת ג"ד | |style="text-align:right;"|ותושבת ב"ג שוה לתושבת ג"ד | ||
|- | |- | ||
| − | | | + | |Therefore angle BAG equals angle GAD. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle BAG=\measuredangle GAD}}</math> | |
|style="text-align:right;"|אם כן זוית בא"ג שוה לזוית גא"ד | |style="text-align:right;"|אם כן זוית בא"ג שוה לזוית גא"ד | ||
|- | |- | ||
| − | | | + | |Angle GAD is right. |
| − | : | + | :<math>\scriptstyle{\color{blue}{\measuredangle GAD=90^\circ}}</math> |
|style="text-align:right;"|וזוית גא"ד נצבת | |style="text-align:right;"|וזוית גא"ד נצבת | ||
|- | |- | ||
| − | | | + | |Therefore angle BAG is right. |
| − | + | :<math>\scriptstyle{\color{blue}{\measuredangle BAG=90^\circ}}</math> | |
|style="text-align:right;"|אם כן זוית בא"ג נצבת | |style="text-align:right;"|אם כן זוית בא"ג נצבת | ||
|- | |- | ||
| − | | | + | |Hence, when the square formed by [one of] the sides of the triangle equals [the sum of] the squares formed by the remaining two sides, then the angle contained by the remaining two sides of the triangle is right. |
|style="text-align:right;"|אם כן כאשר היה המרובע ההוה מצלעות ממשלש שוה לשני המרובעים ההוים משני צלעות הנשארות הנה הזוית אשר יקיפו בה שני הצלעות הנשארות מן המשולש נצבת | |style="text-align:right;"|אם כן כאשר היה המרובע ההוה מצלעות ממשלש שוה לשני המרובעים ההוים משני צלעות הנשארות הנה הזוית אשר יקיפו בה שני הצלעות הנשארות מן המשולש נצבת | ||
|- | |- | ||
| Line 2,263: | Line 2,364: | ||
| | | | ||
|style="text-align:right;"|ונתחיל המאמר השני בג"ה אמן | |style="text-align:right;"|ונתחיל המאמר השני בג"ה אמן | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | == Book | + | == The Second Section of Euclid's Book == |
| − | + | |style="text-align:right;"|<big>המאמר השני מספר אקלידס</big>‫<ref>E: ’מאמר ב; Mu246: מאמר שני<br> | |
| + | מספר אקלידס| Mu246; P1011; P1013; P1014: om.; Mu130: מספר היסודות; Ma1: מספר היסודות לאקלידס; C, AB; P1012: מספר אקלידס; O16: מספר אוקלידיס; W66: מספר אלקידוס; F137: מספר אוקלידס בשרשים</ref> | ||
|- | |- | ||
| | | | ||
| − | * | + | *<span style=color:green>'''Definition 1:'''</span> For any rectangular parallelogram, let the two straight lines containing one of its right angles be called "encompassing it". |
| − | |style="text-align:right;"|‫<ref group=note>titled: F137 הקדמות המאמר; Ma1 הקדמות זה המאמר; W66 הקדמה; Lo; Ma1; P1014: marked א</ref>כל שטח נכחי הצלעות נצב הזויות הנה שני<ref>הנה שני: C, Ma1 om.; F137(marg.), P1012, P1014 הנה כל שני; P1007 הנה ב'< | + | |style="text-align:right;"|‫<ref group=note>titled: F137 הקדמות המאמר; Ma1 הקדמות זה המאמר; W66 הקדמה; Lo; Ma1; P1014: marked א</ref>כל שטח נכחי הצלעות נצב הזויות הנה שני קוים הישרים המקיפים באחת מזויותיו הנצבות יקרא לשניהם המקיפים בו‫ |
| − | + | <ref>הנה שני: C, Ma1 om.; F137(marg.), P1012, P1014 הנה כל שני; P1007 הנה ב‫'<br> | |
| − | קוים המקיפים בו פי' ר"ל ששני אלו הקוים מודיעים לנו שעור שטח ומגבילים אותו<br> | + | באחת: A2 באחד; Ma1 אחת<br> |
| + | מזויותיו: B(except for W66) מזויות; W66 מזויותיה; P1012, P1014 מהזויות<br> | ||
| + | הנצבות: O16 נצבות; W66 om.<br> | ||
| + | יקרא: C, F יאמר<br> | ||
| + | לשניהם: B, C, F להם; P1007 לשניהן<br> | ||
| + | המקיפים: P1012 לשון המקיפים<br> | ||
| + | בו: O16 om.</ref><ref group=note>פי: ר"ל בשטח ולא יקראו המקיפים בו אם לא שיהיה השטח נצב הזוי<sup>ו</sup>ת בעבור שהשני הקוים לא ישערו השטח אם לא שיהיה השטח נצב הזוית <sup>פי' עד כאן</sup><br> | ||
| + | marg.: קוים המקיפים בו פי' ר"ל ששני אלו הקוים מודיעים לנו שעור שטח ומגבילים אותו<br> | ||
המשל בזה אם יהיה אחד מן הקוים ארכו ו' אמות ורחב האחר ג' אמות יהיה כל שעור זה השטח י"ח אמות מהכאת האורך ברחב או אם תרצה תכה הרחב באורך ויהיה י"ח גם כן<br> | המשל בזה אם יהיה אחד מן הקוים ארכו ו' אמות ורחב האחר ג' אמות יהיה כל שעור זה השטח י"ח אמות מהכאת האורך ברחב או אם תרצה תכה הרחב באורך ויהיה י"ח גם כן<br> | ||
וכל זה כשיהיה הקו האחד עומד על חבירו על זוית נצבת מה שאין כן בשטח שאינו נצב הזויות<br> | וכל זה כשיהיה הקו האחד עומד על חבירו על זוית נצבת מה שאין כן בשטח שאינו נצב הזויות<br> | ||
| − | הנה צריך שילקח בזה התנאי שיהיה השטח נצב הזוית שאם לא יהיה כן לא יקראו המקיפים ולא | + | ד"ת ונקרא השטח בשם שתי אותיות המתנגדות<br> |
| + | הנה צריך שילקח בזה התנאי שיהיה השטח נצב הזוית שאם לא יהיה כן לא יקראו המקיפים ולא ישערו את השטח השני קוים המקיפים בו<br> | ||
| + | E: הקוים המקיפי’ באחת הזוית הנצבות מהשטח נצב הזויות נכחי הצלעות יקראו מקיפים בשטח ההוא [כי] הנה מקביליהם ישוו להם<br> | ||
W66: ר"ל ששני אלו הקוים [..] מודיעים לנו שעור השטח ומגבילים אותו<br> | W66: ר"ל ששני אלו הקוים [..] מודיעים לנו שעור השטח ומגבילים אותו<br> | ||
המשל בזה כי אם יהיה אחד מן הקוים ארכו ו' אמות ורחב האחר ג' אמות יהיה כל שעור זה השטח י"ח אמות מהכאת האורך ברחב או הרחב באורך<br> | המשל בזה כי אם יהיה אחד מן הקוים ארכו ו' אמות ורחב האחר ג' אמות יהיה כל שעור זה השטח י"ח אמות מהכאת האורך ברחב או הרחב באורך<br> | ||
וכל זה כשיהיה הקו האחד עומד על חברו על זוי' נצבת מה שאין כן בשטח שאינו נצב הזויות<br> | וכל זה כשיהיה הקו האחד עומד על חברו על זוי' נצבת מה שאין כן בשטח שאינו נצב הזויות<br> | ||
| − | |||
E: ויקרא השטח בשם שתי אותיות המתנגדות אשר בצד קטרו<br> | E: ויקרא השטח בשם שתי אותיות המתנגדות אשר בצד קטרו<br> | ||
P1010 (marg.), PP: ונקרא השטח בשם שתי אותיות הזויות המתנגדות<br> | P1010 (marg.), PP: ונקרא השטח בשם שתי אותיות הזויות המתנגדות<br> | ||
| Line 2,290: | Line 2,398: | ||
|- | |- | ||
| | | | ||
| − | * | + | *<span style=color:green>'''Definition 2:'''</span> For any parallelogram, let any one whatever of the two parallelograms about its diameter with the two complementary areas be called a gnomon. |
| − | |style="text-align:right;"|‫<ref group=note>Ma1: marked השנית</ref>וכל<ref>וכל: F כל; O16 ובכל< | + | |style="text-align:right;"|‫<ref group=note>Ma1: marked השנית</ref>וכל שטח נכחי הצלעות הנה יקרא אחד משני השטחים הנכחי הצלעות אשר הם על קוטרו איזה משניהם היה עם שני השטחים המתמימים<ref group=note>Lo: והמתמימים באור זה מבואר במ”ג מראשון והרושם הוא שני השטחים המתמימים עם אחד מן השטחים שעל קטרו</ref> הרושם‫<ref>וכל: F כל; O16 ובכל<br> |
| + | שטח: F תמונה<br> | ||
| + | נכחי: F נכחית<br> | ||
| + | הנה: C, F, O16 om.<br> | ||
| + | אחד: Ma1 אחד [נ"ל כשאחד‫]<br> | ||
| + | משני: C, F om.; P1007 מב‫'<br> | ||
| + | משני השטחים: B(except for Mu130) מהשני שטחים; F137 <s>הצלעות</s> <sup>מ</sup>השטחים<br> | ||
| + | הנכחי: B(except for Mu130), F נכחיי; C נכוחי<br> | ||
| + | הם: C, F om.<br> | ||
| + | קוטרו: C אלכסונו<br> | ||
| + | משניהם היה: B שיהיה משניהם; C, F מהם שיהיה; P1007 משניהן היה<br> | ||
| + | שני השטחים: A2 השני שטחים; W66 השטחים; P1007 ב' השטחי‫'<br> | ||
| + | המתמימים: B, C, F המשלימים<br> | ||
| + | הרושם: C המסומן</ref> | ||
| + | <ref group=note>Mu 246:א כל שטח שוה הצלעות נצב הזויות יסובבנו השני קוים הסובב בזוית הנצבת וכל שטח נגדיי הצלעות נאמ' כי השני שטחים שעל אלכסונו הנגדיי הצלעות והאלכסון יחצבם כשיצטרף אחד מהם לשני השטחים המשלימין שעל שני צדי האלכסון כל זה יקרא עלם<br> | ||
P1011: כל שטח נכחי הצלעות נצב הזויות הנה יקיפו השני קוים המקיפים בזוית הנצבה<br> | P1011: כל שטח נכחי הצלעות נצב הזויות הנה יקיפו השני קוים המקיפים בזוית הנצבה<br> | ||
וכל שטח נכחי הצלעות הנה השני שטחים אשר יהיו על קטרו [נכח]יי הצלעות והקוטר יחצבם כאשר [...] מהם אל השני שטחים המשלימים אשר [על] צדדי הקוטר יקרא הרושם עד כאן פתי[חה‫]<br> | וכל שטח נכחי הצלעות הנה השני שטחים אשר יהיו על קטרו [נכח]יי הצלעות והקוטר יחצבם כאשר [...] מהם אל השני שטחים המשלימים אשר [על] צדדי הקוטר יקרא הרושם עד כאן פתי[חה‫]<br> | ||
| Line 2,298: | Line 2,420: | ||
|- | |- | ||
| | | | ||
| − | === Proposition 1 === | + | === <span style=color:green>Proposition 1</span> === |
| + | | | ||
| + | |- | ||
| + | |<span style=color:green>'''The distributive law for multiplication over addition:'''</span> | ||
| + | <math>\scriptstyle{\color{OliveGreen}{a\times\left(b_1+b_2\right)=\left(a\times b_1\right)+\left(a\times b_2\right)}}</math> | ||
| | | | ||
|- | |- | ||
| − | | | + | |When there are two straight lines, and one of them is divided into any number of segments, then the rectangle enclosed by the two straight lines is equal to [the sum of] all the rectangles enclosed by the uncut line and each of the segments. |
| − | + | |style="text-align:right;"|<div id="Elements_II_1"></div>‫<ref group=note>F137 titles the propositions’ section: המבוקשים;</ref><big>א</big> <big>כאשר</big> היו שני קוים ישרים וחולק אחד מהם לחלקים איזה מספר שיהיה הנה השטח הנצב הזויות אשר יקיפו בו השני קוים הישרים שוה לכל השטחים הנצבי הזויות אשר יקיף בכל אחד מהם הקו אשר לא נחלק וכל אחד מן החלקים‫<ref group=note>P1011: כל שני קוים יחלק אחד מהם בחלוקה איך שיהיה הנה אשר יהיה מהכאת אחד משני הקוים באחר כמו אשר יהיה מהכאת הקו אשר לא יחלק בכל חלקי הקו המתחלק חלוקה חלוקה<br> | |
| − | |style="text-align:right;"|<div id="Elements_II_1"></div>‫<ref group=note>F137 titles the propositions’ section: המבוקשים;</ref> | ||
E: ‫1 השטח אשר יקיפו בו כל שני קוים שוה למקובץ השטחים יקיפו בם אחד הקוים עם חלקי הקו השני יחד<br> | E: ‫1 השטח אשר יקיפו בו כל שני קוים שוה למקובץ השטחים יקיפו בם אחד הקוים עם חלקי הקו השני יחד<br> | ||
Mu36 adds a marginal note: כונת זה הדרוש שכשהיו לנו שני קוים מונחי’ כמה שיהיו וחולק האחד מהם לחלקים כמה שהיו שהכאת הקו האחד בכל אחד מהחלקים שחולק הקו השני שוה להכאת הקו ההוא בקו המחולק כלו<br> | Mu36 adds a marginal note: כונת זה הדרוש שכשהיו לנו שני קוים מונחי’ כמה שיהיו וחולק האחד מהם לחלקים כמה שהיו שהכאת הקו האחד בכל אחד מהחלקים שחולק הקו השני שוה להכאת הקו ההוא בקו המחולק כלו<br> | ||
The arithmetic version of the proposition is given in marginal notes in a few manuscripts:<br> | The arithmetic version of the proposition is given in marginal notes in a few manuscripts:<br> | ||
| − | Mu91: המשל לתמונת א' משני | + | Mu91: המשל לתמונת א' משני<br> |
| + | כמו עשרה וששה וחולק עשרה לשלשה חלקים כגון חמשה ושלשה ושנים<br> | ||
| + | הנה שטח ששה בעשרה שהוא ס' שוה לשטח חמשה בששה שהוא שלשים ולשטח ששה בשלשה שהוא י"ח ולשטח ששה בשנים שהוא י"ב וקבוץ שלשת שטחים אלו הוא ס‫'<br> | ||
W66: פי’ משל זה במספר כמו עשרה וששה וחולק עשרה לג' חלקים כגון ה' וג' וב' הנה שטח ששה בעשרה שהוא ס' שוה לשטח ששה בחמשה שהוא שלשים ולשטח ששה בשלשה שהוא י"ח ולשטח ששה בשנים שהוא י"ב וקבוץ שלשת שטחים אלו הוא ששים<br> | W66: פי’ משל זה במספר כמו עשרה וששה וחולק עשרה לג' חלקים כגון ה' וג' וב' הנה שטח ששה בעשרה שהוא ס' שוה לשטח ששה בחמשה שהוא שלשים ולשטח ששה בשלשה שהוא י"ח ולשטח ששה בשנים שהוא י"ב וקבוץ שלשת שטחים אלו הוא ששים<br> | ||
Numerical example: <math>\scriptstyle{\color{blue}{\left(2\times6\right)+\left(3\times6\right)+\left(5\times6\right)=12+18+30=60=10\times6}}</math><br> | Numerical example: <math>\scriptstyle{\color{blue}{\left(2\times6\right)+\left(3\times6\right)+\left(5\times6\right)=12+18+30=60=10\times6}}</math><br> | ||
| Line 2,313: | Line 2,440: | ||
המשל בזה הכאת י’ בט”ו הוא ק”נ וכשתחלק ט”ו לג’ חלקים שוים שהוא ה’ ותכה עשרה בה’ ה’ יהיה ק”נ<br> | המשל בזה הכאת י’ בט”ו הוא ק”נ וכשתחלק ט”ו לג’ חלקים שוים שהוא ה’ ותכה עשרה בה’ ה’ יהיה ק”נ<br> | ||
Numerical example: <math>\scriptstyle{\color{blue}{\left(5\times10\right)+\left(5\times10\right)+\left(5\times10\right)=150=15\times10}}</math><br> | Numerical example: <math>\scriptstyle{\color{blue}{\left(5\times10\right)+\left(5\times10\right)+\left(5\times10\right)=150=15\times10}}</math><br> | ||
| − | P1014: וכן במספר שה’ עם ד’ הם כ’ וכולו חולק הה’ על ג’ וב’ ותכה הד’ עם השני חלקים יהיו | + | P1014: וכן במספר שה’ עם ד’ הם כ’ וכולו חולק הה’ על ג’ וב’ ותכה הד’ עם השני חלקים יהיו כ‫’<br> |
| − | Numerical example:<math>\scriptstyle{\color{blue}{\left(3\times4\right)+\left(2\times4\right)=20=5\times4}}</math></ref> | + | Numerical example:<math>\scriptstyle{\color{blue}{\left(3\times4\right)+\left(2\times4\right)=20=5\times4}}</math></ref>‫<ref>א: F137, Lo, O16, P1012 mark is missing; Mu130 למוד א'<br> |
| + | כאשר היו: C כשיהיו; F כאשר יהיו<br> | ||
| + | קוים ישרים: F137 הקוין הישרים; P1013 הקוים הישרים; B(except for W66), C קוים ישרים מונחים<br> | ||
| + | וחולק: B, C ונחלק<br> | ||
| + | מהם: Lo, PP משניהם; P1013 מהן<br> | ||
| + | אחד מהם לחלקים: O16 <s>אותם</s> לחלקים אחד מהם; C אחד מהם חלקים<br> | ||
| + | איזה מספר שיהיה: B, F כמה שיהיו/שהיו; C כמות שהן<br> | ||
| + | הנה: C יהיה<br> | ||
| + | הנצב: B, C, F, P1014 נצב<br> | ||
| + | הזויות: P1010 הזוית<br> | ||
| + | אשר יקיפו: C שיקיפו<br> | ||
| + | בו: A1 בה; O16, P1012 om.<br> | ||
| + | השני קוים: B, C, F שני הקוים; P1007 ב' הקוים<br> | ||
| + | הישרים: C; O16 הישרים המונחים<br> | ||
| + | שוה: F יהיה שוה<br> | ||
| + | לכל השטחים: F לשטחים; W66 לכלל השטחים; O16 כלו לשטחים<br> | ||
| + | הנצבי: B, C, F נצבי; P1012 הנצבים<br> | ||
| + | אשר יקיף: C שיקיפו; O16 אשר יקיפו<br> | ||
| + | בכל אחד מהם: F בהם<br> | ||
| + | הקו: A2 הקו הישר<br> | ||
| + | אשר לא: C שלא<br> | ||
| + | נחלק: F יתחלק<br> | ||
| + | וכל: A2, P1012, P1014 עם כל; P1013 לכל<br> | ||
| + | וכל אחד: C ואחד<br> | ||
| + | מן החלקים: B, P1007 מהחלקים</ref> | ||
|- | |- | ||
| − | | | + | |Let A and BG be two straight lines, and let BG be divided into as many segments at two points D and H. |
| − | |style="text-align:right;"|ויהיו<ref>ויהיו: F המשל יהיו; B הנה יהיה/יהיו< | + | |style="text-align:right;"|ויהיו שני קוי' ישרים על שניהם א' ב"ג ונחלק ב"ג לחלקים כמה שיהיו על שתי נקודות ד'ה‫'‫<ref>ויהיו: F המשל יהיו; B הנה יהיה/יהיו<br> |
| + | שני: P1007 ב‫'<br> | ||
| + | קוים ישרים: A2, F הקוים הישרים; B(except for W66) קוים ישרים מונחים<br> | ||
| + | על שניהם: B, F עליהם<br> | ||
| + | לחלקים: F137 חלקים<br> | ||
| + | כמה שיהיו: B(except for W66) om.; A2 כמה שהוא<br> | ||
| + | שתי: F om.; P1012, P1014 שני; P1007, P1013 ב‫'<br> | ||
| + | נקודות: Ma1 נקודת</ref> | ||
|- | |- | ||
| − | |Supposition: <math>\scriptstyle A\times BG=\left(A\times BD\right)+\left(A\times DH\right)+\left(A\times HG\right)</math> | + | |<span style=color:green>'''Supposition:'''</span> I say that the rectangle enclosed by the two lines A and BG is equal to [the sum of] the rectangle enclosed by the two lines A and BD, the rectangle enclosed by the two lines A and DH, and the rectangle enclosed by A and HG. |
| − | |style="text-align:right;"|הנה אומר כי | + | :<math>\scriptstyle{\color{blue}{A\times BG=\left(A\times BD\right)+\left(A\times DH\right)+\left(A\times HG\right)}}</math> |
| + | |style="text-align:right;"|הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א' ב"ג שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א' ב"ד והשטח הנצב הזויות אשר יקיפו בו שני קוי א' ד"ה והשטח הנצב הזויות גם כן אשר יקיפו בו א' ה"ג‫<ref group=note>C: המשל בזה שקו א' וקו ב"ג נחלק אחד מהם והוא ב"ג על נקודות ד' וה' ואומר שאשר יהיה מהכאת א' בחלק ב"ד ובחלק ד"ה ובחלק ה"ג שוה לאשר יהיה מהכאת א' בב"ג<br> | ||
E: יהיו שני קוי א' ב"ג ונחלק ב"ג על חלקי' איך שנרצה והם ג"ה ה"ד ד"ב ואומ' שהשטח נצב הזויות שיקיפו בו קוי א' ג"ב שוה למקובץ שטחי א'ג"ה וא'ה"ד וא'ד"ב<br> | E: יהיו שני קוי א' ב"ג ונחלק ב"ג על חלקי' איך שנרצה והם ג"ה ה"ד ד"ב ואומ' שהשטח נצב הזויות שיקיפו בו קוי א' ג"ב שוה למקובץ שטחי א'ג"ה וא'ה"ד וא'ד"ב<br> | ||
| − | Mu246: ב שני קוי א'ב"ג חולק ב"ג בחלקי ב"ד ד"ה ה"ג נאמ' כי כפל א' בכל ב"ג ככפל א' בכל אחד מן ב"ד ד"ה ה"ג מקובצי</ref> | + | Mu246: ב שני קוי א'ב"ג חולק ב"ג בחלקי ב"ד ד"ה ה"ג נאמ' כי כפל א' בכל ב"ג ככפל א' בכל אחד מן ב"ד ד"ה ה"ג מקובצי</ref>‫<ref>הנה אומר כי השטח: B הנה נאמר שהשטח; F אומר כי השטח; P1007 הנה אומר כי שטח<br> |
| + | הנצב: B, F, P1007 נצב<br> | ||
| + | הזויות: A2, B(except for W66), P1012 הזוית<br> | ||
| + | בו: A1 בה<br> | ||
| + | שני: F om.; P1007 ב‫'<br> | ||
| + | קוי: P1013 קוים<br> | ||
| + | שוה: Mu130 שוים<br> | ||
| + | הנצב: B, F נצב<br> | ||
| + | הזויות: Mu130 הזוית<br> | ||
| + | שני: P1007 ב‫'<br> | ||
| + | שני קוי: F om.| א' ב"ג ... שני קוי: P1012 om.<br> | ||
| + | א' ב"ד: P1013 אב"ג אב"ד<br> | ||
| + | והשטח הנצב: B, F ולשטח נצב<br> | ||
| + | בו שני: F om.; P1007 בו ב‫'<br> | ||
| + | שני קוי: Mu130, P1014 om.<br> | ||
| + | ד"ה: Lo, PP ה"ד<br> | ||
| + | והשטח הנצב: B, F ולשטח נצב<br> | ||
| + | הזויות: B(except for O16) הזוית<br> | ||
| + | גם כן: B, F om.<br> | ||
| + | בו: A2, P1010, P1013, PP om.; B בו שני קוי; F בו קוי</ref> | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle BG\perp BZ</math> | + | *<span style=color:green>'''I.11:'''</span> We draw a straight line, which is BZ, from point B of the straight line BG at right angles. |
| − | |style="text-align:right;"|ונוציא<ref>ונוציא: A2, B הנה נוציא; F המופת נוציא< | + | :<math>\scriptstyle{\color{blue}{BG\perp BZ}}</math> |
| + | |style="text-align:right;"|<sup>הנה</sup> ונוציא מנקודת ב' מן קו ב"ג הישר קו ישר על זוית נצבת והוא ב"ז <span style=color:red>מי' מא‫’</span>‫<ref>ונוציא: A2, B הנה נוציא; F המופת נוציא<br> | ||
| + | מן קו: A1, B, F, P1007 מקו<br> | ||
| + | הישר: A1, F om.<br> | ||
| + | ישר: P1014 om.<br> | ||
| + | זוית נצבת: B זוית נצבה; A1, F, Lo, P1010, PP זויות נצבות; P1012 זוית קו נצבת<br> | ||
| + | מי' מא‫': Ma1, E, O16, P1007, P1012 om.; F137, Lo, P1010, P1013, PP, W194 מי"א מראשון</ref> | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle BZ=A</math> | + | *<span style=color:green>'''I.3:'''</span> We make the straight line BG equal to the straight line A. |
| − | |style="text-align:right;"|ונשים<ref>ונשים: B(except for Mu130) ויהיה< | + | :<math>\scriptstyle{\color{blue}{BZ=A}}</math> |
| + | |style="text-align:right;"|ונשים קו ב"ז הישר שוה לקו א' הישר <span style=color:red>מג’ מא‫’</span>‫<ref>ונשים: B(except for Mu130) ויהיה<br> | ||
| + | ונשים קו ב"ז: A1, Ma1 om.<br> | ||
| + | שוה: P1010 om.<br> | ||
| + | הישר: A1, W66 om.<br> | ||
| + | מג' מא‫': C, Ma1, E, Mu36, O16, P1007, P1012 om.; F137, P1010, P1013, PP, W194 מב' מראשון; Mu130, P1014 מב' מא‫'</ref> | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle ZC\parallel BG</math> | + | *We draw line ZC from point Z parallel to the straight line BG. |
| − | |style="text-align:right;"|ונוציא מנקודת ז' קו ז"ח נכחי<ref>נכחי: P1013 נכוחי ה[צלע‫]?< | + | :<math>\scriptstyle{\color{blue}{ZC\parallel BG}}</math> |
| + | |style="text-align:right;"|ונוציא מנקודת ז' קו ז"ח נכחי לקו ב"ג הישר <sup>והוא קו ז"ח</sup>‫<ref>נכחי: P1013 נכוחי ה[צלע‫]?<br> | ||
| + | קו ז"ח ... הישר: B קו נכחי לקו ב"ג הישר והוא קו ז"ח; AB קו ז”ח נכחי לקו ב”ג הישר <sup>והוא קו ז”ח</sup>| הישר: Lo om.</ref> | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle DT, | + | *<span style=color:green>'''I.31:'''</span> We draw from D, H, and G lines parallel to line BZ, which are lines DT, KH, GC. |
| − | |style="text-align:right;"|ונוציא מן<ref>מן: B, F מנקודות< | + | :<math>\scriptstyle{\color{blue}{DT,KH,GC\parallel BZ}}</math> |
| + | |style="text-align:right;"|ונוציא מן ד'ה'ג' קוים נכחיים לקו ב"ז והם קוי ד"ט כ"ה ג"ח <span style=color:red>מל”א מא‫’</span>‫<ref>מן: B, F מנקודות<br> | ||
| + | מן ד‫': P1007 מד‫'<br> | ||
| + | ד' ה' ג‫': A1 ד'ה'ג' הישר; F137 ד' ה‫' <sup>וג‫'</sup><br> | ||
| + | קוי: O16 om.<br> | ||
| + | מל"א מא‫': Ma1, E, P1007, P1012 om.; F137, Lo, P1010, P1013, PP, W194 מל"א מראשון</ref> | ||
|- | |- | ||
| − | | | + | |Then, BT, DK, and HC are rectangles. |
| − | |style="text-align:right;"|הנה כל | + | |style="text-align:right;"|הנה כל אחד משטחי ב"ט <s>ד"ה</s> <sup>ד"כ</sup> ה"ח נכחי הצלעות‫<ref>הנה כל: B(except for W66) וכל<br> |
| + | אחד: P1013 אחת</ref> | ||
|- | |- | ||
| − | | | + | |The surface BC is equal to [the sum of] the surfaces BT, DK, and HC. |
| − | + | :<math>\scriptstyle{\color{blue}{\Box_{BC}=\Box_{BT}+\Box_{DK}+\Box_{HC}}}</math> | |
| − | |style="text-align:right;"|ושטח | + | |style="text-align:right;"|ושטח ב"ח שוה לשטחי ב"ט ד"כ ה"ח <span style=color:red>מפתיחת א‫'</span>‫<ref>ושטח: P1013 om.<br> |
| + | לשטחי: O16 לשטח<br> | ||
| + | שוה לשטחי ב"ט: W194 twice<br> | ||
| + | מפתיחת א‫': O561 מהפתיחה מא‫'; P1010 מפ' מרא‫'; P1014 מפת' מא'; PP מפתיחת ראשון; W66 מפתיח' א‫'</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | :But, surface BC is equal to the rectangle enclosed by the two lines A and BG. |
| − | |style="text-align:right;"|ואולם<ref> | + | :<math>\scriptstyle{\color{blue}{\Box_{BC}= A\times BG}}</math> |
| + | |style="text-align:right;"|ואולם שטח ב"ח הנה הוא שוה לשטח הנצב הזויות אשר יקיפו בו ‫<ref>13v</ref>שני קוי א' ב"ג‫<ref>ואולם: F אבל<br> | ||
| + | הנה הוא: F om.<br> | ||
| + | הנצב: A1, B, F נצב<br> | ||
| + | הזויות: Mu130, P1007 הזוית<br> | ||
| + | שני: F om.; P1007 ב‫'</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle BZ=A</math> | + | :For line BZ is equal to line A. |
| − | |style="text-align:right;"|מפני כי קו<ref>מפני כי קו: B מפני שקו; F לפי שקו | + | :<math>\scriptstyle{\color{blue}{BZ=A}}</math> |
| + | |style="text-align:right;"|מפני כי קו<s>י</s> ב"ז שוה לקו א‫'‫<ref>מפני כי קו: B מפני שקו; F לפי שקו; P1012, P1014 מפני כי קוי; PP מפני כי<br> | ||
| + | ואולם ... לקו א‫': P1007 twice, the second recurrence is erased| א‫': O16 <s>ג‫'</s> א‫'</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | :Surface BT is equal to the rectangle enclosed by the two lines A and BD. |
| − | |style="text-align:right;"|ואולם שטח<ref>ואולם שטח: F ושטח< | + | :<math>\scriptstyle{\color{blue}{\Box_{BT}= A\times BD}}</math> |
| + | |style="text-align:right;"|ואולם שטח ב"ט הנה הוא שוה לשטח נצב הזויות אשר יקיפו בו <sup>שני קוי</sup> א' ב"ד‫<ref>ואולם שטח: F ושטח<br> | ||
| + | ב"ט: PP marg.<br> | ||
| + | הנה הוא: F om.; A2, P1007, P1010 הנה<br> | ||
| + | נצב: F137 <sup>ה</sup>זויות נצב; P1014 הנצב<br> | ||
| + | הזויות: Mu130 הזוית<br> | ||
| + | אשר: F om.<br> | ||
| + | שני: F om.; P1007 ב‫'<br> | ||
| + | שני קוי: A2, Lo, P1010, P1012, PP om.</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle BZ=A</math> | + | :For line BZ is equal to line A. |
| − | |style="text-align:right;"|מפני כי קו | + | :<math>\scriptstyle{\color{blue}{BZ=A}}</math> |
| + | |style="text-align:right;"|מפני כי קו ב"ז שוה לקו א‫'‫<ref>מפני כי קו: B מפני שקו<br> | ||
| + | מפני כי קו ב"ז ... א‫': F om.</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | :Surface DK is equal to the rectangle enclosed by the two lines A and DH. |
| − | |style="text-align:right;"|ואולם שטח<ref>ואולם שטח: F ושטח< | + | :<math>\scriptstyle{\color{blue}{\Box_{DK}= A\times DH}}</math> |
| + | |style="text-align:right;"|ואולם שטח ד"כ הנה הוא שוה לשטח הנצב הזויות אשר יקיפו בו <sup>שני קוי</sup> א' ד"ה‫<ref>ואולם שטח: F ושטח<br> | ||
| + | ד"כ: P1014 marg.<br> | ||
| + | הנה הוא: F om.<br> | ||
| + | שוה: P1010 <sup>שוה</sup><br> | ||
| + | הנצב: B, A1, F, P1014 נצב<br> | ||
| + | הזויות: Mu130 הזוית<br> | ||
| + | שני קוי: A2, F, Lo, P1007, P1010, P1014, PP om.<br> | ||
| + | א' ד"ה: P1014 marg.</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle A=DT</math> | + | :For line A is equal to line DT. |
| − | |style="text-align:right;"|מפני כי קו<ref>מפני כי קו: B מפני שקו; F לפי שקו</ref> | + | :<math>\scriptstyle{\color{blue}{A=DT}}</math> |
| + | |style="text-align:right;"|מפני כי קו א' שוה לקו ד"ט‫<ref>מפני כי קו: B מפני שקו; F לפי שקו</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | :Surface HC is equal to the rectangle enclosed by the two lines A and HG. |
| − | |style="text-align:right;"|ואולם שטח<ref>ואולם שטח: F ושטח< | + | :<math>\scriptstyle{\color{blue}{\Box_{HC}= A\times HG}}</math> |
| + | |style="text-align:right;"|ואולם שטח ה"ח הנה הוא שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א' ה"ג‫<ref>ואולם שטח: F ושטח<br> | ||
| + | הנה הוא: F, P1014 om.<br> | ||
| + | שוה: P1010 <sup>שוה</sup><br> | ||
| + | הנצב: B, A1, F נצב<br> | ||
| + | הזויות: Mu130 הזוית<br> | ||
| + | בו: P1013 בהם<br> | ||
| + | א' ד"ה ... שני קוי: P1012 om.| שני קוי: Ma1, O16, P1014 om.; F137 קוי; P1007 ב' קוי</ref> | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle A=HK</math> | + | :<span style=color:green>'''I.34:'''</span> For line A is equal to line HK. |
| − | |style="text-align:right;"|מפני כי קו | + | :<math>\scriptstyle{\color{blue}{A=HK}}</math> |
| + | |style="text-align:right;"|מפני כי קו א' שוה לקו ה"כ‫<ref group=note>AB: פי' זה התבאר מכח מה שאמרנו ששטח ב"ח שוה לשטח ב"ד ד"כ ה"ח</ref> <span style=color:red>מל”ד מא’</span>‫<ref group=note>C: מופת זה שנוציא מקו ב"ג מנקדת ב' קו על זוית נצבה שוה לקו א' והוא קו ב"ז<br> | ||
ונוציא מנקדת ז' קו נכוחי לקו ב"ג והוא קו ז"ח<br> | ונוציא מנקדת ז' קו נכוחי לקו ב"ג והוא קו ז"ח<br> | ||
ונוציא מנקדת ד' וה' וג' קוים נכוחיים לקו ב"ז והם ד"ט וה"כ וג"ח<br> | ונוציא מנקדת ד' וה' וג' קוים נכוחיים לקו ב"ז והם ד"ט וה"כ וג"ח<br> | ||
וכבר התבאר ששטח ז"ג שוה לשלשת שטחי ז"ד וט"ה וכ"ג וכל השטחים הם נכוחי הצלעות<br> | וכבר התבאר ששטח ז"ג שוה לשלשת שטחי ז"ד וט"ה וכ"ג וכל השטחים הם נכוחי הצלעות<br> | ||
| − | ושטח ז"ג הוא מהכאת קו א' בקו ב"ג לפי שיקיפו בו קוי ז"ב ב"ג וז"ב שוה לא'<br> | + | ושטח ז"ג הוא מהכאת קו א' בקו ב"ג לפי שיקיפו בו קוי ז"ב ב"ג וז"ב שוה לא‫'<br> |
| − | ושטח ז"ד יקיפו בו קוי ז"ב <s>וז"ב שוה</s> ב"ד וקו ב"ז שוה לקו א'<br> | + | ושטח ז"ד יקיפו בו קוי ז"ב <s>וז"ב שוה</s> ב"ד וקו ב"ז שוה לקו א‫'<br> |
| − | ושטח ט"ה הוא מהכאת קו א' בקו ד"ה לפי שיקיפו בו קוי ט"ד ד"ה ושקו ט"ד שוה לקו א'<br> | + | ושטח ט"ה הוא מהכאת קו א' בקו ד"ה לפי שיקיפו בו קוי ט"ד ד"ה ושקו ט"ד שוה לקו א‫'<br> |
| − | ושטח כ"ג הוא מהכאת א' בה"ג לפי שכ"ה שוה לקו א'<br> | + | ושטח כ"ג הוא מהכאת א' בה"ג לפי שכ"ה שוה לקו א‫'<br> |
E: מופתו שנוציא מן ג' על קו ג"ב עמוד ג"ח שוה לקו א' ונשלים התמונה<br> | E: מופתו שנוציא מן ג' על קו ג"ב עמוד ג"ח שוה לקו א' ונשלים התמונה<br> | ||
ונוציא מן ה' וד' עמודים על ג"ב והם ה"כ ד"ט<br> | ונוציא מן ה' וד' עמודים על ג"ב והם ה"כ ד"ט<br> | ||
| Line 2,392: | Line 2,626: | ||
וכן ה"ט לאשר יקיפו בו א' עם ה"ד<br> | וכן ה"ט לאשר יקיפו בו א' עם ה"ד<br> | ||
וד"ז לאשר יקיפו א' עם ד"ב<br> | וד"ז לאשר יקיפו א' עם ד"ב<br> | ||
| − | Mu246: כיצד נוציא קוי ב"ז כ"ט ה"כ ג"ח על זויות נצבות וכל אחת מהן שוה לקו א'<br> | + | Mu246: כיצד נוציא קוי ב"ז כ"ט ה"כ ג"ח על זויות נצבות וכל אחת מהן שוה לקו א‫'<br> |
| − | לפי הדבר נראה כי כל שטח ב"ח הוא כפל א' בב"ג ושטח ב"ט הוא כפל א' בד"ה ושטח ה"ח כפל א' בה"ג</ref> | + | לפי הדבר נראה כי כל שטח ב"ח הוא כפל א' בב"ג ושטח ב"ט הוא כפל א' בד"ה ושטח ה"ח כפל א' בה"ג</ref>‫<ref>מפני כי קו: B מפני שקו; F לפי שקו<br> |
| + | לקו ה"כ: A1 לה"כ; Mu130 לקו ה"ד; O16 לקו ה"ג<br> | ||
| + | מל"ד מא‫': A1, Ma1, E, O16, P1007, P1012, P1014 om.; F137, Lo, P1010, P1013, PP, W194 מל"ד מראשון</ref> | ||
|- | |- | ||
| − | |<math>\scriptstyle A\times BG=\left(A\times BD\right)+\left(A\times DH\right)+\left(A\times HG\right)</math> | + | |Therefore the rectangle enclosed by the two lines A and BG is equal to [the sum of] the rectangles enclosed by A and BD, A and DH, and A and HG. |
| − | |style="text-align:right;"|הנה השטח<ref> | + | :<math>\scriptstyle{\color{blue}{A\times BG=\left(A\times BD\right)+\left(A\times DH\right)+\left(A\times HG\right)}}</math> |
| + | |style="text-align:right;"|הנה השטח הנצב הזויות אשר יקיפו בו <sup>שני</sup> קוי א' ב"ג שוה לשטחים נצבי הזויות אשר יקיפו בהם א' ב"ד וא' ד"ה וא' ה"ג‫<ref group=note>C: וכבר התבאר שאשר יהיה מהכאת <s>ק</s> קו א' בקו ב"ג שוה לאשר הוא מהכאת קו א' בקו ב"ד ובקו ד"ה ובקו ה"ג וזה מה שרצינו לבאר<br> | ||
| + | E: יהיה <sup>ה</sup>שטח שיקיפו בו א' עם ב"ג שהוא כמו ב"ה שוה למקובץ שטחי א' עם ג"ה ה"ד ד"ב שהם כמו שטחי ח"ה ה"ט ט"ב והוא המכוון<br> | ||
| + | AB: פי זה התבאר מכח מה שאמרנו ששטח ב"ח שוה לשטח ב"ד ד"כ ה"ח</ref>‫<ref>הנה השטח: F והשטח<br> | ||
| + | הנצב: B, F, P1007 נצב<br> | ||
| + | הזויות: O16 הזוית<br> | ||
| + | יקיפו: P1012 om.; P1014 marg.<br> | ||
| + | שני: F137 om.; P1007 ב‫'<br> | ||
| + | שני קוי: Ma1 om.<br> | ||
| + | א' ב"ג: O16 ב"ג א'<br> | ||
| + | הזויות: P1007 הז<sup>ו</sup>יות<br> | ||
| + | ה"ג: P1012 ג"ה|<br> | ||
לשטחים ... וא' ה"ג: F לשטח נצב הזויות אשר יקיפו בו קוי א' ב"ד והשטח נצב הזויות אשר יקיפו בו קוי א' ד"ה והשטח נצב הזויות אשר יקיפו בו קוי א' ה"ג<br> | לשטחים ... וא' ה"ג: F לשטח נצב הזויות אשר יקיפו בו קוי א' ב"ד והשטח נצב הזויות אשר יקיפו בו קוי א' ד"ה והשטח נצב הזויות אשר יקיפו בו קוי א' ה"ג<br> | ||
B לשטח נצב הזויות אשר יקיפו בו שני קוי א' ב"ד ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ד"ה ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ה"ג [‫הזויות: Mu130 הזוית]<br> | B לשטח נצב הזויות אשר יקיפו בו שני קוי א' ב"ד ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ד"ה ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ה"ג [‫הזויות: Mu130 הזוית]<br> | ||
| − | AB לשטחים נצבי הזויות אשר יקיפו בהם <sup>שני קוי</sup> א' ב"ד | + | AB לשטחים נצבי הזויות אשר יקיפו בהם <sup>שני קוי</sup> <s>א' ב"ד וא' ד"ה וא' ה"ג</s> <sup>ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ד"ה ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ה"ג</sup></ref> |
| − | |||
|- | |- | ||
| − | | | + | |Hence, when there are two straight lines, and one of them is divided into as many segments, then the rectangle enclosed by the two straight lines is equal to [the sum of] all the rectangles enclosed by the uncut line and each of the segments. |
| − | |style="text-align:right;"|הנה<ref>הנה: F137 וא"כ< | + | |style="text-align:right;"|הנה כאשר היו שני קוים ישרים ונחלק אחד משניהם לחלקים כמה שיהיו הנה השטח הנצב הזויות אשר יקיפו בו שני הקוים הישרים <sup>המונחים</sup> שוה לכל השטחים הנצבים הזויות אשר יקיף בהם הקו אשר לא נחלק <s>וכל</s> <sup>עם</sup> אחד מן החלקים‫<ref>הנה: F137 וא"כ<br> |
| + | הנה כאשר: AB הנה <sup>התבאר כי</sup> כאשר<br> | ||
| + | היו: F137 יהיו<br> | ||
| + | שני: P1007 ב‫'<br> | ||
| + | ונחלק: F137 וחולק<br> | ||
| + | Mu130: F137 א‫'<br> | ||
| + | משניהם: F137, B(except for W66), P1010 מהם<br> | ||
| + | לחלקים כמה שיהיו: A2 בחלקים כמה שהיו; Mu130 לאי זה חלק שיהיה; O16 לאי זה חלקים שיהיו; P1007 לחלקים כמה שיהי<s>ה</s><sup>ו</sup><br> | ||
| + | השטח: P1007 om.<br> | ||
| + | הנצב: F137, B(except for W66) נצב<br> | ||
| + | הזויות: Mu130 הזוית, P1007 הז<sup>ו</sup>יות<br> | ||
| + | בו: P1007 בהם, P1010 <sup>בו</sup><br> | ||
| + | שני: P1007 ב‫'<br> | ||
| + | הקוים: F137 הקוין; P1007 קוים<br> | ||
| + | הישרים המונחים: A1 om.<br> | ||
| + | שוה: F137 יהיה שוה; O16 שוים<br> | ||
| + | לכל השטחים: F137, B(except for W66) לשטחים<br> | ||
| + | הנצבים: F137, B(except for W66) נצבי; A1, A2 הנצבי<br> | ||
| + | יקיף: B(except for W66), A2, P1007, P1012 יקיפו<br> | ||
| + | בהם: B(except for W66) בהן<br> | ||
| + | נחלק: F137 יתחלק; Mu130 תחלק; O16 יחלק<br> | ||
| + | וכל: P1014 לכל<br> | ||
| + | וכל אחד: P1012 לאחד<br> | ||
| + | מן החלקים: B(except for W66), P1007 מהחלקים|<br> | ||
הנה כאשר ... מן החלקים: C, Ma1, E, W66 om.</ref> | הנה כאשר ... מן החלקים: C, Ma1, E, W66 om.</ref> | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
| − | |style="text-align:right;"|וזה | + | |style="text-align:right;"|וזה מה שרצינו לבאר‫<ref>וזה: F137 וזהו<br> |
| + | וזה מה שרצינו לבאר: E והוא המכוון; Mu130 ומש"ל; P1007 וזמש"ל; Ma1, P1014 וזה מש"ל; P1010 וזה מה שרצינו לבארו; O16 om.</ref> | ||
|- | |- | ||
| | | | ||
| Line 2,414: | Line 2,684: | ||
| | | | ||
|- | |- | ||
| − | | | + | |<math>\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2}}</math> |
| − | |style="text-align:right;"|<div id="Elements_II_2"></div> | + | | |
| + | |- | ||
| + | |When a straight line is divided randomly, then [the sum of] the rectangles enclosed by the whole line and each of its segments is equal to the square formed by the whole line. | ||
| + | |style="text-align:right;"|<div id="Elements_II_2"></div><big>ב</big> כאשר נחלק קו ישר <sup>מונח</sup> איך שקרה <sup>הנה</sup> השטחים נצבי הזויות אשר יקיף בהם הקו כלו וכל אחד מחלקיו שוה למרובע המתהוה מן הקו כלו‫<ref group=note>P1011: כל קו יחלק לחלקים הנה אשר יהיה מהכאת הקו בכל חלקיו כמו אשר יהיה מהכאת הקו בעצמו<br> | ||
E: ‫2 כשנחלק קו ישר לשני חלקי' איך שהזדמן יהיה השטח נצב הזוית שיקיפו בו הקו <s>כלו</s> כלו עם כל אחד מהחלקים שוי' למרובע כל הקו<br> | E: ‫2 כשנחלק קו ישר לשני חלקי' איך שהזדמן יהיה השטח נצב הזוית שיקיפו בו הקו <s>כלו</s> כלו עם כל אחד מהחלקים שוי' למרובע כל הקו<br> | ||
Mu36: ובנס’ אלחג’אג’ כתו’ כאשר נחלק אי זה מספר שהיה בשני חלקים איך שקרה הנה הכאת המספר כלו בכל אחד מהחלקים להכאת המספר כלו בעצמו<br> | Mu36: ובנס’ אלחג’אג’ כתו’ כאשר נחלק אי זה מספר שהיה בשני חלקים איך שקרה הנה הכאת המספר כלו בכל אחד מהחלקים להכאת המספר כלו בעצמו<br> | ||
| − | ולפי זאת הנס’ צריך להיות המרובע שוה הצלעו’ כמו זה | + | ולפי זאת הנס’ צריך להיות המרובע שוה הצלעו’ כמו זה שלפנינ‫’<br> |
| − | AB: המשל לתמונת ב' כאשר חולק עשרה לשני חלקים כמו ששה וארבעה הנה שטח ששה בעשרה שהוא ס' ושטח ארבעה בעשרה שהוא ארבעים שוה למרובע המתהווה מעשרה אשר הוא מאה<br> | + | AB: המשל לתמונת ב' כאשר חולק עשרה לשני חלקים כמו ששה וארבעה<br> |
| + | הנה שטח ששה בעשרה שהוא ס' ושטח ארבעה בעשרה שהוא ארבעים שוה למרובע המתהווה מעשרה אשר הוא מאה<br> | ||
וזה מתבאר מתמונת א' וזה כי בתמונת א' התבאר שהכאת קו ראשון בקו שני כולו כהכאת הקו הראשון בחלקי הקו השני בין שיהיו שני הקוים ר"ל הראשון והשני שוים או בלתי שוים<br> | וזה מתבאר מתמונת א' וזה כי בתמונת א' התבאר שהכאת קו ראשון בקו שני כולו כהכאת הקו הראשון בחלקי הקו השני בין שיהיו שני הקוים ר"ל הראשון והשני שוים או בלתי שוים<br> | ||
W66: משל זה במספר כשנחלק עשרה לשני מספרי ו' וד' הנה שטח ו' בי' שהוא ס' ושטח ד' בי' שהוא מ' יחד שוים למרובע המתהוה מי' שהוא מאה<br> | W66: משל זה במספר כשנחלק עשרה לשני מספרי ו' וד' הנה שטח ו' בי' שהוא ס' ושטח ד' בי' שהוא מ' יחד שוים למרובע המתהוה מי' שהוא מאה<br> | ||
| Line 2,425: | Line 2,699: | ||
Numerical example: <math>\scriptstyle{\color{blue}{\left(6\sdot10\right)+\left(4\sdot10\right)=60+40=100=10^2}}</math><br> | Numerical example: <math>\scriptstyle{\color{blue}{\left(6\sdot10\right)+\left(4\sdot10\right)=60+40=100=10^2}}</math><br> | ||
P1014: וכן הח’ אם תחלקהו לו’ וב’ מרובע הכל ס”ד ואם תכה הח’ עם הב’ ועם הב’ יהיו ס”ד וכן בשני המספרים איזה שיהיו<br> | P1014: וכן הח’ אם תחלקהו לו’ וב’ מרובע הכל ס”ד ואם תכה הח’ עם הב’ ועם הב’ יהיו ס”ד וכן בשני המספרים איזה שיהיו<br> | ||
| − | Numerical example: <math>\scriptstyle{\color{blue}{\left(8\sdot6\right)+\left(8\sdot2\right)=8^2}}</math></ref> | + | Numerical example: <math>\scriptstyle{\color{blue}{\left(8\sdot6\right)+\left(8\sdot2\right)=8^2}}</math></ref>‫<ref>ב: O16, P1007, P1012 mark is missing; Mu130 למוד ב‫'<br> |
| + | כאשר נחלק: C כשיחלק; F כאשר יתחלק<br> | ||
| + | איך שקרה: C בחלקים כפי אשר קרה; B איך שהזדמן; F איך שיזדמן<br> | ||
| + | הנה: C, F יהיו<br> | ||
| + | השטחים: Mu130 שני השטחים; O16 השני שטחים<br> | ||
| + | נצבי: A1 הנצבי<br> | ||
| + | הזויות: C הזוייות<br> | ||
| + | אשר יקיף: C שיקיפו; P1007 אשר יקיפו<br> | ||
| + | מחלקיו: Mu130, O16 מהחלקים; W66 מן חלקיו<br> | ||
| + | המתהוה: A2, B, F ההוה<br> | ||
| + | המתהוה מן: C om.<br> | ||
| + | מן הקו: P1007, W66 מהקו; O561 מן <s>כלו</s> הקו<br> | ||
| + | כלו: Mu130 om.</ref> | ||
|- | |- | ||
| − | | | + | |Let AB be the straight line and let it be divided randomly at the point G. |
| − | |style="text-align:right;"|ויהיה<ref>ויהיה: F137 יהיה; Ma1 המשל יהיה; B הנה יהיה< | + | |style="text-align:right;"|ויהיה קו ישר <sup>מונח עליו</sup> א"ב ויחלק איך שיקרה על נקודת ג‫'‫<ref>ויהיה: F137 יהיה; Ma1 המשל יהיה; B הנה יהיה<br> |
| + | קו: F, O16, P1014 הקו<br> | ||
| + | ישר: F, P1014 הישר; O16 הישר המונח<br> | ||
| + | עליו: A1, A2, P1012, P1014 om.<br> | ||
| + | א"ב: Mu130, P1014 קו א"ב<br> | ||
| + | ויחלק: F ויתחלק; O16 נחלק; Mu130 ונחלק; W66 שנחלק<br> | ||
| + | איך שיקרה: B איך שהזדמן; F איך שיזדמן; P1013 איך שקרה; O561 איך ש<sup>י</sup>קרה<br> | ||
| + | ג‫': W66 א‫'</ref> | ||
|- | |- | ||
| − | |Supposition: <math>\scriptstyle\left(AB\times BG\right)+\left(AB\times AG\right)=AB^2</math> | + | |<span style=color:green>'''Supposition:'''</span> I say that [the sum of] the rectangle enclosed by the two lines AB and BG with the rectangle enclosed by the two lines AB and AG is equal to the square formed by AB. |
| − | |style="text-align:right;"|הנה<ref> | + | :<math>\scriptstyle{\color{blue}{\left(AB\times BG\right)+\left(AB\times AG\right)=AB^2}}</math> |
| − | + | |style="text-align:right;"|הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב א"ג שוה למרובע המתהוה מן א"ב‫<ref group=note>C:המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר כי אשר יהיה מהכאת קו א"ב בקו א"ג ובקו ג"ב שוה לאשר יהיה מהכאת א"ב בעצמו<br> | |
| + | E: יהיה הקו הישר א"ב ויחלק על ג' ואומ' שמרובע א"ב שוה לשטח א"ב בא"ג וא"ב בג"ב</ref>‫<ref>הנה: F om.<br> | ||
| + | אומר כי: B אומר ש<br> | ||
| + | השטח: P1007, P1014 שטח<br> | ||
| + | הנצב: B, F, P1013 נצב<br> | ||
| + | הזויות: Mu130 הזוית<br> | ||
| + | יקיפו: O16 יקיף<br> | ||
| + | שני: F, O16 om.; P1007 ב‫'<br> | ||
| + | א"ב: F, B(except for W66) ב"א<br> | ||
| + | ב"ג: F, B(except for W66), P1007 א"ג; Lo <s>ג"ד</s> ב"ג<br> | ||
| + | עם: P1007 <s>שוה למרובע המתהווה</s> עם; P1012 וגם<br> | ||
| + | השטח: A2 שטח<br> | ||
| + | הנצב: B, F, A2 נצב<br> | ||
| + | הזויות: Ma1, B(except for W66) הזוית<br> | ||
| + | שני: P1007 ב'; P1012 שתי<br> | ||
| + | שני קוי: F om.; Mu130 שני קו; P1013 שני קוים<br> | ||
| + | א"ג: B(except for W66), F ב"ג; P1010 <sup>א</sup>"ג<br> | ||
| + | שוה: B(except for W66) שוים; W66 שוה<sup>ים</sup><br> | ||
| + | המתהוה: B, F ההוה; O561 ה<sup>מת</sup>הווה<br> | ||
| + | מן א"ב: B(except for W66), F, P1007 מא"ב; W66 <s>מהקו כלו</s> מא"ב</ref> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|והנה | + | *<span style=color:green>'''I.46:'''</span> We construct the square ADHB on line AB. |
| + | |style="text-align:right;"|והנה נעשה <s>על</s> <sup>מ</sup>קו א"ב מרובע עליו א"דה"ב <span style=color:red>מ”ו מראשון</span>‫<ref>והנה: Ma1 המופת; B הנה; F137 om.<br> | ||
| + | מקו א"ב: F מא"ב<br> | ||
| + | עליו: O561 marg.<br> | ||
| + | מ"ו מראשון‫': C בצורת מ"ו; A1, F137, Lo, P1010, PP ממ"ו מראשון; Ma1, E, P1007, P1012, W66 om.</ref> | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle AD,BH\parallel GZ</math> | + | *We draw the straight line GZ from point G parallel to AD and BH. |
| − | |style="text-align:right;"|ונוציא מנקודת ג' קו ישר נכחי | + | :<math>\scriptstyle{\color{blue}{AD,BH\parallel GZ}}</math> |
| + | |style="text-align:right;"|ונוציא מנקודת ג' קו ישר נכחי <s>לקו</s> לכל אחד משני קוי א"ד ב"ה והוא ג"ז <span style=color:red>מל”א מא‫’</span>‫<ref>לכל: Mu36, Mu130 <sup>ל</sup>כל; O561 כל<br> | ||
| + | משני: P1007 מב‫'<br> | ||
| + | משני קוי: F, B(except for Mu130) מקוי<br> | ||
| + | מל"א מא‫': A1, F137, Lo, P1010, PP מל"א מראשון; Mu130 מל"א; AB, C, Ma1, E, P1007, P1012, W66 om.</ref> | ||
| + | |- | ||
| + | |Then, both AZ and GH are parallelograms. | ||
| + | |style="text-align:right;"|הנה כל אחד משני שטחי א"ז ג"ה נכחי הצלעות‫<ref>הנה כל אחד משני: P1014 <s>הנה כל אחד משני קוי א"ד ב"ה והוא ג"ז</s> הנה כל אחד משני; P1007 הנה כל אחד מב‫'<br> | ||
| + | משני שטחי: F, B משטחי</ref> | ||
|- | |- | ||
| − | | | + | |AH equals [the sum of] AZ and GH. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{\Box_{AH}=\Box_{AZ}+\Box_{GH}}}</math> |
| + | |style="text-align:right;"|ושטח א"ה שוה לשני שטחי א"ז ג"ה <sup>נכחיי הצלעות</sup> <span style=color:red>מא’ מזה</span>‫<ref>לשני: A2 לשתי; P1007 לב‫'<br> | ||
| + | לשני שטחי: F137 לשטחי; Ma1 לשטח; W66 לשתי שטחים<br> | ||
| + | מא' מזה: A2 מהקודמת; AB מפתיחת א‫'; P1010 מא‫'; B, C, Ma1, E, P1007, P1012, P1014 om.</ref> | ||
|- | |- | ||
| − | | | + | |AZ is equal to the rectangle enclosed by BA and AG. |
| − | + | :<math>\scriptstyle{\color{blue}{\Box_{AZ}=BA\times AG}}</math> | |
| − | |style="text-align:right;"|ושטח א" | + | |style="text-align:right;"|ושטח א"ז שוה לשטח נצב הזויות אשר יקיפו בו ב"א א"ג‫<ref>שוה: O16 om.<br> |
| + | נצב: O16 הנצב<br> | ||
| + | הזויות: Mu130, P1010 הזוית<br> | ||
| + | יקיפו: B(except for Mu130) יקיף<br> | ||
| + | בו: O561 <sup>בו</sup><br> | ||
| + | ב"א: A2, P1007 א"ב<br> | ||
| + | ב"א א"ג: F137 <s>א"ב ג"ב</s> marg. ב"א א"ג; E א"ג בא"ב; A1 ב"א וא"ג</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | :Because it is enclosed by the two lines AD and AG and line AD equals line AB. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{AD=AB}}</math> |
| + | |style="text-align:right;"|כי הוא יקיפו בו שני קוי א"ד א"ג וקו א"ד שוה לקו א"ב‫<ref>כי הוא: F, B מפני ש<br> | ||
| + | יקיפו: F, B(except for Mu130) מקיף; Mu130 מקיפים<br> | ||
| + | שני: Ma1 om.; P1007 ב‫'<br> | ||
| + | א"ד: F, B ד"א<br> | ||
| + | כי הוא ... א"ד א"ג: Mu36 om.; O561 marg. בו א"ד א"ג וקו א"ד שוה לקו א"ב ושטח ג"ה שוה לשטח<br> | ||
| + | א"ג: P1007 ב"ג; A1 וא"ג<br> | ||
| + | א"ד: F, B ד"א</ref> | ||
|- | |- | ||
| − | | | + | |GH is equal to the rectangle enclosed by the two lines AB and BG. |
| − | + | :<math>\scriptstyle{\color{blue}{\Box_{GH}=AB\times BG}}</math> | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ושטח ג"ה שוה לשטח נצב הזויות אשר יקיפו בו שני קוי א"ב <s>ב"ג</s> <sup>ב"ג</sup>‫<ref>שוה: P1012 om.<br> |
| + | נצב הזויות: F om.<br> | ||
| + | ב"א א"ג ... יקיפו בו: P1014 om.<br>בו: P1010 om.<br> | ||
| + | שני: P1007 ב‫'<br> | ||
| + | שני קוי: Ma1, A1 om.<br> | ||
| + | ב"א א"ג ... א"ב ב"ג: F137 marg.<br> | ||
| + | ב"ג: Ma1 ג"ב; P1007, P1014 א"ג; P1013 ה"ג</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | :Because AB equals BH. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{AB=BH}}</math> |
| + | |style="text-align:right;"|מפני שא"ב שוה לב"ה‫<ref>מפני שא"ב: A2 מפני כי א"ב; P1014 מפני שא"ד; O16 הנה מפני שא"ב<br> | ||
| + | לב"ה: P1014 לב"א<br> | ||
| + | מפני ש... לב"ה: F137 added on top of the line</ref> | ||
|- | |- | ||
| − | | | + | |AH is the square formed by line AB. |
| − | + | :<math>\scriptstyle{\color{blue}{\Box_{AH}=AB^2}}</math> | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ושטח א"ה הוא המרובע ההוה מקו א"ב‫<ref>הוא: O16 om.<br> |
| + | ההוה: P1010, P1012, PP הווה<br> | ||
| + | מקו א"ב: F137 מא"ב</ref> | ||
|- | |- | ||
| | | | ||
| − | : | + | :<math>\scriptstyle{\color{blue}{\left(AB\times AG\right)+\left(AB\times BG\right)=AB^2}}</math> |
| − | + | |style="text-align:right;"|הנה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב א"ג עם השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג שוה למרובע המתהוה מן א"ב‫<ref group=note>מופת זה שנצייר על קו א"ב שטח מרובע והוא שטח א"ה ונוציא מנקודת ג' קו עד ז' נכוחי לקוי א"ד וב"ה ויהיו שטחי א"ז וז"ב נכוחי הצלעות והם שוים לשטח א"ה ושטח א"ז הוא <s>נכוחי</s> אשר היה מהכאת קו ב"א בקו א"ג לפי שיקיפו בו קוי ד"א א"ג וד"א שוה לא"ב ושטח ז"ב הוא אשר היה מהכאת א"ב בג"ב לפי שיקיפו בו ה"ב ב"ג וה"ב שוה לא"ב ושטח א"ה הוא אשר היה מהכאת א"ב בעצמו<br> | |
| − | |||
| − | |||
| − | |style="text-align:right;"|הנה | ||
וכבר התבאר שאשר היה מהכאת א"ב בא"ג ובג"ב שוה לאשר היה מהכאת א"ב בעצמו<br> | וכבר התבאר שאשר היה מהכאת א"ב בא"ג ובג"ב שוה לאשר היה מהכאת א"ב בעצמו<br> | ||
E: מופתו שנעשה על א"ב מרובע א"ה ונוציא ג"ז נכחי לב"ה ולפי ששטח א"ז שוה לשטח שיקיפו בו א"ג בא"ב כי ג"ז כמו א"ב וכן ששטח ג"ה שוה לשטח שיקיף בו א"ב בג"ב ושניהם שו<sup>י</sup>ם למרובע א"ה יהיה מרובע א"ה שהוא ההוה מקו א"ב שוה לשני שטחים ההוים מא"ב בא"ג וא"ב בב"ג<br> | E: מופתו שנעשה על א"ב מרובע א"ה ונוציא ג"ז נכחי לב"ה ולפי ששטח א"ז שוה לשטח שיקיפו בו א"ג בא"ב כי ג"ז כמו א"ב וכן ששטח ג"ה שוה לשטח שיקיף בו א"ב בג"ב ושניהם שו<sup>י</sup>ם למרובע א"ה יהיה מרובע א"ה שהוא ההוה מקו א"ב שוה לשני שטחים ההוים מא"ב בא"ג וא"ב בב"ג<br> | ||
וכבר יתבאר זה בצד אחר כשנניח קו ח' שוה לא"ב ותהיה השטח הנצב הזוית שיקיף בו ח' בא"ב שהוא כמו מרובע א"ב משלפניה' שוה לשטח נצב הזוית <sup>שיקיף</sup> בו ח' בא"ג וח' בג"ב והם כמו שטחי א"ג בא"ב וג"ב בא"ב<br> | וכבר יתבאר זה בצד אחר כשנניח קו ח' שוה לא"ב ותהיה השטח הנצב הזוית שיקיף בו ח' בא"ב שהוא כמו מרובע א"ב משלפניה' שוה לשטח נצב הזוית <sup>שיקיף</sup> בו ח' בא"ג וח' בג"ב והם כמו שטחי א"ג בא"ב וג"ב בא"ב<br> | ||
Mu246: ג כשיוחלק קו א"ב בחלקי א"ג ג"ב נאמ' כי כפל א"ב בפני עצמו ככפלו בכל אחד מן א"ג ג"ב<br> | Mu246: ג כשיוחלק קו א"ב בחלקי א"ג ג"ב נאמ' כי כפל א"ב בפני עצמו ככפלו בכל אחד מן א"ג ג"ב<br> | ||
| − | והדבר בו ברור כשנעשה על קו א"ב מרובע ואחר כך נוציא בו קו ג"ז עמוד</ref> | + | והדבר בו ברור כשנעשה על קו א"ב מרובע ואחר כך נוציא בו קו ג"ז עמוד</ref>‫<ref>הנה: F ואם כן<br> |
| + | השטח: F השטחים<br> | ||
| + | הנצב: F נצבי<br> | ||
| + | הזויות: O561 הזוי<sup>ו</sup>ת<br> | ||
| + | בו: F בהם; P1007, P1010, W194 om.; O561 <sup>בו</sup><br> | ||
| + | שני: F om.; P1007 ב‫'<br> | ||
| + | א"ב: B(except for Mu130) ב"א<br> | ||
| + | א"ג: A1 ב"ג<br> | ||
| + | הנצב: B, F, P1013 נצב<br> | ||
| + | הזויות: Ma1 הזוי<sup>ו</sup>ת; O561 הזוית<br> | ||
| + | בו: A2, P1007, P1010, PP om.<br> | ||
| + | שני קוי: F om.<br> | ||
| + | ב"ג: A1 א"ג<br> | ||
| + | שוה: F שניהם שוים<br> | ||
| + | למרובע: Lo עם המרבע<br> | ||
| + | המתהוה: B, Lo, P1007 ההוה<br> | ||
| + | המתהוה מן: F om.<br> | ||
| + | מן א"ב: B(except for Mu130), P1007 מא"ב; F אדה"ב; Mu130 מן הקו כלו</ref> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה<ref>הנה: F137 ואם כן< | + | |style="text-align:right;"|הנה כאשר נחלק קו ישר <sup>מונח</sup> איך שקרה הנה השטחים הנצבי הזויות אשר יקיף בהם הקו כלו וכל אחד מחלקיו שוה למרובע המתהוה מן הקו כלו‫<ref>הנה: F137 ואם כן<br> |
| + | נחלק: F137 יתחלק<br> | ||
| + | קו: O16 om.<br> | ||
| + | איך שקרה: F137 איך שיזדמן; O16 איך שהזדמן<br> | ||
| + | הנה: F137 יהיו<br> | ||
| + | השטחים: O16 שני השטחים<br> | ||
| + | הנצבי: F137, O16, P1012, P1014 נצבי<br> | ||
| + | בהם: P1007 בו<br> | ||
| + | אחד: P1007 א‫'<br> | ||
| + | מחלקיו: O16 מהחלקים<br> | ||
| + | המתהוה: F137, O16 ההוה; PP המהווה<br> | ||
| + | מן הקו: P1007 מהקו; P1013 מן קו<br> | ||
| + | הנה ... כלו: C, Ma1, E, B(except for O16) om.</ref> | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum. |
|style="text-align:right;"|וזה מה שרצינו לבאר‫<ref>וזה מה שרצינו לבאר: E, Mu130 ומש"ל; P1007 וזמש"ל; F, P1012 וזהו מה שרצינו לבאר; Mu36, P1014 וזה מש"ל; P1010 וזה מה שרצינו בארו</ref> | |style="text-align:right;"|וזה מה שרצינו לבאר‫<ref>וזה מה שרצינו לבאר: E, Mu130 ומש"ל; P1007 וזמש"ל; F, P1012 וזהו מה שרצינו לבאר; Mu36, P1014 וזה מש"ל; P1010 וזה מה שרצינו בארו</ref> | ||
|- | |- | ||
| Line 2,488: | Line 2,865: | ||
|- | |- | ||
|in modern notation: <math>\scriptstyle\left(a+b\right)\sdot a=\left(b\sdot a\right)+a^2</math> | |in modern notation: <math>\scriptstyle\left(a+b\right)\sdot a=\left(b\sdot a\right)+a^2</math> | ||
| − | |style="text-align:right;"|<div id="Elements_II_3"></div>'''ג'''<ref>ג: P1007, P1012 mark is missing; Ma1 ד'; Mu130 למוד ג'; O561 marg. at the end of proposition 2 חסר מכאן תמונת ג’ והיא ‫[...]< | + | |style="text-align:right;"|<div id="Elements_II_3"></div>'''ג''' כאשר נחלק קו ישר בשני חלקים איך שקרה הנה השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד משני חלקיו שוה לשטח הנצב הזויות אשר יקיפו בו השני חלקים והמרובע המתהוה מן החלק אשר זכרנו‫<ref>ג: P1007, P1012 mark is missing; Ma1 ד'; Mu130 למוד ג'; O561 marg. at the end of proposition 2 חסר מכאן תמונת ג’ והיא ‫[...]<br> |
| + | כאשר נחלק: C כשיחלק; F כאשר יתחלק<br> | ||
| + | ישר: C, B ישר מונח; AB ישר <sup>מונח</sup><br> | ||
| + | בשני: P1007 לב'<br> | ||
| + | בשני חלקים: F137 marg.; Ma1 om.<br> | ||
| + | איך שקרה: C כמו שקרה; F137 איך מה שיזדמן; Ma1 איך שהזדמן; B איך שיזדמן<br> | ||
| + | הנה: C, F יהיה<br> | ||
| + | השטח: C שטח<br> | ||
| + | הנצב: B, C, F נצב<br> | ||
| + | אשר יקיף: C שיקיפו; B אשר יקיפו<br> | ||
| + | בו: Mu130 om.<br> | ||
| + | הקו: PP קו<br> | ||
| + | משני: F137 marg.; P1007 מב'<br> | ||
| + | משני חלקיו: C, Ma1 מחלקיו; B(except for Mu130) מן החלקים<br> | ||
| + | הנצב: B, C, Ma1, W194 נצב; F137 <s>נצב לשטח</s> נצב<br> | ||
| + | אשר יקיף ... הזויות: P1013 om.<br> | ||
| + | אשר יקיפו: C שיקיפו<br> | ||
| + | בו: C, P1010 <sup>בו</sup><br> | ||
| + | השני: B(except for W66), C, F, Lo שני; W66 שתי; P1007, P1013 הב'<br> | ||
| + | חלקים: B, C, F, Lo החלקים<br> | ||
| + | והמרובע: C ומרובע<br> | ||
| + | המתהוה: B, F, Lo ההוה<br> | ||
| + | המתהוה מן: C om.<br> | ||
| + | מן החלק: B(except for Mu130), P1007 מהחלק<br> | ||
| + | אשר זכרנו: C שהזכרנו</ref><ref group=note>E:‫3 השטח ההוה מקו מה עם אחד מחלקיו שוה לשטח נ"ה שיקיפו בו השני חלקי' ומרובע החלק הנזכר<br> | ||
P1011: כל קו יחלק בשני חלקים הנה אשר יהיה מהכאת כל הקו באחד החלקים כמו אשר יהיה מאחד מהחלקים בשני והכאת החלק אשר בו הוכה הקו בעצמו<br> | P1011: כל קו יחלק בשני חלקים הנה אשר יהיה מהכאת כל הקו באחד החלקים כמו אשר יהיה מאחד מהחלקים בשני והכאת החלק אשר בו הוכה הקו בעצמו<br> | ||
Mu36: נס’ אלחג’אג’ כאשר נחלק מספר בשני חלקים איך שקרה הנה הכאת המספר כלו באחד מחלקיו שוה להכאת שני החלקים הא[חד] בחבירו עם הכאת החלק ההוא בעצמו<br> | Mu36: נס’ אלחג’אג’ כאשר נחלק מספר בשני חלקים איך שקרה הנה הכאת המספר כלו באחד מחלקיו שוה להכאת שני החלקים הא[חד] בחבירו עם הכאת החלק ההוא בעצמו<br> | ||
| Line 2,504: | Line 2,905: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה<ref>ויהיה: B הנה יהיה; F המשל יהיה< | + | |style="text-align:right;"|ויהיה קו ישר עליו א"ב ויחלק איך שיקרה על נקודת ג‫'‫<ref>ויהיה: B הנה יהיה; F המשל יהיה<br> |
| + | קו: Ma1 הקו<br> | ||
| + | ישר: B ישר מונח; AB ישר <sup>מונח</sup>; Ma1 הישר<br> | ||
| + | עליו: A1 om.<br> | ||
| + | א"ב: A1 om.<br> | ||
| + | ויחלק: AB, B(except for W66) ונחלק; W66 ונחלק אותו; F ויתחלק<br> | ||
| + | איך שיקרה: F איך שיזדמן; B איך שהזדמן; P1007 איך שקרה<br> | ||
| + | על: P1010 <s>עליו</s> על</ref> | ||
|- | |- | ||
|Supposition: <math>\scriptstyle AB\times BG=\left(AG\times GB\right)+GB^2</math> | |Supposition: <math>\scriptstyle AB\times BG=\left(AG\times GB\right)+GB^2</math> | ||
| − | |style="text-align:right;"|הנה<ref>הנה: F om.< | + | |style="text-align:right;"|הנה אומר כי השטח הנצב הזויות אשר יקיפו בו קוי א"ב ב"ג שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב והמרובע המתהוה מן ג"ב‫<ref>הנה: F om.<br> |
| + | כי השטח: B שהשטח; Ma1 ששטח; F137 כי שטח<br> | ||
| + | הנצב: B, F נצב<br> | ||
| + | יקיפו: Mu130 יקיף<br> | ||
| + | קוי: A2, B, P1014 שני קוי; AB <sup>שני</sup> קוי; A1, P1007 קו<br> | ||
| + | שוה: Ma1 שוים<br> | ||
| + | הנצב: B, F נצב<br> | ||
| + | הזויות: P1014 הזוית<br> | ||
| + | בו: Mu130, W194 om.<br> | ||
| + | שני: F om.; P1007 ב'<br> | ||
| + | א"ב ב"ג ... שני קוי: W66 marg.<br> | ||
| + | ג"ב: Mu36, P1007, P1014 ב"ג<br> | ||
| + | המתהוה: B, F ההוה<br> | ||
| + | מן ג"ב: F מב"ג; P1007 מג"ב; Mu36 מן <s>ג"ב</s> ג"ב</ref><ref group=note>C: המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר שאשר יהיה מהכאת קו א"ב בא"ג שוה לאשר יהיה מהכאת א"ג בג"ב ומהכאת א"ג בעצמו<br> | ||
E: יהיה הקו א"ב ונחלק על נקודת ג' ואומ' ששטח א"ב באחד מחלק<sup>י</sup>ו ויהיה ב"ג שוה למרובע ב"ג עם שטח א"ב בב"ג</ref> | E: יהיה הקו א"ב ונחלק על נקודת ג' ואומ' ששטח א"ב באחד מחלק<sup>י</sup>ו ויהיה ב"ג שוה למרובע ב"ג עם שטח א"ב בב"ג</ref> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונעשה<ref>ונעשה: F137 נעשה; Ma1 מופת זה נעשה; B(except for W66) הנה נעשה< | + | |style="text-align:right;"|ונעשה מן קו ג"ב מרובע עליו בגד"ה <span style=color:red>ממ”ו מא‫’</span>‫<ref>ונעשה: F137 נעשה; Ma1 מופת זה נעשה; B(except for W66) הנה נעשה<br> |
| + | מן קו: F על; A1, B, Lo, P1010, PP מקו; P1007 הקו; Mu36 מן <sup>קו</sup><br> | ||
| + | ג"ב: F ב"ג<br> | ||
| + | עליו: F om.<br> | ||
| + | בגד"ה: W66 ה"ג<br> | ||
| + | ממ"ו מא': AB מ"ו מראשון; A1, F137, Lo, P1010, PP ממ"ו מראשון; Mu130 ממ"ו; C, Ma1, E, Mu36, P1007, P1012 om.</ref> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונתמים<ref>ונתמים: B(except for W66), F ונשלים; Lo, AB, P1010, PP ונתמם< | + | |style="text-align:right;"|ונתמים שטח א"ג ד"ז הנכחי הצלעות <span style=color:red>מל”א וממ”ב מא‫’</span>‫<ref>ונתמים: B(except for W66), F ונשלים; Lo, AB, P1010, PP ונתמם<br> |
| + | א"ג ד"ז: F אזד"ג; B(except for W66) ג"א ז"ד<br> | ||
| + | הנכחי: F נכחי<br> | ||
| + | הנכחי הצלעות: B(except for W66) הנכחי הצלעות נצב הזויות<br> | ||
| + | מל"א וממ"ב מא': F137, Lo, P1013, PP מל"א ומ"ב מראשון; P1010 מל"א מרא'; W66 מב"א ומ"ב מא'; W194 מל"א ומ"ה מראשון; AB, B(except for W66), C, Ma1, E, Mu36, P1007, P1012 om.</ref> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה<ref>הנה: O16 marg.< | + | |style="text-align:right;"|הנה כל אחד משני שטחי א"ה א"ד נכחי הצלעות‫<ref>הנה: O16 marg.<br> |
| + | אחד: AB <s>שטח</s> אחד<br> | ||
| + | משני: P1007 מב'; P1010 <s>משטי</s> משני<br> | ||
| + | משני שטחי: F משטחי<br> | ||
| + | א"ה: A1, Mu130 ג"ה<br> | ||
| + | א"ה א"ד: Mu36, P1014 א"ד ג"ה<br> | ||
| + | נכחי: F נכחיי<br> | ||
| + | נכחי הצלעות: B(except for W66) נכחי הצלעות נצב הזויות</ref> | ||
|- | |- | ||
| | | | ||
*<math>\scriptstyle\Box_{AH}=\Box_{AD}+\Box_{GH}</math> | *<math>\scriptstyle\Box_{AH}=\Box_{AD}+\Box_{GH}</math> | ||
| − | |style="text-align:right;"|ושטח א"ה שוה לשטח א"ד עם ג"ה<ref>ג"ה: F שטח ה"ג; B(except for W66), Mu36 שטח ג"ה< | + | |style="text-align:right;"|ושטח א"ה שוה לשטח א"ד עם ג"ה <span style=color:red>מא’ מזה</span>‫<ref>ג"ה: F שטח ה"ג; B(except for W66), Mu36 שטח ג"ה<br> |
| + | מא' מזה: P1010 מא'; AB, B, C, Ma1, E, P1007, P1012, P1013 om.</ref> | ||
|- | |- | ||
| | | | ||
:*<math>\scriptstyle\Box_{AH}=AB\times BG</math> | :*<math>\scriptstyle\Box_{AH}=AB\times BG</math> | ||
| − | |style="text-align:right;"|וא"ה שוה לשטח הנצב<ref>הנצב: AB, B נצב< | + | |style="text-align:right;"|וא"ה שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג‫<ref>הנצב: AB, B נצב<br> |
| + | הנצב הזויות: F om.<br> | ||
| + | בו: P1013 <s>ש</s> בו<br> | ||
| + | שני: F om.; P1007 ב'<br> | ||
| + | ב"ג: Mu130 ג"ב</ref> | ||
|- | |- | ||
| | | | ||
::<math>\scriptstyle BG=BH</math> | ::<math>\scriptstyle BG=BH</math> | ||
| − | |style="text-align:right;"|מפני כי ב"ג<ref>מפני כי ב"ג: F לפי שב"ג; Mu130 מפני שב"ג</ref> | + | |style="text-align:right;"|מפני כי ב"ג שוה לב"ה‫<ref>מפני כי ב"ג: F לפי שב"ג; Mu130 מפני שב"ג</ref> |
|- | |- | ||
| | | | ||
:*<math>\scriptstyle\Box_{AD}=AG\times GB</math> | :*<math>\scriptstyle\Box_{AD}=AG\times GB</math> | ||
| − | |style="text-align:right;"|ושטח א"ד שוה לשטח הנצב<ref>הנצב: A1, B, F נצב< | + | |style="text-align:right;"|ושטח א"ד שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב‫<ref>הנצב: A1, B, F נצב<br> |
| + | שני: F om.<br> | ||
| + | א"ב ב"ג ... שני קוי: O16 marg.; P1007 om.<br> | ||
| + | ג"ב: F, Mu36 ב"ג</ref> | ||
|- | |- | ||
| | | | ||
::<math>\scriptstyle BG=GD</math> | ::<math>\scriptstyle BG=GD</math> | ||
| − | |style="text-align:right;"|מפני כי ב"ג<ref>מפני כי ב"ג: F לפי שב"ג; B(except for W66) מפני שג"ב; P1013 מפני ב"ג< | + | |style="text-align:right;"|מפני כי ב"ג שוה לג"ד‫<ref>מפני כי ב"ג: F לפי שב"ג; B(except for W66) מפני שג"ב; P1013 מפני ב"ג<br> |
| + | ושטח א"ד ... לג"ד: Mu130 moved below; P1014 marg.</ref> | ||
|- | |- | ||
| | | | ||
| Line 2,544: | Line 2,990: | ||
|- | |- | ||
|<math>\scriptstyle AB\times BG=\left(AG\times GB\right)+GB^2</math> | |<math>\scriptstyle AB\times BG=\left(AG\times GB\right)+GB^2</math> | ||
| − | |style="text-align:right;"|הנה<ref>הנה: F אם כן; Mu130 ושטח א"ד [...] לג"ד הנה< | + | |style="text-align:right;"|הנה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב והמרובע המתהוה מן ג"ב‫<ref>הנה: F אם כן; Mu130 ושטח א"ד [...] לג"ד הנה<br> |
| + | הנצב: B(except for W66), F, Mu36 נצב<br> | ||
| + | שני: F om.<br> | ||
| + | הנצב: B(except for W66), F, P1013 נצב<br> | ||
| + | שני: P1007 ב'<br> | ||
| + | שני קוי: A1, F om.<br> | ||
| + | א"ג ג"ב: P1012 א"ב ב"ג; F א"ג ב"ג<br> | ||
| + | והמרובע: Ma1 ומרובע<br> | ||
| + | המתהוה: B(except for W66), A1, AB, F ההוה<br> | ||
| + | מן ג"ב: F מב"ג; P1007 מג"ב</ref><ref group=note>C: מופת זה שנצייר על קו א"ג שטח מרובע עליו א"ז ונוציא קו ז"ד אל ה' ונוציא <sup>מב'</sup> <s>מבית</s> קו נכוחי לקוי א"ד וג"ד והוא קו ב"ה ושטחי ז"ב וז"א נכוחי הצלעות ושטח ב"ד גם כן נכוחי הצלעות והוא שטח ז"ב ושטח ז"א יחד וז"ב הוא שהיה מהכאת א"ג בג"ב לפי שיקיפו בו ב"ג ג"ז וז"ג שוה לג"א וב"ד הוא שהיה מהכאת <s>א"ג בג"ב</s> א"ב בא"ג לפי שיקיפו בו ב"א א"ד וג"א שוה לא"ד וא"ד הוא שהיה מהכאת א"ג בעצמו<br> | ||
והתבאר כבר שאשר היה מהכאת ב"א בא"ג שוה לאשר היה מהכאת א"ג בג"ב ומהכאת א"ג בעצמו<br> | והתבאר כבר שאשר היה מהכאת ב"א בא"ג שוה לאשר היה מהכאת א"ג בג"ב ומהכאת א"ג בעצמו<br> | ||
E: מופתו שנעשה על ב"ג מרובע והוא ב"ד ונוציא קו ד"ה על יושר ונשלים שטח א"ה ויהיה שטח א"ה שוה לשני שטחי א"ד ד"ב ושטח א"ה שוה לשטח שיקיפו בו א"ב ב"ג כי ב"ג שוה לב"ה ושטח א"ד שוה לשטח שיקיפו בו א"ג ג"ב כי ג"ד שוה לג"ב ושטח ג"ה שוה למרובע ג"ב הנה שטח א"ב ב"ג שוה לשני שטחי א"ג בג"ב ומרובע ג"ב<br> | E: מופתו שנעשה על ב"ג מרובע והוא ב"ד ונוציא קו ד"ה על יושר ונשלים שטח א"ה ויהיה שטח א"ה שוה לשני שטחי א"ד ד"ב ושטח א"ה שוה לשטח שיקיפו בו א"ב ב"ג כי ב"ג שוה לב"ה ושטח א"ד שוה לשטח שיקיפו בו א"ג ג"ב כי ג"ד שוה לג"ב ושטח ג"ה שוה למרובע ג"ב הנה שטח א"ב ב"ג שוה לשני שטחי א"ג בג"ב ומרובע ג"ב<br> | ||
| Line 2,551: | Line 3,006: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה<ref>הנה: F137 א"כ< | + | |style="text-align:right;"|הנה כאשר חולק קו ישר בשני חלקים איך שיקרה הנה השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד משני חלקיו שוה לשטח הנצב הזויות אשר יקיפו בו השני חלקים והמרובע המתהוה מן החלק אשר זכרנו‫<ref>הנה: F137 א"כ<br> |
| + | חולק: F137 יתחלק; O16 נחלק<br> | ||
| + | ישר: Mu36, O16 ישר מונח; AB ישר <sup>מונח</sup>; Mu130 ישר <s>על</s> מונח<br> | ||
| + | בשני: P1007 בב'<br> | ||
| + | בשני חלקים: F137 om.<br> | ||
| + | איך שיקרה: F137 איך מה שיזדמן; B(except for W66) איך שהזדמן; P1013 איך שקרה<br> | ||
| + | הנה: F137 יהיה<br> | ||
| + | הנצב: F137, B(except for W66) נצב<br> | ||
| + | יקיף: Mu36, O16 יקיפו<br> | ||
| + | משני: P1007 מב'<br> | ||
| + | משני חלקיו: F137 <sup>מ</sup>חלקיו; O16 מחלקיו<br> | ||
| + | הנצב: F137, B(except for W66) נצב<br> | ||
| + | השני: F137, O16 שני; P1007 הב'<br> | ||
| + | חלקים: F137, O16 החלקים<br> | ||
| + | המתהוה: F137, O16 ההוה<br> | ||
| + | מן החלק: O16, P1007, P1012 מהחלק<br> | ||
| + | אשר זכרנו: F137 שזכרנו<br>הנה כאשר ... זכרנו: C, Ma1, E, W66 om.</ref> | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
|style="text-align:right;"|וזה מה שרצינו לבאר‫<ref>וזה מה שרצינו לבאר: F137, E, Mu130 ומש"ל; Ma1, P1007 וזה מש"ל; Lo, P1010, PP, W194 וזה מה שרצינו באורו; C וזה מה שרצינו</ref> | |style="text-align:right;"|וזה מה שרצינו לבאר‫<ref>וזה מה שרצינו לבאר: F137, E, Mu130 ומש"ל; Ma1, P1007 וזה מש"ל; Lo, P1010, PP, W194 וזה מה שרצינו באורו; C וזה מה שרצינו</ref> | ||
|- | |- | ||
| Line 2,562: | Line 3,033: | ||
|- | |- | ||
|in modern notation: <math>\scriptstyle\left(a+b\right)^2=a^2+b^2+2\sdot\left(a\sdot b\right)</math> | |in modern notation: <math>\scriptstyle\left(a+b\right)^2=a^2+b^2+2\sdot\left(a\sdot b\right)</math> | ||
| − | |style="text-align:right;"|<div id="Elements_II_4"></div>'''ד'''<ref>ד: P1007, P1012 mark is missing; Ma1 ג'; Mu130 למוד ד'< | + | |style="text-align:right;"|<div id="Elements_II_4"></div>'''ד''' כאשר חולק קו ישר בשני חלקים איך שיקרה הנה המרובע המתהוה מן הקו כלו שוה לשני המרובעים המתהוים מן השני חלקים וכפל השטח הנצב הזויות אשר יקיפו בו השני חלקים‫<ref>ד: P1007, P1012 mark is missing; Ma1 ג'; Mu130 למוד ד'<br> |
| + | כאשר חולק: B כאשר נחלק; C כשיחלק; F כאשר יתחלק<br> | ||
| + | ישר: B(except for Mu130), C, P1012; P1014 ישר מונח<br> | ||
| + | בשני: C לשני; P1007 בב'<br> | ||
| + | חלקים: Ma1 חצאים<br> | ||
| + | איך שיקרה: B איך שהזדמן; C כמו שקרה; F איך שיזדמן; O561 <sup>איך</sup> שיקרה; P1007 איך שקרה; PP איך מה שיקרה<br> | ||
| + | הנה: C, F יהיה<br> | ||
| + | המרובע: C מרובע<br> | ||
| + | המתהוה: B(except for Mu130), C ההוה<br> | ||
| + | המתהוה מן: C om.<br> | ||
| + | מן הקו: B(except for Mu130), P1007 מהקו; PP מן קו<br> | ||
| + | לשני: P1007 לב'<br> | ||
| + | המרובעים: C מרובעי<br> | ||
| + | המתהוים: B(except for Mu130), F ההוים; C om.<br> | ||
| + | מן ... המתהוים: O561 marg.<br> | ||
| + | מן השני: B(except for Mu130), F, Lo, P1012, P1013, P1014 משני; C שני; P1007 מהב'; W194 מן שני<br> | ||
| + | חלקים: C, F, Lo, O16, P1012, P1014 החלקים; W66 <sup>ה</sup>חלקים<br> | ||
| + | וכפל: C ולכפל; Mu36, O16, P1012, P1014 ומכפל; O561 ו<sup>מ</sup>כפל<br> | ||
| + | השטח: C שטח<br> | ||
| + | הנצב: B(except for Mu130), C, F נצב; P1014 om.<br> | ||
| + | השני: B(except for Mu130), C, F, PP שני; O561 <sup>ה</sup>שני; P1007 ב'<br> | ||
| + | חלקים: B(except for Mu130), C, F החלקים</ref><ref group=note>P1011: כל קו יחלק בחלקים הנה אשר יהיה מהכאת הקו בעצמו כמו אשר יהיה מהכאת כל חלק בעצמו ומהכאת אחד החלקים באחר שני פעמים<br> | ||
E: ‫4 מרובע כל קו <sup>נחלק לשני חלקים</sup> שוה למרובעי שני חלקיו וכפל שטח אחד מהם באחר | E: ‫4 מרובע כל קו <sup>נחלק לשני חלקים</sup> שוה למרובעי שני חלקיו וכפל שטח אחד מהם באחר | ||
Mu36: נס’ אלחג’אג’ כאשר חולק איזה מספר שיהיה בשני חלקים איך מה שקרה הנה הכאת המספר ההוא בעצמו שוה להכאת כל אחד מהחלקים בעצמו ולהכאת כל אחד משני החלקים בחבירו<br> | Mu36: נס’ אלחג’אג’ כאשר חולק איזה מספר שיהיה בשני חלקים איך מה שקרה הנה הכאת המספר ההוא בעצמו שוה להכאת כל אחד מהחלקים בעצמו ולהכאת כל אחד משני החלקים בחבירו<br> | ||
| Line 2,573: | Line 3,065: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה<ref>ויהיה: B(except for Mu130) הנה יהיה; F137 יהיה; Ma1 המשל יהיה< | + | |style="text-align:right;"|ויהיה קו ישר עליו א"ב ויחולק איך שיקרה על נקודת ג‫'‫<ref>ויהיה: B(except for Mu130) הנה יהיה; F137 יהיה; Ma1 המשל יהיה<br> |
| + | קו ישר: F, Lo הקו הישר; O16 קו<br> | ||
| + | עליו: B(except for Mu130) מונח עליו<br> | ||
| + | ויחולק: F ויתחלק; O16 נחלק; W66 ונחלק<br> | ||
| + | איך שיקרה: B(except for Mu130) איך שהזדמן; F איך שיזדמן; P1007 איך שקרה</ref> | ||
|- | |- | ||
|Supposition: <math>\scriptstyle AB^2=AG^2+GB^2+2\sdot\left(AG\times GB\right)</math> | |Supposition: <math>\scriptstyle AB^2=AG^2+GB^2+2\sdot\left(AG\times GB\right)</math> | ||
| − | |style="text-align:right;"|הנה<ref>הנה: F om.< | + | |style="text-align:right;"|הנה אומר כי המרובע המתהוה מן א"ב שוה לשני המרובעים המתהוים מן א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב‫<ref>הנה: F om.<br> |
| + | המרובע: Mu36 <sup>המרובע</sup><br> | ||
| + | המתהוה: B(except for Mu130), F ההוה<br> | ||
| + | מן א"ב: B(except for Mu130), F, P1007 מא"ב<br> | ||
| + | לשני: P1007 לב'<br> | ||
| + | המתהוים: A1, B(except for Mu130), F ההוים<br> | ||
| + | מן א"ג: B(except for Mu130), F, P1007 מא"ג<br> | ||
| + | ג"ב: F ב"ג<br> | ||
| + | וכפל: P1014 ומכפל<br> | ||
| + | השטח: W66 שטח<br> | ||
| + | הנצב: B(except for Mu130), F נצב<br> | ||
| + | הזויות: Ma1 הזוית<br> | ||
| + | שני: F om.; P1007 ב'<br> | ||
| + | ג"ב: F ב"ג</ref><ref group=note>C: המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר שאשר יהיה מהכאת א"ב בעצמו שוה לאשר יהיה מהכאת א"ג בעצמו וג"ב בעצמו וא"ג בג"ב פעמים<br> | ||
E: יהיה הקו הנחלק א"ג וחלקיו א"ב א"ג אומ' שמרובע א"ג כמו שני מרובעי א"ב ב"ג וכפל שטח א"ב [ב]ב"ג</ref> | E: יהיה הקו הנחלק א"ג וחלקיו א"ב א"ג אומ' שמרובע א"ג כמו שני מרובעי א"ב ב"ג וכפל שטח א"ב [ב]ב"ג</ref> | ||
|- | |- | ||
| Line 2,631: | Line 3,140: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וא"ח שוה ל{{#annot:term| | + | |style="text-align:right;"|וא"ח שוה ל{{#annot:term|1824,591|UxZC}}שטח הנצב הזויות{{#annotend:UxZC}} אשר יקיפו בו א"ג ג"ב מפני שג"ב שוה לג"ח הנה ה"ח שוה ל{{#annot:term|1824,591|PIuX}}שטח נצב הזויות{{#annotend:PIuX}} אשר יקיפו בו א"ג ג"ב הנה שני שטחי א"ח ח"ה שוים לכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב ושני שטחי ט"ז ג"כ שוים לשני המרובעים המתהוים מן קוי א"ג ג"ב הנה כבר התבאר ששטחי ט"ז ג"כ א"ח ח"ה שוים לשני המרובעים המתהוים משני קוי א"ג ג"ב ומכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב אבל שטחי ט"ז ג"כ א"ח ח"ה הם שוים לשטח א"ד ה"ב אשר הוא המרובע המתהוה מן א"ב |
|- | |- | ||
|<math>\scriptstyle AB^2=AG^2+GB^2+2\sdot\left(AG\times GB\right)</math> | |<math>\scriptstyle AB^2=AG^2+GB^2+2\sdot\left(AG\times GB\right)</math> | ||
| Line 2,694: | Line 3,203: | ||
|- | |- | ||
|in modern notation: <math>\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2</math> | |in modern notation: <math>\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2</math> | ||
| − | |style="text-align:right;"|<div id="Elements_II_5"></div>'''ה'''<ref>ה: P1007, P1012 mark is missing; Mu130 למוד ה'< | + | |style="text-align:right;"|<div id="Elements_II_5"></div>'''ה''' כאשר נחלק קו ישר בשני חלקים שוים ושני חלקים בלתי שוים הנה השטח הנצב הזויות אשר יקיפו בו שני חלקי הקו כלו אשר הם בלתי שוים עם המרובע המתהוה מן הקו אשר במה שבין שני מקומות השני חלקים שוה למרובע המתהוה מחצי הקו‫<ref>ה: P1007, P1012 mark is missing; Mu130 למוד ה'<br> |
| + | כאשר: F om.<br> | ||
| + | כאשר נחלק: C כשיחלק<br> | ||
| + | נחלק ... ישר: F כל קו ישר יתחלק<br> | ||
| + | בשני חלקים: C לשני חלקים; O16 בחלקים; F לשני חצאים<br> | ||
| + | שוים: F137 <sup>שוים</sup>; Ma1 om.<br> | ||
| + | ושני: C ולשני; F ובשני; P1007 ולב'<br> | ||
| + | ושני חלקים: O16 וחלקים<br> | ||
| + | בלתי שוים: C שאינם שוים; F מתחלפים<br> | ||
| + | הנה: C; F יהיה<br> | ||
| + | השטח: C שטח<br> | ||
| + | הנצב: B(except for Mu130), C, F137 נצב<br> | ||
| + | אשר יקיפו: C שיקיפו; P1007 אשר יקיף<br> | ||
| + | בו: P1012 om.<br> | ||
| + | שני חלקי: C החלקים; F חלקי; P1007 ב' חלקי; AB שני <s>קוי</s> חלקי<br> | ||
| + | הקו כלו: C om.<br> | ||
| + | אשר הם בלתי: C שאינם; O16 הבלתי<br> | ||
| + | אשר הם בלתי שוים: F המתחלפים<br> | ||
| + | עם המרובע: C עם מרובע; F ומרובע; P1013 מן המרובע; W194 <s>מן</s> <sup>נ' עם</sup> המרובע<br> | ||
| + | המתהוה מן: C om.; B(except for Mu130) ההוה מן<br> | ||
| + | מן הקו: O16, P1007 מהקו; W66 <s>מן הקו</s> מהקו<br> | ||
| + | אשר במה שבין: C כלו שהוא בין; Mu130 אשר במה <s>שני</s> <sup>שבין</sup><br> | ||
| + | שני: B (except for O16), C om.; P1007 ב'; P1013 שכל; P1014 שתי<br> | ||
| + | מקומות: P1007 המקומות<br> | ||
| + | השני חלקים: C <s>שוה</s> החלקים; B(except for Mu130) החלקים<br> | ||
| + | המתהוה מן ... השני חלקים: F יתרון חצי הקו על החלק היותר קצר<br> | ||
| + | שוה: B(except for Mu 130), F, P1012 שוים<br> | ||
| + | למרובע: W66 מרובע<br> | ||
| + | המתהוה: C, F om.; A1, B(except for Mu130), P1014 ההוה<br> | ||
| + | מחצי: C, F חצי; Mu130 מן חצי</ref> | ||
| + | <ref group=note>P1011: <div style="text-align: right; direction: ltr; margin-left: 1em;">כל קו יחלק בחציים ואחר יחלק בחלקים מתחלפים הנה אשר יהיה מהכאת החלק היותר ארוך בחלק היותר קטן ומהכאת יתרון חצי הקו על החלק היותר קצר בעצמו הוא כמו אשר יהיה מהכאת חצי הקו בעצמו</div><br> | ||
For any line divided in half and then divided into two unequal parts, the [sum] of the product of the larger part by the smaller part and the product of the excess of half the line over the smaller part by itself is equal to the product of half the line by itself<br> | For any line divided in half and then divided into two unequal parts, the [sum] of the product of the larger part by the smaller part and the product of the excess of half the line over the smaller part by itself is equal to the product of half the line by itself<br> | ||
E: <div style="text-align: right; direction: ltr; margin-left: 1em;">‫5 הקו הנחלק לחצאיים ולחלקי' בלתי שוים בשטח שיקיפו בו החלקים הבלתי שוים עם מרובע הקו שבן שני המקומות שוים למרובע חצי הקו</div><br> | E: <div style="text-align: right; direction: ltr; margin-left: 1em;">‫5 הקו הנחלק לחצאיים ולחלקי' בלתי שוים בשטח שיקיפו בו החלקים הבלתי שוים עם מרובע הקו שבן שני המקומות שוים למרובע חצי הקו</div><br> | ||
| Line 2,706: | Line 3,245: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה<ref>ויהיה: B (except for Mu130) הנה יהיה; F137 יהיה; Ma1 המשל יהיה< | + | |style="text-align:right;"|ויהיה קו ישר עליו א"ב ויחלק בשני חלקים שוים על נקודת ג' <span style=color:red>מי’ מא‫’</span>‫<ref>ויהיה: B (except for Mu130) הנה יהיה; F137 יהיה; Ma1 המשל יהיה<br> |
| + | קו ישר: F הקו הישר<br> | ||
| + | ויחלק: F ויתחלק; B(except for Mu130) ונחלק<br> | ||
| + | בשני: A2, P1014 לשני; P1007 בב'<br> | ||
| + | בשני חלקים שוים: F לחצאים; O16 בחלקים שוים<br> | ||
| + | נקודת: F om.; P1013 מקומות נקודת<br> | ||
| + | מי' מא': according to AB, W66</ref> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ושני<ref>ושני: Mu130, P1007 וב'; W66 ולשני< | + | |style="text-align:right;"|ושני חלקים בלתי שוים על נקודת ד‫'‫<ref>ושני: Mu130, P1007 וב'; W66 ולשני<br> |
| + | ושני חלקים: F, O16 ובחלקים<br> | ||
| + | בלתי שוים: F מתחלפים<br> | ||
| + | על נקודת ג' ... בלתי שוים: Mu130 marg.<br> | ||
| + | נקודת: F om.</ref> | ||
|- | |- | ||
|Supposition: <math>\scriptstyle \left(AD\times DB\right)+GD^2=GB^2</math> | |Supposition: <math>\scriptstyle \left(AD\times DB\right)+GD^2=GB^2</math> | ||
| − | |style="text-align:right;"|הנה<ref>הנה: F om.< | + | |style="text-align:right;"|הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב עם המרובע המתהוה מן ג"ד שוה למרובע המתהוה מן ג"ב‫<ref>הנה: F om.<br> |
| + | כי השטח: B(except for Mu130), Ma1 שהשטח<br> | ||
| + | הנצב: B, F נצב<br> | ||
| + | בו: P1012 om.<br> | ||
| + | שני: F om.<br> | ||
| + | המתהוה: B(except for Mu130), F ההוה<br> | ||
| + | מן ג"ד: B(except for Mu130), P1007 מג"ד; F מד"ג; Mu130 ג"ד illegible<br> | ||
| + | שוה: F שוים<br> | ||
| + | המתהוה: B(except for Mu130), F, P1014 ההוה<br> | ||
| + | מן ג"ב: B(except for Mu130), P1007, P1013 מג"ב; F מב"ג; AB מן <s>ג"א או מן</s> ג"ב; Mu130 מן ג"א או ג"ב; P1012 מן ג"א או מן ג"ב</ref><ref group=note>C: המשל בזה שקו א"ב נחלק לחלקים שוים על נקדת ג' ולחלקים מתחלפים על נקודת ד' ואומר שאשר היה מהכאת א"ד בד"ב ומהכאת ג"ד בעצמו יחד שוה לאשר יהיה מהכאת ג"ב בעצמו<br> | ||
E: ויהיה קו ישר א"ב ויחלק לחלקי' שוים על ג' ולבלתי שוים על ד' הנה אומר ששטח א"ד בד"ב עם מרובע ג"ד שוה למרובע ג"ב</ref> | E: ויהיה קו ישר א"ב ויחלק לחלקי' שוים על ג' ולבלתי שוים על ד' הנה אומר ששטח א"ד בד"ב עם מרובע ג"ד שוה למרובע ג"ב</ref> | ||
|- | |- | ||
| Line 2,719: | Line 3,277: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונעשה<ref>ונעשה: F137 נעשה; Ma1 המופת נעשה; B(except for Mu130) הנה נעשה< | + | |style="text-align:right;"|ונעשה מקו ג"ב מרובע ג"הז"ב <span style=color:red>ממ”ו מא‫’</span>‫<ref>ונעשה: F137 נעשה; Ma1 המופת נעשה; B(except for Mu130) הנה נעשה<br> |
| + | מקו: AB, Mu130, P1012, P1014 מן קו<br> | ||
| + | ג"ב: F ב"ג<b>r | ||
| + | ג"הז"ב: F ב'ג'ה'ז' ונעשה מב"ד מרובע ד'ב'כ'ח'; P1010 <s>ד"ה</s> ג"ה ז"ב<br> | ||
| + | ממ"ו מא': A2, C, E, Ma1, Mu130, P1007, P1012 om.; A1, AB, F137, Lo, P1010, PP ממ"ו מראשון; O16 ממ"ו</ref> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונרשום התמונה | + | |style="text-align:right;"|ונרשום התמונה ונשלים שטח א"גט"ל הנכחי הצלעות <span style=color:red>מד’ מזה</span>‫<ref>התמונה: F התבנית<br> |
| + | א"גט"ל: F א'ט'ל'ג'<br> | ||
| + | הנכחי: F נכחי; P1013 [..] נכוחי<br> | ||
| + | מד' מזה: A2, B(except for W66), C, E, Ma1, P1007, P1014 om.; Lo, P1010, P1012 מד'</ref> | ||
|- | |- | ||
| | | | ||
:*<math>\scriptstyle\Box_{GC}=\Box_{CZ}\longrightarrow\Box_{GK}=\Box_{DZ}</math> | :*<math>\scriptstyle\Box_{GC}=\Box_{CZ}\longrightarrow\Box_{GK}=\Box_{DZ}</math> | ||
| − | |style="text-align:right;"|הנה מפני<ref>הנה מפני: P1012 twice< | + | |style="text-align:right;"|הנה מפני כי ג"ח שוה לח"ז ונשים ד"כ משותף הנה יהיה ג"כ כלו שוה לד"ז כלו <span style=color:red>ממ”ג מא‫’</span>‫<ref>הנה מפני: P1012 twice<br> |
| + | מפני כי ג"ח: F לפי שג"ח; B(except for Mu130) מפני שג"ח<br> | ||
| + | ג"ח: P1012 ג"ה<br> | ||
| + | לח"ז: P1012 לה"ז<br> | ||
| + | ד"כ: Mu130 ח"ב<br> | ||
| + | משותף: O16 משותפת<br> | ||
| + | הנה: F om.; W66 <s>ה</s> הנה<br> | ||
| + | ג"כ: Mu130 ל"ב<br> | ||
| + | לד"ז: Ma1 לשטח ד"ז<br> | ||
| + | ממ"ג מא': A1, E, F137, P1007, P1010, P1012, PP om.; C מצורת מ"ג מן הראשון; Ma1 מג' מזה המאמר; Lo ממ"ג מראשון; O16 ממ"ג</ref> | ||
|- | |- | ||
| | | | ||
:*<math>\scriptstyle AG=GB\longrightarrow\Box_{LA}=\Box_{GK}</math> | :*<math>\scriptstyle AG=GB\longrightarrow\Box_{LA}=\Box_{GK}</math> | ||
| − | |style="text-align:right;"|ומפני שצלע<ref>ומפני שצלע: AB, P1007, P1012, PP ומפני כי צלע< | + | |style="text-align:right;"|ומפני שצלע א"ג שוה לצלע ג"ב יהיה שטח ל"א שוה לשטח ג"כ <span style=color:red>מל”א מא‫’</span>‫<ref>ומפני שצלע: AB, P1007, P1012, PP ומפני כי צלע<br> |
| + | א"ג: O561 <s>ג"ה</s> <sup>א"ג</sup><br> | ||
| + | ג"כ: Mu130 ל"ב; PP marg. כ"ג<br> | ||
| + | מל"א מא': according to W66; AB מל"ו מראשון</ref> | ||
|- | |- | ||
| | | | ||
:*<math>\scriptstyle\Box_{GK}=\Box_{DZ}\longrightarrow\Box_{LA}=\Box_{DZ}</math> | :*<math>\scriptstyle\Box_{GK}=\Box_{DZ}\longrightarrow\Box_{LA}=\Box_{DZ}</math> | ||
| − | |style="text-align:right;"|וכבר היה שטח ג"כ<ref>ג"כ: Mu130 ל"ב; PP ל"ג< | + | |style="text-align:right;"|וכבר היה שטח ג"כ שוה לשטח ד"ז הנה יהיה שטח ל"א שוה לשטח ד"ז <span style=color:red>מפתיח’ א‫’</span>‫<ref>ג"כ: Mu130 ל"ב; PP ל"ג<br> |
| + | הנה יהיה: B(except for Mu130), AB, F אם כן<br> | ||
| + | ל"א: B(except for Mu130), AB, F א"ל<br> | ||
| + | ומפני שצלע א"ג ... לשטח ד"ז: F137 marg. with the note ונשמט<br> | ||
| + | וכבר היה ... ל"א שוה לשטח ד"ז: AB, PP marg.<br> | ||
| + | הנה יהיה ... לשטח ד"ז: P1012 om.<br> | ||
| + | מפתיח' א': according to W66; AB מפתיחת א'</ref> | ||
|- | |- | ||
| | | | ||
:*<math>\scriptstyle\Box_{AC}=\Gamma_{MNS}</math> | :*<math>\scriptstyle\Box_{AC}=\Gamma_{MNS}</math> | ||
| − | |style="text-align:right;"|ונשים<ref>ונשים: Mu31 starts here (247v; line 2 from the bottom) ונשום< | + | |style="text-align:right;"|ונשים ג"ח משותף הנה א"ח כלו שוה לרושם מנ"ס‫<ref>ונשים: Mu31 starts here (247v; line 2 from the bottom) ונשום<br> |
| + | ג"ח: Lo ד"ח <sup>ג"ח</sup><br> | ||
| + | משותף: B(except for Mu130) משותפת<br> | ||
| + | הנה: F יהיה<br> | ||
| + | כלו: Mu31 ג כלנו<br> | ||
| + | שוה: Mu31 שוים; P1012 om.<br> | ||
| + | לרושם: Mu31 om.; Mu130 <s>לשטח</s> לרושם<br> | ||
| + | מנ"ס: P1012 מנ"ח</ref> | ||
|- | |- | ||
|אד × דב = ‫<math>\scriptstyle\Box</math><sub>אח</sub> → דח = בד | |אד × דב = ‫<math>\scriptstyle\Box</math><sub>אח</sub> → דח = בד | ||
| − | |style="text-align:right;"|אבל א"ח<ref>א"ח: Mu31; Mu130 שטח א"ח< | + | |style="text-align:right;"|אבל א"ח שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב מפני כי ב"ד שוה לד"ח וזה כי ד"כ מרובע <span style=color:red>משלפניה</span>‫<ref>א"ח: Mu31; Mu130 שטח א"ח<br> |
| + | שוה: P1012 שוה לשטח ג”כ וכבר היה שטח ג”כ שוה לשטח ד”ז ונשים ג”ח משותף הנה א”ח כלו לרושם מנ”ח אבל א”ח שוה<br> | ||
| + | הנצב: B, F נצב; P1007 ה[.] הנצב<br> | ||
| + | הזויות: P1007 הזוית<br> | ||
| + | שני: B(except for Mu130), F om. P1007 ב'<br> | ||
| + | מפני כי ב"ד: B(except for Mu130) מפני שב"ד; F לפי שד"ב; O561 marg.; P1007 הנה מפני כי ב"ד; P1012 ומפני כי ב"ד<br> | ||
| + | לד"ח: O16 <s>לשטח</s> לד"ח<br> | ||
| + | וזה כי ד"כ: B(except for Mu130) וזה שד"כ<br> | ||
| + | וזה כי ד"כ מרובע: Ma1 om.<br> | ||
| + | משלפניה: according to B(except for Mu130); C מלפניה; Ma1 מג' מזה; AB מאשר לפניה; O561 מהקודמת; P1014 מסוף תמונה אשר לפניה</ref> | ||
|- | |- | ||
|אד × דב = ‫<math>\scriptstyle\Box^{\Box}</math><sub>מנס</sub> ‫→ | |אד × דב = ‫<math>\scriptstyle\Box^{\Box}</math><sub>מנס</sub> ‫→ | ||
| − | |style="text-align:right;"|הנה<ref>הנה: F אם כן< | + | |style="text-align:right;"|הנה רושם מנ"ס שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב‫<ref>הנה: F אם כן<br> |
| + | רושם: AB <s>כי</s> רושם<br> | ||
| + | מנ"ס: P1012 מנ"ד<br> | ||
| + | שוה לשטח: O561 twice<br> | ||
| + | הנצב: B, F נצב<br> | ||
| + | הזויות: W66 הזוי<sup>ו</sup>ת<br> | ||
| + | בו: Mu31, P1007, P1010, PP om.<br> | ||
| + | שני: B(except for Mu130), F om.; P1007 ב'</ref> | ||
|- | |- | ||
|‫→ ‫<sup>2</sup>גד = ‫<math>\scriptstyle\Box</math><sub>לע</sub> | |‫→ ‫<sup>2</sup>גד = ‫<math>\scriptstyle\Box</math><sub>לע</sub> | ||
‫<sup>2</sup>גד + ‫(אד × דב‫) = ‫<math>\scriptstyle\Box</math><sub>לע</sub> + ‫<math>\scriptstyle\Box^{\Box}</math><sub>מנס</sub> | ‫<sup>2</sup>גד + ‫(אד × דב‫) = ‫<math>\scriptstyle\Box</math><sub>לע</sub> + ‫<math>\scriptstyle\Box^{\Box}</math><sub>מנס</sub> | ||
| − | |style="text-align:right;"|ונשים ל"ע אשר הוא שוה<ref>אשר הוא שוה: Mu31 אשר ראשונה; O16 <sup>שהוא</sup> כמו< | + | |style="text-align:right;"|ונשים ל"ע אשר הוא שוה למרובע המתהוה מן ג"ד משותף ויהיה רושם מנ"ס ושטח ל"ע כמו השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב והמרובע המתהוה מן ג"ד‫<ref>אשר הוא שוה: Mu31 אשר ראשונה; O16 <sup>שהוא</sup> כמו<br> |
| + | למרובע: O16 השטח המרובע<br> | ||
| + | המתהוה: B(except for Mu130), F ההוה<br> | ||
| + | מן ג"ד: B(except for Mu130), F, P1007 מג"ד<br> | ||
| + | משותף: O16 משותפת<br> | ||
| + | ויהיה: B(except for Mu130) הנה יהיה; F יהיה<br> | ||
| + | מנ"ס: P1012 מנ"ד<br> | ||
| + | ושטח: F עם<br> | ||
| + | הנצב: F, W66 נצב<br> | ||
| + | הזויות: O16 הזוית<br> | ||
| + | יקיפו בו: Lo יקיפוהו; A2, F, P1007, P1010, PP, W194 יקיפו<br> | ||
| + | שני: B(except for Mu130), F om.; P1007 ב'<br> | ||
| + | המתהוה: A1, B(except for Mu130), F ההוה<br> | ||
| + | מן ג"ד: B(except for Mu130), F, P1007 מג"ד</ref> | ||
|- | |- | ||
|‫<math>\scriptstyle\Box</math><sub>גז</sub> = ‫<math>\scriptstyle\Box</math><sub>לע</sub> + ‫<math>\scriptstyle\Box^{\Box}</math><sub>מנס</sub> | |‫<math>\scriptstyle\Box</math><sub>גז</sub> = ‫<math>\scriptstyle\Box</math><sub>לע</sub> + ‫<math>\scriptstyle\Box^{\Box}</math><sub>מנס</sub> | ||
| − | |style="text-align:right;"|אבל<ref>אבל: A2, AB, Lo, Mu31, Mu130, P1010, P1012, PP, W194 ויהיה< | + | |style="text-align:right;"|אבל רושם מנ"ס ושטח ל"ע הוא שטח ג"ז כלו‫<ref>אבל: A2, AB, Lo, Mu31, Mu130, P1010, P1012, PP, W194 ויהיה<br> |
| + | רושם: PP marg.<br> | ||
| + | כמו השטח הנצב ... ושטח ל"ע: P1012, P1014 om.<br> | ||
| + | הוא: F הם<br> | ||
| + | כלו: AB om.</ref> | ||
|- | |- | ||
|‫<sup>2</sup>גב = ‫<math>\scriptstyle\Box</math><sub>גז</sub> | |‫<sup>2</sup>גב = ‫<math>\scriptstyle\Box</math><sub>גז</sub> | ||
| − | |style="text-align:right;"|ושטח<ref>ושטח: O561 ג ושטח< | + | |style="text-align:right;"|ושטח ג"ז כלו הוא שטח המרובע המתהוה מן ג"ב‫<ref>ושטח: O561 ג ושטח<br> |
| + | ג"ז: Mu31 כ"ז<br> | ||
| + | ושטח ג"ז כלו: P1012 om.<br> | ||
| + | ושטח ג"ז כלו הוא: F והוא<br> | ||
| + | שטח: B(except for Mu130), F, Mu31 om.; P1007 השטח<br> | ||
| + | המתהוה: B(except for Mu130), F ההוה<br> | ||
| + | מן ג"ב: AB, B(except for Mu130), P1007, P1012 מג"ב; F מב"ג</ref> | ||
|- | |- | ||
|<math>\scriptstyle \left(AD\times DB\right)+GD^2=GB^2</math> | |<math>\scriptstyle \left(AD\times DB\right)+GD^2=GB^2</math> | ||
| − | |style="text-align:right;"|הנה<ref>הנה: F אם כן< | + | |style="text-align:right;"|הנה השטח הנצב הזויות אשר יקיפו בו א"ד ד"ב עם המרובע המתהוה מן ג"ד שוה למרובע המתהוה מן ג"ב‫<ref>הנה: F אם כן<br> |
| + | השטח: Mu31 השוה; Mu130 שטח<br> | ||
| + | הנצב: B(except for Mu130), F נצב<br> | ||
| + | בו: A1 om.<br> | ||
| + | א"ד: F קוי א"ד; P1007 ב' קוי א"ד<br> | ||
| + | המתהוה: B(except for Mu130), F, P1007 ההוה<br> | ||
| + | מן ג"ד: O16, P1007, P1012, P1014 מג"ד; F מד"ג<br> | ||
| + | המתהוה: B(except for Mu130), F, P1007 ההוה<br> | ||
| + | מן ג"ב: O16, P1007 מג"ב; F מב"ג, AB <s>מג"א או</s> <sup>מן</sup> ג"ב; Mu130 מן ג"א או ג"ב; P1010 מן <s>ג"ח</s> ג"ב; P1012, P1013 מן ג"א ג"ב; W194 מן ג"א ג"ב [נ' שהוא אחד‫]</ref><ref group=note>C: מופת זה שנצייר על קו ג"ב שטח מרובע עליו ג"ה[ז"ב] ונדביק ב' בה' ונוציא מד' קו אל ט' נכוחי לקוי ג"ה וב"ז עליו ד'ח'ט' ונוציא מח' קו נכוחי לקוי א"ב וה"ז עליו לח"ב ונוציא מא' קו נכוחי לקוי ג"ל וד"ח וב"כ והוא א"מ ונמשוך קו כ"ל אל מ' ושטח ג"ח המשלים שוה לשטח ח"ז המשלים ויהיה שטח ד"כ משותף ויהיה יחד שטח ג"כ שוה לשטח ד"ז יחד ואמנם ג"כ שוה לג"מ לפי שהם על שתי תושבות שוות ב"ג וג"א ובין שני קוים נכוחים ב"א וכ"מ<br> | ||
ואם כן שטח ג"מ שוה לשטח ד"ז ויהיה ד"ל משותף ויהיה יחד מ"ד שוה לנס"ע המסומן ומ"ד הוא שהיה מהכאת א"ד בד"ב לפי שיקיפו בו א"ד ד"ח וח"ד שוה לב"ד ויהיה נ'ס'ע' המסומן שוה לאשר יהיה מהכאת א"ד בד"ב ונשים אשר יהיה מהכאת ג"ד בעצמו משותף והוא שטח ל"ט המרובע<br> | ואם כן שטח ג"מ שוה לשטח ד"ז ויהיה ד"ל משותף ויהיה יחד מ"ד שוה לנס"ע המסומן ומ"ד הוא שהיה מהכאת א"ד בד"ב לפי שיקיפו בו א"ד ד"ח וח"ד שוה לב"ד ויהיה נ'ס'ע' המסומן שוה לאשר יהיה מהכאת א"ד בד"ב ונשים אשר יהיה מהכאת ג"ד בעצמו משותף והוא שטח ל"ט המרובע<br> | ||
ויתבאר שאשר היה מהכאת א"ד בד"ב ומהכאת ג"ד בעצמו יחד שוה לשטח ג"ז שהיה מהכאת ג"ב בעצמו שהוא חצי הקו [ר”ל מהתבארות צורת ד’ מזה השער]<br> | ויתבאר שאשר היה מהכאת א"ד בד"ב ומהכאת ג"ד בעצמו יחד שוה לשטח ג"ז שהיה מהכאת ג"ב בעצמו שהוא חצי הקו [ר”ל מהתבארות צורת ד’ מזה השער]<br> | ||
| Line 2,766: | Line 3,403: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכאשר<ref>וכאשר: F137 ואם כן; B(except for W66) הנה כאשר; O561 <sup>ו</sup>כאשר< | + | |style="text-align:right;"|וכאשר נחלק קו ישר בשני חלקים שוים ושני חלקים בלתי שוים הנה השטח הנצב הזויות אשר יקיפו בו שני חלקי הקו כלו אשר הם בלתי שוים עם המרובע המתהוה מן הקו אשר במה שבין שני מקומות שני החלקים שוה למרובע המתהוה מחצי הקו‫<ref>וכאשר: F137 ואם כן; B(except for W66) הנה כאשר; O561 <sup>ו</sup>כאשר<br> |
| + | נחלק קו ישר: F137 כל קו ישר יתחלק<br> | ||
| + | בשני חלקים שוים: F137 לשני חצאים; O16 בחלקים שוים; P1007 בב' חלקים שוים<br> | ||
| + | ושני חלקים בלתי שוים: A2 ובלתי שוים; F137 ובשני חלקים מתחלפים; O16 וחלקים בלתי שוים; P1007 om.<br> | ||
| + | הנה: F137 יהיה<br> | ||
| + | הנצב: F137, O16, P1013 נצב<br> | ||
| + | בו: P1010 om.<br> | ||
| + | שני: F137 om.; P1007 ב'<br> | ||
| + | חלקי הקו: Mu31 חלקו ההן; AB חלק קו<br> | ||
| + | כלו: O16 om.<br> | ||
| + | אשר הם בלתי שוים: F137 המתחלפים; O16 אשר אינם שוים<br> | ||
| + | עם המרובע: F137 ומרובע<br> | ||
| + | המתהוה: O16 ההוה<br> | ||
| + | מן הקו: O16, P1007 מהקו<br> | ||
| + | אשר במה: Mu31 twice<br> | ||
| + | מקומות: P1013 המקומות<br> | ||
| + | שני: O16 om.; PP marg.<br> | ||
| + | שני מקומות שני החלקים: A2 שני המקומות שני חלקים; P1007 ב' מקומות ב' החלקים; P1014 שתי מקומות השני חלקים<br> | ||
| + | המתהוה מן הקו אשר במה שבין שני מקומות שני החלקים: F137 יתרון חצי הקו על החלק היותר קצר<br> | ||
| + | שוה: F137 שוים<br> | ||
| + | המתהוה: F137 om.; O16 ההוה<br> | ||
| + | מחצי: F137 חצי; P1012 מהם<br> | ||
| + | וכאשר ... מחצי הקו: C, E, Ma1, W66 om.</ref> | ||
|- | |- | ||
| | | | ||
| Line 3,266: | Line 3,925: | ||
| | | | ||
|- | |- | ||
| − | | | + | |The square formed by the side opposite the acute angle in acute-angled triangles is less than [the sum of] the squares formed by the two sides encompassing the acute angle by twice the rectangle enclosed by one of the lines encompassing the acute angle, on which the perpendicular falls, and the line cut off within by the perpendicular towards the acute angle. |
| − | |style="text-align:right;"|יג המרובע ההוה מן הצלע אשר יהיה מיתר | + | |style="text-align:right;"|<span style=color:red>יג</span> <big>המרובע</big> ההוה מן הצלע אשר יהיה מיתר לזוית החדה מן המשולשים החדים הזויות יותר קטן משני המרובעים ההווים משתי הצלעות המקיפות בזוית החדה בכפל השטח הנצב הזויות אשר יקיף בו הקו אשר יפול עליו העמוד משני קוים המקיפים בזוית החדה והקו אשר יבדילוהו העמוד מחוץ ממה שילוה לזוית החדה‫<ref>deleted: <big>ויהיה</big> המשולש החד הזוית <sup>עליו</sup> א'ב'ג‫' |
| + | ותהיה <s>באג ממנו נרחבת</s> <sup>זוית א'ב'ג ממנו חדה ונוציא מנקודת א' אל קו ב"ג עמוד א"ד ואומר שהמרובע ההווה מן קו א"ג קטן משני המרובעים ההווים משני קוי ב"ג ב"א בכפל השטח נצב הזויות אשר יקיפו בו שני קוי ג"ב וב"ד המופת</sup> ונוציא קו א"ד הישר על יושר קו א"ג הישר ונוציא מנקודת ב' אל קו א"ד הישר עמוד ב"ד הנה אומר כי המרובע ההוה מן ג"ב יותר גדול משני המרובעים ההווים משני קוי א"ב א"ג בכפל השטח הכפל הזויות אשר יקיפו בו שני קוי א"ג וא"ד הנה מפני כי קו ד"ג הישר כבר חולק איך שקרה על נקודת א' היה המרובע ההוה מן ד"ג שוה לשני המרובעים ההוים מן א"ד וא"ג וכפל השטח הנצב מזויות אשר יקיפו בו שני קוי א"ג וא"ד ונשים המרובע ההוה מן ב"ד משותף הנה השני ממרובעים ההוים משני קוי ג"ד וד"ב שוים לשני המרובעים ההוים מקוי ב"ד וד"א וא"ג וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג וא"ד אבל שני המרובעים ההוים משני קוי ב"ד וד"ג שוים למרובע ההוה מן ב"ג מפני כי זוית בד"ג נצבת ושני המרובעים ההוים משני קוי ב"ד וא"ד שוים למרובע תהיה מן א"ב מפני כי בד"א נצבת הנה המרובע ההוה מן ב"ג שוה לשני המרובעים ההוים מן א"ב וא"ג וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד וא"ג הנה יהיה המרובע ההוה מן ב"ג יותר גדול משני המרובעים ההוים משני קוים א"ב וא"ג בכפל השטח הנצב הזויות החדים הזוית יותר קטן משני המרובעים ההוים משתי הצלעות המקיפות בזוית החדה בכפל השטח הנצב הזוית אשר יקיף בו הקו אשר יפול עליו העמוד משני הקוים המקיפים בזוית החדה והקו אשר יגדילהו העמוד ממה שילוה הזוית החדה</ref> | ||
| + | |- | ||
| + | |Let ABG be the acute-angled triangle. | ||
| + | |style="text-align:right;"|<big>ויהיה</big> המשולש החד הזויות אב"ג | ||
|- | |- | ||
| − | | | + | |Let angle ABG be acute angle. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותהיה זוית אב"ג ממנו חדה |
|- | |- | ||
| − | | | + | |<span style=color:green>'''I.12:'''</span> We draw perpendicular AD from point A to BG. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונוציא מנקודת א' אל <sup>קו</sup> ב"ג עמוד א"ד <span style=color:red>מי"ב מא‫'</span> |
|- | |- | ||
| − | | | + | |<span style=color:green>'''Supposition:'''</span> I say that the square formed by line AG is less than [the sum of] the two squares formed by the two lines BG and AB by twice the rectangle enclosed by the two lines GB and BD. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה אומר כי המרובע ההוה מקו א"ג יותר קטן משני המרובעים ההוים משני קוי ב"ג וא"ב בכפל <sup>בשעור כפל</sup> השטח הנצב מהזויות אשר יקיפו בו שני קוי ג"ב וב"ד |
|- | |- | ||
| − | | | + | |The proof: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<sup>המופת</sup> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה מפני כי קו ג"ב הישר כבר חולק לשני חלקים איך שקרה על נקודת ד' | + | |style="text-align:right;"|הנה מפני כי קו ג"ב הישר כבר חולק לשני חלקים איך שקרה על נקודת ד‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|יהיו שני המרובעים ההוים משני קוי ג"ב | + | |style="text-align:right;"|יהיו שני המרובעים ההוים משני קוי ג"ב וב"ד שוים ‫<ref>19r</ref>לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי ג"ב וב"ד <s>ושני</s> <sup>והמרובע ההווה מן ד"ג</sup> <span style=color:red>מז' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונשים המרובע | + | |style="text-align:right;"|<sup>ונשים המרובע ההווה מן א"ד משותף</sup> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה המרובעים | + | |style="text-align:right;"|<sup>הנה המרובעים ההווים מן קוי ג"ב ב"ד ג"א שוים לכפ[ל] השטח נצב הזויות אשר יקיפו בו שני קוי ג"ב ב"ד ושני</sup> המרובעים ההוים משני קוי א"ד וד"ג |
|- | |- | ||
| | | | ||
| Line 3,297: | Line 3,960: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|מפני כי זוית א'ד'ג' נצבת | + | |style="text-align:right;"|מפני כי זוית <s>כי</s> א'ד'ג' נצבת |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<sup>אבל המרובעים ההווים משני קוי א"ד ד"ב שוים למרובע ההווה מן א"ב</sup> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<sup>לפי שזוית א'ד'ב' נצבת</sup> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה שני המרובעים | + | |style="text-align:right;"|<sup>ושני</sup> <s>וכן שני המרובעים ההוים משני קוי ב"ד וא"ד שוים למרובע ההוה מן א"ב מפני כי זוית אד"ב נצבת הנה שני המרובעים מהוים משני קוי ג"ב וא"ב</s> <sup>הנה שני המרובעים ההווים משני קוי ג"ב ב"א שוים</sup> שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי ג"ב ו<s>א</s>ב"ד ולמרובע ההוה מן א"ג |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה המרובע ההוה מן א"ג יותר קטן משני המרובעים ההוים משני קוי ג"ב וא"ב | + | |style="text-align:right;"|הנה המרובע ההוה מן א"ג יותר קטן משני המרובעים ההוים משני קוי ג"ב וא"ב בכפל השטח הנצב הזויות <s>כי</s> אשר יקי<s>פ</s><sup>פו</sup> בו <s>הקו אשר יפול עליו העמוד</s> <sup>שני קוי ג"ב ב"ד</sup> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וזה | + | |style="text-align:right;"|הנה המרובע ההוה מן הצלע אשר יהיה מיתר לזוית החדה מן המשולשים החדים הזויות יותר קטן משני המרובעים ההוים משתי הצלעות המקיפות בזוית החדה בכפל השטח הנצב הזויות אשר יקיף בו הקו אשר יפול עליו העמוד משני הקוים המקיפים בזוית החדה והקו אשר יבדילהו העמוד ממה שילוה לזוית החדה |
| + | |- | ||
| + | |Quod erat demonstrandum. | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 14 === | === Proposition 14 === | ||
| | | | ||
| + | |- | ||
| + | |We wish to construct a square equal to a given rectilinear figure. | ||
| + | |style="text-align:right;"|<span style=color:red>יד</span> <big>נרצה</big> שנעשה מרובע שוה לתמונת ישרת הצלעות מונחת | ||
| + | |- | ||
| + | |Let figure A be the given rectilinear figure. | ||
| + | |style="text-align:right;"|<big>ותהיה</big> התמונה ישרת הצלעות המונחת תמונת א' <s>וראוי</s> | ||
| + | |- | ||
| + | |We wish to construct a square equal to the rectilinear figure A. | ||
| + | |style="text-align:right;"|<big>ונרצה</big> שנעשה מרובע שוה לתמונת <s>ישרת הצלעות ונעמיד</s> <sup>א' ישרת הקוים</sup> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *<span style=color:green>'''I.45:'''</span> We construct rectangle BGDH equal to the rectilinear figure A. |
| + | |style="text-align:right;"|<sup>הנה נעמיד שטח</sup> שטח נכחי <s>עצם נצב הזויות שוה לתמוה ישרת הצלעות</s> <sup>הצלעות נצב הזויות שוה לתמונת א' ישרת הקוים</sup> והוא ב"ג ד"ה <span style=color:red>ממ"ה מא‫'</span> | ||
|- | |- | ||
| − | | | + | |Either BH equals HD |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה אם יהיה ב"ה שוה אל ה"ד |
|- | |- | ||
| − | | | + | |Or one of the two is greater than the other. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|או שיהיה אחד משניהם יותר גדול מן האחר |
|- | |- | ||
| − | | | + | |If they are equal, we have already done what we wanted. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואם היו שוים הנה כבר <s>ידענו</s> <sup>עשינו</sup> מה שרצינו |
|- | |- | ||
| − | | | + | |If they are not equal, than one of the two is greater. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואם לא יהיו שוים <s>הנה שוים</s> הנה <sup>יהיה</sup> אחד משניהם יותר גדול מן האחר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *<span style=color:green>'''I.3:'''</span> Let BH be the greater. |
| + | |style="text-align:right;"|ויהיה היותר גדול ב"ה <span style=color:red>מג' מא‫'</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *We draw the straight line BH in a straight line with line BH. |
| + | |style="text-align:right;"|ונוציא קו ה"ז הישר על יושר קו ב"ה <sup>הישר</sup> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *We make HZ equal to HD. |
| + | :<math>\scriptstyle{\color{blue}{HZ=HD}}</math> | ||
| + | |style="text-align:right;"|ונשים ה"ז שוה אל ה"ד | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונחלק ב"ז בשני | + | *<span style=color:green>'''I.10'''</span> We cut BZ in half at point C. |
| + | |style="text-align:right;"|ונחלק ב"ז בשני חציים על נקודת <s>א' ונקודה על מרכז</s> ח' <span style=color:red>מי' מא‫'</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *We draw the semicircle BTZ with the center C and a radius of [one of] the two lines CB or CZ. |
| + | |style="text-align:right;"|<sup>ונקוה על מרכז ח‫'</sup> ובמרחק שני קוי ח"ב וח"ז חצי עגולה ב'ט'ז‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונוציא ה"ט הישר על יושר קו ד"ה | + | *We draw the straight line HT in a straight line with line DH. |
| + | |style="text-align:right;"|ונוציא <sup>קו</sup> ה"ט הישר על יושר קו ד"ה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *We join line TC. |
| + | |style="text-align:right;"|ונגיע קו ט"ח | ||
|- | |- | ||
| − | | | + | |<span style=color:green>'''II.5'''</span> Since the straight line BZ has been cut into two equal segments at point C and into two unequal segments at point H, the rectangle enclosed by BH and HZ together with the square formed by HC equals the square formed by CZ. |
| − | |style="text-align:right;"|יהיה השטח הנצב הזויות אשר יקיפו בו ב"ה וה"ז עם המרובע ההוה מן ה"ח שוה למרובע ההוה מן ח"ז | + | :<math>\scriptstyle{\color{blue}{\left(BH\times HZ\right)+HC^2=CZ^2}}</math> |
| + | |style="text-align:right;"|הנה מפני כי קו ב"ז הישר כבר נחלק בשני חלקים שוים על נקודת ח' ושני חלקים בלתי שוים על נקודת ה‫' <span style=color:red>מה' מזה</span> יהיה השטח הנצב הזויות אשר יקיפו בו <sup>שני קוי</sup> ב"ה וה"ז עם המרובע ההוה מן ה"ח שוה למרובע ההוה מן ח"ז <span style=color:red>מפתיחת א‫'</span> | ||
|- | |- | ||
| − | | | + | |But, CT equals CZ. |
| − | |style="text-align:right;"|וקו ח"ז שוה לקו ח"ט | + | :<math>\scriptstyle{\color{blue}{CT=CZ}}</math> |
| + | |style="text-align:right;"|<s>וקו ח"ז שוה לקו ח"ט</s> <sup>וח"ט שוה לח"ז</sup> | ||
|- | |- | ||
| − | | | + | |Therefore, the rectangle enclosed by the two lines BH and HZ together with the square formed by HC equals the square formed by CT. |
| − | |style="text-align:right;"|הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה | + | :<math>\scriptstyle{\color{blue}{\left(BH\times HZ\right)+HC^2=CT^2}}</math> |
| + | |style="text-align:right;"|הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה וה"ז עם המרובע ההוה מן ה"ח שוה למרובע ההוה מן ח"ט | ||
|- | |- | ||
| − | | | + | |But, the square formed by CT equals [the sum of] the two squares formed by the two lines TH and HC. |
| + | :<math>\scriptstyle{\color{blue}{CT^2=TH^2+HC^2}}</math> | ||
|style="text-align:right;"|והמרובע ההוה מן ח"ט שוה לשני המרובעים ההוים משני קוי ט"ה וה"ח | |style="text-align:right;"|והמרובע ההוה מן ח"ט שוה לשני המרובעים ההוים משני קוי ט"ה וה"ח | ||
|- | |- | ||
| − | | | + | |Angle THC is right. |
| + | :<math>\scriptstyle{\color{blue}{\measuredangle THC=90^\circ}}</math> | ||
|style="text-align:right;"|מפני כי זוית ט'ה'ח' נצבת | |style="text-align:right;"|מפני כי זוית ט'ה'ח' נצבת | ||
|- | |- | ||
| − | | | + | |Therefore, the rectangle enclosed by the two lines BH and HZ together with the square formed by HC equals [the sum of] the two squares formed by the two lines HC and HT. |
| − | |style="text-align:right;"|הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה וה"ז עם המרובע ההוה מן ה"ח שוה לשני המרובעים ההוים | + | :<math>\scriptstyle{\color{blue}{\left(BH\times HZ\right)+HC^2=HC^2+HT^2}}</math> |
| + | |style="text-align:right;"|הנה השטח הנצב <s>מ</s> הזויות אשר יקיפו בו <s>שוה</s> שני קוי ב"ה וה"ז עם המרובע ההוה מן ה"ח שוה לשני המרובעים ההוים משני קוי ה"ח וה"ט | ||
|- | |- | ||
| − | | | + | |We subtract the common square formed by HC. |
|style="text-align:right;"|ונפיל המרובע המשותף ההוה מן ה"ח | |style="text-align:right;"|ונפיל המרובע המשותף ההוה מן ה"ח | ||
|- | |- | ||
| − | | | + | |Then, the remaining rectangle enclosed by the two lines BH and HZ equals the square formed by line HT. |
| − | |style="text-align:right;"|וישאר השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה וה"ז שוה למרובע | + | :<math>\scriptstyle{\color{blue}{BH\times HZ=HT^2}}</math> |
| + | |style="text-align:right;"|וישאר השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה וה"ז שוה <sup>למרובע ההווה מן קו ה"ט</sup> | ||
|- | |- | ||
| − | | | + | |But, the rectangle enclosed by the two lines BH and HZ equals the parallelogram enclosed by the two lines BH and HD. |
| − | |style="text-align:right;"|והשטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה | + | :<math>\scriptstyle{\color{blue}{BH\times HZ=BD}}</math> |
| + | |style="text-align:right;"|<sup>והשטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה <s>ב"ה</s> ה"ז שוה לשטח ב"ד</sup> לשטח ב"ד הנכחי ‫<ref>19v</ref>הצלעות כי יקיפו בו שני קוי ב"ה וה"ד | ||
|- | |- | ||
| − | | | + | |ZH is equal to DH. |
| + | :<math>\scriptstyle{\color{blue}{ZH=DH}}</math> | ||
|style="text-align:right;"|וז"ה שוה אל ד"ה | |style="text-align:right;"|וז"ה שוה אל ד"ה | ||
|- | |- | ||
| − | | | + | |Therefore, figure BD equals the square formed by HT. |
| + | :<math>\scriptstyle{\color{blue}{BD=HT^2}}</math> | ||
|style="text-align:right;"|הנה שטח ב"ד שוה למרובע ההוה מן ה"ט | |style="text-align:right;"|הנה שטח ב"ד שוה למרובע ההוה מן ה"ט | ||
|- | |- | ||
| − | | | + | |Figure BD equals the rectilinear figure A. |
| − | |style="text-align:right;"|ושטח ב"ד שוה לתמונת ה | + | :<math>\scriptstyle{\color{blue}{BD=A}}</math> |
| + | |style="text-align:right;"|ושטח ב"ד שוה לתמונת א' ישרת הקוים | ||
| + | |- | ||
| + | |So, the rectilinear figure A equals the square formed by HT. | ||
| + | :<math>\scriptstyle{\color{blue}{A=HT^2}}</math> | ||
| + | |style="text-align:right;"|<s>הנה התמונת</s> <sup>אם כן תמונת א'</sup> ישרת הקוים שוה למרובע ההוה מן ה"ט | ||
| + | |- | ||
| + | |Therefore, a square has been constructed equal to the rectilinear figure A, which is the square formed by HT. | ||
| + | |style="text-align:right;"|הנה כבר נעשה מרובע שוה לתמונה ישרת הקוים אשר עליה א' והוא המרובע ההוה מן ה"ט‫<ref>marg.: ר"ל המרובע אשר נוכל לעשות על ה"ט</ref> | ||
|- | |- | ||
| − | | | + | |Quod erat demonstrandum. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה מה שרצינו לבארו |
|- | |- | ||
| − | | | + | |The second discussion of Euclid's book is completed. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>נשלם המאמר השני מספר אקלידס</big> |
|- | |- | ||
| − | | | + | |The number of propositions is fourteen. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ומספר תמונות ארבעה עשר |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| Line 3,870: | Line 4,571: | ||
| | | | ||
*We draw line DG to <math>\scriptstyle\bigcirc_{AG}</math> at random. | *We draw line DG to <math>\scriptstyle\bigcirc_{AG}</math> at random. | ||
| − | |style="text-align:right;"|ו{{#annot: | + | |style="text-align:right;"|ו{{#annot:to draw a line|1843,819|ztOj}}נעביר קו{{#annotend:ztOj}} אל עגולת א"ג איך שיפול והוא ד"ג |
|- | |- | ||
| | | | ||
| Line 8,359: | Line 9,060: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<span style=color:red>טו</span> החלקים אשר כפליהם שוים הנה יחס קצתם כיחס כפלי קצתם אל קצת | + | |style="text-align:right;"|<div id="Elements_V_15"></div><span style=color:red>טו</span> החלקים אשר כפליהם שוים הנה יחס קצתם כיחס כפלי קצתם אל קצת |
|- | |- | ||
| | | | ||
| Line 8,383: | Line 9,084: | ||
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 16 === | === Proposition 16 === | ||
| | | | ||
| Line 8,776: | Line 9,478: | ||
|- | |- | ||
| | | | ||
| − | *The similar rectilinear figures are those whose angles are equal and whose sides about the equal angles are proportional. | + | *{{#annot:surfaces-definition|2532|7gj7}}The similar rectilinear figures are those whose angles are equal and whose sides about the equal angles are proportional. |
| − | |style="text-align:right;"|השטחים המתדמים הם אשר זויותיהם שוות וצלעותיהם המקיפות בזויות השוות מתיחסות | + | |style="text-align:right;"|השטחים המתדמים הם אשר זויותיהם שוות וצלעותיהם המקיפות בזויות השוות מתיחסות{{#annotend:7gj7}} |
|- | |- | ||
| | | | ||
| Line 8,810: | Line 9,512: | ||
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 1 === | === Proposition 1 === | ||
| | | | ||
| Line 9,079: | Line 9,782: | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:definition| | + | *{{#annot:definition|994,1277|ekBL}}The proportional numbers are those of which the first is the same part, or the same parts, of the second, as the third is of the fourth. |
|style="text-align:right;"|<big>והמספרים המתיחסים</big> הם אשר יהיה הראשון מן השני והשלישי מן הרביעי חלק אחד בעצמו או חלקים אחדים בעינם{{#annotend:ekBL}} | |style="text-align:right;"|<big>והמספרים המתיחסים</big> הם אשר יהיה הראשון מן השני והשלישי מן הרביעי חלק אחד בעצמו או חלקים אחדים בעינם{{#annotend:ekBL}} | ||
|- | |- | ||
| Line 9,841: | Line 10,544: | ||
| | | | ||
|- | |- | ||
| − | |11) When two numbers are subtracted from two numbers and the ratio of the subtracted to the subtracted is as the ratio of the whole to the whole, then the ratio of the remainder to the remainder is as the ratio of the whole to the whole. | + | |<div id="Elements_VII_11"></div>11) When two numbers are subtracted from two numbers and the ratio of the subtracted to the subtracted is as the ratio of the whole to the whole, then the ratio of the remainder to the remainder is as the ratio of the whole to the whole. |
|style="text-align:right;"|<span style=color:red>י"א</span> <big>כאשר</big> חוסר משני מספרים שני מספרים והיה יחס המחוסר אל המחוסר כיחס הכל אל הכל הנה יחס הנשאר אל הנשאר כיחס הכל אל הכל | |style="text-align:right;"|<span style=color:red>י"א</span> <big>כאשר</big> חוסר משני מספרים שני מספרים והיה יחס המחוסר אל המחוסר כיחס הכל אל הכל הנה יחס הנשאר אל הנשאר כיחס הכל אל הכל | ||
|- | |- | ||
| Line 9,871: | Line 10,574: | ||
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 12 === | === Proposition 12 === | ||
| Line 10,149: | Line 10,853: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<span style=color:red>י"ח</span> <big>כל</big> מספר יוכה בשני מספרים הנה יחס אחד משני השטחים אל האחר כיחס אחד משני המספרים אל האחר | + | |style="text-align:right;"|<div id="Elements_VII_18"></div><span style=color:red>י"ח</span> <big>כל</big> מספר יוכה בשני מספרים הנה יחס אחד משני השטחים אל האחר כיחס אחד משני המספרים אל האחר |
|- | |- | ||
|Example: <math>\scriptstyle\left(A+B\right)\times G=D+H</math> | |Example: <math>\scriptstyle\left(A+B\right)\times G=D+H</math> | ||
| Line 11,084: | Line 11,788: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<span style=color:red>א</span> <big>כאשר</big> היו מספרים נמשכים על יחס אחד כמה שיהיו והיה כל אחד משתי הקצוות ראשון אצל האחר הנה הם קטני המספרים על יחסם | + | |style="text-align:right;"|<div id="Elements_VIII_1"></div><span style=color:red>א</span> <big>כאשר</big> היו מספרים נמשכים על יחס אחד כמה שיהיו והיה כל אחד משתי הקצוות ראשון אצל האחר הנה הם קטני המספרים על יחסם |
|- | |- | ||
| | | | ||
| Line 11,117: | Line 11,821: | ||
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 2 === | === Proposition 2 === | ||
| Line 12,053: | Line 12,758: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<span style=color:red>יא</span> <big>כל</big> שני מספרים מרובעים הנה יפול בין שניהם מספר מתיחס לשניהם ויחס המרובע אל המרובע הוא יחס צלעו אל צלעו שנוי בכפל | + | |style="text-align:right;"|<div id="Elements_VIII_11"></div><span style=color:red>יא</span> <big>כל</big> שני מספרים מרובעים הנה יפול בין שניהם מספר מתיחס לשניהם ויחס המרובע אל המרובע הוא יחס צלעו אל צלעו שנוי בכפל |
|- | |- | ||
| | | | ||
| Line 12,110: | Line 12,815: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<span style=color:red>יב</span> <big>כל</big> שני מספרים מעוקבים הנה יפול בין שניהם שני מספרים ויהיה הארבעה נמשכים מתיחסים על יחס אחד ויחס המעוקב אל המעוקב הוא ישם צלעו אל צלעו משולשת | + | |style="text-align:right;"|<div id="Elements_VIII_12"></div><span style=color:red>יב</span> <big>כל</big> שני מספרים מעוקבים הנה יפול בין שניהם שני מספרים ויהיה הארבעה נמשכים מתיחסים על יחס אחד ויחס המעוקב אל המעוקב הוא ישם צלעו אל צלעו משולשת |
|- | |- | ||
| | | | ||
| Line 12,191: | Line 12,896: | ||
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 13 === | === Proposition 13 === | ||
| Line 14,801: | Line 15,507: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<big>המופת</big> שילקח מה' מספרים על יחס א"ב ג"ד ועל מניינם והם ה מ' | + | |style="text-align:right;"|<big>המופת</big> שילקח מה' מספרים על יחס א"ב ג"ד ועל מניינם והם ה מ‫' |
|- | |- | ||
| | | | ||
| Line 14,807: | Line 15,513: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן יחס א' אל ד' כיחס ה' אל מ' | + | |style="text-align:right;"|אם כן יחס א' אל ד' כיחס ה' אל מ‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן ה' בד' כמו א' במ' | + | |style="text-align:right;"|אם כן ה' בד' כמו א' במ‫' |
|- | |- | ||
| | | | ||
| Line 14,819: | Line 15,525: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן ז"ח כפל מ' ומ' כפל ל' ול' כפל ט"כ וט"כ כפל ה' | + | |style="text-align:right;"|אם כן ז"ח כפל מ' ומ' כפל ל' ול' כפל ט"כ וט"כ כפל ה‫' |
|- | |- | ||
| | | | ||
| Line 14,828: | Line 15,534: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן יחס הנשאר מן ט"כ והוא ט"ס אל ה' כיחס הנשאר מן ז"ח והוא ז"ע אל כל מ"ל ט"כ ה' | + | |style="text-align:right;"|אם כן יחס הנשאר מן ט"כ והוא ט"ס אל ה' כיחס הנשאר מן ז"ח והוא ז"ע אל כל מ"ל ט"כ ה‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וט"כ כפל ה' וס"כ כמו ה' | + | |style="text-align:right;"|וט"כ כפל ה' וס"כ כמו ה‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן ט"ס כמו ה' | + | |style="text-align:right;"|אם כן ט"ס כמו ה‫' |
|- | |- | ||
| | | | ||
| Line 14,843: | Line 15,549: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וז"ע כבר התבאר שהוא שוה לכל מ"ל ט"כ ה' | + | |style="text-align:right;"|וז"ע כבר התבאר שהוא שוה לכל מ"ל ט"כ ה‫' |
|- | |- | ||
| | | | ||
| Line 14,852: | Line 15,558: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<big>המופת</big> כי הוא אי אפשר שאם היה אפשר הנה ימנהו זולתם והוא נ' וימנהו במספר אחדי פ' | + | |style="text-align:right;"|<big>המופת</big> כי הוא אי אפשר שאם היה אפשר הנה ימנהו זולתם והוא נ' וימנהו במספר אחדי פ‫' |
|- | |- | ||
| | | | ||
| Line 14,858: | Line 15,564: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן שטח פ' בנ' כמו משוטח ה' בד' | + | |style="text-align:right;"|אם כן שטח פ' בנ' כמו משוטח ה' בד‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן יחס פ' אל ק' כיחס ד' אל נ' | + | |style="text-align:right;"|אם כן יחס פ' אל ק' כיחס ד' אל נ‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונ' אינו אחד מן א"ב ג' | + | |style="text-align:right;"|ונ' אינו אחד מן א"ב ג‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן נ' לא ימנה ד' | + | |style="text-align:right;"|אם כן נ' לא ימנה ד‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אבל יחס נ' אל ד' כיחס ה' אל פ' | + | |style="text-align:right;"|אבל יחס נ' אל ד' כיחס ה' אל פ‫' |
|- | |- | ||
| | | | ||
| Line 14,882: | Line 15,588: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן פ' ימנה ד' | + | |style="text-align:right;"|אם כן פ' ימנה ד‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכאשר התיחסו מספרים מן האחד נמשכים כמה שהיו והיה אשר ילוה אל האחד ראשון הנה הוא לא ימנה אחד מהם כי אם המספרים מן היחס ההוא | + | |style="text-align:right;"|וכאשר התיחסו מספרים מן האחד נמשכים כמה שהיו והיה אשר ילוה אל ‫<ref>71r</ref>האחד ראשון הנה הוא לא ימנה אחד מהם כי אם המספרים מן היחס ההוא |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן מספר ד' לא ימנוהו כי אם המספרים ממספרי א'ב'ג' | + | |style="text-align:right;"|אם כן מספר ד' לא ימנוהו כי אם המספרים ממספרי א'ב'ג‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן מספר פ' אחד ממספרי א'ב'ג' | + | |style="text-align:right;"|אם כן מספר פ' הוא אחד ממספרי א'ב'ג‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה ב' וילקח מן ה' מן המספרים על מנין ב'ג'ד' | + | |style="text-align:right;"|ויהיה ב' וילקח מן ה' מן המספרים על <s>מנין</s> <sup>מספר</sup> ב'ג'ד' והוא ה"ט כ"ל והם על יחס ב'ג'ד‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן יחס ב' אל ד' כיחס ה' אל ל' | + | |style="text-align:right;"|אם כן יחס ב' אל ד' כיחס ה' אל ל‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן ה' בד' כמו ב' בל' | + | |style="text-align:right;"|אם כן ה' בד' כמו ב' בל‫' <span style=color:red>מי"ט מז‫'</span> |
|- | |- | ||
| | | | ||
| Line 14,909: | Line 15,615: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן יחס ב' אל פ' כיחס נ' אל ל' | + | |style="text-align:right;"|אם כן יחס ב' אל פ' כיחס נ' אל ל‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ופ' הוא ב' | + | |style="text-align:right;"|ופ' הוא ב‫' |
|- | |- | ||
| | | | ||
| Line 14,924: | Line 15,630: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|נשלם המאמר התשיעי | + | |style="text-align:right;"|נשלם המאמר התשיעי מספר אקלידס החכם |
|} | |} | ||
{| | {| | ||
| Line 14,934: | Line 15,640: | ||
== Book Ten == | == Book Ten == | ||
| − | |style="text-align:right;"|<big>המאמר העשירי</big> | + | |style="text-align:right;"|<big>המאמר העשירי מספר החכם אקלידס</big> |
|- | |- | ||
| | | | ||
| Line 14,943: | Line 15,649: | ||
| | | | ||
*{{#annot:definition|1873,2539|qiVv}}Those that have magnitudes, as lines, surfaces, and solids, that are said to be '''commensurable''', are those that are measured by the same measure. | *{{#annot:definition|1873,2539|qiVv}}Those that have magnitudes, as lines, surfaces, and solids, that are said to be '''commensurable''', are those that are measured by the same measure. | ||
| − | |style="text-align:right;"|בעלי השעורים מן הקוים והשטחים והמוגשמים אשר יאמר להם <big>המשותפים</big> הם אשר ישער אותם כלם שעור אחד{{#annotend:qiVv}} | + | |style="text-align:right;"|בעלי השעורים מן הקוים והשטחים והמוגשמים אשר יאמר להם <s>המשותפים</s> <big>המשותפים</big> הם אשר ישער אותם <s>כלם</s> <sup>יחד</sup> שעור אחד{{#annotend:qiVv}} |
|- | |- | ||
| | | | ||
| − | *{{#annot:definition|2543, | + | *{{#annot:definition-incommensurable|2543,2539|lGqt}}Those that are said to be '''incommensurable''' are those that cannot be measured the same measure. |
|style="text-align:right;"|ואשר יאמר להם <big>בלתי משותפים</big> הם אשר לא ישער אותם כלם שעור אחד{{#annotend:lGqt}} | |style="text-align:right;"|ואשר יאמר להם <big>בלתי משותפים</big> הם אשר לא ישער אותם כלם שעור אחד{{#annotend:lGqt}} | ||
|- | |- | ||
| | | | ||
*{{#annot:definition|2544,2541|shEk}}Straight lines are said to be '''commensurable in square''', when the squares that are generated from them are measured by the same area. | *{{#annot:definition|2544,2541|shEk}}Straight lines are said to be '''commensurable in square''', when the squares that are generated from them are measured by the same area. | ||
| − | |style="text-align:right;"|והקוים הישרים יאמר להם <big>המשותפים בכח</big> כאשר היה למרובעים | + | |style="text-align:right;"|והקוים הישרים אשר יאמר להם <big>המשותפים בכח</big> כאשר היה למרובעים ההוים מהם שטח ישער אותם{{#annotend:shEk}} |
|- | |- | ||
| | | | ||
| − | *{{#annot:definition|2545, | + | *{{#annot:definition-incommensurable in square|2545,2541|zQYu}}They are said to be '''incommensurable in square''', when the squares [that are generated] from them cannot be measured by the same area. |
| − | |style="text-align:right;"|ויאמר להם <big>בלתי משותפים בכח</big> כאשר לא יהיה למרובעים ההווים מהם שטח ישער אותם{{#annotend:zQYu}} | + | |style="text-align:right;"|ויאמר להם <big>בלתי משותפים בכח</big> כאשר לא יהיה למרובעים <s>הנה נבאר</s> [ההווים] מהם שטח ישער אותם{{#annotend:zQYu}} |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכאשר היה זה כן הנה נבאר כי כאשר התחיל והניח קו ישר הנה לו קוים ישרים אין תכלית לרבויים בלתי משותפים לו קצתם באורך לבד וקצתם באורך | + | |style="text-align:right;"|וכאשר היה זה כן הנה נבאר כי כאשר התחיל והניח קו ישר‫<ref>marg.: כמו שיתבאר בתמונה ט‫'</ref> הנה <s>לא</s> <sup>לו</sup> קוים ישרים אין תכלית לרבויים בלתי משותפים לו קצתם באורך לבד וקצתם באורך והכח יחד |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויגיע לקו הישר | + | |style="text-align:right;"|ויגיע לקו הישר איזה קו שיהיה ממה שיתחיל הנחתו וישים תחלה המדבר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה הקוים המשותפים לו הם המדברים | + | |style="text-align:right;"|הנה הקוים המשותפים לו <s>ה ו</s>הם <s>ו</s>המדברים |
|- | |- | ||
| | | | ||
| Line 14,973: | Line 15,679: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|והקוים אשר מהם אלו המרובעים הם כן בלתי מדברים | + | |style="text-align:right;"|והקוים אשר מהם אלו המרובעים הם גם כן בלתי מדברים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|שהקו אשר יהיה מרובעו בלתי מדבר הנה הוא גם כן בלתי מדבר |
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 1 === | === Proposition 1 === | ||
| | | | ||
|- | |- | ||
|When unequal magnitudes are given, and we subtract from the greater a magnitude greater than its half, and from the remainder a magnitude greater than its half, and if this subtraction is repeated continually, then there will be left a magnitude that is less than the smaller given magnitude. | |When unequal magnitudes are given, and we subtract from the greater a magnitude greater than its half, and from the remainder a magnitude greater than its half, and if this subtraction is repeated continually, then there will be left a magnitude that is less than the smaller given magnitude. | ||
| − | |style="text-align:right;"|<span style=color:red>א</span> <big>כאשר</big> היו שעורים מונחים בלתי שוים | + | |style="text-align:right;"|<span style=color:red>א</span> <big>כאשר</big> היו שני שעורים מונחים בלתי שוים ונבדל מהגדול משניהם יותר מחציו ממה ‫<ref>71v</ref>שישאר יותר מחציו ונבדל כן תמיד הנה ישאר ממנו שעור מה יותר קטן מהשעור המונח |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיו שני שעורים בלתי שוים והם א"ב וג' ויהיה היותר קטן מהם ג' | + | |style="text-align:right;"|ויהיו שני שעורים בלתי שוים והם א"ב וג' ויהיה היותר קטן מהם ג‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה אומר כי כאשר הובדל | + | |style="text-align:right;"|הנה אומר כי כאשר הובדל מן א"ב יותר מחציו וממה שישאר יותר מחציו ו<sup>נ</sup>עשה כן פעמים רבות הנה ישאר שעור מהיותר קטן מן הג‫' |
|- | |- | ||
|<math>\scriptstyle\left(n\sdot G\right)>AB\quad n\sdot G=DH</math> | |<math>\scriptstyle\left(n\sdot G\right)>AB\quad n\sdot G=DH</math> | ||
| − | |style="text-align:right;"|וזה כי | + | |style="text-align:right;"|וזה כי הג' כאשר הוכפל פעמים הנה הוא יהיה יותר גדול מן א"ב ויהיה מה שיתקבץ ממנו ד"ה |
|- | |- | ||
| | | | ||
| Line 15,001: | Line 15,708: | ||
|- | |- | ||
|<math>\scriptstyle TK>\frac{1}{2}AT</math> | |<math>\scriptstyle TK>\frac{1}{2}AT</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ומן א"ט יותר מחציו והוא ט"כ |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונבדיל זה תמיד עד שיהיה מנין מה שיתחלק בו א"ב שוה למספר חלקי | + | |style="text-align:right;"|ונבדיל זה תמיד עד שיהיה מנין מה שיתחלק בו א"ב שוה למספר חלקי ח"ה |
|- | |- | ||
|<math>\scriptstyle AB=AK+KT+TB</math> | |<math>\scriptstyle AB=AK+KT+TB</math> | ||
| − | |style="text-align:right;"|ויהיו החלקים אשר | + | |style="text-align:right;"|ויהיו החלקים אשר מן א"ב א"כ וכ"ט ט"ב |
|- | |- | ||
|<math>\scriptstyle AK=SN=NM=ML</math> | |<math>\scriptstyle AK=SN=NM=ML</math> | ||
| − | |style="text-align:right;"|ויהיה א"כ שוה לכל אחד מן ס"נ | + | |style="text-align:right;"|ויהיה א"כ שוה לכל אחד מן ס"נ ונ"מ ומ"ל |
|- | |- | ||
|SN, NM, ML are equal in multitude with DZ, ZC, CH | |SN, NM, ML are equal in multitude with DZ, ZC, CH | ||
| Line 15,016: | Line 15,723: | ||
|- | |- | ||
|<math>\scriptstyle TB>\frac{1}{2}AB\longrightarrow BT>TA</math> | |<math>\scriptstyle TB>\frac{1}{2}AB\longrightarrow BT>TA</math> | ||
| − | |style="text-align:right;"|הנה מפני כי ט"ב יותר מחצי א"ב יהיה ב"ט יותר גדול | + | |style="text-align:right;"|הנה מפני כי ט"ב יותר מחצי א"ב יהיה ב"ט יותר גדול מן ט"א |
|- | |- | ||
|BT is much greater than AK | |BT is much greater than AK | ||
| − | |style="text-align:right;"|ויהיה ב"ט יותר גדול הרבה | + | |style="text-align:right;"|ויהיה ב"ט יותר גדול הרבה <sup>מאד</sup> מן א"כ |
|- | |- | ||
|<math>\scriptstyle AK=LM\longrightarrow BT>LM</math> | |<math>\scriptstyle AK=LM\longrightarrow BT>LM</math> | ||
| Line 15,025: | Line 15,732: | ||
|- | |- | ||
|<math>\scriptstyle KT>\frac{1}{2}TA\longrightarrow TK>KA</math> | |<math>\scriptstyle KT>\frac{1}{2}TA\longrightarrow TK>KA</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה מפני כי כ"ט גם כן יותר מחצי ט"א יהיה ט"כ יותר גדול מן כ"א |
|- | |- | ||
|<math>\scriptstyle KA=MN\longrightarrow TK>MN</math> | |<math>\scriptstyle KA=MN\longrightarrow TK>MN</math> | ||
| − | |style="text-align:right;"|אבל כ"א כמו מ"נ אם כן ט"כ יותר גדול | + | |style="text-align:right;"|אבל כ"א כמו מ"נ אם כן ט"כ יותר גדול מן מ"נ |
|- | |- | ||
|<math>\scriptstyle KT>LM</math> | |<math>\scriptstyle KT>LM</math> | ||
| − | |style="text-align:right;"|וכבר התבאר כי כ"ט גם כן יותר גדול | + | |style="text-align:right;"|וכבר התבאר כי כ"ט גם כן יותר יותר גדול מן ל"מ |
|- | |- | ||
|<math>\scriptstyle KA=NS</math> | |<math>\scriptstyle KA=NS</math> | ||
| Line 15,057: | Line 15,764: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה יחס אחד מהקודמים אל אחד מהנמשכים כיחס כל הקודמים אל כל הנמשכים <span style=color:red>מג' מה'</span> | + | |style="text-align:right;"|ויהיה יחס אחד מהקודמים אל אחד מהנמשכים כיחס כל הקודמים אל כל הנמשכים <span style=color:red>מג' מה‫'</span> |
|- | |- | ||
| | | | ||
| Line 15,065: | Line 15,772: | ||
| | | | ||
:<math>\scriptstyle SL<DH\longrightarrow SN<DZ</math> | :<math>\scriptstyle SL<DH\longrightarrow SN<DZ</math> | ||
| − | |style="text-align:right;"|וס"ל יותר קטן מד"ה אם כן ס"נ יותר קטן מד"ז <span style=color:red>מד' מה'</span> | + | |style="text-align:right;"|וס"ל יותר קטן מד"ה אם כן ס"נ יותר קטן מד"ז <span style=color:red>מד' מה‫'</span> |
|- | |- | ||
| | | | ||
| Line 15,073: | Line 15,780: | ||
| | | | ||
:*<math>\scriptstyle DZ=G</math> | :*<math>\scriptstyle DZ=G</math> | ||
| − | |style="text-align:right;"|ואולם ד"ז הנה הוא כמו ג' | + | |style="text-align:right;"|ואולם ד"ז הנה הוא כמו ג‫' |
|- | |- | ||
| | | | ||
:<math>\scriptstyle AK<G</math> | :<math>\scriptstyle AK<G</math> | ||
| − | |style="text-align:right;"|אם כן א"כ יותר קטן מג' | + | |style="text-align:right;"|אם כן א"כ יותר קטן מג‫' |
|- | |- | ||
| | | | ||
| Line 15,139: | Line 15,846: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיו השיעורים השלשה הידועים המשותפים אשר הם בלתי שוים א' וב' וג' | + | |style="text-align:right;"|ויהיו השיעורים השלשה הידועים המשותפים אשר הם בלתי שוים א' וב' וג‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונקח השיעור היותר גדול משותף אשר ישער שני שיעורי ד' וג' ויהיה ז' | + | |style="text-align:right;"|ונקח השיעור היותר גדול משותף אשר ישער שני שיעורי ד' וג' ויהיה ז‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה מפני כי ז' ישער ד' וד' ישער א' וב' הנה שיעור ז' ישער א' וב' והוא גם כן ישער ג' | + | |style="text-align:right;"|הנה מפני כי ז' ישער ד' וד' ישער א' וב' הנה שיעור ז' ישער א' וב' והוא גם כן ישער ג‫' |
|- | |- | ||
| | | | ||
| Line 15,151: | Line 15,858: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואם היה ד' ישער ג' הנה ד' הוא השיעור היותר גדול המשותף אשר ישער א' וב' וג' | + | |style="text-align:right;"|ואם היה ד' ישער ג' הנה ד' הוא השיעור היותר גדול המשותף אשר ישער א' וב' וג‫' |
|- | |- | ||
| | | | ||
| Line 15,164: | Line 15,871: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיו שני שעורים משותפים והם א' וב' | + | |style="text-align:right;"|ויהיו שני שעורים משותפים והם א' וב‫' |
|- | |- | ||
| | | | ||
| Line 15,170: | Line 15,877: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה מפני כי שיעורי א' וב' משותפים הנה ישער שניהם שיעור מה וישער שניהם שיעור ה' | + | |style="text-align:right;"|הנה מפני כי שיעורי א' וב' משותפים הנה ישער שניהם שיעור מה וישער שניהם שיעור ה‫' |
|- | |- | ||
| | | | ||
| Line 15,176: | Line 15,883: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה ביחס השווי יהיה יחס א' אל ב' כיחס ג' אל ד' | + | |style="text-align:right;"|הנה ביחס השווי יהיה יחס א' אל ב' כיחס ג' אל ד‫' |
|- | |- | ||
| | | | ||
| Line 15,189: | Line 15,896: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיה יחס א' אל ב' כיחס מספר ג' אל מספר ד' | + | |style="text-align:right;"|ויהיה יחס א' אל ב' כיחס מספר ג' אל מספר ד‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<big>הנה</big> אומר כי א' משותף אל ב' | + | |style="text-align:right;"|<big>הנה</big> אומר כי א' משותף אל ב‫' |
|- | |- | ||
| | | | ||
| Line 15,199: | Line 15,906: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונניח האחד הנה מפני כי א' כבר חולק לחלקים כמנין מה שבג' מהאחדים ואחד מחלקיו הוא כמו ה' יהיה חלק האחד ממספר ג' כמו חלק ה' מא' | + | |style="text-align:right;"|ונניח האחד הנה מפני כי א' כבר חולק לחלקים כמנין מה שבג' מהאחדים ואחד מחלקיו הוא כמו ה' יהיה חלק האחד ממספר ג' כמו חלק ה' מא‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן יחס האחד אל ג' כיחס ה' אל א' | + | |style="text-align:right;"|אם כן יחס האחד אל ג' כיחס ה' אל א‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויחס מספר ג' אל מספר ד' כיחס א' אל ב' | + | |style="text-align:right;"|ויחס מספר ג' אל מספר ד' כיחס א' אל ב‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן ביחס השווי יהיה יחס אחד אל מספר ד' כיחס ה' אל ב' והאחד ימנה ד' | + | |style="text-align:right;"|אם כן ביחס השווי יהיה יחס אחד אל מספר ד' כיחס ה' אל ב' והאחד ימנה ד‫' |
|- | |- | ||
| | | | ||
| Line 15,217: | Line 15,924: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן גם כן יהיה יחס ה' אל ז' כיחס האחד אל הד' | + | |style="text-align:right;"|וכן גם כן יהיה יחס ה' אל ז' כיחס האחד אל הד‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן יחס א' אל ז' כיחס ג' אל ד' | + | |style="text-align:right;"|אם כן יחס א' אל ז' כיחס ג' אל ד‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכבר היה יחס א' אל ב' כיחס ג' אל ד' | + | |style="text-align:right;"|וכבר היה יחס א' אל ב' כיחס ג' אל ד‫' |
|- | |- | ||
| | | | ||
| Line 15,263: | Line 15,970: | ||
| | | | ||
|- | |- | ||
| − | | | + | |When there are four proportional magnitudes, and the first is commensurable with the second, then the third is commensurable with the fourth; but, if the first is incommensurable with the second, then the third is incommensurable with the fourth. |
|style="text-align:right;"|<span style=color:red>ח</span> <big>כאשר</big> היו ארבעה שיעורים מתיחסים והיה הראשון משותף לשני הנה השלישי משותף לרביעי ואם היה הראשון בלתי משותף לשני הנה השלישי בלתי משותף לרביעי | |style="text-align:right;"|<span style=color:red>ח</span> <big>כאשר</big> היו ארבעה שיעורים מתיחסים והיה הראשון משותף לשני הנה השלישי משותף לרביעי ואם היה הראשון בלתי משותף לשני הנה השלישי בלתי משותף לרביעי | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויהיו ארבעה שיעורים מתיחסים והם א' וב' וג' וד' ויחס א' אל ב' כיחס ג' אל ד | + | *Let A, B, G, and D be four proportional magnitudes, so that the ratio of A to B is the same as the ratio of G to D. |
| + | :<math>\scriptstyle{\color{blue}{A:B=G:D}}</math> | ||
| + | |style="text-align:right;"|ויהיו ארבעה שיעורים מתיחסים והם א' וב' וג' וד' ויחס א' אל ב' כיחס ג' אל ד‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *Let A be commensurable with B. |
| + | |style="text-align:right;"|ויהיה א' משותף אל ב‫' | ||
|- | |- | ||
| − | | | + | |<span style=color:green>'''Supposition:'''</span> I say that G is commensurable with D. |
| − | |style="text-align:right;"|אבל א' בלתי משותף אל ב' | + | |style="text-align:right;"|<big>הנה</big> אומר כי ג' משותף אל ד‫' |
| + | |- | ||
| + | |Since A is commensurable with B, the ratio of A to B is the same as the ratio of a number to a number. | ||
| + | |style="text-align:right;"|הנה מפני כי א' משותף אל ב' יהיה יחס א' אל ב' כיחס מספר אל מספר | ||
| + | |- | ||
| + | |The ratio of A is to B is the same as the ratio of G to D. | ||
| + | :<math>\scriptstyle{\color{blue}{A:B=G:D}}</math> | ||
| + | |style="text-align:right;"|ויחס א' אל ב' כיחס ג' אל ד‫' | ||
| + | |- | ||
| + | |Therefore, the ratio of G to D is the same as the ratio of a number to a number. | ||
| + | |style="text-align:right;"|אם כן יחס ג' אל ד' כיחס מספר אל מספר | ||
| + | |- | ||
| + | |Hence, G is commensurable with D | ||
| + | |style="text-align:right;"|אם כן ג' משותף אל ד‫' | ||
| + | |- | ||
| + | |Let A be incommensurable with B. | ||
| + | |style="text-align:right;"|ולא יהיה א' משותף אל ב‫' | ||
| + | |- | ||
| + | |<span style=color:green>'''Supposition:'''</span> I say that G is incommensurable with D. | ||
| + | |style="text-align:right;"|הנה אומר כי ג' גם כן בלתי משותף אל ד‫' | ||
| + | |- | ||
| + | |If G is commensurable with D, then A is also commensurable with B. | ||
| + | |style="text-align:right;"|וזה כי הוא אם ג' משותף אל ד' הנה א' גם כן משותף אל ב‫' | ||
| + | |- | ||
| + | |But, A is incommensurable with B. | ||
| + | |style="text-align:right;"|אבל א' בלתי משותף אל ב‫' | ||
|- | |- | ||
| − | | | + | |Therefore, G is incommensurable with D. |
| − | |style="text-align:right;"|אם כן אין ג' משותף אל ד' | + | |style="text-align:right;"|אם כן אין ג' משותף אל ד‫' |
|- | |- | ||
| − | | | + | |Quod erat demonstrandum |
| − | |style="text-align:right;"|וזה | + | |style="text-align:right;"|וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 9 === | === Proposition 9 === | ||
| | | | ||
| Line 16,055: | Line 16,791: | ||
| | | | ||
|- | |- | ||
| − | | | + | |45) We wish to find the first binomial line. |
|style="text-align:right;"|<span style=color:red>מה</span> <big>נרצה</big> שנמצא קו משתי שמות הראשון | |style="text-align:right;"|<span style=color:red>מה</span> <big>נרצה</big> שנמצא קו משתי שמות הראשון | ||
|- | |- | ||
| − | | | + | |We draw a rational line, which is A. |
| − | |style="text-align:right;"|הנה נניח קו מדבר והוא א' ויהיה קו ב"ג משותף לקו א' באורך וקו א' מדבר אם כן קו ב"ג מדבר ויהיו שני מספרים מרובעים והם ה"ד ד"ז ולא יהיה יתרון מה שבין שניהם אשר הוא ה"ז מספר מרובע | + | |style="text-align:right;"|הנה נניח קו מדבר והוא א' |
| − | + | |- | |
| + | |Let line BG be commensurable in length with line A. | ||
| + | |style="text-align:right;"|ויהיה קו ב"ג משותף לקו א' באורך | ||
| + | |- | ||
| + | |Line A is rational, therefore line BG is also rational. | ||
| + | |style="text-align:right;"|וקו א' מדבר אם כן קו ב"ג מדבר | ||
| + | |- | ||
| + | |Let HD and DZ be two square numbers such that the difference between them, which is HZ, is not a square number. | ||
| + | |style="text-align:right;"|ויהיו שני מספרים מרובעים והם ה"ד ד"ז ולא יהיה יתרון מה שבין שניהם אשר הוא ה"ז מספר מרובע | ||
| + | |- | ||
| + | |Hence, line BG is commensurable in length with line T. | ||
| + | |style="text-align:right;"|אם כן קו ב"ג משותף לקו ט' באורך | ||
| + | |- | ||
| + | |The excess of BG over GC in square is the same as the square of the line that is commensurable in length with it. | ||
| + | |style="text-align:right;"|ותוספת ב"ג על ג"ח בכח כמו מרובע יהיה מקו ישתתף עמו באורך | ||
|- | |- | ||
| − | | | + | |Line BG is commensurable with the given rational line, which is A. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וקו ב"ג משותף לקו המדבר המונח אשר הוא א' |
|- | |- | ||
| − | | | + | |Therefore, line BC is the first binomial line. |
|style="text-align:right;"|אם כן קו ב"ח הוא אשר משתי שמות הראשון | |style="text-align:right;"|אם כן קו ב"ח הוא אשר משתי שמות הראשון | ||
|- | |- | ||
| Line 16,072: | Line 16,822: | ||
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 46 === | === Proposition 46 === | ||
| | | | ||
| Line 16,605: | Line 17,356: | ||
| | | | ||
|- | |- | ||
| − | |{{#annot:definition|2538,2358|9THR}}When | + | |{{#annot:definition|2538,2358|9THR}}When a segment measurable in a square is subtracted from a straight line and the two lines are commensurable in square only, then the remaining straight line is unmeasurable; let it be called an apotome. |
|style="text-align:right;"|<span style=color:red>ע</span> <big>כאשר</big> הובדל מקו ישר מדבר בכח והיו השני קוים בכח לבד משותפים הנה הקו הנשאר בלתי מדבר ויקרא הנבדל{{#annotend:9THR}} | |style="text-align:right;"|<span style=color:red>ע</span> <big>כאשר</big> הובדל מקו ישר מדבר בכח והיו השני קוים בכח לבד משותפים הנה הקו הנשאר בלתי מדבר ויקרא הנבדל{{#annotend:9THR}} | ||
|- | |- | ||
| Line 16,819: | Line 17,570: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<big>כאשר</big> הונח קו מדבר | + | |style="text-align:right;"|<big>כאשר</big> הונח קו נבדל וקו מדבר ונדבק בקו הנבדל <sup>הקו</sup> אשר ממנו נבדל <sup>והיה</sup> הכל יוסיף בכח על אשר התחבר כמו מרובע יהיה מקו ישתתף עמו באורך והיה כל הקו משותף באורך לקו המדבר המונח הנה יקרא הקו ההוא נבדל הראשון |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואם היה אשר ישתתף הקו המדבר המונח הוא הקו אשר חובר | + | |style="text-align:right;"|ואם היה אשר ישתתף עם הקו המדבר המונח הוא הקו אשר חובר אליה הנה יקרא הקו הנבדל אשר זכרנו הנבדל השני |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואם לא יהיה אחד משניהם משותף לקו המדבר המונח הנה יקרא הנבדל השלישי | + | |style="text-align:right;"|ואם לא יהיה אחד <ref>98v</ref>משניהם משותף לקו המדבר המונח הנה יקרא הנבדל השלישי |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וגם כן הנה הקו הנבדל עם אשר התחבר בו אם היו כל שניהם יוסיפו בכח על הקו | + | |style="text-align:right;"|וגם כן הנה הקו הנבדל עם אשר התחבר בו אם היו כל שניהם יוסיפו בכח על הקו המונח כמו מרובע יהיה מקו לא ישתתף עמו באורך והיה הכל משותף לקו המדבר הנה יקרא הקו ההוא הנב[ד]ל הרביעי |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואם היה אשר | + | |style="text-align:right;"|ואם היה אשר ישתת<s>ף</s><sup>פהו</sup> <s>עמו הקו המדבר הוא אשר יובא</s> <sup>הקו המדבר הוא אשר יתדבק</sup> הנה יקרא הקו ההוא הנבדל החמישי |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואם לא | + | |style="text-align:right;"|ואם לא יהיה אחד משניהם משותף לקו המדבר הנה יקרא הקו ההוא הנבדל השישי |
|- | |- | ||
| | | | ||
| Line 16,843: | Line 17,594: | ||
| | | | ||
|- | |- | ||
| − | | | + | |82) We wish to find the first apotome. |
|style="text-align:right;"|<span style=color:red>פב</span> <big>נרצה</big> שנמצא הנבדל הראשון | |style="text-align:right;"|<span style=color:red>פב</span> <big>נרצה</big> שנמצא הנבדל הראשון | ||
| + | |- | ||
| + | |We set out a rational line, which is A. | ||
| + | |style="text-align:right;"|הנה נניח קו מדבר והוא א‫' | ||
| + | |- | ||
| + | |We draw line BC commensurable in length with line A | ||
| + | |style="text-align:right;"|ונשים קו ב"ח משותף לקו א' באורך | ||
| + | |- | ||
| + | |Then line BC is rational. | ||
| + | |style="text-align:right;"|ויהיה קו ב"ח אם כן מדבר | ||
| + | |- | ||
| + | |Let DH and HZ be two square numbers, such that the difference between them, which is ZD, is not a square number. | ||
| + | |style="text-align:right;"|ויהיו שני מספרים מרובעים והם ד"ה ה"ז ולא יהיה יתרון מה שבין שניהם אשר הוא ז"ד מספר מרובע | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה | + | |style="text-align:right;"|הנה אין יחס ה"ז אל ד"ז כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונשים יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ג"ח כיחס ז"ה אל ד"ז |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן | + | |style="text-align:right;"|אם כן המרובע ההוה מן ח"ב משותף למרובע ההוה מן ג"ח |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והמרובע ההוה מן ב"ח מדבר |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|אם כן המרובע ההוה מן ח"ג מדבר |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|ומפני כי יחס ה"ז אל ד"ז אינו כיחס מספר מרובע אל מספר מרובע <sup>לא יהיה יחס המרובע ההווה מן ב"ח אל המרובע ההווה מן ח"ג כיחס מספר מרובע אל מספר מרובע</sup> הנה קו ב"ח בלתי משותף לקו ח"ג באורך <span style=color:red>מז' מזה</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן שני קוי ב"ח ח"ג בכח לבד מדברים והם בו לבד משותפים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן קו ב"ג הוא הנבדל <span style=color:red>מע' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואומר כי הוא הנבדל הראשון |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה כי המרובע ההוה מקו ב"ח יותר גדול מן המרובע ההוה מן ג"ח |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותהיה תוספתו עליו כמו המרובע ההוה מקו ט |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכבר היה יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ג"ח כיחס ה"ז אל ד"ז |
|- | |- | ||
| | | | ||
| − | == | + | |style="text-align:right;"|וכאשר הפכנו יהיה יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ט כיחס ה"ז אל ה"ד <span style=color:red>וזה התהפכות היחס בפתיחת ה‫'</span> |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|ויחס ה"ז אל ה"ד כיחס מספר מרובע אל מספר מרובע | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|מפני כי שניהם שני מרובעים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ט כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן קו ב"ח <sup>משותף באורך לקו ט‫'</sup> <span style=color:red>מז' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<sup>הנה קו ב"ח</sup> יוסיף על קו ג"ח בכח כמו מרובע יהיה מקו ישתתף עמו באורך <span style=color:red>מז' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכל קו ב"ח משותף לקו המדבר המונח באורך והוא א‫' |
|- | |- | ||
| − | | | + | |Therefore line BG is the first apotome. |
| − | |style="text-align:right;"|אם כן קו | + | |style="text-align:right;"|אם כן קו ב"ג הוא הנבדל הראשון <span style=color:red>מההקדמה השלישית</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וזה מה שרצינו | + | |style="text-align:right;"|וזה מה שרצינו |
|- | |- | ||
| | | | ||
| − | === Proposition | + | |
| + | === Proposition 83 === | ||
| | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<span style=color:red> | + | |style="text-align:right;"|<span style=color:red>פג</span> <big>נרצה</big> שנמצא הנבדל השני |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונניח קו מדבר והוא א' | + | |style="text-align:right;"|ונניח קו מדבר והוא א‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונשים קו ג"ח משותף אליו |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה קו ג"ח <s>אם</s> <sup>גם</sup> כן מדבר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיו שני מספרים מרובעים והם ד"ה ה"ז ולא יהיה יתרון מה שבין שניהם אשר הוא ד"ז מספר מרובע |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|ויהיה יחס המרובע ההוה מן ג"ח אל המרובע ההוה מן ח"ב כיחס ד"ז אל ד"ה |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|אם כן המרובע ההוה מן ג"ח משותף למרובע ההוה מן ב"ח <span style=color:red>מו' מזה</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והמרובע ההוה מן ג"ח מדבר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן המרובע ההוה מן <s>א"ב</s> ח"ב מדבר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ומפני כי יחס המרובע ‫<ref>99r</ref>ההוה מן ג"ח אל המרובע ההוה מן ב"ח אינו כיחס מספר מרובע אל מספר מרובע יהיה קו ג"ח בלתי משותף לקו ב"ח באורך |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן | + | |style="text-align:right;"|אם כן שני קוי ג"ח ח"ב בכח מדברים והם בו לבד משותפים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן קו ב"ג הוא הנבדל <span style=color:red>מע' מזה</span> |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|ואומר כי הוא שני מן הנבדלים |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|וזה כי המרובע ההוה מן ב"ח יותר גדול מן המרובע ההוה מן ג"ח | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותהיה תוספתו עליו כמו המרובע ההוה מן ט‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה מפני כי יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ג"ח כיחס ד"ה אל ד"ז יהיה כאשר הפכנו יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ט' כיחס ד"ה אל ה"ז <span style=color:red>התהפכות היחס</span> |
| − | |||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכל אחד מן ד"ה ה"ז מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ט' כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן קו | + | |style="text-align:right;"|אם כן קו ב"ח משותף לקו ט' באורך <span style=color:red>מז' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן קו ב"ח יוסיף על ג"ח בכח כמו מרובע יהיה מקו ישתתף עמו באורך |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|וקו ג"ח אשר הובדל מקו ב"ח משותף לקו מדבר |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|אם כן קו <s>ב"ח</s> ב"ג הוא הנבדל השני <span style=color:red>מההקדמה השלישית</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזהו מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| − | |||
| + | === Proposition 84 === | ||
| + | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<span style=color:red>פד</span> <big>נרצה</big> שנמצא הנבדל השלישי |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונניח קו מדבר והוא א‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיו שלשה מספרים עליהם ה' ב"ג ג"ד ולא יתהוה מהם דבר יחסו אל חברו כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה יחס שני מספרי ב"ג ב"ד כל אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה יחס המרובע ההוה מן א' אל המרובע ההוה מן ז"ח כיחס ה' אל ב"ג |
| − | |||
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|ויהיה יחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ח"ט כיחס מספר ב"ג אל מספר ג"ד |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|<s>וישים</s> <sup>ויהיה</sup> המרובע ההוה מן א' משותף למרובע ההוה מן ז"ח <span style=color:red>מו' מזה</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והמרובע ההוה מן א' מדבר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן המרובע ההוה מן ז"ח מדבר |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ז"ח מדבר בכח | |
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ויחס ה' אל ב"ג אינו כיחס מספר מרובע אל מספר מרובע | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<sup>הנה יחס המרובע ההווה מן א' אל המרובע ההווה מן ז"ח אינו כיחס מספר מרובע אל מספר מרובע</sup> <span style=color:red>מו' מזה</span> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו א' בלתי משותף לקו ז"ח באורך | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|וגם כן הנה יחס ב"ג אל ג"ד כיחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ח"ט <span style=color:red>מו' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|והמרובע ההוה מן ז"ח <s>מדבר אם כן</s> <sup>משותף</sup> למרובע ההוה מן ח"ט |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<sup>והמרובע מז"ח מדבר הנה המרובע ההווה מן ח"ט מדבר</sup> | |
| − | |style="text-align:right;"|< | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ויחס ב"ג אל ג"ד אינו כיחס מספר מרובע אל מספר מרובע | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<sup>הנה אין יחס המרובע ההווה מן ז"ח אל המרובע ההווה מן ח"ט כיחס מספר מרובע אל מספר מרובע</sup> | |
| − | |style="text-align:right;"|< | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן קו ז"ח בלתי משותף לקו ח"ט באורך <span style=color:red>מז' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן שני קוי ז"ח ח"ט בכח מדברים והם בו לבד משותפים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|אם כן קו ז"ט נבדל <span style=color:red>מע' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואומר כי הוא השלישי מן הנבדלים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה כי יחס ה' אל ב"ג כיחס המרובע ההווה מן א' אל המרובע ההווה מן ז"ח |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויחס ב"ג אל ג"ד כיחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ח"ט |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|וכיחס השווי יהיה יחס ה' אל ב"ד כיחס המרובע ההוה מן א' אל המרובע ההוה מן ח"ט <span style=color:red>מכ"ב מה‫'</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויחס ה' אל ג"ד אינו כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|אם כן אין יחס המרובע ההוה מן א' אל המרובע ההוה ‫<ref>99v</ref>מן ח"ט כיחס מספר מרובע אל <s>מס</s> מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|אם כן קו א' בלתי משותף לקו ח"ט באורך <span style=color:red>מז' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן אין אחד משני קוי ז"ח ח"ט משותף לקו א' המדבר באורך |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והמרובע ההוה מן ז"ח יותר גדול מן המרובע ההוה מן ח"ט |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|ותהיה תוספתו עליו כמו המרובע ההוה מן קו ב‫' |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|אם כן יחס ב"ג אל ג"ד כיחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ח"ט | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<span style=color:red> | + | |style="text-align:right;"|וכאשר הפכנו היה יחס ב"ג אל ב"ד כיחס המרובע ההוה מן ז"ח אל המרובע ההוה מן <sup>ב‫'</sup> <span style=color:red>התהפכות היחס</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויחס ב"ג אל ב"ד כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן | + | |style="text-align:right;"|אם כן יחס המרובע ההוה מן ז"ח אל המרובע ההוה מב' כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ז"ח משותף לקו ז' ב באורך <span style=color:red>מז' מזה</span> | |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|וקו ז"ח יוסיף על קו ח"ט בכח כמו <sup>המרובע ההווה מב‫'</sup> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|<sup>הנה קו ז"ח מוסיף על קו ט"ח בכח כמו</sup> מרובע יהיה מקו ישתתף עמו באורך |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואין אחד משני קוי ז"ח ח"ט משותף לקו א' המדבר באורך |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן | + | |style="text-align:right;"|אם כן קו ז"ט הוא הנבדל השלישי <span style=color:red>מההקדמה השלישית</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| − | === Proposition | + | === Proposition 85 === |
| | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<span style=color:red>פה</span> <big>נרצה</big> שנמצא הנבדל הרביעי |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונניח קו מדבר והוא א' ונשים קו ב"ח משותף אליו באורך ויהיה קו ב"ח גם כן מדבר ונניח שני מספרים עליהם ד"ה ז"ה ולא יהיה יחס אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכל קו ב"ח משותף לקו א' המדבר המונח באורך אם כן ב"ג הוא הנבדל הרביעי |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|הנה כבר מצאנו הנבדל הרביעי | |
| − | + | |- | |
| | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
|- | |- | ||
| − | | | + | | |
| − | + | === Proposition 86 === | |
| + | | | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|<big> | + | |style="text-align:right;"|<span style=color:red>פו</span> <big>נרצה</big> שנמצא הנבדל החמישי |
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונניח קו מדבר והוא א' ונשים קו ג"ח משותף לקו א' באורך ויהיה קו ג"ח מדבר ונניח שני מספרים עליהם ד"ה ה"ז כמו השני מספרים אשר זכרנו בתמונות אשר קודם זאת ונשים יחס המרובע ההווה מג"ח אל המרובע ההווה מכ"ח כיחס ה"ז אל ד"ה |
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן קו ב"ח יוסיף על קו ח"ג בב"ח כמו מרובע יהיה מקו לא ישתתף עמו באורך וקו ג"ח אשר הובדל מקו ב"ג ישתתף א' המדבר באורך |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ב"ג הוא הנבדל החמשי | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וזה מה שרצינו לבאר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | === Proposition 87 === | |
| − | | | + | | |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<span style=color:red>פז</span> <big>נרצה</big> שנמצא הנבדל הששי | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|הנה נניח קו מדבר והוא א' ויהיו שלשה מספרים עליהם ה' ב"ג ג"ד ולא | |
| − | |style="text-align:right;"| | + | יהיה יחס אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע ולא יהיה גם כן יחס ב"ג אל ב"ד כיחס מספר מרובע אל מספר מרובע |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ואומר שהוא הששי מהנבדלים וזה כי יחס ה' אל ב"ג כיחס המרובע ההווה מא' אל המרובע ההווה מז"ח ויחס ב"ג אל ג"ד כיחס המרובע ההוה מז"ח אל המרובע ההווה מח"ט וביחס ההשואה יהיה יחס ה' אל ג"ד כיחס המרובע ההווה מא' אל המרובע ההווה מח"ט | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ואין אחד משני קוי ז"ח ח"ט משותף לקו א' המדבר המונח באורך | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ז"ט הוא הנבדל הששי | |
| − | |style="text-align:right;"|אם כן | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וזה מה שרצינו לבאר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | === Proposition 88 === | |
| − | |style="text-align:right;"| | + | | |
| + | |- | ||
| + | |When a surface is enclosed by a rational line and a first apotome, then the line of that surface is irrational and it is so-called an apotome. | ||
| + | |style="text-align:right;"|<span style=color:red>פח</span> <big>כאשר</big> הקיף בשטח קו מדבר והנבדל הראשון הנה הקו אשר יגבר על השטח ההוא בלתי מדבר והוא אשר יקרא הנבדל | ||
|- | |- | ||
| | | | ||
| − | * | + | *Let surface AC be enclosed by the rational line AB and the first apotome AZ. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>ויהיה</big> שטח עליו א"ח יקיף בו קו מדבר והוא א"ב והקו הנבדל הראשון והוא א"ז |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ויהיה הקו אשר נבדל ממנו דבק בו והוא ז"ג | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|הנה אומר כי הקו אשר יגבר על שטח א"ח בלתי מדבר הוא אשר יקרא הנבדל | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וזה כי הקו הנבדל והוא הנבדל הראשון א"ז והקו אשר נבדל ממנו הוא ז"ג אם כן קוי א"ג ג"ז בכח מדברים ובו לבד משותפים וקו א"ג יוסיף על קו ג"ז בכח כמו מרובע יהיה מקו ישתתף עמו באורך וקו א"ג משותף באורך לקו א"ב המדבר ואם חובר אל קו ג"א שטח שוה לרבע המרובע ההוה מן ז"ג יחסר משלמות הקו שטח מרובע הנה הוא יחלק קו א"ג בשני חלקים משותפים ויחלק ג"ז בשני חציים על נקודת ד' ונחבר אל קו א"ג שטח שוה למרובע ההוה מן ז"ד יחסר משלמותו שטח מרובע ויהיה השטח המחובר אל קו א"ג השטח אשר יקיפו בו שני קוי א"ה ה"ג אם כן קו א"ה משותף לקו ה"ג באורך ונוציא מנקודת דה"ג קוים נכחיים לשני קוי א"ב ז"ח והם ד"ט ה"כ ג"ל ועוד נוציא קו ב"ח אל ל' ויהיה שטח ע"ק מרובע שוה לשטח בה ויהיה נ"ס מרובע שוה לשטח ה"ל אם כן מרובע נ"ס הוא על קוטר מרובע ע"ק ונוציא הקוטר הזה והוא מ"ס ונשלים לקצ"ו לקוות התמונה ע"מ ק"ס הנה השטח אשר יקיפו בו שני קוי א"ה ה"ג שוה למרובע ההווה מן ג"ד הנה קו ג"ד מתיחס לשני קוי א"ה ה"ב במה שבין שניהם | |
| − | |style="text-align:right;"|אם כן | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ולכן יהיה שטח ג"ט מתייחס לשני שטחי א"ב ב"ג במה שבין שניהם ושטח ע"ד מתייחס לשני שטחי ע"ק נ"ס במה שבין שניהם | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ושטח א"כ שוה לשטח מ"ס ושטח כ"ג שוה לשטח נ"ס אם כן שטח ג"ט שוה לשטח ע"ד אבל שטח ג"ט שוה לשטח ט"ז | |
| − | |style="text-align:right;"| | + | |
| + | |||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אבל מ"ס נ"ס הם שני המרובעים ההוים משני קוי ע"ס ס"פ | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן כל אחד משני קוי ע"ס ס"פ מדבר בכח ושניהם בו משותפים וקו ז"ד שוה לקו ד"ג וקו ז"ג מדבר בכח ובלתי משותף באורך לקו א"ב אם כן אל אחד משני קוי ז"ד ד"ג מדבר בכח בלתי משותף באורך לקו א"ב הנה כל אחד משני משטחי ז"ט ט"ג ממוצע ושטח ט"ג שוה לשטח | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן שטח ע"ד ממוצע ושטח פ"ד מדבר | |
| − | |style="text-align:right;"|אם כן | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן שטח ע"ד בלתי משותף <s>לשטח ד"פ</s> <sup>למרובע פ"ד</sup> ויחס ע"ד אל ד"פ כיחס ע"ס אל ס"פ |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|מא' מו‫' | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ע"ס בלתי משותף לקו ס"פ באורך | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן שני קוי ע"ס ס"פ בכח מדברים ושניהם בו לבד משותפים | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ע"פ נבדל והוא יגבר על שטח א"ח | |
| − | |style="text-align:right;"|אם כן | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|מע' מזה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן הקו אשר יגבר על א"ח בלתי מדבר והוא אשר יקרא הנבדל | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וזה מה שרצינו לבאר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | ||
| − | | | + | === Proposition 89 === |
| + | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<span style=color:red>פט</span> <big>כאשר</big> הקיף בשטח קו מדבר והנבדל השני הנה הקו אשר יגבר על השטח ההוא הוא אשר יקרא נבדל הממוצע הראשון |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<big>ויהיה</big> שטח עליו א"ח יקיף בו קו מדבר והוא א"ב והקו הנבדל השני והוא א"ז | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וידבק בו הקו אשר ממנו נבדל והוא ז"ג | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|הנה אומר כי הקו אשר יגבר על שטח א"ח בלתי מדבר והוא אשר יקרא נבדל הממוצע הראשון | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה כי ‫<ref>101v</ref>קו א"ז הוא הנבדל השני |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והקו אשר יובדל ממנו ד"ך ד"ג |
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|אם כן | + | |style="text-align:right;"|אם כן שני קוי א"ג ג"ז בכח מדברים ושניהם בו לבד משותפים <span style=color:red>מע' מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וקו א"ג יוסיף בכח על קו ג"ז כמו מרובע יהיה מקו ישתתף עמו באורך |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וקו ז"ג ישתתף באורך קו א"ב | |
| − | + | |- | |
| | | | ||
| + | |style="text-align:right;"|ואם חובר אל קו א"ג שטח שוה לרביע המרובע אשר יהיה מקו ז"ג יחסר משלמות הקו שטח מרובע | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה הוא יחלק קו א"ג בשני חלקים משותפים באורך <span style=color:red>מי"ג מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|ויחלק ז"ג בשני חציים על נקודת ד' <span style=color:red>מי' מא‫'</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|ונחבר אל קו א"ג שטח שוה למרובע ההוה מן ד"ג יחסר <s>משותפים</s> משלמותו שטח מרובע והוא השטח אשר יקיפו בו שני קוי א"ה ה"ג |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|אם כן קו א"ה משותף באורך לקו ה"ג |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|ונוציא מנקודות דהג קוים נכחיים לכל אחד משני קוי א"ב ז"ח והם קוי ד"ט ה"כ ג"ל <span style=color:red>מל"א מא‫'</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונוציא קו בכח אל ל ויהיה ק"ע מרובע שוה לשטח א"ב |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|ויהיה פ"ר מרובע שוה לשטח ה"ל | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה מרובע פ"ר על קוטר מרובע ע"ק |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|ונוציא משניהם יחד קוטר מ"ס | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונשלים לקוות התמונה |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|הנה <s>התמונה</s> <sup>השטח</sup> אשר יקיפו בה שני קוי א"ה ה"ג שוה למרובע ההוה מן ד"ג | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן קו | + | |style="text-align:right;"|אם כן קו ג"ד מתיחס לשני קוי א"ה ה"ג במה שבין שניהם <span style=color:red>מי"ז מו‫'</span> |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|ולכן יהיה שטח ג"ט מתיחס לשני שטחי א"ב ב"ג במה שבין שניהם <span style=color:red>יצא מי"א מח‫'</span> | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ושטח ע"ר גם כן מתיחס לשני שטחי ע"ק פ"ד במה שביניהם | |
| − | |style="text-align:right;"| | + | |- |
| | | | ||
| + | |style="text-align:right;"|ושטח א"ב שוה לשטח ע"ק | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ושטח ב"ג שוה לשטח פ"ר | |
| − | |style="text-align:right;"| | + | |- |
| | | | ||
| + | |style="text-align:right;"|אם כן שטח ט"ג שוה לשטח ע"ר | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ואולם שטח ג"ט הנה הוא שוה לשטח ט"ז | |
| − | |style="text-align:right;"| | + | |- |
| | | | ||
| + | |style="text-align:right;"|ואולם שטח ע"ר הנה הוא שוה לשטח פ"ק <span style=color:red>ממ"ג מא‫'</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן שטח ט"ז שוה לשטח פ"ק |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|אם כן כל שטח ז"ל שוה לרושם סנפ עם המרובע <s>נס</s> <sup>פ"ר</sup> | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ושטח ב"ג שוה למרובע פ"ר | |
| − | |style="text-align:right;"| | + | |- |
| | | | ||
| + | |style="text-align:right;"|וישאר שטח ז"כ שוה לרושם סנפ | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וכל א"ב שוה לכל ע"ק | |
| − | |style="text-align:right;"| | + | |- |
| | | | ||
| + | |style="text-align:right;"|וישאר שטח א"ח שוה לשטח מ"נ | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ומרובע מ"נ הוא ההוה מן ע"פ <span style=color:red>מסוף ד' מב‫'</span> | |
| − | |style="text-align:right;"| | + | |- |
| | | | ||
| + | |style="text-align:right;"|אם כן <sup>קו</sup> ע"פ יגבר על שטח א"ח | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ואומר כי ע"פ הוא הנבדל הממוצע הראשון | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה כי קו א"ה משותף לקו ה"ג באורך |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|אם כן כל קו א"ג משותף לכל אחד משני קוי א"ה ה"ג באורך <span style=color:red>מא' מזה</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וקו א"ג בכח מדבר והוא בלתי משותף לקו א"ב באורך |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|אם כן כל אחד משני קוי א"ה ה"ג מדבר בכח והוא בלתי משותף לקו א"ב באורך | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן כל אחד משני <s>קוי א"ה ה"ג מדבר בכח והוא בלתי משותף לקו א"ב באורך אם כל אחד משני</s> שטחי א"ב ב"ג ממוצע ושניהם משותפים <span style=color:red>מי"ז מזה</span> |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ושטח א"כ שוה למרובע ע"ק | |
| − | + | |- | |
| | | | ||
| + | |style="text-align:right;"|ושטח כ"ג שוה למרובע פ"ר | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן כל אחד משני <s>שטחי</s> <sup>מרובעי</sup> ע"ק פ"ד ממוצע ושניהם משותפים והם שני מרוב' ההוים משני קוי ע"ס ס"פ |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן כל אחד משני קוי ע"ס ס"פ ממוצע ושניהם בכח משותפים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וקו ז"ד כמו קו ד"ג |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכל קו ז"ג מדבר בכח משותף לקו א"ב באורך |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן כל אחד משני קוי ז"ד ד"ג מדבר משותף לקו א"ב באורך |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן כל אחד משני שטחי ז"ט ט"ג מדבר | |
| − | + | |- | |
| | | | ||
| + | |style="text-align:right;"|ושטח ט"ג שוה לשטח ע"ר <span style=color:red>מי"א מזה</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן שטח ע"ר מדבר ושטח ע"ר הוא אשר יקיפו בו שני קוי ע"ס ס"פ |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן השטח אשר יקיפו בו שני קוי ‫<ref>101r</ref>ע"ס ס"פ מדבר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה מפני כי שטח ע"ר מדבר ושטח ר"פ ממוצע יהיה השטח ר"ע בלתי משותף לשטח פ"ר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויחס שטח ע"ר אל שטח פ"ר כיחס קו ע"ס אל קו ס"פ <span style=color:red>מא' מו‫'</span> |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ע"ס בלתי משותף לקו ס"פ באורך | |
| − | + | |- | |
| | | | ||
| + | |style="text-align:right;"|אם כן קוי ע"ס ס"פ ממוצע ושניהם בכח לבד משותפים והשטח אשר יקיפו בו מדבר | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן קו ע"פ הוא הנבדל <sup>ה</sup>ממוצע הראשון והוא יגבר על שטח א"ח <span style=color:red>מע"א מזה</span> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן הקו אשר יגבר על שטח א"ח הוא נבדל הממוצע הראשון |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| − | + | === Proposition 107 === | |
| + | | | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<big>הקדמה</big> | |
| − | === | + | |- |
| − | + | |The apotome and the irrational lines following it are not of the same type as the other preceding irrational lines nor are they the same with the medial line or with one another. | |
| + | |style="text-align:right;"|<big>הנבדל</big> ומה שאחריו מן הקוים שאינם מדברים‫<ref>marg.: והם הנזכרים בתמונת צ' וצ"א וצ"ב וצ"ג</ref> אין מהם קו מסוג הקוים האחרים הקודמים אשר אינם מדברים ולא דבר מהם ממוצע ולא מהם דבר מסוג הנשארים מהם | ||
| + | |- | ||
| + | |For the square formed by the medial line, when added to a rational line, generates a rational breadth incommensurable in length with the line to which it is added. | ||
| + | |style="text-align:right;"|וזה כי המרובע <s>וזה כי המרובע</s> ההוה מן הקו הממוצע כאשר חובר אל קו מדבר יחדש רוחב מדבר בכח ובלתי משותף באורך לקו אשר חובר אליו <span style=color:red>מי"ח מזה</span> | ||
|- | |- | ||
| − | | | + | |While the square formed by the apotome, when added to a rational line, generates a breadth which is the first apotome. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואולם המרובע ההוה מן הקו הנבדל הנה הוא כאשר חובר אל קו מדבר יחדש רוחב הוא הנבדל הראשון |
|- | |- | ||
| − | | | + | |The square formed by the first apotome of the medial line, when added to a rational line, generates a breadth which is the second apotome. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואולם המרובע ההו<s>א</s><sup>ה</sup> מנבדל הממוצע הראשון הנה הוא כאשר חובר אל קו מדבר היה הרוחב המתחדש הנבדל השני |
|- | |- | ||
| − | | | + | |The square formed by the second apotome of the medial line, when added to a rational line, generates a breadth which is the third apotome. |
| − | + | |style="text-align:right;"|ואולם המרובע ההוה מנבדל הממוצע השני הנה הוא כאשר חובר אל קו מדבר היה הרוחב המתחדש הנבדל השלישי | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | | | + | |The square formed by the minor line, when added to a rational line, generates a breadth which is the fourth apotome |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואולם המרובע ההוה מן הקו היותר קטן הנה הוא כאשר חובר אל קו מדבר היה הרוחב המתחדש הנבדל הרביעי |
|- | |- | ||
| − | | | + | |The square formed by the line, which produces with a rational area a medial whole, when added to a rational line, generates a breadth which is the fifth apotome. |
| − | |style="text-align:right;"|הנה הוא | + | |style="text-align:right;"|ואולם המרובע ההוה מן הקו אשר עם המדבר ישים הכל ממוצע הנה הוא כאשר חובר אל קו מדבר היה הרוחב המתחדש הנבדל החמישי |
|- | |- | ||
| − | | | + | |The square formed by the line, which produces with a medial area a medial whole, when added to a rational line, generates a breadth which is the sixth apotome, |
| − | + | |style="text-align:right;"|ואולם המרובע ההוה מן הקו אשר עם הממוצע ישים הכל ממוצע הנה הוא כאשר חובר אל קו מדבר הנה <s>הרוחב המתחדש</s> <sup>יחדש</sup> הנבדל הששי | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | | | + | |The breadths we have mentioned differ from each other, none of them are of the same type as the other; this is clear. |
| − | + | |style="text-align:right;"|<s>והרב</s> והרחבים אשר זכרנו <s>שם</s> <sup>אותם הם</sup> מתחלפים אין מהם דבר מסוג חבירו וזה דבר מבואר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ונבאר‫<ref>זה בתמונה הבאה אחר זה</ref> כי אין מאלו הרחבים הנבדלים דבר הוא מסוג הקוים אשר משתי שמות והם הרחבים המתחדשים מן המרובעים ההוים מן הקוים אשר משתי שמות והקוים אשר ימשכו אחריו כאשר יחוברו אל קוים מדברים | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ואם היו אלו הרחבים אשר זכרנו מתחלפים הנה הקוים עצמם אשר התחדשו ממרובעיהם הרחבים האלו אין מהם דבר הוא מסוג חברו | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| Line 17,464: | Line 18,230: | ||
| | | | ||
| − | === Proposition | + | === Proposition 108 === |
| | | | ||
| + | |- | ||
| + | |The apotome is not the binomial line | ||
| + | |style="text-align:right;"|<big>הקו</big> הנבדל לא יהיה <sup>אשר</sup> משתי שמות | ||
| + | |- | ||
| + | |Let A be the apotome. | ||
| + | |style="text-align:right;"|<big>ויהיה</big> הקו הנבדל א‫' | ||
| + | |- | ||
| + | |I say that A is not a binomial line. | ||
| + | |style="text-align:right;"|הנה אומר כי א' אינו משתי שמות | ||
| + | |- | ||
| + | |If possible, let us say that it is a binomial line. | ||
| + | |style="text-align:right;"|שאם היה איפשר נאמר שיהיה משתי שמות | ||
| + | |- | ||
| + | |We construct the rational line BG. | ||
| + | |style="text-align:right;"|ונשים קו ב"ג מדבר | ||
| + | |- | ||
| + | |We add to it surface GD that is equal to the square formed by A. | ||
| + | |style="text-align:right;"|ונחבר אליו שטח שוה למרובע ההוה מן א' והוא ג"ד | ||
| + | |- | ||
| + | |So, BD is a first apotome. | ||
| + | |style="text-align:right;"|אם כן קו ב"ד הוא הנבדל הראשון <span style=color:red>מצ"ד מזה</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונדביק בו הקו אשר הובדל ממנו והוא ד"ה |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן <sup>שני קוי</sup> ב"ה ה"ד בכח מדברים והם בו לבד משותפים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|< | + | |style="text-align:right;"|וקו ב"ה יוסיף על קו ה"ד ‫<ref>108r</ref>בכח כמו מרובע יהיה מקו ישתתף עמו באורך <span style=color:red>מההקדמה השלישית</span> |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וקו ב"ה משותף באורך לקו ב"ג המדבר <span style=color:red>מההקדמה</span> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וגם כן הנה קו א' משתי שמות באורך | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וקו ב"ג <sup>מדבר</sup> וכבר חובר אליו שטח שוה למרובע ההוה מן א' והיה ג"ד | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ב"ד הוא משתי שמות הראשון ויוחלק בשתי שמות על נקודת ז' ויהיה חלקו הגדול ב"ז <span style=color:red>מנ"ח מזה</span> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|הנה שני קוי ב"ג ז"ד בכח מדברים והם בו לבד משותפים <span style=color:red>מל"ג</span> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וקו ב"ז יוסיף על קו ז"ד בכח כמו מרובע יהיה מקו ישתתף עמו באורך <span style=color:red>מההקדמה הראשונה</span> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וקו ב"ז משותף באורך לקו המדבר אשר הוא ב"ג | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ומפני כי כל אחד משני קוי ה"ב ב"ז משותף באורך לקו ב"ג יהיה קו ב"ה משותף באורך לקו ב"ז <span style=color:red>מי"א מזה</span> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ולזה יהיה גם כן משותף באורך לקו ה"ז <span style=color:red>מי"א מזה</span> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ומפני כי קו ב"ה משותף גם כן לקו ה"ז באורך |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וקו ב"ה כבר היה משותף לקו ד"ה בכח לבד | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן קו ה"ז משותף לקו ה"ד בכח לבד |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן שני קוי ז"ה ה"ד מדברים והם בו לבד משותפים | |
| − | |style="text-align:right;"|אם כן | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ד"ז נבדל <span style=color:red>מע' מזה</span> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|והוא גם כן מדבר בכח | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה בלתי אפשר‫<ref>marg.:זה אי אפשר לפי שאחר שד"ז נבדל הוא אלם והשקר אמנם התחייב מהנחתנו שהוא משני שמות אם כן הקו הנבדל לא יהיה אשר משני שמות</ref> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אם כן | + | |style="text-align:right;"|אם כן לא יהיה הקו הנבדל אשר משתי שמות |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| − | + | ||
| − | + | === Proposition 109 === | |
| − | + | ||
| − | |||
| | | | ||
| − | |||
|- | |- | ||
| − | | | + | |An infinite number of irrational lines arise from the medial line, none of which is of the same type as the preceding. |
| − | + | |style="text-align:right;"|<big>הקו</big> הממוצע יתחדשו ממנו קוים בלתי מדברים אין תכלית להם אין אחד מהם מסוג מה שלפניו | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | | | + | |Let AG be a medial line. |
| − | + | |style="text-align:right;"|<big>ויהיה</big> קו א"ג ממוצע | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | | | + | |I say that an infinite number of irrational lines arise from line AG, none of which is of the same type as the preceding. |
| − | + | |style="text-align:right;"|הנה אומר שיהיה מקו א"ג קוים בלתי מדברים מדברים אין תכלית למספרם אין אחד מהם מסוג מה שלפניו | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | *We draw line AB at a right angle from line AG. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה כי אנחנו נוציא קו א"ב על זויות נצבות מקו א"ג <span style=color:red>מי"א מא‫'</span> |
|- | |- | ||
| − | | | + | |Let line AB be irrational. |
| − | + | |style="text-align:right;"|ויהיה קו א"ב מדבר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ונשלים שטח ב"ג | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן שטח ב"ג בלתי מדבר והקו אשר יגבר עליו <s>ע</s> בלתי מדבר ‫<ref>marg.: =וזה יתבאר בהקש החלוף שאם יהיה מדבר יחדש רוחב מדבר והוא א"ג כמבואר בתמונת י"ו וזה שקר</ref> |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה קו ג"ד שוה לקו אשר יגבר על שטח ב"ג |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ג"ד בלתי מדבר ואינו מסוג אחד מן הקוים אשר אינם מדברים ממה שקדם ‫<ref>marg.: וזה שמרובע א"ז כאשר יחובר אל קו מדבר יחדש רוחב מדבר בכח כמבואר בי"ח ואמנם מרובע ג"ד שהוא שוה לשטח ב"ג כאשר יחובר אל א"ב המדבר הוא יחדש רוחב א"ז שהוא ממוצע ואחר שהרחבים מתחלפים הקוים אם כן מתחלפים וכן יתבאר שד"ז אינו מסוג ג"ד וזה שג"ד כאשר יחובר אל ה"ב א"ב הוא יחדש רוחב א"ג וד"ז כאשר יחובר אל א"ב או אל ג"ה הוא יחדש רוחב ג"ד וכבר בארנו שא"ג ג"ד מתחלפים</ref> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |style="text-align:right;"|< | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וגם כן הנה אנחנו נשלים שטח ד"ה |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ושטח ד"ה בלתי מדבר |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן הקו אשר יגבר עליו בלתי מדבר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ויהיה קו ד"ז שוה לקו אשר יגבר על שטח ה"ד | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו ד"ז בלתי מדבר ואינו מסוג אחד מן הקוים אשר אינם מדברים ממה שקדם לו | |
| − | |style="text-align:right;"|אם כן | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|אם כן קו הקו הממוצע יתחדשו ממנו קוים בלתי מדברים אין תכלית לרבויים אין מהם אחד מסוג מה שלפניו | |
| − | |style="text-align:right;"|אם כן | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|וזה מה שרצינו לבאר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<big>נשלם המאמר העשירי מספר אקלידס החכם | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<sup>ומספר תמונותיו מאה ותשעה</sup> | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונשלמה העתקתו ג אב שנת ל לפרט |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|תהלה לאל בורא עולם</big> |
|} | |} | ||
{| | {| | ||
| Line 17,633: | Line 18,388: | ||
| | | | ||
| − | == Book | + | == Book Eleven == |
| − | + | |style="text-align:right;"|<big>המאמר האחד עשר מספר אקלידס החכם</big> | |
| − | |||
|- | |- | ||
| | | | ||
| − | = | + | *A solid is that which has length, breadth, and depth, and everything that has a body. |
| − | | | + | |style="text-align:right;"|<big>התמונה</big> המוגשמת היא אשר לה אורך ורוחב וגובה וכל מה שיש לו גוף |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :The limits of a solid are a surface. |
| + | |style="text-align:right;"|וקצוות המוגשם פשוט | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *When a straight line stands on a plane and straight lines are drawn in that plane that meet the straight line so that every angle contained by one of those lines and the line is a right angle, the straight line is perpendicular to the plane. |
| + | |style="text-align:right;"|וכאשר עמד קו ישר על שטח והוציאו בשטח ההוא קוים ישרים ימששו הקו הנצב והיתה כל זוית יקיף בה קו מאותם הקוים עם הקו הנצב נצבת הנה הקו הנצב ההוא עמוד על השטח | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>כאשר</big> עמד שטח על שטח והיו כל שני עמודים יצאו מן הקו אשר הוא הפרק המשותף מנקודה אחת ממנו אל כל שני השטחים יקיפו בזוית נצבת הנה שני השטחים יקיפו בזוית נצבת |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|<big>השטחים</big> הנכחיים הם אשר לא ימשש שטח מהם האחר ואפילו הוציאו לכל הצדדים עד לאין תכלית |
| − | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *{{#annot:solids-definition|1247,2531|68bD}}The equal similar solid shapes are those that each solid of which is contained by the same number of surfaces as the number of the surfaces containing the other, and each surface is similar and equal in measure to its corresponding surface in the other solid. |
| + | |style="text-align:right;"|<big>התמונות</big> המוגשמות השוות הדומות הם אשר יקיפו בכל מוגשם מהם ממנין השטחים כמו מנין מה שיקיפו באחר ויהיה כל שטח מאחד מהם דומה ושוה השיעור לשטח אשר הוא גילו מן המוגשם האחר ועל בריאתו{{#annotend:68bD}} | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:solids-definition|1397,2532|oKi8}}The similar solid shapes are those that each solid of which is contained by the same number of surfaces as the number of the surfaces containing the other, and each surface is similar to its corresponding surface in the other solid. | ||
| + | |style="text-align:right;"|<big>התמונות</big> המוגשמות הדומות הם אשר יקיף כל מוגשם מהם ממנין השטחים כמו מנין מה שיקיף באחר ויהיה כל שטח מאחד מהם דומה בשטח אשר הוא גילו מן המוגשם האחר ועל בריאתו{{#annotend:oKi8}} | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:triangular-definition|2111,1100|Dfy8}}A prism is a solid figure contained by three rectangles and two triangles. | ||
| + | |style="text-align:right;"|<big>התמונה</big> המוגשמת המגוררת היא אשר יקיפו בה שלשה שטחים נכחיי הצלעות ושני שטחים משולשים{{#annotend:Dfy8}} | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *{{#annot:definition|1892,1098|sI0K}}The sphere is when the semicircle is drawn round with the diameter fixed in two points, so it does not move, and the arc, which is half the perimeter, revolves until it returns to its position; it is the circular solid. The center of the sphare and the center of the circle are the same. |
| + | |style="text-align:right;"|<div id="Elements_XI_def_sphere"></div><big>הכדור</big> הוא מה שיעבור חצי עגולה כאשר יקוים קו הקוטר בין שני כשורים עד שלא יסור וסבבה הקשת אשר היא חצי הקו המקיף עד שתשוב אל מקומה והוא המוגשם העגול ומרכז הכדור ומרכז העגולה אחד{{#annotend:sI0K}} | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>התמונה</big> המוגשמת המחודדת היא אשר יקיפו בה שטחים יעלו משטח אחד אל נקודה אחת מקבילה אותו |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>התמונה</big> המוגשמת העגולה היא אשר שני תושבותיה שני שטחים ושניהם שתי עגולות |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|<big>השוה</big> שתי קצוות והעובי הוא מה שיעבור שטח שוה הצלעות נצב הזויות כאשר יקוים אחת מצלעותיו המקיפות בזוית נצבת בין שני פלכים עד שלא יסור ויעוגל השטח עד שישוב אל מקומו |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|<big>וחץ</big> התמונה הוא הצלע הקים ונקראת התמונה הזאת האסטונה העגולה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>התמונה</big> המוגשמת המחודדת העגולה היא מה שיעבור משולש נצב הזויות כאשר יקוים אחת מצלעותיו המקיפות בזוית הנצבת בין שני כישורים עד שלא יסור ויסובב המשולש עד שישוב אל מקומו |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>ואם</big> היה הצלע הקים שוה לצלע האחר הנה התמונה נצבת הזויות |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>ואם</big> היה יותר ארוך ממנו הנה היא חדה הזוית |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>וכאשר</big> היה יותר קצר ממנו הנה היא נרחבת הזוית |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>וחץ</big> התמונה היא הצלע הקים ותושבתה היא עגולה וזאת התמונה היא מחודדת האסטונה העגולה |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|<big>הזוית</big> המוגשמת היא אשר יקיפו אותה זויות משוטחות יותר משתי זויות ואינם על שטח אחד ויתקבצו בנקודה אחת | |
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|אשר | + | |style="text-align:right;"|<big>התמונות</big> המוגשמות העגולות השוות שתי הקצוות והעובי והמחודדים העגולים הדומים הם אשר יהיה יחס חץ כל תמונה מהם אל קוטר תושבתה כיחס חץ התמונה האחרת אל קוטר תושבתה |
|- | |- | ||
| | | | ||
| Line 17,700: | Line 18,463: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|א | + | |style="text-align:right;"|<span style=color:red>א</span> <big>הקו</big> הישר לא יהיה חלק ממנו בשטח וחלק בגובה |
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<big>מופתו</big> שאי איפשר ונבאר זה במשל הנה אם היה איפשר נאמר שיהיה חלק מקו אב"ג והוא א"ב בשטח וחלק אחר והוא ב"ג והוא בגובה ונוציא מקו א"ב קו בשטח והוא ב"ד הנה אב"ג הוא קו ישר אם כן א"ב דבק ב"ג ובקו ב"ד על יושר זה שקר <span style=color:red>מפתי' א'</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן לא יהיה חלק מקו ישר בשטח וחלק בגובה וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| − | + | ||
| + | === Proposition 2 === | ||
| + | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<span style=color:red>ב</span> <big>כל שני</big> קוים ישרים יחתכו הנה שניהם בשטח אחד וכל משולש הנה הוא בשטח אחד |
|- | |- | ||
| | | | ||
| − | = | + | |style="text-align:right;"|<big>המשל</big> בו כי שני קוי א"ב ג"ד יחתכו על נקודת ה' הנה אומר כי א"ב ג"ד בשטח אחד ונרשום על שני קוי ד"ה ה"ב שתי נקודות ז"ח ונוציא קו ז"ח הנה אומר כי משולש זה"ח הוא בשטח אחד |
| + | |- | ||
| | | | ||
| + | |style="text-align:right;"|<big>המופת</big> כי הוא אי איפשר זולתו ונבאר זה כי אם היה איפשר זה הנה היה חלק ממשולש זה"ח בשטח וחלק בגובה אם כן שני חלקים משני קוי ז"ה ה"ח בשטח ושני חלקים בגובה זה שקר <span style=color:red>מא'</span> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן משולש זה"ח הוא בשטח אחד והשטח אשר בו משולש זה"ח בו שני קוי ז"ה ה"ח ובו שני קוי א"ב ג"ד אם כן שני קוי א"ב ג"ד בשטח אחד |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן כל שני קוים ישרים יחתכו הנה שניהם בשטח אחד וכל משולש הנה הוא בשטח אחד וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 3 === | === Proposition 3 === | ||
| | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ג | + | |style="text-align:right;"|ג <big>כל שני</big> שטחים יחתכו הנה פרק שניהם המשותף הוא קו אחד ישר |
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<big>המשל</big> בו כי שני שטחי א"ב ג"ד ה"ז ח"ט יחתכו ופרקם משותף הוא כ"ל הנה אומ' כי כ"ל קו אחד ישר | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|המופת | + | |style="text-align:right;"|<big>המופת</big> שהוא אי איפשר שיהיה יותר מקו ונבאר זה שאם היה איפשר הנה נוציא מן ל' אל כ' קו בשטח א"ב ג"ד והוא כמ"ל ונוציא מכ' אל ל' קו בשטח ה"ז ח"ט והוא כנ"ל אם כן כמ"ל קו ישר וכנ"ל קו ישר מתחברים אם כן שני קוי כמ"ל כנ"ל ישרים מתקרבים יפגשו קצוות שניהם בכל שתי הצדדים זה שקר אם כן כ"ל הוא קו אחד ישר וזה מה שרצינו לבאר |
|- | |- | ||
| | | | ||
| + | |||
=== Proposition 4 === | === Proposition 4 === | ||
| | | | ||
| + | |- | ||
| + | |When a perpendicular line stands at the intersection point of two intersecting lines, then it is also perpendicular to the plane passing through them. | ||
| + | |style="text-align:right;"|ד <big>כאשר</big> עמד עמוד על פרק שני קוים ישרים יחתכו הנה הוא עמוד על שטח שניהם | ||
| + | |- | ||
| + | |Example: line AB is perpendicular stands at the common intersection point of two lines GD and HZ. | ||
| + | |style="text-align:right;"|<big>המשל</big> בו כי קו א"ב עמוד נצב על פרק שני קוי ג"ד ה"ז המשותף | ||
| + | |- | ||
| + | |Supposition: I say that line AB is perpendicular to plane GD. | ||
| + | |style="text-align:right;"|הנה אומר כי קו א"ב עמוד נצב על שטח ג"ד | ||
| + | |- | ||
| + | |Proof: | ||
| + | |style="text-align:right;"|<big>המופת</big> | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *<math>\scriptstyle BH=BZ=DB=BG</math> |
| + | |style="text-align:right;"|שיהיו קוי ב"ה ב"ז ד"ב ב"ג הנחלקים שוים | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *We draw two lines HG and DZ. |
| + | |style="text-align:right;"|ונוציא שני קוי ה"ג ד"ז | ||
|- | |- | ||
| | | | ||
| − | = | + | *We draw line TK from K on plane GDHZ. |
| + | |style="text-align:right;"|ונוציא מן כ' קו בשטח ג"ד ה"ז והוא ט"כ | ||
| + | |- | ||
| | | | ||
| + | *We place point C on AB. | ||
| + | |style="text-align:right;"|ונרשום על א"ב נקודת ח' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ה | + | *We draw lines HC, DC, CZ, CG, CK and CT. |
| + | |style="text-align:right;"|ונוציא קוים ה"ח ד"ח ח"ז ח"ג ח"כ ח"ט | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :*<math>\scriptstyle CK=BZ</math> |
| + | |style="text-align:right;"|הנה צלע ה"ב כמו ב"ז | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle GB=BD</math> | ||
| + | |style="text-align:right;"|וג"ב כמו ב"ד | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:red>I.4, 15, 27:</span> <math>\scriptstyle HG\parallel DZ\;HG=DZ</math> | ||
| + | |style="text-align:right;"|אם כן ה"ג ד"ז נכחיים ושוים <span style=color:red>מט"ו וד' וכ"ז מא‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle GB=BD</math> | ||
| + | |style="text-align:right;"|וג"ב כמו ב"ד | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle BC\perp GD</math> | ||
| + | |style="text-align:right;"|וב"ח עמוד על ג"ד | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:red>I.4:</span> <math>\scriptstyle CG=CD</math> | ||
| + | |style="text-align:right;"|אם כן ח"ג כמו ח"ד <span style=color:red>מד' מא‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle HB=BZ</math> | ||
| + | |style="text-align:right;"|וגם כן ה"ב כמו ב"ז | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle BC\perp HZ</math> | ||
| + | |style="text-align:right;"|וב"ח עמוד על ה"ז | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:red>I.4:</span> <math>\scriptstyle HC=CZ</math> | ||
| + | |style="text-align:right;"|אם כן ה"ח כמו ח"ז <span style=color:red>מד' מא‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle GC=CD</math> | ||
| + | |style="text-align:right;"|אם כן צלע ג"ח כמו ח"ד | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle HG=DZ</math> | ||
| + | |style="text-align:right;"|וה"ג כמו ד"ז | ||
| + | |- | ||
| + | | | ||
| + | *CG and GH are equal to CD and DZ | ||
| + | |style="text-align:right;"|אם כן שני קוי ח"ג ג"ה שוים לשני קוי ח"ד ד"ז | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle HC=CZ</math> | ||
| + | |style="text-align:right;"|ותושבת ה"ח כמו תושבת ח"ז | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:red>I.8:</span> <math>\scriptstyle\measuredangle CGH=\measuredangle HDZ</math> | ||
| + | |style="text-align:right;"|אם כן זוית חג"ה כמו זוית הד"ז <span style=color:red>מח' מא‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וקו ט"ג ד"ב נכחיים וכבר הוצאו אל שניהם ט"כ ג"ד | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:red>I.29:</span> <math>\scriptstyle\measuredangle GTB=\measuredangle KBD</math> | ||
| + | |style="text-align:right;"|אם כן זוית גט"ב שוה לזוית כב"ד <span style=color:red>מכ"ט מא‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\measuredangle BGT=\measuredangle BDK</math> | ||
| + | |style="text-align:right;"|וזוית בג"ט שוה לזוית בד"כ | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle GB=BD</math> | ||
| + | |style="text-align:right;"|וג"ב כמו ב"ד | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:red>I.26:</span> <math>\scriptstyle TG=DK</math> | ||
| + | |style="text-align:right;"|אם כן ט"ג כמו ד"כ <span style=color:red>מכ"ו מא‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | *CG and GT are equal to CD and DK | ||
| + | |style="text-align:right;"|אם כן שני קוי ח"ג ג"ט שוים לשני קוי ח"ד ד"כ | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\measuredangle CGT=\measuredangle CDK</math> | ||
| + | |style="text-align:right;"|וזוית חג"ט שוה לזוית חד"כ | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:red>I.4:</span> <math>\scriptstyle TC=CK</math> | ||
| + | |style="text-align:right;"|אם כן תושבת ט"ח כמו תושבת ח"כ <span style=color:red>מד' מא‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle TK=BK</math> | ||
| + | |style="text-align:right;"|וצלע ט"כ כמו צלע ב"כ | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכ"ח משותף | ||
| + | |- | ||
| + | | | ||
| + | *TB and BC are equal to KB and KC | ||
| + | |style="text-align:right;"|אם כן שני קוי ט"ב ב"ח יהיו שוים כ"ב כ"ח | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle TC=CK</math> | ||
| + | |style="text-align:right;"|ותושבת ט"ח כמו תושבת ח"כ | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:red>I.8:</span> <math>\scriptstyle\measuredangle CBK=\measuredangle CBT</math> | ||
| + | |style="text-align:right;"|אם כן שתי זויות חב"כ וחב"ט שוות <span style=color:red>מח' מא‫'</span> | ||
| + | |- | ||
| + | |<span style=color:red>def.</span> | ||
| + | |style="text-align:right;"|אם כן שתיהם נצבות <span style=color:red>מפתיחת מא‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן ח"ב עמוד על ט"כ וכן יתבאר כי כל קו יצא מן ב' בשטח שני קוי ג"ד ה"ז הנה הוא יקיף עם ח"ב בזוית נצבת | ||
| + | |- | ||
| + | |<span style=color:red>def.</span> | ||
| + | |style="text-align:right;"|אם כן קו כ"א הוא עמוד על שטח ג"ד ה"ז <span style=color:red>מפתיחת זה</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 5 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ה <big>כאשר</big> עמד קו על פרק משותף לשלשה קוים יקיף עם כל קו מהם בזוית נצבת הנה הקוים השלשה בשטח אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<big>המשל</big> בו כי קו א"ב נצב על פרק משותף לשלשה קוים ב"ג ב"ד ב"ה על זויות נצבות הנה אומר כי ב"ג ב"ד ב"ה בשטח אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<big>המופת</big> כי איפשר שיהיה קו מהם בזולת שטח האחר ונבאר זה שאם היה איפשר הנה היה ב"ד בשטח בגובה הנה שטח א"ב ב"ד הנה יחלק שטח ג"ב ב"ה ויחלקהו ויהיה חלוקם המשותף קו ב"ז [מג'] ותהיה זוית אב"ז נצבת וכבר היתה זוית אב"ד נצבת א"ב ב"ד ב"ז בשטח אחד הנה זוית אב"ז אם כן שוה לזוית אב"ד הגדולה לקטנה זה שקר אם כן ב"ג ב"ד ב"ה בשטח אחד | ||
| + | |- | ||
| + | | | ||
| + | === Proposition 11 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<span style=color:red>י"א</span> <big>נרצה</big> שנוציא מנקודה מונחת בגובה קו יהיה עמוד על שטח מונח | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה נשים הנקודה המונחת נקודת א' ונרצה שנוציא ממנה עמוד נצב על השטח המונח ונתחיל ונקוה בשטח קו ישר איך מה שיפול והוא ב"ג ונוציא מנקודת א' אל קו ב"ג עמוד על קו ב"ג והוא א"ד ונוציא מן ד' בשטח המונח עמוד על ב"ג והוא ד"ה ונוציא מן א' אל קו ד"ה עמוד נצב על ד"ה והוא א"ז הנה אומר כי א"ז עמוד על השטח המונח | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<big>המופת</big> אנחנו נוציא מן ז' קו יהיה נכחי אל ב"ג בשטח המונח והוא ח"ט | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן קו ב"ג עמוד על פרק משותף לשני קוי ז"ד ד"א <span style=color:red>מד' מזה</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle BG\perp ZDDA</math> | ||
| + | |style="text-align:right;"|אם כן קו ב"ג עמוד על שטח ז"ד ד"א | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle BG\parallel CT</math> | ||
| + | |style="text-align:right;"|וב"ג יהיה נכחי אל ח"ט | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle CT\perp ZDDA</math> | ||
| + | |style="text-align:right;"|אם כן ח"ט עמוד נצב על שטח ז"ד ד"א <span style=color:red>מח' מזה</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וז"א הוא בשטח ז"ד ד"א | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle CT\perp AZ</math> | ||
| + | |style="text-align:right;"|אם כן ח"ט עמוד על א"ז | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle AZ\perp CT\quad CT\perp HD</math> | ||
| + | |style="text-align:right;"|וא"ז עמוד על ח"ט והוא גם כן עמוד על ה"ד | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle AZ\perp HD\quad AZ\perp CT</math> | ||
| + | |style="text-align:right;"|אם כן א"ז עמוד נצב על ה"ד ועל ח"ט | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle AZ\perp HZCT</math> | ||
| + | |style="text-align:right;"|אם כן א"ז עמוד על שטח הזח"ט | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ושטח הזח"ט הוא השטח המונח וא"ז עמוד נצב עליו | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה כבר הוצאנו מנקודת א' אשר היא בגובה המונח עמוד נצב על השטח המונח והוא א"ז | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 12 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|י"ב נרצה שנעמיד על שטח מונח על נקודה ידועה ממנו עמוד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונשים הנקודה א' ונרצה שנעמיד על נקודת א' עמוד על השטח המונח ונניח בגובה נקודת ב' איך מה שנפלה ונוציא ממנה עמוד על השטח המונח והוא ב"ג ונוציא מן א' קו יהיה נכחי אל ג"ב והוא א"ד הנה אומר כי א"ד עמוד על השטח המונח | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המופת כי א"ד הוא נכחי אל ב"ג וב"ג עמוד על השטח המונח הנה א"ד עמוד על השטח המונח | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה כבר העמדנו על השטח המונח על נקודת א' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 13 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|י"ג לא יעמוד על שטח אחד שני עמודים על נקודה אחת מן השטח | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המופת שהוא אי איפשר ויתבאר זה במשל שאם היה איפשר הנה נעמיד על נקודת א' שני עמודים על השטח המונח והם א"ב א"ג ויהיה קו ד"ה פרק משותף לשני שטחים אם כן זוית בא"ה נצבת וזוית גא"ה נצבת אם כן שתיהן שוות הגדולה לקטנה זה שקר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן אי איפשר שיעמדו על נקודה אחת שני עמודים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 14 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|י"ד כאשר היה קו אחד עמוד על שני שטחים הנה השני שטחים כאשר הוצאו בכל הצדדים לא יפגשו ואפי' הוצאו בכל הצדדים לאין תכלית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המשל בו שיהיה קו א"ב עמוד על שני שטחי ג"ד ח"ט הנה אומר כי שני שטחי ג"ד ח"ט נכחיים וששניהם כאשר הוצאו עד לאין תכלית לא יפגשו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המופת שהוא אי איפשר ונבאר זה שאם היה איפשר הנה יפגשו ותהיה פגישת שניהם פרק משותף והוא קו כ"ל ונרשום על כ"ל נקודת מ' איך מה שתפול ונוציא שני קוי א"'מ כ"מ הנה כ"ל הוא בשטח ג"ד וכל הנקודות אשר בו הם בשטח ג"ד אם כן א"מ בשטח ג"ד וכל עמוד על שטח הנה הוא עמוד על קו יצא בשטח וימשש העמוד אם כן זוית מא"ב נצבת ולכן זוית אב"מ נצבת אם כן שתי זויות ממשולש אב"מ שתי נצבות זה שקר אם כן שני שטחי ג"ד ח"ט כאשר הוצאו בכל הצדדים לא יפגשו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזהו מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 33 === | ||
| + | | | ||
| + | |- | ||
| + | |Parallelepipedal solids, whose heights are the same: the ratio of the solid to the solid is as the ratio of its base to its base. | ||
| + | |style="text-align:right;"|ל"ג המוגשמים נכחיי השטחים כאשר היה רומם בשיעור אחד הנה יחס המוגשם אל המוגשם כיחס תושבתו אל תושבתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המשל בו כי שני {{#annot:term|2556,2557|5wo6}}מוגשמי כ"ב וז"ל נכחי השטחים{{#annotend:5wo6}} ורומם בשיעור אחד הנה אומר כי יחס תושבת אבג"ד אל תושבת הזח"ט כיחס מוגשם כ"ב אל מוגשם ז"ל | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle DGMN=HZCT</math> | ||
| + | |style="text-align:right;"|המופת כי נשים תושבת ד"ג מ"נ שוה לתושבת הזח"ט | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונשלים מוגשם ס"ג וכל {{#annot:term|2556,2557|w1JC}}מוגשם נכחיי השטחים{{#annotend:w1JC}} יבדילהו שטח על נכחות שני שטחים מקבילים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה הוא יחלקהו בשני חלקים יהיה יחס אחד משניהם אל האחר כיחס תושבתו אל תושבתו [מכ"ה מזה] | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle ABGD:DGMN=KB:GS</math> | ||
| + | |style="text-align:right;"|אם כן יחס תושבת אבג"ד אל תושבת דגמ"נ כיחס מוגשם כ"ב אל מוגשם ג"ס | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle DGMN=HZCT</math> | ||
| + | |style="text-align:right;"|ותושבת דגמ"נ כמו תושבת הזח"ט | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle GS=ZL</math> | ||
| + | |style="text-align:right;"|ומוגשם ג"ס כמו מוגשם ז"ל | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle ABGD:HZCT=KB:ZL</math> | ||
| + | |style="text-align:right;"|אם כן יחס תושבת אבג"ד אל תושבת הזח"ט כיחס כ"ב אל מוגשם ז"ל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 40 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<span style=color:red>מ</span> <big>כל</big> מעוקב יובדלו צלעות שני שטחים משטחיו מקבילים כל צלע בשני חציים אחר כן יצאו ממקומות ההבדלים שני שטחים יבדילו המעוקב ויבדיל כל אחד משניהם האחר הנה הבדל שניהם המשותף יחתוך קוטר המעוקב בשני חציים ויחתכהו הקוטר בשני חציים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המשל בו כי שני שטחי מעוקב א"ב המקבילים ג"ד א"ה ז"ח ט"כ הנה כבר הובדלו צלעות שניהם והם ג"ד ד"א א"ה ה"ג ב"ז ז"ח ח"ט ט"ב כל צלע בשני חציים על נקודת כ' ל' מ' נ' ס' ע' פ' ק' והוצא ממקומות ההבדלים שני שטחים והם כ"מ פ"ס ונ"ל ע"ק יבדילו המעוקב ויבדיל כל אחד משניהם האחר והבדלם המשותף קו ר"ש וקוטר המעוקב קו ב"א הנה אומר כי כל אחד מן ר"ש ב"א יחתוך האחד בשני חציים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<big>המופת</big> כי נוציא קוים ג"ר ר"א ב"ש ש"ח | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle GH=DA</math> | ||
| + | |style="text-align:right;"|הנה ג"ה ישוה ד"א | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\frac{1}{2}GH=GN</math> | ||
| + | |style="text-align:right;"|וחצי ג"ה הוא ג"נ | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\frac{1}{2}DA=LA</math> | ||
| + | |style="text-align:right;"|וחצי ד"א הוא ל"א | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle GN=LA</math> | ||
| + | |style="text-align:right;"|וג"נ ישוה ל"א | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle RN=LR</math> | ||
| + | |style="text-align:right;"|ור"נ ישוה ר"ל | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle\longrightarrow GN+NR=AL+LR</math> | ||
| + | |style="text-align:right;"|הנה כל ג"נ נ"ר כמו כל א"ל ל"ר כל אחד כמו גילו | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle\measuredangle GNR=\measuredangle ALR</math> | ||
| + | |style="text-align:right;"|וזוית גנ"ר כמו זוית אל"ר | ||
| + | |- | ||
| + | | | ||
| + | :I.4: <math>\scriptstyle GR=RA</math> | ||
| + | |style="text-align:right;"|אם כן תושבת ג"ד כמו תושבת ר"א <span style=color:red>מד' מא'</span> | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle\triangle GNR=\triangle ALR</math> | ||
| + | |style="text-align:right;"|ומשולש גנ"ר כמו משולש אל"ר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ושאר הזויות כמו שאר הזויות אשר יהיו מיתריהם הצלעות השוות | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle\measuredangle GRN=\measuredangle LRA</math> | ||
| + | |style="text-align:right;"|זוית גר"נ כמו זוית לר"א | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיה זוית נר"א משותפת | ||
| + | |- | ||
| + | | | ||
| + | ::<math>\scriptstyle\measuredangle GRN+\measuredangle NRA=\measuredangle LRA+\measuredangle ARN</math> | ||
| + | |style="text-align:right;"|אם כן שתי זויות גר"נ נר"א שוות לשתי זויות לר"א אר"נ | ||
| + | |- | ||
| + | | | ||
| + | :I.13: <math>\scriptstyle\measuredangle LRA+\measuredangle ARN=90^\circ+90^\circ</math> | ||
| + | |style="text-align:right;"|אבל שתי זויות לר"א אר"נ ישוו שתי נצבות <span style=color:red>מי"ג מא'</span> | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle\measuredangle GRN+\measuredangle NRA=90^\circ+90^\circ</math> | ||
| + | |style="text-align:right;"|אם כן שתי זויות גר"נ נר"א ישוו שתי נצבות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכבר יצא מקו ר"נ מנקודת ד' שני קוים ר"נ ר"א בשני צדדים מתחלפים ויהיו שתי זויות גר"נ נר"א ישוו שתי נצבות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן יהיו שני קוי ג"ר ר"א קו אחד ישר <span style=color:red>מי"ד מא'</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ולכן יהיו שני קוי ב"ש ש"ח קו אחד ישר | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle GB=HT\quad AC=HT</math> | ||
| + | :<math>\scriptstyle GB\parallel HT\quad AC\parallel HT</math> | ||
| + | |style="text-align:right;"|וכל אחד מן ג"ב א"ח ישוה ה"ט והם נכחיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנכחיים לקו ואינם בשטח אחד הנה הם נכחיים | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle GB=AC\quad GB\parallel AC</math> | ||
| + | |style="text-align:right;"|אם כן ג"ב א"ח נכחיים שוים ונדבקים בקצוות ג"א ב"ח | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle GA=BC\quad GA\parallel BC</math> | ||
| + | |style="text-align:right;"|אם כן ג"א ב"ח שוים נכחים <span style=color:red>מל"ג מא'</span> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\frac{1}{2}GA=RA</math> | ||
| + | |style="text-align:right;"|וחצי ג"א הוא ר"א | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\frac{1}{2}BC=B\hat S</math> | ||
| + | |style="text-align:right;"|וחצי ב"ח הוא ב"ש | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle RA=B\hat S\quad RA\parallel B\hat S</math> | ||
| + | |style="text-align:right;"|אם כן ר"א ב"ש שוים נכחיים ונדבקים בקצוות ר"ש א"ב | ||
| + | |- | ||
| + | | | ||
| + | :I.29; I.46: <math>\scriptstyle RT=T\hat S\quad AT=TB</math> | ||
| + | |style="text-align:right;"|אם כן ר"ת ישוה ת"ש וא"ת ישוה ת"ב <span style=color:red>מכ"ט ומ"ו מא'</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה כבר חתך כל אחד מן א"ב ר"ס האחד בשני חצאים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 41 === | ||
| + | | | ||
| + | |- | ||
| + | |For every two prisms whose heights are equal, if the base of one of them is a triangle, the base of the other is parallelogram, and it is double the base of the other, which is the triangle, then both prisms are equal. | ||
| + | |style="text-align:right;"|<span style=color:red>מא</span> <big>כל</big> שני מגוררים רום שניהם שוים ותושבת אחד משניהם משולש ותושבת האחר נכחית הצלעות והיא כפל תושבת האחר המשולש הנה שני המגוררים שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המשל בו כי שני מגוררי א"ב ג"ד ה"ז ח"ט כ"ל מ"נ רום שניהם שוים ותושבת אחד משניהם משולש והיא נכ"ל ותושבת האחר נכחית הצלעות והוא בגד"ה הנה אומר כי שני המגוררים שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<big>המופת</big> שנשלים שני מוגשמי א"ד ח"ל הנכחיים | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\Box_{BGDH}=2\sdot\triangle_{NKL}</math> | ||
| + | |style="text-align:right;"|הנה נכחי בגד"ה הוא כפל משולש נכ"ל | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\Box_{NL}=2\sdot\triangle_{NKL}</math> | ||
| + | |style="text-align:right;"|ונכחי נ"ל הוא כפל משולש נכ"ל | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle\Box_{BD}=\Box_{NL}</math> | ||
| + | |style="text-align:right;"|אם כן שתי תושבות ב"ד נ"ל הנכחיי הצלעות שוות | ||
| + | |- | ||
| + | | | ||
| + | :XI.32: <math>\scriptstyle AD=CL</math> | ||
| + | |style="text-align:right;"|אם כן מוגשם א"ד ח"ל שוים הרום נכחיי השטחים על שתי תושבות שוות אם כן שתיהן שוות <span style=color:red>מל"ב</span> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\frac{1}{2}AD=ABGDHZ</math> | ||
| + | |style="text-align:right;"|אבל חצי א"ד הוא מגורר א"ב ג"ד ה"ז | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle\frac{1}{2}CL=CTKLMN</math> | ||
| + | |style="text-align:right;"|וחצי ח"ל הוא מגורר ח"ט כ"ל מ"נ | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle ABGDHZ=CTKLMN</math> | ||
| + | |style="text-align:right;"|אם כן שני מגוררי א"ב ג"ד ה"ז ח"ט כ"ל מ"נ שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשלם המאמר האחד עשר ת"ל | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Book Twelve == | ||
| + | |||
| + | !style="text-align:right;"|המאמר השנים עשר מספר אקלידס החכם | ||
| + | |- | ||
| + | | | ||
| + | === Proposition 1 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|א כל שתי שטחים רבי הזויות דומים בשתי עגולות הנה יחס אחד משניהם אל האחר כיחס מרובעי שני קוטרי שתי העגולות אחד מהם אצל האחר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המשל בו כי שני שטחי א"ב גד"ה וח"ט כ"ל רבי הזויות מתדמים בשתי עגולות שני קטריהם ב"ז ט"נ הנה אומר כי יחס שטח א"ב גד"ה אל שטח ח"ט כ"ל מרבי הזויות כיחס מרובע קוטר ב"ז אל מרובע קוטר ט"נ | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המופת שנוציא קוים כ"ה א"ז ט"מ ח"נ הנה יחס ב"א אל ט"ח כיחס א"ה אל ח"מ ושתי זויות בא"ה טח"מ השוות יקיפו בהם צלעות מתיחסות אם כן [מו' ומד' מו'] משולש אב"ה ידמה משולש חט"מ אם כן זויות אה"ב כמו זוית חמ"ט וזוית אה"ב [מכ' מג'] כמו זוית אז"ב וזוית חמ"ט כמו זוית חנ"ט אם כן זוית אז"ב כמו זוית חנ"ט וזוית בא"ז [מל' מג'] נצבת שוה לזוית טח"נ ונשארה זוית אב"ז כמו זוית חט"נ הנשארת אם כן משולש אב"ז שוה הזויות למשולש חט"נ אם כן יחס ז"ב אל נ"ט כיחס ב"א אל ט"ח אם כן [מסוף י"ח מו'] יחס מרובע ב"ז אל מרובע ט"נ הוא יחס ב"ז אל ט"נ שנוי ויחס א"ב גד"ה אל ח"ט כ"ל מרבי הזויות הוא [מי"ט מו'] יחס א"ב אל ח"ט שנוי ויחס ב"ז אל ט"נ כיחס א"ב אל ח"ט אם כן יחס מרובע ב"ז אל מרובע ט"נ כיחס שטח א"ב גד"ה אל שטח ח"ט כל"מ רבי הזויות וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | === Proposition 2 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ב כל שתי עגולות הנה יחס אחד משתיהן אל האחרת כיחס שני מרובעי שני קטריהם אחד מהם אל האחר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המשל בו כי שתי עגולות אבג"ד ה"ז ח"ט קטרי שניהם ב"ד ז"ט הנה אומר כי יחס מרובע קוטר ב"ד אל מרובע קוטר ז"ט כיחס עגולת א"ב ג"ד אל עגולה ה"ז ח"ט | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המופת כי אי איפשר זולתו ונבאר זה כי אם היה איפשר נאמר שיהיה יחס מרובע ב"ד אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל שטח הוא יותר גדול או יותר קטן מעגולת ה"ז ח"ט ויהיה ראשונה אל שטח הוא יותר קטן ממנה ויהיו ת' ויהיו ת"כ מקובצים כמו עגולת ה"ז ח"ט ונקוה בעגולת ה"ז ח"ט מרובע ה"ז ח"ט ויחתכו קשתות ה"ז ז"ח ח"ט ט"ה כל אחת בשני חציים על נקודת כ' ל' מ' נ' ונוציא מיתרי ה"כ כ"ז ז"ל ל"ח ח"מ מ"ט ט"נ נ"ה הנה כל אחד ממשולשי הכ"ז זל"ח חמ"ט טנ"ה הוא יותר גדול מחצי חתיכת העגולה אשר בה המשולש וכאשר עשינו זה פעמים הנה תשאר לנו חתיכות מן העגולה כלם יותר קטן משטח כ' ותשאר ויהיו חתיכות ה"כ כ"ז ז"ל ל"ח ח"מ מ"ט ט"נ נ"ה הנה עגולת ה"ז ח"ט יותר גדולה משטח כ' וכבר חסר מהגדול יותר מחציו ועשה זה פעמים וישאר [מא' מי'] מה שהוא יותר קטן מן כ' ויהיה שטח ה"כ ז"ל ח"מ ט"נ הרב הזויות יותר גדול מן ת' ויקיפו בעגולת א"ג שטח רבי הזויות דומה בשטח ה"כ ז"ל ח"מ ט"נ והוא שטח א"ס ב"ע ג"פ ד"ק הנה יחס מרובע ד' אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל שטח ת' אבל יחס מרובע ב"ד אל מרובע ז"ט כיחס שטח א"ס ב"ע ג"פ ד"ק הרב הזויות אל שטח ה"כ ז"ל ח"נ מ"ט הרב הזויות אם כן [מי"ח מה'] יחס עגולת א"ב ג"ד אל שטח ת' כיחס שטח א"ס ב"ע ג"פ ד"ק אל שטח הכז"ל חנמ"ט וכאשר המירונו [מי"ו מה'] יהיה יחס עגולת א"ב ג"ד אל השטח הרב הזויות אשר בה כיחס שטח ת' אל שטח הכז"ל חמנ"ט הרב הזויות ועגולת א"ב ג"ד היא יותר גדולה מן הרב הזויות אשר בה ושטח ת' אם כן יותר גדול מן הכל"ז חמנ"ט הרב הזויות אבל ת' היה יותר קטן ממנו כמו שבארנו זה שקר אי איפשר אם כן אין יחס מרובע ב"ד אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל שטח הוא יותר קטן מעגולת ה"ז ח"ט | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה אומר ולא אל שטח הוא יותר גדול שאם היה איפשר נאמר שיהיה אל ת' והוא יותר גדול ממנה הנה יחס מרובע ב"ד אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל שטח ת' וכאשר חלפנו היה יחס מרובע ז"ט אל מרובע ב"ד כיחס שטח ת' אל עגולת א"ב ג"ד וכיחס עגולת ה"ז ח"ט אל שטח הוא יותר קטן מעגולת א"ב ג"ד אם כן יחס מרובע ט"ז אל מרובע ד"ב כיחס עגולת ה"ז ח"ט אל שטח הוא יותר קטן מעגולת א"ב ג"ד וכבר ביארנו כי זה שקר אי איפשר אם כן אין יחס מרובע ב"ד אל מרובע ז"ט כיחס מרובע א"ב ג"ד אל שטח הוא יותר גדול מעגולת ה"ז ח"ט וכבר ביארנו ולא אל יותר קטן ממנו אם כן יחס מרובע ב"ד אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל עגולת ה"ז ח"ט וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | === Proposition 6 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<div id="Elements_XII_6"></div>כל מגורר הנה הוא אפשר שיחלקו ממנו שלשה מחודדים שוים ותושבותיהם משולשים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 15 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ט"ו כל שני כדורים הנה יחס אחד משניהם אל האחר הוא יחס קוטרו אל קוטרו משולש | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המשל בו כי נניח שתי כדורים א"ב ג"ד ה"ז ח"ט וקוטרי שניהם ב"ד ז"ט הנה אומר כי יחס כדור א"ב ג"ד אל כדור ה"ז ח"ט הוא יחס קוטר ב"ד אל קוטר ז"ט משולש | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המופת כי אי איפשר זולתו ובאור זה שאם היה איפשר נאמר שיהיה יחס כדור א"ב ג"ד אל כדור הוא יותר קטן או יותר גדול מכדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש ויהיה תחלה אל כדור הוא יותר קטן ממנו והוא כדור א' ויהיה כדור כ"ל מ"נ על מרכז ה"ז ח"ט שוה לכדור א' ויהיו שני כדורים על מרכז אחד ונעשה [מי"ד] בכדור ה"ז ח"ט הגדול מוגשם רב התושבות יקיפו בו בלתי ממשש לפשט כדור כ"ל מ"נ הקטן ונעשה בכדור א"ב ג"ד מוגשם דומה לרב התושבות אשר בכדור ה"ז ח"ט הנה יחס כדור א"ב ג"ד אל כדור א' כיחס ב"ד אל ז"ט משולש ויחס רב התושבות אשר בכדור א"ב ג"ד אל הרב התושבות אשר בכדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש אם כן יחס כדור א"ב ג"ד אל כדור א' כיחס רב התושבות אשר בכדור א"ב ג"ד אל הרב התושבות אשר בכדור ה"ז ח"ט וכאשר המירונו יהיה יחס כדור א"ב ג"ד אל הרב התושבות אשר בו כיחס כדור א' אל הרב התושבות אשר בכדור ה"ז ח"ט הרב התושבות אשר בו וכדור א"ב ג"ד יותר גדול מן הרב התושבות אשר בו אם כן כדור א' יותר גדול מן הרב התושבות אשר בו אם כן כדור א' יותר גדול מן הרב התושבות אשר בכדור ה"ז ח"ט אבל הרב התושבות אשר בכדור ה"ז ח"ט יקיף בכדור כ"ל מ"נ השוה לכדור א' זה שקר אי איפשר אם כן אין יחס כדור א"ב ג"ד אל כדור הוא יותר קטן מכדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואומר ולא אל כדור הוא יותר גדול ממנו ונבאר כי זה אי איפשר שאם היה איפשר נאמר שיהיה אל כדור א' והוא יותר גדול ממנו ונשוב בתואר הנה יחס כדור א' אל כדור א"ב ג"ד הוא יחס ז"ט אל ב"ד משולש ויחס כדור א"ב אל כדור א"ב ג"ד כיחס ה"ז ח"ט אל כדור הוא יותר קטן מכדור א"ב ג"ד אם כן יחס כדור ה"ז ח"ט אל כדור הוא יותר קטן מכדור א"ב ג"ד הוא כיחס ז"ט אל ב"ד משולש זה שקר אי איפשר שכבר ביארנו זה אם כן אין יחס כדור א"ב ג"ד אל כדור הוא יותר קטן ולא אל יותר גדול מכדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש אם כן יחס כדור א"ב ג"ד אל כדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשלם המאמר השנים עשר מספר אקלידס החכם ת"ל | ||
| + | |- | ||
| + | | | ||
| + | == Book Fourteen == | ||
| + | |style="text-align:right;"|<big>המאמר הארבעה עשר</big> אשר יאות באקלידס אשר מספר אספקלאוס | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי אפסלידס אשר היה מאנשי סוראה וטרוגס כאשר בא אלכסנדריה פגש אביו אשר היה בין שניהם מקורבת השתוף בעיון בחכמות הלמודיות העמיד אצלו רוב זמן ימי חיו והכירו ובחנו בקצת מאמריהם מה שכתב אבלניוס בהיקש התמונה אשר לה שתים עשרה תושבות ואשר לה העשרים העשויות בכדור אחד כל אחד מהם אל <s>אחד מהם אל</s> חבירו ואיזה יחס לכל אחת משתיהם אל האחרת <s>וצ"ס</s> וסברו כי ה<s>מ</s>ספר אשר חבר אבלניוס בשער הזה אינו על יושר וחפשו המאמרים אשר בספר הזה <s>ואמונות</s> <sup>ואמתו</sup> וכתבו מה שעשו כמו ששמעתי מאבי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואולם אני הנה נפל בידי אחר זה ספר אחר לאבלניוס עשה בו התמונות אשר זכרנו במופתים אמתיים והועיל בהם תועלת גדולה בידיעה באלו <ref>133v</ref>הדברים אשר זכרנו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואולם הספר אשר חברו אבלוניוס הנה כבר אפשר לנו יחד שנשתתף בעיון וזה כי הוא ספר כבר הגיע לאנשים ונפל ביד רבים מהם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואולם מה שהנחנו אנחנו מאחריו ופרשנו בו עניינים כל מה שראינו שראוי לפרשו והנה ראינו שנכתבנו אליך כי היינו <sup>היית</sup> חזק להכיר מה שיאמר ולהגיעו לך להיותך <s>מקדים</s> <sup>זריז ומהיר</sup> בכל החכמות הלמדיות וביחוד בחכמת התשבורת והיותך <s>אתה הרבה מן הלמוד</s> <sup>ששקידתך והשתדלותך בלמוד הזה</sup> ולפי דעתינו לא שמעת מה שנאמר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה כבר הגיע לעזוב מה שאנו בו מזאת הפתיחת ונתחיל בענין מה שנרצה לדבר בו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונאמר העמוד אשר יצא ממרכז עגולת מה אל צלע המחומש אשר הקיף באותה עגולה <s>אשר יקובצו ותהיה עליה אב"ג</s> הוא שוה לחצי הקו אשר יצא ממרכז אותה העגולה אל הקו המקיף בה עם חצי צלע המעושר אשר יקיף באותה עגולה כאשר יקובצו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ותהיה <sup>עגולה</sup> עליה אב"ג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיה בעגולת אב"ג צלע מחומש שוה הצלעות והוא ב"ג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיה מרכז העגולה ד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונוציא ממנו אל ב"ג עמוד ד"ה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונוציא <sup>קו</sup> ה"ז על יושר קו ד"ה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה אומר כי קו ד"ה שוה לחצי צלע המשושת ו<sup>חצי</sup> צלע המעושר אשר יקיפו בעגולה הזאת כאשר יקובצו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה כי אנחנו נוציא שני קוי ד"ג <s>ג"ח</s> <sup>ג"ח</sup> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיה קו ה"ח שוה לקו ה"ז | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<s>ונגיע במה שבין שתי נקודות ז"ג בקו ז"ג קשת ז"ג ביחס</s> <sup>ונמשיך ה"ג הנה בעבור שיהיה כל הקו המקיף בעגולה חמשה דמיוני קשת ב"ג והיה חצי כל הקו המקיף בעגולה קשת אג"ז וחצי קשת בז"ג קשת א"ג היה קשת אג"ז חמשה דמיוני קשת ג"ז הנה קשת א"ז ארבעה דמיוני קשת ז"ג ויחס קשת א"ג אל קשת ז"ג כיחס זוית אד"ג אל זוית</sup> זוית אד"ג אל זוית זד"ג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן זוית אד"ג ארבעה דמיוני זוית זד"ג | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Book Fifteen by Hyspikleos [hypsicles] which is suitable for Euclid the Wise == | ||
| + | |||
| + | |style="text-align:right;"|<big>המאמר החמשה עשר לאספקלאוס אשר יאות לאקלידס החכם</big> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הקדמה לאספקלוס בהשלמת המאמר על המוגשמים החמשה | ||
| + | |- | ||
| + | | | ||
| + | === Proposition 1 === | ||
| + | | | ||
| + | |- | ||
| + | |When the side of the hexagon is cut in a mean and extreme ratio, the greater segment is a side of the decagon circumscribed by the circle that circumscribes the hexagon. | ||
| + | |style="text-align:right;"|<span style=color:red>א</span> <big>כאשר</big> נחלק צלע המשוש<s>ת</s>ה<sup></sup> על יחס צלע בעל אמצע ושתי קצוות הנה חלק היותר גדול הוא צלע המעושר אשר תקיף בו העגולה אשר תקיף במשושת | ||
| + | |- | ||
| + | |Example: line AB is a side of the hexagon. | ||
| + | |style="text-align:right;"|<big>המשל</big> בזה כי קו א"ב צלע המשושת | ||
| + | |- | ||
| + | |Let it be cut in a mean and extreme ratio at point G | ||
| + | |style="text-align:right;"|וכבר נחלק על יחס בעל אמצע ושתי קצוות על נקודת ג‫' | ||
| + | |- | ||
| + | |Let BG be its greater segment. | ||
| + | |style="text-align:right;"|וחלקו הגדול ב"ג | ||
| + | |- | ||
| + | |I say that BG is the side of the decagon circumscribed by the circle that circumscribes the hexagon. | ||
| + | |style="text-align:right;"|הנה אומר כי ב"ג צלע המעושר אשר תקיף בו העגולה אשר תקיף במשושת | ||
| + | |- | ||
| + | |The proof: | ||
| + | |style="text-align:right;"|<big>המופת</big> | ||
| + | |- | ||
| + | |It has already been proved in Book XIII regarding the sides of the hexagon and the decagon circumscribed by the circle, that when they are joined as a straight line, then that line is cut in a mean and extreme ratio, the greater segment is the side of the hexagon and the smaller segment is the side of the decagon. | ||
| + | |style="text-align:right;"|כי כבר התבאר במאמר הי"ג [בט' ממנו] כי צלע משושת <sup>אשר</sup> בעגולה ומעשורה כאשר נדבקו על יושר אחר כן נחלק הקו על יחס בעל אמצע ושתי קצוות הנה החלק הגדול הוא צלע המשושת והחלק הקטון הוא צלע המעושר | ||
| + | |- | ||
| + | |We join the side of the decagon, which is DB, to line AB. | ||
| + | |style="text-align:right;"|ונגיע בקו א"ב צלע המעושר והוא ד"ב | ||
| + | |- | ||
| + | |So, line AD is cut in a mean and extreme ratio at point B. | ||
| + | |style="text-align:right;"|הנה קו א"ד כבר נחלק על יחס בעל אמצע ושתי קצוות על נקודת ב‫' | ||
| + | |- | ||
| + | |Its greater segment is line AB. | ||
| + | |style="text-align:right;"|וחלקו הגדול יותר קו א"ב <span style=color:red>מט' מי"ג</span> | ||
| + | |- | ||
| + | |We draw line HW equal to line AB. | ||
| + | |style="text-align:right;"|ונרשום קו שוה לקו א"ב והוא קו ה"ו | ||
| + | |- | ||
| + | |We cut it in a mean and extreme ratio at point Z. | ||
| + | |style="text-align:right;"|ונחלקהו ביחס בעל אמצע ושתי קצוות על נקודת ז‫' | ||
| + | |- | ||
| + | |Its greater segment is line WZ. | ||
| + | |style="text-align:right;"|וחלקו הגדול קו <s>א"ב</s> ו"ז ‫<ref>marg.: מי' מי"ד וזה שיחס הקו אל הקו כיחס החלק הגדול אל החלק הגדול</ref> | ||
| + | |- | ||
| + | |WZ is equal to line BG. | ||
| + | |style="text-align:right;"|וו"ז שוה אל קו ב"ג <span style=color:red>מי' מי"ד</span> | ||
| + | |- | ||
| + | |Therefore, the ratio of AD to AB is the same as the ratio of HW to WZ. | ||
| + | |style="text-align:right;"|הנה יחס <s>א"ב</s> א"ד <sup>אל א"ב</sup> כיחס ה"ו אל ו"ז | ||
| + | |- | ||
| + | |When we cut off, then reverse, the ratio of AB to BD is the same as the ratio of WZ to ZH. | ||
| + | |style="text-align:right;"|וכאשר הבדלנו‫<ref>marg.: וזה שנאמר ד"ב אל א"ב וה"ז אל ז"ו עוד הפכנו</ref> אחר כן הפכנו הנה [מי"ו מו'] יחס א"ב אל ב"ד כיחס ו"ז אל ז"ה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן המרובע ההוה מן א"ב בה"ז כמו מרובע אשר יהיה מן ב"ד בו"ז <span style=color:red>מי"ו מו‫'</span> | ||
| + | |- | ||
| + | |AB is the same as HW. | ||
| + | |style="text-align:right;"|וא"ב כמו ה"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואשר [מי"ו מו'] ‫<ref>138v</ref>יהיה מן ה"ו בה"ז שוה לאשר יהיה מן ו"ז בכמוהו‫<ref>נ' בעצמו</ref> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן קו ד"ב הוא כמו ו"ז‫<ref>marg.: וזה שאחר שהכאת ו"ז בעצמו שוה להכאת ד"ב בו"ז אם כן ד"ב הוא כמו ו"ז</ref> | ||
| + | |- | ||
| + | |Line WZ is the same as line BG. | ||
| + | |style="text-align:right;"|וקו ו"ז כמו קו ב"ג | ||
| + | |- | ||
| + | |DB is the side of the decagon. | ||
| + | |style="text-align:right;"|וד"ב צלע המעושר | ||
| + | |- | ||
| + | |Therefore, line BG is the side of the decagon. | ||
| + | |style="text-align:right;"|אם כן קו ב"ג צלע המעושר | ||
| + | |- | ||
| + | |Quod erat demonstrandum | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Proposition 2 === | ||
| + | | | ||
| + | |- | ||
| + | |We wish to draw a polyhedron with four equilateral triangular faces inside a known cube. | ||
| + | |style="text-align:right;"|<span style=color:red>ב</span> <big>נרצה</big> שנרשום בעל ד' תושבות משולשו' שוות הצלעות במעוקב ידוע‫<ref>marg.: אין צריך לעשות כזה כי אם להוציא כל קטרי השטחים</ref> | ||
| + | |- | ||
| + | |Let ABGDHWZC be the known cube. | ||
| + | |style="text-align:right;"|ויהיה המעוקב הידוע א"ב ג"ד ה"ו <sup>ז</sup>"ח | ||
| + | |- | ||
| + | |We join AZ, GZ, GH, AH, and HZ. | ||
| + | |style="text-align:right;"|ונגיע א"ז וג"ז <s>וא"ה</s> <sup>וג"ה וא"ה</sup> וה"ג וה"ז | ||
| + | |- | ||
| + | |I say that we have already constructed a polyhedron with four equilateral triangular faces, which is solid AGZH. | ||
| + | |style="text-align:right;"|הנה אומר כי כבר עשינו בעל ד' תושבות משולשות שות הצלעות והוא מוגשם א"ג ז"ה | ||
| + | |- | ||
| + | |The proof: | ||
| + | |style="text-align:right;"|<big>המופת</big> | ||
| + | |- | ||
| + | |AG is the hypotenuse opposite to the right angle ADG. | ||
| + | |style="text-align:right;"|כי א"ג <sup>כבר</sup> היה מיתר זוית אד"ג <sup>הנצבת</sup> | ||
| + | |- | ||
| + | |AZ is the hypotenuse opposite to the right angle ADZ. | ||
| + | |style="text-align:right;"|<sup>וא"ז</sup> כבר היה מיתר זוית אד"ז הנצבת | ||
| + | |- | ||
| + | |GZ is the hypotenuse opposite to the right angle GDZ. | ||
| + | |style="text-align:right;"|<s>וג"ד</s> <sup>וג"ז</sup> כבר היה מיתר <s>גב"ה הנצבת וה"ז כבר היה מיתר</s> זוית גד"ז הנצבת | ||
| + | |- | ||
| + | |AH is the hypotenuse opposite to the right angle ABH. | ||
| + | |style="text-align:right;"|וא"ה כבר היה מיתר זוית אב"ה הנצבת | ||
| + | |- | ||
| + | |GH is the hypotenuse opposite to the right angle GBH. | ||
| + | |style="text-align:right;"|וג"ה כבר היה מיתר <sup>לזוית</sup> גב"ה הנצבת | ||
| + | |- | ||
| + | |HZ is the hypotenuse opposite to the right angle HWZ. | ||
| + | |style="text-align:right;"|וה"ז כבר היה מיתר לזוית הו"ז הנצבת | ||
| + | |- | ||
| + | |Lines AD, DZ, GD, GB, AB, BH, HW, WZ are equal [to each other]. | ||
| + | |style="text-align:right;"|וקוי א"ד ד"ז ג"ד ג"ב א"ב ב"ה <sup>ה"ו</sup> ו"ז שוים | ||
| + | |- | ||
| + | |So, sides AZ, ZG, AH, AG, ZH, GH are equal [to each other]. | ||
| + | |style="text-align:right;"|אם כן [מד' מא'] צלעות א"ז ז"ג א"ה א"ג ז"ה ג"ה שוות | ||
| + | |- | ||
| + | |Therefore, triangles AGZ, AHG, AHZ, HZG are equal [to each other]. | ||
| + | |style="text-align:right;"|אם כן משולשי אג"ז אה"ג <sup>אה"ז</sup> הז"ג שוים | ||
| + | |- | ||
| + | |Hence, solid AGZH has four equilateral [triangular] faces, its base is triangle AGZ and its apex is point Z. | ||
| + | |style="text-align:right;"|אם כן מוגשם א"ג ז"ה בעל ד' תושבת שוות הצלעות בתושבת משולש אג"ז וראשו נקודת ז‫' | ||
| + | |- | ||
| + | |Quod erat demonstrandum. | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | === Proposition 3 === | ||
| + | | | ||
| + | |- | ||
| + | |We wish to draw a solid shape with eight equilateral triangular faces inside a solid with four equilateral triangular faces. | ||
| + | |style="text-align:right;"|<span style=color:red>ג</span> <big>נרצה</big> שנרשום תמונה <sup>מוגשמת</sup> בעלת ח' תושבות משולשות שוות הצלעות במוגשם בעל ד' תושבות <sup>משולשות</sup> שוות הצלעות | ||
| + | |- | ||
| + | |Let solid ABGD be the solid with four equilateral triangular faces. | ||
| + | |style="text-align:right;"|ויהיה המוגשם אשר לו ארבע תושבות <s>משות</s> משולשות שוות הצלעות מוגשם א"ב ג"ד | ||
| + | |- | ||
| + | |Let triangle ABG be its base. | ||
| + | |style="text-align:right;"|ותהיה תושבתו משולש אב"ג | ||
| + | |- | ||
| + | |Let point D be its apex. | ||
| + | |style="text-align:right;"|וזוית ראשו נקודת ד‫' | ||
| + | |- | ||
| + | |We cut each of its sides in half at points H, W, Z, C, T, L. | ||
| + | |style="text-align:right;"|ונבדיל כל צלע מצלעותיו בשני חציים אצל נקודת ה"ו ז"ח ט"ל | ||
| + | |- | ||
| + | |We join HZ, ZW, WH, CT, TL, LC, CH, HT, TW, WL, LZ, ZC. | ||
| + | |style="text-align:right;"|ונגיע ה"ז ז"ו ו"ה ח"ט ט"ל ל"ח ח"ה ה"ט ט"ו ו"ל ל"ז ז"ח | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה אומר כי אנחנו כבר עשינו במוגשם א"בג"ד בעל ח' תושבות משולשות שוות הצלעות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<big>המופת</big> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי קוי ח"ל ח"ט ח"ז ח"ה ו"ה ו"ז ו"ט ו"ל ז"ל ל"ט ט"ה שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מפני כי הם מיתרי זוית שוות יקיפו בהם קוים שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזוית מוגשם א"ב ג"ד שוות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מפני כי תושבותיהם משולשים שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והקוים המוצאים הנעשים מיתרים לזויות נכחיים לתושבות המשולשות אשר הם מיתרי זויותיהם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם <sup>כן</sup> המשולשים אשר יתחדשו מהם דומים ודומים למשולשי בעל הד' תושבות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן <sup>קו</sup> ז"ה נכחי לקו ג"ב <span style=color:red>מב' מו‫'</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן קוי משולש הז"ו נכחיים לקוי משולש<s>י</s> אב"ג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן קוי משולש חט"ל נכחיים לקוי משולש אב"ג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<sup>וכן</sup> גם כן <s>ו</s>קוי משולש <s>חז"ל</s> <sup>ול"ט</sup> נכחיים לקוי משולשי <s>אד"ב אם כן המוגשם</s> <sup>דג"ב קוי משולש חה"ט נכחיים לקוי משולש אד"ב</sup> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<sup>הנה</sup> מוגשם חה"ט ול"ז בעל ח' תושבות שוות הקוים והזויות המשולשים שוות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומשולשיו השוים הם משולשי זח"ל לח"ט טח"ה הז"ח | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והמשולש<sub>ים</sub> הארבעה הנכחיים להם והם המשולשים טו"ה הו"ז זו"ל טו"ל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והצלעות הד' המרובעות אשר יקיפו באמצעו הם צלעות ט"ל <s>ז"ה</s> <sup>ל"ז ז"ה ה"ט</sup>‫<ref>marg.: רצה בזה שהוא עשוי על שטח מרובע כמו שנעשה במאמר י"ג בתמונת ט"ו</ref> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ושתי זויות ראשי המחודדים שתי נקודות ח"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה כבר עשינו ‫<ref>139r</ref>המוגשם א"ב ג"ד בעל הד' תושבות תמונה בעלת [השמונה] תושבות משולשות שוות הצלעות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | === Proposition 4 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<span style=color:red>ד</span> נרצה שנרצה במעוקב ידוע בעל שמונה תושבות ויהיה המעוקב הידוע מעוקב א"ב ג"ד ה"ו ז"ח בשטחו הששה המרובעים שטח אבג"ד והוא השטח העליון ממנו [ושטח הוז"ח והוא השטח התחתון ממנו והוא הנכחי] לשטח אבג"ד ושטח אהח"ד הנכחי לשטח בגז"ו ושטח אבו"ה הנכחי לשטח חדג"ז ונקח מכל שטח משטחיו הששה הנקודה אשר יחתכו ממנה שני הקוטרים לשטח ההוא ונרשום על הנקודה אשר במרובע אבג"ד רושם מ' ובמרובע הוז"ח רושם ה' ובאבו"ה רושם י' ובגדז"ח רושם ל' ובאהח"ד רושם ט' ובבגז"ו רושם כ' ונוציא קוי י"ט ט"ל ל"כ כ"י מ"י מ"ט מ"ל מ"כ ס"ל ס"ט ס"י ס"כ | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואומר כי אנחנו כבר עשינו במעוקב א"ב ג"ד ה"ו ז"ח בעל שמונה תושבות והוא מוגשם י"ט ל"ב מ"ס | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מופת זה כי אנחנו נקודת ט' אם הוצא עליה קו נכחי לשתי צלעות א"ה ד"ח והוא קו עט"פ וקו אחר לשתי צלעי א"ד ה"ח והוא קו קט"ג יחתכו על זויות נצבות מפני כי שטח א"ה ח"ד שוה צלעות ונכחיים להם ונצב הזויות ולכן [מסוף ד' מב'] יהיו קוי ט"ע ט"פ ט"ק ט"נ שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כל שטחי המעוקב כאשר ננהיגם בזאת ההנהגה יהיו הקוים אשר יצאו מן הנקודות אשר יחתכו עליה קוטריהם אצל צלעיהם ונכחי צלעיהם שוה יחד ויהיה דבקות כל שני קוים מהם בשני שטחים יתמששו על זוית נצבת ויהיו הקוים אשר ידבקו בין כל שתי נקודות מן הנקודות אשר יחתכו עליהם הקוטרים שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיו קוי י"ט י"כ ל"ב ל"ט ס"כ ס"ל ס"י ס"ט מ"כ מ"ל מ"י מ"ט שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיו הזויות אשר יקיפו בהם שוות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן [מח' מא'] משולשי ימ"ט ימ"כ טמ"ל מכ"ל טי"ס טל"ס לכ"ס כי"ס שוי הצלעות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה כבר עשינו תמונה בעל שמונה תושבות יכ"ל טמ"ס אשר רצינו במעוקב א"ב ג"ד ה"ו ז"ח הידוע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | === Proposition 5 === | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|<span style=color:red>ה</span> נרצה שנרשום במוגשם בעל שמונה תושבות ידוע מעוקב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיה המוגשם בעל השמונה תושבות מוגשם א"ב ג"ד ה"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומשולשיו הצלעות משולשי אה"ד דה"ג גה"ב בה"א או"ד דו"ג גו"ב בו"א | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונקח מרכז המשולשים מרכז אח"ד נקודת ז' ומרכז דה"ז נקודת ח' ומרכז גה"ב נקודת ט' ובה"א נקודת י' ואו"ד נקודת ל' וגו"ד נקודת מ' וגו"ב נקודת נ' ובו"א נקודת כ' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונוציא קוי ז"י י"ט ט"ח ל"כ כ"נ נ"מ מ"ל י"כ ז"ל ח"מ ט"נ | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה אומר כי כבר עשינו במוגשם א"ב ג"ד ה"ו בעל השמונה תושבות הידוע מעוקב והוא מעוקב יז"ח טכ"ל מ"נ | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מופת זה אנחנו אם הוצאנו מן הנקודות אשר הם מרכזי המשולשים אשר הם נקודות זי"ט חל"כ מ"נ עמודים אל צלעות משולשיהם יהיו העמודים שוים והיו הזויות אשר יתחדשו ממשוש אותם העמודים היוצאים ממשולש אל משולש אחר שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מפני כי הזויות אשר יתחדשו ממשוש שטחי משולשי בעל השמונה תושבות שוות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיו הקוים אשר הם מיתרי אותם הזויות הם היוצאים מן ז' אל וי ומן י' אל ט' ומן ט' אל ח' ומן ח' אל ז' ומן ז' ל' אל כ' ומן כ' אל נ' ומן נ' אל מ' ומן מ' אל ל' ומן י' אל כ' ומן ט' אל נ' ומן ז' אל ל' ומן ח' אל מ' שוים [מד' מא'] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והזויות אשר יקיפו בהם אותם הקוים שוות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מפני כי מרחק ו"ח מן ה' מרחק אחד ושוה למרחק ט"ז מן ה' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם הוצא מט' אל ז' קו ומן י' אל ח' קו יהיו שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן מרובע י"ז ח"ט נצב הזויות שוה הצלעות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כל מרובעי כ"ל מ"נ וי"כ נ"ט וי"כ ז"ל וז"ל מ"ח וט"נ ח"מ שוי הצלעות נצבי הזויות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן כל המרובעים הששה שוים שוי הצלעות נצבי הזויות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם כן מוגשם זי"ט חל"כ מ"נ מעוקב והוא בבעל שמונה תושבות הידוע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה מה שרצינו לבאר | ||
|} | |} | ||
| Line 17,819: | Line 19,489: | ||
::[http://daten.digitale-sammlungen.de/0010/bsb00103925/images/index.html?id=00103925&groesser=&fip=eayayztsxdsydeayaeayaxseayaenxdsydxdsydqrs&no=2&seite=4 Mu130]<br> | ::[http://daten.digitale-sammlungen.de/0010/bsb00103925/images/index.html?id=00103925&groesser=&fip=eayayztsxdsydeayaeayaxseayaenxdsydxdsydqrs&no=2&seite=4 Mu130]<br> | ||
:2) Oxford, Bodleian Library MS Hunt. 16/1 (IMHM: f 19290) (cat. Neub. 2005, 1), 1r-89v, (15th century)<br> | :2) Oxford, Bodleian Library MS Hunt. 16/1 (IMHM: f 19290) (cat. Neub. 2005, 1), 1r-89v, (15th century)<br> | ||
| − | ::[https://digital.bodleian.ox.ac.uk/ | + | ::[https://digital.bodleian.ox.ac.uk/objects/3bdaec9a-2c1c-42e6-b920-159ec11cb923/surfaces/1fdffb6c-d958-40f5-bfb0-1744903b6836/ O16]<br> |
:3) Wien, Öesterreichische Nationalbibliothek Cod hebr. 66/3 (IMHM: f 1343), ff. 157-233 (16th century)<br> | :3) Wien, Öesterreichische Nationalbibliothek Cod hebr. 66/3 (IMHM: f 1343), ff. 157-233 (16th century)<br> | ||
::[http://web.nli.org.il/sites/NLI/Hebrew/digitallibrary/pages/viewer.aspx?presentorid=MANUSCRIPTS&docid=PNX_MANUSCRIPTS000169510-1#|FL17619849 W66]<br> | ::[http://web.nli.org.il/sites/NLI/Hebrew/digitallibrary/pages/viewer.aspx?presentorid=MANUSCRIPTS&docid=PNX_MANUSCRIPTS000169510-1#|FL17619849 W66]<br> | ||
Latest revision as of 06:46, 3 October 2024
Contents
- 1 Book One
- 1.1 Definitions
- 1.2 Postulates
- 1.3 Common Notions
- 1.4 Proposition 1
- 1.5 Proposition 2
- 1.6 Proposition 3
- 1.7 Proposition 4
- 1.8 Proposition 5
- 1.9 Proposition 6
- 1.10 Proposition 7
- 1.11 Proposition 8
- 1.12 Proposition 9
- 1.13 Proposition 10
- 1.14 Proposition 11
- 1.15 Proposition 12
- 1.16 Proposition 13
- 1.17 Proposition 14
- 1.18 Proposition 15
- 1.19 Proposition 16
- 1.20 Proposition 17
- 1.21 Proposition 18
- 1.22 Proposition 19
- 1.23 Proposition 20
- 1.24 Proposition 21
- 1.25 Proposition 22
- 1.26 Proposition 30
- 1.27 Proposition 31
- 1.28 Proposition 32
- 1.29 Proposition 33
- 1.30 Proposition 34
- 1.31 Proposition 35
- 1.32 Proposition 36
- 1.33 Proposition 37
- 1.34 Proposition 38
- 1.35 Proposition 39
- 1.36 Proposition 40
- 1.37 Proposition 41
- 1.38 Proposition 42
- 1.39 Proposition 43
- 1.40 Proposition 44
- 1.41 Proposition 45
- 1.42 Proposition 46
- 1.43 Proposition 47
- 1.44 Proposition 48
- 2 The Second Section of Euclid's Book
- 3 Book Three
- 3.1 Proposition 1
- 3.2 Proposition 2
- 3.3 Proposition 3
- 3.4 Proposition 4
- 3.5 Proposition 5
- 3.6 Proposition 6
- 3.7 Proposition 7
- 3.8 Proposition 8
- 3.9 Proposition 9
- 3.10 Proposition 10
- 3.11 Proposition 11
- 3.12 Proposition 12
- 3.13 Proposition 13
- 3.14 Proposition 14
- 3.15 Proposition 15
- 3.16 Proposition 16
- 3.17 Proposition 17
- 3.18 Proposition 18
- 3.19 Proposition 19
- 3.20 Proposition 20
- 3.21 Proposition 21
- 3.22 Proposition 22
- 3.23 Proposition 23
- 3.24 Proposition 24
- 3.25 Proposition 25
- 3.26 Proposition 26
- 3.27 Proposition 27
- 3.28 Proposition 28
- 3.29 Proposition 29
- 3.30 Proposition 30
- 3.31 Proposition 31
- 3.32 Proposition 32
- 3.33 Proposition 33
- 3.34 Proposition 34
- 3.35 Proposition 35
- 3.36 Proposition 36
- 4 Book Four
- 4.1 Definitions
- 4.2 Proposition 1
- 4.3 Proposition 2
- 4.4 Proposition 3
- 4.5 Proposition 4
- 4.6 Proposition 5
- 4.7 Proposition 6
- 4.8 Proposition 7
- 4.9 Proposition 8
- 4.10 Proposition 9
- 4.11 Proposition 10
- 4.12 Proposition 11
- 4.13 Proposition 12
- 4.14 Proposition 13
- 4.15 Proposition 14
- 4.16 Proposition 15
- 4.17 Proposition 16
- 4.18 Proposition 17
- 5 Book Five
- 5.1 Definitions
- 5.2 Proposition 1
- 5.3 Proposition 2
- 5.4 Proposition 3
- 5.5 Proposition 4
- 5.6 Proposition 5
- 5.7 Proposition 6
- 5.8 Proposition 7
- 5.9 Proposition 8
- 5.10 Proposition 9
- 5.11 Proposition 10
- 5.12 Proposition 11
- 5.13 Proposition 12
- 5.14 Proposition 13
- 5.15 Proposition 14
- 5.16 Proposition 15
- 5.17 Proposition 16
- 5.18 Proposition 17
- 5.19 Proposition 18
- 5.20 Proposition 19
- 5.21 Proposition 20
- 5.22 Proposition 21
- 5.23 Proposition 22
- 5.24 Proposition 23
- 5.25 Proposition 24
- 5.26 Proposition 25
- 6 Book Six
- 7 Book Seven
- 7.1 Definitions
- 7.2 Proposition 1
- 7.3 Proposition 2
- 7.4 Proposition 3
- 7.5 Proposition 4
- 7.6 Proposition 5
- 7.7 Proposition 6
- 7.8 Proposition 7
- 7.9 Proposition 8
- 7.10 Proposition 9
- 7.11 Proposition 10
- 7.12 Proposition 11
- 7.13 Proposition 12
- 7.14 Proposition 13
- 7.15 Proposition 14
- 7.16 Proposition 15
- 7.17 Proposition 16
- 7.18 Proposition 17
- 7.19 Proposition 18
- 7.20 Proposition 19
- 7.21 Proposition 20
- 7.22 Proposition 21
- 7.23 Proposition 22
- 7.24 Proposition 23
- 7.25 Proposition 24
- 7.26 Proposition 25
- 7.27 Proposition 26
- 7.28 Proposition 27
- 7.29 Proposition 28
- 7.30 Proposition 29
- 7.31 Proposition 30
- 7.32 Proposition 31
- 7.33 Proposition 32
- 7.34 Proposition 33
- 7.35 Proposition 34
- 7.36 Proposition 35
- 7.37 Proposition 36
- 7.38 Proposition 37
- 7.39 Proposition 38
- 7.40 Proposition 39
- 8 Book Eight
- 8.1 Proposition 1
- 8.2 Proposition 2
- 8.3 Proposition 3
- 8.4 Proposition 4
- 8.5 Proposition 5
- 8.6 Proposition 6
- 8.7 Proposition 7
- 8.8 Proposition 8
- 8.9 Proposition 9
- 8.10 Proposition 10
- 8.11 Proposition 11
- 8.12 Proposition 12
- 8.13 Proposition 13
- 8.14 Proposition 14
- 8.15 Proposition 15
- 8.16 Proposition 16
- 8.17 Proposition 17
- 8.18 Proposition 18
- 8.19 Proposition 19
- 8.20 Proposition 20
- 8.21 Proposition 21
- 8.22 Proposition 22
- 8.23 Proposition 23
- 8.24 Proposition 24
- 8.25 Proposition 25
- 8.26 Proposition 26
- 8.27 Proposition 27
- 9 Book Nine
- 9.1 Proposition 1
- 9.2 Proposition 2
- 9.3 Proposition 3
- 9.4 Proposition 4
- 9.5 Proposition 5
- 9.6 Proposition 6
- 9.7 Proposition 7
- 9.8 Proposition 8
- 9.9 Proposition 9
- 9.10 Proposition 10
- 9.11 Proposition 11
- 9.12 Proposition 12
- 9.13 Proposition 13
- 9.14 Proposition 14
- 9.15 Proposition 15
- 9.16 Proposition 16
- 9.17 Proposition 17
- 9.18 Proposition 18
- 9.19 Proposition 19
- 9.20 Proposition 20
- 9.21 Proposition 21
- 9.22 Proposition 22
- 9.23 Proposition 23
- 9.24 Proposition 24
- 9.25 Proposition 25
- 9.26 Proposition 26
- 9.27 Proposition 27
- 9.28 Proposition 28
- 9.29 Proposition 29
- 9.30 Proposition 30
- 9.31 Proposition 31
- 9.32 Proposition 32
- 9.33 Proposition 33
- 9.34 Proposition 34
- 9.35 Proposition 35
- 9.36 Proposition 36
- 9.37 Proposition 37
- 10 Book Ten
- 10.1 Definitions
- 10.2 Proposition 1
- 10.3 Proposition 2
- 10.4 Proposition 3
- 10.5 Proposition 4
- 10.6 Proposition 5
- 10.7 Proposition 6
- 10.8 Proposition 7
- 10.9 Proposition 8
- 10.10 Proposition 9
- 10.11 Proposition 10
- 10.12 Proposition 11
- 10.13 Proposition 12
- 10.14 Proposition 13
- 10.15 Proposition 14
- 10.16 Proposition 15
- 10.17 Proposition 16
- 10.18 Proposition 17
- 10.19 Proposition 18
- 10.20 Proposition 19
- 10.21 Proposition 20
- 10.22 Proposition 21
- 10.23 Proposition 22
- 10.24 Proposition 23
- 10.25 Proposition 24
- 10.26 Proposition 25
- 10.27 Proposition 26
- 10.28 Proposition 27
- 10.29 Proposition 28
- 10.30 Proposition 29
- 10.31 Proposition 30
- 10.32 Proposition 31
- 10.33 Proposition 32
- 10.34 Proposition 33
- 10.35 Proposition 34
- 10.36 Proposition 35
- 10.37 Proposition 36
- 10.38 Proposition 37
- 10.39 Proposition 38
- 10.40 Proposition 39
- 10.41 Proposition 40
- 10.42 Proposition 41
- 10.43 Proposition 42
- 10.44 Proposition 43
- 10.45 Proposition 44
- 10.46 Definitions
- 10.47 Proposition 45
- 10.48 Proposition 46
- 10.49 Proposition 47
- 10.50 Proposition 48
- 10.51 Proposition 49
- 10.52 Proposition 50
- 10.53 Proposition 51
- 10.54 Proposition 52
- 10.55 Proposition 53
- 10.56 Proposition 54
- 10.57 Proposition 55
- 10.58 Proposition 56
- 10.59 Proposition 57
- 10.60 Proposition 58
- 10.61 Proposition 59
- 10.62 Proposition 60
- 10.63 Proposition 61
- 10.64 Proposition 62
- 10.65 Proposition 63
- 10.66 Proposition 64
- 10.67 Proposition 65
- 10.68 Proposition 66
- 10.69 Proposition 67
- 10.70 Proposition 68
- 10.71 Proposition 69
- 10.72 Definitions
- 10.73 Proposition 70
- 10.74 Proposition 71
- 10.75 Proposition 72
- 10.76 Proposition 73
- 10.77 Proposition 74
- 10.78 Proposition 75
- 10.79 Proposition 76
- 10.80 Proposition 77
- 10.81 Proposition 78
- 10.82 Proposition 79
- 10.83 Proposition 80
- 10.84 Proposition 81
- 10.85 Definitions
- 10.86 Proposition 82
- 10.87 Proposition 83
- 10.88 Proposition 84
- 10.89 Proposition 85
- 10.90 Proposition 86
- 10.91 Proposition 87
- 10.92 Proposition 88
- 10.93 Proposition 89
- 10.94 Proposition 107
- 10.95 Proposition 108
- 10.96 Proposition 109
- 11 Book Eleven
- 12 Book Twelve
- 13 Book Fourteen
- 14 Book Fifteen by Hyspikleos [hypsicles] which is suitable for Euclid the Wise
- 15 Appendix: Bibliography
Book One |
|
Definitions |
|
|
הנקודה היא דבר אין לה חלק ולא הנחה |
|
והקו הוא אורך אין רוחב לו |
|
ותכליות הקו שתי נקודות |
|
והקו הישר הוא המוצב על נכוחות אי זה נקודות יהיו עליו קצתם אל קצתם |
|
והשטח הוא אשר לו אורך ורוחב לבד |
|
ותכליות השטח קוים |
|
והפשוט השוה הוא המוצב על נכוחות אי זה קוים ישרים יהיו עליו קצתם אל קצתם |
|
והזוית הפשוטה היא נטיית כל אחד משני קוים מונחים בשטח שוה מדובקים על בלתי יושר האחד מן האחר |
|
וכאשר היו שני קוים מקיפים בזוית הזאת ישרים תקרא ישרת הקוים |
|
וכאשר יעמוד קו ישר על קו ישר ושם שתי הזויות אשר משתי צדדיו שוות הנה כל אחת משתיהן היא זויות נצבת והקו ההוא העומד יקרא העמוד על הקו אשר הוא עומד עליו |
|
ואשר היא גדולה מנצבת תקרא נרוחת |
|
ואשר היא קטנה מנצבת תקרא חדה |
|
והגבול הוא תכלית הדבר |
|
והתמונה היא אשר יקיף אותה גבול או גבולים |
|
והעגולה היא תמונה פשוטה שוה יקיף אותה קו אחד בתוכה נקודה כל הקוים הישרים היוצאים ממנה ויכלו אל הקו ההוא שוים קצתם אל קצתם |
|
והנקודה ההיא הוא מרכז העגולה |
|
וקוטר העגולה הוא קו ישר ילך במרכז העגולה ויכלה בשני הצדדי' אל הקו המקיף אותה והוא יחתכנה בשני חצאים |
|
וחצי העגולה היא תמונה יקיפו בה הקוטר והקשת אשר החזיק בה הקוטר מן הקו המקיף |
|
וחתיכת העגול היא תמונה יקיפו בה קו ישר וקשת ממקיף העגולה אם קטנה מחציה או גדולה |
|
והתמונות ישרות הקוים הם אשר יקיפו בהם קוים ישרים |
|
ואולם בעלות שלש צלעות הם אשר יקיפו בהם קוים ישרים שלשה |
|
ואולם בעלות ארבעה צלעות הם אשר יקיפו בהם ארבעה קוים ישרים |
|
ואולם בעלות צלעות רבות הם אשר יקיפו בהם יותר מארבעה קוים ישרים |
|
ואולם התמונות בעלות שלש צלעות |
|
הנה מהן המשולש השוה הצלעות והוא אשר צלעותיו השלש שוות קצתם אל קצתם |
|
ומהם השוה השוקים והוא אשר שתי צלעותיו לבד שוות |
|
ומהם המתחלף הצלעות והוא אשר צלעותיו השלש בלתי שוות קצתם אל קצתם |
|
ומן התמונות בעלות שלש צלעות |
|
המשולש נצב הזוית והוא אשר לו זוית נצבת |
|
והמשולש הנרוח הזוית והוא אשר לו זוית נרוחת |
|
ומשולש חד הזויות והוא אשר כל אחת מזויותיו השלש חדה |
|
ואולם התמונות בעלות ארבעה צלעות |
|
הנה מהן המרובע הוא השוה הצלעות נצב הזויות |
|
ומהם המתחלף הארכים והוא הנצב הזויות לא שוה הצלעות |
|
ומהם המעויין והוא השוה הצלעות ואינו נצב הזויות |
|
ומהם הדומה למעויין והוא אשר כל שתי צלעות ממנו שזו כנגד זו שוות ואינו שוה הצלעות ואינו נצב הזויות |
|
ומה שהיה על זולת מה שספרנו מן התמונות בעלות ארבע צלעות תקרא הנוטה |
|
והקוים הישרים הנכחיים הם אשר יהיו על שטח אחד שוה ואם הוצאו בשני הצדדים אל לא תכלית לא יפגשו באחד מהם |
Postulates |
|
| The things on which a consensus is needed are five: | הדברים אשר תצטרך ההסכמה עליהם חמשה |
|
מהם שימשך קו ישר מכל נקודה אל כל נקודה |
|
ושיוצא קו ישר בעל תכלית על יושר ודבקות לבלתי תכלית |
|
ושנקוה עגולה על כל נקודה ובשיעור כל מרחק |
|
ושכל הזויות הנצבות שוות קצתם אל קצתם |
|
ואם נפל קו ישר על שני קוים ישרים ושם באחד משני הצדדים שתי הזויות הפנימיות פחות משתי נצבות הנה שני הקוים הישרים כאשר יוצאו בצד ההוא יפגשו |
Common Notions |
|
| דעת כוללת מוסכם עליה | |
|
הדברים השוים לדבר אחד בעצמו הם שוים |
|
ואם הוסף על השוים שוים יהיו כולם שוים |
|
ואם הוסף על הבלתי שוים שוים יהיו הנשארים בלתי שוים |
|
ואם חוסר מהבלתי שוים שוים יהיו הנשארים בלתי שוים |
|
ואם חוסר מן השוים שוים יהיו הנשארים שוים |
| ואשר כל אחד מהם כפל דבר אחד בעצמו הם שוים | |
| ואשר כל אחד מהם חצי דבר אחד בעצמו הם גם כן שוים | |
| ואשר לא יעדיף אחד משניהם על האחר כאשר ידובקו בשווי קצתם אל קצתם הם שוים | |
|
והכלל יותר גדול מחלקו |
|
וכלל הדבר שוה לכל חלקיו |
| ושני קוים ישרים לא יקיפו על שטח | |
Proposition 1 |
|
| We wish to construct an equilateral triangle on a given finite straight line. | א נרצה שנעמיד משולש שוה הצלעות על קו ישר בעל תכלית מונח |
| Example: let line AB be the finite straight line. | המשל שיהיה הקו הישר הבעל תכלי' קו א"ב |
| We wish to construct an equilateral triangle on the straight line AB. | ונרצה שנעמיד על קו א"ב הישר משולש שוה הצלעות |
| The procedure: | המעשה |
|
הנה נקיף על מרכז א' ובמרחק א"ב עגולה והיא עגולת גד"ב |
|
ונקיף גם כן על מרכז ב' ובמרחק ב"א עגולה והיא עגולת אג"ה |
|
ונגיע מנקודת ג' אשר יחתכו עליה שתי העגולות בשתי נקודות א"ב שני קוים ישרים והם ג"ב ג"א מא' מהפתיחה |
|
ונאמ' שכבר העמדנו על קו א"ב משלש שוה הצלעות והוא משלש אג"ב |
| The proof: | המופת |
|
הנה מפני שנקודת א' היא מרכז עגולת בג"ד הנה יהיה קו א"ג שוה לקו א"ב מהפתיחה |
|
וגם כן הנה מפני שנקודת ב' היא מרכז עגולת אג"ה הנה קו ב"ג שוה לקו א"ב |
|
וכבר התבאר כי קו א"ג שוה לקו א"ב |
|
אם כן קו א"ג שוה לקו ג"ב מהפתיחה |
|
אם כן קוי א"ג ג"ב וא"ב השלשה שוים |
|
אם כן משולש אב"ג שוה הצלעות מהפתיחה |
| So, an equilateral triangle has already been constructed on the given finite line AB. | וכבר נעשה על קו א"ב בעל תכלית המונח משולש שוה הצלעות |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 2 |
|
| We wish to attach to a given point a straight line that is equal to a given line. | ב נרצה שנחבר אל נקודה מונחת קו ישר שוה לקו ישר מונח |
| Let A be the given point and BG the given straight line. | תהיה הנקודה המונחת א' והקו הישר המונח ב"ג |
| We wish to attach a straight line to the given point A that is equal to the given straight line BG. | ונרצה שנחבר אל נקודת א' המונחת קו ישר שוה לקו ב"ג הישר המונח |
| We join the straight line AB from point A to point B. | הנה נגיע בין נקודת א' ונקודת ב' קו ישר והוא א"ב |
| I.1: we construct an equilateral triangle DAB on AB. | ונעמיד על א"ב משולש שוה הצלעות והוא משולש דא"ב מאשר לפניה |
|
ונוציא שני קוי א"ה ב"ז הישרים על יושר ב' קוי ד"א ד"ב הישרים |
|
ונקיף על מרכז ב' ובמרחק ב"ג עגולת חז"ג |
|
ונקיף גם כן על מרכז ד' ובמרחק ד"ז עגולת זט"ה |
|
הנה מפני שנקודת ב' מרכז עגולת חז"ג יהיה קו ב"ז שוה לקו ב"ג מהפתיחה |
|
ומפני שנקודת ד' גם כן מרכז עגולת הז"ט יהיה קו ה"ד שוה לקו ד"ז מהפתיחה |
|
וקו א"ד מאחד מהם שוה לקו ב"ד מן האחר מפני שמשולש דא"ב שוה הצלעות |
|
אם כן קו א"ה הנשאר שוה לקו ב"ז הנשאר |
|
וכבר התבאר שקו ב"ג שוה לקו ב"ז |
|
אם כן קו א"ה שוה לקו ב"ג |
|
הנה כבר חברנו אל נקודת א' המונחת קו ישר שוה לקו ב"ג הישר המונח והוא קו א"ה |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 3 |
|
| We wish to cut off from the greater of two given unequal straight lines a line that is equal to the smaller. | ג נרצה שנבדיל מאחד מב' קוי' מונחים ישרים בלתי שוים מן היותר גדול קו שוה ליותר קטן מהם |
| Example: Let the two given unequal straight lines be AB and G, of which line AB is the greater.
|
ויהיו שני הקוים הישרים המונחים אשר הם בלתי שוים א"ב וג' והיותר גדול מהם קו א"ב |
| ונרצה שנבדיל מקו א"ב היותר גדול קו שוה לקו ג' הקטן | |
| I.2: attaching to point A a straight line AD equal to line G.
|
הנה נחבר אל נקודת א' קו ישר שוה לקו ג' והוא קו א"ד מב' מזה |
|
ונקוה על מרכז א' ובמרחק א"ד עגולת הז"ד |
|
הנה מפני כי נקודת א' מרכז עגולת הז"ד יהיה קו א"ז שוה לקו א"ד מהפתיח' |
|
|
אבל קו א"ד שוה לקו ג' |
|
|
אם כן א"ז שוה לקו ג' |
| הנה כבר הבדלנו מן היותר גדול משני קוי א"ב וג' הישרים המונחים אשר הם בלתי שוים והוא א"ב קו שוה ליותר קטן משניהם והוא ג' | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 4 |
|
| When two sides of one triangle are equal to two sides of another triangle respectively, and the two angles contained by the equal straight lines are equal to one another, then the base equals the base, the triangle equals the triangle, and the remaining angles are equal to the remaining angles respectively, whose opposite side is the side that equals the opposite side of the former. | ד כאשר ישתוו שתי צלעות ממשולש אחד לשתי צלעות ממשולש אחר כל צלע לגילו וישתוו שתי הזויות משניהם אשר יקיפו בהם הקוים הישרים השוים הנה התושבת שוה לתושבת והמשולש שוה למשולש ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשנה |
| Let ABG and DHZ be the two triangles. | ויהיו שני המשולשים עליהם אב"ג דה"ז |
| Let the two sides BA and AG of the one be equal to the two sides HD and DZ of the other. | ויהיו שני צלעי ב"א א"ג מאחד משניהם שוים לשני צלעי ה"ד ד"ז מן האחר |
|
אולם צלע א"ב שוה לצלע ד"ה |
|
וצלע א"ג לצלע ד"ז |
| ותהיה הזוית אשר יקיפו בה שתי צלעות ב"א א"ג שוה לזוית אשר יקיפו בה שתי צלעות ה"ד ד"ז | |
| Supposition: I say that the base BG is also equal to the base HZ, triangle ABG is equal to triangle DZH and the remaining angles are equal to the remaining angles respectively, whose opposite side is the side that equals the opposite side of the former. | הנה אומר כי תושבת ב"ג גם כן שוה לתושבת ה"ז ושמשולש אב"ג שוה למשולש דה"ז ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשנה |
| אולם זוית אב"ג שוה לזוית דה"ז | |
| ואולם זוית בג"א לזוית הז"ד | |
| וזה כי כאשר הרכב משולש אב"ג על משולש דה"ז והונח צלע א"ב על צלע ד"ה נפלה נקודת א' על נקודת ד' | |
| וירכב צלע א"ג על צלע ד"ז | |
| מפני כי זוית בא"ג שוה לזוית הד"ז | |
| ונפלה נקודת ב' על נקודת ה' ונקודת ג' על נקודת ז' | |
| ונדבקה בשווי תושבת ב"ג על תושבת ה"ז והיה שוה אליה | |
| ונדבק בשווי משולש אב"ג על משולש דה"ז והיה שוה לו | |
| ונדבקו בשווי שאר הזויות על שאר הזויות והיו קצתם שוות לקצתם כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשון | |
| אולם זוית אב"ג לזוית דה"ז | |
| ואולם זוית אג"ב לזוית דז"ה | |
| הנה כאשר השתוו שתי צלעות ממשולש אחד לשתי צלעות ממשולש אחר כל אחת לגילה והשתוו שתי הזויות מהם אשר יקיפו בהם הקוים הישרים השוים הנה התושבת שוה לתושבת והמשולש שוה למשולש ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר האחרת | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 5 |
|
| The two angles at the base of isosceles triangles are equal to one another; and if the equal straight lines are drawn further, the [external] angles under the base are equal to one another. | ה שתי הזויות אשר על תושבת מן המשולשים שוי השוקים שוות ואם הוצאו הקוים הישרים השוים הנה שתי הזויות אשר תחת התושבת תהיינה שוות |
| Let ABG be an isosceles triangle. | ויהיה משולש שוה שתי השוקים עליו אב"ג |
| Let side AB be equal to side AG.
|
ויהיה צלע א"ב שוה לצלע א"ג |
|
ונוציא שני קוי ב"ד ג"ה הישרים על יושר שני קוי א"ב א"ג הישרים |
| Supposition: I say that angle ABG is equal to angle BGA and angle GBD is equal to angle BGH.
|
הנה אומר כי זוית אב"ג שוה לזוית בג"א וזוית גב"ד שוה לזוית בג"ה |
|
הנה נרשום על ב"ד נקודה איך מה שקרה והיא ז' |
|
ונבדיל מקו א"ה קו ישוה לקו א"ז והוא א"ח |
|
ונגיע שני קוי ג"ז ב"ח |
| Line ZA is equal to line AC.
|
הנה מפני כי קו ז"א שוה לקו א"ח |
| Line GA is equal to line AB.
|
וקו ג"א שוה לקו א"ב |
| Therefore, each of the two lines BA and AC is equal to one of the two lines GA and AZ, respectively. | יהיו כל שני קוי ב"א א"ח שוים לכל שני קוי ג"א א"ז כל אחד לגילו |
| These sides contain a common angle, which is angle ZAC. | ואלו הצלעות יקיפו בזוית אחת משותפת והיא זוית זא"ח |
| Hence, base GZ is equal to base BC.
|
אם כן [1]תושבת ג"ז שוה לתושבת ב"ח |
| Triangle AZG is equal to triangle ABC.
|
ומשולש אז"ג שוה למשולש אב"ח |
| The remaining angles are equal to the remaining angles respectively, namely those that are opposite to the equal sides. | ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר הראשונה |
| Angle AGZ is equal to angle ABC.
|
אולם זוית אג"ז [שוה] לזוית אב"ח |
| Angle AZG is equal to angle ACB.
|
ואולם זוית אז"ג [שוה] לזוית אח"ב |
| Line ZA is also equal to line AC.
|
ומפני כי קו ז"א גם כן שוה לקו א"ח מהפתיחה |
| Lines BA and AG in them are equal.
|
וקוי ב"א א"ג משניהם שוים |
| Therefore, the remainder line BZ is equal to the remainder line GC.
|
יהיה קו ב"ז הנשאר שוה לקו ג"ח הנשאר מד' מפתיחה |
| It has already been proven that line GZ is equal to line BC.
|
|
| Therefore, each of the two lines BZ and ZG is equal to one of the two lines GC and CB, respectively. | הנה כל שני קוי ב"ז ז"ג שוים לכל שני קוי ג"ח ח"ב כל אחד לגילו |
| Angle BZG is equal to angle GCB.
|
וזוית בז"ג שוה לזוית גח"ב |
| Base BG is common to both triangles. | ותושבת ב"ג משותפת לשני המשולשים |
| So, triangle BZG is equal to triangle GCB.
|
אם כן משלש בז"ג שוה למשולש גח"ב מד' |
| The remaining angles are equal to the remaining angles respectively, namely those that are opposite to the equal sides. | ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה הראשונה |
| But, angle BGZ is equal to angle GBC.
|
אולם זוית בג"ז לזוית גב"ח |
| Angle GBZ is equal to angle BGC.
|
ואולם זוית גב"ז לזוית בג"ח |
| It has already been proven that the whole angle AGZ is equal to the whole angle ABC.
|
וכבר התבאר כי כל זוית אג"ז שוה לכל זוית אב"ח |
| The two angles BGZ and GBC are equal.
|
ושתי זויות בג"ז גב"ח |
| Therefore, the remaining angle BGA is equal to the remaining angle GBA, and they are at the base [of the triangle ABG].
|
אם כן זוית בג"א הנשארת שוה לזוית גב"א הנשארת מד' מפתיחה והם שתי הזויות אשר על התושבת |
| But, it has already been proven that angle GBD is equal to the angle BGH, and they are under the base.
|
וכבר התבאר כי זוית גב"ד שוה לזוית בג"ה[2] והם שתי הזויות אשר תחת התושבת |
| Therefore, the two angles at the base of the isosceles triangle are equal to one another; and if the equal straight lines are drawn further, the [external] angles under the base are equal to one another. | אם כן שתי הזויות אשר על התושבת מן המשולש שווי שתי השוקים שוות ואם הוצאו הקוים הישרים השוים ההם הנה יהיו שתי הזויות אשר תחת התושבת שוות |
| Quod erat demonstrandum | וזה מה שרצינו לבאר |
Proposition 6 |
|
| When two angles of a triangle are equal to one another, then the two sides that are opposite to them are equal [to one another]. | ו כאשר השתוו שתי זויות ממשולש הנה שתי הצלעות אשר יהיו מיתר שתיהן יהיו שוות[3] |
| Let angle ABG of triangle ABG be equal to angle AGB.
|
ותהיה זוית אב"ג ממשולש אב"ג שוה לזוית אג"ב ממנו |
| Supposition: I say that side BA is equal to side AG.
|
הנה אומר כי צלע ב"א שוה לצלע א"ג |
| If side BA does not equal side AG, then one of them is greater than the other. | ואם לא יהיה צלע ב"א שוה לצלע א"ג הנה האחד משניהם יותר גדול מן האחר |
| Let AB be the greater if possible.
|
ויהיה היותר גדול א"ב אם אפשר זה |
| We cut off BD from AB the greater equal to AG the less.
|
ונבדיל מן א"ב היותר גדול קו השוה לקו א"ג היותר קטן והוא ב"ד מג' |
| We join DG. | ונגיע ד"ג מפתיחה ל"ז |
| Line DB is equal to line AG.
|
הנה קו ד"ב שוה לקו א"ג |
| Line BG is common | וקו ב"ג משותף |
| Therefore, the two lines DB and BG are equal to the two lines AG and GB respectively. | יהיו כל שני קוי ד"ב ב"ג שוים לכל שני קוי א"ג ג"ב כל אחד לגילו |
| Angle AGB is equal to angle DBG.
|
וזוית דב"ג שוה |
| So, base DG is equal to base AB.
|
אם כן תושבת ד"ג שוה לתושבת א"ב מד' |
| Triangle DBG equals triangle ABG.
|
ומשולש דב"ג שוה למשולש אב"ג |
| The smaller triangle equals the greater, which is impossible. | וישוה המשולש הקטן לגדול וזה בלתי אפשר נ' מפתיחה |
| Therefore, BA is not greater than AG. | אם כן אין ב"א יותר גדול מן א"ג |
| It is also clear that it is not smaller than it. | וכן יתבאר שאינו קטן ממנו |
| Hence, line BA equals line AG.
|
אם כן קו ב"א שוה לקו א"ג |
| Therefore, when two angles of a triangle are equal to one another, then the two sides that are opposite to them are equal [to one another]. | אם כן כאשר השתוו שתי זויות ממשולש הנה שתי הצלעות אשר יהיו מיתרי שתיהן יהיו שוות |
| Quod erat demonstrandum | וזה מה שרצינו לבאר |
Proposition 7 |
|
| Two straight lines that are equal to two other straight lines cannot stand on one straight line, so that their meeting and the meeting of the others are on the same side at two different points, and their two ends are the two ends of the two lines that are equal to them. | ז לא יעמדו על קו אחד ישר שתי קוים ישרים שוים לשני קוים אחרים ישרים כל אחד לגילו ותהיה פגישתם ופגישת האחרים [4]בצד אחד על שתי נקודות מתחלפות ושתי תכליותיהם שתי תכליות שני הקוים השוים לשניהם |
| If possible, let the two straight lines AG and GB stand on the straight line AB. | שאם היה אפשר יעמדו על קו א"ב הישר שני קוים א"ג ג"ב הישרים |
| Let the two other lines AD and DB be equal to the former two respectively. | ושני קוים אחרים שוים לשניהם כל אחד לגילו והם א"ד ד"ב |
| Let their meeting and the meeting of the others be on the same side at the two different points G and D. | ותהיה פגישתם ופגישת האחרים |
| Let their two ends be the two ends of the two lines equal to them. | ושתי תכליות שניהם שני תכליות שני הקוים השוים להם |
| But, the two ends of the two lines AG and AD is point A. | אולם שתי תכליות שני קוי א"ג א"ד הוא נקודת א' |
| Also, the end of the two lines GB and BD is point B. | ואולם תכלית שני קוי ג"ב ב"ד |
| We join line GD. | ונגיע קו ג"ד מהפתיחה |
| Line AG is equal to line AD.
|
הנה מפני כי קו א"ג שוה לקו א"ד |
| Angle GDA equals angle DGA.
|
תהיה זוית גד"א שוה לזוית דג"א מה' |
| Therefore, angle GDA is greater than the angle DGB.
|
אם כן זוית גד"א יותר גדולה מזוית דג"ב |
| So, angle GDB is much greater than angle DGB.
|
אם כן זוית גד"ב יותר גדולה הרבה מזוית דג"ב |
| Line GB equals line DB.
|
ומפני כי קו ג"ב גם כן שוה לקו ד"ב |
| Therefore, angle GDB equals angle DGB.
|
תהיה זוית גד"ב |
| But, it has already been proven that it is much greater than it, which is impossible. | וכבר התבאר שהיא יותר גדולה ממנה וזה בלתי אפשר |
| Therefore, two straight lines that are equal to two other straight lines cannot stand on one straight line, so that their meeting and the meeting of the others are on the same side at two different points, and the ends of both are the ends of the two lines that are equal to them. | אם כן לא יעמדו על קו אחד ישר שני קוים ישרים שוים לשני קוים אחרים ישרים כל אחד לגילו ותהיה פגישת שניהם ופגישת האחרים בצד אחד על שתי נקודות מתחלפות ותכליות שניהם תכליות שני הקוים השוים להם |
| Quod erat demonstrandum | וזה מה שרצינו לבאר |
Proposition 8 |
|
| When two sides of one triangle are equal to two sides of another triangle respectively, and the base of the one is equal to the base of the other, then the two angles, which are contained by the equal sides, are equal. | ח כאשר השתוו שתי צלעות ממשולש אחד לשתי צלעות ממשולש אחר כל אחת לגילה והשתותה תושבתו לתושבתו הנה שתי הזויות אשר יקיפו בהם הצלעות השוות הם שוות |
| Let ABG and DHZ be the two triangles. | ויהיו שני המשלשים אב"ג דה"ז |
| The two sides BA and AG of the one are equal to the two sides HD and DZ of the other, each to its corresponding: | ויהיו שתי הצלעות ב"א א"ג מאחד משניהם שוות לשתי צלעות ה"ד ד"ז מן האחר כל אחת לגילה |
|
|
אולם צלע א"ב לצלע ה"ד |
|
|
ואולם צלע א"ג לצלע ד"ז |
|
|
ותהיה תושבת ב"ג שוה לתושבת ה"ז |
| Supposition: I say that angle BAG is equal to angle HDZ. | הנה אומר כי זוית בא"ג שוה לזוית הד"ז |
| וזה כי כאשר הרכב משלש אב"ג אל משלש דה"ז והושמה תושבת ב"ג על תושבת ה"ז נפלה נקודת ב' על נקודת ה' ונקדת ג' על נקודת ז' | |
| ונפלו שתי צלעות ב"א א"ג על שתי צלעות ה"ד ד"ז | |
| שאם נפלה תושבת ב"ג על תושבת ה"ז ולא יפלו שתי צלעות ב"א א"ג על שתי צלעו' ה"ד ד"ז ונפלו על זולת נקודת ד' כמו שני קוי ה"ח ח"ז | |
| הנה כבר עמדו על קו אחד ישר שני קוים ישרים שוים אל שני קוים אחרים ישרים כל א' לגילו והיתה פגישתם ופגישת האחרים בצד אחד על שתי נקודות מתחלפות ותכלית שניהם תכליות שתי הקוים השוים ואי אפשר זה מהקודמת | |
| אם כן כאשר הורכב משלש אב"ג על משולש דה"ז ונפלה תושבת ב"ג על תושבת ה"ז נפלו שתי צלעות ב"א א"ג על שתי צלעות ה"ד ד"ז ונפלה נקודת א' על נקודת ד' היתה זוית בא"ג שוה לזוית הד"ז | |
| אם כן כאשר ישתוו שתי צלעות ממשולש לשתי צלעות ממשולש אחר כל אחת לגילה והשתוותה תושבתו לתושבתו הנה שתי הזויות אשר יקיפו בהם הצלעות השוות הן שוות | |
| Q.E.D. | ומש"ל |
Proposition 9 |
|
| We wish to bisect a given rectilinear angle. | ט נרצה שנחלק זוית מונחת ישרת הקוים לשני חצאים |
| ותהיה הזוית המונחת ישרת הקוים זוית בא"ג | |
| ונרצה שנחלקה בשני חצאיים | |
| הנה נרשום על קו א"ב נקודה איך שנפלה והיא נקודת ד' | |
| ונבדיל מקו א"ג קו שוה לקו א"ד והוא קו א"ה | |
| ונגיע קו ד"ה | |
| ונעמיד על קו ד"ה הישר משלש שוה הצלעות והוא דז"ה | |
| ונגיע קו א"ז | |
| הנה מפני כי קו א"ד שוה לקו א"ה | |
| Line AZ is common. | וקו א"ז משותף |
| יהיו כל שני קוים ד"א א"ז שוים לכל שני קוים ה"א א"ז כל אחד לגילו | |
| ותושבת ד"ז שוה לתושבת ז"ה | |
| א"כ זוית דא"ז שוה לזוית הא"ז | |
| הנה כבר נחלקה זוית ה"ד המונחת ישרת הקוים לשתי חציים בקו א"ז הישר | |
| Q.E.D. | ומש"ל |
Proposition 10 |
|
| We wish to bisect a given finite straight line. | י נרצה שנחלק קו ישר מונח בעל תכלית לשני חציים |
| ויהיה הקו הישר המונח הבעל תכלית א"ב | |
| ונרצה שנחלק אותו לשני חצאים | |
| הנה נעמיד על קו א"ב משלש שוה הצלעות והוא משולש אג"ב | |
| ונחלק זוית אג"ב לשני חצאים בקו ג"ד הישר | |
| הנה מפני כי קו א"ג שוה לקו ג"ב | |
| Line GD is common. | וקו ג"ד משותף |
| יהיה כל שני קוי א"ג ג"ד שוים לכל שני קוי ב"ג ג"ד כל אחת לגילו | |
| וזוית אג"ד שוה לזוית בג"ד | |
| אם כן תושבת א"ד שוה לתושבת ד"ב | |
| הנה כבר נחלק קו א"ב הישר המונח בעל התכלית לשני חציים על נקודת ד' | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 11 |
|
| יא נרצה שנוציא מנקדה מונחת על קו ישר מונח קו ישר על זוית נצבת | |
| ויהיה הקו הישר המונח א"ב והנקדה המונחת אשר עליו נקדת ג' ונרצה שנוציא מנקדת ג' קו ישר יהיה על זוית נצבת מקו א"ב ונרשום עליו קו ג"א נקדה איך מה שנפלה והיא ד' ונבדיל מקו ג"ב קו שוה לקו ג"ד והוא קו ג"ה ונעמיד על ד"ה משלש שוה הצלעות והוא דה"ז ונגיע קו ז"ג הנה מפני כי קו ד"ג שוה לקו ג"ה וקו ג"ז משתתף יהיו כל שני קוי ה"ג ג"ד כל אחד לגילו ותושבת ד"ז שוה לתושבת ז"ה מפני כי המשלש שוה הצלעות אם כן זוית דג"ז שוה לזוית זג"ה והם אשר משני הצדדים וכאשר עמד קו ישר על קו ישר ושם שתי הזויות אשר משני צדדיו שוות הנה כל אחת משתיהן נצבת אם כן כל אחת משתי זויות דז"ג זג"ה נצבת אם כן קו ג"ז עומד על קו א"ב על זויות נצבות הנה כבר הוצא מנקודת ב' מקו א"ב קו על זוית נצבת והוא ג"ז וזה מה שרצינו לבאר | |
Proposition 12 |
|
| יב נרצה שנוציא על קו ישר מונח בלי תכלית מנקדה איננה עליו קו ישר יהיה עמוד על הקו המונח | |
| ויהיה הקו הישר המונח אשר הוא בלתי בעל תכלית קו א"ב והנקודה המונחת אשר עליו וראוי נקודת מנקודת אל קו א"ב הישר קו יהיה עמוד עליו ונרשום בצד האחד מן הקו הישר נקדה איך מה שנפלה והיה ה' ונקוה על מרכז ג' ומרחק ג"ה עגולת דה"ז ונחלק מן ה"ז הישר בשני חציים על נקדת ח' ונגיע קו ה"ג ג"ה ג"ז הנה אומר כי קו ג"ח עמוד על א"ב הנה מפני כי קו ה"ח ג"ה שוים לכל שני קוי ז"ח ח"ג כל אחד לגילו ותושבת ה"ב שוה לתושבת ג"ז מפני כי נקדת ג' מרכז עגלת דה"ז הנה זוית הח"ג שוה לתושבת ג"ז מפני כי נקדת ג' מרכז עגלת דה"ז הנה זוית הא"ג שוה לזוית דה"ג והם השתי זויות אשר משני הצדדים וכאשר עמד קו ישר על קו ישר ושם שתי הזויות אשר משני צדדיו שוות הנה כל אחת מהן נצבת והקו העומד יקרא העמוד על הקו אשר הוא עומד עליו אם כן קו ג"ח עמוד על קו א"ב הנה כבר הוצא אל הקו א"ב הישר המונח אשר הוא בלי תכלית מנקדת ג' המונחת אשר אינה על קו א"ב קו ישר עמוד עליו והוא קו ג"ח וזה מה שרצינו לבאר | |
Proposition 13 |
|
| יג כאשר עמד קו ישר על קו ישר איך מה שנפל הנה הוא יחדש שתי זויות אם נצבות ואם שוות לשתי נצבות | |
| ויעמוד קו א"ב הישר על קו ג"ד הישר ויחדש שתי זויות גב"א אב"ד הנה אמר כי שתי זויות גב"א אב"ד אם שתי נצבות ואם שוות לשתי זויות נצבות ואם היה א"ב נצב על ג"ד על זויות בלתי נצבות הנה נוציא מנקדת ב' מקו ג"ד קו ב"ח על זויות נצבות הנה שתי זויות גב"ה הב"ד שתי זויות נצבות ומפני כי זויות דב"ח הב"א אב"ג השלשה שוות לשתי זויות גב"ח חב"ד יהיו שתי זויות גב"א אב"ד שוות לשתי זויות גב"ח חב"ד הנצבות הנה שתי זויות גב"ח אב"ד שוות לשתי נצבות הנה כאשר עמד קו ישר על קו ישר איך מה שנפל הנה הוא יחדש שתי זויות אם נצבות ואם שוות לשתי נצבות וזה מה שרצינו לבאר | |
| יג) כאשר יחובר אל נקודה על קו מה ישר שני קוים ישרים אינם בצד אחד וישים שני הזויות משני הצדדים שוות לשתי נצבות הנה כל אחד משני הקוים הישרים על יושר אחד | |
| ונחבר אל נקדת ב' אשר על קו א"ב הישר שני קוי ב"ג ב"ד הישרים אשר אינם מונחים בצד אחד וישימו שתי זויות גב"א אב"ד אשר משני הצדדים שוות לשתי נצבות הנה אומר כי קו ג"ב על יושר ב"ד שאם היה אפשר זולת זה הנה יהיה ב"ה על יושר ג"ב הנה מפני כי קו ב"א הישר כבר עמד על גב"ה וחדש שתי זויות גב"א אב"ה יהיו שתי זויות גב"א אב"ה שוות לשתי זויות ושתי גב"א אב"ד כבר ספרנו שהן שוות לשתי נצבות זויות אם כן שתי זויות גב"א אב"ד שוות לשתי זויות גב"א אב"ה ונשליך זוית גב"א המשותפת הנה זוית אב"ד הנשארת שוה לזוית אב"ה הנשארת הגדולה כמו הקטנה וזה בלתי אפשר אם כן אין ב"ה על יושר ב"ג וכן יתבאר שאין קו אחד על יושר ב"ג זולת ב"ד על יושר קו ב"ג הנה כאשר חובר אל נקדה על קו ישר שני קוים ישרים אינם בצד אחד ושם שתי הזויות אשר משני צדדים שוות לשתי נצבות הנה כל אחד משני הקוים הישרים על יושר האחד וזה מה שרצינו לבאר | |
Proposition 14 |
|
| יד כאשר חתך כל אחד משני קוים ישרים כאחד את האחר הנה הם ישימו כל שתי זויות מתנגדות מן הזויות אשר יתחדשו שוות | |
| ויחתוך כל אחד משני קוי א"ב ג"ד הישרים האחד על נקדת ה' הנה אומר כי זוית גה"ב שוה לזוית אח"ד וזוית בה"א שוה לזוית בה"ד הנה מפני כי כבר עמד קו ישר והוא ג"ה על קו א"ב הישר וחדש שתי זויות בה"ג גה"א יהיו שתי זויות בה"ג גה"א שוות לשתי נצבות וגם כן הנה מפני כי קו א"ה הישר עמד על קו על קו ג"ד הישר ויחדש שתי זויות דה"א אה"ג יהיו שתי זויות דה"א אה"ג שוות לשתי נצבות וכבר התבאר כי שתי זויות בה"ג גה"א שוות לשתי נצבות אם כן שתי זויות בה"ג גה"א שוות לשתי זויות גה"א אה"ד ונשליך זוית גה"א המשותפת אם כן זוית בה"ג הנשארת שוה לזוית דה"א הנשארת והם שני מתנגדים וכן גם כן יתבאר כי זוית גה"א שוה לזוית בה"ד וכאשר חתך כל אחד משני קוים ישרים האחר הנה שניהם ישימו כל שתי זויות מתנגדות מן הזויות אשר יחדשו שוות וזה מה שרצינו לבאר | |
| וכבר התבאר מזה כי כאשר חתך כל אחד משני קוים ישרים האחר הנה שניהם ישימו הזויות אשר אצל חותכיהם שוות לארבע זויות נצבות | |
Proposition 15 |
|
| טו כל משלש יוצא צלע מצלעיו על יושר הנה זוית היוצאת יותר גדולה מכל אחת משתי זויות פנימיות המתנגדות אליה | |
| ויהיה משלש עליו אב"ג ויצא צלע ב"ג מצלעיו אל נקדת ד' הנה אומר כי זוית אג"ד החיצונה ממשלש אב"ג יותר גדולה מכל אחת משתי זויות בא"ג אב"ג הפנימיות המתנגדות אליה ונחלק קו א"ג לשני חצאים על ה' ונגיע בה' ונוציא קו ה"ז הישר על יושר ב"ה ונשים קו ה"ז שוה לקו ב"ה ונגיע ג' ונוציא קו ב"ח הישר על יושר קו א"ג הנה מפני כי קו א"ה שוה לקו ה"ג וקו ב"ה שוה לקו ה"ז יהיו כל שני קוי א"ה ה"ב שוים לכל שני קוי ג"ה ה"ז כל אחד לגילו וזוית אה"ב שוה לזוית גה"ז ותושבת א"ב שוה לתושבת ז"ג ומשלש אב"ה שוה למשלש זה"ג ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע יהיה מיתר האחרת אם כן זוית בא"ה שוה לזוית הג"ז וזוית הג"ד יותר גדולה מזוית הג"ז אם כן זוית אג"ד יותר גדולה מזוית בא"ג וכן יתבאר גם כן מחלוקת קו ב"ג בשתי חציים כי זוית בג"ח יותר גדולה מזוית אב"ג אבל זוית בג"ח שוה לזוית אג"ד מפני כי שניהם מתנגדות אם כן זוית אג"ד יותר גדולה מזוית אב"ג אם כן כל משלש יצא צלע מצלעותיו הנה הזוית החיצונה יותר גדולה מכל אחת מהזויות הפנימיות המתנגדות אליה וזה מה שרצינו לבאר | |
Proposition 16 |
|
| יו כל שתי זויות ממשלש איזה משתי זויות שיהיו הנה הם יותר קטנות משתי נצבות | |
| ויהיה המשלש עליו אב"ג הנה אומר כי כל שתי זויות ממשלש אב"ג איזה שתי זויות שיהיו קטנות משתי נצבות ונוציא קו ג"ד על יושר קו ב"ג הנה מפני כי זוית אג"ד החיצונה ממשלש אב"ג תהיה יותר גדולה מן הזויות הפנימית אשר תתנגד לה והיא זוית אב"ג ונשים זוית בג"א משותפת אם כן שתי זויות דג"א אג"ב יותר גדולות משתי זויות אג"ב גב"א אבל זוית דג"א אג"ב שוות לשתי נצבות אם כן שתי זויות אג"ב גב"א פחות משתי נצבות וכן יתבאר כי שתי זויות גב"א בא"ג פחות משתי נצבות ושתי זויות בא"ג אג"ב גם כן פחות משתי נצבות הנה כל שתי זויות ממשלש איזה שתי זויות שיהיו פחות משתי נצבות וזה מה שרצינו לבאר | |
Proposition 17 |
|
| יז הצלע היותר ארוך מכל משלש יהיה מיתר הזוית הגדולה | |
| ויהיה משלש עליו אב"ג ויהיה צלע א"ב מהם יותר ארוך מצלע א"ג הנה אומר כי זוית אג"ב יותר גדולה מזוית אב"ג הנה מפני כי צלע א"ב יותר ארוך מצלע א"ג הנה אומר כי זוית אג"ב יותר גדולה מזוית אב"ג הנה מפני כי צלע א"ב יותר ארוך מצלע א"ג נשים א"ד כמו א"ג ונציע ד"ג הנה מפני כי קו ד"א שוה לקו א"ג תהיה זוית אד"ג שוה לזוית אג"ד וזוית אג"ב יותר גדולה מזוית אג"ד תהיה זוית אג"ב גדולה מזוית אד"ג ומפני כי זוית אד"ב חיצונה ממשלש דב"ג תהיה יותר גדולה והזוית הפנימית אשר תתנגד לה אשר עליה אב"ג אבל זוית אג"ה יותר גדולה הרבה מזוית אב"ג אם כן הצלע יותר ארוך מכל משלש היא מיתר הזוית הגדולה ונשלם ביאורו | |
Proposition 18 |
|
| יח הזוית היותר גדולה מכל משלש יהיה מיתרה הצלע היותר ארוך | |
| ויהיה משלש עליו אב"ג ותהיה זוית בג"א ממנו יותר גדולה מזוית אב"ג הנה אומר כי צלע א"ב יותר גדולה מצלע א"ג ואם לא תהיה כן הנה היה שוה אליה או קטנה ממנה ואין צלע א"ב שוה לצלע א"ג כי אלו היתה שוה היתה זוית אג"ב כמו זוית אב"ג ואינו כן אם כן אין צלע א"ב שוה לצלע א"ג ואינה יותר קטנה ממנה היתה זוית אג"ב ואינו כן אם כן צלע א"ב שוה לצלע א"ג ואינה יותר קטנה ממנה היתה זוית אג"ב יותר קטנה מזוית אב"ג ואם כן אין צלע א"ב יותר קטנה מצלע א"ג וכבר התבאר שהיה בלתי שוה אם כן צלע א"ב יותר ארוכה מצלע א"ג אם כן הזוית היותר גדולה מכל משלש יהיה מיתרה הצלע היותר ארוך וזה מה שרצינו לבאר | |
Proposition 19 |
|
| יט כל שתי צלעות ממשלש איזה שתי צלעות שיהיו הנה שתיהן יותר ארוכות מן הצלע הנשארת | |
| ויהיה משלש עליו אב"ג הנה אומר כי כל שתי צלעות ממשלש אב"ג איזה שתי צלעות שתהיינה הנה שתיהן יותר ארוכות מן הצלע הנשארת אולם ב"א א"ג הם יותר ארוכות מן ב"ג ואולם א"ב ב"ג ארוכות מא"ג ואולם ב"ג ג"א יותר ארוכות מן א"ב ונוציא קו א"ד הישר על יושר קו ב"א ונשים קו א"ד תהיה זוית אג"ד שוה לזוית אד"ג וזוית דג"ב יותר גדולה מזוית דב"א הנה זוית דג"ב גדולה מזוית בד"ג והזוית היותר גדולה מכל משלש יהיה מיתרה הצלע היותר ארוך אם כן צלע ב"ד יותר ארוך מצלע ב"ג וצלע ב"ד שוה לשתי צלעות ב"א א"ג יותר ארוכות מצלע ב"ג וכן גם כן יתבאר ששתי צלעות א"ב ב"ג ארוכות מצלע א"ג וב"ג ג"א ארוכות מצלע ב"א אם כן כל שתי צלעות ממשלש איזה שתי צלעות שיהיו הנה שתיהן יותר קטנים מן הצלע הנשארת וזה מה שרצינו לבאר | |
Proposition 20 |
|
| כ כאשר עמדו על צלע מצלעות משלש שני קוים ישרים יצאו משני קצוות הצלע בתוך המשלש המשלש הנה שתיהן יותר קטנים משני הצלעות הנשארות מצלעות המשלש ויקיפו בזוית יותר גדולה מן הזוית אשר יקיפו בה השתי צלעות | |
| ויהיה משלש עליו אב"ג ויעמוד על צלע ב"ג מצלעות משלש אב"ג שני קוים ישרים יצאו משני קצותיו ויפלו בתוך המשלש עליהם ב"ד ד"ג הנה אומר כי שני קוי ב"ד ד"ג יותר קטנים משני קוי ב"א א"ג ושזוית בד"ג אשר יקיפו בה יותר גדולה מזוית בא"ג ונוציא קו ד"ה הישר על יושר קו ב"ד הנה מפני כי כל שתי צלעות ממשלש איזה שתי שיהיו הנה שתיהן יותר מהקודמת ארוכות מן הצלע הנשאר יהיו קוי ב"א ה"א ארוכים מקו ה"ב ונשים ה"ב משותף הנה שני קוי ב"א א"ג יותר ארוכים משני קוי ב"ה ה"ג ומפני כי כל שתי צלעות ממשלש איזה שתי צלעות שיהיו הנה שתיהן יותר ארוכים מן הצלע הנשאר יהיו שני קוי ה"ד ה"ג יותר ארוכים מקו ד"ג ונשים קו ד"ב משותף ויהיו שני קוי ג"ה ה"ב יותר ארוכים משני קוי ב"ד ד"ג וכבר התבאר כי שני ב"א א"ג יותר ארוכים משני קוי ב"ה ה"ג אם כן שני קוי ב"א א"ג יותר ארוכים הרבה משני קוי ב"ד וד"ג זוית בא"ג גם כן חוץ ממשלש בא"ה תהיה יותר גדולה מזוית בא"ג הפנימית אשר תקבילה וכבר התבאר כי זוית בד"ג יותר גדולה מזוית בא"ג אם כן כאשר עמדו על צלע מצלעות המשולש קוים יוצאו מקצוות הצלע ויהיו בתוך המשלש הנה הם יותר קצרים משתי צלעות הנשארות מצלעות המשלש ויקיפו בזוית יותר גדולה מן הזוית אשר יקיפו בה שתי הצלעות הנשארות וזה מה שרצינו לבאר | |
Proposition 21 |
|
| כא נרצה שנעמיד משלש משלשה קוים ישרים שוים לשלשה קוים ישרים מונחים וראוי שיהיו כל שני קוים מן הקוים השלשה איזה שני קוים שיהיו יותר ארוכים מן הקו הנשאר | |
| ויהיו השלשה קוים המונחים אב"ג ויהיו כל שני מהם איזה שני קוים שיהיו יותר ארוכים מן הקו הנשאר אם כן א"ב יותר ארוכים מן ג' ואם ב"ג יותר ארוכים מן א' ואם א"ג יותר ארוכים מן ב' ונרצה שנעמיד ממשלש יהיו שוות הצלעות לקו אב"ג הנה נשים קו ד"ה הישר בעל תכלית באחד משני צדדים על נקדת ד' ובלתי בעל תכלית בצד אשר בו ט' ונשים קו ד"ז שוה לקו א' וקו ז"ח שוה לקו ב' וקו ח"ט שוה לקו ג' ונקוה על מרכז ז' ובמרחק ז"ד עגולת דב"ג ונקוה גם כן על מרכז ח' ובמרחק ח"ט עגולת טב"ג ונוציא מנקודת ב' אל שתי נקדות ז"ח שני קוי ב"ז ג"ח הישרים הנה אומר כי משלש בז"ה הוקם משלשה קוים ישרים לקו אב"ג הישרים המונחים הנה מפני כי נקדת ז' מרכז עגולת דב"ג יהיה קו ד"ז שוה לקו ז"ב אבל קו ד"ז שוה לקו א' אם כן קו ז"ב שוה לקו א' וגם כן הנה נקדת ח' מרכז עגולת טב"ג אם כן קו ח"ט שוה לקו ח"ב אבל קו ח"ט שוה לקו ג' אם כן קו ח"ב שוה לקו ג' וקו ז"ח שוה לקו ב' הנה כבר הוקם מקו ד"ז ז"ח ח"ט הישרים השוים לקוי אב"ג הישרים המונחים משלש בז"ח וזה מה שרצינו לבאר | |
Proposition 22 |
|
| כב נרצה שנעמיד על קו ישר מונח על נקודתו ממנו מונחת זוית ישרת שני הקוים שוה לזוית מונחת ישרת שני הקוים | |
| ויהיה הקו הישר המונח א"ב והנקודה המונחת אשר עליו ח' והזוית המונחת ישרת שני הקוים דג"ה ונרצה שנעמיד על קו א"ב הישר המונח על נקודת א' ממנו זוית ישרת שני הקוים שוה לזוית דג"ה המונחת ישרת שני הקוים שוה לזוית דג"ה המונחת ישרת שני הקוים הנה נרשום על כל אחת משני קו ד"ג ג"ה נקדה איך מה שנפלה והם ד"ה ונגיע קו ד"ה ונעמיד מהקו המונח שהוא קו א"ב משולש משלשה קוי א"ז ז"ח א"ח השלשה הישרים השוים לקוי ד"ג ג"ה ה"ד הישרים המונחים והוא משלש אז"ח ויהיה קו א"ז ממנו שוה לקו ג"ד וקו א"ה שוה לקו ג"ה וקו ז"ח לקו ד"ה הנה מפני כי שני קוי ד"ג ג"ה שוים לשני קוי א"ז א"ה כל אחד לגילו ותושבת ד"ה שוה לתושבת זה"ד תהיה זוית דג"ה שוה לזוית זא"ח הנה כבר הוקם על קו א"ב הישר המונח על נקודת א' ממנו זוית ישרת שני הקוים שוה לזוית דג"ה המונחת ישרת הקוים והיא זוית זא"ח וזה מה שרצינו לבאר | |
Proposition 30 |
|
| The lines that are parallel to the same straight line are also parallel to one another. | ל הקוים הנכחים לקו אחד בעינו ישר הנה קצתם נכחי לקצת |
| ויהיה כל אחד מן א"ב ג"ד נכחי לקו ה"ז | |
| Supposition: I say that AB is parallel to GD. | הנה אומר כי א"ב נכחי אל ג"ד |
| ונפל קו ישר והוא חט"כ הנה מפני כי א"ב נכחי אל ה"ז | |
| וכבר נפל עליהם קו חט"כ הישר | |
| תהיה זוית חט"ז שוה לזוית טח"א המומרות | |
| ומפני כי ה"ז נכחי אל ג"ד | |
| תהיה זוית חט"ז החיצונה שוה לזוית טב"ד הפנימית אשר תקבילה | |
| וכבר התבאר כי זוית זט"ח גם כן שוה לזוית טח"א | |
| אם כן זוית אח"ט שוה לזוית טכ"ד והם המומרות | |
| אם כן א"ב נכחי אל ג"ד | |
| אם כן הקוים הנכחיים לקו אחד בעינו ישר הנה קצתם נכחי לקצת | |
| Q.E.D. | וזה מש"ל |
Proposition 31 |
|
| We wish to draw a straight line from a given point, parallel to a given straight line. | לא נרצה שנוציא מנקודה מונחת קו ישר נכחי לקו ישר מונח |
| ותהיה הנקודה המונחת נקדת א' והקו הישר המונח קו ב"ג | |
| ונרצה שנוציא מנקדת א' קו ישר נכחי אל קו ב"ג הישר | |
| ונרשום על קו ב"ג נקדה איך מה שנפלה והיה נקדת ד' | |
| ונגיע קו א"ד | |
| ונעמיד על קו א"ד הישר על נקדת א' ממנו זוית שוה לזוית אד"ג והיא זוית דא"ה | |
| ונוציא קו א"ז על יושר קו ה"א | |
| הנה מפני כי שני קוי ה"ז ב"ג הישרים כבר נפל עליהם קו ישר והוא א"ד | |
| ושם שתי זויות הא"ד אד"ג שוות והם מומרות | |
| יהיה ה"ז נכחי אל ג"ב | |
| הנה כבר הוצא מנקודת א' המונחת קו ישר והוא ה"ז נכחי אל קו ב"ג הישר המונח | |
| Q.E.D. | וזה מש"ל |
Proposition 32 |
|
| For every triangle, if one of its sides is drawn, then the exterior angle equals [the sum of] the two interior opposite angles; and [the sum of] the three interior angles of the triangle equals two right angles. | לב כל משולש תצא צלע מצלעותיו הנה הזוית החיצונה תהיה שוה לשתי הזויות התיכונות אשר יקבילוה והזויות השלשה אשר תוך המשולש שוות לשתי זויות נצבות |
| ויהיה משלש עליו אב"ג ותצא אחת מצלעותיו הוא ב"ג אל נקדת ד' | |
| Supposition: I say that the exterior angle AGD is equal [the sum of] the two interior angles A and B; and that [the sum of] the three interior angles ABG, BGA and GAB of the triangle equals two right angles. | הנה אומר כי זוית אג"ד החיצונה שוה לשתי זויות א"ב הפנימיו' ושזויות אב"ג בג"א גא"ב השלשה אשר תוך המשולש שוות לשתי זויות נצבות |
| ונוציא מנקדת ג' קו נכחי לקו א"ב הישר והוא ג"ה | |
| הנה מפני כי א"ב נכחי אל ג"ה | |
| וכבר נפל עליהם א"ג | |
| יהיו שתי זויות בא"ג אג"ה המומרות שוות | |
| ומפני כי א"ב נכחי אל ג"ה | |
| וכבר נפל עליהם קו בג"ד הישר | |
| תהיה זוית הג"ד החיצונה שוה לזוית אב"ג הפנימית אשר תקבילה | |
| וכבר התבאר כי זוית אג"ה גם כן שוה לזוית בא"ג | |
| אם כן כל זוית אג"ד החיצונה שוה לשתי זויות בא"ג אב"ג הפנימיות אשר יקבילוה | |
We define 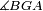 common. common.
|
ונשים זוית בג"א משותפת |
| אם כן שתי זויות דג"א אג"ב שוות לזויות השלשה גב"א בג"א בא"ג | |
| אבל שתי זויות דג"א אג"ב שוות לשתי נצבות | |
| אם כן זויות גב"א בא"ג אג"ב השלשה שוות לשתי זויות נצבות | |
| אם כל משלש יצא צלע מצלעותיו הנה הזוית החיצונה תהיה שוה לשתי הזויות הפנימיות אשר יקבילום והזויות השלשה אשר בתוך המשולש שוות לשתי זויות נצבות | |
| Q.E.D. | וזה מש"ל |
Proposition 33 |
|
| The straight lines, which join the ends of equal and parallel straight lines on the same side, are also equal and parallel. | לג הקוים הישרים אשר יגיעו במה שבין קצוות הקוים הישרים השוים הנכחים אשר בצד אחד הם גם כן שוים נכחיים |
| ונגיע שני קוי א"ג ב"ד הישרים במה שבין קצוות שני קוי א"ב ג"ד אשר בצד אחד | |
| Supposition: I say that AG and BD are also equal and parallel. | הנה אומר כי א"ג ב"ד גם כן שוים נכחיים |
| ונגיע ב"ג | |
| הנה מפני כי א"ב נכחי אל ג"ד | |
| וכבר נפל עליהם קו ישר והוא ב"ג | |
| יהיו שתי זויות אב"ג בג"ד המומרות שוות | |
| ומפני כי א"ב גם כן שוה אל ג"ד | |
| BG is common. | וב"ג משותף |
| יהיו כל שתי קוי א"ב ב"ג שוים לכל שני קוי ד"ג ג"ב כל אחד לגילו | |
| וזוית אב"ג שוה לזוית בג"ד | |
| אם כן תושבת א"ג שוה לתושבת ב"ד | |
| ומשולש אב"ג שוה למשולש בג"ד | |
| ושאר הזויות שוות לשאר הזויות כל אחת לגילה אשר יהיה מיתרה הצלע השוה לצלע אשר יהיה מיתר האחרת | |
| אם כן זוית אג"ב שוה לזוית דב"ג והם מומרות | |
| אם כן א"ג נכחי אל ב"ד | |
| וכבר התבאר כי שניהם שוים | |
| אם כן שני קוי א"ג ב"ד שוים נכחיים | |
| אם כן הקוים הישרים אשר יגיעו במה שבין קצוות הקוים הישרים הנכחים אשר בצד אחד הם גם כן שוים נכחים וזה מה שרצי' לבא' | |
Proposition 34 |
|
| The opposite sides and angles of parallelogrammic areas are equal to one another, and the diameters of these areas bisect them. | לד הצלעות והזויות המתנגדות מן השטחים נכחי הצלעות שוים קצתם אל קצתם וקטרי השטחים יחלקום בשני חצאים |
| ויהיה שטח א"ב ג"ד נכחי הצלעות ויהיה קטרו ד"ב | |
| Supposition: | הנה אומר כי צלעות שטח א"ב ג"ד נכחי הצלעות הצלעות המתנגדות וזויותיו המתנגדות שוות קצתם אל קצתם ושהקוטר יחלקהו לשני חצאיים |
| הנה מפני כי קו א"ד נכחי אל ב"ג | |
| וכבר נפל על שניהם קו ד"ב הישר | |
| יהיו שתי זויות אד"ב גב"ד המומרות שוות | |
| ומפני כי א"ב גם כן נכחי אל ג"ד | |
| וכבר נפל על שניהם קו ד"ב הישר | |
| יהיו שתי זויות גד"ב דב"א המומרות שוות | |
| אם כן שני משולשי אב"ד גד"ב כבר השתוו משתי זויות אד"ב אב"ד מאחד משניהם לשתי זויות גד"ב דב"ג מן האחר כל אחת לגילה | |
| ובשני המשולשים צלע משותף לשניהם מה שילוה הזויות השוות והוא ד"ב | |
| אם כן שאר הצלעות שוות לשאר הצלעות כל אחת לגילה | |
| אולם קו א"ב לקו ג"ד | |
| ואולם קו א"ד לקו ב"ג | |
| וזוית דא"ב הנשארת שוה לזוית בג"ד הנשארת | |
| ומשלש אב"ג שוה למשלש בג"ד | |
| ומפני כי זוית אב"ד גם כן שוה לזוית בד"ג | |
| וזוית גד"ב שוה לזוית אד"ב | |
| תהיה זוית אב"ג כלה שוה לזוית אד"ג | |
| אם כן הצלעות והזויות המתנגדות מן השטחים הנכחים הצלעות שוות קצתם אל קצתם וקטרי השטחים יחלקו' לשני חצאים | |
| Q.E.D. | וזה מש"ל |
Proposition 35 |
|
| The parallelograms, which are on the same base, on the same side, and between the same parallel lines, are equal to one another. | לה השטחים הנכחיי הצלעות אשר על תושבת אחת ובצד אחד ובמה שבין קוים בעינם נכחים שוים קצתם אל קצת |
| ויהיו שני השטחים נכחיי הצלעות א"ב ג"ד ה"ב ג"ז על תושבת אחת והיא ב"ג ובמה שבין שני קוים א"ז ב"ג הנכחים | |
| Supposition: I say that the parallelogram ABGD is equal to the parallelogram BHGZ. | הנה אומר כי שטח א"ב ג"ד נכחי הצלעות שוה לשטח ב"ה ג"ז נכחי הצלעות |
| הנה מפני כי שטח א"ב ג"ד נכחי הצלעות יהיה ב"ג שוה אל ד"א | |
| ומפני זה יהיה ה"ז שוה אל ב"ג | |
| אם כן א"ד שוה אל ה"ז | |
| We define DH common. | ונשים ד"ה משותף |
| אם כן א"ה כולו שוה אל ד"ז כולו | |
| וא"ב גם כן שוה אל ג"ד | |
| אם כן כל שני קוי ב"א א"ה שוים לכל שני קוי ג"ד ד"ז כל אחת לגילה | |
| וזוית בא"ה שוה לזוית גד"ז החיצונה לפנימית | |
| אם כן תושבת ב"ה שוה לתושבת ז"ג | |
| ומשולש הא"ב שוה למשולש זד"ג | |
| ונשליך משלש דח"ה המשותף נשאר שטח א"ב ח"ד שוה לשטח ג"ח ה"ז הנשאר | |
We define 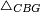 common. common.
|
ונשים משלש חב"ג משותף |
| אם כן כל שטח א"ב ג"ד נכחי הצלעות שוה לכל שטח ה"ב ג"ז נכחי הצלעות | |
| אם כן השטחים נכחי הצלעות אשר על תושבת אחת ובצד אחד ובמה שבין שני קוים בעינם נכחים שוים קצת אל קצת | |
| Q.E.D. | וזה מש"ל |
Proposition 36 |
|
| The parallelograms, which are on equal bases, on the same side, and between the same two parallel lines, are equal to one another. | לו השטחים נכחי הצלעות אשר על תושבות שוות ובצד אחד ובמה שבין שני קוי נכחיים שוים קצתם אל קצתם |
| ויהיו שני שטחים נכחיים הצלעות עליהם א"ב ג"ד ה"ז ח"ט על שתי תושבות שוות והם ב"ג ז"ח ובמה שבין שני קוים א"ט ב"ח הנכחיים | |
| Supposition: I say that the parallelogram ABGD is equal to the parallelogram HZCT. | הנה אומר כי שטח א"ב ג"ד הנכחי הצלעות שוה לשטח ה"ז ח"ט הנכחי הצלעות |
| ונגיע שני קוי ה"ב ט"ג | |
| הנה מפני כי ב"ג שוה אל ז"ח | |
| וז"ח שוה אל ה"ט | |
| יהיה ה"ט שוה אל ב"ג והוא גם כן נכחי לו | |
| והקוים הישרים אשר יגיעו במה שבין קצוות הקוים הישרים השוים הנכחיים אשר בצד אחד הם גם כן שוים נכחיים | |
| אם כן שני קוי ה"ב ט"ג שוים נכחיים | |
| אם כן שטח א"ב ג"ד הנכחי הצלעות שוה גם כן אל שטח ה"ט ג"ב מפני כי שניהם על תושבת אחת והיא ב"ג ובמה שבין שני קוים והם ב"ח א"ט | |
| ולכן יהיה שטח ה"ז ח"ט נכחי הצלעות שוה לשטח ט"ה ב"ג הנכחי הצלעות | |
| אם כן כל אחד משני שטחי א"ב ג"ד ה"ז ח"ט שוה לשטח ט"ה ב"ג | |
| והדברים השוים לדבר אחד בעינו הם שוים | |
| אם כן שטח א"ב ג"ד הנכחי הצלעות שוה לשטח ה"ז ח"ט הנכחי הצלעות | |
| אם כן השטחים הנכחיים הצלעות אשר על תושבות שוות ובצד אחד ובמה שבין קוים בעינם נכחיים שוים קצתם אל קצת | |
| Q.E.D. | וזה מש"ל |
Proposition 37 |
|
| The triangles, which are on the same base, on the same side, and between the same two parallel lines, are equal to one another. | לז המשולשים אשר על תושבת אחת ובצד אחד ובמה שבין קוים נכחיים שוים קצתם אל קצת |
| ויהיו שני משולשים אב"ג דב"ג על תושבת אחת והוא ב"ג | |
| ובמה שבין שני קוי ב"ג א"ד הנכחיים | |
| Supposition: I say that triangle ABG is equal to triangle DBG. | הנה אומר כי משולש אב"ג שוה למשולש דב"ג |
| ונוציא א"ד בשני הצדדים על שתי נקודות ה"ז | |
| ונוציא מנקודת ב' קו ישר נכחי לקו ג"א הישר והוא ב"ה | |
| ומנקודת ג' קו ישר נכחי לקו ב"ד הישר והוא ג"ז | |
| הנה כל אחד משני שטחי ה"ב ג"א ד"ב ג"ז נכחי הצלעות שוים | |
| אם כן שטח ה"ב ג"א הנכחי הצלעות שוה לשטח ז"ד ב"ג הנכחי הצלעות | |
| מפני שהם על תושבת אחת והיא ב"ג | |
| ובמה שבין שני קוי ב"ג ה"ז הנכחים | |
| וחצי שטח ה"ב ג"א הנוכחי הצלעות הוא משולש אב"ג | |
| מפני שא"ב קוטרו | |
| וחצי שטח ד"ב ג"ז הנכחי הצלעות היא משולש דב"ג | |
| מפני שג"ד קטרו | |
| וכאשר נחלקו השוים יהיו גם כן שוים | |
| אם כן משלש אב"ג שוה למשולש דב"ג | |
| הנה כל שני משולשים אשר על תושבת אחת ובצד אחד ובמה שבין שני קוים בעצמם נכחים שוים קצתם אל קצת | |
| ונשלם ביאורו | |
Proposition 38 |
|
| The triangles, which are on equal bases, on the same side, and between the same two parallel lines, are equal to one another. | לח המשולשים אשר הם על שתי תושבות שוות ובצד אחד ובמה שבין שני קוים בעצמם נכחים שוים קצתם לקצת |
| ויהיו שני משולשי אב"ג דה"ז על שתי תושבות שוות והם ב"ג ה"ז | |
| ובמה שבין שני קוי א"ד ב"ז הנכחים | |
| Supposition: I say that triangle ABG is equal to triangle DHZ. | הנה אומר שמשלש אב"ג שוה למשולש דה"ז |
| הנה נוציא א"ד בשני הצדדי' על שתי נקודות ח"ט | |
| ונוציא מנקודת ב' קו ישר נכחי לקו א"ג הישר והוא ב"ח | |
| ומנקודת ז' ישר נכחי לקו ה"ד הישר והוא ז"ט | |
| הנה כל אחד משני שטחי ח"ב ג"א ה"ד ז"ט נכחי הצלעות | |
| אם כן שטח ח"ב ג"א נכחי הצלעות שוה לשטח ה"ד ט"ז הנכחי הצלעות | |
| מפני שהם על תושבת ב"ג ה"ז השוים | |
| ובמה שבין שני קוי ב"ז ח"ט הנכחיים | |
| וחצי שטח ח"ב ג"א הוא משולש אב"ג | |
| מפני שא"ב קטרו | |
| וחצי שטח ז"ט ד"ה הוא משולש דה"ז | |
| מפני שד"ז קטרו | |
| וכאשר נחלקו השוים יהיו גם כן שוים | |
| הנה משולש אב"ג שוה למשולש דה"ז | |
| הנה אם כן שני המשולשים אשר הם על תושבת שוות ובצד אחד ובמה שבין שני קוים בעצמם נכחיים קצתם לקצת | |
| Q.E.D. | וזה מש"ל |
Proposition 39 |
|
| Equal triangles, which are on the same base [and on the same side], are between the same two parallel lines. | לט המשולשים השוים אשר על תושבת אחת במה שבין שני קוים בעינם נכחים |
| יהיו שני משולשי אב"ג דב"ג שוים והם על תושבת אחת והוא ב"ג | |
| ונמשיך קו א"ד | |
| Supposition: I say that AD is parallel to BG. | אומר שא"ד נכחי אל ב"ג |
| שאם לא יהיה כן הנה נוציא מנקודת א' קו ישר נכחי לקו ב"ג והוא א"ה | |
| ונמשיך קו ה"ב | |
| הנה משולש הב"ג שוה למשולש אב"ג | |
| מפני שהם על תושבת אחת והיא ב"ג | |
| ובמה שבין שני קוי ב"ג א"ה נכחים | |
| אבל משולש אב"ג שוה למשולש דב"ג | |
| אם כן משולש דב"ג שוה למשולש הב"ג | |
| הגדול לקטן זה מה שאי אפשר להיות | |
| הנה אין קו א"ה נכחי לקו ב"ג | |
| וכן גם כן יתבאר שלא יוצא מנקודת א' קו נכחי לקו ב"ג זולת קו א"ד | |
| הנה קו א"ד נכחי לקו ב"ג | |
| הנה אם כן שני המשולשים השוים אשר תושבת אחת הם במה שבין שני קוים בעצמם נכחים | |
| Q.E.D. | וזה מש"ל |
Proposition 40 |
|
| Equal triangles, which are on equal bases and both bases are on a straight line and on the same side, are contained between two parallel lines. | מ המשולשים השוים אשר על שתי תושבות שוות ושתי התושבות על קו ישר ובצד אחד יכלו במה שבין שני קוים נכחים |
| יהיו שני משולשי אב"ג דה"ז שוים | |
| ועל שתי תושבות שוות והם ב"ג ה"ז | |
| ונמשיך קו א"ד | |
| Supposition: I say that AD is parallel to BZ. | אומר שא"ד נכחי לב"ז |
| ואם לא יהיה כן הנה יהיה א"ח נכחי לב"ז אם יהיה אפשר זה | |
| ונמשיך קו ח"ה | |
| הנה משולש הח"ז שוה למשלש אב"ג | |
| מפני שהם על תושבות שוות והם ב"ג ה"ז הישרי' | |
| ובמה שבין שני קוי ב"ז א"ח הנכחים | |
| אבל משלש אב"ג שוה למשולש דה"ז | |
| ומשולש דה"ז שוה למשולש הח"ז | |
| הגדול לקטן וזה בלתי אפשר | |
| הנה אין א"ח נכוחי לב"ז | |
| הנה אם כן א"ד נכחי לב"ז | |
| וכן כן יתבאר כי לא יצא מנקודת א' קו נכחי לקו ב"ז זולת א"ד | |
| אם כן א"ד נכחי אל ב"ז | |
| הנה שני המשולשים השוים אשר על שתי התושבות ושתי התושבות על קו ישר ובצד אחד יכלו במה שבין שני קוים נכחים | |
| Quod erat demonstrandum | וזה מש"ל |
Proposition 41 |
|
| When a parallelogram and a triangle are on the same base and are between the same parallel lines, then the parallelogram is double the triangle. | מא כאשר היה שטח נכחי הצלעות ומשולש על תושבת אחת ובין שני קוי בעינם נכחיים הנה השטח הנכחי הצלעות היא כפל המשולש |
|
יהיה שטח נכחי הצלעות עליו א"ב ג"ד ומשלש אב"ג והבעל תושבת אחת והיא ב"ג ובמה שבין שני קוי ב"ג א"ד הנכחיים |
| Supposition: I say that the parallelogram ABGD is double the triangle ABG. | הנה אומר כי שטח א"ב ג"ד נכחי הצלעות כפל משלש אב"ג |
|
מפני כי שניהם על תושבת אחת והיא ב"ג ובמה שבין שני קוי נכחיים והם ב"ג א"ד |
| But, double triangle ABG is parallelogram ABGD.
|
אבל כפל משולש אב"ג הוא שטח אבג"ד הנכחי הצלעות |
|
מפני כי קטרו א"ג |
| So, parallelogram ABGD is double triangle ABG.
|
אם כן יהיה שטח א"ב ג"ד נכחי הצלעות כפל משולש אב"ג |
| Hence, when a parallelogram and a triangle are on the same base and are between the same parallel lines, then the parallelogram is double the triangle. | אם כן כאשר היא שטח נכחי הצלעות ומשולש על תושבת אחת ומה שבין שני קוים בעצמם נכחים הנה השטח הנכחי הצלעות כפל המשולש |
| Quod erat demonstrandum | וזה מש"ל |
Proposition 42 |
|
| We wish to construct a parallelogram equal to a given triangle, whose angle is equal to a given rectilinear angle. | מב נרצה שנעמיד שטח נכחי הצלעות שוה למשולש מונח שוה זויתו לזוית מונחת ישרת הקוים |
|
הנה יהיה המשולש המונח עליו אב"ג והזוית המונחת ישרת הקוים זוית ד' |
| We wish to construct a parallelogram equal to triangle ABG, whose angle is equal to the rectilinear angle D. | ונרצה שנעמיד שטח נכחי הצלעות שוה למשולש אב"ג המונח שוה זויתו לזוית ד' ישרת הקוים |
|
הנה נחלק ב"ג לחציים על נקודת ה' |
|
ונגיע א"ה |
|
ונעמיד על קו ה"ג הישר על נקודת ה' ממנו זוית ישרת הקוים שוה לזוית ד' ישרת הקוים והיא זוית גה"ז |
|
ונוציא מנקודת ג' קו ג"ח נכחי לקו ה"ז הישר ומנקודת ח' קו א"ח נכחי לקו ב"ג הישר |
| Then, ZHGC is a parallelogram. | אם כן שטח ז"ה ג"ח נכחי הצלעות |
| BH equals HG.
|
ומפני כי ב"ה שוה אל ה"ג |
| Therefore triangle ABH equals triangle AHG.
|
יהיה משולש אב"ה שוה למשלש אה"ג |
|
מפני כי שניהם על שתי תושבות שוות ושניהם בין שני קוי ב"ג א"ח הנכחים |
| So, triangle ABG is double triangle AHG.
|
אם כן משלש אב"ג כפל משלש אה"ג |
| But, parallelogram HZGC is also double triangle AHG.
|
ושטח ה"ז ג"ח נכחי הצלעות גם כן כפל משלש אה"ג |
|
מפני כי שניהם על תושבת אחת והיא ה"ג ובמה שבין שני קוי ה"ג א"ח הנכחים |
| Therefore parallelogram ZHGC is equal to triangle ABG.
|
אם כן שטח ז"ה ג"ח נכחי הצלעות שוה למשלש אב"ג |
|
מפני כי מה שהם כפל לדבר אחד בעינו הם שוים |
| Hence, we have already constructed the parallelogram ZCGH equal to triangle ABG, whose angle ZHG is equal to angle D.
|
הנה כבר העמדנו שטח ז"ח ג"ה הנכחי הצלעות שוה למשולש אב"ג וזוית זה"ג ממנו שוה לזוית ד' |
| Quod erat demonstrandum | וזה מש"ל |
Proposition 43 |
|
| For every parallelogram, the complements of the two parallelograms on both sides of its the diameter are equal to one another. | מג כל שטח נכחי הצלעות הנה שתי השטחים נכחי הצלעות אשר משני צדי קטרו אשר יקרא לשניהם המתמימים שוים |
|
ויהיה שטח נכחי הצלעות עליו אב"ג ג"ד |
|
ויהיה קטרו ד"ב |
|
ויהיה על קוטר ד"ב שני שטחי ד"ה ז"ח ז"ט ב"כ נכחי הצלעות |
|
ויהיו שני השטחים אשר יקרא לשניהם המתמימים שטח א"ט ז"ה ז"כ ג"ח |
| Supposition: I say that the two surfaces ATZH and ZKGC are equal.
|
ואומר ששני שטחי א"ט ז"ה ז"כ ג"ח שוים |
| Proof: | |
| ABGD is a parallelogram, and DB is its diameter. | הנה מפני כי א"ב ג"ד נכחי הצלעות וקטרו ד"ב |
| Therefore, triangle ABD is equal to triangle DGB.
|
יהיה משולש אב"ד שוה למשולש דג"ב |
| DHZC is also a parallelogram, and DZ is its diameter. | ומפני כי שטח ד"ה ז"ח גם כן נכחי הצלעות וקטרו ד"ז |
| Therefore, triangle ZHD is equal to triangle ZCD.
|
יהיה משולש זה"ד שוה למשלש זח"ד |
| For the same reason, triangle ZTB is also equal to triangle ZKB.
|
ולזה גם כן יהיה משולש זט"ב שוה למשולש זכ"ב |
| Hence, the two triangles DHZ and ZTB are equal to the two triangles DCZ and ZKB.
|
אם כן שני משלשי דה"ז זט"ב שוים לשני משולשי דח"ז זכ"ב |
| It has already been explained also that the whole triangle ABD is equal to the whole triangle BBG.
|
וכבר התבאר גם כן כי כל משולש אב"ד שוה לכל משולש דב"ג |
| Therefore the remaining complement ATZH must be equal to the remaining complement ZKGC.
|
הנה יחוייב שיהיה שטח א"ט ז"ה המתמים הנשאר שוה לשטח ז"כ ג"ח המתמים הנשאר |
| Thus, for every parallelogram, the complements [of the two parallelograms] on both sides of its the diameter are equal to one another. | אם כן כל שטח נכחי הצלעות אשר משני צדדי קטרו אשר יקרא לשניהם המתמימים שוים |
| Quod erat demonstrandum. | וזמש"ל |
Proposition 44 |
|
| We wish to construct a parallelogram on a given straight line equal to a given triangle, whose angle is equal to a rectilinear angle. | מד נרצה שנעשה על קו ישר מונח שטח נכחי הצלעות שוה למשולש מונח שוה זויתו לזוית מונחת ישרת הקוים |
|
ויהיה הקו הישר המונח א"ב ומשולש המונח גד"ה והזוית המונחת ישרת הקוים זוית ז' |
| We wish to construct on the given straight line AB a parallelogram equal to the given triangle GDH, whose angle is equal to the given rectilinear angle Z. | ונרצה שנעשה על קו א"ב הישר המונח שטח נכחי הצלעות שוה למשולש גד"ה המונח שוה זויתו לזוית ז' המונחת ישרת הקוים |
|
הנה נעמיד שטח נכחי הצלעות עליו ח"ב כ"ט שוה למשולש גד"ה המונח שוה זויתו לזוית ז' |
|
ויהיה ב"כ ממנו על יושר ב"א |
|
ונתמים שטח ל"א ב"ח הנכחי הצלעות |
|
ונגיע קו ל"ב |
| LA is parallel to TB.
|
הנה מפני כי ל"א נכחי אל ט"ב |
| The straight line LT falls upon both. | וכבר נפל על שניהם קו ל"ט הישר |
| Therefore [the sum of] the interior angles ALT and LTK equals two right angles. | יהיו שתי זויות אל"ט לט"כ הפנימיות שוות לשתי נצבות |
| So, [the sum of] the angles BLT and LTK is less than two right angles. | אם כן שתי זויות בל"ט לט"כ פחות משתי זויות נצבות |
| The lines produced indefinitely from [angles] less than two right angles meet. | והקוים אשר יצאו בפחות משתי נצבות אשר לא תכלית יפגשו |
| Therefore the two lines LB and TK, when produced indefinitely, will meet | אם כן שני קוי ל"ב ט"כ כאשר יצאו אל לא תכלית יפגשו |
|
ויוצאו ויפגשו על נקודת מ' |
|
ונוציא מנקודת מ' קו נכחי לשני קוי ב"א ל"ט והוא מ"נ |
|
ונוציא שני קוי א"נ כ"ה על יושר שני קוי ל"א ח"ב |
| LN is a parallelogram and its diameter is ML. | הנה מפני כי ל"נ נכחי הצלעות וקטרו מ"ל |
| LABC and BSMK are two parallelograms on diameter LM. | ועל קוטר ל"מ שני שטחי ל"א ב"ח ב"ס מ"כ נכחי הצלעות |
| ANCB and CBKT are the complements. | ושני שטחי א"נ ח"ב ח"ב כ"ט הם המתמימים |
| Therefore the parallelogram CBKT equals the parallelogram ANHB.
|
אם כן שטח ח"ב כ"ט נכחי הצלעות שוה לשטח א"נ ה"ב נכחי הצלעות |
| But, surface CBTK equals the triangle GDH.
|
אבל שטח ח"ב ט"כ שוה למשולש גד"ה |
| Therefore the parallelogram ANHK equals the triangle GDH.
|
אם כן שטח א"נ ה"כ הנכחי הצלעות שוה למשלש גד"ה |
| Angle CBK equals angle ABH.
|
ומפני כי זוית חב"כ שוה לזוית אב"ה |
| Angle CBK equals angle Z.
|
וזוית חב"כ שוה לזוית ז' |
| Then, angle ABH equals angle Z.
|
תהיה זוית אב"ה שוה לזוית ז' |
| Hence, a parallelogram equal to the given triangle GDH has been constructed on the given straight line AB, whose angle ABH is equal to the given rectilinear angle Z.
|
הנה כבר נעשה על קו א"ב הישר המונח שטח נכחי הצלעות שוה למשולש גד"ה המונח וזוית אב"ה ממנו שוה לזוית ז' המונחת ישרת הקוים |
| Quod erat demonstrandum. | וזה מש"ל |
Proposition 45 |
|
| We wish to construct a parallelogram equal to a rectilinear figure, whose angle is equal to a given rectilinear angle. | מה נרצה שנעמיד שטח נכחי הצלעות שוה לתמונה ישרת הקוים ותהיה שוה זויתה לזוית מונחת ישרת הקוים |
|
ותהיה התמונה ישרת הקוים המונחת א"ב ג"ד |
|
ותהיה הזוית המונחת ישרת הקוים זוית ל' |
| We wish to construct a parallelogram equal to the rectilinear figure ABGD, whose angle is equal to angle L. | ונרצה שנעמיד שטח נכחי הצלעות שוה לתמונה א"ב ג"ד ישרת הקוים שוה זויתו לזוית ל' |
|
הנה נגיע ב"ג |
|
ונעמיד שטח נכחי הצלעות שוה למשולש אב"ג והוא ה"ז כ"ט שוה זוית זה"ט ממנו לזוית ל' |
|
ונעשה על ז"כ שטח נכחי הצלעות שוה למשולש בג"ד והוא ז"ח כ"מ שוה זוית חז"כ ממנו לזוית ל' |
| Since each of the angles ZHT and CZK equals angle L, then angle CZK equals angle ZHT.
|
הנה מפני שכל אחת משתי זויות זה"ט חז"ב שוות לזוית ל' תהיה זוית חז"כ שוה לזוית זה"ט |
| We make angle HZK common [to each]. | ונשים זוית הז"כ משותפת |
| Therefore [the sum of] the two angles ZHT and HZK equals [the sum of] the two angles CZK and KZH. | א"כ שתי זויות זה"ט הז"כ שוות לשתי זויות חז"כ כז"ה |
| But, [the sum of] the two angles ZHT and HZK equals two right angles. | אבל שתי זויות זה"ט הז"כ שוות לשתי נצבות |
| Therefore [the sum of] the angles CZK and KZH =equals two right angles. | אם כן זויות חז"כ כז"ה שוות לשתי נצבות |
| Hence, HZ is in a straight line with line ZC. | אם כן ה"ז על יושר קו ז"ח |
| So, line TB is also in a straight line with line KM. | ולכן גם כן קו ט"ב על יושר קו כ"מ |
| HZ is equal to KT and parallel to it.
|
ומפני כי ה"ז שוה אל כ"ט ונכחי לו |
| ZC is equal to KM and parallel to it.
|
וז"ח שוה אל כ"מ ונכחי לו |
| Therefore, the whole HC is equal to TB and parallel to it.
|
יהיה כל ה"ח שוה אל ט"ב ונכחי לו |
| Hence the parallelogram HCTM is equal to the rectilinear figure ABGD.
|
אם כן שטח ה"ח ט"מ נכחי הצלעות שוה לתמונה א"ב ג"ד ישרת הקוים |
| And angle ZHT is equal to angle L.
|
וזוית זה"ט שוה לזוית ל' |
| Therefore we constructed a parallelogram equal to the rectilinear figure ABGD, whose angle equals the given rectilinear angle. | הנה כבר העמדנו שטח נכחי הצלעות שוה לתמונת א"ב ג"ד ישרת הקוים שוה זויותו לזוית מונחת ישרת הקוים |
| Quod erat demonstrandum. | וזה מש"ל |
Proposition 46 |
|
| We wish to construct a square on a given straight line. | מו נרצה שנעשה על קו ישר מונח מרובע |
| Let AB be the straight line. | ויהיה הקו הישר א"ב |
| We wish to construct a square on line AB. | ונרצה לעשות על קו א"ב מרובע |
|
הנה נוציא מקו א"ב מנקדת א' ממנו קו ישר על זוית נצבת והוא קו א"ג |
|
ונשים א"ג כמו א"ב |
|
ונוציא מנקודת ג' קו ישר נכחי לקו א"ב והוא ג"ד |
|
ונוציא מנקודת ב' קו נכחי לקו א"ג והוא ב"ד |
| Then, GABD is a parallelogram. | אם כן שטח ג"א ב"ד נכחי הצלעות |
|
וקו א"ב שוה לקו ג"ד |
|
וקו א"ג לקו ב"ד |
| But, line AB equals line AG.
|
אבל קו א"ב שוה לקו א"ג |
| So, line GD also equals line DB.
|
אם כן קו ג"ד שוה אל קו ד"ב |
| Therefore, lines AB, BD, DG, GA are equal to one another.
|
אם כן קוי א"ב ב"ד ד"ג ג"א הם שוים |
| Hence, AGDB is equilateral. | אם כן שטח א"ג ד"ב שוה הצלעות |
| Supposition: I say that it is also right-angled. | ואומר גם כן כי הוא נצב הזוי' |
| Line GA falls upon the two parallel lines AB and GD. | כי מפני שהוא כבר נפל על שני קוי א"ב ג"ד הנכחיים קו ג"א |
| Therefore, [the sum of] the two angles BAG and AGD equals [the sum of] two right angles
|
יהיו שתי זויות בא"ג אג"ד שוות לשתי זויות נצבות |
| But, angle BAG is right.
|
אבל זוית בא"ג נצבת |
| So, angle AGD is also right.
|
אם כן זוית אג"ד גם כן נצבת |
| Opposite sides and angles in parallelograms are equal to one another. | והזויות והצלעות המתנגדות מן השטחים נכחי הצלעות שוים |
| Therefore, each of the angles ABD and BDG that are opposite to the above mentioned are right.
|
אם כן כל אחת משתי זויות אב"ד בד"ג המתנגדות לאשר זכרנו שוות |
| So, surface AGDB is right-angled and it was already proved to be equilateral. | אם כן שטח א"ב ג"ד נצב הזויות וכבר התבאר שהוא שוה הצלעות |
| Therefore, surface AGDB is a square and it is constructed on line AB.
|
אם כן שטח א"ב ג"ד מרובע והוא עשוי על קו א"ב |
| Hence, we have constructed a square on the given line AB. | הנה כבר קוינו מקו א"ב המונח מרובע |
| Quod erat demonstrandum. | וזה מה שרצינו לבאר |
Proposition 47 |
|
| The square formed by the hypotenuse in right-angled triangles equals [the sum of] the two squares formed by the two sides containing the right angle. | מז המרובע ההוה מן הצלע אשר יהיה מיתר הזוית הנצבת מן המשולשים נצבי הזויות שוה לשני המרובעים ההוים משתי צלעות המקיפות הזוית הנצבת |
| Let ABG be the right-angled triangle. | ויהיה המשולש נצב הזוית אב"ג |
| Let angle BAG be its right angle.
|
ותהיה זויתו הנצבת זוית בא"ג |
| Supposition: I say that the square formed by BG is equal to [the sum of] the two squares formed by BA and AG.
|
הנה אומר כי המרובע ההווה מן ב"ג שוה לשני המרובעים ההוים מן ב"א וא"ג |
|
הנה נקוה מן ב"ג מרובע ב"ד ה"ג |
|
ומן ב"א א"ג שני מרובעים ב"ח ז"א ג"א ט"כ |
|
ונוציא מנקודת א' קו נכחי לכל אחד משני קוי ב"ד ג"ה והוא א"ל |
|
ונגיע שני קוי ח"ג א"ד |
| Angle BAG is right.
|
הנה מפני זוית בא"ג נצבת |
| Angle BAZ is also right.
|
וזוית בא"ז גם כן נצבת |
| When two straight lines ZA and AG are drawn from point A, but are not lying on the same side, the two [adjacent] angles GAB and BAZ on both sides are equal to two right angles. | יהיה כאשר הוצא מנקודת א' ממנו שני קוי ז"א א"ג הישרים ואינם בצד אחד ויהיו שתי זויות גא"ב בא"ז אשר משני הצדדים שוות לשתי נצבות |
| Therefore line ZA is in a straight line with GA.
|
אם כן קו ז"א על יושר ג"א |
| So, line AT is in a straight line with AB.
|
ולכן יהיה קו א"ט על יושר קו א"ב |
| Angle CBA is equal to the angle DBG, for each is right.
|
ומפני כי זוית חב"א שוה לזוית דב"ג וזה כי כל אחת משתיהן נצבות |
| We add angle ABG common to both. | נשים זוית אב"ג משותפת |
| So, the whole angle CBG is equal to the whole angle ABD.
|
יהיה כל זוית חב"ג שוה לכל זוית אב"ד |
| CB is equal to BA.
|
ומפני כי ח"ב שוה אל ב"א |
| BG [is equal] to BD.
|
וב"ג אל ב"ד |
| Therefore, the two lines CB and BG are equal to the two lines AB and BD respectively. | יהיו כל שני קוי ח"ב ב"ג שוים לכל שני קוי א"ב ב"ד כל אחד לגילו |
| Angle CBG equals angle ABD.
|
וזוית חב"ג שוה לזוית אב"ד |
| So, the base CG is equal to the base AD.
|
אם כן תושבת ח"ג שוה לתושבת א"ד |
| Also, triangle CBG [is equal] to triangle ABD.
|
ומשולש חב"ג למשולש אב"ד |
| But the parallelogram BDLM is double the triangle ABD.
|
אבל שטח ב"ד ל"מ נכחי הצלעות כפל משולש אב"ד |
|
מפני כי שניהם על תושבת אחת והיא ב"ד |
|
ובמה שבין שני קוים נכחיים והם ב"ד א"ל |
| The surface BAZC is double the triangle CBG.
|
ושטח ב"א ז"ח כפל משולש חב"ג |
|
מפני שניהם על תושבת אחת והיא ב"ח |
|
ובמה שבין קוים נכחיים והם ח"ב ז"ג הנכחיים |
| Those that are double the same thing are equal. | ואשר הם כפל לדבר אחד שוה הנה הם גם כן שוים |
| Therefore, the parallelogram BDLM equals the square CBAZ.
|
אם כן שטח ב"ד ל"מ הנכחי הצלעות שוה למרובע חבא"ז |
| Similarly, it is clear that the parallelogram MLHG equals the square TA.
|
וכן יתבאר כי שטח מ"ל ה"ג הנכחי הצלעות שוה למרובע ט"א |
| Therefore, parallelogram BDHG is equal to [the sum of] the two squares CBAZ and TZGB that are formed by BA and AG.
|
אם כן ב"ד ה"ג הנכחיי הצלעות שוה לשני מרובעי ח"ב א"ז ט"ז ג"ב והם הווים מן ב"א א"ג |
| Hence, the square formed by the hypotenuse in right-angled triangles equals [the sum of] the two squares formed by the [two] sides containing the right angle. | אם כן המרובע ההוה מן הצלע אשר תהיה מיתר הזוית הנצבת מן המשולשים נצבי הזויות שוים לשני המרובעים ההוים מהצלעות המקיפות בזוית הנצבת |
| Quod erat demonstrandum. | וזה מה שרצינו לבאר |
Proposition 48 |
|
| When the square formed by one of the sides of the triangle equals [the sum of] the squares formed by the remaining sides, then the angle contained by those remaining two sides of the triangle is right. | מח כאשר היה המרובע ההווה מן הצלע מצלעות המשלש שוה למרובעים ההוים מן הצלעות הנשארות הנה הזוית אשר יקיפו בה שתי צלעות ההם מן המשולש נצבת |
| Let ABG be the triangle. | ויהיה המשלש עליו אב"ג |
| Let the square formed by BG be equal to [the sum of] the two squares formed by AG [and AB]
|
ויהיה המרובע ההוה מן ב"ג ממנו שוה לשני המרובעים ההוים מן א"ג |
| Supposition: I say that the angle BAG is right.
|
הנה אומר כי זוית בא"ג נצבת |
|
ונוציא מנקודת א' קו א"ד נצבת על א"ג על זוית נצבת |
|
ונשים קו א"ד שוה לקו א"ב |
|
ונדביק ג"ד |
|
הנה מפני כי מרובע ב"ג שוה לשני המרובעים ההוים מן ב"א א"ג |
|
וקו ב"א שוה לקו א"ד |
| Therefore the square formed by BG is equal to [the sum of] the two squares formed by AG anf AD.
|
יהיה המרובע ההוה מן ב"ג שוה לשני המרובעים ההוים מן א"ג א"ד |
| But, [the sum of] the two squares formed by AG and AD is equal to the square formed by DG.
|
אבל שני המרובעים ההוים מן א"ג א"ד שוים למרובע ההוה מן ד"ג |
|
מפני כי זוית דא"ג נצבת |
| Therefore the square formed by DG equals the square formed by BG.
|
הנה המרובע ההוה מן ד"ג שוה למרובע ההוה מן ב"ג |
| So, line BG equals line GD.
|
אם כן קו ב"ג שוה לקו ג"ד |
| Line BA equals line AD.
|
ומפני כי קו ב"א שוה אל קו א"ד |
|
וקו א"ג משותף |
|
יהיו כל שני קוי ב"א א"ג שוים לכל שני קוי ד"א א"ג כל אחת לגילו |
| The base BG equals the base GD.
|
ותושבת ב"ג שוה לתושבת ג"ד |
| Therefore angle BAG equals angle GAD.
|
אם כן זוית בא"ג שוה לזוית גא"ד |
| Angle GAD is right.
|
וזוית גא"ד נצבת |
| Therefore angle BAG is right.
|
אם כן זוית בא"ג נצבת |
| Hence, when the square formed by [one of] the sides of the triangle equals [the sum of] the squares formed by the remaining two sides, then the angle contained by the remaining two sides of the triangle is right. | אם כן כאשר היה המרובע ההוה מצלעות ממשלש שוה לשני המרובעים ההוים משני צלעות הנשארות הנה הזוית אשר יקיפו בה שני הצלעות הנשארות מן המשולש נצבת |
| Q.E.D. | וזה מש"ל |
| נשלם המאמר הראשון מספר אקלידס החכם בשרשים | |
| ומספר תמונותיו שמנה וארבעים | |
| ונתחיל המאמר השני בג"ה אמן | |
The Second Section of Euclid's Book |
המאמר השני מספר אקלידס[5] |
|
[note 1]כל שטח נכחי הצלעות נצב הזויות הנה שני קוים הישרים המקיפים באחת מזויותיו הנצבות יקרא לשניהם המקיפים בו |
|
[note 3]וכל שטח נכחי הצלעות הנה יקרא אחד משני השטחים הנכחי הצלעות אשר הם על קוטרו איזה משניהם היה עם שני השטחים המתמימים[note 4] הרושם[7] |
Proposition 1 |
|
| The distributive law for multiplication over addition:
|
|
| When there are two straight lines, and one of them is divided into any number of segments, then the rectangle enclosed by the two straight lines is equal to [the sum of] all the rectangles enclosed by the uncut line and each of the segments. | [note 6]א כאשר היו שני קוים ישרים וחולק אחד מהם לחלקים איזה מספר שיהיה הנה השטח הנצב הזויות אשר יקיפו בו השני קוים הישרים שוה לכל השטחים הנצבי הזויות אשר יקיף בכל אחד מהם הקו אשר לא נחלק וכל אחד מן החלקים[note 7][8] |
| Let A and BG be two straight lines, and let BG be divided into as many segments at two points D and H. | ויהיו שני קוי' ישרים על שניהם א' ב"ג ונחלק ב"ג לחלקים כמה שיהיו על שתי נקודות ד'ה'[9] |
| Supposition: I say that the rectangle enclosed by the two lines A and BG is equal to [the sum of] the rectangle enclosed by the two lines A and BD, the rectangle enclosed by the two lines A and DH, and the rectangle enclosed by A and HG.
|
הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א' ב"ג שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א' ב"ד והשטח הנצב הזויות אשר יקיפו בו שני קוי א' ד"ה והשטח הנצב הזויות גם כן אשר יקיפו בו א' ה"ג[note 8][10] |
|
הנה ונוציא מנקודת ב' מן קו ב"ג הישר קו ישר על זוית נצבת והוא ב"ז מי' מא’[11] |
|
ונשים קו ב"ז הישר שוה לקו א' הישר מג’ מא’[12] |
|
ונוציא מנקודת ז' קו ז"ח נכחי לקו ב"ג הישר והוא קו ז"ח[13] |
|
ונוציא מן ד'ה'ג' קוים נכחיים לקו ב"ז והם קוי ד"ט כ"ה ג"ח מל”א מא’[14] |
| Then, BT, DK, and HC are rectangles. | הנה כל אחד משטחי ב"ט |
| The surface BC is equal to [the sum of] the surfaces BT, DK, and HC.
|
ושטח ב"ח שוה לשטחי ב"ט ד"כ ה"ח מפתיחת א'[16] |
|
ואולם שטח ב"ח הנה הוא שוה לשטח הנצב הזויות אשר יקיפו בו [17]שני קוי א' ב"ג[18] |
|
מפני כי קו |
|
ואולם שטח ב"ט הנה הוא שוה לשטח נצב הזויות אשר יקיפו בו שני קוי א' ב"ד[20] |
|
מפני כי קו ב"ז שוה לקו א'[21] |
|
ואולם שטח ד"כ הנה הוא שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א' ד"ה[22] |
|
מפני כי קו א' שוה לקו ד"ט[23] |
|
ואולם שטח ה"ח הנה הוא שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א' ה"ג[24] |
|
מפני כי קו א' שוה לקו ה"כ[note 9] מל”ד מא’[note 10][25] |
| Therefore the rectangle enclosed by the two lines A and BG is equal to [the sum of] the rectangles enclosed by A and BD, A and DH, and A and HG.
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי א' ב"ג שוה לשטחים נצבי הזויות אשר יקיפו בהם א' ב"ד וא' ד"ה וא' ה"ג[note 11][26] |
| Hence, when there are two straight lines, and one of them is divided into as many segments, then the rectangle enclosed by the two straight lines is equal to [the sum of] all the rectangles enclosed by the uncut line and each of the segments. | הנה כאשר היו שני קוים ישרים ונחלק אחד משניהם לחלקים כמה שיהיו הנה השטח הנצב הזויות אשר יקיפו בו שני הקוים הישרים המונחים שוה לכל השטחים הנצבים הזויות אשר יקיף בהם הקו אשר לא נחלק |
| Quod erat demonstrandum | וזה מה שרצינו לבאר[28] |
Proposition 2 |
|
![\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2}}](/mediawiki/images/math/8/a/a/8aae9db1c4694d4c859578e458487970.png)
|
|
| When a straight line is divided randomly, then [the sum of] the rectangles enclosed by the whole line and each of its segments is equal to the square formed by the whole line. | ב כאשר נחלק קו ישר מונח איך שקרה הנה השטחים נצבי הזויות אשר יקיף בהם הקו כלו וכל אחד מחלקיו שוה למרובע המתהוה מן הקו כלו[note 12][29] |
| Let AB be the straight line and let it be divided randomly at the point G. | ויהיה קו ישר מונח עליו א"ב ויחלק איך שיקרה על נקודת ג'[30] |
| Supposition: I say that [the sum of] the rectangle enclosed by the two lines AB and BG with the rectangle enclosed by the two lines AB and AG is equal to the square formed by AB.
|
הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב א"ג שוה למרובע המתהוה מן א"ב[note 13][31] |
|
והנה נעשה |
|
ונוציא מנקודת ג' קו ישר נכחי |
| Then, both AZ and GH are parallelograms. | הנה כל אחד משני שטחי א"ז ג"ה נכחי הצלעות[34] |
| AH equals [the sum of] AZ and GH.
|
ושטח א"ה שוה לשני שטחי א"ז ג"ה נכחיי הצלעות מא’ מזה[35] |
| AZ is equal to the rectangle enclosed by BA and AG.
|
ושטח א"ז שוה לשטח נצב הזויות אשר יקיפו בו ב"א א"ג[36] |
|
כי הוא יקיפו בו שני קוי א"ד א"ג וקו א"ד שוה לקו א"ב[37] |
| GH is equal to the rectangle enclosed by the two lines AB and BG.
|
ושטח ג"ה שוה לשטח נצב הזויות אשר יקיפו בו שני קוי א"ב |
|
מפני שא"ב שוה לב"ה[39] |
| AH is the square formed by line AB.
|
ושטח א"ה הוא המרובע ההוה מקו א"ב[40] |
|
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב א"ג עם השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג שוה למרובע המתהוה מן א"ב[note 14][41] |
| הנה כאשר נחלק קו ישר מונח איך שקרה הנה השטחים הנצבי הזויות אשר יקיף בהם הקו כלו וכל אחד מחלקיו שוה למרובע המתהוה מן הקו כלו[42] | |
| Quod erat demonstrandum. | וזה מה שרצינו לבאר[43] |
Proposition 3 |
|
in modern notation: 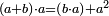
|
ג כאשר נחלק קו ישר בשני חלקים איך שקרה הנה השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד משני חלקיו שוה לשטח הנצב הזויות אשר יקיפו בו השני חלקים והמרובע המתהוה מן החלק אשר זכרנו[44][note 15] |
| ויהיה קו ישר עליו א"ב ויחלק איך שיקרה על נקודת ג'[45] | |
Supposition: 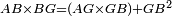
|
הנה אומר כי השטח הנצב הזויות אשר יקיפו בו קוי א"ב ב"ג שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב והמרובע המתהוה מן ג"ב[46][note 16] |
| ונעשה מן קו ג"ב מרובע עליו בגד"ה ממ”ו מא’[47] | |
| ונתמים שטח א"ג ד"ז הנכחי הצלעות מל”א וממ”ב מא’[48] | |
| הנה כל אחד משני שטחי א"ה א"ד נכחי הצלעות[49] | |
|
|
ושטח א"ה שוה לשטח א"ד עם ג"ה מא’ מזה[50] |
|
|
וא"ה שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג[51] |
|
|
מפני כי ב"ג שוה לב"ה[52] |
|
|
ושטח א"ד שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב[53] |
|
|
מפני כי ב"ג שוה לג"ד[54] |
|
|
ושטח ה"ג[55] הוא[56] המרובע[57] המתהוה[58] מן ג"ב[59] |
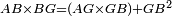
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב והמרובע המתהוה מן ג"ב[60][note 17] |
| הנה כאשר חולק קו ישר בשני חלקים איך שיקרה הנה השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד משני חלקיו שוה לשטח הנצב הזויות אשר יקיפו בו השני חלקים והמרובע המתהוה מן החלק אשר זכרנו[61] | |
| Quod erat demonstrandum | וזה מה שרצינו לבאר[62] |
Proposition 4 |
|
in modern notation: 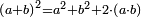
|
ד כאשר חולק קו ישר בשני חלקים איך שיקרה הנה המרובע המתהוה מן הקו כלו שוה לשני המרובעים המתהוים מן השני חלקים וכפל השטח הנצב הזויות אשר יקיפו בו השני חלקים[63][note 18] |
| ויהיה קו ישר עליו א"ב ויחולק איך שיקרה על נקודת ג'[64] | |
Supposition: 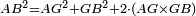
|
הנה אומר כי המרובע המתהוה מן א"ב שוה לשני המרובעים המתהוים מן א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב[65][note 19] |
| הנה נעשה מן א"ב מרובע א"דה"ב ממ"ו מא’ | |
| ונגיע ד"ב ונוציא מנקודת ג' קו נכחי לשני קוי א"ד ב"ה והוא ג"ז מל"א מא’ | |
| ויחתוך קו ד"ב על נקודת ח' ונוציא מנקודת ח' קו נכחי לשני קוי א"ב ד"ה והוא קו ט"כ הנה מפני כי קו ג"ז נכחי לקו א"ד וכבר נפל על שניהם קו ב"ד הישר תהיה זוית ג'ח'ב' החיצונה שוה לזוית א'ד'ב' הפנימית אשר תקבילה מכ”ט מא’ | |
|
|
אבל זוית א'ד'ב' שוה לזוית ד'ב'א' |
|
|
מפני כי צלע א"ד שוה לצלע א"ב מה’ מא’ |
|
|
הנה זוית ג'ח'ב' שוה לזוית א'ב'ד' |
|
|
הנה יהיה צלע ג"ח שוה לצלע ג"ב מו’ מא’ |
| ומפני כי צלע ג"ח שוה לב"כ וג"ב שוה לח"כ יהיו קוי ב"ג ג"ח ח"כ כ"ב הארבעה שוים קצתם אל קצת הנה שטח ג"כ שוה הצלעות מל”ד מא’ | |
| ואומר גם כן כי הוא נצב הזויות הנה מפני כי ג"ח נכחי לב"כ וכבר נפל על שניהם ג"ב יהיו שתי זויות ג'ב'כ' ח'ג'ב' שוות לשתי נצבות מכ”ט מא’ | |
|
|
וזוית כ'ב'ג' נצבת |
|
|
הנה זוית ב'ג'ח' נצבת |
| ויהיו מפני זה שתי זויות ג'ח'כ' ח'כ'ב' המקבילות לשתיהן נצבות מל”ד מא’ | |
| הנה שטח ח"ג כ"ב נצב הזויות וכבר התבאר שהוא שוה הצלעות הנה שטח ג"כ מרובע והוא המתהוה מן ג"ב | |
| וכן התבאר ששטח ט"ז גם כן מרובע והוא המתהוה מן ט”ח אשר הוא שוה לקו א”ג הנה שני שטחי כ"ג ט"ז שני מרובעים והם שוים לשני מרובעים המתהוים מן א"ג ג"ב | |
| אבל ה"ח שוה לא"ח ממ”ג מא’ | |
| וא"ח שוה לשטח הנצב הזויות אשר יקיפו בו א"ג ג"ב מפני שג"ב שוה לג"ח הנה ה"ח שוה לשטח נצב הזויות אשר יקיפו בו א"ג ג"ב הנה שני שטחי א"ח ח"ה שוים לכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב ושני שטחי ט"ז ג"כ שוים לשני המרובעים המתהוים מן קוי א"ג ג"ב הנה כבר התבאר ששטחי ט"ז ג"כ א"ח ח"ה שוים לשני המרובעים המתהוים משני קוי א"ג ג"ב ומכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב אבל שטחי ט"ז ג"כ א"ח ח"ה הם שוים לשטח א"ד ה"ב אשר הוא המרובע המתהוה מן א"ב | |
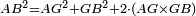
|
הנה המרובע המתהוה מן א"ב שוה לשני המרובעים המתהוים מן א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב[note 20] |
| הנה כאשר נחלק קו ישר איך שיקרה הנה המרובע המתהוה מן הקו כלו שוה לשני המרובעים המתהוים משני החלקים וכפל השטח הנצב הזויות אשר יקיפו בו השני חלקים | |
| וזה מה שרצינו לבאר | |
| ובכאן התבאר כי כל שטח מרובע הנה שני שטחים הנכחי הצלעות אשר על קוטרו גם כן מרובעים | |
| הנה כבר התבאר מן התמונה הזאת כי השטחים הנכחי הצלעות אשר יהיו על קוטרו שני שטחים מרובעים הם גם כן מרובעים[note 21] | |
| אמר תאבת מצאנו בנסחא אחרת שהוא יתבאר על פנים אחרים כי המרובע המתהוה מן א"ב שוה לשני המרובעים המתהוים מן א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב | |
|
|
הנה מפני שא"ב שוה לא"ד |
|
|
תהיה זוית א'ב'ד' שוה לזוית א'ד'ב' מה’ מא’ |
| ומפני כי כל משולש הנה זויותיו השלש שוות לשתי נצבות מל”ב מא’ | |
| יהיו זויות א’ד’ב’ א’ב’ד’ ב’א’ד’ השלש ממשולש א'ד'ב' שוות לשתי זויות נצבות וזוית ב'א'ד' נצבת הנה שתי זויות א'ב'ד' א'ד'ב' הנשארות שוות לזוית נצבת ושתיהן שוות מה’ מא’ | |
| הנה כל אחת מהן חצי נצבת וזוית ב'ג'ח' נצבת כי היא שוה לזוית אשר אצל א' אשר תנגדה מכ”ט מא’ | |
| וזוית ג'ב'ח' חצי נצבת הנה זוית ג'ח'ב' הנשארת חצי נצבת הנה זוית ג'ח'ב' אם כן שוה לזוית ג'ב'ח' ויהיה מפני זה צלע ב"ג שוה לצלע ג"ח מו’ מא’ | |
|
|
אבל ג"ב שוה לח"כ מל”ד מא’ |
| וג"ח שוה לכ"ב הנה שטח ג"כ שוה הצלעות וזוית ב'ג'ח' נצבת הנה ג"כ מרובע והוא המתהוה מן ג"ב ומפני הדברים האלה גם כן התבאר כי ז"ט מרובע והוא שוה למרובע המתהוה מן א"ג הנה ג"כ וט"ז שני מרובעים והם שוים לשני המרובעים המתהוים משני קוי א"ג ג"ב ומפני שא"ח שוה לה"ח ממ”ג מא’ | |
| וא"ח הוא אשר יקיפו בו שני קוי א"ג ג"ב מפני שג"ח שוה לג"ב הנה ה"ח שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב הנה אם כן שני שטחי א"ח ח"ה שוים לכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב ושני שטחי ג"כ ט"ז שוים לשני המרובעים המתהוים משני קוי א"ג ג"ב הנה שטחי ג"כ ט"ז א"ח ח"ה שוים לשני המרובעים המתהוים משני קוי א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב אבל שני שטחי ג"כ ט"ז ושני שטחי א"ח ח"ה הם שטח א"ה הנצב הזויות כלו אשר הוא המרובע המתהוה מן א"ב | |
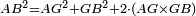
|
הנה המרובע המתהוה מן א"ב שוה לשני המרובעים המתהוים מן א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב |
| וזה מה שרצינו לבאר | |
Proposition 5 |
|
in modern notation: ![\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2](/mediawiki/images/math/6/2/4/6240a40a1b55eec2eca043f4e2218ca7.png)
|
ה כאשר נחלק קו ישר בשני חלקים שוים ושני חלקים בלתי שוים הנה השטח הנצב הזויות אשר יקיפו בו שני חלקי הקו כלו אשר הם בלתי שוים עם המרובע המתהוה מן הקו אשר במה שבין שני מקומות השני חלקים שוה למרובע המתהוה מחצי הקו[66] |
| ויהיה קו ישר עליו א"ב ויחלק בשני חלקים שוים על נקודת ג' מי’ מא’[67] | |
| ושני חלקים בלתי שוים על נקודת ד'[68] | |
Supposition: 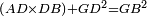
|
הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב עם המרובע המתהוה מן ג"ד שוה למרובע המתהוה מן ג"ב[69][note 23] |
| ונעשה מקו ג"ב מרובע ג"הז"ב ממ”ו מא’[70] | |
| ונרשום התמונה ונשלים שטח א"גט"ל הנכחי הצלעות מד’ מזה[71] | |
|
|
הנה מפני כי ג"ח שוה לח"ז ונשים ד"כ משותף הנה יהיה ג"כ כלו שוה לד"ז כלו ממ”ג מא’[72] |
|
|
ומפני שצלע א"ג שוה לצלע ג"ב יהיה שטח ל"א שוה לשטח ג"כ מל”א מא’[73] |
|
|
וכבר היה שטח ג"כ שוה לשטח ד"ז הנה יהיה שטח ל"א שוה לשטח ד"ז מפתיח’ א’[74] |
|
|
ונשים ג"ח משותף הנה א"ח כלו שוה לרושם מנ"ס[75] |
אד × דב =  אח → דח = בד אח → דח = בד
|
אבל א"ח שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב מפני כי ב"ד שוה לד"ח וזה כי ד"כ מרובע משלפניה[76] |
אד × דב =  מנס → מנס →
|
הנה רושם מנ"ס שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב[77] |
→ 2גד =  לע לע
2גד + (אד × דב) = |
ונשים ל"ע אשר הוא שוה למרובע המתהוה מן ג"ד משותף ויהיה רושם מנ"ס ושטח ל"ע כמו השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב והמרובע המתהוה מן ג"ד[78] |
 גז = גז =  לע + לע +  מנס מנס
|
אבל רושם מנ"ס ושטח ל"ע הוא שטח ג"ז כלו[79] |
2גב =  גז גז
|
ושטח ג"ז כלו הוא שטח המרובע המתהוה מן ג"ב[80] |
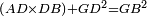
|
הנה השטח הנצב הזויות אשר יקיפו בו א"ד ד"ב עם המרובע המתהוה מן ג"ד שוה למרובע המתהוה מן ג"ב[81][note 24] |
| וכאשר נחלק קו ישר בשני חלקים שוים ושני חלקים בלתי שוים הנה השטח הנצב הזויות אשר יקיפו בו שני חלקי הקו כלו אשר הם בלתי שוים עם המרובע המתהוה מן הקו אשר במה שבין שני מקומות שני החלקים שוה למרובע המתהוה מחצי הקו[82] | |
| וזה מה שרצינו לבאר[83][note 25] | |
Proposition 6in modern notation: |
ו כאשר נחלק קו ישר בחציים ונוסף עליו קו ישר על יושר הנה השטח הנצב הזויות אשר יקיף בו הקו כלו עם התוספת והתוספת עם המרובע המתהוה מחצי הקו שוה למרובע המתהוה מן הקו המורכב מחצי הקו והתוספת[note 26] |
| ויהיה קו ישר עליו א"ב ויחלק בחציים על נקודת ג' מי’ מא’ | |
| ויוסיף עליו קו ישר על יושר והוא ב"ד | |
Supposition: 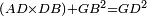
|
הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב עם המרובע המתהוה מן ג"ב שוה למרובע המתהוה מן ג"ד |
| ונעשה מן ג"ד מרובע ג"ה ז"ד ממ”ו מא’ | |
| ונרשום התמונה ונתמים שטח א"גט"כ הנכחי הצלעות מד’ מזה | |
| הנה מפני כי א"ג שוה לג"ב יהיה שטח א"כ הנכחי הצלעות שוה לשטח ג"ח הנכחי הצלעות אבל ג"ח שוה לח"ז הנה שטח א"כ שוה לשטח ח"ז ממ”ג מא’ | |
| We define GL common. | ונשים ג"ל משותף |
| הנה שטח ל"א כלו שוה לרושם מנ"ס כלו אבל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב שוה לשטח ל"א הנצב הזויות מפני שב"ד שוה לד"ל מד’ מזה | |
| הנה רושם מנ"ס שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב ושטח כ"ע שוה למרובע המתהוה מן ג"ב הנה רושם מנ"ס עם שטח כ"ע שוה לשטח אשר יקיפו בו שני קוי א"ד ד"ב והמרובע המתהוה מן ב"ג אבל רושם מנ"ס ומרובע כ"ע הוא ג"ז אשר הוא המרובע המתהוה מן ג"ד | |
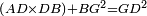
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב עם המרובע המתהוה מן ב"ג שוה למרובע המתהוה מן ג"ד |
| והנה כאשר נחלק קו ישר בשני חציים והוסף עליו קו ישר על יושר הנה השטח הנצב הזויות אשר יקיף בו הקו כלו עם התוספת והתוספת עם המרובע המתהוה מחצי הקו שוה למרובע המתהוה מן הקו המורכב מחצי הקו והתוספת | |
| וזה מה שרצינו לבאר | |
Proposition 7 |
|
in modern notation: ![\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/5/e/f/5ef738b800e1b84fc257df70a83fb86b.png)
|
ז כאשר נחלק קו ישר בשני חלקים איך שיקרה הנה המרובע המתהוה מן הקו כלו והמרובע המתהוה מאחד משני חלקים כאשר התקבצו שוים לכפל השטח הנצב הזויות אשר יקיף בו הקו כלו והחלק אשר זכרנו והמרובע המתהוה מן החלק השני[note 27] |
| ויהיה קו ישר עליו א"ב ויתחלק איך שיקרה על נקודת ג' | |
Supposition: ![\scriptstyle AB^2+BG^2=\left[2\sdot\left(AB\times BG\right)\right]+AG^2](/mediawiki/images/math/8/b/3/8b3bad7fc8aa20f933758fd593165d65.png)
|
הנה אומר כי שני המרובעים המתהוים משני קוי א"ב ב"ג שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג והמרובע המתהוה מן א"ג |
| ונרשום מן א"ב מרובע א"דה"ב ממ”ו מא’ | |
| ונבדיל מן ב"ה כמו ב"ג והוא ב"כ מג’ מא’ | |
| ונרשום התמונה הנה שטח א"ז שוה לשטח ז"ה ממ”ג מא’ | |
| We define GK common. | ונשים ג"כ משותף |
| הנה יהיה א"כ כלו שוה לג"ה כלו הנה א"כ עם ג"ה כפל א"כ | |
| אבל ג"ה עם א"כ הוא רושם למ"נ ומרובע ג"כ הנה רושם למ"נ ומרובע ג"כ שניהם כפל א"כ וא"כ הוא השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב וב"ג כי הוא יקיפו בו שני קוי א"ב ב"כ וב"כ שוה לב"ג הנה רושם למ"נ ומרובע ג"כ שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג ונשים המרובע המתהוה מן א"ג משותף והוא מרובע ח"ט הנה כפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם המרובע המתהוה מן א"ג שוה לרושם למ"נ ושני שטחי ג"כ ט"ח | |
| אבל רושם למ"נ ושני שטחי ג"כ ט"ח הם א"ה וג"כ וא"ה המרובע המתהוה מן א"ב וג"כ הוא המרובע המתהוה מן ג"ב | |
![\scriptstyle AB^2+BG^2=\left[2\sdot\left(AB\times BG\right)\right]+AG^2](/mediawiki/images/math/8/b/3/8b3bad7fc8aa20f933758fd593165d65.png)
|
הנה שני המרובעים המתהוים מן א"ב ב"ג שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג והמרובע המתהוה מן א"ג |
| הנה כאשר נחלק קו ישר בשני חלקים איך שקרה הנה המרובע המתהוה מהקו כלו והמרובע המתהוה מאחד משני החלקים כאשר התקבצו שוים לכפל השטח הנצב הזויות אשר יקיף בו הקו כלו והחלק אשר זכרנו והמרובע המתהוה מן החלק הנשאר | |
| וזה מה שרצינו לבאר | |
Proposition 8 |
|
in modern notation: ![\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2](/mediawiki/images/math/f/6/2/f62f5f20431f619df80a01a1d97e57cf.png)
|
ח כאשר נחלק קו ישר בשני חלקים איך שיקרה הנה ארבעה דמיוני[note 28] השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד משני חלקיו עם המרובע המתהוה מן החלק הנשאר שוה למרובע המתהוה מן הקו כלו והחלק אשר קדם זכרו כאשר הושמו שניהם בקו אחד[note 29] |
| ויהיה קו ישר עליו א"ב ויחולק איך שיקרה על נקודת ג' | |
Supposition: ![\scriptstyle\left[4\sdot\left(AB\times BG\right)\right]+AG^2=\left(AB+BG\right)^2](/mediawiki/images/math/2/6/f/26f5c93d63e08ed80175b13bbd2e238b.png)
|
הנה אומר כי ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם המרובע המתהוה מן א"ג שוה למרובע המתהוה מן א"ב ב"ג כאשר הושמו בקו אחד |
| הנה נוציא א"ב אל נקודת ד' מפתי’ א’ | |
| ויהיה ב"ד שוה לב"ג מג’ מא’ | |
| ונעשה מן א"ד מרובע אדה"ז ממ”ו מא’ | |
| ונמשיך ד"ז ונוציא משתי נקודות ג"ב שני קוים נכחיים לשני קוי א"ז ד"ה והם ג"ח ב"ט מל”א מא’ | |
| ויחתוך ב"ט קו ד"ז על נקודת כ' וג"ח על נקודת ק' ונוציא משתי נקודות כ"ק שני קוים נכחיים לשני קוי א"ד ז"ה והם מ"נ ס"ר מל”ד מא’ | |
| הנה מפני כי ג"ב שוה לב"ד וג"ב שוה לכל אחד מפ"כ ק"ע וב"ד שוה לכל אחד מן כ"נ ר"ע יהיה פ"כ שוה אל כ"נ וק"ע לר"ע הנה שטח כ"ג הנכחי הצלעות שוה לשטח ב"נ הנכחי הצלעות מל”ו מא’ | |
| ופ"ע לכ"ר וק"ט גם כן לה"ע ומפני כי ג"כ הנכחי הצלעות שוה לשטח ב"נ הנכחי הצלעות ופ"ע אל כ"ר וג"כ שוה אל כ"ר ממ”ג מא’ | |
| יהיה ב"נ שוה לכל אחד מן פ"ע כ"ר ויהיה פ"ע שוה לכל אחד מן ג"כ ב"נ הנה שטחי ג"כ ב"נ פ"ע כ"ר ארבעה דמיוני ג"כ אבל שטחי ג"כ ב"נ פ"ע כ"ר הם כל שטח ג"ר אשר הוא ארבעה דמיוני שטח ג"כ ומפני כי ג"ב גם כן שוה אל ב"ד וג"ב שוה אל פ"כ אשר יקבילהו והוא גם כן שוה אל פ"ק מפני כי פ"ע מרובע מד’ מזה | |
| וב"ד שוה אל ב"כ ממרובע ב"נ וב"כ הוא גם כן שוה אל ג"פ וג"פ שוה אל פ"ק והנה שטח א"פ שוה לשטח מ"ק מל”ו מא’ | |
| וק"ט שוה אל ר"ט אבל מ"ק שוה אל ק"ט מפני כי שניהם מתמימים ממ”ג מא’ | |
| הנה א"פ שוה אל ר"ט הנה שטחי א"פ מ"ק ק"ט ע"ה הארבעה ארבעה דמיוני שטח א"פ | |
| ושטח ג"ד הנכחי הצלעות ארבעה דמיוני שטח ג"כ הנה כל רושם שת"ת ארבעה דמיוני שטח א"כ וא"כ הוא השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"כ וב"כ שוה אל ב"ג כי הוא שוה אל ב"ד ממרובע ב"ג הנה רושם שת"ת ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג הנה ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג אם כן שוים לרושם שת"ת ונשים המרובע המתהוה מן א"ג משותף והוא ס"ח הנה ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם המרובע המתהוה מן א"ג שוה לרושם שת"ת ומרובע ס"ח אבל רושם שת"ת וס"ח שניהם יחד שטח א"ה אשר הוא המרובע המתהוה מן א"ד | |
![\scriptstyle\left[4\sdot\left(AB\times BG\right)\right]+AG^2=AD^2=\left(AB+BG\right)^2](/mediawiki/images/math/b/0/7/b078d289f8a024ff549e180cce303114.png)
|
הנה ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם המרובע המתהוה מן א"ג שוה למרובע המתהוה מן א"ד אשר הוא המרובע המתהוה מן א"ב וב"ג כאשר הושמו בקו אחד |
| הנה כאשר חולק קו ישר בשני חלקים איך שקרה הנה ארבעה דמיוני השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד מחלקיו עם המרובע המתהוה מן החלק הנשאר שוה למרובע המתהוה מן הקו כלו והחלק אשר קדם זכרו כאשר הושמו בקו אחד | |
| וזה מה שרצינו לבאר | |
Proposition 9 |
|
in modern notation: ![\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right) \right]^2+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]](/mediawiki/images/math/d/a/a/daab00123b1a8516078d128698e4b24d.png)
|
ט כאשר חולק קו ישר לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים המתהוים משני חלקי הקו כלו אשר הם בלתי שוים שניהם כפל שני המרובעים המתהוים מחצי הקו ומן הקו אשר במה שבין שתי מקומות השני חלקים[note 30] |
| ויהיה קו ישר עליו א"ב ויחלק לשני חלקים שוים על נקודת ג' מי’ מא’ | |
| ושני חלקים בלתי שוים על נקודת ד' | |
Supposition: 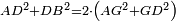
|
הנה אומר כי שני המרובעים המתהוים מן שני קוי א"ד ד"ב כפל שני המרובעים המתהוים מן א"ג ג"ד |
| ונוציא מנקודת ג' מקו א"ב הישר קו ישר על זוית נצבה והוא ג"ה מי”א מא’ | |
| ונשים ה"ג שוה לכל אחד משני קוי א"ג ג"ב מב’ מא’ ונמשיך קו א"ה ה"ב מפתיח’ א’ | |
| ונוציא מנקודת ד' קו נכחי לקו ג"ה והוא ד"ז מל”א מא’ | |
| ונוציא מנקודת ז' קו נכחי לקו ג"ד והוא ז"ח ונמשיך א"ז | |
| הנה מפני כי ה"ג שוה אל א"ג תהיה זוית גה"א שוה לזוית גא"ה מה’ מא’ | |
| ומפני כי זוית אג"ה נצבת יהיו שתי זויות הא"ג אה"ג הנשארות שוות לזוית נצבת מל”ב מא’ | |
| ושתיהם שוות הנה כל אחת משתי זויות גה"א גא"ה חצי נצבת ומפני כי ה"ג גם כן שוה לג"ב תהיה זוית גה"ב שוה לזוית גב"ה מה’ מא’ | |
| וזוית בג"ה נצבת הנה כל אחת משתי זויות גה"ב גב"ה חצי נצבת אבל כל אחת משתי זויות גה"ב אה"ג חצי נצבת תהיה זוית אה"ז נצבת ומפני כי זוית גב"ה חצי נצבת וזוית זד"ב נצבת תהיה זוית דז"ב חצי נצבת מל”ב מא’ | |
| הנה קו ב"ד שוה לקו ד"ז מו’ מא’ | |
| ולכן גם כן יהיה ז"ח שוה אל ח"ה | |
| ומפני כי ה"ג שוה אל א"ג יהיה המרובע המתהוה מן ה"ג שוה למרובע המתהוה מן א"ג הנה שני המרובעים המתהוים משני קוי ה"ג א"ג כפל המרובע המתהוה מן א"ג הנה המרובע המתהוה מן א"ה שוה לשני המרובעים המתהוים משני קוי ה"ג א"ג ממ”ז מא’ | |
| מפני כי זוית הג"א נצבת הנה המרובע המתהוה מן א"ה כפל המרובע המתהוה מן א"ג ומפני כי ה"ח גם כן שוה אל ז"ח יהיה המרובע ההוה מן ה"ח שוה למרובע ההוה מן ח"ז הנה שני המרובעים ההוים משני קוי ה"ח ח"ז כפל המרובע ההוה מן ח"ז והמרובע ההוה מן ה"ז שוה לשני המרובעים ההוים משני קוי ה"ח ח"ז ממ”ז מא’ | |
| הנה המרובע ההוה מן ה"ז כפל המרובע ההוה מן ח"ז וח"ז שוה אל ג"ד הנה המרובע ההוה מן ה"ז כפל המרובע ההוה מן ג"ד | |
| וכבר התבאר גם כן שהמרובע ההוה מן ה"א כפל המרובע ההוה מן א"ג הנה שני המרובעים ההוים משני קוי א"ה ה"ז כפל שני המרובעים ההוים משני קוי א"ג ג"ד והמרובע ההוה מן א"ז שוה לשני המרובעים ההוים משני קוי א"ה ה"ז ממ”ז מא’ | |
| מפני כי זוית אה"ז נצבת הנה המרובע ההוה מן א"ז כפל שני המרובעים ההוים מן א"ג ג"ד והמרובע ההוה מן א"ז כמו שני המרובעים ההוים מן א"ד ד"ז ממ”ז מא’ | |
| מפני כי זוית אד"ז נצבת הנה שני המרובעים ההוים מן א”ד ד”ז כפל שני המרובעים ההוים משני קוי א”ג ג”ד וז”ד שוה לד”ב | |
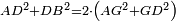
|
הנה שני המרובעים ההוים מן א"ד ד"ב כפל שני המרובעים ההוים משני קוי א"ג ג"ד |
| הנה כאשר חולק קו ישר לשני חלקים שוים ולשני חלקים בלתי שוים הנה שני המרובעים ההוים משני חלקי הקו כלו אשר הם בלתי שוים שניהם כפל שני המרובעים ההוים מחצי הקו כלו ומן הקו אשר במה שבין שני מקומות השני חלקים | |
| וזה מה שרצינו לבאר | |
Proposition 10 |
|
in modern notation: ![\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]](/mediawiki/images/math/b/7/d/b7dd112f5309b8cd4f778bd6269c21f3.png)
|
י כאשר נחלק קו ישר לשני חציים והוסף עליו קו ישר על יושר הנה המרובע ההווה מן הקו כלו עם התוספת והמרובע ההוה מן התוספת כפל שני המרובעים כאשר יחוברו כלומר המרובע ההווה מחצי הקו והמרובע ההווה מן הקו המורכב מחצי הקו והתוספת[note 31] |
| ויהיה הקו הישר א"ב ויחלק לשני חציים על נקודת ג' ויוסיף עליו קו ישר על יושר והוא ב"ד | |
Supposition: 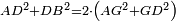
|
הנה אומר כי שני המרובעים ההוים משני קוי א"ד ד"ב כפל שני המרובעים ההוים משני קוי א"ג וג"ד |
| ונוציא מנקודת ג' קו ישר על זוית נצבת והוא ג"ה מי”א מא’ | |
| ויושם שוה לכל אחד משני קוי א"ג וג"ב מג’ מא’ | |
| ונגיע קו א"ה ה"ב ונוציא מנקודת ד' קו ישר נכחי לקו ג"ה והוא ד"ז ומנקודת ה' קו ישר נכחי לקו ג"ד והוא ה"ז מל”א מא’ | |
| הנה מפני כי ה"ג נכחי אל ז"ד וכבר נפל על שניהם קו ה"ז הישר יהיו שתי זויות גה"ז הז"ד הפנימיות שוות לשתי זויות נצבות מכ”ט מא’ | |
| הנה שתי זויות בה"ז והז"ד קטנות משתי זויות נצבות והקוים אשר יצאו מפחות משתי זויות נצבות אל לא תכלית יפגשו מפתיחת א’ | |
| הנה קו ה"ב וז"ד כאשר הוצאו אל לא תכלית יפגשו ויפגשו על נקודת ח' ונגיע א"ח הנה מפני כי ה"ג שוה אל א"ג תהיה זוית גה"א שוה לזוית גא"ה מה’ מא’ | |
| וזוית אג"ה נצבת הנה כל אחת משתי זויות גה"א גא"ה חצי נצבת מל”ב מא’ | |
| ומפני כי ה"ג גם כן שוה לג"ב תהיה זוית גה"ב שוה לזוית גב"ה וזוית בג"ה נצבת הנה כל אחת משתי זויות הב"ג וגה"ב חצי נצבת ומפני כי כל אחת משתי זויות אה"ג בה"ג חצי נצבת תהיה זוית אה"ב נצבת ומפני כי זוית הב"ג חצי נצבת תהיה זוית דב"ח חצי נצבת מט”ו מא’ | |
| וזוית בד"ח נצבת כי היא שוה לזוית דג"ה אשר תמירה מכ”ט מא’ | |
| ותשאר זוית דח"ב חצי נצבת | |
| הנה זוית דח"ב אם כן שוה לזוית דב"ח ויהיה מפני זה צלע ב"ד שוה לצלע ח"ד מו’ מא’ | |
| ומפני כי זוית הח"ז גם כן חצי נצבת ואשר אצל ז' נצבת מפני כי היא שוה לאשר תקבילה מל”ד מא’ | |
| והיא אשר אצל ג' תשאר זוית זה"ח חצי נצבת ותהיה זוית הח"ז שוה לזוית זה"ח ולכן יהיה צלע ח"ז שוה לצלע ה"ז | |
| ומפני כי ה"ג שוה אל א"ג יהיה המרובע ההוה מן ה"ג שוה למרובע ההוה מן א"ג ושני המרובעים ההוים משני קוי ה"ג וא"ג כפל המרובע ההוה מן א"ג והמרובע ההוה מן א"ה שוה לשני המרובעים ההוים משני קוי ה"ג א"ג מפני כי זוית הג"א נצבת ממ”ז מא’ | |
| הנה המרובע ההוה מן א"ה כפל המרובע ההוה מן א"ג | |
| ומפני כי ה"ז גם כן שוה אל ז"ח יהיה המרובע ההוה מן ה"ז שוה למרובע ההוה מן ז"ח הנה שני המרובעים ההוים משני קוי ה"ז ז"ח כפל המרובע ההוה מן ה"ז ושני המרובעים ההוים משני קוי ה"ז ז"ח שוים למרובע ההוה מן ה"ח ממ”ז מא’ | |
| הנה המרובע ההוה מן ה"ח כפל המרובע ההוה מן ה"ז | |
| וה"ז שוה אל ג"ד מל”ד מא’ | |
| הנה המרובע ההוה מן ה"ח כפל המרובע ההוה מן ג"ד וכבר התבאר גם כן כי המרובע ההוה מן א"ה כפל המרובע ההוה מן א"ג הנה שני המרובעים ההוים משני קוי א"ה וה"ח כפל שני המרובעים ההוים משני קוי א"ג ג"ד ושני המרובעים ההוים משני קוי א"ה ה"ח שוים למרובע ההוה מן א"ח מפני כי זוית אה"ח נצבת ממ”ז מא’ | |
| הנה המרובע ההוה מן א"ח כפל שני המרובעים ההוים משני קוי א"ג ג"ד והמרובע ההוה מן א"ח שוה לשני המרובעים ההוים משני קוי א"ד ד"ח מפני כי זוית אד"ח נצבת הנה שני המרובעים ההוים משני קוי א"ד וד"ח כפל שני המרובעים ההוים משני קוי א"ג וג"ד | |
| וקו ח"ד שוה לקו ד"ב | |
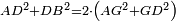
|
הנה שני המרובעים ההוים משני קוי א"ד ד"ב כפל שני המרובעים ההוים משני קוי א"ג וג"ד |
| הנה כאשר חולק קו ישר בשני חציים והוסף עליו קו ישר על יושר הנה המרובע ההווה מן הקו כלו עם התוספת והמרובע ההווה מן התוספת כפל שני המרובעים כאשר יחוברו כלומר המרובע ההווה מחצי הקו והמרובע ההווה מן הקו המורכב מחצי הקו ומן התוספת | |
| וזה מה שרצינו לבאר | |
Proposition 11 |
|
| יא נרצה שנחלק קו ישר מונח ע"ב שיהיה השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד משני החלקים ושוה למרובע ההוה מן החלק הנשאר | |
| המשל יהיה הקו הישר המונח א"ב וראוי שנחלק א"ב עד שיהיה השטח הנצב הזוית אשר יקיף בו הקו כלו ואחד מן שני החלקים שוה למרובע ההוה מן החלק הנשאר | |
| הנה נעשה מקו א"ב מרובע א'ב'ג'ד' | |
| ונחלק קו א"ג בשני חצאים על נקודת ה' | |
| ונגיע קו ב"ה ונוציא על יושר א"ה קו א"ז | |
| ונשים ה"ז שוה אל ב"ה | |
| ונעשה מן א"ז מרובע א'ז'ט'ח' | |
| ונוציא על יושר ח"ט ח'ט'כ' הישר | |
| Supposition: | הנה אומר כי א"ב כבר חולק על ט' חלוקה יהיה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ט שוה למרובע ההוה מן א"ט |
| מופת זה הנה מפני כי קו א"ג הישר כבר חולק בשני חצאים על נקודת ה' והוסף עליו קו ישר והוא א"ז | |
| יהיה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ז ג"ז עם המרובע ההוה מן א"ה שוה למרובע ההוה מן ה"ז וז"ה שוה אל ה"ב | |
| הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ג"ז א"ז עם המרובע ההוה מן א"ה שוה למרובע ההוה מן ה"ב | |
| ושני המרובעים ההוים מן א"ב וא"ה שוים למרובע ההוה מן ה"ב | |
| מפני כי זוית ב'א'ה' נצבת | |
| הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ג"ז וא"ז עם המרובע ההוה מן א"ה שוים למרובעים ההוים משני קוי א"ב וא"ה | |
| ונחסר מהם המרובע המשותף ההוה מן א"ה וישאר השטח הנצב הזויות אשר יקיפו בו שני קוי ג"ז וא"ז שוה למרובע א"ב | |
| אבל השטח הנצב הזויות אשר יקיפו בו שני קוי ג"ז וא"ז שוה לשטח נצב הזויות אשר יקיפו בו שני קוי ג"ז וז"ח | |
| לפי שא"ז שוה לז"ח | |
| והשטח אשר יקיפו ג"ז וז"ח הוא שטח ז"ב | |
| והמרובע ההוה מן א"ב הוא שטח א"ג ד"ב | |
| הנה שטח ז"ב שוה לשטח א"ד | |
| ונחסר מהם א"ב המשותף וישאר ז"ט שוה אל ט"ד הנשאר | |
| אבל ט"ד שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ב וב"ט | |
| מפני כי א"ב שוה אל ב"ד | |
| וז"ט הוא המרובע ההוה מן א"ט | |
| הנה כבר חולק א"ב המונח על נקודת ט' | |
| והיה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב וב"ט שוים למרובע ההוה מן א"ט | |
| וזה מה שרצינו לבאר | |
Proposition 12 |
|
| יב המרובע ההוה מן הצלע אשר יהיה מיתר מן הזוית הנרחבת מן המשולשים הנרוחים יותר משני המרובעים ההוים משני צלעות המקיפות בזוית הנרוחת בכפל השטח הנצב הזויות אשר יקיף בו הקו אשר יפול עליו העמוד באחד משני קוים המקיפים בזוית הנרוחת והקו אשר יגדילהו העמוד מחוץ ממה שילוה לזוית הנרוחת | |
| המשל יהיה המשולש הנרחב הזוית א'ב'ג' | |
| ותהיה ב'א'ג' ממנו נרחבת | |
| ונוציא קו א"ד הישר על יושר קו א"ג הישר | |
| ונוציא מנקודת ב' אל קו א"ד הישר עמוד ב"ד | |
| Supposition: | הנה אומר כי המרובע ההוה מג"ב יותר גדול משני המרובעים ההוים משני קוי א"ב וא"ג ככפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג וא"ד |
| מופת זה הנה מפני כי קו ד"ג הישר כבר חולק איך שקרה על נקודת ה' | |
| יהיה המרובע ההוה מן ד"ג שוה לשני המרובעים ההוים מן א"ד וא"ג וכפל השטח הנצב הזויות אשר יקיפו שני קוי א"ג וא"ד | |
| ונשים המרובע ההוה מן ב"ד משותף | |
| הנה שני המרובעים ההווים משני קוי ג"ד וד"ב שוים למרובעים ההוים מקוי ב"ד וד"א וא"ג וכפל הנצב הזויות אשר יקיפו בו קוי א"ג וא"ד | |
| אבל שני המרובעים ההווים משני קוי ב"ד וד"ג שוים למרובע ההוה מן ב"ג | |
| מפני כי זוית ב'ד'ג' נצבת | |
| ושני המרובעים ההוים משני קוי ב"ד וא"ד שוים למרובע ההוה מן א"ב | |
| מפני כי זוית ב'ד'א' נצבת | |
| הנה המרובע ההוה מן ב"ג שוה לשני המרובעים ההוים מן א"ב וא"ג וכפל שטח הנצב הזויות אשר יקיפו בו א"ד וא"ג | |
| הנה יהיה המרובע ההוה מן ב"ג יותר גדול משני המרובעים ההוים משני קוי א"ב וא"ג ככפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד וא"ג | |
| הנה המרובע ההוה מן הצלע אשר יהיה מיתר הזוית הנרוחת וכו' | |
| וזה מה שרצינו לבאר | |
Proposition 13 |
|
| The square formed by the side opposite the acute angle in acute-angled triangles is less than [the sum of] the squares formed by the two sides encompassing the acute angle by twice the rectangle enclosed by one of the lines encompassing the acute angle, on which the perpendicular falls, and the line cut off within by the perpendicular towards the acute angle. | יג המרובע ההוה מן הצלע אשר יהיה מיתר לזוית החדה מן המשולשים החדים הזויות יותר קטן משני המרובעים ההווים משתי הצלעות המקיפות בזוית החדה בכפל השטח הנצב הזויות אשר יקיף בו הקו אשר יפול עליו העמוד משני קוים המקיפים בזוית החדה והקו אשר יבדילוהו העמוד מחוץ ממה שילוה לזוית החדה[84] |
| Let ABG be the acute-angled triangle. | ויהיה המשולש החד הזויות אב"ג |
| Let angle ABG be acute angle. | ותהיה זוית אב"ג ממנו חדה |
| I.12: We draw perpendicular AD from point A to BG. | ונוציא מנקודת א' אל קו ב"ג עמוד א"ד מי"ב מא' |
| Supposition: I say that the square formed by line AG is less than [the sum of] the two squares formed by the two lines BG and AB by twice the rectangle enclosed by the two lines GB and BD. | הנה אומר כי המרובע ההוה מקו א"ג יותר קטן משני המרובעים ההוים משני קוי ב"ג וא"ב בכפל בשעור כפל השטח הנצב מהזויות אשר יקיפו בו שני קוי ג"ב וב"ד |
| The proof: | המופת |
| הנה מפני כי קו ג"ב הישר כבר חולק לשני חלקים איך שקרה על נקודת ד' | |
| יהיו שני המרובעים ההוים משני קוי ג"ב וב"ד שוים [85]לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי ג"ב וב"ד | |
| ונשים המרובע ההווה מן א"ד משותף | |
| הנה המרובעים ההווים מן קוי ג"ב ב"ד ג"א שוים לכפ[ל] השטח נצב הזויות אשר יקיפו בו שני קוי ג"ב ב"ד ושני המרובעים ההוים משני קוי א"ד וד"ג | |
| ושני המרובעים ההוים משני קוי א"ד וד"ג שוים למרובע ההוה מן א"ג | |
| מפני כי זוית | |
| אבל המרובעים ההווים משני קוי א"ד ד"ב שוים למרובע ההווה מן א"ב | |
| לפי שזוית א'ד'ב' נצבת | |
| ושני | |
| הנה המרובע ההוה מן א"ג יותר קטן משני המרובעים ההוים משני קוי ג"ב וא"ב בכפל השטח הנצב הזויות | |
| הנה המרובע ההוה מן הצלע אשר יהיה מיתר לזוית החדה מן המשולשים החדים הזויות יותר קטן משני המרובעים ההוים משתי הצלעות המקיפות בזוית החדה בכפל השטח הנצב הזויות אשר יקיף בו הקו אשר יפול עליו העמוד משני הקוים המקיפים בזוית החדה והקו אשר יבדילהו העמוד ממה שילוה לזוית החדה | |
| Quod erat demonstrandum. | וזה מה שרצינו לבאר |
Proposition 14 |
|
| We wish to construct a square equal to a given rectilinear figure. | יד נרצה שנעשה מרובע שוה לתמונת ישרת הצלעות מונחת |
| Let figure A be the given rectilinear figure. | ותהיה התמונה ישרת הצלעות המונחת תמונת א' |
| We wish to construct a square equal to the rectilinear figure A. | ונרצה שנעשה מרובע שוה לתמונת |
|
הנה נעמיד שטח שטח נכחי |
| Either BH equals HD | והנה אם יהיה ב"ה שוה אל ה"ד |
| Or one of the two is greater than the other. | או שיהיה אחד משניהם יותר גדול מן האחר |
| If they are equal, we have already done what we wanted. | ואם היו שוים הנה כבר |
| If they are not equal, than one of the two is greater. | ואם לא יהיו שוים |
|
ויהיה היותר גדול ב"ה מג' מא' |
|
ונוציא קו ה"ז הישר על יושר קו ב"ה הישר |
|
ונשים ה"ז שוה אל ה"ד |
|
ונחלק ב"ז בשני חציים על נקודת |
|
ונקוה על מרכז ח' ובמרחק שני קוי ח"ב וח"ז חצי עגולה ב'ט'ז' |
|
ונוציא קו ה"ט הישר על יושר קו ד"ה |
|
ונגיע קו ט"ח |
| II.5 Since the straight line BZ has been cut into two equal segments at point C and into two unequal segments at point H, the rectangle enclosed by BH and HZ together with the square formed by HC equals the square formed by CZ.
|
הנה מפני כי קו ב"ז הישר כבר נחלק בשני חלקים שוים על נקודת ח' ושני חלקים בלתי שוים על נקודת ה' מה' מזה יהיה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה וה"ז עם המרובע ההוה מן ה"ח שוה למרובע ההוה מן ח"ז מפתיחת א' |
| But, CT equals CZ.
|
|
| Therefore, the rectangle enclosed by the two lines BH and HZ together with the square formed by HC equals the square formed by CT.
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה וה"ז עם המרובע ההוה מן ה"ח שוה למרובע ההוה מן ח"ט |
| But, the square formed by CT equals [the sum of] the two squares formed by the two lines TH and HC.
|
והמרובע ההוה מן ח"ט שוה לשני המרובעים ההוים משני קוי ט"ה וה"ח |
| Angle THC is right.
|
מפני כי זוית ט'ה'ח' נצבת |
| Therefore, the rectangle enclosed by the two lines BH and HZ together with the square formed by HC equals [the sum of] the two squares formed by the two lines HC and HT.
|
הנה השטח הנצב |
| We subtract the common square formed by HC. | ונפיל המרובע המשותף ההוה מן ה"ח |
| Then, the remaining rectangle enclosed by the two lines BH and HZ equals the square formed by line HT.
|
וישאר השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה וה"ז שוה למרובע ההווה מן קו ה"ט |
| But, the rectangle enclosed by the two lines BH and HZ equals the parallelogram enclosed by the two lines BH and HD.
|
והשטח הנצב הזויות אשר יקיפו בו שני קוי ב"ה |
| ZH is equal to DH.
|
וז"ה שוה אל ד"ה |
| Therefore, figure BD equals the square formed by HT.
|
הנה שטח ב"ד שוה למרובע ההוה מן ה"ט |
| Figure BD equals the rectilinear figure A.
|
ושטח ב"ד שוה לתמונת א' ישרת הקוים |
| So, the rectilinear figure A equals the square formed by HT.
|
|
| Therefore, a square has been constructed equal to the rectilinear figure A, which is the square formed by HT. | הנה כבר נעשה מרובע שוה לתמונה ישרת הקוים אשר עליה א' והוא המרובע ההוה מן ה"ט[87] |
| Quod erat demonstrandum. | וזה מה שרצינו לבארו |
| The second discussion of Euclid's book is completed. | נשלם המאמר השני מספר אקלידס |
| The number of propositions is fourteen. | ומספר תמונות ארבעה עשר |
Book Three |
המאמר השלישי |
| ההקדמות | |
| א העגולים השוים הם אשר קטריהם שוים קצתם אל קצת או אשר יהיו הקוים אשר יצאו ממרכזיהם אל הקוים המקיפים בהם שוים קצתם אל קצת | |
| ב והקו הישר יקרא לו ממשש לעגולה הוא אשר יפגוש לעגולה וכאשר הוצא לכל אחד משני הצדדים לא יחתכה | |
| ג והעגולות אשר יקרא קצתם ממששות לקצת הם אשר יפגשו קצתם לקצת ולא יתחתכו | |
| ד ויאמר כי רוחק הקוים הישרים מן המרכז בעגולה שוה כאשר היו העמודים המוצאים עליהם מן המרכז שוים | |
| ה והקו אשר יאמר כי מרחקו מהמרכז יותר גדול הוא אשר יהיה העמוד הנופל עליו יותר גדול | |
| A segment of a circle is that which is contained by a straight line that is called a chord and the segment of circumference that is called an arc. | ו חתיכת העגולה היא אשר יקיף בה קו ישר יקרא המיתר והחלק מן הקו המקיף יקרא הקשת |
| ז וזוית חתיכת העגולה היא אשר יקיפו בה קו ישר וקשת מן הקו המקיף בעגולה | |
| ח והזוית אשר בחתיכת העגולה היא אשר יקיפו בה קוים ישרים יגיעו מנקודה תרשם איך שתפול על קשת החתיכה ובין שני קצוות הקו הישר אשר הוא תושבת החתיכה | |
| ט וכאשר יסבבו השני קוים הישרים המקיפים בזוית קשת מה הנה הזוית יקרה לה אשר על הקשת ההיא | |
| A sector of a circle is a shape that is contained by two straight lines containing an angle at the center of the circle, and the arc that is cut off from the circle by these two lines. | י וחתוך העגולה היא תמונה אשר יקיפו בה שני קוים ישרים יקיפו בזוית על מרכז העגולה וקשת יקיפוה אותם שני הקוים מן העגולה |
| יא וחתיכות העגולות המתדמות הם אשר יקבילו זויות שוות | |
| יב וכאשר היו זויותיהן אשר יקבילו שוות הנה הן מתדמות | |
Proposition 1 |
|
| We wish to explain how to find the center of a given circle. | א נרצה לבאר איך נמצא מרכז עגולה מונחת |
Example: 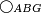 is the given circle and we wish to find its center. is the given circle and we wish to find its center.
|
תהיה העגולה המונחת א"ב ונרצה למצא מרכזה |
|
הנה נקוה בה מיתר איך שיפול והוא ג"ד |
|
ונחלקהו בשני חצאים על ה' מי' מא' |
|
ונוציא מנקודת ה' קו ה"א על זוית נצבת מקו ג"ד מי"א מא' |
|
ונוציאהו אל ב' |
|
ונחלק א"ב על ח' בשני חצאים |
| Supposition: C is the center of the circle and otherwise is impossible. | אומר כי ח' מרכז העגולה ואי אפשר זולתו |
| If possible, let T be the center. | כי אלו היה אפשר זה הנה יהיה זה המרכז נקודת ט' |
|
ונוציא ט"ג וט"ה וט"ד |
|
|
הנה קו ג"ה כמו קו ה"ד |
|
ונשים ה"ט משותף |
|
הנה קו ג"ה וה"ט כמו שני קוי ד"ה וה"ט מפתיחת א' |
|
ותושבת ג"ט כמו תושבת ט"ד מח' מא' |
|
הנה זוית גה"ט כמו זוית דה"ט הנה שתיהם אם כן נצבות מי"ג מא' |
|
|
וזוית דה"א גם כן נצבת |
| It has been proven that all right angles are equal. | וכבר התאמת כי כל הזויות הנצבות שוות |
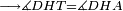
|
אם כן שתי זויות דה"ט דה"א שוות |
| The greater equals the less - it is impossible. | הגדולה לקטנה זה אי אפשר |
| Therefore, point T is not the center of the circle, neither is any other point except point C. | אם כן אין ט' מרכז העגולה ולא זולתה מן הנקודות בלתי נקודת ח' |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 2 |
|
| When you mark two points on the circumference of a circle and draw a straight line from one of them to the other, it falls within the circle. | ב כאשר תרשום על מקיף העגולה שתי נקודות והוצא מאחת משתיהן קו ישר אל האחרת הנה יפול תוך העגולה |
Example: we mark on 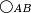 two points G and D two points G and D
|
המשל אנחנו נרשום על עגולת א"ב שתי נקודות ג"ד |
|
ונוציא ג"ד הישר |
| Supposition: it falls within the circle and otherwise is impossible. | הנה אומר כי הוא כבר נפל תוך העגולה אי אפשר זולתו |
| If possible, let it fall outside, as line GHD. | שאם יהיה אפשר הנה יפול חוץ ממנה כמו קו גה"ד |
|
ויהיה מרכז העגולה ז' |
|
ונוציא ז"ג וז"ד |
|
ונוציא מז' אל קשת ג"ד קו ז"ב איך שיפול |
|
ונוציאהו אל ה' |
|
הנה זוית בה"ד יותר גדולה מזוית זג"ה |
|
מפני שהיא חוץ ממשולש זג"ה מי"ו מ' |
|
אבל זוית זג"ה כמו זד"ה |
|
מפני כי צלע ז"ג כמו צלע ז"ד מה' מא' |
|
|
הנה זוית זה"ד יותר גדולה מזוית זד"ה |
| I.19: The side that is opposite to the greatest angle in every triangle is the greatest. | והזוית היותר גדולה מכל משולש יהיה מיתרה הצלע היותר ארוך מי"ט מא' |
|
|
יהיה ז"ד יותר ארוך מצלע ז"ה |
|
|
אבל ז"ד כמו ז"ב |
|
|
אם כן ז"ב יותר ארוך מן ז"ה |
| The smaller is greater than the greater = impossible error. | היותר קצר יותר ארוך מן היותר גדול זה שקר אי אפשר |
| It has been clarified that the line that is drawn from G to D does not fall outside the circle. | הנה כבר התבאר כי הקו אשר יצא מג' אל ד' לא יפול חוץ מן העגולה |
| It has also been clarified that neither does it fall on its circumference. | וכן גם כן התבאר שהוא לא יפול אל הקו המקיף בה |
| Therefore, it falls within as GD. | הנה הוא אם כן יפול בתוכה כמו ג"ד |
| Q.E.D. | וזה מש"ל |
Proposition 3 |
|
| When a chord in a circle does not fall on the center and a straight line that is drawn from the center bisects the chord, then it also cuts it at right angle; and if it cuts it at right angle, then it also bisects it. | ג כאשר נפל מיתר בעגולה על זולת המרכז ויצא מן המרכז קו וחתך המיתר בשני חצאים הנה הוא יחתכהו על זוית נצבת ואם חתך אותו על זוית נצבת הנה יחתכהו בשני חצאים |
Example: chord GD in 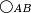 does not pas through the center. does not pas through the center.
|
המשל בו כי נפל בעגולת א"ב מיתר ג"ד על זולת המרכז |
|
והקטר א"ב |
| Supposition: if AB bisects GD, it cuts it at right angles; and if it cuts it at right angles, it bisects it. | אומר כי א"ב אם חתך ג"ד בשני חצאים הנה הוא יחתכהו על זוית נצבת ואם חתכו על זוית נצבת הנה הוא יחתכהו בשני חצאים |
|
ויחתכהו תחלה בשני חצאים על נקודת ה' |
|
הנה אומר כי יחתכהו על זוית נצבת |
|
המופת כאשר נשים המרכז ז' |
|
ונוציא ז"ג וז"ד |
|
|
הנה קו ג"ה כמו ה"ד |
|
ונשים ה"ז משותף |
|
|
הנה קוי ג"ה וה"ז כמו ד"ה וה"ז |
|
ותושבת ג"ז כמו תושבת ז"ד מח' מא' |
|
|
הנה זוית גה"ז כמו זוית דה"ז |
|
הנה שתיהן אם כן נצבות מי"ג מא' |
|
הנה כבר חתך א"ב ג"ד בשני חצאים על זויות נצבות |
|
וגם כן הנה כאשר יחתוך א"ב לג"ד על זויות נצבות |
|
הנה אומר כי הוא יחתכהו בשני חצאים |
|
המופת כי ג"ז כמו ז"ד |
|
אם כן זוית זג"ד כמו זוית זד"ג מה' מא' |
|
אבל זוית גה"ז וזוית דה"ז נצבות |
|
אם כן שתי זויות זג"ה וגה"ז ממשלש זג"ה כמו שתי זויות זד"ה וזה"ד ממשולש זד"ה |
|
|
וצלע ג"ז כמו צלע ז"ד |
|
וקו ה"ז משותף לשני המשולשים |
|
אם כן שתי הצלעות הנשארות והם ג"ה וה"ד שוות מכ"ו מא' |
|
הנה כבר חתך א"ב לג"ד בשני חצאים |
| Its explanation is completed. | ונשלם ביאורו |
Proposition 4 |
|
| Every two chords in a circle that cut one another and do not pass through the center, do not bisect one another. | ד כל שני מיתרים בעגולה יחתוך אחד משניהם האחר ולא יעברו על המרכז הנה לא יחתוך אחד משניהם האחר בשני חצאי' |
Example: the two chords DG and HZ in 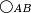 , cut one another at C, do not pass through the center. , cut one another at C, do not pass through the center.
|
דמיון זה כי שני מיתרי ג"ד וה"ז בעגולת א"ב וכבר חתך אחד משניהם האחר על ח' ולא יעברו על המרכז |
| Supposition: neither of the two bisect the other. | הנה אומ' כי הוא לא יחתוך כל אחד משניהם האחר בשני חצאים |
|
ויהיה המרכז ט' |
|
ונוציא ט"ח |
|
הנה כבר יצא מן המרכז קו אל ח' וחתך ג"ד בשני חצאים |
|
הנה הוא יחתכהו על זוית נצבת מג' מזה |
|
|
אם כן זוית דח"ט נצבת |
|
|
וזוית זח"ט גם כן נצבת |
|
מפני כי ח"ט כבר חתך ז"ה בשני חצאי' |
|
|
הנה זוית דח"ט כמו זוית זח"ט |
| The smaller is as the greater = error. | הקטן כמו הגדול זה שקר |
| It has been clarified that neither of the two chords GD and HZ bisect the other. | הנה כבר התבאר כי שני מיתרי ג"ד וה"ז לא יחתוך כל אחד משניהם האחר בשני חצאים |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 5 |
|
| For every two circles that cut one another, their two centers are not the same. | ה כל שתי עגולות תתחתכנה הנה אין שני מרכזיהם אחד |
Example: the two circles 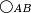 and and 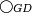 cut one another at the two points A and G. cut one another at the two points A and G.
|
דמיונו כי שתי עגולות א"ב ג"ד תתחתכנה על שתי נקודות א"ג |
| Supposition: their centers are not the same. | הנה אומר כי מרכזיהם אינם אחד |
|
שאם היה אפשר הנה יהיה מרכזיהם ה' |
|
ונוציא מן ה' קו א"ה אל נקודת א' |
|
הנה מן המבואר כי הוא כבר הגיע תכליתו אל מקיף שתי העגולות יחד |
|
ונוציא קו ה"ד אל קשת אד"ג איך שיפול |
|
הנה נקודת ה' מרכז עגולת א"ב |
|
אם כן קו א"ה כמו ה"ז מפתיחת א' |
|
וגם כן הנה מפני כי נקודת ה' מרכז עגלת אד"ג |
|
יהיה קו א"ה שוה לקו ה"ד מפתיחת א' |
|
וכבר התבאר כי קו א"ה שוה לקו ה"ז |
| Those that are equal to the same thing are equal to each other. | והשוים לדבר אחד הנה הם שוים |
|
|
הנה קו ה"ד אם כן שוה לקו ה"ז |
| The greater is as the smaller = impossible error. | הגדול כמו הקטן זה שקר בלתי אפשר |
| Therefore, the center of the two circles is not the same. | אם כן אין מרכז שתי העגולות אחד |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 6 |
|
| For every two circles that touch one another, the centers of both are not the same. | ו כל שתי עגולות תתמששנה הנה אין מרכזי שתיהן אחד |
Example: the two circles 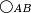 and and 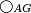 touch one another at A. touch one another at A.
|
דמיונו כי שתי עגולות א"ב וא"ג תתמששנה על א' |
| Supposition: the centers of both are not the same and this is impossible. | הנה אומר כי מרכזי שניהם אינו אחד ואי אפשר זה |
| If possible, let the center of both be one and it is point D. | שאם היה אפשר הנה יהיה מרכז שניהם אחד והוא נקדת ד' |
|
ונוציא א"ד |
|
ונוציא רק ד' קו אל עגולת א"ב איך שיפול והוא ד"ב |
|
ונעביר קו אל עגולת א"ג איך שיפול והוא ד"ג |
|
הנה נקודת ד' מרכז עגולת א"ב |
|
הנה קו א"ד כמו ד"ב מפתיחת א' |
|
ונקודת ד' מרכז עגולת א"ג |
|
הנה קו א"ד כמו קו ד"ג מפתיחת א' |
|
|
וא"ד כבר היה כמו ד"ב |
|
|
הנה ב"ד כמו ד"ג |
| The greater is as the smaller = error. | הגדול כמו הקטן זה שקר |
| It has been clarified that for every two circles that touch one another, the centers of both are not the same. | הנה כבר התבאר כי כל שתי עגולות תתמששנה הנה אין מרכזיהם אחד |
| Its explanation is completed. | ונשלם ביאורו |
Proposition 7 |
|
| For every point in a circle that is not the center, from which lines are drawn to the circumference: the longest of which passes through the center; the shortest is the complement of the diameter from the point to the end of the diameter; the nearer to the line through the center is longer than those that are more remote from it; and only two lines on each side of the shortest line are equal. | ז כל נקדה בעגולה על זולת המרכז יצאו ממנה קוים אל הקו המקיף הנה היותר ארוך מהם אשר יעבור על המרכז והיותר קצר מהם שלימות הקוטר מבין הנקדה וקצה הקטר ומה שקרב מן הקו אשר יעבור על המרכז הנה הוא יותר ארוך ממה שרחק ממנו ושני קוים לבד משני צדדי הקו היותר קצר שוים |
Example: from point H that is not the center on the diameter of 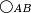 lines are drawn to the circumference, which are: HG, HK, HB, HZ, HC, HA, HD lines are drawn to the circumference, which are: HG, HK, HB, HZ, HC, HA, HD
|
דמיונו כי יצאו מנקודת ה' מן קטר עגולת א"ב והיא על זולת המרכז קוים אל הקו המקיף והם ה"ג ה"כ ה"ב ה"ז ה"ח וה"א וה"ד |
|
וה"ג הוא הקו אשר ילך במרכז |
|
וה"ד שלמות הקוטר |
| Supposition: HG is the longest and HD is the shortest, which is the complement of the diameter. | הנה אומר כי ה"ג הוא היותר ארוך והיותר קצר מהם ה"ד והוא שלמות הקטר |
| As for the rest of the lines: | ואולם הקוים הנשארים |
|
|
הנה ה"ז יותר ארוך מן ה"ח |
|
|
וה"ח יותר ארוך מן א"ה |
| And only two lines on each side of the shortest line are equal. | ושני קוים לבד משני צדדי הקו היותר קצר שוים |
Proof:
|
ומופתו שנשים המרכז ט' |
|
ונוציא ט"ז וט"ח וא"ט |
| [The sum of] any two sides of a triangle is greater than the remaining side. | וכל שתי צלעות ממשולש שניהם יותר ארוכים מן הצלע הנשאר |
|
|
הנה ז"ט וט"ה יותר ארוכים מן ה"ז |
|
|
וז"ט כמו ט"ג |
|
|
הנה ג"ה יותר ארוך מן ה"ז |
|
|
וז"ט כמו ט"ח |
|
|
וט"א כמו ט"ח |
|
וט"ה משותף |
|
|
הנה שני קוי ז"ט וט"ה כמו שני קוי ח"ט וט"ה |
|
|
וזוית זט"ה יותר גדולה מזוית חט"ה |
|
|
הנה תושבת ז"ה יותר ארוכה מתושבת ח"ה |
|
וכן גם כן יתבאר כי ח"ה יותר ארוך מן א"ה |
|
|
וגם כן הנה א"ה וה"ט מקובצים יותר ארוך מן א"ה |
|
|
וגם כן הנה א"ה וה"ט מקובצים יותר ארוך מן א"ט |
|
|
וא"ט כמו ט"ד |
|
|
הנה א"ה וה"ט מחוברים יותר ארוך מן ט"ה וה"ד |
|
ויפול מהם ט"ה המשותף |
|
|
וישאר א"ה יותר ארוך מן ה"ד |
| The longest line is HG, which passes through the center. | הנה היותר ארוך מן הקוים ה"ג והוא אשר עבר על המרכז |
| The shortest is HD, which is the complement of the diameter. | והיותר קצר מהם ה"ד אשר הוא שלמות הקטר |
| As for the rest: the nearer to line HG is longer than the more remote from it. | והנשארים מה שקרב מהם מקו ה"ג יותר ארוך ממה שרחק |
|
|
הנה קו ה"ז יותר ארוך מן ה"ח |
|
|
וה"ח יותר ארוך מן א"ה |
| Supposition: | ואומר כי שני קוים לבד יהיו משני צדדי הקצר שוים |
| המופת אנחנו נעמיד על נקודת ט' מקו ט"ה כמו זוית אט"ה והיא זוית הט"ב | |
| ונוציא ה"ב | |
|
|
הנה קו א"ט כמו ט"ב |
| ונשים ט"ה משותף | |
|
|
הנה קו א"ט וט"ה כמו שני קוי ב"ט וט"ה |
|
|
וזוית אט"ה כמו זוית הט"ב |
|
|
אם כן תושבת ה"ב כמו תושבת א"ה |
| Supposition: | ואומר גם כן כי אי אפשר שיצא מן ה' אל הקו המקיף כמו א"ה כי אם ה"ב |
| ואם יהיה אפשר זה יהיה ה"כ ויצא ט"ב | |
|
|
הנה קו א"ט כמו ט"ב |
| ונשים ה"ט משותף | |
|
|
הנה קו א"ט וט"ה כמו שני קוי ב"ט וט"ה |
|
|
ותושבת א"ה כמו תושבת ה"ב |
|
|
הנה זוית אט"ה כמו זוית כט"ה |
|
|
אבל זוית אט"ה כמו זוית בט"ה |
|
|
הנה זוית כט"ה כמו זוית בט"ה |
| The greater equals the smaller = error. | הגדולה שוה לקטנה זה שקר |
| הנה אי אפשר שיצא מן ה' קו אחר כמו אחד משני קוי א"ה ה"ב זולתם אשר הם מזולתם היותר קצר מהם לבד שוים | |
| וזה מה שרצינו ביאורו | |
Proposition 8 |
|
| For every point outside a circle, from which lines are drawn through to the circle: the longest that enters the circle and cuts lines from it is the one that passes through the center; of the remaining lines, the nearer to the one that passes through the center is longer than those that are more remote; the shortest of the lines that end on the circumference and not entering it is the line that is between the point and the end of the diameter; of the remaining lines the nearer to it is shorter than the more remote; and only two lines on each side of the diameter are equal. | ח כל נקדה יוצאת חוץ מעגולה יצאו ממנה קוים אל העגולה הנה היותר ארוך שיכנס בעגולה ויחתכנה מן הקוים הוא אשר יעבור מן המרכז ומה שקרב מן הקוים הנשארים מן אשר ילך אל המרכז יותר ארוך ממה שרחק והיותר קצר שבקוים אשר יכלו אל העגולה ולא יכנסו בה הוא הקו אשר בין הנקודה ובין קצה הקטר ומה שקרב ממנו מן הקוים הנשארים יותר קצר ממה שרחק ושנים קוים לבד משני צדדי הקטר שוים |
| דמיונו כי הוצאו מנקדת ג' אל תוך עגולת א"ב קוים והם ג"ד וג"ה וג"ז וא"ג והקו אשר יעבור על המרכז ג"ד | |
| Supposition: | הנה אומר שהוא היותר ארוך שבקוים הנכנסים וכי ג"ה יותר ארוך מן ג"ז וכי ג"ז יותר ארוך מן א"ג וכי היותר קצר שבקוי' היוצאים אשר בין הנקודה ובין קצה הקטר הוא ג"ב וכי ג"ב יותר קצר מן ג"ל וג"ל יותר קצר מן ג"ט ושני קוים לבד משני צדדי ג"ב היותר קצר שוים |
| המופת אנחנו נשים המרכז נקודת מ' | |
| ונוציא ממנה קוים מ"ה ומ"ז ומ"א ומ"ט ומ"ל ומ"כ | |
|
|
הנה שני קוי מ"ה ומ"ג מקובצים יותר ארוך מן ג"ה |
|
|
ומ"ה כמו מ"ד |
|
|
הנה ד"ג יותר ארוך מן ג"ה |
|
|
ומ"ה כמו ז"מ |
| ונשים מ"ג משותפים | |
|
|
הנה שני קוי ה"מ ומ"ג כמו שני קוי ז"מ ומ"ג |
|
|
וזוית המ"ג יותר גדולה מזוית זמ"ג |
|
|
הנה תושבת ה"ג יותר ארוכה מתושבת ז"ג |
|
|
וכן גם כן התבאר כי ז"ג יותר ארוך מן א"ג |
|
|
וכי כן הנה מ"כ וכ"ג יותר ארוכים מן מ"ג |
|
|
ומ"כ כמו מ"ב |
|
|
ונשאר ג"כ יותר ארוך מן ג"ב |
|
|
הנה ג"ב יותר קצר מן כ"ג |
| ובמשולש למ"ג שתי צלעות נצבות על תושבת מ"ג והם מ"כ וכ"ג | |
| והנה נפגשו בתוכו | |
|
|
הנה מ"ל ול"ג יותר ארוכים מן מ"כ וכ"ג |
|
|
ואולם מ"כ הוא כמו מ"ל |
|
|
ונשאר ל"ג יותר ארוך מן כ"ג |
|
|
וכן גם כן התבאר כי ג"ט יותר ארוך מן ג"ל |
| הנה היותר ארוך שבקוים הנכנסים ג"ד | |
|
|
ואחר כן ג"ה יותר ארוך מן ג"ז |
|
|
ואחרי כן ג"ז יותר ארוך מן א"ג |
| והיותר קצר שבקוים היוצאים ג"ב | |
|
|
ואחרי כן ג"ב יותר קצר מן ג"כ |
|
|
וג"כ יותר קצר מן ג"ל |
|
|
ואחרי כן ג"ל יותר קצר מן ג"ט |
| Supposition: | ואומר כי שני קוים לבד לשני צדדי ג"ב היות קצר שבקוים שוים |
| המופת שתעמיד על נקודת מ' מקו מ"ג זוית נמ"ג כמו זוית כמ"ג | |
| ונוציא ג"נ | |
|
|
הנה קו כ"מ כמו קו נ"מ |
| ונשים ג"מ משותף | |
|
|
הנה שני קוי כ"מ מ"ג כמו שני קוי מ"נ ומ"ג |
|
|
וזוית כמ"ג כמו זוית נמ"ג |
|
|
אם כן תושבת כ"ג כמו תושבת ג"נ |
| Supposition: | הנה אומר כי לא יצא מן ג' קו אחד כמו כל אחד מן כ"ג ונ"ג |
| שאם היה אפשר יוצא והוא ג"ס | |
| ונוציא מן מ' קו אל ס' | |
|
|
הנה קו כ"מ כמו קו מ"ס |
| ונשים מ"ג משותף | |
|
|
הנה שני קוי כ"מ ומ"ג כמו שני קוי ס"מ ומ"ג |
|
|
ותושבת כ"ג כמו תושבת ג"ס |
|
|
הנה זוית כמ"ג כמו זוית גמ"ס |
|
|
וכבר היתה זוית כמ"ג כמו זוית נמ"ג |
|
|
הנה זוית גמ"ס כמו זוית גמ"נ |
| The greater is as the smaller = error. | הגדולה כמו הקטנה זה שקר |
| ואי אפשר שיצא קו אחר כמו קו ג' זולתי נ"ג | |
| הנה שני קוי כ"ג נ"ג אשר הם משני צדדי הקו היותר קצר לבד שוים | |
| וזה מה שרצינו לבאר | |
Proposition 9 |
|
| When more than two lines are drawn from a point in the circle to the circumference and the lines are equal, then the point is the center of the circle. | ט כאשר הוצא מנקודה בעגלה יותר משני קוים אל הקו המקיף והיו הקוים שוים הנה היא מרכז העגלה |
| המשל בו שיוצא מנקודת ג' מעגלת א"ב קוים שוים יותר משנים והם ג"ד וג"ב וג"ה | |
| Supposition: | הנה אומר כי נקדת ג' מרכז עגלת א"ב |
| המופת אנחנו נוציא ד"ב וב"ה | |
| ונחלק שני קוי ד"ב וב"ה בשני חצאים שוים על ח"ז | |
| ונוציא ג"ז וג"ח ונעביר בשני הצדדים אל הקו המקיף | |
|
|
הנה קו ד"ז כמו קו ז"ב |
| ונשים ז"ג משותף | |
|
|
הנה שני קוי ד"ז וז"ג כמו שני קוי ב"ז וז"ג |
|
|
ותושבת ג"ד כמו תושבת ג"ב |
|
|
אם כן זוית דז"ג כמו זוית בז"ג |
| הנה שתיהן אם כן שתי נצבות | |
| הנה כבר חתך קו א"ט מיתר ב"ד בשני חצאים על שתי זויות | |
| אם כן מרכז העגולה על א"ט | |
| וכן התבאר כי המרכז על כ"מ | |
| והנה המרכז יפול על החתך המשותף לשני הקוים א"ט וכ"מ והוא נקדת ג' | |
| וזה מש"ל | |
| אמ' תבאת מצאנו בקצת הנוסחאות מן היונים לזו התמונה מופת אחר | |
| והוא שאנחנו נשים העגלה א"ב ג"ד | |
| והנקדה אשר בתוכה נקדת ה' | |
| ונוציא מנקדת ה' אל העגלה קוים שוים והם ה"ז וא"ה וח"ה | |
| Supposition: | הנה אומר כי נקדת ה' מרכז עגולת א"ב ג"ד |
| ואם לא יהיה כן הנה יהיה מרכזה ט' אם יהיה אפשר זה | |
| ונגיע קו ט"ה ונעבירהו בשני הצדדים אל שתי נקודות ד"ב | |
| הנה מפני שכבר הורשמה בתוך עגולת א"ב ג"ד נקודה איך שתפול והיא ה' | |
| והוצאו ממנה קוים ה"ב וה"ז וא"ה וה"ח אל העגולה איך מה שנפלו | |
| וקו ב"ה מהם ילך במרכז | |
| יהיה קו ב"ה היותר ארוך מהם | |
| והיותר קצר מהם קו ד"ה | |
| וקו ז"ה יותר ארוך מקו א"ה | |
| וקו א"ה יותר ארוך מקו ה"ח | |
| אבל אלו הקוים השלשה שוים וזה בלתי אפשר | |
| אם כן אין נקדת ט' מרכז לעגולת א"ב ג"ד | |
| וכן גם כן התבאר שאי אפשר שיהיה מרכזה מנקדה אחרת זולת נקודת ה' | |
| אם כן נקודת ה' מרכז עגולת א"ב ג"ד | |
| וזה מש"ל | |
Proposition 10 |
|
| A circle cannot cut a circle at more than two points. | י אי אפשר שתחתוך עגולה עגלה ביותר משתי מקומות |
| שאם היה אפשר זה הנה תחתוך עגולת א"ב עגולת ג"ד ביותר משני מקומות על נקודות ה"ז ח"ט | |
| ונוציא שני קוי ה"ז וז"ח | |
| ונחלקם בשני חצאים על כ"ל | |
| ונוציא כ"ג ול"א על זויות נצבות | |
| ונעביר שניהם אל ב"ד | |
| הנה קו א"ב בעגולת א"ב כבר חתך ז"ח בשני חצאים על זוית נצבת | |
| אם כן מרכז העגולה על א"ב | |
| וג"ד גם כן בעגולת א"ב חתך ז"ה בשני חצאים על זוית נצבת | |
| אם כן מרכז עגולת א"ב על ג"ד | |
| וכבר התבאר כי מרכז עגולת א"ב על קו א"ב | |
| אם כן מרכזה על הנקדה המשותפת לשני קוי א"ב ג"ד | |
| ואינם משותפים בנקודה זולת נקודת נ' אם כן נקודת נ' היא מרכז עגולת א"ב | |
| וכמו כן התבאר שמרכז עגלת ג"ד היא נקודת נ' | |
| אם כן נקודת נ' מרכז עגולות א"ב וג"ד | |
| ושתיהם תתחתכנה אם כן אין מרכז שתיהם אחד | |
| אם כן לא תחתוך עגלה עגלה ביותר משתי מקומות | |
| אמ' תבאת מצאנו בקצת הנוסחאות מהיונים לתמונה הזאת מופת אחר | |
| והוא שאנחנו נשים העגלה אב"ג תחתוך עגלת דה"ז על יותר משתי נקודות והם נקודות ח"ב וז"ט | |
| ויהיה מרכז עגולת אב"ג נקודת כ' | |
| ונגיע קוי ב"כ וח"כ וז"כ | |
| הנה מפני כי כבר הרשמת נקדה בעגולת דה"ז יותר משני קוים והיו שוים והם קוי כ"ב כ"ז כ"ח הנה נקדת כ' מרכז עגולת דה"ז | |
| וכבר היתה גם כן מרכז עגולת אב"ג | |
| הנה כבר נחתכו שתי עגולות והיו מרכזי שתיהן אחד והם נקודת כ' וזה בלתי אפשר | |
| הנה לא תחתוך עגולה עגולה ביותר משני מקומות וזה הוא מה ש"ב | |
Proposition 11 |
|
| For every two circles that touch one another, the line that passes through their centers passes through their point of contact, whether it is inside or outside. | יא כל שתי עגולות תתמששנה הנה הקו אשר יעבור על מרכז שתיהן יעבור במקום המשוש מבפנים היה משושם או מבחוץ |
| המשל בו כי עגולת א"ב תמששה עגולת א"ג מבפנים על נקודת א' ויהיה מרכז עגולת א"ב ה' ומרכז א"ג ז' | |
| Supposition: | הנה אומר כי הקו אשר יעבור על ה"ז יכלה אל נקודת א' אי אפשר זולתו |
| שאם היה אפשר הנה יפול כמו ה"ז ט"ח | |
| ונוציא שני קוי א"ז וז"ה | |
| הנה שני קוי א"ז וז"ה מקובצים יותר ארוך מן א"ה | |
| וא"ז כמו ז"ט | |
| וא"ה כמו ה"ח | |
| אם כן ה"ט יותר ארוך מן ה"ח וזה שקר | |
| הנה כבר התבאר כי הקו אשר יעבור על שתי נקודות ה"ז אין יציאתו כמו יציאת ה"ח ולא יפול במקום אחר כי אם בנקודת א' כאשר תתמששנה שתי העגלות | |
| וגם כן הנה אנחנו נשים עגלת א"ג תמשש עגלת א"ב מחוץ על נקודת א' | |
| ויהיה מרכז עגלת א"ב ה' ומרכז עגלת א"ג ז' | |
| Supposition: | הנה אומר כי הקו אשר יעבור על ה"ז יעבור בנקודת א' |
| ואם לא יהיה כן הנה נפול כמו קו ה"ח ט"ז | |
| ונוציא שני קוי א"ז וא"ה | |
| הנה שני קוי א"ז וא"ה יותר ארוך מן ז"ט ח"ה הישר | |
| ואולם א"ה הנה הוא כמו ה"ח | |
| ואולם א"ז הנה הוא כמו ז"ט | |
| אם כן שני קוי ה"ח וז"ט שוים לשני קוי א"ז וא"ה | |
| וכבר היו שני קוי א"ז וא"ה מחוברי' יותר ארוך מן אח"ז ושניהם יותר קטנים ממנו זה אי אפשר | |
| הנה הקו אשר יגיע בין שתי נקודות ה"ז יעבור בנקודת א' | |
| וזה מש"ל | |
Proposition 12 |
|
| A circle does not touch another circle at more than one point, whether one of them is inside the other or outside it. | יב לא תמשש עגולה עגולה כי אם במקום אחד כאשר תהיה אחת משתיהן תוך האחרת או חוץ ממנה |
| שאם היה אפשר תמששנה בשתי מקומות או יותר הנה תמשש עגולת ג"ד עגולת א"ב בשתי מקומות מבפנים על שתי נקודות ג"ד | |
| והיה מרכז עגולת א"ב נקודת ה' | |
| ומרכז עגולת ג"ד נקודת ז' | |
| הנה הקו אשר יעבור על ה"ז יפול במקום אשר תתמששנה שתי העגולות | |
| ונוציא קו ה"ז ונוציאהו אל שתי נקודות ג"ד | |
| הנה מרכז עגולת א"ב ה' | |
| הנה קו ה"ד כמו קו ה"ג | |
| וד"ה יותר ארוך הרבה מן ז"ד | |
| וגם כן הנה מרכז עגולת ג"ד נקדת ז' | |
| אם כן קו ז"ד כמו קו ז"ג וכבר היה שהתבאר כי ג"ז יותר ארוך הרבה מן ז"ד וזה שקר | |
| אם כן לא תמשש עגולת ג"ד עגולת א"ב כי אם במקום אחד לבד | |
| ותמששנה מחוץ אם היה אפשר זה כמו עגולת ח"ט לעגולת א"ב בשתי מקומות על שתי נקודות א"ב הנה הקו אשר יצא מן א' אל ב' יפול בעגולת א"ב וחוץ מעגולת ח"ט זה שקר | |
| מפני כי שתי נקודות תפולנה על קשת עגולה יהיה הקו הישר אשר יצא מאחת משתיהן אל האחרת יפול בתוך העגולה | |
| הנה לא תמשש עגולה עגולה כי אם במקום אחד אם מבפנים ואם מבחוץ | |
| וזה מש"ל | |
Proposition 13 |
|
| When there are equal chords in a circle, their distances from the center are equal; and those, whose distances from the center are equal, are equal. | יג כאשר נפלו בעגולה מיתרים שוים הנה מרחקיהם מן המרכז שוים ואם היו מרחקיהם מן המרכז שוים הנה הם שוים |
| המשל שהוא נפיל בעגולת א"ב שני מיתרים שוים והם ג"ד וה"ז | |
| Supposition: | הנה אומר כי מרחק שניהם מן המרכז שוה |
| המופת כי נשים המרכז נקודת ח' | |
| ונוציא ממנו אל שני מיתרי ג"ד ה"ז שני עמודים ח"ט וח"כ | |
| ונוציא ה"ח וח"ד וח"ז וח"ג | |
|
|
הנה ג"ד כמו ה"ז |
|
|
וג"ח כמו ה"ח |
|
|
הנה שני קוי ד"ג ג"ח כמו שני קוי ז"ה וח"ה |
|
|
ותושבת ד"ח כמו תושבת ז"ח |
|
|
אם כן זוית טג"ח כמו זוית כה"ח |
|
|
וזוית גט"ח כמו זוית הכ"ח מפני כי שתיהן נצבות |
| אם כן שתי זויות משולש גט"ח כמו שתי זוית משלש הכ"ח | |
|
|
ושתי צלעות ג"ח ה"ח שוות |
| הנה שתי צלעות הנשארות כמו שתי צלעות הנשארות כל אחת כמו הנכחית לה | |
| והזוית הנשארת כמו הזוית הנשארת | |
| אם כן ט"ח כמו כ"ח ושניהם שני העמודים | |
| הנה מרחק ג"ד וה"ז מן המרכז שוה | |
| Supposition: | ואומר כי שניהם שוים |
| המופת כי כבר הוצא מן המרכז קו ט"ח אל ג"ד וחתכו על זוית נצבת | |
| והוא אם כן יחתכהו בשני חצאין | |
|
|
אם כן קו ג"ט כמו קו ט"ד |
|
|
וד"ג כפל ג"ט |
|
|
ולכן יהיה ז"ה כפל ה"כ |
|
|
וג"ח כמו ה"ח |
|
|
אם כן המרובע ההוה מן ג"ח כמו שני המרובעים ההוים מג"ט ט"ח |
|
|
מפני כי זוית גט"ח נצבת |
|
|
והמרובע ההוה מן ה"ח כמו שני המרובעים ההוים מן ה"כ וכ"ח |
|
|
מפני כי זוית הכ"ח נצבת |
|
|
הנה שני המרובעים ההוים מן ט"ח ט"ג כמו שני המרובעים ההוים מן ח"כ וכ"ה |
|
|
והמרובע ההוה מן ט"ח כמו המרובע ההוה מן כ"ח |
|
|
ונשאר המרובע ההוה מן ג"ט כמו המרובע ההוה מן ה"כ |
|
|
הנה קו ג"ט כמו קו ה"כ |
|
|
וג"ד כפל ג"ט |
|
|
וה"ז כפל כ"ה |
| וכל שני קוים שוים כאשר הוכפלו היו שוים | |
|
|
אם כן מיתר ג"ד כמו מיתר ה"ז |
| וזה מה שרצינו ביאורו | |
Proposition 14 |
|
| When there are chords in a circle, the longest of them is the diameter of the circle; and of the rest, the nearer to the center is longer than the more remote. | יד כאשר נפלו בעגולה מיתרים הנה היותר ארוך מהם קוטר העגולה והנשארים הנה היותר קרוב מהם אל המרכז יותר ארוך מן היותר רחוק |
| המשל בו כי נפלו בעגולת א"ב שני מיתרים והם ז"ה וח"ט והקוטר ג"ד וז"ה יותר קרוב אל המרכז מן ח"ט | |
| Supposition: | הנה אומר כי קוטר ג"ד הוא היותר ארוך מהם ושה"ז יותר ארוך מן ט"ח |
| המופת כי נשים המרכז נקדת כ' | |
| ונוציא ממנו שני עמודים אל שני מיתרי ה"ז וח"ט והם כ"ל וכ"מ | |
| הנה מיתר ז"ה יותר קרוב אל המרכז מן ח"ט | |
| אם כן מ"כ יותר קרוב אל המרכז ארוך מן ל"כ | |
| ונבדיל מן כ"מ כמו ל"כ והוא כ"נ | |
| ונקוה על נ' קו נכחי לקו ט"ח והוא ס"ע | |
| הנה שני קוי ה"ז וס"ע מרחק שניהם מן המרכז שוה | |
| אם כן שניהם שוים אם כן קו ה"ז כמו ס"ע | |
| ונוציא קוים כ"ס וכ"ח וכ"ע וכ"ט | |
| הנה ס"כ וכ"ע מחוברים יותר ארוך מן ס"ע | |
| וס"כ כמו כ"ג | |
| וכ"ע כמו כ"ד | |
| הנה קו ג"ד יותר ארוך מן ס"ע | |
| וס"ע כמו ה"ז | |
| אם כן ג"ד יותר ארוך מן ה"ז | |
| וס"ב כמו כ"ח | |
| וע"כ כמו כ"ט | |
| הנה שני קוי ס"כ וכ"ע כמו שני קוי כ"ח וכ"ט | |
| וזוית עכ"ס יותר גדולה מזוית טכ"ח | |
| אם כן תושבת ס"ע יותר ארוכה מתושבת ט"ח | |
| אבל ס"ע כמו ה"ז | |
| אם כן ה"ז יותר ארוך מן ט"ח | |
| הנה המיתרים אשר נפלו בעגולת א"ב היותר ארוך מהם הקוטר והוא ג"ד וה"ז היותר קרוב אל המרכז יותר ארוך מן ט"ח היותר רחוק | |
| ונשלם ביאורו | |
Proposition 15 |
|
| When a straight line is drawn from the end of the diameter of a circle at right angles, it falls outside the circle, and no other straight line falls between it and the circumference; the angle of the semicircle is greater than any acute rectilinear angle, and the angle contained by that line and the circumference is less than any acute rectilinear angle. | טו כאשר הוצא מקצה הקטר העגולה קו ישר על זוית נצבת הנה יוצא מן העגלה ולא יפול בינו ובין הקו מן המקיף קו אחר ישר ותהיה זוית חצי העגולה יותר גדולה מכל זוית חדה ישרת שני הקוים ותהיה זוית אשר יקיף בה הקו ההוא והקו המקיף היותר קטנה מכל זוית חדה ישרת שני הקוים |
| המשל כי עגולת א"ב יצא מקצה קוטרה והוא קו ג"ד קו ד"ז על זוית נצבת מנקודת ד' | |
| Supposition: | הנה אומר כי הוא יפול חוץ מן העגולה אי אפשר זולת זה |
| שאם היה אפשר הנה יפול בתוכה כמו קו ד"ז קו ד"א | |
| ויהיה המרכז ה' | |
| ונוציא א"ה והוא כמו ה"ד | |
| אם כן זוית הא"ד כמו זוית הד"א | |
| וזוית הד"א נצבת אם כן זוית הא"ד גם כן נצבת | |
| אם כן משולש הא"ד נצב שתי הזויות זה שקר | |
| הנה כבר התבאר כי הקו אשר יצא מן ד' והוא קצה ז"ד על זוית נצבת יפול חוץ מן העגולה ויפול כמו ד"ז | |
| Supposition: | הנה אומר כי לא יכנס בינו ובין קשת גא"ד קו אחר ישר |
| שאם היה אפשר הנה יפול בין שניהם כמו קו ד"ח | |
| ונוציא מן ה' עמוד אל קו ד"ח והוא ה"ט | |
| הנה זוית הט"ד נצבת | |
| וזוית הד"ט קטנה מנצבת | |
| אם כן זוית הט"ד יותר גדולה מזוית הד"ט | |
| והזוית היותר גדולה מכל משולש יהיה מיתרה הצלע היותר ארוך | |
| אם כן צלע ה"ד יותר ארוך מן ה"ט | |
| וה"ד כמו ה"א | |
| אם כן ה"א יותר ארוך מן ה"ט זה שקר | |
| הנה כבר התבאר כי לא יפול בין קשת גא"ד ובין קו ד"ז קו אחר ישר | |
| Supposition: | ואומר כי הזוית הנכנסת אשר יקיפו בה הקוטר והקו המקיף אשר עליה בד"ה יותר גדולה מכל זוית חדה ישרת שני הקוים |
| ושזוית בד"ז החיצונה יותר קטנה מכל זוית חדה ישרת שני הקוים | |
| כי אלו היתה זוית חדה ישרת שני הקוים יותר גדולה מן הפנימית ויותר קטנה מן החיצונה אשר זכרנו בשם היה אפשר שיפול בין קו ד"ז ובין קשת גא"ד קו ישר אבל לא יפול | |
| אם כן זוית חצי העגולה אשר עליה גד"ב יותר גדולה מכל זוית חדה ישרת שני הקוים ואשר עליה בד"ז יותר קטנה מכל זוית חדה ישרת שני הקוים | |
| ונשלם ביאורו | |
Proposition 16 |
|
| We wish to draw from a given point a line that touches the circle. | יו נרצה שנוציא מנקודה ידועה קו ימשש העגולה |
| הנה נשים הנקודה הידועה נקודת א' והעגולה עגולת ב"ג | |
| ונרצה שנוציא מן א' קו ימשש עגולת ב"ג | |
| הנה נוציא ממרכז העגולה והוא ד' קו ד"א | |
| ונקוה על מרכז ד' ובמרחק א"ד עגולת א"ח | |
| ונוציא מקו א"ד מנקודת ז' ממנו קו על זוית נצבת והוא ז"ח | |
| ונוציא ד"ח וט"א | |
| הנה קו ד"ח כמו קו א"ד | |
| וד"ז כמו ד"ט | |
| הנה שני קוי א"ד וד"ט כמו שני קוי ח"ד וד"ז | |
| והזויות אשר יקיפו בו שני קוי ח"ד וד"ז ושני קוי א"ד וד"ט אחת | |
| מפני שהם יקיפו זוית אחת והיא ד' | |
| הנה תושבת ז"ח כמו תושבת א"ט | |
| ומשלש זד"ח כמו משלש טד"א | |
| והזויות הנשארות כמו הזויות הנשארות אשר יהיו מיתריהם הצלעות השוות | |
| אם כן זוית דט"א כמו זוית דז"ח הנה שתיהם יחד נצבות | |
| וד"ט קו הקוטר | |
| והקו אשר יצא מקצה הקוטר על זוית נצבת ימשש העגולה | |
| הנה כבר התבאר כי קו א"ט ימשש עגולת ב"ג | |
| וזה מש"ל | |
Proposition 17 |
|
| For every line that touches the circle, when a line is drawn from the touching point to the center, this line is perpendicular to the line that touches the circle. | יז כל קו ימשש העגולה ויצא מן המקום אשר ימששה בו קו אל המרכז הנה הקו יהיה עמוד על הקו הממשש לעגולה |
| המשל בו כי קו ג"ד ימשש עגולת א"ב על נקודת ב' והמרכז ה' ונוציא ב"ה | |
| Supposition: | הנה אומר שהוא עמוד על ג"ד אי אפשר זולתו |
| שאם היה אפשר הנה יצא מן ה' עמוד אל קו ג"ד זולת ב"ה והוא ה"ז | |
| הנה זוית הז"ב אם כן נצבת | |
| וזוית הב"ז חדה | |
| אם כן זוית הב"ז יותר גדולה מזוית הב"ז | |
| והזוית היותר גדולה מכל משלש מיתרה הצלע היותר ארוך | |
| הנה קו ב"ה יותר ארוך מן ה"ז וה"ב כמו ה"א אם כן ה"א יותר ארוך מן ה"ז וזה שקר | |
| אם כן אי אפשר שיהיה ה"ז עמוד על ג"ד ולא זולתו מן הקוים | |
| וזה מה שרצינו לבאר | |
Proposition 18 |
|
| When a straight line touches a circle, and from the touching point a straight line is drawn at right angles to the [line] outside of the circle, then the center falls on it. | יח כאשר ימשש קו ישר עגולה ויצא מן המקום אשר ימששנה קו על זוית נצבת לפנים מן העגולה הנה יהיה עליו המרכז |
| המשל בו כי קו ג"ד ימשש עגולת א"ב על ב' ויצא מנקודת ב' קו א"ב על זוית נצבת | |
| Supposition: | הנה אומר כי המרכז יפול על קו א"ב אי אפשר זולתו |
| שאם יהיה אפשר נאמר שיפול על קו ב"ה אם כן זוית הב"ד נצבת | |
| וזוית דב"א נצבת | |
| ושתיהם נצבות זה שקר | |
| אם כן אין המרכז על ב"ה ולא בזולת קו א"ב | |
| אם כן מרכז העגולה על א"ב | |
| וזהו מה שרצינו לבאר | |
Proposition 19 |
|
| The angle that is at the center of the circle is double the angle that is at the circumference, when the base of both [the angles] is the same arch. | יט הזוית אשר תהיה על מרכז העגולה כמו שני פעמים מאשר תהיה על הקו המקיף כאשר תהיינה תושבות שתיהם קשת אחת |
| המשל בו כי על מרכז עגולת בא"ג זוית בד"ג ועל הקו המקיף זוית בא"ג ותושבת שתיהם יחד קשת ב"ג | |
| Supposition: | הנה אומר כי זוית בד"ג כפל זוית בא"ג |
| המופת כי נוציא קו א"ד ונוציאהו אל ה' | |
| הנה שני קוי א"ד וד"ג שוים | |
| אם כן שתי זויות דא"ג ודג"א שוות | |
| וזוית הד"ג כפל זוית הא"ג | |
| ולכן זוית בד"ה כפל זוית בא"ד | |
| הנה כל זוית בד"ג כפל זוית בא"ג | |
| וזה מש"ל | |
Proposition 20 |
|
| When two angles falls on the same segment of a circle, they are equal to one another. | כ כאשר תהיה בחתיכה אחת מעגלה שתי זויות הנה שתיהן שוות |
| המשל בו כי בעגלת אב"ג חתיכת ג"א ה"ד בה שתי זויות גה"ד וגא"ד | |
| Supposition: | הנה אומר שהן שוות |
| המופת הנה נשים המרכז ז' | |
| ונוציא ג"ז ז"ד | |
| הנה זוית גז"ד על המרכז וזוית גה"ד על הקו המקיף | |
| וזוית גז"ד כפל זוית גה"ד ולכן גם כן יהיה כפל זוית גא"ד | |
| אם כן זוית גה"ד כמו זוית גא"ד | |
| ונשלם ביאורו | |
Proposition 21 |
|
| For every cyclic quadrilateral, [the sum of] each pair of its opposite angles is equal to two right angles. | כא כל עגולה תפול בה תמונה בעלת ארבע צלעות הנה כל שתי זויות מתנגדות מזויותיה הנה שתיהן שוות לשתי זויות נצבות |
| המשל בו כי בעגולת אב"ג תמונה בעלת ארבע צלעות והיא תמונת א"ב ג"ד | |
| Supposition: | הנה אומר כי כל שתי זויות מתנגדות מזויותיה שוות לשתי נצבות |
| המופת אנחנו נוציא א"ג וב"ד | |
| וכל שתי זויות בחתיכה אחת הנה שתיהן שוות | |
| הנה זוית בא"ג כמו זוית בד"ג | |
| וזוית אד"ב גם כן כמו זוית אג"ב | |
| הנה כל זוית אד"ג כמו שתי זויות אג"ב וגא"ב | |
| ונשים זוית גב"א משותפת | |
| אם כן זוית בא"ג ואג"ב וגב"א כמו שתי זויות אב"ג ואד"ג | |
| וזויות גב"א ובא"ג ובג"א יחד כמו שתי זויות נצבות | |
| הנה שתי זויות אד"ג ואב"ג המתנגדות כמו שתי זויות נצבות | |
| ובכמו הצורה הזאת תדע כי שתי זויות בא"ד ודג"ב שוות לשתי נצבות | |
| ונשלם ביאורו | |
Proposition 22 |
|
| כב אי אפשר שיעמודו על קו אחד ישר שתי חתיכות מתדמות מחתיכות העגולות בצד אחד ואחת משתיהן יותר גדולה מן האחרת | |
| שאם היה אפשר נאמר שיקום על קו א"ב הישר שתי חתיכות דומות מחתיכות העגולות בצד אחד והאחת יותר גדולה מן האחרת והם שתי חתיכות אה"ב ואז"ב והיותר גדולה משתיהן חתיכת אז"ב | |
| ונרשום על קשת אה"ב נקדת ה' | |
| ונוציא קו א"ה ונוציאהו עד ז' | |
| ונוציא שני קוי ה"ב וז"ב | |
| הנה חתיכת אה"ב דומה לחתיכת אז"ב | |
| אם כן זוית אה"ב כמו זוית אז"ב היוצאת המשלש כמו הפנימית זה שקר | |
| אם כן לא יעמדו על קו אחד ישר שתי חתיכות דומות מחתיכות העגולים ואחת משתיהם יותר גדולה מן האחרת | |
| וזהו מה שרצינו לבאר | |
Proposition 23 |
|
| כג כאשר יהיו חתיכות העגולות דומות והיו על קוים ישרים שוים הנה החתיכות גם כן שוות | |
| המשל בו כי שתי חתיכות אה"ב וגז"ד דומות ועל שני קוים ישרים שוים והם א"ב ג"ד | |
| Supposition: | הנה אומר כי שתי החתיכות שוות |
| המופת כי אנחנו כאשר הרכבנו חתיכת אה"ב על חתיכת גז"ד ותושבת א"ב על תושבת ג"ד נפלה קשת אה"ב על קשת גז"ד | |
| שאם לא תפול ונפל כמו גה"ד והיה תושבת א"ב כבר נפל על תושבת ג"ד | |
| הנה כבר עמדו על קו ג"ד הישר שתי חתיכות דומות מחתיכות העגולות בצד אחד ואחת משתיהן יותר גדולה מן האחרת והם גז"ד וגה"ד זה שקר אי אפשר | |
| אם כן חתיכת אה"ב תפול על חתיכת גז"ד הנה היא אם כן שוה אליה | |
| וזה מה שרצינו ביאורו | |
Proposition 24 |
|
| כד נרצה שנשלים חתיכה ידועה מהעגולה | |
| ותהיה חתיכת העגולה הידועה אג"ב | |
| הנה כאשר רצינו להשלים עגולתה הנה נגיע א"ב ונחלקהו בשני חצאים על ד' | |
| ונוציא מנקודת ד' עמוד על א"ב והוא ד"ג | |
| ונגיע א"ג | |
| ונעמיד על קו א"ג הישר על נקודת א' ממנו זוית שוה לזוית אג"ד ישרת שתי הצלעות והיא זוית גא"ה | |
| וזוית דג"א יותר קטנה מנצבת | |
| אם כן שתי זויות דג"א וגא"ה יותר קטנות משתי נצבות וירחקו אל לא תכלית יפגשו | |
| ונאמר שיפגשו שני קוי א"ה ג"ד על נקדת ה' | |
| ונגיע קו ב"ה | |
| הנה מפני כי זוית גא"ה שוה לזוית אג"ח יהיה צלע א"ה שוה לצלע ה"ג | |
| וזה כי שתי זויות משולש הא"ג אשר הן על התושבת שוות | |
| וגם כן הנה מפני כי צלע א"ד שוה לצלע ד"ב וקו ד"ה משותף הנה כל אחד משני קוי א"ד ד"ה שוים לכל אחד משני קוי ב"ד ד"ה כל אחד לנכחי אליו | |
| וזוית אד"ה שוה לזוית בד"ה | |
| הנה תושבת א"ה שוה לתושבת ב"ה | |
| והיה כבר התבאר כי קו א"ה שוה לקו ה"ג | |
| הנה קוי א"ה ה"ג ה"ב השלשה שוים | |
| וכאשר שמנו נקודת ה' מרכז וסבבנו עגולה במרחק ה"א ה"ב ה"ג הלכה בנקודת השלש ונקוה העגולה הזאת והיא עגולת אז"ב | |
| הנה קוינו אל עגולת אג"ב חתיכה ממנה והיא עגולת אז"ב | |
| וזה מה שרצינו לבארו | |
Proposition 25 |
|
| כה כאשר היו בעגולות שוות שתי זויות שוות הנה הן על שתי קשתות שוות על המרכז היו או על הקו המקיף | |
| דמיונו כי שתי עגולות אב"ג דה"ז שוות ומרכזי שתיהן ח"ט ובשתיהן שתי זויות שוות על המרכז והם בח"ג הט"ז | |
| Supposition: | הנה אומר כי קשת ב"ג כמו קשת ה"ז |
| המופת אנחנו נוציא משתי נקודות א"ד משתי קשתות בא"ג הד"ז קוי א"ב ב"ג ד"ה ד"ז | |
| הנה קו ח"ב כמו ט"ה | |
| וח"ג כמו ט"ז מפני כי שניהם בעגולות שוות | |
| הנה כל אחת מב"ח ג"ח כמו כל אחת מן ה"ט ט"ז | |
| וזוית בח"ג כמו זוית הט"ז | |
| אם כן תושבת ב"ג כמו תושבת ה"ז | |
| וזוית בח"ג כפל זוית בא"ג | |
| וזוית חט"ז כפל הד"ז | |
| וכבר היתה זוית בח"ג כמו זוית הט"ז | |
| אם כן זוית בא"ג כמו זוית הד"ז | |
| אם כן חתיכת בח"ג דומה לחתיכת הד"ז | |
| ושתי החתיכות שוות | |
| אם כן קשת ב"ג הנשארת כמו קשת ה"ז הנשארת | |
| הנה כבר התבאר כי השתי זויות השוות אשר בעגולת שוות תהיינה על שתי קשתות שוות אם היו על המרכז או היו על הקו המקיף | |
| ונ"ב | |
Proposition 26 |
|
| כו כאשר תהיינה בעגולות שוות שתי זויות על שתי קשתות שוות הנה הזויות שוות היו על המרכז או על הקו המקיף | |
| המשל בו כי שתי עגולות אב"ג דה"ז שוות ושתי קשתות ב"ג ה"ז שוות עליהן שתי זויות בט"ג הח"ז והם על המרכז או לא אבל היו על הקו המקיף | |
| Supposition: | הנה אומר כי שתיהם שוות אי אפשר כי אם זה |
| שאם היה אפשר נאמר שתהיה זוית בט"ג קטנה מזוית הח"ז | |
| ונעמיד על נקודת ח' מקו ה"ח זוית הח"ז כמו בט"ג | |
| הנה קשת ב"ג כמו קשת ה"כ | |
| אבל קשת ה"ז היה כמו קשת ב"ג | |
| הנה קשת ה"ז כמו ה"כ | |
| The greater is as the smaller = error. | הגדולה כמו הקטנה זה שקר |
| הנה אם כן אין בט"ג בלתי שוה לזוית הח"ז | |
| אם כן היא שוה לה | |
| ושתי הזויות אשר תהיינה על קשת בא"ג הד"ז חציי זויות בט"ג הח"ז השוות | |
| אם כן הן שוות | |
| וזה מה שרצינו לבאר | |
Proposition 27 |
|
| כז המיתרים השוים אשר בעגולות השוות יבדילו קשתות שוות הגדולה לגדולה והקטנה לקטנה | |
| המשל בו כי שתי עגולות אב"ג דה"ז שוות ושני מיתרי ב"ג ה"ז הם שוים | |
| Supposition: | הנה אומר כי שניהם יבדילו קשתות שוות |
| אולם קשת ב"ג כמו קשת ה"ז | |
| ואולם קשת בא"ג כמו קשת הד"ז | |
| ויהיו שני המרכזים ט"ח | |
| ונוציא ט"ב ט"ג וה"ח וח"ז | |
| הנה קו ט"ב כמו קו ה"ח | |
| וקו ט"ג כמו קו ח"ז | |
| הנה כל שני קוי ב"ט ט"ג כמו שני קוי ה"ח ח"ז | |
| ותושבת ב"ג כמו תושבת ה"ז | |
| אם כן זוית בט"ג כמו זוית הח"ז | |
| וקשת ב"ג כמו קשת ה"ז | |
| והעגולה כמו העגולה | |
| אם כן בא"ג כמו קשת הד"ג | |
| וזה שרצינו לבארו | |
Proposition 28 |
|
| כח השתי קשתות מן העגולות השוות יבדילום מיתרים שוים | |
| ויהיו שתי עגולות אב"ג דה"ז שוות | |
| ומשתיהן שתי קשתות ב"ג ה"ז שוות | |
| Supposition: | הנה אומר כי השני מיתרים והם ב"ג ה"ז שוים |
| המופת כי נשים המרכזים ט"ח ונוציא ט"ב ט"ג ה"ח ח"ז | |
| הנה קו ט"ב כמו קו ה"ח | |
| וקו ט"ג כמו קו ח"ז | |
| הנה שני קוי ב"ט ט"ג כמו שני קוי ה"ח ח"ז | |
| והזויות אשר יפלו בחתיכות השוות שוות | |
| אם כן זוית בט"ג כמו זוית הח"ז | |
| אם כן תושבת ב"ג כמו תושבת ה"ז | |
| הנה כבר התבאר כי שני מיתרי ב"ג ה"ז שוים | |
| וזה מה שרצינו לבארו | |
Proposition 29 |
|
| כט נרצה לחתוך קשת ידועה בשני חצאים | |
| הנה נשים הקשת הידועה בא"ג | |
| ונרצה לחתוך אותה בשני חציים | |
| הנה נגיע ב"ג ונחלקהו בשני חציים על ד' | |
| ונוציא מן ד' אל קשת בא"ג קו א"ד על זוית נצבת על קו ב"ג | |
| ונוציא שני קוי א"ב א"ג | |
| הנה קו ב"ד כמו קו ג"ד | |
| ונשים א"ד משותף | |
| הנה שני קוי ב"ד ד"א כמו שני קוי ג"ד ד"א | |
| וזוית בד"א כמו זוית גד"א | |
| אם כן תושבת א"ב אשר הוא מיתר קשת א"ב כמו תושבת א"ג אשר הוא מיתר קשת א"ג | |
| הנה קשת א"ב אם כן כמו קשת א"ג | |
| הנה כבר חתכנו קשת בא"ג בשני חציים על נקודת א' | |
| וזה מש"ל | |
Proposition 30 |
|
| ל כאשר היתה בחתיכת העגולה זוית ישרת שני הקוים מורכבת על הקשת והיתה החתיכה חצי עגולה הנה הזוית נצבת ואם היתה יותר גדולה מחצי העגולה הנה היא חדה ואם היתה יותר קטנה מחצי עגולה הנה היא נרחבת וזוית החתיכה אשר היא יותר גדולה מחצי עגולה הנה היא נרחבת | |
| דמיון זה כי עגולת אב"ג קוטרה א"ב | |
| ונרשו' על הקשת נקדת ד' איך שתפול ונוציא ממנה מיתרי א"ד ד"ב | |
| הנה נאמר כי זוית אד"ב אשר בחצי העגולה נצבת וכאשר היתה הזוית ביותר גדולה מחצי העגולה הנה היא חדה וכאשר היתה ביותר קטנה מחצי העגולה הנה היא נרחבת | |
| המופת אנחנו נרשום על קשת א"ד נקדת ז' איך שתפול | |
| ונשים המרכז ה' | |
| ונוציא קוים א"ז ד"ז ד"ה | |
| הנה קו ה"ד כמו קו ה"ב מפני כי המרכז נקודת ה' | |
| אם כן זוית הב"ד כמו זוית הד"ב | |
| הנה שתיהן כפל זוית הד"ב | |
| אבל זוית אה"ד החיצונה מן המשולש כמו שתי זויות הד"ב הב"ד הפנימיות יחד | |
| הנה היא כפל זוית הד"ב | |
| ולכן תהיה זוית דה"ב כפל זוית הד"א | |
| ושתי זויות דה"א דה"ב כמו שתי זויות נצבות | |
| אם כן זוית אד"ב אשר בחצי עגולת אד"ב נצבת | |
| וזוית דב"א יותר קטנה מנצבת והיא בקשת יותר גדולה מחצי עגולה והיא קשת ד"ב ג"א | |
| וכל תמונה בעלת ארבע צלעות תפול בעגולה הנה כל שתי זויות מקבילות מזויותיה שוות לשתי נצבות | |
| וזוית דב"א יותר קטנה מנצבת | |
| ונשאר זוית דז"א יותר גדולה מנצבת והיא בקשת אז"ד אשר היא יותר קטנה מחצי העגולה | |
| Supposition: | ואומר כי הזוית אשר תקיף בה קשת ב"ד ומיתר א"ד נרחבת והיא זוית חתיכת א"ג ב"ד אשר היא יותר גדולה מחצי העגולה ושהזוית אשר יקיפו בה קשת אז"ד ומיתר א"ד חדה והיא זוית חתיכת א"ד והיא יותר קטנה מחצי העגולה |
| המופת אנו נוציא מיתר ב"ד אל ח' | |
| הנה מפני כי זוית אד"ב נצבת היתה הזוית אשר יקיפו בה מיתר א"ד וקשת ד"ב נרחבת | |
| ומפני כי שתי זויות אד"ב אד"ח כמו שתי נצבות וזוית אד"ב נצבת תשאר זוית אד"ח נצבת | |
| והיתה הזוית אשר יקיפו בה קשת אז"ד ומיתר א"ד יותר קטנה מזוית אד"ח | |
| ונשלם ביאורו | |
| אמר תבאת מצאנו בקצת הנוסחאות מהיונים לתמונה הזאת מופת אחר על היות זוית אד"ב נצבת | |
| והוא כי קו א"ה כמו ה"ד אם כן זוית הא"ד כמו זוית הד"א | |
| וקו ה"ד שוה לקו ב"ה אם כן זוית הב"ד כמו זוית הד"ב | |
| הנה כל זוית אד"ב שוה לשתי זויות בא"ד אב"ד | |
| וזוית אד"ח גם כן שוה לשתי זויות בא"ד אב"ד | |
| הנה זוית אד"ב שוה לזוית אד"ח הנה היא אם כן נצבת | |
| וזה מש"ל | |
Proposition 31 |
|
| לא כל קו ימשש העגולה ויצא מן המקום אשר ימששה קו ישר יחתוך העגולה ולא יעבור במרכז הנה השתי זויות אשר משני צדדיו כמו השתי זויות אשר תפולנה בשתי חתיכות העגולה המומרות להם | |
| המשל בו כי קו ד"ה ימשש עגולת אב"ג על ב' | |
| ויצא מב' קו ב"ז וחתך העגולה על זולת המרכז | |
| Supposition: | הנה אומר כי שתי זויות זב"ד זב"ה כמו השתי זויות אשר יפלו בשתי חתיכות זט"ב זא"ב |
| המופת אנחנו נרשום על קשת ז"ב נקודת ט' איך שתפול | |
| ויהיה המרכז ח' | |
| ונוציא ב"ח ויעבור אל א' | |
| ונוציא קוים ב"ט ט"ז א"ז | |
| הנה קו דב"ה ימשש עגולת אב"ג | |
| וכבר הוצא מן המרכז קו א"ב הנה הוא עמוד על קו דה"ב | |
| אם כן זוית אב"ה נצבת | |
| וזוית אז"ב נצבת כי היא בחצי העגולה | |
| ונשים זוית זב"א משותפת | |
| הנה כל זוית זב"ה כמו שתי זויות אז"ב זב"א | |
| ושתי זויות דב"ז זב"ה כמו שתי נצבות | |
| אבל שלש זויות בא"ז אז"ב אב"ז מן המשולש כמו שתי נצבות | |
| אם כן הם יחד כמו שתי זויות דב"ז זב"ה | |
| וזוית זב"ה כמו שתי זויות אז"ב זב"א | |
| אם כן זוית זב"ד הנשארת כמו זוית זא"ב והיא בחתיכת זא"ב | |
| וכל תמונה בעלת ארבע צלעות בעגולה הנה כל שתי זויות מקבילות מזויותיה כמו שתי נצבות | |
| אם כן שתי זויות זט"ב זא"ב כמו שתי נצבות ושתיהן כמו שתי זויות זב"ה זב"ד | |
| וזוית זב"ד כמו זוית זא"ב | |
| אם כן זוית זט"ב הנשארת כמו זוית זב"ה הנשארת והיא בחתיכת זט"ב | |
| וזה מש"ל | |
Proposition 32 |
|
| לב נרצה לעשות על קו ידוע חתיכת עגולה תקביל זוית כמו זוית מונחת ישרת שני הקוים | |
| הנה נשים קו א"ב הידוע | |
| והזוית הידועה גד"ה | |
| ונרצה לעשות על קו א"ב חתיכת עגולה תקביל זוית כמו זוית גד"ה | |
| הנה נעמיד על קו א"ב על נקודת א' ממנו זוית בא"ז כמו זוית גד"ה | |
| ונוציא מנקודת א' ממנו קו א"ח על זוית נצבת | |
| ונעמיד על קו א"ב על נקודת ב' ממנו זוית אב"ח כמו זוית בא"ח | |
| ויפגשו שתי צלעות א"ח א"ב על נקודת ח' מפני כי שתיהן יצאו מפחות משתי זויות נצבות | |
| אם כן צלע א"ח כמו ח"ב | |
| ונשים המרכז ח' | |
| ונקיף עגולה במרחק א"ח ב"ח | |
| הנה בעבור כי זוית זא"ח נצבת הנה קו א"ז ימשש עגולת א"ב | |
| וכבר יצא ממקום משושם קו א"ב וחתך העגולה על זולת המרכז הנה בשתי צדדיו שתי זויות כמו השתי זויות אשר יפלו בשתי חתיכות העגולה המומרות לשתיהן | |
| אם כן זא"ב כמו אשר יפול בחתיכת א"ב | |
| אבל זוית זא"ב כמו זוית גד"ה | |
| אם כן זוית גד"ה כמו אשר תפול בחתיכת א"ב | |
| ונשלם ביאורו | |
Proposition 33 |
|
| לג נרצה שנבדיל מעגולה ידועה חתיכה תקביל זוית ידועה ישרת שני הקוים | |
| ונשים העגולה הידועה עגולת אב"ג | |
| והזוית הידועה ישרת שני הקוים זוית דה"ז | |
| ונרצה שנבדיל מעגולת אב"ג חתיכה תקביל זוית כמו זוית דה"ז | |
| ונעביר על נקודת ג' קו חג"ט ממשש לעגולת אב"ג | |
| ונעמיד על קו ג"ח על נקודת ג' ממנו זוית בג"ח כמו זוית דה"ז | |
| הנה קו חג"ט ימשש עגולת אב"ג | |
| וכבר יצא מהמקום אשר ימששה קו ב"ג יחתוך העגולה על זולת המרכז | |
| הנה משתי צדדיו שתי זויות אשר יפלו בשתי חתיכות העגולה המומרות לשתיהן | |
| אם כן זוית בג"ח כמו אשר תפול בחתיכת גא"ב | |
|
|
אבל זוית בג"ח כמו זוית דה"ז |
| אם כן זוית דה"ז כמו אשר תפול בחתיכת גא"ב | |
| הנה כבר הבדלנו מעגולת אב"ג הידועה חתיכת גא"ב תקביל זוית כמו זוית דה"ז | |
| וזה מש"ל | |
Proposition 34 |
|
| לד כל שני מיתרים יתחתכו בעגולה הנה השטח הנצב הזויות אשר יקיפו בה שני חלקי אחד משניהם המיתרים כמו השטח הנצב הזויות אשר יקיפו בו שני חלקי המיתר האחר | |
| המשל שני חלקי מיתרי א"ג ב"ד יתחתכו בעגולת א"ב ג"ד על נקודת ה' | |
Supposition: 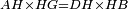
|
הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א"ה ה"ג שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי ד"ה ה"ב |
| המופת שנשים מרכז עגולת א"ב ג"ד נקודת ז' | |
| ונגיע קו ז"ה | |
| ונוציא מן נקודת ז' אל שני קוי א"ג ב"ד שני עמודי ז"ח ז"ט | |
| ונגיע שני קוי ז"ג ז"ב | |
| הנה מפני שכבר יצא ממרכז עגולת א"ב ג"ד קו ישר והוא קו ז"ח וחתך א"ג על זויות נצבות הנה כבר חלקו בשני חצאים על נקודת ח' ובשני חלקים בלתי שוים על נקודת ה' | |
|
|
יהיה השטח הנצב הזויות אשר יקיפו בו א"ה ה"ג עם המרובע המתהוה מן ה"ח שוה למרובע ההוה מן ג"ח |
| ונשים המרובע ההוה מן ז"ח משותף | |
|
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ה ה"ג עם שני המרובעים ההוים משני קוי ה"ח ח"ז שוה לשני המרובעים ההוים משני קוי ז"ח ח"ג |
|
|
אבל שני המרובעים ההוים משני קוי ז"ח ה"ח שוים למרובע ההוה מן ז"ה |
|
|
מפני כי זוית הח"ז נצבת |
|
|
אם כן שני המרובעים ההוים משני קוי ז"ח ח"ג שוים למרובע ההוה מן ז"ג |
|
|
אם כן השטח הנצב הזויות אשר יקיפו בו שני קוי א"ה ה"ג עם המרובע ההוה מן ז"ה שוה למרובע ההוה מן ז"ג |
|
|
וכן גם כן התבאר כי השטח הנצב הזויו' אשר יקיפו בו שני קוי ד"ה ה"ב עם המרובע ההוה מן ז"ה שוה למרובע ההוה מן ז"ב |
|
|
והמרובע ההוה מן ז"ב שוה למרובע ההוה מן ז"ג |
|
|
אם כן השטח הנצב הזויות אשר יקיפו בו שני קוי א"ה ה"ג עם המרובע ההוה מן ז"ה שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי ד"ה ה"ב עם המרובע ההוה מן ז"ה |
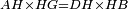
|
וכאשר חסרנו המשותף והוא המרובע ההוה מן ז"ה נשאר השטח הנצב הזויות אשר יקיפו בו שני קוי ד"ה ה"ב |
| וזה מה שרצינו ביאורו | |
Proposition 35 |
|
| לה כאשר רשמת נקודה חוץ מעגולה והוצאו ממנה שני קוים ישרים אל העגולה אחד משתיהם יחתכה והאחר ימששה הנה השטח הנצב הזויות אשר יקיפו בו הקו כלו אשר יחתוך העגולה עם הקו אשר יפול ממנו חוץ לעגולה שוה למרובע ההוה מן הקו הממשש | |
Example:  . .
|
ותהיה העגולה אב"ג |
| והנקודה אשר נרשמה חוץ ממנה נקודת ד' | |
| ונוציא ממנה אל עגולת אב"ג שני קוי ד"א ד"ג הישרים | |
| ויהיה קו ד"ג מהם חותך לעגולה וקו א"ד ממשש אותה | |
Supposition: 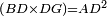
|
הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ד ד"ג שוה למרובע ההוה מן א"ד |
| המופת שנשים המרכז ה' | |
| ונוציא מנקודת ה' אל קו ב"ג עמוד ה"ז | |
| ונגיע קוי א"ה ג"ה ה"ד | |
| הנה מפני כי בעגולת אב"ג קו יצא מן המרכז והוא ה"ז וכבר חתך את ב"ג על זוית נצבת הנה הוא חתכו בשני חצאים | |
|
|
הנה קו ב"ז שוה לקו ז"ג |
| ומפני כי קו ב"ג כבר נחלק בשני חלקים על נקודת ז' ונוסף בו קו ב"ד על יושר | |
|
|
יהיה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ד ד"ג עם המרובע ההוה מן ז"ג כמו המרובע ההוה מן ד"ז בעצמו |
| ונשים המרובע ההוה מן ה"ז משותף | |
|
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ד ד"ג עם שני המרובעים ההוים מן ה"ז ז"ג שוים לשני המרובעים ההוים מן שני קוי ז"ה ז"ד |
|
|
ושני המרובעים ההוים משני קוי ז"ה ז"ג שוים למרובע ההוה מן ה"ג |
|
|
מפני שזוית הז"ג נצבת |
|
|
ושני המרובעים ההוים משני קוי ה"ז ז"ד שוים למרובע ההוה מן ה"ד |
|
|
מפני כי זוית הז"ד נצבת |
|
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ד ד"ג עם המרובע ההוה מן ה"ג שוה למרובע ההוה מן ה"ד |
|
|
אבל המרובע ההוה מן ה"ד שוה לשני המרובעים ההוים משני קוי ה"א א"ד |
|
|
מפני כי זוית הא"ד נצבת |
|
|
הנה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ד ד"ג עם המרובע ההוה מן ה"ג שוה לשני המרובעים ההוים מן א"ה א"ד |
|
|
והמרובע ההוה מן ה"ג שוה למרובע ההוה מן א"ה |
| וזה שהם יצאו מן מרכז העגולה אל הקו המקיף בה | |
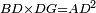
|
הנה נשאר השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ד ד"ג שוה למרובע ההוה מן א"ד |
| ונש"ל ב | |
Proposition 36 |
|
| When there is a circle and a point is placed outside it and two straight lines are drawn from it to the circle, so that one of them cuts it, and the other falls on it, if the rectangle contained by the whole of the straight line which cuts it and its segment that falls outside the circle equals the square on the straight line which falls on the circle, then the straight line which falls on it touches the circle. | לו כאשר היתה עגולה והושמה חוץ ממנה נקודה והוצאו ממנה שני קוים ישרים אל העגולה אחד משניהם יחתכה והאחר יכלה אליה והיה השטח הנצב הזויות אשר יקיף בו הקו אשר יחתכה כלו והחתיכה אשר יפול ממנו חוץ מן העגולה שוה למרובע ההוה מן הקו האחר אשר יכלה אל העגולה הנה הקו אשר יכלה אליה ימשש לעגלה |
| When two lines are drawn from the point, so that both touch the circle, they are equal. | וכאשר יצאו שני קוים מהנקודה האחת ושניהם ימששו העגלה הנה הם שוים |
Example: 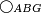 . .
|
ותהיה העגולה אב"ג |
| Point D is drawn outside of it. | ונרשמה חוץ ממנה נקודת ד' |
AD and DB are drawn from it to the circumference of 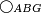 : DB cuts it and DA falls on it. : DB cuts it and DA falls on it.
|
ויצאו ממנה אל מקיף עגלת אב"ג שני קוי א"ד ד"ב הישרים ויהיה ד"ב חותך אותה וד"א כלה אליה |
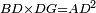
|
ויהיה השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ד ד"ג שוה למרובע ההוה מן א"ד |
Supposition: AD touches 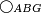
|
הנה אומר כי קו א"ד ממשש לעגלת אב"ג |
|
ונוציא מנקודת ד' קו ממשש לעגלת אב"ג והוא ד"ה מי"ו מזה |
|
ונשים מרכז עגלת אב"ג נקודת ז' |
|
ונגיע קוי א"ז ז"ד ז"ה |
|
הנה מפני כי השטח הנצב הזויות אשר יקיפו בו שני קוי ב"ד ד"ג שוה למרובע ההוה מן ד"ה מל"ה מזה |
|
|
וגם כן יהיה המרובע ההוה מן א"ד שוה למרובע ההוה מן קו ד"ה |
|
|
אם כן יהיה המרובע ההוה מן א"ד שוה למרובע ההוה מן ד"ה |
|
|
אם כן קו א"ד שוה לקו ד"ה |
| ומפני כי קו א"ז שוה לקו ז"ה וזה כי הם יצאו מן המרכז אל המקיף הקו וקו ד"ז משותף יהיו כל שני קוי א"ז ז"ד שוים לכל שני קוי ה"ז ז"ד כל אחד לנכחי אליו | |
|
|
ותושבת א"ד שוה לתושבת ד"ה |
|
תהיה זוית אז"ד שוה לזוית הז"ד מח' מא' |
|
|
ומשולש אז"ד שוה למשולש זד"ה |
| ושאר הזויות שוות לשאר הזויות | |
| אם כן שתי זויות זא"ד אד"ז שוות לשתי זויות זה"ב הד"ז כל אחד לנכחי לו אשר הם מיתריהם הצלעות השוות | |
|
|
אם כן זוית זא"ד שוה לזוית זה"ד |
|
וזוית זה"ד נצבת מי"ז מזה |
|
|
הנה זוית זא"ד נצבת |
| וקו א"ז כאשר הוצא הנה הוא קטר | |
| וכבר הוצא מקצה הקטר קו א"ד על זוית נצבת מי"ז מזה | |
AD touches 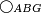
|
הנה קו א"ד ממשש לעגלת אב"ג |
| Q.E.D. | וזה מש"ל |
| נשלם המאמר השלישי מספר אקלידס החכם בשרשים ומספר תמונותיו ששה ושלשים |
Book Four |
המאמר הרביעי |
Definitions |
|
| The figure is said to be inscribed in a figure when each of its angles touches each of the respective sides of the figure in which it is inscribed. | יאמר כי התמונה מורשמת בתמונה כאשר תהיה כל אחת מזויותיה ממששת לכל אחת מצלעות התמונה אשר נרשמת בה |
| The figure is said to be circumscribed about a figure when each of its sides touches each of the respective angles of the figure about which it is circumscribed. | ויאמר כי התמונה נרשמת סביב התמונה כשתהיה כל אחת מצלעותיה ממששת לכל אחת מזויות התמונה אשר היא נרשמת סביבה |
Proposition 1 |
|
| We wish to draw a chord in a given circle equal to a given line, which is not greater than the diameter of the circle. | א נרצה שנקוה בעגלה ידועה מיתר שוה לקו ידוע אינו יותר גדול מקוטר העגולה |
Defining:
|
הנה נשים העגלה הידועה עגלת אב"ג |
|
והקו הישר הידוע אשר לא יהיה יותר גדול מקוטר העגלה קו ד"ה |
We wish to draw a chord in 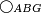 , which is equal to DH. , which is equal to DH.
|
ונרצה שנקוה בעגלת אב"ג מיתר שוה לקו ד"ה |
|
הנה נוציא קוטר העגולה והוא ב"ג מא' מג' |
|
ואם היה ד"ה כמו ב"ג כבר היה מה שרצינו |
|
ואם היה יותר קצר יהיה ז"ג כמו ד"ה מג' מא' |
|
ונשים ג' מרכז ובמרחק ג"ז עגולת א"ח |
|
ונוציא קו ג"א |
|
|
הנה ג"ז כמו ד"ה אם כן א"ג כמו ד"ה |
We have drew in 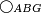 a chord equal to DH, which is not greater than the diameter. a chord equal to DH, which is not greater than the diameter.
|
הנה כבר קוינו בעגלת אב"ג מיתר כמו קו ד"ה שאינו יותר גדול מן הקוטר |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 2 |
|
| We wish to inscribe in a given circle a triangle equiangular with a given triangle. | ב נרצה לעשות בעגולה ידועה משולש שוה זויותיו לזויות משולש ידוע |
Defining:
|
הנה נשים העגולה הידועה עגלת אב"ג |
|
והמשולש הידוע משולש דה"ז |
We wish to inscribe in 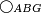 a triangle equiangular with a triangle equiangular with 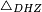 . .
|
ונרצה שנעשה בעגולת אב"ג משולש שוות זויותיו לזוית משולש דה"ז |
|
הנה נעביר על נקודת א' קו א"ח ממשש לעגולה מי"ו מג' |
|
ונעמיד על נקודת א' מקו א"ח זוית בא"ח כמו זוית דה"ז |
|
ונעמיד גם כן על קו א"ט על נקודת א' ממנו כמו זוית דז"ה והיא זוית טא"ג מכ"ג מא' |
|
ונוציא ב"ג |
|
הנה קו א"ח ממשש לעגלת אב"ג |
|
וכבר יצאו ממקום משושו א"ב א"ג יחתכו העגולה |
|
הנה משני צדדי כל אחת מהן שתי זויות כמו אשר יפלו בשתי חתיכות העגולה המומרות מל"א מג' |
|
|
אם כן זוית בא"ח כמו זוית בג"א |
|
|
וזוית גא"ט כמו זוית אב"ג |
|
|
וזוית גא"ט כמו זוית דז"ה |
|
|
וזוית בא"ח כמו זוית דה"ז |
|
אם כן שתי זויות דה"ז דז"ה כמו שתי זויות אב"ג אג"ב |
|
ונשארה זוית הד"ז כמו זוית בא"ג מל"ב מא' |
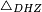 is equiangular with is equiangular with 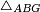 in in 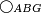
|
אם כן זויות דה"ז שוות למשולש אב"ג העשוי בעגלת אב"ג |
| The explanation is complete. | ונשלם באורו |
Proposition 3 |
|
| We wish to circumscribe about a given circle a triangle equiangular with a given triangle. | ג נרצה לעשות על עגולה ידועה משולש יקיף בה תהיינה זויותיו שוות לזויות משולש ידוע |
Defining:
|
הנה נשים העגולה עגולת אב"ג |
|
והמשולש הידוע משולש דה"ז |
We wish to circumscribe about 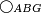 a triangle equiangular with a triangle equiangular with 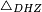 . .
|
ונרצה לעשות על עגלת אב"ג משולש יקיף בה שוות זויותיו לזויות משולש דה"ז |
|
הנה נוציא ה"ז בכל אחד משני הצדדין אל ט"ב |
|
ויהיה המרכז ח' |
|
ונוציא ממנו קו ח"ב אל המקיף איך שיפול |
|
ונעמיד על ח' מקו ב"ח זוית כמו זוית דה"ט והיא זוית בח"ג וכמו זוית דז"ב והיא זוית בח"א מכ"ג מא' |
|
ונעביר על נקודות בג"א קוים ל"מ מ"נ נ"ל ממששים לעגלת אב"ג מי"ו מג' |
|
הנה קו ל"מ ממשש לעגלת אב"ג |
|
וכבר הוצא ממקום המשוש קו ח"ב אל המרכז והוא עמוד על קו לב"מ |
|
|
אם כן זוית לב"ח נצבת מי"ז מג' |
|
|
וזוית מב"ח גם כן נצבת |
|
וכן יהיו שתי זויות אשר אצל ג' נצבות |
|
וכן יהיו זויות אשר אצל א' כל אחת מהן נצבת |
| The four angles of every quadrilateral figure are equal to four right angles. | וכל תמונה בעלת ארבע צלעות הנה זויותיה הארבעה שוות לארבע זויות נצבות |
|
אם כן זויות שטח א"ח ב"ל כמו ארבע זויות נצבות |
|
אבל אשר אצל א"ב נצבות |
|
הנה נשארו אשר אצל ח"ל המתנגדות כמו שתי נצבות |
|
|
אבל שתי זויות דז"ב דז"ה כמו שתי נצבות |
|
אם כן שתי זויות ח"ל כמו שתי זויות דז"ב דז"ה |
|
|
וזוית דז"ב כמו זוית ח' |
|
|
ונשארה זוית דז"ה כמו זוית ל' |
|
|
וכן גם כן יהיו שתי זויות דה"ט דה"ז כמו שתי זויות ח"מ |
|
|
וזוית דה"ט כמו זוית ח' |
|
|
ונשארה זוית מ' כמו זוית דה"ז |
|
וכל משולש הנה זויותיו השלש כמו שתי נצבות מל"ב מא' |
|
|
ושתי זויות דה"ז דז"ה כמו שתי זויות ל"מ |
|
|
ונשארה זוית ד' כמו זוית נ' |
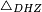 is equiangular with is equiangular with 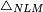 that is circumscribed about that is circumscribed about 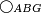
|
אם כן זויות משלש דה"ז שוות לזויות משולש נל"מ העשוי על עגלת אב"ג המקיף בה |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 4 |
|
| We wish to inscribe a circle in a given triangle. | ד נרצה שנעשה במשולש ידוע עגולה יקיף בה |
Defining:
|
הנה נשים המשולש הידוע משולש אב"ג |
| We wish to inscribe a circle in it. | ונרצה שנעשה בו עגולה יקיף בה |
|
הנה נחלק זוית אב"ג בשני חצאים בקו ב"ד וזוית בג"א בשני חצאים בקו ג"ה מט' מא' |
|
ונדביק שני הקוים האלו על ז' |
|
ונוציא מן ז' אל קוי א"ב א"ג ב"ג עמודים ז"ה ז"ח ז"ד מי"ב מא' |
|
ונשים נקודת ז' מרכז ונקיף במרחק ז"ד עגולה במשלש אב"ג |
| Supposition: [the circle] touches the sides [of the triangle] at D, C and H. | הנה אומר כי הוא ימשש צלעותיו על נקודות דח"ה |
| Proof:
|
מופתו כי זוית דג"ז כמו זוית דג"ח |
|
|
וזוית גד"ז נצבת והיא כמו זוית גח"ז |
|
אם כן שתי זויות דג"ז גד"ז ממשולש דג"ז כמו שתי זויות זג"ח גח"ז מן משולש גח"ז |
|
וצלע ג"ז משותף לשתיהם יהיה מיתר שתי זויות שוות מזויות שניהם |
|
אם כן שתי צלעות המשולש הנשארות כמו שתי צלעות המשולש האחר הנשארות כל אחת לנכחי אליה מכ"ו מא' |
|
|
הנה צלע ד"ז כמו צלע ז"ח |
|
|
וכן גם כן יתבאר כי ז"ח כמו ז"ה |
|
אם כן קוי ז"ח ז"ד ז"ה השלשה שוים |
|
והזויות אשר אצל נקודת דח"ה נצבות |
|
אם כן העגולה אשר תסבוב על מרכז ז' ובמרחק ז"ד תלך בשתי נקודות ה"ח מט' מג' |
|
ותשמש צלע המשלש מט"ו מג' |
We have constructed 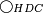 inscribed in the given inscribed in the given 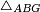 . .
|
הנה כבר עשינו במשולש אב"ג הידוע עגלת הד"ח יקיף בה |
| The explanation is complete. | ונשלם ביאורו |
Proposition 5 |
|
| We wish to circumscribe a circle about a given triangle. | ה נרצה לעשות אל משולש ידוע עגולה תקיף בו |
Defining:
|
הנה יהיה המשולש הידוע משולש אב"ג |
| We wish to circumscribe a circle about it. | ונרצה לעשות עליו עגלה תקיף בו |
|
הנה נחלק כל אחד משתי הצלעות א"ב א"ג בשני חצאים על שתי נקודות ד"ה מי' מא' |
|
ונעמיד על שני קוי א"ב א"ג שני קוים על זויות נצבות והם ד"ז ה"ז מי"א מא' |
|
ונדביק קוי ז"א ז"ג ז"ב |
|
|
הנה מפני כי א"ה שוה לקו ה"ב |
|
וקו ז"ה משותף |
|
יהיו כל שני קוי א"ה ה"ז כמו כל שני קוי ב"ה ה"ז כל אחד אצל הנכחי לו |
|
|
וזוית אה"ז הנצבת שוה לזוית בה"ז הנצבת |
|
אם כן תושבת א"ז שוה לתושבת ב"ז מד' מא' |
|
|
וכן גם כן התבאר כי קו א"ז שוה לקו ג"ז |
|
|
אם כן קוי א"ז ז"ג ז"ב שוים |
|
הנה כאשר שמנו נקודת ז' מרכז וסבבנו במרחק א"ז עגולה הלכה בנקודת אב"ג הנה נקוה העגולה הזאת ויהיה עליה אב"ג מט' מג' |
We have circumscribed a circle about 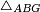 . .
|
הנה כבר עשינו אל משולש אב"ג עגולה תקיף בו |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 6 |
|
| We wish to inscribe a square in a given circle. | ו נרצה לעשות בעגולה ידועה מרובע תקיף בו |
Defining:
|
הנה נשים העגלה הידועה עגולת אב"ג |
| We wish to inscribe a square in it. | ונרצה לעשות בה שטח מרובע תקיף בו |
|
הנה נוציא בה שני קטרים יתחתכו על זוית נצבת והם א"ג ב"ד מא' מג' |
|
ונוציא קוים א"ב א"ד ב"ג ג"ד |
|
|
הנה קו ב"ה כמו קו ה"ד |
|
וקו א"ה משותף |
|
הנה כל שני קוי ב"ה א"ה כמו כל שני קוי ד"ה א"ה |
|
|
וזוית בה"א כמו זוית דה"א |
|
אם כן תושבת א"ב כמו תושבת א"ד מד' מא' |
|
|
וכן גם כן התבאר כי ב"ג כמו ג"ד |
|
|
וכן ג"ד כמו א"ד |
|
אם כן מרובע א"ב ג"ד שוה הצלעות והזויות אשר בחציי העגלות נצבות מל' מג' |
|
הנה כל הזויות אשר אצל נקדות א"ב ג"ד כל אחת מהן נצבת |
We have inscribed a square in the given 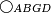 . .
|
הנה כבר התבאר שאנחנו כבר עשינו בעגולת א"ב ג"ד הידועה מרובע |
| Q.E.D. | וזה מש"ל |
Proposition 7 |
|
| We wish to circumscribe a square about a given circle. | ז נרצה לעשות על עגלה ידועה מרובע יקיף בה |
Defining:
|
הנה נשים העגולה הידועה עגלת אב"ג |
| We wish to circumscribe a square about it. | ונרצה לעשו' עליה מרובע יקיף בה |
|
ונוציא בה שני קטרים יתחתכו על זויות נצבות והם א"ג ב"ד מא' מג' |
|
ונוציא מנקודות א'ב'ג'ד' קוי ז"ח ז"ט ט"כ כ"ח ממששים לעגולה |
|
והוא שנוציאם על זויות נצבות על קצות הקטרים מט"ו מג' |
|
הנה ז"ח ימשש לעגולה |
|
וכבר הוצא ממקום אשר ימששה קו א"ה אל המרכז אם כן הוא עמוד על ז"ח מי"ז מג' |
|
|
ושתי זויות זא"ה הא"ח נצבות |
|
וכן תהיינה הזויות אשר אצל נקדות בג"ד נצבות |
|
|
אם כן שתי זויות בה"א זא"ה שתי נצבות |
|
אם כן שני קוי ה"ב ז"א נכחיים וכן יהיו שני קוי ז"ב א"ה נכחיים מכ"ח מא' |
|
הנה שטח ז"ב ה"א נכחי הצלעות הנה צלעותיו וזויותיו המתנגדות שוות מל"ד מא' |
|
|
אם כן צלע ז"א כמו צלע ב"ה |
|
|
וכן יהיה ב"ה כמו ט"ג |
|
|
וא"ח כמו ה"ד וכמו ג"כ |
|
|
הנה ב"ד כמו ז"ח וכמו ט"כ |
|
ולכן א"ג כמו ט"ז וכמו ח"כ מל' מא' |
|
הנה שטח ז"ט כ"ח שוה הצלעות |
|
|
וב"ה ינגד א"ז |
|
וכבר נפל עליהם קו ב"ז |
|
אם כן שתי זויות הב"ז אז"ב הפנימיות כמו שתי נצבות מל"ד מא' |
|
|
וזוית הב"ז נצבת |
|
הנה נשארה זוית אז"ב נצבת מכ"ט מא' |
|
וכן תהיה כל אחת מהזויות אשר אצל נקדות טכ"ח נצבות |
ZTKC is a square that is circumscribed about 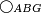 . .
|
אם כן שטח ז"ט כ"ח מרובע והוא עשוי על עגלת א"ב ג"ד |
| The explanation is complete. | ונשלם ביאורו |
Proposition 8 |
|
| We wish to inscribe a circle in a given square. | ח נרצה לעשות במרובע ידוע עגלה יקיף בה |
Defining:
|
הנה נשים המרובע א"ב ג"ד |
|
ונחלק כל אחד מקוי א"ד א"ב בשני חצאים על שתי נקודות ה"ז מי' מא' |
|
ונוציא משתי נקודות ה"ז שני קוי ה"ח ז"ט על זויות נצבות |
|
הנה כל אחד משטחי א"ח ה"ג א"ט ז"ג נכחי הצלעות מכ"ח מא' |
|
אם כן הזויות אשר אצל ח"ט נצבות כי הם יקבילו הזויות הנצבות אשר אצל נקדות בא"ד מן המרבע הידוע מל"ד מא' |
|
והזויות אשר אצל ה"ז נצבות |
|
|
ומפני כי א"ב כמו א"ד יהיה א"ז כמו א"ה |
|
מפני כי א"ז וא"ה חציי א"ב א"ד |
|
|
וקו א"ה כמו ב"ח כי הוא יקבילהו |
|
|
וז"כ כמו א"ה גם כן |
|
|
וז"א כמו כ"ה וד"ט |
|
|
וכן ה"ד כמו ב"ט |
|
וג"ח וז"ב כמו כ"ח וט"ג |
|
אם כן שטחי א"כ ח"ט ז"ח כ"ג הארבעה מרובעים שוים |
|
|
אם כן יהיו קוי כ"ז כ"ה כ"ט כ"ח הארבעה שוים |
|
וכבר התבאר כי הזויות המוצאות מקצוי אלו הקוים נצבות |
|
אם כן כאשר שמנו נקודת כ' מרכז וסבבנו במרחק כל אחד מקוי כ"ז כ"ה כ"ח כ"ט עגולה |
|
הלכה העגולה בנקדות ז"ה ט"ח ותמשש צלעות א"ב ג"ד מט"ו מג' |
|
מפני כי שני קוי ז"ט ה"ח שני קטרי העגולה והזויות אשר אצל קצויהם נצבות |
|
אם כן צלעות מרובע א"ב ג"ד כאשר קוינו העגלה הזאת תמששם |
| We have inscribed the circle in the given square, so that it touches sides AB, GD, BG and AD, since the angles at points H, Z, C and T are right. | אם כן הנה נקוה העגולה במרובע המונח ותהיה ממששת לצלעות א"ב ג"ד ב"ג א"ד מפני כי הזויות אשר אצל נקדות ה"ז ח"ט נצבות |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 9 |
|
| We wish to circumscribe a circle about a given square. | ט נרצה לעשות על מרובע ידוע עגלה מקיף בו |
Defining:
|
הנה נשים המרובע הידוע מרובע א"ב ג"ד |
| We wish to circumscribe [a circle] about it. | ונרצה לעשות עליו תקיף בו |
| הנה נוציא שני קוי א"ג ב"ד | |
| הנה א"ב כמו א"ד | |
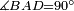
|
וזוית בא"ד נצבת |
| אם כן שתי זויות אד"ב אב"ד כל אחת חצי נצבת | |
| וכן יהיו שתי זויות דא"ג דג"א כל אחת חצי נצבת | |
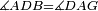
|
אם כן זוית אד"ב כמו זוית דא"ג |
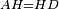
|
אם כן צלע א"ה כמו צלע ה"ד |
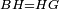
|
וכן יהיה ב"ה כמו ה"ג |
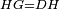
|
וה"ג כמו ד"ה |
| א"כ ה"ד ה"א ה"ב ה"ג שוים | |
| הנה על מרכז ה' ובמרחק ה"ג הקפנו עגולה מוקפת במרובע א"ב ג"ד | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 10 |
|
| We wish to construct an isosceles triangle, such that each of its angles at the base is double the remaining angle. | י נרצה לעשות משולש שוה השוקים תהיה כל אחת מזויותיו אשר על התושבת כפל הזוית הנשארת |
| הנה נקוה קו א"ב ונחלקהו על ג' חלוקה יהיה בה א"ב בב"ג כמו א"ג בעצמו | |
| ונשים נקודת א' מרכז ונקוה על מרכז א' ובמרחק א"ב עגלת הב"ד | |
| ונוציא מן ב' מיתר יהיה שוה אל א"ג והוא ב"ד | |
| ונגיע קוי א"ד ג"ד | |
| ונקוה על משולש אג"ד עגלה תקיף בו והיא עגלת אג"ד | |
| הנה יהיה א"ב בב"ג כמו א"ג בעצמו | |
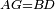
|
וג"א כמו ב"ד |
| אם כן יהיה א"ב בב"ג כמו ב"ד בעצמו | |
| ונקודת ב' חוץ מעגולת אג"ד | |
| וכבר יצאו ממנה אל עגלת אג"ד שני קוים אחד מהם יחתכה והוא א"ב והאחר יכלה אליה והוא ב"ד | |
| ואשר מן א"ב בב"ג כמו ב"ד בעצמו | |
| אם כן ב"ד ימשש עגולת אג"ד | |
| וכבר יצא מהמקום שימששה קו ד"ג ויחתוך העגולה על זולת המרכז | |
| והנה שתי הזויות אשר משני צדדיו כמו אשר יפלו בשתי חתיכות העגולה המומרות לשתיהן | |
| אם כן זוית גד"ב כמו זוית גא"ד וזוית גד"א משותפת אם כן כל זוית בד"א כמו שתי זויות גד"א דא"ג | |
| אבל שתי זויות גד"א דא"ג שתיהן יחד כמו זוית בג"ד החיצונה מן המשולש | |
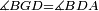
|
אם כן זוית בג"ד כמו זוית בד"א |
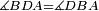
|
וזוית בד"א כמו זוית דב"א |
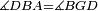
|
אם כן זוית דב"א כמו זוית בג"ד |
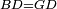
|
אם כן צלע ב"ד כמו צלע ג"ד |
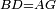
|
וב"ד כמו א"ג |
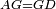
|
אם כן א"ג כמו ג"ד |
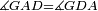
|
אם כן זוית גא"ד כמו זוית גד"א |
| ושתי זויות גא"ד גד"א יחד כפל זוית גא"ד | |
| וזוית בג"ד החיצונה מן משולש אג"ד כמו שתי זויות גא"ד גד"א יחד | |
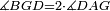
|
אם כן זוית בג"ד כפל זוית דא"ג |
| וזוית בג"ד כמו זוית אב"ד וכמו זוית אד"ב | |
| הנה כל אחת משתי זויות אב"ד אד"ב כפל זוית בא"ד | |
| הנה כבר עשינו משולש שוה השוקים עליו אב"ד תהיה כל אחת מזויותיו אשר על תושבת ב"ד כפל הזויות הנשארות | |
| Q.E.D. | וזה מש"ל |
Proposition 11 |
|
| We wish to inscribe an equilateral and equiangular pentagon in a given circle. | יא נרצה לעשות בעגולה ידועה מחמש שוה הצלעות והזויות אשר תקיף בו |
Defining:
|
הנה נשים העגולה הידועה עגולת אב"ג |
| We wish to inscribe an equilateral and equiangular pentagon in it. | ונרצה לעשות בה מחומש שוה הצלעות והזויות תקיף בו |
| הנה נעשה משולש שוה השוקים תהיה כל אחת מזויותיו אשר על התושבת כפל הזוית הנשארת והוא משולש דה"ז | |
| ונעשה בעגולת אב"ג משולש אב"ג שות זויותיו לזויות משולש דה"ז | |
| הנה כל אחת משתי זויות אב"ג אג"ב כפל זוית בא"ג | |
| ונחלק זוית אב"ג בשני חצאים בקו ב"ח וזוית אג"ב בקו ג"ט | |
| ונוציא קוי א"ט ט"ב ב"ג א"ח ח"ג | |
| הנה כל אחת משתי זויות אב"ג אג"ב כפל זוית בא"ג | |
| וכבר נחלקה כל אחת מהן בשני חצאים אם כן זוית בא"ג אג"ט טג"ב חב"ג חב"א החמש שוות | |
| אם כן קשתות א"ט ט"ב ב"ג ג"ח ח"א החמשה שוים | |
| אם כן מחומש אטבג"ח שוה הצלעות | |
| וקשת ב"ט כמו קשת ג"ח | |
| ונשים קשת טא"ח משותף אם כן כל קשת ב"ט א"ח כמו כל קשת ג"ח א"ט | |
| וזוית גב"ט על קשת ג"ח ט"א וזוית בג"ח על קשת ח"א ט"ב | |
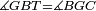
|
אם כן זוית גב"ט כמו זוית בג"ח |
| וכן יהיו זויות גח"א חא"ט אט"ב כמו כל אחת משתי זויות בג"ח וכן גב"ט | |
| אם כן מחומש טבגח"א שוה הצלעות והזויות הנה כבר נעשה בעגולת אב"ג | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 12 |
|
| We wish to circumscribe an equilateral and equiangular pentagon about a given circle. | יב נרצה לעשות על עגולה ידועה מחמש שוה הצלעות והזוית יקיף בה |
| ויהיו נקודות זויות המחמש נקודות א'ב'ג'ד'ה' | |
| ונעביר על אלו הנקודות קוים ממששים לעגלה עליהם כ"ל ל"ז ז"ח ח"ט ט"כ | |
| ונשים מרכז העגולה מ' | |
| ונגיע קוי מ"כ מ"ב מ"ל מ"ג מ"ז מ"ד מ"ח מ"ה מ"ט מ"א | |
| הנה מפני כי שני קוי ג"ז ז"ד כבר יצאו מנקודת ז' ומששו עגולת אבגד"ה יהיה קו ג"ז שוה לקו ז"ד וקו ז"מ משותף הנה כל שני קוי ג"ז ז"מ שוים לכל שני קוי ד"ז ז"מ כל אחת לדומה לו | |
| ותושבת ג"מ שוה לתושבת מ"ד | |
| מפני כי שתיהן יוצאות ממרכז העגולה אל הקו המקיף | |
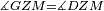
|
אם כן זוית גז"מ שוה לזוית דז"מ |
| הנה קו מ"ז כבר חלק בם זוית גז"ד בשני חצאים | |
| וכן גם כן התבאר כי זויות הח"ד אט"ה בל"א בל"ג כבר חלקום קוי מ"ח מ"ט מ"כ מ"ל בשני חצאי' | |
| וגם כן הנה ג"מ שוה לקו מ"ד וקו מ"ז משותף אם כן כל שני קוי ג"מ מ"ז שוים לכל שני קוי ז"מ מ"ד כל אחד לדומה לו | |
| ותושבת ג"ז שוה לתושבת ז"ד | |
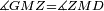
|
אם כן זוית גמ"ז שוה לזוית זמ"ד |
| אם כן זוית גמ"ד כבר נחלקה בשני חצאים בקו מ"ז | |
| וכן גם כן התבאר כי זויות דמ"ה המ"א אמ"כ כמ"ג כבר חלקום קוי מ"ט מ"ח מ"כ מ"ל בשני חצאים | |
| ומפני כי קשת ד"ה שוה לקשת ג"ד כי היה מיתר צלעות מחומש תהיה זוית גמ"ד שוה לזוית דמ"ה | |
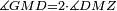
|
ואולם זוית גמ"ד הנה היא כפל זוית דמ"ז |
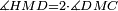
|
ואולם זוית המ"ד הנה היא כפל דמ"ח |
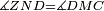
|
אם כן זוית זמ"ד שוה לזוית דמ"ח |
| וזוית מד"ח נצבת מפני כי קו ד"מ אשר יעבור במרכז כבר יצא ממקום המשוש ולכן תהיה מד"ז נצבת | |
| אם כן שתי זויות זמ"ד מד"ז ממשולש זמ"ד שוות לשתי זויות דמ"ח חד"מ ממשולש מד"ח כל אחת לדומה לה וקו מ"ד משותף בין שתיהם אם כן הצלעות הנשארות שוות לצלעות הנשארות כל אחת לדומה לה | |
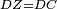
|
אם כן קו ד"ז שוה לד"ח |
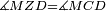
|
וזוית מז"ד שוה לזוית מח"ד הנשארת |
| וכן התבאר כי קו ל"ג שוה לקו ג"ז | |
| ומפני כי קו ג"ז שוה לקו ג"ל וכפל ג"ז הוא ז"ל וכפל ז"ד הוא ז"ח יהיה ז"ח שוה לקו ז"ל | |
| וכן גם כן התבאר כי קו ז"ח שוה לקו ח"ט | |
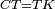
|
ושקו ח"ט שוה לקו ט"כ |
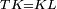
|
ושקו ט"כ שוה לקו כ"ל |
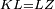
|
ושקו כ"ל שוה לקו ל"ז |
| אם כן קוי כ"ל ל"ז ז"ח ח"ט ט"כ שוים | |
| ומחומש זחטכ"ל שוה הצלעות | |
| Supposition: | ואומר שהוא שוה הזויות |
| ומפני כי כפל זוית מז"ד היא זוית גז"ד וכפל זוית מח"ד היא זוית הח"ד תהיה זוית גז"ד שוה לזוית הח"ד | |
| וכן גם כן התבאר כי זוית זח"ט שוה לזוית כט"ח | |
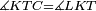
|
ושזוית כט"ח שוה לזוית לכ"ט |
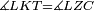
|
ושזוית לכ"ט שוה לזוית לז"ח |
| אם כן זויות אשר עליהן לכ"ט כל"ז לז"ח זח"ט חט"כ שוות | |
| אם כן מחומש זחטכ"ל שוה הזויות | |
| וכבר ביארנו שהוא שוה הצלעות והוא יקיף בעגלת אבג"ד | |
| Q.E.D. | וזה מה שרצינו ביאורו |
Proposition 13 |
|
| We wish to inscribe a circle in a given equilateral and equiangular pentagon. | יג נרצה לעשות במחומש ידוע שוה הצלעות והזויות עגלה יקיף בה |
Defining:
|
הנה נשים המחומש הידוע השוה הצלעות והזויות אבגד"ה |
| We wish to inscribe a circle in it. | ונרצה לעשות בו עגלה יקיף בה |
| הנה נחלק שתי זויות בג"ד דג"ה כל אחת בשני חצאים בשני קוי ז"ג ז"ד | |
| ונגיע קוי א"ז ז"ב ה"ז | |
| ונוציא מנקודת ז' אל קוי א"ב ב"ג ג"ד ה"ד א"ה עמודים ז"ח ז"ט ז"כ ז"ל ז"מ | |
| הנה מפני כי צלע ב"ג שוה לצלע ג"ד כי המחומש הוא שוה הצלעות וקו ז"ג משותף יהיו כל שני קוי ב"ג ג"ז שוים לכל שני קוי ג"ד ג"ז כל אחד לגילו | |
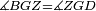
|
וזוית בג"ז שוה לזוית זג"ד |
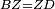
|
אם כן תושבת ב"ז שוה לתושבת ז"ד |
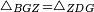
|
ומשולש בג"ז שוה למשולש זד"ג |
| ושאר הזויות שוות לשאר הזויות אשר היו מיתריהם הצלעות השוות | |
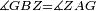
|
אם כן זוית גב"ז שוה לזוית זא"ג |
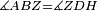
|
ונשארה זוית אב"ז שוה לזוית זד"ה |
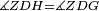
|
ותהיה זוית זד"ה שוה לזוית זד"ג |
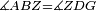
|
הנה זוית אב"ז שוה לזוית זד"ג |
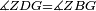
|
וכבר היתה זוית זד"ג שוה לזוית זב"ג |
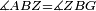
|
אם כן זוית אב"ז שוה לזוית זב"ג |
| אם כן זוית אב"ג כבר נחלקה בשני חצאים כל אחת בקו ב"ז | |
| וכן התבאר כי כל אחת משתי זויות בא"ה אה"ד כבר נחלקה כל אחת בשני חציים בשני קוי א"ז ז"ה | |
| ומפני כי זוית בג"ז שוה לזוית זג"ד וזוית זח"ג נצבת והיא שוה לזוית זמ"ג יהיו כל שתי זויות זמ"ג זג"מ שוות לכל שתי זויות זח"ג זג"ח כל אחת לנכחי לה וקו ז"ג משותף לשני המשולשים יחד יהיו הצלעות הנשארות שוות לשתי הצלעות הנשארות כל אחד לנכחי לו | |
| אם כן קו מ"ז שוה לקו ז"ח | |
| וכן התבאר כי קו ח"ז שוה לקו ז"ט | |
| וקו ז"ט לקו ז"כ | |
| וקו ז"כ לקו ז"ל | |
| וקו ז"ל לקו ז"מ | |
| הנה הקוים החמשה אשר עליהם ח"ז ז"ט ז"כ ל"ז ז"מ שוים | |
| וכאשר שמנו נקודת ז' מרכז וסבבנו במרחק אחת מנקודות ח'ט'כ'ל'מ' עגולה עברה העגולה על שאר הנקודות ומששה צלעות מחומש אבגד"ה מפני כי הזויות אשר אצל נקודות ח'ט'כ'ל'מ' נצבות ונקוה העגולה הזאת והיא עגולת חטכל"מ | |
| הנה כבר עשינו במחומש אבגד"ה עגולה יקיף בה והיא עגולת חטכל"מ | |
| Q.E.D. | וזה מה שרצינו ביאורו |
Proposition 14 |
|
| We wish to circumscribe a circle about a given equilateral and equiangular pentagon. | יד נרצה לעשות על מחומש ידוע שוה הצלעות והזויות עגולה תקיף בו |
Defining:
|
הנה נשים המחומש הידוע מחומש אבגד"ה |
| We wish to circumscribe a circle about it. | ונרצה לעשות עליו עגלה תקיף בו |
| הנה נחלק זוית בג"ד בשני חצאים בקו ג"ז וזוית גד"ה בשני חצאים בקו ד"ז ויפגשו על נקודת ז' | |
| ונוציא קוי ז"ב ז"א ז"ה | |
| הנה קו ב"ג כמו קו ג"ד וג"ז משותף אם כן שני קוי ב"ג ג"ז כמו שני קוי ג"ד ג"ז | |
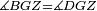
|
וזוית בג"ז כמו זוית דג"ז |
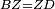
|
אם כן תושבת ב"ז שוה לתושבת ז"ד |
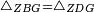
|
ומשולש זב"ג כמו משולש זד"ג |
| ושתי זויות זב"ג בז"ג הנשארות כמו שתי זויות זד"ג דז"ג כל אחת לנכחי לה | |
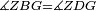
|
אם כן זוית זב"ג כמו זוית זד"ג |
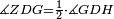
|
וזוית זד"ג חצי זוית גד"ה |
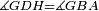
|
וזוית גד"ה כמו זוית גב"א |
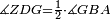
|
אם כן זוית זד"ג חצי זוית גב"א |
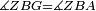
|
אם כן זוית זב"ג כמו זוית זב"א |
| וקו א"ב כמו קו ב"ג וקו ב"ז משותף | |
| אם כן שני קוי א"ב ב"ז כמו שני קוי ג"ב ב"ז | |
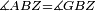
|
וזוית אב"ז כמו זוית גב"ז |
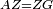
|
אם כן תושבת א"ז כמו תושבת ז"ג |
| וכן גם כן התבאר כי כל אחד מן א"ז ז"ב ז"ג שוים | |
| אם כן קוי א"ז ז"ב ז"ג ז"ד ז"ה החמשה שוים | |
| הנה כאשר שמנו נקודת ז' מרכז והקפנו במרחק ז"א עגולה הלכה בנקודות ב"ג ד"ה והקיפה במחמש שוה הצלעות והזויות הידוע והיא עגולת אבגד"ה | |
| Q.E.D. | וזה הוא מה שרצינו לבאר |
Proposition 15 |
|
| We wish to inscribe an equilateral and equiangular hexagon in a given circle. | טו נרצה לעשות בעגולה ידועה משושה שוה הצלעות והזויות |
Defining:
|
תהיה העגולה הידועה עגולת א"ב ג"ד ה"ז |
| We wish to inscribe an equilateral and equiangular hexagon in it. | ונרצה לעשות בה משושה שוה הצלעות והזויות |
| הנה נוציא קוטר העגולה והוא ג"ז | |
| ויהיה המרכז ח' | |
| ונשים נקודת ז' מרכז ונקיף במרחק ז"ח עגולה עליה חאטב"ה | |
| ונגיע קוי א"ז א"ח ה"ח ה"ז | |
| ונוציא שני קוי א"ח ה"ח אל שתי נקודות ד"ב | |
| ונגיע קוי א"ב ג"ב ג"ד ד"ה | |
| הנה מפני כי נקודת ח' מרכז עגולת אג"ה יהיה קו א"ח שוה לקו ה"ח | |
| ומפני כי נקודת ז' גם כן מרכז עגולת אטב"ה יהיה קו א"ז שוה לקו ז"ה | |
| וכל אחד ממשולשי אח"ז הח"ז שוה הצלעות | |
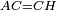
|
וקו א"ח שוה לקו ח"ה |
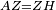
|
וקו א"ז שוה לקו ז"ה |
| וקו ח"ז משותף | |
| הנה כל שני קוי א"ח ח"ז שוים לכל שני קוי ה"ח ח"ז כל אחד לנכחי לו ותושבת א"ז שוה לתושבת ז"ה | |
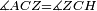
|
אם כן זוית אח"ז שוה לזוית זח"ה |
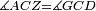
|
אבל זוית אח"ז שוה לזוית גח"ד |
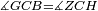
|
וזוית גח"ב שוה לזוית זח"ה |
| אם כן זויות בח"ג גח"ד אח"ז זח"ה הארבעה שוות | |
| ומפני כי קו א"ח שוה לקו ח"ז כי הם יוצאים ממרכז העגולה אל הקו המקיף בהם תהיה זוית חא"ז שוה לזוית אז"ח | |
| אם כן כל שתי זויות חא"ז אז"ח כפל זוית חא"ז | |
| אבל שתי זויות חא"ז אז"ח שוות לזוית אח"ג החיצונה | |
| הנה אם כן זוית אח"ג החיצונה כפל זוית חא"ז | |
| וזוית חא"ז שוה לזוית אח"ז מפני כי המשולש שוה הצלעות | |
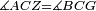
|
וזוית אח"ז שוה לזוית בח"ג |
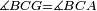
|
אם כן זוית בח"ג שוה לזוית בח"א |
| אבל זוית בח"א שוה לזוית דח"ה | |
| וזוית דח"ה שוה לכל אחת מזויות אח"ז זח"ה גח"ד | |
| הנה כל אחת מזויות בח"ג גח"ד אח"ז זח"ה שוות לכל אחת משתי זויות בח"א דח"ה | |
| אם כן הזויות השש אשר אצל נקודת ח' שוות קצתם אל קצת | |
| והזויות השוות יהיו מיתריהם קשתות שוות | |
| אם כן קשתות א"ב ב"ג ג"ד ד"ה ה"ז ז"א הששה שוים | |
| ומפני כי הקשתות השוות יהיו מיתריהם קוים שוים אם כן משושה א"ב ג"ד ה"ז שוה הצלעות | |
| Supposition: | ואומ' שהוא שוה הזויות |
| הנה מפני כי קשת א"ז שוה לקשת ב"ג וקשת ג"ד ה"ז משותף הנה כל קשת בגדה"ז שוה לכל קשת אזהד"ג | |
| וזוית בא"ז על קשת בגדה"ז וזוית אב"ג על קשת אזהד"ג | |
| והזויות אשר תהיינה על הקשתות השוות הן שוות | |
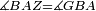
|
אם כן זוית בא"ז שוה לזוית גב"א |
| וכן גם כן התבאר כי זוית גב"א שוה לזוית בג"ד | |
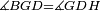
|
וזוית בג"ד שוה לזוית גד"ה |
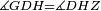
|
וזוית גד"ה לזוית דה"ז |
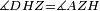
|
וזוית דה"ז לזוית אז"ה |
| אם כן הזויות השש אשר אצל נקודות אב"ג דה"ז שוות | |
| אם כן מששת אב"ג דה"ז שוה הזויות | |
| וכבר ביארנו שהוא שוה הצלעות והוא עשוי בעגולת א"ב ג"ד ה"ז | |
| Q.E.D. | וזה מה שרצינו לבאר |
| וכבר היה אפשר שנעשה על עגולה ידועה משושת שוה הצלעות והזויות יקיף בה ושנעשה עליו עגולה תקיף בו על דמיונו מה שספרנו במחומש | |
| ובכאן התבאר כי חצי קוטר העגולה יהיה מיתר הקו המקיף בה בששה פעמים כי צלע משושת שוה לחצי קוטר העגולה | |
| מצאנו התמונה זאת בנוסחא אחרת במין אחר לפי מה שתראה | |
Proposition 16 |
|
| We wish to circumscribe an equilateral and equiangular hexagon about a circle. | יו נרצה שנעשה בעגולה ידועה משושת שוה הצלעות |
Defining:
|
הנה נשים העגולה אב"ג |
| והקוטר שלה ד"ג ומרכזה ה' | |
| We wish to circumscribe an equilateral and equiangular hexagon about it. | ונרצה לעשות בה משושת שוה הצלעות והזויות תקיף בו |
| הנה נקוה על מרכז ג' ובמרחק ה' עגולת הב"ז | |
| ונוציא א"ה ה"ב ונוציאם אל ח"ט על יושר | |
| ונוציא קוי א"ג ג"ב ב"ח ח"ד ד"ט א"ט | |
| הנה מרכז עגולת א"ב ג"ד נקודת ה' | |
| אם כן קו א"ה כמו קו ה"ג | |
| וגם כן הנה מרכז עגולת אב"ז נקודת ג' | |
| א"כ קו א"ג כמו קו ג"ה | |
| ומשלש אג"ה שוה הצלעות והזויות | |
| וכן התבאר שמשלש גה"ב שוה הצלעות והזויות | |
|
אם כן זוית אה"ג שני שלישי נצבת מל"ב מא' |
|
וזוית גה"ב שני שלישי נצבת מל"ב מא' |
|
|
אם כן כל זוית אה"ב נצבת ושליש נצבת |
|
וזוית טה"א וזוית אה"ב כמו ב' נצבות מי"ג מא' |
|
|
וזוית אה"ב נצבת ושליש נצבת |
|
|
הנה ישאר זוית אה"ט שני שלישי נצבת גם כן |
|
וזוית אה"ט כמו זוית בה"ח מט"ו מא' |
|
|
וזוית אה"ג כמו זוית דה"ח |
|
|
וזוית גה"ב כמו זוית טה"ד |
| הנה כל אחד מהזויות השש אשר אצל נקודות ה' שני שלישי נצבת | |
| אם כן הם שוות | |
| והקשתות השש אשר עליהם א"ט ט"ד ד"ח ח"ב ב"ג ג"ה שוות | |
| ומשושת א"ט ד"ח ב"ג שוה הצלעות | |
| וקשת ד"ח כמו ב"ג וקשת ד"ט א"ג משותף | |
| אם כן כל קשת דט"א ג"ב כמו כל קשת גא"ט ד"ח | |
| אבל קשת דט"א ג"ב עליהם זוית דח"ב ועל קשת ג"א טד"ח זוית חב"ג | |
|
אם כן זוית חב"ג כמו זוית בח"ד מכ"ו מג' |
| וכן הזויות אשר אצל נקודת ד"ט א"ג שוה לשתי הזויות דח"ב חב"ג | |
| הנה כבר התבאר כי המשושת שוה הצלעות והזויות והוא עשוי בעגולת אב"ג | |
| Q.E.D. | וזה מש"ל |
| ובכאן התבאר כי אם נעשה בעגולה משושת שוה הצלעות והזויות הנה צלעו שוה לחצי קוטר העגולה | |
Proposition 17 |
|
| We wish to inscribe an equilateral and equiangular fifteen-angled figure in a given circle. | יז נרצה לעשות בעגולה ידועה תמונה יש לה ט"ו זויות שוה הצלעות והזויות תקיף בה העגולה |
Defining:
|
הנה נשים העגולה הידועה אב"ג |
| We wish to inscribe an equilateral and equiangular fifteen-angled figure in the given circle. | ונרצה שנעשה בה תמונה בעלת ט"ו זויות שוות הצלעות והזויות תקיף בה העגולה |
|
הנה נקוה בעגולה מיתר יהיה צלע המשלש שוה הצלעות והזויות והוא מיתר א"ג מב' מזה |
|
ונוציא מנקודת א' מיתר יהיה צלע מחומש שוה הצלעות והזויות בקשת א"ג והוא מיתר א"ב מי"א מזה |
|
וכאשר חולק הקו המקיף בט"ו חלקים יפול מיתר א"ג על חמשה חלקים מהם ויפול מיתר א"ב על ג' חלקים מהם |
|
וישארו שני חלקים והם קשת ב"ג ונחלקם בשני חצאים על ד' ויצאו שני מיתרי ב"ד ד"ג מכ"ט מג' |
|
|
אם כן קשת ב"ד כמו קשת ד"ג |
|
אם כן מיתר ב"ד כמו מיתר ד"ג מכ"ח מג' |
| אם כן כאשר חלקנו כל הקו המקיף כמו קשת ד"ג ושמנו על כל קשת מיתר הנה כבר עשינו בעגולה תמונה יש לה ט"ו זויות שוות הצלעות והזויות | |
| Q.E.D. | וזה מה שרצינו לבאר |
| והנה אפשר לנו שנעשה על עגולה ידועה תמונה יש לה ט"ו זויות שוות הצלעות והזויות ושנעשה עליה עגולה תקיף בו על דמיון מה שספרנו במחומש | |
| Q.E.D. | וזה מה שרצינו לבאר |
| נשלם המאמר הרביעי מספר אקלידיס החכם בשרשים | |
| ואחריו יבא המאמר הה' בגה"ו |
Book Five |
המאמר החמישי לאקלידס |
Definitions |
הקדמות זה המאמר |
|
השיעור הקטן הוא חלק מן השעור הגדול כאשר ישער הגדול |
| והקצת הוא אשר לא יכלול הגדול כאשר ישערהו | |
|
ויהיה הגדול כפלים לקטן כאשר יפול עליו השעור בקטן |
|
היחס הוא הצטרפות מה בשיעור בין שני שעורים מסוג אחד |
|
ההתיחס הוא הדמות היחסים השעורים אשר יאמר בם כי בין קצתם ובין קצת יחס הם אשר אפשר בהם כשיכפלו שיתוסף קצתם על קצת |
|
יאמר בשעורים שהם על יחס אחד הראשון אל השני והשלישי אל הרביעי כשיהיו כפלי הראשון והשלישי שווי הפעמים איזה מין שיהיו אם שיעדפו יחד על כפלי השני והרביעי השווי הפעמים אי זה כפל שיהיו ואם שישוו עליהם יחד ואם שיגרעו מהם כשיוקשו כסדר קצתם לקצת |
|
ובהפך כשיהיו השיעורים ביחס אחד בעצמו על הסדר הנה כפלי הראשון והשלישי יהיו אם נוספים יחד על כפלי השני והרביעי ואם חסרים יחד מהם ואם שוים יחד לשניהם |
|
ויקראו השעורים אשר יחסם יחס אחד בעצמם המתיחסים |
| וכאשר היו הכפלים שווי הפעמים וכפלי הראשון מהם יעדפו על כפלי השני וכפלי השלישי לא יעדפו על כפלי הרביעי הנה יחס הראשון אז יאמר אל השני שהוא גדול מיחס השלישי אל הרביעי | |
| והמעט שיהיה להתיחסות שלשה שעורים | |
| וכאשר יהיו שלשה שעורים מתיחסים נאמר כי יחס הראשון אל השלישי כפל יחסו אל השני כלומר נשנה בהשנות | |
| וכאשר היו ארבעה שעורים מתיחסים נאמר כי יחס הראשון אל הרביעי שלשה כפלי יחסו אל השני כלומר משולש ועל זה המשל ילך מה שימשך לזה | |
| ויאמר בשעורים שהם מסודרים ביחס ובסדר כאשר הוקשו הראשונים עם הראשונים והנמשכים עם הנמשכים | |
| והפך היחס הוא כשילקח הנמשך במדרגת הראשון | |
| והראשון במדרגת הנמשך | |
| תמורת היחס הוא לקיחת הראשון אל הראשון והנמשך אל הנמשך | |
| הרכבת היחס הוא לקיחת הראשון עם הנמשך במדרגת דבר אחד אצל הנמשך | |
| הבדל היחס הוא לקיחת מותר הראשון על הנמשך אצל הנמשך | |
| הפוך היחס הוא לקיחת הראשון אצל מותרו על הנמשך | |
| יחס השווי הוא כשיהיה כמה שעורים שיהיו ושעורים אחרים כפי מספרם וכשילקחו שנים מאחד משניהם יהיו על יחס שנים מן האחר ונלקחו הקצוות מלבד מה שביניהם | |
| ועל פנים אחרים כשיהיו שיעורים ושעורים אחרים על מספרם הנה יחס השווי הוא יחס הקצוות כשהוכפלו השעורים אשר באמצע | |
| היחס ההולך על סדר הוא כשהראשון אצל הנמשך כראשון אצל הנמשך והנמשך אצל דבר אחד כנמשך אצל דבר אחר | |
| והיחס הנפתל במערכת הוא כשיהיה הראשון אצל הנמשך כראשון אצל הנמשך | |
| והנמשך אצל דבר אחד כדבר אחר אצל הראשון | |
Proposition 1 |
|
| א כאשר יהיו שעורים בהם כפלי שעורים אחרים קרובים להם על מספרם וכפליהם שוים הנה מה שבאחד מכפלי גילו כמו מה שבכל מכפלי הכל | |
| המשל בו כי בשעורי א"ב ג"ד כפלים שוים לשעורי ה'ז' ומה שבא"ב מכפלי ה' כמו מה שבג"ד מכפלי ז' | |
| Supposition: | הנה אומר כי מה שבא"ב מכפלי ה' כמו שבא"ב וג"ד מקובצים מכפלי ה' וז' יחד |
| המופת אנחנו נחלק א"ב בשעור ה' ויהיו חלקיו א"ח וח"ב ונחלק ג"ד בשעור ז' ויהיו חלקיו ג"ט ט"ד | |
|
|
אם כן שעור א"ח כמו ח"ב |
|
|
ושעור ג"ט כמו ט"ד |
|
|
וא"ח כמו ה' |
|
|
וג"ט כמו ז' |
|
|
אם כן כל א"ח וג"ט כמו ה' וז' יחד |
|
|
וכן כל ח"ב וט"ד כמו ה'ז' יחד |
| הנה מה שבא"ב מכפל ה' שוה למה שבא"ב וג"ד מקובצים מכפל ה' וז' יחד וזה מש"ל | |
Proposition 2 |
|
| When the magnitude of the multiple of the second in the first is as the multiple of the fourth in the third, and the multiple of the second in the fifth is as the multiple of the fourth in the sixth, then the multiple of the second in the sum of the first and the fifth is the same as the multiple of the fourth in the sum of the third and the sixth. | ב כשיהיו שעורים בראשון מכפלי השני כמו מה שבשלישי מכפלי הרביעי ובחמישי מכפלי השני כמו מה שבששי מכפלי הרביעי הנה מה שבכפלי הראשון והחמשי מכפלי השני כמו מה שבכפלי השלישי והששי מכפלי הרביעי |
|
|
המשל בו כי בראשון והוא א"ב מכפלי השני והוא ג' כמו מה שבשלישי והוא ד"ה מכפלי הרביעי והוא ז' |
|
|
ובחמשי והוא ב"ח מכפלי השני והוא ג' כמו מה שבששי והוא ט"ה מכפלי הרביעי והוא ז' |
|
הנה אומר כי מה שבראשון והחמישי והוא א"ח מכפלי השני והוא ג' כמו מה שבכל השלישי והששי והוא ד"ט מכפלי הרביעי והוא ז' |
| המופת כי מה שבא"ב מכפלי ג' כמו מה שבד"ה מכפלי ז' | |
| הנה מספר מה שבא"ב מן השעורים השוים אל ג' כמו מספר מה שבד"ה מן השעורים השוים אל ז' ומה שבב"ח מכפלי ג' כמו מה שבה"ט מכפלי ז' | |
| הנה מספר מה שבב"ח מן השעורים השוים אל ג' כמו מספר מה שבה"ט מן השעורים השוים אל ז' | |
| הנה מספר מה שבא"ח אם כן מן השעורים השוים אל ג' כמו מספר מה שבד"ט מן השעורים השוים אל ז' | |
| אם כן מה שבכל א"ח מכפלי ג' כמו מה שבד"ט מכפלי ז' וזה מש"ל' | |
Proposition 3 |
|
| When the multiple of the second in the first is the same as that of the fourth in the third, and if equimultiples are taken of the first and third, then the multiple of the first taken of the second is the same as that of the third taken of the fourth. | ג כשיהיה בראשון מכפלי השני כמו מה שבשלישי מן הרביעי ונלקח לראשון ולשלישי כפלים שוי הפעמי' אי זה מספר שיהיו הנה מה שבכפלי הראשון הלקוח מכפלי השני כמו מה שבשלישי הלקוח מכפלי הרביעי |
|
|
המשל בו כי הראשון א' ובו מכפלי השני והוא ב' כמו מה שבשלישי והוא ג' מכפלי הרביעי והוא ד' |
| וכבר נלקחו כפלים לשעור א' והם ה"ז וכפלים לשעור ג' והם שוים להם במספר הפעמים והם ח"ט | |
|
הנה אומר כי מה שבה"ז מכפלי ב' כמו שבח"ט מכפלי ד' |
| המופת כי מה שבה"ז מכפלי א' כמו מה שבח"ט מכפלי ג' אם כן מספר מה שבה"ז מן השעורים השוים לשעור א' כמו מספר מה שבח"ט מן השעורים השוים לשעור ג' הנה נחלק ה"ז בשעור א' ויהיו חלקיו ה"כ ז"כ ונחלק ח"ט בשעור ג' ויהיו חלקיו ח"ל ול"ט | |
| אם כן מספר ה"כ וכ"ז כמו מספר ח"ל ול"ט | |
| ומה שבא' מכפלי ב' כמו מה שבג' מכפלי ד' וא' כמו ה"כ וג' כמו ח"ל | |
| אם כן מה שבה"כ מכפלי ב' כמו שבח"ל מכפלי ד' | |
| וכן מה שבכ"ז מכפלי ב' כמו מה שבל"ט מכפלי ד' | |
| ונשים הראשון ה"כ ובו מכפלי ב' כמו מה שבשלישי והוא ח"ל מכפלי ד' | |
| והחמישי כ"ז ובו מכפלי ב' כמו מה שבששי והוא ל"ט מכפלי ד' | |
| וכאשר קובץ הראשון והחמישי והם ה"ז היה בשניהם מכפלי ב' כמו מה שבשלישי והשישי והם ח"ט מכפלי ד' אם כן מה שבה"ז מכפלי ב' כמו מה שבח"ט מכפלי ד' וזה מש"ל | |
Proposition 4 |
|
| ד כאשר היה יחס הראשון אל השני הוא השלישי אל הרביעי ונלקח לראשון ולשלישי כפלים שווי הפעמים אי זה מספר שיהיה ולשני ולרביעי כפלים שווי הפעמים אי זה מספר שיהיה הנה יחס כפלי הראשון הלקוחים אל כפלי השני הם יחס כפלי השלישי הלקוחים אל כפלי הרביעי | |
| המשל בו כי יחס הראשון והוא א' אל השני והוא ב' הוא יחס השלישי והוא ג' אל הרביעי והוא ד' | |
| וכבר נלקח לשעורי א"ג כפלים שווי הפעמים והם ח"ט הנה אומר כי יחס ה' אל ח' הוא יחס ז' אל ט' | |
| מופתו אנחנו נקח לשני שעורי ה"ז כפלים שווי הפעמים והם ל"נ ולשני שעורי ח"ט כפלים שווי הפעמים והם מ"ס | |
| הנה כפלי ל' לשעור א' כמו כפלי נ' לשעור ג' וכן כפלי מ' לשעור ב' כמו כפלי ס' לשעור ד' ויחס א' אל ב' הוא יחס ג' אל ד' | |
| וכבר נלקח לשני שעורי א"ג כפלים שווי הפעמים והם מ"ס ל"נ ולשני שעורי ב"ד כפלים שווי הפעמים והם מ"ס | |
| אם כן שעור ל"נ אם מוסיפים יחד על מ"ס ואם שוים יחדל שניהם ואם גורעים יחד מהם ושעור ל"נ כפלים שוים לשני שעורי ה"ו ושעור מ"ס כפלים שוים לשני שעורי ח"ט | |
| אם כן יחס ה' אל ח' הוא יחס ו' אל ט' | |
| וזה מ'ש'ל' | |
Proposition 5 |
|
| ה כאשר יהיו שני שעורים אחד משניהם כפלים לאחר וחוסר משניהם שני שעורים והיה מה שבמחוסר מכפלי המחוסר כמו מה שבכל מכפלי הכל הנה מה שנשאר מכפלי הנשאר כמו מה שבכל מכפלי הכל | |
| המשל בו כי שעור א"ב כפלים לשעור ג"ד והמחוסרים משניהם א"ה וג"ו ומה שבא"ה מכפלי ג"ו כמו מה שבא"ב מכפלי ג"ד | |
| Supposition: | הנה אומר כי מה שבה"ב הנשאר מכפלי ו"ד הנשאר כמו מה שבא"ב מכפלי ג"ד |
| מופתו אנחנו נשים בא"ט מכפלי ו"ד כמו מה שבא"ה מכפלי ג"ו | |
| וכבר היה בא"ב מכפלי ג"ד כמו מה שבא"ה מכפלי ג"ו אם כן מה שבה"ט כלו מכפלי ג"ד כמו מה שבא"ב מכפלי ג"ד | |
| אם כן ה"ט כמו א"ב ותשליך א"ה המשותף וישאר א"ט כמו ה"ב | |
| וכבר היה בא"ט מכפלי ו"ד כמו מה שבא"ה מכפלי ג"ו | |
| אם כן מה שבה"ב מכפלי ו"ד כמו מה שבא"ה מכפלי ג"ו | |
| וכבר היה מה שבא"ב כלו מכפלי ג"ד כמו מה שבא"ה מכפלי ג"ו | |
| אם כן מה שבה"ב מכפלי ו"ד כמו מה שבא"ב מכפלי ג"ד | |
| וזה מה שרצינו לבאר | |
Proposition 6 |
|
| ו כאשר היו שני שעורים בשניהם כפלים שוים לשני שעורים אחרים וחוסר מהשנים הגדולים כפלים שוים לקטנים הנה השנים הנשארים אם שוים לשנים הקטנים ואם כפלים לשניהם שוים | |
| המשל בו כי כפלי א"ב לשעור ה' וכפלי ג"ד לשעור ז' | |
| וכבר חוסר מן א"ב וג"ד כפלים שוים לשעור ה' וז' והם א"ח וג"ט הנה אומר כי ב"ח וט"ד הנשארים אם שוים יחד לשני שעורי ה"ז ואם כפלים לשניהם שוים | |
| ויהיה ב"ח תחלה כפלים לשעור ה' הנה אומר כי ט"ד כפלים כמוהם לשעור ז' | |
| מופתו אנחנו נשים מה שבג"ב מכפלי ז' כמו מה שבח"ב מכפלי ה' והוא השני כמו מה שבג"ט והוא השלישי מכפלי ז' והוא הרביעי | |
| ומה שבח"ב והוא החמישי מכפלי ה' השני כמו מה שבג"ב והוא הששי מכפלי ז' הרביעי | |
| אם כן מה שבא"ב והוא הראשון והחמישי יחד מכפלי ה' השני | |
| כמו מה שבב"ט השלישי והששי יחד מכפלי ז' הרביעי וכבר היה בא"ב מכפלי ה' כמו שבג"ד מכפלי ז' אם כן ב"ט כמו ג"ד | |
| ונשליך ג"ט המשותף וישאר ב"ג כמו מה שבט"ד | |
| וכבר היה מה שבח"ב מכפלי ה' כמו מה שבב"ג מכפלי ז' | |
| אם כן מה שבט"ד מכפלי ז' כמו מה שבח"ב מכפלי ה' | |
| ויהיה גם כן ח"ב שוה אל ה' הנה אומר כי ט"ד שוה אל ז' | |
| המופת אנחנו נשים ג"ב שוה אל ז' | |
| הנה בכמו המעשה הראשון נבאר כי ב"ט כמו ג"ד | |
| הנה כאשר הושלך ג"ט המשותף ישאר ט"ד כמו ב"ג ומפני שב"ג כמו ז' הנה ט"ד אם כן כמו ז' | |
| ומ'ש'ל' | |
Proposition 7 |
|
| ז השעורים השוים יחסם אל שיעור אחד אחד ויחס הוא גם כן אליהם אחד | |
| המשל בו כי שני שעורי א"ב שוים ושיעור ג' שיעור אחד | |
| Supposition: | הנה אומר כי יחס א' אל ג' כיחס ב' אל ג' ויחס ג' גם כן אל א' כיחסו אל ב' |
| מופתו אנחנו נקח לשני שעורי א"ב כפלים שוים והם ד"ה ולשעור ג' כפלים מה שיהיו והם ז' הנה כפלי ד' לשעור א' ככפלי ה' לשעור ב' | |
| וא' כמו ב' אם כן ד' כמו ה' | |
| ושעור ז' שעור אחד אי זה שיהיה אם כן שני שעורי ה"ד אם שוים יחד לשעור ז' ואם נוספים יחד עליו ואם חסרים יחד ממנו ושניהם כפלים שוים לשני שעורי א"ב וז' כפלים לשעור ג' אם כן יחס א' אל ג' כיחס ב' אל ג' | |
| Supposition: | ואומר כי יחס ג' אל א' כיחסו אל ב' מפני כי הנהגת שניהם אחת כי ד"ה שוים |
| וכי ז' אם שוה לשניהם ואם נוסף על שניהם | |
| ואם חסר משניהם יחד | |
| וז' כפלים לשעור ג' וד' ה' כפלים שוים לשני שעורי א"ב | |
| אם כן יחס ג' אל א' כיחסו אל ב' | |
| ומ'ש'ל' | |
Proposition 8 |
|
| ח השעורים המתחלפים כאשר נתיחסו אל שעור אחד הנה הגדול יותר יחסו אליו מן הקטן | |
| וכאשר נתיחס הוא אליהם הנה יחסו אל הקטן יותר מיחסו אל הגדול | |
| המשל בו שעורי א"ב וג' מתחלפים א"ב יותר גדול מן ג' | |
| ושעור ד' שעור אחד | |
| Supposition: | הנה אומר כי א"ב יותר גדול יחסו אל ד' מן ג' אל ד' |
| ושד' יותר גדול יחסו אל ג' מאשר הוא אל א"ב | |
| מופתו שנבדיל מן א"ב כמו ג' והוא ב"ה הנה היותר קטן משני שעורי א"ה ה"ב הנה אפשר שיכפל עד שיהיה יותר גדול מן ד' | |
| ויהיה א"ה יותר קטן משניהם ויהיה כפלו הנוסף על שעור ד' כפל ו"ח | |
| ונקח לשני שעורי ה"ב וג' כפלים שוים לכפלי ו"ח נוסף והוא ח"ט וכ"ל ונשים מ' שני כפלי ד' ונ' שלשה כפלו אחר כן לא תסור נקח כפלי ד' על הסדר עד שיכלה אל הראשון מכפליו עד שיהיה יותר גדול מן כ"ל | |
| ויהיה ס' הוא ראשון מכפלי ד' אשר הוא יותר גדול מן כ"ל הנה כפלי ו"ח לשיעור א"ה ככפלי ח"ט לשעור ה"ב | |
| אם כן כפלי ו"ח לשעור א"ה ככפלי ו"ט לשעור א"ב ושעור ו"ח לשעור א"ה ככפלי כ"ל לשעור ג' | |
| וכפלי ו"ט וכ"ל לשני שעורי א"ב וג' שוה | |
| וגם כן הנה כפלי ח"ט לשעור ה"ב ככפלי כ"ל לשעור ג' וה"ב כמו ג' אם כן ח"ט כמו כ"ל וס' יותר גדול מן כ"ל וכ"ל אינו יותר קטן מן נ' | |
| וכ"ל כמו ח"ט אם כן ח"ט אינו יותר קטן מן נ' וו"ח יותר מן ד' אם כן ו"ט יותר גדול מן ד' ונ' יחד | |
| וס' כמו ד' ונ' יחד | |
| אם כן ו"ט יותר גדול מן ס' אם כן הוא נוסף עליו | |
| וכ"ל בלתי נוסף על ס' וו"ט וכ"ל כפלים שוים לשעורי א"ב וג' וס' כפלים שוים לשעור ד' | |
| אם כן שעור א"ב יותר גדול היחס אל ד' מן ג' אל ד' | |
| ואומר גם כן כי ד' יותר גדול היחס אל ג' מאשר הוא אל ב' מפני כי הנהגתם אחת | |
| והתבאר כי ס' נוסף על כ"ל ואינו נוסף על ו"ט וס' כפל ד' וכ"ל וו"ט כפלים שוים לשעורים א"ב וג' | |
| אם כן יחס ד' אל ג' יותר גדול מיחסו אל א"ב | |
| ומ'ש'ל' | |
Proposition 9 |
|
| ט השעורים אשר יחסם אל שעור אחד אחד הם שוים | |
| ואם היה שעור יחסו אל שעורים אחד הנה השעורים שוים | |
| המשל בו כי שני שעורי א"ב יחסם אל שעור ג' אחד | |
| הנה אומר כי א' כמו ב' | |
| שאם לא יהיה כמוהו הנה הוא יותר גדול ממנו או יותר קטן | |
| ואלו היה יותר גדול יהיה יחסו אל ג' יותר גדול | |
| ואלו היה יותר קטן היה יחסו אל ג' יותר קטן ואינו כן | |
| אם כן אין א' יותר קטן ויותר גדול מן ב' אבל הוא שוה לו | |
| וגם כן הנה יחס ג' אל א' וב' אחד | |
| הנה אומר כי א' כמו ב' שאם לא יהיה כמוהו הנה הוא יותר גדול או יותר קטן ממנו | |
| ואלו היה יותר גדול היה יחס ג' אליו יותר קטן | |
| ואלו היה יותר קטן היה יחס ג' אליו יותר גדול | |
| אם כן אין א' יותר גדול ולא יותר קטן מן ב' אם כן הוא שוה לו | |
| וזה מ'ש'ל' | |
Proposition 10 |
|
| י גדול השעורים יחס אל שעור הוא היותר הוא היותר גדול מהם | |
| ואשר יחס השעור אליו יותר גדול הוא היותר קטן מהם | |
| המשל בו כי א' יותר גדול יחסו אל ג' | |
| הנה אומר כי א' יותר גדול יחסו מן ב' | |
| שאם לא יהיה יותר גדול ממנו הנה הוא כמוהו או יותר קטן ממנו | |
| ואלו היה כמוהו היה יחס שניהם אל ג' אחד | |
| ואלו היה יותר קטן ממנו היה יחסו אל ג' יותר קטן | |
| ואינו כן הנה כבר התבאר כי א' אינו כמו ב' ולא קטן ממנו | |
| הנה אם כן הוא יותר גדול ממנו | |
| וגם כן הנה יחס ג' אל ב' יותר גדול מיחסו אל א' | |
| הנה אומר כי א' יותר גדול מן ב' | |
| שאם לא יהיה יותר גדול ממנו הנה הוא כמוהו או יותר קטן ממנו | |
| ואלו היה כמוהו היה יחס ג' אליו ואל ב' אחד | |
| ואלו היה יותר קטן ממנו היה יחס ג' אליו יותר גדול ואינו כן | |
| אם כן אינו כמו ב' ולא קטן ממנו אבל הוא יותר גדול ממנו | |
| וזה מה שרצינו לבאר | |
Proposition 11 |
|
| יא השעורים אשר יחסם שוים ליחס אחד הנה יחסם שוים | |
| המשל בו כי יחס א' אל ב' כיחס ג' אל ד' ויחס ה' אל ז' כיחס ג' אל ד' הנה אומר כי יחס א' אל ב' כיחס ה' אל ז' | |
| מופתו אנחנו נקח לשיעורי א'ג'ה' כפלים שוים והם ח'ט'ב' ולשעורי ב'ד'ז' כפלים שוים והם ל'מ'נ' הנה יחס א' אל ב' כיחס ג' אל ד' וכבר לוקח לשעורי א"ג כפלים שוים והם ח"ט | |
| ולשעורי ב"ד כפלים שוים והם ל"מ הנה שני שעורי ח"ט אם נוספים יחד על שני שעורי ל"מ ואם שוים לשניהם יחד ואם חסרים משניהם יחד | |
| וגם כן הנה יחס ג' אל ד' כיחס ה' אל ז' | |
| וכבר נלקח לשני שעורי ג"ה כפלים שוים והם ט"כ | |
| ולשני שעורי ד"ז כפלים והם מ"נ | |
| אם כן שני שעורי ט"כ אם נוספים יחד על שני שעורי מ"נ ואם שוים יחד לשניהם | |
| ואם חסרים יחד משניהם וח"כ כפלים שוים לשני שעורי א"ה ול"נ כפלים שוים לשני שעורי ז"ב אם כן יחס א' אל ב' כיחס ה' אל ז' | |
| ומ'ש'ל' | |
Proposition 12 |
|
| יב כאשר היה יחס הראשון אל השני כיחס השלישי אל הרביעי ויחס השלישי אל הרביעי יותר גדול מיחס החמישי על הששי הנה יחס הראשון אל השני יותר גדול מיחס החמשי על הששי | |
| המשל בו כי יחס א' אל ב' כיחס ג' אל ד' ויחס ג' אל ד' יותר גדול מיחס ה' אל ו' הנה אומר כי יחס א' אל ב' יותר גדול מיחס ה' אל ו' | |
| מופתו מפני כי יחס ג' אל ד' יותר גדול מיחס ה' אל ו' הנה יהיה אל ג' וה' כפלים שוים | |
| ואל ד' וו' כפלים שוים ויהיו כפלי ג' נוספים על כפלי ד' וכפלי ה' בלתי נוספים על כפלי ו' הנה יהיו כפלי ג' וה' השוים וכפלי ד' וו' השוים אשר אלו עניינם כפלי ג' וה' הנה ח"ט | |
| ואולם כפלי ד' הנה כ"ל ויהיה מה שבמ' מכפלי א' כמו מה שבח' מכפלי ג' | |
| ומה שבנ' מכפלי ב' כמו מה שבכ' מכפלי ד' | |
| הנה יחס א' אל ב' כיחס ג' אל ד' | |
| וכבר הוסף לשני שעורי א"ג כפלים שוים והם מ"ח ולשני שעורי ב"ד כפלים שוים והם נ"כ הנה שני שעורי מ"ח אם נוספים יחד על שני שעורי נ"ב ואם שוים יחד לשניהם ואם חסרים יחד משניהם | |
| אבל אם היה נוסף ח' על כ' הנה מ' נוסף על נ' וט' בלתי נוסף על ל' הנה מ"ט כפלים שוים לשני שעורי א"ה ונ"ל כפלים שוים לשני שעורי ב' ו' אם כן יחס א' אל ב' יותר גדול מיחס ה' אל ו' | |
| ומ'ש'ל' | |
Proposition 13 |
|
| יג השעורים אשר יחסם אל שעורי' אחרים קרובים להם על מספרם כמה שיהיו אחד הנה יחס האחד אל קרובו כיחס הכל אל הכל | |
| המשל בו כי יחס א' אל ב' וג' אל ד' וה' אל ו' אחד הנה אומר כי יחס א' אל ב' כיחס א'ג'ה' יחד אל ב'ד'ו' יחד | |
| מופתו אנחנו נקח לשעורי א'ג'ה' כפלים שוים והם ח'ט'כ' ולשעורי ב'ד'ו' כפלים שוים והם ל'מ'נ' הנה יחס א' אל ב' כיחס ג' אל ד' | |
| וכיחס ה' אל ו' | |
| וח' וט' וכ' כפלים שוים לשעורי א'ג'ה' ול'מ'נ' כפלים שוים לשעורי ב'ד'ו' אם כן ח'ט'כ' אם נוספים יחד על ל'מ'נ' ואם חסרים מהם יחד ואם שוים להם יחד | |
| ואם היה ח' נוסף על ל' הנה ח'ט'כ' מקובצים נוספים על ל'מ'נ' | |
| ואם היה חסר ממנו הנה הם חסרים מהם | |
| ואם היה שוה לו הנה הם שוים להם | |
| וכפלי ח' לשעור א' ככפלי ח'ט'כ' מקובצים לשעורי א'ג'ה' מקובצים וכפלי ל' לשעור ב' ככפלי ל'מ'נ' לשעור ב'ד'ו' מקובצים | |
| אם כן יחס א' אל ב' כיחס א'ג'ה' מקובצים אל ב'ד'ו' יחד | |
| ומ'ש'ל' | |
Proposition 14 |
|
| יד כאשר היו ארבעה שעורים מתיחסים והיה הראשון יותר גדול מן השלישי הנה השני יותר גדול מן הרביעי ואם היה שוה לו הנה הוא שוה לו ואם היה יותר קטן ממנו הנה הוא יותר קטן ממנו | |
| המשל בו כי שעורי א"ב ג"ד הארבעה מתיחסים יחס א' אל ב' כיחס ג' אל ד' וא' יותר גדול מן ג' הנה אומר כי ב' יותר גדול מן ד' | |
| מופתו כי א' יותר גדול מן ג' אם כן א' גדול היחס אל ב' מג' אל ב' | |
| אבל יחס א' אל ב' כיחס ג' אל ד' אם כן יחס ג' אל ד' יותר גדול מיחסו אל ב' | |
| ואשר יהיה היחס אליו יותר גדול הנה הוא יותר קטן | |
| אם כן ד' יותר קטן מן ב' אם כן ב' יותר גדול מן ד' | |
| וכן התבאר כי אלו היה א' כמו ג' היה ב' כמו ד' | |
| ואלו היה יותר קטן מן ג' היה ב' יותר קטן מן ד' | |
| ומ'ש'ל' | |
Proposition 15 |
|
| טו החלקים אשר כפליהם שוים הנה יחס קצתם כיחס כפלי קצתם אל קצת | |
| המשל בו כי כפלי א"ב אל שעור ג' כשעור ד"ה לשעור ו' הנה אומר כי יחס א"ב אל ד"ה כיחס ג' אל ו' | |
| ד"ת כי יחס ג' אל ו' כיחס א"ב אל ד"ה | |
| המופת אנחנו נחלק א"ב בשעור ג' וחלקיו א"ח וח"ט וט"ב והם שוים ונחלק ד"ה בשעור ו' וחלקיו ד"ל ול"מ ומ"ה והם שוים | |
| ומניין א"ח ח"ט וט"ב כמספר ד"ל ול"מ ומ"ה | |
| אם כן יחס א"ח אל ד"ל כיחס ח"ט אל ל"מ וכיחס ט"ב אל מ"ה ויחס האחר אל קרובו כיחס הכל אל הכל | |
| אם כן יחס א"ח אל ד"ל כיחס א"ב אל ד"ה וא"ח כמו ג' וד"ל כמו ז' אם כן יחס א"ב אל ד"ה כיחס ג' אל ז' | |
| ומ'ש'ל' | |
Proposition 16 |
|
| יו כאשר היו שעורים מתיחסים הם יהיו כאשר הומרו מתיחסים | |
| המשל בו כי שעורי א"ב ג"ד הארבעה מתיחסים יחס א' אל ב' כיחס ג' אל ד' הנה אומר כי יחס א' אל ג' כיחס ב' אל ד' על התמורה | |
| מופתו אנחנו נקח לשעורי א"ב כפלים שוים והם ה"ו ולשעורי ג"ד כפלים שוים והם ח"ט | |
| והחלקים אשר כפליהם שוים | |
| יחס קצתם אל קצתם כיחס כפליהם קצתם אל קצת | |
| וה"ו כפלים לשעורי א"ב אם כן יחס א' אל ב' כיחס ה' אל ו' וגם כן הנה ח' וט' כפלים שוים לשעורי ג' וד' אם כן ג' אל ד' כיחס ח' אל ט' אבל ג' אל ד' כיחס א' אל ב' וכיחס ה' אל ו' | |
| אם כן יחס ה' אל ו' כיחס ח' אל ט' | |
| ואם היה ה' מוסיף אל ח' הנה ו' יוסיף על ט' | |
| ואם היה שוה הנה הוא שוה לו ואם שיחסר ממנו הנה יחסר ממנו אם כן שני שעורי ה' וו' אם נוספים יחד על שני שעורי ח' וט' ואם שוים יחד להם ואם חסרים יחד מהם | |
| וה'ו' כפלים שוים לשני שעורי א"ב וח' וט' כפלים שוים לשני שעורי ג' וד' | |
| אם כן יחס א' אל ג' כיחס ב' אל ד' | |
| ומ'ש'ל' | |
Proposition 17 |
|
| יז כאשר היו שעורים מורכבים מתיחסים הנה הם כאשר נבדלו יהיו מתיחסים | |
| המשל בו כי שעורי א"ב וב"ה וג"ד וד"ו מורכבים מתיחסים יחס א"ב אל ב"ה כיחס ג"ד אל ד"ו הנה אומר שהם כאשר נבדלו יהיו מתיחסים | |
| ויהיה יחס א"ה אל ה"ב כיחס ג"ו אל ו"ד | |
| מופתו אנחנו נקח לשעורי א"ה וה"ב וג"ו וו"ד כפלים שוים והם ח"ט וט"כ ול"מ ומ"נ | |
| אם כן כפלי ח"ט לשעור א"ה ככפלי ח"כ לשעור א"ב וכפלי ח"ט לשעור א"ה ככפלי ל"מ לשעור ג"ו אם כן כפלי ח"כ לשעור א"ב ככפלי ל"מ לשעור ג"ו | |
| וגם כן הנה כפלי ל"מ לשעור ג"ז ככפלי מ"נ לשעור ז"ד אם כן כפלי ל"מ לשעור ג"ז ככפלי ח"כ לשעור א"ב | |
| אם כן כפלי ח"כ לשעור א"ב ככפלי ל"נ לשעור ג"ד | |
| ונקח לשעורי ה"ב וז"ד כפלים שוים והם כ"ס ונ"ע הנה כפלי ט"כ הראשון לשעור ה"ב השני ככפלי מ"נ השלישי לשעור ז"ד הרביעי וכן כפלי כ"ס החמישי לשעור ה"ב השני ככפלי נ"ע הששי לשעור ז"ד הרביעי | |
| אם כן כפלי הראשון והחמישי מקובצים ט"ס לשעור ה"ב השני ככפלי השלישי והששי מקובצים והם מ"ע לשעור ז"ד הרביעי | |
| ויחס א"ב אל ב"ה כיחס ג"ד אל ד"ז ושני שעורי ח"כ ול"נ כפלים שוים לשני שעורי א"ב וג"ד ושני שעורי ט"ס מ"ע כפלים שוים לשני שעורי ה"ב ז"ד | |
| אם כן שני שעורי ח"כ ול"נ אם נוספים יחד על שני שעורי ט"ס ומ"ע ואם שוים יחד לשניהם | |
| ואם חסרים יחד משניהם | |
| ואם חסרנו ט"כ ומ"נ המשותפים הנה שני שעורי ח"ט ול"מ אם נוספים יחד על שני שעורי כ"ס ונ"ע ואם שוים יחד לשניהם ואם חסרים יחד משניהם וח"ט ול"מ כפלים שוים לשני שעורי א"ה וג"ז וכ"ס ונ"ע כפלים שוים לשני שעורי ה"ב וז"ד אם כן יחס א"ה אל ה"ב כיחס ג"ז אל ז"ד | |
| וזה מה שרצינו לבאר | |
Proposition 18 |
|
| יח כאשר היו שעורים נבדלים מתיחסים הנה הם כאשר הורכבו יהיו מתיחסים | |
| המשל בו כי שני שעורי א"ב וב"ג וד"ה וה"ו מתיחסים יחס א"ב אל ב"ג כיחס ד"ה אל ה"ו הנה אומר שהם כאשר הורכבו יהיו מתיחסים א"ג אל ג"ב כיחס ד"ו אל ו"ה | |
| מופתו אם לא יהיה יחס א"ג אל ג"ב כיחס ד"ו אל ו"ה הנה יחס א"ג אל ג"ב כיחס ד"ו אל מה שהוא יותר קטן או יותר גדול מן ו"ה | |
| ויהיה תחלה אל מה שהוא יותר קטן ממנו והוא ז"ח | |
| הנה יחס א"ג אל ג"ב כיחס ד"ז אל ז"ח וכאשר הבדלנו הנה יחס א"ב אל ב"ג כיחס ד"ח אל ח"ז | |
| וכבר היה יחס א"ב אל ב"ג כיחס ד"ה אל ה"ז אם כן יחס ד"ח אל ח"ז כיחס ד"ה אל ה"ז וח"ד הראשון יותר גדול מן ד"ה השלישי | |
| אם כן ח"ז השני יותר גדול מן ז"ה הרביעי וכבר היה יותר גדול מן ז"ח | |
| The smaller is greater than the greater = error. | הנה הקטן אם כן יותר גדול מן הגדול זה שקר |
| אם כן אין יחס א"ג אל ג"ב כיחס ד"ז אל שעור הוא יותר קטן מן ז"ה | |
| וכן יתבאר כי יחס א"ג אל ג"ב אינו כיחס ד"ז אל שעור הוא יותר גדול מן ז"ה | |
| וזה מה שרצינו לבאר | |
Proposition 19 |
|
| יט כאשר חוסר משני שעורים מכל אחד משניהם שעור ויהיה יחס המחוסר אל המחוסר כיחס הכל אל הכל | |
| הנה יחס הנשאר אל הנשאר כיחס הכל אל הכל | |
| המשל בו כי א"ב חוסר ממנו א"ה וג"ד חוסר ממנו ג"ו ויחס א"ה אל ג"ו כיחס א"ב הכל אל ג"ד הכל | |
| הנה אומר כי יחס ה"ב הנשאר אל ו"ד הנשאר כיחס א"ב הכל אל ג"ד | |
| מופתו כי יחס א"ב אל ג"ד כיחס א"ה אל ג"ו וכאשר המירונו הנה יחס א"ב אל א"ה כיחס ד"ג אל ג"ו וכאשר הבדלנו הנה יחס ב"ה אל ו"ד כיחס א"ה אל ג"ו וכבר היה א"ה אל ג"ו כיחס א"ב אל ג"ד אם כן יחס ב"ה אל ו"ד כיחס א"ב אל ג"ד | |
| וזה מה שרצינו לבארו | |
Proposition 20 |
|
| כ כאשר היו שעורים מה שיהיו ושעורים אחרים על מספרם כל שנים מהראשון על יחס שנים מן האחר הנה הראשון מן הראשון ביחס השווי אם היה יותר גדול מן האחרון הנה הראשון מן האחר יותר גדול מן האחרון | |
| ואם היה שוה לו הנה הוא שוה לו | |
| ואם היה יותר קטן ממנו הנה הוא יותר קטן ממנו | |
| המשל בו כי שעורי א'ב'ג' על מספר שעורי ד'ה'ו' | |
| וכל שנים מהם על יחס שנים מהם יחס א' אל ב' כיחס ד' אל ה' ויחס ב' אל ג' כיחס ה' אל ו' | |
| ונשים הראשון מן הראשון והוא א' יותר גדול מן האחרון והוא ג' הנה אומר כי הראשון מן האחר והוא ד' יותר גדול מן האחרון והוא ו' | |
| מופתו כי א' יותר מן ג' ושעור ב' שעור אחד | |
| אם כן שעור א' יותר גדול היחס אל ב' מן ג' אל ב' | |
| אבל יחס א' אל ב' כיחס ד' אל ה' ויחס ג' אל ב' כיחס ה' אל ו' אם כן שעור ד' יותר גדול היחס אל ב' מן ג' אל ב' | |
| אבל יחס א' אל ב' כיחס ד' אל ה' | |
| ויחס ג' אל ב' כיחס ו' אל ה' אם כן שעור ד' יותר גדול היחס אל ה' מן ו' אל ה' ואשר יחסו יותר גדול הנה הוא יותר גדול | |
| אם שעור ד' יותר גדול מן ו' | |
| וכן התבאר כי א' אלו היה שוה אל ג' היה ד' שוה אל ו' ואלו היה יותר קטן מן ג' היה ד' יותר קטן מן ו' | |
| וזה מה שרצינו לבאר | |
Proposition 21 |
|
| כא כאשר היו שעורים מה ושעורים אחרים על מספרם כל שנים מהראשון על יחס שנים מהאחר ונתבלבל היחס הנה הראשון מן הראשון ביחס השווי אם היה יותר גדול מן האחרון הנה הראשון מן האחר יותר גדול מן האחרון | |
| ואם היה שוה לו הנה הוא שוה לו | |
| ואם היה יותר קטן ממנו הנה הוא יותר קטן ממנו | |
| המשל בו כי שעורי א'ב'ג' על מספר שעורי ד'ה'ו' וכל שנים מן הראשון על יחס שנים מן האחר | |
| והיחס מתבלבל יחס א' אל ב' כיחס ה' אל ו' ויחס ב' אל ג' כיחס ד' אל ה' | |
| ונשים א' יותר גדול מג' הנה אומר כי ד' יותר גדול מן ו' | |
| מופתו כי א' יותר גדול מן ג' וב' שעור אחר הנה שעור א' יותר גדול היחס אל ב' מן ג' אל ב' אבל יחס א' אל ב' כיחס ה' אל ו' כי אם כן יחס ה' אל ו' יותר גדול מיחס ג' אל ב' ויחס ג' אל ב' כיחס ה' אל ד' אם כן יחס ה' אל ו' יותר גדול מיחס ה' אל ד' ואשר יהיה היחס אליו יותר גדול הנה הוא יותר קטן אם כן שעור ו' יותר קטן מן ד' | |
| אם כן ד' יותר גדול מן ו' | |
| וכן התבאר כי אלו היה א' שוה לשעור ג' היה ד' שוה לו' | |
| ואלו היה יותר קטן מן ג' היה ד' יותר קטן מן ו' | |
| ומ'ש'ל' | |
Proposition 22 |
|
| כב אשר היו שעורים מה ואחרים על מספרם כל שני שעורים מן הראשון על יחס שני שעורים מן האחר הנה הם ביחס השווי יהיו ביחסם | |
| המשל בו כי שעורי א'ב'ג' ושעורי ד'ה'ו' על מספר אחד וכל שנים מן הראשון על יחס שנים מן האחר יחס א' אל ב' כיחס ד' אל ה' | |
| ויחס ב' אל ג' כיחס ה' אל ו' הנה אומר כי יחס א' אל ג' כיחס ד' אל ו' | |
| מופתו אנחנו נקח לשני שעורי א"ד כפלים שוים והם ח"ט ולשני שעורי ב"ה כפלים שוים והם כ"ל ולשני שעורי ג"ו כפלים שוים והם מ"נ הנה יחס א' אל ב' כיחס ד' אל ה' | |
| וח"ט כפלים שוים לשני שעורי א"ד וכ"ל כפלים שוים לשני שעורי ב"ה | |
| אם כן יחס א' אל ב' כיחס ט' אל ל' | |
| וגם כן הנה יחס ב' אל ג' כיחס ה' אל ו' וכ"ל כפלים שוים לשעורי ב"ה ומ"נ כפלים שוים לשני שעורי ג"ו אם כן יחס כ' אל מ' כיחס ל' אל נ' | |
| וכבר התבאר כי יחס א' אל ב' כיחס ט' אל ל' | |
| אם כן שני שעורי ח"ט אם נוספים יחד על שני שעורי מ"נ | |
| ואם שוים יחד לשניהם ואם חסרים יחד משניהם | |
| וח"ט כפלים שוים לשעורי א"ד ומ"נ כפלים שוים לשני שעורי ג"ו אם כן יחס א' אל ג' כיחס ד' אל ו' וזה מה שרצינו לבארו | |
Proposition 23 |
|
| כג כאשר היו שעורים כמה שיהיו ושעורים אחרים על מספרם כל שנים מהראשון על יחס שנים מן האחר ונתבלבל היחס הנה הם ביחס השווי יהיו על יחסם | |
| המשל בו כי שעורי א'ב'ג' ושעורי ד'ה'ו' על מספר אחד וכל שנים מן הראשון על יחס שנים מן האחרון והיחס מבולבל יחס א' אל ב' כיחס ה' אל ו' ויחס ב' אל ג' כיחס ד' אל ה' הנה אומר כי יחס א' אל ג' כיחס ד' אל ו' | |
| מופתו אנחנו נקח לשעורי א'ב'ד' כפלים שוים והם ח'ט'ל' ולשעורי ה'ו'ג' כפלים שוים והם מנ"כ הנה כפלי ח' לשעור א' ככפלי ט' לשעור ב' | |
| והחלקים אשר כפליהם שוים הנה יחס קצתם אל קצת כיחס כפליהם קצתם אל קצת | |
| אם כן יחס א' אל ב' כיחס ח' אל ט' אבל יחס א' אל ב' כיחס ה' אל ו' | |
| אם כן יחס ה' אל ו' כיחס ח' אל ט' | |
| וגם כן הנה מפני כפלי מ' לשעור ה' ככפלי נ' לשעור ו' אם כן יחס ה' אל ו' כיחס מ' אל נ' אבל יחס ה' אל ו' כיחס ח' אל ט' | |
| אם כן יחס מ' אל נ' כיחס ח' אל ט' | |
| וגם כן הנה יחס ב' אל ג' כיחס ד' אל ה' | |
| וכבר נלקח לשני שעורי ב"ד כפלים שוים והם ט"ל | |
| ולשני שעורי ג"ה כפלים שוים והם כ"מ אם כן יחס ט' אל כ' כיחס ל' אל מ' | |
| וכבר התבאר כי יחס ח' אל ט' כיחס מ' אל נ' | |
| אם כן שני שעורי ח"ל אם נוספים יחד על שני שעורי כ"נ ואם שוים יחד להם | |
| ואם חסרים יחד משניהם וח"ל כפלים שוים לשני שעורי א"ד וכ"נ לשני שעורי ג"ו אם כן יחס א' אל ג' כיחס ד' אל ו' | |
| וזה מה שרצינו לבאר | |
Proposition 24 |
|
| כד כאשר היה יחס הראשון אל השני כיחס השלישי אל הרביעי ויחס החמישי אל השני כיחס הששי אל הרביעי הנה יחס הראשון והחמישי מקובצים אל השני כיחס השלישי והששי מקובצים אל הרביעי | |
| המשל בו כי יחס הראשון והוא א"ב אל השני והוא ג' כיחס השלישי והוא ד"ה אל הרביעי והוא ו' | |
| ויחס החמישי והוא ב"ח אל השני והוא ג' כיחס הששי והוא ה"ט אל הרביעי והוא ו' | |
| הנה אומר כי יחס הראשון והחמישי מקובצים והוא א"ח אל השני והוא ג' כיחס השלישי והששי מקובצים והוא ד"ט אל הרביעי והוא ז' | |
| מופתו כי יחס א"ב אל ג' כיחס ד"ה אל ז' | |
| אבל יחס ג' אל ב"ח כיחס ז' אל ה"ט הנה השווי יהיה יחס א"ב אל ב"ח כיחס ד"ה אל ה"ט | |
| וכאשר הרכבנו יהיה יחס א"ח אל ח"ב כיחס ד"ט אל ט"ה אבל יחס ח"ב אל ג' כיחס ה"ט אל ו' | |
| הנה בשווי יהיה יחס א"ח אל ג' כיחס ד"ט אל ו' | |
| וזה מה שרצינו לבאר | |
Proposition 25 |
|
| כה כאשר יהיו ארבעה שעורים מתיחסים והיה הראשון היותר גדול מהם והאחרון היותר קטן מהם הנה שניהם מקובצים יותר גדולים מן הנשארים מקובצים | |
| המשל בו כי ארבעה שעורי אב'ג'ד' ה'ז' מתיחסים יחס א"ב אל ג"ד כיחס ה' אל ו' וא"ב היותר גדול מהם וו' היותר קטן מהם | |
| הנה אומר כי א"ב וו' מקובצים יותר גדולים מג"ד וה' מקובצים | |
| מופתו אנחנו נבדיל מן א"ב כמו ה' והוא א"ח ומן ג"ד כמו ז' והוא ג"ט הנה יחס א"ב אל ג"ד כיחס ה' אל ז' וה' כמו א"ח וז' כמו ג"ט אם כן א"ב אל ג"ד כיחס א"ח אל ג"ט | |
| אם כן יחס א"ב אל ג"ד כיחס ח"ב הנשאר אל ט"ד הנשאר וכאשר המירונו היה יחס א"ב אל ב"ח כיחס ג"ד אל ד"ט | |
| וא"ב הראשון יותר גדול מן ג"ד השלישי אם כן ב"ח השני יותר גדול מן ט"ד הרביעי ונשים א"ח וט"ג משותפים אם כן שני שעורי א"ב וט"ג יותר גדולים מא"ח וג"ד וג"ט כמו ו' וא"ח כמו ה' אם כן א"ב וו' מקובצים יותר גדולים מן ג"ד וה' מקובצים | |
| וזה מה שרצינו לבאר | |
| נשלם המאמר החמישי מספר אקלידס החכם |
Book Six |
המאמר השישי |
Definitions |
הקדמות המאמר הששי |
|
השטחים המתדמים הם אשר זויותיהם שוות וצלעותיהם המקיפות בזויות השוות מתיחסות |
|
והשטחים המספיקות הצלעות הם אשר צלעותיהם מתיחסות על הקדמה ואחור |
| נמצא בנסחא אחרת | |
| המספיקות הם אשר בכל אחת מהן הקדמות והמשכות | |
|
הגובה בתמונה הוא העמוד המוציא מנקודת ראשו אל תושבתו |
| ומצאתי בקצת הנסחאות | |
| הגובה בתמונה הוא היותר גדול שבעמודים הנופלים מנקודת מה מן הנקודות אשר על מקיף תמונה מן התמונות אי זו תמונה שיהיה על התושבת או על קו אשר יהיה על יושרו | |
|
ויאמר בקו הישר שהוא חלק על יחס בעל אמצעי ושתי קצוות כאשר היה יחס בקו בכללו אל היותר גדול שבחלקיו כיחס היותר גדול שבחלקיו אל היותר קטן משניהם |
| יאמר כי היחס מחובר מיחסים כאשר היו שעורי היחסים אשר נכפלו בעצמיהם עשו יחס מה | |
| נמצא בנסחא אחרת כי היחס מחובר יחלק ליחסים כאשר היו שעורי היחסים קצתם על קצת יחדשו יחס מה | |
Proposition 1 |
|
| The parallelograms and triangles whose heights are the same magnitude, their ratio to one another is as the ratio of their bases to one another. | א השטחים נכחי הצלעות והמשולשים כאשר היה גבהותם בשעור אחד הנה יחס קצתם אל קצת כיחס תושבותיהם קצתם אל קצת |
Proposition 18 |
|
| יח כל שני משולשים דומים הנה יחס אחד משניהם אל האחר הוא יחס צלעו אל צלעו אשר הוא נכחי לו שנוי | |
Proposition 32 |
|
| For every right-angled triangle, the rectilinear figure on the side that is opposite to the right angle equals the sum of the rectilinear figures on the two remaining sides that are similar to it. | לב כל משולש נצב הזוית הנה התמונה ישרת הקוים המחוברת אל מיתר הזויות הנצבת ממנו כמו שתי התמונות ישרות הצלעות המחוברות אל שתי הצלעות הנשארות יחד כאשר היו דומות אליו והיו על מצבו |
| המשל בו כי זוית א' ממשלש אב"ג נצבת | |
| הנה אומר כי התמונה ישרת הצלעות הסמוכה אל מיתר זוית א' והוא צלע ב"ג כמו השתי תמונות ישרות הצלעות הסמוכות אל שתי צלעות א"ב א"ג יחד כאשר היו דומים לה ועל מצבה | |
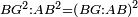
|
הנה מפני כי יחס מרובע ב"ג אל מרובע א"ב כיחס ב"ג אל א"ב שנוי |
| ויחס התמונה ישרת הצלעות הסמוכה אל ב"ג אל התמונה הסמוכה אל א"ב הדומה אליו והמונח במצבו כיחס ב"ג אל א"ב שנוי | |
| אם כן יחס מרובע ב"ג אל מרובע א"ב כיחס התמונה הסמוכה אל ב"ג אל התמונה הסמוכה אל א"ב | |
| הנה אם כן יחס מרובע ב"ג אל שני מרובעי א"ב א"ג כיחס התמונה הסמוכה אל ב"ג אל שתי התמונות הסמוכות אל א"ב א"ג | |
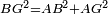
|
אבל מרובע ב"ג כמו שני מרובעי א"ב וא"ג |
| אם כן התמונה ישרת הצלעות הסמוכה אל ב"ג כמו שתי התמונות הישרות הצלעות הדומות אליה והמונחת במצבה הסמוכה אל א"ב | |
| Q.E.D. | וזה מה שרצינו לבאר |
| אחרים והוא שנוציא עמוד א"ד הנה שני משולשי אב"ג אב"ד מתדמים | |
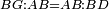
|
אם כן יחס ב"ג אל א"ב כמו יחס א"ב אל ב"ד |
| ויחס ג"ב אל ב"ד כיחס השטח הסמוך אל ג"ב אל השטח הסמוך אל א"ב והדומה אליו | |
| וכן יחס ב"ג אל ג"ד כיחס השטח הסמוך אל ב"ג אל השטח הסמוך אל ג"א הדומה אליו | |
| אם כן יחס ב"ג אל ב"ד וד"ג כיחס השטח שהוא סמוך אל ב"ג אל שני השטחים הסמוכים אל א"ב וא"ג יחד | |
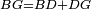
|
וב"ג כמו ב"ד ד"ג יחד |
| אם כן השטח הסמוך אליו כמו שני השטחים הסמוכים אל שניהם יחד | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 33 |
|
| When there are two angles in equal circles that stand at the centers or at the circumferences, the ratio of the angle to the angle is as the ratio of both arcs on which they stand one to the other. | לג כאשר היו בשתי עגולות שוות שתי זויות על המרכז או על הקו המקיף הנה יחס הזויות אל הזויות כיחס שתי הקשתות אשר עליהם אחת אל אחת |
Example: 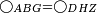
|
המשל בו בשתי עגולות אב"ג דה"ז השוות |
| ועל מרכזיהם שתי זויות גח"ב הט"ז | |
Supposition: 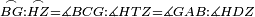
|
הנה אומר כי יחס קשת ב"ג אל קשת ה"ז כיחס זוית בח"ג אל זוית הט"ז וכיחס זוית גא"ב אל זוית הד"ז |
| Proof: | המופת אנחנו נבדיל מעגולת אב"ג כמו קשת ב"ג כמה שרצינו נאמר שנבדיל ג"כ כ"ל ומעגולת דה"ז גם כן כמו קשת ה"ז כמה שנרצה נאמר שנבדיל ז"מ מ"נ ונוציא שני קוי כ"ח ח"ל ושני קוי ט"מ ט"נ |
|
|
הנה קשתות ב"ג ג"כ כ"ל שוות |
|
|
אם כן זויות בח"ג גח"כ כח"ל שוות |
|
|
אם כן כפלי קשת ב"ל לקשת ב"ג ככפלי זוית בח"ל לזוית בח"ג |
|
|
וכן כפלי קשת ה"נ לקשת ה"ז ככפלי זוית הט"נ לזוית הט"ז |
|
|
ואם היה ב"ל תוסיף על קשת ה"נ הנה זוית בח"ל תוסיף על זוית הט"נ |
|
|
ואם יהיה שיהיו שוים אליה הנה היא שוה אליה |
|
|
ואם היה שיוחסרו ממנה הנה היא תחסר ממנה |
The four magnitudes: 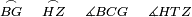 are proportional. are proportional.
|
אם כן השעורים ארבעה קשת ב"ג וקשת ה"ז וזוית בח"ג וזוית הט"ז מתיחסים |
|
וכפלי קשת ב"ג וזוית בח"ג השוה הפעמים היא קשת ב"ל וזוית בח"ל |
|
וכפלי קשת ה"ז וזוית הט"ז השוה הפעמים היא קשת ה"נ וזוית הט"נ |
|
|
וכבר התבאר כי קשת ב"ל אם היתה נוספת על קשת ה"נ הנה זוית בח"ל נוספת על זוית הט"נ |
|
|
ואם היתה שוה אליה הנה היא שוה אליה |
|
|
ואם היתה חסרה ממנו הנה היא חסרה ממנה |
|
|
אם כן יחס קשת ב"ג אל קשת ה"ז כיחס זוית בח"ג אל זוית הט"ז |
|
|
וזוית א' אשר על המקיף הנה היא חצי זוית בח"ג אשר על המרכז |
|
|
וזוית הד"ז היא חצי זוית הט"ז |
|
|
אם כן יחס קשת ב"ג אל קשת ה"ז גם כן כיחס זוית א' אל זוית ד' |
| Q.E.D. | וזה מה שרצינו לבאר |
| והנה נשלם המאמר הששי מספר אקלידס החכם בשרשים | |
| ויבא אחריו המאמ' השביעי מזה הספר בג"ה בעה"ו ובס"ד |
Book Seven |
המאמר השביעי |
Definitions |
הקדמות המאמר |
|
האחדות הוא הדבר אשר יאמר בו לכל דבר אחד מן הנמצאות אחד |
|
המספר הוא הקבוץ המורכב מן האחדים |
|
המספר הקטן יהיה חלק מן המספר הרב כאשר היה שימנה אותו |
|
ויהיה חלקים ממנו כאשר היה שלא ימנה אותו |
|
המספר הרב יהיה כפלים למספר הקטן כאשר היה הקטן מונה אותו |
|
המספר הזוג הוא אשר יחלק בשני חלקים שוים |
|
המספר הנפרד הוא אשר אי אפשר שיחולק לשני חלקים שוים ואשר יתחלף הזוג באחד |
|
המספר אשר יאמר לו זוג הזוג הוא אשר ימנה אותו מספר זוג פעמים מספרם זוג |
|
המספר אשר יאמר לו זוג הנפרד הוא אשר ימנהו מספר נפרד פעמים מספרם זוג |
|
המספר אשר יאמר לו נפרד הנפרד הוא אשר ימנהו מספר נפרד פעמים מספרם נפרד |
|
המספר אשר יקרא ראשון הוא אשר ישיגהו המנין באחד לבד |
|
המספר אשר יאמר לו המספר המורכב הוא אשר ישיגהו המנין במספר זולת אחד |
|
המספרים המשותפים הם אשר ימנה אותם מספר אחד |
|
המספרים המובדלים הם אשר אמנם לא ימנם מספר משותף כי אם אחד לבדו |
|
המספר המוכה במספר הוא אשר יכפל פעמים כמנין מה שבמוכה בו מן האחדים ויהיה מה שיתקבץ מספר אחד |
|
המספר המרובע הוא המקובץ מהכאת מספר בדומה לו או הוא אשר יקיפו בו שני מספרים שוים |
|
המספר המעוקב הוא המקובץ מהכאת מספר במה שיתקבץ מהכאתו בדומה לו או הוא אשר יקיפו בו שלשה מספרים שוים |
|
המספר המשוטח הוא המקובץ מהכאת מספר מה שהיה באחר או אשר יקיפו בו שני מספרים |
|
ויקראו שני המספרים אשר הוכה אחד משניהם באחר והתקבץ משניהם המשוטח ההוא שני צלעי השטח |
|
והמספר המוגשם הוא המקובץ מהכאת מספר במה שיתקבץ מהכאת שני מספרים אחד באחר |
|
והמספרים השלשה צלעות המוגשם |
|
והמספרים המתיחסים הם אשר יהיה הראשון מן השני והשלישי מן הרביעי חלק אחד בעצמו או חלקים אחדים בעינם |
|
המספרים המשוטחים והמוגשמים הדומים הם אשר צלעותיהם מתיחסות |
|
המספר השלם הוא השוה לכל חלקיו |
| The definitions are complete. | תמו ההקדמות |
Proposition 1 |
|
| 1) For every two unequal numbers, such that the multiple of the smaller that is contained in [the greater] is subtracted from the greater, until the remainder is less than the smaller; then the multiple of this remainder that is contained in [the smaller] is subtracted from the smaller and what is left is less than the [first] remainder; then the multiple of second remainder that is contained in [the first remainder] is subtracted from the first remainder and what is left is less than the [second remainder]; and so on [the remainders] are subtracted continually; if what is left from [the two original numbers] never ends with the number that precedes it, but until a unit is left, then the two [original] unequal numbers are relatively prime. | א כל שני מספרים מתחלפים יחסר מהרב משניהם מה שבו מכפלי הקטן עד שיותר פחות מן הקטן אחר כן יחסר מן הקטן מה שבו מכפלי היתרון ההוא ויותר פחות ממנו |
| Example:
|
המשל בו כי שני מספרי א"ב ג"ד יחוסר מן הגדול משניהם והוא א"ב ממנו מדמיוני ג"ד הפחות משניהם והוא ט"ב ונשאר פחות מן ג"ד והוא א"ט |
|
|
עוד חוסר מן ג"ד מה שבו מדמיוני א"ט והוא ד"ח והותיר פחות מן א"ט והוא ג"ח |
|
|
עוד חוסר מן א"ט מה שבו מדמיוני ג"ח והוא כ"ט ונותר א"כ והוא אחד |
| Supposition: AB and GD are relatively prime. | ואומר כי שני מספרי א"ב ג"ד נבדלים |
Proof:
|
המופת כי אם לא יהיו מספרי א"ב ג"ד נבדלים הנה ימנה שניהם מספר מה אם היה אפשר והוא מספר ה' מהפתיחה |
|
אם כן מספר ה' ימנה ג"ד וג"ד ימנה ט"ב |
|
אם כן הוא ימנה ט"ב והוא ימנה כל א"ב |
|
הנה הוא אם כן ימנה כל א"ט וט"א ימנה ח"ד |
|
אם כן ה' ימנה ח"ד וימנה כל ג"ד |
|
הנה אם כן ה' ימנה ח"ג וח"ג ימנה כ"ט |
|
אם כן ה' ימנה כ"ט והוא ימנה כל ט"א |
|
הנה אם כן ימנה א"כ וא"כ אחד וה' מספר זה שקר |
|
אם כן לא ימנה א"ב ג"ד מספר זולת האחד |
| def. relatively prime: Therefore, they are relatively prime. | אם כן שניהם נבדלים מהפתיחה |
| Q.E.D. | וזה מש"ל |
Proposition 2 |
|
| 2) We wish to explain how we find the greatest common number that counts two given relatively composite unequal numbers. | ב נרצה שנבאר איך נמצא גדול מספר משותף ימנה שני מספרים ידועים משותפים בלתי שוים |
|
הנה נשים שני המספרים הידועים המשותפים הבלתי שוים שני מספרי א"ב ג"ד |
|
ונרצה למצוא המספר היותר גדול המשותף אשר ימנה שניהם יחד |
|
הנה אם היה ג"ד ימנה א"ב והוא ימנה עצמו הנה הוא גדול המשותף אשר ימנה שניהם יחד |
|
כי הוא בלתי אפשר שימנה שניהם יחד מספר יותר גדול ממנו |
|
ואם היה ג"ד בלתי מונה א"ב הנה א"ב ג"ד אם כן מתחסרים כמו שספרנו קודם |
| VII.1: | כי הנה אי אפשר שלא יותיר מספר ימנה אשר ילוה אליו לפניו כי הוא אם לא יותיר מספר ימנה אשר ילוה אליו לפניו הנה שניהם אם כן נבדלים משלפניה |
| הנה ג"ד כאשר ימנה ב"א יותיר פחות ממנו והוא א"ה | |
| וה"א כאשר מנה ג"ד יחסר פחות ממנו והוא ז"ג | |
|
אם כן הנה ימנה ז"ג ה"א |
|
אם כן ז"ג ימנה ה"א וה"א ימנה ז"ד |
|
אם כן ז"ג ימנה ז"ד וימנה עצמו |
|
אם כן ז"ג ימנה כל ג"ד וג"ד ימנה ה"ב |
|
אם כן ז"ג ימנה ה"ב וימנה א"ה |
|
אם כן ז"ג ימנה כל א"ב וימנה ג"ד הנה הוא אם כן מספר משותף לשניהם |
| Supposition: it is their greatest common measure. | ואומר כי הוא המספר הגדול המשותף |
| הנה אם לא יהיה ז"ג הוא המספר הגדול המשותף אשר ימנה א"ב ג"ד יחד הנה ימנה אותם מספר אחר יותר מז"ג הוא המספר המשותף והוא ח' | |
|
אם כן ח' ימנה ג"ד וג"ד ימנה ה"ב |
|
אם כן ח' ימנה ה"ב וימנה כל א"ב |
|
הנה ח' אם כן ימנה א"ה |
|
וגם כן הנה ח' ימנה א"ה וה"א ימנה ז"ד |
|
אם כן ח' ימנה ז"ד וימנה כל ג"ד |
| הנה הוא אם כן ימנה ז"ג וז"ג פחות ממנו | |
| הנה אם כן הגדול ימנה הפחות זה שקר | |
| אם כן לא ימנה שני מספרי א"ב ג"ד מספר יותר ממספר ז"ג | |
| אם כן ז"ג גדול מספר ימנה א"ב ג"ד הנה כבר מצאנו גדול מספר משותף ימנה א"ב ג"ד והוא ז"ג | |
| וזה מ'ש'ל' | |
| ובכאן התבאר כי כל מספר ימנה שני מספרים הנה הוא גם כן ימנה המספר הגדול אשר ימנה שניהם יחד מספר משותף | |
| Q.E.D. | ומ'ש'ל' |
Proposition 3 |
|
| 3) We wish to find the greatest common measure of three given relatively composite unequal numbers. | ג נרצה למצא גדול מספר משותף ימנה שלשה מספרים ידועים משותפים בלתי שוים |
|
הנה נשים המספרים הידועים המשותפים הבלתי שוים א'ב'ג' |
| VII.2: We take the greatest common number that counts two numbers of them A and B, which is D. | ונקח גדול מספר משותף ימנה שני מספרים משניהם והם א"ב משותף משניהם והוא מספר ד' משלפניה |
| D either measures G, or does not measure it. | אם כן ד' ימנה ג' או לא ימנה אותו |
|
ונאמר תחלה שימנה אותו והוא ימנה א"ב |
|
אם כן ד' ימנה א'ב'ג' |
|
הנה אומר שהוא גדול מספר משותף ימנה אותם יחד |
|
שאם לא יהיה ד' גדול מספר ימנה א'ב'ג' הנה ימנה אותם מספר גדול מד' והוא מספר ה' |
|
אם כן ה' ימנה א'ב'ג' |
|
אם כן הוא ימנה א"ב |
|
וימנה המספר הגדול היותר אשר ימנה שניהם והוא ד' מסוף אשר לפניה |
|
אם כן ה' ימנה ד' |
|
הגדול ימנה הפחות זה שקר |
|
אם כן לא ימנה א'ב'ג' מספר גדול מן ד' |
|
וגם כן נאמר שיהיה ד' לא ימנה ג' |
| ונקח גדול מספר ימנה שני מספרי ג"ד והוא ה' | |
| אם כן ה' ימנה ד' וד' ימנה שני מספרי א"ב | |
| אם כן ה' ימנה שני מספרי א"ב וימנה ג' אם כן ה' ימנה א'ב'ג' יחד מסוף אשר לפניה | |
|
הנה אומר שהוא המספר הגדול היותר משותף אשר ימנה אותם |
| שאם לא יהיה ה' גדול יותר מספר משותף א'ב'ג' | |
|
אם כן ז' ימנה א"ב |
|
וימנה המספר הגדול המשותף אשר ימנה שניהם יחד והוא ד' |
|
אם כן ז' ימנה ד' והוא ימנה ג' |
|
אם כן ז' ימנה גדול מספר ימנה ג"ד והוא ה' |
|
הנה ז' אם כן ימנה ה' |
|
הגדול ימנה הפחות זה שקר |
|
אם כן לא ימנה א'ב'ג' מספר גדול מן ה' |
| הנה כבר מצאנו גדול מספר משותף ימנה א'ב'ג' השלשה הידועים המשותפים הבלתי שוים | |
| Q.E.D. | ומ'ש'ל' |
Proposition 4 |
|
| 4) For every two unequal numbers, the smaller is either a part or parts of the greater. | ד כל שני מספרים מתחלפים
הנה הקטן אם שיהיה חלק מן הגדול ואם חלקים |
Example: 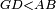
|
המשל בו כי שני מספרי א"ב ג"ד מתחלפים והקטן משניהם ג"ד |
| Supposition: GD is either a part or parts of AB. | הנה אומר כי ג"ד אם חלק מן א"ב ואם חלקים |
Proof:
|
המופת כי ג"ד אם היה שימנה א"ב הנה הוא חלק ממנו |
|
ואם היה שלא ימנה אותו הנה א"ב ג"ד אם שיהיו נבדלים ואם שיהיו משותפים |
|
ואם היו נבדלים הנה אנחנו כאשר חלקנו ג"ד לאחדים בו יהיה כל אחד מן ג"ד חלק מן א"ב |
|
ואם היו משותפים לקחנו גדול מספר משותף ימנה אותם והוא ה"ז מב' מזה |
|
ונחלק ג"ד על ה"ז ויצא ג"ח ח"ט ט"ד |
|
הנה ז"ה ימנה א"ב |
|
|
וישתוה לכל אחד מן ג"ח ח"ט ט"ד |
|
אם כן כל אחד מן ג"ח ח"ט ט"ד חלק מן א"ב הנה ג"ד אם כן חלקים מן א"ב |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 5 |
|
| 5) When a number is a part of a number, and another number is the same part of another number, then the sum of the two smaller is the same part of the sum of the two greater that one of the two smaller is of one of the two greater. | ה כאשר יהיה מספר מה חלק ממספר ומספר אחר כמו החלק ההוא ממספר אחר הנה שנים הקטנים מקובצים מהשנים הגדולים מקובצים הם החלק ההוא אשר היה אחד מן השנים הקטנים מאחד מהשני הגדולים |
| Example: A is a part of GD, and Z is the same part of CT. | המשל בו כי מספר א' חלק ממספר ג"ד ומספר ז' ממספר ח"ט כמו החלק ההוא |
| Supposition: A+Z is the same part of CT+GD that A is of GD. | הנה אומר כי שני מספרי א"ז מקובצים משני מספרי ח"ט ג"ד מקובצים הם החלק ההוא אשר הוא א' מן ג"ד |
| Proof: the part that A is of GD is the same part that Z is of CT. | המופת כי חלק א' מן ג"ד הוא חלק ז' מן ח"ט |
| VII.introduction: the number of multiples of A in GD is as the number of multiples of Z in CT. | אם כן שעור מה שבג"ד מכפלי א' כשעור מה שבח"ט מכפלי ז' מפתיחת זה |
|
הנה נחלק ג"ד על א' ויצא ג"כ כ"ד |
|
ונחלק ח"ט על ז' ויצא ח"ל ל"ט |
|
הנה מספר ג"כ כ"ד כמספר ח"ל ל"ט |
|
|
וג"כ כמו א' |
|
|
וח"ל כמו ז' |
|
|
אם כן ג"כ ח"ל כמו א"ז |
|
|
וכן כ"ד ל"ט כמו א"ז |
| The number of multiples of A in GD is as the number of multiples of A+Z in GD+HT. | אם כן מנין מה שבג"ד מדמיוני א' כמנין מה שבג"ד ח"ט מקובצים מדמיוני א"ז מקובצים |
| The part that A is of GD is the same part that Z+A is of GD+CT. | אם כן חלק א' מן ג"ד הוא חלק ז"א מקובצים מן ג"ד ח"ט מקובצים |
| Q.E.D. | ומ'ש'ל' |
Proposition 6 |
|
| 6) When a number is parts of a number, and another number is the same parts of another number, then the sum of the two smaller is the same parts of the sum of the two greater that one of the two smaller is of one of the two greater. | ו כאשר היה מספר מה חלקים ממספר אחר ומספר אחר כמו החלקים ההם ממספר אחר הנה השנים הקטנים מן השנים הגדולים מקובצים כמו חלקי אחד מן השנים הקטנים מקרובו מן השנים הגדולים |
| Example: AB is parts of G, and HZ is the same parts of C that AB is of G. | המשל בו כי מספר א"ב חלקים ממספר ג' ומספר ה"ז ממספר ח' כמו חלקי א"ב מן ג' |
| Supposition: AB+HZ is the same parts of G+C that AB is of G. | הנה אומר כי כל א"ב ה"ז מכל ג"ח כמו חלקי א"ב מן ג' |
| Proof: the parts that AB is of G are the same parts that HZ is of C. | המופת כי חלקי א"ב מן ג' כמו חלקי ה"ז מן ח' |
|
והנה נחלק א"ב בחלקי ג' א"כ כ"ב |
|
וה"ז בחלקי ח' ויצא ה"ל ל"ז |
|
הנה מנין א"כ כ"ב כמנין ה"ל ל"ז |
|
אם כן חלק א"כ מן ג' הוא חלק ה"ל מן ח' |
VII.5:
|
הנה אם כן כל א"כ ה"ל היו מכל ג"ח כמו חלק א"כ מן ג' מה' מזה |
|
וכן כאשר קבץ כ"ב ל"ז היו מכל ג"ח כמו חלק כ"ב מן ג' |
| AB+HZ is the same parts of G+C that AB is of G. | אם כן א"ב ה"ז כאשר יקובצו היו מן ג"ח מקובצים כמו חלקי א"ב מן ג' |
| Q.E.D. | ו'מ'ש'ל' |
Proposition 7 |
|
| 7) When there are four numbers, such that the first is the same part of the second as the third is of the fourth, when we invert, the first is the same part or parts of the third, as the second is of the fourth. | ז כאשר היו ארבעה מספרים והיה הראשון חלק מן השני והיה השלישי מן הרביעי כמו החלק ההוא הנה אנחנו כאשר המירונו היה החלק או החלקים אשר יהיה הראשון מן השלישי כמו החלק או החלקים אשר יהיה השני מן הרביעי |
| Example: A is a part of GB; D is the same part of HZ as A is of GB. | המשל בו כי מספר א' חלק ממספר ג"ב ומספר ד' חלק ממספר ה"ז כמו חלק א' מן ג"ב |
| Supposition: When we invert, the first, which is A, is the same part or parts of the third, which is D, as the second is of the fourth, which are BG and HZ. | הנה אומר כאשר המירונו היה החלק או החלקים אשר יהיה הראשון והוא א' מן השלישי והוא ד' כמו החלק או החלקים אשר יהיה השני מן הרביעי והם ב"ג וה"ז |
| Proof: A is the same part of GB that D is of HZ. | המופת כי חלק א' מן ב"ג הוא חלק ד' מן ה"ז |
|
אם כן מה שבב"ג מדמיוני א' כמו מה שבה"ז מדמיוני ד' |
|
ונחלק ב"ג מדמיוני א' ויצא ב"ח ח"ג |
|
ונחלק ה"ז כדמיוני ד' ויצא ה"ט ט"ז |
|
הנה מנין ב"ח ח"ג כמו מנין ה"ט ט"ז |
|
וב"ח כמו ח"ג |
|
וה"ט כמו ט"ז |
| VII.5: BC is the same part or parts of HT as BG is of HZ. | אם כן החלק או חלקים אשר הוא ב"ח מן ה"ט הוא החלק או החלקים אשר הוא ב"ג מן ה"ז מה' מזה |
|
וב"ח כמו א' |
|
וה"ט כמו ד' |
| A is the same part or parts of D, as BG is of HZ. | אם כן החלק או החלקים אשר הוא א' מן ד' הוא החלק או החלקים אשר הוא ב"ג מן ה"ז |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 8 |
|
| 8) When there are four numbers, such that the first is the same parts of the second as the third is of the fourth, when we invert, the first is the same part or parts of the third, as the second is of the fourth. | ח כאשר היו ארבעה מספרים והיה הראשון חלקים מן השני והיה השלישי מן הרביעי כמו החלקים ההם הנה כאשר המירונו היו החלקים או החלק אשר היו הראשון מן השלישי כמו החלקים או החלק אשר יהיה השני מן הרביעי |
| Example: AB is parts of G; DH is the same parts of Z as AB is of G. | המשל בו כי מספר א"ב חלקים ממספר ג' ומספר ד"ה ממספר ז' כמו חלקי א"ב מן ג' |
| Supposition: When we invert AB is the same part or parts of DH, as G is of Z. | הנה אומר כי אנחנו כאשר המירונו יהיו החלקים או החלק אשר א"ב מן ד"ה הם החלק או החלקים אשר יהיה ג' מן ז' |
| Proof: AB is the same parts of G that DH is of Z. | המופת כי החלקים אשר הם א"ב מן ג' הם החלקים אשר הם ד"ה מן ז' |
|
הנה מה שבא"ב מדמיוני חלקי ג' כמו מה שבד"ה מדמיוני חלקי ז' |
|
ונחלק א"ב בחלקי ג' ויצא א"ח ח"ב |
|
ונחלק ד"ה בחלקי ז' ויצא ד"ט ט"ה |
|
הנה מנין א"ח ח"ב כמו מנין ד"ט ט"ה |
|
וא"ח כמו ח"ב |
|
וד"ט כמו ט"ה |
| AC is the same part of G as DT is of Z. | אם כן חלק א"ח מן ג' כחלק ד"ט מן ז' |
| When we invert, AC is the same part or parts of DT, as G is of Z. | וכאשר המירונו הנה החלק או החלקים אשר הוא א"ח מן ד"ט הוא החלק או החלקים אשר הוא ג' מן ז' |
| CB is the same part of G as TH is of Z. | והחלק אשר הוא ח"ב מן ג' הוא החלק אשר הוא ט"ה מן ז' |
| When we invert, CB is the same part or parts of TH, as G is of Z. | וכאשר המירונו היה החלק או החלקים אשר הוא ח"ב מן ט"ה הוא החלק או החלקים אשר הוא ג' מן ז' |
| It has been clarified that AB is the same part or parts of DH, as G is of Z. | וכבר התבאר כי החלק או החלקים אשר הוא א"ב מן ד"ה הוא החלק או החלקים אשר הוא ג' מן ז' |
| Q.E.D. | ומ'ש'ל' |
Proposition 9 |
|
| 9) When a number is a part of another number, as the part that a subtracted from the one is of a subtracted from the other, then the remainder from one of them is the same part of the remainder from the other that the whole is of the whole. | ט כאשר היה מספר מה חלק ממספר אחר כחלק מה שיחסר ממנו הנה ממה שיחסר מן האחר הנה הנשאר מאחד משניהם מן הנשאר מן האחר הוא חלק הכל מן הכל |
| In another version: When there are two numbers, such that one is a part of the other, and a number was subtracted from each of them, so that the subtracted from the part is of the subtracted from the whole as the whole is of the whole, then the remainder from the part is the same part of the remainder from the whole that the whole is of the whole. | בנסחא האחרת כאשר היו שני מספרים אחד מהם חלק מן האחר וחוסר מכל אחד מהם מספר והיה המחוסר מהחלק למחוסר מהכל בכל מהכל הנה הנשאר מהחלק מהנשאר מהכל כחלק הכל מהכל |
| Example: AB is a part of GD; AH and GZ are subtracted from them, so that AB is the same part of GD as AH is of GZ. | המשל בו כי מספר א"ב חלק ממספר ג"ד והמחוסרים משניהם א"ה ג"ז וחלק א"ב מן ג"ד כמו חלק א"ה מן ג"ז |
| Supposition: the remainder HB is the same part of the remainder DZ as whole AB is of whole GD. | הנה אומר כי חלק ה"ב הנשאר מן ד"ז הנשאר הוא חלק כל א"ב מכל ג"ד |
| Proof: We set AH as the same part of GZ that BH is of GC. | המופת אנחנו נשים חלק א"ה מן ג"ז הוא חלק ב"ה מן ג"ח |
|
אם כן חלק א"ה מן ג"ז הוא חלק א"ב מן ז"ח |
|
וחלק א"ה מן ג"ז הוא חלק א"ב מן ג"ד |
|
אם כן חלק א"ב מן ח"ז הוא חלק א"ב מן ג"ד |
|
|
אם כן ח"ז כמו ג"ד |
|
|
ויחוסר ג"ז המשותף וישאר ג"ח כמו ז"ד |
|
וכבר היה חלק א"ה מן ג"ז הוא חלק ה"ב מן ג"ח |
|
אם כן חלק א"ה מן ג"ז הוא חלק ה"ב מן ד"ז |
|
וחלק א"ה מן ג"ז הוא חלק א"ב מן ג"ד |
|
אם כן חלק ה"ב מן ז"ד הוא חלק א"ב מן ג"ד |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 10 |
|
| 10) When a number is parts of another number, as the parts that a subtracted from the one is of a subtracted from the other, then the remainder [from one of them] is the same parts of the remainder [from the other] that the whole is of the whole. | י כאשר היה מספר חלקים ממספר אחר כחלקי מה שיחסר ממנו ממה שיחוסר מן האחר הנה הנשאר מן הנשאר הוא חלקי הכל מן הכל |
| Example: AB is parts of GD; AH and GZ are subtracted from them, so that AH is the same part of GZ as AB is of GD. | המשל בו כי מספר א"ב חלקי' ממספר ג"ד והמחוסרים משניהם א"ה ג"ז וחלקי א"ה מן ג"ז כחלקי א"ב מן ג"ד |
| Supposition: the remainder HB is the same parts of the remainder ZD as whole AB is of whole GD. | הנה אומר כי חלקי ה"ב הנשאר מחלקי ז"ד הנשאר הם חלקי כל א"ב מחלקי כל ג"ד |
Proof:
|
המופת אנחנו נשים ח"ט כמו א"ב |
|
אם כן כל חלקי ח"ט מן ג"ד הם חלקי א"ה מן ג"ז |
We divide CT into the parts of GD: 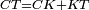
|
ונחלק ח"ט בחלקי ג"ד ויצא ח"כ כ"ט |
We divide AH into the parts of GZ: 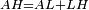
|
ונחלק א"ה בחלקי ג"ז ויצא א"ל ל"ה |
|
הנה מנין ח"כ כ"ט כמו מנין א"ל ל"ה |
|
אם כן חלק ח"כ מן ג"ד הוא חלק א"ל מן ג"ז |
|
|
וג"ד גדול מן ג"ז |
|
|
אם כן חלק ח"כ גדול מן א"ל |
|
ונשים ח"מ כמו א"ל |
|
אם כן חלק ח"כ מן ג"ד כחלק ח"מ מן ג"ז |
|
וישאר מ"כ מן ז"ד כמו חלק ח"כ מן ג"ד |
|
וגם כן הנה חלק כ"ט מן ג"ד כחלק ל"ה מן ג"ז |
|
|
וג"ד גדול מן ג"ז |
|
|
אם כן כ"ט גדול מן ל"ה |
|
ונשים כ"נ כמו ל"ה |
|
אם כן חלק כ"ט מן ג"ד כחלק כ"נ מן ג"ז |
|
ונשאר חלק ט"נ מן ז"ד כמו חלק כל כ"ט מכל ג"ד |
|
וכאשר קובץ מ"כ נ"ט היו מן ז"ד כמו כל ח"ט מכל ג"ד |
|
|
ומ"כ נ"ט יחד כמו ה"ב |
|
|
וח"ט כמו א"ב |
| The remainder HB is the same parts of the remainder ZD as AB is of GD. | הנה נשאר חלקי ה"ב מן ז"ד כמו חלקי א"ב מן ג"ד |
| Q.E.D. | ומ'ש'ל' |
Proposition 11 |
|
| 11) When two numbers are subtracted from two numbers and the ratio of the subtracted to the subtracted is as the ratio of the whole to the whole, then the ratio of the remainder to the remainder is as the ratio of the whole to the whole. | י"א כאשר חוסר משני מספרים שני מספרים והיה יחס המחוסר אל המחוסר כיחס הכל אל הכל הנה יחס הנשאר אל הנשאר כיחס הכל אל הכל |
Example: two numbers AB and GD; AH and GZ are subtracted from them, so that 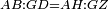 . .
|
המשל בו כי שני מספרי א"ב וג"ד חוסר משניהם א"ה וג"ז והיה יחס א"ב אל ג"ד כיחס
א"ה אל ג"ז |
Supposition: 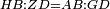
|
הנה אומר כי יחס ה"ב הנשאר אל ז"ד הנשאר כיחס א"ב אל ג"ד |
Proof: 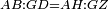
|
המופת כי יחס א"ב אל ג"ד כיחס א"ה אל ג"ז |
|
אם כן החלק או החלקים אשר הם א"ב מן ג"ד הוא החלק או החלקים אשר הם א"ה מן ג"ז |
|
וישאר ה"ב מן ז"ד הוא החלק או החלקים אשר הם א"ב מן ג"ד |
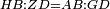
|
אם כן יחס ה"ב אל ז"ד כיחס א"ב אל ג"ד |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 12 |
|
| 12) When there are proportional numbers, as many as there are, then the ratio of one of the antecedents to its corresponding of the consequents is as the ratio of [the sum of] the antecedents to [the sum of] the consequents. | י"ב כאשר היו מספרים מתיחסים כמה שיהיו הנה יחס אחד מן הקודמים אל קרובו מן הנמשכים כיחס הקודמים אל הנמשכים |
Example: A, B, G, D are proportional numbers: 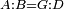 . .
|
המשל בו כי מספרי א"ב ג"ד מתיחסים יחס א' אל ב' כיחס ג' אל ד' |
Supposition: 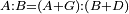
|
הנה אומר כי יחס א' אל ב' כיחס א"ג יחד אל ב"ד יחד |
Proof: 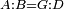
|
המופת כי יחס א' אל ב' כיחס ג' אל ד' |
|
אם כן החלק או החלקים אשר הוא א' מן ב' הוא החלק או החלקים אשר ג' מן ד' |
|
וכאשר קובץ א"ג וקובץ ב"ד היה החלק או החלקים אשר הוא א"ג מן ב"ד יחד הוא החלק או החלקים אשר הוא א' מן ב' יחד |
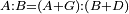
|
אם כן יחס א' אל ב' כיחס א"ג יחד אל ב"ד יחד |
| Q.E.D. | ומ'ש'ל' |
Proposition 13 |
|
| 13) For every four proportional numbers, when they are inverted they are proportional. | י"ג כל ארבעה מספרים מתיחסים הנה הם כאשר הומרו יהיו מתיחסים |
Example: A, B, G, D are proportional numbers: 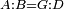
|
המשל בו כי ארבעה מספרי א"בג"ד מתיחסים יחס א' אל ב' כיחס ג' אל ד' |
Supposition: 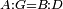
|
הנה אומר שהם כאשר הומרו היה יחס א' אל ג' כיחס ב' אל ד' |
| Proof:
|
המופת כי יחס א' אל ב' כיחס ג' אל ד' |
|
אם כן החלק או החלקים אשר הוא א' מן ב' הוא החלק או החלקים אשר הוא ג' מן ד' |
|
וכאשר המירונו היה החלק או החלקים אשר הוא א' מן ג' הוא החלק או החלקים אשר הוא ב' מן ד' |
|
|
אם כן יחס א' אל ג' כיחס ב' אל ד' |
| Q.E.D. | ומ'ש'ל' |
Proposition 14 |
|
| 14) When there are numbers, as many as there are, and other numbers of the same multitude, such that every two numbers of the first are in the same ratio to two numbers of the others, then they are proportional in the ratio of equality. | י"ד כאשר היו מספרים כמה שיהיו ומספרים אחרים על מספרם כל שני מספרים מן הראשון על יחס שני מספרים מן האחר הנה הם ביחס השווי מתיחסים |
| Example: A, B, G, and D, H, Z are of the same multitude; every two of the first are in the same ratio to two of the others: | המשל כי מספרי א'ב'ג' ומספרי ד'ה'ז' על מנין אחד וכל שני מספרים מן הראשון על יחס שני מספרים מן האחר |
|
|
יחס א' אל ב' כיחס ד' אל ה' |
|
|
ויחס ב' אל ג' כיחס ה' אל ז' |
Supposition: 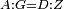
|
הנה אומר שהם ביחס השווי יהיה יחס א' אל ג' כיחס ד' אל ז' |
| Proof:
|
המופת כי יחס א' אל ב' כיחס ד' אל ה' |
|
וכאשר המירונו היה יחס א' אל ד' כיחס ב' אל ה' |
|
|
וכבר התבאר כי יחס א' אל ד' כיחס ב' אל ה' |
|
|
אם כן יחס א' אל ג' כיחס ג' אל ז' |
| Q.E.D. | ומ'ש'ל' |
Proposition 15 |
|
| 15) When the unit measures any number by the measure that [another] number measures another number, then when we invert, the unit measures the measuring number by the measure that the measured number measures the number that is measured by the other. | ט"ו כאשר היה האחד ימנה מספר מה בשעור מה שימנה מספר למספר אחר הנה אנחנו כאשר המירונו היה האחד ימנה המספר המונה בשעור מה שימנה המספר המנוי המספר אשר ימנהו האחר |
| Example: the unit measures AB by the measure that G measures HZ. | המשל בו כי האחד ימנה מספר א"ב בשעור מה שימנה מספר ג' מספר ה"ז |
| Supposition: when we invert, the unit measures G by the measure that AB measures HZ. | הנה אומר כי אנחנו כאשר המירונו האחד ימנה מספר ג' בשעור מה שימנה א"ב מספר ה"ז |
| Proof: there are as many units in AB as the number of times that G is in HZ. | המופת כי מה שבא"ב מן האחד כמו מה שבה"ז מדמיוני ג' |
We divide AB into the units: 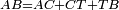
|
ונחלק א"ב באחדים ויצא א"ח ח"ט ט"ב |
And HZ into the G: 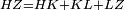
|
וה"ז על ג' ויצא ה"כ כ"ל ל"ז |
| The multitude of the units AC, CT, TB equals the multitude of HK, KL, LZ. | הנה סכום אחדי א"ח ח"ט ט"ב שוים לסכום ה"כ כ"ל ל"ז |
|
אם כן שעור האחד והוא א"ח ממספר ה"כ כשעור האחד והוא ח"ט ממספר כ"ל וכשעור האחד והוא ט"ב ממספר ל"ז |
| The measure of one of the antecedents is to its corresponding of the consequents as the measure of all the antecedents to all the consequents. | ושעור אחד מן הקודמים מקרובו מהנמשכים כשעור כל הקודמים מכל הנמשכים |
|
אם כן שעור האחד והוא א"ח ממספר ה"כ כשעור א"ב מן ה"ז |
|
אם כן חלק א"ח מן ה"כ הוא חלק א"ב מן ה"ז |
|
|
וא"ח שוה לאחד |
|
|
ומספר ה"כ שוה למספר ג' |
| The unit measures G by the measure that AB measures HZ. | אם כן שעור מה שימנה האחד ג' כשעור מה שימנה א"ב ה"ז |
| Q.E.D. | ומ'ש'ל' |
Proposition 16 |
|
| 16) For every two numbers multiplied by one another, their products are equal. | י"ו כל שני מספרים יוכה כל אחד משניהם באחר הנה שני שטחיהם שוים |
| Example:
|
המשל בו כי מספר א' הוכה בו מספר ב' והיה ג' |
|
|
ומספר ב' הוכה בו מספר א' והיה ד' |
Supposition: 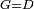
|
הנה אומר כי ג"ד שוים |
| Proof:
|
המופת כי א' הוכה בו מספר ב' והיה ג' |
|
אם כן ב' ימנה ג' בשעור אחדי א' |
|
והאחד ימנה א' בשעור אחדיו |
|
ואם כן שעור מה שימנה האחד א' כשעור מה שימנה ב' ג' |
|
וכאשר המירונו הנה מה שימנה האחד ב' בשעור מה שימנה א' ג' |
|
אם כן שעור האחד מן ב' כשיעור א' מן ג' |
|
ויהיה שעור האחד מן ב' כשעור א' מן ד' |
|
|
מפני כי ב' הוכה בו א' והיה המקובץ ד' |
|
|
אם כן יחס א' אל ג' וד' אחד |
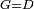
|
אם כן ג"ד שוים |
| Q.E.D. | ומ'ש'ל' |
Proposition 17 |
|
| 17) For every number multiplied by two numbers, the measure of one of the two products to the other is the same measure that one of the two [multiplied] numbers is to the other. | י"ז כל מספר יוכו בו שני מספרים הנה שעור אחד משני השטחים אצל האחר בשעור אחד משני המספרים אצל האחר |
Example: 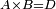 ; ; 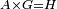
|
המשל בו כי מספר א' הוכו בו שני מספרי ב"ג והתקבץ משניהם שני שטחי ד"ה |
| Supposition: the measure of B to G is as the measure of D to H. | הנה אומר כי שעור ב' מן ג' כשעור ד' מן ה' |
| המופת כי א' הוכה בו ב' והתקבץ בו ד' אם כן ב' ימנה ד' בשעור אחדי א' והאחד ימנה א' בשעור אחדיו | |
| אם כן שעור מה שימנה האחד א' כשעור מה שימנה ב"ד | |
| וגם כן הנה א' הוכה בו ג' והתקבץ ה' | |
| אם כן ג' ימנה ה' בשעור אחדי א' והאחד ימנה א' בשעור אחדיו | |
| אם כן שעור מה שימנה האחד א' כשעור מה שימנה ג"ה | |
| אם כן שעור האחד מן א' כשעור ג' מן ה' וכן שעור האחד מן א' כשעור ב' מן ד' | |
| אם כן שעור ב' מן ד' כשעור ג' מן ה' | |
| וכאשר המירונו היה שעור ב' מן ג' כשעור ד' מן ה' | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 18 |
|
| י"ח כל מספר יוכה בשני מספרים הנה יחס אחד משני השטחים אל האחר כיחס אחד משני המספרים אל האחר | |
Example: 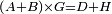
|
המשל בו כי שני מספרי א"ב הוכה בשניהם מספר ג' והיו שני השטחים שני מספרי ד"ה |
Supposition: 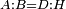
|
הנה אומר כי יחס א' אל ב' כיחס ד' אל ה' |
| Proof:
|
המופת כי א' הוכה בו ג' והיה המקובץ ד' |
|
|
אם כן ג' הוכה בו א' והיה המקובץ ד' |
|
|
וגם כן הנה ב' הוכה בו ג' והיה המקובץ ה' |
|
|
אם כן ג' הוכה בו ב' והיה המקובץ ה' |
|
|
אם כן מספר ג' הוכו בו שני מספרי א"ב והיו מזה שני שטחי ד"ה |
|
|
אם כן יחס א' אל ב' כיחס ד' אל ה' |
| Q.E.D. | ומ'ש'ל' |
Proposition 19 |
|
| י"ט כל מספרים מתיחסים הנה שטח הראשון ברביעי כמו שטח השני בשלישי ואם היה שטח הראשון ברביעי כמו השטח השני בשלישי הנה המספרים הארבעה מתיחסים | |
Example: 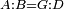
|
המשל בו כי מספרי א"ב ג"ד הארבעה מתיחסים יחס א' אל ב' כיחס ג' אל ד' |
|
|
ושטח א' הראשון בד' הרביעי מספר ז' |
|
|
ושטח ב' השני בג' השלישי מספר ה' |
Supposition: 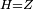
|
הנה אומר כי ה"ז שוים |
| Proof:
|
מופת אנחנו נכה א' בג' ויהיה ח' |
|
|
הנה א' בשני מספרי ג"ד והתקבץ מזה שני שטחי ח"ז |
| אם כן שעור ג' מן ד' כשעור ח' מן ז' | |
| ושעור ג' מן ד' כשעור א' מן ב' | |
| אם כן שעור מן ב' כשעור ח' מן ז' | |
|
|
וגם כן הנה א' הוכה בג' והיה ח' |
|
|
אבל ב' הוכה בג' והיה ה' |
| אם כן שעור א' מן ב' כשעור ח' מן ה' | |
| וכבר התבאר כי שעור א' מן ב' כשעור ח' מן ז' | |
| אם כן יחס ח' אל ה"ז אחד | |
| אם כן ה' כמו ז' | |
| עוד תהיה ה' כמו ז' | |
| Supposition:
|
הנה אומר כי יחס א' אל ב' כיחס ג' אל ד' |
| מופת כי ההנהגה אחת הנה א' הוכה בג' והיה ח' והוכה בד' והיה ז' | |
| אם כן שעור ג' מן ד' כשעור ח' מן ה"ז וז' כמו ה' | |
| אם כן שעור ג' מן ד' כשעור ה' מן ה' | |
| וגם כן הנה א' הוכה בג' והיה ח' וב' הוכה בג' והיה ה' | |
| אם כן שעור א' מן ב' כשעור ח' מן ה' | |
| וכבר התבאר כי שעור ח' מן ה' כשעור ג' מן ד' | |
|
|
אם כן יחס א' אל ב' כיחס ג' אל ד' |
| Q.E.D. | וזה מ'ש'ל' |
Proposition 20 |
|
| כ המעט שבמספרים על יחס הנה הם ימנו המספרים אשר על יחסם המעט למעט והרב לרב | |
| המשל בו כי המעט שבמספרים על יחס א' אל ג' והוא ה"ז אל ח"ט | |
| הנה אומר כי ה"ז ימנה א' בשעור מה שימנה ח"ט ג' | |
| וזה כי אנחנו כבר בארנו כי חלק כל אחד מחברו או חלקיו כחלק אחד מן האחר או חלקיו | |
| שאם לא יהיה ה"ז חלק מן א' הנה הוא חלקים ממנו | |
| כי הוא פחות ממנו ויהיה ח"ט חלקים מן ג' כחלקי ה"ז מן א' ונחלק ה"ז בחלקי א' ויצא ה"כ כ"ז ונחלק ח"ט בחלקי ג' ויצא ח"ל ל"ט | |
| אם כן סכום ה"כ כ"ז כמו סכום ח"ל ל"ט וה"כ כמו כ"ז וח"ל כמו ל"ט | |
| אם כן שעור ה"כ מן ח"ל כשעור ה"ז מן ח"ט | |
| אם כן ה"כ וח"ל על יחס ה"ז וח"ט | |
| וה"כ ח"ל פחות מן ה"ז וח"ט זה שקר מפני כי ה"ז וח"ט היו הקטן שבמספרים על יחסם | |
| אם כן אין ה"ז חלקים מן א' אבל הוא חלק אחד | |
| אם כן ח"ט מן ג' הוא חלק כמו חלק ה"ז מן א' | |
| אם כן ה"ז ימנה א' בשעור מה שימנה ח"ט ג' | |
| Q.E.D. | ומ'ש'ל' |
Proposition 21 |
|
| כ"א שני מספרים הקטנים על יחס הנה הם נבדלים | |
| המשל בו כי שני מספרי א"ב הקטנים שני מספרים על יחס שניהם | |
| הנה אומר כי שניהם נבדלים | |
| המופת אם יהיו משותפים הנה ימנה שניהם מספר ג' | |
| ונאמר שהוא אחדי ד' שיעור מה שימנה ג"א ואחדי ה' שיעור מה שימנה ג"ב | |
| אם כן ג' ימנה א' בשיעור אחדי ד' והנה ג' הוכה בד' והיה א' | |
| וגם כן הנה ג' ימנה ב' בשעור אחדי ה' | |
| והנה ג' הוכה בה' והיה ב' | |
| אם כן ג' הוכה בשני מספרי ד"ה והיה מזה א"ב | |
| אם כן יחס ד' אל ה' כיחס א' אל ב' וד' וה' קטן מא' וב' זה שקר כי א"ב היו שני המספרים הקטנים על יחס שניהם אם כן לא ימנה א"ב מספר אחד | |
| אם כן שניהם נבדלים | |
| Q.E.D. | מ'ש'ל' |
Proposition 22 |
|
| כ"ב כל שני מספרים נבדלים הנה שניהם שני המספרים הקטנים על יחסם המשל בו שני מספרים א"ב נבדלים | |
| הנה אומר שהם הקטנים שבמספרים על יחסם | |
| המופת שאם לא יהיו כן נאמר שיהיו שני מספרים קטנים משניהם ושני מספרים היותר קטנים על יחס שניהם הם ג"ד | |
| אם כן שעור מה שימנה ג"א כשעור מה שימנה ד"ב ויהיו אחדי מספר אחד והוא ה' בשעור מה שימנה ג"א | |
| אם כן ד' ימנה ב' בשעור אחדי ה' וה' ימנה א' בשעור אחדי ג' וה' ימנה ב' בשיעור אחדי ד' | |
| אם כן ה' ימנה א"ב ושניהם נבדלים זה שקר | |
| אם כן א"ב השני מספרים היותר קטנים על יחסם | |
| Q.E.D. | ומ'ש'ל' |
Proposition 23 |
|
| כ"ג כל מספר ימנה אחד משני מספרים נבדלים הנה הוא הנבדל מן המספר האחר | |
| המשל בו כי שני מספרי א"ב נבדלים ומספר ג' ימנה א' | |
| הנה אומר שהוא נבדל מב' | |
| המופת אם היו ב' וג' משותפים הנה ימנה שניהם מספר ד' | |
| אם כן ד' ימנה ג' וג' ימנה א' | |
| אם כן ד' ימנה א'. והוא ימנה ב' ושניהם נבדלים זאת שקר | |
| אם כן לא ימנה ב' ג' מספר אחד אם כן שניהם נבדלים | |
| Q.E.D. | ומ'ש'ל' |
Proposition 24 |
|
| כ"ד כל שני מספרים יובדלו ממספר אחר הנה שטח אחד משניהם באחר יובדל מן המספר ההוא | |
| המשל בו כי שני מספרי א"ב יובדלו ממספר ג' ושטח א' בב' מספר ד' | |
| הנה אומר כי ג"ד נבדלים | |
| המופת כי שניהם אם היו משותפים הנה ימנה שניהם מספר אחד והוא ה' ונאמר שיהיה אחדי ז' בשעור מה שימנה ה' ד' וה' יוכה בז' ויהיה ד' וא' יוכה בב' ויהיה ד' | |
| אם כן שטח ה' בז' כמו שטח א' בב' | |
| אם כן היחס אחד יחס ה' אל א' כיחס ב' אל ז' וא"ג נבדלים וה' ימנה אחד משניהם והוא ג' אם א"ה נבדלים | |
| אם כן שניהם שני מספרים היותר קטנים על יחסם וימנו כל שני מספרים על יחסם בשוה היותר קטן ליותר קטן והרב לרב | |
| אם כן ה' ימנה ב' והוא ימנה ג' וב"ג נבדלים זה שקר | |
| אם כן לא ימנה ג"ד מספר אם כן שניהם נבדלים | |
| Q.E.D. | ומ'ש'ל' |
Proposition 25 |
|
| כ"ה כל שני מספרים נבדלים הנה מרובע הנה מרובע אחד משניהם נבדל מן האחר | |
| המשל בו כי שני מספרי א"ב נבדלים ומרובע א' מספר ג' | |
| הנה אומר כי ג"ב נבדלים | |
| המופת אנחנו נשים ד' כמו א' הנה א"ב נבדלים וא' כמו ד' | |
| אם כן ד"ב נבדלים אם כן א"ד יובדלו מן ב' | |
| אם כן שטח א' בד' יובדל מן ב' ושטח א' בד' הוא ג' אם כן ג"ב נבדלים | |
| Q.E.D. | ומ'ש'ל' |
Proposition 26 |
|
| כ"ו כאשר יהיה כל אחד משני מספרים יובדלו משנים אחרים הנה שטח הראשונים אחד משניהם באחר יובדל גם כן משטח השנים האחרים | |
| המשל בו כי כל אחד משני מספרי א"ב יובדל מכל אחד משני מספרי ג"ד ושטח א' בב' מספר ה' ושטח ג' בד' מספר ז' | |
| הנה אומר כי ה"ז נבדלים | |
| המופת כי א"ב יובדלו מן ג' | |
| אם כן שטח א' בב' והוא ה' יובדל מן ג' | |
| אם כן ה"ג נבדלים וכן יהיו ה"ד נבדלים מן ה' | |
| אם כן ג' בד' הוא ז' יובדל מן ה' אם כן ה"ז נבדלים | |
| Q.E.D. | ומ'ש'ל' |
Proposition 27 |
|
| כ"ז כל שני מספרים נבדלים יוכה כל אחד משניהם בדומה לו הנה שני מרובעיהם נבדלים וכן אם הוכו שני המרובעים בגדריהם והם השני מספרים הראשונים כל מרובע בגדרו הנה השני מעוקבים גם כן נבדלים וכן לא יסורו בקצוות והמספרים האחרונים כי כל מרובע בגדרו הנה השני מעוקבים נבדלים גם כן וכן לא יסורו | |
| המשל בו כי שני מספרי א"ב נבדלים והוכה א' בדומה לו והיה מרובע ג' והוכה ב' בדומה לו והיה מרובע ד' | |
| וגם כן הנה א' הוכה בג' והיה מעוקב ה' וב' הוכה בד' והיה מעוקב ז' | |
| הנה אומר כי שני מרובעי ג"ד נבדלים ושני מעוקבי ה"ז נבדלים גם כן | |
| המופת כי א"ב נבדלים הנה מרובע אחד משניהם נבדל מן האחר ומרובע א' הוא ג' אם כן ג"ב נבדלים | |
| וגם כן הנה ג"ב נבדלים אם כן מרובע אחד משניהם נבדל מן האחר | |
| ומרובע ב' הוא ד' אם כן ג"ד נבדלים | |
| וגם כן הנה א"ב נבדלים ומרובע ב' הוא ד' | |
| אם כן א"ד נבדלים וג"ד נבדלים | |
| אם כן א"ג נבדלים מן ד' ונבדלים מן ב' | |
| אם כן שטח א' בג' והוא מעוקב ה' נבדל משטח ב' בד' והוא ז' | |
| אם כן שני מעוקבי ה"ז נבדלים | |
| וכבר בארנו כי שני מרובעי ג"ד נבדלים וכן לא יסורו בקצוות והמספרים האחרונים אשר יתקבץ מן ההכאה | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 28 |
|
| כ"ח כל שני מספרים נבדלים הנה מקובץ שניהם נבדל מכל אחד משניהם ואם היה מקובץ שניהם נבדל מכל אחד משניהם הנה שניהם נבדלים | |
| המשל בו כי שני מספרי א"ב ב"ג נבדלים | |
| הנה אומר כי כל א"ג נבדל מכל אחד מן א"ב ב"ג | |
| המופת כי אם לא יהיה א"ג נבדל מן ב"ג הנה ימנה שניהם מספר אחד והוא ד' | |
| אם כן ד' ימנה א"ג וימנה ב"ג הנה הוא אם כן ימנה א"ב | |
| אם כן ד' ימנה א"ב ב"ג והם נבדלים זה שקר | |
| אם כן לא ימנה א"ג ב"ג מספר אחד אם כן שניהם נבדלים | |
| וכן התבאר כי א"ג א"ב נבדלים אם כן א"ג נבדל מכל אחד מן א"ב ב"ג ויהיה גם כן א"ג נבדל מכל אחד מן א"ב ב"ג | |
| הנה אומר כי א"ב ב"ג נבדלים | |
| המופת כי שניהם אם לא יהיו כן הנה ימנה שניהם מספר ד' | |
| אם כן ד' ימנה א"ב וימנה ב"ג אם כן הוא ימנה כל א"ג | |
| אם כן ד' ימנה א"ג ב"ג ושניהם נבדלים זה שקר | |
| אם כן לא ימנה א"ב ב"ג מספר אחר אם כן שניהם נבדלים | |
| וכן יתבאר אם היה א"ג נבדל מן א"ב שזה שקר | |
| Q.E.D. | ומ'ש'ל' |
Proposition 29 |
|
| כ"ט כל מספר מורכב הנה ימנה אותו מספר ראשון | |
| המשל בו כי מספר א' מורכב | |
| הנה אומר כי הוא ימנהו מספר ראשון | |
| המופת כי א' מורכב אם כן ימנהו מספר אחר והוא ב' הנה אם היה ב' ראשון הנה התאמת הספור | |
| ואם היה מורכב הנה ימנהו מספר אחר והוא ג' וכן לא יסור יעשה עד שיכלה אל מספר ראשון ימנה אשר לפניו וימנה א' | |
| ואם לא יכלה אל מספר ראשון ימנה אשר לפניו וימנה א' הנה הוא ימנהו מספרים מורכבים בלי תכלית כל אחד מהם קטן מן האחר זה שקר אי אפשר במספר אבל בלא ספק שיכלה אל מספר ראשון ימנה מה שילוה אליו לפניו וימנה א' | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 30 |
|
| ל כל מספר הנה הוא ראשון או ימנהו מספר ראשון | |
| נאמר שהוא מספר מה והוא א' | |
| הנה אומר כי א' ימנהו מספר ראשון | |
| המופת כי א' אם היה ראשון הנה כבר התאמת הספור | |
| ואם היה מורכב הנה ימנהו מספר ראשון וכן כל מספר | |
| Q.E.D. | וזה מ'ש'ל' |
Proposition 31 |
|
| ל"א כל מספר ראשון הנה הוא נבדל לכל מספר לא ימנהו הוא | |
| המשל בו כי מספר א' ראשון ומספר ב' לא ימנהו א' | |
| הנה אומר כי א"ב נבדלים | |
| המופת כי אם היו משותפים הנה ימנה אותם מספר אחד אם כן זה המספר ימנה אם כן מספר א' והוא ראשון זה שקר | |
| אם כן לא ימנה א"ב מספר אחר אם כן שניהם נבדלים | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 32 |
|
| ל"ב כל מספר ראשון ימנה איזה משוטח שיהיה הנה הוא גם כן ימנה אחד משתי צלעות השטח | |
| המשל בו כי מספר א' ראשון והוא ימנה מספר ב' והוא משוטח ושתי צלעותיו ג"ד | |
| הנה אומר כי א' ימנה אחד משני מספרי ג"ד | |
| המופת אם היה א' לא ימנה ג' וא' ראשון הנה א"ג נבדלים | |
| ונאמר שיהיה אחדי מספר אחר הוא ה' בשעור מה שימנה א"ב | |
| אם כן א' ויכה בה' ויהיה ב' | |
| אבל ג' הוכה בד' והוא ב' אם כן שטח א' בה' כמו שטח ג' בד' | |
| אם כן יחס א' אל ג' כיחס ד' אל ה' וא"ג נבדלים | |
| אם כן שניהם שני מספרים היותר קטנים על יחס שניהם וימנו כל שני מספרים בשוה הקטן לקטן והרב לרב | |
| אם כן א' ימנה ד' | |
| וכן יתבאר אם היה א' לא ימנה ד' שהוא ימנה ג' | |
| אם כן א' ימנה אחד משני מספרי ג"ד | |
| Q.E.D. | ומ'ש'ל' |
Proposition 33 |
|
| ל"ג נרצה לבאר איך נמצא הקטן שבמספרים על יחס מספרים ידועים כמה שיהיו | |
| הנה נשים המספרים הידועים מספרי א'ב'ג' | |
| ונרצה לבאר איך נמצא הקטן שבמספרים על יחס א'ב'ג' הנה אם יהיו מספרי א'ב'ג' נבדלים הנה הם המעט שבמספרים על יחסם | |
| ואם היו משותפים יקח גדול מספר שימנם יחד | |
| ונאמר שיהיה המספר ההוא ד' ויהיה באחד בעינו ממספרי ה'ז'ח' מן האחדים בשעור מה שימנה ד' אחד בעינו ממספרי א'ב'ג' הנה כל אחד ממספרי א'ב'ג' ימנהו אחד ממספרי ה'ז'ח' אשר אחדיו בשעור מה שימנהו ד' בשעור אחדי ד' הנה מספר ה'ז'ח' על יחס א'ב'ג' | |
| אם כן יחס מ' אל ד' כיחס ה' אל ט' וה' גדול מן ט' אם כן מ' גדול מן ד' | |
| ואומר שהם המעט שבמספרים על יחסם | |
| ואם לא יהיו כן יהיו מספרים אחרים יותר קטנים מן ה'ז'ח' קטני המספרים על יחס א'ב'ג' והם מספרי ט'כ'ל' | |
| אם כן ט' ימנה א' בשעור מה שימנה כ"ב ובשעור מה שימנה ל"ג | |
| ויהיו אחדי מספר אחד והוא מספר מ' בשעור מה שימנה ט"א הנה כל אחד מספרי כ"ל ימנה בן גילו משני מספרי ב"ג בשעור אחדי מ' וט' ימנה א' בשעור אחדי מ' | |
| אם כן מ' ימנה א' בשעור אחדי ט' | |
| וכן מ' ימנה ב' בשעור אחדי כ' וימנה ג' בשעור אחדי ל' | |
| אם כן מ' ימנה א'ב'ג' ומ' ימנה א' בשעור אחדי ט' הנה מ' | |
| אם כן כאשר הוכה בט' היה א' | |
| וד' כאשר הוכה בה' היה א' | |
| אם כן שטח מ' בט' כמו שטח ד' בה' | |
| אם כן אין מספרים קטנים מן ה'ז'ח' על יחס א'ב'ג' | |
| Q.E.D. | ומ'ש'ל' |
Proposition 34 |
|
| ל"ד נרצה לבאר איך נמצא המספר היותר קטן שימנו אותו שני מספרים ידועים בלתי שוים | |
| הנה יהיו שני המספרים הידועים מספרי א"ב | |
| הנה אם היה הקטן ימנה הגדול משניהם והגדול משניהם ימנה עצמו הנה הגדול הוא קטן המספר שימנוהו | |
| ואם לא יהיה הקטן ימנה הגדול הנה א"ב נבדלים או משותפים ואם היו נבדלים יוכה א' בב' ויהיה ג' | |
| הנה אומר כי ג' המספר הקטן שימנוהו מספרי א"ב | |
| ואם לא יהיה כן הנה ימנו מספר קטן ממנו והוא ד' ויהיו אחדי ה' כשעור מה שימנה א"ד | |
| ואחדי ז' בשעור מה שימנה ב"ד אם כן א' יוכה בה' ויהיה ד' וב' יוכה בז' ויהיה ד' אם כן שטח א' בה' כמו שטח ב' בז' | |
| אם כן יחס א' אל ב' כיחס ז' אל ה' | |
| וא"ב נבדלים אם כן שניהם קטני מספרים על יחסם וימנו כל שני מספרים על יחסם בשוה הקטן לקטן והרב לרב אם כן א' ימנה ז' וב' הוכה בא' ובז' והיו ג"ד | |
| אם כן יחס א' אל ז' כיחס ג' אל ד' | |
| אבל א' ימנה ז' | |
| אם כן ג' ימנה ד' וג' גדול מן ד' הנה הגדול אם כן ימנה הקטן זה שקר | |
| אם כן לא ימנה שני מספרי א"ב מספר הוא קטן מן ג' אם כן ג' היותר קטן שבמספרים שימנהו א"ב | |
| ואם היו א"ב משותפים יהיו ז"ה קטני המספרים על יחסם | |
| אם כן יחס א' אל ב' כיחס ז' אל ה' ויוכה א' בה' ויהיה ג' הנה ב' כאשר הוכה בז' היה ג' אם כן א"ב ימנו ג' | |
| הנה אומר כי ג' קטן מספר ימנוהו א"ב | |
| ואם לא יהיו כן הנה ימנו מספר קטן מן ג' ויהיה מספר ד' ויהיו אחדי ח' כשעור מה שימנה א"ד ואחדי ט' בשעור מה שימנה ב"ד | |
| אם כן א' יוכה בח' ויהיה ד' וב' יוכה בט' ויהיה ד' | |
| אם כן שטח א' בח' כמו שטח ב' בט' | |
| אם כן יחס א' אל ב' כיחס ט' אל ח' ויחס א' אל ב' כיחס ז' אל ה' | |
| אם כן יחס ז' אל ה' כיחס ט' אל ח' וז"ה שני מספרים קטנים על יחסם | |
| אם כן שניהם ימנו כל מספר על יחסם בשוה הקטן לקטן והרב לרב | |
| אם כן ז' ימנה ט' וב' הוכה בז' ובט' והיה ג"ד | |
| אם כן יחס ז' אל ט' כיחס ג' אל ד' | |
| אבל ז' ימנה ט' | |
| אם כן ג' ימנה ד' הגדול ימנה הקטן זה שקר | |
| אם כן לא ימנה א"ב מספר יותר קטן מן ג' | |
| אם כן ג' מספר קטן שימנוהו א"ב | |
| Q.E.D. | ומ'ש'ל' |
Proposition 35 |
|
| ל"ה כאשר היו שני מספרים ימנו מספר הנה קטן מספר שימנהו הוא גם כן ימנה המספר ההוא | |
| ויהיה שני מספרי א"ב ימנו ה"ז ויהיה קטן מספר שימנוהו א"ב מספר ח' | |
| הנה אומר כי ח' ימנה ה"ז | |
| המופת אם לא יהיה שימנהו הנה הוא אם כן מנה ז"ב נשאר כ"ה קטן מן ח' וא"ב ימנו ח' וח' ימנה ז"ב | |
| אם כן א"ב ימנו ז"ב וימנו כל ז"ה | |
| הנה שניהם אם כן ימנו ב"ה וה"ב קטן מן ח' זה שקר מפני כי ח' היה קטן מספר ימנהו א"ב | |
| אם כן ח' ימנה ה"ז | |
| Q.E.D. | ומ'ש'ל' |
Proposition 36 |
|
| ל"ו נרצה לבאר היאך נמצא קטן מספר שימנוהו שלשה מספרים ידועים | |
| ויהיו השלשה מספרים א'ב'ג' | |
| ונרצה שנמצא קטן מספר ימנוהו מספרי א'ב'ג' | |
| הנה נקח קטן מספר שימנוהו שני מספרים מהם והם א"ב ויהיה מספר ד' הנה ג' אם שימנה ד' ואם שלא ימנהו | |
| ואם היה ג' ימנה ד' וא"ב ימנוהו הנה ד' מספר שימנוהו מספרי א'ב'ג' | |
| ואם לא יהיה כן הנה הם ימנו מספר קטן ממנו ויהיה מספר ה' | |
| אם כן ימנוהו א"ב וימנוהו קטן מספר שימנוהו מספרי א"ב והוא מספר ד' | |
| אם כן הגדול ימנה הקטן זה שקר | |
| אם כן אין מספר קטן מן ד' ימנוהו א'ב'ג' | |
| ואם היה ג' קטן מספר ימנוהו ג"ד ויהיה מספר ה' | |
| אם כן ד' ימנה ה' וא"ב ימנו ד' | |
| אם כן שניהם ימנו ה' וג' ימנה ה' | |
| אם כן ה' ימנוהו מספרי א'ב'ג' השלשה | |
| הנה אומר שהוא קטן מספר ימנוהו א'ב'ג' | |
| ואם לא יהיה כן נאמר שיהיה מספר קטן מן ה' ימנוהו א'ב'ג' ויהיה מספר ז' | |
| אם כן ז' ימנוהו מספרי א"ב וימנהו קטן מספר שימנוהו והוא ד' | |
| אם כן ד' ימנה ז' וג' ימנה ז' | |
| אם כן ז' ימנוהו שני מספרי ג"ד וימנהו קטן מספר שימנוהו והוא ה' | |
| אם כן ה' ימנה ז' וה' יותר קטן מז' זה שקר | |
| אם כן אין מספר יותר קטן מן ה' ימנוהו מספרי א'ב'ג' | |
| אם כן ה' קטן מספר ימנוהו מספרי א'ב'ג' | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 37 |
|
| For every number that is counted by another number, the [counted] number has a part named after the number that counts it. | ל"ז כל מספר ימנהו מספר אחר הנה במספר חלק קורא למספר אשר ימנהו |
| ויהיה מספר א' ימנהו מספר ב' | |
| הנה אומר כי בא' חלקים נקראו במספר ב' | |
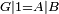
|
ויהיה האחד ימנה ג' בשיעור מה שימנה ב' א' |
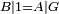
|
וכאשר המירונו הנה שיעור מה שימנה האחד ב' כשעור מה שימנה ג' א' |
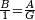
|
אם כן חלק האחד מן ב' הוא חלק ג' מן א' |
| והאחד מן ב' הוא חלק נקרא אל ב' אם כן ג' הוא חלק מן א' נקרא אל ב' אם כן בא' חלק אל ב' | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 38 |
|
| Every number that has any part whatever, is counted by a number after which the part is named. | ל"ח כל מספר שיש לו אי זה חלק היה הנה הוא ימנהו מספר נקרא לחלק ההוא |
| נאמר שיהיה במספר א' חלק מה והוא ב' | |
| הנה אומר כי א' ימנהו מספר נקרא לחלק ב' מן א' | |
| ויהיה חלק האחד מן ג' הוא חלק ב' מן א' אם כן ג' נקרא אל חלק ב' וג' נקרא החלק ממנו וחלק האחד מן ג' הוא חלק ב' מן א' | |
| אם כן שעור מה שימנה האחד ג' בשעור מה שימנה ב' א' | |
| וכאשר המירונו הנה שיעור מה שימנה האחד ב' כשיעור מה שימנה ג"א והאחד ימנה ב' כשיעור אחדי ב' | |
| אם כן ג' ימנה א' בשיעור אחדי ב' וג' מספר נקרא לחלק ב' מן א' | |
| Q.E.D. | וזהו מה שרצינו לבאר |
Proposition 39 |
|
| We wish to explain how to find the number, which is the least that has given parts. | ל"ט נרצה לבאר איך נמצא קטן מספר בו חלקים מונחים |
| ויהיו החלקים המונחים א'ב'ג' ונרצה למצוא אחד קטן מספר בו חלקי א'ב'ג' הנה נקח מספרים נקראים לחלקי א'ב'ג' והם מספרי ד'ה'ז' | |
| ויהיה קטן מספרים שימנוהו ד'ה'ז' מספר ח' אם כן ח' בו חלקים נקראים אל ד'ה'ז' | |
| והחלקים הנקראים אל ד'ה'ז' הם א'ב'ג' אם כן ח' בו חלקי א'ב'ג' | |
| הנה אומר כי ח' קטן מספר בו אלו החלקים | |
| ואם לא יהיה זה הנה יהיה מספר קטן מן ח' בו חלקי א'ב'ג' ויהיה מספר ט' | |
| אם כן ט' בו חלקי א'ב'ג' הנה ט' אם כן ימנוהו מספרים נקראים לחלקי א'ב'ג' והמספרים הנקראים לחלקים האלו הם מספרי ד'ה'ז' | |
| אם כן ט' ימנוהו מספרי ד'ה'ז' והוא קטן מן ח' זה שקר אי איפשר מפני כי ח' קטן מספר ימנו אלה המספרים הנה ח' אם כן קטן מספר בו חלקי א'ב'ג' | |
| Q.E.D. | וזה מה שרצינו לבאר |
| נשלם המאמר השביעי מהחכם אקלידס ת"ל |
Book Eight |
המאמר השמיני |
Proposition 1 |
|
| א כאשר היו מספרים נמשכים על יחס אחד כמה שיהיו והיה כל אחד משתי הקצוות ראשון אצל האחר הנה הם קטני המספרים על יחסם | |
| המשל בו כי מספרי א"ב ג"ד נמשכים על יחס אחד ושתי הקצוות כל אחת משתיהן ראשון אצל האחר ושניהם א"ד | |
| הנה אומר כי א"ב ג"ד הם קטני המספרים על יחסם | |
| המופת כי אם לא יהיה כן הנה יהיו מספרים קטנים מהם ועל מניינם ויחסם והם ה"ז ח"ט | |
| הנה יחס א"ב ג"ד הוא כיחס ה"ז ח"ט מכ"ב מזה | |
| ומנין א'ב'ג'ד' כמניין ה"ז ח"ט | |
| אם כן יחס א' אל ד' כיחס ה' אל ט' | |
| וכל אחד מן א"ד ראשון אצל האחר | |
| אם כן שניהם קטני המספרים על יחס שניהם וימנו כל שני מספרים שהם על יחס שניהם בשוה הקטן לקטן והרב לרב | |
| אם כן א' ימנה ה' הרב ימנה המעט זה שקר | |
| אם כן אין מספרים נמשכים על יחס אחד הם קטנים מן א"ב ג"ד ומ'ש'ל' | |
Proposition 2 |
|
| ב נרצה לבאר איך נמצא קטני המספרים נמשכים על יחס אחד מונח כמה שנרצה הנה נשים היחס המונח בקטן שני מספרים והם יחס א' אל ב' ונרצה למצא קטני מספרים נמשכים על יחס א"ב כמה שנרצה ויהיו המספרים ארבעה | |
|
|
ונכה א' בכמוהו ויהיה ג' |
|
|
ונכה בב' ויהיו ד' |
|
|
ונכה ב' בכמוהו ויהיה ה' |
|
וגם כן הנה אנחנו נכה א' בג' ובד' ובה' ויהיה ז'ח'ט' |
|
|
ונכה ב' בה' ויהיה ל' |
| הנה אומר כי ז"ח ש"ל קטני ארבעה מספרים נמשכים על יחס א' אל ב' | |
|
|
המופת כי א' הוכה בכמוהו והיה ג' |
|
|
והוכה בב' והיה ד' |
|
|
הנה א' הוכה בשני מספרים בכמוהו ובב' והיה ג"ד |
|
|
אם כן יחס א' אל ב' כיחס ג' אל ד' |
|
|
וגם כן הנה ב' הוכה בכמוהו והיה ה' |
|
|
והוכה בא' והיה ד' |
|
|
אם כן יחס א' אל ב' כיחס ד' אל ה' |
|
|
ויחס א' אל ב' כיחס ג' אל ד' |
|
|
אם כן יחס ג' אל ד' כיחס ד' אל ה' |
| אם כן ג'ד'ה' נמשכים על יחס א' אל ב' | |
|
|
וגם כן הנה א' הוכה בג' והיה ז' |
|
|
והוכה בד' והיה ח' |
|
|
הנה א' הוכה בשני מספרי ג"ד והיו מזה ז"ח |
|
|
אם כן יחס ג' אל ד' כיחס ז' אל ח' |
|
|
ויחס ג' אל ד' כיחס א' אל ב' |
|
|
אם כן יחס א' אל ב' כיחס ז' אל ח' |
|
|
וגם כן הנה א' הוכה בד' והיה ח' |
|
|
והוכה בה' והיה ט' |
|
|
אם כן יחס ד' אל ה' כיחס ח' אל ט' |
|
|
ויחס ד' אל ה' כיחס א' אל ב' |
|
|
אם כן יחס א' אל ב' כיחס ח' אל ט' |
|
|
ויחס א' אל ב' כיחס ז' אל ח' |
|
|
אם כן יחס ז' אל ח' כיחס ח' אל ט' |
| אם כן ז'ח'ט' נמשכים על יחס א' אל ב' | |
| וכבר הוכו א"ב ב"ה והיו מזה ט"ל | |
|
|
אם כן יחס א' אל ב' כיחס ט' אל ל' |
|
|
אם כן יחס א' אל ב' כיחס ז' אל ח' וח' אל ט' וט' אל ל' |
| אם כן ז"ח ט"ל נמשכים על יחס אחד והוא יחס א' אל ב' והם ארבעה מספרים ונשלם באורו | |
| והתבאר שהם מעטי המספרים על יחסם כי כל אחד מן א"ב ראשון אצל האחר | |
|
|
וכבר הוכה א' בכמוהו והיה ג' |
|
|
והוכה בג' והיה ז' |
|
|
וכבר הוכה ב' בכמוהו והיה ה' |
|
|
והוכה בה' והיה ל' |
| אם כן כל אחד מן ג"ה ראשון אצל האחר | |
| וכל אחד מן ז"ל ראשון אצל האחר | |
| ואם כן היו מספרים נמשכים על יחס אחד כמה שיהיו המספרים והיתה כל אחת משתי הקצוות ראשון אצל האחר אם כן הם קטני המספרים על יחסם | |
| אם כן מספרי ז"ח ט"ל קטני המספרים | |
| ומ'ש'ל' | |
| ובכאן התבאר כי הם כאשר היו שלשה מספרים קטנים מה שיהיו על יחס אחד הנה שתי הקצוות שני מרובעים א' אל ב' וג' אל ד' וה' אל ז' | |
| וכאשר נמשכו ארבעה מספרים קטנים מה שיהיו על יחס אחד הנה השתי קצוות מעוקבים | |
Proposition 3 |
|
| ג כאשר היו קטני מספרים נמשכים על יחס אחד כמה שיהיו הנה כל אחד משתי הקצוות ראשון אצל האחר | |
| המשל בו כי מספרי א"ב ג"ד הם קטני מספרים נמשכים על יחסם הנה אומר כי כל אחד משתי הקצוות ראשון אצל האחר | |
| המופת אנחנו נקח קטן שני מספרים על יחס א"ב ג"ד והם ה"ז | |
| ונקח שלשה מספרים הם קטני מספרים נמשכים על יחס והם ח'ט'כ' | |
| וכן לא יסור נקח מן המספרים הנמשכים על יחס א"בג"ד עד שיהיה על מניין א"בג"ד | |
| ויהיה ל'מ'נ'ס' נמשכים והם על יחס א'ב'ג'ד' | |
| וא"בג"ד הם קטני המספרים על יחסם | |
| ומנין ל'מ'נ'ס' כמנין א'ב'ג'ד' | |
| אם כן כל אחד מן ל'מ'נ'ס' שוה לבן גילו מן א"בג"ד | |
| אם כן שניהם ל' כמו א' וס' כמו ד' | |
| וה"ז שני מספרים היותר קטנים על יחסם אם כן שניהם נבדלים | |
|
|
וכבר הוכה ה' בכמוהו והיה ח' |
|
|
והוכה ה' בח' והיה ל' |
|
|
והוכה ז' בכמוהו והיה כ' |
| אם כן ח"כ נבדלים וכן ל"ס נבדלים ול' כמו א' וס' כמו ד' אם כן א"ד נבדלים | |
| וזה מ'ש'ל' | |
Proposition 4 |
|
| ד נרצה לבאר איך נמצא
קטני מספרים נמשכים על יחסם כמו יחסים מונחים | |
| ויהיו היחסי' המונחים הם יחס א' אל וג' אל ד' וה' אל ז' ויהיו א"ב קטני שני מספרים על יחס שניהם וכן ג"ד וה"ז | |
| ונרצה למצא קטני מספרים נמשכים על יחס א' אל ב' וג' אל ד' וה' אל ז' | |
| הנה נקח קטן מספר ימנוהו ב"ג והוא ט' | |
| ונשים א' ימנה ח' בשעור מה שימנה ב"ט | |
| וד' ימנה כ' בשעור מה שימנה ג"ט | |
| ונקח קטן מספר ימנוהו ה"ב והוא ל' | |
| ויהיה ז' ימנה מ' בשעור מה שימנה ה"ל | |
| וח"ט ימנו נ' וס' בשעור מה שימנה כ"ל | |
| והנה א' ימנה ח' בשעור מה שימנה כ"ל | |
| והנה א' ימנה ח' בשעור מה שימנה ב"ט | |
|
|
אם כן יחס א' אל ב' כיחס ח' אל ט' |
| וח' ימנה נ' בשעור מה שימנה ט"ס | |
|
|
אם כן יחס ח' אל ט' כיחס נ' אל ס' |
|
|
וכבר היה יחס א' אל ב' כיחס ח' אל ט' |
|
|
אם כן יחס א' אל ב' כיחס נ' אל ס' |
|
|
וכן יחס ג' אל ד' כיחס ס' אל ל' |
| וה' ימנה ל' בשעור מה שימנה ז' מ' | |
|
|
אם כן יחס ה' אל ז' כיחס ל' אל מ' |
| אם כן מספר נ"ס ל"מ נמשכים על יחס א' אל ב' וג' אל ד' וה' אל ז' | |
| ואומר שהם קטני מספרים נמשכים על אלו הששה | |
| ואם לא יהיו אלו נאמר שיהיו ע"פ צ"ק קטני המספרים על אלו הששה על היחס הזה הנה אם כן הם יותר קטנים מן נ"ס ל"מ | |
|
|
אם כן יחס א' אל ב' כיחס ע' אל פ' |
| וא"ב שני מספרים היותר קטנים על יחס שניהם | |
| אם כן ב' ימנה פ' וכן ג' ימנה פ' וקטן מספר ימנוהו ב' וג' הוא ט' | |
| אם כן ט' ימנה פ' | |
|
ויחס ג' אל ד' כיחס פ' אל צ' וכיחס ט' אל כ' |
|
|
אם כן יחס ט' אל כ' כיחס פ' אל צ' |
| וט' ימנה פ' אם כן כ' ימנה צ' | |
|
|
ויחס ה' אל ז' כיחס צ' אל ק' |
| וה"ז שני מספרים היותר קטנים על יחס שניהם | |
| אם כן ה' ימנה צ' | |
| וכבר היה כ' ימנה צ' | |
| אם כן ה' וכ' ימנו צ' | |
| אם כן קטן מספר שימנוהו ה' וכ' והוא ל' ימנה צ' | |
| אם כן ל' הגדול ימנה צ' הקטן זה שקר | |
| אם כן נ"ס ל"מ מעטי מספר נמשכים על יחס א' אל ב' וג' אל ד' וה' אל ט' ונשלם באורו | |
| ולו פנים אחרים והוא זה אנחנו נקח קטן מספר ימנוהו ב"ג והוא ט' | |
| ונשים א' ימנה ח' בשעור מה שימנה ב"ט | |
| ויהיה ד' ימנה כ' בשעור מה שימנה ג"ט | |
| זה אם שיהיה שימנה כ' אם שיהיה שלא ימנהו | |
| ואם היה שימנה כ' הנה יהיה ז' ימנה ל' בשעור מה שימנה ה' כ' | |
| אם כן א' ימנה ח' בשעור מה שימנה ב"ט | |
|
|
אם כן יחס א' אל ב' כיחס ח' אל ט' |
| וגם כן הנה ג' ימנה ט' בשעור מה שימנה ד' כ' | |
|
|
אם כן יחס ג' אל ד' כיחס ט' אל כ' |
| וגם כן הנה ה' ימנה כ' בשעור מה שימנה ז"ל | |
|
|
אם כן יחס ה' אל ז' כיחס כ' אל ל' |
|
|
הנה כבר התבאר כי יחס א' אל ב' כיחס ח' אל ט' |
|
|
ויחס ג' אל ד' כיחס ט' אל כ' |
|
|
ויחס ה' אל ז' כיחס כ' אל ל' |
| אם כן מספרי ח"ט כ"ל נמשכים על יחס א' אל ב' וג' אל ד' וה' אל ז' | |
| הנה אומר כי הם קטני מספרים נמשכים על היחס הזה קטנים מהם והם מספרי מ'נ'ס'ע' | |
|
|
אם כן יחס א' אל ב' כיחס מ' אל נ' |
| וא"ב שני מספרים היותר קטנים על יחס שניהם אם כן ב' ימנה נ' וג' ימנה גם כן נ' | |
| וקטן מספר שימנוהו ב' וג' הוא ימנה נ' | |
| וקטן מספר שימנוהו ב' ג' הוא ט' | |
| אם כן ט' הגדול ימנה נ' הקטן זה שקר | |
| אם כן אין מספרים נמשכים על יחס א' אל ב' וג' אל ד' וה' אל ז' יותר קטנים ממספרי ח"ט כ"ל | |
| אם כן מספרי ח"ט כ"ל הם קטני המספרים על יחס א' אל ב' וג' אל ד' וה' אל ז' | |
| ואם היה ה' לא ימנה כ' נקח קטן מספר שימנוהו ה' וכ' והוא ס' | |
| ויהיה ח' ימנה מ' וט' ימנה נ' כשעור מה שימנה כ"ס | |
| ויהיה ז' ימנה ע' בשעור מה שימנה ה"ס | |
| אם כן ח' ימנה מ' בשעור מה שימנה ט"נ | |
|
|
אם כן יחס ח' אל ט' כיחס מ' אל נ' |
|
|
ויחס ח' אל ט' כיחס א' אל ב' |
|
|
אם כן יחס מ' אל נ' כיחס א' אל ב' |
|
|
וכן יחס ג' אל ד' כיחס נ' אל ס' |
| וגם כן הנה ה' ימנה ס' בשעור מה שימנה ז"ע | |
|
|
אם כן יחס ה' אל ז' כיחס ס' אל ע' |
|
|
וכבר התבאר כי יחס א' אל ב' כיחס מ' אל נ' |
|
|
ושיחס ג' אל ד' כיחס נ' אל ס' |
| אם כן מספרי מ'נ'ס'ע' נמשכים על יחס א' אל ב' וג' אל ד' וה' אל ז' | |
| ואומר כי הם קטני המספרים על היחס הזה קטנים מהם והם מספרי פ"ק ת"צ | |
|
|
אם כן יחס א' אל ב' כיחס פ' אל ק' |
| וא"ב שני מספרים היותר קטנים על יחסם | |
| אם כן ב' ימנה ק' | |
| אם כן ב' וג' ימנו ק' | |
| וקטן מספר שימנוהו גם כן הנה הוא ימנה א' והוא ט' | |
| אם כן ט' ימנה ק' | |
|
|
ויחס ט' אל ק' כיחס כ' אל ת' על התמורה |
| אם כן כ' ימנה ת' וה' ימנה כ' | |
| אם כן ה' וכ' ימנו ת' | |
| וקטן מספר שימנוהו והוא ס' ימנה ת' | |
| אם כן ס' הגדול ימנה ת' הקטן זה שקר | |
| אם כן אין מספרים נמשכים על יחס א' אל ב' וג' אל ד' וה' אל ז' קטנים ממספרי מ'נ'ס'ע' | |
| אם כן מספרי מ'נ'ס'ע' הם קטני מספרים נמשכים על יחס א' אל ב' וג' אל ד' וה' אל ז' | |
| ומ'ש'ל' | |
Proposition 5 |
|
| ה כל שני מספרים משוטחים הנה יחס אחד משניהם אל האחר מחובר משני יחסי צלעות שניהם | |
| ויהיו מספרי א"ב שני שטחים | |
| הנה אומר כי יחס א' אל ב' מחובר משני יחסי צלעות שניהם | |
|
|
ויהיו שתי צלעות א' שני מספרי ג"ד |
|
|
ושתי צלעות ב' שני מספרי ה"ז |
| ושני היחסים הם יחס ג' אל ה' וד' אל ז' | |
| ונקח קטני מספרים נמשכים על שני יחסי ג' אל ה' וד' אל ז' והם מספרי ח'ט'כ' | |
|
|
הנה יחס ג' אל ה' כיחס ח' אל ט' |
|
|
ויחס ד' אל ז' כיחס ט' אל כ' |
|
|
הנה יחס ג' אל ה' שנוי ביחס ד' אל ז' הוא כיחס ח' אל ט' שנוי ביחס ט' אל כ' |
|
|
אבל יחס ח' אל ט' שנוי ביחס ט' אל כ' הוא יחס ח' אל כ' |
| אם כן יחס ח' אל כ' מחובר משני יחסי הצלעות | |
|
|
הנה אומר כי יחס ח' אל כ' הוא יחס א' אל ב' |
|
|
המופת שנכה ד' בה' ויהיה ל' |
|
|
אם כן ד' הוכה בה' והיה ל' |
|
|
והוכה בג' והיה א' |
|
|
אם כן יחס ג' אל ה' כיחס א' אל ל' |
|
|
אבל יחס ג' אל ה' כיחס ח' אל ט' |
|
|
אם כן יחס א' אל ל' הוא כיחס ה' אל ט' |
|
|
וגם כן הנה ה' הוכה בד' והיה ל' |
|
|
והוכה בז' והיה ב' |
|
|
אם כן יחס ד' אל ז' כיחס ל' אל ב' |
|
|
ויחס ד' אל ז' כיחס ט' אל כ' |
|
|
אם כן יחס ל' אל ב' כיחס ט' אל כ' |
|
|
וכבר התבאר כי יחס א' אל ל' כיחס ח' אל ט' |
|
|
הנה ביחס השוים יהיה יחס א' אל ב' כיחס ח' אל כ' |
| אם כן יחס א' אל ב' כמחובר משני יחסי צלעות שניהם | |
| וזה מ'ש'ל' | |
Proposition 6 |
|
| ו איזה מספרים שיהיו
נמשכים על יחס אחד והראשון מהם לא ימנה השני הנה אין מהם מספר ימנה האחר | |
| נאמר שיהיו מספרי א"בג'ד'ה' נמשכים על יחס אחד ויהיה א' לא ימנה ב' | |
| הנה אומר שאין מהם מספר ימנה אחר | |
| ואולם שאין מהם מספר ימנה השני לו הנה זה יתבאר מפני כי יחס כל אחד מהם אל השני לו הוא יחס א' אל ב' | |
| הנה אומר שהוא לא ימנה זולת השני לו גם כן | |
| ואם לא יהיה כן נאמר שימנה ג"ה | |
| ונמצא קטן מספרים על יחס ג'ד'ה' ומניינם והם ז'ח'ט' | |
| הנה ז"ט שתי הקצוות נבדלים | |
|
|
ויחס ז' אל ח' הוא יחס ג' אל ד' |
| אבל ג' לא ימנה ד' אם כן ז' לא ימנה ח' אם כן אין ז' אחד | |
| כי האחד ימנה כל מספר | |
| ומפני כי מספרי ז'ח'ט' על יחס ג'ד'ה' ועל מניינם היו ביחס השוים יחס ג' אל ה' כיחס ז' אל ט' | |
| אבל ג' ימנה ה' אם כן ז' ימנה ט' והוא ימנה עצמו | |
| הנה ז' אם כן ימנה מספרי ז"ט הנבדלים זה שקר | |
| אם כן אין ג' ימנה ה' | |
| ובכמו זה יתבאר כי אין מהם מספר ימנה אחר | |
| ומ'ש'ל' | |
| ויש לו פנים אחרים מן המופת והוא שנעשה כמו שאמרנו במשל ואומר כי ג' לא ימנה ה' | |
| המופת כי מספרי ג'ד'ה' אם היו קטני המספרים על יחסם הנה ג' לא ימנה ה' כי שניהם נבדלים | |
| ואם לא יהיו קטן המספרים על יחסם נקח קטן המספרים על יחסם ומניינם והם ז'ח'ט' | |
| ונבאר כמו שבארנו קודם כי ז' אינו אחד | |
|
|
ויהיה ביחס השוים יחס ז' אל ט' כיחס ג' אל ה' |
| אבל ז' לא ימנה ט' מפני כי שניהם נבדלים כי שניהם שתי הקצוות מקטן מספרים על יחסם אם כן ג' לא ימנה | |
| וכן יתבאר בשני המספרים שאין בהם אחד ימנה אחר | |
| וזה מה שרצינו לבאר | |
Proposition 7 |
|
| ז כאשר נמשכו איזה מספרים שיהיו על יחס אחד כמה שיהיו והיה הראשון ימנה האחרון הנה הוא גם כן ימנה השני | |
| ויהיו א'ב'ג'ד' נמשכים על יחס אחד ויהיה א' ימנה ד' | |
| הנה אומר שהוא גם כן ימנה ב' | |
| וזה כי א' והוא הראשון אם לא יהיה מונה ב' השני לו הנה אין ממספרי אבג"ד מספר ימנה אחר אבל א' ימנה ד' הנה הוא אם כן ימנה ב' | |
| ומ'ש'ל' | |
Proposition 8 |
|
| For every two numbers, between which fall numbers that are all in the same ratio, between every two numbers, which have the same ratio with the [original] numbers, fall numbers that are in the same ratio as the ratio of those that fall between the two [original numbers]. | ח כל שני מספרים יפלו בין שניהם מספרים ויהיו כלם על יחס אחד הנה יפול בין כל שני מספרים על יחס שניהם מן המספרים עד שישובו כלם נמשכים על יחס כמו שנפלו בין שניהם |
| We say that the two numbers G and D fall between the two numbers A and B | ונאמר שיפולו בין שני מספרי א"ב שני מספרי ג"ד |
| Let the numbers A; G; D; B be in the same ratio | הנה יהיו מספרי א"ג ד"ב על יחס אחד |
|
|
ויהיה יחס א' אל ב' כיחס ה' אל ז' |
| Supposition: between H and Z fall numbers that are in the same ratio as the numbers that fall between A and B, which are G and D. | הנה אומר כי יפולו בין ה"ז מן המספרים עד שיהיו כלם נמשכים על יחס אחד כמו מספר מה שנפל בין א"ב והוא ג"ד |
| Proof: | המופת אנחנו נקח קטן מספרים על יחס א"ג ד"ב ומניינם ח"ט כ"ל על מנין א"ג ד"ב |
|
|
ויחסם אם כן יחס ח' אל ל' כיחס א' אל ב' |
|
|
ויחס א' אל ב' כיחס ה' אל ז' |
|
|
אם כן יחס ח' אל ל' כיחס ה' אל ז' |
| וח"ל נבדלים | |
| אם כן שניהם שני מספרים היותר קטנים על יחס שניהם וימנו כל שני מספרים על יחס שניהם בשוה | |
| אם כן ח' ימנה ה' בשעור מה שימנה ל"ז | |
| ויהיה ט' ימנה מ' | |
| וכ' ימנה נ' בשעור מה שימנה ח' ה' | |
| אם כן כל אחד ממספרי ח"ט כ"ל ימנה בן גילו ממספרי ה"מ נ"ז בשוה | |
| אם כן מספרי ח"ט כ"ל על יחס מספרי ה'מ'נ'ז' וח"ט כ"ל על יחס א"ג ד"ב | |
| אם כן א"ג ד"ב על יחס ה'מ'נ'ז' ומניינם אם כן מנין מה שנפל בין ה"ז מן המספרים אשר שבו יחד נמשכים על יחסם כמנין מה שנפל בין א"ב | |
| ומ'ש'ל' | |
Proposition 9 |
|
| ט כל שני מספרים נבדלים יפלו בין שניהם מספרים ויהיו כלם נמשכים על יחס אחד הנה מנין מה שיפול בין שניהם מהמספרים כמו מנין מה שיפול בין כל אחד משניהם ובין האחד מן המספרים עד שישובו כלם נמשכים על יחס אחד | |
| נאמר שיהיו שני מספרי א"ב נבדלים ויפולו בין שניהם שני מספרי ג"ד וישובו מספרי א"ג ד"ב נמשכים על יחס אחד | |
| הנה אומר כי מניין מה שיפול בין א' ובין האחד ובין ב' ובין האחד מן המספרים עד שישובו כלם נמשכים על יחס | |
| המופת אנחנו נקח שני מספרים היותר קטנים על יחס א"ג ד"ב והם ה"ז ושלשה מספרים היותר קטנים על היחס הזה והם ח'ט'כ' לא נסור להוסיף אחד אחד עד שנקח קטני מספרים על יחס א"ג ד"ב ומניינם והם ל'מ'נ'ס' | |
| אם כן מספרי ל'מ'נ'ס' קטני מספרים נמשכים על יחס א"ג ד"ב ושתי הקצוות ממספרי א"ג ד"ב הנמשכים על יחס נבדלים | |
| אם כן א"ג ד"ב קטני המספרים על יחסם | |
| אם כן כל אחד מן ל'מ'נ'ס' שוה לגילו מן א"ג ד"ב | |
| וה' הוכה בכמוהו ושב ח' | |
| אם כן ה' ימנה ח' בשעור אחדי ה' והאחד ימנה אחדיו | |
| אם כן האחד ימנה ה' בשעור מה שימנה ה' ח' | |
| אם כן יחס האחד אל ה' כיחס ה' אל ח' | |
| וגם כן הנה ה' הוכה בח' והיה ל' | |
| אם כן ח' ימנה ל' בשעור אחדי ה' | |
| אם כן האחד ימנה ה' בשעור מה שימנה ח' ל' | |
| אם כן יחס האחד אל ה' כיחס ח' אל ל' | |
| וכבר התבאר כי יחס האחד אל ה' כיחס ה' אל ח' ויחס ח' אל א' | |
| וכן התבאר כי יחס האחד אל ז' כיחס ז' אל כ' . ויחס כ' אל ב' | |
| אם כן מנין מה שנפל בין א' וב' מן המספרים והוא ג"ד כמנין מה שנפל בין א' ובין האחד מן המספרים והוא ז"כ ושבו כלם נמשכים על יחס אחד | |
| ומ'ש'ל' | |
Proposition 10 |
|
| י כל שני מספרים בין כל אחד משניהם ובין האחד מהמספרים כמה שיהיו הנה יהיו כלם נמשכים על יחס אחד הנה יפול בין שניהם מן המספרים עד שיהיו כלם נמשכים על יחס אחד כמו מנין מה שנפל בין כל אחד משניהם ובין האחד מן המספרים אשר יהיו בהם הכל נמשכים על יחס אחד | |
| ונניח שיהיה האחד ל' ויפולו בין א' ובין ל' האחד שני מספרי ג"ד . ובין מספר ב' ובין ל' האחד שני מספרי ה"ז וישובו א"ד ג"ל נמשכים על יחס אחד וכן ב"ז ה"ל נמשכים על יחס אחד | |
| הנה אומר שיפול בין שני מספרי א"ב מן המספרים עד שישובו כלם נמשכים על יחס במנין מה שנפל בין כל אחד משני מספרי א"ב ובין האחד מן המספרים עד שיהיו כלם נמשכים על יחס אחד והם ג"ד ה"ז | |
| המופת כי יחס ל' והוא האחד אל ג' כיחס ג' אל ד' | |
| אם כן האחד ימנה ג' בשעור מה שימנה ג"ד | |
| והאחד ימנה ג' בשעור אחדי ג' | |
| וג' הוכה בדומה לו והיה ד' | |
| וגם כן הנה יחס האחד אל ג' הוא יחס ד' אל א' | |
| אם כן האחד ימנה ג' בשעור מה שימנה ד"א | |
| והאחד ימנה ג' בשעור אחדי ג' | |
| וג' הוכה בד' והיה א' | |
| וכן ה' הוכה בכמוהו ושב ז' | |
| והוכה בז' ושב ב' | |
| וגם כן הנה נכה ג' בה' וישוב ח' | |
| ויוכה בח' וישוב ט' | |
| וה' בח' וישוב כ' | |
| ויתבאר כמו שבאררנו קודם כי ד'ח'ז' מתיחסים ויחסם יחס ג' אל ה' ושא"ט כ"ב נמשכים אל יחס ג' אל ה' | |
| אם כן מנין מה שנפל בין שני מספרי א"ב מן המספרים והוא ט"כ עד כי שבו כלם נמשכים על יחס אחד כמנין מה שנפל בין כל אחד משניהם ובין האחד מן המספרים | |
| ומ'ש'ל' | |
Proposition 11 |
|
| יא כל שני מספרים מרובעים הנה יפול בין שניהם מספר מתיחס לשניהם ויחס המרובע אל המרובע הוא יחס צלעו אל צלעו שנוי בכפל | |
| נניח שיהיו שני מספרים מרובעים והם א"ב | |
| ויהיה צלע א' מספר ג' | |
| וצלע ב' מספר ד' | |
| הנה אומר כי בין א' ובין ב' מספר מתיחס לשניהם ושיחס א' אל ב' הוא יחס ג' אל ד' שנוי בכפל | |
| ויהיה המקובץ מהכאת ג' בד' מספר ה' | |
| הנה מפני כי צלע המרובע הוא מספר ג' יהיה המקובץ מהכאת ג' בכמוהו מספר א' | |
| וכן יהיה המקובץ מהכאת ד' בכמוהו מספר ב' | |
| הנה מפני כי ג' הוכה בשני מספרים והם ג"ד והיו מזה שני מספרי א"ה | |
| יהיה יחס ג' אל ד' כיחס א' אל ה' | |
| וכמו זה גם כן התבאר כי יחס ג' אל ד' כיחס ה' אל ב' | |
| אם כן יחס א' אל ה' כיחס ה' אל ב' | |
| אם כן בין שני מרובעי מספר ה' מתיחס לשניהם מפני כי א'ה'ב' השלשה מתיחסים | |
| יהיה יחס א' אל ב' כיחס א' אל ה' שנוי בכפל | |
| אבל א' אל ה' כיחס ג' אל ד' | |
| אם כן יחס א' אל ב' כיחס ג' אל ד' שנוי בכפל | |
| ומ'ש'ל' | |
Proposition 12 |
|
| יב כל שני מספרים מעוקבים הנה יפול בין שניהם שני מספרים ויהיה הארבעה נמשכים מתיחסים על יחס אחד ויחס המעוקב אל המעוקב הוא ישם צלעו אל צלעו משולשת | |
| ונניח שיהיו שני מספרים מעוקבים והם א"ב ויהיה צלע א' המעוקב מספר ג' וצלע ב' המעוקב מספר ד' | |
| הנה אומר כי בין א' וב' שני מספרים ישיבו הארבעה נמשכים על יחס אחד | |
| ושיחס א' אל ב' הוא יחס ג' אל ד' משולש בכפל | |
| ויהיה המקובץ מהכאת ג' בכמוהו מספר ה' | |
| ומהכאת ג' בד' ז' | |
| ומהכאת ד' בכמוהו ח' | |
| ויהיה המקובץ מהכאת ג' בז' ט' | |
| ומהכאת ד' בז' כ' | |
| הנה מפני כי א' מעוקב וצלעו ג' ומרובע ג' הוא ה' יהיה המקובץ מהכאת ג' בה' מעוקב א' | |
| וכן גם כן יהיה המקובץ מן ד' בח' מעוקב ב' | |
| ומפני כי ג' הוכה בשני מספרי ג"ד והיו מזה שני מספרי ה"ז יהיה יחס ג' אל ד' הוא יחס ה' אל ז' | |
| ויהיה גם כן יחס ג' אל ד' הוא יחס ז' אל ח' | |
| ומפני כי ג' הוכה גם כן ב'ה'ז' והיה מזה א"ט יהיה יחס ה' אל ז' הוא יחס א' אל ט' | |
| אבל כי יחס ה' אל ז' הוא יחס ג' אל ד' | |
| אם כן יחס א' אל ט' הוא יחס ג' אל ד' | |
| ומפני כי ד' הוכה בז' וח' והיה מזה כ' | |
| וב' יהיה ז' אל ח' הוא יחס כ' אל ב' | |
| ויחס ז' אל ח' הוא יחס ג' אל ד' | |
| אם כן יחס כ' אל ב' הוא יחס ג' אל ד' | |
| ויחס ג' אל ד' הוא יחס א' אל ט' וט' אל כ' וכ' אל ב' | |
| אם כן יחס א' אל ט' הוא יחס ט' אל כ' וכ' אל ב' | |
| אם כן בין שני מספרי א"ב המעוקבים שני מספר ט"כ והארבעה נמשכים על יחס אחד | |
| ומפני כי מספרי א"ט כ"ב הארבעה נמשכים על יחס אחד יהיה יחס א' אל ב' הוא יחס א' אל ט' משולש בכפל | |
| אבל יחס א' אל ט' הוא יחס ג' אל ד' | |
| אם כן יחס א' אל ב' הוא יחס ג' אל ד' משולש בכפל | |
| וזה מה שרצינו לבאר | |
Proposition 13 |
|
| יג איזה מספרים שיהיו על יחס אחד והוכה כל אחד בכמוהו הנה מרובעיהם גם נמשכים על יחס אחד | |
| וכן אם הוכה כל מספר מהם במרובעו הנה מעוקביהם גם כן נמשכים על יחס אחד וכן לא יסורו הקצוות והמספרים האחרונים כאשר הוכו בהם על הדרך הזה יהיו נמשכים על יחס אחד | |
| ונניח שיהיו מספרים נמשכים על יחס אחד והם מספרי א'ב'ג' ונכה כל אחד משניהם בדומה לו ויהיו מרובעיהם ד' ה"ז ויוכה כל אחד משניהם במרובעו וישובו מעוקביהם ח'ט'ב' | |
| הנה אומר כי ד'ה'ז' מתיחסים ושח'ט'כ' מתיחסים והיחס הוא הוא א'ב'ג' | |
| ויוכה א' בב' ויהיה ל' | |
| ובל' וה' ויהיה מזה נ' וס' | |
| ויוכה ב' בג' ויהיה מ' | |
| ובמ' וז' ויהיה מזה ע' ופ' | |
| הנה א' הוכה בשני מספרי א"ב והיו מזה ד"ל | |
| אם כן א' אל ב' כיחס ד' אל ל' | |
| וגם כן ב' הנה הוכה בא' והיה ל' | |
| ובדומה לו והיה ה' | |
| אם כן יחס א' אל ב' כיחס ל' אל ה' | |
| וכבר היה יחס א' אל ב' כיחס ד' אל ל' | |
| אם כן יחס ד' אל ל' כיחס ל' אל ה' | |
| אם כן ד'ל"ה מתיחסים ויחסם הוא יחס א' אל ב' | |
| אבל יחס א' אל ב' הוא יחס ב' אל ג' | |
| אם כן יחס ד'ל"ה הוא יחס ב' אל ג' | |
| וגם כן הנה ב' הוכה בדומה לו והיה ה' ובג' והיה מ' | |
| אם כן יחס ב' אל ג' הוא יחס ה' אל מ' | |
| וג' הוכה בב' והיה מ' | |
| והוכה בדומה לו והיה ז' | |
| אם כן יחס ב' אל ג' הוא יחס מ' אל ז' | |
| אם כן יחס ה' אל מ' הוא יחס מ' אל ז' | |
| אם כן ה' ומ"ז מתיחסים הנה יחסם הוא יחס ב' אל ג' | |
| וכבר היו מספרי ד'ל"ה אלו יחסם כמו יחס ב' אל ג' | |
| אם כן ד'ל"ה מתיחסים וה'מ'ז' מתיחסים והיחס אחד והמנין אחד | |
| אם כן ביחס השוים יהיה יחס ד' אל ה' הוא יחס ה' אל ז' וד'ה'ז' מתיחסים והם שלשה מספרים הנה יחסם אל הראשון | |
| וגם כן הנה א' הוכה בד' והיה ח' | |
| ובל' והיה נ' | |
| אם כן יחס ד' אל ל' הוא יחס ח' אל נ' | |
| ויחס ד' אל ל' הוא יחס א' אל ב' | |
| אם כן יחס ח' אל נ' הוא יחס א' אל ב' | |
| וכן יחס א' אל ב' הוא יחס נ' אל ס' | |
| ויחס א' אל ב' הוא יחס ח' אל נ' | |
| אם כן ח'נ'ס' מתיחסים | |
| וא' וב' הוכו בה' והיה מזה ס' וט' | |
| אם כן יחס א' אל ב' הוא יחס נ' אל ס' וס' אל ט' | |
| אם כן מספרי ח'נ'ס'ט' מתיחסים נמשכים על יחס א' אל ב' | |
| וכן ט"עפ"ב נמשכים על יחס ב' אל ג' ושני היחסים אחד | |
| אם כן ח'נ'ס'ט' נמשכים על יחס ט"ע פ"כ והמנין אחד | |
| אם כן יחס ח' אל ט' כיחס ט' אל כ' | |
| אם כן ח'ט'כ' גם כן נמשכים על יחס אחד | |
| וזה הוא מה אשר רצינו לבארו | |
Proposition 14 |
|
| יד כל שני מספרים מרובעים ימנה אחד משניהם האחר הנה צלע המונה משניהם ימנה צלע המנוי | |
| ואם היה מספר ימנה מספר הנה מרובע המונה ימנה מרובע המנוי | |
| נניח שיהיו שני המספרים מרובעים והם א"ב ויהיה צלע א' מספר ג' וצלע ב' מספר ד' ויהיה א' ימנה ב' | |
| הנה אומר כי ג' ימנה ד' | |
| המופת אנחנו נכה ג' בד' ויהיה ה' | |
| וא' מרובע ג' | |
| וב' מרובע ד' | |
| אם כן ה' הוא המספר אשר בין שניהם וא'ה'ב' מתיחסים ויחסם הוא יחס ג' אל ד' | |
| וא' הראשון ימנה ב' האחרון | |
| אם כן הוא ימנה מספר ה' | |
| ויחס א' אל ה' הוא יחס ג' אל ד' | |
| וא' ימנה ה' | |
| אם כן ג' ימנה ד' ואם יהיה ג' ימנה ד' | |
| הנה אומר כי א' ימנה ב' והתבאר כי א'ה'ב' מתיחסים ויחסם יחס ג' אל ד' | |
| אם כן יחס ג' אל ד' כיחס א' אל ה' וג' ימנה ד' | |
| אם כן א' ימנה ה' וה' השני הוא ימנה הוא ימנה ב' האחר | |
| וזה מה שרצינו לבאר | |
| ובכאן התבאר כי אם לא ימנה מרובע מרובע לא ימנה צלעו צלעו ואם לא ימנה הצלע הצלע לא ימנה המרובע המרובע | |
Proposition 15 |
|
| טו כל מספר מעוקב ימנה מספר מעוקב הנה צלע המעוקב המונה ימנה צלע המעוקב המנוי | |
| ואם היה מספר ימנה מספר הנה מעוקב המונה ימנה מעוקב המנוי | |
| ויהיו שני מספרים מעוקבים והם א"ב ושתי צלעותיהם ג"ד ויהיה א' ימנה ב' | |
| הנה אומר כי ג' ימנה ד' | |
| המופת שנכה ג' בדומה לו ויהיה ה' | |
| ונכה ד' בדומה לו ויהיה ז' | |
| הנה ג' כאשר הוכה בה' היה א' | |
| וד' כאשר הוכה בז' היה ב' | |
| היה נכה ג' בד' ויהיה ח' | |
| ונכהו גם כן בח' וז' ויהיו ט' וכ' | |
| הנה מספרי ה'ח'ז' מתיחסים ויחסם הוא יחס ג' אל ד' | |
| וג' הוכה בה' והיה א' | |
| והוכה בח' והיה ט' | |
| אם כן יחס ה' אל ח' הוא יחס א' אל ט' | |
| ויחס ה' אל ח' כיחס ג' אל ד' | |
| אם כן יחס א' אל ט' כיחס ג' אל ד' | |
| וכן יהיה יחס ט' אל כ' הוא יחס ג' אל ד' | |
| ויחס ג' אל ד' הוא יחס א' אל ט' | |
| אם כן יחס א' אל ט' הוא יחס ט' אל כ' | |
| וג"ד הוכו בז' והיה מזה כ"ב | |
| אם כן יחס ג' אל ד' כיחס כ' אל ב' | |
| ויחס ג' אל ד' הוא יחס א' אל ט' וט' אל כ' | |
| אם כן א"ט כ"ב נמשכים על יחס ג' אל ד' | |
| וא' הראשון ימנה ב' האחרון | |
| אם כן הוא ימנה ט' השני | |
| ויחס א' אל ט' כיחס ג' אל ד' וא' ימנה ט' | |
| אם כן ג' ימנה ד' | |
| וגם כן יהיה ג' ימנה ד' | |
| הנה אומר כי א' ימנה ב' | |
| וכן יתבאר כמו שבארנו כי א"ט כ"ב נמשכים על יחס ג' אל ד' ויהיה א' הראשון ימנה ט' השני ויתחייב שימנה ב' | |
| ומ'ש'ל' | |
| ובכאן כי כאשר לא ימנה מעוקב מעוקב לא ימנה צלעו צלעו וכאשר לא ימנה הצלע הצלע לא ימנה המעוקב המעוקב | |
Proposition 16 |
|
| יו כל שני מספרים משוטחים מתדמים יפול בין שניהם מספר מתיחס לשניהם ויחס השטח אל השטח הוא יחס צלעו אל צלעו שנוי | |
| ויהיו שני מספרים משוטחים והם א"ב ויהיו שני צלעי א' שני מספרי ג"ד ושני צלעי ב' שני מספרי ה"ז | |
| הנה אומר כי בין שני מספרי א"ב מספר מתיחס לשניהם ויחס א' אל ב' כיחס צלע א' אל צלע ב' אשר הוא גילו שנוי | |
| המופת כי א"ב שני שטחים מתדמים | |
| אם כן צלעותיהם מתיחסות ושני צלעי א' ג"ד | |
| ושני צלעי ב' ה"ז | |
| הנה יהיה יחס ג' אל ה' כיחס ד' אל ז' | |
| ונכה ד' בה' ויהיה מזה ח' | |
| אבל הכאת ד' בג' הוא מספר א' | |
| וד' הוכה בשני מספרי ג"ה והיה מזה א"ח | |
| אם כן יחס ג' אל ה' כיחס א' אל ח' | |
| ויחס ג' אל ה' כיחס ד' אל ז' | |
| אם כן יחס ד' אל ז' כיחס א' אל ח' | |
| שיחס ד' אל ז' כיחס א' אל ח' | |
| אם כן יחס א' אל ח' הוא יחס ח' אל ב' | |
| אם כן א'ח'ב' מתיחסים הנה כבר נפל בין א' וב' מספר והוא ח' והיו מתיחסים | |
| הנה אומר כי יחס א' אל ב' הוא יחס צלעו אל צלעו אשר הוא גילו שנוי | |
| הנה מפני כי יחס א' אל ח' כיחס ח' אל ב' | |
| הנה יחס א' אל ב' הוא יחס א' אל ח' שנוי | |
| ויחס א' אל ח' הוא יחס הצלע אל הצלע | |
| אם כן יחס א' אל ב' הוא יחס צלעו אל צלעו שנוי | |
| ומ'ש'ל' | |
Proposition 17 |
|
| יז כל שני מספרים מוגשמים מתדמים הנה יפול בין שניהם שני מספרים וימשכו מתיחסים ויחס אחד משני המוגשמים אל האחר הוא יחס צלעו אל צלעו שהוא גילו משולש | |
| המופת כי א"ב שני מוגשמים מתדמים וצלעי איהם ג'ד'ה' וצלעי ב' הם ז'ח'ט' ויחס ג' אל ז' כיחס ד' אל ח' וכיחס ה' אל ט' | |
| וג' כאשר הוכה בד' היה כ' | |
| וז' כאשר הוכה בח' היה ל' | |
| אם כן כ"ל שנים משוטחים מתדמים מפני כי צלעות שניהם מתיחסות הנה יפול בין כ"ל מספר וימשך עם שניהם על יחס אחד ויהיה המספר הזה מ' | |
| וה' כאשר הוכה במ' היה נ' | |
| וט' כאשר הוכה במ' היה ס' | |
| ומשוטח ג' בד' אשר הוא ב' כאשר הוכה בה' היה א' | |
| אבל ה' כאשר הוכה גם כן במ' היה נ' | |
| אם כן יחס א' אל נ' כיחס כ' אל מ' | |
| ויחס כ' אל מ' כיחס מ' אל ל' | |
| ויחס מ' אל ל' כיחס ג' אל ז' וכיחס ד' אל ח' וכיחס ה' אל ט' והוא יחס הצלע אל הצלע שהוא גילו וכן יחס א' אל נ' | |
| וכן כל אחד מן ה"ט הוכה במ' והיה נ"ס | |
| אם כן יחס ה' אל ט' כיחס נ' אל ס' | |
| ויחס ה' אל ט' וג' אל ז' וד' אל ח' הוא יחס הצלע לצלע שהוא גילו | |
| ויחס הצלע אל הצלע כיחס א' אל נ' | |
| אם כן יחס א' אל נ' כיחס נ' אל ס' | |
| וט' כאשר הוכה בל' היה ב' | |
| וכבר הוכה ט' במ' והיה ס' | |
| אם כן יחס מ' אל ל' כיחס ס' אל ב' | |
| ויחס מ' אל ל' הוא יחס הצלע אל הצלע | |
| אם כן יחס ס' אל ב' הוא יחס הצלע אל הצלע | |
| אם כן יחס הצלע אל הצלע הוא כיחס א' אל נ' וכיחס נ' אל ס' וכיחס ה' אל ב' | |
| אם כן מספרי א'נ'ס'ב' נמשכים על יחס הצלע אל הצלע שהוא גילו | |
| וכבר נפלו בין א"ב שני מספרי נ"ס | |
| והנה אומר כי יחס א' אל ב' הוא יחס הצלע אל הצלע אשר הוא גילו משולש | |
| מפני כי יחס א' אל נ' כיחס נ' אל ס' וכיחס ס' אל ב' | |
| אם כן יחס א' אל ב' הוא יחס א' אל נ' משולש | |
| ויהיה א' אל נ' הוא יחס הצלע אל הצלע | |
| אם כן יחס א' אל ב' הוא יחס צלעו אל צלעו אשר הוא גילו משולש | |
| וזה מה שרצינו לבאר | |
Proposition 18 |
|
| יח כאשר נפל מספר בין שני מספרים וימשכו מתיחסים הנה שני המספרים משוטחים מתדמים | |
| המשל בו כי מספר ג' נפל בין שני מספרי א"ב משוטחים מתדמים | |
| המופת אנחנו נקח שני מספרים היותר קטנים על יחס א'ג'ב' והם ד"ה | |
| הנה יחס א' אל ג' כיחס ד' אל ה' | |
| וד"ה שני מספרים היותר קטנים והם ימנו כל שני מספרים על יחס שניהם בשוה הקטן לקטן והרב לרב | |
| הנה ד' ימנה א' וה' ימנה ג' בשוה ויהיו אחדי מספר ז' בשעור מה שימנה ד' א' | |
| אם כן ה' ימנה ג' בשעור אחדי ז' | |
| וד' הוכה בז' והיה א' משוטח ושתי צלעותיו ד"ז | |
| וגם כן הנה יחס ג' אל ב' כיחס ד' אל ה' | |
| וד"ה שני מספרים היותר קטנים על יחס שניהם בשוה הקטן לקטן והרב לרב | |
| אם כן ד' ימנה ג' וה' ימנה ב' | |
| ויהיו אחדי מספר ח' כשעור מה שימנה ה"ב | |
| אם כן ה' ימנה ב' בשעור אחדי ח' | |
| וה' יוכה בח' ויהיה ב' | |
| אם כן ב' משוטח ושתי צלעותיו ה"ח | |
| וד' ימנה ג' בשעור אחדי ח' | |
| הנה ד' הוכה בח' והיה ג' | |
| וכן ז' יוכה בה' ויהיה ג' | |
| אם כן שטח ז' בה' שוה למשוטח ד' בח' | |
| אם כן יחס ז' אל ד' כיחס ח' אל ה' | |
| וד' וז' שתי צלעות א' וה' וח' שתי צלעות ב' אם ^ א"ב שתי שטחים מתדמים מפני כי צלעות שניהם מתיחסים | |
| ומ'ש'ל' | |
Proposition 19 |
|
| יט כל שני מספרים יפלו בין שניהם שני מספרים וימשכו מתיחסים הנה שניהם מוגשמים מתדמים | |
| המשל בו כי שני מספרי א"ב נפלו בין שניהם שני מספרי ג"ד ונמשכו מתיחסים | |
| הנה אומר כי א"ב שניהם מוגשמים מתדמים | |
| המופת אנחנו נקח קטן שלשה מספרים מתיחסים על יחס א"ג ד"ב והם מספרי ה'ז'ח' | |
| אם כן שני הקצוות והם ח"ה כבר נפל בין שניהם מספר ו' ונמשכו מתיחסים | |
| אם כן ה' וח' שני שטחים מתדמים | |
| ויהיו שני צלעי ה' כ"ל | |
| ושני צלעי ח' מ"נ | |
| וה"ח שני שטחים מתדמים וצלעות שניהם מתיחסות יחס כ' אל מ' כיחס ל' אל נ' | |
| וה'ז'ח' על יחס א'ג'ד' | |
| אם כן יחס ה' אל ז' כיחס א' אל ג' | |
| ויחס ז' אל ח' כיחס ג' אל ד' | |
| ומנין ה'ז'ח' כמו מנין א'ג'ד' | |
| אם כן יחס ה' אל ח' כיחס א' אל ד' | |
| וכל אחד מן ה"ח ראשון אצל האחר | |
| אם כן שניהם קטן שני מספרים על יחס שניהם | |
| וימנו כל שני מספרים על יחס שניהם בשווי הקטן לקטן והרב לרב | |
| הנה ה' ימנה א' בשעור מה שימנה ח"ד | |
| ויהיו אחדי מספר ט' בשעור מה שימנה ה"א | |
| אם כן ח' ימנה ד' בשעור אחדי מספר ט' | |
| הנה ט' יוכה בח' ויהיה ד' | |
| וה' ימנה א' בשעור אחדי ט' | |
| וה' יוכה בט' ויהיה א' | |
| וה' הוא שטח כ' בל' | |
| אם כן שטח כ' בל' הוכה בט' והיה מוגשם א' | |
| אם כן צלעותיו כ'ל'ט' | |
| וגם כן הנה מספרי ה'ז'ח' על יחס מספרי ג'ד'ב' | |
| ומנין ה'ז'ח' כמנין ג'ד'ב' | |
| אם כן יחס ה' אל ח' כיחס ג' אל ב' וכל אחד מן ה"ח ראשון אצל האחר | |
| אם כן שניהם קטני שני מספרים על יחס שניהם וימנו כל שני מספרים על יחס שניהם בשווי הקטן לקטן והרב לרב | |
| אם כן ה' ימנה ג' בשעור מה שימנה ח"ב | |
| ויהיו אחדי מספר ס' בשיעור מה שימנה ח"ב | |
| אם כן ה' ימנה ג' בשעור אחדי מספר ס' | |
| וח' יוכה בס' ויהיה ב' | |
| וח' והוא שטח מ' בנ' | |
| אם כן שטח מ' בנ' הוכה בס' והיה מוגשם ב' וצלעיו מ'נ'ס' | |
| וט' הוכה בח' והיה ד' | |
| וס' הוכה בח' והיה ב' | |
| אם כן יחס ט' אל ס' כיחס ד' אל ב' | |
| ויחס ד' אל ב' כיחס ה' אל ז' וכיחס ז' אל ח' | |
| אבל יחס ה' אל ז' וז' אל ח' כיחס כ' אל מ' ול' אל נ' | |
| אם כן יחס ט' אל ס' כיחס כ' אל מ' ול' אל נ' והוא יחס הצלע אל הצלע | |
| וצלעות א' הם כ'ל'ט' | |
| וצלעות ב' הם מ'נ'ס' | |
| אם כן א' וב' שני מוגשמים מתדמים מפני כי צלעות שניהם מתיחסות | |
| ונשלם באורו | |
Proposition 20 |
|
| For every three numbers that are in continued proportion, such that the first is a square, the third is a square. | כ כל שלשה מספרים נמשכים על יחס אחד יהיה הראשון מהם מרובע הנה השלישי מרובע |
| המשל בו כי מספרי א'ב'ג' השלשה נמשכים על יחס אחד והראשון מהם והוא א' הוא מרובע | |
| הנה אומר כי ג' השלישי מרובע | |
| המופת אנחנו נקח קטן מספרים על יחס א'ב'ג' מניינם כמניינם והם ד'ה'ז' ושתי הקצוות והם ד"ז שני מרובעים | |
| ויהיה צלע מרובע א' מספר ח' | |
| וצלע מרובע ז' מספר כ' | |
| וצלע מרובע ד' מספר ט' | |
| הנה מפני כי יחס א'ב'ג' כיחס ד'ה'ז' ומניינם כמניינם יהיו ביחס השוים יחס א' אל ג' כיחס ד' אל ז' | |
| וכל אחד משני מספרי ד"ז ראשון אצל האחר | |
| והמספרים אשר קצתם ראשון אצל קצת הם קטני המספרים על יחסם | |
| וקטן המספרים על יחס ימנו המספרים אשר על יחסם בשווי הקטן לקטן והרב לרב | |
| אם כן ד' ימנה א' בשעור מה שימנה ז"ג | |
| וכאשר ימנה מרובע מרובע הנה צלעו ימנה צלעו | |
| אם כן ט' ימנה ח' וימנה כ"ל בשעור מה שימנה ט"ח | |
| אם כן יחס ט' אל ח' כיחס כ' אל ל' | |
| ויחס המרובע ההווה מן ט' אל המרובע ההווה מן ח' כיחס המרובע ההווה מן כ' אל המרובע ההווה מן ל' | |
| והמרובע ההווה מן ט' הוא ד' | |
| והמרובע ההווה מן ח' הוא א' | |
| והמרובע ההווה מן כ' הוא ז' | |
| אם כן יחס ד' אל המרובע ההווה מן ל' | |
| ויחס ד' אל א' כיחס ז' אל ג' | |
| אם כן יחס ז' אל ג' כיחס ז' אל המרובע ההווה מן ל' | |
| אם כן ג' שוה למרובע ההווה מן ל' | |
| אם כן ג' מרובע | |
| ונשלם באורו | |
Proposition 21 |
|
| For every four numbers that are in continued proportion, such that the first is a cube, the fourth is a cube. | כא כל ארבעה מספרים נמשכים על יחס יהיה הראשון מהם מעוקב הנה הרביעי מעוקב |
| המשל בו כי ארבעה מספרי א'ב'ג'ד' נמשכים על יחס א' אל ב' כיחס ב' אל ג' וכיחס ג' אל ד' ויהיה א' מעוקב | |
| הנה אומר כי ד' מעוקב | |
| המופת אנחנו נקח קטני המספרים על יחס מספרי א'ב'ג'ד' ועל מניינם והם ה'ז'ח'ט' הנה הקצוות והם ה"ט מעוקב | |
| ויהיה צלע מעוקב א"ל וצלע מעוקב ה"ב וצלע מעוקב ט"נ | |
| הנה מפני כי יחס א"בג"ד כיחס ה'ז'ח'ט' והם שוים במנין יהיו ביחס השווי יחס א' אל ד' כיחס ה' אל ט' | |
| וכל אחד מן ה"ט ראשון אצל האחר | |
| אם כן שניהם קטן שני המספרים על יחסם וקטני המספרים על יחס ימנו המספרים על יחסם בשווי הקטן לקטן והרב לרב | |
| אם כן ה' ימנה א' כמו מה שימנה ט"ד | |
| וכאשר מנה מעוקב מעוקב הנה צלעו ימנה צלעו | |
| אם כן ב' ימנה ל' ויהיה מנין מה שימנה נ"מ כמו מנין מה שימנה כ"ל | |
| אם כן יחס כ' אל ל' כיחס נ' אל מ' | |
| ויחס המעוקב ההווה מן נ' אל המעוקב ההווה מן ל' כיחס המעוקב ההווה מן נ' אל המעוקב ההווה מן מ' | |
| והמעוקב ההווה מן כ' הוא ה' | |
| והמעוקב ההווה מן ל' הוא א' | |
| והמעוקב ההווה מן נ' הוא ט' | |
| אם כן יחס ה' אל א' כיחס ט' אל המעוקב ההווה מן מ' | |
| ויחס ה' אל א' כיחס ט' אל ד' | |
| אם כן ד' שוה למעוקב ההווה מן מ' | |
| אם כן ד' מעוקב | |
| Q.E.D. | וזה מ'ש'ל' |
Proposition 22 |
|
| For every two numbers such that the ratio of one of them to the other is as the ratio of a square number to a square number and one of them is a square number, the other is a square number. | כב כל שני מספרים יחס אחד מהם אל האחר כיחס מרובע אל מרובע ואחד משניהם מרובע הנה האחר מרובע |
| המשל בו כי שני מספרי א"ב יחס אחד משניהם אל האחר כיחס מספר ג' המרובע אל מספר ד' המרובע וא' מרובע | |
| אומר כי ב' מרובע | |
| המופת כי שני מספרי ג"ד מרובעים ומשוטחים מתדמים וכבר יפול בין שניהם מספר וימשכו מתיחסים | |
| ויחס ג' אל ד' כיחס א' א' אל ב' | |
| אם כן א"ב הנה יפול בין שניהם מספר ימשכו מתיחסים וא' מרובע | |
| הנה אם כן ב' מרובע | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 23 |
|
| For every two numbers such that the ratio of one of them to the other is as the ratio of a cubic number to a cubic number and one of them is a cubic number, the other is a cubic number. | כג כל שני מספרים יחס אחד מהם אל האחר כיחס מעוקב אל מעוקב ואחד משניהם מעוקב הנה האחר מעוקב |
| המשל בו כי שני מספרי א"ב יחס אחד משניהם אל האחר כיחס מספר ג' המעוקב אל מספר ד' המעוקב וא' מעוקב | |
| הנה אומר כי ב' מעוקב | |
| המופת כי ג"ד מעוקבים ומוגשמים מתדמים והנה יפול בין שניהם שני מספרים וימשכו מתיחסים | |
| ויחס ג' אל ד' כיחס א' אל ב' | |
| הנה כבר יפול בין א"ב שני מספרים וימשכו מתיחסים וא' מעוקב | |
| אם כן ב' מעוקב | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 24 |
|
| When there are two numbers such that the ratio of one of them to the other is as the ratio of a square number to a square number, then they are similar plane numbers. | כד כאשר היו שני מספרים והיה יחס אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע הנה שניהם שני שטחים מתדמים |
| המשל בו כי שני מספרי א"ב יחס אחד משניהם אל האחר כיחס מספר ג' המרובע אל מספר ד' המרובע | |
| הנה אומר כי שני מספרי א"ב שני שטחים מתדמים | |
| המופת כי שני מספרי ג"ד שני מרובעים וכבר יפול בין שניהם מספר מתיחס לשניהם | |
| ויחס א' אל ב' כיחס ג' אל ד' | |
| הנה כבר יפול בין מספרי א"ב מספר מתיחס לשניהם | |
| אם כן מספרי א"ב שני שטחים מתדמים | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 25 |
|
| When there are two numbers such that the ratio of one of them to the other is as the ratio of a cubic number to a cubic number, then they are similar solid numbers. | כה כאשר היו שני מספרים והיה יחס אחד משניהם אל האחר כיחס מספר מעוקב אל מעוקב הנה שניהם מוגשמים מתדמים |
| המשל בו כי שני מספרי א"ב יחס אחד משניהם אל האחר כיחס מספר ג' המעוקב אל מספר ד' המעוקב | |
| הנה אומר כי שני מוגשמי א"ב מוגשמים מתדמים | |
| המופת כי כל אחד משני מספרי ג"ד מעוקב והנה יפול בין שני מספרי ג"ד שני מספרים מתיחסים לשניהם | |
| אם כן מספר א"ב שנים מוגשמים מתדמים | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 26 |
|
| For every two similar plane numbers, the ratio of one of them to the other is as the ratio of a square number to a square number. | כו כל שני מספרים משוטחים מתדמים הנה יחס אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע |
| המשל בו כי שני מספרי א"ב שנים משוטחים מתדמים | |
| הנה אומר כי יחס א' אל ב' כיחס מספר מרובע אל מספר מרובע | |
| המופת כי א"ב שני משוטחים מתדמים וכבר נפל בין שניהם מספר ג' ונמשכו מתיחסים | |
| ונקח קטן שלשה מספרים על יחס א'ג'ב' והוא ד'ה'ז' הנה שתי הקצוות והם ד"ז מרובעים ומנין ד'ה'ז' כמנין א'ג'ב' | |
| אם כן יחס א' אל ב' כיחס מספר מרובע אל מספר מרובע | |
| Q.E.D. | וזה מה שרצינו לבאר |
Proposition 27 |
|
| For every two similar solid numbers, the ratio of one of them to the other is as the ratio of a cubic number to a cubic number. | כז כל שני מספרים מוגשמים מתדמים הנה יחס אחד משניהם אל האחר כיחס מספר מעוקב אל מספר מעוקב |
| המשל בו כי שני מספרי א"ב מוגשמים מתדמים ויפולו בין שניהם שני מספרים והם ג"ד וימשכו מתיחסים | |
| ונקח קטן ארבעה מספרים על יחס א"גד"ב והם ה'ז'ח'ט' הנה שני הקצוות הם ה"ט מעוקבים ומנין ה"זח"ט א"גד"ב | |
|
|
הנה יחס ה' אל ט' כיחס א' אל ב' |
|
ויחס א' אל ב' כיחס מספר ה' המעוקב אל מספר ט' המעוקב |
| Q.E.D. | וזה מה שרצינו לבאר |
| נשלם המאמר השמיני |
Book Nine |
המאמר התשיעי |
Proposition 1 |
|
| א כל שני מספרים משוטחים מתדמים יוכה אחד משניהם באחר הנה הוא ישוב מרובע | |
| המשל בו כי שני מספרי א"ב שני שטחים מתדמים | |
| והוכה א' בב' והיה ג' | |
| הנה אומר כי ג' מרובע | |
| Proof:
|
המופת כי א' הוכה בדומה לו והיה ד' |
|
|
והוכה בב' והיה ג' |
|
|
הנה א' הוכה בשני מספרי א"ב והיה ד"ג |
VII.18: 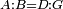
|
אם כן יחס א' אל ב' כיחס ד' אל ג' מי"ח משביעי |
| וא"ב שני משוטחים מתדמים ויפול בין שניהם מספר וימשכו מתיחסים | |
| VIII.17: | הנה יפול גם כן בין שני מספרי ד"ג מספר מי"ז משמיני |
| VIII.18: | אם כן ד"ג שני שטחים מתדמים מי"ח משמיני |
| VIII.20: | וד' מרובע אם כן ג' מרובע מכ' מח' |
| וזה מ'ש'ל' | |
Proposition 2 |
|
| ב כל מספר יוכה במספר אחר ויהיה מרובע הנה השני מספרים משוטחים מתדמים | |
| המשל בו כי א' הוכה במספר ב' והיה ג' וג' מרובע | |
| הנה אומר כי א"ב שני שטחים מתדמים | |
| המופת כי א' הוכה בדומה לו והיה ד' וד' מרובע וא' הוכה בב' והיה ג' | |
VII.18: 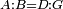
|
הנה יחס א' אל ב' כיחס ד' אל ג' מי"ח מז' |
| וכל אחד מד' ג' מרובע | |
| אם כן יחס א' אל ב' כיחס מספר ד' המרובע אל מספר ג' המרובע | |
| VIII.24: | אם כן מספר א"ב שני שטחים מתדמים מכ"ד משמיני |
| וזה מה שרצינו לבאר | |
| ובכאן התבאר כי כאשר הוכה מספר מרוב' במספר מרובע הנה הוא יהיה מרובע | |
| ואם הוכה מספר מרובע במספר והיה מרובע הנה המוכה בו מרובע | |
| ואם הוכה מספר מרובע במספר והיה בלתי מרובע הנה המוכה בו בלתי מרובע | |
| ואם הוכה מספר מרובע במספר בלתי מרובע הנה הוא בלתי מרובע | |
| ומ'ש'ל' | |
Proposition 3 |
|
| ג כל מספר מעוקב יוכה בדומה לו הנה הוא יהיה מעוקב | |
| המשל בו כי מספר א' הוא מעוקב וכאשר הוכה בכמוהו והיה מספר ב' | |
| הנה אומר כי ב' מעוקב | |
| המופת כי א' מעוקב וצלעו מספר ג' הנה ג' הוכה בכמוהו והיה ד' וג' הוכה בד' והיה א' אם כן ג' ימנה ד' בשעור אחדי ג' והאחד ימנה ג' בשעור אחדי ג' | |
| אם כן האחד ימנה ג' בשעור מה שימנה ג"ד | |
VII.def. proportional numbers: 
|
אם כן יחס האחד אל הג' כיחס ג' אל ד' מפתיחת ז' |
|
|
וגם כן הנה ג' הוכה בד' והיה א' |
| אם כן ד' ימנה א' בשעור אחדי ג' | |
| והאחד ימנה ג' בשעור ג' | |
| אם כן האחד ימנה ג' בשעור מה שימנה ד"א | |
VII.def. proportional numbers: 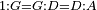
|
אם כן יחס האחד אל ג' כיחס ג' אל ד' וכיחס ד' אל א' מפתיחת ז' |
| הנה בין האחד ובין א' מספר ג"ד והם נמשכים על יחס | |
|
|
וגם כן הנה א' הוכה בכמוהו והיה ב' |
| אם כן א' ימנה ב' בשעור אחדי א' | |
| והאחד ימנה א' בשעור אחדי א' | |
| אם כן האחד ימנה א' בשעור מה שימנה א"ב | |
| אם כן יחס האחד אל א' כיחס א' אל ב' | |
| VIII.8: | ובין האחד ובין א' מספרי ג"ד והם נמשכים על יחס ויפול בין א' ובין ב' שני מספרים וימשכו על יחס מח' מח' |
| VIII.21: | ומספר א' מעוקב אם כן מספר ב' מעוקב מכ"א מח' |
| ומ'ש'ל' | |
Proposition 4 |
|
| ד כל מספר מעוקב יוכה במספר מעוקב אחר הנה הוא מעוקב | |
| המשל בו כי מספר א' מעוקב וכבר הוכה במספר אחר מעוקב והוא ב' והיה ג' הנה אומר כי ג' מעוקב | |
| המופת כי א' הוכה בכמוהו והיה ד' אם כן ד' מעוקב | |
| וא' הוכה בכמוהו והיה ד' והוכה בב' והיה ג' הנה א' הוכה בשני מספרי א"ב והיה ד"ג | |
| אם כן יחס א' אל ב' כיחס ד' אל ג' | |
| אם כן יחס ד' אל ג' כיחס מעוקב א' אל מעוקב ב' וד' מעוקב אם כן ג' מעוקב | |
| וזה מה שרצינו לבאר | |
Proposition 5 |
|
| ה כל מספר מעוקב יוכה במספר ויהיה מעוקב הנה המספר המוכה בו מעוקב | |
| המשל בו כי מספר א' מעוקב וכבר הוכה במספר ב' והיה ג' וג' מעוקב | |
| הנה אומר כי ב' מעוקב | |
| המופת כי א' הוכה בכמוהו והיה ד' אם כן ד' מעוקב | |
| וא' הוכה בכמוהו והיה ד' והוכה בב' והיה ג' הנה א' הוכה בשני מספרי א"ב והיה ד"ג | |
| אם כן יחס א' אל ב' כיחס ד' אל ג' | |
| אם כן יחס א' אל ב' כיחס מעוקב ד' אל מעוקב ג' | |
| וא' מעוקב אם כן ב' מעוקב | |
| ובכאן התבאר כי אם הוכה מספר מעוקב במספר בלתי מעוקב יהיה בלתי מעוקב | |
| ואם הוכה מספר מעוקב במספר והיה בלתי מעוקב הנה המוכה בו בלתי מעוקב | |
| וזה מה שרצינו לבאר | |
Proposition 6 |
|
| ו כל מספר יוכה בכמוהו ויהיה מעוקב הנה הוא מעוקב | |
| המשל בו כי מספר א' הוכה בכמוהו והיה ב' וב' מעוקב הנה אומר כי א' מעוקב | |
| המופת כי א' הוכה בב' והיה ג' הנה ג' מעוקב | |
| וא' הוכה בכמוהו והיה ב' והוכה בב' והיה ג' הנה א' הוכה בשני מספרי א"ב והיה ב"ג | |
| אם כן יחס א' אל ב' כיחס ב' אל ג' וב"ג מעוקבים | |
| אם כן יחס א' אל ב' כיחס מעוקב ב' אל מעוקב ג' | |
| וב' מעוקב אם כן א' מעוקב | |
| וזה מ'ש'ל' | |
Proposition 7 |
|
| ז כל מספר מורכב יוכה במספר
הנה הוא ישוב מוגשם | |
| המשל בו כי מספר א' מורכב וכבר הוכה במספר ב' והיה ג' | |
| הנה אומר כי ג' מוגשם | |
| המופת כי מספר א' מורכב הנה ימנהו מספר ד' ויהיו אחדי ה' בשעור מה שימנה ד"א | |
| אם כן ד' יוכה בה' ויהיה א' וא' יוכה בב' ויהיה ג' אם כן מוגשם | |
| וזה מה שרצינו לבאר | |
Proposition 8 |
|
| ח כאשר היו מספרים מן האחד נמשכים מתיחסים כמה שהיו הנה המספר השלישי מן האחד מרובע מה שימנה זה מן המספרים כאשר עזב מהם אחד ולקח אחד על ההמשכות יהיו המספרים הלקוחים מרובעים והרביעי מן מן האחד מעוקב עוד אחר זה כאשר עזב שני מספרים ולקח מספר יהיו המעוקבים והשביעי מן האחד מרובע מעוקב | |
| עוד אחר זה כאשר עזב חמשה מספרים ולקח מספר יהיו המספרים הלקוחים מרובעים מעוקבים | |
| המשל בו כי מספרי א"בג"דה"ז והאחד יקדם להם נמשכים מתיחסים | |
| הנה אומר כי השלישי מן האחד והוא ב' מרובע | |
| והרביעי מן האחד והוא ג' מעוקב | |
| עוד אחד אחר שנים מעוקב והשביעי מן האחד והוא ז' מרובע מעוקב | |
| עוד אחד אחר מחשה מרובע מעוקב | |
| המופת כי יחס האחד אל א' כיחס א' אל ב' הנה האחד ימנה א' בשיעור מה שימנה א' ב' והאחד ימנה א' בשעור אחדי א' | |
| אם כן א' ימנה ב' בשעור אחדי א' | |
| אם כן א' יוכה בכמוהו ויהיה ב' אם כן ב' מרובע והוא השלישי מן האחד | |
| ויחס ב' אל אל ג' כיחס ג' אל ד' הנה כבר נפל בין ב"ד מספר ג' וימשכו מתיחסים וב' מרובע | |
| אם כן ד' מרובע | |
| וכן יתבאר כי מה שאחר זה מן המספרים כאשר עזב מספר ולקח אחר על ההמשכות יהיו המספרים הלקוחים מרובעים | |
| וגם כן הנה יחס האחד אל א' כיחס ב' אל ג' | |
| אם כן האחד ימנה א' בשעור מה שימנה ב"ג והאחד ימנה א' בשעור אחדי א' | |
| אם כן ב' ימנה ג' בשעור אחדי א' | |
| אם כן א' יוכה בב' ויהיה ג' | |
| אם כן א' יוכה בכמוהו ויהיה ב' ויוכה בב' ויהיה ג' | |
| אם כן ג' מעוקב והוא הרביעי מן האחד | |
| ויחס ג' אל ד' כיחס ד' אל ה' וכיחס ה' אל ז' | |
| הנה כבר נפל בין ג' וז' שני מספרי ד"ה ונמשכו מתיחסים וג' מעוקב אם כן ז' מעוקב | |
| וכן יתבאר כי מה שאחר זה מן המספרים כאשר עזב מהם שני מספרים ולקח מספר יהיו המספרים הלקוחים מעוקבים | |
| ומספר ז' יכנס במספרים המרובעים ובמספרים המעוקבים אם כן הוא מרובע ומעוקב | |
| וז' הוא השביעי מן האחד | |
| וכן יתבאר כי מה שאחר זה מן האחדים אם עזב מהם חמשה מספרים ולקח אחד יהיו המספרים הלקוחים מרובעים מעוקבים | |
| ומ'ש'ל' | |
Proposition 9 |
|
| ט כאשר היו מספרים מן האחד נמשכים מתיחסים כמה שיהיו והיה הנמשך אל האחד מרובע הנה הם כלם מרובעים ואם היה הנמשך אל האחד מעוקב הנה הם כלם מעוקבים | |
| המשל בו כי מספרי א'ב'ג'ד' והאחד יקדם להם נמשכים מתיחסים וא' מרובע | |
| הנה אומר כי הנשארים מרובעים | |
| המופת כי א' מרובע וב' מרובע כי הוא השלישי מן האחד ויחס א' אל ב' כיחס ב' אל ג' | |
| אם כן יחס ב' אל ג' הוא יחס מרובע א' אל מרובע ב' וב' מרובע אם כן ג' מרובע | |
| וכן יתבאר כי כל הנשארים מרובעים וגם כן הנה יהיה הנמשך אל האחד מעוקב | |
| הנה אומר כי הנשארים כלם מעוקבים | |
| המופת כי א' הוכה בכמוהו והיה ב' וא' מעוקב | |
| אם כן ב' מעוקב וג' מעוקב כי הוא הרביעי מן האחד ויחס ב' אל ג' כיחס ג' אל ד' | |
| אם כן יחס ג' אל ד' הוא כיחס מעוקב ב' אל מעוקב ג' וג' מעוקב אם כן ד' מעוקב | |
| וכן יתבאר כי כל הנשארים מעוקבים | |
| וזה מ'ש'ל' | |
Proposition 10 |
|
| י כאשר היו מספרים מן האחד נמשכים מתיחסים כמה שיהיו והיה הנלוה אל האחד בלתי מרובע הנה יהיו הנשארים אין מהם מספר מרובע כי אם השלישי מן האחד עוד אחר זה אחד בלתי מרובע ואחד מרובע ואם היה הנמשך אל האחד בלתי מעוקב הנה הנשארים אין אחד מהם מספר מעוקב כי אם הרביעי מן האחד עוד אחר זה שנים בלתי מעוקבים ואחד מעוקב | |
| המשל בו כי מספרי א'ב'ג'ד'ה'ז' והאחד יקדם להם נמשכים מתיחסים ואשר ילוה אל האחד והוא א' בלתי מרובע | |
| הנה אומר כי אין מהם מספר מרובע כי אם השלישי מן האחד והוא ב' | |
| עוד אחר זה אחד בלתי מרובע ואחד מרובע | |
| המופת אם לא יהיה כן הנה יהיה ג' מרובע אם יהיה אפשר ויחס א' אל ב' כיחס ב' אל ג' | |
| אם כן יחס א' אל ב' כיחס מרובע ב' אל מרובע ג' וב' מרובע אם כן א' מרובע זה שקר | |
| אם כן אין ג' מרובע | |
| וכן יתבאר כי זולתו בלתי מרובע כי אם השלישי מן האחד | |
| עוד אחד בלתי מרובע ואחד מרובע | |
| וגם כן הנה יהיה א' בלתי מעוקב | |
| הנה אומר כי זולתו מאלו המספרים בלתי מעוקב כי אם הרביעי מן האחד | |
| עוד מה שאחר זה שני מספרים בלתי מעוקבים ומספר מעוקב | |
| המופת כי אם לא יהיה כן הנה יהיה ה' מעוקב אם יהיה אפשר ויחס א' אל ג' כיחס ג' אל ה' | |
| אם כן יחס א' אל ג' כיחס מעוקב ג' אל מעוקב ה' וג' מעוקב אם כן א' מעוקב וזה שקר | |
| אם כן אין ה' מעוקב | |
| וכן יתבאר כי זולתו בלתי מעוקב כי אם הרביעי מן האחד | |
| עוד אחר זה שני מספרים בלתי מעוקבים ומספר מעוקב | |
| ומ'ש'ל' | |
Proposition 11 |
|
| יא כאשר היו מספרים נמשכים מן האחד מתיחסים כמה שיהיו הנה הקטן ימנה הרב בשעור מספר מהם | |
| המשל בו כי מספרי א"בג'ד'ה' מן האחד נמשכים מתיחסים הנה נאמר כי הקטן ימנה הרב בשעור מספר מהם | |
| המופת כי מספר ג'ד'ה' כמו מנין האחד וא' וב' על יחס ג'ד'ה' אם כן יחס האחד אל ב' כיחס ג' אל ה' והאחד ימנה ב' בשעור אחדי ב' אם כן ג' ימנה ה' בשעור ב' וזהו שעור ב' | |
| אם כן הקטן ממספרי א'ב'ג'ד'ה' ימנה הרב בשעור מספר מהם | |
| ומ'ש'ל' | |
Proposition 12 |
|
| יב כאשר היו מספרים מן האחד נמשכים מתיחסים כמה שיהיו הנה כל מספר ראשון ימנה האחרון מהם הנה הוא ימנה המספר אשר ילוה לאחד | |
| המשל בו כי מספרי א'ב'ג'ד' והאחד יקדם להם נמשכים מתיחסים | |
| הנה אומר כי כל מספר ראשון ימנה האחרון והוא ד' הנה הוא ימנה א' אשר הוא נלוה אל האחד ונאמר שיהיה ה' ראשון וימנה ד' | |
| הנה אומר כי ה' ימנה א' | |
| המופת אם לא יהיה כן הנה לא ימנהו אם יהיה אפשר הנה כל אחד מן א' וה' ראשון אצל האחר | |
| וה' ימנה ד' | |
| הנה ימנה ה' בשעור אחדי ז' | |
| הנה ה' יוכה בז' ויהיה ד' | |
| אבל א' הוכה בג' והיה ד' | |
| אם כן שטח ה' בז' כמו שטח א' בג' | |
| אם כן יחס ה' אל א' כיחס ג' אל ז' | |
| וכל אחד מן א' וה' ראשון אצל האחר | |
| אם כן שניהם שני קטני מספרים על יחס שניהם וימנו כל שני מספרים על יחס שניהם בשווי הקטן לקטן והרב לרב | |
| אם כן ה' ימנה ג' ויהיו אחדי ח' בשעור מה שימנה הג' | |
| הנה ה' יוכה בח' ויהיה ג' | |
| וא' הוכה בב' והיה ג' | |
| אם כן שטח ה' בח' כמו שטח א' בב' | |
| אם כן יחס ה' אל א' כיחס ב' אל ח' וכל אחד מן א' וה' ראשון אצל האחר | |
| אם כן שניהם שני קטני שני מספרים על יחס שניהם וימנו כל שני מספרים על יחס שניהם | |
| אם כן ה' ימנה ב' ויהיו אחדי ט' בשעור מה שימנה ה' ב' הנה ה' יוכה בט' ויהיה כ' | |
| אבל א' הוכה בכמוהו והיה ב' הנה ה' בט' כמו א' בכמוהו | |
| אם כן יחס ה' אל א' כיחס א' אל ט' וכל אחד מן א' וה' ראשון אצל האחר | |
| אם כן שניהם קטני שני מספרים על יחס שניהם וימנו כל שני מספרים על יחס שניהם | |
| אם כן ה' ימנה א' וכבר היה שלא ימנהו זה שקר | |
| אם כן כל מספר ראשון ימנה ד' הנה הוא ימנה א' אשר ילוה אל האחד | |
| ומ'ש'ל' | |
Proposition 13 |
|
| יג כאשר נתיחסו מספרים מן האחד נמשכים כמה שיהיו והיה הנלוה אל האחד ראשון הנה לא ימנה הרב מהם כי אם מספר מהם | |
| המשל בו כי מספרי א'ב'ג'ד' נמשכים מתיחסים מן האחד ואשר ילוה אל האחד א' והוא ראשון | |
| הנה אומר כי לא ימנה הרב מהם והוא ד' מספר אחר זולת א'ב'ג' | |
| המופת אנחנו נבאר שהוא בלתי אפשר זה שאם היה אפשר זה נאמר שימנהו ה' ואין
ה' כמו אחד מן א'ב'ג' | |
| וה' אם שיהיה ראשון ואם שיהיה מורכב | |
| ואיננו ראשון כי הוא אלו היה ראשון והוא ימנה ד' היה מונה א' אשר ילוה אל האחד אבל הוא לא ימנה א' מפני כי א' ראשון אם כן אין ה' ראשון והנה ימנה ה' אם כן [.] מספר ראשון | |
| והנה אומר שלא ימנהו מספר ראשון כי אם א' | |
| שאם היה אפשר הנה ימנהו כ' | |
| אם כן כ' ימנה ה' וה' ימנה ד' | |
| אם כן כ' ימנה ד' | |
| וכ' ראשון אם כן הוא ימנה א' אשר ילוה אל האחד וא' ראשון זה שקר | |
| אם כן לא ימנהו מספר ראשון כי אם א' וה' ימנה ד' הנה ימנה ד' בשעור אחדי ז' | |
| הנה אומר כי ז' ימנה ג' ושז' איננו כמו אחד מן א'ב'ג' מפני כי ה' ימנה ד' בשעור אחדי ז' | |
| אם כן ה' יוכה בז' ויהיה ד' | |
| אבל א' הוכה בג' והיה ד' | |
| אם כן א' בג' כמו ה' בז' | |
| אם כן יחס א' אל ה' כיחס ז' אל ג' | |
| וא' ימנה ה' אם כן ז' ימנה ג' | |
| ואומר כי ז' אינו כמו אחד מן א'ב'ג' | |
| כי הוא אם כן יתיחס מספרים מן האחד נמשכים הנה הקטן מהם ימנה הרב בשעור אחדי מספר מהם | |
| וז' לא ימנה ד' בשעור אחדי מספר ממספרי א'ב'ג' | |
| כי הוא אם כן ימנה בשעור אחדי מספר ה' ואין ה' כמו אחד מן א'ב'ג' | |
| אם כן ז' אינו כמו אחד מן א'ב'ג' | |
| וכבר התבאר שהוא ימנה ג' וגם כן הנה ז' ימנה ג' נאמר שימנהו בשעור אחדי ח' | |
| ונבאר כמו שבארנו קודם כי א' ימנה ז' וח' ימנה ב' ושא' אינו כמו אחד מן א"ב | |
| אם כן ח' ימנה ב' | |
| ונאמר שימנהו בשעור אחדי ט' וח' ראשון או מורכב | |
| ואם היה ראשון והוא ימנה ב' והנה ח' אינו כמו אחד מן א"ב וח' ימנה ב' הנה הוא ימנה א' וא' ראשון זה שקר | |
| אם כן אין ח' ראשון | |
| ואם היה מורכב נאמר שימנהו מספר ראשון הנה אומר כי לא ימנהו ראשון כי אם א' | |
| מפני שהוא אם היה מספר ראשון ימנה ח' וח' ימנה ב' | |
| אם כן הוא ימנה ב' וימנה א' וא' ראשון זה שקר | |
| אם כן ח' לא ימנהו כי אם א' וא' ימנה ח' | |
| הנה אומר כי ט' אינו כמו הנלוה לאחד ולא ט' ימנה ב' בשעור מספר מן המתיחס כי הוא אמנם ימנהו בשעור ח' | |
| וח' אינו כמו א' וח' ימנה ב' בשעור אחדי ט' | |
| אם כן ח' יוכה בט' ויהיה ב' וא' יוכה בכמוהו ויהיה ב' | |
| אם כן א' בכמוהו כמו ח' בט' | |
| אם כן יחס א' אל ח' כיחס ט' אל א' | |
| וא' ימנה ח' אם כן ט' ימנה א' ואינו כמוהו וזה שקר | |
| אם כן המספרים המתיחסים הנמשכים מן האחד כאשר יהיה אשר ימשך מן האחד ראשון הנה לא ימנה הרב מהם כי אם מספר מהם | |
| וזה מה שרצינו לבאר | |
Proposition 14 |
|
| יד כל מספרים ראשונים ידועי המספר הנה יהיה מן המספרים הראשונים מה שהוא יותר מספר מהם | |
| המשל בו כי מספרי א'ב'ג' ראשונים ידועי המספר | |
| הנה אומר כי הנה יהיה במספרים הראשונים מה שהוא יותר מנין מהם | |
| המופת אנחנו נוציא קטן מספר ימנוהו א'ב'ג' והוא ה"ד ונוסיף עליו אחד והוא ה"ז | |
| הנה אם היה ז"ד ראשון הנה כבר התאמת הספור כי אנחנו כבר מצאנו מספר ראשון איננו כמו אחד ממספרי א'ב'ג' והוא ז"ד | |
| ואם היה ז"ד מורכב הנה ימנהו מספר ראשון והוא ח' | |
| הנה אומר כי ח' מספר אחר בלתי שוה לאחד מן א'ב'ג' כי הוא אם היה כמו אחד מהם הנה הוא ימנה ג"ד ה"ד וימנה האחד הנשאר והוא ז' וח' מספר זה שקר | |
| אם כן ח' ראשון ואינו כמו אחד מן א'ב'ג' | |
| אם כן כל מספרים ידועי המספר הנה יהיה מן המספרים הראשונים מה שהוא יותר ממנין מהם | |
| וזה מ'ש'ל' | |
Proposition 15 |
|
| טו קטן מספר ימנוהו מספרים ראשונים ידועים הנה לא ימנהו זולתם | |
| המשל בו כי מספר א' הוא קטן מספר ימנהו מספרי ב'ג'ד' הראשונים הידועים | |
| הנה אומר כי הוא לא ימנה א' זולת מספרי ב'ג'ד' | |
| המופת כי זה אי אפשר שאם היה אפשר נאמר שימנהו ה' | |
| ואין ה' כמו אחד מן ב'ג'ד' ויהיו אחדי ז' בשעור מה שימנה ה"א | |
| אם כן ה' הוכה בז' והיה א' | |
| וכל שני מספרים יוכה אחד משניהם באחר [....] ומספר ראשון הנה אותו המספר הראשון ימנה אחד משני המספרים המוכים אם כן ב'ג'ד' [....] וימנו אחד מן ז"ה | |
| ואולם ה' הנה לא ימנוהו כי הוא ראשון אם כן ימנה ז' וכן ג"ד ימנו ז' | |
| אם כן מספרי ב'ג'ד' ימנו ז' והוא קטן מן א' זה שקר כי א' היה קטן מספר ימנוהו מספרי ב'ג'ד' | |
| אם כן לא ימנה א' כי אם ב'ג'ד' | |
| וזה מ'ש'ל' | |
Proposition 16 |
|
| יו כאשר היו שלשה מספרים מתיחסים נמשכים והיו קטן המספרים על יחסם הנה כל שני מספרים יתקבצו מהם הנה שניהם מספר ראשון אצל המספר השלישי הנשאר | |
| המשל בו כי מספרי א'ב'ג' השלשה מתיחסים נמשכים והם קטן המספרים על יחסם | |
| הנה אומר כי כל שני מספרים יתקבצו ממספרי א'ב'ג' הנה כלם מספר ראשון אצל המספר השלישי הנשאר | |
| המופת אנחנו נקח קטן שני המספרים על יחס א'ב'ג' והם ז"ה ה"ד הנה כל אחד מן ז"ה ה"ד ראשון אצל האחר | |
| וז"ה אם כן יוכה בכמוהו ויהיה א' | |
| ויוכה בד"ה ויהיה ב' | |
| וגם כן ה"ד יוכה בכמוהו ויהיה ג' | |
| וכל אחד מן ז"ה ה"ד ראשון אצל האחר | |
| אם כן כל ז"ד ראשון אצל ד"ה וה"ז וה"ז ראשון אצל ה"ד | |
| אם כן כל אחד מן ד"ז ז"ה ראשון אצל ד"ה | |
| וכאשר היו שני מספרים ראשונים אצל מספר אחר הנה שטח אחד משניהם באחר ראשון אצל אותו המספר | |
| אם כן משוטח ד"ז בז"ה ראשון אצל ה"ד | |
| וכל שני מספרים יהיה אחד משניהם ראשון אצל האחר הנה מרובע אחד משניהם ראשון אצל האחר | |
| אם כן מרובע ד"ה ראשון אצל משוטח ד"ז בז"ה ומשוטח ד"ז בז"ה ראשון אצל מרובע ה"ד | |
| וכל קו יחלק בשני חלקים | |
| ואם כן הכאת הקו באחד משני החלקים כמו הכאת החלק ההוא בכמוהו ואחד משניהם באחר | |
| אם כן משוטח ד"ז בז"ה כמו מרובע ה"ז וכמו משוטח ז"ה בה"ד | |
| אבל משוטח ד"ה בז"ה הוא ב' | |
| ומרובע ה"ז הוא א' ושניהם יחד כמו משוטח ד"ז בז"ה | |
| אם כן כל א"ב יבדל ממרובע ה"ד בכמוהו | |
| אבל מרובע ה"ד הוא ג' | |
| אם כן כל א"ב ראשון אצל ג' ולכן יהיה כל ג"ב ראשון אצל א' | |
| הנה אומר כי כל א"ג גם כן ראשון אצל ב' | |
| המופת כי כל אחד מן ז"ה ה"ד ראשון אצל האחר וכל ז"ד ראשון אצל כל אחד מן ז"ה ה"ד וכל אחד מן ז"ה ה"ד ראשון אצל ז"ד | |
| וכאשר היו שני מספרים והיה כל אחד משניהם יחד ראשון אצל מספר אחר הנה משוטח אחד משניהם באחר הוא גם כן ראשון אצל המספר ההוא | |
| אם כן משוטח ז"ה בה"ד ראשון אצל ד"ז | |
| וכל שני מספרים אחד משניהם ראשון אצל האחר הנה מרובע אחד מהם ראשון אצל האחר | |
| אם כן מרובע ז"ד ראשון אצל משוטח ז"ה בה"ד | |
| ומרובע ז"ד הוא כמו ז"ה בכמוהו וה"ד בכמוהו | |
| וכפל ז"ה בה"ד יחד אם כן מרובע ז"ה בכמוהו ומרובע ה"ד | |
| וכפל שטח ז"ה בה"ד ראשון אצל שטח ז"ה בה"ד | |
| וכאשר הבדלנו היה מרובע ז"ה ומרובע ה"ד ומשוטח ז"ה בה"ד ראשון אצל משוטח ז"ה בה"ד | |
| וכאשר הבדלנו גם כן היה מרובע ז"ה בכמוהו ומרובע ה"ד בכמוהו יחד ראשון אצל משוטח ז"ה בה"ד אשר הוא ב' | |
| אבל שני מרובעי ז"ה בכמוהו וה"ד בכמוהו הם א' וג' | |
| אם כן כל א' וג' ראשון אצל ב' | |
| וזה מה שרצינו לבאר | |
Proposition 17 |
|
| יז כאשר היו שני מספרים והיה כל אחד משניהם ראשון אצל האחר הנה אין יחס הראשון מהם אל השני כיחס השני אל מספר אחר | |
| המשל בו כי כל אחד משני מספרי א"ב ראשון אצל האחר | |
| הנה אומר כי יחס א' אל ב' אינו כיחס ב' אל מספר אחר | |
| המופת כי זה אי אפשר שאם היה אפשר נאמר שיהיה יחס א' אל ב' כיחס ב' אל ג' | |
| וכל אחד מן א"ב ראשון אצל האחר | |
| אם כן שניהם קטני שני מספרים על יחס שניהם וימנו כל שני מספרים על יחס שניהם הקטן לקטן והרב לרב | |
| אם כן א' ימנה ב' וימנה עצמו | |
| אם כן א' ימנה א' וימנה ב' וכל אחד משניהם ראשון אצל האחר זה שקר | |
| אם כן אין יחס א' אל ב' כיחס ב' אל מספר אחר | |
| וזה מה שרצינו לבאר | |
Proposition 18 |
|
| יח כאשר היו מספרים מתיחסים נמשכים כמה שהיו וכל אחד משתי הקצוות ראשון אצל האחר הנה אין יחס הראשון אל השני כיחס האחרון אל מספר אחר | |
| המשל בו כי מספרי א'ב'ג' מתיחסים נמשכים וכל אחד משתי הקצוות אשר הם א"ג ראשון אצל האחר | |
| הנה אומר כי יחס א' אל ב' אינו כיחס ג' אל מספר אחר | |
| המופת אם היה אפשר נאמר שיהיה כיחס ג' אל ד' | |
| וכאשר המירונו יהיה יחס א' אל ג' כיחס ב' אל ד' וכל אחד מא"ג ראשון אצל האחר | |
| אם כן שניהם קטן שני מספרים על יחס שניהם וימנו כל שני מספרים על יחס שניהם | |
| אם כן א' ימנה ב' | |
| וכאשר היו מספרים מתיחסים נמשכים והיה הראשון ימנה השני הנה הוא ימנה האחר | |
| הנה א' אם כן ימנה ג' וימנה עצמו וכל אחד משניהם ראשון אצל האחר זה שקר | |
| אם כן אין יחס א' אל ב' כיחס ג' אל מספר אחר | |
| ומ'ש'ל' | |
Proposition 19 |
|
| יט נרצה לדעת כאשר היו שני מספרים ידועים אם אפשר שיהיה מספר שלישי לשניהם | |
| ונאמר שיהיו שני המספרים הידועים א"ב | |
| ונרצה שנדע אם אפשר שיהיה מספר שלישי מתיחס לשני מספרי א"ב אם היה כל אחד משני מספרי א"ב ראשון אצל האחר הנה לא יהיה אפשר שיהיה מספר שלישי מתיחס לשניהם | |
| ואם לא יהיה כל אחד משני מספרי א"ב ראשון אצל האחר הנה כאשר נכה ב' בכמוהו ויהיה מרובע ג' הנה שהוא אם יהיה א' ימנה ג' הנה אפשר שיהיה מספר שלישי מתיחס לשני מספרי א"ב ואם לא יהיה א' ימנה ג' הנה לא ימצא מספר מתיחס לשניהם | |
| המופת אנחנו נשים א' ראשון ימנה ג' וימנהו בשעור אחדי ד' | |
| אם כן א' כאשר הוכה בד' היה ממנו ג' | |
| וכאשר הוכה ב' בכמוהו היה ג' | |
| אם כן משוטח א' בד' כמו מרובע ב' בכמוהו | |
| אם כן יחס א' אל ב' כיחס ב' אל ד' | |
| הנה כבר מצאנו מספר שלישי מתיחס לשני מספרי א"ב והוא ד' | |
| וגם כן הנה אנחנו נשים א' לא ימנה ג' | |
| הנה אומר כי לא ימצא מספר שלישי יתיחס א"ב | |
| שאם היה אפשר נאמר שיהיה מספר ד' | |
| אם כן יחס א' אל ב' כיחס ב' אל ד' | |
| ומשוטח א' בד' כמו מרובע ב' ומרובע ב' הוא ג' | |
| אם כן משוטח א' בד' הוא ג' | |
| אם כן א' ימנה ג' וכבר היה שלא ימנהו זה שקר | |
| אם כן אי אפשר שיהיה מספר שלישי מתיחס לשני מספרי א"ב | |
| ומ'ש'ל' | |
Proposition 20 |
|
| כ נרצה לדעת כאשר היו שלשה מספרים ידועים אם אפשר שיהיה מספר רביעי יתיחס להם | |
| ויהיו המספרים השלשה א'ב'ג' | |
| ונרצה שנדע אם יהיה מספר רביעי מתיחס אל א'ב'ג' | |
| הנה אם היה כל אחת משתי הקצוות והם א"ג ראשון אצל האחר הנה אין מספר רביעי יתיחס א'ב'ג' | |
| ואם לא יהיה כל אחד מהם מן א"ג ראשון אצל האחר נכה ב' בג' ויהיה ד' | |
| הנה אומר כי אם היה א' ימנה ד' הנה יהיה מספר רביעי יתיחס א'ב'ג' | |
| ואם היה א' לא ימנה ד' הנה לא יהיה מספר רביעי יתיחס א'ב'ג' | |
| המופת אנחנו נשים תחלה א' ימנה ד' וימנהו בשעור אחדי ה' הנה הוא יוכה בה' ויהיה ד' אבל ב' הוכה בג' והיה ד' | |
| אם כן שטח א' בה' כמו שטח ב' בג' | |
| אם כן יחס א' אל ב' כיחס ג' אל ה' הנה כבר מצאנו מספר רביעי יתיחס א'ב'ג' והוא ה' | |
| ואם לא יהיה א' ימנה ד' הנה לא יהיה אפשר שימצא מספר רביעי יתיחס א'ב'ג' | |
| המופת אם אפשר נאמר שיתיחס להם ה' | |
| אם כן יחס א' אל ב' כיחס ג' אל ה' | |
| הנה שטח א' אם כן בה' כמו משוטח ב' בג' | |
| ומשוטח ב' בג' הוא ד' | |
| אם כן שטח א' בה' הוא ד' | |
| אם כן א' ימנה ד' וכבר היה שלא ימנהו זה שקר | |
| אם כן אי אפשר שיהיה מספר רביעי שלא ימנה א'ב'ג כאשר היה שלא ימנה ג' | |
| ומ'ש'ל' | |
Proposition 21 |
|
| When even numbers are summed, as many one pleases, then their sum is an even number. | כא כאשר נקבצו מספרי זוגות כמה שהיו הנה קבוצם מספר זוג |
| המשל בו כי מספרי א"ב ב"ג ג"ד זוגות | |
| הנה אומר כי א"ד זוגות | |
| המופת כי כל אחד מא"ב ב"ג ג"ד זוג | |
| אם כן לכל אחד מהם חצי מאחדי שעורו | |
| הנה לכל א"ד אם כן חצי מאחדי שעורו | |
| אם כן א"ד זוג | |
| Q.E.D. | וזה מש"ל |
Proposition 22 |
|
| When odd numbers are summed, as many as one pleases, and their multitude is even, then the sum is an even number. | כב כאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם זוג הנה קבוצם מספר זוג |
| המשל בו א"ב ב"ג ג"ד ד"ה נפרדים ומספרם זוג | |
| הנה אומר כי קבוץ א"ה זוג | |
| המופת כי כל אחד מהם בינו ובין הזוג אחד | |
| וכאשר נבדל האחד מכל מספר מהם ישארו המספרים זוגות מנינם זוג מפתיחת ז | |
| ומנין האחרים הנבדלים זוג | |
| אם כן א"ה זוג משלפניה | |
| Q.E.D. | וזמש"ל |
Proposition 23 |
|
| When odd numbers are summed, as many as one pleases, and their multitude is odd, then the sum is an odd number. | כג כאשר נתקבצו מספרים נפרדים כמה שיהיו והיה מספרם נפרד הנה קבוצם נפרד |
| המשל בו כי א"ב ב"ג ג"ד נפרדים ומנינם נפרד | |
| הנה אומר כי קבוץ א"ד נפרד | |
| המופת כי ג"ד נפרד ונבדל ממנו אחד והוא ד"ה | |
| וישאר ג"ה זוג מפתיחת ז | |
| וא"ג זוג כי הוא יקובץ ממספרים נפרדים מניינם זוג והם א"ב ב"ג משלפניה | |
| אם כן כל א"ה זוג | |
| וה"ד אחד | |
| אם כן א"ד נפרד מכ"א | |
| Q.E.D. | ונשלם באורו |
Proposition 24 |
|
| When an even number is subtracted from an even number, then the remainder is even. | כד כאשר נבדל ממספר זוג זוג הנה הנשאר זוג |
| המשל בו כי מספר א"ב זוג וכבר נבדל ממנו מספר זוג והוא ב"ג | |
| הנה אומר כי א"ג הנשאר זוג | |
| המופת כי כל אחד מא"ב ב"ג זוג אם כן לכל אחד מהם חצי מאחדי השלם | |
| אם כן א"ג הנשאר לו חצי מאחדי השלם אם כן הוא זוג | |
| Q.E.D. | ונשלם באורו |
Proposition 25 |
|
| When an odd number is subtracted from an even number, then the remainder is odd. | כה כאשר נבדל ממספר זוג מספר נפרד הנה הנשאר נפרד |
| המשל בו כי מספר א"ב זוג וכבר נבדל ממנו מספר א"ג והוא נפרד | |
| הנה אומר כי גם כן ג"ב הנשאר נפרד | |
| המופת כי א"ג נפרד וכאשר חברנו אחד אליו והוא ג"ד היה א"ד זוג | |
| וכאשר נבדל מא"ב אשר הוא זוג א"ד אשר הוא זוג ישאר ד"ב זוג מאשר לפניה | |
| וג"ד אחד אם כן ג"ב נפרד | |
| Q.E.D. | וזה מש"ל |
Proposition 26 |
|
| When an even number is subtracted from an odd number, then the remainder is odd. | כו כאשר נבדל ממספר נפרד מספר זוג הנה הנשאר נפרד |
| המשל בו כי מספר א"ב נפרד וכבר נבדל ממנו מספר א"ג והוא זוג | |
| הנה אומר כי ג"ב הנשאר נפרד | |
| המופת כי א"ב נפרד וכאשר חברנו אליו אחד והוא ב"ד היה א"ד זוג | |
| וכאשר הבדלנו מא"ד הזוג א"ג הזוג נשאר ג"ד זוג מכ"ד | |
| וב"ד אחד אם כן ג"ב נפרד | |
| Q.E.D. | ונשלם באורו |
Proposition 27 |
|
| When an odd number is subtracted from an odd number, then the remainder is even. | כז כאשר נבדל ממספר נפרד מספר נפרד הנה הנשאר זוג |
| המשל בו כי מספר א"ב נפרד וכבר נבדל ממנו ב"ג והוא נפרד | |
| הנה אומר כי א"ג הנשאר זוג | |
| המופת כי כל אחד מן א"ב ב"ג נפרד וכבר נבדל מכל אחד משניהם אחד והוא ב"ד הנה ישאר כל אחד מא"ד ד"ג זוג | |
| וכבר נבדל מא"ד הזוג ד"ג הזוג וישאר א"ג זוג מכ"ד מזה | |
| Q.E.D. | וזה מש"ל |
Proposition 28 |
|
| When an odd number is multiplied by an even number, then the product is even. | כח כאשר הוכה מספר נפרד במספר זוג הנה המקובץ זוג |
| המשל בו כי מספר א' נפרד והוכה במספר ב' והוא זוג וקובץ ג' אם כן ג' קבוץ
ממספרים נפרדים מנינם זוג אם כן מספר ג' זוג מכ"ב מזה | |
| Q.E.D. | וזה מש"ל |
Proposition 29 |
|
| כט כאשר הוכה מספר נפרד במספר נפרד הנה המקובץ נפרד | |
| המשל בו כי מספר א' נפרד וכבר הוכה במספר ב' והוא נפרד והתקבץ ג' | |
| הנה אומר כי ג' נפרד | |
| המופת כי א' הנפרד הוכה בב' הנפרד והתקבץ ג' | |
| אם כן מספר ג' מקובץ ממספרים נפרדים מניינם נפרד אם כן מנין ג' נפרד | |
| וזה מה שרצינו לבאר | |
| ויתבאר ממה שספרנו כי כאשר היה מספר נפרד ימנה מספר זוג הנה הוא ימנהו במספר זוג | |
| המשל בו כי מספר א' נפרד והוא ימנה מספר ב' וב' זוג | |
| הנה אומר כי הוא ימנהו במספר זוג | |
| המופת אנחנו נשים אחדי ג' בשעור מה שימנה א' הנפרד ב' הזוג | |
| הנה א' יוכה בג' והיה ב' | |
| הנה אומר כי ג' זוג ואם לא יהיה כן נאמר שיהיה ג' נפרד | |
| אם א' הנפרד הוכה בג' הנפרד והיה ב' הנה ב' אם כן נפרד זה שקר כי הוא כבר היה זוג אם כן אין ג' נפרד הנה הוא אם כן זוג | |
| אם כן א' ימנה ב' בשעור ג' הזוג | |
| וזה מה שרצינו לבאר | |
| אמר תאבת והתמונה השלשים והאחת ושלשים לא נמצאם בנסחאות אשר היו בהיכל ומצאנו אותם בכפרים | |
Proposition 30 |
|
| ל כאשר יהיה מספר נפרד ימנה מספר נפרד הנה הוא ימנהו במספר נפרד | |
| המשל בו כי א' נפרד והוא ימנה ב' וב' נפרד הנה ימנהו בשעור ג' | |
| הנה אומר כי ג' נפרד אי אפשר כי אם זה שאם היה אפשר נאמר שיהיה ג' זוג הנה א' מספר נפרד יוכה בג' הזוג ויהיה ב' הנה ב' אם כן זוג זה שקר כי הוא כבר היה נפרד | |
| אם כן אין ג' זוג הנה הוא אם כן נפרד | |
| אם כן א' ימנה ב' בשעור ג' הנפרד | |
| וזה מה שרצינו לבאר | |
Proposition 31 |
|
| לא כאשר היה מספר נפרד ימנה זוג הנה הוא ימנה חציו גם כן ויהיה מספר א' נפרד | |
| ויהיה ב"ג זוג וימנה א' ב"ג ויהיה חצי ב"ג ג"ד | |
| הנה אומר כי א' ימנה ג' ד' | |
| המופת אם הנחנו מספר מה ב'ה'ז' מן האחדים כמו מניין מה שימנה א' מספר ב"ג אם כן מספר ה"ז זוג | |
| ויהיה חציו ז"ח הנה מפני כי א' ימנה ב"ג בשעור האחדים אשר בה"ז יהיה א' אם כן הוכה בה"ז התקבץ ממנו ב"ג ומפני כי חצי ה"ז הוא ח"ז וחצי ב"ג הוא ג"ד יהיה א' כאשר הוכה בז"ח והתקבץ ממנו ג"ד | |
| אם כן א' ימנה ג"ד | |
| וזה מה שרצינו לבאר | |
Proposition 32 |
|
| לב כל מספר נפרד יהיה ראשון אצל מספר אחר הנה הוא ראשון אצל כפלו | |
| המשל בו כי מספר א' נפרד והוא ראשון אצל ג"ד ויהיה ג"ה כפל ג"ד | |
| הנה אומר כי א' ראשון אצל הג' | |
| המופת אם היה אפשר שלא יהיה כן הנה ימנה אותם מספר אחד והוא ב' | |
| אם כן ב' ימנה א' הנפרד | |
| הנה ב' אם כן נפרד והוא ימנה הג' הזוג והוא ימנה חציו וימנה א' | |
| אם כן ב' ימנה א' וימנה ד"ג וכל אחד מהם ראשון אצל האחר זה שקר | |
| אם כן לא ימנה א' וה"ג מספר אחר | |
| אם כן כל אחד משניהם ראשון אצל האחר | |
| ומ'ש'ל' | |
Proposition 33 |
|
| לג המספרים אשר יכפלו משנים הם זוג הזוג לבד | |
| המשל בו כי מספרי ב'ג'ד' כפולים משנים | |
| הנה אומר כי כל אחד מן ב'ג'ד' הוא זוג הזוג | |
| המופת אנחנו נשים האחד קודם הוא שנים והוא כפל האחד וב' הוא כפל א' וג' כפל ב' וד' כפל ג' הנה כל אחד מן א"ב ג"ד הוא זוג וא' הוא שנים והוא ראשון | |
| וכאשר הגענו [...] מספרים מן האחד נמשכים כמה שהיו והיה אשר ילוה אל האחד מהם ראשון לא ימנה הרב מהם כי אם מספרים מהם | |
| אם כן ד' לא ימנהו אלא מספרים ממספרי א'ב'ג' וכל מספר ימנהו מהם הנה הוא אמנם ימנהו במספר מן א'ב'ג' אשר הם זוגות | |
| אם כן מספר ד' זוג הזוג לבד | |
| שאם היה אפשר שיהיה זוג הזוג וזוג הנפרד הנה ימנה אותם מספר נפרד ויתחייב מזה שיהיה מספר אחד ממספרי א'ב'ג'ד' נפרד וזה בלתי אפשר | |
| אם כן אין אחד ממספרי ב'ג'ד' זוג הנפרד | |
| אם כן אין כל אחד מהם זוג הזוג לבד | |
| וזה מ'ש'ל' | |
Proposition 34 |
|
| לד כל מספר חציו נפרד הנה הוא זוג הנפרד לבד | |
| המשל בו כי מספר א"ב חציו נפרד והוא ב"ג | |
| הנה אומר כי א"ב זוג הנפרד לבד | |
| ואולם אם היה א"ב זוג הנפרד הנה הוא מבואר | |
| וזה כי חציו איננו זוג | |
| הנה אומר שהוא אמנם הוא זוג הנפרד לבד | |
| ואם היה אפשר שיהיה עם זה זוג הזוג הנה חציו זוג ואין הדבר כן | |
| אם כן מספר א"ב הוא זוג הנפרד | |
| ומ'ש'ל' | |
Proposition 35 |
|
| לה כל מספר זוג איננו כפול משנים ואין חציו נפרד הנה הוא זוג הזוג וזוג הנפרד | |
| ויהיה מספר עליו א"ב ולא יהיה כפול משנים ולא יהיה חציו אשר הוא ג"ב נפרד | |
| הנה אומר כי א"ב זוג הזוג וזוג הנפרד | |
| ואולם היות מספר א"ב זוג הזוג הנה הוא מבואר | |
| וזה כי חציו זוג ואומר כי הוא זוג הנפרד וזה כי אנחנו חלקנו ב"ג בשני חציים וחציו בשני חציים ולא נסור נעשה כמו זה הנה אנחנו נכלה אל מספר נפרד ימנה אשר לפניו וימנה א"ב ולא יכלה אל האחד | |
| כי אנחנו אם כלינו אל האחד הנה א"ב מכפלי השנים וכבר היה שאמרנו שאינו כן ושיכלה אל מספר ימנה אשר ילוה אליו לפניו וימנה א"ב והוא מבואר שהוא ימנה פעמי מספרם זוג | |
| אם כן מספר א"ב זוג הנפרד וכבר היה זוג הזוג | |
| אם כן מספר א"ב זוג הזוג וזוג הנפרד | |
| ומ'ש'ל' | |
Proposition 36 |
|
| לו כאשרימשכו מספרים מה על יחס כמה שיהיו המספרים ונבדל מן השני ומן האחרון כמו הראשון הנה יחס הנשאר מן השני אל הראשון כיחס הנשאר מן האחרון אל כל המספרים אשר לפניו כאשר נקבצו | |
| המשל בו כי מספרי א"ב ג"ד ח"ז ט"נ נמשכים על יחס וכבר נבדל מן ג"ד השני ומן ט"נ האחרון כמו א"ב והם ה"ד מ"נ | |
| הנה אומר כי יחס ג"ה הנשאר מן השני אל א"ב כיחס ט"מ הנשאר מן האחרון אל כל המספרים אשר לפניו והם א"ב ג"ד ז"ח | |
| המופת אנחנו נשים ל"נ כמו ג"ד וכ"נ כמו ז"ח הנה יחס ט"נ אל ז"ח כיחס ז"ח אל ג"ד וכיחס ג"ד אל א"ב וז"ח כמו כ"נ וג"ד כמו ל"נ וא"ב כמו מ"נ | |
| אם כן יחס ט"נ אל כ"נ כיחס כ"נ אל נ"ל וכיחס ל"נ אל מ"נ | |
| וכאשר הבדלנו היה יחס ט"כ אל כ"נ כיחס כ"ל אל ל"נ וכיחס ל"מ אל מ"נ | |
| ויחס אחד מן הקודמים אל אחד מן הנמשכים כיחס כל הקודמים אל כל הנמשכים | |
| אם כן יחס ל"מ אל מ"נ כיחס כל ט"כ כ"ל ל"מ אל כל כ"נ נ"ל מ"נ ול"מ כמו ג"ה כי כל ל"נ כמו ג"ד ומ"נ כמו כל אחד מן א"ב ה"ד מ"נ וישאר ל"מ כמו ג"ה ומ"נ כמו א"ב | |
| אם כן יחס ג"ה אל א"ב כיחס ט"מ אל כל כ"נ ל"נ מ"נ וכ"נ כמו ח"ז ול"נ כמו ג"ד ומ"נ כמו א"ב | |
| אם כן יחס הנשאר מן ג"ד השני אל א"ב כיחס הנשאר מן ט"נ האחרון אל כל ז"ח ג"ד א"ב והם המספרים אשר לפני ט"נ | |
| וזה מה שרצינו לבאר | |
Proposition 37 |
|
| לז כאשר היו מספרים נמשכים על יחס הכפל מתחילים מן האחד כמה שהיו אחר כן יקובצו יחד והאחד עמהם והיה כל זה מספר ראשון אחר כן הוכה אותו המספר הראשון באחרון מן המספרים אשר נקבצו הנה המספר אשר יתקבץ מן ההכאה הוא מספר שלם | |
| המשל בו כי מספרי א"ב ג"ד נכפלו מן האחד אחר כן נקבצו והאחד עמהם והיו מספר ה' והוא ראשון הנה כאשר הוכה ה' במספר האחרון והוא ד' היה ז"ח | |
| הנה אומר כי ז"ח מספר שלם | |
| המופת שילקח מה' מספרים על יחס א"ב ג"ד ועל מניינם והם ה מ' | |
| אם כן א"ב ג"ד על יחס ה מ' ועל מניינם | |
| אם כן יחס א' אל ד' כיחס ה' אל מ' | |
| אם כן ה' בד' כמו א' במ' | |
| אבל ה' בד' הוא ז"ח | |
| אם כן א' במ' הוא ז"ח וא' הוא שני | |
| אם כן ז"ח כפל מ' ומ' כפל ל' ול' כפל ט"כ וט"כ כפל ה' | |
| ואם כן החמשה מספרים אשר הם ה' ט"כ ל' מ' ז"ח מתיחסים נמשכים | |
| וכאשר נבדל מן השני והאחרון כמו הראשון הנה יחס הנשאר מן השני אל הראשון כיחס הנשאר מן האחרון אל כל המספרים אשר לפניו כאשר נקבצו ונבדל מכל אחד מן ט"כ ז"ח כמו ה' והם כ"ס ע"ח | |
| אם כן יחס הנשאר מן ט"כ והוא ט"ס אל ה' כיחס הנשאר מן ז"ח והוא ז"ע אל כל מ"ל ט"כ ה' | |
| וט"כ כפל ה' וס"כ כמו ה' | |
| אם כן ט"ס כמו ה' | |
| וז"ע אם כן כמו כל מ"ל ט"כ ה' וה' כמו כל ד"ג ב"א והאחד עמהם והוא גם כן שוה לע"ח | |
| אם כן ע"ח שוה לכל ד"ג ב"א והאחד עמהם | |
| וז"ע כבר התבאר שהוא שוה לכל מ"ל ט"כ ה' | |
| אם כן כל ז"ח שוה לכל מ"ל ט'כ' ה' ד"ג ב"א והאחד עמהם | |
| הנה אומר כי לא ימנה ז"ח מספר אחר זולת ד"ג ב"א ה'ט'ב' ל"ח והאחד | |
| המופת כי הוא אי אפשר שאם היה אפשר הנה ימנהו זולתם והוא נ' וימנהו במספר אחדי פ' | |
| אם כן פ' יוכה בנ' ויהיה ז"ח | |
| אם כן שטח פ' בנ' כמו משוטח ה' בד' | |
| אם כן יחס פ' אל ק' כיחס ד' אל נ' | |
| ונ' אינו אחד מן א"ב ג' | |
| אם כן נ' לא ימנה ד' | |
| אבל יחס נ' אל ד' כיחס ה' אל פ' | |
| אם כן ה' לא ימנה פ' וה' ראשון | |
| אם כן כל אחד מן פ' וה' ראשון אצל האחר | |
| אם כן שניהם קטני שני מספרים על יחס שניהם וימנו כל שני מספרים על יחס שניהם בשווי הקטן לקטן והרב לרב | |
| אם כן פ' ימנה ד' | |
| וכאשר התיחסו מספרים מן האחד נמשכים כמה שהיו והיה אשר ילוה אל [88]האחד ראשון הנה הוא לא ימנה אחד מהם כי אם המספרים מן היחס ההוא | |
| אם כן מספר ד' לא ימנוהו כי אם המספרים ממספרי א'ב'ג' | |
| אם כן מספר פ' הוא אחד ממספרי א'ב'ג' | |
| ויהיה ב' וילקח מן ה' מן המספרים על | |
| אם כן יחס ב' אל ד' כיחס ה' אל ל' | |
| אם כן ה' בד' כמו ב' בל' מי"ט מז' | |
| אבל ה' בד' כמו ב' בנ' והוא ז"ח | |
| אם כן ב' בל' כמו פ' בנ' והוא ז"ח | |
| אם כן יחס ב' אל פ' כיחס נ' אל ל' | |
| ופ' הוא ב' | |
| אם כן נ' הוא ל' וכבר היה נ' אינו אחד מן א"ב ג"ד ה'ט'כ' ל"מ זה שקר | |
| אם כן ז"ח לא ימנהו מספר אחר כי אם א'ב'ג'ד' ה"ט כ'ל'מ' והאחד וז"ח שוה לכלם והאחד עמהם | |
| אם כן ז"ח מספר שלם שוה לכל חלקיו | |
| וזה מה שרצינו לבאר | |
| נשלם המאמר התשיעי מספר אקלידס החכם |
Book Ten |
המאמר העשירי מספר החכם אקלידס |
Definitions |
|
|
בעלי השעורים מן הקוים והשטחים והמוגשמים אשר יאמר להם |
|
ואשר יאמר להם בלתי משותפים הם אשר לא ישער אותם כלם שעור אחד |
|
והקוים הישרים אשר יאמר להם המשותפים בכח כאשר היה למרובעים ההוים מהם שטח ישער אותם |
|
ויאמר להם בלתי משותפים בכח כאשר לא יהיה למרובעים |
| וכאשר היה זה כן הנה נבאר כי כאשר התחיל והניח קו ישר[89] הנה | |
| ויגיע לקו הישר איזה קו שיהיה ממה שיתחיל הנחתו וישים תחלה המדבר | |
| הנה הקוים המשותפים לו | |
| ואשר בלתי משותפים לו בלתי מדברים | |
| והקו כאשר היה ממנו מרובע ידובר בו הנה המרובעים המשותפים למרובע ההוא ידובר בהם והבלתי משותפים בלתי מדברים | |
| והקוים אשר מהם אלו המרובעים הם גם כן בלתי מדברים | |
| שהקו אשר יהיה מרובעו בלתי מדבר הנה הוא גם כן בלתי מדבר | |
Proposition 1 |
|
| When unequal magnitudes are given, and we subtract from the greater a magnitude greater than its half, and from the remainder a magnitude greater than its half, and if this subtraction is repeated continually, then there will be left a magnitude that is less than the smaller given magnitude. | א כאשר היו שני שעורים מונחים בלתי שוים ונבדל מהגדול משניהם יותר מחציו ממה [90]שישאר יותר מחציו ונבדל כן תמיד הנה ישאר ממנו שעור מה יותר קטן מהשעור המונח |
| ויהיו שני שעורים בלתי שוים והם א"ב וג' ויהיה היותר קטן מהם ג' | |
| הנה אומר כי כאשר הובדל מן א"ב יותר מחציו וממה שישאר יותר מחציו ונעשה כן פעמים רבות הנה ישאר שעור מהיותר קטן מן הג' | |

|
וזה כי הג' כאשר הוכפל פעמים הנה הוא יהיה יותר גדול מן א"ב ויהיה מה שיתקבץ ממנו ד"ה |
| ויתחלק ד"ה בדמיוני ג' והם ד"ז וז"ח וח"ה | |
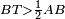
|
ונבדל מא"ב יותר מחציו והוא ב"ט |
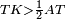
|
ומן א"ט יותר מחציו והוא ט"כ |
| ונבדיל זה תמיד עד שיהיה מנין מה שיתחלק בו א"ב שוה למספר חלקי ח"ה | |
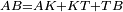
|
ויהיו החלקים אשר מן א"ב א"כ וכ"ט ט"ב |
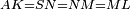
|
ויהיה א"כ שוה לכל אחד מן ס"נ ונ"מ ומ"ל |
| SN, NM, ML are equal in multitude with DZ, ZC, CH | ויהיה סך ס"נ ונ"מ ומ"ל כמו סך ד"ז וז"ח וח"ה |
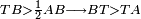
|
הנה מפני כי ט"ב יותר מחצי א"ב יהיה ב"ט יותר גדול מן ט"א |
| BT is much greater than AK | ויהיה ב"ט יותר גדול הרבה מאד מן א"כ |
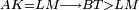
|
אבל א"כ כמו ל"מ אם כן ב"ט יותר גדול מל"מ |
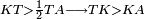
|
הנה מפני כי כ"ט גם כן יותר מחצי ט"א יהיה ט"כ יותר גדול מן כ"א |
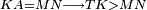
|
אבל כ"א כמו מ"נ אם כן ט"כ יותר גדול מן מ"נ |
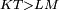
|
וכבר התבאר כי כ"ט גם כן יותר יותר גדול מן ל"מ |
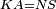
|
וכ"א כמו נ"ס |
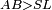
|
אם כן כל א"ב יותר גדול מכל ס"ל |
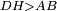
|
וד"ה יותר גדול מן א"ב |
| DH is much greater than LS | אם כן ד"ה יותר גדול הרבה מן ל"ס |
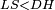
|
ויהיה ל"ס יותר קטן מד"ה |
|
|
ומפני כי שעורי ס"נ ונ"מ ומ"ל שוים |
|
וסך ס"נ ונ"מ ומ"ל שוים לסך ד"ז וז"ח וח"ה |
| ויהיה יחס אחד מהקודמים אל אחד מהנמשכים כיחס כל הקודמים אל כל הנמשכים מג' מה' | |
|
|
הנה יחס ס"נ אל ד"ז כיחס ס"ל אל ד"ה |
|
|
וס"ל יותר קטן מד"ה אם כן ס"נ יותר קטן מד"ז מד' מה' |
|
|
ואולם ס"נ הנה הוא כמו א"כ |
|
|
ואולם ד"ז הנה הוא כמו ג' |
|
|
אם כן א"כ יותר קטן מג' |
| אם כן א"ב כבר נשאר ממנו שעור יותר קטן מג' אשר הוא היותר קטן משני השעורים | |
| Q.E.D. | וזה מש"ל |
Proposition 2 |
|
| ב כאשר היו שעורים מונחים בלתי שוים ויחוסר הקטן מהגדול ויעשה כמו זה למה שיגדל משניהם ולא נסור לחסר ביניהם ולא יכלו אל יתרון משניהם ישער אשר נבדל לפניו הנה השני שעורים בלתי משותפים | |
| ויהיו השני שעורים בלתי שוים והם א"ב וג"ד ונבדל קטן שני שעורי א"ב וג"ד מהגדול משניהם ונעשה כמו זה כמה שיותיר משניהם ולא יסורו יחסרו ולא יכלו אל יתרון ישער אשר נבדל לפניו | |
| הנה אומר כי שני שעורי א"ב וג"ד בלתי משותפים וזה כי הם אם היו משותפים היה להם שעור מה שישער אותם ויאמר שישער אותם ט' וישער ג"ד ב"ה ויותיר קטן ממנו והוא הא' וישער א"ה ד"ז ויותיר הקטן ממנו והוא ז"ג וישער ז"ג ה"ח ויותיר קטן ממנו והוא ח' א' ויובדל זה תמיד עד שיותיר קטן מט' ויותיר קטן ממנו והוא א"ח הנה מפני כי ט' ישער ג"ד וג"ד ישער ב"ה אם כן ט' ישער ב"ה והוא גם כן ישער כל א"ב הנה הוא אם כן ישער הנשאר אשר הוא א"ה אבל א"ה ישער ד"ז אם כן ט' ישער ז"ד והוא גם כן ישער כל ג"ד הנה הוא אם כן ישער הנשאר אשר הוא ג"ז וכל ג"ז ישער ה"ח אם כן ט' ישער ה"ח והוא ישער כל א"ה הנה אם כן ישער הנשאר אם הוא א"ח הגדול לקטן וזה בלתי אפשרי | |
| אם כן אין לשני שעורי א"ב ג"ד שעור ישתף שניהם | |
| אם כן שעורי א"ב וג"ד בלתי משותפים | |
| וזה מש"ל | |
Proposition 3 |
|
| ג נרצה שנמצא שיעור יותר גדול משותף ישער שני שעורים משותפים ידועים בלתי שוים | |
| ויהיו שני שעורים הידועים המשותפים אשר הם בלתי שוים א"ב ג"ד ונרצה שנמצא גדול שעור משותף ישער שניהם | |
| אם כן ג"ז הוא השיעור היותר גדול משותף אשר ישער שני שעורי א"ב וג"ד אם היה ג"ד לא ישער א"ב | |
| ואולם אם היה ג"ד ישער א"ב הנה ג"ד הוא השיעור היותר גדול משותף אשר ישער שני שיעורי א"ב וג"ד | |
| ונשלם באורו | |
| ובכאן התבאר כי כאשר היה שעור ישער שני שיעורים הנה הוא ישער שיעור היותר גדול המשותף אשר ישער שניהם | |
Proposition 4 |
|
| ד נרצה שנמצא שיעור יותר גדול משותף ישער שלשה שיעורים ידועים בלתי שוים משותפים | |
| ויהיו השיעורים השלשה הידועים המשותפים אשר הם בלתי שוים א' וב' וג' | |
| ונקח השיעור היותר גדול משותף אשר ישער שני שיעורי ד' וג' ויהיה ז' | |
| הנה מפני כי ז' ישער ד' וד' ישער א' וב' הנה שיעור ז' ישער א' וב' והוא גם כן ישער ג' | |
| אם כן ז' הוא השיעור היותר גדול המשותף אשר ישער א' וב' וג' אם לא ישער ד"ג | |
| ואם היה ד' ישער ג' הנה ד' הוא השיעור היותר גדול המשותף אשר ישער א' וב' וג' | |
| וזה מש"ל | |
Proposition 5 |
|
| ה השיעורים המשותפים יחס קצתם אל קצת כיחס מספר אל מספר | |
| ויהיו שני שעורים משותפים והם א' וב' | |
| הנה אומר כי יחס א' אל ב' כיחס מספר אל מספר | |
| הנה מפני כי שיעורי א' וב' משותפים הנה ישער שניהם שיעור מה וישער שניהם שיעור ה' | |
| וכבר התבאר גם כן כי יחס א' אל ה' כיחס ג' אל האחד | |
| הנה ביחס השווי יהיה יחס א' אל ב' כיחס ג' אל ד' | |
| וזה מש"ל | |
Proposition 6 |
|
| ו השיעורים אשר יחס קצתם אל קצת כיחס מספר אל מספר הם משותפים | |
| ויהיה יחס א' אל ב' כיחס מספר ג' אל מספר ד' | |
| הנה אומר כי א' משותף אל ב' | |
| וזה כי אנחנו נחלק א' לחלקים בשיעור האחדים אשר בג' ויהיה ה' שוה לאחד מחלקיו | |
| ונניח האחד הנה מפני כי א' כבר חולק לחלקים כמנין מה שבג' מהאחדים ואחד מחלקיו הוא כמו ה' יהיה חלק האחד ממספר ג' כמו חלק ה' מא' | |
| אם כן יחס האחד אל ג' כיחס ה' אל א' | |
| ויחס מספר ג' אל מספר ד' כיחס א' אל ב' | |
| אם כן ביחס השווי יהיה יחס אחד אל מספר ד' כיחס ה' אל ב' והאחד ימנה ד' | |
| אם כן ה' ימנה ב' והוא גם כן ימנה א' אם כן א' משותף לב' ונשלם ביאורו | |
| ובחלוף יהיה יחס א' אל ה' כיחס ג' אל האחד | |
| וכן גם כן יהיה יחס ה' אל ז' כיחס האחד אל הד' | |
| אם כן יחס א' אל ז' כיחס ג' אל ד' | |
| וכבר היה יחס א' אל ב' כיחס ג' אל ד' | |
| אם כן יחס א' אל ז' ואל ב' אחד | |
| אם כן ז' כמו ב' וא' וז' משותפים | |
| אם כן א' וב' גם כן משותפים | |
| וזה מש"ל | |
Proposition 7 |
|
| ז המרובעים ההוים מהקוים הישרים המשותפים באורך יחס קצתם אל קצת כיחס מספר מרובע אל מספר מרובע והמרובעים אשר יחס קצתם אל קצת כיחס מספר מרובע אל מספר מרובע הנה צלעות שניהם משותפות באורך | |
| וגם כן הנה אנחנו נשים יחס המרובע ההוה מא' אל המרובע ההוה מב' אינו כיחס מספר מרובע אל מספר מרובע | |
| הנה אומר כי א' וב' בלתי משותפים באורך | |
| המופת כי הוא בלתי אפשר כי אם היה אפשר הנה שניהם משותפים באורך וכאשר היו כן הנה יחס המרובע ההוה מא' אל המרובע ההוה מב' כיחס מספר מרובע אל מספר מרובע ואינו כן | |
| אם כן א' בלתי משותף אל ב' באורך | |
| וזה מש"ל | |
Proposition 8 |
|
| When there are four proportional magnitudes, and the first is commensurable with the second, then the third is commensurable with the fourth; but, if the first is incommensurable with the second, then the third is incommensurable with the fourth. | ח כאשר היו ארבעה שיעורים מתיחסים והיה הראשון משותף לשני הנה השלישי משותף לרביעי ואם היה הראשון בלתי משותף לשני הנה השלישי בלתי משותף לרביעי |
|
ויהיו ארבעה שיעורים מתיחסים והם א' וב' וג' וד' ויחס א' אל ב' כיחס ג' אל ד' |
|
ויהיה א' משותף אל ב' |
| Supposition: I say that G is commensurable with D. | הנה אומר כי ג' משותף אל ד' |
| Since A is commensurable with B, the ratio of A to B is the same as the ratio of a number to a number. | הנה מפני כי א' משותף אל ב' יהיה יחס א' אל ב' כיחס מספר אל מספר |
| The ratio of A is to B is the same as the ratio of G to D.
|
ויחס א' אל ב' כיחס ג' אל ד' |
| Therefore, the ratio of G to D is the same as the ratio of a number to a number. | אם כן יחס ג' אל ד' כיחס מספר אל מספר |
| Hence, G is commensurable with D | אם כן ג' משותף אל ד' |
| Let A be incommensurable with B. | ולא יהיה א' משותף אל ב' |
| Supposition: I say that G is incommensurable with D. | הנה אומר כי ג' גם כן בלתי משותף אל ד' |
| If G is commensurable with D, then A is also commensurable with B. | וזה כי הוא אם ג' משותף אל ד' הנה א' גם כן משותף אל ב' |
| But, A is incommensurable with B. | אבל א' בלתי משותף אל ב' |
| Therefore, G is incommensurable with D. | אם כן אין ג' משותף אל ד' |
| Quod erat demonstrandum | וזה מה שרצינו לבאר |
Proposition 9 |
|
| ט נרצה שנמצא שני קוים ישרים בלתי משותפים לקו ישר ידוע אחד מהם באורך לבד והאחר באורך ובכח | |
| ויהיה הקו הישר הידוע א' ונרצה שנמצא לקו א' הישר שני קוים ישרים בלתי משותפים אליו אחד משניהם באורך לבד והאחר באורך ובכח | |
| אם כן א' בלתי משותף אל ה' בכח | |
| הנה כבר מצאנו לקו א' הידוע שני קוים בלתי משותפים אליו אולם באורך לבד ד' ואולם באורך והכח ה' | |
| וזה מש"ל | |
Proposition 10 |
|
| י השיעורים המשותפים לשיעור א' הנה קצתם משותף לקצת | |
| ויהיה כל אחד מא"ג משותף אל ב' | |
| הנה אומר כי א' משותף אל ג' | |
| הנה מפני כי א' משותף אל ב' יהיה יחס א' אל ב' כיחס מספר ד' אל מספר ה' | |
| וכן גם כן התבאר כי יחס ב' אל ג' כיחס כ' אל ל' הנה כיחס השווי יהיה יחס א' אל ג' כיחס ט' אל ל' | |
| אם כן יחס א' אל ג' כיחס מספר ט' אל מספר ל' | |
| אם כן א' משותף אל ג' | |
| וזמש"ל | |
Proposition 11 |
|
| יא כאשר היו שני שיעורים משותפים והורכבו הנה כלל שניהם משותף לכל אחד משניהם ואם היה הכל משותף לאחד משניהם השני שיעורים הראשונים משותפים | |
| ויהיו שני שיעורים משותפים עליהם א"ב וב"ג | |
| הנה אומר כי כל א"ג משותף לכל אחד מא"ב וב"ג | |
| ונאמר שיהיה שיעור ד' הנה מפני כי ד' ישער כל אחד משני שיעורי א"ג וב"ג הנה הוא ישער הנשאר אשר הוא א"ב והוא גם כן שיעור ד' ישער שני שיעורי א"ב ב"ג אם כן א"ב משותף אל ב"ג | |
| וזה מה שרצינו לבאר | |
Proposition 12 |
|
| יב כאשר היו ארבעה קוים מתיחסים והיה הראשון משניהם יוסיף על השני בכח ורוצה באומרו בכח כי מרובעו יוסיף על מרובעו כמו מרובע יהיה מקו משותף לו באורך הנה השלישי יוסיף על הרביעי בכח כמו מרובע יהיה מקו משותף לו באורך ואם היה הראשון יוסיף על השני בכח כמו מרובע יהיה מקו לא ישתתף עמו באורך הנה השלישי יוסיף על הרביעי בכח כמו מרובע יהיה מקו לא ישתתף עמו באורך | |
| ואם היה בלתי משותף אל ה' הנה ג' בלתי משותף אל ז' | |
| וזה מש"ל | |
Proposition 13 |
|
| יג כאשר היו שני קוים ישרים בלתי שוים וחובר אל היותר ארוך משניהם שטח שוה לרביע המרובע ההוה מהקו הקצר יחסר משלימות הקו שטח מרובע הנה אם חולק הקו היותר ארוך בשני חלקים משותפים הנה הקו היותר ארוך יוסיף על הקצר בכח כמו מרובע יהיה מקו משותף לקו הארוך ואם היה הקו הארוך יוסיף על קו הקצר בכח כמו מרובע יהיה מקו משותף לקו הארוך הנה אם חובר מהארוך שטח שוה לרביע המרובע ההוה מהקו הקצר וחסר משלימות הקו שטח מרובע הנה יחלק הקו בשני חלקים משותפים | |
| ויהיו שני קוי ישרים עליהם א"ב וגו | |
| הנה אומר כי א"ב יוסיף על ג' בכח כמו מרובע יהיה מקו משותף לקו א"ב ויהיה ד"ה כמו ב"ד הנה מפני כי קו א"ד כבר חולק בשני חלקים איך שנפל על ה' ונוסף באורכו כמו אחת משתי החלוקות והוא ד"ב יהיו ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד וד"ה עם המרובע ההוה מהא' שוה למרובע ההוה מקו א"ב | |
| וזה כי אנחנו כאשר הלכנו כמו הדרך הקודם הנה נבאר בזה כי א"ב יוסיף על ג' בכח כמו המרובע ההוה מא"ה ויהיה א"ב משותף אל ב"ד באורך וישאר ה"ב גם כן משותף אל א"ב וה"ב כפל ב"ד אם כן א"ב משותף אל ב"ד באורך | |
| וכאשר הבדלנו יהיה א"ד משותף אל ב"ד באורך | |
| וזה מש"ל | |
Proposition 14 |
|
| יד כל שני קוים בלתי שוים יחובר אל הארוך שטח שוה לרביע המרובע ההוה מהקו הקצר יחסר משלימות הקו שטח מרובע ויחלק הקו הארוך לשני חלקים בלתי משותפים הנה הקו הארוך יוסיף על הקו הקצר בכח כמו מרובע יהיה מקו בלתי משותף אליו באורך | |
| ויהיו שני קוי א' וב"ג בלתי שוים והקצר משניהם קו א' ונחבר אל ב"ג הארוך שטח שוה לרביע המרובע ההוה מקו א' יחסר משלימות שטח מרובע והוא שטח ב"ד בד"ג ויהיה ב"ד בלתי משותף אל ד"ג באורך | |
| הנה אומר כי ב"ג יוסיף על א' בכח כמו מרובע יהיה מקו לא ישתתף עמו באורך | |
| המופת שאנחנו נשים ד"ה כמו ג"ד והתבאר כמו שביארנו בתמונה הקודמת כי ב"ג יוסיף על א' בכח כמו המרובע ההוה מב"ה | |
| [הנה אומר] כי ב"ג בלתי משותף אל ב"ה באורך כי אלו היה משותף אל ב"ה היה ב"ד משותף אל ד"ג ואין זה כן | |
| אם כן לא ישתתף אליו באורך | |
| וגם כן הנה אנחנו נשים ב"ג יוסיף על א' בכח כמו מרובע יהיה מקו לא ישתתף אל ב"ג באורך | |
| אם כן אין ב"ד משותף אל ד"ג באורך | |
| הנה הוא אם כן בלתי משותף אליו באורך | |
| וזה מה שרצינו לבאר | |
Proposition 15 |
|
| טו כל שטח נצב הזויות יקיפו בו שני קוים ישרים משותפים באורך מדברים הנה הוא מדבר | |
| ויקיפו שני קוי ב"א וא"ג הישרים אשר ידבר לשניהם בשטח ב"ג | |
| הנה אומר כי שטח ב"ג מדבר ונעשה על קו א"ב מרובע עליו ב"ד הנה מרובע ב"ד מדבר | |
| הנה שטח ב"ד משותף לשטח ב"ג ומרובע ב"ד מדבר | |
| אם כן שטח ב"ג מדבר | |
| וזה מה שרצינו לבאר | |
Proposition 16 |
|
| יו כאשר חובר שטח מדבר אל קו מדבר הנה הוא יחדש רוחב מדבר ישתתף אל הקו אשר חובר אליו השטח באורך | |
| ויהיה הקו המדבר א"ב והשטח המדבר אשר חובר אליו ב"ג ויחדש ב"ג רוחב א"ג | |
| המופ' הנה אומר כי א"ג מדבר משותף לקו א"ב באורך | |
| אם כן קו ד"א מדבר משותף לקו א"ג וקו ד"א מדובר | |
| אם כן קו א"ג מדובר והוא משותף לקו ב' בארך | |
| וזה מש"ל | |
Proposition 17 |
|
| יז כאשר היה שטח נצב הזויות יקיפו בו שני קוים ישרים מדברים בכח והיו בהם לבד משותפים הנה הוא בלתי מדבר והקו הישר אשר יחזיק עליו גם כן בלתי מדבר ויקרא הממוצע | |
| ויקיפו בשטח ב"ג שני קוי ב"א א"ג הישרים ויהיו בכח מדברים ובהם לבד משותפים | |
| אם כן ד"ב בלתי משותף אל ב"ג וד"ב מדבר | |
| אם כן ב"ג בלתי מדבר והקו אשר יחזיק עליו גם כן בלתי מדבר ויקרא הממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 18 |
|
| יח כאשר יחובר אל קו מדבר שטח שוה למרובע יהיה מקו ממוצע הנה יתחדש ממנו רוחב מדובר בכח והוא באורך בלתי משותף לקו אשר חובר אליו השטח | |
| ויהיה קו א' ממוצע והקו המדבר ב"ג | |
| ויהיה זה השטח אשר יחזיק עליו קו א' שטח ה"ח והוא יקיפו בו שני קוי ה"ז וז"ח ושניהם מדברים בכח בהם לבד משותפים וא' גם כן יחזיק על ג"ד הנה ג"ד כמו ה"ח וזויותיו כמו זויותיו והשטחים הנכחי הצלעות השוים אשר זויותיהם שוות צלעות שניהם המקיפות בזויות השוות מספיקות | |
| אם כן קו ד"ב בלתי משותף לקו ב"ג באורך | |
| אם כן קו ד"ב מדבר בכח והוא בלתי משותף לקו ב"ג באורך | |
| וזה מש"ל | |
Proposition 19 |
|
| יט כל קו משותף לממוצע הנה הוא ממוצע | |
| ויהיה א' ממוצע ויהיה משותף לקו ב' | |
| הנה אומר כי ב' ממוצע ויהיה קו ג"ד מדבר ונחבר אל קו ג"ד שטח שוה למרובע ההוה מא' והוא שטח ד"ה | |
| וקו ב' יחזיק על שטח ד"ז | |
| אם כן קו ב' בלתי מדבר ויקרא ממוצע | |
| וזה מש"ל | |
Proposition 20 |
|
| כ יתרון הממוצע על הממוצע בלתי מדבר | |
| ויהיה שטח א"ב ממוצע ושטח א' ממוצע ויותיר מה שבין שניהם שטח ב' | |
| הנה אומר כי ב' בלתי מדבר | |
| שאם היה אפשר שלא יהיה כן נאמר שיהיה מדבר ויהיה קו ג"ד גם כן מדבר | |
| ולכן יהיה שטח ג"ז בז"ה בלתי משותף למרובע ההוה מז"ה | |
| ואולם שטח ג"ז בז"ה הוא משותף לכפל שטח ג"ז בז"ה | |
| ואולם המרובע ההוה מז"ה הנה הוא משותף למרובע ההוה מג"ז | |
| אם כן המרובע ההוה מג"ה בלתי מדבר וזה בלתי אפשר מפני כי ג"ה מדבר בכח | |
| אם כן אין תוספת הממוצע על הממוצע שטח מדבר וזה מש"ל
היה שעור אחד בלתי משותף לשני שעורים לכל אחד בעצמו והיו שני השעורים ההם משותפים הנה הוא בלתי משותף לשניהם מקובצים . דמיון זה כי שעור א' בלתי משותף לשעור ב' ולשעור ג' ושני שעורי ב"ג משותפים ואומר כי א' בלתי משותף לשני ב"ג מקובצים . המופת שאי אפשר בלתי זה . שאם היה אפשר הנה יהיה ב' משותף לג' אם כן הוא משותף לכל ב"ג וא' משותף לכל ב"ג אם כן ב"ג משותף לשני שעורי א"ב אם כן א"ב משותפים זה שקר אם כן אין א' משותף לכל ב"ג ומ'ש'ל' | |
Proposition 21 |
|
| כא נרצה שנמצא שני קוים ממוצעים משותפים בכח לבד יקיפו בשטח מדבר | |
| ויהיו שני קוים משותפים בכח לבד וידובר בשניהם בו והם א' וב' ויהיה המרובע ההוה מג' שוה לשטח ההוה מא' בב' | |
| אם כן שני קוי ג' וד' ממוצעים ושניהם משותפים בכח לבד ויקיפו בשטח מדבר והוא שטח ג"ד | |
| וזה מש"ל | |
Proposition 22 |
|
| כב נרצה שנבאר איך נמצא שני קוים ממוצעים משותפים בכח לבד יקיפו בשטח ממוצע | |
| ויהיו שלשה קוים בכח לבד מדברים משותפים והם א'ב'ג' ויהיה המרובע ההוה מד' שוה לשטח ההוה מא' בב' | |
| אם כן השטח ההוה מד' בה' ממוצע | |
| ומפני כי השטח ההוה מא' בב' שוה למרובע ההוה מד' והשטח ההוה מב' בג' שוה לשטח ההוה מד' בה' יהיה יחס השטח ההוה מא' בב' אל המרובע ההוה מד' כיחס השטח ההוה מב' בג' אל השטח ההוה מד' בה' | |
| אם כן קו ד' משותף לקו ה' בכח לבד וקו ד' ממוצע אם כן ה' ממוצע | |
| אם כן שני קוי ד"ה ממוצעים משותפים בכח לבד ויקיפו בשטח ד' בה' אשר הוא ממוצע | |
| וזה מש"ל | |
Proposition 23 |
|
| כג כאשר הקיפו בשטח נצב הזויות שני קוים ממוצעים משותפים לבד בכח הנה השטח ההוא אם שיהיה מדבר ואם שיהיה ממוצע | |
| ויקיף בשטח ב"ג שני קוים ממוצעים משותפים בכח לבד והם ב"א וא"ג | |
| אם כן שטח כ"ל אם שיהיה מדבר ואם שיהיה ממוצע וכ"ל כמו ב"ג | |
| אם כן שטח ב"ג אם שיהיה מדבר ואם שיהיה ממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 24 |
|
| כד נרצה שנמצא שני קוים מדברים בכח משותפים בהם לבד ויוסיף היותר ארוך משניהם על הקצר בכח כמו מרובע יהיה מקו ישתתף עמו באורך | |
| ויהיו שני מספרים מרובעים והם א"ב וא"ג ולא יהיה יתרון מה שבין שניהם והוא ב"ג מרובע | |
| מפני כי יחס א"ב אל ב"ג כיחס המרובע ההוה מד"ה אל המרובע ההוה מד"ז ויחס א"ב אל ב"ג כיחס מספר אל מספר ולא יהיה כיחס מספר מרובע אל מספר מרובע | |
| אם כן יחס המרובע ההוה מד"ה אל המרובע ההוה מז"ה כיחס מספר מרובע אל מספר מרובע הנה קו ד"ה משותף לקו ז"ה באורך | |
| אם כן קו ד"ה יוסיף על קו ד"ז בכח כמו מרובע יהיה מקו משותף אליו באורך | |
| וזמש"ל | |
| ומצאתי אני המעתיק זאת הנסחא בשני ספרים אחרים במקום מה שסיימתי כן | |
| אם כן יחס המרובע ההוה מד"ה אל המרובע ההוה מד"ז כיחס מספר אל מספר ולא יהיה כיחס מספר מרובע אל מספר מרובע | |
| ומפני כי יחס א"ב אל ב"ג כיחס המרובע ההוה מד"ה אל המרובע ההוה מד"ז והיה כאשר הפכנו יחס א"ב אל א"ג כיחס המרובע ההוה מד"ה אל המרובע ההוה מז"ה וכו' כמו שהשלים | |
Proposition 25 |
|
| כה נרצה שנמצא שני קוים מדברים בכח ומשותפים בהם לבד ויוסיף הארוך משניהם על הקצר בכח כמו מרובע יהיה מקו לא ישתתף עמו באורך | |
| ויהיו שני מספרים בלתי מרובעים והם א"ג ג"ב ויהיה קבוץ שניהם קו א"ב ואינו מרובע ויהיה קו ד"ה מדבר ונקוה עליו חצי עגולה דז"ה | |
| אם כן קו ד"ה בלתי משותף לקו ז"ה באורך | |
| אם כן קו ד"ה יוסיף על קו ד"ז בכח כמו מרובע יהיה מקו בלתי משותף אליו באורך | |
| וזה מש"ל | |
Proposition 26 |
|
| כו נרצה שנמצא שני קוים ממוצעים משותפים בכח לבד יקיפו בשטח מדבר ויוסיף אחד משניהם על האחר בכח בתוספת מרובע מקו ישתתף עמו באורך | |
| ויהיו שני קוים מדברים בכח ובהם לבד משותפים והם א"ב ויוסיף הגדול מהם והוא א' על הקטן והוא ב' כמו מרובע מקו ישתתף עמו באורך ונקח מה שבין שני קוי א' וב' קו מתיחס להם והוא ג' | |
| ויהיה יחס ב' אל ד' כיחס א' אל ג' | |
| אם כן שני קוי ג' וד' ממוצעים בכח ובהם לבד משותפים ויקיפו בשטח מדבר ויוסיף ג' על ד' בכח כמו מרובע יהיה מקו ישתתף עמו באורך | |
| וזה מש"ל | |
Proposition 27 |
|
| כז נרצה שנמצא שני קוים ממוצעים משותפים בכח לבד יקיפו בשטח מדבר ויוסיף אחד משניהם על האחר כמו מרובע יהיה מקו לא ישתתף עמו באורך | |
| ומעשה זה יתבאר כמו שבארנו על התמונה אשר לפני זאת כאשר נשים שני הקוים הראשונים אשר בהם עשינו זה מדברים בכח משותפים בה יוסיף הגדול משניהם על הקטן כמו מרובע יהיה מקו לא ישתתף עמו באורך | |
| וזה מה שרצינו לבאר | |
Proposition 28 |
|
| כח נרצה שנמצא שני קוים ממוצעים משותפים בכח לבד יקיפו בשטח ממוצע ויוסיף אחד משניהם על האחר כמו מרובע יהיה מקו ישתתף עמו באורך | |
| ויהיו שלשה קוים מדברים בכח ויהיו בו לבד משותפים והם א' וב' וג' | |
| ומפני כי יחס א' אל ג' כיחס ד' אל ה' וקו א' יוסיף על קו ג' בכח כמו מרובע יהיה מקו ישתתף עמו באורך הנה שני קוי ד"ה ממוצעים משותפים בכח לבד יקיפו בממוצע ויוסיף ד' על ה' בכח כמו מרובע יהיה מקו ישתתף עליו באורך | |
| וזה מש"ל | |
Proposition 29 |
|
| כט נרצה שנמצא שני קוים ממוצעים משותפים בכח לבד יקיפו בשטח ממוצע ויוסיף אחד משניהם על האחר בכח כמו מרובע יהיה מקו לא ישתתף עמו בארך | |
| והמעשה הזה יתבאר כמו שהתבאר מעשה התמונה אשר לפני זאת כאשר יעשה השלשה קוים אשר בהם עשינו אותו מדברים בכח משותפים השיעור בו לבד יוסיף אחד משניהם על האחר בכח כמו מרובע יהיה בקו ולא ישתתף עמו באורך | |
| וזה מש"ל | |
Proposition 30 |
|
| ל נרצה שנמצא שני קוים ישרים בלתי משותפים בכח וכאשר יקובצו שני המרובעים ההוים משניהם יהיה מה שיתקבץ מדבר ויהיה כפל השטח אשר יקיפו בו ממוצע | |
| ויהיו שני קוים מדברים בכח ובו לבד משותפים והם א"ב ב"ג | |
| וכאשר יקובצו שני המרובעים ההוים משניהם יהיה מה שיתקבץ מדבר ויהיה כפל אשר יקיפו בו ממוצע | |
| וזה מש"ל | |
Proposition 31 |
|
| לא נרצה שנמצא שני קוים ישרים בלתי משותפים בכח וכאשר יקובצו שני המרובעים ההוים משניהם היה מה שיתקבץ ממוצע ויהיה כפל השטח אשר יקיפו בו מדבר | |
| ויהיו שני קוים ממוצעים משותפים בכח לבד והם א"ב ב"ג ויהיה השטח אשר יקיפו בו והוא ההוה מא"ב בב"ג מדבר | |
| ומפני כי המרובע ההוה מא"ב שוה לשני המרובעים ההוים מא"ז א"ב והמרובע ההוה מא"ב ממוצע הנה יהיו שני המרובעים ההוים מא"ז ז"ב כאשר יקובצו ממוצע | |
| ומפני כי השטח אשר יקיפו בו שני קוי א"ב ב"ג מדבר יהיה השטח אשר יקיפו שני קוי א"ב ב"ד מדבר ולכן יהיה מה שיהיה מא"ב בב"ד שתי פעמים מדבר | |
| אם כן אשר יהיה מא"ב בז"ה שתי פעמים מדבר והוא שוה לכפל השטח אשר יקיפו בו שני קוי א"ז ז"ב אם כן שני קוי א"ז ז"ב בלתי משותפים בכח | |
| וכאשר יקובצו שני המרובעים ההוים משניהם יהיו ממוצעים וכפל השטח אשר יקיפו בו מדבר | |
| וזה מה שרצינו לבאר | |
Proposition 32 |
|
| לב נרצה שנמצא שני קוים ישרים בלתי משותפים בכח וכאשר יקובצו שני המרובעים ההוים משניהם היה מה שיקובץ ממוצע ויהיה כפל השטח אשר יקיפו בו ממוצע ויהיו מרובעיהם כאשר יקובצו בלתי משותפים לכפל השטח אשר יקיפו בו | |
| ואולם קבוץ המרובעים ההוים משניהם היה מה שיתקבץ ממוצע וכפל השטח אשר יקיפו בו הוא גם כן ממוצע והוא בלתי משותף לשני המרובעים ההוים משני קוים א"ז ז"ב כאשר יקובצו | |
| וזה מש"ל | |
Proposition 33 |
|
| When a line is composed of two straight lines measurable in square only, then the whole straight line is unmeasurable; let it be called binomial. | לג כאשר הורכב קו משני קוים ישרים מדברים בכח והיו בו לבד משותפים הנה כל הקו בלתי מדבר ויקרא אשר משתי שמות |
| ויורכב קו מה משני קוים ישרים מדברים בכח משותפים בו לבד והם א"ב ב"ג | |
| אם כן המרובע ההוה מא"ג בלתי מדבר הנה קו א"ג אם כן בלתי מדבר ויקרא אשר משתי שמות | |
| וזה מה שרצינו לבאר | |
Proposition 34 |
|
| When a line is composed of two medial straight lines commensurable in square only, and the rectangle contained by them is measurable, then the whole straight line is unmeasurable; let it be called first bimedial. | לד כאשר הורכב קו משני קוים ישרים ממוצעים משותפים בכח לבד ויהיה השטח אשר יקיפו בו מדבר הנה כל הקו בלתי מדבר ויקרא אשר משתי הממוצעים הראשון |
| ויורכב קו משני קוים ישרים ממוצעים משותפים בכח לבד והם א"ב ב"ג ויקיפו בשטח מדבר והוא שטח א"ב בב"ג | |
| אם כן המרובע ההוה מא"ג בלתי מדבר ויקרא אשר משני האמצעים הראשון | |
| וזה מה שרצינו לבאר | |
Proposition 35 |
|
| לה כאשר הורכב קו משני קוים ישרים ממוצעים משותפים בכח לבד ויהיה השטח אשר יקיפו בו ממוצע הנה כל הקו בלתי מדבר ויקרא אשר משני ממוצעים השני | |
| ויורכב קו משני קוים ישרים ממוצעים משותפים בכח לבד והם א"ב ב"ג ויקיפו בשטח ממוצע והוא שטח א"ב בב"ג | |
| והקו אשר יחזיק על השטח אשר יקיפו בו בלתי מדבר וקו א"ג יחזיק על שטח ה"ט | |
| אם כן קו א"ג בלתי מדבר ויקרא אשר משני הממוצעים השני | |
| וזה מה שרצינו לבאר | |
Proposition 36 |
|
| When a line is composed of two straight lines incommensurable in square, so that the rectangle that equals the sum of their two squares is measurable and the rectangle contained by them is medial, then the whole straight line is unmeasurable; let it be called major. | לו כאשר הורכב קו משני קוים ישרים בלתי משותפים בכח והיה השטח השוה לשני מרובעיהם כאשר קובצו מדבר והיה השטח אשר יקיפו בו ממוצע הנה כל הקו בלתי מדבר ויקרא היותר גדול |
| ויהיו שני קוים ישרים בלתי משותפים בכח והם א"ב ב"ג ויהיה השטח השוה לשני מרובעי א"ב ב"ג מדבר | |
| אם כן המרובע ההוה מא"ג בלתי מדבר | |
| הנה א"ג אם כן בלתי מדבר ויקרא היותר גדול | |
| וזה מה ש"ל | |
Proposition 37 |
|
| When a line is composed of two straight lines incommensurable in square, so that the rectangle that equals the sum of their two squares is medial and the rectangle contained by them is measurable, then the whole straight line is unmeasurable; let it be called the sum of a measurable and a medial area. | לז כאשר הורכב קו משני קוים ישרים בלתי משותפים בכח והיה השטח השוה לשני מרובעיהם ממוצע והיה השטח אשר יקיפו בו מדבר הנה כל הקו בלתי מדבר ויקרא אשר יחזיק על מדבר וממוצע |
| אם כן המרובע ההוה מא"ג בלתי מדבר | |
| אם כן קו א"ג בלתי מדבר ויקרא אשר יחזיק על מדבר וממוצע | |
| וזהו מה שרצינו לבאר | |
Proposition 38 |
|
| When two straight lines incommensurable in square are combined, so that the rectangle that equals the sum of their two squares is medial and the rectangle contained by them is medial and the sum of their two squares is incommensurable with the rectangle contained by them, then the whole straight line is unmeasurable; let it be called the sum of two medial areas. | לח כאשר הורכבו שני קוים ישרים בלתי משותפים בכח והיה השטח השוה לשני מרובעיהם ממוצע והיה השטח אשר יקיפו בו ממוצע ויהיו שני המרובעים ההוים משניהם כאשר יקובצו בלתי משותפים לשטח אשר יקיפו בו הנה כל הקו בלתי מדבר ויקרא אשר יחזיק על שני ממוצעים |
| ויהיו שני קוים בלתי משותפים בכח והם א"ב ב"ג ויהיה השטח השוה לשני המרובעים ההוים ממוצע ויהיה גם כן השטח אשר יקיפו בו ממוצע ויהיו שני המרובעים ההוים משניהם כאשר יקובצו בלתי משותפים לשטח אשר יקיפו בו | |
| הנה אומר כי כל א"ג בלתי מדבר ויקרא אשר יחזיק על שני ממוצעים | |
| אם כן ד"ט בלתי מדבר והוא אשר יקרא משתי שמות וקו ד"ה מדבר והשטח הנצב הזויות אשר יקיפו בו קו מדבר וקו בלתי מדבר הנה הוא בלתי מדבר והקו אשר יחזיק עליו בלתי מדבר וקו א"ג יחזיק על שטח ה"ט | |
| אם כן קו א"ג בלתי מדבר ויקרא אשר יחזיק על שני ממוצעים | |
| וזה מה שרצינו לבאר | |
Proposition 39 |
|
| The binomial straight line is divided into its two terms at one point only. | לט הקו אשר משתי שמות אמנם יחלק בשתי שמות על נקודה אחת לבד |
| ויהיה הקו אשר משתי שמות א"ג ויתחלק בשתי שמות על נקודת ב' | |
| הנה אומר כי א"ג לא יתחלק בשתי שמות על נקודה אחרת | |
| שאם היה אפשר הנה יתחלק על נקודת ד' גם כן | |
| אם כן הקו אשר משני שמות לא יתחלק בשתי שמות בשתי מקומות | |
| וזהו מה שרצינו לבאר | |
Proposition 40 |
|
| The first bimedial straight line is divided into two medial areas at one point only. | מ הקו אשר משני ממוצעים הראשון אמנם יתחלק בשני הממוצעים על נקודה אחת לבד |
| ויהיה הקו אשר משני ממוצעים הראשון א"ג ויתחלק בשני ממוצעים על נקודת ב' | |
| הנה אומר כי הוא לא יתחלק בשני ממוצעים על נקודה אחרת שאם היה אפשר יתחלק גם כן על נקודת ד' הנה מפני כי יתרון מה שבין מרובעי א"ב ב"ג כאשר יקובצו ובין שני מרובעי א"ד ד"ג כאשר יקובצו שוה ליתרון מה שבין כפל השטח אשר יקיפו בו שני קוי א"ב ב"ג ובין כפל השטח אשר יקיפו בו א"ד ד"ג ויתרון מה שבין כפל השטח אשר יקיפו א"ב ב"ג ובין כפל השטח אשר יקיפו בו א"ד ד"ג מדבר | |
| אם כן הקו אשר משני הממוצעים הראשון לא יתחלק בשני הממוצעים בשני מקומות מתחלפות | |
| וזהו מה שרצינו לבאר | |
Proposition 41 |
|
| The second bimedial straight line is divided into two medial areas at one point only. | מא הקו אשר משני הממוצעים השני אמנם יתחלק בשני ממוצעים על נקודה אחת לבד |
| ויהיה הקו אשר משני ממוצעים השני א"ג ויתחלק בשני ממוצעים על נקודת ב' | |
| הנה אומר כי א"ג לא יתחלק בשני ממוצעים על נקודה אחרת | |
| וכן גם כן התבאר שהוא כבר חולק בשתי שמות על נקודת ל' | |
| הנה הקו אשר משתי שמות כבר חולק בשתי שמות על שתי נקודות מתחלפות | |
| וכבר התבאר כי זה בלתי אפשר | |
| אם כן לא יתחלק הקו אשר משני ממוצעים השני על שתי נקודות מתחלפות | |
| וזהו מה שרצינו לבאר | |
Proposition 42 |
|
| The major straight line is divided at one point only. | מב הקו היותר גדול אמנם יתחלק על נקודה אחת לבד |
| ויהיה הקו היותר גדול א"ג ויתחלק על נקודת ב' הנה קוי א"ב ב"ג שניהם בכח בלתי משותפים ושני מרובעיהם כאשר יקובצו יהיה משניהם מדבר | |
| אם כן אי אפשר שיתחלק הקו היותר גדול על שתי נקודות מתחלפות | |
| וזה מש"ל | |
Proposition 43 |
|
| The line of a measurable plus a medial area is divided at one point only. | מג הקו אשר יחזיק על מדבר וממוצע אמנם יתחלק על נקודה אחת לבד |
| ויהיה הקו אשר יחזיק על מדבר ממוצע א"ג ויתחלק על נקודת ב' הנה שני קוי א"ב ב"ג בלתי משותפים בכח ושניהם המרובעים ההוים משניהם כאשר יקובצו יהיה ממוצע | |
| וזה בלתי אפשר מפני כי כל אחד משניהם ממוצע הנה לא יתחלק הקו אשר יחזיק על מדבר וממוצע על שתי נקודות מתחלפות | |
| וזה מש"ל | |
Proposition 44 |
|
| The line of the sum of two medial areas is divided at one point only. | מד הקו אשר יחזיק על שני ממוצעים אמנם יתחלק על נקודה אחת |
| ויהיה הקו אשר יחזיק על שני ממוצעים א"ד ויתחלק על נקודת ב' הנה קוי א"ב ב"ד בלתי משותפים בכח ושני המרובעים ההוים מב' קוי א"ב ב"ד כאשר יקובצו היה ממוצע והשטח אשר יקיפו בו ב' קוי א"ב ב"ד גם כן ממוצע ושני המרובעים ההוים מב' קוי א"ב ב"ד כאשר יקובצו בלתי משותפים לשטח אשר יקיפו בו א"ב ב"ד | |
| אם כן הקו אשר יחזיק על שני ממוצעים אמנם יתחלק על נקודה אחת לבד | |
| וזה מה שרצינו לבאר | |
Definitions |
הקדמה |
| כאשר היה קו מה מדבר וקו משתי שמות והיה כבר חולק משתי שמות והיה היותר גדול מהחלקים יוסיף על הקטן מהם בכח כמו מרובע יהיה מקו ישתתף עמו באורך והיה החלק הגדול משותף באורך לקו המדבר הנה יקרא הקו כלו אשר משתי שמות הראשון | |
| ואם היה החלק הקטן משותף באורך לקו המדבר הנה יקרא אשר משתי שמות החמשי | |
| ואם לא יהיה אחד משתי השמות משותף באורך לקו המדבר הנה יקרא אשר משתי שמות הששי | |
Proposition 45 |
|
| 45) We wish to find the first binomial line. | מה נרצה שנמצא קו משתי שמות הראשון |
| We draw a rational line, which is A. | הנה נניח קו מדבר והוא א' |
| Let line BG be commensurable in length with line A. | ויהיה קו ב"ג משותף לקו א' באורך |
| Line A is rational, therefore line BG is also rational. | וקו א' מדבר אם כן קו ב"ג מדבר |
| Let HD and DZ be two square numbers such that the difference between them, which is HZ, is not a square number. | ויהיו שני מספרים מרובעים והם ה"ד ד"ז ולא יהיה יתרון מה שבין שניהם אשר הוא ה"ז מספר מרובע |
| Hence, line BG is commensurable in length with line T. | אם כן קו ב"ג משותף לקו ט' באורך |
| The excess of BG over GC in square is the same as the square of the line that is commensurable in length with it. | ותוספת ב"ג על ג"ח בכח כמו מרובע יהיה מקו ישתתף עמו באורך |
| Line BG is commensurable with the given rational line, which is A. | וקו ב"ג משותף לקו המדבר המונח אשר הוא א' |
| Therefore, line BC is the first binomial line. | אם כן קו ב"ח הוא אשר משתי שמות הראשון |
| וזה מה שרצינו לבאר | |
Proposition 46 |
|
| מו נרצה שנמצא קו משתי שמות השני | |
| הנה נניח קו מדבר והוא א' ויהיה קו ג"ח משותף לקו א' באורך אם כן קו ג"ח מדבר ויהיו שני מספרים מרובעים והם ה"ד ד"ז ולא יהיה יתרון מה שבין שניהם אשר הוא ה"ז מספר מרובע | |
| וזה כי יחס המרובע ההווה מן ג"ח אל המרובע ההווה מן ג"ב כיחס מספר ה"ז אל מספר ד"ה ומספר ה"ז קטן ממספר ד"ה אם כן המרובע ההווה מן ג"ח קטן מן המרובע ההווה מן ב"ג | |
| ונבאר כמו שבארנו במה שקדם כי ט' משותף לקו ב"ג באורך אם כן ב"ג יוסיף על קו ג"ח בכח כמו מרובע יהיה מקו ישתתף עמו באורך וקו ג"ח הוא הקטן משני קוי ב"ג ג"ח והוא ישתתף באורך לקו המדבר אשר הוא א' | |
| אם כן קו ב"ח הוא אשר משתי השמות השני | |
| וזה מה שרצינו לבאר | |
Proposition 47 |
|
| מז נרצה שנמצא קו משתי שמות השלישי הנה נניח קו מדבר והוא א' ושלשה מספרים כי אין יחס אחד מהם אל האחר כיחס מספר מרובע אל מספר מרובע והם ב"ג ג"ד ה' | |
| יהיה כאשר הפכנו יחס ב"ג אל ב"ד כיחס המרובע ההווה מן ז"ח אל המרובע ההווה מן כ' ויחס ב"ג אל ב"ד כיחס מספר מרובע אל מספר מרובע | |
| אם כן יחס המרובע ההווה מן ז"ח אל המרובע ההווה מן כ' כיחס מספר מרובע אל מספר מרובע | |
| אם כן קו ז"ח משותף לקו כ' באורך | |
| אם כן קו ז"ח יוסיף על ח"ט בכח כמו מרובע יהיה מקו ישתתף עמו באורך ואין אחד משני קוי ז"ח ח"ט משותף באורך לקו המדבר המונח אשר הוא א' | |
| אם כן קו ז"ט הוא אשר משתי שמות השלישי | |
| וזמש"ל | |
Proposition 48 |
|
| מח נרצה שנמצא קו אשר משתי שמות הרביעי | |
| הנה נניח קו מדבר והוא א' ויהיה קו ב"ג משותף לקו א' באורך וקו א' מדבר הנה קו ב"ג מדבר ויהיו שני מספרים מרובעים והם ד"ז ז"ה | |
| והיותר גדול שבשני קוי ב"ג ג"ח אשר הוא ב"ג משותף באורך לקו המדבר אשר הוא א' אם כן קו ב"ח הוא אשר משתי שמות הרביעי | |
| וזה מש"ל | |
Proposition 49 |
|
| מט נרצה שנמצא קו אשר משתי שמות החמישי | |
| הנה נניח קו מדבר והוא א' ויהיה קו ג"ח משותף לקו א' באורך וקו א' מדבר אם כן קו ג"ח מדבר ויהיו שני מספרים מרובעים והם ד"ז ז"ה ולא יהיו שניהם יחד אשר הוא ד"ה מרובע | |
| ונבאר כמו שביארנו במה שקדם כי קו ב"ג בלתי משותף לקו ט' באורך וכי ב"ג יוסיף על ג"ח בכח כמו מרובע ההוה מקו ט' אשר לא ישתתף עמו באורך והיותר קטן מב' קוי ב"ג ג"ח אשר הוא ג"ח משותף לקו המדבר אשר הוא א' באורך | |
| וזמש"ל | |
Proposition 50 |
|
| נ נרצה שנמצא קו משתי שמות הששי | |
| הנה נניח קו מדבר והוא א' ויהיו שלשה מספרים אין יחס אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע והם ב"ג ג"ד ה' ולא יהיו גם כן יחס ב"ג אל ג"ד כיחס מספר מרובע אל מספר מרובע ויהיה יחס המרובע ההוה מא' אל המרובע ההוה מז"ח כיחס ה' אל ב"ג | |
| יתבאר לנו כי שני קוי ז"ח ח"ט בכח מדברים ושהם בו לבד משותפים ושאינו משותף אחד משניהם באורך לקו א' המדבר ושהיותר גדול הוא ז"ח יוסיף על הקצר והוא ח"ט כמו מרובע יהיה מקו לא ישתתף עמו באורך | |
| אם כן ז"ח ז"ט הוא אשר משתי שמות הששי | |
| וזה מה שרצינו לבאר | |
Proposition 51 |
|
| נא כאשר הקיף בשטח קו מדבר וקו משתי שמות הראשון הנה הקו אשר יחזיק על השטח ההוא בלתי מדבר והוא אשר יקרא אשר משתי שמות | |
| ויהיה שטח עליו ב"ג יקיף בו קו מדבר והוא א"ב וקו משתי שמות הראשון והוא קו א"ג | |
| הנה אומר כי קו ע"ס הוא אשר משתי שמות הנה מפני כי קו א"ז משותף לקו ז"ד באורך יהיה קו א"ד משותף לכל אחד מב' קוי א"ז ז"ד באורך וקו א"ד מדבר ומשותף לקו א"ב באורך אם כן כל אחד משני קוי א"ז ז"ד מדבר משותף באורך לקו א"ב | |
| אם כן קו ע"פ בלתי משותף לקו פ"ס באורך הנה שניהם בכח לבד משותפים והם בו מדברים אם כן קו ע"ס הוא אשר מב' שמות והוא יחזיק על שטח ב"ג | |
| אם כן הקו אשר יחזיק על שטח ב"ג בלתי מדבר והוא אשר משתי שמות | |
| וזה מה שרצינו לבאר | |
Proposition 52 |
|
| נב כאשר הקיף בשטח קו מדבר וקו משתי שמות השני הנה הקו אשר יחזיק על השטח ההוא בלתי מדבר והוא אשר יקרא אשר משני הממוצעים הראשון | |
| ויהיה שטח עליו א"ל ויקיפו בו קו מדבר והוא א"ב וקו משתי שמות השני והוא א"ג | |
| הנה מפני כי השטח הנצב אשר יקיפו בו שני קוי א"ז ז"ד כמו המרובע ההוה מד"ה יהיה קו ד"ה מתיחס לב' קוי א"ז ז"ד במה שבין שניהם ושטח נ"ע גם כן מתיחס לשני מרובעי מ"נ נ"ס הנה שטח ד"כ אם כן שוה לשטח נ"ע אבל שטח ד"כ שוה לשטח כ"ג ושטח נ"ע שוה לשטח נ"ק אם כן שטח כ"ג שוה לשטח נ"ק אם כן שטח כ"ג שוה לכל שטח ע"ק ושטח ע"ק מרובע אם כן קו ע"ס יחזיק על שטח ב"ג | |
| אם כן ע"ס הוא אשר משתי ממוצעים הראשון והוא יחזיק על שטח ב"ג | |
| אם כן הקו אשר יחזיק על ב"ג בלתי מדבר והוא אשר משני ממוצעים הראשון | |
| וזהו מה שרצינו לבאר | |
Proposition 53 |
|
| נג כאשר הקיף בשטח קו מדבר וקו משתי שמות השלישי הנה הקו אשר יחזיק על השטח הוא בלתי מדבר והוא אשר יקרא אשר משני ממוצעים השני | |
| ויהיה השטח עליו ב"ג ויקיף בו קו מדבר והוא א"ב וקו משתי שמות השלישי והוא א"ג | |
| הנה אומר כי קו ע"ס הוא אשר משני ממוצעים השני הנה מפני כי קו א"ז משותף לקו ז"ד באורך יהיה קו א"ד משותף לכל אחד מב' קוי א"ז ז"ד באורך וקו א"ד בכח מדבר ובלתי משותף לקו א"ב באורך | |
| אם כן כל אחד מב' קוי א"ז ז"ד מדבר בכח ובלתי משותף לקו א"ב באורך | |
| אם כן כל אחד משני שטחי א"ח ח"ד ממוצע והם משותפים | |
| אם כן קו ע"ס אמנם הוא אשר משתי שמות ממוצעים השני והוא יחזיק על שטח ב"ג | |
| אם כן הקו אשר יחזיק על שטח ב"ג הוא אשר משני ממוצעים השני | |
| והוא מש"ל | |
Proposition 54 |
|
| נד כאשר הקיף בשטח קו מדבר וקו משתי שמות הרביעי הנה הקו אשר יחזיק על השטח ההוא בלתי מדבר והוא אשר יקרא היותר גדול | |
| ויהיה עליו שטח ב"ג יקיף בו קו מדבר והוא א"ב וקו משתי שמות הרביעי והוא א"ג ויתחלק א"ג בשתי שמות ויהיה השם היותר גדול א"ד | |
| ואומר שהוא היותר גדול | |
| ומפני כי קו א"ז בלתי משותף לקו ז"ד באורך יהיה שטח א"ח בלתי משותף לשטח ח"ד | |
| אם כן שני מרובעי מ"נ נ"ס אשר הם כמו [שני] שטח[י] א"ח ח"ד בלתי משותפים | |
| וכבר בארנו כי שני קוי ע"פ פ"ס בלתי משותפים בכח ושטחי שניהם כאשר יקובצו מדבר | |
| אם כן קו ע"ס הוא היותר גדול | |
| וזהו מה שרצינו לבאר | |
Proposition 55 |
|
| נה כאשר הקיף בשטח קו מדבר וקו משתי שמות החמישי הנה הקו אשר יגבר על השטח ההוא בלתי מדבר והוא אשר יקרא אשר יגבר על מדבר וממוצע | |
| ויהיה שטח עליו ב"ג יקיפו בו קו מדבר והוא א"ב | |
| ומפני כי קו א"ד בלתי משותף לקו א"ב באורך ושניהם בכח מדברים יהיה שטח א"ט ממוצע והוא כמו שני מרובעי ע"פ פ"ס כאשר יקובצו | |
| אם כן קו ע"ס הוא אשר יגבר על מדבר וממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 56 |
|
| נו כאשר הקיף בשטח קו מדבר וקו משתי שמות הששי הנה הקו אשר יגבר על השטח ההוא בלתי מדבר ויקרא אשר יגבר על שני ממוצעים | |
| ויהיה שטח עליו ב"ג יקיף בו קו מדבר והוא א"ב | |
| אם כן קו ע"ס הוא אשר יגבר על שטח ב"ג והקו אשר יגבר על שטח ב"ג הוא אשר יגבר על שני הממוצעים | |
| וזה מה שרצינו לבאר | |
Proposition 57 |
|
| נז כאשר חובר שטח שוה למרובע ההוה מקו משתי שמות אל קו מדבר הנה הרוחב אשר יתחדש הוא משתי שמות הראשון | |
| ויהיה קו משתי שמות והוא א"ב ויחלק בשתי שמות על נקודת ג' ויהיה השם היותר גדול ב"ג | |
| וזה כי אנחנו כאשר הבדלנו מן ה"ז שטח שוה לשני המרובעים ההוים משני קוי א"ג ג"ב והוא ה"כ ונשאר שטח ל"ז שוה לכפל השטח אשר יקיפו בו שני קוי א"ג ג"ב ויתחלק קו כ"ז בשני חציים על נקודת מ' ונוציא מנקודת מ' קו נכחי לכל אחד משני קוי ד"ה ז"ס והוא קו מ"נ | |
| חלק אותו על נקודת ח' בשני חלקים ד"ח ח"כ אשר הם משותפים יהיה קו ד"ב יותר גדול מקו כ"ז בכח כמו מרובע יהיה מקו ישתתף עמו באורך וקו ד"כ משותף באורך לקו ד"ה המדבר המונח | |
| אם כן קו ד"ז הוא אשר משתי שמות הראשון | |
| ונשלם ביאורו | |
Proposition 58 |
|
| נח כאשר חובר שטח שוה למרובע ההוה מקו משני הממוצעים הראשון אל קו מדבר הנה הרוחב אשר יתחדש הוא משתי שמות השני | |
| [ויהיה קו משני הממוצעים הראשון והוא א"ב ויחלק בשני אמצעיים על נקודת ג'] ויהיה קו ד"ה מדבר | |
| הנה אומר כי קו ז"ד הוא משתי שמות השני וזה כי אנחנו כאשר הבדלנו מן ה"ז שטח שוה לשני המרובעים ההוים משני קוי א"ג ג"ב ושמנו אותם ה"כ נשאר שטח ל"ז שוה לכפל השטח אשר יקיפו בו שני קוי א"ג ג"ב ויתחלק קו כ"ז בשני חציים על נקודת מ' ונוציא מנקודת מ' קו נכחי לכל אחד משני קוי ד"ה ז"ס והוא קו מ"נ | |
| ומפני שהוא כאשר חובר אל קו ד"ב שטח שוה לרביע המרובע ההוה מן כ"ז יחסר משלימותו שטח מרובע חלק השטח ההוא קו ד"ב על נקודת שני חלקים משותפים יהיה קו ד"ב נוסף על כ"ז בכח כמו מרובע יהיה מקו ישתתף עמו באורך וקו כ"ז משותף לקו ד"ה המדבר המונח | |
| אם כן קו ד"ז הוא משתי שמות השני | |
| וזה מה שרצינו לבאר | |
Proposition 59 |
|
| נט כאשר חובר שטח שוה למרובע ההווה מקו משני הממוצעים השני [אל קו מדבר הנה] הרוחב אשר יתחדש הוא משתי [השמות] השלישי | |
| ויהיה קו משני ממוצעים השני והוא א"ב ויתחלק בשני ממוצעים על נקודת ג' | |
| ונוציא קו מ"נ נכחי לכל אחד משני שטחי ד"ה ז"ס | |
| הנה השטח אשר יקיפו בו שני קוי א"ג ג"ב שוה לכל אחד משני שטחי כ"נ נ"ז | |
| וגם כן הנה אנחנו כאשר שמנו שטח ה"ח שוה למרובע ההווה מן ב"ג ישאר שטח כ"ט שוה למרובע ההוה מן ג"א | |
| ומפני שהוא כאשר חובר אל קו ד"ב שטח שוה לרביע המרובע ההוה מן קו כ"ז יחסר משלמותו שטח מרובע וחלק השטח ההוא קו ד"ב על נקודת ח' בשני חלקים משתתפים יהיה קו ד"ב נוסף על קו כ"ז בכח כמו מרובע יהיה מקו ישתתף עמו באורך | |
| ואין אחד משני קוי כ"ד כ"ז משותף לקו ד"ה באורך | |
| אם כן קו ד"ז הוא אשר משתי שמות השלישי | |
| וזה מה שרצינו לבאר | |
Proposition 60 |
|
| ס כאשר חובר שטח שוה למרובע ההוה מן הקו היותר גדול אל קו מדבר הנה הרוחב אשר יתחדש הוא משתי שמות הרביעי | |
| ויהיה הקו היותר גדול א"ב ויחלק בשני חלקיו על נקודת ג' ויהיה א"ג יותר גדול מן ג"ב | |
| אם כן קו ד"ב יוסיף על קו כ"ז בכח כמו מרובע יהיה מקו לא ישתתף עמו באורך ושני קוי ד"כ כ"ז בכח מדברים ובו לבד משותפים וקו ד"כ משותף לקו ד"ה המדבר | |
| אם כן קו ד"ז הוא אשר משתי שמות הרביעי | |
| וזה מה שרצינו לבאר | |
Proposition 61 |
|
| סא כאשר חובר שטח שוה למרובע ההווה מן הקו אשר יגבר על מדבר וממוצע אל קו מדבר הנה הרוחב אשר יתחדש הוא משתי שמות
החמישי | |
| ויהיה הקו אשר יגבר על מדבר וממוצע א"ב ויחלק בשני חלקיו על נקודת ג' | |
| אם כן שני קוי ד"כ כ"ז בכח מדברים ובו לבד משותפים וקו כ"ז משותף באורך לקו ד"ה המדבר | |
| אם כן קו ד"ז הוא אשר משתי שמות החמישי | |
| וזה מה שרצינו לבאר | |
Proposition 62 |
|
| סב כאשר חובר שטח שוה למרובע ההווה מן הקו אשר יגבר על שני ממוצעים אל קו מדבר הנה הרוחב אשר יתחדש הוא משתי שמות הששי | |
| ויהיה הקו אשר יגבר על שני ממוצעים א"ב ויחלק בשני חלקיו על נקודת ג' ויהיה א"ג יותר גדול מן ג"ב ויהיה קו ד"ה מדבר | |
| וזה כי אנחנו נבאר כמו שביארנו במה שקדם כי השטח אשר יקיפו בו שני קוי ד"ח ח"כ שוה למרובע ההווה מן קו כ"מ ושקו ד"ח בלתי משותף לקו ח"כ באורך | |
| ויהיה קו ד"כ נוסף על קו כ"ז בכח כמו מרובע יהיה מקו לא ישתתף עמו באורך ואין אחד משני קוי ד"כ כ"ז משותף באורך לקו ד"ה המדבר | |
| אם כן קו ד"ז הוא אשר משתי שמות הששי | |
| וזה מה שרצינו לבאר | |
Proposition 63 |
|
| סג הקו אשר ישתתף באורך לקו משתי שמות הנה הוא גם כן משתי שמות ומדרגתו כמדרגתו | |
| ויהיה הקו אשר משתי שמות א"ב ויחלק בשתי שמות על נקודת ג' ויהיה קו ד"ה משותף באורך לקו א"ב | |
| ואם לא יהיה אחד משני קוי א"ג ג"ב משותף לקו המדבר הנה הוא לא היה אחד משני קוי ד"ז ז"ה משותף לקו המדבר | |
| אם כן קו ד"ה הוא משתי שמות ומדרגתו כמדרגת קו א"ב | |
| וזה מה שרצינו | |
Proposition 64 |
|
| סד הקו אשר ישתתף קו משני ממוצעים באורך הוא גם כן משני ממוצעים ומדרגתו כמדרגתו | |
| ויהיה הקו אשר משני ממוצעים א"ב ויחלק בשני ממוצעים על נקודת ג' ויהיה קו ד"ה משותף לקו א"ב באורך | |
| הנה אומר כי קו ד"ה הוא משני אמצעיים ומדרגתו כמדרגת קו א"ב | |
| ואם היה שטח אשר יקיפו בו שני קוי א"ג ג"ב מדבר הנה השטח אשר יקיפו בו שני קוי ד"ז ז"ה גם כן מדבר | |
| ואם היה שטח אשר יקיפו בו שני קוי א"ג ג"ב ממוצע הנה השטח אשר יקיפו בו שני קוי ד"ז ז"ה גם כן ממוצע | |
| אם כן קו ד"ז הוא אשר משני ממוצעים ומדרגתו כמדרגת קו א"ב | |
| וזה מה שרצינו לבאר | |
Proposition 65 |
|
| סה הקו אשר ישתתף הקו היותר גדול באורך הוא גם כן קו יותר גדול | |
| ויהיה היותר גדול א"ב ויחלק בשני חלקיו על נקודת ג' הנה שני קוי א"ג ג"ב הם בכח בלתי משותפים ושני מרובעיהם כאשר יקובצו מדבר והשטח אשר יקיפו ממוצע | |
| אם כן כל קו ד"ה בלתי מדבר והוא אשר יקרא היותר גדול | |
| ונשלם ביאורו | |
Proposition 66 |
|
| סו הקו אשר ישתתף הקו אשר יגבר על מדבר וממוצע הוא גם כן יגבר על מדבר וממוצע | |
| ויהיה הקו אשר יגבר על מדבר וממוצע א"ב ויחלק בשני חלקיו על נקודת ג' הנה שני קוי א"ג ג"ב שניהם בכח בלתי משותפים ושני מרובעיהם כאשר יקובצו ממוצע | |
| ונבאר כי כל אחד משני קוי א"ג ג"ב משותף לגילו משני קוי ד"ז ז"ה ושיחס המרובע ההוה מן א"ב אל המרובע ההוה מן ד"ה כיחס שני המרובעים ההווים משני קוי א"ג ג"ב אל שני המרובעים ההווים מן ד"ז ז"ה | |
| והמרובע ההווה מן א"ב משותף למרובע ההווה מן ד"ה | |
| אם כן שני המרובעים ההווים מן א"ג ג"ב משותפים לשני המרובעים ההווים מן ד"ז ז"ה | |
| אם כן השטח אשר יקיפו בו ד"ז ז"ה מדבר | |
| אם כן כל ד"ה בלתי מדבר והוא אשר יגבר על מדבר וממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 67 |
|
| סז הקו אשר ישתתף באורך הקו אשר יגבר על שני ממוצעים הוא גם כן יגבר על שני ממוצעים | |
| ויהיה הקו אשר יגבר על שני ממוצעים א"ב ויחלק הקו אשר יגבר בשני חלקיו על נקודה ג' | |
| אם כן שני קוי ד"ז ז"ה בלתי משותפים בכח ושני המרובעים ההווים משניהם כאשר יקובצו ממוצע והשטח אשר יקיפו בו גם כן ממוצע ושני המרובעים ההווים משניהם בלתי משותפים לשטח אשר יקיפו בו | |
| אם כן קו ד"ז הוא אשר יגבר על שני ממוצעים | |
| ונשלם ביאורו | |
Proposition 68 |
|
| סח כאשריקובצו שני שטחים אחד משניהם מדבר והאחר ממוצע הנה הקו אשר יגבר על שניהם הוא אחד מארבעה קוים בלתי מדברים אם שיהיה משתי שמות ואם אשר משני ממוצעים הראשון ואם היותר גדול ואם אשר יגבר על מדבר וממוצע | |
| הנה אומר כי שני שטחי אבג"ד כאשר יקובצו יהיה הקו אשר יגבר על שניהם אחד מהארבעה קוים אשר זכרנו | |
| ויהיה קו ז"ה מדבר ונחבר אליו שטח שוה לשטח א"ב והוא ה"ח ונחבר אל ט"ח שטח שוה לשטח ג"ד והוא ח"כ הנה מפני כי שטח א"ב מדבר יהיה ה"ח מדבר | |
| הנה כאשר יקובצו שני שטחים אחד משניהם מדבר והאחר ממוצע הנה הקו אשר יגבר על כל שניהם כאשר יקובצו הוא אחד מארבעה קוים בלתי מדברים אם שיהיה אשר משתי שמות ואם שיהיה אשר משני ממוצעים הראשון ואם שיהיה יותר גדול ואם שיהיה אשר יגבר על מדבר וממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 69 |
|
| סט כאשר יקובצו שני שטחים ממוצעים בלתי משותפים הנה הקו אשר יגבר על שניהם אחד משני קוים בלתי מדברים אם שיהיה אשר משני ממוצעים השני ואם שיהיה אשר יגבר על שני ממוצעים | |
| אם כן הקו אשר יגבר על שטח אבג"ד אם שיהיה אשר משני ממוצעים השני ואם שיהיה אשר יגבר על שני ממוצעים | |
| וזה מה שרצינו לבאר | |
Definitions |
הקדמה |
| הקו אשר משתי שמות ומה שאחריו מסוגי הקוים אשר אינם מדברים אין מהם קו ממוצע ואין בהם דבר מסוג הנשארים | |
| וזה כי המרובע ההווה מן הקו הממוצע כאשר חובר אל קו מדבר יחדש רוחב מדבר בכח | |
| והרחבים אשר זכרנו הם מתחלפים אין מהם דבר מסוג חבירו | |
| והקוים אשר מרובעיהם יחדשו הרחבים ההם המתחלפים אין מהם דבר מסוג חבירו | |
Proposition 70 |
|
| When a segment measurable in a square is subtracted from a straight line and the two lines are commensurable in square only, then the remaining straight line is unmeasurable; let it be called an apotome. | ע כאשר הובדל מקו ישר מדבר בכח והיו השני קוים בכח לבד משותפים הנה הקו הנשאר בלתי מדבר ויקרא הנבדל |
| ויהיה קו מדבר בכח והוא א"ג ונבדיל ממנו קו מדבר בכח והוא ב"ג ויהיה בכח לבד משותף לכל קו א"ג | |
| וישאר המרובע ההווה מן א"ב בלתי משותף לשני המרובע ההווים משני קוי א"ג ג"ב ושני המרובעים ההווים משני קוי א"ג ג"ב מדברים אם כן המרובע ההוה מקו א"ב בלתי מדבר ויקרא הנבדל | |
| וזה מה שרצינו לבאר | |
Proposition 71 |
|
| עא כאשר הובדל מממוצע ממוצע והיו בכח לבד משותפים והיה השטח אשר יקיפו בו מדבר הנה הקו הנשאר בלתי מדבר ויקרא נבדל הממוצע הראשון | |
| ויהיה קו ממוצע והוא א"ג | |
| וישאר המרובע ההווה מן א"ב בלתי משותף לכפל השטח אשר יקיפו בו שני קוי א"ג ג"ב אם כן המרובע ההווה מן א"ב בלתי מדבר הנה קו א"ב אם כן בלתי מדבר ויקרא נבדל הממוצע הראשון | |
| וזה מה שרצינו לבאר | |
Proposition 72 |
|
| עב כאשר נבדל מממוצע ממוצע והיו בכח לבד משותפים והיה השטח אשר יקיפו בו ממוצע הנה הקו הנשאר בלתי מדבר ויקרא נבדל הממוצע השני | |
| ויהיה קו ממוצע והוא א"ג ויובדל ממנו קו ממוצע והוא ג"ב | |
| ויחס א"ג אל ג"ב כיחס המרובע ההווה מן א"ג אל השטח אשר יקיפו בו שני קוי א"ג ג"ב | |
| ואולם המרובע ההווה מן א"ג הנה הוא משותף לשני המרובעים ההווים מן א"ג ג"ב | |
| והקו אשר יגבר על ד"ז הוא א"ב אם כן קו א"ב בלתי מדבר ויקרא נבדל הממוצע השני | |
| וזה מה שרצינו לבאר | |
Proposition 73 |
|
| עג כאשר נבדל מקו ישר קו ישר והיו בכח בלתי משותפים והיו שני המרובעים ההווים משניהם כאשר יקובצו מדבר והיה השטח אשר יקיפו בו ממוצע הנה הקו הנשאר בלתי מדבר ויקרא היותר קטן | |
| הנה קו א"ג אם כן בלתי מדבר ויקרא היותר קטן | |
| וזה מה שרצינו לבאר | |
Proposition 74 |
|
| עד כאשר נבדל מקו ישר קו ישר והיו בכח בלתי משותפים והיו שני המרובעים ההווים משניהם כאשר יקובצו ממוצא והיה השטח אשר יקיפו בו מדבר הנה הקו הנשאר בלתי מדבר ויקרא אשר עם המדבר יהיה הכל ממוצע | |
| ויהיה קו מה ישר והוא א"ב ונבדיל ממנו קו ב"ג ויהיו שני קוי א"ב ב"ג בכח בלתי משותפים ויהיו שני המרובעים ההווים משניהם כאשר יקובצו ממוצע | |
| אם כן המרובע ההווה מן א"ג בלתי מדבר | |
| אם כן קו א"ג בלתי מדבר ויקרא אשר עם המדבר יהיה הכל ממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 75 |
|
| עה כאשר נבדל מקו ישר קו ישר והיו בכח בלתי משותפים והיו שני המרובעים ההווים משניהם כאשר יקובצו ממוצע והיה השטח אשר יקיפו בו גם כן ממוצע והיו שני המרובעים ההווים משניהם כאשר יקובצו בלתי משותפים לשטח אשר יקיפו בו גם כן הנה הנשאר בלתי מדבר | |
| והקו אשר יגבר על ד"ז הוא א"ג אם כן קו א"ג בלתי מדבר ויקרא אשר עם הממוצע יקרא הכל ממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 76 |
|
| עו אמנם ידבק בקו הנבדל קו אחד לבד מדבר בכח | |
| ויהיה קו א"ב נבדל וידבק בו קו על הדרך שספרנו והוא ב"ג הנה אומר שהוא לא ידבק בקו א"ב קו אחד מדבר בכח ישתתף הכל בכח | |
| וכאשר המירונו יהיה יתרון מה שבין שני מרובעי שני קוי א"ג ג"ב ובין שני מרובעי שני קוי א"ד ד"ב שוה ליתרון מה שבין כפל השטח אשר יקיפו בו שני קוי א"ג ג"ב ובין כפל השטח אשר יקיפו בו שני קוי א"ד ד"ב ויתרון מה שבין שני מרובעי שני קוי א"ג ג"ב ובין שני מרובעי שני קוי א"ד ד"ב מדבר | |
| מפני כי שניהם ממוצעים ולא יוסיף ממוצע על ממוצע מדבר אם כן הקו הנבדל אמנם ידבק בו קו אחד לבד מדבר בכח לבד | |
| וזה מה שרצינו לבאר | |
Proposition 77 |
|
| עז אמנם ידבק בנבדל הממוצע הראשון קו אחד לבד ממוצע ישתתף הכל בכח לבד ויקיף עם הכל במדבר | |
| ויהיה הקו א"ב נבדל הממוצע הראשון וידבק בו קו על הדרך שספרנו והוא ב"ג | |
| הנה אומר שהוא לא ידבק בו קו אחר ממוצע ישתתף הכל בכח לבד | |
| אם כן נבדל הממוצע הראשון אמנם ידבק בו קו אחד לבד ויקיף עמו במדבר | |
| וזה מה שרצינו לבאר | |
Proposition 78 |
|
| עח אמנם ידבק בנבדל הממוצע השני קו אחד לבד ממוצע ישתתף הכל בכח לבד ויקיף עם הכל בממוצע | |
| ויהיה קו א"ב נבדל הממוצע השני וידבק בו קו על הדרך שספרנו והוא ב"ג | |
| אם כן שני מרובעי שני קוי א"ג ג"ב כאשר יקובצו בלתי משותפים לכפל השטח אשר יקיפו בו שני קוי א"ג ג"ב אבל שני המרובעים ההווים משני קוי א"ג ג"ב הוא כמו שטח ז"כ וכפל השטח אשר יקיפו בו
שני קוי א"ג ג"ב הוא כמו שטח כ"ט | |
| הנה אמנם ידבק בנבדל הממוצע ישתתף הכל בכח לבד ויקיפו עם הכל בממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 79 |
|
| עט אמנם ידבק בקו היותר קטן קו אחד לא ישתתף הכל בכח ויהיה מרובעו עם מרובע הכל מדבר ויהיה השטח אשר יקיפו
בו ממוצע ויהיה הקו היותר קטן א"ב וידבק בו קו ב"ג ויהיו שני קוי א"ג ב"ג בלתי משותפים בכח | |
| אם כן הקו היותר קטן אמנם ידבק בו קו אחד לבד לא ישתתף הכל בכח ויהיה מרובעו עם מרובע הכל מדבר ויהיה השטח אשר יקיפו בו ממוצע | |
| וזה מה שרצינו לבאר | |
Proposition 80 |
|
| פ אמנם ידבק באשר עם המדבר ויהיה הכל ממוצע קו אחד לא ישתתף הכל בכח ויהיה מרובע עם מרובע הכל ממוצע | |
| ויהיה השטח אשר יקיפו בו מדבר ויהיה קו אשר עם המדבר יהיה הכל ממוצע והוא א"ב וידבק בו קו ב"ג | |
| אם כן שני קוי א"ד ד"ב כאשר יקובצו ממוצע והשטח אשר יקיפו בו שני קוי א"ד ד"ב מדבר הנה יתרון מה שבין שני מרובעי שני קוי א"ד ד"ב ושני מרובעי שני קוי א"ג ג"ב שוה ליתרון מה שבין כפל השטח אשר יקיפו בו שני קוי א"ד ד"ב וכפל השטח אשר יקיפו בו שני קוי א"ג ג"ב ויתרון מה שבין כפל השטח אשר יקיפו בו שני קוי א"ד ד"ב וכפל השטח אשר יקיפו בו שני קוי א"ג ג"ב מדבר | |
| הנה יתרון מה שבין שני מרובעי שני קוי א"ד ד"ב ושני מרובעי שני קוי א"ג ג"ב מדבר וזה בלתי איפשר | |
| מפני כי שני מרובעי שני קוי א"ד ד"ב כאשר יקובצו ממוצע וכן שני מרובעי שני קוי א"ג ג"ב אם כן הקו אשר עם המדבר ישוב הכל ממוצע לא ידבק בו כי אם קו אחד לא ישתתף הכל בכח ויהיה מרובעו עם מרובע הכל ממוצע ויהיה השטח אשר יקיף בו מדבר | |
| וזה מה שרצינו לבאר | |
Proposition 81 |
|
| פא אמנם ידבק בקו אשר עם הממוצע יהיה הכל ממוצע קו אחד לא ישתתף הכל בכח ויהיה מרובעו עם מרובע הכל ממוצע ויהיה השטח אשר יקיפו בו לבד גם כן ממוצע ויהיו שני מרובעיהם כאשר יקובצו בלתי משותפים לשטח אשר יקיפו בו ויהיה קו עם הממוצע ישים הכל ממוצע והוא א"ב | |
| אם כן הקו אשר עם הממוצע ישיב הכל ממוצע אמנם ידבק בו קו אחד לבד לא ישתתף עמו הכל בכח | |
| ויהיה מרובעו עם מרובע הכל ממוצע ויהיה השטח אשר יקיפו גם כן ממוצע | |
| ויהיו שני מרובעי שניהם כאשר יקובצו בלתי משותף לשטח אשר יקיפו | |
| וזה מה שרצינו לבאר | |
Definitions |
הקדמה |
| כאשר הונח קו נבדל וקו מדבר ונדבק בקו הנבדל הקו אשר ממנו נבדל והיה הכל יוסיף בכח על אשר התחבר כמו מרובע יהיה מקו ישתתף עמו באורך והיה כל הקו משותף באורך לקו המדבר המונח הנה יקרא הקו ההוא נבדל הראשון | |
| ואם היה אשר ישתתף עם הקו המדבר המונח הוא הקו אשר חובר אליה הנה יקרא הקו הנבדל אשר זכרנו הנבדל השני | |
| ואם לא יהיה אחד [91]משניהם משותף לקו המדבר המונח הנה יקרא הנבדל השלישי | |
| וגם כן הנה הקו הנבדל עם אשר התחבר בו אם היו כל שניהם יוסיפו בכח על הקו המונח כמו מרובע יהיה מקו לא ישתתף עמו באורך והיה הכל משותף לקו המדבר הנה יקרא הקו ההוא הנב[ד]ל הרביעי | |
| ואם היה אשר ישתת | |
| ואם לא יהיה אחד משניהם משותף לקו המדבר הנה יקרא הקו ההוא הנבדל השישי | |
| וזה מה שרצינו לבאר | |
Proposition 82 |
|
| 82) We wish to find the first apotome. | פב נרצה שנמצא הנבדל הראשון |
| We set out a rational line, which is A. | הנה נניח קו מדבר והוא א' |
| We draw line BC commensurable in length with line A | ונשים קו ב"ח משותף לקו א' באורך |
| Then line BC is rational. | ויהיה קו ב"ח אם כן מדבר |
| Let DH and HZ be two square numbers, such that the difference between them, which is ZD, is not a square number. | ויהיו שני מספרים מרובעים והם ד"ה ה"ז ולא יהיה יתרון מה שבין שניהם אשר הוא ז"ד מספר מרובע |
| הנה אין יחס ה"ז אל ד"ז כיחס מספר מרובע אל מספר מרובע | |
| ונשים יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ג"ח כיחס ז"ה אל ד"ז | |
| אם כן המרובע ההוה מן ח"ב משותף למרובע ההוה מן ג"ח | |
| והמרובע ההוה מן ב"ח מדבר | |
| אם כן המרובע ההוה מן ח"ג מדבר | |
| ומפני כי יחס ה"ז אל ד"ז אינו כיחס מספר מרובע אל מספר מרובע לא יהיה יחס המרובע ההווה מן ב"ח אל המרובע ההווה מן ח"ג כיחס מספר מרובע אל מספר מרובע הנה קו ב"ח בלתי משותף לקו ח"ג באורך מז' מזה | |
| אם כן שני קוי ב"ח ח"ג בכח לבד מדברים והם בו לבד משותפים | |
| אם כן קו ב"ג הוא הנבדל מע' מזה | |
| ואומר כי הוא הנבדל הראשון | |
| וזה כי המרובע ההוה מקו ב"ח יותר גדול מן המרובע ההוה מן ג"ח | |
| ותהיה תוספתו עליו כמו המרובע ההוה מקו ט | |
| וכבר היה יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ג"ח כיחס ה"ז אל ד"ז | |
| וכאשר הפכנו יהיה יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ט כיחס ה"ז אל ה"ד וזה התהפכות היחס בפתיחת ה' | |
| ויחס ה"ז אל ה"ד כיחס מספר מרובע אל מספר מרובע | |
| מפני כי שניהם שני מרובעים | |
| אם כן יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ט כיחס מספר מרובע אל מספר מרובע | |
| אם כן קו ב"ח משותף באורך לקו ט' מז' מזה | |
| הנה קו ב"ח יוסיף על קו ג"ח בכח כמו מרובע יהיה מקו ישתתף עמו באורך מז' מזה | |
| וכל קו ב"ח משותף לקו המדבר המונח באורך והוא א' | |
| Therefore line BG is the first apotome. | אם כן קו ב"ג הוא הנבדל הראשון מההקדמה השלישית |
| וזה מה שרצינו | |
Proposition 83 |
|
| פג נרצה שנמצא הנבדל השני | |
| ונניח קו מדבר והוא א' | |
| ונשים קו ג"ח משותף אליו | |
| ויהיה קו ג"ח | |
| ויהיו שני מספרים מרובעים והם ד"ה ה"ז ולא יהיה יתרון מה שבין שניהם אשר הוא ד"ז מספר מרובע | |
| ויהיה יחס המרובע ההוה מן ג"ח אל המרובע ההוה מן ח"ב כיחס ד"ז אל ד"ה | |
| אם כן המרובע ההוה מן ג"ח משותף למרובע ההוה מן ב"ח מו' מזה | |
| והמרובע ההוה מן ג"ח מדבר | |
| אם כן המרובע ההוה מן | |
| ומפני כי יחס המרובע [92]ההוה מן ג"ח אל המרובע ההוה מן ב"ח אינו כיחס מספר מרובע אל מספר מרובע יהיה קו ג"ח בלתי משותף לקו ב"ח באורך | |
| אם כן שני קוי ג"ח ח"ב בכח מדברים והם בו לבד משותפים | |
| אם כן קו ב"ג הוא הנבדל מע' מזה | |
| ואומר כי הוא שני מן הנבדלים | |
| וזה כי המרובע ההוה מן ב"ח יותר גדול מן המרובע ההוה מן ג"ח | |
| ותהיה תוספתו עליו כמו המרובע ההוה מן ט' | |
| והנה מפני כי יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ג"ח כיחס ד"ה אל ד"ז יהיה כאשר הפכנו יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ט' כיחס ד"ה אל ה"ז התהפכות היחס | |
| וכל אחד מן ד"ה ה"ז מספר מרובע | |
| אם כן יחס המרובע ההוה מן ב"ח אל המרובע ההוה מן ט' כיחס מספר מרובע אל מספר מרובע | |
| אם כן קו ב"ח משותף לקו ט' באורך מז' מזה | |
| אם כן קו ב"ח יוסיף על ג"ח בכח כמו מרובע יהיה מקו ישתתף עמו באורך | |
| וקו ג"ח אשר הובדל מקו ב"ח משותף לקו מדבר | |
| אם כן קו | |
| וזהו מה שרצינו לבאר | |
Proposition 84 |
|
| פד נרצה שנמצא הנבדל השלישי | |
| ונניח קו מדבר והוא א' | |
| ויהיו שלשה מספרים עליהם ה' ב"ג ג"ד ולא יתהוה מהם דבר יחסו אל חברו כיחס מספר מרובע אל מספר מרובע | |
| ויהיה יחס שני מספרי ב"ג ב"ד כל אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע | |
| ויהיה יחס המרובע ההוה מן א' אל המרובע ההוה מן ז"ח כיחס ה' אל ב"ג | |
| ויהיה יחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ח"ט כיחס מספר ב"ג אל מספר ג"ד | |
| והמרובע ההוה מן א' מדבר | |
| אם כן המרובע ההוה מן ז"ח מדבר | |
| אם כן קו ז"ח מדבר בכח | |
| ויחס ה' אל ב"ג אינו כיחס מספר מרובע אל מספר מרובע | |
| הנה יחס המרובע ההווה מן א' אל המרובע ההווה מן ז"ח אינו כיחס מספר מרובע אל מספר מרובע מו' מזה | |
| אם כן קו א' בלתי משותף לקו ז"ח באורך | |
| וגם כן הנה יחס ב"ג אל ג"ד כיחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ח"ט מו' מזה | |
| והמרובע ההוה מן ז"ח | |
| והמרובע מז"ח מדבר הנה המרובע ההווה מן ח"ט מדבר | |
| ויחס ב"ג אל ג"ד אינו כיחס מספר מרובע אל מספר מרובע | |
| הנה אין יחס המרובע ההווה מן ז"ח אל המרובע ההווה מן ח"ט כיחס מספר מרובע אל מספר מרובע | |
| אם כן קו ז"ח בלתי משותף לקו ח"ט באורך מז' מזה | |
| אם כן שני קוי ז"ח ח"ט בכח מדברים והם בו לבד משותפים | |
| אם כן קו ז"ט נבדל מע' מזה | |
| ואומר כי הוא השלישי מן הנבדלים | |
| וזה כי יחס ה' אל ב"ג כיחס המרובע ההווה מן א' אל המרובע ההווה מן ז"ח | |
| ויחס ב"ג אל ג"ד כיחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ח"ט | |
| וכיחס השווי יהיה יחס ה' אל ב"ד כיחס המרובע ההוה מן א' אל המרובע ההוה מן ח"ט מכ"ב מה' | |
| ויחס ה' אל ג"ד אינו כיחס מספר מרובע אל מספר מרובע | |
| אם כן אין יחס המרובע ההוה מן א' אל המרובע ההוה [93]מן ח"ט כיחס מספר מרובע אל | |
| אם כן קו א' בלתי משותף לקו ח"ט באורך מז' מזה | |
| אם כן אין אחד משני קוי ז"ח ח"ט משותף לקו א' המדבר באורך | |
| והמרובע ההוה מן ז"ח יותר גדול מן המרובע ההוה מן ח"ט | |
| ותהיה תוספתו עליו כמו המרובע ההוה מן קו ב' | |
| אם כן יחס ב"ג אל ג"ד כיחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ח"ט | |
| וכאשר הפכנו היה יחס ב"ג אל ב"ד כיחס המרובע ההוה מן ז"ח אל המרובע ההוה מן ב' התהפכות היחס | |
| ויחס ב"ג אל ב"ד כיחס מספר מרובע אל מספר מרובע | |
| אם כן יחס המרובע ההוה מן ז"ח אל המרובע ההוה מב' כיחס מספר מרובע אל מספר מרובע | |
| אם כן קו ז"ח משותף לקו ז' ב באורך מז' מזה | |
| וקו ז"ח יוסיף על קו ח"ט בכח כמו המרובע ההווה מב' | |
| הנה קו ז"ח מוסיף על קו ט"ח בכח כמו מרובע יהיה מקו ישתתף עמו באורך | |
| ואין אחד משני קוי ז"ח ח"ט משותף לקו א' המדבר באורך | |
| אם כן קו ז"ט הוא הנבדל השלישי מההקדמה השלישית | |
| וזה מה שרצינו לבאר | |
Proposition 85 |
|
| פה נרצה שנמצא הנבדל הרביעי | |
| ונניח קו מדבר והוא א' ונשים קו ב"ח משותף אליו באורך ויהיה קו ב"ח גם כן מדבר ונניח שני מספרים עליהם ד"ה ז"ה ולא יהיה יחס אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע | |
| וכל קו ב"ח משותף לקו א' המדבר המונח באורך אם כן ב"ג הוא הנבדל הרביעי | |
| הנה כבר מצאנו הנבדל הרביעי | |
| וזה מה שרצינו לבאר | |
Proposition 86 |
|
| פו נרצה שנמצא הנבדל החמישי | |
| ונניח קו מדבר והוא א' ונשים קו ג"ח משותף לקו א' באורך ויהיה קו ג"ח מדבר ונניח שני מספרים עליהם ד"ה ה"ז כמו השני מספרים אשר זכרנו בתמונות אשר קודם זאת ונשים יחס המרובע ההווה מג"ח אל המרובע ההווה מכ"ח כיחס ה"ז אל ד"ה | |
| אם כן קו ב"ח יוסיף על קו ח"ג בב"ח כמו מרובע יהיה מקו לא ישתתף עמו באורך וקו ג"ח אשר הובדל מקו ב"ג ישתתף א' המדבר באורך | |
| אם כן קו ב"ג הוא הנבדל החמשי | |
| וזה מה שרצינו לבאר | |
Proposition 87 |
|
| פז נרצה שנמצא הנבדל הששי | |
| הנה נניח קו מדבר והוא א' ויהיו שלשה מספרים עליהם ה' ב"ג ג"ד ולא
יהיה יחס אחד משניהם אל האחר כיחס מספר מרובע אל מספר מרובע ולא יהיה גם כן יחס ב"ג אל ב"ד כיחס מספר מרובע אל מספר מרובע | |
| ואומר שהוא הששי מהנבדלים וזה כי יחס ה' אל ב"ג כיחס המרובע ההווה מא' אל המרובע ההווה מז"ח ויחס ב"ג אל ג"ד כיחס המרובע ההוה מז"ח אל המרובע ההווה מח"ט וביחס ההשואה יהיה יחס ה' אל ג"ד כיחס המרובע ההווה מא' אל המרובע ההווה מח"ט | |
| ואין אחד משני קוי ז"ח ח"ט משותף לקו א' המדבר המונח באורך | |
| אם כן קו ז"ט הוא הנבדל הששי | |
| וזה מה שרצינו לבאר | |
Proposition 88 |
|
| When a surface is enclosed by a rational line and a first apotome, then the line of that surface is irrational and it is so-called an apotome. | פח כאשר הקיף בשטח קו מדבר והנבדל הראשון הנה הקו אשר יגבר על השטח ההוא בלתי מדבר והוא אשר יקרא הנבדל |
|
ויהיה שטח עליו א"ח יקיף בו קו מדבר והוא א"ב והקו הנבדל הראשון והוא א"ז |
| ויהיה הקו אשר נבדל ממנו דבק בו והוא ז"ג | |
| הנה אומר כי הקו אשר יגבר על שטח א"ח בלתי מדבר הוא אשר יקרא הנבדל | |
| וזה כי הקו הנבדל והוא הנבדל הראשון א"ז והקו אשר נבדל ממנו הוא ז"ג אם כן קוי א"ג ג"ז בכח מדברים ובו לבד משותפים וקו א"ג יוסיף על קו ג"ז בכח כמו מרובע יהיה מקו ישתתף עמו באורך וקו א"ג משותף באורך לקו א"ב המדבר ואם חובר אל קו ג"א שטח שוה לרבע המרובע ההוה מן ז"ג יחסר משלמות הקו שטח מרובע הנה הוא יחלק קו א"ג בשני חלקים משותפים ויחלק ג"ז בשני חציים על נקודת ד' ונחבר אל קו א"ג שטח שוה למרובע ההוה מן ז"ד יחסר משלמותו שטח מרובע ויהיה השטח המחובר אל קו א"ג השטח אשר יקיפו בו שני קוי א"ה ה"ג אם כן קו א"ה משותף לקו ה"ג באורך ונוציא מנקודת דה"ג קוים נכחיים לשני קוי א"ב ז"ח והם ד"ט ה"כ ג"ל ועוד נוציא קו ב"ח אל ל' ויהיה שטח ע"ק מרובע שוה לשטח בה ויהיה נ"ס מרובע שוה לשטח ה"ל אם כן מרובע נ"ס הוא על קוטר מרובע ע"ק ונוציא הקוטר הזה והוא מ"ס ונשלים לקצ"ו לקוות התמונה ע"מ ק"ס הנה השטח אשר יקיפו בו שני קוי א"ה ה"ג שוה למרובע ההווה מן ג"ד הנה קו ג"ד מתיחס לשני קוי א"ה ה"ב במה שבין שניהם | |
| ולכן יהיה שטח ג"ט מתייחס לשני שטחי א"ב ב"ג במה שבין שניהם ושטח ע"ד מתייחס לשני שטחי ע"ק נ"ס במה שבין שניהם | |
| ושטח א"כ שוה לשטח מ"ס ושטח כ"ג שוה לשטח נ"ס אם כן שטח ג"ט שוה לשטח ע"ד אבל שטח ג"ט שוה לשטח ט"ז
| |
| אבל מ"ס נ"ס הם שני המרובעים ההוים משני קוי ע"ס ס"פ | |
| אם כן כל אחד משני קוי ע"ס ס"פ מדבר בכח ושניהם בו משותפים וקו ז"ד שוה לקו ד"ג וקו ז"ג מדבר בכח ובלתי משותף באורך לקו א"ב אם כן אל אחד משני קוי ז"ד ד"ג מדבר בכח בלתי משותף באורך לקו א"ב הנה כל אחד משני משטחי ז"ט ט"ג ממוצע ושטח ט"ג שוה לשטח | |
| אם כן שטח ע"ד ממוצע ושטח פ"ד מדבר | |
| אם כן שטח ע"ד בלתי משותף | |
| מא' מו' | |
| אם כן קו ע"ס בלתי משותף לקו ס"פ באורך | |
| אם כן שני קוי ע"ס ס"פ בכח מדברים ושניהם בו לבד משותפים | |
| אם כן קו ע"פ נבדל והוא יגבר על שטח א"ח | |
| מע' מזה | |
| אם כן הקו אשר יגבר על א"ח בלתי מדבר והוא אשר יקרא הנבדל | |
| וזה מה שרצינו לבאר | |
Proposition 89 |
|
| פט כאשר הקיף בשטח קו מדבר והנבדל השני הנה הקו אשר יגבר על השטח ההוא הוא אשר יקרא נבדל הממוצע הראשון | |
| ויהיה שטח עליו א"ח יקיף בו קו מדבר והוא א"ב והקו הנבדל השני והוא א"ז | |
| וידבק בו הקו אשר ממנו נבדל והוא ז"ג | |
| הנה אומר כי הקו אשר יגבר על שטח א"ח בלתי מדבר והוא אשר יקרא נבדל הממוצע הראשון | |
| וזה כי [94]קו א"ז הוא הנבדל השני | |
| והקו אשר יובדל ממנו ד"ך ד"ג | |
| אם כן שני קוי א"ג ג"ז בכח מדברים ושניהם בו לבד משותפים מע' מזה | |
| וקו א"ג יוסיף בכח על קו ג"ז כמו מרובע יהיה מקו ישתתף עמו באורך | |
| וקו ז"ג ישתתף באורך קו א"ב | |
| ואם חובר אל קו א"ג שטח שוה לרביע המרובע אשר יהיה מקו ז"ג יחסר משלמות הקו שטח מרובע | |
| הנה הוא יחלק קו א"ג בשני חלקים משותפים באורך מי"ג מזה | |
| ויחלק ז"ג בשני חציים על נקודת ד' מי' מא' | |
| ונחבר אל קו א"ג שטח שוה למרובע ההוה מן ד"ג יחסר | |
| אם כן קו א"ה משותף באורך לקו ה"ג | |
| ונוציא מנקודות דהג קוים נכחיים לכל אחד משני קוי א"ב ז"ח והם קוי ד"ט ה"כ ג"ל מל"א מא' | |
| ונוציא קו בכח אל ל ויהיה ק"ע מרובע שוה לשטח א"ב | |
| ויהיה פ"ר מרובע שוה לשטח ה"ל | |
| ויהיה מרובע פ"ר על קוטר מרובע ע"ק | |
| ונוציא משניהם יחד קוטר מ"ס | |
| ונשלים לקוות התמונה | |
| הנה | |
| אם כן קו ג"ד מתיחס לשני קוי א"ה ה"ג במה שבין שניהם מי"ז מו' | |
| ולכן יהיה שטח ג"ט מתיחס לשני שטחי א"ב ב"ג במה שבין שניהם יצא מי"א מח' | |
| ושטח ע"ר גם כן מתיחס לשני שטחי ע"ק פ"ד במה שביניהם | |
| ושטח א"ב שוה לשטח ע"ק | |
| ושטח ב"ג שוה לשטח פ"ר | |
| אם כן שטח ט"ג שוה לשטח ע"ר | |
| ואולם שטח ג"ט הנה הוא שוה לשטח ט"ז | |
| ואולם שטח ע"ר הנה הוא שוה לשטח פ"ק ממ"ג מא' | |
| אם כן שטח ט"ז שוה לשטח פ"ק | |
| אם כן כל שטח ז"ל שוה לרושם סנפ עם המרובע | |
| ושטח ב"ג שוה למרובע פ"ר | |
| וישאר שטח ז"כ שוה לרושם סנפ | |
| וכל א"ב שוה לכל ע"ק | |
| וישאר שטח א"ח שוה לשטח מ"נ | |
| ומרובע מ"נ הוא ההוה מן ע"פ מסוף ד' מב' | |
| אם כן קו ע"פ יגבר על שטח א"ח | |
| ואומר כי ע"פ הוא הנבדל הממוצע הראשון | |
| וזה כי קו א"ה משותף לקו ה"ג באורך | |
| אם כן כל קו א"ג משותף לכל אחד משני קוי א"ה ה"ג באורך מא' מזה | |
| וקו א"ג בכח מדבר והוא בלתי משותף לקו א"ב באורך | |
| אם כן כל אחד משני קוי א"ה ה"ג מדבר בכח והוא בלתי משותף לקו א"ב באורך | |
| אם כן כל אחד משני | |
| ושטח א"כ שוה למרובע ע"ק | |
| ושטח כ"ג שוה למרובע פ"ר | |
| אם כן כל אחד משני | |
| אם כן כל אחד משני קוי ע"ס ס"פ ממוצע ושניהם בכח משותפים | |
| וקו ז"ד כמו קו ד"ג | |
| וכל קו ז"ג מדבר בכח משותף לקו א"ב באורך | |
| אם כן כל אחד משני קוי ז"ד ד"ג מדבר משותף לקו א"ב באורך | |
| אם כן כל אחד משני שטחי ז"ט ט"ג מדבר | |
| ושטח ט"ג שוה לשטח ע"ר מי"א מזה | |
| אם כן שטח ע"ר מדבר ושטח ע"ר הוא אשר יקיפו בו שני קוי ע"ס ס"פ | |
| אם כן השטח אשר יקיפו בו שני קוי [95]ע"ס ס"פ מדבר | |
| הנה מפני כי שטח ע"ר מדבר ושטח ר"פ ממוצע יהיה השטח ר"ע בלתי משותף לשטח פ"ר | |
| ויחס שטח ע"ר אל שטח פ"ר כיחס קו ע"ס אל קו ס"פ מא' מו' | |
| אם כן קו ע"ס בלתי משותף לקו ס"פ באורך | |
| אם כן קוי ע"ס ס"פ ממוצע ושניהם בכח לבד משותפים והשטח אשר יקיפו בו מדבר | |
| אם כן קו ע"פ הוא הנבדל הממוצע הראשון והוא יגבר על שטח א"ח מע"א מזה | |
| אם כן הקו אשר יגבר על שטח א"ח הוא נבדל הממוצע הראשון | |
| וזה מה שרצינו לבאר | |
Proposition 107 |
|
| הקדמה | |
| The apotome and the irrational lines following it are not of the same type as the other preceding irrational lines nor are they the same with the medial line or with one another. | הנבדל ומה שאחריו מן הקוים שאינם מדברים[96] אין מהם קו מסוג הקוים האחרים הקודמים אשר אינם מדברים ולא דבר מהם ממוצע ולא מהם דבר מסוג הנשארים מהם |
| For the square formed by the medial line, when added to a rational line, generates a rational breadth incommensurable in length with the line to which it is added. | וזה כי המרובע |
| While the square formed by the apotome, when added to a rational line, generates a breadth which is the first apotome. | ואולם המרובע ההוה מן הקו הנבדל הנה הוא כאשר חובר אל קו מדבר יחדש רוחב הוא הנבדל הראשון |
| The square formed by the first apotome of the medial line, when added to a rational line, generates a breadth which is the second apotome. | ואולם המרובע ההו |
| The square formed by the second apotome of the medial line, when added to a rational line, generates a breadth which is the third apotome. | ואולם המרובע ההוה מנבדל הממוצע השני הנה הוא כאשר חובר אל קו מדבר היה הרוחב המתחדש הנבדל השלישי |
| The square formed by the minor line, when added to a rational line, generates a breadth which is the fourth apotome | ואולם המרובע ההוה מן הקו היותר קטן הנה הוא כאשר חובר אל קו מדבר היה הרוחב המתחדש הנבדל הרביעי |
| The square formed by the line, which produces with a rational area a medial whole, when added to a rational line, generates a breadth which is the fifth apotome. | ואולם המרובע ההוה מן הקו אשר עם המדבר ישים הכל ממוצע הנה הוא כאשר חובר אל קו מדבר היה הרוחב המתחדש הנבדל החמישי |
| The square formed by the line, which produces with a medial area a medial whole, when added to a rational line, generates a breadth which is the sixth apotome, | ואולם המרובע ההוה מן הקו אשר עם הממוצע ישים הכל ממוצע הנה הוא כאשר חובר אל קו מדבר הנה |
| The breadths we have mentioned differ from each other, none of them are of the same type as the other; this is clear. | |
| ונבאר[97] כי אין מאלו הרחבים הנבדלים דבר הוא מסוג הקוים אשר משתי שמות והם הרחבים המתחדשים מן המרובעים ההוים מן הקוים אשר משתי שמות והקוים אשר ימשכו אחריו כאשר יחוברו אל קוים מדברים | |
| ואם היו אלו הרחבים אשר זכרנו מתחלפים הנה הקוים עצמם אשר התחדשו ממרובעיהם הרחבים האלו אין מהם דבר הוא מסוג חברו | |
| וזה מה שרצינו לבאר | |
Proposition 108 |
|
| The apotome is not the binomial line | הקו הנבדל לא יהיה אשר משתי שמות |
| Let A be the apotome. | ויהיה הקו הנבדל א' |
| I say that A is not a binomial line. | הנה אומר כי א' אינו משתי שמות |
| If possible, let us say that it is a binomial line. | שאם היה איפשר נאמר שיהיה משתי שמות |
| We construct the rational line BG. | ונשים קו ב"ג מדבר |
| We add to it surface GD that is equal to the square formed by A. | ונחבר אליו שטח שוה למרובע ההוה מן א' והוא ג"ד |
| So, BD is a first apotome. | אם כן קו ב"ד הוא הנבדל הראשון מצ"ד מזה |
| ונדביק בו הקו אשר הובדל ממנו והוא ד"ה | |
| אם כן שני קוי ב"ה ה"ד בכח מדברים והם בו לבד משותפים | |
| וקו ב"ה יוסיף על קו ה"ד [98]בכח כמו מרובע יהיה מקו ישתתף עמו באורך מההקדמה השלישית | |
| וקו ב"ה משותף באורך לקו ב"ג המדבר מההקדמה | |
| וגם כן הנה קו א' משתי שמות באורך | |
| וקו ב"ג מדבר וכבר חובר אליו שטח שוה למרובע ההוה מן א' והיה ג"ד | |
| אם כן קו ב"ד הוא משתי שמות הראשון ויוחלק בשתי שמות על נקודת ז' ויהיה חלקו הגדול ב"ז מנ"ח מזה | |
| הנה שני קוי ב"ג ז"ד בכח מדברים והם בו לבד משותפים מל"ג | |
| וקו ב"ז יוסיף על קו ז"ד בכח כמו מרובע יהיה מקו ישתתף עמו באורך מההקדמה הראשונה | |
| וקו ב"ז משותף באורך לקו המדבר אשר הוא ב"ג | |
| ומפני כי כל אחד משני קוי ה"ב ב"ז משותף באורך לקו ב"ג יהיה קו ב"ה משותף באורך לקו ב"ז מי"א מזה | |
| ולזה יהיה גם כן משותף באורך לקו ה"ז מי"א מזה | |
| ומפני כי קו ב"ה משותף גם כן לקו ה"ז באורך | |
| וקו ב"ה כבר היה משותף לקו ד"ה בכח לבד | |
| אם כן קו ה"ז משותף לקו ה"ד בכח לבד | |
| אם כן שני קוי ז"ה ה"ד מדברים והם בו לבד משותפים | |
| אם כן קו ד"ז נבדל מע' מזה | |
| והוא גם כן מדבר בכח | |
| וזה בלתי אפשר[99] | |
| אם כן לא יהיה הקו הנבדל אשר משתי שמות | |
| וזה מה שרצינו לבאר | |
Proposition 109 |
|
| An infinite number of irrational lines arise from the medial line, none of which is of the same type as the preceding. | הקו הממוצע יתחדשו ממנו קוים בלתי מדברים אין תכלית להם אין אחד מהם מסוג מה שלפניו |
| Let AG be a medial line. | ויהיה קו א"ג ממוצע |
| I say that an infinite number of irrational lines arise from line AG, none of which is of the same type as the preceding. | הנה אומר שיהיה מקו א"ג קוים בלתי מדברים מדברים אין תכלית למספרם אין אחד מהם מסוג מה שלפניו |
|
וזה כי אנחנו נוציא קו א"ב על זויות נצבות מקו א"ג מי"א מא' |
| Let line AB be irrational. | ויהיה קו א"ב מדבר |
| ונשלים שטח ב"ג | |
| אם כן שטח ב"ג בלתי מדבר והקו אשר יגבר עליו | |
| ויהיה קו ג"ד שוה לקו אשר יגבר על שטח ב"ג | |
| אם כן קו ג"ד בלתי מדבר ואינו מסוג אחד מן הקוים אשר אינם מדברים ממה שקדם [101] | |
| וגם כן הנה אנחנו נשלים שטח ד"ה | |
| ושטח ד"ה בלתי מדבר | |
| אם כן הקו אשר יגבר עליו בלתי מדבר | |
| ויהיה קו ד"ז שוה לקו אשר יגבר על שטח ה"ד | |
| אם כן קו ד"ז בלתי מדבר ואינו מסוג אחד מן הקוים אשר אינם מדברים ממה שקדם לו | |
| אם כן קו הקו הממוצע יתחדשו ממנו קוים בלתי מדברים אין תכלית לרבויים אין מהם אחד מסוג מה שלפניו | |
| וזה מה שרצינו לבאר | |
| נשלם המאמר העשירי מספר אקלידס החכם | |
| ומספר תמונותיו מאה ותשעה | |
| ונשלמה העתקתו ג אב שנת ל לפרט | |
| תהלה לאל בורא עולם |
Book Eleven |
המאמר האחד עשר מספר אקלידס החכם | |
|
התמונה המוגשמת היא אשר לה אורך ורוחב וגובה וכל מה שיש לו גוף | |
|
וקצוות המוגשם פשוט | |
|
וכאשר עמד קו ישר על שטח והוציאו בשטח ההוא קוים ישרים ימששו הקו הנצב והיתה כל זוית יקיף בה קו מאותם הקוים עם הקו הנצב נצבת הנה הקו הנצב ההוא עמוד על השטח | |
| כאשר עמד שטח על שטח והיו כל שני עמודים יצאו מן הקו אשר הוא הפרק המשותף מנקודה אחת ממנו אל כל שני השטחים יקיפו בזוית נצבת הנה שני השטחים יקיפו בזוית נצבת | ||
| השטחים הנכחיים הם אשר לא ימשש שטח מהם האחר ואפילו הוציאו לכל הצדדים עד לאין תכלית | ||
|
התמונות המוגשמות השוות הדומות הם אשר יקיפו בכל מוגשם מהם ממנין השטחים כמו מנין מה שיקיפו באחר ויהיה כל שטח מאחד מהם דומה ושוה השיעור לשטח אשר הוא גילו מן המוגשם האחר ועל בריאתו | |
|
התמונות המוגשמות הדומות הם אשר יקיף כל מוגשם מהם ממנין השטחים כמו מנין מה שיקיף באחר ויהיה כל שטח מאחד מהם דומה בשטח אשר הוא גילו מן המוגשם האחר ועל בריאתו | |
|
התמונה המוגשמת המגוררת היא אשר יקיפו בה שלשה שטחים נכחיי הצלעות ושני שטחים משולשים | |
|
הכדור הוא מה שיעבור חצי עגולה כאשר יקוים קו הקוטר בין שני כשורים עד שלא יסור וסבבה הקשת אשר היא חצי הקו המקיף עד שתשוב אל מקומה והוא המוגשם העגול ומרכז הכדור ומרכז העגולה אחד | |
| התמונה המוגשמת המחודדת היא אשר יקיפו בה שטחים יעלו משטח אחד אל נקודה אחת מקבילה אותו | ||
| התמונה המוגשמת העגולה היא אשר שני תושבותיה שני שטחים ושניהם שתי עגולות | ||
| השוה שתי קצוות והעובי הוא מה שיעבור שטח שוה הצלעות נצב הזויות כאשר יקוים אחת מצלעותיו המקיפות בזוית נצבת בין שני פלכים עד שלא יסור ויעוגל השטח עד שישוב אל מקומו | ||
| וחץ התמונה הוא הצלע הקים ונקראת התמונה הזאת האסטונה העגולה | ||
| התמונה המוגשמת המחודדת העגולה היא מה שיעבור משולש נצב הזויות כאשר יקוים אחת מצלעותיו המקיפות בזוית הנצבת בין שני כישורים עד שלא יסור ויסובב המשולש עד שישוב אל מקומו | ||
| ואם היה הצלע הקים שוה לצלע האחר הנה התמונה נצבת הזויות | ||
| ואם היה יותר ארוך ממנו הנה היא חדה הזוית | ||
| וכאשר היה יותר קצר ממנו הנה היא נרחבת הזוית | ||
| וחץ התמונה היא הצלע הקים ותושבתה היא עגולה וזאת התמונה היא מחודדת האסטונה העגולה | ||
| הזוית המוגשמת היא אשר יקיפו אותה זויות משוטחות יותר משתי זויות ואינם על שטח אחד ויתקבצו בנקודה אחת | ||
| התמונות המוגשמות העגולות השוות שתי הקצוות והעובי והמחודדים העגולים הדומים הם אשר יהיה יחס חץ כל תמונה מהם אל קוטר תושבתה כיחס חץ התמונה האחרת אל קוטר תושבתה | ||
Proposition 1 |
||
| א הקו הישר לא יהיה חלק ממנו בשטח וחלק בגובה | ||
| מופתו שאי איפשר ונבאר זה במשל הנה אם היה איפשר נאמר שיהיה חלק מקו אב"ג והוא א"ב בשטח וחלק אחר והוא ב"ג והוא בגובה ונוציא מקו א"ב קו בשטח והוא ב"ד הנה אב"ג הוא קו ישר אם כן א"ב דבק ב"ג ובקו ב"ד על יושר זה שקר מפתי' א' | ||
| אם כן לא יהיה חלק מקו ישר בשטח וחלק בגובה וזה מה שרצינו לבאר | ||
Proposition 2 |
||
| ב כל שני קוים ישרים יחתכו הנה שניהם בשטח אחד וכל משולש הנה הוא בשטח אחד | ||
| המשל בו כי שני קוי א"ב ג"ד יחתכו על נקודת ה' הנה אומר כי א"ב ג"ד בשטח אחד ונרשום על שני קוי ד"ה ה"ב שתי נקודות ז"ח ונוציא קו ז"ח הנה אומר כי משולש זה"ח הוא בשטח אחד | ||
| המופת כי הוא אי איפשר זולתו ונבאר זה כי אם היה איפשר זה הנה היה חלק ממשולש זה"ח בשטח וחלק בגובה אם כן שני חלקים משני קוי ז"ה ה"ח בשטח ושני חלקים בגובה זה שקר מא' | ||
| אם כן משולש זה"ח הוא בשטח אחד והשטח אשר בו משולש זה"ח בו שני קוי ז"ה ה"ח ובו שני קוי א"ב ג"ד אם כן שני קוי א"ב ג"ד בשטח אחד | ||
| אם כן כל שני קוים ישרים יחתכו הנה שניהם בשטח אחד וכל משולש הנה הוא בשטח אחד וזה מה שרצינו לבאר | ||
Proposition 3 |
||
| ג כל שני שטחים יחתכו הנה פרק שניהם המשותף הוא קו אחד ישר | ||
| המשל בו כי שני שטחי א"ב ג"ד ה"ז ח"ט יחתכו ופרקם משותף הוא כ"ל הנה אומ' כי כ"ל קו אחד ישר | ||
| המופת שהוא אי איפשר שיהיה יותר מקו ונבאר זה שאם היה איפשר הנה נוציא מן ל' אל כ' קו בשטח א"ב ג"ד והוא כמ"ל ונוציא מכ' אל ל' קו בשטח ה"ז ח"ט והוא כנ"ל אם כן כמ"ל קו ישר וכנ"ל קו ישר מתחברים אם כן שני קוי כמ"ל כנ"ל ישרים מתקרבים יפגשו קצוות שניהם בכל שתי הצדדים זה שקר אם כן כ"ל הוא קו אחד ישר וזה מה שרצינו לבאר | ||
Proposition 4 |
||
| When a perpendicular line stands at the intersection point of two intersecting lines, then it is also perpendicular to the plane passing through them. | ד כאשר עמד עמוד על פרק שני קוים ישרים יחתכו הנה הוא עמוד על שטח שניהם | |
| Example: line AB is perpendicular stands at the common intersection point of two lines GD and HZ. | המשל בו כי קו א"ב עמוד נצב על פרק שני קוי ג"ד ה"ז המשותף | |
| Supposition: I say that line AB is perpendicular to plane GD. | הנה אומר כי קו א"ב עמוד נצב על שטח ג"ד | |
| Proof: | המופת | |
|
|
שיהיו קוי ב"ה ב"ז ד"ב ב"ג הנחלקים שוים | |
|
ונוציא שני קוי ה"ג ד"ז | |
|
ונוציא מן כ' קו בשטח ג"ד ה"ז והוא ט"כ | |
|
ונרשום על א"ב נקודת ח' | |
|
ונוציא קוים ה"ח ד"ח ח"ז ח"ג ח"כ ח"ט | |
|
|
הנה צלע ה"ב כמו ב"ז | |
|
|
וג"ב כמו ב"ד | |
|
אם כן ה"ג ד"ז נכחיים ושוים מט"ו וד' וכ"ז מא' | |
|
|
וג"ב כמו ב"ד | |
|
|
וב"ח עמוד על ג"ד | |
|
אם כן ח"ג כמו ח"ד מד' מא' | |
|
|
וגם כן ה"ב כמו ב"ז | |
|
|
וב"ח עמוד על ה"ז | |
|
אם כן ה"ח כמו ח"ז מד' מא' | |
|
|
אם כן צלע ג"ח כמו ח"ד | |
|
|
וה"ג כמו ד"ז | |
|
אם כן שני קוי ח"ג ג"ה שוים לשני קוי ח"ד ד"ז | |
|
|
ותושבת ה"ח כמו תושבת ח"ז | |
|
אם כן זוית חג"ה כמו זוית הד"ז מח' מא' | |
| וקו ט"ג ד"ב נכחיים וכבר הוצאו אל שניהם ט"כ ג"ד | ||
|
אם כן זוית גט"ב שוה לזוית כב"ד מכ"ט מא' | |
|
|
וזוית בג"ט שוה לזוית בד"כ | |
|
|
וג"ב כמו ב"ד | |
|
אם כן ט"ג כמו ד"כ מכ"ו מא' | |
|
אם כן שני קוי ח"ג ג"ט שוים לשני קוי ח"ד ד"כ | |
|
|
וזוית חג"ט שוה לזוית חד"כ | |
|
אם כן תושבת ט"ח כמו תושבת ח"כ מד' מא' | |
|
|
וצלע ט"כ כמו צלע ב"כ | |
| וכ"ח משותף | ||
|
אם כן שני קוי ט"ב ב"ח יהיו שוים כ"ב כ"ח | |
|
|
ותושבת ט"ח כמו תושבת ח"כ | |
|
אם כן שתי זויות חב"כ וחב"ט שוות מח' מא' | |
| def. | אם כן שתיהם נצבות מפתיחת מא' | |
| אם כן ח"ב עמוד על ט"כ וכן יתבאר כי כל קו יצא מן ב' בשטח שני קוי ג"ד ה"ז הנה הוא יקיף עם ח"ב בזוית נצבת | ||
| def. | אם כן קו כ"א הוא עמוד על שטח ג"ד ה"ז מפתיחת זה | |
| וזה מה שרצינו לבאר | ||
Proposition 5 |
||
| ה כאשר עמד קו על פרק משותף לשלשה קוים יקיף עם כל קו מהם בזוית נצבת הנה הקוים השלשה בשטח אחד | ||
| המשל בו כי קו א"ב נצב על פרק משותף לשלשה קוים ב"ג ב"ד ב"ה על זויות נצבות הנה אומר כי ב"ג ב"ד ב"ה בשטח אחד | ||
| המופת כי איפשר שיהיה קו מהם בזולת שטח האחר ונבאר זה שאם היה איפשר הנה היה ב"ד בשטח בגובה הנה שטח א"ב ב"ד הנה יחלק שטח ג"ב ב"ה ויחלקהו ויהיה חלוקם המשותף קו ב"ז [מג'] ותהיה זוית אב"ז נצבת וכבר היתה זוית אב"ד נצבת א"ב ב"ד ב"ז בשטח אחד הנה זוית אב"ז אם כן שוה לזוית אב"ד הגדולה לקטנה זה שקר אם כן ב"ג ב"ד ב"ה בשטח אחד | ||
Proposition 11 |
||
| י"א נרצה שנוציא מנקודה מונחת בגובה קו יהיה עמוד על שטח מונח | ||
| הנה נשים הנקודה המונחת נקודת א' ונרצה שנוציא ממנה עמוד נצב על השטח המונח ונתחיל ונקוה בשטח קו ישר איך מה שיפול והוא ב"ג ונוציא מנקודת א' אל קו ב"ג עמוד על קו ב"ג והוא א"ד ונוציא מן ד' בשטח המונח עמוד על ב"ג והוא ד"ה ונוציא מן א' אל קו ד"ה עמוד נצב על ד"ה והוא א"ז הנה אומר כי א"ז עמוד על השטח המונח | ||
| המופת אנחנו נוציא מן ז' קו יהיה נכחי אל ב"ג בשטח המונח והוא ח"ט | ||
| אם כן קו ב"ג עמוד על פרק משותף לשני קוי ז"ד ד"א מד' מזה | ||
|
|
אם כן קו ב"ג עמוד על שטח ז"ד ד"א | |
|
|
וב"ג יהיה נכחי אל ח"ט | |
|
|
אם כן ח"ט עמוד נצב על שטח ז"ד ד"א מח' מזה | |
| וז"א הוא בשטח ז"ד ד"א | ||
|
|
אם כן ח"ט עמוד על א"ז | |
|
|
וא"ז עמוד על ח"ט והוא גם כן עמוד על ה"ד | |
|
|
אם כן א"ז עמוד נצב על ה"ד ועל ח"ט | |
|
|
אם כן א"ז עמוד על שטח הזח"ט | |
| ושטח הזח"ט הוא השטח המונח וא"ז עמוד נצב עליו | ||
| הנה כבר הוצאנו מנקודת א' אשר היא בגובה המונח עמוד נצב על השטח המונח והוא א"ז | ||
| וזה מה שרצינו לבאר | ||
Proposition 12 |
||
| י"ב נרצה שנעמיד על שטח מונח על נקודה ידועה ממנו עמוד | ||
| ונשים הנקודה א' ונרצה שנעמיד על נקודת א' עמוד על השטח המונח ונניח בגובה נקודת ב' איך מה שנפלה ונוציא ממנה עמוד על השטח המונח והוא ב"ג ונוציא מן א' קו יהיה נכחי אל ג"ב והוא א"ד הנה אומר כי א"ד עמוד על השטח המונח | ||
| המופת כי א"ד הוא נכחי אל ב"ג וב"ג עמוד על השטח המונח הנה א"ד עמוד על השטח המונח | ||
| הנה כבר העמדנו על השטח המונח על נקודת א' | ||
| וזה מה שרצינו לבאר | ||
Proposition 13 |
||
| י"ג לא יעמוד על שטח אחד שני עמודים על נקודה אחת מן השטח | ||
| המופת שהוא אי איפשר ויתבאר זה במשל שאם היה איפשר הנה נעמיד על נקודת א' שני עמודים על השטח המונח והם א"ב א"ג ויהיה קו ד"ה פרק משותף לשני שטחים אם כן זוית בא"ה נצבת וזוית גא"ה נצבת אם כן שתיהן שוות הגדולה לקטנה זה שקר | ||
| אם כן אי איפשר שיעמדו על נקודה אחת שני עמודים | ||
| וזה מה שרצינו לבאר | ||
Proposition 14 |
||
| י"ד כאשר היה קו אחד עמוד על שני שטחים הנה השני שטחים כאשר הוצאו בכל הצדדים לא יפגשו ואפי' הוצאו בכל הצדדים לאין תכלית | ||
| המשל בו שיהיה קו א"ב עמוד על שני שטחי ג"ד ח"ט הנה אומר כי שני שטחי ג"ד ח"ט נכחיים וששניהם כאשר הוצאו עד לאין תכלית לא יפגשו | ||
| המופת שהוא אי איפשר ונבאר זה שאם היה איפשר הנה יפגשו ותהיה פגישת שניהם פרק משותף והוא קו כ"ל ונרשום על כ"ל נקודת מ' איך מה שתפול ונוציא שני קוי א"'מ כ"מ הנה כ"ל הוא בשטח ג"ד וכל הנקודות אשר בו הם בשטח ג"ד אם כן א"מ בשטח ג"ד וכל עמוד על שטח הנה הוא עמוד על קו יצא בשטח וימשש העמוד אם כן זוית מא"ב נצבת ולכן זוית אב"מ נצבת אם כן שתי זויות ממשולש אב"מ שתי נצבות זה שקר אם כן שני שטחי ג"ד ח"ט כאשר הוצאו בכל הצדדים לא יפגשו | ||
| וזהו מה שרצינו לבאר | ||
Proposition 33 |
||
| Parallelepipedal solids, whose heights are the same: the ratio of the solid to the solid is as the ratio of its base to its base. | ל"ג המוגשמים נכחיי השטחים כאשר היה רומם בשיעור אחד הנה יחס המוגשם אל המוגשם כיחס תושבתו אל תושבתו | |
| המשל בו כי שני מוגשמי כ"ב וז"ל נכחי השטחים ורומם בשיעור אחד הנה אומר כי יחס תושבת אבג"ד אל תושבת הזח"ט כיחס מוגשם כ"ב אל מוגשם ז"ל | ||
|
|
המופת כי נשים תושבת ד"ג מ"נ שוה לתושבת הזח"ט | |
| ונשלים מוגשם ס"ג וכל מוגשם נכחיי השטחים יבדילהו שטח על נכחות שני שטחים מקבילים | ||
| הנה הוא יחלקהו בשני חלקים יהיה יחס אחד משניהם אל האחר כיחס תושבתו אל תושבתו [מכ"ה מזה] | ||
|
|
אם כן יחס תושבת אבג"ד אל תושבת דגמ"נ כיחס מוגשם כ"ב אל מוגשם ג"ס | |
|
|
ותושבת דגמ"נ כמו תושבת הזח"ט | |
|
|
ומוגשם ג"ס כמו מוגשם ז"ל | |
|
|
אם כן יחס תושבת אבג"ד אל תושבת הזח"ט כיחס כ"ב אל מוגשם ז"ל | |
| וזה מה שרצינו לבאר | ||
Proposition 40 |
||
| מ כל מעוקב יובדלו צלעות שני שטחים משטחיו מקבילים כל צלע בשני חציים אחר כן יצאו ממקומות ההבדלים שני שטחים יבדילו המעוקב ויבדיל כל אחד משניהם האחר הנה הבדל שניהם המשותף יחתוך קוטר המעוקב בשני חציים ויחתכהו הקוטר בשני חציים | ||
| המשל בו כי שני שטחי מעוקב א"ב המקבילים ג"ד א"ה ז"ח ט"כ הנה כבר הובדלו צלעות שניהם והם ג"ד ד"א א"ה ה"ג ב"ז ז"ח ח"ט ט"ב כל צלע בשני חציים על נקודת כ' ל' מ' נ' ס' ע' פ' ק' והוצא ממקומות ההבדלים שני שטחים והם כ"מ פ"ס ונ"ל ע"ק יבדילו המעוקב ויבדיל כל אחד משניהם האחר והבדלם המשותף קו ר"ש וקוטר המעוקב קו ב"א הנה אומר כי כל אחד מן ר"ש ב"א יחתוך האחד בשני חציים | ||
| המופת כי נוציא קוים ג"ר ר"א ב"ש ש"ח | ||
|
|
הנה ג"ה ישוה ד"א | |
|
|
וחצי ג"ה הוא ג"נ | |
|
|
וחצי ד"א הוא ל"א | |
|
|
וג"נ ישוה ל"א | |
|
|
ור"נ ישוה ר"ל | |
|
|
הנה כל ג"נ נ"ר כמו כל א"ל ל"ר כל אחד כמו גילו | |
|
|
וזוית גנ"ר כמו זוית אל"ר | |
|
אם כן תושבת ג"ד כמו תושבת ר"א מד' מא' | |
|
|
ומשולש גנ"ר כמו משולש אל"ר | |
| ושאר הזויות כמו שאר הזויות אשר יהיו מיתריהם הצלעות השוות | ||
|
|
זוית גר"נ כמו זוית לר"א | |
| ויהיה זוית נר"א משותפת | ||
|
|
אם כן שתי זויות גר"נ נר"א שוות לשתי זויות לר"א אר"נ | |
|
אבל שתי זויות לר"א אר"נ ישוו שתי נצבות מי"ג מא' | |
|
|
אם כן שתי זויות גר"נ נר"א ישוו שתי נצבות | |
| וכבר יצא מקו ר"נ מנקודת ד' שני קוים ר"נ ר"א בשני צדדים מתחלפים ויהיו שתי זויות גר"נ נר"א ישוו שתי נצבות | ||
| אם כן יהיו שני קוי ג"ר ר"א קו אחד ישר מי"ד מא' | ||
| ולכן יהיו שני קוי ב"ש ש"ח קו אחד ישר | ||
|
|
וכל אחד מן ג"ב א"ח ישוה ה"ט והם נכחיים | |
| והנכחיים לקו ואינם בשטח אחד הנה הם נכחיים | ||
|
|
אם כן ג"ב א"ח נכחיים שוים ונדבקים בקצוות ג"א ב"ח | |
|
|
אם כן ג"א ב"ח שוים נכחים מל"ג מא' | |
|
|
וחצי ג"א הוא ר"א | |
|
|
וחצי ב"ח הוא ב"ש | |
|
|
אם כן ר"א ב"ש שוים נכחיים ונדבקים בקצוות ר"ש א"ב | |
|
אם כן ר"ת ישוה ת"ש וא"ת ישוה ת"ב מכ"ט ומ"ו מא' | |
| הנה כבר חתך כל אחד מן א"ב ר"ס האחד בשני חצאים | ||
| וזה מה שרצינו לבאר | ||
Proposition 41 |
||
| For every two prisms whose heights are equal, if the base of one of them is a triangle, the base of the other is parallelogram, and it is double the base of the other, which is the triangle, then both prisms are equal. | מא כל שני מגוררים רום שניהם שוים ותושבת אחד משניהם משולש ותושבת האחר נכחית הצלעות והיא כפל תושבת האחר המשולש הנה שני המגוררים שוים | |
| המשל בו כי שני מגוררי א"ב ג"ד ה"ז ח"ט כ"ל מ"נ רום שניהם שוים ותושבת אחד משניהם משולש והיא נכ"ל ותושבת האחר נכחית הצלעות והוא בגד"ה הנה אומר כי שני המגוררים שוים | ||
| המופת שנשלים שני מוגשמי א"ד ח"ל הנכחיים | ||
|
|
הנה נכחי בגד"ה הוא כפל משולש נכ"ל | |
|
|
ונכחי נ"ל הוא כפל משולש נכ"ל | |
|
|
אם כן שתי תושבות ב"ד נ"ל הנכחיי הצלעות שוות | |
|
אם כן מוגשם א"ד ח"ל שוים הרום נכחיי השטחים על שתי תושבות שוות אם כן שתיהן שוות מל"ב | |
|
|
אבל חצי א"ד הוא מגורר א"ב ג"ד ה"ז | |
|
|
וחצי ח"ל הוא מגורר ח"ט כ"ל מ"נ | |
|
|
אם כן שני מגוררי א"ב ג"ד ה"ז ח"ט כ"ל מ"נ שוים | |
| וזה מה שרצינו לבאר | ||
| נשלם המאמר האחד עשר ת"ל | ||
Book Twelve |
המאמר השנים עשר מספר אקלידס החכם | |
|---|---|---|
Proposition 1 |
||
| א כל שתי שטחים רבי הזויות דומים בשתי עגולות הנה יחס אחד משניהם אל האחר כיחס מרובעי שני קוטרי שתי העגולות אחד מהם אצל האחר | ||
| המשל בו כי שני שטחי א"ב גד"ה וח"ט כ"ל רבי הזויות מתדמים בשתי עגולות שני קטריהם ב"ז ט"נ הנה אומר כי יחס שטח א"ב גד"ה אל שטח ח"ט כ"ל מרבי הזויות כיחס מרובע קוטר ב"ז אל מרובע קוטר ט"נ | ||
| המופת שנוציא קוים כ"ה א"ז ט"מ ח"נ הנה יחס ב"א אל ט"ח כיחס א"ה אל ח"מ ושתי זויות בא"ה טח"מ השוות יקיפו בהם צלעות מתיחסות אם כן [מו' ומד' מו'] משולש אב"ה ידמה משולש חט"מ אם כן זויות אה"ב כמו זוית חמ"ט וזוית אה"ב [מכ' מג'] כמו זוית אז"ב וזוית חמ"ט כמו זוית חנ"ט אם כן זוית אז"ב כמו זוית חנ"ט וזוית בא"ז [מל' מג'] נצבת שוה לזוית טח"נ ונשארה זוית אב"ז כמו זוית חט"נ הנשארת אם כן משולש אב"ז שוה הזויות למשולש חט"נ אם כן יחס ז"ב אל נ"ט כיחס ב"א אל ט"ח אם כן [מסוף י"ח מו'] יחס מרובע ב"ז אל מרובע ט"נ הוא יחס ב"ז אל ט"נ שנוי ויחס א"ב גד"ה אל ח"ט כ"ל מרבי הזויות הוא [מי"ט מו'] יחס א"ב אל ח"ט שנוי ויחס ב"ז אל ט"נ כיחס א"ב אל ח"ט אם כן יחס מרובע ב"ז אל מרובע ט"נ כיחס שטח א"ב גד"ה אל שטח ח"ט כל"מ רבי הזויות וזה מה שרצינו לבאר | ||
Proposition 2 |
||
| ב כל שתי עגולות הנה יחס אחד משתיהן אל האחרת כיחס שני מרובעי שני קטריהם אחד מהם אל האחר | ||
| המשל בו כי שתי עגולות אבג"ד ה"ז ח"ט קטרי שניהם ב"ד ז"ט הנה אומר כי יחס מרובע קוטר ב"ד אל מרובע קוטר ז"ט כיחס עגולת א"ב ג"ד אל עגולה ה"ז ח"ט | ||
| המופת כי אי איפשר זולתו ונבאר זה כי אם היה איפשר נאמר שיהיה יחס מרובע ב"ד אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל שטח הוא יותר גדול או יותר קטן מעגולת ה"ז ח"ט ויהיה ראשונה אל שטח הוא יותר קטן ממנה ויהיו ת' ויהיו ת"כ מקובצים כמו עגולת ה"ז ח"ט ונקוה בעגולת ה"ז ח"ט מרובע ה"ז ח"ט ויחתכו קשתות ה"ז ז"ח ח"ט ט"ה כל אחת בשני חציים על נקודת כ' ל' מ' נ' ונוציא מיתרי ה"כ כ"ז ז"ל ל"ח ח"מ מ"ט ט"נ נ"ה הנה כל אחד ממשולשי הכ"ז זל"ח חמ"ט טנ"ה הוא יותר גדול מחצי חתיכת העגולה אשר בה המשולש וכאשר עשינו זה פעמים הנה תשאר לנו חתיכות מן העגולה כלם יותר קטן משטח כ' ותשאר ויהיו חתיכות ה"כ כ"ז ז"ל ל"ח ח"מ מ"ט ט"נ נ"ה הנה עגולת ה"ז ח"ט יותר גדולה משטח כ' וכבר חסר מהגדול יותר מחציו ועשה זה פעמים וישאר [מא' מי'] מה שהוא יותר קטן מן כ' ויהיה שטח ה"כ ז"ל ח"מ ט"נ הרב הזויות יותר גדול מן ת' ויקיפו בעגולת א"ג שטח רבי הזויות דומה בשטח ה"כ ז"ל ח"מ ט"נ והוא שטח א"ס ב"ע ג"פ ד"ק הנה יחס מרובע ד' אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל שטח ת' אבל יחס מרובע ב"ד אל מרובע ז"ט כיחס שטח א"ס ב"ע ג"פ ד"ק הרב הזויות אל שטח ה"כ ז"ל ח"נ מ"ט הרב הזויות אם כן [מי"ח מה'] יחס עגולת א"ב ג"ד אל שטח ת' כיחס שטח א"ס ב"ע ג"פ ד"ק אל שטח הכז"ל חנמ"ט וכאשר המירונו [מי"ו מה'] יהיה יחס עגולת א"ב ג"ד אל השטח הרב הזויות אשר בה כיחס שטח ת' אל שטח הכז"ל חמנ"ט הרב הזויות ועגולת א"ב ג"ד היא יותר גדולה מן הרב הזויות אשר בה ושטח ת' אם כן יותר גדול מן הכל"ז חמנ"ט הרב הזויות אבל ת' היה יותר קטן ממנו כמו שבארנו זה שקר אי איפשר אם כן אין יחס מרובע ב"ד אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל שטח הוא יותר קטן מעגולת ה"ז ח"ט | ||
| הנה אומר ולא אל שטח הוא יותר גדול שאם היה איפשר נאמר שיהיה אל ת' והוא יותר גדול ממנה הנה יחס מרובע ב"ד אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל שטח ת' וכאשר חלפנו היה יחס מרובע ז"ט אל מרובע ב"ד כיחס שטח ת' אל עגולת א"ב ג"ד וכיחס עגולת ה"ז ח"ט אל שטח הוא יותר קטן מעגולת א"ב ג"ד אם כן יחס מרובע ט"ז אל מרובע ד"ב כיחס עגולת ה"ז ח"ט אל שטח הוא יותר קטן מעגולת א"ב ג"ד וכבר ביארנו כי זה שקר אי איפשר אם כן אין יחס מרובע ב"ד אל מרובע ז"ט כיחס מרובע א"ב ג"ד אל שטח הוא יותר גדול מעגולת ה"ז ח"ט וכבר ביארנו ולא אל יותר קטן ממנו אם כן יחס מרובע ב"ד אל מרובע ז"ט כיחס עגולת א"ב ג"ד אל עגולת ה"ז ח"ט וזה מה שרצינו לבאר | ||
Proposition 6 |
||
| כל מגורר הנה הוא אפשר שיחלקו ממנו שלשה מחודדים שוים ותושבותיהם משולשים | ||
Proposition 15 |
||
| ט"ו כל שני כדורים הנה יחס אחד משניהם אל האחר הוא יחס קוטרו אל קוטרו משולש | ||
| המשל בו כי נניח שתי כדורים א"ב ג"ד ה"ז ח"ט וקוטרי שניהם ב"ד ז"ט הנה אומר כי יחס כדור א"ב ג"ד אל כדור ה"ז ח"ט הוא יחס קוטר ב"ד אל קוטר ז"ט משולש | ||
| המופת כי אי איפשר זולתו ובאור זה שאם היה איפשר נאמר שיהיה יחס כדור א"ב ג"ד אל כדור הוא יותר קטן או יותר גדול מכדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש ויהיה תחלה אל כדור הוא יותר קטן ממנו והוא כדור א' ויהיה כדור כ"ל מ"נ על מרכז ה"ז ח"ט שוה לכדור א' ויהיו שני כדורים על מרכז אחד ונעשה [מי"ד] בכדור ה"ז ח"ט הגדול מוגשם רב התושבות יקיפו בו בלתי ממשש לפשט כדור כ"ל מ"נ הקטן ונעשה בכדור א"ב ג"ד מוגשם דומה לרב התושבות אשר בכדור ה"ז ח"ט הנה יחס כדור א"ב ג"ד אל כדור א' כיחס ב"ד אל ז"ט משולש ויחס רב התושבות אשר בכדור א"ב ג"ד אל הרב התושבות אשר בכדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש אם כן יחס כדור א"ב ג"ד אל כדור א' כיחס רב התושבות אשר בכדור א"ב ג"ד אל הרב התושבות אשר בכדור ה"ז ח"ט וכאשר המירונו יהיה יחס כדור א"ב ג"ד אל הרב התושבות אשר בו כיחס כדור א' אל הרב התושבות אשר בכדור ה"ז ח"ט הרב התושבות אשר בו וכדור א"ב ג"ד יותר גדול מן הרב התושבות אשר בו אם כן כדור א' יותר גדול מן הרב התושבות אשר בו אם כן כדור א' יותר גדול מן הרב התושבות אשר בכדור ה"ז ח"ט אבל הרב התושבות אשר בכדור ה"ז ח"ט יקיף בכדור כ"ל מ"נ השוה לכדור א' זה שקר אי איפשר אם כן אין יחס כדור א"ב ג"ד אל כדור הוא יותר קטן מכדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש | ||
| ואומר ולא אל כדור הוא יותר גדול ממנו ונבאר כי זה אי איפשר שאם היה איפשר נאמר שיהיה אל כדור א' והוא יותר גדול ממנו ונשוב בתואר הנה יחס כדור א' אל כדור א"ב ג"ד הוא יחס ז"ט אל ב"ד משולש ויחס כדור א"ב אל כדור א"ב ג"ד כיחס ה"ז ח"ט אל כדור הוא יותר קטן מכדור א"ב ג"ד אם כן יחס כדור ה"ז ח"ט אל כדור הוא יותר קטן מכדור א"ב ג"ד הוא כיחס ז"ט אל ב"ד משולש זה שקר אי איפשר שכבר ביארנו זה אם כן אין יחס כדור א"ב ג"ד אל כדור הוא יותר קטן ולא אל יותר גדול מכדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש אם כן יחס כדור א"ב ג"ד אל כדור ה"ז ח"ט הוא יחס ב"ד אל ז"ט משולש וזה מה שרצינו לבאר | ||
| נשלם המאמר השנים עשר מספר אקלידס החכם ת"ל | ||
Book Fourteen |
המאמר הארבעה עשר אשר יאות באקלידס אשר מספר אספקלאוס | |
| כי אפסלידס אשר היה מאנשי סוראה וטרוגס כאשר בא אלכסנדריה פגש אביו אשר היה בין שניהם מקורבת השתוף בעיון בחכמות הלמודיות העמיד אצלו רוב זמן ימי חיו והכירו ובחנו בקצת מאמריהם מה שכתב אבלניוס בהיקש התמונה אשר לה שתים עשרה תושבות ואשר לה העשרים העשויות בכדור אחד כל אחד מהם אל | ||
| ואולם אני הנה נפל בידי אחר זה ספר אחר לאבלניוס עשה בו התמונות אשר זכרנו במופתים אמתיים והועיל בהם תועלת גדולה בידיעה באלו [102]הדברים אשר זכרנו | ||
| ואולם הספר אשר חברו אבלוניוס הנה כבר אפשר לנו יחד שנשתתף בעיון וזה כי הוא ספר כבר הגיע לאנשים ונפל ביד רבים מהם | ||
| ואולם מה שהנחנו אנחנו מאחריו ופרשנו בו עניינים כל מה שראינו שראוי לפרשו והנה ראינו שנכתבנו אליך כי היינו היית חזק להכיר מה שיאמר ולהגיעו לך להיותך | ||
| הנה כבר הגיע לעזוב מה שאנו בו מזאת הפתיחת ונתחיל בענין מה שנרצה לדבר בו | ||
| ונאמר העמוד אשר יצא ממרכז עגולת מה אל צלע המחומש אשר הקיף באותה עגולה | ||
| ותהיה עגולה עליה אב"ג | ||
| ויהיה בעגולת אב"ג צלע מחומש שוה הצלעות והוא ב"ג | ||
| ויהיה מרכז העגולה ד | ||
| ונוציא ממנו אל ב"ג עמוד ד"ה | ||
| ונוציא קו ה"ז על יושר קו ד"ה | ||
| הנה אומר כי קו ד"ה שוה לחצי צלע המשושת וחצי צלע המעושר אשר יקיפו בעגולה הזאת כאשר יקובצו | ||
| וזה כי אנחנו נוציא שני קוי ד"ג | ||
| ויהיה קו ה"ח שוה לקו ה"ז | ||
| אם כן זוית אד"ג ארבעה דמיוני זוית זד"ג | ||
Book Fifteen by Hyspikleos [hypsicles] which is suitable for Euclid the Wise |
המאמר החמשה עשר לאספקלאוס אשר יאות לאקלידס החכם | |
| הקדמה לאספקלוס בהשלמת המאמר על המוגשמים החמשה | ||
Proposition 1 |
||
| When the side of the hexagon is cut in a mean and extreme ratio, the greater segment is a side of the decagon circumscribed by the circle that circumscribes the hexagon. | א כאשר נחלק צלע המשוש | |
| Example: line AB is a side of the hexagon. | המשל בזה כי קו א"ב צלע המשושת | |
| Let it be cut in a mean and extreme ratio at point G | וכבר נחלק על יחס בעל אמצע ושתי קצוות על נקודת ג' | |
| Let BG be its greater segment. | וחלקו הגדול ב"ג | |
| I say that BG is the side of the decagon circumscribed by the circle that circumscribes the hexagon. | הנה אומר כי ב"ג צלע המעושר אשר תקיף בו העגולה אשר תקיף במשושת | |
| The proof: | המופת | |
| It has already been proved in Book XIII regarding the sides of the hexagon and the decagon circumscribed by the circle, that when they are joined as a straight line, then that line is cut in a mean and extreme ratio, the greater segment is the side of the hexagon and the smaller segment is the side of the decagon. | כי כבר התבאר במאמר הי"ג [בט' ממנו] כי צלע משושת אשר בעגולה ומעשורה כאשר נדבקו על יושר אחר כן נחלק הקו על יחס בעל אמצע ושתי קצוות הנה החלק הגדול הוא צלע המשושת והחלק הקטון הוא צלע המעושר | |
| We join the side of the decagon, which is DB, to line AB. | ונגיע בקו א"ב צלע המעושר והוא ד"ב | |
| So, line AD is cut in a mean and extreme ratio at point B. | הנה קו א"ד כבר נחלק על יחס בעל אמצע ושתי קצוות על נקודת ב' | |
| Its greater segment is line AB. | וחלקו הגדול יותר קו א"ב מט' מי"ג | |
| We draw line HW equal to line AB. | ונרשום קו שוה לקו א"ב והוא קו ה"ו | |
| We cut it in a mean and extreme ratio at point Z. | ונחלקהו ביחס בעל אמצע ושתי קצוות על נקודת ז' | |
| Its greater segment is line WZ. | וחלקו הגדול קו | |
| WZ is equal to line BG. | וו"ז שוה אל קו ב"ג מי' מי"ד | |
| Therefore, the ratio of AD to AB is the same as the ratio of HW to WZ. | הנה יחס | |
| When we cut off, then reverse, the ratio of AB to BD is the same as the ratio of WZ to ZH. | וכאשר הבדלנו[104] אחר כן הפכנו הנה [מי"ו מו'] יחס א"ב אל ב"ד כיחס ו"ז אל ז"ה | |
| אם כן המרובע ההוה מן א"ב בה"ז כמו מרובע אשר יהיה מן ב"ד בו"ז מי"ו מו' | ||
| AB is the same as HW. | וא"ב כמו ה"ו | |
| ואשר [מי"ו מו'] [105]יהיה מן ה"ו בה"ז שוה לאשר יהיה מן ו"ז בכמוהו[106] | ||
| אם כן קו ד"ב הוא כמו ו"ז[107] | ||
| Line WZ is the same as line BG. | וקו ו"ז כמו קו ב"ג | |
| DB is the side of the decagon. | וד"ב צלע המעושר | |
| Therefore, line BG is the side of the decagon. | אם כן קו ב"ג צלע המעושר | |
| Quod erat demonstrandum | וזה מה שרצינו לבאר | |
Proposition 2 |
||
| We wish to draw a polyhedron with four equilateral triangular faces inside a known cube. | ב נרצה שנרשום בעל ד' תושבות משולשו' שוות הצלעות במעוקב ידוע[108] | |
| Let ABGDHWZC be the known cube. | ויהיה המעוקב הידוע א"ב ג"ד ה"ו ז"ח | |
| We join AZ, GZ, GH, AH, and HZ. | ונגיע א"ז וג"ז | |
| I say that we have already constructed a polyhedron with four equilateral triangular faces, which is solid AGZH. | הנה אומר כי כבר עשינו בעל ד' תושבות משולשות שות הצלעות והוא מוגשם א"ג ז"ה | |
| The proof: | המופת | |
| AG is the hypotenuse opposite to the right angle ADG. | כי א"ג כבר היה מיתר זוית אד"ג הנצבת | |
| AZ is the hypotenuse opposite to the right angle ADZ. | וא"ז כבר היה מיתר זוית אד"ז הנצבת | |
| GZ is the hypotenuse opposite to the right angle GDZ. | ||
| AH is the hypotenuse opposite to the right angle ABH. | וא"ה כבר היה מיתר זוית אב"ה הנצבת | |
| GH is the hypotenuse opposite to the right angle GBH. | וג"ה כבר היה מיתר לזוית גב"ה הנצבת | |
| HZ is the hypotenuse opposite to the right angle HWZ. | וה"ז כבר היה מיתר לזוית הו"ז הנצבת | |
| Lines AD, DZ, GD, GB, AB, BH, HW, WZ are equal [to each other]. | וקוי א"ד ד"ז ג"ד ג"ב א"ב ב"ה ה"ו ו"ז שוים | |
| So, sides AZ, ZG, AH, AG, ZH, GH are equal [to each other]. | אם כן [מד' מא'] צלעות א"ז ז"ג א"ה א"ג ז"ה ג"ה שוות | |
| Therefore, triangles AGZ, AHG, AHZ, HZG are equal [to each other]. | אם כן משולשי אג"ז אה"ג אה"ז הז"ג שוים | |
| Hence, solid AGZH has four equilateral [triangular] faces, its base is triangle AGZ and its apex is point Z. | אם כן מוגשם א"ג ז"ה בעל ד' תושבת שוות הצלעות בתושבת משולש אג"ז וראשו נקודת ז' | |
| Quod erat demonstrandum. | וזה מה שרצינו לבאר | |
Proposition 3 |
||
| We wish to draw a solid shape with eight equilateral triangular faces inside a solid with four equilateral triangular faces. | ג נרצה שנרשום תמונה מוגשמת בעלת ח' תושבות משולשות שוות הצלעות במוגשם בעל ד' תושבות משולשות שוות הצלעות | |
| Let solid ABGD be the solid with four equilateral triangular faces. | ויהיה המוגשם אשר לו ארבע תושבות | |
| Let triangle ABG be its base. | ותהיה תושבתו משולש אב"ג | |
| Let point D be its apex. | וזוית ראשו נקודת ד' | |
| We cut each of its sides in half at points H, W, Z, C, T, L. | ונבדיל כל צלע מצלעותיו בשני חציים אצל נקודת ה"ו ז"ח ט"ל | |
| We join HZ, ZW, WH, CT, TL, LC, CH, HT, TW, WL, LZ, ZC. | ונגיע ה"ז ז"ו ו"ה ח"ט ט"ל ל"ח ח"ה ה"ט ט"ו ו"ל ל"ז ז"ח | |
| הנה אומר כי אנחנו כבר עשינו במוגשם א"בג"ד בעל ח' תושבות משולשות שוות הצלעות | ||
| המופת | ||
| כי קוי ח"ל ח"ט ח"ז ח"ה ו"ה ו"ז ו"ט ו"ל ז"ל ל"ט ט"ה שוים | ||
| מפני כי הם מיתרי זוית שוות יקיפו בהם קוים שוים | ||
| וזוית מוגשם א"ב ג"ד שוות | ||
| מפני כי תושבותיהם משולשים שוים | ||
| והקוים המוצאים הנעשים מיתרים לזויות נכחיים לתושבות המשולשות אשר הם מיתרי זויותיהם | ||
| אם כן המשולשים אשר יתחדשו מהם דומים ודומים למשולשי בעל הד' תושבות | ||
| אם כן קו ז"ה נכחי לקו ג"ב מב' מו' | ||
| וכן קוי משולש הז"ו נכחיים לקוי משולש | ||
| וכן קוי משולש חט"ל נכחיים לקוי משולש אב"ג | ||
| וכן גם כן | ||
| הנה מוגשם חה"ט ול"ז בעל ח' תושבות שוות הקוים והזויות המשולשים שוות | ||
| ומשולשיו השוים הם משולשי זח"ל לח"ט טח"ה הז"ח | ||
| והמשולשים הארבעה הנכחיים להם והם המשולשים טו"ה הו"ז זו"ל טו"ל | ||
| והצלעות הד' המרובעות אשר יקיפו באמצעו הם צלעות ט"ל | ||
| ושתי זויות ראשי המחודדים שתי נקודות ח"ו | ||
| הנה כבר עשינו [110]המוגשם א"ב ג"ד בעל הד' תושבות תמונה בעלת [השמונה] תושבות משולשות שוות הצלעות | ||
| וזה מה שרצינו לבאר | ||
Proposition 4 |
||
| ד נרצה שנרצה במעוקב ידוע בעל שמונה תושבות ויהיה המעוקב הידוע מעוקב א"ב ג"ד ה"ו ז"ח בשטחו הששה המרובעים שטח אבג"ד והוא השטח העליון ממנו [ושטח הוז"ח והוא השטח התחתון ממנו והוא הנכחי] לשטח אבג"ד ושטח אהח"ד הנכחי לשטח בגז"ו ושטח אבו"ה הנכחי לשטח חדג"ז ונקח מכל שטח משטחיו הששה הנקודה אשר יחתכו ממנה שני הקוטרים לשטח ההוא ונרשום על הנקודה אשר במרובע אבג"ד רושם מ' ובמרובע הוז"ח רושם ה' ובאבו"ה רושם י' ובגדז"ח רושם ל' ובאהח"ד רושם ט' ובבגז"ו רושם כ' ונוציא קוי י"ט ט"ל ל"כ כ"י מ"י מ"ט מ"ל מ"כ ס"ל ס"ט ס"י ס"כ | ||
| ואומר כי אנחנו כבר עשינו במעוקב א"ב ג"ד ה"ו ז"ח בעל שמונה תושבות והוא מוגשם י"ט ל"ב מ"ס | ||
| מופת זה כי אנחנו נקודת ט' אם הוצא עליה קו נכחי לשתי צלעות א"ה ד"ח והוא קו עט"פ וקו אחר לשתי צלעי א"ד ה"ח והוא קו קט"ג יחתכו על זויות נצבות מפני כי שטח א"ה ח"ד שוה צלעות ונכחיים להם ונצב הזויות ולכן [מסוף ד' מב'] יהיו קוי ט"ע ט"פ ט"ק ט"נ שוים | ||
| וכן כל שטחי המעוקב כאשר ננהיגם בזאת ההנהגה יהיו הקוים אשר יצאו מן הנקודות אשר יחתכו עליה קוטריהם אצל צלעיהם ונכחי צלעיהם שוה יחד ויהיה דבקות כל שני קוים מהם בשני שטחים יתמששו על זוית נצבת ויהיו הקוים אשר ידבקו בין כל שתי נקודות מן הנקודות אשר יחתכו עליהם הקוטרים שוים | ||
| ויהיו קוי י"ט י"כ ל"ב ל"ט ס"כ ס"ל ס"י ס"ט מ"כ מ"ל מ"י מ"ט שוים | ||
| ויהיו הזויות אשר יקיפו בהם שוות | ||
| אם כן [מח' מא'] משולשי ימ"ט ימ"כ טמ"ל מכ"ל טי"ס טל"ס לכ"ס כי"ס שוי הצלעות | ||
| הנה כבר עשינו תמונה בעל שמונה תושבות יכ"ל טמ"ס אשר רצינו במעוקב א"ב ג"ד ה"ו ז"ח הידוע | ||
| וזה מה שרצינו לבאר | ||
Proposition 5 |
||
| ה נרצה שנרשום במוגשם בעל שמונה תושבות ידוע מעוקב | ||
| ויהיה המוגשם בעל השמונה תושבות מוגשם א"ב ג"ד ה"ו | ||
| ומשולשיו הצלעות משולשי אה"ד דה"ג גה"ב בה"א או"ד דו"ג גו"ב בו"א | ||
| ונקח מרכז המשולשים מרכז אח"ד נקודת ז' ומרכז דה"ז נקודת ח' ומרכז גה"ב נקודת ט' ובה"א נקודת י' ואו"ד נקודת ל' וגו"ד נקודת מ' וגו"ב נקודת נ' ובו"א נקודת כ' | ||
| ונוציא קוי ז"י י"ט ט"ח ל"כ כ"נ נ"מ מ"ל י"כ ז"ל ח"מ ט"נ | ||
| הנה אומר כי כבר עשינו במוגשם א"ב ג"ד ה"ו בעל השמונה תושבות הידוע מעוקב והוא מעוקב יז"ח טכ"ל מ"נ | ||
| מופת זה אנחנו אם הוצאנו מן הנקודות אשר הם מרכזי המשולשים אשר הם נקודות זי"ט חל"כ מ"נ עמודים אל צלעות משולשיהם יהיו העמודים שוים והיו הזויות אשר יתחדשו ממשוש אותם העמודים היוצאים ממשולש אל משולש אחר שוים | ||
| מפני כי הזויות אשר יתחדשו ממשוש שטחי משולשי בעל השמונה תושבות שוות | ||
| ויהיו הקוים אשר הם מיתרי אותם הזויות הם היוצאים מן ז' אל וי ומן י' אל ט' ומן ט' אל ח' ומן ח' אל ז' ומן ז' ל' אל כ' ומן כ' אל נ' ומן נ' אל מ' ומן מ' אל ל' ומן י' אל כ' ומן ט' אל נ' ומן ז' אל ל' ומן ח' אל מ' שוים [מד' מא'] | ||
| והזויות אשר יקיפו בהם אותם הקוים שוות | ||
| מפני כי מרחק ו"ח מן ה' מרחק אחד ושוה למרחק ט"ז מן ה' | ||
| ואם הוצא מט' אל ז' קו ומן י' אל ח' קו יהיו שוים | ||
| אם כן מרובע י"ז ח"ט נצב הזויות שוה הצלעות | ||
| וכן כל מרובעי כ"ל מ"נ וי"כ נ"ט וי"כ ז"ל וז"ל מ"ח וט"נ ח"מ שוי הצלעות נצבי הזויות | ||
| אם כן כל המרובעים הששה שוים שוי הצלעות נצבי הזויות | ||
| אם כן מוגשם זי"ט חל"כ מ"נ מעוקב והוא בבעל שמונה תושבות הידוע | ||
| וזה מה שרצינו לבאר |
Notes
- ↑ titled: F137 הקדמות המאמר; Ma1 הקדמות זה המאמר; W66 הקדמה; Lo; Ma1; P1014: marked א
- ↑ פי: ר"ל בשטח ולא יקראו המקיפים בו אם לא שיהיה השטח נצב הזויות בעבור שהשני הקוים לא ישערו השטח אם לא שיהיה השטח נצב הזוית פי' עד כאן
marg.: קוים המקיפים בו פי' ר"ל ששני אלו הקוים מודיעים לנו שעור שטח ומגבילים אותו
המשל בזה אם יהיה אחד מן הקוים ארכו ו' אמות ורחב האחר ג' אמות יהיה כל שעור זה השטח י"ח אמות מהכאת האורך ברחב או אם תרצה תכה הרחב באורך ויהיה י"ח גם כן
וכל זה כשיהיה הקו האחד עומד על חבירו על זוית נצבת מה שאין כן בשטח שאינו נצב הזויות
ד"ת ונקרא השטח בשם שתי אותיות המתנגדות
הנה צריך שילקח בזה התנאי שיהיה השטח נצב הזוית שאם לא יהיה כן לא יקראו המקיפים ולא ישערו את השטח השני קוים המקיפים בו
E: הקוים המקיפי’ באחת הזוית הנצבות מהשטח נצב הזויות נכחי הצלעות יקראו מקיפים בשטח ההוא [כי] הנה מקביליהם ישוו להם
W66: ר"ל ששני אלו הקוים [..] מודיעים לנו שעור השטח ומגבילים אותו
המשל בזה כי אם יהיה אחד מן הקוים ארכו ו' אמות ורחב האחר ג' אמות יהיה כל שעור זה השטח י"ח אמות מהכאת האורך ברחב או הרחב באורך
וכל זה כשיהיה הקו האחד עומד על חברו על זוי' נצבת מה שאין כן בשטח שאינו נצב הזויות
E: ויקרא השטח בשם שתי אותיות המתנגדות אשר בצד קטרו
P1010 (marg.), PP: ונקרא השטח בשם שתי אותיות הזויות המתנגדות
W194 (marg.): ד"ת ונקרא בשטח בשם שתי אותיות הזויות המתנגדות
Lo (marg.): ונקרא השטח בשם שתי אותיות הזויות המתנגדות בו - ↑ Ma1: marked השנית
- ↑ Lo: והמתמימים באור זה מבואר במ”ג מראשון והרושם הוא שני השטחים המתמימים עם אחד מן השטחים שעל קטרו
- ↑ Mu 246:א כל שטח שוה הצלעות נצב הזויות יסובבנו השני קוים הסובב בזוית הנצבת וכל שטח נגדיי הצלעות נאמ' כי השני שטחים שעל אלכסונו הנגדיי הצלעות והאלכסון יחצבם כשיצטרף אחד מהם לשני השטחים המשלימין שעל שני צדי האלכסון כל זה יקרא עלם
P1011: כל שטח נכחי הצלעות נצב הזויות הנה יקיפו השני קוים המקיפים בזוית הנצבה
וכל שטח נכחי הצלעות הנה השני שטחים אשר יהיו על קטרו [נכח]יי הצלעות והקוטר יחצבם כאשר [...] מהם אל השני שטחים המשלימים אשר [על] צדדי הקוטר יקרא הרושם עד כאן פתי[חה]
E: כל שטח נכחי הצלעות יחתכהו הקוטר והוציאו מנקודו’ ממנו קוים נכחיים לצלעות יחתכם הקוטר ועומדי’ מצדו יקראו השטחי’ אשר יחתכם הקוטר אשר על הקוטר ואשר מצדו המתמימים ומקובץ אחד השטחים שית[ח]כהו הקוטר עם שני המתמימים אשר משני צדיו יקראו הרושם
Ma1: באור להקדמה ב’ הנה נעשה מרובע עליו א’ב’ג’ד’ ובתוכו קוטר אחד והוא קוטר ב”ד ונרשום עליו נקודה איך שתזדמן והיא נקודת ח’ ונגיע מנקודת ח’ קו ט’ח’כ’ על נוכח א”ב וקו ה’ח’ז’ על נוכח ב”ג הנה חלקנו מרובע א’ב’ג’ד’ לארבעה מרובעי’ והם א”ח ה”כ ט”ז ח”ג שנים מהם על קוטר ב”ד ושנים חוצה לו ויאמר שאם נקח אחד משני מרובעי ט”ז ה”כ אשר על הקוטר איזה מהם שנרצה עם שני המרובעי’ אשר חוץ לקוטר הנקראים המשלימים כמבואר בלמוד מ”ג מהמאמר הראשון יקראו אלה השלשה מרובעים רושם ויהיה שעור דבריו כך כל תמונה נכחית הצלעות אחד השטחים וכו’ יקרא הרושם - ↑ F137 titles the propositions’ section: המבוקשים;
- ↑ P1011: כל שני קוים יחלק אחד מהם בחלוקה איך שיהיה הנה אשר יהיה מהכאת אחד משני הקוים באחר כמו אשר יהיה מהכאת הקו אשר לא יחלק בכל חלקי הקו המתחלק חלוקה חלוקה
E: 1 השטח אשר יקיפו בו כל שני קוים שוה למקובץ השטחים יקיפו בם אחד הקוים עם חלקי הקו השני יחד
Mu36 adds a marginal note: כונת זה הדרוש שכשהיו לנו שני קוים מונחי’ כמה שיהיו וחולק האחד מהם לחלקים כמה שהיו שהכאת הקו האחד בכל אחד מהחלקים שחולק הקו השני שוה להכאת הקו ההוא בקו המחולק כלו
The arithmetic version of the proposition is given in marginal notes in a few manuscripts:
Mu91: המשל לתמונת א' משני
כמו עשרה וששה וחולק עשרה לשלשה חלקים כגון חמשה ושלשה ושנים
הנה שטח ששה בעשרה שהוא ס' שוה לשטח חמשה בששה שהוא שלשים ולשטח ששה בשלשה שהוא י"ח ולשטח ששה בשנים שהוא י"ב וקבוץ שלשת שטחים אלו הוא ס'
W66: פי’ משל זה במספר כמו עשרה וששה וחולק עשרה לג' חלקים כגון ה' וג' וב' הנה שטח ששה בעשרה שהוא ס' שוה לשטח ששה בחמשה שהוא שלשים ולשטח ששה בשלשה שהוא י"ח ולשטח ששה בשנים שהוא י"ב וקבוץ שלשת שטחים אלו הוא ששים
Numerical example:
P1010: דמיון במספר כאשר תכה מספר בעצמו יהיה המרובע ההווה ממנו כמרובע ההוה מהכאת המספר ההוא בכל אחד מחלקיו השוים
המשל בזה הכאת י’ בט”ו הוא ק”נ וכשתחלק ט”ו לג’ חלקים שוים שהוא ה’ ותכה עשרה בה’ ה’ יהיה ק”נ
Numerical example:
P1014: וכן במספר שה’ עם ד’ הם כ’ וכולו חולק הה’ על ג’ וב’ ותכה הד’ עם השני חלקים יהיו כ’
Numerical example: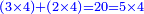
- ↑ C: המשל בזה שקו א' וקו ב"ג נחלק אחד מהם והוא ב"ג על נקודות ד' וה' ואומר שאשר יהיה מהכאת א' בחלק ב"ד ובחלק ד"ה ובחלק ה"ג שוה לאשר יהיה מהכאת א' בב"ג
E: יהיו שני קוי א' ב"ג ונחלק ב"ג על חלקי' איך שנרצה והם ג"ה ה"ד ד"ב ואומ' שהשטח נצב הזויות שיקיפו בו קוי א' ג"ב שוה למקובץ שטחי א'ג"ה וא'ה"ד וא'ד"ב
Mu246: ב שני קוי א'ב"ג חולק ב"ג בחלקי ב"ד ד"ה ה"ג נאמ' כי כפל א' בכל ב"ג ככפל א' בכל אחד מן ב"ד ד"ה ה"ג מקובצי - ↑ AB: פי' זה התבאר מכח מה שאמרנו ששטח ב"ח שוה לשטח ב"ד ד"כ ה"ח
- ↑ C: מופת זה שנוציא מקו ב"ג מנקדת ב' קו על זוית נצבה שוה לקו א' והוא קו ב"ז
ונוציא מנקדת ז' קו נכוחי לקו ב"ג והוא קו ז"ח
ונוציא מנקדת ד' וה' וג' קוים נכוחיים לקו ב"ז והם ד"ט וה"כ וג"ח
וכבר התבאר ששטח ז"ג שוה לשלשת שטחי ז"ד וט"ה וכ"ג וכל השטחים הם נכוחי הצלעות
ושטח ז"ג הוא מהכאת קו א' בקו ב"ג לפי שיקיפו בו קוי ז"ב ב"ג וז"ב שוה לא'
ושטח ז"ד יקיפו בו קוי ז"בוז"ב שוהב"ד וקו ב"ז שוה לקו א'
ושטח ט"ה הוא מהכאת קו א' בקו ד"ה לפי שיקיפו בו קוי ט"ד ד"ה ושקו ט"ד שוה לקו א'
ושטח כ"ג הוא מהכאת א' בה"ג לפי שכ"ה שוה לקו א'
E: מופתו שנוציא מן ג' על קו ג"ב עמוד ג"ח שוה לקו א' ונשלים התמונה
ונוציא מן ה' וד' עמודים על ג"ב והם ה"כ ד"ט
הנה לפי ששטח ב"ח שוה לשלשה שטחי ח"ה ה"ט ט"ב
לפי שמקובץ חלקי השטח שוה לכל השטח ושטח ח"ב שוה לה אשר יקיפו בו א' עם ג"ב
וח"ה שוה לה אשר יקיפו בו א' עם ג"ה
וכן ה"ט לאשר יקיפו בו א' עם ה"ד
וד"ז לאשר יקיפו א' עם ד"ב
Mu246: כיצד נוציא קוי ב"ז כ"ט ה"כ ג"ח על זויות נצבות וכל אחת מהן שוה לקו א'
לפי הדבר נראה כי כל שטח ב"ח הוא כפל א' בב"ג ושטח ב"ט הוא כפל א' בד"ה ושטח ה"ח כפל א' בה"ג - ↑ C: וכבר התבאר שאשר יהיה מהכאת
קקו א' בקו ב"ג שוה לאשר הוא מהכאת קו א' בקו ב"ד ובקו ד"ה ובקו ה"ג וזה מה שרצינו לבאר
E: יהיה השטח שיקיפו בו א' עם ב"ג שהוא כמו ב"ה שוה למקובץ שטחי א' עם ג"ה ה"ד ד"ב שהם כמו שטחי ח"ה ה"ט ט"ב והוא המכוון
AB: פי זה התבאר מכח מה שאמרנו ששטח ב"ח שוה לשטח ב"ד ד"כ ה"ח - ↑ P1011: כל קו יחלק לחלקים הנה אשר יהיה מהכאת הקו בכל חלקיו כמו אשר יהיה מהכאת הקו בעצמו
E: 2 כשנחלק קו ישר לשני חלקי' איך שהזדמן יהיה השטח נצב הזוית שיקיפו בו הקוכלוכלו עם כל אחד מהחלקים שוי' למרובע כל הקו
Mu36: ובנס’ אלחג’אג’ כתו’ כאשר נחלק אי זה מספר שהיה בשני חלקים איך שקרה הנה הכאת המספר כלו בכל אחד מהחלקים להכאת המספר כלו בעצמו
ולפי זאת הנס’ צריך להיות המרובע שוה הצלעו’ כמו זה שלפנינ’
AB: המשל לתמונת ב' כאשר חולק עשרה לשני חלקים כמו ששה וארבעה
הנה שטח ששה בעשרה שהוא ס' ושטח ארבעה בעשרה שהוא ארבעים שוה למרובע המתהווה מעשרה אשר הוא מאה
וזה מתבאר מתמונת א' וזה כי בתמונת א' התבאר שהכאת קו ראשון בקו שני כולו כהכאת הקו הראשון בחלקי הקו השני בין שיהיו שני הקוים ר"ל הראשון והשני שוים או בלתי שוים
W66: משל זה במספר כשנחלק עשרה לשני מספרי ו' וד' הנה שטח ו' בי' שהוא ס' ושטח ד' בי' שהוא מ' יחד שוים למרובע המתהוה מי' שהוא מאה
וזהמתפארמתבאר מתמונת א' כי שם התבאר שהכאת קו ראשון בקו שני בקו שני כלו כהכאת הקו הראשון בחלקי הקו השני בין שהיוהשני הקוים ר"ל הראשון והשני שוים או בלתי שוים
Numerical example: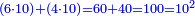
P1014: וכן הח’ אם תחלקהו לו’ וב’ מרובע הכל ס”ד ואם תכה הח’ עם הב’ ועם הב’ יהיו ס”ד וכן בשני המספרים איזה שיהיו
Numerical example: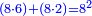
- ↑ C:המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר כי אשר יהיה מהכאת קו א"ב בקו א"ג ובקו ג"ב שוה לאשר יהיה מהכאת א"ב בעצמו
E: יהיה הקו הישר א"ב ויחלק על ג' ואומ' שמרובע א"ב שוה לשטח א"ב בא"ג וא"ב בג"ב - ↑ מופת זה שנצייר על קו א"ב שטח מרובע והוא שטח א"ה ונוציא מנקודת ג' קו עד ז' נכוחי לקוי א"ד וב"ה ויהיו שטחי א"ז וז"ב נכוחי הצלעות והם שוים לשטח א"ה ושטח א"ז הוא
נכוחיאשר היה מהכאת קו ב"א בקו א"ג לפי שיקיפו בו קוי ד"א א"ג וד"א שוה לא"ב ושטח ז"ב הוא אשר היה מהכאת א"ב בג"ב לפי שיקיפו בו ה"ב ב"ג וה"ב שוה לא"ב ושטח א"ה הוא אשר היה מהכאת א"ב בעצמו
וכבר התבאר שאשר היה מהכאת א"ב בא"ג ובג"ב שוה לאשר היה מהכאת א"ב בעצמו
E: מופתו שנעשה על א"ב מרובע א"ה ונוציא ג"ז נכחי לב"ה ולפי ששטח א"ז שוה לשטח שיקיפו בו א"ג בא"ב כי ג"ז כמו א"ב וכן ששטח ג"ה שוה לשטח שיקיף בו א"ב בג"ב ושניהם שוים למרובע א"ה יהיה מרובע א"ה שהוא ההוה מקו א"ב שוה לשני שטחים ההוים מא"ב בא"ג וא"ב בב"ג
וכבר יתבאר זה בצד אחר כשנניח קו ח' שוה לא"ב ותהיה השטח הנצב הזוית שיקיף בו ח' בא"ב שהוא כמו מרובע א"ב משלפניה' שוה לשטח נצב הזוית שיקיף בו ח' בא"ג וח' בג"ב והם כמו שטחי א"ג בא"ב וג"ב בא"ב
Mu246: ג כשיוחלק קו א"ב בחלקי א"ג ג"ב נאמ' כי כפל א"ב בפני עצמו ככפלו בכל אחד מן א"ג ג"ב
והדבר בו ברור כשנעשה על קו א"ב מרובע ואחר כך נוציא בו קו ג"ז עמוד - ↑ E:3 השטח ההוה מקו מה עם אחד מחלקיו שוה לשטח נ"ה שיקיפו בו השני חלקי' ומרובע החלק הנזכר
P1011: כל קו יחלק בשני חלקים הנה אשר יהיה מהכאת כל הקו באחד החלקים כמו אשר יהיה מאחד מהחלקים בשני והכאת החלק אשר בו הוכה הקו בעצמו
Mu36: נס’ אלחג’אג’ כאשר נחלק מספר בשני חלקים איך שקרה הנה הכאת המספר כלו באחד מחלקיו שוה להכאת שני החלקים הא[חד] בחבירו עם הכאת החלק ההוא בעצמו
W66: משל זה במספר כשחולק קו עשרה לשני חלקים כמו ששה וארבעה הנה שטח ד' בי’ שהוא מ’ שוה לשטח ו' בד’ שהוא כ”ד עם מרובע ד’ שהוא י”ו
Mu91: המשל לתמונת ג' כאשר חולק קו עשרה לשני חלקים כמו ששה וארבעה הנה שטח ארבעה בעשרה שהוא מ’ שוה לשטח ששה בארבעה שהוא כ”ד עם מרובע ד’ שהוא י”ו
וזה מתבאר מתמונת א’ וזה כי בתמונת א’ התבאר שהכאת קו ראשון בקו שני כמו הכאת קו ראשון עם חלקי הקו השני
וכן בתמונה הזאת כי הכאת קו ארבע שהוא הראשון עם עשרה השני כהכאת הקו ד’ הראשון עם ששה וארבעה שהם חלק הקו השני
Numerical example: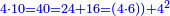
Mu130: יהיה הקו כלו עשרה ונחלק לשבעה וג’ הנה הכאת עשרה בג’ שהם ל’ כמו הכאת ז’ בג’ שהם כ”א עם הכאת ג’ בעצמו שהם ט’ שהמקובץ מכ”א וט’ יעלו ל’
Another example: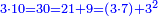
P1010: דמיון במספר המרובע המתהוה מהכאת עשרה בששה כמרובע ההווה מהכאת ששה בארבעה שהוא כ”ד וכמרובע ההווה מששה בעצמו שהוא החלק אשר זכרנו והיה ל”ו והכל ששים וכך מרובע עשרה בששה
Example: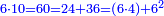
P1014: וכן הח’ על ו’ וב’ הח’ עם הב’ יעלו י”ו וכן הו’ בב’ ומרובע הב’ יעלו י”ו וכן בכל מן מספר
Example: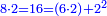
- ↑ C: המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר שאשר יהיה מהכאת קו א"ב בא"ג שוה לאשר יהיה מהכאת א"ג בג"ב ומהכאת א"ג בעצמו
E: יהיה הקו א"ב ונחלק על נקודת ג' ואומ' ששטח א"ב באחד מחלקיו ויהיה ב"ג שוה למרובע ב"ג עם שטח א"ב בב"ג - ↑ C: מופת זה שנצייר על קו א"ג שטח מרובע עליו א"ז ונוציא קו ז"ד אל ה' ונוציא מב'
מביתקו נכוחי לקוי א"ד וג"ד והוא קו ב"ה ושטחי ז"ב וז"א נכוחי הצלעות ושטח ב"ד גם כן נכוחי הצלעות והוא שטח ז"ב ושטח ז"א יחד וז"ב הוא שהיה מהכאת א"ג בג"ב לפי שיקיפו בו ב"ג ג"ז וז"ג שוה לג"א וב"ד הוא שהיה מהכאתא"ג בג"בא"ב בא"ג לפי שיקיפו בו ב"א א"ד וג"א שוה לא"ד וא"ד הוא שהיה מהכאת א"ג בעצמו
והתבאר כבר שאשר היה מהכאת ב"א בא"ג שוה לאשר היה מהכאת א"ג בג"ב ומהכאת א"ג בעצמו
E: מופתו שנעשה על ב"ג מרובע והוא ב"ד ונוציא קו ד"ה על יושר ונשלים שטח א"ה ויהיה שטח א"ה שוה לשני שטחי א"ד ד"ב ושטח א"ה שוה לשטח שיקיפו בו א"ב ב"ג כי ב"ג שוה לב"ה ושטח א"ד שוה לשטח שיקיפו בו א"ג ג"ב כי ג"ד שוה לג"ב ושטח ג"ה שוה למרובע ג"ב הנה שטח א"ב ב"ג שוה לשני שטחי א"ג בג"ב ומרובע ג"ב
וכבר יתבאר זה בהניחנו קו ח' שוה לקו ג"ב ויהיה שטח ח' בא"ב שוה לשני שטחי ח' בא"ג וח' בג"ב וח' בג"ב הוא כמו מרובע ג"ב כי ח' שוה לג"ב וא"ג בח' כמו שטח א"ג בג"ב הנה שטח א"ב בב"ג שוה לשטחי א"ג בג"ב ומרובע ג"ב
Mu246: ד [כמו של מעלה] קו א"ב חולק בשני חלקי' על ג' נאמ' כי כפל א"ב בא"ג ככפל א"ג בג"ב וכפל א"ג [בפני] עצמו מקובצי' נוציא עמוד א"ד שוה לא"ג וכמו כן כיוצא ב"ה ג"ז והוא כפל א"ג בפני עצמו ושטח ג"ה הוא א"ג בג"ב וכל שטח א"ה הוא כפל א"ב בא"ג - ↑ P1011: כל קו יחלק בחלקים הנה אשר יהיה מהכאת הקו בעצמו כמו אשר יהיה מהכאת כל חלק בעצמו ומהכאת אחד החלקים באחר שני פעמים
E: 4 מרובע כל קו נחלק לשני חלקים שוה למרובעי שני חלקיו וכפל שטח אחד מהם באחר Mu36: נס’ אלחג’אג’ כאשר חולק איזה מספר שיהיה בשני חלקים איך מה שקרה הנה הכאת המספר ההוא בעצמו שוה להכאת כל אחד מהחלקים בעצמו ולהכאת כל אחד משני החלקים בחבירו
Mu130: יהיה הקו עשרה נחלק על שלשה וז’ נכה שלשה בשבעה עלו כ"א והכפל מ"ב ומרובע שבעה מ"ט נוסיפם עלו צ"א נוסיף מרובעכל הקוג’ שהוא ט’ עלו מאה וכן מרובע כל הקו מאה
Numerical example:![\scriptstyle{\color{blue}{\left[2\sdot\left(3\sdot7\right)\right]+72+32=\left(2\sdot21\right)+49+9=42+49+9=91+9=100=102}}](/mediawiki/images/math/1/1/3/113ef37869cb07a63959a68cc09af144.png)
P1010: דמיון במספר כאשר תכה עשרה על דרך משל בעצמו יהיה מאה אחר כן תחלק עשרה לשני חלקים על דרך משל לז’ וג’ ותרבע ז’ בעצמו יהיה מ"ט עוד ג’ בעצמו יהיה ט’ והכל נ"ח עוד תכה ג’ בז’ ב’ פעמים יהיה מ"ב הכל מאה
Numerical example:![\scriptstyle{\color{blue}{\left[2\sdot\left(3\sdot7\right)\right]+72+32=\left(2\sdot21\right)+49+9=42+58=100=102}}](/mediawiki/images/math/4/1/c/41c82e0003478bf24398273435235086.png)
P1014: העשרה כלו חולק על ו’ וד’ מרובע הכל ק’ שוה למרובע הו’ והד’ וכפל שטח ו' בד’ וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{102=100=\left[2\sdot\left(6\sdot4\right)\right]+62+42}}](/mediawiki/images/math/2/e/6/2e682b264718f78a3fc3fde0b8b0dbbd.png)
- ↑ C: המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר שאשר יהיה מהכאת א"ב בעצמו שוה לאשר יהיה מהכאת א"ג בעצמו וג"ב בעצמו וא"ג בג"ב פעמים
E: יהיה הקו הנחלק א"ג וחלקיו א"ב א"ג אומ' שמרובע א"ג כמו שני מרובעי א"ב ב"ג וכפל שטח א"ב [ב]ב"ג - ↑ E: מופתו שנעמיד על קו א"ג מרובע א"ה ונוציא בו קוטר א"ה ומן ב' עמוד ב"ד נכחי לג"ה יחתוך קוטר א"ה על ז' ונוציא מז' קו נכחי לקו א"ג והוא ח'ז'ט' ויתבאר ששטחי א"ז ז"ה שעל הקוטר מרובעים לפי שזוית ג' נצבת וזויות ג'א'ה' ג'ה'א' שוות כי קוי ג"א ג"ה שוות הנה כל אחת מהן חצי נצבת הנה קוי א"ב ב"ז שוים ולכן א"ז מרובע וכן קוי ז"ט ט"ה שוים ולכן ז"ה מרובע וקו ז"ט שוה לקו ב"ג הנה שטח ז"ה כמו מרובע ב"ג ולפי שמרובע א"ה ההוה מן א"ג שוה לשני מרובעי א"ז ז"ה ושני מתמימים כ"ט ח"ד ושני אלה המרובעים הם כמו מרובעי א"ב ב"ג ומתמים כ"ט כמו השטח שיקיף בו ב"ג בב"ז השוה לא"ב והוא שוה למתמים ח"ז יהיה מרובע א"ג שוה לשני המרובעים ההווים מן א"ב ב"ג וכפל שטח א"ב בב"ג
ולו מופת קרוב והוא שנניח קו דה"ז שוה לא'ב'ג' ד"ה שוה לא'ב'ג' וה"ז לב"ג והנה יהיה שטח א"ב בכל ד"ז שוה לשטח א"ג בד"ה וא"ג בה"ז ואבל שטח א"ג בד"ה כמו שטח א"ב בד"ה שהוא כמו מרובע א"ב וב"ג בד"ה וכן שטח א"ג בה"ז שוה לשטח ב"ג בה"ז שהוא כמו מרובע ב"ג ושטח א"ב בה"ג הנה שטח א"ג בד"ז השוה לא"ג כמו מרובע א"ב ומרובע ב"ג וכפל שטח א"ב בב"ג ומשל - ↑ E: והתבאר בזה שהשטחים שעל קוטר המרובע הם מרובעים ואם הם מרובעי' הקוטר קוטר למרובעי' ושמרובע כל קו ד' דמיוני מרובע חציו וט' דמיוני מרובע שלישיתו
- ↑ P1011: כל קו יחלק בחציים ואחר יחלק בחלקים מתחלפים הנה אשר יהיה מהכאת החלק היותר ארוך בחלק היותר קטן ומהכאת יתרון חצי הקו על החלק היותר קצר בעצמו הוא כמו אשר יהיה מהכאת חצי הקו בעצמו
For any line divided in half and then divided into two unequal parts, the [sum] of the product of the larger part by the smaller part and the product of the excess of half the line over the smaller part by itself is equal to the product of half the line by itself
E:
5 הקו הנחלק לחצאיים ולחלקי' בלתי שוים בשטח שיקיפו בו החלקים הבלתי שוים עם מרובע הקו שבן שני המקומות שוים למרובע חצי הקו
Mu36:ובנס’ אלחג’אג’ כאשר חולק אי זה מספר שיהיה בשני חלקים שוים ובשני חלקים בלתי שוים הנה הכאת החלקים הבלתי שוים כל אחד בחבירו עם הכאת המספר אשר מה שבין בעצמו שוים להכאת חצי המספר בעצמו
In the version of al-Ḥajjāj: when a number is divided into two equal parts and into two unequal parts, [the sum of] the product of the unequal parts one by the other together with the product of the number that is the difference by itself [is] equal to the product of half the number by itself
Mu130:
יהיה הקו עשרה ונחלק בשווי על חמשה ובבלתי שיווי על שלש נכה שלשה בשבעה עלה כ”א נוסיף מרובע שבין שלשה וחמשה והוא ארבע כי המרחק שנים עלו כ”ה וכן מרובע חצי הקו שהוא חמשה עולה כ”ה
P1010:דמיון במספר כשנחלק עשרה על ה’ ה’ חלקים שוים עוד נחלק עשרה לג’ וז’ על [דרך] משל הנה המרובע המתהוה מחלק השוה באחר שהוא [...] כ”ה [...] המרובע המתהוה מג’ על ז’ שהוא כ”א עם המרובע המתהוה מתוספת ז’ על ה’ שהוא ב’ ומרובעו ד’ והכל כ”ה
Numerical example:
P1014:![\scriptstyle{\color{blue}{\left(3\sdot7\right)+\left[\left(\frac{1}{2}\sdot10\right)-3\right]^2=21+\left(5-3\right)^2=21+2^2=21+4=25=5^2=\left(\frac{1}{2}\sdot10\right)^2}}](/mediawiki/images/math/1/5/3/153fd747e25cb09c6de8b6414c49e8d6.png) העשרה אם תחלקהו על ה’ ועל ו’ וד’ הנה שטח ו’ בד’ עם מרובע אחד שבין ה' לו’ שוה למרובע ה’ה’ שהם כ”ה וכן בשיעורים
העשרה אם תחלקהו על ה’ ועל ו’ וד’ הנה שטח ו’ בד’ עם מרובע אחד שבין ה' לו’ שוה למרובע ה’ה’ שהם כ”ה וכן בשיעורים
Numerical example:
![\scriptstyle{\color{blue}{\left(6\sdot4\right)+\left[6-\left(\frac{1}{2}\sdot10\right)\right]^2=24+\left(6-5\right)^2=24+1^2=24+1=25=5^2=\left(\frac{1}{2}\sdot10\right)^2}}](/mediawiki/images/math/1/5/3/153a80898ac8207e134965131113b24f.png)
- ↑ C: המשל בזה שקו א"ב נחלק לחלקים שוים על נקדת ג' ולחלקים מתחלפים על נקודת ד' ואומר שאשר היה מהכאת א"ד בד"ב ומהכאת ג"ד בעצמו יחד שוה לאשר יהיה מהכאת ג"ב בעצמו
E: ויהיה קו ישר א"ב ויחלק לחלקי' שוים על ג' ולבלתי שוים על ד' הנה אומר ששטח א"ד בד"ב עם מרובע ג"ד שוה למרובע ג"ב - ↑ C: מופת זה שנצייר על קו ג"ב שטח מרובע עליו ג"ה[ז"ב] ונדביק ב' בה' ונוציא מד' קו אל ט' נכוחי לקוי ג"ה וב"ז עליו ד'ח'ט' ונוציא מח' קו נכוחי לקוי א"ב וה"ז עליו לח"ב ונוציא מא' קו נכוחי לקוי ג"ל וד"ח וב"כ והוא א"מ ונמשוך קו כ"ל אל מ' ושטח ג"ח המשלים שוה לשטח ח"ז המשלים ויהיה שטח ד"כ משותף ויהיה יחד שטח ג"כ שוה לשטח ד"ז יחד ואמנם ג"כ שוה לג"מ לפי שהם על שתי תושבות שוות ב"ג וג"א ובין שני קוים נכוחים ב"א וכ"מ
ואם כן שטח ג"מ שוה לשטח ד"ז ויהיה ד"ל משותף ויהיה יחד מ"ד שוה לנס"ע המסומן ומ"ד הוא שהיה מהכאת א"ד בד"ב לפי שיקיפו בו א"ד ד"ח וח"ד שוה לב"ד ויהיה נ'ס'ע' המסומן שוה לאשר יהיה מהכאת א"ד בד"ב ונשים אשר יהיה מהכאת ג"ד בעצמו משותף והוא שטח ל"ט המרובע
ויתבאר שאשר היה מהכאת א"ד בד"ב ומהכאת ג"ד בעצמו יחד שוה לשטח ג"ז שהיה מהכאת ג"ב בעצמו שהוא חצי הקו [ר”ל מהתבארות צורת ד’ מזה השער]
E: מופתו שנעשה על ג"ב מרובע ג"ז ונוציא ד"ע עמוד על א"ב וקוטר ה"ב ויתחתכו על ח' ונוציא קו ט'ח'ב' נכחי לא"ב ונשלים התמונה הנה מרובע ג"ז ההוה מקו ג"ב שוה לשני מתמימי ג"ח ח"ז עם מרובעי ב"ח ח"ד ולפי שמתמים ג"ח עם [מרובע] ד"כ העושה שטח ג"כ ישוה לשטח ג"ט יהיה שטח ג"ט עם מתמימי ח"ז שהוא כמו שטח א"ח עם מרובע ח"ה [שוה לשטח ג"כ [עם] מרובע ח"ה ומת[מים] ח"ז אבל שטח ג[כ] עם מרובע ח"ה] ומתמים ח"ז כמו המרובע ההווה מן ג"ב ושטח א"ח הוא ההווה מהכאת א"ד בד"ב [כי] ד"ח ד"ב שוים ומרובע ח"ה הוא כמו המרובע ההווה מן ג"ד הנה שטח [א"ד] בד"ב עם מרובע ג"ד כמו המרובע ההווה מן ג"ב
ויתבאר גם כן שלפי שג"ב נחלק בנקודת ד' איך שיזדמן היה מרובע ג"ב כמו המרובע ההווה מן ג"ד עם [כפל] שטח ג"ד בד"ב ומרובע ד"ב [כפל] ושטח ג"ד בד"ב עם מרובע ד"ב כמו שטח ג"ד בב"ד והוא כמו שטח א"ג בד"ב [הנה] שטח א"ג בד"ב עם שטח ג"ד בד"ב שזה כמו א"ד בד"ב כשקובץ עם מרובע ג"ד היה כמו מרובע ג"ב
Mu246: ו קו א”ב חולק בחציו על ג’ ובשני חלקים שאינם שוים על ד’ נאמ’ כי כפל א”ד בד”ב וכפל ג”ד בפני עצמו מקובצים ישוו לג”ב בפני עצמו
נעשה על ג”ב מרובע ג”ז ונחוק בו מרובע ב”ח ושני שטחי ג”ח ח”ז וגם נעשה שטח א”ל על יושר קו מל”כ וקו א”מ כמו ד”ב ומפני שא”ג שוה לב”ז הילכך שטח א”ל כמו ד”ז וכפל א”ד בד”ב הוא שטח א”ח ונשים שטח ג”ח שותף ויהא נס”ע שוה לשטח א”ח שהוא כפל א”ד בד”ב ומרובע ה”ח הוא כפל ג”ד בעצמו - ↑ C adds: והתבאר לך הנה ששני מרובעי החלקים המתחלפים יעדפו על כפל שטח נצב הזויות שיקיפו בו החלקים ארבעה דמיוני מרובע הקו שבין מקומות החלקים
תקון המעתיק ועוד יתבאר לך הנה כי כשיחלק קו בשני מקומות לחלקים שאינם שוים שהשטח שיקיפו בו שני קוי החלוקה האחד בלתי שוה לשטח שיקיפו בו שני קוי החלוק האחר
כי כל אשר ירחק מקום החלוק מחצי הקו יחסר השטח שיקיפו בו שני קוי החלוק
ומתוך הצורה אשר לפני זו התבאר כי כשיעור אשר יחסר כפל שטח שיקיפו בו קוי החלוק האחד מן האחר יוסיפו שני מרובעי הקוים ההם על שני מרובעי הקוים האחרים ולפי ביאור זה נעשו מופתים רבים בשער העשירי - ↑ P1011: כל קו יחלק בחציים עוד נוסף עליו קו אחר בארכו הנה אשר יהיה מהכאת כל זה בקו הנוסף ומהכאת חצי הקו הראשון בעצמו הוא כמו אשר יהיה מחצי הקו הראשון כאשר יחובר הקו הנוסף ואחר הוכה כלו בעצמו יחד
Mu36: נ’ אלחג’אג’ כאשר נחלק אי זה מספר שהונח בחציים והוספנו עליו מספר מו[נח] הנה הכאת המספר המקובץ במספר הנוסף עם מרובע חצי המ[ספר] שוים למרו[בע] חצי המספ[ר] והתוספת כשחוברו והושמו מ[ספר] אחד
Mu130: [...] יהיה הקו עשרה ונוסיף עליו ארבע נכה ארבע
P1010: דמיון במספר כשנחלק עשרה לחציין והוא ה’ ותוסיף על עשרה שנים על דרך משל הנה מרובע המתהוה מהמספר כולו שהוא י”ב כאשר תכה אותו בשנים שהוא התוספת ויהיו עשרים וארבע [..] המרובע המתהוה מ[חצי] [מספר] הראשון שהוא ה’ ומרובעו כ”ה והכל מ”ט כמרובע המתהוה מחצי המספר עם התוספת שהוא ז’ ומרובעו מ”ט
Numerical example:![\scriptstyle{\color{blue}{\left[\left(10+2\right)\sdot2\right]+\left(\frac{1}{2}\sdot10\right)^2=\left(12\sdot2\right)+5^2=24+25=49=7^2=\left(5+2\right)^2=\left[\left(\frac{1}{2}\sdot10\right)+2\right]^2}}](/mediawiki/images/math/d/3/1/d31d0d74b15499bed8abd54a866f974f.png)
P1014: וכן במספר אם תחלק הי”ב ות[ו]סיף עליו ב’ הנה השטח י”ד עם ב’ ומרובע ו' שהו’ חצי י”ב והכל ס”ד שוה למרובע הח’ שהו’ תוספת הקו עם חציו כמש[.] התמונה וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{\left[\left(12+2\right)\sdot2\right]+\left(\frac{1}{2}\sdot12\right)^2=\left(14\sdot2\right)+6^2=64=8^2=\left(6+2\right)^2=\left[\left(\frac{1}{2}\sdot12\right)+2\right]^2}}](/mediawiki/images/math/d/b/f/dbff83c5299277fd73a904ad1f1f3a68.png)
- ↑ P1011: כל קו יחלק בחלקים הנה אשר יהיה מהכאת הקו בעצמו והכאת אחד משני החלקים בעצמם יחד הוא כמו אשר יהיה מהכאת הקו כלו בחלק אשר תכה בעצמו שני פעמים ומהכאת החלק האחד בעצמו
Mu36: נס’ אל חג’אג’ כאשר נחלק אי זה מספר שיהיה בשני חלקים איך מה שקרה ה[נה] המרובעי’ ההווים מהמספר כלו ומאחד מהחלקים כאש[ר] קובצו שוים לכפל הכאת המספר כלו בחלק אשר זכרנו [עם] הכאת החלק הנשאר בעצמו
Mu130: ויהיה הקו עשרה ויחלק על ששה נכה ששה בעשרה עלה ס’ וכפלו ק”כ ועם מרובע ארבע שהוא י”ו עלה [...] קל”ו וכן מרובע כל הקו שהוא עשרה עם מרובע החלק הנזכר שהוא ששה עלו [...]
P1010: דמיון במספר כשנחלק מספר עשרה לד’ ו’ יהיה המרובע המתהוה מכל המספר מאה והמרובע המתהוה מו’ על דרך משל ל”ו והכל קל”ו ויהיה שוה למרובע המתהוה מהכאת עשרה בששה שני פעמים שהם ק”כ והמרובע המתהוה מן החלק הנשאר שהוא ד’ ומרובעו י”ו ועם ק”כ יהיו קל”ו
Numerical example:![\scriptstyle{\color{blue}{10^2+6^2=100+36=136=120+16=\left(2\sdot60\right)+16=
\left[2\sdot\left(10\sdot6\right)\right]+4^2}}](/mediawiki/images/math/3/a/b/3ab19fd72438ca4bb72c921369fc9aaa.png)
P1014: וכן עשרה אם חולק על ח’ וב’ מרובע הי’ שהו’ ק’ ומרובע הב’ שהו’ ד’ והכל ק”ד שוה לכפל י’ עם ב’ שהו’ מ’ ומרובע ח’ בין הכל ג”כ ק”ד וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{10^2+2^2=100+4=104=40+64=
\left[2\sdot\left(10\sdot2\right)\right]+8^2}}](/mediawiki/images/math/5/0/c/50ca39d8b1c1632a6ce0b882cb22620d.png)
- ↑ דמיוני: AB פי’ כפולי
- ↑ P1011: כל קו יחלק בחלקים עוד נוסף באורך הקו כמו אחד מהחלקים הנה אשר יהיה מהכאת כל זה בעצמו כמו אשר יהיה מהכאת הקו הראשון בחלק הנוסף ארבע פעמים והכאת החלק האחד בעצמו
Mu36: נס’ אל חג’אג’ כאשר חולק אי זה מספר שיהיה בשני חלקים איך שקרה הנה ארבעה דמיוני כפל המספר כלו באחד משני חלקיו עם הכאת החלק הנשאר בעצמו שוי[ם] למרובע המספר הנקבץ מהמספר המונח והחלק אשר זכרנו
Mu130: [יהיה הקו עשרה ונחלקהו על ג’ ונכה ד’] פעמים ג’ בעשרה עלה ק”ך [נרבע] שבעה ויעלה מ”ט נוסיפהו על ק”ך עלה קס”ט וכן [מרובע] כל הקו המונח שהוא עשרה א”כ נוסיף עליו שלושה שחולק עליו יהיה כל הקו י”ג ומרובעו קס”ט
Numerical example:![\scriptstyle{\color{blue}{\left[4\sdot\left(10\sdot3\right)\right]+7^2=120+49= 169=13^2=\left(10+3\right)^2}}](/mediawiki/images/math/1/1/9/119c63c57a6f45b75bf018ff924f1131.png)
P1010: דמיון במספר כש[נחלק] עשרה על דרך משל לב’ וח’ ונוסיף [על] עשרה שנים שה[ם] כמו החלק ה[...] ויהיה הכל י”ב ומרובעו קמ”[ד] ויהיה שוה להכאת המספר הראש[ון] שהוא עשרה ב[שנים] שהוא החלק הנ[שאר] ד’ פעמים שה[ם] שמנים ומרוב[ע] החלק עשרה הנשאר שמנה ומרובעו ס”ד והכל קמ”ד
Numerical example:![\scriptstyle{\color{blue}{\left[4\sdot\left(10\sdot2\right)\right]+8^2=80+64=144 =12^2=\left(10+2\right)^2}}](/mediawiki/images/math/3/5/7/3572c6c2fff1368f77750977b208cbff.png)
P1014: אם הי’ יחולק לו’ וד’ הנה ד’ פעמי’ הי’ עם הד’ שהם ק”ס עם מרובע הו’ ס”ד ובין הכל קצ”ו שוה למרובע י”ד שהו’ ג”כ קצ”ו וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{\left[4\sdot\left(10\sdot4\right)\right]+6^2=160+36=196 =14^2=\left(10+4\right)^2}}](/mediawiki/images/math/b/c/6/bc69367f2c839dd02ac2d7e8e1216d85.png)
- ↑ P1011: כל קו יחלק בחציים עוד יתחלק גם כן לחלקים מתחלפים הנה אשר יהיה מהכאת שני החלקים המתחלפים כל אחד מהם בעצמו הוא כפל מה שיהיה מהכאת חצי הקו בעצמו וכפל מה שיהיה מהכאת חצי הקו על החלק היותר קצר בעצמו יחד
Mu36: נס’ אל חג’אג’ כאשר חולק אי זה מספר שיהיה בשני חלקים שוים ושני חלקים בלתי שוים הנה הכאת כל אחד מהשני חלקים הבלתי שוים בעצמו מקובצים הנה הם שוים להכאת חצי המספר בעצמו עם הכאת המספר אשר מה שבין בעצמו
Mu130: [...]
P1010: דמיון במספר כשנחלק עשרה לה’ ה’ שהם שנים ונחלקהו לז’ וג’ שהם חלקים בלתי שוים הנה המרובע המתהוה מהכאת ז’ בעצמו שהוא מ”ט ומהכאת ג’ בעצמו שהוא ט’ והכל נ”ח כמרובע המתהוה מחצי הקו שהוא ה’ ורבועו כ”ה וכפלו נ’ ועוד כפל מרובע מותר החלק הגדול הבלתי שוה על החלק השוה שהיה המותר ב’ ורבועו ד’ וכפלו ח’ והכל נ”ח
Numerical example:
P1014: וכן הי”ד אם חולק לז’ ז’ וחולק לח’ וו’ מרובעי ח’ ס”ד ומרובע ו’ ל”ו בין הכל הו’ ק’ שוה לכפל מרובע ז’ שהם צ”ח וכפל מרובע א’ ובין הכל ק’ וכן בשיעורים
Numerical example: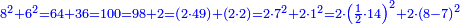
- ↑ P1011: כל קו יחלק בחציים עוד נוסף באורך הקו קו אחר הנה אשר יהיה מהכאת זה כלו בעצמו והקו הנוסף בעצמו מקבצים הוא כפל מה שיהיה מחצי הקו הראשון כאשר תחבר אליו הקו הנוסף ותכה בעצמו והכאת חצי הקו הראשון בעצמו
Mu36: נ’ אל חג’אג’ כאשר נחלק אי זה מספר מונח שיהיה בשני חלקים שוים והוספנו עליו אי זה מספר מונח שהיה הנה המרובע ההווה מהמספרהמונחהמקובץ מהמספר המונח והמספר המוסף עם הכאת המספר המוסף בעצמו הנה הם כפל המרובע ההווה מחצי המספר המונח עם הכאת המספר המקובץ מחצי המספר המונח והתוספת בעצמו
Mu130: [...]
P1010: דמיון במספר כשנחלק מספר עשרה על דרך משל לה’ ה’ והוסף עליו מספר [ב'] והוא י”ב יהיה הכאת י”[ב] שה[וא] המספר עם התוספת בעצמו והוא קמ”ד ורבוע התוספת שהוא ב’ ורבועו ד’ והכל קמ”ח שוה לכפל מרובע ההוה מחצי המספר הבלתי נוסף שהיה חציו ה’ ורבועו כ”ה וכפלו נ’ עם כפל מרובע ה’ מורכב עם ב’ שהוא הנוסף והכל ז’ ורובעו מ”ט וכפלו צ”ח והכל קמ”ח
Numerical example:![\scriptstyle{\color{blue}{\left(10+2\right)^2+2^2=12^2+2^2=144+4=148=50+98=
\left(2\sdot25\right)+\left(2\sdot49\right)=\left(2\sdot5^2\right)+\left(2\sdot7^2\right)=\left(2\sdot5^2\right)+\left[2\sdot\left(5+2\right)^2\right]=\left[2\sdot\left(\frac{1}{2}\sdot10\right)^2\right]+\left[2\sdot\left[\left(\frac{1}{2}\sdot10\right)+2\right]^2\right]}}](/mediawiki/images/math/b/a/9/ba91ead41879ce09af12af17781c287b.png)
P1014: הי’ אילו חולק לה’ ה’ והוסף עליו ד’ שהו’ י”ד הנה מרובע הכל שהו’ קצ”ו עם י”ו שהו’ מרובע ד’ בין הכל רי”ב שוה לכפל מרובע הה’ שהו’ נ’ ולכפל מורכב מה’ וד’ שהו’ ט’ וכפל מרו’ ט’ יהיה קס”ב ובין הכל רי”ב וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{\left(10+4\right)^2+4^2=14^2+4^2=196+16=212=50+162=
\left(2\sdot25\right)+\left(2\sdot81\right)=\left(2\sdot5^2\right)+\left(2\sdot9^2\right)=\left(2\sdot5^2\right)+\left[2\sdot\left(5+4\right)^2\right]=\left[2\sdot\left(\frac{1}{2}\sdot10\right)^2\right]+\left[2\sdot\left[\left(\frac{1}{2}\sdot10\right)+4\right]^2\right]}}](/mediawiki/images/math/f/8/9/f891e0ea124a956a8e6d7ca572734a4f.png)
Apparatus
- ↑ 2r
- ↑ marg.: פי' מאמרו אולם זוית גב"ז שוה לזוית בג"ח ומ"ח ל"ה כמו ל"ז ל"ד
- ↑ marg.: הפוך התמונה הנזכרת
- ↑ 2v
- ↑ E: ’מאמר ב; Mu246: מאמר שני
מספר אקלידס| Mu246; P1011; P1013; P1014: om.; Mu130: מספר היסודות; Ma1: מספר היסודות לאקלידס; C, AB; P1012: מספר אקלידס; O16: מספר אוקלידיס; W66: מספר אלקידוס; F137: מספר אוקלידס בשרשים - ↑ הנה שני: C, Ma1 om.; F137(marg.), P1012, P1014 הנה כל שני; P1007 הנה ב'
באחת: A2 באחד; Ma1 אחת
מזויותיו: B(except for W66) מזויות; W66 מזויותיה; P1012, P1014 מהזויות
הנצבות: O16 נצבות; W66 om.
יקרא: C, F יאמר
לשניהם: B, C, F להם; P1007 לשניהן
המקיפים: P1012 לשון המקיפים
בו: O16 om. - ↑ וכל: F כל; O16 ובכל
שטח: F תמונה
נכחי: F נכחית
הנה: C, F, O16 om.
אחד: Ma1 אחד [נ"ל כשאחד]
משני: C, F om.; P1007 מב'
משני השטחים: B(except for Mu130) מהשני שטחים; F137הצלעותמהשטחים
הנכחי: B(except for Mu130), F נכחיי; C נכוחי
הם: C, F om.
קוטרו: C אלכסונו
משניהם היה: B שיהיה משניהם; C, F מהם שיהיה; P1007 משניהן היה
שני השטחים: A2 השני שטחים; W66 השטחים; P1007 ב' השטחי'
המתמימים: B, C, F המשלימים
הרושם: C המסומן - ↑ א: F137, Lo, O16, P1012 mark is missing; Mu130 למוד א'
כאשר היו: C כשיהיו; F כאשר יהיו
קוים ישרים: F137 הקוין הישרים; P1013 הקוים הישרים; B(except for W66), C קוים ישרים מונחים
וחולק: B, C ונחלק
מהם: Lo, PP משניהם; P1013 מהן
אחד מהם לחלקים: O16אותםלחלקים אחד מהם; C אחד מהם חלקים
איזה מספר שיהיה: B, F כמה שיהיו/שהיו; C כמות שהן
הנה: C יהיה
הנצב: B, C, F, P1014 נצב
הזויות: P1010 הזוית
אשר יקיפו: C שיקיפו
בו: A1 בה; O16, P1012 om.
השני קוים: B, C, F שני הקוים; P1007 ב' הקוים
הישרים: C; O16 הישרים המונחים
שוה: F יהיה שוה
לכל השטחים: F לשטחים; W66 לכלל השטחים; O16 כלו לשטחים
הנצבי: B, C, F נצבי; P1012 הנצבים
אשר יקיף: C שיקיפו; O16 אשר יקיפו
בכל אחד מהם: F בהם
הקו: A2 הקו הישר
אשר לא: C שלא
נחלק: F יתחלק
וכל: A2, P1012, P1014 עם כל; P1013 לכל
וכל אחד: C ואחד
מן החלקים: B, P1007 מהחלקים - ↑ ויהיו: F המשל יהיו; B הנה יהיה/יהיו
שני: P1007 ב'
קוים ישרים: A2, F הקוים הישרים; B(except for W66) קוים ישרים מונחים
על שניהם: B, F עליהם
לחלקים: F137 חלקים
כמה שיהיו: B(except for W66) om.; A2 כמה שהוא
שתי: F om.; P1012, P1014 שני; P1007, P1013 ב'
נקודות: Ma1 נקודת - ↑ הנה אומר כי השטח: B הנה נאמר שהשטח; F אומר כי השטח; P1007 הנה אומר כי שטח
הנצב: B, F, P1007 נצב
הזויות: A2, B(except for W66), P1012 הזוית
בו: A1 בה
שני: F om.; P1007 ב'
קוי: P1013 קוים
שוה: Mu130 שוים
הנצב: B, F נצב
הזויות: Mu130 הזוית
שני: P1007 ב'
שני קוי: F om.| א' ב"ג ... שני קוי: P1012 om.
א' ב"ד: P1013 אב"ג אב"ד
והשטח הנצב: B, F ולשטח נצב
בו שני: F om.; P1007 בו ב'
שני קוי: Mu130, P1014 om.
ד"ה: Lo, PP ה"ד
והשטח הנצב: B, F ולשטח נצב
הזויות: B(except for O16) הזוית
גם כן: B, F om.
בו: A2, P1010, P1013, PP om.; B בו שני קוי; F בו קוי - ↑ ונוציא: A2, B הנה נוציא; F המופת נוציא
מן קו: A1, B, F, P1007 מקו
הישר: A1, F om.
ישר: P1014 om.
זוית נצבת: B זוית נצבה; A1, F, Lo, P1010, PP זויות נצבות; P1012 זוית קו נצבת
מי' מא': Ma1, E, O16, P1007, P1012 om.; F137, Lo, P1010, P1013, PP, W194 מי"א מראשון - ↑ ונשים: B(except for Mu130) ויהיה
ונשים קו ב"ז: A1, Ma1 om.
שוה: P1010 om.
הישר: A1, W66 om.
מג' מא': C, Ma1, E, Mu36, O16, P1007, P1012 om.; F137, P1010, P1013, PP, W194 מב' מראשון; Mu130, P1014 מב' מא' - ↑ נכחי: P1013 נכוחי ה[צלע]?
קו ז"ח ... הישר: B קו נכחי לקו ב"ג הישר והוא קו ז"ח; AB קו ז”ח נכחי לקו ב”ג הישר והוא קו ז”ח| הישר: Lo om. - ↑ מן: B, F מנקודות
מן ד': P1007 מד'
ד' ה' ג': A1 ד'ה'ג' הישר; F137 ד' ה' וג'
קוי: O16 om.
מל"א מא': Ma1, E, P1007, P1012 om.; F137, Lo, P1010, P1013, PP, W194 מל"א מראשון - ↑ הנה כל: B(except for W66) וכל
אחד: P1013 אחת - ↑ ושטח: P1013 om.
לשטחי: O16 לשטח
שוה לשטחי ב"ט: W194 twice
מפתיחת א': O561 מהפתיחה מא'; P1010 מפ' מרא'; P1014 מפת' מא'; PP מפתיחת ראשון; W66 מפתיח' א' - ↑ 13v
- ↑ ואולם: F אבל
הנה הוא: F om.
הנצב: A1, B, F נצב
הזויות: Mu130, P1007 הזוית
שני: F om.; P1007 ב' - ↑ מפני כי קו: B מפני שקו; F לפי שקו; P1012, P1014 מפני כי קוי; PP מפני כי
ואולם ... לקו א': P1007 twice, the second recurrence is erased| א': O16ג'א' - ↑ ואולם שטח: F ושטח
ב"ט: PP marg.
הנה הוא: F om.; A2, P1007, P1010 הנה
נצב: F137 הזויות נצב; P1014 הנצב
הזויות: Mu130 הזוית
אשר: F om.
שני: F om.; P1007 ב'
שני קוי: A2, Lo, P1010, P1012, PP om. - ↑ מפני כי קו: B מפני שקו
מפני כי קו ב"ז ... א': F om. - ↑ ואולם שטח: F ושטח
ד"כ: P1014 marg.
הנה הוא: F om.
שוה: P1010 שוה
הנצב: B, A1, F, P1014 נצב
הזויות: Mu130 הזוית
שני קוי: A2, F, Lo, P1007, P1010, P1014, PP om.
א' ד"ה: P1014 marg. - ↑ מפני כי קו: B מפני שקו; F לפי שקו
- ↑ ואולם שטח: F ושטח
הנה הוא: F, P1014 om.
שוה: P1010 שוה
הנצב: B, A1, F נצב
הזויות: Mu130 הזוית
בו: P1013 בהם
א' ד"ה ... שני קוי: P1012 om.| שני קוי: Ma1, O16, P1014 om.; F137 קוי; P1007 ב' קוי - ↑ מפני כי קו: B מפני שקו; F לפי שקו
לקו ה"כ: A1 לה"כ; Mu130 לקו ה"ד; O16 לקו ה"ג
מל"ד מא': A1, Ma1, E, O16, P1007, P1012, P1014 om.; F137, Lo, P1010, P1013, PP, W194 מל"ד מראשון - ↑ הנה השטח: F והשטח
הנצב: B, F, P1007 נצב
הזויות: O16 הזוית
יקיפו: P1012 om.; P1014 marg.
שני: F137 om.; P1007 ב'
שני קוי: Ma1 om.
א' ב"ג: O16 ב"ג א'
הזויות: P1007 הזויות
ה"ג: P1012 ג"ה|
לשטחים ... וא' ה"ג: F לשטח נצב הזויות אשר יקיפו בו קוי א' ב"ד והשטח נצב הזויות אשר יקיפו בו קוי א' ד"ה והשטח נצב הזויות אשר יקיפו בו קוי א' ה"ג
B לשטח נצב הזויות אשר יקיפו בו שני קוי א' ב"ד ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ד"ה ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ה"ג [הזויות: Mu130 הזוית]
AB לשטחים נצבי הזויות אשר יקיפו בהם שני קויא' ב"ד וא' ד"ה וא' ה"גולשטח נצב הזויות אשר יקיפו בו שני קוי א' ד"ה ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ה"ג - ↑ הנה: F137 וא"כ
הנה כאשר: AB הנה התבאר כי כאשר
היו: F137 יהיו
שני: P1007 ב'
ונחלק: F137 וחולק
Mu130: F137 א'
משניהם: F137, B(except for W66), P1010 מהם
לחלקים כמה שיהיו: A2 בחלקים כמה שהיו; Mu130 לאי זה חלק שיהיה; O16 לאי זה חלקים שיהיו; P1007 לחלקים כמה שיהיהו
השטח: P1007 om.
הנצב: F137, B(except for W66) נצב
הזויות: Mu130 הזוית, P1007 הזויות
בו: P1007 בהם, P1010 בו
שני: P1007 ב'
הקוים: F137 הקוין; P1007 קוים
הישרים המונחים: A1 om.
שוה: F137 יהיה שוה; O16 שוים
לכל השטחים: F137, B(except for W66) לשטחים
הנצבים: F137, B(except for W66) נצבי; A1, A2 הנצבי
יקיף: B(except for W66), A2, P1007, P1012 יקיפו
בהם: B(except for W66) בהן
נחלק: F137 יתחלק; Mu130 תחלק; O16 יחלק
וכל: P1014 לכל
וכל אחד: P1012 לאחד
מן החלקים: B(except for W66), P1007 מהחלקים|
הנה כאשר ... מן החלקים: C, Ma1, E, W66 om. - ↑ וזה: F137 וזהו
וזה מה שרצינו לבאר: E והוא המכוון; Mu130 ומש"ל; P1007 וזמש"ל; Ma1, P1014 וזה מש"ל; P1010 וזה מה שרצינו לבארו; O16 om. - ↑ ב: O16, P1007, P1012 mark is missing; Mu130 למוד ב'
כאשר נחלק: C כשיחלק; F כאשר יתחלק
איך שקרה: C בחלקים כפי אשר קרה; B איך שהזדמן; F איך שיזדמן
הנה: C, F יהיו
השטחים: Mu130 שני השטחים; O16 השני שטחים
נצבי: A1 הנצבי
הזויות: C הזוייות
אשר יקיף: C שיקיפו; P1007 אשר יקיפו
מחלקיו: Mu130, O16 מהחלקים; W66 מן חלקיו
המתהוה: A2, B, F ההוה
המתהוה מן: C om.
מן הקו: P1007, W66 מהקו; O561 מןכלוהקו
כלו: Mu130 om. - ↑ ויהיה: F137 יהיה; Ma1 המשל יהיה; B הנה יהיה
קו: F, O16, P1014 הקו
ישר: F, P1014 הישר; O16 הישר המונח
עליו: A1, A2, P1012, P1014 om.
א"ב: Mu130, P1014 קו א"ב
ויחלק: F ויתחלק; O16 נחלק; Mu130 ונחלק; W66 שנחלק
איך שיקרה: B איך שהזדמן; F איך שיזדמן; P1013 איך שקרה; O561 איך שיקרה
ג': W66 א' - ↑ הנה: F om.
אומר כי: B אומר ש
השטח: P1007, P1014 שטח
הנצב: B, F, P1013 נצב
הזויות: Mu130 הזוית
יקיפו: O16 יקיף
שני: F, O16 om.; P1007 ב'
א"ב: F, B(except for W66) ב"א
ב"ג: F, B(except for W66), P1007 א"ג; Loג"דב"ג
עם: P1007שוה למרובע המתהווהעם; P1012 וגם
השטח: A2 שטח
הנצב: B, F, A2 נצב
הזויות: Ma1, B(except for W66) הזוית
שני: P1007 ב'; P1012 שתי
שני קוי: F om.; Mu130 שני קו; P1013 שני קוים
א"ג: B(except for W66), F ב"ג; P1010 א"ג
שוה: B(except for W66) שוים; W66 שוהים
המתהוה: B, F ההוה; O561 המתהווה
מן א"ב: B(except for W66), F, P1007 מא"ב; W66מהקו כלומא"ב - ↑ והנה: Ma1 המופת; B הנה; F137 om.
מקו א"ב: F מא"ב
עליו: O561 marg.
מ"ו מראשון': C בצורת מ"ו; A1, F137, Lo, P1010, PP ממ"ו מראשון; Ma1, E, P1007, P1012, W66 om. - ↑ לכל: Mu36, Mu130 לכל; O561 כל
משני: P1007 מב'
משני קוי: F, B(except for Mu130) מקוי
מל"א מא': A1, F137, Lo, P1010, PP מל"א מראשון; Mu130 מל"א; AB, C, Ma1, E, P1007, P1012, W66 om. - ↑ הנה כל אחד משני: P1014
הנה כל אחד משני קוי א"ד ב"ה והוא ג"זהנה כל אחד משני; P1007 הנה כל אחד מב'
משני שטחי: F, B משטחי - ↑ לשני: A2 לשתי; P1007 לב'
לשני שטחי: F137 לשטחי; Ma1 לשטח; W66 לשתי שטחים
מא' מזה: A2 מהקודמת; AB מפתיחת א'; P1010 מא'; B, C, Ma1, E, P1007, P1012, P1014 om. - ↑ שוה: O16 om.
נצב: O16 הנצב
הזויות: Mu130, P1010 הזוית
יקיפו: B(except for Mu130) יקיף
בו: O561 בו
ב"א: A2, P1007 א"ב
ב"א א"ג: F137א"ב ג"בmarg. ב"א א"ג; E א"ג בא"ב; A1 ב"א וא"ג - ↑ כי הוא: F, B מפני ש
יקיפו: F, B(except for Mu130) מקיף; Mu130 מקיפים
שני: Ma1 om.; P1007 ב'
א"ד: F, B ד"א
כי הוא ... א"ד א"ג: Mu36 om.; O561 marg. בו א"ד א"ג וקו א"ד שוה לקו א"ב ושטח ג"ה שוה לשטח
א"ג: P1007 ב"ג; A1 וא"ג
א"ד: F, B ד"א - ↑ שוה: P1012 om.
נצב הזויות: F om.
ב"א א"ג ... יקיפו בו: P1014 om.
בו: P1010 om.
שני: P1007 ב'
שני קוי: Ma1, A1 om.
ב"א א"ג ... א"ב ב"ג: F137 marg.
ב"ג: Ma1 ג"ב; P1007, P1014 א"ג; P1013 ה"ג - ↑ מפני שא"ב: A2 מפני כי א"ב; P1014 מפני שא"ד; O16 הנה מפני שא"ב
לב"ה: P1014 לב"א
מפני ש... לב"ה: F137 added on top of the line - ↑ הוא: O16 om.
ההוה: P1010, P1012, PP הווה
מקו א"ב: F137 מא"ב - ↑ הנה: F ואם כן
השטח: F השטחים
הנצב: F נצבי
הזויות: O561 הזויות
בו: F בהם; P1007, P1010, W194 om.; O561 בו
שני: F om.; P1007 ב'
א"ב: B(except for Mu130) ב"א
א"ג: A1 ב"ג
הנצב: B, F, P1013 נצב
הזויות: Ma1 הזויות; O561 הזוית
בו: A2, P1007, P1010, PP om.
שני קוי: F om.
ב"ג: A1 א"ג
שוה: F שניהם שוים
למרובע: Lo עם המרבע
המתהוה: B, Lo, P1007 ההוה
המתהוה מן: F om.
מן א"ב: B(except for Mu130), P1007 מא"ב; F אדה"ב; Mu130 מן הקו כלו - ↑ הנה: F137 ואם כן
נחלק: F137 יתחלק
קו: O16 om.
איך שקרה: F137 איך שיזדמן; O16 איך שהזדמן
הנה: F137 יהיו
השטחים: O16 שני השטחים
הנצבי: F137, O16, P1012, P1014 נצבי
בהם: P1007 בו
אחד: P1007 א'
מחלקיו: O16 מהחלקים
המתהוה: F137, O16 ההוה; PP המהווה
מן הקו: P1007 מהקו; P1013 מן קו
הנה ... כלו: C, Ma1, E, B(except for O16) om. - ↑ וזה מה שרצינו לבאר: E, Mu130 ומש"ל; P1007 וזמש"ל; F, P1012 וזהו מה שרצינו לבאר; Mu36, P1014 וזה מש"ל; P1010 וזה מה שרצינו בארו
- ↑ ג: P1007, P1012 mark is missing; Ma1 ד'; Mu130 למוד ג'; O561 marg. at the end of proposition 2 חסר מכאן תמונת ג’ והיא [...]
כאשר נחלק: C כשיחלק; F כאשר יתחלק
ישר: C, B ישר מונח; AB ישר מונח
בשני: P1007 לב'
בשני חלקים: F137 marg.; Ma1 om.
איך שקרה: C כמו שקרה; F137 איך מה שיזדמן; Ma1 איך שהזדמן; B איך שיזדמן
הנה: C, F יהיה
השטח: C שטח
הנצב: B, C, F נצב
אשר יקיף: C שיקיפו; B אשר יקיפו
בו: Mu130 om.
הקו: PP קו
משני: F137 marg.; P1007 מב'
משני חלקיו: C, Ma1 מחלקיו; B(except for Mu130) מן החלקים
הנצב: B, C, Ma1, W194 נצב; F137נצב לשטחנצב
אשר יקיף ... הזויות: P1013 om.
אשר יקיפו: C שיקיפו
בו: C, P1010 בו
השני: B(except for W66), C, F, Lo שני; W66 שתי; P1007, P1013 הב'
חלקים: B, C, F, Lo החלקים
והמרובע: C ומרובע
המתהוה: B, F, Lo ההוה
המתהוה מן: C om.
מן החלק: B(except for Mu130), P1007 מהחלק
אשר זכרנו: C שהזכרנו - ↑ ויהיה: B הנה יהיה; F המשל יהיה
קו: Ma1 הקו
ישר: B ישר מונח; AB ישר מונח; Ma1 הישר
עליו: A1 om.
א"ב: A1 om.
ויחלק: AB, B(except for W66) ונחלק; W66 ונחלק אותו; F ויתחלק
איך שיקרה: F איך שיזדמן; B איך שהזדמן; P1007 איך שקרה
על: P1010עליועל - ↑ הנה: F om.
כי השטח: B שהשטח; Ma1 ששטח; F137 כי שטח
הנצב: B, F נצב
יקיפו: Mu130 יקיף
קוי: A2, B, P1014 שני קוי; AB שני קוי; A1, P1007 קו
שוה: Ma1 שוים
הנצב: B, F נצב
הזויות: P1014 הזוית
בו: Mu130, W194 om.
שני: F om.; P1007 ב'
א"ב ב"ג ... שני קוי: W66 marg.
ג"ב: Mu36, P1007, P1014 ב"ג
המתהוה: B, F ההוה
מן ג"ב: F מב"ג; P1007 מג"ב; Mu36 מןג"בג"ב - ↑ ונעשה: F137 נעשה; Ma1 מופת זה נעשה; B(except for W66) הנה נעשה
מן קו: F על; A1, B, Lo, P1010, PP מקו; P1007 הקו; Mu36 מן קו
ג"ב: F ב"ג
עליו: F om.
בגד"ה: W66 ה"ג
ממ"ו מא': AB מ"ו מראשון; A1, F137, Lo, P1010, PP ממ"ו מראשון; Mu130 ממ"ו; C, Ma1, E, Mu36, P1007, P1012 om. - ↑ ונתמים: B(except for W66), F ונשלים; Lo, AB, P1010, PP ונתמם
א"ג ד"ז: F אזד"ג; B(except for W66) ג"א ז"ד
הנכחי: F נכחי
הנכחי הצלעות: B(except for W66) הנכחי הצלעות נצב הזויות
מל"א וממ"ב מא': F137, Lo, P1013, PP מל"א ומ"ב מראשון; P1010 מל"א מרא'; W66 מב"א ומ"ב מא'; W194 מל"א ומ"ה מראשון; AB, B(except for W66), C, Ma1, E, Mu36, P1007, P1012 om. - ↑ הנה: O16 marg.
אחד: ABשטחאחד
משני: P1007 מב'; P1010משטימשני
משני שטחי: F משטחי
א"ה: A1, Mu130 ג"ה
א"ה א"ד: Mu36, P1014 א"ד ג"ה
נכחי: F נכחיי
נכחי הצלעות: B(except for W66) נכחי הצלעות נצב הזויות - ↑ ג"ה: F שטח ה"ג; B(except for W66), Mu36 שטח ג"ה
מא' מזה: P1010 מא'; AB, B, C, Ma1, E, P1007, P1012, P1013 om. - ↑ הנצב: AB, B נצב
הנצב הזויות: F om.
בו: P1013שבו
שני: F om.; P1007 ב'
ב"ג: Mu130 ג"ב - ↑ מפני כי ב"ג: F לפי שב"ג; Mu130 מפני שב"ג
- ↑ הנצב: A1, B, F נצב
שני: F om.
א"ב ב"ג ... שני קוי: O16 marg.; P1007 om.
ג"ב: F, Mu36 ב"ג - ↑ מפני כי ב"ג: F לפי שב"ג; B(except for W66) מפני שג"ב; P1013 מפני ב"ג
ושטח א"ד ... לג"ד: Mu130 moved below; P1014 marg. - ↑ ה"ג: F ג"ה
- ↑ הוא: Mu36 om.
- ↑ המרובע: Mu36 מרובע; AB המרובע
- ↑ המתהוה: B(except for W66), Ma1 ההוה; F137
המההווה; Mu36 מתהוה - ↑ מן ג"ב: F, Mu36, P1007 מג"ב
ושטח ה"ג ... מן ג"ב: P1014 ושטח מרובע מתהוה מן ב"ג; marg. ושטח ה"ג הוא המרובע המתהוה מן ג"ב - ↑ הנה: F אם כן; Mu130 ושטח א"ד [...] לג"ד הנה
הנצב: B(except for W66), F, Mu36 נצב
שני: F om.
הנצב: B(except for W66), F, P1013 נצב
שני: P1007 ב'
שני קוי: A1, F om.
א"ג ג"ב: P1012 א"ב ב"ג; F א"ג ב"ג
והמרובע: Ma1 ומרובע
המתהוה: B(except for W66), A1, AB, F ההוה
מן ג"ב: F מב"ג; P1007 מג"ב - ↑ הנה: F137 א"כ
חולק: F137 יתחלק; O16 נחלק
ישר: Mu36, O16 ישר מונח; AB ישר מונח; Mu130 ישרעלמונח
בשני: P1007 בב'
בשני חלקים: F137 om.
איך שיקרה: F137 איך מה שיזדמן; B(except for W66) איך שהזדמן; P1013 איך שקרה
הנה: F137 יהיה
הנצב: F137, B(except for W66) נצב
יקיף: Mu36, O16 יקיפו
משני: P1007 מב'
משני חלקיו: F137 מחלקיו; O16 מחלקיו
הנצב: F137, B(except for W66) נצב
השני: F137, O16 שני; P1007 הב'
חלקים: F137, O16 החלקים
המתהוה: F137, O16 ההוה
מן החלק: O16, P1007, P1012 מהחלק
אשר זכרנו: F137 שזכרנו
הנה כאשר ... זכרנו: C, Ma1, E, W66 om. - ↑ וזה מה שרצינו לבאר: F137, E, Mu130 ומש"ל; Ma1, P1007 וזה מש"ל; Lo, P1010, PP, W194 וזה מה שרצינו באורו; C וזה מה שרצינו
- ↑ ד: P1007, P1012 mark is missing; Ma1 ג'; Mu130 למוד ד'
כאשר חולק: B כאשר נחלק; C כשיחלק; F כאשר יתחלק
ישר: B(except for Mu130), C, P1012; P1014 ישר מונח
בשני: C לשני; P1007 בב'
חלקים: Ma1 חצאים
איך שיקרה: B איך שהזדמן; C כמו שקרה; F איך שיזדמן; O561 איך שיקרה; P1007 איך שקרה; PP איך מה שיקרה
הנה: C, F יהיה
המרובע: C מרובע
המתהוה: B(except for Mu130), C ההוה
המתהוה מן: C om.
מן הקו: B(except for Mu130), P1007 מהקו; PP מן קו
לשני: P1007 לב'
המרובעים: C מרובעי
המתהוים: B(except for Mu130), F ההוים; C om.
מן ... המתהוים: O561 marg.
מן השני: B(except for Mu130), F, Lo, P1012, P1013, P1014 משני; C שני; P1007 מהב'; W194 מן שני
חלקים: C, F, Lo, O16, P1012, P1014 החלקים; W66 החלקים
וכפל: C ולכפל; Mu36, O16, P1012, P1014 ומכפל; O561 ומכפל
השטח: C שטח
הנצב: B(except for Mu130), C, F נצב; P1014 om.
השני: B(except for Mu130), C, F, PP שני; O561 השני; P1007 ב'
חלקים: B(except for Mu130), C, F החלקים - ↑ ויהיה: B(except for Mu130) הנה יהיה; F137 יהיה; Ma1 המשל יהיה
קו ישר: F, Lo הקו הישר; O16 קו
עליו: B(except for Mu130) מונח עליו
ויחולק: F ויתחלק; O16 נחלק; W66 ונחלק
איך שיקרה: B(except for Mu130) איך שהזדמן; F איך שיזדמן; P1007 איך שקרה - ↑ הנה: F om.
המרובע: Mu36 המרובע
המתהוה: B(except for Mu130), F ההוה
מן א"ב: B(except for Mu130), F, P1007 מא"ב
לשני: P1007 לב'
המתהוים: A1, B(except for Mu130), F ההוים
מן א"ג: B(except for Mu130), F, P1007 מא"ג
ג"ב: F ב"ג
וכפל: P1014 ומכפל
השטח: W66 שטח
הנצב: B(except for Mu130), F נצב
הזויות: Ma1 הזוית
שני: F om.; P1007 ב'
ג"ב: F ב"ג - ↑ ה: P1007, P1012 mark is missing; Mu130 למוד ה'
כאשר: F om.
כאשר נחלק: C כשיחלק
נחלק ... ישר: F כל קו ישר יתחלק
בשני חלקים: C לשני חלקים; O16 בחלקים; F לשני חצאים
שוים: F137 שוים; Ma1 om.
ושני: C ולשני; F ובשני; P1007 ולב'
ושני חלקים: O16 וחלקים
בלתי שוים: C שאינם שוים; F מתחלפים
הנה: C; F יהיה
השטח: C שטח
הנצב: B(except for Mu130), C, F137 נצב
אשר יקיפו: C שיקיפו; P1007 אשר יקיף
בו: P1012 om.
שני חלקי: C החלקים; F חלקי; P1007 ב' חלקי; AB שניקויחלקי
הקו כלו: C om.
אשר הם בלתי: C שאינם; O16 הבלתי
אשר הם בלתי שוים: F המתחלפים
עם המרובע: C עם מרובע; F ומרובע; P1013 מן המרובע; W194מןנ' עם המרובע
המתהוה מן: C om.; B(except for Mu130) ההוה מן
מן הקו: O16, P1007 מהקו; W66מן הקומהקו
אשר במה שבין: C כלו שהוא בין; Mu130 אשר במהשנישבין
שני: B (except for O16), C om.; P1007 ב'; P1013 שכל; P1014 שתי
מקומות: P1007 המקומות
השני חלקים: Cשוההחלקים; B(except for Mu130) החלקים
המתהוה מן ... השני חלקים: F יתרון חצי הקו על החלק היותר קצר
שוה: B(except for Mu 130), F, P1012 שוים
למרובע: W66 מרובע
המתהוה: C, F om.; A1, B(except for Mu130), P1014 ההוה
מחצי: C, F חצי; Mu130 מן חצי - ↑ ויהיה: B (except for Mu130) הנה יהיה; F137 יהיה; Ma1 המשל יהיה
קו ישר: F הקו הישר
ויחלק: F ויתחלק; B(except for Mu130) ונחלק
בשני: A2, P1014 לשני; P1007 בב'
בשני חלקים שוים: F לחצאים; O16 בחלקים שוים
נקודת: F om.; P1013 מקומות נקודת
מי' מא': according to AB, W66 - ↑ ושני: Mu130, P1007 וב'; W66 ולשני
ושני חלקים: F, O16 ובחלקים
בלתי שוים: F מתחלפים
על נקודת ג' ... בלתי שוים: Mu130 marg.
נקודת: F om. - ↑ הנה: F om.
כי השטח: B(except for Mu130), Ma1 שהשטח
הנצב: B, F נצב
בו: P1012 om.
שני: F om.
המתהוה: B(except for Mu130), F ההוה
מן ג"ד: B(except for Mu130), P1007 מג"ד; F מד"ג; Mu130 ג"ד illegible
שוה: F שוים
המתהוה: B(except for Mu130), F, P1014 ההוה
מן ג"ב: B(except for Mu130), P1007, P1013 מג"ב; F מב"ג; AB מןג"א או מןג"ב; Mu130 מן ג"א או ג"ב; P1012 מן ג"א או מן ג"ב - ↑ ונעשה: F137 נעשה; Ma1 המופת נעשה; B(except for Mu130) הנה נעשה
מקו: AB, Mu130, P1012, P1014 מן קו
ג"ב: F ב"גr ג"הז"ב: F ב'ג'ה'ז' ונעשה מב"ד מרובע ד'ב'כ'ח'; P1010ד"הג"ה ז"ב
ממ"ו מא': A2, C, E, Ma1, Mu130, P1007, P1012 om.; A1, AB, F137, Lo, P1010, PP ממ"ו מראשון; O16 ממ"ו</span> </li>- ↑ התמונה: F התבנית
א"גט"ל: F א'ט'ל'ג'
הנכחי: F נכחי; P1013 [..] נכוחי
מד' מזה: A2, B(except for W66), C, E, Ma1, P1007, P1014 om.; Lo, P1010, P1012 מד'- ↑ הנה מפני: P1012 twice
מפני כי ג"ח: F לפי שג"ח; B(except for Mu130) מפני שג"ח
ג"ח: P1012 ג"ה
לח"ז: P1012 לה"ז
ד"כ: Mu130 ח"ב
משותף: O16 משותפת
הנה: F om.; W66ההנה
ג"כ: Mu130 ל"ב
לד"ז: Ma1 לשטח ד"ז
ממ"ג מא': A1, E, F137, P1007, P1010, P1012, PP om.; C מצורת מ"ג מן הראשון; Ma1 מג' מזה המאמר; Lo ממ"ג מראשון; O16 ממ"ג- ↑ ומפני שצלע: AB, P1007, P1012, PP ומפני כי צלע
א"ג: O561ג"הא"ג
ג"כ: Mu130 ל"ב; PP marg. כ"ג
מל"א מא': according to W66; AB מל"ו מראשון- ↑ ג"כ: Mu130 ל"ב; PP ל"ג
הנה יהיה: B(except for Mu130), AB, F אם כן
ל"א: B(except for Mu130), AB, F א"ל
ומפני שצלע א"ג ... לשטח ד"ז: F137 marg. with the note ונשמט
וכבר היה ... ל"א שוה לשטח ד"ז: AB, PP marg.
הנה יהיה ... לשטח ד"ז: P1012 om.
מפתיח' א': according to W66; AB מפתיחת א'- ↑ ונשים: Mu31 starts here (247v; line 2 from the bottom) ונשום
ג"ח: Lo ד"ח ג"ח
משותף: B(except for Mu130) משותפת
הנה: F יהיה
כלו: Mu31 ג כלנו
שוה: Mu31 שוים; P1012 om.
לרושם: Mu31 om.; Mu130לשטחלרושם
מנ"ס: P1012 מנ"ח- ↑ א"ח: Mu31; Mu130 שטח א"ח
שוה: P1012 שוה לשטח ג”כ וכבר היה שטח ג”כ שוה לשטח ד”ז ונשים ג”ח משותף הנה א”ח כלו לרושם מנ”ח אבל א”ח שוה
הנצב: B, F נצב; P1007 ה[.] הנצב
הזויות: P1007 הזוית
שני: B(except for Mu130), F om. P1007 ב'
מפני כי ב"ד: B(except for Mu130) מפני שב"ד; F לפי שד"ב; O561 marg.; P1007 הנה מפני כי ב"ד; P1012 ומפני כי ב"ד
לד"ח: O16לשטחלד"ח
וזה כי ד"כ: B(except for Mu130) וזה שד"כ
וזה כי ד"כ מרובע: Ma1 om.
משלפניה: according to B(except for Mu130); C מלפניה; Ma1 מג' מזה; AB מאשר לפניה; O561 מהקודמת; P1014 מסוף תמונה אשר לפניה- ↑ הנה: F אם כן
רושם: ABכירושם
מנ"ס: P1012 מנ"ד
שוה לשטח: O561 twice
הנצב: B, F נצב
הזויות: W66 הזויות
בו: Mu31, P1007, P1010, PP om.
שני: B(except for Mu130), F om.; P1007 ב'- ↑ אשר הוא שוה: Mu31 אשר ראשונה; O16 שהוא כמו
למרובע: O16 השטח המרובע
המתהוה: B(except for Mu130), F ההוה
מן ג"ד: B(except for Mu130), F, P1007 מג"ד
משותף: O16 משותפת
ויהיה: B(except for Mu130) הנה יהיה; F יהיה
מנ"ס: P1012 מנ"ד
ושטח: F עם
הנצב: F, W66 נצב
הזויות: O16 הזוית
יקיפו בו: Lo יקיפוהו; A2, F, P1007, P1010, PP, W194 יקיפו
שני: B(except for Mu130), F om.; P1007 ב'
המתהוה: A1, B(except for Mu130), F ההוה
מן ג"ד: B(except for Mu130), F, P1007 מג"ד- ↑ אבל: A2, AB, Lo, Mu31, Mu130, P1010, P1012, PP, W194 ויהיה
רושם: PP marg.
כמו השטח הנצב ... ושטח ל"ע: P1012, P1014 om.
הוא: F הם
כלו: AB om.- ↑ ושטח: O561 ג ושטח
ג"ז: Mu31 כ"ז
ושטח ג"ז כלו: P1012 om.
ושטח ג"ז כלו הוא: F והוא
שטח: B(except for Mu130), F, Mu31 om.; P1007 השטח
המתהוה: B(except for Mu130), F ההוה
מן ג"ב: AB, B(except for Mu130), P1007, P1012 מג"ב; F מב"ג- ↑ הנה: F אם כן
השטח: Mu31 השוה; Mu130 שטח
הנצב: B(except for Mu130), F נצב
בו: A1 om.
א"ד: F קוי א"ד; P1007 ב' קוי א"ד
המתהוה: B(except for Mu130), F, P1007 ההוה
מן ג"ד: O16, P1007, P1012, P1014 מג"ד; F מד"ג
המתהוה: B(except for Mu130), F, P1007 ההוה
מן ג"ב: O16, P1007 מג"ב; F מב"ג, ABמג"א אומן ג"ב; Mu130 מן ג"א או ג"ב; P1010 מןג"חג"ב; P1012, P1013 מן ג"א ג"ב; W194 מן ג"א ג"ב [נ' שהוא אחד]- ↑ וכאשר: F137 ואם כן; B(except for W66) הנה כאשר; O561 וכאשר
נחלק קו ישר: F137 כל קו ישר יתחלק
בשני חלקים שוים: F137 לשני חצאים; O16 בחלקים שוים; P1007 בב' חלקים שוים
ושני חלקים בלתי שוים: A2 ובלתי שוים; F137 ובשני חלקים מתחלפים; O16 וחלקים בלתי שוים; P1007 om.
הנה: F137 יהיה
הנצב: F137, O16, P1013 נצב
בו: P1010 om.
שני: F137 om.; P1007 ב'
חלקי הקו: Mu31 חלקו ההן; AB חלק קו
כלו: O16 om.
אשר הם בלתי שוים: F137 המתחלפים; O16 אשר אינם שוים
עם המרובע: F137 ומרובע
המתהוה: O16 ההוה
מן הקו: O16, P1007 מהקו
אשר במה: Mu31 twice
מקומות: P1013 המקומות
שני: O16 om.; PP marg.
שני מקומות שני החלקים: A2 שני המקומות שני חלקים; P1007 ב' מקומות ב' החלקים; P1014 שתי מקומות השני חלקים
המתהוה מן הקו אשר במה שבין שני מקומות שני החלקים: F137 יתרון חצי הקו על החלק היותר קצר
שוה: F137 שוים
המתהוה: F137 om.; O16 ההוה
מחצי: F137 חצי; P1012 מהם
וכאשר ... מחצי הקו: C, E, Ma1, W66 om.- ↑ וזה מה שרצינו לבאר: E om.; Mu130 ומש"ל; P1007 וזמש"ל; W66 וזה מה שרצינו לבאר ונשלם באורו; Ma1, P1014 וזה מש"ל; F137 וזהו מה שרצי' לבאר
- ↑ deleted: ויהיה המשולש החד הזוית עליו א'ב'ג' ותהיה
באג ממנו נרחבתזוית א'ב'ג ממנו חדה ונוציא מנקודת א' אל קו ב"ג עמוד א"ד ואומר שהמרובע ההווה מן קו א"ג קטן משני המרובעים ההווים משני קוי ב"ג ב"א בכפל השטח נצב הזויות אשר יקיפו בו שני קוי ג"ב וב"ד המופת ונוציא קו א"ד הישר על יושר קו א"ג הישר ונוציא מנקודת ב' אל קו א"ד הישר עמוד ב"ד הנה אומר כי המרובע ההוה מן ג"ב יותר גדול משני המרובעים ההווים משני קוי א"ב א"ג בכפל השטח הכפל הזויות אשר יקיפו בו שני קוי א"ג וא"ד הנה מפני כי קו ד"ג הישר כבר חולק איך שקרה על נקודת א' היה המרובע ההוה מן ד"ג שוה לשני המרובעים ההוים מן א"ד וא"ג וכפל השטח הנצב מזויות אשר יקיפו בו שני קוי א"ג וא"ד ונשים המרובע ההוה מן ב"ד משותף הנה השני ממרובעים ההוים משני קוי ג"ד וד"ב שוים לשני המרובעים ההוים מקוי ב"ד וד"א וא"ג וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג וא"ד אבל שני המרובעים ההוים משני קוי ב"ד וד"ג שוים למרובע ההוה מן ב"ג מפני כי זוית בד"ג נצבת ושני המרובעים ההוים משני קוי ב"ד וא"ד שוים למרובע תהיה מן א"ב מפני כי בד"א נצבת הנה המרובע ההוה מן ב"ג שוה לשני המרובעים ההוים מן א"ב וא"ג וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד וא"ג הנה יהיה המרובע ההוה מן ב"ג יותר גדול משני המרובעים ההוים משני קוים א"ב וא"ג בכפל השטח הנצב הזויות החדים הזוית יותר קטן משני המרובעים ההוים משתי הצלעות המקיפות בזוית החדה בכפל השטח הנצב הזוית אשר יקיף בו הקו אשר יפול עליו העמוד משני הקוים המקיפים בזוית החדה והקו אשר יגדילהו העמוד ממה שילוה הזוית החדה- ↑ 19r
- ↑ 19v
- ↑ marg.: ר"ל המרובע אשר נוכל לעשות על ה"ט
- ↑ 71r
- ↑ marg.: כמו שיתבאר בתמונה ט'
- ↑ 71v
- ↑ 98v
- ↑ 99r
- ↑ 99v
- ↑ 101v
- ↑ 101r
- ↑ marg.: והם הנזכרים בתמונת צ' וצ"א וצ"ב וצ"ג
- ↑ זה בתמונה הבאה אחר זה
- ↑ 108r
- ↑ marg.:זה אי אפשר לפי שאחר שד"ז נבדל הוא אלם והשקר אמנם התחייב מהנחתנו שהוא משני שמות אם כן הקו הנבדל לא יהיה אשר משני שמות
- ↑ marg.: =וזה יתבאר בהקש החלוף שאם יהיה מדבר יחדש רוחב מדבר והוא א"ג כמבואר בתמונת י"ו וזה שקר
- ↑ marg.: וזה שמרובע א"ז כאשר יחובר אל קו מדבר יחדש רוחב מדבר בכח כמבואר בי"ח ואמנם מרובע ג"ד שהוא שוה לשטח ב"ג כאשר יחובר אל א"ב המדבר הוא יחדש רוחב א"ז שהוא ממוצע ואחר שהרחבים מתחלפים הקוים אם כן מתחלפים וכן יתבאר שד"ז אינו מסוג ג"ד וזה שג"ד כאשר יחובר אל ה"ב א"ב הוא יחדש רוחב א"ג וד"ז כאשר יחובר אל א"ב או אל ג"ה הוא יחדש רוחב ג"ד וכבר בארנו שא"ג ג"ד מתחלפים
- ↑ 133v
- ↑ marg.: מי' מי"ד וזה שיחס הקו אל הקו כיחס החלק הגדול אל החלק הגדול
- ↑ marg.: וזה שנאמר ד"ב אל א"ב וה"ז אל ז"ו עוד הפכנו
- ↑ 138v
- ↑ נ' בעצמו
- ↑ marg.: וזה שאחר שהכאת ו"ז בעצמו שוה להכאת ד"ב בו"ז אם כן ד"ב הוא כמו ו"ז
- ↑ marg.: אין צריך לעשות כזה כי אם להוציא כל קטרי השטחים
- ↑ marg.: רצה בזה שהוא עשוי על שטח מרובע כמו שנעשה במאמר י"ג בתמונת ט"ו
- ↑ 139r
</ol>
- ↑ התמונה: F התבנית
Appendix: Bibliography
Manuscripts:
A) Moses ibn Tibbon - the main translation
- 1) London, British Library Add. 20746 (IMHM: f 5053), (cat. Margo. 1001) (15th century)
- translation: 6 September 1270; Book X – 2 August 1270
- Lo
- translation: 6 September 1270; Book X – 2 August 1270
- 2) Paris, Bibliothèque Nationale de France heb. 1007/3 (IMHM: f 15710), ff. 37r-65v (16th century)
- 3) Paris, Bibliothèque Nationale de France heb. 1010 (IMHM: f 15712), (15th-16th century)
- translation: 6 September 1270; Book X – 2 August 1270
- P1010
- translation: 6 September 1270; Book X – 2 August 1270
- 4) Paris, Bibliothèque Nationale de France heb. 1012/1 (IMHM: f 15713), ff. 1-254 (15th century)
- translation: 16 September 1270
- P1012
- translation: 16 September 1270
- 5) Paris, Bibliothèque Nationale de France heb. 1014/1 (IMHM: f 15714), ff. 1r-157r (16th century)
- 6) Paris, Private collection (IMHM: f 39116) (1470-1475)
- A1)
- 1) Paris, Bibliothèque Nationale de France heb. 1013 (IMHM: f 15018), (15th century)
- 2) Wien, Öesterreichische Nationalbibliothek Cod hebr. 194/1 (IMHM: f 1456), ff. 1-82 (16th century)
- A2)
- 1)München, Bayerische Staatsbibliothek, Cod. hebr. 36/3 (IMHM: f 1166), ff. 8r-17r, 22r-85r, 87r-100r (Istanbul, 1485)
- translation: 16 September 1270
- Mu36
- translation: 16 September 1270
- 2) Oxford, Bodleian Library MS Hunt. 561 (IMHM: f 19288) (cat. Neub. 2003) (Candia, 1375)
Unchecked
- Jerusalem, Jewish National and University Library Ms. Heb. 8°2339 (IMHM: B 449 (8°2339)), (19th century)
- Leiden, Bibliotheek der Rijksuniversiteit Cod. Or. 4785 (IMHM: f 27910) (14th-15th century) (similar to MS Oxford 405?)
- Madrid, Biblioteca Nacional 5474/1 (IMHM: f 7233), 1-190 (14th-15th century)
- translation: 16 September 1270
- Montecassino, Archivio di Stato 510/1 (IMHM: f 34894), ff. 1v-132v (15th century)
- translation: 2 August 1270
- translation: 2 August 1270
- New York, Jewish Theological Seminary Ms. 2613 (IMHM: f 28866), ff. 1r-30r (list of propositions of Books I-XV); 31r-38r (Book I until proposition 19) (18th century)
- New York, Jewish Theological Seminary Ms. 9545/2 (IMHM: f 49965), ff. 16r, 18v-21v (15th century)
- Oxford, Bodleian Library MS Mich. 358/1 (IMHM: f 19289) (cat. Neub. 2004, 1), ff. 1r-72v, (13th-14th century)
- Oxford, Bodleian Library MS Mich. 400/1 (IMHM: f 19291) (cat. Neub. 2006, 1), 1r-10v, (15th century) (list of definitions and propositions)
- Oxford, Bodleian Library MS Mich. 405 (IMHM: f 19287) (cat. Neub. 2002) (1573) (similar to MS Leiden?)
- Philadelphia, University of Pennsylvania Ms. Codex 1787
- Roma, Accademia Nazionale dei Lincei, Biblioteca Corsiniana, Or. 259/1 (IMHM: f 73284), ff. 1r-68v, (Mantova, 1441)
- Roma, Biblioteca Nazionale Centrale Vittorio Emanuele II Or. 78 (IMHM: f 415) (15th century) (with comments by Gersonides)
- St. Petersburg, Inst. of Oriental Studies of the Russian Academy B 16 (IMHM: f 52919), (15th century)
- St. Petersburg, Inst. of Oriental Studies of the Russian Academy B 191/2 (IMHM: f 53338), ff. 167v-178v (Volga, 1392)
- St. Petersburg, Inst. of Oriental Studies of the Russian Academy C 127 (IMHM: f 69382), (Istanbul, 17th century)
B) Jacob ben Makir - revision of ibn Tibbon's translation
- 1) München, Bayerische Staatsbibliothek, Cod. hebr. 130 (IMHM: f 1195), (15th century)
- 2) Oxford, Bodleian Library MS Hunt. 16/1 (IMHM: f 19290) (cat. Neub. 2005, 1), 1r-89v, (15th century)
- 3) Wien, Öesterreichische Nationalbibliothek Cod hebr. 66/3 (IMHM: f 1343), ff. 157-233 (16th century)
AB)
- München, Bayerische Staatsbibliothek, Cod. hebr. 91/1 (IMHM: f 1157), ff. 1r-141v (14th century)
C)
- Cambridge, Trinity College R 14 61 (IMHM: f 12598), (14th century)
F)
- 1) Firenze, Biblioteca Nazionale Centrale Magl. III. 137/1 (IMHM: f 11976), ff. 4v-199r (15th century)
- translation: 6 September 1270
- F137
- translation: 6 September 1270
- 2) Mantova, Comunita Israelitica MS ebr. 1 (IMHM: f 782) (15th century)
- translation: 6 September 1270
- Ma1
- translation: 6 September 1270
E)
- Mantova, Comunita Israelitica MS ebr. 2 (IMHM: f 783) (14th-15th century)
lists
- München, Bayerische Staatsbibliothek, Cod. hebr. 246/6 (IMHM: f 1102), ff. 56r-64r (1429-1431)
- Paris, Bibliothèque Nationale de France heb. 1011/1 (IMHM: f 15017), ff. 1r-64r (13th-14th century)
Campanus de Novare?
- Moscow, Russian State Library, Ms. Guenzburg 539/2 (IMHM: f 47860), ff. 67r-91r (16th century) (Moses Provenṣali ?)
- München, Bayerische Staatsbibliothek, Cod. hebr. 31/3; 31/5 (IMHM: f 1165), ff. 113r-122v; 242v-254r (16th century)
- Paris, Bibliothèque Nationale de France heb. 1015/1 (IMHM: f 15019), ff. 1-29 (16th century)
Bibliography:
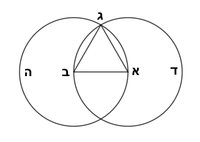



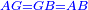

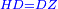

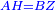
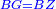
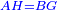

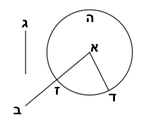
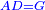
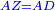

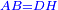 .
.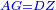 .
.

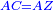




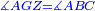
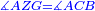
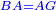

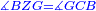
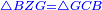
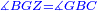
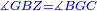
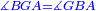
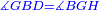
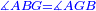

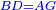
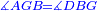
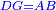

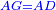
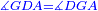



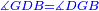


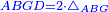




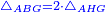
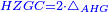
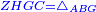

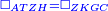
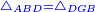
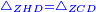


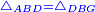
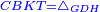
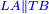
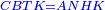
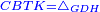
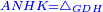
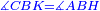
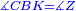
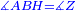
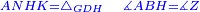
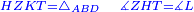
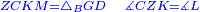




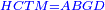

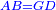







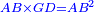
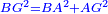



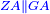
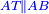
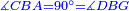
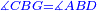
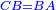

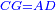

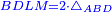
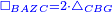
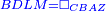
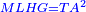
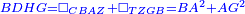
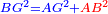
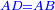
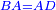

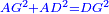

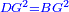

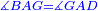
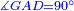
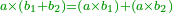
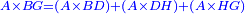
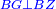
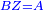
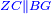
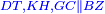

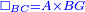
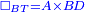
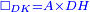
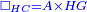
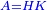
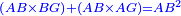
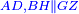
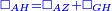
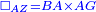


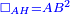
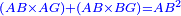
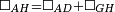
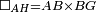
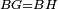
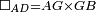
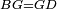
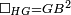
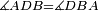
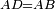
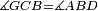
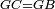
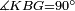
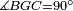
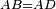
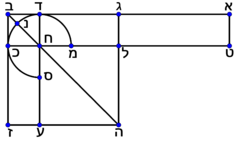
![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
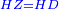

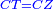

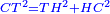

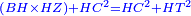
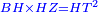

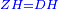

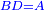
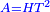
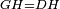
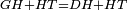
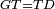
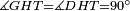
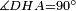
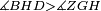
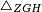
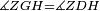
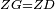
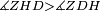
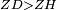
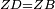
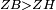
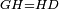
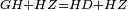
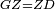
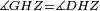
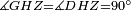
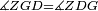
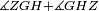 of
of 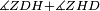 of
of 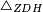
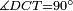
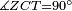
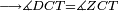
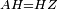
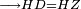
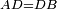
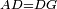
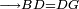
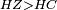
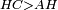
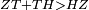
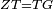
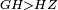
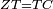
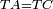
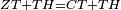
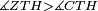
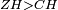
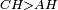
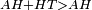
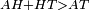
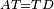
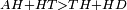
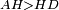
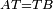
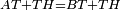
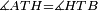
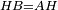
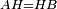
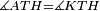
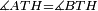
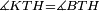
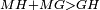
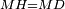
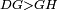
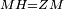
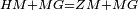
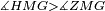
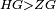
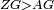
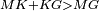
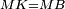
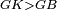
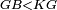
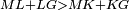
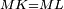
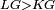
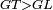
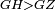
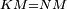
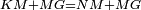
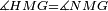
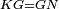
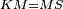
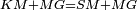
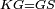
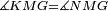
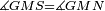
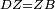
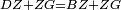
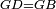
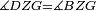
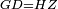
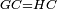
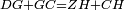
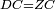
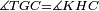
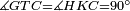
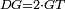
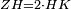
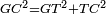
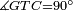
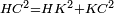
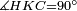
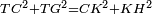
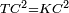
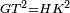
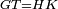
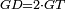
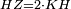
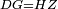
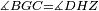
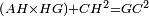
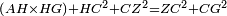
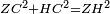
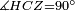
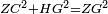
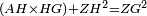
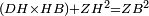
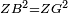
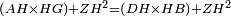
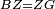
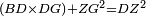
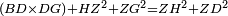
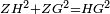
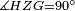
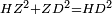
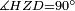
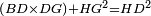
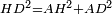
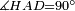
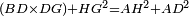
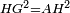
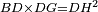
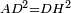
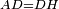
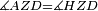
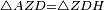
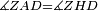
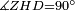
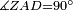
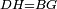 , the required has been achieved.
, the required has been achieved.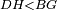 , [defining]
, [defining] 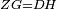
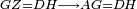
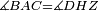
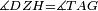
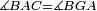
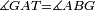
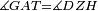
 are equal to
are equal to 
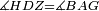
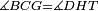 and
and 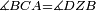
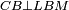
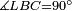
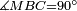
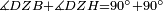
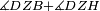 .
.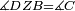
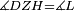
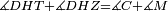
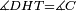
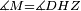
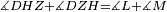
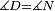
 by line BD and
by line BD and 
 of
of  are equal to
are equal to  of
of 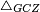
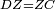
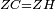
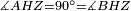
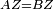
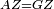
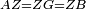
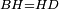
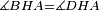
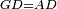
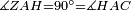
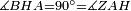
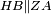 and
and 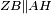
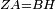
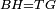
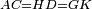
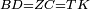
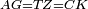
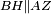
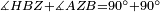
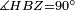
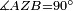
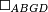 the [known] square.
the [known] square.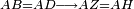
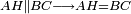
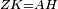
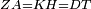
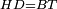
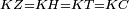
 the known circle.
the known circle.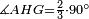
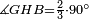
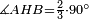
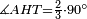
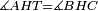
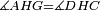
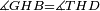
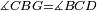
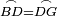
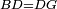
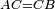
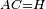
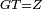
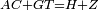
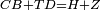





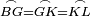
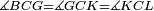
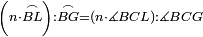
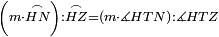
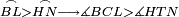
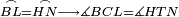
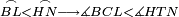
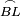 and
and 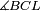 are equimultiples of
are equimultiples of 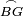 and
and 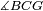
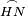 and
and 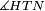 are equimultiples of
are equimultiples of 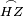 and
and 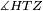
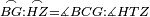
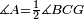
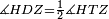
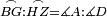
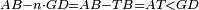
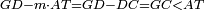
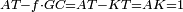
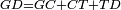
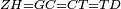
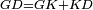
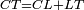
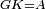
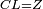
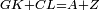
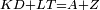
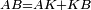
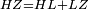
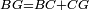
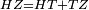
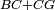 equals the multitude of
equals the multitude of 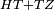 .
.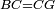 .
.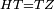 .
.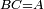 .
.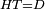 .
.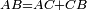
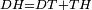
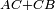 equals the multitude of
equals the multitude of 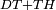 .
.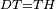 .
.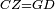
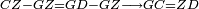
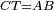
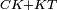 equals the multitude of
equals the multitude of 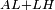 .
.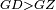
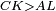
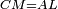
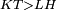
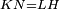
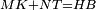
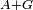 is the same part or parts of
is the same part or parts of 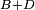 that A is of B.
that A is of B.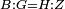
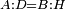
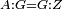
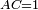
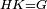
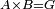
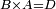
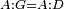
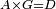
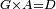
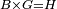
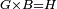
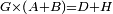
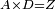
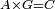
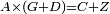
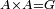
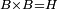
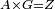 ;
; 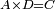 ;
; 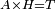
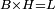
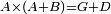
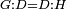
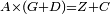
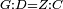
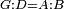
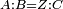
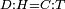
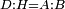
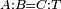
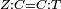
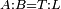
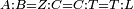
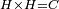
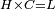
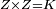
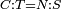
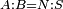
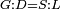
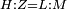
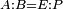
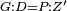 ;
; 
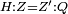
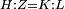
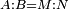
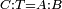
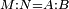
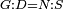
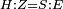
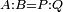
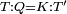
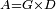
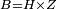
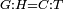
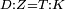
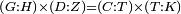
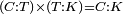
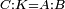
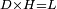
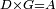
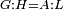
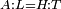
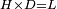
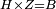
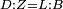
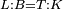
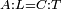
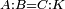
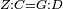
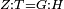
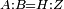
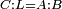
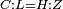
 = cubic number H to cubic number T
= cubic number H to cubic number T