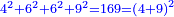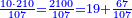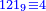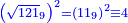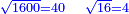Difference between revisions of "פירוש אנונימי לספר המספר"
(→Has not yet reached the ranks of the units) |
|||
| (176 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | == [Chapter One] == |
| − | == האות על זה == | + | |
| + | | | ||
| + | |- | ||
| + | | | ||
| + | === The sign for this === | ||
| + | |||
| + | |style="width:45%;text-align:right;"|‫<ref>39r</ref>[[ספר_המספר_/_אברהם_אבן_עזרא#the_sign_for_this|<span style=color:blue>'''האות על זה'''</span>]] | ||
| + | |- | ||
| + | |I.e. the sign that all numbers revolve around nine is when you draw a circle etc. | ||
| + | |style="text-align:right;"|ר"ל האות על היות כל המספר סובב על תשעה כשתעשה עגול וכו‫' | ||
| + | |- | ||
| + | |He could have given another difference: when you multiply 9 by itself, or by 8, or by 7, or by 6, you find that the units of the tens position exceed the units themselves and from 5 and up it is the opposite as a general rule. | ||
| + | |style="text-align:right;"|וכן היה יכול ליתן הבדל אחר כי כשתכפול ט' על עצמו או על ח' או על ז' או על ו' תמצא האחדים שבמקום העשרות יתרים במספרם מן האחדים עצמם ומה' ולמעלה ככלל הדבר בהפך | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Therefore five is called round number, for it revolves around itself === | ||
| + | |||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#five_is_called_round_number|<span style=color:blue>'''על כן נקרא חמשה חשבון עגול כי הוא מתגלגל על עצמו'''</span>]] | ||
| + | |- | ||
| + | |I.e. it is found in its square. | ||
| + | |style="text-align:right;"|ר"ל שימצא במרובעו | ||
| + | |- | ||
| + | |Although it is also found in six, the square of six is not preserved in its cube. | ||
| + | |style="text-align:right;"|וא'ע'פ' שבששה ימצא כן אמנם ששה לא ישמר מרובעו במעוקבו | ||
| + | |- | ||
| + | |Because when you multiply 6 by 6, it is 36. | ||
| + | :<math>\scriptstyle{\color{blue}{6\times6=36}}</math> | ||
| + | |style="text-align:right;"|כי כשתכפול ו' על ו' ויהיו ל"ו | ||
| + | |- | ||
| + | |Next, you multiply 6 by 36; but it does not stay in its shape. | ||
| + | :<math>\scriptstyle{\color{blue}{6\times36}}</math> | ||
| + | |style="text-align:right;"|ואחר תכפול ו' על ל"ו לא ישאר בצורתו | ||
| + | |- | ||
| + | |But, [5] times 5, which is 25, if you multiply it by 5, it retains itself; the result is 125 and this is the absolute product, since after multiplying its length by its width, we multiply it by its depth. | ||
| + | :<math>\scriptstyle{\color{blue}{5\times25=125}}</math> | ||
| + | |style="text-align:right;"|אך פעמים ה' שהם כ"ה אם תכפלם על ה' ישמר עצמו ויעלה ק'כ'ה' וזהו הכפל הגמור כי אחר שכפלנו ארכו על רחבו שהוא השטח נכפלנו בעמקו | ||
| + | |- | ||
| + | |So, the height is divided into five equal parts, each of which is 5 by 5. | ||
| + | |style="text-align:right;"|ונחלק הגובה לה' חלקים שוים שכל אחד ה' על ה‫' | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === For 1, 10, 100 repeat in the thousands === | ||
| + | |||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#1_10_100_repeat_as_thousands|<span style=color:blue>'''כי א'י'ק' יחזור באלפים וכו‫''''</span>]] | ||
| + | |- | ||
| + | |1, 10, 100 are apart of all numbers, because every number is either one [= units], or 10 [= tens], or 100 [= hundreds]. | ||
| + | |style="text-align:right;"|א'י'ק' הוא חוץ לכל המספרים כי כל מספר הוא אם אחד או י' או ק‫' | ||
| + | |- | ||
| + | |For a thousand is one, 10 thousand returns to 10 and 100 thousand to 100. | ||
| + | |style="text-align:right;"|כי אלף הוא באחד וי' אלפים ישובו לי' וק' אלפים לק‫' | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === To multiply a number by itself === | ||
| + | |||
| + | |style="text-align:right;"|לכפול חשבון על עצמו | ||
| + | |- | ||
| + | |As 25 by 25. | ||
| + | |style="text-align:right;"|כמו כ"ה על כ"ה | ||
| + | |- | ||
| + | |Or by other | ||
| + | |style="text-align:right;"|או על אחר | ||
| + | |- | ||
| + | |Such as 25 by 44. | ||
| + | |style="text-align:right;"|כמו כ"ה על מ"ד | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Or multiplication of one number by two numbers === | ||
| + | |||
| + | |style="text-align:right;"|או כפל חשבון אחד על שנים חשבונות | ||
| + | |- | ||
| + | |As the multiplication of tens by hundreds and tens. | ||
| + | |style="text-align:right;"|ככפל עשרות על מאות ועשרות | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Or multiplication of multiple numbers by multiple numbers === | ||
| + | |||
| + | |style="text-align:right;"|או כפל רבים על רבים | ||
| + | |- | ||
| + | |As units, tens and hundreds by units, tens and hundreds. | ||
| + | |style="text-align:right;"|כמו אחדים ועשרות ומאות עם אחדים ועשרות ומאות | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === About the scales === | ||
| + | |||
| + | |style="text-align:right;"|על המאזנים | ||
| + | |- | ||
| + | |I.e. the sign indicating the truth of multiplication, or division, or vice versa. | ||
| + | |style="text-align:right;"|ר"ל האות המעיד המורה על אמתת הכפל או החלוק או חלופו | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Addition of a number to a number === | ||
| + | |||
| + | |style="text-align:right;"|בחבור מספר אל מספר | ||
| + | |- | ||
| + | |For example, if you want to add many numbers together with many numbers, we write those numbers in rows and add the digits in order as if they were units. | ||
| + | |style="text-align:right;"|כגון שתרצה לחבר יחד מספרים רבים במספרים רבים נכתוב אלו המספרים בשורות שורות ונחבר האותיות ביושר כאלו היו אחדים | ||
| + | |- | ||
| + | |If the result that exceeds ten has no units, we write zero and keep it. | ||
| + | |style="text-align:right;"|והעולה על עשר אם אין בו אחדים נכתוב גלגל ונשמור | ||
| + | |- | ||
| + | |If it has units, we write the units; we write the tens in another position and keep it as will be explained in its place. | ||
| + | |style="text-align:right;"|ואם יש עמו אחדים נכתוב האחדים ונניח הכלל במקום אחד ונשמרהו כמו שיתבאר במקומו | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Subtraction of a number from a number === | ||
| + | |||
| + | |style="text-align:right;"|לחסר מספר ממספר | ||
| + | |||
| + | |- | ||
| + | |Meaning to subtract a number from another number greater than it and know the remainder. | ||
| + | |style="text-align:right;"|כלו' לגרוע מספר ממספר אחר רב ממנו ולדעת הנשאר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Always subtract one for the foundation === | ||
| + | |||
| + | |style="text-align:right;"|וגרע לעולם אחד למוסד | ||
| + | |- | ||
| + | |For the units do not generate any rank for any number, because every number multiplied by units does not go out of its rank, which is not the case when multiplying by another number that rises the rank. | ||
| + | |style="text-align:right;"|כי אחדים לא יחדשו מדרגה בשום מספר ‫<ref>39v</ref>כי כל מספר הנכפל על אחדים לא יצא ממדרגתו מה שאין כן בהכפלו על מספר אחר שיוסיף מדרגה | ||
| + | |- | ||
| + | |A table to know the rank of the product of the numbers that are multiplied by each other | ||
| + | |style="text-align:right;"|לוח לדעת המספרים הכפולים אלו על אלו באיזו מדרגה ישאר הנכפל | ||
| + | |- | ||
| + | |Know that the rubric corresponding to both is the total and it indicates both. | ||
| + | |style="text-align:right;"|דע כי הנקודה הנכחית לשניהם הוא סך המספר המורה והיא המזכרת אותם | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
| + | |- | ||
| + | |מאה אלף||רבבות||אלפים||מאות||עשרות||אחדים | ||
| + | |- | ||
| + | |אלף אלפים||מאה אלף||רבבות||אלפים||מאות||עשרות | ||
| + | |- | ||
| + | |עשרת אלפי אלפים||אלף אלפים||מאה אלף||רבבות||אלפים||מאות | ||
| + | |- | ||
| + | |מאה אלף אלפים||עשרות אלף||אלף אלפים||מאה אלף||רבבות||אלפים | ||
| + | |- | ||
| + | |אלף אלפי אלפים||ק' אלף אלפים||עשרות אלף||אלף אלפים||מאה אלף||רבבות | ||
| + | |- | ||
| + | |רבבות אלפי אלפים||אלף אלפי אלפים||ק' אלף אלפים||עשרות אלף||אלף אלפים||מאה אלף | ||
| + | |} | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :{|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; color:blue; text-align:center;" | ||
| + | |- | ||
| + | |hundreds of thousands||tens of thousands||thousands||hundreds||tens||units | ||
| + | |- | ||
| + | |thousands of thousands||hundreds of thousands||tens of thousands||thousands||hundreds||tens | ||
| + | |- | ||
| + | |tens of thousands of thousands||thousands of thousands||hundreds of thousands||tens of thousands||thousands||hundreds | ||
| + | |- | ||
| + | |hundreds of thousands of thousands||tens of thousands of thousands||thousands of thousands||hundreds of thousands||tens of thousands||thousands | ||
| + | |- | ||
| + | |thousands of thousands of thousands||hundreds of thousands of thousands||tens of thousands of thousands||thousands of thousands||hundreds of thousands||tens of thousands | ||
| + | |- | ||
| + | |tens of thousands of thousands of thousands||thousands of thousands of thousands||hundreds of thousands of thousands||tens of thousands of thousands||thousands of thousands||hundreds of thousands | ||
| + | |} | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
| + | |- | ||
| + | |י||ט||ח||ז||ו||ה||ד||ג||ב||א | ||
| + | |- | ||
| + | |כ||יח||יו||יד||יב||י||ח||ו||ד||ב | ||
| + | |- | ||
| + | |ל||כז||כד||כא||יח||טו||יב||ט||ו||ג | ||
| + | |- | ||
| + | |מ||לו||לב||כח||כד||כ||יו||יב||ח||ד | ||
| + | |- | ||
| + | |נ||מה||מ||לה||ל||כה||כ||טו||י||ה | ||
| + | |- | ||
| + | |ס||נד||מח||מב||לו||ל||כד||יח||יב||ו | ||
| + | |- | ||
| + | |ע||ס[ג]||נו||מט||מב||לה||כח||כא||יד||ז | ||
| + | |- | ||
| + | |פ||עב||סד||נו||מח||מ||ל[ב]||כד||יו||ח | ||
| + | |- | ||
| + | |צ||פ[א]||עב||סג||נד||מה||לו||כז||יח||ט | ||
| + | |- | ||
| + | |ק||צ||פ||ע||ס||נ||מ||ל||כ||י | ||
| + | |} | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :{|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; color:blue; text-align:center;" | ||
| + | |- | ||
| + | |10||9||8||7||6||5||4||3||2||1 | ||
| + | |- | ||
| + | |20||18||16||14||12||10||8||6||4||2 | ||
| + | |- | ||
| + | |30||27||24||21||18||15||12||9||6||3 | ||
| + | |- | ||
| + | |40||36||32||28||24||20||16||12||8||4 | ||
| + | |- | ||
| + | |50||45||40||35||30||25||20||15||10||5 | ||
| + | |- | ||
| + | |60||54||48||42||36||30||24||18||12||6 | ||
| + | |- | ||
| + | |70||63||56||49||42||35||28||21||14||7 | ||
| + | |- | ||
| + | |80||72||64||56||48||40||32||24||16||8 | ||
| + | |- | ||
| + | |90||81||72||63||54||45||36||27||18||9 | ||
| + | |- | ||
| + | |100||90||80||70||60||50||40||30||20||10 | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Example: we wish to multiply 29 by 31 === | ||
| + | |||
| + | |style="text-align:right;"|‫<ref>40r</ref>[[ספר_המספר_/_אברהם_אבן_עזרא#29 by 31|<span style=color:blue>'''דמיון רצינו לכפול כ"ט על ל"א'''</span>]] | ||
| + | |||
| + | |- | ||
| + | |According to this way, for all those that are similar, such as the multiplication of 70 by 90, whose distance from 80 is the same. | ||
| + | :<math>\scriptstyle{\color{blue}{70\times90=\left(80-10\right)\times\left(80+10\right)}}</math> | ||
| + | |style="text-align:right;"|ועל זה הדרך כל הדמים לאלה כגון כפל ע' על צ' שמרחקם מפ' אחד | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === If the number does not have a whole third and there is an excess of one === | ||
| + | |||
| + | |style="text-align:right;"|ואם לא היה למספר שלישית שלימה ויהיה בו תוספת אחד | ||
| + | |- | ||
| + | |Such as ten and you wish to know its square: | ||
| + | |style="text-align:right;"|כגון עשר ותרצה לידע מרובעו | ||
| + | |- | ||
| + | |Subtract the one from the number; 9 remains. | ||
| + | |style="text-align:right;"|חסר האחד מהמספר ישאר ט‫' | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Calculate the sought number in the procedure that I have shown you === | ||
| + | |||
| + | |style="text-align:right;"|ותוציא המספר המבוקש כמשפטו שהראיתיך | ||
| + | |||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שתקח שליש ט' שהוא ג' ומרובעו ט' נעלהו במדרגה שלפניו ויהיו צ' חסר ממנו ט' וישאר פ"א ואחר תוסיף עליו מספר ט' והמספר בעצמו שהוא י' ויעלה ק‫' | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === If there are two between our number and the number that has a third === | ||
| + | |||
| + | |style="text-align:right;"|ואם היו שנים בין המספר שלנו ובין המספר שיש לו שלישית | ||
| + | |||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' שיעדף מספרנו על שלישית שנים כי כל מספר או יש לו שלישית שיעדף יעדיף אחד או שנים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === We do the opposite === | ||
| + | |||
| + | |style="text-align:right;"|נעשה להפך | ||
| + | |||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לפי שזה התוספת יקרא חסרון בערך המספר שלאחריו כי הוא יחסר אחד משלישית שהוא החלק הקטן והוא הפך מה שאמ' למעלה נוסיף על מספר שלנו אחד כי יותר יתכן זה משנחסר שנים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Know that if there are two digits to multiply by one another === | ||
| + | |||
| + | |style="text-align:right;"|ודע כי אם יהיו שני מספרים לכפול זה על זה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל מספרם בין שניהם כגון ב' פעמים די לו בהכאה אחת כגון שתאמר ב' פעמים ב' כמו שאמור למעלה | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === If you have one digit by two digits === | ||
| + | |||
| + | |style="text-align:right;"|ואם יהיה לך מספר אחד על שני מספרים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון ש' פעמים מ"ה אתה צריך להכות פעמים שתכה תחלה הש' על המ' כן ג' על ד' י"ב והנה עשרות במאות הם במדרגה רביעית שהם אלפים והוא י"ב אלף | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עוד נכה ג' על ה' והם ט"ו מאות שהם אלף ות"ק נמצא הכל י"ג אלפים ות"ק | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === If three by three === | ||
| + | |||
| + | |style="text-align:right;"|ואם על שלשה שלשה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' אם תרצה לכפול מספר אחד על ג' מספרים כגון ש' על ת'כ'ה' ג' פעמים ככה ‫<ref>40v</ref>ג' פעמים ד' הם י"ב הם במדרגה חמישית שהיא רבבות והם ק"כ אלף | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עוד נכה ג' על ב' הם ו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עוד נכה ג' על ה'ט"ו והם מאות והכל ק'כ'ז' אלפים ות'ק‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומאה אם המספר אחד תן שיהיה המספר הנכפל אחד או רבים ראה אם הוא זוג שאם הוא זוג גם המחובר זוג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואף אם האחד נפרד בכפל בזוג כגון ט' פעמים ח' יהיה העולה זוג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אף אם שניהם נפרדים כגון ט' על ט' או ט"ו על ט"ו אז המספר נפרד | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === The paved way === | ||
| + | |||
| + | |style="text-align:right;"|והדרך סלולה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שתשים למעלה עוד המספר כי זה יותר ישר ונאות ר"ל שכללו ומועט ולא נחוש אם יהיו הפרטים העליונים גדולים בכמות מפרטי הטור השפל אחר שכלל העליון בלתי גדול וכן לא נחוש בהיות מספרי הטור העליון שכללו קטן יותר רבים ממספרי הטור השפל | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Write it corresponding to the top row === | ||
| + | |||
| + | |style="text-align:right;"|כתוב אותו כנגד טור העליון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומר כנגד קו המספר העליון הראשון כי אחדים עם אחדים אחדים וכתוב בטור שלישי כנגד המספר השני העליון כי אחדים בעשרות יעלו עשרות | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Write the units in the place to which they belong === | ||
| + | |||
| + | |style="text-align:right;"|תכתוב הפרט במקום הראוי לו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' כפרט העודף כתבהו במדרגתו ושמור תחת הכלל אחדים כמספר וחברם וכתבם עם המספר הבא אחריו במדרגת המספר ההוא הבא אחר כן עד תום להכות הראשון עליון עם כל השפלים ואם ישאר שם כלל ופרט יכתוב הפרט וא' ואחריו הכלל כי שם תכלית הטור ההוא | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Start to multiply the second digit and write the result in the third row === | ||
| + | |||
| + | |style="text-align:right;"|תחל לכפול המספר השני והעולה כתבהו בטור השלישי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומר תחל לכתוב בטור אחד למטה ולא באותו ‫<ref>41r</ref>טור | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לפי שעשרות עם אחדים יהיו עשרות ואין ראוי לשים מדרגת עשרות במדרגה גבוהה ממנה על כן נכתבם במקום העשרות | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Then, multiply the second top by the second and write it in the third row === | ||
| + | |||
| + | |style="text-align:right;"|ואחר כך תכפול השני העליון על שני וכו' ותכתבהו בטור השלישי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל כנגד המספר השלישי שבטור העליון אבל זה טור שם הוא מהעולה מן הכפל | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === As the third digit === | ||
| + | |||
| + | |style="text-align:right;"|במספר שלישי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' במדרגה שלישית כי העולה מכפל עשרות בעשרות מאות | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Which is second to the digit from with which I have started === | ||
| + | |||
| + | |style="text-align:right;"|שהוא שני למספר שהחלותי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי מן השני התחיל | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === With the rule that the units are in the lower rank === | ||
| + | |||
| + | |style="text-align:right;"|עם משפט הפרט להיותו תחתון וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' ר"ל שתכתוב הפרט תחלה במדרגתו השפלה ואחר כן תכתוב הכלל במקום גבוה ממנו שהוא שני לפרט | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === If there is zero, whether in the top row === | ||
| + | |||
| + | |style="text-align:right;"|ואם היה גלגל בין בטור העליון וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' כשתכה באות או אות בגלגל כתוב גלגל להוסיף מדרגה ושימהו במקומו כדרך שתעשה מן המספרים שלפני הגלגל או לאחריו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הא למדת שכפי מנין מספר הטור העליון תכתוב טורים תחת שני הטורים שמהם הכפל יוצא וכל אלו הטורים זולת קורא טור שלישי | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Then, start adding up === | ||
| + | |||
| + | |style="text-align:right;"|אחר כן תחל לחבר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' אחר שהשלמת כל ההכאות תחל לחבר העולה מן הטורים השלישי שכתבת ותכתבהו בטור אחד שפל כגון שיש לך מן העולה בכפל ג' טורים חבר בקו היושר מה שנמצא בהם במדרגה הראשונה וכתבהו ואחר כן חבר מה שנמצא במדרגתם השנית וכתבהו וכן כולם עד סופם | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === If there is ten, write one after it === | ||
| + | |||
| + | |style="text-align:right;"|ואם יש בו עשרה תכתוב אחד אחריו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' אם מן שתחבר מאותה מדרגה יעלו עשרה בכוון יכתוב ספרא וישמור אחד וא' יחברהו עם מה שיבא אחריו ואם יעלה החבור כלל ופרט כתוב היושר על הכלל בחבור שיש לך וכתוב אחריו במקום הכלל אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>41v</ref>ואם לא ימצא באיזה מן הטורים רק גלגל כתבהו ואחר שתשלים טור החבור ותרצה לבחון אמתת מספרך ספור מנין מדרגותיו וכאיזה יהיה מעלות השני טורים בלי מדרגת אחד כי הכלל יעשהו מדרגה אחרת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עוד ילמדך מאזנים להבחין מספרך שתמנה סכום האותיות שבטור העליון ואם הוא פחות מט' ישמרהו ואם הוא יתר מט' שמור היתר וכן תעשה ממנין אותיות הטור השפל והנשאר מט' כפלהו עם הנשאר מן הטור הראשון ואם לא ישאר על ט' באחד משני טורים אין צריך לבדוק האחד כי מה שנכפל על ט' יצא ט'ט' וככה יהיה הפחות מט' או היתר מט' ממנין טור החבור ואם לאו תדע כי טעית בחשבונך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשלם השער הראשון | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Chapter Two == | ||
| + | |||
| + | |style="text-align:right;"|<big>השער השני</big> | ||
| + | |- | ||
| + | | | ||
| + | === One alone does not assume any change === | ||
| + | |||
| + | |style="text-align:right;"|האחד לבדו לא יקבל שנוי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כל שנוי בא מצד ההרכבה וההפך והאחד לפי [שהוא]‫<ref>marg.</ref> פשוט אין דבר שישנהו | ||
| + | |- | ||
| + | | | ||
| + | === No increase === | ||
| + | |||
| + | |style="text-align:right;"|ולא רבוי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי כפל אחד על אחד אחד | ||
| + | |- | ||
| + | | | ||
| + | === And no division === | ||
| + | |||
| + | |style="text-align:right;"|ולא חלוק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי מצד שהוא אחד לא יתחלק | ||
| + | |- | ||
| + | | | ||
| + | === One is eternal === | ||
| + | |||
| + | |style="text-align:right;"|והאחד קדמון לבדו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי הוא קודם אל המספר קדימה טבעית | ||
| + | |- | ||
| + | | | ||
| + | === They did this === | ||
| + | |||
| + | |style="text-align:right;"|ועשו זה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל למה חלקו הגלגל לי"ב מזלות בעבור כי שנת השמש שהיא זמן סבובה מנקודה ידועה מגלגל המזלות עד שובה אליה ושנותה לסוב מהנקודה ההיא באותו הזמן סבבה הלבנה גלגלה ודבקה עמו י"ב פעם כי י"ב פעם חדושי הלבנה והמולדה שלמים יש בשנת החמה | ||
| + | |- | ||
| + | | | ||
| + | === They divided each sign to thirty degrees, because this number has more whole units than 12; for it has one-half, one-third etc. === | ||
| + | |||
| + | |style="text-align:right;"|וחלקו המזל לשלשים מעלות כי זה המספר יש לו אחדים שלמים יותר מי"ב כי יש לו חצי ‫<ref>42r</ref>חצי ושלישית וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|זה מוסיף על י"ב אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וש"ס מוסיף עוד שמינית שהוא מ"ה ותשיעית שהוא מ‫' | ||
| + | |- | ||
| + | | | ||
| + | === Each according to its rank === | ||
| + | |||
| + | |style="text-align:right;"|כל אחד כפי מעלתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל כפי מדרגתו | ||
| + | |- | ||
| + | | | ||
| + | === The number by which you divide should be less than the dividend === | ||
| + | |||
| + | |style="text-align:right;"|וראוי להיות המספר שתחלק עליו פחות מהמספר המחולק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי כשתרצה לחלק מספר אחד על אחר ראוי להיות המספר העליון גדול מהמספר השפל ואז תחלקנו עליו לידע כמה חלקים מחלקי המספר המועט ימצאו בגדול | ||
| + | |- | ||
| + | | | ||
| + | === Return back as the number of the distance === | ||
| + | |||
| + | |style="text-align:right;"|וכפי מספר המרחק תשוב אחורנית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שהמספר שבטור השפל במדרגה השלישית תכתוב העולה בחילוק במדרגה באמצע אחורנית מהאחרון שבטור העליון עד שאם היה האחרון השפל כנגד האחרון העליון נכתוב העולה בחילוק כנגד הראשון העליון | ||
| + | |- | ||
| + | | | ||
| + | === If a number that cannot be divided remains from the last digit === | ||
| + | |||
| + | |style="text-align:right;"|ואם ישאר במספר אחרון חשבון שלא נתחלק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' אחר שחלקת המספר העליון על השפל ונתת לו חלקו והנה נשאר עדין חשבון שלא יקבל חלוק לקטנותו באחדים כגון שלקח השפל חלק או חלקים במספר מהאות העליון ונשאר קצת מהאות והוא שלא יוכל להתחלק | ||
| + | |- | ||
| + | | | ||
| + | === Has not yet reached the rank of the units === | ||
| + | |||
| + | |style="text-align:right;"|ולא הגיע למעלת האחדים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שלא ירד עדין כל כך שיחבר כמותו מהמחולק עליו אבל גבוה במדרגה ממנו שאם כן לא נחלקהו עוד כי כבר יצא לחוץ | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Return the remaining number back to the preceding rank, which is lower than it === | ||
| + | |||
| + | |style="text-align:right;"|השב אחורנית מהמספר הנשאר אצל המדרגה הראשונה המדרגה שהיא פחותה ממנה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והעולה בחילוק תכתוב אותו אחורנית רחוק מהמדרגה שחלקת עתה ממנה כמרחק השפל מדרגתו הראשונה וכתבהו לפני מה שיעלה בחילוק בראשונה | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Write the remainder above the top row according to its rank === | ||
| + | |||
| + | |style="text-align:right;"|ואותו הנשאר תכתבהו למעלה מן הטור העליון כפי מעלתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' שאם הוא עשרות או מאות כתבהו למעלה במקום מדרגתו | ||
| + | |- | ||
| + | | | ||
| + | === In the fifth chapter === | ||
| + | |||
| + | |style="text-align:right;"|ובשער החמישי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יפרש כיצד נחלק אותו הנשאר | ||
| + | |- | ||
| + | | | ||
| + | === We give it 1 === | ||
| + | |||
| + | |style="text-align:right;"|ונתן לו א‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' נקח מן הט' שביעית אחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשיבם אחורנית על ‫<ref>42v</ref>הגלגל שלפני ט' נשארו ששה נשיבהו אחורנית על הגלגל השני | ||
| + | |- | ||
| + | | | ||
| + | === Calculate from this position === | ||
| + | |||
| + | |style="text-align:right;"|ותחשוב מאותו המקום | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' משם התחיל לחלוק על השפל | ||
| + | |- | ||
| + | | | ||
| + | === According to the distance of the divisor === | ||
| + | |||
| + | |style="text-align:right;"|וכפי מרחק המספר המחולק עליו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' כפי מרחק המספר האחרון שבטור השפל מהראשון תשיב זה העולה אחורנית מהמספר שחלקת ממנו | ||
| + | |- | ||
| + | | | ||
| + | === If there is a zero in one of the positions === | ||
| + | |||
| + | |style="text-align:right;"|ואם היה גלגל באחד המקומות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שהוא מפסיק בין מספרים חלוקים מגלגל אי איפשר ליקח כלום ולא לתת לו כלום | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכשיגיע המספר הגדול המחולק לתכלית החלוקה כגון שיחסר מהמספר התחתון שנחלק עליו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או יאמר עליו שכבר יצא לחוץ | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כל זמן שיהיה העליון פחות מהשפל נשיב לו כל אותו העליון אחורנית ונשיבם עשרות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומשם נמנה החלק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלל הדבר כל מה שנוכל לתת מהאחרון העליון על האחרון השפל נתן והוא שיהיה אפשר להגיע במספר חלקים לשני שהוא שני אחורנית מן השני ומן השלישי לשלישי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם לא נחלק בפעם ראשון נשוב לחלק מן הראשון לאחרון אם לא נשאר באחרון כלום או אם נשאר פחות מהשפל ואז נשיבהו אחורנית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונתן לאחרון שבטור השפל ומן השלישי לאחרון לשני מן השפל ומן הרביעי לשלישי עד שנתחיל לחלק מהעליון שהוא כנגד האחרון ונחלק כלם על כלם כנגד וכזאת החלוקה נעשה הכל כי המחולק נשאר פחות ואז נכתוב מה שעלה בחלוק באחרונה במדרגת האחדים ושוב אי איפשר לדחות כי כבר יצא לחוץ | ||
| + | |- | ||
| + | | | ||
| + | === Give the last in the bottom row of the top row === | ||
| + | |||
| + | |style="text-align:right;"|תן לאחרון שבטור השפל מהטור העליון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' שהוא שפל מהטור העליון | ||
| + | |- | ||
| + | | | ||
| + | === Give the preceding in the bottom row === | ||
| + | |||
| + | |style="text-align:right;"|ותתן לראשון מן הטור השפל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' במספר החלקים שנתת לאחרון שהוא ‫<ref>43r</ref>שהוא אחרון מהמספר מטור השפל כזה תן לראשון מן האחרון שבטור השפל מן הראשון לאחרון שבטור העליון | ||
| + | |- | ||
| + | | | ||
| + | === If you cannot do this === | ||
| + | |||
| + | |style="text-align:right;"|ואם לא תוכל לעשות ככה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' לא תוכל לתת לו כל החלקים שנתת לו כי יגרע מן האחדים מנינם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שוב וגרע מהמספרים שחשבת לתת לו בתחלה | ||
| + | |- | ||
| + | | | ||
| + | === When you have to take any digit from the digit that precedes the last === | ||
| + | |||
| + | |style="text-align:right;"|וכשאתה צריך לקחת שום מספר מהטור הראשון לאחרון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שלא יספיק לך המספר ההוא בהיותו במקום האחרון השיבהו לאחור במקום שלפני האחרון וחשוב כל אחד עשרה ולא תקח ממנו רק כפי מה שתגזרהו החלוקה | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Return back from the higher rank === | ||
| + | |||
| + | |style="text-align:right;"|השב מן הגבוה ממנו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' שלא תחלק כל המספר הגבוה על השפל רק תשאיר ממנו קצת ותשפיל מן הנשאר שם והניחהו במעלות הגלגל כפי שתצטרך וחלק ממנו לאשר כנגד מדרגתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי כפי מדרגת האחרון העליון לאחרון השפל יהיו מדרגות הראשונים העליונים לראשונים התחתונים | ||
| + | |- | ||
| + | | | ||
| + | === Return back the higher that corresponds to the digit === | ||
| + | |||
| + | |style="text-align:right;"|השב אחורנית הגבוה שהוא כנגד החשבון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שיש בטור העליון סיפרא לפני האחרון הנה נשיב הגבוה האחרון אחורנית אל גלגל אחרון אשר לפניו ותקח ממנו מה שתצטרך או כלו | ||
| + | |- | ||
| + | | | ||
| + | === From the remainder there === | ||
| + | |||
| + | |style="text-align:right;"|ומהנשאר שם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל בגלגל ההוא השיב כפי <s>רצונך</s> צרכך אחורנית לגלגל הראשון ותחלוק ממנו מה שצריך אל השפל הראוי לו כפי מדרגתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ולעולם לא נכתוב אלו מה שיעלה נחלוק בתחלה ונתן לו כפי מספר החלוקות שנשוב לעשות ובכל חלוק נכוין שיגיע לכל אח' אחד חלקו על דרך כפל שלקח תחלה האחרון מהאחרון | ||
| + | |- | ||
| + | | | ||
| + | === Two are left on the two === | ||
| + | |||
| + | |style="text-align:right;"|נשארו שנים על השנים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל על מקום הב' שהיה שם תחלה | ||
| + | |- | ||
| + | | | ||
| + | === We return on the 8 back === | ||
| + | |||
| + | |style="text-align:right;"|נשיב של הח' אחורנית | ||
| + | |||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' הא' שהוא עתה על מקום הח' שהיה תחלה נשיבהו אחורנית על מקום הב' שיש עתה עליו א' והיו ‫<ref>43v</ref>י"א | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחלק אותם על ג' שהוא בטור השפל כנגד מדרגתו ומעתה יקח כל אחד ממדרגתו ביושר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי אינו יכול לקחת הג' הד' הראשונים מהי' מבלי השבת אחד אחורנית וזהו אמרו בתשובה כלומ' בראשית שתקח אחד מהי' ונשיבהו אחורנית לפי שאינו מעלתו עכשו כמו שביארנו | ||
| + | |- | ||
| + | | | ||
| + | === Because it was first third to it === | ||
| + | |||
| + | |style="text-align:right;"|כי בראשונה היה שלישי לו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' מקום הא' היה נחשב מחלוק ראשון שלישי והיה נחלק על ג' הראשון באלכסון שהוא שלישי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכאשר תשיבהו אחורנית הנה עם הג' י"ג וט"ו ד' פעמים ל"ו על כן לא יכולנו לתת ל"כ מן הט' ד' על כן לא נתן לו רק ג‫' | ||
| + | |- | ||
| + | | | ||
| + | === Two, which is one === | ||
| + | |||
| + | |style="text-align:right;"|שנים שהם אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' נקח מאותם הה' ב' שהוא חלק אחד לב' השפלים | ||
| + | |- | ||
| + | | | ||
| + | === We take one from the 3 that is above the three === | ||
| + | |||
| + | |style="text-align:right;"|נקח מן השלשה שעל השלשה אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' שעל מקום הג' בתחלה וישארו שנים כנגד אותו מקום הג' הקודם ויש לנו לחלק על ט' ולא יספיק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אך נתן לו אחד ונכתבהו כנגד ט' נתן לב' שהוא רביעי ח' פעמים ב' שהוא י"ו נשארו ח' על הד‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם נאמר נשיב מהם שבעה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|סדר הדברים הנה באמת נאמר שנשיב מהח' שנשארו על מקום הד' ז' אצל הו' שהנחנו על הגלגל שלא נוכל להשיב מהם אחורנית אל הד' שעל מקום הט' שלשה <s>לבד</s> לבד מן הטעם שמבאר | ||
| + | |- | ||
| + | | | ||
| + | === Eight remains on the 4 that is on the 9 === | ||
| + | |||
| + | |style="text-align:right;"|וישארו שמנה על הד' שהם על הט‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' ישארו שמנה על מקום הט' שהנחנו עליו אחר כן בחלוקתנו ארבעה | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === It is taken as tens for us but that is still not enough === | ||
| + | |||
| + | |style="text-align:right;"|יצא לנו בעשרות ועוד לא יספיק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' עדין לו יספיק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' עדין לו יספיק לפי שהוא גלגל בגלגל על כן נצטרך עוד שנקח ג' מהם ונשיבם אחורנית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והשלשה הם שלשים על הד' והם ל"ד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשארו שבעה במקום ד‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי יש לנו לקחת ממנו ג' פעמים ט' ‫<ref>44r</ref>והם כ"ז ואז ישארו י"ו על הד' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ועתה נשלם חלוק ראשון [.]גלגל שלפני הד' וב' שבטור העליון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לפי שהניח בד' הזכיר הנשאר לפניו ואחר כן יזכיר הנשאר לאחריו | ||
| + | |- | ||
| + | | | ||
| + | === We give it three === | ||
| + | |||
| + | |style="text-align:right;"|נתן לו שלשה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' נתן לב' ג' חלקים כמהו שהם ו' מז' שעל הח' וישאר שם אחד והג' נכתבם תחת הגלגל הראשון | ||
| + | |- | ||
| + | | | ||
| + | === And it is impossible to return the digit back on the two, because the two is not in its rank === | ||
| + | |||
| + | |style="text-align:right;"|וגם לא נוכל להשיב אות אחורנית על השנים כי השנים אינם מעלתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|זה לא היה צריך להזכיר ועוד כי אין על הגלגל כלום | ||
| + | |- | ||
| + | | | ||
| + | === 3 remains above the zero === | ||
| + | |||
| + | |style="text-align:right;"|נשארו ג' על הגלגל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל אחר שנקח מן השלשים כ"ז שהוא חלקו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מאזני החלוק הוא שתמנה המספר השפל שעליו נחלק ונקח הנשאר בו על ט' ט' ונמנה כמה ישאר מט' ט' ושמרהו ואם נשאר למעלה דבר לחלק והוא הכתוב למעלה נראה מה שבו על ט' ונחברהו עם השמור וכזה יעדף על ט' במספר הגדול המחולק אם ימנה כהוגן | ||
| + | |- | ||
| + | | | ||
| + | === If you multiply the quotient === | ||
| + | |||
| + | |style="text-align:right;"|ואם תכפול מה שעלה בחלוק וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|זהו בוחן אחד והוא פשוט | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Chapter Three == | ||
| + | |||
| + | |style="text-align:right;"|<big>השער השלישי</big> | ||
| + | |- | ||
| + | | | ||
| + | === Every number is in accordance with these two ways === | ||
| + | |||
| + | |style="text-align:right;"|ועל אלו שני הדרכים כל החשבון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל דרך הזוגות שנחשב בו ב' חשבונות כפל כל החשבון על חציו וכפלו על חצי אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ודרך הנפרדים שנכפול על חציו לבד | ||
| + | |- | ||
| + | | | ||
| + | === Another way === | ||
| + | |style="text-align:right;"|דרך אחרת | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<ref> | + | |style="text-align:right;"|שנקח סוף החשבון שנרצה לידע המחובר מהמספרים שעברו לפניו ונכפלהו על עצמו ואחר כן ‫<ref>44v</ref>נוסיף על המרובע הזה שרשו שהוא סוף החשבון והנה חצי זה הוא המבוקש |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|דרך אחרת שנכפול מרובע חצי המספר ונוסיף עליו שרש זה המרובע שהוא חצי החשבון והוא המבוקש המבוקש |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הרוצה לידע מספרים מחוברים בדלוג אחד עד מספר ידוע כמו שירצה |
| − | == | + | |- |
| + | | | ||
| + | |style="text-align:right;"|לידע הנפרדים שהם עד ט' יוסיף על החשבון אחד והיו עשרה נכפול עשרה על רביע' רביעיתם שהוא ב' וחצי <s>והוכה</s> והיו כ"ה וככה המחובר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונחבר אליו שלישית הסכום שהוא כ"ו כי כפל אחד ע"ח הוא ע"ח וכפל אחד על ע"ח הוא שליש ע"ח שהוא כ"ו | ||
| + | |- | ||
| + | | | ||
| + | === Add the scale of the top row === | ||
| + | |style="text-align:right;"|חבר מאזני הטור העליון | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ר"ל הנשאר בו מתשעיות |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | === In the tables of the planets there is no [more fractions] === |
| + | |||
| + | |style="text-align:right;"|ואין בלוחות המשרתים | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|לא ידקדקו יותר מזה |
|- | |- | ||
| | | | ||
| − | + | === One according to the solar years === | |
| − | == | ||
| + | |style="text-align:right;"|האחד על שנות השמש | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|כגון האמות המונים לשמש ועושים מחזורים מעשרים עשרים שנה שיזכרו מהלך כל משרת בזה המספר מן השנים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | === The same is done with the whole hours that have passed after the middle of the day === |
| + | |||
| + | |style="text-align:right;"|וככה תעשה בשעות השלמות שעברו אחר חצי היום | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|כי הם ימנו תחלת היום מחצי היום |
| − | == | + | |- |
| + | | | ||
| + | === Write them alone === | ||
| + | |style="text-align:right;"|כתבם לבדד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי הוא רוצה לדעת מקום המשרת בזה השעה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|על כן יכתוב העולה מן המחובר בטור מיוחד השם . כתוב השניים המחוברים מטורי השניים לפניהם הראשונים ולפניהם המעלות וכן <s>כולם</s> כולם וישמור כל העולה למה שרצהו |
|- | |- | ||
| | | | ||
| − | |||
| − | |||
| + | == Chapter Four == | ||
| + | |||
| + | |style="text-align:right;"|<big>השער הרביעי</big> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כשנרצה לגרוע מספרים ממספרים נכתוב המספרים שנרצה לגרוע מהם עליונים ותחתיהם טור הנגרעים וצריך שיהיה אחרון שבטור העליון כללו גדול משכנגדו השפל ולא נפקד בגודל הפרטים השפלים כי הכל תלוי בכלל | ||
| + | |- | ||
| + | | | ||
| + | === If you find in one of the ranks === | ||
| + | |||
| + | |style="text-align:right;"|והנה אם מצות באחדות המעלות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>45r</ref>פי' כי כשנמצא במדרגות האחדות שהן לפני האחרון שהשפל גדול ממספר הטור העליון שכנגדו נקח אחד מהעליון ונחשבהו ונחל לגרוע מהאחרונים הגבוהים במדרגה זהו דרך אבן עזרא ואין זה סדר נכון שאחר שיכתוב הנשאר מן הראשון יצטרך לפעמים לגרוע ממנו ולהוסיף לראשון ויצטרך לפי זה שבטרם יכתוב האחרון אם יעדיף השפל שלפניו ויתן לו אחד ויגיע אחד מהמספר האחרון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אבל הסדר היותר נאות שנחל נמנות מן האחדים ומה שיתחבר מהם כלל יחברהו עם הכלל שלאחריו וכן כולם כדרך שנעשה בשניים ובראשונים ובמעלות ובמזלות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון חסרון אחד מב' וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שתרצה לגרוע י"ז מכ' ונכתוב שני הטורים כן | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחסר א' מב' ונשאר א' והנה אין על הז' כלום נשיב ז' א' הא' כנגד הז' והוא י' נחסר ממנו ז' ונשאר ג‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה מאזני הטור העליון ב' ומאזני הטור השני ח' ולא נוכל לחסר ח' מב' על כן נוסיף ט' עם הב' יהיו י"א נגרע ממנו ח' ועתה נשאר מאזני שני הטורים ג' וכן מאזני השלישי |
|- | |- | ||
| | | | ||
| − | + | === He adds six to the scale of the upper seconds === | |
| − | == | ||
| + | |style="text-align:right;"|יוסיף על מאזני השנים העליונים ששה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|כי כך ישאר מששים על ט' ט‫' |
|- | |- | ||
| | | | ||
| − | + | === Add three to the scale of the degrees that were written first === | |
| − | == | ||
| + | |style="text-align:right;"|הוסף על מאזני המעלות הכתובים בראשונה שלשה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|כי כן ישאר מל' מעלות הנוספות |
|- | |- | ||
| | | | ||
| − | + | === Add three to the scale of the signs that were written first === | |
| − | == | ||
| + | |style="text-align:right;"|הוסף על מאזני המזלות הכתובים בראשונה שלשה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי כן ישאר מי"ב מזלות | ||
| + | |- | ||
| + | | | ||
| + | === One thing that is necessary when subtracting: the last [digit] at the end of the upper row must always be greater === | ||
| + | |||
| + | |style="text-align:right;"|דבר שהוא צורך למגרעת לעולם אותו בסוף הטור העליון יהיה גדול | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|זה מדבר על דעת חכמי החשבון כי האחרונים גבוהים במדרגה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |
| + | == Chapter Five == | ||
| + | |||
| + | |style="text-align:right;"|<big>השער החמישי</big> | ||
|- | |- | ||
| | | | ||
| − | + | === One is as a point in a circle === | |
| − | == | ||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#one_is_as_a_point_in_a_circle|<span style=color:blue>'''האחד כמו נקודה בתוך עגולה'''</span>]] | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ר"ל כי האחד אמצעי בין השלמים והשברים על כן לא יתכן להיות האחד נשבר כי מאשר הוא אמצעי לא יתחלק |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | === The whole is named with one name, as the shape represents the entire body === |
| − | = | + | |
| + | |style="text-align:right;"|‫<ref>45r</ref>[[ספר_המספר_/_אברהם_אבן_עזרא#the_whole_has_one_name|<span style=color:blue>'''רק בעבור שיקרא הכלל בשם אחד כמו צורת הגוף ותבניתו שהיא כוללת כל הגוף'''</span>]] | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונקרא הכל בגוף אחד וא'ע'פ' שהוא מורכב מאברים רבים שכל אבר הוא אחד כן האחד נקחנו כולל ותחתיו שברים רבים שהם אחדים רק בערך אל האחד הכולל יקראו שברים וכל זה במחשבה כי האחד האמתי לא יתחלק |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | === Therefore they take the half from two === |
| + | |||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#arithmeticians_take_half_from_two|<span style=color:blue>'''על כן יוציאו החצי משנים'''</span>]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי החצי הוא אחד משני חלקי הדבר | ||
|- | |- | ||
| | | | ||
| − | + | === The analogous number from which they derive is called the "denominator" === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#the_analogous_is_called_denominator|<span style=color:blue>'''ואותו שיקחו הדמיון ממנו יקראו המורה'''</span>]] | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כמו השלשה לשליש וארבעה לרביעית | |
| − | + | |- | |
| − | + | | | |
| − | + | === For the product is divided by its square === | |
| − | |||
| − | |||
| − | |||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#the_product_is_divided_by_its_square|<span style=color:blue>'''כי כל מרובע יחלקו העולה בחשבון'''</span>]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שנכפול שני רביעיים על שני רביעית הנה הנכפל ד' והמורה ומרובעו י"ו שהוא אחד שלם ונכפול ב' על ב' והם ד' נחלק ד' על ט' יגיע לכל אחד שליש ותשיעית אחד | ||
| + | |- | ||
| + | | | ||
| + | === The remainder that cannot be divided === | ||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#the_remainder_that_cannot_be_divided|<span style=color:blue>'''והנשאר שלא יתחלק'''</span>]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' אחר שנחלק מרובע המורה על החשבון הנכפל אם ישאר חשבון שלא יוכל להתחלק לחלקים שלמים אלא כשנחלק אחד מהם לחלקים רבים כגון המשל השני שהמשלנו נכנה אותו החלק בשם רביעית או תשיעית כפי מה שיהיה החשבון | ||
| + | |- | ||
| + | | | ||
| + | === The one, on the one hand, is not a number === | ||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#one_is_not_a_number|<span style=color:blue>'''האחד מפאה אחת איננו מספר'''</span>]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל כי אינו מספר כי אם בהתחברו למספרים | ||
| + | |- | ||
| + | | | ||
| + | === Because when you sum all the odd numbers === | ||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#the_sum_of_odd_numbers|<span style=color:blue>'''כי בחברך כל הנפרדים'''</span>]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי אם א[.] וג' הם ד' והוא מרובע שנים ד' וה' הם ט' והוא מרובע ג' ט' וז' הם י"ו והם מרובע ד' וכן כולם על הסדר וכל זה ככה האחד ושתותיו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"| | ||
| + | === ודברים רבים === | ||
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ימצאו באחד | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"| | |
| − | + | === אין צורך להזכירם והנה נשארו במערכה הראשונה כו‫' === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|מערכת הראשונה הם ט' האחדים והנה דבר על האחד והנה נשאר לדבר על שמונה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"| | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === והנה חציים ראשונים === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ראשון נקרא כל חשבון פשוט שאינו מתחלק בשוה | |
| − | + | אלא לאחדים במספרו כגון שנים שנים ‫<ref>46r</ref>שנים לשני אחדים וג' לג' וכן כלם . המספר [...........] למספרים שוים | |
| − | + | |- | |
| − | + | | | |
| − | + | === When there is a need for two fractions that are not of one kind === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"| | |
| − | + | [[ספר_המספר_/_אברהם_אבן_עזרא#2_fractions_of_different_kinds|<span style=color:blue>'''וכאשר יצטרכו שברים שאינם ממין אחד וכו‫''''</span>]] | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כגון שנרצה לכפול שני שלישים על שני רביעיים הנה כפל שנים על שנים ד' והנה נבקש לכל אחד המורה שיצא ממנו שהוא שלשה וארבעה ונכפול המורה האחד על המורה האחר והוא המורה ואליו נחלק כפל החשבון הראשון | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | === If there are 3 types === | ||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#3_types_of_fractions|<span style=color:blue>'''ואם היו שלשה מינים'''</span>]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שנרצה לכפול ב' שלישיים וב' רביעיים וב' חמישיים זה על זה נכפול שלשה על ארבעה והם י"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נכפול י"ב על חמשה והם ס' וזהו המורה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונכפול החשבון שהוא י"ב ב' על ב' והם ד' נכפול ד' על ב' והם ח' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחלק ח' על ס' . [.] שנרצה לכפול ב' שלישים על ג' רביעיים וד' חמשים נעשה מורה אחד לרביעים ולחמישיים והוא כ' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נכפול מורה שלישיים על ד' עלה ח‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נכפול ג' רביעיים על ד' חמישיים והם י"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נכפול ב' שלישיים על י"ב והם כ"ד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה החשבון כערך כ"ד אל ס‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או אם נרצה אחר שעשינו תחלה מורה מכ‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכפלנו ג' על ד' שהוא י"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נסיר מהם ב' שלישיות והוא ח‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והכל שוה כי ערך ח' אל כ' כערך כ"ד אל ס' והוא ב' חמישיות אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ודע כי בקשת המורה כדי שנדע אי זה חשבון הוא שימצאו בו חלקים אלו ונחלוק אותו על מרובע המורה כדי שנדע אי זה <s>חשבון הוא שימצאו בו חלקים</s> ערך יש לחשבון מן האחד כשיכפול אדם שני שלישים על ג' רביעים צריך שנבקש לשניהם מורה אחד והוא העולה מכפל שניהם והנה יעשה לו מרובע בדרך שנעשה במורה אחד ויעשה כפי השני במספר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם ירצה יקח כפל השני מורים מקום מרובע כי הוא מרובע אמצעי ביניהם כי כפל ג' הוא ט' ומרובע ד' י"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה המורה הוא י"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואחר שנדע המורה נראה כמה הוא ג' רביעיותיו ונקח <ref>46ב</ref>מהם ב' שלישיים כי הוא כאמרו קח ב' שלישיים מב' רביעיים או בהפך והכל שוה | ||
| + | |- | ||
| + | | | ||
| + | === The multiplication of fractions is opposite to the multiplication of integers === | ||
| + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#multiplication_of_fractions_is_opposite_to_multiplication_of_integers|<span style=color:blue>'''כפל השברים הפך כפלי השלמים'''</span>]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי השלמים הנכפלים אלה על אלה יוסיפו בחשבון כפי מה שיעלה | ||
| + | מכפל אבל שברים על שברים יהיה העולה שבר אחד מהשברים הנכפלים וכפי התוספת בשלמים נכוין לגרוע בשברים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי האחד הנכפל על איזה חשבון לא יוסיף על אותו חשבון כלום כי אחד על שנים שנים ואחד על חצי כלו' פעם פעם אחד חצי הוא חצי אם כן חצי על חצי הוא רביע כאלו תאמר חצי החצי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן שלישית על שלישית כאלו תאמר שלישית השלישית שהוא תשיעית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכפל רביעית על רביעית יהיה חלק אחד מי"ו והוא חצי שמינית שהוא השלם ועל כן אמר והנכפל אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי לעולם ירד ממדרגה אחת בדרך שכפל ראשונים בראשונים יהיו שניים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"| | ||
| + | === ועל זה הדרך תכפול שברי המין האחד על שברי המין בעצמו === | ||
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כמו שהמשלנו משלישיות על שלישיות או מרביעיות על רביעיות | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"| | |
| − | + | === בין שיהיו שוים === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כגון ב' רביעית על ב' רביעיות | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|או שיהיו שברי אחד מהם גדולים כגון ב' רביעיות על ג' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"| | |
| − | + | === ואם תרצה חלק תשעה על הארבעה === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | על | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|שהוא המורה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"| | |
| − | + | === והדבר יצא בשוה === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כי העולה בחלוק לכל אחד הוא ב' ורובע שהוא ב' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
רביעיים ורביעית רביעית והוא חצי וחצי [.] שמינית כי האר' | רביעיים ורביעית רביעית והוא חצי וחצי [.] שמינית כי האר' | ||
הארבעה שנחלק עליהם הם רביעית מרובע המורה . ל"א כי | הארבעה שנחלק עליהם הם רביעית מרובע המורה . ל"א כי | ||
| Line 477: | Line 1,171: | ||
שלישיות שמונה . כי ח' ב' שלישי י"ב שהוא המורה . והוא חצי | שלישיות שמונה . כי ח' ב' שלישי י"ב שהוא המורה . והוא חצי | ||
ק'מ'ד' שהוא מרובע הי"ב ואם עשית זה משנים מורים כלומ' אתה | ק'מ'ד' שהוא מרובע הי"ב ואם עשית זה משנים מורים כלומ' אתה | ||
| − | 47א | + | <ref>47א</ref>אתה רשאי להעריך חשבונך לכפל השני מורים [........]מרובע |
| − | אתה רשאי להעריך חשבונך לכפל השני מורים [........]מרובע | ||
בענין שהקדמנו . כי העולה שהוא ששה נקח ערכו אליו . ר"ל אל הי"ב | בענין שהקדמנו . כי העולה שהוא ששה נקח ערכו אליו . ר"ל אל הי"ב | ||
שהוא המורה והוא חציו . כי השביעית הם תשעה . כלומ' כי אחר ש' | שהוא המורה והוא חציו . כי השביעית הם תשעה . כלומ' כי אחר ש' | ||
| Line 491: | Line 1,184: | ||
לקחנו אותו כלומ' בעבור כל צורה נקח המספר המיוחד לו כי | לקחנו אותו כלומ' בעבור כל צורה נקח המספר המיוחד לו כי | ||
לולי ג' לא היה נאמר ב' שלישיים ולולי מורה ד' לא יתכן לו' | לולי ג' לא היה נאמר ב' שלישיים ולולי מורה ד' לא יתכן לו' | ||
| − | לומר ג' רביעיים | + | לומר ג' רביעיים |
| − | חמישיות וכו' | + | |- |
| − | מעלות על ראשונים שהם ראשונים על כן נקח המורה שהוא ה' | + | | |
| − | ומרובעו כ"ה וד' פעמים ג' הם י"ב והנה ערך י"ב אל כ"ה הם [ב'] | + | === Example: we wish to multiply 4 integers by 3 fifths === |
| − | שלמים וב' חמישיות | + | |
| − | ראשונים והיו ת'ר'י'ו' שנים ר"ל שכל אחד חלק מכ"ה . עלו | + | |style="text-align:right;"|[[ספר_המספר_/_אברהם_אבן_עזרא#4_by_3_fifths|<span style=color:blue>'''דמיון רצינו לכפול ד' שלמים על ג' חמישיות וכו''''</span>]] |
| − | כ"ד שלמים וישארו י"ו שניים והט"ו הם ג' חמישיים | + | |- |
| − | והאחד חומש החומש שהוא חלק מכ"ה באחד . כי הם | + | | |
| − | חלקי המורה כי מהשברים וקח המורה . לכן המחובר | + | |style="text-align:right;"|והנה שלמים על נשברים עלו נשברים בע[..] מעלות על ראשונים שהם ראשונים על כן נקח המורה שהוא ה' ומרובעו כ"ה וד' פעמים ג' הם י"ב והנה ערך י"ב אל כ"ה הם [ב'] שלמים וב' חמישיות |
| − | מהם הוא חלקים ממנו | + | |- |
| − | מ"א אלף ות"ת והנה כל ארבעים מהם הוא אחד שלם כי הם | + | | |
| + | |style="text-align:right;"|נכפול כ"ב על כ"ח שהם נשברים ראשונים והיו ת'ר'י'ו' שנים ר"ל שכל אחד חלק מכ"ה . עלו כ"ד שלמים וישארו י"ו שניים והט"ו הם ג' חמישיים והאחד חומש החומש שהוא חלק מכ"ה באחד . כי הם חלקי המורה כי מהשברים וקח המורה . לכן המחובר מהם הוא חלקים ממנו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה נכפול זה על זה ועלה מ"א אלף ות"ת והנה כל ארבעים מהם הוא אחד שלם כי הם <ref>47v</ref>במדרגה שנית מארבעים גם כן ועל כן שבו הנשארים ה' חלקים ממ' עלו אלף קנ"ה שכל ע"ז הוא אחד מע"ז הראשונים על כן ט"ו פעמים ע"ז הם ט"ו מע"ז שהוא המורה . והוא מנין שהיה יכול לעשות מרובע למורה שהוא ע"ז ויהיה ה' אלפים ות'ת'ק'כ'ט' ויהיה ערך אלף קנ"ה אליו כ' כערך ט"ו אל ע"ה (ע"ז) כי מרחק ט"ו מע"ה (ע"ז) ס"ב ומרחק אלף קנ"ה מה' אלפים | ||
| + | ת'ת'ק'כ'ט' ס"ב פעמים ע"ז . כל שבר נפרד שהוא למעלה מי' שיש בו שני מספרים כגון י"א או י"ג וי"ט נקרא חשבון שלא יוכל אדם לב' לבטא בו . אבל כל זוג יכול לבטא כי אם יש לנו ב' חלקים מי"ב נקח ששית אחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון כמה ג' שביעיות על ה' חלקים מאחד עשר וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והדרך הקרובה שאחר שמענו שהמורה ע"ז ושה' חלקים מי"א מע"ז הם ל"ה נחסר ג' שביעיות מל"ה שהם ט"ו מע"ז והוא המבוקש כי הוא כאמרנו ג' שביעיות מה' חלקים מי"א | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או כפול מספר ג' על ה' והוא ט"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נכפול קע"א על רכ"א יעלו ל"ז אלפים ות'ש'צ'א‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחלקים על ר'מ'ז' והנם ק'נ'ג‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל ק'נ'ג' פעמים ר'מ'ז' שכל ר'מ'ז' חלקים מאלו באחד מחלקי ר'מ'ז' שהוא המורה נמצא שיש לנו ק'נ'ג' חלקים מר'מ'ז‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכערך ק'נ'ג' מר'מ'ז' שיחסר ממנו צ'ד' כן ערך המספר הראשון שהוא ל"ז אלפים ות'ש'צ'א' אל מרובע ר'מ'ז‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי כן יחסר ממנו צ"ד פעמים ר'מ'ז‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומרובע ר'מ'ז' הוא ששים ואחד אלף ותשעה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כפל ט' בי"ז שהוא המספר יעלה ק'נ'ג‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן אם תקח מר'כ'א' הוא י"ז וט' פעמים י"ז הוא ק'נ'ג‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אחר שיש לנו ששיות אין צריך לשלשה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי שלשה הם בכלל ששה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|גם זה על שבעה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל גם שלשים על ז‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|גם זה על ח' ר"ל [ר"י] ורביעיותיו פ"ד ר"ל רביעית של"ו הוא פ"ד ושתי שלישיות פ"ד הוא נ"ו כי הוא כאלו אמרנו נכפול שני שלישיות הלקוחות מרביעית הלקוח מחמישית על שש רביעיות הלקוחות משמינית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|על כן נקח‫<ref>48r-49r: illegible</ref> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>49v</ref>בספר [...] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ועוד כי מצאו בשנת ה[שמש] וכו' זה טעם למה חלקו הגלגל לי"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כאומר חשבון חברנו אליו כל החלקים מחצי עד עשירית מה ערך המספר אליו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל אם ישאלך אדם ממון היה אצלי וחברתי עמו חציו ושלישיתו וכל החלקים עד עשירית והיה כך כמה היה החשבון תחלה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי אם נצטרך לכפול כל החלקים אלו על אלו כדרך שעשינו במה שעבר היה טורח גדול ואמ' שלא נצטרך לזה רק שנקח זה החשבון תחת המורה שהוא אלפים ותק"כ כי בו נמצאו כל אלו החלקים ולא בפחות ממנו ואע"פ שימצאו בגובה ממנו כי צורך בקשת המורה כדי שנמצא חשבון שיהיו החלקים הנרצים והוא הדין שאם נמצא חשבון פחות מזה הנכפל שיהיו בו אלו החלקים בעצמם שזה יספיק לנו ויגיענו למבוקשנו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון זה ממון חברנו אליו שלישיתו ורביעיתו (וחמישיתו) וששיתו והיה השלם כ"א נכפול המורה בחשבון והוא ש"ס נחלק ש"ס על כ"א עלו [י"ז] שלמים וג' חלקים מכ"א שהן שביעית אחד כך היה סך הממון הראשון ובחן זה ותמצא | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כשנצטרך למצוא כל החלקים לא נצטרך לכפול כל החלקים אבל נקח אלפים ותק"כ ואע"פ שהוא פחות הרבה מהנכפל מאלה החלקים ונוסיף מע מחציתו ושלישיתו ורביעיתו וכל החלקים והמחובר א"ח ג"ז וזהו השלם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונחשוב שהחשבון ס' נכפול המורה בחשבון ויהיה העולה נחלק על זה הנכפל על השלם הנה נבחן זה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה חצי השלמים ורביעיתם וחמישיתם ד' ועשיריתם ב' ושלישיתם ו' וישארו שניים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשיבם אל שברי השלם שהוא א"ח ג"ז ונחבר עמהם החלקים הנשארים למעלה שהם ג' אלפים ותק"ף ומן המחובר נקח השלישי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן נעשה מן השתות ומן התשיעית כי כשלקחנו בעבור השתות | ||
| + | ג' ובעבור התשיעית ב' ישארו ב' שלמים וכשלקחנו בעבור השמינית <ref>50א</ref>השמינית ב' ישארו ד' וכשלקחנו בעבור התשיעית (שביעית) ב' ישארו ו' שנשיבם לשברים הנה כל השלמים נ"ו נעשה מן השלמים הנשארים | ||
| + | חלקים הנה השער ב"ו זד"א ועם 0 ח הג יהיה בדג חא עם 0 | ||
| + | והג' הם ד 0 אג ג וג' שלמים [........] ועם החלקים הנשארים | ||
| + | הנזכרים וו ח זד וזה מספר כל חלק החלקים שהם מחצי עד עשירי | ||
| + | נחבר עם 0 ח ה ג ויעלה דבהט"ב נחלק על אחגז ויעלו ד' שלמים נחברם עם הי"ו (נ"ו) שהיו לנו והנה כל המספר ס' | ||
| + | |- | ||
| + | | | ||
| + | === The rule: the product of degrees by any type is the same type itself === | ||
| + | |||
| + | |style="text-align:right;"|והכלל כפל מעלות על אי זה מין שיהיה ישאר אותו המין בעצמו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כמו כפל אחדים על השברים שיהיה ישאר אותו המין בעצמו כמו העולה אותו המין מן השברים | ||
| + | |- | ||
| + | | | ||
| + | === The product of minutes by minutes is seconds === | ||
| + | |||
| + | |style="text-align:right;"|וכפל ראשונים על ראשונים יהיה העולה שנים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כמו שהחצי על חצי העולה יהיה רביעית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וראשונים על שנים יהיה העולה שלישיים וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עד שיהיה כפל שלישים על רביעים וחמישיים על חמישיים עשרים כי לעולם נחבר מספר השתי מדרגות והוא היוצא וכן מבואר בלוח המעלות והשברים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואחר שנכפול ראשונים בראשונים שהם שניים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון ל' ראשונים יהיה העולה הת"ק נחלקנו על ס' יעלה ט"ו והם ראשונים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן אם נכפול ראשונים על שניים והיו שלישיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחלק השלישיים על ס' ומה שיעלה יעלה למדרגת השניים כי לעולם יעלה בחלוק מדרגה אחת והנשאר הוא מן השלישיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שנכפול מ"ה ראשונים על נ' שניים יעלה אלפים וכן שלישים נחלקם על ששים עלו ל"ז שניים וישארו ‫<ref>50v</ref>ל' שלישים שלישיים באיזו מעלה מן השברים ר"ל באיזו מדרגה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם יהיו שנים חשבונים כלומ' אם יהיה לך ב' מעלות תכתוב 0ב במקומו ואם יש לך שני חשבונות כגון כ"ה תכתוב שם ה"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כדרך שתעשה בשלמים ‫<ref>51r</ref>כפול המספר הטור העליון במספר הטור אשר תחתיו והחל לכפול מעלות במעלות וכתוב במדרגת המעלות ואחר מעלות בראשונים וכתבם תחת הראשונים וכן כל אחד במדרגתו כמשפט ואם היה היו שם שני מספרים בכלם ביחד וכתבהו במקומו וכתוב האחדים ראשונה ואחר העשרות ואחר המאות כל אחד באותו הטור אם יעלה כל כך הכפל ההוא תכתוב הכל על הסדר ולא תתערבב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם תרצה כפול האות האחת באות הראשון שבאותו הטור וכתבהו לבד במקומו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואחר כן כפול האות ההוא באות השני וכתבהו סמוך לו באותו טור | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם נשאר מכפל האות הראשון עשרה חשבהו כאחדים וחברהו עם | ||
| + | כפל האות שאחריו וכתבהו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם ישאר לסוף עשרה כתוב שם בסוף א' בדרך שלמדך החכם אבן עזרא בשער הכפל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם תרצה <s>[..]ל</s> תוכל לעשות בדרך האלכסונות ולא תצטרך רק לטור אחד ולא תצטרך לחבור כי הוא העולה רק יכבד הדבר עליך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואחר חבר הכל וכתוב העולה הכל טור למטה כנגדו מהאחדים שבאותו טור על הסדר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם ישאר לך כלל שמרהו וחברהו עם העולה מהמספר שאחריו באותו טור | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן תעשה מכל טור וטור כמו שתראה בצורה בטור השפל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אחר תחל לחלק על ששים הטור האחרון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שהוא חמישיים ולכל ששים קח אחד וחברהו עם המדרגה שלפניו שהם רביעיים והנשאר פחות מס' השאר שם במקומו שהוא חמישיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן תעשה מהרביעים הוציאם ס' ס' ומכל ששים חבר אחד עם השלישיים והנשאר תכתבהו במעלת הרביעיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כולם עד שתעלה המספר למדרגת המעלות והנשאר בכל מעלה ישאר וזה הנשאר אחר החלוק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>51v</ref>זהו דרך חכמי המזלות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אבל דרך חכמי החשבון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כשיגיעו לכפול הטור העליון שבצורה ראשונה על הטור השפל שבו כל מה שבטור העליון למדרגת המספר הקטן שהוא בכאן השלישיים וכן כל מה שבטור השפל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכיצד יעשו יכפלו המעלות על ששים והנם ראשונים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחברם עם הראשונים ונכפלם על ס' יהיו שלישיים כי לעולם ירד ממדרגה אחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן נעשה בכאן | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply 2 by 60; they are 120 primes. | ||
| + | ::<math>\scriptstyle{\color{blue}{2\sdot60^{\prime}=120^{\prime}}}</math> | ||
| + | |style="text-align:right;"|נכפול ב' על ס' והם ק"כ ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::We add them to the 9, which are also primes; they are 129. | ||
| + | ::<math>\scriptstyle{\color{blue}{120^{\prime}+9^{\prime}=129^{\prime}}}</math> | ||
| + | |style="text-align:right;"|נחברם עם ט' שהם ראשונים כמו כן והם קכ"ט | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply 129 by sixty; with the 4, they are 7 thousand and 744 seconds. | ||
| + | ::<math>\scriptstyle{\color{blue}{129^{\prime}\sdot60^{\prime}+7^{\prime\prime}=7744^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|נכפול קכ"ט על ששים ועם הד' הם ז' אלפים תשמ"ד שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply them by 60; with the 3, they are 464 thousand and 643 thirds. | ||
| + | ::<math>\scriptstyle{\color{blue}{7744^{\prime\prime}\sdot60^{\prime}+3^{\prime\prime\prime}=464643^{\prime\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|נכפול זה על ס' ועם הג' הם תס"ד אלפים [...] אלפים ותרמ"ג שלישיים | ||
| + | |- | ||
| + | | | ||
| + | ::We do the same with the second line; the result is 715 thousand and 451 thirds. | ||
| + | |style="text-align:right;"|וכן נעשה מן הטור <s>נעשה מן</s> השני ויעלה תשט"ו אלפים ותנ"א שלישיים | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply them by each other; the result is 332429[29]8993 sixths. | ||
| + | ::<math>\scriptstyle{\color{blue}{464643^{\prime\prime\prime}\times715451^{\prime\prime\prime}=332429298993^{vi}}}</math> | ||
| + | |style="text-align:right;"|נכפול אלו על אלו ועלה גטטחטבדבגג והם ששיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אחר נחלקם על ס' ותן לו מכל אחד מה שתוכל וכתבהו במקום הראוי לו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם היה העליון פחות השיבהו אחורנית בעשרות ותן לו מה שתוכל ומה שישאר השיבהו אחורנית שלפניו וכן תמיד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכשיקרה באחד מן האמצעיים שיכלה בכוון אל הו' והאות שלפניו פחות מו' כתוב בספרא כנגדו בטור האמצעי והאות שלפניו השיבהו אחורנית וחלק ממנו כמשפט עד שתגיע כנגד הראשון שהיא מדרגת האחדים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומה שישאר לחלק שהוא פחות מששיים ישאר במדרגתו והעולה בחלוק יהיה רביעיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומה שישאר לחלק הוא חמשים כבתחלה וכן נעתיקנו תמיד ממדרגה והעולה בחלוק יהיה רביעיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומה שישאר לחלק הוא למדרגה עד הגיעו למעלות כי בכל חלק יעלה מדרגה אחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם תחשוב כראוי תמצא הנשאר מכל המדרגות שוה ‫<ref>52r</ref>לחשבון הראשון וזה הדרך השני הוא שקרא דרך המבטא | ||
| + | |- | ||
| + | | | ||
| + | ::When we divide the line of the sixths by sixty, the result of division is 5540[4]88316 fifths and 33 sixths remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{332429298993^{vi}\div60=5540488316^{v}+33^{vi}}}</math> | ||
| + | |style="text-align:right;"|וכשנחלק טור הששים על ששים יצאו בחלוק מן החמישיים ואגחח0דהה וישארו מן הששים גג | ||
| + | |- | ||
| + | | | ||
| + | ::When we divide these fifths by sixty, the result is 92341471 fourths and 56 fifths remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{5540488316^{v}\div60=92341471^{iv}+56^{v}}}</math> | ||
| + | |style="text-align:right;"|וכשנחלק אלו החמישיים על ששיים יעלו הרביעים אזדאדגבט וישאר מן החמישיים וה | ||
| + | |- | ||
| + | | | ||
| + | ::When we divide these fourths by 60, the result is 1539024 thirds and 31 fourths remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{92341471^{iv}\div60=1539024^{\prime\prime\prime}+31^{iv}}}</math> | ||
| + | |style="text-align:right;"|וכשנחלק אלו הרביעיים על ס' יעלו השלישיים דב0טגהא וישאר ממין הרביעים אג | ||
| + | |- | ||
| + | | | ||
| + | ::When we divide the thirds, the result of division is 25650 seconds and 24 thirds remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{1539024^{\prime\prime\prime}\div60=25650^{\prime\prime}+24^{\prime\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|וכשנחלק השלישיים יצא בחלוק מהשניים 0הוהב וישאר מהשלישיים דב | ||
| + | |- | ||
| + | | | ||
| + | ::When we divide the seconds by 60, the result is 427 primes and 30 seconds remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{25650^{\prime\prime}\div60=427^{\prime}+30^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|וכשנחלק השניים על ס' יצא זבד ראשונים וישאר מהשניים 0ג | ||
| + | |- | ||
| + | | | ||
| + | ::When we divide the primes by [60], they are 7 degrees and 7 primes remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{427^{\prime}\div60=7+7^{\prime}}}</math> | ||
| + | |style="text-align:right;"|נחלק הראשונים על מעלות ויהיו המעלות ז' וישארו ז' ראשונים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והיה זה שוה לנשאר תחלה | ||
| + | |- | ||
| + | | | ||
| − | + | === The chords of the arcs === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |style="text-align:right;"|יתרי הקשתות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שנדע המרחק מנקודה ידועה מהקשת עד נקודה ידועה ממנו ונרצה לידע אורך היתר שמנקודה זו אל נקודה האחרת מהקשת ביושר או כמה אלכסון המיתר ההוא | ||
| + | |- | ||
| + | | | ||
| + | === The perimeter should be three times the diameter === | ||
| + | |style="text-align:right;"|הקו הסובב ראוי שלשה מהאלכסון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שלשה מקטרו ושביעית וא'ע'פ' שלפי החוג שהקיפו שלשה ממנו לבד אין ראיה כי החוג [....] מיתר ברחב העגול שהוא קו ישר שאין [....] שעקם העגול שבין שתי נקודות אלו יותר גדול | ||
| + | |- | ||
| + | | | ||
| + | == Chapter Six == | ||
| + | |style="text-align:right;"|<big>השער הששי</big> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כונת זה השער לזכור ערכי המדות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ומתוך כך רצה להודיע מיני הערכים כמה הם ערכי החשבון והם על הסדר שכפי היתרון שיש לשני על הראשון יש לשלישי על השני | ||
| + | |- | ||
| + | | | ||
| + | === The second way is the geometric proportions as 4 6 9 === | ||
| + | |style="text-align:right;"|והדרך השני ערכי המדות כמו ד'ו'ט‫' | ||
| + | |- | ||
| + | |As the ratio of 6 to 4, which exceeds it by its third, so is the ratio of 9 to 6, which exceeds it by its third. | ||
| + | :<math>\scriptstyle{\color{blue}{6:4=\left[4+\left(\frac{1}{3}\sdot6\right)\right]:4=\left[6+\left(\frac{1}{3}\sdot9\right)\right]:6=9:6}}</math> | ||
| + | |style="text-align:right;"|שכערך שיש לו' אל ד' שמידתו גדולה ממנו השליש כן ערך ט' אל ו' שעודף עליו שלישו | ||
| + | |- | ||
| + | | | ||
| + | === So the product of the smaller number by the greater number === | ||
| + | |style="text-align:right;"|על כן כפל הקטן על הגדול | ||
| + | |- | ||
| + | |I.e. since 4 is smaller than 6 by the same as 9 exceeds 6 | ||
| + | :<math>\scriptstyle{\color{blue}{4=6-\left(\frac{1}{3}\sdot6\right)\quad6=9-\left(\frac{1}{3}\sdot9\right)}}</math> | ||
| + | |style="text-align:right;"|ר"ל אחר שיחסר ד' מן הו' כמו שיעדיף ט' על ו‫' | ||
| + | |- | ||
| + | |So the product of the smaller number by the greater number. | ||
| + | |style="text-align:right;"|על כן כפל הקטן על הגדול וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | === Know that these three numbers are like four numbers === | ||
| + | |style="text-align:right;"|ודע כי אלה ‫<ref>52v</ref>השלשה מספרים כמו ארבעה הם | ||
| + | |- | ||
| + | |Since the means are the same when extracting the ratio. | ||
| + | |style="text-align:right;"|לפי שאמצעי לשוה <s>בעשירית</s> בעשיית הערך | ||
| + | |- | ||
| + | | | ||
| + | :Because we say the ratio of 4 to 6 is the same as the ratio of 8 to 12. | ||
| + | :<math>\scriptstyle{\color{blue}{4:6=8:12}}</math> | ||
| + | |style="text-align:right;"|כי נאמר ערך ד' אל ו' כערך ח' אל י"ב | ||
| + | |- | ||
| + | | | ||
| + | :So, if you consider the squares of 4, 6, 9 as if they are four numbers [their sum] is equal to the square of the sum of the first and the fourth, which is 169. | ||
| + | :<math>\scriptstyle{\color{blue}{4^2+6^2+6^2+9^2=169=\left(4+9\right)^2}}</math> | ||
| + | |style="text-align:right;"|על כן אם תחשב מרובע ד'ו'ט' כאלו היה ד' מספרים יהיה שוה אל העולה ממרובע מחובר הראשון והרביעי והוא ק'ס'ט‫' | ||
| + | |- | ||
| + | | | ||
| + | === The means are regarded === | ||
| + | |style="text-align:right;"|כי האמצעי יחשב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' ואם תאמר אלה השלשה כמו ארבעה והלא ארבעה יש בו ב' אמצעיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דע כי אותם השנים יחשבו כאלו הם מספר אחד כמו שיאמר למטה כי שניהם חברים על כן אמ' שנקח מרובע המחובר משניהם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ועוד כי כמו שאמרנו [ב]ג' מספרים שכפל הקטן על הגדול ככפל | ||
| + | התיכון על עצמו כן נאמר בד' מספרים שנכפול האמצעי האחד על חברו כמו שנכפול התיכון על עצמו | ||
| + | |- | ||
| + | | | ||
| + | *Example: 4, 6, 8, 12 | ||
| + | |style="text-align:right;"|המשל בזה ד ו ח יב | ||
| + | |- | ||
| + | | | ||
| + | :Because the product of 4 by 12 is 48 and so is the product of 6 by 8. | ||
| + | :<math>\scriptstyle{\color{blue}{4\times12=48=6\times8}}</math> | ||
| + | |style="text-align:right;"|כי כפל ד' על י"ב הוא מ"ח וככה כפל ו' על ח‫' | ||
| + | |- | ||
| + | | | ||
| + | === Example 2 3 6 === | ||
| + | |style="text-align:right;"|דמיון ב' ג' ו‫' | ||
| + | |- | ||
| + | | | ||
| + | :As the ratio of the difference between 2 and 3 to the difference between 3 and 6, which is a third, so is the ratio of the first, which is 2, to the last, which is 6. | ||
| + | :<math>\scriptstyle{\color{blue}{\left(3-2\right):\left(6-3\right)=\frac{1}{3}=2:6}}</math> | ||
| + | |style="text-align:right;"|שכפי יחס היתרון שבין ב' וג' אל היתרון שבין ג' וו' שהוא שלישיתו כן הוא ערך הראשון שהוא ב' אל האחרון שהוא ו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי לעולם ערך האמצעי האחד אל האמצעי השני כערך הראשון אל האחרון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכל אלו הדמיונות שיעשה מב'ג'ו' ומג'ד'ו' הם על דרך ערכי הנגינות שהם ג' מספרים ב'ג'ו' קורא דמיון ראשון וג'ד'ו' דמיון שני <s>וע</s> | ||
| + | |- | ||
| + | | | ||
| + | === We double the quotient === | ||
| + | |style="text-align:right;"|והעולה בחלוק נכפלנו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שנמנהו ב' פעמים היו בערכי הנגינות דין כל אחד מהג' בפני עצמו | ||
| + | |- | ||
| + | | | ||
| + | === They are ten === | ||
| + | |style="text-align:right;"|והיו עשרה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל אלו החלקים המחוברים כמה היה כל הממון שהיו העשרה בכללם | ||
| + | |- | ||
| + | | | ||
| + | === We multiply the extremes that are ten and 210; they are two thousand and one hundred === | ||
| + | |style="text-align:right;"|כפלנו הקצוות שהם עשרה ור"י והיו אלפים ומאה | ||
| + | |- | ||
| + | |We divide it by the known mean, which is 106; we receive the unknown mean, which is the whole amount; the resulting total amount is 19 integers and 67 parts. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{10\sdot210}{107}=\frac{2100}{107}=19+\frac{67}{107}}}</math> | ||
| + | |style="text-align:right;"|חלקנום על האמצעי הנודע שהוא ק"ז ויצא לנו האמצעי הנעלם שהוא כל הממון יעלה כל הממון י"ט שלמים וס"ז חלקים | ||
| + | |- | ||
| + | | | ||
| + | === Another example: We take its seventh and its ninth; they are seven === | ||
| + | |style="text-align:right;"|דמיון אחר לקחנו ‫<ref>53r</ref>שביעיתו ותשיעיתו והיו שבעה | ||
| + | |- | ||
| + | |How much is the amount? | ||
| + | |style="text-align:right;"|כמה היה הממון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה המורה ס"ג ושביעיתו ותשיעיתו י"ו וערך ז' אל הממון כערך י"ו אל ס"ג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נכפול הקצוות שהם ז' וס"ג והיו ת'מ'א‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחלק זה על י"ו ועלה כ"ז שלמים וט' חלקים מי"ו | ||
| + | |- | ||
| + | | | ||
| + | === If one reversed the saying === | ||
| + | |||
| + | |style="text-align:right;"|<s>עם</s> ואם הפך הדבר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל כשנדע החלקים לבד נחלק כפל הקצוות על חלקי המורה ויודע הנשאר אבל כשיהיה בהפך שלא נדע רק הנשאר מן החלקים גם אנו נחלק על הנשאר אחד חלקי המורה ויודע לנו סך החלקים | ||
| + | |- | ||
| + | | | ||
| + | === We sum up their amounts of money === | ||
| + | |style="text-align:right;"|נחבר ראשי ממונם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל חשבונות ממונם יעלו שלשה נ"ו שלמים שהם ג' דינ' ומ"א חלקים מנ"ו שהם מ"א חלקים מדינר שכל נ"ו בכאן נחשב כאחד מחלקי המורה | ||
| + | |- | ||
| + | | | ||
| + | === The result is 4 pešuṭim === | ||
| + | |style="text-align:right;"|עלה ד' פשו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל לכל חלק מנ"ו שהוא דינר אחד על כן כל אחד יקח לכל דינר מממונו ד' פשו‫' | ||
| + | |- | ||
| + | | | ||
| + | === Also 4 parts of 56 === | ||
| + | |style="text-align:right;"|גם ד' חלקים מנ"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שישארו עוד ד' פשו' לחלק שיש לכל דינר ודינר שיקח מהם ד' חלקים מנ"ו | ||
| + | |- | ||
| + | | | ||
| + | === Because each pašuṭ is divided to 56 === | ||
| + | |style="text-align:right;"|כי כל פשו' יתחלק לנ"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם יש לכל דינר שיקח מפשו' אחד חלק אחד מנ"ו אם כן יקח מד' פשו' ד' חלקים מנ"ו שהם חלק אחד מי"ד שהוא חצי שביעית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן אם נשיב ארבעתם לנ"ו נ"ו שהם ר'כ'ב' ונחלקם על נ"ו יעלה לכל אחד ד' מאותם החלקים ומד' חלקי פשו' מנ"ו חלקים שבו | ||
| + | |- | ||
| + | | | ||
| + | === We sum all the parts === | ||
| + | |style="text-align:right;"|והנה נחבר החלקים כלם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל אותם שנשארו מהחלקים יהיו שנים פשו' ושנים שחברנו מהחלקים היו ד' ונחבר עתה הפשוט כלם היו ב' דינ‫' | ||
| + | |- | ||
| + | | | ||
| + | === All the mentioned parts === | ||
| + | |style="text-align:right;"|וכל החלקים הנזכרים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שלישית ורביעית וששית מי"ב הם טא והוא הדינר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי לעולם החלקים הם דינר אחד והמורה הוא כל הדינר | ||
| + | |- | ||
| + | | | ||
| + | === We ask what is the ratio of 12 to 9 === | ||
| + | |style="text-align:right;"|ונבקש מה ערך י"ב אל ט‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כאלו אמ' נחלק י"ב על ט‫' | ||
| + | |- | ||
| + | | | ||
| + | === It is the same as it and its third, we add 4 pešuṭim to 12 pešuṭim, which is the dinar === | ||
| + | |style="text-align:right;"|והנה הוא כמהו ושלישיתו והנה נוסיף על י"ב פשו' שהוא הדינר ד' פשו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי ט' הוא הדינר אחד ועם שליש הדינר והוא י"ו ונוכל לעשות ערכים שנאמר ערך י"ב שהוא המורה אל ‫<ref>53v</ref>אל ט' כערך כל הסך אל הדינר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|על כן נכפול הקצוות שהוא י"ב על י"ב והם ק'מ'ד‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחלק על ט' עלו י"ו והוא הדינר המחובר מג' הערכים | ||
| + | |- | ||
| + | | | ||
| + | === We divide the denominator by this number; the result is 2 dinar and 29 === | ||
| + | |style="text-align:right;"|ונחלק המורה על זה המספר יהיו ב' דינ' וכ"ט | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל מכל מטבע מהשלשה | ||
| + | |- | ||
| + | | | ||
| + | === We convert the dinar to parts of 143 === | ||
| + | |style="text-align:right;"|נשיב הדינר חלקים מק'מ'ג‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל מהב' דינ' וכ"ט חלקים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה נכפול ש'י'ה' על ה' שהם הקצוות ויהיו אלף ות'ק'ע'ה‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונחלק אותם על שבעה יהיו בדנר ר'כ'ה‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכפי ערך ה' אל ז' יהיה הערך ר'כ'ה' אל ש'י'ה וכן תאמר בכלם | ||
| + | |- | ||
| + | | | ||
| + | === When we exchange this number of coin seven === | ||
| + | |style="text-align:right;"|וכאשר החלפנו זה המספר ממטבע שבעה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל כי לעולם נקח המורה במקום סך המטבע שנרצה להשיב הכל אליו והנה שביעית המורה מה שהוא ז' פעמים מ"ה כי השבעה ישובו ל"ה והם ר'כ'ה' ממטבע הוא שהוא דינ' אחד ופ"ב חלקים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כשנרצה להשיב הב' דינ' וכ"ט חלקים ממטבע ט' אל מטבע ה' נמנה ה' פעמים ל"ה שהוא התשיעית והוא קע"א | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כשנרצה להשיב הכל למטבע ז' נקח בעבור ז' ש'י'ה‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובעבור שנרצה לעשות מ"ה ז' נחשוב ז' פעמים ס"ג והיו ת'מ'ה' ממטבע ז' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן נחשוב ז' פעמים ל"ה יהיו ר'מ'ה' ועל זה הדרך תשיב הכל למטבע ט‫' | ||
| + | |- | ||
| + | | | ||
| + | === We want to know how many parts he takes of coin five === | ||
| + | |style="text-align:right;"|ונרצה לדעת כמה חלקים יקח ממטבע חמשה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל כמה חלקים יקח מזה המטבע שהוא מטבע ז' בעבור מה שיהיה לנו ממטבע חמשה כלו' כמה יהיה ממטבע ז‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או נעשה כן כשנרצה להשיב ב' דינ' וכ"ט של מטבע ז' למטבע ה' ונסיר מש'י'ה' שהיו מנין חלקיו שיש בו ז' פעמים מ"ה ב' שביעיות שהן צ' כי יתרון ז' על הב‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כשנרצה להחזיר ט' ל"ה נסיר תשיעית ש'י'ה' שהם ד' פעמים ל"ה שהם ק"ם ביתרון ט' מ"ה והנשאר יהיה של י"ה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכשתרצה לגרוע המטבע ולהשיב כנל לז' או לט' הוסף על חלקי האחד כיתרון האחד עליו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון ‫<ref>54r</ref>זה אם תרצה להשיב הכל למטבע ז' הוסף בעבור מטבע ה' ב' חמישיות שהם ק'נ'ו' ובעבור מטבע ט' גרע ממנו ב' תשיעיות שהם ע' ועל זה הדרך הכל והכל יוצא שוה | ||
| + | |- | ||
| + | | | ||
| + | === We think as if the 7 measures are carried 17 miles === | ||
| + | |style="text-align:right;"|נחשוב כי הז' מדות הולך כל י"ז מילין | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ולכן לא נזכרם בערך א' אבל נעשה הערך מהמדות שלא השלים ומהסך שלא הרויח כלו כי כערך ז' אל י"ג כן ערך מה שיוצא לי"ט ובעבור שלא ידענו הריוח נכתוב תחתיו גלגל ונעשה הצורה כן והנה בזה הסדר היו הקצוות ז' וי"ט על כן נכפלם והיו ק'ל'ג' נחלקם על י"ג שהוא האמצעי הנודע יעלה י' שלמים ונשארו ג' חלקים מי"ג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ולפי שחסר תנאי המילין נעשה ערך אחר ולא נזכר מדות כלל אבל נאמר כערך י"א מילין אל ז' יהיה ערך מה שיקח אל הריוח הנזכר שהוא י' וג' על זה הדמיון נכפול י"א על י' עלו ק'י' נכפול י"א על ג' שהם חלקים והיו ל"ג חלקי י"ג והנה הנ"ו ב' שלמים נחברם ק'י' והיו ק'י'ב' ונשארו ז' חלקים מי"ג והנה נחלקם על י"ז שהוא האמצעי הנה נחלק העולה ק'י'ב' על י"ז עלו ו' פשו' ונשארו י' לחלק נשיבם לחלקים מי"ג ונחברם עם הז' שהם כמו כן חלקים מי"ג ויעלה ק'ל'ז' נשיב ק'ל'ז' לחלקים מי"ג (מי"ז) שנכפלם על י"ז ועלה ט ב ג ב נחלקם על ר'כ'א' שהוא כפל י"ג על י"ז והוא אחד שלם ועלה ק'ל'ה' (קל"ז) שהם חלקים מרכ"א והם ח' חלקים מי"ג עם חלק אחד מי"ז בחלק או אם תרצה הם י' חלקים מי"ז עם ז' חלקים מי"ג בחלק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או אם תרצה תחשוב י' פעמים רכ"א ולא תצטרך אלא לשום בראש ר'כ'ה' (רכ"א) גלגל שבעשותך כן העלית כל אות ממנו מדרגה אחת שהיא עשרה ותחבר עמו כפל הז' בי"ז שהוא ‫<ref>54v</ref>ק'י'ט‫' | ||
| + | |- | ||
| + | | | ||
| + | === We multiply the first number === | ||
| + | |style="text-align:right;"|והנה נכפול המספר הראשון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|רצה במספר ראשון התנאי ובמספר השני המעשה ר"ל מדת הספירה | ||
| + | |- | ||
| + | | | ||
| + | === Now we set the proportion diagram === | ||
| + | |style="text-align:right;"|ועתה נעשה דמיון הערכים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיו קצוות בקשתם שהוא המספר הקטן ומעורב בתנאי שהוא הגדול שבד' המספרים הנערכים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונאמר כי ערך הריוח המבוקש אל י"א כערך ק"כ אל ר"י | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|על כן נכפול האמצעיים שהם ק"כ וי"א ונחלק על ר"י שהוא הקצה האחרון הנודע והעולה יהיה הקצה הראשון הנעלם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או אם נרצה נעשה אלו האמצעיים קצוות שנאמר ערך ק"כ אל ר"י כערך המבוקש אל י"א והכל שוה | ||
| + | |- | ||
| + | | | ||
| + | === You can convert them into hours of the day === | ||
| + | |style="text-align:right;"|ותוכל להשיבם לשעות היום | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל תוכל להשיב הז' תשיעיות לשעות היום בדרך הערכין ותכתוב כן כי כערך ז' תשיעיות אל ט' יש לשעור היום המבוקש מי"ב | ||
| + | |- | ||
| + | | | ||
| + | === We know that the ratio of 12 to 9 is the same as it plus its third === | ||
| + | |style="text-align:right;"|ידענו כי ערך י"ב אל ט' כמהו ושלישיתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלו' תשיעית יום הוא יותר מחלק י"ב מיום השלישית והוא שעה ושליש על כן נחשוב בעבור ז' תשיעיות ז' שעות וז' שלישי שעה | ||
| + | |- | ||
| + | | | ||
| + | === Since we have a third, we convert all to thirds === | ||
| + | |style="text-align:right;"|והנה בעבור שיש לנו שלישית נשיב הכל לדרך שלישית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' נעשה מכל הימים שלישיים והנה כערך י"ג אל מ"ז כן ערך מה שיקח מן הזהוב | ||
| + | |- | ||
| + | | | ||
| + | === We want to know how much each one has to work for the 13 === | ||
| − | + | |style="text-align:right;"|ונבקש לדעת כמה חייב כל אחד שיעבוד בעבור י"ג וכו‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ונאמר כערך י"ג אל מ"[ז] שהוא הזהוב הנה ערך עבודתו אל כ' שלישיים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|עלו ה' שלישיות נשארו כ"ה חלקים ממ"ז שהוא שלישית ששלישית יום הוא ד' שעות | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|אם כן הכ"ה חלקים הם כ"ה חלקים ממ"ז חלקים שבד' שעות היום | |
| − | + | |- | |
| − | + | | | |
| − | + | === We multiply also 25 parts by four; the product is one hundred === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|גם נכפול כ"ה חלקים על ארבעה עלו מאה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כי אם יש לו כ"ה חלקים מד' שעות שבמ"ז הנה מכל שעה כ"ה חלקים ממ"ז בשעה יעלה לד' שעות ה' ‫<ref>55r</ref>ה' חלקים ממ"ז שבשעה נחלקם על מ"ז שנחשבהו עתה שעה אחת ונשארו ו' חלקים ממ"ז בשעה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|והנה נעשה הערך לשמעון | |
| − | ג | + | |- |
| − | ו | + | | |
| − | + | |style="text-align:right;"|כי כערך י"ג אל מ"ז כן ערך עבודתו אל ט"ו שלישיות | |
| − | + | |- | |
| − | + | | | |
| − | + | === We divide them by three === | |
| − | |||
| + | |style="text-align:right;"|נחלקם על שלשה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כלומ' שנחזירם לשלמים | ||
| + | |- | ||
| + | | | ||
| + | === We multiply also 7 by 4 === | ||
| + | |style="text-align:right;"|גם נכפול ז' על ד‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי הז' הם חלקים ממ"ז שבו ד' שעות וכשנקח כן מכל שעה יהיו כ"ח ממ"ז בשעה | ||
| + | |- | ||
| + | | | ||
| + | === Make the diagram like this === | ||
| + | |style="text-align:right;"|תעשה הדמיון ככה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי כערך ו' אל א' הוא ערך הנשאר אל ג' ושליש | ||
| + | |- | ||
| + | | | ||
| + | === Another example: he has 9 measures of must and he wants them to be cooked until the third part of it remains === | ||
| + | |style="text-align:right;"|דמיון אחר היו לו ט' מדות תירוש ורצה שיתבשלו עד שישאר השליש וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונשארו שנים והנה כערך ב' אל ו' כן ערך הנשאר אל ג‫' | ||
| + | |- | ||
| + | | | ||
| + | === Question: an amount of money, we sum its fifth === | ||
| + | |style="text-align:right;"|שאלה ממון חברנו חמישיתו וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נעשה הערך כי כערך ק'מ'ג' על ש'ט'ו' כן ערך י' אל הממון והנה נרצה לידע הקצה האחד על כן נכפול האמצעיים זה על זה שהוא ש'ט'ו' על י' נחלקנו על הקצה הידוע | ||
| + | |- | ||
| + | | | ||
| + | === We do the opposite: An amount of money - we have subtracted from it === | ||
| + | |style="text-align:right;"|נעשה להפך ממון חסרנו ממנו וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נעשה הערך ונאמר כי ערך י' שהוא הנשאר אל כל הממון כערך ק'ע'ב' אל ש'ט'ו‫' | ||
| + | |- | ||
| + | | | ||
| + | === Five remain === | ||
| + | |style="text-align:right;"|ישארו חמשה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה אם היה הנשאר מן האילן ה' לבד היה י"ב הוא כל הגובה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אך בעבור שהוא י' נעשה הערך ונאמר כי כערך ה' אל י"ב ערך י' אל כל האילן | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונכפול האמצעיים שהם י' על י"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או נשיב האמצעיים קצוות כשנאמר כן ערך אל כל האילן כערך ה' אל י"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונכפול הקצוות שהן י' וי"ב והכל אחד | ||
| + | |- | ||
| + | | | ||
| + | === The Gentile sages divide the money according to the ratio of the share of each === | ||
| + | |style="text-align:right;"|וחכמי הגויים יחלקו זה הממון על דרך ערך ממון כל אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל כדרך חכמי החשבון | ||
| + | |- | ||
| + | | | ||
| + | === The wise men of Israel divide it === | ||
| + | |style="text-align:right;"|וחכמי ישראל מחלקים אותו וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|למטה יפרש זה | ||
| + | |- | ||
| + | | | ||
| + | === The arithmeticians === | ||
| + | |style="text-align:right;"|וחכמי החשבון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יבקשו ממון שיהיו בו אלו החלקים ויקחו ממנו ערך לזה הממון אם לא כמהו שאם היה כמהו הנה נמצא | ||
| + | |- | ||
| + | | | ||
| + | === The total is two and one-half of one-sixth === | ||
| + | |style="text-align:right;"|יהיה הכל שניים וחצי ששית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי השלישית הוא רביע וחלק מי"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והשברים ‫<ref>55v</ref>והנ השברים י"ג ובקש הכל כ"ה | ||
| + | |- | ||
| + | | | ||
| + | === We set the proportion at [60] === | ||
| + | |style="text-align:right;"|נעשה הערך ככה על דרך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שנקח האחד ששים ונחבר אליו החלקים השברים | ||
| + | |- | ||
| + | | | ||
| + | === This is the proportion of the money that Reuven takes === | ||
| − | + | |style="text-align:right;"|וזה צורת ערך הממון שיקח ראובן | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כלומ' שאם היה הממון קכ"ה הנה היה נוטל ששים שהוא כל האחד אך עתה שאינו רק ק"כ אין ספק כי פחות מס' יקח לפי חסרון ק"כ מן [.] ק'כ'ה' על כן נעריך ונאמר כי כערך ק"כ אל ק'כ'ה' יהיה ערך מה שיקח מס' או נאמר ערך ס' אל מה שיקח כערך ק'כ'ה' אל ק"כ ומכל מקום נכפול הקצוות שהם על ק"כ ועל זה הדרך צורת כל אחד כי אלו היה ק'כ'ה' היה שמעון נוטל עתה יחסר מזה כפי גרעון ק'כ'ה' מק'כ'ה' ונעשה צורתו ככה וצורת חלק לו | |
| − | + | |- | |
| − | + | | | |
| − | + | === In a shorter way Shimon takes a half of Reuven's share === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | כי | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|ובדרך קצרה יקח לעולם שמעון חצי חלק ראובן | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כמו שהיה אלו היו ק'כ'ה' על כן לעולם אחר שנדע חלק ראובן על דרך הערך אין צריך להעריך האחרים | |
| − | + | |- | |
| − | + | | | |
| − | + | === According to the procedure of the sages of Israel === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|ועל דרך חכמי ישראל וכו‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|איפשר שאמ' כן לפי מה ששנינו זה אומר כלה שלי וזה אומר חציה שלי (בבלי, בבא מציעא א ד"ב ע"א, משנה) וכו‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | === You have already took your share of the thirty === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|וכבר לקחת חלקת מהשלישים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כלו' באותם מ' שהיית תובע בל' היינו ד' חולקים ועל כן לקחנו כל אחד רביע ונשאר מהם י' שאתה תובע והנה בהם ג' חולקים על כן תקח שלושים | |
| − | + | |- | |
| − | + | | | |
| − | + | === Which all four of us have claimed === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|שארבעתנו ערערנו עליהם | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כי הגדולים מערערים בכל חלקי הקטנים כי בכלל חצי השליש והרביע ולא בהפך | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | בכל חלקי הקטנים כי בכלל חצי השליש והרביע ולא בהפך | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === When determining the moon and also when determining 5 planets === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|כי בתיקון לבנה בתיקון ה' משרתים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|אך לא בתיקון חמה | |
| − | + | |- | |
| − | + | | | |
| − | + | === There is a row that is called the row of ratio === | |
| − | + | ||
| − | + | |style="text-align:right;"|טור יקרא טור הערך | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|טור הערך טור אחד שבו מספרים רבים על הסדר זה למעלה מזה שכנגד כל מספר מהם ימצא ‫<ref>56r</ref>ימצא מספר אחד בטור אחד שבו מספרים שהם בסדר זה למעלה מזה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ואותו טור הבא אחר טור הערך יקרא טור חמישי או שביעי | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ונראה איזה מספר יש בטור הערך ונביט מה ערך יש לו אל ס' אם שליש או רביע וכפי זה נקח מטור החמישי או השביעי ואם היה בו ס' נקח כל הכתו' בטור החמישי | |
| − | + | |- | |
| − | + | | | |
| − | + | === Example: you have 40 fractions exceeding over the degrees and in the row of the ratio there is 15 === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|דמיון יש עמך חלקים יתרים על המעלות מ' ובטור הערך ט"ו | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|לא הוצרך להראות לקיחת הערך מן המעלות כי נקל הוא | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|אך הוצרך להראות בחלקים וכל שכן כשלא ימצא להם ערך | |
| − | + | |- | |
| − | + | | | |
| − | + | === They are 22 and one-half that are 30 seconds === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |style="text-align:right;"|והנם כ"ב וחצי שהם ל' שניים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי לא נכתוב בלוחות חצי | ||
| + | |- | ||
| + | | | ||
| + | === We multiply 3 by 20; they are 60 === | ||
| + | |style="text-align:right;"|נכפול ג' על כ' יהיו ששים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן נוכל להפך ולומר כמה ערך כ' אל ס' שליש כן נקח שליש אחד והוא ראשון אחד | ||
| + | |- | ||
| + | | | ||
| − | + | === Since we have add two === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |style="text-align:right;"|ובעבור שהוספנו שנים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל בחשבוננו שמנינו אותם יותר מן הראוי | ||
| + | |- | ||
| + | | | ||
| + | === Always see if there are any fractions added to the degrees of the determined center === | ||
| + | |||
| + | |style="text-align:right;"|ולעולם ראה אם היו חלקים נוספים על מעלות המוצק המתוקן | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|טור אחד יש לפני טור הערך שבו מספרים רבים זה למעלה מזה כל מספר שבו כנגד מספר שבטור הערך וממנו יכנסו ‫<ref>56v</ref>לטור הערך ויקרא המוצק המתוקן | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שבטור המוצק כ' וכנגדו בטור הערך ט"ו ולמטה בטור המוצק כ"א וכנגדו בטור הערך י"ו וכן על הסדר הולך ומוסיף | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה אם היו יותר מל' חשבם במעלה אחת והכנס בטור הערך למטה | ||
| + | |- | ||
| + | | | ||
| + | === If you find the determined quotient between 4 constellations === | ||
| + | |||
| + | |style="text-align:right;"|ואם נמצאת המנה המתוק' שהוא ב' ד' מזלות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שאם היה פחות מד' או יותר מח' עשה כדרך שהראיתיך במעלות המוצק שאם אין לך לא תחוש אך מד' ועד ח' דקדק באלו החלקים ליקח ערך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שהיו לך ל' חלקים נוספים על ד' מעלות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה אם לא היו הל' היה נכנס בט"ו בטור הערך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם היה לנו מעלה אחת יותר היה נכנס בי"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי בעבור כל מעלה יוסיף אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עכשיו שיש לנו חצי מעלה נוסיפנו עם הכתוב במעלת הד' ונראה מה ערך ט"ו וחצי אל ס' ונעשה בדרך הכפל כפי צרכנו | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Chapter Seven == | ||
| + | |||
| + | |style="text-align:right;"|<big>השער השביעי</big> | ||
| + | |- | ||
| + | | | ||
| + | === The first way is roots === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''הדרך האחד שרשים וכו‫''''</span> | ||
| + | |- | ||
| + | |Meaning: every number is required due to being a roots, or due to being a square, or required due to neither of those two. | ||
| + | |style="text-align:right;"|ר"ל כל חשבון יבוקש מצד שהוא שורש או מצד שהוא מרובע או ‫<ref>57r</ref> או לא יבוקש מטעם אחד מאלו השנים | ||
| + | |- | ||
| + | | | ||
| + | === There are numbers that have no true root at all === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''ויש חשבון שאין לו שורש אמת כלל'''</span> | ||
| + | |- | ||
| + | |Meaning: we do not know its true and exact root. | ||
| + | |style="text-align:right;"|ר"ל שלא ידענו שרשו באמת ובדקדוק | ||
| + | |- | ||
| + | | | ||
| + | === One is a root and a square === | ||
| + | |||
| + | |style="text-align:right;"|והיה האחד שרש מרובע | ||
| + | |- | ||
| + | |Because, one [multiplied] by one [is one]. | ||
| + | |style="text-align:right;"|כי אחד על אחד | ||
| + | |- | ||
| + | | | ||
| + | === Check if the scales of the square === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''הסתכל אם לא היו מאזני המרובע וכו‫''''</span> | ||
| + | |- | ||
| + | |Meaning: if you find a number and you wish to know if it is a square or not: | ||
| + | |style="text-align:right;"|כלומ' אם תמצא מספר אחד ותרצה לדעת האם הוא מרובע אם לא | ||
| + | |- | ||
| + | |Check if it is all cast out by nines, or how much remains. | ||
| + | |style="text-align:right;"|הסתכל אם יהיה הכל ט'ט' או כמה ישאר | ||
| + | |- | ||
| + | |Look at the remainder from the nines in the root and multiply it by itself. | ||
| + | |style="text-align:right;"|וראה בשורש הנשאר מט' וכפלהו על עצמו | ||
| + | |- | ||
| + | |If the remainder from the nines after the multiplication is the same as the remainder from the square, it can be a square. | ||
| + | |style="text-align:right;"|ואם יהיה הנשאר מט' אחר הכפל כנשאר מן המרובע אפשר להיותו מרובע | ||
| + | |- | ||
| + | |Because when the root is multiplied, the scales are multiplied, and the remainder from their product remains in the square. | ||
| + | |style="text-align:right;"|כי בהכפל השורש נכפלו המאזנים והנשאר מכפלם ישאר במרובע | ||
| + | |- | ||
| + | |If it is not found so, you know for sure that it is not square. | ||
| + | |style="text-align:right;"|ואם לא ימצא כן תדע באמת שאינו מרובע | ||
| + | |- | ||
| + | |Example: if someone tells you: 121 is a square. | ||
| + | |style="text-align:right;"|המשל בזה אם יאמר לך אדם ק'כ'א' הוא מרובע | ||
| + | |- | ||
| + | |Check its scales; they are 4. | ||
| + | :<math>\scriptstyle{\color{blue}{121_9\equiv4}}</math> | ||
| + | |style="text-align:right;"|הסתכל במאזניו והנם ד‫' | ||
| + | |- | ||
| + | |You find the same in the product of the scales of its root, which is 11. | ||
| + | :<math>\scriptstyle{\color{blue}{\left(\sqrt{121}_9\right)^2=\left(11_9\right)^2\equiv4}}</math> | ||
| + | |style="text-align:right;"|ככה תמצא בכפל מאזני שרשו שהוא י"א | ||
| + | |- | ||
| + | |Therefore, his statement is correct. | ||
| + | |style="text-align:right;"|על כן נאותו דבריו | ||
| + | |- | ||
| + | |But, if he says that 122 is a square, deny it. | ||
| + | |style="text-align:right;"|אך אם אמר כי ק'כ'ב' הוא מרובע הכחישהו | ||
| + | |- | ||
| + | | | ||
| + | === Other scales === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''מאזנים אחרים'''</span> | ||
| + | |- | ||
| + | |Examined only by the knowledge of the remainder from the scales of the square and there is no need to look at the root | ||
| + | |style="text-align:right;"|יבחנו מידיעת הנשאר על מאזני המרובע בלבד ולא יצטרך להסתכל בשרש | ||
| + | |- | ||
| + | |If the remainder is 2, or 3, or 5, or 6, or 8, it is not a square. | ||
| + | |style="text-align:right;"|שאם ישאר כגב' או ג' או ה' או ו' או ח' אינו מרובע | ||
| + | |- | ||
| + | |For, the scales of the square are always derived from the scales of the root, which are from 1 to 8. | ||
| + | |style="text-align:right;"|כי לעולם יצאו מאזני המרובע ממאזני השורש שהם מא' עד ח‫' | ||
| + | |- | ||
| + | |The product of one of them [by itself] never produces in the square any of the mentioned numbers, which are 2, 3, 5, 6, 8. | ||
| + | |style="text-align:right;"|והנה מכפל אחד מהם לא יולד לעולם במרובע אחד מהמספרים ‫<ref>57v</ref>הנזכרים שהם ב'ג'ה'ו'ח‫' | ||
| + | |- | ||
| + | |The result of the product is only 1, or 4, or 9, or 7. | ||
| + | |style="text-align:right;"|רק היוצא מן הכפל א' או ד' או ט' או ז‫' | ||
| + | |- | ||
| + | |Therefore, if you find that the scales are one of these, it may be a square. | ||
| + | |style="text-align:right;"|על כן אם תמצא המאזנים אחד מאלו אפשר היותו מרובע | ||
| + | |- | ||
| + | |Examine all of them and you will find that it is so. | ||
| + | |style="text-align:right;"|עיין בכולם אחד ותמצא כן | ||
| + | |- | ||
| + | |He said: "seven is also among them". | ||
| + | |style="text-align:right;"|אמר גם שבעה עמהם | ||
| + | |- | ||
| + | |Meaning: even though it is not a square. | ||
| + | |style="text-align:right;"|כלו' א'ע'פ' שאיננו מרובע | ||
| + | |- | ||
| + | |Know that 1 or 4 or 7 each results from one of two numbers, but 9 can result from three and here is a table for you to know this: | ||
| + | |style="text-align:right;"|ודע כל אחד מא' או ד' או ז' יצאו מאחד משני אותיות והט' תוכל לצאת משלשה והנה לך לוח לדעת זה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; color:blue; text-align:center;" | ||
| + | |- | ||
| + | |8||1||1 | ||
| + | |- | ||
| + | |7||2||4 | ||
| + | |- | ||
| + | |5||4||7 | ||
| + | |- | ||
| + | |96||3||9 | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
| + | |- | ||
| + | |ח||א||א | ||
| + | |- | ||
| + | |ז||ב||ד | ||
| + | |- | ||
| + | |ה||ד||ז | ||
| + | |- | ||
| + | |וט||ג||ט | ||
| + | |} | ||
| + | |- | ||
| + | |Other scales | ||
| + | |style="text-align:right;"|מאזנים אחרים | ||
| + | |- | ||
| + | |If the units of our number are 2, or 3, or 7, or 8, know that the number is not a square. | ||
| + | |style="text-align:right;"|אם היה הנשאר מאחדים על מספרנו ב' או ג' ז' או ח' תדע כי אין המספר מרובע | ||
| + | |- | ||
| + | |Because the units of the square are always generated from the units [of the root] that are one of nine digits. [The units] of their product [by themselves] are not 2, nor 3, nor 7, not 8; only 1, or 4, or 9, or of the round numbers that are 5 and 6, since they are found in the squares. | ||
| + | |style="text-align:right;"|כי לעולם לא יולדו הפרטים על כלל המרובע אלא מתוספת אחדים על כלל ואותו התוספת יהיה אחת מט' אותיות והנם מכפלם לא ישאר ב' ולא ג' ז' וח' רק א' או ד' או ט' או מן המתגלגלים שהם ה' וו' כי ימצאו במרובעים | ||
| + | |- | ||
| + | |The same way for the tens, which are as units of the hundreds. | ||
| + | |style="text-align:right;"|ועל זה הדרך בנותר מעשרות שהם כאחדים על מאות | ||
| + | |- | ||
| + | |If you find one [as units] in the required number, know that there is either 1 or 9 in the root. | ||
| + | |style="text-align:right;"|אם מצאת במספר המבוקש שהנוסף בו אחד דע כי יש בשרש א' או ט‫' | ||
| + | |- | ||
| + | |Because 1 is always generated from the product of one of them. | ||
| + | |style="text-align:right;"|כי לעולם <s>מכ</s> מכפל אחד מאלו יולד א‫' | ||
| + | |- | ||
| + | |4 is generated from 2 or 8 in the root. | ||
| + | |style="text-align:right;"|ויצא ד' מב' שהוא בשרש או מח‫' | ||
| + | |- | ||
| + | |6 is generated in the square from the product of 6 or 4. | ||
| + | |style="text-align:right;"|ויתחדש ו' במרובע מהכפל ו' או ד‫' | ||
| + | |- | ||
| + | |9 is generated from the product of 3 or 7. | ||
| + | |style="text-align:right;"|וט' יפול מכפל ג' או ז‫' | ||
| + | |- | ||
| + | |5 is generated from the product of 5. | ||
| + | |style="text-align:right;"|וה' יצא מכפל ה‫' | ||
| + | |- | ||
| + | |As our lord, our teacher, "May his Rock protect him and grant him life" said regarding that: | ||
| + | |style="text-align:right;"|‫<ref>58r</ref><span style=color:blue>'''לשון אדננו מורנו יצ"ו על זה'''</span> | ||
| + | |- | ||
| + | |If you have a square and [its units are] 1, know that there is either 1 or 9 in the root. | ||
| + | |style="text-align:right;"|אם יש בידך מרובע ויש בתוספת הכללים א' דע שיש בשורש א' או ט‫' | ||
| + | |- | ||
| + | |If you wish to know which of the two, know the scales of the number, then know the scales of the root. [If the scales of the number are equal to the scales of the root], know that there is 9 in the root. | ||
| + | |style="text-align:right;"|ואם תרצה לידע אחד משניהם דע מאזני המספר ואחר דע מאזני השורש כי אם תקחהו עם א' ויהיו מאזני המספר שוה כשתקחהו עם ט' ושוה למאזני המספר דע שיש בשרש ט'ט‫' | ||
| + | |- | ||
| + | |End of quote. | ||
| + | |style="text-align:right;"|ע"ד לשונו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; color:blue; text-align:center;" | ||
| + | |- | ||
| + | |9||1||1 | ||
| + | |- | ||
| + | |8||2||4 | ||
| + | |- | ||
| + | | ||5||5 | ||
| + | |- | ||
| + | |6||4||6 | ||
| + | |- | ||
| + | |[7]||3||9 | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
| + | |- | ||
| + | |ט||א||א | ||
| + | |- | ||
| + | |ח||ב||ד | ||
| + | |- | ||
| + | | ||ה||ה | ||
| + | |- | ||
| + | |ו||ד||ו | ||
| + | |- | ||
| + | |[ז]||ג||ט | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === Every rank that is non-even === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''כל מעלה שאינה זוג'''</span> | ||
| + | |- | ||
| + | |As hundreds, tens of thousands, thousands of thousands. | ||
| + | |style="text-align:right;"|כמו מאות רבבות אלפים אלפים | ||
| + | |- | ||
| + | |Their squares are according to the squares of the first rank and by their number. | ||
| + | |style="text-align:right;"|הנה מרובעיהם על דרך מרובעי המעלה הראשונה ובמספרם | ||
| + | |- | ||
| + | |For, the squares of the hundreds are 100, 400, 900. | ||
| + | |style="text-align:right;"|כי מרובעי המאות ק' ת' ת'ת'ק‫' | ||
| + | |- | ||
| + | |The squares of the tens of thousands are ten thousand, forty thousand, 90 thousand. | ||
| + | |style="text-align:right;"|ומרובעי הרבואות עשרת אלפים וארבעים אלף וצ' אלף | ||
| + | |- | ||
| + | |And so on this way. | ||
| + | |style="text-align:right;"|ועל זה הדרך הכל | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === The analogous squares === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''ולעולם יהיו המרובעים הנמשלים וכו‫''''</span> | ||
| + | |- | ||
| + | |Meaning: in the square of any rank that is non-even, there is always only one number, as it is in the first rank. | ||
| + | |style="text-align:right;"|ר"ל לעולם במרובע כל מעלה שהיא בלתי זוג לא ימצא רק מספר אחד על דרך שהוא במעלה הראשונה | ||
| + | |- | ||
| + | |But, in the squares of the even ranks, there are always two numbers. | ||
| + | |style="text-align:right;"|ומרובעי המעלות בעלות הזוג לעולם ימצא בהם ב' מספרים | ||
| + | |- | ||
| + | |As in the thousands: one thousand and 600. | ||
| + | |style="text-align:right;"|כמו באלפים אלף ות"ר | ||
| + | |- | ||
| + | |And so on. | ||
| + | |style="text-align:right;"|וכן כולם | ||
| + | |- | ||
| + | | | ||
| + | === From the analogous squares you can know all those that precede them or succeed them === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''ומהנמשלים תוכל לדעת כל שהם לפניהם או אחריהם'''</span> | ||
| + | |- | ||
| + | |Meaning: if you know the perfect squares and their ranks, you know their roots. | ||
| + | |style="text-align:right;"|ר"ל שאם ידעת מרובעי אמת ומדרגות ותדע שרשם | ||
| + | |- | ||
| + | |Because, since you know the squares of the hundreds: 100, [400] and 900; the root of 100 is 10, and the root of 400 is 20; then the number of squares between 100 and 400 is the same as the numbers from 10 to 20; and the same for the means between four hundred and nine hundred. | ||
| + | |style="text-align:right;"|כי אחר שידעת כי מרובעי המאות ק' ות'ת'ק' והנה שורש ק' י' ושרש ת' כ' אם כן מספר המרובעים שבין ק' ות' כמספרים שהם מי' עד כ' ובין ק' ות' יפולו וכן מהאמצעיים שבין ארבעה מאות לתשע מאות | ||
| + | |- | ||
| + | |The analogous are the ranks after the tens, for the non-even [ranks] are analogous to the first [rank] and the even ranks [are analogous] to the second [rank]. | ||
| + | |style="text-align:right;"|הנמשלים יקראו המדרגות הבאות אחר העשרות כי אשר אינם בעלי זוג נמשלו לראשונה והמדרגות הזוגיות לשנית | ||
| + | |- | ||
| + | | | ||
| + | === Know that the units that are in the first rank === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''דע כי ההווה במעלה הראשונה מהאחדים וכו‫''''</span> | ||
| + | |- | ||
| + | |Meaning: as 1 is [the root of] 1 in the first rank, so is 10, which is the root of 100. | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{1}=1\quad\sqrt{100}=10}}</math> | ||
| + | |style="text-align:right;"|ר"ל כגון א' שהוא א' במעלה הראשונה כן י' הוא שורש ק‫' | ||
| + | |- | ||
| + | |Also, as in the first [rank] the root of 4 is 2 and the root of 9 is 3, so in the ranks of hundreds, the root of 400 is [20] and the root of 900 is 30. | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{4}=2\quad\sqrt{9}=3}}</math> | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{400}=20\quad\sqrt{900}=30}}</math> | ||
| + | |style="text-align:right;"|וכמו שבראשונה שרש ד' הוא ב' ‫<ref>58v</ref> ושרש ט' הוא ג' כן במעלת המאות שורש ת' הוא (כ') ושרש ת'ת'ק' ל‫' | ||
| + | |- | ||
| + | |The roots of the squares in the fifth rank, which is the tens of thousands, that is analogous to the first [rank], are found in the rank of hundreds: because the root of 10 thousand is one hundred and the root of 40 thousand is 200. | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{10000}=100\quad\sqrt{40000}=200}}</math> | ||
| + | |style="text-align:right;"|ושרשי מרובעי המדרגה החמישית שהיא רבבות הנמשלת לראשונה ימצאו במדרגת המאות כי שרש י' אלפים הוא מאה ושרש מ' אלפים הוא ר‫' | ||
| + | |- | ||
| + | |The roots [of the squares] in the seventh rank, which is two ranks up from the fifth, that is similar to it, since it is odd, are found in the rank that follows the hundreds, which is the thousands: because the root of a thousand of a thousand is a thousand and the root of 4 thousand of thousands is two thousand. | ||
| + | |style="text-align:right;"|ושרשי המדרגה השביעית שהיא דולגת מהחמישית שתי מדרגות הדומה אליה בהיותה נפרדת ימצאו במדרגה הבאה אחר המאות שהיא אלפים כי שרש אלף אלפים אלף ושרש ד' אלפי אלפים | ||
| + | |- | ||
| + | |And so for all of them. | ||
| + | |style="text-align:right;"|וככה בכולם | ||
| + | |- | ||
| + | |The units that are the roots of [the squares] in the second rank: | ||
| + | |style="text-align:right;"|והאחדים שהם במעלה השנית בשרש | ||
| + | |- | ||
| + | |As 16, whose root is 4: in the fourth rank that is analogous to it, the root of the square one thousand and 600 is the digit 4 in the tens. | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{1600}=40\quad\sqrt{16}=4}}</math> | ||
| + | |style="text-align:right;"|כגון י"ו ששרשם ד' כן במדרגה הרביעית הדומה לה במרובע אלף ות"ר יהיה שרשו אות ד' בעשרות | ||
| + | |- | ||
| + | |The root of the square two thousand and 500 that is analogous to 25, is 50, which is analogous to 5. | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{2500}=50\quad\sqrt{25}=5}}</math> | ||
| + | |style="text-align:right;"|ובמרובע אלפים ות"ק הדומה לכ"ה יהיה השרש נ' שהוא כמו ה‫' | ||
| + | |- | ||
| + | |The roots of the squares in the sixth rank that is analogous to the second rank, are hundreds. | ||
| + | |style="text-align:right;"|ובמרובעו המדרגה הששית הנמשלת למדרגה השנית יהיה שרשם מאות | ||
| + | |- | ||
| + | |As the square 160 thousand that is analogous to 16, whose root is 400 that is analogous to 4, which is the root of 16. | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{160000}=400\quad\sqrt{16}=4}}</math> | ||
| + | |style="text-align:right;"|כגון מרובע ק"ס אלפים הדומה לי"ו ששרשו ת' הדומה לד' שהוא שרש י"ו | ||
| + | |- | ||
| + | |Say the same for all of them. | ||
| + | |style="text-align:right;"|וכן תאמר בכלם | ||
| + | |- | ||
| + | |As our lord, our teacher, "May his Rock protect him and grant him life" said: | ||
| + | |style="text-align:right;"|לשון מורנו רבינו יצ"ו | ||
| + | |- | ||
| + | |If you have a known square and you wish to find another square using it: | ||
| + | |style="text-align:right;"|אם יש לך [...] מרובע ידוע ותרצה לדעת ממנו מרובע אחר | ||
| + | |- | ||
| + | |If it follows it: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2+b}}</math> | ||
| + | |style="text-align:right;"|אם הוא אחריו | ||
| + | |- | ||
| + | |Double the root of the former. | ||
| + | |style="text-align:right;"|כפול השורש הראשון | ||
| + | |- | ||
| + | |Know how much is the distance of the number, whose square you wish to know, from it. | ||
| + | |style="text-align:right;"|ודע כמה מרחק המספר שתרצה לדעת מרובעו ממנו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכפול הכפל ההוא במספר המרחק עוד תוסיף עליו מרובע מה שעלה בחלוק והוסף הכל על השרש הראשון ויצא המבוקש | ||
| + | |- | ||
| + | |If the number you wish to find precedes the known number: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2-b}}</math> | ||
| + | |style="text-align:right;"|ואם המספר שתרצה לדעת הוא לפני המספר הידוע | ||
| + | |- | ||
| + | |Double the root of the known square. | ||
| + | |style="text-align:right;"|כפול שרש המרובע הידוע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ועוד תכה אותו במרחק מה שיש <s>בו</s> בין מספר אשר תרצה לדעת מרובעו ובינו ומה שיצא תגרע ממנו מרובע מה שעלה בחלוק והנשאר תגרענו ממרובע המספר הידוע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם יש לך מרובע ידוע ותרצה לדעת ממספר אחר כמה הוא קרוב אל מרובע אם ‫<ref>59r</ref>אם המספר ההוא הוא א אחרי המספר הידוע דע כמה המרחק וחלק אותו על כפל שורש המרובע הידוע והשאר בידך מה שיצא במרובע החלוק וחבר הכפל ותוספת מרובע החלוק עם המרובע הידוע ויצא המבוקש | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או אם המספר אשר בידך הוא לפני המרובע הידוע ראה כמה מרחקו ממספר הידוע והמרחק ההוא חלקהו על כפל שרש המרובע הידוע ותן לו מהחלוקה כדי שנוכל לגרוע ממנו מרובע מה שעלה בחלוק ולא ישאר כי אם פחות מכפל שורש המרובע ומה שיצא בכ בכפילת החלוק אחר שתגרע ממנו מרובע החלוק חסר אותו מהמרובע הנמשל ויהיה המבוקש | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ע"כ וכל זה שוה עם הכתוב בספר אלא שהספר יצוה לגרוע כל כפל החלוק מהמרובע הנמשל ולהוסיף על הנשאר מרובע החלוק ולגרוע הנשאר מהמרובע העתיד והכל שוה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אלא שמלמדנו כמות תוספת החלוקה והכונה בתוספת לגרוע כל המרחק עד שנגיע אל המרובע שעבר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ודע כי כל [ב]כל אחד משני הדרכים לא נמצא רק מרובע שעבר הקרוב למספרנו ובדרך הראשון נמצאנו בין שהיה מספרנו יותר קרוב ממרובע שעבר או שהיה יותר קרוב ממרובע שאחריו והדרך השני לא יועילו רק בהיות מספרנו בלתי קרוב אל מרובע שעבר יהיו ק"נ שהוא שרש ו' ומרובע כ"ב אלף ות"ק וממנו נדע מהנשאר מרובע הקרוב על כן נחלק על כפל שרשו ונתן לו א' ו שהוא שם ונוסיפנו על מרובע הראשון שהיה לנו והיו כ"ב אלפים ותת"א עם מרובע א' שעלה בחילוק . נתן לו יותר מה שנוכל . שנתן לו ט' שהם ה' אלפים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === We cannot give it 5 === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''לא נוכל לתת לו ה‫''''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל נסיר ממנו אלף ות"ר שהוא מרובע מ' ונוסיפנו על המספר יהיו ל"ג אלפים ות"ר ועתה יהיה לנו ת"ם ‫<ref>59v</ref> ר"ל שנעשה מרובע קרוב ונחלק על כפלו מה שנשאר לנו שהוא אלפים ות' נתן לז' שהם ו' אלפים וק"ס | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחסר עוד מרובע ז' שעלה בחילוק ר"ל ונוסיפנו על מה שהיה לנו ויהיו ו' אלפים ור"ט | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נחבר זה אל ל"ג אלף ות"ר שהיה לנו ועם הכל עלה קצ"ט אלפים ות"ר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשארו קצ"א נחסרנו ממאתים אלף ישארו קצ"ט אלפים ותת"ט והדבר יצא שוה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ולידע השורש נוסיף ז' שעלה בחלוק על השרש שהוא ת"ם היה תמ"ז והוא השרש | ||
| + | |- | ||
| + | | | ||
| + | === We give it all we can === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''נתנו לו כל מה שיכולנו'''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נתנו לו כל מה שיכולנו והנה המ' אלף עלה בחלוק כ"ה בצמצום והנה נתן לו יותר חלק אחד שנחברהו מן השש מאות אלף נוכל ליקח מרובע מה שעלה בחלוק והיו כ"ו וכן נחסר כ"ו משרש ומרובע הנמשל שהוא ת"ת והנה שרש מספרנו תשע"ד נחלק המספר הנשאר שהוא אלף אלפים על ד' אלפים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה לא נתן לו רק רל"ו שהם תת"קמ"ד אלפים ונשארו נ"ו אלפים נקח מהם מרובע מה שיעלה בחלוק שהוא נ"ה אלפים ותרצ"ו וזהו המרובע ונשאר ש"ר ואם ד' אלפי אלפים תחסרנו מאלף אלפים שאר המבוקש שהזכרנו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונחבר רל"ו שעלה בחלוק עם שרש ראשון שהוא אלפים והוא השרש המבוקש | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה גם כן העולה מחשבון הספר אלא שמחלק זה חלוקת רבות חלוק אחר חלוק ערך מרובע אל מרובע מרובע אותו הערך העולה הוא מרובע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והמבחן שאם תחלק השרש הגדול על השרש יצא שרש ערך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון חלקנו ס"ד על י"ו עלה ד' וזה הערך הוא מרובע ושרשו הוא היוצא מערך ד' אל ח' שהוא ב' והנה הוא כפלו וב' שביעיות שביעיות וזהו מרובע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם נחזירנו לשביעיות שביעית ותחבר עמהם הב' היו ק' ושרשם י' שביעיות שהוא אחד ש' שלם וד' שביעיות כי שרש הנשברים גדול ממרובע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|בקשנו לדעת מרובע מספר ידוע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כגון שנרצה לידע מרובע ממרובע כ"ה ‫<ref>60r</ref>כ"ה שהוא ידוע למספר ה' שהוא ידוע נחלק י' על ה' ועלה שנים ומרובעם ד' נכפול ד' על כ"ה ועלה ק' שהוא מרובע ד' ועל זה הדרך בכלם | ||
| + | |- | ||
| + | | | ||
| + | === If we sum three squares, we triple them === | ||
| − | + | |style="text-align:right;"|<span style=color:blue>'''ואם חברנו שלשה מרובעים ונכפלם ג' פעמים'''</span> | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ר"ל אם נחבר ג' מרובעים ונכפלם המחובר על ג' ונשמור זה העולה ונקח מרובע היתרון שבין הראשון לשני ומרובע היתרון שבין השני לשלישי ומרובע היתרון שבין הראשון לשלישי ותחבר אלה הג' מרובעים והמחובר חסרהו מהעולה תחלה והנשאר מהעולה הוא מרובע ושרשו המחובר מג' המרובעים הראשונים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ועל זה הדרך אם חברת ד' מספרים ותכפלם ד' פעמים או אם חברת ה' מספרים ותכפלם ה' פעמים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ואומר לך כלל שתוכל לדעת ממנו וכו‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|לעולם חסר אחד מהמספר המחוברים וראה סך המחובר מא' עד סוף מספר הנשאר בדרך שאמר בשער החיבור וככה מספר היתרונים כגון שהיו המספרים ד' חסר אחד והיו ג' והמחוברים מא' עד ג"ו וכן היתרונים ו‫' | |
| − | + | |- | |
| − | ואם | + | | |
| − | + | |style="text-align:right;"|רק אם יהיה בו רביעית כלומ' אם נמצא במרובע רביעית ידענו כי בשרש היה חצי ממנו יצא אם היה בו ששית ששית מששית יצא וכן בשאר | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ואם היה בו חצי שמינית שהוא חלוק מי"ו הנה מהרביעית יצא | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וכן שניים שהם כמו רביעית יצאו מראשונים שהם חצי ורביעים יצאו משניים אבל שלישיים וחמשיים ושביעיים ושמניים אין להם שורש אמת | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|הסתכל אם היה מרובע רביעית דע כי בשרש חצי | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כגון שהיו לך י"ב שלמים ורביעית הנה בשרש היה חצי נשיב הכל לרביעיות היו מ"ט ושרשם ז' חצאים שהם ג' וחצי והנה כאשר נכפול ג' וחצי על עצמם יצא לך י"ב ורביעית | |
| − | + | |- | |
| − | ונכפלם המחובר על ג' ונשמור זה העולה ונקח מרובע היתרון שבין | + | | |
| − | הראשון לשני ומרובע היתרון שבין השני לשלישי ומרובע היתרון שבין | + | |style="text-align:right;"|תכפול מ' על מ' ראשונים שהם שתי שלישית מעלה יהיו אלף ות"ר |
| − | הראשון לשלישי ותחבר אלה הג' מרובעים והמחובר חסרהו מהעולה | + | |- |
| − | תחלה והנשאר מהעולה הוא מרובע ושרשו המחובר מג' המרובעים | + | | |
| − | |||
| − | או אם חברת ה' מספרים ותכפלם ה' פעמים | ||
| − | לדעת ממנו וכו' | ||
| − | המחובר מא' עד סוף מספר הנשאר בדרך שאמר בשער החיבור וככה | ||
| − | מספר היתרונים כגון שהיו המספרים ד' חסר אחד והיו ג' והמחוברים | ||
| − | מא' עד ג"ו וכן היתרונים ו' | ||
| − | במרובע רביעית ידענו כי בשרש היה חצי ממנו יצא אם היה | ||
| − | ששית ששית מששית יצא וכן בשאר | ||
| − | שהוא חלוק מי"ו הנה מהרביעית יצא | ||
| − | יצאו מראשונים שהם חצי ורביעים יצאו משניים אבל שלישיים | ||
| − | וחמשיים ושביעיים ושמניים אין להם שורש אמת | ||
| − | אם היה מרובע רביעית דע כי בשרש חצי | ||
| − | ורביעית הנה בשרש היה חצי נשיב הכל לרביעיות היו מ"ט ושרשם | ||
| − | ז' חצאים שהם ג' וחצי והנה כאשר נכפול ג' וחצי על עצמם יצא לך | ||
| − | י"ב ורביעית | ||
| − | יהיו אלף ות"ר | ||
| − | |||
| − | + | === If we convert this number to thirds === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|<span style=color:blue>'''ואם עשינו מזה המספר שלישיות'''</span> | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ר"ל בעבור שהזכרנו שלישיות נשיב הו' ראשונים שנעשה מכל ראשון שהוא ס"ג שלישיות <ref>60v</ref>יהיה עם הב' שלישיות עשרים וכבר אמרנו שהם כ"ו ראשונים ומ' שניים הם תשיעית אחת מס' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|שוב וחשוב כי הם ראשונים כי שרש שניים הוא מראשונים יהיו אלף ות"ר שניים שכל ע' הם ראשון אחר נכפול מ' על ס' ונחלק העולה על ע' כי כערך מ' אל ע' יהיה ערך העולה מס' על כן נכפול הקצוות שהם מ' על ס' ונחלק על ע' שהוא האמצעי ומה שיצא יהיה ערכו מס' יעלו ל"ד ראשונים וישארו ב' שהוא שניים יעלו ז' שהם <s>ראשונים</s> שניים וישאר לנו מהשלישיים י' שהם שביעית אחת מע' נעשה ממנו ששים והם רביעיים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|נכפלנו עוד ויהיו ג' אלפים ות"ר חמישיים נחלקם על ע' יעלו כ"א רביעיים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ונעשה חלקנו תשעים ר"ל נעשה אחד מצ' חלקים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כפלנוהו על עצמו והם ת'ת'ק' נחלקם על צ' ועלה י' חלקים ראשונים והם המרובע ושרשם ל' ראשונים אם אמת כי המרובע חלק אחד ומ' שניים ר"ל הוא נכון שהוא מרובע כי חלק מס' ומ' שניים הוא ששית הששית מס' כי הששית הוא וששית י' הוא ראשון אחד ומ' שניים אם כן השורש הוא י' כי מכפל ששית יצא ששית הששית ומרובע י' ראשונים הוא ק' שניים שהוא ראשון אחד ומ' שניים | |
| − | ראשונים | + | |- |
| − | + | | | |
| − | + | === As for the numbers that are divisible by sixty === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | על | ||
| − | |||
| − | |||
| − | |||
| − | שהוא | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | מרובע | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|<span style=color:blue>'''והנה במספר שיש לו ערך אל ששים'''</span> | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ר"ל א'ע'פ' שקצת המספרים שלא יאותו במקום אחד להיות מרובעים ובכאן לפי שיש להם ערך אל ס' הם מרובעים כמו ט"ו כי הוא רביעית ס' ושרשו ל' ראשונים שהם חצי אך לא יתכן זה בכל המספרים כי י' שהוא ששית אינם מרובע כל שכן המספרים שאין להם ערך כלל אל ס' שאינם מרובע כגון י"א גד יד יט נחלקם על כפל השרש שעבר שהוא ששה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כי לעולם כשנעלם ממנו שרש מרובע אחד כגון שלא נדע שרש ק' על דרך משל נבקש מרובע שעבר שהוא פ"א ששרשו ט' ונביט מה המרחק שבינו לבין ק' ‫<ref>61r</ref>ק' והוא י"ט נחלקם על כפל השרש שעבר שהוא י"ח ונוסיף עליו המרחק שבין ט' לי' ועלה אחד נוסיף האחד <s>עש</s> על שרש ה' ראשון והיה י' והוא שרש ק' וכן בכאן נחלק המרחק על ו' יהיו ב' ראשונים והנה השרש ג' שלמים וב' ראשונים שהם שלישית אחת נכפלם ועלה י"א שלמים ותשיעית | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ואם תרצה השב הי"א לתשיעיות והם עם התשיעיות ק' ושרשם י' שלישיות שהם ג' שלמים ושליש | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וזה שנניח השבר לפי שכל השאר נחלק ולא נקח ממנו מרובע החלוק כי לא יתכן והנה במרובע תוסף אם בשלמים נחלקים כל המרחק ונניח כדי מרובע החלוק ונוסיף הנשאר בשרש והכל שוה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ידענו כי יש בחשבון חומש החומש כי הכ"ד שניים ה' הם ב' חמישיות מראשון והנה חמישית לא יתכן היותו מרובע על כן הוא חומש החומש וכמה הוא חומש החומש שיש בכלל זה המרובע ב' חלקים וכ"ד שניים כי באמת חומש חומש היה בשורש שהוא י"ב וחומש הוא ב' ומק"כ ראשונים נעשה שניים שמן ק"כ וחמישיתם כ"ד והנה המרחק מהמרובע שהוא אחריו שהוא ט‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|דע כי לעולם יהיה בין שנים מספרים ר"ל המרחק בין שני מרובעים הסדורים במספר שרשיהם על כן כשתדע מרובע אחד ולא השני לו חבר שרשיהם עם מרובע הנודע | |
| − | + | |- | |
| − | + | | | |
| − | + | === Look at the number you want === | |
| − | |||
| − | י | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|<span style=color:blue>'''והנה הסתכל המספר שתרצה'''</span> | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וכו' ר"ל אם תבקש לידע שרש אי זה מרובע שיהיה כגון שתרצה לידע מרובע י"ב שהוא בין ובין י"ו והנה הסתכל מרחקו ממרובע שעבר שהוא ט' אם היה בשרש ט' שהוא ג' והמספר נקרא אמצעי לפי שאם תחלק המרחק על אי זה משני המרובעים שתרצה תהיה חלוקתך שוה שאם תחלוק ג' על ו' שהוא כפל שרש שעבר יצא בחלוק חצי וכן אם תחלוק ד' שהוא המרחק שאחריו על כפל השרש שאחריו שהוא ח' יהיה חצי והדבר שוה | |
| − | + | |- | |
| − | + | | | |
| − | + | === Extract any number that is less than the mean, as 11, from the preceding square number === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|‫<ref>61v</ref><span style=color:blue>'''וכל מספר שיהיה פחות מהאמצעי כגון י"א הוציאהו ממספר המרובע שעבר'''</span> | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ר"ל שתקח המרחק שבין מספרך ובין המרובע שעבר וחלקהו על כפל שרשו ואם היה המרחק יותר משרש שעבר עשה חשבונך במרובע העתיד | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ואם חשבונך היה במאות ובאלפים זה השרש יספיק לך כי לרבויו לא יוכר בו הטעות והחסרון ויותר יוכר בו אם נקחהו מהקטן כי החסרון והשגגה הולך ורב עד כי גדל מאד רק אם היה המספר קטן אתה צריך למספר שני לפי שלא לקחת ממנו מרובע החלוק | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ופעם נקח השורש בקטן מהגדול ויצא מדוייק כמו שעתיד לבאר לפי שטענת הגדול יתמעט כל אשר ירד ויחלק ויבלע מאד | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ואם רצית לדעת שרש עשרים אלף כפול זה השרש על עשרה לפי שה<s>ש</s>שרש גם כן יכפול ויעלה למדרגה אחרת כי שרש המאות עשרות ושרש הרבבות מאות והנה שביעית מל"ד | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וזה בקירוב כי עדיין ישארו ב' שניים שלא לקחנו שביעיתם יהיו ת'ק'י'ד' ועשיריתם ר"פ וזה בקירוב | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|נעשה מהנשארים שהם ק'י'ט' ראשונים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|נחלקם על ר'פ'ב' שהוא כפל ק'מ'א' עלו כ"ה חלקים ראשונים וישארו צ' חלקים והנה לא נוכל לחלקם על ר'פ'ב' נשיבם שניים והם ה' מב' נחלקם על ר'פ'ב' שהם שרשנו עלו י"ט שניים וישארו מ"ב שלא יתחלקו ואלו ראשונים וי"ט שניים נוספים על שרשנו שהוא ק'מ'א' ואם רצה לדקדקו עוד ישיב המ"ב לשלישיים ויחלקם על ר'פ'ב‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ודע כי כל שברים שתחלק על שלמים יעלה אותו המין מן השבר וכשתחלק מין שברים פחות על מין שבר יותר גדול נחסר מספר הגדול ממספר הפחות והנשאר הוא העולה החלוק | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|נחלק כל מה שאמרנו מן השלמים והשנים על מאה כי כמו שאמרנו כשבקשנו שרש שניים משרש ‫<ref>62r</ref>משרש מאתים שלקחנו עשירית שרש מאתים לפי שהוא כפלו י' פעמים כן נאמר עכשו כשנוציא שרש שניים משרש עשרים אלף שהוא כפלו מאה פעם שנקח אחד ממאה שבו הנה מן המאה קח אחד שלם ונקח בעבור המ"ב חמישיות ז' שהן כ"ד מס' לפי שערכם אל מאה כן והאחד שנשאר מק'מ'א' נעשנו ס' ראשונים ועם הכ"ה היה פ"ה והנה בעבור הפ' תקח ד' חמישיות מס' ובעבור הה' שהוא רביעית חמישית ק' נקח רביעית חמישית ס' שהוא ג' והרי לנו נ"א ובעבור הי"ט שהוא פחות אחד מחמישית מאה לקח חמישית ס' פחות א' והוא י"א | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ואם תכפול כל חשבון שהוא כפל מרובע נראה שכך הוא סדר הדבר אם תרצה לידע שרש חשבון שהוא כפל מרובע כפול שרש חציו על זה ושרש ר"ל שרש ב' השבר | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כי כל חשבון שתכפול על שרש מאחד יהיה מרובע אותו הנכפל נכפל אותו חשבון על עצמו מדמיוני מרובע השרש הראשון המיוחד ר"ל שכפי מספר כפל החשבון נחשוב כך פעמים המרובע הראשון | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|המשל בזה כפלנו ב' שהוא שרש ד' על ג' והוא ו' הנה כפל ג' ט' נכפול ט' על מרובע ראשון שהוא ד' והוא ל"ו שהוא מרובע ו' ואם נכפול ה' על ב' שהוא י' הנה מרובע ו נכפל ה' שהוא כ"ה כפול על ד‫' | |
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|רצינו לדעת כמה שרש י"ח הנה כפלנו שרש המרובע שעבר שהוא ג' על זה המספר שהוא א'נ"ד כ"א י"א שוה המספר שהוא י"ח כפלו ר"ל ממרובע ג' שהוא יעלה ד' שלמים י"ד ראשונים ל"ג שניים ל"ג שלישיים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם כפלנו זה המספר שהוא שרש י"ח יהיה זה הנשנה שרש ע"כ כי לעולם כפל שרש מרובע אם יהיה מרובעם כפל מרובע ראשון כמו שרמזנו למעלה מן חציו הוא שרש רביעית מרובע ראשון | ||
| + | |- | ||
| + | | | ||
| + | === If we take the square of 7 thousand and 200 === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''ואם נקח מרובע ז' אלפים ור‫''''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל אם נקח זה המספר מקום מרובע ונבקש לידע שרשו נעשה על הדרך הנזכר שנקח שרש חציו שהוא ס' ‫<ref>62v</ref>ונכפלהו על א'נ"ד נ"א י"א יהיה שרש ז' אלפים ור' פ"ד נ"א י"א וזהו שרש שנים בעצמו אלא שהעלינו כל מספר למדרגה עליונה ממדרגתו שהוא מס' לס' עד ששבו השלישיים שניים והשניים ראשונים והראשונים שלמים | ||
| + | |- | ||
| + | | | ||
| + | === Because we convert them to minutes, consider these as integers === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''כי השיבונו אותם בדרך ראשונים והנה חשוב אלה שיהיו שלמים'''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה רצה באמרו כי השיבונו אותם בדרך ראשונים והנה חשוב אלה שיהיו שלמים ר"ל שאם היה לנו זה השורש שהוא פ"ד נ"א י"א ולא היה לנו שרש ב' נוריד זה השרש מס' לס' ונתיכהו כדרך שהרכבנוהו ויגיע לנו שורש ב‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם תכפול זה המספר על עצמו ר"ל המבחן על זה השרש שנכפלהו על עצמו ונשיב הכל אם נרצה למדרגה שהוא שלישיים ונכפלם על עצמם והם ששיים ונחלקם על ס' עד שנשיבם לשניים וראשונים ומעלות וישאר בכל אחד מה שלא יתחלק על הדרך שהורינו בסוף שער חמישי תמצא בסוף שלא ישאר אפי' שני אחד וכל שכן ראשון כל זה אמר להראות דיוק זה השרש | ||
| + | |- | ||
| + | | | ||
| + | === We go back to extract the root of two === | ||
| + | |style="text-align:right;"|<span style=color:blue>'''נשוב להוציא שורש שנים'''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל בדרך אחרת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויספוק לנו השרש הראשון ר"ל לא נצטרך להוציא שרש ב' מד' או מעשרים אלף כי יספיק לנו להדריכנו אל האמת השרש הראשון במה שנעשה בו כמו שמבאר והולך ובעבור שיש לנו ששיות כי הנ' הם ה' ששיות וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשיבם הכל מערך ו' והיו י"ז וכן נשיב הנ"ה לששיות שנכפלם על ו' ועלה ק"נ ועתה יכשר לחלקם על הי"ו עלו מ"ט שלישיים ונשארו א' שלא יתחלקו | ||
| + | |- | ||
| + | | | ||
| + | === If we calculate even more precisely by taking the square of 49 === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''ואלו היינו מדקדקים עוד מדרך מרובע המ"ט'''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שנקח מרובעם ונחלקם על כפל השרש שהיה לנו שהוא ב' מ"ט מ"ב כ"ב ונחשוב כי הכל בנ' ובעבור שהנ' הם ד' ששיות נשים הכל ששיות והיו י"ז ונשיב אצל המ"ט והקי לנו ת'ק'כ'ט' שלישיים נעשה מהם מרובע ויהיו ששיים נחלקם ונגיעם עד רביעיים ונשיבם מערך ששיות ‫<ref>63r</ref>ששיות ונחלקם על י"ז שהיה לנו נתן לו כ"ז רביעיים כ"ז חמישיים נחסרם משרש שלנו וישאר א'כ"ד נ"א י' ל"ט ל"ד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואנחנו דקדקנוהו יותר ולקחנוהו משרש ב' אלפי אלפים ויצא מדוייק בתכלית הדיוק א'כ"ד נ"א י' ז' מ"ז כי לא ישאר אפילו רביעי ולא חמשים רק ב' ושרש נ' המוצא ממנו זד טו ד' לח נה ושרש ה' אלפים עד מב כג לא כט | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונשיב הכל מערך שלשה והיו י"ט וכן נשיב ק'ה'ק' לשלישיות שהם ש' ועלו ט"ו נשיבם שניים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נראה שהוא שלישיים יהיו שלש מאות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נראה זה טעות כי השניים הנשארים הם ט"ו וכשנשיבם שלישיים יעלו ת'ת'ק' וכשנחלקם על י"ט יעלו מז שלישיים מעשרה חלקים ישארו ט' מ"ד י"ג וכשנדקדקהו ונעשה מרובע מה שעלה בחילוק ונחלק על כפלם השרש יעלה בחלוק שלישי אחד נחסרהו מי"ג וישאר השורש כ"ט מ"ד י"ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכשנכפול זה החשבון על עשרה וכו' כי מה שהוא במעלה הראשונה אחדים יהיה באלפים עשרות | ||
| + | |- | ||
| + | | | ||
| + | === We divide the root of 18 === | ||
| + | |||
| + | |style="text-align:right;"|<span style=color:blue>'''חלקנוהו שרש י"ח'''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל אם נרצה לדעת שרש י"ח משרש כבר ידענוהו משרש כשכפלנוהו ושרשו אחד וחצי ככה שרש י"ח הוא כפל שרש ח' וחצי הכפל שהוא ג' פעמים שורש ב‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נקח מרובע החילוק שנשיב הכ"ב ראשונים למתכונה הל' שהם שניים יעלו ת'ת'ד' שין ומרובעם אלף אלפים ות"ר שהם שלשים אלף שע"ה שלישיים נחלקם על כפל השורש שהוא <s>תק"ה</s> ת'ק'כ'ה' ראשונים יעלה כ"ח שניים בקרוב כי שלישיים על ראשונים יצאו שניים כמו שהקדמנו נחסרם מן השרש הראשון שהוא ד'כ'כ'ל' הנה נשליך הל' שהם שניים ונחסר הכ"ח שניים הנשארים מראשון אחד שנקח וישאר השרש השני ד'כ'א' ל"ה | ||
| + | |- | ||
| + | |As the ratio of the versed sine to the entire diameter so is the ratio of the [sum of] the square of the versed sine with the square of half the chord to the square of the diameter and so is the ratio of the square of versed sine to the square of half the chord. | ||
| + | |style="text-align:right;"|לעולם כערך החץ אל כל האלכסון יהיה ערך מרובע החץ עם מרובע חצי המיתר ממרובע האלכסון וככה ערך מרובע החץ אל המרובע חצי היתר | ||
| + | |- | ||
| + | |The reason is that if you make a circle and you draw a chord | ||
| + | |style="text-align:right;"|‫<ref>63v</ref>והטעם שאם תעשה עיגול ותוציא ממנו יתר בנקודה ידועה מהאלכסון ותעשה אלכסון מתחלת האלכסון שהוא ראש החץ אל קצה היתר ותמשיך קו אחד מקצה היתר עד סוף הקוטר תמצא שמרובע הקוטר הוא כנגד שני הקוים שהוא הכאת שני הזויות ומרובע <s>שנים</s> שניהם הוא ברבוע האלכסון ומה שיחסר האחד ממרובע האלכסון ישלים חברו אם כן אם היה אלכסון החץ וחצי המיתר שלישיות שני הקוים כגון שהונח בשלישית האלכסון יהיה אם כן מרובעו החץ וחצי המיתר שלישית רבוע כל הא' האלכסון כי מרובע קטרם שקול בשניהם וזה הצורה לדמיון לעולם מרובע מה שנשאר מן החץ על הנקודה וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והטעם שאם תוציא קו אחד מקצה המיתר עד הנקודה שהוא חצי האלכסון תראה שהוא קוטר חצי המיתר ומה שאחרי החץ מהאלכסון עד הנקודה ולכן מרובען כרבוע שניהם יהיה מרובע חצי המיתר שלשת כפלי מרובע החץ | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שכן הקוטר כפלי החץ כי הוא רביעיתו ונמצא החץ ד' חלקים ומרובעו ו' ראשונים ומ' שניים שהוא תשיעית אחת והוא אחד מל' מנ' ונ' הנה מרובע חצי היתר הנשאר מג' שלישית שהוא ג' י"ג כ‫' | ||
| + | |- | ||
| + | | | ||
| + | === If you multiply the requested diameter by 22 === | ||
| + | |style="text-align:right;"|<span style=color:blue>'''אם כפל האלכסון שתראה על כ"ב'''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל מאי זה אלכסון שתדע הערך לידע הקו הסובב כגון שהקוטר עשרה תעריך ותאמר כערך י' אל ז' יהיה ערך העגול אל כ"ב ונכפול הקצוות ונחלק על ז' והנה הנוסף אל הג' שלמים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שאם היה הנוסף ז' חלקים מע' וחצי יהיה הנוסף על הג' שלמים ח' ר"ל שאם היה הנוסף כ"ד ל"ה אך אינו כן כי הוא נתן ראיה כי ראוי להיות יותר וכיצד נחשוב נעשה הערך ככה בעבור ד' אל ק'מ'א' יהיה זה מס' ונכפול ב' על ס' שהם הקצוות ונחלק על ק'מ'א' והעולה הוא כך חלקים מס' והנשאר גם כן נשוב לכפול על ס' ונחלק על ק'מ'א' כי ‫<ref>64r</ref>כי התוספת ח"ל ולעשות ערך נעשה מהכל ראשונים ר"ל ה'ג' ח"ל והם ק'פ'ח' וחצי ובעבור החצי נשיב הכל לשניים ונעשה האחד מק"כ ויהיה הכל ש'ע'ז' וכן נעשה האלכסון ק"כ ונעריך ונאמר כערך האלכסון אל ק"כ יהיה ערך קו העגול מש'ע'ז‫' | ||
| + | |- | ||
| + | | | ||
| + | === If we set the diameter as 10, the square of the chord is as one-third === | ||
| + | |style="text-align:right;"|<span style=color:blue>'''אם שמנו האלכסון י' יהיה מרובע היתר כשלישית'''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל כשנוציא יתר בשלישית הקוטר ונרבע אותו יותר עם השלישית יהיה כמספר הקו הסובב כי לפי זה מרובע חצי המיתר כ"ב וב' תשיעיות ושרשם ד' וב' שלישיות בקרוב נמצא כל המיתר ט' ושליש נכפלם על שליש האלכסון שהוא ג' ושליש יעלה ל"ז ותשיעית ויותר מעט כי בקרוב מנינו כל המיתר ונמצא שהוא כשעור הקו הסובב וזו הצורה | ||
| + | |- | ||
| + | | | ||
| + | === Likewise, if you make the square between the upper third and the lower third === | ||
| + | |style="text-align:right;"|<span style=color:blue>'''וככה אם עשית מרובע בשלישית העליונה ובשלישית השפלה'''</span> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ר"ל שנוציא שני יתרים אחד למעלה בשלישית ואחד למטה בשליש הקוטר גם כן יהיו שבריו כמספר הקו כי אין חלוק בין מרובע החץ שהיא שליש האלכסון עם היתר ובין מרובע היתר ההוא למטה בשלישית האלכסון כזה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכל מספר שהוא לפני עשרה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כל זה הוא ספור מעלות עשרה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שאם תוציא משולש שוה השוקים בתוך העיגול ותשים תושבתו במיתר ששלישית אם יהיה הקוטר העובר באמצעו עשרה יהיה רבוע המשולש בקו הסובב כי רבוע כל משולש הוא הכאת הקו האמצעי מחציו על כלו כי משולש הוא חצי מרובע תראה זה אם תעשה בתושבתו שארכו כאורך המשולש ואין הפרש בין שתכה שליש האלכסון על כל היתר או שתכה שני שלישיו על חציו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם היה האלכסון פחות מי' בערך מה שיחסר מעשרה יגרע מדעת המשולש שבשלישית מהיות כקו הסובב ואם היה האלכסון יותר לפי ערך מספרו מעשרה יהיה ערך גודל מספר המשולש על הקו הסובב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>64v</ref>המשל בזה אם תעשה אלכסון ט"ו ותוציא יתר בשלישית יהיה | ||
| + | רבוע כל האלכסון רכ"ה ושלישיתו ע"ה וזהו מרובע חצי היתר ומרובע החץ נחסר ממנו השליש שהוא מרובע החץ וישאר נ' ויהיה שרש ז' שלמים ומשהו נכה אותו בשני שלישי האלכסון הוא שנים ושביעית אחת אם כן יהיה הקו המקיף מ"ז ויותר מעט וערכו אל ע' שהוא תשבורת המשולש כערך י' אל ט"ו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והמשל בפחות מי' כגון שהיה האלכסון שבעה יהיה מרובע כל האלכסון מ"ט ושלישיתו י"ו כ' והוא כולל מרובע החץ וחצי היתר נוציא מהם מרובע החץ והוא ה' ושלישית ותשיעית שהוא כ"ו מ' נחסר אותו מי"ו כ' ישאר י"א פחות תשיעית ושרשו ג' י"ח ככה זה המספר בשני שלישי האלכסון שהוא ד' מ' ויהיה ט"ו כ"ד והוא תשבורת המשולש אל כ"ב שהוא הקו המקיף כערך ז' אל ז‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם תעשה זה דקדוק רב תמצא בפי' שהנוסף על השלשה הוא פחות משביעית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכאשר נחפש הקו הסובב לדעתי לפי ערך המשולש שבשלישית ימצא מסכים לדברי ארשמידס | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וממעלות העשרה כי בהיות קו העיגול עשרה יהיה האלכסון שרש י' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם ידעת האלכסון כפול מרובעו כגון שהאלכסון י' ומרובעו ה' נכפול על י"א וכו' כלל אחר טוב לדעת השברים מהקו הסובב כפול חצי הקוטר על חצי העגול וככה הם השברים ויצא הדבר שוה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לעולם כערך י"א אל י"ד יחסרו שברי העגול ממרובע האלכסון נמצא מרובע יתר על העיגול שביעית חצי שביעית שהוא פחות מרביע ורבותי שאמרו רביע נמשכו אחר כללם שאמרו כל שיש ברחבו טפחיים וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ודע והנה הנמשלים שהם מי' ולמעלה ‫<ref>65r</ref>ראוי שנקח המדרגות מהם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|בקשנו לכפול מאתים על ש' והנה הנמשלים ב' וג' שהם במקום ת'ש' כפלנו זה על זה והיו ו' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן המדרגות <s>המבוקשות</s> המקובצות משניהם ו' בחשבון האמת תחלק המדרגה הרביעית היא עשרת אלפים וכשנכפול מאות במאות לא יצטרך לחשוב אלא ד' מדרגות ונשמע מהמדרגה הרביעית עשרת אלפים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תם ונשלם תהלה לאל עולם | ||
| + | |} | ||
פרוש ספר המספר של ראב"ע | פרוש ספר המספר של ראב"ע | ||
| − | + | Genève, Bibliothèque de Genève, MS héb. 10/2 (IMHM: f 2320), ff. 39r-65r (14th-15th century) | |
| − | + | ::[http://www.e-codices.unifr.ch/en/bge/heb0010/39r Ms. heb. 10] | |
| − | |||
| − | |||
נראה שחסר מעט בהתחלה | נראה שחסר מעט בהתחלה | ||
בדף 58ב: "לשון מורינו ורבינו יצ"ו. אם יש לך אות(?) מרובע ידוע ...". | בדף 58ב: "לשון מורינו ורבינו יצ"ו. אם יש לך אות(?) מרובע ידוע ...". | ||
Latest revision as of 11:51, 2 November 2024
Contents
[Chapter One] |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The sign for this |
[1]האות על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I.e. the sign that all numbers revolve around nine is when you draw a circle etc. | ר"ל האות על היות כל המספר סובב על תשעה כשתעשה עגול וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| He could have given another difference: when you multiply 9 by itself, or by 8, or by 7, or by 6, you find that the units of the tens position exceed the units themselves and from 5 and up it is the opposite as a general rule. | וכן היה יכול ליתן הבדל אחר כי כשתכפול ט' על עצמו או על ח' או על ז' או על ו' תמצא האחדים שבמקום העשרות יתרים במספרם מן האחדים עצמם ומה' ולמעלה ככלל הדבר בהפך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Therefore five is called round number, for it revolves around itself |
על כן נקרא חמשה חשבון עגול כי הוא מתגלגל על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I.e. it is found in its square. | ר"ל שימצא במרובעו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Although it is also found in six, the square of six is not preserved in its cube. | וא'ע'פ' שבששה ימצא כן אמנם ששה לא ישמר מרובעו במעוקבו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because when you multiply 6 by 6, it is 36.
|
כי כשתכפול ו' על ו' ויהיו ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Next, you multiply 6 by 36; but it does not stay in its shape.
|
ואחר תכפול ו' על ל"ו לא ישאר בצורתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But, [5] times 5, which is 25, if you multiply it by 5, it retains itself; the result is 125 and this is the absolute product, since after multiplying its length by its width, we multiply it by its depth.
|
אך פעמים ה' שהם כ"ה אם תכפלם על ה' ישמר עצמו ויעלה ק'כ'ה' וזהו הכפל הגמור כי אחר שכפלנו ארכו על רחבו שהוא השטח נכפלנו בעמקו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| So, the height is divided into five equal parts, each of which is 5 by 5. | ונחלק הגובה לה' חלקים שוים שכל אחד ה' על ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For 1, 10, 100 repeat in the thousands |
כי א'י'ק' יחזור באלפים וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1, 10, 100 are apart of all numbers, because every number is either one [= units], or 10 [= tens], or 100 [= hundreds]. | א'י'ק' הוא חוץ לכל המספרים כי כל מספר הוא אם אחד או י' או ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For a thousand is one, 10 thousand returns to 10 and 100 thousand to 100. | כי אלף הוא באחד וי' אלפים ישובו לי' וק' אלפים לק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
To multiply a number by itself |
לכפול חשבון על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As 25 by 25. | כמו כ"ה על כ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Or by other | או על אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Such as 25 by 44. | כמו כ"ה על מ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Or multiplication of one number by two numbers |
או כפל חשבון אחד על שנים חשבונות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As the multiplication of tens by hundreds and tens. | ככפל עשרות על מאות ועשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Or multiplication of multiple numbers by multiple numbers |
או כפל רבים על רבים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As units, tens and hundreds by units, tens and hundreds. | כמו אחדים ועשרות ומאות עם אחדים ועשרות ומאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
About the scales |
על המאזנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I.e. the sign indicating the truth of multiplication, or division, or vice versa. | ר"ל האות המעיד המורה על אמתת הכפל או החלוק או חלופו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Addition of a number to a number |
בחבור מספר אל מספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For example, if you want to add many numbers together with many numbers, we write those numbers in rows and add the digits in order as if they were units. | כגון שתרצה לחבר יחד מספרים רבים במספרים רבים נכתוב אלו המספרים בשורות שורות ונחבר האותיות ביושר כאלו היו אחדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the result that exceeds ten has no units, we write zero and keep it. | והעולה על עשר אם אין בו אחדים נכתוב גלגל ונשמור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If it has units, we write the units; we write the tens in another position and keep it as will be explained in its place. | ואם יש עמו אחדים נכתוב האחדים ונניח הכלל במקום אחד ונשמרהו כמו שיתבאר במקומו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subtraction of a number from a number |
לחסר מספר ממספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meaning to subtract a number from another number greater than it and know the remainder. | כלו' לגרוע מספר ממספר אחר רב ממנו ולדעת הנשאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Always subtract one for the foundation |
וגרע לעולם אחד למוסד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For the units do not generate any rank for any number, because every number multiplied by units does not go out of its rank, which is not the case when multiplying by another number that rises the rank. | כי אחדים לא יחדשו מדרגה בשום מספר [2]כי כל מספר הנכפל על אחדים לא יצא ממדרגתו מה שאין כן בהכפלו על מספר אחר שיוסיף מדרגה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A table to know the rank of the product of the numbers that are multiplied by each other | לוח לדעת המספרים הכפולים אלו על אלו באיזו מדרגה ישאר הנכפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that the rubric corresponding to both is the total and it indicates both. | דע כי הנקודה הנכחית לשניהם הוא סך המספר המורה והיא המזכרת אותם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example: we wish to multiply 29 by 31 |
[3]דמיון רצינו לכפול כ"ט על ל"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| According to this way, for all those that are similar, such as the multiplication of 70 by 90, whose distance from 80 is the same.
|
ועל זה הדרך כל הדמים לאלה כגון כפל ע' על צ' שמרחקם מפ' אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If the number does not have a whole third and there is an excess of one |
ואם לא היה למספר שלישית שלימה ויהיה בו תוספת אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Such as ten and you wish to know its square: | כגון עשר ותרצה לידע מרובעו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Subtract the one from the number; 9 remains. | חסר האחד מהמספר ישאר ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Calculate the sought number in the procedure that I have shown you |
ותוציא המספר המבוקש כמשפטו שהראיתיך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שתקח שליש ט' שהוא ג' ומרובעו ט' נעלהו במדרגה שלפניו ויהיו צ' חסר ממנו ט' וישאר פ"א ואחר תוסיף עליו מספר ט' והמספר בעצמו שהוא י' ויעלה ק' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If there are two between our number and the number that has a third |
ואם היו שנים בין המספר שלנו ובין המספר שיש לו שלישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' שיעדף מספרנו על שלישית שנים כי כל מספר או יש לו שלישית שיעדף יעדיף אחד או שנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We do the opposite |
נעשה להפך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שזה התוספת יקרא חסרון בערך המספר שלאחריו כי הוא יחסר אחד משלישית שהוא החלק הקטן והוא הפך מה שאמ' למעלה נוסיף על מספר שלנו אחד כי יותר יתכן זה משנחסר שנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Know that if there are two digits to multiply by one another |
ודע כי אם יהיו שני מספרים לכפול זה על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל מספרם בין שניהם כגון ב' פעמים די לו בהכאה אחת כגון שתאמר ב' פעמים ב' כמו שאמור למעלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If you have one digit by two digits |
ואם יהיה לך מספר אחד על שני מספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון ש' פעמים מ"ה אתה צריך להכות פעמים שתכה תחלה הש' על המ' כן ג' על ד' י"ב והנה עשרות במאות הם במדרגה רביעית שהם אלפים והוא י"ב אלף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נכה ג' על ה' והם ט"ו מאות שהם אלף ות"ק נמצא הכל י"ג אלפים ות"ק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If three by three |
ואם על שלשה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' אם תרצה לכפול מספר אחד על ג' מספרים כגון ש' על ת'כ'ה' ג' פעמים ככה [4]ג' פעמים ד' הם י"ב הם במדרגה חמישית שהיא רבבות והם ק"כ אלף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נכה ג' על ב' הם ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נכה ג' על ה'ט"ו והם מאות והכל ק'כ'ז' אלפים ות'ק' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומאה אם המספר אחד תן שיהיה המספר הנכפל אחד או רבים ראה אם הוא זוג שאם הוא זוג גם המחובר זוג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואף אם האחד נפרד בכפל בזוג כגון ט' פעמים ח' יהיה העולה זוג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אף אם שניהם נפרדים כגון ט' על ט' או ט"ו על ט"ו אז המספר נפרד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The paved way |
והדרך סלולה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שתשים למעלה עוד המספר כי זה יותר ישר ונאות ר"ל שכללו ומועט ולא נחוש אם יהיו הפרטים העליונים גדולים בכמות מפרטי הטור השפל אחר שכלל העליון בלתי גדול וכן לא נחוש בהיות מספרי הטור העליון שכללו קטן יותר רבים ממספרי הטור השפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Write it corresponding to the top row |
כתוב אותו כנגד טור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומר כנגד קו המספר העליון הראשון כי אחדים עם אחדים אחדים וכתוב בטור שלישי כנגד המספר השני העליון כי אחדים בעשרות יעלו עשרות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Write the units in the place to which they belong |
תכתוב הפרט במקום הראוי לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' כפרט העודף כתבהו במדרגתו ושמור תחת הכלל אחדים כמספר וחברם וכתבם עם המספר הבא אחריו במדרגת המספר ההוא הבא אחר כן עד תום להכות הראשון עליון עם כל השפלים ואם ישאר שם כלל ופרט יכתוב הפרט וא' ואחריו הכלל כי שם תכלית הטור ההוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Start to multiply the second digit and write the result in the third row |
תחל לכפול המספר השני והעולה כתבהו בטור השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומר תחל לכתוב בטור אחד למטה ולא באותו [5]טור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שעשרות עם אחדים יהיו עשרות ואין ראוי לשים מדרגת עשרות במדרגה גבוהה ממנה על כן נכתבם במקום העשרות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Then, multiply the second top by the second and write it in the third row |
ואחר כך תכפול השני העליון על שני וכו' ותכתבהו בטור השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כנגד המספר השלישי שבטור העליון אבל זה טור שם הוא מהעולה מן הכפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
As the third digit |
במספר שלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' במדרגה שלישית כי העולה מכפל עשרות בעשרות מאות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Which is second to the digit from with which I have started |
שהוא שני למספר שהחלותי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי מן השני התחיל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
With the rule that the units are in the lower rank |
עם משפט הפרט להיותו תחתון וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' ר"ל שתכתוב הפרט תחלה במדרגתו השפלה ואחר כן תכתוב הכלל במקום גבוה ממנו שהוא שני לפרט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If there is zero, whether in the top row |
ואם היה גלגל בין בטור העליון וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' כשתכה באות או אות בגלגל כתוב גלגל להוסיף מדרגה ושימהו במקומו כדרך שתעשה מן המספרים שלפני הגלגל או לאחריו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הא למדת שכפי מנין מספר הטור העליון תכתוב טורים תחת שני הטורים שמהם הכפל יוצא וכל אלו הטורים זולת קורא טור שלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Then, start adding up |
אחר כן תחל לחבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' אחר שהשלמת כל ההכאות תחל לחבר העולה מן הטורים השלישי שכתבת ותכתבהו בטור אחד שפל כגון שיש לך מן העולה בכפל ג' טורים חבר בקו היושר מה שנמצא בהם במדרגה הראשונה וכתבהו ואחר כן חבר מה שנמצא במדרגתם השנית וכתבהו וכן כולם עד סופם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If there is ten, write one after it |
ואם יש בו עשרה תכתוב אחד אחריו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' אם מן שתחבר מאותה מדרגה יעלו עשרה בכוון יכתוב ספרא וישמור אחד וא' יחברהו עם מה שיבא אחריו ואם יעלה החבור כלל ופרט כתוב היושר על הכלל בחבור שיש לך וכתוב אחריו במקום הכלל אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [6]ואם לא ימצא באיזה מן הטורים רק גלגל כתבהו ואחר שתשלים טור החבור ותרצה לבחון אמתת מספרך ספור מנין מדרגותיו וכאיזה יהיה מעלות השני טורים בלי מדרגת אחד כי הכלל יעשהו מדרגה אחרת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד ילמדך מאזנים להבחין מספרך שתמנה סכום האותיות שבטור העליון ואם הוא פחות מט' ישמרהו ואם הוא יתר מט' שמור היתר וכן תעשה ממנין אותיות הטור השפל והנשאר מט' כפלהו עם הנשאר מן הטור הראשון ואם לא ישאר על ט' באחד משני טורים אין צריך לבדוק האחד כי מה שנכפל על ט' יצא ט'ט' וככה יהיה הפחות מט' או היתר מט' ממנין טור החבור ואם לאו תדע כי טעית בחשבונך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נשלם השער הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Two |
השער השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
One alone does not assume any change |
האחד לבדו לא יקבל שנוי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כל שנוי בא מצד ההרכבה וההפך והאחד לפי [שהוא][7] פשוט אין דבר שישנהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
No increase |
ולא רבוי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כפל אחד על אחד אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
And no division |
ולא חלוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי מצד שהוא אחד לא יתחלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
One is eternal |
והאחד קדמון לבדו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הוא קודם אל המספר קדימה טבעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
They did this |
ועשו זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל למה חלקו הגלגל לי"ב מזלות בעבור כי שנת השמש שהיא זמן סבובה מנקודה ידועה מגלגל המזלות עד שובה אליה ושנותה לסוב מהנקודה ההיא באותו הזמן סבבה הלבנה גלגלה ודבקה עמו י"ב פעם כי י"ב פעם חדושי הלבנה והמולדה שלמים יש בשנת החמה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
They divided each sign to thirty degrees, because this number has more whole units than 12; for it has one-half, one-third etc. |
וחלקו המזל לשלשים מעלות כי זה המספר יש לו אחדים שלמים יותר מי"ב כי יש לו חצי [8]חצי ושלישית וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זה מוסיף על י"ב אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וש"ס מוסיף עוד שמינית שהוא מ"ה ותשיעית שהוא מ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Each according to its rank |
כל אחד כפי מעלתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כפי מדרגתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The number by which you divide should be less than the dividend |
וראוי להיות המספר שתחלק עליו פחות מהמספר המחולק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כשתרצה לחלק מספר אחד על אחר ראוי להיות המספר העליון גדול מהמספר השפל ואז תחלקנו עליו לידע כמה חלקים מחלקי המספר המועט ימצאו בגדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Return back as the number of the distance |
וכפי מספר המרחק תשוב אחורנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שהמספר שבטור השפל במדרגה השלישית תכתוב העולה בחילוק במדרגה באמצע אחורנית מהאחרון שבטור העליון עד שאם היה האחרון השפל כנגד האחרון העליון נכתוב העולה בחילוק כנגד הראשון העליון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If a number that cannot be divided remains from the last digit |
ואם ישאר במספר אחרון חשבון שלא נתחלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' אחר שחלקת המספר העליון על השפל ונתת לו חלקו והנה נשאר עדין חשבון שלא יקבל חלוק לקטנותו באחדים כגון שלקח השפל חלק או חלקים במספר מהאות העליון ונשאר קצת מהאות והוא שלא יוכל להתחלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Has not yet reached the rank of the units |
ולא הגיע למעלת האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שלא ירד עדין כל כך שיחבר כמותו מהמחולק עליו אבל גבוה במדרגה ממנו שאם כן לא נחלקהו עוד כי כבר יצא לחוץ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Return the remaining number back to the preceding rank, which is lower than it |
השב אחורנית מהמספר הנשאר אצל המדרגה הראשונה המדרגה שהיא פחותה ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והעולה בחילוק תכתוב אותו אחורנית רחוק מהמדרגה שחלקת עתה ממנה כמרחק השפל מדרגתו הראשונה וכתבהו לפני מה שיעלה בחילוק בראשונה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Write the remainder above the top row according to its rank |
ואותו הנשאר תכתבהו למעלה מן הטור העליון כפי מעלתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' שאם הוא עשרות או מאות כתבהו למעלה במקום מדרגתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In the fifth chapter |
ובשער החמישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יפרש כיצד נחלק אותו הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We give it 1 |
ונתן לו א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' נקח מן הט' שביעית אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נשיבם אחורנית על [9]הגלגל שלפני ט' נשארו ששה נשיבהו אחורנית על הגלגל השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Calculate from this position |
ותחשוב מאותו המקום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' משם התחיל לחלוק על השפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
According to the distance of the divisor |
וכפי מרחק המספר המחולק עליו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' כפי מרחק המספר האחרון שבטור השפל מהראשון תשיב זה העולה אחורנית מהמספר שחלקת ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If there is a zero in one of the positions |
ואם היה גלגל באחד המקומות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שהוא מפסיק בין מספרים חלוקים מגלגל אי איפשר ליקח כלום ולא לתת לו כלום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכשיגיע המספר הגדול המחולק לתכלית החלוקה כגון שיחסר מהמספר התחתון שנחלק עליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או יאמר עליו שכבר יצא לחוץ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כל זמן שיהיה העליון פחות מהשפל נשיב לו כל אותו העליון אחורנית ונשיבם עשרות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומשם נמנה החלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלל הדבר כל מה שנוכל לתת מהאחרון העליון על האחרון השפל נתן והוא שיהיה אפשר להגיע במספר חלקים לשני שהוא שני אחורנית מן השני ומן השלישי לשלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם לא נחלק בפעם ראשון נשוב לחלק מן הראשון לאחרון אם לא נשאר באחרון כלום או אם נשאר פחות מהשפל ואז נשיבהו אחורנית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונתן לאחרון שבטור השפל ומן השלישי לאחרון לשני מן השפל ומן הרביעי לשלישי עד שנתחיל לחלק מהעליון שהוא כנגד האחרון ונחלק כלם על כלם כנגד וכזאת החלוקה נעשה הכל כי המחולק נשאר פחות ואז נכתוב מה שעלה בחלוק באחרונה במדרגת האחדים ושוב אי איפשר לדחות כי כבר יצא לחוץ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Give the last in the bottom row of the top row |
תן לאחרון שבטור השפל מהטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' שהוא שפל מהטור העליון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Give the preceding in the bottom row |
ותתן לראשון מן הטור השפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' במספר החלקים שנתת לאחרון שהוא [10]שהוא אחרון מהמספר מטור השפל כזה תן לראשון מן האחרון שבטור השפל מן הראשון לאחרון שבטור העליון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If you cannot do this |
ואם לא תוכל לעשות ככה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' לא תוכל לתת לו כל החלקים שנתת לו כי יגרע מן האחדים מנינם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שוב וגרע מהמספרים שחשבת לתת לו בתחלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
When you have to take any digit from the digit that precedes the last |
וכשאתה צריך לקחת שום מספר מהטור הראשון לאחרון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שלא יספיק לך המספר ההוא בהיותו במקום האחרון השיבהו לאחור במקום שלפני האחרון וחשוב כל אחד עשרה ולא תקח ממנו רק כפי מה שתגזרהו החלוקה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Return back from the higher rank |
השב מן הגבוה ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' שלא תחלק כל המספר הגבוה על השפל רק תשאיר ממנו קצת ותשפיל מן הנשאר שם והניחהו במעלות הגלגל כפי שתצטרך וחלק ממנו לאשר כנגד מדרגתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כפי מדרגת האחרון העליון לאחרון השפל יהיו מדרגות הראשונים העליונים לראשונים התחתונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Return back the higher that corresponds to the digit |
השב אחורנית הגבוה שהוא כנגד החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שיש בטור העליון סיפרא לפני האחרון הנה נשיב הגבוה האחרון אחורנית אל גלגל אחרון אשר לפניו ותקח ממנו מה שתצטרך או כלו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
From the remainder there |
ומהנשאר שם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל בגלגל ההוא השיב כפי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולעולם לא נכתוב אלו מה שיעלה נחלוק בתחלה ונתן לו כפי מספר החלוקות שנשוב לעשות ובכל חלוק נכוין שיגיע לכל אח' אחד חלקו על דרך כפל שלקח תחלה האחרון מהאחרון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Two are left on the two |
נשארו שנים על השנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל על מקום הב' שהיה שם תחלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We return on the 8 back |
נשיב של הח' אחורנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' הא' שהוא עתה על מקום הח' שהיה תחלה נשיבהו אחורנית על מקום הב' שיש עתה עליו א' והיו [11]י"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחלק אותם על ג' שהוא בטור השפל כנגד מדרגתו ומעתה יקח כל אחד ממדרגתו ביושר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אינו יכול לקחת הג' הד' הראשונים מהי' מבלי השבת אחד אחורנית וזהו אמרו בתשובה כלומ' בראשית שתקח אחד מהי' ונשיבהו אחורנית לפי שאינו מעלתו עכשו כמו שביארנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Because it was first third to it |
כי בראשונה היה שלישי לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' מקום הא' היה נחשב מחלוק ראשון שלישי והיה נחלק על ג' הראשון באלכסון שהוא שלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר תשיבהו אחורנית הנה עם הג' י"ג וט"ו ד' פעמים ל"ו על כן לא יכולנו לתת ל"כ מן הט' ד' על כן לא נתן לו רק ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Two, which is one |
שנים שהם אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' נקח מאותם הה' ב' שהוא חלק אחד לב' השפלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We take one from the 3 that is above the three |
נקח מן השלשה שעל השלשה אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' שעל מקום הג' בתחלה וישארו שנים כנגד אותו מקום הג' הקודם ויש לנו לחלק על ט' ולא יספיק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אך נתן לו אחד ונכתבהו כנגד ט' נתן לב' שהוא רביעי ח' פעמים ב' שהוא י"ו נשארו ח' על הד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם נאמר נשיב מהם שבעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| סדר הדברים הנה באמת נאמר שנשיב מהח' שנשארו על מקום הד' ז' אצל הו' שהנחנו על הגלגל שלא נוכל להשיב מהם אחורנית אל הד' שעל מקום הט' שלשה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Eight remains on the 4 that is on the 9 |
וישארו שמנה על הד' שהם על הט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' ישארו שמנה על מקום הט' שהנחנו עליו אחר כן בחלוקתנו ארבעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
It is taken as tens for us but that is still not enough |
יצא לנו בעשרות ועוד לא יספיק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' עדין לו יספיק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' עדין לו יספיק לפי שהוא גלגל בגלגל על כן נצטרך עוד שנקח ג' מהם ונשיבם אחורנית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשלשה הם שלשים על הד' והם ל"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נשארו שבעה במקום ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי יש לנו לקחת ממנו ג' פעמים ט' [12]והם כ"ז ואז ישארו י"ו על הד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועתה נשלם חלוק ראשון [.]גלגל שלפני הד' וב' שבטור העליון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שהניח בד' הזכיר הנשאר לפניו ואחר כן יזכיר הנשאר לאחריו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We give it three |
נתן לו שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' נתן לב' ג' חלקים כמהו שהם ו' מז' שעל הח' וישאר שם אחד והג' נכתבם תחת הגלגל הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
And it is impossible to return the digit back on the two, because the two is not in its rank |
וגם לא נוכל להשיב אות אחורנית על השנים כי השנים אינם מעלתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זה לא היה צריך להזכיר ועוד כי אין על הגלגל כלום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 remains above the zero |
נשארו ג' על הגלגל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל אחר שנקח מן השלשים כ"ז שהוא חלקו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מאזני החלוק הוא שתמנה המספר השפל שעליו נחלק ונקח הנשאר בו על ט' ט' ונמנה כמה ישאר מט' ט' ושמרהו ואם נשאר למעלה דבר לחלק והוא הכתוב למעלה נראה מה שבו על ט' ונחברהו עם השמור וכזה יעדף על ט' במספר הגדול המחולק אם ימנה כהוגן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If you multiply the quotient |
ואם תכפול מה שעלה בחלוק וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זהו בוחן אחד והוא פשוט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Three |
השער השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Every number is in accordance with these two ways |
ועל אלו שני הדרכים כל החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל דרך הזוגות שנחשב בו ב' חשבונות כפל כל החשבון על חציו וכפלו על חצי אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודרך הנפרדים שנכפול על חציו לבד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Another way |
דרך אחרת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שנקח סוף החשבון שנרצה לידע המחובר מהמספרים שעברו לפניו ונכפלהו על עצמו ואחר כן [13]נוסיף על המרובע הזה שרשו שהוא סוף החשבון והנה חצי זה הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דרך אחרת שנכפול מרובע חצי המספר ונוסיף עליו שרש זה המרובע שהוא חצי החשבון והוא המבוקש המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הרוצה לידע מספרים מחוברים בדלוג אחד עד מספר ידוע כמו שירצה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לידע הנפרדים שהם עד ט' יוסיף על החשבון אחד והיו עשרה נכפול עשרה על רביע' רביעיתם שהוא ב' וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונחבר אליו שלישית הסכום שהוא כ"ו כי כפל אחד ע"ח הוא ע"ח וכפל אחד על ע"ח הוא שליש ע"ח שהוא כ"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Add the scale of the top row |
חבר מאזני הטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל הנשאר בו מתשעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In the tables of the planets there is no [more fractions] |
ואין בלוחות המשרתים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לא ידקדקו יותר מזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
One according to the solar years |
האחד על שנות השמש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון האמות המונים לשמש ועושים מחזורים מעשרים עשרים שנה שיזכרו מהלך כל משרת בזה המספר מן השנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The same is done with the whole hours that have passed after the middle of the day |
וככה תעשה בשעות השלמות שעברו אחר חצי היום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הם ימנו תחלת היום מחצי היום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Write them alone |
כתבם לבדד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הוא רוצה לדעת מקום המשרת בזה השעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| על כן יכתוב העולה מן המחובר בטור מיוחד השם . כתוב השניים המחוברים מטורי השניים לפניהם הראשונים ולפניהם המעלות וכן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Four |
השער הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כשנרצה לגרוע מספרים ממספרים נכתוב המספרים שנרצה לגרוע מהם עליונים ותחתיהם טור הנגרעים וצריך שיהיה אחרון שבטור העליון כללו גדול משכנגדו השפל ולא נפקד בגודל הפרטים השפלים כי הכל תלוי בכלל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If you find in one of the ranks |
והנה אם מצות באחדות המעלות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [14]פי' כי כשנמצא במדרגות האחדות שהן לפני האחרון שהשפל גדול ממספר הטור העליון שכנגדו נקח אחד מהעליון ונחשבהו ונחל לגרוע מהאחרונים הגבוהים במדרגה זהו דרך אבן עזרא ואין זה סדר נכון שאחר שיכתוב הנשאר מן הראשון יצטרך לפעמים לגרוע ממנו ולהוסיף לראשון ויצטרך לפי זה שבטרם יכתוב האחרון אם יעדיף השפל שלפניו ויתן לו אחד ויגיע אחד מהמספר האחרון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל הסדר היותר נאות שנחל נמנות מן האחדים ומה שיתחבר מהם כלל יחברהו עם הכלל שלאחריו וכן כולם כדרך שנעשה בשניים ובראשונים ובמעלות ובמזלות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון חסרון אחד מב' וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שתרצה לגרוע י"ז מכ' ונכתוב שני הטורים כן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחסר א' מב' ונשאר א' והנה אין על הז' כלום נשיב ז' א' הא' כנגד הז' והוא י' נחסר ממנו ז' ונשאר ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה מאזני הטור העליון ב' ומאזני הטור השני ח' ולא נוכל לחסר ח' מב' על כן נוסיף ט' עם הב' יהיו י"א נגרע ממנו ח' ועתה נשאר מאזני שני הטורים ג' וכן מאזני השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
He adds six to the scale of the upper seconds |
יוסיף על מאזני השנים העליונים ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כך ישאר מששים על ט' ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Add three to the scale of the degrees that were written first |
הוסף על מאזני המעלות הכתובים בראשונה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כן ישאר מל' מעלות הנוספות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Add three to the scale of the signs that were written first |
הוסף על מאזני המזלות הכתובים בראשונה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כן ישאר מי"ב מזלות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
One thing that is necessary when subtracting: the last [digit] at the end of the upper row must always be greater |
דבר שהוא צורך למגרעת לעולם אותו בסוף הטור העליון יהיה גדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זה מדבר על דעת חכמי החשבון כי האחרונים גבוהים במדרגה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Five |
השער החמישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
One is as a point in a circle |
האחד כמו נקודה בתוך עגולה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כי האחד אמצעי בין השלמים והשברים על כן לא יתכן להיות האחד נשבר כי מאשר הוא אמצעי לא יתחלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The whole is named with one name, as the shape represents the entire body |
[15]רק בעבור שיקרא הכלל בשם אחד כמו צורת הגוף ותבניתו שהיא כוללת כל הגוף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונקרא הכל בגוף אחד וא'ע'פ' שהוא מורכב מאברים רבים שכל אבר הוא אחד כן האחד נקחנו כולל ותחתיו שברים רבים שהם אחדים רק בערך אל האחד הכולל יקראו שברים וכל זה במחשבה כי האחד האמתי לא יתחלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Therefore they take the half from two |
על כן יוציאו החצי משנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי החצי הוא אחד משני חלקי הדבר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The analogous number from which they derive is called the "denominator" |
ואותו שיקחו הדמיון ממנו יקראו המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו השלשה לשליש וארבעה לרביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For the product is divided by its square |
כי כל מרובע יחלקו העולה בחשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שנכפול שני רביעיים על שני רביעית הנה הנכפל ד' והמורה ומרובעו י"ו שהוא אחד שלם ונכפול ב' על ב' והם ד' נחלק ד' על ט' יגיע לכל אחד שליש ותשיעית אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The remainder that cannot be divided |
והנשאר שלא יתחלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' אחר שנחלק מרובע המורה על החשבון הנכפל אם ישאר חשבון שלא יוכל להתחלק לחלקים שלמים אלא כשנחלק אחד מהם לחלקים רבים כגון המשל השני שהמשלנו נכנה אותו החלק בשם רביעית או תשיעית כפי מה שיהיה החשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The one, on the one hand, is not a number |
האחד מפאה אחת איננו מספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כי אינו מספר כי אם בהתחברו למספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Because when you sum all the odd numbers |
כי בחברך כל הנפרדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם א[.] וג' הם ד' והוא מרובע שנים ד' וה' הם ט' והוא מרובע ג' ט' וז' הם י"ו והם מרובע ד' וכן כולם על הסדר וכל זה ככה האחד ושתותיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ודברים רבים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ימצאו באחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
אין צורך להזכירם והנה נשארו במערכה הראשונה כו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מערכת הראשונה הם ט' האחדים והנה דבר על האחד והנה נשאר לדבר על שמונה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
והנה חציים ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשון נקרא כל חשבון פשוט שאינו מתחלק בשוה
אלא לאחדים במספרו כגון שנים שנים [16]שנים לשני אחדים וג' לג' וכן כלם . המספר [...........] למספרים שוים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
When there is a need for two fractions that are not of one kind |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שנרצה לכפול שני שלישים על שני רביעיים הנה כפל שנים על שנים ד' והנה נבקש לכל אחד המורה שיצא ממנו שהוא שלשה וארבעה ונכפול המורה האחד על המורה האחר והוא המורה ואליו נחלק כפל החשבון הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If there are 3 types |
ואם היו שלשה מינים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שנרצה לכפול ב' שלישיים וב' רביעיים וב' חמישיים זה על זה נכפול שלשה על ארבעה והם י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכפול י"ב על חמשה והם ס' וזהו המורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונכפול החשבון שהוא י"ב ב' על ב' והם ד' נכפול ד' על ב' והם ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחלק ח' על ס' . [.] שנרצה לכפול ב' שלישים על ג' רביעיים וד' חמשים נעשה מורה אחד לרביעים ולחמישיים והוא כ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכפול מורה שלישיים על ד' עלה ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכפול ג' רביעיים על ד' חמישיים והם י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכפול ב' שלישיים על י"ב והם כ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה החשבון כערך כ"ד אל ס' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או אם נרצה אחר שעשינו תחלה מורה מכ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפלנו ג' על ד' שהוא י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נסיר מהם ב' שלישיות והוא ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והכל שוה כי ערך ח' אל כ' כערך כ"ד אל ס' והוא ב' חמישיות אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי בקשת המורה כדי שנדע אי זה חשבון הוא שימצאו בו חלקים אלו ונחלוק אותו על מרובע המורה כדי שנדע אי זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ירצה יקח כפל השני מורים מקום מרובע כי הוא מרובע אמצעי ביניהם כי כפל ג' הוא ט' ומרובע ד' י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה המורה הוא י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שנדע המורה נראה כמה הוא ג' רביעיותיו ונקח [17]מהם ב' שלישיים כי הוא כאמרו קח ב' שלישיים מב' רביעיים או בהפך והכל שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The multiplication of fractions is opposite to the multiplication of integers |
כפל השברים הפך כפלי השלמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי השלמים הנכפלים אלה על אלה יוסיפו בחשבון כפי מה שיעלה
מכפל אבל שברים על שברים יהיה העולה שבר אחד מהשברים הנכפלים וכפי התוספת בשלמים נכוין לגרוע בשברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי האחד הנכפל על איזה חשבון לא יוסיף על אותו חשבון כלום כי אחד על שנים שנים ואחד על חצי כלו' פעם פעם אחד חצי הוא חצי אם כן חצי על חצי הוא רביע כאלו תאמר חצי החצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן שלישית על שלישית כאלו תאמר שלישית השלישית שהוא תשיעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפל רביעית על רביעית יהיה חלק אחד מי"ו והוא חצי שמינית שהוא השלם ועל כן אמר והנכפל אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי לעולם ירד ממדרגה אחת בדרך שכפל ראשונים בראשונים יהיו שניים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ועל זה הדרך תכפול שברי המין האחד על שברי המין בעצמו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו שהמשלנו משלישיות על שלישיות או מרביעיות על רביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
בין שיהיו שוים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון ב' רביעית על ב' רביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או שיהיו שברי אחד מהם גדולים כגון ב' רביעיות על ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ואם תרצה חלק תשעה על הארבעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שהוא המורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
והדבר יצא בשוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי העולה בחלוק לכל אחד הוא ב' ורובע שהוא ב'
רביעיים ורביעית רביעית והוא חצי וחצי [.] שמינית כי האר' הארבעה שנחלק עליהם הם רביעית מרובע המורה . ל"א כי התשעה הם רביעיים . והיו שתי חמישיות המרובע וכו' . כי עשר שתי חמישיות מרובע המורה שהוא כ"ה והשנים שתי חמישיות חמישית שהם בשנים . והנה נקח בעבור שתי ש' שלישיות שמונה . כי ח' ב' שלישי י"ב שהוא המורה . והוא חצי ק'מ'ד' שהוא מרובע הי"ב ואם עשית זה משנים מורים כלומ' אתה [18]אתה רשאי להעריך חשבונך לכפל השני מורים [........]מרובע בענין שהקדמנו . כי העולה שהוא ששה נקח ערכו אליו . ר"ל אל הי"ב שהוא המורה והוא חציו . כי השביעית הם תשעה . כלומ' כי אחר ש' שהמורה הוא ס"ג שיש בו ז' תשיעיות או ט' שביעיות אם כן שביעיותיו הוא ט' ותשיעיתו הוא ז' . וכאשר חלקנו חשבוננו הראשון ת'ת'ר' ת'ש'ס'ד' על ס"ג עלו כ"ח . אם כן ערך ת'ת'ר' ת'ש'ס'ד' אל ג' אלפים ות'ת'ק'ס'ט' כערך כ"ח אל ס"ג כי כמו שתחלק כ"ח מס"ג ישאר ל"ה כי כשתחלק ת'ת'ר' ת'ש'ס'ד' שהם כ"ח פעמים ס"ג מג' אלפים ות'ת'ק'ס'ט' שהם ס"ג פעמים ס"ג ישאר ל"ה פעמים ס"ג . ואם לקחנו בשנים מורים יהיה הנכפל ס"ג וכו' . ואם נרצה נסיר משבע תשיעיות ס"ג שהם מ"ט והנה העולה כ"ח שהוא פחות מחצי האחד . וקח שנים כי משלשה לק' לקחנו אותו כלומ' בעבור כל צורה נקח המספר המיוחד לו כי לולי ג' לא היה נאמר ב' שלישיים ולולי מורה ד' לא יתכן לו' לומר ג' רביעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example: we wish to multiply 4 integers by 3 fifths |
דמיון רצינו לכפול ד' שלמים על ג' חמישיות וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה שלמים על נשברים עלו נשברים בע[..] מעלות על ראשונים שהם ראשונים על כן נקח המורה שהוא ה' ומרובעו כ"ה וד' פעמים ג' הם י"ב והנה ערך י"ב אל כ"ה הם [ב'] שלמים וב' חמישיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכפול כ"ב על כ"ח שהם נשברים ראשונים והיו ת'ר'י'ו' שנים ר"ל שכל אחד חלק מכ"ה . עלו כ"ד שלמים וישארו י"ו שניים והט"ו הם ג' חמישיים והאחד חומש החומש שהוא חלק מכ"ה באחד . כי הם חלקי המורה כי מהשברים וקח המורה . לכן המחובר מהם הוא חלקים ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה נכפול זה על זה ועלה מ"א אלף ות"ת והנה כל ארבעים מהם הוא אחד שלם כי הם [19]במדרגה שנית מארבעים גם כן ועל כן שבו הנשארים ה' חלקים ממ' עלו אלף קנ"ה שכל ע"ז הוא אחד מע"ז הראשונים על כן ט"ו פעמים ע"ז הם ט"ו מע"ז שהוא המורה . והוא מנין שהיה יכול לעשות מרובע למורה שהוא ע"ז ויהיה ה' אלפים ות'ת'ק'כ'ט' ויהיה ערך אלף קנ"ה אליו כ' כערך ט"ו אל ע"ה (ע"ז) כי מרחק ט"ו מע"ה (ע"ז) ס"ב ומרחק אלף קנ"ה מה' אלפים
ת'ת'ק'כ'ט' ס"ב פעמים ע"ז . כל שבר נפרד שהוא למעלה מי' שיש בו שני מספרים כגון י"א או י"ג וי"ט נקרא חשבון שלא יוכל אדם לב' לבטא בו . אבל כל זוג יכול לבטא כי אם יש לנו ב' חלקים מי"ב נקח ששית אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון כמה ג' שביעיות על ה' חלקים מאחד עשר וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והדרך הקרובה שאחר שמענו שהמורה ע"ז ושה' חלקים מי"א מע"ז הם ל"ה נחסר ג' שביעיות מל"ה שהם ט"ו מע"ז והוא המבוקש כי הוא כאמרנו ג' שביעיות מה' חלקים מי"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או כפול מספר ג' על ה' והוא ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכפול קע"א על רכ"א יעלו ל"ז אלפים ות'ש'צ'א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחלקים על ר'מ'ז' והנם ק'נ'ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל ק'נ'ג' פעמים ר'מ'ז' שכל ר'מ'ז' חלקים מאלו באחד מחלקי ר'מ'ז' שהוא המורה נמצא שיש לנו ק'נ'ג' חלקים מר'מ'ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכערך ק'נ'ג' מר'מ'ז' שיחסר ממנו צ'ד' כן ערך המספר הראשון שהוא ל"ז אלפים ות'ש'צ'א' אל מרובע ר'מ'ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כן יחסר ממנו צ"ד פעמים ר'מ'ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומרובע ר'מ'ז' הוא ששים ואחד אלף ותשעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כפל ט' בי"ז שהוא המספר יעלה ק'נ'ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תקח מר'כ'א' הוא י"ז וט' פעמים י"ז הוא ק'נ'ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר שיש לנו ששיות אין צריך לשלשה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי שלשה הם בכלל ששה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם זה על שבעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל גם שלשים על ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם זה על ח' ר"ל [ר"י] ורביעיותיו פ"ד ר"ל רביעית של"ו הוא פ"ד ושתי שלישיות פ"ד הוא נ"ו כי הוא כאלו אמרנו נכפול שני שלישיות הלקוחות מרביעית הלקוח מחמישית על שש רביעיות הלקוחות משמינית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| על כן נקח[20] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [21]בספר [...] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועוד כי מצאו בשנת ה[שמש] וכו' זה טעם למה חלקו הגלגל לי"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאומר חשבון חברנו אליו כל החלקים מחצי עד עשירית מה ערך המספר אליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל אם ישאלך אדם ממון היה אצלי וחברתי עמו חציו ושלישיתו וכל החלקים עד עשירית והיה כך כמה היה החשבון תחלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם נצטרך לכפול כל החלקים אלו על אלו כדרך שעשינו במה שעבר היה טורח גדול ואמ' שלא נצטרך לזה רק שנקח זה החשבון תחת המורה שהוא אלפים ותק"כ כי בו נמצאו כל אלו החלקים ולא בפחות ממנו ואע"פ שימצאו בגובה ממנו כי צורך בקשת המורה כדי שנמצא חשבון שיהיו החלקים הנרצים והוא הדין שאם נמצא חשבון פחות מזה הנכפל שיהיו בו אלו החלקים בעצמם שזה יספיק לנו ויגיענו למבוקשנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון זה ממון חברנו אליו שלישיתו ורביעיתו (וחמישיתו) וששיתו והיה השלם כ"א נכפול המורה בחשבון והוא ש"ס נחלק ש"ס על כ"א עלו [י"ז] שלמים וג' חלקים מכ"א שהן שביעית אחד כך היה סך הממון הראשון ובחן זה ותמצא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כשנצטרך למצוא כל החלקים לא נצטרך לכפול כל החלקים אבל נקח אלפים ותק"כ ואע"פ שהוא פחות הרבה מהנכפל מאלה החלקים ונוסיף מע מחציתו ושלישיתו ורביעיתו וכל החלקים והמחובר א"ח ג"ז וזהו השלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונחשוב שהחשבון ס' נכפול המורה בחשבון ויהיה העולה נחלק על זה הנכפל על השלם הנה נבחן זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה חצי השלמים ורביעיתם וחמישיתם ד' ועשיריתם ב' ושלישיתם ו' וישארו שניים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נשיבם אל שברי השלם שהוא א"ח ג"ז ונחבר עמהם החלקים הנשארים למעלה שהם ג' אלפים ותק"ף ומן המחובר נקח השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן נעשה מן השתות ומן התשיעית כי כשלקחנו בעבור השתות
ג' ובעבור התשיעית ב' ישארו ב' שלמים וכשלקחנו בעבור השמינית [22]השמינית ב' ישארו ד' וכשלקחנו בעבור התשיעית (שביעית) ב' ישארו ו' שנשיבם לשברים הנה כל השלמים נ"ו נעשה מן השלמים הנשארים חלקים הנה השער ב"ו זד"א ועם 0 ח הג יהיה בדג חא עם 0 והג' הם ד 0 אג ג וג' שלמים [........] ועם החלקים הנשארים הנזכרים וו ח זד וזה מספר כל חלק החלקים שהם מחצי עד עשירי נחבר עם 0 ח ה ג ויעלה דבהט"ב נחלק על אחגז ויעלו ד' שלמים נחברם עם הי"ו (נ"ו) שהיו לנו והנה כל המספר ס' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The rule: the product of degrees by any type is the same type itself |
והכלל כפל מעלות על אי זה מין שיהיה ישאר אותו המין בעצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו כפל אחדים על השברים שיהיה ישאר אותו המין בעצמו כמו העולה אותו המין מן השברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The product of minutes by minutes is seconds |
וכפל ראשונים על ראשונים יהיה העולה שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו שהחצי על חצי העולה יהיה רביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וראשונים על שנים יהיה העולה שלישיים וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עד שיהיה כפל שלישים על רביעים וחמישיים על חמישיים עשרים כי לעולם נחבר מספר השתי מדרגות והוא היוצא וכן מבואר בלוח המעלות והשברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שנכפול ראשונים בראשונים שהם שניים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון ל' ראשונים יהיה העולה הת"ק נחלקנו על ס' יעלה ט"ו והם ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם נכפול ראשונים על שניים והיו שלישיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחלק השלישיים על ס' ומה שיעלה יעלה למדרגת השניים כי לעולם יעלה בחלוק מדרגה אחת והנשאר הוא מן השלישיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שנכפול מ"ה ראשונים על נ' שניים יעלה אלפים וכן שלישים נחלקם על ששים עלו ל"ז שניים וישארו [23]ל' שלישים שלישיים באיזו מעלה מן השברים ר"ל באיזו מדרגה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יהיו שנים חשבונים כלומ' אם יהיה לך ב' מעלות תכתוב 0ב במקומו ואם יש לך שני חשבונות כגון כ"ה תכתוב שם ה"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כדרך שתעשה בשלמים [24]כפול המספר הטור העליון במספר הטור אשר תחתיו והחל לכפול מעלות במעלות וכתוב במדרגת המעלות ואחר מעלות בראשונים וכתבם תחת הראשונים וכן כל אחד במדרגתו כמשפט ואם היה היו שם שני מספרים בכלם ביחד וכתבהו במקומו וכתוב האחדים ראשונה ואחר העשרות ואחר המאות כל אחד באותו הטור אם יעלה כל כך הכפל ההוא תכתוב הכל על הסדר ולא תתערבב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה כפול האות האחת באות הראשון שבאותו הטור וכתבהו לבד במקומו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר כן כפול האות ההוא באות השני וכתבהו סמוך לו באותו טור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם נשאר מכפל האות הראשון עשרה חשבהו כאחדים וחברהו עם
כפל האות שאחריו וכתבהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ישאר לסוף עשרה כתוב שם בסוף א' בדרך שלמדך החכם אבן עזרא בשער הכפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר חבר הכל וכתוב העולה הכל טור למטה כנגדו מהאחדים שבאותו טור על הסדר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ישאר לך כלל שמרהו וחברהו עם העולה מהמספר שאחריו באותו טור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה מכל טור וטור כמו שתראה בצורה בטור השפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר תחל לחלק על ששים הטור האחרון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שהוא חמישיים ולכל ששים קח אחד וחברהו עם המדרגה שלפניו שהם רביעיים והנשאר פחות מס' השאר שם במקומו שהוא חמישיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה מהרביעים הוציאם ס' ס' ומכל ששים חבר אחד עם השלישיים והנשאר תכתבהו במעלת הרביעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כולם עד שתעלה המספר למדרגת המעלות והנשאר בכל מעלה ישאר וזה הנשאר אחר החלוק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [25]זהו דרך חכמי המזלות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל דרך חכמי החשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כשיגיעו לכפול הטור העליון שבצורה ראשונה על הטור השפל שבו כל מה שבטור העליון למדרגת המספר הקטן שהוא בכאן השלישיים וכן כל מה שבטור השפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכיצד יעשו יכפלו המעלות על ששים והנם ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחברם עם הראשונים ונכפלם על ס' יהיו שלישיים כי לעולם ירד ממדרגה אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן נעשה בכאן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכפול ב' על ס' והם ק"כ ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחברם עם ט' שהם ראשונים כמו כן והם קכ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכפול קכ"ט על ששים ועם הד' הם ז' אלפים תשמ"ד שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכפול זה על ס' ועם הג' הם תס"ד אלפים [...] אלפים ותרמ"ג שלישיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן נעשה מן הטור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכפול אלו על אלו ועלה גטטחטבדבגג והם ששיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר נחלקם על ס' ותן לו מכל אחד מה שתוכל וכתבהו במקום הראוי לו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היה העליון פחות השיבהו אחורנית בעשרות ותן לו מה שתוכל ומה שישאר השיבהו אחורנית שלפניו וכן תמיד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכשיקרה באחד מן האמצעיים שיכלה בכוון אל הו' והאות שלפניו פחות מו' כתוב בספרא כנגדו בטור האמצעי והאות שלפניו השיבהו אחורנית וחלק ממנו כמשפט עד שתגיע כנגד הראשון שהיא מדרגת האחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומה שישאר לחלק שהוא פחות מששיים ישאר במדרגתו והעולה בחלוק יהיה רביעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומה שישאר לחלק הוא חמשים כבתחלה וכן נעתיקנו תמיד ממדרגה והעולה בחלוק יהיה רביעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומה שישאר לחלק הוא למדרגה עד הגיעו למעלות כי בכל חלק יעלה מדרגה אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תחשוב כראוי תמצא הנשאר מכל המדרגות שוה [26]לחשבון הראשון וזה הדרך השני הוא שקרא דרך המבטא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנחלק טור הששים על ששים יצאו בחלוק מן החמישיים ואגחח0דהה וישארו מן הששים גג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנחלק אלו החמישיים על ששיים יעלו הרביעים אזדאדגבט וישאר מן החמישיים וה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנחלק אלו הרביעיים על ס' יעלו השלישיים דב0טגהא וישאר ממין הרביעים אג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנחלק השלישיים יצא בחלוק מהשניים 0הוהב וישאר מהשלישיים דב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנחלק השניים על ס' יצא זבד ראשונים וישאר מהשניים 0ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחלק הראשונים על מעלות ויהיו המעלות ז' וישארו ז' ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיה זה שוה לנשאר תחלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The chords of the arcs |
יתרי הקשתות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שנדע המרחק מנקודה ידועה מהקשת עד נקודה ידועה ממנו ונרצה לידע אורך היתר שמנקודה זו אל נקודה האחרת מהקשת ביושר או כמה אלכסון המיתר ההוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The perimeter should be three times the diameter |
הקו הסובב ראוי שלשה מהאלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שלשה מקטרו ושביעית וא'ע'פ' שלפי החוג שהקיפו שלשה ממנו לבד אין ראיה כי החוג [....] מיתר ברחב העגול שהוא קו ישר שאין [....] שעקם העגול שבין שתי נקודות אלו יותר גדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Six |
השער הששי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כונת זה השער לזכור ערכי המדות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומתוך כך רצה להודיע מיני הערכים כמה הם ערכי החשבון והם על הסדר שכפי היתרון שיש לשני על הראשון יש לשלישי על השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The second way is the geometric proportions as 4 6 9 |
והדרך השני ערכי המדות כמו ד'ו'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As the ratio of 6 to 4, which exceeds it by its third, so is the ratio of 9 to 6, which exceeds it by its third.
|
שכערך שיש לו' אל ד' שמידתו גדולה ממנו השליש כן ערך ט' אל ו' שעודף עליו שלישו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
So the product of the smaller number by the greater number |
על כן כפל הקטן על הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I.e. since 4 is smaller than 6 by the same as 9 exceeds 6
|
ר"ל אחר שיחסר ד' מן הו' כמו שיעדיף ט' על ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| So the product of the smaller number by the greater number. | על כן כפל הקטן על הגדול וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Know that these three numbers are like four numbers |
ודע כי אלה [27]השלשה מספרים כמו ארבעה הם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Since the means are the same when extracting the ratio. | לפי שאמצעי לשוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי נאמר ערך ד' אל ו' כערך ח' אל י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
על כן אם תחשב מרובע ד'ו'ט' כאלו היה ד' מספרים יהיה שוה אל העולה ממרובע מחובר הראשון והרביעי והוא ק'ס'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The means are regarded |
כי האמצעי יחשב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' ואם תאמר אלה השלשה כמו ארבעה והלא ארבעה יש בו ב' אמצעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי אותם השנים יחשבו כאלו הם מספר אחד כמו שיאמר למטה כי שניהם חברים על כן אמ' שנקח מרובע המחובר משניהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועוד כי כמו שאמרנו [ב]ג' מספרים שכפל הקטן על הגדול ככפל
התיכון על עצמו כן נאמר בד' מספרים שנכפול האמצעי האחד על חברו כמו שנכפול התיכון על עצמו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל בזה ד ו ח יב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי כפל ד' על י"ב הוא מ"ח וככה כפל ו' על ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example 2 3 6 |
דמיון ב' ג' ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שכפי יחס היתרון שבין ב' וג' אל היתרון שבין ג' וו' שהוא שלישיתו כן הוא ערך הראשון שהוא ב' אל האחרון שהוא ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי לעולם ערך האמצעי האחד אל האמצעי השני כערך הראשון אל האחרון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל אלו הדמיונות שיעשה מב'ג'ו' ומג'ד'ו' הם על דרך ערכי הנגינות שהם ג' מספרים ב'ג'ו' קורא דמיון ראשון וג'ד'ו' דמיון שני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We double the quotient |
והעולה בחלוק נכפלנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שנמנהו ב' פעמים היו בערכי הנגינות דין כל אחד מהג' בפני עצמו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
They are ten |
והיו עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל אלו החלקים המחוברים כמה היה כל הממון שהיו העשרה בכללם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We multiply the extremes that are ten and 210; they are two thousand and one hundred |
כפלנו הקצוות שהם עשרה ור"י והיו אלפים ומאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We divide it by the known mean, which is 106; we receive the unknown mean, which is the whole amount; the resulting total amount is 19 integers and 67 parts.
|
חלקנום על האמצעי הנודע שהוא ק"ז ויצא לנו האמצעי הנעלם שהוא כל הממון יעלה כל הממון י"ט שלמים וס"ז חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Another example: We take its seventh and its ninth; they are seven |
דמיון אחר לקחנו [28]שביעיתו ותשיעיתו והיו שבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| How much is the amount? | כמה היה הממון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה המורה ס"ג ושביעיתו ותשיעיתו י"ו וערך ז' אל הממון כערך י"ו אל ס"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכפול הקצוות שהם ז' וס"ג והיו ת'מ'א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחלק זה על י"ו ועלה כ"ז שלמים וט' חלקים מי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If one reversed the saying |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כשנדע החלקים לבד נחלק כפל הקצוות על חלקי המורה ויודע הנשאר אבל כשיהיה בהפך שלא נדע רק הנשאר מן החלקים גם אנו נחלק על הנשאר אחד חלקי המורה ויודע לנו סך החלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We sum up their amounts of money |
נחבר ראשי ממונם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל חשבונות ממונם יעלו שלשה נ"ו שלמים שהם ג' דינ' ומ"א חלקים מנ"ו שהם מ"א חלקים מדינר שכל נ"ו בכאן נחשב כאחד מחלקי המורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The result is 4 pešuṭim |
עלה ד' פשו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל לכל חלק מנ"ו שהוא דינר אחד על כן כל אחד יקח לכל דינר מממונו ד' פשו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Also 4 parts of 56 |
גם ד' חלקים מנ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שישארו עוד ד' פשו' לחלק שיש לכל דינר ודינר שיקח מהם ד' חלקים מנ"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Because each pašuṭ is divided to 56 |
כי כל פשו' יתחלק לנ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יש לכל דינר שיקח מפשו' אחד חלק אחד מנ"ו אם כן יקח מד' פשו' ד' חלקים מנ"ו שהם חלק אחד מי"ד שהוא חצי שביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם נשיב ארבעתם לנ"ו נ"ו שהם ר'כ'ב' ונחלקם על נ"ו יעלה לכל אחד ד' מאותם החלקים ומד' חלקי פשו' מנ"ו חלקים שבו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We sum all the parts |
והנה נחבר החלקים כלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל אותם שנשארו מהחלקים יהיו שנים פשו' ושנים שחברנו מהחלקים היו ד' ונחבר עתה הפשוט כלם היו ב' דינ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
All the mentioned parts |
וכל החלקים הנזכרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שלישית ורביעית וששית מי"ב הם טא והוא הדינר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי לעולם החלקים הם דינר אחד והמורה הוא כל הדינר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We ask what is the ratio of 12 to 9 |
ונבקש מה ערך י"ב אל ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו אמ' נחלק י"ב על ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
It is the same as it and its third, we add 4 pešuṭim to 12 pešuṭim, which is the dinar |
והנה הוא כמהו ושלישיתו והנה נוסיף על י"ב פשו' שהוא הדינר ד' פשו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי ט' הוא הדינר אחד ועם שליש הדינר והוא י"ו ונוכל לעשות ערכים שנאמר ערך י"ב שהוא המורה אל [29]אל ט' כערך כל הסך אל הדינר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| על כן נכפול הקצוות שהוא י"ב על י"ב והם ק'מ'ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחלק על ט' עלו י"ו והוא הדינר המחובר מג' הערכים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We divide the denominator by this number; the result is 2 dinar and 29 |
ונחלק המורה על זה המספר יהיו ב' דינ' וכ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל מכל מטבע מהשלשה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We convert the dinar to parts of 143 |
נשיב הדינר חלקים מק'מ'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל מהב' דינ' וכ"ט חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה נכפול ש'י'ה' על ה' שהם הקצוות ויהיו אלף ות'ק'ע'ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונחלק אותם על שבעה יהיו בדנר ר'כ'ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפי ערך ה' אל ז' יהיה הערך ר'כ'ה' אל ש'י'ה וכן תאמר בכלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
When we exchange this number of coin seven |
וכאשר החלפנו זה המספר ממטבע שבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כי לעולם נקח המורה במקום סך המטבע שנרצה להשיב הכל אליו והנה שביעית המורה מה שהוא ז' פעמים מ"ה כי השבעה ישובו ל"ה והם ר'כ'ה' ממטבע הוא שהוא דינ' אחד ופ"ב חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כשנרצה להשיב הב' דינ' וכ"ט חלקים ממטבע ט' אל מטבע ה' נמנה ה' פעמים ל"ה שהוא התשיעית והוא קע"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כשנרצה להשיב הכל למטבע ז' נקח בעבור ז' ש'י'ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובעבור שנרצה לעשות מ"ה ז' נחשוב ז' פעמים ס"ג והיו ת'מ'ה' ממטבע ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן נחשוב ז' פעמים ל"ה יהיו ר'מ'ה' ועל זה הדרך תשיב הכל למטבע ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We want to know how many parts he takes of coin five |
ונרצה לדעת כמה חלקים יקח ממטבע חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כמה חלקים יקח מזה המטבע שהוא מטבע ז' בעבור מה שיהיה לנו ממטבע חמשה כלו' כמה יהיה ממטבע ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או נעשה כן כשנרצה להשיב ב' דינ' וכ"ט של מטבע ז' למטבע ה' ונסיר מש'י'ה' שהיו מנין חלקיו שיש בו ז' פעמים מ"ה ב' שביעיות שהן צ' כי יתרון ז' על הב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כשנרצה להחזיר ט' ל"ה נסיר תשיעית ש'י'ה' שהם ד' פעמים ל"ה שהם ק"ם ביתרון ט' מ"ה והנשאר יהיה של י"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכשתרצה לגרוע המטבע ולהשיב כנל לז' או לט' הוסף על חלקי האחד כיתרון האחד עליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון [30]זה אם תרצה להשיב הכל למטבע ז' הוסף בעבור מטבע ה' ב' חמישיות שהם ק'נ'ו' ובעבור מטבע ט' גרע ממנו ב' תשיעיות שהם ע' ועל זה הדרך הכל והכל יוצא שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We think as if the 7 measures are carried 17 miles |
נחשוב כי הז' מדות הולך כל י"ז מילין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולכן לא נזכרם בערך א' אבל נעשה הערך מהמדות שלא השלים ומהסך שלא הרויח כלו כי כערך ז' אל י"ג כן ערך מה שיוצא לי"ט ובעבור שלא ידענו הריוח נכתוב תחתיו גלגל ונעשה הצורה כן והנה בזה הסדר היו הקצוות ז' וי"ט על כן נכפלם והיו ק'ל'ג' נחלקם על י"ג שהוא האמצעי הנודע יעלה י' שלמים ונשארו ג' חלקים מי"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולפי שחסר תנאי המילין נעשה ערך אחר ולא נזכר מדות כלל אבל נאמר כערך י"א מילין אל ז' יהיה ערך מה שיקח אל הריוח הנזכר שהוא י' וג' על זה הדמיון נכפול י"א על י' עלו ק'י' נכפול י"א על ג' שהם חלקים והיו ל"ג חלקי י"ג והנה הנ"ו ב' שלמים נחברם ק'י' והיו ק'י'ב' ונשארו ז' חלקים מי"ג והנה נחלקם על י"ז שהוא האמצעי הנה נחלק העולה ק'י'ב' על י"ז עלו ו' פשו' ונשארו י' לחלק נשיבם לחלקים מי"ג ונחברם עם הז' שהם כמו כן חלקים מי"ג ויעלה ק'ל'ז' נשיב ק'ל'ז' לחלקים מי"ג (מי"ז) שנכפלם על י"ז ועלה ט ב ג ב נחלקם על ר'כ'א' שהוא כפל י"ג על י"ז והוא אחד שלם ועלה ק'ל'ה' (קל"ז) שהם חלקים מרכ"א והם ח' חלקים מי"ג עם חלק אחד מי"ז בחלק או אם תרצה הם י' חלקים מי"ז עם ז' חלקים מי"ג בחלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או אם תרצה תחשוב י' פעמים רכ"א ולא תצטרך אלא לשום בראש ר'כ'ה' (רכ"א) גלגל שבעשותך כן העלית כל אות ממנו מדרגה אחת שהיא עשרה ותחבר עמו כפל הז' בי"ז שהוא [31]ק'י'ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We multiply the first number |
והנה נכפול המספר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| רצה במספר ראשון התנאי ובמספר השני המעשה ר"ל מדת הספירה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Now we set the proportion diagram |
ועתה נעשה דמיון הערכים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויהיו קצוות בקשתם שהוא המספר הקטן ומעורב בתנאי שהוא הגדול שבד' המספרים הנערכים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמר כי ערך הריוח המבוקש אל י"א כערך ק"כ אל ר"י | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| על כן נכפול האמצעיים שהם ק"כ וי"א ונחלק על ר"י שהוא הקצה האחרון הנודע והעולה יהיה הקצה הראשון הנעלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או אם נרצה נעשה אלו האמצעיים קצוות שנאמר ערך ק"כ אל ר"י כערך המבוקש אל י"א והכל שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
You can convert them into hours of the day |
ותוכל להשיבם לשעות היום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל תוכל להשיב הז' תשיעיות לשעות היום בדרך הערכין ותכתוב כן כי כערך ז' תשיעיות אל ט' יש לשעור היום המבוקש מי"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We know that the ratio of 12 to 9 is the same as it plus its third |
ידענו כי ערך י"ב אל ט' כמהו ושלישיתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' תשיעית יום הוא יותר מחלק י"ב מיום השלישית והוא שעה ושליש על כן נחשוב בעבור ז' תשיעיות ז' שעות וז' שלישי שעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Since we have a third, we convert all to thirds |
והנה בעבור שיש לנו שלישית נשיב הכל לדרך שלישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' נעשה מכל הימים שלישיים והנה כערך י"ג אל מ"ז כן ערך מה שיקח מן הזהוב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We want to know how much each one has to work for the 13 |
ונבקש לדעת כמה חייב כל אחד שיעבוד בעבור י"ג וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמר כערך י"ג אל מ"[ז] שהוא הזהוב הנה ערך עבודתו אל כ' שלישיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עלו ה' שלישיות נשארו כ"ה חלקים ממ"ז שהוא שלישית ששלישית יום הוא ד' שעות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם כן הכ"ה חלקים הם כ"ה חלקים ממ"ז חלקים שבד' שעות היום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We multiply also 25 parts by four; the product is one hundred |
גם נכפול כ"ה חלקים על ארבעה עלו מאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם יש לו כ"ה חלקים מד' שעות שבמ"ז הנה מכל שעה כ"ה חלקים ממ"ז בשעה יעלה לד' שעות ה' [32]ה' חלקים ממ"ז שבשעה נחלקם על מ"ז שנחשבהו עתה שעה אחת ונשארו ו' חלקים ממ"ז בשעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה נעשה הערך לשמעון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כערך י"ג אל מ"ז כן ערך עבודתו אל ט"ו שלישיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We divide them by three |
נחלקם על שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' שנחזירם לשלמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We multiply also 7 by 4 |
גם נכפול ז' על ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הז' הם חלקים ממ"ז שבו ד' שעות וכשנקח כן מכל שעה יהיו כ"ח ממ"ז בשעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Make the diagram like this |
תעשה הדמיון ככה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כערך ו' אל א' הוא ערך הנשאר אל ג' ושליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Another example: he has 9 measures of must and he wants them to be cooked until the third part of it remains |
דמיון אחר היו לו ט' מדות תירוש ורצה שיתבשלו עד שישאר השליש וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונשארו שנים והנה כערך ב' אל ו' כן ערך הנשאר אל ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Question: an amount of money, we sum its fifth |
שאלה ממון חברנו חמישיתו וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נעשה הערך כי כערך ק'מ'ג' על ש'ט'ו' כן ערך י' אל הממון והנה נרצה לידע הקצה האחד על כן נכפול האמצעיים זה על זה שהוא ש'ט'ו' על י' נחלקנו על הקצה הידוע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We do the opposite: An amount of money - we have subtracted from it |
נעשה להפך ממון חסרנו ממנו וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נעשה הערך ונאמר כי ערך י' שהוא הנשאר אל כל הממון כערך ק'ע'ב' אל ש'ט'ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Five remain |
ישארו חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה אם היה הנשאר מן האילן ה' לבד היה י"ב הוא כל הגובה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אך בעבור שהוא י' נעשה הערך ונאמר כי כערך ה' אל י"ב ערך י' אל כל האילן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונכפול האמצעיים שהם י' על י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או נשיב האמצעיים קצוות כשנאמר כן ערך אל כל האילן כערך ה' אל י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונכפול הקצוות שהן י' וי"ב והכל אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וחכמי הגויים יחלקו זה הממון על דרך ערך ממון כל אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כדרך חכמי החשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The wise men of Israel divide it |
וחכמי ישראל מחלקים אותו וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| למטה יפרש זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The arithmeticians |
וחכמי החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יבקשו ממון שיהיו בו אלו החלקים ויקחו ממנו ערך לזה הממון אם לא כמהו שאם היה כמהו הנה נמצא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The total is two and one-half of one-sixth |
יהיה הכל שניים וחצי ששית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי השלישית הוא רביע וחלק מי"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשברים [33]והנ השברים י"ג ובקש הכל כ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We set the proportion at [60] |
נעשה הערך ככה על דרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שנקח האחד ששים ונחבר אליו החלקים השברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This is the proportion of the money that Reuven takes |
וזה צורת ערך הממון שיקח ראובן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלומ' שאם היה הממון קכ"ה הנה היה נוטל ששים שהוא כל האחד אך עתה שאינו רק ק"כ אין ספק כי פחות מס' יקח לפי חסרון ק"כ מן [.] ק'כ'ה' על כן נעריך ונאמר כי כערך ק"כ אל ק'כ'ה' יהיה ערך מה שיקח מס' או נאמר ערך ס' אל מה שיקח כערך ק'כ'ה' אל ק"כ ומכל מקום נכפול הקצוות שהם על ק"כ ועל זה הדרך צורת כל אחד כי אלו היה ק'כ'ה' היה שמעון נוטל עתה יחסר מזה כפי גרעון ק'כ'ה' מק'כ'ה' ונעשה צורתו ככה וצורת חלק לו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ובדרך קצרה יקח לעולם שמעון חצי חלק ראובן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו שהיה אלו היו ק'כ'ה' על כן לעולם אחר שנדע חלק ראובן על דרך הערך אין צריך להעריך האחרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
According to the procedure of the sages of Israel |
ועל דרך חכמי ישראל וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| איפשר שאמ' כן לפי מה ששנינו זה אומר כלה שלי וזה אומר חציה שלי (בבלי, בבא מציעא א ד"ב ע"א, משנה) וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכבר לקחת חלקת מהשלישים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כלו' באותם מ' שהיית תובע בל' היינו ד' חולקים ועל כן לקחנו כל אחד רביע ונשאר מהם י' שאתה תובע והנה בהם ג' חולקים על כן תקח שלושים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Which all four of us have claimed |
שארבעתנו ערערנו עליהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הגדולים מערערים בכל חלקי הקטנים כי בכלל חצי השליש והרביע ולא בהפך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
When determining the moon and also when determining 5 planets |
כי בתיקון לבנה בתיקון ה' משרתים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אך לא בתיקון חמה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
There is a row that is called the row of ratio |
טור יקרא טור הערך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| טור הערך טור אחד שבו מספרים רבים על הסדר זה למעלה מזה שכנגד כל מספר מהם ימצא [34]ימצא מספר אחד בטור אחד שבו מספרים שהם בסדר זה למעלה מזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואותו טור הבא אחר טור הערך יקרא טור חמישי או שביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונראה איזה מספר יש בטור הערך ונביט מה ערך יש לו אל ס' אם שליש או רביע וכפי זה נקח מטור החמישי או השביעי ואם היה בו ס' נקח כל הכתו' בטור החמישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example: you have 40 fractions exceeding over the degrees and in the row of the ratio there is 15 |
דמיון יש עמך חלקים יתרים על המעלות מ' ובטור הערך ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לא הוצרך להראות לקיחת הערך מן המעלות כי נקל הוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אך הוצרך להראות בחלקים וכל שכן כשלא ימצא להם ערך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
They are 22 and one-half that are 30 seconds |
והנם כ"ב וחצי שהם ל' שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי לא נכתוב בלוחות חצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We multiply 3 by 20; they are 60 |
נכפול ג' על כ' יהיו ששים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן נוכל להפך ולומר כמה ערך כ' אל ס' שליש כן נקח שליש אחד והוא ראשון אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Since we have add two |
ובעבור שהוספנו שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל בחשבוננו שמנינו אותם יותר מן הראוי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Always see if there are any fractions added to the degrees of the determined center |
ולעולם ראה אם היו חלקים נוספים על מעלות המוצק המתוקן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| טור אחד יש לפני טור הערך שבו מספרים רבים זה למעלה מזה כל מספר שבו כנגד מספר שבטור הערך וממנו יכנסו [35]לטור הערך ויקרא המוצק המתוקן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שבטור המוצק כ' וכנגדו בטור הערך ט"ו ולמטה בטור המוצק כ"א וכנגדו בטור הערך י"ו וכן על הסדר הולך ומוסיף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה אם היו יותר מל' חשבם במעלה אחת והכנס בטור הערך למטה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If you find the determined quotient between 4 constellations |
ואם נמצאת המנה המתוק' שהוא ב' ד' מזלות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שאם היה פחות מד' או יותר מח' עשה כדרך שהראיתיך במעלות המוצק שאם אין לך לא תחוש אך מד' ועד ח' דקדק באלו החלקים ליקח ערך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שהיו לך ל' חלקים נוספים על ד' מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה אם לא היו הל' היה נכנס בט"ו בטור הערך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היה לנו מעלה אחת יותר היה נכנס בי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי בעבור כל מעלה יוסיף אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עכשיו שיש לנו חצי מעלה נוסיפנו עם הכתוב במעלת הד' ונראה מה ערך ט"ו וחצי אל ס' ונעשה בדרך הכפל כפי צרכנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Seven |
השער השביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The first way is roots |
הדרך האחד שרשים וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meaning: every number is required due to being a roots, or due to being a square, or required due to neither of those two. | ר"ל כל חשבון יבוקש מצד שהוא שורש או מצד שהוא מרובע או [36] או לא יבוקש מטעם אחד מאלו השנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
There are numbers that have no true root at all |
ויש חשבון שאין לו שורש אמת כלל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meaning: we do not know its true and exact root. | ר"ל שלא ידענו שרשו באמת ובדקדוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
One is a root and a square |
והיה האחד שרש מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because, one [multiplied] by one [is one]. | כי אחד על אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Check if the scales of the square |
הסתכל אם לא היו מאזני המרובע וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meaning: if you find a number and you wish to know if it is a square or not: | כלומ' אם תמצא מספר אחד ותרצה לדעת האם הוא מרובע אם לא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check if it is all cast out by nines, or how much remains. | הסתכל אם יהיה הכל ט'ט' או כמה ישאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Look at the remainder from the nines in the root and multiply it by itself. | וראה בשורש הנשאר מט' וכפלהו על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the remainder from the nines after the multiplication is the same as the remainder from the square, it can be a square. | ואם יהיה הנשאר מט' אחר הכפל כנשאר מן המרובע אפשר להיותו מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because when the root is multiplied, the scales are multiplied, and the remainder from their product remains in the square. | כי בהכפל השורש נכפלו המאזנים והנשאר מכפלם ישאר במרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If it is not found so, you know for sure that it is not square. | ואם לא ימצא כן תדע באמת שאינו מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example: if someone tells you: 121 is a square. | המשל בזה אם יאמר לך אדם ק'כ'א' הוא מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check its scales; they are 4.
|
הסתכל במאזניו והנם ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You find the same in the product of the scales of its root, which is 11.
|
ככה תמצא בכפל מאזני שרשו שהוא י"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Therefore, his statement is correct. | על כן נאותו דבריו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But, if he says that 122 is a square, deny it. | אך אם אמר כי ק'כ'ב' הוא מרובע הכחישהו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Other scales |
מאזנים אחרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examined only by the knowledge of the remainder from the scales of the square and there is no need to look at the root | יבחנו מידיעת הנשאר על מאזני המרובע בלבד ולא יצטרך להסתכל בשרש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the remainder is 2, or 3, or 5, or 6, or 8, it is not a square. | שאם ישאר כגב' או ג' או ה' או ו' או ח' אינו מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For, the scales of the square are always derived from the scales of the root, which are from 1 to 8. | כי לעולם יצאו מאזני המרובע ממאזני השורש שהם מא' עד ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The product of one of them [by itself] never produces in the square any of the mentioned numbers, which are 2, 3, 5, 6, 8. | והנה מכפל אחד מהם לא יולד לעולם במרובע אחד מהמספרים [37]הנזכרים שהם ב'ג'ה'ו'ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The result of the product is only 1, or 4, or 9, or 7. | רק היוצא מן הכפל א' או ד' או ט' או ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Therefore, if you find that the scales are one of these, it may be a square. | על כן אם תמצא המאזנים אחד מאלו אפשר היותו מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examine all of them and you will find that it is so. | עיין בכולם אחד ותמצא כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| He said: "seven is also among them". | אמר גם שבעה עמהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meaning: even though it is not a square. | כלו' א'ע'פ' שאיננו מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that 1 or 4 or 7 each results from one of two numbers, but 9 can result from three and here is a table for you to know this: | ודע כל אחד מא' או ד' או ז' יצאו מאחד משני אותיות והט' תוכל לצאת משלשה והנה לך לוח לדעת זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Other scales | מאזנים אחרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the units of our number are 2, or 3, or 7, or 8, know that the number is not a square. | אם היה הנשאר מאחדים על מספרנו ב' או ג' ז' או ח' תדע כי אין המספר מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because the units of the square are always generated from the units [of the root] that are one of nine digits. [The units] of their product [by themselves] are not 2, nor 3, nor 7, not 8; only 1, or 4, or 9, or of the round numbers that are 5 and 6, since they are found in the squares. | כי לעולם לא יולדו הפרטים על כלל המרובע אלא מתוספת אחדים על כלל ואותו התוספת יהיה אחת מט' אותיות והנם מכפלם לא ישאר ב' ולא ג' ז' וח' רק א' או ד' או ט' או מן המתגלגלים שהם ה' וו' כי ימצאו במרובעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The same way for the tens, which are as units of the hundreds. | ועל זה הדרך בנותר מעשרות שהם כאחדים על מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you find one [as units] in the required number, know that there is either 1 or 9 in the root. | אם מצאת במספר המבוקש שהנוסף בו אחד דע כי יש בשרש א' או ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because 1 is always generated from the product of one of them. | כי לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 is generated from 2 or 8 in the root. | ויצא ד' מב' שהוא בשרש או מח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 is generated in the square from the product of 6 or 4. | ויתחדש ו' במרובע מהכפל ו' או ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 is generated from the product of 3 or 7. | וט' יפול מכפל ג' או ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 is generated from the product of 5. | וה' יצא מכפל ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As our lord, our teacher, "May his Rock protect him and grant him life" said regarding that: | [38]לשון אדננו מורנו יצ"ו על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you have a square and [its units are] 1, know that there is either 1 or 9 in the root. | אם יש בידך מרובע ויש בתוספת הכללים א' דע שיש בשורש א' או ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you wish to know which of the two, know the scales of the number, then know the scales of the root. [If the scales of the number are equal to the scales of the root], know that there is 9 in the root. | ואם תרצה לידע אחד משניהם דע מאזני המספר ואחר דע מאזני השורש כי אם תקחהו עם א' ויהיו מאזני המספר שוה כשתקחהו עם ט' ושוה למאזני המספר דע שיש בשרש ט'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| End of quote. | ע"ד לשונו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Every rank that is non-even |
כל מעלה שאינה זוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As hundreds, tens of thousands, thousands of thousands. | כמו מאות רבבות אלפים אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Their squares are according to the squares of the first rank and by their number. | הנה מרובעיהם על דרך מרובעי המעלה הראשונה ובמספרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For, the squares of the hundreds are 100, 400, 900. | כי מרובעי המאות ק' ת' ת'ת'ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The squares of the tens of thousands are ten thousand, forty thousand, 90 thousand. | ומרובעי הרבואות עשרת אלפים וארבעים אלף וצ' אלף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on this way. | ועל זה הדרך הכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The analogous squares |
ולעולם יהיו המרובעים הנמשלים וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meaning: in the square of any rank that is non-even, there is always only one number, as it is in the first rank. | ר"ל לעולם במרובע כל מעלה שהיא בלתי זוג לא ימצא רק מספר אחד על דרך שהוא במעלה הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But, in the squares of the even ranks, there are always two numbers. | ומרובעי המעלות בעלות הזוג לעולם ימצא בהם ב' מספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As in the thousands: one thousand and 600. | כמו באלפים אלף ות"ר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on. | וכן כולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
From the analogous squares you can know all those that precede them or succeed them |
ומהנמשלים תוכל לדעת כל שהם לפניהם או אחריהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meaning: if you know the perfect squares and their ranks, you know their roots. | ר"ל שאם ידעת מרובעי אמת ומדרגות ותדע שרשם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because, since you know the squares of the hundreds: 100, [400] and 900; the root of 100 is 10, and the root of 400 is 20; then the number of squares between 100 and 400 is the same as the numbers from 10 to 20; and the same for the means between four hundred and nine hundred. | כי אחר שידעת כי מרובעי המאות ק' ות'ת'ק' והנה שורש ק' י' ושרש ת' כ' אם כן מספר המרובעים שבין ק' ות' כמספרים שהם מי' עד כ' ובין ק' ות' יפולו וכן מהאמצעיים שבין ארבעה מאות לתשע מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The analogous are the ranks after the tens, for the non-even [ranks] are analogous to the first [rank] and the even ranks [are analogous] to the second [rank]. | הנמשלים יקראו המדרגות הבאות אחר העשרות כי אשר אינם בעלי זוג נמשלו לראשונה והמדרגות הזוגיות לשנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Know that the units that are in the first rank |
דע כי ההווה במעלה הראשונה מהאחדים וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meaning: as 1 is [the root of] 1 in the first rank, so is 10, which is the root of 100.
|
ר"ל כגון א' שהוא א' במעלה הראשונה כן י' הוא שורש ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Also, as in the first [rank] the root of 4 is 2 and the root of 9 is 3, so in the ranks of hundreds, the root of 400 is [20] and the root of 900 is 30.
|
וכמו שבראשונה שרש ד' הוא ב' [39] ושרש ט' הוא ג' כן במעלת המאות שורש ת' הוא (כ') ושרש ת'ת'ק' ל' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The roots of the squares in the fifth rank, which is the tens of thousands, that is analogous to the first [rank], are found in the rank of hundreds: because the root of 10 thousand is one hundred and the root of 40 thousand is 200.
|
ושרשי מרובעי המדרגה החמישית שהיא רבבות הנמשלת לראשונה ימצאו במדרגת המאות כי שרש י' אלפים הוא מאה ושרש מ' אלפים הוא ר' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The roots [of the squares] in the seventh rank, which is two ranks up from the fifth, that is similar to it, since it is odd, are found in the rank that follows the hundreds, which is the thousands: because the root of a thousand of a thousand is a thousand and the root of 4 thousand of thousands is two thousand. | ושרשי המדרגה השביעית שהיא דולגת מהחמישית שתי מדרגות הדומה אליה בהיותה נפרדת ימצאו במדרגה הבאה אחר המאות שהיא אלפים כי שרש אלף אלפים אלף ושרש ד' אלפי אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so for all of them. | וככה בכולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The units that are the roots of [the squares] in the second rank: | והאחדים שהם במעלה השנית בשרש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As 16, whose root is 4: in the fourth rank that is analogous to it, the root of the square one thousand and 600 is the digit 4 in the tens.
|
כגון י"ו ששרשם ד' כן במדרגה הרביעית הדומה לה במרובע אלף ות"ר יהיה שרשו אות ד' בעשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The root of the square two thousand and 500 that is analogous to 25, is 50, which is analogous to 5.
|
ובמרובע אלפים ות"ק הדומה לכ"ה יהיה השרש נ' שהוא כמו ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The roots of the squares in the sixth rank that is analogous to the second rank, are hundreds. | ובמרובעו המדרגה הששית הנמשלת למדרגה השנית יהיה שרשם מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As the square 160 thousand that is analogous to 16, whose root is 400 that is analogous to 4, which is the root of 16.
|
כגון מרובע ק"ס אלפים הדומה לי"ו ששרשו ת' הדומה לד' שהוא שרש י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Say the same for all of them. | וכן תאמר בכלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As our lord, our teacher, "May his Rock protect him and grant him life" said: | לשון מורנו רבינו יצ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you have a known square and you wish to find another square using it: | אם יש לך [...] מרובע ידוע ותרצה לדעת ממנו מרובע אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If it follows it:
|
אם הוא אחריו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Double the root of the former. | כפול השורש הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know how much is the distance of the number, whose square you wish to know, from it. | ודע כמה מרחק המספר שתרצה לדעת מרובעו ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפול הכפל ההוא במספר המרחק עוד תוסיף עליו מרובע מה שעלה בחלוק והוסף הכל על השרש הראשון ויצא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the number you wish to find precedes the known number:
|
ואם המספר שתרצה לדעת הוא לפני המספר הידוע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Double the root of the known square. | כפול שרש המרובע הידוע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועוד תכה אותו במרחק מה שיש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יש לך מרובע ידוע ותרצה לדעת ממספר אחר כמה הוא קרוב אל מרובע אם [40]אם המספר ההוא הוא א אחרי המספר הידוע דע כמה המרחק וחלק אותו על כפל שורש המרובע הידוע והשאר בידך מה שיצא במרובע החלוק וחבר הכפל ותוספת מרובע החלוק עם המרובע הידוע ויצא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או אם המספר אשר בידך הוא לפני המרובע הידוע ראה כמה מרחקו ממספר הידוע והמרחק ההוא חלקהו על כפל שרש המרובע הידוע ותן לו מהחלוקה כדי שנוכל לגרוע ממנו מרובע מה שעלה בחלוק ולא ישאר כי אם פחות מכפל שורש המרובע ומה שיצא בכ בכפילת החלוק אחר שתגרע ממנו מרובע החלוק חסר אותו מהמרובע הנמשל ויהיה המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ע"כ וכל זה שוה עם הכתוב בספר אלא שהספר יצוה לגרוע כל כפל החלוק מהמרובע הנמשל ולהוסיף על הנשאר מרובע החלוק ולגרוע הנשאר מהמרובע העתיד והכל שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אלא שמלמדנו כמות תוספת החלוקה והכונה בתוספת לגרוע כל המרחק עד שנגיע אל המרובע שעבר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי כל [ב]כל אחד משני הדרכים לא נמצא רק מרובע שעבר הקרוב למספרנו ובדרך הראשון נמצאנו בין שהיה מספרנו יותר קרוב ממרובע שעבר או שהיה יותר קרוב ממרובע שאחריו והדרך השני לא יועילו רק בהיות מספרנו בלתי קרוב אל מרובע שעבר יהיו ק"נ שהוא שרש ו' ומרובע כ"ב אלף ות"ק וממנו נדע מהנשאר מרובע הקרוב על כן נחלק על כפל שרשו ונתן לו א' ו שהוא שם ונוסיפנו על מרובע הראשון שהיה לנו והיו כ"ב אלפים ותת"א עם מרובע א' שעלה בחילוק . נתן לו יותר מה שנוכל . שנתן לו ט' שהם ה' אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We cannot give it 5 |
לא נוכל לתת לו ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל נסיר ממנו אלף ות"ר שהוא מרובע מ' ונוסיפנו על המספר יהיו ל"ג אלפים ות"ר ועתה יהיה לנו ת"ם [41] ר"ל שנעשה מרובע קרוב ונחלק על כפלו מה שנשאר לנו שהוא אלפים ות' נתן לז' שהם ו' אלפים וק"ס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחסר עוד מרובע ז' שעלה בחילוק ר"ל ונוסיפנו על מה שהיה לנו ויהיו ו' אלפים ור"ט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחבר זה אל ל"ג אלף ות"ר שהיה לנו ועם הכל עלה קצ"ט אלפים ות"ר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נשארו קצ"א נחסרנו ממאתים אלף ישארו קצ"ט אלפים ותת"ט והדבר יצא שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולידע השורש נוסיף ז' שעלה בחלוק על השרש שהוא ת"ם היה תמ"ז והוא השרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We give it all we can |
נתנו לו כל מה שיכולנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נתנו לו כל מה שיכולנו והנה המ' אלף עלה בחלוק כ"ה בצמצום והנה נתן לו יותר חלק אחד שנחברהו מן השש מאות אלף נוכל ליקח מרובע מה שעלה בחלוק והיו כ"ו וכן נחסר כ"ו משרש ומרובע הנמשל שהוא ת"ת והנה שרש מספרנו תשע"ד נחלק המספר הנשאר שהוא אלף אלפים על ד' אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה לא נתן לו רק רל"ו שהם תת"קמ"ד אלפים ונשארו נ"ו אלפים נקח מהם מרובע מה שיעלה בחלוק שהוא נ"ה אלפים ותרצ"ו וזהו המרובע ונשאר ש"ר ואם ד' אלפי אלפים תחסרנו מאלף אלפים שאר המבוקש שהזכרנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונחבר רל"ו שעלה בחלוק עם שרש ראשון שהוא אלפים והוא השרש המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה גם כן העולה מחשבון הספר אלא שמחלק זה חלוקת רבות חלוק אחר חלוק ערך מרובע אל מרובע מרובע אותו הערך העולה הוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמבחן שאם תחלק השרש הגדול על השרש יצא שרש ערך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון חלקנו ס"ד על י"ו עלה ד' וזה הערך הוא מרובע ושרשו הוא היוצא מערך ד' אל ח' שהוא ב' והנה הוא כפלו וב' שביעיות שביעיות וזהו מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם נחזירנו לשביעיות שביעית ותחבר עמהם הב' היו ק' ושרשם י' שביעיות שהוא אחד ש' שלם וד' שביעיות כי שרש הנשברים גדול ממרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| בקשנו לדעת מרובע מספר ידוע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שנרצה לידע מרובע ממרובע כ"ה [42]כ"ה שהוא ידוע למספר ה' שהוא ידוע נחלק י' על ה' ועלה שנים ומרובעם ד' נכפול ד' על כ"ה ועלה ק' שהוא מרובע ד' ועל זה הדרך בכלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If we sum three squares, we triple them |
ואם חברנו שלשה מרובעים ונכפלם ג' פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל אם נחבר ג' מרובעים ונכפלם המחובר על ג' ונשמור זה העולה ונקח מרובע היתרון שבין הראשון לשני ומרובע היתרון שבין השני לשלישי ומרובע היתרון שבין הראשון לשלישי ותחבר אלה הג' מרובעים והמחובר חסרהו מהעולה תחלה והנשאר מהעולה הוא מרובע ושרשו המחובר מג' המרובעים הראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועל זה הדרך אם חברת ד' מספרים ותכפלם ד' פעמים או אם חברת ה' מספרים ותכפלם ה' פעמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואומר לך כלל שתוכל לדעת ממנו וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לעולם חסר אחד מהמספר המחוברים וראה סך המחובר מא' עד סוף מספר הנשאר בדרך שאמר בשער החיבור וככה מספר היתרונים כגון שהיו המספרים ד' חסר אחד והיו ג' והמחוברים מא' עד ג"ו וכן היתרונים ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| רק אם יהיה בו רביעית כלומ' אם נמצא במרובע רביעית ידענו כי בשרש היה חצי ממנו יצא אם היה בו ששית ששית מששית יצא וכן בשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היה בו חצי שמינית שהוא חלוק מי"ו הנה מהרביעית יצא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן שניים שהם כמו רביעית יצאו מראשונים שהם חצי ורביעים יצאו משניים אבל שלישיים וחמשיים ושביעיים ושמניים אין להם שורש אמת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסתכל אם היה מרובע רביעית דע כי בשרש חצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שהיו לך י"ב שלמים ורביעית הנה בשרש היה חצי נשיב הכל לרביעיות היו מ"ט ושרשם ז' חצאים שהם ג' וחצי והנה כאשר נכפול ג' וחצי על עצמם יצא לך י"ב ורביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תכפול מ' על מ' ראשונים שהם שתי שלישית מעלה יהיו אלף ות"ר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If we convert this number to thirds |
ואם עשינו מזה המספר שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל בעבור שהזכרנו שלישיות נשיב הו' ראשונים שנעשה מכל ראשון שהוא ס"ג שלישיות [43]יהיה עם הב' שלישיות עשרים וכבר אמרנו שהם כ"ו ראשונים ומ' שניים הם תשיעית אחת מס' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שוב וחשוב כי הם ראשונים כי שרש שניים הוא מראשונים יהיו אלף ות"ר שניים שכל ע' הם ראשון אחר נכפול מ' על ס' ונחלק העולה על ע' כי כערך מ' אל ע' יהיה ערך העולה מס' על כן נכפול הקצוות שהם מ' על ס' ונחלק על ע' שהוא האמצעי ומה שיצא יהיה ערכו מס' יעלו ל"ד ראשונים וישארו ב' שהוא שניים יעלו ז' שהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכפלנו עוד ויהיו ג' אלפים ות"ר חמישיים נחלקם על ע' יעלו כ"א רביעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונעשה חלקנו תשעים ר"ל נעשה אחד מצ' חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפלנוהו על עצמו והם ת'ת'ק' נחלקם על צ' ועלה י' חלקים ראשונים והם המרובע ושרשם ל' ראשונים אם אמת כי המרובע חלק אחד ומ' שניים ר"ל הוא נכון שהוא מרובע כי חלק מס' ומ' שניים הוא ששית הששית מס' כי הששית הוא וששית י' הוא ראשון אחד ומ' שניים אם כן השורש הוא י' כי מכפל ששית יצא ששית הששית ומרובע י' ראשונים הוא ק' שניים שהוא ראשון אחד ומ' שניים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
As for the numbers that are divisible by sixty |
והנה במספר שיש לו ערך אל ששים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל א'ע'פ' שקצת המספרים שלא יאותו במקום אחד להיות מרובעים ובכאן לפי שיש להם ערך אל ס' הם מרובעים כמו ט"ו כי הוא רביעית ס' ושרשו ל' ראשונים שהם חצי אך לא יתכן זה בכל המספרים כי י' שהוא ששית אינם מרובע כל שכן המספרים שאין להם ערך כלל אל ס' שאינם מרובע כגון י"א גד יד יט נחלקם על כפל השרש שעבר שהוא ששה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי לעולם כשנעלם ממנו שרש מרובע אחד כגון שלא נדע שרש ק' על דרך משל נבקש מרובע שעבר שהוא פ"א ששרשו ט' ונביט מה המרחק שבינו לבין ק' [44]ק' והוא י"ט נחלקם על כפל השרש שעבר שהוא י"ח ונוסיף עליו המרחק שבין ט' לי' ועלה אחד נוסיף האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה השב הי"א לתשיעיות והם עם התשיעיות ק' ושרשם י' שלישיות שהם ג' שלמים ושליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שנניח השבר לפי שכל השאר נחלק ולא נקח ממנו מרובע החלוק כי לא יתכן והנה במרובע תוסף אם בשלמים נחלקים כל המרחק ונניח כדי מרובע החלוק ונוסיף הנשאר בשרש והכל שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ידענו כי יש בחשבון חומש החומש כי הכ"ד שניים ה' הם ב' חמישיות מראשון והנה חמישית לא יתכן היותו מרובע על כן הוא חומש החומש וכמה הוא חומש החומש שיש בכלל זה המרובע ב' חלקים וכ"ד שניים כי באמת חומש חומש היה בשורש שהוא י"ב וחומש הוא ב' ומק"כ ראשונים נעשה שניים שמן ק"כ וחמישיתם כ"ד והנה המרחק מהמרובע שהוא אחריו שהוא ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי לעולם יהיה בין שנים מספרים ר"ל המרחק בין שני מרובעים הסדורים במספר שרשיהם על כן כשתדע מרובע אחד ולא השני לו חבר שרשיהם עם מרובע הנודע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Look at the number you want |
והנה הסתכל המספר שתרצה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכו' ר"ל אם תבקש לידע שרש אי זה מרובע שיהיה כגון שתרצה לידע מרובע י"ב שהוא בין ובין י"ו והנה הסתכל מרחקו ממרובע שעבר שהוא ט' אם היה בשרש ט' שהוא ג' והמספר נקרא אמצעי לפי שאם תחלק המרחק על אי זה משני המרובעים שתרצה תהיה חלוקתך שוה שאם תחלוק ג' על ו' שהוא כפל שרש שעבר יצא בחלוק חצי וכן אם תחלוק ד' שהוא המרחק שאחריו על כפל השרש שאחריו שהוא ח' יהיה חצי והדבר שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Extract any number that is less than the mean, as 11, from the preceding square number |
[45]וכל מספר שיהיה פחות מהאמצעי כגון י"א הוציאהו ממספר המרובע שעבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שתקח המרחק שבין מספרך ובין המרובע שעבר וחלקהו על כפל שרשו ואם היה המרחק יותר משרש שעבר עשה חשבונך במרובע העתיד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם חשבונך היה במאות ובאלפים זה השרש יספיק לך כי לרבויו לא יוכר בו הטעות והחסרון ויותר יוכר בו אם נקחהו מהקטן כי החסרון והשגגה הולך ורב עד כי גדל מאד רק אם היה המספר קטן אתה צריך למספר שני לפי שלא לקחת ממנו מרובע החלוק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ופעם נקח השורש בקטן מהגדול ויצא מדוייק כמו שעתיד לבאר לפי שטענת הגדול יתמעט כל אשר ירד ויחלק ויבלע מאד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם רצית לדעת שרש עשרים אלף כפול זה השרש על עשרה לפי שה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה בקירוב כי עדיין ישארו ב' שניים שלא לקחנו שביעיתם יהיו ת'ק'י'ד' ועשיריתם ר"פ וזה בקירוב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נעשה מהנשארים שהם ק'י'ט' ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחלקם על ר'פ'ב' שהוא כפל ק'מ'א' עלו כ"ה חלקים ראשונים וישארו צ' חלקים והנה לא נוכל לחלקם על ר'פ'ב' נשיבם שניים והם ה' מב' נחלקם על ר'פ'ב' שהם שרשנו עלו י"ט שניים וישארו מ"ב שלא יתחלקו ואלו ראשונים וי"ט שניים נוספים על שרשנו שהוא ק'מ'א' ואם רצה לדקדקו עוד ישיב המ"ב לשלישיים ויחלקם על ר'פ'ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי כל שברים שתחלק על שלמים יעלה אותו המין מן השבר וכשתחלק מין שברים פחות על מין שבר יותר גדול נחסר מספר הגדול ממספר הפחות והנשאר הוא העולה החלוק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחלק כל מה שאמרנו מן השלמים והשנים על מאה כי כמו שאמרנו כשבקשנו שרש שניים משרש [46]משרש מאתים שלקחנו עשירית שרש מאתים לפי שהוא כפלו י' פעמים כן נאמר עכשו כשנוציא שרש שניים משרש עשרים אלף שהוא כפלו מאה פעם שנקח אחד ממאה שבו הנה מן המאה קח אחד שלם ונקח בעבור המ"ב חמישיות ז' שהן כ"ד מס' לפי שערכם אל מאה כן והאחד שנשאר מק'מ'א' נעשנו ס' ראשונים ועם הכ"ה היה פ"ה והנה בעבור הפ' תקח ד' חמישיות מס' ובעבור הה' שהוא רביעית חמישית ק' נקח רביעית חמישית ס' שהוא ג' והרי לנו נ"א ובעבור הי"ט שהוא פחות אחד מחמישית מאה לקח חמישית ס' פחות א' והוא י"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תכפול כל חשבון שהוא כפל מרובע נראה שכך הוא סדר הדבר אם תרצה לידע שרש חשבון שהוא כפל מרובע כפול שרש חציו על זה ושרש ר"ל שרש ב' השבר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כל חשבון שתכפול על שרש מאחד יהיה מרובע אותו הנכפל נכפל אותו חשבון על עצמו מדמיוני מרובע השרש הראשון המיוחד ר"ל שכפי מספר כפל החשבון נחשוב כך פעמים המרובע הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל בזה כפלנו ב' שהוא שרש ד' על ג' והוא ו' הנה כפל ג' ט' נכפול ט' על מרובע ראשון שהוא ד' והוא ל"ו שהוא מרובע ו' ואם נכפול ה' על ב' שהוא י' הנה מרובע ו נכפל ה' שהוא כ"ה כפול על ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| רצינו לדעת כמה שרש י"ח הנה כפלנו שרש המרובע שעבר שהוא ג' על זה המספר שהוא א'נ"ד כ"א י"א שוה המספר שהוא י"ח כפלו ר"ל ממרובע ג' שהוא יעלה ד' שלמים י"ד ראשונים ל"ג שניים ל"ג שלישיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם כפלנו זה המספר שהוא שרש י"ח יהיה זה הנשנה שרש ע"כ כי לעולם כפל שרש מרובע אם יהיה מרובעם כפל מרובע ראשון כמו שרמזנו למעלה מן חציו הוא שרש רביעית מרובע ראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If we take the square of 7 thousand and 200 |
ואם נקח מרובע ז' אלפים ור' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל אם נקח זה המספר מקום מרובע ונבקש לידע שרשו נעשה על הדרך הנזכר שנקח שרש חציו שהוא ס' [47]ונכפלהו על א'נ"ד נ"א י"א יהיה שרש ז' אלפים ור' פ"ד נ"א י"א וזהו שרש שנים בעצמו אלא שהעלינו כל מספר למדרגה עליונה ממדרגתו שהוא מס' לס' עד ששבו השלישיים שניים והשניים ראשונים והראשונים שלמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Because we convert them to minutes, consider these as integers |
כי השיבונו אותם בדרך ראשונים והנה חשוב אלה שיהיו שלמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה רצה באמרו כי השיבונו אותם בדרך ראשונים והנה חשוב אלה שיהיו שלמים ר"ל שאם היה לנו זה השורש שהוא פ"ד נ"א י"א ולא היה לנו שרש ב' נוריד זה השרש מס' לס' ונתיכהו כדרך שהרכבנוהו ויגיע לנו שורש ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תכפול זה המספר על עצמו ר"ל המבחן על זה השרש שנכפלהו על עצמו ונשיב הכל אם נרצה למדרגה שהוא שלישיים ונכפלם על עצמם והם ששיים ונחלקם על ס' עד שנשיבם לשניים וראשונים ומעלות וישאר בכל אחד מה שלא יתחלק על הדרך שהורינו בסוף שער חמישי תמצא בסוף שלא ישאר אפי' שני אחד וכל שכן ראשון כל זה אמר להראות דיוק זה השרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We go back to extract the root of two |
נשוב להוציא שורש שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל בדרך אחרת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויספוק לנו השרש הראשון ר"ל לא נצטרך להוציא שרש ב' מד' או מעשרים אלף כי יספיק לנו להדריכנו אל האמת השרש הראשון במה שנעשה בו כמו שמבאר והולך ובעבור שיש לנו ששיות כי הנ' הם ה' ששיות וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נשיבם הכל מערך ו' והיו י"ז וכן נשיב הנ"ה לששיות שנכפלם על ו' ועלה ק"נ ועתה יכשר לחלקם על הי"ו עלו מ"ט שלישיים ונשארו א' שלא יתחלקו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If we calculate even more precisely by taking the square of 49 |
ואלו היינו מדקדקים עוד מדרך מרובע המ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שנקח מרובעם ונחלקם על כפל השרש שהיה לנו שהוא ב' מ"ט מ"ב כ"ב ונחשוב כי הכל בנ' ובעבור שהנ' הם ד' ששיות נשים הכל ששיות והיו י"ז ונשיב אצל המ"ט והקי לנו ת'ק'כ'ט' שלישיים נעשה מהם מרובע ויהיו ששיים נחלקם ונגיעם עד רביעיים ונשיבם מערך ששיות [48]ששיות ונחלקם על י"ז שהיה לנו נתן לו כ"ז רביעיים כ"ז חמישיים נחסרם משרש שלנו וישאר א'כ"ד נ"א י' ל"ט ל"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואנחנו דקדקנוהו יותר ולקחנוהו משרש ב' אלפי אלפים ויצא מדוייק בתכלית הדיוק א'כ"ד נ"א י' ז' מ"ז כי לא ישאר אפילו רביעי ולא חמשים רק ב' ושרש נ' המוצא ממנו זד טו ד' לח נה ושרש ה' אלפים עד מב כג לא כט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונשיב הכל מערך שלשה והיו י"ט וכן נשיב ק'ה'ק' לשלישיות שהם ש' ועלו ט"ו נשיבם שניים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נראה שהוא שלישיים יהיו שלש מאות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נראה זה טעות כי השניים הנשארים הם ט"ו וכשנשיבם שלישיים יעלו ת'ת'ק' וכשנחלקם על י"ט יעלו מז שלישיים מעשרה חלקים ישארו ט' מ"ד י"ג וכשנדקדקהו ונעשה מרובע מה שעלה בחילוק ונחלק על כפלם השרש יעלה בחלוק שלישי אחד נחסרהו מי"ג וישאר השורש כ"ט מ"ד י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכשנכפול זה החשבון על עשרה וכו' כי מה שהוא במעלה הראשונה אחדים יהיה באלפים עשרות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We divide the root of 18 |
חלקנוהו שרש י"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל אם נרצה לדעת שרש י"ח משרש כבר ידענוהו משרש כשכפלנוהו ושרשו אחד וחצי ככה שרש י"ח הוא כפל שרש ח' וחצי הכפל שהוא ג' פעמים שורש ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נקח מרובע החילוק שנשיב הכ"ב ראשונים למתכונה הל' שהם שניים יעלו ת'ת'ד' שין ומרובעם אלף אלפים ות"ר שהם שלשים אלף שע"ה שלישיים נחלקם על כפל השורש שהוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As the ratio of the versed sine to the entire diameter so is the ratio of the [sum of] the square of the versed sine with the square of half the chord to the square of the diameter and so is the ratio of the square of versed sine to the square of half the chord. | לעולם כערך החץ אל כל האלכסון יהיה ערך מרובע החץ עם מרובע חצי המיתר ממרובע האלכסון וככה ערך מרובע החץ אל המרובע חצי היתר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The reason is that if you make a circle and you draw a chord | [49]והטעם שאם תעשה עיגול ותוציא ממנו יתר בנקודה ידועה מהאלכסון ותעשה אלכסון מתחלת האלכסון שהוא ראש החץ אל קצה היתר ותמשיך קו אחד מקצה היתר עד סוף הקוטר תמצא שמרובע הקוטר הוא כנגד שני הקוים שהוא הכאת שני הזויות ומרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והטעם שאם תוציא קו אחד מקצה המיתר עד הנקודה שהוא חצי האלכסון תראה שהוא קוטר חצי המיתר ומה שאחרי החץ מהאלכסון עד הנקודה ולכן מרובען כרבוע שניהם יהיה מרובע חצי המיתר שלשת כפלי מרובע החץ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שכן הקוטר כפלי החץ כי הוא רביעיתו ונמצא החץ ד' חלקים ומרובעו ו' ראשונים ומ' שניים שהוא תשיעית אחת והוא אחד מל' מנ' ונ' הנה מרובע חצי היתר הנשאר מג' שלישית שהוא ג' י"ג כ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If you multiply the requested diameter by 22 |
אם כפל האלכסון שתראה על כ"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל מאי זה אלכסון שתדע הערך לידע הקו הסובב כגון שהקוטר עשרה תעריך ותאמר כערך י' אל ז' יהיה ערך העגול אל כ"ב ונכפול הקצוות ונחלק על ז' והנה הנוסף אל הג' שלמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שאם היה הנוסף ז' חלקים מע' וחצי יהיה הנוסף על הג' שלמים ח' ר"ל שאם היה הנוסף כ"ד ל"ה אך אינו כן כי הוא נתן ראיה כי ראוי להיות יותר וכיצד נחשוב נעשה הערך ככה בעבור ד' אל ק'מ'א' יהיה זה מס' ונכפול ב' על ס' שהם הקצוות ונחלק על ק'מ'א' והעולה הוא כך חלקים מס' והנשאר גם כן נשוב לכפול על ס' ונחלק על ק'מ'א' כי [50]כי התוספת ח"ל ולעשות ערך נעשה מהכל ראשונים ר"ל ה'ג' ח"ל והם ק'פ'ח' וחצי ובעבור החצי נשיב הכל לשניים ונעשה האחד מק"כ ויהיה הכל ש'ע'ז' וכן נעשה האלכסון ק"כ ונעריך ונאמר כערך האלכסון אל ק"כ יהיה ערך קו העגול מש'ע'ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If we set the diameter as 10, the square of the chord is as one-third |
אם שמנו האלכסון י' יהיה מרובע היתר כשלישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כשנוציא יתר בשלישית הקוטר ונרבע אותו יותר עם השלישית יהיה כמספר הקו הסובב כי לפי זה מרובע חצי המיתר כ"ב וב' תשיעיות ושרשם ד' וב' שלישיות בקרוב נמצא כל המיתר ט' ושליש נכפלם על שליש האלכסון שהוא ג' ושליש יעלה ל"ז ותשיעית ויותר מעט כי בקרוב מנינו כל המיתר ונמצא שהוא כשעור הקו הסובב וזו הצורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Likewise, if you make the square between the upper third and the lower third |
וככה אם עשית מרובע בשלישית העליונה ובשלישית השפלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שנוציא שני יתרים אחד למעלה בשלישית ואחד למטה בשליש הקוטר גם כן יהיו שבריו כמספר הקו כי אין חלוק בין מרובע החץ שהיא שליש האלכסון עם היתר ובין מרובע היתר ההוא למטה בשלישית האלכסון כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל מספר שהוא לפני עשרה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כל זה הוא ספור מעלות עשרה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שאם תוציא משולש שוה השוקים בתוך העיגול ותשים תושבתו במיתר ששלישית אם יהיה הקוטר העובר באמצעו עשרה יהיה רבוע המשולש בקו הסובב כי רבוע כל משולש הוא הכאת הקו האמצעי מחציו על כלו כי משולש הוא חצי מרובע תראה זה אם תעשה בתושבתו שארכו כאורך המשולש ואין הפרש בין שתכה שליש האלכסון על כל היתר או שתכה שני שלישיו על חציו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היה האלכסון פחות מי' בערך מה שיחסר מעשרה יגרע מדעת המשולש שבשלישית מהיות כקו הסובב ואם היה האלכסון יותר לפי ערך מספרו מעשרה יהיה ערך גודל מספר המשולש על הקו הסובב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [51]המשל בזה אם תעשה אלכסון ט"ו ותוציא יתר בשלישית יהיה
רבוע כל האלכסון רכ"ה ושלישיתו ע"ה וזהו מרובע חצי היתר ומרובע החץ נחסר ממנו השליש שהוא מרובע החץ וישאר נ' ויהיה שרש ז' שלמים ומשהו נכה אותו בשני שלישי האלכסון הוא שנים ושביעית אחת אם כן יהיה הקו המקיף מ"ז ויותר מעט וערכו אל ע' שהוא תשבורת המשולש כערך י' אל ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמשל בפחות מי' כגון שהיה האלכסון שבעה יהיה מרובע כל האלכסון מ"ט ושלישיתו י"ו כ' והוא כולל מרובע החץ וחצי היתר נוציא מהם מרובע החץ והוא ה' ושלישית ותשיעית שהוא כ"ו מ' נחסר אותו מי"ו כ' ישאר י"א פחות תשיעית ושרשו ג' י"ח ככה זה המספר בשני שלישי האלכסון שהוא ד' מ' ויהיה ט"ו כ"ד והוא תשבורת המשולש אל כ"ב שהוא הקו המקיף כערך ז' אל ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תעשה זה דקדוק רב תמצא בפי' שהנוסף על השלשה הוא פחות משביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר נחפש הקו הסובב לדעתי לפי ערך המשולש שבשלישית ימצא מסכים לדברי ארשמידס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וממעלות העשרה כי בהיות קו העיגול עשרה יהיה האלכסון שרש י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם ידעת האלכסון כפול מרובעו כגון שהאלכסון י' ומרובעו ה' נכפול על י"א וכו' כלל אחר טוב לדעת השברים מהקו הסובב כפול חצי הקוטר על חצי העגול וככה הם השברים ויצא הדבר שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לעולם כערך י"א אל י"ד יחסרו שברי העגול ממרובע האלכסון נמצא מרובע יתר על העיגול שביעית חצי שביעית שהוא פחות מרביע ורבותי שאמרו רביע נמשכו אחר כללם שאמרו כל שיש ברחבו טפחיים וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע והנה הנמשלים שהם מי' ולמעלה [52]ראוי שנקח המדרגות מהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| בקשנו לכפול מאתים על ש' והנה הנמשלים ב' וג' שהם במקום ת'ש' כפלנו זה על זה והיו ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן המדרגות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תם ונשלם תהלה לאל עולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
פרוש ספר המספר של ראב"ע Genève, Bibliothèque de Genève, MS héb. 10/2 (IMHM: f 2320), ff. 39r-65r (14th-15th century)
נראה שחסר מעט בהתחלה בדף 58ב: "לשון מורינו ורבינו יצ"ו. אם יש לך אות(?) מרובע ידוע ...". דף 65א, שהוא ככל הנראה סוף הפרוש, בכתיבה אחרת, נראה שחסר בין דפים 64 ו-65. בדף 65ב השיר הקצר הידוע "שאל רופא שאל אל שואליך". בדף 1ב חתימת בעלים: BARTOLOMEO ROBERTI=] ROBERTI]. אלוני. נ. וקופפר. א., רשימת תצלומי כתבי-היד העבריים במכון. חלק ב (ירושלים תשכ"ד) מס. 13-15.
Senebier, J. Catalogue raisonne des manuscrits conserves dans la Bibliotheque de la Ville et Republique de Geneve (Geneva 1779).- ↑ 39r
- ↑ 39v
- ↑ 40r
- ↑ 40v
- ↑ 41r
- ↑ 41v
- ↑ marg.
- ↑ 42r
- ↑ 42v
- ↑ 43r
- ↑ 43v
- ↑ 44r
- ↑ 44v
- ↑ 45r
- ↑ 45r
- ↑ 46r
- ↑ 46ב
- ↑ 47א
- ↑ 47v
- ↑ 48r-49r: illegible
- ↑ 49v
- ↑ 50א
- ↑ 50v
- ↑ 51r
- ↑ 51v
- ↑ 52r
- ↑ 52v
- ↑ 53r
- ↑ 53v
- ↑ 54r
- ↑ 54v
- ↑ 55r
- ↑ 55v
- ↑ 56r
- ↑ 56v
- ↑ 57r
- ↑ 57v
- ↑ 58r
- ↑ 58v
- ↑ 59r
- ↑ 59v
- ↑ 60r
- ↑ 60v
- ↑ 61r
- ↑ 61v
- ↑ 62r
- ↑ 62v
- ↑ 63r
- ↑ 63v
- ↑ 64r
- ↑ 64v
- ↑ 65r


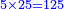
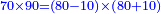
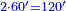
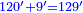
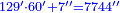
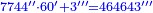
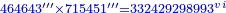
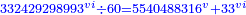
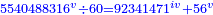
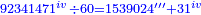
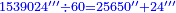
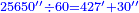
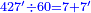
![\scriptstyle{\color{blue}{6:4=\left[4+\left(\frac{1}{3}\sdot6\right)\right]:4=\left[6+\left(\frac{1}{3}\sdot9\right)\right]:6=9:6}}](/mediawiki/images/math/c/4/3/c43c7c0237c19df5f8d69daf6dbcff52.png)