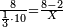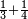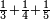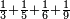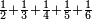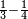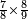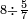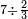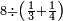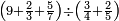Difference between revisions of "Arithmetic Textbook by Meir Shapira"
From mispar
(→Chapter Four: Division) |
(→Chapter on Fractions) |
||
| (92 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{#annotpage: time="1400-1500"}} | ||
{| | {| | ||
|- | |- | ||
| Line 4: | Line 5: | ||
== Introduction == | == Introduction == | ||
| − | |style="text-align:right;"|פתיחה | + | |style="width:45%;text-align:right;"|פתיחה |
|- | |- | ||
| | | | ||
| Line 15: | Line 16: | ||
|style="text-align:right;"|כמה שו"ת בחכמה זו ‫[...] | |style="text-align:right;"|כמה שו"ת בחכמה זו ‫[...] | ||
|- | |- | ||
| − | | | + | |In the name of He Who ''gives light to the whole world'' [Berakhot 60b] |
| − | |style="text-align:right;"|‫<ref>59r</ref>בשם המאיר לעולם | + | |style="text-align:right;"|‫<ref>59r</ref>בשם ''המאיר לעולם''‫<ref>ברכות ס, ב</ref> |
|- | |- | ||
| − | | | + | |He is hidden from all and nothing is hidden from Him. |
|style="text-align:right;"|והוא מכל נעלם ואין עמו העלם | |style="text-align:right;"|והוא מכל נעלם ואין עמו העלם | ||
|- | |- | ||
| − | | | + | |I start to explain some of the calculation methods in arithmetic and some of geometrical issues. |
|style="text-align:right;"|אחל לבאר קצת דרכי החשבון בחכמת המספר והקצת התשבורות | |style="text-align:right;"|אחל לבאר קצת דרכי החשבון בחכמת המספר והקצת התשבורות | ||
|- | |- | ||
| − | | | + | |My intention is to simplify the explanation as much as I can, so that it will be easier for the reader who is not well versed and will undoubtedly receive a great benefit in a short time without getting weary by the unfamiliar words, because every unfamiliar word that needs to be discussed - I will explain it in an explanatory note, in order not to confuse it with an explanation of a word that is not intended to be clarified in the work, and where necessary, I will add an additional explanation on the intended matter in an explanatory note, but I will not elaborate in the text itself, so that the reader can comprehend the matter intended in his knowledge and understanding without the misunderstanding that will occur from the length and the explanation of words, meaning in general an intentional explanation. |
|style="text-align:right;"|וכוונתי להקל בביאור תכלית האיפשר אצלי למען יקל על המעיין אשר לא הורגל ובלי ספק יקבל תועלת גדולה בזמן קצר בלי ליאות מן המלות הזרות כי כל מלה זרה אשר יבא הצרך לדבר בה אבאריה בהגהה כדי שלא אבלבל מכוון לבאר בביאו' המלה אשר אין כוונת החבור לבארה וכן במקום הצורך אבאר בהגה אחת תוספת ביאור על ענין המכוון ולא אאריך בעצם החבור כדי שיוכל המעיין לכלול [במ]דעו ובשכלו העניין המכוון בבלתי הטעאה אשר תקרה מצד האריכות ומצד ביאור דברי' ורי' בכלל ביאור מכוון | |style="text-align:right;"|וכוונתי להקל בביאור תכלית האיפשר אצלי למען יקל על המעיין אשר לא הורגל ובלי ספק יקבל תועלת גדולה בזמן קצר בלי ליאות מן המלות הזרות כי כל מלה זרה אשר יבא הצרך לדבר בה אבאריה בהגהה כדי שלא אבלבל מכוון לבאר בביאו' המלה אשר אין כוונת החבור לבארה וכן במקום הצורך אבאר בהגה אחת תוספת ביאור על ענין המכוון ולא אאריך בעצם החבור כדי שיוכל המעיין לכלול [במ]דעו ובשכלו העניין המכוון בבלתי הטעאה אשר תקרה מצד האריכות ומצד ביאור דברי' ורי' בכלל ביאור מכוון | ||
| + | |- | ||
| + | |The unfamiliar words that apear in this work are the words that I need to state, in order to designate a special term for the matter intended, so that we do not have to refer the intended matter with many words, but the intention will always be addressed by one or two word at most. | ||
| + | |style="text-align:right;"|ואמנם המלות הזרות אשר יקרו בזה החבור הם מלות אשר יבואוני הצורך לדבר בהם כדי להניח שם נפרד אל העניין המכוון כדי שלא נצטרך לזכר המכוון מלות רבות שיבא [..] אלא המכוון יבא תמיד זכרונו במלה א' או שתים על הרוב | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|כי יראה לי שבזה ג"כ תועלת גדולה למעיין כי העניין אשר יתכן זכרו במלה אחת ואם יבא זכרו במלות רבות הוא מעם גדול מבלבל בלי ספק בקלות מפני שלא יכלול עליו המדע אלא בטורח ואע"פ שהמלות רבות יבארו העניין המכוון ביאור מכוון מ"מ מפני שאין הכוונ' לבאר מהות העניין אשר יביא הצורך זכרו |
| − | מכוון מ"מ מפני שאין הכוונ' לבאר מהות העניין אשר יביא הצורך זכרו | ||
|- | |- | ||
| | | | ||
|style="text-align:right;"|והכוונ' לבאר עניין אחד אשר אל העניין ההוא ראוי להיות ידוע כל הנרצה בכל מה אשר | |style="text-align:right;"|והכוונ' לבאר עניין אחד אשר אל העניין ההוא ראוי להיות ידוע כל הנרצה בכל מה אשר | ||
| − | יבאו מן זכר הענייני' אשר ישתתפו בביאור העניין המכוון לבארו ואין ראוי להכניס בכלל הביאור ההוא ביאור הענייני' אשר ישתתף זכרם בביאור העניין המכוון לבארו כי זה מבלבל בלי ספק | + | יבאו מן זכר הענייני' אשר ישתתפו בביאור העניין המכוון לבארו |
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואין ראוי להכניס בכלל הביאור ההוא ביאור הענייני' אשר ישתתף זכרם בביאור העניין המכוון לבארו כי זה מבלבל בלי ספק | ||
|- | |- | ||
| | | | ||
|style="text-align:right;"|לכן ראוי להשים אל אלו הענייני' אשר יביא הצורך לזכרם הגהות יבואר בהם הכוונ' במלה הזרה אשר יביא הצורך לדבר בה | |style="text-align:right;"|לכן ראוי להשים אל אלו הענייני' אשר יביא הצורך לזכרם הגהות יבואר בהם הכוונ' במלה הזרה אשר יביא הצורך לדבר בה | ||
|- | |- | ||
| − | | | + | |And from the Lord of the world who stands at the top of the ladder, |
| − | |style="text-align:right;"|ומאת אדון העולם הנצב בראש הסלם והוא הסבה במציאות הנמצאות כלם אשאל העזר ואליו השבח וההודאה שהגדיל חסדו עמנו בתתו לנו שכל ומדע להשאיר לנו ברכה והנה אחר השבח וההודאה לאל ית' ושאלת העזר מאתו אחל בביאור המכוון לבארו ואומר | + | |style="text-align:right;"|ומאת אדון העולם הנצב בראש הסלם |
| + | |- | ||
| + | |Who is the cause of the existence of all beings, | ||
| + | |style="text-align:right;"|והוא הסבה במציאות הנמצאות כלם | ||
| + | |- | ||
| + | |I ask for help and to Him the praise and gratitude, | ||
| + | |style="text-align:right;"|אשאל העזר ואליו השבח וההודאה | ||
| + | |- | ||
| + | |For He has increased His grace upon us by giving us wisdom and knowledge, | ||
| + | |style="text-align:right;"|שהגדיל חסדו עמנו בתתו לנו שכל ומדע | ||
| + | |- | ||
| + | |To grant us a blessing. | ||
| + | |style="text-align:right;"|להשאיר לנו ברכה | ||
| + | |- | ||
| + | |So, after the praise and gratitude to the exalted God, | ||
| + | |style="text-align:right;"|והנה אחר השבח וההודאה לאל ית‫' | ||
| + | |- | ||
| + | |And asking Him for help, | ||
| + | |style="text-align:right;"|ושאלת העזר מאתו | ||
| + | |- | ||
| + | |I begin the explanation of what should be explained, | ||
| + | |style="text-align:right;"|אחל בביאור המכוון לבארו | ||
| + | |- | ||
| + | |And say: | ||
| + | |style="text-align:right;"|ואומר | ||
| + | |- | ||
| + | |This is how the number is explained according to the ways of every nation and language: | ||
| + | |style="text-align:right;"|<big>הנה</big> המספר מצד מה שמבואר מעניינו לפי דרכי כל אומה ולשון | ||
|- | |- | ||
| − | | | + | |1 is the beginning of all numbers and 9 is the end of all of them. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה א' הוא ראש המספרים כלם וט' סוף המספרי' כלם |
|- | |- | ||
| − | | | + | |Because, when we start counting 1, 2, 3, up to 9, we have no more units other than those chosen from these 9s up to the tens. |
|style="text-align:right;"|כי כאשר אנו מתחילי' למנות אב"ג עד ט' אין לנו מן האחדי' יותר זולת מה שנבחר מאלו הט' אל העשריות | |style="text-align:right;"|כי כאשר אנו מתחילי' למנות אב"ג עד ט' אין לנו מן האחדי' יותר זולת מה שנבחר מאלו הט' אל העשריות | ||
|- | |- | ||
| − | | | + | |When we start counting the tens - 10, 20, 30, up to 90 - the tens are 9. |
| − | |style="text-align:right;"|וכן כאשר נתחיל למנות העשיריות יכ"ל עד צ' הנה העשריות הם ט' | + | |style="text-align:right;"|וכן כאשר נתחיל למנות העשיריות יכ"ל עד צ' הנה העשריות הם ט‫' |
|- | |- | ||
| − | | | + | |Then, we reach the rank of hundreds and the hundreds also end in 9 hundreds. |
|style="text-align:right;"|ואח"כ נכנסים לכלל המאות וכן המאות סופם ט' מאות | |style="text-align:right;"|ואח"כ נכנסים לכלל המאות וכן המאות סופם ט' מאות | ||
|- | |- | ||
| − | | | + | |After that, we reach the rank of thousands and the end of the thousands is 9 thousands. |
| − | |style="text-align:right;"|אז אנו נכנסי' לכלל האלפי' וסוף האלפים הם ט' אלפי' | + | |style="text-align:right;"|אז אנו נכנסי' לכלל האלפי' וסוף האלפים הם ט' אלפי‫' |
|- | |- | ||
| − | | | + | |From there, we reach the rank of tens of thousands and the end of the tens of thousands is 9 tens of thousands. |
|style="text-align:right;"|משם אנו לכלל הרבבות וכן סוף הרבבות ט' רבבות | |style="text-align:right;"|משם אנו לכלל הרבבות וכן סוף הרבבות ט' רבבות | ||
|- | |- | ||
| − | | | + | |From there, we reach the hundreds of thousands and the hundreds of thousands also end in 9. |
| − | |style="text-align:right;"|ומשם אנו נכנסי' אל המאות באלפי' וכן המאות אלפים יכלו על ט' | + | |style="text-align:right;"|ומשם אנו נכנסי' אל המאות באלפי' וכן המאות אלפים יכלו על ט‫' |
|- | |- | ||
| − | | | + | |From there, we reach the millions [lit. thousands of thousands] and they also end in 9. |
| − | |style="text-align:right;"|ומשם אנו נכנסים אל האלף אלפי' וסופם ג"כ ט' | + | |style="text-align:right;"|ומשם אנו נכנסים אל האלף אלפי' וסופם ג"כ ט‫' |
|- | |- | ||
| − | | | + | |From there, we reach the tens of millions [lit. tens of thousands of thousands] and they also end in 9. |
| − | |style="text-align:right;"|ומשם אנו נכנסים אל הרבבות מאלף אלפים וסופם ג"כ ט' | + | |style="text-align:right;"|ומשם אנו נכנסים אל הרבבות מאלף אלפים וסופם ג"כ ט‫' |
|- | |- | ||
| − | | | + | |From there, we reach the hundreds of millions [lit. hundreds of thousands of thousands] . |
| − | |style="text-align:right;"|ומשם אנו נכנסי' אל המאות אלף אלפי' | + | |style="text-align:right;"|ומשם אנו נכנסי' אל המאות אלף אלפי‫' |
|- | |- | ||
| | | | ||
| Line 75: | Line 108: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<big>והנה</big> מפני שראו חכמי זאת המלאכה שכל מין ממיני המספר לפי זה האופן אינו מוסיף על ט' שמו ט' אותיות למנות בהם המספרי' כלם והם אבגד"הוזח"ט והאומות אשר אינם מאומתינו לוקחים מקום אלו ט' אותיות אחרי אשר הם ‫<ref>59v</ref>משתמשים בהם בכת' שלהם או מיחדים מקום ט' האותיות ט' סימנים מיוחדי' כל סימן עומד מקום אות מאלו האותיות והמכוון מכלם הוא כוונ' א' והנה כל אות מאלו האותיות לפעמי' הוא רומז כולל אחדי' כפי המספר אשר הוא מונח לו ולפעמי' רומז כך עשריות ולפעמי' מאות ולפעמי' אלפי' ולפעמי' רבבות אלפי' ולפעמי' מאות אלפים ולפעמי' אלפי אלפי' | + | |style="text-align:right;"|<big>והנה</big> מפני שראו חכמי זאת המלאכה שכל מין ממיני המספר לפי זה האופן אינו מוסיף על ט' שמו ט' אותיות למנות בהם המספרי' כלם והם אבגד"הוזח"ט והאומות אשר אינם מאומתינו לוקחים מקום אלו ט' אותיות אחרי אשר הם ‫<ref>59v</ref>משתמשים בהם בכת' שלהם או מיחדים מקום ט' האותיות ט' סימנים מיוחדי' כל סימן עומד מקום אות מאלו האותיות והמכוון מכלם הוא כוונ' א' והנה כל אות מאלו האותיות לפעמי' הוא רומז כולל אחדי' כפי המספר אשר הוא מונח לו ולפעמי' רומז כך עשריות ולפעמי' מאות ולפעמי' אלפי' ולפעמי' רבבות אלפי' ולפעמי' מאות אלפים ולפעמי' אלפי אלפי‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<big>וזה הכלל</big> כל אות רומז על איזה מין שתרצה ממיני המספר במקצת הפעמי' | + | |style="text-align:right;"|<big>וזה הכלל</big> כל אות רומז על איזה מין שתרצה ממיני המספר במקצת הפעמי‫' |
|- | |- | ||
| | | | ||
| Line 90: | Line 123: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן הג' על שלשה ועל שלשי' ועל ג' מאות ועל ג' אלפי' וכן על ג' מכל מין מן המספרי' | + | |style="text-align:right;"|וכן הג' על שלשה ועל שלשי' ועל ג' מאות ועל ג' אלפי' וכן על ג' מכל מין מן המספרי‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן הד' על על ד' מכל מין מן המספרי' | + | |style="text-align:right;"|וכן הד' על על ד' מכל מין מן המספרי‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן ה' על חמשה מכל מין מן המספרי' | + | |style="text-align:right;"|וכן ה' על חמשה מכל מין מן המספרי‫' |
|- | |- | ||
| | | | ||
| Line 111: | Line 144: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואמנם כל אלו אות מאלו האותיות אם הוא ראשון בסדר האותיות אשר עמ[ל] או שהוא יחידי אז הוא מורה על אחדי' מפני שאחדי' הם הקודמי' בטבע המספר כי לא ימצא עשריות זולת אחדי' כי עניין העשריות הוא שהם קבוץ אחדי' | + | |style="text-align:right;"|ואמנם כל אלו אות מאלו האותיות אם הוא ראשון בסדר האותיות אשר עמ[ל] או שהוא יחידי אז הוא מורה על אחדי' מפני שאחדי' הם הקודמי' בטבע המספר כי לא ימצא עשריות זולת אחדי' כי עניין העשריות הוא שהם קבוץ אחדי‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואם א' מאלו האותיות שני בסדר אז הוא מורה על עשריות כי העשריות קודמי' לשאר מספרי' כי המאה אינו אלא קבוץ עשריות ומאוחרי' לאחדי' ולכן כאשר הם שניים בסדר אז יורו על העשריו' | + | |style="text-align:right;"|ואם א' מאלו האותיות שני בסדר אז הוא מורה על עשריות כי העשריות קודמי' לשאר מספרי' כי המאה אינו אלא קבוץ עשריות ומאוחרי' לאחדי' ולכן כאשר הם שניים בסדר אז יורו על העשריו‫' |
|- | |- | ||
| | | | ||
| Line 123: | Line 156: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן כל אות שהוא חמישי בסדר הוא רבבות כי הרבבות אחר האלפי' | + | |style="text-align:right;"|וכן כל אות שהוא חמישי בסדר הוא רבבות כי הרבבות אחר האלפי‫' |
|- | |- | ||
| | | | ||
| Line 129: | Line 162: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן האות שהוא שביעי בסדר הוא מורה על אלפי אלפי' | + | |style="text-align:right;"|וכן האות שהוא שביעי בסדר הוא מורה על אלפי אלפי‫' |
|- | |- | ||
| | | | ||
| Line 153: | Line 186: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|והנה אם יחובר לאלו האותיות אות רביעי היה מורה האות הרביעית אלפי' | + | |style="text-align:right;"|והנה אם יחובר לאלו האותיות אות רביעי היה מורה האות הרביעית אלפי‫' |
|- | |- | ||
| | | | ||
| Line 159: | Line 192: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואם היה סדרם כך ה'ב'א'ג' אז יורו אל חמשה עשרים ומאה וג' אלפי' ‫<ref>60r</ref>אלפי' | + | |style="text-align:right;"|ואם היה סדרם כך ה'ב'א'ג' אז יורו אל חמשה עשרים ומאה וג' אלפי' ‫<ref>60r</ref>אלפי‫' |
|- | |- | ||
| | | | ||
| Line 165: | Line 198: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן הששי מאות אלפי' | + | |style="text-align:right;"|וכן הששי מאות אלפי‫' |
|- | |- | ||
| | | | ||
| Line 177: | Line 210: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ע'ד'מ' הנה רצינו מספ' עשיריות בזולת מין אחר והנה האותיות אשר יורו על העשריות הם אשר הם שניים | + | |style="text-align:right;"|ע'ד'מ' הנה רצינו מספ' עשיריות בזולת מין אחר והנה האותיות אשר יורו על העשריות הם אשר הם שניים ב{{#annot:term|206,2446|C7oL}}מערכה{{#annotend:C7oL}} ואם נשים לפניהם א' מן האותיות התשעה שזכרנו שהם א'ב'ג' ד'ה'ו' ז'ח'ט' הנה אותו האות אשר הוא ראשון במערכה הוא מורה ג"כ על מין מן המספר והוא שיורה על אחדי' והרצון לנו שלא יהיו לנו מיני אחדים קודמים בזה המספר אשר אנו רומזי' עליו אלא יהיה רק עשריות ובעבור שלא יתכן לנו אות רומז על העשריות אלא האות אשר הוא שנית במערכה הנה כאשר נרצה שלא ישותף אליו מין מן המספר קודם לו ושיהיה הוא עם זה מכוון שנית למערכה הנה אנו צריכים לכתו' לפניו אות א' או רושם אחר שלא יורה בעצמו מאומה ושלא יהיה האות ההוא או הרושם ההוא מכוון לדבר רק להורות שהוא הראשון במערכה כדי שיראה המערכת המכוונת באותיות אשר יבאו אחריו וכן הדין בעצמו באי זה מקום שיהיה במערכה כאשר יהיה המכוון באותו המקום שלא יהיה שם מספר כלל נשים במקום ההוא האות אשר לא יורה בעצמו מאומה או רושם |
|- | |- | ||
| | | | ||
| Line 228: | Line 261: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ולמאות אלפי' בזולת מספר קודם תשים 00000 ואח"כ א' למאה אלפים ב' לשני מאות אלפי' וכן שאר האותיות לשאר המאות אלפי' | + | |style="text-align:right;"|ולמאות אלפי' בזולת מספר קודם תשים 00000 ואח"כ א' למאה אלפים ב' לשני מאות אלפי' וכן שאר האותיות לשאר המאות אלפי‫' |
|- | |- | ||
| | | | ||
| Line 243: | Line 276: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|המשל בזה הנה א'0'ג' | + | |style="text-align:right;"|המשל בזה הנה א'0'ג‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה הא' מורה אחד מן האחדי' | + | |style="text-align:right;"|הנה הא' מורה אחד מן האחדי‫' |
|- | |- | ||
| | | | ||
| Line 252: | Line 285: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|משל אחר 0'ב'ג' | + | |style="text-align:right;"|משל אחר 0'ב'ג‫' |
|- | |- | ||
| | | | ||
| Line 258: | Line 291: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ובעבור זה הב' שנית למערכה ומורה עשרי' | + | |style="text-align:right;"|ובעבור זה הב' שנית למערכה ומורה עשרי‫' |
|- | |- | ||
| | | | ||
| Line 264: | Line 297: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|משל אחר 0'ד'0'ה' | + | |style="text-align:right;"|משל אחר 0'ד'0'ה‫' |
|- | |- | ||
| | | | ||
| Line 279: | Line 312: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הנה כבר יספיק למשכיל אופן הצורך ב0' | + | |style="text-align:right;"|הנה כבר יספיק למשכיל אופן הצורך ב0‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ועל איזה אופן ישתמשו אלו העשרה אותיות לרמוז בהם כל מספר הן מספר ממין אחד או מורכב ממין אחד או מינים רבים עד שלא ימלט שום מספר מלרמוז אליו באלו האותיות העשרה ר"ל א'ב'ג' ד'ה'ו' ז'ח'ט' 0' | + | |style="text-align:right;"|ועל איזה אופן ישתמשו אלו העשרה אותיות לרמוז בהם כל מספר הן מספר ממין אחד או מורכב ממין אחד או מינים רבים עד שלא ימלט שום מספר מלרמוז אליו באלו האותיות העשרה ר"ל א'ב'ג' ד'ה'ו' ז'ח'ט' 0‫' |
|- | |- | ||
| | | | ||
| Line 291: | Line 324: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויספיק מה שבארתי להבנת אופן הוראת אלו העשרה אותיות על המספרי' לפי | + | |style="text-align:right;"|ויספיק מה שבארתי להבנת אופן הוראת אלו העשרה אותיות על המספרי' לפי דרך חכמי החשבון |
| − | דרך חכמי החשבון | ||
|- | |- | ||
| | | | ||
| Line 315: | Line 347: | ||
== Chapter One: Addition == | == Chapter One: Addition == | ||
| − | |style="text-align:right;"|‫<ref>61r</ref><big>השער הראשון</big> הוא שער | + | |style="text-align:right;"|‫<ref>61r</ref><big>השער הראשון</big> הוא שער ה{{#annot:term|154|hayQ}}חבור{{#annotend:hayQ}} |
|- | |- | ||
| | | | ||
| Line 324: | Line 356: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ואחר זאת ההודעה נשוב אל עניין השער שהוא לחבר שני מספרי' או יותר יחד | + | |style="text-align:right;"|ואחר זאת ההודעה נשוב אל עניין השער שהוא {{#annot:term|178|gFRx}}לחבר{{#annotend:gFRx}} שני מספרי' או יותר יחד |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ונאמר על דרך הכלל שלעולם נכתו' כל המספרי' אשר אנו רוצים לחברם זה תחת זה ונכוין בדרך הכתיבה שיהיו נכתבי' באפן שיהיו כל האותיות אשר הם ממערכ' אחת זה למעלה מזה בטור אחת ואחר שיהיה הכת' על זה האופן אז נתחיל במה שהוא בטור הראשון שהם | + | |style="text-align:right;"|ונאמר על דרך הכלל שלעולם נכתו' כל המספרי' אשר אנו רוצים לחברם זה תחת זה ונכוין בדרך הכתיבה שיהיו נכתבי' באפן שיהיו כל האותיות אשר הם ממערכ' אחת זה למעלה מזה בטור אחת ואחר שיהיה הכת' על זה האופן אז נתחיל במה שהוא בטור הראשון שהם ב{{#annot:term|203|Thbp}}מערכה{{#annotend:Thbp}} הראשונה ותחבר כל אותיות המערכה ההיא וכל מה שיעלה לעשיריות תכתו' אותם העשיריות בטור הסמוכה לה שהיא מן המערכה שאחריה ומה שישאר בטור הראשונה מן האחדי' או שלא הגיע לכלל עשיריות אותו תכתו' באות א' כולל מחובר המספר אשר עלה ממקובץ האותיות שהיו במערכה הראשונ' או הנשאר על העשיריות בטור הראשונ' ממקובץ אותיותיה ואח"כ תקבץ ג"כ כל מה שתמצא בטור השנית שהוא מן המערכה השנית ואם עלה אות מן העשיריות של הראשונ' הוא בכלל זה הטור ולעולם תחשוב מקובץ אותיות של איזה טור אשר תשתמש בה כאילו הם אחדי' ואין צורך להביט מאיזה מין אותיות הטור אשר תקבץ וכל פעם אשר יעלו לך עשיריות אז תכתוב האות אשר יורה על העשיריות ההם בטור שאחריה ר"ל הטור שהיא מהמערכה הסמוכה לה וכן תעשה באותיות בטור השלישי והרביעי ובאותיות כל טור מאיזה מערכה שהיא ר"ל הטור ולעולם העשיריות אשר יעלו ממקובץ תכתו' באות אשר כולל אותם בטור שאחר הטור ההיא וכל אשר לא יגיע לעשיריות או שישאר על העשיריות תבתו' באות כולל אותם האחדי' בטור ההיא אשר המקובץ מן האותיות מאותה הטור כדי שישארו אותם האחדים ממין המערכה אשר נולדו בה |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|והמשל הנה רצינו לחבר מספר א'ב'ג'ד' ומספר ב'ג'ד'ה'ו' ומספר ג'ד'ה'ו'ז' ומספר ה'ו'ז'ח'ט' | + | *Example: we wish to sum up the numbers 4321, 65432, 76543, and 98765 |
| + | :<math>\scriptstyle4321+65432+76543+98765</math> | ||
| + | |style="text-align:right;"|והמשל הנה רצינו לחבר מספר א'ב'ג'ד' ומספר ב'ג'ד'ה'ו' ומספר ג'ד'ה'ו'ז' ומספר ה'ו'ז'ח'ט‫' | ||
|- | |- | ||
| | | | ||
| Line 382: | Line 416: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|והב' שהם עשיריות תכתוב בטור החמישית ויעלה המקובץ מאותיות הטור החמישי ד' ב' | + | |style="text-align:right;"|והב' שהם עשיריות תכתוב בטור החמישית ויעלה המקובץ מאותיות הטור החמישי ד' ב‫' |
|- | |- | ||
| | | | ||
| Line 388: | Line 422: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ולפי זה יעלה המחובר מאלו הד' מספרי' א'ו'0'ה'ד'ב' שהם אחד וששים וחמשה וארבעי' אלף ומאתים אלפי' | + | |style="text-align:right;"|ולפי זה יעלה המחובר מאלו הד' מספרי' א'ו'0'ה'ד'ב' שהם אחד וששים וחמשה וארבעי' אלף ומאתים אלפי‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|משל אחר הרי שרצינו לחבר א'ב'ג'ד'ה' עם א'ב'ג'ד'ה' | + | *Another example: we wish to sum 54321 with 54321 |
| + | :<math>\scriptstyle54321+54321</math> | ||
| + | |style="text-align:right;"|משל אחר הרי שרצינו לחבר א'ב'ג'ד'ה' עם א'ב'ג'ד'ה‫' | ||
|- | |- | ||
| | | | ||
| Line 420: | Line 456: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויעלה המקובץ מאלו השני מספרי' ב'ד'ו'ח'0'א' | + | |style="text-align:right;"|ויעלה המקובץ מאלו השני מספרי' ב'ד'ו'ח'0'א‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|משל אחר הרי שרצינו לחבר ג' | + | *Another example: we wish to sum 103 with 280 |
| + | :<math>\scriptstyle103+280</math> | ||
| + | |style="text-align:right;"|משל אחר הרי שרצינו לחבר ג'0'א' עם 0'ח'ב‫' | ||
|- | |- | ||
| | | | ||
| Line 452: | Line 490: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויעלה המקובץ מהם ג'ח'ג' | + | |style="text-align:right;"|ויעלה המקובץ מהם ג'ח'ג‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|משל אחר הנה רצינו לחבר א'ג'0'ד' עם ד'0'ג'א' ועם 0'ג'א'ד' ועם 0'ד'ג'ט' ועם א'0'ד'ג' | + | *Another example: we wish to sum 4031 with 1304, 4130, 9340, and 3401 |
| + | :<math>\scriptstyle4031+1304+4130+9340+3401</math> | ||
| + | |style="text-align:right;"|משל אחר הנה רצינו לחבר א'ג'0'ד' עם ד'0'ג'א' ועם 0'ג'א'ד' ועם 0'ד'ג'ט' ועם א'0'ד'ג‫' | ||
|- | |- | ||
| | | | ||
| Line 496: | Line 536: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ויעלה המחובר מאלו המספרי' ו'0'ב'ד'א' | + | |style="text-align:right;"|ויעלה המחובר מאלו המספרי' ו'0'ב'ד'א‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|משל אחר הרי שרצינו לחבר א' עם ט'ט'ט'ט'ט' ויהיה תמונת הכת' כך | + | *Another example: we wish to sum 1 with 99999 |
| + | :<math>\scriptstyle1+99999</math> | ||
| + | |style="text-align:right;"|משל אחר הרי שרצינו לחבר א' עם ט'ט'ט'ט'ט‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויהיה תמונת הכת' כך | ||
|- | |- | ||
| | | | ||
| Line 525: | Line 570: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|והנה כאשר נחבר א' על ט' שלמעלה ממנו יעלה 0א' נניח ה0 מקום ט' העליונה והא' נכתו' במערכה השנית ולשם ג"כ ט' | + | |style="text-align:right;"|והנה כאשר נחבר א' על ט' שלמעלה ממנו יעלה 0א' נניח ה0 מקום ט' העליונה והא' נכתו' במערכה השנית ולשם ג"כ ט‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכאשר נחבר הא' עם הט' יעלה 0'א' ישאר ה0' במערכה השנית מקום הט' והא' נכתו' במערכה השלישית ולשם ג"כ ט' | + | |style="text-align:right;"|וכאשר נחבר הא' עם הט' יעלה 0'א' ישאר ה0' במערכה השנית מקום הט' והא' נכתו' במערכה השלישית ולשם ג"כ ט‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכאשר נחבר הא' עמה יעלה 0"א ישאר ה0 במערכה השלישית מקום הט' והא' נכתו' במערכ הרביעית ולשם ג"כ ט' | + | |style="text-align:right;"|וכאשר נחבר הא' עמה יעלה 0"א ישאר ה0 במערכה השלישית מקום הט' והא' נכתו' במערכ הרביעית ולשם ג"כ ט‫' |
|- | |- | ||
| | | | ||
| Line 551: | Line 596: | ||
== Chapter Two: Subtraction == | == Chapter Two: Subtraction == | ||
| − | |style="text-align:right;"|השער השני והוא שער | + | |style="text-align:right;"|<big>השער השני</big> והוא שער ה{{#annot:term|155|LCca}}חסור{{#annotend:LCca}} |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|והכוונה בו לחסר מספר ממספר שהוא יותר גדול ממנו או שוה לו הדרך לחסר מספר ממספר אחר הוא שלעולם תכתו' לפניך המספר אשר תרצה לחסר ממנו ותכתו' תחתיו המספר אשר תרצה לחסר אותו ותכוין בכתיבה לכתו' אות תחת אות ר"ל מערכה תחת מערכה ואח"כ תתחיל לחסר האות האחרון של המספר אשר תרצה לחסר אות מן האות אשר למעלה המנו ולעולם תחשוב האות אשר תרצה לחסר אותו כאילו הוא אחדים ‫<ref>62r</ref>ולא תביט מאיזה מן הוא וכן תחשוב גם לאחדי' האות שלמעלה המנו | + | |style="text-align:right;"|והכוונה בו {{#annot:term|181|ydpy}}לחסר{{#annotend:ydpy}} מספר ממספר שהוא יותר גדול ממנו או שוה לו הדרך לחסר מספר ממספר אחר הוא שלעולם תכתו' לפניך המספר אשר תרצה לחסר ממנו ותכתו' תחתיו המספר אשר תרצה לחסר אותו ותכוין בכתיבה לכתו' אות תחת אות ר"ל מערכה תחת מערכה ואח"כ תתחיל לחסר האות האחרון של המספר אשר תרצה לחסר אות מן האות אשר למעלה המנו ולעולם תחשוב האות אשר תרצה לחסר אותו כאילו הוא אחדים ‫<ref>62r</ref>ולא תביט מאיזה מן הוא וכן תחשוב גם לאחדי' האות שלמעלה המנו |
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה אם האות התחתון אחד פחות במספרו מן האות העליון כאשר רואים שניהם כאילו הם מין אחדים אז תגרע מן העליון ומה שישאר מן העליון תרשום מקום האות העליון אשר גרעת ממנו ולא תביט לדבר אחר |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואמנם אם האות התחתון יותר מן העליון אז מ"מ תחשוב האות העליון כאילו הוא ממין אחדי' ומה שאחריו תחשוב לעשיריות כי הם עשיריות בערך אל מה שקדם בסמוך וכן תחשוב בשלישיים לאות העליון למאות והרביעית לאלפי' אם תצטרך אל האות הרביעי אחריו וכן שאר כל האותיו' תשים אותם במערכה שראש המערכה האות אשר למעלה מהתחתון אשר אנו מכוונים לגרוע אותו ואח"כ תתחיל {{#annot:term|181|x9f0}}לגרוע{{#annotend:x9f0}} האות התחתון מן האות העליון ומה שיבא אחריו והנשאר אחר הגרעון הנח מקום מה שהיה למעלה קודם הגרעון ועל דמות זה האופן תגרע כל אותיות של המספר התחתון מן האות מה שעומד למעלה ממנו והלאה וישאר לך אחר גרעון המבוקש |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *Example: we wish to subtract 8888 from 9999 |
| + | :<math>\scriptstyle9999-8888</math> | ||
| + | |style="text-align:right;"|המשל הנה רצינו לגרוע ח'ח'ח'ח' מן ט'ט'ט'ט‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה נכתו' למעלה מספר ט'ט'ט'ט' אשר אנו רוצים לגרוע מהם ונכתו' תחתיהם ח'ח'ח'ח' אשר אנו רוצים לגרוע אותו ויהיה תמונת הכת‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align: | + | :{|class="wikitable" style="color:blue; text-align:center;" |
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
|- | |- | ||
| + | |9||9||9||9 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |8||8||8||8 | ||
| + | |} | ||
| + | |} | ||
| | | | ||
| − | |style="text-align: | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" |
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
|- | |- | ||
| − | | | + | |ט||ט||ט||ט |
| − | |style=" | + | |-style="border-bottom: 1px solid black;" |
| − | + | |ח||ח||ח||ח | |
| + | |} | ||
| + | |} | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה הנשאר מן העליון אחר שאנו גורעים התחתון ממנו א'א'א'א‫' |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *Another example: we wish to subtract 2030 from 2103 |
| + | :<math>\scriptstyle2103-2030</math> | ||
| + | |style="text-align:right;"|משל אחר הנה אנו רוצים לגרוע 0'ג'0'ב' מן ג'0'א'ב‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה תמונת הכת' כך |
|- | |- | ||
| | | | ||
| − | |style="text-align: | + | :{|class="wikitable" style="color:blue; text-align:center;" |
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
|- | |- | ||
| + | |2||1||0||3 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |2||0||3||0 | ||
| + | |} | ||
| + | |} | ||
| | | | ||
| − | |style="text-align: | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" |
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
| + | |- | ||
| + | |ב||א||0||ג | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ב||0||ג||0 | ||
| + | |} | ||
| + | |} | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|והנה לא | + | |style="text-align:right;"|הנה כאשר אנו מתחילי' לגרוע ב' של 0'ג'0'ב' מן ב' של ג'0'א'ב' לא ישאר במעלה הרביעי דבר וגרעון 0 מן הא' ישאר א' מפני שאין הם מספר לעצמו והנה כאשר אנו רוצים לגרוע ג' מן 0' שהוא למעלה ממנו לא יתכן מפני שאין ה0' בעצמו מספר ולכן נגרע הג' מן הא' אשר היא אחר ה0' והיא ממין עשיריות בערך למה שהיא ממערכה קודם לה והנה כאשר נחסר ג' מן 0א ישאר ז' ונכתו' הז' מקום ה0' מפני שאילו הז' הם ממקום ממין המערכה אשר ה0' בה ואח"כ נגרע ה0' מן ג' שעליה וישאר ג' מפני שאין ה0' מספר ובעבור זה לא יחסר גרעונו מן המספר הנגרע ממנו כי אין אנו גורעים ממנו ויהיה לפי זה מן ג'0'א'ב' אחר שגרענו ממנו 0'ג'0'ב' הנשאר ג"ז |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|משל אחר הרי שרצינו | + | *Another example: we wish to subtract 5432 from 54321 |
| + | :<math>\scriptstyle54321-5432</math> | ||
| + | |style="text-align:right;"|משל אחר הרי שרצינו לגרוע מן המספר של א'ב'ג'ד'ה' מספר ב'ג'ד'ה‫' | ||
|- | |- | ||
| | | | ||
| Line 619: | Line 684: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align: | + | :{|class="wikitable" style="color:blue; text-align:center;" |
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
|- | |- | ||
| + | |5||4||3||2||1 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | ||5||4||3||2 | ||
| + | |} | ||
| + | |} | ||
| | | | ||
| − | |style="text-align: | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" |
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
| + | |- | ||
| + | |ה||ד||ג||ב||א | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | ||ה||ד||ג||ב | ||
| + | |} | ||
| + | |} | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה כאשר נתחיל לגרוע מן ד' שלמעלה המנה לא יתכן ובעבור זה נגרע הה' מן ד'ה' שהוא ארבע וחמשים כערך לה' התחתונה וכאשר נגרע ה' מן ד'ה' ישאר מקום ד"ה ט"ד |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואח"כ נגרע ד' מן ג' שלמעלה המנה ולא יתכן ולכן נגרע ד' מן ג' ומה שאחריה והוא ט' מפני שכך נשאר מצד מה שגרענו מקום והנה כאשר אנו גורעים ד' מן ג'ט' ישאר מקום ג"ט ט"ח |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואח"כ אנו גורעים ג"כ ג' מן ב"ט בעבור שלא נוכל לגרוע הג' מן הב' לבד וישאר מקום ב"ט ט"ח |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואח"כ נגרע ב' מן א"ט וישאר מקום א"ט ט"ח ולפי זה ישאר מקום ‫<ref>62v</ref>א'ב'ג'ד'ה' אחר שגרענו מהם ב'ג'ד'ה' ט'ח'ח'ח'ד' והוא המבוקש |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *Another example: we wish to subtract 54 from 4321 |
| − | + | :<math>\scriptstyle4321-54</math> | |
| − | + | |style="text-align:right;"|משל אחר הרי שרצינו לחסר ד'ה' מן אבגד | |
|- | |- | ||
| | | | ||
| − | + | |style="text-align:right;"|ויהיה תמונת הכתב כך | |
| − | |||
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | |style="text-align: | + | :{|class="wikitable" style="color:blue; text-align:center;" |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| + | |4||3||2||1 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || ||5||4 | ||
| + | |} | ||
| + | |} | ||
| | | | ||
| − | |style="text-align: | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
| − | + | |- | |
| − | ג | + | |ד||ג||ב||א |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | | || ||ה||ד | |
| − | + | |} | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה לא נוכל לחסר ה' מן ב' שלמעלה המנה לבד ולכן נחסר אותה מן ב'ג' וישאר מקום ב'ג' ז'ב' וכן נחסר ד' מן א'ז' ישאר מקום א'ז' ז'ו' ולפי זה יהיה הנשאר מן א'ב'ג'ד' אחר שגרענו מהם ד'ה' ז'ו'ב'ד‫' |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ב' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ג | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | *Another example: we wish to subtract 54 from 4321 |
| − | + | :<math>\scriptstyle4321-54</math> | |
| − | + | |style="text-align:right;"|משל אחר הנה רצינו לחסר ד'ה' מן א'ב'ג'ד‫' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ג' | ||
| − | |||
| − | ד | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה תמונת הכת' כך |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | + | :{|class="wikitable" style="color:blue; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| + | |4||3||2||1 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || ||5||7 | ||
| + | |} | ||
| + | |} | ||
| | | | ||
| − | |style="text-align: | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style=" | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
| − | + | |- | |
| − | + | |ד||ג||ב||א | |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | | || ||ה||ז | |
| − | + | |} | |
| − | + | |} | |
| − | |||
| − | ב | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה לא נוכל לחסר ה' מן ב' שלמעלה המנה |
| − | + | |- | |
| − | + | | | |
| − | + | *Another example: we wish to subtract 43 from 4021 | |
| − | + | :<math>\scriptstyle4021-43</math> | |
| − | + | |style="text-align:right;"|משל אחר הרי שרצינו לחסר מן א'ב'0'ד' ג'ד‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ויהיה תמונת הכת' כך | |
| − | + | |- | |
| − | + | | | |
| − | + | :{|class="wikitable" style="color:blue; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | + | |- | |
| − | + | |4||0||2||1 | |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | | || ||4||3 | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | אחר | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | הרי שרצינו | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | לחסר | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ויהיה | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | |style="text-align: | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" |
| − | + | |- | |
| − | + | | | |
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | + | |- | |
| − | + | |ד||0||ב||ד | |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | | || ||ד||ג | |
| − | + | |} | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|והנה לא נוכל לחסר ד' מן ב' שלמעלה ממנה לבד וכאשר נצטרך לגרוע הד' מן ב0' כי ה0' הוא האות שאחר הב' הנה ה0' אינ' מספר בעצמו וא"כ לא יתכן לגרוע הד' גם מאלו השנים ולכן נגרע הד' מן ב'0'ד' ויהיה הד' של ב'0'ד' מאות בערך אל ד' התחתונה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וכאשר נחסר ד' מן ב'0'ד' ישאר מקום ב'0'ד' ח'ט'ג‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כי כאשר לקחנו מן ד' מאות מאה נשארו ג' מאות | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וכאשר לקחנו מן המאה עשרה ליקח מהם ה' נשא' ט' מקום העשיריות | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וכאשר לקחנו מן העשרה ד' נשארו ו' ועו' יש ב' אחדי' שהם למעלה מהד' הרי ח' וא"כ נשארו ח'ט'ג' מקום ב'0'ד' ואח"כ נחסר ג' מן א'ח' וישארו ח'ז' מקום א'ח' ויהיה הנשאר בכלל לפי זה ח'ז' ט'ג‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | *Another example: we wish to subtract 1 from 100000 | |
| − | + | :<math>\scriptstyle100000-1</math> | |
| − | + | |style="text-align:right;"|משל אחר הרי שרצינו לגרוע א' מן 0'0'0'0'0'א‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ויהיה תמונת הכת' כך | |
| − | + | |- | |
| − | + | | | |
| − | + | :{|class="wikitable" style="color:blue; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | + | |- | |
| − | + | |1||0||0||0||0||0 | |
| − | מן | + | |-style="border-bottom: 1px solid black;" |
| − | + | | || || || || ||1 | |
| − | + | |} | |
| − | + | |} | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | + | |- | |
| − | + | |א||0||0||0||0||0 | |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | | || || || || ||א | |
| − | + | |} | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|והנה לא נוכל לחסר הא' מן ה0 שלמעלה המנה וכן לא נוכל לחסר אותה מן ה0 ולא מן 000 ולא מן 0000 ולא מן 00000 ולכן אנו צריכים לחסר אותה מן 00000א וככה נעשה הנה הא' של 00000א היא מאות אלפי' נכתו' במערכה במעלה החמישית ט' מקום שהיה א' במערכה הששית ולא יהיה במערכה הששי' דבר והנה ט' במערכה החמישית היא תשעים אלף וא"כ יש עוד בידינו עשרה אלפים לגרוע מהם אחד ולא נצטרך לכלום ולכן נשאיר בידינו אלף לגרוע מהם ונכתו' ט' אלפים במערכה הרביעית מקום ה0' שהיה שם והנה ג"כ לא נצטרך אל האלף בכלל ולכן נכתו' ט' במערכה השלישית מקום ה0' שהיה שם ויהיה הט' ההיא רומז לט' מאות וישארו עוד בידינו מאה לגרוע מהם אחד ולא נצטרך אל כל המאה בכלל ולכן נכתו' ט' במערכה השנית מקום ה0' שהוא שם וישארו עוד בידינו עשרה ליקח מהם הא' וכאשר נחסר א' מעשרה ישאר ט' נכתו' אותם במערכה הראשונה מקום ה0' שהוא שם ויהיה הנשאר בכלל ט'ט'ט'ט'ט‫' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|הנה זה מה שזכרנו מביאור זה השער ומשליו לתוספת הביאור יספיק מאד לכל בעל הבנה כי הדברי' מושכלי' קרובים למושכל ראשון ולכן ראיתי כי אין צורך להאריך יות' כי כבר הארכנו מאד בהרבות המשל אלא שכוונתנו להיות זה הביאור רחב שנה שאיפשר שישתבש המעיין ‫<ref>63r</ref>בעצמות ביאור דרך החסור יקח רושם מן המשלים עד שיקיף המכוון ומעתה נפסוק דבור מזה השער ונחל בביאור שער הכפל | |
| − | + | |} | |
| − | + | {| | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | נוכל | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | == Chapter Three: Multiplication == | ||
| − | + | |style="text-align:right;"|<big>השער הג' והוא שער ה{{#annot:term|156|GjWo}}כפל{{#annotend:GjWo}}</big> | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|לדעת לכפול מספר איזה מספר שיהיה אל איזה מספר שיהיה ר"ל לדעת המקובץ מן המספר כאשר ילקח אותו המספר שני פעמי' או ג' פעמי' או מספר פעמים הרבה איזה ריבוי שיהיה | |
| − | + | |- | |
| − | + | | | |
| − | אותו המספר | + | |style="text-align:right;"|ע'ד'מ' הרי שרצינו לדעת מספר העשרי' כמה יעלה מקובצו שלשים פעמ' או פעמי' יתרי' או פחותי' כפי מה שרצינו וכן כל מספר אשר אנו רומזי' אליו לדעת קבוצו מפעמי' יותר מפעם איזה פעמי' שאנו רוצים |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|והנה לך לדעת שאין צורך להטריד המחשבה בחשבון הכפל רק בכפל האחדים על האחדי' כי מצד מה שיבואר לנו המקובץ מכפל אחדים על אחדים יבואר לנו ג"כ יבואר לנו ג"כ המקובץ מכפל מינים אחרי' זולת האחדי' על האחדים או זולתם | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|והמשל מצד מה שאנו יודעים שג' פעמי' ג' הם של ט' אחדים כאשר היו כאשר היו שני הג' אשר כפלנו אחדי' מאותו הצד אנו יודעי' שג' אחדים פעמי' פעמי' ג' עשיריות הם ט' אבל ט' ממין מערכה מיוחדת וכן ג' עשיריות פעמי' ג' מאות הם ט' ממין מערכה מיוחדת וכן ג' עשריות פעמי' ג' מאות וכן מאיזה מין או מינים שהיו שני הג' אשר נכפלו יהיה לעולם המקובץ ט' כמו שהוא מן האחדי' אלא שיהיה חלוף ביניהם מצד המערכה ולא בזולת זה וכל בכל שאר ט' האותיות מאיזה מערכה שיהיו יהיה מקובץ הכפל מהם שוה מצד המספר אלא שיתחלפו במערכה ובעבור זה יהיה חילוף בין מיני המספר ר"ל ע'ד'מ' שקצת יהיו אחדים וקצתם עשיריות או מאות או אלפי' וזולת אלו והנה אחר שהענין כן אין אנו צריכים להטריד המחשבה בחשבון רק להוציא כמות כפל האחדי' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כי הנה אם אנו רוצים לדעת ע'ד'מ' כמה שלשים פעמי' שלשים לא נצטרך לחשוב רק כמות שלשה פעמי' שלשה ר"ל ג"פ ג' שהם האותיות אשר ירמוז לשלשים פעמים שלשים | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וכן אם אנו רוצים לדעת שלשים פעמים ששים לא נצטרך לדעת רק כמות ג' פעמי' ו' שהם האותיות אשר ירמזו לשלשים ולששים וכן בכל מיני שאר מיני המספר | |
| − | אנו | + | |- |
| − | + | | | |
| − | + | |style="text-align:right;"|ואמנם לדעת מאיזה מערכה הם האותיות אשר יעלו ממקובץ הכפל זה יבואר מצד סדר הכתיבה אשר ראוי לכתו' אל אופני שני המספרי' אשר הכוונה לכפול האחד על האחר | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וסדר הכת' הוא כך שיהיה אחד מן המספרי' נרשם לפניך ואח"כ תברור לך מן המספר ההוא אות א' שהוא האות הראשון ותכתוב תחת האות ההיא המספר שתרצה לכפול אליו באופן שיהיה התחלת המספר השני תחת האות ההוא ומשם והלאה ישאר סדרו אות תחת אות ר"ל אותיות המספר השני יהיו מהתחלתם מכוונים אות תחת אות ואז אנו ‫<ref>63v</ref>מתחילי' {{#annot:term|185|VH0l}}לכפול{{#annotend:VH0l}} האות מן המספר הראשון על כל אות ואות מן המספר השני ביחוד ומקובץ הכפל נכתוב בשורה מיוחדת למעלה מאלו השני מספרי' ונכוין שיהיה כל מקובץ כפל האות מהמספר הראשון על אחד מאותיות המספר השני | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|‫<ref>marg.</ref>הג"ה המספר אשר אנו כותבים תחלה לפנינו אנו קוראי' אותו המספר הראשון והמספר אשר אנו רוצים לכפול אותו על זה המספר על כל אות ואות ביחוד הוא הנקרא המספר השני ע"כ | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|התחלתו למעלה מן האות התחתון שהוא מן המספר השני ולא יהיה התחלה נוטה לא לפניו ולא לאחריו כדי שיהיה המערכה הראשונ' ממקובץ הכפל מסודרת נגד המערכה אשר נרשם בה האות של המספר השני ולא תחוש אם יזדמן לך שתכתו' שני אותיות מכלל המקובצי' זה למעלה מזה כאשר יתן לך סדר הכתיבה לכתו' אות אחד במערכה שכבר נמצא בה אות או אותיות שעלו מצד הכפל ואחר שכפלת האות מן המספר הראשון על כל אות של מספר השני וכתבת מקובץ הכפולי' למעלה מאלו שני המספרי' על האופן אשר זכרתי אז תכתו' המספר השני שיהיה התחלתו תחת האות השני מהמספר הראשון ותמיד מן ההתחלה והלאה יהיו אותיות של המספר השני מכווני' אות תחת אות מן האותיות אשר למעלה מהמספר השני ואחר שכתבת המספר השני על זה האופן אז תכפול ג"כ על כל אות של המספר השני האות של המספר הראשון אשר התחלת המספר השני תחתיו ותכתו' לעולם ג"כ מקובץ הכפל למעלה מאלו שני המספרי' ר"ל למעלה ממספר הראשון והשני ויהיה בתחלת כל מקובץ למעלה מן האות שהוא מן המספר השני אשר כפל המקובץ ממנו ואח"כ תתחיל לכתו' שלישית המספר השני שיהיה התחלתו <s>תחלת</s> תחת אות שלישי מהמספ' הראשון אם יהיו למספר הראשון יותר אותיות ותנהג גם באות השלישי של המספר הראשון עם המספר השני המנהג אשר נהגת בשנים הראשונים עם מספר השני וכן תעשה על זה האופן בלי חלוף עם כל אותיות של המספר הראשון כי כל אות של המספר ראשון צריך שיהיה כפול על כל אות של המספר השני והמספר השני יהיה התחלתו תחת האות אשר יהיה נכפל עליו ומקובצי הכפל צריכים שיהיה ההתחלה מהם תמיד למעלה מן האות של המספר השני שהמקובץ ממנו | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|והנה נוסיף בזה ביאור מצד המשלים | |
| − | + | |- | |
| − | + | | | |
| − | + | *Example: we wish to multiply 11 by 12 | |
| − | + | :<math>\scriptstyle11\times12</math> | |
| − | + | |style="text-align:right;"|<big>הנה</big> רצינו לכפול א'א' על ב'א' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|הנה נכתו' תחלה לפנינו א'א' ואנו קורים להם המספר הראשון וב'א' אנו קוראים המספר השני אחר שקראנו א'א' המספר הראשון והנה נכתו' תחלה ב'א' שיהיה התחלתם תחת הא' הראשון של א'א' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|‫<ref>marg.</ref>הג"ה ואם היינו כותבי' תחלה ב"א והיינו קוראי' להם מספר ראשו' לא יומר דבר | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ויהיה תמונת הבת' כך | |
| − | + | |- | |
| − | + | | | |
| − | ה' | + | :{|class="wikitable" style="color:blue; text-align:center;" |
| − | + | |- | |
| − | + | | | |
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | + | |- | |
| − | + | |1||1 | |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | |1||2 | |
| − | + | |} | |
| − | + | |} | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | + | |- | |
| − | + | |א||א | |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | |א||ב | |
| − | + | |} | |
| − | + | |} | |
| − | הראשון | + | |- |
| − | + | | | |
| − | + | |style="text-align:right;"|ואח"כ נתחיל לכפול הא' העליונ' על הב' ונאמר א' פעמים ב' הוא ב' ונכתב זה הב' למעלה מאלו שני המספרים שתהיה מעמדה מכוון ממעל של ב' מן ב'א' שהיא האות של המספר השני אשר זה הב' בא מצד שכפלנו א' עליה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ויהיה דמות הכתב אשר לפניך תמונתו כך | |
| − | + | |- | |
| − | + | | | |
| − | + | :{|class="wikitable" style="color:blue; text-align:center;" | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | הראשון | ||
| − | |||
| − | |||
| − | |||
| − | הראשון | ||
| − | |||
| − | הראשון | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | + | |- | |
| − | + | |1||1 | |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | |1||2 | |
| − | + | |} | |
| − | + | |} | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | |
| − | + | |- | |
| − | + | |א||א | |
| − | + | |-style="border-bottom: 1px solid black;" | |
| − | + | |א||ב | |
| − | + | |} | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|‫<ref>64r</ref>ואח"כ נאמר ג"כ א' פעמי' הא' של ב'א' והוא א' ונכתו' זה הא' בשורה העליונה ממעל א' של ב'א' ויהיה תמונת הכת' העולה כך | |
| − | + | |- | |
| − | + | | | |
| − | + | :{|class="wikitable" style="color:blue; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |1||2 | ||
| + | |- | ||
| + | |1||1 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |1||2 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |א||ב | ||
| + | |- | ||
| + | |א||א | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |א||ב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ועתה נכתו' המספר השני באופן שיהיה התחלתו תחת הא' השנית של א'א' ויהיה תמונת הכת' אשר יקרה לפניך תמונת כך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כי אנו מוחקים עתה האות הראשון מן המספר הראשון וגם המספר השני שיהיה התחלתו תחתיו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ועתה אנו כופלים הא' השנייה של המספר הראשון על ב' של המספר השני וכפל א' על ב' הוא ב' נכתו' זה הב' למעלה לב' של המספר השני ויעלה בידך תמונת הכת' ממעל המספר הראשון והשני תמונת כך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | ||2|| | ||
| + | |- | ||
| + | |1||1||2 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | | ||ב|| | ||
| + | |- | ||
| + | |א||א||ב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואח"כ נכפול עוד הא' השני של המספר הראשון על הא' של המספר השני והנה א' פעמים א' הוא א' נכתו' זה הא' אשר עלה מהכפל ממעל לא' של המספר השני ויעלה בידך ממקובצי הכפל ממעל למספר הראשון והשני אותיות תמונת כך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה חבר יחד כל האותיות שהם ממערכה אחת ר"ל שהם ממערכה אחת לפי סדר האותיות הנולדים למעלה ויקרה לך מן א' וב' שהם בטור השנית לעשות מהם ג' ויהיה אשר עלה לך מהכפל ב"א על א'א' ב'ב'א' | ||
| + | |- | ||
| + | | | ||
| + | *Another example: we wish to multiply 543 by 654 | ||
| + | :<math>\scriptstyle543\times654</math> | ||
| + | |style="text-align:right;"|<big>משל</big> אחר הנה רצינו לכפול ג'ד'ה' על ד'ה'ו' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ונכתו' לפנינו ג'ד'ה' למספר הראשון ונכפול תחלה ד'ה'ו' על ג' של ג'ד'ה' ויהיה תמונת הכת' כך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |5||4||3 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |6||5||4 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |ה||ד||ג | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ו||ה||ד | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה כאשר נכפול ד' על ג' יעלה הכפל ב'א' ונכתו' אלו הב'א' למעלה ממספר הראשון והשני שיהיה התחלתם ממעל הד' של המספר השני ויקרה לפניך כתב תמונת כך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||1||2 | ||
| + | |- | ||
| + | |5||4||3 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |6||5||4 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||א||ב | ||
| + | |- | ||
| + | |ה||ד||ג | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ו||ה||ד | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואח"כ תכפול עוד ג' של ג'ד'ה' על ה' של ד'ה'ו' ותכתו' מקובץ הכפל שיהיה התחלתו ממעל ה' של ד'ה'ו' שהוא המספר השני ויקרה לפניך כתב תמונת כך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||5|| | ||
| + | |- | ||
| + | |1||1||2 | ||
| + | |- | ||
| + | |5||4||3 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |6||5||4 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||ה|| | ||
| + | |- | ||
| + | |א||א||ב | ||
| + | |- | ||
| + | |ה||ד||ג | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ו||ה||ד | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואח"כ תכפול עוד ג' על ו' של ד'ה'ו' ויקרה לפניך כתב תמונת כך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||8||5|| | ||
| + | |- | ||
| + | |1||1||1||2 | ||
| + | |- | ||
| + | | ||5||4||3 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | ||6||5||4 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||ח||ה|| | ||
| + | |- | ||
| + | |א||א||א||ב | ||
| + | |- | ||
| + | | ||ה||ד||ג | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | ||ו||ה||ד | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואח"כ תמחוק הג' של ג'ד'ה' וגם ד'ה'ו' שהיו מתחילים תחת הג' ותכתו' ד'ה'ו' שנית שיהיה התחלתו תחת ד' של ג'ד'ה' ויקרה לפניך תואר הכת' בתמונת כך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||8||5|| | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |1||1||1||2 | ||
| + | |- | ||
| + | | ||5||4||3 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | ||6||5||4 | ||
| + | |- | ||
| + | |6||5||4|| | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||ח||ה|| | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |א||א||א||ב | ||
| + | |- | ||
| + | | ||ה||ד||ג | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | ||ו||ה||ד | ||
| + | |- | ||
| + | |ו||ה||ד|| | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ותכפול ד' של ג'ד'ה' על ד' של ד'ה'ו' ויעלה לפניך הכת' העליון שהוא ממקובצי הכפולי' תמונת כך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | ||1||6|| | ||
| + | |- | ||
| + | | ||8||5|| | ||
| + | |- | ||
| + | |1||1||1||2 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | | ||א||ו|| | ||
| + | |- | ||
| + | |& | ||
| − | + | == Bibliography == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Meir Shapira'''<br> | |
| − | + | 15th century?<br> | |
| − | + | '''''Beur Darkei ha-Ḥeshbon'''''<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Manuscript:'''<br> | |
| − | + | *MS Oxford, Bodleian Library MS Opp. 211 (IMHM: f 17281), ff. 59r-103v; 117r124r (Cat. Neub. 362, 7); (15th century)<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Bibliography:'''<br> | |
| − | + | *Steinschneider, Moritz. 1893–1901. Mathematik bei den Juden. Berlin-LeipzigFrankfurt: Kaufmann, p. 209 (h75); repr. Hildesheim: G. Olms, 1964 and 2001. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 05:39, 24 July 2024
Contents[hide]Introduction |
פתיחה |
| ביאור דרכי חשבון להחכם השלם ר' מאיר אלסנזי המכונה שפירא | |
| והוא מבאר חכמת המספר כולה מסודר לז' שערים ולכל שער ושער | |
| כמה שו"ת בחכמה זו [...] | |
| In the name of He Who gives light to the whole world [Berakhot 60b] | [1]בשם המאיר לעולם[2] |
| He is hidden from all and nothing is hidden from Him. | והוא מכל נעלם ואין עמו העלם |
| I start to explain some of the calculation methods in arithmetic and some of geometrical issues. | אחל לבאר קצת דרכי החשבון בחכמת המספר והקצת התשבורות |
| My intention is to simplify the explanation as much as I can, so that it will be easier for the reader who is not well versed and will undoubtedly receive a great benefit in a short time without getting weary by the unfamiliar words, because every unfamiliar word that needs to be discussed - I will explain it in an explanatory note, in order not to confuse it with an explanation of a word that is not intended to be clarified in the work, and where necessary, I will add an additional explanation on the intended matter in an explanatory note, but I will not elaborate in the text itself, so that the reader can comprehend the matter intended in his knowledge and understanding without the misunderstanding that will occur from the length and the explanation of words, meaning in general an intentional explanation. | וכוונתי להקל בביאור תכלית האיפשר אצלי למען יקל על המעיין אשר לא הורגל ובלי ספק יקבל תועלת גדולה בזמן קצר בלי ליאות מן המלות הזרות כי כל מלה זרה אשר יבא הצרך לדבר בה אבאריה בהגהה כדי שלא אבלבל מכוון לבאר בביאו' המלה אשר אין כוונת החבור לבארה וכן במקום הצורך אבאר בהגה אחת תוספת ביאור על ענין המכוון ולא אאריך בעצם החבור כדי שיוכל המעיין לכלול [במ]דעו ובשכלו העניין המכוון בבלתי הטעאה אשר תקרה מצד האריכות ומצד ביאור דברי' ורי' בכלל ביאור מכוון |
| The unfamiliar words that apear in this work are the words that I need to state, in order to designate a special term for the matter intended, so that we do not have to refer the intended matter with many words, but the intention will always be addressed by one or two word at most. | ואמנם המלות הזרות אשר יקרו בזה החבור הם מלות אשר יבואוני הצורך לדבר בהם כדי להניח שם נפרד אל העניין המכוון כדי שלא נצטרך לזכר המכוון מלות רבות שיבא [..] אלא המכוון יבא תמיד זכרונו במלה א' או שתים על הרוב |
| כי יראה לי שבזה ג"כ תועלת גדולה למעיין כי העניין אשר יתכן זכרו במלה אחת ואם יבא זכרו במלות רבות הוא מעם גדול מבלבל בלי ספק בקלות מפני שלא יכלול עליו המדע אלא בטורח ואע"פ שהמלות רבות יבארו העניין המכוון ביאור מכוון מ"מ מפני שאין הכוונ' לבאר מהות העניין אשר יביא הצורך זכרו | |
| והכוונ' לבאר עניין אחד אשר אל העניין ההוא ראוי להיות ידוע כל הנרצה בכל מה אשר
יבאו מן זכר הענייני' אשר ישתתפו בביאור העניין המכוון לבארו | |
| ואין ראוי להכניס בכלל הביאור ההוא ביאור הענייני' אשר ישתתף זכרם בביאור העניין המכוון לבארו כי זה מבלבל בלי ספק | |
| לכן ראוי להשים אל אלו הענייני' אשר יביא הצורך לזכרם הגהות יבואר בהם הכוונ' במלה הזרה אשר יביא הצורך לדבר בה | |
| And from the Lord of the world who stands at the top of the ladder, | ומאת אדון העולם הנצב בראש הסלם |
| Who is the cause of the existence of all beings, | והוא הסבה במציאות הנמצאות כלם |
| I ask for help and to Him the praise and gratitude, | אשאל העזר ואליו השבח וההודאה |
| For He has increased His grace upon us by giving us wisdom and knowledge, | שהגדיל חסדו עמנו בתתו לנו שכל ומדע |
| To grant us a blessing. | להשאיר לנו ברכה |
| So, after the praise and gratitude to the exalted God, | והנה אחר השבח וההודאה לאל ית' |
| And asking Him for help, | ושאלת העזר מאתו |
| I begin the explanation of what should be explained, | אחל בביאור המכוון לבארו |
| And say: | ואומר |
| This is how the number is explained according to the ways of every nation and language: | הנה המספר מצד מה שמבואר מעניינו לפי דרכי כל אומה ולשון |
| 1 is the beginning of all numbers and 9 is the end of all of them. | הנה א' הוא ראש המספרים כלם וט' סוף המספרי' כלם |
| Because, when we start counting 1, 2, 3, up to 9, we have no more units other than those chosen from these 9s up to the tens. | כי כאשר אנו מתחילי' למנות אב"ג עד ט' אין לנו מן האחדי' יותר זולת מה שנבחר מאלו הט' אל העשריות |
| When we start counting the tens - 10, 20, 30, up to 90 - the tens are 9. | וכן כאשר נתחיל למנות העשיריות יכ"ל עד צ' הנה העשריות הם ט' |
| Then, we reach the rank of hundreds and the hundreds also end in 9 hundreds. | ואח"כ נכנסים לכלל המאות וכן המאות סופם ט' מאות |
| After that, we reach the rank of thousands and the end of the thousands is 9 thousands. | אז אנו נכנסי' לכלל האלפי' וסוף האלפים הם ט' אלפי' |
| From there, we reach the rank of tens of thousands and the end of the tens of thousands is 9 tens of thousands. | משם אנו לכלל הרבבות וכן סוף הרבבות ט' רבבות |
| From there, we reach the hundreds of thousands and the hundreds of thousands also end in 9. | ומשם אנו נכנסי' אל המאות באלפי' וכן המאות אלפים יכלו על ט' |
| From there, we reach the millions [lit. thousands of thousands] and they also end in 9. | ומשם אנו נכנסים אל האלף אלפי' וסופם ג"כ ט' |
| From there, we reach the tens of millions [lit. tens of thousands of thousands] and they also end in 9. | ומשם אנו נכנסים אל הרבבות מאלף אלפים וסופם ג"כ ט' |
| From there, we reach the hundreds of millions [lit. hundreds of thousands of thousands] . | ומשם אנו נכנסי' אל המאות אלף אלפי' |
| ועל זה הדמותנו תמיד סוף כל מספר ומספר ואחריה אנו נכנסי' אחד ממיני המספר | |
| והנה מפני שראו חכמי זאת המלאכה שכל מין ממיני המספר לפי זה האופן אינו מוסיף על ט' שמו ט' אותיות למנות בהם המספרי' כלם והם אבגד"הוזח"ט והאומות אשר אינם מאומתינו לוקחים מקום אלו ט' אותיות אחרי אשר הם [3]משתמשים בהם בכת' שלהם או מיחדים מקום ט' האותיות ט' סימנים מיוחדי' כל סימן עומד מקום אות מאלו האותיות והמכוון מכלם הוא כוונ' א' והנה כל אות מאלו האותיות לפעמי' הוא רומז כולל אחדי' כפי המספר אשר הוא מונח לו ולפעמי' רומז כך עשריות ולפעמי' מאות ולפעמי' אלפי' ולפעמי' רבבות אלפי' ולפעמי' מאות אלפים ולפעמי' אלפי אלפי' | |
| וזה הכלל כל אות רומז על איזה מין שתרצה ממיני המספר במקצת הפעמי' | |
| עד"מ הא' לפעמי' רומז על א' ממש ולפעמים על אחד מהעשריות ולפעמי' על אחד מן המאות ולפעמי' על א' מן האלפי' וע"ד זה היא רומזת על א' מאי זה מין מן המספר אי זה שיהיה | |
| וכן הב' על שנים ממש ולפעמי' על ב' עשיריות ולפעמי' על ב' מאות או ב' אלפי' או ב' רבבות או ב' מאי זה מין שתרצה | |
| [4]הג"ה מיני המספר אחדי' מין אחד עשריות מין א' מאות מין א' אלפי' מין א' רבבות מין א' מאו' אלפי' מין א' אלפי אלפי' מין א' רבבות אלפי אלפי' מ"א מאות אלפי אלפי' מ"א אלפי אלף אלפי' מ"א ועל ה הדרך מסדר המינים עד לאין תכלית | |
| וכן הג' על שלשה ועל שלשי' ועל ג' מאות ועל ג' אלפי' וכן על ג' מכל מין מן המספרי' | |
| וכן הד' על על ד' מכל מין מן המספרי' | |
| וכן ה' על חמשה מכל מין מן המספרי' | |
| וכן ו' על ששה מכל מין | |
| וכן ז' על שבעה מכל מין | |
| וכן ח' על ח' מכל מין | |
| וכן ט' על ט' מכל מין | |
| ואמנם כל אלו אות מאלו האותיות אם הוא ראשון בסדר האותיות אשר עמ[ל] או שהוא יחידי אז הוא מורה על אחדי' מפני שאחדי' הם הקודמי' בטבע המספר כי לא ימצא עשריות זולת אחדי' כי עניין העשריות הוא שהם קבוץ אחדי' | |
| ואם א' מאלו האותיות שני בסדר אז הוא מורה על עשריות כי העשריות קודמי' לשאר מספרי' כי המאה אינו אלא קבוץ עשריות ומאוחרי' לאחדי' ולכן כאשר הם שניים בסדר אז יורו על העשריו' | |
| וכן כל אות מהאותיות האלו כאשר הוא שלישי בסדר אז יורה על מאות כי המאות הם אחר העשריות וקודמי' לאלפי' כי אין מספר האלפי' אלא קבוץ המאות | |
| וכל אות שהוא רביעי בסדר הוא אלפי' כי הוא אחר המאות | |
| וכן כל אות שהוא חמישי בסדר הוא רבבות כי הרבבות אחר האלפי' | |
| וכן כל אות מאלו האותיות כאשר הוא ששית בסדר הוא מורה על מאות אלפי' כי הם אחר הרבבות | |
| וכן האות שהוא שביעי בסדר הוא מורה על אלפי אלפי' | |
| ועל זה הדרך יורו האותיות על כל מין כפי סדר המין מההתחלה של המספר כך צרי' להיות האות המורה על המין ההוא כסדר מהתחלת האותיות אשר מסודרי' בשורה | |
| והמשל בזה הנה מסודרי' א'א'א' בשורה א' הנה הא' הראשונ' היא אחדים והשנייה עשר והשלישית מאה ולפי זה יכללו אלו האותיות אא' עשר ומאה | |
| ואם בשורה א' ב'ב'ב' הנה שניים אחדי' וב' עשרות דהיינו עשרי' וב' מאות דהיינו מאתים | |
| ואם בשורה א' ג'ג'ג' יהיה המספר שלשה שלשים ושלש מאות | |
| ואין הפרש בין שיהיו האותיות אשר בשורה אחת ממין אות א' או ממין אותיות מתחלפי' עד"מ א'ב'ג' הנה בעבור שהאלף בראשונה היא א' ושהשני שנייה בסדר היא עשרי' שהם ב' עשריות ובעבור שהג' שלישית בסדר היא ג' מאות | |
| ואם היה סדרם כך ב'א'ג' אז היה המספר שניים עשר ושלש מאות | |
| ואם היה סדרם כך ג'ב'א' אז היה המספר שלשה עשרי' ומאה | |
| והנה אם יחובר לאלו האותיות אות רביעי היה מורה האות הרביעית אלפי' | |
| עד"מ ג'א'ב'ה' הם שלשה עשר מאתים וחמש אלפים | |
| ואם היה סדרם כך ה'ב'א'ג' אז יורו אל חמשה עשרים ומאה וג' אלפי' [5]אלפי' | |
| וע"ד זה אם יחובר אל ארבע אותיות אות חמישי הוא יורה רבבות | |
| וכן הששי מאות אלפי' | |
| וכן כל אשר יוסיפו אותיות יורה תמיד הנוסף ר"ל האות האחרון על מין מהמספר שהוא אחד מיני המספר אשר יורו עליו הקדומים | |
| [6]הג"ה במערכה הרצון בו כל אות שהוא ראשון לשאר אותיות הוא נקרא ראשון במערכה והאו' שהוא שני לשאר אותיות הוא נקר' שני במערכ' וכן האות שהוא שלישי' לשאר אותיות שלישית למערכה ועד"ז כלם | |
| ואמנם חכמי זאת המלאכה משתתפים עוד לאלו ט' אותיות רושם א' מקום אות והיא תמונת גלגל כזה 0 או כזה ס וקראו לו סיפרא בהרב' מחמ[ש]ת מספריהם וזה האות הניחו שיהיה עומד מקום אות רק שזה האות אינו מורה בעצמו על שום מספר אלא שיעמוד בעבור צורך האות אז האותיות אשר יבאו אחריו שיהיו האותיות ההם מסודרי' במערכה על אופן שיורו כל א' מהם על מן המספר המכוון בהם | |
| ע'ד'מ' הנה רצינו מספ' עשיריות בזולת מין אחר והנה האותיות אשר יורו על העשריות הם אשר הם שניים במערכה ואם נשים לפניהם א' מן האותיות התשעה שזכרנו שהם א'ב'ג' ד'ה'ו' ז'ח'ט' הנה אותו האות אשר הוא ראשון במערכה הוא מורה ג"כ על מין מן המספר והוא שיורה על אחדי' והרצון לנו שלא יהיו לנו מיני אחדים קודמים בזה המספר אשר אנו רומזי' עליו אלא יהיה רק עשריות ובעבור שלא יתכן לנו אות רומז על העשריות אלא האות אשר הוא שנית במערכה הנה כאשר נרצה שלא ישותף אליו מין מן המספר קודם לו ושיהיה הוא עם זה מכוון שנית למערכה הנה אנו צריכים לכתו' לפניו אות א' או רושם אחר שלא יורה בעצמו מאומה ושלא יהיה האות ההוא או הרושם ההוא מכוון לדבר רק להורות שהוא הראשון במערכה כדי שיראה המערכת המכוונת באותיות אשר יבאו אחריו וכן הדין בעצמו באי זה מקום שיהיה במערכה כאשר יהיה המכוון באותו המקום שלא יהיה שם מספר כלל נשים במקום ההוא האות אשר לא יורה בעצמו מאומה או רושם | |
| וכאשר יעמוד האות או הרושם ההוא מקום מין מן המספרי' אז ישארו כל האותיות אשר יבאו על המערכ' אשר המכוון בהם ולא ישותף אליהם מספר אשר אין הרצון אל שותפו | |
| וחכמי זאת המלאכה הניחו ע"ד ההנחה להיות תמונת גלגל כזה ס או כזה 0 תמיד מקום אות או רושם אשר בעצמו לא יורה על דבר | |
| [7]בחרו לתמונת גלגל מפני שלא נצטרך לזה האות אלא מפני שהאותיות התשעה חוזרי' כי אחר אשר כלו האחדי' באלו ט' אותיות שהם א'ב'ג' ד'ה'ו' ז'ח'ט' אז חוזרי' הם בעצמם להורות על העשריות שהם י'כ'ל' מ'נ'ס' ע'פ'ץ' ויורה הרושם אשר הונח ראשון במערכה על שאינם אחדי' אלא חזרו ושבו להיות עשריות וכן עניינם במאות ובשאר המינים ולכן שמו זה האות הרומז אל הגלגל שלהם תמונ' גלגל | |
| וקראו לו ספרא במקצת הלשונות ואנו קוראי' לו גלגל מפני שתמונתו תמונת גלגל | |
| והנה לך משלים לתוספת ביאור אל אשר כווננו אליו לבאר | |
| הנה רצינו מספר שיהי' עשיריות ולא יהיו אחדים לפניו הנה נשים ראשון במערכה 0 שהוא בעצמו לא יורה מאומה ונשים אחריו אות אשר יורה על מספר כפי מספר העשריות אשר אנו רוצים | |
| ע'ד'מ' אם אנו רוצים עשר לבד אנו עושי' 0"א | |
| ואם אנו רוצים ב' עשריות אנו עושים 0"ב | |
| ואם ג' עשריות 0"ג | |
| ועל זה הדרך על איזה מספר מן העשריות אשר אנו רוצים נשים תמיד שנית למערכה האות אשר יורה על המספר ההוא | |
| וכן אם אנו רוצים מאות ולא מספר קודם נניח במערכה 0' בראשון ועו' 0' בשנית ואות בשלישית אשר יורה על המאות אשר המכוון אליהם | |
| המשל אם אנו רוצים מאה אנו עושי' 0'0'א' ואם מאתים אנו עושה 0'0'ב' | |
| וכן שאר האותיות לשאר המאות | |
| ואם תחפוץ אלפי' נשים ראשונה ג' גלגלי' כך 000 ואח"כ אות אשר יורה על האלפים | |
| [8]ע'ד'מ' אלף לאלף ב' לאלפי' ג' לשלשה אלפי' וכן שאר האותיות לשאר האלפים | |
| ואם תרצה רבבות בזולת מספר קודם תשים ראשונ' 0000 ואח"כ אות מורה הרבבות א' לרבבה ב' לשני רבבות וכן לשאר האותיות לשאר הרבבות | |
| ולמאות אלפי' בזולת מספר קודם תשים 00000 ואח"כ א' למאה אלפים ב' לשני מאות אלפי' וכן שאר האותיות לשאר המאות אלפי' | |
| וע'ד'ז' תעשה לכל המינים כאשר תרצה שלא יקדם מספר תשים קודם להם מאלו הגלגלים כפי הצורך כמותם | |
| ואם תרצה מין מן המינים ועוד מין או מינים קח לו אי זה מין שתרצה קודם לו תשים במערכה מקום המין ההוא אות יורה על המין ועל איש המין הנרצה והוא יורה לך המין וגם הוא יספיק אל המערכה למה שיבא אחריו | |
| ויבדלו מכאן אלו הט' אותיות שזכרנו שהם א'ב'ג' ד'ה'ו' ז'ח'ט' מן האות העשירי שהוא 0 ר"ל גלגל כשהגלגל לא יורה בעצמו דבר אבל הוא מכלל אשר ישלימו המערכה למה שיבא אחריהם | |
| והאותיות האחדי' הם מורי' בעצמם על מין מן המספר וגם הם מכלל המספר אשר ישלימו המערכה לאותיות אשר יבאו אחריהם | |
| המשל בזה הנה א'0'ג' | |
| הנה הא' מורה אחד מן האחדי' | |
| וה0' לא יורה על דבר אלא שנדע בעבורו שהג' שלישית למערכה וזה יורה ג"כ הא' עם שהיא מורה בעצמה אל אחד מן האחדי' ג"כ | |
| משל אחר 0'ב'ג' | |
| הנה ה0' ראשון במערכה ולא יורה בעצמו דבר אלא שהוא מכלל המערכה | |
| ובעבור זה הב' שנית למערכה ומורה עשרי' | |
| והג' שלישית למערכ' ומורה מאות | |
| משל אחר 0'ד'0'ה' | |
| הנה ה0' הא' ראשון למערכה ואינו מורה דבר | |
| והד' שנית ומורה ד' עשיריות | |
| וה0' השנית שלישית למערכה ואינו מורה דבר בעצמו | |
| והה' הוא רביעית למערכה ומורה על אלפים | |
| הנה כבר יספיק למשכיל אופן הצורך ב0' | |
| ועל איזה אופן ישתמשו אלו העשרה אותיות לרמוז בהם כל מספר הן מספר ממין אחד או מורכב ממין אחד או מינים רבים עד שלא ימלט שום מספר מלרמוז אליו באלו האותיות העשרה ר"ל א'ב'ג' ד'ה'ו' ז'ח'ט' 0' | |
| באפן אשר יובן המכוון נבדל מכל מספר זולתו עם שהמספר' אין להם תכלית ואפי' הפשוטי' וכ"ש המורכבים | |
| [9]הפשוטי' ר"ל המינים כל מין נקרא פשוט בערך המורכב משני מינים או יותר כי האחדי' הם מין אחד העשיריות מין אחר המאות מין אחר וכן האחדי' וכל א' מהם תשעה וכאשר יורכבו רק האחדי' עם העשיריות יולדו מהם בהכרח א"ח מספרי' וזה מובן מצד מה שיחובר כל א' מן האחדי' אל כל א' מן העשיריות | |
| ויספיק מה שבארתי להבנת אופן הוראת אלו העשרה אותיות על המספרי' לפי דרך חכמי החשבון | |
| ונתחיל עתה בביאור דרכי החשבון כפי מה שדרכו בו אנשי זאת החכמה | |
| ונחלק הביאורי' האלה על שבעה שערי' כאשר חלקום ג"כ הקדמוני' אשר חברו ספרי' בזאת המלאכה | |
| ואמנם חלקו דורכי החשבונות בזאת החכמ' לז' שערי' כי על ז' דרכים יבואר כל המבוקש מזאת החכמה וא'ע'פ' שיכלול כל א' מאלו הדרכי' דרכי' רבים מ"מ אלו הדרכי' כלם יכללו בז' סוגים ומה שהם ישתלשלו אליהם הם מיניהם ואסדר סדרם כפי הנאות אצלי וא'ע'פ' שקצת המחברי' סדרום על סדר אחר | |
| והנה אבאר ראשונ' שער החבור ואח"כ שער החסור ואח"כ שער הכפל ואח"כ שער החלוק ואח"כ שער השברי' ואח"כ שער הערך ואח"כ שער השרשים | |
| ועניין כל שער יבואר בפתחתו באר היטב בע"ה |
Chapter One: Addition |
[10]השער הראשון הוא שער החבור | ||||||||||||||||||||||||||||||||||||||||||
| והוא שיש לך שני מספרי' ותרצה לחברם | |||||||||||||||||||||||||||||||||||||||||||
| וכאשר נאמר מכאן ואילך מספ' או מספרי' בזולת תנאי בכוונה בו שלא נבדיל אם יהיה המספר ההוא ממין א' או משני מינים או יות' כי כלל המספר המרוצה אלינו מצד עצמו נקרא מספר בסתם ואמנם שאנו קוראי' אותו מין או סוג הוא בערך אל המספרים אחדי' ואין צורך לנו לפי המכוון מאלו ההבדלי' ולכן נקרא כל מספר מספר ואם הוא מחובר מן אחדים ועשיריות ומאות ואלפי' ויותר מן המינים או מיני' זולת אלו עם אלו ממקצת מאלו או מינים זולת אלו | |||||||||||||||||||||||||||||||||||||||||||
| ואחר זאת ההודעה נשוב אל עניין השער שהוא לחבר שני מספרי' או יותר יחד | |||||||||||||||||||||||||||||||||||||||||||
| ונאמר על דרך הכלל שלעולם נכתו' כל המספרי' אשר אנו רוצים לחברם זה תחת זה ונכוין בדרך הכתיבה שיהיו נכתבי' באפן שיהיו כל האותיות אשר הם ממערכ' אחת זה למעלה מזה בטור אחת ואחר שיהיה הכת' על זה האופן אז נתחיל במה שהוא בטור הראשון שהם במערכה הראשונה ותחבר כל אותיות המערכה ההיא וכל מה שיעלה לעשיריות תכתו' אותם העשיריות בטור הסמוכה לה שהיא מן המערכה שאחריה ומה שישאר בטור הראשונה מן האחדי' או שלא הגיע לכלל עשיריות אותו תכתו' באות א' כולל מחובר המספר אשר עלה ממקובץ האותיות שהיו במערכה הראשונ' או הנשאר על העשיריות בטור הראשונ' ממקובץ אותיותיה ואח"כ תקבץ ג"כ כל מה שתמצא בטור השנית שהוא מן המערכה השנית ואם עלה אות מן העשיריות של הראשונ' הוא בכלל זה הטור ולעולם תחשוב מקובץ אותיות של איזה טור אשר תשתמש בה כאילו הם אחדי' ואין צורך להביט מאיזה מין אותיות הטור אשר תקבץ וכל פעם אשר יעלו לך עשיריות אז תכתוב האות אשר יורה על העשיריות ההם בטור שאחריה ר"ל הטור שהיא מהמערכה הסמוכה לה וכן תעשה באותיות בטור השלישי והרביעי ובאותיות כל טור מאיזה מערכה שהיא ר"ל הטור ולעולם העשיריות אשר יעלו ממקובץ תכתו' באות אשר כולל אותם בטור שאחר הטור ההיא וכל אשר לא יגיע לעשיריות או שישאר על העשיריות תבתו' באות כולל אותם האחדי' בטור ההיא אשר המקובץ מן האותיות מאותה הטור כדי שישארו אותם האחדים ממין המערכה אשר נולדו בה | |||||||||||||||||||||||||||||||||||||||||||
|
והמשל הנה רצינו לחבר מספר א'ב'ג'ד' ומספר ב'ג'ד'ה'ו' ומספר ג'ד'ה'ו'ז' ומספר ה'ו'ז'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||
| והנה הם ד' מספרי' ונכתו' אותם על הצורה שביארנו ויהיה תמונת המעמד מהם כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| והנה מקובץ הטור הראשונה הוא א'א' וישאר הא' בטור הראשונ' מקום כל האותיות והא' השנית תכתו' בטור השנית מפני שהיא מכלל העשיריות | |||||||||||||||||||||||||||||||||||||||||||
| ואחר זה תחבר אותיות הטור השנית ויעלה המקובץ ממנה עם הא' אשר נוסף עליה בסבת [11]המקובץ של הטור שלפניה ו'א' וישאר הו' שהיא המות' על העשיריות בטור השני והא' תכתו' בטור שאחריה שהיא השלישית | |||||||||||||||||||||||||||||||||||||||||||
| ואז תקבץ כל האותיות של הטור השלישית ויעלה 0"בה0 תניח בטור השלישית וב' העשיריות תרשום בטור שאחריה שהיא הרביעית | |||||||||||||||||||||||||||||||||||||||||||
| ותקבץ גם אותיות הטור הרביעית ויעלה מהמקובץ ה"ב | |||||||||||||||||||||||||||||||||||||||||||
| הה' ישאר בטור הרביעית מקום האותיות שהיו בה | |||||||||||||||||||||||||||||||||||||||||||
| והב' שהם עשיריות תכתוב בטור החמישית ויעלה המקובץ מאותיות הטור החמישי ד' ב' | |||||||||||||||||||||||||||||||||||||||||||
| כתו' הד' בטור החמישית אשר היא נולדה שם מקום כל האותיות שהיו בה והב' עשיריות בטור ששית | |||||||||||||||||||||||||||||||||||||||||||
| ולפי זה יעלה המחובר מאלו הד' מספרי' א'ו'0'ה'ד'ב' שהם אחד וששים וחמשה וארבעי' אלף ומאתים אלפי' | |||||||||||||||||||||||||||||||||||||||||||
|
משל אחר הרי שרצינו לחבר א'ב'ג'ד'ה' עם א'ב'ג'ד'ה' | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| הנה נכתו' אלו שני המספרי' על האופן אשר זכרנו ויהיה תמונת הכתיבה כך | |||||||||||||||||||||||||||||||||||||||||||
| ויעלה המקובץ מאלו השני מספרי' ב'ד'ו'ח'0'א' | |||||||||||||||||||||||||||||||||||||||||||
|
משל אחר הרי שרצינו לחבר ג'0'א' עם 0'ח'ב' | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ויהיה תמונת הכת' מהם | |||||||||||||||||||||||||||||||||||||||||||
| ויעלה המקובץ מהם ג'ח'ג' | |||||||||||||||||||||||||||||||||||||||||||
|
משל אחר הנה רצינו לחבר א'ג'0'ד' עם ד'0'ג'א' ועם 0'ג'א'ד' ועם 0'ד'ג'ט' ועם א'0'ד'ג' | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| והנה כאשר אנו כותבי' אלו המספרי' על האופן אשר זכרנו אז יהיה תמונת הכת' כך | |||||||||||||||||||||||||||||||||||||||||||
| ויעלה המחובר מאלו המספרי' ו'0'ב'ד'א' | |||||||||||||||||||||||||||||||||||||||||||
|
משל אחר הרי שרצינו לחבר א' עם ט'ט'ט'ט'ט' | ||||||||||||||||||||||||||||||||||||||||||
| ויהיה תמונת הכת' כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| והנה כאשר נחבר א' על ט' שלמעלה ממנו יעלה 0א' נניח ה0 מקום ט' העליונה והא' נכתו' במערכה השנית ולשם ג"כ ט' | |||||||||||||||||||||||||||||||||||||||||||
| וכאשר נחבר הא' עם הט' יעלה 0'א' ישאר ה0' במערכה השנית מקום הט' והא' נכתו' במערכה השלישית ולשם ג"כ ט' | |||||||||||||||||||||||||||||||||||||||||||
| וכאשר נחבר הא' עמה יעלה 0"א ישאר ה0 במערכה השלישית מקום הט' והא' נכתו' במערכ הרביעית ולשם ג"כ ט' | |||||||||||||||||||||||||||||||||||||||||||
| וכאשר נחבר הא' עמה יעלה 0"א ישאר ה0' במערכ' הרביעית והא' נכתו' במערכה החמשית | |||||||||||||||||||||||||||||||||||||||||||
| הנה עלה לנו מחבור א' על ט'ט'ט'ט'ט' 0'0'0'0'א | |||||||||||||||||||||||||||||||||||||||||||
| והנה אין צורך להאריך העניין השער הזה כי הוא פשוט הרבה | |||||||||||||||||||||||||||||||||||||||||||
| ואמנם היה ראוי לזכור בו דרך חבור שברי' עם שברי' ושברי' עם שלמים אלא שאלו הענייני' יהיו מבוארים בשער השברים ביאור מבואר מצד מה שהביאור לשם יותר נאות |
Chapter Two: Subtraction |
השער השני והוא שער החסור | ||||||||||||||||||||||||||
| והכוונה בו לחסר מספר ממספר שהוא יותר גדול ממנו או שוה לו הדרך לחסר מספר ממספר אחר הוא שלעולם תכתו' לפניך המספר אשר תרצה לחסר ממנו ותכתו' תחתיו המספר אשר תרצה לחסר אותו ותכוין בכתיבה לכתו' אות תחת אות ר"ל מערכה תחת מערכה ואח"כ תתחיל לחסר האות האחרון של המספר אשר תרצה לחסר אות מן האות אשר למעלה המנו ולעולם תחשוב האות אשר תרצה לחסר אותו כאילו הוא אחדים [12]ולא תביט מאיזה מן הוא וכן תחשוב גם לאחדי' האות שלמעלה המנו | |||||||||||||||||||||||||||
| והנה אם האות התחתון אחד פחות במספרו מן האות העליון כאשר רואים שניהם כאילו הם מין אחדים אז תגרע מן העליון ומה שישאר מן העליון תרשום מקום האות העליון אשר גרעת ממנו ולא תביט לדבר אחר | |||||||||||||||||||||||||||
| ואמנם אם האות התחתון יותר מן העליון אז מ"מ תחשוב האות העליון כאילו הוא ממין אחדי' ומה שאחריו תחשוב לעשיריות כי הם עשיריות בערך אל מה שקדם בסמוך וכן תחשוב בשלישיים לאות העליון למאות והרביעית לאלפי' אם תצטרך אל האות הרביעי אחריו וכן שאר כל האותיו' תשים אותם במערכה שראש המערכה האות אשר למעלה מהתחתון אשר אנו מכוונים לגרוע אותו ואח"כ תתחיל לגרוע האות התחתון מן האות העליון ומה שיבא אחריו והנשאר אחר הגרעון הנח מקום מה שהיה למעלה קודם הגרעון ועל דמות זה האופן תגרע כל אותיות של המספר התחתון מן האות מה שעומד למעלה ממנו והלאה וישאר לך אחר גרעון המבוקש | |||||||||||||||||||||||||||
|
המשל הנה רצינו לגרוע ח'ח'ח'ח' מן ט'ט'ט'ט' | ||||||||||||||||||||||||||
| הנה נכתו' למעלה מספר ט'ט'ט'ט' אשר אנו רוצים לגרוע מהם ונכתו' תחתיהם ח'ח'ח'ח' אשר אנו רוצים לגרוע אותו ויהיה תמונת הכת' | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ויהיה הנשאר מן העליון אחר שאנו גורעים התחתון ממנו א'א'א'א' | |||||||||||||||||||||||||||
|
משל אחר הנה אנו רוצים לגרוע 0'ג'0'ב' מן ג'0'א'ב' | ||||||||||||||||||||||||||
| ויהיה תמונת הכת' כך | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| הנה כאשר אנו מתחילי' לגרוע ב' של 0'ג'0'ב' מן ב' של ג'0'א'ב' לא ישאר במעלה הרביעי דבר וגרעון 0 מן הא' ישאר א' מפני שאין הם מספר לעצמו והנה כאשר אנו רוצים לגרוע ג' מן 0' שהוא למעלה ממנו לא יתכן מפני שאין ה0' בעצמו מספר ולכן נגרע הג' מן הא' אשר היא אחר ה0' והיא ממין עשיריות בערך למה שהיא ממערכה קודם לה והנה כאשר נחסר ג' מן 0א ישאר ז' ונכתו' הז' מקום ה0' מפני שאילו הז' הם ממקום ממין המערכה אשר ה0' בה ואח"כ נגרע ה0' מן ג' שעליה וישאר ג' מפני שאין ה0' מספר ובעבור זה לא יחסר גרעונו מן המספר הנגרע ממנו כי אין אנו גורעים ממנו ויהיה לפי זה מן ג'0'א'ב' אחר שגרענו ממנו 0'ג'0'ב' הנשאר ג"ז | |||||||||||||||||||||||||||
|
משל אחר הרי שרצינו לגרוע מן המספר של א'ב'ג'ד'ה' מספר ב'ג'ד'ה' | ||||||||||||||||||||||||||
| ויהיה תמונת הכת' כך | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה כאשר נתחיל לגרוע מן ד' שלמעלה המנה לא יתכן ובעבור זה נגרע הה' מן ד'ה' שהוא ארבע וחמשים כערך לה' התחתונה וכאשר נגרע ה' מן ד'ה' ישאר מקום ד"ה ט"ד | |||||||||||||||||||||||||||
| ואח"כ נגרע ד' מן ג' שלמעלה המנה ולא יתכן ולכן נגרע ד' מן ג' ומה שאחריה והוא ט' מפני שכך נשאר מצד מה שגרענו מקום והנה כאשר אנו גורעים ד' מן ג'ט' ישאר מקום ג"ט ט"ח | |||||||||||||||||||||||||||
| ואח"כ אנו גורעים ג"כ ג' מן ב"ט בעבור שלא נוכל לגרוע הג' מן הב' לבד וישאר מקום ב"ט ט"ח | |||||||||||||||||||||||||||
| ואח"כ נגרע ב' מן א"ט וישאר מקום א"ט ט"ח ולפי זה ישאר מקום [13]א'ב'ג'ד'ה' אחר שגרענו מהם ב'ג'ד'ה' ט'ח'ח'ח'ד' והוא המבוקש | |||||||||||||||||||||||||||
|
משל אחר הרי שרצינו לחסר ד'ה' מן אבגד | ||||||||||||||||||||||||||
| ויהיה תמונת הכתב כך | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה לא נוכל לחסר ה' מן ב' שלמעלה המנה לבד ולכן נחסר אותה מן ב'ג' וישאר מקום ב'ג' ז'ב' וכן נחסר ד' מן א'ז' ישאר מקום א'ז' ז'ו' ולפי זה יהיה הנשאר מן א'ב'ג'ד' אחר שגרענו מהם ד'ה' ז'ו'ב'ד' | |||||||||||||||||||||||||||
|
משל אחר הנה רצינו לחסר ד'ה' מן א'ב'ג'ד' | ||||||||||||||||||||||||||
| ויהיה תמונת הכת' כך | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה לא נוכל לחסר ה' מן ב' שלמעלה המנה | |||||||||||||||||||||||||||
|
משל אחר הרי שרצינו לחסר מן א'ב'0'ד' ג'ד' | ||||||||||||||||||||||||||
| ויהיה תמונת הכת' כך | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה לא נוכל לחסר ד' מן ב' שלמעלה ממנה לבד וכאשר נצטרך לגרוע הד' מן ב0' כי ה0' הוא האות שאחר הב' הנה ה0' אינ' מספר בעצמו וא"כ לא יתכן לגרוע הד' גם מאלו השנים ולכן נגרע הד' מן ב'0'ד' ויהיה הד' של ב'0'ד' מאות בערך אל ד' התחתונה | |||||||||||||||||||||||||||
| וכאשר נחסר ד' מן ב'0'ד' ישאר מקום ב'0'ד' ח'ט'ג' | |||||||||||||||||||||||||||
| כי כאשר לקחנו מן ד' מאות מאה נשארו ג' מאות | |||||||||||||||||||||||||||
| וכאשר לקחנו מן המאה עשרה ליקח מהם ה' נשא' ט' מקום העשיריות | |||||||||||||||||||||||||||
| וכאשר לקחנו מן העשרה ד' נשארו ו' ועו' יש ב' אחדי' שהם למעלה מהד' הרי ח' וא"כ נשארו ח'ט'ג' מקום ב'0'ד' ואח"כ נחסר ג' מן א'ח' וישארו ח'ז' מקום א'ח' ויהיה הנשאר בכלל לפי זה ח'ז' ט'ג' | |||||||||||||||||||||||||||
|
משל אחר הרי שרצינו לגרוע א' מן 0'0'0'0'0'א' | ||||||||||||||||||||||||||
| ויהיה תמונת הכת' כך | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה לא נוכל לחסר הא' מן ה0 שלמעלה המנה וכן לא נוכל לחסר אותה מן ה0 ולא מן 000 ולא מן 0000 ולא מן 00000 ולכן אנו צריכים לחסר אותה מן 00000א וככה נעשה הנה הא' של 00000א היא מאות אלפי' נכתו' במערכה במעלה החמישית ט' מקום שהיה א' במערכה הששית ולא יהיה במערכה הששי' דבר והנה ט' במערכה החמישית היא תשעים אלף וא"כ יש עוד בידינו עשרה אלפים לגרוע מהם אחד ולא נצטרך לכלום ולכן נשאיר בידינו אלף לגרוע מהם ונכתו' ט' אלפים במערכה הרביעית מקום ה0' שהיה שם והנה ג"כ לא נצטרך אל האלף בכלל ולכן נכתו' ט' במערכה השלישית מקום ה0' שהיה שם ויהיה הט' ההיא רומז לט' מאות וישארו עוד בידינו מאה לגרוע מהם אחד ולא נצטרך אל כל המאה בכלל ולכן נכתו' ט' במערכה השנית מקום ה0' שהוא שם וישארו עוד בידינו עשרה ליקח מהם הא' וכאשר נחסר א' מעשרה ישאר ט' נכתו' אותם במערכה הראשונה מקום ה0' שהוא שם ויהיה הנשאר בכלל ט'ט'ט'ט'ט' | |||||||||||||||||||||||||||
| הנה זה מה שזכרנו מביאור זה השער ומשליו לתוספת הביאור יספיק מאד לכל בעל הבנה כי הדברי' מושכלי' קרובים למושכל ראשון ולכן ראיתי כי אין צורך להאריך יות' כי כבר הארכנו מאד בהרבות המשל אלא שכוונתנו להיות זה הביאור רחב שנה שאיפשר שישתבש המעיין [14]בעצמות ביאור דרך החסור יקח רושם מן המשלים עד שיקיף המכוון ומעתה נפסוק דבור מזה השער ונחל בביאור שער הכפל |
Chapter Three: Multiplication |
השער הג' והוא שער הכפל | ||||||||||||||||||||||||||||||||||||||||||
| לדעת לכפול מספר איזה מספר שיהיה אל איזה מספר שיהיה ר"ל לדעת המקובץ מן המספר כאשר ילקח אותו המספר שני פעמי' או ג' פעמי' או מספר פעמים הרבה איזה ריבוי שיהיה | |||||||||||||||||||||||||||||||||||||||||||
| ע'ד'מ' הרי שרצינו לדעת מספר העשרי' כמה יעלה מקובצו שלשים פעמ' או פעמי' יתרי' או פחותי' כפי מה שרצינו וכן כל מספר אשר אנו רומזי' אליו לדעת קבוצו מפעמי' יותר מפעם איזה פעמי' שאנו רוצים | |||||||||||||||||||||||||||||||||||||||||||
| והנה לך לדעת שאין צורך להטריד המחשבה בחשבון הכפל רק בכפל האחדים על האחדי' כי מצד מה שיבואר לנו המקובץ מכפל אחדים על אחדים יבואר לנו ג"כ יבואר לנו ג"כ המקובץ מכפל מינים אחרי' זולת האחדי' על האחדים או זולתם | |||||||||||||||||||||||||||||||||||||||||||
| והמשל מצד מה שאנו יודעים שג' פעמי' ג' הם של ט' אחדים כאשר היו כאשר היו שני הג' אשר כפלנו אחדי' מאותו הצד אנו יודעי' שג' אחדים פעמי' פעמי' ג' עשיריות הם ט' אבל ט' ממין מערכה מיוחדת וכן ג' עשיריות פעמי' ג' מאות הם ט' ממין מערכה מיוחדת וכן ג' עשריות פעמי' ג' מאות וכן מאיזה מין או מינים שהיו שני הג' אשר נכפלו יהיה לעולם המקובץ ט' כמו שהוא מן האחדי' אלא שיהיה חלוף ביניהם מצד המערכה ולא בזולת זה וכל בכל שאר ט' האותיות מאיזה מערכה שיהיו יהיה מקובץ הכפל מהם שוה מצד המספר אלא שיתחלפו במערכה ובעבור זה יהיה חילוף בין מיני המספר ר"ל ע'ד'מ' שקצת יהיו אחדים וקצתם עשיריות או מאות או אלפי' וזולת אלו והנה אחר שהענין כן אין אנו צריכים להטריד המחשבה בחשבון רק להוציא כמות כפל האחדי' | |||||||||||||||||||||||||||||||||||||||||||
| כי הנה אם אנו רוצים לדעת ע'ד'מ' כמה שלשים פעמי' שלשים לא נצטרך לחשוב רק כמות שלשה פעמי' שלשה ר"ל ג"פ ג' שהם האותיות אשר ירמוז לשלשים פעמים שלשים | |||||||||||||||||||||||||||||||||||||||||||
| וכן אם אנו רוצים לדעת שלשים פעמים ששים לא נצטרך לדעת רק כמות ג' פעמי' ו' שהם האותיות אשר ירמזו לשלשים ולששים וכן בכל מיני שאר מיני המספר | |||||||||||||||||||||||||||||||||||||||||||
| ואמנם לדעת מאיזה מערכה הם האותיות אשר יעלו ממקובץ הכפל זה יבואר מצד סדר הכתיבה אשר ראוי לכתו' אל אופני שני המספרי' אשר הכוונה לכפול האחד על האחר | |||||||||||||||||||||||||||||||||||||||||||
| וסדר הכת' הוא כך שיהיה אחד מן המספרי' נרשם לפניך ואח"כ תברור לך מן המספר ההוא אות א' שהוא האות הראשון ותכתוב תחת האות ההיא המספר שתרצה לכפול אליו באופן שיהיה התחלת המספר השני תחת האות ההוא ומשם והלאה ישאר סדרו אות תחת אות ר"ל אותיות המספר השני יהיו מהתחלתם מכוונים אות תחת אות ואז אנו [15]מתחילי' לכפול האות מן המספר הראשון על כל אות ואות מן המספר השני ביחוד ומקובץ הכפל נכתוב בשורה מיוחדת למעלה מאלו השני מספרי' ונכוין שיהיה כל מקובץ כפל האות מהמספר הראשון על אחד מאותיות המספר השני | |||||||||||||||||||||||||||||||||||||||||||
| [16]הג"ה המספר אשר אנו כותבים תחלה לפנינו אנו קוראי' אותו המספר הראשון והמספר אשר אנו רוצים לכפול אותו על זה המספר על כל אות ואות ביחוד הוא הנקרא המספר השני ע"כ | |||||||||||||||||||||||||||||||||||||||||||
| התחלתו למעלה מן האות התחתון שהוא מן המספר השני ולא יהיה התחלה נוטה לא לפניו ולא לאחריו כדי שיהיה המערכה הראשונ' ממקובץ הכפל מסודרת נגד המערכה אשר נרשם בה האות של המספר השני ולא תחוש אם יזדמן לך שתכתו' שני אותיות מכלל המקובצי' זה למעלה מזה כאשר יתן לך סדר הכתיבה לכתו' אות אחד במערכה שכבר נמצא בה אות או אותיות שעלו מצד הכפל ואחר שכפלת האות מן המספר הראשון על כל אות של מספר השני וכתבת מקובץ הכפולי' למעלה מאלו שני המספרי' על האופן אשר זכרתי אז תכתו' המספר השני שיהיה התחלתו תחת האות השני מהמספר הראשון ותמיד מן ההתחלה והלאה יהיו אותיות של המספר השני מכווני' אות תחת אות מן האותיות אשר למעלה מהמספר השני ואחר שכתבת המספר השני על זה האופן אז תכפול ג"כ על כל אות של המספר השני האות של המספר הראשון אשר התחלת המספר השני תחתיו ותכתו' לעולם ג"כ מקובץ הכפל למעלה מאלו שני המספרי' ר"ל למעלה ממספר הראשון והשני ויהיה בתחלת כל מקובץ למעלה מן האות שהוא מן המספר השני אשר כפל המקובץ ממנו ואח"כ תתחיל לכתו' שלישית המספר השני שיהיה התחלתו | |||||||||||||||||||||||||||||||||||||||||||
| והנה נוסיף בזה ביאור מצד המשלים | |||||||||||||||||||||||||||||||||||||||||||
|
הנה רצינו לכפול א'א' על ב'א' | ||||||||||||||||||||||||||||||||||||||||||
| הנה נכתו' תחלה לפנינו א'א' ואנו קורים להם המספר הראשון וב'א' אנו קוראים המספר השני אחר שקראנו א'א' המספר הראשון והנה נכתו' תחלה ב'א' שיהיה התחלתם תחת הא' הראשון של א'א' | |||||||||||||||||||||||||||||||||||||||||||
| [17]הג"ה ואם היינו כותבי' תחלה ב"א והיינו קוראי' להם מספר ראשו' לא יומר דבר | |||||||||||||||||||||||||||||||||||||||||||
| ויהיה תמונת הבת' כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ואח"כ נתחיל לכפול הא' העליונ' על הב' ונאמר א' פעמים ב' הוא ב' ונכתב זה הב' למעלה מאלו שני המספרים שתהיה מעמדה מכוון ממעל של ב' מן ב'א' שהיא האות של המספר השני אשר זה הב' בא מצד שכפלנו א' עליה | |||||||||||||||||||||||||||||||||||||||||||
| ויהיה דמות הכתב אשר לפניך תמונתו כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| [18]ואח"כ נאמר ג"כ א' פעמי' הא' של ב'א' והוא א' ונכתו' זה הא' בשורה העליונה ממעל א' של ב'א' ויהיה תמונת הכת' העולה כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ועתה נכתו' המספר השני באופן שיהיה התחלתו תחת הא' השנית של א'א' ויהיה תמונת הכת' אשר יקרה לפניך תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| כי אנו מוחקים עתה האות הראשון מן המספר הראשון וגם המספר השני שיהיה התחלתו תחתיו | |||||||||||||||||||||||||||||||||||||||||||
| ועתה אנו כופלים הא' השנייה של המספר הראשון על ב' של המספר השני וכפל א' על ב' הוא ב' נכתו' זה הב' למעלה לב' של המספר השני ויעלה בידך תמונת הכת' ממעל המספר הראשון והשני תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ואח"כ נכפול עוד הא' השני של המספר הראשון על הא' של המספר השני והנה א' פעמים א' הוא א' נכתו' זה הא' אשר עלה מהכפל ממעל לא' של המספר השני ויעלה בידך ממקובצי הכפל ממעל למספר הראשון והשני אותיות תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| והנה חבר יחד כל האותיות שהם ממערכה אחת ר"ל שהם ממערכה אחת לפי סדר האותיות הנולדים למעלה ויקרה לך מן א' וב' שהם בטור השנית לעשות מהם ג' ויהיה אשר עלה לך מהכפל ב"א על א'א' ב'ב'א' | |||||||||||||||||||||||||||||||||||||||||||
|
משל אחר הנה רצינו לכפול ג'ד'ה' על ד'ה'ו' | ||||||||||||||||||||||||||||||||||||||||||
| ונכתו' לפנינו ג'ד'ה' למספר הראשון ונכפול תחלה ד'ה'ו' על ג' של ג'ד'ה' ויהיה תמונת הכת' כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| והנה כאשר נכפול ד' על ג' יעלה הכפל ב'א' ונכתו' אלו הב'א' למעלה ממספר הראשון והשני שיהיה התחלתם ממעל הד' של המספר השני ויקרה לפניך כתב תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ואח"כ תכפול עוד ג' של ג'ד'ה' על ה' של ד'ה'ו' ותכתו' מקובץ הכפל שיהיה התחלתו ממעל ה' של ד'ה'ו' שהוא המספר השני ויקרה לפניך כתב תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ואח"כ תכפול עוד ג' על ו' של ד'ה'ו' ויקרה לפניך כתב תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ואח"כ תמחוק הג' של ג'ד'ה' וגם ד'ה'ו' שהיו מתחילים תחת הג' ותכתו' ד'ה'ו' שנית שיהיה התחלתו תחת ד' של ג'ד'ה' ויקרה לפניך תואר הכת' בתמונת כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ותכפול ד' של ג'ד'ה' על ד' של ד'ה'ו' ויעלה לפניך הכת' העליון שהוא ממקובצי הכפולי' תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ויהיה מקובץ הכפל ד' על ד' ו'א' אלו ו'א' תכתו' ממעל ד' של ד'ה'ו' ויעלה לפניך הכת' העליון שהוא ממקובצי הכפולי' תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| ואח"כ תכפול עוד ד' של ג'ד'ה' על ה' של ד'ה'ו' ויעלה לפניך כפל ד' על ה' 0'ב' ותכתו' אותם שיהיה התחלתם ממעל ה' של ד'ה'ו' ויקרה לפניך תמונת האותיות שעלו ממקובצי הכפולי' תמונ' כך | |||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
| ואח"כ תכפול עוד ד' של ד'ה'ו' והכפל של ד' על ו' הוא ד'ב' תכתו' אותם שיהיה התחלתם [19]ממעל ו' של ד'ה'ו' שהוא המספר השני ויקרה לפניך תמונת הכתב ממקובצי הכפולי' תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| ואח"כ תמחוק ג"כ ד' של ג'ד'ה' וגם תמחוק ד'ה'ו' השנית ותכתו' ד'ה'ו' שיהיה התחלתו תחת ה' של גדה ויהיה לפניך תמונת הכת' הזה תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| כי הנשאר שאין לנו צורך יותר הוא מחוק | |||||||||||||||||||||||||||||||||||||||||||
| ועתה תכפול ה' של ג'ד'ה' על ד' של ד'ה'ו' ויקרו לפניך האותיות
ממקובצי הכפולים על תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| כי כפל ד' על ה' הוא 0'ב' ואח"כ תכפול ה' של ג'ד'ה' על ה' של ד'ה'ו' וכפל ה' על ה' הוא ה'ב' ותכתו' אותם שיהיה התחלתם ממעל לה' של ד'ה'ו' ויעלה בידך תמונת הכת' של אותיות מקובצי הכפולים על תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| ואח"כ תכפול עוד ה' של ג'ד'ה' על ו' של ד'ה'ו וכפל ה' על ו' הוא 0'ג' ותכתו' אותם שיהיה התחלתם ממעל לו' של ד'ה'ו' ויעלה לפניך תמונת הכת' מן אותיות שעלו ממקובצי הכפולים על תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| והנה במערכה הראשונ' ב' ובשנית המקובץ מן אותיות הטור השנית שהיא מן המערכה השנית הוא ב'א' וישאר הב' במערכה השנית והא' נכתו' אל הטור השלישית ויצא בטור השלישי' בכלל עם זה הא' הנוסף לה א'א' וישאר הא' בטור השלישית מקום מה שהיה בה והא' השנית נוסיף אותה לטור הרביעית ויצא בכל מן הטור הרביעית עם הא' הנוסף ה'א' וישאר הה' מקום מה שהיה בה וה'א' נוסיף אותה אל הטור החמישית ויצא בטור החמשית בכלל עם הא' הנוסף לה ה' ותשאר מקום מה שהיה בה ובטור הששית רק ג' ולפי זה עלה המקובץ מכפל ג'ד'ה' על ד'ה'ו' בבא ההג והנה הכלל שאתה צריך לכפול אחד משני המספרי' אשר אתה רוצה לכפול אות' זה על זה האחד על כל אות של המספר השני ביחוד ועל איזה אות אשר תכפול אותו המספר האחד עליו תחתיו יהיה התחלתו ואתה צרי' מאותו המספר התחתון לכפול כל אות ממנו ביחוד על האות [20]האות אשר התחלת המספר התחתון תחתיו ומקובץ הכפל הוא יהיה לעולם התחלתו ממעל האות של המספר התחתון וביאור זה שהנה אם אנו כופלים ב' על ג' והנם שניהם אחדים יהיו עומדי' אלו שני האותיות על תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| וכאשר תכפול אותם זה על זה יעלה לך ו' במערכה ההיא בלי ספק ואמנם אם יהיה האחד מהם מן המעלה השנית ע'ד'מ' שיהיה האחד 0'ג' הנה כאשר תכתו' הב' תחת הג' יהיה לפניך תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| וכאשר תאמ' ב' פעמי' ג' במקום ההוא ר"ל בטור שהב' תחת הג' אז יעלה בידך מהכפל ו' בלי ספק בטור ההיא והיא הטור שהיא מן המערכה השנית ויהיה א"כ הו' מן המערכה השנית וזה מובן שראוי להיות באופן הזה דרך החשבון ראוי כי כמו שפעם אחד א' הוא א' במערכה הראשונ' וב' פעמים א' הוא ב' כן ראוי ג"כ א' פעם עשרה להיות א' פעם עשרה וב' פעמים עשרה ב' פעמי' עשרה | |||||||||||||||||||||||||||||||||||||||||||
| וכן פעם א' מאה א' פעם מאה וב' פעמים מאה ב' פעמי' מאה ולכן איזה מן האותיות אשר תכתו' תחת אות אחד ותכפול אותו על האות ההוא שהוא ממעל לו לא יוליד הכפל ההוא דבר אחר אלא מספר מיני המספר ממין המספר העליון כמו שיוליד כפל האות התחתון על אות עליון מן האחדים מספר אחדים כך יוליד ג"כ מספר ממיני המספר שהעליון ממנו ר"ל מאותו המין ואם מיני המספר פחות מ0'א' ישארו במערכה ההיא ר"ל כאשר יתכן לכתוב המספר הנולד מהכפל באות אחת כאשר נניח התחלתו בטור תולדתו אז ישאר הכל בטור תולדתו ואמנם מה שיהיה ממנו יותר מאות אחת צרי' שיהיה רשומו בטור אחר הטור אשר נולד בה כמו שג"כ בכפל אחדים על אחדים כאשר יהיה המקובץ יותר מט' ישאר | |||||||||||||||||||||||||||||||||||||||||||
| ויספיק זה הביאור אשר ביארתי [תיארתי] למשכיל והאריכות יותר ליאות ואינו תוספת ביאור | |||||||||||||||||||||||||||||||||||||||||||
| ואתחיל בזכרון קצת שאלות להרחיב הביאור להתעורר על מה שנשתמש בו בזה השער בזולת האחרים אשר יבאו אחריו | |||||||||||||||||||||||||||||||||||||||||||
| שאלה הנה יש לנו חמשה עשר פרחים ונרצה לעשות מהם פרוטות והפרוטות הם 0'ב'א' על פרח א' | |||||||||||||||||||||||||||||||||||||||||||
| הנה תכפול [21]בא על ה"א ויעלה המבוקש | |||||||||||||||||||||||||||||||||||||||||||
| והנה אתה צריך לכפול תחלה 0בא על ה' של ה"א ואח"כ על א' של ה"א | |||||||||||||||||||||||||||||||||||||||||||
| ואין הפרש בזה אם תרצה לכפול ראשונה 0בא על א' של ה"א ואח"כ על הה' | |||||||||||||||||||||||||||||||||||||||||||
| גם אין הפרש אם תרצ' להניח 0בא למספר ראשון ולכפול על כל אות ממנו ה"א | |||||||||||||||||||||||||||||||||||||||||||
| ואין הפרש במאמ' וגם במעשה בין שתאמ' לכפול המספר השני על כל אות מן המספר הראשון או שתאמ' לכפול כל אות מן המספר הראשון על כל המספר השני | |||||||||||||||||||||||||||||||||||||||||||
| והנה כאשר תכפול ה"א על 0ב"א יעלה מכפל 0בא על ה' של ה"א תמונת כך | |||||||||||||||||||||||||||||||||||||||||||
| ומכפל 0בא על א' של ה"א יעלה 0בא ויהיה תמונת הכת' כאשר יהיה נולד מסדר אשר זכרתי על תמונת כך וכאשר תחבר כל מה שהוא ממערכה אחת יעלה המבוקש 00חא | |||||||||||||||||||||||||||||||||||||||||||
| שאלה הנה השנה ב'ה' שבועות כמה ימים בכלל השנה | |||||||||||||||||||||||||||||||||||||||||||
| הנה תכפול ז' על ב'ה' ויעלה המבוקש כי ז' ימי' הם שבוע א' והנה המבוקש ד'ו'ג' | |||||||||||||||||||||||||||||||||||||||||||
| שאלה הנה יש לנו ג'ו'ב' מחזורי' מבריאת עולם ועוד שנים עשר שנים והמחזור הוא ט'א' שנים כמה הפרט | |||||||||||||||||||||||||||||||||||||||||||
| תכפול ט'א' על ג'ז'ב' ויעלה ז'ח'א'ה' חבר עליהם עוד כ"א שנים אשר היו בידך יותר מן ג'ז'ב' מחזורים ויעל ט'ט'א'ה' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||
| שאלה הנה יש לנו ה'ח'ט' מחזורי' ועוד ט'א' שנה והמחזור הוא ח'ב' שנה כמה הפרט | |||||||||||||||||||||||||||||||||||||||||||
| הנה תכפול ה'ח'א' על ח'ב' ומה שעלה ממקובץ הכפל עליו תחבר ט'א' שנים הנותרי' ויעלה המבוקש והוא ט'ט'א'ה' | |||||||||||||||||||||||||||||||||||||||||||
| שאלה הנה השעה 0'ח'0'א' חלקים והיום ד'ב' שעות כמה חלקים ביום | |||||||||||||||||||||||||||||||||||||||||||
| תכפול ד'ב' על 0'ח'0'א' ויעלה המבוקש בטהב | |||||||||||||||||||||||||||||||||||||||||||
| שאלה הנה היתרון מן המחזור הוא שעה וה'ח'ז' חלקים כמה יהיו החלקים | |||||||||||||||||||||||||||||||||||||||||||
| כאשר נשים השעה ג"כ לחלקים הנה תחבר ה'ח'ד' עם 0ח0א ויעלה המבוקש ה'ו'ב'א' | |||||||||||||||||||||||||||||||||||||||||||
| שאלה שארית החדש הוא א' ב'א' ג'0'ז' ר"ל יום וב'א' שעו' ג'ט'ז' חלקים כמה חלקים יהיה | |||||||||||||||||||||||||||||||||||||||||||
| כאשר נשים היום והשעות ג"כ חלקים הנה היום הוא ד"ב שעות וב"א שעות הרי ו"ג שעו' תכפול ו"ג על 0'ח'0'א' על ו"ג ויעלו לך 0חחחג חבר עליהם גטז שהם החלקי' הנותרי' על הימים והשעות ויעלה בידך גזוטג | |||||||||||||||||||||||||||||||||||||||||||
| שאלה החדש החדש הוא ט"ב ימים ב"א שעות גטז חלקי' כמה [22]יהיה החדש כאשר נשים אותו הכל חלקי' | |||||||||||||||||||||||||||||||||||||||||||
| הנה בראשונה נעשה מן הימים שעות והוא שנכפול ד"ב על ט"ב ויעלה בידך וטו שעו' חבר עליהם ב'א' שעות אשר הם בכלל החדש נותרי' על הימים השלמים ויהיו שעות החדש ח0ז תכפול ח0ז על 0ח0א שהם חלקי השעה ויעלה בידך 0דודוז חלקים חבר עליהם גטז חלקי' אשר בכלל החדש נותרים על הימי' והשעות ויעלה בידך המבוקש גגדהוז | |||||||||||||||||||||||||||||||||||||||||||
| והנה זכרתי ממין אלו השאלות להתעודד על מיני החשבונות אשר יועילו בחשבון התקופות והמולדות עם מה שיתרחב ג"כ בזה הדעת ליכנס בעניינים אשר שעריהם נעולים לרוב בני אדם לא מפני עומק אלו הדברי' אלא מפני מיעוט העסק להם בדברים שהם זולת רדיפת המותרות ותאוות הבהמיות | |||||||||||||||||||||||||||||||||||||||||||
| ומעתה נפסיק מזה ונחל בביאור שער החלוק | |||||||||||||||||||||||||||||||||||||||||||
| וטרם שאחל בה ראיתי להשכילך בדרך אחרת בשער ה[נזכ] ר"ל בשער הכפל |
Chapter Four: Division |
השער הרביעי והוא שער החלוק |
| לחלק מספר גדול על מספר קטן ממנו ולדעת כמה פעמי' שימצא הקטן בכלל הגדול | |
| הנה דע לך כאשר תרצה לחלק המספר הגדול על המספר הקטן אז תכתו' המספר הקטן תחת המספר הגדול באפן אשר אבארהו | |
| ואבאר ראשונה כאשר יהיה המספר הקטן נכלל רק באות א' והוא כאשר יהיה המספר הקטן רק אחדים | |
| והנה כאשר תרצה לחלק מספר קטן שהוא בעל אות אחת מן מספר שהוא ג"כ בעל אות אחת זה צריך לך להיות המשער שלך משיג אותו ואין צורך להמציא לזה תחבולה | |
| ע'ד'מ' אם תרצה לחלק ח' על ב' ותרצה לדעת כמה פעמים שימצא הב' בח' זה מובן שהוא ד' פעמי' | |
| וכן מובן היות הד' ב' פעמי' בח' והא' בח' ח' פעמי' בח' | |
| וכן מובן היות הג' ג' פעמי' בט' והא' ט' פעמי' בט' | |
| וכן מובן שהג' ב' פעמי' בח' ושישאר עוד ב' | |
| ונוכל לומ' בעבור זה המותר שהג' בכלל הח' שני פעמי' ושני שליש פעם | |
| אלא שאין כוונתינו ליכנס בזה השער רק בביאור עניין השלמים כמו שעשיתי בשאר השערי' הקדומים | |
| ואמנם עניין השברי' יתבאר בשער השברי' אשר הוא מיוחד להם | |
| והנה אחר שהקדמתי לך זה שכאשר יהיה המספר הגדול רק אות אחת וכן המספר הקטן רק אות אחת שאז ההבנ' מקיף בעניין החלוק הנני אומ' עוד כאשר יהיה המספר [23]הגדול שני אותיות והמספר הקטן אות אחת אם יהיה אותיות המספר הגדול כל אחד מהם יותר מן המספר הקטן באפן אשר יכלה כל אחד
מן האותיות הגדולות על מספר האות הקטן | |
| ע'ד'מ' ט'ט' המספר הגדול והמספר הקטן ג' הנה הט' יחלק על ג' ולא ישאר דבר | |
| וכאשר יהיה תמי' המספרי' על זה האופן אז תכתו' המספר הקטן תחלה תחת האות האחרון מן המספר הגדול ותחשוב כאילו האות האחרון ג"כ אחדים ולא תביט מאיזה מין שהוא וראה כמה פעמי' האות התחתון כתוב ותכתו' למעלה מן האות העליון מספר הפעמי' אשר ימצא התחתון כמו בו ותמחוק האות של המספר הגדול וגם של המספר הקטן ותכתו' שנית האות של המספר הקטן תחת האות הראשון ונהג לשם זה המנהג בעצמו אשר נהגת תחת האות השני | |
| והמשל הרי שרצינו לדעת כמה פעמי' שימצא ג' בתוך ט"ט | |
| הנה ג' פעמי' נכתו' ג' תחת הט' השנית ונאמר הנה הג' ימצא ג' פעמי' בתוך ט' וא"כ נכתוב ג' למעלה מט' ונמחוק הט' וגם הג' שתחתיה | |
| ואחר זה נכתו' עו' הג' שהיא המספר הקטן תחת הט' הראשונה ונאמר כמה פעמי' ימצא ג' בט' והוא ג' פעמים וא"כ נכתו' למעלה מהט' ג' ונמחוק הט' וגם הג' שתחתיה ויהי' אשר עלה למעלה ג'ג' והוא המבוקש ר"ל ג'ג' פעמי' ימצא ג' בתוך ט'ט' | |
| משל אחר הרי שרצינו לדעת כמה פעמי' ימצא ג' בתוך ט"ו | |
| הנה נכתו' ג' תחת הו' ונאמר ג' ימצא שני פעמי' בתוך ו' ולכן נכתו' ממעל לו' ב' ונמחוק הו' וגם הג' שתחתיה | |
| אחר זה נכתו' עוד הג' תחת הט' ונאמר הג' ימצא בתוך הט' ג' פעמי' וא"כ נכתו' ג' ממעל הט' ונמחוק הט' הרי שעלה המבוקש ג"ב | |
| משל אחר הרי שרצינו לדעת כמה פעמי' ימצא ג' בתוך ט"ג | |
| נכתו' ג' תחת הג' שלט'ג' ונאמר הנה ג' ימצא בתוך ג' א' פעם וא"כ נכתו' ממעל לג' של ט'ג' א' ונמחוק הג' של ו'ג' וגם הג' שתחתיה | |
| ואחר זה נכתו' עוד ג' תחת הט' ונאמ' הנה ג' ימצא ג' פעמי' בתוך ט' וא"כ נכתו' ממעל הט' ג' ונמחוק הט' וגם הג' שתחתיה הנה עלה המבוקש ג"א | |
| משל אחר הרי שרצינו לדעת כמה פעמי' ימצא ב' בתוך ו"ח | |
| הנה נכתו' הב' תחת הח' ונאמ' הנה ב' ימצא ד' פעמי' בתוך ח' וא"כ נכתוב ממעל הח' ד' ונמחוק הח' וגם הב' שתחתיה | |
| ואחר זה נכתוב גם כן הב' תחת הו' ונאמ' הנה ב' ימצא בתוך הו' ג' פעמים וא"כ נכתו' ממעל לו' ג' ונמחוק הו' וגם הב' שתחתיה הרי שעלה המבוקש ג'ד' | |
| ואמנם כאשר יהיה האות השני של המספר הגדול פחות מן האות של המספר הקטן אז אתה צריך לכתו' המספר הקטן תחת האות הראשון ולאמר כמה ימצא המספר הקטן תחת האות הראשון כזה המספר הגדול בכללו ר"ל כמה פעמים שימצא המספר הקטן במספר הגדול הנרמז בשני אותיו' [24]וכמספר הפעמי' אשר תבין שימצא המספר הקטן במספר הגדול האות הרומז אל אותו המספר תכתו' ממעל לאותו האות הראשון של המספר הגדול ואח"כ תמחוק המספר הגדול והמספר הקטן אשר תחתיו | |
| המשל הרי שרצינו לדעת כמה פעמי' שימצא ד' בתוך ו'א' | |
| הנה אנו צריכים לכתו' ד' תחת של ו'א' ונאמר הנה ד' ימצא ד' פעמי' בתוך ו'א' וא"כ אנו כותבי' ד' ממעל לו' אל ו'א' ואנו מוחקים ו'א' וגם הד' אשר תחתיהם והד' העליונה היא המבוקש | |
| משל אחר הרי שרצינו לדעת כמה פעמי' שימצא ג' בתוך ב'א' | |
| הנה אנו צריכי' לכתו' הג' תחת ב' של ב'א' ונאמר ג"כ כמה פעמים ימצא ג' בתוך ב'א' והנה תמצא ד' פעמי' וא"כ נכתו' ד' ממעל לב' של ב"א ונמחוק ב"א וגם הג' שתחתיהם והד' שעליהם הוא המבוקש | |
| משל אחר הרי שרצינו לדעת כמה פעמי' שימצא ח' בתוך ב'ז' | |
| הנה נכתו' הח' תחת הב' של ב"ז ונאמר כמה פעמים ימצא ח' בתוך ב"ז והנה ימצא ט' פעמי' וא"כ נכתו' הט' ממעל לב' של ב"ז שהוא ממעל לאות הראשון של המספר הגדול ונמחוק ב"ז שהם המספר הגדול וגם הח' שתחתיהם ויהיה הט' שעליהם המבוקש | |
| הנה כבר ראית שאין לנו תחבולה להקל עלינו החשבון בחלוק כאשר יהיה המספ' הגדול שני אותיות על זה האופן אשר רמזתי באלו הג' משלים כי כמו שתחשוב אותו כן יחשוב אותו מי שלא ידע חכמת המספר וסדר הכתב אשר נתתי אינו רק ליאות ומעמס אין צורך בו כי האדם צריך לחשוב אותו לפי הבנתו בבלתי תחבולה וא"כ מה תועלת הכת' במין אלו החשבונו' | |
| ואמנם אע"פ שלא יהיה תועלת בסדר הכת' אשר זכרתי כאשר יהיו השאלות כמו שרמזתי באלו המשלים מ"מ יהיה לנו תועלת גדולה בסדר הכת' אשר נתתי לך כאשר יזדמנו השאלות על מעט חילוף המשלים שזכרתי ולכן ביארתי זה הסדר ואם אין צורך לו באותם השאלו' אשר המשלתי | |
| והמשל במה שיועיל לנו הסדר הנה אנו רוצים לדעת כמה פעמים שימצא ג' בתוך ב'ד' | |
| הנה אנו כותבים ראשונה הג' תחת הד' ואומרי' כמה פעמי' ימצא ג' בתוך ד' והוא פעם א' וא"כ ראוי לך להסיר מן הד' ג' פעם אחת וישאר מקום הד' א' והאות הרומז לפעם א' הוא א' וא"כ אנו כותבי' א' ממעל האות אשר הג' תחתיו | |
| ואחר זה נמחוק הג' ונכתו' אותה תחת האות הראשון של המספר הגדול והוא תחת הב' ויהיה עתה העומד לפנינו עדיין מן המספר הגדו' בא כי כבר נגרע קצת ממנו ועתה נאמר כמה פעמי' ימצאו ג' בתוך ב'א' והוא ד' פעמי' ונלך בזה המנהג כאילו שהיה המספר בראשונה ב'א' ע"ד אשר ביארתי הסדר וא"כ צרי' שנכתו' האות הרומז לד' פעמים ממעל לב' של ב'א' ונמחוק הב'א' והג' שתחתיהם והאות הרומז לד' פעמי' [25]הוא ד' וא"כ ישאר המבוקש ממעל שהיה המספר הגדול ד"א | |
| הנה כבר הגיע לנו תועלת מהדרכי' אשר זכרתי בלי ספק | |
| משל אחר הרי שרצינו לדעת כמה פעמי' ימצא ב' בתוך בט | |
| הנה נכתו' ראשונה ב' תחת הט' | |
| ונאמר כמה פעמי' ימצא ב' בתוך הט' והוא ד' פעמי' וישאר א' וא"כ נסיר מן הט' ד' פעמי' הב' שהוא ח' ונכתוב מקום הט' א' הנשארת | |
| והאות הרומז נכתו' ממעל האות אשר הב' תחתיו שהוא עתה הא' וקודם לכן היה ט' ואחר זה נמחוק הב' התחתונה ונכתו' אותה תחת הב' של ב'א' אשר נשארו לפנינו | |
| ונאמר כמה פעמי' ב' [נ]מצא בתוך ב'א' והוא ו' פעמי' וא"כ נכתו' ממעל לב' ב'א' ונסיר ו' פעמי' ב' מן ב'א' וא"כ לא ישאר דבר ולכן אמרתי במשלים הקודמי' ותמחוק המספר הגדול ויהיה המבוקש מה שעלה ממעל למספר הגדול והוא ו'ד' | |
| משל אחר הנה רצינו לדעת כמה פעמי' ימצא ד' בתוך ו'ו' | |
| הנה תכתו' ד' תחת הו' השנית של ו'ו' | |
| ואמור כמה פעמי' ימצא ד' בתוך ו' והוא פעם א' תכתו' א' ממעל הו' השנית ותחסר א' פעמי' ותחסר א' פעמי' ד' מן הו' שהד' תחתיה וישאר מקום הו' ב' | |
| ואחר זה תמחוק הד' ותכתוב אותה תחת הו' הראשונה והנה נשאר לפניך ו'ב' | |
| ואמור כמה פעמים ימצא ד' בתוך ו'ב' והוא ו' פעמי' וישאר ב' וא"כ תכתו' ו' ממעל לו' של ו'ב' ותחסר מן ו'ב' ו' פעמי' ד' שהוא ד'ב' וישאר ב' | |
| הרי שעלה המבוקש ו'א' ונשארו עוד ב' | |
| וכאשר יהיה המספר הגדול ג' אותיות או יותר אז תכתו' המספר הקטן ראשונה תחת האות האחרון אם האות האחרון אינו פחות מן המספר הקטן ונהג תחת האות האחרון מה שנהגת תחת האות השני או תחת האות הראשון ואח"כ תכתו' המספר הקטן תחת האות שלפני האחרון ונהג ג"כ שמה וכן תעשה תחת כל אות שלאותיות המספר הגדול | |
| המשל הרי שרצינו לדעת כמה פעמים שימצא ד' בתוך ג'ד'ט' | |
| הנה תכתו' הד' תחת הט' ראשונ' ותאמר כמה פעמי' ימצא ד' בתוך ט' והוא ב' פעמי' וא"כ תכתו' ב' ממעל הט' ותחסר מן הט' ב' פעמי' ד' שהוא ח' וישאר מקום הט' א' ואח"כ מחוק הד' ותכתו' אותה תחת הד' ויהיה העומד לפניך מן הד' ההוא והלאה מהמספר הגדול ד'א' | |
| ולכן תאמ' כמה פעמ' ימצא ד' בתוך ד'א' והוא ג"פ וא"כ תכתו' ד' ממעל הד' אשר תחתיה המספר הקטן שהוא ג"פ ד' ותחסר מן ד'א' שהם לפניך מהמספר הגדול ג"פ ד' שהם ב'א' וישארו מקום ד'א' ב' ואחר זה תמחוק המספר הקטן שהוא ד' ותכתו' אותו תחת אות קודם האות שהיה תחתיו והוא הג' בזה המשל ויהיה העומד עוד לפניך מהמספר הגדול ג'ב' ולכן תאמר כמה פעמים ימצא ד' בתוך ג'ב' והוא ה' פעמים ולכן תכתו' ה' ממעל האות אשר המספר הקטן תחתיו והוא ממעל הג' בזה המשל ותחסר ה' פעמי' ד' שהוא 0'ב' מן ג'ב' שהם לפניך וישארו עוד ג' הרי שעלה המבוקש ה'ג'ב' ונשארו עוד ג' | |
| משל אחר הרי [26]הרי שרצינו לדעת כמה פעמי' ימצא ג' בתוך ה'ו'ז'ח' | |
| הנה נכתו' ראשונה הג' תחת הח' שהוא האות האחרון של המספר הגדול ונאמר כמה פעמי' ימצא ג' בח' והוא ב' פעמי' וא"כ תכתו' ב' ממעל לח' ותחסר ב' פעמי' ג' מן הח' וישאר מקום הח' ב' ותמחוק האות התחתון שהוא ג' ותכתו' אותו תחת אות מוקדם לאחרון מפני שנחסר מן האחרון שהוא שנעשה הוא יותר פחות מהמספר הקטן והנה יהיה לפניך מהמספר הגדול ז'ב' ממקום המספר הקטן והלאה | |
| ותאמר כמה פעמי' ימצא המספר הקטן שהוא ג' בתוך ז'ב' והוא ט' פעמי' וא"כ כתו' ט' ממעל הז' אשר המספר הקטן תחתיה ותחסר ט' פעמי' ג' שהו' המספר הקטן מז'ב' שהוא ממעל המספר הקטן והלאה וט' פעמי' ג' הם ז'ב' וא"כ תחסר ז'ב' מן ז'ב' לא ישאר דבר | |
| ואחר זה תחזור עוד המספר הקטן תחת אות מוקדם ממה שהיה תחתיו מקודם כי לא נשאר דבר ממעל המקו' שהיה שם המספר הקטן ולא ממעל והלאה וכאשר תעשה כן יקרה מעמ' המספר הקטן תחת ו' של המספר הגדול והנה ג' שהוא המספר הקטן הוא שני פעמים בו' וא"כ תכתו' ב' ממעל הו' ותחסר ב' פעמי' ג' מהו' ולא ישאר דבר | |
| ואחר זה תזיר עו' הג' שהיא המספר הקטן תחת אות מוקדם ממה שהיה ויהיה מעמדו תחת הה' ומשם והלאה אין מספר יותר והנה ג' א' פעם תוך ה' וא"כ נכתו' א' ממעל הה' ונחסר א' פעמי' ג' מן הה' וישאר ב' והנה א"כ המבוקש א"ב ט"ב ונשארו עוד ב' | |
| ואמנם כאשר יהיה המספר הקטן יותר גדול מן האות האחרון של המספר הגדול אז נזיר המספר הקטן תחת אות מוקדם לאות האחרון | |
| והמשל הרי שרצינו לדעת כמה פעמי' ימצא ה' בתוך א"בג"ד | |
| הנה האות האחרון ד' והוא יותר קטן מהמספר הקטן שהוא ה' ולכן נכתוב המספר הקטן תחת ג' של אבגד שהוא האות המוקדם בסמוך לאות האחרון | |
| ונאמר כמה פעמי' ימצא ה' בתוך ג'ד' והנה תמצא ח' פעמים וא"כ נכתו' ח' ממעל האות שהמספר הקטן תחתיו והוא הג' ונחסר מן ג'ד' 0'ח' פעמים ה' שהוא 0'ד' וישאר ג' ואחר זה נזיר ה' של המספר הקטן תחת אות סמוך מוקדם ויהיה לפי זה מעמדו תחת ב' ומשם והלאה יהיה ב'ג' | |
| ונאמר כמה פעמי' ימצא ה' בתוך ב'ג' והוא ו' פעמי' וא"כ תכתו' ו' ממעל האות שהמספר הקטן תחתיו ונחסר מן ב'ג' ו"פ ה' שהוא 0'ג' וישארו מקום ב'ג' ב' | |
| ונזיר אחר זה עוד המספר תחת האות הסמוך מוקדם ויהיה משם והלאה א"כ נאמ' כמה פעמים ימצא ה' בתוך א'ב' וימצאו ד' פעמים וא"כ תכתו' ד' ממעל האות שהמספר הקטן תחתיו ותחסר ד' פעמי' ה' שהוא 0'ב' מן א'ב' וישאר מקום א"ב א' וא"כ עלה המבוקש ד'ו'ח' וישאר עוד אחד | |
| משל אחר הנה רצינו לדעת כמה פעמי' ימצא ו' בתוך ז'0'ח'ט'א' | |
| הנה האות האחרון פחות מן המספר הקטן וא"כ נכתו' המספר הקטן [27]שהוא ו' תחת האות הסמוך מוקדם והוא הט' ויהיה משם והלאה ט'א' | |
| ונאמר הנה ו' ימצא ג' פעמי' בתוך ט'א' וא"כ תכתו' ג' ממעל הט' שהאות האחרון תחתיה ותחסר מן ט'א' ג' פעמי' ו' וישאר מקום הט'א' א' והנה נזיר המספר הקטן תחת אות מוקדם סמוך ויהיה מעמדו א"כ תחת הח' ומשם והלאה ימצא ח'א' | |
| וא"כ נאמר כמה פעמי' ימצא המספר הקטן שהוא ו' בתוך ח'א' והנה ימצא ג' פעמי' וא"כ כתו' ג' ממעל הח' שהמספר הקטן תחתיו ותחסר מח'א' ג' פעמי' ו' ולא ישאר דבר מקום ח'א' ואחר זה תזיר המספר הקטן תחת אות מוקדם סמוך ויהיה מעמדו תחת ה0' ומ0' והלאה אינו דבר יותר כי כבר נתן החשבון למחוק הכל וא"כ תאמר כמה פעמי' ימצא ו' בתוך 0 והוא ימצא 0' פעמי' ר"ל לנו שום פעם וא"כ תכתו' 0 ממעל האות שהמספר הקטן תחתיו | |
| ואחר זה תזיר עו' המספר הקטן ויהיה מעמדו תחת הז' ומשם והלאה אין מספר יותר | |
| וא"כ תאמר כמה פעמים ימצא ו' בתוך ז' ותמצא א' פעם וא"כ תכתו' א' ממעל הז' שהמספ' הקטן תחתיו ותחסר א' פעם ו' מן הז' וישאר א' וא"כ עלה המבוקש ממעל שהיה שם המספר הגדול והוא א'0'ג'ג' ונשאר עוד א' | |
| והנה כל מה שביארנו מדרך החלוק הוא כאשר המספר הקטן אות אחת | |
| ואמנם כאשר יהיה המספר הקטן יותר מאות אחת אז אתה צרי' לכתו' האות המספר הקטן תחת המספר הגדול כראשונה באופן שיהיה האות האחרון של המספר הקטן תחת האות האחרון של המספר הגדול ותראה כמה פעמי' שימצ' האות האחרון של המספר הקטן באות האחרון של המספר הגדול והאות הרומז אל הפעמי' ההם תכתו' ממעל למספר הגדול ממעל האות שתחתיו התחלת המספר הקטן ותכפול אותו האות על כל אות של המספר הקטן מקום אשר שם אותיות של המספר הקטן ומקובץ הכפל תכתוב ממעל המספר הקטן בין המספר הגדול והקטן מקום אשר נולד שם מקובץ הכפל ואחר זה תוציא מקובץ הכפל כל אות ממנו מן האות שהו' ממעל לו והלאה מאותיות של המספר הגדול ואח"כ תזיר המספר הקטן באפן שיהיה התחלתו תחת אות מוקדם סמוך ותעשה שם כל המנהג אשר עשית במקום הראשון שהיה שם המספר הקטן ואח"כ תזיר עוד המספר הקטן תחת אות מוקדם וסמוך למה שהיה ונהג ג"כ שם אותו המנהג וכן תזיר תמיד המספר הקטן עד שאין לך אותיות להזירו יותר ויעלה לך ממעל המספר הגדול המבוקש | |
| המשל הרי שרצינו לדעת כמה פעמי' שימצאו ב"ב בתוך באוז הנה נכתו' ב"ב תחת ו'ז' של באוז כדי שיהיה האות האחרון של המספ' הקטן תחת האות האחרון של המספר הגדול והנה ב' האחרונה של המספר הקטן ימצא בתוך הז' ג' פעמי' וא"כ תכתו' ג' ממעל הו' אשר תחתיה התחלת המספר הקטן ואחר זה תכפול זה הג' על המספר הקטן ויעלה המקובץ מן הכפל ו'ו' ממעל המספר הקטן בינו ובין הגדול [28]הגדול והם מכווני' תחת ו'ז' של המספר הגדול ולכן נחסר אלו הו'ו' מן ו'ז' שהם תחתיהם וישאר מקום ו'ז'א' | |
| ועתה נזיר המספר הקטן אחורני' שיהיה התחלתו תחת אות מוקדם סמוך ויהיה מעמד המספר הקטן לפי זה תחת א'א' ונאמר כמה פעמי' ימצא ב' האחרונ' של המספר הקטן בתוך א' שהוא תחתיה והנה תמצא 0 פעמים וא"כ תכתו' 0 ממעל האות אשר התחלת המספר הקטן תחתיו ותכפול ה0' ההוא על המספר הקטן ויעלה מקובץ הכפל 00 ממעל למספר בין המספר הקטן והגדול תחת א'א' ותחסר 0'0' מא'א' וישאר א'א' ואחר זה תזיר עוד המספר הקטן תחת אות מוקדם סמוך ויהיה מעמדו תחת ב'א' של המספר הגדול והנה בעבור שאחר הא' אשר האות האחרון של המספר תחתיה עוד אות והוא ג"כ א' נאמ' כמה פעמים ימצא האות האחרון של המספר הקטן בתוך א'א' והוא ימצא ה' פעמי' כי האות האחרון של המספר הקטן הוא ב' וא"כ נכתו' ה' ממעל האות אשר התחלת המספר הקטן תחתיו ונכפול אותה הה'א' על המספר הקטן ויהיה מקובץ הכפל 0'0'א' ממעל המספר הקטן בין הקטן והגדול תחת ב'א'א' ונחסר זה המקובץ ר"ל 0'0'א' מן ב'א'א' אשר הם תחתיו וישאר מקום ב'א'א' רק ב'א' והנה אין אותיות יותר קדומים להזיר המספר הקטן וא"כ המבוקש הוא מה שעלה ממעל שהיה שם המספר הגדול והוא ה'0'א' ונשארו ב'א' | |
| משל אחר הנה רצינו לדעת כמה פעמים ימצא ד"ה בתוך א'ב'ג'ד'א' | |
| הנה כאשר נכתו' ד'ה' תחת המספר הגדול באופן שיהיה האות האחרון של המספר הקטן תחת האות האחרון של המספר הגדול יהיה אז מעמד המספר הקטן תחת ד"א והנה כאשר תאמר כמה פעמים ימצא ה' שהוא האות האחרון בתוך א' הנה לא ימצא כי אם 0 פעם שהוא פי' לא פעם כלל | |
| וכאשר יזדמן בראשונה כן שלא ימצא האות האחרון של המספר הקטן באות האחרון של המספר הגדול אז אנו צריכים לכתוב המספר הקטן באופן שיהיה האות האחרון של המספר הקטן תחת אות מוקדם וסמוך לאות האחרון מהמספר הגדול ונאמ' אח"כ כמה פעמי' ימצא האות האחרון של המספ' הקטן בתוך מספר אשר ירמזו אליו שני אותיות אשר האות האחרון של המספר הקטן תחת הראשון מהם | |
| והנה לפי מה שביארתי הנה צריך שיהיה המספר הקטן תחת ג'ד' ויהיה האות האחרון של המספר הקטן תחת הד' שהיא האות הקודם וסמוך לאות האחרון של המספר הגדול | |
| והנה בעבור שאחר האות אשר האות האחרון של המספר הקטן תחתיו עוד אות אחד והוא א' אתה צרי' לאמר כמה פעמים ימצא ה' שהיא האות האחרון של המספר הקטן תוך הד' שהיא ממעל לה ובמה שאחר הד' ר"ל כמה פעמי' ימצא הה' בתוך ד'א' והנה תמצא ב' פעמים וא"כ תכתו' ב' ממעל המספר הגדול ממעל האות אשר [29]התחלת המספר הקטן תחתיו ותכפול הב' ההיא על המספר הקטן ויעל' מקובץ הכפל ממעל המספר הקטן בין הקטן והגדול ח'0'א' ויהיה מעמד המקובץ הכפל שהוא ח'0'א' תחת ג'ד'א' מהמספר הגדול וא"כ נחסר ח'0'א' מן ג'ד'א' וישאר מקום ג'ד'א' ה'ג' ונזיר עתה המספר הקטן ויקרה מעמדו תחת ב'ה' של המספר הגדול ואחר הה' עוד ג' ויהיה מקום האות האחרון של המספר הקטן תחת הה' שאחריה עוד ג' ולכן נאמר כמה פעמים ימצא האות האחרון של המספר הקטן שהוא ה' תוך ה'ג' והנה תמצא ז' פעמים וא"כ נכתו' ז' ממעל אות של המספר הגדול אשר התחלת המספר הקטן תחתיו ונכפול אותו הז' על המספר הקטן ויעלה מקובץ הכפל ח'ז'ב' ממעל המספר הקטן בין הקטן והגדול תחת ב'ה'ג' של המספר הגדול והנה מקובץ הכפל הוא מספר יותר גדול מן המספר אשר הוא תחתיו מן המספר הגדול ולכן אנו צריכים למחוק זה מקובץ הכפל וגם ז' אשר הוליד זה המקובץ הכפל אנו צריכים למחוק אותה ונכתוב מקום הז' אות יותר פחות ממנה במספר ושהוא האות הסמוך לה לאחר והוא הו' וכן אנו עושים בכל מקובץ הכפל אשר הוא יותר גדול מהמספר אשר הוא תחתיו אז אנו מוחקים אותו וגם האות שהוא ממעל למספר הגדול אשר הוליד המקובץ ההוא אנו מוחקים ונכתו' מקום האות ההוא אות שהוא פחות ממנו במספר וקרוב לו ואותו האות אשר נכתו' מקומו של הנמחק אותו נכפול על המספר הקטן כמו שעשינו באות הראשון אשר הוצרכנו למחוק והנה הו' אשר כתב' אותה מקום הז' שמחק' כאשר תכפול אות' על המספר הקטן יעלה מקובץ הכפל ד'ב'ג' ממעל המספר הקטן בין הקט' והגדול תחת ב'ה'ג' של המספר הגדול במקום שהיה מקובץ הכפל אשר הוצרכנו למחוק אותו | |
| והנה תחסר עתה המקובץ הכפל הזה מן ב'ה'ג' אשר תחתיהם וישאר מקום ב'ה'ג' ח'ב' ואחר זה תזיר המספר הקטן ויקרה מעמדו תחת א'ח' של א'ח'ב' שהם עוד לפנינו מן המספר הנשאר במספר הגדול ותאמר כמה פעמי' ימצא ה' בתוך ח'ב' ותמצא ה' פעמי' וא"כ תכתו' ה' ממעל אות א' של המספר הגדול אשר תחת האות ההוא התחלת המספר הקטן ואחר זה תכפול אותו הה' על המספר הקטן ויעלה מקובץ הכפל 0'ז'ב' בין המספר הקטן והגדול תחת אח'ב' ותחסר 0זב מן אחב שהוא ממעל לו וישאר מקום אח'ב' א'א' והנה אין אותיות קודמת למספר הגדול להזיר המספר הקטן יותר וא"כ המבוקש הוא מה שעלה ממעל אשר היה שם המספר הגדול והוא ה'י'ב' ונשארו עוד א'א' | |
| משל אחר הנה אנו רוצים לדעת כמה פעמים שימצ' ד'ו'ד' בתוך בט ו'ט'ב'ה'א'ב' הנה אנו צריכים לכתו' המספר הקטן שיהיה האות האחרון ממנו תחת האות שהוא סמוך לאות האחרון של המספר הגדול מפני שהאות האחרון של המספר הגדול [30]הקטן הוא יותר במספר מהאות האחרון של המספר הגדול ויהיה מעמד המספר הקטן לפי זה תחת ב'ה'א' מהמספר הגדול ונאמ' כמה פעמי' ימצא ד' בתוך א'ב' והנה תמצא ה' פעמי' וא"כ נכת' ה' ממעל המספר הגדול ממעל אות ממנו אשר תחתיו התחלת המספר הקטן ונכפול אותה הה' על המספר הקטן ויעלה מקובץ הכפל הקטן ונכפול אותה הה' על המספר הקטן ויעלה מקובץ הכפל בין המספר הגדול והקטן תחת ב'ה' א'ב' 0'ו'ב'ב' והוא מספר יותר גדול מן ב'ה' א'ב' אשר הוא תחתיו ולכן נמחוק זה המקובץ הכפל וגם הה' אשר הולידה אותו ונכתו' מקום ה' אות ד' שהוא אות יותר פחות במספר ונכפול אותה הד' על דוד שהוא המספר הקטן ויעלה מקובץ הכפל מקום שהיה שם מקובץ הכפל הקודם תחת ב'ה' א'ב' ממספר הגדול וה'ח'א' נחסר אותו מן בהאב אשר הוא תחתיו וישאר מקום ב'ה' א'ב' וט'ב' ונזיר אחר זה המספר הקטן ויהיה מעמדו תחת ט'ו'ט'ב' ונאמ' כמה פעמי' ימצא ד' שהוא האות האחרון מן המספר הקטן בתוך ט'ב' אשר הד' תחת הט' מהם והנה תמצא ז' פעמי' ואם כן היה ראוי לנו לכתו' אותו הז' על המספר העליון ממעל אות אשר התחלת המספר הקטן תחתיו ולכפול אחר זה אותו הז' על המספר הקטן אבל לא נעשהו מפני שאנו שיהיה המקובץ הכפל מספר יותר גדול מן ט'ו'ט'ב' אשר יקרה מעמ' מקובץ הכפל תחתיו וא"כ מקום שרצינו לכתו' הז' שם נכתו' ו' שהוא אות יותר פחות במספר מן הז' ונכפול אותו הו' על המספר הקטן כפי מה שהיינו עושים אחר שהיינו מוחקים מקובץ הכפל שהיה בא מתולדות הז' והנה מקובץ הכפל מן ו' על ד'ו'ד' הוא ד'ח'ז'ב' ויקרה מעמדו תחת ט'ו'ט'ב' ונחסרנו מן ט'ו'ט'ב' שהוא ממעל לו וישאר ה'ח'א' מקום ט'ו'ט'ב' ונזיר המספר הקטן עוד ויקרה מעמדו תחת ו'ה'ח' של ו'ה'ח'א' שהם מהמספר הגדול ונאמ' כמה פעמים ימצא ד' שהיא האות האחרון של המספר הקטן בתוך ח'א' אשר הד' תחת הח' ממנו והנה תמצא ד' פעמי' וא"כ תכתו' ד' ממעל האות אשר התחלת המספר הקטן תחתיו ותכפול הד' ההיא על המספר הקטן ויעלה כפל המקובץ והח'א' ויקד' מעמד של ו'ה'ח'א' הזה שהוא כפל המקובץ תחת והחא אשר עדיין לפנינו מן המספר הגדול וא"כ לא ישאר מהמספר הגדול דבר יותר ואין לנו להזיר א"כ המספר הקטן יותר ויהיה המבוקש מה שעלה ממעל אשר היה שם המספר הגדול והוא ד'ו'ד' | |
| הנה לך לדעת לעולם באשר יקרה שלא תוכל להזיר הקטן יותר מפני שאין אותיות יותר קודמות אז יעלה לך המבוקש והוא מה שעלה ממעל המספר הגדול ואם עדיין לפניך דבר מן המספר הגדול הוא מה שישאר שלא לכלל המספר הקטן | |
| ועוד לך לדעת כי כאשר תזיר המספר [31]הקטן ויתן לך החשבון שלא ימצא המספר הקטן אפי' פעם אחת בתוך המספר אשר הקטן תחתיו ואינו כמספר שהקטן תחתיו אותיות אחר סוף המספר הקטן אז תכתו' 0 ממעל האות אשר התחלת המספר הקטן תחתיו ותזיר הקטן אם יש עוד בגדול אותיות קודמות | |
| ואם אחר אשר תזיר אותו עדיין לא תוכל למצא המספר אפילו פעם אחת [הגה זה לא יקרה אלא כאשר היו האותיות הבינונים בחשבון 0] המספר הקטן בתוך המספר הגדול כמה שממנו ממעל הקטן והלאה אז תכתוב ממעל האות אשר התחלת המספר הקטן תחתיו ג"כ 0 | |
| ותזיר אח"כ עוד המספר הקטן וכן תעשה תמיד כל זמן שלא ימצא המספר הקטן כמה שממעל לו והלאה מהמספר הגדול אז תכתו' ממעל המספר הגדול 0 ממעל האות אשר התחלת הקטן תחתיו עד שלא תוכל להזיר יותר ומה שעלה לך אז ממעל הוא המבוקש | |
| ועוד תדע תמיד כאשר יקרה לך להסיר מספר ממספר אם לא תוכל להוציא כל אות מן האות שהוא ממעל לו אז תוכל ליקח לך לעזר האותיות אשר יבאו אחריו אבל לא האותיות אשר קודם לאות אשר תרצה לחסר | |
| והמשל על מה שרמזתי לך הנה מהכללים | |
| הנה רצינו לחסר ז'ה'ב' מן א'0'0'0'ג'א' הנה יקרה מעמדי המספר הקטן תחת 00ג מהמספר הגדול והנה כאשר תאמר כמה ימצא ב' בתוך ג'א' והוא ו' פעמים אלא שזה הו' יוליד מקובץ כפל שהוא יותר גדול מן המספר שהוא יזדמן להיות תחתיו ולכן נכתו' ממעל המספר הגדול ממעל האות אשר התחלת המספר הקטן תחתיו ה' מקום שהיה לנו לכתו' ו' לולי המונע שזכרתי ותכפול ה' על ז'ה'ב' ויעלה מקובץ הכפל ה'ח'ב'א' נחסר ה'ח'ב'א' מן 0'0'ג'א' שהם ממעל להם וישאר ה'א' מקום 0'0'ג'א' והנה נזיר המספר הקטן ויקרה מעמדו תחת 0'ה'א' והנה 0'ה'א' הוא מספר יותר פחות מן המספר הקטן ואין אותיות כמספר הגדול אחר 0'ה'א' כי אם היו אותיות אחר 0'ה'א' לא היה מזיק היות 0'ה'א' יותר פחות מן המספר הקטן כי האות האחרון שהוא אחר התנגדות המספר הקטן הוא תמיד יותר כולל מם המספר הקטן בכלל | |
| והנה אחר שאין אותיות אחר 0'ה'א' שהמספר הקטן תחתיו ו0'ה'א' פחות מן המספר הקטן א"כ נכתו' 0 ממעל המספר הגדול ממעל האות אשר התחלת המספר הקטן תחתיו [הגה מה שאינו מזכיר לכפול ה0' הנכת' ממעל המספ' הגדול על המספר הקטן הוא שכפל ה0' על איזה מספר שיהיה לא יולד ממנו מספר] ואחר זה נזיר המספר הקטן ויקרה מעמדו תחת א'0'ה'א' ונאמ' כמה פעמים ימצא ב' תוך הא' ותמצא ז' פעמים אלא שיקרה לנו למחוק הז' ולכתוב מקומה ו' וגם ו' יביא ההכרח למחוק מפני שתוליד היא על ידי הכפל הראוי לעשות ג"כ מספר יותר גדול מן א'0'ה'א' אשר יזדמן להיותו תחתיו ויביא בסוף הצורך לכתו' ה' מקום הו' אשר רצינו להעמידה מקום הז' ואחר שיביא הצורך לכתו' הה' ומה שיעשה זולתה [32]זולתה יהיה פועל א"כ אחר שאנו משערי' בזה נכתו' הה' עתה וננצל מפועל הבטלה ונכתו' הה' ממעל המספר הגדול ממעל האות אשר התחלת המספר הקטן תחתיו ונכפול הה' על המספר הקטן ויעלה מקובץ הכפל תחת א'0'ה'א' אחבט נחסר אותו מן א0הא וישאר ו'א'ב' מקום א0הא ואין להזיר יותר וא"כ מה שעלה ממעל המספר הגדול הוא המבוקש והוא ה0ה ונשארו עוד ו'א'ב' | |
| והנה אחר שזכרתי לך דרך חשבון זה השער אזכיר קצת שאלות אשר יתכן החשבון להם ממנו וממה שקדם בזולת הצורך למה שיבא מן השערים אחר אלו | |
| שאלה הנה יש לנו פרוטות דהוזח ונרצה לדעת כמה פרחי' ערכם והנה הפרח גדא פרוטו' | |
| הנה נחלק ד'ה'ו'ז'ח' שהם הפרוטות על ג'ד'א' שהוא הפרח ויעלה המבוקש ב'א'ו' וישארו עוד חגא פרוטות שלא הגיעו לכלל פרח | |
| שאלה הנה השנה ו'ו'ג' ימים כמה שבועות הם | |
| תחלק ו'ו'ג' על ז' שהוא שבוע ויעלה המבוקש והוא ב"ה וישארו עוד ב' ימים שלא הגיעו לכלל שבוע | |
| שאלה הנה השנים שעברו מבריאת עולם עם השנה שאנו עומדים בה הם טטאה כמה מחזורי' הם ממחזור של ט"א וכמה אנו במחזור אשר היום בלתי שלם עדין | |
| הנה תחלק ט"טא"ה על ט"א ויעלה המבוקש מן המחזורי' ג'ז'ב' וישאר עוד ב"א וא"כ אנו היום בשנת הבא למחזור הקטן | |
| שאלה הנה הפרט טטאה כמה מחזורי' עברו ממחזור ח"ב וכמה שנים אנו היום במחזור ההוא | |
| תחלק ט'ט'א'ה' שהוא הפרט על ח"ב שהוא המחזור ויצא לך המבוקש במחזורים ה'ח'א' וישאר ט'א' וככה אנו עומדי' במחזור הגדול של ח"ב | |
| שאלה שארית של חדש א' הוא יום א' וב"א שעות וג'ט'ז' חלקי' כמה שארית השנה | |
| הנה נשים היום והשעות הכל חלקי' ונחבר אליהם ג'ט'ז' החלקים ואז נכפול ב"א על אותם החלקים ומה שיעלה מן הכפל הם הכל חלקים נחלקם על חלקים של יום אחד ויעלו ימים ומה שישאר שלא יגיע לכלל יום חלק על חלקי שעה אחת ויעלו לך שעות ומה שישאר עוד שלא יגיע לכלל שעה הם חלקים | |
| וככה נעשה הנה היום והב"א שעות הם ו"ג שעות נכפול אותם על 0'ח'0'א' שהם חלקי השעה ויעלה בידך 0חחחג והם חלקים של ו"ג שעות נחבר עליהם עוד ג'ט'ז' החלקים ויעלה בידך גזוטג והם [33]החלקי' אשר יכלול אותם שארית החדש נכפול עליו ב"א שהוא מספר חדשי השנה פשוטה ויעלה בידך וז0וזד נחלקם על 0בטהב יעלה לך חא ימים וישארו עוד ו'א'ה'ט' חלקים שלא הגיעו לכלל יום נחלקם על 0ח0א שהם חלקי השעה ויעלו לך ח' שעות וישארו עוד ו'ז'ח' חלקי' והנה א"כ אחר אשר תשליך השביעיות מן החא ימים יהיה שארית השנה הפשוטה ד' ימים ח' שעו' וזח חלקים | |
| [34]הג"ה 0'ד'ד' א'ח'א' הם חלקי ז' ימי' וחלקי יום א' הם 0בטהב וחלקי השעה הם 0ח0א | |
| שאלה הנה חלקים של שארית החדש הם גזוטג כמה שארי' החדש המחזור שהם ה'ג'ב' חדשי' | |
| הנה תכפול הגב שהוא מספר חדשי המחזור על גזוטג שהוא שארית החדש ויעלו לך מקובץ הכפל הכל חלקים חלק מקובץ הכפל כל 0בטהב שהם חלקי יום ויעלו לך מן החלקים ימים השלך מן הימים השביעיות ותפוס הנשאר והחלקים אשר ישארו שלא יגיעו לכלל יום תחלק על 0ח0א שהם חלקי השעה ויעלו לך שעות והחלקים שלא יגיעו לכלל השעה הם חלקי השארית ויעלה לך לפי זה שארית המחזור ב' ימים ו'א' שעות הטה חלקים | |
| שאלה הנה חלקי' של שארית המחזור הוא האזטו ונרצה לדעת כמה שארית ג'ז'ב' מחזורים | |
| תכפול ג'ז'ב' שהוא מספר המחזורי' על האזטו וחלק מקובץ הכפל על 0'ב'ט'ה'ב' שהם חלקי היום והעולה בחלוק הם ימים השלך מהם השביעיות כמו שהדין בחשבון המולדו' ומה שלא יגיע לכלל ימים חלק על 0ח0א שהם חלקי השעה ותפוס גם הנשאר שלא יגיע לכלל שעה ויהיה לך המבוקש והוא ו' ימים ו' שעות ה'ג'ד' חלקים | |
| שאלה יתרון חדש החמה על חדשי הלבנה הוא ז0הגב חלקי' אחר ששמנו כל היתרון לחלקי' כמה יתרון חדשי החמה על ה'ג'ב' חדשי הלבנה שהם חדשי המחזור של ט'א' | |
| הנה תכפול ה'ג'ב' על ז0הגב וחלק מקובץ הכפל על חלקי יום לעשות ימים והנשאר על חלקי השעה לעשות שעות ותפוס ג"כ החלקים הנשארי' והשלך אחר זה ממה שעלה כ"ט ימים ב"א שעות גטז חלקים שהם מדת החדש הירחי וכן תשליך מדת החדש תמיד עד שישאר לך למטה ממדת החדש הירחי והוא היתרון והוא שעה א' ועו' ה'ח'ד' חלקים שהם בכלל הוהא חלקים | |
| שאלה הוהא חלקים הם יתרון חדשי חמה על חדשי הירח למחזור א' כמה היתרון לגזב מחזורי' | |
| הנה תכפול ג'ז'ב' הוהא ומקובץ החלק הכפל תחלק על ימים ומה שלא יגיע לכלל ימים תחלק על שעות ותפוס ג"כ הנשאר ויהיה לך יתרון חדשי החמה לגוב מחזורים והנה אין לנו צורך להזכיר [35]להזכיר להפיל מדת החדש כי לא יגיע לכלל מדת החדש והנה יעלה זה היתרון המבוקש ה'א' ימים א'ב' שעות ה'ו'ז' חלקי' ואמנם אנשי זאת החכמה ישליכו מזה היתרון ב'א' 0'ב' שעות ד0ב חלקי' כאשר רוצי' בו יתרון החמה גזב מחזורים אחר מולד ב'ה' ר'ד' שהוא מולדתהו מפני שאומרי' שכך קדמה המולד הירחי קודם ראש חדש השמשי ויהיה לפי אלו אותו היתרון | |
| שאלה הנה יש לנו מספרי' הראשון א' וכל א' מוסיף א' על הקוד' עד תשעה עשר כמה המחובר מהם | |
| הנה כאשר המספרי' נפרדי' כמו עתה שהם ט'א' בלי ספר אותם המספרי' שיבאו אחר האמצעי מהם יוסיפו על האמצעי כמה שיחסרו הקודמים וא"כ ניחס כל אלו הט'א' מספרי' אל האמצעי וא'ע'פ' שקצתם יותר וקצתם פחות אחר שתוספ' הא' משלים החסרון האחר נוכל להניח כאילו הם כלם שוים | |
| ומבואר זה שהוא כן שתוספת א' משלים חסרון אחר שהנה בזה הנשאל האמצעי הוא 0'א' והנה כפי מה שיוסיפו א'א' שהם הסמוכים אחר האמצעי כך יחסרו ט' שהם הסמוכים קודם האמצעי | |
| [36]הג"ה דע לך לעולם המספר האחרון הוא כלל המספרי' מאחר שהראשון הוא א' | |
| ולפי זה הכלל כמין זאת השאלה שכל מספר שיש לו אמצעי אנו כופלי' אמצעיתו על כולו ויעלה המבוקש | |
| המשל בנשאל הנה אמצעית ט'א' הוא 0'א' תכפול ט'א' שהוא כלו על 0'א' שהוא אמצעיתו ויעלה 0טא והוא המבוקש | |
| ואמנם כאשר יהיה המספר האחרון זוגות אתה כופל חציו ר"ל חצי המספר האחרון ויעלה המבוקש | |
| והמשל ששאל השואל כמה מחובר המספרי' מא' עד 0'ב' | |
| הנה נכפול 0'ב' על 0'א' אשר הוא חציו ויעלה 00ב | |
| נחבר עליהם עוד 0'א' שהם חצי המספר האחרון ויעלה 0'א'ב' והוא המבוקש | |
| שאלה כמה המחובר המספרי' מב"א עד א"ג | |
| הנה בעבור שאין התחלת אלו המספרי' מא' אנו צריכי' לחסר ראשונה מהמספר האחרון המספר אשר הוא קודם התחלת המספרי' בסמוך ותחשוב הנשאר כאילו הוא כל ונהג עמו המנהג אשר בארתי לך לעשות כאשר ההתחלה בא' | |
| והמשל בזה הנשאל שהמספר האחרון הוא א"ג והתחלת המספרי' ב"א וא"כ א"א קודמים להם וסמוכי' חסר אותם מן א"ג ישארו 0"ב תחשוב עתה כאילו שאל כמה מחובר המספרי' מא' עד 0'ב' ומבוקשו הוא ג"כ מבוקש לזה הנשאל והוא 0'א'א' כי כפל חצי 0"ב על 0"ב עם תוספת חצי 0"ב הוא 0'א'א' | |
| שאלה כמה המחובר מן מספרי' שהולכים ומוסיפים מג' לג' עד שלשי' | |
| דע לך בכל שאלה מזה המין אשר יתחיל המספר הראשון באחד המספרי' [37]שהמספרי' הולכי' ומוסיפי' באותו המספר שהוא ראשון להם אז תחלק המספר האחרון על אותו המספר שהמספרי' הולכי' ונוספי' עמו והעול' בחלוק תשים אותו מקום המספר האחרון כאשר השאלה ממחובר המספרי' אשר תחילים בא' והולכים ומוסיפי' בא' עד סוף אותו המספר אשר עלה בחלוק ומה שיעלה לך כמנהג ההוא עליו תכפול המספר אשר תוספת המספרי' בו | |
| המשל כנשאל הנה ג' היא המספר אשר המספרי' הולכי' ונוספי' בה ו0'ג' המספר האחרון נחלק 0'ג' על ג' יעלו 0'א' | |
| נניח עתה כאילו שאל כמה המחובר ממספרי' מא' עד סוף עשרה ונכפול חצי עשרה שהוא ה' על 0'א' ויעלה 0'ה' נוסיף עוד ה' עליהם שהוא חצי עשרה ויעלה ה'ה' וזה היה המבוקש אם היתה השאלה כפי המונח ונכפול מבוקש המונח הזה על ג' שהיא תוספת הנשאל ויעלה הוא והוא מבוקש הנשאל | |
| משל אחר כמה מחובר המספרי' אשר התחלת' ז' ותוספת' ז'ז' עד ז'ז' | |
| הנה נחלק ז'ז' על ז' ויעלה א'א' תכפול א'א' על ו' שהוא אמצעיתם ויעלה ו'ו' תכפול אלו ו'ו' על ז' בו"ז והוא המבוקש | |
| שאלה כמה מחובר המספרי' שהם הולכים על זה הסדר א'ג'ה' עד סוף א'ב' | |
| כל שאלה שהיא מזה המין תכפול החצי ממנו על עצמו ויעלה המבוקש | |
| המשל בנשאל חצי א"ב הוא א"א תכפול א"א על א"א ויעלה א'ב'א' והוא המבוקש | |
| [38]תכפול בנפרדים חציו על חציו בתוספת חצי כי חצי כא י' וחצי תוסיף חצי ויהיו יא ותכפלם על עצמם ויצא המבוקש | |
| או אמור י' פעמים יב בתוספת א' שהוא התחלת הכל | |
| ובזוגות תכפול חצים על חצים ותוסיף על העולה חצים המשל כב חצים יא כפלנום על עצמם והיו קכא הוספנו יא ועלו קלב והוא המבוקש | |
| או אמור יא פעמים יב בלי תוספת א' כי כבר [...] מההתחלה [....] בכלל |
Chapter Five: Fractions |
[39]השער החמישי הוא שער השברים |
| והוא שער שיכלול עיין על כל מה שזכרנו באלו השערי' הארבע כאשר יזדמן החשבון בשברי' הן שיהיה החשבון בשברי' לבד או שלמי' עם שברי' יבוארו ענייני' זה בזה השער אשר ישתתפו ג"כ לפעמי' לשאר השערי' כי ענייני זה השער יתנו דרכים להכנס בכל חשבון שהוא מין שברים או משותף כמין שברי' ונחל בענייני זה השער במה שהוא היותר קל והיותר מועיל למה שיבא אחריו כי בזה האופן יקל העיון הרבה למעיין ולכן נסדר זה השער על האופן הזה ואבאר המכוון ע"ד שאלות ותשובות כי דרך החשבון כנשאל למצא המבוקש הוא המכוון והאל יהיה בעזרי להפיק רצוני לעשות [...] בקשתי ולתת את שאלתי | |
| והנה לך לדעת שהרצון בעניין השברי' הוא חלק או חלקים מכלל הכל ומספר החלקים אשר יכלול הכל אותו המספר הוא הנקרא המורה כלומ' הוא מורה מאיזה מין אילו החלקי' ר"ל אם הם ממין שנים באחד אשר כל א' מהם נקרא החצי או הם ממין ג' באחד שכל א' נקרא שליש או הם ממין ארבע באחד שכל א' נקרא רביעית או מאיזה מין הם זולת אלו או מאלו לעולם המספר אשר יורה על כמות מספר באחד שלם הוא נקרא המורה כי המספר ההוא מורה מאיזה מין הם בערך אל השלם והאות או האותיות הרומזים אל המספר ההוא הוא רומז ג"כ על מין השבר אשר כלל המספר ממין אותם השברי' הוא א' שלם | |
| המשל ב' רומז על חצי וג' על שליש וד' אל רביעית מפני שד' רביעיות בשלם וע"ד זה יורו כל אותיות על מין ממיני השברי' וכן יורו ג"כ על מין ממיני שברי השבר או שברי שברי' של שבר או שברי שברי' עד אין סוף כי כל שבר יונח הוא כל בעצמו והשברים ממנו בערך אל עצמו כמו שברי השברי' אל השלם בעצמו | |
| והנה אחר אשר ביארנו עניין השברי' ועניין המספר המורה על מין מהם אומ' שהאות או האותיות אשר יורו על מין מהם אני קורא אותו רומז מזה הצד רומז ל לפי שהוא רומז אליהם | |
| ע'ד'מ' ב' רומז של החצי ג' רומז של השליש ד' רומז של הרביעית 0'א' רומז של העשירית ב'א' רומז לחלק ב'א' בשלם 0'0'א' רומז לחלק ממאה בשלם 000א רומז לחלק מאלף בשלם וע"ד זה כל המספרי' שהם אין אלו המספרי' או אחריהם | |
| והנה מה שראוי להקדי' הוא לדעת איזה מספר אשר ימצא בו שני מיני שברי' או יותר משני מינים כפי המבוקש ושנוכל לחלק המספר ההוא על כל מין ממיני השברי' המבוקשים במספר שלם שלא נצטרך להשים בחלוקה שברים עד"מ ד' לרביעית וחמשה לחומש כי אחד מד' הוא רביעית מספר הד' וא' מן חמשה הוא חומש החמשה | |
| והנה לא שמשנו בשברי' ע"ד שהיה מחוייב לעשות אם היינו אומרי' הרביעית משלשה או הרביעית [40]מן החמשה כי הרביעית משלשה הוא שלשה רביעיות האחד והרביעי' מן החמשה הוא אחד ורביעי' והנה כמו אלו צריכי' אנו להודיע מיני אלו השברי' במספר בלתי הכל שלמי' מה שאין כן הד' או ח' או ב'א' לרביעית כי רביעית הד' הוא א' שלם והרביעית מח' הוא שני שלמים ורביעית ב'א' הוא ג' שלמים וכן ב'א' תמצא בהם שליש ורביעית ושתות בשלמים כי הרביעית ג' והשליש ד' והשתות ו' | |
| והנה באשר תרצה למצוא חשבון אשר יחלק אל כל אחד ממיני השברי' אשר המבוקש שיחלק המספר אליהם אז תכתוב לפניך רומזי השברי' ההם אשר תרצה מספר שיחלק להם ותכפול שני רומזים ראשונה זה על זה ואם היו הרומזים רק שנים הנה כבר זה המקובץ הכפל הוא המספר המבוקש ואמנם אם הרומזי' יותר [הג"ה והוא כאשר יהיו מיני השברי' יותר מן שנים אז הרומזים ג"כ יותר] משנים אז תכפול השלישית על מקובץ הכפל של השנים ומקובץ הכפל של השלשה עליו תכפול הרומז הרביעית אם יש בידך רומז רביעי ועל מקובץ הכפל של הארבע תכפול הרומז החמישית וכן תכפול הרומז הששית על מקובץ הכפל של החמשה וכן תמיד על כל מקובץ הכפל תכפול הרומז אשר אחר הרומז המוקדם בכפל עד שלא יהיה לך רומז יותר והשתתפות כל הרומזים אל הכפל וכאשר יהיה לך רומז יותר המקובץ הכפל הוא המבוקש בלי ספק ומהנה אכתו' לך המשלים ע"ד השאלות ומסדר השאלות יבואר לך המכוון על אופנו בלי ספק | |
| [41]הג"ה דע לך כאשר תכפול ג' על ד' יעלה בידך ב"א שהוא חשבון שימצא בו שליש ורביעית בלי ספק וכמו שימצא בו שליש כן תמצא בו שליש הרביעית וכן רביעית השליש כי אותם הרומזי' אשר תכפלם יחד ר"ל השנים אשר תכפול אותם יחד ימצא כל אחד מהם במספר שלם כמספר אשר יכלול חבירו והמשל הרי שכפלנו ג' על ד' עלו ב"א השליש מהם ד' ורביעית ד' הוא א' הנה במספר אשר יכלול עליו השליש והוא ד' כן תמצא הרביעית וכן תמצא בג' שהוא הרביעית שליש וזה מובן ואם תכפול על 0א איזה מספר שלם שיהיה לא תפסד זה לעולם ימצא בשליש הרביעית וברביעית השליש והמשל הרי שתכפול על בא ה' יעלו 0א 0ו השליש | |
| שאלה איזה חשבון הוא שימצא בו שליש ורביעית | |
| הנה רומז השליש ג' ורומז הרביעית ד' וא"כ תכפול ג' על ד' יעלה ב'א' והוא המבוקש כי הרביעית ג' והשליש ד' | |
| שאלה איזה חשבון הוא שימצא בו חצי ושביעית | |
| הנה רומז השלי החצי הוא ב' ושל השביעי ז' וא"כ תכפול ב' על ז' ויעלה ד'א' והוא המבוקש כי ב' הוא השביעית והחצי הוא ז ז' | |
| שאלה איזה חשבון שימצא בו שליש ורביעית וחומש הנה הרומזים לאלו השברים הם ג' ד' ה' והנה תכפול ראשונה ג' על על ד' יעלה ב'א' ותכפול על ב'א' ה' אשר עוד בידך מהרומזים ויעלה 0'ו' והוא המבוקש כי 0'ב' הוא השליש וה'א' הרביעית וב'א' החומש | |
|
שאלה איזה חשבון שיחלק על חצי ושליש ורביעית וחומש ושתות ועשירית וחלק שנים עשר |
|
הנה רומז החצי ב' ושל השליש ג' ושל הרביעית ד' ושל החומש ה' ושל השתות ו' ושל העשירית 0'א' ושל חלק שנים עשר ב'א' |
| והנה כאשר תכפול ב' על ג' יעלה ו' וד' תכפול על ע ו' שעלה יעלה ד'ב' | |
| ותכפול עליהם ה' שהוא רומז הסמוך אחר הרומזים שמכלל כפל שלהם עלו הד'ב' ויעלה 0'ב'א' תכפול עליהם הרומז הסמוך אשר עדיין בידך והוא 0'א' ויעלה בידך 00בז תכפול עליהם ב'א' שהוא הרומז אשר נשאר עוד 00דוח [42]וזהו המספר המבוקש | |
| ואמנם יש לדעת כי יש לזה המבוקש מספר יותר קרוב והדרך לדעת המספר היותר קרוב הוא שתעיין ברומזים ותראה איזה מהם יקבל חלוקה שיחלק על אחד האחדי' במספר שלמים ואותו שיקבל החלוקה על זה האופן אותו תתפוס והוא יעמוד מקום עצמו וגם יעמוד מקום הרומז אשר הוא יחלק אליו ואין צורך לאותו הרומז האחר שזה הרומז אשר אנו תופסי' אותו יקבל החלוקה למספרי' של הרומז אשר נניחהו וכן אם יכלול הרבה מן הרומזי' על זה האופן ר"ל שיהיה רומז בכלל הרומזים שיתכן לו החלוקה לכל אחד מקצת הרומזים הנשארי' והמשל כנשאל שזכרנו שהרומזים ב'ג'ד'ה'ו'0'א' ב'א' הנה ב'א' איפשר שיחלק על ב' בלי שישאר או יחסר דבר וכן יחלק ב'א' על ג' וג"כ על ד' וג"כ על ו' הנה ראוי לנו שנקח ב'א' לבד מקום כל אילו ר"ל מקום ב'ג'ד'ו' וישארו לפי זה עוד מן הרומזי' ה'0'א' ב'א' והנה ג"כ לא נצטרך אל הה' מפני ש0'א' יעמוד ג"כ מקום הה' לפי ש0'א' יקבל החלוק על הה' וא"כ ישארו מקום הרומזים כלם 0'א' ב'א' וא"כ תכפול 0'א' על ב'א' ויעלה 0בא והוא המבוקש בלי ספר ר"ל הוא חשבון שימצא בו חצי ושליש ורביעית וחומש ושתות ועשירית וחלק ב'א' | |
| ואמנם יתכן בזה הנשאל לילך דרך שימצא חשבון עוד יותר קרוב אשר ימצא בו כל אלו השברי' והדרך הזה הוא שאחר שנשארו רק שני הרומזים שהם ב'א' ו0'א' נוכל לתפוז מקום א' מהם חציו מפני שישאר עוד רומז שמספרו זוגות ומספר זוג אשר תכפול על חצי מספר מן המספרי' יוליד הכפל אותו המספר שיהיה חצי שיהיה שלם ואם הזוגות אשר תכפול על חציו רבים יוליד לך מספרי' שלמי' רבים ואין היזק בזה לעניין אשר אנו בו כי על כל פנים יעלו מהמספרי' ההם שלמי' יותר מעטי' משיעלו מכפל אותם הזוגות על כולו וכוונתינו שיהיה לנו המספר היותר קרוב שיתכן בו מבוקשנו | |
| והנה לפי זה כאשר תכפול 0'א' וב'א' אחד על חצי השני יעלה לך 0'א' 0'ו' והוא המבוקש בלי ספק כי הנה חצי 0'ו' הוא 0'ג' והשליש הוא 0'ב' והרביעית ה'א' והחומש ב'א' והשתות 0'א' והעשירית ו' והחלק ב'א' הוא ה' | |
| שאלה איזה חשבון שימצא בו חצי ושליש ורביעית ושתות ושמינית ותשיעית | |
| הנה הרומזי' לאלו הם בגדוחט והנה לפי מה שזכרנו מעמד הט' הוא מקום הג' ומע[מ]ד הח' מקום ב'ד' וישארו הרומזים לפי זה ו'ח'ט' והנה שבכלל אלו הרומזים מהם זוגות ניקח מקום האחד חציו ויהיה לנו הרומזים לפי זה ג'ח'ט' | |
| ואם תרצה יהיו ו'ד'ט' | |
| והעניין לפי מה שאנחנו בו עתה הוא הכל אחד ר"ל הם שתשים הרומזי' ג'ח'ט' הן שתשים אותם ו'ד'ט' | |
| כי מכפל ג' על ח' יעלה ד"ב וכן יעלה בעצמו מכפל ד' על ו' וכאשר [43]לששים שברי' וקוראי' לכל חלק מן הששים ראשון או חלק ראשון או שבר | |
| [44]שאלה כמה ז' שניים פעמים ה' שלישיי' | |
| הנה ז' פעמי' ה' הוא ה'ג' ורומז השניים ב' ושל השלישיים ג' והמחובר מהם הוא ה' וא"כ אלו ה'ג' הם ה'ג' חמשיים | |
| שאלה כמה ה' פעמי' ג' רביעיי' | |
| הנה ה' פעמי' ג' הם ב'א' והם רביעיים בעבור שהשברי' המשותפים בשאלה הם רביעיים והם נכפלים בשלמים | |
| שאלה כמה ט' פעמים ט' שניים | |
| הנה ט' פעמים ט' הם א'ח' והם שניים מפני שהשברי' הנכפלי' היו שניים ונכפלים בשלמים | |
| [45][46] |
Chapter Six: Proportions |
השער הששי והוא שער הערך |
| To know the required unknown number, to find it using the other known numbers. | והוא לדעת מספר אחד המבוקש ונעלם לדעת אותו ממספרי' אחרי' ידועים |
| Sometimes the others are also unknown, but the arithmetician assumes numbers by supposition, since the required can be found using the assumed numbers, as will be explained. | ולפעמים לא יהיו ג"כ האחרי' ידועי' אלא שהחכם בחשבון מניח מספרי' ע"ד ההנחה שמאותן המספרי' המונחים יתכן לדעת המבוקש כמו שיבא הביאור במקומו |
| The investigation of the required unknown number is necessarily by association of the other three numbers. | והנה המספר הנעלם המבוקש לא תמלט החקירה עליו מהשתוף משלשה מספרי' אחרי' |
| Pricing Problems | |
|---|---|
|
והמשל שאם יאמר האדם קניתי ח' חביות יין עבור ו"א פרחים איך יבאו ג' חביות |
|
הנה ח' חביות הם מספר אחד |
|
והנה ו"א פרחים הוא מספר שני |
|
והנה ג' חביות הוא מספר שלישי |
|
ואיך שיבאו השלש' חביות הוא המבוקש והוא המספר הרביעי ועליו החקירה והדריש' |
| We always call this required "the sought-after", or "the result", because by this name we separate it from the other numbers. | והנה אנו קוראי' לזה המבוקש תמיד מבוקש כי בזה השם נפרידהו משאר המספרי' או קוראים לו תולדה |
| These are the three numbers that reveal the required to us in the way that I will explain. | ואלו השלשה מספרי' אשר יורו לנו המבוקש בדרך אשר אבאר |
| We specify each of them by a name that distinguishes it from the others. | גם אנו מיחדי' כל אחד מהם בשם אשר יבדילהו מזולתו |
| This is that we call every number that stands in the position of the 8 barrels an "indicator". | וזה שכל מספר אשר יעמוד מעמד הח' חביות אנו קוראי' לו מורה |
| We call the number that stands in the position of the 16 peraḥim the "associated". | והמספר אשר יעמוד מעמד ו'א' פרחים אנו קוראי' לו משותף |
| We call the number that stands in the position of the 3 barrels the "unknown". | והמספר אשר יעמוד מעמד ג' חביות אנו קוראי' לו נעלם |
| When we have associated numbers mentioned in the question, as these three, yet the sought-after does not derive from them directly, but through other numbers resulting from them which are closer factors, these numbers are not called by these absolute names, but they are called by an additional name - we call them a "remote indicator", a "remote associated", and a "remote unknown". | ואמנם כאשר יהיו לנו מספרי' משותפים מצד הזכר בשאלה כמו אלו הג' אבל לא יגיע המבוקש מהם בעצם אלא יגיע מהם המבוקש מצד מה שהם יולידו מספרי' אחרי' אשר הם הסבות הקרובות אז לא נקראו אלו המספרי' באלו השמות במוחלט אבל יקראו בהם עם תוספ' כנוי והוא שאנו קוראי' להם לאחד מורה רחוק ולאחד משותף רחוק ולאחד נעלם רחוק |
| However those numbers that result from them, which are the closer factors, are those that are always called by these names. | אבל אותם המספרי' אשר יתילדו מהם שהם הסבות הקרובות הם הם אשר נקראו תמיד באילו השמות |
| The numbers that are the factors that are closer to causing the result are called accidental and when they are named by the "remote" word, they are named "remote accidental". | ואותם המספרים שהם הסבות הקרובות להוליד התולדה הם הנקראים בכלל משרתים וכאשר יפול להם הכינוי שמכנים אותם במלת רחוק אז נקראים משרתים רחוקי' |
| Whenever we say "accidental" without the word "remote" there is no doubt that the intention is to the closer factors. | אבל בכל מקום אשר נזכיר משרתים בזולת כנוי רחוק בלי ספק הרצון בהם הסבות הקרובות |
| וכן כאשר אני זוכר המורה או המשותף או הנעלם בזולת כנוי רחוק אז הרצון בהם הסבות הקרובות | |
| וזה הכלל יהיה בין עיניך להשען בו כי על זאת ההקדמה אשען בביאור כדי לקצר תכלית מה שאיפר לי לקצר | |
| After the introduction I presented to you and the explanation I explained, turn Your ear to me, hear what I say [Psalms 17, 6]. | ואחרי זאת ההקדמה אשר הקדמתי לך וההצעה אשר הצעתי הט אזניך לי שמע אמרתי[47] |
| ואומ' דע לך לעולם בכל שאלה כאשר תכפול הנעלם במשותף ותחלק מקובץ הכפל על המורה אז יעלה לך המבוקש בלי חלוף | |
| ונציע לך שאלות שונות ומהם יתבאר המכוון בע"ה ביאור רחב הרבה | |
|
שאלה קניתי ח' חביות יין עבור ו'א' פרחים איך יבאו ג' חביות |
|
הנה כבר הקדמתי שהוא ח' הוא המורה וו'א' הוא המשותף וג' הוא הנעלם |
|
והנה כאשר תכפול ג' שהוא הנעלם על ו'א' שהוא המשותף אז יעלה בידך מקובץ הכפל ח'ד' |
|
והנה כאשר תחלק אלו ח'ד' על ח' שהוא המורה יעלה בידך המבוקש והוא [48]ו' וא"כ ג' החביות יבאו בו' פרחים |
|
שאלה קניתי ט' חביות יין עבור ז'ב' פרחים איך יבאו ב'א' |
|
הנה ט' המורה ז'ב' המשותף ב'א' הנעלם |
|
וכאשר תכפול הנעלם על המשותף יעלה מקובץ הכפל ד'ב'ג' |
|
חלקהו על ט' המורה ויעלה בידך המבוקש והוא ו'ג' |
| והנה נתעורר על הסבה אשר בעבורה אנו הולכים זה הדרך בחשבון | |
| ואומר הנה כאשר תאמר ע'ד'מ' קניתי ט' חביות עבור ז'ב' פרחי' | |
| הנה בהכרח כמספר הפרחים כן יגיעו שברי' לחבית אחד משברי' שהם בשלם המספר החביות אשר קנית כי לו הונח פרח א' לט' חביות היה מגיע בלי ספק תשיעית פרח לחבית א' | |
| וא"כ כאשר הונחו פרחים הרבה לט' חביות מגיעים ג"כ תשיעיות הרבה לחבית אחד ואם הונחו החביות עשרה יהיה לחבית אחד עשיריות מקום התשיעיות בלי ספק | |
| וכן אם הונחו החביות מספר אחר יהיו ג"כ שברי חבית אחד מין אחר | |
| והנה בעבור אשר יורו החביות על מין ממיני השברים אשר יגיעו לחבית אחד אנו קוראים להם מורה ר"ל שהן יורו לנו מין השברי' ובעבור שהפרחים יורו על מספר השברי' אשר יגיעו לאחד ויורו ג"כ על מספר אשר יגיע אל החביות כלם הנה אנו קוראים להם משותף | |
| והנה אחר שמספר הפרחים אשר קראנוהו המושתף יורה על מספר שברי' אשר יגיעו לחבית אחד | |
| הנה כאשר נרצה לדעת מה יגיע לחביות הרבה אנו כופלים מספר החביות אשר אנו רוצים לדעת אותם על שבר חבית אחד שהמשותף יורה עליהם ויעלה בידינו שברי החביות אשר כפלנו על המשותף וכאשר נחלק אותם השברי' על המורה הנה בלי ספק יצא לנו מן השברים שלמים זהו ביאור הסבה אשר על קוטבה סובב זה הדרך אשר זכרנו | |
| ונחזור עתה לעניין השאלות | |
|
שאלה קניתי ח' אמות בגד עבור ד'ב' פרחים איך יבאו ו' אמות |
| When the subjects of the number change the meaning of the number does not change. | הנה בהתחלף נושאי המספר לא יומר עניין המספר |
|
והנה ח' המורה ד'ב' המשותף ו' הנעלם |
|
והנה ד'ב' פעמים ו' יעלה ד'ד'א' |
|
חלק ד'ד'א' על ח' שהוא המורה ויעלה המבוקש ח'א' |
|
שאלה קניתי ה'א' אמו' עבור ז' פרחי' איך יבאו ט' |
|
הנה ה'א' המור' ז' המשותף ט' הוא הנעלם |
|
והנה כאשר תכפול ז' על ט' יעלה המקובץ הכפל ג'ו' |
|
חלק אותו על ה'א' שהוא המורה ויעלה בידך ד' וישארו ג' וא"כ המבוקש ד' פרחי' וג' שברים מה'א' בשלם שהם חומש אחד |
|
שאלה קניתי ה'א' ליטרי' פלפל עבור א'ג' פשיטים איך יבאו ז' ליטרי' |
|
הנה ז' פעמים א'ג' הוא ז'א'ב' |
|
וחלקם על המורה שהוא ה'א' ויעלה בידך המבוקש ד'א' פשיטי' וז' שברים מן ה'א' בשלם |
| Payment Problems | |
|
שאלה |
|
הנה ב'א' פעמים ג'א' הוא ו'ה'א' |
|
חלקם על ט' שהוא המורה ויעלה בידך המבוקש ז'א' פשיטים וג' שברי' מט' בשלם |
| ואמנם הם שברים מט' בשלם מפני היות המורה ט' וג' שברי מט' הם שליש אחד | |
|
שאלה נתתי לרגלי ח' פשיטים בעבור מהלך ב'א' פרסאות כמה יגיע לה פרסאו' |
|
הנה ה' פעמים ב'א' הוא 0'ו' |
|
ונחלקם על ח' יעלה המבוקש ז' פשיטים [49]פשיטים וד' שברי' מח' בשלם והם חצי א' |
| Interest Problems | |
|
שאלה אדם שהלוה עשר פרחים ברבית ו' פרחים מה יגיע לז' פרחי' |
|
הנה ו' פעמים ז' הוא ב'ד' |
|
נחלקם אל 0'א' שהוא המורה ויעלה בידך המבוקש ד' פרחים וב' שברים ממין 0'א' בשלם והוא חומש אחד |
|
שאלה שנים שהלוו ג'א' פרחי' עבור רבית ז' פרחים ולאחד שלו ו' פרחי' ולשני ז' כמה יגיע לכל אחד |
|
הנה אין חילוף בעניין זאת השאלה אלא שהרכיב שני שאלות |
|
האחד היא שאלת ג'א' פרחים בז' איך יבאו ו' |
|
והנה המורה ג'א' והמשותף ז' והנעלם ו' |
|
עשה כמשפט ויעלה המבוקש לזאת השאלה האחת ג' פרחים וג' שברים מג'א' בשלם |
|
והשאלה השנית היא ג'א' פרחים עבור ז' איך יבאו ז' |
|
הנה המורה ג"כ ג'א' והמשותף ג"כ ז' אלא שהנעלם ז' |
|
עשה כמשפט ויעלה המבוקש ג' פרחים ועוד 0'א' שברים מג'א' בשלם |
|
שאלה אחד שהלוה ו' פרחים ואחד ז' פרחים ולקחו שניהם לריבית ב'א' פרחים כמה יבא לכל אחד |
| הנה זה ג"כ שתי שאלות | |
| האחת היא ג'א' פרחים עבור ב'א' איך יבואו ו' עשה כמשפט ויעלה לך המבוקש | |
| והשאלה השנית ג'א' פרחים עבור ב'א' איך יבאו ז' | |
| עשה כמשפט ויעלה לך המבוקש כי לא חדש השואל בעניין השאלה אלא שלא זכר המורה בפירוש | |
| מ"מ הוא מובן שכלל ממון שניהם הוא המור' כמו בשאלה הקודמת | |
| שאלה שנים השתתפו אחד ו' פרחים ואחד ז' פרחים והרויחו ב'א' פרחים כמה יגיע לכל אחד | |
| הנה זאת השאלה אין שום הבדל בינה ובין הקודמת בשום אופן אלא שחלף קצת הנושאים ושם מקום רבית הרויחו ומקום הלוו שם השתתפו ומבואר לכל בעל דעת שמחלוף הנושאים בזה האופן לו יומר שום דבר בעבור זה בעצם המספר כי כאשר תאמר קניתי ה' חביות אין הפרש אם תמיר מקום קניתי השכרתי או הלותי או שתפתי או הרוחתי וכל מה שידמה לאלו החילופים אם תשאר הה' על מקומה לא ימיר עניינה מחילוף הנושאים מאופן אלו החלופי' | |
| וכן אם תאמר מקום חביות בגד או פלפל או שאר דברים הן מילין ימי' שנים לא יומר עניין הה' ע"ד משל | |
| וכן כאשר תאמר קניתי ה' עבור א'א' פרחים לא יומר עניין א'א' אם תשים מקום פרחים עניין אחר כאשר תחליף הנושאים למורה יזדמן ג"כ חלוף לפעמים למשותף | |
| ע'ד'מ' שתאמר בה ימיר הלך א'א' פרסאות וכן העניין בנעלם | |
| ואמנם אם תמיר המספר הנה מצד שתמיר הכמות לא יצא בעבור זה מה שיעמוד מקום הה' ע'ד'מ' הוא נקרא המורה ומה שיעמוד מקום א'א' הוא הנעלם | |
| ע'ד'מ' אם תאמר קניתי א'א' בעבור ה' הנה כבר שבו א'א' מקום ה' וה' מקום א'א' הנה א'א' המורה הוא ה' המשותף וכן הענין ג"כ בנעלם | |
|
שאלה א'א' פרחי' עבור ה' חביות כמה חביות יגיעו לו' פרחים |
| הנה א'א' המורה ה' המשותף ו' פרחים הנעלם | |
| עשה כמשפט ויעלה המבוקש והנה בזאת השאלה הומרו נושאי השאלות עד שמה שהיה המשותף בשאלות הקודמי' [50]נעשה מורה והמורה נעשה משותף והמבוקש נעלם והנעלם מבוקש וזה עשה שמקום קנה חביות היה משים קנה פרחים ומקום שאמר עבור פרחים אמר עבור חביות ומקום אמרו איך יבאו חביות אמר איך יבאו פרחים | |
|
שאלה ו' פרחים עבור א'א' אמות איך יבא עבור ז' פרחי' |
| הנה ו' המורה א'א' המשותף ז' הנעלם | |
| עשה עם המשרתים כמשפט ויעלה המבוקש | |
|
שאלה ה' פרחים רבית מא'א' פרחי' ח' פרחים רבית מכמה |
| הנה ה' המורה א'א' המשותף ח' הנעלם | |
| עשה עם אלו המשרתים כמשפט ויעלה המבוקש | |
|
שאלה ב'א' פרסאות בב' ימים ה'א' פרסאות בכמה ימים |
| ב'א' המור' ב' המשותף ה'א' הנעלם | |
| עשה עם אלו המשרתים כמשפט ויעלה המבוקש | |
|
שאלה ו' פרחים עבור 0'ה' ליטרי' פלפל איך יבאו ז' פרחים |
| ו' פרחי' המורה 0'ה' המשותף ז' פרחי' הנעלם | |
| עשה עם אלו המשרתי' כמשפט ויעלה המבוקש | |
|
שאלה קניתי 0'א' אמות ושליש עבור ז' פרחים איך יבאו ג' אמו' |
| הנה בזאת השאלה תשים האמות כלם שלישיות עבור היות עם 0'א' אמות שליש אמה ויעלה בידך מ0'א' אמות ושליש א'ג' שלישיות ומן הג' אמות ט' שלישיות ויהיה שאלתך כאילו שאל א'ג' שלישיות עבור ז' פרחי' איך יבאו ט' שלישיות הנה א'ג' המור' ז' המשותף ט' הנעלם | |
| והנה תעשה עם אלו המשרתים כמשפט ויעלה המבוקש | |
|
שאלה קניתי א'א' אמות עבור ח' פרחים ושליש איך יבאו ה' אמו' |
| תשים הפרחים הכל שלישיות עבור השליש שעמהם וחבר אליהם השליש שעמהם ויעלה בידך ה'ב' שלישיות | |
| וידמה שאלתך כאילו שאל קניתי א'א' אמות עבור ה'ב' איך יבאו ה' | |
| הנה א'א' המור' ה'ב' המשותף ה' הנעלם עשה עמהם כמשפט ויעלה בידך המבוקש אלא מה שיעלה לך השלמים הם שלישיות פרחים והנשאר יהיו חלקי השליש אם ישאר | |
| והנה נוציא זה החשבון לתוספת ביאור כאשר נכפול ה'ב' שהוא המשותף על ה' הנעלם יעלה מקובץ הכפל ה'ב'א' נחלקם על א'א' המורה ויעלה בידינו א'א' שלמים ועוד ד' שלמים שברי' מא'א' בשלם | |
| ואמנם אלו השלמים הם שלישיות של פרח והד' חלקים הם חלקים מא'א' בשליש פרח | |
| והנה כאשר תחלק השלישיות על ג' יעלו לך מא'א' ג' שלמים ושני שלישיות ועוד ד' שברי' מא'א' בשליש והם בכלל ג' שלמים ועו' ו'ב' שברים ממין ג'ג' בשלם | |
|
שאלה קניתי ד' חביות ושליש עבור ז' פרחים איך יבאו ה' חביות ורביעית |
| הנה בעבור שזאת השאלה משותפים ב' מיני שברי' צריכים אנו לבקש להם מורה ר"ל המורה אשר שמשנו בו בשער השברי' והוא המספר אשר ימצאו בו שני מיני השברי' בשלמים ונקרא זה המורה לכאן מורה ראשון להבדיל בינו ובין המורה אשר אנו משתמשים בו בזה השער אשר אנו קוראים לו מורה בסתם | |
| והנה המורה הראשון לאלה השברי' הוא ב'א' ולכן אנו צריכים לחלק [51]החביות כלם כל א' לב'א' חלקי' ויהיה לפי זה מן הד' חביות עם השליש שעמהם ב'ה' שברי' מן ב'א' בשלם ומן הה' חביות יהיו ג'ו' שברי' מב'א' בשלם עם הרביעית שעמהם | |
| וידמה עתה שאלתך כאילו שאל קניתי ב'ה' חביות עבור ז' פרחים איך יבואו ג'ו' חביות הנה ב'ה' המורה ז' המשותף ג'ו' הנעלם עשה עם אלו המשרתים כמשפט ויעלה לך המבוקש בלי חלוף | |
| [52]הג"ה המבוקש בלי חלוף ר"ל שלא יהיה העולה העולה שברי פרח וזה מפני שלא יבא שינוי בפרחים כי ז' פרחי' היו ולא הוחלפו ולכן יבוא המורה בלי חלוף אבל בשאלה הקדמת שם הפרחים שלישיות ועלה המבוקש ג"כ שלישיות פרחים | |
|
שאלה קניתי ד' חביות ושליש עבור ה' פרחי' ורביעית איך יבאו ו' חביות וחומש |
| הנה אע"פ שמיני השברי' אשר הם משותפים בשאלה הם ג' מ"מ אין אנו צריכי' לבקש מורה ראשון אלא לשני מיני השברי' אשר הם עם החביות אבל הפרחים נשים אותם שברי' ממין השברי' שעמהם אשר הם בזה השאלה רביעיות ויהיה מן ה' פרחים עם הרביעית שעמהם א'ב' רביעיות והמורה ר"ל המורה הראשון לשלשיות וחמשיות הוא ה'א' וא"כ אנו צריכים לכפול ה'א' על כל א' מן החביות כדי לעשות כל חבית לחלקי ה'א' בשלם ויעלה מן ד' חביות עם השליש שעמהם ה'ו' ומן ו' חביות וחומש יעלה ג'ט' | |
| ויהיה א"כ השאלה כאילו שאל קניתי ה'ו' חביות עבור א'ב' איך יבואו ג'ט' | |
| הנה ה'ו' הוא המורה א'ב' המשותף ג'ט' הנעלם | |
| וכאשר תעשה עמהם כמשפט יעלה המבוקש והוא יהיה רביעיות וחלקי רביעיות מא'ב' מרביעית אם יהיה נשאר בחלוקה דבר ואמנם אם תכפול המורה על ד' ומקובץ כפלו תחלק על המקובץ הכפול שעלה מן הנעלם והמשותף ואז יבא המבוקש באופן שלם ואמנם אמר לכפול המורה על ד' מפני שהמשותף היה רביעיות וכאשר לא יהיה המורה נכפל על ד' אז יהיה תולדות המבוקש רביעיי' | |
| Find a Quantity Problem - Whole from Parts - Tree | |
| Question: A tree, a third of it and a quarter of its is [ingrained] in the soil, and 4 cubits of it stand up above, how much is the length of the whole tree?
|
שאלה אילן העומד הארץ שליש ורביעית וד' אמות ממנו הוא עומד מבחוץ כמה אורך כל האילן |
| הנה בזאת השאלה לא הודיע לנו השואל שום מורה אבל אנחנו נשתדל מצד התחבולה שיהיה לנו מורה על דרך ההנחה וזה שנבקש איזה מספר שיהיה ונראה הנשאר ממנו על השליש ועל הרביעית ונשים הנשאר מורה וכולו משותף וד' אמות אשר הם הנשאר על השליש ועל הרביעית נשימ' נעלם ובעבור שמשותף בשאלתינו שליש ורביעית ראוי שנקח בידינו מספר שימצא שליש ורביעית ונקרא למספר ההוא מורה ראשון והנה המורה הראשון הוא ב'א' והשליש והרביעית ממנו הוא ז' וא"כ הנשאר הוא ה' | |
| ונניח עתה כאילו שאל אילן ששלישיתו ורביעיתו בארץ וה' מבחוץ אורך כל אותו אילן הוא ב'א' אילן שד' אמות מבחוץ והשליש והרביעית מבחוץ בארץ כמה ארכו | |
| והנה דמות זאת השאלה בלי חלוף קניתי ה' בעבור ב'א' איך יבאו ד' והנה א"כ ה' המורה ב'א' המשותף ד' הנעלם | |
| והנה כאשר נכפול ד' הנעלם על ב'א' המשותף יעלה ח'ד' נחלקם על ה' ויעלה ט' וג' חמשיות וזהו אורך כל האילן אשר אורכו המבוקש | |
| First from Last Problem - Money | |
|
[53]שאלהחסרתי מן ממון השליש והרביעית והיה הנשאר ד' כמה כל הממון |
| ואין הפרש בין זאת השאלה ובין שאלת האילן שקדמה אלא חילוף נושאי המספרי' וזה ששם מקום אילן ממון ומקום מלת בארץ שם מלת חסרתי ומקום מלת מבחוץ שם מלת הנשאר ובעבור אילו החלופי' לא יומר מענייני המספרי' דבר ויהיה ד' המורה וב'א' המשותף וה' הנעלם ותעש' עם אלו המשרתים כמשפט ויעלה המבוקש | |
| שאלה הנה אילן בארץ שליש [54]קניתי ז'ד' עבור ג'א' איך יבאו 0'ב' | |
| הנה ז'ד' המורה ג'א' המשותף ט'ב' הנעלם עשה במשפט עם אלו המשרתים ויעלה מבוקשך | |
| How Much Problem - Money | |
|
שאלה הנה ממון והוספנו עליו השליש והרביעית והתשיעית ונעשה המקובץ 0'ג' כמה היה הממון בראשונה |
| הנה המורה הראשון | |
| [55]שאלה חסרנו ממון רביעית ושתות והוספנו שמינית ושליש והיה 0'ג' כמה היה הממון אחר החסרון קודם התוספת | |
| הנה ממון שנשאר ה'ב' היה הממון אחר החסרון ד'א' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ה'ב' עבור ד'א' איך יבאו 0'ג' הנה ה'ב' המורה ד'א' המשותף 0'ג' והנעלם עשה עם אלו המשרתים כמשפט ויעלה מבוקשך | |
| שאלה הוספנו על ממון שליש ושמינית וחסרנו רביעית ושתות מערך הממון לפי מה היה הממון בראשונה ואחר התוס' והגרעון נשאר 0'ג' כמה היה הממון בראשונה | |
| הנה המורה הראשון [56]כמה החלוף אשר היה בכמות הממון אחר התוספת והגרעון ובין מה שהיה הממון בראשונ' קודם התוספת והגרעון | |
| הנה ממון שהיה בכלל מספר השברי' שחוסרו 0'א' היה החילוף א' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי 0'א' בעבור א' איך יבאו 0'ב' | |
| הנה 0'א' המורה א' המשותף 0'ב' הנעלם תעשה עם אלו המשרתי' כמשפט ויעלה המבוקש | |
| שאלה הוספנו על ממון שליש ושמינית וחסרנו רביעית וששית והיה החסרון שחוסר 0'ב' כמה היתה התוספת | |
| הנה ממון אשר היה מספר [57]0'ב' כמה היה הממון אחר התוספת והגרעון | |
| הנה ממון שהיתה התוספת א'א' היה הנשאר ה'ב' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי א'א' עבור ה'ב' איך יבאו 0'ב' | |
| הנה א'א' המורה ה'ב' המשותף 0'ב' הנעלם | |
| עשה עם אלו המשרתים כמשפט ויעלה המבוקש | |
| שאלה הנה חסרנו מממון רביעית ושתות והוספנו שליש ושמינית והיתה התוספת 0'ב' כמה היה הממון אחר החסרון וקודם התוספת | |
| [58]התוספת והגרעון ר"ל התוספת והגרעון הנזכרי' בשאר אלו השאלות | |
| הנה ממון אשר החלוף א' היה קודם התוספת והגרעון ד'ב' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי א' עבור ד'ב' איך יבאו 0'ב' | |
| הנה א' המורה ד'ב' המשותף ס'ב' הנעלם תעשה עם אלה המשרתים כמשפט ויעלה המבוקש | |
| שאלה הנה החלוף 0'ב' כמה היה הממון אחר התוספת קודם הגרעון | |
| הנה ממון שהיה החלוף א' היה הממון אחר התוספת קודם הגרעון ה'ג' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי א' עבור ה'ג' | |
| [59]שאלה הנה סך הממון אחר החסרון קודם התוספת 0'ב' כמה התוספ' | |
| הנה ממון ד'א' אחר חסרון התוספת א'א' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ד'א' עבור א'א' איך יבאו 0'ב' | |
| הנה ד'א' המורה א'א' המשותף 0'ב' הנעלם עשה עם אלו המשרתים כמשפט וב'ה' | |
| שאלה סך הממון אחר החסרון 0'ב' כמה החסרון | |
| הנה ממון האחר החסרון ד'א' החסרון הוא 0'א' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ד'א' עבור 0'א' איך יבאו 0'ב' | |
| הנה ד'א' המורה 0'ב' המשותף 0'ב' הנעלם עשה עם אלה המשרתים כמשפט ויעלה המבוקש | |
| שאלה הנה סך הממון אחר החסרון 0'ב' כמה הנשאר אחר התוס' והגרעון | |
| הנה ממון שהוא אחר החסרון ד'א' הנשאר ה'ב' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ד'א' עבור ה'ב' איך יבאו 0'ב' | |
| הנה ד'א' המורה ה'ב' המשותף 0'ב' הנעלם עשה עם אלה הכוב"ה | |
| שאלה סך הממון אחר החסרון הוא 0'ב' כמה החלוף אשר בין הנשאר אחר התוספת והגרעון ובין מה שהיה הממון בראשונה | |
| הנה ממון אשר היה אחר החסרון ד'א' היה החילוף בין הנשאר ממנו אחר התוספת והגרעון ובין מה שהיה הממון ההוא בראשונ' קודם התוספת והגרעון א' ר"ל החלוף היה א' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ד'א' עבור א' איך יבאו 0'ב' | |
| תעשה עם אלו הכוב"ה | |
| שאלה הנה הוספנו על ממון שליש ושמינית וחסרנו רביעית ושתות והיה הממון אחר התוספת קודם החסרון 0'ב' כמה היה החסרון | |
| הנה ממון שהיה אחר התוספ' ה'ג' היה החסרון 0'א' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ה'ג' עבור 0'א' איך יבאו 0'ב' | |
| הנה ה'ג' המורה 0'א' המשותף 0'ב' הנעלם עעא"ה כזה | |
| שאלה המקובץ 0'ב' כמה הנשאר אחר התוספת והחסרון | |
| הנה ממון שהמקובץ ה'ג' הנשאר ה'ב' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ה'ג' עבור ה'ב' איך יבאו 0'ב' | |
| הנה ה'ג' המורה ה'ב' המשותף 0'ב' הנעלם עשה עם אלו המשרתים כמשפט ויעלה ב'ה' | |
| שאלה הנה המקובץ 0'ב' כמה החילוף | |
| הנה ממון שהמקובץ ה'ג' החילוף הוא אחד | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ה'ג' עבור א' איך יבאו 0'ב' | |
| הנה ה'ג' המורה א' המשותף 0'ב' הנעלם עשה עם אלו המשרתים כמשפט ויעלה בידך המבוקש | |
| שאלה הנה המקובץ 0'ב' כמה סך הממון אחר החסרון קודם התוספת | |
| הנה ממון שהמקובץ ה'ג' סך הממון אחר החסרון ד'א' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ה'ג' עבור ד'א' איך יבאו 0'ב' | |
| הנה ה'ג' המורה ד'א' המשותף 0'ב' הנעלם עעא"ה כזה | |
| הנה זכרתי לך ל"ו שאלות אשר כלם היו ממון שנוסף עליו ונחסר ממנו ושמתי השאלות כלם באופן [60]באופן אשר המורה הראשון בהם אחד ר"ל המספר אשר נמצאו בו מיני השברי' ושמתי התוספת והחסרון בכלם ענין א' ר"ל התוספת בכלם שליש ושמינית והחסרון רביעית ושתות ועם כל זה נתחלפו אלו השאלות כלם עד שלא נמצא בהם שנים שהמשרתים בהם שוה וכל זה החילוף בא לפי הנחת השאלה כפי מה שתוכל להבין בהם כי לעולם צרי' שיהיה המורה והנעלם ממין אחד והמשותף והמבוקש ממין אחר
ר"ל אם המורה ע'ד'מ' חביות גם הנעלם צרי' להיות חביות | |
| וכן אם המשותף ע'ד'מ' ממון גם צרי' שיהיה המבוקש ממון | |
| וכן אם המורה כמות כלל ממון אשר נוסף עליו גם הנעלם צרי' להיות כמות כלל ממון אשר נוסף עליו גם הנעלם צרי' להיות כמות ממון שנוסף עליו אם המורה דבר נשאר מכלל דבר גם צרי' להיות הנעלם דבר נשאר מכלל דבר שהוא המשותף שמורה כמין מדה או אורך מדבר גם צרי' להיות הנעלם מדה או אורך וכן שאר הענייני' צרי' להיות המורה והנעלם משותפים כמין ממיני נושאי המספר אבל לא בעצם המספר וכן הדבר בעניין המשותף והמבוקש ותוכל להתעורר על הבנת זה מכלל אלו השאלות אשר הוקדמו כי העניין הזה אשר אני מעורר אותך עליו הוא מבואר ביאור רחב בלי ספק מכלל השאלות אשר הקדמתי משאלות האילן והלא וגם מאשר קדם מהשאלות קודם שאלת האילן בזה השער | |
| שאלה הנה הוספנו על ממון שליש ושמינית וחסרנו רביעית ושתות והיה הנשאר אחר התוספת והגרעון 0'ב' כמה היה הממון בראשונ' וכמה היה הממון אחר התוספת וכמה היה הממון אחר החסרון בזולת התוספת וכמה היה החלוף וכמה היתה התוספת וכמה היה החסרון | |
| הנה זה השואל שאל ו' שאלות בלי ספק וכבר הקדמנו כל שאלה מאלו הששה בפרט | |
| והנה השואל לא רמז לנו שום דבר רק שזכר הנעלם ושהוא עניין נשאר ויהיה זה הנשאר שאמר שהוא 0'ב' הנעלם לכל אלו השאלות וצרי' שיהיה המור' ג"כ דבר נשאר ממון אשר נוסף עליו ונחסר ממנו מיני אלו השברי' אשר הם השליש והשמינית לתוספת והרביעית והשתות לחסרון ויהיה המור' הראשון לאלו השברי' ד'ב' ויהיה ממון ד'ב' הנשאר על זה האופן ה'ב' וא"כ ה'ב' המורה לכל אחת מאלו השאלות ואמנם מצד מה שהמבוקשי' שונים במין ר"ל שהמבוקש האחד הוא כמות הממון בראשונ' והמבוקש האחר כמות הממון אחר התוספת וכן מתחלפי' המבוקשי' כלם כן צרי' בלי ספק שיתחלפו המשותפי' כלם כי לכל מבוקש אנו צריכי' משותף שהוא ממין המבוקש בנושאיו מנושאי המספר | |
| הנה א"כ לעניין המבוקש לדעת כמות הממון בראשונ' צרי' להיות המשותף כמות הממון הראשון מזה הממון אשר הנחנו אותו להיות המורה הראשון שהוא ד'ב' ויהיה א"כ המשותף ד'ב' וכבר הנזכר המורה שהוא ה'ב' והנעלם שהוא 0'ב' עשה עם אלה המשרתים כמשפט ויעלה בידך המבוקש | |
| ולעניין [61]לדעת הממון אחר התוספת יהיה המשותף ה'ג' כי כאשר תעשה התוספת והחסרון במורה הראשון יעלה ה'ג' עשה עם זה המשרת ועם שאר המשרתים כמשפט ויעלה המבוקש וכן תבקש שאר המשותפי' לשאר המבוקשי' מצד המורה הראשון ושתף שאר המשרתים ר"ל עם המשותף כמשפט ויעלה מבוקש כל משותף וכבר זכרתי שהמורה והנעלם הם שוים בכלם | |
| שאלה הנה ממון הוספנו עליו השליש והשמינית וחסרנו הרביעית והשתות והתוספת היתה 0'ב' כמה היה הממון בראשונה וכמה היה הנשאר אחר התוספת והגרעון וכמה היה הממון אחר התוספת וכמה היה הממון אחר החסרון וכמה היה החילוף וכמה היה התוספת וכמה היה החסרון | |
| הנה אין הפרש בין זאת השאלה והקודמת אלא ששם הנעלם התוספת וא"כ צריך שיהיה המורה ג"כ התוספת ויהיה המורה מורה לכל השאלות והנעלם ג"כ נעלם לכל השאלות והמשותפי' יתחלפו לפי המבוקשים | |
| וזכרתי לך אלו שני השאלות לתוספת ביאור ואע"פ שכבר נזכרו כל אלו השאלות כל א' בפרט וכמו העניין באלו השאלות שתשים מורה אחד להרבה שאלות ונעלם אחד להרבה שאלות על דרך שעשינו באלו השאלות ששמנו הנעלם הנשאר והמורה ג"כ הנשאר באחת השאלות ובשנית שמנו הנעלם הנשאר התוספת והמורה ג"כ התוספת כן נוכל להשים הנעלם החילוף והמורה ג"כ החילוף או הנעלם החסרון והמוה ג"כ החסרון או הנעלם ממספר מיוחס אל הכלל איזה יחס שיהיה והמורה ג"כ מאותו היחס | |
| ודע לעולם על אותו הדבר אשר יפול בו מליצת היה כך ואיך היה כך ע'ד'מ' כמו אמ' בשאלה והתו' היה כך ואיך היה הנשאר או איך היה החסרון דע החלק מהמליצ' הזאת אשר הוא מעמד והתוספת היה כך הוא הנעלם ואין הפרש איזה מלה תשים מקו' תוספ' כי כל מה שהוא עומד מעמד מלת תוספת הוא המספר הנשוא במלה [62]במלה ההיא הוא הנעלם בלי ספק ותבקש מספר נשוא ג"כ במלה שהיא עומ' מקום תוספת למורה וכל מספר אשר הוא בה בתשובה להחלק מם המליצ' שהוא איך היה כמו מלת חסרון כאשר תאמ' איך היה החסרון אותו המספר שיבא בתשובה ההיא הוא המבוקש ותבקש המשותף שיהיה ממין נשוא איך היה אשר הנשוא ההוא בזה המשל מלת חסרון ואם יהיה הנשוא מקום חסרון מלה אחרת איזה שיהיה תבקש המשותף שיהיה ממנה | |
| שאלה הוספנו על ממון השליש והרביעית וחסרנו מן המחוב' השליש והרביעית של המחובר ונשאר הממון 0'ב' כמה היה הממון בראשונ' | |
| הנה אנו צריכים לבקש לזאת השאלה מספר שימצא בו שליש ורביעית ושימצא ג"כ בכל שבר מאלו השברי' שליש ורביעית | |
| והנה המספר אשר בו ימצא שליש ורביעית הוא ב'א' ונקח מרובעו והוא המספ' אשר ימצא בכל חלק ממנו מאלו השברי' שליש ורביעית בשלמים והנה מרובע ב'א' הוא ד'ד'א וזה המספר אנו קוראים במין זאת השאלה המורה הנכון והנה שליש ד'ד'א' ח'ד' והרביעית ו'ד' ומחובר ו'ג' וגם ו'ד' אשר הם השליש והרביעית של דדא עם ד'ד'א' יעלה המחובר ח'ב'ב' והנה שליש ח'ב'ב' הוא ו'ז' והד' של חבב הוא ז'ה' והנה כאשר נחסר מן ח'ב'ב' ו'ז' וגם ז'ה' שהם השליש והרביעית של ח'ב'ב' מן ח'ב'ב' יהיה הנשאר ה'ט' ובעבור זה הנשאר עשינו כל החשבונות מפני שנתן לנו בשאלה הנעלם בממון הנשאר שאמר שהנשאר 0'ב' ולכן אנו צריכי' [63]להשים המורה מספר הנשאר ומצאנו נשאר א' שהוא ה'ט' ובעבור שהשאלה לדעת מספר הממון הראשון נשים ג"כ למשותף מספר הממון הראשון מזה הממון אשר ה'ט' הנשאר ממנו | |
| ויהיה א"כ דמות זאת השאלה כאילו שאל קניתי ה'ט' עבור ד'ד'א' איך יבאו 0'ב' | |
| הנה 0'ב' הנעלם ה'ט' המורה ד'ד'א' המשותף עשה עמהם כמשפט ויעלה המבוקש | |
| ואם היתה שאלתו והיה הנשאר 0'ב' כמה היה המחובר אז | |
| היה המשותף ח'ב'ב' שהוא המחובר לממון הנשאר ה'ט' והמורה נשאר ה'ט' וגם הנעלם 0'ב' | |
| ואם היה השאלה כמה היה התוספת כאשר הנשאר 0'ב' היה המור' ה'ט' שהוא ג"כ הנשאר והיה הנעלם 0'ב' והמשותף היה ד'ח' שהם התוספת לממון הנשאר ה'ט' | |
| ואם היה שואל כמה היה החסרון אז היה המשותף ג'ג'א' אשר הוא החסרון לממון הנשאר ה'ט' וה'ט' המורה 0'ב' הנעלם בכל אלו השאלות | |
| ואם היה השאלה מחובר התוספת והחסרון אז היה המשותף ז'א'ב' אשר הם המחובר מן התוספת והחסרון לממון הנשאר ה'ט' | |
| ואם היה שואל כמה החילוף בין הנשאר והממון הראשון אז היה המשותף ט'ד' אשר הוא החילוף בין הנשאר והממון הראשון אשר הנשאר ממנו ה'ט' | |
| ואם היה שואל כמה החילוף בין המחובר ובין הנשאר אז היה המשותף ג'ג'א' | |
| ואם היה שואל כמה החלוף בין המחובר ובין הממון הראשון אז היה המשותף [64]המשותף ד'ח' והנה בכל אלו השאלות המורה והנעלם לא יתחלפו יען אשר שם הנעלם 0'ב' ושהוא הנשאר | |
| ואמנם אם ישאל שהיה הממון [..] הראשון 0'ב' כמה נשאר א'ז'ב' היה המורה ד'ד'א' אשר הוא ממון ראשון מממון אשר נוסף עליו ונחסר ממנו התוספת והחסרון אשר זכרנו בראש אלה השאלות כי הרצון בכל אלו השאלות שיהיה בהם משותפים התוספת והחסרון על האופן אשר הם משותפי' בשאלה הראשונה מאלו השאלות והיה המשותף ה'ט' אשר הוא הנשאר לזה הממון הראשון והיה הנעלם 0'ב' | |
| ואם היה שואל לפי הנחת זאת השאלה שאמרנו ר"ל לדעת המבוקש מהממון הראשון שהיתה השאלה על התוספת יחזור המשותף ד'ח' שהוא התוס' לזה הממון הראשון כי מה שהיתה התוס' בשאלות הקודמות לממון שהיה הנשאר ה'ט' היא ג"כ התוספת לממון אשר ד'ד'א' הממון הראשון וע'ד' זה חוזרי' כל היחסים אשר נזכרו במשותפים בשאלות הקודמות להיותם משותפים ג"כ לשאלות אשר נמשכים לזאת ההנחה אשר חפץ ידיעת המבוקש מצד הממון הראשון | |
| ואם חפץ ידיעת המבוקשים מהמחובר אז יהיה המורה ח'ב'ב' שהוא המחובר מן ממון אשר נעשה בו התוספת והחסרון אשר הוזכר ו0'ב' יהיה הנעלם תמיד והמשותפים יהיו ג"כ חוזרים לפי בקשת המבוקשים | |
| ואם ואם יהיה החפץ לדעת המבוקשים מהתוספת אז יהיה המורה ד'ח' [65]שהם תוספת לממון אשר נוסף עליו ונחסר התוספת והחסרון שהוזכר והנעלם ישאר 0'ב' והמשותפי' חוזרי' לפי עניין המבוקשים | |
| ואם חפץ ידיעת המבוקשים מהחסרון אז יהיה המורה ג'ג'א' אשר הם החסרון מממון אשר נוסף עליו ונגרע ממנו התוספת והחסרון הנזכר והנעלם ישאר 0'ב' | |
| המשותפים חוזרי' לפי עניין המבוקשי' | |
| ואם חפץ ידיעת המבוקשי' ממחובר התוספת והחסרון אז יהיה המורה ז'א'ב' שהוא מחובר התוספת והחסרון מממון שנוסף עליו ונחסר ממנו התוספת והחסרון הנז' והנעלם יהיה 0'ב' והמשותפים חוזרי' כפי הנחת המבוקשים | |
| שאלה שאל השואל הנה חסרנו מממון השליש והרביעית והוספנו עליו שליש ורביעית הנשאר והיה המחובר אחר התוספת ג'א' כמה היה הממון בראשונה | |
| הנה בזאת השאלה אנו צריכי' מספר שימצא בו שליש ורביעי' ושימצא ג"כ בנשאר ממנו על השליש והרביעית שליש ורביעית והנה החשבון אשר ימצא בו השליש והרביעית הוא ב'א' ומרובעו הוא החשבון אשר אנו צריכים והוא ד'ד'א' והוא נקרא המורה הנכון והנה השליש והרביעי' ממנו הוא ד'ח' וכאשר תחסר ד'ח' מן ד'ד'א' ישאר 0'ו' | |
| והשליש והרביעית של 0'ו' הוא ה'ג' וכאשר תוסיף ה'ג' על ה'ו' יהיה המחובר ה'ט' ובעבור זה היה הטורח למצוא מחובר בזה מממון אשר נוסף עליו ונחסר ממנו והממון אשר אלו ה'ט' המחובר לו הנה היה בראשונ' דדא | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי ה'ט' [66]ה'ט' עבור ד'ד'א' איך יבאו ג'א' | |
| הנה ה'ט' המורה ד'ד'א המשותף ג'א' הנעלם תעשה עם אלו המשרתים כמשפט ויעלה בידך המבוקש | |
| והנה בהנחת זאת השאלה לדעת המבוקש מהמחובר אחר התוספת יהיה לעולם הט המורה וג'א' הנעלם אבל המשותף יחלף לפי הנחת המבוקשים ע'ד'מ' אם הרצון לדעת מהמחובר סך הממון אחר החסרון צריך שיהיה המשותף 0'ו' שהוא הנשאר אחר החסרון מן הממון שהמחובר אחר התוספ' ה'ט' | |
| ואם הרצון לדעת מהמחובר התוס' אז המשותף ה'ג' לפי שהתוספת ה'ג' מממון שהמחובר ה'ט' | |
| ואם הרצון לדעת מהמחו' החסרון אז המשו' ד'ח' לפי הד'ח' הם החסרו' מממון שהמחובר ה'ט' | |
| ואמנם אם נפשך לדעת המבוקשים מהממון הראשון אז ד'ד'א' הוא הממון המורה וג'א' הנעלם והמשותפי' לפי הנחת המבוקשים | |
| ואם הרצון לדעת המבוקשים מן החסרון אז המורה ד'ח' והנעלם ג'א' | |
| והמשותף לפי הנחת המבוקשים וע'ד'ז' אם נפשך לדעת המבוקשים מיחס אחד זולת אלו היחסים תשים המורה ממין היחס ההוא ונעלם יהיה לעולם לפי הנחת אלו השאלות והמשותפי' יהיו לעולם לפי הנחת המבוקשי' | |
| שאלה הנה ממון אשר הוספנו עליו החצי והשתות וחסרנו ממנו השליש מן המחובר והיה הממון אחר התוספת והגרעון ו'א' כמה היה הממון בראשונ' | |
| הנה מספר שימצא בו שליש וחצי ושתות הוא ו' ומרובע ו' הוא ו'ג' וחצי ו'ג' הוא ח'א' והשתות ו' ומחובר השליש והשתות הזה הוא ד'ב' [67]וכאשר תחבר ד'ב' על ו'ג' יהיה המחובר 0'ו' וכאשר תחסר מן 0'ו' השליש ישאר 0'ד' הנה א"כ ממון אשר הנשאר אחר התוספ' והגרעון 0'ד' היה בראשונ' ו'ג' | |
| וא"כ דמות זאת השאלה כאילו שאל קניתי 0'ד' עבור ו'ג' איך יבאו ו'א' | |
| הנה 0'ד' המורה ו'ג' המשותף ו'א' הנעלם תעשה עם אלו המשרתים כמשפט ויעלה בידך המבוקש | |
| ואם הוא רוצה לדעת מהמחובר החצי אז יהיה המשותף ח'א' והמורה 0'ד' והנעלם ו'א' | |
| ואם הוא רוצה לדעת מן המחובר החצי אז יהיה המשותף ח'א' והמורה 0'ד' והנעלם ו'א' | |
| ואם הוא רוצה לדעת מן המחוב' השתו' אז המשותף ו' והמורה 0'ד' והנעלם ו'א' וכן ע'ד'ז' בשאר המבוקשי' המשותף לפי ה[כח] המבוקש | |
| ואם הוא רוצה לדעת המבוקשי' מערך אחד הן עשרי' של אחד מאלו היחסים או משאר אחד היחסים במיוחסי' או היחסי' המיוחסי' לממון תשים תמיד המורה ממין היחס ההוא הנעלם ישאר תמיד ו'א' לפי זאת השאלה והמשותף לפי הנחת המבוקשים | |
| שאלה הנה חסרנו [68]שאלה הנה חסרנו מממון החצי והשתות והוספנו על הנשאר השליש מהנשאר התוספת 0"א כמה היה החסרון | |
| הנה המספר אשר בו ימצאו אילו השברים הוא ו' ומרובע הו' הוא ו"ג וזהו המורה הנכון נניחהו להיות ממון והנה החצי והשתות ממנו ה"ו הו ד"ב וכאשר נחסר ד"ב מן ו"ג ישאר ב"א והנה ד"ב החסרון מן הממון כאשר תוסיף על הנשאר שהוא ב"א השליש יעלה לך ו"א כיד' הוא השליש והוא התוספת ואם כן ואם כן ממון שד' ת התוספת החסרון ב"ד | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ד' עבור ד"ב איך יבוא 0"א הנה ד' המורה ד"ב המשותף ב"א הנ' הנעלם תעשה אם אילו המשרתים כמשפט ויעלה בידך המבוקש | |
| שאלה הנה בִישַלְתִי ט' מדות יין וחסרו השליש והוספתי עליהם עוד ב' מדות והנחתי לבשל אותן עד שחסר הרביעית ממה שהיה היין אחר שהוספתי עליו הב' מדות | |
| הנה זאת השאלה נחלקת לשתי שאלות אומנם השאלה הראשונה היא היין ט' מדות שנחסרו שליש כמה הנשאר וזה שאלה פשוטה אין צורך ערך בה כי היא מבוארת אבל אנו רוצים לבאר אותה בדרך הערך בעבור שאלות אשר ממינה | |
| ואמנם השאלה השנית אין ידיעת השאלה אלא אחר הגעת המבוקש בשאלה הראשונה | |
| והנה השאלה הראשונה צריכים אנו לה מספר שימצא בו שליש והוא המורה הראשון והמספר ההוא ג' | |
| ונניחהו להיות ג' מדות יין וכאשר יחסר מג' מדות יין השליש ישאר ב' | |
| ואם כן דמות זאת השאלה הראשונה כאילו שאל קניתי ג' מדות יין עבור ב' איך יכתו' ט' הנה ג' המורה ב' המשותף ט' הנעלם וכאשר תעשה [69]עם אלו המשרתים כמשפט יעלה המבוקש ו' והנה אחר שהגיע לנו להיות המבוקש ו' | |
| השאלה השנית היא כאשר הוספנו על ו' ד' וחסרנו הרביעית כמה הנשאר והנה מחובר ו' עם ד' הוא 0"א ואם כן השאלה היא נחסר מ0"א הרביעית כמה הנשאר הנה החשבון אשר ימצא בו רביעי' הוא ד' נניחהו להיות ד' מדות והנה כאשר נחם מד' הרביעי' ישאר ג' | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ד' עבור ג' איך יבואו 0"א | |
| הנה ד' המורה ג' המשותף 0"א הנעלם עשה עם אילו המשרתים כמשפט ויעלה בידך מבוקש ז' שלמי' וב' שברי' מד' כשלם והוא המבוקש אשר אליו כיון השואל בכלל אילו השאלות השתים | |
| שאלה הנה ט' מדות יין יתבשלו עד שיחסר מהם השליש והרביעי' ונוסיף מקום החסרון 0"א ויתבשל עד שיחסר השליש והשתות כמה ישאר עוד מן היין | |
| הנה בשאלה הראשונה מאילו שתי שאלות הנכללים אנו צריכים למספר שיש בו שליש מאילו שתי שאלות ורביעית והוא ב"א ונניחנו מדות יין וכאשר נחסר ממנו ה השליש והרביעי' ישאר ה' ואם כן דמות זאת השאלה הראשונה כאילו שאל קניתי ב"א בשלם בעבור ה' איך יבו[א] ט' הנה המורה ב"א המשותף ה' המשותף ט' הנעלם וכאשר נעשה עם אילו המשרתים כמשפט יעלה המבוקש לזאת השאלה הראשונה ג' מדות שלמו' ועוד ט' שברי' ממון ב"א נשלם והם ג' רביעיות מדה | |
| ולפי זה יהיה השאלה השנית כאשר תוסיף על ג' מדות וג' רביעיות עוד 0"א מדות ויתבשלו עד שיחסר הרביעית והשתות כמה יהיה הנשאר והנה בעבור שאצל המדות רביעיות נעשה מןן הש השלמי' גם כן רביעיות ויהיו לנו מג' שלמי' וג' רביעיות ה"א רביעיות ועשרה שלמי' אשר נוסיף הם 0"ד רביעיות ו ויהיו וכאשר 0"ד רביעיות על ה"א רביעיות יעלה לנו ה"ה רביעיות | |
| ואם כן השאלה שלנו ה"ה רביעיות כאשר נחסר מהם הרביעיות והשתות כמה יחסרו הנה החשבון שימצא בו הרביעיות והשתות הוא [ו' והרביע....] והשתות [70]היין בג' שעות ואם תוציא השני לבד יצא כל היין בד' שעות ואם תוציא השלישי יצא כל היין בה' שעות וכאשר תוציא שלשתן בפעם אחת באיזהו זמן יצא החבית הנה החשבון אשר יתחלק ג'ד'ה' הוא 0"ו ובאשר נניח 0"ו זמן 0"ו שעות יצאו החביות ממון ברזא האחת 0"ב חביות וממון הברזא השנית יצאו ה"א חביות וממון הברזא השלישית יצאו ב"א חביות הנה שאלה קניתי יצאו ז"ד חביות ב0וו ב0"ו שעות ואם כו' דמות זאת השאלה כאילו שאל קניתי ז"ד עבור 0"ו איך יביא אחד והנה כאשר תעשה עם אילו המשרתי' כמשפט אז יצאו לך המבוקש א' שעה וג"א שברים ממון 0"ו בשלם | |
| שאלה הנה חביות שלכל אחד מהם שלשה ברזאות של ג' ד' ה' שעות על דרך שזכרתי בשאלה הסמוכה ב"א חביות מאילו בכמה זמן יצאו כאשר יוציאו בכל חבית ג' הברזאות בבת אחת ונציאם ב' באחד כאשר יצא החבית המוקדם הנה בזאת השאלה אתה צריך ללכת בה בדרך הוצאת הערך על דרך שביארנו בסמוך וזה שתא[.]' ז"ד חביות קניתי עבור 0"ו איך [יבוא] כ"א הנה ז"ד המורה 0"ו המשותף ב"א הנעלם עשה עם אילו המשרתים כמשפט ויצא לך המבוקש | |
| שאלה הנה ב"א שעות יצאו חביות של ברזאות גד"ה על דרך שזכרנו כמה חביות יצאו הנה 0"ו שעות יצאו בהם ז"ד חביות ואם כן דמות זאת השאלה כאילו שאל קניתי 0"ו עבור ז"ד איך יבוא ב"א תעשה עם אילו המשרתי' כמשפט ויעלה בידך המבוקש והנה הוא ט' חביות וד"ב ש[ב]רים ממון 0"ו בשלם שהם שני חומשים של השלם | |
| Purchase Problem – Moneychanger | |
| Question: a shopkeeper exchanges coins and there are three [kinds of] coins in front of him. One of them [is worth] 3 dinar in one peraḥ; the second [kind] [is worth] 4 dinar in one peraḥ; the third [kind] [is worth] 6 dinar in one peraḥ. A man said to him: give me from each of these three [kinds of] coins equally, so that you do not give me from one of the coins more in the number than you give me from the second and you will repay the peraḥ without addition or deficiency. How much should he give him from each coin according to his request.
|
שאלה הנה יש חנווני שמחליף מטבעות והנה לפניו ג' מטבעות אחת מהם ג' דינרי' בפרח והשנית ד' דנרי' בפרח והשלישית ו' דנרי' בפרח ואמר לו אדם אחד תן לי מאילו השלשה מטבעות מכל אחת מספר שוה שלא תתן לי מאחד המטבעות יותר במספר משתתן לי מנ' מהשנית ותפרע לי הפרח בלי תוספת או חסרון [71]כמה הוצרך ליתן לו מכל מטבע לפי שאלתו |
| הנה החשבון אשר יחלק לג' וה' וו' הוא ב"א והנה כאשר נתן לו מכל מטבע דינר הנה נותן לו בלי ספק שליש ורבעית ושתות והם שברים מב"א כפרח שלם הנה אם כן דמות זאת השאלה כאילו שואל קניתי ט' ב"א איך יבואו ב"א הנה ט' המורה ב"א המשותף גם ב"א הנעלם והנה כאשר תכפול המשותף על הנעלם יעלה דד"א וכ וכאשר תכפול ט' המורה על דד"א יעלה המבוקש ו"א הנה אם כן כאשר יתן לו ו"א מכל מטבע אז פרע לו המטבע הפרח בשוה | |
| שאלה הנה שלשה המטבעות האחת אחד בפרח והשנית ב' בפרח והשלישי ג' בפרח כמה יתן לו מכל מטבע שיתן לו מספר שוה ויפרע לו הפרח בשוה | |
| הנה מספר שימצא בו א'ב'ג' הוא וכאשר יתן לו אחד מכל פרח יתן לו כל וחצי ושליש והנה הוא ו' והשליש ב' והחצי ג' וזה בכלל א'א' ואם כן דמות זאת השאלה כאילו שאל קניתי א"א עבור א' איך יבואו ו' והנה א"א המורה א' המשותף ו' הנעלם וכאשר תעשה עם אילו המשרתי[ם] כמשפט יעלה המבוקש ו' שברי' מא"א בשלם צריך ליתן לו [בלי] ספק מכל מטבע וביאור ו' שברי' מא"א כשלם הנה ו' שברים פרח מא"א בפרח מן המטבע ב' יהיו הו' שברי' ו' שברים ב"ב פרחי' והנה ו' מא"א כשלם משלשה בפרח הם ו' שברים ג"ג בפרח ואם כן לא לקח ו' מא"א בפרח וו' מב"ב בפרח וו' מ[ג"ג] בפרח והנה שברי ג"ג בפרח ג' מהם הוא אחד ממון א"א ב[פרח] ואם כן ו' מהם הם ב' ממון א"א בפרח והנה מאותם שב"ב בפרח מהם הוא אחד ממון א"א בשלם ואם כן ו' מהם הם ג' ממון א"א בפרח הנה ב"ג מחובר עם ו' הוא א"א | |
| שאלה הנה נתן לו מ[ט] מטבע ג"א מ[ן] מטבעות ג'ד'ו' כמה פרחי' נתן לו הנה כאשר נתן מכל מטבע א' נתן לו שליש ורביעית וחומש והם ז"ד מ0"ו משלם | |
| ואם כן דמות זאת השאלה כאלו שאל קניתי א' עבור ז"ד 0"ו בשלם איך יבוא ג"א הנה א' המורה ז"ד המשותף ג"א הנעלם והנה כאשר [72]מן ו הוא הוא ג' רביעיות איך יבואו הה' רביעיות הנה ו' המורה | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ו' רביעיות עבור ג' רביעיות איך יבואו הה' רביעיות הנה ו' המורה ג' המשותף הה' הנעלם ואמנם יותר ראוי לכפול המורה על ד' ראשונ' ויעלו ד"ב ונניחם להיות מורה כי זה המורה יוציא לנו המבוקש בשלמים ואמנם מה שיגיע מן המורה כאשר נניח אותו ו' הם רביעיי' ויצטריך נכפול המורה הראשונ' על ד' ואחרי כן נעשה עם המשרתי' לחלקם עוד על ד' לעשות מהם כ[...] וזה לא יהיה צריך כאשר נפכ נכפול כמשפט ויעל לנו המבוקש והנה כאשר נכפול המשותף שהוא ג' על הה' שהוא הנעלם יעלה מקום הכפל הו"א וכאשר נחלק על הו"א ג' ד"ב שהוא המורה לפי הנחתינו ו' שלמי' ועוד א"ב שברי' מן ד"ב בשלם וזהו המבוקש על דרך האמת ואמנם אם היינו נשארים בהנחת המורה ו' אז יהיה עולה בידינו מחלוק הו"א על ו' אז יהיה עולה לנו ז"ב רביעיות ועוד ג' מו רביעיות | |
| שאלה הנה היינו מבשלים יין עד שנחסר שליש ושתות ואחר שנחסר כך חסרנו עוד ממנו הרביעית מן הנשאר והיין היה בראשונה ח"א מדות כמה היה היין אחר הבשול וכמה היה היין אחר החסרון השני וכמה היה היין אשר נחסר על ידי הבישול וכמה היה היין אשר חסרנו אחר הבישול | |
| הנה זאת השאלה נחלקת לארבע שאלות אבל א"ב המורה הוא אחד לכולם וכן הנעלם אחד לכולם כי הרצון לדעת המבוקשים לכולם מן הממון הראשון והנה אנו צריכי' חשבון שימצא בו שליש ושתות ואחר החסרון ממנו שליש ושתות שימצא בנשאר הרביעית והנה החשבון אשר ימצא בו שליש ושתות הוא ו' ובעבור שאנו רוצים שימצא בו אחר החסרון רביעית נכפול אותו על ד' כדי שיהיה כל אחד מן האחדי' של ו' ד' כי אז ימצא בלי ספק אחר החסרון בנשאר רביעיות והנה כפל ד' על ו' הוא ד"ב והנה כאשר נחסר מן ד"ב השליש והרביעית ישאר ב"א ומה שחסרנו הוא גם כן ב"א [73]וכאשר נחסר מן ב"א הרביעית ישאר ט' והרביעית אשר הוא החסרון השני הוא ג' והנה אם כן כאשר נניח הד"ב להיות ממון הראשון יהיה דמות אילו הארבע שאילות הראשונה מהם קניתי ד"ב עבור ב"א איך יבואו ח"א ודמות השאלה השנית קניתי ד"ב עבור ט' איך יבואו ח"א ודמות השאלה השלישית קניתי ד"ב עבור ב"א איך יבואו ודמות השאלה הרביעית קניתי ד"ב עבור ג' איך יבואו ח"א הנך רואה שהמורה והנעלם הם שוים בכל ארבע השאלות [.] ונתחלפו רק המבוקשי' ותעשה בכל שאלה עם המשרתים כמשפט ויעלה לך המבוקש לכל משרתי' אשר אתה משתמש עמהם כמשפט ואם תרצה לדעת אילו המבקשים מיחס אחד זולת הסך הראשון עד"מ מאחד החסרונות או זולתם הנה תלך הדרך המבואר מכלל אשר הוקדם מהביאור בשאלות א אשר קדמו ואין צורך להכפיל הדבר תמיד כי כבר הוזכר הדרך פעמים רבים | |
| שאלה הנה יש חבית יין שיש לו שלשה בַרְזֵאוֹת אם תפתח האחד לבדו אז יצא כל היין אשר בחבית בשעה אחת ואם תפתח השני לבדו אז ייצא כל היין מן החבית בשני שעות ואם תפתח השלשי אז ייצא כל היין בשלשה שעות והנה כאשר תוצא את כל שלש' הברזאות בבת אחת בכמה זמן ייצא כל היין הנה אנו צריכים החשבון אשר יתחלק על אב"ג על כל אחד מהם בשלמים וזה החשבון הוא ו' והנה כאשר נניח זאת הו' שעות ונאמ' הנה בו' שעות ייצאו כולם ששה חביות כאשר יפתח הברזא של א' ומברזא של ב' ייצאו ג' ומברזא של ג' יצאו ב' באילו השש שעו' ואם כן א"א חביות יצאו בו' שעות ואם כן דמות זאת השאלה כאילו שאל קניתי א"א בו' ואיך יבואו אחד וכאשר תעשה עם אילו המשרתים כמשפט אז יעלה המבוקש ו' חלקים [ממין] א"א בשעה | |
| שאלה הנה חבית שיש לו ג' ברזאות אם תוציא האחד ייצא [בו] [74]תכפול ד"ד המשותף על ג"א המורה יעלה עליך בידך מקובץ הכפל אא"ו חלקם על המורה שהוא ג"ו ויעלה המבוקש א'א'ו' שברים ממין 0'ו בשלם יען שהיה המשותף ממין אילו השברים והנה אם כן כאשר תחלקם על ס"ו שהוא השלם יעלה בידך 0"א פרחי' ועוד א"א שברים ממין ס"ו בשלם וזהו המבוקש האמתי | |
| How Many Problem - Group of People | |
|
שאלה הנה אדם עובר עבר על האנשים ואמר שלו' עליכם מאה איש והשיב אחד הנה אכן היו עוד עמנו כמו החצי ממנו והשליש ואתה עמנו אז היינו מאה כמה היו |
| הנה החצי והשליש ימצא בו' והחצי ג' והשליש ב' וכאשר תחברם על ו' יעלה א"א ואם כן כאשר יאמר אם אנו עוד החצי והשליש אז היינו א"א אז היו בראשונ ו' | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי א"א עבור ו' איך יבואו ט"ט | |
| הנה א"א המורה ו' משותף ט"ט הנעלם וכאשר (וכאשר) תכפול ו' המשותף על ט"ט הנעלם יעלה מקובץ הכפל ד'ט'ה' וכאשר תחלקם על א"א המורה יעלה בידך ד"ה והוא והוא המבוקש ר"ל ד"ה היו האנשי ההם | |
| שאלה הנה ראובן שמעון לוי ירשו ממון אביהם ולקח ראובן מ"ו הממון יותר מהחצי והשאר לקח לוי אמרו שמעון ולוי לראובן לטעון עמו בדין עבור המותר אז נתן ראובן לכל אחד כפי מה שהיה בידו ואז היה לשמעון החלק הגדול חלקו ראובן ולוי על שמעון נתן להם שמעון שמעון גם כן לכל אחד כפי מה שהיה בידו בשעה שחלקו עליו כי אז תפס ולוי החלק היותר גדול אז חלקו ראובן ושמעון על לוי ונתן להם לוי גם כן לכל אחד כפי מה שהיה בידו בשעה שחלקו עליו ואז תפס כל אחד מהם חלק שווה לשאר החלקי' כמה היה הממון וכמה תפס כל אחד מהם ראשונה המבוקש לדעת הממון שיתכן זה בשלמים ושיהיה גם כן החלקי' של כל אחד שלמי' ושא[.] ושוא[.] זה בממון היותר הפחות שאפשר | |
| הנה ראוי בראשונה לבקש החשבון ה' היותר הפחות שאפשר אשר יתכן לחלקו לשלשה מספרים שכל א אחד יותר מהשני כשלמים שהראשון יותר והחצי מהחצי ולא ימצא לזאת הבקשה חשבון יותר פחות מז' כי בו אפשר שיקח אחד ד' ואחד ב' ואחד ג' א' והנה לא יתכן להיות המספר רק ז' כי צריך להיות המספר אשר יסבול החלוקה לשלשה חלקי' שוים יען אשר להם באחרונה לכל אחד משלשה האחים חלק שוה לאחד מחלקי אחיו ונעשה [75]הדרך המורגל במספרי' שנכפול הז' על ג' ויעלה א"ב גם א"ב לא יתכן שיהיה המספר מפני שבהכרח החלק אשר תפס לוי הוא היה חציו בלי ספק כי פחות מרביעית לא יהיה מגיע לו משני נתינות חלקו והרביעית לא יספיק לו להגעת לו חלקו והנה לוי בהכרח לכפל חלקו בשתי הנתינות אשר נתנו לו אחיו כי לראובן לא נשאר לו אחר שנתן רק רביעית וגם לא פחות כי שתי הנתינות הביאו שלשה פעמי' מה שהיה בידו ושמעון נתן לו אחד ולוי שנים הנה לא ימלנו החשבון מהיותו חשבון שימצא בו חצי ורביעית וכבר זכרנו שצריך להיות בו גם כן שליש מאחר שיחלק הממון בא באחרונה לשלשה חלקים שוים ואמנם מה שהנחנו כבר להיות החשבון א"ב הוא בעבור כפל על ד' ואמנם לא הנחנו הז' אלא מפני שלא ימלט החשבון מהיות פחות מז' ואמנם אחר שיגדור לנו החצי והשליש והרביעית חשבון יותר מן בזולת הז' נניח הז' ומה שבנוי ממנה אשר הם א"ב ונתפוס חשבון שיש בו שליש ורביע וחצי והוא ב"א והיה ראוי לפי הבחינה אשר זכרנו להיות זה המספר החשבון המבוקש אבל הדבר אינו כן וזה מפני שאם היה החשבון ב"א והיינו מניחים לראובן ז' שהוא יותר מן החצי היה נשאר ל לאילו השנים ה' | |
| והנה מבואר שאם היה המספר החשבון ב"א היה חלק שכל אחד מהם ד' והיה אם כן חצי חלק ב' וכבר זכרנו שב' שבהכרח יגיע ללוי בראשונה חצי חלק שלו והיה זה ב' ואם כן היה בהכרח מגיע לשמעון ג' ואם היה הדבר כן לא היה נשאר לשמעון דבר וגם לראובן היה נשאר שנים אחר אחר הנתינה שלו וזה היה יותר מן רביעית חלק ולא יתכן שישאר לראובן יותר מרביעית חלקו אחר הנתינה אשר הוא נותן ולכך ולכן אנו צריכים בהכרח ליתן לראובן מב"א חלקים פחות מז' ומה שאנו פותחי' לו נוסיף לשמעון ואשר פותחי' לראובן הוא צריך להיות חצי היתור אשר היה לו נשאר יותר על הרביעית לפי הנחת ז' לראובן כי אז יזדמן שיתן לו ראובן בעבור אותו חצי היתור עוד חצי היתור השני בנתינה אשר הוא נותן וזה יבוא יביא לו שיכלה היתור לגמרי והנה היתור הוא בהכרח אחר כי בהנחת ז' לראובן ישארו לו שנים בהכרח והנה הרביעית הוא רק אחד מאחד שחלק כל אחד ד' ואם כן זה היתור הוא א' והוא [76]גם כן הרביעית וכאשר יזדמן זה היתור לשמעון חצי מצד מה שאנו פוחתים אותו לראובן וחצי השנית מן היתור יזדמן לו לו מה שיוסיף לו ראובן בנתינה הנה יהיה מזה הצד ביד שמעון אחר נתינת ראובן בהכרח רביעית אחד החלקי' יותר משהיה לו לפי הנחת ז' שלמי' לראובן וזה הרביעית יהיה נפחת לראובן מה נשאר אשר הונח לו ומזה הצד יקרה לשמעון עוד השארה בידו רביעית אחר שכבר נתן אותו לראובן בעבור מה שהיה לראובן יותר ובעבור זה יזדמן ההשארה לשמעון אחר מה שיתן לאחיו חציו רביעית מצד מה שהונח יותר ומה (ומה) שנתן לו ראובן יותר ורביעית מצד מה שלא הוציא לראובן כפי מה שהית גודר הנחת ז' לראובן וזהו מה שיגדור עינייו זאת החלוקה להיות הכרחי והנה בעבור שיביא הצריך להיות חלק ראובן בתחלה פחות מז' חצי אחד מאילו הב"א נכפול ב' על ב"א ויעלה לנו ד"ב ונניח ד"ב מקום שהנחנו ב"א וכל מה שהנחנו אחד בהנחת ב"א כל הממון יהיה שנים ולפי מה שביארנו בחלק ראובן בראשונ' מהיותו הכרחי להיות פחות מז' חצי אחד מב"א יהיה חלקו ג"א מד"ב בכלל הממון ומקום שהנחנו ללוי ב' יהיה חלקו ד' בראשונ' ומקום שהנחנו לשמעון ג' יהיה לו ז' ו' מצד הג' ואחד מצד מב' שנפחת לראובן וזהו המבוקש בלי ספק ובניתי לך כלל זה הממון להתעורר על מין זאת שאלה וגם שיהיו לך אילו המספרי' מזומנים לקחת אותם למורה ולמשותף לשאלות אשר יבואו במין זאת השאלה ר"ל שיקח ראובן בראשון מן הממון על הדרך אשר זכרנו וכן שמעון ולוי ובסוף יהיה לכל אחד מהם חלק שוה על הדרך שביארנו מנתינותיהם ואילו הם השאלות ואזכיר אותם בקיצור בלי הכפל אופן השאלה כי אין הכוונה אלא האופן אשר זכרנו אותו מלבד מה שיתחדש מאופן הנחת הנעלם ומה שישח שימשך לזה | |
| שאלה כאשר היו ראובן שמעון ולוי תופסי' מממו' א' אביהם על הדרך שזכרנו והיה החלק הראוי לכל אחד מהם 0"ב פרחים כמה היה הפרחי' הממון הכל | |
| הנה נשים הממון אשר זכרנו בשאלה הקודמת שה[יה] ד"ב למורה ראשון ליקח מחלק המורה חלק ממון ראוי ממון שהוא ח"0 היה הממון ד"ב | |
| ואם כן דמות זאת השאלה כאלו שאל קניתי ח' עבור ד"ב איך יבואו 0"ב הנה [77]ח' מורה ד"ב המשותף 0"ב הנעלם | |
| שאלה ואם יהיה הממון 0"ב כמה היה החלק הראוי לכל אחד | |
| הנה ממון ד"ב החלק הראוי ח' | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ד"ב עבור ח' 0"ב איך יבואו הנה דב המורה ח' המשותף 0"ב הנעלם תעשה עם אילו המשרתי' כמשפט ויעל המבוקש | |
| שאלה ואם ישאל החלק אשר תפס ראובן בראשונ' הוא היה 0"ב כמה היה הממון | |
| הנה כאשר היה חלק ראובן ג"א היה הממון ד"ב | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ג"א עבור ד"ב איך יבואו 0"ב | |
| שאלה ואם שאל החלק אשר תפס שמעון בראשונה היה 0"ב כמה היה החלק אשר תפס ראובן בתחלה | |
| הנה כאשר תפס שמעון ז' היה ראובן תופס ג"א | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ז' עבור ג"א איך יבוא 0"ב | |
| שאלה ואם היה החלק אשר נשאר ביד שמעון 0"ב אחר נתינתו לאחיו הנתינה הנ' הנזכרת כמה היה הממון הכל | |
| הנה כאשר היה הנשאר לשמעון ז' אז יהיה הממון ד"ב | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ד' עבור ד"ב איך יבואו 0"ב | |
| שאלה אם יהיה החלק אשר תפס לוי קודם שנתן לאחיו 0"ב כמה היה כל הממון | |
| הנה כאשר היה החלק אשר תפס לוי ו"א קודם שנתן אז היה הממון ד"ב | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ו"א עבור ד"ב איך יבואו 0"ב | |
| שאלה אם היה כל הממון 0"ב כמה היה חלק שמעון אשר היה לו קודם שנתן לאחיו | |
| הנה כאשר היה הממון ד"ב היה חלק שמעון ד"א | |
| ואם כן דמות השאלה הזאת כאילו שאל קניתי ד"ב עבור ד"א איך יבואו 0"ב | |
| שאלה ואם היה מה שתפס ראובן ולוי בראשונה 0"ב כמה היה מה שתפס שמעון | |
| הנה כאשר תפסו ראובן ולוי ד"א תפס שמעון ז' | |
| ואם כן דמות זאת השאלה קניתי ד"א עבור ד' איך יבואו 0"ב | |
| ועל דמות זה תנהג עם שאר היחסי' להוצא המבוקש כי זאת השאלה תתהפך לפעם רבים מצד חילוף היחסי' המתחלפים חילוף המשותף וגם למורה ואמנם האופן כאילו שאלות שיתחלף המורה להרבה פנים וכל יעמוד להיות מורה לשאלות הרבה אבל אין צורך להאריך [78]בביאור כל זה מצד מה שהתעוררנו באילו השאלות וגם בשאלות אשר קדמו | |
| Find a Quantity Problem - Whole from Parts – Fish | |
|
שאלה הנה דג ראשונו שליש ורביעית הדג והזנב משקל חמשית הדג והנה הגוף נמכר עבור 0"א פשיטי' איך יבוא הראש ואיך יבוא הזנב ומהו משקל הגוף בערך על כל הדג ומהו משקל כל הדג ואיך נמכר כל הדג |
| הנה המספר אשר בו ימצא שליש ורביעית וחומש אותו נוכל להניח להיות הדג במשקלו כך ואם לא יהיה המשקל ליטרי' יהיה משקל זולת הליטר' מ'מ' לא ימלט הדג מלהניח משקלו ב"א שקלים אזהו משקל שיהי' | |
|
והנה המשקל אשר בו ימצא שליש ורביעית וחומש הוא 0"ו |
|
והנה השליש ורביעית ממנו הוא ה"ג ואם כן משקל הראש ה"ג |
|
והחומש מ0"ו הוא ב"א ואם כן משקל הזנב ב"א שקלי' משקלים שהם 0"ו בכל הדג |
| והנה אם הראש משקלו ה"ג הזנב משקלו ב"א אם כן המשקל הראש והזנב משקלם ז"ד ואם כן הנשאר מן הדג שהוא הגוף הוא ג"א שקלי' בלי ספק והנה אחר שאמר שהגוף נמכר עבור 0"א הנה אם כן ג"א שקלי' מ0"ו בכל הדג נמכר עבור 0"א | |
| והנה מה ששאל איך יבוא הראש יהיה דמות השאלה ההיא כאילו שאל קניתי ג"א עבור 0"א איך יבואו ה"ג | |
| בעבור שמשקל הראש הוא ה"ג שקלי' עשה עמי עם המשרתי' כמשפט ויעלה המבוקש | |
| ואשר שאל איך קנה הזהב יהיה דמות השאלה ההיא כאילו קניתי ג"א עבור 0"א איך יבואו ב"א | |
| עשה עם המשרתי' כמשפט ויעלה המבוקש שמשקל הזנב ב"א שקלי' | |
| ואשר שאל איך נמכר כל הדג אז יהיה דמות השאלה כאילו שאל קניתי ג"א עבור 0"ו איך יבואו 0"א | |
| עשה עם המשרתי' של כל השאלה כמשפט ויעלה בידך המבוקשי' והנה ג"א בכל אילו השאלות המורה והנעלם 0"א והמשותפי' יתחלפו בכל | |
| שאלה ואם היה השואל אומ' מקום מלת והגוף נמכר הראש נמכר אז היה המורה ה"ג והנעלם 0"א והמשפט [79]והמשותפי' יתחלפו בכל שאלה | |
| ואם היה השואל אומר מקום והמשותפי' יתחלפו בכל שאלה מלת והגוף נמכר הראש נמכר אז יהיה המורה ה"ג ונעלם 0"א והמשותפי' לפי הנחת המבוקשים | |
| ואם היה אומ' מקום הגוף נמכר הזנב נמכר | |
| אז היה המורה ב"א מפני שמשקל הזנב ב"א ואם היה אומר מקום אמרו הגוף נמכר וכל הדג נמכר היה 0"ו המורה ו0"א הנעלם המשותפי' חוזרים | |
|
שאלה הנה דג שראשו שליש ורביעית כל הדג והזנב החומש ומשקל הגוף ח' ליטרי' ונמכר עבור ב"א פשיטי' איך נמכר הראש ואיך נמכר הזנב או איך דמי מכר כולו וכמה משקל הראש וכמה משקל הזנב וכמה משקל כל הדג |
| הנה מספר שימצא בו שליש ורביעית וחומש הוא 0"ו ונניחהו להיותו משקל דג אחד בכלל והנה שליש ורביעית ממנו שהוא משקל ראש הדג הוא ה"ג והחומש שהוא משקל הזנב הוא ב"א ויהיה אם כן משקל הגוף ג"א | |
| ואחר הנחת זאת ההנחה מדג שמשקל כולו 0"ו ושהראש משקל ה"ג והזנב משקל ב"א והגוף משקל ג"א נשוב אל השאלת השואל והנה נאמר מה ששאל איך נמכר כל הדג זהו שאלה אחת ולא נוכל לעמוד על עניין זאת השאלה אלא מצד שנידע קודם כמה משקלם הדג ההוא אמ' אשר אמ' שמשקל גופו ח' ליטר' וזה יודע לנו ממשקל גוף של הדג אשר לקחנוהו בידינו על דרך ההנחה והגוף מאותו הדג הוא ג"א וכל הדג ההוא שמשקל גופו ג"א ב' הוא בעבור 0"ו | |
| ואם כן דמות זאת השאלה כאילו שאל קניתי ג"א בעבור 0"ו איך יבואו ח' | |
| הנה ג"א המורה 0"ו המשותף ח' הנעלם וכאשר נכפול ח' הנעלם על 0"ו המשותף יעלה מקובץ הכפל 0'ח'ד' ובאשר אותו על ג"א שהוא המורה יעלה המבוקש ו'ג' ליטר' וב"א חלקים מג"א ליטר | |
| והנה אחר שאנו יודעי' משקל כל הדג הזה שמשקל גופו ח' ליטר ונודע ממשקל כולו ו"ג ליטר' וב"א שברי מג"א בליטרא [80]כאילו שאל קניתי 0"ו עבור ה"א איך יבואו 0"ב הנה 0"ו המורה ה"א המשותף 0"ב הנעלם תעשה עם אילו המשרתים כמשפט ויעלה בידך המבוקש | |
| ואם שאל על ימי עבודת לוי | |
| הנה דמות זאת השאלה כאילו שואל קניתי 0"ו עבור ב"א איך יבואו 0"ב | |
| הנה 0"ו המור' ב"א המשותף 0"ב הנעלם | |
| ותעשה עם אילו המשרתים כמשפט ויעלה בידך המבוקש | |
| ואם שאל הנה היו ימי ראובן 0"ב כמה היו ימי עבודת שלשתם | |
| הנה דמות השאלה הזאת כאילו שאל קניתי 0"ב עבור 0"ו איך יבואו 0"ב | |
| ואם שאל והנה ימי ראובן 0"ב כמה חלק כל אחד | |
| הנה דמות זאת השאלה כאילו שאל קניתי 0"ב עבור ז"ד איך יבואו 0"ב | |
| ואם שאל הנה ימי עבודת ראובן 0"ב יום כמה ימי עבודת שמעון | |
| הנה דמות זאת השאלה כאילו שאל קניתי 0"ב עבו' ה"א איך יבואו 0"ב | |
| הנה המורה 0"ב והמשותף ה"א והנעלם 0"ב | |
| ואמנם אם שאל הנה ימי עבודת לוי 0"ב כמה ימי עבודת ראובן | |
| הנה דמות זאת השאלה כאילו שאל קניתי ב"א עבור 0"ב איך יבואו 0"ב | |
| הנה ב"א המורה 0"ב המשותף 0"ב הנעלם | |
| תעשה עם אלו המשרתי' כמשפט ויעלה בידך המבוקש | |
| Give and Take Problem | |
|
שאלה אדם ייצא מעירו ונדר נדר בכל יום שיכפיל השם ממונו שרצה ליתן לצדקה ב' פשיטי' והש' מלא שאלתו והוא קיים נדרו וביום הרביעי צריך שיאמר השלישי לא יהיה לו יותר כמה היה ממונו בראשונה |
| הנה בהכרח שהיה ממונו פחות מב' פשיטי' ואיזהו פחיתות שהיה ממונו פחות יחוייב שיפחות ממונו בסוף שלשה ימים פחת א' ב' ד' ר"ל ביום הראשון חלק א' וביום השני ב' חלקי' וביום השלישי ד' חלקי' ואם היו כלל ממונו מפני שלא נשאר הנה יפחות ממונו בג' ימי' ד' חלקי' והם היו כלל ממונו מפני שלא נשאר לו אחר פחת אילו הד' מאומה ואילו הד' חלקי' היו פחות מב' פשיטי' חלק אחד ממין חלקי אילו הד' ואם כן ב' פשיטי' הם שמונה חלקים ואם כן אילו הד' חלקי' הם ד' חלקים משמונה בשנים ואם כן היו לו ד"א חלקים מח' בשלם כאשר יבאר לפנים לא"כ ה0"ב [...............] | |
| [81]שאלה הנה נדר כל מה שיכפיל ממונו [רצה] ליתן שני פשוטים ובסוף ה' ימים לא היה לו יותר | |
| הנה הלך ממונו הולך ופוחת א' ב' ב' ח' ו"א שהם א"ג חלקי' ואם כן יהיה ממונו כ"ו חלקי' ממון א"ג ב"ג בשלם | |
| שאלה נדר בכל יום שיוכפל לו ממונו רצה ליתן שלשה פשיטים והנה בסוף ו' ימי' לא נשאר לו דבר | |
| הנה עבור היות הימים ו' תקח מחובר ו' מספרים שהראשון א' והאחרי' נוספי' על סדר ב' ד' ח' ו"א ב"ג והנה מחובר אלה המספרי' הוא ג"ו ובעבור שהיתה הצדקה ג' תכפול ג' על המחובר הזה והוא יהיה הממון אשר היה בידו ראשונה והם חלקו שהם ממון מספר השביעי' בשלם ר"ל המספר השביעי מן המספרים שהולכי' על סדר א' ד' ח' ו"א אם תרצה תוכל לאמר שהם שברים שהם בשלם כמספר המחובר מו' המספרי' בתוספת אחד על המחובר [..] כי לעולם המחובר מן המספרי' האילו הוא חסר אחד מן המספר שיבא על הסדר הזה אחר מספר האחרון מו' המספרי' המחוברי' ואם כן הכלל כמין זאת השאלה שנכפול מחובר המספרי' על הצדקה ויעלה מספר החלקים אשר היה ביד הנודר והחלקי' היו בשלם כמספר המחובר בתוספת אחד והמספרי' המחוברי' יהיו כמספר הימים אשר בהם כלה ממונו והכלל אשר נתנו בזאת השאלה הוא כאשר יכפל ממו[נו] | |
| שאלה הנה נדר כשאר יושלש ממונו אז הוא רוצה ליתן שלשה והנה אזל כל ממונו בד' ימי' כממה היה לו בראשונ[ה] | |
| הנה בהכרח שיהיה לו פחות מחצי כי [........] ובעבור שאמ' מממונו שיושלש אנו מתחילין בא' והולכי' בממספר על סדר א' ג' ט' ז"ב כמ' שהלכנו בעניין הממון המוכפל על סדר א' ב' ד' ח' ונקח מסדר אילו המספ' כמספר הימי' והמחובר מהמספרים האילו תכפול אותו על הצדקה ויעלה בידך מספר הממון שהיה בידו ראשונה והם חלקי' שהם בשלם כמו המספר אשר יבא על הסדר הנזכר אחר המספר האחרון המספרי' שנעשה מהם המחובר הנזכר ולפי זה היה הממון שהיה בידו ראשונה [82]לפי זאת השאלה היה 0ב"א מא"ה בשלם זה כי הימי' ארבע וארבע המספרי הם א' ג' ט' ז"ב והמחובר מהם הוא 0"ד והצדקה ג וג' פעמי' 0"ד הוא 0ב"א והמספר אשר יבא אחר ז"ב שהוא האחרון מן המחוברים הוא א"ח ואם כן החלקי' שהם 0ב"א הם מאה בשלם שהוא אחד שלם ועוד ט"ג חלקי' מא"ח בשלם | |
| שאלה הנה נדר כאשר יוסיף ממונו בכל יום שיהיה ארבע פעמי' כמו שהוא אז הוא רוצה ליתן לצדקה ג' ובסוף חמשה ימי' לא נשאר דבר | |
| הנה נקח מספרים כפי מספר הימים ובעבור שיהיה התוספת ארבע פעמי' נקח המספרי' על סדר הארבע ר"ל א' ד' ח' ו"א ד"ו וה"ב ונכפול מחובר אלה חמשה המספרי' על ג' שהוא הצדקה והנה המחובר הוא אד"ג וכפלו על ג' הוא ג"כ ס"א וזה היה ממונו והם חלקי' מ"ד פעמי' וה"ב בשלם כי וה"ב הוא המספר האחרון מן המחוברי' וד' פעמי' וה"ב ד"ב ס"א | |
| Boiling Problem | |
|
שאלה הנה אדם רוצה לבשל י' מדות תו תירוש ורצה לבשלם עד שיפחתו השליש וכאשר בשלו עד שנשארו ח' מדות נשפחך מהם ב מדות ושפך אליהם עוד ב' מדות אחרי' והניחם לבשל עד שכלה מצד הבישול מה שהיה כוונתו הראשונה שיהיה נפחת מן התירוש בערך הנפחת אל הכל במה שנשאר לו מן התירוש לפי זה באחרונה |
| הנה כאשר נחסר השליש מן עשרה הוא ג' ושליש יהיה הנשא ו' ושני שלישיות וזה מה שהיה ראוי להשאר [נא] מן העשרה מדות אם לא היה נשפך דבר והנה בעבור שמשותף השליש בזה הנשאר ראוי להשאר נעריך העשרה על חשבון שיש בו שליש והוא 0"ג והנה יהיה לפי זה מכל מדה ג' שברים ולפי זה אחר שחסרו שני המדות נשארו עוד ד"ב שברי' והיה ראוי שיפחתו אילו עוד ד' שברי' וזה היה מכל מדה שבר ד' שברים מד"ב בשבר והנה אחר שנשפך לו ו' שברי' ואם כן ישארו ח"א שברים וצריך שיתבשלו אילו ח"א שברי' עד שיחסר מכל שברי' ד' שברי שברים [83]מד"ב מבשבר והם ד' פעמי' ח"א שברי' שברים והם ב"ד שברי' שברים ונבקש המורה על שברי שברים והוא ד"ב פעמי' ג' מפני שהשברים מג' בשלם והנה ג' פעמים ד"ב הם ב"ז ואם כן מה שהיה ראוי להתחסר מן ח"א שברי' שהם שישה מדות שלמים הוא [.]"ח ב"ז שברי' ממון ב"ז בשלם ואם כן ישארו מן העשרה ה' ואם הוסיף עליהם שנים אחר שנשפך הנה אחר שיחסרו השנים שליש מצד הבישול ישאר מהם אחד ושליש והנה חמש והמחובר מהם ששה ושליש והוא המבוקש | |
| [84] [85] [86] [87]בשם המאי[ר ל]עולם | |
| ואין עמ[.] העלם והוא מכל נעלם | |
| אבאר דרכי חשבונות השברי' והערכים והשרשים עם ביאור תוצאות מקצת הכללים בדרכי חשבונותיהם וגם א[...] קצת כללים מן התשבורת יען אשר תוצאותיהם מן השרשי' | |
| וכוונ[ת]י להקל בביאור תכלית האפשר אצלי למען יקל על המעיין אשר לא הורגל ויקבל תועלת גדולה בזמן קצר בלי ליאות מן ה[כללת] המלות הזרות כי כל מלה זרה אשר יביא הצורך לדבר בה אבארה וגם אחדש מלות עד השאלה כוללי הענין המכון | |
| כדי שלא יבא על ענין אחד בזכירתו מלות כוללים הענין רבות רק יבא זכר הענין במלה א' מונחת לו לשם רבות רק יבא זכר העניין מצד ההשאלה | |
| בזה תועלת גדולה למעיין שיבא העניין הנרצה מבואר בלשון קצר | |
| כל ביאור שהוא באריכו[ת] הדברי' ילאה האדם בו ליאות גדול מפני האריכות ומפני שלפעמי' לא תשלוט הזכירה על כללי הדברי' מראשם ועד [..]מ[ם] אשר כלל הדברי' ההם רק ספור א' כי כאשר יקרא האדם סוף הסיפור לפעמי' שכח מה שהיה בראש הספור והספור המחובר [...] לעניין א' אי אפשר ממנו הבנת המכוון אלא כאשר יהיה כלל הספור נרשם בדמיון בא מן המכוון מן הספור ולכן צרי' לכל מחבר [....] בכל ספור תכלית מה שאפשר באופן שלא יחסר הביאור מהמכוון [....] אשר יביא הצורך זכרו בספור מן הספור ראוי לו להיות כל אל העניין ההוא שם מיוחד בו יובן עניינו ושלא יצטרך המספר להאריך בעניין אשר אין הכוונ' בו לבארו בספור ההוא כי העניינים אשר יבאו בספור מן הספורי' צרי' שתקדים ההבנה בהם על הבנת הספור ולא [...] ביאורם בכלל הספור אשר כוונתו לבאר עניין אחר ולכן ראוי שיקדים המחבר ביאור שמות מונחים אל העניינים אשר יביא הצורך לזכרם בכלל הספור המכוין הבנתו שלא יבלבל ביאור העניין בכלל הספור אשר בלתי מכוין המכוון ואל ה[...] אני נותן ההודאה והשבח על כל שכל ודעת [...]ט[ו]ב אשר [......] כי מאתו הכל ומאתו אשאל העזר להיישיר דרכי בהפקת רצוני וההצלה מהשגיאות ברוך הוא הטוב והמטיב והנני מקדים בעניין השברי' כי הם הם המ[.]מי' בטבע עכ"פ כי זולתם לא יתכן לא ביאור הערכים ולא השרשי' על השלימות כי הם המשותפים ברוב השאל[ות] |
Chapter on Fractions |
שער השברים |
| הוא שידע אדם לכפול שברי' על שברים או שברים ושלמים על שברים ושלמי' או שברי' על שלמים ושברי' וכן העניין בעניין החלוק שיכול לחלק שברי' או שברים ושלמים ממספר אחר הן שהוא שלמי' או שברי' או שלמי' ושברי' | |
| וכן בכלל זה השער שידע האדם אי זה חשבון אשר אפשר לחלקו לשברי' מ[.....] שיבאו מספר כל שבר ושבר בשלמי' | |
| וידמ י"ב לשליש ולרביעית ולשת[.] [88]ולחלק י"ב שהשליש ממנו ד' והרביעית לשליש ג' והשתות ב' וחלק י"ב א' | |
| וכן בכלל זה השער שידע האדם שבר השבר או השברי' בשלמי' | |
| עדמ י"ו שימצא בו רביעית הרביעית ורביעית החצי וחצי החצי וחצי השמינית בשלמי' | |
| כי רביעית ו"א הוא ד' ורביעי' הד' אחד וא"כ א' הוי רביעית הרביעית וכן חצי הוא ח' | |
| וחצי הח' ד' ורביעי' הח' ב' וא"כ ב' הוא רביעית וחצי וד' הוא חצי החצי | |
| והנה שמינית ו"א הוא ב' וחצי הב' הוא א' וא"כ חצי השמינית הוא א' | |
| והראוי להקדים בזה השער הוא דרך מציאות המספר אשר ימצאו בו השברי' בשלמים או שברי שברי' | |
| וקודם ביאור זה הדרך אקדי' ואומ' כל שבר מהשברי' הן שהוא ש[בר] או שברי שברי' צרי' שיונח לו אות או אותיות רומז על השבר המרוצה ויקרא אותו האות או האותיות הרומזים על השברי' רומז בעבור שהאות או האותיות הם עניין רומז על מין מן השברי' ולכן נשאיל זה השם ר"ל שם רומז נשאיל או' האותיות ההם כדי שיהיה מובן בזה הש' אל מה שנרצה בו כאשר יבא הערך לזכרו כאילו הג' שערי' אשר כוונתי לבאר בהם | |
| והנה האות הרומז לחצי הוא ב' בעבור שכאשר יחלק השלם לחציים יהיה ממנו ב' חלקים וכן האות הרומ[ז] לשליש הוא ג' בעבור שכאשר יחלק השלם לשלישיות יהיו ממנו ג' ח[לקים] וכן האות הרומז לרביעית הוא ד' כי כאשר יחלק הא' לרביעי[.] הוא ד' כי כאשר יהיו ממנו ד' חלקי' | |
| ומזה הטעם בעצמו ה' רומז [לחמישית] ו' לשתות ז' לשביעית ח' לשמינית ט' לתשיעית ס"א 0"א לעשירית א"א לחלק של א' עשר ב"א לחלק של שנים עשר וכן עד אין סוף האותיות אשר יורו על מספר ערך השברי' אל השלם הם רומזים ג"כ לאחד מן השברי' מן המין ההוא כי כמו שיורה ג' על הש[לו]ש כן יורה 0"ב על חלק העשרים ו00"א על חלק המאה ו000"א על חלק האלף | |
| והאותיות הרומזים אל השברי' הם רומזים בעצמם אל שברי שברי' | |
| עד"מ כמו שיורה הב' על חצי שלם וכן והג' על שליש השלם כן יורה הב' על חצי שבר וכן הג' על שליש שבר עד"מ בשליש מורה הב' על חצי השליש והג' על שליש השליש וכן הדין על לשברי שברי' ולשברי שברי שברים עד אין קץ אם יביאך הצורך או החשק לחשבון מהחשבונות למין שברי' ראוי מן השבר הראש[ון] ואמנם השבר הראשון נקרא שבר בסתם ושברי שברי' הראשונים נקראים שניים ושברי השניים שלישים ושברי השלישים חמשיים וכן הדבר עד אין סוף | |
| ויש במקצת החשבונות שמחלקים השלם לש[...] וקוראים לכל חלק שבר או ראשון או דק או חלק | |
| וכן מחלקים כל הל[...] מן החלקים ההם לשניים וקוראים לו שניים וכן מחלקי' כל שניי לשניים שלישיי' וכל שלישיים לששים רביעיי' וכן נעשים חמשיים וששיים עד אין סוף ואמנם הדרכים האלו נמצא בדרכי חכמ[..] המזלות ומה שנכלל בחכמתם אבל כוונתינו הנה ע"ד חכמי החשבון ואח"כ נזכיר ג"כ מעט מן השאלות אשר יפלו בצורך חכמי המזלות בחשבונות שלהם | |
| והנה אחר הקדימי זאת נתחיל [89]נתחיל לבאר המכוון בדרך השאלות ויתבאר המבוקש מהשאלו' ומסדרם ולכן תקיף בשאלות המונחי' על הסדר ראשון ראשון ואז יתבאר המבוקש באופן השלם תכלית מה שאפשר אצלינו ביאורו היום | |
| [90]הג"ה בכל מקום אשר יבא הזכר תכפול או כפול הרצון בו ע"ד שער הכפל שהוא עד"מ כפל ג' על ד' הוא פי' ג"פ ד' | |
|
שאלה אי זה חשבון הוא שימצא בו שליש ורביעית במספ' שלמים |
| הנה לעולם כאשר תכפול הרומזים זה על זה יעלה מכפלם החשבון אשר בו מבוקשך | |
| והמשל בזאת השאלה שהרומזים הם ג' וד' תכפול ג' על ד' ויעלה בא והוא המבוקש ר"ל הוא חשבון שימצא בו שליש ורביע בשלמים כי השליש הוא ג ד והרביעית ג' | |
|
שאלה איזה חשבון שימצא בו שליש וחומש בשלמים |
| הנה הרומזים ג' וה' וכפלם ה'א' והוא המבוקש כי השליש הוא ה' והחומש ג' | |
|
שאלה אי זה חשבון ימצא בו חומש ושתות בשלמים |
| הנה הרומזים ה' ו' בעבור שהייתה השאלה מן חמשיות וששיות וכפל ה' על ו' הוא 0'ג' והוא המבו[קש] כי החומש הוא ו' והשתות הוא ה' | |
|
שאלה אי זה חשבון ימצא בו שתות וחצי |
| הנה הרומזי' הם ב' וו' כפלם ב'א' והוא חשבון שימצא בו חצי ושתות בשלמים כי השתות הוא ב' והחצי הוא ו' | |
| ואמנם בזאת השאלה ימ[צא] חשבון יותר קרוב והוא ו' וסימנך לעולם כאשר יהיה א' המרומזי' [....] שוה על מספר הרמז הקטן אז אינך צריך אל כפל שני הרומזים כי מספר הרומז הגדול הוא בעצמו המבוקש | |
| [91]הג"ה הרומז הקטן הוא אשר יורה על מספר קטן ואם השבר אשר הוא יורה עליו הוא היות[ר] גדול בלי ספק והרומז הגדול הוא אשר יורה על מספר יותר גדול ואם השבר אשר הוא יורה עליו יותר קטון ספק | |
| והמשל בזאת השאלה ששאל על חשבון שימצא בו חצי ושתות | |
| הנה הרמזים ב' ו' ב' | |
| והנה מספר הו' שהוא הרומז הגדול הוא יכלה בב' בשוה ולכן ו' בעצמו הוא חשבון שימצא בו שתות וחצי | |
| שאלה אי זה חשבון שימצא בו שליש ושתות | |
| הנה הרומ' ג' ו' והנה הו' יכלה על ג' בשוה וא"כ הו' בעצמו המבוקש כי השתות הוא א' והשליש ב' | |
| שאלה אי זה חשבון ימצא בו שמינית ורביעית | |
| הנה הרומזי' ד' וח' והנה הח' יכלה על ד' א"כ הח' הוא המבוקש | |
|
שאלה אי זה חשבון שימצא בו שליש ורביעית וחומש בשלמי' |
| הנה הרומזים אל השליש והרביעית והחומש הם ג' וד' וה' ובעבור שהרומזים ג' אתה צרי' לכפול מהם ראשונ' שנים רומזים זה על זה ועל מוכפל השנים תכפול הרומז השלישי ויעלה מבוקשך | |
| והמשל בזאת השאלה שהרומזים ג' ד' ה' תכפול ראשונ' ג' על ד' ויעלה ב"א והנה ב"א מוכפל שני הרומזים תכפול עליהם הרומז השלישי שהוא ה' ויעלה 0"ו והוא המבוקש ר"ל חשבון שימצא בו שליש ורביעית וחומש בשלמים והשליש הוא 0"ב והחומש הוא ב"א והרביעי' ה"א | |
| [92]הג"ה אין הפרט באי זה שני הרומזים אשר תת[...] הכפל ראשונה כי אם תתחיל ראשונ' ותאמר ה' פעמי' ד' יעלו 0"ב וג' פעמים 0"ב יעלה 0"ו הנה תראה שיעלה לחשבון א' מאי זה שתתחיל | |
|
שאלה אי זה חשבון שימצא בו רביעית וחומש ושתות בשלמים |
| הנה הרומזים הם ד' וה' וו' | |
| וכפל ד' על ה' הוא 0"ב וכפל ו' על זה המוכפל הוא 0ב"א והוא המבוקש [93]והוא המבוקש | |
| והרביעית ממנו ר"ל מ0ב"א הוא 0"ג והחומש ממנו ד'ב' והשתות 0"ב | |
| ואמנם לכאן בזאת בשאלה ששאל לחש[בון] שימצא בו רביעית וחומש ושתות יש חשבון יותר קרוב וראוי להמציא לעולם החשבון היותר קרוב במספר וככה נדע אותו הנה הרומזי' ד' ה' ו' והנה בעבור ששנים מן הרומזים הם זוגות נוכל ליקח מקום א' מן השנים מספר חצי הרומז והוא יספיק כי מצד שיקר' עליו כפל הזוג הנה יחזור | |
| [94]הג"ה ואם היינו לקחים חצי ה'ו' לא היה בא הפר[ש] בעבור זה כי לא תוכל לי[קח] לעולם חצי א' של שני הרומזי' שהם מספר זוג אי זה שיהיה והמשל בזה כי אם היינו לוקחים ג' וכפל ג' על ד' הוא ב"א כן כפל ו' על ב' וא"כ אין הפרש | |
| והמשל בזאת השאלה שהיו רומזי' ד' ה' ו' והנה נקח חצי מן הד' והוא ב' ונכפול ב' על ה' יעלה 0"א ו' על 0"א יעלה 0"ו והוא המבוקש כי השליש ממנו הוא 0"ב והרביעי' ה"א והחומש ב"א | |
| שאלה אי זה חשבון שימצא בו עשור ורביעית ושליש | |
| הנה הרומזי' 0"א וד' וג' ונקח מקום אחד שני הרומזים שהם מספר זוג חציו ויהיה מקום 0"א ה' ונכפול ד' על ה' יעלה 0"ב וג' על 0"ב יעלה [0]"ו והוא המבוקש | |
| שאלה אי זה חשבון שימצא בו עשור וחומש ושתות | |
| הנה הרומזים 0"א ה"ו ונקח מקום 0"א ה' יהיו א"כ הרומזים הה"ו הנה בעבור ששנים מן הרומזים לפי זאת ההנחה שוים ר"ל ששנים מהם ה' נניח ה' ר"ל א' מן השוים וישאר לנו עוד ה'ו' ובמלה 0"ג והוא המבוקש | |
| [95]הג"ה וצרי' להיות המספ' השלישי דומה לא' הנשארי' כגון הה' הרומזת על החומש אבל אם היו שוי' שני המספרי' אשר הא' הג' והא' מקום הזוג האח' [אז] לא תוכל להניח א' מן [ה]מספרי' השוים כי לקחת מספר הא' השוה מקום מספר הזוג והוא רק חצי [ש]ל המספר אשר לקחת אותו במקומו ואמנם טעית זה מפני שתשען [ע]ל חזרתו שלם מכפל מספ' [ה]ג עליו ואם תניח אותו [ה]מספר לא ישוב להיות שלם לעולם | |
| שאלה אי זה חשבון שימצא בו שליש ורביעית ושמינית | |
| הנה הרומזים ג' ד' ח' | |
| ונקח מקום הח' ד' ויהיו הרומזים ג'ד'ד' ולא נוכל להניח הד' הא' כי לא יחזור מכפל ג' על ד' מספר יכלה על ח' כי מה שלקחנו חצי הח' סמכנו בזה על מספר זוג שיהיה נכפל עליו וכאשר נניחנו לא יבא בתוך הכפלים מספר זוג עליו ולכן לא נוכל להשליכו וא"כ תכפול ד' על ד' יעלה ו"א ותכפול ג' על המוכפל שהוא ו"א ויעלה ח"ד והוא המבוקש והשליש ו"א והשמינית ו' והרביעית כ"א | |
| ואמנם יש בזא[ת] השאלה מספר יותר קרוב כי אע"פ שלא נוכל להניח א' מן השני רומזים השוים מ"מ אחד שהם זוגות נקח מקרי הא' חציו והוא ב' ויהיו הרומזים ב' ג' ד' וכפל ב' על ד' ח' וכפל ג' על המוכפל שהוא ח' ד"ב והוא המבוקש | |
| שאלה אי זה חשבון שימצא בו חלק שליש ורבי' ושמינית | |
| והנה אודיעך דרך אחר בזאת השאלה מן הד[רך] אשר זכרתי הנה הרומזים ח' ד' ג' ובעבור אשר יכלה הח' על ד"ד הנח הד' לגמרי וישאר לך ח' וג' תכפול הח' על הג' אז יעלה ד"ב והוא המבוקש ולעול' כאשר יספיק שני רומזים אל תתעסק בשלשה כי כל מה שיהיו הרומזים יותר יתקבץ מכפלם חשבון יותר גדול | |
| שאלה אי זה חשבון שימצא בו שליש ורביעית וחומש ושביעי' הנה בעבור שאלו המספרי' אז מן הרומזים ארבע צרי' אתה לכפול ראשונה שנים ועל מוכפל השנים תכפו' רומז השלישי ועל מוכפל שלשה הרומזי' תכפול הרביעי ויעלה מבוקשך ואם יעלו היו הרומזים הרבה לעולם תכפול על מוכפל הראשונ' ‫ [96]הראשונים הרומז שאחריהם עד שיכלו כלם ויהיה בזאת השאלה הרומזי' ג' ד' ה' ז' וכפל ג' על ד' ב"א וה' על ב"א 0"ו וז' על 0"ו יעלה 0ב"ד והוא המבוקש והשליש הוא 0ד"א והרביעית ה0"א והחומש ד"ח והשביעית 0"ו | |
| שאלה אי זה חשבון שימצא בו שליש ורביעי' וחומש ושתות ועשור וחלק ב"א | |
| הנה הרומזים ג' ד' ה' ו' 0"א ב"א | |
| והנה נקח מקום ב"א ו' ומקום 0"א ה' בעבור שיש מספר זוג בכלל הרומזים האחרי' ויהיו הרומזים לפי זאת ההנחה ג' ד' ה' ו' ו' ה' ונוכל להניח הו' האחד והה' הא' כי נשאר מספר זוג לכפול עליהם וישארו הרומזים ג' ד' ה' ו' והנה יעלה מכפל ג' על ד' ב"א וכפל ה' על זה המוכפל ר"ל על ב"א יעלה 0"ו וכפל ו' על זה המוכפל ר"ל 0"ו יעלה 0ו"ג והוא המבוקש והשליש ממנו 0ב"א והרביעית 0"ט והחומש ב"ז והשתות 0"ו | |
| ואמנם יש בזא[ת] השאלה חשבון יותר שתניח גם הו האחרת כי אע"פ שהיא עומד מקום הרומז של השתות ומקום הרומז של חל[ק] ב"א מ"מ בעבור שישאר בכלל הרומזים ג' ד' אינך צריך אל הו' כי מכפל ג' ד' יעלה מספר אשר בכללו ו' וגם ב"א והוא מספר ב"א כי ג' פעמי' ד' הוא ב"א ולפי זה יהיו הרומזים בזאת השאלה ג' ד' ה' ויעלה מכפלם לפי משפט כפלם 0"ו והשליש ממנו 0"ב והרביעית ה"א והחומש ב"א והעשור ו' וחלק ב"א הוא ה' | |
| שאלה אי זה חשבון שימצא בו חצי ושליש ורביעית וחומש ושתות ושמינית ותשיעית ועשור | |
| הנה הרומזי' ב' ג' ד' ה' ו' ח' ט' 0"א | |
| והנה אין א[נו] צריכים ל0"א מפני שיש בתוך הרומזי' חציו ומספר זוג וכפל מספר זוג על חציו הוא יבא במקומן ומספר חציו הוא ה' גם אין אנו צריכי' לט' כי יש בכלל הרומזים ג' וגם ו' וכפל ג' על ו' יהיו ח"א וח"א יכלו ט' ט' | |
| ולעולם כאשר יבא מכלל כפל קצת הרומזים מספ' שיכלה על מספר אחד שאר הרומזי' הנה כל [מס] רומז אשר יכלה המוכפל עליו אין צורך אל הרומזים ההם גם הח' אין אנו צריכים מפני שיש בכלל הרומזים חצי ח' שהוא ד' ובזולת הד' והוא הו' או הב' ומכפל זוג על חצי מספר יעלה מספר שלם וגם נניח הב' כי היא אינה צורך לא בעבורה כי היא בכלל הו' מפני שהו' יכלה על ב' ב' וגם אינה צריכה בעבור צורך למספר זוג מחמת הרומזים שהנחנו וסמכנו על מספר זוג כגון הח' ו0"א כי יש עו' ו' והיא מספר זוג ומספיק אע"פ שהד' לא מספיק כי הי[א] עומדת ג"כ מקום ח' מ"מ הו' מספיק | |
| ולפי זאת ההנחה אשר ישאר לנ[ו] מכל אלה הרומזים אשר אנו צריכים להם עכ"פ הם ג' ד' ה' ו' ויעלה מכפלם כמשפט 0ו"ג וזהו המבוקש ר"ל חשבון שימצא בו חצי ושליש ורבי' וחומש ושתות ושמינית ותשיעית והחצי 0ח"א והשליש 0ב"א והרביעית 0"ט והחומש ב"ז והשתות 0"ו והשמינית ה"ד והתשיעית 0"ד | |
| שאלה אי זה חשבון שימצא בו שליש ושליש השליש והרביעי' | |
| הנה הרומזי' ג' ג' ד' ויעלה מכפלם ו"ג והוא המבוקש כי [97]כי הרביעית ט' והשליש ב"א ושליש השליש הוא ד' | |
| שאלה אחד שאל לנו חשבון שימצא בו השליש והרביעית והחומש איך נדע כמה השליש ממנו או החומש או הרביעית | |
| הנה אי זה שתרצה לדעת תחלק עליו ר"ל בחשבון שימצאו בו החלקי' הרומז של השבר אשר תרצה לדעת אותו ויעלה מן החלוק מבוקשך | |
| והמשל הנה 0"ו הוא החשבן אשר בו השברי' המבוקשי' | |
| והנה תרצה לדעת השליש ממנו תחלק לתוך 0ו"ג שהיא רומז השליש ממנו תחל[.] ומה שיעלה בחלוק הוא המבוקש והנה יעלה 0"ב | |
| ואם תרצה לדעת הרביעית ממנו תחלוק לתוכו ד שהוא הרומז לרביעי ויעלה מבוק[ש] והוא ה"א | |
| ואם תרצה לדעת החומש תחלק לתוכו ה שהוא רומז החומש ויעלה ב"א והוא המבוקש | |
| וכן תעשה לכל מין ומין מן השברי' בכ[..] החשבון | |
| שאלה אי זה חשבון שימצא בו שליש הרביעית ורביעית החומש | |
| הנה הרומזי' הם ג' ד' ד' ה' ונוכ[ל] ליקח מקום אחד הדלתין חצי ד' שהוא ב' בעבור שיש מספר זוג בתוך המורים זולת אותה הד' והוא הד' האחרת ויהיו הרומזים לפי זה ג' ד' ב' ה' ויעלה מכפלם 0ב"א והרביעית הוא [0]"ג ושליש [0"ג] הוא 0"א והם שליש של הרביעית והחומש הוא ד"ב ורביעית ד"ב הוא ו' [וא"כ] ו' הוא רביעית החומש | |
|
שאלה כמה המחובר מן הש[ליש] והרביעי' |
| הנה נבקש חשבון שיש בו שליש ורביעית והוא נקרא לעולם המורה במין אלו השאלות מפני שיורה לנו על מספר [שנוכל] להוציא ממנו מיני השברי' המשותפי' בשאלה ר"ל הוא יורה [...] מספר שנוכל להוציא ממנו מיני השברי' המשותפי' בשאלה במין שברי' שיש להם ערך אחד אל השלם | |
| והנה לך המשל בזאת השאלה אשר שאלנו שהשברי' המשותפי' בה הם שליש ורביעית והנה החשבון אשר ימצא בו שליש ורביעית הוא ב"א | |
| הנה השליש ממנו ג' חלקי' מן חלקים ב"א בשלם והרביעית הוא ג' חלקים מן ב"א בשלם הנה השליש ד' והרביעית ג' חלקי' שערכם ערך א' לשלם והוא ב"א כי הג' חלקים הם ג' מן ב"א בשלם והד' ד' חלקים שהם ג"כ חלקים מן ב"א בשלם | |
| והנה אחר שתדע שהשליש הוא ד' חלקי' והרביעית הוא ג' חלקים הנה א"כ המחובר מהם ז' חלקים מן ב"א בשלם וזה יהיה חצי אחד וחלק אחד מן ב"א בשלם | |
|
שאלה כמה המחובר מן השליש והרביעית והחומש |
| נבקש חשבון שימצא בו שליש ורביעית וחומש בשלמים והוא המורה והוא 0"ו והשליש ממנו הוא 0"ב והרביעית ממנו הוא ה"א והחומש ממנו הוא ב"א ומחובר ב"א וה"א ו0"ב הוא ז"ד וא"כ מחובר [98]מחובר השליש והרביעית והחומש הוא ז"ד חלקי' מן 0"ו בשלם והוא ג' רביעיות השלם ועו' שני חלקי' מן 0"ו בשלם כי הרביעית הוא ה"א וג' פעמי' ה"א הוא ה"ד והמחובר של שליש ורביעית וחומש היה ז"ד וא"כ הם ג' רביעיות של השלם וב' חלקים | |
| [99]הג"ה והם שני שליש השלם ועו' ג' חלקים מן תשעים בשלם שהוא חלק א' מן 0"ג בשלם כי 0"ג פעמי' ג' הוא תשעי' | |
|
שאלה כמה המחובר מן השליש והחומש ושתות ותשיעי' |
| הנה הרומזי' לזה המורה הם ג' ה' ו' ט' ונניח הט' מפני שהיא בכלל ג' פעמי' ו' וישארו לנו מן הרומזים ג' ה' ו' ויעלה כפלם 0"ט והוא המורה והתשיעית ממנו 0"א והש[תו]ת ה"א והחומש ח"א והשליש 0"ג וא"כ המחובר מן 0"א וה"א וח"א ו0"ג הוא ג"ז והוא המבוקש | |
|
שאלה כמה המחובר מן חצי ושליש ורביעית וחומש ושתות |
| הנה הרומזים ואלו השברי' הם ב' ג' ד' ה' ו' ולא נצטרך אל הב' מפני שהיא בכלל ד' וכן לא נצטרך אל הו' מפני שג' היא חצי ו' ויש ברומזי' זולת הו' מספר זוג הנה א"כ הרומזי' הנשארי' הם ג' ד' ה' וכפלם כמשפט הוא 0"ו והם המור' והחצי ממנו 0"ג והשליש 0"ב והרביעית ה"א והחומש ב"א והשתות 0"א והמחובר של אלו הוא ז"ז (?) והם ז"ז חלקי' מן 0"ו בשלם [..........] המורה הוא 0"ו וא"כ הם א' שלם וז"א חלקי' מן 0"ו בשלם שהם [ר]ביעית השלם וב' חלקי' מן 0"ו בשלם וב' חלקי' מן 0"ו בשלם הוא חלק א' ממין 0"ג בשלם וא"כ המבוקש הוא אחד שלם ורביעית וחלק 0"ג בשלם | |
| שאלה כמה המחובר משלושה שלמי' וחצי וארבע שלמי' וחצי ושליש וחמשה שלמים וחומש ושתות | |
| הנה המחובר השלמי' הוא ב"א והמורה לשליש וחצי וחומש הוא 0"ג והחצי ממנו ה"א והחומש ו' | |
| והנה צריכים אנו לחבר שני חצאי' וחומש וחצי א' הוא ה"א וא"כ שני חצאי' הם 0"ג והשתות ו' מחובר הו' אל 0"ג שהם מחובר שני חצאי' הוא ו"ג והמורה 0"ג א"כ ו"ג [ה]וא א' שלם ועו' ו' חלקי' מן 0"ג בשלם וכבר היה לנו ממחובר השלמי' ב"א שלמי' נחבר עליהם האחד השלם שעלה לנו ממחובר השברים ויעלה לנו המבוקש ג"א שלמים וו' חלקי' מן 0"ג בשלם שהם חלק אחד מן 0"א בשלם כי 0"א פעמי' ימצא ג' בתוך 0"ג | |
| שאלה כמה המחובר מחצי ושני שלישיות וג' רביעיות וארבע חמשיות וחמש ששיות הנה המורה לאלו השברים 0"ו והחצי ממנו 0"ג והשליש השליש הוא 0"ב וא"כ שני שלישיות הם 0"ד והרביעית ממנו הוא ה"א וא"כ ג' רביעיות הם ה"ד והחומש ב"א וא"כ ד' חומשי' הם ח"ד והשתו' 0"א וא"כ ה' ששיות הם 0"ה ולפי זה 0"ג שהוא חצי ו0"ד שהוא שני שלישיות וה"ד שהוא שלשה רביעיות וח"ד שהוא ד' חמשיות ו0"ה שהוא ה' ששיות יהיה המחובר מהם גא"ב חלקי' מן 0"ו בשלם כי 0"ו הוא המורה והנה כאשר תחלק 0"ו לתוך גא"ב חלקים מן 0"ו בשלם לדעת כמה שלמים יעלו מן אלו [100]החלקי' יעלו לך ג' שלמי' וג"ג חלקים מן 0"ו בשלם וג"ג חלקים הם חצי א' וחלק עשרי' וא"כ המבוקש הוא ג' שלמים וחצי ועו' חלק א' מעשרי' בשלם | |
| שאלה כמה המחובר משלשה שלמים ושני שלישיו' וחמש שלמי' וה' שביעיות | |
| הנה מחובר השלמים ח' שלמים והמורה לאלו השברי' הוא א"ב ושני שלישיות א"ב הוא ד"א וחמשה שביעיות א"ב הוא ה"א ומחובר ה"א וד"א הוא ט"ב מן א"ב בשלם נעשה א' שלם מקו' א"ב מכלל הט"ב ונחברהו אל ח' השלמי' שעלו ממחובר השלמי' ויהיו לנו ט' שלמי' ועו' ח' חלקי' מן א"ב בשלם שהם שליש א' ועו' חלק א' מן א"ב בשלם ויהיה המבוקש א"כ ט' שלמים ושליש ועוד חלק מן א"ב בשלם | |
| שאלה כמה מחובר ד' שלמי' וד' חמשי' ושליש חומש וחמשה שלמים וארבע ששיות וחצי שתות | |
| הנה הרומזי' לאלו השברי' המשותפי' בזאת השאלה הם ה' ג' ו' ב' ואמנם נוכל ליקח מקום הו' ב' כי ג' חצי ו' ויבא הב' לכפול הג' שיהיה הו' שלם ולא יספיק לנו ב' א' מקום הב' ומקום הו' כי מכפל ב' על ג' לא יעלה רק ו' ואנו צריכי' ג"כ לחצי שתות ולא ימצא זה מכל ה' אשר נעשה מן הג' ואכן אם היה מספר זוג אחד לא היינו צריכים לב' ולפי זה יהיו הרומזים ב' ב' ג' ה' ואם תרצה יהיו הרומזים ג' ד' ה' כי הד' יעמוד מקו[ם] שני הביתין כי ב' פעמי' ב' הוא ד' | |
| והנה בזאת השאלה מחובר השלמים הוא ט' שלמים והמורה אל השברי' הוא 0"ו וד' חומשין 0"ו הוא ח"ד כי החומש ב"א ושליש החומש ד' נחברהו על ח"ד יעלה לנו ב"ה והם ד' חומשין ושליש וד' ששיות 0"ו הם 0"ד כי השתות 0"א וחצי השתות הוא ה' נחברהו על 0"ד יעלה ה"ד והם ד' ששיות וחצי נחברם אל ב"ה שהם ד' חמשיות ושליש ויעלה לנו ז"ט והם חלקי' מן 0"ו בשלם כי המורה 0"ו נוציא מקום 0"ו מהם אחד שלם ונחברהו אל ט' השלמי' ויעלו לנו 0"א שלמים וישארו ז"ג חלקים ממין 0"ו בשלם שהם חצי אחד ועשירית וחלק מ0"ו בשל' וא"כ המבוקש הוא 0"א שלמים וחצי ועשירית וחלק א' מן 0"ו בשלם | |
| ואם תרצה אמור המבוקש הוא 0"א שלמים וחצי וז' חלקים מן 0"ו בשלם | |
| ואם תרצה אמור המבוקש הוא 0"א שלמים וז"ג חלקים מן 0"ו בשלם | |
| שאלה כמה היתרון על השלם אחר שחוסר ממנו השליש והרביעי' | |
| הינה המורה לאלו השברי' הוא ב"א והשליש ד' והרביעי[ת ג'] וכאשר תסיר מן ב"א אלו החלקים ר"ל ג' וד' שהם השליש והרביעית ישאר ה' והוא המבוקש | |
| שאלה כמה היתרון ממחובר השליש והרביעית אחר שהוסר ממנו החומש והשתות | |
| הנה המורה לאלו השברי' 0"ו והשליש ממנו 0"ב והרביעית ה"א ומחובר השליש שהוא 0"ב עם ה"א שהוא הרביעית הוא ה"ג א"כ מחובר השליש והרביעית ה"ג והחומש הוא ב"א והשתות 0"א והמחובר מהם הוא ב"ב וא"כ תחסר ב"ב שהוא מחובר החומש והשתות מן ה"ג שהוא המחובר השליש והרביע[ית] וישארו ג"א וא"כ המבוקש ג"א חלקים מן 0"ו בשלם | |
| שאלה כמה הית[רון] מן מחובר הרביעית והחומש אחר שחוסר ממנו השלי[ש] [101]ושליש השליש | |
| הנה הרומז' לאלו השברי' הם ג' ג' ד' ה' ויעלה מכפלם 0ח"א והוא המורה | |
| והנה הרביעית ה"ד והחומש ו"ג ומחובר ה"ד ו"ג א"ח והשליש 0"ו ושליש השליש הוא 0"ב ומחובר 0"ב ו0"והוא 0"ח וא"כ תחסר 0"ח שהוא מחובר של השליש ושליש השליש מן א"ח שהוא המחובר של הרביעית והחומש וישאר א' והוא המבוקש והוא חלק א' מן 0ח"א בשלם | |
|
שאלה כמה השליש יותר מן הרביעית |
| הנה המורה לאלה החלקי' ב"א והשליש ד' והרביעית ג' תחסר ג' מן ד' וישאר א' וא"כ השליש יותר מן הרביעי' חלק אחד מן ב"א בשלם | |
| שאלה כמה השליש והרביעית יותר מן השתות והשביעית | |
| הנה הרומזים גדו"ז ויספיק לנו גד"ז מפני כפל ג' על ד' שהוא יביא ווין ויהיה המורה ד"ח והשליש והרביעי' מן ה ד"ח הוא ט"ד והשתות והשביעית מן ד"ח הוא ו"ב וא"כ תחסר ו"ב מן ט"ד וישאר המבוקש ג"ב חלקי' מן ד"ח בשלם | |
| שאלה כמה המחובר מתוספת שליש ורביעית על השלם | |
| הנה המורה לאלה החלקים הוא ב"א והשליש והרביעי' ממנו ז' וא"כ המחוב' מתוספת השליש והרביעית על השלם הוא א' שלם וז' חלקי' מן ב"א בשלם | |
| שאלה כמה המחובר מן תוספת ג' רביעיות וד' חמשיות של השלם על השלם | |
| הנה מורה לאלה השברי' הוא 0"ב וג' רביעיותיו הוא ה"א כי הרביעית ה' וד' חומשיות ממנו הוא ו"א כי החומש ד' ומחובר ה"א ו"א שהם שלשה רביעיות וד' חמשיות הוא א"ג נוציא מהם מקום 0"ב אחד שלם ויהיה א"כ המבוקש שני שלמים וא"א חלקים מן 0"ב בשלם | |
| שאלה כמה שלשה רביעיות פעמי' ד' חמשיות | |
| הנה דע לך בזאת השאלה וכל מה שידמה לה שהוא מענין כפל שברי' על שברי' אין הפרש במספר שיעלה מכפל שברים על שברים ובין מספר שיעלה מכפל שלמים על שלמים | |
| כי כמו שהמספר אשר בא מכפל ג' שלמי' על ד' שלמי' הוא ב"א כן המספר אשר יעלה מכפל ג' רביעיות על ד' חמשיות הוא ב"א | |
| ואין הפרש בין שיהיו שני בתי השברים שתדרוש על כפלם זה על זה ממין אחד או משני מינים כי לעול' יהיה המספר המגיע מכפלם במניין כמו המספר המגיע מכפל השלמי' | |
| ואבל אמנם יש הפרש במין המספר שיעלה מכפל השלמי' ובין מין המספ' שיעלה מכפל השברי' וזה שמכפל שלמי' על שלמים מספר שהוא ממין הנכפלים והם שלמים בעבור שהיו הנכפלים שלמים | |
| ואמנם המספר שיעלה מכפל שברי' על שברי' הוא מין שברי' זולת מיני השברי' הנכפלים וצריכין בזה חקירה בכל שאלה מאיזה מין הם השברי' | |
| ודרך החקירה הזאת הוא שנבקש להם מורה ר"ל חשבון שיורה לנו ערכם אל השלם וככה נדע המורה שנכפיל הרומזים של מיני השברי' המשותפים בשאל' בדרך אשר הקדמתיך משפט הכפל הרומזים והחשבון העולה הוא המו[רה] מאי זה מין הם החלקים | |
| המשל בזאת השאלה אשר שאל כמה ג' רביעיות על ד' חמשיות | |
| הנה ג' פעמי' ד' ב"א והרומזים הם ד' ה' ויעלה מכפלם 0"ב והוא המורה וא"כ ג' רביעיות על ד' חמשיותהם ב"א שברים ממין 0"ב שברים בשלם | |
| [102]שאלה כמה ג' רביעיות על ג' רביעיות הנה ג' פעמי' ג' הוא ט' והרומזי' ד' על ד' ד' וכפל ד' על ד' ו"א וא"כ ו"א הוא המורה וא"כ ג' רביעיו' על ג' רביעיו' הם ט' חלקים מן ו"א בשלם | |
| שאלה כמה כפל שלשה רביעיות על ב' רביעיות | |
| הנה ב' על ג' הוא ו' והמורה ו"א כפי מה שהקדמנו בשאלה הקודמת וא"כ כפל ב' רביעיות על ג' רביעיות הוא ו' שברי' מן ו"א בשלם | |
| שאלה כמה שלשה רביעיות על רביעי' אחד | |
| הנה ג' פעמים א' הוא ג' והמורה ו"א כפי מה שהוקדם וא"כ כפל ג' רביעיות על רביעית אחד הוא ג' חלקים מן ו"א בשלם | |
| שאלה כמה כפל רביעית אחד על רביעית אחד | |
| הנה א' פעם א' הוא א' והמורה לאילו השברי' ו"א וא"כ כפל רביעית אחד על רביעית א' הוא א' מן ו"א בשלם | |
| שאלה כמה כפל שליש א' על רביעית א' | |
| הנה א' פעמי' א' הוא א' והמורה לאילו השברים ב"א מפני שהרומזי' הם ג' ד' וא"כ כפל השליש על הרביעית הוא חלק אחד מן ב"א בשלם | |
| וביאור אמיתת הדרך באלו השאלות מכפל שברים על שברי' הוא מה שאומר הנה מבואר שא' פע' אחד שלם הוא א' וחצי פע' א' הוא חצי רביעית פעמי' א' הוא רביעית ושליש פעמי' הרביעי' הוא שליש של הרביעית וא"כ שנים שלשיות פעמי' רביעית אחד הוא שני שלשיות של הרביעית ושני שלשיות פעמים שני רביעיות הם בהכרח ד' שלישיות של הרביעית כי שני שלישיות פעם רביעי' א' הוא שני שלישיות של רביעית וא"כ שני פעמי' שני שלישיות פעמים שני רביעיות הוא ד' והנה יצא לך אלו השברים שהזכרנו ר"ל השליש והרביעית כפל א' על א' הוא א' וכפל ב' על א' על א' הוא ב' | |
| וכפל ב' על ב' הוא ד' וזהו כמו הענין בכפל שלמים על שלמים אלא שמין המספר היה שלשיות של רביעיות ולהוציא זה המין ליחס השלם צריך אתה לבקש חשבון שיש לו שליש ורביעית כדי שתדע מה ערך שליש על הרביע אל השלם וזהו ב"א שהרביעית ג' ושליש[ה] הוא א' ואם יהיו לך מן החשבון הרבה שלישיות של רביעית יהיו לך הרבה ח[לקי'] של ב"א בשלם | |
| כי חלק ב"א בשלם הוא שליש הרביעי' וכן הענין כאשר תאמר רביעית פעמי' רביעית אתה צרי' לבקש חשבון שתמצא בו רביעי' הרביעית כדי שתדע ערך רביעית הרביעית אל השלם והחשבון הזה הוא ו"א והרביעית הוא ד' ורביעית הרביעית הוא א' מן ו"א בשלם | |
| הנה כפי מה שיעלה בידך מכפל רביעיות על רביעיות יהיו הכל רבעי רביעי' שהם חלקים מן ו"א בשלם | |
|
שאלה כמה ז' שמיניות על [שמנה] תשעיות |
| הנה ז' פעמים ח' הם ו"ה והמורה ב"ז וא"כ הם ו"ה חלקים מן ב"ז בשלם | |
|
שאלה כמה ג' שביעיות על חמש תשעיות |
| הנה המורה ג"ו וג' פעמי' ה' ה"א וא"כ המבוקש ה"א חלקים מן ג"ו בשלם | |
|
שאלה כמה כפל ג' רביעיות על שלשה חמשיות של שליש אחד |
| הנה אנו צריכים [לבקש] תחלה חשבון שיש בו רביעית ושליש וחומש השליש מפני שאלו השברים משותפים בשאלה והרומזים לאלו השברי' הם ד'ה'ג' וכפלם כמשפט כפל [103]א"א רביעיות וג' שלמי' ושני שלישיות הם ח' שלישיות והנה שבה השאלה לשאלת מי ששאל כמה כפל א"א רביעיות על ח' שלישיות והנה המורה ב"א כי ה[רו]מזי' ג'ד' וכפל ח' על א"א יעלה ח"ח תחלקם על ב"א שהוא המורה יעלה לך ז' של[מי]ם וד' חלקים מן ב"א בשלם | |
|
שאלה כמה ג' שלמים וחומש על ב' שלמים ושתות |
| הנה ג' שלמים וחומש על ב' שלמים הם ו"א חומשים וב' שלמים ושתות הם ג"א ששיות ושבה עתה השאלה אל שאלת כמה כפל ו"א חומשי' על ג"א ששיות והנה המורה 0"ג וכפל ו"א על ג"א הוא ח0"ב וחלק המורה עליה ויעלה לך ו' שלמים וח"ב שברי' מן 0"ג בשלם | |
|
שאלה כמה כפל ג' שלמים ושליש על ב' שלמי' וחומש |
| הנה ג' שלמי' ושליש הוא 0"א שלשיות וב' שלמים וחומש הם א"א חומשי' ושבה שאלתינו אל שאלת מי ששאל כמה כפל 0"א שלישיות על א"א חומשיות | |
| הנה המור' ה"א וכפל 0"א על א"א הוא 0א"א תחלקם על המורה שהוא ה"א ויעלו לך שלמים ז' וגם ה' חלקים מן ה"א בשלם | |
|
שאלה כמה פעמי' ימצאו ג' רביעיות בה' שלמים |
| תשים השלמי' ראשונ' שברים ממין השברי' שתרצה לחלק השלמי' עליהם ובתוך מספר השברי' אשר יבא מן השלמי' תחלק מספר השברי' אשר תשאל כמה פעמים הם כמספר הקצוב מן השלמי' ויעלה מבוקשך המשל בזאת השאלה הנה ה' שלמי' ברביעיות נחלקם על ג' רביעיות אשר שאל בעבורם יעלה ו' וישאר ב' וא"כ ג' רביעיות הם ו' פעמי' בה' שלמים ועוד שני שליש פעם | |
|
שאלה כמה פעמים ימצא חמש שביעיות בח' שלמים |
| הנה ח' שלמים הם ו"ה שביעיות וחלקם על ה' ויעלה א"א וישאר א' וא"כ המבוקש א"א פעמים וחומש | |
|
שאלה כמה פעמים ימצאו ב' שלישיות בז' שלמי' |
| הנה ז' שלמים הם א"ב שלישיות וחלק אותם על ב' ויעלה 0"א וישאר א' וא"כ המבוקש 0"א פעמי' וחצי פעם | |
|
שאלה כמה פעמי' תמצא שלישית ורביעית בשמנה שלמים |
| הנה אתה צריך להוציא זאת השאלה לשאלה אחרת [ש]מין השברי' מין אחד וככה תעשה בקש חשבון שיש בו שליש ורביעית בעבור היות השברי' אשר משותפי' בשאלה משלישיות ורביעיות והנה זה החשבון ב"א והשליש ממנו ד' והרביעית כמה פעמי' ג' והמח[ובר] מהם ז' וא"כ שבה שאלה לשאלת מי ששאל כמה פעמים תמצא ז' חלקים מב"א בשמנה שלמים וא"כ תכפול ח' על ב"א ויעלה לך מן השלמי' חלקים ב"א והנה יעלה ו"ט חלקם על ז' ויעלה מבוקשך והנה יעלה ג"א פעמי' וה' שביעיות פעם | |
|
שאלה כמה פעמי' ימצא ג' רביעיו' וב' חומשיות בתוך ט' שלמי' וב' שלישיות וחמש שביעיות |
| הנה אנו צריכי' לבקש חשבון שימצאו בו כל אלו השברי' המשותפים בשל[מי'] והנה [104]והנה הרומזי' להם דהג"ז ויעלה מהם המורה 0ב"ד הנה הרביעית ה0"א ויהיו לפי זה ג' רביעיות ה0"א והחומש הוא ד"ח ויהיו א"כ ב' חומשי' חו"א והנה מחובר ב' שלמי' חומשי' וג' רביעיות הם גז"ב שברי' [..]מין 0ב"ד בשלם ונשים הט' שלמים ושני שלישיות וחמש שביעיות ל[....] אלו השברי' ויהיו מן הט' שלמים 0חז"ג שברי' מן 0ב"ד בשלם והשלם הוא 0ד"א וא"כ שני שלישיות הם 0ח"ב והשביעית 0"ו וא"כ ה' שביעיות הם 00"ג ועתה תחבר 0ח"ב שהוא שני שלישיות וגם 00"ג שהוא חמש שביעיות עם 0חז"ג שהם תשעה השלמים ויעלה בידך 0וג"ד והנה 0וג"ד שברי' [.....] 0ב"ד בשלם הם ט' שלמים וב' שלשיות וחמש שביעיות וכבר ביארנו שג' רביעיו' וב' חומשיות המחובר מהם גז"ב שברי' מן 0ב"ד בשלם | |
| וא"כ שבה עתה שאלתינו אל שאלת כמה פעמי' תמצא גז"ב שברים מן 0ב"ד בשלם תוך 0וג"ד שברים מן 0ב"ג (ד) בשלם | |
| והנה תמצאם ה"א פעמי' וישארו הו"ב שלא הגיעו לכלל 0ב"ד שהוא המורה | |
| והנה לפי זה המבוקש הוא ה"א פעמי' והו"ב חלקי פעם שהוא 0ב"ד בשלם |
Chapter on Proportions |
[105]שער הערך |
| שידע האדם הדבר הנעלם מסבת דבר הידוע אשר יודיע השואל ולפעמים שלא יודיע השואל דבר רק ישאל עניין נעלם אפשר לעמוד עליו | |
| וצרי' החכם [.]חכמת החשבון לעשות ידוע עד"מ אשר יתכן להוציא הנעלם בסבת [.] ידוע ההוא כמו שיבא הביאור באלו העניינים בע"ה | |
| והמשל שישאל השואל הנה קניתי מספר ענייני' מן העניינים בממון כללו כך וכך איך יבא מספר אחד מן הענייני' | |
| הנה מתי שיאמ' השואל קניתי מספר כך עבור ממון כך הנה אותו המספר שקנה הוא ידוע לך איך שבא יען שיאמר קניתי בעבור כך | |
| ומה ששואל איך יבא לפי הערך מספר כך וכך אותו המספר הוא נעלם ממך תחלה איך יבא וצריך אתה להוציא הנעלם מבוקשו מן הידוע | |
| והנה נדבר תחלה מזה להוציא הנעלם המבוקש מתוך הידוע שיודיע השואל ואח"כ נזכיר ג"כ אופן הענייני' אשר לא יגלה השואל בהם דבר ודרך המצאת התחבולות אשר ראויי' לאותם השאלות | |
| והנני אומ' לך כלל לעולם הדבר הידוע לך אני קורא אותו המורה ויבא ביאור הסבה אשר בעבורה נקרא המורה והדבר המשותף עם המורה עד"מ הממון אשר בעבורו קנוי הידוע אני קורא אותו המשותף ויבא בביאו' הסבה אשר בעבורה נקרא משותף | |
| והדבר אשר אתה שואל אני קור' אותו הנעלם וההודעה אשר אתה מבקש אני קורא אותו המבוקש | |
| והמשל בזה השאלה אשר אזכיר אותה הנה ישאל השואל קניתי ה' חביות יין בעבור פרח א' איך יבאו לפי הערך א חבית יין | |
| הנה ה' חביות אשר אמר השואל שקנה אותם הם נקראים המורה והפרח אשר בעבורם קנה אותם הה' חביות הוא נקרא המשותף וא' חבי' אשר אתה שואל איך יבאו הם נקראי' הנעלם והדומי' אשר בעבורם יבואו אותם הו' חביות נקרא המבוקש כי זהו מבוקש לשואל לדעת אותו והנה בזאת השאלה שאמ' קניתי ה' חביות בעבור פרח איך יבואו א' חבית הנה אם קנה ה' בעבור א' הנה נגלה שאחד שייך בעבור חומש אחד בעבור שבחביות ה' והוא המבוקש | |
| ואמנם אם היה שואל איך שייכים ו' חביות הנה אחר שהוא מבואר אם היה שואל על אחד היה שייך חומש אחד א"כ אי זה מספר מן החביות אשר תחפוץ לדעת איך יבאו תכפול אותו המספר על מה שבעבורו יבא א' ויעלה מבוקשך והוא בזאת השאלה חומש א' | |
| ואמנם אם היה אומ' השואל קנה הה' בעבור ב' פרחים הנה היה שייך חבית א' בעבור שני חמשיות וזה קל להבין כי כאשר היה קונה הה' בעבור חומש א' ואם הפרחי' שקנה בעבורם שני פעמים א' הנה יגיע לחבית אחד שני חומשים | |
| וכן אם היה קונה בעבור ג' פרחים החמשה היה מגיע לחבית א' ג' חומשים | |
| וכן אם קנה בעבור ד' היה מגיע לאחד ד' חומשים | |
| ולפי זה אנו רואים בזאת השאלה [106]שכפי מספר הפרחי' אשר בעבורם קנויים החמ[ש]ה חביות כן החומש אשר יגיעו לחבית א' ולפי זה מספר הפרחים הוא יורה על מספר השברי' אשר יגיעו לחבית אחד | |
| והנה זה המספר מגיד לנו שני [ענייני..] כלומר מספר הפרחים אשר בעבורם נקנה הה' חביות כי הוא מגיד מספר הפרחי' אשר בעבורם נקנה החמשה חביות כי השלמים אשר בעבורם נקנה יבואו החמשה חביות ויגיד ג"כ מספר ה[....]ים אשר יגיעו לחבית אחד לפי הערך והשברי' בזאת הש[אל]ה [....] ואמו' אם היה מאמר השואל קניתי ו' חביות בעבור פרח אז היה מגיע לחבית שתות פרח | |
| ואם היו הפרחי' ב' לו' חביות אז היה מגיע לח[בית] א' ב' ששיות | |
| ואם היו הפרחי' ג' אז היה מגיע לחבית א' ג' ששיות הנה אתה רואה שמספר הפרחי' אשר בעבור [.........] הו' חביו' יורו על מספר השברי' אשר יגיעו לאחד מן החביות אלא שהשברי' ששיות | |
| ואמנם אם היה מא[מ'] השואל קניתי ז' חביות בעבור פרח א' הנה בלי ספק היה מגיע לחבית א' שביעית אחד מן הפרח ואם היה קונה הז' עבור שני פרחים היה מגיע לחבית אחד שני שביעיות פרח | |
| ואם היה קונה הז' חביות בעבור ג' זהובים אז היה מגיע לחבית א' ג' שביעיות | |
| הנה אתה רואה מאי זה מספר שהיו החביות אשר קנה השואל לעולם יורה מספר הפרחים על מספר מן השברים אשר יגיעו לחבית א' | |
| וא"כ מספר הפרחי' לעולם משותף ר"ל שהוא יורה לעולם מספר השלמי' אשר בעבורם באו כלל החביות אשר קנה ויורה ג"כ מספר השברי' אשר יגיעו לאחד ולכן נקרא המספר ההוא המשותף | |
| והנה כבר ראית באלו הדמיונו[.] אשר זכרתי שכאשר היו החביות שקנה השואל חמשה בעבור פרח א' היה מגיע לחבית א' פרח חומש אחד | |
| ואם היו הפרחי' יותר מא' היו החומשים אשר הגיעו לחבית א' כפי מספר הפרחים והיו הפרחים השברים אשר הגיעו לחבית א' חומשים [ב]עבור שהיו החביות ה' | |
| ואמנם אם היו החביות ששה בעבור פרח א' אז היה מגיע לחבית א' שבר א' והשבר היה שתות וכפי מספר הפרחי' אשר באו בעבור ששה חביות כן היה מספר הששיות אשר הגיעו לא' | |
| ואמנם אם היו החביות שקנה שבעה בעבור פרח הגיע לחבית א' שבר א' שהוא שביעית בעבור שהיו החביות ז' | |
| ואם היו הפרחי' הרבה היו השביעיות אשר הגיעו לחבית אחד הרבה כפי מספר הפרחים ולפי זה אתה רואה אע"פ שהפרחים אשר כבר קראנו המשותף הם יורו על מספר שברים אשר יגיע לא' הנה הם לא יורו ולא יודע מהם מאי זה מין הם השברים בערך לשלם ואמו' יורה על מין השברים החביות אשר קנה כי כאשר היו החביות [107]החביות ה' היו השברי' ממין חמשיות וכאשר היו החביות ו' היו השברי' ממין ששיות | |
| וכאשר היו החביות שקנה ז' היו השברי' ממין שביעיו' וא"[כ] מספר החביות יורה לעולם על אי זה מין הם השברי' הראויים לא' כי המספר של החביות הוא הרומז למין ממין השברי' אשר יגיע לא' ולכן יקרא מספר החביות מורה כי הוא יורה מאי זה מין הם השברי' אשר יגיעו לא' | |
| ואמנם מספר הפרחי[ים] יורה על מספר השברי' ממין אשר יורו עליו החביות | |
| והיה ראוי לקרא ג"כ מספר הפרחי' מורה ואם היינו קוראי' אותו ג"כ מורה לא היה ביניהם הבדל וכאשר יבא זכר אחד [....] היה המכוון מסופק ולכן קראנו מספר הפרחי' משותף לפי הסמך שזכרנו כדי להבדיל ביניהם בשם שיהיה המכוון ידוע כאשר יבא זכרו | |
| ואמנם היינו יכולים לקרא המשותף שברים מפני שהוא יורה על מספר השברי' אשר יגיעו לאחד אבל לא עשינו זה מפני ששם שברי' משותף לענייני' אחרי' אשר יבא זכרם באלו החשב[ונות] כי כל מיני שברי' נקראו שברי' ואנו בורחי' משמות המשותפים אשר אשר אפשרות הזכר מהם בזה השער וכבר קראנו ג"כ המורה בשער השברים המספר אשר יורה על מין השברי' מאי זה ערך הם לשלם ולכן נשארנו בזה השער בשם קריאת המורה מורה על אותו האופן ר"ל שיורה המורה על מין ממין השברים כלומ' מאי זה ערך השברים אל השלם הנה אחר אשר זכרתי לך אפן ההבנה לעולם כמה מספר השברים אשר יגיעו לאחד קל להבין ולהוציא מה שיגיע לרבים כי המספ' המגיע לאחד כאשר תכפול אותו על מספר אחר אז יעלה לך בלי ספק מה ש[מגי]ע לאותו המספר אשר כפלת אותו במספר המגיע לאחד אלא [.ע]ל מה שיעלה מן הכפל הוא מספר ממין שברי' מפני שהיה שברי' המספר הראוי לאחד ולפי זה כאשר תחלוק המספר שעלה הכפל על המורה יעלו לך כמה שלמים אשר יכללו השברי' וכמה שברי' שישארו שלא הגיעו לכלל השלם | |
| והמשל הנה שאל השואל קניתי ה' חביות יין עבור ז' פרחי' איך שייכים ד' חביות | |
| הנה כבר ידעת בעבור שהפרחים ז' שיגיעו ז' שברים לחבית א' וא"כ כאשר תרצה לדעת המגיע לד' חביות אתה צריך לכפול ד' על ד' ז' אשר הם שברי חבית אחד ויעלה בידך שברי ד' חביות והם ז"ב שברי' והנה אלה השברי' כלם חמשיות בעבור שהיו החביות שקנה ה' וא"כ ה' המורה | |
| וא"כ תחלק ז"ב על ה' [.....] לך ה' וג' חלקי' מן ה' בשלם והם המבוקש והנה המבוקש ה' שלמים וג' חלקים מן ה' בשלם | |
| והנה יצא לך מכלל מה שזכרתי שבכל שאלה אתה צריך לכפול הנעלם על המשותף ולחלק הנכפל על המורה ומה שיעלה מן החלוק הוא המבוקש | |
| וזה הכלל תקחנו בידך כי עליו מסתובב כל זה השער ותבנה מזה בנייני' מופלאים בחכמת החשבון כפי מה שתראה מעניין השאלות אשר אזכיר ואהיה תמיד נשען בכל שאלה שיהיה ידוע לך המכוון |
Notes
[Expand]
Appendix I: Glossary of Terms
| rank | מעלה, מערכה |
| addition | חבור |
| to add | לחבר |
| division | חלוק |
| to divide | לחלק |
| multiplication | כפל |
| to multiply | לכפול |
| subtraction | חסור |
| to subtract | לחסר, לגרוע |
Bibliography
Meir Shapira
15th century?
Beur Darkei ha-Ḥeshbon
Manuscript:
- MS Oxford, Bodleian Library MS Opp. 211 (IMHM: f 17281), ff. 59r-103v; 117r124r (Cat. Neub. 362, 7); (15th century)
Bibliography:
- Steinschneider, Moritz. 1893–1901. Mathematik bei den Juden. Berlin-LeipzigFrankfurt: Kaufmann, p. 209 (h75); repr. Hildesheim: G. Olms, 1964 and 2001.
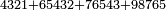
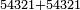
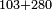
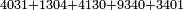
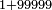
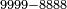
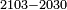
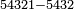
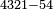
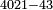
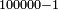
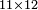
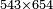
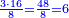
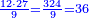
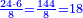
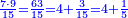
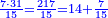
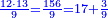
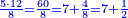
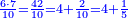
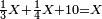
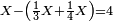
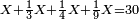
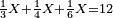
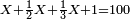
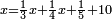
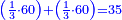

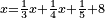
![\scriptstyle2\sdot\left[2\sdot\left[2\sdot\left(2X-2\right)-2\right]-2\right]=2](/mediawiki/images/math/a/c/0/ac095356b36a77f4fb4a1ac6de9f4dd9.png)