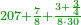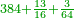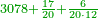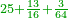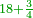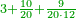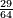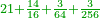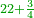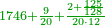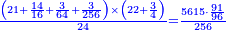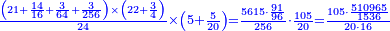Difference between revisions of "Anonymous text from Latin"
(→Division) |
|||
| (240 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{| | {| | ||
| + | |- | ||
| + | |With good luck | ||
| + | |style="width=45%; text-align:right;"|‫<ref>125r / ל"ד</ref>גדא טוב | ||
| + | |- | ||
| + | |My help is from the Lord, the Maker of heaven and earth [Psalms 121, 2]. | ||
| + | |style="text-align:right;"|עמי עשו | ||
| + | |- | ||
| + | |Translated into the Assyrian script and the Hebrew language. | ||
| + | |style="text-align:right;"|בעתק לכתב אשורית ולשון עברית | ||
| + | |- | ||
| + | |From the Latin script and language. | ||
| + | |style="text-align:right;"|מכתב ולשון גלחות | ||
| + | |- | ||
| + | |As it is said: ''the tongue of the stammerers shall speak with fluent eloquence'' [Isaiah 32, 4]. | ||
| + | |style="text-align:right;"|ע"ד ''ולשון עלגים תדבר צחות''‫<ref group=note>ישעיה לב, 4</ref> | ||
|- | |- | ||
| | | | ||
| − | + | == Addition == | |
| − | + | ||
| | | | ||
| − | |||
|- | |- | ||
| − | | | + | |{{#annot:definition|154,1208|zq5n}}The addition indicates how much are separate numbers summed to one number. |
| − | |style="text-align:right;"|חבור הוא המורה כמה מספרי' פרטיי' להביא ולכולל למספר אחד | + | |style="text-align:right;"|חבור הוא המורה כמה מספרי' פרטיי' להביא ולכולל למספר אחד{{#annotend:zq5n}} |
|- | |- | ||
| − | | | + | |First, one must make sure to write the numbers one below the other, correspondingly, units beneath units, the second rank beneath the second [rank] and and under them a line that is called "lina", for example: |
| − | |style="text-align:right;"|בראשונה יש ליזהר ליכתוב המספרים זה תחת זה מכוני' אחדים תחת אחדים | + | |style="text-align:right;"|בראשונה יש ליזהר ליכתוב המספרים זה תחת זה מכוני' אחדים תחת אחדים וה{{#annot:term|203,1316|wamR}}מעלה{{#annotend:wamR}} השנייה תחת השניי' ותחתיהם שורה שקורין לֵינָא ודמיונה כזה |
|- | |- | ||
| | | | ||
| Line 18: | Line 32: | ||
|- | |- | ||
| | | | ||
| − | {| | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
|- | |- | ||
|4||4||8||9||6 | |4||4||8||9||6 | ||
| Line 37: | Line 51: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | |Then, take the first number on the right and the one below it and add them together. |
|style="text-align:right;"|ואז קח המספר ראשונה בצד ימין לאשר תחתיה וחבר' יחד | |style="text-align:right;"|ואז קח המספר ראשונה בצד ימין לאשר תחתיה וחבר' יחד | ||
|- | |- | ||
| − | | | + | |If the resulting number consists of two ranks, write the first rank below the drawn line and keep the other in your hand. Go to the place you choose, which is the second number. Write it above its digit. Consider it as a digit, although it is of the tenths, for example: |
|style="text-align:right;"|ואם יעלה מספר משני מעלות כתוב המעלה ראשונה תחת השורה הנרשמ' והשניי' תקח בידך והלכת אל המקום אשר תבחר והיא המספר השניי' תשימה על מספרה אמנם לא תחשביה אלא כמו צורות האו' ואם כי היא ממספר העשיריות וכן דמיוני | |style="text-align:right;"|ואם יעלה מספר משני מעלות כתוב המעלה ראשונה תחת השורה הנרשמ' והשניי' תקח בידך והלכת אל המקום אשר תבחר והיא המספר השניי' תשימה על מספרה אמנם לא תחשביה אלא כמו צורות האו' ואם כי היא ממספר העשיריות וכן דמיוני | ||
|- | |- | ||
| Line 47: | Line 61: | ||
|- | |- | ||
| | | | ||
| − | {| | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
|- | |- | ||
|4||8||9||6 | |4||8||9||6 | ||
| Line 66: | Line 80: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | |If your calculation is complete, write the resulting sum of the two numbers. |
| − | |style="text-align:right;"|ואם ככלות חשבונך לאחרונה אז ת ‫<ref>125v</ref>תכתוב החשבון כאשר יעלה שני מספרי' | + | |style="text-align:right;"|ואם ככלות חשבונך לאחרונה אז ת ‫<ref>125v</ref>תכתוב החשבון כאשר יעלה שני מספרי‫' |
|- | |- | ||
| | | | ||
| Line 73: | Line 87: | ||
|- | |- | ||
| | | | ||
| − | {| | + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" |
|-style="border-bottom: 1px solid black;" | |-style="border-bottom: 1px solid black;" | ||
|1||2||7||0||8 | |1||2||7||0||8 | ||
| Line 89: | Line 103: | ||
|- | |- | ||
| | | | ||
| + | :<math>\scriptstyle{\color{blue}{4896+7812=12708}}</math> | ||
| + | | | ||
| + | |- | ||
| + | |The scales of justice that strengthen every test: | ||
|style="text-align:right;"|מאזני צדק המחזקת כל בדק | |style="text-align:right;"|מאזני צדק המחזקת כל בדק | ||
|- | |- | ||
| − | | | + | |Cast out the nines from the numbers you summed, and keep what remains. |
|style="text-align:right;"|השליך המספרים אשר חברתם בט' ט' ואשר יוותר לך תהא ארוכה ושמורה בבטנך | |style="text-align:right;"|השליך המספרים אשר חברתם בט' ט' ואשר יוותר לך תהא ארוכה ושמורה בבטנך | ||
|- | |- | ||
| − | | | + | |Do the same with the number resulting from your calculation. |
|style="text-align:right;"|וכן תעשה למספר אשר יצאה מתוך חשבונך | |style="text-align:right;"|וכן תעשה למספר אשר יצאה מתוך חשבונך | ||
|- | |- | ||
| − | | | + | |If one is the same as the other, know that your calculation is correct. |
|style="text-align:right;"|ואם יהיה לזה כמו לזה תדע כי אמת חשבונך | |style="text-align:right;"|ואם יהיה לזה כמו לזה תדע כי אמת חשבונך | ||
|- | |- | ||
| − | | | + | |If the remainder of one of them is greater, then it is false. |
|style="text-align:right;"|ואם יוותר לאחד יותר אז הוא פסול בנותר | |style="text-align:right;"|ואם יוותר לאחד יותר אז הוא פסול בנותר | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|מולטי פליציטיאן | + | |
| + | == Multiplication == | ||
| + | |||
| + | |style="text-align:right;"|{{#annot:term|156|4Ict}}מולטי פליציטיאן{{#annotend:4Ict}} | ||
|- | |- | ||
| | | | ||
| Line 110: | Line 131: | ||
|- | |- | ||
| | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |8<br>10<br>12<br>12<br>16<br>18|| ||4<br>5<br>6<br>7<br>8<br>9||2 times | ||
| + | |- | ||
| + | |9<br>12<br>15<br>18<br>21<br>24<br>27|| ||3<br>4<br>5<br>6<br>7<br>8<br>9||3 times | ||
| + | |- | ||
| + | |16<br>20<br>24<br>28<br>[32]<br>36|| ||4<br>5<br>6<br>7<br>8<br>9||4 times | ||
| + | |- | ||
| + | |25<br>30<br>35<br>40<br>45|| ||5<br>6<br>7<br>8<br>9||5 times | ||
| + | |} | ||
|style="text-align:right;"|‫<ref>126r / ל"ה</ref> | |style="text-align:right;"|‫<ref>126r / ל"ה</ref> | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:right;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:right;" | ||
|- | |- | ||
| − | |ח<br>‫0א<br>בא<br>דא<br>וא<br>חא|| ||ד<br>ה<br>ו<br>ז<br>ח<br>ט||ב' פעמי' | + | |ח<br>‫0א<br>בא<br>דא<br>וא<br>חא|| ||ד<br>ה<br>ו<br>ז<br>ח<br>ט||ב' פעמי‫' |
|- | |- | ||
| − | |ט<br>בא<br>הא<br>חא<br>אב<br>דב<br>זב|| ||ג<br>ד<br>ה<br>ו<br>ז<br>ח<br>ט||ג' פעמי' | + | |ט<br>בא<br>הא<br>חא<br>אב<br>דב<br>זב|| ||ג<br>ד<br>ה<br>ו<br>ז<br>ח<br>ט||ג' פעמי‫' |
|- | |- | ||
| − | |וא<br>‫0ב<br>דב<br>חב<br>[בג]<br>וג|| ||ד<br>ה<br>ו<br>ז<br>ח<br>ט||ד' פעמי' | + | |וא<br>‫0ב<br>דב<br>חב<br>[בג]<br>וג|| ||ד<br>ה<br>ו<br>ז<br>ח<br>ט||ד' פעמי‫' |
|- | |- | ||
| − | |הב<br>‫0ג<br>הג<br>‫0ד<br>הד|| ||ה<br>ו<br>ז<br>ח<br>ט||ה' פעמי' | + | |הב<br>‫0ג<br>הג<br>‫0ד<br>הד|| ||ה<br>ו<br>ז<br>ח<br>ט||ה' פעמי‫' |
|} | |} | ||
|- | |- | ||
| | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |36<br>42<br>48<br>54|| ||6<br>7<br>8<br>9||6 times | ||
| + | |- | ||
| + | |49<br>56<br>63|| ||7<br>8<br>9||7 times | ||
| + | |- | ||
| + | |64<br>[7]2|| ||8<br>9||8 times | ||
| + | |- | ||
| + | |81|| ||9||9 times | ||
| + | |} | ||
|style="text-align:right;"|‫<ref>[126v]</ref> | |style="text-align:right;"|‫<ref>[126v]</ref> | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:right;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:right;" | ||
|- | |- | ||
| − | |וג<br>בד<br>חד<br>דה|| ||ו<br>ז<br>ח<br>ט||ו' פעמי' | + | |וג<br>בד<br>חד<br>דה|| ||ו<br>ז<br>ח<br>ט||ו' פעמי‫' |
|- | |- | ||
| − | |טד<br>וה<br>גו|| ||ז<br>ח<br>ט||ז' פעמי' | + | |טד<br>וה<br>גו|| ||ז<br>ח<br>ט||ז' פעמי‫' |
|- | |- | ||
| − | |דו<br>ב[ז]|| ||ח<br>ט||ח' פעמי' | + | |דו<br>ב[ז]|| ||ח<br>ט||ח' פעמי‫' |
|- | |- | ||
| − | |אח|| ||ט||ט' פעמי' | + | |אח|| ||ט||ט' פעמי‫' |
|} | |} | ||
|- | |- | ||
| Line 148: | Line 189: | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:right;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:right;" | ||
|- | |- | ||
| − | |ה ה<br>ד ו||ה ה<br>ג ז||ה ה<br>0 ח | + | |ה ה<br>‫0 ח||ה ה<br>ג ז||ה ה<br>ד ו |
| + | |- | ||
| + | |‫0 ד||ה ג||‫0 ג | ||
| + | |- | ||
| + | |ה ה<br>א ט||ד ו<br>ד ו||ו ד<br>ג ז | ||
| + | |- | ||
| + | |ה ד||ו ג||ב ד | ||
| + | |- | ||
| + | |ד ו<br>ב ח||ד ו<br>א ט||ג ז<br>ג ז | ||
| + | |- | ||
| + | |ח ד||ד ה||ט ד | ||
| + | |- | ||
| + | |ג ז<br>ב ח||ג ז<br>א ט||ב ח<br>ב ח | ||
| + | |- | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>[127v]</ref> | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:right;" | ||
| + | |- | ||
| + | |ו ה||ג ו||ד ו | ||
| + | |- | ||
| + | | ||ב א<br>ח ט||א ט<br>א ט | ||
| + | |- | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם יושם אליך מספר שמרחק יותר מהמספר אש' תכפול תעמוד המספרים זו למעלה מזו לרשו' פני המספר {{#annot:term|205,1472|fYsr}}גלגל{{#annotend:fYsr}} 0 והמספר אשר יעלה תחסר מונה אותה מספר עצמה במעלת היחידים כפי המרחק מעשר' ואשר יוותר הוא המבוקש | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון | ||
| + | |- | ||
| + | | | ||
| + | *2 times 2 is obtained from 20 minus 2 times 8. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times2=20-\left(2\sdot8\right)}}</math> | ||
| + | |style="text-align:right;"|ב' פעמים ב' מראיתו 0"ב חס' ב' פעמי' ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *2 times 3 is obtained from 30 minus 3 times 8. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times3=30-\left(3\sdot8\right)}}</math> | ||
| + | |style="text-align:right;"|ב' פעמי' ג מראי' 0ג חסר ג' פע' ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *2 times 4 is obtained from 40 minus 4 times 8. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times4=40-\left(4\sdot8\right)}}</math> | ||
| + | |style="text-align:right;"|ב' פעמי' ד מראי' 0ד חסר ד' פע' ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *2 times 5 is obtained from 50 minus 5 times 8. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times5=50-\left(5\sdot8\right)}}</math> | ||
| + | |style="text-align:right;"|ב' פעמי' ה מראי' 0ה חסר ה' פע' ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *2 times 6 is obtained from 60 minus 6 times 8. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times6=60-\left(6\sdot8\right)}}</math> | ||
| + | |style="text-align:right;"|ב' פעמי' ו מראי' 0ו חסר ו' פע' ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *2 times 7 is obtained from 70 minus 7 times 8. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times7=70-\left(7\sdot8\right)}}</math> | ||
| + | |style="text-align:right;"|ב' פעמי' ז מראי' 0ז חסר ז' פע' ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *2 times 8 is obtained from 80 minus 8 times 8. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times8=80-\left(8\sdot8\right)}}</math> | ||
| + | |style="text-align:right;"|ב' פעמי' ח מראי' 0ח חסר ח' פע' ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *2 times 9 is obtained from 90 minus 9 times 8. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times9=90-\left(9\sdot8\right)}}</math> | ||
| + | |style="text-align:right;"|‫<ref>128r / ל"ז</ref>ב' פעמי' ט מראי' 0ט חסר ט' פע' ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *3 times 3 is obtained from 30 minus 3 times 7. | ||
| + | :<math>\scriptstyle{\color{blue}{3\times3=30-\left(3\sdot7\right)}}</math> | ||
| + | |style="text-align:right;"|ג' פעמי' ג מראי' 0ג חסר ג' פע' ז‫' | ||
| + | |- | ||
| + | | | ||
| + | *4 times 5 is obtained from 50 minus 5 times 6. | ||
| + | :<math>\scriptstyle{\color{blue}{4\times5=50-\left(5\sdot6\right)}}</math> | ||
| + | |style="text-align:right;"|ד' פעמי' ה מראי' 0ה חסר ה' פע' ו‫' | ||
| + | |- | ||
| + | | | ||
| + | *5 times 6 is obtained from 60 minus 6 times 5. | ||
| + | :<math>\scriptstyle{\color{blue}{5\times6=60-\left(6\sdot5\right)}}</math> | ||
| + | |style="text-align:right;"|ה' פעמי' ו מראי' 0ו חסר ו' פע' ה‫' | ||
| + | |- | ||
| + | | | ||
| + | *6 times 7 is obtained from 70 minus 4 times 7. | ||
| + | :<math>\scriptstyle{\color{blue}{6\times7=70-\left(4\sdot7\right)}}</math> | ||
| + | |style="text-align:right;"|ו' פעמי' ז מראי' 0ז חסר ד' פע' ז‫' | ||
| + | |- | ||
| + | | | ||
| + | *[9] times 8 is obtained from 80 minus 2 times 4. | ||
| + | :<math>\scriptstyle{\color{blue}{9\times8=80-\left(2\sdot4\right)}}</math> | ||
| + | |style="text-align:right;"|ז' פעמי' ח מראי' 0ח חסר ב' פע' ד‫' | ||
| + | |- | ||
| + | | | ||
| + | *8 times 9 is obtained from 90 minus 2 times 9. | ||
| + | :<math>\scriptstyle{\color{blue}{8\times9=90-\left(2\sdot9\right)}}</math> | ||
| + | |style="text-align:right;"|ח' פעמי' ט מראי' 0ט חסר ב' פע' ט‫' | ||
| + | |- | ||
| + | | | ||
| + | *9 times 9 is obtained from 90 minus 1 time 9. | ||
| + | :<math>\scriptstyle{\color{blue}{9\times9=90-\left(1\sdot9\right)}}</math> | ||
| + | |style="text-align:right;"|ט' פעמי' ט מראי' 0ט חסר א' פע' ט‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויש לדעת תחילה לכתוב המספר הנפלת ואח"כ הכפול | ||
| + | |- | ||
| + | | | ||
| + | *Example: you wish to multiply 98765 by 43210 | ||
| + | :<math>\scriptstyle98765\times43210</math> | ||
| + | |style="text-align:right;"|דמיון רצונך לכפול הוזחט ע"י 0אבגד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תעמיד המספרים זה למעל מזה וככו מראיתו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |9||8||7||6||5 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |4||3||2||1||0 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |ט||ח||ז||ו||ה | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ד||ג||ב||א||0 | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אמו' גלגל פעמ' ה' עולה גלגל רשום גלגל תחת השורה הנרשמת ג תמחה הכתוב למעלה ע"ז עברת קולמוס כי באם תכפלנה על כל המספר לא מעלה ולא מורדת ואחר זה תעבר על כל המספרי' ‫<ref>[128v]</ref>המספרים הכתוב למעלה ואינו עולה יותר ושום השתנו' מאשר מאשר כתוב למעלה אמו' יש לזה שיהא ה' כתוב תחת הא' אשר למעלה ממנה ושאר המספרים יהיה מראיתו ככה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||9||8||7||6||5 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | ||4||3||2||1||0 | ||
| + | |- | ||
| + | |9||8||7||6||5||0 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | ||ט||ח||ז||ו||ה | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | ||ד||ג||ב||א||0 | ||
| + | |- | ||
| + | |ט||ח||ז||ו||ה||0 | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תלך משום ותאמר עו' ב' פע' ה' עולה 0' א' תעמיד 0 למטה תחת ב' שהיא למעל' שלישי' והא' תהיה ארוכה ושמור' בבטנך | ||
| + | |- | ||
| + | | | ||
| + | :Then, say: 2 times 6; the result is 12. Add the reserved 1 to it; the result is 13. | ||
| + | |style="text-align:right;"|אח"כ אמור ב' פעם ו' עולה ב'א' חבר עליו א' השמור עמך עולה ג'א‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|רשום ג' אחר הגלגל כמבואר וא' נעימ' ו' כי תשמר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תאמר עוד ב' פעמי' ז' עולה ז"א חבר עליו א' השמורה עולה ה"א כתוב ה' אחר ג' הרשומה וא' שעונה עמך עד בא עתה גם ב' פע' ח' עולה ו"א חבר אליו א' יהיה ז"א אחר ה' כתוב ז' עוד עמך א' ובאחרונ' אמור ב' פע' ט' עולה ח"א וא' הוא ט"א כתוב אות' מספר כלה העולה אחרי ז' והב' תמח' ע"י עברת קולמוס ומראיתו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | || || ||9||8||7||6||5 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || || ||4||3||2||1||0 | ||
| + | |- | ||
| + | | || ||9||8||7||6||5||0 | ||
| + | |- | ||
| + | |1||9||7||5||3||0|| || | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | || || ||ט||ח||ז||ו||ה | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || || ||ד||ג||ב||א||0 | ||
| + | |- | ||
| + | | || ||ט||ח||ז||ו||ה||0 | ||
| + | |- | ||
| + | |א||ט||ז||ה||ג||0|| || | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>129r / ל"ח</ref>ובזה כפֵלת ג' מספרי' אלו 0 א ב קח עוד ג' והעבירנה על כל המספרים כמבואר וככה מראיתו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
|- | |- | ||
| + | | || || || ||9||4||5||6||5 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || || || ||4||3||2||1||0 | ||
| + | |- | ||
| + | | || || ||9||8||7||6||5||0 | ||
| + | |- | ||
| + | | ||1||9||7||5||3||0|| || | ||
| + | |- | ||
| + | |[2]||9||6||2||9||5|| || || | ||
|} | |} | ||
|} | |} | ||
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | || || || ||ט||ח||ז||ו||ה | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || || || ||ד||ג||ב||א||0 | ||
| + | |- | ||
| + | | || || ||ט||ח||ז||ו||ה||0 | ||
| + | |- | ||
| + | | ||א||ט||ז||ה||ג||0|| || | ||
| + | |- | ||
| + | |א||ט||ו||ב||ט||ה|| || || | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן לעשות עם הד' ומראה הכפל עם החבו' ככה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | || || || || ||9||8||7||6||5 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || || || || ||4||3||2||1||0 | ||
| + | |- | ||
| + | | || || || ||9||8||7||6||5||0 | ||
| + | |- | ||
| + | | || ||1||9||7||5||3||0|| || | ||
| + | |- | ||
| + | | ||[2]||9||6||2||9||5|| || || | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |3||9||5||0||[6]||0|| || || || | ||
| + | |- | ||
| + | |4||2||[6]||7||6||3||5||6||5||0 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | | || || || || ||ט||ח||ז||ו||ה | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || || || || ||ד||ג||ב||א||0 | ||
| + | |- | ||
| + | | || || || ||ט||ח||ז||ו||ה||0 | ||
| + | |- | ||
| + | | || ||א||ט||ז||ה||ג||0|| || | ||
| + | |- | ||
| + | | ||א||ט||ו||ב||ט||ה|| || || | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ג||ט||ה||0||ט||0|| || || || | ||
| + | |- | ||
| + | |ד||ב||ג||ז||ו||ג||ה||ו||ה||0 | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מאזני צדק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תשליך הכפל והנכפל ט' ט' וחבר הנותר משני' יחד וכן תעשה למספר הבאה ואם יוותר לזה כמו לזה ידוע תדע כי כוונתך האמת | ||
| + | |- | ||
| + | | | ||
| − | + | == Subtraction == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|{{#annot:term|155,1657|lthR}}חיסור{{#annotend:lthR}} או {{#annot:term|155,2391|EKVU}}נכוי{{#annotend:EKVU}} {{#annot:term|155|xiXX}}זוכט רַצטיאן{{#annotend:xiXX}} | |
| − | + | | | |
| − | ו ד | + | |- |
| − | ג ז | + | |Teaching how to subtract a number from a number. |
| − | + | |style="text-align:right;"|‫<ref>[129v]</ref>הוא המורה {{#annot:term|181|bUjh}}לנכות{{#annotend:bUjh}} חשבון מחשבון | |
| − | + | |- | |
| − | + | | | |
| − | + | *For example: 324 from 485 | |
| − | + | |style="text-align:right;"|דמיון דוג מתוך החד | |
| − | + | |- | |
| − | + | | | |
| − | א ט | + | :Its diagram is like this: |
| + | |style="text-align:right;"|מראיתו כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |4||8||5 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |3||6||4 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |ד||ח||ה | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ג||ו||ד | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | |The number on the bottom line will never be greater than [the number on] the upper line. | ||
| + | |style="text-align:right;"|לעולם לא יהיה מספר הטור השפלה למטה עלה יותר מהטור אשר במעלה הגבוהה ממנה | ||
| + | |- | ||
| + | |You start your calculation from the right and subtract the first bottom digit from the first upper digit. | ||
| + | |style="text-align:right;"|תחילת חשבונך תתחיל מצד ימין וחסר מספר ראשונה התחתונה ממספר ראשונה עליונה | ||
| + | |- | ||
| + | |The place of what remains is below the written line. | ||
| + | |style="text-align:right;"|ואשר יוותר מקומו' תחת השורה הנרשמת | ||
| + | |- | ||
| + | | | ||
| + | *Example: | ||
| + | |style="text-align:right;"|דימיון | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |9||8||2||7 | ||
| + | |- | ||
| + | |6||5||0||5 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |ט||ח||ב||ז | ||
| + | |- | ||
| + | |ו||ה||0||ה | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::Say: 5 from 7; 2 remains. | ||
| + | |style="text-align:right;"|אמו' ה' מז' ישאר ב‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Write it beneath the written diagram. | ||
| + | |style="text-align:right;"|העמידה תחת השירטוט הנרשמת | ||
| + | |- | ||
| + | | | ||
| + | ::Say also: 0 from 2; 2 remains. | ||
| + | |style="text-align:right;"|אמו' עוד 0' מב' נשאר ב‫' | ||
| + | |- | ||
| + | | | ||
| + | ::It is also written in its place. | ||
| + | |style="text-align:right;"|גם הוא אל מקומו יושב | ||
| + | |- | ||
| + | | | ||
| + | ::5 from 8; 3 remains. | ||
| + | |style="text-align:right;"|ה' מח' ישאר ג‫' | ||
| + | |- | ||
| + | | | ||
| + | ::6 from 9; 3 remains. | ||
| + | |style="text-align:right;"|ו' מט' ישאר ג‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Its diagram is like this: | ||
| + | |style="text-align:right;"|ומראהו ככה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |9||8||2||7 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |6||5||0||5 | ||
| + | |- | ||
| + | |3||3||2||2 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |ט||ח||ב||ז | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ו||ה||0||ה | ||
| + | |- | ||
| + | |ג||ג||ב||ב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | |If you cannot subtract the first bottom [digit] from the first one in the upper line, do this way ''For whoever finds me finds life'' [Proverbs 8, 35]. | ||
| + | |style="text-align:right;"|ובאם לא תוכל לנכות הראשונה אשר למטה מראשונה אשר בטור העליון ‫<ref>130r / ל"ט</ref>בזה הדרך תלך ''כי מוצאיו מוצא חיים''‫<ref group=note>משלי ח, לה</ref> | ||
| + | |- | ||
| + | |Subtract the first digit in the bottom row from the one in the second rank, which is the rank of tens and add the remainder to the preceding digit. Its place is beneath the row. | ||
| + | |style="text-align:right;"|תחסר האות הראשון אשר בשור' התחתון מאותו אשר במעלה שניי' שהיא במעלה העשיריי' ואשר יוותר תחבר אל המספר אשר לפניה ומקו' מעמדה למטה תחת השורה | ||
| + | |- | ||
| + | |Add 1 to the second digit in the bottom row. | ||
| + | |style="text-align:right;"|ואל המספר' השניי' אשר בטור השפל תחבר אליה א‫' | ||
| + | |- | ||
| + | |And so on. This is enough for the one who understands. | ||
| + | |style="text-align:right;"|וכן עד עולם ולמבין די | ||
| + | |- | ||
| + | | | ||
| + | *Example: | ||
| + | |style="text-align:right;"|דמיון | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |9||7||2||1 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |6||8||9||2 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |ט||ז||ב||א | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ו||ח||ט||ב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::Say: it is impossible to take 2 from 1. So, take 2 from 10; 8 remains. | ||
| + | |style="text-align:right;"|אמור א' מב' אי אפשר לקח' אך לקחת ב' מ0'א' ישאר ח‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Add to it 1, which is the digit you could not subtract from; the result is 9 and its place is beneath the bottom 2. | ||
| + | |style="text-align:right;"|חבר אליו א' אות' מספר שלא יכלת לחסר ממנה והעולה הוא ט' ומקום ישוב' תחת הב' למטה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תחב עוד להולאה א' לט' אשר במעלה שניי' יעלה 0'א‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מב' אמנ' לקחת 0'א' מ0'א' טוב והנותר 0' חבר אליה ב' והעמידה למטה הקרוב א' אליו שהיא ח' תחבר א' מראיתו ט' וט' מז' אי אפשר לקחת רק מ0'א' ישאר א' עם התחבר אליה הז' עולה ח' תעמיד' במקומה כמשפטה ובאחרונה תוסיף על ו'ט'א' יהיה ‫<ref>[130v]</ref>ז' וז' מט' יוותר לך ב' ויראה ככה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center; border-collapse: collapse;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |9||7||2||1 | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |6||8||9||2 | ||
| + | |- | ||
| + | |2||8||2||9 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |ט||ז||ב||א | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ו||ח||ט||ב | ||
| + | |- | ||
| + | |ב||ח||ב||ט | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מאזני צדק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|חבר שני מספרי' התחתוני' יחד ואם יעלה בדרך המספר הראשון אמת חשבונך ע"א השליך שני המספרי' התוחתונים יחד ט' ט' ואם ישאר למספר ראשונה כמו כן כוונתך האמת | ||
| + | |- | ||
| + | | | ||
| − | + | == Division == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|{{#annot:term|157,1223|IqRw}}חילוק{{#annotend:IqRw}} {{#annot:term|157|evwb}}דיוידירו{{#annotend:evwb}} | |
| − | + | |- | |
| − | ג ז | + | |A very nice chapter called division because it divides a general number by a number of units as many times it is found in it. |
| − | ג | + | |style="text-align:right;"|שער נחמד מאד ונקרא חלוק כי הוא מחלק מספר כוללים ע"י מספר פרטיים לכמה פעמים שהוא בתוכו |
| − | + | |- | |
| − | + | |Whoever wants to truly know this chapter and acquire it in its entirety, should be careful and aim that the last digit of the divisor be corresponding beneath the last digit of the upper row, which is the dividend and write the rest [of the digits] close to it from left to right. | |
| − | ד ו | + | |style="text-align:right;"|הרוצה לדעת אמיתי' זה שער ולקנות שלימתו צריך ליזהר ולכוון שיהא האות האחרון ממספר {{#annot:term|604,1966|ERvy}}החולק{{#annotend:ERvy}} מכוון תחת האות אחרונ' מטור העליון שהוא {{#annot:term|605,1226|rMzk}}הנחלק{{#annotend:rMzk}} והשנייה לשארו הקרוב אליו מצד שמאל לצד ימין |
| − | א ט | + | |- |
| − | + | | | |
| − | + | *Example: you wish to divide 396 by 36. | |
| − | + | |style="text-align:right;"|דמיון רצונך לחלק וטג על יד וג | |
| − | ב ח | + | |- |
| + | | | ||
| + | :Like this: | ||
| + | |style="text-align:right;"|דמיוני כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |3||9||6 | ||
| + | |- | ||
| + | | ||3||6 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |ג||ט||ו | ||
| + | |- | ||
| + | | ||ג||ו | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכאשר ‫<ref>131r / מ</ref>וכאשר יקרא לפניך שהחולק עולה יותר ממספר אותיות אשר למעלה ממנה אם נעמידהו כמבואר צריך להשים כל מספר החולק לאחוריו לצד ימין כמלוא' מעלה אחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דימיון רצונך לחלוק והג ע"י וג ממקומו כרשום לפניך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |3||5||6 | ||
| + | |- | ||
| + | | ||3||6 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |ג||ה||ו | ||
| + | |- | ||
| + | | ||ג||ו | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויש לדעת כי כמו הרבה פעמים אי לקח החולק האחרון ממספר אחרונ' למעלה ממנה כמו כן יש לקחת כל אותיות מאות' המספר מהספרים אשר למעלה מהן ומספר כמה פעמי' אשר יוחלק יכתב בתוך חצי העיגול הנרשם לך בזה רצוני לחלוק והג ע"י וג דימיון מראהו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |3||5||6 | ||
| + | |- | ||
| + | | ||3||6 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |ג||ה||ו | ||
| + | |- | ||
| + | | ||ג||ו | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכה תאמר כמה פעמי' ו'ו' ג' מה"ג באשר או אוכל ליקח ה"ו כמו כן פעמי' יוקח ט' פע' ג‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Say: 9 times 3 is 27. | ||
| + | |style="text-align:right;"|ואמו' ט' פעמי' ג' עולה ז"ב | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract [it] from 35; 8 remains. | ||
| + | |style="text-align:right;"|נחסר מה"ג וישאר ח‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תשימ' למעלה במעלה הגבוהה מן הה' ומחוק ה"ג ע"י העבר' קולמוס | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply 6 by 9; the result is 54. | ||
| + | |style="text-align:right;"|כפול ו' על ט' והעולה הוא ד'ה‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Subtract it from 86; you are left with 32. | ||
| + | |style="text-align:right;"|חסרה מו'ח' יוותר לך ב'ג‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם עדיין יש לך לקחת החולק מהנחלק אמנם אין במספר ‫<ref>[131v]</ref>אשר למעלה ממנה כדי לנכות' תמשך החולק במעלה אחת לאחוריה וככה מראיתו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | ||3|| | ||
| + | |- | ||
| + | | ||8||2 | ||
| + | |- | ||
| + | |3||5||6 | ||
| + | |- | ||
| + | | ||3||6 | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | |9 | ||
| + | |- | ||
| + | | | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | ||ג|| | ||
| + | |- | ||
| + | | ||ח||ב | ||
| + | |- | ||
| + | |ג||ה||ו | ||
| + | |- | ||
| + | | ||ג||ו | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | |ט | ||
| + | |- | ||
| + | | | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם יקרא לפניך הן בתחילה הן בסופה הן באמצע שלא שתוכל לקח המספר הקטנה מאותה אשר למעלה ממנה תמשוך אותה מעלה אחת לאחוריה ובמקומ' תרשום בתוך חצי עיגול גלגל 0 וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | *Example: to divide 3210 by 32. | ||
| + | |style="text-align:right;"|דימיון לחלוק 0אבג ע"י בג | ||
| + | |- | ||
| + | | | ||
| + | :Its diagram is as follows: | ||
| + | |style="text-align:right;"|מראיתו ככה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |3||2||1||0 | ||
| + | |- | ||
| + | | ||3||2||2 | ||
| + | |- | ||
| + | | || ||3|| | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |ג||ב||א||0 | ||
| + | |- | ||
| + | | ||ג||ב||ב | ||
| + | |- | ||
| + | | || ||ג|| | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מאזני צדק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|קח החולק גם המספר העולה ממנה וחברם יחד והשליכם ט' ט' ואם נשאר דבר מאות' למעלה תחבר ג"כ אליה והעולה כתוב לפניך וכן תעשה למספר אשר היא למעלה ממנה ואם ישאר לזה כמו לזה אמת חשבונך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|חלוק דוידיריו תאל ‫<ref>132r / מא</ref>תאל ואשכילך ואראך דמיון לחלוק בבטבחא ע"י א0ב מראיתו ככה וכן תעשה עד סוף הדורות | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |1||8||2||9||2||2 | ||
| + | |- | ||
| + | | || ||2||0||1|| | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |א||ח||ב||ט||ב||ב | ||
| + | |- | ||
| + | | || ||ב||0||א|| | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|האמור כמבואר לעיל כמה פעמי' נוכל ליקח ב' מח"א באופן זה שגם לאותה אשר לפניה יעשה כן והוא ט' פעמים ב' פע' ט' הוא ח"א נכנו מח"א לא ישאר בידך מאומה ט' פעמי' גלגל אינו עולה שום מספר ואותה <s>ש</s> אשר למעלה ממנה תעמוד במקומה תאמר עוד ט' פע' א' נחסר מט' ישאר גלגל 0' וככה מראיתו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | || || ||0|| || | ||
| + | |- | ||
| + | |1||8||2||9||2||2 | ||
| + | |- | ||
| + | | ||2||0||1|| || | ||
| + | |- | ||
| + | | ||2||0|| || || | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | |9 | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | || || ||0|| || | ||
| + | |- | ||
| + | |א||ח||ב||ט||ב||ב | ||
| + | |- | ||
| + | | ||ב||0||א|| || | ||
| + | |- | ||
| + | | ||ב||0|| || || | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | |ט | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תמשוך השורה התחתונה מעלה אחת לאחוריה כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |1||8||2||9||2||2 | ||
| + | |- | ||
| + | | ||2||0||1||1|| | ||
| + | |- | ||
| + | | || ||2||0|| || | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |א||ח||ב||ט||ב||ב | ||
| + | |- | ||
| + | | ||ב||0||א||א|| | ||
| + | |- | ||
| + | | || ||ב||0|| || | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>[132v]</ref>תאמר עוד כמה פע' תוכל ליקח ב' מב' אשר היא בשורה העליונה למעלה ממנה מכוון אינו כ"א פעמי' אחת ולא ישאר לך מאומה א' פע' 0 הוא 0' א' פע' א' הוא א' נחסרנו מב' ישאר א' ומראהו כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | || || ||0|| ||1 | ||
| + | |- | ||
| + | |1||8||2||9||2||2 | ||
| + | |- | ||
| + | | ||2||0||1||1|| | ||
| + | |- | ||
| + | | || ||2||0|| || | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | |91 | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | || || ||0|| ||א | ||
| + | |- | ||
| + | |א||ח||ב||ט||ב||ב | ||
| + | |- | ||
| + | | ||ב||0||א||א|| | ||
| + | |- | ||
| + | | || ||ב||0|| || | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | |אט | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והיא באחרונה תשנה החולק עו' מעל' אחת וככה מראיתו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |1||8||2||9||2||2 | ||
| + | |- | ||
| + | | ||2||0||1||1||1 | ||
| + | |- | ||
| + | | || ||2||0||0|| | ||
| + | |- | ||
| + | | || || ||2|| || | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |א||ח||ב||ט||ב||ב | ||
| + | |- | ||
| + | | ||ב||0||א||א||א | ||
| + | |- | ||
| + | | || ||ב||0||0|| | ||
| + | |- | ||
| + | | || || ||ב|| || | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והיה אם לא תוכל ליקח עוד החולק מהנחלק וכלית חשבונך לפני א"ט תעמיד 0 ומראיתו כזה 0אט והנותר הוא ב"א | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מאזני צדק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|השליך ט' ט' מהמספר העלה בתוך חצי העיגול וישאר א' וכן אותה אשר חלקת בה ‫<ref>133r / מב</ref>בה ישאר ג' תאמר א' פע' ג' חבר אליו הנותר על ט' מאות' מספר אשר נשארה לך בשורה עליונה והוא ג' עולה ו' ואם יוותר לעליונה כמו כן אמת חשבון | ||
| + | |- | ||
| + | | | ||
| − | + | == Progression == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |style="text-align:right;"|שער לשער החבור פראגרעשיא | |
| − | + | |- | |
| − | ב ח | + | | |
| − | ב ח | + | |style="text-align:right;"|הוא המורה לחבר דרך קצרה אשר הוא קרוב אל השכל להשיג לחבר כמה מספרי' יחד שהם כתוב בזה אחר זה בין הראשונים בין האמצעיים בין הסופיים |
| − | + | |- | |
| − | + | | | |
| − | ג | + | |style="text-align:right;"|עשהו כן חבר הראשונה אל הסופי' והעולה תחציהו באם הוא באפשרו' אח"כ תכפול מספר המעלת כמה הם והעולה הוא סך מחבר כל המעלות |
| − | א | + | |- |
| − | + | | | |
| − | + | |style="text-align:right;"|ובאם לא תוכל לחצהו תחלוק מספר המעלות למחציתו וכפול בהן כאשר אראך בציור דמיוני אלו ודו"ק בהן | |
| − | + | |- | |
| − | ב ח | + | | |
| + | *Example: 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, [22], 23, 24, 25 | ||
| + | :How much is the sum of all together? | ||
| + | |style="text-align:right;"|דמיון ז ח ט 0א אא בא גא דא הא וא זא חא טא 0ב בא בג בד בה<br> | ||
| + | כמה עולה מספר כולם ביחד | ||
| + | |- | ||
| + | | | ||
| + | ::Add 7 to 25; the result is 32. | ||
| + | |style="text-align:right;"|‫<ref>[133v]</ref>תחבר ז' לכ"ה והעולה הוא ב"ג | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תחצית' יעלה ו"א | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כפלום על מספר המעלת והם ט"א והעולה הוא ד0ג ככה מספר המעלות הכתוב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם אי אפשר לחצות | ||
| + | |- | ||
| + | | | ||
| + | *Example: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48 | ||
| + | |style="text-align:right;"|דמיון ג ו ט בא הא חא אב דב זב 0ג גג וג טג בד הד חד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|חבר ג' אל חד עולה אה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואינ' נחלקי' בשוה לכן תמנה מספר המעלות והם וא | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תחצית עולה ח' כפלם על אה עולה ח0ד כל המספר כולה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם המספריי' כל אחת כפולות משלפניה שניי' אי שלשיי' או רביעי' חמשיי' עד עולה קח המספר האחרונה כפליים ומ<sup>ה</sup>עולה תקח מספר ראשונה פחת א' כאשר אצייר לך בדמיונו | ||
| + | |- | ||
| + | | | ||
| + | *Example: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 | ||
| + | |style="text-align:right;"|דמיון ב ד ח וא בג דו חבא והב באה דב0א חד0ב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כפול חד0ב ובו0ד חסר ב' ראשונה עולה דט0דח חלקם ע"י פחות א' דהיינו א' וישאר אותה מספר עצמה ואם לאחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>134r / מג</ref>ואם לאחת שלש על חברתה | ||
| + | |- | ||
| + | | | ||
| + | *Example: 3, 9, 27, 81, 243, 729, 2187, 6561 | ||
| + | :How much is the sum of all together? | ||
| + | |style="text-align:right;"|דמיון ג' ט' זב אח גדב טבז זחאב אוהו<br> | ||
| + | כמה עולה מספר כולם ביחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תכפול מספר אחרונה ע"י ג' גחוטא חסר מנה ג' דהיינו מספר ראשונה נשאר 0חוטא חלוק ע"י ג' פחות א' דהיינו ע"י ב' עולה 0דחד וכן עד כל הדורות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נשלם שער פרמיגירעשיא | ||
| + | |- | ||
| + | |A short way to know weights and measures of coins and of time - belongs to division | ||
| + | |style="text-align:right;"|דרך קצרה לדעת משקלות ומדה ממטבעות גם על העתיד שייך לחלוק | ||
| + | |- | ||
| + | | | ||
| + | {|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |colspan=3 |weights|| ||result | ||
| + | |- | ||
| + | |1||kikkar||=||1000||liter | ||
| + | |- | ||
| + | |1||liter||=||32||lot | ||
| + | |- | ||
| + | |1||lot||=||4||quenten | ||
| + | |- | ||
| + | |1||quenten||=||4||pešiṭim | ||
| + | |- | ||
| + | |1||zaquq||=||16||lot | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |עולה|| || ||השקלו‫' | ||
| + | |- | ||
| + | |לטר‫'||‫000א|| ||ככר | ||
| + | |- | ||
| + | |לאט||בג||לט||לטר‫' | ||
| + | |- | ||
| + | |קווינטן||ד||לו||לוט | ||
| + | |- | ||
| + | |פ‫'||ד||קווי‫'||קווי‫' | ||
| + | |- | ||
| + | |לו‫'||וא||זקוק||זקוק | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=5 style="border-bottom: 1px solid black;"|Austrian Measurement | ||
| + | |- | ||
| + | |1||Fuder<ref>measure of volume for liquids and solids</ref>||=||32||Hin | ||
| + | |- | ||
| + | |1||Dreiling<ref>an Austrian volume measure for liquids, especially for wine</ref>||=||24||Hin | ||
| + | |- | ||
| + | |1||Eimer||=||32||Achtring<ref>Achtring or Aechtring = an Austrian measure of volume for beverages</ref> | ||
| + | |- | ||
| + | |1||Seidel<ref>measure of volume for liquids and a measure of grain</ref>||=||4||[Achtring?] | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=3|מדה אוישטרייך | ||
| + | |- | ||
| + | |הין||בג||בודר בו | ||
| + | |- | ||
| + | |הין||דב||דריילינג | ||
| + | |- | ||
| + | |עכטרינג||בג||איימר | ||
| + | |- | ||
| + | |זיידלינג||ד||אנטרינג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=5 style="border-bottom: 1px solid black;"|Hungarian Coin | ||
| + | |- | ||
| + | |1||zahuv||=||100||pešiṭim | ||
| + | |- | ||
| + | |1||pešiṭ||=||2||halishim | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=3|אונגרש מטבע | ||
| + | |- | ||
| + | |פשיטי‫'||‫00א||זהוב | ||
| + | |- | ||
| + | |חלשין||ב||פשי‫' | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>[134v]</ref> | ||
| + | |- | ||
| + | | | ||
| + | {|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=5 style="border-bottom: 1px solid black;"|Nuremberg Measurement | ||
| + | |- | ||
| + | |1||Fuder||=||12||Hin | ||
| + | |- | ||
| + | |1||Hin||=||68||measures | ||
| + | |- | ||
| + | |1||measure||=||2||Seidel | ||
| + | |- | ||
| + | |1||viertel?||=||2||measures | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=3|מדה ניירבערג | ||
| + | |- | ||
| + | |הין||בא||בודר | ||
| + | |- | ||
| + | |מידות||חו||הין | ||
| + | |- | ||
| + | |זיידל||ב||מידה | ||
| + | |- | ||
| + | |מידות||ב||וירטייל | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=3|מטבע ניירבערג | ||
| + | |- | ||
| + | |פשי‫'||בא||זהו' ח תרי‫' | ||
| + | |- | ||
| + | |פשי‫'||‫0ג||דינר | ||
| + | |- | ||
| + | |פשיטי‫'||בהב||זהו‫' | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=5 style="border-bottom: 1px solid black;"|Austrian Coin | ||
| + | |- | ||
| + | |1||zahuv||=||8||dinar | ||
| + | |- | ||
| + | |1||dinar||=||30||pešiṭim | ||
| + | |- | ||
| + | |1||pašuṭ||=||2||halishim | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=3 |מטבע אוישטרך | ||
| + | |- | ||
| + | |דינרי||ח||זהו‫' | ||
| + | |- | ||
| + | |פשיטי‫'||‫0ג||דינר | ||
| + | |- | ||
| + | |חלישי‫'||ב||פשוט | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=5 style="border-bottom: 1px solid black;"|Gold? Coin | ||
| + | |- | ||
| + | |1||zahuv||=||20||dinar | ||
| + | |- | ||
| + | |1||dinar||=||21||halishim | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |colspan=3 |מטבע בדהב | ||
| + | |- | ||
| + | |דינר‫'||‫0ב||זהוב | ||
| + | |- | ||
| + | |חלישין||כא||דינר | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |colspan=3 |measure|| ||time | ||
| + | |- | ||
| + | |1||year||=||55||weeks | ||
| + | |- | ||
| + | |1||week||=||7||days | ||
| + | |- | ||
| + | |1||day||=||24||hours | ||
| + | |- | ||
| + | |1||hour||=||16||minutes | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |עתים|| ||מדה | ||
| + | |- | ||
| + | |שבועו‫'||נה||שנה | ||
| + | |- | ||
| + | |ימים||ז‫'||שבועו‫' | ||
| + | |- | ||
| + | |שעות||דב||יום | ||
| + | |- | ||
| + | |מנוטן||וא||שעה | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| − | + | == Chapter on Proportions - Rule of Three == | |
| − | + | |style="text-align:right;"|שער הערכין רגולא רעטלי | |
| − | + | |- | |
| − | + | |Very nice [rule], all its results are respectable. | |
| − | + | |style="text-align:right;"|נחמד מאד נכבדות כל תוצאותיה | |
| − | + | |- | |
| − | + | |These are three numbers by which the eye can reach the fourth number that is hidden from the eyes of the entire community. | |
| − | + | |style="text-align:right;"|והוא ‫<ref>135r / מד</ref>משלש ספרים וע"י יוכל העיין להגיע אל מספ' הרביעי' אשר הוא נעלמה מעיני העדה | |
| − | + | |- | |
| − | + | | | |
| − | + | *{{#annot:saffron|629|8zJi}}Example: You bought one kikkar of saffron for 800 zehuivim. How much is the price of 2 liṭra of saffron? | |
| + | |style="text-align:right;"|דמיון קנית ככר זפרן בעד 00ח זהובי' כמה מגיע דמי מקח הב' לטראו' זפראן{{#annotend:8zJi}} | ||
| + | |- | ||
| + | | | ||
| + | :The resulting number is 200 zehuvim and it was unknown for you. | ||
| + | |style="text-align:right;"|מספר העולה 00ב זהו' והיא נעלמה ממך | ||
| + | |- | ||
| + | |As the first number contains the second, so the third contains the fourth, and as the third is contained in the first, so the fourth is contained in the second. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a_1:a_2=a_3:a_4\quad a_3:a_1=a_4:a_2}}</math> | ||
| + | |style="text-align:right;"|וכמו' אשר כולל המספר הראשונה השניי' גם השלישי' ורביעי' ככה וכאשר נכלל השלישית בראשונה כמו כן נכלל הרביעי' בשניי‫' | ||
| + | |- | ||
| + | | | ||
| + | *Example: 18 liṭra for 9 zehuvim, how much are 24 liṭra worth? | ||
| + | |style="text-align:right;"|דמיון חא ליטראו' בעד ט' זהו' כמה עולה ד"ב ליטראות | ||
| + | |- | ||
| + | | | ||
| + | :The resulting number is 12 zehuvim. | ||
| + | |style="text-align:right;"|מספר העולה הוא ב"א זהו‫' | ||
| + | |- | ||
| + | | | ||
| + | :As the first number contains the second twice, so the third contains the fourth twice. | ||
| + | :<math>\scriptstyle{\color{blue}{a_1:a_2=18:9=2=24:12=a_3:a_4}}</math> | ||
| + | |style="text-align:right;"|והנה המספר הראשונה כוללת השניי' ב' פעמי' כמו כן כוללת השלישי' לרביעית ב' פעמי‫' | ||
| + | |- | ||
| + | | | ||
| + | :As the first is contained in the third one time and a third, so the [fourth] is contained in the [second] one time and a [third]. | ||
| + | :<math>\scriptstyle{\color{blue}{a_3:a_1=24:18=1+\frac{1}{3}=12:9=a_4:a_2}}</math> | ||
| + | |style="text-align:right;"|והנה הראשונה נכלל בשלישי פע' א' ושלישי וכן השלישי נכלל ברביעי' פע' א' ורביעי‫' | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |זהו‫'||<u>ד</u><br>וא||לטראו‫'||[[File:three eighths.png|12 px]]||זהו‫'||[[File:two eighths.png|12 px]]||לטראות [[File:quarter.png|12 px]] | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכאשר מרחק א' מב' כמו כן המרחק מג' לד‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכאשר המרחק א' לג' ככה ב' לד‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה לדעת המספר הנעלמה ‫<ref>[135v]</ref>כפול מספר השאלה על האמצעי אח"כ חלוק העולה ע"י הראשונה והוא מורה המבוקש | ||
| + | |- | ||
| + | | | ||
| + | *Example: 32 liṭra for 24 zehuvim, how much are 8 liṭra worth? | ||
| + | |style="text-align:right;"|דמיון בג לטראו' דב זהובי' כמה עולה ערך ח' לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | || || | ||
| + | |- | ||
| + | |א||ט||ה | ||
| + | |- | ||
| + | | ||ג||ב | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | || ||ח | ||
| + | |- | ||
| + | |א||ט||ב | ||
| + | |- | ||
| + | | || || | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ו' זהו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם יקרא לפניך באמצעת איזו מיני מטבעות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|בראשונה כפול המספר השלישי על המטבע הגדולה <s>ע</s> אשר ערכה עולה יותר מל חברת והעולה תחלוק ע"י מספר הראשונ' ואשר יוותר לך תחלוק ע"י המטבע הקטנה ממנה דמיון אם יש לפניך דינרי' ואותה תהא שמורה בבטנך עד בא עתה אח"כ כפול השלישי' על האמצעי' שהיא דינרין ואל העולה תחבר הדינרי' השמרין עמך והעול' מכולם תחלוק ג"כ ע"י הראשונו' ואשר יוותר לך עוד תעשה למספר הק[טן] שהוא פשיטי' ותשמר תחברם עוד כאמנ' אל הפשיטי' אשר יעלה בחשבונך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ותן לחכם עוד ‫<ref>136r / מה</ref>ותן לחכם עוד כי כן לעשות לכל הדומים לו במטבע אוישטרייך ד' דריילינג הן 0ט זהו' ג' דינרי' חא פשיטי' כמה עולה דמי ערך ז' דריילינג | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; border-collapse: collapse;" | ||
| + | |- | ||
| + | |חא פשיטי‫'||ג' דנרי‫'||‫0ט זהו‫' | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | | || ||ז | ||
| + | |-style="border-bottom: 1px solid black;" | ||
| + | |ובא||אב||‫0גו | ||
| + | |- | ||
| + | | || ||ב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|זהא זהו' וא' דינרי' יהא שמור‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ט דנרי' 0ג פשיטי' שמורים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מספר העולה הוא תהא זהו' ב' דנרי' ט' פשיטי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|במטבע אונגריש קנייני דהב | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |זקו‫'||בא||זהוב||וו||זקו‫'||א | ||
| + | |- | ||
| + | |זקוקי‫'||ו||זהו‫'||גג||לוט||ד‫' | ||
| + | |- | ||
| + | |זקו‫'||סהכ ג‫'||זהו‫'||וא||לוט||א | ||
| + | |- | ||
| + | |לו‫'||פ' א' זק' ח‫'||זהו||ח||קוו||א | ||
| + | |- | ||
| + | |לוט||כא פ א בא||זהו‫'||ד||פ||א | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מספרם בטז זהובים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|קנייני יין במדה ובמטבעו' נוירבורג | ||
| + | |- | ||
| + | | | ||
| + | |‫<ref>[136v]</ref> | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:right;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |בודר||בז||זהו‫'||‫0בז||בודר||‫0בז | ||
| + | |- | ||
| + | |בודר||וג||זהו‫'||‫וג||בודר||‫0חא | ||
| + | |- | ||
| + | |בודר||חא||זהו‫'||‫0חא||בודר||הד | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |בודר||ט||זהו‫'||‫0ט||איימר||ג||בודר||א | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |הין||ו||בודר||ד||זהו'||הד||מידו'||ה||הין||ט||בודר||ב | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |דנרי'||ד||זהו‫'||ד||זייד‫'||א||מידות||הב||הין||ג‫' | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |הין||ו||בודר||ד||פשיטי‫'||ו | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |בודר||וג||זהו'||וג||בודר||חא | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |בודר||חא||זהו‫'||חא||הין||ו||בודר||ד | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |בודר||ט||זהו‫'||ט||מדו||דג||הין||א||בודר||א | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מספר העולה ב"ז זהו' מטבעו' בדהב קנייני בגד ו"ג אמות טד זהו' ב"א אמות ט' אמות דב זהו' 0"א דינרי' ו' אמו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מספר העולה וא זהו' ו' דינ' ת חלושי' סך העולה 0א ה' דינרי' 0א פשיטי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עתים עד מטבעות אוישטריך שנה נותן חבא זהו' כמה שנה אח' ב' שני‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דו זהו' וב' שבועו' כ"ג זהו' כמה הא שבועה ט' שבועות ג' ימי' ב"א שעות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|באם יושם לפניך ‫<ref>137r / מו</ref>באם יושם לפניך חשבון גדול ורצונך לידע ולראות אחר מספר קטנה שהוא דמיונה דוק וראה ובקש איז מספר אשר המספרי' השניי' לו נחלקי' ע"י בשוה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון דב לטר' דו זהו' ז' דנרי' חא פשיטי' בא לטראו' מספרים אלו תוכל להקטונה עי"ד קח חצי מדב לטר' עולה מ בא לטר' וחצי מספר' האמצעי הוא בג' ג' דנרי' דב פשיטי' ומראיתו ככה בא לטר' בג' זהו' ג' דנרי' דב פשיטי' בכמה בא ליט‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או נלך בדרך זה כי אורחת חיים תחצי המספרי' הראשון ואחרון ואמצעי כרקאי קאי ויהא מראי' כזה בא ליטר' דו זהו' ז' דנרי' ח"א פ' ו' ליטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ותוכל עוד להקטין המספר הראשון ע"י ד' ג"כ לחצות האחרונה וירא ג' ליטר' בג' זהו' ג' דנרי' דב פש' ג' ליטראו' עושה הדמיונת הכתוב לפניך כמבואר לעיל כי מספר כולם שוה כאשר הראית בדמיונ' הכתוב למעלה ובהיות כאשר יקרא לפניך גלגל כזה 0 לפני המס' תדע ‫<ref>[137v]</ref>ותבין כמה מספרי' מחקת מהספרי' הראשונ' כמו כן יש למחוק מהאמצעי' או מאחרונ' כאשר תרצה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון <s>‫0א</s> 00בא כפו' 000וז בכמה 00א ככ' כזה מראיתו 0בא ככ' 00ו זהו' 0א ככ' בא ככ' או כזה 00ו זהו' 0א ככרי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שער הערכין רעגילא דעטרי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תקשין המספר הלזה עוד כאשר הראיתך ו ככ' 00ג זהו' 0א ככרים א ככר 0ה לטר' 0הא זהו' ה' ככרים זג לטר' וא לוט הז זהו' ב' ככר 0ה לטר' וכו' וסך העולה מכולם אחד והוא 00א זהו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מאזני צדק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תחליף הדמיון באופן זה הפנים לאחור ואחור לפני' והמספר העלת ביני לאמצע ועשה כאשרה ראית ואם התוך העולה הוא המספר אשר לפני' הרת' אמצעית אז ‫<ref>138r / מז</ref>תדע כי אמת חשבונך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון דב לט' חא זהו' בא לטר' הסך המגיע לו הוא ט' לחלופו בא לט' ט' זהו' דב לטר' והמגיע לו חא | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם נשאר לך בחושבנך אשר לא עלה לחלק הנותר אל תזיז ממקומו עד אם כפלת האחרונ' על המטבעו' הדומו' לו ואז חבר אל המספר הבא' הנשאר' ועשהו כאשר הראיתך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון בג לטר' ט' זהו' בא לטראו' עולה ח' זהו' ב' דינרי' גא פשיטי' עוד נשארו חא פשיטי' שלא באו לחשבון וחלופו בא לטר' ח' זהו' ג' דנרי' ג"א פשיטי' ג"ב לטראות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם אין הדמיונות כתוב כהלכתן או שום מעות בעולם בקש וראה השאלה ואותה תעמיד חוצה באחרונ' ושם הדומה לו ראשונה ובכן בא לך השלישי באמצע | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון דב לט' כל ‫<ref>[138v]</ref>לטר' בעד ב' זהו' עד כמה מגיע דמי מקחו והנה דב היא השאלה לכן יש לצידו בציור זה אשר אצייר לך והא לך דמיונו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|א' לט' ב' זהו' דב לטראות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וסליק לך שער ערכין כאשר מצאתיו | ||
| + | |- | ||
| + | | | ||
| − | + | == Fractions == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | | | |
| − | + | |- | |
| − | + | |With good fortune I start to translate this chapter of fractions from Latin, to the best of my ability, although it is little, I do my best with the help of God in Heaven. | |
| − | + | |style="text-align:right;"|בטוב גדא אתחיל דא שער השברי' להעתיק מלשון גלחות כפי יכולתי ואם כי היא קטנה אנא דידי עבידנ' בעזר' אלקי' דשמיא | |
| − | + | |- | |
| − | + | |One should understand that every fraction, which is called fraction in Latin, has two letters and between them a line, called linea or ? | |
| − | + | |style="text-align:right;"|יש להבין שכל השברין הנקרא בלשון לטינא פַראַצְטיָאן יש לו ב' אותיות וביניהם שורה אחת הנקרא לִינַא או פירגיל | |
| − | + | |- | |
| − | + | |The upper letter is called the numerator [lit. number], which is the number of the parts. | |
| − | + | |style="text-align:right;"|האות העליונה נקרא' המספ' שהוא מספר מספר החלקי' | |
| − | ב' פעמי' | + | |- |
| − | ב' פעמי' ו | + | |The bottom [letter] is called the denominator [lit. dissolving], for it divides the integers by its number. |
| − | + | |style="text-align:right;"|והתחתון הפורט כי הוא מחלק השלמי' ע"י מספרי | |
| − | + | |- | |
| + | | | ||
| + | *Example: <math>\scriptstyle{\color{blue}{\frac{3}{4}}}</math>, the 3 is the numerator and the 4 is the denominator. | ||
| + | |style="text-align:right;"|וזה דמיונו [[File:three quarters.png|12 px]] הג' היא המספ' והד' היא הפורטת וקריאתו נתפרש בראשונה ע"י האו' הראשונ' וכן התחתונ' וע"י שיפר' לומר חלק כגון [[File:quarter.png|12 px]] חלק [[File:two thirds.png|12 px]] חלקי' וכן עד עולם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לחלוק השבר ‫<ref>139r / מח</ref>לחלוק השבר ולחצותו ולהקטינו עד האפשרו' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דנא ואראך דרך אשר תלך בו ואז תשכיל בעז"ה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|בקש מספר אשר שני המספרי' נחלקי' ע"י מכוון | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{4}{3}}}</math>||<math>\scriptstyle{\color{blue}{\frac{6}{3}}}</math>||<math>\scriptstyle{\color{blue}{\frac{8}{6}}}</math> | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>ד</u><br>ג||<u>ו</u><br>ג||<u>ח</u><br>ו | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יחלק וישבר למחציתו דהיינו בשנים <s>ור</s> ויראה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{8}{16}}}</math>||<math>\scriptstyle{\color{blue}{\frac{4}{8}}}</math> | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>ח</u><br>וא||<u>ד</u><br>ח | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יחלק עוד למחציתו בשני' ויעלה בידך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{4}{8}}}</math>||<math>\scriptstyle{\color{blue}{\frac{2}{4}}}</math> | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |[[File:four eighths.png|12 px]]||[[File:two quarters.png|12 px]] | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עוד בשני' | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{2}{4}}}</math>||<math>\scriptstyle{\color{blue}{\frac{1}{2}}}</math> | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |[[File:two quarters.png|12 px]]||[[File:half.png|12 px]] | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואי אפשר עוד למחציתו בב' נקטין אותו ונעשנו לשלישי' והעולה הוא | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{7}{14}}}</math> | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |ז | ||
| + | |- | ||
| + | |דא | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נכה ממנה עו' השביעיו' ויוותר לך ‫[[File:half.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן עולמי' ובזה הדרך נלך ללו"ד וכן מלו"ד דהיינו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{70}{80}}}</math> | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |‫0ז | ||
| + | |- | ||
| + | |‫0ח | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יחלק בעשריו' ועו' בה עשרי' <s>בה</s> דהיינו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{1}{1}}}</math> | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |א | ||
| + | |- | ||
| + | |א | ||
| + | |} | ||
| + | |- | ||
| + | |the tongue of the stammerers shall speak clearly [Isaiah 32, 4] | ||
| + | |style="text-align:right;"|לכתיב אשורי' וללשון עברי' מכתב ולשון גלחת ע"ד ולשון עלגים תדבר צחות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|להביא כמה מיני שברי' אל כח המדבר להיות אחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|באם יקרא לפניך שים או שלשה ‫<ref>139v</ref>מיני שברי' ואין קריאת' ופרטיהם שוין לך בדרך אשר אראך כי הוא ארוכה וקצרה ושמץ לא נשמע פה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כפול תחילה הפרטי' הפרטי' הפורטים המספר והעולה יקרא הפרטיי' והוה ממוצע השוה לכולם לשניהם ור וירשם לפניך העול ב' פעמי' אח"כ המספר הראשונה אשר הוא בטור העליונה תכפול על הפרטיי' השני אשר הוא מושפל למטה והעולה הוא המספר הכוללי' מהראשון ותכתבהו על הפרטיי' הממוצע הרשום לפניך ראשונה וכן ל תעשה למספַר השני נקט האי כללא המספר הראשונה תכפל על הפרטי השני והמספ' השני תכפול על הפרטי הראשון והעולה מכל אחד ואחד תכתוב על אחד מה פרטיי' הנרשמי' לפניך הראשון ראשון ואחרון אחרון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דומיונו [[File:five sixths.png|12 px]][[File:four fifths.png|12 px]] אמור ו' פע' ה' הרי 0ג והוא הפרטיי' ד תרשמהו ב' פעמי' ‫<ref>140r / מט</ref> פע' ד' פעמי' ו' יעלה דב העלהו על 0ג הנרשמ' ראשונ' ואח"כ ה' פעמי' ה' הב תכתבהו על 0ג הנרשם שניי' ויראה כך | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |[[File:five sixths.png|12 px]]||<u>דב</u><br>‫0ג||[[File:four fifths.png|12 px]] | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הוא | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>הב</u><br>‫0ג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכזה [[File:four fifths.png|12 px]] וגם | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>דב</u><br>‫0ג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שוים שוים זה לזה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן [[File:five sixths.png|12 px]] וגם | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>הב</u><br>‫0ג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שוים זה לזה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובקל תוכל לבדוק אם כוונתך לאמת חשבונך באם תביא | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>דב</u><br>‫0ג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|למספ' הקטנה יעלה [[File:four fifths.png|12 px]] וכן השנייה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם יקרא לפניך שלמי' ושברי' להביאה וכח המדבר ע"י שברי' או שברי' ושלמים יש להשוות השלמים והשברי' יחד באופן זה כפול השלימי' עם הפרטיי' מאות' מספר והעולה תחבר אל המספר ותח' הכלל העולה תרשום הפרטיי' אשר כפלת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ודמיונ' [[File:three quarters.png|12 px]]ב עם [[File:half.png|12 px]] ומראיתו ככה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>אא</u><br>ד | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובהשוותך המדות יהיה מראיתו | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>ד</u><br>ח||<u>בב</u><br>ח | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן ב[[File:half.png|12 px]] ‫<ref>140v</ref>עם ג[[File:quarter.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואמנם אם יש להשוותו שברים עם שלמים תשבר השלם ברשימות תחתיו אחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיונו ח עם [[File:three quarters.png|12 px]] רשמהו כך | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |[[File:three quarters.png|12 px]]||<u>ח</u><br>א | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>בג</u><br>ד||[[File:three quarters.png|12 px]] | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | === Fractions of Fractions === | ||
| + | |style="text-align:right;"|שביר' משבירות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שבירה משבירות הוא חלק מחלק דמיונו אם לקחתי חצי זהו' ורצוני לחצות והצומח הוא רביעי' מזהו' שלם עשהו כך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כפול הכללים העליונים הנקראי' מסַפרים ואח"כ הפרטיים והשבירה אחרונה מורה תשובה על שאילתו שאלת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון יש לי [[File:two thirds.png|12 px]] מעם [[File:half.png|12 px]] מתוך [[File:seventh.png|12 px]] מזהוב כמה חלקים יעלה מספרו מזהו' שלם וסך המספר | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>א</u><br>אב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | |Which is 10 pešiṭim in Augsburg's coin. | ||
| + | |style="text-align:right;"|שהוא 0א פשיטי' במטבע אויגשבורג | ||
| + | |- | ||
| + | |True scales that strengthen every check <ref>based on Ezekiel 27, 9 and 27</ref> | ||
| + | |style="text-align:right;"|מאזני צדק המחזיק כל בדק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תתחיל ‫<ref>141r / נ</ref>תתחיל במספר האחרונה ואמו' קח שביעי מזהו' שלם ה' דינרי' ואות חצי עולה ב' דנרי' וח' דהיינו ט"ו פשי' נכה עוד ממנו [[File:two thirds.png|12 px]] וישאר עוד 0"א פשי' ואז תדע כי אמת חשבונך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לידע בשני שברי' איזה מהם עולה מספרו יותר מחבירו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תצייר פני כל מסַפר שהוא הכוללי' ב' גלגלים 00 וחלוק אותו מספר כולה בכתיבת וקריאה ע"י מספרו הפרטיי' ואותו שעולה מספרה יותר גם מספר' עולה יותר מחברת' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון [[File:three quarters.png|12 px]] גם ‫[[File:seven eighths.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תצייר אצל ג' ב' גלגלים הנקראי' נולא ויעלה 00ג תחלקם בד' ומספר כלה הז' וכן לז' תעשה כן צייר לפניה 00 עולה 00ז תחלק' בח' והצומח זח [[File:half.png|12 px]] ובבירור [[File:seven eighths.png|12 px]] עולה יותר [[File:three quarters.png|12 px]] וטוב הוא מאוד וחסר ולנכות שבירה משביר' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>141v</ref>ולא דבר רק הוא חכם הגם כי אפשר לידע ע"י הכאה בפרטיי' אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון ‫[[File:three quarters.png|12 px]] [[File:five eighths.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תביא' לפרטיי אחד ויהיה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>‫0ב</u><br>בג||<u>דב</u><br>בג | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ולפי חשבון זה [[File:three quarters.png|12 px]] עולה יותר [[File:eighth.png|12 px]] מ | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>‫0ב</u><br>בג | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מכאן ואילך אראך בקיצור דרך תלך על חבור חסר חלוק כפל ערכין | ||
| + | |- | ||
| + | | | ||
| + | === Chapter on Addition === | ||
| + | |style="text-align:right;"|שער ה{{#annot:term|154,1208|cq4h}}חבור{{#annotend:cq4h}} | ||
| + | |- | ||
| + | |First know for sure and also see if the denominators are equal, then you will be successful in all your ways. <ref>based on Samuel I, 18, 14</ref> | ||
| + | |style="text-align:right;"|בתחילה ידוע תדע גם תראה עם הפרטיי' שוים ואז תהיה בכל דרכיך משכיל | ||
| + | |- | ||
| + | | | ||
| + | *If the denominators are equal, sum the numerators together, with one denominator beneath them. | ||
| + | |style="text-align:right;"|אם הפרטיי' שוים תחבר המספרי' הכוללי' יחד ופרטי אחד יהיה תחתיהם | ||
| + | |- | ||
| + | | | ||
| + | *If not, multiply the first numerator by the denominator of the other and vice versa, then sum the two [products] together, with the product of the denominators by each other beneath. | ||
| + | |style="text-align:right;"|ואם אין תכפלם הכוללי הראשון לפרטי אחרון והפוך בה ותחבר שניהם יחד והפרטי' כפולי' תחתיהם | ||
| + | |- | ||
| + | |As here: | ||
| + | |style="text-align:right;"|כאשר לפניך | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{11}{13}}}</math>||<math>\scriptstyle{\color{blue}{\frac{8}{13}}}</math>||<math>\scriptstyle{\color{blue}{\frac{5}{13}}}</math> | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>אא</u><br>גא||<u>ח</u><br>גא||<u>ה</u><br>גא | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::Sum 8, 5 and 11 together; the result is 24. Write beneath it 13. | ||
| + | |style="text-align:right;"|תחבר יחד ח ה אא יעלה דב תרשום תחתיהם גא | ||
| + | |- | ||
| + | | | ||
| + | ::It looks like this: | ||
| + | |style="text-align:right;"|ומראיתו ככה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{24}{13}}}</math> | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>דב</u><br>גא | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::Or: | ||
| + | |style="text-align:right;"|או | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{1\frac{11}{13}}}</math> | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |א||<u>אא</u><br>גא | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם אינו שוות ‫<ref>142r / נא</ref>ואם אינם שווים הפרטיי' [[File:five sevenths.png|12 px]] [[File:seven ninths.png|12 px]] כמה עולה עשהו כמבואר ויעלה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{\frac{94}{63}}}</math> | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>דט</u><br>גו | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::Or: | ||
| + | |style="text-align:right;"|או | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{1\frac{31}{63}}}</math> | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |[א]||<u>אג</u><br>גו | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם [או תדמי] בחשבונך יותר מב' שברי' לחבר יחד ואין פרוטיהם שווים תחבר זה אחר זה ובכפל כמבואר וכאשר אראך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה לפניך לחבר [[File:two thirds.png|12 px]] [[File:three quarters.png|12 px]] גם [[File:four fifths.png|12 px]] כמה מספרים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תחבר השני המספרים הראשונים יחד דהיינו [[File:two thirds.png|12 px]] [[File:three quarters.png|12 px]] ויעלה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>זא</u><br>בא | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עוד תחבר [[File:four fifths.png|12 px]] הצמח הוא | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |חלקים||<u>גא</u><br>‫0ו||ב | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | === Subtraction of Fractions === | ||
| + | |style="text-align:right;"|חסר בשברים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|באם שני הפרטים שוים קח כוללי או מספר מכוללי ואשר הוא כתוב תחתיו פרטי אחד ובאים אינם שוים תכפול הכלולי כמבואר שתי וערב ועולה משניה' תנכה ותחסר זה מזה והנשאר כתוב תחתיו הפרטים כפולים כאשר הוא ‫<ref>142v</ref>לפניך דמיון תחסר | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>ד</u><br>אא||ישאר||<u>ט</u><br>אא||מ||<u>ה</u><br>אא | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם אין הפרטי' שוים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תנכה [[File:two thirds.png|12 px]] מ [[File:four fifths.png|12 px]] ישאר | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>ב</u><br>הא | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|באם תחסר שברי' משלמי' קח הכוללי' מהפרטי' ואשר יוותר בידך תרשום תחת הפרטי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דימיונו | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |מא'||<u>ה</u><br>אא | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תפול ה' מא"א וישא' ו' ותחתיהם ע תעמיד א"א וככה תבניתו | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |חלקי'||<u>ו</u><br>אא | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דרך אחרת נלך בו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תשבר השלם בסמיכה תחתו או כזה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכפול כדלמעלה בתבניתו [[File:five sevenths.png|12 px]] מ <math>\scriptstyle\frac{\aleph}{\aleph}</math> חסר וישאר בידך [[File:two sevenths.png|12 px]] חלקי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לחסור שלמי' ושברי' משלמי' ושברי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תכפול השלמי' עם הפרטי' תחבר הכוללי ועולה כדעיל במקום הכוללי ואח"כ תכפלהו וחסרהו ‫<ref>143r / נב</ref>וחסרהו כמו למעלה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תבניתו ג[[File:two thirds.png|12 px]] תחסר מ' ד‫[[File:quarter.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כפול שלמי' ופרטיי' ומראיתו | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>אא</u><br>ג | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|גם | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>זא</u><br>ד | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ועשהו כמבואה והנשאר הוא | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>[ז]</u><br>בא | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | === Doubling === | ||
| + | |style="text-align:right;"|כפל בשנים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תכפול או תחלק הפרטיי' למחצית תבנית ב' פעמי' [[File:three fifths.png|12 px]] עולה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>ו</u><br>ה | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או א‫[[File:fifth.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן ב' פעמי' [[File:three quarters.png|12 px]] עולה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>ג</u><br>ב | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או א‫[[File:half.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | === Halving === | ||
| − | + | |style="text-align:right;"|למחלק למחציתו | |
| − | + | |- | |
| + | | | ||
| + | |style="text-align:right;"|חצי הכוללי באם הוא באפשרי ואם אין כפול הפרט' כאשר אבאר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון חצי [[File:six sevenths.png|12 px]] הוא [[File:three sevenths.png|12 px]] חלקי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן [[File:three fifths.png|12 px]] עולה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>ג</u><br>‫0א | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כל הדומה לו | ||
| + | |- | ||
| + | | | ||
| + | === Multiplication of Fractions === | ||
| − | + | |style="text-align:right;"|כפל גדול בשברי' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|‫<ref>143v</ref>כפול יחד הכוללי' ואח"כ הפרטיי' כל אחד ואחד בפני עצמו אמו' כמדומה לי יש לדעת לחלוק הסך העולה משניהם במעלה השפולו' שאפרוש אך יחלק במכוון בשלמי' ולא בחצאין והנשאר הוא המבוקש כך נעלד ואף כי לא בפירש איתמר אמנם מכללא אתמר | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וכן מצאתי דמיונו [[File:three quarters.png|12 px]] יכפול ע"י [[File:four fifths.png|12 px]] ומצאת בתוך שהסך העולה הוא ‫[[File:three fifths.png|12 px]] | |
| − | + | |- | |
| + | | | ||
| + | |style="text-align:right;"|ואיך זה באשרו' אם לא שנעשנו כאשר אמרת גם מצאתי בספר אחר כתוב אל תתמה על מה שהסך העולה מועט מהסך הנכפל ואין בכך הפסד והטעם לא ידעתי ודוק ותמצא כאשר אמרתי וד"ל ואח"כ דקדקתי בו יותר ומצאתי כי הכל אחד כי הפרטי יחלק כמו הכוללי ואח"כ חשבונך מכוון וד"ל כך <s>נעל</s> נלע"ד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לכפול שלמים עם שברי' וחתיכו' כמראה כתוב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שבור השלמי' ע"י בכתיב' א ואח"כ עשהו כאשר הראיתך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שלמי' ‫<ref>144r / נג</ref>שלמים עם שברי' ושלמי' או שברי' ושלמי' עם שברי' ושלמי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עשהו כאשר הראתיך אך כפול השלמי' על הפרטי' וחברוהו אל הכוללי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיונו ז[[File:three quarters.png|12 px]] על [[File:five eighths.png|12 px]] עשהו כמבו' ויעלה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>זב</u><br>בג||ד||מספרו||<u>ההא</u><br>בג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ותן לחכם ויחכם עוד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן דמיונו ג[[File:two thirds.png|12 px]] על ג[[File:three quarters.png|12 px]] כפלים בחלקי' ויעלה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>הא</u><br>ד||ו||<u>אא</u><br>ג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עשהו כמבואר יבא בחשבונך גא ‫[[File:three quarters.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | === Division === | ||
| − | + | |style="text-align:right;"|דוידירו הוא חלק | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|בהיות הפרטיי' שווי' חלק בכוללי ואם אינם שווים כפלם כמבואר והמספר אשר תחלק תעמיד במעלה הגבוה והחלק במעלה המושפל כאשר בשלמי' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וזה תבניתו | |
| − | + | |- | |
| − | + | | | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {| | |
| + | |- | ||
| + | |<u>ג</u><br>טא||ע"י||תחלק||<u>בא</u><br>טא | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והעולה הוא ד' מכוון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן [[File:six sevenths.png|12 px]] ע"י [[File:five sevenths.png|12 px]] עולה א‫[[File:fifth.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>144v</ref>ואם שאינם שוים הפרטים דמיונו כזה [[File:two thirds.png|12 px]] ו [[File:three quarters.png|12 px]] ויעלה בידך [[File:eight ninths.png|12 px]] חלקי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן [[File:three quarters.png|12 px]][[File:half.png|12 px]] עולה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |א"ב||או||<u>ג</u><br>[ב] | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|רצונך לחלק שברים במספר שלמה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אם תוכל לחלק די כלולי מכוון בלא השארים אחרי' ע"י השלמה עשהו וזהו בנקל ותחת העולה כתוב הפרטם ואם ואין כפול המספר השלמה על הפרטיי' והכוללו יעמיד בארשונה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה דמיון השוה לחלק | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>בא</u><br>[ג] | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ע"י ד' שלמים חלק ב"א ע"י ד' עולה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |א||<u>ג</u><br>ג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה דמיון אחרים הנה לפניך [[File:seven eighths.png|12 px]] ע"י ג' עולה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>ז</u><br>דב | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן כל הדומי' לו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|לחלק השברים ע"י שברים ושלמים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עשה השלמים לחלוקים כמבואר ואח"כ חלקוהו כמראה אשר הראיתך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון ג[[File:two thirds.png|12 px]] תחלק ע"י ד[[File:four fifths.png|12 px]] לחלקים עולה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<u>דב</u><br>ה||ע"י||לחלק||<u>אא</u><br>ג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עשהו כמבואר עולה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>הה</u><br>בז | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה יגד די עי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שייך לשער כפל גדול | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שברי' בלי ‫<ref>145r / נד</ref>שברי' בלי שלמי' בצדם עם שלמי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון [[File:three quarters.png|12 px]] ע"י ב' זהו' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|חלוק ג' בשני חלקי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון [[File:quarter.png|12 px]][[File:two quarters.png|12 px]] אמור [[File:quarter.png|12 px]] מתוך ב' זהו' הוא | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |מזהו'||<u>ד</u><br>[[File:half.png|12 px]] | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אח"כ [[File:two quarters.png|12 px]] עולה כפלים כמוהו דהיינו זהו' שלם העולה הוא א' זהו‫' [[File:half.png|12 px]] | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שברים עם שלימי' בצדם עם שלמי' בלי שברי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ב [[File:half.png|12 px]] זהו' ע"י ג' אמו' ב' פעמי' ג' הוא ו' זהו' אח"כ בקש החצי זהו' מג' זהו' דהיינו א' זהו' ד' דינרי' אוישטריך עולה ז' זהו' ד' דנרי' אוישטרייך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שברי' עם שלמי' בצדם עם שלמי' ושברי' בצדה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון ג [[File:quarter.png|12 px]] זהו' ע"י ב[[File:three quarters.png|12 px]] אמו' ב' פעמי' ג' הוא ו' זהו' קח ג"כ [[File:quarter.png|12 px]] מתוך ב' זהו' הוא ד' דנרי' אוישטרייך ובכן כפלת הג' ע"י העליונה אח"כ כפול כמו כן [[File:three quarters.png|12 px]] ע"י ג [[File:quarter.png|12 px]] זהו' החצי [[File:three quarters.png|12 px]] בב' חלקים | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון [[File:quarter.png|12 px]][[File:two quarters.png|12 px]] אמו' [[File:quarter.png|12 px]] מג' זהו' הוא דנרי' ‫<ref>145v</ref>אוישטרייך עוד [[File:quarter.png|12 px]] מתוך [[File:quarter.png|12 px]] מזהו' או 0ו' פשיטי' הוא הא פשי' ובאחרונה יעלה מתו' [[File:two quarters.png|12 px]] כפלים מאשר עולה מתוך [[File:quarter.png|12 px]] ומספרו א זהו' ה' דנרי' אויש' חבר שני המספרי' יחד ח' זהו' ז' דנרי' הא פשיטי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שברי' בלי שלמי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הדרך הטוב הוא לכפול יחד המספרי' העליונה אח"כ התחתוני' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון [[File:three quarters.png|12 px]] ע"י [[File:half.png|12 px]] עולה [[File:three eighths.png|12 px]] או ג' דנרי' | ||
| + | |- | ||
| + | | | ||
| + | === Proportions === | ||
| − | + | |style="text-align:right;"|ערכין | |
| − | הוא | + | |- |
| − | + | | | |
| − | + | |style="text-align:right;"|יש לעשותו כמו בשלמי' לכפול האחרון ע"י האמצעי' ואח"כ לחולקו ע"י הראשון | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|דמיון קנית [[File:three quarters.png|12 px]] מלטר' בעד [[File:four fifths.png|12 px]] מזהו' כמה המגיע [[File:three sevenths.png|12 px]] מלטר' | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כפול ג' ע"י ד' עולה בא הוא המספר או כוללי כמו כן כפול ז' ע"י ה' עולה ה"ג הוא הפרטיי מראיתו | |
| − | + | |- | |
| − | + | | | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | |<u>בא</u><br>הג | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| + | |style="text-align:right;"|חלקוהו ע"י [[File:three quarters.png|12 px]] מספר הוא | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |מזהו'||<u>וה</u><br>אג | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והתבררנ' שברי' כנ"ל הוא המתבקשו' ג' מספרי' שלמי' הנשוואות עם ‫<ref>146r / נה</ref>עם דמיון השברי' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון ‫[[File:three quarters.png|12 px]] <s>מיל</s> מלטר' בעד ‫[[File:four fifths.png|12 px]] מזהו' כמה הגיע על ‫[[File:three sevenths.png|12 px]] וכאשר תגיע אל שלמיות אלו ככה יהיה תבניתו ה0א לטר' עולה דמיה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וא' זהו' כמה המגיע על ג' לטראו' או הא' לטראו' דמי מקח' וא' זהו' כמה מגיע על א' לטרא | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אמנם החשבון הנוהגים עכשיו ככה הוא | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה כל השברי' עומדין כל אחד בפני עצמו או יש לו שלמיו' בצדו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם יועמד לחוד כמראי' ככה יהיה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יש לו שלמי' בצדו אז כפול הפרטיי' ע"י שלם כמבו' והעולה חבר אל הכוללי' ותחתיו הפרטי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובאם יהיה לפניך שלם בלי שברי' בצדו העמוד תחתיו א' במקום בפרטיי | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|להביא הציורי' השבורי' ולעשות שלמי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כפול הפרטי' האחרון אשר לצד שמאלי' ‫<ref>[146v]</ref>ע"י האמצעי העולה כפול על הכללי הראשון ובאחרונה כפול הפרטיי הראשון על הכללי האמצעי והפרטיי האמצעי על הכללי האחרון וככה יועמד הציור הלזה בשלמי' ולעשתו כאשר כתבתי לך לעיל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והא לך ציורי' אילו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫[[File:half.png|12 px]] לטר' ב' זהו' ו' ליט ככה יועמד | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |לטר'||<u>ו</u><br>א||זהו'||<u>ב</u><br>א||לט||[[File:half.png|12 px]] | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובהקנותך שלמיות ככה יהיו אי לטר' ד' זהו' ו' לטראות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|העולה הוא דב זהו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ב' לט' [[File:half.png|12 px]] מזהו' ו' לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ככה יועמד | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |מלט‫'||<u>ו</u><br>א||מזהו‫'||[[File:half.png|12 px]]||מלט‫'||<u>ב</u><br>א | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובשלימותו ‫<ref>147r / נו</ref> ובשלימותו זה יהיה תבניתו ד' לטר' א' זה' ו' לט‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|העולה הוא א' זהו' ד'ד' דנרי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ולטראו' דא זהו' ‫[[File:quarter.png|12 px]] מלטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יועמד ככה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |מלטראו‫'||[[File:quarter.png|12 px]]||מזהו'||א||<u>ד</u><br>א||לטר‫'||<u>ו</u><br>א | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובשלימותו דב לטר' דא זה' א' לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|העולה הוא ד' דנרי' 0ב פשי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ב ‫[[File:third.png|12 px]] לטר' ו' זהו' ט' לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יועמד ככה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |מלטראו‫'||<u>ט</u><br>א||מזהו'||לטר‫'||<u>ז</u><br>ג | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובשלימותו ז' לטר' חא זהו' ט' לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הסך העולה גב זהו' א' דינר ד ‫[[File:five sevenths.png|12 px]] פשיטי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>[147v]</ref>ו' לטר' ב[[File:third.png|12 px]] זהו' בא לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מראיתו ככה יהיה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |לטראו‫'||<u>א</u><br> ||<u>ב</u><br>א||<u>ז</u><br>ב||לטר‫'||<u>ו</u><br>א | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובשלימתו חא לט' ז' זהו' בא לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הסך העולה הוא ד' זהו' ה' דנרי' 0"א פשי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ט' לטר' ו' זהו' ח ‫[[File:quarter.png|12 px]] לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|זה תבניתו | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |לטראו‫'||<u>ג</u><br> ||<u>ג</u><br>ד||זהו‫'||<u>ו</u><br>א||לטר‫'||<u>ט</u><br>א | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וזה תבניתו בהיותו במלואו וג' לט' ו' זהו' גג לטראות | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|העולה הוא ה' זהו' ד' דנרי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ט[[File:half.png|12 px]] לטר' ג[[File:quarter.png|12 px]] זהו' ו' לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יועמד ככה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |לטראות||<u>ו</u><br>א||זהו‫'||<u>א</u><br> ||<u>ג</u><br>ח||לט‫'||<u>א</u><br> ||||<u>ט</u><br>ב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובעמדו ‫<ref>148r / נז</ref> ובעמדו בשלימתו ו"ז לטר' גא זהו' בא לט‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המספר העולה הוא ב' זהו' 0 דנרי‫' | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |פשיטים||<u>א</u><br>א||<u>ב</u><br>ט||בא | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ו' לטר' ב[[File:quarter.png|12 px]] זהו' ג[[File:half.png|12 px]] לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יועמד ככה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |לטראות||<u>ז</u><br>ב||זהו‫'||<u>ט</u><br>ז||לטרי'||ו | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובהשלמתו <s>העולה</s> חד לט' ט' זהו' ז' לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המספר העולה י"ו זהו' ב' דנרי' הא לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דא[[File:half.png|12 px]] לט' 00ב זהו' ט[[File:quarter.png|12 px]] לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יועמד ככה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |לטראו‫'||<u>זג</u><br>ד||זהו‫'||<u>‫00ב</u><br>א||לטראו‫'||<u>ג</u><br> ||<u>ב</u><br>ב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|בהשלמתו דבא לטר' 00ד לט' זג לט‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|העולה טאא זהו' ב' דנרי‫' | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |פשי||<u>א</u><br>אג||הב | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>[148v]</ref>ג[[File:quarter.png|12 px]] לט' ד[[File:quarter.png|12 px]] זהו' ט[[File:half.png|12 px]] לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מראיתו ככה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |לטראות||<u>ב</u><br> ||<u>ח</u><br>ג||זהו‫'||<u>א</u><br> ||<u>ז</u><br>ד||לטר'||ז | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והיה בהשלימך המספרי' דח לט' ז"א זהו' ו"ה לטראו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|העולה הוא אא זהו' וב' דנרי' 0ב פשיט | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ד[[File:half.png|12 px]] לט' ח' זהו' ז' דנרי' ב[[File:half.png|12 px]] פשי' ה[[File:quarter.png|12 px]] לט' במטבע אחת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ד[[File:half.png|12 px]] לטר' בד אב[[File:half.png|12 px]] פשי' ה[[File:quarter.png|12 px]] לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ובהשוואות לשלימות בז לט' הח כד פשי' כד לטר' מספרם 0א זהו' ג דנרי' ‫[...] | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |פשי||<u>ז</u><br>בא||ט | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ד[[File:half.png|12 px]][[File:three quarters.png|12 px]][[File:five sixths.png|12 px]] לט' ו[[File:half.png|12 px]] פחו' [[File:third.png|12 px]] זהו' ב[[File:half.png|12 px]] מתוך [[File:quarter.png|12 px]] מעם [[File:three quarters.png|12 px]] לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|יועמד ככה ה[[File:seven eighths.png|12 px]] לטר' ו[[File:sixth.png|12 px]] זהו' וז לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מספר ‫<ref>149r / נח</ref>מספר העולה ב' זהו' א' דינר זא[[File:seventh.png|12 px]][[File:two quarters.png|12 px]] פשי‫' | ||
| + | |- | ||
| + | |Exchange: Hungarian gold coin and Rheinos gold coin | ||
| + | |style="text-align:right;"|חלוף לעשות זהו' אונגריש במטבע גם זהו' רינוס במטבע | ||
| + | |- | ||
| + | |Multiply the Hungarian gold coins by the number of Austrian dinar in a Hungarian gold coin, then divide the product by the number of dinar in a Rheinos gold coin, which is 8. | ||
| + | |style="text-align:right;"|תכפול זהו' אונגריש על מספר כמה דינרי' אוישטרייך בזהו' אונגריש ואשר יעלה במצודתך תחלקהו ע"י מספר הדינרי' מזהו' רינוס והיא ח‫' | ||
| + | |- | ||
| + | | | ||
| + | *If one asks, for example: one has 248 Hungarian gold coins and the question is how much are they worth in Rheinos gold coins? | ||
| + | |style="text-align:right;"|אם ישאל השואל דמיון יש לאחד חדב זהו' אונגריש במטבע והשאלה <s>כמה</s> עד כמה יגיע דמיהם לזהו' רינוס במטבע | ||
| + | |- | ||
| + | | | ||
| + | :Multiply 248 by 10; the result is 2480. Divide them by 8; the result is 310 Rheinos gold coins. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{248\sdot10}{8}=\frac{2480}{8}=310}}</math> | ||
| + | |style="text-align:right;"|כפול חדב על 0א יעלה 0חדב תחלקם בח ויעל 0אג זהו רינוס במטבע | ||
| + | |- | ||
| + | |I shall teach you also to calculate Hungarian gold coin from Rheinos gold coin | ||
| + | |style="text-align:right;"|תא ואאלפך עוד לחשוב זהו' אונגריש במטבע מתוך זהו' רינוס במטבע | ||
| + | |- | ||
| + | |Multiply the Rheinos gold coins by 8 dinar, then divide the product by 10 dinar etc. | ||
| + | |style="text-align:right;"|כפול זהו' רינוס על ח' דינרי' וחלוק העולה ע"י 0א דינרי' וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | *Example: you have 310 Rheinos gold coins and you wish to know how much are they worth in Hungarian gold coins? | ||
| + | |style="text-align:right;"|דימיון הרי לפניך 0אג זהו' רינוס במטבע ו ‫<ref>[149v]</ref>ובקשתו לדעת כמה יעלה מנינ' וזהו' אונגריש במטבע | ||
| + | |- | ||
| + | | | ||
| + | :Multiply 310 gold coins by 8 dinar; the result is 2480. Divide them by 10; the required is 248 Hungarian gold coins. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{310\sdot8}{10}=\frac{2480}{10}=248}}</math> | ||
| + | |style="text-align:right;"|כפול 0אג זהו' על ח' דנרי' וי' ויעלה 0חדב תחלקם ע"י 0א והמבוקש הוא חדב זהו אונגריש במטבע | ||
| + | |- | ||
| + | |To find the [value of] Rheinos gold coins in Hungarian gold coins. | ||
| + | |style="text-align:right;"|למצא זהו' רינוס במטבע בתוך זהו' דהב אונגריש | ||
| + | |- | ||
| + | |Multiply the Hungarian gold coins by 11 dinar, then the units by the exchange rate. Convert the pašuṭim into dinar, add them to the former, and seek for the gold coins in the dinar that are divided by 8. | ||
| + | |style="text-align:right;"|כפול זהו' אונגריש על אא דינר ואח"כ ביחידי' על שבח החלוף ומן הפשי' תעשה דנרי' וחברם אל הראשוני' ובקש מתוך הדנרי' זהו' נחלקי' בח' וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | *Example: one has 360 Hungarian gold coins, the rate of a Hungarian gold coin is 11 dinar and the exchange rate is 12 pašuṭim. The question is how many Rheinos gold coins is this amount of Hungarian gold coins worth? | ||
| + | |style="text-align:right;"|דמיון יש לו 0וג זהו' אונגריש בדהב ודמי זהו' אונגריש בדהב אא דינרי' ושבח החילוף בא פשי' השאלה כמה עולה סך זהו' אונגריש הנ"ל זהו' רינוס במטבע | ||
| + | |- | ||
| + | | | ||
| + | :Multiply these 3[6]0 gold coins by 11 dinar; the result is 3960 dinar. Multiply them also by 12 pašuṭim; the result is 4320 pašuṭim. Divide them by the dinar; the result is 144 dinar. Add them to the 3960 dinar and divide the whole sum, which is 4104, by 8; the result is 513 Rheinos gold coins. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{\left(360\sdot11\right)+\frac{360\sdot12}{30}}{8}=\frac{3960+\frac{4320}{30}}{8}=\frac{3960+144}{8}=\frac{4104}{8}=513}}</math> | ||
| + | |style="text-align:right;"|כפול 0הג זהו' דהב הנ"ל על א'א' דינרי' ויעלה 0וטג דינרי‫'<br> | ||
| + | כפלם עוד על בא פשיטי' ויצמח 0בגד פשי‫'<br> | ||
| + | חלקם לדינרי' והצומח הוא דדא ‫<ref>150r / נט</ref>הוא דדא דינרי' חברם על 0וטג דינרי' וחלק הסך כולו כגון ד0אד דינר' בח' ועולה מורה גאה זהו' רינוס במטבע | ||
| + | |- | ||
| + | |Comparing Two Types of Cubits | ||
| + | |style="text-align:right;"|השוואות שני מיני אמות | ||
| + | |- | ||
| + | | | ||
| + | *I bought 24 cubits for 9610 in the city of Vienna [at a rate of] a cubit for 4 Rheinos gold coins and when they were brought to Ofen [= Buda] in the country of Hungary, I sold one cubit for 4 Hungarian gold coins. <math>\scriptstyle\frac{3}{4}</math> of a cubit in Vienna is one cubit in Ofen. I ask: how much is the profit? | ||
| + | |style="text-align:right;"|קניתי דב אמות 0אוט בעיר ווין והאמה בעד ד' זהו' רינוס ובהביאם לאובן במדינת אונגרן נתתי האמה בד' זהו' <s>רינוס</s> אונגריש במטבע והנה [[File:three quarters.png|12 px]] אמו' בווין הוא אמה באובן ושאלת כמה עולה הריווח | ||
| + | |- | ||
| + | | | ||
| + | :Say: at 4 Rheinos gold coins [for one cubit], how much is the price of 24 cubits? The result is 96 Rheinos gold coins. | ||
| + | :<math>\scriptstyle{\color{blue}{4\sdot24=96}}</math> | ||
| + | |style="text-align:right;"|תאמר האמר בעד ד' זהו' רינוס כמה מגיע דמי מקח דב אמות הצומח וט זהו' רינוס בחוץ יהיה מושבת | ||
| + | |- | ||
| + | | | ||
| + | :Seek also how many cubits of Ofen are 24 cubits of Vienna: | ||
| + | |style="text-align:right;"|בקש עוד כמה עולה דב אמו' בווינא אמו' אובן | ||
| + | |- | ||
| + | | | ||
| + | :Say: 3 cubits of Vienna are 4 cubits of Ofen, how many are 24 cubits of Vienna? The result is 32 cubits of Ofen. | ||
| + | :<math>\scriptstyle{\color{red}{4\sdot\frac{24}{3}}}{\color{blue}{=32}}</math> | ||
| + | |style="text-align:right;"|תאמר ג' אמו' בווינא הם ד' אמו' באובן כמה עולה על דב אמו' ווינ' הצומח בג אמו' אובן | ||
| + | |- | ||
| + | | | ||
| + | :Say also: at 1 cubit for 4 Hungarian gold coins, how much are 32 cubits worth? 128 Hungarian gold coins <math>\scriptstyle{\color{blue}{4\sdot32=128}}</math>, which are 160 Rheinos gold coins <math>\scriptstyle{\color{red}{\frac{10\sdot128}{8}=160}}</math>. | ||
| + | |style="text-align:right;"|תאמר עוד תאמר עוד א' אמה בעד ד' זהו' אונגריש כמה יגיע על ב"ג אמו' מספרי' חבא זהו' אונגריש והם 0וא זהו' רינוס | ||
| + | |- | ||
| + | | | ||
| + | :Subtract the 96 Rheinos gold coins from them; you are left with 64 Rheinos gold coins and this is the profit. | ||
| + | :<math>\scriptstyle{\color{blue}{160-96=64}}</math> | ||
| + | |style="text-align:right;"|‫<ref>[150v]</ref>חסר ממנו וט זהו' ריינוס יוותר לך דו זהו' ריינוס והוא הריווח | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אמנם יש לדעת ולברר אמיתתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן לעשות במדה במשקל ובמשורה לחשוב חשבונו' אילו לידע הריווח יוסף על דמי המקח ההוצא' אשר הוציא עליהם בהליכתו למקום אחר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שבירות עגלי' למדינו' מרחק משקל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|נתתי שבירו' על בא ככרים וג' פרסאות הא זהו' רינוס ובקשת למצו' שכירות המגיע על דב ככרי' חא פרסאו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ויש להעמידו ב' פעמי' על אופניו בתחילה בא ככרי' שכרו הא זהו' רינוס כמה המגיע על דב ככרי' מספרו 0ג זהו' רינוס ובשניי' וג ככרי' נותני' 0ג זהו' רינוס כמה מגיע חא פרסאות מספרו הצומח הא זהו' רינוס | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|חשבון זה שייך לחייטין ‫<ref>151r / ס'</ref>חשבון זה שייך לחייטין | ||
| + | |- | ||
| + | | | ||
| + | *I bought 6 cubits of cloth for wearing; the width of the cubit is <math>\scriptstyle1+\frac{1}{2}</math> cubits; and I wish to buy another cloth instead of <math>\scriptstyle1+\frac{1}{2}</math> cubits. The question is how much of that cloth should be taken instead of the garment? | ||
| + | |style="text-align:right;"|קניתי ו' אמות בגד למלבוש ורוחב האמה א[[File:half.png|12 px]] אמות ורציתי לקנות עוד בגד אחר תחתיו א[[File:half.png|12 px]] אמו' והנה השאלה כמה צריכ' מאותו בגד לעשותו תחת המלבוש | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אראך אשר תעשה תרבע הבגד על דרך זה כפול ארכו אפותיו והעולה ט' תרבע כמו כן הבגד אשר תחתיו והעולה הוא | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |<u>ה</u><br>ד | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|רוחבו ובו תחלק ט' רוחב הראשונה ומראה מספרו הוא ז[[File:fifth.png|12 px]] אמות וככה יהיה מספר הבגד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הרוצה לחשוב ולידע ריווח בדבר כאשר תרצה להרוויח כך תוסיף על דמי מקנתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|דמיון קניתי 0בא ככרי' שעוה בעד וטבא זהו' רינוס כמה מגיע על א' לטר' אשר תוכל להרוויח בכל הסחורה כולו וטא זהובי' רינוס | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תאמר 0בא ככרי' בעד בטדא זהו' רינוס כמה עולה א' לטר‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>[151v]</ref>ריווח | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מכרתי בגד האמה בעד ה' דינרי' אויש' והרווחתי ב0א אמו' א' זהו' ב' דינרי' ובקש' לדעת בכמה קנית | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תאמ' בראשונה תאמר 0א אמו' מרויחי' א[[File:quarter.png|12 px]] זהו' כמה עולה א' אמו' העולה א' דינר תחסרנו מעל ה' דינרי' עולה ד' דנרי' והוא דמי מקח הראשונה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הפסד בדבר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|מכרתי בגד האמה בעד ה' דנרי' והפסיד ב0ב אמו' ז[[File:half.png|12 px]] זהו' והשאלה בכמה קנית האמ' בקניין ראשון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אמו' 0ב אמו' עולין ז[[File:half.png|12 px]] זהו' בכמה א' אמה עולה ג' דנרי' חברם על ה' עולה א' זהו' וכן קנית' אמה בראשונה | ||
| + | |- | ||
| + | |I bought 6 kikkar of peppers, each fine quality kikkar is worth 50 Rheinos. If there are 5 damaged liters in each kikkar and you want to know how much the fine quality peppers are worth without the damaged ones. | ||
| + | |style="text-align:right;"|קניתי ו' ככרי' פלפלין וכל ככר מזוקק ומנופ' בעד 0ה זהו' ריינוס ובאם יש בכל ככר ה' לטר' פסולו' ובקשת לדעת בכמה הפלפלין <s>המחקק</s> המזוקק ומנופה בלתי הפסולו‫' ‫<ref>152r / ס"א</ref>הפסולו‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תאמר א' ככר יש בתוכו ה' ליט' פסולו' וקח מכל ככר ה' לטר' עולה 0ג לטר' חסר' מעל ו' ככרי' יוותר לך ה' ככרי' 0ז לטר' נקרי' באחרונה תאמר א' ככר בעד 0"ה זהו' רינוס בכמה ה' ככרים 0ז ליטר' עולה מספרו החב | ||
| + | |- | ||
| + | | | ||
| + | == Barter == | ||
| − | + | |style="text-align:right;"|חלוף | |
| − | ז' | + | |- |
| − | + | |One has 7 liters of turmeric and he sells the liter for 6 Rheinos gold coins and in barter he sells it for a price of 7 Rheinos gold coins. The other has 30 liters of peppers in barter, each liter is worth 5 Austrian dinar. By how much will he raise the price of a liter of peppers and how much will he give to his friend? | |
| − | + | |style="text-align:right;"|יש לאחד ז' לטר' כרכום ומוכרי' הלטר' בעד ו' זהו' רינוס ובהחלוף נותן ערכו עליו בעד ז' זהו' רינוס ויש לאחר בחלופו 0ג לטר' פלפלין וכל לט' בעד ה' דינרי' אוישטרייך בכמה יאריך זה לפי ערכו א' לטר' פלפלין ואיזה מהם יתן עוד לחבירו | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|דמיון תאמר ו' זהו' רינוס נעשי' בחלוף ז' זהו' רינוס ומה יהיה על ה' דנרי' עולין ה' דינרי' ה[..] פשי' וחשוב אכ אח"כ כל סחורה וסחורה בפני עצמה כגון א' לטר' כרכום בעד ז' זהו' רינוס בכמה עולה על לטר' עולה טד זהו' רינוס נלך עוד משם ונאמר א' לטר' פ ‫<ref>[152v]</ref>פלפלין בעד דינרי' הב פשי' בכמה 0ג לטר' עולה אב זהו' רינוס ז' דינרי' חסר' מעל טז זהו' רינוס יוותר לך זב זהו' רינוס א' דינר וזהו חיוב בעל הפלפלין לבעל הכרכום | |
| − | על | + | |- |
| − | + | | | |
| − | |||
| − | + | == Partnership == | |
| − | |||
| − | + | |style="text-align:right;"|שותפות | |
| − | + | |- | |
| − | + | |Three form a partnership together | |
| − | + | |style="text-align:right;"|שלוש' עושים שותפות ביחד | |
| − | + | |- | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {| | |
| − | + | |- | |
| − | + | |Rheinos||zehuvim||24||rowspan="3"|contributes to the partnership||the first | |
| − | + | |- | |
| − | + | |Rheinos||zehuvim||36||the second | |
| − | + | |- | |
| − | + | |Rheinos||zehuvim||48||the third | |
| − | + | |} | |
| − | + | |} | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {| | |
| + | |- | ||
| + | |רינוס||זהו‫'||דב||rowspan="3"|מניח בשותפו‫'||הראשון | ||
| + | |- | ||
| + | |רינוס||זהו‫'||וג||השני | ||
| + | |- | ||
| + | |רינוס||זהו‫'||חד||שלישי | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | |They earn 720 Rheinos zehuvim together. | ||
| + | |style="text-align:right;"|והרוויחו ביחד 0בז זהו' רינוס | ||
| + | |- | ||
| + | |One wishes to know how much is owed to each according to what he contributed. | ||
| + | Want to know how much is owed to each person based on what they contributed. | ||
| + | |style="text-align:right;"|והרוצה לדעת המגיע לכל אחד לפי ערך אשר הניח | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ילך בדרך זה חבר יחד מה שהניחו בשותפו' והעולה תשמור ביך בידך והוא יהיה החולק כפול הריווח שהרוויח על אשר הניח לכל אחד בפני עצמו והעולה חלוק במספר השמור לך לחולק ואז תשכיל | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |רי‫'||זהו‫'||‫0וא||לראשון||רינוס||זהו‫'||‫דב | ||
| + | |- | ||
| + | |רי‫'||זהו‫'||‫0זב||לשני||רינוס||זהו‫'||‫זג | ||
| + | |- | ||
| + | |רי‫'||זהו‫'||‫0בג||לשלישי||רינוס||זהו‫'||‫חד | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | |Three made a joint deal to divide between them 360 Hungarian coins: | ||
| + | |style="text-align:right;"|‫<ref>153r / ס"ב</ref>ג' שעשו עיסקא בהדדי ויש לחלק ביניהם 0וג זהו' אונגריש במטבע | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |ב||rowspan="3"|שייך||ראשון||rowspan="3"|ול | ||
| + | |- | ||
| + | |[[File:third.png|12 px]]||שני | ||
| + | |- | ||
| + | |[[File:half.png|12 px]]||שלישי | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עשהו כאשר הראיתך והיה ככה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שלשה שהטילו לכיס<br> | ||
| + | הראשון מניח גרוטאו' של כסף<br> | ||
| + | והשני ג"כ 0א זהו' גרוטאו' של כסף<br> | ||
| + | והשלישי הטיל דו זהו' רינוס<br> | ||
| + | והשכיחו 00ד זהו' פעמים לראשון מגיע 0ד זהו' לשני 0ח זהו' לשלישי 0הב זהו' כמה הטילו השניי' הראשוני‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אשכילך את אשר תעשה תאמר 0ח"ב באי' ע"י דו זהו' רינוס כמה הטיל הראשון שבאו לו 0ד לוטא' עולה דמיו ט[[File:seventh.png|12 px]] זהו' רינוס וזה דמי ערך גרוטאות הראשון בשווים תאמר ‫<ref>153v</ref>עוד 0חב זהו' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכמה מגיע אשר ממנו באו 0ח לוטא' עולה 0ח[[File:two sevenths.png|12 px]] זהוב רינוס לוט חסר ממנו 0א זהו' רינוס ישאר לך ח[[File:two sevenths.png|12 px]] זהו' רינוס וזה דמי שוה הגרוטאות של שני | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שלשה שעשו שותפין ביחד<br> | ||
| + | הראשון נתן 0א זהו' רינוס ונותן ונוש' בו 0ב שבועות<br> | ||
| + | השני הטיל 0ד זהו' רינוס ונושא ונותן ה' שבועות<br> | ||
| + | השלישי הטיל 0ה זהו' ונשא ונתן בו ד' שבועו' <s>והרב</s> והרוויח בו 000א זהו' מטבע ברחב<br> | ||
| + | כמה מגיע לכל אחד לפי הטיל מעותיו גם לפי הימי‫' | ||
| + | |- | ||
| + | | | ||
| + | == Currency calculations == | ||
| + | |style="text-align:right;"|חשבון כסף | ||
| + | |- | ||
| + | | | ||
| + | :{|style="color:green;" | ||
| + | |- | ||
| + | |1 zaquq = 16 lot | ||
| + | |- | ||
| + | |1 lot = 4 quenten | ||
| + | |- | ||
| + | |1 quenten = 4 pešiṭim | ||
| + | |} | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *A piece of silver weighs 12 zequqim, 13 lot, 3 quenten, and 1 pašuṭ. When you remove the slag from it and melt it, there is in a refined pure silver zaquq 14 lot, 3 quenten, 2 pešiṭim. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{14}{16}+\frac{3}{64}+\frac{2}{256}}}</math> | ||
| + | :How much pure silver is included in 12 zequqim, 13 lot, 3 quenten, and 1 pašuṭ? | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{12+\frac{13}{16}+\frac{3}{64}+\frac{1}{256}}}</math> | ||
| + | |style="text-align:right;"|חתיכה כסף משקלו בא זקוקי' גא לוט ג' קווינטן א' פשי' וכשתסיר ממנו הסיגי' ותצרפנו יש בזקוק כסף מזוקק דא לוט ג' קווינטן ב' פשי‫'<br>כמה כסף ‫<ref>154r / ס"ג</ref>כמה כסף מצורף בתוך בא זקוקי' גא לוט ג' קווינטן א' פשי‫' | ||
| + | |- | ||
| + | |rowspan=2 | | ||
| + | :The result is: 11 zequqim, 15 lot, 1 quenten, and <math>\scriptstyle1\frac{5{\color{red}{9}}}{128}</math> pešiṭim | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{11+\frac{15}{16}+\frac{1}{64}+\frac{1+\frac{59}{128}}{256}}}</math> | ||
| + | |style="text-align:right;"|עולה אא זקוקי' הא לוט א' קווינטן | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |פשי‫'||<u>חה</u><br>חבא||א | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | :{|style="color:green;" | ||
| + | |- | ||
| + | |1 zahuv = 8 dinar | ||
| + | |- | ||
| + | |1 dinar = 30 pešiṭim | ||
| + | |} | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *A piece of silver weighs 20 zequqim, 12 lot, 2 quenten, and 2 pešiṭim. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{20+\frac{12}{16}+\frac{2}{64}+\frac{2}{256}}}</math> | ||
| + | :Each lot is worth 5 Austrian dinar. How much is the price of the whole [piece of] silver? | ||
| + | |style="text-align:right;"|חתיכה כסף משקלו 0ב זקוקי' בא לוט ב' קווינטן ב' פשי' וכל לוט בעד ה' דינרי' אוישטרייך מטבע וכמה עולה דמי כל הכסף הנ"ל | ||
| + | |- | ||
| + | | | ||
| + | :Say: [If] 1 lot is worth 5 dinar, how much [is the price of] 20 zequqim, 12 lot, 2 quenten, and 2 pešiṭim? | ||
| + | |style="text-align:right;"|תאמר א' לוט בעד ה' דינרי' בכמה 0ב זקוקי' בא לוט ב' קווינטן ב' פשי‫' | ||
| + | |- | ||
| + | |rowspan=2 | | ||
| + | :The result is: 207 zehuvim, 7 dinar, and <math>\scriptstyle3{\color{red}{\frac{3}{4}}}</math> pešiṭim | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{207+\frac{7}{8}+\frac{3+\frac{3}{4}}{8\sdot30}}}</math> | ||
| + | |style="text-align:right;"|מספר העולה ז0ב זהו' ז' דינרי‫' | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |פשי‫'||<u>ד</u><br>ב||ג | ||
| + | |} | ||
| + | |- | ||
| + | |I found in another book a calculation of silver and gold | ||
| + | |style="text-align:right;"|מצאתי בספר אחר חשבון כסף וזהוב | ||
| + | |- | ||
| + | |The silver weights are explained above, but you should know that the calculation of the weights is as follows: | ||
| + | |style="text-align:right;"|ואמנם משקלו' כסף מבואר לעיל אך יש לדעת כי חשבון המשקלו' כך הן | ||
| + | |- | ||
| + | | | ||
| + | :24 carat = 1 marc | ||
| + | |style="text-align:right;"|דב קראטן א' מרקא | ||
| + | |- | ||
| + | | | ||
| + | :4 gran = 1 carat | ||
| + | |style="text-align:right;"|ד' גראן א קרַאטא | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ג גֶרען א' גרַאן | ||
| + | |- | ||
| + | | | ||
| + | *If one asks: 384 zequqim, 13 lot, 3 quenten of pure silver. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{384+\frac{13}{16}+\frac{3}{64}}}</math> | ||
| + | :You bought the zaquq for 8 zehuvim. | ||
| + | |style="text-align:right;"|אם ישאל השואל דחג זקוקי' גא לוט ג' קווינט כסף מזוקק וקנית הזקוק בעד ח' זהו‫' | ||
| + | |- | ||
| + | | | ||
| + | :The price is 3078 [zehuvim] 17 dinar, and 6 halusim. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{3078+\frac{17}{20}+\frac{6}{20\sdot12}}}</math> | ||
| + | |style="text-align:right;"|מספר ‫<ref>154v</ref>מספר חז0ג זא דינרי' ו' חלושי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תעשה כאשר אראך אמו' זקוק בעד ח' זהו' בכמה דחג זקוק גא לוט' ג' קווינטן תעשה מכולם קווינטן ויהיה מראיתו ככה | ||
| + | |- | ||
| + | | | ||
| + | :This calculation is for Frankfurt dinars | ||
| + | |style="text-align:right;"|וזה חשבון ורנקבורט דינרי‫' | ||
| + | |- | ||
| + | | | ||
| + | :{|style="color:green;" | ||
| + | |- | ||
| + | |1 zahuv = 20 dinar | ||
| + | |- | ||
| + | |1 dinar = 12 halish | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|קנית הב"א זקוקי' ג' לוט' א' קווינטן כסף ודמי מקח הכסף ח' זהו' וחצי רביעי‫' | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והצומח זא 0א זהו' ה' דנרי' ו' חלישין חלקים עשהו כאשר הראית ובהשבתו מראיתו ככה | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |גא0ח||הו זהו‫'||באה | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | *You bought 1256 zaquq at one lot of pure silver; the zaquq contains 9 lot and 3 quenten of pure silver. You bought one zaquq of pure silver for 8 zehuvim and 3 dinar; the result is 62641 zehuvim, 10 dinar, 7 halish and 14 parts of 63. | ||
| + | |style="text-align:right;"|קנית והבא זקוק בא לוט כסף מצורף והזקוק יש בתוכו ט' לוט ג' קווינטן כסף מזוקק וקנית זקוק כסף המזוקק בעד ח' זהו' ג' דנרי' והצומח הוא אדובו זהו' 0א דינרי' ז' חלישין גם | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |חלקי‫'||‫<u>דא</u><br>גו | ||
| + | |} | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עשהו כמראה הזה חשוב בראשונה כמה המספר הנ"ל עולה כסף מזוקק | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תאמר א' זקוק יש בתוכו ט' לוט ג' קווינטן כמה ישנו בתוך והבא זקוקי' בא לוט בתחילה וקצה ‫<ref>155r / ס"ד</ref>וקצה השיטה עשהו לוט ובאמצעי קווינטן כזה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תחשבהו ובהעלותך קווינט עשהו לוט ואח"כ לוט לזקוקי' עולה הוז זקוקי' גא לוט' א קווינ' ומשקל א' פשי' תאמר עוד הזקוק בעד ח' זהו' ג' דנרי' בכמה הוז זקוקי' גא לוט' א' קווינ' א' פשי' תעשה ראשי' ואחרית שהשיטה פשי' ואמציע דינרי' יועמד ככה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה לפניך גרוטאות של כסף משקלו דחג' זקוקי' גא לוט' ג' קווינט ובכל זקוק יש בתוכו ז' לוט' ג' קווינט ומשקל א' פשי' ודמי מקח זקוק כסף מזוקק ז' זהו' ג' רביעית וחצי והצומח הוא טזדא זהו' זא דינרי' ח' חלישין גם חלקי' עשהו כאשר הראיתך | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|או נלך בדרך אחרת ותא אראך דרך תלך אמור א' זקוק יש בתוכו ז' לוט ג' קווינטן משקל א' פ' כמה בתוך דחג זקוקי' ‫<ref>155v</ref> גא לוט ג' קווינטן ותעשה שוים ראשית ואחרית השיטה תביא אל המספר הקטנה ואמציעתו משקלו פשי' ותבניתו ככה יהיה | ||
| + | כפלהו וכתוב המחלק תחתיו כזה הזחַחַז0ג משקלי פשי' כסף מזוקק תוסיף עוד דו לאמר זקוק כסף מזוקק עולה דמיו זהו' בכמה ה משקלי פשי' ראשי' השיטה תעשה משקלי פשוט ותוליך שני השברי' ע"י אמצעי' שברהו על עצמו ואחרי' השיטה תעמיד המספר הכוללי ותעביר הפרטיי מעל פני וזה תבניתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|עד כאן משקלי כסף א"ם משקלי זהוב | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|הנה לפניך זקוק זהב וכבדיקתו הוא זא קרַט ודמי מקח הקראט ג' זהו' ט' דינרי' העולה חה זהו' גא דינרי' אשכילך אשר תעשה תאמר הקראט דמיו ג' זהו' ט' דינרי' כמה עולה זא קרַאט אמציעתו תעשה דינרי' וז תבניתו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|קנית גרוטאו' ‫<ref>156r / ס"ה</ref>קנית גרוטאות של זהו' ומשקלו עולה חב זקוקי' בא לוט והזקוק בהבדקו יש בתוכו וא קרַאט זהו' טהור ודמי קראט ג' זהו' רביעי' וחצי והצומח בההוא זהו' 0א דינרי' תלך בדרך זה ואז תשכיל ר ראשונה חשוב כמה עולה זהב טהור ואח"כ כמה עולה דמי זהו' טהור ויעלה המספר כמבואר | ||
| + | |- | ||
| + | | | ||
| + | *One bought scraps of gold weighing 25 zequqin, 13 lot, and 3 quenten. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{25+\frac{13}{16}+\frac{3}{64}}}</math> | ||
| + | |style="text-align:right;"|קנה הקונה גרוטאות של זהו' משקלם הב זקוקין גא לוט' ג' קווינט | ||
| + | |- | ||
| + | | | ||
| + | :One zaquq is 18 carat and 3 gran of pure gold. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{18+\frac{3}{4}}}</math> | ||
| + | |style="text-align:right;"|והזקוק הוא חא קרַאט ג' גראן זהו' מזוקק | ||
| + | |- | ||
| + | | | ||
| + | :The price of one carat is 3 zehuvim, 10 dinar and 9 halushim. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{3+\frac{10}{20}+\frac{9}{20\sdot12}}}</math> | ||
| + | |style="text-align:right;"|ודמי הקרַאטי ג' זהו' 0א דנרי' ט חלושי‫' | ||
| + | |- | ||
| + | | | ||
| + | :The result is: 1715 [zehuvim], 4 dinar, 0 halishim, and <math>\scriptstyle\frac{237}{2{\color{red}{56}}}</math> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{1715+\frac{4}{20}+\frac{\frac{237}{256}}{20\sdot12}}}</math> | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |חלקים||<u>זגב</u><br>הוב||גם||חלישי‫'||0||דינרי‫'||האזאד||עולה | ||
| + | |} | ||
| + | |- | ||
| + | |I will show you a nice method, all its results are respected | ||
| + | |style="text-align:right;"|תא אראך דרך נחמדה נכבודות כל תוצאתיה | ||
| + | |- | ||
| + | |Calculate how much pure gold scraps are worth, in gold weight. | ||
| + | |style="text-align:right;"|חשוב כמה עולה גרוט(ר)או' זהב טהור משקלו כזהב | ||
| + | |- | ||
| + | | | ||
| + | :Say: one zaquq contains 18 carat and 3 gran, how much are 25 zequqim, 13 lot, and 3 quenten worth? | ||
| + | |style="text-align:right;"|תאמר הזקוק יש בתוכו חא קראט ג' <s>ק</s> גראן כמה עולה על הב' זקוקי' גא לוט' ג' קווינ‫' | ||
| + | |- | ||
| + | | | ||
| + | :Write the beginning and the end of the line and in the middle [the conversion of] carat to gran. Its diagram is as follows: | ||
| + | |style="text-align:right;"|ראשי' ואחרית השיטה תעשה ואמציעתו ה קרַאטן לגראן ומראיתו כזה | ||
| + | |- | ||
| + | | | ||
| + | :1655 — [parts of] — 64 | ||
| + | :<math>\scriptstyle{\color{blue}{25+\frac{13}{16}+\frac{3}{64}=\frac{1655}{64}}}</math> | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |ההוא||—||זא||—||דו | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | :Multiply and divide; the result is gran. Convert to carat: | ||
| + | |style="text-align:right;"|‫<ref>156v</ref>כפול וחלק עולה גראן תעשה קראטן | ||
| + | |- | ||
| + | | | ||
| + | :The result is: 484 carat, 3 gran, and <math>\scriptstyle\frac{29}{64}</math> | ||
| + | :<math>\scriptstyle{\color{blue}{\left(25+\frac{13}{16}+\frac{3}{64}\right)\times\left(18+\frac{3}{4}\right)=484+\frac{3+\frac{29}{64}}{4}}}</math> | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |חלקי‫'||<u>טב</u><br>דו||גם||גראן||ג‫'||קראט||דחד||עולה | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|חשוב כמה עולה דמי מקחו הקראט בעד ג' זהו' 0א דינרי' ט' חלושין ועשהו גראן ואמציעתו פשי' וככה מראהו | ||
| + | |- | ||
| + | | | ||
| + | :124125 — 849 pešiṭim — 256 | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |והב||—||טדח פשי'||—||הבאדבא | ||
| + | |} | ||
| + | |- | ||
| + | | colspan=2 | | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{124125}{256}\times\frac{849}{20\sdot12}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *Scraps of gold weighing 21 zequqin, 14 lot, 3 quenten, and 3 pešiṭim. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{21+\frac{14}{16}+\frac{3}{64}+\frac{3}{256}}}</math> | ||
| + | :One zaquq weighs 22 carat and 3 gran of pure gold. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{22+\frac{3}{4}}}</math> | ||
| + | |style="text-align:right;"|גרוטאות של זהו' משקלו אב זקוקי' דא לוט' ג' קווינט ומשקל ג' פשיטי' זקוק הוא בב קראט ג' גראן עולה זהו' טהור לעשרים וארבע קראט 0ב זקוקי' בא לוט' ב' קווינ' ב' פשי' א' חליש חלקי‫' | ||
| + | |- | ||
| + | | | ||
| + | :The price of one lot of pure gold is 5 zehuvim and 5 dinar. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{5+\frac{5}{20}}}</math> | ||
| + | |style="text-align:right;"|ודמי לוט זהב טהור ה' זהו' ה דינרי‫' | ||
| + | |- | ||
| + | | | ||
| + | :The result is: 1746 zehuvim, 9 dinar, 2 halishim <math>\scriptstyle\frac{125}{128}</math> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{1746+\frac{9}{20}+\frac{2+\frac{125}{128}}{20\sdot12}}}</math> | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |colspan=9 style="text-align:right;"| עולה מספר כולו | ||
| + | |- | ||
| + | |חלקי‫'||<u>הבא</u><br>חבא||גם||חלישין||ב‫'||דינרי‫'||ט‫'||זהו‫'||ודזא | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|תעשהו לזהו' טהור ע"י הפיכה הדימיון הלזה תאמר דב קראט עולה אב זקוקי' ד' לוט ג' קווי' משקל ג' פשיט' עד כמה עולה בב קרַאט ג' גראן ראשי' ואחרי' תעשה גראן ואמציעתו משקלי פשו' וככה יועמד | ||
| + | |- | ||
| + | | | ||
| + | :91 — 5615 — 96 | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |אט||—||האוה||—||וט | ||
| + | |} | ||
| + | |- | ||
| + | | colspan=2 | | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{\left(21+\frac{14}{16}+\frac{3}{64}+\frac{3}{256}\right)\times\left(22+\frac{3}{4}\right)}{24}=\frac{5615\sdot\frac{91}{96}}{256}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|‫<ref>157r / ס"ו</ref>כפלה וחלקהו יעלה משקלו פשיטי' תעשם קווינטן והקווינטן תעשה לוט' לזקוקי' ויעלה הא דלעיל | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וחשוב דמי ממכרו אמור א' לוט ממכרו ה' זהו' ה' דינרי' בכמה 0ב זקוקה בא לוט' וכו' תכנם בשם אחד | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שברם ואמציעתו תעשה דינרי' ויועמד ככה | ||
| + | |- | ||
| + | | | ||
| + | :510965 — 105 — 153[6] | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |הוט0אה||—||ה0א||—||הגהא | ||
| + | |} | ||
| + | |- | ||
| + | | colspan=2 | | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{\left(21+\frac{14}{16}+\frac{3}{64}+\frac{3}{256}\right)\times\left(22+\frac{3}{4}\right)}{24}\times\left(5+\frac{5}{20}\right)=\frac{5615\sdot\frac{91}{96}}{256}\sdot\frac{105}{20}=\frac{105\sdot\frac{510965}{1536}}{20\sdot16}}}</math> | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | == Appendix I: Glossary of Terms == | ||
| + | {| | ||
| + | |- | ||
| + | |rank | ||
| + | |style="text-align:right;"|מעלה | ||
| + | |- | ||
| + | |addition | ||
| + | |style="text-align:right;"|חבור | ||
| + | |- | ||
| + | |division | ||
| + | |style="text-align:right;"|דיוידירו, חילוק | ||
| + | |- | ||
| + | |multiplication | ||
| + | |style="text-align:right;"|מולטי פליציטיאן | ||
| + | |- | ||
| + | |subtraction | ||
| + | |style="text-align:right;"|חיסור, נכוי, זוכט רַצטיאן | ||
| + | |} | ||
| − | + | == Notes == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div style="text-align: right;"><div class="mw-collapsible mw-collapsed"><div class="mw-collapsible-content"> | ||
| + | <br> | ||
| + | <references group=note/> | ||
| + | </div></div></div> | ||
| − | + | == Apparatus == | |
| + | <div class="mw-collapsible mw-collapsed"><div class="mw-collapsible-content"> | ||
| + | <references/> | ||
| + | </div></div> | ||
| − | + | == Bibliography == | |
| − | [[https://www.nli.org.il/he/manuscripts/NNL_ALEPH000105392/NLI#$FL30387087]] | + | '''Manuscript:'''<br> |
| + | *MS New York, Jewish Theological Seminary Ms. 2634/6 (IMHM: f F 28887), ff.125r-157r | ||
| + | [[https://www.nli.org.il/he/manuscripts/NNL_ALEPH000105392/NLI#$FL30387087 JTS2634]] | ||
Latest revision as of 04:28, 14 October 2024
| With good luck | [1]גדא טוב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| My help is from the Lord, the Maker of heaven and earth [Psalms 121, 2]. | עמי עשו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Translated into the Assyrian script and the Hebrew language. | בעתק לכתב אשורית ולשון עברית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| From the Latin script and language. | מכתב ולשון גלחות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As it is said: the tongue of the stammerers shall speak with fluent eloquence [Isaiah 32, 4]. | ע"ד ולשון עלגים תדבר צחות[note 1] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Contents[hide]Addition |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The addition indicates how much are separate numbers summed to one number. | חבור הוא המורה כמה מספרי' פרטיי' להביא ולכולל למספר אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First, one must make sure to write the numbers one below the other, correspondingly, units beneath units, the second rank beneath the second [rank] and and under them a line that is called "lina", for example: | בראשונה יש ליזהר ליכתוב המספרים זה תחת זה מכוני' אחדים תחת אחדים והמעלה השנייה תחת השניי' ותחתיהם שורה שקורין לֵינָא ודמיונה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Then, take the first number on the right and the one below it and add them together. | ואז קח המספר ראשונה בצד ימין לאשר תחתיה וחבר' יחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the resulting number consists of two ranks, write the first rank below the drawn line and keep the other in your hand. Go to the place you choose, which is the second number. Write it above its digit. Consider it as a digit, although it is of the tenths, for example: | ואם יעלה מספר משני מעלות כתוב המעלה ראשונה תחת השורה הנרשמ' והשניי' תקח בידך והלכת אל המקום אשר תבחר והיא המספר השניי' תשימה על מספרה אמנם לא תחשביה אלא כמו צורות האו' ואם כי היא ממספר העשיריות וכן דמיוני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If your calculation is complete, write the resulting sum of the two numbers. | ואם ככלות חשבונך לאחרונה אז ת [2]תכתוב החשבון כאשר יעלה שני מספרי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The scales of justice that strengthen every test: | מאזני צדק המחזקת כל בדק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cast out the nines from the numbers you summed, and keep what remains. | השליך המספרים אשר חברתם בט' ט' ואשר יוותר לך תהא ארוכה ושמורה בבטנך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Do the same with the number resulting from your calculation. | וכן תעשה למספר אשר יצאה מתוך חשבונך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If one is the same as the other, know that your calculation is correct. | ואם יהיה לזה כמו לזה תדע כי אמת חשבונך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the remainder of one of them is greater, then it is false. | ואם יוותר לאחד יותר אז הוא פסול בנותר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiplication |
מולטי פליציטיאן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם יש לדעת הלוח הנרשמ' לך כזה כי מבלעד' לא תוכל להוציא הדבר מן הכח אל הפועל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[3]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[4]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועתה אבאר בע'ה'י' בקצרה דרך נחמד מאוד כפל שהוא פחות מעשרה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועתה שמע [..]ני עדי כי לא יבורר הדבר מכל עדי כאשר אומר לך תעמיד הט המספרים מכוונים זה למטה מזה בצד ימין והמרחק אשר בינו לבין עשרה לכל אחד בצידו לצד שמאל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יעלה בידך מספר מעלה אחת אז כתוב אותו תחתיו מכוון תחת השורה הנרשמת תחתיו ואם יעלה משני [5]משני מספרי' אז תכתוב מעלה ראשונה ראשונה לצד ימין והשני כמוסה עמך עד בא עתה ואח"כ הרי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[6]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם יושם אליך מספר שמרחק יותר מהמספר אש' תכפול תעמוד המספרים זו למעלה מזו לרשו' פני המספר גלגל 0 והמספר אשר יעלה תחסר מונה אותה מספר עצמה במעלת היחידים כפי המרחק מעשר' ואשר יוותר הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ב' פעמים ב' מראיתו 0"ב חס' ב' פעמי' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ב' פעמי' ג מראי' 0ג חסר ג' פע' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ב' פעמי' ד מראי' 0ד חסר ד' פע' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ב' פעמי' ה מראי' 0ה חסר ה' פע' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ב' פעמי' ו מראי' 0ו חסר ו' פע' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ב' פעמי' ז מראי' 0ז חסר ז' פע' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ב' פעמי' ח מראי' 0ח חסר ח' פע' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[7]ב' פעמי' ט מראי' 0ט חסר ט' פע' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ג' פעמי' ג מראי' 0ג חסר ג' פע' ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ד' פעמי' ה מראי' 0ה חסר ה' פע' ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ה' פעמי' ו מראי' 0ו חסר ו' פע' ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ו' פעמי' ז מראי' 0ז חסר ד' פע' ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ז' פעמי' ח מראי' 0ח חסר ב' פע' ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ח' פעמי' ט מראי' 0ט חסר ב' פע' ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ט' פעמי' ט מראי' 0ט חסר א' פע' ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויש לדעת תחילה לכתוב המספר הנפלת ואח"כ הכפול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון רצונך לכפול הוזחט ע"י 0אבגד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעמיד המספרים זה למעל מזה וככו מראיתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמו' גלגל פעמ' ה' עולה גלגל רשום גלגל תחת השורה הנרשמת ג תמחה הכתוב למעלה ע"ז עברת קולמוס כי באם תכפלנה על כל המספר לא מעלה ולא מורדת ואחר זה תעבר על כל המספרי' [8]המספרים הכתוב למעלה ואינו עולה יותר ושום השתנו' מאשר מאשר כתוב למעלה אמו' יש לזה שיהא ה' כתוב תחת הא' אשר למעלה ממנה ושאר המספרים יהיה מראיתו ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תלך משום ותאמר עו' ב' פע' ה' עולה 0' א' תעמיד 0 למטה תחת ב' שהיא למעל' שלישי' והא' תהיה ארוכה ושמור' בבטנך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ אמור ב' פעם ו' עולה ב'א' חבר עליו א' השמור עמך עולה ג'א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| רשום ג' אחר הגלגל כמבואר וא' נעימ' ו' כי תשמר' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר עוד ב' פעמי' ז' עולה ז"א חבר עליו א' השמורה עולה ה"א כתוב ה' אחר ג' הרשומה וא' שעונה עמך עד בא עתה גם ב' פע' ח' עולה ו"א חבר אליו א' יהיה ז"א אחר ה' כתוב ז' עוד עמך א' ובאחרונ' אמור ב' פע' ט' עולה ח"א וא' הוא ט"א כתוב אות' מספר כלה העולה אחרי ז' והב' תמח' ע"י עברת קולמוס ומראיתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [9]ובזה כפֵלת ג' מספרי' אלו 0 א ב קח עוד ג' והעבירנה על כל המספרים כמבואר וככה מראיתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן לעשות עם הד' ומראה הכפל עם החבו' ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מאזני צדק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תשליך הכפל והנכפל ט' ט' וחבר הנותר משני' יחד וכן תעשה למספר הבאה ואם יוותר לזה כמו לזה ידוע תדע כי כוונתך האמת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subtraction |
חיסור או נכוי זוכט רַצטיאן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Teaching how to subtract a number from a number. | [10]הוא המורה לנכות חשבון מחשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון דוג מתוך החד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מראיתו כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The number on the bottom line will never be greater than [the number on] the upper line. | לעולם לא יהיה מספר הטור השפלה למטה עלה יותר מהטור אשר במעלה הגבוהה ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You start your calculation from the right and subtract the first bottom digit from the first upper digit. | תחילת חשבונך תתחיל מצד ימין וחסר מספר ראשונה התחתונה ממספר ראשונה עליונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The place of what remains is below the written line. | ואשר יוותר מקומו' תחת השורה הנרשמת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דימיון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמו' ה' מז' ישאר ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
העמידה תחת השירטוט הנרשמת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמו' עוד 0' מב' נשאר ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם הוא אל מקומו יושב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ה' מח' ישאר ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ו' מט' ישאר ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומראהו ככה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you cannot subtract the first bottom [digit] from the first one in the upper line, do this way For whoever finds me finds life [Proverbs 8, 35]. | ובאם לא תוכל לנכות הראשונה אשר למטה מראשונה אשר בטור העליון [11]בזה הדרך תלך כי מוצאיו מוצא חיים[note 2] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Subtract the first digit in the bottom row from the one in the second rank, which is the rank of tens and add the remainder to the preceding digit. Its place is beneath the row. | תחסר האות הראשון אשר בשור' התחתון מאותו אשר במעלה שניי' שהיא במעלה העשיריי' ואשר יוותר תחבר אל המספר אשר לפניה ומקו' מעמדה למטה תחת השורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Add 1 to the second digit in the bottom row. | ואל המספר' השניי' אשר בטור השפל תחבר אליה א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on. This is enough for the one who understands. | וכן עד עולם ולמבין די | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמור א' מב' אי אפשר לקח' אך לקחת ב' מ0'א' ישאר ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חבר אליו א' אות' מספר שלא יכלת לחסר ממנה והעולה הוא ט' ומקום ישוב' תחת הב' למטה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחב עוד להולאה א' לט' אשר במעלה שניי' יעלה 0'א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מב' אמנ' לקחת 0'א' מ0'א' טוב והנותר 0' חבר אליה ב' והעמידה למטה הקרוב א' אליו שהיא ח' תחבר א' מראיתו ט' וט' מז' אי אפשר לקחת רק מ0'א' ישאר א' עם התחבר אליה הז' עולה ח' תעמיד' במקומה כמשפטה ובאחרונה תוסיף על ו'ט'א' יהיה [12]ז' וז' מט' יוותר לך ב' ויראה ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מאזני צדק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר שני מספרי' התחתוני' יחד ואם יעלה בדרך המספר הראשון אמת חשבונך ע"א השליך שני המספרי' התוחתונים יחד ט' ט' ואם ישאר למספר ראשונה כמו כן כוונתך האמת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Division |
חילוק דיוידירו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A very nice chapter called division because it divides a general number by a number of units as many times it is found in it. | שער נחמד מאד ונקרא חלוק כי הוא מחלק מספר כוללים ע"י מספר פרטיים לכמה פעמים שהוא בתוכו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Whoever wants to truly know this chapter and acquire it in its entirety, should be careful and aim that the last digit of the divisor be corresponding beneath the last digit of the upper row, which is the dividend and write the rest [of the digits] close to it from left to right. | הרוצה לדעת אמיתי' זה שער ולקנות שלימתו צריך ליזהר ולכוון שיהא האות האחרון ממספר החולק מכוון תחת האות אחרונ' מטור העליון שהוא הנחלק והשנייה לשארו הקרוב אליו מצד שמאל לצד ימין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון רצונך לחלק וטג על יד וג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיוני כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר [13]וכאשר יקרא לפניך שהחולק עולה יותר ממספר אותיות אשר למעלה ממנה אם נעמידהו כמבואר צריך להשים כל מספר החולק לאחוריו לצד ימין כמלוא' מעלה אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דימיון רצונך לחלוק והג ע"י וג ממקומו כרשום לפניך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויש לדעת כי כמו הרבה פעמים אי לקח החולק האחרון ממספר אחרונ' למעלה ממנה כמו כן יש לקחת כל אותיות מאות' המספר מהספרים אשר למעלה מהן ומספר כמה פעמי' אשר יוחלק יכתב בתוך חצי העיגול הנרשם לך בזה רצוני לחלוק והג ע"י וג דימיון מראהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכה תאמר כמה פעמי' ו'ו' ג' מה"ג באשר או אוכל ליקח ה"ו כמו כן פעמי' יוקח ט' פע' ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמו' ט' פעמי' ג' עולה ז"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחסר מה"ג וישאר ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תשימ' למעלה במעלה הגבוהה מן הה' ומחוק ה"ג ע"י העבר' קולמוס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול ו' על ט' והעולה הוא ד'ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חסרה מו'ח' יוותר לך ב'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם עדיין יש לך לקחת החולק מהנחלק אמנם אין במספר [14]אשר למעלה ממנה כדי לנכות' תמשך החולק במעלה אחת לאחוריה וככה מראיתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם יקרא לפניך הן בתחילה הן בסופה הן באמצע שלא שתוכל לקח המספר הקטנה מאותה אשר למעלה ממנה תמשוך אותה מעלה אחת לאחוריה ובמקומ' תרשום בתוך חצי עיגול גלגל 0 וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דימיון לחלוק 0אבג ע"י בג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מראיתו ככה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מאזני צדק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח החולק גם המספר העולה ממנה וחברם יחד והשליכם ט' ט' ואם נשאר דבר מאות' למעלה תחבר ג"כ אליה והעולה כתוב לפניך וכן תעשה למספר אשר היא למעלה ממנה ואם ישאר לזה כמו לזה אמת חשבונך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלוק דוידיריו תאל [15]תאל ואשכילך ואראך דמיון לחלוק בבטבחא ע"י א0ב מראיתו ככה וכן תעשה עד סוף הדורות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| האמור כמבואר לעיל כמה פעמי' נוכל ליקח ב' מח"א באופן זה שגם לאותה אשר לפניה יעשה כן והוא ט' פעמים ב' פע' ט' הוא ח"א נכנו מח"א לא ישאר בידך מאומה ט' פעמי' גלגל אינו עולה שום מספר ואותה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תמשוך השורה התחתונה מעלה אחת לאחוריה כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [16]תאמר עוד כמה פע' תוכל ליקח ב' מב' אשר היא בשורה העליונה למעלה ממנה מכוון אינו כ"א פעמי' אחת ולא ישאר לך מאומה א' פע' 0 הוא 0' א' פע' א' הוא א' נחסרנו מב' ישאר א' ומראהו כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיא באחרונה תשנה החולק עו' מעל' אחת וככה מראיתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיה אם לא תוכל ליקח עוד החולק מהנחלק וכלית חשבונך לפני א"ט תעמיד 0 ומראיתו כזה 0אט והנותר הוא ב"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מאזני צדק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| השליך ט' ט' מהמספר העלה בתוך חצי העיגול וישאר א' וכן אותה אשר חלקת בה [17]בה ישאר ג' תאמר א' פע' ג' חבר אליו הנותר על ט' מאות' מספר אשר נשארה לך בשורה עליונה והוא ג' עולה ו' ואם יוותר לעליונה כמו כן אמת חשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Progression |
שער לשער החבור פראגרעשיא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הוא המורה לחבר דרך קצרה אשר הוא קרוב אל השכל להשיג לחבר כמה מספרי' יחד שהם כתוב בזה אחר זה בין הראשונים בין האמצעיים בין הסופיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשהו כן חבר הראשונה אל הסופי' והעולה תחציהו באם הוא באפשרו' אח"כ תכפול מספר המעלת כמה הם והעולה הוא סך מחבר כל המעלות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם לא תוכל לחצהו תחלוק מספר המעלות למחציתו וכפול בהן כאשר אראך בציור דמיוני אלו ודו"ק בהן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון ז ח ט 0א אא בא גא דא הא וא זא חא טא 0ב בא בג בד בה כמה עולה מספר כולם ביחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[18]תחבר ז' לכ"ה והעולה הוא ב"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחצית' יעלה ו"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפלום על מספר המעלת והם ט"א והעולה הוא ד0ג ככה מספר המעלות הכתוב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אי אפשר לחצות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון ג ו ט בא הא חא אב דב זב 0ג גג וג טג בד הד חד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר ג' אל חד עולה אה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואינ' נחלקי' בשוה לכן תמנה מספר המעלות והם וא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחצית עולה ח' כפלם על אה עולה ח0ד כל המספר כולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם המספריי' כל אחת כפולות משלפניה שניי' אי שלשיי' או רביעי' חמשיי' עד עולה קח המספר האחרונה כפליים ומהעולה תקח מספר ראשונה פחת א' כאשר אצייר לך בדמיונו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון ב ד ח וא בג דו חבא והב באה דב0א חד0ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול חד0ב ובו0ד חסר ב' ראשונה עולה דט0דח חלקם ע"י פחות א' דהיינו א' וישאר אותה מספר עצמה ואם לאחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [19]ואם לאחת שלש על חברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון ג' ט' זב אח גדב טבז זחאב אוהו כמה עולה מספר כולם ביחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תכפול מספר אחרונה ע"י ג' גחוטא חסר מנה ג' דהיינו מספר ראשונה נשאר 0חוטא חלוק ע"י ג' פחות א' דהיינו ע"י ב' עולה 0דחד וכן עד כל הדורות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נשלם שער פרמיגירעשיא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A short way to know weights and measures of coins and of time - belongs to division | דרך קצרה לדעת משקלות ומדה ממטבעות גם על העתיד שייך לחלוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [24] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter on Proportions - Rule of Three |
שער הערכין רגולא רעטלי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Very nice [rule], all its results are respectable. | נחמד מאד נכבדות כל תוצאותיה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| These are three numbers by which the eye can reach the fourth number that is hidden from the eyes of the entire community. | והוא [25]משלש ספרים וע"י יוכל העיין להגיע אל מספ' הרביעי' אשר הוא נעלמה מעיני העדה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון קנית ככר זפרן בעד 00ח זהובי' כמה מגיע דמי מקח הב' לטראו' זפראן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מספר העולה 00ב זהו' והיא נעלמה ממך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As the first number contains the second, so the third contains the fourth, and as the third is contained in the first, so the fourth is contained in the second.
|
וכמו' אשר כולל המספר הראשונה השניי' גם השלישי' ורביעי' ככה וכאשר נכלל השלישית בראשונה כמו כן נכלל הרביעי' בשניי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון חא ליטראו' בעד ט' זהו' כמה עולה ד"ב ליטראות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מספר העולה הוא ב"א זהו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה המספר הראשונה כוללת השניי' ב' פעמי' כמו כן כוללת השלישי' לרביעית ב' פעמי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה הראשונה נכלל בשלישי פע' א' ושלישי וכן השלישי נכלל ברביעי' פע' א' ורביעי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר מרחק א' מב' כמו כן המרחק מג' לד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר המרחק א' לג' ככה ב' לד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה לדעת המספר הנעלמה [26]כפול מספר השאלה על האמצעי אח"כ חלוק העולה ע"י הראשונה והוא מורה המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון בג לטראו' דב זהובי' כמה עולה ערך ח' לטראו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ו' זהו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם יקרא לפניך באמצעת איזו מיני מטבעות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| בראשונה כפול המספר השלישי על המטבע הגדולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותן לחכם עוד [27]ותן לחכם עוד כי כן לעשות לכל הדומים לו במטבע אוישטרייך ד' דריילינג הן 0ט זהו' ג' דינרי' חא פשיטי' כמה עולה דמי ערך ז' דריילינג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זהא זהו' וא' דינרי' יהא שמור' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ט דנרי' 0ג פשיטי' שמורים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מספר העולה הוא תהא זהו' ב' דנרי' ט' פשיטי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| במטבע אונגריש קנייני דהב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מספרם בטז זהובים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קנייני יין במדה ובמטבעו' נוירבורג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[28]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מספר העולה ב"ז זהו' מטבעו' בדהב קנייני בגד ו"ג אמות טד זהו' ב"א אמות ט' אמות דב זהו' 0"א דינרי' ו' אמו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מספר העולה וא זהו' ו' דינ' ת חלושי' סך העולה 0א ה' דינרי' 0א פשיטי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתים עד מטבעות אוישטריך שנה נותן חבא זהו' כמה שנה אח' ב' שני' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דו זהו' וב' שבועו' כ"ג זהו' כמה הא שבועה ט' שבועות ג' ימי' ב"א שעות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| באם יושם לפניך [29]באם יושם לפניך חשבון גדול ורצונך לידע ולראות אחר מספר קטנה שהוא דמיונה דוק וראה ובקש איז מספר אשר המספרי' השניי' לו נחלקי' ע"י בשוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון דב לטר' דו זהו' ז' דנרי' חא פשיטי' בא לטראו' מספרים אלו תוכל להקטונה עי"ד קח חצי מדב לטר' עולה מ בא לטר' וחצי מספר' האמצעי הוא בג' ג' דנרי' דב פשיטי' ומראיתו ככה בא לטר' בג' זהו' ג' דנרי' דב פשיטי' בכמה בא ליט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או נלך בדרך זה כי אורחת חיים תחצי המספרי' הראשון ואחרון ואמצעי כרקאי קאי ויהא מראי' כזה בא ליטר' דו זהו' ז' דנרי' ח"א פ' ו' ליטר' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותוכל עוד להקטין המספר הראשון ע"י ד' ג"כ לחצות האחרונה וירא ג' ליטר' בג' זהו' ג' דנרי' דב פש' ג' ליטראו' עושה הדמיונת הכתוב לפניך כמבואר לעיל כי מספר כולם שוה כאשר הראית בדמיונ' הכתוב למעלה ובהיות כאשר יקרא לפניך גלגל כזה 0 לפני המס' תדע [30]ותבין כמה מספרי' מחקת מהספרי' הראשונ' כמו כן יש למחוק מהאמצעי' או מאחרונ' כאשר תרצה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שער הערכין רעגילא דעטרי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תקשין המספר הלזה עוד כאשר הראיתך ו ככ' 00ג זהו' 0א ככרים א ככר 0ה לטר' 0הא זהו' ה' ככרים זג לטר' וא לוט הז זהו' ב' ככר 0ה לטר' וכו' וסך העולה מכולם אחד והוא 00א זהו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מאזני צדק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחליף הדמיון באופן זה הפנים לאחור ואחור לפני' והמספר העלת ביני לאמצע ועשה כאשרה ראית ואם התוך העולה הוא המספר אשר לפני' הרת' אמצעית אז [31]תדע כי אמת חשבונך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון דב לט' חא זהו' בא לטר' הסך המגיע לו הוא ט' לחלופו בא לט' ט' זהו' דב לטר' והמגיע לו חא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם נשאר לך בחושבנך אשר לא עלה לחלק הנותר אל תזיז ממקומו עד אם כפלת האחרונ' על המטבעו' הדומו' לו ואז חבר אל המספר הבא' הנשאר' ועשהו כאשר הראיתך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון בג לטר' ט' זהו' בא לטראו' עולה ח' זהו' ב' דינרי' גא פשיטי' עוד נשארו חא פשיטי' שלא באו לחשבון וחלופו בא לטר' ח' זהו' ג' דנרי' ג"א פשיטי' ג"ב לטראות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם אין הדמיונות כתוב כהלכתן או שום מעות בעולם בקש וראה השאלה ואותה תעמיד חוצה באחרונ' ושם הדומה לו ראשונה ובכן בא לך השלישי באמצע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון דב לט' כל [32]לטר' בעד ב' זהו' עד כמה מגיע דמי מקחו והנה דב היא השאלה לכן יש לצידו בציור זה אשר אצייר לך והא לך דמיונו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| א' לט' ב' זהו' דב לטראות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וסליק לך שער ערכין כאשר מצאתיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| With good fortune I start to translate this chapter of fractions from Latin, to the best of my ability, although it is little, I do my best with the help of God in Heaven. | בטוב גדא אתחיל דא שער השברי' להעתיק מלשון גלחות כפי יכולתי ואם כי היא קטנה אנא דידי עבידנ' בעזר' אלקי' דשמיא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| One should understand that every fraction, which is called fraction in Latin, has two letters and between them a line, called linea or ? | יש להבין שכל השברין הנקרא בלשון לטינא פַראַצְטיָאן יש לו ב' אותיות וביניהם שורה אחת הנקרא לִינַא או פירגיל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The upper letter is called the numerator [lit. number], which is the number of the parts. | האות העליונה נקרא' המספ' שהוא מספר מספר החלקי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The bottom [letter] is called the denominator [lit. dissolving], for it divides the integers by its number. | והתחתון הפורט כי הוא מחלק השלמי' ע"י מספרי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה דמיונו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לחלוק השבר [33]לחלוק השבר ולחצותו ולהקטינו עד האפשרו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דנא ואראך דרך אשר תלך בו ואז תשכיל בעז"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| בקש מספר אשר שני המספרי' נחלקי' ע"י מכוון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יחלק וישבר למחציתו דהיינו בשנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יחלק עוד למחציתו בשני' ויעלה בידך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד בשני' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואי אפשר עוד למחציתו בב' נקטין אותו ונעשנו לשלישי' והעולה הוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נכה ממנה עו' השביעיו' ויוותר לך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן עולמי' ובזה הדרך נלך ללו"ד וכן מלו"ד דהיינו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יחלק בעשריו' ועו' בה עשרי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the tongue of the stammerers shall speak clearly [Isaiah 32, 4] | לכתיב אשורי' וללשון עברי' מכתב ולשון גלחת ע"ד ולשון עלגים תדבר צחות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| להביא כמה מיני שברי' אל כח המדבר להיות אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| באם יקרא לפניך שים או שלשה [34]מיני שברי' ואין קריאת' ופרטיהם שוין לך בדרך אשר אראך כי הוא ארוכה וקצרה ושמץ לא נשמע פה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול תחילה הפרטי' הפרטי' הפורטים המספר והעולה יקרא הפרטיי' והוה ממוצע השוה לכולם לשניהם ור וירשם לפניך העול ב' פעמי' אח"כ המספר הראשונה אשר הוא בטור העליונה תכפול על הפרטיי' השני אשר הוא מושפל למטה והעולה הוא המספר הכוללי' מהראשון ותכתבהו על הפרטיי' הממוצע הרשום לפניך ראשונה וכן ל תעשה למספַר השני נקט האי כללא המספר הראשונה תכפל על הפרטי השני והמספ' השני תכפול על הפרטי הראשון והעולה מכל אחד ואחד תכתוב על אחד מה פרטיי' הנרשמי' לפניך הראשון ראשון ואחרון אחרון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דומיונו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שוים שוים זה לזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שוים זה לזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובקל תוכל לבדוק אם כוונתך לאמת חשבונך באם תביא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| למספ' הקטנה יעלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם יקרא לפניך שלמי' ושברי' להביאה וכח המדבר ע"י שברי' או שברי' ושלמים יש להשוות השלמים והשברי' יחד באופן זה כפול השלימי' עם הפרטיי' מאות' מספר והעולה תחבר אל המספר ותח' הכלל העולה תרשום הפרטיי' אשר כפלת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודמיונ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהשוותך המדות יהיה מראיתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם אם יש להשוותו שברים עם שלמים תשבר השלם ברשימות תחתיו אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיונו ח עם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fractions of Fractions |
שביר' משבירות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שבירה משבירות הוא חלק מחלק דמיונו אם לקחתי חצי זהו' ורצוני לחצות והצומח הוא רביעי' מזהו' שלם עשהו כך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול הכללים העליונים הנקראי' מסַפרים ואח"כ הפרטיים והשבירה אחרונה מורה תשובה על שאילתו שאלת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון יש לי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Which is 10 pešiṭim in Augsburg's coin. | שהוא 0א פשיטי' במטבע אויגשבורג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| True scales that strengthen every check [37] | מאזני צדק המחזיק כל בדק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תתחיל [38]תתחיל במספר האחרונה ואמו' קח שביעי מזהו' שלם ה' דינרי' ואות חצי עולה ב' דנרי' וח' דהיינו ט"ו פשי' נכה עוד ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לידע בשני שברי' איזה מהם עולה מספרו יותר מחבירו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תצייר פני כל מסַפר שהוא הכוללי' ב' גלגלים 00 וחלוק אותו מספר כולה בכתיבת וקריאה ע"י מספרו הפרטיי' ואותו שעולה מספרה יותר גם מספר' עולה יותר מחברת' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תצייר אצל ג' ב' גלגלים הנקראי' נולא ויעלה 00ג תחלקם בד' ומספר כלה הז' וכן לז' תעשה כן צייר לפניה 00 עולה 00ז תחלק' בח' והצומח זח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [39]ולא דבר רק הוא חכם הגם כי אפשר לידע ע"י הכאה בפרטיי' אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תביא' לפרטיי אחד ויהיה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולפי חשבון זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מכאן ואילך אראך בקיצור דרך תלך על חבור חסר חלוק כפל ערכין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter on Addition |
שער החבור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First know for sure and also see if the denominators are equal, then you will be successful in all your ways. [40] | בתחילה ידוע תדע גם תראה עם הפרטיי' שוים ואז תהיה בכל דרכיך משכיל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם הפרטיי' שוים תחבר המספרי' הכוללי' יחד ופרטי אחד יהיה תחתיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם אין תכפלם הכוללי הראשון לפרטי אחרון והפוך בה ותחבר שניהם יחד והפרטי' כפולי' תחתיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As here: | כאשר לפניך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחבר יחד ח ה אא יעלה דב תרשום תחתיהם גא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומראיתו ככה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אינו שוות [41]ואם אינם שווים הפרטיי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם [או תדמי] בחשבונך יותר מב' שברי' לחבר יחד ואין פרוטיהם שווים תחבר זה אחר זה ובכפל כמבואר וכאשר אראך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה לפניך לחבר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחבר השני המספרים הראשונים יחד דהיינו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תחבר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subtraction of Fractions |
חסר בשברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| באם שני הפרטים שוים קח כוללי או מספר מכוללי ואשר הוא כתוב תחתיו פרטי אחד ובאים אינם שוים תכפול הכלולי כמבואר שתי וערב ועולה משניה' תנכה ותחסר זה מזה והנשאר כתוב תחתיו הפרטים כפולים כאשר הוא [42]לפניך דמיון תחסר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם אין הפרטי' שוים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תנכה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| באם תחסר שברי' משלמי' קח הכוללי' מהפרטי' ואשר יוותר בידך תרשום תחת הפרטי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דימיונו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תפול ה' מא"א וישא' ו' ותחתיהם ע תעמיד א"א וככה תבניתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דרך אחרת נלך בו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תשבר השלם בסמיכה תחתו או כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
וכפול כדלמעלה בתבניתו  חסר וישאר בידך חסר וישאר בידך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לחסור שלמי' ושברי' משלמי' ושברי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תכפול השלמי' עם הפרטי' תחבר הכוללי ועולה כדעיל במקום הכוללי ואח"כ תכפלהו וחסרהו [43]וחסרהו כמו למעלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תבניתו ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול שלמי' ופרטיי' ומראיתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועשהו כמבואה והנשאר הוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Doubling |
כפל בשנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תכפול או תחלק הפרטיי' למחצית תבנית ב' פעמי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן ב' פעמי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Halving |
למחלק למחציתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חצי הכוללי באם הוא באפשרי ואם אין כפול הפרט' כאשר אבאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון חצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כל הדומה לו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiplication of Fractions |
כפל גדול בשברי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [44]כפול יחד הכוללי' ואח"כ הפרטיי' כל אחד ואחד בפני עצמו אמו' כמדומה לי יש לדעת לחלוק הסך העולה משניהם במעלה השפולו' שאפרוש אך יחלק במכוון בשלמי' ולא בחצאין והנשאר הוא המבוקש כך נעלד ואף כי לא בפירש איתמר אמנם מכללא אתמר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מצאתי דמיונו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואיך זה באשרו' אם לא שנעשנו כאשר אמרת גם מצאתי בספר אחר כתוב אל תתמה על מה שהסך העולה מועט מהסך הנכפל ואין בכך הפסד והטעם לא ידעתי ודוק ותמצא כאשר אמרתי וד"ל ואח"כ דקדקתי בו יותר ומצאתי כי הכל אחד כי הפרטי יחלק כמו הכוללי ואח"כ חשבונך מכוון וד"ל כך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לכפול שלמים עם שברי' וחתיכו' כמראה כתוב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שבור השלמי' ע"י בכתיב' א ואח"כ עשהו כאשר הראיתך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שלמי' [45]שלמים עם שברי' ושלמי' או שברי' ושלמי' עם שברי' ושלמי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשהו כאשר הראתיך אך כפול השלמי' על הפרטי' וחברוהו אל הכוללי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיונו ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותן לחכם ויחכם עוד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן דמיונו ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשהו כמבואר יבא בחשבונך גא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Division |
דוידירו הוא חלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| בהיות הפרטיי' שווי' חלק בכוללי ואם אינם שווים כפלם כמבואר והמספר אשר תחלק תעמיד במעלה הגבוה והחלק במעלה המושפל כאשר בשלמי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה תבניתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והעולה הוא ד' מכוון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [46]ואם שאינם שוים הפרטים דמיונו כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| רצונך לחלק שברים במספר שלמה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תוכל לחלק די כלולי מכוון בלא השארים אחרי' ע"י השלמה עשהו וזהו בנקל ותחת העולה כתוב הפרטם ואם ואין כפול המספר השלמה על הפרטיי' והכוללו יעמיד בארשונה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה דמיון השוה לחלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ע"י ד' שלמים חלק ב"א ע"י ד' עולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה דמיון אחרים הנה לפניך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כל הדומי' לו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לחלק השברים ע"י שברים ושלמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה השלמים לחלוקים כמבואר ואח"כ חלקוהו כמראה אשר הראיתך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשהו כמבואר עולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה יגד די עי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שייך לשער כפל גדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שברי' בלי [47]שברי' בלי שלמי' בצדם עם שלמי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלוק ג' בשני חלקי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שברים עם שלימי' בצדם עם שלמי' בלי שברי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שברי' עם שלמי' בצדם עם שלמי' ושברי' בצדה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שברי' בלי שלמי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הדרך הטוב הוא לכפול יחד המספרי' העליונה אח"כ התחתוני' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proportions |
ערכין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יש לעשותו כמו בשלמי' לכפול האחרון ע"י האמצעי' ואח"כ לחולקו ע"י הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון קנית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ג' ע"י ד' עולה בא הוא המספר או כוללי כמו כן כפול ז' ע"י ה' עולה ה"ג הוא הפרטיי מראיתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלקוהו ע"י | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והתבררנ' שברי' כנ"ל הוא המתבקשו' ג' מספרי' שלמי' הנשוואות עם [49]עם דמיון השברי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וא' זהו' כמה המגיע על ג' לטראו' או הא' לטראו' דמי מקח' וא' זהו' כמה מגיע על א' לטרא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם החשבון הנוהגים עכשיו ככה הוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה כל השברי' עומדין כל אחד בפני עצמו או יש לו שלמיו' בצדו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם יועמד לחוד כמראי' ככה יהיה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יש לו שלמי' בצדו אז כפול הפרטיי' ע"י שלם כמבו' והעולה חבר אל הכוללי' ותחתיו הפרטי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאם יהיה לפניך שלם בלי שברי' בצדו העמוד תחתיו א' במקום בפרטיי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| להביא הציורי' השבורי' ולעשות שלמי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול הפרטי' האחרון אשר לצד שמאלי' [50]ע"י האמצעי העולה כפול על הכללי הראשון ובאחרונה כפול הפרטיי הראשון על הכללי האמצעי והפרטיי האמצעי על הכללי האחרון וככה יועמד הציור הלזה בשלמי' ולעשתו כאשר כתבתי לך לעיל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והא לך ציורי' אילו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהקנותך שלמיות ככה יהיו אי לטר' ד' זהו' ו' לטראות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| העולה הוא דב זהו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ב' לט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ככה יועמד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובשלימותו [51] ובשלימותו זה יהיה תבניתו ד' לטר' א' זה' ו' לט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| העולה הוא א' זהו' ד'ד' דנרי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולטראו' דא זהו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יועמד ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובשלימותו דב לטר' דא זה' א' לטר' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| העולה הוא ד' דנרי' 0ב פשי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יועמד ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובשלימותו ז' לטר' חא זהו' ט' לטראו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסך העולה גב זהו' א' דינר ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [52]ו' לטר' ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מראיתו ככה יהיה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובשלימתו חא לט' ז' זהו' בא לטראו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסך העולה הוא ד' זהו' ה' דנרי' 0"א פשי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ט' לטר' ו' זהו' ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זה תבניתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה תבניתו בהיותו במלואו וג' לט' ו' זהו' גג לטראות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| העולה הוא ה' זהו' ד' דנרי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יועמד ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובעמדו [53] ובעמדו בשלימתו ו"ז לטר' גא זהו' בא לט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המספר העולה הוא ב' זהו' 0 דנרי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ו' לטר' ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יועמד ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהשלמתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המספר העולה י"ו זהו' ב' דנרי' הא לטראו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יועמד ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| בהשלמתו דבא לטר' 00ד לט' זג לט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| העולה טאא זהו' ב' דנרי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [54]ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מראיתו ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיה בהשלימך המספרי' דח לט' ז"א זהו' ו"ה לטראו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| העולה הוא אא זהו' וב' דנרי' 0ב פשיט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהשוואות לשלימות בז לט' הח כד פשי' כד לטר' מספרם 0א זהו' ג דנרי' [...] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יועמד ככה ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מספר [55]מספר העולה ב' זהו' א' דינר זא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Exchange: Hungarian gold coin and Rheinos gold coin | חלוף לעשות זהו' אונגריש במטבע גם זהו' רינוס במטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiply the Hungarian gold coins by the number of Austrian dinar in a Hungarian gold coin, then divide the product by the number of dinar in a Rheinos gold coin, which is 8. | תכפול זהו' אונגריש על מספר כמה דינרי' אוישטרייך בזהו' אונגריש ואשר יעלה במצודתך תחלקהו ע"י מספר הדינרי' מזהו' רינוס והיא ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם ישאל השואל דמיון יש לאחד חדב זהו' אונגריש במטבע והשאלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול חדב על 0א יעלה 0חדב תחלקם בח ויעל 0אג זהו רינוס במטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I shall teach you also to calculate Hungarian gold coin from Rheinos gold coin | תא ואאלפך עוד לחשוב זהו' אונגריש במטבע מתוך זהו' רינוס במטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiply the Rheinos gold coins by 8 dinar, then divide the product by 10 dinar etc. | כפול זהו' רינוס על ח' דינרי' וחלוק העולה ע"י 0א דינרי' וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דימיון הרי לפניך 0אג זהו' רינוס במטבע ו [56]ובקשתו לדעת כמה יעלה מנינ' וזהו' אונגריש במטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול 0אג זהו' על ח' דנרי' וי' ויעלה 0חדב תחלקם ע"י 0א והמבוקש הוא חדב זהו אונגריש במטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| To find the [value of] Rheinos gold coins in Hungarian gold coins. | למצא זהו' רינוס במטבע בתוך זהו' דהב אונגריש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiply the Hungarian gold coins by 11 dinar, then the units by the exchange rate. Convert the pašuṭim into dinar, add them to the former, and seek for the gold coins in the dinar that are divided by 8. | כפול זהו' אונגריש על אא דינר ואח"כ ביחידי' על שבח החלוף ומן הפשי' תעשה דנרי' וחברם אל הראשוני' ובקש מתוך הדנרי' זהו' נחלקי' בח' וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון יש לו 0וג זהו' אונגריש בדהב ודמי זהו' אונגריש בדהב אא דינרי' ושבח החילוף בא פשי' השאלה כמה עולה סך זהו' אונגריש הנ"ל זהו' רינוס במטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול 0הג זהו' דהב הנ"ל על א'א' דינרי' ויעלה 0וטג דינרי' כפלם עוד על בא פשיטי' ויצמח 0בגד פשי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Comparing Two Types of Cubits | השוואות שני מיני אמות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קניתי דב אמות 0אוט בעיר ווין והאמה בעד ד' זהו' רינוס ובהביאם לאובן במדינת אונגרן נתתי האמה בד' זהו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תאמר האמר בעד ד' זהו' רינוס כמה מגיע דמי מקח דב אמות הצומח וט זהו' רינוס בחוץ יהיה מושבת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
בקש עוד כמה עולה דב אמו' בווינא אמו' אובן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תאמר ג' אמו' בווינא הם ד' אמו' באובן כמה עולה על דב אמו' ווינ' הצומח בג אמו' אובן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תאמר עוד תאמר עוד א' אמה בעד ד' זהו' אונגריש כמה יגיע על ב"ג אמו' מספרי' חבא זהו' אונגריש והם 0וא זהו' רינוס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[58]חסר ממנו וט זהו' ריינוס יוותר לך דו זהו' ריינוס והוא הריווח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם יש לדעת ולברר אמיתתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן לעשות במדה במשקל ובמשורה לחשוב חשבונו' אילו לידע הריווח יוסף על דמי המקח ההוצא' אשר הוציא עליהם בהליכתו למקום אחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שבירות עגלי' למדינו' מרחק משקל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נתתי שבירו' על בא ככרים וג' פרסאות הא זהו' רינוס ובקשת למצו' שכירות המגיע על דב ככרי' חא פרסאו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויש להעמידו ב' פעמי' על אופניו בתחילה בא ככרי' שכרו הא זהו' רינוס כמה המגיע על דב ככרי' מספרו 0ג זהו' רינוס ובשניי' וג ככרי' נותני' 0ג זהו' רינוס כמה מגיע חא פרסאות מספרו הצומח הא זהו' רינוס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חשבון זה שייך לחייטין [59]חשבון זה שייך לחייטין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קניתי ו' אמות בגד למלבוש ורוחב האמה א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אראך אשר תעשה תרבע הבגד על דרך זה כפול ארכו אפותיו והעולה ט' תרבע כמו כן הבגד אשר תחתיו והעולה הוא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| רוחבו ובו תחלק ט' רוחב הראשונה ומראה מספרו הוא ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הרוצה לחשוב ולידע ריווח בדבר כאשר תרצה להרוויח כך תוסיף על דמי מקנתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון קניתי 0בא ככרי' שעוה בעד וטבא זהו' רינוס כמה מגיע על א' לטר' אשר תוכל להרוויח בכל הסחורה כולו וטא זהובי' רינוס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר 0בא ככרי' בעד בטדא זהו' רינוס כמה עולה א' לטר' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [60]ריווח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מכרתי בגד האמה בעד ה' דינרי' אויש' והרווחתי ב0א אמו' א' זהו' ב' דינרי' ובקש' לדעת בכמה קנית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמ' בראשונה תאמר 0א אמו' מרויחי' א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הפסד בדבר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מכרתי בגד האמה בעד ה' דנרי' והפסיד ב0ב אמו' ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמו' 0ב אמו' עולין ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I bought 6 kikkar of peppers, each fine quality kikkar is worth 50 Rheinos. If there are 5 damaged liters in each kikkar and you want to know how much the fine quality peppers are worth without the damaged ones. | קניתי ו' ככרי' פלפלין וכל ככר מזוקק ומנופ' בעד 0ה זהו' ריינוס ובאם יש בכל ככר ה' לטר' פסולו' ובקשת לדעת בכמה הפלפלין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר א' ככר יש בתוכו ה' ליט' פסולו' וקח מכל ככר ה' לטר' עולה 0ג לטר' חסר' מעל ו' ככרי' יוותר לך ה' ככרי' 0ז לטר' נקרי' באחרונה תאמר א' ככר בעד 0"ה זהו' רינוס בכמה ה' ככרים 0ז ליטר' עולה מספרו החב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Barter |
חלוף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| One has 7 liters of turmeric and he sells the liter for 6 Rheinos gold coins and in barter he sells it for a price of 7 Rheinos gold coins. The other has 30 liters of peppers in barter, each liter is worth 5 Austrian dinar. By how much will he raise the price of a liter of peppers and how much will he give to his friend? | יש לאחד ז' לטר' כרכום ומוכרי' הלטר' בעד ו' זהו' רינוס ובהחלוף נותן ערכו עליו בעד ז' זהו' רינוס ויש לאחר בחלופו 0ג לטר' פלפלין וכל לט' בעד ה' דינרי' אוישטרייך בכמה יאריך זה לפי ערכו א' לטר' פלפלין ואיזה מהם יתן עוד לחבירו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון תאמר ו' זהו' רינוס נעשי' בחלוף ז' זהו' רינוס ומה יהיה על ה' דנרי' עולין ה' דינרי' ה[..] פשי' וחשוב אכ אח"כ כל סחורה וסחורה בפני עצמה כגון א' לטר' כרכום בעד ז' זהו' רינוס בכמה עולה על לטר' עולה טד זהו' רינוס נלך עוד משם ונאמר א' לטר' פ [62]פלפלין בעד דינרי' הב פשי' בכמה 0ג לטר' עולה אב זהו' רינוס ז' דינרי' חסר' מעל טז זהו' רינוס יוותר לך זב זהו' רינוס א' דינר וזהו חיוב בעל הפלפלין לבעל הכרכום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Partnership |
שותפות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Three form a partnership together | שלוש' עושים שותפות ביחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| They earn 720 Rheinos zehuvim together. | והרוויחו ביחד 0בז זהו' רינוס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| One wishes to know how much is owed to each according to what he contributed.
Want to know how much is owed to each person based on what they contributed. |
והרוצה לדעת המגיע לכל אחד לפי ערך אשר הניח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ילך בדרך זה חבר יחד מה שהניחו בשותפו' והעולה תשמור ביך בידך והוא יהיה החולק כפול הריווח שהרוויח על אשר הניח לכל אחד בפני עצמו והעולה חלוק במספר השמור לך לחולק ואז תשכיל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Three made a joint deal to divide between them 360 Hungarian coins: | [63]ג' שעשו עיסקא בהדדי ויש לחלק ביניהם 0וג זהו' אונגריש במטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשהו כאשר הראיתך והיה ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שלשה שהטילו לכיס הראשון מניח גרוטאו' של כסף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אשכילך את אשר תעשה תאמר 0ח"ב באי' ע"י דו זהו' רינוס כמה הטיל הראשון שבאו לו 0ד לוטא' עולה דמיו ט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמה מגיע אשר ממנו באו 0ח לוטא' עולה 0ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שלשה שעשו שותפין ביחד הראשון נתן 0א זהו' רינוס ונותן ונוש' בו 0ב שבועות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Currency calculations |
חשבון כסף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חתיכה כסף משקלו בא זקוקי' גא לוט ג' קווינטן א' פשי' וכשתסיר ממנו הסיגי' ותצרפנו יש בזקוק כסף מזוקק דא לוט ג' קווינטן ב' פשי' כמה כסף [65]כמה כסף מצורף בתוך בא זקוקי' גא לוט ג' קווינטן א' פשי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עולה אא זקוקי' הא לוט א' קווינטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חתיכה כסף משקלו 0ב זקוקי' בא לוט ב' קווינטן ב' פשי' וכל לוט בעד ה' דינרי' אוישטרייך מטבע וכמה עולה דמי כל הכסף הנ"ל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תאמר א' לוט בעד ה' דינרי' בכמה 0ב זקוקי' בא לוט ב' קווינטן ב' פשי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מספר העולה ז0ב זהו' ז' דינרי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I found in another book a calculation of silver and gold | מצאתי בספר אחר חשבון כסף וזהוב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The silver weights are explained above, but you should know that the calculation of the weights is as follows: | ואמנם משקלו' כסף מבואר לעיל אך יש לדעת כי חשבון המשקלו' כך הן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דב קראטן א' מרקא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ד' גראן א קרַאטא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ג גֶרען א' גרַאן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם ישאל השואל דחג זקוקי' גא לוט ג' קווינט כסף מזוקק וקנית הזקוק בעד ח' זהו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מספר [66]מספר חז0ג זא דינרי' ו' חלושי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעשה כאשר אראך אמו' זקוק בעד ח' זהו' בכמה דחג זקוק גא לוט' ג' קווינטן תעשה מכולם קווינטן ויהיה מראיתו ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה חשבון ורנקבורט דינרי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קנית הב"א זקוקי' ג' לוט' א' קווינטן כסף ודמי מקח הכסף ח' זהו' וחצי רביעי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והצומח זא 0א זהו' ה' דנרי' ו' חלישין חלקים עשהו כאשר הראית ובהשבתו מראיתו ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קנית והבא זקוק בא לוט כסף מצורף והזקוק יש בתוכו ט' לוט ג' קווינטן כסף מזוקק וקנית זקוק כסף המזוקק בעד ח' זהו' ג' דנרי' והצומח הוא אדובו זהו' 0א דינרי' ז' חלישין גם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשהו כמראה הזה חשוב בראשונה כמה המספר הנ"ל עולה כסף מזוקק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר א' זקוק יש בתוכו ט' לוט ג' קווינטן כמה ישנו בתוך והבא זקוקי' בא לוט בתחילה וקצה [67]וקצה השיטה עשהו לוט ובאמצעי קווינטן כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחשבהו ובהעלותך קווינט עשהו לוט ואח"כ לוט לזקוקי' עולה הוז זקוקי' גא לוט' א קווינ' ומשקל א' פשי' תאמר עוד הזקוק בעד ח' זהו' ג' דנרי' בכמה הוז זקוקי' גא לוט' א' קווינ' א' פשי' תעשה ראשי' ואחרית שהשיטה פשי' ואמציע דינרי' יועמד ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה לפניך גרוטאות של כסף משקלו דחג' זקוקי' גא לוט' ג' קווינט ובכל זקוק יש בתוכו ז' לוט' ג' קווינט ומשקל א' פשי' ודמי מקח זקוק כסף מזוקק ז' זהו' ג' רביעית וחצי והצומח הוא טזדא זהו' זא דינרי' ח' חלישין גם חלקי' עשהו כאשר הראיתך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או נלך בדרך אחרת ותא אראך דרך תלך אמור א' זקוק יש בתוכו ז' לוט ג' קווינטן משקל א' פ' כמה בתוך דחג זקוקי' [68] גא לוט ג' קווינטן ותעשה שוים ראשית ואחרית השיטה תביא אל המספר הקטנה ואמציעתו משקלו פשי' ותבניתו ככה יהיה
כפלהו וכתוב המחלק תחתיו כזה הזחַחַז0ג משקלי פשי' כסף מזוקק תוסיף עוד דו לאמר זקוק כסף מזוקק עולה דמיו זהו' בכמה ה משקלי פשי' ראשי' השיטה תעשה משקלי פשוט ותוליך שני השברי' ע"י אמצעי' שברהו על עצמו ואחרי' השיטה תעמיד המספר הכוללי ותעביר הפרטיי מעל פני וזה תבניתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עד כאן משקלי כסף א"ם משקלי זהוב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה לפניך זקוק זהב וכבדיקתו הוא זא קרַט ודמי מקח הקראט ג' זהו' ט' דינרי' העולה חה זהו' גא דינרי' אשכילך אשר תעשה תאמר הקראט דמיו ג' זהו' ט' דינרי' כמה עולה זא קרַאט אמציעתו תעשה דינרי' וז תבניתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קנית גרוטאו' [69]קנית גרוטאות של זהו' ומשקלו עולה חב זקוקי' בא לוט והזקוק בהבדקו יש בתוכו וא קרַאט זהו' טהור ודמי קראט ג' זהו' רביעי' וחצי והצומח בההוא זהו' 0א דינרי' תלך בדרך זה ואז תשכיל ר ראשונה חשוב כמה עולה זהב טהור ואח"כ כמה עולה דמי זהו' טהור ויעלה המספר כמבואר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קנה הקונה גרוטאות של זהו' משקלם הב זקוקין גא לוט' ג' קווינט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והזקוק הוא חא קרַאט ג' גראן זהו' מזוקק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ודמי הקרַאטי ג' זהו' 0א דנרי' ט חלושי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I will show you a nice method, all its results are respected | תא אראך דרך נחמדה נכבודות כל תוצאתיה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calculate how much pure gold scraps are worth, in gold weight. | חשוב כמה עולה גרוט(ר)או' זהב טהור משקלו כזהב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תאמר הזקוק יש בתוכו חא קראט ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ראשי' ואחרית השיטה תעשה ואמציעתו ה קרַאטן לגראן ומראיתו כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[70]כפול וחלק עולה גראן תעשה קראטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חשוב כמה עולה דמי מקחו הקראט בעד ג' זהו' 0א דינרי' ט' חלושין ועשהו גראן ואמציעתו פשי' וככה מראהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גרוטאות של זהו' משקלו אב זקוקי' דא לוט' ג' קווינט ומשקל ג' פשיטי' זקוק הוא בב קראט ג' גראן עולה זהו' טהור לעשרים וארבע קראט 0ב זקוקי' בא לוט' ב' קווינ' ב' פשי' א' חליש חלקי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ודמי לוט זהב טהור ה' זהו' ה דינרי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעשהו לזהו' טהור ע"י הפיכה הדימיון הלזה תאמר דב קראט עולה אב זקוקי' ד' לוט ג' קווי' משקל ג' פשיט' עד כמה עולה בב קרַאט ג' גראן ראשי' ואחרי' תעשה גראן ואמציעתו משקלי פשו' וככה יועמד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [71]כפלה וחלקהו יעלה משקלו פשיטי' תעשם קווינטן והקווינטן תעשה לוט' לזקוקי' ויעלה הא דלעיל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וחשוב דמי ממכרו אמור א' לוט ממכרו ה' זהו' ה' דינרי' בכמה 0ב זקוקה בא לוט' וכו' תכנם בשם אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שברם ואמציעתו תעשה דינרי' ויועמד ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Appendix I: Glossary of Terms
| rank | מעלה |
| addition | חבור |
| division | דיוידירו, חילוק |
| multiplication | מולטי פליציטיאן |
| subtraction | חיסור, נכוי, זוכט רַצטיאן |
Notes
Apparatus
Bibliography
Manuscript:
- MS New York, Jewish Theological Seminary Ms. 2634/6 (IMHM: f F 28887), ff.125r-157r
[JTS2634]
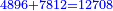
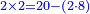
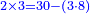
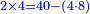
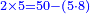
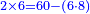
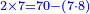
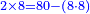
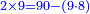
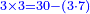
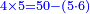
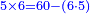
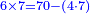
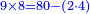
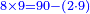
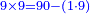
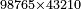


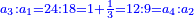
 , the 3 is the numerator and the 4 is the denominator.
, the 3 is the numerator and the 4 is the denominator. 


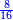



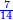
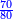

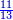
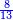
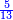
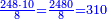
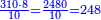
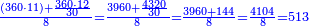
 of a cubit in Vienna is one cubit in Ofen. I ask: how much is the profit?
of a cubit in Vienna is one cubit in Ofen. I ask: how much is the profit? 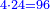
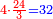
 , which are 160 Rheinos gold coins
, which are 160 Rheinos gold coins 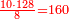 .
.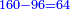
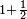 cubits; and I wish to buy another cloth instead of
cubits; and I wish to buy another cloth instead of 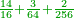
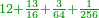
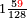 pešiṭim
pešiṭim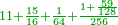
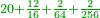
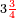 pešiṭim
pešiṭim