Difference between revisions of "Commentary of al-Nayrīzī on Euclid’s Elements"
From mispar
(→Proposition 5) |
(→Proposition 5) |
||
| (25 intermediate revisions by the same user not shown) | |||
| Line 100: | Line 100: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|مثاله ان خط اب المستقيم قسم بقسمين متساوين على نقطة ج وبقسمين مختلفين على نقطة د فأقول ان السطح الذي يحيط به قسما اد دب مع مربع ﺟد مساو لمربع ﺟب | + | |style="text-align:right;"|مثاله ان خط اب المستقيم قسم بقسمين متساوين على نقطة ج وبقسمين مختلفين على نقطة د فأقول ان السطح الذي يحيط به قسما اد دب مع مربع ﺟد مساو لمربع ﺟب |
|- | |- | ||
| − | |5 = اب = 10 | + | | |
| − | + | |[[File:Elements II-5 Nayrîzî.png|thumb|250px]] | |
| − | |style="text-align:right;"|مثاله في الاعداد نفرض اب عشرة من العدد وقسمي اﺟ جب كل واحد منهما خمسة وقسم اد سبعة فيبقى دب ثلثة فيحصل جد اثنين فمن المبين ان المجتمع من ضرب قسم | + | |- |
| + | | | ||
| + | |style="text-align:right;"|برهانه انا نعمل على خط ﺟب سطحا مربعا قائم الزوايا كما بين ببرهان مه من ا وليكن مربع ﺟز ونخرج قطر به ونخرج من نقطة د خطا موازيا لضلعي ﺟه بز كما بينا إخراجه ببرهان لا من ا ونخرج من نقطة ا خطا موازيا لخطوط ﺟل دح بﻛ يلقى خط ﻜﻝﻡ وننزل انه لقيه على نقطة م كما بينا إخراجه ببرهان لا من ا ونبين كما بينا في شكل د من ب وبمثل ما استشهدنا فيه من الاشكال ان سطحي دﻜ ﻝط مربعان قائما الزوايا وهما على قطر به فبحسب برهان مﺟ من ا فان سطح ﺟح المتمم مثل سطح حز المتمم ونأخذ سطح دﻛ مشتركا فسطح ﺟﻛ باسره مساو لسطح دز باسره وسطح ﺟﻛ مثل سطح ﺟﻡ لانهما على قاعدتين متساويتين وهما بﻝ ﻝﻡ وبين خطين متوازيين وهما ﻜﻡ اب وذلك بين ببرهان لو من ا فسطح ﺟﻡ إذا مساو لسطح دز لان الأشياء المساوية لشيء واحد تكون متساوية ونأخذ سطح دل مشتركا فسطح ﻡﺟ باسره مساو لعلم ﻦﺲﻉ لكن سطح ﻡد يحيط به خطا اد دح وخط دح مثل خط دب لان سطح دﻜ مربع قائم الزوايا فسطح ﻡد يحيط به خطا اد دب فعلم ﻦﺲﻉ مساو للذي يحيط به خطا اد دب ومربع ہح مساو لمربع خط جد فمربع جز باسره مساو لعلم ﻦﺲﻉ ولمربع ہح لكن مربع جز هو مربع خط جب فالسطح الذي يحيط به قسما اد دب مع مربع خط جد الذي بين العلامتين مساو لمربع خط جب وذلك ما اردنا ان نبين | ||
| + | |- | ||
| + | |<span style=color:blue>اب = 10<br> | ||
| + | اﺟ = جب = 5<br> | ||
| + | اد = 7; دب = 3; جد = 2<br> | ||
| + | ‫<sup>2</sup>جب = 25 = 21 + 4 = ‫<sup>2</sup>جد + ‫(اد × دب‫)</span> | ||
| + | |style="text-align:right;"|مثاله في الاعداد نفرض اب عشرة من العدد<br> | ||
| + | وقسمي اﺟ جب كل واحد منهما خمسة<br> | ||
| + | وقسم اد سبعة فيبقى دب ثلثة فيحصل جد اثنين<br> | ||
| + | فمن المبين ان المجتمع من ضرب قسم جب في مثله خمسة وعشرون وهو مساو للذي يجتمع من ضرب اد في دب وذلك أحد وعشرون ومن ضرب جد في مثله وذلك أربعة وجميعها خمسة وعشرون وذلك ما مردنا ان نبين | ||
|- | |- | ||
| | | | ||
Latest revision as of 06:41, 21 June 2018
Contents
Book Two |
المقالة الثانية من كتاب اوقليدس في الأصول |
|---|---|
| بسم الله الرحمان الرحيم | |
| قال اوقليدس كل سطح متواري الاضلاع قائم الزوايا فانه يحيط به الخطان المحيطان بإحدى زواياه القائمة | |
| قال المفسر قال ايرن انما خص اوقليدس السطح المتوازي الاضلاع القائم الزوايا بانه يحيط به الضلعان المحيطان بالزاوية القائمة دون المتوازي الاضلاع الذي ليس تقام الزوايا لان مساحة المتوازي القائم الزوايا هو ما يجتمع من ضرب أحد الضلعين المحيطين بالزاوية القائمة في الضلع الاخر فهو السطح الذي يحيط به الضلعان المحيطان بالزاوية القائمة | |
| قال اوقليدس وكل سطح متوازي الاضلاع فان السطحين اللذين تكونان على قطره المتوازيين الاضلاع والقطر يقطعهما اذا اضيف احدهما الى السطحين المتممين اللذين عن جنبتي القطر فان جميع ذلك يسمى العلم | |
Proposition 1 |
الشكل الأول من المقالة الثانية كل خطين مستقيمين يقسم أحدهما بأقسام كم كانت فان السطح الذي يحيط به الخطان مساو لجماعة السطوح التي يحيط به الخط الذي لم يقسم وكل واحد من اقسام الخط الاخر المقسوم |
| مثاله ان خطى ا بﺟ مفروضان وقد قسم خط بﺟ على نقطتي ده فأقول ان السطح الذي يحيط به خطا ا بﺟ مساو لجماعة السطوح التي يحيط بها خط ا واقسام بد ده ہﺟ برهانه انا نقسم على نقطة ب عمود بز وليكن مساويا لخط ا كما بينا عمله ببرهان الشكل المضاف الى با من ا ونجيز على نقطة ز خط زه موازيا لخط بﺟ ومساويا له كما بين برهان لا من ا وبمثل هذا البرهان نخرج خطوط دط ہﻜ ﺟح موازية لخط بز فمن البين ان سطح ﺟز يحيط به خطا بﺟ بز لكن بز مثل ا فسطح ﺟز يحيط حطا ا بﺟ وهو مساو لجماعة السطوح الثلثة ﺟﻜ ہط دز المتوازية الاضلاع لكن سطح ﺟﻜ يحيط به خطا ﺟه ہﻜ وسطح ہط يحيط به خطا ہد دط وسطح دز يحيط به خطا دب بز وكل واحد من خطوط ﺟح ہﻜ دط بز مساو لخط ا فجماعة سطوح ﺟﻜ ہط دز يحيط بها خط ا واقسام بد دہ ہﺟ وجماعتها مساوية لسطح ﺟز وسطح ﺟز يحيط به كما بينا خطا ا بﺟ فقد يبين ان السطح الذي يحيط به خطا ا بﺟ مساو لجماعة السطوح التي يحيط بها خط ا وكل واحد من اقسام بد ده ہﺟ وذلك ما أردنا ان نبين | |
| زيادة | |
| ومثال هذا الشكل من الاعداد | |
|
|
ليكن خط ا ستة من العدد وخط بﺟ عسرة وليكن بد اثنين وده ثلثة وﺟه خمسة فمن البين انا متى ضربنا الستة في العشرة بلغت ستين وهو مساو للذي يجتمع من ضرب الستة في الاثنين وفي الثلثة وفي الخمسة لان الستة في اثنين اثنا عشر وستة في ثلثة ثمانية عشر وستة في خمسة ثلثون ومجموع هذه الاعداد ستون |
| قال ايرن ان هذا الشكل ليس يمكن ان يبرهن عليه الا بان يرسم الخطان جميعا فأما الاشكال الباقية فقد يمكن ان يبين برسم خط واحد فقط وأيضا فقد يمكن ان تأتي من وضعنا خطا واحدا بطريقي البرهان اللذين أحدهما طريق التحليل والأخر طريق التركيب اما التحليل فانه متى فرضت منا مسئلة ما قلنا ننزلها منزلة التي المطلوب انه موجود ثم نفضه الى شيء قد تقدم برهانه فاذا بين لنا قلنا انه قد وجد المطلوب بالتحليل واما التركيب فانه ان يبتدأ بأشياء معروفة ثم تركب الى ان توجد الشيء المطلوب فضد ذلك يكون المطلوب قد يبين بالتركيب وإذ قد أخبرنا بهذا فلنصر الى مطلوبنا على ما وصفنا ووعدنا يريد بذلك ان نبين ما وعدها هنا في سائر الاشكال التي يأتي بها اوقليدس في هذه المقالة الثانية | |
Proposition 2 |
الشكل الثاني من المقالة الثانية كل خط مستقيم يقسم بأقسام كم كانت فان مربع الخط كله مساو لجماعة السطوح التي يحيط بها الخط كله مع كل واحد من اقسامه |
| مثاله ان خط اب قد قسم على ج بقسمين فأقول ان مربع خط اب مساو لمجموع السطحين اللذين يحيط بهما خط اب وكل واحد من خطى اﺟ ﺟب برهانه انا نعمل على خط اب سطحا مربعا قائم الزوايا كما بين عمله ببرهان مه من ا وليكن مربع بد ونخرج من نقطة ج خطا موازيا لخطى اد به كما بين إخراجه ببرهان لا من ا وليكن خط ﺟز فسطحا از ﺟه متوازيا الاضلاع اما سطح دﺟ فيحيط خطا دا اﺟ وسطح زب ويحيط به زﺟ ﺟب وخط ﺟز مثل خط اد وخط اد مثل خط اب فمجموع سطحي دﺟ زب يخيط بهما خط اب وكل واحد من خطي اﺟ ﺟب ومجموع سطحي دﺟ زب مساو لمربع دب الكائن من خط اب فقد تبين ان المربع الكائن من خط اب مساو لمجموع السطحين اللذين يحيط بهما خط اب وكل واحد من خطي اﺟ ﺟب وذلك ما أردنا ان نبين | |
|
|
مثاله من الاعداد يفرض خط اب عشرة من العدد وقد قسم على نقطة ج بقسمين فصار اﺟ ثلثة من العدد وخط ﺟب سبعة فمن المبين ان مضروب اب الذي هو عشرة في مثله مساو للذي يجتمع من ضرب اب الذي هو عشرة في كل واحد من ثلثة وسبعة لان عشرة في مثلها مائة وعشرة في ثلثة ثلثون وفي سبعة سبعون ومجموعهما مائة وذلك ما أردنا ان نبين |
| قال ايرن مثال ذلك ان نفرض الخط المستقيم خط اب ونقسمه قسمة كيف كانت على نقطة ج فنريد ان نبين ان مربع اب مساو للسطح الذي يحيط به خطا اب بﺟ مع السطح الذي يحيط به خطا اب اﺟ ف... ان يتوهم خط اب خطين متساوين أحدهما منقسم والاخر غير منقسم فمن البين ان الخطين يكونان متساويا مكونا بسطح الذي يحيط به هذان الخطان المتساويان مساويا لمربع أحدهما فليكن مساويا لمربع اب فمما بينا ببرهان ا من ب يكون مجموع السطحين الكائنين من الخط الذي لم يقسم مع اقسام اﺟ ﺟب مساويا للسطح الذي يحيط به الخط الذي لم يقسم وخط اب ومربع اب مساو لذلك السطح كما بينا والخط الذي لم يقسم مساو لخط اب كما وصفنا فالسطحان اللذان يحيط بهما خط اب وكل من قسمي اﺟ ﺟب مساويان لمربع خط اب وذلك ما أردنا ان نبين | |
Proposition 3 |
الشكل الثالث من المقالة الثانية كل خط يقسم بقسمين أي قسمين كانا فان السطح الذي يحيط به الخط كله واحد القسمين مساو للسطح الذي يحيط به قسما الخط مع مربع ذلك القسم |
| مثاله ان خط اب قد قسم بقسمين على نقطة ج فأقول ان السطح الذي يحيط به خط اب وقسم بﺟ مساو للسطح الذي يحيط به قسما اﺟ ﺟب مع مربع ﺟب برهانه انا نعمل على خط ﺟب سطحا مربعا كما بين عمله ببرهان مه من ا وليكن مربع ﺟہ ونخرج من نقطة ا خطا موازيا لخط ﺟز كما بين ببرهان لا من ا وليكن خط اد ونخرج خط ہز على الاستقامة وننزل انه لقى خط اد على نقطة د فمن الظاهر ان سطح اه متوازي الاضلاع وهو مساو لسطحي از زب المتوازي الاضلاع لكن سطح از يحيط به خطا اﺟ ﺟز وخط ﺟز مثل خط ﺟب لان سطح زب عمل مربعا فسطح از يحيط به خطا اﺟ ﺟب وسطح زب هو مربع خط ﺟب فالسطح الذي يحيط به خطا اﺟ ﺟب مع المربع الكائن من خط ﺟب مساو لسطح اه المتوازي الاضلاع باسره لكن سطح اه يحيط به خطا اب بہ وخط بہ مساو لخط ﺟب لان سطح بز عمل مربعا فسطح اه باسره يحيط به خطا اب بﺟ فقد يبين ان السطح الذي يحيط به خطا اب بﺟ مساو للسطح الذي يحيط به قسما اﺟ ﺟب مع مربع ﺟب وذلك ما أردنا ان نبين | |
|
|
مثاله من الاعداد انا نفرض خط اب عشرة من الاعداد ونقسمه على نقطة ج بقسمين يكون اﺟ ثلثة من العدد وﺟب سبعة فضرب اب الذي هو عشرة في بﺟ الذي هو سبعة يكون سبعون من العدد وهو مساو للمجتمع من ضرب اﺟ الذي هو ثلثة في ﺟب الذي هو سبعة ومن ضرب ﺟب السبعة في نفسه وذلك ان اﺟ في ﺟب أحد وعشرون وخط ﺟب في مثله تسعة واربعون ومجموعهما سبعون وذلك ما أردنا ان نبين |
| قال ايرن وبرهان هذا الشكل يبين بلا صورة ببرهان الشكل الأول من هذه المقالة فنفرض ان لنا خطين موضوعين وهما خطا اب بﺟ أحدهما غير منقسم وهو بﺟ والأخر مقسوم على نقطة ج وهو اب فمن البين انه يكون السطح الذي يحيط به الخط غير المنقسم وخط اب مساويا لمجموع السطوح التي يحيط بها الخط غير المنقسم واقسام الخط المنقسم أعنى بالأقسام قسمي اﺟ ﺟب ولكن الخط غير المنقسم مساو لخط ﺟب فالسطح الذي يحيط به الخط غير المنقسم وخط ﺟب مساو لمربع خط ﺟب فالسطح الذي يحيط به الخط غير المنقسم وخط ﺟب مساو لمربع خط ﺟب فاذا السطح الذي يحيط به خطا اب بﺟ مساو للسطح الذي يحيط به خط اﺟ ﺟب مع مربع خط ﺟب وذلك ما أردنا ان نبين | |
Proposition 4 |
الشكل الرابع من المقالة الثانية كل خط يقسم بقسمين قسمة كيف وقفت فان مربع الخط كله مساو لمربعي قسميه مع ضعف السطح الذي يحيط به قسما الخط |
| مثاله ان خط اب قسم بقسمين على نقطة ج فأقول ان مربع خط اب مساو لمربعي قسمي اﺟ ﺟب مع ضعف السطح الذي تحيط به قسما اﺟ ﺟب برهانه انا نعمل على خط اب سطحا مربعا كما بين عمله ببرهان مه من ا وليكن مربع ادهب ونخرج قطر بد وخط ﺟح موازيا خطى اد بہ كما بين إخراجه ببرهان لا من ا وليقطع قطر بد على نقطة ز ونجيز على نقطة ز خطا موازيا لخطى اب ده بحسب ما استشهدنا وهو خط طﻜ فلان خط بد قد اجيز على خطى اد ﺟح الموازين فحسب برهان كط من ا تكون زاوية ﺟزب الخارجة مساوية لزاوية ادز الداخلة ولان مثلث ادب متساوي الساقين فبحسب برهان ه من ا تكون زاوية ابد مساوية لزاوية ادب والاشياء المتساوية لشيء فهي متساوية فزاوية ﺟزب مساوية لزاوية جبز فبحسب برهان و من ا يكون ضلع ﺟب مثل ضلع ﺟز ولان سطح ﺟﻜ متوازي الاضلاع فبحسب برهان لد من ا يكون خط ﺟز مثل خط بﻜ وخط ﺟب مثل خط ﻜز وقد كنا بينا ان خط ﺟب مثل خط ﺟز والاشياء المساوية لشيء واحد فهي متساوية فخط زﻜ مثل خط ﺟز فهو مثل خط ﻜب فالأضلاع الأربعة ﺟب ﺟز زﻜ ﻜب متساوية فسطح ﺟﻜ متساوي الاضلاع قائم الزوايا لان زاوية ج القائمة مثل زاوية ك القائمة فزاويتا بز كل واحدة منهما قائمة وذلك بين ببرهان لد من ا فسطح ﺟﻜ هو مربع خط ﺟب ولان ضلع اب مثل ضلع بہ وخط ﺟب مثل خط ﻜب فاذا اسقطنا من المتساوية متساوية فان الذي بقي مساو فخط اﺟ مثل ہﻜ لكن بحسب برهان لد من ا يكون اﺟ مثل طز فخط ﻜہ مثل خط زح وخط طز مثل خط حز وخط طز يوازي خط دح وخط زح يوازي خط دط فسطح طح متساوي الاضلاع قائم الزوايا وهو مساو لمربع خط اﺟ فسطحا طح ﺟﻜ هما مربعا خطى اﺟ ﺟب فلان سطح اه متوازي الاضلاع وعلى قطره سطحان متوازيا الاضلاع فبحسب برهان مج من ا يكون السطحان اللذان عن جنابي قطر بد المتممان متساويين فسطح از مثل سطح زه لكن سطح طﺟ يحيط به خطا اﺟ ﺟز وخط ﺟز مثل خط ﺟب فسطح از يحيط به خطا اﺟ ﺟب فضعف السطح الذي يحيط به خطا اﺟ ﺟب مساو لمجموع سطحي از زه فمربع اه باسره مساو لمربعي قسمي اﺟ ﺟب ولضعف السطح الذي يحيط به قسما اﺟ ﺟب لكن مربع اه هو مربع خط اب فقد تبين ان مربع خط اب مساو لمربعي قسمي اﺟ ﺟب ولضعف السطح الذي يحيط به خطا اﺟ ﺟب وذلك ما أردنا ان نبين | |
|
|
ومثاله من الاعداد ان نفرض اب عشرة من العدد ونقسمه على نقطة ج بقسمين وليكن اﺟ سبعة وﺟب ثلثة فضرب اب في مثله ماية وهو مساو لضرب اﺟ الذي هو سبعة في مثله وهو تسعة واربعون ولضرب ﺟب الذي هو ثلثة في مثله وهو تسعة ولضعف المجتمع من ضرب اﺟ السبعة في ﺟب الثلثة وهو اثنان واربعون فهو ماية وذلك ما أردنا ان نبين |
| واما البرهان على هذا الشكل من غير صورة على مذهب ايرن على مريق الحل فنطلب هل يحل المربع الكائن من خط اب الى مجموع المربعين الكائنين من اﺟ ﺟب مع ضعف السطح الذي يحيط به خطا اﺟ ﺟب فلان خط اب قد انقسم الى خطي اﺟ ﺟب فببرهان ب من ب يحل المربع الكائن من خط اب الى مجموع السطحين اللذين يحيط بأحدهما خطا با اﺟ وبالأخر خطا اب بﺟ لأنه مثلهما وهذان السطحان يحلان الى برهان شكل ج من ب وذلك لان السطح الذي يحيط به خطا اب اﺟ مساو للسطح الذي يحيط به خطا بﺟ ﺟا مع مربع اﺟ والسطح الذي يحيط به خطا اب بﺟ مساو للسطح الذي يحيط به خطا اﺟ ﺟب مع مربع ﺟب فمجموع المربعين الكائنين من خطا اﺟ ﺟب مع ضعف السطح الذي يحيط به خطا اﺟ ﺟب مساو لمجموع السطحين اللذين يحيط بأحدهما خطا با اﺟ وبالأخر خطا اب بﺟ وقد كنا بينا ان مربع خط اب مساو لهذين السطحين فقد انحل المربع الكائن من خط اب الى مجموع المربعين الكائنين من خطي اﺟ ﺟب مع ضعف السطح الذي يحيط به خطا اﺟ ﺟب واستويا وذلك ما أردنا ان ابين | |
| واما على طريق التركيب فنبدأ الان فنركب من حيث انتهى بنا الحل فنقول ان بحسب برهان ج من ب فان السطح الذي يحيط به خطا بﺟ ﺟا مع مربع اﺟ مساو للسطح الذي يحيط به خطا با اﺟ وكذلك السطح الذي يحيط به خطا اﺟ جب مع مربع بﺟ مساو للسطح الذي يحيط به خطا اب بﺟ مع المربع الكائن من خط بﺟ فقد تركب المربعان الكائنان من خطى اﺟ ﺟب مع ضعف السطح الذي يحيط به خطا اﺟ ﺟب وساويا السطحين اللذين يحيط بأحدهما خطا با اﺟ وبالأخر خطا اب بﺟ وهذان السطحان يتركبان ويساويان المربع الكائن من خط اب بحسب برهان ب من ب فمجموع المربعين الكائنين من خطى اﺟ ﺟب مع ضعف السطح الذي يحيط به خطا اﺟ ﺟب قد تركب وساوي بأجمعه المربع الكائن من خط اب وذلك ما أردنا ان نبين | |
Proposition 5 |
الشكل الخامس من المقالة الثانية كل خط مستقيم يقسم بقسمين متساوين ويقسم أيضا بقسمين مختلفين فان السطح الذي يحيط به القسمان المختلفان مع مربع الخط الذي بين نقطتي القسمين مساو لمربع نصف الخط |
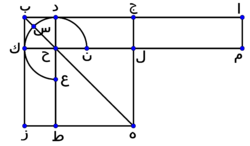
| مثاله ان خط اب المستقيم قسم بقسمين متساوين على نقطة ج وبقسمين مختلفين على نقطة د فأقول ان السطح الذي يحيط به قسما اد دب مع مربع ﺟد مساو لمربع ﺟب | |
| برهانه انا نعمل على خط ﺟب سطحا مربعا قائم الزوايا كما بين ببرهان مه من ا وليكن مربع ﺟز ونخرج قطر به ونخرج من نقطة د خطا موازيا لضلعي ﺟه بز كما بينا إخراجه ببرهان لا من ا ونخرج من نقطة ا خطا موازيا لخطوط ﺟل دح بﻛ يلقى خط ﻜﻝﻡ وننزل انه لقيه على نقطة م كما بينا إخراجه ببرهان لا من ا ونبين كما بينا في شكل د من ب وبمثل ما استشهدنا فيه من الاشكال ان سطحي دﻜ ﻝط مربعان قائما الزوايا وهما على قطر به فبحسب برهان مﺟ من ا فان سطح ﺟح المتمم مثل سطح حز المتمم ونأخذ سطح دﻛ مشتركا فسطح ﺟﻛ باسره مساو لسطح دز باسره وسطح ﺟﻛ مثل سطح ﺟﻡ لانهما على قاعدتين متساويتين وهما بﻝ ﻝﻡ وبين خطين متوازيين وهما ﻜﻡ اب وذلك بين ببرهان لو من ا فسطح ﺟﻡ إذا مساو لسطح دز لان الأشياء المساوية لشيء واحد تكون متساوية ونأخذ سطح دل مشتركا فسطح ﻡﺟ باسره مساو لعلم ﻦﺲﻉ لكن سطح ﻡد يحيط به خطا اد دح وخط دح مثل خط دب لان سطح دﻜ مربع قائم الزوايا فسطح ﻡد يحيط به خطا اد دب فعلم ﻦﺲﻉ مساو للذي يحيط به خطا اد دب ومربع ہح مساو لمربع خط جد فمربع جز باسره مساو لعلم ﻦﺲﻉ ولمربع ہح لكن مربع جز هو مربع خط جب فالسطح الذي يحيط به قسما اد دب مع مربع خط جد الذي بين العلامتين مساو لمربع خط جب وذلك ما اردنا ان نبين | |
| اب = 10 اﺟ = جب = 5 |
مثاله في الاعداد نفرض اب عشرة من العدد وقسمي اﺟ جب كل واحد منهما خمسة |
| واما على مذهب ايرن في برهان هذا الشكل بالتحليل فمن اجل انا نطلبه ان نعلم هل السطح الذي يحيط به قسما اد دب مع مربع خط جد مساو لمربع خط جب فلنأخذ خطين قد قسم أحدهما بأقسام وهو خط اد على نقطة ﺟ والأخر لم يقسم وهو خط دب فبحسب برهان ا من ب يكون السطح الذي يحيط به خطا اد دب مساويا لمجموع السطحين اللذين يحيط بهما خط بد وقسما اﺟ جد فلان اﺟ مثل جب فان مجموع السطحين اللذين يحيط بهما خطا جب بد وخطا جد دب مساو للسطح الذي يحيط به خطا اد دب فقد بقي لنا مربع جد فنجعله مشتركا فيكون مجموع السطحين اللذين يحيط بهما جب بد وخطا جد دب مع مربع جد مساويا للسطح الذي يحيط به خطا اد دب مع مربع جد لكن السطح الذي يحيط به خطا جد دب مع مربع جد مساو للسطح الذي يحيط به خطا بﺟ جد وذلك ببرهان ﺟ من ب فمجموع السطحين اللذين يحيط بأحدهما خطا بﺟ جد وبالأخر خطا جب بد مساو للسطح الذي يحيط به خطا اد دب مع مربع جد لكن بحسب برهان ب من ب يكون مجموع السطحين اللذين يحيط بهما خطا جب بد وخطا بﺟ جد مساويا لمربع خط جد فمربع خط جب اذن مساو للسطح الذي يحيط به قسما اد دب مع مربع جد وذلك ما أردنا ان نبين فقد انحل الى برهان ب من ب ونبدا الان فنركب من حيث انتهى بنا الحل فبحسب برهان ب من ب فان السطح الذي يحيط به خطا جب جد مع السطح الذي يحيط به خطا بﺟ جد مثل مربع خط جب لكن بحسب برهان ﺟ من ب يكون السطح الذي يحيط به خطا بﺟ جد مساويا للسطح الذي يحيط به خطا جد دب مع مربع جد فمربع خط جب اذا مساو للسطحين اللذين يحيط بأحدهما حط ﺟب بد وبالأخر خطا جد دب مع مربع جد فلان خط اﺟ مساو لخط جب يكون السطح الذي يحيط به خطا اﺟ دب مع السطح الذي يحيط به خطا اد دب فالسطح الذي يحيط به خطا اد دب مع مربع جد مساو للمربع الكائن من خط جب وذلك ما أردنا ان نبين |
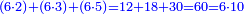
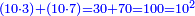
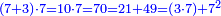
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle
3^2+7^2+\left[2\sdot\left(3\sdot7\right)\right]&\scriptstyle=9+49+\left(2\sdot21\right)=9+49+42\\&\scriptstyle=100=10^2\\&\scriptstyle=\left(3+7\right)^2\\\end{align}}}](/mediawiki/images/math/8/4/8/8485bf1fc7542ef51ab16602c07e9c8b.png)