Difference between revisions of "Anonymous"
(→Partnership) |
(→Chapter Seven: Conversion of One to the Other) |
||
| Line 1: | Line 1: | ||
| + | {{#annotpage: time="1200-1300", peshat_title="00002161"}} | ||
<div style="text-align: right; direction: ltr; margin-left: 1em;"> | <div style="text-align: right; direction: ltr; margin-left: 1em;"> | ||
| − | תהלה לאל הנעלה | + | </div> |
| − | אשר אין לו תחלה ותכלה | + | __TOC__ |
| − | ויצר עולמו חוזר חלילה | + | <br> |
| − | יומם ולילה | + | {| |
| − | ושם | + | |- |
| − | לחשב מספר מאחד ועד תשעה | + | |Praise be to the wonderful Almighty God, |
| − | =< | + | |style="text-align:right;"|‫<ref>2r</ref>תהלה לאל הנעלה הנפלא |
| − | ==< | + | |- |
| − | גם הוא | + | |Who has no beginning or end, |
| − | כי כאשר תערוך תשעה על תשעה יהיה מספר העולה בין שני צדיו האחדים מצד שמאל והעשרות מצד ימין וכן על ח' ועל ז' ועל ו' | + | |style="text-align:right;"|אשר אין לו תחלה ותכלה |
| − | אך כאשר תגיע לחמשה יתהפכו העשרות לשמאל והאחדים לימין ועל זה הדרך על ד' ועל ג' ועל ב' | + | |- |
| − | ואם תערכנו על א' יצא לך ט' בעצמו | + | |Who created His world repeating itself, |
| − | ואם תכתוב תשעה בתחלת העגול תוציאם על זה הדרך רק שיתהפך הדבר לימין ולשמאל | + | |style="text-align:right;"|ויצר עולמו חוזר חלילה |
| + | |- | ||
| + | |Day and night, | ||
| + | |style="text-align:right;"|יומם ולילה | ||
| + | |- | ||
| + | |And put wisdom and knowledge in the human heart, | ||
| + | |style="text-align:right;"|ושם [בלב] האדם חכמה ודעה | ||
| + | |- | ||
| + | |To calculate a number from one to nine. | ||
| + | |style="text-align:right;"|לחשב מספר מאחד ועד תשעה | ||
| + | |- | ||
| + | | | ||
| + | == <span style=color:Green>Introduction</span> == | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | === <span style=color:Green>Presentation of the products of units by nine through the arrangement of the nine digits in a circle</span> === | ||
| + | | | ||
| + | |- | ||
| + | |When you write it on a circle you find it recurrent. | ||
| + | |style="width: 45%; text-align:right;"|גם הוא [כאשר] תכתבנו בעגולה תמצאנו חוזר חלילה | ||
| + | |- | ||
| + | |[[File:products of nine.png|thumb|200px|left]] | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *<span style="color:Green>9×9; 9×8; 9×7; 9×6:</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :For, when you multiply nine by nine the number obtained will be on its both sides: the units to the left and the tens to the right. | ||
| + | |style="text-align:right;"|כי כאשר תערוך תשעה על תשעה יהיה מספר העולה בין שני צדיו האחדים מצד שמאל והעשרות מצד ימין | ||
| + | |- | ||
| + | | | ||
| + | :Likewise by 8, by 7 and by 6. | ||
| + | |style="text-align:right;"|וכן על ח' ועל ז' ועל ו‫' | ||
| + | |- | ||
| + | | | ||
| + | *<span style="color:Green>9×5; 9×4; 9×3; 9×2:<span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :But, when you reach five the tens will turn to the left and the units to the right | ||
| + | |style="text-align:right;"|אך כאשר תגיע לחמשה יתהפכו העשרות לשמאל והאחדים לימין | ||
| + | |- | ||
| + | | | ||
| + | :In the same way by 4, by 3 and by 2. | ||
| + | |style="text-align:right;"|ועל זה הדרך על ד' ועל ג' ועל ב‫' | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply it by 1, you will get 9 itself, as every number that is multiplied by 1 has no increment. | ||
| + | |style="text-align:right;"|ואם תערכנו על א' יצא לך ט' בעצמו כי כל חשבון הנערך על א' אין לו תוספת | ||
| + | |- | ||
| + | |If you write nine on the beginning of the circle, you extract them according to this way, only that it will be vice versa to the right and to the left. | ||
| + | |style="text-align:right;"|ואם תכתוב תשעה בתחלת העגול תוציאם על זה הדרך רק שיתהפך הדבר לימין ולשמאל | ||
| + | |- | ||
| + | | | ||
| − | ==< | + | === <span style=color:Green>One is not a number</span> === |
| − | + | | | |
| − | + | |- | |
| − | + | |If the number is like a circle - the one is like a point. | |
| − | + | |style="text-align:right;"|ואם המספר כעגלה האחד כנקדה | |
| − | + | |- | |
| − | + | |For, it is the foundation and the cause of all numbers, but it is not a number - it is the essence of a thing. | |
| − | + | |style="text-align:right;"|כי הוא יסוד וסבת כל מספר ואיננו מספר והוא עצם דבר | |
| − | ואם | + | |- |
| − | + | |The similar to this are the words of the language that are the secret of every speaker and the source of every reason, but do not utter any reason. | |
| − | + | |style="text-align:right;"|והדומה לזה תבות הלשון שהם סוד כל מדבר ומוצא כל דבר ואינם משמיעים דבר מעניני הדבר | |
| − | + | |- | |
| − | + | |From the categories of number it is clear that the one is not a number, for every number is either even or odd, but one is neither. | |
| − | + | |style="text-align:right;"|וממחלקות המספר יתבאר כי האחד איננו מספר כי כל מספר יתחלק ל{{#annot:term|1333,63|j0hi}}זוג{{#annotend:j0hi}} ול{{#annot:term|1336,65|vJmF}}נפרד{{#annotend:vJmF}} ולא כן האחד | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | כל | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | כל | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==< | + | === <span style=color:Green>One is a number</span> === |
| + | | | ||
| + | |- | ||
| + | |From another aspect it is also a number. | ||
| + | |style="text-align:right;"|ומפאה אחרת גם הוא מספר | ||
| + | |- | ||
| + | | | ||
| + | ==== <span style=color:Green>General properties of numbers that apply to one</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *Every number, even or odd, is summed from it. | ||
| + | |style="text-align:right;"|ובו {{#annot:term|178,2436|VXAj}}נתחבר{{#annotend:VXAj}} כל זוג וכל נפרד | ||
| + | |- | ||
| + | | | ||
| + | *If we sum the odd numbers, when they are in a sequence one by one, the squares are generated and one is included with them. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left(2k-1\right)=n^2}}</math> | ||
| + | |style="text-align:right;"|ואם חברנו הנפרדים כאשר הם במערכת זה אחר זה יולדו המרובעים והנה האחד עמהם | ||
| + | |- | ||
| + | | | ||
| + | *Every number is half the sum of its two sides. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{n=\left[\frac{1}{2}\sdot\left(n-1\right)\right]+\left[\frac{1}{2}\sdot\left(n+1\right)\right]}}</math> | ||
| + | |style="text-align:right;"|וכל מספר מחצית שתי פאותיו | ||
| + | |- | ||
| + | | | ||
| + | :One applies on one side what every number applies on two [sides] and in this respect its conduct is the same as every number. | ||
| + | :<math>\scriptstyle{\color{blue}{1=\frac{1}{2}\sdot2}}</math> | ||
| + | |style="text-align:right;"|והאחד יעשה בפאה אחת מעשה כל מספר בשתים והנו בדרך כל המספר | ||
| + | |- | ||
| + | | | ||
| + | *There are three fundamental types for all number: | ||
| + | |style="text-align:right;"|יסוד כל מספר על שלש דרכים | ||
| + | |- | ||
| + | | | ||
| + | :1) [Identifiable] in one: its addition to itself is greater than its product by itself. | ||
| + | ::<math>\scriptstyle{\color{blue}{1\sdot1<1+1}}</math> | ||
| + | |style="text-align:right;"|האחת באחד להיות {{#annot:term|1346,388|Cezq}}הנחבר{{#annotend:Cezq}} יותר מהנערך | ||
| + | |- | ||
| + | | | ||
| + | :2) [Identifiable] in two: its addition to itself is equal to its product by itself. | ||
| + | ::<math>\scriptstyle{\color{blue}{2\sdot2=2+2}}</math> | ||
| + | |style="text-align:right;"|והשנית בשנים להיותם שוים | ||
| + | |- | ||
| + | | | ||
| + | :3) [Identifiable] in three: its product by itself is greater than its addition to itself. | ||
| + | ::<math>\scriptstyle{\color{blue}{3\sdot3>3+3}}</math> | ||
| + | |style="text-align:right;"|והשלישית בשלשה להיות {{#annot:term|1282,241|ijKL}}הנערך{{#annotend:ijKL}} רב מהמחובר | ||
| + | |- | ||
| + | | | ||
| + | :Every number greater than three follows the conduct of three. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\forall n>3: n\sdot n>n+n}}</math> | ||
| + | |style="text-align:right;"|ומשפט כל מספר אחר השלשה בדרך השלשה | ||
| + | |- | ||
| + | |So, [from this aspect] one is [considered] with the numbers. | ||
| + | |style="text-align:right;"|והנה האחד עם כל מספר | ||
| + | |- | ||
| + | | | ||
| − | + | ==== <span style=color:Green>Properties of the numbers 2-10 that pertain to one</span> ==== | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | ===== <span style=color:Green>The number two</span> ===== | |
| − | + | | | |
| − | + | |- | |
| − | + | |Two is the beginning of the numbers. | |
| − | + | |style="text-align:right;"|ושנים תחלת המספר | |
| − | + | |- | |
| − | + | |It is the root of four. | |
| − | <math>\ | + | ::<math>\scriptstyle{\color{blue}{\sqrt{4}=2}}</math> |
| − | + | |style="text-align:right;"|והוא שורש ארבעה | |
| − | < | + | |- |
| − | + | |<span style="color:Green>As the first root of a square number, it represents the properties of the roots:</span> | |
| − | + | | | |
| − | + | |- | |
| − | <math> | + | | |
| − | + | *The ratio that is generated from the product of one of the roots by the other to the first square is as the ratio of the second square to the mentioned product. Likewise for the one, which is a root and a square. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a\sdot b}{a^2}=\frac{b^2}{a\sdot b}}}</math> | |
| − | + | |style="text-align:right;"|וערך {{#annot:term|1346,241|PvrY}}הנחבר{{#annotend:PvrY}} מעריכת אחד השרשים על האחר אל המרובע הראשון כערך המרובע השני אל הנחבר הנזכר וככה האחד והנו שרש ומרובע | |
| − | + | |- | |
| − | + | | | |
| − | + | *For every number, if we sum the root with its square, [the sum] is as the product of the root by the succeeding number. Likewise for the one, which is a root and a square. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{a+a^2=a\sdot\left(a+1\right)}}</math> | |
| − | <math>\ | + | |style="text-align:right;"|וכל חשבון אם חברנו השרש עם מרובעו יהיה כעריכת השורש על המספר שהוא שני וככה האחד והנו שרש ומרובע |
| − | + | |- | |
| − | + | | | |
| − | + | *For every root that you double its square and add its quarter to it, [the sum] is a square and its root is as the original root summed with its half. Likewise for the one. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{2a^2+\frac{1}{4}a^2=\left(a+\frac{1}{2}a\right)^2}}</math> | |
| − | + | |style="text-align:right;"|כל שרש שתכפול מרובעו ותוסיף עליו ‫<ref>2v</ref>רביעיתו יהיה מרובע ושרשו כמו השרש הראשון מחובר עם חציו וככה האחד | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | <math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | ===== <span style="color:Green>The number three</span> ===== |
| − | < | + | | |
| − | + | |- | |
| − | == | + | |<span style="color:Green>It represents a special property of the proportional triad:</span> |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | *[For every] three numbers, such that the ratio of the mean to the first is as the ratio of the last to the mean, if we multiply the first by the last it is the same as the square of the mean. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a_2}{a_1}=\frac{a_3}{a_2}\longrightarrow a_1\sdot a_3=a_2^2}}</math> | |
| − | + | |style="text-align:right;"|שלשה מספרים ערך התיכון אל הראשון כערך האחרון אל התיכון אם ערכנו הראשון על האחרון יהיה כמרובע התיכון | |
| − | + | |- | |
| − | <math>\ | + | | |
| − | + | |style="text-align:right;"|‫[ו]‫אם הראשון כן יהיה האחרון וככה האחד | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==< | + | ===== <span style="color:Green>The number four</span> ===== |
| − | + | | | |
| − | === | + | |- |
| − | + | |Four is a square number | |
| − | + | |style="text-align:right;"|וארבעה מרובע | |
| − | <math>\ | + | |- |
| − | + | |<span style="color:Green>As the first square number, it represents the properties of the square numbers:</span> | |
| − | <math>\ | + | | |
| − | + | |- | |
| − | <math>\ | + | | |
| − | + | *Between every square to double-double the square there is a number that is not a square. Likewise for the one. | |
| − | <math>\ | + | :<math>\scriptstyle{\color{OliveGreen}{\forall n\in N, \exists b\neq n^2:a^2<b<\left(2\sdot2\sdot a^2\right)}}</math> |
| − | + | |style="text-align:right;"|ובין כל מרובע לכפל כפל המרובע אחד שאיננו מרובע וככה האחד | |
| − | + | |- | |
| − | + | | | |
| − | <math>\ | + | *If we subtract a square from its successive square, the remainder is as the sum of both their roots together. Likewise for the one. |
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(n+1\right)^2-n^2=\left(n+1\right)+n}}</math> | ||
| + | |style="text-align:right;"|אם חסרנו מרובע ממרובע הקרוב אליו יהיה הנשאר כשנים השרשים {{#annot:term|1346,178|PfY5}}הנחברים{{#annotend:PfY5}} וככה האחד | ||
| + | |- | ||
| + | | | ||
| + | *For every number, if we multiply the number preceding it by the number succeeding it and add one, [the result] is as the square of that number. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[\left(n-1\right)\sdot\left(n+1\right)\right]+1=n^2}}</math> | ||
| + | |style="text-align:right;"|כל חשבון אם ערכנו החשבון שהוא לפניו על החשבון שהוא לאחריו ונוסיף אחד יהיה כמרובע החשבון | ||
| + | |- | ||
| + | | | ||
| + | *For every square, when you take its root and the number preceding it and subtract them from it, a square remains. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{n^2-n-\left(n-1\right)=a^2}}</math> | ||
| + | |style="text-align:right;"|כל מרובע שתקח שרשו והחשבון שלפניו ותחסרם ממנו ישאר מרובע | ||
| + | |- | ||
| + | | | ||
| + | *And if you add to it its root and the number succeeding [the sum] is a square. Likewise for the one. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{n^2+n+\left(n+1\right)=b^2}}</math> | ||
| + | |style="text-align:right;"|ואם תוסיף עליו שרשו והחשבון שלאחריו יהיה מרובע וככה האחד | ||
| + | |- | ||
| + | | | ||
| − | ===< | + | ===== <span style="color:Green>The number five</span> ===== |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | <math>\ | + | *Five is a circular number, for its first square is found in every power of [five].<ref><math>\scriptstyle{\color{blue}{n>1;a\in N: 5^n=a25}}</math><br> |
| − | + | <math>{\color{blue}{\begin{cases}\scriptstyle5^2=\color{Red}{25}\\\scriptstyle5^3=1\color{Red}{25}\\\scriptstyle5^4=6\color{Red}{25}\\\scriptstyle5^5=31\color{Red}{25}\\\scriptstyle\ldots\end{cases}}}</math></ref> | |
| − | + | |style="text-align:right;"|החמשה {{#annot:term|95,1470|vcGf}}חשבון עגול{{#annotend:vcGf}} כי ימצא בכל חשבונו המרובע הראשון | |
| − | + | |- | |
| − | + | | | |
| − | + | ||
| − | + | ===== <span style="color:Green>The number six</span> ===== | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | *The same for six, only that six itself is found in each of its powers instead of its first square.<ref><math>\scriptstyle{\color{blue}{a\in N: 6^n=a6}}</math><br> | |
| − | ואם | + | <math>{\color{blue}{\begin{cases}\scriptstyle6^2=3\color{Red}{6}\\\scriptstyle6^3=21\color{Red}{6}\\\scriptstyle6^4=129\color{Red}{6}\\\scriptstyle6^5=777\color{Red}{6}\\\ldots\end{cases}}}</math></ref> |
| − | + | |style="text-align:right;"|גם כן ששה רק ששה ימצא בכל חשבונו ולא מרובעו הראשון | |
| − | + | |- | |
| − | + | | | |
| − | + | :Likewise the one. | |
| − | + | |style="text-align:right;"|והנה האחד ככה | |
| − | + | |- | |
| − | + | | | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | ||
| − | + | ===== <span style="color:Green>The number seven</span> ===== | |
| − | + | | | |
| − | + | |- | |
| − | + | |<span style="color:Green>Holds the following property:</span> | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | *If we sum seven with all the numbers preceding it, the sum is the same as the square of its double and it includes the one. | |
| − | + | :<math>\scriptstyle{\color{blue}{\left(1+2+3+4+5+6+7\right)\sdot7=\left(2\sdot7\right)^2}}</math> | |
| − | + | |style="text-align:right;"|אם ערכנו שבעה על עצמו ועל כל מספר שלפניו יהיה הנחבר כמרובע כפלו והנה האחד עמהם | |
| − | + | |- | |
| − | + | | | |
| − | + | ||
| − | + | ===== <span style="color:Green>The number eight</span> ===== | |
| − | + | | | |
| − | + | |- | |
| + | |Eight is a cube number [guf šaveh] | ||
| + | |style="text-align:right;"|השמונה {{#annot:term|91,1446|VNkE}}גוף שוה{{#annotend:VNkE}} | ||
| + | |- | ||
| + | |<span style="color:Green>As the first cube number it represents the following properties of the cube numbers:</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *If we sum up all the cube numbers successively, including the one, the sum is a square number. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^n i^3=a^2}}</math> | ||
| + | |style="text-align:right;"|ואם חברנו כל חשבון שהוא גוף שוה כאשר הם {{#annot:term|2576,1357|NFbm}}בתולדת זה אחר זה{{#annotend:NFbm}} יהיה מרובע והנה אחד עמהם | ||
| + | |- | ||
| + | | | ||
| + | *Between two square numbers there is always a cube number. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\forall a<b; \exists n: a^2<n^3<b^2}}</math> | ||
| + | |style="text-align:right;"|ולעולם ימצא גוף שוה בין שנים מרובעים | ||
| + | |- | ||
| + | | | ||
| + | :*When we subtract one half from half the cube root and multiply the remainder by the cube root, we find the root of the smaller square. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a=\left[\left(\frac{1}{2}n\right)-\frac{1}{2}\right]\sdot n}}</math> | ||
| + | |style="text-align:right;"|כשנחסר מחצי {{#annot:term|558,1450|HT70}}קו הגוף{{#annotend:HT70}} חצי אחד ונערוך הנשאר על הקו נמצא שרש המרובע הקטן | ||
| + | |- | ||
| + | | | ||
| + | :*When we add one half to half the cube root and multiply [the sum] by the cube root, we find the root of the greater square. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{b=\left[\left(\frac{1}{2}n\right)+\frac{1}{2}\right]\sdot n}}</math> | ||
| + | |style="text-align:right;"|וכאשר נוסיף חצי אחד על חצי {{#annot:term|558,1450|fqgq}}הקו{{#annotend:fqgq}} ונעריכנו על הקו נמצא שרש המרובע הגדול | ||
| + | |- | ||
| + | | | ||
| + | :*If you subtract the smaller square from the greater square, you will find the cube number. The same for one, which is a cube. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{b^2-a^2=n^3}}</math> | ||
| + | |style="text-align:right;"|ואם תחסר מרובע הקטן ממרובע הגדול נמצא הגוף השוה וככה האחד שהוא גוף שוה | ||
| + | |- | ||
| + | | | ||
| + | *If you want to extract the difference between two successive cube numbers, take the square of the cube root of the first [cube] and the square of the cube root of the second [cube], multiply the cube root of the first by [the cube root of] the second, then sum all and you will find the difference between the two cube numbers. The same for one. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(n+1\right)^3-n^3=\left(n+1\right)^2+n^2+\left[\left(n+1\right)\sdot n\right]}}</math> | ||
| + | |style="text-align:right;"|ואם תרצה להוציא המרחק שיש בין שני {{#annot:term|91,1445|qHD4}}הגופות{{#annotend:qHD4}} שהם זה אחר זה קח מרובע קו הגוף הראשון גם מרובע הקו השני וערוך הקו הראשון על השני וחבר הכל אז תמצא המרחק שיש בין שני הגופות וככה האחד | ||
| + | |- | ||
| + | | | ||
| − | =< | + | ===== <span style="color:Green>The number nine</span> ===== |
| − | < | + | | |
| − | + | |- | |
| − | ==< | + | |Nine is a square number. |
| − | + | |style="text-align:right;"|התשעה {{#annot:term|1263,86|r3kW}}חשבון מרובע{{#annotend:r3kW}} | |
| − | + | |- | |
| + | |<span style="color:Green>As the second square it represents the following properties of square numbers:</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *The difference between one square and another square is always an odd number. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2-b^2=2n-1}}</math> | ||
| + | |style="text-align:right;"|והיתרון שיש בין מרובע אחד ובין מרבע אחר לעולם נפרד | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply the difference between two squares by each of their two roots: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[\left(a^2-b^2\right)\sdot a\right]+\left[\left(a^2-b^2\right)\sdot b\right]}}</math> | ||
| + | |style="text-align:right;"|ואם תערוך היתרון שיש בין שני {{#annot:term|1263,86|GLSP}}המרובעים{{#annotend:GLSP}} על שני השרשים כל אחד בפני עצמו | ||
| + | |- | ||
| + | | | ||
| + | :*If the greater is second to the first in succession, [the sum of both products] is the same as the square of the difference. | ||
| + | |style="text-align:right;"|אם הגדול ‫<ref>3r</ref>שני לראשון יהיה כמרובע היתרון | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a=b+1\longrightarrow\left[\left(a^2-b^2\right)\sdot a\right]+\left[\left(a^2-b^2\right)\sdot b\right]=\left(a^2-b^2\right)^2}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*If it is third to it, multiply [the sum] of both products of the difference by both roots by two. | ||
| + | |style="text-align:right;"|אם היה שלישי לו תערוך היוצא מעריכת היתרון על שני השרשים על שנים | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a=b+2\longrightarrow2\sdot\left[\left[\left(a^2-b^2\right)\sdot a\right]+\left[\left(a^2-b^2\right)\sdot b\right]\right]=\left(a^2-b^2\right)^2}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*If it is fourth to it, multiply [the sum] by three. | ||
| + | |style="text-align:right;"|ואם רביעי לו על שלשה וככה האחד | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a=b+3\longrightarrow3\sdot\left[\left[\left(a^2-b^2\right)\sdot a\right]+\left[\left(a^2-b^2\right)\sdot b\right]\right]=\left(a^2-b^2\right)^2}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If we divide the square of the smaller by the [square of the] greater or the [square of the] greater by the [square of the] smaller, the result is always a square. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a<b\longrightarrow\frac{b^2}{a^2}=\left(\frac{b}{a}\right)^2}}</math> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a<b\longrightarrow\frac{a^2}{b^2}=\left(\frac{a}{b}\right)^2}}</math> | ||
| + | |style="text-align:right;"|אם חלקנו מרובע הקטן על הגדול או הגדול על הקטן לעולם יהיה כמרובע | ||
| + | |- | ||
| + | | | ||
| + | :*When you divide nine by the square of seven, the result of division is a seventh and two-sevenths of a seventh and its root is 3 sevenths. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{\frac{9}{7^2}}=\sqrt{\frac{1}{7}+\left(\frac{2}{7}\sdot\frac{1}{7}\right)}=\frac{3}{7}}}</math> | ||
| + | |style="text-align:right;"|וכאשר תחלק תשעה על מרובע שבעה יצא בחלוק שביעית ושתי שביעיות שביעית ושרשו ג' שביעיות | ||
| + | |- | ||
| + | | | ||
| + | ::The Check: consider the parts of one as seventy, so the seventh and two-sevenths of a seventh are 12 minutes and 60 seconds. Convert the minutes to seconds and add the seconds to them; the result is nine hundred seconds. Divide them by seventy, the result of division is thirty minutes, which are 3 sevenths. Likewise for the one. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{7}+\left(\frac{2}{7}\sdot\frac{1}{7}\right)=\frac{12}{70}+\frac{60}{70^2}=\frac{900}{70^2}=\left(\frac{30}{70}\right)^2=\left(\frac{3}{7}\right)^2}}</math> | ||
| + | |style="text-align:right;"|והבחינה שתחשב חלקי האחד שבעים יהיה השביעית ושתי שביעיות י"ב ראשונים ס' שניים<br> | ||
| + | תשיב הראשונים לשניים ותחבר השניים עמהם יעלה תשע מאות שניים<br> | ||
| + | תחלקם על שבעים יצא בחלוק שלשים ראשונים והם ג' שביעיות וככה האחד | ||
| + | |- | ||
| + | | | ||
| + | :*If we divide the square of seven by nine, the result of division is five and four-ninths and their root is two and one-third; for the nine, by which we divided, is generated from its root, which is three. Likewise the one. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{\frac{7^2}{9}}=\sqrt{5+\frac{4}{9}}=2+\frac{1}{3}}}</math> | ||
| + | |style="text-align:right;"|אם חלקנו מרובע שבעה על תשעה יצא בחלק חמשה וארבע תשיעיות ושרשם שנים ושלישית<br> | ||
| + | כי תשעה שחלקנו עליו קם משרש שלשה וככה האחד | ||
| + | |- | ||
| + | | | ||
| + | *If you want to know the square whose root is known using a known square whose root is also known, multiply the difference between the two roots by each of the roots, then add the result to the known square, if it is less than that sought; | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a>b\longrightarrow a^2=\left[\left(a-b\right)\sdot a\right]+\left[\left(a-b\right)\sdot b\right]+b^2}}</math> | ||
| + | |style="text-align:right;"|אם תרצה לדעת מרובע שרשו ידוע ממרובע ידוע גם שרשו ידוע ערוך המרחק שהוא בין שני השרשים על כל אחד מהשרשים ואשר יהיה תחברם למרובע הידוע אם היה פחות מהמבוקש | ||
| + | |- | ||
| + | | | ||
| + | :or subtract the result [from the known square] if it exceeds over it. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a<b\longrightarrow a^2=b^2-\left[\left(b-a\right)\sdot a\right]-\left[\left(b-a\right)\sdot b\right]}}</math> | ||
| + | |style="text-align:right;"|או תחסרם אם היה {{#annot:term|1351,420|UrqP}}יתר עליו{{#annotend:UrqP}} וככה האחד | ||
| + | |- | ||
| + | !<span style="color:Green>Approximation method for finding a root of a square number</span> | ||
| + | | | ||
| + | |- | ||
| + | |If you want to know the root of a square, integer or fraction, from the preceding square: | ||
| + | |style="text-align:right;"|אם תרצה לדעת שרש ממרובע שלם או נשבר מהמרובע שלפניו | ||
| + | |- | ||
| + | | | ||
| + | :*Such as the root of 9 from the square of 2. | ||
| + | ::<math>\scriptstyle\sqrt{9}</math> | ||
| + | |style="text-align:right;"|כמו שרש תשעה‫<ref>MS Geneva: here starts the interpolated excerpt</ref> ‫<ref>MS Geneva continues 4v</ref>ממרובע שנים | ||
| + | |- | ||
| + | | | ||
| + | ::Divide the [difference between the two squares] by twice the [known] root. The result of division is 1° 15′. We add them to the [known] root and the approximate root is 3° 15′.[This is when] we use sexagesimal fractions. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{9}\approx\sqrt{2^2}+\frac{9-2^2}{2\sdot\sqrt{2^2}}=2+\left(1+15^\prime\right)=3+15^\prime}}</math> | ||
| + | |style="text-align:right;"|חלק המרובע על כפל השרש יצא בחלוק א' ט"ו<br> | ||
| + | חברנום עם השרש ויהיה {{#annot:term|1393,2485|FBUc}}השורש המיוחד{{#annotend:FBUc}} ג' ט"ו<br> | ||
| + | וחלקנו כ{{#annot:term|1441,19|XVRP}}חלקי חכמי המזלות{{#annotend:XVRP}} | ||
| + | |- | ||
| + | | | ||
| + | ::We want to correct it: we multiply 1 by itself and [twice] by 15, it is 1° 30′; 15 by 15, [the result is 3° 45′]. We double the result, because we always double the fractions, and divide the product by 60 it is 7′ 30′′. We add them to 1° 30′, the result is 1° 37′ 30′′. We convert them to minutes, the result is 97′ 30′′. We double them for the half, it is 195′. We divide them by 13, which is twice the approximate root. The result of division is 15. We subtract it from the approximate root and the remainder is 3, which is the [sought] root. | ||
| + | |style="text-align:right;"|רצינו לתקנו ערכנו א' על עצמו ועם ט"ו והנה א"ל וט"ו על ט"ו<br> | ||
| + | וכפלנו העולה כי לעולם נכפול השברים וחלקנו {{#annot:term|1346,241|WdtT}}הנחבר{{#annotend:WdtT}} על ששים והנה ז"ל<br> | ||
| + | חברנום עם א"ל עלה א'ל"זל‫'<br> | ||
| + | החזרנום לראשונים עלה צ"ז ל‫'<br> | ||
| + | וכפלנום בעבור החצי והנה קצ"ה<br> | ||
| + | חלקנום על י"ג שהוא כפל השרש המיושר בחלקיו יצא בחלק ט"ו<br> | ||
| + | חסרנום מ{{#annot:term|2166,2485|nXz7}}השרש המיושר{{#annotend:nXz7}} והנה ג' הוא השרש | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{2\sdot\left[1^2+\left(2\sdot15^\prime\right)+\left[2\sdot\left(15^\prime\right)^2\right]\right]}{2\sdot\left[2\sdot\left(3+15^\prime\right)\right]}=\frac{2\sdot\left[1+30^\prime+\left(7^\prime+30^{\prime\prime}\right)\right]}{13}=\frac{2\sdot\left(1+37^\prime+30^{\prime\prime}\right)}{13}=\frac{2\sdot\left(97^\prime+30^{\prime\prime}\right)}{13}=\frac{195^\prime}{13}=15^\prime}}</math> | ||
| + | :<math>\scriptstyle{\color{blue}{\sqrt{9}=\left(3+15^\prime\right)-\frac{2\sdot\left[1^2+\left(2\sdot15^\prime\right)+\left[2\sdot\left(15^\prime\right)^2\right]\right]}{2\sdot\left[2\sdot\left(3+15^\prime\right)\right]}=\left(3+15^\prime\right)-15^\prime=3}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *<span style="color:Green>First approximation:</span> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sqrt{a^2+b}\approx a+\frac{b}{2a}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :For every square, do as follows: divide the difference between the two squares by double the first root, then add the result to the root and this is the approximate root. | ||
| + | |style="text-align:right;"|וככה תעשה לכל מרובע שתחלוק היתרון שבין שני המרובעים על כפל השרש הראשון ותשמור היוצא הוסיפנו על השרש ויהיה {{#annot:term|2166,2485|k2cu}}מיושר{{#annotend:k2cu}} | ||
| + | |- | ||
| + | | | ||
| + | *<span style="color:Green>Second approximation:</span> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sqrt{a^2+b}\approx\left(a+\frac{b}{2a}\right)-\frac{1^2+2\sdot\left(\frac{b}{2a}-1\right)+2\sdot\left(\frac{b}{2a}-1\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :Afterwards take the quotient and multiply it by itself. Double the square of the quotient [...] Divide the total by double the approximate root, then subtract the result from the approximate root; the root of the greater square remains. | ||
| + | |style="text-align:right;"|ואחר כן קח היוצא בחלוק וערוך אותו על עצמו ותכפול מרובע השבר ותחלק הכל על כפל השרש המיושר והיוצא תגרע מ{{#annot:term|2166,2485|Ofvh}}השורש המיושר{{#annotend:Ofvh}} ישאר השרש מהמרובע הגדול | ||
| + | |- | ||
| + | | | ||
| + | :*This is the case with one, because the difference between it and four is three. We divide it by double the root; the result is one and a half. We add it to the root; the approximate root is two and a half. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{4}\approx\sqrt{1}+\frac{4-1}{2\sdot\sqrt{1}}=1+\frac{3}{2}=1+\left(1+\frac{1}{2}\right)=2+\frac{1}{2}}}</math> | ||
| + | |style="text-align:right;"|וכן משפט האחד כי המרחק בינו ובין ארבעה שלשה<br> | ||
| + | חלקנום על כפל השרש יצא אחד וחצי<br> | ||
| + | הוספנום על השרש ויהיה השרש המיושר שנים וחצי | ||
| + | |- | ||
| + | | | ||
| + | ::We take the square of the quotient; the result is [a quarter]. We double the quarter, which is [the square of] the quotient [...] it is two and a half. We divide it by double the approximate root; the result is a half. Subtract it from the approximate [root]; two remains and it is the root of four. | ||
| + | |style="text-align:right;"|לקחנו מרובע היוצא בחלוק עלה שנים ורביע<br> | ||
| + | כפלנו הרביע שהם השברים והנה שנים וחצי<br> | ||
| + | חלקנום על כפל השרש המיושר יצא חצי<br> | ||
| + | תגרענו מ{{#annot:term|2166,2485|2oyj}}המיושר{{#annotend:2oyj}} ישארו שנים והם שרש ארבעה | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{4}=\left(2+\frac{1}{2}\right)-\frac{1^2+\left(2\sdot\frac{1}{2}\right)+\left[2\sdot\left(\frac{1}{2}\right)^2\right]}{2\sdot\left(2+\frac{1}{2}\right)}=\left(2+\frac{1}{2}\right)-\frac{2+\frac{1}{2}}{2\sdot\left(2+\frac{1}{2}\right)}=\left(2+\frac{1}{2}\right)-\frac{1}{2}=2}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *For every square, when you take its root and the number that precedes the root and subtract them from it, the remainder is a square. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2-\left[a+\left(a-1\right)\right]=b^2}}</math> | ||
| + | |style="text-align:right;"|כל מרובע שתקח שרשו והחשבון שלפני השרש ותחסרם ממנו ישאר מרובע | ||
| + | |- | ||
| + | | | ||
| + | :If you add to it its root and the number that follows [its root], the result is a square. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2+\left[a+\left(a+1\right)\right]=c^2}}</math> | ||
| + | |style="text-align:right;"|ואם תוסיף עליו שרשו והחשבון שלאח' אחריו יהיה מרובע | ||
| + | |- | ||
| + | | | ||
| + | :The same for one. | ||
| + | |style="text-align:right;"|וככה האחד | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style="color:Green>The number ten</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | |Ten is analogous to one <span style="color:Green>[= as a unit in the rank of tens]</span> | ||
| + | |style="text-align:right;"|ומספר עשרה דומה לאחד | ||
| + | |- | ||
| + | |<span style="color:green>As such it represents the following properties:</span> | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2=10a-\left[\left(10-a\right)\sdot a\right]}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*When you wish to know the square of nine, multiply it by one, which is the difference [from ten], and subtract it from ninety, which is similar to nine, so it is eighty-one. | ||
| + | ::<math>\scriptstyle{\color{blue}{9^2=\left(9\sdot10\right)-\left[\left(10-9\right)\sdot9\right]=90-\left(1\sdot9\right)=81}}</math> | ||
| + | |style="text-align:right;"|וכאשר תרצה לדעת מרובע תשעה תערכנו על אחד שהוא המרחק ותחסרנו מתשעים {{#annot:term|1397,2506|mDS8}}הדומה ל{{#annotend:mDS8}}תשעה והנה שמונים ואחד | ||
| + | |- | ||
| + | | | ||
| + | :The same for every number [including] one. | ||
| + | |style="text-align:right;"|וכן כל המספר לפי המרחק וככה האחד | ||
| + | |- | ||
| + | | | ||
| + | *Since ten is analogous to one, we can extract the squares - whether integers or fractions - from their ratio to ten, or to one hundred, or to one thousand. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2=\left(\frac{a}{10}\sdot a\right)\sdot10}}</math> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2=\left(\frac{a}{100}\sdot a\right)\sdot100}}</math> | ||
| + | |style="text-align:right;"|ובעבור היות עשרה דומה לאחד נוכל ‫<ref>5r</ref>להוציא המרובעים {{#annot:term|1376,20|q4zm}}התמימים{{#annotend:q4zm}} והנשברים מהערך שיש לו אל עשרה או אל מאה או אל אלף | ||
| + | |- | ||
| + | | | ||
| + | :*Such as 75 - how much is its square? | ||
| + | |style="text-align:right;"|כמו ע"ה כמה מרובעו | ||
| + | |- | ||
| + | | | ||
| + | ::Take its ratio to one hundred; it is 3-quarters. Take 3-quarters of 75; it is 18 and three-quarters. Subtract them from 75; fifty-six and a quarter remain; so it is five thousand 600 and twenty-five. | ||
| + | |style="text-align:right;"|קח ערכו אל מאה והוא ג' רביעיותיו<br> | ||
| + | וכמו כן קח ג' רביעיות ע"ה והם י"ח ושלש רביעיות<br> | ||
| + | חסרם מע"ה נשארו חמשים וששה ורביעית והם חמשת אלפים ות"ר מאות וחמשה ועשרים | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{75^2=\left(\frac{75}{100}\sdot75\right)\sdot100=\left(\frac{3}{4}\sdot75\right)\sdot100=\left[75-\left(18+\frac{3}{4}\right)\right]\sdot100=\left(56+\frac{1}{4}\right)\sdot100=5625}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :The same rule for the fractions, including the one. | ||
| + | |style="text-align:right;"|וככה משפט הנשברים עם האחד | ||
| + | |- | ||
| + | | | ||
| + | *For every square greater than ten, its ratio to the square is the same as the ratio of another square smaller than ten to [ten]. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\forall{a^2>10},\exists{b^2<10}:\quad 10:a^2=b^2:10}}</math> | ||
| + | |style="text-align:right;"|וכל מרובע שהוא אחר העשרה יש מערכת המרובע אליו כערך מרובע אחר טרם העשרה אליו | ||
| + | |- | ||
| + | | | ||
| + | :*Such as sixteen with six and a quarter: | ||
| + | |style="text-align:right;"|כמו ששה עשר עם ששה ורביע | ||
| + | |- | ||
| + | | | ||
| + | ::The ratio of 16 to ten is as one time and 3-fifths. | ||
| + | |style="text-align:right;"|שערך י"ו אל עשרה כמוהו וג' חמישיותיו | ||
| + | |- | ||
| + | | | ||
| + | ::When you add to six and a quarter its three-fifths, which is 3 to 5, the result is ten. | ||
| + | |style="text-align:right;"|וכאשר תוסיף על ששה ורביע שלש חמישיותיו שהם ג' מה' יעלה עשרה | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{16:10=1+\frac{3}{5}=\frac{\left(6+\frac{1}{4}\right)+\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]}{6+\frac{1}{4}}=10:\left(6+\frac{1}{4}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::<span style="color:green>Check:</span> The roots prove it, because the one is divided by the other: When you divide ten by the root of 16, the result is two and a half. Multiply it by itself; the result is 6 and a quarter and the ratio of ten to it is the same as the ratio of 16 to ten. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(\frac{10}{\sqrt{16}}\right)^2=\left(2+\frac{1}{2}\right)^2=6+\frac{1}{4}}}</math> | ||
| + | |style="text-align:right;"|והשרשים יוכיחו כי זה {{#annot:term|784,1225|FWr3}}יתחלק על{{#annotend:FWr3}} זה כי כשתחלק עשרה על שרש י"ו יעלה שנים וחצי<br> | ||
| + | תערכם על עצמם יעלה ו' ורביע וערך עשרה אליו כערך י"ו אל עשרה | ||
| + | |- | ||
| + | | | ||
| + | :*Likewise, if you take the ratio of ten to 16, which is five-eighths, and we wish to find a number smaller than ten that is 5-eighths of ten, this is how you find it: | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{10}{16}=\frac{a}{10}}}</math> | ||
| + | |style="text-align:right;"|וכן אם תקח מהערך עשרה אל י"ו והוא חמש שמניותיו רצינו להוציא חשבון טרם העשרה שיהיה ה' שמיניות עשרה וככה תמצאנו | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply 10 by 5; the result is fifty. Divide it by eight; the result of division is six and two remains, which is one quarter and it is five-eighths of ten. | ||
| + | ::<math>\scriptstyle{\color{blue}{a=\frac{10}{16}\sdot10=\frac{5}{8}\sdot10=\frac{10\sdot5}{8}=\frac{50}{8}=6+\frac{2}{8}=6+\frac{1}{4}}}</math> | ||
| + | |style="text-align:right;"|ערוך י' על ה' יעלה חמשים<br> | ||
| + | חלק על שמונה יצא בחלוק ששה נשארו שנים שהם רביע אחד והם חמש שמיניות עשרה | ||
| + | |- | ||
| + | | | ||
| + | ::<span style="color:green>Check:</span> When we take the ratio of 16 to 10; it is one time and three-fifths. We add to six and a quarter its three-fifths; the result is ten. | ||
| + | |style="text-align:right;"|וכאשר נקח ערך י"ו אל י' והוא כמוהו ושלש חמישיותיו ונוסיף על ששה ורביע שלש חמישיותיו יעלה עשרה | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{16}{10}\sdot\left(6+\frac{1}{4}\right)=\left(1+\frac{3}{5}\right)\sdot\left(16+\frac{1}{4}\right)=\left(16+\frac{1}{4}\right)+\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=10}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :For every number you find it the same way. | ||
| + | |style="text-align:right;"|וכן תמצא לכל חשבון | ||
| + | |- | ||
| + | | | ||
| + | :*Also for seven by seven with one and three-sevenths. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{7^2}{10}=\frac{10}{\left(1+\frac{3}{7}\right)^2}}}</math> | ||
| + | |style="text-align:right;"|וכן שרש שבעה על שבעה עם אחד ושלש שביעיות | ||
| + | |- | ||
| + | | | ||
| + | :The same for all. | ||
| + | |style="text-align:right;"|וככה כלם | ||
| + | |- | ||
| + | | | ||
| + | *<span style="color:green>This property is also applicable to one:</span> The same for one with the squares that precede it and follow it. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\forall{b^2>1},\exists{a^2<1}: \frac{b^2}{1}=\frac{1}{a^2}}}</math> | ||
| + | |style="text-align:right;"|גם כן משרש האחד עם המרובעים לפניו ואחריו | ||
| + | |- | ||
| + | | | ||
| + | ::This is clear: as one quarter, whose root is half, so they are similar to four and two. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{2^2}{1}=4=\frac{1}{\frac{1}{4}}=\frac{1}{\left(\frac{1}{2}\right)^2}}}</math> | ||
| + | |style="text-align:right;"|וזה יתברר כרביע אחד ששרשו חצי והנה הם כארבעה ושנים | ||
| + | |- | ||
| + | | | ||
| + | :Likewise the rule of the fractions of fractions and so on endlessly. | ||
| + | |style="text-align:right;"|וכן משפט שברי השברים עד אין קץ | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style="color:Green>The uniqueness of one – as mean between the proper fractions and the improper fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |The proper fractions before one are the inverses to the improper fractions after one | ||
| + | |style="text-align:right;"|ובעבור היות השרשים בנשברים שהם טרם האחד הפך הנמצאים אחרי האחד | ||
| + | |- | ||
| + | |<span style="color:Green>Therefore one has the following properties:</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *One is a root, a square number, and a cubic number. | ||
| + | :<math>\scriptstyle{\color{blue}{1=\sqrt{1}=1^2=1^3}}</math> | ||
| + | |style="text-align:right;"|על כן האחד שורש ומרובע וגוף שוה | ||
| + | |- | ||
| + | | | ||
| + | *''His hand will be upon all, and the hand of everyone upon him'' [Genesis 16, 12]; it is the beginning and the end of all. | ||
| + | |style="text-align:right;"|''{{#annot:Gen16-12|494|QDE2}}ידו בכל ויד כל בו{{#annotend:QDE2}}''‫<ref group=note>בראשית טז, יב</ref> והוא ראשית הכל ואחרית הכל | ||
| + | |- | ||
| + | | | ||
| + | *It has no addition [<math>\scriptstyle{\color{blue}{1\times1=1;\;1\times a=a}}</math>] and no subtraction [<math>\scriptstyle{\color{blue}{1\div1=1;\;a\div1=a}}</math>]. | ||
| + | |style="text-align:right;"|ולא יקבל תוספת ומגרעת | ||
| + | |- | ||
| + | | | ||
| + | *No number resembles to it. | ||
| + | |style="text-align:right;"|ואין לו דמות במספר | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === <span style="color:Green>The Twelve Names that Form Every Number</span> === | ||
| + | | | ||
| + | |- | ||
| + | |The names of all numbers are formed by twelve words: | ||
| + | |style="text-align:right;"|{{#annot:||vkGr}}יסוד כל מספר נכלל בשנים עשר שמות {{#annotend:vkGr}} | ||
| + | |- | ||
| + | | | ||
| + | *Nine of them repeat themselves and they are [the names] of the units from ''one'' to ''nine''. | ||
| + | |style="text-align:right;"|תשעה מהם חוזרים חלילה והם האחדים מאחד ועד תשעה | ||
| + | |- | ||
| + | | | ||
| + | *Three form the names of the ranks - tens, hundreds, and thousands. | ||
| + | |style="text-align:right;"|והשלשה שמות בונים {{#annot:term|1316,203|hUiz}}מעלותיו{{#annotend:hUiz}} והם העשרות והמאות והאלפים | ||
| + | |- | ||
| + | | | ||
| + | :For, every number higher than the thousands reiterate these [three] names, such as ten thousand, one hundred thousand, one thousand thousand. | ||
| + | |style="text-align:right;"|‫<ref>5v</ref>כי כל חשבון אשר על האלפים חוזרים חלילה על אלו השמות כמו עשרת אלפים ומאת אלף ואלף אלפי אלפים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == <span style="color:Green>Table of Contents</span> == | ||
| + | | | ||
| + | |- | ||
| + | |<span style="color:Green>The chapters representing the eight arithmetical operations applied to all numbers - integers and fractions:</span> | ||
| + | | | ||
| + | |- | ||
| + | |Every number - integer or fraction - is divided into eight chapters and they are: addition of one to another; subtraction of one from another; multiplication of one by another; division of one by another; ratio of one to another; deducing one from another; conversion of one into another; root of one and another. | ||
| + | |style="text-align:right;"|וכל מספר השלם והנשבר נחלק לשמנה שערים והם {{#annot:term|1166,154|WXEA}}מחברת זה עם זה{{#annotend:WXEA}} {{#annot:term|1193,155|L8O7}}מגרעת זה מזה{{#annotend:L8O7}} {{#annot:term|1345,156|GOSD}}מערכת זה על זה{{#annotend:GOSD}} {{#annot:term|1370,157|RJWg}}מחלוקת זה על זה{{#annotend:RJWg}} ערך זה אל זה הוצאת זה מזה {{#annot:term|1430,1551|fagX}}השבת זה לזה{{#annotend:fagX}} שורש זה וזה | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == <span style="color:Green>Interpolated Excerpt</span> == | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |style="width:45%; text-align:right;"|שהיה י"ו ישאר ד‫' | ||
| + | |- | ||
| + | |If the scales of the remainder we have to subtract from the greater number are greater than the scales of the greater number, we add 9 to the scales of the greater number and then we subtract. | ||
| + | |style="text-align:right;"|ואלו היה {{#annot:term|1453,354|kRMI}}מאזני{{#annotend:kRMI}} הנשאר שיש לנו לחסר מהחשבון הגדול יותר ממאזני החשבון הגדול היינו מוסיפים על מאזני החשבון הגדול ט' ואחר כן היינו מחסרים | ||
| + | |- | ||
| + | | | ||
| + | :Another example with odd numbers: | ||
| + | |style="text-align:right;"|דמיון אחר בנפרדים | ||
| + | |- | ||
| + | | | ||
| + | :*We say that the number is eighty thousand, seven thousand, six hundred and fifty four, which is of the odds. | ||
| + | ::<math>\scriptstyle\sqrt{87654}</math> | ||
| + | |style="text-align:right;"|נאמר החשבון שמנים אלף ושבעת אלפים ושש מאות וחמשים וארבעה והוא מן {{#annot:term|1336,65|1B3Z}}הנפרדים{{#annotend:1B3Z}} | ||
| + | |- | ||
| + | | | ||
| + | ::The analogous of eighty thousand in the units is eight; the closest preceding square is four and its root is two. Since it is in the fifth rank, the root is two hundred. | ||
| + | |style="text-align:right;"|והדומה לשמנים אלף הוא שמונה באחדים והמרובע הקרוב שעבר הוא ארבעה ושרשו שנים ובעבור היותו ‫<ref>3v</ref>במערכת חמישית הנה השרש מאתים | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract the square, which is 4, from eight, which is eighty thousand; we are left with [47] thousand and 654. | ||
| + | |style="text-align:right;"|ונסיר המרובע שהוא ד' משמונה שהם שמונים אלף אז ישארו לנו [מ"ז] אלף גם תרנ"ד | ||
| + | |- | ||
| + | | | ||
| + | ::We double the root; it is 400. | ||
| + | |style="text-align:right;"|ונכפול השרש ויהיו ת‫' | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::{| | ||
| + | |- | ||
| + | |<span style="color:red>8</span>7654||rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{8}}-{\color{blue}{2^2}}=8-4={\color{blue}{4}}}</math>||<span style="color:#0000FF>4</span>7654||rowspan="2"|<math>\scriptstyle\xrightarrow{2\sdot200={\color{blue}{4}}00}</math>||<span style="color:red>47</span>654 | ||
| + | |- | ||
| + | | ||<span style="color:#0000FF>2</span>    || <span style="color:#0000FF>4</span>    | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::We divide 47 by it, but we cannot give it a ten, since it is a hundred and we must subtract its square, which is ten thousand. So, we give it 9, which is 90; the result is 36000 and we are left with 11654. | ||
| + | |style="text-align:right;"|ונחלק מ"ז עליו ולא נוכל לתת לו עשרה ובעבור שיהיו מאה ויש לנו להסיר מרובעו שהוא עשרת אלפים והנה נתן לו ט' שהם צ' ועלה המספר ל"ו אלפים ונשארו לנו י"א אלף גם תרנ"ד | ||
| + | |- | ||
| + | | | ||
| + | ::The root is 290. | ||
| + | |style="text-align:right;"|והשרש ר"צ | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::{| | ||
| + | |- | ||
| + | |rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{47}}000-\left(400\sdot{\color{blue}{9}}0\right)=47000-36000={\color{blue}{11}}000}</math>||<span style="color:#0000FF>11</span>654 | ||
| + | |- | ||
| + | | 4<span style="color:#0000FF>9</span>   | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::We must subtract the square of 90, which is 8 thousand and one hundred; 3[5]54 remain. | ||
| + | |style="text-align:right;"|ויש לנו להסיר מרובע צ' שהוא ח' אלפים ומאה ונשארו ג' אלפים גם תרנ"ד | ||
| + | |- | ||
| + | | | ||
| + | ::We double the root; it is five hundred and eighty. | ||
| + | |style="text-align:right;"|נכפול השרש והנו חמש מאות ושמנים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::{| | ||
| + | |- | ||
| + | |rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{116}}00-90^2=11600-8100={\color{blue}{35}}00}</math>||<span style="color:#0000FF>35</span>54||rowspan="2"|<math>\scriptstyle\xrightarrow{2\sdot290={\color{blue}{58}}0}</math>||<span style="color:red>35</span>54 | ||
| + | |- | ||
| + | |49  || <span style="color:#0000FF>58</span>  | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::<span style="color:Green>missing stages of calculation:</span> | ||
| + | | | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::{| | ||
| + | |- | ||
| + | |rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{35}}00-\left(500\sdot{\color{blue}{6}}\right)=3500-3000={\color{blue}{5}}00}</math>||<span style="color:#0000FF>5</span>54||rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{55}}0-\left(80\sdot{\color{blue}{6}}\right)=550-480={\color{blue}{7}}0}</math>|| <span style="color:#0000FF>7</span>4 | ||
| + | |- | ||
| + | |58<span style="color:#0000FF>6</span>||586 | ||
| + | |} | ||
| + | ::{| | ||
| + | |- | ||
| + | |rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{74}}-6^2=74-36={\color{blue}{38}}}</math>|| <span style="color:#0000FF>38</span> | ||
| + | |- | ||
| + | |586 | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | ::We divide the remaining number by it; the result is 6. | ||
| + | |style="text-align:right;"|נחלק החשבון הנשאר עליו ויצא ו‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Subtract a square of six from the remainder, which is 74; 38 remains. | ||
| + | |style="text-align:right;"|הסר מרובע ששה מהנשאר שהיה ע"ד ונשאר ל"ח | ||
| + | |- | ||
| + | | | ||
| + | ::So, the root is 296 and its square is 87616. | ||
| + | ::<math>\scriptstyle{\color{blue}{296^2=87616}}</math> | ||
| + | |style="text-align:right;"|והנה השרש רצ"ו ומרובעו פ"ז אלפים תרי"ו | ||
| + | |- | ||
| + | | | ||
| + | ::<span style="color:Green>'''Check:'''</span> The scales of the root are one, we add it to the scales of 38, which is the remainder added to the square, that is two; the result is three. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(296^2=87616\equiv_91\right)+\left(38\equiv_92\right)=3}}</math> | ||
| + | |style="text-align:right;"|ו{{#annot:term|1451,2139|SqpY}}משקל{{#annotend:SqpY}} השרש א' חברנו אותו עם משקל ל"ח שהוא הנשאר יותר מהמרובע שהוא שנים עליו שלשה | ||
| + | |- | ||
| + | | | ||
| + | ::Look at the scales of the original number, which is the greater; it is three. | ||
| + | ::<math>\scriptstyle{\color{blue}{87654\equiv_93}}</math> | ||
| + | |style="text-align:right;"|והנה הסתכל משקל החשבון הראשון שהוא הגדול היה שלשה | ||
| + | |- | ||
| + | | | ||
| + | ::We also look how much is [the scales of] 38; it is two. We subtract it from the scales of the greater number, which is 3; 1 remains. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(87654\equiv_93\right)-\left(38\equiv_92\right)=1}}</math> | ||
| + | |style="text-align:right;"|ועוד בקשנו כמה ל"ח שהוא לחסר והנו שנים חסרנוהו ממשקל החשבון הגדול שהיה ג' ונשאר א‫' | ||
| + | |- | ||
| + | | | ||
| + | ::So should be the scales of the square as well as the scales of the root multiplied by itself and so they are. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(296\equiv_91\right)=\left(296^2=87616\equiv_91\right)}}</math> | ||
| + | |style="text-align:right;"|וככה ראוי להיות משקל המרובע גם משקל שרשו ערוך על עצמו וככה הוא | ||
| + | |- | ||
| + | |<span style="color:Green>'''The three algebraic species: root, square, and number'''</span> | ||
| + | | | ||
| + | |- | ||
| + | |All numbers are divided into three categories, which are: root, square, and a number that is neither root nor square. | ||
| + | |style="text-align:right;"|וכל המספרים הם נפרדים לשלשה ענינים והם שרש ומרובע ומספר שלא יעשה לא שרש ולא מרובע | ||
| + | |- | ||
| + | |You can extract them from each other: | ||
| + | |style="text-align:right;"|ואתה יכול להוציאם זה מזה | ||
| + | |- | ||
| + | | | ||
| + | *As saying: a square is equal to its five roots. | ||
| + | :<math>\scriptstyle x^2=5x</math> | ||
| + | |style="text-align:right;"|כאמרך מרובע שוה לחמשת שרשיו | ||
| + | |- | ||
| + | | | ||
| + | :Know that its root is 5 and its square is 25 <math>\scriptstyle{\color{blue}{x=5;\ x^2=25}}</math> | ||
| + | |style="text-align:right;"|דע כי שרשו ה' ומרובעו כ"ה | ||
| + | |- | ||
| + | | | ||
| + | *Also, a third of a square is equal to its five roots. | ||
| + | :<math>\scriptstyle\frac{1}{3}x^2=5x</math> | ||
| + | |style="text-align:right;"|וכן שלישית מרובע שוה לחמשת שרשיו | ||
| + | |- | ||
| + | | | ||
| + | :Know that its root is [15] and its square is [2]25. | ||
| + | |style="text-align:right;"|דע כי שרשו ה' ומרובעו כ"ה | ||
| + | |- | ||
| + | | | ||
| + | *Also, a third of a square is equal to its 4 roots. | ||
| + | :<math>\scriptstyle\frac{1}{3}x^2=4x</math> | ||
| + | |style="text-align:right;"|וכן שלישית מרובע שוה לד' שרשיו | ||
| + | |- | ||
| + | | | ||
| + | :Know that there are 12 roots in the square and the square is [14]4. | ||
| + | :<math>\scriptstyle{\color{blue}{x^2=12x}}</math> | ||
| + | |style="text-align:right;"|דע כי המרובע יהיה בו י"ב שרשים והמרובע ד‫' | ||
| + | |- | ||
| + | !<span style="color:Green>'''The six canonical equations'''</span> | ||
| + | | | ||
| + | |- | ||
| + | |<span style="color:Green>Three simple types of equations</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *One category is a square equals roots. | ||
| + | :<math>\scriptstyle ax^2=bx</math> | ||
| + | |style="text-align:right;"|והנה ענין אחד הוא מרובע שוה לשרשים | ||
| + | |- | ||
| + | | | ||
| + | *The second category is a square equals a number. | ||
| + | :<math>\scriptstyle ax^2=c</math> | ||
| + | |style="text-align:right;"|והענין השני מרובע שוה למספר | ||
| + | |- | ||
| + | | | ||
| + | :*As saying 5 squares equal 80. | ||
| + | ::<math>\scriptstyle5x^2=80</math> | ||
| + | |style="text-align:right;"|כאמרך ה' מרובעים שוים לפ‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Know that one square is a fifth of 80, which is 16. | ||
| + | ::<math>\scriptstyle{\color{blue}{x^2=\frac{1}{5}\sdot80=16}}</math> | ||
| + | |style="text-align:right;"|דע לך כי המרובע האחד הוא חמישית פ' שהוא י"ו | ||
| + | |- | ||
| + | | | ||
| + | :*Also half a square equals 18. | ||
| + | ::<math>\scriptstyle\frac{1}{2}x^2=18</math> | ||
| + | |style="text-align:right;"|וכן חצי מרובע שוה לי"ח | ||
| + | |- | ||
| + | | | ||
| + | ::Know that the square is 36. | ||
| + | ::<math>\scriptstyle{\color{blue}{x^2=36}}</math> | ||
| + | |style="text-align:right;"|דע כי המרובע הוא ל"ו | ||
| + | |- | ||
| + | | | ||
| + | *The third category is roots equal a number. | ||
| + | :<math>\scriptstyle bx=c</math> | ||
| + | |style="text-align:right;"|והענין השלישי שרשים שוים למספר | ||
| + | |- | ||
| + | | | ||
| + | :*As saying 9 roots equal 81. | ||
| + | ::<math>\scriptstyle9x=81</math> | ||
| + | |style="text-align:right;"|כאמרך ט' שרשים שוים פ"א | ||
| + | |- | ||
| + | | | ||
| + | ::Know that the number is the square and its root is 9. | ||
| + | ::<math>\scriptstyle{\color{blue}{x=9;\ x^2=81}}</math> | ||
| + | |style="text-align:right;"|דע המספר ‫<ref>4r</ref>הוא המרובע ושרשו ט‫' | ||
| + | |- | ||
| + | | | ||
| + | :*Also half a root equals 10. | ||
| + | ::<math>\scriptstyle\frac{1}{2}x=10</math> | ||
| + | |style="text-align:right;"|וכן חצי שרש שוה לי‫' | ||
| + | |- | ||
| + | | | ||
| + | ::The [root] is 20 and the square is two hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{x=20;\ x^2=200}}</math> | ||
| + | |style="text-align:right;"|השני עשרים והמרובע מאתים | ||
| + | |- | ||
| + | |You can also find three other composite [types of equations] and they are: | ||
| + | |style="text-align:right;"|וגם תוכל להוציא מזה שלשה ענינים אחרים מורכבים והם | ||
| + | |- | ||
| + | | | ||
| + | *A square and a root equal a number. | ||
| + | :<math>\scriptstyle ax^2+bx=c</math> | ||
| + | |style="text-align:right;"|מרובע ושרש שניהם שוים למספר | ||
| + | |- | ||
| + | | | ||
| + | *Or, a square and a number equal roots. | ||
| + | :<math>\scriptstyle ax^2+c=bx</math> | ||
| + | |style="text-align:right;"|או מרובע ומספר שוים לשרשים | ||
| + | |- | ||
| + | | | ||
| + | *Or, root and a number equal a square. | ||
| + | :<math>\scriptstyle bx+c=ax^2</math> | ||
| + | |style="text-align:right;"|או שרשים ומספר שוים למרובע | ||
| + | |- | ||
| + | |The first category: | ||
| + | :<math>\scriptstyle ax^2+bx=c</math> | ||
| + | |style="text-align:right;"|הענין הראשון | ||
| + | |- | ||
| + | | | ||
| + | *As saying: a square summed its ten roots are 39 - how much is the square and how much is the root? | ||
| + | :<math>\scriptstyle x^2+10x=39</math> | ||
| + | |style="text-align:right;"|כאמרך מרובע עם עשרת שרשיו מחוברים עלו ל"ט כמה המרובע וכמה השרש | ||
| + | |- | ||
| + | | | ||
| + | ::Take half [the number of] the roots and multiply it by itself; the result is 25. | ||
| + | |style="text-align:right;"|קח חצי השרשים וערכם על עצמם יעלה כ"ה | ||
| + | |- | ||
| + | | | ||
| + | ::Add it to 39; the result is 64. | ||
| + | |style="text-align:right;"|הוסיפם על ל"ט יעלה ס"ד | ||
| + | |- | ||
| + | | | ||
| + | ::Extract the root; it is 8. | ||
| + | |style="text-align:right;"|הוצא השרש והוא ח‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Subtract from it half [the number of] the roots, which is 5; 3 remains, which is the required root and the square is 9. | ||
| + | |style="text-align:right;"|וחסר מהם חצי השרשים שהוא ה' ישאר ג' והוא השרש המבוקש ומרובע ט‫' | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{x=\sqrt{\left(\frac{1}{2}\sdot10\right)^2+39}-\left(\frac{1}{2}\sdot10\right)=\sqrt{5^2+39}-5=\sqrt{25+39}-5=\sqrt{64}-5=8-5=3}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :<span style="color:Green>'''Normalization:'''</span> also if it is said: 2 squares, or 3, or more, plus so and so of its roots are equal to a certain number. Do as follows: | ||
| + | |style="text-align:right;"|וכן אם יאמר ב' מרובעים או ג' או יותר עם שרשיו כך וכך שוין למספר כך וכך ככה תעשה | ||
| + | |- | ||
| + | | | ||
| + | :Take one square and take its ratio to [the number of] the squares from the roots and the number. Then, proceed according to the rule: half, multiply, add, extract the root, and subtract; the remainder will be the root of a single square. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{ax^2+bx=c\longrightarrow x^2+\frac{b}{a}x=\frac{c}{a}}}</math> | ||
| + | |style="text-align:right;"|קח מרובע אחד וכערכו מן המרובעים קח מן השרשים ומן המספר ועשה כמשפט לחצות ולערוך ולהוסיף ולהוציא השרש ולחסר והנשאר יהיה שרש המרובע האחד | ||
| + | |- | ||
| + | | | ||
| + | :The same if it is said: half a square, or its third, plus so and so of its roots are equal to a certain number. Do as follows: | ||
| + | |style="text-align:right;"|וכן אם יאמר חצי מרובע או שלישיתו עם גדריו כך שוים למספר כך ככה תעשה | ||
| + | |- | ||
| + | | | ||
| + | :Complete the square and add to the roots and the number as the value you add to [the square]. Then, proceed according to the rule and you will receive the root of the whole square. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{1}{a}x^2+bx=c\longrightarrow x^2+a\sdot bx=a\sdot c}}</math> | ||
| + | |style="text-align:right;"|{{#annot:term|970,1267|PY3H}}השלם{{#annotend:PY3H}} המרובע וכערך שהוספת עליו הוסף על השרשים ועל המספר ועשה כמשפט יצא לך שרש המרובע השלם | ||
| + | |- | ||
| + | |The second category: | ||
| + | :<math>\scriptstyle ax^2+c=bx</math> | ||
| + | |style="text-align:right;"|הענין השני | ||
| + | |- | ||
| + | | | ||
| + | *A square plus 21 equal ten roots of the square. | ||
| + | :<math>\scriptstyle x^2+21=10x</math> | ||
| + | |style="text-align:right;"|מרובע עם כ"א שוים לעשרת שרשי המרובע | ||
| + | |- | ||
| + | | | ||
| + | ::Take half [the number of] the roots and multiply it by itself; it is 25. | ||
| + | |style="text-align:right;"|קח חצי השרשים וערכם על עצמם יהיה כ"ה | ||
| + | |- | ||
| + | | | ||
| + | ::Subtract from it the number, which is 21; 4 remains. | ||
| + | |style="text-align:right;"|{{#annot:term|1232,181|UdlW}}הוצא מהם{{#annotend:UdlW}} המספר שהוא כ"א ישאר ד‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Its root is 2. | ||
| + | |style="text-align:right;"|ושרשם ב‫' | ||
| + | |- | ||
| + | | | ||
| + | ::If you subtract it from half [the number of] the roots, which is 5, 3 remains and this is a root of the square. | ||
| + | |style="text-align:right;"|אם תגרעהו מחצי השרשים שהוא ה' ישאר ג' והוא שרש המרובע | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{x=\left(\frac{1}{2}\sdot10\right)-\sqrt{\left(\frac{1}{2}\sdot10\right)^2-21}=5-\sqrt{25-21}=5-\sqrt{4}=5-2=3}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::If you add it to half [the number of] the roots, the result is 8 and this is also a root of the square. | ||
| + | ::<math>\scriptstyle{\color{blue}{x=\left(\frac{1}{2}\sdot10\right)+\sqrt{\left(\frac{1}{2}\sdot10\right)^2-21}=5+2=7}}</math> | ||
| + | |style="text-align:right;"|ואם תוסיפהו על חצי השרשים יעלה ח' והוא כמו כן שרש המרובע | ||
| + | |- | ||
| + | | | ||
| + | ::<span style="color:Green>'''Check:'''</span> when you add it to the 21, they will be equal to 10 roots of the square. | ||
| + | ::<math>\scriptstyle{\color{blue}{3^2+21=10\sdot3}}</math> | ||
| + | ::<math>\scriptstyle{\color{blue}{7^2+21=10\sdot7}}</math> | ||
| + | |style="text-align:right;"|כשתחברהו עם כ"א ההם יחד יהיו שוים לי' שרשי המרובע | ||
| + | |- | ||
| + | | | ||
| + | ::Sometimes it does not have two results. | ||
| + | |style="text-align:right;"|ופעמים שאינו יוצא לשני הפנים האלה | ||
| + | |- | ||
| + | |Know that if the product of half [the number of] the roots is less than the number, then the question is wrong. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(\frac{1}{2}\sdot b\right)^2<c\longrightarrow\varnothing}}</math> | ||
| + | |style="text-align:right;"|ודע שאם יהיה היוצא מערך חצי השרשים פחות מן המספר שהשאלה {{#annot:term|463,1395|Jf2K}}משובשת{{#annotend:Jf2K}} | ||
| + | |- | ||
| + | |If the product is equal to the number, know that the root of the square is half [the number of] the roots mentioned in the question. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(\frac{1}{2}\sdot b\right)^2=c\longrightarrow x=\frac{1}{2}\sdot b}}</math> | ||
| + | |style="text-align:right;"|ואם יהיה היוצא שוה למספר דע כי שרש המרובע הוא חצי השרשים הנזכרים בשאלה | ||
| + | |- | ||
| + | |The third category | ||
| + | :<math>\scriptstyle bx+c=ax^2</math> | ||
| + | |style="text-align:right;"|הענין השלישי | ||
| + | |- | ||
| + | | | ||
| + | *As saying: 3 roots plus four equal a square. | ||
| + | :<math>\scriptstyle3x+4=x^2</math> | ||
| + | |style="text-align:right;"|כאמרך ג' שרשים וארבעה שוים למרובע | ||
| + | |- | ||
| + | | | ||
| + | ::Take half [the number of] the roots and multiply it by itself; the result is 2 and a quarter. | ||
| + | |style="text-align:right;"|קח חצי השרשים וערכם על עצמם יעלה ב' ורביע | ||
| + | |- | ||
| + | | | ||
| + | ::Add it to the number, which is 4; it is 6 and a quarter. | ||
| + | |style="text-align:right;"|‫<ref>4v</ref>הוסיפם על המספר שהוא ד' יהיה ו' ורביע | ||
| + | |- | ||
| + | | | ||
| + | ::Its root is 2 and a half. | ||
| + | |style="text-align:right;"|ושרשי ב' וחצי | ||
| + | |- | ||
| + | | | ||
| + | ::Add it to half [the number of] the roots, which is one and a half; the result is 4 and this is the root of the square. | ||
| + | |style="text-align:right;"|הוסף על חצי השרשים שהם אחד וחצי יעלה ד' והוא שרש המרובע | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle=\sqrt{\left(\frac{1}{2}\sdot3\right)^2+4}+\left(\frac{1}{2}\sdot3\right)=\sqrt{\left(2+\frac{1}{4}\right)+4}+\left(1+\frac{1}{2}\right)=\sqrt{6+\frac{1}{4}}+\left(1+\frac{1}{2}\right)\\&\scriptstyle=\left(2+\frac{1}{2}\right)+\left(1+\frac{1}{2}\right)=4\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ודע כי לעולם כפל כפל המרובע | ||
| + | |- | ||
| + | |} | ||
| − | + | {| | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | == Chapter One: Addition == |
| − | + | !style="width:45%; text-align:right;"|<big>השער</big> הראשון ב{{#annot:term|1166,154|cjIw}}מחברת{{#annotend:cjIw}} | |
| − | + | |- | |
| − | + | |It is divided into two categories: | |
| − | + | |style="text-align:right;"|והוא נחלק לשני ענינים | |
| − | + | |- | |
| − | + | | | |
| − | + | *Addition of integers with integers | |
| − | + | |style="text-align:right;"|{{#annot:term|1208,154|fHVb}}חבור{{#annotend:fHVb}} שלמים עם שלמים | |
| − | <math>\ | + | |- |
| − | + | | | |
| − | + | *Addition of fractions of fractions with fractions | |
| − | <math> | + | |style="text-align:right;"|וחבור שברי שברים עם שברים |
| − | + | |- | |
| − | + | | | |
| − | + | === The First Category: [Addition of] Integers === | |
| − | + | !style="text-align:right;"|הענין הראשון בשלמים | |
| − | + | |- | |
| − | + | | | |
| − | + | ==== <span style=color:Green>Sums</span> ==== | |
| − | + | | | |
| − | + | |- | |
| − | + | !<span style=color:Green>sum of arithmetic progression of consecutive numbers</span> | |
| − | + | | | |
| − | + | |- | |
| − | + | |When you want to sum numbers increasing by progression as much as you wish. | |
| − | + | |style="text-align:right;"|שתרצה לחבר חשבון הולך וגדל {{#annot:term|1355,2576|KBdx}}על דרך המספר{{#annotend:KBdx}} עד כמה שתרצה | |
| − | + | |- | |
| − | + | | | |
| − | + | *If the number of terms is odd | |
| − | + | |style="text-align:right;"|אם החשבון מן הנפרדים | |
| − | + | |- | |
| − | + | | | |
| − | + | :*Multiply the [last] number by its half plus one half and the result is the sum | |
| − | + | ::<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n-1} i=\left(2n-1\right)\sdot\left[\left[\frac{1}{2}\sdot \left(2n-1\right)\right]+\frac{1}{2}\right]}}</math> | |
| − | + | |style="text-align:right;"|ערוך החשבון שהגיע עדיו על חציו {{#annot:term|1207,878|POyO}}בתוספת{{#annotend:POyO}} חצי אחד והעולה הוא המחובר | |
| + | |- | ||
| + | | | ||
| + | :Example: question: we summed the units by progression up to 11, how much are they? | ||
| + | ::<math>\scriptstyle\sum_{i=1}^{11} i</math> | ||
| + | |style="text-align:right;"|והמשל <big>שאלה</big> חברנו האחדים {{#annot:term|1355,2576|ZAwr}}על דרך המספר{{#annotend:ZAwr}} עד י"א כמה הם | ||
| + | |- | ||
| + | | | ||
| + | ::The answer: take half the last number, add to it one half, it is 6. Multiply it by the [last] number, the result is 66 and so is the sought. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{11} i=n\sdot\left[\left(\frac{1}{2}\sdot11\right)+\frac{1}{2}\right]=11\sdot6=66}}</math> | ||
| + | |style="text-align:right;"|<big>התשובה</big> קח חצי המספר האחרון ו{{#annot:term|1206,178|ghsv}}הוסף עליו{{#annotend:ghsv}} חצי אחד והנה ו‫'<br> | ||
| + | ערכם על המספר עלה ס"ו וככה המבוקש | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n-1} i=\left[\left(2n-1\right)+1\right]\sdot\left[\frac{1}{2}\sdot\left(2n-1\right)\right]}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::Know it by adding one to 11, then multiply the result by a half of 11 and so is the sought. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{11} i=\left(11+1\right)\sdot\left(\frac{1}{2}\sdot11\right)}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתוסיף על י"א אחד ותערוך העולה על חצי י"א וככה המבוקש | ||
| + | |- | ||
| + | | | ||
| + | *If the number of terms is even | ||
| + | |style="text-align:right;"|ואם החשבון מן ה{{#annot:term|1333,63|bXwy}}זוגות{{#annotend:bXwy}} | ||
| + | |- | ||
| + | | | ||
| + | :*Multiply the last [number] by its half and add to it half the [last] number. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n} i=\left[2n\sdot\left(\frac{1}{2}\sdot2n\right)\right]+\left(\frac{1}{2}\sdot2n\right)}}</math> | ||
| + | |style="text-align:right;"|ערוך האחרון על חציו והוסף עליו חצי החשבון | ||
| + | |- | ||
| + | | | ||
| + | :Example: we summed from 1 to 10 | ||
| + | ::<math>\scriptstyle\sum_{i=1}^{10} i</math> | ||
| + | |style="text-align:right;"|והמשל חברנו מא' עד י‫' | ||
| + | |- | ||
| + | | | ||
| + | ::We take its half, which is 5, multiply it by 10, then add five, which is a half of 10, the result is 55 and so it the sought. | ||
| + | |style="text-align:right;"|לקחנו חציו והוא ה‫'<br> | ||
| + | ערכנו אותו על י' והוספנו חמשה שהוא חצי י' ועלה נ"ה וככה המבוקש | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=\left[10\sdot\left(\frac{1}{2}\sdot10\right)\right]+\left(\frac{1}{2}\sdot10\right)=\left(10\sdot5\right)+5=55}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n} i=\left(2n+1\right)\sdot\left(\frac{1}{2}\sdot2n\right)}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::Know it by adding one to 10, then multiply the result by half the 10. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=\left(10+1\right)\sdot\left(\frac{1}{2}\sdot10\right)}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתוסיף אחד על י' והעולה תערוך במחצית הי‫' | ||
| + | |- | ||
| + | !<span style=color:Green>sum of arithmetic progression of consecutive even integers</span> | ||
| + | | | ||
| + | |- | ||
| + | |If you add the numbers [two by two] | ||
| + | |style="text-align:right;"|ואם תוסיף החשבון בב‫' | ||
| + | |- | ||
| + | | | ||
| + | *Start from two to 10. | ||
| + | ::<math>\scriptstyle\sum_{i=1}^{10} 2i</math> | ||
| + | |style="text-align:right;"|ותתחיל בשנים עד י' פעם | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 2i=\left(2n+2\right)\sdot\left(\frac{1}{2}\sdot n\right)}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::It is known that the last [number] is 20, add to it 2, then multiply the result by half the 10 and the result is the sought, which is 110. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} 2i=\left(20+2\right)\sdot\left(\frac{1}{2}\sdot10\right)=110}}</math> | ||
| + | |style="text-align:right;"|ידוע הוא כי האחרון הוא כ' הוסף עליהם ב' והעולה תערוך על חצי הי' והעולה הוא המבוקש והוא ק"י | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{k=1}^{n} 2k=\left[\left(\frac{1}{2}\sdot2n\right)+\left(\frac{1}{2}\sdot2\right)\right]\sdot\left(\frac{1}{2}\sdot2n\right)}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::Or, take half the last number, which is 10, add a half of 2, it is 11, multiply it by 10 and the result is the sought. | ||
| + | |style="text-align:right;"|או קח חצי ‫<ref>6r</ref>המספר האחרון והוא י' הוסף חצי ב' והוא י"א<br> | ||
| + | ערכם על י' והעולה הוא המבוקש | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} 2i=\left[\left(\frac{1}{2}\sdot20\right)+\left(\frac{1}{2}\sdot2\right)\right]\sdot\left(\frac{1}{2}\sdot20\right)=\left[10+\left(\frac{1}{2}\sdot2\right)\right]\sdot10=11\sdot10}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 2i=\left[\left(\frac{1}{2}\sdot n\right)+\frac{1}{2}\right]\sdot2n}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::Or, take half the last [number], which is 5, add to it one half and multiply by the last [number]. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} 2i=\left[\left(\frac{1}{2}\sdot10\right)+\frac{1}{2}\right]\sdot20=\left(5+\frac{1}{2}\right)\sdot20}}</math> | ||
| + | |style="text-align:right;"|או קח חצי האחרון והוא ה' הוסיף עליהם חצי אחד והערך על האחרון | ||
| + | |- | ||
| + | !<span style=color:Green>sum of arithmetic progression of consecutive triples</span> | ||
| + | | | ||
| + | |- | ||
| + | |If you add three by three | ||
| + | |style="text-align:right;"|ואם תוסיף ג"ג | ||
| + | |- | ||
| + | | | ||
| + | *Start from 3 to 10. | ||
| + | ::<math>\scriptstyle\sum_{k=1}^{10} 3k</math> | ||
| + | |style="text-align:right;"|ותתחיל בג' עד י' פעם | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 3i=\left(3n+3\right)\sdot\left(\frac{1}{2}\sdot n\right)}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::It is known that the last number is 30, add to it 3, then multiply the result by half the 10, the result is 165 and it is the sought. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} 3i=\left(30+3\right)\sdot\left(\frac{1}{2}\sdot10\right)=165}}</math> | ||
| + | |style="text-align:right;"|ידוע הוא כי החשבון האחרון הוא ל' הוסף עליהם ג' והעולה תערוך על חצי הי' יעלה קס"ה והוא המבוקש | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 3i=\left[\left(\frac{1}{2}\sdot3n\right)+\left(\frac{1}{2}\sdot3\right)\right]\sdot n}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::Or, take half the last number, which is 15, add to it a half of 3, it is 16 and one half, multiply it by 10 and the result is the sought. | ||
| + | |style="text-align:right;"|או קח חצי מספר האחרון והוא ט"ו {{#annot:term|1206,178|3Bta}}הוסף עליהם{{#annotend:3Bta}} חצי ג' והוא י"ו וחצי ערכם על י' והעולה הוא המבוקש | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} 3i=\left[\left(\frac{1}{2}\sdot30\right)+\left(\frac{1}{2}\sdot3\right)\right]\sdot\left(\frac{1}{3}\sdot30\right)=\left[15+\left(\frac{1}{2}\sdot3\right)\right]\sdot10=\left(16+\frac{1}{2}\right)\sdot10}}</math> | ||
| + | |- | ||
| + | !<span style=color:Green>sum of arithmetic progression of consecutive quadruples</span> | ||
| + | | | ||
| + | |- | ||
| + | |If [you] add four by four | ||
| + | |style="text-align:right;"|ואם מוסיף ד"ד | ||
| + | |- | ||
| + | | | ||
| + | :*Take a half of its quarter. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 4i=\left[\left(\frac{1}{2}\sdot\frac{1}{4}\sdot an\right)+\frac{1}{2}\right]\sdot 4n}}</math> | ||
| + | |style="text-align:right;"|קח חצי רביעיתו | ||
| + | |- | ||
| + | !<span style=color:Green>sum of arithmetic progression of consecutive quintuples</span> | ||
| + | | | ||
| + | |- | ||
| + | |If five by five | ||
| + | |style="text-align:right;"|ואם ה"ה | ||
| + | |- | ||
| + | | | ||
| + | :*Take a half of its fifth. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 5i=\left[\left(\frac{1}{2}\sdot\frac{1}{5}\sdot 5n\right)+\frac{1}{2}\right]\sdot 5n}}</math> | ||
| + | |style="text-align:right;"|קח חצי חמישיתו | ||
| + | |- | ||
| + | !<span style=color:Green>sum of arithmetic progression of consecutive integers when the first number is equal to the excess</span> <math>\scriptstyle{\color{OliveGreen}{a_1=d}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *Always add one half and multiply by the last [term] - the way is one [and the same] for all excesses. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} ai=\left[\left(\frac{1}{2}\sdot\frac{1}{a}\sdot an\right)+\frac{1}{2}\right]\sdot an}}</math> | ||
| + | |style="text-align:right;"|ולעולם תוסיף חצי אחד והערך על האחרון ודרך אחד לכל ה{{#annot:term|1207,2412|75Lg}}תוספות{{#annotend:75Lg}} | ||
| + | |- | ||
| + | |This sum of progression is true when adding one by one, starting from 1, or for all excesses, [when the first number is the excess itself] <math>\scriptstyle{\color{OliveGreen}{a_1=d}}</math> | ||
| + | |style="text-align:right;"|וזה {{#annot:term|1208,388|w79b}}חבור{{#annotend:w79b}} {{#annot:term|1214,787|4xfy}}המוספים{{#annotend:4xfy}} הוא הנכון כשתוסיף א"א תתחיל בא' וכן לכל התוספות תתחיל בחשבונם | ||
| + | |- | ||
| + | !<span style=color:Green>sum of arithmetic progression of consecutive integers when the first number is not equal to the excess</span> <math>\scriptstyle{\color{OliveGreen}{a_1\ne d}}</math> | ||
| + | | | ||
| + | |- | ||
| + | |If you start from 10 and add one by one, or two by two, or three by three, as much as you want, do like this: | ||
| + | :Extract the [total] sum up to the last, as instructed above for the odds and for the evens, and save it. | ||
| + | *<math>\scriptstyle{\color{OliveGreen}{\sum_{k=m}^{n} ak=\left(\sum_{i=1}^{n} ai\right)-\left(\sum_{i=1}^{m-1} ai\right)}}</math> | ||
| + | |style="text-align:right;"|אך אם תתחיל מי' ותוסיף א"א או ב"ב או ג"ג עד שתרצה ככה תעשה שתוציא לעולם חשבונך מהאחרון כמו שהורתיך למעלה משפט הנפרדים המשפט הזוגות ושמרהו | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:Green>sum of consecutive natural numbers</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*Then is you added one by one until reaching 19, which is of the odds | ||
| + | ::<math>\scriptstyle\sum_{i=10}^{19} i</math> | ||
| + | |style="text-align:right;"|ואחר כן אם א"א הוספת עד שהגעת לי"ט והוא מן הנפרדים | ||
| + | |- | ||
| + | | | ||
| + | ::You apply on it the rule of the odds, then subtract 1 from 10, take half the remainder, multiply it by the 10, subtract the result from the reserved, which is 190 and the remainder is your sum. | ||
| + | |style="text-align:right;"|וכבר עשית בו משפט הנפרדים<br> | ||
| + | אחר כן תפחות א' מן י' וקח מחצית הנשאר וערכם על הי' והעולה תחסר מן השמור שהיה ק"צ והנשאר הוא חשבונך | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=10}^{19} i=\left(\sum_{i=1}^{19} i\right)-\left[\left[\frac{1}{2}\sdot\left(10-1\right)\right]\sdot10\right]=190-\left[\left[\frac{1}{2}\sdot\left(10-1\right)\right]\sdot10\right]}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:Green>sum of consecutive even numbers</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*If you added two by two and the last number is 20 | ||
| + | ::<math>\scriptstyle\sum_{i=5}^{10} 2i</math> | ||
| + | |style="text-align:right;"|ואם ב"ב הוספת והיה החשבון האחרון כ‫' | ||
| + | |- | ||
| + | | | ||
| + | ::I have already demonstrated how much is [the total sum], which is 110 and it is the reserved. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} 2i=110}}</math> | ||
| + | |style="text-align:right;"|וכבר הורתיך כמה יעלה והוא ק"י והוא השמור | ||
| + | |- | ||
| + | | | ||
| + | ::Now, subtract 2 from 10, take half the remainder, multiply it by a half of 10, subtract the result from the reserved and the remainder is the sum from 10 to 20. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=5}^{10} 2i=110-\left[\left[\frac{1}{2}\sdot\left(10-2\right)\right]\sdot\left(\frac{1}{2}\sdot10\right)\right]}}</math> | ||
| + | |style="text-align:right;"|עכשו חסר ב' מן י' וקח מחצית הנשאר<br> | ||
| + | ערכם על מחצית י' והעולה חסר מהשמור והנשאר הוא {{#annot:term|1220,388|GP8R}}המחובר{{#annotend:GP8R}} מי' עד כ‫' | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:Green>sum of consecutive triples</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*If you added three by three, started your sum from 12 and the last [term] is 30, as it is impossible to start from 10. | ||
| + | ::<math>\scriptstyle\sum_{i=4}^{10} 3i</math> | ||
| + | |style="text-align:right;"|ואם ג"ג הוספת והתחלת בחשבונך מי"ב והיה האחרון ל' אך לא יתכן להתחיל בי‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Extract your sum from 3 to the last [number], which is 465 and save it. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{10} 3i=465}}</math> | ||
| + | |style="text-align:right;"|הוצא חשבונך מן ג' עד האחרון והוא תס"ה ושמרהו | ||
| + | |- | ||
| + | | | ||
| + | ::Subtract 3 from 12, then take half the remainder and multiply it by a third of 12, subtract the result from the reserved and the remainder is the sought. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=4}^{10} 3i=465-\left[\left[\frac{1}{2}\sdot\left(12-3\right)\right]\sdot\left(\frac{1}{3}\sdot12\right)\right]}}</math> | ||
| + | |style="text-align:right;"|ושוב חסר ג' מי"ב וקח מחצית הנשאר וערכם על שלישית י"ב וחסר העולה מן השמור והנשאר הוא המבוקש | ||
| + | |- | ||
| + | |Apply this for all the excesses. | ||
| + | |style="text-align:right;"|וככה תעשה לכל התוספות שתשמר השמות | ||
| + | |- | ||
| + | !<span style=color:Green>Finding the number of terms in a given sum of multiples</span> | ||
| + | | | ||
| + | |- | ||
| + | |If you want to sum a known number multiplied by the units successively, their [number] is unknown and their sum is so and so, by how many numbers it was multiplied? | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} ai=m}}</math> | ||
| + | |style="text-align:right;"|ואם תרצה לחבר מספר ידוע הספור במספר האחדים {{#annot:term|1401,2494|laQt}}על הסדר{{#annotend:laQt}} ואינם ידועים ועלו ככה על כמה מספרים ספר אותו | ||
| + | |- | ||
| + | | | ||
| + | :Divide the result [= the given sum] by the said number, then observe from how many units the quotient is summed and as the number of the units so is the number of terms | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{k=1}^{n} k=\frac{m}{a}}}</math> | ||
| + | |style="text-align:right;"|חלק המספר העולה על המספר שאמר ומה שיצא בחלוק ראה מכמה אחדים יעלה וכמספר האחדים כך ‫<ref>6v</ref>מספרים תפש | ||
| + | |- | ||
| + | | | ||
| + | :*Example: 15 multiplied by the numbers successively and the sum is 315, by how many numbers it was multiplied? | ||
| + | ::<math>\scriptstyle\sum_{i=1}^{n} 15i=315</math> | ||
| + | |style="text-align:right;"|והמשל ט"ו ערוכים על החשבון על הסדר ועלה המחבר שט"ו על כמה מספרים ספר אותו | ||
| + | |- | ||
| + | | | ||
| + | ::Divide 315 by 15, the result is 21. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{n} i=\frac{315}{15}=21}}</math> | ||
| + | |style="text-align:right;"|חלק שט"ו על ט"ו יצא כ"א | ||
| + | |- | ||
| + | | | ||
| + | ::We know that the units that are summed from 1 to 6 are 21. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{6} i=21}}</math> | ||
| + | |style="text-align:right;"|וידענו מהאחדים הספורים מא' ועד ו' הם כ"א | ||
| + | |- | ||
| + | | | ||
| + | ::Hence, it was multiplied by six numbers <math>\scriptstyle{\color{blue}{n=6}}</math> and the sum is 315. | ||
| + | |style="text-align:right;"|והנה על ששה מספרים ספר אותו והיה המחובר שט"ו | ||
| + | |- | ||
| + | | | ||
| + | ::*If you want to know the sum of 15 multiplied successively by 1 to 6. | ||
| + | :::<math>\scriptstyle\sum_{i=1}^{6} 15i</math> | ||
| + | |style="text-align:right;"|ואם תרצה לדעת כמה המחובר מט"ו ספורים {{#annot:term|1401,2494|1GdV}}על סדר חשבון{{#annotend:1GdV}} מא' ועד ו‫' | ||
| + | |- | ||
| + | | | ||
| + | :::We know that up to six the result is 21. | ||
| + | :::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{6} i=21}}</math> | ||
| + | |style="text-align:right;"|ידענו כי עד ששה יעלה כ"א | ||
| + | |- | ||
| + | | | ||
| + | :::Multiply 15 by 21, the result is 315. | ||
| + | :::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{6} 15i=15\sdot21=315}}</math> | ||
| + | |style="text-align:right;"|וערוך ט"ו על כ"א יעלה שט"ו | ||
| + | |- | ||
| + | !<span style=color:Green>sum of geometrical progressions of even-times-even numbers</span> | ||
| + | | | ||
| + | |- | ||
| + | |If you want to sum the even-times-even numbers from one to however you wish successively. | ||
| + | :<math>\scriptstyle\sum_{i=1}^{n} 2^{i-1}</math> | ||
| + | |style="text-align:right;"|ואם תרצה לחבר {{#annot:term|69,2508|bvwq}}חשבון כפל הכפל{{#annotend:bvwq}} מאחד ועד כמה שתרצה על סדר החשבון | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:Green>odd number of even-times-even terms</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :Take the square of the mean even-times-even term, which is the last even-times-even term if the number of the even-times-even terms is odd, double the number, subtract from it one, which is the first term, and the remainder is the sum. | ||
| + | |style="text-align:right;"|קח מרובע הכפל האמצעי והוא הכפל האחרון אם הכפולים נפרדים וכפול החשבון ו{{#annot:term|1362,181|TmDO}}חסר ממנו{{#annotend:TmDO}} אחד שהוא החלק הראשון והנשאר הוא המחובר | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n+1} 2^{i-1}=\left[2\sdot\left(2^{\frac{\left(2n+1\right)-1}{2}}\right)^2\right]-1=\left[2\sdot2^{2n}\right]-1}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*Example: 1, 2, 4 | ||
| + | |style="text-align:right;"|והמשל א' ב' ד‫' | ||
| + | |- | ||
| + | | | ||
| + | ::The square of the 2 is 4 and it is the last even-times-even term <math>\scriptstyle{\color{blue}{a_n=2^2=4}}</math> | ||
| + | |style="text-align:right;"|מרובע הב' הוא ד' והוא הכפל האחרון לעולם | ||
| + | |- | ||
| + | | | ||
| + | *even number of even-times-even terms | ||
| + | |style="text-align:right;"|ואם הכפולים זוגות | ||
| + | |- | ||
| + | | | ||
| + | :Take the square of the greater mean, subtract one from it and the remainder is the sum. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n} 2^{i-1}=\left(2^{n}\right)^2-1}}</math> | ||
| + | |style="text-align:right;"|קח מרובע הכפל האמצעי הגדול וחסר ממנו אחד והנשאר הוא המחובר | ||
| + | |- | ||
| + | | | ||
| + | *''And if the way be too long for you'' [Deuteronomy 14, 24], as if you want to know [the sum of] the even-times-evens from [the first term] to the sixty-fourth [term] by sequence of the numbers, it will be difficult for you to extract the mean even-times-even term and its square. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{k=1}^{n+1} 2^{k-1}=2^{n+1}-1}}</math> | ||
| + | :*<math>{\color{blue}{\scriptstyle1+2+2^2+\ldots+2^{64}=2^{64+1}-1}}</math> | ||
| + | |style="text-align:right;"|''{{#annot:Deu14-24|494|8ktL}}וכי ירבה ממך דרך{{#annotend:8ktL}}''‫<ref group=note>דברים יד, כד</ref> החשבון שתרצה לדעת מאחד ועד ס"ד {{#annot:term|69,2508|AxYM}}כפל הכפל{{#annotend:AxYM}} על סדר החשבון ויתקשה עליך להוציא הכפל האמצעי ומרובעו | ||
| + | |- | ||
| + | | | ||
| + | ::*<span style=color:Green>repetitive process of squaring:</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::You can find it this way: | ||
| + | :::Start with two and multiply it by itself. The result, which is 4, is the number that is the second term and the sum [of all the numbers] preceding it is equal to it, minus 1. | ||
| + | :::<math>\scriptstyle{\color{blue}{2^{2}=4\longrightarrow1+2=2^2-1}}</math> | ||
| + | |style="text-align:right;"|ככה תדענו שתתחיל מן השנים וערכם על עצמם והעולה שהוא ד' הוא חשבון שבמדרגה השניה לה וכל החשבון שלפניה כמוה {{#annot:term|1366,879|DRZq}}פחות{{#annotend:DRZq}} אחד | ||
| + | |- | ||
| + | | | ||
| + | :::Again, multiply 4 by itself, the result is 16, which is the number that is the fourth term, and the sum [of all the numbers] preceding it is equal to it, minus 1. | ||
| + | :::<math>\scriptstyle{\color{blue}{2^{4}=4^2=16\longrightarrow1+2+2^2+2^3=2^4-1}}</math> | ||
| + | |style="text-align:right;"|ושוב וערוך הד' על עצמם יעלה י"ו והוא חשבון שבמדרגה הרביעית לשנית וכל חשבון שלפניה כמוה פחות אחד | ||
| + | |- | ||
| + | | | ||
| + | :::Again, multiply 16 by itself; the result is 256, which is the number that is the eighth term, and the sum [of all the numbers] preceding it is equal to it, minus 1. | ||
| + | :::<math>\scriptstyle{\color{blue}{2^{8}=16^2=256\longrightarrow1+2+\ldots+2^7=2^8-1}}</math> | ||
| + | |style="text-align:right;"|ושוב וערוך הי"ו על עצמם יעלה רנ"ו והוא חשבון שבמדרגה השמינית לשניה והחשבון שלפניה כמוה פחות אחד | ||
| + | |- | ||
| + | | | ||
| + | :::Again, multiply 256 by itself; the result will be 65536, which is the 16th term, and the sum [of all the numbers] preceding it is equal to it, minus 1. | ||
| + | :::<math>\scriptstyle{\color{blue}{2^{16}=256^2=65536\longrightarrow1+2+\ldots+2^{15}=2^{16}-1}}</math> | ||
| + | |style="text-align:right;"|ושוב וערוך רנ"ו על עצמם יעלה ס"ה אלפים וחמש מאות ושלשים וששה והוא מדרגת י"ו לשניה והחשבון שלפניה כמוה פחות אחד | ||
| + | |- | ||
| + | | | ||
| + | :::Again, multiply the result in the 16th term by itself, the result will be the number that is the 32nd term; and the sum [of all the numbers] preceding it is equal to it, minus 1. | ||
| + | :::<math>\scriptstyle{\color{blue}{2^{32}=\left(2^{16}\right)^2\longrightarrow1+2+\ldots+2^{31}=2^{32}-1}}</math> | ||
| + | |style="text-align:right;"|ושוב וערוך העולה במדרגת י"ו על עצמם ומה שעלה הוא חשבון שבמדרגת ל"ב לשניה והחשבון שלפניה כמוה פחות אחד | ||
| + | |- | ||
| + | | | ||
| + | :::Again, multiply the result in the 32nd term [by itself], the result will be the number that is the 64th term, and the sum [of all the numbers] preceding it is equal to it, minus 1. | ||
| + | :::<math>\scriptstyle{\color{blue}{2^{64}=\left(2^{32}\right)^2\longrightarrow1+2+\ldots+2^{63}=2^{64}-1}}</math> | ||
| + | |style="text-align:right;"|ושוב וערוך העולה במדרגת ל"ב ומה שיעלה הוא חשבון שבמדרגת ס"ד והחשבון שלפניה כמוה פחות אחד | ||
| + | |- | ||
| + | !<span style=color:Green>sum of squares</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{k=1}^{n} k^2=\left[\left(n+1\right)\sdot\left(\frac{1}{2}\sdot n\right)\right]\sdot\left[\left(\frac{2}{3}\sdot n\right)+\frac{1}{3}\right]}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :If you want to add up the square of one, the square of two [and so on] by the sequence of the numbers up to the square of 10. | ||
| + | ::<math>\scriptstyle\sum_{k=1}^{10} k^2</math> | ||
| + | |style="text-align:right;"|ואם תרצה לחבר ‫<ref>7r</ref>מרובע אחד ומרובע שנים {{#annot:term|1356,2576|IXVK}}על דרך החשבון{{#annotend:IXVK}} עד מרובע עשרה | ||
| + | |- | ||
| + | | | ||
| + | ::Do as follows: add one to ten, then multiply the sum by half the ten; the result will be 55 — keep it. Then take two-thirds of the ten and add one third to it; the result is seven. Multiply this by the 55 you kept and the result will be the sough. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{k=1}^{10} k^2=\left[\left(10+1\right)\sdot\left(\frac{1}{2}\sdot10\right)\right]\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{1}{3}\right]=55\sdot7}}</math> | ||
| + | |style="text-align:right;"|ככה תעשה הוסף אחד על עשרה ו{{#annot:term|1220,388|DrP0}}המחובר{{#annotend:DrP0}} תערוך בחצי העשרה יהיו נ"ה ושמרם<br> | ||
| + | ואחר כן קח שני שלישי העשרה ותוסיף עליהם שליש אחד יהיה שבעה<br> | ||
| + | ערכם על נ"ה ששמרת והעולה הוא המבוקש | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{k=m}^{n} k^2=\sum_{k=1}^{n} k^2-\left[\left[\left[\left(m-1\right)\sdot\frac{1}{2}\right]\sdot m\right]\sdot\left[\left[\frac{2}{3}\sdot\left(m-1\right)\right]+\frac{1}{3}\right]\right]}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :If you wish to sum from four up to ten. | ||
| + | ::<math>\scriptstyle\sum_{k=4}^{10} k^2</math> | ||
| + | |style="text-align:right;"|ואם רצית לחבר מארבעה ואילך עד עשרה | ||
| + | |- | ||
| + | | | ||
| + | ::Extract the sum from one to ten. Then subtract one from four, take half the remainder and multiply it by four and multiply the result by two thirds of three plus one third. Subtract the result from the number that you have in your hand and the remainder is the sought. | ||
| + | |style="text-align:right;"|הוצא כל החשבון מאחד ועד עשרה<br> | ||
| + | אחר כך חסר האחד מן הארבעה וקח חצי הנשאר וערכהו בארבעה והעולה תערוך בשני שלישי שלשה בתוספת שליש אחד<br> | ||
| + | והעולה חסר מהחשבון שעלה בידך והנשאר הוא שאלתך | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{k=4}^{10} k^2=\sum_{k=1}^{10} k^2-\left[\left[\left[\left(4-1\right)\sdot\frac{1}{2}\right]\sdot4\right]\sdot\left[\left(\frac{2}{3}\sdot3\right)+\frac{1}{3}\right]\right]}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\sum_{k=m}^{n} k^2=\sum_{k=1}^{n} k^2-\sum_{k=1}^{m-1} k^2}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::Know it by extracting the sum from 1 to 10, then extract the sum from 1 to 3, according to the way you have seen. Subtract the result from the total sum and the remainder is the sought. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{k=4}^{10} k^2=\sum_{k=1}^{10} k^2-\sum_{k=1}^{3} k^2}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתוציא כל החשבון מא' עד י' ואחר כך הוצא החשבון מא' ועד ג' כל על הדרך שראית והעולה חסר מכל החשבון והנשאר הוא שאלתך | ||
| + | |- | ||
| + | | | ||
| + | :If you wish to sum from five up to ten. | ||
| + | ::<math>\scriptstyle\sum_{k=5}^{10} k^2</math> | ||
| + | |style="text-align:right;"|ואם מחמשה ועד עשרה רצית לחבר | ||
| + | |- | ||
| + | | | ||
| + | ::Always extract the total sum. Then subtract one from the five, take half the remainder and multiply it by the five and multiply the result by two thirds of 4 plus one third. Subtract the result from the [total sum] and the remainder is the sought. | ||
| + | |style="text-align:right;"|הוצא לעולם כל החשבון ואחר כך חסר האחד מן החמשה ומהנשאר קח מחציתם וערכם על החמשה ותערוך העולה בשני שלישי ד' בתוספת שליש אחד לעולם והעולה חסר מן החשבון והנשאר הוא שאלתך | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{k=5}^{10} k^2=\sum_{k=1}^{10} k^2-\left[\left[\left[\left(5-1\right)\sdot\frac{1}{2}\right]\sdot5\right]\sdot\left[\left(\frac{2}{3}\sdot4\right)+\frac{1}{3}\right]\right]}}</math> | ||
| + | |- | ||
| + | |According to this way for all, keeping the names and the terms. | ||
| + | |style="text-align:right;"|ועל זה הדרך לכלם שתשמר השמות והמדרגות | ||
| + | |- | ||
| + | | | ||
| − | = | + | === The Second Category: Addition of Fractions === |
| − | < | + | !style="text-align:right;"|הענין השני ב{{#annot:term|1208,154|Tp2r}}חבור{{#annotend:Tp2r}} השברים |
| − | + | |- | |
| − | == | + | | |
| − | + | ==== <span style=color:green>Sexagesimal Fractions</span> ==== | |
| − | + | | | |
| − | + | |- | |
| − | + | |If you have fractions as the fractions of the astrologers | |
| − | + | |style="text-align:right;"|אם היו בידך שברים כ{{#annot:term|1440,19|Iq0j}}שברי חכמי המזלות{{#annotend:Iq0j}} | |
| − | + | |- | |
| − | + | | | |
| − | + | :*Who divide the sign [of the zodiac] into thirty degrees <math>\scriptstyle{\color{blue}{1=30^\circ}}</math> | |
| + | |style="text-align:right;"|שמחלקים המזל אל שלשים מעלות | ||
| + | |- | ||
| + | | | ||
| + | :*The degree into sixty minutes <math>\scriptstyle{\color{blue}{1^\circ=60'}}</math> | ||
| + | |style="text-align:right;"|והמעלה לששים ראשונים | ||
| + | |- | ||
| + | | | ||
| + | :*The minute into sixty seconds <math>\scriptstyle{\color{blue}{1'=60''}}</math> | ||
| + | |style="text-align:right;"|והראשון לששים שניים | ||
| + | |- | ||
| + | | | ||
| + | *Let there be 8 signs, 24 degrees, 24 minutes and 44 seconds, and you wish to sum them with 7 signs, 18 degrees, 48 minutes and 28 seconds. | ||
| + | :<math>\scriptstyle\left(8+24^\circ+24^\prime+44^{\prime\prime}\right)+\left(7+18^\circ+48^\prime+28^{\prime\prime}\right)</math> | ||
| + | |style="text-align:right;"|ויהיו ח' מזלות כ"ד מעלה כ"ד ראשונים מ"ד שניים ותרצה לחברם עם ז' מזלות י"ח מעלה מ"ח ראשונים כ"ח שניים | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Seconds:'''</span> first, sum the seconds, which are 72, add one to the minutes, 12 remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{44^{\prime\prime}+28^{\prime\prime}=72^{\prime\prime}=1^\prime+12^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|חבר בתחלה השניים והם ע"ב הוסף אחד על הראשונים ישארו י"ב | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Minutes:'''</span> then, sum the minutes, which are 73, add one to the degrees, 13 remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{24^\prime+48^\prime+1^\prime=73^\prime+1^\prime=1^\circ+13^\prime}}</math> | ||
| + | |style="text-align:right;"|ושוב חבר הראשונים והם ע"ג הוסף אחד על המעלות ישארו י"ג | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Degrees:'''</span> sum the degrees, which are 43, add one to the signs, 13 degrees remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{24^\circ+18^\circ+1^\circ=43^\circ=1+13^\circ}}</math> | ||
| + | |style="text-align:right;"|ושוב ו{{#annot:term|1165,178|aTlG}}חבר{{#annotend:aTlG}} המעלות והם מ"ג הוסף על אחד על המזלות ישארו י"ג מעלה | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Signs:'''</span> sum the signs, which are 16, extract from them 12 signs that are recurrent. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(8+7+1\right)-12=16-12=4}}</math> | ||
| + | |style="text-align:right;"|ושוב וחבר המזלות והם י"ו הוצא מהם י"ב מזלות שהם חוזרים חלילה | ||
| + | |- | ||
| + | | | ||
| + | :4 signs, 13 degrees, 13 minutes and 12 seconds remain. | ||
| + | |style="text-align:right;"|ישארו ד' מזלות י"ג מעלות י"ג ראשונים י"ב שניים | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(8+24^\circ+24^\prime+44^{\prime\prime}\right)+\left(7+18^\circ+48^\prime+28^{\prime\prime}\right)=4+13^\circ+13^\prime+12^{\prime\prime}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Simple Fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |But, the geometricians divide one into a half, a third, a quarter, a fifth, a sixth, a seventh, an eighth, a ninth, and a tenth. | ||
| + | |style="text-align:right;"|אך {{#annot:term|1512,846|3f0H}}חכמי המדות{{#annotend:3f0H}} הם מחלקים אחד לחצי ולשליש ולרביע ולחומש ולששית ולשביעית ולשמינית ולתשיעית ולעשירית | ||
| + | |- | ||
| + | | | ||
| + | *If you add four sixths to three ninths. | ||
| + | :<math>\scriptstyle\frac{4}{6}+\frac{3}{9}</math> | ||
| + | |style="text-align:right;"|ואם {{#annot:term|1165,178|cO31}}תחבר{{#annotend:cO31}} ד' ‫<ref>7v</ref>שתותין אל שלשה תשיעיות | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Seek a number that has a sixth and a ninth, this is by multiplying six by nine, the result is 54 and this is the denominatorץ | ||
| + | ::<math>\scriptstyle{\color{blue}{6\sdot9=54}}</math> | ||
| + | |style="text-align:right;"|בקש חשבון שיהיה לו שתות ותשיעית והוא שתערוך ששה על תשעה יעלה נ"ד והוא ה{{#annot:term|1239,571|zHyZ}}מורה{{#annotend:zHyZ}} | ||
| + | |- | ||
| + | | | ||
| + | :*Take 4 sixths of the denominator, which is 36, add it to its three ninths, which are 18, the result is 54, and it is one integer. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{4}{6}+\frac{3}{9}=\frac{\left(\frac{4}{6}\sdot54\right)+\left(\frac{3}{9}\sdot54\right)}{54}=\frac{36+18}{54}=\frac{54}{54}=1}}</math> | ||
| + | |style="text-align:right;"|קח ד' שתותין מן המורה והוא ל"ו וחברם אל שלשת תשיעיותיו שהם י"ח יעלה נ"ד והוא אחד שלם | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Another way:'''</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> you will know it by knowing from which number the sixth is derived, which is from six. | ||
| + | |style="text-align:right;"|ותדענו שתדע מאי זה חשבון יצא השתות והוא מששה | ||
| + | |- | ||
| + | | | ||
| + | :*Take its 4 sixths, which is 4: | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{4}{6}\sdot6=4}}</math> | ||
| + | |style="text-align:right;"|קח ד' ששיותיו והוא ד‫' | ||
| + | |- | ||
| + | | | ||
| + | :*Take its 3 ninths, which is 2: | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{9}\sdot6=2}}</math> | ||
| + | |style="text-align:right;"|וקח ג' תשיעיותיו והוא ב‫' | ||
| + | |- | ||
| + | | | ||
| + | :Sum them and divide by 6, the result is one. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{4}{6}+\frac{3}{9}=\frac{4+2}{6}=\frac{6}{6}=1}}</math> | ||
| + | |style="text-align:right;"|חברם וחלקם עליו על ו' יצא אחד | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Another way:'''</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> you will know it by knowing from which number the ninth is derived, which is from nine. | ||
| + | |style="text-align:right;"|ותדענו שתדע מאיזה חשבון התשיעית והוא מתשעה | ||
| + | |- | ||
| + | | | ||
| + | :*Take its 3 ninths, which is 3: | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{9}\sdot9=3}}</math> | ||
| + | |style="text-align:right;"|קח ג' תשיעיותיו והוא ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :*Take its 4 sixths, which is 6: | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{4}{6}\sdot9=6}}</math> | ||
| + | |style="text-align:right;"|וקח ד' ששיותיו והוא ו‫' | ||
| + | |- | ||
| + | | | ||
| + | :Sum them and divide by 9, the result is one. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{4}{6}+\frac{3}{9}=\frac{3+6}{9}=\frac{9}{9}=1}}</math> | ||
| + | |style="text-align:right;"|חברם וחלקם על ט' יצא אחד | ||
| + | |- | ||
| + | | | ||
| + | *If you add 3 eighths to 7 tenths. | ||
| + | :<math>\scriptstyle\frac{3}{8}+\frac{7}{10}</math> | ||
| + | |style="text-align:right;"|ואם תחבר ג' שמיניות אל ז' עשיריות | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Take the denominator, which is eighty. | ||
| + | |style="text-align:right;"|קח המורה והוא שמנים | ||
| + | |- | ||
| + | | | ||
| + | :*Its 3 eighths are thirty, add them to 56, which are its 7 tenths, the result is eighty six, which is one and six eighths of a tenth. | ||
| + | |style="text-align:right;"|וג' שמיניותיו הם שלשים חברם אל נ"ו שהם ז' עשיריותיו יעלה ששה ושמונים והוא אחד וששה שמיניות העשירית | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{8}+\frac{7}{10}=\frac{\left(\frac{3}{8}\sdot80\right)+\left(\frac{7}{10}\sdot80\right)}{80}=\frac{30+56}{80}=\frac{86}{80}=1+\left(\frac{6}{8}\sdot\frac{1}{10}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If you add 4 eighths and a seventh to 3 sixths and a fifth. | ||
| + | :<math>\scriptstyle\left(\frac{4}{8}+\frac{1}{7}\right)+\left(\frac{3}{6}+\frac{1}{5}\right)</math> | ||
| + | |style="text-align:right;"|ואם תחבר ד' שמיניות ושביעית אל ג' ששיות וחמישית | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Seek for a number that is divisible by the four fractions, this is by multiplying them one by the other, the result is 1680 and it is the denominator. | ||
| + | ::<math>\scriptstyle{\color{blue}{8\sdot7\sdot6\sdot5=1680}}</math> | ||
| + | |style="text-align:right;"|בקש חשבון שיחלק על ארבעת השברים והוא שתערכם זה על זה ויעלה אלף ושש מאות ושמונים והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | ::*Its eighth is 210: | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{8}\sdot1680=210}}</math> | ||
| + | |style="text-align:right;"|ושמיניתו והוא ר"י | ||
| + | |- | ||
| + | | | ||
| + | ::*Its seventh is 240: | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{7}\sdot1680=240}}</math> | ||
| + | |style="text-align:right;"|ושביעיתו והוא ר"מ | ||
| + | |- | ||
| + | | | ||
| + | ::*Its sixth 280: | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{6}\sdot1680=280}}</math> | ||
| + | |style="text-align:right;"|וששיתו ר"פ | ||
| + | |- | ||
| + | | | ||
| + | ::*Its fifth 336: | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot1680=336}}</math> | ||
| + | |style="text-align:right;"|וחמישיתו של"ו | ||
| + | |- | ||
| + | | | ||
| + | :*Add its four eighths and a seventh, which are 1080, to its three sixths and a fifth, which are 1176, the result is 2256, which is one and 2 sevenths, a quarter of a seventh, half the quarter of a seventh, and a tenth of a quarter of a seventh. | ||
| + | |style="text-align:right;"|חבר ארבעת שמיניותיו ושביעית שהם אלף ושמנים אל שלשת ששיותיו וחמישית שהם אלף וקע"ו יעלו אלפים רנ"ו והוא אחד וב' שביעיות ורביעית שביעית וחצי רביעית השביעית ועשירית רביעית השביעית | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle\left(\frac{4}{8}+\frac{1}{7}\right)+\left(\frac{3}{6}+\frac{1}{5}\right)&\scriptstyle=\frac{\left[\left(\frac{4}{8}\sdot1680\right)+\left(\frac{1}{7}\sdot1680\right)\right]+\left[\left(\frac{3}{6}\sdot1680\right)+\left(\frac{1}{5}\sdot1680\right)\right]}{1680}\\&\scriptstyle=\frac{1080+1176}{1680}=\frac{2256}{1680}=1+\frac{2}{7}+\left(\frac{1}{4}\sdot\frac{1}{7}\right)+\left(\frac{1}{2}\sdot\frac{1}{4}\sdot\frac{1}{7}\right)+\left(\frac{1}{10}\sdot\frac{1}{4}\sdot\frac{1}{7}\right)\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If you sum the fractions from one half up to a tenth. | ||
| + | :<math>\scriptstyle\sum_{k=2}^{10} \frac{1}{k}</math> | ||
| + | |style="text-align:right;"|ואם תחבר השברים מחצי עד עשירית | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Seek for a number that has all these fractions, it is 2520 | ||
| + | |style="text-align:right;"|בקש חשבון שיהיו לו כל השברים והוא אלפים וחמש מאות ועשרים | ||
| + | |- | ||
| + | | | ||
| + | :*When you sum all the fractions the result is 4861, which is one and 7 eighths, half a tenth, ?, and a fifth of a seventh of an eighth. | ||
| + | |style="text-align:right;"|וכשתחבר כל השברים יעלה ד' אלפים תתס"א שהם אחד וז' שמיניות וחצי עשירית ושמינית שלישית וחמישית שביעית שמינית | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{k=2}^{10} \frac{1}{k}=\frac{\sum_{k=2}^{10} \left(\frac{1}{k}\sdot\prod_{i=2}^{10} i\right)}{\prod_{i=2}^{10} i}=\frac{\sum_{k=2}^{10} \left(\frac{1}{k}\sdot2520\right)}{2520}=\frac{4861}{2520}=1+\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)+?+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If you wish to know how much is the number whose sixth and quarter are 5. | ||
| + | :<math>\scriptstyle\frac{1}{6}a+\frac{1}{4}a=5</math> | ||
| + | |style="text-align:right;"|ואם תרצה לדעת חשבון שתיתו ורביעיתו היו ה' כמה סך החשבון | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> the denominator is 24. | ||
| + | |style="text-align:right;"|הנה המורה הוא כ"ד | ||
| + | |- | ||
| + | | | ||
| + | :*Take its sixth and its quarter, they are 10, divide the denominator by it, the result is two and 4 tenths, multiply the outcome by five, the result is twelve. | ||
| + | :<math>\scriptstyle{\color{blue}{a=5\sdot\frac{24}{\left(\frac{1}{6}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)}=5\sdot\frac{24}{10}=5\sdot\left(2+\frac{4}{10}\right)=12}}</math> | ||
| + | |style="text-align:right;"|קח שתותו ורביעיתו והיו י' חלק עליו המורה יצא שנים וד' עשיריות ערוך היוצא על חמשה יעלה שנים עשר | ||
| + | |- | ||
| + | | | ||
| + | :*Or, multiply the denominator by five, then divide by ten, the result is twelve. | ||
| + | :<math>\scriptstyle{\color{blue}{a=\frac{24\sdot5}{\left(\frac{1}{6}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)}=\frac{24\sdot5}{10}=12}}</math> | ||
| + | |style="text-align:right;"|או ערוך המורה על חמשה והעולה חלק על עשרה ‫<ref>8r</ref>עלה שנים עשר | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Another way:'''</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> You can also extract it from one, by taking its sixth and its quarter, which is 2 sixths and a half of a sixth, and it is the denominator. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{6}\sdot1\right)+\left(\frac{1}{4}\sdot1\right)=\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}}</math> | ||
| + | |style="text-align:right;"|גם תוכל להוציא מאחד שתקח שתיתו ורביעיתו והוא ב' ששיות וחצי ששית והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | :*We divide one by it, the result is two and a sixth remains, i.e. we convert [the one] into sixths, then divide them without a fraction by each sixth, the result is two sixths for each sixth and a sixth remains that is not divided. Multiply by 5, the result is ten and 5 sixths. Divide 5 sixths by the denominator, the quotient is two, add them to the ten and they are twelve. | ||
| + | |style="text-align:right;"|נחלק עליו אחד יצא שנים ונשאר ששית<br> | ||
| + | כלו' נעשה ממנו ששיות ונחלקם בלא שבר על כל ששית וששית<br> | ||
| + | יצא שני ששיות לכל ששית וששית ונשאר ממנו ששית שלא נתחלק<br> | ||
| + | ערוך על ה' יעלה עשרה וה' ששיות<br> | ||
| + | חלק ה' ששיות על המורה יצא בחלוק שנים<br> | ||
| + | חברם עם העשרה והנה שנים עשר | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{a=5\sdot\frac{1}{\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=5\sdot\frac{\frac{6}{6}}{\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=5\sdot\left(2+\frac{\frac{1}{6}}{\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}\right)=10+\frac{\frac{5}{6}}{\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=10+2=12}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If you add its fifth to its seventh they are two, how much is the whole number? | ||
| + | :<math>\scriptstyle\frac{1}{5}a+\frac{1}{7}a=2</math> | ||
| + | |style="text-align:right;"|ואם תחבר חמישיתו עם שביעיתו ויהיו שנים כמה כל החשבון | ||
| + | |- | ||
| + | | | ||
| + | :*Multiply the denominator by two, then divide by twelve, which are a fifth and a seventh of the denominator, the result is five integers and five sixths. | ||
| + | :<math>\scriptstyle{\color{blue}{a=\frac{35\sdot2}{\left(\frac{1}{5}\sdot35\right)+\left(\frac{1}{7}\sdot35\right)}=\frac{2\sdot35}{12}=5+\frac{5}{6}}}</math> | ||
| + | |style="text-align:right;"|ערוך המורה על השנים וחלק על השנים עשר שהם חמשית ושביעית המורה יצא חמשה שלמים וחמש ששיות אחד | ||
| + | |- | ||
| + | | | ||
| + | :*Or, divide by the denominator, i.e. 35 by twelve, then multiply the result, which is 3 minus half a sixth, by two, the result is five and five sixths. | ||
| + | :<math>\scriptstyle{\color{blue}{a=2\sdot\frac{35}{\left(\frac{1}{5}\sdot35\right)+\left(\frac{1}{7}\sdot35\right)}=2\sdot\frac{35}{12}=2\sdot\left[3-\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]=5+\frac{5}{6}}}</math> | ||
| + | |style="text-align:right;"|או חלק המורה כלו' ל"ה על שנים עשר והיוצא שהוא ג' פחות חצי שתות תערוך על שנים יעלה חמשה וחמש ששיות אחד | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Another way:'''</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Also extract it from one, by taking its fifth and its seventh, which is 2 sevenths and 2 fifths of a seventh, and it is the denominator. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{5}\sdot1\right)+\left(\frac{1}{7}\sdot1\right)=\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}}</math> | ||
| + | |style="text-align:right;"|גם תוציאנו מאחד והוא שתקח חמישיתו ושביעיתו ויהיו ב' שביעיות וב' חמישיות השביעית והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | :*We divide one by it, the quotient is two, and two sevenths and a fifth of a seventh remain. We multiply them by two and they are four integers, 4 sevenths and 2 fifths of a seventh. Divide the four sevenths and 2 fifths of a seventh by the denominator, the result is one. Add it to the four and ten fifths of a seventh remain, which are 2 sevenths, and one seventh is five [fifths of a seventh]. Thus, ten parts remain, which are 10 parts of twelve. | ||
| + | |style="text-align:right;"|נחלק עליו אחד יצא בחלוק שנים וישאר שתי שביעיות וחומש שביעית<br> | ||
| + | נערכם על שנים והם ארבעה שלמים וד' שביעיות וב' חמישיות השביעית<br> | ||
| + | חלק הארבעה שביעיות והב' חמישיות שביעית על המורה יצא אחד<br> | ||
| + | וחברהו עם הארבעה ונשארו עשרה חמישיות שביעית שהם ב' שביעיות והשביעית הוא חמשה<br> | ||
| + | והנה נשארו עשרה חלקים שהם י' חלקים משנים עשר | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{a=2\sdot\frac{1}{\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}=2\sdot\left[2+\frac{\frac{2}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)}{\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}\right]=4+\frac{\frac{4}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}{\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}=4+\left[1+\frac{\frac{10}{5}\sdot\frac{1}{7}}{\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}\right]=5+\frac{10}{12}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If you add a third of a quarter of its fifth to a seventh of an eighth of its ninth they are two, and you wish to know how much is the whole number. | ||
| + | :<math>\scriptstyle\left[\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\sdot a\right]+\left[\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\sdot a\right]=2</math> | ||
| + | |style="text-align:right;"|ואם תחבר שלישית רביעית חמישיתו עם שביעית שמינית תשיעיתו ויהיו שנים ותרצה לדעת כמה כל החשבון | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Seek for a number that has all these fractions, the number that has all these fractions is 2520 and this is the denominator. | ||
| + | |style="text-align:right;"|בקש חשבון שיהיו לו כל השברים האלה והוא החשבון שיש לו כל החלקים אלפים וחמש מאות ועשרים והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | :*Then, take a third of a quarter of its fifth, which is 42, add it to a seventh of an eighth of its ninth, which is 5, the sum is 47. Divide the denominator by it, the result is fifty three and 29 remains. Multiply them by two, the result is 106 [integers], 58 [fractions]. Divide 58 by 47, the result is one, add it to 106, the sum is 107 integers and eleven parts of 47 remain, and this is the whole number. | ||
| + | |style="text-align:right;"|ואחר כן קח שלישית רביעית חמישיתו והוא מ"ב וחברהו עם שביעית שמינית תשיעיתו שהוא ה' יהיה הכל מ"ז<br> | ||
| + | וחלק עליו המורה יצא חמשים ושלשה וישאר כ"ט<br> | ||
| + | ערוך אותם בשנים יעלה ק"ו נ"ח<br> | ||
| + | חלק הנ"ח על מ"ז יהיה אחד חברהו עם הק"ו יעלה ק"ז שלמים וישאר אחד עשר חלקים ממ"ז באחד וכן היה כל החשבון | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle a&\scriptstyle=2\sdot\frac{2520}{\left[\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\sdot2520\right]+\left[\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\sdot2520\right]}=2\sdot\frac{2520}{42+5}=2\sdot\frac{2520}{47}\\&\scriptstyle=2\sdot\left(53+\frac{29}{47}\right)=106+\frac{58}{47}=106+1+\frac{11}{47}=107+\frac{11}{47}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*Or, double the denominator, then divide by 47, the result is 107 and 11 remain, as in the other method. | ||
| + | |style="text-align:right;"|או כפול המורה וחלק על מ"ז יצא ק"ז וישאר י"א כמו ‫<ref>8v</ref>הענין האחר | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{a=\frac{2\sdot2520}{\left[\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\sdot2520\right]+\left[\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\sdot2520\right]}=\frac{2\sdot2520}{47}=107+\frac{11}{47}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :Its check: | ||
| + | :*Multiply 107 by 47 and add 11 to the product, the result is 5040. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(107\sdot47\right)+11=5040}}</math> | ||
| + | |style="text-align:right;"|ובחינתו שתערוך ק"ז על מ"ז ותחבר עם העולה הי"א יהיה הכל חמשת אלפים וארבעים | ||
| + | |- | ||
| + | | | ||
| + | :*When you take a third of a quarter of its fifth the result is 84, which is one integer and 37 parts of 47. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\sdot5040}{47}=\frac{84}{47}=\left(1+\frac{37}{47}\right)}}</math> | ||
| + | |style="text-align:right;"|וכשתקח שלישית רביעית חמישיתו יהיה פ"ד והוא אחד שלם ול"ז חלקים ממ"ז באחד | ||
| + | |- | ||
| + | | | ||
| + | :*When you take a seventh of an eighth of its ninth the result is ten parts of 47. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\sdot5040}{47}=\frac{10}{47}}}</math> | ||
| + | |style="text-align:right;"|וכשתקח שביעית שמינית תשיעיתו יהיה עשרה חלקים ממ"ז באחד | ||
| + | |- | ||
| + | | | ||
| + | ::Sum them with 37 and it is one integer. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{37}{47}+\frac{10}{47}=1}}</math> | ||
| + | |style="text-align:right;"|חברם עם הל"ז והנה אחד שלם | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Chapter Two: Subtraction == | ||
| + | !style="width: 45%; text-align:right;"|<big>השער</big> השני במגרעת | ||
| + | |- | ||
| + | |It is divided into two categories: | ||
| + | |style="text-align:right;"|והוא נחלק לשני ענינים | ||
| + | |- | ||
| + | | | ||
| + | *Subtraction of integers from integers | ||
| + | |style="text-align:right;"|{{#annot:term|1193,155|pUkT}}מגרעת{{#annotend:pUkT}} שלמים משלמים | ||
| + | |- | ||
| + | | | ||
| + | *Subtraction of fractions from fractions | ||
| + | |style="text-align:right;"|ומגרעת שברים משברים | ||
| + | |- | ||
| + | | | ||
| + | === The First Category: [Subtraction] of Integers === | ||
| + | !style="text-align:right;"|הענין הראשון בשלמים | ||
| + | |- | ||
| + | |When you wish to know a number that is subtracted repeatedly by the succession of the [natural] numbers, one by one, or two by two, or three by three, from ten to one, the way to extract it is the same as explained for addition, so there is no need to elaborate on that. | ||
| + | |style="text-align:right;"|שתרצה לדעת {{#annot:term|1362,181|qrBI}}חשבון הולך הלוך וחסור{{#annotend:qrBI}} על דרך המספר אחד אחד או שנים שנים או שלשה שלשה מעשרה ועד אחד<br> | ||
| + | הדרך להוציאו שוה כמו שפרשתי בחבור ואין צורך להאריך בו | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === The Second Category: Subtraction of Fractions from Fractions === | ||
| + | !style="text-align:right;"|הענין השני מגרעת שברים משברים | ||
| + | |- | ||
| + | | | ||
| + | ==== <span style=color:green>Sexagesimal Fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |If you have fractions of the astrologers. | ||
| + | |style="text-align:right;"|ואם שברי חכמי המזלות יהיו בידך | ||
| + | |- | ||
| + | | | ||
| + | *Such as 2 signs, 20 degrees, 40 minutes, and 40 seconds, and you wish to subtract from them one number and know the reminder, such as 1 sign, 10 degrees, 45 minutes and 30 seconds. | ||
| + | :<math>\scriptstyle\left(2+20^\circ+40'+40''\right)-\left(1+10^\circ+45'+30''\right)</math> | ||
| + | |style="text-align:right;"|כמו ב' מזלות כ' מעלות מ' ראשונים ומ' שניים ותרצה לגרוע מהם חשבון אחד ולדעת הנשאר כמו א' מזלות י' מעלה מ"ה ראשונים ל' שניים | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Seconds:'''</span> you start from the seconds, 10 seconds remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{40''-30''=10''}}</math> | ||
| + | |style="text-align:right;"|אתה מתחיל בשניים וישארו י' שניים | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Minutes:'''</span> then, minutes from minutes, but you cannot subtract the greater from the smaller, so take one degree from the degrees, it will be 60 minutes. Add them to the minutes and subtract from them 45 minutes. 55 minutes remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(1^\circ+40'\right)-45'=\left(60'+40'\right)-45'=55'}}</math> | ||
| + | |style="text-align:right;"|ושוב הראשונים מהראשונים ולא תוכל לגרוע הרב מהמעט [..] ומפני זה קח מהמעלות מעלה אחת תהיה ס' ראשונים ותחברם עם הראשונים ו{{#annot:term|1192,181|prjt}}גרע מהם{{#annotend:prjt}} מ"ה ראשונים ישארו נ"ה ראשונים | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Degrees:'''</span> subtract also degrees from degrees. 9 degrees remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(20^\circ-1^\circ\right)-10^\circ=9^\circ}}</math> | ||
| + | |style="text-align:right;"|ושוב וגרע המעלות מהמעלות וישארו ט' מעלות | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Signs:'''</span> then subtract one sign from the 2 signs. | ||
| + | ::<math>\scriptstyle{\color{blue}{2-1}}</math> | ||
| + | |style="text-align:right;"|ושוב וגרע מזל אחד מהב' מזלות | ||
| + | |- | ||
| + | | | ||
| + | :1 [sign], 9 [degrees], 55 [minutes] and 10 [seconds] remain. | ||
| + | |style="text-align:right;"|ישאר א' ט' נ"ה י‫' | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(2+20^\circ+40'+40''\right)-\left(1+10^\circ+45'+30''\right)=1+9^\circ+55'+10''}}</math> | ||
| + | |- | ||
| + | |If the signs of the subtrahend excceed the minuend signs, you add to them 12 signs, which are the cyclic zodiac signs, then you subtract from the sum and keep the remainder: signs, degrees, minutes and seconds. | ||
| + | |style="text-align:right;"|ואם מזלות {{#annot:term|1365,789|qM5I}}חשבון הנגרעים{{#annotend:qM5I}} {{#annot:term|1352,996|7f8a}}עודפים על{{#annotend:7f8a}} המזלות שאתה גורע ממנו ולא לגרוע אתה מוסיף עליהם י"ב מזלות שהם מזלות הגלגל שהם חוזרים חלילה ומן ה{{#annot:term|1347,388|kKah}}נאסף{{#annotend:kKah}} תגרע ותשמור הנשאר בידך מזלות מעלות ראשונים ושניים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Simple Fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |If you have fractions of the geometricians. | ||
| + | |style="text-align:right;"|ואם שברי חכמי המדות יהיו בידך | ||
| + | |- | ||
| + | | | ||
| + | *Such as when you wish to subtract from ten its sixth and its quarter and know the remainder. | ||
| + | :<math>\scriptstyle10-\left[\left(\frac{1}{6}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)\right]</math> | ||
| + | |style="text-align:right;"|כמו שתרצה לגרוע מעשרה ששיתו ורביעיתו ולדעת הנשאר | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Seek a number that has a sixth and a quarter, it is 12 and it is the denominator. | ||
| + | |style="text-align:right;"|בקש חשבון שיהיה לו ששית ורביעית והוא י"ב והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | :*Subtract from it its sixth and its quarter, 7 remains. | ||
| + | ::<math>\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{6}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=7}}</math> | ||
| + | |style="text-align:right;"|גרע ממנו ששיתו ורביעיתו ישאר ז‫' | ||
| + | |- | ||
| + | | | ||
| + | :*Know their ratio, and as their ratio, take from the ten, it is five [and five] sixths. | ||
| + | :<math>\scriptstyle{\color{blue}{10-\left[\left(\frac{1}{6}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)\right]=\frac{7}{12}\sdot10=5+\frac{5}{6}}}</math> | ||
| + | |style="text-align:right;"|ודע ערכם ‫<ref>9r</ref>והוא חציו וכזה הערך קח מן העשרה והוא חמשה שתותין | ||
| + | |- | ||
| + | | | ||
| + | :*Or, take the ratio of ten to 12, which is 5 sixths, and as this ratio, take from the seven, it is 5 and 5 sixths. | ||
| + | :<math>\scriptstyle{\color{blue}{10-\left[\left(\frac{1}{6}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)\right]=\frac{10}{12}\sdot7=\frac{5}{6}\sdot7=5+\frac{5}{6}}}</math> | ||
| + | |style="text-align:right;"|או קח מהערך עשרה אל י"ב והוא ה' ששיותיו וקח כזה הערך מן השבעה והוא ה' וה' שתותין | ||
| + | |- | ||
| + | | | ||
| + | *If you wish to subtract 3 quarters from 4 fifths and know how much is the remainder. | ||
| + | :<math>\scriptstyle\frac{4}{5}-\frac{3}{4}</math> | ||
| + | |style="text-align:right;"|ואם תרצה לגרוע ג' רביעיות אחד מן ד' חומשין ולדעת כמה הנשאר | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Know from which number the fifth is [derived]. It is from five. | ||
| + | |style="text-align:right;"|דע מאיזה חשבון החומש והוא מחמשה | ||
| + | |- | ||
| + | | | ||
| + | :*Take [its] 4 fifths, which is 4, then 3 quarters of the five, which is 3 and 3 quarters. Subtract them from the 4, the remainder is a quarter. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(\frac{4}{5}\sdot5\right)-\left(\frac{3}{4}\sdot5\right)=4-\left(3+\frac{3}{4}\right)=\frac{1}{4}}}</math> | ||
| + | |style="text-align:right;"|קח ד' חומשין והוא ד' ואחר כך ג' רביעיות החמשה והוא ג' וג' רביעיות {{#annot:term|1362,181|imnV}}תחסרם מן{{#annotend:imnV}} הד' ישאר רביע | ||
| + | |- | ||
| + | | | ||
| + | :*Know the ratio of the quarter from the 5, it is half a tenth. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{4}{5}-\frac{3}{4}=\frac{1}{4}:5=\frac{1}{2}\sdot\frac{1}{10}}}</math> | ||
| + | |style="text-align:right;"|ודע מה ערך הרובע מן הה' והוא חצי עשירית | ||
| + | |- | ||
| + | | | ||
| + | :*Or, take from the denominator, which is twenty, its 3 quarters, which are 15, subtract them from its 4 fifths, which are 16, one remains, which is half a tenth and this is the remainder. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(\frac{4}{5}\sdot20\right)-\left(\frac{3}{4}\sdot20\right)=16-15=1}}</math> | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{4}{5}-\frac{3}{4}=\frac{1}{20}=\frac{1}{2}\sdot\frac{1}{10}}}</math> | ||
| + | |style="text-align:right;"|או נקח מן המורה שהוא עשרים ג' רביעיותיו והם ט"ו וגרעם מד' חומשיו שהם י"ו ישאר אחד שהוא חצי עשירית וככה השאר | ||
| + | |- | ||
| + | | | ||
| + | *If you wish to subtract four fifths from 5 sixths and 3 quarters and know the remainder. | ||
| + | :<math>\scriptstyle\left(\frac{5}{6}+\frac{3}{4}\right)-\frac{4}{5}</math> | ||
| + | |style="text-align:right;"|ואם תרצה לגרוע ארבע חומשיו מן ה' שתותין וג' רביעיות ולדעת הנשאר | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Seek a number that has a fifth and a sixth, it is thirty. | ||
| + | |style="text-align:right;"|בקש חשבון שיהיה לו חומש ושתות והוא שלשים | ||
| + | |- | ||
| + | | | ||
| + | :*Take [its] four fifths, which are 24, subtract them from its five sixths and its three quarters, which are 47 and a half, the remainder is 23 and a half. | ||
| + | |style="text-align:right;"|קח ארבע חמישיות והם כ"ד ו{{#annot:term|1192,181|fMF7}}תגרעם מ{{#annotend:fMF7}}חמשה שתותיו ומשלש רביעיותיו שהם מ"ז וחצי יהיה הנשאר כ"ג וחצי | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\left[\left(\frac{5}{6}\sdot30\right)+\left(\frac{3}{4}\sdot30\right)\right]-\left(\frac{4}{5}\sdot30\right)=\left(47+\frac{1}{2}\right)-24=23+\frac{1}{2}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*Know their ratio to thirty, it is 7 tenths and half a sixth. | ||
| + | :<math>\scriptstyle{\color{blue}{\left(\frac{5}{6}+\frac{3}{4}\right)-\frac{4}{5}=\left(23+\frac{1}{2}\right):30=\frac{7}{10}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}}</math> | ||
| + | |style="text-align:right;"|ודע ערכם משלשים והוא ז' עשיריות וחצי השתות | ||
| + | |- | ||
| + | | | ||
| + | *If you subtract its third and its quarter, eight remains and you wish to know how much is the whole number. | ||
| + | :<math>\scriptstyle a-\frac{1}{3}a-\frac{1}{4}a=8</math> | ||
| + | |style="text-align:right;"|ואם תגרע שלישיתו וריביעיתו ונשאר שמונה ותרצה לדעת כמה היה כל החשבון | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Take the denominator, which is 12. | ||
| + | |style="text-align:right;"|קח המורה והוא י"ב | ||
| + | |- | ||
| + | | | ||
| + | :*Subtract from it its third and its quarter. Five remains. | ||
| + | ::<math>\scriptstyle{\color{blue}{12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)=5}}</math> | ||
| + | |style="text-align:right;"|וגרע ממנו שלישיתו ורביעיתו ישאר חמשה | ||
| + | |- | ||
| + | | | ||
| + | :*Divide the denominator by it, the result is 2 and 2 fifths. Multiply them by eight, the result is 19 and a fifth. | ||
| + | :<math>\scriptstyle{\color{blue}{a=\frac{12}{5}\sdot8=\left(2+\frac{2}{5}\right)\sdot8=19+\frac{1}{5}}}</math> | ||
| + | |style="text-align:right;"|חלק עליו המורה יצא ב' וב' חומשין ערכם בשמונה יעלה י"ט וחומש | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{a-\left(\frac{1}{n}\sdot a\right)-\left(\frac{1}{m}\sdot a\right)=b}}</math> | ||
| + | | | ||
| + | |- | ||
| + | |According to this way for every remaining number, whether two, or three, or whichever number that remains: extract the denominator, subtract from it the subtracted parts - whether sixths, or fifths, or quarters, or whichever is subtracted - then divide the denominator by the remainder and multiply by the stated remainder. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a=\frac{n\sdot m}{\left(n\sdot m\right)-\left[\left[\frac{1}{n}\sdot\left(n\sdot m\right)\right]+\left[\frac{1}{m}\sdot\left(n\sdot m\right)\right]\right]}\sdot b}}</math> | ||
| + | |style="text-align:right;"|ועל זה הדרך לכל חשבון שישאר שנים או שלשה או איזה חשבון שישאר שתוציא המורה ותגרע ממנו הערכים שגרע הן שתותין או חמישיות או רביעיות או כל מה שגרע ועל הנשאר תחלק המורה והיוצא תערוך בנשאר שאמר | ||
| + | |- | ||
| + | |Or, divide the stated remainder by what remains from the denominator, after subtracting the subtracted from it, then multiply the result by the denominator. It is the same thing. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a=\frac{b}{\left(n\sdot m\right)-\left[\left[\frac{1}{n}\sdot\left(n\sdot m\right)\right]+\left[\frac{1}{m}\sdot\left(n\sdot m\right)\right]\right]}\sdot\left(n\sdot m\right)}}</math> | ||
| + | |style="text-align:right;"|או חלק הנשאר שאמר על מה שישאר מן המורה כשתוציא ממנו מה שגרע והיוצא תערוך על המורה והדבר שוה | ||
| + | |- | ||
| + | | | ||
| + | *If you subtract its fifth, then a seventh of the remainder, 24 remains. How much is the whole? | ||
| + | :<math>\scriptstyle\left(a-\frac{1}{5}a\right)-\left[\frac{1}{7}\sdot\left(a-\frac{1}{5}a\right)\right]=24</math> | ||
| + | |style="text-align:right;"|ואם תגרע חמישיתו ומהנותר שביעיתו ונשאר כ"ד כמה היה הכל | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Know the denominator, which is 35. | ||
| + | |style="text-align:right;"|דע המורה והוא ל"ה | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply it by the remainder, i.e. according to the rule mentioned above, the result is 35 and it is the sought. | ||
| + | ::<math>\scriptstyle{\color{blue}{a=\frac{35\sdot24}{24}=35}}</math> | ||
| + | |style="text-align:right;"|וערכהו על הנשאר כלומ' כמשפט אשר הזכיר למעלה יצא ל"ה והוא המבוקש | ||
| + | |- | ||
| + | |This way is correct when the [unknown] number is equal to the denominator like this. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[a-\left(\frac{1}{n}\sdot a\right)\right]-\left[\frac{1}{m}\sdot\left[a-\left(\frac{1}{n}\sdot a\right)\right]\right]=b}}</math> | ||
| + | *<math>\scriptstyle{\color{OliveGreen}{a=n\sdot m \longrightarrow a=\frac{\left(n\sdot m\right)\sdot b}{b}}}</math> | ||
| + | |style="text-align:right;"|וזה הדרך הוא נכון כשיהיו סך החשבון והמורה שוים כמו זה | ||
| + | |- | ||
| + | | | ||
| + | :*Also if one takes 30, subtract its fifth and a sixth of what remains, so the remainder is twenty. Thus, the [unknown] number and the denominator are equal. | ||
| + | |style="text-align:right;"|וכמו אם יקח ל' ויחסר חמישיתו ומן הנותר ששית וישאר עשרים שהחשבון והמורה שוים | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{5\sdot6=30\longrightarrow\left[30-\left(\frac{1}{5}\sdot30\right)\right]-\left[\frac{1}{6}\sdot\left[30-\left(\frac{1}{5}\sdot30\right)\right]\right]=20}}</math> | ||
| + | |- | ||
| + | |For every number like this, the denominator leads you to the truth. | ||
| + | |style="text-align:right;"|ובכל חשבון כאלו יוציאך המורה אל האמת | ||
| + | |- | ||
| + | | | ||
| + | :*<math>\scriptstyle{\color{OliveGreen}{\left(a-\frac{1}{5}a\right)-\left[\frac{1}{7}\sdot\left(a-\frac{1}{5}a\right)\right]=17+\frac{1}{7}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::But, if one takes 25, then subtracts its fifth and a seventh of the remainder, 17 and one-seventh remain, so the denominator and the [unknown] number are unequal. | ||
| + | |style="text-align:right;"|אך אם יקח כ"ה ויגרע חמישיתו ומן הנשאר שביעיתו וישאר י"ז <sup>ו</sup>שביעית שהמורה והחשבון אינם ‫<ref>9v</ref>שוים | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{5\sdot7\ne25\longrightarrow\left[25-\left(\frac{1}{5}\sdot25\right)\right]-\left[\frac{1}{7}\sdot\left[25-\left(\frac{1}{5}\sdot25\right)\right]\right]=17+\frac{1}{7}}}</math> | ||
| + | |- | ||
| + | |For every number such as this if "your eyes shall see thy Teacher and your ears shall hear a word from behind thee... This is the way; walk in it" [Isaiah 30, 20-21]. | ||
| + | |style="text-align:right;"|ובכל חשבון כיוצא בו אם ''{{#annot:Isa30-20|494|JQZP}}יהיו עיניך רואות את מוריך אזניך תשמענה דבר מאחריך זה הדרך תלכו בה{{#annotend:JQZP}}''‫<ref group=note>ישעיה ל, כ-כא</ref> | ||
| + | |- | ||
| + | | | ||
| + | ::The way for every number is that you seek a number that is divisible by seven after you subtract its fifth from it: | ||
| + | |style="text-align:right;"|והדרך לכל חשבון שתבקש חשבון שיהיה לו שביעיות אחרי שתגרע ממנו חמישית | ||
| + | |- | ||
| + | | | ||
| + | ::Such as 35, whose fifth is 7. 28 remain, whose seventh is 4. We sum them and the result is 11. | ||
| + | |style="text-align:right;"|כגון ל"ה שחומשו ז‫'<br> | ||
| + | וישאר כ"ח<br> | ||
| + | ששביעיתו ד‫'<br> | ||
| + | ונחברם יעלה י"א | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{5}\sdot35\right)+\left[\frac{1}{7}\sdot\left[35-\left(\frac{1}{5}\sdot35\right)\right]\right]=7+\left[\frac{1}{7}\sdot\left(35-7\right)\right]=7+\left(\frac{1}{7}\sdot28\right)=7+4=11}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::24 remain: <math>\scriptstyle{\color{blue}{35-11=24}}</math> | ||
| + | |style="text-align:right;"|וישאר כ"ד | ||
| + | |- | ||
| + | | | ||
| + | ::Know the ratio of 11 to [24] - it is a quarter and 5 sixths of a quarter. | ||
| + | ::<math>\scriptstyle{\color{blue}{11:24=\frac{1}{4}+\left(\frac{5}{6}\sdot\frac{1}{4}\right)}}</math> | ||
| + | |style="text-align:right;"|ודע מה ערך י"א אל והוא רביעית וה' ששיות רביעית | ||
| + | |- | ||
| + | | | ||
| + | ::Take this ratio from 17 and one-seventh, which is the [given] remainder, and the result is 7 plus 6 sevenths. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(17+\frac{1}{7}\right)\sdot\left[\frac{1}{4}+\left(\frac{5}{6}\sdot\frac{1}{4}\right)\right]=7+\frac{6}{7}}}</math> | ||
| + | |style="text-align:right;"|וכזה הערך קח מי"ז ושביעית שהוא הנשאר והיוצא שהוא ז' ועוד ו' שביעיות | ||
| + | |- | ||
| + | | | ||
| + | ::Add [it] to 17 and one-seventh, the result is 25 and this is what you asked for. | ||
| + | ::<math>\scriptstyle{\color{blue}{a=\left(17+\frac{1}{7}\right)+\left(7+\frac{6}{7}\right)=25}}</math> | ||
| + | |style="text-align:right;"|הוסף על י"ז ושביעית יעלה כ"ה והוא מה ששאלת | ||
| + | |- | ||
| + | |Know it by maintaining the degrees of the fractions and adding one degree to each fraction. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a=b+\left(\frac{1}{n-1}\sdot b\right)+\left[\frac{1}{m-1}\sdot\left[b+\left(\frac{1}{n-1}\sdot b\right)\right]\right]}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתשמור מדרגות השברים ותוסיף על כל שבר ושבר מדרגה אחת | ||
| + | |- | ||
| + | | | ||
| + | ::Do so: take the remainder, add to it its sixth, which exceeds by one degree over the seventh that was stated. Add to the sum a quarter of the sum, which exceeds by one degree over the fifth that was stated at first, and the sum is the sought. | ||
| + | |style="text-align:right;"|וכן תעשה קח הנשאר והוסף ששיתו שהוא {{#annot:term|1213,420|gUhh}}נוסף{{#annotend:gUhh}} מדרגה אחת מן השביעית שאמר באחרונה ועל המחובר תוסיף רביעית המחובר שהוא {{#annot:term|1352,996|YLfG}}עודף{{#annotend:YLfG}} מדרגה אחת על החמישית שאמ' בתחלה והמחובר הוא המבוקש | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{a=\left(17+\frac{1}{7}\right)+\left[\frac{1}{6}\sdot\left(17+\frac{1}{7}\right)\right]+\frac{1}{4}\sdot\left[17+\left(\frac{1}{7}\right)+\left[\frac{1}{6}\sdot\left(17+\frac{1}{7}\right)\right]\right]}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If you take two numbers, such that are not equal to one another. You subtract a fifth of the one from a third of the other and six remain. You wish to know how much is each of the numbers? | ||
| + | :<math>\scriptstyle\frac{1}{3}a-\frac{1}{5}b=6</math> | ||
| + | |style="text-align:right;"|ואם תקח שני חשבונות שאין האחד שוה לחברו ותגרע חמישית האחד משלישית האחר וישארו ששה ותרצה לדעת כמה היה כל אחד ואחד מהחשבונות | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Seek a number that has a fifth and a third, it is 15 and it is the denominator. | ||
| + | |style="text-align:right;"|בקש חשבון שיהיה לו חמישית ושלישית והוא ט"ו והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | ::Take its fifth, which is three, add it to the six, it is 9. Multiply it by the three, the result is 27, which is the number from which you subtract. Since you know it, you can extract the number that is subtracted, which is 15, for its fifth is three. | ||
| + | ::<math>\scriptstyle{\color{blue}{\begin{cases}\scriptstyle a=\left[\left(15\sdot\frac{1}{5}\right)+6\right]\sdot3=\left(3+6\right)\sdot3=9\sdot3=27\\\scriptstyle \frac{1}{5}b=3\longrightarrow b=15\end{cases}}}</math> | ||
| + | |style="text-align:right;"|וקח חמישיתו והוא שלשה והוסף על הששה ויהיה ט' ותערכם על השלשה ויעלה כ"ז וזה הוא החשבון שגרעת ממנו<br> | ||
| + | ואחר שידעת זה תוכל להוציא {{#annot:term|1365,789|jTt2}}החשבון הנגרע{{#annotend:jTt2}} שהוא ט"ו אחרי שחמישיתו שלשה | ||
| + | |- | ||
| + | |This way is not a general way for every number "and your Teacher shall no longer hide Himself" [Isaiah 30, 20], except when one number is equal to the denominator, such as this and the like, but if none is equal to the denominator it does not apply. | ||
| + | |style="text-align:right;"|וזה הדרך אינו דרך כלל לכל חשבון ''{{#annot:Isa30-20|494|iprg}}ולא יכנף עוד מוריך{{#annotend:iprg}}''‫<ref group=note>ישעיה ל, כ</ref> זולתי כשיהיה החשבון האחד שוה למורה כגון זה וכיוצא בו אך אם לא ישוו המורה אל יורה | ||
| + | |- | ||
| + | | | ||
| + | ::Such as when one is 10 and the other is 24 and when you subtract a fifth of the ten from a third of 24, six remains. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot24\right)-\left(\frac{1}{5}\sdot10\right)=6}}</math> | ||
| + | |style="text-align:right;"|כגון שהיה האחד י' והשני כ"ד וכשתגרע חמישית עשרה משלישית כ"ד ישאר ששה | ||
| + | |- | ||
| + | | | ||
| + | ::Whereas if you look at the denominator it leads you to 27 and 15 and this number is known if the first number is known. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot27\right)-\left(\frac{1}{5}\sdot15\right)=6}}</math> | ||
| + | |style="text-align:right;"|ואם תביט אל המורה יוציאך אל כ"ז ואל ט"ו וזה החשבון יודיע אם החשבון האחד ידוע | ||
| + | |- | ||
| + | | | ||
| + | :*As when it is said that the one is ten, we subtract its fifth from a third of an unknown number and six remains. How much is the unknown number? | ||
| + | ::<math>\scriptstyle\frac{1}{3}a-\left(\frac{1}{5}\sdot10\right)=6</math> | ||
| + | |style="text-align:right;"|כמו שיאמר האחד עשרה גרעונו חמישיתו משלישית חשבון שאינו ידוע ונשאר ששה<br> | ||
| + | כמה החשבון שאינו ידוע | ||
| + | |- | ||
| + | | | ||
| + | ::The way for this and for every number is that you add a fifth of the known to the remainder and multiply the sum by three, since the third is denominated from three and the result is the unknown number. | ||
| + | ::<math>\scriptstyle{\color{blue}{a=\left[6+\left(\frac{1}{5}\sdot10\right)\right]\sdot3}}</math> | ||
| + | |style="text-align:right;"|הדרך בו ולכל חשבון שתוסיף חמישית ‫<ref>10r</ref>הידוע על הנשאר והמחובר תערך על שלשה בעבור כי שלישית יוצאת משלשה והעולה הוא החשבון שאינו ידוע | ||
| + | |- | ||
| + | |You can also extract the two numbers. | ||
| + | |style="text-align:right;"|וגם תוכל להוציא שני החשבונות | ||
| + | |- | ||
| + | | | ||
| + | *If it is said: when we subtract one-fifth of the one from one-third of the other, 6 remains. We sum them and the result is ten. | ||
| + | :<math>\scriptstyle\begin{cases}\scriptstyle\frac{1}{3}a-\frac{1}{5}b=6\\\scriptstyle\frac{1}{3}a+\frac{1}{5}b=10\end{cases}</math> | ||
| + | |style="text-align:right;"|אם יאמר כאשר גרענו חמישית האחד משלישית האחר נשאר ו‫'<br> | ||
| + | חברנום יעלו עשרה | ||
| + | |- | ||
| + | | | ||
| + | ::The way of this is that you subtract the remainder from the sum, then take half of what remains and so is the number of the fifth that was subtracted. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{5}b=\frac{1}{2}\sdot\left(10-6\right)}}</math> | ||
| + | |style="text-align:right;"|הדרך בזה שתחסר הנשאר מהמחובר ומן הנותר קח המחצית וככה מספר החמישית שגרע | ||
| + | |- | ||
| + | | | ||
| + | ::Since you know its fifth, you know its whole and you can extract the second from the first. | ||
| + | |style="text-align:right;"|ואחר שידעת חמישיתו ידעת כלו ומן האחד תוציא השני | ||
| + | |- | ||
| + | |According to this way for every number. | ||
| + | |style="text-align:right;"|ועל זה הדרך לכל חשבון | ||
| + | |- | ||
| + | | | ||
| + | *If it is said: if we subtract one-quarter of the one from one-fifth of the other, 1 remains and if we sum them together, the result is 11. | ||
| + | :<math>\scriptstyle\begin{cases}\scriptstyle\frac{1}{5}a-\frac{1}{4}b=1\\\scriptstyle\frac{1}{5}a+\frac{1}{4}b=11\end{cases}</math> | ||
| + | |style="text-align:right;"|שאם יאמר אם גרענו רביעית האחד מחמישית האחר נשאר אחד ואם חברנום יעלו י"א | ||
| + | |- | ||
| + | | | ||
| + | ::Do as follows: subtract one from 11, 10 remain. Take its half; it is 5, which is the number of the quarter that was subtracted. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{4}b=\frac{1}{2}\sdot\left(11-1\right)=\frac{1}{2}\sdot10}}</math> | ||
| + | |style="text-align:right;"|ככה תעשה גרע אחד מי"א ונשאר עשרה<br> | ||
| + | קח מחציתם והוא מספר הרביעית שגרע | ||
| + | |- | ||
| + | | | ||
| + | ::It is discovered that one number is twenty, and from it you can deduce the other, which is thirty. | ||
| + | ::<math>\scriptstyle{\color{blue}{\begin{cases}\scriptstyle b=20\\\scriptstyle a=30\end{cases}}}</math> | ||
| + | |style="text-align:right;"|מתברר שהחשבון האחד הוא עשרים וממנו תוכל להוציא השני והוא שלשים | ||
| + | |- | ||
| + | |This way will lead you to the truth and to the correct. | ||
| + | |style="text-align:right;"|וזה הדרך ידריכך אל האמת ואל הנכון | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Chapter Three: Multiplication == | ||
| + | !style="width:45%; text-align:right;"|<big>השער</big> השלישי במערכת | ||
| + | |- | ||
| + | |It is divided into three categories: | ||
| + | |style="text-align:right;"|ונחלק לשלשה ענינים | ||
| + | |- | ||
| + | | | ||
| + | *Multiplication of integers by integers | ||
| + | |style="text-align:right;"|{{#annot:term|1345,156|CHKw}}מערכת{{#annotend:CHKw}} שלמים על שלמים | ||
| + | |- | ||
| + | | | ||
| + | *Multiplication of integers by fractions | ||
| + | |style="text-align:right;"|ומערכת שלמים על שברים | ||
| + | |- | ||
| + | | | ||
| + | *Multiplication of fractions by fractions | ||
| + | |style="text-align:right;"|ומערכת שברים על שברים | ||
| + | |- | ||
| + | | | ||
| + | === The First Category: [Multiplication of] Integers by Integers === | ||
| + | !style="text-align:right;"|הענין הראשון בשלמים על שלמים | ||
| + | |- | ||
| + | |You should know that every number is built and established on ten ranks: | ||
| + | |style="text-align:right;"|יש לך לדעת כי כל חשבון יבנה ויכונן בעשרה {{#annot:term|203,1344|WfnU}}מדרגות{{#annotend:WfnU}} | ||
| + | |- | ||
| + | | | ||
| + | *The first rank are the units | ||
| + | |style="text-align:right;"|וה{{#annot:term|203,1344|CscP}}מדרגה{{#annotend:CscP}} הראשונה הם האחדים | ||
| + | |- | ||
| + | | | ||
| + | *The second - the tens | ||
| + | |style="text-align:right;"|והשניה העשרות | ||
| + | |- | ||
| + | | | ||
| + | *The third - the hundreds | ||
| + | |style="text-align:right;"|והשלישית המאות | ||
| + | |- | ||
| + | | | ||
| + | *The fourth - the thousands | ||
| + | |style="text-align:right;"|והרביעית האלפים | ||
| + | |- | ||
| + | | | ||
| + | *The fifth - the tens of thousands | ||
| + | |style="text-align:right;"|והחמישית העשרות אלפים | ||
| + | |- | ||
| + | | | ||
| + | *The sixth - the hundreds of thousands | ||
| + | |style="text-align:right;"|והששית במאות אלף | ||
| + | |- | ||
| + | | | ||
| + | *The seventh - the thousands of thousands | ||
| + | |style="text-align:right;"|והשביעית באלף אלפים | ||
| + | |- | ||
| + | | | ||
| + | *The eighth - the tens thousands of thousands | ||
| + | |style="text-align:right;"|והשמינית עשרת אלפי אלפים | ||
| + | |- | ||
| + | | | ||
| + | *The ninth - the hundreds thousands of thousands | ||
| + | |style="text-align:right;"|והתשיעית במאת אלף אלפים | ||
| + | |- | ||
| + | | | ||
| + | *The tenth - the thousands thousands of thousands | ||
| + | |style="text-align:right;"|והעשירית באלף אלפי אלפים | ||
| + | |- | ||
| + | |And so on endlessly. | ||
| + | |style="text-align:right;"|וכן עד אין קץ | ||
| + | |- | ||
| + | |<span style=color:green>'''Definition of the multiplication operation:'''</span> {{#annot:definition|1345,156|BNPE}}the multiplication of a number by a number is that you count the first number by the multitude of the second number. | ||
| + | |style="text-align:right;"|ומערכת מספר על מספר הוא שתהיה מונה המספר האחד במנין המספר השני{{#annotend:BNPE}} | ||
| + | |- | ||
| + | !<span style=color:green>Multiplication of units by units</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *Every number that you multiply by one persists and does not increase. | ||
| + | |style="text-align:right;"|וכל מספר שאתה עורך אותו באחד הוא עומד ואינו נוסף | ||
| + | |- | ||
| + | | | ||
| + | :Indeed, if you multiply one by one it is one, two by one are two, and so every number that you multiply by one does not increase. | ||
| + | |style="text-align:right;"|ואכן אם תערוך אחד על אחד הוא אחד ושנים על אחד הם שנים וכן כל מספר שתערכנו על אחד אינו נוסף | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply two by two, you double it. | ||
| + | |style="text-align:right;"|ואם תערוך שנים על שנים אתה כופל אותו | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply by three, you will find it three [times] the number. | ||
| + | |style="text-align:right;"|ואם בשלשה תערכנו תמצאנו שלשה מן המספר | ||
| + | |- | ||
| + | | | ||
| + | *So on up to ten that if you multiply if by itself it is one-hundred. | ||
| + | |style="text-align:right;"|וכן עד עשרה שאם תערכנו על ‫<ref>10v</ref>עצמו יהיו מאה | ||
| + | |- | ||
| + | |If you multiply a number by a number that are greater than ten, you should master the multiplication of units, for every number is calculated this way. | ||
| + | |style="text-align:right;"|ואם תרצה לערוך מספר על מספר למעלה מעשרה אתה צריך שיהיה {{#annot:term|1200,156|YSqP}}חשבון{{#annotend:YSqP}} האחדים סדורים על פיך כי כל חשבון {{#annot:term|1460,229|b1kl}}מתחשב{{#annotend:b1kl}} על זה הדרך | ||
| + | |- | ||
| + | !<span style=color:green>Full multiplication table:</span> | ||
| + | | | ||
| + | |- | ||
| + | |To make it easier for the reader, I have drawn a table for you from 1 to 10, by which you may find out every number. | ||
| + | |style="text-align:right;"|ולהקל על הקורא ציירתי לך זה המכבר מא' ועד י' שתברור לך בו כל חשבון | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | {|class="wikitable" style="color: blue; text-align:center; margin-left: auto; margin-right: auto; border: none;" | ||
| + | |- | ||
| + | | 10 || 9 || 8 || 7 || 6 || 5 || 4 || 3 || 2 || 1 | ||
| + | |- | ||
| + | | 20 || 18 || 16 || 14 || 12 || 10 || 8 || 6 || 4 || 2 | ||
| + | |- | ||
| + | | 30 || 27 || 24 || 21 || 18 || 15 || 12 || 9 || 6 || 3 | ||
| + | |- | ||
| + | | 40 || 36 || 32 || 28 || 24 || 20 || 16 || 12 || 8 || 4 | ||
| + | |- | ||
| + | | 50 || 45 || 40 || 35 || 30 || 25 || 20 || 15 || 10 || 5 | ||
| + | |- | ||
| + | | 60 || 54 || 48 || 42 || 36 || 30 || 24 || 18 || 12 || 6 | ||
| + | |- | ||
| + | | 70 || 63 || 56 || 49 || 42 || 35 || 28 || 21 || 14 || 7 | ||
| + | |- | ||
| + | | 80 || 72 || 64 || 56 || 48 || 40 || 32 || 24 || 16 || 8 | ||
| + | |- | ||
| + | | 90 || 81 || 72 || 63 || 54 || 45 || 36 || 27 || 18 || 9 | ||
| + | |- | ||
| + | | 100 || 90 || 80 || 70 || 60 || 50 || 40 || 30 || 20 || 10 | ||
| + | |- | ||
| + | |} | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
|- | |- | ||
| י || ט || ח || ז || ו || ה || ד || ג || ב || א | | י || ט || ח || ז || ו || ה || ד || ג || ב || א | ||
| Line 359: | Line 2,285: | ||
|- | |- | ||
|} | |} | ||
| − | + | |- | |
| − | וכאשר תרצה לערוך חשבון על חשבון מא' ועד י' | + | !<span style=color:green>Instructions for using the multiplication table:</span> |
| − | + | | | |
| − | וכן לכל החשבון.< | + | |- |
| − | ואם תרצה לחשוב משאר המדרגות אחת על אחת יחשוב אותם כאלו הם אחדים.< | + | | |
| − | כמו שתרצה שש מאות על ארבעת אלפים | + | *When you wish to multiply a number by a number from 1 to 10 |
| − | מאיזה חשבון הם המאות מששה והאלפים מארבעה ערוך ששה על ארבעה כאלו הם אחדים והם כ"ד ושמרם | + | |style="text-align:right;"|וכאשר תרצה {{#annot:term|1280,185|zAiS}}לערוך{{#annotend:zAiS}} חשבון על חשבון מא' ועד י‫' |
| − | וכן אם תקח מדרגת האלפים והוא ארבעה ותמנה אתו מן המאות ולמעלה אתה מגיע אל המדרגה הששית ושים שם חשבון האחדים ששמרת והעשרות במדרגה אשר אחריה והיא השביעית.< | + | |- |
| − | ומפני זה אתה אומר כי הכ"ד ששמרת הם ב' אלפי אלפים וארבע מאות אלף.< | + | | |
| − | דרך אחרת שתהיה חושב מדרגות בב' חשבונות ותפחות אחד מהם והנשאר יהיה מדרגת המספר. | + | :*Such as when you wish to multiply 8 by 7 |
| − | כמו שתקח מדרגת המאות והוא שלשה ומדרגת האלפים ארבעה תחברם יהיו שבעה תחסר מהם אחד לעולם וישארו בידך ששה | + | ::<math>\scriptstyle8\times7</math> |
| − | והטעם שאתה מחסר משתי המדרגות בהתקבצם מפני שמדרגת האחד עולה לכאן ולכאן. | + | |style="text-align:right;"|כמו שתרצה לערוך ח' על ז‫' |
| − | ואם תערוך אחדים ועשרות על אחדים ועשרות | + | |- |
| − | כמו כ"ה על כ"ח | + | | |
| − | דע מה ערך כ"ה ממאה והוא רובע קח רובע כ"ח והוא ז' יהיו האחדים מאות.< | + | ::You place your fingers orderly on the first two lines [lengthwise and breadthwise], in which 1 to 10 are written: one finger on 8 and your other finger on 7. Lead them and where the fingers meet there you will find the result, which is 56. |
| − | ואם תערוך נ"ד בס"ו. | + | |style="text-align:right;"|אתה נותן אצבעותיך בשני הטורים הראשונים אשר כתוב בהם מא' ועד י' על הסדר<br> |
| − | דע מה ערך החמשים ממאה והוא חצי קח חצי מספר ששה וששים יהיו ל"ג העשרות הם האלפים והאחדים הם מאות ואחר כך תערוך הארבעה הנותרים על | + | האצבע האחד על ח' ואצבעך השני על ז‫'<br> |
| − | ואם תערוך קכ"ה על עצמו. | + | הולך אותם ובמקום אשר יפגשו האצבעות שם תמצא העולה והוא נ"ו |
| − | דע מה ערכו מאלף והיא שמינית קח שמינית קכ"ה והוא ט"ו וחמשה שמיניות ערוך אותם באלף יעלה ט"ו אלפים ותרכ"ה | + | |- |
| − | ואם תערוך אחדים על עשרות.< | + | | |
| − | כמו חמשה על שבעים.< | + | :Likewise for every number. |
| − | ערוך חמשה על שבעה יעלה ל"ה יהיו העשרות מאות והאחדים עשרות והוא ג' מאות וחמשים.< | + | |style="text-align:right;"|וכן לכל החשבון |
| − | גם תדענו שתחשוב מהו חמשה מעשרה והוא חציו קח מחצית השבעים והוא ל"ה. | + | |- |
| − | או תדענו שתחשוב מהו השבעים ממאה והוא שבע עשיריות קח שבע עשיריות מחמשה והוא ג' וחצי תערכם על מאה יהיו ג' מאות וחמשים | + | | |
| − | ואם תערוך אחדים על מאות.< | + | *If you wish to multiply the other ranks one by the other, consider them as if they are units. |
| − | כמו חמשה על שלש מאות.< | + | :<math>\scriptstyle{\color{OliveGreen}{\left(a\sdot10^n\right)\times\left(b\sdot10^m\right)}}</math> |
| − | ערוך חמשה על ג' יעלה ט"ו יהיו העשרות אלפים והאחדים מאות. | + | |style="text-align:right;"|ואם תרצה לחשוב משאר המדרגות אחת על אחת יחשוב אותם כאלו הם אחדים |
| − | ותדענו שתחשב מהו חמשה ממאה והוא חצי עשיריות קח חצי עשירית של ג' מאות והוא ט"ו | + | |- |
| − | ותדענו שתחלק הג' מאות על מאה ותערוך היוצא על חמשה יעלה ט"ו | + | | |
| − | ואם תערוך עשרות על עשרות.< | + | :*{{#annot:600×4000|156|ZjcQ}}As if you want to [multiply] six hundred by four thousand. |
| − | כמו כ' על ל'.< | + | ::<math>\scriptstyle600\times4000</math> |
| − | ערוך שנים על שלשה יהיו ששה האחדים יהיו מאות.< | + | |style="text-align:right;"|כמו שתרצה שש מאות על ארבעת אלפים{{#annotend:ZjcQ}} |
| − | ותדענו שתחשוב מהו כ' ממאה וקח | + | |- |
| − | או תדע מה שהם הל' ממאה וקח ערכו מן עשרים והדבר שוה | + | | |
| − | ואם תערוך עשרות על מאות.< | + | ::*What is the number of the hundreds? six. And the thousands? four. Multiply six by four as if they were units; the result is 24, save it. |
| − | כמו מ' בשש מאות.< | + | :::<math>\scriptstyle{\color{blue}{6\sdot4=24}}</math> |
| − | ערוך ד' על | + | |style="text-align:right;"|מאיזה חשבון הם המאות מששה והאלפים מארבעה<br> |
| − | ותדענו שתחשב מהן ו' מאות מאלף והוא ו' עשיריות קח זה הערך ממ' יעלה כ"ד | + | ערוך ששה על ארבעה כאלו הם אחדים והם כ"ד ושמרם |
| − | או תדע מהן הארבעים מאלף חלק אחד מן כ"ה וכערכו קח משש מאות והדבר שוה | + | |- |
| − | ואם תערוך עשרות על אלפים.< | + | | |
| − | כמו נ' בז' אלפים.< | + | ::<span style=color:green>Determining the place of 6·4 in the product 600×4000</span> |
| − | וערוך ה' על זה שבעה יעלה ל"ה יהיו האחדים עשרות אלפים והעשרות מאות אלפים.< | + | ::*Then take the rank of hundreds, which is three, and count up three ranks from the thousands, it is the sixth rank. |
| − | ותדענו שתחשב מהן ז' אלפים מי' אלפים וקח אותו הערוך מחמשים והוא ל"ה. | + | :::<span style=color:green>(rank of hundreds)+[(rank of thousands)-1]=3+(4-1)=6</span> |
| − | או תדע מהם הנ' מי' אלפים וכערכו קח מן הז' אלפים והדבר שוה. | + | |style="text-align:right;"|ואחר כך קח מדרגת המאות והוא שלשה ומנה מהאלפים ולמעלה ג' מדרגות והוא מדרגה הששית |
| − | ועל אלו הדרכים תוכל לדעת כל חשבון עד אין קץ שתשמר השמות והמדרגות | + | |- |
| + | | | ||
| + | ::*Likewise, if you take the rank of thousands, which is four, and count up from the hundreds, you reach the sixth rank. | ||
| + | :::<span style=color:green>(rank of thousands)+[(rank of hundreds)-1]=4+(3-1)=6</span> | ||
| + | |style="text-align:right;"|וכן אם תקח מדרגת האלפים והוא ארבעה ותמנה אתו מן המאות ולמעלה אתה מגיע אל המדרגה הששית | ||
| + | |- | ||
| + | | | ||
| + | ::Put there the number of units that you kept, and the tens in the succeeding rank, which is the seventh. | ||
| + | |style="text-align:right;"|ושים שם חשבון האחדים ששמרת והעשרות במדרגה אשר אחריה והיא השביעית | ||
| + | |- | ||
| + | | | ||
| + | :::Hence, you say that the 24 that you kept are 2 thousand of thousand and four hundred of thousand. | ||
| + | :::<math>\scriptstyle{\color{blue}{600\times4000=2400000}}</math> | ||
| + | |style="text-align:right;"|ומפני זה אתה אומר כי הכ"ד ששמרת הם ב' אלפי אלפים וארבע מאות אלף | ||
| + | |- | ||
| + | | | ||
| + | ::*Another way is that you count the ranks of the two numbers and subtract one from [the sum]; the remainder will be the rank of the number [sought]. | ||
| + | :::<span style=color:green>[(rank of hundreds)+(rank of thousands)]-1=(3+4)-1=7-1=6</span> | ||
| + | |style="text-align:right;"|דרך אחרת שתהיה חושב מדרגות בב' חשבונות ותפחות אחד מהם והנשאר יהיה מדרגת המספר | ||
| + | |- | ||
| + | | | ||
| + | :::*Such as, when you take the rank of hundreds, which is three, and the rank of thousands, which is four, and add them, they are seven. Always subtract one from them; you are left with six. This is equal to the first number. | ||
| + | |style="text-align:right;"|כמו שתקח מדרגת המאות והוא שלשה ומדרגת האלפים ארבעה תחברם יהיו שבעה<br> | ||
| + | תחסר מהם אחד לעולם וישארו בידך ששה<br> | ||
| + | זה דבר שוה ‫<ref>11r</ref>לחשבון הראשון | ||
| + | |- | ||
| + | | | ||
| + | ::The reason you subtract [one] from the sum of the two ranks is that the rank of the units appears here and here [= the rank of the units is counted twice] | ||
| + | |style="text-align:right;"|והטעם שאתה מחסר משתי המדרגות {{#annot:term|1216,178|exwB}}בהתקבצם{{#annotend:exwB}} מפני שמדרגת האחד עולה לכאן ולכאן | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply units and tens by units and tens. | ||
| + | |style="text-align:right;"|ואם תערוך אחדים ועשרות על אחדים ועשרות | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:25×28|156|BQkO}}Such as 25 by 28. | ||
| + | ::<math>\scriptstyle25\times28</math> | ||
| + | |style="text-align:right;"|כמו כ"ה על כ"ח{{#annotend:BQkO}} | ||
| + | |- | ||
| + | | | ||
| + | ::Know the ratio of 25 to 100, it is a quarter. Take a quarter of 28, which are 7. The units will be hundreds | ||
| + | ::<math>\scriptstyle{\color{blue}{25\times28=\left(\frac{25}{100}\sdot28\right)\sdot100=\left(\frac{1}{4}\sdot28\right)\sdot100=7\sdot100}}</math> | ||
| + | |style="text-align:right;"|דע מה ערך כ"ה ממאה והוא רובע<br> | ||
| + | קח רובע כ"ח והוא ז‫'<br> | ||
| + | יהיו האחדים מאות | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:54×66|156|KaQ7}}If you multiply 54 by 64. | ||
| + | ::<math>\scriptstyle54\times66</math> | ||
| + | |style="text-align:right;"|ואם תערוך נ"ד בס"ו{{#annotend:KaQ7}} | ||
| + | |- | ||
| + | | | ||
| + | ::Know the ratio of fifty to one-hundred, it is a half. Take a half of sixty-six, it is 33. The tens are thousands and the units are hundreds. Then multiply the remaining four by sixty-six, the result is 264. Add it to the 33, the result is 3 thousand, 5 hundred and sixty-four. | ||
| + | |style="text-align:right;"|דע מה ערך החמשים ממאה והוא חצי<br> | ||
| + | קח חצי מספר ששה וששים יהיו ל"ג<br> | ||
| + | העשרות הם האלפים והאחדים הם מאות<br> | ||
| + | ואחר כך תערוך הארבעה הנותרים על בששה וששים יעלה רס"ד<br> | ||
| + | חברם על הל"ג יעלה ג' אלפים וה' מאות וארבע וששים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle54\times66&\scriptstyle=\left[\left(\frac{50}{100}\sdot66\right)\sdot100\right]+\left(4\sdot66\right)=\left[\left(\frac{1}{2}\sdot66\right)\sdot100\right]+264\\&\scriptstyle=\left(33\sdot100\right)+264=3300+264=3564\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:125×125|156|GRmk}}If you multiply 125 by itself. | ||
| + | ::<math>\scriptstyle125\times125</math> | ||
| + | |style="text-align:right;"|ואם תערוך קכ"ה על עצמו{{#annotend:GRmk}} | ||
| + | |- | ||
| + | | | ||
| + | ::Know its ratio to one-thousand, it is an eighth. Take an eighth of 125, it is 15 and five eighths. Multiply it by one-thousand, the result is 15 thousand and 625. | ||
| + | |style="text-align:right;"|דע מה ערכו מאלף והיא שמינית<br> | ||
| + | קח שמינית קכ"ה והוא ט"ו וחמשה שמיניות<br> | ||
| + | ערוך אותם באלף יעלה ט"ו אלפים ותרכ"ה | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{125\times125=\left(\frac{125}{1000}\sdot125\right)\sdot1000=\left(\frac{1}{8}\sdot125\right)\sdot1000=\left(15+\frac{5}{8}\right)\sdot1000=15625}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply units by tens | ||
| + | |style="text-align:right;"|ואם תערוך אחדים על עשרות | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:5×70|156|kmOR}}If you multiply five by seventy. | ||
| + | ::<math>\scriptstyle5\times70</math> | ||
| + | |style="text-align:right;"|כמו חמשה על שבעים{{#annotend:kmOR}} | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply five by seven, the result is 35. The tens are hundreds and the units are tens. So, it is 3 hundred and fifty. | ||
| + | ::<math>\scriptstyle{\color{blue}{5\times70=\left(5\sdot7\right)\sdot10=35\sdot10=350}}</math> | ||
| + | |style="text-align:right;"|ערוך חמשה על שבעה יעלה ל"ה<br> | ||
| + | יהיו העשרות מאות והאחדים עשרות<br> | ||
| + | והוא ג' מאות וחמשים | ||
| + | |- | ||
| + | | | ||
| + | ::Know it also by calculating how much is five from ten, it is its half. Take a half of seventy, it is 35. | ||
| + | ::<math>\scriptstyle{\color{blue}{5\times70=\left(\frac{5}{10}\sdot70\right)\sdot10=\left(\frac{1}{2}\sdot70\right)\sdot10=35\sdot10}}</math> | ||
| + | |style="text-align:right;"|גם תדענו שתחשוב מהו חמשה מעשרה והוא חציו<br> | ||
| + | קח מחצית השבעים והוא ל"ה | ||
| + | |- | ||
| + | | | ||
| + | ::Or, know it by calculating how much is seventy from one-hundred, it is seven tenths. Take seven tenths of a five, it is 3 and a half. Multiply it by one-hundred, it is 3 hundred and fifty. | ||
| + | |style="text-align:right;"|או תדענו שתחשוב מהו השבעים ממאה והוא שבע עשיריות<br> | ||
| + | קח שבע עשיריות מחמשה והוא ג' וחצי<br> | ||
| + | תערכם על מאה יהיו ג' מאות וחמשים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{5\times70=\left(5\sdot\frac{70}{100}\right)\sdot100=\left(5\sdot\frac{7}{10}\right)\sdot100=\left(3+\frac{1}{2}\right)\sdot100=350}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply units by hundreds | ||
| + | |style="text-align:right;"|ואם תערוך אחדים על מאות | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:5×300|156|dnZv}}Such as five by three hundred. | ||
| + | ::<math>\scriptstyle5\times300</math> | ||
| + | |style="text-align:right;"|כמו חמשה על שלש מאות{{#annotend:dnZv}} | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply five by 3, the result is 15. The tens are thousands and the units are hundreds. | ||
| + | ::<math>\scriptstyle{\color{blue}{5\times300=\left(5\sdot3\right)\sdot100=15\sdot100}}</math> | ||
| + | |style="text-align:right;"|ערוך חמשה על ג' יעלה ט"ו<br> | ||
| + | יהיו העשרות אלפים והאחדים מאות | ||
| + | |- | ||
| + | | | ||
| + | ::Know it by calculating how much is five of one-hundred, it is half the tenth. Take half the tenth of 3 hundred, it is 15. | ||
| + | |style="text-align:right;"|ותדענו שתחשב מהו חמשה ממאה והוא חצי עשיריות<br> | ||
| + | קח חצי עשירית של ג' מאות והוא ט"ו | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{5\times300=\left(\frac{5}{100}\sdot300\right)\sdot100=\left[\left(\frac{1}{2}\sdot\frac{1}{10}\right)\sdot300\right]\sdot100=15\sdot100}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Know it by dividing the 3 hundred by one-hundred, then multiplying the result by five, the result is 15. | ||
| + | ::<math>\scriptstyle{\color{blue}{5\times300=\left(5\sdot\frac{300}{100}\right)\sdot100=15\sdot100}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתחלק הג' מאות על מאה ותערוך היוצא על חמשה יעלה ט"ו | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply tens by tens | ||
| + | |style="text-align:right;"|ואם תערוך עשרות על עשרות | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:20×30|156|CSsq}}Such as 20 by 30. | ||
| + | ::<math>\scriptstyle20\times30</math> | ||
| + | |style="text-align:right;"|כמו כ' על ל‫'{{#annotend:CSsq}} | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply two by three, they are six. The units are hundreds. | ||
| + | ::<math>\scriptstyle{\color{blue}{20\times30=\left(2\sdot3\right)\sdot100=6\sdot100}}</math> | ||
| + | |style="text-align:right;"|ערוך שנים על שלשה יהיו ששה<br> | ||
| + | האחדים יהיו מאות | ||
| + | |- | ||
| + | | | ||
| + | ::Know it by calculating how much is 20 of one-hundred, take its ratio from 30 and multiply the result by one-hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{20\times30=\left(\frac{20}{100}\sdot30\right)\sdot100}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתחשוב מהו כ' ממאה וקח ערכו מל' ומה שיהיה תערכנו במאה | ||
| + | |- | ||
| + | | | ||
| + | ::Or, know how much is the 30 of one-hundred and take its ratio from twenty. It is the same thing. | ||
| + | ::<math>\scriptstyle{\color{blue}{20\times30=\left(20\sdot\frac{30}{100}\right)\sdot100}}</math> | ||
| + | |style="text-align:right;"|או תדע מה שהם הל' ממאה וקח ערכו מן עשרים והדבר שוה | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply tens by hundreds | ||
| + | |style="text-align:right;"|ואם תערוך עשרות על מאות | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:40×600|156|X9sf}}Such as 40 by six hundred. | ||
| + | ::<math>\scriptstyle40\times600</math> | ||
| + | |style="text-align:right;"|כמו מ' בשש מאות{{#annotend:X9sf}} | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply 4 by six, the result is 24. The units are thousands and the tens are tens of thousands. | ||
| + | ::<math>\scriptstyle{\color{blue}{40\times600=\left(4\sdot6\right)\sdot1000=24\sdot1000}}</math> | ||
| + | |style="text-align:right;"|ערוך ד' על ‫<ref>11r</ref>ששה יעלה כ"ד יהיו האחדים אלפים והעשרות עשרות אלפים | ||
| + | |- | ||
| + | | | ||
| + | ::Know it by calculating how much is 6 hundred of one-thousand, which is 6 tenths, take this ratio from 40, the result is 24. | ||
| + | |style="text-align:right;"|ותדענו שתחשב מהן ו' מאות מאלף והוא ו' עשיריות<br> | ||
| + | קח זה הערך ממ' יעלה כ"ד | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{40\times600=\left(40\sdot\frac{600}{1000}\right)\sdot1000=\left(40\sdot\frac{6}{10}\right)\sdot1000=24\sdot1000}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Or, know how much is the forty of one-thousand, [it is] one part of 25 and take its ratio from six hundred. It is the same thing. | ||
| + | ::<math>\scriptstyle{\color{blue}{40\times600=\left(\frac{40}{1000}\sdot600\right)\sdot1000=\left(\frac{1}{25}\sdot600\right)\sdot1000}}</math> | ||
| + | |style="text-align:right;"|או תדע מהן הארבעים מאלף חלק אחד מן כ"ה וכערכו קח משש מאות והדבר שוה | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply tens by thousands | ||
| + | |style="text-align:right;"|ואם תערוך עשרות על אלפים | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:50×7000|156|DsCO}}Such as 50 by 7 thousand. | ||
| + | ::<math>\scriptstyle50\times7000</math> | ||
| + | |style="text-align:right;"|כמו נ' בז' אלפים{{#annotend:DsCO}} | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply 5 by seven, the result is 35. The units are tens of thousands and the tens are hundreds of thousands. | ||
| + | ::<math>\scriptstyle{\color{blue}{50\times7000=\left(5\sdot7\right)\sdot10000=35\sdot10000}}</math> | ||
| + | |style="text-align:right;"|וערוך ה' על זה שבעה יעלה ל"ה<br> | ||
| + | יהיו האחדים עשרות אלפים והעשרות מאות אלפים | ||
| + | |- | ||
| + | | | ||
| + | ::Know it by calculating how much is 7 thousand of 10 thousand, take this ratio from fifty, it is 35. | ||
| + | ::<math>\scriptstyle{\color{blue}{50\times7000=\left(50\sdot\frac{7000}{10000}\right)\sdot10000}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתחשב מהן ז' אלפים מי' אלפים וקח אותו הערוך מחמשים והוא ל"ה | ||
| + | |- | ||
| + | | | ||
| + | ::Or, know how much is the 50 of 10 thousand and take its ratio from the 7 thousand. It is the same thing. | ||
| + | ::<math>\scriptstyle{\color{blue}{50\times7000=\left(\frac{50}{10000}\sdot7000\right)\sdot10000}}</math> | ||
| + | |style="text-align:right;"|או תדע מהם הנ' מי' אלפים וכערכו קח מן הז' אלפים והדבר שוה | ||
| + | |- | ||
| + | |By these ways you can know every number endlessly, keeping the names and the ranks. | ||
| + | |style="text-align:right;"|ועל אלו הדרכים תוכל לדעת כל חשבון עד אין קץ שתשמר השמות והמדרגות | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === The Second Category: Multiplication of Integers by Fractions=== | ||
| + | !style="width: 45%; text-align:right;"|<big>הענין</big> השני מערכת שלמים על שברים | ||
| + | |- | ||
| + | | | ||
| + | ==== <span style=color:green>Sexagesimal Fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |If you have fractions of the astrologers: degrees, minutes and seconds | ||
| + | |style="text-align:right;"|אם יהיו בידך שברי חכמי המזלות מעלות ראשונים ושניים | ||
| + | |- | ||
| + | | | ||
| + | *If you mulnitply degrees by degrees, the product are degrees | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^\circ\times b^\circ=\left(a\sdot b\right)^\circ}}</math> | ||
| + | |style="text-align:right;"|אם אתה עורך מעלות <sup>על</sup> מעל[ו]ת יהיה {{#annot:term|1219,241|2rFl}}הנקבץ{{#annotend:2rFl}} מעלות | ||
| + | |- | ||
| + | | | ||
| + | *If you multiply degrees by fractions, the product are fractions: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a\times\frac{b}{60^n}=\frac{a\sdot b}{60^n}}}</math> | ||
| + | |style="text-align:right;"|ואם אתה עורך מעלות על שברים יהיה הנקבץ שברים | ||
| + | |- | ||
| + | | | ||
| + | :*If you multiply by minutes, they are minutes. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a^\circ\times b^\prime=\left(a\sdot b\right)^\prime}}</math> | ||
| + | |style="text-align:right;"|אם ערכת על ראשונים הם ראשונים | ||
| + | |- | ||
| + | | | ||
| + | :*If by seconds, they are seconds. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a^\circ\times b^{\prime\prime}=\left(a\sdot b\right)^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|ואם על שניים הם שניים | ||
| + | |- | ||
| + | | | ||
| + | :*If by thirds, they are thirds. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a^\circ\times b^{\prime\prime\prime}=\left(a\sdot b\right)^{\prime\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|ואם על שלישיים הם שלישיים | ||
| + | |- | ||
| + | | | ||
| + | :And so on for all the fractions that are multiplied by degrees. | ||
| + | |style="text-align:right;"|וכן למעלה מהם לכל השברים הנערכים על מעלות | ||
| + | |- | ||
| + | | | ||
| + | :*Such as when you wish to multiply 20 degrees by 50 minutes. | ||
| + | ::<math>\scriptstyle20^\circ\times50^\prime</math> | ||
| + | |style="text-align:right;"|כמו שתרצה לערוך כ' מעלות על נ' ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::The result is one-thousand, which are minutes. Divide them by sixty, the result of the division is 16 and 40 minutes remain, which are 5 sixths. Take this ratio from the 20, they are 16 degrees and 40 minutes. | ||
| + | ::<math>\scriptstyle{\color{blue}{20^\circ\times50^\prime=1000^\prime=20^\circ\sdot\frac{5}{6}^\circ=16^\circ+40^\prime}}</math> | ||
| + | |style="text-align:right;"|יעלו אלף והם ראשונים<br> | ||
| + | תחלקם על ששים יצא בחלוק י"ו וישאר מ' ראשונים והוא ה' ששיותיו וכאותו הערך קח מן הב' יהיו י"ו מעלות מ' ראשונים | ||
| + | |- | ||
| + | |According to this calculate the seconds, thirds and all the fractions endlessly. | ||
| + | |style="text-align:right;"|ועל זה תחשב לשניים ולשלישיים ולכל השברים עד אין קץ | ||
| + | |- | ||
| + | |Since the calculation of the integers that are multiplied by fractions is decreasing. | ||
| + | |style="text-align:right;"|כי כל חשבון השלמים הנערכים בשברים הוא {{#annot:term|1364,1585|vany}}פחות פוחת והולך{{#annotend:vany}} | ||
| + | |- | ||
| + | | | ||
| + | ::The saying: "multiply ten by a third or a quarter" is the same as the saying: "how much is a third or a quarter of the ten" and so on to all fractions. | ||
| + | |style="text-align:right;"|והאומר {{#annot:term|1269,185|KApw}}חשוב{{#annotend:KApw}} עשרה בשליש או ברביע דומה כמי שאומר כמה חלק שליש או רביע מהעשרה וכן לכל השברים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Integers by integers and fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ===== <span style=color:green>Simple Fractions</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | |If you have fractions of the geometricians and you wish to multiply integers by integers and fractions. | ||
| + | |style="width: 45%; text-align:right;"|ואם יהיו בידך שברי חכמי המדות ותרצה לערוך שלמים על שלמים ושברים | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:2×(3+¼)|17|rNFH}}Such as two by three and a quarter. | ||
| + | :<math>\scriptstyle2\times\left(3+\frac{1}{4}\right)</math> | ||
| + | |style="text-align:right;"|כגון שנים על שלשה ורביע{{#annotend:rNFH}} | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> We seek a number that has a third and a quarter, which is twelve and it is the denominator. | ||
| + | |style="text-align:right;"|נבקש חשבון שיש לו שלישית ורביעית והוא שנים עשר והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | ::Take 12 for each integer: | ||
| + | |style="text-align:right;"|ותקח לכל אחד שלם י"ב | ||
| + | |- | ||
| + | | | ||
| + | ::*They are 24 in the first number <math>\scriptstyle{\color{blue}{2\sdot12=24}}</math> | ||
| + | |style="text-align:right;"|והם כ"ד בחשבון האחד | ||
| + | |- | ||
| + | | | ||
| + | ::*In the second number the result is 36, add to them 3 for the quarter, the result is 39 <math>\scriptstyle{\color{blue}{\left(3\sdot12\right)+3=36+3=39}}</math>. | ||
| + | |style="text-align:right;"|‫<ref>12r</ref>והחשבון השני השלשה יעלו ל"ו הוסף עליהם ג' בעבור הרביע יעלו ל"ט | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply 24 by 39, the result is 936 <math>\scriptstyle{\color{blue}{24\sdot39=936}}</math> | ||
| + | |style="text-align:right;"|ונערוך כ"ד על ל"ט יעלו תתקל"ו חלקים | ||
| + | |- | ||
| + | | | ||
| + | ::Divide them by 144, which is the square of the denominator, the result is six and 72 remain, which are half of 144, thus six and a half. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times\left(3+\frac{1}{4}\right)=\frac{936}{12^2}=\frac{936}{144}=6+\frac{72}{144}=6+\frac{1}{2}}}</math> | ||
| + | |style="text-align:right;"|חלקם על קמ"ד שהוא מרובע המורה יצא ששה ונשארו ע"ב שהוא חצי קמ"ד והנה ששה וחצי | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by leaving [aside] the two as they are two and take four for each of the three for the fraction of the quarter, the result is 12. We add one for the quarter, they are 13. We multiply them by two that we have, the result is 26. We divide by four, the result is six and a half. | ||
| + | |style="text-align:right;"|ותדענו שתעזב השניים כמו שהם שנים ובעבור שבר הרביעית וקח לכל אחד מן השלשה ארבעה יעלו י"ב<br> | ||
| + | נוסיף אחד בעבור הרביעית הנה י"ג<br> | ||
| + | ערכנום על שנים שהיה לנו עלה כ"ו<br> | ||
| + | נחלק על ארבעה יצא ששה וחצי | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{2\times\left(3+\frac{1}{4}\right)=\frac{2\sdot\left[\left(3\sdot4\right)+1\right]}{4}=\frac{2\sdot\left(12+1\right)}{4}=\frac{2\sdot13}{4}=\frac{26}{4}=6+\frac{1}{2}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:Green>'''common denominator:'''</span> Know it by taking [the number] by which the quarter is denominated, which is four and it is the denominator. | ||
| + | |style="text-align:right;"|ותדענו שתקח מה שיצא ממנו הרביע והוא ארבעה והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | ::*We multiply two by 4, the result is eight. <math>\scriptstyle{\color{blue}{2\sdot4=8}}</math> | ||
| + | |style="text-align:right;"|נערוך שנים על ד' יעלו שמונה | ||
| + | |- | ||
| + | | | ||
| + | ::*The three by 4, the result is 12 and with the quarter, 13. <math>\scriptstyle{\color{blue}{\left(3\sdot4\right)+1=12+1=13}}</math>. | ||
| + | |style="text-align:right;"|ושלשה על ד' יעלו י"ב ועם הרביעית י"ג | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them one by the other, the result is 104. Divide by the square of the denominator, which is 16, the result is six and eight remain, which are one-half. | ||
| + | :<math>\scriptstyle{\color{blue}{2\times\left(3+\frac{1}{4}\right)=\frac{8\sdot13}{4^2}=\frac{104}{16}=6+\frac{8}{16}=6+\frac{1}{2}}}</math> | ||
| + | |style="text-align:right;"|ערכם זה על זה יצא ק"ד וחלק על מרובע המורה שהוא י"ו יצא ששה וישאר שמונה שהוא חצי אחד | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by multiplying two by three, the result is six. <math>\scriptstyle{\color{blue}{2\sdot3=6}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתערך שנים על שלשה עלה ששה וישוב ו‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply two by a quarter, the result is two quarters, which is one-half, and it will be the reserved. <math>\scriptstyle{\color{blue}{2\sdot\frac{1}{4}=\frac{2}{4}=\frac{1}{2}}}</math> | ||
| + | :<math>\scriptstyle{\color{red}{2\times\left(3+\frac{1}{4}\right)=6+\frac{1}{2}}}</math> | ||
| + | |style="text-align:right;"|וערוך על שנים על רביעית עלה שנים רביעיות שהוא חצי וזה יהיה שמור בידך | ||
| + | |- | ||
| + | |For the one when it is multiplied by a fraction is the same [as the fraction]. <math>\scriptstyle1\sdot\frac{a}{b}=\frac{a}{b}</math> | ||
| + | |style="text-align:right;"|כי האחד הנערך על שבר הרי הוא כמוהו | ||
| + | |- | ||
| + | |It is like saying one in length by one-half in width, which is really nothing but one-half. The same by one-third and by all fractions. | ||
| + | |style="text-align:right;"|ודומה כמי שאומר אחד באורך על חצי ברוחב וזה באמת אינו כי אם חציו וכן על שליש ועל כל השברים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Integers by fractions fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |If you multiply integers by fractions | ||
| + | |style="width:45%; text-align:right;"|ואם תערוך שלמים על שברים | ||
| + | |- | ||
| + | | | ||
| + | ===== <span style=color:green>Simple Fractions</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:¾×9|17|lhz8}}Such as three quarters by nine. | ||
| + | :<math>\scriptstyle\frac{3}{4}\times9</math> | ||
| + | |style="text-align:right;"|כגון שלשה רביעיות בתשעה{{#annotend:lhz8}} | ||
| + | |- | ||
| + | | | ||
| + | :*Know by which number the quarters are denominated, it is four. | ||
| + | |style="text-align:right;"|דע מאיזה מספר הרביעיות והוא מארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::Divide the nine by it; the result is two and one-quarter for each. Multiply the result by three; it is six and three-quarters. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{3}{4}\times9=3\sdot\frac{9}{4}=3\sdot\left(2+\frac{1}{4}\right)=6+\frac{3}{4}}}</math> | ||
| + | |style="text-align:right;"|חלק התשעה עליהם יצא לכל אחד שנים ורובע<br> | ||
| + | ערוך היוצא על שלשה יהיה ששה וג' רביעיות | ||
| + | |- | ||
| + | | | ||
| + | :*Know it [by knowing] by which number the quarters are denominated, it is four and it is the denominator. | ||
| + | |style="text-align:right;"|ותדענו מאיזה מספר הרביעית והוא מארבעה והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply the nine by four; the result is 36. | ||
| + | ::<math>\scriptstyle{\color{blue}{9\sdot4=36}}</math> | ||
| + | |style="text-align:right;"|נערוך התשעה על ארבעה יעלה ל"ו | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply them by three for the quarters, which are three; the result is 108. | ||
| + | ::<math>\scriptstyle{\color{blue}{3\sdot36=108}}</math> | ||
| + | |style="text-align:right;"|ונערכם על שלשה בעבור הרביעיות שהם שלשה יעלה ק"ח | ||
| + | |- | ||
| + | | | ||
| + | ::Divide them by 16, which is the square of the denominator, the result is six integers and 12 remain, which are 3 quarters. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{3}{4}\times9=\frac{108}{4^2}=\frac{108}{16}=6+\frac{12}{16}=6+\frac{3}{4}}}</math> | ||
| + | |style="text-align:right;"|חלקם על י"ו שהוא מרובע המורה יצא ששה שלמים וישארו י"ב שהם ג' רביעיות אחד | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Integers and fractions by integers and fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |If you multiply integers and fractions by integers and fractions | ||
| + | |style="text-align:right;"|ואם תערוך שלמים ושברים על שלמים ושברים | ||
| + | |- | ||
| + | | | ||
| + | ===== <span style=color:green>Simple Fractions</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:(3+⅐)×(5+⅛)|17|t8Al}}Such as three and a seventh by five and an eighth. | ||
| + | :<math>\scriptstyle\left(3+\frac{1}{7}\right)\times\left(5+\frac{1}{8}\right)</math> | ||
| + | |style="text-align:right;"|כגון שלשה ושביעית על חמשה ושמינית{{#annotend:t8Al}} | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Seek for a number that has the two fractions, i.e. a seventh and an eighth, it is 56 and it is the denominator. | ||
| + | |style="text-align:right;"|בקש חשבון שיש לו שני השברים כלומ' שביעית ושמינית והוא נ"ו והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | ::*We multiply the first number, which is three, by the denominator; the result is 168. We add to it 8, for the seventh; the result is 176. | ||
| + | :::<math>\scriptstyle{\color{blue}{\left(3\sdot56\right)+8=168+8=176}}</math> | ||
| + | |style="text-align:right;"|ונערוך החשבון האחד שהוא שלשה על המורה ויעלה קס"ח ונוסיף עליו ח' בעבור השביעית ועלה קע"ו | ||
| + | |- | ||
| + | | | ||
| + | ::*We further multiply the first number, which is five, by the denominator; the result is 280. For the eighth we add seven; it is 287. | ||
| + | :::<math>\scriptstyle{\color{blue}{\left(5\sdot56\right)+7=280+7=287}}</math> | ||
| + | |style="text-align:right;"|ועוד ‫<ref>12v</ref>נערוך החשבון האחד שהוא חמשה על המורה יעלה ר"פ ובעבור השמינית נוסיף שבעה והנה רפ"ז | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply 176 by 287; the result is fifty thousand five hundred and twelve. | ||
| + | ::<math>\scriptstyle{\color{blue}{176\times287=50512}}</math> | ||
| + | |style="text-align:right;"|נערוך קע"ו על רפ"ז עלה חמשים אלף וחמש מאות ושנים עשר | ||
| + | |- | ||
| + | | | ||
| + | ::We divide it by three thousand one hundred and thirty-six, which is the square of the denominator; the result of the division is sixteen and 336 remain, which are three-quarters of one-seventh | ||
| + | |style="text-align:right;"|חלקנום על שלשת אלפים ומאה ושלשים ושש שהוא מרובע המורה יצא בחלוק ששה עשר ונשארו של"ו והם שלש רביעיות שביעית אחד | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(3+\frac{1}{7}\right)\times\left(5+\frac{1}{8}\right)=\frac{50512}{56^2}=\frac{50512}{3136}=16+\frac{336}{3136}=16+\left(\frac{3}{4}\sdot\frac{1}{7}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|שהאחד הוא מרובע המורה שהם ושביעיתו הם ב{{#annot:term|1636,1432|J6jU}}אותיות הודו{{#annotend:J6jU}} ובאותיותנו הם ת'מ'ח‫' | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by taking forty for the [five] that have one-eighth with them and add one; the result is 41. | ||
| + | :::<math>\scriptstyle{\color{blue}{\left(5\sdot8\right)+1=40+1=41}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתקח לשלשה שיש עמהם שמינית ארבעים והוסף אחד הנה מ"א | ||
| + | |- | ||
| + | | | ||
| + | :::<math>\scriptstyle{\color{red}{\left(3\sdot7\right)+1=21+1=22}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply them by each other; the result is nine hundred and two. | ||
| + | ::<math>\scriptstyle{\color{blue}{22\times41=902}}</math> | ||
| + | |style="text-align:right;"|ערכנום זה על זה עלו תשע מאות ושנים | ||
| + | |- | ||
| + | | | ||
| + | ::We divide them by 56, which is the product of seven by eight; the result is 16 and 6 remain, which are three-quarters of one-seventh, because one-seventh of 56 is 8. | ||
| + | |style="text-align:right;"|חלקנום על נ"ו שהוא ערך שבעה על שמונה ויצא י"ו ונשארו ו' שהם שלש רביעיות שביעית אחד כי שביעית נ"ו הם ח‫' | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(3+\frac{1}{7}\right)\times\left(5+\frac{1}{8}\right)=\frac{902}{7\sdot8}=\frac{902}{56}=16+\left(\frac{6}{8}\sdot\frac{1}{7}\right)=16+\left(\frac{3}{4}\sdot\frac{1}{7}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by multiplying three by five; the result is 15. | ||
| + | :::<math>\scriptstyle{\color{blue}{3\times5=15}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתערוך שלשה על חמשה עלה ט"ו | ||
| + | |- | ||
| + | | | ||
| + | ::*Multiply three again by one-eighth; the result is 3 eighths. | ||
| + | :::<math>\scriptstyle{\color{blue}{3\times\frac{1}{8}=\frac{3}{8}}}</math> | ||
| + | |style="text-align:right;"|ועוד תערוך ג' על שמינית עלה ג' שמיניות | ||
| + | |- | ||
| + | | | ||
| + | ::*Five by one-seventh is five-sevenths. | ||
| + | :::<math>\scriptstyle{\color{blue}{5\times\frac{1}{7}=\frac{5}{7}}}</math> | ||
| + | |style="text-align:right;"|וחמשה על שביעית הנה חמש שביעית | ||
| + | |- | ||
| + | | | ||
| + | ::We count them as eighths and add them to the three; the result is one unit and five-eighths of one-seventh remain from the excess of the seventh over the eighth. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{8}+\frac{5}{7}=1+\left(\frac{5}{8}\sdot\frac{1}{7}\right)}}</math> | ||
| + | |style="text-align:right;"|ונחשוב שהם שמיניות ונחברם עם השלש עלה אחד שלם ונשאר מיתרון השביעית על השמינית חמש שמיניות שביעית | ||
| + | |- | ||
| + | | | ||
| + | ::Still you have to multiply one-seventh by one-eighth; the result is one-seventh of one-eighth. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{7}\times\frac{1}{8}=\frac{1}{7}\sdot\frac{1}{8}}}</math> | ||
| + | |style="text-align:right;"|ועוד יש לך לערוך שביעית על שמינית והוא שביעית שמינית | ||
| + | |- | ||
| + | | | ||
| + | ::Add this to the five that you have and the result is six-eighths of one-seventh. | ||
| + | |style="text-align:right;"|תחברם עם החמש שיש לך והנה שש שמיניות שביעית | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(3+\frac{1}{7}\right)\times\left(5+\frac{1}{8}\right)=15+1+\left(\frac{5}{8}\sdot\frac{1}{7}\right)+\left(\frac{1}{7}\sdot\frac{1}{8}\right)=16+\left(\frac{6}{8}\sdot\frac{1}{7}\right)}}</math> | ||
| + | |- | ||
| + | |All of these ways yield the same. | ||
| + | |style="text-align:right;"|וכל הדרכים יצאו שוה | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Sexagesimal Fractions</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | |For the way of the astrologers, as sixty is indivisible by seven nor by eight, do as follows: | ||
| + | |style="text-align:right;"|ולדרך חכמי המזלות שלא יחלקו ששים על שבעה ולא על שמונה ככה תעשה | ||
| + | |- | ||
| + | | | ||
| + | :*Divide one degree into 56 minutes <math>\scriptstyle{\color{blue}{1^\circ=56^\prime}}</math> | ||
| + | |style="text-align:right;"|שתעשה מן מעלה אחת נ"ו ראשונים | ||
| + | |- | ||
| + | | | ||
| + | :*And one minute into 56 seconds <math>\scriptstyle{\color{blue}{1^\prime=56^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|ומראשון נ"ו שניים | ||
| + | |- | ||
| + | | | ||
| + | :Since 56 has a seventh and an eighth [= divisible by 7 and 8]. | ||
| + | |style="text-align:right;"|בעבור שנ"ו יש להם שביעית ושמינית | ||
| + | |- | ||
| + | | | ||
| + | ::Thus, you should multiply three degrees and 8 minutes, which are one-seventh of 56, by five degrees and 7 minutes, which are one-eighth of 56. | ||
| + | |style="text-align:right;"|והנה יש לך לערוך שלשה מעלות וח' ראשונים שהם שביעית נ"ו על חמשה מעלות ז' ראשונים שהם שמינית נ"ו | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(3+\frac{1}{7}\right)\times\left(5+\frac{1}{8}\right)=\left(3+\frac{\frac{1}{7}\sdot56}{56}\right)\sdot\left(5+\frac{\frac{1}{8}\sdot56}{56}\right)=\left(3^\circ+8^\prime\right)\times\left(5^\circ+7^\prime\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::*Multiply 3 by 5, which are degrees; the result is 15. | ||
| + | :::<math>\scriptstyle{\color{blue}{3^\circ\times5^\circ=15^\circ}}</math> | ||
| + | |style="text-align:right;"|תערוך ג' על ה' שהם מעלות עלה ט"ו | ||
| + | |- | ||
| + | | | ||
| + | ::*Multiply the three integers by seven minutes; the result is 21 minutes. | ||
| + | :::<math>\scriptstyle{\color{blue}{3^\circ\times7^\prime=21^\prime}}</math> | ||
| + | |style="text-align:right;"|ותערוך השלשה שלמים על שבעה ראשונים ועלה כ"א ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::*Then, multiply 8 by 5 integers; the result is 40 minutes. | ||
| + | :::<math>\scriptstyle{\color{blue}{8^\prime\times5^\circ=40^\prime}}</math> | ||
| + | |style="text-align:right;"|ואחר כן תערוך ח' על ה' שלמים יעלה מ' ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::*We multiply 8 minutes by 7 minutes; the result is 56 seconds. | ||
| + | :::<math>\scriptstyle{\color{blue}{8^\prime\times7^\prime=56^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|ונערוך ח' ראשונים על ז' ראשונים יעלה נ"ו שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We divide the seconds by 56; the result is one minute, which we add to the minutes, so [they are] 62. | ||
| + | ::<math>\scriptstyle{\color{blue}{21^\prime+40^\prime+56^{\prime\prime}=21^\prime+40^\prime+1^\prime=62^\prime}}</math> | ||
| + | |style="text-align:right;"|נחלק השניים על נ"ו עלה ראשון אשר חברנו עם הראשונים והנה ס"ב | ||
| + | |- | ||
| + | | | ||
| + | ::We convert 56 to one degree; the result is sixteen degrees and 6 minutes remain, which are 3 quarters of one-seventh of 56. | ||
| + | |style="text-align:right;"|נעשה מהם מעלה אחת מנ"ו עלה שש עשרה מעלות ונשארו ו' ראשונים ‫<ref>13r</ref>שהם ג' רביעיות משביעית נ"ו במעלה אחת | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(3+\frac{1}{7}\right)\times\left(5+\frac{1}{8}\right)=15^\circ+62^\prime=15^\circ+1^\circ+6^\prime=16^\circ+6^\prime=\left[16+\left(\frac{3}{4}\sdot\frac{1}{7}\right)\right]^\circ}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Integers and fractions by integers and fractions of fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |If you multiply integers and fractions by integers and fractions of fractions | ||
| + | |style="width: 50%; text-align:right;"|ואם תערוך שלמים ושברים על שלמים ושברי שברים | ||
| + | |- | ||
| + | | | ||
| + | ===== <span style=color:green>Simple Fractions</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:(3+¼)×(5+⅙·⅐)|17|ubkD}}Such as three and a quarter by five and one-sixth of one-seventh. | ||
| + | :<math>\scriptstyle\left(3+\frac{1}{4}\right)\times\left[5+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]</math> | ||
| + | |style="text-align:right;"|כמו שלשה ורביעית על חמשה וששית שביעית{{#annotend:ubkD}} | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Take a number that has a sixth and a seventh, which is 42, multiply it by four, for the quarter, the result is 168 and it is the denominator <math>\scriptstyle{\color{blue}{6\sdot7\sdot4=42\sdot4=168}}</math> | ||
| + | |style="text-align:right;"|קח חשבון שיש לו ששית ושביעית והוא מ"ב גם נערכנו על הארבעה בעבור הרביעית יעלו קס"ח והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | ::Convert all the integers to the denominator, sum the fractions [= numerators] with each of the numbers, multiply the sums one by the other, then divide by the square of the denominator - the result of division are the integers and the remainder are the parts of the denominator. | ||
| + | |style="text-align:right;"|והשב כל השלמים על המורה ותחבר השברים עם כל אחד מהחשבונות והעולה תערוך זה על זה ותחלק על מרובע המורה והיוצא בחלוק הם שלמים והנשאר הם חלקים מהמורה | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by multiplying 3 by 5; it is 15 integers. | ||
| + | ::<math>\scriptstyle{\color{blue}{3\times5=15}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתערך ג' על ה' והוא ט"ו שלמים | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply three by one-sixth of one-seventh; it is 3 sixths of one-seventh. | ||
| + | ::<math>\scriptstyle{\color{blue}{3\times\left(\frac{1}{6}\sdot\frac{1}{7}\right)=\frac{3}{6}\sdot\frac{1}{7}}}</math> | ||
| + | |style="text-align:right;"|ותערוך שלשה על ששית שביעית והוא ג' ששיות שביעית | ||
| + | |- | ||
| + | | | ||
| + | ::*<span style=color:green>'''common denominator:'''</span> Since you find all the fractions that are needed for this calculation, take 84, that has a sixth, a seventh and a quarter, and it is the denominator. | ||
| + | |style="text-align:right;"|ובעבור שתמצא כל השברים שצריכים לזה החשבון קח פ"ד שיש לו ששית ושביעית ורביעית והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | :::*Its quarter is 21: <math>\scriptstyle{\color{blue}{\frac{1}{4}\sdot84=21}}</math> | ||
| + | |style="text-align:right;"|ורביעיתו כ"א | ||
| + | |- | ||
| + | | | ||
| + | :::*Its seventh is 12: <math>\scriptstyle{\color{blue}{\frac{1}{7}\sdot84=12}}</math> | ||
| + | |style="text-align:right;"|ושביעיתו י"ב | ||
| + | |- | ||
| + | | | ||
| + | :::*Its sixth is 14: <math>\scriptstyle{\color{blue}{\frac{1}{6}\sdot84=14}}</math> | ||
| + | |style="text-align:right;"|וששיתו י"ד | ||
| + | |- | ||
| + | | | ||
| + | ::Hence, the 3 sixths of one-seventh resulting by the ratio are six. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{6}\sdot\frac{1}{7}=\frac{6}{84}}}</math> | ||
| + | |style="text-align:right;"|והנה ג' ששיות שביעית שיצאו בערך הם ששה | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply a quarter by 5, which are quarters, they are 105 | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{4}\times5=\frac{105}{84}}}</math> | ||
| + | |style="text-align:right;"|ושוב וערוך רביעית על ה' והם רביעיות שהם ק"ה | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply a quarter by one-sixth of one-seventh; it is one half. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{4}\times\left(\frac{1}{6}\sdot\frac{1}{7}\right)=\frac{\frac{1}{2}}{84}}}</math> | ||
| + | |style="text-align:right;"|ושוב וערוך רביעית על ששית שביעית והוא חצי אחד | ||
| + | |- | ||
| + | | | ||
| + | ::*When you sum them, the result is 111 and a half. | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{6}{84}+\frac{105}{84}+\frac{\frac{1}{2}}{56}=\frac{111+\frac{1}{2}}{84}}}</math> | ||
| + | |style="text-align:right;"|וכאשר תחברם יעלה קי"א וחצי | ||
| + | |- | ||
| + | | | ||
| + | ::Take one integer from them, which is 84, and add it to the 15 integers; the result is 16 integers and 27 and a half still remain. Twenty-one is one-quarter; 6 and a half remain: the six are 2 sevenths of one-quarter and the remaining half is one-sixth of one-seventh of one-quarter. It becomes clear that the result is 16 integers, one-quarter, 2 sevenths of one-quarter and one-sixth of one-seventh of one-quarter. | ||
| + | |style="text-align:right;"|קח מהם אחד שלם שהוא פ"ד וחברהו עם הט"ו שלמים יעלו י"ו שלמים ונשארו עדין כ"ז וחצי<br> | ||
| + | ועשרים ואחד הוא רביעית נשאר ו' וחצי<br> | ||
| + | והששה הם ב' שביעיות רביעית<br> | ||
| + | והחצי שנשאר הוא ששית שביעית רביעית<br> | ||
| + | ונתברר שעלה י"ו שלמים ורביעית וב' שביעיות רביעית וששית שביעית הרביעית | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>{\color{blue}{\begin{align}\scriptstyle\left(3+\frac{1}{4}\right)\times\left[5+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]&\scriptstyle=15+\frac{111+\frac{1}{2}}{84}=15+\frac{84+27+\frac{1}{2}}{84}=15+1+\frac{27+\frac{1}{2}}{84}\\&\scriptstyle=16+\frac{21+6+\frac{1}{2}}{84}=16+\frac{1}{4}+\frac{6+\frac{1}{2}}{84}\\&\scriptstyle=16+\frac{1}{4}+\left(\frac{2}{7}\sdot\frac{1}{4}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{4}\right)\\\end{align}}}</math> | ||
| + | |- | ||
| + | |You can extract it in all ways. | ||
| + | |style="text-align:right;"|ובכל הדרכים תוכל להוציאו | ||
| + | |- | ||
| + | | | ||
| − | == | + | === The Third Category: Multiplication of Fractions by Fractions === |
| − | + | !style="text-align:right;"|<big>הענין</big> השלישי מערכת שברים על שברים | |
| − | + | |- | |
| − | + | | | |
| − | + | ==== <span style=color:green>Sexagesimal Fractions</span> ==== | |
| − | + | | | |
| − | + | |- | |
| − | + | |If you have fractions of the astrologers, such as minutes and seconds and you wish to multiply them by minutes and seconds. | |
| − | + | |style="text-align:right;"|אם יהיו בידך שברי חכמי המזלות כגון ראשונים ושניים ותרצה להעריכם על ראשונים ושניים | |
| − | + | |- | |
| − | + | | | |
| − | + | :*When you multiply minutes by minutes the result are seconds. | |
| − | + | ::<math>\scriptstyle{\color{OliveGreen}{a'\times b'=\left(a\sdot b\right)''}}</math> | |
| − | + | |style="text-align:right;"|כשאתה עורך ראשונים על ראשונים יעלה מן הערך שניים | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ====< | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | אם יהיו בידך שברי חכמי המזלות כגון ראשונים ושניים ותרצה להעריכם על ראשונים ושניים | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | חמשיים || רביעיים || שלישיים || שניים || ראשונים || מעלות || | + | | |
| + | :*If minutes by seconds the result are thirds. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a'\times b''=\left(a\sdot b\right)'''}}</math> | ||
| + | |style="text-align:right;"|ואם ראשונים בשניים יעלה שלישיים | ||
| + | |- | ||
| + | | | ||
| + | :*If minutes by thirds the result are fourths | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a'\times b'''=\left(a\sdot b\right)^{iv}}}</math> | ||
| + | |style="text-align:right;"|ואם ראשונים בשלישים יעלה רביעים | ||
| + | |- | ||
| + | | | ||
| + | :*If you multiply thirds by thirds the result are sixths | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a'''\times b'''=\left(a\sdot b\right)^{vi}}}</math> | ||
| + | |style="text-align:right;"|ואם שלישים בשלישים אתה עורך יעלה ששיים | ||
| + | |- | ||
| + | | | ||
| + | :*If by fourths the result are sevenths | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{a'''\times b^{iv}=\left(a\sdot b\right)^{vii}}}</math> | ||
| + | |style="text-align:right;"|ואם ברביעים יעלה שביעים | ||
| + | |- | ||
| + | |Since, every number that you multiply by fractions is decreasing from its value by the rank of the fraction by which we multiply. | ||
| + | <math>\scriptstyle{\color{OliveGreen}{\frac{1}{60^n}\sdot\frac{1}{60^m}=\frac{1}{60^{n+m}}}}</math> | ||
| + | |style="text-align:right;"|כי כל מספר שאתה עורך אותו בשברים שברים בשברים הוא {{#annot:term|1364,1585|kxA9}}פוחת{{#annotend:kxA9}} ‫<ref>13v</ref>ומתרחק מחשבונו כמרחק השבר אשר נערוך בו | ||
| + | |- | ||
| + | !<span style=color:green>Multiplication table of sexagesimal fractions</span> | ||
| + | | | ||
| + | |- | ||
| + | |To make it easier for the reader, I have drawn a table in order to understand the product of fractions by fractions. | ||
| + | |style="text-align:right;"|ולהקל על הקורא ציירתי לוח להבין העולה משברים על שברים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | |||
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
| + | |- | ||
| + | | חמשיים || רביעיים || שלישיים || שניים || ראשונים || מעלות || <sub>רוחב</sub>/<sup>אורך</sup> | ||
|- | |- | ||
| חמשיים || רביעיים || שלישיים || שניים || ראשונים || מעלות || מעלות | | חמשיים || רביעיים || שלישיים || שניים || ראשונים || מעלות || מעלות | ||
| Line 485: | Line 3,048: | ||
|- | |- | ||
|} | |} | ||
| − | + | |- | |
| − | + | | colspan="2"| | |
| − | + | {|class="wikitable" style="color: blue; margin-left: auto; margin-right: auto; border: none; text-align:center;" | |
| − | + | |- | |
| − | + | | fifths || fourths || thirds || seconds || minutes || degrees|| <sup>length</sup>/<sub>width</sub> | |
| − | + | |- | |
| − | + | | fifths || fourths || thirds || seconds || minutes || degrees || degrees | |
| − | + | |- | |
| − | + | | sixths || fifths || fourths || thirds || seconds || minutes || minutes | |
| − | + | |- | |
| − | + | | sevenths || sixths || fifths || fourths || thirds || seconds || seconds | |
| − | + | |- | |
| − | + | | eighths || sevenths || sixths || fifths || fourths || thirds || thirds | |
| − | + | |- | |
| − | + | | ninths || eighths || sevenths || sixths || fourths || fourths || fourths | |
| − | + | |- | |
| + | | tenths|| ninths || eighths || sevenths || sixths || fifths || fifths | ||
| + | |- | ||
| + | |} | ||
| − | + | |- | |
| − | + | |<span style=color:green>'''Instructions for using the multiplication table:'''</span> when you wish to know the product of one of the types of the fractions that are written in the lines breadthwise [and lengthwise], look at where the two lines meet and this is where the product of both is. | |
| − | + | |style="width: 50%; text-align:right;"|וכאשר תרצה לדעת העולה מאחד ממיני השברים שהם כתובים בטור הרוחב הסתכל במקום אשר ייפגשו שני הטורים זה בזה ושם העולה משניהם | |
| − | + | |- | |
| − | + | |When you multiply fractions by fractions: | |
| − | + | |style="text-align:right;"|וכאשר תערוך שברים על שברים | |
| − | + | |- | |
| − | + | | | |
| − | + | *If the result is less than sixty, you keep it and count it as belonging to the species that resulting from that product. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{ab<60\longrightarrow\frac{a}{60^n}\sdot\frac{b}{60^m}=\frac{a\sdot b}{60^{n+m}}}}</math> | |
| − | + | |style="text-align:right;"|אם יהיה העולה פחות מששים אתה מחזיק בו ומונה אותו מאותו המין היוצא מהערך ההוא | |
| − | + | |- | |
| − | + | | | |
| − | + | *But, if it exceeds sixty, you divide it by sixty and the result of the division belongs to the species, which is higher than the species you divided. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{ab>60\longrightarrow\frac{a}{60^n}\sdot\frac{b}{60^m}=\frac{\frac{a\sdot b}{60}}{60^{n+m-1}}}}</math> | |
| − | + | |style="text-align:right;"|ואם יהיה {{#annot:term|1206,420|8f0E}}מוסיף על{{#annotend:8f0E}} ששים אתה מחלק אותו על ששים והיוצא בחלוק הוא מן המין אשר למעלה מאותו המין אשר חלקת אותו | |
| − | + | |- | |
| − | + | | | |
| − | + | :*As if you multiply 50 seconds by 50 seconds. | |
| − | + | :<math>\scriptstyle50^{\prime\prime}\times50^{\prime\prime}</math> | |
| − | + | |style="text-align:right;"|כאלו היית עורך נ' שניים בנ' שניים | |
| − | + | |- | |
| − | ואם | + | | |
| − | + | ::The result is two thousand and 500 fourths. Divide them by sixty. The result of division is 41, which are thirds, and 40 fourths remain, which can not be divided. | |
| − | + | ::<math>\scriptstyle{\color{blue}{50^{\prime\prime}\times50^{\prime\prime}=2500^{iv}=\frac{2500^{\prime\prime\prime}}{60}=41^{\prime\prime\prime}+40^{iv}}}</math> | |
| − | + | |style="text-align:right;"|יהיה העולה אלפים ות'ק' מאות רביעיים<br> | |
| − | + | חלקם על ששים יצא בחלוק מ"א והם שלישים ונשארו מ' רביעיים שלא נתחלקו | |
| − | + | |- | |
| − | + | |According to this way for all fractions. | |
| − | + | |style="text-align:right;"|ועל זה הדרך לכל השברים | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ועל זה הדרך | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==< | + | ==== <span style=color:green>Simple Fractions</span> ==== |
| − | + | | | |
| − | ===< | + | |- |
| − | + | |If you divide the fractions of the geometricians one by another. | |
| − | + | |style="text-align:right;"|ואם שברי חכמי המדות תערוך <sup>זה</sup> על זה | |
| − | כגון | + | |- |
| − | + | | | |
| − | + | ===== <span style=color:green>Fraction by Fraction</span> ===== | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | *{{#annot:⅔×⅖|17|Tlt0}}Such as two thirds by two fifths. | |
| − | + | :<math>\scriptstyle\frac{2}{3}\times\frac{2}{5}</math> | |
| − | + | |style="text-align:right;"|כגון שני שלישיים על שני חמישיים{{#annotend:Tlt0}} | |
| − | + | |- | |
| − | + | |This is the sign that you keep the names of the fractions: | |
| + | |style="text-align:right;"|זה לך האות שתשמור שמות השברים | ||
| + | |- | ||
| + | | | ||
| + | ::Know that the thirds are derived from three and the fifths from five. | ||
| + | |style="text-align:right;"|ודע כי השלישים הם חצובים משלשה והחמישיים מהחמשה | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''common denominator:'''</span> Multiply 3 by five, they are 15 and it is the denominator <math>\scriptstyle{\color{blue}{3\sdot5=15}}</math> | ||
| + | |style="text-align:right;"|וערוך ג' על חמשה והם ט"ו והוא המורה | ||
| + | |- | ||
| + | | | ||
| + | :*Then multiply two by two, they are four <math>\scriptstyle{\color{blue}{2\sdot2=4}}</math> | ||
| + | |style="text-align:right;"|ואחר כן תערוך שנים על שנים והם ארבעה | ||
|- | |- | ||
| − | | | + | | |
| + | :*As the ratio of four to 15 so is the ratio of this number to one, which is a fifth and a third of a fifth. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{2}{3}\times\frac{2}{5}=4:15=\frac{1}{5}+\left(\frac{1}{3}\sdot\frac{1}{5}\right)}}</math> | ||
| + | |style="text-align:right;"|וכערך ארבעה מט"ו כן ערך חשבון זה מאחד והוא חמישית ושליש חמישית | ||
|- | |- | ||
| − | | | + | |The reason is that saying a third by a fifth is as saying a third of a fifth, which is one part of 15. |
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{3}\times\frac{1}{5}=\frac{1}{3}\sdot\frac{1}{5}=\frac{1}{15}}}</math> | ||
| + | |style="text-align:right;"|והטעם כי האומר שלישי על חמישי דומה כמי שאומר שלישית מחמישית שהוא חלק אחד מט"ו | ||
|- | |- | ||
| − | | | + | |Or it is as saying a third lengthwise by a fifth breadthwise and it is clear that it is one part of 15. |
| + | |style="text-align:right;"|או דומה כמי שאומר שלישי באורך על חמישי ברוחב וידוע וברור שהוא חלק אחד מט"ו | ||
|- | |- | ||
| − | | | + | | |
| + | |||
| + | ===== <span style=color:green>Fraction by fraction of fraction</span> ===== | ||
| + | |||
| + | *{{#annot:⅖×⅒×⅔|17|j0VS}}If you multiply 2 parts of five by a tenth by 2 thirds. | ||
| + | :<math>\scriptstyle\frac{2}{5}\times\frac{1}{10}\times\frac{2}{3}</math> | ||
| + | |style="width: 50%; text-align:right;"|ואם תערוך ב' חלקים מחמשה בעשירית האחד בב' שלישי אחד{{#annotend:j0VS}} | ||
|- | |- | ||
| − | | | + | | |
| + | :*Know that the name of one part is fifty, as the number of five by ten. | ||
| + | ::<math>\scriptstyle{\color{blue}{5\sdot10=50}}</math> | ||
| + | |style="text-align:right;"|דע כי שם החלק האחד הוא חמשים כמספר חמשה בעשרה | ||
|- | |- | ||
| − | | | + | | |
| + | :*Multiply the 50 by 3, which is the name of the other part; the result is 150 and it is the denominator. | ||
| + | ::<math>\scriptstyle{\color{blue}{50\sdot3=150}}</math> | ||
| + | |style="text-align:right;"|ותערוך הנ' בג' שהוא שם החלק השני ויעלה ק"נ והוא המורה | ||
|- | |- | ||
| − | | | + | | |
| + | :As the ratio of 4, which is the [common numerator of] both numbers, to 150 so is its ratio to one and it is two-thirds of one-fifth of one-fifth. | ||
| + | :<math>\scriptstyle{\color{blue}{\left(\frac{2}{5}\times\frac{1}{10}\right)\times\frac{2}{3}=\left(2\sdot2\right):150=4:150=\frac{2}{3}\sdot\frac{1}{5}\sdot\frac{1}{5}}}</math> | ||
| + | |style="text-align:right;"|וכערך ד' שהם שני החשבונות מן ק"נ כן ערך ערכו מן האחד והוא שני שלישי ‫<ref>14r</ref>חמישית החמישית | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Fraction of integer and fraction by fraction of integer</span> ===== | ||
| + | |||
| + | *{{#annot:(¾·(3+⅓))×(⁶/₇·5)|17|Na7V}}If you multiply three-quarters of three and one-third by six-sevenths of five. | ||
| + | :<math>\scriptstyle\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)</math> | ||
| + | |style="width: 50%; text-align:right;"|ואם תערוך שלשה רביעיות [ש]ל שלשה ושליש על ששה שביעיות חמשה{{#annotend:Na7V}} | ||
| + | |- | ||
| + | | | ||
| + | :*Know from which number the quarter is derived - it is from four. | ||
| + | |style="text-align:right;"|דע מאיזה מספר יצא הרביע והוא מארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::*Take its three-quarters, they are three. Multiply them by three and one-third; the result is ten, keep it. | ||
| + | :::<math>\scriptstyle{\color{blue}{\left(\frac{3}{4}\sdot4\right)\sdot\left(3+\frac{1}{3}\right)=3\sdot\left(3+\frac{1}{3}\right)=10}}</math> | ||
| + | |style="text-align:right;"|קח שלשת רביעיותיו יהיו שלשה<br> | ||
| + | ערכם בשלשה ושליש יעלה עשרה ושמרם | ||
| + | |- | ||
| + | | | ||
| + | ::*Then, take six-sevenths of five, it is four and 2-sevenths. | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{6}{7}\sdot5=4+\frac{2}{7}}}</math> | ||
| + | |style="text-align:right;"|ואחר כך תקח ששה שביעיות חמשה והוא ארבעה וב' שביעיות | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them by the reserved; the result is 42 and six-sevenths. | ||
| + | ::<math>\scriptstyle{\color{blue}{10\sdot\left(4+\frac{2}{7}\right)=42+\frac{6}{7}}}</math> | ||
| + | |style="text-align:right;"|ערכם על השמור יעלה מ"ב וששה שביעיות | ||
| + | |- | ||
| + | | | ||
| + | ::Divide them by four; the result of the division is ten integers and 5-sevenths. | ||
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)=\frac{42+\frac{6}{7}}{4}=10+\frac{5}{7}}}</math> | ||
| + | |style="text-align:right;"|תחלקם על ארבעה יצא בחלוק עשרה שלמים וה' שביעיות | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by knowing from which number the seventh is derived - it is from seven. | ||
| + | |style="text-align:right;"|ותדענו דע מאיזה מספר הוא השביעית והוא משבעה | ||
| + | |- | ||
| + | | | ||
| + | ::*Take its six-sevenths and multiply them by five; the result is thirty, keep them. | ||
| + | :::<math>\scriptstyle{\color{blue}{\left(\frac{6}{7}\sdot7\right)\sdot5=30}}</math> | ||
| + | |style="text-align:right;"|קח ששה שביעיותיו ותערכם בחמשה יעלה שלשים ושמרם | ||
| + | |- | ||
| + | | | ||
| + | ::*Then, take three-quarters of three and one-third, it is two and a half. | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)=2+\frac{1}{2}}}</math> | ||
| + | |style="text-align:right;"|ואחר כך תקח שלשה רביעיות משלשה ושליש והוא שנים וחצי | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them by the reserved, which are 30; the result is 75. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(2+\frac{1}{2}\right)\sdot30=75}}</math> | ||
| + | |style="text-align:right;"|ערכם על השמור שהם ל' יעלה ע"ה | ||
| + | |- | ||
| + | | | ||
| + | ::Divide them by 7; the result of the division is ten and five-sevenths. | ||
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)= | ||
| + | \frac{75}{7}=10+\frac{5}{7}}}</math> | ||
| + | |style="text-align:right;"|חלקם על ז' יצא בחלוק עשרה וחמשה שביעיות | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by multiplying two and a half, which is the first number, by four and 2-sevenths, which is the [second] number; the result is ten and 5-sevenths. | ||
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)=\left(2+\frac{1}{2}\right)\sdot\left(4+\frac{2}{7}\right)=10+\frac{5}{7}}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתערוך שנים וחצי שהוא החשבון האחד על ארבעה וב' שביעיות שהוא החשבון יעלה עשרה ‫<ref>14v</ref>וה' שביעיות | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Fraction of integer and fraction by fraction of integer and fraction</span> ===== | ||
| + | |||
| + | *{{#annot:(⅞·(5+⅓))×(⅗·(6+¼))|17|tInL}}If you multiply seven eighths of 5 and a third by 3 fifths of 6 and a quarter. | ||
| + | :<math>\scriptstyle\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]</math> | ||
| + | |style="width: 50%; text-align:right;"|ואם תערוך שבעה שמיניות של ה' ושליש בג' חמישיות של ו' ורובע{{#annotend:tInL}} | ||
| + | |- | ||
| + | | | ||
| + | :*Know by which number the eighth is [denominated], it is eight. Take 7 eighths from eight, it is 7. Multiply it by 5 and one-third; the result is 37 and one-third. Keep them. | ||
| + | ::<math>\scriptstyle{\color{blue}{8\sdot\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)=7\sdot\left(5+\frac{1}{3}\right)=37+\frac{1}{3}}}</math> | ||
| + | |style="text-align:right;"|דע מאיזה מספר השמינית והוא משמנה<br> | ||
| + | קח ז' שמיניות והוא ז‫'<br> | ||
| + | ערכם בה' ושליש יעלה ל"ז ושליש ושמרם | ||
| + | |- | ||
| + | | | ||
| + | ::Know by which number the fifth is [denominated], it is five. Take its 3 fifths, they are 3. Multiply them by six and one-quarter; the result is [18] and 3 quarters. | ||
| + | ::<math>\scriptstyle{\color{blue}{5\sdot\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)=3\sdot\left(6+\frac{1}{4}\right)=18+\frac{3}{4}}}</math> | ||
| + | |style="text-align:right;"|ואחר כך דע מאיזה מספר החומש והוא מחמשה<br> | ||
| + | קח ג' חמישיותיו והם ג‫'<br> | ||
| + | ערכם בששה ורביע יעלה [י"ח] וג' רביעיות | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them by the reserved, the result is 139 and 4 quarters. Divide them by eight and the result of the division is seventeen and a half. | ||
| + | |style="text-align:right;"|תערכם על השמור יעלה קל"ט וד' רביעיות<br> | ||
| + | תחלקם על שמונה יצא בחלוק שבעה עשר וחצי | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=\frac{37+\frac{1}{3}}{8}\sdot\frac{18+\frac{3}{4}}{5}=\frac{139+\frac{4}{4}}{8}=17+\frac{1}{2}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*Or, if you wish, divide the reserved, which is 37 and one-third, by eight. Multiply the result, which is 4 and 2 thirds, by 18 and three-quarters. Divide the result, which is 87 and a half, by five and the result is 17 and a half. | ||
| + | |style="text-align:right;"|או אם תרצה תחלק השמור שהוא ל"ז ושליש על שמונה והעולה שהוא ד' וב' שלישים תערוך על י"ח ושלשה רביעיות והעולה שהוא פ"ז וחצי תחלק על חמשה יצא י"ז וחצי | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=\frac{37+\frac{1}{3}}{8}\sdot\frac{18+\frac{3}{4}}{5}=\frac{\left(4+\frac{2}{3}\right)\sdot\left(18+\frac{3}{4}\right)}{5}=\frac{87+\frac{1}{2}}{5}=17+\frac{1}{2}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by converting the five and one-third to thirds; they are 16 thirds. Take their 7 eighths; the result is 14. Keep it. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)=\frac{7}{8}\sdot\frac{16}{3}=\frac{14}{3}}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתשיב החמשה ושליש כלם שלישים יהיו י"ו שלישים<br> | ||
| + | קח ז' שמיניותיו והעולה שהוא י"ד ושמרם | ||
| + | |- | ||
| + | | | ||
| + | ::Return to the six and one-quarter and convert them to quarters; they are 25. Take their three fifths. Divide the result, which is 15, by four. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)=\frac{3}{5}\sdot\frac{25}{4}=\frac{15}{4}}}</math> | ||
| + | |style="text-align:right;"|ושוב אל הששה ורביע תשיבם כלם רביעיות ויהיו כ"ה<br> | ||
| + | קח שלשת חמישיותיו והעולה שהוא ט"ו תחלק על ארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply the result of the division, which is three and three-quarters, by the reserved, then divide the result by three; the result is 17 and a half. | ||
| + | |style="text-align:right;"|והיוצא בחלוק שהוא שלשה ושלשה רביעיות תערכם על השמור והעולה תחלק על שלשה יצא י"ז וחצי | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=\frac{14}{3}\sdot\frac{15}{4}=\frac{14\sdot\left(3+\frac{3}{4}\right)}{3}=17+\frac{1}{2}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*Or, if you wish, divide the resereved, which is 14, by three. Multiply the result, which is 4 and two-thirds, by 15. Divide the result, which is 70, by 4 and the result is 17 and a half. | ||
| + | |style="text-align:right;"|או אם תרצה תחלק השמור שהם י"ד על שלשה והיוצא שהוא ארבעה ושני שלישיים תערוך בט"ו והעולה שהוא ע' תחלק על ד' יצא י"ז וחצי | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=\frac{14}{3}\sdot\frac{15}{4}=\frac{\left(4+\frac{2}{3}\right)\sdot15}{4}=\frac{70}{4}=17+\frac{1}{2}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Fraction of fraction by fraction of fraction</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:(¾·⅗)×(⅚·³/₇)|17|ySC3}}If you multiply 3 quarters of 3 fifths by 5 sixths of 3 sevenths. | ||
| + | :<math>\scriptstyle\left(\frac{3}{4}\sdot\frac{3}{5}\right)\times\left(\frac{5}{6}\sdot\frac{3}{7}\right)</math> | ||
| + | |style="width: 50%; text-align:right;"|ואם תערוך ג' רביעיות של ג' חומשין בה' שתותין של ג' רביעיות{{#annotend:ySC3}} | ||
| + | |- | ||
| + | | | ||
| + | :*Know from which number the quarter and the fifth are derived, it is twenty. Its 3 fifths are 12. Take its three-quarters, which is 9, they are 2 fifths and one-quarter of one-fifth. Keep them. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{4}\sdot\frac{3}{5}=\frac{\frac{3}{4}\sdot\frac{3}{5}\sdot20}{20}=\frac{\frac{3}{4}\sdot12}{20}=\frac{9}{20}=\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)}}</math> | ||
| + | |style="text-align:right;"|דע מאיזה מספר הרובע והחומש והוא מעשרים<br> | ||
| + | וג' חומשיו הוא י"ב<br> | ||
| + | קח שלשה רביעיותיו והוא ט' שהם ב' חמישיות ורביעית חמישית ושמרם | ||
| + | |- | ||
| + | | | ||
| + | ::Then, take the second number and know from which number the sixth and the seventh are derived, it is 42. When you take its five-sixths of three-sevenths the result is 15, which are two-sevenths and one-half of one-seventh. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{5}{6}\sdot\frac{3}{7}=\frac{\frac{5}{6}\sdot\frac{3}{7}\sdot42}{42}=\frac{15}{42}=\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)}}</math> | ||
| + | |style="text-align:right;"|ואחר תקח החשבון השני ודע מאיזה מספר השתות והשביעית והוא מ"ב<br> | ||
| + | וכאשר תקח חמשה שתותין של שלשה שביעיות יעלה ט"ו שהם שתי שביעיות וחצי שביעית | ||
| + | |- | ||
| + | | | ||
| + | ::When you multiply the reserved 2 fifths and one-quarter of one-fifth by two-sevenths and one-half of one-seventh, look for a number that has a quarter, a fifth and a seventh; it is 140 and this is the denominator. You get from the multiplication of the one by the other 22 and a half, which are parts of the denominator, and they are one-seventh and one-eighth of one-seventh. | ||
| + | |style="text-align:right;"|וכאשר תערוך הב' חמישיות ורביעית חמישית השמורים על שתי שביעיות וחצי שביעית בקש לך חשבון שיהיה לו רביעית וחמישית ושביעית והוא ק"מ והוא המורה<br> | ||
| + | ועלה בידך ממערכת זה על זה כ"ב וחצי והם חלקים מהמורה והם שביעית ושמינית שביעית | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}\sdot\frac{3}{5}\right)\times\left(\frac{5}{6}\sdot\frac{3}{7}\right)&\scriptstyle=\left[\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]=\frac{140\sdot\left[\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]}{140}\\&\scriptstyle=\frac{22+\frac{1}{2}}{140}=\frac{1}{7}+\left(\frac{1}{8}\sdot\frac{1}{7}\right)\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by knowing the three-quarters of three fifths, which are 9, as said. Then take five-sixths of three-sevenths, which are two-sevenths and one-half of one-seventh. Take the ratio of two-sevenths and one-half of one-seventh from the nine; the result is three and one-seventh and one-half of one-seventh. Take the ratio of the result from the twenty, from which the quarter and the fifth are derived, and so is the ratio of the number to the one, which is one-seventh and one-eighth of one-seventh. | ||
| + | |style="text-align:right;"|ותדענו שתדע השלשה ‫<ref>15r</ref>רביעיות של שלשה חומשין שהוא ט' כאשר אמרנו<br> | ||
| + | ואחר כך תקח חמשה שתותין של שלשה שביעיות שהם שני שביעיות וחצי שביעית ותקח מן התשעה כערכם שתי שביעיות וחצי שביעית יעלה שלשה ושביעית וחצי שביעית<br> | ||
| + | וכערך העולה קח מן העשרים אשר יצאו הרביע והחומש ממנו וכן החשבון מן האחד והוא שביעית ושמינית שביעית | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(\frac{3}{4}\sdot\frac{3}{5}\right)\times\left(\frac{5}{6}\sdot\frac{3}{7}\right)=\frac{9}{20}\sdot\left[\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]=\frac{9\sdot\left[\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]}{20}=\frac{3+\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)}{20}=\frac{1}{7}+\left(\frac{1}{8}\sdot\frac{1}{7}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:(⅖·⅒)×(²/₈·⅓)|17|bfok}}If you multiply two parts of a five by one-tenth by two parts of an eight by one-third. | ||
| + | :<math>\scriptstyle\left(\frac{2}{5}\sdot\frac{1}{10}\right)\times\left(\frac{2}{8}\sdot\frac{1}{3}\right)</math> | ||
| + | |style="text-align:right;"|ואם תערוך שני חלקים מחמשה בעשירית האחד בשני חלקים משמונה בשלישית האחד{{#annotend:bfok}} | ||
| + | |- | ||
| + | | | ||
| + | :*know the names of the parts of the second number, which are eight and three. Multiply them by each other, the result is 24. | ||
| + | ::*<math>\scriptstyle{\color{blue}{8\sdot3=24}}</math> | ||
| + | |style="text-align:right;"|דע שמות החלקים חלקי החשבון השני והם שמונה ושלשה<br> | ||
| + | ערכם <sup>זה</sup> בזה יעלה כ"ד | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply 50 by 24, the result is one thousand and two hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{50\sdot24=1200}}</math> | ||
| + | |style="text-align:right;"|ותערוך נ' בכ"ד ויעלה אלף ומאתים | ||
| + | |- | ||
| + | | | ||
| + | ::As the ratio of the numerators of both numbers, which are two by two, to one thousand and two hundred, so is their ratio to one, which is one part of three hundred. | ||
| + | :<math>\scriptstyle{\color{blue}{\left(\frac{2}{5}\sdot\frac{1}{10}\right)\times\left(\frac{2}{8}\sdot\frac{1}{3}\right)=\left(2\sdot2\right):1200=\frac{1}{300}}}</math> | ||
| + | |style="text-align:right;"|וכערך שמות שני החשבונות שהם שנים שנים מן אלף ומאתים כן ערכם מן האחד והוא חלק אחד משלש מאות | ||
| + | |- | ||
| + | | | ||
| + | :*Know it by taking from the 50 two parts a five of one-tenth, which are two, and it is one-fifth of one-fifth by one-quarter of one-third. It is the same as to say one-fifth of one-fifth from one-quarter of one-third. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{2}{5\sdot10}\sdot\frac{2}{8\sdot3}=\left(\frac{1}{5}\sdot\frac{1}{5}\right)\sdot\left(\frac{1}{4}\sdot\frac{1}{3}\right)}}</math> | ||
| + | |style="text-align:right;"|ותדענו שתקח מן הנ' שני חלקים מחמשה בעשירית והם שנים והוא חומש החומש על רביעית השליש הוא כמי שיאמר חומש החומש מרביעית השליש | ||
| + | |- | ||
| + | | | ||
| + | ::Now, look for a number that has a third, a quarter, a fifth, and one-fifth of one-fifth. It is 300. | ||
| + | |style="text-align:right;"|ועתה בקש חשבון שליש ורביע וחומש וחומש החומש והוא שלש מאות | ||
| + | |- | ||
| + | | | ||
| + | ::Take its third, which is 100. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{3}\sdot300=100}}</math> | ||
| + | |style="text-align:right;"|קח שלישיתו והוא ק‫' | ||
| + | |- | ||
| + | | | ||
| + | ::From the 100 [take] its quarter, it is 25. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{4}\sdot100=25}}</math> | ||
| + | |style="text-align:right;"|ומן הק' רביעיתו והוא כ"ה | ||
| + | |- | ||
| + | | | ||
| + | ::From 25 [take] its fifth, it is 5. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot25=5}}</math> | ||
| + | |style="text-align:right;"|ומן כ"ה חמישיתו והוא ה‫' | ||
| + | |- | ||
| + | | | ||
| + | ::From 5 [take] its fifth, it is one. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot5=1}}</math> | ||
| + | |style="text-align:right;"|ומן ה' חמישיתו והוא אחד | ||
| + | |- | ||
| + | | | ||
| + | ::It has been found that [the answer] is one part of three hundred. | ||
| + | :<math>\scriptstyle{\color{blue}{\left(\frac{2}{5}\sdot\frac{1}{10}\right)\times\left(\frac{2}{8}\sdot\frac{1}{3}\right)=\frac{1}{300}}}</math> | ||
| + | |style="text-align:right;"|ונתברר שהוא חלק אחד משלש מאות | ||
| + | |- | ||
| + | |From these examples and ways you can understand the fractions of fractions and all of them are present for the one who understands. | ||
| + | |style="text-align:right;"|ומן הדמיונות והדרכים האלה תוכל להבין בשברי השברים וכולם נכוחים למבין | ||
|- | |- | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | {| |
| − | + | |- | |
| − | === | + | | |
| − | + | ||
| − | + | == Chapter Four: Division == | |
| − | + | !style="width:45%; text-align:right;"|<big>השער</big> הרביעי ב{{#annot:term|1370,157|J9rH}}מחלוקת{{#annotend:J9rH}} | |
| − | + | |- | |
| − | + | |It is divided into three categories: | |
| − | + | |style="text-align:right;"|והוא נחלק לשלשה ענינים | |
| − | + | |- | |
| − | + | | | |
| − | + | === <span style=color:green>[The First Category]:</span> Division of Integers by Integers === | |
| − | + | !style="text-align:right;"|{{#annot:term|1221,157|PV7k}}חלוקת{{#annotend:PV7k}} שלמים על שלמים | |
| − | + | |- | |
| − | + | | | |
| − | + | ==== <span style=color:green>Sexagesimal Fractions</span> ==== | |
| − | + | | | |
| − | + | |- | |
| − | + | |If you wish to divide degrees by degrees according to the calculation of the astrologers: | |
| − | + | |style="text-align:right;"|אם תרצה לחלק מעלות על מעלות לחשבון חכמי המזלות | |
| − | + | |- | |
| − | + | | | |
| − | + | *<span style=color:green>'''greater by smaller:'''</span> If you divide a greater number by a smaller [number], the result of division are degrees. | |
| − | + | |style="text-align:right;"|אם תחלק חשבון רב על מעט יהיה היוצא בחלוק מעלות | |
| − | + | |- | |
| − | + | | | |
| − | + | :*If there is a remainder that cannot be divided, multiply the remainder by sixty - they are minutes; then it is divided by the [original divisor] and the result of division are minutes. | |
| − | + | ::<math>\scriptstyle{\color{OliveGreen}{a>b\longrightarrow a\div b=n+\frac{r_1\sdot60}{60}}}</math> | |
| − | + | |style="text-align:right;"|ואם ישאר שלא יתחלק ערוך הנשאר על ששים יהיו ראשונים ו{{#annot:term|2187,1225|W47r}}יתחלק{{#annotend:W47r}} על מה שחלקת בראשונה והיוצא בחלוק הם ראשונים | |
| − | + | |- | |
| − | + | | | |
| − | + | :*If there is still a remainder that cannot be divided, multiply it by sixty, then divide by the [original divisor] and the result are seconds. | |
| − | + | ::<math>\scriptstyle{\color{OliveGreen}{a>b\longrightarrow a\div b=n+\frac{r_1\sdot60}{60}+\frac{r_2\sdot60}{60^2}}}</math> | |
| − | + | |style="text-align:right;"|ואם ישאר שלא יתחלק תערכם על ששים ותחלק על מה שחלקת והיוצא הם שנים | |
| − | + | |- | |
| − | + | | | |
| − | + | ::And so on, as much as you wish. | |
| − | + | |style="text-align:right;"|וכן עד כמה שתרצה | |
| − | + | |- | |
| − | + | | | |
| − | + | *<span style=color:green>'''smaller by greater:'''</span> If you wish to divide a smaller number by a greater [number], multiply the smaller [number] by sixty - they are minutes; then, divide [by the greater number] and the result of division are minutes. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{a<b\longrightarrow a\div b=\frac{\frac{a\sdot60}{b}}{60}}}</math> | |
| − | + | |style="text-align:right;"|ואם רצית לחלק חשבון מועט על רב תערוך המועט על ששים יהיו ראשונים ואחר כן ‫<ref>15v</ref>תחלוק והיוצא בחלוק הם ראשונים | |
| − | + | |- | |
| − | + | | | |
| − | + | :*If there is a remainder that cannot be divided, multiply it by sixty, then divide by the [original divisor] and the result are seconds. | |
| − | + | |style="text-align:right;"|ואם ישאר שלא יחלק ערכם על ששים ותחלק על מה שחלקת יהיה היוצא שניים | |
| − | + | |- | |
| − | + | | | |
| − | + | ::And so on for thirds, fourths and to infinity. | |
| − | + | |style="text-align:right;"|וכן לשלישיים ולרביעיים עד אין קץ | |
| − | ואם | + | |- |
| − | + | | | |
| − | + | ||
| − | + | ==== <span style=color:Green>Simple Fractions</span> ==== | |
| − | + | | | |
| − | + | |- | |
| − | + | |If according to the calculation of the geometricians. | |
| − | + | |style="text-align:right;"|ואם לחשבון חכמי המדות | |
| − | + | |- | |
| − | + | | | |
| − | + | *<span style=color:Green>'''greater by smaller:'''</span> If you wish to divide a greater number by a smaller [number]. | |
| − | + | |style="text-align:right;"|תרצה לחלק חשבון רב על מועט | |
| − | + | |- | |
| − | + | | | |
| − | + | :*{{#annot:100÷15|157|SXQ5}}Such as when you wish to divide one-hundred by 15. | |
| − | + | ::<math>\scriptstyle100\div15</math> | |
| − | + | |style="text-align:right;"|כגון שתרצה לחלק מאה על ט"ו{{#annotend:SXQ5}} | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Look for a number that counts both, it is five. Take a fifth of one-hundred, it is 20. Divide by a fifth of 15, which is 3; the result of the division is six and two-thirds and so is [the quotient of] 100 by 15. | |
| − | + | ::<math>\scriptstyle{\color{blue}{100\div15=\frac{\frac{1}{5}\sdot100}{\frac{1}{5}\sdot15}=\frac{20}{3}=6+\frac{2}{3}}}</math> | |
| − | + | |style="text-align:right;"|בקש חשבון שהיה מונה לשניהם והוא חמשה<br> | |
| − | | | + | קח חמישית מאה והוא כ' וחלק על חמישית ט"ו והוא ג' יצא בחלוק ששה ושני שלישיות וככה מק' על ט"ו |
| + | |- | ||
| + | | | ||
| + | :*{{#annot:1000÷72|157|WAFS}}If you divide one-thousand by seventy-two. | ||
| + | ::<math>\scriptstyle1000\div72</math> | ||
| + | |style="text-align:right;"|ואם תחלק אלף על שנים ושבעים{{#annotend:WAFS}} | ||
| + | |- | ||
| + | | | ||
| + | ::The number that counts both is eight. One-eighth of 72 is nine and one-eighth of one-thousand is 125. Divide the greater by the smaller; the result of the division is 14 minus one-ninth and so is [the quotient of] one-thousand by 72. | ||
| + | ::<math>\scriptstyle{\color{blue}{1000\div72=\frac{\frac{1}{8}\sdot1000}{\frac{1}{8}\sdot72}=\frac{125}{9}=14-\frac{1}{9}}}</math> | ||
| + | |style="text-align:right;"|החשבון שמונה לשניהם הוא שמונה ושמינית ע"ב תשעה ושמינית אלף קכ"ה<br> | ||
| + | חלק המרובה על המועט יצא בחלוק י"ד פחות תשיעית וככה מאלף על ע"ב | ||
| + | |- | ||
| + | | | ||
| + | :If you cannot find a number that counts the two numbers: | ||
| + | |style="text-align:right;"|ואם יהיו שני החשבונות שלא תמצא להם חשבון שמונה לשניהם | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:40÷7|157|LN7a}}Such as when you wish to divide 40 by 7. | ||
| + | ::<math>\scriptstyle40\div7</math> | ||
| + | |style="text-align:right;"|כגון שתרצה לחלק מ' על ז‫'{{#annotend:LN7a}} | ||
| + | |- | ||
| + | | | ||
| + | ::The result of the division is 5 and you are left with 5. Make sevenths from them, so the result of the division is 5 integers and 5-sevenths. | ||
| + | ::<math>\scriptstyle{\color{blue}{40\div7=5+\frac{5}{7}}}</math> | ||
| + | |style="text-align:right;"|יצא בחלוק ה' וישארו לך ה‫'<br> | ||
| + | עשה מהם שביעיות יצא בחלוק ה' שלמים וה' שביעיות | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:Green>'''smaller by greater:'''</span> If you divide a smaller [number] by a greater [number]. | ||
| + | |style="text-align:right;"|ואם מספר מועט תחלק על רב | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:15÷100|157|S5mt}}Such as 15 by 100. | ||
| + | ::<math>\scriptstyle15\div100</math> | ||
| + | |style="text-align:right;"|כמו ט"ו על ק‫'{{#annotend:S5mt}} | ||
| + | |- | ||
| + | | | ||
| + | :This category is derived from the ratios: | ||
| + | |style="text-align:right;"|זה הענין יצא מהערכים | ||
| + | |- | ||
| + | | | ||
| + | ::You already know that the five counts both: 3 times for 15 and [20] times for 100. Hence, as the ratio of 3 to 20, which is one-tenth and one-half of one-tenth, so is the ratio of 15 to one-hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{15\div100=\frac{\frac{1}{5}\sdot15}{\frac{1}{5}\sdot100}=\frac{3}{20}=\frac{1}{10}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}}</math> | ||
| + | |style="text-align:right;"|וכבר ידעת כי החמשה מונה לשניהם למספר ט"ו ג' פעם ולמספר ק' פעם וכערך ג' אל כ' שהוא עשור וחצי עשור כך ערך ט"ו אל מאה | ||
| + | |- | ||
| + | | | ||
| + | :If you cannot find a number that counts both: | ||
| + | |style="text-align:right;"|ואם לא תמצא מספר שיהיה מונה לשניהם | ||
| + | |- | ||
| + | | | ||
| + | :*{{#annot:7÷40|157|zZxW}}Such as 7 by 40. | ||
| + | ::<math>\scriptstyle7\div40</math> | ||
| + | |style="text-align:right;"|כגון ז' על מ‫'{{#annotend:zZxW}} | ||
| + | |- | ||
| + | | | ||
| + | :Take one part of the greater number, then take its ratio from the smaller [number]. | ||
| + | |style="text-align:right;"|קח חלק אחד מהמספר הרב ותערוך המועט אליו | ||
| + | |- | ||
| + | | | ||
| + | ::In this example, take one-tenth of the 40, which is 4; or its fifth, which is 8; or its eighth, which is 5. | ||
| + | |style="text-align:right;"|ובדמיון זה תקח עשור המ' והוא ד' או חמישיתו והוא ח' או שמיניתו והוא ה‫' | ||
| + | |- | ||
| + | | | ||
| + | ::If you took its tenth, when you take its ratio from the 7, you find in it two-tenths minus one-quarter of one-tenth. Hence, each part of the 40 is two-tenths minus one-quarter of one-tenth. | ||
| + | ::<math>\scriptstyle{\color{blue}{7\div40=\frac{7}{\frac{1}{10}\sdot40}\sdot\frac{1}{10}=\frac{7}{4}\sdot\frac{1}{10}=\frac{2}{10}-\left(\frac{1}{4}\sdot\frac{1}{10}\right)}}</math> | ||
| + | |style="text-align:right;"|אם עשיריתו לקחת כאשר תערוך הז' אליו תמצא בו שנים עשיריות פחות רביע העשור וכן יגיע לכל אחד מן המ' שני עשיריות אחד פחות רביע העשור | ||
| + | |- | ||
| + | | | ||
| + | ::Or one-fifth minus one-eighth of one-fifth. | ||
| + | ::<math>\scriptstyle{\color{blue}{7\div40=\frac{7}{\frac{1}{5}\sdot40}\sdot\frac{1}{5}=\frac{7}{8}\sdot\frac{1}{5}=\frac{1}{5}-\left(\frac{1}{8}\sdot\frac{1}{5}\right)}}</math> | ||
| + | |style="text-align:right;"|או חומש פחות שמינית החומש | ||
| + | |- | ||
| + | | | ||
| + | ::Or one-eighth plus two-fifths of one-eighth. | ||
| + | ::<math>\scriptstyle{\color{blue}{7\div40=\frac{7}{\frac{1}{8}\sdot40}\sdot\frac{1}{8}=\frac{7}{5}\sdot\frac{1}{8}=\frac{1}{8}+\left(\frac{2}{5}\sdot\frac{1}{8}\right)}}</math> | ||
| + | |style="text-align:right;"|או שמינית וב' חמישיות שמינית | ||
| + | |- | ||
| + | | | ||
| + | :This is the result of the division for each. | ||
| + | |style="text-align:right;"|וככה יצא בחלוק לכל אחד | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Check:'''</span> | ||
| + | ::Its check is when you multiply two-tenths minus one-quarter of one-tenth by 40. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left[\frac{2}{10}-\left(\frac{1}{4}\sdot\frac{1}{10}\right)\right]\sdot40=7}}</math> | ||
| + | |style="text-align:right;"|ובחינתו שכשתערוך שנים עשיריות אחד פחות רביע העשור על מ‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Or, one-fifth minus one-eighth of one-fifth by 40. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left[\frac{1}{5}-\left(\frac{1}{8}\sdot\frac{1}{5}\right)\right]\sdot40=7}}</math> | ||
| + | |style="text-align:right;"|או חומש אחד פחות שמינית החומש על מ‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Or, one-eighth and 2-fifths of one-eighth by 40. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left[\frac{1}{8}+\left(\frac{2}{5}\sdot\frac{1}{8}\right)\right]\sdot40=7}}</math> | ||
| + | |style="text-align:right;"|או שמינית וב' חמישיות שמינית על מ‫' | ||
| + | |- | ||
| + | | | ||
| + | ::The result is 7 integers no more and no less. | ||
| + | |style="text-align:right;"|יעלה ז' שלמים בלי ‫<ref>16r</ref>חסר ויתר | ||
| + | |- | ||
| + | !<span style=color:Green>Word Problems - Divide a Quantity Problems</span> | ||
| + | | | ||
| + | |- | ||
| + | |<span style=color:Green>Dividing a known quantity among a known number of people in given ratios</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:green>'''double ratio - each one receives double the previous'''</span> | ||
| + | :If you wish to divide a known number among a known [number of] people and give each double of [the share of] his friend. You wish to know how much should you give the first, so that the whole number is divided no more and no less. | ||
| + | :<math>\scriptstyle\begin{cases}\scriptstyle S_n=m\\\scriptstyle a_n=2\sdot a_{n-1}\end{cases}</math> | ||
| + | |style="text-align:right;"|ואם תרצה לחלק מספר ידוע על אנשים ידועים ולתת לכל אחד ואחד כפל חברו ותרצה לדעת כמה תתן לראשון ש{{#annot:term|2187,1225|LyjR}}יתחלק{{#annotend:LyjR}} כל המספר בלא תוספת ובלא מגרעת | ||
| + | |- | ||
| + | | | ||
| + | :*Such as when you divide 100 among 4, so that each has double of [the share of] his friend. | ||
| + | ::<math>\scriptstyle\begin{cases}\scriptstyle S_4=100\\\scriptstyle a_n=2\sdot a_{n-1}\end{cases}</math> | ||
| + | |style="text-align:right;"|כמו שתחלק מספר ק' על ד' כל אחד ואחד כפל חבירו | ||
| + | |- | ||
| + | | | ||
| + | ::Know how much is the sum of the even-times-evens from one up to four people, then divide the number by the sum and the result is the share of the first. | ||
| + | ::<math>\scriptstyle a_1=\frac{m}{\sum_{i=1}^{n} 2^{i-1}}</math> | ||
| + | |style="text-align:right;"|זה תדע מאחד כמה {{#annot:term|178,1215|bTMn}}יתחבר{{#annotend:bTMn}} בתוספת הכפל לארבעה אנשים ועל המחובר תחלק המספר והיוצא הוא חלק הראשון | ||
| + | |- | ||
| + | | | ||
| + | ::It is known that the sum of the even-times-evens for four people is 15. Divide the 100 by it; the result of the division is six and 2-thirds and so is the share of the first. | ||
| + | ::<math>\scriptstyle{\color{blue}{a_1=\frac{100}{\sum_{i=1}^{4} 2^{i-1}}=\frac{100}{15}=6+\frac{2}{3}}}</math> | ||
| + | |style="text-align:right;"|וכפל הכפל לארבעה אנשים ידוע הוא שהם ט"ו חלק עליהם הק' יצא בחלוק ששה וב' שלישיים וככה חלק הראשון | ||
| + | |- | ||
| + | | | ||
| + | :*likewise if it is said to add to the second a half of what the first has, to the third a third of what the the second has, and to the fourth a quarter of what the third has | ||
| + | ::<math>\scriptstyle\begin{cases}\scriptstyle S_4=100\\\scriptstyle a_2=a_1+\frac{1}{2}a_1\\\scriptstyle a_3=a_2+\frac{1}{3}a_2\\\scriptstyle a_4=a_3+\frac{1}{4}a_3\end{cases}</math> | ||
| + | |style="text-align:right;"|וכן אם יאמר להוסיף לשני חצי הראשון ולשלישי שלישית השני ולרביעית רביעית השלישי | ||
| + | |- | ||
| + | | | ||
| + | ::Know how much is summed from one up to four, it is known that it is summed to 7 integers. | ||
| + | |style="text-align:right;"|תדע זה מאחד כמה יתחבר עד ארבעה וידוע הוא שיתחבר ז' שלמים | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{1+\left(1+\frac{1}{2}\right)+\left[\left(1+\frac{1}{2}\right)+\frac{1}{3}\sdot\left(1+\frac{1}{2}\right)\right]+\left[\left[\left(1+\frac{1}{2}\right)+\frac{1}{3}\sdot\left(1+\frac{1}{2}\right)\right]+\frac{1}{4}\sdot\left[\left(1+\frac{1}{2}\right)+\frac{1}{3}\sdot\left(1+\frac{1}{2}\right)\right]\right]=7}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Divide the 100 by them; the result of division is 14 and two-sevenths and so is the share of the first. | ||
| + | ::<math>\scriptstyle{\color{blue}{a_1=\frac{100}{7}=14+\frac{2}{7}}}</math> | ||
| + | |style="text-align:right;"|תחלק עליהם הק' יצא בחלוק י"ד ושתי שביעיות וככה חלק הראשון | ||
| + | |- | ||
| + | |According to this way for every number whether great or small. | ||
| + | |style="text-align:right;"|ועל זה הדרך לכל מספר בין רב למעט | ||
| + | |- | ||
| + | | | ||
| + | :*If you divide 10 by 2, then you divide the result of the first division by 3, then by 4 and then by 5. You wish to know how much the share of the fifth is. | ||
| + | ::<math>\scriptstyle\begin{cases}\scriptstyle a_1=100\\\scriptstyle a_2=\frac{a_1}{2}\\\scriptstyle a_3=\frac{a_2}{3}\\\scriptstyle a_4=\frac{a_3}{4}\\\scriptstyle a_5=\frac{a_4}{5}\end{cases}</math> | ||
| + | |style="text-align:right;"|ואם תחלק ק' על ב' והיוצא בחלוק האחד תחלק על ג' והיוצא על ד' והיוצא על ה' ותרצה לדעת כמה חלק החמישי | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply the two by three, then by 4, then by 5; the result is 120. | ||
| + | ::<math>\scriptstyle{\color{blue}{2\sdot3\sdot4\sdot5=120}}</math> | ||
| + | |style="text-align:right;"|ערוך השנים בשלשה והעולה בד' והעולה בה' יעלה ק"כ | ||
| + | |- | ||
| + | | | ||
| + | ::When you divide the 100 by the result, which is 120, the result is one minus one-sixth and so is the share of the fifth. | ||
| + | ::<math>\scriptstyle{\color{blue}{a_5=\frac{100}{120}=1-\frac{1}{6}}}</math> | ||
| + | |style="text-align:right;"|וכאשר תחלק הק' על העולה שהוא ק"כ יצא אחד פחות שתות וככה חלק החמישי | ||
| + | |- | ||
| + | | | ||
| + | :*<span style=color:green>'''arithmetic progression:'''</span> If you divide 90 between 9 people, so that each one exceeds over his friend by one. How much will be given to the first? | ||
| + | ::<math>\scriptstyle\begin{cases}\scriptstyle S_9=90\\\scriptstyle d=1\end{cases}</math> | ||
| + | |style="text-align:right;"|ואם תחלק צ' על ט' אנשים ושיוסיף כל אחד על חברו אחד<br> | ||
| + | כמה יתן לראשון ויצא שוה | ||
| + | |- | ||
| + | | | ||
| + | ::This is the rule that you have: subtract one from the number of the people; the remainder is eight. Know how much is the sum from one up to eight, by adding one to eight, then multiplying the sum by half the eight; the result is 36. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sum_{i=1}^{9-1} i=\sum_{i=1}^{8} i=\left[\left(8+1\right)\sdot\left(\frac{1}{2}\sdot8\right)\right]=36}}</math> | ||
| + | |style="text-align:right;"|זה הכלל יהיה בידך שתגרע אחד מחשבון האנשים והנשאר שהם שמונה דע כמה יתחבר מאחד ועד שמונה והוא שתוסיף אחד על שמונה והמחובר תערוך על חצי השמונה יעלה ל"ו | ||
| + | |- | ||
| + | | | ||
| + | ::Subtract it from ninety and divide the remainder, which is fifty-four, by the nine. The result, which is six, is the share of the first. | ||
| + | ::<math>\scriptstyle{\color{blue}{a_1=\frac{90-36}{9}=\frac{54}{9}=6}}</math> | ||
| + | |style="text-align:right;"|גרע אותם מהתשעים והנשאר שהוא ארבעה וחמשים חלקם על התשעה והיוצא שהוא שוה ששה הוא חלק הראשון | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>[this is the general rule for arithmetic progression:]</span> This is the rule that will guide you in all the questions that are similar to this one, when all the excesses are equal, so that the excess of the third over the second is the same as the excess of the fourth over the third and of the fifth over the fourth and so on. | ||
| + | :[<math>\scriptstyle{\color{OliveGreen}{a_3-a_2=a_4-a_3=a_5-a_4=\ldots}}</math>] | ||
| + | :[<math>\scriptstyle{\color{OliveGreen}{a_n=a_1+\left(n-1\right)\sdot d}}</math>] | ||
| + | :[<math>\scriptstyle{\color{OliveGreen}{a_1=\frac{S_n-\sum_{i=1}^{n-1} i}{n}=\frac{S_n-\left[n\sdot\left[\frac{1}{2}\sdot\left(n-1\right)\right]\right]}{n}}}</math>] | ||
| + | |style="text-align:right;"|וזה הכלל ידריכך בכל השאלות הדומות לזו שיהיו כל התוספות שוות שיהיה {{#annot:term|1207,877|Ku0r}}תוספת{{#annotend:Ku0r}} השלישי על השני כתוספת רביעי על השלישי והחמישי על הרביעי וכן כלם | ||
| + | |- | ||
| + | | | ||
| + | :*If you divide eighty between five people, so that the second exceeds over the first by 3, the third [exceeds] over the second by one, the fourth [exceeds] over the third by two, and the fifth [exceeds] over the fourth by six. You wish to know how much will be given to the first. | ||
| + | ::<math>\scriptstyle\begin{cases}\scriptstyle S_5=80\\\scriptstyle a_2=a_1+3\\\scriptstyle a_3=a_2+1\\\scriptstyle a_4=a_3+2\\\scriptstyle a_5=a_4+6\end{cases}</math> | ||
| + | |style="text-align:right;"|ואם תחלק שמונים על חמשה אנשים ושיוסיף השני על הראשון ג' והשלישי על השני אחד והרביעי על השלישי שנים והחמישי על הרביעי ששה ותרצה לדעת כמה יתן לראשון | ||
| + | |- | ||
| + | | | ||
| + | ::Sum up all the excesses over the first, they are 25. Subtract them from the eighty and divide the remainder by the number of the people. The result of division is 11 and it is the share of the first. | ||
| + | |style="text-align:right;"|חבר ‫<ref>16v</ref>כל התוספות שיש על הראשון יעלו כ"ה וגרעם מהשמונים והנשאר שהוא נ"ה חלק על האנשים יצא בחלוק י"א וככה חלק הראשון | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{a_1=\frac{80-\left[3+\left(3+1\right)+\left(3+1+2\right)+\left(3+1+2+6\right)\right]}{5}=\frac{80-25}{5}=\frac{55}{5}=11}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*If you divide a known number between three people. You wish to know how much will be given to each. | ||
| + | ::<math>\scriptstyle S_3=a_1+a_2+a_3</math> | ||
| + | |style="text-align:right;"|ואם תחלק מספר ידוע לשלשה אישים ותרצה לדעת כמה נתן לכל אחד | ||
| + | |- | ||
| + | | | ||
| + | ::Do as follows: tell him to double the share of the first; multiply the whole share of the second by the [known] number minus one; divide the share of the third by the whole [known] number; and sum up all. | ||
| + | |style="text-align:right;"|ככה תעשה שתצוה לו לכפול חלק הראשון וחלק השני כלו יערוך על המספר פחות אחד וחלק השלישי על המספר כלו ויחבר הכל | ||
| + | |- | ||
| + | | | ||
| + | ::Then, ask him what is the complement to the square of the number he divided. | ||
| + | |style="text-align:right;"|ואחר כן תשאל ממנו כמה יש להשלמת מרובע החשבון אשר חילק | ||
| + | |- | ||
| + | | | ||
| + | ::Divide it by the number he divided minus two; the result of division is the share of the first. | ||
| + | ::<math>\scriptstyle a_1=\frac{S_3^2-\left[2a_1+\left[a_2\sdot\left(S_3-1\right)\right]+\left(a_3\sdot S_3\right)\right]}{S_3-2}</math> | ||
| + | |style="text-align:right;"|ומה שיהיה חלק על המספר ההוא אשר חילק פחות שנים והיוצא בחלוק הוא חלק הראשון | ||
| + | |- | ||
| + | | | ||
| + | ::What remains that cannot be divided into integers is the share of the second and from this you know [the share of] the third. | ||
| + | |style="text-align:right;"|ומה שישאר ולא יוכל לחלקו עד שיעשנו ש[למ]ים הוא חלק השני ו[מז]ה תדע השלישי | ||
| + | |- | ||
| + | | | ||
| + | ::Sometimes this calculation goes wrong, so that [there is no remainder] in the division. | ||
| + | |style="text-align:right;"|וזה החשבון פעמים שישתבש שיצא הכל בחלוק | ||
| + | |- | ||
| + | | | ||
| + | ::When this happens, know that he gave only one to the first. Give all the remainder to the second and from them you will know the [share] of the third. | ||
| + | |style="text-align:right;"|וכאשר יקרך זה תדע שלא נתן לראשון כי אם אחד בלבד והנשאר כלו תן לשני ומהם תדע השלישי | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === The Second Category: Division of Fractions by Integers or Integers by Fractions === | ||
| + | !style="text-align:right;"|<big>הענין השני</big> {{#annot:term|1221,157|kTLd}}חלוקת{{#annotend:kTLd}} שברים על שלמים או שלמים על שברים | ||
| + | |- | ||
| + | | | ||
| + | ==== <span style=color:green>Sexagesimal Fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |If you have sexagesimal fractions [lit. fractions of the astrologers] and you wish to divide them by degrees, the result of division will be of the same type of the fractions: if they are primes, [the result will be] primes; if seconds [the result are] seconds; and so on for all the fractions | ||
| + | |style="text-align:right;"|אם יהיו בידך שברי חכמי המזלות ותרצה לחלקם על מעלות יהיה היוצא בחלוק ממין השבר אם ראשונים ראשונים ואם [שניים] שניים וכן לכל השברים | ||
| + | |- | ||
| + | |Because, for every fraction you multiply by a degree, the result is of the same type of that fraction. | ||
| + | |style="text-align:right;"|מפני שכל שבר אשר אתה עורך אותו במעלה יהיה העולה ממין השבר ההוא | ||
| + | |- | ||
| + | |If something remains that cannot be divided, multiply the remainder by sixty and divide by what you have divided; the result will be fractions that are lower than the first type by one rank. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{b}{60^n}\div a=\frac{\frac{b}{a}}{60^n}=\frac{k}{60^n}+\frac{\frac{m\sdot60}{a}}{60^{n+1}}}}</math> | ||
| + | |style="text-align:right;"|ואם ישאר שלא יתחלק תערוך הנשאר על ששים ותחלק על מה שחלקת והיוצא יהיו שברים יורדים מדרגה אחת מן המין הראשון | ||
| + | |- | ||
| + | |If you divide degrees by [sexagesimal] fractions, you convert the degrees into the type by which you want to divide, then divide this type by its own type and the result of division is degrees. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a\div\frac{b}{60^n}=\frac{a\sdot60^n}{60^n}\div\frac{b}{60^n}=\frac{a\sdot60^n}{b}}}</math> | ||
| + | |style="text-align:right;"|ואם תחלק מעלות על שברים אתה משיב המעלות אל המין אשר אתה רוצה לחלוק עליו ותחלק מין על מינו ויהיה היוצא בחלוק מעלות | ||
| + | |- | ||
| + | |You must always convert the degrees into the type by which you want to divide, even if the degrees are many. | ||
| + | |style="text-align:right;"|ואתה צריך לעולם להשיב המעלות אל המין אשר תרצה לחלק עליו וגם אם יהיו המעלות רבות | ||
| + | |- | ||
| + | | | ||
| + | *As if you wish to divide ten degrees by five primes. | ||
| + | :<math>\scriptstyle10^\circ\div5^\prime</math> | ||
| + | |style="text-align:right;"|כגון שתרצה לחלק עשרה מעלות על חמשה ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::It is impossible to say: divide ten by five, so that the result of division will be 2 degrees. | ||
| + | ::<math>\scriptstyle{\color{blue}{10^\circ\div5^\prime\ne10\div5=2^\circ}}</math> | ||
| + | |style="text-align:right;"|אי איפשר לומ' שתחלק עשרה על חמשה ויצא בחלוק ב' מעלות | ||
| + | |- | ||
| + | | | ||
| + | ::Since when you multiply degrees by primes they are primes, as we have said in the Chapter on [Multiplication]. | ||
| + | |style="text-align:right;"|כי כאשר תערוך מעלות על ראשונים יהיו ראשונים כאשר אמרנו בשער המגרעת | ||
| + | |- | ||
| + | | | ||
| + | ::In addition, for every number, when you multiply the result of division by the divisor, the result will be the divided number. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}=c\longrightarrow c\sdot b=a}}</math> | ||
| + | |style="text-align:right;"|‫<ref>17r</ref>וכל חשבון כאשר תערוך מה שיצא בחלוק על {{#annot:term|1226,604|pHVT}}הנחלק עליו{{#annotend:pHVT}} יעלה {{#annot:term|1227,605|vZNL}}החשבון המחולק{{#annotend:vZNL}} | ||
| + | |- | ||
| + | | | ||
| + | ::Therefore, you multiply the ten by sixty, the result is 600. Then, divide [them] by five, the result of division is 120, which are degrees. | ||
| + | ::<math>\scriptstyle{\color{blue}{10^\circ\div5^\prime=10\div\frac{5}{60}=\frac{10\sdot60}{5}=\frac{600}{5}=120^\circ}}</math> | ||
| + | |style="text-align:right;"|ומפני זה אתה עורך העשרה על ששים יעלו ת"ר ותחלק על חמשה יצא בחלוק ק"כ והם מעלות | ||
| + | |- | ||
| + | | | ||
| + | ::Because the one who divides ten degrees by 5 primes should to do as follows: he should divide the 10 degrees, so that the breadth on one side will be only 5 primes. You find that there are 120 degrees lengthwise. | ||
| + | |style="text-align:right;"|כי המחלק עשרה מעלות על ה' ראשונים כך הוא רוצה לעשות שיחלק הי' מעלות שלא יהיה בצד האחד שהוא הרחב כי אם ה' ראשונים ותמצא שיהיה באורך ק"כ מעלות | ||
| + | |- | ||
| + | | | ||
| + | ::If something remains indivisible, multiply the remainder by sixty, then divide by what you have divided; the result will be fractions that are lower than the first type by one rank. | ||
| + | |style="text-align:right;"|ואם ישאר שלא יתחלק תערוך הנשאר על ששים ותחלק מה שחלקת והיוצא יהיו שברים יורדים מדרגה מן המין הראשון | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Simple Fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |If you divide simple fractions [lit. fractions of the geometricians]: | ||
| + | |style="text-align:right;"|ואם שברי חכמי המדות תחלק | ||
| + | |- | ||
| + | | | ||
| + | ===== <span style=color:green>Integer by integer and fraction</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *As the one who divides 100 by two and a quarter. | ||
| + | :<math>\scriptstyle100\div\left(2+\frac{1}{4}\right)</math> | ||
| + | |style="text-align:right;"|כגון מי שמחלק ק' על שנים ורביע | ||
| + | |- | ||
| + | | | ||
| + | ::Find the ratio of one to two and a quarter; it is four-ninths. | ||
| + | |style="text-align:right;"|דע מה ערך האחד מן השנים ורביע והוא ארבע תשיעיות | ||
| + | |- | ||
| + | | | ||
| + | ::Take four-ninths of 100, which is 44 integers and 4-ninths and this is the part of every unit of two and a quarter. | ||
| + | ::<math>\scriptstyle{\color{blue}{100\div\left(2+\frac{1}{4}\right)=100\sdot\frac{1}{2+\frac{1}{4}}=100\sdot\frac{4}{9}=44+\frac{4}{9}}}</math> | ||
| + | |style="text-align:right;"|וקח ארבעת תשיעיות הק' שהם מ"ד שלמים וד' תשיעיות וכן יגיע לכל אחד מהשנים ורביע | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Integer by fraction of integer and fraction</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *If you divide twenty by two-thirds of seven and one-fifth. | ||
| + | :<math>\scriptstyle20\div\left[\frac{2}{3}\sdot\left(7+\frac{1}{5}\right)\right]</math> | ||
| + | |style="text-align:right;"|ואם תחלק עשרים על שני שלישי שבעה וחומש | ||
| + | |- | ||
| + | | | ||
| + | ::know how much two-thirds of seven and one-fifth are. They are 4 and four-fifths, which are 24 fifths. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{2}{3}\sdot\left(7+\frac{1}{5}\right)=4+\frac{4}{5}=\frac{24}{5}}}</math> | ||
| + | |style="text-align:right;"|דע כמה שני שלישי ז' וחומש והוא ארבעה וארבע חומשין שהם כ"ד חומשין | ||
| + | |- | ||
| + | | | ||
| + | ::Know what the ratio of one to them is. It is one-sixth and one-quarter of one-sixth. | ||
| + | ::<math>\scriptstyle{\color{blue}{1:\frac{24}{5}=\frac{1}{6}+\left(\frac{1}{4}\sdot\frac{1}{6}\right)}}</math> | ||
| + | |style="text-align:right;"|ודע מה ערך האחד מהם והוא שתות ורובע השתות | ||
| + | |- | ||
| + | | | ||
| + | ::Take from twenty its one-sixth and one-quarter of one-sixth. They are four and one-sixth and so is the part of each. | ||
| + | :<math>\scriptstyle{\color{blue}{\scriptstyle20\div\left[\frac{2}{3}\sdot\left(7+\frac{1}{5}\right)\right]=20\sdot\left[\frac{1}{6}+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]=4+\frac{1}{6}}}</math> | ||
| + | |style="text-align:right;"|וקח מהעשרים שתותם ורובע שתותם והם ארבעה ושתות וככה חלק כל אחד | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Integer and fraction by fraction</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *If you divide 2 by 3-sevenths. | ||
| + | :<math>\scriptstyle\left(2+\frac{6}{7}\right)\div\frac{3}{7}</math> | ||
| + | |style="text-align:right;"|ואם תחלק ב' על ג' שביעיות | ||
| + | |- | ||
| + | | | ||
| + | ::Know how much is the complement of 3-sevenths to one; it is two and a third. | ||
| + | |style="text-align:right;"|דע בכמה {{#annot:term|1945,1268|u2bz}}ישלמו{{#annotend:u2bz}} הג' שביעיות עד שי' שיהיו אחד והוא שנים פעמים ושליש פעם | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply it by twenty-sevenths; the result is 7 minus a third and this is the part of each unit. | ||
| + | :<math>\scriptstyle{\color{blue}{\left(2+\frac{6}{7}\right)\div\frac{3}{7}=\left(2+\frac{6}{7}\right)\sdot\frac{1}{\frac{3}{7}}=\frac{20}{7}\sdot\left(2+\frac{1}{3}\right)=7-\frac{1}{3}}}</math> | ||
| + | |style="text-align:right;"|ערכם בעשרים שביעיות יעלה ז' פחות שליש וככה חלק כל אחד | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Integer and fraction by fraction and fraction of fraction</span> ===== | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *If you divide twenty by 7-eighths and half an eighth. | ||
| + | :<math>\scriptstyle\left(2+\frac{1}{2}\right)\div\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]</math> | ||
| + | |style="text-align:right;"|ואם תחלק עשרים על ז' שמיניות וחצי שמיניות | ||
| + | |- | ||
| + | | | ||
| + | ::Know how much is the complement of 7-eighths and half and eighth to one; it is one and a third of a fifth. | ||
| + | |style="text-align:right;"|דע בכמה ישלמו הז' שמיניות וחצי שמיניות עד שיהיו אחד והוא אחד ושליש חומש | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply it by twenty-eighths; the result is 21-eighths and a third [of an eighth], which are two, 5-eighths and a [third] of an eighth that are 3 minus a third. | ||
| + | |style="text-align:right;"|תערכם על עשרים שמיניות יעלה כ"א שמיניות ושליש שהם שנים וה' שמיניות ושלש שמינית שהם ג' פחות שליש | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | :<math>{\color{blue}{\begin{align}\scriptstyle\left(2+\frac{1}{2}\right)\div\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{20}{8}\sdot\frac{1}{\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)}=\frac{20}{8}\sdot\left[1+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]=\frac{21}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\\&\scriptstyle=2+\frac{5}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)=3-\frac{1}{3}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === <span style=color:green>Completion of Fractions</span> === | ||
| + | | | ||
| + | |- | ||
| + | |The way to know the multiplicative inverses of fractions so that they become one: | ||
| + | |style="text-align:right;"|ודרך לדעת {{#annot:term|1418,1550|bgPF}}תשלומי{{#annotend:bgPF}} השברים עד אשר יהיו אחד ככה תדענו | ||
| + | |- | ||
| + | | | ||
| + | :*Such as when you wish to know how 3-eighths are completed until they become one one. | ||
| + | ::<math>\scriptstyle a\sdot\frac{3}{8}=1</math> | ||
| + | |style="text-align:right;"|כגון שתרצה לדעת איך ג' שמיני האחד ישלמו עד שיהיו אחד שלם | ||
| + | |- | ||
| + | | | ||
| + | ::Know that the name of the eighths is derived from eight and the number of the times that the three are counting the eight, is 3 times minus one-third. By this number you multiply the three-eighths and the result is one. | ||
| + | ::<math>\scriptstyle{\color{blue}{a\sdot\frac{3}{8}=1\longrightarrow a=\frac{8}{3}=3-\frac{1}{3}}}</math> | ||
| + | |style="text-align:right;"|דע כי שם השמיניות הוא משמונה ומספר הפעמים אשר השלשה מונים את השמונה הם ג' פעמים פחות שליש ‫<ref>17v</ref>וכמספר הזה אתה {{#annot:term|1269,185|bBid}}חושב את{{#annotend:bBid}} שלשת השמיניות ויהיו אחד | ||
| + | |- | ||
| + | |For The number of times that one number [i.e., the numerator] counts the denominator is the same as [the number of times that] the part counts the one. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}=\frac{1}{\frac{b}{a}}}}</math> | ||
| + | |style="text-align:right;"|כי כמנין הפעמים אשר מספר אחד מונה את {{#annot:term|1443,571|C79S}}המספר המוכיח{{#annotend:C79S}} כמוהם החלק מונה את האחד | ||
| + | |- | ||
| + | | | ||
| + | :*Such as if you wish to complete 2-fifths and one-tenth of the fifth until they become one. | ||
| + | ::<math>\scriptstyle a\sdot\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]=1</math> | ||
| + | |style="text-align:right;"|כגון שתרצה להשלים ב' חמישיות ועשירית החומש עד שיהיו אחד | ||
| + | |- | ||
| + | | | ||
| + | ::Look for a number that has a fifth and a tenth, which is 50, and it is the denominator which in this book is called "moreh". | ||
| + | |style="text-align:right;"|בקש חשבון שיהיה לו חמישית ועשירית והוא נ' והוא ה{{#annot:term|1443,571|YnO1}}מוכיח{{#annotend:YnO1}} אשר נקרא בספר הזה המורה | ||
| + | |- | ||
| + | | | ||
| + | ::2-fifths of this number and one-tenth of its fifth is 21. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]\sdot50=21}}</math> | ||
| + | |style="text-align:right;"|וב' חמישי המספר הזה ועשירית חמישיתו הוא כ"א | ||
| + | |- | ||
| + | | | ||
| + | ::This number counts the fifty 2 times and one-third and one-seventh of one-third of one time. According to this will be the complementary fraction of 2-fifths and one-tenth of one-fifth so it becomes one. | ||
| + | ::<math>\scriptstyle{\color{blue}{a\sdot\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]=1\longrightarrow a=\frac{50}{21}=2+\frac{1}{3}+\left(\frac{1}{7}\sdot\frac{1}{3}\right)}}</math> | ||
| + | |style="text-align:right;"|והמספר הזה מונה את החמשים ב' פעמים ושליש פעם ושביעית השליש וכענין הזה יהיו {{#annot:term|1418,1550|dz28}}תשלומי{{#annotend:dz28}} ב' חמישיות ועשירית החומש ויהיה אחד | ||
| + | |- | ||
| + | |For an integer you can also say the same way. | ||
| + | |style="text-align:right;"|וגם במספר השלם אתה יכול לומר על זה הדרך | ||
| + | |- | ||
| + | | | ||
| + | :*Such as if you wish to complete the seven until they become 16. | ||
| + | ::<math>\scriptstyle a\sdot7=16</math> | ||
| + | |style="text-align:right;"|כגון שתרצה להשלים את השבעה עד שיהיו י"ו | ||
| + | |- | ||
| + | | | ||
| + | ::You know that the seven counts 16 two times and two-sevenths of a time and this is its complementary number to 16. | ||
| + | ::<math>\scriptstyle{\color{blue}{a\sdot7=16\longrightarrow a=\frac{16}{7}=2+\frac{2}{7}}}</math> | ||
| + | |style="text-align:right;"|אתה יודע כי השבעה מונה את י"ו שני פעמים ושני שביעי פעם ובהם {{#annot:term|1945,1268|jhIl}}ישלמו{{#annotend:jhIl}} י"ו | ||
| + | |- | ||
| + | | | ||
| + | :This way you can find every number. | ||
| + | |style="text-align:right;"|ועל זה הדרך תוכל למצא לכל חשבון | ||
| + | |- | ||
| + | | | ||
| + | *If you divide three-quarters of three-fifths of nine by 24: | ||
| + | :<math>\scriptstyle\left[\frac{3}{4}\sdot\left(\frac{3}{5}\sdot9\right)\right]\div24</math> | ||
| + | |style="text-align:right;"|ואם תחלק שלשה רביעיות של שלשה חומשי תשעה על כ"ד | ||
| + | |- | ||
| + | | | ||
| + | ::It is known that three-fifths of nine are 27-fifths and their three-quarters are 4 integers and half a tenth. | ||
| + | :<math>\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(\frac{3}{5}\sdot9\right)\right]\div24=\left(\frac{3}{4}\sdot\frac{27}{5}\right)\div24=\frac{4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}{24}}}</math> | ||
| + | |style="text-align:right;"|וידוע כי שלשה חומשי תשעה הם כ"ז חומשין ושלשה רביעיותיהם הם ד' שלמים וחצי עשירית אחד | ||
| + | |- | ||
| + | | | ||
| + | ::Therefore, <span style=color:blue>'''the author'''</span> said: "take" etc. | ||
| + | |style="text-align:right;"|ולפיכך אמ' המחבר תקח וכו‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Take one part from 24: its eighth, which is 3; or its third, which is 8; or its quarter, which is 6. | ||
| + | |style="text-align:right;"|תקח חלק אחד מכ"ד שמיניתו והוא ג' או שלישיתו והוא ח' או רביעיתו והוא ו‫' | ||
| + | |- | ||
| + | | | ||
| + | ::If you take its eighth, when you multiply the 4 and half a tenth by it, you find in it an eighth, a third of an eighth, and half a tenth of a third of an eighth. | ||
| + | |style="text-align:right;"|אם שמיניתו לקחת כאשר תערוך הד' וחצי עשירית אחד אליו תמצא בו פעם אחת שמינית ושליש שמינית וחצי עשירית שליש שמינית | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}{24}=\frac{\frac{8\sdot\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]}{24}}{8}=\frac{1}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{3}\sdot\frac{1}{8}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::If you take its third, you find in it half a third and half a tenth of an eighth of a third. | ||
| + | |style="text-align:right;"|ואם שלישיתו לקחת תמצא בו חצי שלישיתו וחצי עשירית שמינית שלישית | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}{24}=\frac{\frac{3\sdot\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]}{24}}{3}=\left(\frac{1}{2}\sdot\frac{1}{3}\right)+\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{3}\sdot\frac{1}{8}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::If you take its quarter, you find in it two-thirds of a [quarter] and half a tenth of a sixth of a quarter. | ||
| + | |style="text-align:right;"|ואם רביעיתו לקחת תמצא בו שני שלישי שלישית וחצי עשירית ששית רביעית | ||
| + | |- | ||
| + | | | ||
| + | ::This is the result of division by 24. | ||
| + | |style="text-align:right;"|וככה יצא בחלוק לכל אחד מכ"ד | ||
| + | |- | ||
| + | | colspan=2| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}{24}=\frac{\frac{4\sdot\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]}{24}}{4}=\left(\frac{2}{3}\sdot\frac{1}{4}\right)+\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{4}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::The check is by multiplying whichever fraction you wish of the fractions we mentioned by 24; the result is 4 and half a tenth. | ||
| + | ::<math>\scriptstyle{\color{blue}{result\times24=4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}}</math> | ||
| + | |style="text-align:right;"|והבחינה כשתערוך איזה שתרצה מהחלקים שהזכרנו על כ"ד יעלה ד' וחצי עשירית אחד | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === The Third Category: Division of Fractions by Fractions === | ||
| + | !style="width:45%; text-align:right;"|<big>הענין</big> השלישי חלוקת שברים על שברים | ||
|- | |- | ||
| − | | | + | | |
| + | ==== <span style=color:green>Sexagesimal Fractions</span> ==== | ||
| + | | | ||
|- | |- | ||
| − | | | + | !<span style=color:green>The first rule</span> |
| + | | | ||
|- | |- | ||
| − | | | + | |If you divide sexagesimal fractions [lit. fractions of the astrologers] by each other: |
| + | |style="text-align:right;"|אם שברי חכמי המזלות תחלק זה על זה | ||
|- | |- | ||
| − | | | + | | |
| + | *If you divide primes by primes, the result of division will be degrees. | ||
| + | |style="text-align:right;"|אם ראשונים על ראשונים תחלק יהיה היוצא בחלוק מעלות | ||
| + | |- | ||
| + | | | ||
| + | *If you divide seconds by seconds, the result will be degrees. | ||
| + | |style="text-align:right;"|וכן אם שניים על שניים תחלק היוצא מעלות | ||
| + | |- | ||
| + | |The same for the rest of the [sexagesimal] fractions: if you divide them by their type, the result will be degrees - this is the first rule of the division of [sexagesimal] fractions. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a}{60^n}\div\frac{b}{60^n}=\frac{a}{b}}}</math> | ||
| + | |style="text-align:right;"|וכן שאר ‫<ref>18r</ref>השברים אם אתה מחלק אותם על מיניהם יהיה היוצא מעלות וזה כלל אחד ב{{#annot:term|1223,157|09hR}}חלוק{{#annotend:09hR}} השברים | ||
| + | |- | ||
| + | !<span style=color:green>The second rule</span> | ||
| + | | | ||
| + | |- | ||
| + | |The second rule: know that if you divide one type of fractions by another type that is lower: | ||
| + | |style="text-align:right;"|וכלל שני דע שאם אתה מחלק מין אחד מן השברים על מין אחר שהוא תחתיו | ||
| + | |- | ||
| + | | | ||
| + | *As if you wish to divide primes by seconds, or by thirds: | ||
| + | |style="text-align:right;"|כגון שתרצה לחלק ראשונים על שניים או על שלישיים | ||
| + | |- | ||
| + | | | ||
| + | :You multiply the primes by sixty; they become seconds, then you divide seconds by seconds. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a}{60}\div\frac{b}{60^2}=\frac{a\sdot60}{60^2}\div\frac{b}{60^2}=\frac{a\sdot60}{b}}}</math> | ||
| + | |style="text-align:right;"|אתה עורך הראשונים על ששים ויהיו שניים ותחלק שניים על שניים | ||
| + | |- | ||
| + | | | ||
| + | :If you divide by thirds, multiply them by sixty another time; they become thirds, then divide thirds by thirds and the result is degrees. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a}{60}\div\frac{b}{60^3}=\frac{a\sdot60\sdot60}{60^3}\div\frac{b}{60^3}=\frac{a\sdot60\sdot60}{b}}}</math> | ||
| + | |style="text-align:right;"|ואם על שלישיים תחלק ערכם על ששים פעם אחרת ויהיו שלישיים ותחלק שלישיים על שלישיים ויהיה היוצא מעלות | ||
| + | |- | ||
| + | | | ||
| + | :The same for everything similar to it. | ||
| + | |style="text-align:right;"|וכן כל הדומה לזה | ||
| + | |- | ||
| + | !<span style=color:green>The third rule</span> | ||
| + | | | ||
| + | |- | ||
| + | |The third rule: if you divide one type of fractions by another type higher than it, the result of division will be of a lower type than the type [that is divided] according to the type by which you divide. | ||
| + | |style="text-align:right;"|וכלל שלישי אם תחלק מין אחד מן השברים על מין אחר שהוא גדול ממנו יהיה היוצא בחלוק מן המין אשר תחתיו של המין אשר אתה מחלק עליו | ||
| + | |- | ||
| + | | | ||
| + | *As if you divide by primes, the result of division will be seconds. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^{\prime\prime\prime}\div b^\prime=\left(\frac{a}{b}\right)^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|כאלו חלקת שלישיים על ראשונים יהיה היוצא בחלוק שניים | ||
| + | |- | ||
| + | | | ||
| + | *Or, seconds by primes will be primes. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^{\prime\prime}\div b^\prime=\left(\frac{a}{b}\right)^\prime}}</math> | ||
| + | |style="text-align:right;"|או שניים על ראשונים יהיו ראשונים | ||
| + | |- | ||
| + | |Because, when you multiply the result of division by the divisor, the result should be the original dividend. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}=c\longrightarrow c\sdot b=a}}</math> | ||
| + | |style="text-align:right;"|מפני שכשתערוך מה שיצא בחלוק על מה שחלקת עליו צריך שיצא הראשון {{#annot:term|1226,605|bSCg}}הנחלק{{#annotend:bSCg}} | ||
| + | |- | ||
| + | !<span style=color:green>Remainder</span> | ||
| + | | | ||
| + | |- | ||
| + | |If something remains that cannot be divided, you multiply the remainder by sixty, then divide by what you have divided; the result will be of a type that is one rank lower than the type of the number that initially resulted from the division. | ||
| + | |style="text-align:right;"|ואם ישאר שלא יתחלק אתה עורך הנשארים בששים ותחלק על מה שחלקת ויהיה היוצא ממין שירד מדרגה אחת ממין המספר שיצא בחלוק בראשונה | ||
| + | |- | ||
| + | | | ||
| + | *As if you divide fifty primes by seven primes. | ||
| + | :<math>\scriptstyle50^\prime\div7^\prime</math> | ||
| + | |style="text-align:right;"|כאלו תחלק חמשים ראשונים על שבעה ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::The result of division is seven degrees and one remains indivisible. | ||
| + | |style="text-align:right;"|יצא בחלוק שבע מעלות וישאר שלא יתחלק אחד | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply it by sixty; they are seconds. | ||
| + | |style="text-align:right;"|ערכהו על ששים יהיו שניים | ||
| + | |- | ||
| + | | | ||
| + | ::Divide them by the seven, by which you have divided at first; the result of division is eighth primes and 4 seconds remain indivisible. | ||
| + | |style="text-align:right;"|חלקם על שבעה אשר חלקת בראשונה יצא בחלוק שמונה ראשונים וישאר שלא יתחלק ד' שניים | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them by sixty; the result is 240 thirds. | ||
| + | |style="text-align:right;"|ערכם על ששים יעלו ר"מ שלישיים | ||
| + | |- | ||
| + | | | ||
| + | ::Divide them by 7; the result is 34 seconds and two-thirds remain. | ||
| + | |style="text-align:right;"|חלקם על ז' יעלה ל"ד שניים וישאר שני שלישיים | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them by sixty and divide them by what you have divided; the result is thirds. | ||
| + | |style="text-align:right;"|ערכם בששים וחלקם על מה שחלקת ויעלו שלישיים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>{\color{blue}{\begin{align}\scriptstyle50^\prime\div7^\prime&\scriptstyle=\left(7+\frac{1}{7}\right)^\circ=7+\frac{\frac{1\sdot60}{7}}{60}=7+\frac{8}{60}+\frac{\frac{4}{7}}{60}=7+\frac{8}{60}+\frac{\frac{4\sdot60}{7}}{60^2}=7+\frac{8}{60}+\frac{\frac{240}{7}}{60^2}\\&\scriptstyle=7+\frac{8}{60}+\frac{34}{60^2}+\frac{\frac{2}{7}}{60^2}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::You can convert them into fourths, fifths, and so on as much as you like. | ||
| + | |style="text-align:right;"|וכן אתה יכול לחקרן לרביעיים ולחמישיים עד כמה שתרצה | ||
| + | |- | ||
| + | !<span style=color:green>division table of sexagesimal fractions</span> | ||
| + | | | ||
| + | |- | ||
| + | |To make it easier for the reader, I have drawn for you a table of primes to sixths. | ||
| + | |style="text-align:right;"|ולהקל על הקורא ציירתי לך לוח מראשונים עד ששיים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | |||
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
| + | |- | ||
| + | | ששיים | ||
| + | | חמשיים | ||
| + | | רביעיים | ||
| + | | שלישיים | ||
| + | | שניים | ||
| + | | ראשונים | ||
| + | |<sub>רוחב</sub>/<sup>אורך</sup> | ||
| + | |- | ||
| + | | חמשיים | ||
| + | | רביעיים | ||
| + | | שלישיים | ||
| + | | שניים | ||
| + | | ראשונים | ||
| + | | מעלות | ||
| + | | ראשונים | ||
| + | |- | ||
| + | | רביעיים | ||
| + | | שלישיים | ||
| + | | שניים | ||
| + | | ראשונים | ||
| + | | מעלות | ||
| + | | ראשונים | ||
| + | | שניים | ||
| + | |- | ||
| + | | שלישיים | ||
| + | | שניים | ||
| + | | ראשונים | ||
| + | | מעלות | ||
| + | | ראשונים | ||
| + | | שניים | ||
| + | | שלישיים | ||
| + | |- | ||
| + | | שניים | ||
| + | | ראשונים | ||
| + | | מעלות | ||
| + | | ראשונים | ||
| + | | שניים | ||
| + | | שלישיים | ||
| + | | רביעיים | ||
| + | |- | ||
| + | | ראשונים | ||
| + | | מעלות | ||
| + | | ראשונים | ||
| + | | שניים | ||
| + | | שלישיים | ||
| + | | רביעיים | ||
| + | | חמשיים | ||
| + | |- | ||
| + | | מעלות | ||
| + | | ראשונים | ||
| + | | שניים | ||
| + | | שלישיים | ||
| + | | רביעיים | ||
| + | | חמשיים | ||
| + | | ששים | ||
|- | |- | ||
| − | |||
|} | |} | ||
| − | + | |- | |
| + | | colspan="2"| | ||
| + | {|class="wikitable" style="color: blue; margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
| + | |- | ||
| + | | sixths | ||
| + | | fifths | ||
| + | | fourths | ||
| + | | thirds | ||
| + | | seconds | ||
| + | | primes | ||
| + | |<sup>length</sup>/<sub>width</sub> | ||
| + | |- | ||
| + | | fifths | ||
| + | | fourths | ||
| + | | thirds | ||
| + | | seconds | ||
| + | | primes | ||
| + | | degrees | ||
| + | | primes | ||
| + | |- | ||
| + | | fourths | ||
| + | | thirds | ||
| + | | seconds | ||
| + | | primes | ||
| + | | degrees | ||
| + | | primes | ||
| + | | seconds | ||
| + | |- | ||
| + | | thirds | ||
| + | | seconds | ||
| + | | primes | ||
| + | | degrees | ||
| + | | primes | ||
| + | | seconds | ||
| + | | thirds | ||
| + | |- | ||
| + | | seconds | ||
| + | | primes | ||
| + | | degrees | ||
| + | | primes | ||
| + | | seconds | ||
| + | | thirds | ||
| + | | fourths | ||
| + | |- | ||
| + | | primes | ||
| + | | degrees | ||
| + | | primes | ||
| + | | seconds | ||
| + | | thirds | ||
| + | | fourths | ||
| + | | fifths | ||
| + | |- | ||
| + | | degrees | ||
| + | | primes | ||
| + | | seconds | ||
| + | | thirds | ||
| + | | fourths | ||
| + | | fifths | ||
| + | | sixths | ||
| + | |- | ||
| + | |} | ||
| + | |- | ||
| + | |If you want to divide degrees and fractions by degrees and fractions: convert the two numbers into one rank, then divide. | ||
| + | |style="text-align:right;"|ואם תרצה לחלק מעלות ושברים על מעלות ושברים השב שני החשבונים למדרגה אחת ואחר תחלק | ||
| + | |- | ||
| + | | | ||
| + | *Such as if you wish to divide eight degrees and twenty primes by 3 degrees and 15 primes. | ||
| + | :<math>\scriptstyle\left(8^\circ+20^\prime\right)\div\left(3^\circ+15^\prime\right)</math> | ||
| + | |style="text-align:right;"|כגון שתרצה לחלק שמנה מעלות ועשרים ראשונים על ג' ‫<ref>18v</ref>מעלות וט"ו ראשונים | ||
| + | |- | ||
| + | | | ||
| + | :We convert all of them to primes: the first number is 500, which is the dividend, and the other is 195. We divide the greater by the smaller. The result of division is two, which are degrees, and 110 remain. | ||
| + | :<math>\scriptstyle{\color{blue}{\left(8^\circ+20^\prime\right)\div\left(3^\circ+15^\prime\right)=500^\prime\div195^\prime=\left(2+\frac{110}{195}\right)^\circ}}</math> | ||
| + | |style="text-align:right;"|נשיבם כלם ראשונים והנה החשבון האחד ת"ק והוא {{#annot:term|1227,605|SyYf}}המחולק{{#annotend:SyYf}} והשני קצ"ה<br> | ||
| + | חלקנו הגדול על הקטן יצא בחלוק שנים והם מעלות ונשארו ק"י | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them by sixty and divide by 195. The result of division is 33, which are primes, and 165 remain. | ||
| + | |style="text-align:right;"|ערוך אותם על ששים וחלק על קצ"ה<br> | ||
| + | יצא בחלוק ל"ג והם ראשונים וישאר קס"ה | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(8^\circ+20^\prime\right)\div\left(3^\circ+15^\prime\right)=2^\circ+\left(\frac{110\sdot60}{195}\right)^\prime=2^\circ+\left(33+\frac{165}{195}\right)^\prime}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them by 60 and divide by 195. The result of division is 50 and they are seconds. | ||
| + | |style="text-align:right;"|ערכם על ס' וחלק על קצ"ה ראשונים יצא בחלוק נ' והם שניים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(8^\circ+20^\prime\right)\div\left(3^\circ+15^\prime\right)=2^\circ+33^\prime+\left(\frac{165\sdot60}{195}\right)^{\prime\prime}=2^\circ+33^\prime+\left(50+\frac{150}{195}\right)^{\prime\prime}}}</math> | ||
| + | |- | ||
| + | |If you want to make it more accurate with thirds and fourths, do it in this way. | ||
| + | |style="text-align:right;"|ואם תרצה לדקדק כן לשלישיים ולרביעיים תעשה על זה הדרך | ||
| + | |- | ||
| + | | | ||
| + | :*Or, know the ratio of the remaining 110 to the divided 390. Their quarter is 97 and a half and 12 and a half remain. The 6 and a half are one-third of one-fifth of one-quarter [of 390] and 6 remain, which are 6 parts of 13 of two-thirds of one-fifth of one-quarter [of 390]. | ||
| + | |style="text-align:right;"|או תדע מה ערך ק"י הנשארים אל ש"צ {{#annot:term|1226,605|nmhU}}הנחלקים{{#annotend:nmhU}} והנה רביעיתם צ"ז וחצי נשארו י"ב וחצי והו' וחצי הם שלישית חמישית הרביעית ונשארו ו' שהם ו' חלקים מי"ג בשני שלישי חמישית רביעית | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle\frac{110}{195}&\scriptstyle=\frac{\left(97+\frac{1}{2}\right)+\left(12+\frac{1}{2}\right)}{195}=\frac{\frac{1}{4}\sdot390}{195}+\frac{\left(6+\frac{1}{2}\right)+6}{195}=\frac{\frac{1}{4}\sdot390}{195}+\frac{\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot390}{195}+\frac{6}{195}\\&\scriptstyle=\frac{\frac{1}{4}\sdot390}{195}+\frac{\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot390}{195}+\frac{\frac{6}{13}\sdot\frac{2}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot390}{195}=\left(\frac{1}{4}\sdot2\right)+\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot2\right)+\left(\frac{6}{13}\sdot\frac{2}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot2\right)\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::For the quarter add one-quarter of 2 degrees, so that the result of division are 30 primes. For the 6, which are 6 parts of 13 of two-thirds of one-fifth of one-quarter add one prime and [50] seconds. The result of division is 33 primes and 50 seconds, as in the first calculation | ||
| + | |style="text-align:right;"|ובעבור הרביעית הוסף רביעית ב' מעלות שיצאו בחלוק והם ל' ראשונים<br> | ||
| + | ובעבור ו' חלקם מי"ג בשני שלישי חמישית רביעית הוסף ראשון אחד לשניים והנה יצא בחלוק ל"ג ראשונים נ' שניים כמו החשבון הראשון | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>{\color{blue}{\begin{align}\scriptstyle\left(8^\circ+20^\prime\right)\div\left(3^\circ+15^\prime\right)&\scriptstyle=2+\left(\frac{1}{4}\sdot2\right)+\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot2\right)+\left(\frac{6}{13}\sdot\frac{2}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot2\right)\\&\scriptstyle\approx2+30^\prime+2^\prime+\left(1^\prime+50^{\prime\prime}\right)=2+33^\prime+50^{\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| − | =< | + | ==== <span style=color:green>Simple Fractions</span> ==== |
| − | + | | | |
| − | ==< | + | |- |
| − | + | | | |
| − | + | ===== <span style=color:green>Integer and fraction by integer and fraction</span> ===== | |
| − | + | | | |
| − | + | |- | |
| − | + | |If you divide simple fractions [lit. fractions of the geometricians]: | |
| − | + | |style="text-align:right;"|ואם שברי חכמי המדות תחלק | |
| − | + | |- | |
| − | + | | | |
| − | + | *Such as three and three-quarters by one and a fifth. | |
| − | + | :<math>\scriptstyle\left(3+\frac{3}{4}\right)\div\left(1+\frac{1}{5}\right)</math> | |
| − | + | |style="text-align:right;"|כגון שלשה ושלשה רביעיות על אחד וחומש | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Find the ratio of one to one and a fifth; it is five-sixths. | |
| − | + | |style="text-align:right;"|דע מה ערך האחד מן אחד וחומש והוא חמשה שתותיו | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Take 5-sixths from 3 and 3-quarters that are six-eighths; the result is three and an eighth. | |
| − | + | |style="text-align:right;"|קח ה' שתותין מג' וג' רביעיות אחד שהם שש שמיניות יעלה ‫<ref>19r</ref>שלשה ושמינית וככה חלק האחד | |
| − | + | |- | |
| − | + | | colspan="2"| | |
| − | + | :<math>\scriptstyle{\color{blue}{\left(3+\frac{3}{4}\right)\div\left(1+\frac{1}{5}\right)=\left(3+\frac{3}{4}\right)\sdot\frac{1}{1+\frac{1}{5}}=\left(3+\frac{3}{4}\right)\sdot\frac{5}{6}=3+\frac{1}{8}}}</math> | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | כגון | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ====< | + | ===== <span style=color:green>Integer and fraction by fraction</span> ===== |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | *If you divide 7 and a fifth by three-quarters. | |
| − | + | :<math>\scriptstyle\left(7+\frac{1}{5}\right)\div\frac{3}{4}</math> | |
| − | + | |style="text-align:right;"|ואם תחלק ז' וחומש על שלש רביעיות אחד | |
| − | <math>\ | + | |- |
| − | + | | | |
| − | + | ::Find the complement of the 3-quarters to one; it is one and a third, meaning add to 7 and a fifth its third. | |
| − | + | |style="text-align:right;"|דע בכמה ישלמו הג' רביעיות לאחד כלו' שתוסיף על ז' וחומש שלישיתם והוא אחד ושליש | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Multiply [one and a third] by 7 and a fifth; the result is nine and 3-fifths and their quarter is the part of each quarter. | |
| − | + | :<math>\scriptstyle{\color{blue}{\left(7+\frac{1}{5}\right)\div\frac{3}{4}=\left(7+\frac{1}{5}\right)\sdot\frac{1}{\frac{3}{4}}=\left(7+\frac{1}{5}\right)\sdot\left(1+\frac{1}{3}\right)=9+\frac{3}{5}}}</math> | |
| − | <math> | + | |style="text-align:right;"|תערכם על ז' וחומש יעלה תשעה וג' חומשין ורביעיתם הוא חלק כל רביע ורביע |
| − | + | |- | |
| − | + | | | |
| − | + | ::Or, convert the 7 and a fifth into fifths; you have 36-fifths. | |
| − | + | |style="text-align:right;"|או תשיב הז' וחומש לחומשין יהיו בידך ל"ו חומשין | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Divide them by the 3-quarters; the result of division is 12-fifths, which are two and 2-fifths for each quarter, which is 9 and 3-fifths for one unit. | |
| − | + | :<math>\scriptstyle{\color{blue}{\left(7+\frac{1}{5}\right)\div\frac{3}{4}=\frac{36}{5}\div\frac{3}{4}=\frac{\frac{12}{5}}{\frac{1}{4}}=\frac{2+\frac{2}{5}}{\frac{1}{4}}=9+\frac{3}{5}}}</math> | |
| − | + | |style="text-align:right;"|חלקם על הג' רביעיות יצא בחלוק י"ב חומשין שהם שנים וב' חומשין לכל רביע ורביע שהוא לאחד שלם ט' וג' חומשין | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ====< | + | ===== <span style=color:green>Fraction by fraction</span> ===== |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | *If you divide six-sevenths by eight-tenths. | |
| − | + | :<math>\scriptstyle\frac{6}{7}\div\frac{8}{10}</math> | |
| − | + | |style="text-align:right;"|ואם תחלק ששה שביעיות על שמונה עשיריות | |
| − | ואם | + | |- |
| − | + | | | |
| − | + | ::find its complement to one; it is one and a quarter. | |
| − | + | |style="text-align:right;"|דע בכמה {{#annot:term|1945,1267|OrbI}}ישלים{{#annotend:OrbI}} אחד והוא אחד ורביע | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Multiply them by six-sevenths; the result is [seven] and a half. | |
| − | + | |style="text-align:right;"|תערכם על ששה שביעיות יעלה א' שביעיות וחצי | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Divide them [by seven]; the result is one and half a seventh and this is one part. | |
| − | + | |style="text-align:right;"|חלקם יצא אחד וחצי שביעית וככה חלק האחד | |
| − | + | |- | |
| − | + | | colspan=2| | |
| − | + | :<math>\scriptstyle{\color{blue}{\frac{6}{7}\div\frac{8}{10}=\frac{6}{7}\sdot\frac{1}{\frac{8}{10}}=\frac{6}{7}\sdot\left(1+\frac{1}{4}\right)=\frac{7+\frac{1}{2}}{7}=1+\left(\frac{1}{2}\sdot\frac{1}{7}\right)}}</math> | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Or, if you divide six by eight, the result is one minus a quarter. | |
| − | + | |style="text-align:right;"|או אם תרצה חלק ששה על שמונה יצא אחד פחות רובע | |
| − | + | |- | |
| − | + | | | |
| − | + | ::So, now the result is one seventh minus a quarter of a seventh divided by a tenth, which is 10 to one; 7-sevenths and half a seventh. | |
| − | + | |style="text-align:right;"|לפיכך יצא עכשו שביעית אחד פחות רובע שביעית לחלק העשירית והם י' לאחד ז' שביעי<sup>ו</sup>ת וחצי שביעית | |
| − | + | |- | |
| − | + | | colspan=2| | |
| − | + | :<math>\scriptstyle{\color{blue}{\frac{6}{7}\div\frac{8}{10}=\frac{\frac{6}{8}}{7}\div\frac{1}{10}=\frac{1-\frac{1}{4}}{7}\div\frac{1}{10}=\left[\frac{1}{7}-\left(\frac{1}{4}\sdot\frac{1}{7}\right)\right]\div\frac{1}{10}=\frac{7}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)}}</math> | |
| − | + | |- | |
| − | <math>\frac{ | + | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | ====< | + | ===== <span style=color:green>Fraction of integer and fraction by fraction of integer and fraction</span> ===== |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | *If you divide six-sevenths of five and a quarter by three-eighths of one and one-fifth. | |
| − | + | :<math>\scriptstyle\left[\frac{6}{7}\sdot\left(5+\frac{1}{4}\right)\right]\div\left[\frac{3}{8}\sdot\left(1+\frac{1}{5}\right)\right]</math> | |
| − | + | |style="text-align:right;"|ואם תחלק ששה שביעיות חמשה ורובע על שלשה שמיניות מאחד וחומש | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Convert the five and a quarter to quarters. They are 21. Their six-sevenths are 18, which are 4 integers and a half. | |
| − | ואם | + | ::<math>\scriptstyle{\color{blue}{\frac{6}{7}\sdot\left(5+\frac{1}{4}\right)=\frac{6}{7}\sdot\frac{21}{4}=\frac{18}{4}=4+\frac{1}{2}}}</math> |
| − | <math>\ | + | |style="text-align:right;"|השב החמשה ורובע כלם לרביעיות יעלו כ"א וששה שביעיותיו י"ח שהם ד' שלמים וחצי |
| − | + | |- | |
| − | + | | | |
| − | + | ::Convert also the one and one-fifth to fifths. They are six-fifths. Their three-eighths are 2-fifths and one-quarter of one-fifth. | |
| − | <math>\frac{ | + | ::<math>\scriptstyle{\color{blue}{\frac{3}{8}\sdot\left(1+\frac{1}{5}\right)=\frac{3}{8}\sdot\frac{6}{5}=\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)}}</math> |
| − | + | |style="text-align:right;"|ועוד השב האחד וחומש לחמישיות והם ששה חמישיות ושלשה שמיניותיו ב' חומשין ורביע חומש | |
| − | + | |- | |
| − | + | | | |
| − | + | :::Know how much of them are 1, it is two and two-ninths. | |
| − | + | :::<math>\scriptstyle{\color{blue}{\left[\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\right]\sdot\left(2+\frac{2}{9}\right)=1}}</math> | |
| − | + | |style="text-align:right;"|ותדע בכמה יהיו אחד והוא בשנים ושני תשיעיותיו | |
| − | + | |- | |
| − | + | | | |
| − | + | :::For, one-quarter of one-fifth is one-ninth of two-fifths and one-quarter of one-fifth. | |
| − | + | :::<math>\scriptstyle{\color{blue}{\frac{1}{4}\sdot\frac{1}{5}=\frac{1}{9}\sdot\left[\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\right]}}</math> | |
| − | + | |style="text-align:right;"|כי רביעית חומש הוא תשיעית ב' חומשין ורביע חומש | |
| − | + | |- | |
| − | + | | | |
| − | + | ::Multiply them by four and a half, i.e. take twice of 4 and a half and two-ninths of them. The result is 10 of 5 fifths. We find that each fifth gets two integers and from them you know the part. | |
| − | + | :<math>\scriptstyle{\color{blue}{\left[\frac{6}{7}\sdot\left(5+\frac{1}{4}\right)\right]\div\left[\frac{3}{8}\sdot\left(1+\frac{1}{5}\right)\right]=\left(4+\frac{1}{2}\right)\sdot\left(2+\frac{2}{9}\right)=10}}</math> | |
| − | + | |style="text-align:right;"|תערכם בארבעה וחצי כלו' תקח שני פעמים ד' וחצי ותקח שני תשיעיותיהם יעלה עשרה והם ה' חומשין<br> | |
| − | + | נמצא מגיע שנים שלמים לכל חומש וחומש ומהם תדע חלק אחד שלם | |
| − | + | |- | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | == Chapter Five: Ratios == |
| − | + | !style="width:45%; text-align:right;"|<big>השער החמישי</big> בערך | |
| − | + | |- | |
| − | + | | | |
| − | + | ==== <span style=color:green>Sexagesimal Fractions</span> ==== | |
| − | + | | | |
| − | <math>\ | + | |- |
| − | + | |The method of the astrologers is to calculate all their calculations by sixty, since it has most of the divisors. | |
| − | + | |style="text-align:right;"|דרך חכמי המזלות לחשוב כל חשבונם על ששים מפני שיש לו רוב החלקים | |
| − | + | |- | |
| − | + | | | |
| − | + | *We wish to multiply thirty by twenty and divide by sixty. | |
| − | + | :<math>\scriptstyle\frac{30\sdot20}{60}</math> | |
| − | + | |style="text-align:right;"|רצינו לערוך שלשים על עשרים ולחלק על ששים | |
| − | + | |- | |
| + | | | ||
| + | ::Know the ratio of one number, which is thirty, to sixty, by which we divide; it is its half. Take half the other number; it is ten and this is the result of division. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{30\sdot20}{60}=\frac{30}{60}\sdot20=\frac{1}{2}\sdot20=10}}</math> | ||
| + | |style="text-align:right;"|דע מה ערך החשבון האחד שהוא שלשים <s>על עשרים</s> אל ששים אשר עליו נחלק והוא חציו וקח חצי חשבון ‫<ref>19v</ref>האחר והנה עשרה וככה יצא בחלוק | ||
| + | |- | ||
| + | | | ||
| + | ::Or, know the ratio of twenty to sixty, which is its third. Take a third of the other number; it is ten. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{30\sdot20}{60}=\frac{20}{60}\sdot30=\frac{1}{3}\sdot30=10}}</math> | ||
| + | |style="text-align:right;"|או דע מה ערך עשרים אל ששים והוא שלישיתו תקח שלישית החשבון האחר והנה עשרה | ||
| + | |- | ||
| + | | | ||
| + | *If one number is 50 and the other is 40 and we divide the product by 60. | ||
| + | :<math>\scriptstyle\frac{50\sdot40}{60}</math> | ||
| + | |style="text-align:right;"|ואם החשבון האחד נ' והשני מ' ונחלק העולה על ששים | ||
| + | |- | ||
| + | | | ||
| + | ::Take the ratio of 50 to sixty, which is five-sixths, and as this ratio [take] from forty: from thirty-six take its five-sixths; the result is thirty and four remain. | ||
| + | |style="text-align:right;"|קח ערך נ' אל ששים והוא חמש ששיות וכזה הערך מארבעים והנה מששה ושלשים קח חמש ששיותיו והם שלשים ונשארו ארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply it by five; the result is twenty. | ||
| + | |style="text-align:right;"|ערכם על חמשה עלו עשרים | ||
| + | |- | ||
| + | | | ||
| + | ::Divide this by six; the result is three integers and one-third, which are twenty fractions and the number is 33 and one-third. | ||
| + | |style="text-align:right;"|תחלקם על ששה יצא שלשה שלמים ושליש שהם עשרים שברים והנה המספר ל"ג ושליש | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{50\sdot40}{60}=\frac{50}{60}\sdot40=\frac{5}{6}\sdot40=\left(\frac{5}{6}\sdot36\right)+\left(\frac{5}{6}\sdot4\right)=30+\frac{20}{6}=30+\left(3+\frac{1}{3}\right)=33+\frac{1}{3}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Or, take the ratio of 40 to 60; it is its two-thirds. | ||
| + | |style="text-align:right;"|או קח ערך מ' אל ס' והוא שני שלישיותיו | ||
| + | |- | ||
| + | | | ||
| + | ::Take two-thirds of 50: of 48 it is thirty-two and two remain. | ||
| + | |style="text-align:right;"|קח שני שלישיות נ' והנה מן מ"ח שנים ושלשה ונשארו שנים | ||
| + | |- | ||
| + | | | ||
| + | ::Multiply them by 2, which are the two-thirds, the result is 4. | ||
| + | |style="text-align:right;"|נערכים על שנים שהם שתי שלישיות ועלו ארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::We divide them by three; the result is one and one-third. | ||
| + | |style="text-align:right;"|נחלקם על שלשה יצא אחד ושליש | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{50\sdot40}{60}=\frac{40}{60}\sdot50=\frac{2}{3}\sdot50=\left(\frac{2}{3}\sdot48\right)+\left(\frac{2}{3}\sdot2\right)=32+\frac{4}{6}=32+\left(1+\frac{1}{3}\right)=33+\frac{1}{3}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If the two numbers are not related to sixty, as 14 and 39. | ||
| + | :<math>\scriptstyle\frac{14}{60}\sdot\frac{39}{60}</math> | ||
| + | |style="text-align:right;"|ואם שני חשבונים שאין לאחד מהם ערך אל ששים כמו י"ד ול"ט | ||
| + | |- | ||
| + | | | ||
| + | ::We do as follows: we add one part to 14, its ratio [to sixty] is a quarter. | ||
| + | |style="text-align:right;"|ככה נעשה נוסיף על חשבון י"ד חלק אחד והנה ערכו רביעית | ||
| + | |- | ||
| + | | | ||
| + | ::We add one to 39; its quarter is ten. | ||
| + | |style="text-align:right;"|וככה נוסיף על ל"ט אחד ויהיה רביעיתו עשרה | ||
| + | |- | ||
| + | | | ||
| + | ::We have two subtractive, because we added two: for the one we added to 39, we have to subtract fifteen seconds. We multiply the one we added by 39; the result is 39 seconds. | ||
| + | |style="text-align:right;"|ויש לנו לחסר שני חסרונים כי שנים הוספנו והנה בעבור האחד שהוספנו על ל"ט יש לנו לחסר חמשה עשר שניים ונערוך האחד שהוספנו על ל"ט ויעלו ל"ט שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We add them to the 15 we have; the result is 54. | ||
| + | |style="text-align:right;"|נחברם עם ט"ו שהיו לנו עלו נ"ד | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract them from one prime; the result is 9 primes and 6 seconds. | ||
| + | |style="text-align:right;"|נחסרם מראשון אחד ועלה החשבון ט' ראשונים גם ו' שניים | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{14}{60}\sdot\frac{39}{60}&\scriptstyle=\left(14^\prime\sdot39^\prime\right)+\left(1^\prime\sdot39^\prime\right)-39^{\prime\prime}=\left(15^\prime\sdot39^\prime\right)-39^{\prime\prime}=\left(\frac{1}{4}\sdot39^\prime\right)-39^{\prime\prime}\\&\scriptstyle=\left(\frac{1}{4}\sdot39^\prime\right)+\left(\frac{1}{4}\sdot1^\prime\right)-\left(\frac{1}{4}\sdot1^\prime\right)-39^{\prime\prime}=\left(\frac{1}{4}\sdot40^\prime\right)-15^{\prime\prime}-39^{\prime\prime}\\&\scriptstyle=10^\prime-15^{\prime\prime}-39^{\prime\prime}=10^\prime-54^{\prime\prime}=9^\prime+\left(1^\prime-54^{\prime\prime}\right)=9^\prime+6^{\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Or, we add one to 39. | ||
| + | |style="text-align:right;"|או נוסיף על ל"ט אחד | ||
| + | |- | ||
| + | | | ||
| + | ::Know its ratio to sixty; it is two-thirds. | ||
| + | |style="text-align:right;"|ודע מה ערכו אל ששים והנו שתי שלישיות | ||
| + | |- | ||
| + | | | ||
| + | ::We take two-thirds of fourteen; it is 9', 20'': | ||
| + | |style="text-align:right;"|והנה נקח שתי שלישיות ארבעה עשר והנו ט"כ | ||
| + | |- | ||
| + | | | ||
| + | ::Because, two-thirds of 15 are ten. | ||
| + | |style="text-align:right;"|כי מט"ו יהיו שתי שלישיות עשרה | ||
| + | |- | ||
| + | | | ||
| + | ::We have to subtract two-thirds of one prime, which are 40 seconds, so the number is 9', 20''. | ||
| + | |style="text-align:right;"|ויש לנו לחסר שתי שלישיות ראשון אחד שהם מ' שניים והנה המספר ט"כ | ||
| + | |- | ||
| + | | | ||
| + | ::Since we added one to 39, we multiply it by 14; the result is 14 seconds. | ||
| + | |style="text-align:right;"|ובעבור שהוספנו על ל"ט אחד נערכנו על י"ד ויעלו י"ד שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract them from twenty; you are left with 6 seconds. | ||
| + | |style="text-align:right;"|נחסרם מעשרים נשארו לך ו' שניים | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle\frac{14}{60}\sdot\frac{39}{60}&\scriptstyle=\left(14^\prime\sdot39^\prime\right)+14^{\prime\prime}-14^{\prime\prime}=\left(14^\prime\sdot\frac{2}{3}\right)-14^{\prime\prime}=\left(14^\prime\sdot\frac{2}{3}\right)+\left(1^\prime\sdot\frac{2}{3}\right)-\left(1^\prime\sdot\frac{2}{3}\right)-14^{\prime\prime}\\&\scriptstyle=\left(15^\prime\sdot\frac{2}{3}\right)-\left(1^\prime\sdot\frac{2}{3}\right)-14^{\prime\prime}=10^\prime-\left(1^\prime\sdot\frac{2}{3}\right)-14^{\prime\prime}=10^\prime-40^{\prime\prime}-14^{\prime\prime}\\&\scriptstyle=9^\prime+60^{\prime\prime}-40^{\prime\prime}-14^{\prime\prime}=9^\prime+20^{\prime\prime}-14^{\prime\prime}=9^\prime+6^{\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If we wish to multiply 35 by thirteen, then divide by sixty. | ||
| + | :<math>\scriptstyle\frac{35}{60}\sdot\frac{13}{60}</math> | ||
| + | |style="text-align:right;"|ואם רצינו לערוך ל"ה על שלשה עשר ונחלק על ששים | ||
| + | |- | ||
| + | | | ||
| + | ::We seek for the ratio of twelve, which is close to 13, to sixty; it is its fifth. | ||
| + | |style="text-align:right;"|בקשנו מה ערך שנים עשר שהוא הקרוב אל י"ג אל ששים והוא חמישיתו | ||
| + | |- | ||
| + | | | ||
| + | ::We take a fifth of 35; it is seven. | ||
| + | |style="text-align:right;"|לקחנו חמישית ל"ה והנה שבעה | ||
| + | |- | ||
| + | | | ||
| + | ::One remains; we multiply it by 35 and they are seconds. | ||
| + | |style="text-align:right;"|ונשאר אחד ערכנוהו על ל"ה והנם שניים | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{35}{60}\sdot\frac{13}{60}=\left(35^\prime\sdot13^\prime\right)-35^{\prime\prime}+35^{\prime\prime}=\left(35^\prime\sdot12^\prime\right)+35^{\prime\prime}=\left(35^\prime\sdot\frac{1}{5}\right)+35^{\prime\prime}=7^\prime+35^{\prime\prime}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::The Check: we know that 35 is three-fifths plus one. | ||
| + | |style="text-align:right;"|והבחינה ידענו כי ל"ה שלש חמישיות בתוספת ‫<ref>20r</ref>אחד | ||
| + | |- | ||
| + | | | ||
| + | ::We take 3-fifths of fifteen, which is the number closest to 13; they are 9. | ||
| + | |style="text-align:right;"|לקחנו ג' חמישיות חמשה עשר שהוא המספר הקרוב אל י"ג והיו ט‫' | ||
| + | |- | ||
| + | | | ||
| + | ::We add two, since we had 13, and we multiplied them by 35; it is one [prime] and [twelve] seconds. | ||
| + | |style="text-align:right;"|והוספנו שנים כי י"ג היו לנו ערכנום על ל"ה והוא חלק אחד ועשרה שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We added one at first, because we took thirty-six; they are 15. | ||
| + | |style="text-align:right;"|והוספנו בתחלה אחד כי לקחנו ששה ושלשים והיו ט"ו | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract all from nine; the remainder is the number. | ||
| + | |style="text-align:right;"|חסרנו הכל מתשעה ונשאר החשבון | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle\frac{35}{60}\sdot\frac{13}{60}&\scriptstyle=\left(36^\prime-1^\prime\right)\sdot13^\prime=\left(\frac{3}{5}-1^\prime\right)\sdot13^\prime=\left(\frac{3}{5}\sdot13^\prime\right)-13^{\prime\prime}=\left(\frac{3}{5}\sdot15^\prime\right)-\left(\frac{3}{5}\sdot2^\prime\right)-13^{\prime\prime}\\&\scriptstyle=9^\prime-\left(\frac{3}{5}\sdot2^\prime\right)-13^{\prime\prime}=9^\prime-\left(36^\prime\sdot2^\prime\right)-13^{\prime\prime}=9^\prime-\left(1^\prime+12^{\prime\prime}\right)-13^{\prime\prime}=7^\prime+35^{\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Or, we take a half of 13, for the thirty; they are six and a half, which is thirty seconds. | ||
| + | |style="text-align:right;"|או לקחנו חצי י"ג בעבור השלשים והנם ששה וחצי שהוא שלשים שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply five by 13; the result is one [prime] and five seconds. | ||
| + | |style="text-align:right;"|וערכנו חמשה על י"ג עלה חלק אחד וחמשה שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We add them and the result is the number. | ||
| + | |style="text-align:right;"|חברנום ועלה המספר | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle\frac{35}{60}\sdot\frac{13}{60}&\scriptstyle=\left(30^\prime\sdot13^\prime\right)+\left(5^\prime\sdot13^\prime\right)=\left(30^\prime\sdot\frac{\frac{1}{2}\sdot13}{30}\right)+\left(5^\prime\sdot13^\prime\right)=\left(30^\prime\sdot\frac{6+\frac{1}{2}}{30}\right)+\left(5^\prime\sdot13^\prime\right)\\&\scriptstyle=\left(6+\frac{1}{2}\right)^\prime+\left(5^\prime\sdot13^\prime\right)=6^\prime+30^{\prime\prime}+\left(5^\prime\sdot13^\prime\right)=6^\prime+30^{\prime\prime}+1^\prime+5^{\prime\prime}=7^\prime+35^{\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | *If one of the two numbers is 46 and the other is 25. | ||
| + | :<math>\scriptstyle\frac{46}{60}\sdot\frac{25}{60}</math> | ||
| + | |style="text-align:right;"|ואם שני חשבונים האחד מ"ו והשני כ"ה | ||
| + | |- | ||
| + | | | ||
| + | ::We do not find a ratio of 46 to sixty. | ||
| + | |style="text-align:right;"|והנה לא מצאנו ערך למ"ו עם ששים | ||
| + | |- | ||
| + | | | ||
| + | ::So, we subtract one from the number; 45 remains and its ratio [to sixty] is three-quarters. | ||
| + | |style="text-align:right;"|נחסר אחד מהחשבון ישאר מ"ה וערכו שלש רביעיות | ||
| + | |- | ||
| + | | | ||
| + | ::We take 25 from 24; its three-quarters are 18 and 3-quarters of one remain, which are 45 seconds. | ||
| + | |style="text-align:right;"|ונקח מכ"ה כ"ד ושלש רביעיותיו י"ח נשארו ג' רביעיות אחד שהם מ"ה שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply the one added to 45 by 25; the result is 25. | ||
| + | |style="text-align:right;"|וערכנו האחד שיש תוספת על מ"ה על כ"ה ועלה כ"ה | ||
| + | |- | ||
| + | | | ||
| + | ::We add them to the 45 seconds; the result is one prime and ten seconds remain. The number is 19', 10''. | ||
| + | |style="text-align:right;"|הוספנום על מ"ה שניים שהיו לנו ועלה ראשון אחד ונשארו עשרה שניים והנה החשבון י"ט י‫' | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle\frac{46}{60}\sdot\frac{25}{60}&\scriptstyle=\left(45^\prime\sdot25^\prime\right)+\left(1^\prime\sdot25^\prime\right)=\left(\frac{3}{4}\sdot25^\prime\right)+\left(1^\prime\sdot25^\prime\right)=\left(\frac{3}{4}\sdot24^\prime\right)+\left(\frac{3}{4}\sdot1^\prime\right)+25^{\prime\prime}\\&\scriptstyle=18^\prime+45^{\prime\prime}+25^{\prime\prime}=18^\prime+1^\prime+10^{\prime\prime}=19^\prime+10^{\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Or, we take the ratio of 25 to 60; it is its third and a quarter of its third. | ||
| + | |style="text-align:right;"|או נקח מה ערך כ"ה אל ס' והיו שלישיתו ורביע שלישיתו | ||
| + | |- | ||
| + | | | ||
| + | ::We take from 46 its third, which is 15 [primes] and twenty seconds. | ||
| + | |style="text-align:right;"|נקח ממ"ו שלישיתו שהוא ט"ו ועשרים שניים | ||
| + | |- | ||
| + | | | ||
| + | ::A quarter of 15 [primes] and twenty seconds are three [primes] and 50 [seconds]. | ||
| + | |style="text-align:right;"|ורביעית ט"ו ועשרים שניים הם שלשה וגם נ' שברים | ||
| + | |- | ||
| + | | | ||
| + | ::We add them to the above; the result is 19', 10''. | ||
| + | |style="text-align:right;"|חברנום עם אשר למעלה עלה י"ט י‫' | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle\frac{46}{60}\sdot\frac{25}{60}&\scriptstyle=46^\prime\sdot\left[\frac{1}{3}+\left(\frac{1}{4}\sdot\frac{1}{3}\right)\right]=46^\prime\sdot\frac{1}{3}\sdot\left(1+\frac{1}{4}\right)=\left(15^\prime+20^{\prime\prime}\right)\sdot\left(1+\frac{1}{4}\right)\\&\scriptstyle=\left(15^\prime+20^{\prime\prime}\right)+\left(15^\prime+20^{\prime\prime}\right)\sdot\frac{1}{4}=15^\prime+20^{\prime\prime}+3^\prime+50^{\prime\prime}=19^\prime+10^{\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Or, we subtract one from 25 and we know the ratio of 24 to sixty, which is two-fifths. | ||
| + | |style="text-align:right;"|או נחסר אחד מכ"ה ונדע מה ערך כ"ד אל ששים והנו שתי חמישיות | ||
| + | |- | ||
| + | | | ||
| + | ::Two-fifths of 45 are 18. | ||
| + | |style="text-align:right;"|ושתי חמישיות מ"ה הם י"ח | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply the one that remains to complete the 25 by 45; it is [one] second | ||
| + | |style="text-align:right;"|והאחד שנשאר ל{{#annot:term|1422,598|hmsG}}השלמת{{#annotend:hmsG}} כ"ה נערכנו על מ"ה יהיו שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply the one added by 25 also. | ||
| + | |style="text-align:right;"|גם נערוך האחד שהוא תוספת על כ"ה | ||
| + | |- | ||
| + | | | ||
| + | ::We sum up all the seconds and the result is the number. | ||
| + | |style="text-align:right;"|ונחבר כל השניים ועלה המספר | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>{\color{blue}{\begin{align}\scriptstyle\frac{46}{60}\sdot\frac{25}{60}&\scriptstyle=\left(46^\prime\sdot24^\prime\right)+\left(46^\prime\sdot1^\prime\right)=46^\prime\sdot\left(\frac{2}{5}+1^\prime\right)=\left[45^\prime\sdot\left(\frac{2}{5}+1^\prime\right)\right]+\left[1^\prime\sdot\left(\frac{2}{5}+1^\prime\right)\right]\\&\scriptstyle=18^\prime+45^{\prime\prime}+\left[1^\prime\sdot\left(24^\prime+1^\prime\right)\right]=18^\prime+45^{\prime\prime}+24^{\prime\prime}+1^{\prime\prime}=19^\prime+10^{\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::Or, we add two to 46; the result is 48 and its ratio to sixty is four-fifths. | ||
| + | |style="text-align:right;"|או נוסיף על מ"ו שנים ועלה מ"ח וערכו אל ששים ארבע חמישיות | ||
| + | |- | ||
| + | | | ||
| + | ::We take four-fifths of 25; they are twenty. | ||
| + | |style="text-align:right;"|נקח ארבע חמישיות כ"ה והנם עשרים | ||
| + | |- | ||
| + | | | ||
| + | ::Since we added two, we multiply it by 25; the result is 50 seconds. | ||
| + | |style="text-align:right;"|ואנחנו הוספנו שנים נערכם על כ"ה עלו נ' שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract them from twenty [primes]; 19 remain. | ||
| + | |style="text-align:right;"|נחסרם מעשרים ישאר י"ט | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{46}{60}\sdot\frac{25}{60}=\left(48^\prime\sdot25^\prime\right)-\left(2^\prime\sdot25^\prime\right)=\left(\frac{4}{5}\sdot25^\prime\right)-50^{\prime\prime}=20^\prime-50^{\prime\prime}=19^\prime+10^{\prime\prime}}}</math> | ||
| + | |- | ||
| + | |Always do as follows: find a number that has a ratio to sixty, or an approximate ratio, whether by adding to it, or by subtracting. Take the ratio from that number. Subtract finally if you added at first, or add finally if you subtracted at first. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{60a+n}{60}=a+\frac{n}{60}}}</math> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{60b-m}{60}=b-\frac{m}{60}}}</math> | ||
| + | |style="text-align:right;"|וככה תעשה לעולם שהסתכל איזה חשבון יש לו ערך אל ששים או ערך קרוב אליו בין להוסיף עליו בין לגרוע ומאותו החשבון תקח הערך ואם הוספת בראשונה גרע באחרונה ואם גרעת בראשונה תוסיף ‫<ref>20v</ref>באחרונה | ||
| + | |- | ||
| + | |If one of the numbers is greater than the divisor, or both are greater than it, find the ratio of the divisor to one of the numbers and take its ratio from the other number. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a\sdot b}{60}=\frac{a}{60}\sdot b=\frac{b}{60}\sdot a}}</math> | ||
| + | |style="text-align:right;"|ואם היה אחד החשבונים גדול מ{{#annot:term|2322,604|JrfP}}המחולק עליו{{#annotend:JrfP}} או שניהם גדולים ממנו הסתכל מה ערך חשבון שיחלק עליו אל אחד החשבונים וכערכו קח מן החשבון האחר | ||
| + | |- | ||
| + | | | ||
| + | *As eighty by ninety divided by sixty. | ||
| + | :<math>\scriptstyle\frac{80\sdot90}{60}</math> | ||
| + | |style="text-align:right;"|כגון שמונים על תשעים מחולקים על ששים | ||
| + | |- | ||
| + | | | ||
| + | ::We find the ratio of sixty to eighty; it is one and a third. We add to ninety its third; the result is one hundred and twenty. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{80\sdot90}{60}=\frac{80}{60}\sdot90=\left(1+\frac{1}{3}\right)\sdot90=90+30=120}}</math> | ||
| + | |style="text-align:right;"|נסתכל מה ערך ששים אל שמונים והוא כמהו ושלישיתו ונוסיף על תשעים שלישיתו יעלו מאה ועשרים | ||
| + | |- | ||
| + | | | ||
| + | ::Or, find the ratio of 60 to 90; it is one and a half. We add to 80 its half; the result is 120. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{90\sdot90}{60}=\frac{90}{60}\sdot80=\left(1+\frac{1}{2}\right)\sdot80=80+40=120}}</math> | ||
| + | |style="text-align:right;"|או הסתכל מה ערך ס' אל צ' והוא כמוהו וחציו והנה נוסיף על פ' חציו יעלו ק"כ | ||
| + | |- | ||
| + | | | ||
| + | *If one number is 80 and the other is 88. | ||
| + | :<math>\scriptstyle\frac{80\sdot88}{60}</math> | ||
| + | |style="text-align:right;"|ואם החשבון האחד פ' והשני פ"ח | ||
| + | |- | ||
| + | | | ||
| + | ::We think of it as 90, because it has a ratio to 60; the resulting number is 120. | ||
| + | |style="text-align:right;"|נחשוב שהוא צ' מפני שיש לו ערך אל ס' ויצא החשבון ק"כ | ||
| + | |- | ||
| + | | | ||
| + | ::Since we added two, we relate it to eighty, which is the other number; the result is one hundred and sixty primes, which are two degrees and 40 primes. | ||
| + | |style="text-align:right;"|ובעבור שהוספנו שנים נערכם על שמונים שהוא החשבון האחר יעלו מאה וששים ראשונים והם שתי מעלות מ' ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::Subtract them from 120; the remainder is 117⁰ 20' and this is the number. | ||
| + | |style="text-align:right;"|חסרם מק"כ ישאר קי"ז כ' וככה החשבון | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{80\sdot88}{60}=\frac{90\sdot80}{60}-\frac{2\sdot80}{60}=120-\frac{160}{60}=120-\left(2+\frac{40}{60}\right)=117+\frac{20}{60}}}</math> | ||
| + | |- | ||
| + | | | ||
| − | + | ==== <span style=color:green>Simple Fractions</span> ==== | |
| − | + | | | |
| − | + | |- | |
| − | + | |The geometricians said that there are five kinds of ratios and they are derived from the units and they are: | |
| + | |style="text-align:right;"|וחכמי המדות אמרו שחמשה ערכים הם ונלקחים מן האחדים והם | ||
| + | |- | ||
| + | |The first is the '''multiple ratio''': | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a:\left(n\sdot a\right)}}</math> | ||
| + | |style="text-align:right;"|האחד ערך הכפל | ||
| + | |- | ||
| + | | | ||
| + | :Such as two of three to one. | ||
| + | :<math>\scriptstyle{\color{blue}{1:2;\ 1:3}}</math> | ||
| + | |style="text-align:right;"|כמו שנים או שלשה עם אחד | ||
| + | |- | ||
| + | |The second is the '''superparticular ratio''' [lit. the same and a part]: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a:\left[\left(1+\frac{1}{m}\right)\sdot a\right]}}</math> | ||
| + | |style="text-align:right;"|והשני {{#annot:term|1419,125|Qnb8}}כמוהו וחלק ממנו{{#annotend:Qnb8}} | ||
| + | |- | ||
| + | | | ||
| + | :Such as two to three and this ratio is not found [in smaller numbers]. | ||
| + | :<math>\scriptstyle{\color{blue}{2:3}}</math> | ||
| + | |style="text-align:right;"|כמו שנים עם שלשה וזה הערך לא ימצא קודם זה | ||
| + | |- | ||
| + | |The third is the '''multiple superparticular ratio''': | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a:\left[\left(n+\frac{1}{m}\right)\sdot a\right]}}</math> | ||
| + | |style="text-align:right;"|והשלישי כפלו וחלק ממנו | ||
| + | |- | ||
| + | | | ||
| + | :Such as five to two | ||
| + | :<math>\scriptstyle{\color{blue}{2:5}}</math> | ||
| + | |style="text-align:right;"|כמו חמשה עם שנים גם הוא | ||
| + | |- | ||
| + | |The fourth ratio is the '''superpartient ratio''' [lit. the same and parts]: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a:\left[\left(1+\frac{r}{m}\right)\sdot a\right]}}</math> | ||
| + | |style="text-align:right;"|הערך הרביעי שהוא {{#annot:term|1420,128|eYgJ}}כמוהו וחלקים ממנו{{#annotend:eYgJ}} | ||
| + | |- | ||
| + | | | ||
| + | :Such as five to three | ||
| + | :<math>\scriptstyle{\color{blue}{3:5}}</math> | ||
| + | |style="text-align:right;"|והיו כמו חמשה עם שלשה | ||
| + | |- | ||
| + | |The fifth is the '''multiple superpartient ratio''': | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a:\left[\left(n+\frac{r}{m}\right)\sdot a\right]}}</math> | ||
| + | |style="text-align:right;"|והחמישי שהוא {{#annot:term|1416,131|xtWA}}הכפל וחלקים ממנו{{#annotend:xtWA}} | ||
| + | |- | ||
| + | | | ||
| + | :Which is not found [in numbers smaller] than eight to three. | ||
| + | :<math>\scriptstyle{\color{blue}{3:8}}</math> | ||
| + | |style="text-align:right;"|לא ימצא עד שמונה עם שלשה | ||
| + | |- | ||
| + | |There are no ratios other than these. | ||
| + | |style="text-align:right;"|ואין ערכים אלא אלו | ||
| + | |- | ||
| + | !<span style=color:green>All kinds of ratios are divided into three categories of progressions:</span> | ||
| + | | | ||
| + | |- | ||
| + | |The science of ratio is according to three ways: | ||
| + | |style="text-align:right;"|וחכמת הערכין על שלש דרכים | ||
| + | |- | ||
| + | |<span style=color:green>'''Arithmetic Progression:'''</span> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a_2-a_1=a_3-a_2}}</math> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a_n=a_1+\left(n-1\right)\sdot d}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :One is as four, six, and eight - where the increment is the same and this is the arithmetic progression. | ||
| + | :<math>\scriptstyle{\color{blue}{4,6,8}}</math> | ||
| + | |style="text-align:right;"|האחת כמו ארבעה וששה ושמונה שה{{#annot:term|1207,2412|ZsOM}}תוספת{{#annotend:ZsOM}} היא שוה והוא דרך החשבון | ||
| + | |- | ||
| + | |<span style=color:green>'''Geometric Progression'''</span> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a_2:a_1=a_3:a_2}}</math> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a_n=a_1\sdot q^{n-1}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :The second is as 4, 6, 9 - where the ratio of 6 to 4 is one and its half, and so is the ratio of 9 to 6. | ||
| + | |style="text-align:right;"|והשנית כמו ד' ו' ט' שערך ו' אל ד' כמהו וחציו וככה ערך ט' אל ו‫' | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{9:6:4\longrightarrow q=1+\frac{1}{2}\longrightarrow6:4=\left[4\sdot\left(1+\frac{1}{2}\right)\right]:4=\left[6\sdot\left(1+\frac{1}{2}\right)\right]:6=9:6}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :Or, you can say that the ratio of 4 to 6 is two-thirds and so is 6 to 9. | ||
| + | :<math>\scriptstyle{\color{blue}{4:6:9\longrightarrow q=\frac{2}{3}\longrightarrow4:6=\left(6\sdot\frac{2}{3}\right):6=\left(9\sdot\frac{2}{3}\right):9=6:9}}</math> | ||
| + | |style="text-align:right;"|או תוכל לומ' כי ערך ד' אל ו' שתי שלישיותיו וככה ו' עם ט‫' | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:green>'''Proportional Triad:'''</span> always if we multiply the smallest by the greatest, it is the same as the square of the mean. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a_1}{a_2}=\frac{a_2}{a_3}\longrightarrow a_1\sdot a_3=a_2^2}}</math> | ||
| + | |style="text-align:right;"|ולעולם אם ערכנו קטן על גדול יהיה כמרובע התיכון | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:green>'''Rule of Three:'''</span> likewise, if we take four numbers, such that the ratio of the fourth to the third is the same as the ratio of the second to the first: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a_2}{a_1}=\frac{a_4}{a_3}}}</math> | ||
| + | |style="text-align:right;"|וככה אם לקחנו ארבעה ומספרים שיהיה ערך הרביעי אל השלישי כערך השני אל הראשון | ||
| + | |- | ||
| + | | | ||
| + | :If we multiply the first by the fourth, the product is the same as the product of the second by the third. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a_2}{a_1}=\frac{a_4}{a_3}\longrightarrow a_1\sdot a_4=a_2\sdot a_3}}</math> | ||
| + | |style="text-align:right;"|אם ערכנו הראשון על הרביעי יהיה {{#annot:term|1220,241|1RGU}}המחובר{{#annotend:1RGU}} כמחובר העולה מערך השני על השלישי | ||
| + | |- | ||
| + | |<span style=color:green>'''Harmonic Progression'''</span> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a_2-a_1}{a_3-a_2}=\frac{a_1}{a_3}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :The third is as 3, 4, 6 - where the difference between 3 and 4 is one, whereas between 4 and 6 is two, so the ratio of the differences is double, as the ratio of the smallest to the greatest. | ||
| + | :<math>\scriptstyle{\color{blue}{3:4:6\longrightarrow\frac{4-3}{6-4}=\frac{1}{2}=\frac{3}{2\sdot3}=\frac{3}{6}}}</math> | ||
| + | |style="text-align:right;"|והשלישית כמו ג'ד'ו' שה{{#annot:term|1207,877|uuzM}}תוספת שיש בין{{#annotend:uuzM}} ג' וד' הוא אחד ובין ד' וו' שנים ‫<ref>21r</ref>שערך התוספת היא כפל כערך הקטן אל הגדול | ||
| + | |- | ||
| + | | | ||
| + | *<math>\scriptstyle{\color{OliveGreen}{a_3=\frac{a_1\sdot a_2}{a_1-\left(a_2-a_1\right)}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :If we know two of them, we can extract the third: we multiply 3 by 4; the result is twelve. We subtract from the smallest the difference between it and the second, then divide 12 by the remainder; the result is six. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{3\sdot4}{3-\left(4-3\right)}=\frac{12}{2}=6}}</math> | ||
| + | |style="text-align:right;"|ואם ידענו השנים מהם נוכל להוציא השלישי נערך ג' על ד' עלו שנים עשר ונחסר מן הקטן התוספת שיש בינו ובין השני ועל הנשאר נחלק י"ב יצא ששה | ||
| + | |- | ||
| + | | | ||
| + | *<math>\scriptstyle{\color{OliveGreen}{a_1=\frac{a_2\sdot a_3}{a_3+\left(a_3-a_2\right)}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :Similarly, if we know the second and the third, 4 and 6, and we want to extract the smallest: we multiply 4 by 6; the result is 24. We add to the greatest its excess over the second; the result is eight. We divide 24 by it; the result is three. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{4\sdot6}{6+\left(6-4\right)}=\frac{24}{8}=3}}</math> | ||
| + | |style="text-align:right;"|וכן אם ידענו שהשני והשלישי ד'ו' ורצינו להוציא הקטן נערך ד' על ו' עלו כ"ד ונוסיף על הגדול התוספת שיש לו על השני ועלו שמונה ועליו נחלק כ"ד יעלה שלשה | ||
| + | |- | ||
| + | | | ||
| + | *<math>\scriptstyle{\color{OliveGreen}{a_2=\frac{a_1\sdot a_3}{a_1+a_3}\sdot2}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :If we know the smallest and the greatest, 3 and 6, and we want to know the mean: we multiply 3 by 6; the result is 18. We add the smallest to the greatest; it is nine. We divide eighteen by it; the result is two. We always double the result and this is the mean. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{3\sdot6}{3+6}\sdot2=\frac{18}{9}\sdot2=2\sdot2=4}}</math> | ||
| + | |style="text-align:right;"|ואם ידענו שהקטן והגדול ג'ו' ונרצה לדעת האמצעי נערוך ג' על ו' יעלו י"ח ונחבר הקטן עם הגדול יהיו תשעה ונחלק עליו שמונה עשר יצא שנים ונכפול העולה לעולם וככה האמצעי | ||
| + | |- | ||
| + | | | ||
| + | :Or, we add to the smallest a quarter of the greatest, then divide by it [???]. | ||
| + | |style="text-align:right;"|או נוסיף על הקטן רביעית הגדול ונחלק עליו והיוצא לאחד מהשלמים הוא האמצעי | ||
| + | |- | ||
| + | !<span style=color:green>Instructions for creating a table of arithmetic progressions based on the set of the natural numbers</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :If you wish to extract the multiples from the units, write the sequence of the [natural] numbers from 1 to whichever you want. | ||
| + | |style="text-align:right;"|ואם תרצה להוציא חשבון הכפול מן האחדים תכתוב החשבון מא' ועד כמה שתרצה על סדר החשבון | ||
| + | |- | ||
| + | | | ||
| + | :Write beneath them, starting from 2, then 4, always adding 2 by 2 - this line is double the first correspondingly, as the two rows, the first and the second, in the table. | ||
| + | |style="text-align:right;"|ואחר כך תכתוב תחתיו ותתחיל בב' ואחריו ד' שתוסיף לעולם ב'ב' וזו השטה תהיה כפל מן הראשונה על הסדר כגון שני שטין שבמכבר הראשונה והשניה | ||
| + | |- | ||
| + | | | ||
| + | :If you want to extract the multiples from the units, write their same and a part [= superparticular ratio], which is a half, derived from two and three: write the sequence of the even numbers, starting from two, which is the first of the even numbers. Then, multiply the sequence of the units by three, meaning always add three, as the third row of the table, which is the same and a half of the second row. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{3n=2n+\left(\frac{1}{2}\sdot2n\right)=\left(1+\frac{1}{2}\right)\sdot2n}}</math> | ||
| + | |style="text-align:right;"|ואם תרצה להוציא חשבון הכפל מן האחדים תכתוב החשבון כמוהו וחלק ממנו שהוא חצי היוצא משנים עם שלשה תכתוב הזוגות על הסדר ותתחיל משנים שהם ראש הזוגות ואחר כן תערך האחדים על הסדר על שלשה שתוסיף לעולם שלשה כמו הטור השלישי שבמכבר והוא יהיה כמוהו וחציו אל הטור השני | ||
| + | |- | ||
| + | | | ||
| + | :If you want to extract its double and a part [= double superparticular ratio], which is a half, derived from five to two: write 2 first. Add 2 [by 2] after it, as the second row in the table. Then, multiply the units by 5, as the fifth row of the table, which is double and a half of the second row. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{5n=\left(2\sdot2n\right)+\left(\frac{1}{2}\sdot2n\right)=\left(2+\frac{1}{2}\right)\sdot2n}}</math> | ||
| + | |style="text-align:right;"|ואם תרצה להוציא {{#annot:term|1415,130|gdw0}}כפלו וחלק ממנו{{#annotend:gdw0}} שהוא חצי היוצא מחמשה אל שנים תכתוב ב' בתחלה והוסף בב' אחריה כמו הטור השני שבמכבר ואחר כן תערוך האחדים על ה' כמו הטור החמישי שבמכבר והוא יהיה כפלו וחלק ממנו אל הטור השני | ||
| + | |- | ||
| + | | | ||
| + | :If you want to extract its same and parts [= superpartient ratio], which are two-thirds, derived from five to three: it is as the fifth row of the table to the third row. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{5n=3n+\left(\frac{2}{3}\sdot3n\right)=\left(1+\frac{2}{3}\right)\sdot3n}}</math> | ||
| + | |style="text-align:right;"|ואם תרצה להוציא כמוהו וחלקים ממנו שהם שתי שלישיות היוצא מחמשה אל שלשה הוא כמו הטור החמישי שבמכבר אל הטור השלישי | ||
| + | |- | ||
| + | | | ||
| + | :If you want to extract its double and parts [= double superpartient ratio], which are two-thirds, derived from eight to three: it is as the eighth row to the third row of the table. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{8n=\left(2\sdot3n\right)+\left(\frac{2}{3}\sdot3n\right)=\left(2+\frac{2}{3}\right)\sdot3n}}</math> | ||
| + | |style="text-align:right;"|ואם תרצה להוציא {{#annot:term|1416,131|VTES}}כפלו וחלקים ממנו{{#annotend:VTES}} שהוא שתי שלישיות היוצא משמונה אל שלשה כמו הטור השמיני ‫<ref>21v</ref>אל הטור השלישי שבמכבר הוא | ||
| + | |- | ||
| + | | | ||
| + | *For every number that has a divisor, the divisor counts it by its own multitude, or by the multitude of another divisor. | ||
| + | |style="text-align:right;"|וכל מספר שיש לו {{#annot:term|1259,604|Go1q}}חלק{{#annotend:Go1q}} החלק מונה אותו כמנינו או כמנין חלק אחר | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:green>'''Definition of a square number:'''</span> {{#annot:definition|86,1263|7eUa}}the number whose part counts it by its number is called a square number [<math>\scriptstyle{\color{OliveGreen}{n^2}}</math>], since its one side is equal to its other side, and when you count its side by its multitude the product is the square number. | ||
| + | |style="text-align:right;"|והמספר אשר חלקו מונה אותו כמספרו נקרא מספר מרובע מפני שצלעו האחד שוה לצלעו השני וכשאתה מונה את צלעו כמנינה תקבץ המספר הרבוע{{#annotend:7eUa}} | ||
| + | |- | ||
| + | | | ||
| + | ::Such as the numbers 4, 9, 16 and their like. | ||
| + | |style="text-align:right;"|כמספר ד' וט' וי"ו וכדומה להם | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:green>'''Definition of a plane number:'''</span> {{#annot:definition|83,1456|coqV}}that whose part counts it as the multitude of one of its parts is called a plane number and it has two sides [<math>\scriptstyle{\color{OliveGreen}{a=n\sdot m}}</math>]. | ||
| + | |style="text-align:right;"|ואשר חלקו מונה אותו כמנין אחד מחלקיו נקרא מספר שטוח ויש לו שתי צלעות{{#annotend:coqV}} | ||
| + | |- | ||
| + | | | ||
| + | ::Such as the number 15, whose one side is 3 and the other is 5. | ||
| + | |style="text-align:right;"|כמספר ט"ו אשר צלעו האחת ג' והשנית ה‫' | ||
| + | |- | ||
| + | | | ||
| + | ::When you count its side by the multitude of the other side, the product is the plane number, which is 15. | ||
| + | ::<math>\scriptstyle{\color{blue}{3\sdot5=15}}</math> | ||
| + | |style="text-align:right;"|וכשאתה מונה צלעו כמנין הצלע השנית תקבץ {{#annot:term|83,1456|AcuH}}מספרו השטוח{{#annotend:AcuH}} שהוא ט"ו | ||
| + | |- | ||
| + | | | ||
| + | *<span style=color:green>'''Definition of a prime number:'''</span> {{#annot:definition|76,1457|cltb}}every number that you count by one alone is called a prime number [lit. lengthy number <math>\scriptstyle{\color{OliveGreen}{p=1\sdot p}}</math>], since it has no other side but one, which is not a number. | ||
| + | |style="text-align:right;"|וכל מספר שאתה מונה אותו באחד לבדו נקרא מספר ארוך מפני שאין לו צלע שני כי אם האחד שאינו מספר{{#annotend:cltb}} | ||
| + | |- | ||
| + | |All square numbers are formed successively by the sum of one, which is the first square, with the sequence of the odd numbers. | ||
| + | |style="text-align:right;"|וכל {{#annot:term|86,1263|TMvg}}המספרים המרובעים{{#annotend:TMvg}} נמצאים על סדרם מ{{#annot:term|1211,388|gZOi}}קבוץ{{#annotend:gZOi}} האחד אשר הוא המרובע הראשון עם המספרים הנפרדים על סדרם | ||
| + | |- | ||
| + | | | ||
| + | :Meaning that if you add one, which is the first square, to three, which is the beginning of the odd [numbers], you find the second square, which is 4, whose factor is 2. | ||
| + | :<math>\scriptstyle{\color{blue}{1+3=1^2+3=4=2^2}}</math> | ||
| + | |style="text-align:right;"|וענין זה אם אתה {{#annot:term|1210,178|Mgyh}}מקבץ{{#annotend:Mgyh}} האחד שהוא {{#annot:term|86,1263|jKkY}}המרובע{{#annotend:jKkY}} הראשון אל השלש שהוא תחלת הנפרדים אתה מוצא {{#annot:term|86,1531|JaRl}}הרבוע{{#annotend:JaRl}} השני והוא ד' אשר צלעו ב‫' | ||
| + | |- | ||
| + | | | ||
| + | :If you add the second odd number, which is 5, to the second square, the total is 9, which is the third square, whose factor is 3. | ||
| + | :<math>\scriptstyle{\color{blue}{1+3+5=2^2+5=9=3^2}}</math> | ||
| + | |style="text-align:right;"|ואם אתה מוסיף על מרובע השני {{#annot:term|1336,65|anpd}}המספר הנפרד{{#annotend:anpd}} השני והוא ה' יהיה הכל ט' והוא המרובע השלישי אשר צלעו ג‫' | ||
| + | |- | ||
| + | | | ||
| + | :Also if you add the third odd [number], which is 7, to the third square, the result is the fourth square, which is 16. | ||
| + | :<math>\scriptstyle{\color{blue}{1+3+5+7=3^2+7=16=4^2}}</math> | ||
| + | |style="text-align:right;"|וכן אם אתה מוסיף על המרובע השלישי הנפרד השלישי והוא ז' יצא המרובע הרביעי והוא י"ו | ||
| + | |- | ||
| + | | | ||
| + | :And so on endlessly, you add to the square its corresponding odd number successively, the result is the square that follows it. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{1+3+5+7+\ldots+\left(2n+1\right)=n^2+\left(2n+1\right)=\left(n+1\right)^2}}</math> | ||
| + | |style="text-align:right;"|וכן על הסדר הזה אתה מוסיף על המרובע המספר הנפרד אשר במעלתו יצא המרובע התלוי אליו עד אין סוף | ||
| + | |- | ||
| + | |You find the five different kinds of ratios depend on the equivalence ratio and return to it, when you dissolve their relation, as the odd numbers create the square numbers. | ||
| + | |style="text-align:right;"|וכן אתה מוצא חמשה ערכי המספר אשר הם נחלפים תלויים בערך הישר וחוזרים אליו כשאתה מתיר את קשרם כאשר {{#annot:term|1336,65|S0a2}}המספרים הנפרדים{{#annotend:S0a2}} קושרים את המרובע במספר | ||
| + | |- | ||
| + | |I draw for you a diagram, in which you can see the six different ratios, including the equivalence ratio, arranged with three numbers for each ratio: | ||
| + | |style="text-align:right;"|והנה אני מצייר לך צורה תראה בה שש הערכים אשר הם הנחלפים עם הישר סדורים בשלשה מספרים בכל ערך וערך | ||
| + | |- | ||
| + | | | ||
| + | :If you want to dissolve an inequivalence ratio to the equivalence ratio, you subtract the first number from the second; you are left with three [numbers] that are equal, or proportional by a ratio closer to the equivalence ratio. | ||
| + | |style="text-align:right;"|ואם אתה רוצה להתיר הערך הנחלף אל ישר אתה פוחת ראש מספרו מן השני וישאר בידך שלשה ‫<ref>22r</ref>שהם שוים או {{#annot:term|1405,994|8IsM}}מוערכים{{#annotend:8IsM}} על שרש אחד שהוא קרוב אל השוה | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | {|class="wikitable" style="color: blue; text-align:center; margin-left: auto; margin-right: auto; border: none;" | ||
| + | | 1 | ||
| + | | 1 | ||
| + | | 1 | ||
| + | |Equivalence Ratio | ||
| + | | 1 | ||
| + | |- | ||
| + | | 4 | ||
| + | | 2 | ||
| + | | 1 | ||
| + | |Multiple Ratio | ||
| + | | 2 | ||
| + | |- | ||
| + | | 9 | ||
| + | | 6 | ||
| + | | 4 | ||
| + | |Superparticular Ratio | ||
| + | | 3 | ||
| + | |- | ||
| + | | 21 | ||
| + | | 10 | ||
| + | | 4 | ||
| + | |Multiple Superparticular Ratio | ||
| + | | 4 | ||
| + | |- | ||
| + | | 25 | ||
| + | | 15 | ||
| + | | 9 | ||
| + | |Superpartient Ratio | ||
| + | | 5 | ||
| + | |- | ||
| + | | 64 | ||
| + | | 24 | ||
| + | | 9 | ||
| + | |Multiple Superpartient Ratio | ||
| + | | 6 | ||
| + | |} | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; border: none; text-align:center;" | ||
| + | | א | ||
| + | | א | ||
| + | | א | ||
| + | |ערך ישר | ||
| + | | א | ||
| + | |- | ||
| + | | ד | ||
| + | | ב | ||
| + | | א | ||
| + | | ערך כפל | ||
| + | | ב | ||
| + | |- | ||
| + | | ט | ||
| + | | ו | ||
| + | | ד | ||
| + | | ערך חלק | ||
| + | | ג | ||
| + | |- | ||
| + | | כא | ||
| + | | י | ||
| + | | ד | ||
| + | | {{#annot:term|1415,130|eaey}}כפל וחלק{{#annotend:eaey}} | ||
| + | | ד | ||
| + | |- | ||
| + | | כה | ||
| + | | טו | ||
| + | | ט | ||
| + | | חלקים | ||
| + | | ה | ||
| + | |- | ||
| + | | סד | ||
| + | | כד | ||
| + | | ט | ||
| + | | {{#annot:term|1416,131|3YUC}}כפל וחלקים{{#annotend:3YUC}} | ||
| + | | ו | ||
| + | |} | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | {| class="wikitable" style="text-align:left: auto; margin-left: auto; margin-right: auto; border: none;" | ||
| + | ! <math>\scriptstyle{\color{blue}{\left(4,6,9\right)\longrightarrow\left(1,2,4\right)}}</math> | ||
| + | ! <math>\scriptstyle{\color{blue}{\left(1,2,4\right)\longrightarrow\left(1,1,1\right)}}</math> | ||
| + | |- | ||
| + | | <math>\scriptstyle{\color{OliveGreen}{x_1=a_3-\left[a_2+\left(a_2-a_1\right)\right]}}{\color{blue}{=9-\left[6+\left(6-4\right)\right]=1}}</math> | ||
| + | | <math>\scriptstyle{\color{OliveGreen}{ x_1=a_1}}{\color{blue}{=1}}</math> | ||
| + | |- | ||
| + | | <math>\scriptstyle{\color{OliveGreen}{x_2=a_2-a_1}}{\color{blue}{=6-4=2}}</math> | ||
| + | | <math>\scriptstyle{\color{OliveGreen}{x_2=a_2-a_1}}{\color{blue}{=2-1=1}}</math> | ||
| + | |- | ||
| + | | <math>\scriptstyle{\color{OliveGreen}{x_3=a_1}}{\color{blue}{=4}}</math> | ||
| + | | <math>\scriptstyle{\color{OliveGreen}{x_3=a_3-\left[a_2+\left(a_2-a_1\right)\right]}}{\color{blue}{=4-\left[2+\left(2-1\right)\right]=1}}</math> | ||
| + | |} | ||
| + | |||
| + | |- | ||
| + | | | ||
| + | ::As the superparticular ratio, which is the third level in this diagram, and its numbers are 4, 6, 9: | ||
| + | |style="text-align:right;"|כגון ערך החלק אשר היא המעלה השלישית בצורה הזאת ומספרנו ד' ו' ט‫' | ||
| + | |- | ||
| + | | | ||
| + | ::If you subtract 4 from 6, you are left with 2. | ||
| + | |style="text-align:right;"|אם אתה {{#annot:term|1364,181|BhEN}}פוחת{{#annotend:BhEN}} ד' מן ו' ישארו בידך ב‫' | ||
| + | |- | ||
| + | | | ||
| + | ::If you subtract 1 from 2, then subtract 1 and 2 from 4, which is the greatest number, you are left with one three times and this is the equivalence ratio. | ||
| + | |style="text-align:right;"|ואם אתה פוחת מן ב' א' ואחר כך {{#annot:term|1364,181|fNvT}}תפחות מ{{#annotend:fNvT}}ד' שהוא המספר הגדול א' וב' ישאר לך אחד ג' פעמים והוא הערך הישר | ||
| + | |- | ||
| + | |All ratios return to the equivalence ratio, when you dissolve their relation and inequivalence. | ||
| + | |style="text-align:right;"|והנה כל הערכים כאשר אתה מתיר את קשרם ואת חלופם חוזרים אל ערך הישר | ||
| + | |- | ||
| + | |The sages deduce from this an allusion about the human: if he keeps himself once in the virtues of the ascetics and restrains himself from the passions of the world, the next time will be easier for him until reaching the definition of righteousness that is derived from the image of the one that corresponds the form of the Most High; Who dwells alone; Who is everything and everything is from Him, the beginning of all and the end of all; Who knows everything in particular and in general; to Whom the spirit of everything returns; the Secret of praises and the Reason of | ||
| − | == | + | == Appendix II: Bibliography == |
| − | + | '''Anonymous Textbook''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Manuscripts:''' | |
| − | + | #Budapest, Magyar tudomanyos akademia, MS Kaufmann A 507/2 (IMHM: f 15161), ff. 20-43 (15th-16th century) | |
| − | + | #Genève, Bibliothèque de Genève, MS héb. 10/1 (IMHM: f 2320), ff. 2r-38r (14th-15th century)<br> | |
| − | + | ::[http://www.e-codices.unifr.ch/en/bge/heb0010/1v Ms. heb. 10] | |
| − | + | #Vatican, Biblioteca Apostolica, MS ebr. 171/18 (IMHM: f 8630), f. 104r, line 3 – f. 105v, line 19 (Canea, 1493)<br> | |
| − | + | ::[https://digi.vatlib.it/view/MSS_Vat.ebr.171 Vat.ebr.171]<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <span style=color:blue>The transcript is based mainly on manuscript Genève 10</span> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Bibliography:''' | |
| − | + | *Aradi, Naomi. 2013. An Unknown Medieval Hebrew Anonymous Treatise on Arithmetic, Aleph 13.2, pp. 235-309. | |
| − | + | *Lévy, Tony. 2002. A Newly Discovered Partial Hebrew Version of al-Khwārizmı̄’s Algebra, Aleph 2, pp. 225–34. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 10:58, 30 December 2022
Contents
- 1 Introduction
- 1.1 Presentation of the products of units by nine through the arrangement of the nine digits in a circle
- 1.2 One is not a number
- 1.3 One is a number
- 1.4 The Twelve Names that Form Every Number
- 2 Table of Contents
- 3 Interpolated Excerpt
- 4 Chapter One: Addition
- 5 Chapter Two: Subtraction
- 6 Chapter Three: Multiplication
- 6.1 The First Category: [Multiplication of] Integers by Integers
- 6.2 The Second Category: Multiplication of Integers by Fractions
- 6.3 The Third Category: Multiplication of Fractions by Fractions
- 7 Chapter Four: Division
- 8 Chapter Five: Ratios
- 9 Chapter Six: Deducing One from Another
- 10 Chapter Seven: Conversion of One to the Other
- 11 Chapter Eight: Roots
- 12 Notes
- 13 Apparatus
- 14 Appendix I: Glossary of Terms
- 15 Appendix II: Bibliography
| Praise be to the wonderful Almighty God, | [1]תהלה לאל הנעלה הנפלא |
| Who has no beginning or end, | אשר אין לו תחלה ותכלה |
| Who created His world repeating itself, | ויצר עולמו חוזר חלילה |
| Day and night, | יומם ולילה |
| And put wisdom and knowledge in the human heart, | ושם [בלב] האדם חכמה ודעה |
| To calculate a number from one to nine. | לחשב מספר מאחד ועד תשעה |
Introduction |
|
Presentation of the products of units by nine through the arrangement of the nine digits in a circle |
|
| When you write it on a circle you find it recurrent. | גם הוא [כאשר] תכתבנו בעגולה תמצאנו חוזר חלילה |
|
|
|
כי כאשר תערוך תשעה על תשעה יהיה מספר העולה בין שני צדיו האחדים מצד שמאל והעשרות מצד ימין |
|
וכן על ח' ועל ז' ועל ו' |
|
|
|
אך כאשר תגיע לחמשה יתהפכו העשרות לשמאל והאחדים לימין |
|
ועל זה הדרך על ד' ועל ג' ועל ב' |
|
ואם תערכנו על א' יצא לך ט' בעצמו כי כל חשבון הנערך על א' אין לו תוספת |
| If you write nine on the beginning of the circle, you extract them according to this way, only that it will be vice versa to the right and to the left. | ואם תכתוב תשעה בתחלת העגול תוציאם על זה הדרך רק שיתהפך הדבר לימין ולשמאל |
One is not a number |
|
| If the number is like a circle - the one is like a point. | ואם המספר כעגלה האחד כנקדה |
| For, it is the foundation and the cause of all numbers, but it is not a number - it is the essence of a thing. | כי הוא יסוד וסבת כל מספר ואיננו מספר והוא עצם דבר |
| The similar to this are the words of the language that are the secret of every speaker and the source of every reason, but do not utter any reason. | והדומה לזה תבות הלשון שהם סוד כל מדבר ומוצא כל דבר ואינם משמיעים דבר מעניני הדבר |
| From the categories of number it is clear that the one is not a number, for every number is either even or odd, but one is neither. | וממחלקות המספר יתבאר כי האחד איננו מספר כי כל מספר יתחלק לזוג ולנפרד ולא כן האחד |
One is a number |
|
| From another aspect it is also a number. | ומפאה אחרת גם הוא מספר |
General properties of numbers that apply to one |
|
|
ובו נתחבר כל זוג וכל נפרד |
|
ואם חברנו הנפרדים כאשר הם במערכת זה אחר זה יולדו המרובעים והנה האחד עמהם |
|
וכל מספר מחצית שתי פאותיו |
|
והאחד יעשה בפאה אחת מעשה כל מספר בשתים והנו בדרך כל המספר |
|
יסוד כל מספר על שלש דרכים |
|
האחת באחד להיות הנחבר יותר מהנערך |
|
והשנית בשנים להיותם שוים |
|
והשלישית בשלשה להיות הנערך רב מהמחובר |
|
ומשפט כל מספר אחר השלשה בדרך השלשה |
| So, [from this aspect] one is [considered] with the numbers. | והנה האחד עם כל מספר |
Properties of the numbers 2-10 that pertain to one |
|
The number two |
|
| Two is the beginning of the numbers. | ושנים תחלת המספר |
| It is the root of four.
|
והוא שורש ארבעה |
| As the first root of a square number, it represents the properties of the roots: | |
|
וערך הנחבר מעריכת אחד השרשים על האחר אל המרובע הראשון כערך המרובע השני אל הנחבר הנזכר וככה האחד והנו שרש ומרובע |
|
וכל חשבון אם חברנו השרש עם מרובעו יהיה כעריכת השורש על המספר שהוא שני וככה האחד והנו שרש ומרובע |
|
כל שרש שתכפול מרובעו ותוסיף עליו [2]רביעיתו יהיה מרובע ושרשו כמו השרש הראשון מחובר עם חציו וככה האחד |
The number three |
|
| It represents a special property of the proportional triad: | |
|
שלשה מספרים ערך התיכון אל הראשון כערך האחרון אל התיכון אם ערכנו הראשון על האחרון יהיה כמרובע התיכון |
| [ו]אם הראשון כן יהיה האחרון וככה האחד | |
The number four |
|
| Four is a square number | וארבעה מרובע |
| As the first square number, it represents the properties of the square numbers: | |
|
ובין כל מרובע לכפל כפל המרובע אחד שאיננו מרובע וככה האחד |
|
אם חסרנו מרובע ממרובע הקרוב אליו יהיה הנשאר כשנים השרשים הנחברים וככה האחד |
|
כל חשבון אם ערכנו החשבון שהוא לפניו על החשבון שהוא לאחריו ונוסיף אחד יהיה כמרובע החשבון |
|
כל מרובע שתקח שרשו והחשבון שלפניו ותחסרם ממנו ישאר מרובע |
|
ואם תוסיף עליו שרשו והחשבון שלאחריו יהיה מרובע וככה האחד |
The number five |
|
|
החמשה חשבון עגול כי ימצא בכל חשבונו המרובע הראשון |
The number six |
|
|
גם כן ששה רק ששה ימצא בכל חשבונו ולא מרובעו הראשון |
|
והנה האחד ככה |
The number seven |
|
| Holds the following property: | |
|
אם ערכנו שבעה על עצמו ועל כל מספר שלפניו יהיה הנחבר כמרובע כפלו והנה האחד עמהם |
The number eight |
|
| Eight is a cube number [guf šaveh] | השמונה גוף שוה |
| As the first cube number it represents the following properties of the cube numbers: | |
|
ואם חברנו כל חשבון שהוא גוף שוה כאשר הם בתולדת זה אחר זה יהיה מרובע והנה אחד עמהם |
|
ולעולם ימצא גוף שוה בין שנים מרובעים |
|
כשנחסר מחצי קו הגוף חצי אחד ונערוך הנשאר על הקו נמצא שרש המרובע הקטן |
|
וכאשר נוסיף חצי אחד על חצי הקו ונעריכנו על הקו נמצא שרש המרובע הגדול |
|
ואם תחסר מרובע הקטן ממרובע הגדול נמצא הגוף השוה וככה האחד שהוא גוף שוה |
|
ואם תרצה להוציא המרחק שיש בין שני הגופות שהם זה אחר זה קח מרובע קו הגוף הראשון גם מרובע הקו השני וערוך הקו הראשון על השני וחבר הכל אז תמצא המרחק שיש בין שני הגופות וככה האחד |
The number nine |
|
| Nine is a square number. | התשעה חשבון מרובע |
| As the second square it represents the following properties of square numbers: | |
|
והיתרון שיש בין מרובע אחד ובין מרבע אחר לעולם נפרד |
|
ואם תערוך היתרון שיש בין שני המרובעים על שני השרשים כל אחד בפני עצמו |
|
אם הגדול [5]שני לראשון יהיה כמרובע היתרון |
|
| |
|
אם היה שלישי לו תערוך היוצא מעריכת היתרון על שני השרשים על שנים |
|
| |
|
ואם רביעי לו על שלשה וככה האחד |
|
| |
|
אם חלקנו מרובע הקטן על הגדול או הגדול על הקטן לעולם יהיה כמרובע |
|
וכאשר תחלק תשעה על מרובע שבעה יצא בחלוק שביעית ושתי שביעיות שביעית ושרשו ג' שביעיות |
|
והבחינה שתחשב חלקי האחד שבעים יהיה השביעית ושתי שביעיות י"ב ראשונים ס' שניים תשיב הראשונים לשניים ותחבר השניים עמהם יעלה תשע מאות שניים |
|
אם חלקנו מרובע שבעה על תשעה יצא בחלק חמשה וארבע תשיעיות ושרשם שנים ושלישית כי תשעה שחלקנו עליו קם משרש שלשה וככה האחד |
|
אם תרצה לדעת מרובע שרשו ידוע ממרובע ידוע גם שרשו ידוע ערוך המרחק שהוא בין שני השרשים על כל אחד מהשרשים ואשר יהיה תחברם למרובע הידוע אם היה פחות מהמבוקש |
|
או תחסרם אם היה יתר עליו וככה האחד |
| Approximation method for finding a root of a square number | |
|---|---|
| If you want to know the root of a square, integer or fraction, from the preceding square: | אם תרצה לדעת שרש ממרובע שלם או נשבר מהמרובע שלפניו |
|
כמו שרש תשעה[6] [7]ממרובע שנים |
|
חלק המרובע על כפל השרש יצא בחלוק א' ט"ו חברנום עם השרש ויהיה השורש המיוחד ג' ט"ו |
|
רצינו לתקנו ערכנו א' על עצמו ועם ט"ו והנה א"ל וט"ו על ט"ו וכפלנו העולה כי לעולם נכפול השברים וחלקנו הנחבר על ששים והנה ז"ל |
|
| |
|
|
|
וככה תעשה לכל מרובע שתחלוק היתרון שבין שני המרובעים על כפל השרש הראשון ותשמור היוצא הוסיפנו על השרש ויהיה מיושר |
|
|
|
ואחר כן קח היוצא בחלוק וערוך אותו על עצמו ותכפול מרובע השבר ותחלק הכל על כפל השרש המיושר והיוצא תגרע מהשורש המיושר ישאר השרש מהמרובע הגדול |
|
וכן משפט האחד כי המרחק בינו ובין ארבעה שלשה חלקנום על כפל השרש יצא אחד וחצי |
|
לקחנו מרובע היוצא בחלוק עלה שנים ורביע כפלנו הרביע שהם השברים והנה שנים וחצי |
|
| |
|
כל מרובע שתקח שרשו והחשבון שלפני השרש ותחסרם ממנו ישאר מרובע |
|
ואם תוסיף עליו שרשו והחשבון שלאח' אחריו יהיה מרובע |
|
וככה האחד |
The number ten |
|
| Ten is analogous to one [= as a unit in the rank of tens] | ומספר עשרה דומה לאחד |
| As such it represents the following properties: | |
|
|
|
|
וכאשר תרצה לדעת מרובע תשעה תערכנו על אחד שהוא המרחק ותחסרנו מתשעים הדומה לתשעה והנה שמונים ואחד |
|
וכן כל המספר לפי המרחק וככה האחד |
|
ובעבור היות עשרה דומה לאחד נוכל [8]להוציא המרובעים התמימים והנשברים מהערך שיש לו אל עשרה או אל מאה או אל אלף |
|
כמו ע"ה כמה מרובעו |
|
קח ערכו אל מאה והוא ג' רביעיותיו וכמו כן קח ג' רביעיות ע"ה והם י"ח ושלש רביעיות |
|
| |
|
וככה משפט הנשברים עם האחד |
|
וכל מרובע שהוא אחר העשרה יש מערכת המרובע אליו כערך מרובע אחר טרם העשרה אליו |
|
כמו ששה עשר עם ששה ורביע |
|
שערך י"ו אל עשרה כמוהו וג' חמישיותיו |
|
וכאשר תוסיף על ששה ורביע שלש חמישיותיו שהם ג' מה' יעלה עשרה |
|
| |
|
והשרשים יוכיחו כי זה יתחלק על זה כי כשתחלק עשרה על שרש י"ו יעלה שנים וחצי תערכם על עצמם יעלה ו' ורביע וערך עשרה אליו כערך י"ו אל עשרה |
|
וכן אם תקח מהערך עשרה אל י"ו והוא חמש שמניותיו רצינו להוציא חשבון טרם העשרה שיהיה ה' שמיניות עשרה וככה תמצאנו |
|
ערוך י' על ה' יעלה חמשים חלק על שמונה יצא בחלוק ששה נשארו שנים שהם רביע אחד והם חמש שמיניות עשרה |
|
וכאשר נקח ערך י"ו אל י' והוא כמוהו ושלש חמישיותיו ונוסיף על ששה ורביע שלש חמישיותיו יעלה עשרה |
|
| |
|
וכן תמצא לכל חשבון |
|
וכן שרש שבעה על שבעה עם אחד ושלש שביעיות |
|
וככה כלם |
|
גם כן משרש האחד עם המרובעים לפניו ואחריו |
|
וזה יתברר כרביע אחד ששרשו חצי והנה הם כארבעה ושנים |
|
וכן משפט שברי השברים עד אין קץ |
The uniqueness of one – as mean between the proper fractions and the improper fractions |
|
| The proper fractions before one are the inverses to the improper fractions after one | ובעבור היות השרשים בנשברים שהם טרם האחד הפך הנמצאים אחרי האחד |
| Therefore one has the following properties: | |
|
על כן האחד שורש ומרובע וגוף שוה |
|
ידו בכל ויד כל בו[note 1] והוא ראשית הכל ואחרית הכל |
|
ולא יקבל תוספת ומגרעת |
|
ואין לו דמות במספר |
The Twelve Names that Form Every Number |
|
| The names of all numbers are formed by twelve words: | יסוד כל מספר נכלל בשנים עשר שמות |
|
תשעה מהם חוזרים חלילה והם האחדים מאחד ועד תשעה |
|
והשלשה שמות בונים מעלותיו והם העשרות והמאות והאלפים |
|
[9]כי כל חשבון אשר על האלפים חוזרים חלילה על אלו השמות כמו עשרת אלפים ומאת אלף ואלף אלפי אלפים |
Table of Contents |
|
| The chapters representing the eight arithmetical operations applied to all numbers - integers and fractions: | |
| Every number - integer or fraction - is divided into eight chapters and they are: addition of one to another; subtraction of one from another; multiplication of one by another; division of one by another; ratio of one to another; deducing one from another; conversion of one into another; root of one and another. | וכל מספר השלם והנשבר נחלק לשמנה שערים והם מחברת זה עם זה מגרעת זה מזה מערכת זה על זה מחלוקת זה על זה ערך זה אל זה הוצאת זה מזה השבת זה לזה שורש זה וזה |
Interpolated Excerpt |
||||||||||
| שהיה י"ו ישאר ד' | ||||||||||
| If the scales of the remainder we have to subtract from the greater number are greater than the scales of the greater number, we add 9 to the scales of the greater number and then we subtract. | ואלו היה מאזני הנשאר שיש לנו לחסר מהחשבון הגדול יותר ממאזני החשבון הגדול היינו מוסיפים על מאזני החשבון הגדול ט' ואחר כן היינו מחסרים | |||||||||
|
דמיון אחר בנפרדים | |||||||||
|
נאמר החשבון שמנים אלף ושבעת אלפים ושש מאות וחמשים וארבעה והוא מן הנפרדים | |||||||||
|
והדומה לשמנים אלף הוא שמונה באחדים והמרובע הקרוב שעבר הוא ארבעה ושרשו שנים ובעבור היותו [10]במערכת חמישית הנה השרש מאתים | |||||||||
|
ונסיר המרובע שהוא ד' משמונה שהם שמונים אלף אז ישארו לנו [מ"ז] אלף גם תרנ"ד | |||||||||
|
ונכפול השרש ויהיו ת' | |||||||||
| ||||||||||
|
ונחלק מ"ז עליו ולא נוכל לתת לו עשרה ובעבור שיהיו מאה ויש לנו להסיר מרובעו שהוא עשרת אלפים והנה נתן לו ט' שהם צ' ועלה המספר ל"ו אלפים ונשארו לנו י"א אלף גם תרנ"ד | |||||||||
|
והשרש ר"צ | |||||||||
| ||||||||||
|
ויש לנו להסיר מרובע צ' שהוא ח' אלפים ומאה ונשארו ג' אלפים גם תרנ"ד | |||||||||
|
נכפול השרש והנו חמש מאות ושמנים | |||||||||
| ||||||||||
|
||||||||||
| ||||||||||
|
נחלק החשבון הנשאר עליו ויצא ו' | |||||||||
|
הסר מרובע ששה מהנשאר שהיה ע"ד ונשאר ל"ח | |||||||||
|
והנה השרש רצ"ו ומרובעו פ"ז אלפים תרי"ו | |||||||||
|
ומשקל השרש א' חברנו אותו עם משקל ל"ח שהוא הנשאר יותר מהמרובע שהוא שנים עליו שלשה | |||||||||
|
והנה הסתכל משקל החשבון הראשון שהוא הגדול היה שלשה | |||||||||
|
ועוד בקשנו כמה ל"ח שהוא לחסר והנו שנים חסרנוהו ממשקל החשבון הגדול שהיה ג' ונשאר א' | |||||||||
|
וככה ראוי להיות משקל המרובע גם משקל שרשו ערוך על עצמו וככה הוא | |||||||||
| The three algebraic species: root, square, and number | ||||||||||
| All numbers are divided into three categories, which are: root, square, and a number that is neither root nor square. | וכל המספרים הם נפרדים לשלשה ענינים והם שרש ומרובע ומספר שלא יעשה לא שרש ולא מרובע | |||||||||
| You can extract them from each other: | ואתה יכול להוציאם זה מזה | |||||||||
|
כאמרך מרובע שוה לחמשת שרשיו | |||||||||
|
דע כי שרשו ה' ומרובעו כ"ה | |||||||||
|
וכן שלישית מרובע שוה לחמשת שרשיו | |||||||||
|
דע כי שרשו ה' ומרובעו כ"ה | |||||||||
|
וכן שלישית מרובע שוה לד' שרשיו | |||||||||
|
דע כי המרובע יהיה בו י"ב שרשים והמרובע ד' | |||||||||
| The six canonical equations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Three simple types of equations | ||||||||||
|
והנה ענין אחד הוא מרובע שוה לשרשים | |||||||||
|
והענין השני מרובע שוה למספר | |||||||||
|
כאמרך ה' מרובעים שוים לפ' | |||||||||
|
דע לך כי המרובע האחד הוא חמישית פ' שהוא י"ו | |||||||||
|
וכן חצי מרובע שוה לי"ח | |||||||||
|
דע כי המרובע הוא ל"ו | |||||||||
|
והענין השלישי שרשים שוים למספר | |||||||||
|
כאמרך ט' שרשים שוים פ"א | |||||||||
|
דע המספר [11]הוא המרובע ושרשו ט' | |||||||||
|
וכן חצי שרש שוה לי' | |||||||||
|
השני עשרים והמרובע מאתים | |||||||||
| You can also find three other composite [types of equations] and they are: | וגם תוכל להוציא מזה שלשה ענינים אחרים מורכבים והם | |||||||||
|
מרובע ושרש שניהם שוים למספר | |||||||||
|
או מרובע ומספר שוים לשרשים | |||||||||
|
או שרשים ומספר שוים למרובע | |||||||||
| The first category:
|
הענין הראשון | |||||||||
|
כאמרך מרובע עם עשרת שרשיו מחוברים עלו ל"ט כמה המרובע וכמה השרש | |||||||||
|
קח חצי השרשים וערכם על עצמם יעלה כ"ה | |||||||||
|
הוסיפם על ל"ט יעלה ס"ד | |||||||||
|
הוצא השרש והוא ח' | |||||||||
|
וחסר מהם חצי השרשים שהוא ה' ישאר ג' והוא השרש המבוקש ומרובע ט' | |||||||||
|
| ||||||||||
|
וכן אם יאמר ב' מרובעים או ג' או יותר עם שרשיו כך וכך שוין למספר כך וכך ככה תעשה | |||||||||
|
קח מרובע אחד וכערכו מן המרובעים קח מן השרשים ומן המספר ועשה כמשפט לחצות ולערוך ולהוסיף ולהוציא השרש ולחסר והנשאר יהיה שרש המרובע האחד | |||||||||
|
וכן אם יאמר חצי מרובע או שלישיתו עם גדריו כך שוים למספר כך ככה תעשה | |||||||||
|
השלם המרובע וכערך שהוספת עליו הוסף על השרשים ועל המספר ועשה כמשפט יצא לך שרש המרובע השלם | |||||||||
| The second category:
|
הענין השני | |||||||||
|
מרובע עם כ"א שוים לעשרת שרשי המרובע | |||||||||
|
קח חצי השרשים וערכם על עצמם יהיה כ"ה | |||||||||
|
הוצא מהם המספר שהוא כ"א ישאר ד' | |||||||||
|
ושרשם ב' | |||||||||
|
אם תגרעהו מחצי השרשים שהוא ה' ישאר ג' והוא שרש המרובע | |||||||||
|
| ||||||||||
|
ואם תוסיפהו על חצי השרשים יעלה ח' והוא כמו כן שרש המרובע | |||||||||
|
כשתחברהו עם כ"א ההם יחד יהיו שוים לי' שרשי המרובע | |||||||||
|
ופעמים שאינו יוצא לשני הפנים האלה | |||||||||
| Know that if the product of half [the number of] the roots is less than the number, then the question is wrong.
|
ודע שאם יהיה היוצא מערך חצי השרשים פחות מן המספר שהשאלה משובשת | |||||||||
| If the product is equal to the number, know that the root of the square is half [the number of] the roots mentioned in the question.
|
ואם יהיה היוצא שוה למספר דע כי שרש המרובע הוא חצי השרשים הנזכרים בשאלה | |||||||||
| The third category
|
הענין השלישי | |||||||||
|
כאמרך ג' שרשים וארבעה שוים למרובע | |||||||||
|
קח חצי השרשים וערכם על עצמם יעלה ב' ורביע | |||||||||
|
[12]הוסיפם על המספר שהוא ד' יהיה ו' ורביע | |||||||||
|
ושרשי ב' וחצי | |||||||||
|
הוסף על חצי השרשים שהם אחד וחצי יעלה ד' והוא שרש המרובע | |||||||||
|
| ||||||||||
| ודע כי לעולם כפל כפל המרובע | ||||||||||
Chapter One: Addition |
השער הראשון במחברת |
|---|---|
| It is divided into two categories: | והוא נחלק לשני ענינים |
|
חבור שלמים עם שלמים |
|
וחבור שברי שברים עם שברים |
The First Category: [Addition of] Integers |
הענין הראשון בשלמים |
Sums |
|
| sum of arithmetic progression of consecutive numbers | |
| When you want to sum numbers increasing by progression as much as you wish. | שתרצה לחבר חשבון הולך וגדל על דרך המספר עד כמה שתרצה |
|
אם החשבון מן הנפרדים |
|
ערוך החשבון שהגיע עדיו על חציו בתוספת חצי אחד והעולה הוא המחובר |
|
והמשל שאלה חברנו האחדים על דרך המספר עד י"א כמה הם |
|
התשובה קח חצי המספר האחרון והוסף עליו חצי אחד והנה ו' ערכם על המספר עלה ס"ו וככה המבוקש |
|
|
|
|
ותדענו שתוסיף על י"א אחד ותערוך העולה על חצי י"א וככה המבוקש |
|
ואם החשבון מן הזוגות |
|
ערוך האחרון על חציו והוסף עליו חצי החשבון |
|
והמשל חברנו מא' עד י' |
|
לקחנו חציו והוא ה' ערכנו אותו על י' והוספנו חמשה שהוא חצי י' ועלה נ"ה וככה המבוקש |
|
| |
|
|
|
|
ותדענו שתוסיף אחד על י' והעולה תערוך במחצית הי' |
| sum of arithmetic progression of consecutive even integers | |
| If you add the numbers [two by two] | ואם תוסיף החשבון בב' |
|
ותתחיל בשנים עד י' פעם |
|
|
|
|
ידוע הוא כי האחרון הוא כ' הוסף עליהם ב' והעולה תערוך על חצי הי' והעולה הוא המבוקש והוא ק"י |
|
|
|
|
או קח חצי [13]המספר האחרון והוא י' הוסף חצי ב' והוא י"א ערכם על י' והעולה הוא המבוקש |
|
| |
|
|
|
|
או קח חצי האחרון והוא ה' הוסיף עליהם חצי אחד והערך על האחרון |
| sum of arithmetic progression of consecutive triples | |
| If you add three by three | ואם תוסיף ג"ג |
|
ותתחיל בג' עד י' פעם |
|
|
|
|
ידוע הוא כי החשבון האחרון הוא ל' הוסף עליהם ג' והעולה תערוך על חצי הי' יעלה קס"ה והוא המבוקש |
|
|
|
|
או קח חצי מספר האחרון והוא ט"ו הוסף עליהם חצי ג' והוא י"ו וחצי ערכם על י' והעולה הוא המבוקש |
|
| |
| sum of arithmetic progression of consecutive quadruples | |
| If [you] add four by four | ואם מוסיף ד"ד |
|
קח חצי רביעיתו |
| sum of arithmetic progression of consecutive quintuples | |
| If five by five | ואם ה"ה |
|
קח חצי חמישיתו |
sum of arithmetic progression of consecutive integers when the first number is equal to the excess 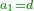
|
|
|
ולעולם תוסיף חצי אחד והערך על האחרון ודרך אחד לכל התוספות |
This sum of progression is true when adding one by one, starting from 1, or for all excesses, [when the first number is the excess itself] 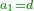
|
וזה חבור המוספים הוא הנכון כשתוסיף א"א תתחיל בא' וכן לכל התוספות תתחיל בחשבונם |
sum of arithmetic progression of consecutive integers when the first number is not equal to the excess 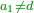
|
|
If you start from 10 and add one by one, or two by two, or three by three, as much as you want, do like this:
|
אך אם תתחיל מי' ותוסיף א"א או ב"ב או ג"ג עד שתרצה ככה תעשה שתוציא לעולם חשבונך מהאחרון כמו שהורתיך למעלה משפט הנפרדים המשפט הזוגות ושמרהו |
|
|
|
ואחר כן אם א"א הוספת עד שהגעת לי"ט והוא מן הנפרדים |
|
וכבר עשית בו משפט הנפרדים אחר כן תפחות א' מן י' וקח מחצית הנשאר וערכם על הי' והעולה תחסר מן השמור שהיה ק"צ והנשאר הוא חשבונך |
|
| |
|
|
|
ואם ב"ב הוספת והיה החשבון האחרון כ' |
|
וכבר הורתיך כמה יעלה והוא ק"י והוא השמור |
|
עכשו חסר ב' מן י' וקח מחצית הנשאר ערכם על מחצית י' והעולה חסר מהשמור והנשאר הוא המחובר מי' עד כ' |
|
|
|
ואם ג"ג הוספת והתחלת בחשבונך מי"ב והיה האחרון ל' אך לא יתכן להתחיל בי' |
|
הוצא חשבונך מן ג' עד האחרון והוא תס"ה ושמרהו |
|
ושוב חסר ג' מי"ב וקח מחצית הנשאר וערכם על שלישית י"ב וחסר העולה מן השמור והנשאר הוא המבוקש |
| Apply this for all the excesses. | וככה תעשה לכל התוספות שתשמר השמות |
| Finding the number of terms in a given sum of multiples | |
| If you want to sum a known number multiplied by the units successively, their [number] is unknown and their sum is so and so, by how many numbers it was multiplied?
|
ואם תרצה לחבר מספר ידוע הספור במספר האחדים על הסדר ואינם ידועים ועלו ככה על כמה מספרים ספר אותו |
|
חלק המספר העולה על המספר שאמר ומה שיצא בחלוק ראה מכמה אחדים יעלה וכמספר האחדים כך [14]מספרים תפש |
|
והמשל ט"ו ערוכים על החשבון על הסדר ועלה המחבר שט"ו על כמה מספרים ספר אותו |
|
חלק שט"ו על ט"ו יצא כ"א |
|
וידענו מהאחדים הספורים מא' ועד ו' הם כ"א |
|
והנה על ששה מספרים ספר אותו והיה המחובר שט"ו |
|
ואם תרצה לדעת כמה המחובר מט"ו ספורים על סדר חשבון מא' ועד ו' |
|
ידענו כי עד ששה יעלה כ"א |
|
וערוך ט"ו על כ"א יעלה שט"ו |
| sum of geometrical progressions of even-times-even numbers | |
| If you want to sum the even-times-even numbers from one to however you wish successively.
|
ואם תרצה לחבר חשבון כפל הכפל מאחד ועד כמה שתרצה על סדר החשבון |
|
|
|
קח מרובע הכפל האמצעי והוא הכפל האחרון אם הכפולים נפרדים וכפול החשבון וחסר ממנו אחד שהוא החלק הראשון והנשאר הוא המחובר |
|
| |
|
והמשל א' ב' ד' |
|
מרובע הב' הוא ד' והוא הכפל האחרון לעולם |
|
ואם הכפולים זוגות |
|
קח מרובע הכפל האמצעי הגדול וחסר ממנו אחד והנשאר הוא המחובר |
|
וכי ירבה ממך דרך[note 2] החשבון שתרצה לדעת מאחד ועד ס"ד כפל הכפל על סדר החשבון ויתקשה עליך להוציא הכפל האמצעי ומרובעו |
|
|
|
ככה תדענו שתתחיל מן השנים וערכם על עצמם והעולה שהוא ד' הוא חשבון שבמדרגה השניה לה וכל החשבון שלפניה כמוה פחות אחד |
|
ושוב וערוך הד' על עצמם יעלה י"ו והוא חשבון שבמדרגה הרביעית לשנית וכל חשבון שלפניה כמוה פחות אחד |
|
ושוב וערוך הי"ו על עצמם יעלה רנ"ו והוא חשבון שבמדרגה השמינית לשניה והחשבון שלפניה כמוה פחות אחד |
|
ושוב וערוך רנ"ו על עצמם יעלה ס"ה אלפים וחמש מאות ושלשים וששה והוא מדרגת י"ו לשניה והחשבון שלפניה כמוה פחות אחד |
|
ושוב וערוך העולה במדרגת י"ו על עצמם ומה שעלה הוא חשבון שבמדרגת ל"ב לשניה והחשבון שלפניה כמוה פחות אחד |
|
ושוב וערוך העולה במדרגת ל"ב ומה שיעלה הוא חשבון שבמדרגת ס"ד והחשבון שלפניה כמוה פחות אחד |
| sum of squares | |
|
|
|
|
ואם תרצה לחבר [15]מרובע אחד ומרובע שנים על דרך החשבון עד מרובע עשרה |
|
ככה תעשה הוסף אחד על עשרה והמחובר תערוך בחצי העשרה יהיו נ"ה ושמרם ואחר כן קח שני שלישי העשרה ותוסיף עליהם שליש אחד יהיה שבעה |
|
| |
|
ואם רצית לחבר מארבעה ואילך עד עשרה |
|
הוצא כל החשבון מאחד ועד עשרה אחר כך חסר האחד מן הארבעה וקח חצי הנשאר וערכהו בארבעה והעולה תערוך בשני שלישי שלשה בתוספת שליש אחד |
|
| |
|
|
|
|
ותדענו שתוציא כל החשבון מא' עד י' ואחר כך הוצא החשבון מא' ועד ג' כל על הדרך שראית והעולה חסר מכל החשבון והנשאר הוא שאלתך |
|
ואם מחמשה ועד עשרה רצית לחבר |
|
הוצא לעולם כל החשבון ואחר כך חסר האחד מן החמשה ומהנשאר קח מחציתם וערכם על החמשה ותערוך העולה בשני שלישי ד' בתוספת שליש אחד לעולם והעולה חסר מן החשבון והנשאר הוא שאלתך |
|
| |
| According to this way for all, keeping the names and the terms. | ועל זה הדרך לכלם שתשמר השמות והמדרגות |
The Second Category: Addition of Fractions |
הענין השני בחבור השברים |
Sexagesimal Fractions |
|
| If you have fractions as the fractions of the astrologers | אם היו בידך שברים כשברי חכמי המזלות |
|
שמחלקים המזל אל שלשים מעלות |
|
והמעלה לששים ראשונים |
|
והראשון לששים שניים |
|
ויהיו ח' מזלות כ"ד מעלה כ"ד ראשונים מ"ד שניים ותרצה לחברם עם ז' מזלות י"ח מעלה מ"ח ראשונים כ"ח שניים |
|
חבר בתחלה השניים והם ע"ב הוסף אחד על הראשונים ישארו י"ב |
|
ושוב חבר הראשונים והם ע"ג הוסף אחד על המעלות ישארו י"ג |
|
ושוב וחבר המעלות והם מ"ג הוסף על אחד על המזלות ישארו י"ג מעלה |
|
ושוב וחבר המזלות והם י"ו הוצא מהם י"ב מזלות שהם חוזרים חלילה |
|
ישארו ד' מזלות י"ג מעלות י"ג ראשונים י"ב שניים |
|
| |
Simple Fractions |
|
| But, the geometricians divide one into a half, a third, a quarter, a fifth, a sixth, a seventh, an eighth, a ninth, and a tenth. | אך חכמי המדות הם מחלקים אחד לחצי ולשליש ולרביע ולחומש ולששית ולשביעית ולשמינית ולתשיעית ולעשירית |
|
ואם תחבר ד' [16]שתותין אל שלשה תשיעיות |
|
בקש חשבון שיהיה לו שתות ותשיעית והוא שתערוך ששה על תשעה יעלה נ"ד והוא המורה |
|
קח ד' שתותין מן המורה והוא ל"ו וחברם אל שלשת תשיעיותיו שהם י"ח יעלה נ"ד והוא אחד שלם |
|
|
|
ותדענו שתדע מאי זה חשבון יצא השתות והוא מששה |
|
קח ד' ששיותיו והוא ד' |
|
וקח ג' תשיעיותיו והוא ב' |
|
חברם וחלקם עליו על ו' יצא אחד |
|
|
|
ותדענו שתדע מאיזה חשבון התשיעית והוא מתשעה |
|
קח ג' תשיעיותיו והוא ג' |
|
וקח ד' ששיותיו והוא ו' |
|
חברם וחלקם על ט' יצא אחד |
|
ואם תחבר ג' שמיניות אל ז' עשיריות |
|
קח המורה והוא שמנים |
|
וג' שמיניותיו הם שלשים חברם אל נ"ו שהם ז' עשיריותיו יעלה ששה ושמונים והוא אחד וששה שמיניות העשירית |
|
| |
|
ואם תחבר ד' שמיניות ושביעית אל ג' ששיות וחמישית |
|
בקש חשבון שיחלק על ארבעת השברים והוא שתערכם זה על זה ויעלה אלף ושש מאות ושמונים והוא המורה |
|
ושמיניתו והוא ר"י |
|
ושביעיתו והוא ר"מ |
|
וששיתו ר"פ |
|
וחמישיתו של"ו |
|
חבר ארבעת שמיניותיו ושביעית שהם אלף ושמנים אל שלשת ששיותיו וחמישית שהם אלף וקע"ו יעלו אלפים רנ"ו והוא אחד וב' שביעיות ורביעית שביעית וחצי רביעית השביעית ועשירית רביעית השביעית |
|
| |
|
ואם תחבר השברים מחצי עד עשירית |
|
בקש חשבון שיהיו לו כל השברים והוא אלפים וחמש מאות ועשרים |
|
וכשתחבר כל השברים יעלה ד' אלפים תתס"א שהם אחד וז' שמיניות וחצי עשירית ושמינית שלישית וחמישית שביעית שמינית |
|
| |
|
ואם תרצה לדעת חשבון שתיתו ורביעיתו היו ה' כמה סך החשבון |
|
הנה המורה הוא כ"ד |
|
קח שתותו ורביעיתו והיו י' חלק עליו המורה יצא שנים וד' עשיריות ערוך היוצא על חמשה יעלה שנים עשר |
|
או ערוך המורה על חמשה והעולה חלק על עשרה [17]עלה שנים עשר |
|
|
|
גם תוכל להוציא מאחד שתקח שתיתו ורביעיתו והוא ב' ששיות וחצי ששית והוא המורה |
|
נחלק עליו אחד יצא שנים ונשאר ששית כלו' נעשה ממנו ששיות ונחלקם בלא שבר על כל ששית וששית |
|
| |
|
ואם תחבר חמישיתו עם שביעיתו ויהיו שנים כמה כל החשבון |
|
ערוך המורה על השנים וחלק על השנים עשר שהם חמשית ושביעית המורה יצא חמשה שלמים וחמש ששיות אחד |
|
או חלק המורה כלו' ל"ה על שנים עשר והיוצא שהוא ג' פחות חצי שתות תערוך על שנים יעלה חמשה וחמש ששיות אחד |
|
|
|
גם תוציאנו מאחד והוא שתקח חמישיתו ושביעיתו ויהיו ב' שביעיות וב' חמישיות השביעית והוא המורה |
|
נחלק עליו אחד יצא בחלוק שנים וישאר שתי שביעיות וחומש שביעית נערכם על שנים והם ארבעה שלמים וד' שביעיות וב' חמישיות השביעית |
|
| |
|
ואם תחבר שלישית רביעית חמישיתו עם שביעית שמינית תשיעיתו ויהיו שנים ותרצה לדעת כמה כל החשבון |
|
בקש חשבון שיהיו לו כל השברים האלה והוא החשבון שיש לו כל החלקים אלפים וחמש מאות ועשרים והוא המורה |
|
ואחר כן קח שלישית רביעית חמישיתו והוא מ"ב וחברהו עם שביעית שמינית תשיעיתו שהוא ה' יהיה הכל מ"ז וחלק עליו המורה יצא חמשים ושלשה וישאר כ"ט |
|
| |
|
או כפול המורה וחלק על מ"ז יצא ק"ז וישאר י"א כמו [18]הענין האחר |
|
| |
|
ובחינתו שתערוך ק"ז על מ"ז ותחבר עם העולה הי"א יהיה הכל חמשת אלפים וארבעים |
|
וכשתקח שלישית רביעית חמישיתו יהיה פ"ד והוא אחד שלם ול"ז חלקים ממ"ז באחד |
|
וכשתקח שביעית שמינית תשיעיתו יהיה עשרה חלקים ממ"ז באחד |
|
חברם עם הל"ז והנה אחד שלם |
Chapter Two: Subtraction |
השער השני במגרעת |
|---|---|
| It is divided into two categories: | והוא נחלק לשני ענינים |
|
מגרעת שלמים משלמים |
|
ומגרעת שברים משברים |
The First Category: [Subtraction] of Integers |
הענין הראשון בשלמים |
| When you wish to know a number that is subtracted repeatedly by the succession of the [natural] numbers, one by one, or two by two, or three by three, from ten to one, the way to extract it is the same as explained for addition, so there is no need to elaborate on that. | שתרצה לדעת חשבון הולך הלוך וחסור על דרך המספר אחד אחד או שנים שנים או שלשה שלשה מעשרה ועד אחד הדרך להוציאו שוה כמו שפרשתי בחבור ואין צורך להאריך בו |
The Second Category: Subtraction of Fractions from Fractions |
הענין השני מגרעת שברים משברים |
Sexagesimal Fractions |
|
| If you have fractions of the astrologers. | ואם שברי חכמי המזלות יהיו בידך |
|
כמו ב' מזלות כ' מעלות מ' ראשונים ומ' שניים ותרצה לגרוע מהם חשבון אחד ולדעת הנשאר כמו א' מזלות י' מעלה מ"ה ראשונים ל' שניים |
|
אתה מתחיל בשניים וישארו י' שניים |
|
ושוב הראשונים מהראשונים ולא תוכל לגרוע הרב מהמעט [..] ומפני זה קח מהמעלות מעלה אחת תהיה ס' ראשונים ותחברם עם הראשונים וגרע מהם מ"ה ראשונים ישארו נ"ה ראשונים |
|
ושוב וגרע המעלות מהמעלות וישארו ט' מעלות |
|
ושוב וגרע מזל אחד מהב' מזלות |
|
ישאר א' ט' נ"ה י' |
|
| |
| If the signs of the subtrahend excceed the minuend signs, you add to them 12 signs, which are the cyclic zodiac signs, then you subtract from the sum and keep the remainder: signs, degrees, minutes and seconds. | ואם מזלות חשבון הנגרעים עודפים על המזלות שאתה גורע ממנו ולא לגרוע אתה מוסיף עליהם י"ב מזלות שהם מזלות הגלגל שהם חוזרים חלילה ומן הנאסף תגרע ותשמור הנשאר בידך מזלות מעלות ראשונים ושניים |
Simple Fractions |
|
| If you have fractions of the geometricians. | ואם שברי חכמי המדות יהיו בידך |
|
כמו שתרצה לגרוע מעשרה ששיתו ורביעיתו ולדעת הנשאר |
|
בקש חשבון שיהיה לו ששית ורביעית והוא י"ב והוא המורה |
|
גרע ממנו ששיתו ורביעיתו ישאר ז' |
|
ודע ערכם [19]והוא חציו וכזה הערך קח מן העשרה והוא חמשה שתותין |
|
או קח מהערך עשרה אל י"ב והוא ה' ששיותיו וקח כזה הערך מן השבעה והוא ה' וה' שתותין |
|
ואם תרצה לגרוע ג' רביעיות אחד מן ד' חומשין ולדעת כמה הנשאר |
|
דע מאיזה חשבון החומש והוא מחמשה |
|
קח ד' חומשין והוא ד' ואחר כך ג' רביעיות החמשה והוא ג' וג' רביעיות תחסרם מן הד' ישאר רביע |
|
ודע מה ערך הרובע מן הה' והוא חצי עשירית |
|
או נקח מן המורה שהוא עשרים ג' רביעיותיו והם ט"ו וגרעם מד' חומשיו שהם י"ו ישאר אחד שהוא חצי עשירית וככה השאר |
|
ואם תרצה לגרוע ארבע חומשיו מן ה' שתותין וג' רביעיות ולדעת הנשאר |
|
בקש חשבון שיהיה לו חומש ושתות והוא שלשים |
|
קח ארבע חמישיות והם כ"ד ותגרעם מחמשה שתותיו ומשלש רביעיותיו שהם מ"ז וחצי יהיה הנשאר כ"ג וחצי |
|
| |
|
ודע ערכם משלשים והוא ז' עשיריות וחצי השתות |
|
ואם תגרע שלישיתו וריביעיתו ונשאר שמונה ותרצה לדעת כמה היה כל החשבון |
|
קח המורה והוא י"ב |
|
וגרע ממנו שלישיתו ורביעיתו ישאר חמשה |
|
חלק עליו המורה יצא ב' וב' חומשין ערכם בשמונה יעלה י"ט וחומש |
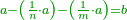
|
|
| According to this way for every remaining number, whether two, or three, or whichever number that remains: extract the denominator, subtract from it the subtracted parts - whether sixths, or fifths, or quarters, or whichever is subtracted - then divide the denominator by the remainder and multiply by the stated remainder.
|
ועל זה הדרך לכל חשבון שישאר שנים או שלשה או איזה חשבון שישאר שתוציא המורה ותגרע ממנו הערכים שגרע הן שתותין או חמישיות או רביעיות או כל מה שגרע ועל הנשאר תחלק המורה והיוצא תערוך בנשאר שאמר |
| Or, divide the stated remainder by what remains from the denominator, after subtracting the subtracted from it, then multiply the result by the denominator. It is the same thing.
|
או חלק הנשאר שאמר על מה שישאר מן המורה כשתוציא ממנו מה שגרע והיוצא תערוך על המורה והדבר שוה |
|
ואם תגרע חמישיתו ומהנותר שביעיתו ונשאר כ"ד כמה היה הכל |
|
דע המורה והוא ל"ה |
|
וערכהו על הנשאר כלומ' כמשפט אשר הזכיר למעלה יצא ל"ה והוא המבוקש |
| This way is correct when the [unknown] number is equal to the denominator like this.
|
וזה הדרך הוא נכון כשיהיו סך החשבון והמורה שוים כמו זה |
|
וכמו אם יקח ל' ויחסר חמישיתו ומן הנותר ששית וישאר עשרים שהחשבון והמורה שוים |
|
| |
| For every number like this, the denominator leads you to the truth. | ובכל חשבון כאלו יוציאך המורה אל האמת |
|
|
|
|
אך אם יקח כ"ה ויגרע חמישיתו ומן הנשאר שביעיתו וישאר י"ז ושביעית שהמורה והחשבון אינם [20]שוים |
|
| |
| For every number such as this if "your eyes shall see thy Teacher and your ears shall hear a word from behind thee... This is the way; walk in it" [Isaiah 30, 20-21]. | ובכל חשבון כיוצא בו אם יהיו עיניך רואות את מוריך אזניך תשמענה דבר מאחריך זה הדרך תלכו בה[note 3] |
|
והדרך לכל חשבון שתבקש חשבון שיהיה לו שביעיות אחרי שתגרע ממנו חמישית |
|
כגון ל"ה שחומשו ז' וישאר כ"ח |
|
| |
|
וישאר כ"ד |
|
ודע מה ערך י"א אל והוא רביעית וה' ששיות רביעית |
|
וכזה הערך קח מי"ז ושביעית שהוא הנשאר והיוצא שהוא ז' ועוד ו' שביעיות |
|
הוסף על י"ז ושביעית יעלה כ"ה והוא מה ששאלת |
| Know it by maintaining the degrees of the fractions and adding one degree to each fraction.
|
ותדענו שתשמור מדרגות השברים ותוסיף על כל שבר ושבר מדרגה אחת |
|
וכן תעשה קח הנשאר והוסף ששיתו שהוא נוסף מדרגה אחת מן השביעית שאמר באחרונה ועל המחובר תוסיף רביעית המחובר שהוא עודף מדרגה אחת על החמישית שאמ' בתחלה והמחובר הוא המבוקש |
|
| |
|
ואם תקח שני חשבונות שאין האחד שוה לחברו ותגרע חמישית האחד משלישית האחר וישארו ששה ותרצה לדעת כמה היה כל אחד ואחד מהחשבונות |
|
בקש חשבון שיהיה לו חמישית ושלישית והוא ט"ו והוא המורה |
|
וקח חמישיתו והוא שלשה והוסף על הששה ויהיה ט' ותערכם על השלשה ויעלה כ"ז וזה הוא החשבון שגרעת ממנו ואחר שידעת זה תוכל להוציא החשבון הנגרע שהוא ט"ו אחרי שחמישיתו שלשה |
| This way is not a general way for every number "and your Teacher shall no longer hide Himself" [Isaiah 30, 20], except when one number is equal to the denominator, such as this and the like, but if none is equal to the denominator it does not apply. | וזה הדרך אינו דרך כלל לכל חשבון ולא יכנף עוד מוריך[note 4] זולתי כשיהיה החשבון האחד שוה למורה כגון זה וכיוצא בו אך אם לא ישוו המורה אל יורה |
|
כגון שהיה האחד י' והשני כ"ד וכשתגרע חמישית עשרה משלישית כ"ד ישאר ששה |
|
ואם תביט אל המורה יוציאך אל כ"ז ואל ט"ו וזה החשבון יודיע אם החשבון האחד ידוע |
|
כמו שיאמר האחד עשרה גרעונו חמישיתו משלישית חשבון שאינו ידוע ונשאר ששה כמה החשבון שאינו ידוע |
|
הדרך בו ולכל חשבון שתוסיף חמישית [21]הידוע על הנשאר והמחובר תערך על שלשה בעבור כי שלישית יוצאת משלשה והעולה הוא החשבון שאינו ידוע |
| You can also extract the two numbers. | וגם תוכל להוציא שני החשבונות |
|
אם יאמר כאשר גרענו חמישית האחד משלישית האחר נשאר ו' חברנום יעלו עשרה |
|
הדרך בזה שתחסר הנשאר מהמחובר ומן הנותר קח המחצית וככה מספר החמישית שגרע |
|
ואחר שידעת חמישיתו ידעת כלו ומן האחד תוציא השני |
| According to this way for every number. | ועל זה הדרך לכל חשבון |
|
שאם יאמר אם גרענו רביעית האחד מחמישית האחר נשאר אחד ואם חברנום יעלו י"א |
|
ככה תעשה גרע אחד מי"א ונשאר עשרה קח מחציתם והוא מספר הרביעית שגרע |
|
מתברר שהחשבון האחד הוא עשרים וממנו תוכל להוציא השני והוא שלשים |
| This way will lead you to the truth and to the correct. | וזה הדרך ידריכך אל האמת ואל הנכון |
Chapter Three: Multiplication |
השער השלישי במערכת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| It is divided into three categories: | ונחלק לשלשה ענינים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מערכת שלמים על שלמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומערכת שלמים על שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומערכת שברים על שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The First Category: [Multiplication of] Integers by Integers |
הענין הראשון בשלמים על שלמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You should know that every number is built and established on ten ranks: | יש לך לדעת כי כל חשבון יבנה ויכונן בעשרה מדרגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה הראשונה הם האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשניה העשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשלישית המאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והרביעית האלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והחמישית העשרות אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והששית במאות אלף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשביעית באלף אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשמינית עשרת אלפי אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והתשיעית במאת אלף אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והעשירית באלף אלפי אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on endlessly. | וכן עד אין קץ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of the multiplication operation: the multiplication of a number by a number is that you count the first number by the multitude of the second number. | ומערכת מספר על מספר הוא שתהיה מונה המספר האחד במנין המספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiplication of units by units | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכל מספר שאתה עורך אותו באחד הוא עומד ואינו נוסף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואכן אם תערוך אחד על אחד הוא אחד ושנים על אחד הם שנים וכן כל מספר שתערכנו על אחד אינו נוסף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך שנים על שנים אתה כופל אותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם בשלשה תערכנו תמצאנו שלשה מן המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן עד עשרה שאם תערכנו על [22]עצמו יהיו מאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you multiply a number by a number that are greater than ten, you should master the multiplication of units, for every number is calculated this way. | ואם תרצה לערוך מספר על מספר למעלה מעשרה אתה צריך שיהיה חשבון האחדים סדורים על פיך כי כל חשבון מתחשב על זה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Full multiplication table: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| To make it easier for the reader, I have drawn a table for you from 1 to 10, by which you may find out every number. | ולהקל על הקורא ציירתי לך זה המכבר מא' ועד י' שתברור לך בו כל חשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Instructions for using the multiplication table: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תרצה לערוך חשבון על חשבון מא' ועד י' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שתרצה לערוך ח' על ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אתה נותן אצבעותיך בשני הטורים הראשונים אשר כתוב בהם מא' ועד י' על הסדר האצבע האחד על ח' ואצבעך השני על ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן לכל החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תרצה לחשוב משאר המדרגות אחת על אחת יחשוב אותם כאלו הם אחדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שתרצה שש מאות על ארבעת אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מאיזה חשבון הם המאות מששה והאלפים מארבעה ערוך ששה על ארבעה כאלו הם אחדים והם כ"ד ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך קח מדרגת המאות והוא שלשה ומנה מהאלפים ולמעלה ג' מדרגות והוא מדרגה הששית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם תקח מדרגת האלפים והוא ארבעה ותמנה אתו מן המאות ולמעלה אתה מגיע אל המדרגה הששית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושים שם חשבון האחדים ששמרת והעשרות במדרגה אשר אחריה והיא השביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומפני זה אתה אומר כי הכ"ד ששמרת הם ב' אלפי אלפים וארבע מאות אלף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דרך אחרת שתהיה חושב מדרגות בב' חשבונות ותפחות אחד מהם והנשאר יהיה מדרגת המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שתקח מדרגת המאות והוא שלשה ומדרגת האלפים ארבעה תחברם יהיו שבעה תחסר מהם אחד לעולם וישארו בידך ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והטעם שאתה מחסר משתי המדרגות בהתקבצם מפני שמדרגת האחד עולה לכאן ולכאן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך אחדים ועשרות על אחדים ועשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו כ"ה על כ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מה ערך כ"ה ממאה והוא רובע קח רובע כ"ח והוא ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך נ"ד בס"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מה ערך החמשים ממאה והוא חצי קח חצי מספר ששה וששים יהיו ל"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך קכ"ה על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מה ערכו מאלף והיא שמינית קח שמינית קכ"ה והוא ט"ו וחמשה שמיניות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך אחדים על עשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו חמשה על שבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערוך חמשה על שבעה יעלה ל"ה יהיו העשרות מאות והאחדים עשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם תדענו שתחשוב מהו חמשה מעשרה והוא חציו קח מחצית השבעים והוא ל"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או תדענו שתחשוב מהו השבעים ממאה והוא שבע עשיריות קח שבע עשיריות מחמשה והוא ג' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך אחדים על מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו חמשה על שלש מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערוך חמשה על ג' יעלה ט"ו יהיו העשרות אלפים והאחדים מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתחשב מהו חמשה ממאה והוא חצי עשיריות קח חצי עשירית של ג' מאות והוא ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתחלק הג' מאות על מאה ותערוך היוצא על חמשה יעלה ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך עשרות על עשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו כ' על ל' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערוך שנים על שלשה יהיו ששה האחדים יהיו מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתחשוב מהו כ' ממאה וקח ערכו מל' ומה שיהיה תערכנו במאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או תדע מה שהם הל' ממאה וקח ערכו מן עשרים והדבר שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך עשרות על מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו מ' בשש מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערוך ד' על [24]ששה יעלה כ"ד יהיו האחדים אלפים והעשרות עשרות אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתחשב מהן ו' מאות מאלף והוא ו' עשיריות קח זה הערך ממ' יעלה כ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או תדע מהן הארבעים מאלף חלק אחד מן כ"ה וכערכו קח משש מאות והדבר שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך עשרות על אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו נ' בז' אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וערוך ה' על זה שבעה יעלה ל"ה יהיו האחדים עשרות אלפים והעשרות מאות אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתחשב מהן ז' אלפים מי' אלפים וקח אותו הערוך מחמשים והוא ל"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או תדע מהם הנ' מי' אלפים וכערכו קח מן הז' אלפים והדבר שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| By these ways you can know every number endlessly, keeping the names and the ranks. | ועל אלו הדרכים תוכל לדעת כל חשבון עד אין קץ שתשמר השמות והמדרגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The Second Category: Multiplication of Integers by Fractions |
הענין השני מערכת שלמים על שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sexagesimal Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you have fractions of the astrologers: degrees, minutes and seconds | אם יהיו בידך שברי חכמי המזלות מעלות ראשונים ושניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם אתה עורך מעלות על מעל[ו]ת יהיה הנקבץ מעלות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם אתה עורך מעלות על שברים יהיה הנקבץ שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם ערכת על ראשונים הם ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם על שניים הם שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם על שלישיים הם שלישיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן למעלה מהם לכל השברים הנערכים על מעלות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שתרצה לערוך כ' מעלות על נ' ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יעלו אלף והם ראשונים תחלקם על ששים יצא בחלוק י"ו וישאר מ' ראשונים והוא ה' ששיותיו וכאותו הערך קח מן הב' יהיו י"ו מעלות מ' ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| According to this calculate the seconds, thirds and all the fractions endlessly. | ועל זה תחשב לשניים ולשלישיים ולכל השברים עד אין קץ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Since the calculation of the integers that are multiplied by fractions is decreasing. | כי כל חשבון השלמים הנערכים בשברים הוא פחות פוחת והולך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והאומר חשוב עשרה בשליש או ברביע דומה כמי שאומר כמה חלק שליש או רביע מהעשרה וכן לכל השברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Integers by integers and fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Simple Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you have fractions of the geometricians and you wish to multiply integers by integers and fractions. | ואם יהיו בידך שברי חכמי המדות ותרצה לערוך שלמים על שלמים ושברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שנים על שלשה ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נבקש חשבון שיש לו שלישית ורביעית והוא שנים עשר והוא המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותקח לכל אחד שלם י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והם כ"ד בחשבון האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[25]והחשבון השני השלשה יעלו ל"ו הוסף עליהם ג' בעבור הרביע יעלו ל"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונערוך כ"ד על ל"ט יעלו תתקל"ו חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על קמ"ד שהוא מרובע המורה יצא ששה ונשארו ע"ב שהוא חצי קמ"ד והנה ששה וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתעזב השניים כמו שהם שנים ובעבור שבר הרביעית וקח לכל אחד מן השלשה ארבעה יעלו י"ב נוסיף אחד בעבור הרביעית הנה י"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתקח מה שיצא ממנו הרביע והוא ארבעה והוא המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נערוך שנים על ד' יעלו שמונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושלשה על ד' יעלו י"ב ועם הרביעית י"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכם זה על זה יצא ק"ד וחלק על מרובע המורה שהוא י"ו יצא ששה וישאר שמונה שהוא חצי אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתערך שנים על שלשה עלה ששה וישוב ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וערוך על שנים על רביעית עלה שנים רביעיות שהוא חצי וזה יהיה שמור בידך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For the one when it is multiplied by a fraction is the same [as the fraction]. 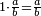
|
כי האחד הנערך על שבר הרי הוא כמוהו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| It is like saying one in length by one-half in width, which is really nothing but one-half. The same by one-third and by all fractions. | ודומה כמי שאומר אחד באורך על חצי ברוחב וזה באמת אינו כי אם חציו וכן על שליש ועל כל השברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Integers by fractions fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you multiply integers by fractions | ואם תערוך שלמים על שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Simple Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שלשה רביעיות בתשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מאיזה מספר הרביעיות והוא מארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלק התשעה עליהם יצא לכל אחד שנים ורובע ערוך היוצא על שלשה יהיה ששה וג' רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו מאיזה מספר הרביעית והוא מארבעה והוא המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נערוך התשעה על ארבעה יעלה ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונערכם על שלשה בעבור הרביעיות שהם שלשה יעלה ק"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על י"ו שהוא מרובע המורה יצא ששה שלמים וישארו י"ב שהם ג' רביעיות אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Integers and fractions by integers and fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you multiply integers and fractions by integers and fractions | ואם תערוך שלמים ושברים על שלמים ושברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Simple Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שלשה ושביעית על חמשה ושמינית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
בקש חשבון שיש לו שני השברים כלומ' שביעית ושמינית והוא נ"ו והוא המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונערוך החשבון האחד שהוא שלשה על המורה ויעלה קס"ח ונוסיף עליו ח' בעבור השביעית ועלה קע"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד [26]נערוך החשבון האחד שהוא חמשה על המורה יעלה ר"פ ובעבור השמינית נוסיף שבעה והנה רפ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נערוך קע"ו על רפ"ז עלה חמשים אלף וחמש מאות ושנים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקנום על שלשת אלפים ומאה ושלשים ושש שהוא מרובע המורה יצא בחלוק ששה עשר ונשארו של"ו והם שלש רביעיות שביעית אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שהאחד הוא מרובע המורה שהם ושביעיתו הם באותיות הודו ובאותיותנו הם ת'מ'ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתקח לשלשה שיש עמהם שמינית ארבעים והוסף אחד הנה מ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכנום זה על זה עלו תשע מאות ושנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקנום על נ"ו שהוא ערך שבעה על שמונה ויצא י"ו ונשארו ו' שהם שלש רביעיות שביעית אחד כי שביעית נ"ו הם ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתערוך שלשה על חמשה עלה ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד תערוך ג' על שמינית עלה ג' שמיניות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחמשה על שביעית הנה חמש שביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחשוב שהם שמיניות ונחברם עם השלש עלה אחד שלם ונשאר מיתרון השביעית על השמינית חמש שמיניות שביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד יש לך לערוך שביעית על שמינית והוא שביעית שמינית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחברם עם החמש שיש לך והנה שש שמיניות שביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| All of these ways yield the same. | וכל הדרכים יצאו שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sexagesimal Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For the way of the astrologers, as sixty is indivisible by seven nor by eight, do as follows: | ולדרך חכמי המזלות שלא יחלקו ששים על שבעה ולא על שמונה ככה תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שתעשה מן מעלה אחת נ"ו ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומראשון נ"ו שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
בעבור שנ"ו יש להם שביעית ושמינית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יש לך לערוך שלשה מעלות וח' ראשונים שהם שביעית נ"ו על חמשה מעלות ז' ראשונים שהם שמינית נ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תערוך ג' על ה' שהם מעלות עלה ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותערוך השלשה שלמים על שבעה ראשונים ועלה כ"א ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן תערוך ח' על ה' שלמים יעלה מ' ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונערוך ח' ראשונים על ז' ראשונים יעלה נ"ו שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נחלק השניים על נ"ו עלה ראשון אשר חברנו עם הראשונים והנה ס"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נעשה מהם מעלה אחת מנ"ו עלה שש עשרה מעלות ונשארו ו' ראשונים [27]שהם ג' רביעיות משביעית נ"ו במעלה אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Integers and fractions by integers and fractions of fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you multiply integers and fractions by integers and fractions of fractions | ואם תערוך שלמים ושברים על שלמים ושברי שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Simple Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שלשה ורביעית על חמשה וששית שביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח חשבון שיש לו ששית ושביעית והוא מ"ב גם נערכנו על הארבעה בעבור הרביעית יעלו קס"ח והוא המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשב כל השלמים על המורה ותחבר השברים עם כל אחד מהחשבונות והעולה תערוך זה על זה ותחלק על מרובע המורה והיוצא בחלוק הם שלמים והנשאר הם חלקים מהמורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתערך ג' על ה' והוא ט"ו שלמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותערוך שלשה על ששית שביעית והוא ג' ששיות שביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שתמצא כל השברים שצריכים לזה החשבון קח פ"ד שיש לו ששית ושביעית ורביעית והוא המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ורביעיתו כ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושביעיתו י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וששיתו י"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה ג' ששיות שביעית שיצאו בערך הם ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושוב וערוך רביעית על ה' והם רביעיות שהם ק"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושוב וערוך רביעית על ששית שביעית והוא חצי אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תחברם יעלה קי"א וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח מהם אחד שלם שהוא פ"ד וחברהו עם הט"ו שלמים יעלו י"ו שלמים ונשארו עדין כ"ז וחצי ועשרים ואחד הוא רביעית נשאר ו' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You can extract it in all ways. | ובכל הדרכים תוכל להוציאו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The Third Category: Multiplication of Fractions by Fractions |
הענין השלישי מערכת שברים על שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sexagesimal Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you have fractions of the astrologers, such as minutes and seconds and you wish to multiply them by minutes and seconds. | אם יהיו בידך שברי חכמי המזלות כגון ראשונים ושניים ותרצה להעריכם על ראשונים ושניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כשאתה עורך ראשונים על ראשונים יעלה מן הערך שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ראשונים בשניים יעלה שלישיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ראשונים בשלישים יעלה רביעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם שלישים בשלישים אתה עורך יעלה ששיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ברביעים יעלה שביעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Since, every number that you multiply by fractions is decreasing from its value by the rank of the fraction by which we multiply.
|
כי כל מספר שאתה עורך אותו בשברים שברים בשברים הוא פוחת [28]ומתרחק מחשבונו כמרחק השבר אשר נערוך בו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiplication table of sexagesimal fractions | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| To make it easier for the reader, I have drawn a table in order to understand the product of fractions by fractions. | ולהקל על הקורא ציירתי לוח להבין העולה משברים על שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Instructions for using the multiplication table: when you wish to know the product of one of the types of the fractions that are written in the lines breadthwise [and lengthwise], look at where the two lines meet and this is where the product of both is. | וכאשר תרצה לדעת העולה מאחד ממיני השברים שהם כתובים בטור הרוחב הסתכל במקום אשר ייפגשו שני הטורים זה בזה ושם העולה משניהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| When you multiply fractions by fractions: | וכאשר תערוך שברים על שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם יהיה העולה פחות מששים אתה מחזיק בו ומונה אותו מאותו המין היוצא מהערך ההוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיה מוסיף על ששים אתה מחלק אותו על ששים והיוצא בחלוק הוא מן המין אשר למעלה מאותו המין אשר חלקת אותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כאלו היית עורך נ' שניים בנ' שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יהיה העולה אלפים ות'ק' מאות רביעיים חלקם על ששים יצא בחלוק מ"א והם שלישים ונשארו מ' רביעיים שלא נתחלקו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| According to this way for all fractions. | ועל זה הדרך לכל השברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Simple Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you divide the fractions of the geometricians one by another. | ואם שברי חכמי המדות תערוך זה על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fraction by Fraction |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שני שלישיים על שני חמישיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is the sign that you keep the names of the fractions: | זה לך האות שתשמור שמות השברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ודע כי השלישים הם חצובים משלשה והחמישיים מהחמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וערוך ג' על חמשה והם ט"ו והוא המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן תערוך שנים על שנים והם ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכערך ארבעה מט"ו כן ערך חשבון זה מאחד והוא חמישית ושליש חמישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The reason is that saying a third by a fifth is as saying a third of a fifth, which is one part of 15.
|
והטעם כי האומר שלישי על חמישי דומה כמי שאומר שלישית מחמישית שהוא חלק אחד מט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Or it is as saying a third lengthwise by a fifth breadthwise and it is clear that it is one part of 15. | או דומה כמי שאומר שלישי באורך על חמישי ברוחב וידוע וברור שהוא חלק אחד מט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fraction by fraction of fraction
|
ואם תערוך ב' חלקים מחמשה בעשירית האחד בב' שלישי אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע כי שם החלק האחד הוא חמשים כמספר חמשה בעשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותערוך הנ' בג' שהוא שם החלק השני ויעלה ק"נ והוא המורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכערך ד' שהם שני החשבונות מן ק"נ כן ערך ערכו מן האחד והוא שני שלישי [29]חמישית החמישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fraction of integer and fraction by fraction of integer
|
ואם תערוך שלשה רביעיות [ש]ל שלשה ושליש על ששה שביעיות חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מאיזה מספר יצא הרביע והוא מארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח שלשת רביעיותיו יהיו שלשה ערכם בשלשה ושליש יעלה עשרה ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך תקח ששה שביעיות חמשה והוא ארבעה וב' שביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכם על השמור יעלה מ"ב וששה שביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלקם על ארבעה יצא בחלוק עשרה שלמים וה' שביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו דע מאיזה מספר הוא השביעית והוא משבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח ששה שביעיותיו ותערכם בחמשה יעלה שלשים ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך תקח שלשה רביעיות משלשה ושליש והוא שנים וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכם על השמור שהם ל' יעלה ע"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על ז' יצא בחלוק עשרה וחמשה שביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתערוך שנים וחצי שהוא החשבון האחד על ארבעה וב' שביעיות שהוא החשבון יעלה עשרה [30]וה' שביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fraction of integer and fraction by fraction of integer and fraction
|
ואם תערוך שבעה שמיניות של ה' ושליש בג' חמישיות של ו' ורובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מאיזה מספר השמינית והוא משמנה קח ז' שמיניות והוא ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך דע מאיזה מספר החומש והוא מחמשה קח ג' חמישיותיו והם ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תערכם על השמור יעלה קל"ט וד' רביעיות תחלקם על שמונה יצא בחלוק שבעה עשר וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או אם תרצה תחלק השמור שהוא ל"ז ושליש על שמונה והעולה שהוא ד' וב' שלישים תערוך על י"ח ושלשה רביעיות והעולה שהוא פ"ז וחצי תחלק על חמשה יצא י"ז וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתשיב החמשה ושליש כלם שלישים יהיו י"ו שלישים קח ז' שמיניותיו והעולה שהוא י"ד ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושוב אל הששה ורביע תשיבם כלם רביעיות ויהיו כ"ה קח שלשת חמישיותיו והעולה שהוא ט"ו תחלק על ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והיוצא בחלוק שהוא שלשה ושלשה רביעיות תערכם על השמור והעולה תחלק על שלשה יצא י"ז וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או אם תרצה תחלק השמור שהם י"ד על שלשה והיוצא שהוא ארבעה ושני שלישיים תערוך בט"ו והעולה שהוא ע' תחלק על ד' יצא י"ז וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fraction of fraction by fraction of fraction |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך ג' רביעיות של ג' חומשין בה' שתותין של ג' רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מאיזה מספר הרובע והחומש והוא מעשרים וג' חומשיו הוא י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר תקח החשבון השני ודע מאיזה מספר השתות והשביעית והוא מ"ב וכאשר תקח חמשה שתותין של שלשה שביעיות יעלה ט"ו שהם שתי שביעיות וחצי שביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תערוך הב' חמישיות ורביעית חמישית השמורים על שתי שביעיות וחצי שביעית בקש לך חשבון שיהיה לו רביעית וחמישית ושביעית והוא ק"מ והוא המורה ועלה בידך ממערכת זה על זה כ"ב וחצי והם חלקים מהמורה והם שביעית ושמינית שביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתדע השלשה [31]רביעיות של שלשה חומשין שהוא ט' כאשר אמרנו ואחר כך תקח חמשה שתותין של שלשה שביעיות שהם שני שביעיות וחצי שביעית ותקח מן התשעה כערכם שתי שביעיות וחצי שביעית יעלה שלשה ושביעית וחצי שביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך שני חלקים מחמשה בעשירית האחד בשני חלקים משמונה בשלישית האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע שמות החלקים חלקי החשבון השני והם שמונה ושלשה ערכם זה בזה יעלה כ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותערוך נ' בכ"ד ויעלה אלף ומאתים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכערך שמות שני החשבונות שהם שנים שנים מן אלף ומאתים כן ערכם מן האחד והוא חלק אחד משלש מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדענו שתקח מן הנ' שני חלקים מחמשה בעשירית והם שנים והוא חומש החומש על רביעית השליש הוא כמי שיאמר חומש החומש מרביעית השליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה בקש חשבון שליש ורביע וחומש וחומש החומש והוא שלש מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח שלישיתו והוא ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן הק' רביעיתו והוא כ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן כ"ה חמישיתו והוא ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן ה' חמישיתו והוא אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונתברר שהוא חלק אחד משלש מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| From these examples and ways you can understand the fractions of fractions and all of them are present for the one who understands. | ומן הדמיונות והדרכים האלה תוכל להבין בשברי השברים וכולם נכוחים למבין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Four: Division |
השער הרביעי במחלוקת | |||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| It is divided into three categories: | והוא נחלק לשלשה ענינים | |||||||||||||||||||||||||||||||||||||||||||||||||
[The First Category]: Division of Integers by Integers |
חלוקת שלמים על שלמים | |||||||||||||||||||||||||||||||||||||||||||||||||
Sexagesimal Fractions |
||||||||||||||||||||||||||||||||||||||||||||||||||
| If you wish to divide degrees by degrees according to the calculation of the astrologers: | אם תרצה לחלק מעלות על מעלות לחשבון חכמי המזלות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
אם תחלק חשבון רב על מעט יהיה היוצא בחלוק מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ישאר שלא יתחלק ערוך הנשאר על ששים יהיו ראשונים ויתחלק על מה שחלקת בראשונה והיוצא בחלוק הם ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ישאר שלא יתחלק תערכם על ששים ותחלק על מה שחלקת והיוצא הם שנים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן עד כמה שתרצה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם רצית לחלק חשבון מועט על רב תערוך המועט על ששים יהיו ראשונים ואחר כן [32]תחלוק והיוצא בחלוק הם ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ישאר שלא יחלק ערכם על ששים ותחלק על מה שחלקת יהיה היוצא שניים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן לשלישיים ולרביעיים עד אין קץ | |||||||||||||||||||||||||||||||||||||||||||||||||
Simple Fractions |
||||||||||||||||||||||||||||||||||||||||||||||||||
| If according to the calculation of the geometricians. | ואם לחשבון חכמי המדות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
תרצה לחלק חשבון רב על מועט | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שתרצה לחלק מאה על ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
בקש חשבון שהיה מונה לשניהם והוא חמשה קח חמישית מאה והוא כ' וחלק על חמישית ט"ו והוא ג' יצא בחלוק ששה ושני שלישיות וככה מק' על ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק אלף על שנים ושבעים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
החשבון שמונה לשניהם הוא שמונה ושמינית ע"ב תשעה ושמינית אלף קכ"ה חלק המרובה על המועט יצא בחלוק י"ד פחות תשיעית וככה מאלף על ע"ב | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיו שני החשבונות שלא תמצא להם חשבון שמונה לשניהם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שתרצה לחלק מ' על ז' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
יצא בחלוק ה' וישארו לך ה' עשה מהם שביעיות יצא בחלוק ה' שלמים וה' שביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם מספר מועט תחלק על רב | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ט"ו על ק' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
זה הענין יצא מהערכים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר ידעת כי החמשה מונה לשניהם למספר ט"ו ג' פעם ולמספר ק' פעם וכערך ג' אל כ' שהוא עשור וחצי עשור כך ערך ט"ו אל מאה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם לא תמצא מספר שיהיה מונה לשניהם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון ז' על מ' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
קח חלק אחד מהמספר הרב ותערוך המועט אליו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ובדמיון זה תקח עשור המ' והוא ד' או חמישיתו והוא ח' או שמיניתו והוא ה' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
אם עשיריתו לקחת כאשר תערוך הז' אליו תמצא בו שנים עשיריות פחות רביע העשור וכן יגיע לכל אחד מן המ' שני עשיריות אחד פחות רביע העשור | |||||||||||||||||||||||||||||||||||||||||||||||||
|
או חומש פחות שמינית החומש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
או שמינית וב' חמישיות שמינית | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וככה יצא בחלוק לכל אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ובחינתו שכשתערוך שנים עשיריות אחד פחות רביע העשור על מ' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
או חומש אחד פחות שמינית החומש על מ' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
או שמינית וב' חמישיות שמינית על מ' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
יעלה ז' שלמים בלי [33]חסר ויתר | |||||||||||||||||||||||||||||||||||||||||||||||||
| Word Problems - Divide a Quantity Problems | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Dividing a known quantity among a known number of people in given ratios | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תרצה לחלק מספר ידוע על אנשים ידועים ולתת לכל אחד ואחד כפל חברו ותרצה לדעת כמה תתן לראשון שיתחלק כל המספר בלא תוספת ובלא מגרעת | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שתחלק מספר ק' על ד' כל אחד ואחד כפל חבירו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
זה תדע מאחד כמה יתחבר בתוספת הכפל לארבעה אנשים ועל המחובר תחלק המספר והיוצא הוא חלק הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכפל הכפל לארבעה אנשים ידוע הוא שהם ט"ו חלק עליהם הק' יצא בחלוק ששה וב' שלישיים וככה חלק הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם יאמר להוסיף לשני חצי הראשון ולשלישי שלישית השני ולרביעית רביעית השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||
|
תדע זה מאחד כמה יתחבר עד ארבעה וידוע הוא שיתחבר ז' שלמים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק עליהם הק' יצא בחלוק י"ד ושתי שביעיות וככה חלק הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
| According to this way for every number whether great or small. | ועל זה הדרך לכל מספר בין רב למעט | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק ק' על ב' והיוצא בחלוק האחד תחלק על ג' והיוצא על ד' והיוצא על ה' ותרצה לדעת כמה חלק החמישי | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ערוך השנים בשלשה והעולה בד' והעולה בה' יעלה ק"כ | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תחלק הק' על העולה שהוא ק"כ יצא אחד פחות שתות וככה חלק החמישי | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק צ' על ט' אנשים ושיוסיף כל אחד על חברו אחד כמה יתן לראשון ויצא שוה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
זה הכלל יהיה בידך שתגרע אחד מחשבון האנשים והנשאר שהם שמונה דע כמה יתחבר מאחד ועד שמונה והוא שתוסיף אחד על שמונה והמחובר תערוך על חצי השמונה יעלה ל"ו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
גרע אותם מהתשעים והנשאר שהוא ארבעה וחמשים חלקם על התשעה והיוצא שהוא שוה ששה הוא חלק הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה הכלל ידריכך בכל השאלות הדומות לזו שיהיו כל התוספות שוות שיהיה תוספת השלישי על השני כתוספת רביעי על השלישי והחמישי על הרביעי וכן כלם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק שמונים על חמשה אנשים ושיוסיף השני על הראשון ג' והשלישי על השני אחד והרביעי על השלישי שנים והחמישי על הרביעי ששה ותרצה לדעת כמה יתן לראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
|
חבר [34]כל התוספות שיש על הראשון יעלו כ"ה וגרעם מהשמונים והנשאר שהוא נ"ה חלק על האנשים יצא בחלוק י"א וככה חלק הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק מספר ידוע לשלשה אישים ותרצה לדעת כמה נתן לכל אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ככה תעשה שתצוה לו לכפול חלק הראשון וחלק השני כלו יערוך על המספר פחות אחד וחלק השלישי על המספר כלו ויחבר הכל | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן תשאל ממנו כמה יש להשלמת מרובע החשבון אשר חילק | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שיהיה חלק על המספר ההוא אשר חילק פחות שנים והיוצא בחלוק הוא חלק הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שישאר ולא יוכל לחלקו עד שיעשנו ש[למ]ים הוא חלק השני ו[מז]ה תדע השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה החשבון פעמים שישתבש שיצא הכל בחלוק | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר יקרך זה תדע שלא נתן לראשון כי אם אחד בלבד והנשאר כלו תן לשני ומהם תדע השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||
The Second Category: Division of Fractions by Integers or Integers by Fractions |
הענין השני חלוקת שברים על שלמים או שלמים על שברים | |||||||||||||||||||||||||||||||||||||||||||||||||
Sexagesimal Fractions |
||||||||||||||||||||||||||||||||||||||||||||||||||
| If you have sexagesimal fractions [lit. fractions of the astrologers] and you wish to divide them by degrees, the result of division will be of the same type of the fractions: if they are primes, [the result will be] primes; if seconds [the result are] seconds; and so on for all the fractions | אם יהיו בידך שברי חכמי המזלות ותרצה לחלקם על מעלות יהיה היוצא בחלוק ממין השבר אם ראשונים ראשונים ואם [שניים] שניים וכן לכל השברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| Because, for every fraction you multiply by a degree, the result is of the same type of that fraction. | מפני שכל שבר אשר אתה עורך אותו במעלה יהיה העולה ממין השבר ההוא | |||||||||||||||||||||||||||||||||||||||||||||||||
| If something remains that cannot be divided, multiply the remainder by sixty and divide by what you have divided; the result will be fractions that are lower than the first type by one rank.
|
ואם ישאר שלא יתחלק תערוך הנשאר על ששים ותחלק על מה שחלקת והיוצא יהיו שברים יורדים מדרגה אחת מן המין הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
| If you divide degrees by [sexagesimal] fractions, you convert the degrees into the type by which you want to divide, then divide this type by its own type and the result of division is degrees.
|
ואם תחלק מעלות על שברים אתה משיב המעלות אל המין אשר אתה רוצה לחלוק עליו ותחלק מין על מינו ויהיה היוצא בחלוק מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||
| You must always convert the degrees into the type by which you want to divide, even if the degrees are many. | ואתה צריך לעולם להשיב המעלות אל המין אשר תרצה לחלק עליו וגם אם יהיו המעלות רבות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שתרצה לחלק עשרה מעלות על חמשה ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
אי איפשר לומ' שתחלק עשרה על חמשה ויצא בחלוק ב' מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כי כאשר תערוך מעלות על ראשונים יהיו ראשונים כאשר אמרנו בשער המגרעת | |||||||||||||||||||||||||||||||||||||||||||||||||
|
[35]וכל חשבון כאשר תערוך מה שיצא בחלוק על הנחלק עליו יעלה החשבון המחולק | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ומפני זה אתה עורך העשרה על ששים יעלו ת"ר ותחלק על חמשה יצא בחלוק ק"כ והם מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כי המחלק עשרה מעלות על ה' ראשונים כך הוא רוצה לעשות שיחלק הי' מעלות שלא יהיה בצד האחד שהוא הרחב כי אם ה' ראשונים ותמצא שיהיה באורך ק"כ מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ישאר שלא יתחלק תערוך הנשאר על ששים ותחלק מה שחלקת והיוצא יהיו שברים יורדים מדרגה מן המין הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
Simple Fractions |
||||||||||||||||||||||||||||||||||||||||||||||||||
| If you divide simple fractions [lit. fractions of the geometricians]: | ואם שברי חכמי המדות תחלק | |||||||||||||||||||||||||||||||||||||||||||||||||
Integer by integer and fraction |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון מי שמחלק ק' על שנים ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מה ערך האחד מן השנים ורביע והוא ארבע תשיעיות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח ארבעת תשיעיות הק' שהם מ"ד שלמים וד' תשיעיות וכן יגיע לכל אחד מהשנים ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||
Integer by fraction of integer and fraction |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק עשרים על שני שלישי שבעה וחומש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דע כמה שני שלישי ז' וחומש והוא ארבעה וארבע חומשין שהם כ"ד חומשין | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ודע מה ערך האחד מהם והוא שתות ורובע השתות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח מהעשרים שתותם ורובע שתותם והם ארבעה ושתות וככה חלק כל אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
Integer and fraction by fraction |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק ב' על ג' שביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דע בכמה ישלמו הג' שביעיות עד שי' שיהיו אחד והוא שנים פעמים ושליש פעם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכם בעשרים שביעיות יעלה ז' פחות שליש וככה חלק כל אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
Integer and fraction by fraction and fraction of fraction |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק עשרים על ז' שמיניות וחצי שמיניות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דע בכמה ישלמו הז' שמיניות וחצי שמיניות עד שיהיו אחד והוא אחד ושליש חומש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
תערכם על עשרים שמיניות יעלה כ"א שמיניות ושליש שהם שנים וה' שמיניות ושלש שמינית שהם ג' פחות שליש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Completion of Fractions |
||||||||||||||||||||||||||||||||||||||||||||||||||
| The way to know the multiplicative inverses of fractions so that they become one: | ודרך לדעת תשלומי השברים עד אשר יהיו אחד ככה תדענו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שתרצה לדעת איך ג' שמיני האחד ישלמו עד שיהיו אחד שלם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דע כי שם השמיניות הוא משמונה ומספר הפעמים אשר השלשה מונים את השמונה הם ג' פעמים פחות שליש [36]וכמספר הזה אתה חושב את שלשת השמיניות ויהיו אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
| For The number of times that one number [i.e., the numerator] counts the denominator is the same as [the number of times that] the part counts the one.
|
כי כמנין הפעמים אשר מספר אחד מונה את המספר המוכיח כמוהם החלק מונה את האחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שתרצה להשלים ב' חמישיות ועשירית החומש עד שיהיו אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
בקש חשבון שיהיה לו חמישית ועשירית והוא נ' והוא המוכיח אשר נקרא בספר הזה המורה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וב' חמישי המספר הזה ועשירית חמישיתו הוא כ"א | |||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספר הזה מונה את החמשים ב' פעמים ושליש פעם ושביעית השליש וכענין הזה יהיו תשלומי ב' חמישיות ועשירית החומש ויהיה אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
| For an integer you can also say the same way. | וגם במספר השלם אתה יכול לומר על זה הדרך | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שתרצה להשלים את השבעה עד שיהיו י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
אתה יודע כי השבעה מונה את י"ו שני פעמים ושני שביעי פעם ובהם ישלמו י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל זה הדרך תוכל למצא לכל חשבון | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק שלשה רביעיות של שלשה חומשי תשעה על כ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וידוע כי שלשה חומשי תשעה הם כ"ז חומשין ושלשה רביעיותיהם הם ד' שלמים וחצי עשירית אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפיכך אמ' המחבר תקח וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
תקח חלק אחד מכ"ד שמיניתו והוא ג' או שלישיתו והוא ח' או רביעיתו והוא ו' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
אם שמיניתו לקחת כאשר תערוך הד' וחצי עשירית אחד אליו תמצא בו פעם אחת שמינית ושליש שמינית וחצי עשירית שליש שמינית | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם שלישיתו לקחת תמצא בו חצי שלישיתו וחצי עשירית שמינית שלישית | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם רביעיתו לקחת תמצא בו שני שלישי שלישית וחצי עשירית ששית רביעית | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וככה יצא בחלוק לכל אחד מכ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והבחינה כשתערוך איזה שתרצה מהחלקים שהזכרנו על כ"ד יעלה ד' וחצי עשירית אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
The Third Category: Division of Fractions by Fractions |
הענין השלישי חלוקת שברים על שברים | |||||||||||||||||||||||||||||||||||||||||||||||||
Sexagesimal Fractions |
||||||||||||||||||||||||||||||||||||||||||||||||||
| The first rule | ||||||||||||||||||||||||||||||||||||||||||||||||||
| If you divide sexagesimal fractions [lit. fractions of the astrologers] by each other: | אם שברי חכמי המזלות תחלק זה על זה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
אם ראשונים על ראשונים תחלק יהיה היוצא בחלוק מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם שניים על שניים תחלק היוצא מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||
| The same for the rest of the [sexagesimal] fractions: if you divide them by their type, the result will be degrees - this is the first rule of the division of [sexagesimal] fractions.
|
וכן שאר [37]השברים אם אתה מחלק אותם על מיניהם יהיה היוצא מעלות וזה כלל אחד בחלוק השברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| The second rule | ||||||||||||||||||||||||||||||||||||||||||||||||||
| The second rule: know that if you divide one type of fractions by another type that is lower: | וכלל שני דע שאם אתה מחלק מין אחד מן השברים על מין אחר שהוא תחתיו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שתרצה לחלק ראשונים על שניים או על שלישיים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
אתה עורך הראשונים על ששים ויהיו שניים ותחלק שניים על שניים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם על שלישיים תחלק ערכם על ששים פעם אחרת ויהיו שלישיים ותחלק שלישיים על שלישיים ויהיה היוצא מעלות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן כל הדומה לזה | |||||||||||||||||||||||||||||||||||||||||||||||||
| The third rule | ||||||||||||||||||||||||||||||||||||||||||||||||||
| The third rule: if you divide one type of fractions by another type higher than it, the result of division will be of a lower type than the type [that is divided] according to the type by which you divide. | וכלל שלישי אם תחלק מין אחד מן השברים על מין אחר שהוא גדול ממנו יהיה היוצא בחלוק מן המין אשר תחתיו של המין אשר אתה מחלק עליו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כאלו חלקת שלישיים על ראשונים יהיה היוצא בחלוק שניים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
או שניים על ראשונים יהיו ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||
| Because, when you multiply the result of division by the divisor, the result should be the original dividend.
|
מפני שכשתערוך מה שיצא בחלוק על מה שחלקת עליו צריך שיצא הראשון הנחלק | |||||||||||||||||||||||||||||||||||||||||||||||||
| Remainder | ||||||||||||||||||||||||||||||||||||||||||||||||||
| If something remains that cannot be divided, you multiply the remainder by sixty, then divide by what you have divided; the result will be of a type that is one rank lower than the type of the number that initially resulted from the division. | ואם ישאר שלא יתחלק אתה עורך הנשארים בששים ותחלק על מה שחלקת ויהיה היוצא ממין שירד מדרגה אחת ממין המספר שיצא בחלוק בראשונה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כאלו תחלק חמשים ראשונים על שבעה ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
יצא בחלוק שבע מעלות וישאר שלא יתחלק אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכהו על ששים יהיו שניים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על שבעה אשר חלקת בראשונה יצא בחלוק שמונה ראשונים וישאר שלא יתחלק ד' שניים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכם על ששים יעלו ר"מ שלישיים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על ז' יעלה ל"ד שניים וישאר שני שלישיים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכם בששים וחלקם על מה שחלקת ויעלו שלישיים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אתה יכול לחקרן לרביעיים ולחמישיים עד כמה שתרצה | |||||||||||||||||||||||||||||||||||||||||||||||||
| division table of sexagesimal fractions | ||||||||||||||||||||||||||||||||||||||||||||||||||
| To make it easier for the reader, I have drawn for you a table of primes to sixths. | ולהקל על הקורא ציירתי לך לוח מראשונים עד ששיים | |||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| If you want to divide degrees and fractions by degrees and fractions: convert the two numbers into one rank, then divide. | ואם תרצה לחלק מעלות ושברים על מעלות ושברים השב שני החשבונים למדרגה אחת ואחר תחלק | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שתרצה לחלק שמנה מעלות ועשרים ראשונים על ג' [38]מעלות וט"ו ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיבם כלם ראשונים והנה החשבון האחד ת"ק והוא המחולק והשני קצ"ה חלקנו הגדול על הקטן יצא בחלוק שנים והם מעלות ונשארו ק"י | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ערוך אותם על ששים וחלק על קצ"ה יצא בחלוק ל"ג והם ראשונים וישאר קס"ה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכם על ס' וחלק על קצ"ה ראשונים יצא בחלוק נ' והם שניים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| If you want to make it more accurate with thirds and fourths, do it in this way. | ואם תרצה לדקדק כן לשלישיים ולרביעיים תעשה על זה הדרך | |||||||||||||||||||||||||||||||||||||||||||||||||
|
או תדע מה ערך ק"י הנשארים אל ש"צ הנחלקים והנה רביעיתם צ"ז וחצי נשארו י"ב וחצי והו' וחצי הם שלישית חמישית הרביעית ונשארו ו' שהם ו' חלקים מי"ג בשני שלישי חמישית רביעית | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור הרביעית הוסף רביעית ב' מעלות שיצאו בחלוק והם ל' ראשונים ובעבור ו' חלקם מי"ג בשני שלישי חמישית רביעית הוסף ראשון אחד לשניים והנה יצא בחלוק ל"ג ראשונים נ' שניים כמו החשבון הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Simple Fractions |
||||||||||||||||||||||||||||||||||||||||||||||||||
Integer and fraction by integer and fraction |
||||||||||||||||||||||||||||||||||||||||||||||||||
| If you divide simple fractions [lit. fractions of the geometricians]: | ואם שברי חכמי המדות תחלק | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון שלשה ושלשה רביעיות על אחד וחומש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מה ערך האחד מן אחד וחומש והוא חמשה שתותיו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
קח ה' שתותין מג' וג' רביעיות אחד שהם שש שמיניות יעלה [39]שלשה ושמינית וככה חלק האחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Integer and fraction by fraction |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק ז' וחומש על שלש רביעיות אחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דע בכמה ישלמו הג' רביעיות לאחד כלו' שתוסיף על ז' וחומש שלישיתם והוא אחד ושליש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
תערכם על ז' וחומש יעלה תשעה וג' חומשין ורביעיתם הוא חלק כל רביע ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||
|
או תשיב הז' וחומש לחומשין יהיו בידך ל"ו חומשין | |||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על הג' רביעיות יצא בחלוק י"ב חומשין שהם שנים וב' חומשין לכל רביע ורביע שהוא לאחד שלם ט' וג' חומשין | |||||||||||||||||||||||||||||||||||||||||||||||||
Fraction by fraction |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק ששה שביעיות על שמונה עשיריות | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דע בכמה ישלים אחד והוא אחד ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||
|
תערכם על ששה שביעיות יעלה א' שביעיות וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם יצא אחד וחצי שביעית וככה חלק האחד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
או אם תרצה חלק ששה על שמונה יצא אחד פחות רובע | |||||||||||||||||||||||||||||||||||||||||||||||||
|
לפיכך יצא עכשו שביעית אחד פחות רובע שביעית לחלק העשירית והם י' לאחד ז' שביעיות וחצי שביעית | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Fraction of integer and fraction by fraction of integer and fraction |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלק ששה שביעיות חמשה ורובע על שלשה שמיניות מאחד וחומש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
השב החמשה ורובע כלם לרביעיות יעלו כ"א וששה שביעיותיו י"ח שהם ד' שלמים וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד השב האחד וחומש לחמישיות והם ששה חמישיות ושלשה שמיניותיו ב' חומשין ורביע חומש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדע בכמה יהיו אחד והוא בשנים ושני תשיעיותיו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כי רביעית חומש הוא תשיעית ב' חומשין ורביע חומש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
תערכם בארבעה וחצי כלו' תקח שני פעמים ד' וחצי ותקח שני תשיעיותיהם יעלה עשרה והם ה' חומשין נמצא מגיע שנים שלמים לכל חומש וחומש ומהם תדע חלק אחד שלם | |||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Five: Ratios |
השער החמישי בערך | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Sexagesimal Fractions |
|||||||||||||||||||||||||||||||
| The method of the astrologers is to calculate all their calculations by sixty, since it has most of the divisors. | דרך חכמי המזלות לחשוב כל חשבונם על ששים מפני שיש לו רוב החלקים | ||||||||||||||||||||||||||||||
|
רצינו לערוך שלשים על עשרים ולחלק על ששים | ||||||||||||||||||||||||||||||
|
דע מה ערך החשבון האחד שהוא שלשים | ||||||||||||||||||||||||||||||
|
או דע מה ערך עשרים אל ששים והוא שלישיתו תקח שלישית החשבון האחר והנה עשרה | ||||||||||||||||||||||||||||||
|
ואם החשבון האחד נ' והשני מ' ונחלק העולה על ששים | ||||||||||||||||||||||||||||||
|
קח ערך נ' אל ששים והוא חמש ששיות וכזה הערך מארבעים והנה מששה ושלשים קח חמש ששיותיו והם שלשים ונשארו ארבעה | ||||||||||||||||||||||||||||||
|
ערכם על חמשה עלו עשרים | ||||||||||||||||||||||||||||||
|
תחלקם על ששה יצא שלשה שלמים ושליש שהם עשרים שברים והנה המספר ל"ג ושליש | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
או קח ערך מ' אל ס' והוא שני שלישיותיו | ||||||||||||||||||||||||||||||
|
קח שני שלישיות נ' והנה מן מ"ח שנים ושלשה ונשארו שנים | ||||||||||||||||||||||||||||||
|
נערכים על שנים שהם שתי שלישיות ועלו ארבעה | ||||||||||||||||||||||||||||||
|
נחלקם על שלשה יצא אחד ושליש | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
ואם שני חשבונים שאין לאחד מהם ערך אל ששים כמו י"ד ול"ט | ||||||||||||||||||||||||||||||
|
ככה נעשה נוסיף על חשבון י"ד חלק אחד והנה ערכו רביעית | ||||||||||||||||||||||||||||||
|
וככה נוסיף על ל"ט אחד ויהיה רביעיתו עשרה | ||||||||||||||||||||||||||||||
|
ויש לנו לחסר שני חסרונים כי שנים הוספנו והנה בעבור האחד שהוספנו על ל"ט יש לנו לחסר חמשה עשר שניים ונערוך האחד שהוספנו על ל"ט ויעלו ל"ט שניים | ||||||||||||||||||||||||||||||
|
נחברם עם ט"ו שהיו לנו עלו נ"ד | ||||||||||||||||||||||||||||||
|
נחסרם מראשון אחד ועלה החשבון ט' ראשונים גם ו' שניים | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
או נוסיף על ל"ט אחד | ||||||||||||||||||||||||||||||
|
ודע מה ערכו אל ששים והנו שתי שלישיות | ||||||||||||||||||||||||||||||
|
והנה נקח שתי שלישיות ארבעה עשר והנו ט"כ | ||||||||||||||||||||||||||||||
|
כי מט"ו יהיו שתי שלישיות עשרה | ||||||||||||||||||||||||||||||
|
ויש לנו לחסר שתי שלישיות ראשון אחד שהם מ' שניים והנה המספר ט"כ | ||||||||||||||||||||||||||||||
|
ובעבור שהוספנו על ל"ט אחד נערכנו על י"ד ויעלו י"ד שניים | ||||||||||||||||||||||||||||||
|
נחסרם מעשרים נשארו לך ו' שניים | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
ואם רצינו לערוך ל"ה על שלשה עשר ונחלק על ששים | ||||||||||||||||||||||||||||||
|
בקשנו מה ערך שנים עשר שהוא הקרוב אל י"ג אל ששים והוא חמישיתו | ||||||||||||||||||||||||||||||
|
לקחנו חמישית ל"ה והנה שבעה | ||||||||||||||||||||||||||||||
|
ונשאר אחד ערכנוהו על ל"ה והנם שניים | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
והבחינה ידענו כי ל"ה שלש חמישיות בתוספת [41]אחד | ||||||||||||||||||||||||||||||
|
לקחנו ג' חמישיות חמשה עשר שהוא המספר הקרוב אל י"ג והיו ט' | ||||||||||||||||||||||||||||||
|
והוספנו שנים כי י"ג היו לנו ערכנום על ל"ה והוא חלק אחד ועשרה שניים | ||||||||||||||||||||||||||||||
|
והוספנו בתחלה אחד כי לקחנו ששה ושלשים והיו ט"ו | ||||||||||||||||||||||||||||||
|
חסרנו הכל מתשעה ונשאר החשבון | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
או לקחנו חצי י"ג בעבור השלשים והנם ששה וחצי שהוא שלשים שניים | ||||||||||||||||||||||||||||||
|
וערכנו חמשה על י"ג עלה חלק אחד וחמשה שניים | ||||||||||||||||||||||||||||||
|
חברנום ועלה המספר | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
ואם שני חשבונים האחד מ"ו והשני כ"ה | ||||||||||||||||||||||||||||||
|
והנה לא מצאנו ערך למ"ו עם ששים | ||||||||||||||||||||||||||||||
|
נחסר אחד מהחשבון ישאר מ"ה וערכו שלש רביעיות | ||||||||||||||||||||||||||||||
|
ונקח מכ"ה כ"ד ושלש רביעיותיו י"ח נשארו ג' רביעיות אחד שהם מ"ה שניים | ||||||||||||||||||||||||||||||
|
וערכנו האחד שיש תוספת על מ"ה על כ"ה ועלה כ"ה | ||||||||||||||||||||||||||||||
|
הוספנום על מ"ה שניים שהיו לנו ועלה ראשון אחד ונשארו עשרה שניים והנה החשבון י"ט י' | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
או נקח מה ערך כ"ה אל ס' והיו שלישיתו ורביע שלישיתו | ||||||||||||||||||||||||||||||
|
נקח ממ"ו שלישיתו שהוא ט"ו ועשרים שניים | ||||||||||||||||||||||||||||||
|
ורביעית ט"ו ועשרים שניים הם שלשה וגם נ' שברים | ||||||||||||||||||||||||||||||
|
חברנום עם אשר למעלה עלה י"ט י' | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
או נחסר אחד מכ"ה ונדע מה ערך כ"ד אל ששים והנו שתי חמישיות | ||||||||||||||||||||||||||||||
|
ושתי חמישיות מ"ה הם י"ח | ||||||||||||||||||||||||||||||
|
והאחד שנשאר להשלמת כ"ה נערכנו על מ"ה יהיו שניים | ||||||||||||||||||||||||||||||
|
גם נערוך האחד שהוא תוספת על כ"ה | ||||||||||||||||||||||||||||||
|
ונחבר כל השניים ועלה המספר | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
או נוסיף על מ"ו שנים ועלה מ"ח וערכו אל ששים ארבע חמישיות | ||||||||||||||||||||||||||||||
|
נקח ארבע חמישיות כ"ה והנם עשרים | ||||||||||||||||||||||||||||||
|
ואנחנו הוספנו שנים נערכם על כ"ה עלו נ' שניים | ||||||||||||||||||||||||||||||
|
נחסרם מעשרים ישאר י"ט | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
| Always do as follows: find a number that has a ratio to sixty, or an approximate ratio, whether by adding to it, or by subtracting. Take the ratio from that number. Subtract finally if you added at first, or add finally if you subtracted at first.
|
וככה תעשה לעולם שהסתכל איזה חשבון יש לו ערך אל ששים או ערך קרוב אליו בין להוסיף עליו בין לגרוע ומאותו החשבון תקח הערך ואם הוספת בראשונה גרע באחרונה ואם גרעת בראשונה תוסיף [42]באחרונה | ||||||||||||||||||||||||||||||
| If one of the numbers is greater than the divisor, or both are greater than it, find the ratio of the divisor to one of the numbers and take its ratio from the other number.
|
ואם היה אחד החשבונים גדול מהמחולק עליו או שניהם גדולים ממנו הסתכל מה ערך חשבון שיחלק עליו אל אחד החשבונים וכערכו קח מן החשבון האחר | ||||||||||||||||||||||||||||||
|
כגון שמונים על תשעים מחולקים על ששים | ||||||||||||||||||||||||||||||
|
נסתכל מה ערך ששים אל שמונים והוא כמהו ושלישיתו ונוסיף על תשעים שלישיתו יעלו מאה ועשרים | ||||||||||||||||||||||||||||||
|
או הסתכל מה ערך ס' אל צ' והוא כמוהו וחציו והנה נוסיף על פ' חציו יעלו ק"כ | ||||||||||||||||||||||||||||||
|
ואם החשבון האחד פ' והשני פ"ח | ||||||||||||||||||||||||||||||
|
נחשוב שהוא צ' מפני שיש לו ערך אל ס' ויצא החשבון ק"כ | ||||||||||||||||||||||||||||||
|
ובעבור שהוספנו שנים נערכם על שמונים שהוא החשבון האחר יעלו מאה וששים ראשונים והם שתי מעלות מ' ראשונים | ||||||||||||||||||||||||||||||
|
חסרם מק"כ ישאר קי"ז כ' וככה החשבון | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
Simple Fractions |
|||||||||||||||||||||||||||||||
| The geometricians said that there are five kinds of ratios and they are derived from the units and they are: | וחכמי המדות אמרו שחמשה ערכים הם ונלקחים מן האחדים והם | ||||||||||||||||||||||||||||||
| The first is the multiple ratio:
|
האחד ערך הכפל | ||||||||||||||||||||||||||||||
|
כמו שנים או שלשה עם אחד | ||||||||||||||||||||||||||||||
| The second is the superparticular ratio [lit. the same and a part]:
|
והשני כמוהו וחלק ממנו | ||||||||||||||||||||||||||||||
|
כמו שנים עם שלשה וזה הערך לא ימצא קודם זה | ||||||||||||||||||||||||||||||
| The third is the multiple superparticular ratio:
|
והשלישי כפלו וחלק ממנו | ||||||||||||||||||||||||||||||
|
כמו חמשה עם שנים גם הוא | ||||||||||||||||||||||||||||||
| The fourth ratio is the superpartient ratio [lit. the same and parts]:
|
הערך הרביעי שהוא כמוהו וחלקים ממנו | ||||||||||||||||||||||||||||||
|
והיו כמו חמשה עם שלשה | ||||||||||||||||||||||||||||||
| The fifth is the multiple superpartient ratio:
|
והחמישי שהוא הכפל וחלקים ממנו | ||||||||||||||||||||||||||||||
|
לא ימצא עד שמונה עם שלשה | ||||||||||||||||||||||||||||||
| There are no ratios other than these. | ואין ערכים אלא אלו | ||||||||||||||||||||||||||||||
| All kinds of ratios are divided into three categories of progressions: | |||||||||||||||||||||||||||||||
| The science of ratio is according to three ways: | וחכמת הערכין על שלש דרכים | ||||||||||||||||||||||||||||||
| Arithmetic Progression:
|
|||||||||||||||||||||||||||||||
|
האחת כמו ארבעה וששה ושמונה שהתוספת היא שוה והוא דרך החשבון | ||||||||||||||||||||||||||||||
| Geometric Progression
|
|||||||||||||||||||||||||||||||
|
והשנית כמו ד' ו' ט' שערך ו' אל ד' כמהו וחציו וככה ערך ט' אל ו' | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
|
או תוכל לומ' כי ערך ד' אל ו' שתי שלישיותיו וככה ו' עם ט' | ||||||||||||||||||||||||||||||
|
ולעולם אם ערכנו קטן על גדול יהיה כמרובע התיכון | ||||||||||||||||||||||||||||||
|
וככה אם לקחנו ארבעה ומספרים שיהיה ערך הרביעי אל השלישי כערך השני אל הראשון | ||||||||||||||||||||||||||||||
|
אם ערכנו הראשון על הרביעי יהיה המחובר כמחובר העולה מערך השני על השלישי | ||||||||||||||||||||||||||||||
| Harmonic Progression
|
|||||||||||||||||||||||||||||||
|
והשלישית כמו ג'ד'ו' שהתוספת שיש בין ג' וד' הוא אחד ובין ד' וו' שנים [43]שערך התוספת היא כפל כערך הקטן אל הגדול | ||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
ואם ידענו השנים מהם נוכל להוציא השלישי נערך ג' על ד' עלו שנים עשר ונחסר מן הקטן התוספת שיש בינו ובין השני ועל הנשאר נחלק י"ב יצא ששה | ||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
וכן אם ידענו שהשני והשלישי ד'ו' ורצינו להוציא הקטן נערך ד' על ו' עלו כ"ד ונוסיף על הגדול התוספת שיש לו על השני ועלו שמונה ועליו נחלק כ"ד יעלה שלשה | ||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
ואם ידענו שהקטן והגדול ג'ו' ונרצה לדעת האמצעי נערוך ג' על ו' יעלו י"ח ונחבר הקטן עם הגדול יהיו תשעה ונחלק עליו שמונה עשר יצא שנים ונכפול העולה לעולם וככה האמצעי | ||||||||||||||||||||||||||||||
|
או נוסיף על הקטן רביעית הגדול ונחלק עליו והיוצא לאחד מהשלמים הוא האמצעי | ||||||||||||||||||||||||||||||
| Instructions for creating a table of arithmetic progressions based on the set of the natural numbers | |||||||||||||||||||||||||||||||
|
ואם תרצה להוציא חשבון הכפול מן האחדים תכתוב החשבון מא' ועד כמה שתרצה על סדר החשבון | ||||||||||||||||||||||||||||||
|
ואחר כך תכתוב תחתיו ותתחיל בב' ואחריו ד' שתוסיף לעולם ב'ב' וזו השטה תהיה כפל מן הראשונה על הסדר כגון שני שטין שבמכבר הראשונה והשניה | ||||||||||||||||||||||||||||||
|
ואם תרצה להוציא חשבון הכפל מן האחדים תכתוב החשבון כמוהו וחלק ממנו שהוא חצי היוצא משנים עם שלשה תכתוב הזוגות על הסדר ותתחיל משנים שהם ראש הזוגות ואחר כן תערך האחדים על הסדר על שלשה שתוסיף לעולם שלשה כמו הטור השלישי שבמכבר והוא יהיה כמוהו וחציו אל הטור השני | ||||||||||||||||||||||||||||||
|
ואם תרצה להוציא כפלו וחלק ממנו שהוא חצי היוצא מחמשה אל שנים תכתוב ב' בתחלה והוסף בב' אחריה כמו הטור השני שבמכבר ואחר כן תערוך האחדים על ה' כמו הטור החמישי שבמכבר והוא יהיה כפלו וחלק ממנו אל הטור השני | ||||||||||||||||||||||||||||||
|
ואם תרצה להוציא כמוהו וחלקים ממנו שהם שתי שלישיות היוצא מחמשה אל שלשה הוא כמו הטור החמישי שבמכבר אל הטור השלישי | ||||||||||||||||||||||||||||||
|
ואם תרצה להוציא כפלו וחלקים ממנו שהוא שתי שלישיות היוצא משמונה אל שלשה כמו הטור השמיני [44]אל הטור השלישי שבמכבר הוא | ||||||||||||||||||||||||||||||
|
וכל מספר שיש לו חלק החלק מונה אותו כמנינו או כמנין חלק אחר | ||||||||||||||||||||||||||||||
|
והמספר אשר חלקו מונה אותו כמספרו נקרא מספר מרובע מפני שצלעו האחד שוה לצלעו השני וכשאתה מונה את צלעו כמנינה תקבץ המספר הרבוע | ||||||||||||||||||||||||||||||
|
כמספר ד' וט' וי"ו וכדומה להם | ||||||||||||||||||||||||||||||
|
ואשר חלקו מונה אותו כמנין אחד מחלקיו נקרא מספר שטוח ויש לו שתי צלעות | ||||||||||||||||||||||||||||||
|
כמספר ט"ו אשר צלעו האחת ג' והשנית ה' | ||||||||||||||||||||||||||||||
|
וכשאתה מונה צלעו כמנין הצלע השנית תקבץ מספרו השטוח שהוא ט"ו | ||||||||||||||||||||||||||||||
|
וכל מספר שאתה מונה אותו באחד לבדו נקרא מספר ארוך מפני שאין לו צלע שני כי אם האחד שאינו מספר | ||||||||||||||||||||||||||||||
| All square numbers are formed successively by the sum of one, which is the first square, with the sequence of the odd numbers. | וכל המספרים המרובעים נמצאים על סדרם מקבוץ האחד אשר הוא המרובע הראשון עם המספרים הנפרדים על סדרם | ||||||||||||||||||||||||||||||
|
וענין זה אם אתה מקבץ האחד שהוא המרובע הראשון אל השלש שהוא תחלת הנפרדים אתה מוצא הרבוע השני והוא ד' אשר צלעו ב' | ||||||||||||||||||||||||||||||
|
ואם אתה מוסיף על מרובע השני המספר הנפרד השני והוא ה' יהיה הכל ט' והוא המרובע השלישי אשר צלעו ג' | ||||||||||||||||||||||||||||||
|
וכן אם אתה מוסיף על המרובע השלישי הנפרד השלישי והוא ז' יצא המרובע הרביעי והוא י"ו | ||||||||||||||||||||||||||||||
|
וכן על הסדר הזה אתה מוסיף על המרובע המספר הנפרד אשר במעלתו יצא המרובע התלוי אליו עד אין סוף | ||||||||||||||||||||||||||||||
| You find the five different kinds of ratios depend on the equivalence ratio and return to it, when you dissolve their relation, as the odd numbers create the square numbers. | וכן אתה מוצא חמשה ערכי המספר אשר הם נחלפים תלויים בערך הישר וחוזרים אליו כשאתה מתיר את קשרם כאשר המספרים הנפרדים קושרים את המרובע במספר | ||||||||||||||||||||||||||||||
| I draw for you a diagram, in which you can see the six different ratios, including the equivalence ratio, arranged with three numbers for each ratio: | והנה אני מצייר לך צורה תראה בה שש הערכים אשר הם הנחלפים עם הישר סדורים בשלשה מספרים בכל ערך וערך | ||||||||||||||||||||||||||||||
|
ואם אתה רוצה להתיר הערך הנחלף אל ישר אתה פוחת ראש מספרו מן השני וישאר בידך שלשה [45]שהם שוים או מוערכים על שרש אחד שהוא קרוב אל השוה | ||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
|
כגון ערך החלק אשר היא המעלה השלישית בצורה הזאת ומספרנו ד' ו' ט' | ||||||||||||||||||||||||||||||
|
אם אתה פוחת ד' מן ו' ישארו בידך ב' | ||||||||||||||||||||||||||||||
|
ואם אתה פוחת מן ב' א' ואחר כך תפחות מד' שהוא המספר הגדול א' וב' ישאר לך אחד ג' פעמים והוא הערך הישר | ||||||||||||||||||||||||||||||
| All ratios return to the equivalence ratio, when you dissolve their relation and inequivalence. | והנה כל הערכים כאשר אתה מתיר את קשרם ואת חלופם חוזרים אל ערך הישר | ||||||||||||||||||||||||||||||
| The sages deduce from this an allusion about the human: if he keeps himself once in the virtues of the ascetics and restrains himself from the passions of the world, the next time will be easier for him until reaching the definition of righteousness that is derived from the image of the one that corresponds the form of the Most High; Who dwells alone; Who is everything and everything is from Him, the beginning of all and the end of all; Who knows everything in particular and in general; to Whom the spirit of everything returns; the Secret of praises and the Reason of prayers; may God's name be blessed forever and ever. | ואמרו מכאן החכמים רמז על האדם אם ישמור נפשו במעלות הפרושים ויכבוש את עצמו מתאות העולם פעם אחת יקל עליו באחרת עד שיגיע לגדר היושר היוצא מדמות האחד אשר דמות העליון כנגדו והוא שוכן לבדו והוא הכל ומאתו הכל ראשית הכל ואחרית הכל ויודע הכל בפרט וכל ואליו תשוב רוח הכל על כן סוד התהלות וטעם התפלות יהי שם יי' מבורך לעולם ועד | ||||||||||||||||||||||||||||||
Chapter Six: Deducing One from Another |
השער הששי הוצאת זה מזה |
|---|---|
In Astrology |
|
| It is known in the science of the zodiacal constellation of the seven planets. | ידוע בחכמת המזלות לשבעת המשרתים שהם כוכבי לכת |
| The mean motion of Saturn each day is approximately 2 minutes, of Jupiter 5 minutes, of Mars 32 minutes, of the Sun and Venus 29 minutes, of Mercury 3 degrees and 11 minutes, and of the Moon 13 degrees and 11 minutes. | ומהלך השוה בכל יום בדרך קרובה לשבתי ב' ראשונים ולצדק ה' ראשונים ולמאדים ל"ב ראשונים ולחמה ונוגה כ"ט ראשונים ולכוכב חמה ג' מעלות י"א ראשונים וללבנה י"ג מעלות י"א ראשונים |
|
ואם ידעת יום ידוע שנכנס אחד מן המשרתים שמהלכם במתון בראש טלה ולאחר ט"ו יום נכנס אחד מן הקלים שמהלכם במרוצה בראש ו' טלה ותרצה להוציא מתוך חשבון מהלכם בכמה ימים וכמה שעות ישיגנו ויתחבר עמו |
|
הערך המעלות או החלקים כפי מה [46]שיהיו בימים שהלך וחלק על היתרון שיש בין שתי ההליכות ומה שיצא הם ימים ומה שישאר הם חלקים מהיתרון חלק חלקי היתרון על י"ב ומה שיצא חלק חלקי היתרון עליו והם שעות וחלקי שעה |
|
ובחינתו להעריך מהלך הראשון על הימים שעברו מחוברים עם הימים שירדף אחריו השני |
|
והערך חלקי היתרון על חשבון המעלות או החלקים שילך וחלק על היתרון והם מעלות או חלקים וישארו חלקים מחלקי היתרון |
|
וכן תעשה במהלך השני שתערוך חלקי היתרון על מהלכו וחלקם על היתרון |
|
תמצאם שוים |
|
ואם ילך האחד והשני יבא כנגדו כגון שיהיה נזור ותרצה להוציא מתי יתחברו |
|
חבר מהלך שניהם והוא היום וחלק הדרך עליו |
|
ועל זה הדרך תוכל לחשב לרצים ולשלוחים אשר תדע מהלכם בלא תוספת ובלא מגרעת |
|
וגם ידוע הוא שיש למשרתים מחברות פעמים שיתחברו כלם במזל אחד ופעמים ששה מהם או ה' או ד' או ג' או ב' מהם במזל אחד ותרצה להוציא כמה הם כל המחברות שלא ידמה זה לזה |
|
וככה תוכל לדעתם דע כי כל חשבון שיחובר מאחד עד איזה מספר שתרצה תוכל להוציאו מערכו אל חצי ואל חצי אחד |
|
ונחל לספור כמה יהיו המחברות השניות והטעם שיתחברו שני כוכבים לבדם |
|
והנה יש לשבתי עם המשרתים מחברות ששה ונערוך ששה על חציו וחצי אחד יעלה כ"א וככה מספר המחברות השניות |
|
רצינו להוציא השלישיות |
|
ושמנו צדק עם שבתי ועמהם אחד מהאחרים החמשה ויעלה מספרם חמשה ערכנום על שלשה שהוא חצי המספר וחצי אחד יעלה ט"ו וזאת מחברת שבתי |
|
וראוי להיות מחברות צדק ארבעה ערכנוהו על שנים וחצי עלה עשרה |
|
ומחברות מאדים שלשה ערכנוהו על שנים עלה ששה |
|
ומחברות חמה שנים ערכנום על אחד וחצי עלה שלשה |
|
ומחברות נגה אחת |
|
והנה מספר מחברות[47] השלישיות חמשה ושלשים |
|
רצינו להוציא הרביעיות |
|
ונחל משבתי וצדק ומאדים עמו ובעבור שצריך לשלשה שיתחברו עמו תחלת המחברת ארבעה ערכנו על שנים וחצי עלו עשרה |
|
ואחר כן יהיה מחברת שבתי וצדק עם האחרים ויהיו בתחלה שלשה ערכנום על שנים עלה ששה |
|
ואחר כן יחל שבתי עם מאדים ויהיו שנים ערכנום על אחד וחצי עלה שלשה |
|
ואחרי כן מחברת אחת |
|
ועלה מספר מחברות שבתי עשרים |
|
והנה יחל צדק משלשה ערכנום על שנים עלה ששה |
|
ואחר כן שנים ערכנום על אחד וחצי עלה שלשה |
|
ואחר כן מחברת אחת |
|
והנה מחברת צדק עשר |
|
ויחל מאדים משנים ערכנום על אחד וחצי עלה שלשה |
|
ואחר כן מחברת אחת |
|
הנה ארבע מחברות למאדים |
|
ומחברת חמה עם השפלים אחת |
|
והנה מספר הרביעיות חמשה ושלשים |
|
רצינו להוציא החמישיות ומצאנו לשבתי ט"ו ולצדק ה' ולמאדים אחת והנה מספר החמישיות כ"א |
|
והמחברות הששיות יש לשבתי שש ואחת לצדק והנם שבע |
|
ומחברות השבעה אחת |
|
ועלה מספר כלם מאה ועשרים מחברות |
| In many issues the astrologers need to extract the unknown from the known: | ובעינינים רבים יצטרכו חכמי המזלות להוציא הנסתר מהידוע |
|
כמו בחשבון הקשתות והיתרים והחצים להוציא זה מזה ועם גזור האל אפרשנו במקומו בזה הספר |
|
וכאשר בחשבון צללי השמש להוציא הישר מן ההפוך וההפוך מן הישר ומן כל אחד ואחד הגובה ומן הגובה כל אחד ואחד מהם אך אין זה מקומו להאריך בו |
| Reference to Abraham Ibn Ezra's works: This is explained in Sefer Keli ha-Neḥošet [Book on the Astrolabe] and Sefer ha-Luḥot le-Šivʿah ha-Mešaretim [Tables of the Seven Planets]. | והנה מפורש בספר כלי הנחשת ובספר הלוחות לשבעה המשרתים |
In Mathematics |
|
| In the mathematicians' way you extract the unknown from the known as you have seen in the preceding chapters on addition, subtraction, multiplication, division, ratio of one to another, and we find it also in the issue of roots. By the decree of God I will explain it in its place. | ולענין חכמי המדות אתה מוציא הנסתר מן הגלוי כאשר ראית בשערים שעברו במחברת ובמגרעת [48]ובמערכת ובמחלוקת ובערך זה אל זה וגם בענין השרשים נמצאנו ועם גוזר האל במקומו אפרשנו |
| In bargaining and in human affairs you find also the extraction of the unknown from the known. | וגם בחשבוני מקח וממכר ובעסקי בני אדם אתה מוצא להוציא הנסתר מהידוע |
| For, all human affairs associated with the calculations of commerce, employment of workers, and exchange are based on four numbers in two orders of ratio [= "Rule of Three"] | כי כל עסקי בני אדם בחשבוני מקחם וממכרם ושכירות כל מעשיהם ושעור חלופיהם הם עומדים בין ארבעה מספרים בשני סדרי הערך |
| The Rule of Three is built on four numbers that are in the two orders of the equivalence ratio | |
| For every four numbers that are in the two orders of the equivalence ratio: | כי כל ארבעה מספרים בשני סדרי ערך שוה |
|
והוא שיהיה חלק האחד מן השני כחלק השלישי מן הרביעי |
|
אם אתה עורך הראשון ברביעי יהיה מספרו כמספר השני בשלישי |
|
והמשל כגון שני מספר ד' ט"ו עם שני מספרי י"ב מ"ה |
|
והראשון שהוא ד' הוא חלק מן מספר ט"ו אשר הוא השני כמו י"ב שהוא המספר השלישי מן מספר מ"ה והוא הרביעי והוא חמישיתו ושליש חמישיתו |
|
ואם אתה עורך ד' והוא הראשון במספר מ"ה והוא הרביעי יהיה מספרו כמספר ט"ו השני במספר י"ב השלישי |
|
ועוד אם תקח ערך ד' אל י"ב השלישי יהיה כערך ט"ו אל מ"ה הרביעי |
|
ואתה מוצא מספר ד' והוא הראשון נערך אל שני המספרים אל השני ואל השלישי ואינו נערך אל הרביעי |
|
וכן השני נערך אל הראשון ואל הרביעי ואינו נערך אל השלישי |
|
והמספרים הנערכים זה אל זה נקראים חברים |
|
ושאינם נערכים נקראים נכריים |
| Hence, you learn that every four numbers that are equal in ratio, if you multiply one of the ratio’s orders by its stranger from the second order, it will be equal to the product of its companion in the ratio [multiplied] by its own stranger from the other ratio.
|
ומכאן אתה למד שכל ד' מספרים שהם שוים בערך אם אתה עורך האחד מסדרי הערך עם הנכרי לו מסדר השני יהיה שוה לחשבון חברו בהקשה באשר הוא נכרי לו מן הערך השני |
Word Problems |
|
Trade |
|
| Trade is based on the "Rule of Three" | |
| All human affairs are based on the two orders of the equivalence ratio: | וכל עסקי בני אדם עומדים בשני סדרי הערך הזה |
The [amount of goods offered in] business and trade are one [term] [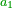 ]; the corresponding price is the second [term] [ ]; the corresponding price is the second [term] [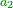 ]. ].
|
כי העסק והמסחר הוא האחד ושני לו השער המסור לו |
The second order is the taken or sold [amount of goods] [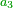 ] and its second [term] is the money [paid for the amount of goods which was actually sold] [ ] and its second [term] is the money [paid for the amount of goods which was actually sold] [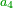 ]. ].
|
והסדר השני הוא הנלקח או הנמכר ושני לו הדמים |
| The [amount of goods offered in] business is proportional to the price, as the sold [amount of goods] is proportional to the money [paid]. | והעסק נערך אל השער כאשר הנמכר נערך אל הדמים |
| The ratio of the [amount of goods offered in] business to the sold merchandise is equal to the ratio of the price to the money [paid] and they are the "companions". | ועוד ערך העסק אל המכר כערך השער אל הדמים ואלו הם החברים |
|
| |
| You find the [amount of goods offered in] business stranger to the money [paid] and the sold merchandise stranger to the price. | ותמצא לעולם העסק נכרי [49]לדמים והמכר נכרי לשער |
| In all human affairs three of these values are known and the fourth is unknown, but we can deduce it from the three that are known: | ובכל עסקי בני אדם שלשה מאלה הארבעה ידועים והרביעי נסתר ונוציאנו מכח השלשה הידועים |
| For, if you multiply one of the three knowns by its stranger and you get the product, then you divide the product by the third known, you find the fourth unknown. | שאם אתה עורך אחד מהשלשה הידועים בנכרי לו מהם ותדע המספר הנכלל בחשבון ותחלק אותו על השלישי הידוע אתה מוצא הרביעי הנסתר |
|
| |
| Examples | |
|
כגון האומר עשרה כורי החטה בו' דינ' כמה כורים אוכל לקחת בארבעה דינ' |
|
והמסחר הוא הי' כורים והוא הנקרא עסק |
|
והשער המסור לו הוא ו' דינ' |
|
ואלה שניהם עומדים בערך אחד |
|
והערך השני הוא הד' דינ' והוא הדמים |
|
ואתה רוצה להוציא המכר הנסתר |
|
ובזה הענין שני הנכרים אשר בשלשה הידועים הם הדמים והעסק והם י' וד' |
|
ולפיכך תערוך י' בד' ויהיו מ' |
|
חלקם על השער הידוע שהוא ו' ויהיה ששה ושני שלישי אחד והוא מספר המכר שהיה נסתר |
|
או דע מה ערך ד' שהם הדמים מן ו' שהם השער והם החברים ויהיה ב' שלישיותיו |
|
קח שני שלישיותיו העשרה שהוא העסק וככה הוא המכר שהיה נסתר |
|
או חלק העשרה על הו' והיוצא תערוך על ד' והעולה הוא המכר אשר היה נסתר |
Here, the third number [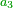 ], which is the sold merchandise, was unknown. ], which is the sold merchandise, was unknown.
|
ובכאן היה המספר השלישי נסתר והוא המכר |
If the fourth number [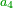 - the money paid] is unknown: - the money paid] is unknown:
|
ואם היה המספר הרביעי נסתר |
|
כגון האומר י' כורים בו' דינ' כמה הוא דמי ד' כורים |
|
ובכאן הם הדמים נסתרים |
|
ותדענו שתערוך השער שהוא ו' במכר שהוא ד' יעלה כ"ד |
|
חלקם על המסחר והוא הנקרא עסק והם הי' כורים יצא ב' דינ' וב' חומשי דינ' והוא הדמים שהיו נסתרים |
|
גם תדענו שתדרוש מה ערך הד' שהם המכר מן הי' שהם העסק והם החברים והוא שני חמישיותיו |
|
קח שני חמישיות ו' והוא הדמים הנסתרים |
|
או חלק הו' דינ' על הי' והיוצא שהם שלשה חומשין ערכם על הד' והעולה הם הדמים הנסתרים |
If the price [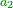 ] is unknown: ] is unknown:
|
ואם היה השער נסתר |
|
כגון האומר קניתי ג' כורים בד' דינ' בכמה הייתי קונה עשרה כורים |
|
[50]ובכאן המכר ודמיו ידועים והם ג' כורים וד' דינ' |
|
וכן המסחר שנקרא העסק ידוע והם הי' כורים |
|
ונסתר ממך שער הי' כורים |
|
ותדענו שתערוך המסחר שהם י' כורים בד' שהם דמי המכר ועלה מ' |
|
חלקם על ג' והם המכר ושא השער הנסתר והוא י"ג דינ' ושליש |
|
גם תדענו ראה מה ערך הי' מן הג' והוא כפלו ג' פעם ושליש |
|
ערכם על הד' כלו' כפול ד' ג' פעמים ושליש יעלה י"ג ושליש |
|
או חלק הד' על הג' יצא אחד ושליש |
|
ערכם על הי' יעלה י"ג ושליש |
If the [amount of goods offered in the] business [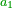 ] is unknown: ] is unknown:
|
ואם היה המסחר שהוא הנקרא עסק נסתר |
|
כגון האומר קניתי ו' כורים בד' דינ' כמה כורים אקנה בז' דינ' |
|
נמצא שאתה יודע המכר ודמיו והם ו' כורים וד' דינ' והם כערך אחד |
|
וגם אתה יודע מן הערך הראשון השער שהוא ז' דינ' |
|
ונסתר ממך העסק והוא המסחר |
|
ותדענו שתערוך השער שהם ז' בו' שהוא המכר והם הנכריים ועלו מ"ב |
|
חלקם על ד' שהם הדמים יצא המסחר שהוא העסק והוא י' כורים וחצי |
|
ותדענו שתדע מה ערך ז' אל ד' והוא כמוהו וג' רביעיותיו |
|
ערכם אל הו' והוא י' וחצי |
|
או חלק הו' על הד' יצא אחד וחצי |
|
ערכם אל על הז' יעלה י' וחצי |
| Now I have explained to you the extraction of the unknown number from the known [numbers]. | ועתה בארתי לך הוצאת המספר הנסתר מתוך הידועים |
| If you want to extract both the [amount of goods offered in the] business and the corresponding price: | ואם רצית להוציא הכורים והדמים |
|
כגון שישאל השואל ג' כורים בה' דינ' וקנה כורים נעלמים וכאשר תחבר הדמים עם הכורים יעלו ששים כמה היו הכורים והדמים |
|
חבר הג' והה' יעלה ח' |
|
ודע מה ערך הג' מן הח' והוא ג' שמיניות |
|
קח ג' שמיניות הששים והוא כ"ב וחצי והם הכורים |
|
ולהוציא הדמים דע מה ערך הה' מן הח' והוא ה' שמיניות |
|
קח ה' שמיניות הששים והם ל"ז וחצי והם הדמים |
|
או חלק הששים על שמונה יהיה היוצא ז' וחצי |
|
אם תערכם על הג' יעלה חשבון הכורים |
|
[51]ואם תערכם על ה' יעלה חשבון הדמים |
|
ואם תרצה להוציא ג' כורים בז' דינ' וקנה כורים נעלמים כשתגרע מהם הדמים ישאר כ' כמה היו הכורים והדמים |
|
גרע הג' מן הז' ישאר ד' |
|
ודע מה ערך הג' מן הד' והוא ג' רביעיות |
|
קח ג' רביעיות הכ' והוא ט"ו והם הכורים |
|
ולהוציא הדמים דע מה ערך הז' מן הד' והוא כמוהו וג' רביעיותיו |
|
קח כערכם מן הכ' והוא ל"ה והם הדמים |
|
או אם תחלק הכ' על ד' יצא ה' |
|
אם תערכם על ג' יעלה חשבון הכורים |
|
ואם תערכם בז' יעלה חשבון הדמים |
|
ואם תוציא ג' כורים בה' דינ' וקנה כורים נעלמים כשתערוך הכורים על הדמים יעלה ששים |
|
ערוך הג' בה' יעלה ט"ו |
|
וחלק עליהם הששים ומהעולה קח השורש והוא ב' |
|
וערכם על ג' יהיה ששה והם הכורים |
|
ואם תערוך הב' על הה' יעלה י' והם הדמים |
|
או אם תערוך הג' בששים יצא ק"פ |
|
אם תחלקם על הה' יצא ל"ו |
|
ומהיוצא תקח השרש והעולה הוא חשבון הכורים |
|
ואם תחלקם על הג' ומהיוצא תקח שרש והעולה הוא חשבון הדמים |
|
ואם תוציא ד' כורים בט' דינ' וקנה כורים נעלמים אם תחבר שורש הכורים עם שורש הדמים יעלה ז' וחצי |
|
קח שורש הד' והוא ב' |
|
וקח שורש הט' והוא ג' |
|
חבר ב' עם ג' יהיה ה' |
|
חלק עליהם הז' וחצי והיוצא תערוך בשנים יעלה ג' והם שורש הכורים ומספרם ט' |
|
ואם תערוך היוצא בחלוק בג' יהיה ד' וחצי והם שורש הדמים |
|
תערכם על עצמם יעלה כ' דינ' ורובע דינ' |
|
או אם תחלק הט' על הד' יצא ב' ורובע |
|
קח השורש והוא אחד וחצי |
|
הוסף עליו אחד לעולם יהיה שנים וחצי |
|
חלק עליהם הז' וחצי והיוצא שהם ג' תערוך [52]על עצמם והעולה הוא חשבון הכורים |
|
| |
|
ולדעת הדמים תחלק הד' על הט' יצא ד' תשיעיות |
|
קח השרש והוא ב' שלישיות שהם שורש ד' תשיעיות |
|
הוסף עליהם אחד יהיה אחד וב' שלישיות |
|
חלק עליהם הז' וחצי יצא לאחד שלם ד' וחצי |
|
ערכם על עצמם והוא חשבון הדמים |
|
ואם תוציא ד' כורים בט' דינ' כשתפחות שרשו משורש הדמים ישאר אחד וחצי |
|
קח שורש הד' והוא ב' |
|
וחסרם משרש הט' ישאר א' |
|
חלק עליו אחד וחצי יצא הכל |
|
אם תערכנו עם שנים יעלה שורש הכורים |
|
ואם תערכנו על שלשה יצא שרש הדמים |
|
ותוכל להוציאו בדרך האחר |
|
ואם תוציא ד' כורים בט' דינ' כשתערוך שורש הכורים על שורש הדמים יהיה כ"ד |
|
קח שרש הד' והוא ב' |
|
ערכם בגדר הט' יעלה ששה |
|
חלק עליהם הכ"ד והיוצא תח תערוך בד' יהיה י"ו והוא חשבון הכורים |
|
ואם תערוך היוצא בחלוק על ט' יעלה ל"ו והוא חשבון הדמים |
|
ואם תוציא כורים נעלמים ודמיהם ששים ודמי הכור כשיתחברו עם חשבון הכורים יהיה י"ו |
|
קח חצי הי"ו והוא ח' |
|
ערכם על עצמם ומהעולה חסר הששים ישאר ארבעה |
|
קח השורש והוא ב' |
|
והוסף על הח' יהיו י' והם הכורים |
|
| |
|
וחסר הב' מן הח' ישאר ו' והם הדמים |
|
ואם תוציא כורים נעלמים ודמיהם ששים אם תחסר דמי הכור מחשבון הכורים ישאר ארבעה |
|
קח חצי הד' ותערכנו על עצמו יהיה ד' |
|
חברם עם הששים וקח השרשים והוא ח' |
|
הוסף עליהם השנים והוא י' והם הכורים |
|
או אם תחסר הב' מן הח' ישאר ששה והם דמי הכור |
|
ואם תוציא כור בג' וכור בז' ורוצה לקנות משניהם כור בו' כמה יקח מכל אחד ואחד |
|
דע מה [53]בין הג' והז' והוא ד' |
|
ואחר כך תגרע הו' מן הז' ישאר אחד |
|
ודע מה ערכו מן הד' והוא רביע וככה יקח מן הכור שהוא בג' רביע |
|
ומותר הכור שהם ג' רביעיות יקח מן הכור שהוא בז' |
|
ואם תוציא כור בג' וכור בד' וכור בה' ורוצה ליקח בב' דינ' מכל כור וכור בשוה כמה יקח מכל אחד |
|
חבר הג' והד' והה' יהיו י"ב |
|
ודע מה |
|
ואם תוציא כור בג' וכור בד' וכור בה' ולקח משלשתם כור וחצי מכל אחד בשוה כמה הם הדמים |
|
חבר הג' והד' והה' יהיו י"ב |
|
ודע מה ערך הכור וחצי מן הג' כורים וכערכם קח מן הי"ב והוא ו' והם הדמים |
|
ואם תוציא כור בג' וכור בז' וכור בי"ב וירצה לקח כור בי' דינ' כמה יקח מכל מין ומין |
|
חבר הג' והז' והוא עשרה ושמרם |
|
ואחר כך כפול הי"ב יהיו כ"ד |
|
וחסר מהם הי' ששמרת ישאר י"ד |
|
ואחר חסר הי' אשר לקח מהם הכור מן הי"ב ישאר שנים |
|
ודע מה ערכם מן הי"ד והוא שביעית וככה קח מן הכור שהוא בג' וכמו כן מן הכור שהוא בז' |
|
והנשאר שהוא ה' שביעיות נקח מן הכור שהוא בי"ב |
|
ואם תוציא כור בב' דינ' וכור בג' וכור בה' וכור בי"ד ורוצה לקח כור בי"ב דינ' כמה יקח מכל מין ומין |
|
חבר הב' והג' וה' יעלו עשרה |
|
ואחר כך כ"כ כפול הי"ד שלשה פעמים לפי שעלו הדמים בדמי ג' המינין אך למעלה לא כפלנוהו אלא פעם אחת לפי שלא עלו הדמים לדמי ג' המינין וכשכפלנו הי"ד ג' פעם עלה מ"ב |
|
חסר מהם הי' ישאר ל"ב |
|
ואחר חסר הי"ב מן הי"ד ישאר שנים |
|
ודע מה ערכם מן הל"ב והוא חצי שמינית וככה יקח מן הכור שהוא בב' דינ' וכן מן הג' וכן מן הה' |
|
והנשאר שהוא ו' שמיניות וחצי שמינית יקח מן הכור שהוא בי"ד |
|
ואם תוציא עשרה כורים בעשרים ושנים עשר בעשרים וחמשה עשר כורים בעשרים וירצה לקח בעשרים חלק שוה מכל מין ומין כמה יתן לו |
|
חלק העשרים [54]על עשרה יצא שנים ועל י"ב יצא אחד ושני שלישיות ועל ט"ו יצא אחד ושליש |
|
חבר הכל יהיו חמשה |
|
חלק עליהם העשרים יצא ארבעה וכן יקח מכל מין ומין |
|
ואם תוציא ד' כורים בח' זוז פחות דבר שאינו ידוע ולקח שני כורים בשאינו ידוע וזוז כמה היה מה שאינו ידוע |
|
הוסף הב' כורים על הד' יהיו ו' |
|
ואחר כך חבר שאינו ידוע וזוז עם הח' פחות דבר שאינו ידוע יהיו תשעה |
|
ודע מה ערך שני הכורים מן הששה והוא שליש |
|
קח שליש התשעה וחסר ממנו הזוז והנשאר שהוא שני זוזים הוא הדבר שאינו ידוע |
|
| |
|
ואם תוציא חמשה כורים בעשרה דינ' פחות משהו ולקח ג' כורים במשהו שאינו ידוע פחות דינ' עם כמה זה המשהו |
|
חבר הג' עם הה' יהיו ח' |
|
ואחר כך חבר המשהו פחות דינ' עם הי' פחות משהו יהיה ט' דינ' |
|
ודע מה ערך הג' כורים מן השמונה והוא רביעית וחצי רביעית |
|
וכערכם קח מן הט' והוא ג' ושלשה שמיניות |
|
הוסף עליהם הדינר הפחות והם ד' וג' שמיניות והוא המשהו |
|
| |
Employment of workers |
|
| Likewise you find in the employment issue. | וכן אתה מוצא בענין השכירות |
|
כגון האומר שכרתי פועל לשלשים יום בי' דינ' ועשה על ח' ימים כמה שכרו |
|
ובכאן אתה חושב ל' ימי השכירות למסחר |
|
והי' דינ' לשער |
|
וח' ימים שעשה מלאכתו למכר |
|
ויהיה המספר הנסתר דמי המכר |
|
ותוציאנו שתערך הח' בי' יהיו פ' |
|
חלקם על הל' יצא ג' פחות שליש |
|
ותדענו שתדע מה ערך ח' אל ל' והוא ד' חמשיות שלישית וכערכם קח מן הי' יצא ג' פחות שליש |
|
ותדענו שתחלק הי' על הל' יצא שליש |
|
ערכהו על ח' יצא והוא ח' שלישיות והדבר שוה |
| With these methods you solve when the sold merchandise, or price, or [amount of goods offered in the] business are unknown. There is no need to elaborate. | ועל אלו הדרכים תוציא כשיהיו המכר או השער או המסחר נסתרים ואין צריך להאריך בזה |
|
ואם תוציא שכיר בימים נעלמים בדינר נעלמים וכשתחבר הימים והדינ' יהיו מ' ועשה ימים נעלמים כשתערכם בשכרם יעלה י"ב ואם תערך הנשאר [55]מן הימים בנשאר מן השכר יעלה קצ"ב כמה הם הימים הנעלמים וכמה הדינ' וכמה עשה מן הימים |
|
|
|
|
|
|
|
חלק הקצ"ב על י"ב יצא י"ו |
|
קח שרשם והוא ד' והוסף עליהם אחד יהיה ה' |
|
וחלק עליהם המ' יצא ח' |
|
קח חצים והוא ד' וערכם על עצמם ומהעולה חסר הי"ב ישאר ד' |
|
קח שרשם והוא ב' הוסיפם על הד' שהם חצי הח' והעולה שהוא ו' הם הימים הנעלמים אשר עשה |
|
| |
|
|
|
|
או דע מה ערך הי"ב מן הק'צ'ב' והוא חצי שמינית קח השרש והוא רובע הוסף עליו אחד לעולם יהיה אחד ורובע |
|
חלק עליהם המ' יצא ל"ב |
|
קח חצים והוא י"ו וערכם על עצמם יעלה רנ"ו |
|
חסר מהם הק'צ'ב' יהיה הנשאר ס"ד |
|
קח שרשם והוא ח' הוסיפם על הי"ו יהיו כ"ד |
|
חברם עם הו' ראשונים והמחובר שהוא ל' הם הימים הנעלמים מן השכירות |
|
| |
|
וחסרם מן המ' והנשאר שהוא י' הם הדינ' הנעלמים |
|
ואם תוציא שכיר בחדש בי' דינ' ואם יבטל ישלם חצי שכרו ועשה ובטל ויצא שכרו בהפסדו |
|
חבר הה' שהוא חצי השכר עם הי' יהיה ט"ו |
|
ודע מה ערך הה' מהם והוא שליש וכערכם קח ממי החדש והיוצא שהוא י' הוא הימים שעשה |
|
ובטל שאר הימים והם כ' |
|
או תחלק הי' דינ' על הה' דינ' יצא ב' |
|
הוסף עליהם אחד לעולם יהיה ג' |
|
וחלק עליהם ימי החדש והיוצא שהוא י' הם הימים שעשה |
|
ואם תוציא שכיר בחדש בי' דינ' ואם יבטל ישלם ה' דינ' בחדש ועשה ובטל והיה שכרו זוזים נעלמים |
|
חבר הה' עם הי' יהיו ט"ו |
|
הוסף הזוזים על הה' יהיו ו' |
|
גרע ודע מה ערכם מן הט"ו וכערכם קח מימי החדש והוא י"ב והם הימים שעשה |
|
ובטל הנשאר והם י"ח |
|
ולקח בשכרו שכר ב' ימים |
|
או חלק הי' על ה' והיוצא שהוא ב' הוסף עליהם אחד לעולם ויהיה ג' |
|
ודע מה ערך הזוזים מן הה' והוא חומש |
|
הוסיפם על ימי החדש חמישיתם יהיה ל"ו |
|
חלקם על הג' והיוצא הם הימים שעשה |
|
ואם תוציא שכיר בחדש בי' דינ' ואם יבטל ישלם ה' דינ' בחדש ועשה ובטל ונתחייב לשלם זוזים נעלמים |
|
[56]חבר הה' עם הי' יהיה ט"ו |
|
ואחר כן חסר דינ' מן הה' ישאר ד' |
|
ודע מה ערכם מן הט"ו וכערכם קח מימי החדש והוא ח' והם הימים שעשה |
|
ובטל כ"ב יום ונתחייב לשלם שכר ב' ימים |
|
או חלק הי' על הה' יצא ב' |
|
הוסף עליהם אחד יהיה ג' ושמרם |
|
ואחר דע מה ערך דינ' מן הה' דינ' והוא חמשים |
|
וקח מימי החדש חמישיתם ישאר כ"ד |
|
חלקם על הג' ששמרת והיוצא שהוא ח' הם הימים שעשה |
|
ואם תוציא שכיר בחדש בדינ' נעלמים ואם יבטל ישלם ה' דינ' בחדש ועשה ימים נעלמים וכשתערוך הימים הנעלמים על הדינ' הנעלמים היה פ' וכשיצא ממלאכתו נתחייב דינ' נעלמים |
|
חסר הדינר מן הה' ישארו ד' |
|
ערכם על הל' ומהמחובר חסר פ' ישאר מ' |
|
חלקם על ה' והיוצא שהוא הם הימים שעשה |
|
חלק עליהם הפ' והיוצא שהוא י' הם הדינ' הנעלמים |
|
ונתחייב לשלם שכר ב' ימים |
|
ואם תערוך הדינ' בל' ותחבר העולה עם הפ' יהיה ק"י |
|
חלקם על הה' והיוצא שהוא כ"ב הם ימי הבטלה |
|
ואם תוציא שכר ג' פועלים אחד ג' דינ' בחדש והשני ו' דינ' והשלישי י' דינ' ועשו בין שלשתם חדש אחד ולקחו כל אחד בשוה כמה עשה כל אחד מהם |
|
דע מה ערך הג' מן הי' והוא ג' עשיריות |
|
ודע מה ערך הג' מן הו' והוא חצי |
|
חברהו אל הג' עשיריות יהיה ד' חומשין |
|
הוסף עליהם אחד לעולם יהיה אחד וד' חומשין |
|
ודע מה האחד מהם והוא חמשה תשעיות |
|
קח חמש תשעיות ימי החדש שהם י"ו ושני שלישי יום והם הימים שעשה הראשון |
|
| |
|
וקח חצי מלאכת הראשון והוא ח' ושליש והם הימים שעשה השני |
|
או חלק הל' על הג' ודע מה ערך הל' מי"ח והוא כמוהו ושני שלישיותיו |
|
וכערך הזה קח מכל מה שיצא בחלוק לכל אחד ואחד והם הימים שעשה כל אחד ואחד |
|
ואם תוציא שכר ג' פועלים האחד ל' יום בדבר שאינו ידוע והשני בחצי הדבר שאינו ידוע והשלישי [57]בשלישית הדבר שאינו ידוע ועשו ל' יום בין שלשתם ולקח הראשון ב' דינ' והשני ג' די' והשלישי ד' די' כמה היה הדבר שאינו ידוע וכמה עשה כל אחד |
|
ערוך חלק הראשון בימי החדש יעלה ס' |
|
וערוך חלק השני בימי החדש והעולה תכפול ג' פעם יעלה ש"ס |
|
חבר הכל יהיה ת"ר |
|
חלקם על ימי החדש והיוצא שהוא כ' הוא הדבר שאינו ידוע |
|
| |
|
ולדעת הימים שעשה הראשון דע מה ערך ס' מת"ר והוא עשירית |
|
וכערכו קח מימי החדש והם ג' והם הימים שעשה הראשון |
|
ודע מה ערך הק"פ מת"ר וכערכם קח מימי החדש[58] והם ט' ימים שעשה השני |
|
ודע מה ערך הש"ס מת"ר והוא ג' חמישיותיו |
|
וכערכם קח מימי החדש והם י"ח ימים שעשה השלישי |
|
ואם תוציא שם שכיר בו' דינ' ובדבר שאינו ידוע חדש אחד ועשה עשרה ימים ולקח הדבר שאינו ידוע כמה הוא |
|
ערוך ימי החדש בו' דינ' עלה ק"פ ושמרם |
|
ואחר כן חסר י' ימים שעשה מימי החדש והנשאר שהם כ' הוא המורה |
|
וחלק ק"פ ששמרת על המורה יצא ט' והוא הכל הידוע |
|
ושאינו ידוע חסר הידוע ישאר מה שאינו ידוע והוא ג' |
|
דרך אחרת חסר הימים שעשה מימי החדש והנשאר שהוא כ' הוא המורה |
|
ואחר כן ערוך הימים שעשה על הו' דינ' יעלה ס' |
|
חלקם על המורה יצא ג' והוא הדבר שאינו ידוע |
|
דרך אחרת דע מה ערך הימים שעשה אל המורה והוא חצי |
|
וכערך זה קח מן הו' דינ' הידוע והוא ג' והם הדבר שאינו ידוע |
|
ואם היה חשבון שלא היה לו ערך |
|
ערוך הימים שעשה על הו' דינ' והעולה חלק על המורה אז תמצא הדבר שאינו ידוע |
|
ואם אמר ולקח בשכרו הדבר שאינו ידוע ונתן לו עוד דינר |
|
הוסף על הדבר הידוע אחד ועשה כמשפט |
Partnership |
|
| You also find two orders of ratio in the issue of partnership: | וכן לענין שתוף אתה מוצא שני סדרי הערך |
For, all the parts of the money that are contributed to the partnership are as [the amount of goods offered in] business, which is the trade [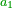 ]. ].
|
כי כל ראשי הממון שמכניסים בשתוף הם כעין העסק שהוא [59]המסחר |
The total profit is as the corresponding price. [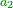 ]. ].
|
וכל הריוח הוא כעין השער המסור לו |
The share of each [of the partners] in the capital is as the sold [amount of goods] [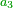 ]. ].
|
וחלק כל אחד מהממון כעין המכר |
And the part owed to each [of the partners] from the profit is as the money paid [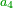 ]. ].
|
והחלק המגיע לכל אחד מן הריוח כעין הדמים |
| If the money paid [= the part owed to each of the partners from the profit] is unknown: | ואם הדמים הנסתרים |
|
כגון שנשתתפו האחד בי' והשני בכ' והשלישי בל' והרויחו ל' |
|
ערוך השער על המכר וחלק על העסק יצא חלק |
| If the sold merchandise [= share of each of the partners in the money] is unknown: | ואם המכר נסתר |
|
כגון שנשתתפו בין כלם בששים ורוחו ל' ולקח האחד ה' והשני י' והשלישי ט"ו |
|
ערוך המסחר בדמי האחד וחלק על השער יצא חלקו |
| If the price [= total profit] is unknown: | ואם השער נסתר |
|
כגון האחד י' והשני כ' והשלישי ל' ורוח בעל הי' חמשה |
|
ערוך העסק בדמי המכר וחלק על המכר |
| If the business [= all the parts of the money given to the partnership] is unknown: | ואם העסק נסתר |
|
כגון שידוע שחלק האחד היה י' ורוחו בין כלם ל' ולקח בעל הי' חמשה מן הריוח |
|
ערוך השער על המכר וחלק על הדמים |
| In all the other ways you can extract them also as it is in employment and trade. | וגם בשאר כל הדרכים תוכל להוציאם כאשר הם בשכיר ובמקח וממכר |
|
וכן אם היו ד' שותפים לכל אחד ראש ממון שאינו שוה לחברו [כלו' ה' וי' וט"ו וכ'] ויצא להם ריוח |
|
הערך ראש ממון כל אחד בפני עצמו בריוח וחלק על המחובר מראש ממון כלם שהוא נ' והיוצא הוא בחלק חלקו המגיעו מן הריוח |
|
ואם ישאר שלא יתחלק השב הדי' לפשיטים וחלק על מה שחלקת |
|
או חלק המחובר שהוא נ' על החלק ועל היוצא שהוא י' תחלק הריוח |
|
ובדרך אחרת תוכל לדעת כמה חלק כל אחד מן הריוח |
|
שתחבר ראש ממונם ודע מה ערך הריוח מראש ממונם וכערכו קח מראש כל אחד והוא חלקו |
|
ותדענו שתחלק ראש ממון הגדול על הקטן ושמור היוצא |
|
ועוד חלק ראש ממון האמצעי על הקטן והיוצא הוא חלק הראשון |
|
וראה מה ערך ראש ממון הקטן אל האמצעי וכערכו תוסיף על חלקו מן הריוח והוא חלק האמצעי |
|
וכן תוסיף לשלישי כערכו אל הקטן |
|
ואם תרצה להוציא ג' נשתתפו האחד כ' והשני ל' והשלישי מ' והריוח בעל הכ' ג' כמה הגיע לחלק האחרים |
|
חלק הל' על הכ' והיוצא תערכנו בג' שרוח והעולה [60]הוא חלק בעל הל' והוא ד' וחצי |
|
וכן תחלק המ' על הכ' והיוצא תערוך בג' והעולה שהוא ו' הוא חלקו |
|
ותדענו שתדע מה ערך הג' אל הכ' והוא ג' רביעיות חמישית |
|
וכערכו קח מראש ממון השני והשלישי |
|
ואם תוציא האחד כ' והשני ל' והשלישי מ' וריוח בעל הכ' כשתחברנו אל ריוח בעל הל' יעלה עשרה |
|
חבר הכ' והל' יהיו חמשים |
|
חלק עליהם הי' יצא חומש |
|
קח חומש ראש ממון כל אחד |
|
יקח בעל הכ' ד' |
|
ובעל הל' ו' |
|
ובעל המ' ח' |
|
ואם תוציא האחד י' והשני ל' והשלישי נ' וכשתחבר ריוח הראשון והשני ותחסרם מריוח השלישי ישאר ג' |
|
חבר הי' והל' יהיו מ' |
|
ותגרעם מן הנ' ישאר י' |
|
ודע מה ערך ג' מי' והוא ג' עשיריות |
|
קח ג' עשיריות ראש ממון כל אחד וככה חלקו |
|
הראשון ג' |
|
והשני ט' |
|
והשלישי ט"ו |
|
ואם תוציא האחד י' והשני כ' והשלישי מ' וכשתערוך ריוח הראשון והשני בריוח השלישי עלה מ"ח כמה היה ריוח כל אחד |
|
חבר הי' עם הכ' והעולה תערוך על המ' יעלה אלף ומאתים |
|
דע מה ערך המ"ח מהם והוא חמישית החומש |
|
חשוב אותם כאלו הם שברים וקח השרש והוא חומש |
|
וקח חומש ראש ממון כל אחד מהם |
|
יקח הראשון ב' |
|
והשני ד' |
|
והשלישי ח' |
|
ואם תוציא שני שותפין האחד ח' והשני י"ח ורוחו וכשתערוך שורש ריוח האחד בשורש ריוח השני יהיה ו' |
|
ערוך הו' על עצמם יעלה ל"ו |
|
ואחר כן ערוך הח' על הי"ח יעלה קמ"ד |
|
חלק עליהם הל"ו והיוצא שהוא רוביע קח שרשו והוא חצי |
|
אם תערכהו על השמונה יעלה ד' והוא הריוח של בעל הח' |
|
ואם תערכהו על י"ח יעלה ט' והוא הריוח של בעל הי"ח |
|
ותדענו שתחלק הי"ח על הח' יצא ב' ורביע |
|
קח שרשם והוא אחד וחצי |
|
חלק עליו הו' והיוצא שהוא ד' הוא ריוח הראשון |
|
ואם תערוך הד' בשנים ורובע יעלה ט' והוא ריוח השני |
|
ואם תוציא שני אנשים נשתתפו זה בה' ככר וזה בג' ככר ונשתתף עמהם השלישי שלא הביא [61]כלום והוציאו שלשתם אותם הח' ככר ושלם להם השלישי ח' ליטרין כסף כמה יקח כל אחד |
|
קח שליש הח' ככר והוא ב' וב' שלישיים |
|
חסרם מן הה' ישארו ב' ושליש |
|
ודע מה ערכם מן הב' וב' שלישיים והוא ז' שמיניות |
|
קח ז' שמיניות הח' שהוא והוא יהיה חלק בעל הה' ככר |
|
ואם תחסר הב' וב' שלישים מן הג' ישאר שליש |
|
ותדע ערכו אל ב' ושליש והוא שמינית |
|
וקח שמינית הח' והוא אחד והוא חלק בעל הג' ככרים |
|
ואם תרצה תוציא ג' אנשים נשתתפו האחד בט' ככר והשני בח' והשלישי בז' ונשתתף עמהם הרביעי שלא הביא כלום והוציאו בין שלשתם הכל ושלם הרביעי להם י"ח ליט' כסף כמה יקח כל אחד |
|
חלק כל הככרים על הד' אנשים יצאו ו' |
|
חסרם מן הט' ישאר ג' |
|
ומן הח' ישאר ב' |
|
ומן הז' ישאר אחד |
|
חבר כל השיורין וחלק עליהם הי"ח יצא ג' |
|
אם תערכם בג' יעלה ט' והוא חלק בעל הט' |
|
ואם תערכנו בב' יעלה ו' והוא חלק בעל הח' |
|
ואם תערכהו באחד יהיה ג' והוא חלק בעל הז' |
|
ואם תוציא שלשה נשתתפו בראש ממון שוה כל אחד לחבירו ומה שהביא האחד היה ארבע חומשי ממונו והשני הביא חמש שביעיות ממונו והשלישי שש תשיעיות ממונו כמה היה לכל אחד ואחד |
|
הערך השנים הראשונים זה על זה באלכסון והטעם שתערוך שברי האחד על חשבון חברו ותחשבם כאלו הם שלמים |
|
והנה הראשון כ"ה |
|
והשני כ"ח |
|
ועשה כן לשני גם לשלישי |
|
והנה השני מ"ב |
|
והשלישי מ"ה |
|
ודע כמה הוסיף השני על הראשון והוא שלש רביעיות שביעית |
|
חסר כן ממ"ב ישארו ל"ז וחצי והוא ראש ממון הראשון |
|
וד' חמשיותיו ל' |
|
וראש ממון השני מ"ב |
|
וה' שביעיותיו ל' |
|
וראש ממון השלישי [62]מ"ה |
|
ושש תשיעיותיו ל' |
Coinage |
|
| You also find two orders of ratio in the issue of coinage: | וגם בענין קשור המטבע אתה מוצא שני סדרי ההקשה |
| For the liṭra is a kind of [goods offered in the] business. | כי הליטרא כעין המסחר |
| The silver [in it] is a kind of its price. | והכסף הראוי לה כעין השער |
| The ՚oqya are a kind of a sold merchandise. | והאוקיאות כעין המכר |
| The silver in the ՚oqya is a kind of money [paid]. | והכסף המגיע לאוקיא כעין הדמים |
|
ואם היו הדמים נסתרים |
|
כגון האומר ליט' מטבעות שהיא י"ב אוקיאות ויש בהם ד' אוקיאות כסף כמה כסף יש בג' אוקיאות |
|
ערוך השער במכר וחלק על המסחר |
|
ואם היה המכר נסתר |
|
כגון האומר ליט' בד' אוקיאות כסף בכמה יש אוקיא מכסף |
|
ערוך המסחר בדמים וחלק על השער |
|
ואם היה השער נסתר |
|
כגון האומר קניתי ג' אוקיאות באוקיא כסף בכמה אקנה הליטרא |
|
ערוך המסחר בדמים וחלק על המכר |
|
ואם היה המסחר נסתר |
|
כגון האומר קניתי ג' אוקיאות מטבעות באוקיא כסף כמה אקח מן המטבעות בד' אוקיא כסף |
|
ערוך השער במכר וחלק על הדמים |
|
ואם תרצה לקשור מטבע מא' אוקיאות כסף בליט' והשני מב' אוקיאות כסף בליט' והשלישי מו' אוקי' בליטרא ואתה צריך לדעת כמה תקח מכל מטבע ומטבע ויהיה המחובר לד' אוק' אוקיאות בליט' |
|
ככה תדענו שתחבר הכסף שיש בשני המטבעות הפחותות ויעלה שלשה |
|
ואחר תכפול המטבע השלישי ויהיה הכפול י"ב |
|
וגרע מהם העולה מהמחובר משני המטבעות ישאר ט' ושמרהו |
|
ואחר תגרע הד' שהוא רוצה לקשור מן הששה שהוא סך המטבע השלישי ישאר ב' |
|
ודע מה ערך זה הנשאר אל הנשאר השמור והוא ב' תשיעיות וככה תקח מכל אחד ואחד משני המטבעות |
|
ויעלה בין שניהם ה' אוקיאות ושליש |
|
ויש בהן כסף ב' שלישי אוקיא |
|
ומן המטבע השלישי יקח ו' אוקי' וב' שלישי אוקי' |
|
שיש בהן כסף ג' אוקי' ושליש אוקי' |
|
ותעלה בידך ליט' שיש בה ארבע אוקיאו' כסף |
|
ואם יש בידך מן המטבעות ליט' באוקי' כסף וליט' בה' אוקי' וליט' בז' אוקי' ותרצה לקשור ליט' בד' אוקי' כסף |
|
[63]כן תעשה חבר שני המטבעות הגדולות מן המטבעות שהוא רוצה לקשור ויעלה י"ב |
|
וכפול השלישי ויעלה ב' |
|
וגרע אותו מהעולה מהמחובר ישאר י' ושמרהו |
|
ואחר גרע האחד שהוא המטבע היחידי מן הד' שהוא רוצה לקשור ישאר ג' |
|
ודע מה ערך זה הנשאר אל הנשאר השמור והוא ג' עשיריותיו וככה יקח מכל אחד ואחד משני המטבע |
|
ויעלה בין שניהם שבעה אוקי' וחומש אוקי' |
|
יש בהם כסף ג' אוקיאות וחצי וחצי חומש |
|
ומן המטבע השלישי ד' אוקיאות וד' חומשין |
|
יש בהם כסף ב' חומשין |
|
והנה מה שרצינו |
|
ואם יש בידך ליט' בג' רביעיות אוקי' וליטר' באוקיא ורביע וליט' בו' אוקיאו' ותרצה לקשור בד' אוקי' בליט' |
|
ככה תדענו חבר שני המטבע הפחותות יהיה ב' |
|
וכפול השלישי ויעלה י"ב |
|
וגרע ממנו המחובר ישאר י' ושמרהו |
|
ואחר גרע הד' מן הו' ישאר ב' |
|
ודע ערכם מהנשאר השמור והוא חומש וככה תקח מכל אחד ואחד משני המטבעות שחברת |
|
ויעלה בין שניהם ארבעה וד' חמישיות |
|
ויש בהם כסף ב' חומשין |
|
ומהמטבע השלישי ז' וחומש |
|
יש בהם כסף ג' וחצי וחצי חומש |
|
והנה מה שרצינו |
|
ואם יש בידך ליט' בשני אוקי' וליט' בה' ורביע וליט' בו' וג' רביעיות וקושר בד' בליטר' |
|
ככה תדענו חבר השנים הגדולים יעלה י"ב |
|
וכפול השלישי יעלה ד' |
|
וגרע הכפול מהמחובר ישאר ח' ושמרם |
|
ואחר כן גרע הב' מן הד' ישאר ב' |
|
וערכם אל הנשאר השמור והם רביע וככה יקח מכל אחד ואחד משני המטבע |
|
ויעלה בין שניהם ו' אוקי' |
|
ויש בהם כסף ג' אוקי' |
|
ומן השלישי יקח ו' אוקי' |
|
יש בהם כסף אוקי' |
|
והנה מה שרצינו |
|
ואם יש בידך ליט' ברביע אוקי' וליט' בחצי אוקי' וליט' באוקי' ורביע וליט' בה' אוקי' וקושר בד' אוקי' בליט' |
|
ככה תעשה חבר הג' מטבע הפחותות ויעלה ב' |
|
וכפול השלישי ג' פעמים בעבור שחברת ג' מטבעו' ויעלה [64]ט"ו |
|
וגרע המחובר מהכפול ישאר י"ג ושמרם |
|
ואחר כך גרע הד' מן ה' ישאר אחד |
|
וערכו מהנשאר השמור חלק אחד מי"ג וככה יקח מכל אחד מהשלשה המטבעו' המחוברות |
|
ויעלה בין שלשתם ב' אוקי' ועשרה חלקים מי"ג באחד |
|
ויש בהם כסף ב' חלקים מי"ג באחד |
|
ומן השלישי יקח ט' אוקי' וג' חלקים מי"ג |
|
יש בהם כסף ג' אוקי' ואחד עשר חלקים מי"ג באחד |
|
ונתברר מה שרצינו |
|
ואם יש בידך ליט' בג' אוקי' וליט' בחמשה ורביע וליט' בששה וחצי ליט' בז' ורביע וקושר בד' בליט' |
|
ככה תעשה חבר הג' מטבעו' הגדולות ויעלו י"ט |
|
וכפול השלישי ג' פעם ויעלה ט' |
|
וגרע הכפול מהמחובר ישאר י' ושמרם |
|
ואחר גרע הג' מן הד' ישאר אחד |
|
וערכו אל הנשאר השמור עשירית וככה יקח מכל אחד ואחד מהשלשה המחוברות |
|
ויעלה בין שלשתם ג' אוקי' וג' חומשין |
|
ויש בהם כסף ב' אוקי' וחצי חומש |
|
והנה מה שרצינו |
| ואם יש בידך ליט' בב' אוקי' | |
|
ואם יש בידך ליט' בחצי אוקי' וליט' בג' רביעיות וליט' בב' וחצי וליט' בג' ורביע וליט' בה' וג' רביעיות וקושר בג' וג' רביעיות |
|
| |
|
ככה תדענו חבר הד' מטבעו' הפחותות ויעלה ז' |
|
וכפול החמישי ד' פעם ויעלה כ"ג |
|
וגרע המחובר מהכפול ישאר י"ו ושמרם |
|
ואחר חסר הג' וג' רביעיות מן הה' וג' רביעיות ישאר ב' |
|
וערכם אל הנשאר השמור והם שמינית וכן יקח מכל אחד מהד' מטבעו' |
|
| |
|
ויעלה מארבעתם ו' אוקי' |
|
ויש בהם כסף [65]ז' שמיניות אחד |
|
ומן החמישי יקח ו' אוקי' |
|
ויש בהם כסף ב' אוקי' וז' שמיניות |
|
וזה שרצינו |
|
ואם הוא רוצה לקשור בד' אוקי' בליט' ויש מטבעות שכלם פחותות מד' כגון שיש בידו ליט' מג' רביעיות אוקי' כסף בליט' וליט' באוקי' ורביע וליט' באוקי' וחצי וליט' בב' אוקי' וחצי ורוצה להתיך מכלם בשוה וצריך לערב בהם כסף |
|
| |
|
ככה תדענו חבר הד' מטבעו' ויעלה ששה |
|
וכפול ליט' של כסף ד' פעם יעלה מ"ח אוקי' |
|
חסר המחובר מהכפול ישאר מ"ב ושמרם |
|
ואחר כך חסר הד' מן הליט' כסף ישאר ח' אוקי' |
|
וערכם מהנשאר השמור שביעית ושליש שביעית וככה יקח מכל אחד מהם |
|
| |
|
ויעלה מארבעים ט' אוקי' ושביעית |
|
ויש בהם כסף אוקי' ושביעית |
|
ומן הכסף ישים ב' אוקי' וו' שביעיות |
|
והנה מה שרצינו |
|
ואם רוצה לקשור בד' אוקי' בליט' ויש לו מטבעות שכלם גדולות מד' כגון שיש לו ליט' מה' אוקי' ורביע כסף וליט' מו' וחצי וליט' מז' וג' רביעיות וליט' מח' וחצי ורוצה להתיך מכלם בשוה וצריך לערב נחשת |
|
| |
|
ככה תדענו שתהפוך הענין ותקח חשבון הנחשת אשר במטבעו וחשבון נחשת המטבע אשר הוא רוצה לקשור |
|
וכך הוא החשבון ליט' בג' וחצי נחושת וליט' בד' ורביע נחשת וליט' בה' וחצי נחשת וליט' בו' וג' רביעיות נחשת וליט' מנחושת שהיא י"ב אוקי' ורוצה לקשור מכל זה ד' אוקי' כסף בח' מנחשת |
|
| |
|
כן תעשה חבר נחשת הד' מטבעו יעלה כ' אוקי' |
|
וכפול ליט' הנחשת ד' פעם יעלה מ"ח |
|
חסר המחובר מהכפול ישאר כ"ח ושמרם |
|
ואחר כן חסר הד' מן הי' ישאר ד' |
|
וערכם מהנשאר השמור שביעיות וככה יקח מכל אחד ואחד מהמטבעו' |
|
| |
|
ויעלה לו מארבעתם ו' אוקי' וו' שביעיות |
|
יש בהם מנחשת ב' אוקי' וו' שביעיות |
|
ומן הנחשת ישים ה' אוקי' ושביעית |
|
ויצא מה שרצינו |
| If one produce [a coin] with four [types of coins] and he has some that are less valuable and some that are more valuable, he should sum the less valuable [coins] and multiply one of the most valuable or sum the most valuable [coins] and multiply one of the [less] valuable, then he should proceed according to the rule. | ואם הוא קושר בד' ויש בידו פחותות ויתרות [66]יחבר הפחותות ויכפול אחת מהיתרות או יחבר היתרות ויכפול אחת מהיתרות ויעשה כמשפט |
| You should apply the following rule: multiply according to the number of the coins you mix. | וכלל זה יהא בידך שתכפול הכפול לפי חשבון המטבעות שחברת |
| When you sum the most valuable [coins], subtract the product from the sum, then subtract the one that is less valuable [coin] from the remainder. | ובחברך היתרות תגרע הכפול מהמחובר ותגרע היחידי שהוא פוחת מן הנקשר |
| Vice versa when you sum up the less valuable [coins]: subtract the sum from the product, then subtract the remainder from the one that is the most valuable [coin]. | והפך הדבר בחברך הפחותות שתחסר המחובר מהכפול ותחסר הנקשר מן היחידי היתר |
| From these examples you can deduce for all [kinds of] coins and all human affairs. | ומאלו הדמיונות תוכל להוציא לכל המטבעות ולכל עסקי בני אדם בין רב למע' למעט |
| Instruct a wise man, and he will become wiser [Proverbs 9, 9]. | ותן לחכם ויחכם עוד[note 5] |
Chapter Seven: Conversion of One to the Other |
השער השביעי השבת זה לזה |
|---|---|
The example:
|
והדמיון שאמ' אברכז כי מעלות נטיית הגלגל אשר לשמש אחד עשר חלק משמונים ושלשה בכל הגלגל |
|
ותלמי אמ' כי מעלות הנטייה ארבעים ושבע מעלות ממעלות הגלגל שהם ש"ס ועוד שנים וארבעים חלק ראשונים |
| We wish to know if [their estimates] are equal or different, so do like this: | ונרצה לדעת אם הם שוים או שונים ככה תעשה |
|
ערוך י"א שהוא חשבון אברכז הקטן על מעלות הגלגל שהוא חשבון תלמי הגדול והעולה שהוא ג' אלפים ותשע מאות וששים חלק על פ"ג שהוא חשבון הגדול של אברכז יצא בחלוק מ"ז כדברי תלמי ונשארו נ"ט שלא יתחלקו ערכנום על ששים והעולה שהוא ג' אלפים וחמש מאות וארבעים חלק על פ"ג יצא בחלוק שנים וארבעים חלק כדברי תלמי ונתברר ששני החשבונים שוים |
|
| |
|
והפך הדבר ערכנו מ"ז שהם מעלות תלמי על פ"ג והעולה שהוא ג' אלפים ותשע מאות ואחד וערכנו מ"ב על פ"ג והעולה שהוא ג' אלפים וד' מאות ושמונים וששה חלקנום על ש"ס שהוא החשבון הגדול של תלמי ויצא בחלוק י"א שהוא החשבון הקטן של אברכז והנה שני החשבונים שוים |
Simple fractions to simple fractions |
|
| If you have fractions of the geometricians and you wish to convert them to other fractions | ואם יהיו בידך שברי חכמי המדות ותרצה להשיבם לשברים אחרים |
|
כגון שלשה רובעים כמה שתותים הם |
|
דע מאיזה מספר הוא השתות והוא מששה |
|
קח שלשה רביעיותיו והם ארבעה וחצי וככה שתותים הם |
|
[67]ותדענו שתערוך שלשה על ששה והעולה תחלק על ארבעה והיוצא הם שתותים |
|
ותדענו שתערוך ארבעה על ששה יעלה כ"ד והוא המורה |
|
קח ג' רביעיותיו והם י"ח |
|
חלקם על ששית המורה יצא בחלוק ד' וחצי וככה שתותים הם |
|
ואם תרצה לידע ששה שביעיות כמה תשיעיות הם |
|
דע מאיזה מספר הוא התשיעית והוא מט' |
|
קח ששה שביעיותיו והם שבעה וה' שביעיות תשיעית |
|
או ערוך הששה על תשעה והעולה חלק על שבעה |
|
או ערוך השבעה על תשעה והעולה שהם ס"ג הוא המורה |
|
קח ששה שביעיותיו שהם נ"ד וחלקם על תשיעית המורה שהם ז' יצא שבעה וה' שביעיות |
|
אם כן מצאנו ששה שביעיות הם שבעה תשיעיות וה' שביעיות תשיעית |
|
או דע מאיזה מספר הוא השביעית משבעה |
|
קח ששת שביעיותיו והם ששה |
|
ערכם על תשעה והעולה שהם נ"ד חלק על שבעה יצא לחשבון אחד |
|
ואם תרצה להשיב שבעה שמיניות וחצי שמינית לעשיריות |
|
דע מאיזה מספר הוא העשירית מעשרה |
|
קח שבעה שמיניותיו וחצי שמיניתו יעלה תשעה עשרות ושלשה שמיניות עשירית |
|
ובכל הדרכים האחרים תוכל להוציאו |
| You can solve in these ways if you want to convert sixths into quarters, or ninths into quarters, whether you convert the fractions into smaller or into larger fractions; the [method] is the same. | ועל אלו הדרכים כמו כן תוכל להוציא אם תרצה להשיב ששיות לרביעיות או תשיעיות לרביעיות בין שתשיב השברים לפחותים מהם בין שתשיבם לגדולים מהם הדבר שוה |
Simple fractions to sexagesimal fractions |
|
| If you have simple fractions [= fractions of the geometricians] and you wish to convert them into fractions of the astrologers that are sexagesimal. | ואם יהיו בידיך שברי חכמי המדות ותרצה להשיבם לשברי חכמי המזלות שהם ששים |
| If the fractions you have are a half, a third, a quarter, a fifth, a sixth, or a tenth, it is easy to convert them into sexagesimal [fractions], because they are [divisors of sixty]. | ואם השברים שבידך הם חצי או שליש או רביע או חומש או ששית ועשירית דבר קל להשיב אל ששים מפני שיתחלקו עליו |
| But, if you have a seventh, an eighth, or a ninth, which [are not divisors of] sixty, and you need to know how you can convert them into sexagesimal [fractions]: | אך אם יש בידך שביעית ושמינית ותשיעית לא [68]יתחלקו עליהם ששים ואתה צריך לדעת איך תוכל להשיבם אל ששים |
|
כגון שהיו בידך ב' שביעיות ותרצה להשיבם לחשבון ששים |
|
ככה תעשה ערוך מספר השביעיות על ששים והעולה שהוא ק"כ חלק על שבעה יצא י"ז וישאר אחד |
|
וערוך הנשאר על ששים וחלק על ז' יצא ח' והם שניים ישאר ד' |
|
וערכם על ששים וחלק על ז' יצא ל"ד והם שלשים |
|
| |
|
ועל זה הדרך תוכל לדקדק אותו לרביעים או לחמישיים עד אין קץ |
|
או אם תרצה ערוך מספר השביעיים על ח' ל"ד י"ז שהם שביעית ששים יעלה י"ז ח' ל"ד כדרך הראשון |
| In these ways you also solve for eighths, and ninths. | ובאלו הדרכים תוציא כמו כן לשמיניות ולתשיעיות |
| If you have fractions of seventy and you want to convert them into a sexagesimal number: | ואם יהיו בידך חלקים משבעים ותרצה להשיבם לחשבון ששים |
|
ערוך החלקים על ששים וחלק העולה על שבעים |
|
ואם ישאר שלא יתחלק ערוך על ס' וחלק על ע' יהיו שניים מחשבון ששים |
|
או ערוך החלקים שיש בידך על ח' ראשונים ל"ד שניים י"ז שלישיים שהם שביעית ששים וחלק העולה על ששים והיוצא הוא המבוקש |
|
או חסר שביעית החשבון והנשאר הם חלקים מששים |
Chapter Eight: Roots |
השער השמיני שרש זה וזה |
|---|---|
| [Extracting] roots - of integers or fractions - is difficult. | השרשים הם קשים בין בשלמים בין בשברים |
| Most of them do not have a known root in the units, the tens, or the consequent ranks, therefore we extract them by approximation. | ורבם אין להם שורש ידוע באחדים ובעשרות ובכל המערכות הבאות אחריהן ונלקחום בדרך קרובה אל האמת |
Integers |
|
| Shortcuts for finding the root of a perfect square | |
| We start to explain the [extraction of roots of] integers that have a known root and give introductions and checks, as eyes for their seekers. | ונחל לפרש השלמים שיש להם שורש ידוע ונתן מפתחות ומאזנים להיות למבקשיהם עינים |
| The roots [of perfect squares] are found in two ways: | והשרשים ימצאו על שני דרכים |
|
האחד על דרך מספר האחדים |
|
והמרובעים הנמצאים בשלמים במערכתם הם שלשה והם א'ד'ט' ושרשם א'ב'ג' |
|
והדרך השני על דרך מספר העשרות |
|
והמרובעים הנמצאים במערכתם ששה והם י"ו כ"ה ל"ו מ"ט ס"ד פ"א ושרשם ד'ה'ו' ז'ח'ט' |
| These are the foundations of all the roots. | ואלה הם מוסדי [69]כל השרשים |
| From here on: every rank that is not even [i.e. every odd rank] takes after the units and every even [rank] takes after the tens. | ומכאן ואילך כל מעלה שאינה זוג היא כאחדים ומה שהיה זוג היא כעשרות |
|
כי המאות כמו האחדים כי הם כמערכת השלישית כמספר נפרד |
|
והאלפים כמו העשרות |
|
ועשרות אלפים כאחדים |
|
ומאות אלפים כעשרות |
|
ואלפי אלפים כאחדים |
|
ועשרות אלפי אלפים כעשרות |
|
ומאות אלפי אלפים כאחדים |
|
ואלף אלפים כעשרות |
|
ככה עד אין קץ ובין כזוג ובין כמה שאינה זוג |
| The [units] that are [roots] of the first rank become ten[s] [as roots] of the third rank, which is analogous to it; hundreds [as roots] of the fifth rank; and thousands [as roots] of the seventh rank. | האחד שהוא במערכת הראשונה ישוב עשרה במעלה השלישית שהיא דומה לה ובמעלה חמישית ממנה מאות ובשביעית ממנה אלפים |
|
ששרש אחד הוא אחד ישוב המעלה השלישית עשרה והוא שורש מאה ששניהם דומים לאחד |
|
ושרש ארבעה שנים על כן שרש ד' מאות עשרים |
|
ועל זה הדרך שרש תשע מאות ל' |
|
והמעלה הרביעית שהיא זוג דומה לשנית |
|
והנה אלף ושש מאות דומה לי"ו על כן שרשו ארבעים |
|
כי שב האחד עשרה כמערכת השלישית מן השנית |
|
והנה עשרת אלפים יהיה שרשו מאה כי הוא במעלה החמישית מן הראשונה |
|
ויהיה אלף אלפים שהיא המעלה השביעית שרשו אלף |
|
והנה ארבעים אלף כדמות ארבעה |
|
ומאה וששים אלף כדמות ששה עשר |
| This way for all the squares. | ועל זה הדרך לכל המרובעים |
|
וכאשר יהיה בידך חשבון ותרצה לדעת אם יש לו שרש שלם שקלו במאזני תשעה והוא שתחשב האחדים והעשרות והמאות וכל החשבונות כאלו הם אחדים והוציאם ט'ט' |
|
ואם נשאר א' או ד' או ט' או ז' יתכן להיותו מרובע |
|
ואם נשאר ב' או ג' או ה' או ח' דע שאיננו מרובע |
|
והנה דרך אחד |
|
ודרך שנית שתסתכל בחשבון אם יש שם ממספרי האחדים שהם במערכת הראשונה |
|
ואם מצאת שם א' או ד' או ה' או ו' או טיתין [70]ט' יתכן להיות מרובע |
|
ודרך שלישית |
|
שתדע כי אם יהיה בחשבון א' ראוי להיות בשרש א' או ט' |
|
ותוכל לדעת איזה יהיה בשרש החשבון לאיזה חשבון הוא קרוב אל הדומה למרובע האחדים |
|
ואם יהיה המרובע הדומה קודם החשבון ויש ביניהם כפל שרש המרובע הוסף על השרש הדומה אחד |
|
ואם היה פחות גרע משרש הדומה אחד |
|
ואם יהיה בשרש ט' |
|
כמו מרבע ת'מ'א' |
|
שקלנוהו במאזני ט' ויצא כלו ט'ט' והנה לאות שיתכן להיותו מרבע |
|
והדומה הקרוב הוא ד' מאות ושרשו כ' |
|
ובעבור שהחשבון גדול ממנו כפל השרש נוסיף בשרש אחד והנה השרש כ"א |
|
| |
|
ובחינתו שתסיר מרבע התוספת מן החשבון ישאר ת"מ |
|
ולו היה החשבון פחות ממרובע הדומה |
|
כגון שס"א |
|
ובעבור שהוא פחות תחסר אחד משורש מרובע הדומה הקרוב שהוא כ' וישאר בשרש ט' והוא י"ט |
|
| |
|
והבחינה להסיר מהחשבון מרובע החסרון וישאר ש"ס ונכפול השרש הדומה והוא מ' וככה מרחק החשבון מן הדומה |
|
ואם במרובע ד' יהיה בשרש ב' שהוא שני לאחד או ח' שהוא שני לי"ט |
|
ואם חשבון הדומה לפניו כמו מרובע ת'פ'ד' יהיה בשרש ב' והשרש כ"ב |
|
וכשתחסר מרובע התוספת מהחשבון ישאר ת"פ והנה המרחק מן הדומה פ' וככה ראוי להיות כפל הכפל מהשרש הדומה |
|
ואם חשבון הדומה אחריו כמו מרובע ש'כ'ד' שהדומה הקרוב כ' ובעבור שהחשבון פחות חסר ממנו ב' יהיה בשרש ח' והשרש י"ח |
|
וכשתסיר מרובע החסרון מהחשבון ישאר ש"כ ונכפול פעמים שרש הדומה וככה המרחק |
|
| |
|
ואם יש במרובע ט' יהיה בשרש ג' או ז' שהוא רחוק מעשרה ג' לאחורי' |
|
[71]ואם הדומה הקרוב הוא לפניו כגון מרובע ת'ק'כ'ט' שהדומה הקרוב הוא ד' מאות יהיה בשרש ג' והשרש כ"ג |
|
וכשתסיר מרובע התוספת מן החשבון ישאר ת'ק' והנה המרחק ק"כ ונכפול שרש הדומה והוא מ' וראוי להיות המרחק ג' פעמים כפל השרש וכן הוא |
|
| |
|
ואם הדומה הקרוב לאחריו כגון מרובע ת'ש'כ'ט' שהדומה הקרוב הוא ל' ובעבור שהוא פחות חסר ממנו ג' יהיה בשרש ז' והשרש כ"ז |
|
ואם תסיר מרובע החסרון מהחשבון ישאר ת'ש'כ' והנה המרחק ק'פ' ונכפול שרש הדומה והוא מ' וראוי להיות המרחק ג' פעמים כפל השרש וככה הוא |
|
| |
|
ואם במרובע ה' יהיה בשרש ה' בין לפניו בין לאחריו |
|
ואם הוא לפניו כגון אלף ור'כ'ה' שהדומה הוא ל' |
|
וכשתסיר מרובע ה' ישאר אלף ור' ותוספת המרחק הוא ש' |
|
ונכפול השורש הדומה והוא ס' וראוי להיות המרחק ה' פעם ס' וככה הוא |
|
| |
|
ואם הדומה הקרוב לאחריו כגון ת'ר'כ'ה' שהדומה הוא כ' |
|
וכשתסיר מרובע ה' ישאר ת'ר' וחסרון המרחק וכן ראוי להיות |
|
| |
|
כי כל מרובע ה' בין שני מרובעים הדומים |
|
כי מספר ת'ר'כ'ה' כאשר נסיר מרובעו שהוא כ"ה נשאר ת"ר והוא בין ד' מאות שהוא הדומה ובין ט' מאות שהוא הדומה האחד לפנים והאחד לאחור מן השרש |
|
| |
Approximations |
|
| [It seems that the beginning of the discussion concerning this issue is missing though there is no indication for that in the manuscript] | |
|
|
|
|
שאינו מתוקן ישאר אחד וב' ששיות וחצי ששית והוא השרש המתוקן |
|
ואם תרצה לתקן אותו תקנהו פעם אחרת וערוך חצי הששית שיצא בחלוק על עצמו והעולה חלק על כפל השרש המתוקן והיוצא בחלוק חסר מן השורש המתוקן והנשאר הוא השרש המדוקדק |
| If you want, you can correct [the "corrected root"] as you wish, but you cannot reach the truth, only approximately. | ואם תרצה תוכל לדקדק אותו כרצונך אך לא תוכל להגיע אל האמת כי לעולם יהיה בדרך קרובה |
|
ואם החשבון שתרצה להוציא שרשו יותר קרוב מהמרובע [72]אשר לאחריו מן המרבע אשר לפניו |
|
כמו שלשה שהוא קרוב אל המרובע ארבעה אשר לאחריו יותר ממרובע אחד אשר לפניו |
|
לעולם תקח מן הקרוב וככה תעשה |
|
|
|
קח השרש אשר לארבעה והוא שנים ואחר כן קח המרחק אשר בין חשבונך ובין המרובע שלקחת שרשו וחלקהו על כפל השרש |
|
|
|
ותקנהו פעם אחרת שתקח מרובע מה שיצא בחלוק וחלקהו על כפל השרש והיוצא תחסר מהשרש המתוקן |
| You can correct it and make it more accurate as you wish. | ותוכל לתקנו ולדקדק אותו כרצונך |
|
|
|
ואם החשבון שתרצה להוציא שרשו הוא מן הזוגות |
|
והדומה לו במעלה הרביעית אלף והמרובע הקרוב אליו ת'ת'ק'ס'א' ושרשו ל"א ונשאר ל"ט |
|
חלקנום על כפל השרש שהוא ס"ב ויצא חצי אחד ונשארו ח' |
|
עשינו מהם שביעיות והנם נ"ו חלקנום על כפל השרש ונתן לו בדרך קרובה אחד והנה שרש אלף ל"א וחצי ושביעית |
|
| |
|
ועשיריתם בדרך קרובה אל האמת שלשה ושביעית שביעית |
|
ותדענו שתקח שורש המרובע הקרוב אליו והוא ט' ושרשו ג' חלק הנשאר שהוא אחד על כפל השרש יצא ששית |
|
ותקן אותו שתערוך מה שיצא בחלוק על עצמו יעלה ששית הששית חסרהו מן השרש שאינו מתוקן ישאר ג' והם ששיות הששית |
|
תקנהו פעם אחרת שתערוך ששית הששית על עצמו ותחסרהו מן השרש המתוקן והנשאר הוא מדוקדק |
| If the following square is closer than the preceding square, do as I showed you. It is the same whether the [number of ranks] is odd or even. | ואם המרובע הבא לאחריו הוא יותר קרוב מהמרובע שעבר שהוא לפניו תעשה כאשר הראיתיך והדבר שוה בין בנפרדים בין בזוגות |
Fractions |
|
Simple Fractions |
|
|
ואם תרצה להוציא שרש ו' שמיניות ושמינית שמינית |
|
דע מאיזה חשבון יצא שמיניתו שמינית השמינית והוא ס"ד ושרשו ח' |
|
וקח מן ס"ד ו' שמיניות ושמינית שמיניתו והוא מ"ט |
|
קח שרשם והוא ז' |
|
חלק על ח' [73]יצא ז' שמיניות וככה השרש |
|
| |
|
ותדענו שתקח כפל כפלו והוא ג' וחצי שמינית |
|
ושרשו א' וג' רביעיות |
|
קח חציו והוא ז' שמיניות וככה השרש |
|
| |
|
ואם תרצה להוציא שרש שנים וחצי |
|
דע כי החצי יצא משנים ואין לשנים שרש ידוע |
|
ונעשה מהכל חציים ויעלו ה' |
|
נערכם על שנים ויעלו י' |
|
ושרשם ג' וששית בדרך קרובה |
|
ונחלק זה השרש על שנים יצא אחד וחצי וחצי ששית והוא דרך קרובה |
|
| |
|
ואם תרצה להוציא שרש אחד וג' חומשים |
|
דע כי החומש יצא מה' |
|
נעשה מכלם חמישיות יהיו ח' |
|
נערכם על ה' יעלו מ' ושרשם בדרך קרובה ו' שליש |
|
חלקם על ה' יצא אחד וחומש ושליש חומש |
|
| |
|
ותדענו שתערוך המ' בק' וקח שרש העולה וחלקהו על העולה מערך ה' על שרש ק' והיוצא הוא השרש |
| In these ways the geometricians used to extract roots of integers, fractions, and fractions of fractions endlessly. | ועל אלו הדרכים נהגו חכמי המדות להוציא השרשים בשלמים ובנשברים ובשברי השברים עד אין קץ |
Sexagesimal Fractions |
|
| The astrologers extract it by degrees, primes, seconds, thirds, and they approximate it up to tenths or up to whatever they want. | וחכמי המזלות מוציאים אותו למעלות לראשונים ולשניים ולשלישיים ומדקדקים עד עשיריים ועד כמה שירצו |
| Eventually they do not reach the truth, only approximately. | וסוף הכל לא יגיעו אל האמת רק בדרך קרובה |
| When you extract a root of degrees, you extract it in the way of extracting roots of integers, and the root are degrees also. | וכאשר אתה מוציא שרש מספר מעלות אתה מוציאו בדרך הוצאת שרשי המספר השלם ויהיה השרש מעלות כמוהו |
| When you extract a root of [sexagesimal] fractions, you should know that the [sexagesimal] fractions are divided in two kinds: | וכאשר תוציא שרש מספר שברים יש לך לדעת כי השברים נחלקים לשני מינין |
|
יש מהם שיש להם שרש ידוע ומפורסם |
|
כגון השניים והרביעים ששורש השניים הם ראשונים ושרש רביעיים הם שניים |
|
מפני כי כאשר תערוך ראשונים על ראשונים יעלו שניים |
|
וכאשר תערוך שניים על שניים יעלו רביעים |
|
ויש מהם שאין להם שרש ידוע ומפורסם |
|
כגון הראשונים והשלישיים והחמישיים וכל הדומה להם |
|
כי אין אתה מוצא שברים שתהיה עריכתם על עצמם מוציאה אל השברים האלה |
| Therefore, the way of extracting the root of [sexagesimal fractions]: | ומיכן היה הדרך בהוצאת שרשי השברים |
|
אם יהיו השברים [74]שתרצה להוציא שרשם מן המין ששרשם ידוע ומפורסם אתה מוצא שרשם בדרך הוצאת שרשי מספרי השלמים |
|
אך שאתה קורא שם השרש ממין השברים אשר עריכתו על עצמו מוציאך אל שם השברים שאתה רוצה להוציא שרשם |
|
כגון שהיית רוצה להוציא ט' שניים |
|
ואתה יודע כי שרש ט' במספר השלם הוא ג' שלמים ובכאן אתה אומר כי השרש ו' ראשונים |
|
ועל זה הדרך לכל השברים אשר שרשם ידוע ומפורסם |
|
ואם היו השברים שאתה מוציא שרשיהם מן השברים הסתומים והנעלמים שאין שרשיהם מפורסמים |
|
אתה משיב השברים ההם אל השברים הקרובים אשר פחותים מהם ששרשיהם ידועים ויהיה שרש המספר ההוא מן המין אשר עריכתו על עצמו מוציאך אל המין אשר החזרת חשבונך אליו |
|
כאלו רצית להוציא שרש ט"ו שלישיים והם מן השברים הסתומים |
|
ואתה מחזיר אותם אל רביעיים אשר הוא הקרובים אליהם והם מהידועים |
|
וכשנערוך ט"ו על ששים יעלו תת"ק רביעיים ושרשם הוא שלשים והם שניים |
|
כי שניים על שניים מוציאך אל רביעים |
|
ונמצא אתה אומ' כי ט"ו שלישיים שרשם שלשים שניים |
|
ועל זה הדרך לכל השברים שאין שרשם מפורסם |
|
ולעולם אם יהיה במרובע שניים יהיה בשרש ראשונים |
|
ואם רביעיים יהיה בשרש שניים |
|
והכלל כי בשרש יהיה מספר חצי השברים |
Sexagesimal approximations of integers |
|
| Here are two methods of the astrologers to extract very accurate roots by approximation: | והנה לך שני דרכים על דרך חכמי המזלות להוציא השרשים בדרך קרובה מדוקדקים היטב |
First approximation method |
|
|
| |
|
הדרך האחד שתוציא שרש המרובע שעבר הקרוב אליו והנשאר שהוא המרחק שיש בין חשבונך ובין המרובע תערך אל ששים יקראו ראשונים והעולה תחלק על כפל השרש |
|
והשמר שישאר שתוכל לחסר מרובע מה שיצא בחלוק |
|
וככה עד שתגיע אל השלישים והוא מדוקדק |
|
והדמיון רצינו להוציא שרש שנים |
|
והמרובע הקרוב שעבר הוא אחד ושרשו אחד ונשאר אחד ונשאר א' נשיבהו ראשונים והוא ששים |
|
והנה יוסיפו כ"ה שניים |
|
ובעבור זה לא נתננו לו כי אם כ"ד ונשארו י"ב ומרובע כ"ד הוא ט' ראשונים ל"ו שניים |
|
| |
|
השיבונו ב' ראשונים כ"ד שניים לשלישיים בעבור שנוכל לחלק על כפל השרש שהם ק'ס'ח' ראשונים יצא בחלוק נ"א שניים ונשארו לנו ע"ב שלישיים |
|
| |
|
ועל זה הדרך תדקדקהו תמצא השרש א'כ'ד' נ"א י'ח' רביעיים והוא מדוקדק |
| If you multiply a root of any number you wish by this number, the result will by the root of the product. | ואם תערוך על זה המספר שרש חשבון שתרצה שיהיה העולה שרש כפל החשבון |
|
ואם תשיב האחד לס' ראשונים ותחבר עמהם הכ"ד ראשונים יהיו פ"ד ותחשבם שהם שלמים ותחשב כמו כן השניים ראשונים והשלישיים שניים והרביעיים שלישיים אז תמצא שרש שבעת אלפים ומאתים כי שלשת אלפים ושש מאות הוא מרובע ששים והנו חשוב כאחד והמספר הנזכר והוא כפלו |
|
| |
| If we know the root of a number and we wish to know the root of a number that is twice its double, we always double the root and so it is.
|
ולעולם אם ידענו שרש מספר ונרצה לדעת שרש מספר שהוא כפל כפלו נכפול השרש וככה [76]הוא |
| And vice versa, if we know the root of a known number and we wish to know how much is the root of a number that is its quarter, we take half the root and so it is.
|
והפך הדבר אם ידענו שרש מספר ידוע ונרצה לדעת כמה שרש מספר שהוא רביעיתו נקח חצי השרש וככה הוא |
Second approximation method |
|
|
והדרך האחרת |
|
|
|
חלק המרחק מהמרובע הקרוב על כפל השרש ותן לו הכל והיוצא תחבר עם השרש הקרוב אשר לפניו וככה השרש שאיננו מתוקן |
|
אך אם היה המרובע הבא אשר לאחריו יותר קרוב |
|
תחלק המרחק על שרש המרובע הבא והיוצא תחסר מהשורש מן המרובע הבא והנשאר הוא השרש שאיננו מתוקן |
|
ואחר כן קח מה שעלה בחלוק על איזה דרך שיהיה וערוך אותו על עצמו והעולה תחלק על כפל השרש שאיננו מתוקן |
|
| |
|
ועל זה הדרך תקנהו עד שתגיע לשלישיים והוא מדוקדק קרוב אל האמת |
|
ובהוציאך השרש תוכל לדעת ולהכיר אם לקחת חשבון קרוב אל המרובע שעבר או אל הבא |
|
כי כאשר תחלק המרחק ממרובע הראשון על כפל השרש אם עלה יותר משלשים אז תדע כי הוא קרוב אל המרובע הבא |
|
ואם עלה שלשים או פחות דע כי הוא קרוב אל המרובע שעבר |
|
והדמיון רצינו להוציא שרש שניים |
|
|
|
|
יהיה המרחק אחד והוא ס' ראשונים חלקנום על כפל השרש שהוא שנים |
|
|
|
|
רצינו לתקנו ערכנו ל' על עצמו וחלקנום על ס' יצא ט"ו |
|
| |
|
|
|
|
נתקן אותו פעם שנית ונערוך ה' ראשונים שיצאו בחלוק על עצמם עלו כ"ה והם שניים |
|
השיבונו אותם שלישיים עלו אלף וחמש מאות |
|
וחלקנום על כפל השרש המתוקן והוא ק"ע ראשונים יצא בחלוק ח' והם שניים ונשארו ק"מ |
|
השיבונום לרביעים עלו ח' אלפים [77]וארבע מאות |
|
חלקנום על ק"ע ויצא מ"ט ונשארו עוד לחלק אך אין צריך להטריח יותר |
|
| |
|
והנה יש לנו לחסר מהשרש המתוקן ח' שניים מ"ט שלישיים וישאר א'כ"ד כ"א י"א והוא מדוקדק |
|
|
|
ואם תרצה להוציא שרשו שתקח דמיונו במעלה השלישית והוא במאות והנכון במעלה החמישית ואם תקחנו במעלה השביעית יהיה יותר נכון |
|
וכאשר תוציא שרש שנים מן המעלה החמישית תוציא שרש עשרים אלף שהוא הדומה כמשפט |
|
ולדעת שרש שנים חלק הכל על מאה והיוצא הוא שרש שנים והוא אחד שלם כ"ד ראשונים נ"א שניים י' שלישיים ז' רביעיים מ"ח חמישיים |
|
ואם ידעת שרש שנים תערכנו על מאה והעולה הוא שרש כ' אלף |
|
ואם הוצאת שרש שנים מן המעלה השלישית שהיא המאות הוציא שרש מאתים שהוא הדומה |
|
והיוצא חלק על עשרה ונמצא שרש שנים |
|
ואם ידעת שרש שנים תערכנו על מאה והעולה הוא שרש כ' אלף |
|
ואם הוצאת שרש שנים מן עשרה והעולה הוא שורש מאתים |
|
ואם תרצה להוציא שרש עשרה תוציאנו בכל הדרכים כמשפטם תמצאנו ג' שלמים כ"ו ראשונים מ"ד שניים י"ב שלישיים |
Shortcuts |
|
| For every number that we know its root, if we multiply it by ten and we wish to know how much is the root of the product, multiply the root of the number by the root of ten and the result is the required.
|
וכל מספר שנדע שרשו אם נערכנו על עשרה ונרצה לדעת כמה שרש המחובר מהמערכות תערוך השרש של המספר על שרש עשרה והעולה הוא המבוקש |
| There are tables [of roots] from one integer to two and a half and the square [the range] up to six integers and a quarter, with which you can correct all the roots.
|
והנה יש לוחות עשויות מאחד שלם עד שנים וחצי ויעלה המרובע עד ששה שלמים ורביע ומהם תוכל לתקן כל השרשים |
| Guidelines for finding roots using these tables: | |
|
ואם היו לך חלקים פחותים מאחד ערכם על ארבעה וקח בלוח שרש העולה ומה שיהיה קח חציו |
|
ואם כפלנוהו כל ככה ולא עלה עד אחד ערכהו על שמונה וקח רביעית השרש |
|
ואם היה חשבונך מאחד ועד ששה ורביע ותרצה להוציא השרש בקש מספר חשבונך |
|
ואם לא תמצאנו קח השרש בלוח [78]שהוא כנגד החשבון הקרוב הנמצא לפניו או לאחריו וקח הקרוב אל חשבונך בין לפניו בין לאחריו וערוך המרחק הנמצא בין החשבון ובין חשבונך על ששים וחלק העולה על המרחק הנמצא בין שני המרובעים וההוה תוסיפנו על השרש הנמצא אם היה החשבון בלוחות שלקחת פחות מחשבונך ואם יותר תגרענו אז תמצא המבוקש |
|
ואם היה המספר יותר מששה ורביעית עד חמשה ועשרים שלמים קח שרש רביעיתו וההוה בשרש כפלהו תמצא השרש |
|
ואם היה יותר מכ"ה עד מאה כפלהו ארבעה פעמים וקח שרש הדומה וההוה קח חציו וככה שרש המבוקש |
| The hundreds are analogous to the units: | והנה המאות דומות לאחדים |
|
ואם היה לך מספר יותר ממאה ערכהו על ששה וחלק העולה על עשרה וההוה קח שרשו וקח לכל מאה אחד במרובע וכאשר תדע השרש תערכנו על עשרה אז תמצא השרש המבוקש |
|
ואם היה חשבונך באלפים חשוב כי הוא בעשרות והוצא דמיונו והיוצא ערכנו על עשרה אז תמצא רצונך |
|
ואם החשבון בעשרות אלפים הוציא הדומה וההוה תערכנו על מאה |
|
ואם במאות אלפים הוצא הדומה בעשרות וההוה תערכנו על מאה |
| This way you can extract the root of any number you want. | ועל זה הדרך תוכל להוציא שרש כל חשבון שתרצה |
|
ואלף אלפים דומה לאחדים וההוה בשרש ערכנו על אלף |
| From there on proceed according to this method. | ומשם והלאה תעשה על זה הדרך |
| The book is complete. | הספר |
| Glory be to God of the world. | תהלה לאל עולם |
Notes
Apparatus
- ↑ 2r
- ↑ 2v
- ↑
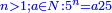
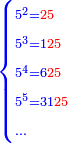
- ↑
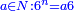
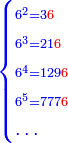
- ↑ 3r
- ↑ MS Geneva: here starts the interpolated excerpt
- ↑ MS Geneva continues 4v
- ↑ 5r
- ↑ 5v
- ↑ 3v
- ↑ 4r
- ↑ 4v
- ↑ 6r
- ↑ 6v
- ↑ 7r
- ↑ 7v
- ↑ 8r
- ↑ 8v
- ↑ 9r
- ↑ 9v
- ↑ 10r
- ↑ 10v
- ↑ 11r
- ↑ 11r
- ↑ 12r
- ↑ 12v
- ↑ 13r
- ↑ 13v
- ↑ 14r
- ↑ 14v
- ↑ 15r
- ↑ 15v
- ↑ 16r
- ↑ 16v
- ↑ 17r
- ↑ 17v
- ↑ 18r
- ↑ 18v
- ↑ 19r
- ↑ 19v
- ↑ 20r
- ↑ 20v
- ↑ 21r
- ↑ 21v
- ↑ 22r
- ↑ 22v
- ↑ 23r ומחברות מאדים ... והנה מספר מחברות: again
- ↑ 23v
- ↑ 24r
- ↑ 24v
- ↑ 25r
- ↑ 25v
- ↑ 26r
- ↑ 26v
- ↑ 27r
- ↑ 27v
- ↑ 28r
- ↑ והם ג' והם... וכערכם קח מימי החדש: twice
- ↑ 28v
- ↑ 29r
- ↑ 29v
- ↑ 30r
- ↑ 30v
- ↑ 31r
- ↑ 31v
- ↑ 32r
- ↑ 32v
- ↑ 33r
- ↑ 33v
- ↑ 34r
- ↑ 34v
- ↑ 35r
- ↑ 35v
- ↑ 36r
- ↑ 36v
- ↑ 37r
- ↑ 37v
- ↑ 38r
Appendix I: Glossary of Terms
| author | המחבר |
| book | ספר |
| introduction | מפתחות |
| chapter | שער, שערים, השער ה... ב |
| Decimal Dystem | |
|---|---|
| rank | מדרגה, מדרגת (ה), מדרגות (ה), במדרגה (ה), במדרגת, במדרגת... ל, במדרגה ה... ל |
| מעלה ה, מעלות, מעלותיו | |
| rank | מערכת, מערכות, במערכתם |
| units | אחדים |
| tens | עשרות |
| hundreds | מאות, מדרגת המאות |
| thousands | אלפים, מדרגת האלפים |
| tens of thousands | עשרות אלפים |
| hundreds of thousands | מאות אלף, מאות אלפים |
| thousands of thousands | אלף אלפים, אלפי אלפים |
| tens of thousands of thousands | עשרת אלפי אלפים, עשרות אלפי אלפים |
| hundreds of thousands of thousands | מאת אלף אלפים, מאות אלפי אלפים |
| thousands of thousands of thousands | אלף אלפי אלפים, אלף אלפים |
| Arithmetic Operations | |
| Addition | |
| addition | מחברת, מחברת זה עם זה, חבור (ה / ... עם) |
| to add | בחברך ה, לחבר, לחבר מ... ואילך עד, לחברם עם, חבר (ה / הכל, כל ה), חבר ... (אל / ה / עם), חבר ה... עם ה, חברו, חברהו (אל ה / עם ה), חברם (אל / על ה / עם ה), חברנו (אותו עם / ה / ה... עם / עם ה), חברנו מ... עד, חברנום (עם), חברת, יחבר ה, נחבר ה... עם ה, נחברם עם, תחבר (ה / כל ה / עם / עמהם), תחבר ... (אל / עם / ה... עם / ה... עמהם), תחברהו עם... יחד, תחברם (ל / עם ה), תחברנו אל |
| תחבר ה... מ... עד | |
| חבר בתחלה ה | |
| להוסיף (ל / עליו), הוסף (ב / ל / על / עליו / עליהם), הוסף ... על, הוסף ה... על, הוסיף עליהם, הוסיף ה... על ה, הוסיפם על, הוסיפנו על, הוספנו (על), הוספנום על, הוספת (עליו), מוסיף (על / על ה... ה / עליהם), נוסיף (ב / על / עליו), נוסיף... על, תוסיף (ל / על / עליהם / עליו), תוסיף ... על, תוסיפהו על, תוסיפנו על | |
| מוסיפים על | |
| קבוץ ה... עם | |
| מקבץ ה... אל, תקבץ ה | |
| to add one by one | תוסיף א"א, א"א הוספת |
| to add two by two | תוסיף החשבון בב, ב"ב הוספת, תוסיף לעולם בב' |
| to add three by three | תוסיף ג"ג, ג"ג הוספת, תוסיף לעולם שלשה |
| to add four by four | מוסיף ד"ד |
| נוסף ... מן ה | |
| to sum | חברנו כל חשבון, חבר הכל, יחבר הכל |
| to be summed | בו נתחבר, יחובר מ... עד, יתחבר (עד), יתחבר מ... ועד, יתחברו עם, מחובר שם, מחוברים (עם), מחוברות, נחברים |
| sum | מחובר (ל / מ), המחובר מ... עד, המחבר, חבור ה, הנחבר, הנאסף |
| sum | בהתקבצם |
| total sum | כל החשבון |
| Progression | |
| progression | מוספים |
| progression of multiples | חשבון הכפול |
| progression of doubles | חשבון הכפל |
| excess | התוספת, תוספת (ה / על), התוספת שיש בינו ובין ה, התוספת שיש לו על ה, תוספות |
| excess | תוספת ה... על ה... כתוספת ... על ה |
| to exceed | יוסיף (... על / ה... על ה), יוסיפו, יתר עליו, עודף ... על ה, עודפים על, מוסיף על |
| has no addition and no subtraction | לא יקבל תוספת ומגרעת, בלא תוספת ובלא מגרעת |
| בלי חסר ויתר | |
| last term | החשבון שהגיע עדיו, המספר האחרון, החשבון האחרון, אחרון |
| succession of numbers | על דרך המספר, על דרך החשבון |
| according to | על דרך, על דרך מספר ה |
| approximately | בדרך קרובה, בדרך קרובה אל האמת |
| successively | על הסדר, על סדר ה, על סדר החשבון, על סדר חשבון, על סדרם |
| sequence | בתולדת, במערכת |
| successive | זה אחר זה |
| plus | עם |
| plus | בתוספת |
| increment | תוספת, התוספת שיש בין |
| Subtraction | |
| subtraction | מגרעת, מגרעת ... מ, מגרעת זה מזה |
| subtraction | הגרעון |
| to subtract | לגרוע (מ / מהם / ... מ / ... מן / ה... מ), גורע ממנו, גרע (אותו מ / אותם מה / ה / מ / מהם / ממנו / ... מ / ... מה / ה... מ / ה... מן), גרעם מ, גרענו ... מ, גרעת, יגרע |
| גרעונו ... מ | |
| תגרע (מ / מהם / ממנו / ה... מ / ה... מן / ... מ), תגרעהו מ, תגרעם (מ / מן), תגרענו מ | |
| לחסר (מ / ממנו), חסר (ה / כן מ / מ / מה / מן ה / מהם / ממנו / מכל ה), חסר ... (מ / מן), חסר ה... (מ / מן ה / מה), חסרהו מן | |
| חסרם מן ה, חסרנו ... מ, חסרנוהו מ, חסרנום (מ / מן), חסרם מ, יחסר, מחסר מ, נחסר (מ / מן / ... מ / ... מה), נחסרם מ | |
| תחסר (מ / מהם / מן ה / ... מ / ... מה / ... מן ה / ה... מ / ה... מן / ה... מן ה), תחסרהו מן ה, תחסרם (מ / מן ה / ממנו), תחסרנו מ | |
| מחסרים | |
| subtracted repeatedly | הולך הלוך וחסור |
| to subtract | פוחת (... מן / ... מן ה), תפחות ... (מ / מן / מהם) |
| להסיר (מ), הסר ... מ, נסיר ה... מ, תסיר (מהם), תסיר ... (מ / מן) | |
| הוצא מהם (ה), הוצאת ממנו | |
| subtrahend | חשבון הנגרעים, החשבון הנגרע |
| החשבון שגרעת ממנו | |
| minus | פחות |
| Multiplication | |
| multiplication | חשבון ה |
| multiplication | מערכת זה על זה, מערכת ... על, מערכת מספר על מספר, עריכת ... על, עריכת ה... על ה, ערכו אל |
| to multiply | להעריך... על, להעריכם על, לערוך, לערוך מספר על מספר, לערוך חשבון על חשבון, לערוך... על |
| הערך (ה / על ה / ... על), הערך ה... זה על זה | |
| יערוך על | |
| נערוך... על, נערוך ה... על, נעריכנו על ה, נערכים על, נערך ... על, נערכם על, נערכנו על | |
| עורך (אותו ב), עורך... ב, עורך... על, עורך ה... ב, עורך ה... על, עורך ה... עם | |
| ערוך (על), ערוך אותם ב, ערוך אותם על, ערוך... ב, ערוך ... על, ערוך ה... ב, ערוך ה... על, ערוך ה... על ה, ערוך על, ערכהו (ב / על) | |
| ערכם (ב / על), ערכם זה בזה, ערכם זה על זה | |
| ערכנו (אותו על / על), ערכנו... על, ערכנו ה... על | |
| ערכנוהו על, ערכנום על, ערכנום זה על זה | |
| ערכת על | |
| תערוך (ב / על), תערוך ה... ב, תערוך ה... על, תערוך... ב, תערוך ... על, תערוך זה על זה | |
| תערך (ה... ב / ה... על / על / ... על), תערכהו (ב / על), תערכם (ב / על), תערכנו (ב / על / עם) | |
| תערכם זה על זה | |
| to multiply | לחשוב... על, חושב את, חשוב... ב |
| to duplicate | יכפול, תכפול הכפול, כפלנוהו |
| to triple | כפול ה... שלשה פעמים, כפול ה... ג' פעמים, כפול ... ג' פעמים, כפול ה.... ג' פעם, כפלנו ה... ג' פעם, תכפול ג' פעם |
| to quadruple | כפול ה... ד' פעם, כפלהו ארבעה פעמים |
| duplication | כפלו |
| ערכם על עצמם | |
| ערוך על עצמו, ערוך אותו על עצמו, ערוך... על עצמו, ערוך ... על עצמם, ערוך ה... על עצמם, ערכנו... על עצמו, נערוך... על עצמם, תערוך... על עצמו, תערוך על עצמם, תערכם על עצמם, תערכנו על עצמו | |
| עריכתו על עצמו, עריכתם על עצמם | |
| to be multiplied | הנערך (על), הערוך, ערוכים על ה, אשר נערוך בו, הנערכים (ב / על) |
| product | עריכת ה... על, ערך ... על |
| product | היוצא מערך, העולה מערך ה... על ה |
| product | המחובר (מ), הנחבר (מ), הנקבץ |
| product | הכפול |
| product | חשבון... ב, המספר הנכלל בחשבון |
| power | חשבונו |
| Doubling | |
| to double | כופל אותו, כפול ה, כפלהו, כפלנו ה, כפלנוהו, כפלנום, נכפול ה, תכפול (ה), נכפול פעמים |
| double | הכפול, כפל (ה / ב / מן ה), כפלו |
| double of a double | כפל כפל ה, כפל כפלו |
| Halving | |
| to half | לחצות, קח חצי (ה), נקח חצי ה, לקחנו חציו, קח מחצית (ה), קח המחצית, קח מחציתם, קח חציו, קח חצים |
| half | חצי (ה), חציו, חציים, מחצית (ה) |
| Division | |
| division | מחלוקת, מחלוקת זה על זה, חלוקת ... על, בחלוק ה |
| to divide | לחלוק עליו, לחלק (על / עליו / ... על), לחלקו, לחלקם על, חלק (על / על ה / עליו / עליהם / ה... על / ה... עליהם / ה... עליו / ... על / ... עליו), חלקהו על, חלקם (על / עליו), חלקנו (... על / ה... על / כ), חלקנום על, חלקת ... על, יחלק ה, מחלק (אותו על / אותם על / ... על / עליו), מחלקים (... ל / ה... אל), נחלק (על / עליו), נחלק (... עליו / ה... על / ה... עליו / זה ה... על), נחלקם על |
| תחלוק (ה... על), תחלק (אותו על / ה / על / עליהם ה), תחלק... ל, תחלק ... על, תחלק ה... על, תחלק זה על זה, תחלקם על | |
| ונחלקם בלא שבר על | |
| divided into | נחלק ל, נחלקים ל, יחלק על, יחלקו ... על, זה יתחלק על זה, יתחלק על, יתחלקו (על / עליו / עליהם) |
| quotient | מה שיצא בחלוק, יצא בחלוק, יצא בחלק, היוצא בחלוק, שיצאו בחלוק, מה שעלה בחלוק |
| dividend | המחולק, הנחלק, הנחלקים |
| מחולקים על, המחולק עליו | |
| הנחלק עליו | |
| החשבון המחולק | |
| אשר חילק, אשר חלקת (אותו), מה שחלקת | |
| מה שחלקת עליו, שחלקנו עליו, אשר עליו נחלק | |
| שיחלק עליו | |
| יצא הכל בחלוק | |
| תתן לו הכל בחלוק | |
| לתת בחלוק | |
| שלא יחלק, שלא יתחלק, שלא יתחלקו, שלא נתחלק, שלא נתחלקו | |
| divisible | יתחלק ל, יתחלק כל המספר |
| divisible by | יהיו לו כל השברים, שיש לו כל החלקים, יש לו רוב החלקים, שיש לו חלק |
| divisor | חלק, חלקים |
| divisible by seven | יהיה לו שביעיות |
| Extraction of Roots | |
| גדר ה, שורש (ה), שרש (ה), שרשו, שרשי ה, שרשיו, שרשם, שרשיהם, שרש המרובע, השורש מן המרובע | |
| הוצאת שרשי (ה) | |
| to extract a root | בהוציאך השרש, להוציא השרש, להוציא השרשים, להוציא שרש, להוציא שרשו, להוציא שרשם (מן), הוצא השרש, הוציא שרש, הוצאת שרש ... מן, מוציא שרש, מוציא שרשו, מוציא שרשיהם, תוציא שרש |
| to extract a root | מוציאו |
| לקחת שרשו, קח שורש, קח השורש, קח שרש, קח שרשו, קח שרשם, קח השרש, קח השרשים, תקח השרש, תקח שורש, תקח שרש, תקח שרשו | |
| לקחת שרש המרובע | |
| לדעת שרש מספר, ידענו שרש מספר, ידענו שרש מספר ידוע | |
| root | שרש ה, שרשו, שרשם, שרש ממרובע, שרש מה, שרשים, השרש של ה, שרש מספר |
| square | מרבע, מרובע (ה), מרובעים, מרובעו, מרובע שרשו, הרבוע |
| קח מרובע ה, תקח מרובע, לקחנו מרובע ה | |
| none-square | איננו מרובע |
| perfect square | המרובעים התמימים |
| הסתומים | |
| אין ל... שרש, אין להם שורש | |
| יש להם שורש | |
| to correct | לתקן (אותו), לתקנו, תקן אותו ש, תקנהו, נתקן אותו |
| uncorrected root | השרש שאיננו מתוקן, השרש שאינו מתוקן, שאינו מתוקן |
| corrected root | השרש המתוקן, השורש המתוקן, השרש המדוקדק |
| השורש המיוחד | |
| approximate root | השורש המיושר, השרש המיושר, השרש המיושר בחלקיו, מיושר |
| השורש הדומה, השרש הדומה, שרש הדומה | |
| השרש הקרוב | |
| לדקדק אותו (ל), לדקדק כן ל, מדקדקים עד, תדקדקהו | |
| מדוקדק, מדוקדק קרוב אל האמת | |
| מדוקדקים היטב | |
| corrected | מתוקן |
| wrong, incorrect | משובשת |
| Ratio and Proportion | |
| to take ratio, to relate | תערוך ה... אליו, הערך ... כ |
| relation | הקשה, ערך, ערך זה אל זה |
| ratio | ערך (אל / ה / ... אל / ... אל ה / ה... אל / ה ... אל ה / ... על / ל... עם), ערכים, ערכו (אל / מ / מן), ערכם (מה / מן ה), ערכי המספר |
| ערך ה... מן ה | |
| הערך שיש לו אל | |
| ערך זה אל זה | |
| ערך ה... אל ה... כערך ה... אל ה, ערך ... אליו כערך ... אל | |
| כערך (ה), כערך ... אל... כך ערך ... אל, כערך ... מ... כן ערך ... מ, כערך ... מן ... כן ערך | |
| כערכו אל ה | |
| יש לו ערך אל | |
| ratio | מערכת ה... אליו כערך ... אליו |
| proportion | ערכים, ערכין |
| to take the ratio | ערכם אל ה |
| נקח ערך ... אל, נקח מה ערך ... אל | |
| קח ערך ... אל, קח מהערך ... אל, קח ערכו (אל / מ / מן), קח זה הערך מ | |
| תקח הערך, תקח ערך ... אל ... יהיה כערך ... אל, תקח מן ה... כערכם | |
| כערכו קח מ, כערכו קח מן ה, כערכו מן ה... קח מן ה | |
| וכערכם קח מ, וכערכם קח מן ה | |
| תערך אל | |
| כזה הערך קח מ, כזה הערך קח מן ה, קח כזה הערך מן ה | |
| כערך זה קח מן ה, כערך הזה קח מכל | |
| כאותו הערך קח מן ה | |
| וכזה הערך מ | |
| דע מה ערך ...(אל / מ / מן), דע מה ערך ה... (אל / מ / מהם / מן), ודע מה ערך האחד מהם | |
| נדע מה ערך ... אל, תדע מה ערך ... אל, תדע מה ערך ה... אל ה | |
| תדע מה שהם ה... מ, תדע מהן ה... מ, תדע מהם ה... מ | |
| resulting by the ratio | יצאו בערך |
| order | סדרי ה |
| to be arranged | סדורים ב |
| proportional | נערך אל ה, מוערכים על |
| not proportional | אינו נערך אל ה |
| related to, depend on | התלוי אליו, תלויים ב |
| proportional | נערך אל ה, נערכים זה אל זה |
| disproportionate | שאינם נערכים |
| order of ratio | סדר (ה), סדרי הערך |
| companion | חברו בהקשה, חברים |
| stranger | נכריים, נכרים, נכרי ל, נכרי לו |
| to resolve | להתיר הערך ... אל, מתיר את קשרם |
| relation | קשרם |
| to join, to relate | קושרים את ה... ב |
| הערך הנחלף | |
| Equivalence Ratio | ישר, ערך ישר, ערך שוה, ערך הישר, הערך הישר, השוה |
| Multiple Ratio | ערך כפל, ערך הכפל |
| Superparticular Ratio | ערך חלק, כמוהו וחלק ממנו, ערך החלק |
| Multiple Superparticular Ratio | כפל וחלק, כפלו וחלק ממנו, כפלו וחלק ממנו אל ה |
| Superpartient Ratio | חלקים, כמוהו וחלקים ממנו |
| Multiple Superpartient Ratio | כפל וחלקים, הכפל וחלקים ממנו, כפלו וחלקים ממנו |
| כמהו וחציו, כמוהו וחציו (אל) | |
| כמהו ושלישיתו | |
| כמוהו ושני שלישיותיו | |
| כמוהו וג' רביעיותיו | |
| כמוהו וג' חמישיותיו, כמוהו ושלש חמישיותיו | |
| Completion | |
| multiplicative inverse | תשלומי (ה) |
| completion | להשלמת |
| to complete | להשלים (את ה), השלם ה, ישלים |
| to be completed | ישלמו (ה), ישלמו ה... ל, נשלם |
| Conversion | |
| to convert | נעשה (מהכל / מהם / מכלם / ממנו), עשה מהם, עשינו מהם, תעשה מן |
| החזרנום ל, החזרת חשבונך אליו, מחזיר אותם אל | |
| השבת זה לזה | |
| להשיב (אל), להשיב... ל, להשיב ה... אל, להשיבם (אל / ל), להשיבם לחשבון, השב ... על ה, השיבונו אותם, השיבונו ... ל, השיבונום ל, השב (... ל / ה... ל / ה... כלם ל), נשיבהו, נשיבם כלם, תשיב ה... ל, תשיבם (כלם / ל) | |
| משיב ה... אל | |
| Algebraic Terms | |
| x | שרש, שרשים, שרשיו, שרשם, שרשי ה, גדריו |
| thing, x | דבר, משהו |
| x² | מרובע, מרובעים |
| constant | מספר |
| Arithmetic Terms | |
| numeral | באותיותנו |
| Indian numerals | באותיות הודו |
| number | חשבון (ה), חשבונך, חשבונם, חשבונות, חשבונים |
| מספר (ה), מספרי ה, מספרים, מספרם, מספרנו | |
| מנין ה | |
| multitude | כמנינה |
| amount | סך ה |
| integer | שלם, שלמים, המספר השלם, במספר השלם |
| fraction | נשבר, נשברים, שבר (ה), שברים, שברי (ה) |
| fraction of fraction | שברי שברים, שברי השברים |
| sexagesimal fractions | שברי חכמי המזלות, חלקי חכמי המזלות, מחשבון ששים |
| part | חלקו, חלקי (ה), חלקיו, חלקים |
| part of | חלק אחד (מן / מ), חלק ... מה, חלקים (מ), חלקים מ... באחד, חלקי ה, חלק ה... מן ה, חלק מן |
| portion | חלק |
| denominator | מורה, המוכיח, המספר המוכיח |
| יורה | |
| "round" number | חשבון עגול |
| cube number | גוף שוה, הגופות |
| cubic root | קו הגוף, הקו |
| square number | מספר מרובע, המספר הרבוע, חשבון מרובע, המספרים המרובעים |
| plane number | מספר שטוח, מספרו השטוח |
| prime number | מספר ארוך |
| congruent modulo | משקל ה |
| מאזני ה | |
| שקלו במאזני תשעה | |
| שקלנוהו במאזני ט' | |
| יצא כלו ט'ט' | |
| הוציאם ט'ט' | |
| even | זוג, זוגות |
| odd | נפרד, נפרדים, מספר נפרד, המספר הנפרד, המספרים הנפרדים |
| sequence of the even-times-evens | בתוספת הכפל |
| even-times-even term | הכפל, הכפולים |
| even-times-even number | כפל הכפל |
| to calculate | לחשב, לחשוב, תחשוב מהו ה... מ, תחשוב מהו... מ, תחשב (ל / מהו), תחשב מהן... מ |
| to be calculated | מתחשב |
| calculation | חשבון (ה), החשבונים, חשבונך, חשבונם |
| to count | חושב |
| to count | מונה (את ה / אותו / אותו ב / אותו כמנין / אותו כמנינו / אותו כמספרו), מונה את ... פעמים, מונה ... כמנין ה, מונה ה... במנין ה, מונים את ה... פעמים, מנה מה, תמנה אתו מן ה |
| לספור, ספר אותו | |
| counted by | הספור ב, ספורים |
| common factor | מונה לשניהם, חשבון שמונה לשניהם |
| same, equal | שוה (ל / ... ל), שוים (ל), שוות |
| to be equal | שוים (ב), שוין ל, יהיו שוים (ל), ישוו ה |
| unequal | אינם שוים |
| to recognize | ולהכיר (אם) |
| to bother | להטריח |
| reason | הטעם (כי / ש) |
| extraction, deducing | הוצאת זה מזה, הוצאת ה... מתוך ה |
| to deduce | להוציא מתוך, להוציא מתי, נוציאנו מכח ה |
| to extract | להוציא (ה / מ / מזה / ... מן ה / ה... מה / ה... מן ה / לכל ה / זה מזה), להוציאו (ב / מ), להוציאם (זה מזה) |
| הוצא (ה / מהם), הוציא (ה), תוציא (ה / ממנו / ... מ / ... ל), תוציאם, תוציאנו (מ) | |
| מן ה... תוציא ה | |
| הוצא החשבון מ... ועד, הוצא חשבונך מן ... עד האחרון, תוציא כל החשבון מ... עד | |
| מוציאים אותו ל | |
| מוציאך אל, מוציאה אל ה | |
| מוציא ה... מן הגלוי | |
| [goods offered in the] business | מסחר, עסק |
| affairs | עסקי |
| profit | ריוח (ה), הריוח של, רוח |
| corresponding | המסור לו |
| corresponding | כנגד ה, כנגדו |
| corresponding to | הראוי לה |
| corresponding to | המגיע ל |
| to contribute | הביא (ה) |
| to share | נשתתפו (ב), נשתתפו בין כלם ב, נשתתף עמהם (ה) |
| partnership | שתוף |
| partner | שותפים, שותפין |
| to invest | מכניסים ב |
| to earn | הרויחו ל, רוחו, רוחו בין כלם, יצא להם ריוח, שרוח |
| to spend | הוציאו |
| share | חלק (ה), חלק כל אחד מן ה, חלקו, חלקו מן ה |
| capital | הממון |
| owed to | המגיע ל, מגיע ... ל, מגיעו מן ה |
| amount, money | ממונו, ראש ממון (ה), ראש ממונם, ראשי הממון, ראש כל אחד, ראש ממון כל אחד, ראש ממון כלם |
| people | אנשים, אישים |
| human | אדם, בני אדם |
| share | חלק, חלקו |
| בעל ה | |
| kikkar | ככר, ככרים |
| liṭra | ליטרא, ליט', ליטרין |
| ՚oqya | אוקיא (מ), אוקיאות |
| kor | כור, כורים, כורי ה |
| silver | כסף, של כסף |
| copper | נחושת, נחשת, מנחשת |
| wheat | חטה |
| coin | מטבע, מטבעות |
| coinage | קשור המטבע, לקשור מטבע מ, לקשור (מ), קושר ב, קושר ב... בליטר |
| הנקשר | |
| להתיך מכלם בשוה | |
| לערב, לערב בהם | |
| zuzim | זוז, זוזים |
| dinar | דינר, דינ' |
| pešiṭim | פשיטים |
| to persist | עומד |
| to exist | עומדים בין, עומדים ב |
| to buy | לקנות מ, קנה, קניתי, אקנה (ב / ה), קניתי ... ב, קונה |
| to pay | לשלם, ישלם, שלם להם ה, שלם ה... להם |
| to be payed | ולקח בשכרו (ה) |
| price | שער, שער ה |
| measure | שעור |
| exchange | חלופיהם |
| sold merchandise | מכר, הנמכר, הנלקח |
| money [paid] | דמים, דמי (ה), דמיו, דמיהם |
| trade | במקח וממכר |
| trading calculation | בחשבוני מקח וממכר, בחשבוני מקחם וממכרם |
| payment | שכר, שכרו, שכרם |
| to hire | תוציא שכיר ב, שכרתי... ל... ב |
| תוציא שכר ... פועלים, תוציא שם שכיר ב | |
| worker, salaried | שכיר |
| worker | פועל |
| employment | שכירות, בשכיר |
| to be unemployed | בטל |
| to cancel | יבטל, בטל |
| unemployment | בטלה |
| to work together | ועשו ... יום בין שלשתם, ועשו בין שלשתם |
| to work | עשה, עשה מלאכתו |
| days of work | ימים שעשה (ה), עשה מן הימים |
| work | מלאכתו, מלאכת ה |
| נתחייב, נתחייב ל | |
| month | חדש |
| day | יום, ימים, ימי ה, ימי החדש, בכל יום |
| hour | שעה, שעות |
| equally | בשוה |
| name | שם ה, שמות (ה) |
| saying | כדברי |
| to give | לתת (ל / לו), יתן (ל / לו), נתן (ל / לו), נתננו לו, תן (ל / לו הכל), תתן ל... ש |
| to be able | אוכל ל, יוכל ל, יכול ל, יכולנו ל, נוכל ל, תוכל ל |
| have to, need to | צריך (ל / ש), יש לך ל, יש לנו ל, יש לו ל, יצטרכו ... ל |
| to be needed | צריכים ל |
| no need | ואין צורך ל |
| to have | היה ל, יש, יש בידך מן ה, היה לו, היה לך, היה לנו, היו לנו, היו לך, יהיה לו, יהיו לו, יש ל, יש להם, יש לו, יש לנו, היו בידך, יהיו בידך, יהיה בידך, שיש לך, יש בידו, שבידך, שיש בידך |
| have no | אין ל, אין לו, אין להם |
| to know by heart | סדורים על פיך |
| remainder | הנותר, הנותרים |
| remainder | מותר ה |
| to keep | מחזיק בו |
| explained | מפורש ב |
| to understand | להבין (ב), מבין |
| to ease | להקל על ה |
| to ease | יקל עליו ב |
| easy | דבר קל |
| to be difficult | יתקשה עליך ל |
| difficult | קשים |
| to mention | הזכרנו, הזכיר למעלה |
| to draw | מצייר לך, ציירתי (לך) |
| diagram | צורה |
| table | לוח (ל), לוחות, לוח מ... עד, מכבר (מ... ועד) |
| line | טור, טורים, שטה, שטין |
| row | בטור הרוחב |
| width | רוחב, ברוחב |
| length | אורך, באורך |
| derived | חצובים מ |
| sage | החכמים |
| geometricians | חכמי המדות |
| astrologers | חכמי המזלות |
| Astrology | חכמת המזלות |
| חשבון חכמי המזלות | |
| דרך חכמי המזלות (ל / ש) | |
| Hipparchus | אברכז |
| Ptolemy | תלמי |
| sign | מזל, מזלות, מזלות הגלגל |
| degree | מעלה, מעלות |
| minute | ראשון, ראשונים, חלק אחד, חלקים ראשונים |
| second | שניים |
| third | שלישים, שלישיים |
| fourth | רביעים, רביעיים |
| fifth | חמישיים |
| sixth | ששיים |
| sevenths | שביעיים |
| eighths | שמיניים |
| ninths | תשיעיים |
| tenths | עשיריים |
| sign of Aries | טלה |
| Saturn | שבתי |
| Mars | מאדים |
| Mercury | כוכב חמה, חמה |
| Venus | נגה, נוגה |
| Jupiter | צדק |
| moon | לבנה |
| sun | שמש |
| planets | משרתים, כוכבים, כוכבי לכת |
| שבעת המשרתים | |
| planets beneath | השפלים |
| runner | רצים |
| messenger | שלוחים |
| mean motion | מהלך השוה |
| motion | מהלך ה, מהלכו, מהלך שניהם, מהלכם ב, הליכות |
| quick motion | מהלכם במרוצה |
| quick | הקלים |
| slow motion | מהלכם במתון |
| to conjoin | יתחבר עמו, יתחברו (עמו / כלם ב) |
| conjunction | מחברת, מחברות |
| double conjunctions | המחברות השניות |
| triple conjunctions = conjunctions of three planets | השלישיות, מחברות השלישיות |
| quadruple conjunctions = conjunctions of four planets | הרביעיות |
| quintuple conjunctions = conjunctions of five planets | החמישיות |
| sextuple conjunctions = conjunctions of six planets | המחברות הששיות |
| septuple conjunctions | מחברות השבעה |
| the arc of the Sun's inclination | מעלות הנטייה, מעלות נטיית הגלגל אשר לשמש |
| degrees of the circle | מעלות הגלגל, מעלות מ |
| to enter | נכנס |
| to catch up | ישיגנו |
| to chase | ירדף אחריו |
| have passed | עברו |
| to move | הלך, ילך (ה) |
| to come | יבא כנגדו |
| retrograde | נזור |
| arcs | קשתות |
| chord | היתרים |
| sagittae | החצים |
| shadow | צללי ה |
| tangent | הפוך |
| cotangent | הישר |
| height | הגובה |
| circle | גלגל |
| circle | עגלה, עגולה, עגול |
| point | נקדה |
| side | פאה, פאותיו, צדיו |
| aspect | פאה |
| side, divisor, factor | צלע, צלעו, צלעות |
| א.מ.ר. | |
| האומר | |
| דומה כמי שאומר, הוא כמי שיאמר | |
| שאמר | |
| to say | לומר, אמר, יאמר, נאמר, אמרו (ש), אמ' (ה / כי / ... כי), אומר כי, אומ' כי, לומ' כי, לומ' ש |
| כאמרך, כאשר אמרנו ב | |
| ב.א.ר | |
| to explain | לפרש ה, אפרשנו במקומו, במקומו אפרשנו, פרשתי ב, בארתי לך |
| יתבאר כי | |
| ב.ר.ר. | |
| it becomes clear | יתברר כ, מתברר ש, נתברר (ש) |
| תברור לך בו | |
| ח.ש.ב | |
| to think | חשוב כי |
| to consider | חושב ... ל, חשוב אותם כאלו הם, נחשוב ש, תחשב (ה), תחשבם (שהם), יחשוב אותם כאלו הם |
| to be considered | חשוב כ |
| י.ד.ע. | |
| to know | לדעת (ה / כי / איזה / איך / כמה), לדעתם, לידע |
| דע (ה / כי / לך כי / ש / כמה / בכמה / מה), ידענו (כי / ש / מ), ידענו ה... מהם, ידעת (זה / כי), יודע (כי / מן ה... ה), נדע, תדע (ה / כי / ש / בכמה / מ / זה מ), תדענו (ש), מהם תדע (ה) | |
| יודע ה | |
| to be known | יודיע |
| known | ידוע הוא (כי / ש), ידוע (כי / ש / מ / ב) |
| ככה תדענו (ש) | |
| לדעת מ... ועד | |
| דע מאיזה מספר (ה / הוא ה / יצא ה), דע מאיזה חשבון (ה / יצא), תדע מאיזה חשבון (ה / יצא ה) | |
| וידוע וברור ש | |
| י.צ.א. | |
| result | מה שיצא |
| יצא (ה / הכל / ל / לך / מ), יצאו | |
| יצא לחשבון אחד | |
| יצא ... לכל | |
| היוצא (ל / מ) | |
| to be solved | יוצא ל |
| to be derived | יצא (מ / מה / ממנו ה), יוצאת מ, יצאו ה |
| כ.ת.ב. | |
| to write | תכתבנו ב, תכתוב (ה / תחתיו) |
| written | כתוב בהם, כתובים ב |
| ל.ק.ח. | |
| to take | אקח מן ה, יקח (ה / מ / מן ה), ליקח ב...מ, לקח (ב / ה / מ / מהם ה / ... ב), לקחו, לקחנו, לקחת (ב), נקח (מ / מן ה), קח (אותו ב / ה... מ / ה / כ / מ / מה / מהם / מן / מן ה / ... מ / ... מן ה), תקח (ה / ל / מ / מן ה), תקחנו ב, נלקחום |
| קח לכל, תקח לכל אחד שלם, קח לכל אחד מן ה | |
| שלקחת | |
| to be derived | נלקחים מן ה |
| מ.צ.א. | |
| to find | למצא ל, מוצא (ב / ה), מצאנו (ל), מצאת, נמצא (ה / ש), נמצאנו, תמצא (בו / ה / ש / להם), תמצאם, תמצאנו (ב) |
| to be found | ימצא (ב), ימצא... בין, ימצאו, נמצאים (אחרי ה) |
| הנמצא, הנמצאים (ב) | |
| נ.ג.ע. | |
| to reach | הגעת ל, יגיע ל, תגיע (אל / ל), מגיע אל ה |
| להגיע אל האמת, יגיעו אל האמת | |
| to be owed | הגיע ל, יגיע לכל אחד (מה / מן ה) |
| ע.ל.ה. | |
| to result | עלה (ה / עד), עלו, עלו ה... (ב / ל), עולה, יעלה (ה / מ / מן ה / לו מ), יעלו, ויעלה בין שניהם, ויעלה בין שלשתם, תעלה בידך |
| result, obtained | העולה (ב / מ / משניהם), מה שיעלה, מה שעלה, המספר העולה, החשבון שעלה בידך, עלה בידך מ |
| ע.ש.ה. | |
| to do, to apply | לעשות, יעשה ב, תעשה ל, תעשה ש, עשית בו |
| to make | יעשה |
| יעשנו | |
| conduct | מעשה |
| doing, action | מעשיהם |
| עשה כן ל, כן תעשה (ל), ככה תעשה (ל / ש), ככה נעשה | |
| to be formed | עשויות |
| ק.ר.א. | |
| to be called | נקראים, נקרא, הנקרא, שנקרא ה, יקראו |
| to denominate | קורא שם ה |
| to read | קורא |
| reader | קורא |
| ר.א.ה. | |
| to see | ראה (מה), ראית ב, תראה בה |
| to show | כאשר הראיתיך |
| ר.צ.ה. | |
| to want | נרצה ל, רוצה ל, תרצה (ל / ש), רצינו ל, רצית (ל), ירצה ל |
| זה שרצינו, מה שרצינו | |
| רצונך | |
| as much as you wish | כרצונך, עד כמה שתרצה, עד כמה שירצו, עד איזה מספר שתרצה |
| whichever you wish | איזה שתרצה מה, כל ... שתרצה |
| ש.א.ר. | |
| to remain | ישאר (ב / מן ה / לך / בידך), ישארו (בידך / לך / לנו), נשאר (בידך / ל / מ / ממנו), נשארו (לך / לנו / עוד ל) |
| remainder | הנשאר (מן ה), הנשארים, שיורין, הנשאר בידך, מה שישאר, השאר |
| ש.מ.ר. | |
| to keep | שמור ה, שמרהו, שמרם, תשמר ה, תשמור (ה) |
| reserved | השמור, השמורים, ששמרת, שמור בידך |
| preserve | ישמור |
| be careful | השמר ש |
| to investigate | תדרוש |
| to learn | למד ש |
| to instruct | תצוה לו |
| to instruct | הורתיך |
| כמו שהורתיך למעלה | |
| to look at, to observe | הסתכל (איזה / ב / מה), נסתכל (מה), תסתכל ב |
| to look | תביט אל ה |
| friend | חברו, חבירו |
| to be used to | נהגו... ל |
| to lead | יוציאך אל |
| to lead | הולך אותם |
| to lead | ידריכך ב |
| יוציאך ה... אל האמת, ידריכך אל האמת ואל הנכון | |
| to return | אליו תשוב, ושוב אל ה |
| to return | חוזרים אל, חוזרים אליו |
| to return | ישוב (ה / ... ב), שב ה |
| to put | ישים |
| to place | ושם ב, ושים... ב, ושמנו ... עם |
| to place | נותן... ב |
| place | במקומו (ב), מקומו |
| אין זה מקומו ל | |
| to meet | יפגשו ה, ייפגשו... זה בזה |
| to leave aside | תעזב ה... כמו שהם |
| case | ענין |
| category | ענין, ענינים |
| issue | ענין (ה / ה... ב), ענינים, עינינים |
| type | מין, מינו, מיני ה, מינין, מיניהם, ממין (ה / ש), מן המין אשר |
| example | משל, דמיון (ש), בדמיון זה, דמיונות |
| example | כגון (ה / ש) |
| כגון זה וכיוצא בו | |
| question | שאלה, שאלות |
| הוא שאלתך, והוא מה ששאלת | |
| ישאל השואל | |
| תשאל ממנו | |
| answer | תשובה |
| to be confusing, to go wrong | ישתבש |
| to happen | יקרך זה |
| to elaborate | להאריך בזה, להאריך בו |
| to prove | יוכיחו כי |
| check | בחינתו (ל / ש), הבחינה (ל / ש / כש) |
| check | מאזנים |
| sought | מבוקש, הוא המבוקש, וככה המבוקש, והעולה הוא המבוקש |
| seeker | מבקשיהם |
| to seek | בקש חשבון (ש), בקש לך חשבון ש, תבקש חשבון ש, בקש מספר חשבונך |
| בקשנו כמה, בקשנו מה | |
| way | פנים |
| way, method | דרך (ה / ל / ל... ש / ב / בזה ש), דרכים (ל), בדרך (ה), כדרך ה, הדרך בו |
| דרך אחרת (ש) | |
| בדרך כל המספר | |
| על הדרך שראית | |
| דרך החשבון (ש) | |
| ודרך אחד לכל ה | |
| general way | דרך כלל ל |
| rule | כלל (... ב), והכלל כי |
| וכלל זה יהא בידך ש | |
| זה הכלל יהיה בידך ש | |
| rule | משפט ה |
| כמשפט, כמשפטם, עשה כמשפט, יעשה כמשפט | |
| difference | מרחק (מ) |
| המרחק שהוא בין, המרחק שיש בין, המרחק הנמצא בין, המרחק בינו ובין | |
| המרחק מן ה, מרחק החשבון מן ה | |
| המרחק שיש בין חשבונך ובין ה, המרחק אשר בין חשבונך ובין ה | |
| מתרחק מחשבונו כמרחק ה | |
| difference | יתרון, יתרון ה... על ה, היתרון שיש בין ... ובין , היתרון שיש בין שני ה, היתרון שיש בין שתי ה, היתרון שבין שני ה |
| difference, deficiency | החסרון, חסרון ה, חסרונים |
| foundation | יסוד, מוסדי |
| element, basis | שרש |
| cause | סבת |
| letter | תבות ה |
| language | לשון |
| essence | עצם דבר |
| secret | סוד (ה) |
| origin | מוצא |
| speaking | מדבר |
| express | משמיעים |
| word | דבר |
| thing | דבר (מ) |
| sense | עניני ה |
| category | מחלקות ה |
| to start | להתחיל ב, התחלת ב... מ, תתחיל (ב / מ / מן ה), נחל ל, יחל... מ, יחל ... עם, נחל מ |
| מתחיל ב | |
| first, at first | בתחלה |
| at first | בראשונה |
| beginning | בתחלת, תחלת ה |
| beginning | בראש |
| the beginning and the end of all | ראשית הכל ואחרית הכל |
| beginning and end | תחלה ותכלה |
| to turn | יתהפכו, יתהפך ה, תהפוך ה |
| vice versa | והפך הדבר (ב) |
| inverse | הפך ה |
| to increase | נוסף |
| to increase | הולך וגדל |
| to decrease | פחות פוחת והולך, פוחת |
| to be lowered | יורדים ... מן ה, ירד |
| time | פעם, פעמים |
| once | פעם אחת |
| twice | שני פעמים |
| three times | שלשה מן ה |
| exalted | הנעלה |
| wonderful | הנפלא |
| virtue | מעלות ה |
| ascetic | פרושים |
| to subdue | ויכבוש את עצמו מ |
| earthly desire | תאות העולם |
| form, shape | דמות ה |
| the Most High | העליון |
| from Him | ומאתו |
| Knower | יודע הכל |
| glory | התהלות |
| reason | טעם ה |
| prayer | תפלות |
| definition, category | גדר ה |
| righteousness | יושר |
| to create | יצר |
| to be generated | יולדו ה |
| to be generated | קם מ |
| world | עולמו |
| day and night | יומם ולילה |
| dwell | שוכן |
| alone | לבדו, לבדם |
| allusion | רמז על ה |
| sign | זה לך האות ש, לאות ש |
| similarity | דמות ב |
| included | נכלל ב |
| to form | בונים |
| to be built | יבנה |
| to be established | יכונן ב |
| soul | נפשו |
| eye | עינים |
| heart | לב ה |
| finger | אצבע, אצבעך, אצבעות, אצבעותיך |
| wisdom, science | חכמה, חכמת ה |
| knowledge | דעה |
| אני, אנחנו, אתה, הוא, הם | |
| to be | להיות (ה / ל), להיותם |
| to be | היות ה... ב, היותו ב |
| to be | היה (ה / ה... ב), שהיה, יהיה (ב / ה), היו (ה), יהיו (ה / כל ה), היית, הייתי, היינו, תהיה |
| there is / are | יש (ב / מהם ש / שם מ), יהיה בו |
| הוא (ה / מ / ש), שהוא (ב / ה / ל), היא (ה), שהיא, הם (ה), שהם (ה) | |
| ההוא, ההם | |
| זה (ה / הוא ה), הזה, זו, זאת, הזאת, האלה, אלה (ה / הם), אלו (ה / הם ה), הנו, הנם | |
| אותו ה, אותם ה, מאותו ה | |
| אשר | |
| as much as | עד כמה ש, עד ש |
| kind of | כעין ה |
| endlessly | עד אין קץ, עד אין סוף |
| because | כי, בעבור (זה / כי / ש), מפני (כי / ש), לפי ש |
| hence | ומכאן |
| therefore | על כן, לפיכך, ומפני זה |
| how many, how much | כמה (ה / הוא / הם ה / הם כל ה / היה / היה ה / היה הכל / זה ה / יש / ... הם), בכמה, מכמה |
| what | מה, מה ש |
| every | כל, בכל |
| everything | הכל |
| all, total | כל ה, כל מה ש, הכל, יהיה הכל, בכל ה, לכל ה, כלם, כולם |
| whole | כל ה, כלו, שלם |
| the same for all | וככה כלם |
| יש, יש ב, יש בהם (מ), יש בהן, שיש ב, שיש בה, שיש בהן | |
| שיש עמהם | |
| each | כל אחד (מ / מה / מהם / מן ה), כל אחד ואחד (מ / מהם), לכל אחד מ, מכל אחד |
| each | לכל ... ו..., בכל ... ו |
| on its own | בפני עצמו |
| both | שני ה, שניהם |
| one of | אחד (ה / מה / מהם / מן ה), אחת מ |
| of the | מן ה, הם מן ה, הם מה, מהם |
| also | גם (הוא), וגם ב, גם כן, וכן (הוא / ל), וכן היה |
| only | רק ש |
| לא ... רק | |
| likewise | וכן (ה / כלם / לכל ה), וככה (ה), וככה הוא (ה) |
| על זה הדרך (ל / לכלם / לכל), ובאלו הדרכים, ועל אלו הדרכים, על... דרכים | |
| so | וכן, כן |
| so | ככה (ה / הוא), כך (הוא ה) |
| as… so | וכמספר ה... כך |
| so and so | כך, כך וכך, ככה |
| between | בין, ובין כל ... ל, ביניהם, בין שלשתם |
| בין ... ובן, בין ה... ובין, בין ה... וה..., בין ל ... בין ל | |
| בין ... בין ..., בין ש... בין ש, בין ב... בין ב | |
| left | מצד שמאל, לשמאל |
| right | מצד ימין, לימין |
| itself | בעצמו, בפני עצמו |
| still | עדין |
| known | ידוע, ידועים |
| known | מפורסם, מפורסמים |
| unknown | נסתר, נסתרים, נעלמים, נסתר ממך (ה), אינם ידועים, שאינו ידוע |
| mentioned | הנזכר, הנזכרים ב |
| compound | מורכבים |
| as if | כאלו |
| if | אלו, ולו, וכי, אם, ואם, שאם |
| והנה (ה), והנה לך | |
| first | ראשון, ראשונים |
| second | שני (ל / לו / לו ה), שניה, שנית, השניה לה |
| half | חצי ה, חציו, מחצית ה |
| third | שליש, שלישי, שלישית, שלישי לו, שלישי..., שלישיות |
| fourth | רביעי, רביעית, רביעי לו |
| quarter | רביע, רובע, רביעית |
| fifth | חמישית (ממנה), חומש, חומשין |
| sixth | ששית, שתות, שתותים, שתותין |
| seventh | שביעית (ממנה), שביעיות |
| eighth | שמינית |
| ninth | תשיעית |
| tenth | עשירית, עשור |
| different | שונים |
| differ | נפרדים ל |
| differ | נחלפים, הנחלפים עם ה |
| diversity, difference | חלופם |
| similar to | כמו ה, כדמות |
| to be similar, to resemble | ידמה זה לזה |
| דומה (ל / לה), דומות ל, דומים ל | |
| דמיונו (ב), הדומה ל, הדומה לזה, והדומה לו ב, הדומים | |
| וכן כל הדומה לזה, וכל הדומה להם, וכדומה להם | |
| כיוצא בו | |
| up to, until | עד, עד ש, עד אשר |
| or | או |
| always | לעולם, לעולם ועד |
| true | הנכון, הוא הנכון |
| when | מתי |
| when | כאשר, כש |
| as | כאשר |
| as | יהיה כ, יהיה ה... כ |
| but | אך |
| כמו (ה / זה / ש), היא כ | |
| such as | כמו ב |
| כמו כן | |
| same | כמוה, כמוהו, כמוהם |
| closest | הקרוב (אל / אל ה / אליו), קרוב (אל ה / אליו), הקרובים (אליהם) |
| closer | יותר קרוב (מה / מה... מן ה) |
| לפנים, לפניו | |
| לאחור מן ה, אחריו, לאחריו | |
| רחוק מ... לאחורי | |
| preceding | אשר לפניו, שלפני ה, שלפניה, שלפניו, שהוא לפניו, אשר עבר, שעבר, שעברו, שעבר שהוא לפניו, הנמצא לפניו |
| succeeding, following, consecutive | אשר אחריה, אשר לאחריו, שלאחריו, שהוא לאחריו, הבא, הבא לאחריו, הבא אשר לאחריו, הבאות אחריהן |
| שלאח' אחריו | |
| above | למעלה, אשר למעלה |
| more than | למעלה מ, למעלה מהם |
| greater than, more | יותר (מ), רב מ |
| less than | פחות (מ / מן) |
| small | פוחת, הפחות, הפחותות, מועט, חשבון מועט, מספר מועט, מעט, הקטן, החשבון הקטן |
| smaller | פחותות (מ), פחותים (מ / מהם) |
| first, first term | הראשון, ראש ה, ראש מספרו, האחד |
| consecutive term | השני |
| last | האחרון |
| mean | אמצעי, תיכון |
| האמצעי הגדול | |
| great | הגדול, הגדולים, הגדולות, החשבון הגדול |
| greater | גדול (מ / ממנו), גדולות מ, גדולים (מהם / ממנו), יתרות, היתר, המרובה, רב, חשבון רב, המספר הרב |
| בין רב למעט | |
| then | אז, ואז |
| then, afterwards | אחר, אחר כן, אחרי כן, אחר כך, אחר ש, אחרי ש, לאחר |
| after | אחר ה, אחרי ש, אחריה, אחריו |
| already | כבר |
| now | עכשו, ועתה |
| impossible | לא יתכן ל, אי איפשר |
| possible | יתכן להיות, יתכן להיותו |
| further, still | ועוד |
| before | טרם ה |
| before | קודם ה, קודם זה |
| upon | בכל, בו |
| where | במקום אשר |
| there | שם (ה) |
| here | ובכאן |
| henceforth | ומכאן ואילך |
| thenceforth | משם והלאה |
| according | ועל זה |
| according, as | כפי מה ש |
| according | לפי (ה) |
| again | ושוב, שוב, ושוב ו |
| recurrent | חוזר חלילה, חוזרים חלילה |
| indeed | ואכן |
| indeed | הרי (הוא) |
| towards | כנגדו |
| to catch | תפש |
| to be too long | ירבה ממך |
| from which | מאיזה ... הם ה |
| i.e. | כלו', כלו' ש, כלומ' |
| for | בעבור ה |
| since | בעבור היות |
| since | ואחר ש, אחרי ש |
| with, including | עם (ה), עמו, עמהם |
| should be | וראוי להיות (ב / ה / כי), וככה ראוי להיות |
| rest | שאר (ה), משאר ה |
| most | ורבם, רוב ה |
| numerous, many | רבות, רבים |
| here and here | לכאן ולכאן |
| for all | לכל ה |
| really | וזה באמת |
| sometimes | פעמים ש |
| correct | נכון |
| like this | כאלו |
| recently, lastly | באחרונה |
| except | זולתי |
| other | חבירו, חברו, אחר, אחרת, אחרים |
| others | אחרים |
| another | אחר, אחרת |
| another | עוד |
| crosswise | באלכסון |
| from | וממנו, ומהם, מן ה |
| in front of | נכוחים ל |
| who | מי ש |
| how | איך |
| etc. | וכו' |
| beneath, lower | תחתיו, אשר תחתיו של ה |
| himself | עצמו |
| particularly and generally | בפרט וכל |
| כ"כ | |
| then | אם כן |
| finally | וסוף הכל |
| hence | ומיכן |
| no longer | לא... עוד |
| no | אין |
| not | אין (ה), אינה, אינו, איננו, אינם |
| does not | אינו |
| ולא כן ה | |
| לא ... ולא | |
| לא ... זולתי | |
| לא... אלא | |
| לא ... כי אם | |
| לא ... כי אם ... בלבד | |
| anything | לא ... כלום |
| ואין ... אלא | |
| אין לו... כי אם ה | |
| אינו כי אם | |
| which | איזה |
| whichever | איזה ... ש, איזה ... שיהיה |
| whether… or | בין ש... בין ש |
| או ... או | |
| secluded, separated | היחידי (ה / מן ה) |
| accurate | נכון, והנכון ב |
| from … to | מ... ועד, מ... עד |
| in | הוא ב |
| ההוה (ב) | |
| בצד ה | |
| הרחב | |
| לחקרן ל | |
| His hand will be upon all, and the hand of everyone upon him [Genesis 16, 12] | ידו בכל ויד כל בו |
| and your Teacher shall no longer be concealed from you [Isaiah 30, 20] | ולא יכנף עוד מוריך |
| your eyes shall see your Teacher and your ears shall hear a word behind you, saying, "This is the way; walk in it" [Isaiah 30, 20-21] | יהיו עיניך רואות את מוריך אזניך תשמענה דבר מאחריך זה הדרך תלכו בה |
| may the name of the Lord be blessed [Job 1, 21] | יהי שם יי' מבורך |
| the spirit returns to God [Ecclesiastes 12, 7] | תשוב רוח |
| instruct a wise man, and he will grow wiser [Proverbs 9, 9] | ותן לחכם ויחכם עוד |
| his gain disappears in his loss [Mishnah, Avot 5, 10] | ויצא שכרו בהפסדו |
| Praise be to God | תהלה לאל, תהלה לאל עולם |
| by the decree of God | ועם גזור האל, ועם גוזר האל |
| Sefer Keli ha-Neḥošet | ספר כלי הנחשת |
| Sefer ha-Luḥot le-Šivʿah ha-Mešaretim | ספר הלוחות לשבעה המשרתים |
Appendix II: Bibliography
Anonymous Textbook
Manuscripts:
- Budapest, Magyar tudomanyos akademia, MS Kaufmann A 507/2 (IMHM: f 15161), ff. 20-43 (15th-16th century)
- Genève, Bibliothèque de Genève, MS héb. 10/1 (IMHM: f 2320), ff. 2r-38r (14th-15th century)
- Vatican, Biblioteca Apostolica, MS ebr. 171/18 (IMHM: f 8630), f. 104r, line 3 – f. 105v, line 19 (Canea, 1493)
The transcript is based mainly on manuscript Genève 10
Bibliography:
- Aradi, Naomi. 2013. An Unknown Medieval Hebrew Anonymous Treatise on Arithmetic, Aleph 13.2, pp. 235-309.
- Lévy, Tony. 2002. A Newly Discovered Partial Hebrew Version of al-Khwārizmı̄’s Algebra, Aleph 2, pp. 225–34.

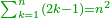
![\scriptstyle{\color{OliveGreen}{n=\left[\frac{1}{2}\sdot\left(n-1\right)\right]+\left[\frac{1}{2}\sdot\left(n+1\right)\right]}}](/mediawiki/images/math/e/c/f/ecf15d858a99040f9ad8e644b76e7a48.png)

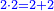

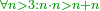
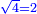
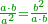
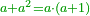
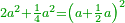

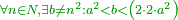
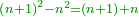
![\scriptstyle{\color{OliveGreen}{\left[\left(n-1\right)\sdot\left(n+1\right)\right]+1=n^2}}](/mediawiki/images/math/1/f/b/1fbc3c3780f1396f2a3d7dff682a2226.png)
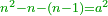
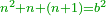
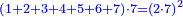
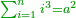
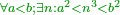
![\scriptstyle{\color{OliveGreen}{a=\left[\left(\frac{1}{2}n\right)-\frac{1}{2}\right]\sdot n}}](/mediawiki/images/math/a/9/a/a9acadf85e2c5569112d90a372248590.png)
![\scriptstyle{\color{OliveGreen}{b=\left[\left(\frac{1}{2}n\right)+\frac{1}{2}\right]\sdot n}}](/mediawiki/images/math/a/d/b/adb0d5616a4ba87fdc754424d4df6844.png)
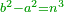
![\scriptstyle{\color{OliveGreen}{\left(n+1\right)^3-n^3=\left(n+1\right)^2+n^2+\left[\left(n+1\right)\sdot n\right]}}](/mediawiki/images/math/7/8/b/78b7139239f29f3d86631815640809f2.png)
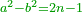
![\scriptstyle{\color{OliveGreen}{\left[\left(a^2-b^2\right)\sdot a\right]+\left[\left(a^2-b^2\right)\sdot b\right]}}](/mediawiki/images/math/3/0/c/30c95e1da47187a6465db586a4250f87.png)
![\scriptstyle{\color{OliveGreen}{a=b+1\longrightarrow\left[\left(a^2-b^2\right)\sdot a\right]+\left[\left(a^2-b^2\right)\sdot b\right]=\left(a^2-b^2\right)^2}}](/mediawiki/images/math/1/b/3/1b33b258ee33352763bbcc76bbdf6a89.png)
![\scriptstyle{\color{OliveGreen}{a=b+2\longrightarrow2\sdot\left[\left[\left(a^2-b^2\right)\sdot a\right]+\left[\left(a^2-b^2\right)\sdot b\right]\right]=\left(a^2-b^2\right)^2}}](/mediawiki/images/math/0/c/a/0ca8b2f020d853c550a4fd704dba85b8.png)
![\scriptstyle{\color{OliveGreen}{a=b+3\longrightarrow3\sdot\left[\left[\left(a^2-b^2\right)\sdot a\right]+\left[\left(a^2-b^2\right)\sdot b\right]\right]=\left(a^2-b^2\right)^2}}](/mediawiki/images/math/8/0/8/808ea48f0d81c8301bbca84aa263e5f9.png)
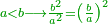
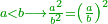
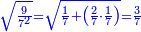
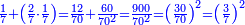

![\scriptstyle{\color{OliveGreen}{a>b\longrightarrow a^2=\left[\left(a-b\right)\sdot a\right]+\left[\left(a-b\right)\sdot b\right]+b^2}}](/mediawiki/images/math/b/f/a/bfa549196c3269dad8f2a3750f64ec25.png)
![\scriptstyle{\color{OliveGreen}{a<b\longrightarrow a^2=b^2-\left[\left(b-a\right)\sdot a\right]-\left[\left(b-a\right)\sdot b\right]}}](/mediawiki/images/math/6/9/7/697653ecf969cbfa9e3f21cf93250796.png)
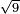
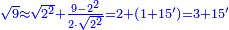
![\scriptstyle{\color{blue}{\frac{2\sdot\left[1^2+\left(2\sdot15^\prime\right)+\left[2\sdot\left(15^\prime\right)^2\right]\right]}{2\sdot\left[2\sdot\left(3+15^\prime\right)\right]}=\frac{2\sdot\left[1+30^\prime+\left(7^\prime+30^{\prime\prime}\right)\right]}{13}=\frac{2\sdot\left(1+37^\prime+30^{\prime\prime}\right)}{13}=\frac{2\sdot\left(97^\prime+30^{\prime\prime}\right)}{13}=\frac{195^\prime}{13}=15^\prime}}](/mediawiki/images/math/1/0/0/10033b77bba0b955971292c46fc87f44.png)
![\scriptstyle{\color{blue}{\sqrt{9}=\left(3+15^\prime\right)-\frac{2\sdot\left[1^2+\left(2\sdot15^\prime\right)+\left[2\sdot\left(15^\prime\right)^2\right]\right]}{2\sdot\left[2\sdot\left(3+15^\prime\right)\right]}=\left(3+15^\prime\right)-15^\prime=3}}](/mediawiki/images/math/6/7/9/67903f0c471f4b35f08226743216c2ca.png)

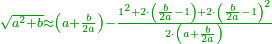
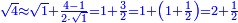
![\scriptstyle{\color{blue}{\sqrt{4}=\left(2+\frac{1}{2}\right)-\frac{1^2+\left(2\sdot\frac{1}{2}\right)+\left[2\sdot\left(\frac{1}{2}\right)^2\right]}{2\sdot\left(2+\frac{1}{2}\right)}=\left(2+\frac{1}{2}\right)-\frac{2+\frac{1}{2}}{2\sdot\left(2+\frac{1}{2}\right)}=\left(2+\frac{1}{2}\right)-\frac{1}{2}=2}}](/mediawiki/images/math/6/b/8/6b8ad8f5d55d03e88ce26fcf7a247423.png)
![\scriptstyle{\color{OliveGreen}{a^2-\left[a+\left(a-1\right)\right]=b^2}}](/mediawiki/images/math/6/3/2/6329c80cd4e2d19fd96fa02f79b37aec.png)
![\scriptstyle{\color{OliveGreen}{a^2+\left[a+\left(a+1\right)\right]=c^2}}](/mediawiki/images/math/2/9/7/2970beb5f398434f29290ae0322a3feb.png)
![\scriptstyle{\color{OliveGreen}{a^2=10a-\left[\left(10-a\right)\sdot a\right]}}](/mediawiki/images/math/6/0/5/605517108bb09392281d796df0be0449.png)
![\scriptstyle{\color{blue}{9^2=\left(9\sdot10\right)-\left[\left(10-9\right)\sdot9\right]=90-\left(1\sdot9\right)=81}}](/mediawiki/images/math/e/4/1/e41fa1d31a6cf398eef9c61aa78e26cf.png)
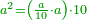
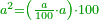
![\scriptstyle{\color{blue}{75^2=\left(\frac{75}{100}\sdot75\right)\sdot100=\left(\frac{3}{4}\sdot75\right)\sdot100=\left[75-\left(18+\frac{3}{4}\right)\right]\sdot100=\left(56+\frac{1}{4}\right)\sdot100=5625}}](/mediawiki/images/math/1/5/3/153a2cb31735bfe4e95a8391abe4d365.png)

![\scriptstyle{\color{blue}{16:10=1+\frac{3}{5}=\frac{\left(6+\frac{1}{4}\right)+\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]}{6+\frac{1}{4}}=10:\left(6+\frac{1}{4}\right)}}](/mediawiki/images/math/7/a/3/7a3bd5130ce987474d6469769499dfbb.png)
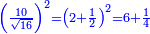
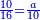
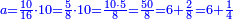
![\scriptstyle{\color{blue}{\frac{16}{10}\sdot\left(6+\frac{1}{4}\right)=\left(1+\frac{3}{5}\right)\sdot\left(16+\frac{1}{4}\right)=\left(16+\frac{1}{4}\right)+\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=10}}](/mediawiki/images/math/f/e/d/fedf7320425943539905a4f6efb65aa1.png)
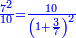
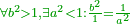
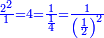
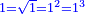
 ] and no subtraction [
] and no subtraction [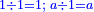 ].
].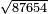
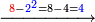
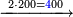
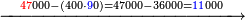
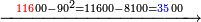
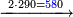
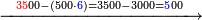
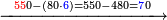
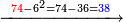

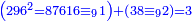
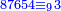
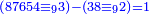
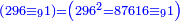
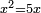
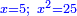
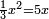
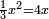
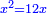
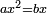
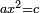
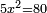
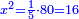
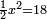
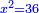
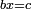
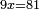
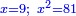
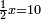
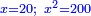
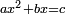
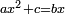
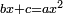



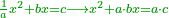

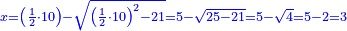
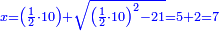
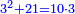
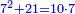
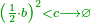

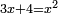
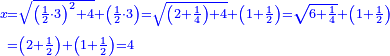
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n-1} i=\left(2n-1\right)\sdot\left[\left[\frac{1}{2}\sdot \left(2n-1\right)\right]+\frac{1}{2}\right]}}](/mediawiki/images/math/5/6/b/56bb680020be3e2fc0e2790841bd4562.png)
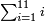
![\scriptstyle{\color{blue}{\sum_{i=1}^{11} i=n\sdot\left[\left(\frac{1}{2}\sdot11\right)+\frac{1}{2}\right]=11\sdot6=66}}](/mediawiki/images/math/0/6/f/06f970bc7137159a2ab14aa652cfbfa6.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n-1} i=\left[\left(2n-1\right)+1\right]\sdot\left[\frac{1}{2}\sdot\left(2n-1\right)\right]}}](/mediawiki/images/math/d/6/b/d6ba7a681352b67fe283573e33b7f63d.png)
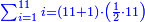
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n} i=\left[2n\sdot\left(\frac{1}{2}\sdot2n\right)\right]+\left(\frac{1}{2}\sdot2n\right)}}](/mediawiki/images/math/3/d/8/3d8aae7e2ed76f3d5ec4c12b2f4f1f5c.png)
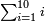
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=\left[10\sdot\left(\frac{1}{2}\sdot10\right)\right]+\left(\frac{1}{2}\sdot10\right)=\left(10\sdot5\right)+5=55}}](/mediawiki/images/math/b/b/6/bb68f216b91f76482347d0d5dfe0b742.png)

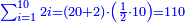
![\scriptstyle{\color{OliveGreen}{\sum_{k=1}^{n} 2k=\left[\left(\frac{1}{2}\sdot2n\right)+\left(\frac{1}{2}\sdot2\right)\right]\sdot\left(\frac{1}{2}\sdot2n\right)}}](/mediawiki/images/math/2/8/d/28d76309c66cfd0f833d5ca1c298f741.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} 2i=\left[\left(\frac{1}{2}\sdot20\right)+\left(\frac{1}{2}\sdot2\right)\right]\sdot\left(\frac{1}{2}\sdot20\right)=\left[10+\left(\frac{1}{2}\sdot2\right)\right]\sdot10=11\sdot10}}](/mediawiki/images/math/a/0/a/a0aef8c7a8ea1e69a3e9ff5f91feb418.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 2i=\left[\left(\frac{1}{2}\sdot n\right)+\frac{1}{2}\right]\sdot2n}}](/mediawiki/images/math/3/9/b/39b705c06ca37b802afeb48889b6ded8.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} 2i=\left[\left(\frac{1}{2}\sdot10\right)+\frac{1}{2}\right]\sdot20=\left(5+\frac{1}{2}\right)\sdot20}}](/mediawiki/images/math/1/e/7/1e7a8c3e9658295cde7f79d3fb27ef4f.png)
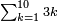
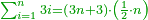
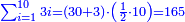
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 3i=\left[\left(\frac{1}{2}\sdot3n\right)+\left(\frac{1}{2}\sdot3\right)\right]\sdot n}}](/mediawiki/images/math/1/0/1/10162f6c170194f0bae48da061d06c26.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} 3i=\left[\left(\frac{1}{2}\sdot30\right)+\left(\frac{1}{2}\sdot3\right)\right]\sdot\left(\frac{1}{3}\sdot30\right)=\left[15+\left(\frac{1}{2}\sdot3\right)\right]\sdot10=\left(16+\frac{1}{2}\right)\sdot10}}](/mediawiki/images/math/8/7/6/876200dd8bf8a7613490421edf150e14.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 4i=\left[\left(\frac{1}{2}\sdot\frac{1}{4}\sdot an\right)+\frac{1}{2}\right]\sdot 4n}}](/mediawiki/images/math/c/5/e/c5ec303844b7e9b62f1e7c81b5f0b32c.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} 5i=\left[\left(\frac{1}{2}\sdot\frac{1}{5}\sdot 5n\right)+\frac{1}{2}\right]\sdot 5n}}](/mediawiki/images/math/b/a/f/baf5de85497a8a52fd9baaf877bdc75e.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} ai=\left[\left(\frac{1}{2}\sdot\frac{1}{a}\sdot an\right)+\frac{1}{2}\right]\sdot an}}](/mediawiki/images/math/4/1/6/416d0cd5481e534c789cc5ad432c5d33.png)
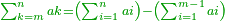
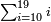
![\scriptstyle{\color{blue}{\sum_{i=10}^{19} i=\left(\sum_{i=1}^{19} i\right)-\left[\left[\frac{1}{2}\sdot\left(10-1\right)\right]\sdot10\right]=190-\left[\left[\frac{1}{2}\sdot\left(10-1\right)\right]\sdot10\right]}}](/mediawiki/images/math/a/1/5/a155b42978ccbefa5bb6188b676c9234.png)
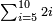
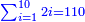
![\scriptstyle{\color{blue}{\sum_{i=5}^{10} 2i=110-\left[\left[\frac{1}{2}\sdot\left(10-2\right)\right]\sdot\left(\frac{1}{2}\sdot10\right)\right]}}](/mediawiki/images/math/9/8/a/98a419691d798e578b4a89b09cc4dfab.png)
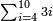
![\scriptstyle{\color{blue}{\sum_{i=4}^{10} 3i=465-\left[\left[\frac{1}{2}\sdot\left(12-3\right)\right]\sdot\left(\frac{1}{3}\sdot12\right)\right]}}](/mediawiki/images/math/6/9/b/69bb994c6027afd7ff801965e6f09024.png)
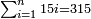
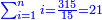
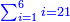
 and the sum is 315.
and the sum is 315.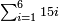
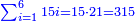
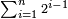
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n+1} 2^{i-1}=\left[2\sdot\left(2^{\frac{\left(2n+1\right)-1}{2}}\right)^2\right]-1=\left[2\sdot2^{2n}\right]-1}}](/mediawiki/images/math/6/c/9/6c9437ea6fc92be61b5a01c7a0e95f42.png)
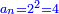
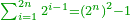
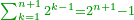
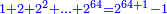
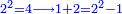
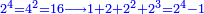
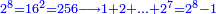
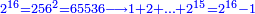
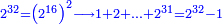
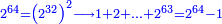
![\scriptstyle{\color{OliveGreen}{\sum_{k=1}^{n} k^2=\left[\left(n+1\right)\sdot\left(\frac{1}{2}\sdot n\right)\right]\sdot\left[\left(\frac{2}{3}\sdot n\right)+\frac{1}{3}\right]}}](/mediawiki/images/math/8/c/a/8ca1d983fcff11845ed7123640c7c7cf.png)
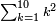
![\scriptstyle{\color{blue}{\sum_{k=1}^{10} k^2=\left[\left(10+1\right)\sdot\left(\frac{1}{2}\sdot10\right)\right]\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{1}{3}\right]=55\sdot7}}](/mediawiki/images/math/e/4/6/e462dcd61583e0b569458db8623e1619.png)
![\scriptstyle{\color{OliveGreen}{\sum_{k=m}^{n} k^2=\sum_{k=1}^{n} k^2-\left[\left[\left[\left(m-1\right)\sdot\frac{1}{2}\right]\sdot m\right]\sdot\left[\left[\frac{2}{3}\sdot\left(m-1\right)\right]+\frac{1}{3}\right]\right]}}](/mediawiki/images/math/7/b/7/7b70c413dcf9fd97d3582bafa9d3a611.png)
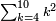
![\scriptstyle{\color{blue}{\sum_{k=4}^{10} k^2=\sum_{k=1}^{10} k^2-\left[\left[\left[\left(4-1\right)\sdot\frac{1}{2}\right]\sdot4\right]\sdot\left[\left(\frac{2}{3}\sdot3\right)+\frac{1}{3}\right]\right]}}](/mediawiki/images/math/3/0/8/308b968aa002a8d3bacc0210087a52ab.png)
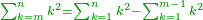
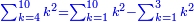
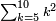
![\scriptstyle{\color{blue}{\sum_{k=5}^{10} k^2=\sum_{k=1}^{10} k^2-\left[\left[\left[\left(5-1\right)\sdot\frac{1}{2}\right]\sdot5\right]\sdot\left[\left(\frac{2}{3}\sdot4\right)+\frac{1}{3}\right]\right]}}](/mediawiki/images/math/5/7/8/578c2c53ee5ee93be3e312bdda94bd4b.png)
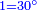
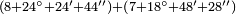
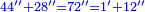
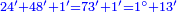
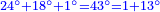
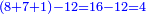

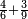
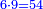
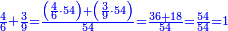
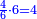
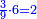
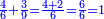
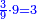
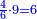
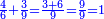
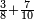
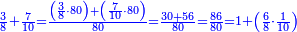
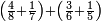
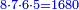




![{\color{blue}{\begin{align}\scriptstyle\left(\frac{4}{8}+\frac{1}{7}\right)+\left(\frac{3}{6}+\frac{1}{5}\right)&\scriptstyle=\frac{\left[\left(\frac{4}{8}\sdot1680\right)+\left(\frac{1}{7}\sdot1680\right)\right]+\left[\left(\frac{3}{6}\sdot1680\right)+\left(\frac{1}{5}\sdot1680\right)\right]}{1680}\\&\scriptstyle=\frac{1080+1176}{1680}=\frac{2256}{1680}=1+\frac{2}{7}+\left(\frac{1}{4}\sdot\frac{1}{7}\right)+\left(\frac{1}{2}\sdot\frac{1}{4}\sdot\frac{1}{7}\right)+\left(\frac{1}{10}\sdot\frac{1}{4}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/9/e/0/9e0906e615770823e29a177630299753.png)
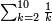
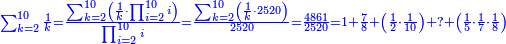
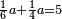
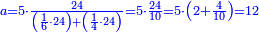
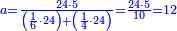
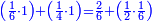
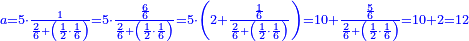
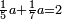
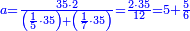
![\scriptstyle{\color{blue}{a=2\sdot\frac{35}{\left(\frac{1}{5}\sdot35\right)+\left(\frac{1}{7}\sdot35\right)}=2\sdot\frac{35}{12}=2\sdot\left[3-\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]=5+\frac{5}{6}}}](/mediawiki/images/math/f/6/8/f6820c46198e5ece587b1f47daa1711f.png)
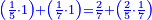
![\scriptstyle{\color{blue}{a=2\sdot\frac{1}{\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}=2\sdot\left[2+\frac{\frac{2}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)}{\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}\right]=4+\frac{\frac{4}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}{\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}=4+\left[1+\frac{\frac{10}{5}\sdot\frac{1}{7}}{\frac{2}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)}\right]=5+\frac{10}{12}}}](/mediawiki/images/math/a/c/b/acb8488409ce44a0500121d10d911df0.png)
![\scriptstyle\left[\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\sdot a\right]+\left[\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\sdot a\right]=2](/mediawiki/images/math/7/9/4/794cfeb38a33298248c8beb2bbcaaf4d.png)
![{\color{blue}{\begin{align}\scriptstyle a&\scriptstyle=2\sdot\frac{2520}{\left[\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\sdot2520\right]+\left[\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\sdot2520\right]}=2\sdot\frac{2520}{42+5}=2\sdot\frac{2520}{47}\\&\scriptstyle=2\sdot\left(53+\frac{29}{47}\right)=106+\frac{58}{47}=106+1+\frac{11}{47}=107+\frac{11}{47}\\\end{align}}}](/mediawiki/images/math/3/5/0/350b83ba141d1a45e93d53d160a416b9.png)
![\scriptstyle{\color{blue}{a=\frac{2\sdot2520}{\left[\left(\frac{1}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\sdot2520\right]+\left[\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\sdot2520\right]}=\frac{2\sdot2520}{47}=107+\frac{11}{47}}}](/mediawiki/images/math/3/d/a/3da4de584f88ba936061416abf22589b.png)
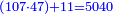
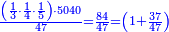
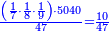
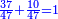
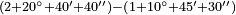
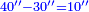
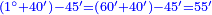
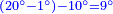
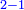
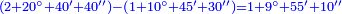
![\scriptstyle10-\left[\left(\frac{1}{6}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)\right]](/mediawiki/images/math/a/1/d/a1d97ff50871513400365ebcd487aa8a.png)
![\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{6}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=7}}](/mediawiki/images/math/3/3/d/33dfcec01093bb32ff598181b158bec3.png)
![\scriptstyle{\color{blue}{10-\left[\left(\frac{1}{6}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)\right]=\frac{7}{12}\sdot10=5+\frac{5}{6}}}](/mediawiki/images/math/d/1/c/d1c612b2ceb20e7224afa166cbae0b72.png)
![\scriptstyle{\color{blue}{10-\left[\left(\frac{1}{6}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)\right]=\frac{10}{12}\sdot7=\frac{5}{6}\sdot7=5+\frac{5}{6}}}](/mediawiki/images/math/0/4/4/044287a70b44b8ce604ae271f631ad0a.png)
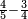
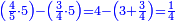
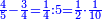

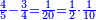
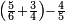
![\scriptstyle{\color{blue}{\left[\left(\frac{5}{6}\sdot30\right)+\left(\frac{3}{4}\sdot30\right)\right]-\left(\frac{4}{5}\sdot30\right)=\left(47+\frac{1}{2}\right)-24=23+\frac{1}{2}}}](/mediawiki/images/math/2/9/c/29c8ab403d3dd1af213d159271381551.png)
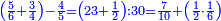
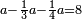
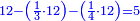
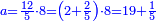
![\scriptstyle{\color{OliveGreen}{a=\frac{n\sdot m}{\left(n\sdot m\right)-\left[\left[\frac{1}{n}\sdot\left(n\sdot m\right)\right]+\left[\frac{1}{m}\sdot\left(n\sdot m\right)\right]\right]}\sdot b}}](/mediawiki/images/math/d/5/a/d5af5089a39514224807c0286cdbbcce.png)
![\scriptstyle{\color{OliveGreen}{a=\frac{b}{\left(n\sdot m\right)-\left[\left[\frac{1}{n}\sdot\left(n\sdot m\right)\right]+\left[\frac{1}{m}\sdot\left(n\sdot m\right)\right]\right]}\sdot\left(n\sdot m\right)}}](/mediawiki/images/math/e/c/7/ec7c26c4065e4cb6a216e65f85134659.png)
![\scriptstyle\left(a-\frac{1}{5}a\right)-\left[\frac{1}{7}\sdot\left(a-\frac{1}{5}a\right)\right]=24](/mediawiki/images/math/3/7/4/374076552ffc3b65b582bafe02e38a00.png)
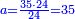
![\scriptstyle{\color{OliveGreen}{\left[a-\left(\frac{1}{n}\sdot a\right)\right]-\left[\frac{1}{m}\sdot\left[a-\left(\frac{1}{n}\sdot a\right)\right]\right]=b}}](/mediawiki/images/math/5/2/1/521bc9ccb2f87c9a4835c93b82a68977.png)
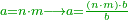
![\scriptstyle{\color{blue}{5\sdot6=30\longrightarrow\left[30-\left(\frac{1}{5}\sdot30\right)\right]-\left[\frac{1}{6}\sdot\left[30-\left(\frac{1}{5}\sdot30\right)\right]\right]=20}}](/mediawiki/images/math/a/8/b/a8b4fb85ba2061c2ee6fd40301c0cb64.png)
![\scriptstyle{\color{OliveGreen}{\left(a-\frac{1}{5}a\right)-\left[\frac{1}{7}\sdot\left(a-\frac{1}{5}a\right)\right]=17+\frac{1}{7}}}](/mediawiki/images/math/f/7/0/f706b47807e8bb8aad8176e20d20442a.png)
![\scriptstyle{\color{blue}{5\sdot7\ne25\longrightarrow\left[25-\left(\frac{1}{5}\sdot25\right)\right]-\left[\frac{1}{7}\sdot\left[25-\left(\frac{1}{5}\sdot25\right)\right]\right]=17+\frac{1}{7}}}](/mediawiki/images/math/9/4/e/94ee8615f27ff9c0e073190ccc9aa7b8.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{5}\sdot35\right)+\left[\frac{1}{7}\sdot\left[35-\left(\frac{1}{5}\sdot35\right)\right]\right]=7+\left[\frac{1}{7}\sdot\left(35-7\right)\right]=7+\left(\frac{1}{7}\sdot28\right)=7+4=11}}](/mediawiki/images/math/b/e/7/be7af84c599a9702a27a9cdea4852dd5.png)
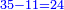
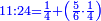
![\scriptstyle{\color{blue}{\left(17+\frac{1}{7}\right)\sdot\left[\frac{1}{4}+\left(\frac{5}{6}\sdot\frac{1}{4}\right)\right]=7+\frac{6}{7}}}](/mediawiki/images/math/f/b/7/fb74968c1148d7314c945145d0608788.png)
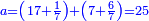
![\scriptstyle{\color{OliveGreen}{a=b+\left(\frac{1}{n-1}\sdot b\right)+\left[\frac{1}{m-1}\sdot\left[b+\left(\frac{1}{n-1}\sdot b\right)\right]\right]}}](/mediawiki/images/math/0/f/2/0f2bddd324df91c36cffacf202099513.png)
![\scriptstyle{\color{blue}{a=\left(17+\frac{1}{7}\right)+\left[\frac{1}{6}\sdot\left(17+\frac{1}{7}\right)\right]+\frac{1}{4}\sdot\left[17+\left(\frac{1}{7}\right)+\left[\frac{1}{6}\sdot\left(17+\frac{1}{7}\right)\right]\right]}}](/mediawiki/images/math/b/d/e/bdece7a97d81b3c13872ad944dfb533f.png)
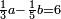
![\scriptstyle{\color{blue}{\begin{cases}\scriptstyle a=\left[\left(15\sdot\frac{1}{5}\right)+6\right]\sdot3=\left(3+6\right)\sdot3=9\sdot3=27\\\scriptstyle \frac{1}{5}b=3\longrightarrow b=15\end{cases}}}](/mediawiki/images/math/3/a/b/3ab9475039c685a7c96f52c9e3661694.png)
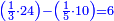
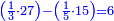
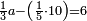
![\scriptstyle{\color{blue}{a=\left[6+\left(\frac{1}{5}\sdot10\right)\right]\sdot3}}](/mediawiki/images/math/9/f/b/9fb3e3e07b1461f5218f62f52845d28d.png)
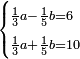
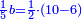
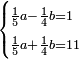
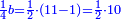
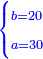
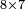
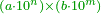
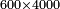
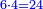
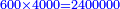
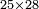

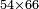
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle54\times66&\scriptstyle=\left[\left(\frac{50}{100}\sdot66\right)\sdot100\right]+\left(4\sdot66\right)=\left[\left(\frac{1}{2}\sdot66\right)\sdot100\right]+264\\&\scriptstyle=\left(33\sdot100\right)+264=3300+264=3564\\\end{align}}}](/mediawiki/images/math/d/2/d/d2dcff5ce76e67e6b7bd557d89eafbb5.png)
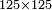
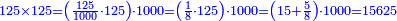

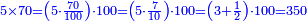
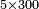
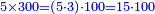
![\scriptstyle{\color{blue}{5\times300=\left(\frac{5}{100}\sdot300\right)\sdot100=\left[\left(\frac{1}{2}\sdot\frac{1}{10}\right)\sdot300\right]\sdot100=15\sdot100}}](/mediawiki/images/math/1/4/6/14612faaf59a164181a05ac6636a133f.png)
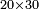
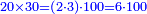
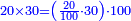

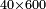
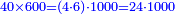

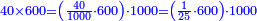
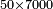
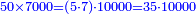
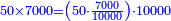

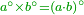
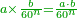
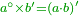
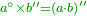
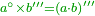
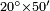
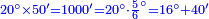
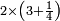
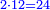
 .
.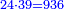
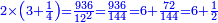
![\scriptstyle{\color{blue}{2\times\left(3+\frac{1}{4}\right)=\frac{2\sdot\left[\left(3\sdot4\right)+1\right]}{4}=\frac{2\sdot\left(12+1\right)}{4}=\frac{2\sdot13}{4}=\frac{26}{4}=6+\frac{1}{2}}}](/mediawiki/images/math/9/e/b/9ebb902113adb9c9b6516f8d3a5d9422.png)
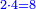
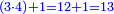 .
.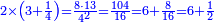

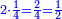
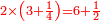
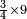
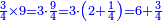
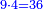
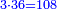
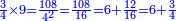
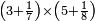
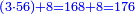
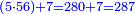
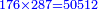

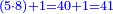

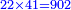
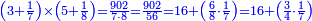
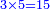
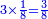
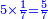
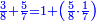
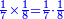
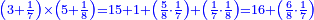
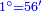
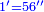
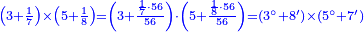
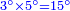
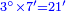
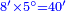
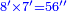
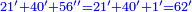
![\scriptstyle{\color{blue}{\left(3+\frac{1}{7}\right)\times\left(5+\frac{1}{8}\right)=15^\circ+62^\prime=15^\circ+1^\circ+6^\prime=16^\circ+6^\prime=\left[16+\left(\frac{3}{4}\sdot\frac{1}{7}\right)\right]^\circ}}](/mediawiki/images/math/a/b/8/ab85e5551c1c68da951d5d947c330f97.png)
![\scriptstyle\left(3+\frac{1}{4}\right)\times\left[5+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/a/e/2/ae2eb1d97e60b3daefe628a8a4333262.png)

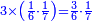
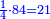
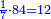
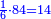
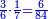

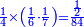
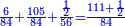
![{\color{blue}{\begin{align}\scriptstyle\left(3+\frac{1}{4}\right)\times\left[5+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]&\scriptstyle=15+\frac{111+\frac{1}{2}}{84}=15+\frac{84+27+\frac{1}{2}}{84}=15+1+\frac{27+\frac{1}{2}}{84}\\&\scriptstyle=16+\frac{21+6+\frac{1}{2}}{84}=16+\frac{1}{4}+\frac{6+\frac{1}{2}}{84}\\&\scriptstyle=16+\frac{1}{4}+\left(\frac{2}{7}\sdot\frac{1}{4}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{4}\right)\\\end{align}}}](/mediawiki/images/math/6/7/0/67063b710aa1ec41ea429525fe874aea.png)


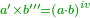
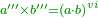
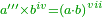

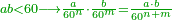
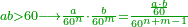
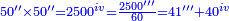
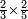
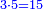


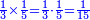
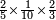
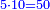

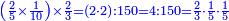
![\scriptstyle\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)](/mediawiki/images/math/1/a/c/1ac4f88a6d78fe1ca6efd685e4d7383f.png)
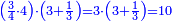
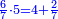
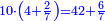
![\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)=\frac{42+\frac{6}{7}}{4}=10+\frac{5}{7}}}](/mediawiki/images/math/f/8/9/f8955275d28af1f3362cd09d8774bd51.png)
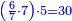
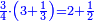
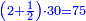
![\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)=
\frac{75}{7}=10+\frac{5}{7}}}](/mediawiki/images/math/4/2/f/42feda1496f4369722717e3f35bdaba7.png)
![\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)=\left(2+\frac{1}{2}\right)\sdot\left(4+\frac{2}{7}\right)=10+\frac{5}{7}}}](/mediawiki/images/math/e/9/5/e95370870e15985c0bf40ea4eb7e0f20.png)
![\scriptstyle\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]](/mediawiki/images/math/3/c/4/3c44a996a735d16f077b6f5636f1fd0a.png)
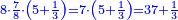
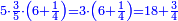
![\scriptstyle{\color{blue}{\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=\frac{37+\frac{1}{3}}{8}\sdot\frac{18+\frac{3}{4}}{5}=\frac{139+\frac{4}{4}}{8}=17+\frac{1}{2}}}](/mediawiki/images/math/1/4/2/14226c70721156a36c475d7ed7ea74a5.png)
![\scriptstyle{\color{blue}{\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=\frac{37+\frac{1}{3}}{8}\sdot\frac{18+\frac{3}{4}}{5}=\frac{\left(4+\frac{2}{3}\right)\sdot\left(18+\frac{3}{4}\right)}{5}=\frac{87+\frac{1}{2}}{5}=17+\frac{1}{2}}}](/mediawiki/images/math/2/3/9/23948e19af1ed84f590521c31540bb01.png)
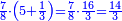
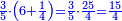
![\scriptstyle{\color{blue}{\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=\frac{14}{3}\sdot\frac{15}{4}=\frac{14\sdot\left(3+\frac{3}{4}\right)}{3}=17+\frac{1}{2}}}](/mediawiki/images/math/4/9/e/49e74c31c3372c8d3ebc3970f1c8b37f.png)
![\scriptstyle{\color{blue}{\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]=\frac{14}{3}\sdot\frac{15}{4}=\frac{\left(4+\frac{2}{3}\right)\sdot15}{4}=\frac{70}{4}=17+\frac{1}{2}}}](/mediawiki/images/math/9/8/a/98a6dd3ddabf531dc87d83441bfb8660.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}\sdot\frac{3}{5}\right)\times\left(\frac{5}{6}\sdot\frac{3}{7}\right)&\scriptstyle=\left[\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]=\frac{140\sdot\left[\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]}{140}\\&\scriptstyle=\frac{22+\frac{1}{2}}{140}=\frac{1}{7}+\left(\frac{1}{8}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/7/3/1/731b480409a79c84beb1d2839dddade1.png)
![\scriptstyle{\color{blue}{\left(\frac{3}{4}\sdot\frac{3}{5}\right)\times\left(\frac{5}{6}\sdot\frac{3}{7}\right)=\frac{9}{20}\sdot\left[\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]=\frac{9\sdot\left[\frac{2}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]}{20}=\frac{3+\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)}{20}=\frac{1}{7}+\left(\frac{1}{8}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/1/1/c/11c0904770226283a50ad33b476ea128.png)
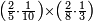
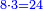
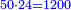
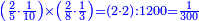
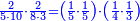
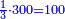
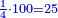
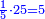
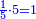
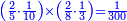
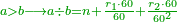
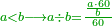
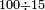
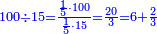
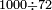
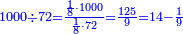
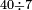
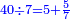
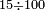
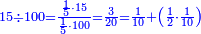
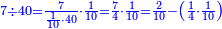
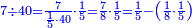
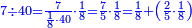
![\scriptstyle{\color{blue}{\left[\frac{2}{10}-\left(\frac{1}{4}\sdot\frac{1}{10}\right)\right]\sdot40=7}}](/mediawiki/images/math/e/3/7/e37b262131999cf0c3e5d10be7365d57.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{5}-\left(\frac{1}{8}\sdot\frac{1}{5}\right)\right]\sdot40=7}}](/mediawiki/images/math/0/2/9/029e15d45923fbee4bbda30e80fa69c8.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{8}+\left(\frac{2}{5}\sdot\frac{1}{8}\right)\right]\sdot40=7}}](/mediawiki/images/math/f/9/f/f9fc4f8fb00d95d78afdbce6f5bab3a2.png)
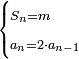
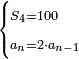
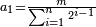
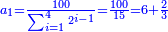
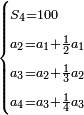
![\scriptstyle{\color{blue}{1+\left(1+\frac{1}{2}\right)+\left[\left(1+\frac{1}{2}\right)+\frac{1}{3}\sdot\left(1+\frac{1}{2}\right)\right]+\left[\left[\left(1+\frac{1}{2}\right)+\frac{1}{3}\sdot\left(1+\frac{1}{2}\right)\right]+\frac{1}{4}\sdot\left[\left(1+\frac{1}{2}\right)+\frac{1}{3}\sdot\left(1+\frac{1}{2}\right)\right]\right]=7}}](/mediawiki/images/math/e/e/3/ee333d0a1e3daaccc1b747ff0a5db333.png)
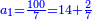
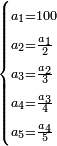
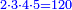
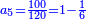
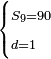
![\scriptstyle{\color{blue}{\sum_{i=1}^{9-1} i=\sum_{i=1}^{8} i=\left[\left(8+1\right)\sdot\left(\frac{1}{2}\sdot8\right)\right]=36}}](/mediawiki/images/math/4/9/0/490595aaecc6da7c8c1107abcdf56489.png)
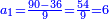
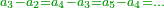 ]
]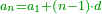 ]
]![\scriptstyle{\color{OliveGreen}{a_1=\frac{S_n-\sum_{i=1}^{n-1} i}{n}=\frac{S_n-\left[n\sdot\left[\frac{1}{2}\sdot\left(n-1\right)\right]\right]}{n}}}](/mediawiki/images/math/7/4/d/74d1638f038ded38066b767ecff46acd.png) ]
]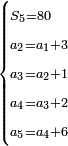
![\scriptstyle{\color{blue}{a_1=\frac{80-\left[3+\left(3+1\right)+\left(3+1+2\right)+\left(3+1+2+6\right)\right]}{5}=\frac{80-25}{5}=\frac{55}{5}=11}}](/mediawiki/images/math/3/1/1/3117596a6b3e1b03ad8e76096769ff87.png)
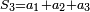
![\scriptstyle a_1=\frac{S_3^2-\left[2a_1+\left[a_2\sdot\left(S_3-1\right)\right]+\left(a_3\sdot S_3\right)\right]}{S_3-2}](/mediawiki/images/math/7/4/b/74b406a92903345a162d5a49fefd60be.png)
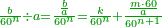
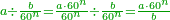
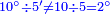

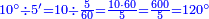
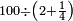
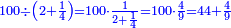
![\scriptstyle20\div\left[\frac{2}{3}\sdot\left(7+\frac{1}{5}\right)\right]](/mediawiki/images/math/2/4/c/24c083330efd4b6463fe3289713dd1a5.png)
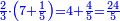
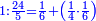
![\scriptstyle{\color{blue}{\scriptstyle20\div\left[\frac{2}{3}\sdot\left(7+\frac{1}{5}\right)\right]=20\sdot\left[\frac{1}{6}+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]=4+\frac{1}{6}}}](/mediawiki/images/math/a/d/a/ada019ee97e0df4b80c349cdf8f539a1.png)
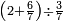
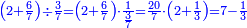
![\scriptstyle\left(2+\frac{1}{2}\right)\div\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/d/8/e/d8e83feda1d6610aa137ca89b047e05e.png)
![{\color{blue}{\begin{align}\scriptstyle\left(2+\frac{1}{2}\right)\div\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{20}{8}\sdot\frac{1}{\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)}=\frac{20}{8}\sdot\left[1+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]=\frac{21}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\\&\scriptstyle=2+\frac{5}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)=3-\frac{1}{3}\\\end{align}}}](/mediawiki/images/math/a/e/b/aeb22c83f7afacafcd9a79a7e5e607e9.png)
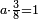
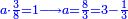
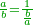
![\scriptstyle a\sdot\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]=1](/mediawiki/images/math/3/7/7/3778176acc4bf275d05b23058a9d3c17.png)
![\scriptstyle{\color{blue}{\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]\sdot50=21}}](/mediawiki/images/math/5/a/6/5a62aaa9b864834e8b9a434ccd6637d7.png)
![\scriptstyle{\color{blue}{a\sdot\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]=1\longrightarrow a=\frac{50}{21}=2+\frac{1}{3}+\left(\frac{1}{7}\sdot\frac{1}{3}\right)}}](/mediawiki/images/math/6/7/1/671108f23ce267b018217d47dc4431ee.png)
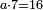
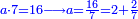
![\scriptstyle\left[\frac{3}{4}\sdot\left(\frac{3}{5}\sdot9\right)\right]\div24](/mediawiki/images/math/f/d/5/fd5da07e5ee7c1d16ab429c699e3a165.png)
![\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(\frac{3}{5}\sdot9\right)\right]\div24=\left(\frac{3}{4}\sdot\frac{27}{5}\right)\div24=\frac{4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}{24}}}](/mediawiki/images/math/2/5/b/25bc66f9b17c777073d5d4939e202a09.png)
![\scriptstyle{\color{blue}{\frac{4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}{24}=\frac{\frac{8\sdot\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]}{24}}{8}=\frac{1}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{3}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/2/2/8/228b3484f8b9a8825d222f1daefb5ce6.png)
![\scriptstyle{\color{blue}{\frac{4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}{24}=\frac{\frac{3\sdot\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]}{24}}{3}=\left(\frac{1}{2}\sdot\frac{1}{3}\right)+\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{3}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/7/0/f/70fb2be6e47e7834af1a1bd5811ee4fd.png)
![\scriptstyle{\color{blue}{\frac{4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}{24}=\frac{\frac{4\sdot\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]}{24}}{4}=\left(\frac{2}{3}\sdot\frac{1}{4}\right)+\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{4}\right)}}](/mediawiki/images/math/f/4/e/f4e230dc5199ceaee1aa5ab8073b1949.png)

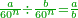
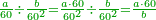
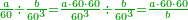
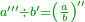
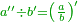
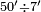
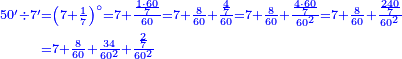
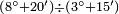
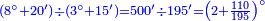
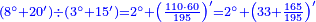
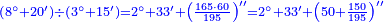
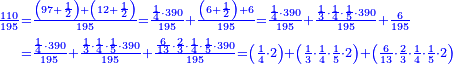
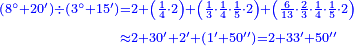
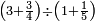
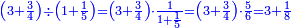
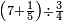
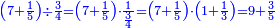
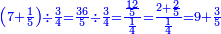
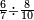
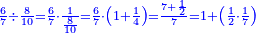
![\scriptstyle{\color{blue}{\frac{6}{7}\div\frac{8}{10}=\frac{\frac{6}{8}}{7}\div\frac{1}{10}=\frac{1-\frac{1}{4}}{7}\div\frac{1}{10}=\left[\frac{1}{7}-\left(\frac{1}{4}\sdot\frac{1}{7}\right)\right]\div\frac{1}{10}=\frac{7}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/b/1/7/b17759b34258c56758a694f42702a9d7.png)
![\scriptstyle\left[\frac{6}{7}\sdot\left(5+\frac{1}{4}\right)\right]\div\left[\frac{3}{8}\sdot\left(1+\frac{1}{5}\right)\right]](/mediawiki/images/math/a/c/7/ac790ab4f0c5e266ccc6cb6b836c03b1.png)
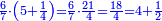
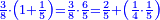
![\scriptstyle{\color{blue}{\left[\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\right]\sdot\left(2+\frac{2}{9}\right)=1}}](/mediawiki/images/math/0/5/9/0594e524801206478f581c1e90e3ea1d.png)
![\scriptstyle{\color{blue}{\frac{1}{4}\sdot\frac{1}{5}=\frac{1}{9}\sdot\left[\frac{2}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\right]}}](/mediawiki/images/math/7/1/2/712a2bb1daa78bf98f67982635a279e7.png)
![\scriptstyle{\color{blue}{\left[\frac{6}{7}\sdot\left(5+\frac{1}{4}\right)\right]\div\left[\frac{3}{8}\sdot\left(1+\frac{1}{5}\right)\right]=\left(4+\frac{1}{2}\right)\sdot\left(2+\frac{2}{9}\right)=10}}](/mediawiki/images/math/5/c/0/5c0630351a5a57e6b1a4c41e1256d012.png)
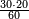


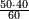
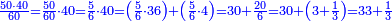
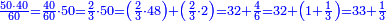
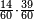
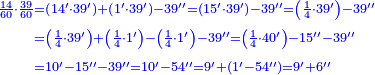
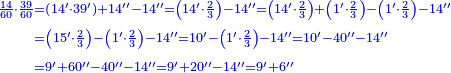
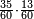
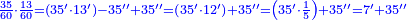
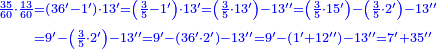
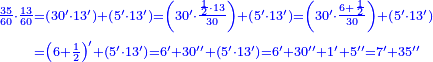
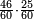
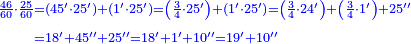
![{\color{blue}{\begin{align}\scriptstyle\frac{46}{60}\sdot\frac{25}{60}&\scriptstyle=46^\prime\sdot\left[\frac{1}{3}+\left(\frac{1}{4}\sdot\frac{1}{3}\right)\right]=46^\prime\sdot\frac{1}{3}\sdot\left(1+\frac{1}{4}\right)=\left(15^\prime+20^{\prime\prime}\right)\sdot\left(1+\frac{1}{4}\right)\\&\scriptstyle=\left(15^\prime+20^{\prime\prime}\right)+\left(15^\prime+20^{\prime\prime}\right)\sdot\frac{1}{4}=15^\prime+20^{\prime\prime}+3^\prime+50^{\prime\prime}=19^\prime+10^{\prime\prime}\\\end{align}}}](/mediawiki/images/math/b/2/4/b242e0b3a88a8979f61e74ae450a26a7.png)
![{\color{blue}{\begin{align}\scriptstyle\frac{46}{60}\sdot\frac{25}{60}&\scriptstyle=\left(46^\prime\sdot24^\prime\right)+\left(46^\prime\sdot1^\prime\right)=46^\prime\sdot\left(\frac{2}{5}+1^\prime\right)=\left[45^\prime\sdot\left(\frac{2}{5}+1^\prime\right)\right]+\left[1^\prime\sdot\left(\frac{2}{5}+1^\prime\right)\right]\\&\scriptstyle=18^\prime+45^{\prime\prime}+\left[1^\prime\sdot\left(24^\prime+1^\prime\right)\right]=18^\prime+45^{\prime\prime}+24^{\prime\prime}+1^{\prime\prime}=19^\prime+10^{\prime\prime}\\\end{align}}}](/mediawiki/images/math/5/f/4/5f41627b7f4ed9e8a2a97d01463117d8.png)
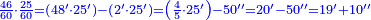
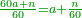
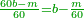
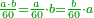
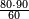
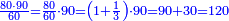
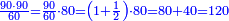
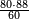
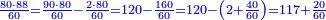
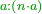
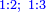
![\scriptstyle{\color{OliveGreen}{a:\left[\left(1+\frac{1}{m}\right)\sdot a\right]}}](/mediawiki/images/math/f/c/4/fc4d1259c62a36e18bfa2717d538557b.png)

![\scriptstyle{\color{OliveGreen}{a:\left[\left(n+\frac{1}{m}\right)\sdot a\right]}}](/mediawiki/images/math/4/9/f/49ffeb341070689e9bd7477550d14286.png)

![\scriptstyle{\color{OliveGreen}{a:\left[\left(1+\frac{r}{m}\right)\sdot a\right]}}](/mediawiki/images/math/8/8/1/881413e48793148bcf7349859fda67c3.png)

![\scriptstyle{\color{OliveGreen}{a:\left[\left(n+\frac{r}{m}\right)\sdot a\right]}}](/mediawiki/images/math/b/b/e/bbe4ec31fcd206b9fcf1bc44b6803a41.png)

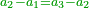
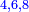
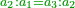
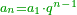
![\scriptstyle{\color{blue}{9:6:4\longrightarrow q=1+\frac{1}{2}\longrightarrow6:4=\left[4\sdot\left(1+\frac{1}{2}\right)\right]:4=\left[6\sdot\left(1+\frac{1}{2}\right)\right]:6=9:6}}](/mediawiki/images/math/7/5/6/756be9b5b3e5a8677075f50931c07469.png)
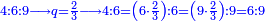

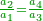
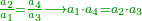
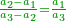
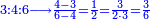
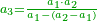
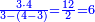
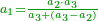
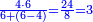
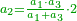
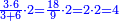
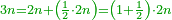
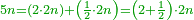

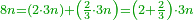
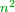 ], since its one side is equal to its other side, and when you count its side by its multitude the product is the square number.
], since its one side is equal to its other side, and when you count its side by its multitude the product is the square number. ].
]. ], since it has no other side but one, which is not a number.
], since it has no other side but one, which is not a number.
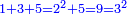
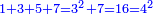
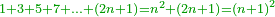


![\scriptstyle{\color{OliveGreen}{x_1=a_3-\left[a_2+\left(a_2-a_1\right)\right]}}{\color{blue}{=9-\left[6+\left(6-4\right)\right]=1}}](/mediawiki/images/math/c/6/d/c6d3dc69d0bc528ebf471016106220a5.png)
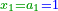
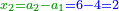
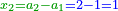
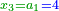
![\scriptstyle{\color{OliveGreen}{x_3=a_3-\left[a_2+\left(a_2-a_1\right)\right]}}{\color{blue}{=4-\left[2+\left(2-1\right)\right]=1}}](/mediawiki/images/math/b/8/b/b8bb8e5a3852eeef74fd7287e34f27f8.png)
![\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n k=n\sdot\left[\left(\frac{1}{2}\sdot n\right)+\frac{1}{2}\right]}}](/mediawiki/images/math/f/a/6/fa6baa34b565d43b5520a33eb7e7b4dc.png)
![\scriptstyle{\color{blue}{6\sdot\left[\left(\frac{1}{2}\sdot6\right)+\frac{1}{2}\right]=21}}](/mediawiki/images/math/a/e/a/aea414d9e1212dae3c7a94b10896734c.png)
![\scriptstyle{\color{blue}{5\sdot\left[\left(\frac{1}{2}\sdot5\right)+\frac{1}{2}\right]=5\sdot3=15}}](/mediawiki/images/math/9/3/b/93b7a01eee210e0c8b3564be3a95258b.png)
![\scriptstyle{\color{blue}{4\sdot\left[\left(\frac{1}{2}\sdot4\right)+\frac{1}{2}\right]=4\sdot\left(2+\frac{1}{2}\right)=10}}](/mediawiki/images/math/8/d/c/8dcb9fc5daf2d06f013534f9070a4a28.png)
![\scriptstyle{\color{blue}{3\sdot\left[\left(\frac{1}{2}\sdot3\right)+\frac{1}{2}\right]=3\sdot2=6}}](/mediawiki/images/math/8/4/9/8498e8411722f69ceec740ca7148af49.png)
![\scriptstyle{\color{blue}{2\sdot\left[\left(\frac{1}{2}\sdot2\right)+\frac{1}{2}\right]=2\sdot\left(1+\frac{1}{2}\right)=3}}](/mediawiki/images/math/6/5/1/6519f9961d55250aa0c0e946d8d00aa1.png)
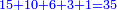
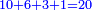
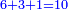
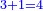


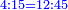
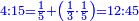
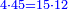
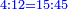

![\scriptstyle{\color{OliveGreen}{\frac{\left[amount\ of\ goods\ offered\ in\right]\ business}{price}=\frac{sold\ \left[amount\ of\ goods\right]}{money\ \left[paid\right]}}}](/mediawiki/images/math/6/a/4/6a4de5708c8e2857cb12749f97b5fd4d.png)
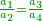
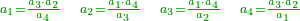
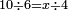
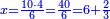
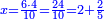
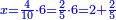
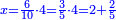
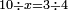
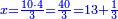
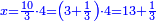
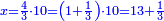
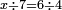
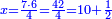
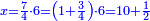
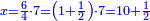
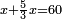
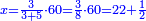
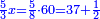
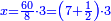
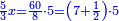
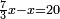
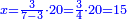
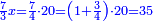
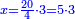
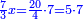
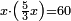
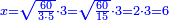
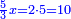

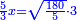
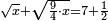
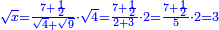
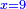
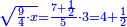
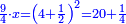
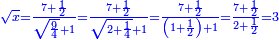
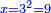
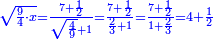
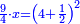
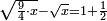
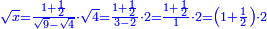
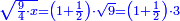
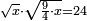
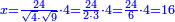
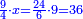
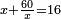
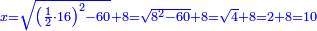
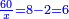
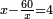
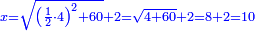
![\scriptstyle3x+\left[7\sdot\left(1-x\right)\right]=6](/mediawiki/images/math/0/3/8/03896ab071ff585de4d04aa27ed3415e.png)
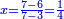
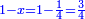
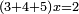
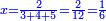
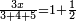
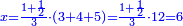
![\scriptstyle\left[\left(3+7\right)\sdot x\right]+\left[12\sdot\left(1-2x\right)\right]=10](/mediawiki/images/math/8/0/2/8025bb98c833778586376b3608eac629.png)
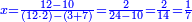
![\scriptstyle\left[\left(2+3+5\right)\sdot x\right]+\left[14\sdot\left(1-3x\right)\right]=12](/mediawiki/images/math/b/f/3/bf35d2d99dd4cbfbb45254630ea49227.png)
![\scriptstyle{\color{blue}{1-3x=1-\left[3\sdot\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]=\frac{6}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/b/e/9/be982293d267e02fe60ed804f20d2e26.png)
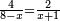
![\scriptstyle{\color{blue}{x=\left[\left[\left(8-x\right)+\left(x+1\right)\right]\sdot\frac{2}{2+4}\right]-1=\left(9\sdot\frac{2}{6}\right)-1=\left(9\sdot\frac{1}{3}\right)-1=2}}](/mediawiki/images/math/d/4/2/d42b90936bb2eba7513ff2d1773924bb.png)
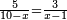
![{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle=\left[\left[\left(x-1\right)+\left(10-x\right)\right]\sdot\frac{3}{3+5}\right]+1=\left(9\sdot\frac{3}{8}\right)+1=\left[9\sdot\left[\frac{1}{4}+\left(\frac{1}{2}\sdot\frac{1}{4}\right)\right]\right]+1=\left(3+\frac{3}{8}\right)+1\\&\scriptstyle=4+\frac{3}{8}\\\end{align}}}](/mediawiki/images/math/d/e/a/dea0e61a0b9149869024b1b1ae347ab5.png)
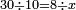
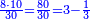
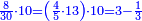
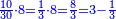
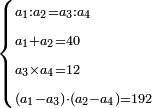

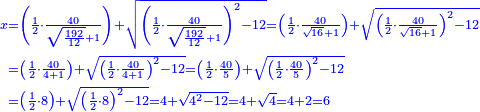

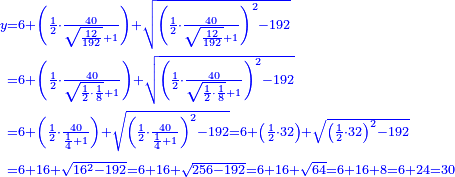

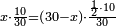
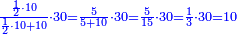
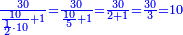
![\scriptstyle\left(x\sdot\frac{10}{30}\right)-\left[\left(30-x\right)\sdot\frac{5}{30}\right]=1](/mediawiki/images/math/3/4/6/346922a7313f2cbdbdec4b3250f5981e.png)
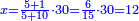
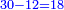
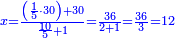
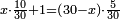


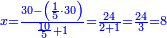
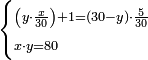
![\scriptstyle{\color{blue}{y=\frac{\left[\left(5-1\right)\sdot30\right]-80}{5}=\frac{\left(4\sdot30\right)-80}{5}=\frac{40}{5}=8}}](/mediawiki/images/math/0/4/e/04ef367b12d05fc6cb75960e54fe97bd.png)
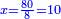
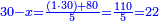
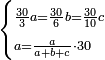
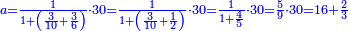
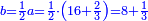
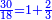
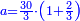
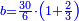
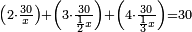
![\scriptstyle{\color{blue}{x=\frac{\left(2\sdot30\right)+\left[\left(3\sdot30\right)\sdot2\right]+\left[\left(4\sdot30\right)\sdot3\right]}{30}=\frac{60+180+360}{30}=\frac{600}{30}=20}}](/mediawiki/images/math/5/6/2/562fda47469492be1aa79eec119908b6.png)
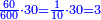
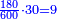
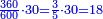
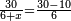
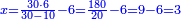
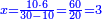
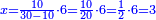
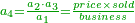
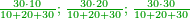

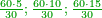

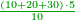
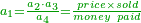
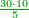
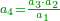
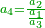

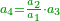
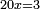

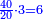
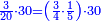
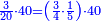
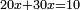
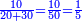


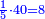
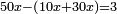
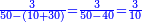
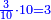
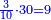

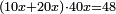
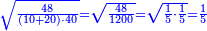
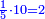
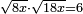
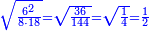

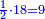
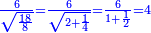
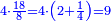
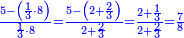

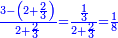
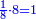
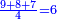


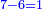
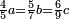
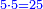
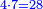
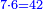
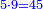
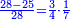
![\scriptstyle{\color{blue}{a=42-\left[\left(\frac{3}{4}\sdot\frac{1}{7}\right)\sdot42\right]=37+\frac{1}{2}}}](/mediawiki/images/math/8/a/4/8a4cc703188e80aec577434c60184cdb.png)
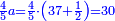
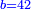

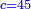
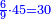
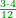
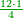
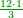
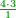
![\scriptstyle\left(2x\sdot6\right)-\left[x\sdot\left(1+2\right)\right]=6-4](/mediawiki/images/math/a/1/a/a1a3080a03d2b52fc41377b632dd56a1.png)
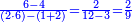
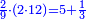
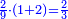
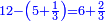
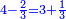
![\scriptstyle\left[x\sdot\left(5+7\right)\right]-\left(2x\sdot1\right)=4-1](/mediawiki/images/math/a/3/b/a3b4865ffc423e382f8577a723762bdc.png)
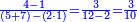
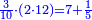
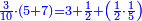
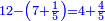
![\scriptstyle{\color{blue}{4-\left[3+\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]=\frac{2}{5}}}](/mediawiki/images/math/8/a/a/8aa11d0bf6e1875a1242afc9dac56e76.png)
![\scriptstyle\left(2x\sdot6\right)-\left[x\sdot\left[\frac{3}{4}+\left(1+\frac{1}{4}\right)\right]\right]=6-4](/mediawiki/images/math/c/8/0/c8067ad9007f3a7cda8edbd70f832bbe.png)
![\scriptstyle{\color{blue}{\frac{6-4}{\left(2\sdot6\right)-\left[\frac{3}{4}+\left(1+\frac{1}{4}\right)\right]}=\frac{2}{12-2}=\frac{2}{10}=\frac{1}{5}}}](/mediawiki/images/math/f/7/1/f7120260ad540faf61afc12a17ca71a6.png)
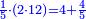
![\scriptstyle{\color{blue}{\frac{1}{5}\sdot\left[\frac{3}{4}+\left(1+\frac{1}{4}\right)\right]=\frac{2}{5}}}](/mediawiki/images/math/2/b/3/2b3267957a45ab5a0e4f837c40f745c6.png)
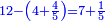
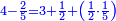
![\scriptstyle\left[x\sdot\left[\left(5+\frac{1}{4}\right)+\left(6+\frac{3}{4}\right)\right]\right]-\left(2x\sdot2\right)=4-2](/mediawiki/images/math/3/4/5/345afae745fd9cc75c453b9aabbf4fe1.png)
![\scriptstyle{\color{blue}{\frac{4-2}{\left[\left(5+\frac{1}{4}\right)+\left(6+\frac{3}{4}\right)\right]-\left(2\sdot2\right)}=\frac{2}{12-4}=\frac{2}{8}=\frac{1}{4}}}](/mediawiki/images/math/e/9/7/e97cddba5666298a7ab4407e7bfb239f.png)
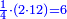
![\scriptstyle{\color{blue}{\frac{1}{4}\sdot\left[\left(5+\frac{1}{4}\right)+\left(6+\frac{3}{4}\right)\right]=3}}](/mediawiki/images/math/8/2/6/826bece0bd15376a8f55506f242f8dc6.png)
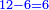

![\scriptstyle\left(3x\sdot5\right)-\left[x\sdot\left[\frac{1}{4}+\frac{1}{2}+\left(1+\frac{1}{4}\right)\right]\right]=5-4](/mediawiki/images/math/4/e/b/4eb0927ce361b75f8b3baf535c21318f.png)
![\scriptstyle{\color{blue}{\frac{5-4}{\left(3\sdot5\right)-\left[\frac{1}{4}+\frac{1}{2}+\left(1+\frac{1}{4}\right)\right]}=\frac{1}{15-2}=\frac{1}{13}}}](/mediawiki/images/math/9/c/5/9c5c95b523f39c1b26e6b5856cb86e3b.png)
![\scriptstyle{\color{blue}{\frac{1}{13}\sdot\left[\frac{1}{4}+\frac{1}{2}+\left(1+\frac{1}{4}\right)\right]=\frac{2}{13}}}](/mediawiki/images/math/4/2/3/423de9f88d80f84b155e54b8772e55f8.png)
![\scriptstyle\left[x\sdot\left[\left(5+\frac{1}{4}\right)+\left(6+\frac{1}{2}\right)+\left(7+\frac{1}{4}\right)\right]\right]-\left(3x\sdot3\right)=4-3](/mediawiki/images/math/f/5/d/f5d280babd1c03df9b2ee340c2f82645.png)
![\scriptstyle{\color{blue}{\frac{4-3}{\left[\left(5+\frac{1}{4}\right)+\left(6+\frac{1}{2}\right)+\left(7+\frac{1}{4}\right)\right]-\left(3\sdot3\right)}=\frac{1}{19-9}=\frac{1}{10}}}](/mediawiki/images/math/d/b/9/db95614cdb6ceb7cc5861b1397207e39.png)
![\scriptstyle{\color{blue}{4-\left[\frac{1}{10}\sdot\left[\left(5+\frac{1}{4}\right)+\left(6+\frac{1}{2}\right)+\left(7+\frac{1}{4}\right)\right]\right]=2+\left(\frac{1}{2}\sdot\frac{1}{5}\right)}}](/mediawiki/images/math/4/b/d/4bd6a1017a84c6d09562d1901ef0ae2c.png)
![\scriptstyle\left[4x\sdot\left(5+\frac{3}{4}\right)\right]-\left[x\sdot\left[\frac{1}{2}+\frac{3}{4}+\left(2+\frac{1}{2}\right)+\left(3+\frac{1}{4}\right)\right]\right]=\left(5+\frac{3}{4}\right)-\left(3+\frac{3}{4}\right)](/mediawiki/images/math/6/2/8/6281af632a6c43529673337ff9e95a22.png)
![\scriptstyle{\color{blue}{x=\frac{\left(5+\frac{3}{4}\right)-\left(3+\frac{3}{4}\right)}{\left[4\sdot\left(5+\frac{3}{4}\right)\right]-\left[\frac{1}{2}+\frac{3}{4}+\left(2+\frac{1}{2}\right)+\left(3+\frac{1}{4}\right)\right]}=\frac{2}{23-7}=\frac{2}{16}=\frac{1}{8}}}](/mediawiki/images/math/d/e/d/ded43f5fb915555a080b1de4f9c1ef4e.png)
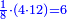
![\scriptstyle{\color{blue}{\frac{1}{8}\sdot\left[\frac{1}{2}+\frac{3}{4}+\left(2+\frac{1}{2}\right)+\left(3+\frac{1}{4}\right)\right]=\frac{7}{8}}}](/mediawiki/images/math/1/2/c/12cc4230f3ecd1287b595695b3141c40.png)
![\scriptstyle{\color{blue}{\frac{1}{8}\sdot\left[4\sdot\left(5+\frac{3}{4}\right)\right]=2+\frac{7}{8}}}](/mediawiki/images/math/1/9/3/193a763fd916da00b03ce872ab8db939.png)
![\scriptstyle4x\sdot12-\left[x\sdot\left[\frac{3}{4}+\left(1+\frac{1}{4}\right)+\left(1+\frac{1}{2}\right)+\left(2+\frac{1}{2}\right)\right]\right]=12-4](/mediawiki/images/math/1/0/b/10b5b7964f1a5a51a2d28692a15d7481.png)
![\scriptstyle{\color{blue}{x=\frac{12-4}{\left(4\sdot12\right)-\left[\frac{3}{4}+\left(1+\frac{1}{4}\right)+\left(1+\frac{1}{2}\right)+\left(2+\frac{1}{2}\right)\right]}=\frac{8}{48-6}=\frac{8}{42}=\frac{1}{7}+\left(\frac{1}{3}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/b/8/2/b82678cfe92167e0c8be52f20bc23f81.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{7}+\left(\frac{1}{3}\sdot\frac{1}{7}\right)\right]\sdot\left(4\sdot12\right)=9+\frac{1}{7}}}](/mediawiki/images/math/c/8/7/c87d62c86ac0cbd46985e02ee0f8b6fd.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{7}+\left(\frac{1}{3}\sdot\frac{1}{7}\right)\right]\sdot\left[\frac{3}{4}+\left(1+\frac{1}{4}\right)+\left(1+\frac{1}{2}\right)+\left(2+\frac{1}{2}\right)\right]=1+\frac{1}{7}}}](/mediawiki/images/math/f/8/9/f89fe031ec446389c11a11681d8da0c7.png)
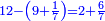
![\scriptstyle4x\sdot12-\left[x\sdot\left[\left[12-\left(8+\frac{1}{2}\right)\right]+\left[12-\left(7+\frac{3}{4}\right)\right]+\left[12-\left(6+\frac{1}{2}\right)\right]+\left[12-\left(5+\frac{1}{4}\right)\right]\right]\right]=12-\left(12-4\right)](/mediawiki/images/math/1/7/6/176fc78a09bb823d327cff56957f2455.png)
![\scriptstyle4x\sdot12-\left[x\sdot\left[\left(3+\frac{1}{2}\right)+\left(4+\frac{1}{4}\right)+\left(5+\frac{1}{2}\right)+\left(6+\frac{3}{4}\right)\right]\right]=12-8](/mediawiki/images/math/f/f/b/ffb05c32fd2cc4ec70ac2fac0ff9c0e8.png)
![\scriptstyle{\color{blue}{x=\frac{12-8}{\left(4\sdot12\right)-\left[\left(3+\frac{1}{2}\right)+\left(4+\frac{1}{4}\right)+\left(5+\frac{1}{2}\right)+\left(6+\frac{3}{4}\right)\right]}=\frac{4}{48-20}=\frac{4}{28}=\frac{1}{7}}}](/mediawiki/images/math/f/2/b/f2b727fa41789725a2d1854914de2dd6.png)
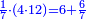
![\scriptstyle{\color{blue}{\frac{1}{7}\sdot\left[\left(3+\frac{1}{2}\right)+\left(4+\frac{1}{4}\right)+\left(5+\frac{1}{2}\right)+\left(6+\frac{3}{4}\right)\right]=2+\frac{6}{7}}}](/mediawiki/images/math/b/e/6/be6152bd21ff14f9ac2f4d5a12f57463.png)
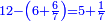
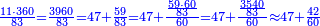
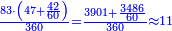
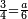
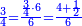
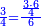
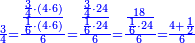
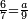
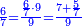
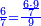
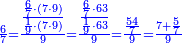
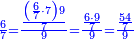
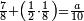
![\scriptstyle{\color{blue}{\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)=\frac{\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\sdot10}{10}=\frac{9}{10}+\left(\frac{3}{8}\sdot\frac{1}{10}\right)}}](/mediawiki/images/math/6/2/0/620d0016d0da06ef18a40d3d9a967edd.png)
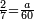
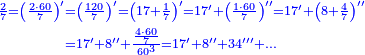
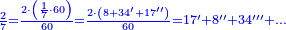
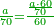
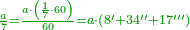
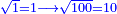
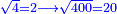
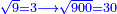
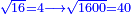


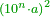
![\scriptstyle{\color{OliveGreen}{x^2=\left(10a\right)^2+\left[2\sdot\left(10a\right)\right]+1\longrightarrow x=10a+1}}](/mediawiki/images/math/2/a/5/2a5e4934cad9769d5202b0d5628780bd.png)
![\scriptstyle{\color{OliveGreen}{x^2=\left(10a\right)^2-\left[2\sdot\left(10a\right)\right]+1\longrightarrow x=10a-1}}](/mediawiki/images/math/b/a/1/ba18f1518910e2c1f135f2c4c40e5791.png)
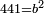

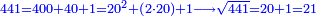
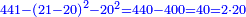
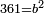
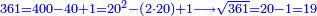
![\scriptstyle{\color{blue}{20^2-\left[361-\left(20-19\right)^2\right]=400-360=40=2\sdot20}}](/mediawiki/images/math/c/2/c/c2c27f2d1246b8105b3326c2e2bb0d87.png)
![\scriptstyle{\color{OliveGreen}{x^2=\left(10a\right)^2+\left[2\sdot2\left(10a\right)\right]+4\longrightarrow x=10a+2}}](/mediawiki/images/math/f/c/9/fc9f4628b27f8f0ce5b976fdc272c66e.png)
![\scriptstyle{\color{OliveGreen}{x^2=\left(10a\right)^2-\left[2\sdot2\left(10a\right)\right]+4\longrightarrow x=10a-2}}](/mediawiki/images/math/d/e/1/de1d443f2a3bea2ba84d48521238a53d.png)
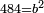
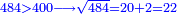
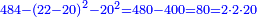

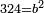
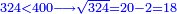
![\scriptstyle{\color{blue}{20^2-\left[324-\left(20-18\right)^2\right]=400-320=80=2\sdot2\sdot20}}](/mediawiki/images/math/e/9/5/e95964a1fed2285c919ecc9238d3ab87.png)

![\scriptstyle{\color{OliveGreen}{x^2=\left(10a\right)^2+\left[2\sdot3\left(10a\right)\right]+9\longrightarrow x=10a+3}}](/mediawiki/images/math/3/8/5/38592c0a7541791300eaa374d24f62d2.png)
![\scriptstyle{\color{OliveGreen}{x^2=\left(10a\right)^2-\left[2\sdot3\left(10a\right)\right]+9\longrightarrow x=10a-3}}](/mediawiki/images/math/2/f/d/2fda45c85939259a46aad2549a06466d.png)
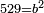
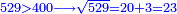
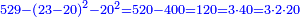
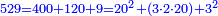
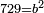
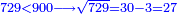
![\scriptstyle{\color{blue}{30^2-\left[729-\left(30-27\right)^2\right]=900-720=180=3\sdot2\sdot30}}](/mediawiki/images/math/c/c/1/cc17220e49784d7225993f7962ed1324.png)
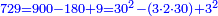
![\scriptstyle{\color{OliveGreen}{\left(10a+5\right)^2=\left[\left[10\sdot\left(a+1\right)\right]-5\right]^2}}](/mediawiki/images/math/5/b/e/5be21e907a7d68d5d2514150e24f965a.png)
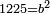
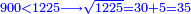
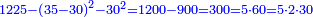
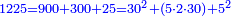
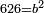
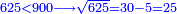
![\scriptstyle{\color{blue}{30^2-\left[625-\left(30-25\right)^2\right]=900-600=300=5\sdot2\sdot30}}](/mediawiki/images/math/3/7/3/373b859db08c1448562e0332e897e6e9.png)
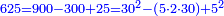
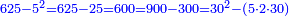
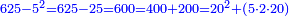
![\scriptstyle{\color{blue}{\left[\left(2\sdot10\right)+5\right]^2=\left(20+5\right)^2=625=\left(30-5\right)^2=\left[\left(3\sdot10\right)-5\right]^2}}](/mediawiki/images/math/9/1/2/9129b10118885049df632bd2d40d63ae.png)
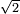
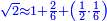
![\scriptstyle{\color{blue}{\sqrt{2}\approx1+\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)-\frac{\left(\frac{1}{2}\sdot\frac{1}{6}\right)^2}{2\sdot\left[1+\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]}}}](/mediawiki/images/math/0/2/a/02a5749a5be75d8750bee2f6ca4401f2.png)
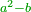
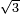


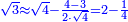
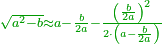
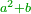 ]
]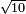
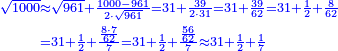
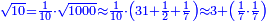
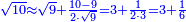
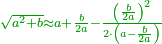
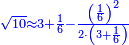
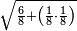
![\scriptstyle{\color{blue}{\sqrt{\frac{6}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)}=\frac{1}{8}\sdot\sqrt{8^2\sdot\left[\frac{6}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)\right]}=\frac{1}{8}\sdot\sqrt{64\sdot\left[\frac{6}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)\right]}=\frac{1}{8}\sdot\sqrt{49}=\frac{7}{8}}}](/mediawiki/images/math/a/d/1/ad1a1b4f26ded493b5b94fda2c99b55c.png)
![\scriptstyle{\color{blue}{\sqrt{\frac{6}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)}=\frac{1}{2}\sdot\sqrt{2^2\sdot\left[\frac{6}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)\right]}=\frac{1}{2}\sdot\sqrt{3+\left(\frac{1}{2}\sdot\frac{1}{8}\right)}=\frac{1}{2}\sdot\left(1+\frac{3}{4}\right)=\frac{7}{8}}}](/mediawiki/images/math/1/d/f/1df6109380b8df4b9dc4c8c6154e409b.png)
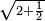
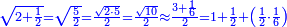
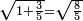
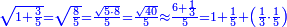
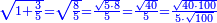
 .
.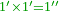
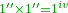
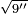
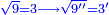
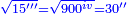
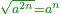
![\scriptstyle{\color{OliveGreen}{\sqrt{a^2+\left[\left(2\sdot a\sdot n\right)+m\right]^\prime}=\sqrt{\left(a+n^\prime\right)^2+\left[m^\prime-\left(n^\prime\right)^2\right]}\approx a+n^\prime}}](/mediawiki/images/math/a/5/9/a591799418260af4e1aebab8fd3b6628.png)
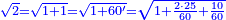
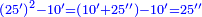
![{\color{blue}{\begin{align}\scriptstyle\sqrt{2}&\scriptstyle=\sqrt{1+1}=\sqrt{1+60^\prime}=\sqrt{1+\frac{2\sdot24}{60}+12^\prime}=\sqrt{\left(1+24^\prime\right)^2+\left[12^\prime-\left(24^\prime\right)^2\right]}\\&\scriptstyle=\sqrt{\left(1+24^\prime\right)^2+\left[12^\prime-\left(9^\prime+36^{\prime\prime}\right)\right]}=\sqrt{\left(1+24^\prime\right)^2+\left(2^\prime+24^{\prime\prime}\right)}\approx1+24^\prime\\\end{align}}}](/mediawiki/images/math/1/9/a/19a5e62bfc43b5d1333713069849f88d.png)
![{\color{blue}{\begin{align}\scriptstyle\sqrt{2}&\scriptstyle=\sqrt{\left(1+24^\prime\right)^2+\left(2^\prime+24^{\prime\prime}\right)}=\sqrt{\left(1+24^\prime\right)^2+\left(\frac{168\sdot51}{60^3}+72^{\prime\prime\prime}\right)}\\&\scriptstyle=\sqrt{\left(1+24^\prime\right)^2+\left[\left[2\sdot\left(1+24^\prime\right)\sdot51^{\prime\prime}\right]+72^{\prime\prime\prime}\right]}=\sqrt{\left(1+24^\prime+51^{\prime\prime}\right)^2+\left[72^{\prime\prime\prime}-\left(51^{\prime\prime}\right)^2\right]}\\&\scriptstyle=\sqrt{\left(1+24^\prime+51^{\prime\prime}\right)^2+\left[72^{\prime\prime\prime}-\left(43^{\prime\prime}+21^{\prime\prime\prime\prime}\right)\right]}\\&\scriptstyle=\sqrt{\left(1+24^\prime+51^{\prime\prime}\right)^2+\left(28^{\prime\prime\prime}+39^{\prime\prime\prime\prime}\right)}\approx1+24^\prime+51^{\prime\prime}\\\end{align}}}](/mediawiki/images/math/6/1/e/61e5dc28b8cf5063a933a4f80db978b3.png)
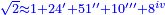
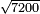
![{\color{blue}{\begin{align}\scriptstyle\sqrt{7200}&\scriptstyle=\sqrt{2\sdot3600}=\sqrt{2\sdot60^2}=60\sdot\sqrt{2}\approx60\sdot\left(1+24^\prime+51^{\prime\prime}+\ldots\right)\\&\scriptstyle=60\sdot\left[\left(60+24\right)^\prime+51^{\prime\prime}+\ldots\right]=60\sdot\left(84^\prime+51^{\prime\prime}+\ldots\right)=84+51^\prime+\ldots\\\end{align}}}](/mediawiki/images/math/d/d/f/ddf4daa2baeb054cf4ce7b82841458e0.png)

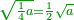
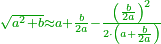
![\scriptstyle{\color{OliveGreen}{\frac{b}{2a}>30^\prime\longrightarrow\left[\left(a+1\right)^2-\left(a^2+b\right)\right]<\left(a^2+b\right)-a^2}}](/mediawiki/images/math/2/0/0/200d3db83eaf9d79f5857f2b89703dff.png)
![\scriptstyle{\color{OliveGreen}{\frac{b}{2a}<30^\prime\longrightarrow\left[\left(a+1\right)^2-\left(a^2+b\right)\right]>\left(a^2+b\right)-a^2}}](/mediawiki/images/math/0/e/8/0e8535ccaa17614915593b7f3491cc60.png)

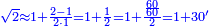
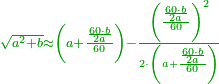
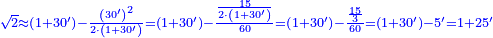
![\scriptstyle{\color{OliveGreen}{\sqrt{a^2+b}\approx a+\frac{b}{2a}-\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}-\frac{\left[\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\right]^2}{2\sdot\left[a+\frac{b}{2a}-\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\right]}}}](/mediawiki/images/math/8/9/6/8966db37705ce5b03d2f73262fe412d1.png)
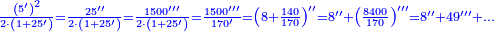
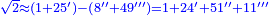
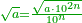
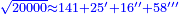
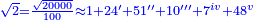
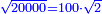
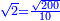
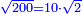
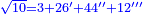
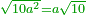
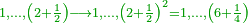
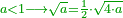
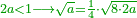
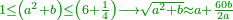
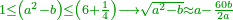


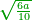 ]. Take a unit from each hundred in the square. When you know the root [from the tables], multiply it by ten and then you will find the required root.
]. Take a unit from each hundred in the square. When you know the root [from the tables], multiply it by ten and then you will find the required root.