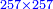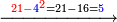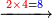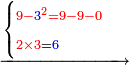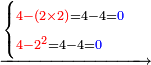Difference between revisions of "ספר ציפרא"
(→Chapter Seven: Proportions) |
(→Chapter Seven: Proportions) |
||
| Line 5,241: | Line 5,241: | ||
== Chapter Seven: Proportions == | == Chapter Seven: Proportions == | ||
| − | + | |style="text-align:right;"|<big>שער עירוכין</big> | |
|- | |- | ||
|The purpose of this chapter - deducing and estimating a thing from another thing | |The purpose of this chapter - deducing and estimating a thing from another thing | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|שער הנכבד ונקרא שער הערך אשר לכולי עלמא צריך למנות ולחשוב ולחכם ולהשכיל לדעת ולהבין דבר מתוך דבר ולהעריך דבר אחר דבר ולעמוד על יסודו ועל בוריו |
|- | |- | ||
| | | | ||
*Estimating the price of a small amount of goods based on the given price of a larger amount of the same goods | *Estimating the price of a small amount of goods based on the given price of a larger amount of the same goods | ||
| − | |style="text-align:right;"|כיצד אם לקחת מקח גדול בדמים מרובים | + | |style="text-align:right;"|כיצד אם לקחת מקח גדול בדמים מרובים ואת צריך להעריך מקח קטן לפי אותה דמים פי' כמה מגיע לפי אותה הדמים למקח הקטן שקנית |
|- | |- | ||
| | | | ||
*Estimating the price of a large amount of goods based on the given price of a smaller amount of the same goods | *Estimating the price of a large amount of goods based on the given price of a smaller amount of the same goods | ||
| − | |style="text-align:right;"|או | + | |style="text-align:right;"|או להיפך שקנית מקח קטן בדמים מועטי' ואתה רוצה להעריך אחריו מקח גדול |
|- | |- | ||
|The procedure: | |The procedure: | ||
| − | |style="text-align:right;"|הילך היאך | + | |style="text-align:right;"|הילך היאך תחשוב ותמנה ותעריך |
|- | |- | ||
| | | | ||
*Calculating the price of a small amount of goods based on a given price of a larger amount of the goods: | *Calculating the price of a small amount of goods based on a given price of a larger amount of the goods: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|תכתו' המקח גדול וסכו דמים מן הגדול המקח תכתוב תחת המקח גדול ואח"כ תכתוב המקח הקטן תחת הסכום |
|- | |- | ||
|<math>\scriptstyle\frac{\left(price\ of\ large\ amount\ of\ goods\right)\times\left(small\ amount\ of\ goods\right)}{large\ amount\ of\ goods}</math> | |<math>\scriptstyle\frac{\left(price\ of\ large\ amount\ of\ goods\right)\times\left(small\ amount\ of\ goods\right)}{large\ amount\ of\ goods}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותכפול דמי המקח הגדול אשר כתבת למעלה אחר המקח הגדול תכפול אותו על מניין מקח קטן והעולה קח בידך ותחלוק אותו בשער החילוק על המקח הגדול ומה שיעלה בידך כל כך ערך המקח הקטן |
|- | |- | ||
| | | | ||
:If there is a remainder - the price is represented by [an integer and] fractions | :If there is a remainder - the price is represented by [an integer and] fractions | ||
| − | |style="text-align:right;"|ואם יותר לך חלקים שלא | + | |style="text-align:right;"|ואם יותר לך חלקים שלא יעלו לחלק המבוקש אז תאמר עוד נשאר לי חלקים כך וכך שסכום כך וכך עולה לחלק אחד של המבוקש |
|- | |- | ||
| | | | ||
*Calculating the price of a large amount of goods based on a given price of a smaller amount of the goods: | *Calculating the price of a large amount of goods based on a given price of a smaller amount of the goods: | ||
| − | |style="text-align:right;"|ואם להיפך שאתה רוצה להעריך חשבון מקח גדול אחר חשבון מקח קטן אז | + | |style="text-align:right;"|ואם להיפך שאתה רוצה להעריך חשבון מקח גדול אחר חשבון מקח קטן אז תכתוב חשבון הקטן למעלה ואח"כ תכתוב דמים הידועים לאותו מקח והחשבון הגדול תכתוב למטה <s>נ</s> תחת דמיו של חשבון הקטן |
|- | |- | ||
|<math>\scriptstyle\frac{\left(price\ of\ small\ amount\ of\ goods\right)\times\left(large\ amount\ of\ goods\right)}{small\ amount\ of\ goods}</math> | |<math>\scriptstyle\frac{\left(price\ of\ small\ amount\ of\ goods\right)\times\left(large\ amount\ of\ goods\right)}{small\ amount\ of\ goods}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותכפול חשבון <s>הקטן</s> הגדול על דמים הידועי' של מקח הקטן והעולה תחלק בשער החילוק על מקח הקטן ‫<ref>115r</ref>שלמעלה כדלעיל |
|- | |- | ||
|The writing rule of the calculation procedure:<br> | |The writing rule of the calculation procedure:<br> | ||
| Line 5,279: | Line 5,279: | ||
::*its price<br> | ::*its price<br> | ||
::*the amount of goods of which the price is unknown | ::*the amount of goods of which the price is unknown | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה הכלל<br> |
| − | המקח אשר ידעת | + | המקח אשר ידעת תכתוב תחילה<br> |
| − | + | ואח"כ תכתוב דמיו<br> | |
| − | + | ואח"כ המקח אשר בקשת לידע להעריך ותכפול ואח"כ תעריך כמו שציויתיך | |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| Line 5,301: | Line 5,299: | ||
*{{#annot:cloth|629|k21g}}A man who asks you: I bought 70 cubits of cloth for 40 dinar, how much will 55 cubits cost? | *{{#annot:cloth|629|k21g}}A man who asks you: I bought 70 cubits of cloth for 40 dinar, how much will 55 cubits cost? | ||
:<math>\scriptstyle\frac{70}{40}=\frac{55}{X}</math> | :<math>\scriptstyle\frac{70}{40}=\frac{55}{X}</math> | ||
| − | |style="text-align:right;"|איש אשר ישאלך הנה קניתי ע' אמות בגד | + | |style="text-align:right;"|איש אשר ישאלך הנה קניתי ע' אמות בגד עבור מ' דינרים כמה מגיע לנ"ה אמות{{#annotend:k21g}} |
|- | |- | ||
| | | | ||
:*First write 70 cubits, then the price of the bargain, and then the 55 cubits, whose price you wish to know, as this: | :*First write 70 cubits, then the price of the bargain, and then the 55 cubits, whose price you wish to know, as this: | ||
| − | |style="text-align:right;"|אז תכתוב תחילה | + | |style="text-align:right;"|אז תכתוב תחילה הע' אמות ואח"כ דמי הע' אמות ואח"כ הנ"ה אמות אשר בקשת לידע ערכיהן כזה |
|- | |- | ||
| | | | ||
| Line 5,678: | Line 5,676: | ||
| | | | ||
:*First write 21 cubits, then 43 dinar, then 65 cubits that you wish to evaluate, like this: | :*First write 21 cubits, then 43 dinar, then 65 cubits that you wish to evaluate, like this: | ||
| − | |style="text-align:right;"|כתוב בתחילה כ"א אמות ואח"כ מ"ג דינרין ואחר כך ס"ה אמות אשר בקשת | + | |style="text-align:right;"|כתוב בתחילה כ"א אמות ואח"כ מ"ג דינרין ואחר כך ס"ה אמות ‫<ref>116r</ref>אשר בקשת לחשוב כזה |
|- | |- | ||
| | | | ||
| Line 5,712: | Line 5,710: | ||
::<span style=color:Green>Rule of Three</span> | ::<span style=color:Green>Rule of Three</span> | ||
:*Multiply 65 by 43, meaning how much is 43 times 65, the result is 2795. | :*Multiply 65 by 43, meaning how much is 43 times 65, the result is 2795. | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותכפול ה"ו על ג"ד פי' כמה עולה ג"ד פעמי' ה"ו ויעלה <s>הטז"ב</s> הטז"ב |
|- | |- | ||
| | | | ||
:*Then, divide 2795 according to the chapter of division: how many times 21 is [in it]? You find that there are 133 times 21 in it and 2 parts remain, of which 21 are a whole unit, i.e. one dinar. | :*Then, divide 2795 according to the chapter of division: how many times 21 is [in it]? You find that there are 133 times 21 in it and 2 parts remain, of which 21 are a whole unit, i.e. one dinar. | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואח"כ חלוק הטז"ב בשער החילוק כמה פעמי' שיש בהן א"ב ותמצא ג'ג'א' פעמי' ועוד נשארו ב' חלקי' קטני' שא"ב מהן עושי' חלק אחד דהיינו דינר |
|- | |- | ||
| | | | ||
:We find that if you bought 21 cubits for 43 dinar, 65 cubits cost 133 dinar and 2 parts, of which 21 are one dinar. | :We find that if you bought 21 cubits for 43 dinar, 65 cubits cost 133 dinar and 2 parts, of which 21 are one dinar. | ||
:<math>\scriptstyle{\color{blue}{X=\frac{65\sdot43}{21}=\frac{2795}{21}=133+\frac{2}{21}}}</math> | :<math>\scriptstyle{\color{blue}{X=\frac{65\sdot43}{21}=\frac{2795}{21}=133+\frac{2}{21}}}</math> | ||
| − | |style="text-align:right;"|נמצא אם קנית א"ב אמות | + | |style="text-align:right;"|נמצא אם קנית א"ב אמות עבור ג"ד דנרי' מגיע לה"ו אמות ג'ג'א' דינרי' וב' חלקי' שא"ב מהן דינר |
|- | |- | ||
| | | | ||
| Line 5,731: | Line 5,729: | ||
:*See by how much 65 exceeds 21, i.e. by 44. | :*See by how much 65 exceeds 21, i.e. by 44. | ||
::<math>\scriptstyle{\color{blue}{65-21=44}}</math> | ::<math>\scriptstyle{\color{blue}{65-21=44}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הבט וראה כמה ה"ו עולה יותר מא"ב דהיינו ד"ד |
|- | |- | ||
| | | | ||
::<span style=color:Green>Rule of Three</span> | ::<span style=color:Green>Rule of Three</span> | ||
:*[Multiply] 44 by 43, according to the chapter of division, meaning: 43 times 44, i.e. 1892. | :*[Multiply] 44 by 43, according to the chapter of division, meaning: 43 times 44, i.e. 1892. | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|השליכהו בשער הכפל על ג"ד פי' ג"ד פעמי' ד"ד דהיינו בטח"א |
|- | |- | ||
| | | | ||
:*Then, divide it, according to the chapter of division: how many times 21 is in it? We find 90 times and 2 small parts remain, of which 21 is a whole unit. | :*Then, divide it, according to the chapter of division: how many times 21 is in it? We find 90 times and 2 small parts remain, of which 21 is a whole unit. | ||
::<math>\scriptstyle{\color{blue}{\frac{44\sdot43}{21}=\frac{1892}{21}=90+\frac{2}{21}}}</math> | ::<math>\scriptstyle{\color{blue}{\frac{44\sdot43}{21}=\frac{1892}{21}=90+\frac{2}{21}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואח"כ חלקיהו בשער החילוק כמה פעמי' יש בהן א"ב ותמצא 0"ט פעמי' ועוד נשארו ב' חלקי' קטני' שא"ב מהן חלק אחד שלם |
|- | |- | ||
| | | | ||
:*Add 90 and 2 small parts to 43, i.e. the dinar for the 21 cubits, and it is 133 and 2 small parts, like this: | :*Add 90 and 2 small parts to 43, i.e. the dinar for the 21 cubits, and it is 133 and 2 small parts, like this: | ||
::<math>\scriptstyle{\color{blue}{43+\left(90+\frac{2}{21}\right)=133+\frac{2}{21}}}</math> | ::<math>\scriptstyle{\color{blue}{43+\left(90+\frac{2}{21}\right)=133+\frac{2}{21}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|חבר 0"ט וב' חלקי' קטני' על ג"ד דהיינו הדינרי' השייכי' לא"ב זהו ויהיה גג"א וב' חלקי' קטני' כזה |
|- | |- | ||
| | | | ||
| Line 5,783: | Line 5,781: | ||
| | | | ||
:So, the calculation is correct. Note well. | :So, the calculation is correct. Note well. | ||
| − | |style="text-align:right;"|והיינו כוונת החשבון | + | |style="text-align:right;"|והיינו כוונת החשבון ולמבין די |
|- | |- | ||
|} | |} | ||
| Line 5,802: | Line 5,800: | ||
:<math>\scriptstyle\frac{50}{7}=\frac{50-5}{X}</math> | :<math>\scriptstyle\frac{50}{7}=\frac{50-5}{X}</math> | ||
:<math>\scriptstyle\frac{50}{7}=\frac{45}{X}</math> | :<math>\scriptstyle\frac{50}{7}=\frac{45}{X}</math> | ||
| − | |style="text-align:right;"|הנה לפניך נ' סאין ועתה | + | |style="text-align:right;"|הנה לפניך נ' סאין מים ואם אתה ש' אבשל אות' על האור מתבשלין ונחסרי' בכל יום ז' סאין ועתה שואלי' <s>ועתה</s> אם נשכפו ה' סאין ואנו ממעטי' האור לפי זה כמה יחסרו המ"ה סאין הנותרי' ביום אחד{{#annotend:VxeG}} |
|- | |- | ||
| | | | ||
| Line 5,810: | Line 5,808: | ||
| | | | ||
:*First write 50 se'ah, then write 7 se'ah that evaporate each day and beneath the 7 se'ah write the remaining 45 se'ah, like this: | :*First write 50 se'ah, then write 7 se'ah that evaporate each day and beneath the 7 se'ah write the remaining 45 se'ah, like this: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|תכתוב תחילה הנ' סאין ואח"כ תכתוב הז' סאין הנחסרי' ביום אחד ותחת הז' סאין תכתוב המ"ה סאין הנשארי' כזה |
|- | |- | ||
| | | | ||
| Line 5,844: | Line 5,842: | ||
::<span style=color:Green>'''Rule of Three:'''</span> | ::<span style=color:Green>'''Rule of Three:'''</span> | ||
:*Multiply what is beneath by 7 that is above it, meaning, calculate: how much is 45 times 7? The result is 315. | :*Multiply what is beneath by 7 that is above it, meaning, calculate: how much is 45 times 7? The result is 315. | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותכפול מ"ה שלמטה על ז' שלמעלה הימנה פי' חשוב כמה עולה מ"ה פעמי' ז' ויעלה שט"ו |
|- | |- | ||
| | | | ||
:*Divide it by 50, meaning, calculate: how many times 50 there are in 315? You find in it 6 times 50 and 15 parts remain, of which 50 is a whole unit. | :*Divide it by 50, meaning, calculate: how many times 50 there are in 315? You find in it 6 times 50 and 15 parts remain, of which 50 is a whole unit. | ||
::<math>\scriptstyle{\color{blue}{X=\frac{45\sdot7}{50}=\frac{315}{50}=6+\frac{15}{50}}}</math> | ::<math>\scriptstyle{\color{blue}{X=\frac{45\sdot7}{50}=\frac{315}{50}=6+\frac{15}{50}}}</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|תחלוק אות' שט"ו לנ' פי' כמה פעמי' יש בשט"ו ותמצא בו ו' פעמי' נ' ועוד נשארו ט"ו חלקי' קטני' שנ' מהן חלק אחד שלם |
|- | |- | ||
| | | | ||
| − | :We find that when 50 se'ah are reduced by 7 se'ah each day, 45 se'ah are reduced by 6 se'ah and 15 parts, of which 50 are a whole | + | :We find that when 50 se'ah are reduced by 7 se'ah each day, 45 se'ah are reduced by 6 se'ah and 15 parts, of which 50 are a whole se'ah. |
| − | |style="text-align:right;"|נמצא כשנ' סאין יחסרו ז' סאין ביום אחד מ"ה סאין יחסרו ו' סאין וט"ו | + | |style="text-align:right;"|נמצא כשנ' סאין יחסרו ז' סאין ביום אחד מ"ה סאין יחסרו ו' סאין וט"ו חלקי' קטני' שנ' מהן סיאה שלם |
|- | |- | ||
| | | | ||
:Another question: | :Another question: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|שאלה אחרת |
|- | |- | ||
| | | | ||
| Line 5,863: | Line 5,861: | ||
:<math>\scriptstyle\frac{91}{9}=\frac{91+11}{X}</math> | :<math>\scriptstyle\frac{91}{9}=\frac{91+11}{X}</math> | ||
:<math>\scriptstyle\frac{91}{9}=\frac{102}{X}</math> | :<math>\scriptstyle\frac{91}{9}=\frac{102}{X}</math> | ||
| − | |style="text-align:right;"|אם ישאל השואל הנה יש צ"א סאין מים ואם | + | |style="text-align:right;"|<big>אם</big> ישאל השואל הנה יש צ"א סאין מים ואם מתבשלין על האור יחסרו ביום אחד ט' סאין ואם נוסיף עליהם עוד י"א סאין שיהיה הכל ק"ב סאי' ואנו מרבין את האש לפי זה שאם לא היינו מרבי' את האש אז לא היו המים מתמעטי' וחסירי' לפי החשבון הזה כי האור אינו שולט כל כך כשהמים הרבה כמו שאם היו המים מועטי' לפיכך כשמרבי' המים אז ‫<ref>116v</ref>צריכי' להרבות האש או אם מתמעטי' אז צריכי' למעט האש<br> |
נחזור לשאלה ששאלנו כמה יחסרו ק"ב סאין ביו' אחד כשצ"א חסירי' ט' סאין{{#annotend:8v4H}} | נחזור לשאלה ששאלנו כמה יחסרו ק"ב סאין ביו' אחד כשצ"א חסירי' ט' סאין{{#annotend:8v4H}} | ||
|- | |- | ||
Revision as of 16:05, 25 November 2022
Contents
- 1 Prologue
- 2 Introduction
- 3 Chapter One: Multiplication of Units - Shortcuts
- 4 Chapter Two: Addition
- 5 Chapter Three: Subtraction
- 6 Chapter Four: Multiplication
- 7 Chapter Five: Gelosia
- 8 Chapter Six: Division
- 9 Chapter Seven: Proportions
- 9.1 Word Problems
- 9.1.1 Pricing Problems - Find the Price
- 9.1.2 Boiling Problem
- 9.1.3 Find a Quantity Problems - Whole from Parts
- 9.1.4 Joint Purchase Problems - If You Give Me
- 9.1.5 Find a Quantity Problems - Whole from Parts
- 9.1.6 Shared Work Problems - Filling/Draining a Vessel
- 9.1.7 Multiple Quantities Problems - Selling Eggs
- 9.1.8 Proportional Division - Inheritance
- 9.1.9 Payment Problem - Digging a Hole
- 9.1.10 Find a Quantity Problem - Stolen Purse
- 9.1.11 Find a Quantity Problem - How Much Problem - Amount of Money
- 9.1.12 Divide a Quantity - Loans Repayment
- 9.1.13 Multiple Quantities - Weights
- 9.1.14 Divide a Quantity - Money
- 9.1.15 Find a Quantity Problem - Whole from Parts - Fish
- 9.1.16 Multiple Quantities - Selling Cloth
- 9.1.17 Partnership Problems - for the Same Time - Three Partners
- 9.1.18 Multiple Quantities
- 9.1.19 Motion Problem - Pursuit
- 9.1.20 Ordering Problem - Stock of Coins
- 9.1.21 Proportional Division - Three Men Sharing Food
- 9.1.22 Multiple Quantities - Men, Women, Children
- 9.1.23 Find a Quantity Problem - How Much Problem - Money
- 9.2 Additional Word Problems
- 9.1 Word Problems
- 10 Chapter On Cubic Roots [P1088 2r-v]
- 11 Chapter on Square Roots [P1088 6v-7v]
- 12 Notes
- 13 Appendix I: Glossary of Terms
- 14 Appendix II: Bibliography
Prologue |
|||||||||||||||
| [MS Paris, Séminaire Israélite de France (École Rabbinique) 158/1 (IMHM 4102) f. 197r, lines 1-16] | |||||||||||||||
| This is a book on mathematics [called] Ṭeshifra. | זה ספר חכמת התשבורת [הנקרא] טשיפרא | ||||||||||||||
| Its cause: I myself, already from youth, my soul desired to acquire wisdom and to seek for arithmetic, if only I will find them in a book engraved by a pen of a skilled writer. For the reason that this is an external science, which is not found before us in Israel and the very least that is available is gathered inside the house in utmost discretion, my thoughts therefore aroused me to collect the sayings from any one that has them […] for recollection. | סיבתו אני את לבי גם מנעורי גרסה נפשי לדעת חכמה ובקש חשבון ומי יתן ואמצאם בספר ויחקו בעט סופר מהיר [1] ולסבה שזאת היא חכמת החיצוניות לא נמצאת לפנינו בישראל והמיעוט שבמיעוט הנמצא נאסף אל תוך הבית בחדרי חדרים לכן העירוני רעיוני ללקט האמרים מיד כל אשר ימצא אתו ולכל[...] לזכרון | ||||||||||||||
| Before I start, I ask all its readers not to condemn me and say: what is it with you? Go study havayot d'Abbaye ve-Rabba! God forbid […]. Since I did not undertake it for any cause or purpose, but sharpening the mind and obtaining arithmetic by accident and learning and by the wittiness of Abbaye ve-Rabba primarily. On that said those who speak in parables: come to Ḥeshbon [Numbers 21, 27]. As is written in Maimonides, chapter five of the introduction to Tractate Avot: | וקודם שאתחיל אבקש מיד כל רואיו לבל יכרעני לכף חובה ולומר מה לך פה כלך בהוייות דאביי ורבא חלילה וחס [לי'] לזרעא דאבא כי לא לקחתי זאת לשום עיקר ותכלית רק לחדד השכל ולבא בחשבון במקרה ושנייה ובחידוד דאביי ורבא בעצם וראשונה ועל זאת אמרו המושלים באו חשבון [2] כמו שכתוב הרמבם ז"ל פרק חמישי מה[קדמת] ה פרקי אבות [3] וז"ל | ||||||||||||||
| What has no benefit in it for that purpose – as the arithmetic problems, the Book of Conics, the numerous techniques for questions on geometry, the measuring of weights, and many like those – the intention in them is to sharpen the mind and train the rational faculty through methods of proof, until a person acquires the knowledge of demonstrative reasoning from other, and this will be his way whereby he will reach the knowledge of the truth of His existence, The Exalted. | ומה שאין בו תועלת לו בתכלית ההוא כשאלות החשבון וספר החר[וט]ים והתחבולות הרבות משאלות אל ההנד[ס]ה ומשיכת המשקלים והרבה כיוצא בא[ילו] יהיה הכוונה בהם לחדד השכל ולהרגיל כח השכלי בדרכי המופת עד שיגיע לו לאדם קניין ידיעת ההיקש המופתי מזולתו ויהיה לו זה הדרך שיגיע בה לידעת אמיתות מציאתו ית' עכל' | ||||||||||||||
| So, for my part it will not be inaccessible. | גם מצדי לא יבצר | ||||||||||||||
Introduction |
|||||||||||||||
| With good luck | בטוב גדא | ||||||||||||||
| I shall start this | אתחיל דא | ||||||||||||||
| Sefer Ṣifra | ספר ציפרא | ||||||||||||||
| To know and explain the book of number that has 9 chapters. | לידע ולפרש ספר המספר שיש בו ט' שערים | ||||||||||||||
| First I shall explain the teachings that the one who calculates should know, so that he can know all the calculations [practice]. | ואפרש תחילה הקבלות אשר צריך לידע המחשב הוא המפתח ויכול אחר כך לידע כל החשבונות | ||||||||||||||
The Positional Decimal System |
|||||||||||||||
| The numerals | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Know that you do not have any number [= numeral] smaller than one and you do not have any number [= numeral] greater than nine. | דע כי אין לך חשבון קטן מן א' שהוא אחד ואין לך חשבון גדול מן ט' | ||||||||||||||
| By these nine numerals from א to ט [the nine first Hebrew letters] all numbers in the world [are formed] infinitely. How?: | ובאלו ט' אותיות מן א' ועד ט' יש בו כל החשבונות שבעולם עד אין מספר כיצד | ||||||||||||||
| The written ranks [= decimal places] | |||||||||||||||
|
מעלה הראשונה היא נקראת מעלת היחידים כי כאשר יקראו האות כך מניינם פי' א' אחד ב' שנים ג’ שלש וכן עד ט' שהיא תשע | ||||||||||||||
|
|||||||||||||||
|
וכשתחשוב עשרה אז צריך אתה לכתוב ב' מעלות א' במעלה שנייה | ||||||||||||||
|
ולפניו ציפרא שהוא גלגל כזה 0 שאין בו ממש אלא שומר המעלות וזכר לדבר כגלגל לפני רוח [4] | ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
כי הא' הראשונה מן היחידים שהיא במעלה ראשונה וא' שנייה היא מן העשיריות הרי י"א | ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
ומעלה השלישית היא מעלת המאות כזה | ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
ומעלה הרביעית היא מעלת האלפים | ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
וככה עד ט' אלפים שהוא 000"ט | ||||||||||||||
|
ומעלה החמישית היא מעלת הרבבות שהוא י' אלפים | ||||||||||||||
|
ומעלה ששית היא מעלת מאה אלפים | ||||||||||||||
|
ומעלה שביעית היא מעלת אלף אלפים | ||||||||||||||
| And so you can write endlessly. | וככה עד אין מספר תוכל לכתוב | ||||||||||||||
| Every rank is ten times the preceding rank. | וכל מעלה היא עשרה פעמים יותר מן המעלה שלפניה | ||||||||||||||
|
| ||||||||||||||
|
תשיב אל לבך כי הגלגל אין לו מניין רק שומר המעלות והנה החשבון עשרים וג' אלפים | ||||||||||||||
| Thus, I have explained to you the number and the meaning of the writing. | והנה ביארתי לך מניין ועניין הכתיבה | ||||||||||||||
| 1 2 3 4 5 6 7 8 9 0 10 20 30 |
| ||||||||||||||
Chapter One: Multiplication of Units - Shortcuts |
שער הכפל הקטן |
| If you wish to know how much is the result of 9 times 9, or 9 times 8, or 5 times 9, or 6 times 9 and so on for all that is less than ten, I will teach you: | אם תרצה לידע כמה עולה ט' פעמים ט' או ט' פעמים ח' או ה' פעמים ט' או ו' פעמים ט' וכן כל כיוצא בזה שכל אחד פחות מעשרה אשכילך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם תחפוץ לידע כמה ט’ פעמים ט’ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אז כתוב כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך חשוב כמה יותר על עשרה ויהיה ח' ואותה ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתוב אצל הט' העליונה בצד שמאל כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך חשוב כמה ט' העליונה יותר על ח' ותמצא רק אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אותו א’ כתוב בצד ט’ התחתונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך חשוב כמה ט’ התחתונה יותר על הח’ ויהיה א’ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתוב אותה א’ ג”כ בצד ט’ תחתונה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותחשוב א' פעמים א' היינו אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתוב א' לפני הח' כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומחוק הט' למטה ולמעלה ויהיו אחד ושמונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם תרצה לידע כמה ט' פעמים ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתוב כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחשוב כמה ח'ט' יותר על עשרה דהיינו ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתוב הז' אצל הט' כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחשוב כמה הט' עודף על הז' דהיינו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמה הח' עודף על ז' א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכתוב כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תכפול א' על ב' היינו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אותה ב' כתוב קודם הז’ כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נמצא ט' פעמים ח' יהיה ע"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דומיון אם תחפוץ לידע כמה ו' פעם ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אז כתו' הו' תחת הו' כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואז תאמר כמה השני ו' למעלה מי' זהו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואותו ב' תכתו' לאחר הו' כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואז תאמ' כמה הו' יתיר על הב' זהו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והו' השנייה נמי למעל' מב' זהו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואז תכפול ד' פעמי' ד' זהו ו"א פי' י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואז תכתוב שים הא' על הב' כי הב' מעלה שניי' ויהיה ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד הוה ו' ואות' ו' תכתו' לפני הג' כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נמצא שו' פעמ' ו' עולה ו"ג פי' ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Always do as this. | וכן עשה לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiply always the excess of this by the excess of this and write the result before the excess [of the sum of the multipliers over ten], then you will become wise in all that you do. | וכן לעולם תכפול המותר מזה ומזה והעולה כתוב קודם העודף עליו ואז תשכיל בכל אשר תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר שהעתקתי מספר גלחות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חברם יחד הב' אותיות והשליך עשרה והמניין הקטון כתוב ואח"כ תכפול יחד החשבון שיש מכל אחד עד עשרה וכתוב זה לפני המנין הקטן שבידך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון אילו החשבונות החרו[ת]ים לפניך ממנו תשכיל ותחכם עוד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או כלך לדרך זו כתוב לפני המניין קטון שבשני אותיות גלגל כזה 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון את"ל ז'פ'ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתוב כזה 0ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח ממנו מה שבא מן הכפל שתכפול המניין מאות הגדול עד עשרה עם האות הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון מה שלפניך אמור ז'פ'ב' הם ד"א ותקח ד"א מן 0"ז ונשאר ו"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכגון אילו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תרצה לידע ולחשוב כמה ג' פעמים ג' או ד' פעמים ד' וכן כל כיוצא בזה שאפילו צירופו אינו מגיע לעשרה אשכילך לעשות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שתלוה לו כמה שצריך שיהיה בכל פעם אחד יותר מעשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וככלות חשבונך קח מה שהלוית לו וישאר מתכונך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון בקשנו ד' פעמים ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- [Illustration of the procedure:]
4 ![\scriptstyle\xrightarrow{{\color{red}{\left[4+4+\left[11-\left(4+4\right)\right]\right]-10}}={\color{blue}{1}}}](/mediawiki/images/math/3/f/a/3faacadf1089c902d319654aa049b711.png)
14 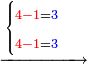
14 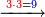
19 ![\scriptstyle\xrightarrow{{\color{red}{9-\left[11-\left(4+4\right)\right]}}={\color{blue}{6}}}](/mediawiki/images/math/2/1/1/211ec1ed49b06c80e5f87cd6b93c9500.png)
16 4 4 4 4 4 33
|
והנה תלוה לו ג' שיעלה י"א | |||||||||||||||
|
והשלך עשרה וישאר בידך א' | |||||||||||||||
|
ורשום כזה | |||||||||||||||
|
| |||||||||||||||
|
ואחר כך חשוב כמה ד' הראשונה יותר על הא' הוי אומר ג' | |||||||||||||||
|
וכן ד' השנייה גם כן יותר ג' | |||||||||||||||
|
| |||||||||||||||
|
כפול ג' על ג' הרי ט' | |||||||||||||||
|
כתוב הט' לפני הא’ כזה | |||||||||||||||
|
| |||||||||||||||
|
והנה קח ג' שהלוית לו וישאר ו"א והם י"ו | |||||||||||||||
|
ותמצא חשבונך מכוון | |||||||||||||||
|
| |||||||||||||||
|
עניין אחר אם תרצה לידע כמה ג’ פעמים ג’ או ד’ פעמים ד’ וכן כל כיוצא בזה שאפילו צירופו אינו מגיע לעשרה אשכילך | |||||||||||||||
|
דמיון אם תרצה לחשוב ד’ פעמים ד’ | |||||||||||||||
|
אז תכתוב אותו כזה | |||||||||||||||
|
| |||||||||||||||
|
||||||||||||||||
|
וחשוב כמה ד’ ראשונה פחות מי’ ויהיה ו’ | |||||||||||||||
|
וחשוב גם השנייה כמה השנייה פחות מי’ ותמצא ג”כ ו’ | |||||||||||||||
|
ואז תכפול ו’ על ו’ ויעלה בידך ו”ג | |||||||||||||||
|
אז חשוב כמה השני ד’ פחותים מעשרה ויהיה ב’ | |||||||||||||||
|
השלך ב’ ממעלה שנייה מהג’ וישאר לך ו”א | |||||||||||||||
|
נמצא ד’ פעמים ד’ הוא ו”א | |||||||||||||||
|
וכן כולם ודוק | |||||||||||||||
|
ואם יהיה המספר אשר תרצה לכפול זע"ז פחות מי' כשתצרף שני המספרים יחד | |||||||||||||||
|
דימיון אם בקשת לכפול ד' על ג' | |||||||||||||||
|
||||||||||||||||
|
אז תקח המרחק מן י' מכל אחד דהיינו מד' עד י' ו' ומג' עד י' ז' ופ"ז ב"ד | |||||||||||||||
|
אותו ב"ד כתו' לזכרון [בד] | |||||||||||||||
|
ואח"כ צרוף ד' ג' יחד ויהיה ז' | |||||||||||||||
|
אות ז' כתוב לצד שמאל אצל ב"ד כזה [בדז] | |||||||||||||||
|
ואח"כ השלך י' מצד אותיות של שמאל וישאר ב'א' היינו החשבון אשר בקשת לידע | |||||||||||||||
|
וכפי זה תקיש | |||||||||||||||
|
והנה כתבתי זה אף כי הוא מושכל ראשון החשבון אשר בקשת להודיעך שאין בדרך הזה [...] | |||||||||||||||
| I have found another method for the multiplication of units in another book [MS New York, 94r-v; MS Oxford 60, 161r; MS Oxford 440, 115r, 124r]: | דרך אחרת לכפל קטן בספר אחר מצאתי | |||||||||||||||
|
או כלך בדרך זו קח המרחק עד י’ מן כל אחד ואחד שתרצה לכפול יחד וחשוב אותו ב’ מרחקים זה על זה ומה שיעלה בידך כתוב לזכרון | |||||||||||||||
|
דמיון הנה רצונך לכפול ז’ פעמים ט’ | |||||||||||||||
|
||||||||||||||||
|
קח המרחק מן הז' עד י' דהיינו ג' והמרחק מן ט’ עד י’ דהיינו א’ ואמור ג’ פעמים א’ היינו ג’ | |||||||||||||||
|
אותו ג’ כתוב לזכרון כזה ג | |||||||||||||||
|
אחר כך חבור ז' על ט' ויעלה ו"א פי' י"ו השלך הי’ והו’ קח בידך | |||||||||||||||
|
וכתוב אותה בצד שמאל אצל הג’ הנשארת ויהיה כזה גו | |||||||||||||||
|
ועיין | |||||||||||||||
|
דמיון אחר הנה רצונך לכפול ו’ פעמים ח’ | |||||||||||||||
|
||||||||||||||||
|
קח המרחק מן ו’ עד י’ דהיינו ד’ והמרחק מן ח’ היינו ב’ ואמור ב’ פעמים ד’ היינו ח’ | |||||||||||||||
|
אותו ח’ כתוב לזכרון [ח] | |||||||||||||||
|
אחר כך חבור ו’ על ח’ ויעלה י”ד השלך י’ וקח ד’ בידך | |||||||||||||||
|
וכתוב ד’ בצד שמאל אל ח’ אשר כתבת כבר ויעלה מ”ח היינו חשבון ח’פ’ו’ [חד] | |||||||||||||||
|
עיין ודוק | |||||||||||||||
|
דמיון אחר אם תרצה לידע הפ"ו | |||||||||||||||
|
||||||||||||||||
|
קח המרחק מן ה' עד י' ויהיה ה' | |||||||||||||||
|
צרפם יחד הה’ והו’ ויהיה א' השלך עשרה ונשאר לך א' | |||||||||||||||
|
צרפם 0"ב ויהיה ג' נמצא ל' ודוק | |||||||||||||||
| Multiplication Table | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||
| I will write to you a precise table of multiplication of units, in order that you will be able to observe easily all that you want without any calculation, from 1 times 1 to 9 times 9. Note well. | והנה ארשום לך לוח מתוקנת על שער הכפל קטן כדי שתוכל לראות בקלות כל מה שתרצה בלא שום חשבון מן א' פעמים א' עד ט' פעמים ט' ודוק | |||||||||||||||
|
||||||||||||||||
| I made a half table in order to find every number, since you do not need that much. | והחצי לוח עשיתי למצוא כל חשבון ואינך צריך הרבה כל כך | |||||||||||||||
| The chapter on the multiplication of units is completed. | סליק שער כפל קטן | |||||||||||||||
| You shall become wise in all that you do. | ואז תשכיל כל אשר תעשה |
Chapter Two: Addition |
שער החיבור | ||||||||||||||||||
|
אם תרצה לחבר שנים ושבעים וג' מאות וג' אלפים עם שנים ותשעים וג' מאות וג' אלפים | ||||||||||||||||||
|
תכתוב כזה | ||||||||||||||||||
|
|
- [Illustration of the procedure:]
3372 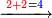
[3372] 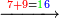
[3372] 
[3372] 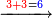
[3372] 3392 [3392] [3392] [3392] [3392] 4 64 764 6764
|
תחבר ב' תחתונה על ב' עליונה ויהי ד' | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
תחבר ט' תחתונה על ז' עליונה ויהיה ו"א הו' כתוב במעלה שניה אחר ד' שכתבת כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
והא' הנשארת חבור אל הג'ג' שלאחריו שהם למעלה מזו כזה במעלה השלישי | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ויהיה הכל ז' כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ואחר כך תחבר שני הג'ג' האחרונים במעלה הרביעי' ויהיה חבורם ו' אות' ו' כתוב במעלה הרביעי' אחר דוז שכתבת כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ותשלם המלאכה ויהיה חבורו ארבע וששי' ז' מאות ו' אלפי' דהיינו כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| The highest rank of the sum exceeds the addend by one rank to the left at most, sometimes it does not exceed [its ranks] at all. | לעולם לא תמצא הטור מן החיבור אשר בעליונה שעברת על המחובר רק מעלה לשמאל לכל היותר ולפעמים לא תעבור כלל | ||||||||||||||||||||||||||
| [MS Paris 1088, 7v:] Here follows a chapter on addition, to add every thing and to establish its methods | הילך שער חיבור לחבר כל דבר [..] ולישב על אופניו | ||||||||||||||||||||||||||
| Such as, if you wish to sum some numbers together. | כגון אם תרצה לחבר כמה חשבונות יחד | ||||||||||||||||||||||||||
| Now, I sum one number and according to this you shall apply for others: | ועתה אחבר חשבון אחד ומהם תבין אחר | ||||||||||||||||||||||||||
|
ותכתו' אות תחת אות ולא תכתו' כאשר כותבין בשער כפל אלא תכתו' כזה שאראך בע"ה | ||||||||||||||||||||||||||
|
דומיון בקשנו לחבר ע"ב וג' מאות וג' אלפי' עם צ"ב וח' מאות וט' אלפים | ||||||||||||||||||||||||||
|
הילך היאך תכתוב אותו וצורתו כזה | ||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
3372 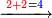
3372 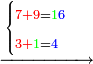
3472 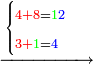
4472 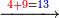
3372 9892 9892 9892 9892 9892 4 64 264 13264
| נחבר ב' תחתונ' עם ב' עליונ' הרי ד' אות' ד' נכתוב נגד ב' תחתונ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחבר כמו כן ט' תחתונ' עם ז' עליונ' ויעלה ו"א נכתוב ו' תחת הט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונוסיף א' על אות שבשיט' עליונ' הסמוכ' לה ושם יש ג' ונוסיף א' עליה ויהיה כאילו נכתו' ד' במקום ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונחבר ד' עליונ' עם ח' תחתונ' ויעלה ב"א נכתו' ב' למטה תחת הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונוסיף א' על אות הסמוך לד' עליונ' ושם יש ג' ונוסיף א' עליה ויהא ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחבר ד' עליונ' על ט' שלמטה ויעלה ג"א נכתוב ג' למט' תחת הט' וא' נכתוב לאחריה ויהיה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זה הכלל לא ימוש מפיך כשמותר הא' משיט' ראשונ' אני מוסיף אות' על שיט' שלאחריה כי הא' הנותרת לי היא כמו כן מן העשיריות נגד שיט' ראשונ' לכך אני מוסיף אות' תדיר עליה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [MS Paris158, 198v] | ציור זה בגלחת ונקרא אדירין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Checking Methods |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, know that I shall write you two checking method [lit. scales]: | ועתה תדע שאכתוב לך שני משקלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [MS Paris158, 198v] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הא' השלך ט"ט כל כמה שתוכל מב' שיטות עליונות ומה שנשמר לך למטה מט' קח בידך לאבני המשקל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואח"כ השלך ג"כ השיטה התחתונה בט"ט ומה שנשאר לך אם משקלו כאבן הראשון דע שכוינת חשבונך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
משקל השני יקח השני שיטות העליונות מהשיטה התחתונה אם יצא במבוקש בלי חסרון ויתרון אז חשבונך מכוון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examine and you will find [that it is true]. | ודוק ותמצא |
Chapter Three: Subtraction |
שער החיסור | ||||||||||||||||||
| If you want to subtract and deduct a number from a number, here is how you do that: | אם תרצה לחסור ולנכות חשבון מן חשבון הילך איך תעשה | ||||||||||||||||||
| Write the number from which you wish to subtract and deduct above, according to its ranks, and write the number you subtract from it beneath, according to its ranks. | תכתוב החשבון שאתה רוצה לנכות ולחסר ממנו אותו חשבון כתוב למעלה כפי מעלותיו והחשבון שאתה מנכה הימנו כתוב למטה כפי מעלותיו | ||||||||||||||||||
| Then subtract it from the number above. | ואחר כך תנכה מן החשבון שלמעלה | ||||||||||||||||||
| Now, I shall write you an example to teach you: | ועתה אכתוב לך הדמיון להשכילך | ||||||||||||||||||
|
הנה בקשנו לחסור ט' מאות ותשעים ותשע מאלף | ||||||||||||||||||
|
הילך היאך תכתוב אותו כזה | ||||||||||||||||||
|
| ||||||||||||||||||
| |||||||||||||||||||
|
נמצא הא' שבשיטה העליונה במעלה רביעי' עולה עשרה לגבי ט' שלישית שבתחתונה | ||||||||||||||||||
|
עתה נחסר מאותו עשרה ט' וישאר לך א' | ||||||||||||||||||
|
אותו א' כתוב במקום גלגל השלישי נגד הט' שחסרת ואותו ט' מחוק כזה | ||||||||||||||||||
|
| ||||||||||||||||||
|
ועכשיו כמו כן הא' שבמעלה שלישית שבשיטה העליונה עולה עשרה לגבי ט' שבשיטה תחתונה | ||||||||||||||||||
|
נחסר ט' שנייה ונשאר א' | ||||||||||||||||||
|
ואותו א' כתוב במקום הגלגל השני ותמחוק ט' שנייה שחסרנו וגם תמחוק הא' העליונה שבמעלה שלישית שחסרנו ממנו ויהיה כזה | ||||||||||||||||||
|
| ||||||||||||||||||
|
שוב נחסר ט' תחת הגלגל מן א' שלמעלה במעלה השנייה כי גם היא עולה עשרה לגבי ט' כדלעיל | ||||||||||||||||||
|
והנה כשנחסר ט' מן י' וישאר א' | ||||||||||||||||||
|
אותו א' כתוב במקום הגלגל ומחק הא' העליונה אשר במעלה שנייה וגם הט' מחק | ||||||||||||||||||
|
ואז נשאר רק א' | ||||||||||||||||||
|
נמצא כשחסרנו ט' מאות וצ"ט מאלף נשאר א' | ||||||||||||||||||
|
דמיון אחר אם בקשנו לחסור אב"ג מן דה"ו | ||||||||||||||||||
|
כתוב כזה | ||||||||||||||||||
|
| ||||||||||||||||||
| |||||||||||||||||||
|
נחסר ג' התחתונה מן ו' העליונה שכנגדה וישאר ג' | ||||||||||||||||||
|
מחק הו' וכתוב במקומה הג' שנשאר ומחק גם כן הג' שנשאר שלמטה | ||||||||||||||||||
|
ויהיה כזה | ||||||||||||||||||
|
| ||||||||||||||||||
|
שוב נחסר ב' התחתונה מן ה' עליונה שכנגדה וישאר ג' | ||||||||||||||||||
|
אותו ג' כתוב במקום הה' ומחק הב' שלמטה וגם ה' שלמעלה | ||||||||||||||||||
|
ויהיה כזה | ||||||||||||||||||
|
| ||||||||||||||||||
|
שוב נחסר א' התחתונה מן ד' עליונה שכנגדה וישאר ג' | ||||||||||||||||||
|
ומחוק ד' שלמעלה וגם א' שלמטה וכתוב ג' במקום ד' שלמעלה | ||||||||||||||||||
|
ויהיה כזה | ||||||||||||||||||
|
| ||||||||||||||||||
|
נמצא כשחסרנו אב"ג מן דה"ו לא נשאר כי אם ג'ג'ג' | ||||||||||||||||||
|
וכאשר תמצא שהאות העליון אשר בקשנו לחסר ממנו פחות מן האות התחתון שתרצ' לחסר | ||||||||||||||||||
|
|
כגון אם תרצ' לחסר ז ו ח מן ו ה ט כזה | ||||||||||||||||||
|
| ||||||||||||||||||
|
היאך תחסור מרובה ממועט כזה ז' מן ו' לא תוכל וכן ו' מן ה' בדרך זה תעשה: טול א' מן ה' אשר אצל ו' ומחוק הה' וכתוב ד' אותו א' כמה עולה לחבירו עם הו' י"ו כי היא במעלה שנייה מן הו' הרי י"ו חסר ז' אשר בטור השפל מן י"ו וישאר ט' אחר כך צריך לחסר ו' מן ד' עשר ג"כ כמו שצויתיך מחוק א' מן ט' ויהיה במעלה שלפניו י"ד וחסר ממנו ו' וישאר ח' ול"ד זה שייך לשער הכפל קטון | ||||||||||||||||||
| [MS Oxford 60, 153r-v] | |||||||||||||||||||
|
אשכילך היאך תעשה כי לא תוכל לחסר ז' מן ו' וכן ו' מה' בדרך זה תעשה: בתחילה חסר ח' תחתונה מט' עליונ' וישאר א' מחוק הט' וכתוב א' במקומ' גם ח' תחתונ' מחוק ויהיה כזה | ||||||||||||||||||
|
| ||||||||||||||||||
| עתה צריכין אנו לחסר ו' תחתונ' מה' עליונ' ולא יכולנ' לכן לך לך אל הא' אשר לשמאל ה' עליונ' וצרפ' יחד א' וה' ויהיה ט"ו ונחסור הו' ממנו וישאר ט' מחוק הא' העליונ' גם ה' העליונ' וכתוב במקומם ט' גם ו' תחתונ' תמחוק וישאר כזה | |||||||||||||||||||
|
| ||||||||||||||||||
| שוב צריכין אנו לחסר ז' תחתונ' מו' ולא יכולנ' עתה לך לך וקח אחד מן הט' שבצד הו' בשיט' עליונ' וצרפ' יחד הו' גם הא' והיא עשרה אצל הו' ויהיה י"ו ועתה חסר ז' מן י"ו וישאר ט' מחק ו' ט' עליונ' וכתוב ט' ח' במקומם כאשר ציויתיך ומחוק ג"כ הז' התחתונ' ויהיה כזה | |||||||||||||||||||
|
| ||||||||||||||||||
| ותשלם המלאכה עיין היטב | |||||||||||||||||||
Checking Methods |
|||||||||||||||||||
|
ואם תרצה לידע אם אמת חשבת אז תחבר בשער החיבור אב"ג עם גג"ג אז תמצא דה"ו אז החיסור מכוון | ||||||||||||||||||
|
ואם תרצ' לידע אם אמת חשבת אז חבר בשער החיבור ז ו ח עם ט ח הנשארי' ואם תמצא ו ה ט אז כיוונת | ||||||||||||||||||
| The checking method of addition is subtraction and the checking method of subtraction is addition | זה הכלל שער החיסור מאזני צדק לשער החיבור ושער החיבור מאזני צדק לשער החיסור | ||||||||||||||||||
Chapter Four: Multiplication |
שער הכפל | ||||||||||||||||||
|
אם תרצה לכפול רל"ד ואלף על ד' אלפים ושכ"א |
- [Illustration of the procedure:]
4321 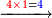
4 4321 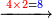
48 4321 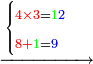
4924321 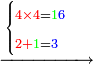
4936321 1234 234 34 4
| הילך צורתו כאשר תכתבנו חשבון האחד בצד השני ומכוון אות ראשון בחשבון התחתון תחת אות האחרון שבחשבון העליון כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| וכפול א' תחתונה על ד' עליונה פי' חשוב א' פעמים ד' זה ד' אות ד' כתוב נגד א' התחתונה ומחוק א' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד כפול ב' תחתונה על ד' עליונה ויעלה ח' אותו ח' כתוב נגד ב' התחתונה ומחק ב' התחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד נכפל ג' תחתונה על ד' עליונה ויעלה ב"א פי' י"ב עתה כתוב ב' נגד ג' תחתונה וא' על ח' אחריה ויעלה ט' כי הוא מעלה אחת שהיא עשרה אחר ב' שלפניה ומחוק ג' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד נכפל ד' תחתונה על ד' עליונה ויעלה ו"א פי' י"ו עתה נכתב ו' נגד ד' תחתונה במקום ד' עליונה כי עתה חשבנו ד' עליונה בכל חלקים וכתוב א' על ב' שלאחריה ויהיה ג' כזה | |||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
4936321 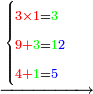
5236321 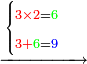
5296321 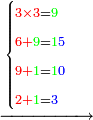
5305321 1234 234 34 4
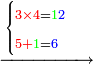
5306221
| ועתה נמשך ד"ג ב"א מעלה לאחורית תחת ג' עליונה כדי לחשוב ג' עליונה כדי לחשוב ג' גם בכל תוצאותיה ד"גב"א כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| כפול א' תחתונה על ג' עליונה פי' ג' פעמים א' זהו ג' ושים אותו ג' על ט' שעל א' התחתונה ויעל ב"א פי' י"ב עתה כתוב ב' במקום ט' א' שהיא עשרה שים אותו במעלה שנייה דהיינו ד' ועשה ד' אחרונה ה' ומחוק א' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד כפול ב' תחתונה על ג' עליונה ויעלה ב' פעמים ג' דהיינו ו' ושים אותו ו' על ג' שעליה ויהיה ט' ומחוק ב' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד כפול ג' תחתונה על ג' עליונה ג' פעמים יעלה ט' ושים אותו ט' על ו' שעליה ויעלה ה"א ה' כתוב במקום ו' א' כתוב במעלה שנייה דהיינו אל ט' שלאחריה ויהיה עשרה אך אין ראוי לכתוב עשרה כי אין כותבין בחשבונות הציפרא עשרה רק ט' לכן כתוב גלגל כזה במקום ט' וכת' א' במעלה שלאחריה דהיינו אל ב' | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| ועתה יהיה ג' מחוק ג' תחתונה כזה עוד כפול ד' תחתונה על ג' עליונה ויעלה ב"א עתה כתב ב' במקום ג' עליונה כי חשבונו גם כן ג' בכל חילוקה א' כתוב במעלה שנייה אל ה' ויהיה ו' ומחוק ד' תחתונה כזה | |||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
5306221 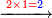
5326221 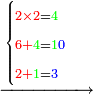
5330221 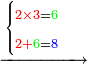
5330821 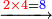
5330881 1234 234 34 4
| ועתה נמשך ד"ג ב"א מעלה אחת לאחורית תחת ב' עליונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד כפול א' תחתונה על ב' עליונ' א' פעמים ב' דהיינו ב' כתוב אותו ב' נגד א' תחתונה במקום גלגל ומחוק א' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול תחתונה על ב' עליונה ב' פעמים ב' היינו ד' אותו ד' כתוב למעלה נגד ב' תחתונה דהיינו אל ו' הרי י' כתוב במקום ו' גלגל ואחר הגלגל תוסיף א' היינו אל ב' ויהיה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ג' תחתונה על ב' עליונה ג' פעמים ב' היינו ו' אותה ו' כתו' נגד ג' תחתונה דהיינו אל ב' עליונה ויהיה ח' ומחוק ג' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ד' תחתונה על ב' עליונה ד' פעמים ב' ויעלה ח' כתוב ח' במקום ב' עליונה כי חשבנו ב' בכל חילוקיה ומחוק ד' תחתונה כזה | |||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
5330881 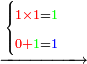
5331881 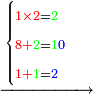
5332081 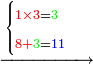
5332111 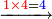
5332114 1234 234 34 4
| ועתה נמשך דגב"א מעלה לאחורית כדי לכפול אותו על א' ראשונה ויהיה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| כפול א' תחתונה על א' עליונה א' פעמים א' זה א' אותו א' כתוב נגד א' תחתונה במקום גלגל ומחק א' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ב' תחתונה על א' עליונה ב' פעמים א' היינו ב' אותו ב' כתוב על התחתונה דהיינו אל ח' ויהיה עשרה כתוב במקום ח' גלגל אחר גלגל תוסיף א' על א' ויהיה ב' ומחוק ב' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ג' תחתונה על א' עליונה ג' פעמים א' זה ג' אותו ג' כתוב נגד ג' תחתונה דהיינו אל ח' הרי י"א מחוק ח' וכתוב במקומה א' ואחריה במקום גלגל א' ומחוק ג' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ד' תחתונה אל א' עליונה ד' פעמים א' היינו ד' אותו ד' כתוב במקום א' שכנגדה אבל לא תצרף אותו א' עם ד' כמו שצויתיך כבר כי על אותו א' כפלנו עכשיו דגב"א ולא היתה א' רק לסימן לכן לא חיידיא לצירוף ומחוק ד' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| נמצא כי א"בג"ד פעמים דגב"א עולה בחשבון דא"אב"ג ג"ה היינו י"ד ומאה וגם ב' אלפים גם ל' אלפים וגם מאה אלפים וגם ה' מאות רבבות וד"ל |
|
דמיון אחר הנה בקשנו לכפול ט' ומאתים על ג' אלפים ושלשים | ||||||||||||||||||||||||||
|
הילך היאך תכתוב צורתו כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| כפול ב' תחתונה על ג' עליונה ב' פעמים ג' היינו ו' אותו ו' כתוב נגד ב' תחתונה ומחוק ב' תחתונה וגם הגלגל שלפני ב' מחוק וכתוב גלגל לפניו כזה כי נכפול גלגל ג' פעמים ויהיה גלגל | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| שוב כפול ט' על ג' שעליה ט' פעמים ג' היינו ז"ב אותו ז' כתוב למעלה במקום ג' אחרונה ויהיה ז' במקום וגם ב' כתוב במקום גלגל ומחק ט' תחתונה כזה | |||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
627030 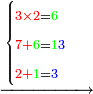
633030 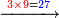
633270 209 9
| ועתה משוך 0ט"ב לאחוריו ב' מעלות כדי שתהא ט' תחתונה שהיא אות ראשונה שבשיטה תחתונה נגד ג' עליונה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואת"ל למה לא כתבנו ט0"ב תחת גלגל עליון ודאי עשינו כך אבל מ"מ לא עלה יותר מגלגל כי כאשר תמצא אותיות כתובים ואת' צריך לצרף עמהם גלגל אין צירופין עמהם ול"ד כמו שפי' לקמן | |||||||||||||||||||||||||||
| כפול ב' תחתונה על ג' עליונה ב' פעמים ג' היינו ו' אותו ו' כתוב נגד ב' תחתונה דהיינו אל ז' ויהיה י"ג מחוק ז' וכתוב במקומה ג' ואחריה תוסיף א' על ב' כי הוא עשרה כמו שכתבתי לעיל ויהיה ג"כ ג' ומחוק ב' תחתונה וגם גלגל שלפניה | |||||||||||||||||||||||||||
| Zero cannot replace a non-zero digit in the upper line (the result line) in this erasing and shifting procedure -as this will decrease the numerical value of the rank, and there is no need for the zero as a place holder, since the current non-zero digit is already holding the place | ואין אתה צריך לצייר אותו הגלגל למעלה כמו שעשית כבר כי בלאו הכי יש גלגל כנגדו וכ"ש אם היה אות נגד הגלגל שלא היינו מוחקים האות לצייר שם גלגל שאם היינו מוחק' האות כדי לצייר שם גלגל אז היינו ממעטים החשבון ואם לעשות כדי להרחיק המעלה זה אינו כי בלאו הכי האות מרחיק המעלה כללא דמילתא לעולם אין אנו מציירין גלגל התחתון למעלה אלא אם אין כנגדו שום דבר | ||||||||||||||||||||||||||
| Zero does not need to replace a zero in the upper line as it is only a place holder, and the rank is already held by the current zero | אבל אם יש שום גלגל או אות נגד אותו גלגל התחתון אז אין אנו צריכין לצייר שום גלגל כי ציורו אינו אלא שומר המעלה כמו שכתבתי לעיל כי הגלגל מודיע שאות אחריו עולה מעלה אחת יותר ממה שהיית עושה אם לא היית שם שום ציור גלגל | ||||||||||||||||||||||||||
| ועתה נחזור לחשבון דלעיל כמו שפרטתי אז יהיה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| שוב כפול ט' תחתונה על ג' עליונה ט' פעמים ג' היינו ז"ב כתוב במקום ג' עליונה ז' ואחריה במקום גלגל כתוב ב' ומחק ט' תחתונה כזה וגם ג' עליונה מחק | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| תמצא שמאתים וט' פעמים ג' אלפים ול' יש ס"ג רבבות וג' אלפים ומאתים ושבעים | |||||||||||||||||||||||||||
| הנה אראך בדרך אחר לכפול | |||||||||||||||||||||||||||
|
אם תרצה לידע כמה ט"ו פעמים תתר"ף |
- [Illustration of the procedure:]
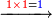
1 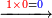
10 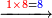
108 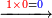
1080 1080 1080 1080 1080 1080 15 15 15 15 15
| עשה טור ראשון מתתר"ף ושים תחתיו ט"ו ה' תחת הא' וא' לשמאלו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| אז תכפול הא' על כל הטור העליון ואחר כך ה' על כל הטור העליון וכה תאמר א' פעם א' הרי א' שים א' כנגד א' השפל מן הכפלות כל כך גבוה שיהא הוא למעלה מן התתר"ף מכוון כנגד הא' התחתונ' ויהיה צורת' כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך כפול א' פעמי' גלגל הרי גלגל שים אותו גלגל לפני הא' אשר כתבתי למעלה מן התתר"ף מכוונ' נגד הא' בשיט' ראשונ' ויהיה כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך כפול א' פעמי' ח' יעלה ח' כתוב ח' לפני ה0' שכתבת בשיט' עליונ' מכוונת נגד הציפר' שבשיט' אמצעי' ויהיה כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך כפול א' פעם 0' ויעלה 0' שימהו לפני הח' אשר כתבת בשיט' עליונ' מכוון נגד 0' שבשיט' אמצעי' גם תמחוק הא' כי נכפל על כל התתר"ף ויהיה כזה דמיונו | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| והנה כפלת הא' על כל התתר"ף |
- [Illustration of the procedure:]
1080 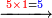
1580 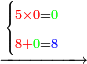
1580 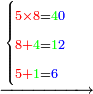
1620 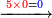
16200 1080 1080 1080 1080 15 15 15 15
| ואחר כך כפול הה' על כל התתרף ותתחיל לכופלו כנגדו ממש למעלה כאשר התחלת לכפול הא' כנגד א' כן תכפול הה' ועלה כך ה' פעמים א' היינו ה' שים אות ה' נגד הא' למעלה הימנו דהיינו במקום גלגל כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך אמור ה' פעמים 0' אם לא היה נכתב מאומה על הגלגל היית נותן שם גלגל עכשיו שרשום עליו ח' לא תעשה מהגלגל כלום כי אוחז מקומו ואחר כך אמור ה' פעמים ח' יעלה ארבעים ולא תשימהו במקום הגלגל כי תצטרך לגלגל אלא כתוב ד' על הח' לשמאל אז תמצא ד"ח זה על זה תמחוק שניהם ותכתוב במקומו ב' ועל הה' אשר כתבת לשמאל כתוב א' הרי ו' כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך אמור ה' פעמים גלגל היינו גלגל שים גלגל על גלגל ויהא דמיונו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| תבין שלא נשלם הטור העליון נגד הטור השפל עד אשר תכפול כל האותיות מן הכפולות על כל החשבון ולמבין די ודו"ק |
Checking Methods |
ואם לבך מפקפק לומר מאן יאמר שכך הוא הילך מאזני צדק היאך תשקול ותבחין אם טעות אם לאו |
|
בראשונה קח חשבון שבשיטה העליונה אשר בקשת לכפול והשלך אותו ט"ט והמותר קח בידך |
| ואם לא תמצא אפילו פעם אחת ט' אז תקח הכל | |
| ואחר כך קח החשבון התחתון והשלך גם כן בט"ט | |
| ומה שנשאר בידך קח נא והשלך אותו בשער הכפל על מה שנשאר לך בשיטה עליונה אחר שהשלכת ממנו ט"ט ומה שיעלה בידך השלך אותו ג"כ בט"ט ומה שנשאר שלא הגיע לכלל ט' קח נא בידך | |
| ואחר כך קח החשבון היוצא לך כבר כשכפלת הב' חשבונות יחד והשלך ג"כ אותו בט"ט | |
| ומה שנשאר בידך אם הוא מכוון כנגד מה שנשאר לך כבר ידוע תדע שאמת חשבת ואם לאו בודאי טעית | |
|
|
ועתה שקול חשבון דלעיל למען יבין המבין ויוסיף לקח הדמיון היה 0"ג0"ג פעמים ט0"ב |
|
|
בתחילה נחבר ב' פעמים ג' היינו ו' ואין כאן אפילו פעם אחת ט' |
|
|
ואחר כך חבר חשבון התחתון דהיינו ט0"ב חיבור ט"ב היינו י"א השלך ט' וישאר ב' |
|
|
כפול ב' על ו' ב' פעמים ו' היינו י"ב השלך ט' וישאר ג' וזה יהיה לך לזכרון |
|
|
זה הכלל ראה בכפל מה שנשאר לך כגון עתה הוצרכת לכפול ב' פעמים ו' ויהיה י"ב כתוב י"ב בציפור ויהיה ב"א היינו יתיר על ט' ג' וכן לעולם |
|
|
ואחר כך ראה מה שיעלה בידך כשכפלתה 0"ג0"ג על ט0"ב דהיינו 0'ז'ב'ג'ג'ו' חבור אותו יחד ויהיה כ"א השלך אותו ט"ט וישאר ג' כמו שנשאר לך כבר ואם כן החשבון מכוון |
Chapter Five: Gelosia |
שער הכפל בסולם |
|---|---|
| ציור נקרא סולם ויפה לשער הכפל גדול | |
| The number of cells corresponds to the number of ranks of the multiplicands | וכמה שתרצה לכפול חשבון על חשבון כן עשה מניין הבתים |
|
אם תכפול חשבון בן ג' מעלות על ג' מעלות כמו כן תצייר שליבות הסולם ג' בתים לארכה ולרחבה |
|
ואם תכפל סך בן ג' אותיות על ב' אותיות עשה ג' בתים לרחבה וב' בתים לארכה |
| וכן להיפך מלמעלה למטה אחד המרבה ואחד הממעיט ובלבד שיכווין לבו כל אות במקומו לפי הציור | |
|
|
דמיון אם תרצה לידע כמה כ"א וג' מאות פעמים נ"ד וגם ת"ר שרשימתו א'ב'ג' ד'ה'ו' |
| The multiplier is written in the top line and the multiplicand in the rightmost column | רשום למעלה על הבתים כאשר תראה בסולם שרשמתי והנכפול כתוב בצדו זה תחת זה כמצוייר |
|
ובראשונה חשוב כמה ד' פעמים א' ויעלה ד' וכתוב אות בחצי הבית ראשון שמכוון תחת הא' וגם נגד הד' |
| Every cell is divided to two: the upper part is for the units of the interim product and the bottom part is for the tens | כי כל בית נחלק מחציתו העליון אחדים והתחתוני' עשיריים |
|
|
ואחר כך חשוב כמה ד' פעמים ב' ויעלה ח' רשומיהו בחצי בית העליון שתחת ב' |
|
|
ואחר כך חשוב כמה ד' פעמים ג' ויעלה ב"א רשומיהו באותו בית שתחת הג' וכתוב ב' בחצי' בית העליון וא' בחצי השניי' |
| ומעתה מחוק הד' כי היא נחשבת בכל חילוקים | |
|
מעתה תצטרך לחשוב ה' פעמים א' ויעלה ה' רשומיהו בבית שבצד הה' מכוון תחת הא' |
|
|
ואחר כך חשוב ה' פעמים ב' ויעלה 0"א רשומיהו בחצי בית התחתון בבית חמישי |
|
|
ואחר כך חשוב ה' פעמים ג' ויעלה ה"א רשומיהו בבית ששי ה' בחצי העליון א' בחצי תחתון |
| ומעתה מחוק ה' | |
|
והנה חשוב ו' פעמים א' ויעלה ו' רשומיהו בצדו מכוון בטור שתחת הא' |
|
|
ו' פעמים ב' כ"א רשומיהו בבית השמיני |
|
|
ו' פעמים ג' היינו ח"א רשומיהו בבית האחרון |
| והנה כפלנו כולה | |
| ואשכילך כמה יעלה סכום שלה קח אות ראשון שבבית ראשון שהיא ד' וכתביהו במקום מיוחד | |
| ואחר כך חשוב בשליבה שנייה בכל השיפוע מאות ח' עד אות ה' וצירוף אות הה' עם הח' ויעלה ג'א' הג' כתוב בצד הד' הנרשמת כבר כזה ד ג | |
| וגם הא' שהיא עשרה צרוף לשליבה שתחתיו וחבריהו אל הב' בתחילת שליבה שלישית ויעלה ג' וחבור אחר כך גם הו' שבסוף השיפוע ויהיה ט' רשומיהו אצל ד"ג כזה ד ג ט | |
| ואחר כך חשוב וצרוף אותיות שבשליבה רביעי' מראש ועד סוף ויעלה ט' כתוב ט' אצל דג"ט כזה ד ג ט ט | |
| והנה חשוב אותיות שבשליבה חמישית בשיפוע ויעלה צירופו עשרה | |
| The tens in the sum of the interim products are added to the subsequent sum of interim products | וכבר אמרתי שלעולם העשירי מצטרף לשליבה שתחתיו ואין רושמין אותה בצד המיוחדין |
| If there are no units left in the sum - zero should be written in order to hold the rank | אבל תצטרך להשיב גלגל במקום העשרה לשמור המעלה הואיל ולא נשאר אפילו אחד לשמור המורה המעלה |
| והנה כשתצטרף העשרה לא' שבשליבה אחרונה יעלה ב' וכתביהו בצד ד'ג'ט'ט' המיוחדים ויהיה כזה ד ג ט ט 0 ב | |
| זה מכוון חשבון של כפולת אב"ג על דה"ו | |
| The checking method of the result is the same method as in the previous chapter on multiplication | ומאזנים שלו כמו שכתבתי לעיל בשער הכפל הגדול |
|
|
ד'ו'ד' פעמים ד'ו'ד' עולה חשבונו ו'ט'ב'ה'א'ב' ודוק |
| סליק שער הכפל |
Multiplication - CheckMS Mantova f. 69r |
כשתרצה לידע משקל אם אתא שפיר כשיש לפניך הכפל |
|---|---|
|
|
כגו' א דוד פעם דוד כגו' ו'ט'ב'ה'א'ב' או כל כפלים אם הן שפיר או לאו |
|
|
אז קח לפניך דוד במניין נמצא י"ד ואמ' כמה הוא יותר מט' נמצא ה' ותשליך הט' ממך ואמ' כמה ה' פעמי' ה' נמצא כ"ה ותשליך ממך כל הט' שבתוך כ"ה ויתר לך ז' |
|
|
אז תשליך נמי ו'ט'ב'ה'א'ב' בט' אז ישאר לך ז' וכן תעשה לכל הכפולים שבעולם ודו"ק |
Chapter Six: Division |
שער החילוק | ||||||||||||||||||||||||||
| Dividing a large number into a few smaller numbers | והוא טוב לחלק חשבון גדול לכמה חשבונות קטנים | ||||||||||||||||||||||||||
| ועתה ידוע תדע שאין כותבין בשער זה כמו בשער הכפל אות ראשונה משורה תחתונה נגד אות אחרונה משורה עליונה אלא כותבין שורה עליונה כפי מעלותיה ושורה תחתונה כמו כן כפי מעלותיה ויכוון אות אחרונה שבשורה תחתונה נגד אות אחרונה שבשורה עליונה | |||||||||||||||||||||||||||
|
ואם אות אחרונה שבשורה תחתונה יותר מאות אחרונה שבשורה עליונה אז יסיג שורה תחתונה מעלה אחת לאחוריה אלא א"כ דאותו שורה תחתונה יש בה יותר מאות אחת | ||||||||||||||||||||||||||
|
אבל אם עלו שוות לא יסוג לאחריה אלא אם כן דאותו שורה יש בה יותר מאות אחת | ||||||||||||||||||||||||||
|
וכשיש בה יותר מאות אחת יסיג כל השורה מעלה אחת לאחוריה ואז יכול לחלק אותיות עליונה על אותיות תחתונות | ||||||||||||||||||||||||||
|
והחילוק שחילקו יכתוב נגד מעלה ראשונה שבשורה תחתונה הן אם אותו מעלה אות או גלגל | ||||||||||||||||||||||||||
| All the digits of the divisor should be subtracted from the dividend the same number of times as the digit in the highest rank is subtracted | וכשתחלוק ב' אותיו' פי' שהיו בשורה תחתונה ב' אותיות אז אין חילוק של שתיהם רק מנין אחד יהיה ג' אותיות או ד' וכן עד סוף כל הדורות וכל כך כמה פעמים שחלקת האות האחרונה מן החשבון כן תקח כל שאר אותיות ול"ד | ||||||||||||||||||||||||||
| Examples | ועתה אכתוב דמיונים למען יבין המבין ותן לחכם ויחכם עוד ויוסיף לקח | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
ועתה אתחיל בחילוק קטן אם ישאל השואל כמה פעמים ז' יש במאתים וי"ח | ||||||||||||||||||||||||||
|
הילך היאך תעשה כתוב המאתים וי"ח כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והז' היה מן הדין לכתוב תחת הב' כדי לחלק הב' לז' ז' פי' למנה כמה פעמים ז' יש בב' אלא שאין הב' מגיע לחילוק של ז' לכן נסוג הז' לאחור כדי שתהא הב' במעלה שנייה לה ותעלה לנגדה עשרים ואחת כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואותו עשרים ואחת תחלוק לז'ז' פי' מנה כמה פעמים ז' יש באחת ועשרים ונמצא שיש בהם ג' פעמים ז' אותו ג' כתוב למעלה על הא' שבשורה עליונה נגד ז' שבשורה התחתונה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואחר כך מחוק הא"ב שמצאת בהם ג' פעמי' ז' ואחר כך סוג הז' מעלה אחת לאחוריה ויהיה תחת הח' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ומנה כמה פעמי' ז' יש בח' ולא מצאת בה רק פעם אחת ז' ועוד יש א' יותר אז כתוב א' נגד הז' על הח' כזה והאחד העודפת כתוב במקום הח' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| נמצא ברי"ח יש ל"א פעמים ז' וישאר אחת וכן לעולם ועיין | |||||||||||||||||||||||||||
|
דמיון אחר הנה יש לי עשרת אלפים פצין ומאה ועשרים ושבע פצין ואבקש לידע כמה זהובי' יש בתוכם שכל אחד יש ט"ו פצין | ||||||||||||||||||||||||||
| והנה רשומיהו כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
והנה רשום תחת זה הז'ב'א'0'א' החשבון ה'א' ואם תכתבהו תחת הסופיים כמחוייב נמצא א' תחת א' ולא ישאר לך דבר וא"כ מאין תקח ה'פעמים א' כי כמה פעמים שתקח אות אחת כמו כן תקח חבירתה כמו שכתבתי לעיל וא"כ סוג ה'א' אחור וכתו' א' תחת גלגל וכתו' ה' תחת א' שלפני גלגל ויהיה כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה צריכין אנו לשער באם נקח הא' מהאותיות שעליו שגם יעדיף למצא הה' בעודף בחשבון הזה ואם תרצה לומר ליקח ט' פעמים מן י' א"כ לא ישאר רק אחד ותבא א' במקום גלגל ויהיה א"א ומעתה לא תוכל ליקח ט' פעמים ה' מן א"א וכן אם תקח ח' פעמים א' לא ישאר רק ב' ולא תוכל ליקח ח' פעמים ה' מן ב"א וכן אם תיקח ז' לא ישאר רק ג' ולא תוכל ליקח ז' פעמים ה' מן ג"א אלא קח ו' וישאר ד' כתוב ו' על הא' ויהיה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תוכל ליקח ו' פעמים ה' מן א"ד וישאר לך מן הד' שהיא א' עשרה ואם כן כתוב א' במקום הד' ומחק ה' ויהיה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ואחר כך בקשנו ליקח הא' מן החשבון הזה י' פעמים לא תוכל ליקח כמו שפירשתי וגם זה הכלל נקוט בידך לעולם לא תוכל ליקח י' רק ט' או ח' או ז' ולמטה לכן עשה כך: כתוב ה'א' תחת ב'א' כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| וקח ז' פעמים וישאר ד' שעודף י"א על ז' ד' וכתוב ז' למעלה נגד הה' תחתונה ומחק הא' תחתונה ומחק ג"כ הא'א' עליונה וכתב תחתיהן ד' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
והנה קח ז' פעמים ה' מן ד' שבצידה דהיינו ל"ה וישאר ה' כי הד' היא במעלה שנייה מן הה' עולה ארבעים ועתה קח ממנה ל"ה וישאר ה' צרוף הה' אל הב' שלפניה ויהיה ז' כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| וקח ה' פעמים א' מן ז' כי ז' פעמים לא נוכל ליקח כמו שפי' לעיל שאז לא נוכל ליקח ז' פעמים או ו' פעמים ה' ודו"ק לכן קח ה' פעמי' וכתוב למעלה ה' בצד הז' נגד ה' תחתונה ויעדיף ב' אותו ב' כתוב במקום ז' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה קח ה' פעמי' ה' מן ז"ב וישאר ב' שאינו מגיע לחשבון הא' וצורתו כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| נמצא מכוון שעשרת אלפים ומאה וכ"ז פצין עולה ה' זהו' וגם ת"ר זהו' ושני פצין | |||||||||||||||||||||||||||
Checking Methods |
ואם לבך מגמגם כפול העודף האחרון על ה'א' ויצא לך חשבון הראשון ששאלת | ||||||||||||||||||||||||||
| The checking method of division is multiplication and the checking method of multiplication is division | וזהו מאזני צדק על שער החילוק נמצא כפל מברר החילוק והחילוק מברר הכפל |
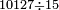 → Check:
→ Check: 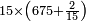
- [Illustration of the procedure:]
15 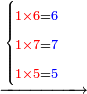
6755 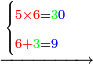
9755 
10105 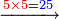
10125 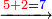
10127 675 675 75 5
| דמיון למאזנים כתוב ה'א' וכתוב תחתיו ה'ז'ו' הנשאר באחרונה חוץ מן הב' שלא הגיע לחשבון ט"ו אל תצטרף עמהן עד סופו חיבורו לאות ראשונה כזה | |||||||||||||||||||||||
|
| ||||||||||||||||||||||
| כפול ו' על א' יעלה ו' כפול ז' על א' יעלה ז' כפול ה' על א' ויעלה ה' כזה | |||||||||||||||||||||||
|
| ||||||||||||||||||||||
| והנה כתוב ה'ז'ו' תחת ה' של ה'א' כזה | |||||||||||||||||||||||
|
| ||||||||||||||||||||||
| כפול ו' על ה' ויעלה ל' חבור על ז' שעליו כמו שצויתיך בשער הכפול אם כן צריך אתה ליתן הג' אל הו' ויהיה ט' כזה | |||||||||||||||||||||||
|
| ||||||||||||||||||||||
| ואחר כך כפול ז' על ה' ויעלה ה"ג ועליו ה' דהיינו 0"ד עשה גלגל במקום ה' ותן ד' לז' ויהיה א"א כתוב במקום ז"א ותן א' על הט' ויהיה י' אז צריך אתה לעשות גלגל במקום הט' ואחריו א' כזה | |||||||||||||||||||||||
|
| ||||||||||||||||||||||
| ואחר כך כפול ה' על ה' ויעלה ה"ב כתוב ה' במקום ה' העליונה ואל תצטרף ה' ראשונה עליה כמו שצויתיך בשער הכפל ואחר כך כתוב ב' במקום גלגל כזה | |||||||||||||||||||||||
|
| ||||||||||||||||||||||
| והנה חבר ב' שלא הגיע לכלל ט"ו אל הה' הראשונה ויהיה ז' ואז יהיה החשבון כזה | |||||||||||||||||||||||
|
| ||||||||||||||||||||||
| והיינו כיון השאלה | |||||||||||||||||||||||
| סליק שער החילוק | |||||||||||||||||||||||
|
ועוד אראה לך דומיון חושבתי מן חו"ה פעמי' חו"ה הכי | ||||||||||||||||||||||
|
|
- [Illustration of the procedure:]

5 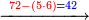
5 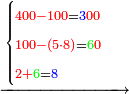
5 322624 72624 42624 38624 568 68 8
| ורציתי לחלק אם חושבתי שפיר וכה תעשה תכתוב לפניך החשבון שעולה ממנה ותכתוב תחתיו חו"ה וצורתו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| כי לא אתה יכול לחלק ה' מן ג' כי ג' לא מגיע אפי' פעם אחת לה' לפיכך סוג הה' לאחרי' ואז תאמר כמה פעמים ה' בב"ג זהו ה' פעמים אע"ג שיש לי לקח עוד פעם אחת ה' אלא מטעם זה אני לקח נוטל אות' ה' פעמים ולא יותר כי אם אני נוטל ו' פעמי' אז לא היה נשאר מן הב"ג אלא ב' ואז לא היה יכול לקח הו' מן חו"ה נמי ו' פעמי' מן ב"ב פי' מן כ"ב והדין בזה השער כי כמה פעמי' שתחלק האות ראשו' אז אתה עושה לכל האותיות לפי זה אני נוטל ה' פעמי' ואז נשאר ז' ואז אני יכול לנטול גם הו' ה' פעמים ואות' ה' תכתוב למעלה על הו' נגד הח' התחתונ' ונמחוק הב"ג ותכתוב במקומ' הז' וצורתו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ושוב תחלוק הו' מן חו"ה נמי ה' פעמים מן ב"ז ואז נשאר לך ב"ד ותמחוק הז' ותכתוב במקו' ד' וצורתו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואז תחלוק הח' נמי ה' פעמי' מן ו'ב"ד פי' כ"ו ד' מאות אז תקח מאה מן הד' מאו' ועוד נשאר ג' מאות ואז קח מן המאה הח' פעם ה' וזהו 0"ד פי' מ' ועוד נשאר 0"ו ואותו ו' תשים על הב' ויהיה ח' וצורתו כזה | |||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
5 
56 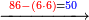
56 
56 38624 8624 5024 4544 568 68 8
| נמשוך חו"ה לאחריה תחת הב' וצורתו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואז תאמר כמה פעמי' ה' בח"ג ויעלה ו' ועוד נשאר ח' ותמחוק הג' שאחר הח' והו' העולה מן הח"ג תכתו' על הב' בשור' עליונ' נגד הח' שלמטה וצורתו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואז תקח הו' נמי ו' פעמי' מן ו"ח פי' מן פ"ו ועשה הכי תקח ה"ג פי' ה"ל מן ה"ח ואז נשאר נ' וקח הו' שלפני הח' ושים במקומ' גלגל כי ו' פעמי' ו' זהו ו"ג וצורתו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ותמחוק הו' של חו"ה כמו שציירתי ושוב קח הח' נמי ו' פעמים מן ה' מאות ואז שוב עשה הכי קח מאה מן הה' מאות ועוד נשאר ד' מאות וקח מן המאה ח' פעמי' ו' וזהו ח"ד פי' מ"ח ואז קח מן המאה נ' ואז נשאר נ' ואות' נ' תכתו' במקו' הגלגל שלפני הד' ועוד יש ב' יותר שאני צריך אלא מ"ח ואני לקחתי נ' ואות' ב' תשים על הב' של אחר הד' הראשונ' ונמחוק הח' מן חו"ה וצורתו כזה | |||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
56 
568 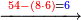
568 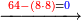
568 4544 544 64 568 68 8
| נמשוך חו"ה לאחריה תח הח' תחת הד' והו' תחת הד' השניי' והה' תחת הה' וצורתו כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תאמר כמה פעמי' ה' בה"ד פי' מ"ה ויעלה ח' פעמי' ואות' ח' תכתו' למעלה על הד' נגד ח' התחתונ' ועוד נשאר ה' ותמחוק הד' שאחר הה' ותמחוק הה' של חו"ה וצורתו כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ושוב נחלק הו' נמי ח' פעמים מן ד"ה פי' מן נ"ה וע ועשה הכי קח מן הנ' ח' פעמי' ו' ועוד נשאר ב' כי ח' פעמי' ו' זהו ח"ד פי' מ"ח ועוד נשאר ב' ואות' ב' תשים על הד' שלפני הה' והוה ו' וצור ונמחק ו' של חו"ה והה' אחר הד' וצורת' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תאמר ח' פעמי' ח' וזהו ד"ו פי' ס"ד
סליק דומיון של שער החילוק | |||||||||||||||||||||||||||
| נמצא כשחלקתי חו"ה מן ד'ב'ו'ב'ב'ג' אז לא נשאר מאומה | |||||||||||||||||||||||||||
| וכן בכל מקום אשר אתה מחשב דבר השוה כגו' ח'ו'ה' פעמי' ח'ו'ה' או דו"ד פעמי' דו"ד וכשתחלק ממנ' אות' שחשבת ולא נשאר לך מאומה אז החשבון אמת ודו"ק ותמצא | |||||||||||||||||||||||||||
| ועוד אראה לך דומיון שאינ' חשבון שוה כגו' א"ב פעמי' ה"ד | |||||||||||||||||||||||||||
| ואז אתה לא עושה כדרך זה קח חד מן הפרטות הא"ב או הה"ד ותחלק מן החשבון ואז עולה הפרט השיני ודו"ק | |||||||||||||||||||||||||||
|
דומיון חשבנו ה"ד פעמים א"ב ועולה ממנ' כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ואז נחלק אם חשבנו אמת אז קח הכלל העולה ותכתוב תחתיו חד פרט ותאמר כמה פעם זה הפרט בזה הכלל אז עולה הפרט השני' והילך צורתו אשר תכתביהו הכלל ותחתיו הד פרט איזה שתרצה ועת' נרא' קח הכלל ה' ד' ט' ותכתוב תחתיו הפרט ה"ד וצורתו כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ותאמר כמה פעמים ד' בט' נמצא ב' פעמי' ולא יותר אות' ב' תכתוב על הד' נגד הה' שלמט' ותמחוק הט' ותכתוב במקומ' א' ואז קח ותמחוק ד' תחתונ' וצורת' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז קח הה' נמי ב' פעמי' מן ד"א ונשאר הד' ונמחוק הא' והה' שלמט' וצורתו כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ואז תמשוך הה"ד מעלה אחת לאחריה הה' תחת הה' והד' תחת הד' וצורתו כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תאמר כמה פעמי' ד' בד' נמצא רק א' ואות' א' תכתו' על השני ה' קודם הב' וצורתו כזה ונמחק השני ד' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תאמר תקח הה' נמי א' פעם אז לא נשאר לך מאומה נמצא כשחלקתי חד פרט אז עולה הפרט השיני וכן תמצא בכל פעם אשר אתה מחלק | |||||||||||||||||||||||||||
|
והילך שער טוב לראות אם חלקתי אמת וטוב מאד מאד ואראה לך דומיון רציתי לחלק כמה פעם ז' בב' מאות וי"ח כאשר נחלק כבר בתחילת שער החילוק והוה עולה [א"ג] ונשאר א' ואז ראה אם חלקתי אמת | ||||||||||||||||||||||||||
|
קח הז' שחלקתי ושים אותה תחת הג' [כזה] | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ותאמר כמה ז' פעמים ג' זהו כ"א א"ב פי' כ"א | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז קח הז' ושים אות' תחת הא' ותאמ' ז' פעמי' א' זהו ז' ואות' ז' תכתו' קודם הא"ב שעולין מן ג' פעמי' ז' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז קח הא' שלא חלקת לז' ושים עתה על ה ז' שעולה השת' מן א"ג פעם ז' ויהיה ויהיה ח' וצורתו כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| נמצא כשלקחתי הח'א'ב' וחלקתי ממנ' כמה פעמי' ז' ועולה א"ג ונשאר א' ואז לקחתי הא"ג וזרקתי ג' ל[...] הז' וחשבתי כמה פ' ז' פעמים א"ג ועולה ממנ' זא"ב ואז לקחתי הא' שנשאר כבר וזרקתי על זה הז' והוה ח' כמו נמצא ח'א'ב' כמו בראשון |
Chapter Seven: Proportions |
שער עירוכין | ||||||||||||||
| The purpose of this chapter - deducing and estimating a thing from another thing | שער הנכבד ונקרא שער הערך אשר לכולי עלמא צריך למנות ולחשוב ולחכם ולהשכיל לדעת ולהבין דבר מתוך דבר ולהעריך דבר אחר דבר ולעמוד על יסודו ועל בוריו | ||||||||||||||
|
כיצד אם לקחת מקח גדול בדמים מרובים ואת צריך להעריך מקח קטן לפי אותה דמים פי' כמה מגיע לפי אותה הדמים למקח הקטן שקנית | ||||||||||||||
|
או להיפך שקנית מקח קטן בדמים מועטי' ואתה רוצה להעריך אחריו מקח גדול | ||||||||||||||
| The procedure: | הילך היאך תחשוב ותמנה ותעריך | ||||||||||||||
|
תכתו' המקח גדול וסכו דמים מן הגדול המקח תכתוב תחת המקח גדול ואח"כ תכתוב המקח הקטן תחת הסכום | ||||||||||||||
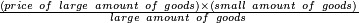
|
ותכפול דמי המקח הגדול אשר כתבת למעלה אחר המקח הגדול תכפול אותו על מניין מקח קטן והעולה קח בידך ותחלוק אותו בשער החילוק על המקח הגדול ומה שיעלה בידך כל כך ערך המקח הקטן | ||||||||||||||
|
ואם יותר לך חלקים שלא יעלו לחלק המבוקש אז תאמר עוד נשאר לי חלקים כך וכך שסכום כך וכך עולה לחלק אחד של המבוקש | ||||||||||||||
|
ואם להיפך שאתה רוצה להעריך חשבון מקח גדול אחר חשבון מקח קטן אז תכתוב חשבון הקטן למעלה ואח"כ תכתוב דמים הידועים לאותו מקח והחשבון הגדול תכתוב למטה | ||||||||||||||
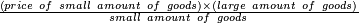
|
ותכפול חשבון | ||||||||||||||
The writing rule of the calculation procedure:
|
וזה הכלל המקח אשר ידעת תכתוב תחילה | ||||||||||||||
Word Problems |
|||||||||||||||
| Now I will write two or three examples so you may understand and become wise. | ועתה אכתוב לך ב' או ג' דמיונות כדי שתוכל להבין ולהשכיל | ||||||||||||||
Pricing Problems - Find the Price |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
איש אשר ישאלך הנה קניתי ע' אמות בגד עבור מ' דינרים כמה מגיע לנ"ה אמות | ||||||||||||||
|
אז תכתוב תחילה הע' אמות ואח"כ דמי הע' אמות ואח"כ הנ"ה אמות אשר בקשת לידע ערכיהן כזה | ||||||||||||||
|
| ||||||||||||||
|
וכפול נ"ה על מ' ועולה הוא ב' אלפים וב' מאות כזה | ||||||||||||||
|
| ||||||||||||||
|
ואחר כך תחלק ב' אלפים וב' מאות לע'ע' פי' חלוק בשער החילוק כמה פעמים ע' יש בהן והחילוק הוא ל"א פעמים ע' ועוד ל' חלקים קטנים שע' מהם הם חלוק שלם דהיינו דינר | ||||||||||||||
|
נמצא השאלה ששואל לך כשקנה ע' אמות עבור מ' דינרין כמה מגיע לנ"ה אמות ל"א דינרין ועוד ל' חלקים שע' עושין חלק שלם שהוא דינר | ||||||||||||||
|
ואם תעלה על דעתך מאן מוכח ומאן לימא לן שכך הוא שמא הערך אינו כמו שחשבת | ||||||||||||||
|
אז צא וחשוב ט"ו אמות העודפים על נ"ה כי מן נ"ה עד ע' יש ט"ו | ||||||||||||||
|
ותעריך כמה מגיע לט"ו אמות כשע' אמות באו עבור מ' דינרין | ||||||||||||||
|
והילך היאך תעשה | ||||||||||||||
|
כתוב ע' אמות ואחר כך ט"ו אמות כזה | ||||||||||||||
|
| ||||||||||||||
|
וכפול ט"ו על מ' פי' חשוב כמה ט"ו פעמים מ' ועולה ו' מאות | ||||||||||||||
|
ואחר חלוק ו' מאות לע"ע פי' מנה כמה פעמים ע' יש בו' מאות ויעלה שמונה פעמים ע' ועוד ישארו מ' חלקים שע' מהם עושין חלק שלם פי' דינר אחד | ||||||||||||||
|
נמצא כשקנית ע' אמות בעד מ' דינרין מגיע לט"ו אמות ח' דינרין ומ' חלקים שע' מהם עושין דינר שלם | ||||||||||||||
|
ולמעלה חשבנו שמגיע לנ"ה אמות ל"א דינרין ול' חלקים שע' מהם עושין דינר שלם עתה חבור הערך יחד ל"א דינרין וח' דינרין הרי ל"ט דינרין | ||||||||||||||
|
צרוף נ"ה וט"ו ויהיה ע' | ||||||||||||||
|
נמצא שעכשיו אתה יודע ומבין שחשבת כדין וביושר ול"ד ע"א | ||||||||||||||
|
דמיון אחר אם ישאלך אדם הנה קניתי ק' חבית בעד צ' ליטרות כמה מגיע לחבית אחת | ||||||||||||||
|
אז כתוב תחילה ק' חבית ואחר כך דמיהם דהיינו צ' ליטרות ותחת צ' ליטרו' כתוב החבית האחד כזה | ||||||||||||||
|
| ||||||||||||||
|
וכפול א' התחתונה על צ' שלמעלה הימנה א' פעמים צ' יעלה צ' | ||||||||||||||
|
ואחר כך תחלק אותו צדיק לק"ק פי' כמה פעמים ק' יש בצ' ולא תשיג ידך אפי' פעם אחת ק' אדרבה חסר לך עשרה וזה הערך המגיע לחבית אחד צדיק חלקי' שק' מהן עולין ליטרו' | ||||||||||||||
|
זה מוצא מהר"ר וייזל בספר אחר וזה לשונו | ||||||||||||||
|
ולפי דעתי שאין צריך לטעם זה כי אין מחשבתו של אדם לחלק צ' חלקים שק' מהן חלק א' | ||||||||||||||
|
וזה הטעם ראוי יותר בעיני גם חשבונות של גוים נמי כזה שאכתוב הנה שאלת ק' חבית בעד צ' ליטרו' כמה מגיע לאחד | ||||||||||||||
|
כתוב כזה | ||||||||||||||
|
| ||||||||||||||
|
חשוב בדעתך כמה פשוטים יש בצ' ליטרו' אם היה בליטר' כ' פשוטים | ||||||||||||||
|
חשוב כ' פעמים צ' ויעלה ח' מאות ואלף כזה | ||||||||||||||
|
| ||||||||||||||
|
חשוב בשער החילוק כמה פעמים מאה יש באלף וח' מאות ותמצא י"ח פעמים מכוון כך היא החשבון י"ח פשיטי' לחבית אחד | ||||||||||||||
|
ואם ישארו לך חלקי' קטנים אמור כך וכך חלקים שכך וכך עולה לחלק שלם פי' פשי' ודוק ע"א | ||||||||||||||
| We wish to evaluate: | הנה בקשנו להעריך | ||||||||||||||
|
אם ישאל אדם קניתי י"ט אמות בגד עבור י"ג דינרין כמה מגיע לי"ג אמות | ||||||||||||||
|
אז תערוך כך | ||||||||||||||
|
וכתוב תחילה י"ט אמות אחר כך דמיו דהיינו י"ג דינרין ואחר כך י"ג אמות כזה | ||||||||||||||
|
| ||||||||||||||
|
וכפול י"ג שלמעלה על י"ג שלמטה פי' מנה כמה עולה י"ג פעמים י"ג ותמצא שיעלה קס"ט כזה | ||||||||||||||
|
| ||||||||||||||
|
ואז תחלק קס"ט לי"ט י"ט פי' כמה פעמים י"ט יש בקס"ט ותמצא שיש בו ח' פעמים י"ט ונשארו י"ז חלקים שי"ט מהן עולה חלק אחד | ||||||||||||||
|
וזה הערך המגיע לי"ג אמות כשקונין י"ט אמות בעד י"ג דינרין אז מגיע לי"ג אמו' ח' דינרין וי"ז חלקים שי"ט מהן עושין חלק שלם דהיינו דינר אחד ול"ד | ||||||||||||||
| Likewise, if you wish to evaluate a large amount of merchandise through a small amount of merchandise, I will teach how: | וכן אם תרצה להעריך מקח גדול אחר מקח קטן אשכילך היאך | ||||||||||||||
|
הנה קנית כ"א אמות מ"ג דינרין כמה מגיע לס"ה אמות | ||||||||||||||
|
כתוב בתחילה כ"א אמות ואח"כ מ"ג דינרין ואחר כך ס"ה אמות [6]אשר בקשת לחשוב כזה | ||||||||||||||
|
| ||||||||||||||
|
ותכפול ה"ו על ג"ד פי' כמה עולה ג"ד פעמי' ה"ו ויעלה | ||||||||||||||
|
ואח"כ חלוק הטז"ב בשער החילוק כמה פעמי' שיש בהן א"ב ותמצא ג'ג'א' פעמי' ועוד נשארו ב' חלקי' קטני' שא"ב מהן עושי' חלק אחד דהיינו דינר | ||||||||||||||
|
נמצא אם קנית א"ב אמות עבור ג"ד דנרי' מגיע לה"ו אמות ג'ג'א' דינרי' וב' חלקי' שא"ב מהן דינר | ||||||||||||||
|
ואם תרצה לידע אם אמת חשבת אם לאו | ||||||||||||||
|
הבט וראה כמה ה"ו עולה יותר מא"ב דהיינו ד"ד | ||||||||||||||
|
השליכהו בשער הכפל על ג"ד פי' ג"ד פעמי' ד"ד דהיינו בטח"א | ||||||||||||||
|
ואח"כ חלקיהו בשער החילוק כמה פעמי' יש בהן א"ב ותמצא 0"ט פעמי' ועוד נשארו ב' חלקי' קטני' שא"ב מהן חלק אחד שלם | ||||||||||||||
|
חבר 0"ט וב' חלקי' קטני' על ג"ד דהיינו הדינרי' השייכי' לא"ב זהו ויהיה גג"א וב' חלקי' קטני' כזה | ||||||||||||||
|
| ||||||||||||||
|
והיינו כוונת החשבון ולמבין די |
Boiling Problem |
|||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
שאלה היוצא משער הערך הזה | ||||||||||||||||||||||||||||||||
|
הנה לפניך נ' סאין מים ואם אתה ש' אבשל אות' על האור מתבשלין ונחסרי' בכל יום ז' סאין ועתה שואלי' | ||||||||||||||||||||||||||||||||
|
הילך היאך תעשה | ||||||||||||||||||||||||||||||||
|
תכתוב תחילה הנ' סאין ואח"כ תכתוב הז' סאין הנחסרי' ביום אחד ותחת הז' סאין תכתוב המ"ה סאין הנשארי' כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
ותכפול מ"ה שלמטה על ז' שלמעלה הימנה פי' חשוב כמה עולה מ"ה פעמי' ז' ויעלה שט"ו | ||||||||||||||||||||||||||||||||
|
תחלוק אות' שט"ו לנ' פי' כמה פעמי' יש בשט"ו ותמצא בו ו' פעמי' נ' ועוד נשארו ט"ו חלקי' קטני' שנ' מהן חלק אחד שלם | ||||||||||||||||||||||||||||||||
|
נמצא כשנ' סאין יחסרו ז' סאין ביום אחד מ"ה סאין יחסרו ו' סאין וט"ו חלקי' קטני' שנ' מהן סיאה שלם | ||||||||||||||||||||||||||||||||
|
שאלה אחרת | ||||||||||||||||||||||||||||||||
|
אם ישאל השואל הנה יש צ"א סאין מים ואם מתבשלין על האור יחסרו ביום אחד ט' סאין ואם נוסיף עליהם עוד י"א סאין שיהיה הכל ק"ב סאי' ואנו מרבין את האש לפי זה שאם לא היינו מרבי' את האש אז לא היו המים מתמעטי' וחסירי' לפי החשבון הזה כי האור אינו שולט כל כך כשהמים הרבה כמו שאם היו המים מועטי' לפיכך כשמרבי' המים אז [7]צריכי' להרבות האש או אם מתמעטי' אז צריכי' למעט האש נחזור לשאלה ששאלנו כמה יחסרו ק"ב סאין ביו' אחד כשצ"א חסירי' ט' סאין | ||||||||||||||||||||||||||||||||
|
הילך היאך תעשה | ||||||||||||||||||||||||||||||||
|
תכתוב תחילה הצ"א ואח"כ הט' ואח"כ הק"ב כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
ותכפול ק"ב שלמט' על ט' שלמעלה פי' כמה עולה ט' פעמי' ק"ב ויעלה תתקי"ח | ||||||||||||||||||||||||||||||||
|
תחלוק תתקי"ח לצ"א פי' כמה פעמי' צ"א יש בתתקי"ח והיינו י' פעמי' צ"א וח' חלקי' קטנים שצ"א מהן חלק שלם | ||||||||||||||||||||||||||||||||
|
נמצא כשצ"א חסירי' ביום אחד ט' סאין יחסרו ק"ב י' סאין וח' חלקי' שצ"א מהן עולי' חקל שלם | ||||||||||||||||||||||||||||||||
| The checking procedure is as written above regarding the cloth. | והמאזנים על זה כמו שכתבתי לעיל עם הבג' | ||||||||||||||||||||||||||||||||
| This is the rule: the [boiling] water problems are similar to the cloth [pricing] problems, therefore their checking procedure and solving method are similar. | זה הכלל זה השאלות עם המים אות באות כמו השאלו' עם הבגד לכן יש להם מאזני צדק אחד וחשבון אחד ול"ד | ||||||||||||||||||||||||||||||||
Find a Quantity Problems - Whole from Parts |
|||||||||||||||||||||||||||||||||
| Many sciences and problems are derived from this chapter that cannot be counted. | והרבה חכמות ושאלות יוצאין משער זה אשר לא יוכל הסופר לכתוב | ||||||||||||||||||||||||||||||||
| Now, I will explain a few of them with God's help. | ועתה אפרש קצת ממנה בע"ה | ||||||||||||||||||||||||||||||||
| I start by saying: | [ובזה אתחיל ואומר][8] | ||||||||||||||||||||||||||||||||
| Tree | |||||||||||||||||||||||||||||||||
|
א הנה לך אילן שחציו בארץ ושלישיתו במים ומעל המים הוא ה' אמות כמה ארכו של כל האילן | ||||||||||||||||||||||||||||||||
|
הילך היאך תעשה ותבין העניין | ||||||||||||||||||||||||||||||||
|
חשוב כל כך איזה חשבון הקרוב שיכולין לחלק לשני חלקי' ולג' חלקי' זה ו' | ||||||||||||||||||||||||||||||||
|
הסר מן ו' החציה וישאר ג' הסר ג"כ השלישי וישאר א' | ||||||||||||||||||||||||||||||||
|
אותה א' תכתוב תחילה ואחריה בצד שמאלית אצל הא' תכתוב ו' ותחת הא' תכתוב ה' אמות כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
ותכפול ה' שתחת הא' על ו' שעומד אחר הא' בשיטה עליונה פי' מנה כמה עולה ה' פעמי' ו' והעולה הוא ל' | ||||||||||||||||||||||||||||||||
|
אות' ל' תחלק לא'א' פי' מנה כמה פעמי' א' יש בל' ודבר ידוע הוא לכל שיש בל' ל' פעמי' א' וזהו אורך האילן אשר שאלת אם תצא בארץ ושלישו עומד במים ומעל המים הוא ה' אמות וששאלת כמה ארכו הנה ארכו ל' אמות והדמיון כך כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
ואם אתה ירא שאינו כך אז קח רומח שארכו ל' אמו' | ||||||||||||||||||||||||||||||||
|
הסר ממנו חציו זהו ט"ו | ||||||||||||||||||||||||||||||||
|
אח"כ הסר ממנו השליש זהו עשרה | ||||||||||||||||||||||||||||||||
|
וט"ו הרי כ"ה | ||||||||||||||||||||||||||||||||
|
נמצא שאין נשאר כ"א ה' אמות | ||||||||||||||||||||||||||||||||
| Another example, in order that the reader will be well taught in it and understand its virtues and profit, and it is the question asked: | דומיון אחר למען ירוץ הקורא בו ויבין מעלתו וטובו והוא שאלה ששואלין | ||||||||||||||||||||||||||||||||
| Lance | |||||||||||||||||||||||||||||||||
|
הנה לך רומח שעומד השליש והרביעי' והחומש בארץ ולמעלה מן הארץ ארכו ז' אמות כמה ארכו של כל הרומח | ||||||||||||||||||||||||||||||||
|
אז חשוב איזה חשבון שיש בו [9]שליש ורביע וחומש וזהו ס' שיכולי' לחלק לג' ולד' ולה' | ||||||||||||||||||||||||||||||||
|
והסר מס' שליש וזהו כ' | ||||||||||||||||||||||||||||||||
|
הסר כמו כן הרביע הוא ט"ו | ||||||||||||||||||||||||||||||||
|
והסיר ג"כ החומש זהו י"ב | ||||||||||||||||||||||||||||||||
|
ס"ה מ"ז | ||||||||||||||||||||||||||||||||
|
עוד נשאר לך מס' י"ג | ||||||||||||||||||||||||||||||||
|
אז תכתוב תחלה י"ג שנשארו ואחר הי"ג בצדו רחוק מעט תכתוב הס' ותחת הי"ג תכתוב ז' אמות שהרומח עומד למעלה מן הארץ ויהיה כך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
תכפול ז' שלמטה על 0"ו שבשיטה עליונה פי' חשוב ומנה כמה עולה ז"פ 0"ו ויעלה ת"ך | ||||||||||||||||||||||||||||||||
|
תחלק ת"ך לי"ג י"ג פי' חשוב ומנה כמה י"ג יש בת"ך ותמצא שיש בו ל"ב פעמי' י"ג ועוד נשארו ד' שלא יכולנו לעשות מהם י"ג והם ד' מי"ג בשלם | ||||||||||||||||||||||||||||||||
|
נמצא שהרומח ששאלת כשהשליש והרביע והחומש בארץ ולמעלה מן הארץ אכרו ז' אמות ושאלת כמה אורך של כל הרומח ארכו ל"ב אמות וד' חלקי' שי"ג מהן חלק שלם | ||||||||||||||||||||||||||||||||
| Wall | |||||||||||||||||||||||||||||||||
|
ב שאלה אחרת הנה חומה שיסודה שקוע' בקרקע ה' אמו' ולמעלה מן הארץ היא גבוה החציה והשלישי והשביעי' כמה גובהה של כל החומה | ||||||||||||||||||||||||||||||||
|
אז חשוב איזה חשבון שיכולין לחלקו לב' ולג' ולז' בקל לפי רגע | ||||||||||||||||||||||||||||||||
|
והנה לך דרך היאך תמצא אותו חשבון המתחלק לב' ולג' ולז' תמנה זפ"ג כמה כ"א | ||||||||||||||||||||||||||||||||
|
כ"א פעמי' שנים כמה הם מ"ב הרי שמ"ב מתחלקי' לשנים ולשבעה ולשלשה | ||||||||||||||||||||||||||||||||
|
[או כלך לדרך זו והכל אחד ב' פעמים ג' הרי ו' ו' פעמים ו' הרי ל"ו וכבר היו לך ו' צרוף ו' עם ל"ו הרי מ"ב הוא] | ||||||||||||||||||||||||||||||||
|
או נלך לדרך זו והכל אחד חשוב בפ"ג הרי ו' ו'פ"ז הרי מ"ב | ||||||||||||||||||||||||||||||||
|
נמצא שמ"ב הוא דבר המתחלק הוא לשביעיו' או לתשיעיות ולעשיריו' | ||||||||||||||||||||||||||||||||
|
[וכן לעולם כשישאלך דבר המתחלק לשביעי ולתשיעי ולעשירי] או לכל דבר המתחלק אז תכפול אותו חלק על האחד | ||||||||||||||||||||||||||||||||
|
כגון אם שאל דבר המתחלק לעשיריו' ולתשיעיו' אז תכפול י' על ט' פי' מנה כמה עולה י' פעמי'' | ||||||||||||||||||||||||||||||||
|
ואם ישאלך דבר המתחלק לחמישיות ולרביעיו' או למאות ולאלפי' או לכל דבר המתחלק תכפול זה על זה או לכל דבר שישאל השואל שמתחלק כך וכך תכפול זה על זה | ||||||||||||||||||||||||||||||||
|
ואם ישאל השואל דבר המתחלק לג' ד' וה' אז תכפול ג' על ד' והעולה שיעלה תכפול על ה' או איפכא תכפול תחילה ה' על ד' והעולה שיעלה בידך תכפול על ג' | ||||||||||||||||||||||||||||||||
|
ועתה נחזור לשאילתינו דלעיל החומה אשר היא חצייה ושליש ושביעי' גבוה על הקרקע ויסודה שקועה בקרקע ה' אמות כמה גובהה של כל החומה | ||||||||||||||||||||||||||||||||
|
נמצא ששאלנו על דבר המתחלק [10]לב' ולג' ולז' ב"פ ג' היינו ו' ופ"ז היינו מ"ב נמצא שמ"ב הוא חשבון המתחלק לב' ולג' ולז' | ||||||||||||||||||||||||||||||||
|
ועתה נסיר החציה ממ"ב והוא כ"א | ||||||||||||||||||||||||||||||||
|
נסיר כמו כן השליש ממ"ב זהו יהיה | ||||||||||||||||||||||||||||||||
|
נסיר כמו כן השביעי' ממ"ב זהו יהיה ו' | ||||||||||||||||||||||||||||||||
|
ס"ה מ"א | ||||||||||||||||||||||||||||||||
|
עוד נשאר ממ"ב א' | ||||||||||||||||||||||||||||||||
|
נמצא אם היינו שואלי' גובה החמה שיסודה שקוע אמה אחת וחצי ושלישי' ושביעי' למעלה למעלה מן הקרקע אז יהיה | ||||||||||||||||||||||||||||||||
|
אבל עכשיו צריכין אנו ללמוד ולהעריך כמה מגיע לה' אמו' פי' שיהיה שקוע ה' אמות בקרקע | ||||||||||||||||||||||||||||||||
|
וכן נעשה הערך | ||||||||||||||||||||||||||||||||
|
נכתוב תחיל' האמה האחת ואח"כ רחוק ממנו מעט נכתוב מ"ב אמות ותחת האמה האח' נכתוב הה' אמות ששאלנו ויהיה כך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
נכפול ה' על מ"ב פי' נמנה כמה עולה ה' פעמי' מ"ב והעולה הוא ר"י | ||||||||||||||||||||||||||||||||
|
נחלק ר"י לא'א' פי' נמנה כמה פעמי' א' יש בר"י ונמצא בו ר"י פעמים א' והנה גובה החומה ששאלנו והדמיון כך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וזה לך דרך אחר בקוצר היאך תוכל לידע כמה גובהה של כל החומה כשהיא משוקעת בארץ ה' אמות ולמעלה מן הקרקע היא גבוה החציה ושליש ושביעי' | ||||||||||||||||||||||||||||||||
|
תקח ב' פעמי' ה' הרי י' י' פעמי' ג' הרי ל' פעמי' ז' הרי ר"י | ||||||||||||||||||||||||||||||||
|
או נלך לדרך זו ב' פעמי' ה' הרי י' יפ"ג ג' הרי ל' לפ"ז הרי ר"י | ||||||||||||||||||||||||||||||||
Joint Purchase Problems - If You Give Me |
|||||||||||||||||||||||||||||||||
|
ג הא לך שאלה אם אדם אחד אומר לך הנה יש כאן דג אחד למכור והנה ג' ואחד מהן אמר לחבירו אתן כל אשר לי וכל אחד מכם יתן החציה ממה שלו ואז יהיה הדג פרוע | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
תשובה הדג רוצי' ליתן עבור י"ז פשי' | ||||||||||||||||||||||||||||||||
|
והראשון יש לו ה' פשי' | ||||||||||||||||||||||||||||||||
|
והשני י"א פשי' | ||||||||||||||||||||||||||||||||
|
והשלישי יש לו י"ג פשי' | ||||||||||||||||||||||||||||||||
|
זהו בשלימי' | ||||||||||||||||||||||||||||||||
|
אבל השברי' כגון אם ישאל השואל כשהדג נקנה עבור ח' פשי' או ט' פשי' או י"ח פשי' או ל' פשי' או מ' פשי' או איזה סכום שירצה לשאול [11]ולאותו סכום ששואל אמר האחד אתן כא"ל ואתם תנו שליש שלכם | ||||||||||||||||||||||||||||||||
|
והנה אכתוב לך ב' או ג' דמיונות כדי שתוכל להבין כל כיוצא בזה | ||||||||||||||||||||||||||||||||
|
אם הדג נקנה עבור ח"פ ואמר הראשון אתן כא"ל ואתם תנו החציה שלכם והשני אמר תנו הג' שלכם והשלישי אמר תנו הרביעי | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
צריך שיהא לראשון ב"פ וששה חלקי' שי"ז מהן עושי' חלק שלם | ||||||||||||||||||||||||||||||||
|
ולשני ה"פ וג' חלקי' שי"ז מהן עושי' חלק שלם | ||||||||||||||||||||||||||||||||
|
[ולשלישי ו' פשיטי' וב' חלקים שי"ז עושין חלק שלם] | ||||||||||||||||||||||||||||||||
|
ועתה אראה לך הדרך שתמצא שכן הוא | ||||||||||||||||||||||||||||||||
|
הנה אם היה בשלימי' אז היה לראשון ה"פ כמו שפירשתי לעיל ועתה שהוא בשברי' ועתה כשהדג נקנה בח' פשי' | ||||||||||||||||||||||||||||||||
|
אתה צריך להטותו בשער הכפל חפ"ה זהו מ' | ||||||||||||||||||||||||||||||||
|
ואח"כ צריך אתה להטותו בשער החילוק ולחלק כמה פעמי' י"ז יש במ' והנה יש ב"פ וששה עודפי' שלא הגיע | ||||||||||||||||||||||||||||||||
|
נמצא שיש לראשון ב"פ וששה חלקי' שי"ז מהן חלק שלם | ||||||||||||||||||||||||||||||||
|
ועתה נפרש כמה שיש לשיני | ||||||||||||||||||||||||||||||||
|
אם היה בשליש' כמה היו לו י"א עתה שהוא בשברי' אז תאמר לו כמו שאמרת לראשון | ||||||||||||||||||||||||||||||||
|
פי' לראשון אמרת ח' פ"ה כן תאמר לשני ח"פ י"א והעולה פ"ח | ||||||||||||||||||||||||||||||||
|
ואח"כ תחלוק פ"ח לי"ז י"ז פי' כמה פעמי' י"ז יש בפ"ח ו והנה יש בו ה' פעמי' י"ז וג' עודפי' | ||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
וכן תעשה לשלישי | ||||||||||||||||||||||||||||||||
|
ותאמר אם היה בשלימי' היו לו י"ג פשי' ועכשיו שהוא בשברי' אז תאמר לו ח' פעמי' י"ג הרי ק"ד | ||||||||||||||||||||||||||||||||
|
ואח"כ [תחלק] ק"ד לי"ז י"ז [פי'] כמה פעמי' י"ז יש בק"ד ותמצא בו ו' פעמי' שי"ז [ב'] מהן עודפי' | ||||||||||||||||||||||||||||||||
|
נמצא שיש לשלישי ו"פ וב' חלקי' שי"ז מהן חלק שלם | ||||||||||||||||||||||||||||||||
|
ואם השאלה מדג הנקנה בל' פשי' | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
אז תאמר לראשון ל' פעמי' והעולה כתוב ואח"כ תחלקיהו כמו שציויתיך | ||||||||||||||||||||||||||||||||
|
וכן לשני וכן לשלשי כדלעיל | ||||||||||||||||||||||||||||||||
|
ועתה כתבת לעיל שיש לראשון ה' ולשני י"א ולשלישי י"ג בשלימי' הנה אראך הדרך שתמצא [12]שהכלל כך הוא של כולם יש כ"ט | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
קח ג' חשבונות כשתסיר מהן החציי' והשליש והרשביעי' וישאר בידך ג' ואילו הן ד'ד' וחצי ו' | ||||||||||||||||||||||||||||||||
|
תסיר הרביע מן הד' [וישאר ג'] | ||||||||||||||||||||||||||||||||
|
והשליש מן ד' וחצי [וישאר ג'] | ||||||||||||||||||||||||||||||||
|
והחצי מן ו' וישאר ג' מכל ג' אחד ואחד | ||||||||||||||||||||||||||||||||
|
וזה המורה תועי רוח בינה[13] | ||||||||||||||||||||||||||||||||
|
ועתה יען כי אין במור' שלימי' כי ד' וחצי אינו שלם | ||||||||||||||||||||||||||||||||
|
כפול ד' ויהיה ח' | ||||||||||||||||||||||||||||||||
|
כפול ד' וחצי ויהיה ט' | ||||||||||||||||||||||||||||||||
|
כפול | ||||||||||||||||||||||||||||||||
|
ס"ה כ"ט | ||||||||||||||||||||||||||||||||
|
ועדיין אין אנו יודעין כמה מגיע לכל אחד לחלקו ועתה אשכילך | ||||||||||||||||||||||||||||||||
|
הסיר ב' פעמי' י"ב מכ"ט וישאר ה' והוא חלק של ראשון | ||||||||||||||||||||||||||||||||
|
וכן הסר ב' פעמי' ט' מכ"ט וישאר י"א והוא של שני | ||||||||||||||||||||||||||||||||
|
וכן הסר בפ"ח מכ"ט וישאר י"ג והוא חלק של שלישי | ||||||||||||||||||||||||||||||||
|
נמצא כשהראשון אומר אתן כא"ל וכ"א"מ יתן החציה יהיה ס"ה י"ז | ||||||||||||||||||||||||||||||||
|
נמצא שהדג נקנה בי"ז פשי' וכן כולם ודוק | ||||||||||||||||||||||||||||||||
|
וכן אם הקוני' ד' או ה' עד אין סוף הרוצה לקנות דג קח מניין השוה בכולם פי' או קונין ג' אז קח המניין כשתסיר השליש והרביע וחציי' וישאר ג' כמו שפירשנו או אם הקוני' ד' קח המניין כשתסיר החציי' והשליש והרביעי' והחמישי' וישאר ד' וכן ה' קח המניין כשתסיר חצי של רביעי' חמישי' ששית ונשאר ה' וכן כולם | ||||||||||||||||||||||||||||||||
|
וכשאין המניין בשלימים תכפול אות' שיהא החשבון שלם ואח"כ כעשית החשבון שלם אם הקוני' ג' תסיר ב' פעמי' ואם ד' תסיר ג' פעמי' הכפיל וכן לעולם | ||||||||||||||||||||||||||||||||
| MS P1088, margin: | |||||||||||||||||||||||||||||||||
|
ואם הקוני' ד' והרביעי אומ' אתן כא"ל וכל אחד יתן רק החומש | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
אז קח ד' מנינים | ||||||||||||||||||||||||||||||||
|
אחר תסיר ממנו חצי וישאר ד' וזהו ח' | ||||||||||||||||||||||||||||||||
|
ואחר תסיר ממנו שליש וישאר ד' זהו ו' | ||||||||||||||||||||||||||||||||
|
ואחר תסיר ממנו רביעי וישאר ד' זהו ה' ושלישי | ||||||||||||||||||||||||||||||||
|
ואחר תסיר ממנו החומש וישאר ד' זהו ה' | ||||||||||||||||||||||||||||||||
|
וצריך לקח' זה החשבונות ג' פעמים ואז יהא השליש שלם | ||||||||||||||||||||||||||||||||
|
ועתה קח ח' ג' פעמי' זהו ד"ב | ||||||||||||||||||||||||||||||||
|
קח ו' ג"פ זהו ח"א | ||||||||||||||||||||||||||||||||
|
קח ה' ושלי' ג"פ זהו ו"א | ||||||||||||||||||||||||||||||||
|
קח ה' ג"פ זהו ה"א | ||||||||||||||||||||||||||||||||
|
סך הכל ג"ז | ||||||||||||||||||||||||||||||||
|
ועתה הסר ג"פ ד"ב מג"ז וישאר א' נמצא ש[......] ראובן א' | ||||||||||||||||||||||||||||||||
|
והסר ג"פ ח"א מג"ז וישאר ט"א זה סך שמעון | ||||||||||||||||||||||||||||||||
|
והסר ו"א ג"פ מג"ז וישאר ה"ב זהו סך לוי | ||||||||||||||||||||||||||||||||
|
והסר ה"א ג"פ מג"ז וישאר ח"ב זהו סך יודא | ||||||||||||||||||||||||||||||||
|
הכל ג"ז והדג נקנה בעד ז"ג | ||||||||||||||||||||||||||||||||
|
ודוק ותמצא | ||||||||||||||||||||||||||||||||
|
ד הנה ג' אנשים הולכי' על השוק ראובן שמעון ולוי לקנות דבר והנה ראובן אמר אתן כל אשר לי וכל אחד מכם יתן הג' שבכיסו | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
ועתה אשכילך הדרך | ||||||||||||||||||||||||||||||||
|
הנה יש לך ג' אנשי' ראובן שמעון ולוי ראובן שואל שליש ושמעון ששית ולוי תשיעי' נגדו | ||||||||||||||||||||||||||||||||
|
כתוב ג' אותיו' לפי שאילת' כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וקח חשבון המועט תקח ממנו השלישי' וישאר ג' נגד בני החיד' זהו ד' וחצי | ||||||||||||||||||||||||||||||||
|
וכותבו תחת הג' הד' וחצי כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וקח חשבון המועט שתקח ממנו הששית [14]וישאר ג' כנגד בני החידה וזהו ג' וג' חומשיהו | ||||||||||||||||||||||||||||||||
|
ותכתבהו תחת הו' כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
ותקח חשבון המועט שכשתיקח התשיעי' וישאר ג' כנגד בני החידה זהו ג' וג' שמניות | ||||||||||||||||||||||||||||||||
|
ותכתבהו ג"כ תחת הט' כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
ועתה קח חשבון המועט שתמצא בו חשבון שלם נגד אותן חלקי' שברים שיש לך | ||||||||||||||||||||||||||||||||
|
כגון חצי חמישי' שמיני' עתה קח חשבון שתמצא בו חצי שלם זהו ב' | ||||||||||||||||||||||||||||||||
|
וקח חשבון שתמצא חמישי' שלם זהו ה' | ||||||||||||||||||||||||||||||||
|
וג"כ קח חשבון המועט שתמצא בו שמיני' שלם זהו ח' | ||||||||||||||||||||||||||||||||
|
תכפול ב' על ה' ויהיה עשרה כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
בזה תמצא שניהם חצי שלם וחמישי' שלם | ||||||||||||||||||||||||||||||||
|
עתה תכפול ותאמר יפ"ד דהיינו חצי ח' זהו מ' כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
בזה תמצא חצי שלם חמישי' שלם שמיני' שלם | ||||||||||||||||||||||||||||||||
|
ובדו' לפכול ה' עם העשר' נגד חלקי שברי' דהן ג' שמי' ואז היה עולה כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
אך היית מצוא יותר מצרכך כי כמה תמצא חשבון כמו ב"פ | ||||||||||||||||||||||||||||||||
|
ולעולם קח חשבון המועט תפשת מרובה לא תפשת תספת מועט תפסת[15] | ||||||||||||||||||||||||||||||||
|
ועתה כפול המ' על שכתוב תחת כל אחד | ||||||||||||||||||||||||||||||||
|
הנה מצאת תחת ראובן ד' וחצי כפול 0'ד' על ד' וחצי ויעלה כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וכפול 0"ד על שכתוב תחת שמעון דהיינו ג' וג' חומשי' ויעלה כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וכפול 0'ד' על שכתוב תחת לוי דהיינו ג' וג' שמיניו' ויעלה כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
עת' חבר אילו ג' חשבונות יחד ויעלה כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וזהו המורה את החידה | ||||||||||||||||||||||||||||||||
|
כפול 0ח"א ב' פעמי' ויעלה 0ו"ג ונכיהו מן המורה את החידה שהוא טה"ד ויוותר לך ט"ט כך מעות יש לראובן | ||||||||||||||||||||||||||||||||
|
ואח"כ כפול ב"פ דד"א והוא הייה כפול לשמעון ויעלה חח"ב נכיהו מן המורה ויוותר לך אז"א כך מעות יש לשמעון | ||||||||||||||||||||||||||||||||
|
ואח"כ כפול ב"פ הג"א שהוא כפול לוי ויעלה 0ז"ב נכיהו מן המורה ויוותר לך טח"א כך מעות יש ללוי | ||||||||||||||||||||||||||||||||
|
עתה מצאת הכל לראובן ט'ט' ולשמעון אז"א וללוי טח"א | ||||||||||||||||||||||||||||||||
|
והמבין יבין | ||||||||||||||||||||||||||||||||
Find a Quantity Problems - Whole from Parts |
|||||||||||||||||||||||||||||||||
| Tree | |||||||||||||||||||||||||||||||||
|
ה אילן התקוע בארץ שלישיתו חמישיתו ותשיעיתו ונותר למעלה מן הארץ י' אמות כמה הית | ||||||||||||||||||||||||||||||||
|
והא לך דמות אשר תעריך כתוב כזה דהיינו נגד החלקי' ששאלת | ||||||||||||||||||||||||||||||||
|
עתה שים דעתך [16]למצא חשבון המועט שנמצא בו החלקי' ששאלת שליש שלם חמישי' שלם תשיעי' שלם | ||||||||||||||||||||||||||||||||
|
וכה תאמר ג"פ ה' היינו ה"א ט' פעמי' ה"א יעלה הג"א | ||||||||||||||||||||||||||||||||
|
ואינך צריך כ"כ כי תמצאנה בה"ד שהו שליש מן הג"א | ||||||||||||||||||||||||||||||||
|
קח המועט ולא המרובה | ||||||||||||||||||||||||||||||||
|
תחסור מן ה"ד כל החלקי' ששאלת דהיינו שלישי' חמישית תשיעי' | ||||||||||||||||||||||||||||||||
|
שליש ה"ד ה"א חמישי' ט' תשיעי' ה' תסרם מן המורה שהיה ה"ד ונותר ו"א | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
עתה כפול האמות הנותרי' למעלה מן הארץ והם 0"א על המורה שהיה ה"ד ויעלה 0ה"ד | ||||||||||||||||||||||||||||||||
|
עתה [חלוק ממנו][17] ו"א הנותרי' [בשער החילוק פי' כמה פעמים יש ו"א ב0'ה'ד'] ויעלה החילוק ח"ב וב' חלקי' שו"א מהן עושי' חלק שלם | ||||||||||||||||||||||||||||||||
|
וכן כל האילן ח"ב אמו' וב' חלקי' שו"א מהן עושין חלק שלם | ||||||||||||||||||||||||||||||||
| Lance | |||||||||||||||||||||||||||||||||
|
ו' הנה רומח לפניך ובא אחד ותוקעו בארץ חציו של כל הרומח ובא אחד והגביה שלישיתו של כל הרומח ובא אחד ותוקעו רביעיתו של כל הרומח ובא אחד והגביה שישיתו של כל הרומח ולאחר מן הארץ הגבהה וזה הגביה הנמוך נותר למעלה מן הארץ א'א' אמות כמה אמות ארכו של כל הרומח | ||||||||||||||||||||||||||||||||
|
וזה לך הדרך | ||||||||||||||||||||||||||||||||
|
כתוב נגד החלקי' ששאלת נגד החצי ב' נגד השליש ג' נגד רביעי' ד' נגד הששית ו' | ||||||||||||||||||||||||||||||||
|
וכתוב עליו א'א' אמות הנותרי' כזה | ||||||||||||||||||||||||||||||||
|
וקח החשבון המועט שתמצא בו אילו שלם דהיינו ב"א וזה המורה | ||||||||||||||||||||||||||||||||
|
הסיר מב"א החציה וישאר ו' | ||||||||||||||||||||||||||||||||
|
הוסיף השליש מב"א על הו' [דהיינו ד'] ויהיה 0"א | ||||||||||||||||||||||||||||||||
|
הסיר הרביע מב"א [דהיינו ג'] מ0"א וישאר ז' | ||||||||||||||||||||||||||||||||
|
הוסיף הששית [של][18] ב"א [דהיינו ב'] על ז' ויהיה ט' | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
אות' [ט'] כתוב בצד אחר ויהיו עיניך רואות את פני מוריך [19] שהוא ב"א | ||||||||||||||||||||||||||||||||
|
וכפול עליו הא"א הנותרי' למעלה מן הארץ ויעלה כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
תחלוק ממנו [בשער החילוק] מה שנותר לך מן המורה שלאחר שחסרת והוסף כל החלקי' זהו ט' כמה פעמים ט' יש בבג"א זהו ד"א פעמי' ונותרי' ו' שאינ' מגיעי' לכלל ט' | ||||||||||||||||||||||||||||||||
|
וכן אורך הרומח ד"א אמו' ו' חלקי' שט' מהן עולין חלק שלם דהיינו אמה | ||||||||||||||||||||||||||||||||
| This is the rule - when you say: add to it one-third, or one-fifth, or one-quarter, or as much as you want and it is so and so, how much was it originally?
|
זה הכלל כשתאמר שים שליש עליו או חומש או רביע או כל מה שתרצה ויהיה כך וכך כמה היה בתחילה | ||||||||||||||||||||||||||||||||
| I will show you the way to proceed: | אראה לך הדרך אשר תלך בה | ||||||||||||||||||||||||||||||||
| Always subtract from the specified number a fraction [whose denominator is smaller by one than] what you intended to add to the unknown number.
|
[20]לעולם הסר מן החשבון המפורשי' חלק אחד יותר מחשבון הנעלם שדעתך לצרף עליו | ||||||||||||||||||||||||||||||||
|
כגון אם תאמר עשה שליש עליו ויהיה ה' זהו המפורש כמה היה בתחילה | ||||||||||||||||||||||||||||||||
|
אז הסר מן | ||||||||||||||||||||||||||||||||
|
וכשתעשה עליו שליש יהיה ה' | ||||||||||||||||||||||||||||||||
|
או אם תאמר עשה שביעי' עליו ויהיה ג' זהו ג' המפורש | ||||||||||||||||||||||||||||||||
|
אז הסר מג' המפור' שמי' ומה שנשאר הוא הסכום מה שהיה בתחילה | ||||||||||||||||||||||||||||||||
|
ואת"ל אם אמת חשבת צרוף שביעי' על הנשאר ויהיה ג' | ||||||||||||||||||||||||||||||||
| And so on do as I showed you. | וכן לעולם כשאר | ||||||||||||||||||||||||||||||||
| But, if you wish to say: subtract one-third and so and so remains, or subtract as much as you want and so and so remains, how much was it originally?
|
אבל אם ת"ל כשתקח שליש ממנו וישאר כך וכך או תיקח ממנו כל מה שתרצה וישאר כך וכך כמה שהיה בתחילה | ||||||||||||||||||||||||||||||||
| Divide the remaining number by a [denominator] smaller by one than that of the fraction you subtract, then add the fraction to the remainder, and you will find how much it was originally.
|
אז תחלק | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
| Well | |||||||||||||||||||||||||||||||||
|
ז' שאלה הנה לך בור שמימיו נכנסי' בו בג' קני' ויוצאי' ממנו דרך ב' קני' ומהאח' מג' קנים שמימיו נכנסי' בו היה הבור מתמלא מששית היום אם לא היו יוצאין מן הבור מים כלל | ||||||||||||||||||||||||||||||||
|
תשובה בעשירי' היום מתמלא | ||||||||||||||||||||||||||||||||
|
ואשכילך הדרך כיצד | ||||||||||||||||||||||||||||||||
|
קנה האחד שממלא הבור בששי' היום יכול למלא ששה בורות ביו' אחד | ||||||||||||||||||||||||||||||||
|
והשני שממלא הבור בחמישי' היום יכול למלא חמשה בורות ביום אחד | ||||||||||||||||||||||||||||||||
|
והשלישי שמתמלא הבור ברביעי' היום יכול למלא ד' בורו' ביום אחד | ||||||||||||||||||||||||||||||||
|
הרי ט"ו בורות שג' קני' הללו ממלאי' ביום אחד אם [21]לא היו אלו ב' קני' מריקי' | ||||||||||||||||||||||||||||||||
|
ובכמה הן מריקי' | ||||||||||||||||||||||||||||||||
|
האחד המריק' בחצי היום ממריקי' ב' ליום אחד | ||||||||||||||||||||||||||||||||
|
והשני שממריקי' בשלישי' היום ממריק ג' ליום אחד | ||||||||||||||||||||||||||||||||
|
הרי ה' בורות שאילו ב' קני' ממריקי' ביום אחד | ||||||||||||||||||||||||||||||||
|
ועדיין נשארו י' בורות שהג' ממלאי' ביום אחד כשהב' מריקי' | ||||||||||||||||||||||||||||||||
|
נמצא שהבור מתמלא בעשירי' היום | ||||||||||||||||||||||||||||||||
|
ובזה תוכל להבין כל כזה וכיוצא בזה | ||||||||||||||||||||||||||||||||
| Barrel | |||||||||||||||||||||||||||||||||
|
כגון ח' אם ישאל השואל יש כאן חבית של ג' ברזות שהוא זב ממנו דרך ברזא האחד זב היא ביום שלם ודרך ברזא השני' זב היא בחצי היום ודרך ברזא השלישי היא בשליש יום וכשהן זבין כולן כאחד בכמה החבית יוצא | ||||||||||||||||||||||||||||||||
|
תשובה שבשישי' היום יוצא | ||||||||||||||||||||||||||||||||
|
היאך הברזא שהוא זב ממנו ביום שלם מריק' חבית אחת ביום אחד | ||||||||||||||||||||||||||||||||
|
והשני שהוא זב בחצי יום מריקה ב' חביות ביום אחד | ||||||||||||||||||||||||||||||||
|
והשלישי שהוא מריקה בשליש היום מריק' ג' חביות [ביום אחד] | ||||||||||||||||||||||||||||||||
|
ס"ה כשמריקי' יחד מריקי' ו' חביות ביום אחד | ||||||||||||||||||||||||||||||||
|
נמצא שמתרוקן בשישית היום | ||||||||||||||||||||||||||||||||
|
ט' אם ישאל השואל הנה בחבית ג' ברזות האחד כשזב לבדו מריקו בשעה והשני לבד ממריקו בב' שעו' והשלישי מריקו בג' שעות וכשיזובו כולם כאחד בכמה מריק' | ||||||||||||||||||||||||||||||||
|
אבקש לך דמיונות [בחבית המחזיק][22] י"ב הינין שממורק בחצי שעה ובחלק א"א שבחצי שעה | ||||||||||||||||||||||||||||||||
|
וכה תעשה | ||||||||||||||||||||||||||||||||
|
אמור בתחילה הברזא שממריק בשעה כמה ממריק בחצי שעה ו' הינין | ||||||||||||||||||||||||||||||||
|
והממריק בב' שעות כמה ממריק בחצי שעה ג' | ||||||||||||||||||||||||||||||||
|
והממריק בג' שעות ממריק בחצי שעה ב' הינין | ||||||||||||||||||||||||||||||||
|
נמצא שג' ברזות המריקי' א' ב' ג' מריקי' בחבית המחזיק י"ב הינין בחצי י"א היני' | ||||||||||||||||||||||||||||||||
|
כמה נשאר עוד הין נמצא שאותו הין שאותו ממריק בחלק י"א שבחצי שעה | ||||||||||||||||||||||||||||||||
| Note well and you will understand. | ודוק ותבין | ||||||||||||||||||||||||||||||||
| Fountain | |||||||||||||||||||||||||||||||||
|
י' ועוד שאלו ד' נהרות רצים אל מעיין אחד הראשון ממלאו ביום אחד והב' בב' והג' בג' והד' בד' ואם רצו כולם ביחד בכמה מתמלא | ||||||||||||||||||||||||||||||||
|
עשה על דרך זה | ||||||||||||||||||||||||||||||||
|
אמור אחד חצי שליש רביע [23]אנה ימצאון [ר"ל על דרך המועט כדלעיל דהיינו] בי"ב האחד | ||||||||||||||||||||||||||||||||
|
נמצא בי"ב ימי' ימלאו כ"ה מענייות | ||||||||||||||||||||||||||||||||
|
כיצד הראשון ממלאו' בי"ב ימים י"ב מענייות | ||||||||||||||||||||||||||||||||
|
השני בי"ב ימי' ו' מעיינות | ||||||||||||||||||||||||||||||||
|
השלישי בי"ב ימי' ד' מעיינות | ||||||||||||||||||||||||||||||||
|
הרביעי' בי"ב ימי' ג' מעיינות | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
א"כ כ"ה מעיינות בי"ב ימי' מעיין אחד בכמה | ||||||||||||||||||||||||||||||||
|
אז כפול א' בי"ב ויעלה י"ב חלקי' בשער החילוק [בכ"ה פי' כמה פעמים כ"ה יש בי"ב כנ"ל אש'] נמצא שמעיין האחד מתמלא בי"ב חלקי' שכ"ה מהן יום שלם | ||||||||||||||||||||||||||||||||
|
לידע כמה חלק מים של כל נהרות לראשון כפול י"ב בא' ויעלה י"ב חלקי' [בשער החילוק] בכ"ה נמצא שמימיו י"ב חלקי' מכ"ה | ||||||||||||||||||||||||||||||||
|
כפול ו' לשנים בא' ויעלה ו' חלקי' [בשער החילוק] בכ"ה הרי ו' חלקי' מכ"ה | ||||||||||||||||||||||||||||||||
|
לשלישי כפול ד' בא' | ||||||||||||||||||||||||||||||||
|
לרביעי ג' בא' | ||||||||||||||||||||||||||||||||
|
ודוק ותבין | ||||||||||||||||||||||||||||||||
Multiple Quantities Problems - Selling Eggs |
|||||||||||||||||||||||||||||||||
|
י"א חוד חידה ג' נשי' מוכרות ביצי' לאחת יש י' ביצים לשנית יש ל' ולשלישי' נ' וכל אחת תתן ביצה בחליש אחד כמו חבירת' ויפדו מעות שוות | ||||||||||||||||||||||||||||||||
|
תשובה כל אחת תתן ז' בחליש וכל מה שנותר על השביעיות תתן ביצה אחת בעד ג' חלישים | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
ואם היית' ארבע לרביעי' לה ע' ביצים והחשבון כמו כן | ||||||||||||||||||||||||||||||||
Proportional Division - Inheritance |
|||||||||||||||||||||||||||||||||
|
י"ב שאלה אם נפלה ירושה לפני ג' אחים הראשון לקח כל מה שירצה וכן השני וכן השלישי | ||||||||||||||||||||||||||||||||
|
תשובה הכל היה כ"ד הראשו' לקח י"ג והשני ז' והשלישי ד' | ||||||||||||||||||||||||||||||||
|
והילך המורה את החידה | ||||||||||||||||||||||||||||||||
|
אם הם רק ג' אז קח לאחרון ג' ואחד יותר הרי זהו ד' | ||||||||||||||||||||||||||||||||
|
ולאמצעי קח כפלים כמו לאחרון וזהו ח' רק אחת תסיר ויהיה ז' | ||||||||||||||||||||||||||||||||
|
ולראשון קח כפלים כמו לאמצעי דהיינו י"ד רק אחת תסיר | ||||||||||||||||||||||||||||||||
|
וכן לעולם כמה הן אז קח לאחרון כמניין כולם וא' יותר ואח"כ כפול המבוקש ותסיר אחת | ||||||||||||||||||||||||||||||||
|
וכן אם הם ד' | ||||||||||||||||||||||||||||||||
|
קח לאחרון ד' וא' יותר וזהו ה' | ||||||||||||||||||||||||||||||||
|
ולשלישי י' ואחד תסיר זהו ט' | ||||||||||||||||||||||||||||||||
|
לשני י"ח ואחד תסיר זהו י"ז | ||||||||||||||||||||||||||||||||
|
לראשון ל"ד ואחד תסיר זהו ל"ג | ||||||||||||||||||||||||||||||||
|
בין תבין את אשר לפניך[24] | ||||||||||||||||||||||||||||||||
Payment Problem - Digging a Hole |
|||||||||||||||||||||||||||||||||
|
[25]יג[26] שוכר את הפועל לחפור בור ארוכה י"ז אמות ברוחב ז' אמות בעד ל"ג זהו' והפועל חפר ג' אמו' במשך י"ז כמה שכרו | ||||||||||||||||||||||||||||||||
|
תשובה כפול בתחילה בשער הכפל ז"פ י"ז ויעלה טא"א | ||||||||||||||||||||||||||||||||
|
נמצא ששכר את הפועל לחפור קי"ט אמו' ברוחב אמה בעד ל"ג זהו' | ||||||||||||||||||||||||||||||||
|
והפועל חפר ג' אמות במשך י"ז כפול ג' בי"ז ויעלה א"ה | ||||||||||||||||||||||||||||||||
|
נמצא שלא חפר רק נ"א אמות והיה לו לחפור קי"ט אמות | ||||||||||||||||||||||||||||||||
|
ואח"כ כתוב קי"ט אמו' ולמטה הימנו כתוב נ"א אמו' כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
וכפול בשער הכפל א"ה על ג'ג' ויעלה תרפ"ג | ||||||||||||||||||||||||||||||||
|
[חלוק ג"חו"א] לקי"ט פי' כמה פעמי' קי"ט איתא בתרפ"ג ותמצא י"ד פעמי' קי"ט דהיינו טא"א וי"ז חלקי' שלא הגיעו לקי"ט שהוא חלק שלם | ||||||||||||||||||||||||||||||||
|
נמצא שכר הפועל י"ד זהו' וי"ז החלקי' שקי"ט מהן חלק זהוב שלם | ||||||||||||||||||||||||||||||||
Find a Quantity Problem - Stolen Purse |
|||||||||||||||||||||||||||||||||
|
יד אדם הפקיד לחבירו כיסו מלא מעות ונגנב בפשיעה והמפקיד והנפקד אינם יודעי' כמה היו המעות אשר בו אלא המפקיד זוכר כשמנה המעות בב"ב נשאר א' בג"ג נשאר א' בד'ד' נשאר א' בה"ה נשאר א' בו'ו' נשאר א' בז' יצא מכוון [והנה חוד כמה היו המעות הללו] | ||||||||||||||||||||||||||||||||
|
תשובה | ||||||||||||||||||||||||||||||||
|
והנה אשכילך הדרך היאך תעשה | ||||||||||||||||||||||||||||||||
|
כתוב כנגד כל מניין השאלה מספר המעוט שתצא בו השאלה פי' שאלת מניין הנמנה בב'ב' וישאר א' נגד [.] זה כתוב ב' ושאלת מניין הנמנה ג'ג' נגד זה כתוב ג' וששאלת מניין הנמנה ד'ד' נגד זה כתוב ד' וששאלת מניין הנמנה ה'ה' נגד זה כתוב ה' ושאלת מנין הנמנה ו'ו' נגד זה כתוב ו' | ||||||||||||||||||||||||||||||||
|
ואח"כ כפול ב' על ג' ויעלה ו' | ||||||||||||||||||||||||||||||||
|
כפול ו' על ד' ויעלה ד'ב' | ||||||||||||||||||||||||||||||||
|
כפול ד'ב' על ה' ויעלה 0ב"א | ||||||||||||||||||||||||||||||||
|
כפול 0ב"א על ו' ויעלה 0ב"ז פי' עשרי' וז' מאות זהו מספר המתחלק לב' ולג' ולד' ולה' ולו' | ||||||||||||||||||||||||||||||||
|
ובהוסיפך עוד אחד שיהיה א"ב אז כשתחלקהו לבגדה"ו ישאר בכל המניין אחת וכשתחלקהו לז'ז' יצא [.] מכוון | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
וכן אם ישאל השואל מספר המתחלק לבגדהוז"ח וישאר א' ובט' יצא מכוון | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
אזי כפול ז"ח ויעלה ו"ה | ||||||||||||||||||||||||||||||||
|
ואח"כ כפול ו"ה על 0ב"ז והעולה הוא המתחלק לבגדהוז"ח | ||||||||||||||||||||||||||||||||
|
[27]ובהוסיפך אחת עליו ישאר א' בכל המניין וב' יוצא מכוון | ||||||||||||||||||||||||||||||||
|
ואם ישאלך מניין הנותרי' ג' בכל המנייני' אזי תוסיף ג' על העולה אחר כופלך מספרי' המועטי' | ||||||||||||||||||||||||||||||||
|
וכן אם ישאלך [מניין הנותר] ד' אזי תוסיף ד' וכן לעולם | ||||||||||||||||||||||||||||||||
Find a Quantity Problem - How Much Problem - Amount of Money |
|||||||||||||||||||||||||||||||||
|
ט"ו שאלה ממון הוספנו עליו מחציתו שלישיתו רביעיתו חמישיתו שישיתו והכל הוא מ' כמה היה הממון | ||||||||||||||||||||||||||||||||
|
בתחילה אשכילך את אשר בלבבי קח מספר המועט המתחלק לחצאין לשליש ולרביע ולחומשי' ולששין וזהו 0"ו פי' ששים | ||||||||||||||||||||||||||||||||
|
ותוסיף על ששים כל החלקי' ששאלת החצי הוא ל' והשליש הוא עשרי' והרביעי הוא ט"ו והחמשי' י"ב והששית י' וצרפם הכל יחד ויהיה פ"ז חבור פ"ז עם ששים ויעלה קמ"ז | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
נמצא אם היו שואלי' אותך ממון שהוספת עליו מחציתו שלישיתו ורביעיתו חמשיתו ששיתו ובין הכל קמ"ז כמה תחילת הממון היינו משיבי' תחילתו ששים ועתה שהוא בין הכל רק א' כמה היה תחילתו | ||||||||||||||||||||||||||||||||
|
אז כתוב אותן קמ"ז בטור העליון ורחוק ממנו קצת כתוב הששים ותחת הס' כתוב המ' שאנו שואלי' ויהיה כך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
כפול 0"ד ב 0"ו שעליהם ויעלה 00ד"ב פי' כ"ד מאות | ||||||||||||||||||||||||||||||||
|
תחלק כמה פעמי' זד"א בכ"ד מאות ותמצא שיש בו י"ו פעמי' זד"א ונותר מ"ח חלקי' (חלקי') קטני' שאינן מגיעי' לזד"א | ||||||||||||||||||||||||||||||||
|
נמצא שתחילת הממון י"ו שלמי' ומ"ח חלקי' שזד"א עושי' חלק שלם | ||||||||||||||||||||||||||||||||
|
ואם תחפוץ לשקול אם חשבונך מכוון אז כפול זד"א על י"ו פי' כמה י"ו פעמי' זד"א ויעלה בהג"ב פי' ב' אלפי' וג' מאות ונ"ב | ||||||||||||||||||||||||||||||||
|
חבר עמהם מ"ח הנותרי' למעלה שלא עלו לזד"א ויהיה 00ד"ב פי' כ"ד מאות | ||||||||||||||||||||||||||||||||
|
תוסיף עליהם החציה השלישי' והרביעי' החמישי' והששי' וחבור הכל עם הכ"ד מאות | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
ואח"כ כפול 0"ד פי' מ' פעמי' בזד"א | ||||||||||||||||||||||||||||||||
|
ואם תמצא מכוון מה שיעלה לך אחר שתכפול מ' בקמ"ז כמו החשבון שמצאת [28]בהוסיפך אבגדה"ו על כ"ד מאות אז חשבונך מכוון ואם לאו ודאי
טעית | ||||||||||||||||||||||||||||||||
|
והבמין יבין | ||||||||||||||||||||||||||||||||
Divide a Quantity - Loans Repayment |
|||||||||||||||||||||||||||||||||
|
י"ו אם ישאלך השואל הנה ראובן שמעון הלוי' שני חובות ראובן הלויה ל"ז זהו' ועלה על כל זהב פשי' לשבוע ועמדו נ"ה שבועו' ושמעו' הלוה לאותו חייב כ"ג זהו' ועמדו ל"ג זהו' ואח"כ בא הבעל חוב ואמ' להן אתן לכם ג' זהו' מן הכל ואתם התפשרו יחד | ||||||||||||||||||||||||||||||||
|
ואשכילך הדרך אשר תמצא בו כמה מגיע לראובן וכמה מגיע לשמעון מן הי"ג זהו' כאשר קבלתי מרבי' | ||||||||||||||||||||||||||||||||
|
חשבון כמה רבותו של ראובן שהוא ל"ז על נ"ה ויעלה הג0"ב פשי' פי' ב' אלפי' ול"ה זה היה ריבית שהיה שייך מדינה לראובן | ||||||||||||||||||||||||||||||||
|
ואח"כ כפול הכ"ג זהו' של שמעון בל"ג שבועות ויעלה טהג"ז שהיה ראוי לשמעון | ||||||||||||||||||||||||||||||||
|
ואח"כ חבר טה"ז עם הג0"ב ויעלה דט0"ב וזהו המורה את החידה | ||||||||||||||||||||||||||||||||
|
אח"כ כפול הי"ג זהו' על הג0"ב שהיה רבי' שהיה שייך | ||||||||||||||||||||||||||||||||
|
אח"כ נכהו מן המורה שהוא דטז"ב פי' כמה פעמי' דטז"ב ב' ההדו"ב ותמצא שיש בו ט' פעמי' ונותרי' ט' וג' מאות ואלף שלא יעלו למניין דטז"ב | ||||||||||||||||||||||||||||||||
|
נמצא של ראובן שייך מן הי"ג זהו' ט' זהו' ואלף וש"ט חלקי' שלא הגיעו לכלל דטז"ב | ||||||||||||||||||||||||||||||||
|
ואם תרצה לידע כמה מגיע לשמעון על הדרך שאמרנו על ראובן אז כפול י"ג בטה"ז שהוא רביתו של שמעון ויעלה זוח"ט | ||||||||||||||||||||||||||||||||
|
נכיהו מן המורה שהוא דטז"ב פי' כמה פעמי' דטז"ב בזוח"ט ותמצא שיש בו ג' פעמי' ונותרי' אלף ותפ"ה חלקי' שדטז"ב מהן עושין חלק שלם דהיינו זהב | ||||||||||||||||||||||||||||||||
|
נמצא ששייך לשמעון ג' זהו' והחד"א חלקי' שדטז"ב מהן זהב שלם | ||||||||||||||||||||||||||||||||
|
חבר החד"א עם אלף וש"ט הנותרי' בראובן ויעלה דטז"ב | ||||||||||||||||||||||||||||||||
|
ואם תחפוץ לידע חשבון בצימצום אז חלק הי"ג זהו' לפשיטי' [29]ואח"כ כפול בהן ההדו"ב ריביתו של ראובן או דטז"ב רביתו של שמעון ואז יתחלק דטז"ב לחלקי' פשוט' | ||||||||||||||||||||||||||||||||
|
ודוק | ||||||||||||||||||||||||||||||||
Multiple Quantities - Weights |
|||||||||||||||||||||||||||||||||
|
י"ז אם ישאלך אדם איך תמצא ארבע משקולות שמשקל כולן רק ארבעי' ואת' תוכל לשקול בהן הן רב הן מעט עד ארבעי' כמה משקל כל אחד בפני עצמו או אם ה' משקל שמשקלם קכ"א ואתה תוכל לשקול בהן הן רב הן מעט כמה משקל כל אחד בפני עצמו | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
כה תעשה | ||||||||||||||||||||||||||||||||
|
אם תחפוץ להוסיף משקלות הראשון משקלו לטרא השני משקלו ג' לטרין השלישי משקלו ט' לטרי' החמשי פ"א ליטרין הרביעי כ"ז לטרין | ||||||||||||||||||||||||||||||||
|
וככה תעשה כתוב בתחילה א' משקלו של משקל הראשון ואח"כ כתוב כך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
חברם יחד ויהיה ב' תוסיף עוד א' עליה ויהיה ג' זהו משקל השני | ||||||||||||||||||||||||||||||||
|
אח"כ כתוב כך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
חברם יחד ויהיה ח' תוסיף עוד אחת ויהיה ט' זהו משקל השלישי | ||||||||||||||||||||||||||||||||
|
אח"כ כתוב כך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
חברם יחד ויהיה כ"ו תוסיף עוד אחת ויהיה כ"ז זהו משקל רביעי | ||||||||||||||||||||||||||||||||
|
אח"כ כתוב כך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
חברם יחד ויהיה פ' תוסיף עוד אחת ויהיה פ"א זהו משקל חמישי | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
ס"ה קכ"א | ||||||||||||||||||||||||||||||||
|
ועל דרך זה תוכל להוסיף | ||||||||||||||||||||||||||||||||
|
או נלך אצל דרך זה למשקל הראשו' קח את אחת לשנים גפ"א לשלישי' ג'פג' לרביעי' גפ"ט לחמישי' ג"פ כ"ז וכן לעולם וסימניך ושלישי' על כולו פי' ג"פ משקל הראשון | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
Divide a Quantity - Money |
|||||||||||||||||||||||||||||||||
|
י"ח אם תרצה לחלק ה"פ לשליש ולרביע ולא ישאר מהן כלום | ||||||||||||||||||||||||||||||||
|
אמור תחילה שליש ורביע בכמה ימצאון בי"ב השליש הוא ד' הרביע הוא ג' חברם יחד הרי ז' וזהו המורה | ||||||||||||||||||||||||||||||||
|
ואם תרצה לידע בכמה מגיע לזה שיש לו השליש שהוא ד' כפול ד' בה' פשי' ויעלה כ' תחלק בז' ותמצא בו ב' פ"ז ועודף ו' חלקי' שז' מהן חלק שלם הרי שיש לזה ב' פשי' שלימי' וו' שברי' שז' מהן חלק שלם | ||||||||||||||||||||||||||||||||
|
ומי שיש לו הרביעי כפול ג' בה' ויעלה ט"ו תחלק ממנו ו' ויעלה ב' פשי' וחלק אחד שז' פשי' שלם | ||||||||||||||||||||||||||||||||
|
הרי שנחלקו ה' [פשוטים] [30]לג' ולד' ולא נשאר מהן כלום | ||||||||||||||||||||||||||||||||
|
וכן אם בידך י"ב פשי' ותרצה לחלקם לחצאין לשליש ולרביעי ולא ישאר כלום | ||||||||||||||||||||||||||||||||
|
אמור חצי שליש ורביע אָנה ימצאון בי"ב החצי ו' השליש ד' הרביע ג' צרוף יחד הרי י"ג וזהו המורה | ||||||||||||||||||||||||||||||||
|
אח"כ כפול ו' שהוא החציה בי"ב | ||||||||||||||||||||||||||||||||
|
אח"כ כפול השליש שהוא ד' בי"ב ויעלה מ"ח תחלק ממנו י"ג תמצא ג' וט' שברי' מי"ג | ||||||||||||||||||||||||||||||||
|
וכן כפול ג' בי"ב ויעלה ל"ו חלק מהן י"ג ותמצא ב' וי' שברי' מי"ג | ||||||||||||||||||||||||||||||||
|
וכן לעולם | ||||||||||||||||||||||||||||||||
Find a Quantity Problem - Whole from Parts - Fish |
|||||||||||||||||||||||||||||||||
|
י"ט הרי יש לפניך דג שמשקל גופו | ||||||||||||||||||||||||||||||||
|
תשובה מנה מספר המתחלק לגדה"ו וזהו ס' | ||||||||||||||||||||||||||||||||
|
וכשתסיר מס' גדה"ו פי' השליש והרבי' והחומש והשישי' ותצרפם יחד ויעלה נ"ז ועודף ג' זהו המורה | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
כפול י' בס' ויעלה ת"ר | ||||||||||||||||||||||||||||||||
|
תחלק ממנו ג' ותמצא בו ר' פעמי' ג' | ||||||||||||||||||||||||||||||||
|
וכן כל משקלו של דג ששאלנו מאתם | ||||||||||||||||||||||||||||||||
Multiple Quantities - Selling Cloth |
|||||||||||||||||||||||||||||||||
|
כ' שאלה אדם נתן לג' בניו [ל'] אמות בגד למכור והאחד מכר האמה עבור ד' זהו' והשני עבור ה' והג' עבור ו' זהו' וכולם מביאי' מעות שוות זה כזה חוד כמה מעות להג' מן המקח וכמה אמות מכר כל אחד | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
תשובה בתחילה אראך כמה שהיה לזה שנתן אמה עבור ד' זהו' | ||||||||||||||||||||||||||||||||
|
אמור תחילה | ||||||||||||||||||||||||||||||||
|
בס' רביעי' ט"ו חמישי' י"ב ששות י' חברם יחד ויהיה ל"ז זהו המורה | ||||||||||||||||||||||||||||||||
|
ואח"כ כפול הט"ו שהוא הרביעי' בל' כמדת הבגד ותמצא ת"נ | ||||||||||||||||||||||||||||||||
|
תחלק ת"ן לל"ז ותמצא בו י"ב פעמי' ל"ז וששה חלקי' של"ז אמה שלימה נמצא שהיה לזה שנתן אמה עבור ד' זהו' י"ב אמות וששה חלקי' של"ז מהן אמה שלימה | ||||||||||||||||||||||||||||||||
|
ואם תחפוץ לידע כמה מעות גבהו לזה שנתן אמה עבור ד' זהובי' | ||||||||||||||||||||||||||||||||
|
[31]י"ב אמות היו לו וששה חלקים של"ז מהן אמה שלימה | ||||||||||||||||||||||||||||||||
|
הרי י"ב ד"פ י"ב עולה מ"ח ומן הו' חלקי' הנותרי' עשה כך | ||||||||||||||||||||||||||||||||
|
חלוק כל זהב בז' תפוחי' ותאמר כך אילו היו הו' חלקי' ל"ז [דהיינו דמיהם של בגד אמה] אז היה דמיהן כ"ח תפוחי' עתה שהם רק ו' כמה הם | ||||||||||||||||||||||||||||||||
|
אז כפול בכ"ח [ויעלה ח'ו'א'] | ||||||||||||||||||||||||||||||||
|
וחלוק אותו לל"ז ותמצא בו ד' פעמי' ל"ז [ועשרים חלקים] של"ז עושי' תפוח שלם | ||||||||||||||||||||||||||||||||
|
נמצא שזה גבה מ"ח | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
לדעת כמה אמו' מכר זה שנתן אמה עבור ה' זהו' עשה כך | ||||||||||||||||||||||||||||||||
|
כפול החומש משישית דהיינו י"ב במניין אמו' הבגד שהם ל' [ויעלה 0'ו'ג'] | ||||||||||||||||||||||||||||||||
|
ותחלק ממנו ל"ז [שהוא] המורה ותמצא בו ט' אמות וכ"ז חלקי' של"ז מהן עושי' אמה שלמה | ||||||||||||||||||||||||||||||||
|
ואם תחפוץ לידע כמה מעות גבה ט' אמות היינו מ"ה זהו' וכ"ז חלקי' | ||||||||||||||||||||||||||||||||
|
אילו היה ל"ז היו נמכרי' בעד ל"ה תפ | ||||||||||||||||||||||||||||||||
|
עשה מכ"א [.] תפוחי' ג' זהו' וחברם יחד עם מ"ה ויהיה מ"ח ויוותרו לך ד' תפוחי' וך' חלקי' של"ז תפוח שלם | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
נמצא שמעו' הראשונות כשיני | ||||||||||||||||||||||||||||||||
|
לדעת המעו' ואמו[ת][32] המוכר אמה עבור ל' זהו' כפול חלק ששי' מס' בל' מניין האמות [דהיינו ל' ויעלה 0'0'ג'] ומן העולה תחלוק ל"ז ותמצא ח' אמות וד' חלקי' של"ז עושי' חלק שלם | ||||||||||||||||||||||||||||||||
|
ולדעת כמה מעותיו ח' פעמי' ו' זהו' היינו מ"ח ד' חלקי' הנותרי' אילו היה ל"ז היו נמכרי' במ"ב תפוחי' עתה שהם רק ד' בכמה כפול ד' במ"ב [ויעלה חו"א] ומן העולה תחלק [ל"ז] זהו' ותמצא ד' תפוחי' וך' חלקי' של"ז תפוח שלם | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
נמצא שאין בין זה לזה [במנין][33] המעות | ||||||||||||||||||||||||||||||||
|
והראשון מכר י"ב אמו' יותר ו' חלקי' ושני מכר ט' אמו' וכ"ז חלקי' והשלישי מכר ח' אמו' וד' חלקי' | ||||||||||||||||||||||||||||||||
| וזהו סימנם | |||||||||||||||||||||||||||||||||
Partnership Problems - for the Same Time - Three Partners |
|||||||||||||||||||||||||||||||||
|
כ"א ועוד שאלה ג' חבירי' רצו לתת בחבורה מ' לטרי' זהו' לראשון יש לו זהב ששוה הלטרי' ג' זהו' לשני ששוה ה' זהו' ולשלישי יש לו זהב ששוה הלטר' ח' זהו' כמה יש כל אחד לטרי' שוה בשוה | ||||||||||||||||||||||||||||||||
|
תשובה עשה מספ' המתחלק לגה"ח כיצד כפול ג' על ה' הרי ט"ו כפול ח' על ט"ו ויעלה ק"כ | ||||||||||||||||||||||||||||||||
|
הסר מק"כ | ||||||||||||||||||||||||||||||||
|
לדעת כמה לטרי' צריך לשום זה שזה שוה ג' זהו' קח השליש מק"כ [34]וזהו מ' כפול מ' על מ' מניין הליטרין ומן העולה תחלק ע"ט | ||||||||||||||||||||||||||||||||
|
וכן לכולם | ||||||||||||||||||||||||||||||||
|
לשני כפול החומש מק"ך במ' | ||||||||||||||||||||||||||||||||
|
לשלישי' כפול מק"כ | ||||||||||||||||||||||||||||||||
|
כמה כבר הארכתי בעניין זה | ||||||||||||||||||||||||||||||||
Multiple Quantities |
|||||||||||||||||||||||||||||||||
| Four Coins | |||||||||||||||||||||||||||||||||
|
כב הרי שיש לפניך ד' מטבעות ששוים מ' פשי' הראשונה שוה החצי והשתות מן השנייה | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
עשה כך | ||||||||||||||||||||||||||||||||
|
הראשונה ששוה החצי והשתו' מן השנייה באיזה מספר נמצאי' חצי ושתות שלמי' בששה החצי מהחצי ג' והשתות א' הרי ד' מן הוי' כאילו אמר הראשונ' ב' שליש מן השני | ||||||||||||||||||||||||||||||||
|
ושלישית[35] ששוה [שליש][36] ורביע ושתות מן הראשון אילו החלקי' בכמה נמצאון בי"ב השליש ד' הרביע ג' השתות ב' כלול יחד הרי ט' הוי כאילו אמר השליש ג' רבי' מן הראשונה | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
[והד'][37] ששוה ד' חומשי' מן (מן) השני אין צריך ביאור דהא מבואר היטב | ||||||||||||||||||||||||||||||||
|
לדעת איך תמצאם החלקי' חלוקי' בפי' הבן איזה חלקי' הזכרנו בשאל' חצי ושתות ובכל מקום שתמצא שתות שליש גם תמצא גם הוזכרנו רביעי' וחומש וכל אילו החלקי' נמצא בששי' נמצאת מטבע שנייה ס' | ||||||||||||||||||||||||||||||||
|
החצי והשתות גם ל' וי' כללם יחד הרי מ' זו היא מטבע הראשונה | ||||||||||||||||||||||||||||||||
|
כמה עודף ס' יותר על מ' כ' זהו' שאמרנו בשאלה והנשאר מן השני עודף על הראשון הוא שני שליש מן השלישי' כי מטבע [שלישי ל'][38] כשתסיר גד"ו פי' שליש רביעי' שישית ממ' תמצא שלישי | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
לדעת מטבע רביעי' תחלק לה' חלקי' נמצא ה' פעמי' ו' ד' חומשי' מל' הרי כ"ד | ||||||||||||||||||||||||||||||||
|
וזהו סדורן מ' ס' ל' כ"ד צרוף אותם יחד הרי קנ"ד זהו המורה את החידה | ||||||||||||||||||||||||||||||||
|
לדעת כמה מטבע ראשונה למלאו' מניין ארבעי' כפול מ' במ' שהוא מניין המעות ומן העולה תחלק קנ"ד ותמצא צורתו כך | ||||||||||||||||||||||||||||||||
|
פי' י' פשי' וששי' [חלקים] שקנ"ד פשי' שלם זהו סך מטבע ראשונ' | ||||||||||||||||||||||||||||||||
|
אח"כ כפול ס' במ' ומן העולה תחלק קנ"ד ויהיה צורתו כך | ||||||||||||||||||||||||||||||||
|
פי' ט"ו פשי' וצ' חלקי' שקנ"ד פשי' שלם זהו סך מטבע שנייה | ||||||||||||||||||||||||||||||||
|
אח"כ כפול ל' על מ' וחלקהו בקנ"ד ויהיה צורתו כך | ||||||||||||||||||||||||||||||||
|
פי' ז' פשי' קכ"ב חלקי' שקנ"ד פשי' שלם זהו סך מטבע ג' | ||||||||||||||||||||||||||||||||
|
אח"כ כפול כ"ד במ' ומן העולה תחלק קנ"ד וצורתו כך | ||||||||||||||||||||||||||||||||
|
פי' ו' פשי' ל"ו חלקי' שקנ"ד פשי' שלם | ||||||||||||||||||||||||||||||||
|
צרוף יחד י' וט"ו וז' וו' הרי ל"ח[39] [40]צרוף יחד החלקי' שתחתיהן ויעלו ח' וג' מאות דהיינו ב"פ קנ"ד וזהו ב' פשי' וד"ק | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
| Sons | |||||||||||||||||||||||||||||||||
|
כ"ג חידה אדם עשיר המחלק נכסיו על פה ואומר לאחד מבניו טול מכיסי זהב בראש ואח"כ טול המעשר מן הנותרי' לשני אמר טול אתה ב' זהו' ועישור נכסי' מן הנותרי' | ||||||||||||||||||||||||||||||||
|
תשובה אמור לפי שהחשבון השבור שבזה הוא עשירי תפחת א' מעשר' ישארו ט' הרי שט' היו הבני' | ||||||||||||||||||||||||||||||||
|
אמור אחר זה ט'פ"ט ויעלה פ"א הרי שפ"א היו הזהובי' | ||||||||||||||||||||||||||||||||
|
ולכל אחד הגיע ט' זהו' | ||||||||||||||||||||||||||||||||
|
וכן לעולם היאך שהיה | ||||||||||||||||||||||||||||||||
Motion Problem - Pursuit |
|||||||||||||||||||||||||||||||||
|
כ"ד אדם שמהלך בכל יו' י' מילין וחבירו מהלך ביום ראשון מיל יום שני ב' מילין וכן בכל ימים מוסיף והולך מיל בכמה ימים מגיע למהלך י' מיל | ||||||||||||||||||||||||||||||||
|
תשובה חבר י' עם י' ויהיה כ' הסר ממנו אחת וישאר י"ט הרי שבי"ט ימים מגיע [לחבירו] | ||||||||||||||||||||||||||||||||
|
וכן לעולם תכפול מהלכו של המהלך קביעיתו והסר אחת ובאילו ימי' הגיעו | ||||||||||||||||||||||||||||||||
|
ואם השני מהלך אגה"ז | ||||||||||||||||||||||||||||||||
|
תחוסר מן המהלך י' וישיגו בי' ימי' | ||||||||||||||||||||||||||||||||
|
ואם הוא מהלך | ||||||||||||||||||||||||||||||||
|
ישיגו [בט'] ימים | ||||||||||||||||||||||||||||||||
|
והא לך סימן לעולם על המהלך אב"ג שתדע בקיצור כמה מילין הלך | ||||||||||||||||||||||||||||||||
Ordering Problem - Stock of Coins |
|||||||||||||||||||||||||||||||||
|
כ"ה אז אם ישאלך אדם הנה צבור מעות מונחי' כאן וכולם הונחו על דרך אבגד"הו | ||||||||||||||||||||||||||||||||
|
תבין בסוף השיטה הזאת ח' | ||||||||||||||||||||||||||||||||
|
אז קח אמצעי' אותה שיט' שהוא חמשה ואמור ה' פעמי' ט' הרי מ"ה וכך המעות מ"ה | ||||||||||||||||||||||||||||||||
|
ואם סוף השיט' [י'] | ||||||||||||||||||||||||||||||||
|
אז קח אחת מאמצעי' השיטה ואמור ה"פ י' הרי נ' ותוסיף עוד חצי שיטה דהיינו [ה'] היינו הכל נ"ה | ||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||
|
נקוט האי כללא בידך | ||||||||||||||||||||||||||||||||
|
כשסוף השיטה בזוגות אז כפול אמצע השיטה על שיטה שלימה ותוסיף חצי שיטה | ||||||||||||||||||||||||||||||||
|
ואם סוף השיטה בפרודות כגו' ז' ט' י"א י"ג ט"ו אז כפול אמצעי' השיטה על כל השיטה ואינך צריך להוסיף | ||||||||||||||||||||||||||||||||
Proportional Division - Three Men Sharing Food |
|||||||||||||||||||||||||||||||||
|
[41]כ"ו חידה שנים הסיבו לאכול לחם האחד יש לו ג' ככרות ולשני יש לו ב' ככרות ובא עוד שלישי ואכל עמהם ובגמר סעודה הלך לו והניח לפני השנים ה' פשי' חוד איך יחלקו אילו השנים הה' פשי' | ||||||||||||||||||||||||||||||||
|
דע והבן כמה שהגיע לכל אחד מן הלחמניות תצטרך לומר כיכר שלם ושני שלישי | ||||||||||||||||||||||||||||||||
|
כמה הפסיד בעל ב' ככרות רק שליש | ||||||||||||||||||||||||||||||||
|
וכמה הפסיד בעל ג' ככרות ככר ושליש | ||||||||||||||||||||||||||||||||
|
נמצא שנתן עבור ה' שלישיות ה' פשי' זה נוטל ארבע פשי' וזה נוטל פשי' | ||||||||||||||||||||||||||||||||
|
סליק | ||||||||||||||||||||||||||||||||
| MS München | |||||||||||||||||||||||||||||||||
| This is not the language of the book, but the language of the late R. Weysil. | אין זה לשון הספר רק לשון מהר"ר ווייזיל ז"ל | ||||||||||||||||||||||||||||||||
| I have found this in another book. | זה מצאתי בספר אחר | ||||||||||||||||||||||||||||||||
|
יחשוב החושב איזה סכום שירצה עד ל"ב והנשאל יתן לו חצי מחשבתו פעם ראשון | ||||||||||||||||||||||||||||||||
| ויאמר לו אם יש בו חצי | |||||||||||||||||||||||||||||||||
|
כגון אם היה מחשבתו ה' ונתן זה לו ב' וחצי דהיינו ז' וחצי | ||||||||||||||||||||||||||||||||
| וכך יאמר לו עשה החצי לאחד שלם ואותו פעם ראשון אשר היה בו מחצה יתן למשמרת | |||||||||||||||||||||||||||||||||
| ואם לא היה בו חצי | |||||||||||||||||||||||||||||||||
| כגון אם היה מחשבתו ד' דהיינו החצי ב' מה טוב ומה נעים | |||||||||||||||||||||||||||||||||
| ואח"כ יאמר לו קח עוד חצי על חשבון אשר בידך וישאל לו אם יש בו מחצה אם לא כמו שכתבתי | |||||||||||||||||||||||||||||||||
| וככה יתן לו החצי על החשבון אשר בידו חמשה פעמי' | |||||||||||||||||||||||||||||||||
| וכל פעם אשר עלה בידו מחצה יתן למשמרת | |||||||||||||||||||||||||||||||||
| ואח"כ ילך אל זה השורה וכל פעם אשר היה בו מחצה יקח לו אותו מספר אשר כתוב כאן וישלך אותו בל"ב ל"ב ומה שנשאר בידו הוא המספר | |||||||||||||||||||||||||||||||||
| [42]וכן אם ירצה השואל יחשוב חשבון עד קכ"ח והנשאל אמור לו כמה | |||||||||||||||||||||||||||||||||
| כגון אם חושב השואל חשבון שבפעם ראשון ובפעם שלישי ובפעם חמישי ובפעם שביעי' היה בו מחצה דהיינו חשבונם לשורה ראשונה ג"ד ולשלישי ו"ח ולחמשי ח"ד ולשביעי ד"ו צרוף יחד ויהיה אד"ב השליכהו בל"ב ל"ב וישאר ז"א דהיינו החשבון הראשון אשר חשב השואל | |||||||||||||||||||||||||||||||||
|
סימניך | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
Multiple Quantities - Men, Women, Children |
|||||||||||||||||||||||||||||||||
|
חוד חידה הנה באו הנה נפשות לאכול ויש ביניהם אנשים ונשים וטף וסך כולם עשרים ובא להן בעל אושפיזן ואמר להן תנו לי איש אחד מכם ג' פשי' ואשה ב' פשי' ותינוק חצי פשי' וכן עשו ויעלה הסך של מעות כולם עשרים פשי' חוד כמה היו האנשים וכמה הנשים וכמה הטף | ||||||||||||||||||||||||||||||||
|
תשוב איש אחד חמשה נשים י"ד תינוקות | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
ודוק | ||||||||||||||||||||||||||||||||
|
דרך אחר הנה באו מאה נפשות למלון אחד וישבו יחד לאכול ויהיה ג"כ ביניהם [אנשים][43] [ונשים][44] וטף ובא ג"כ להן בעל אושפיזין ואמר להן תנו לי כל איש עשרה פשי' ואשה ה' פשי' ותינוק חצי פשי' וכן עשו ויעלה הסך של מעות מאה פשי' חוד כמה אנשים וכמה הנשי' וכמה תינוקות | ||||||||||||||||||||||||||||||||
|
תשובה איש אחד ותשעה נשים ותשעים תינוקו' | ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
| Double False Position | |||||||||||||||||||||||||||||||||
| Question by R. Israel from Prague: | שאלה מפי הר"ר ישראל מפראג ממון שהוספנו עלינו כמה שהיה בתחלה כגון אם הוא ג' תוסיף עליו ג' וגם מחציתו ורביעתו ויהיה הכל עשרים או ל' או מ' או כפי רצונך כמה שתרצה ותכתוב שני חשבונות שקרים ותחשוב מהם האמת כמה היה בתחילה | ||||||||||||||||||||||||||||||||
Find a Quantity Problem - How Much Problem - Money |
|||||||||||||||||||||||||||||||||
|
והנה לך דימיון כגון ממון שהוספנו עליו כמו שהיה בתחילה ומחציתו ורביעתו ויהיה הכל עשרים | ||||||||||||||||||||||||||||||||
|
אז חשוב אם היה בתחלה המעות ד' זהו' והוספנו עליו עוד ד' ועוד מחציתו שהוא ב' ורביעתו שהוא א' והנה הכל ביחד א'א' | ||||||||||||||||||||||||||||||||
|
|
והנה הוא שקר כי היה ראוי להיות הכל 0"ב כי שאילתינו כשהוספנו עליו כמו שהיה בתחילה ומחציתו ורביעתו ויהיה הכל עשרים וזה אינו רק א'א' אז חשוב כמה הוא מן א'א' עד 0"ב ויהיה ט' אותו ט' כתוב תחת ד' שאמרנו שהיו המעות בתחילה כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
ואח"כ חשוב אם היו המעו' בתחילה ח' והוספנו עליו כפי שאילתינו עוד ח' ומחציתו שהוא ד' ורביעיתו שהוא ב' והנה הכל ביחד ב'ב' | ||||||||||||||||||||||||||||||||
|
|
א"כ זהו ג"כ שקר כי הוא ראוי להיות הכל ביחד 0"ב כמו ששאלנו כי שאלנו כשהוספנו עליו כמו שהיה בתחילה ומחציתו ורביעתו ויהיה הכל 0"ב אז תנכה 0"ב מן החשבון כפי שאילתנו ויהיה יותר ב' אותו ב' כתוב תחת ח' שאמרנו שהיה המעות בתחילה וכתוב ח' בצד שמאל של ד' וגם ב' הנשאר מן החשבון כתוב בצד שמאל על ט' כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
|
והנה צרוף ט"ב ביחד כי הם נשארים מן החשבונות השקרים ויהיה א'א' וזה המורה אח"כ כפל ב' שתחת על ד' ויהיה ח' אותו ח' כתוב שלא תשכח ואח"כ כפול ט' שתחת ד' על ח' ויהיה ב"ז וקח ח' שכתבת כבר ושים אותו על ב' ויהיה עשרה כתוב גלגל במקום ב' ומחוק ד' וכתוב במקומה ח' ויהיה 0"ח פי' פ' ואח"כ חלוק בשער החילוק כמה פעמים א'א' יש בשמונים כי הוא המורה ותמצא בו ז' פעמים ועוד ג' חלקים שא'א' מהן חלק שלם פי' שלם זהב שלם וכך היא המעות בתחילה ששאלנו והמבין יבין | ||||||||||||||||||||||||||||||||
| וזה החשבון דלעיל מכוון כששני חשבונות השקרים אחד פחות ואחד יותר אבל אם שני חשבונות שקרים כל אחד יותר על חשבון היוצא או שניהם חסרים אשכילך האיך תעשה אז תנכה החשבון המועט הנשאר מן חשבון המרובע ומה שישאר לך זהו המורה וכשכפלת שני חשבונות יחד אז תנכה גם כן חשבון המועט מן המרובה | |||||||||||||||||||||||||||||||||
|
והנה אכתוב לך דימיון כגון אם יש לך סך מעות וכפלת עליו סך שהיה כבר ומחציתו ורביעתו ויהיה בין הכל 0"ב | ||||||||||||||||||||||||||||||||
|
אשכילך האיך תעשה אם תאמר שהיה סך מעות ח' זהו' והוספנו עליו עוד ח' ומחציתו שהוא ד' ורביעתו שהוא ב' ויהיה [ס]ך הכל ב'ב' | ||||||||||||||||||||||||||||||||
|
|
וזה שקר כי היה ראוי להיות סך הכל 0"ב אז תנכה 0"ב וישאר ב' אותו ב' כתוב שלא [ת]שכח | ||||||||||||||||||||||||||||||||
|
ואז תחשוב חשבון השני ותאמר אם היו סך המעות ו"א והוספנו עליו ו"א ומחציתו שהוא ח' ורביעיתו שהוא ד' ויהיה בין הכל ד"ד | ||||||||||||||||||||||||||||||||
|
|
וזה שקר גמור כי היה ראוי להיות 0"ב אז תנכה 0"ב שהוא סך היוצא מן מעות מן ד"ד וישאר ד"ב | ||||||||||||||||||||||||||||||||
|
|
ואח"כ ב' הנשאר מן חשבון הראשון מן ד"ב הנשאר מן חשבון השני וישאר ב"ב וזהו המורה ואז כפול ב' שתחת ח' על ו"א ויהיה ב"ג כתוב שלא תשכח ואח"כ כפול ד'ב' על ח' ויעלה ב'ט'א' אז תנכה החשבון הראשון אשר כפלת שהוא ב"ג מן החשבון השני שהוא ב'ט'א' כי הוא חשבון המועט וישאר 0'ו'א' אז חלוק בשער החילוק כמה פעמים ב'ב' יש בו כי הוא המורה ותמצא שיש בו ז' פעמים וגם ו' חלקים שב'ב' מהן חלק שלם דהיינו זהו' והמבין יבין סליק | ||||||||||||||||||||||||||||||||
Additional Word Problems |
||||
Mantova, Comunità Ebraica MS ebr. 8/16 |
||||
| Into how many parts you should divide a piece [of bread] so that [the parts] will be divisible by 3, 4, and 5 | והנה אגלה לך שער השברים אם נשאל לך השואל על פת אחת לכמה חלקים שצריך אתה לשבר הפת שתמצא בה שלישית ורביעית וחמישית אז תכתוב כך השאלה
| |||
| ותאמ' ג' פעמים ד' ויעלה ב"א ותכפול פעם אחת הב"א תוך הה' אז יעל' לך ס"ו וזה חלוקים שתמצא שלישית ורביעית וחמישית דהא 0"ב שלישית מס"ו ורביעית ה"א וחמישית זהו ב"א סליק | ||||
| 12 barrels are bought for 6 zehuvim, how much are 9 barrels cost? | והנה אגלה לך שער הערך וזהוא דמיונו אם נשאל לך השואל הנה לפניך ב"א חביות שנקנין עבור ו' זהובי' ט' חביות כמה הן עולין אז תכתו' כך השאלה
| |||
| ואז תאמר ו' פעמי' ט' ויעלה לך ד"ה אז תחלוק הב"א מד"ה ותאמר כמה א' בה' והא' הוי תוך הה' ה' פעמים אבל לא תוכל ליקח ה' פעמים דאל"כ לא תוכל ליקח הב' מן הד' ה' פעמים וכמה פעמים שתקח הא' מן הה' כך הרבה פעמים צריך אתה ליקח הב' מן הד' אלא לא תוכל ליקח הא' מן הה' אלא ד' פעמים ואז נשאר לך ד"א והד' תכתו' למעלה דה"ד הוי הזהו' ואז צריך ליקח הב' מן ד"א נמי ד' פעמי' אז נשאר לך ו' וזהו ג' גדולי' שעולי' י"ב על הזהוב אחד ונמצא לכשתקנה ב"א חביות עבור ו' זהובי' שט' חביות עולים ד' זהובי' וחצי כן תעשה לכל פעם | ||||
| Two lent a loan of 34 zehuvim - one had a debt of 15 zehuvim and the other had a debt of 19 zehuvim and they charged an interest of 13 zehuvim, how much will each have of the interest? | ועוד אפרש לך ערך אחר שנים שהלוו על חוב אחד ד"ג זהובי' ולאחד יש לו בחוב ה"א זהובי' ולשיני יש לו בחוב ט"א זהובי' ולקחו שנים לרבית ג"א זהובי' כמה יש לכל אחד בה ג"א זהובי' לפי הערך | |||
| והנה אפרש לך בקיצור איך תעשה שתמצא היושר אז תכתו' כל אחד לחוד וכך תכתו' הריבי' למעלה ואח"כ המעות שיש לו ב' בחוב ואח"כ הסך כולה וזה דומיונו שכתו' מבראי ותכפל המעות שלו תוך הריבית ותאמ' פ' א'פ'א' ואח"כ תאמ' א'פ'ה' שהוא ה' ואח"כ תכתו' עוד פעם אחת ה"א תחת הג' שלמעלה ויהיה כך דמיונו ותאמ' גפ"א שהוא ג' ותשים על הה' שלמעלה אז יהיה ח' ותאמ' עוד פ"א גפ"ה שהוא ה"א אז תמצא הט' א' אז תחליק הד"ג מן הט"א ותאמ' כמה יש ג' בתוך ט"א והוא הוי ביה ו'פ' אבל תוכל לקח ו' פ' כי אז אין נשאר לך אלא ה' א' ולא תוכל ליקח ו'פ'ד' מה"א אלא לא תוכל ליקח אל ה'פ' אז נשאר לך הד' והה' תכתו' למעלה כמו כן ותקח ה'פ'ד' מן ה'ד' אז תשאר לך ה"ב אז יהיה לזה בחלקו ה' זהוב' והב' גדולי' שעולים ד"ג על זהוב אחד ועשית' גם כן לצד השני ותמצא שיהיה לשני בחלקו ז' זהובי' וט' גדולי' שעולי' ד"ג על זהוב אחד סליק | ||||
|
הנה אפרש לך ערך אחר אם ישאל לך השואל כי הנה ה"א סאין מים לפניך ואם מתבשלין על האור יום אחד אז הוי מתמעטין ז' סאין הנה אם היו רק ג"א סאין על האש והאש הוי מממועט לפי זה הערך כמה הוי מתמעט מן הג"א סאין ביום אחד אז תכתו' כך השאלה כדכתי' מבדאי | |||
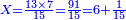
|
ותעשה כמו שפרשתי לעיל תכפול הג"א תוך הז' ותמצא א"ט אז תחלוק ה"א מן הא"ט ותמצא שהוי הג"א סאין מתמעט ביום אחד ו' סאין וחלק אחד שה"א עושין על סאה אחת סליק | |||
| השורש מערך שנים שהלוו על חוב ט' זהו' לאחד יש ה' זהו' ולאחד ד' זהו' ולקחו לרבית י"ג ונמצא דשייך לכל אחד ב' זהוב י"ג תשיעיו' לרבית ונמצא דשייך לזה שיש לו ה' זהו' ה'פ' י"ג תשיעיו' שהם וו' תשיעיו' וכשתחלוק ממנו ט' שהוא המור' פי' כל ט' תשיעיות הם רבי' זהוב וכך תעשה גם לשני סליק | ||||
| והנה אפרש לך ערך מתוך ערך והנה אחד שלוה על חוב ט' זהובי' והם עומדים ד"א שבועות ואחד שלוה על חוב א"א זהובי' והם עומדי' ה"א שבועות ולקחו שניהם ליחד ריבית ז' זהובי' כמה יש לכל אחד בחלקו לפי הערך הנה אפרש לך בקיצור איך שתעשה שתמצ' האמת תכתו' לכל אחד לבדו כמה שהכתב מבדאי הריבי' לעי' ואח"כ המעות ואח"כ השובועו' ותשים צד אחד לפניך איזי שתרצה ותכפל המעות תוך השבועות ותאמ' ט'פ'א' שהוא ט' ואח"כ תאמ' טפ"ד ותמצא הוא אז תחבר וב"א ותעשה ג"כ לצד השיני ותמצא הוא אז תחבר אותם ליחד וב"א והוא ותמצא אט"ב וזה תרשום לפניך כי הוא המור' ואח"כ תכפול כל אחד ואחד וב"א והוא תוך הריבית וכשתכפול וב"א תוך הז' אז תמצא בח"ח ותחליק אט"ב הנזכרים לעיל מן בח"ח ותמצ' אט"ב תוך בח"ח ג"פ והג' הוא הזהו' שיהיו לו בחלקו וגם ט' נשאר לך מן החילק הוא הוי ט' גדולי' שעולי' אט"ב על אט"ב על אט"ב זהוב אחד ותעשה ג"כ לצד השני ותיכפול הוא תוך הז' ותמצא ה"ה א"א ותחליק ג"כ אט"ב מן ה"ה א"א ותמצא אטב תוך ה"א א"א ג"פ שהוא הזהו' שיהיו לו בחלקו וגם נשאר לך בח"ב שלא יכולים להשיג לכלל אט"ב שהוא גדולים שעולים אט"ב על זהו' אחד ונמצא שיהיו לזה בחלקו ג' זהו' ובח"ב גדולי' שעולי' אט"ב על זהוב אחד סליק דוק | ||||
| ואם נשאל לך על זה העיגול כמה כי יאמר לך החץ וחצי היתור אותו אז תאמר כמה היתור חצי הוא הד' אמות אז תאמ' ד'פ'ד' והוא ו"א ותאמ' כמה אורך החץ והוא אמה אז תחלק האמ' מן הו"א ותאמר כמה א' בתוך ו"א והוא ו"א והוא ו"א פ' בתוכה אז תעשה אורך החץ שהוא א' על הו"א אז יהיה ז"א וקח הו"א אורכו העיגול וכן תעשה לכל פעם תכפול היתור תחלק החץ מן ה' הנכפל ודוק | ||||
| הנה אפרש לך שאלה שנקר' הסולם אם נשאל לך על סולם אחד שהיא גבוה עשרה אמות ואם נישג הסולם למעלה ב' אמות כמה אמות השיג למטה מחומה כמה זה אז תעשה כך תאמ' כמה אורך הסול' אורכה עשרה ותאמ' י'פ'י' שהי' ק' ותאמ' כמה אורך החומה מן הארץ עד ראש הסולם והיא ח' אמות ותאמ' ח'פ'ח' והוא ד"ו ותחלק הח' מן ה0'0'א' ונשאר ו"ג ותעשה שורת בה'ו'ג' והשורת בהוג הוא ו' זה אורך הקרקע מן החומה עד הסולם. זליק | ||||
| בזה הוכיח דלאכח מה שבריבוע מאה על אמה שהאלכסון שלו אמ' ותרי חומשין כי זה 0"א אמות על 0"א אמו' ודוק |
Moscow, Russian State Library, Ms. Guenzburg 714/4 |
|
| Question: here are many bulls one after another, meaning that every time I bought the first for a certain amount, I then bought the bull that follows it for double the first and likewise the third bull I bought also for double [the price] that I bought the one that preceded it and so the fourth bull and the fifth bull. | [45]שאלה הנה שוורים הרבה בזה אחר זה ובענין זה בכל פעם כשקניתי הראשון בעד סך א' אז קניתי אותו שור של אחריו בעד כפל הראשון וכן השור השלישי קניתי ג"כ בעד כפל שקניתי אותו שלפניו וכן השור הד' וכן השור הה' |
| כגון הא' קניתיו בעד א' זהוב הב' בב' זהובי' הג' בד' וכן כולם והנה השאלה כמה כל המעות הללו בסך אחת | |
| תשובה זאת ועוד אחרת דוגמא זה למצוא ולחשוב ולעמוד על בוריו תעשה בענין זה ואופן זה בתחלה תראה ותבין כמה הוא סך הראשון שקנית בו השור הראשון ואח"כ תראה ג"כ כמה הוא הסך האחרון ב' פעמים בשער הכפל גדול ותחסר ממנו בשער החיסור הסך הראשון שקנית בו השור הראשון ומה שישאר בידך כשחסרת ממנו הסך הא' הוא סכום כל המעות שקנית בהם כל השוורים | |
| והנה לך הדמיון כגון הראשון קנית בעד א' זהוב והשני בעד ב' והשלישי בעד ד' והרביעי בעד ח' והה' בעד י"ו והו' בעד ל"ב והז' בעד ס"ד . והנה תראה אתה שהסך האחרון שקנית בו השור הז' היינו השור האחרון הוא ס"ד זהובים א"כ תחשוב בשער הכפול הגדול ב' פעמים ס"ד ויהיה [46]ס"ד ויהיה קכ"ח אז תחסר מן קכ"ח הסך הראשון שקנית בו השור הא' שהוא א' זהוב וישאר בידך קכ"ז זה כל כך מעות קנית כל השוורים וכן כל פעם תחסר מן הסך האחרון סך הראשון אחרי אשר כפלת אותו ב' פעמים ולאו דוקא אם הסך הראשון א' שהוא הדין אם הסך הא' ב' או ג' או ד' או כמה שהוא בתחלה תחסר מן הסך האחרון כשכפלת אותו ב"פ ואל תשנה מעניין זה כי חשבון א' הוא ואמת | |
| שאלה אם תרצה לידע ולחשוב חשבון מה שתרצה בעניין זה בכל פעם אותו חשבון שלאחריו הוא ד' פעמים כמו אותו חשבון שלפניו כגון א' ד' י"ו . ס"ד . ס"ד . רנ"ו . ותרצה לידע ולחשוב כמה הוא סך אחד . אשכילך בדרך זו הילך למען תצליח שתשכיל . והנה אראך הדרך אשר תלך בה בתחלה תראה ותבין ג"כ על הסך הראשון ועל הסך האחרון כמה הם אמנם אינו צריך לכפול סך האחרון כמו שהראיתיך לעיל . רק קח בידך כמו שתמצא אותו עתה ותחסר ממנו סך הראשון מן סך האחרון אז תוכל לחלק הנשאר בידך לג' חלקים שוים וזה קל להבין לכל בר משכיל אשר הערה את נפשו למלאכה היקרה הזאת . כי אמשול לך [47]משל בדמיון קטן ואשכילך בו למען תבין ממנו ותראה בעיניך שתוכל לחלק הנשאר בידך לג' חלקים אחרי שחסרת ממנו הסך הראשון | |
| והנה לך הדמיון כגון אם תרצה לידע ולחשוב בסך א' א' ד' י"ו ס"ד רנ"ו [...] תראה עתה שהסך האחרון הוא רנ"ו והסך הא' הוא א' ותרצה לחשוב כל הסכומין בסך אחד אז קח הסך האחרון היינו רנ"ו ותחסר ממנו הסך הראשון היינו א' וישאר לך רנ"ה ואח"כ תחלק בשער החלוק כמה יש ברנ"ה הג' כי תמצא שיצא החשבון לג' חלקים שוים ולא ישאר לך מהם כלום . אחר אשר חסרת ממנו הסך הראשון היינו א' . ואם אתה עושה כן תמצא שיש בו פ"ה פעמים ג' ברנ"ה והיינו השליש מן הרנ"ה כי פ"ה פעמים ג' היינו רנ"ה . אם כן תראה עתה שיצא החשבון בג' חלקים שוים אחרי שחסרת ממנו הסך הראשון אח"כ קח אותו השליש מן רנ"ה דהיינו פ"ה וחבר אותו אל רנ"ו כי כן היה הסך האחרון מתחלה קודם שחסרת ממנו הסך הראשון ותמצא אחר החיבור שיצא לך תר"ל (?) והיינו כל החשבון אשר חפצת לידע כי כשתחבר ביחד א' ד' י"ו ס"ד ס"ד רנ"ו יעלה לך תר"ל (?) . ותן לבך להבין ולא לשכוח בכל [48]פעם לחסר החשבון הראשון מן סך האחרון ויצא אחר החיסור לג' חלקים שוים אח"כ תוכל ליקח החלק הג' היינו השליש ולחברו אל הסך האחרון כמו שהיה בתחלה ולאו דוקא אם הסך הראשון א' הוא הדין אם הסך הראשון ב' או ג' או ד' או ה' או כמה שתרצה . תוכל בכל פעם לחסר אותו מן הסך האחרון ויצא לך הסך בכל פעם אחר החיסור לג' חלקים שוים וחבור אותו השליש לסך האחרון כמו שהיה בתחלה וזהו חשבון ודוק תם | |
| Give and Take Problems | |
|---|---|
|
[49]אדם הלך לשוק וכפל מעותיו והוציא י"ב פשוטים ועוד הלך לשוק אחר וכפל הנשאר בידו והוציא י"ב פשוטים ועוד הלך לשוק אחר וכפל הנשאר בידו והוציא [י"ב פשוטים] [...] בידו כלום כמה היה הקרן שהוליך כמו בשוק הראשון |
|
עשה כך |
|
בעבור הראשון נצטרך להוציא החצי מן הי"ב שהוציא |
|
ובעבור השני נקח הרביעי |
|
ובעבור השלישי נקח השמינית מי"ב שהוא פשוט וחצי |
|
הסר א' פשוט וחצי מי"ב ישארו י' וחצי וכן היה הקרן שהוליך לשוק הראשון |
|
ועל זה הדרך תוכל לעשות ואם ילך לכמה שווקים |
|
כי בעבור השוק הרביעי נסיר מן הי"ב פ' שהיה מוציא בכל פעם חלק א' מי"ו |
|
ובעבור החמישי נסיר חלק א' מל"ב |
|
ובעבור השישי נסיר חלק א' מס"ד |
|
וכאשר תרבה השווקים כן תכפול מה שיש בידך ועל הכפול חלק מה שהוציא ומה שיעלה בחילוק הסר ממה שהוציא והוא המבוקש |
|
אדם א' הלך לפרדס א' ללקוט תפוחים ויש לו ללקוט מהם כל כך שיתן לשוער הפנימי [50]של הפרדס חצי התפוחים שלקט וא' יותר ולשוער השני מן השער הב' יש לו ליתן החצי מן התפוחים שנשארו בידו וא' יותר וכן יש לו [...] לששה שערים שיש לפרדס דהיינו לתת לכל שוער החצי וא' יותר [...] תפוחים לא פחות ולא יותר עשה כך |
|
תפוש מספר הה' שהוא חייב להביא ותוסיף עליו א' הרי ו' |
|
כפול ו' ויהא י"ב הרי שער א' |
|
הוסיף עליו א' הרי י"ג |
|
כפול אותם ויהיו כ"ו הרי ב' שערים |
|
תוסיף עליו א' ויהיו כ"ז |
|
כפול אותם ויהיו נ"ד הרי ג' שערים |
|
תוסיף עליהם א' ויהיו נ"ה |
|
כפול אותם ויהיו ק"י הרי ד' שערים |
|
תוסיף עליהם א' ויהיו קי"א |
|
כפול אותם ויהיו רכ"ב הרי ה' שערים |
|
תוסיף עליהם א' ויהיו רכ"ג |
|
כפול אותם ויהיו תמ"ו הרי ו' שערים |
|
הרי שיש לו ללקט תמ"ו תפוחים בין הכל וישארו בידו ה' תפוחים להביא לא פיחות ולא יותר |
| ואם יש לו ללקט מהם כל כך שיתן לשוער הפנימי החצי ממה שלקט וא' יותר ולשוער הב' חצי הנשאר וב' יותר ולשוער הג' חצי הנשאר וג' יותר [51]ולשוער הד' חצי הנשאר וד' יותר וד' תפוחים יש לו להביא לא פחות ולא יותר | |
|
עשה כך |
| תפוח משער הד' שיש לו להביא הוסף עליהם ד' שיש לו להוסיף לשו[ער] [...] שער א' | |
|
הוסף [עליהם ג' וי]היו י"ט |
|
כפלם ויהיו ל"ח הרי ב' שערים |
|
הוסף עליהם ב' ויהיו מ' |
|
כפלם ויהיו פ' הרי ג' שערים |
|
הוסף עליהם א' יהיו פ"א |
|
כפלם ויהיו קס"ב הרי ד' שערים |
|
והתפוחים שלקט היו קס"ב והנשארים בידו ד' תפוחים |
| Find a Quantity Problems - Whole from Parts | |
|
חנית מעוכה בארץ שלישיתה ורביעיתה ולמעלה מן הארץ היא פ' אמה כמה אמות היא בין כולה |
|
עשה כך |
|
תמצא מספר שיש לו שליש ורביע והוא י"ב |
|
ושליש ורביע מי"ב הוא ז' והוא התחוב בארץ |
|
ולמעלה מן הארץ נשאר ה' |
|
אם כך אמור כך אם ה' שווה י"ב כמה ישוה כ' |
|
כפול אותם כ"פ י"ב יעלו ר"מ |
|
חלקם על ה' יעלו מ"ח בחלוק |
|
א"כ אורך החנית מ"ח אמות |
| Reuven hired Shimon to build him a house in 30 days - for a day working in construction he will earn 9 liṭra, and for an unemployment day he will lose 4 liṭra. At the end of 30 days he did not earn or lose. How many days did he work and how many days he did not work?
|
ראובן שכר שמעון שיבנה לו בית א' בל' יום והיום שיעבוד בבנין ירויח ג' ליט' והיום שלא יעבוד יפסיד ד' ליט' ובסוף ל' יום לא הרויח ולא הפסיד כלום כמה ימים עבד וכמה ימים לא [52]עבד |
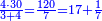
|
[53][י"ב ימים חלקים של ז' והם הימים שלא עבד בה ואחר הכפיל ד"פ ל' ויעלו ק"כ חלקם עם ז' ויעלו י"ז יום וחלק א' מז' ביום] |
| עשה כך אין ספק כי מה שירויח בד' ימים לחשבון ג' ליט' ליום יפסיד בג' ימים לחשבון ד' ליט' ליום חבר ד' עם הג' יהיו ז' כפול ג"פ ל' יהיו צ' חלקם על [...] יעלו [...] [...] וכן ימים עבד בה | |
| If for a day working in building the house he will earn 36 pešuṭim, for an unemployment day he will lose 41 pešuṭim and at the end of 30 days he did not earn or lose
|
ואם יאמר כי היום שיעבוד בבית ירויח ל"ו פשוט והיום שלא יעבוד יפסיד מ"א פשוטים ובסוף ל' יום לא הרויח ולא הפסיד כלום |
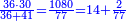
|
עשה כך אין ספק כי מה שירויח במ"א יום לחשבון ל"ו פשוטים ליום יפסיד בל"ו יום לחשבון מ"א פשוטים ליום תחבר ל"ו עם מ"א יעלו ע"ז כפול ל"ו פעמים ל' יהיו לך י"ד יום שלמים יעלה לך אלף ופ' חלקם על ע"ז ויעלו בחלוק י"ד יום שלם וב' חלקים מע"ז ביום וכך ימים לא עבד בבית |
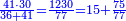
|
ועוד כפול מ"א פעמים ל' ויעלה אלף ור"ל חלקם על ע"ז ויעלו בחלוק ט"ו ימים שלמים וע"ה חלקים מע"ז ביום |
Two men sat down to eat. One had two loafs of bread and the second had three loafs of bread. A third came and ate with them. [The three ate the five loafs of bread and after they ate and drank, the third who came to eat with them gave five pešiṭim for the two. How should they share the five pešiṭim]?
|
[54]ב' אנשים היו יושבין לאכול לאחד היו ב' לחמים ולשני ג' לחמים בא אדם שלישי ואכל עמהם ואכלו בין שלשתם אלו הה' לחמים לאחר שאכלו נתן אותו השלישי שאכל עמהם לאותם השנים ה' פשוטים [...] ביניהם [...] כמה חלק מכל לחם אכל כל א' מהם א' לחם וב' שלישיות מלחם א"כ אותו שהיו לו ב' לחמים ואכל א' לחם וב' שלישיות לא הפסיד כי אם שליש לחם ואותו שהיו לו ג' לחמים ואכל א' לחם וב' שלישיות הפסיד א' לחם ושליש שהם ד' שלישיות לחם א"כ אותו שהיו לו ב' לחמים יקח א' פשוט כי הפסיד שליש לחם ואותו שהיו לו ג' לחמים יקח ד' פשוטים כי הפסיד לחם א' ושליש שהם ד' שלישי לחם |
A tower is 20 cubits tall. An ant wants to climb up. Every day it climbs up one third of a cubit and every night it goes down a quarter of a cubit. How much further up it moves each day and in how many days it will reach to the top? |
מגדל שהוא גבוה כ' אמה ונמלה א' רוצה לעלות למעלה ובכל יום עולה שליש אמה ובכל לילה יורדה רביע אמה כמה יתרון יש לה בכל יום ובכמה ימים תעלה למעלה |
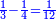
|
אמור תחלה כמה הוא יותר השליש מן הרביע א' חלק מי"ב |
| הרי שבי"ב ימים היא עולה א' אמה | |
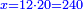
|
ובעבור שהמגדל היא גבוה כ' אמות אמור י"ב פעמים כ' הרי ר"מ הרי שבר"מ ימים היא עולה לראש המגדל |
You have some money. You take a third, a quarter, and a fifth of it and their sum is nine. How much remains?
|
הרי שיש לך מעות והוצאת מהם השליש והרביע [55]והחומש והם ט' פשוטים כמה יהיו הנשארים |
| אמור תחלה שליש ורביע וחומש ימצאו בס' השליש הוא כ' הרביע הוא ט"ו החומש הוא י"ב וכללם יהיו מ"ז הרי שהשליש והרביע והחומש שהם ט' פשוטים הם מ"ז חלקים מס' נמצא שהנשאר [...] י"ג חלקים מס' ולכן אמור אם מ"ז חלקים מס' שוים ט' פשוטים י"ג חלקים מס' כמה שוים אמור י"ג פעמים ט' הם קי"ז חלקם במ"ז יבואו כ"ג חלקים ממ"ז נמצא שהיו בכיס י"א פשוטים וכ"ג חלקים ממ"ז ומה שהוציא הוא ט' ומה שנשאר היו ב' וכ"ג חלקים ממ"ז וכן לכל חשבון שתרצה | |
| A man has a jug with maximum capacity of 8 cups of wine and he wants to divide its content between two people, giving each 4 cups, but he has only two jars – one with a maximum capacity of 3 cups and the other [with a maximum capacity of] 5 [cups]. How will he divide it, giving each 4 [cups]? | אדם א' יש לו קנקן שמחזיק ח' כוסות של יין ורוצה לחלקו לשני אנשים וליתן לכל א' ד' כוסות ואין לו רק שני כלים שהא' מחזיק ג' כוסות וא' ה' היאך יעשה לחלק אותם וליתן ד' לכל א' |
|
תחלה ימלא הכלי שמחזיק ג' כוסות וישים אותם בתוך הכלי המחזיק ה' |
|
ואח"כ ימלא פעם אחר הכלי המחזיק ג' ויריק כמו כן באותו הכלי המחזיק ה' הרי שהכלי המחזיק ה' מלא ונשאר בכלי המחזיק ג' כוס א' |
|
אח"כ יריק הכלי מלא של ה' כוסות בתוך הקנקן המחזיק ח' ונמצא [56]שבתוך הקנקן גדול יש בו ז' כוסות ובכלי המחזיק ג' יש בו כוס א' |
|
אח"כ יריק הכלי של ג' כוסות שיש בו כוס א' בתוך הכלי המחזיק ה' ויחזור וימלא הכלי המחזיק ג' מתוך הכלי המחזיק ח' ויריק בתוך הכלי המחזיק ה' ונמצא עכשיו ד' כוסות בתוך הכלי המחזיק ח' וד' כוסות בתוך הכלי המחזיק ה' ועם זה היין חלוק בשוה |
|
שלשה חברים היו ואמר הא' לשני חבריו דעו כי כל מה שבכיסי והחצי משניכם עולה ס' ויען השני ויאמר כל מה שבכיסי ורביע משניכם עולה ס' ויען השלישי כל מה שבכיסי ושליש משניכם עולה ס' |
|
מצאנו ג' מספרים והם ה' י"א וי"ג שהם כעין השאלה הזאת |
|
כי ה' אומר לי"א ולי"ג אני וחצי שניכם י"ז וי"א אומר לה' ולי"ג אני ושליש שניכם י"ז |
|
והנך רואה שאלו אמרו מחובר שלשתנו י"ז יהיה לא' ה' ולשני י"א ולשלישי י"ג |
|
ועכשיו שאמרו מחובר שלשתנו יחד ס' נשוב לערכים ונאמר |
|
כערך ה' לי"ז כן ערך הקטן אל ס' הוא ששאל לחבריו החצי |
|
וכערך י"א לי"ז כן ערך השני לס' והוא ששאל [57]לחבריו השליש |
|
וכערך י"ג לי"ז כן ערך הגדול אל ס' והוא ששאל לחביריו הרביע |
| וכן תערוך לכל הסכומים שיאמרו שלשתם תשים המורה ה' וי"א וי"ג ודרך הערכים הוא כענין | |
|
|
אמור אם בעת שהמחובר הוא י"ז יהיה חלק הקטן ה' בהיות המחובר ס' כמה הם חלקיו אמור ספ"ה הוא ש' וחלקם בי"ז יהיו י"ז וי"א חלקים מי"ז |
|
|
ולדעת החלק האמצעי אמור אם בעת שהמחובר הוא י"ז שוה חלק האמצעי י"א בהיות המחובר ס' כמה הם חלקו אמור ס"פ י"א הם תר"ס חלקם בי"ז יהיו ל"ח וי"ד חלקים מי"ז |
|
|
ולדעת חלקי הגדול אמור אם בעת שהמחובר הוא י"ז יהיה החלק הגדול י"ג בהיות המחובר ס' כמה יהיה חלקו אמור ס"פ י"ג תש"פ חלקם בי"ז יהיו מ"ה וט"ו חלקים מי"ז |
|
ויהיה סדר הענין כך אומר הקטן אני שאני י"ז וי"א חלקים וחצי האמצעי שהם י"ט וז' חלקים מי"ז וחצי הגדול שהם כ"ב וי"ו חלקים מי"ז מחובר שלשתם ס' |
|
| |
| ואומר האמצעי אני שאני ל"ח וי"ד חלקים מי"ז ושליש הקטן שהם ה' וט"ו חלקים מי"ז ושליש הגדול שהם ט"ו וה' חלקים מי"ז מחובר שלשתנו ס' | |
|
| |
| ואומר הגדול אני שאני מ"ה וט"ו [58]חלקים מי"ז ורביע הקטן שהוא ד' וז' חלקים מי"ז ורביע האמצעי שהוא ט' וי"ב חלקים מי"ז מחובר שלושתנו עולה ס' | |
|
| |
| Jacob divided [a certain amount] between his three sons. The share of Reuven was greater than the share of Shimon and the share of Shimon was greater than the share of Levi. Reuven gave his two brothers from his shares as much as their shares, Shimon gave his brothers also as much as their shares and Levi gave his brothers also as much as their shares, then the shares of the three were equal. How much was the [original] share of each? | שאלה יעקב חלק לבניו ג' והיה חלק ראובן גדול משל שמעון ושל שמעון גדול משל לוי נתן ראובן לשני אחיו מחלקו כפי מה שהיה חלקם ושמעון גם הוא נתן לאחיו כפי חלקם ולוי גם כן נתן לאחיו כפי חלקם ואז נמצא חלק שלשתם שוה כמה היה חלק כל א' מהם |
| אמור כי חלק הראשון היה ד' וחלק השני ז' וחלק השלישי י"ג ונמצא בסוף חלקם שוה והיה ח' פשוטים לכל א' כיצד דרך משל חלק ראובן היה י"ג וחלק שמעון ז' וחלק לוי ד' והנה התחיל ראובן ונתן מחלקו לשמעון ז' כפי שהיה לו וללוי ד' ושנים נשאר בידו ואח"כ שמעון שעכשיו היה לו י"ד נתן ללוי ח' כפי מה שהיה בידו ולראובן ב' כפי מה שהיה עכשיו בידו ואח"כ לוי שעכשיו היה לו י"ו נתן מאלו לראובן ד' ונמצא שיש לו ח' וד' לשמעון ועם זה נמצא שביד כולם יש ח' פשוט' וחלקם שוה | |
| Buy and Sell Problems | |
|
אדם א' אמר הנה שני כלכלות של תאנים ובכל א' יש ק תאנים משל היפות כ' לפשוט והרעות [59]ל' לפשוט עולה חשבונם ח' פשוטים ושליש בא א' לקנות ואמר היאך אתה מוכר אמר מאלו אתן לך לז' ומאלו כ' השיב הקונה אם כן תן לי מאלו ומאלו ב' בב' פשוטים ונתן הכל בח' פשוטים והפסיד שליש פשוט |
| אדם שכר שכיר לל' יום בשכר [...] פשוט לכל יום והיה צריך לפרוע מידי יום ביום ולא היה לו כי אם ששה מטבעות ששוויים בין הכל ל' פשוטים ועכשיו שואלים מה יהיה שווי המטבעות כדי שיוכל לפרוע מידי יום ביומו | |
| תשובה שיווי המטבעות צריך להיות כזה א' ב' ג' ד' ח' י"ב | |
|
אדם היה לו זאב ועז וכרוב והיה לו לעבור מעבר מים ולא היה כי אם ספינה קטנה מאד שאינה מחזיק כי אם האדם ודבר אחד ולא יותר ואם תניח העז והכרוב ויעביר הזאב העז אכל הכרוב |
|
תחלה יעביר העז ויניח הזאב והכרוב ואחר יעביר הכרוב ויחזור להעביר העז עמו [60]למקום הראשון |
|
ראובן אמר לשמעון אם אתה נותן לי אלף זהובים יעלה הקרן שלי כסכום מעותיך ושמעון משיב לראובן ואם אתה נותן לי אלף זהובים אני אכפול מעותי לסכום מעותיך |
|
|
תשובה ראובן יש לו ה' אלפים זהובים ושמעון יש לו ז' אלפים וזה פי' ראובן שואל לשמעון אלף זהובים ואם שמעון יתן לו נשאר ביד שמעון ו' אלפים וראובן שהיה לו ה' אלפים תחלה עכשיו עם האלף שנותן לו שמעון יש לו ו' אלפים נמצא שלכל א' יש להם ו' אלפים |
Chapter On Cubic Roots [P1088 2r-v] |
והילך שער על דבר מרובע על כל עבריו | |||||||||
|
|
כגון שתחשוב חוה פעם חוה וזהו רבוע | |||||||||
|
|
כמו שתאמר ב פעמים ב' זהו ד' כזה | |||||||||
|
|
ואם תאמר ותחשוב הד' חתיכות גם ב' פעמים [...] ויהיו ח' זהו רבוע על כל עבריו ב' פעם ב' זהו ד' | |||||||||
|
|
כשתחשוב דוד פעם דוד עולה וטבהאב | |||||||||
|
|
תאמר דוד פעם וטבהאב ועולה דדגזטחטט כו' | |||||||||
|
|
דומיון הנה הכלל העולה מן החשבון המרובע [לג'] צדדין הוא כזה
|
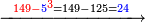
5 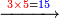
5 149721291 24721291 24721291 5 15
| ותמנה לעולם ברביעיות [....] [אטב]א אבזט טדא ומה שלא עולה לרבעיות מאות[...] תוכל להבין החשבון עתה בכלל הנרשם טדא ג' אותיות ותאמר [מה] הריבוע המרובע על כל עבריו אטדא באה ג' אותיות טדא ע"כ לא יותר מן ה' כי ה' פעמי' ה' זהו ה"ב ה' פעמים ה"ב זהו הבא ועתה הסר הבא מן טדא ונשאר ד"ב ויהא כזה ותכתוב ה' תחת הד' ועל הד' כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| ומעתה תשלש האות הנמצא ר"ל ה' ונסוג שלש מעלות לאחריך דהיינו מן ה' יהיה ה"א ותכתוב ה' תחת ב' וא' תחת ז' כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
53 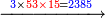
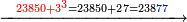
24721291 15 2385 23877
| ועתה תעיין מה אות מצורף לאות ה' שממנה בא זה החשבון הכלל הנרשם ואז תנסה ותצרף אליה אות שאם תחשוב כאשר אשכילך שיהא מכוון אות האחרון מן חשבון העולה לאות אחרון מן חשבון אשר אנו מתעסקים בו או בקרוב דומה לאות אחרון ועתה הילך הדרך תלך בו תקח ג' וכתוב למעלה על הא' אחד לפני הה' העומדת על הב' כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| ועתה נסה אם אמת הדבר תצרף ג"ה של מעלה עם ה"א של מטה ויעלה ה ט ז ועתה תאמר תצרף ג' העולה עם הט"ז ג' פעמים ז' ג' פעמי' ט' ג' פעמי' ה' כו ויעלה כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואז תוסיף עליו על זה החשבון ג' פעמי' ג' על כל עבריו זהו ז"ב אותו ז"ב שים על החג"ב וככה תעשה אות ראשון מן ז"ב ר"ל הז' כתוב קו לפני החג"ב [...] דהיינו ב' שים על ה' כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ו[...] ה' אות [ה] שים נגד האותיות [..]כלל הנרשם דהוא כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| ו[תחסר] כלל התחתון מן העליון ונש[אר] כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה יהיה החשבון צורתו כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| ועתה [...] ג' מעלות לאחריך ונסוג ג' ג"כ לאחריך ג' מעלות ותשלש ויהיה ט' וצורתו כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה תאמר מה היה אות ראשון ע"כ היה א' כי לעולם כשיהיה א' אות ראשון מן הכלל העולה היה הפרט א' ואם אות ראשון ח' אז היה השרש ב' [..] ועתה תחשב אג"ה עם טה"א ויעלה טבדדח | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה תצרף הא' ג"כ עם כל אות אטבדד"ח ותשים לפניו א' פעמים א' ויהיה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| נמצא שהם מכוונים זה העולה מן אג"ה פעמים טה"א אחד צרופך והכלל הנרשם למעלה ולעולם כשהם מכוונים אז החשבון אמת ואם יוותר לך אפי' אות אחת תוכל להבין שלא [נאות] | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
דומיון אחר הכלל העולה ד ד ג ז ט ח ט ט | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
נתחיל מאות ט' הראשונה כי היא אות רביעית ונקח מן ט"ט הריבוע והוא ע"כ ד' כי לא תוכל ליקח יותר והוא ד' פעמים ד' עלה ד"ו חסר ד"ו מן ט"ט ונשאר ה"ג אותו ד' תכתוב למטה תחת הט' ולמעלה נסוג ד' ג' מעלות ותשלש לאחריך ויהיה ב"א תכתוב ב' תחת הט' וא' תחת ח' כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואח' תצרף אל הד' ד' מנין השוה בדעתך וזהו ו' ואם תצרף אליו ה' אז אינו מכוון פרט העולה לחשבון הכלל ולפעמים לפי האמת אינו מכוון אך תדקדק על אות הסמוך לאות אחרון שהוא דומה קצת ועתה קח ו' ותצרף לד' ותאמר ו"ד פעמי' ב"א ויעלה בה"ה תצרף ו' עם בה"ה ויעלה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושים עליו ו' פעמים ו' ויהיה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחסר זה העולה מן ה' אותיות החשבון הנרשם ויהיה אחר חסרונך כזה ועתה צורתו כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה נסוג עם ו' העולה ג' מעלות לאחריך ותשלש וב"א ג"כ ג' מעלות לאחריך ויהיה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה מה היה אות ראשון ע"כ ד' ותחבר [...] עם חג"א ויעלה [...] ושים עליו ד' פעמי' ד' ויעלה הפרט אות באות [...] הכלל ודוק |
Chapter on Square Roots [P1088 6v-7v] |
הילך שער ונקר' שער השורש ושייך על דבר כשחשבת ריבוע כגו' | ||||||||||||||||||||||||||||||||
|
|
חו"ה פעם חו"ה | ||||||||||||||||||||||||||||||||
|
|
או זה"ב פעם זה"ב | ||||||||||||||||||||||||||||||||
| שתראה מה תחילת החשבון אע"ג שלא ידעת בתחילה הפרט | |||||||||||||||||||||||||||||||||
|
|
ועת' אכתו' דומיון חשבתי דבר ועולה ממנה כזה הוה הכלל
| ||||||||||||||||||||||||||||||||
| וראה מה היה מתחילה הפרט שעולה ממנ' ועתה אשכילך ותן לחכם ויחכם עוד ויסף לקח [61] קח הכלל לפניך ואראה לך דבר לעולם תתחיל מן האו' שלא מכוון כגו' | |||||||||||||||||||||||||||||||||
|
ועתה אראה חשב' הכלל ו' אותיות ו"טב"הא"ב אז תתחיל באו' ה' וזהו א' ותאמ' מה הריבוע בא"ב פי' מה אות אתה יכול ליקח זה פעם זה אי אתה יכול ליקח ה' פעם ה' מן א"ב כי ה' פעם ה' זהו כ"ה והשו' אין לך אלא כ"א אלא אתה יכול [לומ'] ליקח ד' פעם ד' כי ד' פעם ד' זהו ו"א פי' י"ו ועוד נשאר לך ה' ואות' ד' העולה כי הריבוע בא"ב זהו ד' פעם ד' ואות' ד' תכתוב על הא' מן ו'ט'ב'ה'א'ב' ותחת הא' | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואז תכפול הד' הריבוע העומד [ותמשוך] הח' לאחריה תחת ה' השנייה ויהא ח' והד' העומדת על הה' תמשוך ג"כ לאחריה על ה' השניי' אבל לא תכפול אות' וצורתו כזה | |||||||||||||||||||||||||||||||||
|
|
46 
46 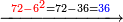
46 55296 7296 3696 86 86 86
| ואז תאמר כמה פעם ח' בה"ה פי' בנ"ה והוה בה ו' פעמים אות' ו' תכתוב למעלה מן הב' ולמטה מן הב' כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ועוד נשאר ז' וז' מן ה"ה ותמחוק השני ה' ותכתו' במקומ' הז' ויהא צורתו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| והו' העולה מן השני ה' העומדת על הב' ולמט' מן הב' תקח אות' נמי ו' פעמי' ו' פעם ו' זהו ו"ג פי' ל"ו וקח הו"ג מן הב"ז קח ארבעי' מן הע' כי הב"ז הוה ע"ב ועוד נשאר ב' ודע שלקחת ארבעי' ולא אתה צרך אל צריך אלא ל"ו אז קח הד' מן המ' ושים אות' על הב' שלפני הז' ויהא צורתו כזה | |||||||||||||||||||||||||||||||||
|
|
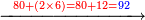
46 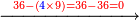
464 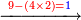
464 3696 96 16 92 24 4
| ועתה תכפול הו' ג"כ לאחריה ויהא י"ב ואז תכתו' הכי שים הב"א לאחריה והח' נמי לאחרי' ואז תעשה הכי שים הב' תחת הט' והא' שים על הח' ויהיה ט' ותשים נמי למפריע הו' העליונ' ולא תכפול ושי' אות' על הט' והד' העליונ' תמשוך נמי לאחריה על הו' נגד הט' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תאמ' כמה פעמים ט' בו"ג פי' בל"ו והוה בו ד' פעמים ולא נשארי' לך מאומה ואות' ד' תכתו' על הו' הראשונ' ותחת הו' ותמחק הו"ג של מעלה והט' של מטה וצורת' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז קח הב' נמי ד' פעמים מן הט' ועוד נשאר לך א' ונמח' הט' ותכתוב במקו' א' ונמח' הב' תחתונ' כי לקחנו נמי ד' פעמי' ועוד נשאר כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ואז קח הד' נמי ד' פעמי' מן ו"א פי' מן י"ו ואז לא נשאר לך מאומה נמצא שהפרט היה בתחילה דו"ד פעם דו"ד ועולה הכלל ו"טב"הא"ב | ||||||||||||||||||||||||||
| ודע לעולם כשתעשה בדרך זה ולא נשאר לך מאומ' אז מה שעולה בידך זה היה תחילת החשבון |
|
|
ועוד אראה לך דומיון החשבון עולה כזה
| ||||||||||||||||||||||||||||||||
|
אז תתחיל בט' כי הט' אות חמיש' ואז תאמר כמה הריבוע בט' ודע שהריבוע בט' הוה ג' כי ג' פעמי' ג' זהו ט' ולא נשאר לך מאומה והג' תכתוב תחת הט' ועל הט' כזה | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואז תכפול הג' לאחריה והוה ו' ותשים לאחריה תחת הז' והג' שלמעלה תמשוך לאחריה על הז' אבל [לא] תכפול כמו שתעשה לג' תחתונ' והילך צורתו ונמחק הט' כזה | |||||||||||||||||||||||||||||||||
|
|
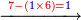
31 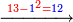
31 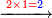
31 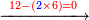
312 1344 1244 1244 44 61 61 62 22
| ואז תאמ' כמה פעמי' ו' בז' ואינ' אלא פעם א' ועוד נשאר א' ואות' א' שעולה מן הז' תכתוב על הג' שלפני הז' ותחת הג' ונמח' הז' ותכתו' במקומ' א' הנשארת מן הז' שלא מגיע נמי לז' וזה וצורת' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תקח הא' נמי א' פעם מן ג"א ועדיין הוה ב"א | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תכפול הא' שתחת הב' לאחריה תחת הד' ויהא ב' והו' תשים ג"כ לאחרי' אבל לא תכפול שכבר כפלת הו' ותשים אות' ו' תחת הב' שכבר עומד שם הא' והא' למעלה על הב' נמי תמשוך לאחריה על הד' ולא תכפול והג' במקו' הא' על הב' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תאמר כמה פעמים ו' בב"א פי' בי"ב והוה בו ב' פעמים אות' ב' תכתוב על הד' הראשונ' ותחת הד' ותמחוק הב"א ויהא צורתו כזה והו' של מט' נמי תמחוק ויהא כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ואז תקח הב' נמי ב' פעמים והוה ד' ולא נשאר מאומ' והב' השנייה נמי תקח ב' פעמים מן הד' ואז לא נשאר לך מאומא נמצא הפרט הוה ב'א'ג' פעם ב'א'ג' ויוצא ממנ' כלל ד'ד'ג'ז'ט' | ||||||||||||||||||||||||||
| ודוק ותובין לעולם בדרך זה |
Notes
| |
Appendix I: Glossary of Terms
| to know | לידע, דע כי, דע שתדע ש |
| to explain | לפרש, ביארתי |
| chapter | שערים |
| teaching | הקבלות |
| one who calculates | המחשב, המפתח |
| calculation | החשבונות |
| numeral | חשבון, אותיות, ציפרא |
| zero | גלגל |
| place holder | שומר המעלות |
| first rank | מעלה הראשונה |
| units | מעלת היחידים |
| third rank | מעלה השלישית |
| hundreds | מעלת המאות |
| fourth rank | מעלה הרביעית |
| thousands | מעלת האלפים |
| fifth rank | מעלה החמישית |
| tens of thousands | מעלת הרבבות, י' אלפים |
| sixth rank | מעלה ששית |
| hundreds of thousands | מעלת מאה אלפים |
| seventh rank | מעלה שביעית |
| millions | מעלת אלף אלפים |
| smaller than | קטן מן |
| greater than | גדול מן |
| more than | יותר מ |
| to exceed by | יותר על, יתיר על, עודף על, למעלה מ |
| bottom numeral | התחתונה, תחתונה |
| upper numeral | העליונה, עליונה |
| infinitely, endlessly | עד אין מספר |
| times | פעמים |
| to multiply | לחשוב, לכפול זע"ז |
| rank | מעלות, מעלה |
| המעלה שנייה | |
| עליונה | |
| שיט' | |
| שבשיט' עליונ', שיטות עליונות, שיטות העליונות | |
| שיט' ראשונ' | |
| השיטה התחתונה | |
| דומיון, דמיון | |
| מגיע ל | |
| עולה, יעלה, יעלה בידך, מה שיעלה בידך, העולה בידך | |
| יצא | |
| נקראת, נקרא | |
| יקראו | |
| אות, האות | |
| מניינם, מניין | |
| תחשוב | |
| חשוב | |
| חשוב אותו | |
| חשבונך | |
| תאמר, אמור | |
| ישאלך | |
| שואל | |
| תשיב אל לבך | |
| לכתוב, כתוב, כתוב (אותו / אותה / ב), כתבתי, כתבת, תכתוב (אותו), נכתוב, אכתוב לך, כותבין | |
| כתיבה | |
| שכתבת | |
| רשום, ארשום לך | |
| חרו[ת]ים | |
| העתקתי | |
| לראות | |
| שאראך | |
| אדירין | |
| חברם יחד | |
| לחבר, לחבר ... עם, תחבר...אל, תחבר... על, תחבר... ה, חבור... על, חבור אל ה, נחבר... עם, נחבר... על, אחבר | |
| לחבר כמה חשבונות יחד | |
| חבורם, חבורו, חיבור שחברנו | |
| הטור מן החיבור | |
| צירופו | |
| תצרף, צרוף (...יחד), צורפם יחד, צרפם (יחד) | |
| נוסיף... על, נוסיף... עליה | |
| מוסיף ...על, מוסיף... עליה | |
| בשער החיבור, שער חיבור | |
| המחובר | |
| השליך, השלך (...מ / ה), השלך מידך, קח ממנו, תקח ... מן, קח מה ש | |
| השלך ט"ט... מ, השלך ... בט"ט | |
| נשאר, ישאר, ישאר בידך, ישאר לך, הנשארת | |
| בלי חסרון ויתרון | |
| ומה שנשאר לך, ומה שנשמר לך | |
| הנותרת לי | |
| משקלו, משקל ה, משקלים | |
| אבני המשקל, אבן הראשון | |
| תכפול יחד, לכפול יחד | |
| תכפול | |
| כפל | |
| כפל קטן | |
| מה שבא מן הכפל | |
| בשער כפל | |
| לוח | |
| חצי לוח | |
| מתוקנת | |
| שער הכפל קטן, שער כפל קטן | |
| ציור | |
| צורתו | |
| עברת על ה, תעבור | |
| תקח ה, קח ה, קח בידך, קח בידך ל, יקח ה... מה | |
| ומהם תבין | |
| מרחק מן, המרחק עד, מרחקים | |
| מכל אחד, מן כל אחד ואחד | |
| זה על זה | |
| דהיינו, היינו | |
| הילך | |
| היאך | |
| המניין הקטון, מניין קטון, המנין הקטן, האות הקטן | |
| אות הגדול | |
| tens | העשיריות |
| ספר | |
| גלחות, בגלחת | |
| מחוק | |
| עניין | |
| כלל | |
| פי' | |
| המותר מ, עודף עליו | |
| לעשות, עשה, תעשה, עשיתי | |
| כאשר, כש | |
| עתה | |
| תדיר | |
| לעולם | |
| ולפעמים | |
| לא ... כלל | |
| לא ימוש מפיך | |
| תוכל ל | |
| כל כמה שתוכל | |
| אינך צריך | |
| צריך ל | |
| צריך ש | |
| תלוה לו, הלוית לו | |
| תרצה (ל), תחפוץ ל, בקשת ל, רצונך, בקשנו ל | |
| אשר בקשת, מבוקש | |
| מתכונך | |
| מכוון | |
| כוינת חשבונך | |
| אשכילך | |
| תשכיל, תחכם | |
| מושכל ראשון | |
| עיין | |
| תקיש | |
| ודוק | |
| להודיעך ש | |
| למצוא, תמצא (ה), נמצא, מצאתי, נמצא ה | |
| לזכרון | |
| וככלות | |
| תשלם | |
| המלאכה | |
| סליק | |
| הוי אומר | |
| בדרך הזה, דרך אחרת ל | |
| ואז, אז | |
| כבר | |
| כדי ש | |
| מה ש | |
| כל מה ש, כל אשר | |
| אשר ב | |
| אף כי | |
| כי | |
| לכך | |
| והנה | |
| נמי | |
| אחר כך, אח"כ | |
| ואם... אז | |
| אם | |
| אפילו | |
| רק | |
| כמה | |
| יהיה בכל פעם | |
| פעמים | |
| לכל היותר | |
| יותר מן | |
| מותר ה... מ | |
| פחות מ, פחותים מ, מה שלמטה מן, למטה מ | |
| הרבה כל כך | |
| ויהיה, ויהי, ויהא | |
| שם | |
| יש | |
| הרי | |
| ויהיה הכל | |
| הוה | |
| שהם | |
| אני | |
| הוא, היא | |
| או כלך לדרך זו, או כלך בדרך זו | |
| זה, זה ה | |
| כזה | |
| הזה | |
| אילו ה | |
| האחרונים | |
| חשבונות, חשבון | |
| שבידך | |
| בא לידך מ | |
| לפניך, מה שלפניך | |
| הסמוכ' לה, הסמוך ל | |
| מצד אותיות של שמאל | |
| לצד שמאל, בצד שמאל (ל), לשמאל | |
| אצל, אל | |
| נגד | |
| במקום | |
| אחר | |
| עוד | |
| ועוד | |
| וכן, ג”כ | |
| וכפי זה | |
| כגון | |
| כאילו | |
| כמו כן | |
| כל כיוצא בזה | |
| שלאחריו, לאחריה, שלאחריה | |
| שלפניה, לפני ה, קודם ה | |
| מן ה | |
| תחת, תחת ה | |
| למטה, שלמטה | |
| למעלה, למעלה מזו | |
| לעיל | |
| שאין בו ממש | |
| בקלות | |
| ולא ... אלא | |
| בלא שום | |
| זכר ל | |
| דבר | |
| כל דבר | |
| את"ל | |
| בע"ה | |
| לישב על אופניו |
Appendix II: Bibliography
Anonymous
Sefer Ṣifra
Manuscripts:
- 1) Budapest, Magyar Tudományos Akadámia, Ms. Kaufmann A 520/10 (IMHM: f 15170), ff. 179-200; 217-218 (16th century)
- Kaufmann A 520/10
- 2) Cincinnati, Hebrew Union College 890/1 (IMHM: f 30901), ff. 4r-18v (Hanau, 1641)
- Cincinnati 890
- 3) Mantova, Comunità Ebraica MS ebr. 8/16 (IMHM: f 788), ff. 69r-71v (Porto, 1464-1471)
- Mantova 8
- 4) Moscow, Russian State Library, Ms. Guenzburg 714/4 (IMHM: f 27994), ff. 64r-83v (17th-18th century)
- Guenzburg 714
- 5) München, Bayerische Staatsbibliothek, Cod. hebr. 394/4 (IMHM: f 1223), ff. 109v-127r (1566)
- München Cod. hebr. 394
- 6) New York, Jewish Theological Seminary Ms. 2634/6 (IMHM: f 28887), ff. 94r-124v
- JTS 2634
- 7) Oxford, Bodleian Library MS Mich. 60/11 (IMHM: f 22085), ff. 151r-176v (cat. Neub. 2171); (Frankfurt am Main, 1537)
- 8) Oxford, Bodleian Library MS Mich. 440/4 (IMHM: f 19984), ff. 114v-124v (cat. Neub. 2170); (1645)
- 9) Paris, Bibliothèque Nationale heb. 1088/1 (IMHM: f 14921), ff. 1r-23v (15th century)
- heb.1088
- 10) Paris, Séminaire Israélite de France (École Rabbinique) 158/1 (IMHM: f 4102), ff. 197r-211v (1604)
- École Rabbinique 158
- 11) Warszaw, Żydowski Instytut Historyczny 288/1 (IMHM: f 12013), ff. 1r-5v (15th century)
- 12) Warszaw, Żydowski Instytut Historyczny 295/4 (IMHM: f 10129), f. 56v (16th century)
The transcript is based mainly on manuscript München 394
Bibliography:
- Steinschneider, Moritz (Moshe). 1893–1901. Die Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann; repr. Hildesheim: G. Olms, 1964 and 2001. pp. 216-217 [i478-i479]
- ———. 1905. Mathematik bei den Juden, Band II: 1551-1840. Monatsschrift für die Geschichte und Wissenschaft des Judenthums 49, pp. 85-86. repr.: ed. Gad Freudenthal, Hildesheim, Zürich, New York: Olms, 2014, pp. 8-9.
![\scriptstyle{\color{red}{x,y<10\quad x\sdot y=\left[10\sdot\left[\left(x+y\right)-10\right]\right]+\left[\left[x-\left[\left(x+y\right)-10\right]\right]\sdot\left[y-\left[\left(x+y\right)-10\right]\right]\right]}}](/mediawiki/images/math/9/4/f/94f68b3edd7a5de8373da91368968ab4.png)
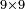
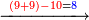
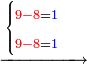

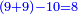

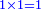
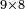
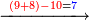
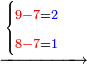
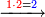
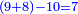


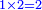
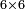
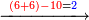
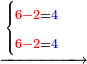
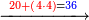
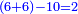

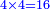
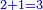
![\scriptstyle{\color{red}{x,y<10\quad x\sdot y=\left[10\sdot\left[\left(x+y\right)-10\right]\right]+\left[\left(10-y\right)\sdot\left(10-x\right)\right]}}](/mediawiki/images/math/b/a/4/ba47b3ce6e602ae8b4e44a762172704c.png)



![\scriptstyle{\color{red}{x<y<10\quad x\sdot y=\left(x\sdot10\right)-\left[x\sdot\left(10-y\right)\right]}}](/mediawiki/images/math/3/7/9/379821fa6258d1d24574dbe3c30f6dca.png)
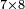
![\scriptstyle{\color{blue}{7\times8=\left(7\sdot10\right)-\left[7\sdot\left(10-8\right)\right]=70-\left(7\sdot2\right)=70-14=56}}](/mediawiki/images/math/c/f/8/cf82d668175564f785f54108257ef5e3.png)



![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=10+\left[\left(x-1\right)\sdot\left(y-1\right)\right]-\left[11\left(x+y\right)\right]}}](/mediawiki/images/math/d/e/b/deb3a15bab1027d790aee3e499ce8951.png)
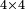
![\scriptstyle{\color{blue}{4+4+\left[11-\left(4+4\right)\right]=4+4+3=11}}](/mediawiki/images/math/b/4/2/b42c664ab942373f7f7104da31b46a3d.png)
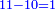
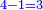


![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]-\left[10\sdot\left[10-\left(x+y\right)\right]\right]}}](/mediawiki/images/math/f/a/5/fa50d116d61f078f4565958da778fb21.png)
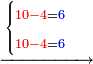
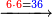
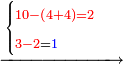
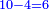

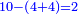
![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left(x+y\right)\right]-\left(10\sdot10\right)}}](/mediawiki/images/math/0/0/9/009964355db1dd5f0f49cfb6586fc299.png)
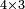
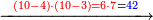
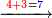
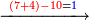
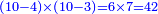
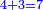
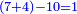

![\scriptstyle{\color{red}{x,y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left[\left(x+y\right)-10\right]\right]}}](/mediawiki/images/math/0/a/6/0a68457b8baa2872f5fd92e1bf4d30a1.png)
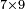
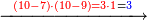
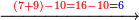
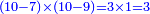
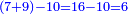
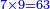
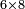
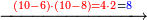
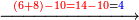
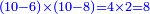
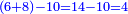

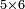
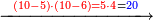

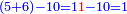

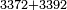

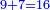
 :
: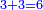
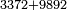



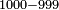
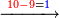
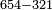
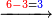
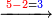
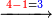
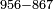
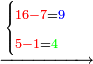
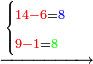
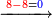
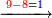
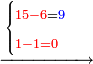
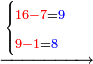
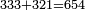
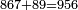
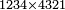
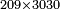
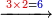
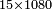
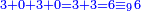
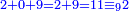
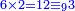

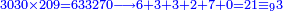
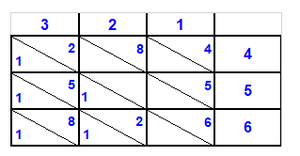
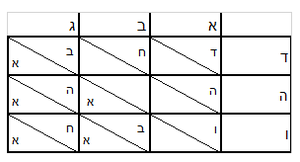






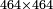
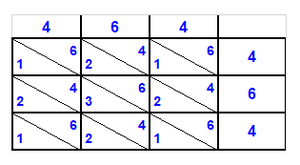
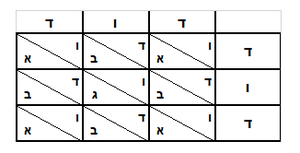
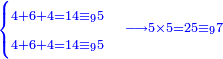
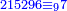
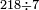
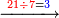
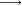

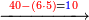
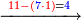
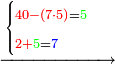

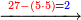
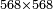 → Check:
→ Check: 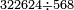
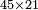 → Check:
→ Check: 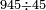

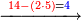

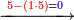
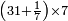
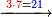
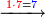
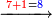
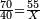
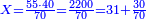 dinar
dinar
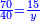
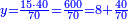 dinar
dinar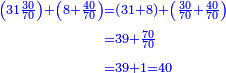
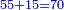
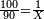
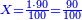
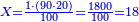
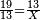
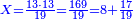 dinar
dinar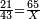
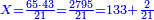
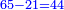
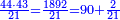
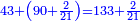
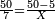
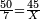
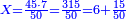
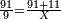
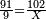
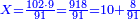
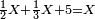
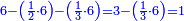
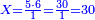
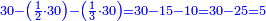
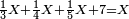




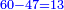
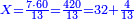
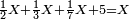
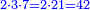
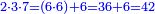
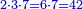
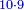
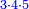
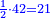

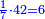
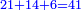
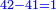
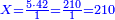
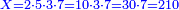
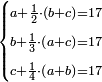
 ].
].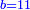 ].
].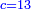 ]
]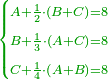
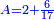

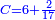
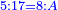
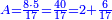
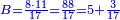
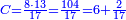
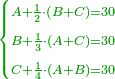
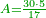
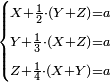

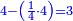
![\scriptstyle{\color{blue}{\left(4+\frac{1}{2}\right)-\left[\frac{1}{3}\sdot\left(4+\frac{1}{2}\right)\right]=3}}](/mediawiki/images/math/b/2/c/b2c7654e9e36456843cf38a9cefba0f9.png)
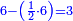
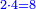
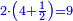
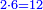
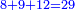
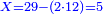
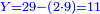
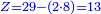
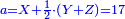
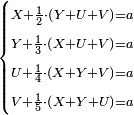
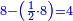
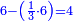
![\scriptstyle{\color{blue}{\left(5+\frac{1}{3}\right)-\left[\frac{1}{4}\sdot\left(5+\frac{1}{3}\right)\right]=4}}](/mediawiki/images/math/2/f/8/2f8b0ce274ed2357653f5bbb5b2e2059.png)
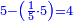
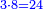
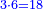
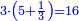
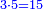
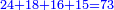

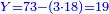
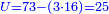
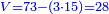
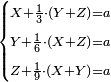
![\scriptstyle{\color{blue}{\left(3+\frac{3}{5}\right)-\left[\frac{1}{6}\sdot\left(3+\frac{3}{5}\right)\right]=3}}](/mediawiki/images/math/d/b/8/db875db8eb50eca9108eb5f305313319.png)
![\scriptstyle{\color{blue}{\left(3+\frac{3}{8}\right)-\left[\frac{1}{9}\sdot\left(3+\frac{3}{8}\right)\right]=3}}](/mediawiki/images/math/7/f/1/7f1cf2e5edc0dd92725597fe77ab6fbe.png)
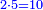
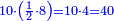

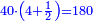
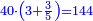
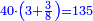

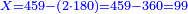
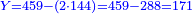
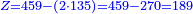
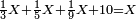
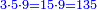
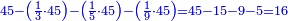
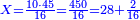
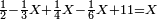
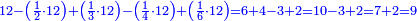
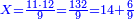
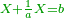
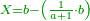
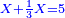
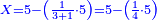
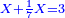
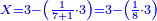
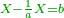
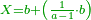
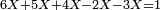

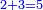
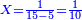
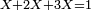

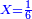
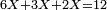
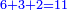
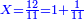
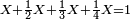
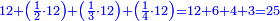
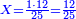
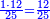
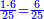
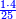
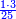
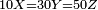
![\scriptstyle{\color{OliveGreen}{\begin{cases}\scriptstyle1+\left[3\sdot\left[10-\left(1\sdot7\right)\right]\right]=1+\left[3\sdot\left(10-7\right)\right]=1+\left(3\sdot3\right)\\\scriptstyle4+\left[3\sdot\left[30-\left(4\sdot7\right)\right]\right]=4+\left[3\sdot\left(30-28\right)\right]=4+\left(3\sdot2\right)\\\scriptstyle7+\left[3\sdot\left[50-\left(7\sdot7\right)\right]\right]=7+\left[3\sdot\left(50-49\right)\right]=7+\left(3\sdot1\right)\end{cases}}}](/mediawiki/images/math/9/e/a/9eae4ff1a7d19532b4c04b80bbf4a91a.png)

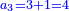
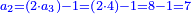
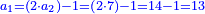
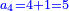
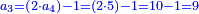
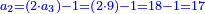
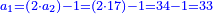
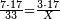
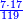
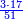
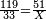
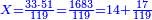
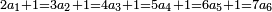
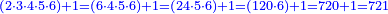
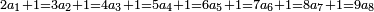
![\scriptstyle{\color{blue}{\left[720\sdot\left(7\sdot8\right)\right]+1=\left(720\sdot56\right)+1}}](/mediawiki/images/math/4/7/7/4771f98330aab4d54b098ef66e8365c0.png)
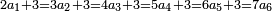
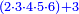
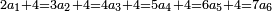
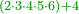
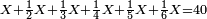
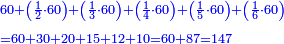

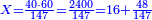
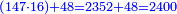
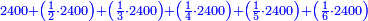
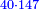
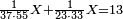
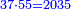

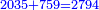

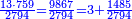
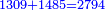
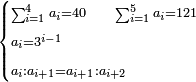
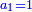


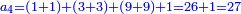
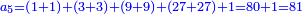
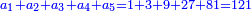
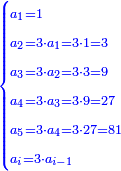
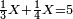
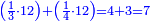
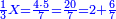
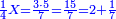
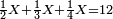
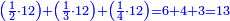
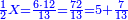
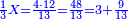
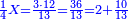
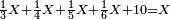
![\scriptstyle{\color{blue}{60-\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)\right]=60-57=3}}](/mediawiki/images/math/a/f/0/af01839e49ad14fc9850f6d812f5b8cb.png)
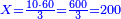
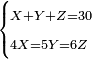
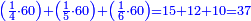
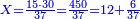
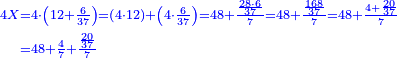
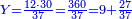
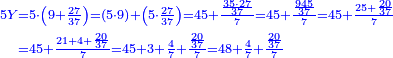
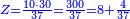
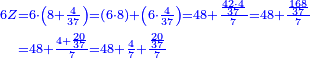
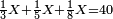
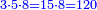
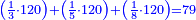
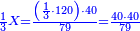
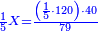
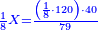
![\scriptstyle\begin{cases}\scriptstyle\sum_{i=1}^4 a_i =40\\\scriptstyle a_1=\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\\\scriptstyle a_2-\left[\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\right]=a_2-a_1=\frac{2}{3}a_3\\\scriptstyle a_3=\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{6}\right)\sdot a_1\\\scriptstyle a_4=\frac{4}{5}\sdot{\color{red}{a_3}}\end{cases}](/mediawiki/images/math/c/1/e/c1e254f07692c6845aa08397f170e7e7.png)
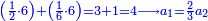
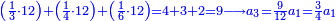
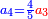
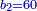
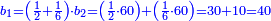
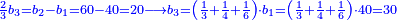
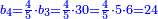
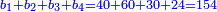
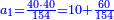
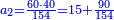
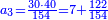
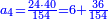
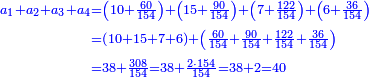
![\scriptstyle1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]=2+\frac{1}{10}\sdot\left[X-\left[\left[1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]\right]+2\right]\right]](/mediawiki/images/math/0/4/e/04ec9fa2f7109a05d7c4e8fa7ce5d879.png)
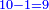
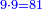
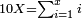
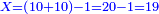
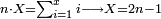
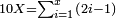
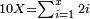
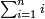
![\scriptstyle{\color{blue}{\sum_{i=1}^9 i={\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(9+1\right)\right]\sdot9}}=5\sdot9=45}}](/mediawiki/images/math/6/f/0/6f09e82bc29722bd17b0356389427645.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=\left[\left(\frac{1}{2}\sdot10\right)\sdot10\right]+\left(\frac{1}{2}\sdot10\right)=\left(5\sdot10\right)+5=50+5=55}}](/mediawiki/images/math/8/0/b/80b5dca53c99289503b8c13b342ab214.png)
![\scriptstyle n=2m\longrightarrow\sum_{k=1}^n k=\left[\left(\frac{1}{2}\sdot n\right)\sdot n\right]+\frac{1}{2}n](/mediawiki/images/math/a/8/a/a8a5babcd3a6eea49bd9b762c7395e9b.png)
![\scriptstyle n=2m+1\longrightarrow\sum_{k=1}^n k=\left[\frac{1}{2}\sdot\left(n+1\right)\right]\sdot n](/mediawiki/images/math/1/e/4/1e4ea38423bb671340fbd2275e275e63.png)
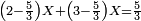
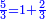
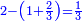
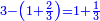
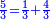
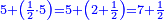
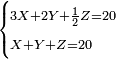
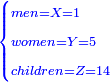
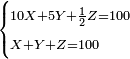
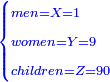
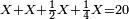
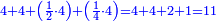
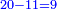
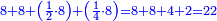

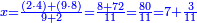
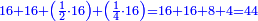

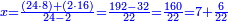
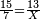
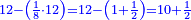
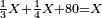
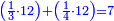
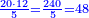
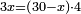
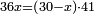
![\scriptstyle\left[\left(2-\frac{5}{3}\right)\sdot X\right]+\left[\left(3-\frac{5}{3}\right)\sdot X\right]=5](/mediawiki/images/math/b/3/9/b39a89f5f9f01ae578ff87165913ffb8.png)
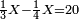
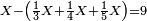
![\scriptstyle\begin{cases}\scriptstyle X+\left[\frac{1}{2}\sdot\left(Y+Z\right)\right]=60\\\scriptstyle Y+\left[\frac{1}{4}\sdot\left(X+Z\right)\right]=60\\\scriptstyle Z+\left[\frac{1}{3}\sdot\left(X+Y\right)\right]=60\end{cases}](/mediawiki/images/math/f/7/e/f7ed4efec08d6ecaa27c9fc465bdae6d.png)
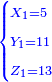
![\scriptstyle{\color{blue}{\begin{cases}\scriptstyle X_1+\left[\frac{1}{2}\sdot\left(Y_1+Z_1\right)\right]=17\\\scriptstyle Y_1+\left[\frac{1}{4}\sdot\left(X_1+Z_1\right)\right]=17\\\scriptstyle Z_1+\left[\frac{1}{3}\sdot\left(X_1+Y_1\right)\right]=17\end{cases}}}](/mediawiki/images/math/9/7/d/97d57b8ac4e8a9dbe8f698d6b961bdee.png)
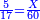
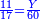
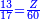
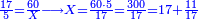
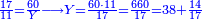
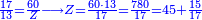
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle X+\left[\frac{1}{2}\sdot\left(Y+Z\right)\right]&\scriptstyle=\left(17+\frac{11}{17}\right)+\left[\frac{1}{2}\sdot\left[\left(38+\frac{14}{17}\right)+\left(45+\frac{15}{17}\right)\right]\right]\\&\scriptstyle=\left(17+\frac{11}{17}\right)+\left(19+\frac{7}{17}\right)+\left(22+\frac{16}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/1/1/5/1151c1953e5eeefb1128f4a9ae687afb.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Y+\left[\frac{1}{3}\sdot\left(X+Z\right)\right]&\scriptstyle=\left(38+\frac{14}{17}\right)+\left[\frac{1}{3}\sdot\left[\left(17+\frac{11}{17}\right)+\left(45+\frac{15}{17}\right)\right]\right]\\&\scriptstyle=\left(38+\frac{14}{17}\right)+\left(5+\frac{15}{17}\right)+\left(15+\frac{5}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/8/c/5/8c51fcde67c49f9f297096f4fcd9e029.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Z+\left[\frac{1}{4}\sdot\left(X+Y\right)\right]&\scriptstyle=\left(45+\frac{15}{17}\right)+\left[\frac{1}{4}\sdot\left[\left(17+\frac{11}{17}\right)+\left(38+\frac{14}{17}\right)\right]\right]\\&\scriptstyle=\left(45+\frac{15}{17}\right)+\left(4+\frac{7}{17}\right)+\left(9+\frac{12}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/5/a/2/5a2cd999d16458b3c413355c1586917a.png)
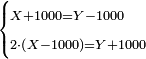
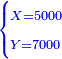
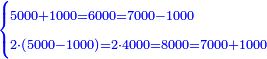
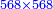

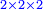
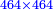

![\scriptstyle{\color{blue}{\sqrt[3]{149721291}}}](/mediawiki/images/math/2/8/8/28889c07ec72df83ee96c8d036f89e7d.png)

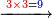


![\scriptstyle{\color{blue}{\sqrt[3]{99897344}}}](/mediawiki/images/math/7/3/e/73e3d56a32f3f45e418253824810fdba.png)
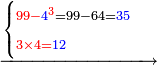
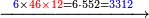
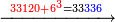

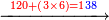
![\scriptstyle\xrightarrow{{\color{red}{\left[\left[4\times\left(464\times138\right)\right]\sdot10\right]+4^3}}={\color{blue}{2561344}}}](/mediawiki/images/math/9/8/5/98577a9d90a199749f7fe8e04eebab1f.png)