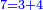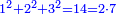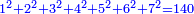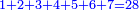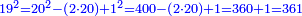Difference between revisions of "ספר האחד"
From mispar
(→Appendix: Bibliography) |
|||
| Line 789: | Line 789: | ||
:22) Wien, Öesterreichische Nationalbibliothek Cod hebr. 152/1 (IMHM: f 1422), ff. 1r-3v (18th-19th century)<br> | :22) Wien, Öesterreichische Nationalbibliothek Cod hebr. 152/1 (IMHM: f 1422), ff. 1r-3v (18th-19th century)<br> | ||
| − | + | <span style=color:blue>The transcript is based mainly on manuscript London 27153</span> | |
'''<u>Edition</u>''':<br> | '''<u>Edition</u>''':<br> | ||
Latest revision as of 17:19, 8 July 2022
| [1]בשם האחד לבדו יחל אברהם עבדו | |
Contents[hide]One |
|
|
האחד סופר את עצמו ואין אחר סופרו[2] והוא יספור כל מספר[3] |
|
והוא שורש ויסוד ומרובע ומעוקב[4] |
|
והוא דומה לעצם הדבר הנושא כל המקרים[5] |
|
וכל מספר בכחו[6] והוא בכל מספר במעשה[7] |
|
והוא ההוה וכל מספר הוה בעבורו[8] |
|
והוא קדמון לכל וכל מספר מתחדש[9] |
|
והוא סבת כל מספר זוג ושאינו זוג |
|
והוא אינו מספר[10] |
|
ולא ירבה ולא יתחלק והוא סבת כל רבוי וחילוק[11] |
|
ואין לו דמיון גם אין לו הפך ולא שינוי[12] |
|
והוא יעשה בפאה אחת מה שיעשה כל חשבון בשתי פאות[13] |
|
והוא כולל כל כלל וכל חלק כי הוא ראשון[14] ואחרון ואין לו שבר[15] כי אם במחשבת חלק הכלל שיהיה אחד |
|
והוא תחלת כל מספר שאינו זוג המחוברים[16] על סדר המולידים המרובעים[17] |
|
גם הוא תחלת כל זוג שתהיינה הקצוות כפל זה על זה שוות[18] |
|
ואם המספר איננו זוג יהיה הכפל ומרובע האמצעי[19] |
|
ובין מרובע למרובע דמות חלק וחצי חלק[20] |
|
ובעבור שאחד אינו שבור היו השנים חלקים נכונים[21] וכן כל חלק וחלק כשנים[22] |
|
וכל צורה משולשת שהיא תחלת הצורות ועליה תתחלק כל הצורה[23] |
|
ואם היה הצלע האחר ג' אחד לא יתכן להיות המשולש כי [24]אם שוה כולו או שוה השוקים רק חדי המקצוע כי המכונה תהיה אחת |
|
וחשבון עשרה דומה לאחת וככה מאה ואלף על הסדר[25] |
|
וחכמי המספר ברצותם לכפול חשבון על חשבון במערכה אחת או בשתים יחסרו אחד למוסד והאריכו לתת טעם |
|
והעקר כי המערכת השנית שם יחל הדמיון |
|
ובעבור הקל על התלמידים חשבו המערכת הראשונה שהם האחדים והוסיפו השנים על השנים כמספרם על כן הוצרכו לחסר אחת |
|
כי מערכת העשרות באמת אחת והמאות שנים והאלפים שלשה והדבר שוה |
Two |
|
|
השנים תחלת כל מספר |
|
ונקרא כן בעבור שהוא מקבל שינוי מגזרת ודתיהם שונות[26] |
|
ומחברתו כמו כפלו בעצמו |
|
וכל [יש][27] עצם וצורה ולא כן האחד |
|
וכל משולש שתהא הצלע האחת שתים ולא יתכן להיותו כי אם שוה כולו או שוקיו שוות או המקצוע רחב |
|
ודע כי כל משולש מתחלק לשנים חלקים שונים |
|
האחד שוה והוא על שנים דרכים שוה כולו או שתי שוקיו ולעולם יהיו כל המקצועים חדים |
|
והחלק השני תהיינה הצלעות משתנות והוא על שלשה דרכים |
|
האחד שיהיה המקצוע רחב כי שתי המקצועות לעולם חדים |
|
ומרובע הצלע הגדול הוא מוסיף על שני מרובעי הצלעות [הקטנות][28] ככפל אחד חלקי קו הצלע על החלק השני עם התוספת על הצלע עד היותה לנוכח העמוד שהוא מבחוץ |
|
ותחלת כל משולש רחב המקצוע על הסדר בג"ד |
|
והדרך השני להיות המקצוע האחד ישר גם השנים מקצועות יהיו חדים |
|
ומרובעי השנים הקטנות כמרובע היתר שהוא הצלע הגדול |
|
והדרך השלישי יקרא חד[29] המקצוע כי כל מקצועותיו חדים |
Three |
|
|
השלשה הפך האחד כי מחברת אחד אל אחד גדול מכפלו בעצמו וחשבון השנים שוה ומחברת ג' אל ג' קטן מכפלו בעצמו ועל דרך שלשה הוא בכל חשבון |
|
והוא תחלת מספר משולש שוה |
|
ומרובעו כמספר תחלת משולש [בלתי שוה][30] |
|
ומעקבו[31] מספר צלעות השוה שהם במערכת הראשונה |
|
ומספר שלשה תחלת כל מספר שאיננו זוג וכפלו על עצמו גדול ממנו |
|
ואין מספר שיהיה המספרים לפניו כמותו רק הוא לבדו |
|
על כן היה חשבון ששה שהוא מורכב ממנו ישר עם חלקיו |
|
והמורכב מהשלשה תחלת החשבון שחלקיו רבים ממנו |
|
ואם תחברנו עם חלקיו יהיה מספר המחובר חשבון ישר |
|
ודע כי האחד כמו אורך שהוא קו |
|
[והשנים שטח][32] |
|
[והשלשה][33] גוף כי יש לו אֹרך ורֹחב ועומק |
|
ואמרו חכמי התושייה כי הזמן מתחלק על שלשה |
|
הנפש הצומחת והחיה והחכמה שלש |
|
והוא תחלת משלש ישר המקצוע |
Four |
|
|
הארבעה מרובע ראשון נראה |
|
והוא תחלת החשבון זוג הזוג |
|
והוא תחלת החשבון מורכב |
|
כי מערכת הראשונה הם ט' והנה האחד יסוד החשבון ונשארו ארבעה ראשונים והם בגה"ז והארבעה האחרים הם מורכבים |
|
ובחשבון המספרים לפניו הם עשרה שהוא תחלת הכלל הדומה והשורש ד' |
|
ובעבור היות האחדים אל הראשון לאחד שאינו מתחלק על כן הוא להפך |
|
וככה ב' עם ה' וג' עם ו' וד' עם ז' וככה [34]עד אין קץ |
|
על כן המזל הרביעי הפך הראשון כי החֹם והקֹר הם הפועלים והשנים האחרים לח ויבש פעולים |
|
והנה כל רביעי במזלות הפך הראשון בפֹעל ומזלות האש לבדה הפך בפֹעל ובפעול |
|
ועל כן אמרו חכמי המזלות כי מבט רביעית הגלגל שנאה ומבט ששית חצי אהבה |
|
כי השלישי מהמזלות על הראשון בתולדת אחד בפֹעל והפך בפעול על כן אמרו כי הוא חצי אהבה |
|
ומבט שלישית אהבה גמורה כי מבט שלישית הגלגל שהוא החמישי בתולדת הראשון על כן מבט אהבה גמורה בפֹעל ובפעול |
|
וככה א' עם ה' כי שניהם שומרים עצמם |
|
וככה ב' עם ו' כי שניהם זוג הנפרד |
|
וככה ג' עם ז' כי שניהם אינם זוגות ומחלקיהן שוה |
|
ולא כן הא' עם הג' וב' עם הד' וג' עם ה' |
|
ומבט חצי הגלגל ומבט רביעית בחציו והוא מבט איבה בפעול |
|
ואל תתמה כי גם הבית השביעי יורה על העזר בדרך שהזכיר בעל ספר יצירה אמ"ש בזכר ואש"מ בנקבה |
|
והנה הגלגל שהוא אחד יחלקהו האלכסון |
|
גם יתחלק האלכסון והנה מבטו רביעית |
|
ואם תשים נקדה ברביעית יתחלק הגלגל לשלשה חלקים שוים למשלש וחציו ששית הגלגל |
|
ולא ימצא מספר אחר שיחלקהו במחשבה בשברים רבים |
|
והארבעה תחלת משלש משתנה חד המקצוע |
|
ואחריו כל המספר הולך על הסדר בכל דרכיו |
|
והנה בעל הרֹחב הראשון יהיה תוספת היתר על השתים כמספר האמצעית והמקצוע החד יחסר מהיתר כמספר האמצעית |
|
והנה אתן לך כלל אם יהיו שלשה מספרים סמוכים על הסדר מארבעה ולמעלה ותרצה לדעת כמה יתרון השתים על היתר חסר לעולם מהאמצעית ארבעה וכפֹל הנשאר על האמצעית |
|
וככה יהיה דמיון יו"ד י"א י"ב |
|
חסרנו ד' מי"א נשארו ז' כפלנוהו על י"א עלה ע"ז והוא חסרון מרבע היתר |
|
ודע כי יש מקצוע רחב מאד ויש קרוב מישר |
|
כמו ד' ח' ט' |
|
וככה יש חד שהוא חצי ישר או שלישיתו או פחות |
|
ואל תחשֹׁב שתוכל לעשות משלש מכל מספר שתרצה |
|
כי החד לא יתכן להיות בו פחות מד' |
|
ולא משלש שתהיה הצלע גדולה מן השתים |
|
ולא לעשות ישר אם היו מספרי המקצועות רחוקים |
|
רק על מרכבת אחת כמו ג' ד' ה' או במֹרכב ממנה |
|
או שתהיינה הצלעות הקטנות סמוכות כמו כ' כ"א כ"ט |
|
או הגדולות סמוכות כמו ה' י"ב י"ג |
|
ויש רחב המקצוע רב כמו י' י"ז כ"ו |
|
ויש מעט כמו י' כ"ג כ"ו |
|
והנה י' כ"ד כ"ו |
|
רק י' כ"ה כ"ו חד מעט |
|
על כן לא נוכל לעשות גם רחב גם חד שתהיינה הצלעות רחוקות |
| I shall give you a rule: | והנה אתן לך כלל |
|
דע כי מדרך החשבון היו המשלשים משֻני צלעות שהם במערכה ראשונה ע"ט והנה אין נכונים מהם רק ל"ג |
|
גם המשלשים בעלי השוקים השוות אין כלם נכונים |
|
והנה חשבון ד' תחלת חשבון שני |
|
על כן כל מספר זוג לעולם יהיה מספר שני שהוא מֻרכב חוץ מחשבון שתים בעבור כח האחד כי הוא ראש מעשיו |
|
והנה כל חשבון ערוך על אחד לא יוסיף כי הוא עצם כל חשבון |
|
על כן תחלת המרבע ד' |
|
וכל מרבע כפול על מרבע מרבע |
|
גם מחֻלק על מרבע מרבע |
|
וערך מרבע אל מרבע מרבע |
|
על כן מדות כל החכמים במרבעים |
Five |
|
|
החמשה חשבון עגול והיה כן יען כי סוף המערכת הראשונה ט' על כן הוא מתגלגל על עצמו כאשר אפרש |
|
וכשתחבר האחד שהוא דומה למרובע אל מרובע ראשון הזוגות יהיה ה' |
|
ואם תחברנו אל מרובע ראשון מחשבון שאינו זוג יהיה כפלו |
|
וכשתחבר מרובעו אל מרובע כפלו יהיה המחובר כמספר מעוקבו |
|
ואם כפלת זה המספר יהיה מרובעו עם מרובע כפלו חצי מעוקבו |
|
ועוד אם בקשת לדעת ערך מרובע איזה מספר שתרצה ומרובע כפלו אל מעוקבו לעולם יהיה כערך המספר אל ה' אם הוא פחות ממנו או ערך ה' אליו אם הוא גדול ממנו |
|
כמו ג' כי מרובעו כפלו מ"ה והמעוקב כ"ז וערכו אל המרובעים כערך ג' אל ה' |
|
וערך ו' מרובעו וכפלו ק"פ והמעוקב רי"ו והנה המספר ה' ששיות המעוקב |
|
ועל זה הדרך הכל |
|
וזה המספר מחובר מתחלת זוג ומתחלת שאינו זוג |
|
ויש אומרים כי חמש הרגשות כנגד זה המספר |
|
ואמרו כי מראה העין מתולדות הכוכבים ע"כ תראה העין בלא זמן |
|
והריח מתולדות האש כי הוא כמי הדם |
|
והטעם מתולדות המים והעקר הליחה |
|
והשמע מתולדות הרוח |
|
והמשוש מתולדות הארץ |
Six |
|
|
הששה מורכב מן ג' כי גבול הגוף ג' |
|
מן האורך יצא פנים ואחור |
|
מן הרוחב ימין ושמאל |
|
ומן העומק מעלה ומטה |
|
והנה מן ג' פיאות נכבדות הפנים |
|
כי תנועת כל החיים לפנים גם לימין כי כן תנועת הגלגל הגדול גם מעלה כי כן תנועת כל צומח למעלה |
|
וכבר הזכרתי שהוא ישר |
Seven |
|
|
השבעה מחובר מתחלת מספר שאיננו זוג עם שני לזוג |
|
וככה הוא מחובר מתחלת זוג עם שני לאשר איננו זוג |
|
ובעבור זה קראוהו חכמי התושיה חשבון שלם |
|
ואמר עליו בעל ספר יצירה כי הוא מכוון באמצע והנה הוא סוד האחד שאינו גוף עם הגוף שיש לו ו' פיאות |
|
והנה ידמה לאחד כי אין אחריו מורכב אך משנים גם אח"כ ט' שהוא מורכב מן ג' |
|
והנה הוא כתחלת חשבון |
|
גם ידמה לשנים כי מאזני מרובעיהם שוים |
|
גם ידמה לג' כי מרחקו מהדומה ג' ע"כ במרובעו ט' |
|
גם ידמה לארבעה כי כל מאזני מרובע מרובע או ז' |
|
גם דומה לחמשה כי המחובר מרובע אחד ומרובע תחלת הזוג ואשר איננו זוג כפול ז' שהוא י"ד |
|
ויגיע עד מרובע ז' ק"מ כדמות י"ד |
|
גם ידמה לששה כי אל ז' המחובר שלפניו חשבון ישר עם חלקיו בשוה |
|
ועוד כי כחשבון שלושה המשרתים ויש לו סוד |
|
כי אם יהיו ד' לא יהיו שנים במספר |
|
וככה אם יהיו ה' לא יהיו השנים כן עשרה ואם הוא מחמשה הנה לא יהיה זוג הפך תולדותו |
|
וככה ששה וכל מספר אחרי שבעה |
|
כי השנים בחשבון שבעה כ"א שהוא כפל ג' שאינו זוג על ז' |
|
וככה הם הרבעיים |
Eight |
|
|
השמונה ידוע כי האורך בין שתי נקודות והנה המרחב ד' נקודות והגוף ח' והוא העובי |
|
על כן שמונה מגזרת מאשר שמנה לחמו[35] |
|
גם הוא חשבון מעוקב |
|
ובעבור שהם ח' גלגלים גדולים שהם העגולות |
|
הנה מאזני ח' כמו אחד |
|
ומאזני ז' כמו שנים |
|
ומאזני ו' כמאזני ג' |
|
ומאזני ד' כמאזני ה' |
|
וכנגד הח' האש והרוח והמים והעפר כי לכל אחד ואחד ב' תולדות כי הם מורכבים מארבע יסודות |
Nine |
|
|
התשעה סוף המערכת הראשונה |
|
על כן מאזני כל מספר הכפול על עצמו או על אחר הם ט' |
|
והוא תחלת מרובע מספר שאינו זוג |
|
ואם תעשה עגול ותכתוב בו הט' מספרים הנה ט' מתגלגל על כל המספרים שהם לפניו |
|
כי ט' על ט' פ"א הנה הא' בשמאל שהוא האחדים ובימין הפ' שהוא העשרות כנגד ח' |
|
ואח"כ מהשמאל ט' על ח' ע"ב ב' בשמאל וז' בימין בעשרות |
|
ואח"כ מהשמאל ג' ובימין ו' שהוא ט' על ז' ס"ג |
|
ואח"כ מהשמאל ד' באחדים ובימין ה' בעשרות והוא כפל ו' על ט' נ"ד |
|
ואחר כך בשמאל ה' ושב מספר מ' כנגד הד' שיהיו אחדים כי תהפוך הגלגל ושבו החמשים חמשה |
|
גם הט' על ד' עלו ל"ו והנה האחדים בימין והעשרות בשמאל |
|
ג"כ כ"ז |
|
גם י"ח |
|
ועוד נחשוב כי שתים עגולות הם כנגד העליונות האחת מזרחית והשנית מערבית ונאמר כי גם הט' בראש התלי מהגלגל וזאת הולכת לצד אחד והאחרת לצד אחר |
|
והנה מרובע ט' יש בו א' וככה כלם ע"כ היה חשבון ה' באמצע כאלו היא בזנב התלי ע"כ הוא חשבון עגול |
| I will show you a method for the squares: | והנה אראה לך דרך במרובעים |
| We know that the hundreds are similar to the units and the squares are also similar to those that are in the first rank. | ידענו כי המאות דומות לאחדים ושבו מרובעים דומים לאשר הם במערכת הראשונה |
|
והנה בקשנו לדעת כמה מרובע י"ט |
|
כי הקרוב אליו ת' וחשבונו לפניו והנה נחסר אחד מהשלמת העשרים והנה נכפלנו ונחסרנו אחורנית יעלה המספר ש"ס ונוסיף מרובע הא' שחסרנו והנה עלה הכל שס"א וזה מרובע י"ט |
Notes
[Expand]
Appendix: Bibliography
Abraham ben Meir Ibn ‛Ezra
b. 1089, Tudela, Spain – d. 1167
Sefer ha-ʼEḥad (The Book of One)
Prior to 1148, possibly in Béziers
Manuscripts:
- 1) Berlin, Staatsbibliothek (Preußischer Kulturbesitz) Or. Oct. 244/12 (IMHM: f 1996), ff. 57v-59v (15th-16th century)
- 2) Budapest, Magyar Tudományos Akadámia, MS. Kaufmann A 271/6 (IMHM: fiche 76), ff. 417-424 (15th century)
- 3) Cambridge, University Library Add. 1215, 3/3 (IMHM: f 17078), ff. 25v-28v (1532)
- 4) Hamburg, Staats- und Universitätsbibliothek, Ms. Levy 113/3 (IMHM: f 1559), ff. 24v-27v (15th century)
- 5) London, British Library Add. 27038/6 (IMHM: f 5716), ff. 41v-44v (cat. Margo. 1073, 6) (16th century)
- 6) London, British Library Add. 27153/8 (IMHM: f 5826), ff. 37v-40v (cat. Margo. 1085, 8) (Siena, 1431)
- [London 27153]
- 7) Moscow, Russian State Library, Ms. Guenzburg 338/6 (IMHM: f 47620), ff. 51r-54v (16th-17th century)
- 8) München, Bayerische Staatsbibliothek, Cod. hebr. 36/9 (IMHM: f 1166), ff. 136r-137v (Istanbul, 1485)
- 9) Napoli, Biblioteca Nazionale Vittorio Emanuele III F 12/33 (IMHM: f 11526), ff. 187r-190r (Benevento, 1492)
- 10) New York, Jewish Theological Seminary Ms. 2316/2 (IMHM: f 28569), ff. 1v-5r (15th century)
- 11) New York, Jewish Theological Seminary Ms. 2321/6 (IMHM: f 28574), ff. 44r-46v (1555)
- 12) New York, Jewish Theological Seminary Ms. 2349/2 (IMHM: f 28602), ff.?? (16th century)
- 13) New York, Jewish Theological Seminary Ms. 2497/3 (IMHM: f 28750), ff. 7r-8v (15th century)
- 14) New York, M. Lehmann 43/1 (IMHM: f 23218), ff. 1-4 (19th century)
- 15) Oxford, Bodleian Library MS Mich. 238/6 (IMHM: f 22048), ff. 52v-56r (cat. Neub. 1234, 6) (17th century)
- 16) Oxford, Bodleian Library MS Mich. 400/6 (IMHM: f 19291), ff. 14r-15r (cat. Neub. 2006, 3) (15th century)
- 17) Oxford, Bodleian Library MS Poc. 209/3 (IMHM: f 22049), ff. 23r-26r (cat. Neub. 1235, 3) (15th century)
- 18) Paris, Bibliothèque Nationale de France heb. 1085/5 (IMHM: f 14919), ff. 53v-55v (15th-16th century)
- 19) Roma, Biblioteca Casanatense 3104/3 (IMHM: f 74), ff. 17r-21r (15th-16th century)
- 20) Vatican, Biblioteca Apostolica ebr. 429/19 (IMHM: f 502), ff. 75r-77v (14th-15th century)
- 21) Warszaw, Żydowski Instytut Historyczny 150/5 (IMHM: f 30154), ff. 33r-35r (19th century)
- 22) Wien, Öesterreichische Nationalbibliothek Cod hebr. 152/1 (IMHM: f 1422), ff. 1r-3v (18th-19th century)
The transcript is based mainly on manuscript London 27153
Edition:
- Ibn ‛Ezra, Abraham. Sefer ha-’Eḥad. In: Yalqut Avraham Ibn ‛Ezra, ed. Israel Levin. New York, Tel Aviv: Israel Matz Hebrew Classics Ltd. 1985, pp. 399-414.
- Ibn Ezra, Abraham. Sepher ha-Echad: liber de novem numeris cardinalibus. Ed. Simchae Pinsker and Michael Abba Goldhardt. Odessa: 1867.
Bibliography:
- Langermann, Y. Tzvi. 2001. Studies in Medieval Hebrew Pythagoreanism: Translations and Notes to Nicomachus; Arithmological Texts, Micrologus IX, pp. 219–236.
- Sela, Shlomo, and Gad Freudenthal. 2006. Abraham Ibn Ezra’s scholarly writings: a chronological listing, Aleph 6, pp. 13-55.
Commentary on Sefer ha-ʼEḥad
Mordecai ben Eliezer Comṭino
Constantinople & Adrianople c. 1402-1482
Manuscripts:
- 1) Moscow, Russian State Library, Ms. Guenzburg 469/5 (IMHM: f 43040), ff. 184r-211r (16th century)
- 2) New York, Jewish Theological Seminary Ms. 2577/1 (IMHM: f 28830), ff. 1r-31v (19th century)
- 3) New York, M. Lehmann 43/2 (IMHM: f 23218), ff. 6-24 (19th century)
- 4) Paris, Bibliothèque Nationale de France heb. 681/3 (IMHM: f 11559), ff. 79v-101r (15th century)
- 5) Parma, Biblioteca Palatina Cod. Parm. 2446/3 (IMHM: f 13450), ff. [72r]-[89v] (15th century)
- 6) St. Petersburg, Inst. of Oriental Studies of the Russian Academy A 221/3 (IMHM: f 69628), ff. :24v-42v (1472)
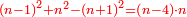
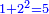
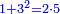
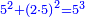
![\scriptstyle{\color{blue}{\left(2\sdot5\right)^2+\left[2\sdot\left(2\sdot5\right)\right]^2=\frac{1}{2}\sdot\left(2\sdot5\right)^3}}](/mediawiki/images/math/c/c/8/cc8d772d9367fc32e176a5ca9156e880.png)