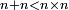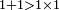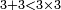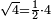Difference between revisions of "ספר המלכים"
(→Four) |
(→Tetrad in the existences) |
||
| Line 587: | Line 587: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|כבר ביארו אפלטון בס' טימאוס הרוחניי כשאמר שהנמצאות כלם בלתי האלוה אחר הבדלם בישיותהם ישתתפו בארבעה דברים בהיותם בלתי שלמים בהיותם עלולים בהיותם בעלי רבוי בהיות כח כל א' מהם בלתי מתפשט בכל הנשארים | + | *things shared by the existents apart from God: imperfect; caused; have multitude; the faculty of each does not spread to the rest (Plato, Timaeus) |
| + | |style="text-align:right;"|כבר ביארו '''אפלטון''' בס' טימאוס הרוחניי כשאמר שהנמצאות כלם בלתי האלוה אחר הבדלם בישיותהם ישתתפו בארבעה דברים בהיותם בלתי שלמים בהיותם עלולים בהיותם בעלי רבוי בהיות כח כל א' מהם בלתי מתפשט בכל הנשארים | ||
|- | |- | ||
| | | | ||
| + | *things in the orbs: orb; star; essence; separate mover | ||
|style="text-align:right;"|'''ובגלגלים ד' דברים''' הגלגל והכוכב הנפש והמניע הנבדל | |style="text-align:right;"|'''ובגלגלים ד' דברים''' הגלגל והכוכב הנפש והמניע הנבדל | ||
|- | |- | ||
| | | | ||
| + | *natures in the orbs: stars, planets; the two luminaries (Maimonides, Guide II.9) | ||
|style="text-align:right;"|'''בגלגלים המצויים ד' טבעים''' המכוכב כוכבי הנבוכה שני המאורות כמו שבי' הר"מ ז"ל פי י"א משני | |style="text-align:right;"|'''בגלגלים המצויים ד' טבעים''' המכוכב כוכבי הנבוכה שני המאורות כמו שבי' הר"מ ז"ל פי י"א משני | ||
|- | |- | ||
| | | | ||
| + | *faculties emanate from the orbs: inanimate; vegetative; animal; rational | ||
|style="text-align:right;"|'''הכוחות השופעות מן הגלגל ד'''' הדומם הצומח החי המדבר | |style="text-align:right;"|'''הכוחות השופעות מן הגלגל ד'''' הדומם הצומח החי המדבר | ||
|- | |- | ||
| | | | ||
| + | *skills of analogy: proof; argumentation; refutation; rhetorics | ||
|style="text-align:right;"|'''המלאכות אשר תעשנה ההקש ד'''' והן המופת והנצוח וההטעמה וההלצה | |style="text-align:right;"|'''המלאכות אשר תעשנה ההקש ד'''' והן המופת והנצוח וההטעמה וההלצה | ||
|- | |- | ||
| | | | ||
| + | *seasons: cold; hot; summer; winter | ||
|style="text-align:right;"|'''התקופות ארבעה''' קור וחום קיץ וחורף | |style="text-align:right;"|'''התקופות ארבעה''' קור וחום קיץ וחורף | ||
|- | |- | ||
| | | | ||
| + | *astrological aspects: opposition; triplicity; quartile; sextile | ||
|style="text-align:right;"|'''מיני המבטים אשר כפיהם יתמזגו ניצוצות הכוכבים ארבעה''' נכח שליש רביע שתות | |style="text-align:right;"|'''מיני המבטים אשר כפיהם יתמזגו ניצוצות הכוכבים ארבעה''' נכח שליש רביע שתות | ||
|- | |- | ||
| | | | ||
| + | *opposites: contradiction; correlation; privation and possession; affirmation and negation | ||
|style="text-align:right;"|'''המקבילות ארבעה''' ההפכים המצטרפים ההעדר והקנין החיוב והשוללות | |style="text-align:right;"|'''המקבילות ארבעה''' ההפכים המצטרפים ההעדר והקנין החיוב והשוללות | ||
|- | |- | ||
| | | | ||
| + | *qualities: hot; cold; moist; dry | ||
|style="text-align:right;"|'''האיכיות ארבעה''' החום והקור הלחות והיובש | |style="text-align:right;"|'''האיכיות ארבעה''' החום והקור הלחות והיובש | ||
|- | |- | ||
| | | | ||
| + | *created mixtures | ||
|style="text-align:right;"|'''וההמזגות המתילדות מהם ד'''' כמ"ש החכמים | |style="text-align:right;"|'''וההמזגות המתילדות מהם ד'''' כמ"ש החכמים | ||
|- | |- | ||
| | | | ||
| + | *types of “how”: possetion; meaning; natural faculty and nonnatural faculty; causing and effecting | ||
|style="text-align:right;"|'''מיני האיך''' קנין ענין כח טבעי ולא כח טבעי הפעל וההפעלות | |style="text-align:right;"|'''מיני האיך''' קנין ענין כח טבעי ולא כח טבעי הפעל וההפעלות | ||
|- | |- | ||
| | | | ||
| + | *phlegms: red; black; white; blood | ||
|style="text-align:right;"|'''הליחות ד'''' אדומה שחורה לבנה ודם | |style="text-align:right;"|'''הליחות ד'''' אדומה שחורה לבנה ודם | ||
|- | |- | ||
| | | | ||
| + | *causes: matter; form; act; purpose | ||
|style="text-align:right;"|'''הסבות ד'''' החומר והצורה והפעל והתכלית | |style="text-align:right;"|'''הסבות ד'''' החומר והצורה והפעל והתכלית | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|'''הרוחות ד'''' ימה וקדמה צפונה ונגבה והם מוגבלות כמ"ש הפילוסוף בתחלת השני מס' השמים והעולם כשביאר שלגלגל פאות | + | *directions: west; east; north; south (Aristotle, ?) |
| − | מוגבלות בטבע | + | |style="text-align:right;"|'''הרוחות ד'''' ימה וקדמה צפונה ונגבה והם מוגבלות כמ"ש הפילוסוף בתחלת השני מס' השמים והעולם כשביאר שלגלגל פאות מוגבלות בטבע |
|- | |- | ||
| | | | ||
| + | *perfections | ||
| + | |style="text-align:right;"|מיני השלמויות ד' | ||
| + | |- | ||
| + | | | ||
| + | *acting powers: attraction; retentive; digestion; repulsion | ||
| + | |style="text-align:right;"|הכוחות העובדות הכח ד' מושך מחזיק מעכל ודוחה | ||
| + | |- | ||
| + | | | ||
| + | *heavenly cardines: ascendant; line of the lower midheaven; setting point; midheaven | ||
|style="text-align:right;"|'''יתדות הרקיע ד'''' הצומח וקו התהום והשוקע וחצי השמים | |style="text-align:right;"|'''יתדות הרקיע ד'''' הצומח וקו התהום והשוקע וחצי השמים | ||
|- | |- | ||
| | | | ||
| + | *primary mental faculties: intellect; mixing; strength; righteousness | ||
|style="text-align:right;"|'''כחות הנפש הראשונים ד'''' והם השכל וההמזגה והחוזק והצדק | |style="text-align:right;"|'''כחות הנפש הראשונים ד'''' והם השכל וההמזגה והחוזק והצדק | ||
|- | |- | ||
| | | | ||
| + | *trees: those that have waters; those that have resins; those that have oils; those that have milky saps | ||
|style="text-align:right;"|'''טבעי האילנות ד'''' בעלי מימות בעלי שרפים בעלי שמנים בעלי חלבים כמ"ש בס' עבודת האדמה | |style="text-align:right;"|'''טבעי האילנות ד'''' בעלי מימות בעלי שרפים בעלי שמנים בעלי חלבים כמ"ש בס' עבודת האדמה | ||
|- | |- | ||
| | | | ||
| + | *primary organs: brain; heart; liver; testicles | ||
|style="text-align:right;"|'''האיברים הראשונים ד'''' מוח לב כבד אשכים | |style="text-align:right;"|'''האיברים הראשונים ד'''' מוח לב כבד אשכים | ||
|- | |- | ||
| | | | ||
| + | *medicine faculties (Ibn Rushd) | ||
|style="text-align:right;"|'''מיני הכחות המיוחסות לרפואות כפי פעולתם בנו ד'''' כפי דעת האחרונים ובפרט בן רשד בס' הכליות | |style="text-align:right;"|'''מיני הכחות המיוחסות לרפואות כפי פעולתם בנו ד'''' כפי דעת האחרונים ובפרט בן רשד בס' הכליות | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|'''מיני הדרישות ד'''' אם פשוט אם מורכב ומה ולמה כמ"ש הפילוסופ בתחלת השני מס' המופת ואחרים אמרו שהם אם ומה איך ולמה | + | *constructions of the figure (Aristotle) |
| + | | | ||
| + | |style="text-align:right;"|חבורי התמונה ד' ואין בכל חבורי שאר התמונות טבעי, אלא כי זאת התמונה יש שאמר ארסטו בהקש ממה שת[..]ול מחשבת בני אדם בטבע והיא תנליו בלא מלאכה ותוליד כל מיני הסותרים ושאר התמונות בהפך כל אלו כמו שהתבאר בספר ההקש | ||
| + | |- | ||
| + | | | ||
| + | *questions: simple "if"; complex "if"; what; why (Aristotle, Posterior Analytics, II, 1, 89b23-24) | ||
| + | |style="text-align:right;"|'''מיני הדרישות ד'''' אם פשוט אם מורכב ומה ולמה כמ"ש הפילוסופ בתחלת השני מס' המופת | ||
| + | |- | ||
| + | | | ||
| + | :other have said these are: if; what; how; why | ||
| + | |style="text-align:right;"|ואחרים אמרו שהם אם ומה איך ולמה | ||
| + | |- | ||
| + | | | ||
| + | *animals of the chariot | ||
| + | |style="text-align:right;"|'''חיות המרכבה ד'''' | ||
| + | |- | ||
| + | | | ||
| + | *Zacariah’s chariots | ||
| + | |style="text-align:right;"|ומרכבות זכריה ד' והם מורות על עניינים נכבדים זכרו מהם החכמים שלפנינו הרבה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ועדין נשאר הרבה אבל אין בזה הספר מקום לדבר בם וכ"ש שסובלות דברים ארוכים ועמוקים ואם יניח השם לנו ניחד בהם מאמר בפני עצמו |
|- | |- | ||
| | | | ||
Revision as of 18:18, 12 September 2017
שער המספר וסגולתו (לא ידוע מחברו)
ContentsIntroduction |
|
| דע שזה השער הוא הנכבד שבזאת החכמה וכאלו הוא התכלית בה ולרוב מעלת זאת החקירה טעו בה הקדמונים והניחו מספרים נבדלים ושמום התחלות המציאות המוחש וזה שמפני שהם מצאו הכמה נאמר בכל הדברים גשמיים או רוחניים | |
| וזה שבאלוה יאמר גודל ההשגה והיכולת או אין תכליות ביכולת ודומה לזה | |
| ואין תכלית הוא כמה בלתי מוגבל בין בשיעור בין במספר וכן מצאו בשכלים מהנפרדים רבוי וספירה לפחות מצד עלה ועלול או מציאות ומהות | |
| וג"כ מצאו רוב הנמצאות המוחשות שומרות יחסים מוגבלים כענין בגודל גרמי הכוכבים ועובי גלגליהם ויציאת מרכזיהם וכן בעגולים המוגבלים בכדור הח' וכן בעובי גרמי היסודות וכן באברי הב"ח כמו פרקי איבריהם וקצוות המין בגודל אישיו כמו שנעיר על קצת מאלו בזה השער הביאם הענין להגדיל המספר עד שייחסו אליו היותו התחלה וכן עשו בשעור כמו שאמרנו | |
| אמנם שזה הסברה טעות ושהמספר מקרה בספורים מה שבמקרה אי אפשר לשומו התחלה אין כאן מקומו וכבר האריך בזה הפילוסוף בקצת מקומות מהשמע ובהרבה ממה שאחר הטבע | |
| והרחיבו בו מפרשי ספריו וכמה מחברים אחרונים יווניים וערביים ונצרים | |
| ועל האמת יש במספר סגולות נפלאות וטבעים משונים | |
| מהם גלויי הסבות ומהם נעלמי הסבות אבל הם ידועי המציאות ורובם שנעלמו מאתנו אלו ואלו | |
| ואין ספק שכל ענין וענין מענייני הטבע הכוללים כשתשיגהו הנפש ותדעהו תשמח ותתענג בזה מאד לפי שזה תכליתה ולזה הכינה הכח האלהי לקבול פיתוחי הנמצאות וציוריהן | |
| ומפני זה אמר הפילוסוף בשלישי מן הנפש שהיא כמו הלוח החלק המקבל כל ציור וכתיבה | |
| ואלגזאלי אמר בתחלת ספרו בכונות שהיא כמו מראה זכה מלוטשת מקבלת דמות המציאות כלו כל עת שלא יחול מסך בינה ובינם בכל או בקצת | |
| וכמו שתהוה הנפש מידיעת סגולות העצים והאבנים ואברי הב"ח המתדמים והכליים אע"פ שתסכל ברובם הסבות תתענג הרבה בהשיגה המציאות ותצטער בסכלה הרבה ותצטער יותר כשתסכל אלו ואלו כן כשתדע הנפש סגולות הכמה המתחלק והמתדבק אע"פ שתסכל בקצתם הסבות תתענג הנפש תענוג גדול במה שהשיגה ולזה אמר אחד מחכמי ישמעאל מי יתן ונדע טבעי כל הנמצאות ונסכל סבותיהם | |
| ונשוב למה שהיינו בו ונאמר שמי שידע טבעי המספר וסגולותיו ידע הרבה מטבעי המציאות אין ראוי שיוסכלו לשלם | |
| ועל הכונה הב' יקח מהם כמה הערות יקרות בעולם | |
| באלוה ובמלאכי' ובגלגלים ובנפש ובנמצאות השפלות | |
| ואנחנו בלא ספק נדע מעט מהם ונסכל הרבה ואף גם זאת במעט אשר נודע לחכמים ואמרו בו כמה רמזים יקרים משמחי לב ומאירי נפש | |
| ודע שזה הענין כן הוא בהנדסה ר"ל שיש בה סגולות נפלאות יעי[דנו] על סודות נכבדים וכאלו ב' אלה הטבעים שמם האלוה ית' על הכונה השנית | |
| דמיון ודוגמא למציאות כולו ואחר שהקדמנו זה נתחיל לדבר בזה כפי מה שמצאנו לחכמים לפנינו מעט שהושקף לנו מבלתי שנעמיק ונטה אל קצת הערות דחוקות זכרום קצת אנשים מצורף למה שהסכמנו לקצר כפי כחנו מבלתי שנשמיט ההכרחי | |
Section One - Discussion on the Numbers One - Ten |
|
One |
|
| The numerical one testifies to issues related to God – | ומעתה נתחיל ונאמר שמהאחד המספריי נוכל להכיר כמה עניינים בבורא |
|
מהם שכמו שהאחד המספרי מצד שהוא א' לא מתרבה ולא מקבל חלוק ושנוי ולזה לא יתרבה בהכפלו בעצמו כן הבורא ית' שהוא אחדות אחת יותר פשוט לא יתואר בצד מן הצדדים ברבוי בעצמו רק ביחס השלמיות אליו או בצירוף פעולתו בנמצאות |
|
וכמו שהא' המספרי הוא בעצמו בפעל ובמספר בכח כן האלוה ית' הוא בעצמו בפעל גמור אחר שהוא עלת הכל ונבדל והוא בכח בכל אחד מן הנמצאות |
|
ומזה הצד אמרו החכמים שהבורא בכל ולזה אחד מהחכמים כששאלו תלמידו אנה הוא האלוה השיבו אנה אינו ר"ל שהכח האלהי מצוי בכל נמצא כפי מה שבטבעו שיקבל ממנו וזה הוא מה שאמר א' מחכמי הנוצרים שהאלוה מתנדב עצמו לכל מצוי |
|
וכמו שהא' המספרי עלת המספר והתחלתו ואינו מספר ולא יצדק בו גדר המספר ובו קיום המספר ולא עד שיחולק המספר בחלוקו והוא לא יחולק בהסתלק המספר כן האלוה האחד הוא עלת כל הנמצאות כלן והתחלת היותן וקיומן ואינו משאר הנמצאות ולא חלק מהן אבל הוא נבדל מעלוליו עם היותו עלה ובהסתלקו יסתלקו שאר הנמצאות ולא יסולק הוא בהסתלקן |
|
וכמו שהאחד המספריי אין לו רק פאה א' לפי שהוא גבול הספירה וממנו ימשך הרבוי עד לאין תכלית בכח וכלה הוא בכל גבול הנמצאות אין אחריו כלום לא בפעל ולא במחשבה |
| וזה שאפי' המחשבה אינה הולכת לאין תכלית אבל מכח אלהותו ירבו ויתמעטו הנמצאות ויאצלו עד תכליתן בהדרגה במין ולאין תכלית באישים באים זה אחר זה בכח | |
|
ומה שאמרו קצת אנשים שהאחד שרש ומרובע ומעוקב ומשולש הוא טעות |
|
וזה שהאחד המספריי לקוח בשכל מופשט מכל נושא חוץ לנפש ומצד שהוא כן אין רבוי בו בשום פנים ואיך א"כ יתואר במה שיסבול ההחלק והרבוי כמו מרובע ומעוקב שהם דברים מתחלקים בכח לאין תכלית ואם נאמר שהאחדות המונח חוץ לנפש כמו אמה וזרת שומרים אותו האחדות ברבוע ועקוב אנו אומרים שזה הבל שכבר נתרבו אלו באלכסוניהם |
|
ואם ישאל שואל למה לא יתואר הבורא ית' באחדות המספריי אחר שטבעיו דומים לטבע האלהות |
|
נשיב לו שאלו הדמויים אינם כלם ולא רובם על טבע אחד |
|
ועוד שהאחדות המספריי ישיגהו שלפעמים ילבש מלבוש נכרי וישתתף לריבוי ר"ל למספר בקצת טבעיו כמ"ש בקצת מקומות מב' שערים שעברו ויתבאר יותר בזה השער כשנדבר בסגולות הפרטיות וזה שיש טבעים שישיגו המספרים והאחד עמהם וברוב המקומות טבעו טבע הנפרד |
| The fact that one shares the characteristics of numbers at times, but in other occasions not - is among of the things related to number whose reason is very mysterious | וזה א' מהדברים הנמצאים במספר שסבתו נעלמת מאד ר"ל היות האחד פעם טבעו טבע מספר ופעם לא |
| Hence, the unity of God is different than the numerical unity | יתבאר א"כ מזה שאחדות האלוה מתחלף מהאחדות המספריי |
| The unity of God does not cease in any aspect and relation, it is a simple unity permanent forever almost inaccessible for the intellect due to its depth and subtlety | וזה שאחדות האלוה לא יפסד בשום בחינה וצירוף אבל הוא אחדות פשוט שמור לעולם כמעט שיבצר מן השכל לעומקו ודקותו |
Monad in the existences |
|
| The worthy existences are united in receiving the quality of unity - their species exists as one individual | וכמו שהאחדות המספריי יכלול כל המעלות הנזכרות ויותר הרבה נתיחדו הנמצאות הנכבדות לקבל טבע האחדות כפי כחן והיה מינם מתקיים באיש א' כמו האלוה ית' והשכלים הנפרדים לפי שהם יתחלפו ב[מ]יניהם במין והשמש והירח יתחלפו כלם כן וזה שאחר שיש להם פעולות מתחלפות במהות המקבל א' בעצמו הנה הם בלא ספק יתחלפו במהות ובמין אם כן כל א' מהם יחידי במינו |
| The universe as a whole is one from this aspect - as explained by Aristotle, On the Heavens, I.8, 277b8-13 | גם העולם בכללו מצד זה א' לבד כמו שביאר הפילוסוף בראשון מהשמים והעולם |
Two |
השנים |
|---|---|
|
תחלת הרבוי המספריי |
|
וכן תחלת הרבוי הישיי |
|
וזה שאחר אחדות האלוה הוא השכל הנפרד ואין בו רק השניות והוא העלול הא' שיש בו הרכבה ויש בו הרכבה |
|
מעלה ועלול |
|
וממציאות ומהות |
|
לפי שהוא עלול וזה שכל נמצא עלול המציאות מקרה בו והמקרה ובעל המקרה שוים אבל האלוה לפי שאינו עלול המציאות והמהות בו אחד לגמרי |
Properties of the number two |
|
|
ומטבע השנים שמחברתו כמערכתו ר"ל שרבוי העלול הראשון אינו רבוי גמור רק בהצטרף לא רבוי מהויות ולזה הוא דומה לטבע השניות המספרי שמערכתו לא יותיר על מחברתו |
|
וזה בחלוף כל המספרים שאחריו וזה שכולם יעדיף מערכתם על מחברתם |
|
וכאלו הוא ממוצע בין טבע האחדות והרבוי ולזה בטבעו הוא מונח בין האחד והשלשה |
|
|
וזה שהאחד מחברתו יותר ממערכתו |
|
|
והג' בהפך |
|
ולפי שהשנים ממוצע ביניהם יש לו טבע ממוצע בין עניין העלול הראשון שאינו א' לגמרי ולא רב לגמרי |
|
והנה השנים הזוג הראשון |
Dyad in the existences |
וכמה דברים כוללים במציאות והנה השנים הזוג הראשון שירוץ מספרם בשנים בין בשכלים בין בגלגלים בין ביסודות והמורכב מהם |
|
באלוה בחינת שניות האחד בבחינת עצמו השני בבחינת זולתו |
|
כמו שהוא עלה או פועל מזה שהתחלות הדברים המוחשים זוג השניות |
|
אם בגשמים היסודים החומר והצורה |
|
ואם ברקיעים הנושא והצורה |
|
וכל מי המגבילות זוג השנים |
|
והגבלת האמתיות ובשוללות ולזה היא היותר קודמת שבמושכלות כמו שביאר הפילוסוף בשני ממה שאחר |
|
והאמת והשקר שנים |
|
חלקי הזמן שנים עבר ועתיד וזה שההוה בלתי מוגבל ולא קיים |
|
החיים והמות שנים |
|
הכח והפועל שנים |
|
השנוי בשנים הפעל וההתפעלות ר"ל הקבול |
|
הגופות שנים היסודי והרקיעי |
|
היסודיי שנים פשוט ומורכב |
|
הרקיעיי שנים הגלגל והכוכב וזה שהם מתחלפים במהות לפי שהגלגל ספירי והכוכב לא והגלגל מתנועע בעצם והכוכב במקרה |
|
תנועות הגלגלים הגלגלים |
|
בארך שנים ימה וקדמה |
|
וברוחב שנים צפונה ונגבה |
|
הגלגלים יתחלפו ישתתפו בטבעיהם שנים שנים כמו שיאמרו האצטגנינים |
|
וזה שמהם שנים מאורות |
|
ושנים מצליחים צדק ונגה |
|
ושנים מזיקים שבתי ומאדים |
| וכותב אין לו טבע מוגבל אבל הוא לפי דבריהם מתהפך | |
|
טבע הסוגיות בשנים זכר ונקבה ואין ביניהם שלישי ממוצע רק בשגיאת הטבע כמו הטומטום והאנדרוגינוס וזה אשר אמרנו בנולד מכמוהו במין אבל במגילד מהעיפוש אע"פ שהוא ממה שבטבע הנה אינו טבעי |
|
מיני האברים המורכבים שנים מתדמה וכליי |
|
סוגי ההקשה שנים השתוף וההבדל |
|
מיני החיים שנים פעליים ומחשביים |
|
מיני הנימוסים שנים טבעי וקנסי כמו שביאר הפילוסוף בשני מס' ההליכה |
|
המשכות הנמצאות בשנים בזמן או בנצחות |
|
בחינת הנמצאות אלו עם אלו בשנים והם ההאותות והחלוף וזה סוג כולל יכנסו תחתיו כל מיני טבעי הנמצאות כמו שביארו מחברי אחואן אלצפא וגאבר בן חיאן מלמד הכימיא בספרו בסגולות הדברים |
|
סוגי האשור שנים מחשביי ומדותיי כמו שביאר הפילוסוף בראש המאמר [א]ב' מהמדות |
Three |
השלושה |
|---|---|
Properties of the number three |
|
|
הוא ראשון למספרים הנפרדים |
|
ובו נשלם כל טבע המספר וזה שבו האחד ושני מיני הריבוי שהם הזוג והנפרד |
Triad in the existences |
|
| וכמו שהשלשה בסדור המספר אחר שנים כן בהשתלשלות המציאות טבע השלוש מגיע אחר השניות | |
|
וזה שאחר שנניח האלוה ושהוא ממשיך המציאות מאתו יתואר בשהוא צורת העולם ופועלו ותכליתו |
|
ושלשה אלו הם א' לא יתנו רבוי בעצמו ית' כמו שביאר בן רשד בסוף השני מקצורו למה שאחר |
|
וגם בדברים הטבעיים הוא כן כי הצורה והפועל והתכלית א' בנושא שלשה בבחינה כמ"ש ארסטו בשני מהשמע |
|
וכן יתואר הבורא בשלוש שהוא שכל ומשכיל ומושכל |
|
ולא יביאו אל הרבוי כמו שביארו גדולי החכמים |
|
ולזה אמר ארסטו בתחלת הראשון מספר השמים כשביאר שהג' כל ושלם אחר שיש לו ב' הקצוות ואמצעי שראוי מפני זה שנגדיל האלוה בזה המספר כדי שנמשך לפעל הטבע ויהיה זה כאלו הוא תורה לנו |
|
ובן רשד המפרש פי' בו מספר התפלות והקרבנות ואולי זאת היתה כוונת מיסדי תפלותינו שהם שלש אנחנו הישראלים |
|
תארי הבורא בשלמות שלשה חכמה ויכולת ורצון |
|
והעלה השניה ממשיכה אחריה ג' והם הגלגל הראשון ונפשו ומניע הגלגל השני |
|
ובגרמים השמימים טבע השלוש וזה ששבעת הכדורים בכל א' גלגלים רבים להניע כוכב א'
ובשמיני גלגל א' יניע אלפ וכ"ב כוכבים ובט' אין בו כוכב |
|
ומצד אחר כוכבי הרקיע השמיני תנועתם פשוטה מתדמה סביב מרכז העולם ובמאורות בלתי מתדמה ולא סביב מרכז העולם אבל ישיגם נזורות ובה' כוכבי הנבוכה ישיגם הנזורות הנה נבדלו הגופים הרקיעים בג' טבעים בתנועתם באורך |
|
ומצד אחר בתנועת הרחב וזה שהשמש אין לו תנועה ברוחב מאזור המזלות והירח יתנועע ברוחב בכל גלגלו הנוטה ברוחב קיים הנטיה ובחמשת הכוכבים גלגלם הנוטה בלתי קיים |
|
ומצד אחר השמש לפשיטותו יספיק בו יציאת המרכז או גלגל הקפה והששה הנשארים צריכים לשניהם וכוכבי שבת אין בהם לא זה ולא זה |
|
ומצד אחר השמש תקרהו הסתרה והירח לקות והוא אבוד האור לגמרי והנשארים לא זה ולא זה |
|
ויש בהם שלוש מפנים אחרים אבל אלו שזכרנו די |
|
טבעי המזלות שלשה קיים מתהפך בעל ב' גופות |
|
וכן ביסודות שלש |
|
מהם קל במוחלט מהם כבד במוחלט מהם כבד וקל בהצטרף |
|
ומצד אחר מהם עב במוחלט ומהם דק במוחלט ומהם עבים ודקים בהצטרף |
|
ומצד אחר מהם קצוות באיך כמו החם והיבש והקר והלח והנשארים מתמצעים בין ב' אלו להשתתפם עם הנשארים בא' מאיכיותיהם |
|
מיני תנועות הגשמים ג' |
|
מן האמצע אל האמצע סביב האמצע |
|
מיני התנועות מצד אחר שלשה ישרה וסבובית ומורכבת משתיהן הנקראת סלזונית |
|
הנה התבאר שהעולמות ג' ושבכל א' מהם מצוי טבע השלוש בדרך שביארנו גם באלוה בתאריו כמו שזכרנו לא זולת זה |
|
גם בנמצאות מצוי טבע השלוש כי הנפשות ג' במין הצומחת והחיונית והמדברת |
|
מיני הצומח ג' האילן והעשב והירק והעשב נשאר זמן כמו האילן והירק מזריע ומתיבש בתוך שנה |
|
מיני החי ג' המהלך והמעופף והשח והמדבר לא יחלק לפי שלא יתרבה במין |
|
מיני הכחות ג' טבעי חיוני ונפשיי |
|
המרחקים ג' האורך ורחב והעומק |
|
ולוקחים התחלותיהם מג' הקו והשטח והגשם |
|
התמונות הישרות הקוים השטוחות הראשונה מג' גבולים והוא המשולש וכל שאר התמונות ישרות הצלעות הרבות אליו יותרו ולזה חשבוהו הראשונים יסוד כמ"ש הפילוסוף בב' מהשמים והעולם |
|
החכמות ג' הלמודיות והטבעיות והאלהיות |
|
תמונות ההקש המולידות ג' כמ"ש בראשון מספר ההקש |
|
מיני ההקשה הראשונים ג' אם שווי אם תוספת אם חסרון |
|
מיני היחס הכוללים ג' המספריי המדותיי הנגוניי |
|
הדבור אצל הפילוסופים שלשה שם ופעל ומלה
כמו שהתבאר בתחלת ספר המ |
|
מיני הטבעים בהתמדה ולא התמדה שלשה לא הוה ולא נפסד באלוה מתמיד במין נפסד באיש כיסודות והמורכב מהם מתמיד באים כמו המלאכים והגלגלים והכוכבים |
|
הכחות המנהיגות הראשית ג' מוליד ומגדל וזן |
|
הדברים הנמצאים בנפש ג' מקרים כחות ותכונות כמ"ש הפילוסוף בשני מספר המדות |
|
מיני האהבה ג': אהבת מעלה אהבת הנאה אהבת תועלת כמ"ש ארסטו בתחלת הח' מס' המדות |
|
בנפש ג' חלקים אחד לפועל והוא התאוה ושנים לשפוט והם החוש והשכל ומה שהוא בשכל חיוב ושוללות הוא בתאוה דרישה ובריחה כמ"ש בו' מס' המדות |
|
החמרים בגזרות ג' מחויב ונמנע ואפשר שהמשולח מטבע האפשר והא מין ממיניו לפי דעת האחרונים |
|
החתוכים הנופלים במחודד בעגול ג' המספיק הנוסף והחסר כמ"ש במאמר הראשון מספר אבולוניוס בחרוטים |
|
מיני מנהגי המדינות כפי מה שיראה ארסטו בא' מס' המדות ג' והם התענוג הכבוד העיון |
Four |
הארבעה | |
|---|---|---|
Properties of the number four |
||
|
תחלת מספר מורכב | |
|
ותחלת זוג הזוג | |
|
ותחלת מרובע שיהיה בפועל | |
|
וחבורו משלים י' שהם בפנים מספרי המעלה הראשונה | |
|
|
ושרשו חציו | |
|
|
והוא חצי מעוקבו | |
Tetrad in the existences |
אמנם בנמצאות איך ימצא רבוע אחר השלוש | |
|
כבר ביארו אפלטון בס' טימאוס הרוחניי כשאמר שהנמצאות כלם בלתי האלוה אחר הבדלם בישיותהם ישתתפו בארבעה דברים בהיותם בלתי שלמים בהיותם עלולים בהיותם בעלי רבוי בהיות כח כל א' מהם בלתי מתפשט בכל הנשארים | |
|
ובגלגלים ד' דברים הגלגל והכוכב הנפש והמניע הנבדל | |
|
בגלגלים המצויים ד' טבעים המכוכב כוכבי הנבוכה שני המאורות כמו שבי' הר"מ ז"ל פי י"א משני | |
|
הכוחות השופעות מן הגלגל ד' הדומם הצומח החי המדבר | |
|
המלאכות אשר תעשנה ההקש ד' והן המופת והנצוח וההטעמה וההלצה | |
|
התקופות ארבעה קור וחום קיץ וחורף | |
|
מיני המבטים אשר כפיהם יתמזגו ניצוצות הכוכבים ארבעה נכח שליש רביע שתות | |
|
המקבילות ארבעה ההפכים המצטרפים ההעדר והקנין החיוב והשוללות | |
|
האיכיות ארבעה החום והקור הלחות והיובש | |
|
וההמזגות המתילדות מהם ד' כמ"ש החכמים | |
|
מיני האיך קנין ענין כח טבעי ולא כח טבעי הפעל וההפעלות | |
|
הליחות ד' אדומה שחורה לבנה ודם | |
|
הסבות ד' החומר והצורה והפעל והתכלית | |
|
הרוחות ד' ימה וקדמה צפונה ונגבה והם מוגבלות כמ"ש הפילוסוף בתחלת השני מס' השמים והעולם כשביאר שלגלגל פאות מוגבלות בטבע | |
|
מיני השלמויות ד' | |
|
הכוחות העובדות הכח ד' מושך מחזיק מעכל ודוחה | |
|
יתדות הרקיע ד' הצומח וקו התהום והשוקע וחצי השמים | |
|
כחות הנפש הראשונים ד' והם השכל וההמזגה והחוזק והצדק | |
|
טבעי האילנות ד' בעלי מימות בעלי שרפים בעלי שמנים בעלי חלבים כמ"ש בס' עבודת האדמה | |
|
האיברים הראשונים ד' מוח לב כבד אשכים | |
|
מיני הכחות המיוחסות לרפואות כפי פעולתם בנו ד' כפי דעת האחרונים ובפרט בן רשד בס' הכליות | |
|
חבורי התמונה ד' ואין בכל חבורי שאר התמונות טבעי, אלא כי זאת התמונה יש שאמר ארסטו בהקש ממה שת[..]ול מחשבת בני אדם בטבע והיא תנליו בלא מלאכה ותוליד כל מיני הסותרים ושאר התמונות בהפך כל אלו כמו שהתבאר בספר ההקש | |
|
מיני הדרישות ד' אם פשוט אם מורכב ומה ולמה כמ"ש הפילוסופ בתחלת השני מס' המופת | |
|
ואחרים אמרו שהם אם ומה איך ולמה | |
|
חיות המרכבה ד' | |
|
ומרכבות זכריה ד' והם מורות על עניינים נכבדים זכרו מהם החכמים שלפנינו הרבה | |
| ועדין נשאר הרבה אבל אין בזה הספר מקום לדבר בם וכ"ש שסובלות דברים ארוכים ועמוקים ואם יניח השם לנו ניחד בהם מאמר בפני עצמו | ||
Five |
החמשה |
|---|---|
| מספר עגול סובב על עצמו וזה שהוא שומר עצמו במרובעו ובמעוקבו כי מרובע ה' כ"ה ומעוקבו קכ"ה ואם יכפל יותר ימצא בו פרט ה' וזה שהחמשה כנקודה אמצעית בין המספרים הט' והוא חבור המרובע הראשון בכח עם המרובע הראשון בפעל | |
| ויש בו סגולה נפלאה מעידה שהמספרים ט' לבד והיא שהחמשה מרובעו ומרובע מרובעו ומרובע כפלו כמו מעוקבו וזה שמרובעו כ"ה ומרובע כפלו ק' הרי קכ"ה והוא מעוקב ה' | |
| וכל מספר שלפני ה' ערך מרובע ומרובע כפלו אל מעוקבו כערך אותו המספר אל ה' | |
| וכל מספר שאחר ה' הדבר בהפך והנה נאריך בזה במקומו הראוי לו | |
| ויש בנמצאות דברים כוללים ירוצו מרוצת הה' מהם כמ"ש אפלטון בס' תימאוס שהחמשה הם שרשי המציאות והם השכל והצורה והחומר והמקום והזמן | |
| נושאי ההנדסה ה' הנקודה הקו והשטח הגשם והזוית | |
| נשואי הגזרות ה' והם הסוג המין ההבדל הסגולה המקרה | |
| ההרגשות הגשמיות ה' הראות והשמע והריח והטעם והמשוש | |
| סימני החיים במולדות אצל ההוברים ה' והם מקומות שני המאורות והצומח וחצי השמים וגורל היופי | |
| ירידת הכח הגלגליי בעולם השפל תלוי במצבי ה' עגולים והם עגול המזלות ועגול ב' ההפוכים ועגול המבדיל בין הנראה תמיד מהגלגל והעגול המבדיל בין הנסתר תמיד | |
| התנועות שיבוטאו [...] הגזרים ה' והם פתח צרי חירק שורק חולם והשאר אינם טבעיות ויקראו בעלי הנקוד בתנועות כמו שיאמר רמב"ן בקצורו לנקוד ואבן עזרא בס' ואלה שמות | |
| התמונות הגשמיות שוות התושבות וימוששו מכל צד הם ה' לבד וכבר התבאר עניינם בי"ג מאיקלידס | |
| מיני ההקשה האחרונים בין הדברים שיפול ביניהם הם ה' וכבר התבאר עניינם בשער השני | |
| הכוכבים שהשתתפו בנזורות ורחב בלתי קיים הם ה' שצמנ"כ | |
| חלקי הדבור הפשוטים והמורכבים ה' והם הקול האות הגזר התיבה הגזרה | |
| מיני האשור ה' ג' במחשבי וכו' כמ"ש בסוף הא' מס' המדות | |
| התולדה בב"ח תמצא על ה' פנים | |
| הא' שיוליד בגופו חי כמותו בצורה | |
| והב' שיוליד בגופו בצים וחוץ מגופו בע"ח | |
| הג' שיוליד בגופו וחוץ מגופו בצים שלמים | |
| הד' שיוליד בגופו בצים בלתי שלמים וישלמו בחוץ | |
| והה' שיוליד בחוץ תולעים כמ"ש הפילוסוף בי"ו מס' ב"ח | |
| סבות הזכרות והנקבות בב"ח ה' והם המזג השנים הרוחות טבע המקום טבע המים והאויר כמ"ש ארסט"ו בי"ח מב"ח | |
Six |
הששה |
|---|---|
| תחלת זוג הנפרד והוא כמו כן מספר כדוריי מתגלגל על עצמו כמו החמשה וזה שהששה שומר ג"כ עצמו במרובעו ובמעוקבו כמו החמשה וזה כי ו' על ו' ל"ו
וו' על ל"ו רי"ו ואם יכפל עוד ישמר בכפל ההוא וכן לעולם והששה מספר שלם ר"ל שחלקיו שוים לכולו לא פחות ולא יותר וזה שחציו ג' ושלישיתו ב' וששיתו א' הרי ששה ואין בלעדיו מספר שלם במדרגה הראשונה ובשנית ימצא אחד והוא כ"ח ובשלישית תצ"ו ובד' שמות אלפים ר"פ ומן הוא והלאה לא ימצא מספר שלם רק בדלוג מדרגות וכל המספרים אם נוספים ואם חסרים וחכמי העיון הוציאו מזה רמז כי השלמים ימצאו מעטים ובפליאה ובדלוג מדינות ודורות ואמנם קראו זה המספר שלם לפי שגדר השלם כמ"ש הפילוסופ הוא אשר אין להוסיפ עליו ולא לגרוע ממנו ולזה נק' העגול שלם בתמונות השטוחות והכדור במוגשמות והאנשים שעניינם כך מעטים ואמנם רוב האנשים אם חסרים מהראוי להיות בם ואם שיהיו בם דבר לא יתכן שיהיו ואמנם הדרך בהוצאתם נבארהו כשנגיע אל הסגולות הפרטיות וכמה דברים כוללים בנמצאות ירוצו מרוצת הששה כמ"ש אלפראבי בתחלת ספרו הנק' התחלות הנמצאות שאמר שהתחלות המציאות ששה והם האלוה השכל הנפש הגלגל הצורה ההיולי הפאות ששה מעלה ומטה ימין ושמאל פנים ואחור המזלות הצפוניים ו' והם טש"ת סא"ב והדרומיים ו' מע"ק גד"ד חבור היחסים הל[קוחי]ם בנושאים מפורדים אמנם הוא בו' קולות הנגון ו' ובד' מהם מתחיל הטבע האחד מהנעימה והולך עד ששה וכן משם ולמעלה עד לאין תכלית כי מה שאין תכלית לו אי אפשר שיצא אל הפעל לעולם הקוים האלמים מדובקים או נבדלים המתילדים בכל סוג מסוגי הנבדלים הם לעולם ששה ששה מוצאי המותר בגופ האדם ו' והם העין האזן האפ הפה מוצא המותר הדק ומוצא המותר העב ואין ראוי למנות הכפולים רק אחדים כי כמ"ש הפילוסופ לא נכפלו רק מפני היותר טוב כחות הנפש האנושית הכוללים ששה והם צמיחה הזנה הרגש חוש משותפ דמיון שכל פרקי הזרוע והיד וכל אצבע ששה וזה שמהכתפ עד תחלת היד שנים ומתחלת היד עד ראש כל אצבע א' ובכל אצבע ג' הרי ו' וכלם מתיחסים בהדרגה ביחס מוגבל בטבע אם לא שישנה הטבע על הזרות וכן מתחלת הרגל עד קצות כל אצבעות הרגל האיברים הבולטים בפנים ו' והם שתי עינים שתי אזנים שתי נחירים ואין ראוי למנות השפתים לפי שהאדם יכול לקפוץ פיו ושפתיו ולא יוכר בם שנוי משאר שטח הפנים גדלי כוכבי הרקיע כלם יחלקו לו' כמ"ש החכמים הסבות המשותפות לבריאות והחולי ששה האויר המקיפ מאכל ומשתה תנועה ומנוחה שינה ויקיצה הרקה והסגר חדושים נפשיים | |
Seven |
השבעה |
|---|---|
| הוא מספר ראשון שבמדרגה ראשונה וזה שהמספרים הראשונים שבמדרגה היא בגה"ז ומספר הז' מורכב מתחלת הזוגות עם שני לנפרדים ומתחלת הנפרדים עם שני לזוגות ולזה קראוהו קדמוני החכמים מספר כולל והוא אמצעי בין ארבעת המספרים המורכבים שנים לפניו ושנים לאחריו
לפניו ד"ו ואחריו ח"ט ואם תכפול שבעה יהיו י"ד וזה עולה במחובר מרובעי אב"ג שהם כל טבע המספר כמ"ש למעלה וחבור ז' מספר שלם ואין במדרגת העשרות זולתו ויש בנמצאות דברים רבים ירוצו מרוצת השבעה מהם שהכוכבים ז' והם מנהיגי העולם הראשונים ולזה קראום מקדם חכמי ישראל המשרתים ימי כל רבוע מרבועי הירח ז' ובהם יעתקו האוירים והטבעים בבריאות ובחולי אקלימי הארץ שבעה ואינה חלוקה הנחית אבל נמשכת לכח עליוני כמ"ש חכמי הכוכבים מיני המתכות ז' הזהב הכספ הנחשת הבדיל העופרת הברזל הכספ חי ואע"פ שהברזל לא יותך כפי מה שיחשב הנה איפשר להתיכו בתחבולה נעלמת עד שיותך מהרה כמו העופרת סוגי טבעי הב"ח הבלתי מדברים שבעה חיות טורפות בלתי טורפות עופות דורסים בלתי דורסים שרץ העופ זוחלי עפר ר"ל שקצים ורמשים חיות המים ותחת כל א' מאלו ישתרגו מינים רבים החכמות שיחלקו כפי דעת הפילוסופ ז' והם הטבע והאלהות והמספר וההנדסה וחכמת התכונה הגלגליית וחכמת המוסיקה והחכמה המדינית ויש בחלוקה הזאת חלופ דעות לאחרונים ולא מנו ההגיון לפי שאינו חכמה אבל כלי לבד והאמת כמ"ש הר"ס ז"ל בפ' מ"ג מג' שלשבעה מבוא גדול בעניינים הטבעים והתוריים וכן יאמר בעל ספר התמר סופ ספרו וזה מכלל הדברים הכרתם מחויבת שנויי שנות האדם שבעה כמ"ש בן סינא בראש ספרו בקאנון ואבוקראט בספריו בשביעיות מיני הכמה שבעה הקו השטח הגשם המקום הזמן המספר הדבור חדשי עמידת העובר לפחות שיוכל לחיות בו הילוד שבעה וטעם זה ארוך והתבאר היטב בספרי חכמי הכוכבים כי אין בחכמת הטבע די להשלים סבת זה | |
Eight |
השמנה |
|---|---|
| תחלת מעוקב בפעל ר"ל מספר שארכו ורחבו וגבהו שוה והוא זוג הזוג כמו הד' ולזה הוא מספר חסר ר"ל שחלקיו פחות מכלו כי כן דרך מספרי זוג הזוג ר"ל שהם חוסרים לעולם [.]' מכללם
וחבור ח' במרובע הזוג הזוג שלפניו וחבור חבורו עולה ק"כ שחלקיו כפלו והוא סך מרובעי הזוגות שבמדרגה הראשונה וכל מעוקב מחובר מששה שטחים וי"ב צלעות וכ"ד זויות שטוחות וכל אלו מתיחסים ביחס כפל וכשתחבר שטחי ח' צלעותיו וזויותיו יעלה מ"ב וזה ככפל מחובר הזוג שלפני שמנה ויש בנמצאות דברים ירוצו במספרם על שמנה מהם שהרקיעים המכוכבים שמנה וחלקי הדבור אצל מדקדק קצת הלשונות שמנה קצוות התנועות שמנה לפי שהשנוי בארבעת המאמרות שהם העצם והכמה והאיך והאנה ובכל א' מה ממנו ומה אליו היו גבולי התנועה הטבעית שמנה טבעי האילנות שמנה והם אילן סרק אילן שפריו נאכל כלו שנאכל מה שבחוץ שנאכל מה שבפנים שאין שומר לפריו שיש לו שומר אחד שיש לו שני שומרים שיש לו שלשה | |
Nine |
התשעה |
|---|---|
| תחלת מרובע מספר נפרד וחלקיו הם כמספר מרובע תחלת זוג לפי שחלקיו שלשה וא' והם ד' שהוא מרובע ב' ומחוברו כמו הכאתו במספר האמצעי והוא ה' וחבור חבורו עולה רס"ה והוא סך מרובעי הנפרדים שבמעלה הא' כמ"ש בן עזרא בס' השם
ותשעה סופ המדרגה הראשונה מהמספר וזה שהמספרים ט' והאחד עמהם והאות ע"ז שאם תעשה עגול ותניח סביבו תשעת המספרים ותתחיל ותכפול ט' על עצמו תמצא המרובע פ"א ותמצא ח' שהוא כנגד פ' אל הימין והא' אל השמאל ואם תכפול ט' על ח' יעלו ע"ב ותמצא ז' שהוא כנגד ע' מימין והב' אל השמאל וכן כל ארבעת מספרים אשר לפני ה' עגול הכלל מימין והפרט משמאל לארבעתם וחמשה לפי שהוא חשבון עגול אמצעי הוא מתגלגל על עצמו והוא בזה הענין כנקודה אמצעית עגול ולזה כאשר תכפול ט' על ד' יעלה ל"ו ותמצא ג' שהוא כנגד ל' עגול אל השמאל וו' שהוא הפרט אל הימין וכן כל הד' שאחר ה' כמו שתראה הנה יתבאר א"כ מזה כי בתשעה טבע הסבוב ולפי שה' באמצע יתחיל ממנו לנטות אל צד אחר מהעגול כי כן משפט מתנועע בסבוב שמנוקדה מהעגול עד חצי העגול ירוץ במצב א' ומשם והלאה מחליפ המצב וכמו שהיות המספרים ט' עם הא' התבאר מצד המספרים עצמם יתבאר מצד מרובעיהם ומצד מעוקביהם אמנם מצד מרובעיהם שאם תסדר בטור במספרים הטבעים עד ט' ותניח עליהם או תחתיהם מרובעיהם על הסדר תמצא שהפרטים ההוים במרובעים עד מרובע ה' חוזרים אחורנית במרובעים שאחריו וזה שהפרטים שאחר שלפני מרובע ה' הם אד"ט וה' שבאמצע שומר עצמו ואחר חוזרים לאחוריהם כאלו הם הולכים חצי עגול אחר וזה שהפרטים שאחר מרובע ה' הם ו' ט' ד' א' ואמנם במעוקבים יתבאר הדבר כן אם תסדר מעוקבי המספרים הטבעיים על הסדר עד ט' תמצא פרט המעוקב הראשון עם פרט האחרון הוא כלל והוא ראש המדרגה השנית והשני לא' עם השני לאחרון לפניו עושים כלל וכן תמיד עד האמצעי שהוא ה' שהוא הנקודה לאמצע זה הענין כאלו הוא בחצי קשת העיגול ותמצא בכאן דבר מופלא שכל החלקים השלמין שאפשר שיחלק בם מספר העשרה נמצאים באלו הפרטים פרט לפני ה' עם פרט לאחריו וזה כמו א' וט', ח' וב', ז' וג', ובאמצע שהוא א' מחלקיו בהתחלקו לחצי ומדרך אחרת מצד המעוקב נבאר שהמספרים ט' שכמו שאמרנו במספר ה' שמרובעו ומרובע כפלו שוה אל מעוקבו וכל מספר שלפניו ערך מרובעו ומרובע כפלו אל מעוקבו כערך אותו המספר פשוט אל חמשה ואחר החמשה יתהפך הענין וזה שאז יהיה ערך מרובע המספר ומרובע כפלו אל מעוקבו כערך חמשה אל אותו המספר וזה לאות שהט' שלמות המספר והוא כדמות עגול שלם סובב על עצמו וממה שיחזק מה שאמרנו עתה והוא שאם תסדר תשעה המספרים בטור ותשים על כל א' מהם מרובעו ומרובע כפלו תמצא בראשון פרט ה' ובשני כלל וכן עד ט' וערך כל מרובע מספר מה עם מרובע כפלו אל מרובע אי זה מספר עם מרובע כפלו כערך המספר הפשוט אל המספר הפשוט שנוי בכפל ואם תסדר מרובעי המספרים הטבעיים עם מרובעי כפליהם בטור הנה הכאת איזו מדרגה שתהיה מהם עם איזו מדרגה אחרת לעולם מרובע אמנם ידיעת שרשי אלו המרובעים היא ע"ז הדרך תכה הראשון שהוא ה' בשני לו ואחר בג' ואחר בד' וכן ע"ז הסדר תמצא המרובע הראשון שרשו כפל ה' והוא י' ושרש השני יוסיפ ה' ושרש ה' יוסיפ ה' וכן כלם וזה יקרא הסבוב הראשון ובכל זה הסבוב תמצא המרובעים האחד פרטו והשני כללו וכן לעולם ובסבוב השני והוא שתכה השני מהטור הנז' בכל הבאים אחריו תמצא המרובעים היוצאים ד' דמיוני המרובעים הראשונים ולזה שרשיהם כפלי שרשיהם ולזה הם כלם כללים ובסבוב הג' והוא שתכה הג' בכל הבאים אחריו יהיו המרובעים היוצאים ארבעה דמיוני השניים ולזה שרשיהם כפלי שרשיהם ותמצא האחד כלל והשני פרטו ה' וכן תמיד כדרך הסבוב הראשון וכן החמישי והשביעי והט' סופ דבר הסבובים הזוגות בדרך אחת והנפרדים בדרך אחרת וייראה באלו המספרים ר"ל מרובעי המספרים הטבעיים על מרובעי כפליהם שאם תחבר כל א' מהם אל מספרו פשוט תמצא הפרט הראשון ו' עוד ב' עוד ח' עוד ד' והאמצעי שהוא קכ"ה עם מספרו יהיה כלל והמספרים הארבעה שאחריו ה' הענין בם כמו במספרים שלפני ה' וזה אות מופלא שהמספרים ט' לבד הנה כבר ביארנו שהמספרים ט' לבד ולזה נקח מהקדמות הנזכרות ראשונה מאזנים למרובעים ולמעוקבים וזה שאי אפשר בשום מרובע שיהיה בו פרט ב' או ג' או ז' ואם הוא כן אינו מרובע ואם יש בו א' או ט' היה בשורש ואם יש בו ד' ב' או ח' היה בשורש ואם היה בו ו' ד' או ז' היה בשורש ואם בפרט ה' בשורש ה' ג"כ וכן תמיד ואמנם במעוקבים אם יש במספר פרט א' הנה במספר בשורש א' ואם יש בו ב' בשורש היה ב' ואם יש בו ג' בשורש היה ז' ואם יש בו ד' בשורש ד' ואם יש בו ה' בשורש ה' ואם ו' בשורש ו' ואם יש בו ג' בשורש ז' ואם יש בו ט' בשורש ט' ודי בזה ראיות שהמספרים ט' לבד ודע שיש בנמצאות דברים הרבה ירוצו במספרי הט' מהם כי הרקיעים לא יותר גם בתשיעי ספק לא מעט השכלים הנפרדים אחר האלוה ית' לפחות ט' וזה כפי דעת הפילוסופי אבל כפי דעת התורה רבו מלמנות המזגים ט' אחד פשוט שוה וארבעה פשוטים וארבעה מורכבים המהויות הפשוטים ט' אלוה השכל הנפש הגלגל הכוכב היסודות הארבעה מיני האותות והחילופ שיש בין דבר וזולתו ט' והם טבע יאהב טבע וטבע ישנא טבע, טבע רודפ טבע, טבע בורח מטבע, טבע יתגדר על טבע טבע יכנע לטבע, טבע מקיים טבע, טבע מפסיד טבע, והתשעי הוא טבע נכרי לטבע ר"ל שאין ביניהם האותות והתנגדות ואלו הם ט' סוגים יכנסו תחתיהם כל מיני הפעל וההפעלות בעניינים הטבעיים ובס' אכואן אלספא הובאו משלים מפרטי הטבע בכל א' מהם והראשונים היו מונים אלו הסוגים י"ג והאחרונים השיבום אל ט' והנה התבארו דברים אלו בס' השתנות הטבעים האיברים שייחדם הטבע במין האנושי חוץ מהגופ לפעולות מיוחדות וכפל אותם הם ט' והם העין האזן האפ השפה השניים היד הרגל השדים האשכים סוגי המקרים ט' והם שביארם הפילוסופ בס' המאמרות בהגיון טבעי המתדמי החלקים אשר ספרם הפילוסופ ברביעי מאותות השמים שהם כדמות הבדלים צוריים הם ט' וזה שהוא מנאם י"ח שישובו לט' וזה שהוא מנה הקניינים והעדריהם וההעדרים אינם דברים ישיים ובמקומו יתבאר בבירור חדשי עמידת העובר האנושי בבטן ט' וזה דבר הסכימו בו חכמי הטבע ולא נתנו לזה טעם מספיק אבל האיצטגנינים האריכו בזה בדברים נכונים כמ"ש בספרים הרבה והיותר מספיק בה מה שזכרו מחברי אכואן אלצפא מיני הטעמים שמנה מתוק מר מליח חריפ חמוץ קובץ דשן תפל ואין למנות העפוץ טעם בפני עצמו לפי שהוא אינו אלא תכלית ה[ק]ביצות כמ"ש בן רשד בס' הכליאת | |
Ten |
העשרה |
|---|---|
| תחלת המדרגה השנית והוא כאחד והשני בה עשרים והשלישי שלשים וכן עד צ' ולזה נגזרו לאלו שמות משמות אחד המדרגה הראשונה והפרטים שבין אלו הם מורכבים משתי המדרגות כמו י"ב כ"ג ל"ד מ"ה וכמו שהוא תחלת מדרגה שנית כן המאה תחלת מדרגה שלישית והאלף רביעית וכן תמיד ואם תחבר המרובעים שיש עד חציו ר"ל תמצאם כמחובר עשרה פשוט | |
| ונהגו ההמון והספרים לגמור בעשרה מפני שהוא כלל וכאלו הביאם הרצון האלהי לזה להורות שהוא סוף הספורים וזה שהספורים עשרה האלוה והשכל והגלגל והכוכב והנפש והיסוד והדומם והצומח והחי והמדבר והמאמרות עשרה ודברות התורה הקדושה שנמסרו לנו בסיני הם עשרה והם סוד אלהי נכבד בהנהגם בזה המספר וזה הוא שנרמז בס' יצירה עשר ספירות בלי מה ופארות אילן האדם עשרה למעלה ועשרה למטה והם עשר אצבעות הידים ועשר אצבעות הרגלים | |
| ומן הפלא הגמור בהמשך הספורים למספר שכמו שהמספר לא יעבור ט' או עשרה כן לא תמצא בכוללי הנמצאות דבר שיעבור זה המספר כי אם בדרך חלוקה הנחית כמו י"ב מזלות וכ"ח מחנות הלבנה וכיוצא באלו שאינה חלוקה מוגבלת יישיית וזה א' מנפלאות הטבע בלא ספק | |
| ולולא יראתיהו מהאריכות ושלא נצא ממה שאנחנו בו הייתי מאריך בביאור עניינים נפלאים גדולים ויקרים על זה הדרוש אבל ייעדנו לו מקום אחר בס' הסכמנו לדבר בו בטבע המציאות | |
| ומפני הפליאה הזאת עם אחרות רבות טעו המניחים המספר התחלה | |
| ודע שאותם הכוללים שזכרנו בכל מספר ומספר הם מעט מהרבה כי קצרה יד השכל האנושי להשיגם כ"ש לרחוקים מהשלמות ודי הערה גלויה באותם שזכרנו | |
General Properties of Numbers |
|
Introduction |
|
| ואחר שהגענו לזה המקום נביא קצת סגולות פרטיות מטבע המספר בדרך הגדה וספור | |
| לא כדרך שעשה אקלידס בז' ושמיני ותשיעי מספרו כי המספר אינו צריך לזה אחר שהספירה המעשית תאמת כל הקדמה מונחת גם שם לא ינוח לב הקורא עד יבחננו במבחן הספירה וכן תמצא מפרש אוקלידס בסוף פי' כל הקדמה מהם מביא משל מספריי | |
| ולא בהקדמות המספריות לבד אבל גם בהנדסיות כל מה שאפשר לבחון הענין במספר יושב אל מספר כמו רוב הקדמות המאמר השני מאקלידס | |
| וקצת אנשים אמרו שהוצרך אקלידס לזה להיות לו בהקדמה לקצת מקומות מהמאמר העשירי מספרו ואנחנו חפשנו ולא מצאנו הענין כן א"כ דרך אקלידס בשלשת המאמרים הנז' היא נגיעת השכל לא זולת וזה ממה שראוי שירוחק בכל מקום וכ"ש באשר אנחנו בו להפיס בו דעת אדונינו המלך הגדול יצליחהו ה' | |
| ולזה נביא ההקדמות ספוריות ותעיד בהם ונלקט מה שמצאנו מזה לאשר קדמונו | |
| ומה שחדשנוהו אנחנו והמוסיף אחרינו שנות חיים ושלום יוסיפו לו | |
A list of arithmetical statements concerning general properties of the numbers – without demonstrations or proofs |
|
| כל שלשה מספרים מתיחסים הנה הכאת הא' בג' כהכאת האמצעי בעצמו | |
| ואם היו ארבעה תהיה הכאת הקצוות כהכאת האמצעיים | |
| קטני המספרים על יחס מה הנה הם ימנו המספרים אשר על יחסם הקטן לקטן והרב לרב | |
| קטני המספרים על יחס מה הנה כל א' מהם ראשון אצל האחר וזאת ההקדמה מתהפכת | |
| כאשר היו ב' מספרים כל א' מהם ראשון אצל האחר והוכה כל א' מהם בעצמו הנה כל א' משתי ההכאות ראשון אצל האחר וכן אם היו שנים ראשונים אצל שנים אחרים והוכו זה בזה והשנים האחרים זה בזה הנה שתי ההכאות ראשונות זו לזו | |
| כאשר היו ב' מספרים כל א' מהם ראשון אצל האחר והוכו זה בזה הנה אותה ההכאה מספר ראשון אצל כל א' משני המספרים | |
| כאשר היו מספרים כמה שיהיו וימשכו על יחס מה והראשון מהם לא ימנה השני אין מהם מספר ימנה האחר ואם היה הראשון מונה האחרון הנה הוא מונה השני | |
| כאשר נפלו מספרים בין מספרים וימשכו קצתם לקצתם ביחס מה הנה כסך מה שיפול מן המספרים בין ב' אותם המספרים כן יפול בין כל שני מספרים מאותו היחס וימשכו כלם ביחס א' | |
| כאשר היו ב' מספרים כל א' מהם ראשון אצל האחר ונפלו ביניהם מספרים ונמשכו ביחס מה הנה כסך המספרים שיפלו בין שניהם כן יפלו בין הא' וכל א' מהם וזאת ההקדמה מתהפכת | |
| המספרים המרובעים יחס קצתם אל קצת כיחס שרשיהם קצתם אל קצת | |
| שנוי המספרים המתיחסים כשהוכה כל א' בעצמו הנה כל ההכאות ג"כ מתיחסות ואם תכה ההכאות במספרים הראשונים יהיו כמו כן ההכאות השניות שהם מעוקבים מתיחסים וכן אם יוכו עוד לעולם יתיחסו כאשר ימנה המרובע מרובע אחר הנה צלעו ימנה צלעו ובהפך וכן במעוקב כל שני מספרים שהאחד מהם ראשון אצל האחר אין יחס הראשון אל השני כיחס השני אל מספר אחר | |
| כאשר היו ב' מספרים שטחים מתדמים ל ר"ל ששני צלעות המספר האחד השטוח על יחס שני צלעות המספר השטוח האחר הנה יפול ביניהם מספר יתמצע ביחס ואותו האמצעי נולד מקטן צלע א' מהשטחים עם גדול צלע האחר וזאת ההקדמה מתהפכת | |
| כאשר היו ב' מספר מוגשמים מתדמים הנה יפלו ביניהם ב' מספרים וימשכו ארבעתם ביחס והוצאת אלו השנים בשתכה תחלה קטן שתי צלעות א' מהמוגשמים בשני מהמוגשם האחר והיוצא תכהו בצלע הגדול מכל א' מהמוגשמים והשניים שיצאו הם האמצעיים וזאת ההקדמה ג"כ מתהפכת | |
| כאשר היו ב' מספרים והיה יחס א' מהם אל האחר כיחס מספר מרובע אל מספר מרובע והיה א' מרובע | |
| ואם היו ביחס מספר מעוקב אל מספר מעוקב והיה הא' מעוקב הנה האחר מעוקב | |
| המספרים השטוחים המתדמים יחס א' אל האחר כיחס מספר מרובע אל מספר מרובע והמוגשמים המתדמים יחס א' מהם אל האחר כיחס מספר מעוקב אל מספר מעוקב | |
| המספרים השטוחים המתדמים כשיוכו זה בזה יתקבץ מההכאה מספר מרובע ושרשו הכאת קטן צלע מא' מהם בגדול האחר | |
| המספרים המוגשמים המתדמים כשיוכו זה בזה יתקבץ מספר מעוקב ושרשו שתכה שורש א' מהמוגשמים בשורש האחר והיוצא הוא השרש המבוקש ואמנם אמרתי השרש לפי שהוא מספר נגדר לעולם | |
| כאשר היו מספרים מתיחסים מתחילים מהאחד הנה הג' מרובע והד' מעוקב והחמישי מרובע והששי מעוקב והז' מרובע וכן ימשך לעולם | |
| כאשר היו מספרים מתיחסים מתחילים מהא' והיה השני מרובע הנה הנשארים כלם מרובעים ואם היה מעוקב יהיו כולם מעוקבים | |
| ואם לא היה השני מרובע אין בהם שום מרובע | |
| ואם לא היה השני מעוקב אין בהם שום מעוקב | |
| כאשר היו מספרים מתיחסים מתחילים מהאחד הנה כל מספר א' ימנה האחרון מהם הנה הוא ימנה אשר ילוה לאחד ואם היה אשר ילוה לאחד א' הנה לא ימנה הרב מהם כי אם מספר מהם | |
| כשהיה קטן מספר ימנוהו מספרים ראשונים ידועים הנה לא ימנהו מספר אחר זולתם | |
| כאשר היו שלשה מספרים מתיחסים והיו קטני המספרים על אותו היחס הנה כל שנים מהם מחוברים ראשונים אצל הנשאר | |
| כל שני מספרים ראשונים זה אל זה הנה אין יחס הראשון אל השני כיחס השני אל מספר אחר | |
| כאשר היו מספרים ימשכו קצתם לקצת ביחס מה והיו הקצוות ראשונים זה לזה הנה אין שעור הראשון אצל השני כשעור האחד אל המספר האחר | |
| כאשר היו מספרים נמשכים אל יחס מה וחוסר מכל א' מהשני והאחרון כמו הראשון הנה שעור מה שישאר מהשני אצל הראשון כשעור מה שישאר מהאחרון אצל כל המספרים אשר לפניו כאשר יקובצו | |
| כל מספר נפרד ראשון אצל מספר אחר הנה הוא ראשון אצל כפלו | |
| כשהיו שני מספרים ראשונים זה אל זה הנה אשר ימנה א' מהם הוא ראשון לאחר | |
| כל ב' מספרים יוכה א' מהם באחר וימנה אותה ההכאה מספר ראשון הנה אותו המספר הראשון ימנה א' משני המספרים אשר הוכו זה בזה | |
| המספרים המתיחסים הנה הם בחילוף ובתמורה ובהבדל ובהרכבה יתיחסו | |
| כשהוכה מספר בשני מספרים הנה יחס שתי ההכאות א' מהן לאחרת כיחס המספר למספר | |
| כל מספר שטוח יהיה א' מצלעותיו מספר ראשון והמספר השני מורכב הנה הוא ימנוהו צלעותיו וכל מספר ימנה צלעו המורכב | |
| וכל מספר יתקבץ מהכאת צלעו הראשון | |
| בכל מספר ימנה צלעו המורכב ולא ימנהו מספר אחר בלתי אלו | |
| כל מספר שטוח צלעותיו מספרים מורכבים הנה ימנוהו צלעותיו וכל מספר ימנה כל א' מצלעותיו וכל מספר יתקבץ מהכאת כל א' מצלעותיו בכל מספר ימנה צלע האחר מהם ולא ימנהו מספר אחר בלתי אלו | |
| כשקובצו מספרים נמשכים על יחס הכפל מן הא' עם האחד והתקבץ מהם כלל והוכה הרב מספר מאותם המספרים במספר א' בלתי השנים הנה אם היה המספר הראשון שוה לכלל אשר קובץ הנה המספר המתקבץ מזה מספר שלם ואם היה אותו המספר הראשון פחות מהכלל אשר קובץ הנה הוא מספר נוסף ואם היה המספר הראשון יותר מהכלל אשר קובץ מספר חסר והגעת תוספתו אם היה נוסף וחסרונו אם היה חוסר כמו יתרון מה שבין אותו הכלל אשר קובץ ואותו המספר הראשון | |
| ויש בהוצאת המספר השלם תחבולה א' יותר קצרה והוא שתסדר מספרי זוג הזוג בטור ותניח תחתיו טור הנפרדים הטבעיים מתחיל כנגד ב' מהזוגות הנה כל מספר זוג מהטור העליון שתמצא תחתיו נפרד ראשון ותכהו בו יצא לך מספר שלם | |
| ובזה הדרך יצאו המספרים השלימים על סדרם ומסגולתם שאם יסודרו אלו השלמים כפי מה שנולדו בטבע תמצא האחד פרטו ה' ואשר אחריו פרטו ח' ואחר ו' ואחר ח' וכן לעולם | |
| כאשר קובצו מספרים נמשכים על יחס הכפל מהאחד עמהם והתקבץ מהם כלל והוכה גדול מספר מאותם המספרים במספר שטוח צלעותיו שני מספרים ראשונים בלתי השנים הנה אשר יתקבץ מזה מספר נוספ או מספר חסר אמנם אם היה אותו המספר השטוח פחות מהכלל אשר קובץ עם אשר יתקבץ מהכאתם בצלעי אותו המספר השטוח מקובצים הנה המתקבץ מספר נוסף והגעת תוספתו בהגעת תוספתם על המספר השטוח | |
| אמנם אם היה אותו המספר השטוח יותר מהכלל אשר קובץ עם אשר יתקבץ מהכאתו בב' צלעי אותו המספר השטוח מקובצים הנה המספר המתקבץ חסר והגעת חסרונו בהגעת חסרוניהם מהמספר השטוח | |
| כל ארבעה מספרים נמשכים על יחס הכפל והראשון מהם היותר קטן הנה המשוטח ההוה מהכאת הב' והג' מקובצים בשלישי והד' מקובצים הוא כמו המשוטח ההוה מהכאת המספר הרביעי בראשון והרביעי מקובצים | |
| ואם היה המספר המשוטח ההוה מהכאת הב' והב' מקובצים ברביעי והג' מקובצים כמו המשוטח ההוה מהכאת הרביעי בראשון והרביעי מקובצים הנה המספר המוגשם אשר א' מצלעותיו המספר הג' מהם וצלעו הב' והג' והד' מקובצים וצלעו הב' המספר הב' והג' מקובצים כמו המספר המוגשם אשר א' מצלעותיו המספר הג' מהם והב' המספר הד' מהם והג' המספר הא' והרביעי מקובצים | |
| כל ד' מספרים מתיחסים ביחס הכפל יהיה הא' מהם היותר קטן הנה המספר המשוטח ההווה מהכאת האחרון בראשון והאחרון מקובצים מלבד א' מהם כמו המתקבץ מהכאת המספר הג' מהם במותר מה שבין השטח ההוה מהכאת האחרון בא' והאחרון מקובצים מלבד אחד ובין השטח ההוה מהכאת המספר הג' והרביעי מהם בלתי א' מקובצים בג' והב' בלתי א' מקובצים | |
| כל מספר יחלק בחלקים כמו שיהיו הנה הכאת המספר כלו בעצמו כמו הכאת כל א' משני החלקים בעצמו וכפל הכאת א' משני החלקים באחר כאשר יקובצו | |
| כל ב' מספרים יחלק א' מהם בחלקים כמו שיהיו הנה המספר שלא חולק במספר של[א ש]חולק כמו הכאתו בכל חלקי המספר הנחלק כא[ש]ר יקובצו | |
| כל מספר זוג יחלק לחציים ולחלקים מתחלפים הנה אשר יהיה מהכאת (חצי) המספר בעצמו כמו ההוה מהכאת החלק הגדול בקטן עם הכאת מותר חצי המספר על החלק הקטן בכמהו | |
| כל מספר זוג יחלק בשני חציים ויתוספ בו מספר אחר הנה הכאת חצי המספר עם התוספת בכמוהו כהכאת המספר עם התוספת בתוספת והכאת חצי המספר הא' בעצמו | |
| כל מספר יחלק בב' חלקים הנה הכאת המספר בכמהו וא' משני החלקים בכמהו כמו ההוה מהכאת המספר בחלק המוכה בכמהו ב"פ והחלק הב' בכמהו | |
| כל מספר יחלק בב' חלקים הנה הכאת המספר בכמהו ונוספ עליו כמו א' משני החלקים הנה הכאת המספר עם התוספת בכמהו כמו הכאת בתוספת ארבעה פעמים והכאת החלק האחר בכמוהו | |
| כל מספר זוג יחלק בב' חלקים חצאים ובב' מתחלפים הנה כל א' משני החלקים המתחלפים בכמהו כהכאת חצי המספר בכמהו ב' פעמים והכאת מותר חצי המספר על החלק הקטן בכמהו ב"פ | |
| כל מספר זוג יחלק לחצאים ונוספ בו מספר אחר הנה ההוה מהכאת חצי המספר בכמהו ב"פ והכאת חצי המספר עם התוספת בכמהו ב"פ כהכאת המספר עם התוספת בכמהו והתוספת בכמהו | |
| כל מספר יחלק בשני חלקים מתחלפים ובב' חלקים אחרים מתחלפים הנה הכאת קטן הקטנים בגדול הגדולים ותספת הכאת מותר מה שבין הקטנים במותר מה שבין שני הקטנים והמספר כולו כמו הכאת רב הקטנים בקטן הגדולים כשהיו ב' מספרים משותפים מתחלפים והובדלו מהגדול דמיוני הקטן עד שישאר פחות ממנו או הוא עצמו וכן בסור הקטן מהגדול עד שיכלה אל מספר הנה הוא גדול משותפ בין ב' מספרים | |
| אם רצינו למצוא קטן מספר ימנוהו ב' מספרים ידועים אם היו המספרים ראשונים נכה האחד באחר ויגיע דרושינו | |
| ואם היו משותפים נקח גדול מספר משותפ ביניהם ונקח מספר האחדים שהוא מונה הקטן ושהוא מונה הגדול ותכה הקטן מאלו בגדול המספרים המשותפים או הגדול בקטן המספרים המשותפים כי הכל א' ואותו המספר הוא המבוקש | |
| כשנרצה למצוא מספר קטן ימנוהו מספרים ידועים כאלו נאמר ב'ג'ד' הנה נקח קטן ימנוהו ב"ג והוא ו' ואם היה ו' ימנוהו בג"ד טוב ואם לא נקח קטן מספר ימנוהו ו' וד' והוא כ"ד והוא הדרוש | |
| כשנרצה למצוא קטן מספר בו חלקים ידועים הנה נת' מפני ההקדמה שלפני זאת | |
| כשנרצה למצוא קטני מספרים על יחס מוגבל אם היו ראשונים הנה הם קטני המספרים על אותו היחס ואם היו משותפים הנה נקח גדול מספר ימנם וכאלו אלו המספרים הם ח' י"ב י"ח וגדול מספר ימנם ב' ונקח מספר אחדים שימנה ב' ח' ומספר השעור שימנה ב' י"ב וכשעור שימנה י"ח ותמצא דו"ט והם קטני המספרים על אותו היחס | |
| כשנרצה למצוא קטני מספרים על יחסים ידועים בנושאים מפורדים כמו ב' אל ד' חצי ד' אל י"ב שליש ו' אל כ"ד רביע נבקשהו בנושאים נלוים הנה נקח קטן מספר שיש לו חצי נרצה לידע כשהיו ב' מספרים אם ימצא להם מתיחס הנה אם היו ראשונים לא ימצא שלישי על יחסם ואם היו משותפים נכה הב' בעצמו ואם ימנהו הראשון הנה ימנה להם ג' מתיחס אחריהם ואם לא לא' | |
| ואם היו ג' ונרצה לידע אם יש להם רביעי הנה אם היו הראשון והג' ראשונים זה לזה אין להם רביעי ואם היו משותפים נכה השני בג' ויצא מספר מה הנה אם ימנהו הראשון ימצא להם מספר מספר רביעי ואם לא לא | |
| כשנרצה למצוא מספרים נאהבים כמו שנרצה הנה נניח מספרים נלוים על יחס הכפל מן האחד והאחד עמהם ויקובצו המספרים אשר קודם האחרון והאחד עמהם ונוספ על המקובץ המספר אשר קודם האחרון וחסר מהנוספ עליו המספר אשר ילוה מה שקודם האחרון הנה יהיו המספרים המתחדשי' אחר התוספת והחסרון מספרים ראשונים ואין אחד מהם שנים ואם לא יהיו ראשונים תעבור הלאה עד שיצאו אלו המספרים ראשונים והכה משוטח א' מהם באחר במספר אשר קודם האחרון ושמור מה שיצא והוספ על האחרון המספר הרביעי [או] האחד אם היה הא' רביעי ממנו והנה מה שיתקבץ במספר האחרון וחסר מן היוצ[א] מן ההכאה ויהיה הנשאר מספר ראשון תכה זה המספר הראשון אשר קודם האחרון הנה היוצא מן ההכאה עם המספר השמור ישוה כל א' מהם כל חלקי האחר ואלו המספרים המתילדים מזאת התחלה נקראו נאהבים | |
| הכאת זוג במספר זוג הוא זוג | |
| הכאת זוג בנפרד נפרד | |
| הכאת נפרד בנפרד נפרד | |
| כשיוכה מרובע במרובע היוצא יהיה מרובע ושרשו כפל השרש על השרש וערך מרובע על מרובע ושרשו היוצא בחלוק השרש הגדול על השרש הקטן | |
| כל מרובע רביעיתו מרובע וארבעה דמיוניו מרובע | |
| כל מרובע שתחסר ממנו השרש והמספר שלפניו הוא מרובע ואם תוסיף בו השרש והמספר שלאחריו יהיה מרובע | |
| מרחק מרובע ממרובע סמוך לו כמחובר ב' השרשים | |
| כל שני מרובעים סמוכים או רחוקים יוכה שרש א' מהם באחר יגיע מספר מתיחס בין שני המרובעים ההם | |
| אם תסדר החבור הטבעי בטור ותצרף כל מדרגה עם אשר אחריה יתילדו המרובעים | |
| אם תקבץ המספרים עד גבול ותחזור לאחור ותקבץ הכל יעלה כמרובע המספר אשר עמדת בו | |
| אם תסדר המספרים הנפרדים כסדרם והאחד עמהם ותחברם א' א' יתילדו המרובעים הטבעיים כמו שתניח בטור א' ג' ה' ז' ט' י"א הנה א' מרובע א' תחבר אליו ג' יהיו ד' והוא מרובע ב' תחבר אליהם ה' יהיו ט' והוא מרובע ג' וכן תמיד | |
| אם תניח הזוגות הטבעים בטור ותחברם כמו שעשינו בנפרדים יתילדו המרובעים הטבעיים ושרשיהם כמו ב' ד' ו' ח' י' הנה ב' א' וצלעו נחבר אליו ד' יהיו ו' שהם מרובע ב' וצלעו תחבר אליהם ו' יהיו י"ב והוא כמרובע ג' וצלעו וכן לעולם | |
| אם תסדר הנפרדי' הטבעיים בטור כסדרם הנה הנפרד הראשון והוא א' מעוקב א' וחבור ב' נפרדים אחריו שהם ג' ה' יהיה מעוקב ב' ושלשה נפרדים אחר ה' שהם ז' ט' י"א יולידו מעוקב ג' וארבעה אחר י"א יולידו המעוקב הרביעי וכן תמיד | |
| ואם תחבר בזה הדרך הזוגות יתילדו המעוקבים כסדרן וצלעותיהם | |
| אם תסדר המספר הטבעי ותצרף כל מדרגה אל אשר אחריה יתילדו הנפרדים הטבעיים | |
| אם תחבר המעוקבים כסדרם כמו שתרצה והאחד עמהם הנה המקובץ מרובע ושרשו מרובע החבור עד שרש המעוקב שעמדת | |
| חבור המרובעים הנלוים יודע כשתקח מחובר המספר שהוא שורש לאותו המרובע שעמדת בו שמרהו וקח שני שלישי אותו ב שורש א המרובע עם תוספת שלישית אחד ונכפלהו בשמור והעולה הוא מחובר המרובעים עד סוף חבור המספר פשוט הוא שתכפול איזה מספר שתרצה חבורו בחצי המספר הבא אחריו או בחציו וחצי אחד והעולה הוא חבור הנפרדים לבד הוא שתכה המספר האמצעי בעצמו ב' פעמים ותוסיף עליו השרש והוא המבוקש | |
| חבור הזוגות לבד בחשבון ותכהו בעצמו ותוסיף עליו השרש שלו והוא המבוקש | |
| החבור הטבעי הוא חצי מרובע המספר שעמדנו בו וצלעו | |
| אם תשים המספר הטבעי בטור ותשים על כל א' חבורו ותקיש כל א' אל חבורו תמצא כל חבור יוסיף על המספר חצי דמיון המשל בו שתמצא בכאן א' כמו א' וג' כמו ב' וחציו וו' ב' דמיוני ג' וי' שני דמיוני ד' וחציו | |
| וט"ו שלשה דמיוני ה' וכן תמיד יוסיפ בחצי דמיון א ג ו י טו כא כח לו א ב ג ד ה ו ז ח כל מספר שתחלקהו בשני חלקים איך שיהיה ותחלק כולו על כל אחד מחלקיו ותכה היוצא מכל אחת משתי החלוקות זה בזה ותשמרהו ואחר תכה אחד משני החלקים באחר ותכהו בשמור יעלה כמרובע המספר | |
| כל חשבון שתקח שלישיתו ותכהו בעצמו ותעלהו מדרגה א' ותחסר ממנו מרובע השלישית יעלה כמרובע המספר | |
| ואם לא היה לו שלישית אבל הוא מוסיפ אחד חסר ממנו האחד ותעשה בנשאר כאשר ביארנו והוסף עליו אח"כ המספר שיש לו שלישית והמספר עצמו ויגיע מרובע המספר | |
| ואם יוסיף שנים על שלישית המספר נעשה בהיפך וזה שיוסיפ אחד ויהיה מספר שלישי ונעשה כבראשונה ונחסר ממנו בסוף מה שהיינו מוסיפים ויעלה המבוקש | |
| הכאת מעוקב על מעוקב מעוקב ושרשו הכאת שרש א' מהם בשני | |
| חלוק מעוקב על מעוקב מעוקב ואם תחלק שרש הגדול על שרש הקטן תמצא שרשו | |
| אם תסדר המספר הטבעי והא' עמהם ותתחיל ותכה הא' בשני והשני בג' והג' בד' וכן תמיד יתילדו המספרים שהם אמצעיים ביחס בין המרובעים הטבעיים | |
| כל ג' מספרים מתיחסים שתכה שלשתם זה בזה יתקבץ מספר מעוקב ושרשו המספר האמצעי | |
| כל מרובע מעוקב יש מצדדיו שני מרובעים | |
| אם תחסר ממנו שרש המעוקב חצי א' ותכהו שרש הנשאר בשרש המעוקב תמצא המרובע הקטן ואם תוסיף על חצי שרש המעוקב חצי א' ותכהו בשרש המעוקב תמצא שרש המרובע הגדול | |
| ואם תחסר המרובע הקטן ממרובע הגדול תמצא המעוקב | |
| תראה בזה פליאה נשגבה מאד שאם תסדר המרובעים הטבעיים בטור ותבין בהם ענין זאת ההקדמה תמצא שהמעוקב הראשון ההוה מחסרון מרובע ממנו תמצא שאותם השני מרובעים שזה דרכם ביניהם מרובע א' והמעוקב השני שמצדדיו שני מרובעים הנה ביניהם שני מרובעים והמעוקב הג' בין ב' מרובעים ביניהם ג' מרובעים וכן תמיד יוסיף המרחק בא' כמו זאת הצורה | |
| אם תסדר המספר הטבעי ותשים תחתיו הזוגות הטבעיים על הסדר ותחבר הראשון והוא א' בזוג הראשון והוא ב' יעלה ג' והוא המספר הא' עם מרובעו ומעוקבו | |
| תחבר אל הג' הזוג הב' והוא ד' יהיו ז' תכם במספר הב' והוא ב' יעלו י"ד והוא המספר השני עם מרובעו ומעוקבו תוסיף על הז' הזוג הג' והוא ו' יהיו י"ג תכהו במספר הג' שהוא י"ג יעלו ל"ט והוא המספר הג' עם מרובעו ומעוקבו וכן לעולם | |
| ונחתום עתה זה החלק בביאור סגלה נפלאה מהמספר והיא שמרובעי המספרים הט' שהם במדרגה הראשונה הם נשלמים בשתי מדרגות ר"ל האחדים והעשרות וזה שבאחדים לא ימצאו רק מג' מספרים והם אב"ג שמרובעיהם אד"ט והנשארים ישלמו בעשרות | |
| ולפי שהמדרגה הא' התחלה ויסוד לכל המספרים המתחדשים היו מרובעיה דוגמא ומשל לכל המדרגות שאחריה לאין תכלית ולפי שמרובעי אחדי המדרגה הראשונה לוקחים משתי המדרגות שהם אחדים עשרות תחזור השלישית אל הראשונה והרביעית לשנית והחמישית לראשונה והששית לשנית וכן תמיד המדרגות הנפרדות מהראשונה והזוגות מהשנית וזה לך הפי' במדרגה הראשונה אד"ט מרובעים ובשלישית מאה ד' מאות ט' מאות ג"כ מרובעים ושרשיהם דמיון שרשיהם אלא שיעלו מדרגה א' כי שרשי אד"ט אב"ג ושרשי אלו יהיו יכ"ל וא[ו]ן במדרגה הג' מרובעים ראשי כללים רק אלה כאשר אין באחדים רק אד"ט ושלמות מרובעי שאר המספרים הטבעיים הם י"ו כ"ה ל"ו וכו' וכן במדרגה הרביעית אלפ ות"ר אלפים ות"ק ג' אלפים ות"ר ושרשיהם דמיוני שרשי מרובעי האחדים אלא שיעלו מדרגה א' ויהיו ארבעים חמשים ששים וזה שומר הסדר בכל המדרגות עד אין קץ | |
| ודע שכמו שיש נמשלים במרובעים כן יש במעוקבים ומרובעי ט' המספרים ישלמו בב' מדרגות ר"ל באחדים והעשרות ולזה ידלגו משתים לב' עד לאין תכלית ואמנם המעוקבים הפליא בם הטבע וזה לפי שהמרובע הוא משני מרחקים ישלמו נמשליו בשתי מדרגות ולפי שהמעוקב הוא בעל ג' רחקים ישלמו נמשליו בג' מדרגות וידלגו אח"כ מג' לג' מדרגות עד לאין תכלית כאשר היה דולג במרובעים משנים לשנים וזה שאחד מעוקב אחד ושרשו א' כן אלפ שהוא רביעי לו מעוקב ושרשו עשרה שהוא אחד שעלה מדרגה וכן שמנת אלפים מעוקב שמנה ושרשו עשרים שהוא כנגד שנים ומשם והלאה תשמור הסדר שזכרנו לך ומכאן ראיה חזקה שהמספרים ט' לבד | |
| ולפי שהסגולות המספריות כמעט שאין להם תכלית ולזה ההפלגה בם אבוד הזמן די לנו עתה במה שהבאנו לפי ומה שנצטוינו מהמלך הגדול אדונינו שיחיה ויאריך ימים בהשקט ובטחה ולא רצינו לחבר אל זה חלק מלא לפי שחובר על זה הרבה אצל כל האומות לצרכם אליו בענייניהם המדיניים ולזה הסכמנו שיהיה בכאן סוף דברינו בזה החלק הראשון | |
|
בר"ד |
נשלמה העתקת ספרי הראב"ע ז"ל באלול הרמ"ג בקצ"ד לשטרי הצעיר יחיא בן סלי'
אלקאפח יצ"ו |
 :
: